lOMoARcPSD|46342985 130 BÀI 10 Bài 10
KHẢO SÁT CÁC QUÁ TRÌNH CÂN BẰNG NHIỆT ĐỘNG
XÁC ĐỊNH TỶ SỐ NHIỆT DUNG PHÂN TỬ CP/CV CỦA CHẤT KHÍ
DỤNG CỤ THÍ NGHIỆM
1. Bình thủy tinh hình trụ (10 lít);
2. Van xả khí ba chạc K1K2 bằng đồng;
3. Áp kế cột nước chữ U bằng thủy tinh;
4. Giá đỡ áp kế cột nước có thước milimét;
5. Bơm nén khí dùng quả bóp cao su;
6. Ống dẫn khí bằng cao su silicon;
7. Hệ van nạp và xả khí;
8. Hộp chân đế 30x45x7cm, bằng kim loại, sơn tĩnh điện.
Hình 1: Bộ thí nghiệm đo tỷ số Cp/Cv lOMoARcPSD|46342985
KHẢO SÁT CÁC QUÁ TRÌNH CÂN BẰNG NHIỆT ĐỘNG… 131
MỤC ĐÍCH THÍ NGHIỆM
Khảo sát các quá trình biến đổi trạng thái cân bằng nhiệt động của
một khối không khí chứa trong bình và xác định tỷ số nhiệt dung phân tử 
= Cp /CV của khối khí.
1. CƠ SỞ LÝ THUYẾT
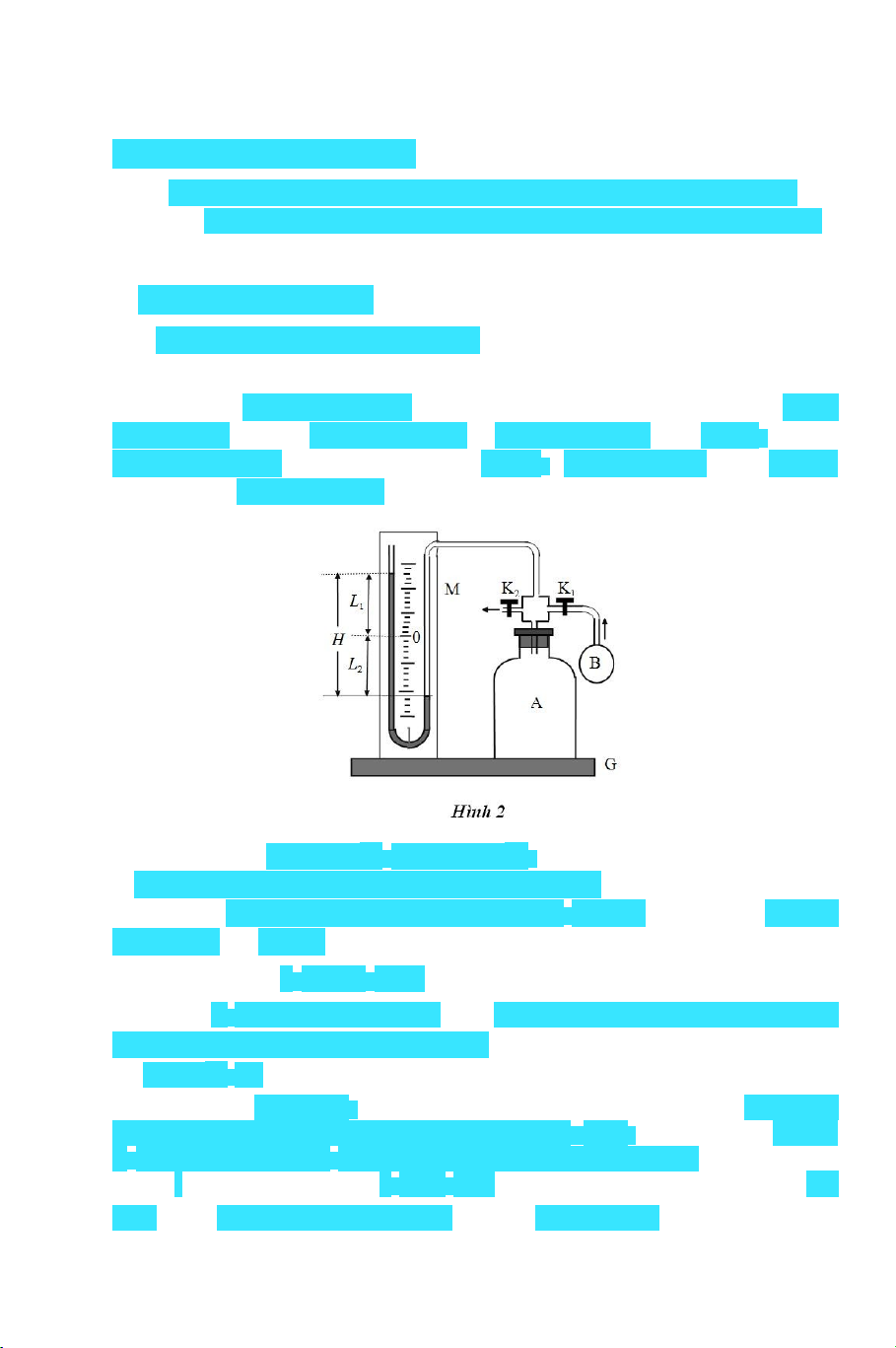
1.1. Cấu tạo và hoạt động bộ thiết bị
Cấu tạo và hoạt động bộ thiết bị dùng trong thí nghiệm này (Hình
2) gồm: một bình thuỷ tinh A chứa không khí được nối thông với áp kế
cột nước M, đồng thời nối thông với bơm nén khí B qua van K1 và nối
thông với khí qu yển bên ngoài qua van K2. Toàn bộ dụng cụ này được
lắp đặt trên hộp chân đế G.
Lúc đầu, đóng van K2 và mở van K1 để nối thông bình A với bơm
B. Dùng bơm B , bơm không khí vào bình A, làm tăng dần áp suất
trong bình. Sau đó dừng bơm và đóng van K1. Chờ vài phút cho áp suất
trong bình đạt giá trị ổn định p1: p1 = H0 + H (14)
Với H0 là áp suất khí quyển, còn H là độ tăng áp suất của không khí
trong bình A so với áp suất khí quyển và đọc trực tiếp trên áp kế M. Các
đại lượng H0 và H được tính theo đơn vị milimét cột nước (mmH2O).
Tiếp đó, mở van K2 để không khí phụt nhanh ra ngoài cho tới khi áp
suất không khí trong bình A giảm tới giá trị p 2 = H0, thì đóng nhanh van
K2 lại. Sau khi đóng K2 , ta thấy áp suất chất khí trong bình tăng lên từ từ
và đạt đến giá trị ổn định p3 = H0 + h. Căn cứ các giá trị H và h, ta xác
định được tỷ số nhiệt dung phân tử hay hệ số Poisson của không khí. lOMoARcPSD|46342985 132 BÀI 10
1.2. Nhiệt dung phân tử của chất khí
Trạng thái của khối khí được đặc trưng bởi các đại lượng: áp suất
p, thể tích V, nhiệt độ T. Đối với 1 mol khí, các đại lượng này liên hệ với
nhau bởi phương trình trạng thái: pV RT (1)
Ở đây R = 8,31J/mol.K là hằng số chất khí.
Khi truyền lượng nhiệtQ cho khối khí có khối lượng m, khối khí sẽ
nóng lên và nhiệt độ của nó tăng thêm một lượng dT. Theo định nghĩa,
nhiệt dung riêng c của chất khí là đại lượng đo bằng lượng nhiệt cần
truyền cho 1 kilogram chất khí để nhiệt độ của nó tăng thêm 1 độ. Do đó:  Q c = (2) m.dT
Nếu là khối lượng của 1 mol
chất khí thì nhiệt dung phân tử c của chất khí sẽ là :  Q c =.c = (3) dT
Đơn vị đo của c là J/kg.K, của C là J/mol.K và của là kg/mol.
Nhiệt dung của chất khí phụ thuộc đặc điểm quá trình nung nóng. Để
chứng minh điều này, ta áp dụng phương trình trạng thái khí lý tưởng và
nguyên lý thứ nhất của nhiệt động lực học. Theo nguyên lý này: Độ biến thiên
nội năng dU của một hệ nhiệt động trong quá trình biến đổi trạng thái nào
đó đúng bằng lượng nhiệtQ và côngA mà hệ nhận từ ngoài vào trong
quá trình đó, nghĩa là:
dU AQ (4)
Ở đâyA = - pdV, với p là áp suất và dV là độ biến thiên thể tích của khối khí.
RútQ từ (4) và thay vào (3), ta tìm được: C = dU p.dV  (5) dT dT
Trong quá trình đẳng tích : V = const, nên dV = 0 vàA = 0. Khi
đó từ (5) ta suy ra nhiệt dung phân tử đẳng tích CV lOMoARcPSD|46342985
KHẢO SÁT CÁC QUÁ TRÌNH CÂN BẰNG NHIỆT ĐỘNG… 133 C dU  (6) V dT
Trong quá trình đẳng áp: p = const, nên dp = 0 và lấy vi phân của
phương trình (1) ta có :
p.dV R.dT . (7)
Thay (6) và (7) vào (4), ta suy ra nhiệt dung phân tử đẳng áp Cp :
C p CV R (8) C
Công thức (7) cho thấy C p p > CV nên > 1 CV
1.3. Quá trình đoạn nhiệt
Quá trình đoạn nhiệt là quá trình biến đổi trạng thái mà hệ không
trao đổi nhiệt với ngoài, tức làQ = 0. Khi đó (4) viết thành: dU =A (9)
Rút dU từ (5) và thay vào (9), ta được: CV. dT = - p. dV (10)
Chia (7) cho (10) và chú ý đến (8), ta tìm được :
1 V dp  C  C  C   1 P V P p dV C C V V hay dp  Cp dV (11)  p C V V
Thực hiện phép tích phân đối với (11), ta tìm được phương trình đoạn nhiệt:
p.V  const (12)  C với p  (13) CV
là tỷ số nhiệt dung phân tử của chất khí - còn gọi là hệ số Poisson. Phương
trình (12) chứng tỏ trong quá trình dãn nở đoạn nhiệt, khi thể tích V tăng thì
áp suất p giảm nhanh hơn nhiều so với trong quá trình đẳng nhiệt (p.V =
const). Nghiên cứu quá trình đoạn nhiệt có ý nghĩa rất quan trọng trong lý lOMoARcPSD|46342985 134 BÀI 10
thuyết nhiệt động học, nó cho phép xây dựng một chu trình hoạt động cho
loại động cơ nhiệt đặc biệt, có hiệu suất cao nhất, đó là chu trình Carnot.
Trong thí nghiệm này, ta sẽ xác định tỷ số nhiệt dung phân tử γ
của không khí theo phương pháp dãn đoạn nhiệt.
1.4. Phân tích các quá trình nhiệt động
Sau khi bơm không khí vào bình A, đóng van K1 và chờ khoảng
vài phút để khối khí đạt tới trạng thái cân bằng ổn định: khối không
khí trong bình có khối lượng là m0, chiếm toàn bộ thể tích V0 của bình
A, có áp suất p1 = H0+ H và nhiệt độ T1 = T0 (bằng nhiệt độ phòng).
Khi mở van K2: khối khí phụt nhanh ra ngoài một lượng ∆m. Do
đó khối lượng khí còn lại trong bình là m = m0 - Δm, vẫn chiếm toàn bộ
thể tích bình, tức là V 2 = V0 và có áp suất p2 = H0 < p1 . Như vậy, suy ra
trước khi mở van K2 , khối lượng khí m trong bình A (ở áp suất p1 và
nhiệt độ T0) chỉ chiếm một phần thể tích của bình: V1 < V0 . Trạng thái
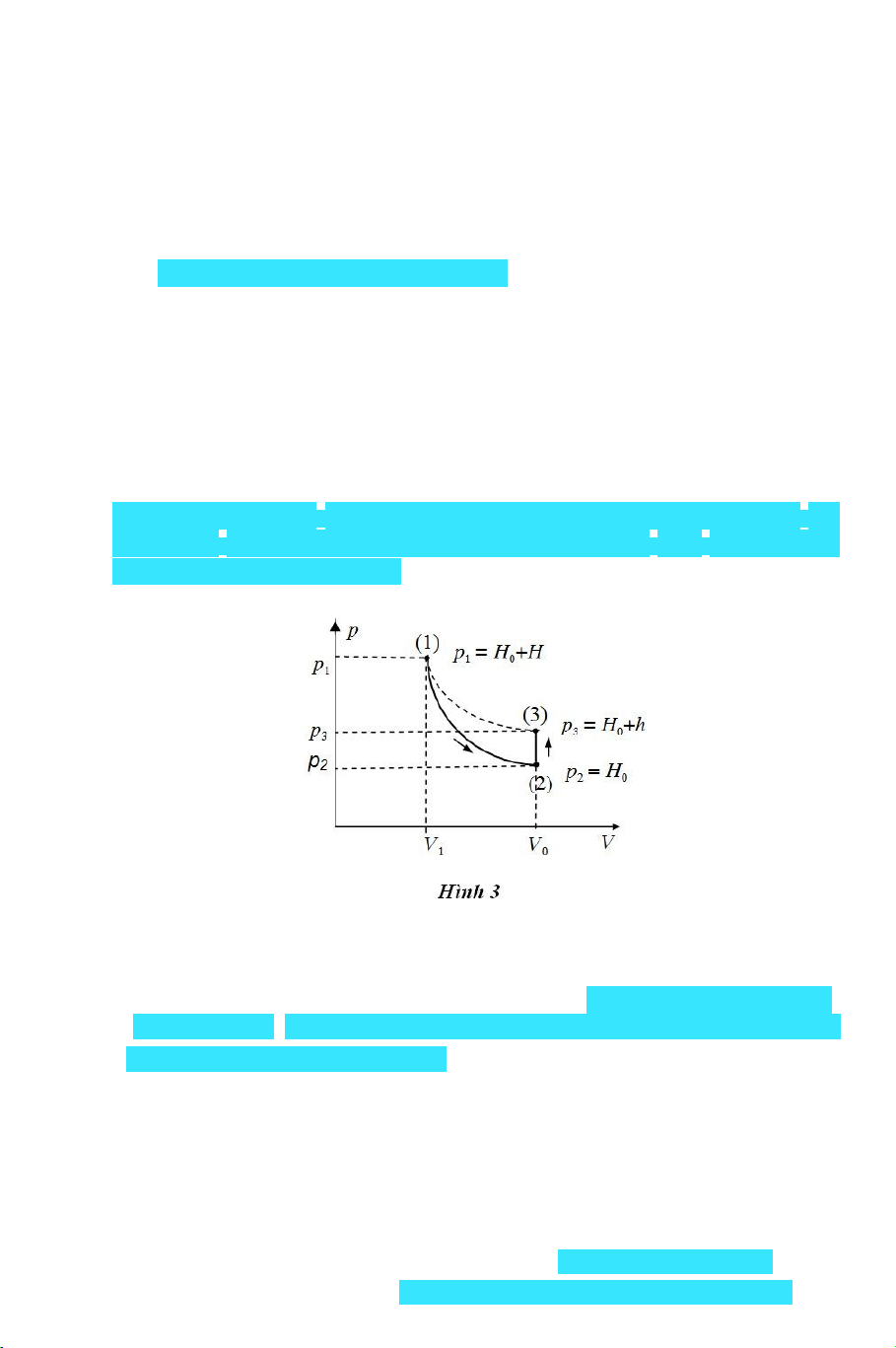
này của khối khí m được mô tả bởi điểm (1) trên đồ thị Hình 3.
Vì quá trình dãn nở của khối lượng khí m trong bình từ trạng thái (1) có
(p1 , V1 , T0 ) sang trạng thái (2) có (p2 =H0 , V2 =V0 ) xảy ra rất nhanh, không
kịp trao đổi nhiệt với ngoài (  Q = 0) nên có thể coi gần đúng là quá trình
dãn đoạn nhiệt, được biểu diễn bởi đường đoạn nhiệt 1-2 trên đồ thị Hình
3. Áp dụng phương trình Poisson (12) cho quá trình dãn đoạn nhiệt 1-2, ta có: p1V p2V (15) 1 0
Trong quá trình này, khí bị lạnh đi và nhiệt độ của nó giảm từ nhiệt độ
phòng T0 xuống đến nhiệt độ T2 < T0. Do đó, khối khí m trong bình sẽ thu
nhiệt từ ngoài qua thành bình, thực hiên một quá trình biến đổi đẳng tích, để lOMoARcPSD|46342985
KHẢO SÁT CÁC QUÁ TRÌNH CÂN BẰNG NHIỆT ĐỘNG… 135
nhiệt độ của nó tăng dần từ T2 đến T0, còn áp suất tăng từ p2 = H0 đến p3 bằng:
p3 = H0 + h (16)
Trên đồ thị Hình 3, ta nhận thấy trạng thái 1 và 3 thuộc cùng một
quá trình đẳng nhiệt T0 , biểu diễn bởi đường cong đứt nét 1-3.
Áp dụng định luật Boyle - Mariotte (pV = const) cho khối khí m trong
quá trình biến đổi đẳng nhiệt từ trạng thái 1 ( p1,V1 , T0 ) đến trạng thái 3 (p3,
V2 = V0 , T0 ), ta có:
p1V1 p3V0 (17) V Rút ra tỷ số 0
V từ (17) thay vào (15), và thay thế các giá trị của áp suất 1
p1 , p2 , p3
theo độ chênh milimét cột nước H0 , H , h , đồng thời chú ý đến
điều kiện H, h << H0 . áp dụng hệ thức gần đúng ln (1 + x )  x khi x << 1, ta tìm được:  H  (18) H h C
Công thức (18) cho phép ta xác định tỷ số nhiệt dung phân p tử CV
của không khí một cách đơn giản.
2. TRÌNH TỰ THÍ NGHIỆM
2.1. Quan sát các van K1, K2 để tìm hiểu các vị trí đóng mở chúng.
Trong một số trường hợp người ta dùng khoá ba chạc bằng thuỷ
tinh hoặc kim loại, cần tìm hiểu cách xoay khoá để nối thông bình
A với bơm nén khí B hoặc với khí quyển bên ngoài.
2.2. Đóng van K2 và mở van K1. Bơm không khí vào bình A (không
bơm quá mạnh, tránh làm nước trong áp kế M phụt ra ngoài) tới
khi độ chênh cột nước trong hai nhánh áp kế M đạt khoảng 250
300 mmH2O thì ngừng lại. Vặn van K1 để đóng kín bình A.
Chờ 4 5 phút để nhiệt độ và áp suất của khối khí trong bình đạt
trạng thái cân bằng ổn định. Để đo nhiều lần với áp suất p1 ban đầu như
nhau, ta mở từ từ van K2 để giảm bớt lượng không khí trong bình A sao
cho độ chênh cột nước trong hai nhánh áp kế M đạt giá trị chọn trước H
= L1 + L2 (trong khoảng 250 300 mmH2O). Đọc các giá trị của L1, L2
trên thước milimét của giá đỡ áp kế M để xác định giá trị của H và lOMoARcPSD|46342985 136 BÀI 10 ghi vào Bảng 1.
2.3. Mở nhanh van K2 để không khí trong bình A phụt ra ngoài. Khi
áp suất không khí trong bình A cân bằng với áp suất khí quyển H0
bên ngoài, ta đóng nhanh van K2. Muốn kết quả đo được chính
xác, ta cần quan sát và đóng nhanh van K2 ngay khi mực nước
trong hai nhánh áp kế M vừa đạt ngang nhau, kết hợp với tai nghe
tiếng “xì xì” của không khí thoát ra khỏi bình A vừa dứt.
Chờ 4 5 phút cho nhiệt độ của khối khí trong bình A cân bằng với
nhiệt độ phòng. Khi đó độ chênh cột nước trong hai nhánh áp kế M / /
đạt giá trị ổn định h L1  L2. Đọc các giá trị của L1/, L2/ trên thước
milimét của giá đỡ áp kế M để xác định giá trị của h và ghi vào Bảng 1.
2.4. Lặp lại 5 lần các động tác 2 và 3 ứng với cùng (hoặc xấp xỉ) giá trị đã
chọn của H. Ghi các kết quả đo tương ứng của h trong mỗi lần đo vào Bảng 1.
3. CÂU HỎI KIỂM TRA
3.1. Định nghĩa và viết biểu thức của nhiệt dung riêng và nhiệt dung
phân tử. Nhiệt dung của chất khí có phụ thuộc điều kiện của quá
trình nung nóng không?
3.2. Phân biệt nhiệt dung phân tử đẳng tích Cv và đẳng áp CP . Tìm biểu
thức liên hệ giữa chúng để chứng tỏ C  p Cv .
3.3. Trong thực tế, khi nào có thể coi gần đúng các quá trình nén hoặc
dãn khí là đẳng nhiệt hoặc đoạn nhiệt? Sau khi nén hoặc dãn khí
chứa trong bình A, tại sao lại phải chờ một khoảng thời gian nào
đó (khoảng 4 - 5 phút) thì độ chênh cột nước trên hai nhánh áp kế
M mới đạt giá trị ổn định?
3.4. Tại sao trong thí nghiệm này, ta phải dùng áp kế cột nước mà không
dùng áp kế thuỷ ngân để đo áp suất khí trong bình thuỷ tinh A?
3.5. Muốn đảm bảo kết quả đo được chính xác, tại sao phải đóng kín van K2
ngay khi cột nước trong hai nhánh áp kế M vừa đạt mức ngang nhau?
3.6. Chứng minh công thức tính sai số tương đối của tỷ số nhiệt dung phân tử chất H 
Hh khí có dạng: h  H H h 
H ( H h) lOMoARcPSD|46342985
KHẢO SÁT CÁC QUÁ TRÌNH CÂN BẰNG NHIỆT ĐỘNG… 137
3.7. Tính giá trị lý thuyết của tỷ số nhiệt dung phân tử không khí khô
(coi như chỉ gồm các phân tử ôxy O2 và nitơ N2) theo số bậc tự do i
của các phân tử khí.
3.8. Nếu không khí trong bình có độ ẩm cao chứa nhiều hơi nước thì giá trị
lý thuyết của tỷ số nhiệt dung phân tử của không khí sẽ thay đổi như thế
nào (tăng hay giảm so với không khí khô)? Giải thích tại sao?
Cho biết số bậc tự do i phụ thuộc cấu tạo của các phân tử khí: phân
tử đơn nguyên tử (khí trơ.): i = 3, phân tử lưỡng nguyên tử (O2,
N2,..): i = 5, phân tử đa nguyên tử (H2O, CO2,...): i = 6. lOMoARcPSD|46342985 138 BÀI 10
HƯỚNG DẪN BÁO CÁO THÍ NGHIỆM
BÀI 10: XÁC ĐỊNH TỶ SỐ NHIỆT DUNG PHÂN TỬ
CP / CV CỦA CHẤT KHÍ Xác nhận của
Giáo viên hướng dẫn
Lớp:..................Tổ.....................
Họ tên:........................................
1. LÝ THUYẾT (trình bày tóm tắt ngắn gọn lý thuyết, hình vẽ nếu có)
..........................................................................................................................
..........................................................................................................................
..........................................................................................................................
..........................................................................................................................
..........................................................................................................................
..........................................................................................................................
..........................................................................................................................
2. TRÌNH TỰ THÍ NGHIỆM (bao gồm cả dụng cụ đo và sai số dụng cụ)
..........................................................................................................................
..........................................................................................................................
..........................................................................................................................
..........................................................................................................................
..........................................................................................................................
..........................................................................................................................
..........................................................................................................................
3. CÔNG THỨC TÍNH VÀ CÔNG THỨC KHAI TRIỂN SAI SỐ
..........................................................................................................................
..........................................................................................................................
..........................................................................................................................
.......................................................................................................................... lOMoARcPSD|46342985
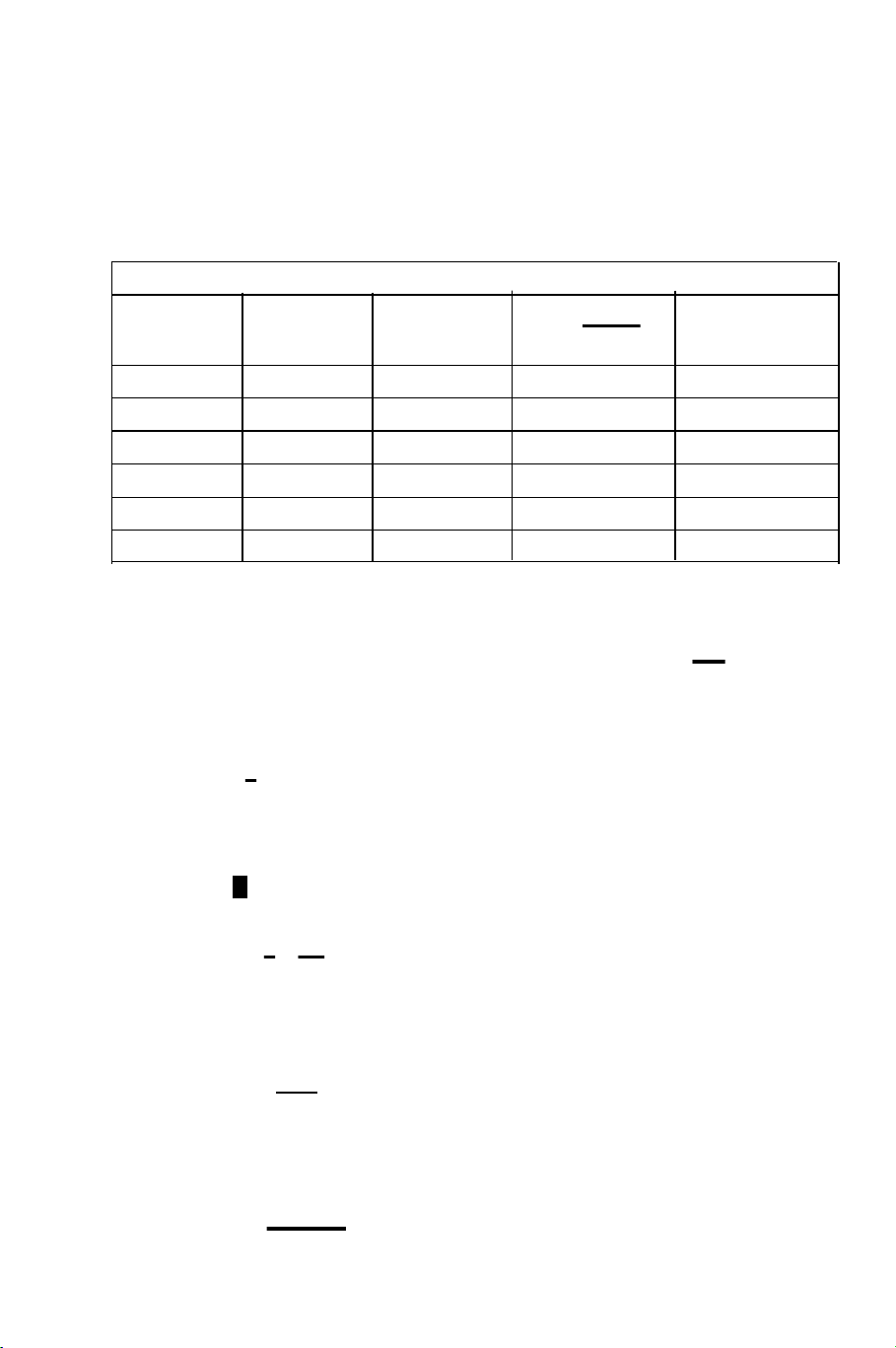
KHẢO SÁT CÁC QUÁ TRÌNH CÂN BẰNG NHIỆT ĐỘNG… 139 4. BẢNG SỐ LIỆU
4.1.Xác định số liệu Bảng 1
- Độ chính xác của thước milimét trên giá đỡ áp kế M:
........................(mm) H h Lần đo   H  (mmH2O) (mmH2O) H h 1 2 … 9 10 Trung bình C
4.2. Tính kết quả của phép đo tỷ số nhiệt dung phân p của không tử CV khí
a) Tính giá trị trung bình:  =
b) Tính sai số tuyệt đối trung bình:
 ...............................................
c) Viết kết quả phép đo:
 ...................................
d) Tính giá trị lí thuyết của tỷ số của không khí theo công thức:  i 2 lt  ………. i
e) So sánh giá trị đođo với giá trị lí thuyếtlt bằng các tính độ lệch tỉ đối: 
  lt d o  lt