Khảo Sát Mô Men Xoắn Hồi Phục Trong Thí Nghiệm Thiết Bị | Vật lý đại cương 1 | Trường Đại học Khoa học Tự nhiên, Đại học Quốc gia Hà Nội

II. Kết quả thực nghiệm
1. Xác định mômen xoắn hồi phục của con lắc lò xo xoắn
a. Lắp đặt thí nghiệm 
Bố trí thí nghiệm như hình 4 trong tài liệu 
Giữ thanh đồng nằm ngang trên trục xoắn bằng ốc vít. Lắp hai vật nặng vào
hai đầu thanh, mỗi vật cách tâm của trục xoắn một khoảng r = 30 cm. Khối
lượng của một vật nặng m = 0,24 kg. 
Điều chỉnh vị trí của thanh sao cho khi dao động thanh sẽ đi qua cổng quang
điện trên cảm biến hình chữ U.  Bật máy tính  Mở Cassy Lab 2 
Kích chuột vào cổng kết nối giữa cảm biến ánh sáng chữ U với cassy trên
màn hình máy, giả sử cổng EA1.  Đóng cửa sổ Cassy 
Trên cửa sổ setting chọn:
Period TA1(E) → Pendulum (Every other edge) → Append new meas.series
(lưu trữ số liệu lần đo trước).
Displays → Standard →TA1(t) →x-axis→ n (khi đó trên cửa sổ “Standard”
sẽ xuất hiện hai cột: một là n và một là TA1 (s)).
b. Tiến hành đo đạc 
Xoay thanh ngang sang bên phải một góc bằng 180o và thả ra. 
Ấn F9 để thực hiện phép đi ngay sau khi thanh chắn đi qua vị trí cân bằng và
dừng lại phép đo sau khi đo được 5 chu kỳ dao động. Ghi lại giá trị T bằng giá
trị trung bình của 6 chu kỳ đó vào bảng 1.
Bảng 1. Sự phụ thuộc của chu kỳ dao động T vào khoảng cách r của các chất
điểm gắn trên thanh nằm ngang quay quanh trục xoắn T (s) r(cm) T (s ) Lần 1 Lần 2 Lần 3 Lần 4 Lần 5 30 6.57 6.558 6.554 6.584 6.582 6.5696 25 5.556 5.506 5.562 5.528 5.594 5.5492 20 4.614 4.602 4.62 4.602 4.596 4.6068 15 3.66 3.7 3.692 3.682 3.672 3.6812 10 2.832 2.852 2.85 2.85 2.83 2.8428 5 2.22 2.242 2.226 2.25 2.232 2.234 Không có 1.952 1.938 1.946 1.946 1.958 1.948 vật nặng 
Lặp lại phép đo bốn lần, luân phiên làm lệch hướng của thanh ngang sang bên
trái và bên phải (lò xo dãn hoặc nén), ghi lại các kết quả vào bảng 1. 
Thay đổi khoảng cách r với các giá trị 25 cm, 20 cm, 15 cm, 10 cm và 5 cm,
với mỗi giá trị r, lặp lại các phép đo tương tự như với r= 30 cm. Các kết quả ghi lại vào bảng 1. 
Bỏ 2 vật nặng ra khỏi thanh, xác định chu kỳ dao động T0 của thanh. Cách đo
tương tự như khi có vật nặng trên thanh. Kết quả ghi vào bảng 1.
2. Khảo sát ảnh hưởng của khối lượng, hình dạng và mô men quán tính đến
chu kỳ dao động của vật rắn.
Hình ảnh lắp đặt thí nghiệm được minh họa trong hình 6. 
Đặt quả cầu trên trục xoắn và đánh dấu vị trí cân bằng trên bàn. 
Xoay quả cầu sang phía bên phải 180o và thả cho nó chuyển động. 
Ấn F9 để đo chu kỳ dao động của quả cầu ngay sau khi quả cầu đi qua vị trí
cân bằng. Dừng phép đo sau khi đo được 5 chu kỳ dao động. Ghi giá trị T
bằng giá trị của các chu kỳ đó vào bảng 2. 
Lặp lại phép đo với đĩa tròn, trụ đặc, trụ rỗng và ghi lại vào bảng 2:
Bảng 2. Chu kỳ dao động của các vật rắn có hình dạng khác nhau T (s) Vật rắn Lần 1 Lần 2 Lần 3 Lần 4 Lần5 Quả cầu đặc 1.4221 1.425 1.419 1.424 1.424 Đĩa tròn đặc 1.4201 1.4201 1.4196 1.4223 1.4235 Hình trụ đặc+đế 0.6988 0.7007 0.701 0.7021 0.7040 Hình trụ rỗng+đế 0.9396 0.9397 0.9435 0.9408 0.9425 Đế 0.44521 0.4371 0.4425 0.4334 0.4406 
Lặp lại phép đo 4 lần, luân phiên làm lệch hướng sang trái và phải (lò xo dãn
hoặc nén), ghi lại các kết quả vào bảng 2. 
Thay quả cầu bằng đĩa tròn, trụ đặc, trụ rỗng rồi làm tương tự 
Cuối cùng thực hiện với vật “Empty supporting plate”. 
Xác định khối lượng và đường kính các vật rắn. Kết quả điền vào bảng 2.
Bảng 3. Bảng khối lượng, đường kính và chu kỳ của các vật rắn Vật rắn M ± ∆ M (g)
2R ± ∆ 2R (cm) T (s) Quả cầu đặc 930 14.5 1.4228 Đĩa tròn đặc 340 22 1.4211 Hình trụ đặc 330 9 0.7013 Hình trụ rỗng 360 9 0.9412 Đế   0.4398
3. Xác định mô men quán tính của một đĩa tròn đối với các trục quay song
song với trục đối xứng của đĩa. Nghiệm lại định lý Huyghen - Steiner 
Lắp đặt thí nghiệm theo hình 5. 
Gắn đĩa tròn lên trục xoắn sao cho tâm của đĩa nằm trên trục quay. Đánh dấu
vị trí cân bằng trên bàn. 
Xoay đĩa lệch khỏi vị trí cân bằng 180o và thả ra. 
Ấn F9 để thực hiện phép đo ngay sau khi đĩa đi qua vị trí cân bằng và dừng lại
phép đo sau khi đo được 5 chu kì dao động. Ghi lại giá trị T bằng giá trị trung
bình cũng 5 chu kỳ sau đó ghi vào bảng 4. 
Lặp lại phép đo 4 lần, luân phiên làm lệch hướng của thanh sang bên trái và
bên phải (lò xo dãn hoặc nén), ghi lại các kết quả vào bảng 4. 
Gắn đĩa tròn lên trục xoắn sao cho tâm của đĩa cách trục quay một khoảng là a. 
Lần lượt lặp lại các kết quả với các khoảng cách a = 4,6,8,10,12,14 và16 cm
Bảng 4. Sự phụ thuộc của chu kỳ dao động T vào khoảng cách a giữa trục
quay và trục song song đi qua khối tâm của đĩa tròn T a (cm) A (s) T A(s) Lần 1 Lần 2 Lần 3 Lần 4 Lần 5 0 3.5720 3.5569 3.5643 3.550 3.5725 3.56314 2 3.5925 3.5822 3.59 3.5809 3.5942 3.58796 4 3.775 3.7193 3.7732 3.779 3.776 3.7645 6 3.983 3.990 3.992 4.007 4.013 3.997 8 4.329 4.339 4.361 4.364 4.369 4.3524 10 4.533 4.544 4.554 4.563 4.573 4.5534 12 5.016 5.065 5.073 5.084 5.096 5.0668 14 5.415 5.463 5.478 5.483 5.498 5.4674 16 6.222 6.314 6.370 6.450 6.502 6.3716
III. Xử lý số liệu
1. Xác định mômen xoắn hồi phục D 
Tính chu kỳ dao động T của con lắc từ giá trị trung bình của 5 lần đo ứng với
mỗi giá trị của r, các vật rắn và a điền vào vảng 1,2,4 tương ứng. 
Từ kết quả ở bảng 2, lập bảng 5 thể hiện sự phụ thuộc của T2 vào r2
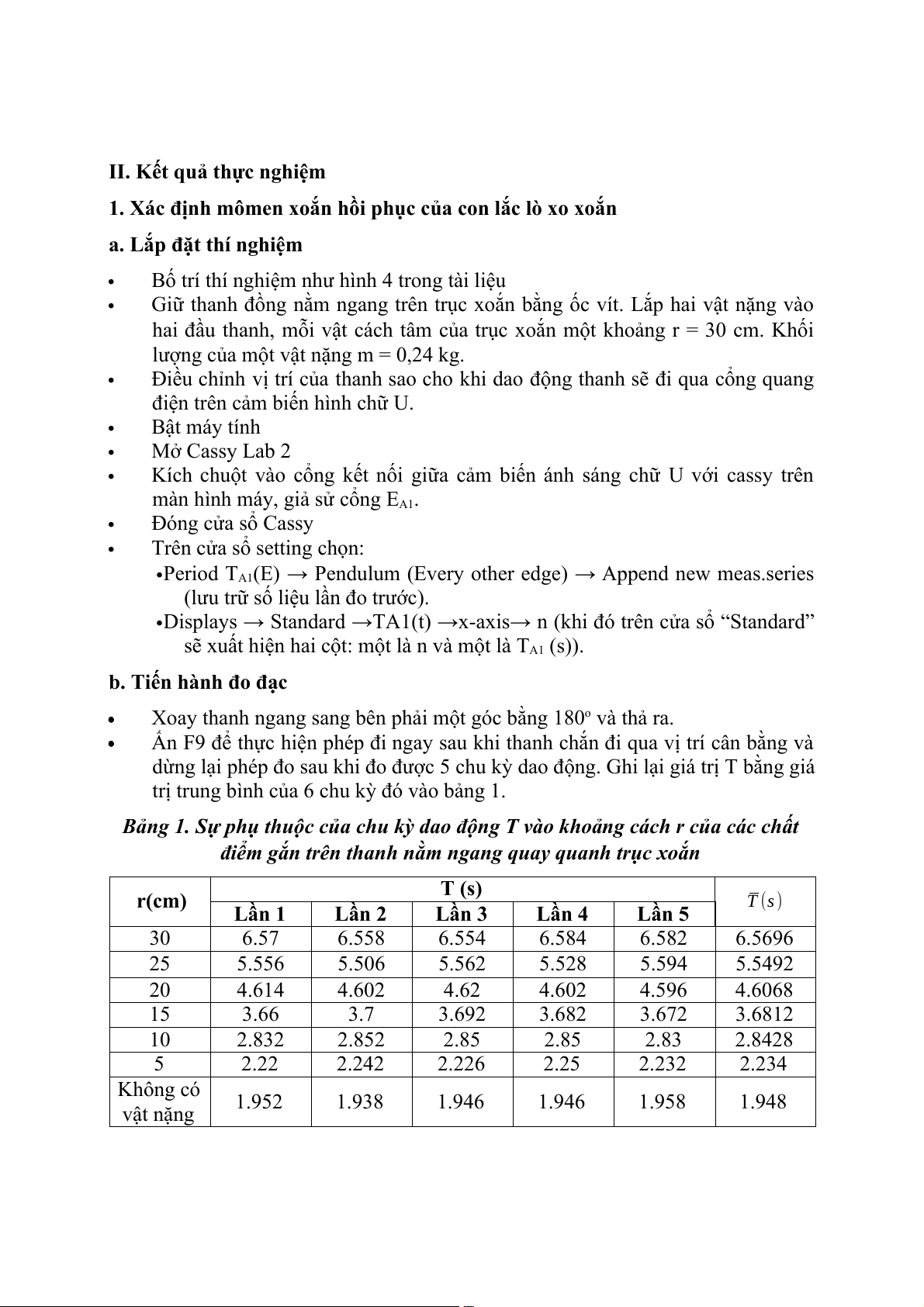
Bảng 5: Sự phụ thuộc của T2 vào r2 r (cm) r2 (m2) T2 (s2) 30 0.09 43.1596 25 0.063 30.7936 20 0.04 21.2226 15 0.023 13.55123 10 0.01 8.0815 5 0.003 4.9907
ĐỒ THỊ MÔ TẢ SỰ PHỤ THUỘC CỦA T2 (s2) vào r2 (m2) 2
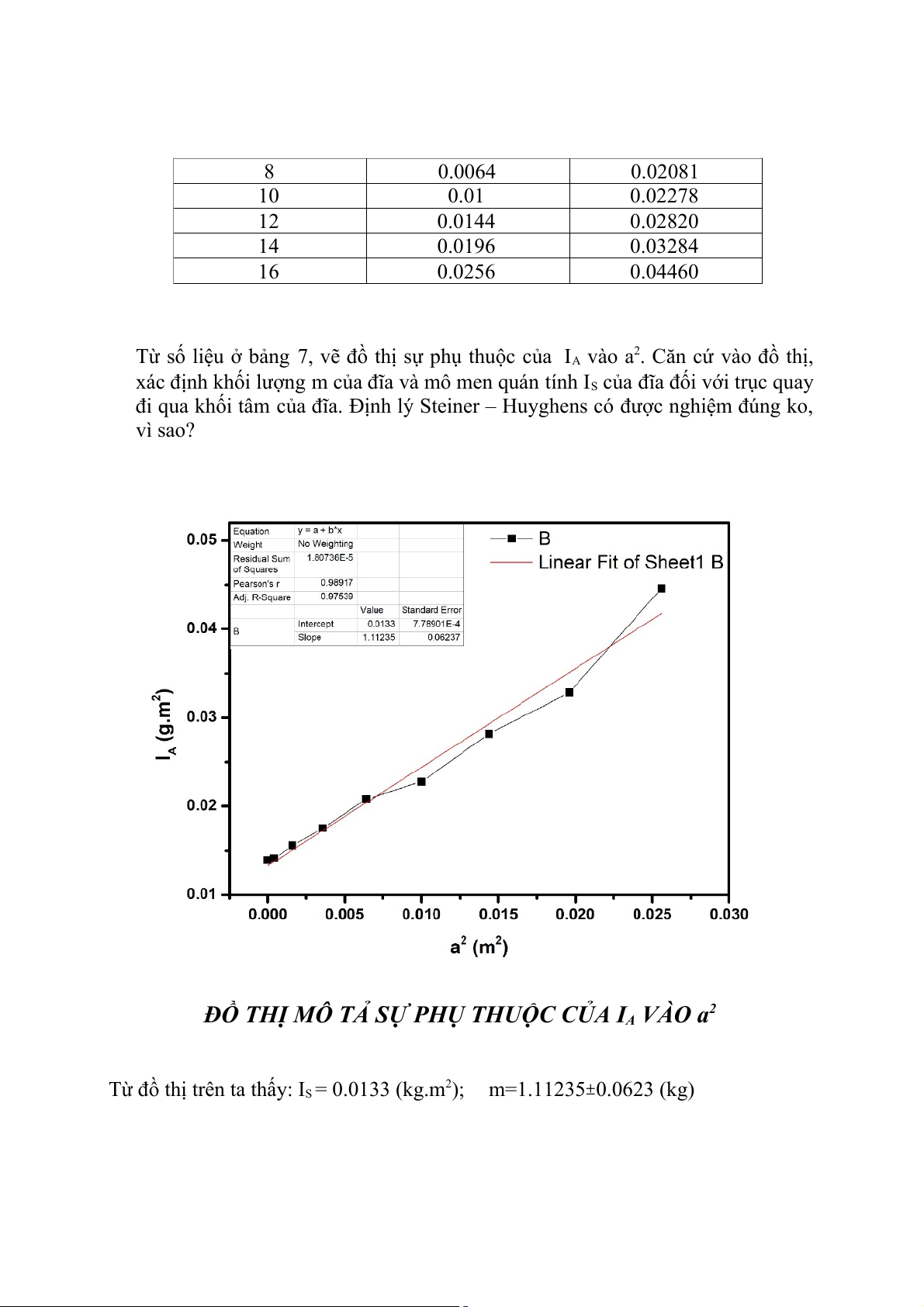
Ta có: T2= 8 m π r2+ 2 T 0 D 2
Từ đồ thị ta thấy: 8m π = 436.88385 ⇔ D= 0.04337 (Nm) D
Nhận xét: phần thực hành xác định mômen xoắn hồi phục khá tốt, ta có thể thấy
độ chính xác của đường fit trên đồ thị ≈ 1.
2. Xác định mômen quán tính của các vật rắn từ chu kỳ dao động của chúng 
Từ bảng 2, tính giá trị chu kỳ dao động trung bình của mỗi vật rắn. Kết quả điền vào bảng 3. 
Xác định mô men quán tính các vật rắn từ chu kỳ dao động của chúng và từ
các công thức tính toán, kết quả điền vào bảng 6. 
So sánh chu kỳ dao động của 2 vật có khối lượng khác nhau, nhưng có mô men quán tính giống nhau. 
So sánh chu kỳ dao động của vật rỗng và vật rắn có cùng khống lượng và có cùng kích thước. 
So sánh chu kỳ dao động của hai vật có cùng khối lượng và hình dạng nhưng khác kích thước.
Bảng 6: Mô men quan tính của các vật rắn xác định từ chu kỳ và khối lượng,
bán kính của chúng Vật rắn Jthực nghiệm Jlý thuyết Quả cầu đặc 2.2239 x 10-3 1.9553 x 10-3 Đĩa tròn đặc 2.2186 x 10-3 2.057 x 10-3 Hình trụ đặc 0.3278 x 10-3 0.3441 x 10-3 Hình trụ rỗng 0.7607 x 10-3 0.7290 x 10-3 Đế 0.2125 x 10-3 
Hình trụ đặc và hình trụ rỗng có cùng kích thước và khối lượng nhưng hình
trụ đặc có chu kỳ quay nhỏ hơn hình trụ rỗng. 
Hình trụ đặc và đĩa tròn đặc có cùng momen quán tính, nhưng mà hình trụ đặc
có khối lượng nhỏ hơn đĩa tròn đặc nên chu kỳ quay của hình trụ đặc lớn hơn đĩa tròn đặc.
3. xác định khối lượng m của đĩa và mômen quán tính Is của đĩa đối với trục
quay đi qua khối tâm đĩa, nghiệm lại định luật Huyghens – steiner. 
Căn cứ vào kết quả trong bảng 4, sử dụng giá trị D đã xác định trong phần
trên, tính mô men quán tính IA của hệ đối với các trục quay A ứng với các giá
trị bình phương khoảng cách a2 giữa trục A và trục đi qua khối tâm của đĩa
theo các công thứ (18) (19). Ghi lại kết quả vào bảng 7.
Bảng 7: Sự phụ thuộc của I a2
A vào các giá trị a (cm) a2 (m2) I 2 A (kg.m ) 0 0 0.01395 2 0.0004 0.01414 4 0.0016 0.01557 6 0.0036 0.01755 8 0.0064 0.02081 10 0.01 0.02278 12 0.0144 0.02820 14 0.0196 0.03284 16 0.0256 0.04460
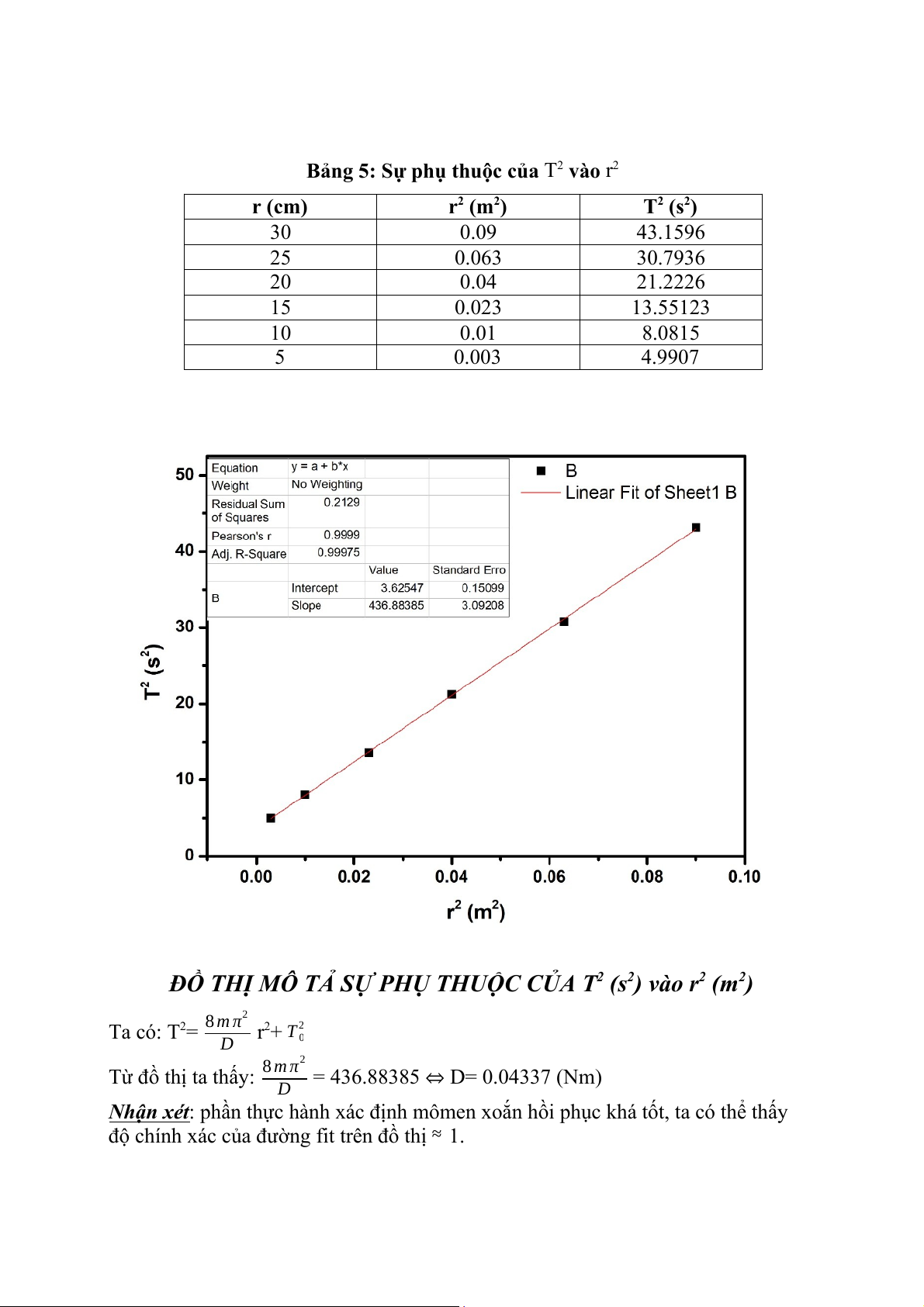
Từ số liệu ở bảng 7, vẽ đồ thị sự phụ thuộc của I 2
A vào a . Căn cứ vào đồ thị,
xác định khối lượng m của đĩa và mô men quán tính IS của đĩa đối với trục quay
đi qua khối tâm của đĩa. Định lý Steiner – Huyghens có được nghiệm đúng ko, vì sao?
ĐỒ THỊ MÔ TẢ SỰ PHỤ THUỘC CỦA I 2 A VÀO a
Từ đồ thị trên ta thấy: I 2 S = 0.0133 (kg.m ); m=1.11235±0.0623 (kg)
Định lý Steiner-Huyghens được nghiệm gần đúng, sai số xảy ra hầu hết là do ma
sát giữa vật với trục quay khi quay, nhưng bên cạnh đó, việc chưa xác định được
thời điểm có chu kỳ ổn định cũng là 1 yếu tố gây đến sai số này.