Kiểm định thống kê và bài tập áp dụng môn Xác suất thống kê| Trường Đại học Ngoại Thương

Bài 7.1. Bột mỳ được đóng bao bằng máy tự động có trọng lượng đóng bao theo quy định
là 16 kg và độ lệch chuẩn là 1,2 kg. Lấy ngẫu nhiên 25 bao bột để kiểm tra tìm được
trọng lượng đóng gói trung bình của chúng là 16,5 kg. Với mức ý nghĩa 0,05:
a) có cần dừng máy để điều chỉnh hay không?
b) Phi chăng trọng lượng thực t đóng gói lớn hơn trọng lượng quy định?
c) Phi chăng trọng lượng thực t đóng gói b hơn trọng lượng quy định?
Bài 7.2. Định mức thời gian hoàn thành một sn phẩm là 14 phút. Có cần thay đổi định mức
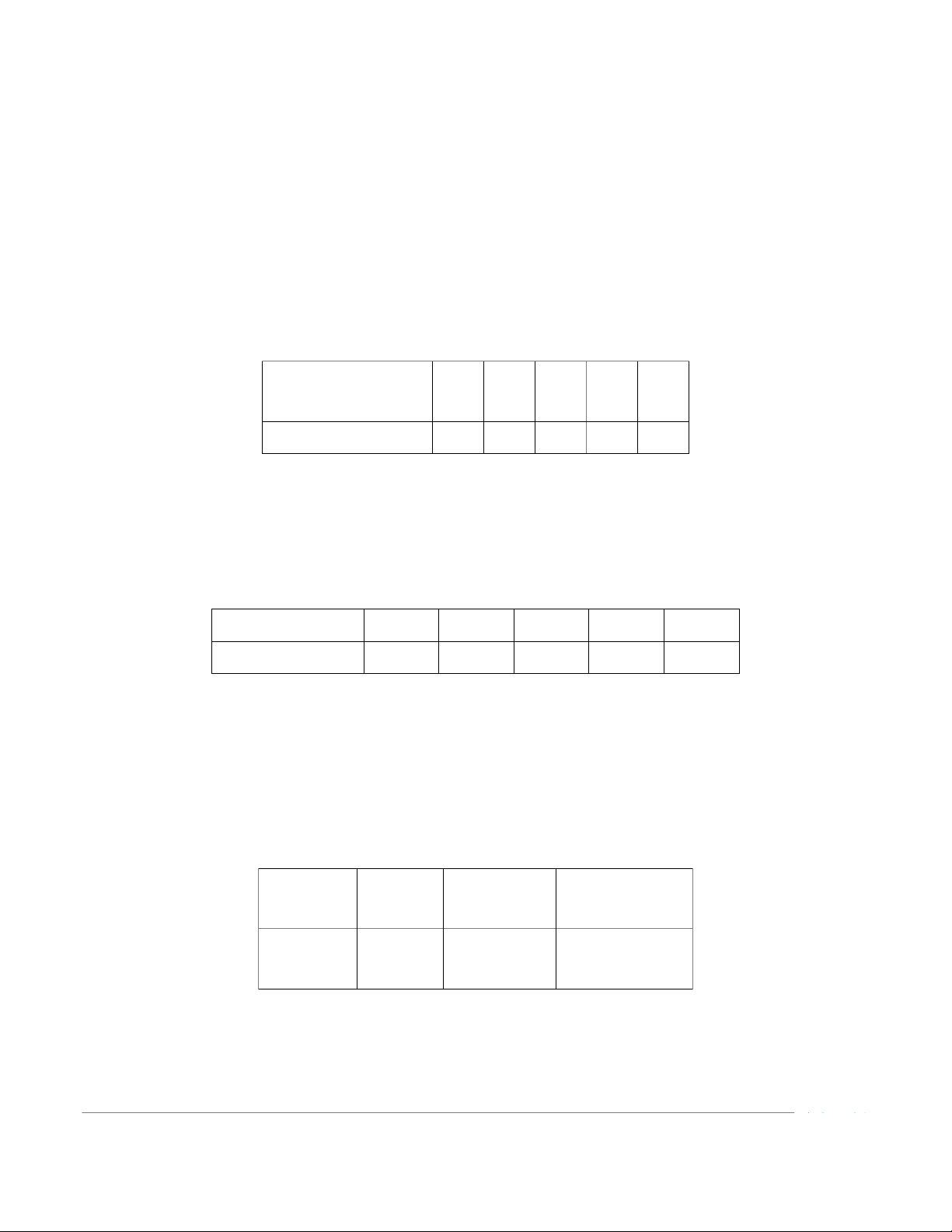
không, nu theo dõi thời gian hoàn thành sn phẩm ở 25 công nhân, ta thu được bng số liệu sau: Thời gian sn xuất 10-12 12-14 14-16 16-18 18-20 một sn phẩm (phút)
Số công nhân tương ứng 2 6 10 4 3
Yêu cần kt luận với mức ý nghĩa 0,05, bit rằng thời gian hoàn thành một sn phẩm là bin
ngẫu nhiên phân phối chuẩn.
Bài 7.3. Trọng lượng đóng bao của các bao go trong kho là bin ngẫu nhiên phân phối
chuẩn với trọng lượng trung bình theo quy định là 50 kg. Nghi ngờ go bị đóng thiu,
người ta đem cân ngẫu nhiên 25 bao và thu được các số liệu sau:
Trọng lượng bao (kg) 48,0-48,5 48,5-49,0 49,0-49,5 49,5-50,0 50,0-50,5 Số bao tương ứng 2 5 10 6 2 Với  = 0,01:
a) Hy kt luận về điều nghi ngờ trên.
b) Tìm xác suất mc sai lầm loi 2 nu trọng lượng đóng bao trung bình thực sự là 49,5 kg.
c) Hy đánh giá điều nghi ngờ trên bằng kiểm định P.
Bài 7.4. Người ta thí nghiệm hai phương pháp chăn nuôi gà khác nhau. Sau một tháng kt qu tăng trọng như sau:
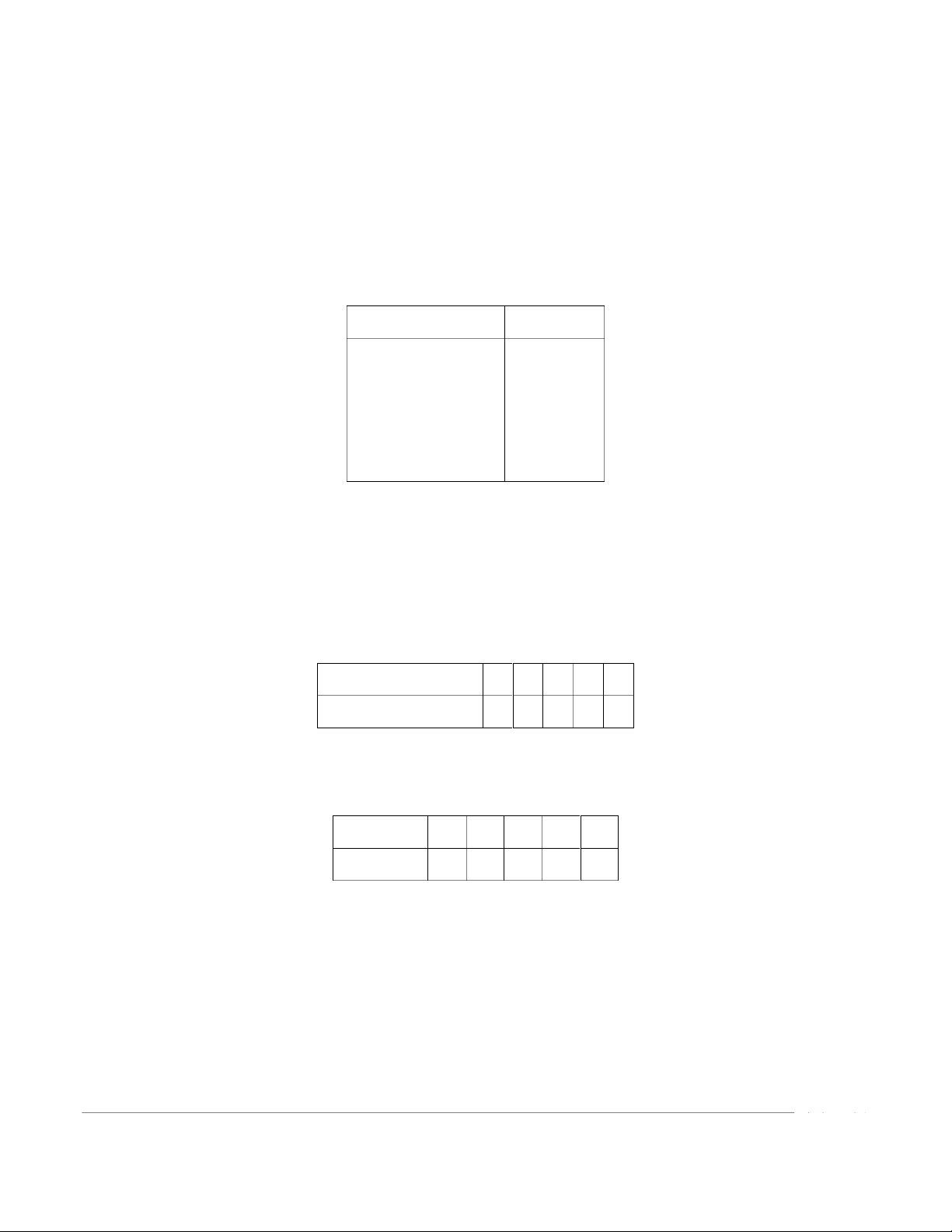
Phương pháp Số gà được Mức tăng trọng Độ lệch chuẩn (kg) theo dõi trung bình (kg) I 100 1,1 0,2 II 150 1,2 0,3
Với mức ý nghĩa 0,05, có thể kt luận:
a) phương pháp II hiệu qu hơn phương pháp I hay không?
b) phương pháp II không hiệu qu bằng phương pháp I hay không?
b) phương pháp II không hiệu qu hơn phương pháp I hay không?
c) hiệu qu của phương pháp II và I như nhau hay không?
Gi thit mức tăng trọng gà phân phối chuẩn.
Bài 7.5. Trọng lượng đóng bao theo qui định của 1 loi sn phẩm A là 50 kg. Kiểm tra ngẫu
nhiên 100 bao của một lô hàng thu được kt qu sau: Trọng lượng (kg) 48 - 48,5 48,5 - 49 49 - 49,5 49,5 - 50 50 - 50,5 Số bao 9 18 35 23 15
a. Với mức ý nghĩa 5% có thể cho rằng trọng lượng sn phẩm có xu hướng bị đóng thiu hay không?
b. Lô hàng sẽ không được php xuất kho nu tỉ lệ bao có trọng lượng dưới 48,5 kg vượt quá
10%. Vậy lô hàng này có được php xuất kho không? Hy kt luận với mức ý nghĩa 5%.
Gi thit rằng trọng lượng bao sn phẩm tuân theo qui luật chuẩn.
Bài 7.6. Công ty A bán được 2000 chic bp ga mang nhn hiệu của công ty trên địa bàn
vùng B. Điều tra 1000 hộ ở vùng B thấy có 750 hộ dùng bp ga, trong đó có 250 hộ
dùng bp ga mang nhn hiệu của công ty A. Gi thit rằng mỗi hộ chỉ dùng một bp ga.
a. Với độ tin cậy 95%, hy cho bit trong toàn vùng có ít nhất bao nhiêu hộ dùng bp ga.
b. Với mức ý nghĩa 5% có thể cho rằng tỷ lệ hộ dùng bp ga của vùng B là dưới 80% được không?
Bài 7.7. Điều tra 100 hộ ti vùng A thấy có 7 hộ thuộc diện nghèo. Có ý kin cho rằng số 1
hộ nghèo trong toàn vùng bằng 9 số hộ không thuộc diện nghèo. Hy đánh giá ý
kin trên với mức ý nghĩa 5%.
Bài 7.8. Mức tiêu hao xăng/100 km của xe A (XA) thuộc Công ty 3A là bin ngẫu nhiên
phân phối chuẩn. Điều tra ngẫu nhiên mức tiêu hao xăng/100 km của 100 xe loi
trên, người ta thu được bng số liệu sau:
XA (lít) 6,0 6,5 7,0 7,5 8,0 8,5 9,0 9,5 Số xe 5 10 15 20 29 10 6 5
a) Với xác suất 95%, mức tiêu hao xăng tối thiểu cho 100 km là bao nhiêu?
b) Trước đây tỷ lệ xe A tiêu hao xăng ít nhất 8 lít/100 km là 0,45. Với mức ý nghĩa 5%, hy
cho bit tỷ lệ này có lớn hơn trước đây không?
Bài 7.9. Doanh thu (X- triệu đồng) của các cửa hàng bán đồ điện trong một tháng trong một
tháng là bnn pp chuẩn. Điều tra ngẫu nhiên 144 cửa hàng kinh doanh mặt hàng trên
ở địa phương A trong tháng 2, người ta thu được các số liệu sau đây: 144 144 2 x  2736; ( x x ) 3575  i i  . i i1  1
a) Tỷ lệ các cửa hàng cùng loi trong toàn quốc có doanh thu từ 20 triệu đồng/tháng trở lên
bằng 42%. Với mức ý nghĩa 5%, hy cho bit sự khác biệt về tỷ lệ này của địa phương A trong
tháng 2 so với toàn quốc hay không? Bit rằng trong mẫu 144 cửa hàng nói trên có 58 cửa hàng
có doanh thu ít nhất 20 triệu/tháng.
b) Hy tìm khong tin cậy đối xứng cho mức doanh thu trung bình với hệ số tin cậy 95%.
c) Theo thống kê, trước đây độ phân tán () của doanh thu/tháng của các cửa hàng trên bằng
5,2 triệu. Với mức ý nghĩa 5%, hy cho bit độ phân tán trong tháng 2 có nhỏ hơn so với trước đây không?
d) Từ mẫu ngẫu nhiên gồm 169 cửa hàng kinh doanh mặt hàng tương tự ở địa phương B, người
ta thu được sai số tiêu chuẩn mẫu bằng 5,5. Với mức ý nghĩa 5% hy cho bit độ phân tán của
doanh thu ở A có nhỏ hơn ở B hay không? Doanh thu các cửa hàng vùng B cũng là bin ngẫu nhiên phân bố chuẩn.
Bài 7.10. Năng suất một giống lúa ti
vùng A là bin ngẫu nhiên phân phối chuẩn. Người
ta đ thu hoch ngẫu nhiên 100 khu ruộng, được số liệu sau:
Năng suất (tấn/ha) 2,5 3,0 3,5 4,0 4,5 5,0 5,5 Số điểm thu hoch 8 13 22 24 15 10 8
a) Trước đây năng suất trung bình của giống lúa trên bằng 3,8 tấn/ha, với mức ý nghĩa 5% hy
cho bit năng suất có tăng lên hay không?
b) Với hệ số tin cậy 95%, tìm khong tin cậy cho phương sai của năng suất.
c) Thu hoch ngẫu nhiên 100 điểm ở vùng B người ta tính được năng suất trung bình là 3,7 tấn
và độ lệch tiêu chuẩn là 0,9 tấn. Với mức ý nghĩa 5% có thể cho rằng năng suất giống lúa ở
vùng A lớn hơn năng suất vùng B hay không? Năng suất vùng B cũng là bnn pp chuẩn.
Bài 7.11. Điều tra ngẫu nhiên 200 sinh viên của một trường đi học thấy có 110 sinh viên
nữ và 90 nam. Trong số sinh viên nữ, có 20 người đi làm thêm ngoài giờ học, trong
số sinh viên nam có 19 người đi làm thêm ngoài giờ học. Với mức ý nghĩa 5% hy
cho kt luận về điều nghi ngờ sau:
a) Tỷ lệ giới trong sinh viên của trường đi học này là như nhau.
b) Tỷ lệ sinh viên nam đi làm ngoài giờ lớn hơn tỷ lệ nữ đi làm ngoài giờ.
Kiểm định tham số 
Bài 7.12. Mức hao phí xăng (X) cho một loi xe ô tô chy trên đon đường AB là bin ngẫu
nhiên phân phối chuẩn có kỳ vọng toán là 50 lít. Do đường được tu sửa li, người ta
cho rằng mức hao phí xăng trung bình đ gim xuống. Quan sát 30 chuyn xe chy
trên đường AB ta thu được bng số liệu sau đây:
Mức xăng hao phí (lít) Số chuyn xe 48,5 49,0 – 5 49,0 49,5 – 10 49,5 50,0 – 10 50,0 50,5 – 3 50,5 51,0 – 2
a) Với mức ý nghĩa 0,05, hy kt luận về ý kin nêu trê n.
b) Tìm xác suất mc sai lầm loi hai nu mức xăng hao phí trung bình thực sự là 48 lít.
Bài 7.13. Trọng lượng sn phẩm (X) do nhà máy sn xuất ra là bin ngẫu nhiên phân phối
chuẩn với độ lệch chuẩn σx = 2 kg và trọng lượng trung bình là 20kg. Nghi ngờ máy
hot động không bình thường làm thay đổi trọng lượng trung bình của sn phẩm
người ta cân thử 100 sn phẩm và thu được kt qu sau:
Trọng lượng sn phẩm 19 20 21 22 23
Số sn phẩm tương ứng 10 60 20 5 5 Với mức ý nghĩa α =
0,05 hy kt luận về điều nghi ngờ nói trên.
Bài 7.14. Điều tra chất lượng X (gam) của 1 loi sn phẩm, kt qu cho trong bng Xi ( gam) 200 220 240 260 280 Số sn phẩm 3 7 16 17 7
a) Có tài liêu cho rằng trung bình chỉ tiêu X các sn phẩm loi này là 250 gam. Hy đánh giá
về nhận xt của tài liệu này với mức ý nghĩa 5%.
b) Những sn phẩm có chỉ tiêu X không vượt quá 240 gam là loi 2. Có tài liệu cho rằng trung
bình chỉ tiêu X của các sn phẩm loi 2 là 220 gam. Hy cho nhận xt về kt luận của tài liệu
này với mức ý nghi 2%. Gi thit chỉ tiêu X của các loi sn phẩm 2 có phân phối chuẩn.
Bài 7.15. Một tổ kiểm tra muốn xác định thời gian trung bình từ lúc công ty A nhân được ý
kin của khách hàng đn lúc gii quyt là bao nhiêu ngày. Mẫu điều tra 15 trường
hợp thời gian khiu kiện được gii quyt trong năm kt qu như sau: 114 78 96 137 78 103 117 126 86 99 114 72 104 73 96
Với mức nghĩa 1% có thể cho rằng thời gian trung bình để 1 khiu kiện được gii quyt bởi
công ty A không vượt qúa 90 ngày không? Gi sử thời gian gii quyt khiu kiện có phân phối chuẩn.
Kiểm định hai tham số 1,  2
Bài 7.16. Hai lớp sinh viên cùng học môn thống kê và kt qu thi ht môn như sau: Lớp A Lớp B n1 = 64 n2 = 68 𝑥1= 73,2 𝑥2 = 76,6 s1 = 10,9 s2 = 11,2.
Với mức ý nghĩa 0,05 có thể cho rằng kt qu thi trung bình của lớp B cao hơn lớp A được không.
Bài 7.17. Để so sánh trọng lượng trung bình của trẻ sơ sinh ở thành thị và nông thôn người
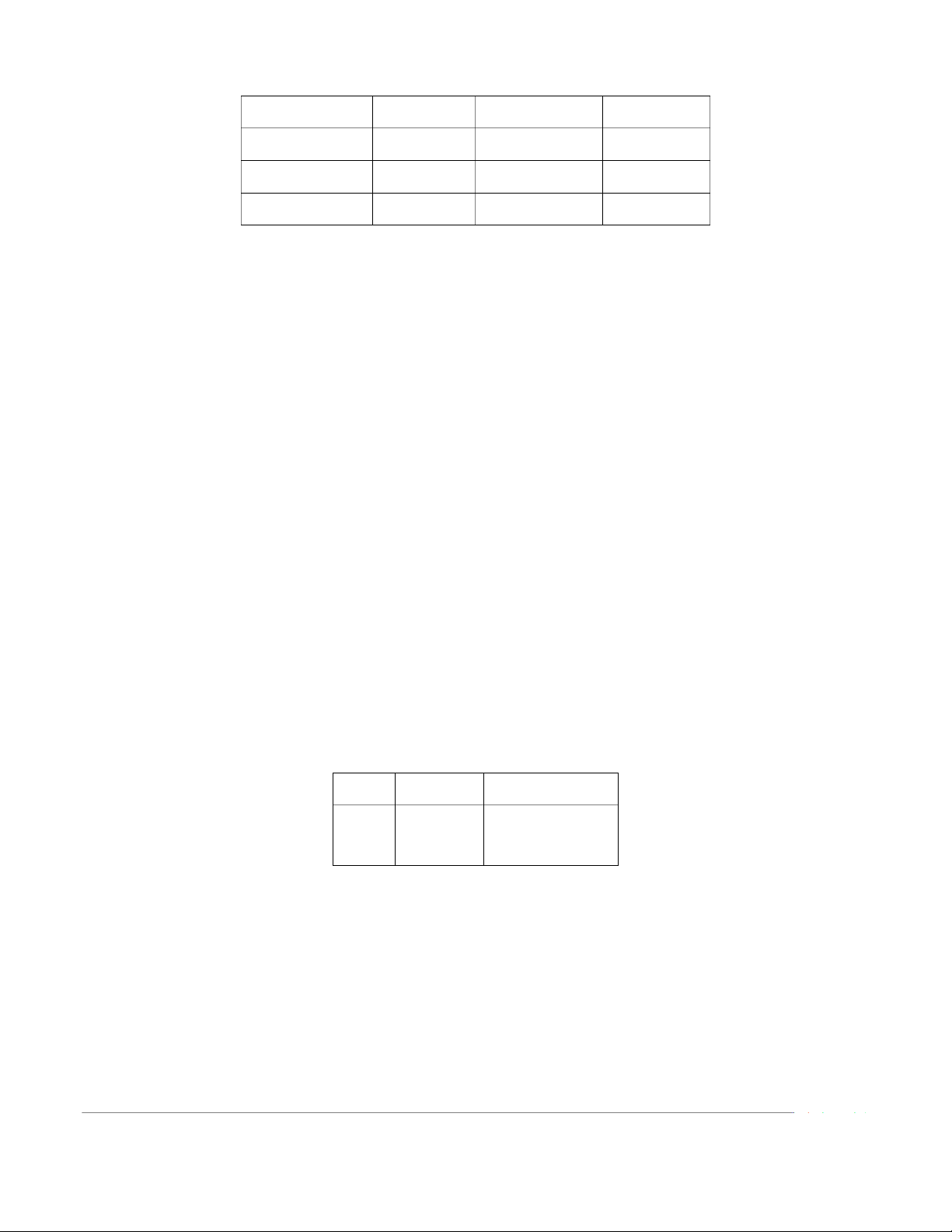
ta cân thử trọng lượng của 10.000 cháu và thu được kt qu như sau: Số cháu Trọng lượng Vùng Độ lệch chuẩn Được cân trung bình Nông thôn 8.000 3,0 (kg) 0,9 (kg) Thành Thị 2.000 3,2 (kg) 0,4 (kg)
Với mức ý nghĩa α = 0,05, có thể coi trọng lượng trung bình của trẻ sơ sinh ở thành phố cao
hơn ở nông thôn hay không? Gia thit trọng lượng trẻ sơ sinh là bin ngẫu nhiên phân phối chuẩn.
Bài 7.18. Trồng cùng một giống lúa trên hai thửa ruộng như nhau và bón hai lọa phân khác
nhau. Đn ngày thu hoch ta có kt qu như sau:Thửa thứ nhất lấy mẫu 1000 bông
lúa thấy số ht trung bình là 𝑥1 = 70 ht và độ lệch chuẩn mẫu s1 =10. Thửa thứ hai
lấy mẫu 500 bông thấy số ht trung bình mỗi bông là 𝑥2 = 72 ht và s2 = 20. Hỏi sự
khác nhau giữa 𝑥1và 𝑥2 là ngẫu nhiên hay bn chất. Hy kt luận với mức ý nghĩa α = 0,05.
Bài 7.19. Nu áp dụng biện pháp kĩ thuật thứ nhất thì điều tra ngẫu nhiên n1 = 100 thửa
ruộng trồng giống lúa A thu được năng suất 𝑥1 =100 t/ha. Và s1 = 10 t/ha. Còn nu
áp dụng biện pháp kĩ thuật thứ hai thì điều tra ngẫu nhiên n2 = 50 thửa, thu được
năng suất trung bình 𝑥2 = 95 t/ha, và s2 = 9 t/ha. Hy kt luận với mức ý nghĩa α
= 0,05 xem nu áp dụng biện pháp kĩ thuật thứ nhất thì năng suất giống lúa A cao
hơn thực sự so với kt qu áp dụng biện pháp kĩ thuật hai không? Gi thit năng suất
lúa tuân theo quy luật chuẩn.
Kiểm định tham số p
Bài 7.20. Tỷ lệ ph phẩm do một máy tự động sn xuất là 5%. Kiểm tra ngẫu nhiên 300 sn
phẩm thấy có 24 sn phẩm là ph phẩm. Từ đó có ý kin cho rằng tỷ lệ ph phẩm do
máy đó sn xuất có chiều hướng tăng lên. Hy kt luận ý kin nêu trên với mức ý nghĩa α = 0,05.
Bài 7.21. Nu áp dụng phương pháp công nghệ thứ nhất thì tỷ lệ ph phẩm là 6%; còn nu
áp dụng phương pháp công nghệ thứ hai thì trong100 sn phẩm có 5 ph phẩm. Vậy
có thể kt luận áp dụng phương pháp công nghệ thứ hai thì tỷ lệ ph phẩm thấp hơn
tỷ lệ ph phẩm của phương pháp công nghệ thứ nhất không? Yêu cầu kêt luận với mức ý nghĩa α = 0,05.
Bài 7.22. Tỷ lệ bệnh nhân khỏi bệnh T khi điều trị bằng thuốc A là 85%. Thí nghiệm dùng
loi thuốc B để chữa bệnh thì trong số 900 người mc bệnh T có 810 người được
chữa khỏi. Như vậy có thể kt luận thuốc B hiệu qu hơn thuốc A hay không?
Bài 7.23. Nu áp dụng phương pháp công nghệ thứ nhất thì tỉ lệ ph phẩm là 8%, còn áp
dụng phương pháp công nghệ thứ 2 thì trong 100 sn phẩm có 3 ph phẩm. Với ý
nghĩa 5%, có thể áp dụng phương pháp công nghệ thứ 2 cho ti lệ ph phẩm thấp hơn không?
Bài 7.24. Năng suất trung bình trong những vụ trước là 5,5 tấn/ha.Vụ lúa năm nay người ta
áp dụng 1 phương pháp trồng lúa cho toàn bộ diện tích lúa của vùng.Mẫu điều tra
100 ha lúa trong vùng thu được kt qu:
Năng suất ( t/ha ) Diện tích (ha) Năng suất ( t/ha) Năng suất (ha) 40-45 7 60-65 20 45-50 12 65-70 8 50-55 18 70-75 5 55-60 27 75-80 3
a) Những ha lúa có năng suất trên 60 t/ha là hecta có năng suất cao. Có báo cáo cho rằng tỉ lệ
hecta có năng suất lúa cao của vùng năm nay là 45%. Cho nhận xt về báo cáo đó với mức ý nghĩa 3%.
b) Với mức ý nghĩa 5%, hy cho kt luận về phương pháp kĩ thuật mới làm tăng năng suất lúa
của vùng năm nay lên hay không?
Kiểm định hai tham số p1, p2
Bài 7.25. Ti hai xí nghiệp A và B có số liệu sau về nhân công. Xí nghiệp A có 200 nhân
công thì năm 1997 có 30 người xin chuyển đi chỗ khác. Xí nghiệp B có 350 nhân
công thì năm 1997 có 65 người thôi việc. Vậy với mức ý nghĩa 0.05 có thể cho rằng
tỷ lệ công nhân thôi việc ở xí nghiệp A thấp hơn xí nghiệp B hay không?
Bài 7.26. Từ dây truyền thứ nhất khi kiểm tra 100 chi tit người ta loi đi 30 chi tit, từ dây
chuyền thứ 2 khi kiểm tra 150 chi tit người ta loi đi 40 chi tit. Vậy nu cho rằng
chất lượng sn phẩm của hai dây chuyền là như nhau thì P-Value bằng bao nhiêu?
Bài 7.27. Bài 7.62. Vào lúc 9 giờ lấy ngẫu nhiên 50 chi tit do một máy sn xuất thì có 5
chi tit hỏng. Và lúc 12 giờ lấy ngẫu nhiên 40 chi tit cũng do máy đó sn xuất thì
có 7 chi tit hỏng. Vậy với mức ý nghĩa 0,01 có thể cho rằng tỷ lệ chi tit hỏng đ
thực sự tăng lên theo thời gian sn xuất hay không.
Bài 7.28. Hiện tượng học sinh bỏ học là vấn đề đang được đặc biệt quan tâm, nhất là ở nông
thôn. Ti hai trường trung học ở hai vùng nông thôn A và B trong năm học 1996 –
1997 có các số liệu thống kê sau:
Trường Số học sinh Số học sinh bỏ học A 1900 175 B 2600 325
a. Với mức ý nghĩa 0,05 có thể cho rằng tình trng bỏ học ở trường B là nghiêm trọng hơn ở trường A hay không.
b. Tìm xác suất mc sai lầm li 2 nu tỷ lệ học sinh bỏ học ở hai trường thật sự chênh lệch nhau là 2%.
Bài 7.29. Có 2 lô ht giống. Từ lô thứ nhất gieo thử ngẫu nhiên 850 ht thấy 680 ht ny
mầm. Từ lô thứ 2 gieo thử 1200 ht thấy có 1020 ht ny mầm. Với mức ý nghĩa 5%
có thể coi tỉ lệ ht giống ny mầm của 2 lô là khác biệt không?
Bài 7.30. Để đánh gi tỉ lệ học sinh đỗ kì thi tốt nghiệp trung học cơ sỏ (THCS) của 2 tỉnh
A và B, người ta điểu tra ngẫu nhiên được:
Tỉnh Số em thi THCS Số em đỗ A 198 173 B 210 195
Với mức ý nghĩa 4%, hay xem:
a) Tỉ lễ đỗ kì thi THCS của 2 tỉnh có khác nhau không?
b) Tỉ lệ đỗ kì thi trung học cơ sở của B có cao hơn A không?
Kiểm định tham số 2
Bài 7.31. Một nhà sn xuất bóng đèn tuýp cho rằng chất lượng bóng đèn sẽ được coi là đồng
đều nu tuổi thọ các bóng đèn có độ lệch chuẩn bằng 1000 giờ hoặc ít hơn. Lấy ngẫu
nhiên 10 bóng để kiểm tra thì tìm được độ lệch chuẩn của mẫu s=1150. Vậy với mức
ý nghĩa 0,05 có thể coi chất lượng bóng đèn do công ty đó sn xuất là đồng đều hay
không? Bit tuổi thọ bóng đèn phân phối chuẩn.
Bài 7.32. Kiểm tra ngẫu nhiên 16 viên thuốc từ một lô thuốc mới nhập về tìm được độ phân
tán của thành phần chính trong mỗi viên thuốc là s² = 0,0775 gr². Gi sử độ phân tán
của thành phần chính trong mỗi viên thuốc theo quy định không được vượt quá 0,05
gr² thì với mức ý nghĩa 0,01 có thể chấp nhận lô thuốc mới nhập về hay không?Bit
trọng lượng thành phần chính trong mỗi viên thuốc phân phối chuẩn.
Bài 7.33. Nu máy móc hot động bình thường thì trọng lượng sn phẩm tuân theo quy luật
chuẩn với độ lệch chuẩn 1 kg. Có thể coi máy móc hot động tôt hay không nu cân
thử 30 sm phẩm ta thấy độ lệch chuẩn mẫu tăng lên tới 1,1 (kg). Yêu cầu kt luận
với mức ý nghĩa α = 0,01.
Bài 7.34. Độ lệch tiêu chuẩn của 1 trọng lượng 1 loi sn phẩm là 0,1 kg, Nghi ngờ độ đồng
đều trọng lượng sn phẩm gim sút, người ta cân thử 25 sn phẩm và thu được số liệu:
Trọng lượng (kg) 2,1 2,2 2,3 2,4 2,5 Số sn phẩm 2 4 15 3 1
Với mức ý nghĩa 5% cho kt luận về nghi ngờ trên. Gi thit trọng lượng sn phẩm có phân phối tiêu chuẩn.
Bài 7.35. Đường kính chi tit của 1 loi chi tit do 1 máy sn xuất là 1 bin ngâu nhiên có
phân phối chuẩn voies độ lệch tiêu chuẩn là 0,15mm. Sau 1 thời gian sn xuất, nghi
ngờ máy làm việc không bình thường làm cho độ đồng đều của các chi tit co xu
hướng gim sút, người ta kiêm tra ngẫu nhiên đường kính các chi tit do máy sn
xuât ra và thu được kt qu (đơn vị: mm).
19,80; 19,83; 19,84; 19,85; 19,88; 19,86; 19,89; 19,90; 20,10; 20,12; 20,15; 20,18; 20,05;
20,20; 19,78; 19,75; 19,74; 20,25; 20,30; 20,28; 19,77; 19,72; 20,35; 19,82; 19,76; 19,74;
20,38; 20,26; 19,92; 20,35; 20,38.
Với mức ý nghĩa 1%, hy xem nghi ngờ trên có cơ sở hay không?
Kiểm định hai tham số 2 2  , 1 2 
Bài 7.36. Hai máy cùng gia công 1 loi chi tit. Người ta muốn kiểm tra xem hai máy này
có độ chính xác như nhau hay không. Để làm điều đó người ta lấy ngẫu nhiên 7 chi
tit từ mỗi máy, đem đo và thu được kt qu sau:
Máy A: 135 138 136 140 138 135 139
Máy B: 140 135 140 138 135 138 140
Với mức ý nghĩa 0,05 có thể cho rằng 2 máy có độ chính xác như nhau hay không. Bit kích
thước chi tit phân phối chuẩn.
Bài 7.37. Để so sánh độ phân tán về trọng lượng đóng gói của 2 máy đóng bao người ta lấy
từ 2 máy đó 2 mẫu và thu được kt qu sau: Máy A Máy B 𝑛1= 12 𝑛2= 15 𝑥1 = 1,5 𝑥2 = 2,0 ∑𝑋 12 2 15 2 𝑖 𝑖
= 1 = 49 ∑𝑋𝑖2𝑖=1 =158
Với mức ý nghĩa 0,05, kiểm định xem độ phân tán về trọng lượng đóng bao của 2 máy có như
nhau hay không. Bit trọng lượng đóng bao là bin ngẫu nhiên phân phối chuẩn.
Bài 7.38. Độ rủi ro trong đầu tư thường được đo bằng phương sai của tỉ lệ thu hồi vốn. Để
quyt định xem nên đầu tư vào ngành nào một người đ thu thập số liệu về hai ngành
kinh t và thu được kt qu sau Ngành A Ngành B
Số dự án điều tra:10 Số dự án điều tra:15
Tốc độ hoàn vốn trung bình:10,48 Tốc độ hoàn vốn trung bình:11
Phương sai:1,44 Phương sai:16
Vậy với mức ý nghĩa 0,05 có thể cho rằng rủi ro đầu tư ở ngành B cao hơn ngành A hay không.
Gi thit tỉ lệ thu hồi vốn là bin ngẫu nhiên phân phối chuẩn.
Bài 7.39. Theo dõi giá cổ phiu ( đơn vị: ngàn đồng) của công ty A trong 31 phên và giá cổ
phiu của công ti B trong 41 phiên người ta tính được:
Trung bình mẫu Độ lệch tiêu chuẩn Công ty A 37,58 1,50 Công ty B 38,24 2,20
Với mức ý nghĩa 5% và gỉa sử giá cổ phiu của các công ty có phân phối chuẩn.
a) Sự khác nhau hay không về giá cổ phiu trung bình của 2 công ty?
b) Nu dùng phương sai của giá cổ phiu làm độ đo sự rủi ro của 2 công ty thì rủi ro của công
ty A có thấp hơn B hay không?