LẬP TRÌNH ĐỘNG TRONG LÝ THUYẾT TRÒ CHƠI (ngành khoa học máy tính)

lOMoAR cPSD| 45148588
BỘ GIÁO DỤC VÀ ĐÀO TẠO
TRƯỜNG ĐẠI HỌC XÂY DỰNG HÀ NỘI
KHOA CÔNG NGHỆ THÔNG TIN -------- -- ------ ĐỒ ÁN
TỐT NGHIỆP ĐẠI HỌC
NGÀNH KHOA HỌC MÁY TÍNH
LẬP TRÌNH ĐỘNG TRONG LÝ THUYẾT TRÒ CHƠI
Sinh viên thực hiện Lê Thị Lâm Oanh Mã sinh viên 153365 Lớp 65CS3
Giảng viên hướng dẫn TS Phạm Hồng Phong
H愃 Nôi : 04/2024 MỤC LỤC lOMoAR cPSD| 45148588
LỜI CẢM ƠN....................................................................................................................3
DANH MỤC CÁC BẢNG.................................................................................................4
DANH MỤC HÌNH..........................................................................................................4
LỜI MỞ ĐẦU...................................................................................................................5
CHƯƠNG 1: TỔNG QUAN VỀ LẬP TRÌNH ĐỘNG.....................................................8 1.1
Giới thiệu chung................................................................................................8
1.1.1 Khái niệm về quy hoạch động..........................................................................8 1.1.2
Lập trình động hoạt động như thế n愃o?.......................................................8
1.1.3 Khi nào sử dụng lập trình động........................................................................9
1.1.4 Các phương pháp lập trình động....................................................................10
1.1.5 Ứng dụng của lập trình động..........................................................................10
1.2 Đặc điểm của lập trình động...........................................................................11
1.3 Lập trình động dựa trên các nguyên tắc........................................................11
1.4 Các bước giải b愃i toán bằng lập trình động...................................................12
1.4.1 Xem xét bài toán............................................................................................12
1.4.2 Xác định hệ thức xã hội.................................................................................12 1.4.3
Tìm nghiệm tối ưu.........................................................................................12 1.5
Một số kỹ thuật giải b愃i toán lập trình động.................................................12
1.5.1 Top-Down (Từ trên xuống – Ghi nhớ).............................................................13
1.5.2 Bottom-Up (Từ dưới lên – Lập bảng)..............................................................13
CHƯƠNG 2: TÌM HIỂU VỀ LÝ THUYẾT TRÒ CHƠI...............................................16
2.1 Các khái niệm chung............................................................................................16
2.2 Trạng thái trò chơi...............................................................................................17
2.3 Đồ thị trạng thái của trò chơi (State graph).......................................................18
2.4 Trò chơi tổ hợp cân bằng.....................................................................................19
2.4.1 Mô tả................................................................................................................20
2.4.2 Tập P, tập N và cách tìm.................................................................................20
2.4.3 Tổng Nim và trò chơi Nim...............................................................................21
2.4.5 Định lý Bouton.................................................................................................24
2.4.6 Trò chơi trên đồ thị..........................................................................................25
2.4.7 Định lý Sprague – Grundy...............................................................................25
2.4.8 Cách tính Grundy Numbers.............................................................................26
2.4.9 Trò chơi phụ.....................................................................................................28
2.5 Trò chơi hai người có tổng điểm bằng 0.............................................................30
2.5.1 Định lý Minimax..............................................................................................30
2.5.2 Cân bằng Nash.................................................................................................34 lOMoAR cPSD| 45148588
CHƯƠNG 3: ỨNG DỤNG LẬP TRÌNH ĐỘNG TRONG LÝ THUYẾT TRÒ CHƠI N
ĐỒNG XU.......................................................................................................................37
3.1 Giới thiệu về trò chơi n đồng xu..........................................................................37
3.2 Các khía cạnh của lý thuyết trò chơi trong b愃i toán
n愃y...................................37 3.3 B愃i
toán.............................................................................................................38 3.4 Khởi
tạo v愃 Định nghĩa...................................................................................39
3.4.1 Khởi tạo ma trận dp.........................................................................................39
3.4.2 Cập nhật ma trận..............................................................................................40
3.4.3 Tính giá trị tối ưu cho các đoạn đồng xu có độ dài lớn hơn 1..........................41
Giải b愃i toán trò chơi n đồng xu bằng phương pháp đệ
quy...................................42 So sánh lập trình động v愃 đệ
quy..............................................................................43
KẾT LUẬN TÀI LIỆU THAM KHẢO...........................................................................44 lOMoAR cPSD| 45148588 LỜI CẢM ƠN
Trong thời gian làm đồ án tốt nghiệp, em đã nhận được nhiều sự giúp đỡ, đóng góp ý
kiến và chỉ bảo tận tình của thầy cô, gia đình và bạn bè. Em xin gửi lời cảm ơn chân thành
đến TS Phạm Hồng Phong, người đã hướng dẫn và giúp đỡ em trong suốt quá trình hoàn
thiện đồ án tốt nghiệp.
Em cũng xin chân thành cảm ơn các thầy cô giáo trong trường Đại học Xây Dựng Hà
Nội nói chung và các thầy cô trong khoa Khoa Học Máy Tính nói riêng đã giảng dạy cho
em những kiến thức về các môn đại cương cũng như những môn chuyên ngành, giúp em
có cơ sở lý thuyết vững vàng và tạo điều kiện cho em trong suốt quá trình học tập.
Với điều kiện thời gian cũng như kinh nghiệm còn hạn chế nên đồ án này không thể
tránh những thiếu sót. Em rất mong nhận được sự đóng góp ý kiến của thầy cô để em có
điều kiện bổ sung, nâng cao kiến thức và có thể hoàn thành tốt công tác thực tế sau này.
Em xin trân thành cảm ơn!
Hà Nội, ngày tháng 05 năm 2024 Sinh viên thực hiện lOMoAR cPSD| 45148588 DANH MỤC CÁC BẢNG STT Bảng Tên bảng 1 1
So sánh lập bảng và ghi nhớ 2 2 Trạng thái W-L 3 3
Trạng thái W-L của đồ thị trạng thái DANH MỤC HÌNH STT Hình Tên hình 1 1 Dãy Fibonacci 2 2
Trạng thái của trò chơi trên đồ thị trạng thái 3 3 Đồ thị trạng thái 4 4
Đồ thị trạng thái có các số Grundy 5 5
Trạng thái khởi đầu của trò chơi mê cung 6 6
Trạng thái khởi đầu của trò chơi mê cung có số Grundy 7 7
Trạng thái khởi đầu trò chơi phụ 8 8
Trạng thái khởi đầu của trò chơi phụ có số Grundy LỜI MỞ ĐẦU
1. Tính cấp thiết của đề tài
Trong cuộc sống, tất cả chúng ta đều có lý do cá nhân cho sự lựa chọn của mình.
Chúng ta lựa chọn dựa theo tình huống hoặc những gì chúng ta nghĩ là phù hợp với
bản thân mình hoặc cả với những người khác. Mục đích chính của các sự lựa chọn
này là làm những gì tốt nhất (hay có lợi nhất) cho bản thân. Lý thuyết trò chơi
(Game theory) đã ra đời từ đó, là mô hình để nghiên cứu các tình huống mang tính
mâu thuẫn mà trong đó các bên tham gia sẽ lựa chọn các hành động khác nhau để
cố gắng làm tối ưu hóa các kết quả nhận được. Ngày nay, nó được áp dụng rộng rãi
trong mọi khía cạnh của đời sống, đặc biệt là trong kinh tế, chính trị, lý luận, khoa
học máy tính,... Vì thế, người nào nắm rõ được các quy tắc và áp dụng hiệu quả Lý
thuyết trò chơi sẽ có nhiều khả năng nâng cao được quyền lực, địa vị trong xã hội,
cũng như kiếm và tiết kiệm được nhiều tiền hơn. lOMoAR cPSD| 45148588
Lý thuyết trò chơi là một công cụ thuộc Toán học ứng dụng, vì thế nó có thể được
biểu diễn dưới dạng toán. Tuy nhiên ở bài viết này, tôi chỉ muốn giải thích một cách
đơn giản và chỉ ra một số các ứng dụng của Lý thuyết trò chơi trong thực tế. Nhìn
chung, “Trò chơi” (Game) ở đây chính là các tình huống đòi hỏi những người tham
gia (hay người chơi) phải đưa ra các quyết định, ví dụ như liệu sẽ ra đấm, kéo hay
lá khi oẳn tù tì; quyết định sẽ mua hay bán khi đầu tư chứng khoán; quyết định sẽ
tấn công hay phòng ngự trong trận bóng;... Điều quan trọng là kết quả và lợi ích đạt
được sẽ phụ thuộc vào quyết định của tất cả các bên tham gia, ví dụ tôi ra đấm thì
đối phương phải ra kéo thì tôi mới thắng; hoặc khi tôi mua chứng khoán thì những
người khác cũng phải mua theo thì tôi mới có lãi. Do đó, xây dựng mô hình Lý
thuyết trò chơi sẽ giúp chúng ta đưa ra được phương án tốt nhất khi bị buộc phải lựa chọn.
Các dạng cơ bản của Lý thuyết trò chơi có thể bao gồm dạng đối xứng (Symmetric),
tổng bằng không (Zero-sum), đồng thời (Simultaneous),... Tuy nhiên, nhìn chung
thì nó giúp ta thấy được bản chất của các tình huống được tạo ra và các lựa chọn có
thể giúp giải quyết tình huống đó một cách tốt nhất cho chính mình cũng như những
người khác. Lý thuyết trò chơi có thể được áp dụng vào rất nhiều trường hợp thực
tế trong cuộc sống một cách tương tự. Do đó đề tài “Lập trình động trong lý thuyết
trò chơi” được chọn để thực hiện đồ án tốt nghiệp. Lý thuyết trò chơi và lập trình
động là hai lĩnh vực có sự quan điểm rất mạnh mẽ trong khoa học máy tính. Sự kết
hợp giữa chúng cung cấp các công cụ hữu ích để nghiên cứu, phân tích và giải quyết
các vấn đề phức tạp liên quan đến tối ưu hóa chiến lược và đưa ra quyết định trong
các trò chơi và ứng dụng thực tế. Lập trình động trong lý thuyết trò chơi cung cấp
một loạt các bài toán phong phú và đa dạng. Từ việc tính toán giá trị Grundy cho
các trò chơi phức tạp như Nim, đến tìm kiếm chiến lược tối ưu trong các trò chơi
bàn cờ như tic-tac-toe, chess, hay tối ưu hóa các chiến lược trong các mô hình thực
tế, những bài toán này thú vị và mang tính thử thách cao. Nghiên cứu và thực hiện
các bài toán lập trình động trong lý thuyết trò chơi mang lại trải nghiệm thú vị và
hấp dẫn. Việc tìm hiểu cách máy tính "suy nghĩ" và đưa ra quyết định trong các tình lOMoAR cPSD| 45148588
huống đối kháng như trong trò chơi mang lại sự hứng thú và khám phá liên tục. Tóm
lại, lựa chọn đề tài "Lập trình động trong lý thuyết trò chơi" là một sự kết hợp tuyệt
vời giữa lý thuyết và thực tiễn, giúp phát triển kỹ năng nghiên cứu và lập trình trong
lĩnh vực lý thuyết trò chơi và khoa học máy tính. 2. Mục đích nghiên cứu
Mục đích chính của nghiên cứu này là nâng cao hiểu biết về lý thuyết trò chơi và
các phương pháp tính toán trong lý thuyết này. Lý thuyết trò chơi là một lĩnh vực
quan trọng trong khoa học máy tính, và việc nghiên cứu về lập trình động trong ngữ
cảnh này giúp củng cố kiến thức về các thuật toán và kỹ thuật quan trọng. Nghiên
cứu về lập trình động trong lý thuyết trò chơi cung cấp cơ hội áp dụng các kiến thức
và kỹ năng vào giải quyết các vấn đề thực tế. Ví dụ, áp dụng các thuật toán lập trình
động để tối ưu hóa chiến lược trong các ứng dụng game, hoặc trong các lĩnh vực
khác như trí tuệ nhân tạo và tối ưu hóa. Tăng cường kỹ năng lập trình và khả năng
giải quyết các bài toán phức tạp. Việc thực hiện các thuật toán lập trình động trong
các trò chơi cạnh tranh (competitive programming) cũng giúp rèn luyện tư duy logic và sáng tạo.
3. Kết cấu của đề tài
Chương 1: Tổng quan kiến thức về lập trình động.
Chương 2: Tìm hiểu về lý thuyết trò chơi.
Chương 3: Tìm hiểu trò chơi n đồng xu. lOMoAR cPSD| 45148588
CHƯƠNG 1: TỔNG QUAN VỀ LẬP TRÌNH ĐỘNG 1.1 Giới thiệu chung
1.1.1 Khái niệm về quy hoạch động
Lập trình động (Dynamic Programming) là một phương pháp được sử dụng trong
toán học và khoa học máy tính để giải quyết các vấn đề phức tạp bằng cách chia
chúng thành những bài toán con đơn giản hơn. Bằng cách giải mỗi bài toán con chỉ
một lần và lưu trữ kết quả, nó tránh được các phép tính dư thừa, dẫn đến giải pháp
hiệu quả hơn cho nhiều bài toán.
1.1.2 Lập trình động hoạt động như thế nào?
Xác định các vấn đề phụ: chia vấn đề chính thành các vấn đề phụ nhỏ hơn, độc lập.
Lưu trữ giải pháp: giải quyết từng bài toán con và lưu trữ giải phpas trong một bảng hoặc mảng.
Xây dựng giải pháp: sử dụng các giải pháp được lưu trữ để xây dựng giải pháp cho vấn đề chính.
Tránh dư thừa: bằng cách lưu trữ lời giải, quy hoạch động đảm bảo rằng mỗi bài
toán con chỉ được giải một lần, giảm thời gian tính toán.
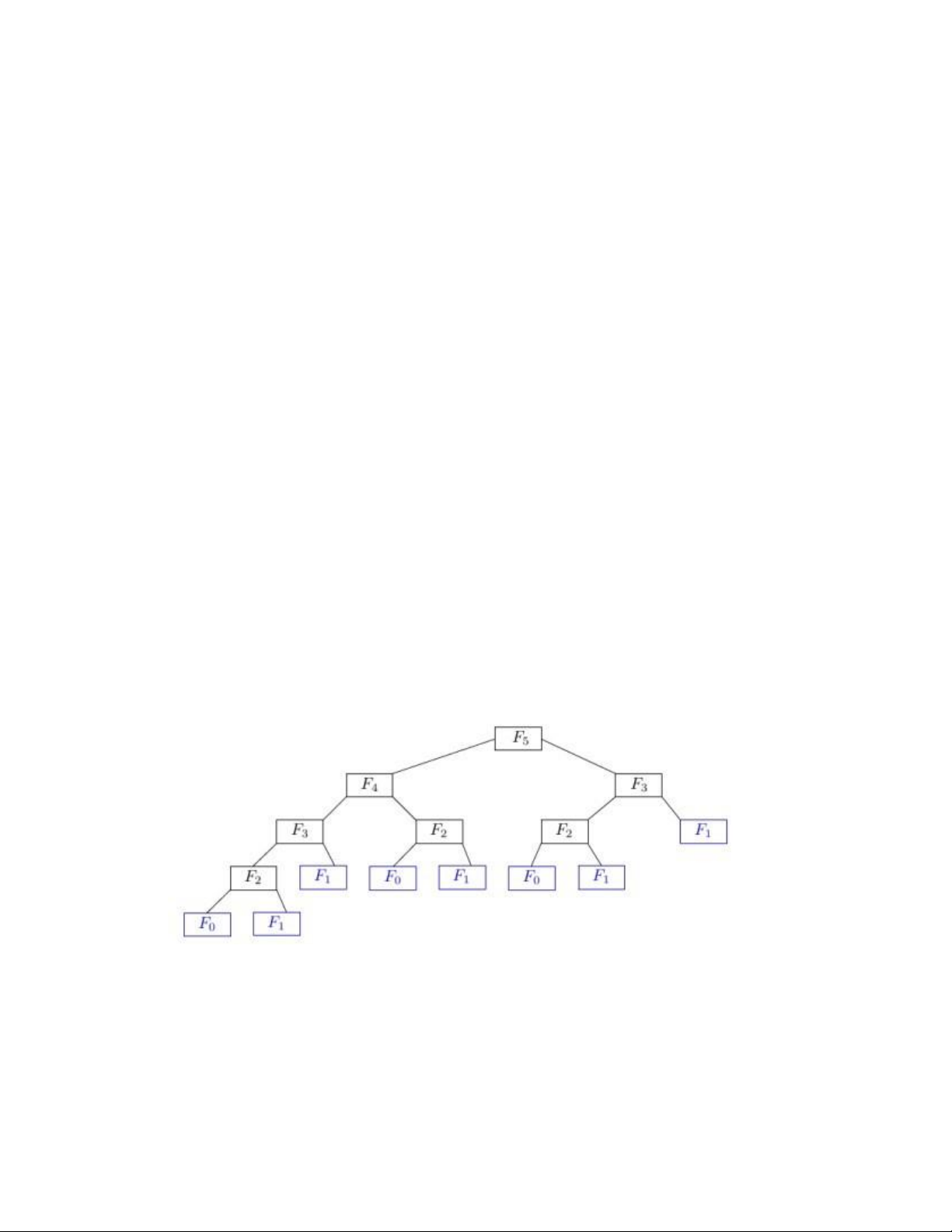
Ví dụ về lập trình động: Xét bài toán tìm dãy Fibonacci Hình 1: Dãy Fibonacci
Chuỗi Fibonacci sử dụng lập trình động:
• Các bài toán con: F(0), F(1), F(2), F(3),….
• Giải pháp lưu trữ: Tạo một bảng để lưu trữ các giá trị của F(n) khi chúng được tính toán. lOMoAR cPSD| 45148588
• Xây dựng lời giải: Đối với F(n), hãy tra cứu F(n-1) và F(n-2) trong bảng và cộng chúng lại.
• Tránh dư thừa: Bảng đảm bảo rằng mỗi bài toán con (ví dụ F(2)) chỉ được giải một lần.
Bằng cách sử dụng lập trình động, chúng ta có thể tính toán dãy Fibonacci một
cách hiệu quả mà không cần phải tính toán lại các bài toán con.
1.1.3 Khi nào sử dụng lập trình động
Lập trình động là một kỹ thuật tối ưu hóa được sử dụng khi giải quyết các vấn đề bao gồm đặc điểm sau: 1.1.3.1 Cấu trúc tối ưu:
Cấu trúc tối ưu có nghĩa là chúng ta kết hợp các kết quả tối ưu của các bài toán
con để đạt được kết quả tối ưu của bài toán lớn hơn. Ví dụ:
Xét vấn đề tìm đường dẫn chi phí tối thiểu trong biểu đồ có trọng số từ nút
nguồn đến nút đích. Chúng ta chia bài toán này thành các bài toán con nhỏ hơn:
• Tìm đường đi có chi phí tối thiểu từ nút nguồn đến mỗi nút trung gian.
• Tìm đường đi có chi phí tối thiểu từ mỗi nút trung gian đến nút đích. 1.1.3.2
Các bài toán con chồng chéo
Các bài toán con giống nhau được giải lặp đi lặp lại ở các phần khác nhau của bài toán.
Ví dụ:Xét bài toán tính dãy Fibonacci. Để tính số Fibonacci tại chỉ số n, chúng
ta cần tính số Fibonacci tại chỉ số n-1 và n-2. Điều này có nghĩa là bài toán con
tính số Fibonacci tại chỉ số n-1 được sử dụng hai lần trong lời giải cho bài toán
lớn hơn là tính số Fibonacci tại chỉ số n
1.1.4 Các phương pháp lập trình động
Lập trình động có thể đạt được bằng hai cách tiếp cận: 1.1.4.1
Cách tiếp cận từ trên xuống (Top-Down) lOMoAR cPSD| 45148588
Trong cách tiếp cận từ trên xuống, còn được gọi là ghi nhớ (memoization), chúng
ta bắt đầu với lời giải cuối cùng và chia nó thành các bài toán con nhỏ hơn một
cách đệ quy. Để tránh tính toán dư thừa, chúng tôi lưu trữ kết quả của các bài
toán con đã giải trong bảng ghi nhớ.
Phân tích cách tiếp cận từ trên xuống:
• Bắt đầu với lời giải cuối cùng và chia thành các bài toán con nhỏ hơn.
• Lưu trữ lời giải của các bài toán con trong một bảng để tránh tính toán dư thừa.
• Thích hợp khi số lượng bài toán con lớn và nhiều bài toán con được sử dụng lại. 1.1.4.2
Cách tiếp cận từ dưới lên (Bottom-Up)
Trong cách tiếp cận từ dưới lên, còn được gọi là lập bảng (tabulation), chúng ta
bắt đầu với các bài toán nhỏ nhất và dần dần xây dựng đến lời giải cuối cùng.
Chúng ta lưu trữu kết quả của các bài toán con đã giải trong một bảng để tránh tính toán dư thừa.
Phân tích cách tiếp cận từ dưới lên:
• Bắt đầu với những bài toán nhỏ nhất và dẫn dần xây dựng lời giải cuối cùng.
• Điền vài bảng các giải pháp cho các bài toán con theo cách từ dưới lên.
• Thích hợp khi số lượng bài toán con nhỏ và lời giải tối ưu có thể được
tính trực tiếp từ lời giải của bài toán con nhỏ hơn.
1.1.5 Ứng dụng của lập trình động
Lập trình động có nhiều ứng dụng, bao gồm:
• Tối ưu hóa: bài toán balo, đường đi ngắn nhất, mảng con tối đa.
• Khoa học máy tính: dãy con chung dài nhất, chỉnh sửa khoảng cách, khớp chuỗi.
• Nghiên cứu hoạt động: quản lý hàng tồn kho, lập kế hoạch, phân bổ nguồn lực. lOMoAR cPSD| 45148588
1.2 Đặc điểm của lập trình động
Lập trình động là một trong những kỹ thuật mạnh mẽ nhất để giải quyết một loại vấn đề nhất định.
Có một cách hay để hình thành cách tiếp cận và quy trình tư duy rất đơn giản, đồng
thời phần mã hóa cũng rất dễ dàng.
Về cơ bản, đó là một lý tưởng đơn giản, sau khi giải quyết một vấn đề với một đầu vào
nhất định, lưu jeets quả làm tài liệu tham khảo để sử dụng cho tương lai. Lời giải của
các bài toán con được lưu trữu trong một bảng hoặc mảng(ghi nhớ) hoặc theo cách từ
dưới lên (lập bảng) để tránh tính toán dư thừa.
Lời giải bài toán có thể được xây dựng từ lời giải của các bài toán con.
Lập trình động có thể được triển khai bằng thuật toán đệ quy, trong đó giải pháp cho
các bài toán con được tìm thấy đệ quy hoặc sử dụng thuật toán lặp, giải pháp được tìm
thấy bằng cách giải quyết các bài toán con theo một thứu tự cụ thể.
1.3 Lập trình động dựa trên các nguyên tắc
Đặc trung cấu trúc của lời giải tối ưu, tức là xây dựng mô hình toán học của lời giải.
Xác định đệ quy giá trị của giải pháp tối ưu.
Sử dụng phương phápt iếp cận từ dưới lên, tính toán giá trị của lời giải tối ưu cho từng
bài toán con có thể xảy ra.
Xây dựng giải pháp tối ưu cho bài toán ban đầu bằng cách sử dụng thông tin được tính toán ở bước trước.
1.4 Các bước giải bài toán bằng lập trình động
Bước 1: xem xét bài toán có thể chia thành các bài toán con thảo mãn nguyên lý Bellman không.
Bước 2: Xác định hệ thức truy hồi cho bài toán tối ưu.
Bước 3: Tìm nghiệm tối ưu của bài toán bằng hai phương pháp Top-Down hoặc Bottom-Up. 1.4.1 Xem xét bài toán lOMoAR cPSD| 45148588
Xác định xem bài toán có thể chia thành các bài toán con nhỏ hơn không, có thể giải
quyết độc lập với nhau.
Kiểm tra xem bài toán có thỏa mãn nguyên lý Bellman hoặc các đặc điểm của quy
hoạch động hay không. Những đặc điểm bao gồm bài toán con chồng chéo và cấu
trúc tối ưu phụ thuộc.
1.4.2 Xác định hệ thức xã hội
Xây dựng một hệ thống truy hồi để tính toán giá trị tối ưu của bài toán từ các bài toán con nhỏ hơn.
Định nghãi cách biểu diễn các trạng thái và cách chuyển đổi giữa chúng.
Xác định công thức hoặc quy tắc để tính toán giá trị tối ưu dựa trên các giá trị của các trạng thái con. 1.4.3 Tìm nghiệm tối ưu
Có hai phương pháp chính để tìm nghiệm tối ưu của bài toán: Top-Down (Đệ quy
với ghi nhớ) và Bottom-Up (Lập bảng).
Trong phương pháp Top-Down, chúng ta sử dụng đệ quy và lưu trữ các giá trị đã
tính toán trước đó để không phải tính lại.
Trong phương pháp Bottom-Up, chúng ta sử dụng một bảng để lưu trữ các giá trị
tối ưu và điền vào bảng theo thứ tự các trường hợp cơ bản đến phức tạp.
1.5 Một số kỹ thuật giải bài toán lập trình động
Có hai hướng tiếp cận để giải quyết một bài toán bằng lập trình động
1.5.1 Top-Down (Từ trên xuống – Ghi nhớ)
Theo hướng tiếp cận Top-Down chúng ta sẽ bắt đầu bằng bài toán lớn nhất hay bài toán
ở mức trên cùng sau đó dùng phương pháp đệ quy để gọi lời giải cho các bài toán con
ở mức thấp hơn tiếp theo. Quá trình tiếp tục cho đến khi gặp bài toán nhỏ nhất. Đệ quy
sẽ tự động tổ hợp kết quả các bài toán con để được kết quả bài toán ban đầu. Cách này
đòi hỏi tốn nhiều thời nguyên để ghi nhớ tất cả kết quả của các bài toán con. lOMoAR cPSD| 45148588
Việc thực hiện các loại ghi nhớ phụ thuộc vào các tham số thay đổi chịu trách nhiệm
giải quyết vấn đề. Có nhiều kích thuốc khác nhau của bộ nhớ đệm được sử dụng trong
kỹ thuật ghi nhớ. Dưới đây là một trong số đó:
Ghi nhớ 1D: Hàm đệ quy chỉ có một đối số có giá trị không đổi sau mỗi lần gọi hàm.
Ghi nhớ 2D: Hàm đệ quy chỉ có hai đối số có giá trị không đổi sau mỗi lần gọi hàm.
Ghi nhớ 3D: Hàm đệ quy chỉ có ba đối số có giá trị không đổi sau mỗi lệnh gọi hàm.
Kết luận: Ghi nhớ là một khái niệm lập trình và có thể được áp dụng cho bất kỳ ngôn
ngữ nào. Mục tiêu tuyệt đối của nó là tối ưu hóa chương trình. Thông thường vấn đề
này xuất hiện khi các chương trình thực hiện các phép tính nặng. Kỹ thuật này được
lưu trữ tát cả kết quả được tính toán trước đó để không phải tính toán lại cho cùng một vấn đề.
1.5.2 Bottom-Up (Từ dưới lên – Lập bảng)
Hướng tiếp cận Bottom-Up đầu tiên chúng ta giải các bài toán con ở mức thấp nhất sau
đó dùng các kết quả này để tính bài toán ở mức trên. Quá trình tiếp tục cho đến khi
chúng ta tìm được kết quả bài toán mức cao nhất. Hướng này không đòi hỏi phải lưu
lại kết quả của tất cả các bài toán con.
Chiến lược từ dưới lên trong lập trình động là lập bảng
Kết quả của các bài toán con được lưu trữ trong một bảng, thường là một mảng So sánh
việc lập bảng với việc ghi nhớ về độ phức tạp về thời gian, việc lập bảng thường sẽ hiệu quả hơn.
Việc lập bảng được thực hiện theo các bước sau:
• Xác định các yếu tố cần tối ưu và xác định rõ ràng vấn đề cần giải quyết.
• Tạo một bảng để chứa kết quả của các bài toán con (thường là một mảng). Sự cố
xác định kích thước của bảng.
• Tạo trường hợp cơ sở hoặc giá trị ban đầu cho bảng. Những con số này đại diện
cho câu trả lời cho các bài toán con nhỏ nhất. lOMoAR cPSD| 45148588
• Điền vào bảng từ các bài toán con nhỏ nhất đến bài toán lớn nhất bằng cách sử
dụng phép lặp (thường là các vòng lặp). Dựa trên các bài toán con đã tính toán
trước đó, hãy xác định lời giải cho từng bài toán con.
• Khi bảng được điền đầy đủ, kết quả cuối cùng thường được tìm thấy ở mục cuối cùng của bảng.
Kết luận: Lập bảng là một kỹ thuâth mạnh mẽ trong quy hoạch động để giải quyết các
vấn đề phức tạp một cách hiệu quả bằng cách lưu trữ kết quả các bài toán con trong mảng.
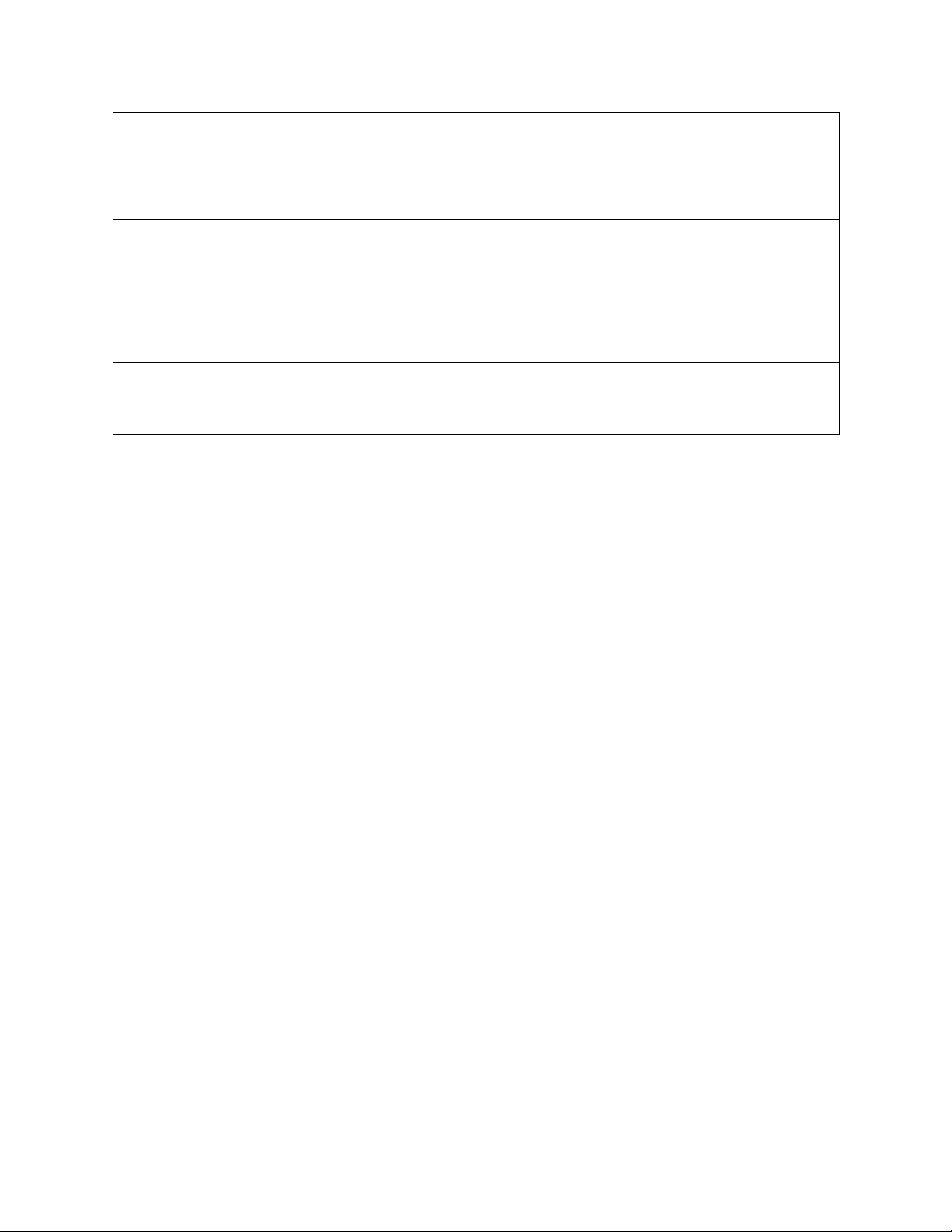
1.5.2 So sánh lập bảng và ghi nhớ Ghi
nhớ: Cách tiếp cận từ trên xuống
Lưu trữ kết quả của lệnh gọi Hàm triển khai đệ quy
Rất phù hợp cho các bài toán có tập hợp đầu vào tương đối nhỏ
Được sử dụng khi các bài toán con có các bài toán con chồng chéo.
Lập bảng: Cách tiếp cận từ dưới lên
Lưu trữ kết quả của các bài toán con trong một bảng Triển khai lặp lại
Phù hợp cho ácc bài toán có tập hợp đầu vào lớn
Được sử dụng khi các bài toán con không trùng nhau. Lập bảng Ghi nhớ Tình trạng
Quan hệ chuyển trnagj thái rất
Quan hệ chuyển trạng thái dễ nghĩ khó nghĩ Mã số
Mã trở nên phứuc tạp khi yêu cầu Mã dễ dàng và ít phức tạp hơn nhiều điều kiện lOMoAR cPSD| 45148588 Tốc độ
Nhanh chóng, vì truy cập trực Chậm do có nhiều lệnh gọi đệ quy
tiếp vào các trạng thái trước đó từ và báo cáo trả về bảng Giải quyết vấn
Nếu một số bài toán con trong đề phụ không gian bài Các mục trong bảng Tiếp cận
Lập bảng là một cách tiếp cận lặp Ghi nhớ là một cách tiếp cận đệ đi lặp lại quy
Bảng 1: So sánh lập bảng và ghi nhớ
CHƯƠNG 2: TÌM HIỂU VỀ LÝ THUYẾT TRÒ CHƠI 2.1 Các khái niệm chung
Lý thuyết trò chơi là một mô hình toán học được sử dụng để ra quyết định. Nó có ứng dụng
trong mọi lĩnh vực khoa học xã hội, cũng như logic và khoa học máy tính. Lý thuyết trò
chơi ngày càng đóng một vai trò quan trọng trong logic và khoa học máy tính. Để được lOMoAR cPSD| 45148588
xác định đầy đủ, một trò chơi phải xác định rõ các yếu tố sau: người chơi trong trò chơi,
thông tin hành động có sẵn cho mỗi người chơi tại mỗi thời điểm quyết định và phần thưởng
cho mỗi kết quả. Hầu hết các trò chơi hợp tác được trình bày dưới dạng hàm đặc trưng,
trong khi dạng mở rộng và thông thường được sử dụng để xác định các trò chơi không hợp tác.
Trong lý thuyết trò chơi, dạng thông thường hay còn được gọi là dạng chiến lược là sự mô
tả về một trò chơi. Trò chơi thông thường thường được thể hiện bằng một ma trận hiển thị
người chơi, chiến lược và phần thưởng. Khi một trò chơi được trình bày ở dạng bình
thường, người ta cho rằng mỗi người chơi hành động đồng thời hoặc ít nhất là không biết
hành động của người kia.
Lý thuyết trò chơi là một chủ đề trong lập trình cạnh tranh liên quan đến một loại vấn đề
nhất định, trong đó có một số người chơi trò chơi dựa trên các nguyên tắc nhất định và
nhiệm vụ thường là tìm ra người chiến thắng hoặc nước đi chiến thắng
Mục tiêu lý thuyết trò chơi cho lập trình cạnh tranh
• Ở đây chúng ta sẽ tập trung vào các trò chơi hai người chơi không chứa các yếu tố ngẫu nhiên
• Mục tiêu của chúng ta là tìm ra một chiến lược mà chúng ta có thể áp dụng để dành
chiến thắng trong trò chơi bất kể đối thủ có làm gì nếu chiến lược đó tồn tại
• Lý thuyết trò chơi hoặc lý thuyết trò chơi tổ hợp trong đó chúng ta có thông tin hoàn
hảo(không có sự ngẫu nhiên như tung đồng xu) chẳng hạn như luậy trò chơi, lượt
của người chơi, mức tối thiểu và tối đa liên quan đến các phát biểu vấn đề cũng như
một số điều kiện và ràng buộc
• Sẽ có ba trường hợp có thể xảy ra là thắng, thua hoặc hòa
• Điều kiện đầu cuối được xác định rõ ràng
• Người ta cho rằng trò chơi sẽ kết thúc vào một thời điểm nào đó sau một số nước đi
cố định. Không giống như cờ vua, nơi bạn có thể có vô số nước đi lOMoAR cPSD| 45148588 2.2 Trạng thái trò chơi
Chúng ta cùng xem xét một trò chơi khi ban đầu có n gậy. Người chơi A và B di chuyển
luân phiên, và người chơi A bắt đầu. Mối lần đi, người chơi phải loại bỏ 1,2 hoặc 3 cây
gậy cuối cùng sẽ chiến thắng trò chơi.
Ví dụ: n=10 thì trò chơi sẽ được tiến hành như sau
Người A loại bỏ 2 cây gậy (còn 8 cây gậy) Người
B loại bỏ 3 cây gậy (còn 5 cây gậy)
Người A loại bỏ 1 cây gậy (còn 4 cây gậy)
Người B loại bỏ 2 cây gậy (còn 2 cây gậy)
Người A loại bỏ 2 cây còn lại và chiến thắng.
Trò chơi này bao gồm cacs trạng thái 0,1,2,…,n số lượng trạng thái phụ thuộc vào số gậy còn lại.
Các trạng thái chiến thắng và thua cuộc (Winning - Losing)
Trạng thái chiến thắng là trạng thái khi người chơi sẽ thắng trò chơi nếu họ chơi tối ưu,
và trạng thái thua là trạng thái khi người người chơi sẽ thua trò chơi nếu đối thủ tối ưu.
Chúng ta có thể phân loại tất cả các trạng thái của trò chơi sao cho mỗi trạng thái có cả
trạng thái thắng và trạng thái thua.
Trong trò chơi trên, trạng thái 0 là trạng thái thua cuộc vì người chơi không thể thực
hiện bất kỳ nước đi nào.
• Trạng thái 1, 2 và 3 là trạng thái chiến thắng vì chúng ta có thể loại bỏ 1,2 hoặc 3
gậy và giành chiến thắng trong trò chơi
• Ngược lại, trạng thái 4 là trạng thái thua, vì bất kỳ nước đi nào cũng dẫn đến trạng
thái thắng của đối phương.
Tổng quát hơn, nếu có một động thái dẫn đến từ trạng thái hiện tại sang trạng thái thua
cuộc thù trạng thái hiện tại là trạng thái thắng, còn ngược lại là thì trạng thái thua cuộc. lOMoAR cPSD| 45148588
Bằng cách sử dụng quan sát này, chúng ta có thể phân loại tất cả các trạng thái của một
trò chơi bắt đầu bằng những trạng thái thua khi không có nước đi nào có thể thực hiện được.
Các trạng thái 0,1,2,…9 của trò chơi trên có thể được phân loại như sau (W- Thắng và L- Thua) Trạng 0 1 2 3 4 5 6 7 8 9 thái Kết L W W W L W W W L W quả Bảng 2: Trạng thái W - L
Từ cách phân loại này, chúng ta có thể rút ra một chiến lược tối ưu: luôn để lại số gậy
chia hết cho 4. Chiến thuật này đảm bảo rằng đối thủ luôn rơi vào tình trạng thua cuộc,
với điều kiện số gậy ban đầu không chia hết cho 4.
2.3 Đồ thị trạng thái của trò chơi (State graph)
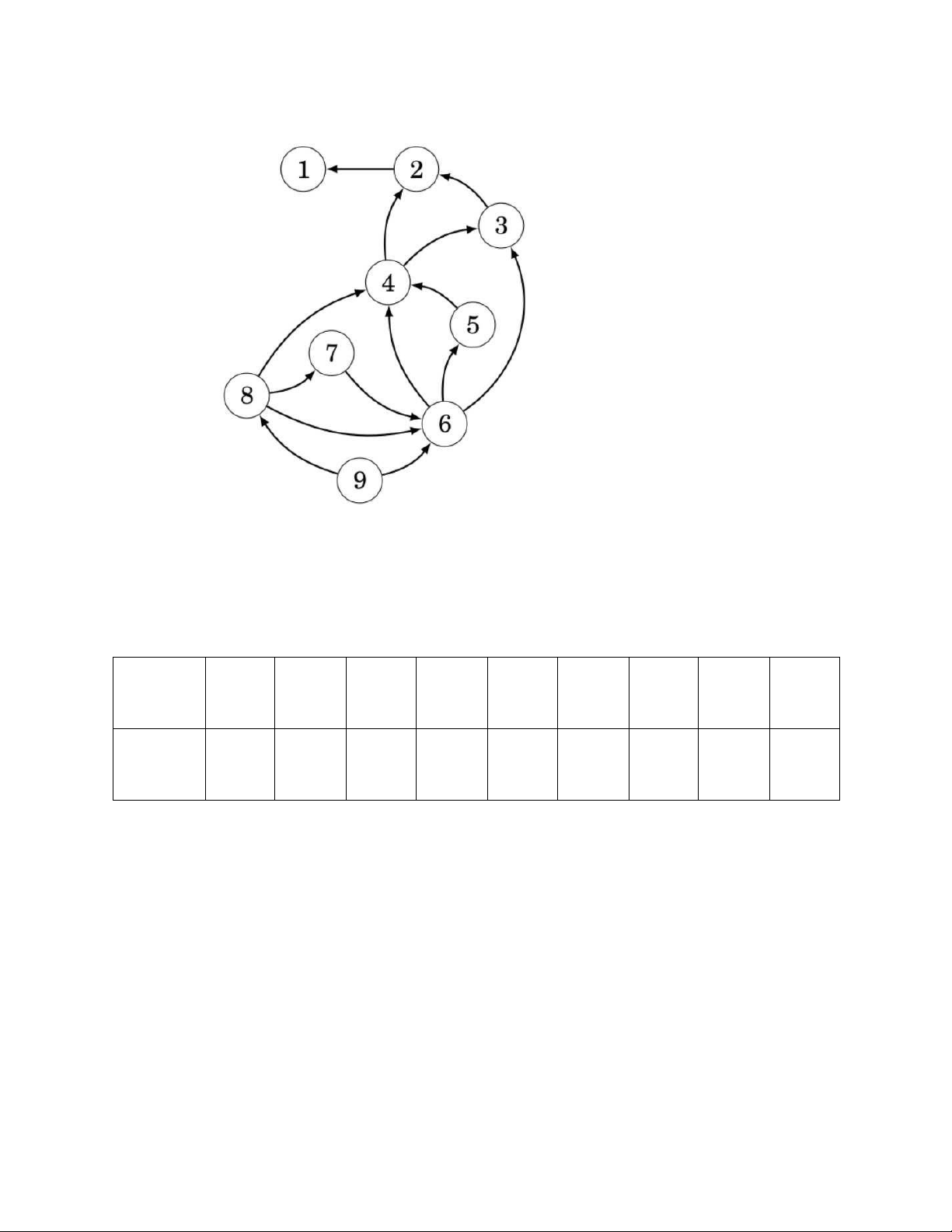
Xét một trò chơi gậy khác, khi trong mỗi trạng thái k, ta được phép loại bỏ số lượng x
gậy bất kỳ nào sao cho x nhỏ hơn k và chia hết cho k
Ví dụ trong trạng thái 8 chúng ta có thể bỏ 1,2 hoặc 4 gậy, nhưng trong trạng thái 7
chúng ta chỉ được loại bỏ 1 gậy.
Hình sau chỉ ra các trạng thái 1…9 của trò chơi bằng đồ thị trạng thái, khi mỗi đỉnh là
một trạng thái và các cạnh là các đường đi giữa chúng. lOMoAR cPSD| 45148588
Hình 2: Trạng thái của trò chơi trên đồ thị trạng thái
Trạng thái cuối cùng trong trò chơi này luôn là trạng thái 1, là trạng thái thua vì không
có nước đi hợp lệ. Việc phân loại các trạng thái 1…9 như sau: Trạn 1 2 3 4 5 6 7 8 9 g thái Kết L W L W L W L W L quả
Bảng 3: Trạng thái L -W của đồ thị trạng thái
Trong trò chơi này, tất cả các trạng thái sỗ chẵn là các trạng thái số chẵn đều là trạng
thái thắng và tất cả các trạng thái số lẻ là trạng thái thua.
2.4 Trò chơi tổ hợp cân bằng 2.4.1 Mô tả
Trò chơi tổ hợp là trò chơi gồm: hai người chơi (ở đây gọi người chơi trước là 𝐴 và
người chơi sau là 𝐵), một tập hữu hạn các trạng thái 𝑆 (viết tắt của State) có thể đạt
được của trò chơi. Mỗi người chơi có một tập các bước di chuyển hợp lệ 𝑄 để di chuyển lOMoAR cPSD| 45148588
từ trạng thái này sang trạng thái khác (gọi là luật chơi) và một tập các trạng thái kết
thúc gọi là 𝑇⊂𝑆 (viết tắt của Terminal). Hai người chơi sẽ luân phiên di chuyển từ trạng
thái này sang trạng thái khác. Người đến được trạng thái kết thúc trước sẽ là người chiến thắng.
Trò chơi tổ hợp cân bằng là trò chơi đối kháng thỏa mãn những điều kiện sau: • Có 2 người chơi
• Có một tập hữu hạn các vị trí có thể xảy ra (các trạng thái) của trò chơi
• Có quy luật chơi áp dụng cho hai người chơi là cân bằng, nghĩa là mỗi người
chơi đến lượt mình đều có quyền chọn một phép di chuyển hợp lệ tùy ý
• Hai người chơi lần lượt, mỗi lần thực hiện một phép di chuyển hợp lệ
• Trò chơi kết thúc khi đạt tới vị trí kết thúc. Thông thường quy định người
chơi di chuyển được cuối cùng là người chiến thắng, người nào đến lượt mà
k di chuyển được nữa thì thua
• Nếu trò chơi không bao giờ kết thúc sẽ có một thông báo rút thăm. Có thể bổ
sung thêm điều kiện nào đó để trò chơi kết thúckhoong câng thông báo rút
thăm nhưP trò chơi sẽ kết thúc khi đã có đủ số lần di chuyển nhất định mà
không ai thắng thì hai đấu thủ hòa.
2.4.2 Tập P, tập N và cách tìm
Để thuận tiện cho việc xây dựng thuật toán (giành thắng) của trò chơi, người ta đưa ra
khái niệm tập P và tập N. Đó là hai tập thỏa mãn các tính chất sau:
• N: tập các trạng thái x S sao cho nếu trạng thái ban đầu của trò chơi là x thì
người chơi trước luôn chiến thắng
• P: tập các trạng thái x S sao cho nếu trạng thái ban đầu của trò chơi là x thì
người chơi sau luôn ở trạng thái thắng.
Từ định nghĩa trên, N và P sẽ thỏa mãn ba tính chất sau:
Tập P phải chứa toàn bộ trạng thái kết thúc
Với mỗi trạng thái s thuộc tập N, tồn tại ít nhất một trạng thái s’ đến được từ s mà thuộc tập P