Lectures 9-10. QuicksortIntroduction to AlgorithmsDa Nang University of Science and Technology | Tài liệu Tiếng Anh

Lectures 9-10. Quicksort Introduction to Algorithms
Da Nang University of Science and Technology Dang Thien Binh dtbinh@dut.udn.vn
Intelligent Networking Laboratory Copyright 2000-2022 DANG Intelligent Ne THIEN BIN two H rking Labo 1/44 ratory Introduction of Quicksort
 Worst-case running time: Θ(𝑛²)
 Expected running time: Θ(𝑛 lg 𝑛)
 Constants hidden in Θ(𝑛 lg 𝑛) are small
 Another divide-and-conquer algorithm
Intelligent Networking Laboratory DANG THIEN BINH 2/44 Quicksort
 To sort the subarray 𝐴[𝑝 . . 𝑟]  Divide
 Partition 𝐴[𝑝. . 𝑟], into two (possibly empty) subarrays 𝐴[𝑝 . . 𝑞 − 1]
and 𝐴[𝑞 + 1 . . 𝑟], such that each element of 𝐴[𝑝 . . 𝑞 − 1] is less
than or equal to each element of 𝐴[𝑞 + 1 . . 𝑟]  Conquer
 Sort the two subarrays by recursive calls to QUICKSORT  Combine
 No work is needed to combine the subarrays because they are already sorted
 Perform the divide step by a procedure PARTITION,
which returns the index 𝑞 that marks the position separating the subarrays
Intelligent Networking Laboratory DANG THIEN BINH 3/44 N e t w o Quicksort Pseudocode (1/2) r k i n g L a b o r a t o r y 4 / 4 8
Intelligent Networking Laboratory DANG THIEN BINH 4/44 N e t w o Quicksort Pseudocode (2/2) r k i n g L a b o r a t o r y 5 / 4 8
Intelligent Networking Laboratory DANG THIEN BINH 5/44 Partition (1/2)
 Clearly, all the action takes place in the partition() function
 Rearrange the subarray 𝐴[𝑝 . . 𝑟] in place  End result:  Two subarrays
 All values in first subarray  all values in second one
 Return index of the “𝑝𝑖𝑣𝑜𝑡” element separating the two subarrays
Intelligent Networking Laboratory DANG THIEN BINH 6/44 Partition (2/2)
 PARTITION always selects the last element 𝐴[𝑟] in the
subarray 𝐴[𝑝 . . 𝑟] as the 𝒑𝒊𝒗𝒐𝒕
 The element around which to partition
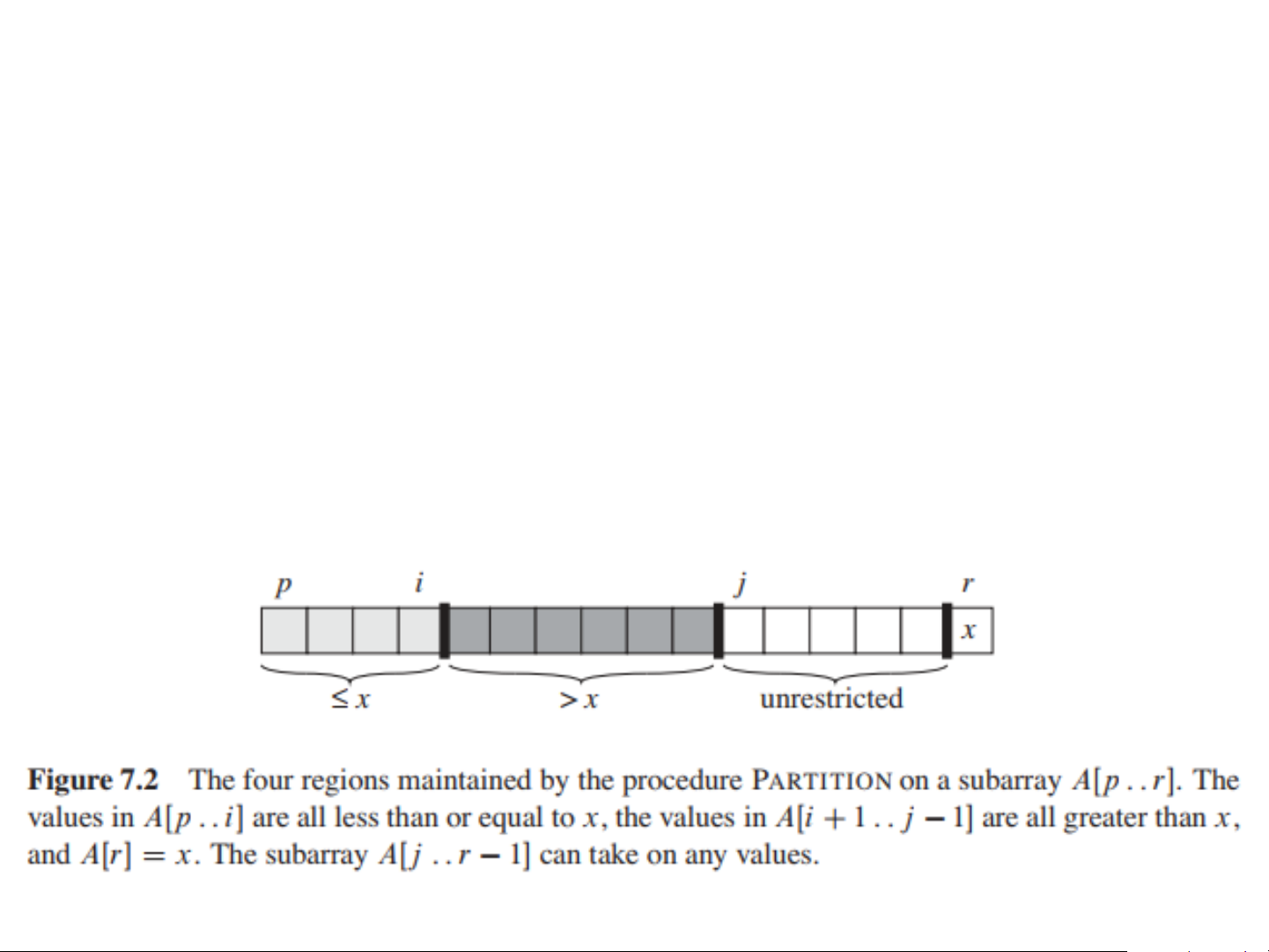
 As the procedure executes, the array is partitioned
into four regions, some of which may be empty
Intelligent Networking Laboratory DANG THIEN BINH 7/44 Partition Property
 Loop invariant: For any array index i
1. All entries in 𝐴[𝑝 . . 𝑖]  𝑝𝑖𝑣𝑜𝑡
2. All entries in 𝐴[𝑖 + 1 . . 𝑗 − 1] > 𝑝𝑖𝑣𝑜𝑡
3. 𝐴[𝑟] = 𝑝𝑖𝑣𝑜𝑡
 It’s not needed as part of the loop invariant, but the
fourth region is 𝐴[ 𝑗 . . 𝑟 − 1], whose entries have not
yet been examined, and so we don’t know how they compare to the pivot.
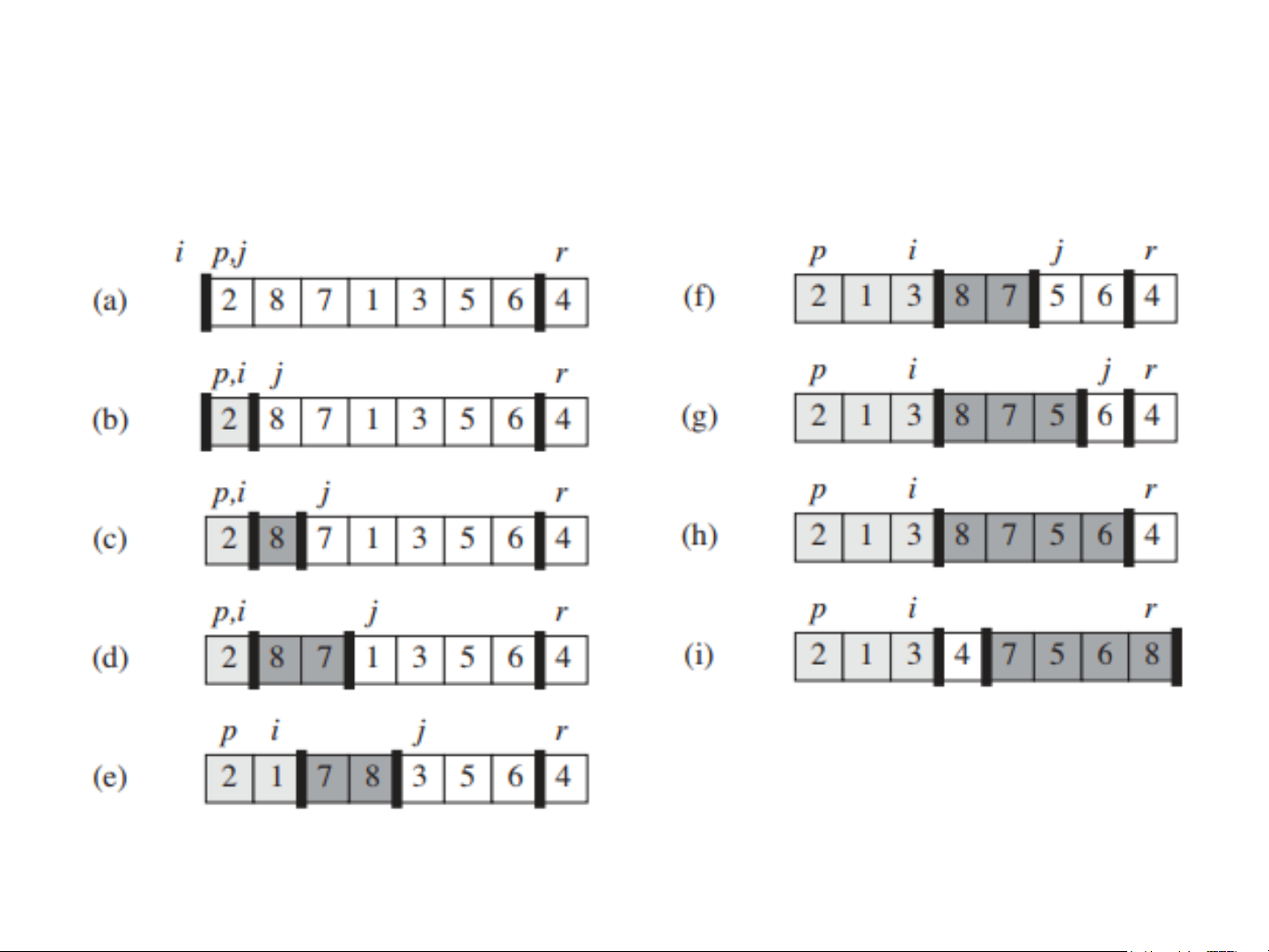
Intelligent Networking Laboratory DANG THIEN BINH 8/44 Partition Example
Intelligent Networking Laboratory DANG THIEN BINH 9/44
Correctness of Loop Invariant (1/3)  Initialization:
 Before the loop starts, all the conditions of the loop invariant
are satisfied, because 𝐴[𝑟] is the pivot and the subarrays
𝐴[𝑝 . . 𝑖] and 𝐴[𝑖 + 1 . . 𝑗 − 1] are empty
Intelligent Networking Laboratory DANG THIEN BINH 10/44
Correctness of Loop Invariant (2/3)
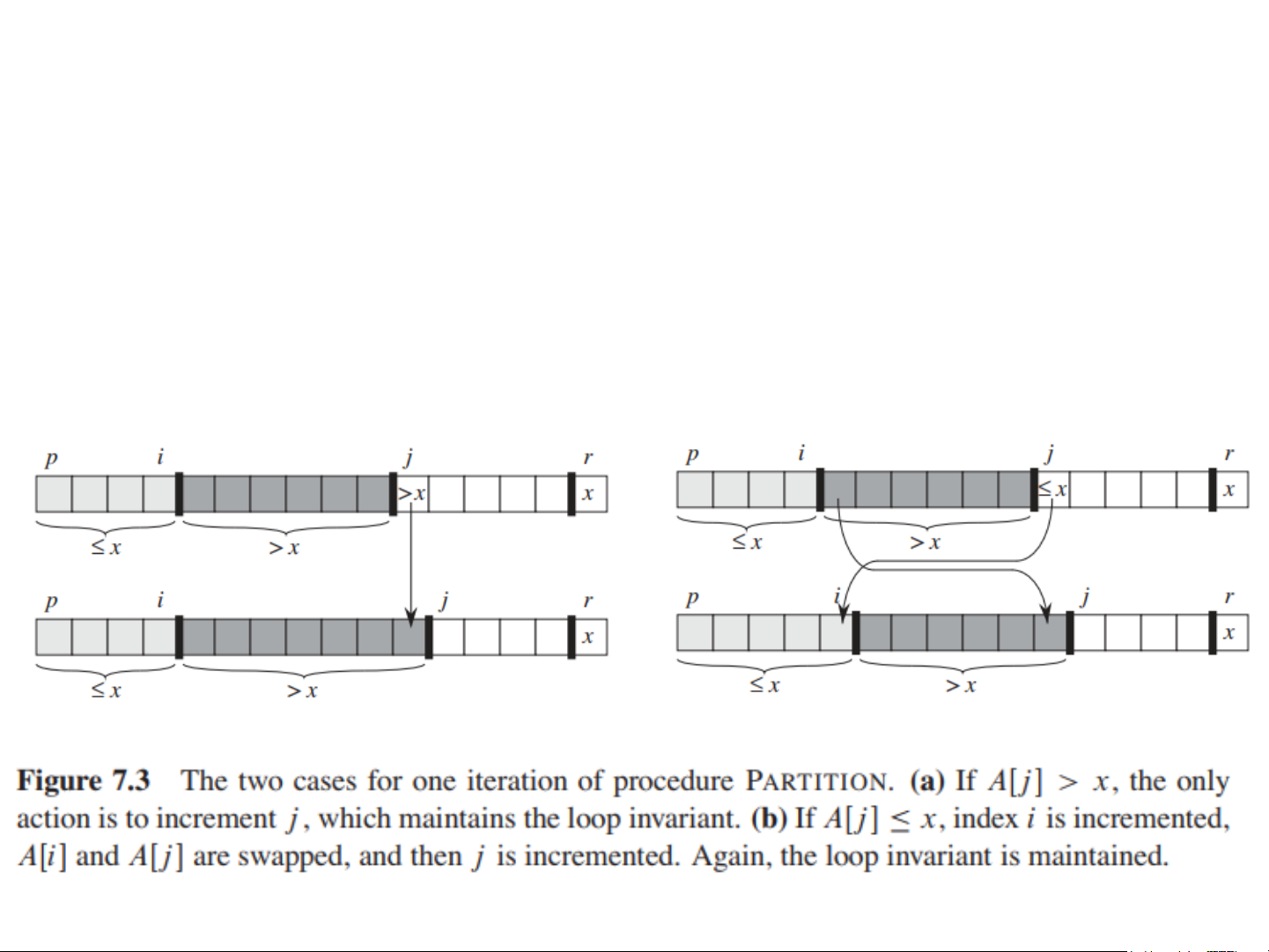
 Maintenance: while the loop is running,
 if 𝐴[𝑗] ≤ 𝑝𝑖𝑣𝑜𝑡, then 𝐴[ 𝑗] and 𝐴[𝑖 + 1] are swapped and 𝑖 and 𝑗 are incremented
 If 𝐴[𝑗] > 𝑝𝑖𝑣𝑜𝑡, then increment only 𝑗 (a) (b)
Intelligent Networking Laboratory DANG THIEN BINH 11/44
Correctness of Loop Invariant (3/3)  Termination:
 When the loop terminates, 𝑗 = 𝑟, so all elements in 𝐴 are
partitioned into one of the three cases:
 𝐴[𝑝 . . 𝑖 ] ≤ 𝑝𝑖𝑣𝑜𝑡, 𝐴[𝑖 + 1 . . 𝑟 − 1] > 𝑝𝑖𝑣𝑜𝑡, and 𝐴[𝑟] = 𝑝𝑖𝑣𝑜𝑡
 The last operation of PARTITION is to move the pivot
from the end of the array to a position between two subarrays:
 swapping the 𝑝𝑖𝑣𝑜𝑡 𝐴[𝑟] and the first element of the second subarray 𝐴[𝑖 + 1]  Time for partitioning:
 (𝑛) to partition an 𝑛-element subarray
Intelligent Networking Laboratory DANG THIEN BINH 12/44 Quicksort Algorithm  Video Content
 An illustration of Quick Sort.
Intelligent Networking Laboratory DANG THIEN BINH 13/44 Quicksort Algorithm
Intelligent Networking Laboratory DANG THIEN BINH 14/44 Practice Problem  The operation of PARTITION on an array
𝐴 1. . 12 = [13,19,9,5,12,8,7,4,21,2,6,11] is performed.
Then the given array is divided into 𝐴[1. . 𝑞] and 𝐴[𝑞 + 1. . 12] such that 𝐴[𝑖] ≤ 𝐴[𝑗] for all
1 ≤ 𝑖 ≤ 𝑞 and 𝑞 + 1 ≤ 𝑗 ≤ 12. What are 𝑞 and 𝐴[𝑞]?  𝑞 = 8  𝐴[𝑞] = 11
Intelligent Networking Laboratory DANG THIEN BINH 15/44 Performance of Quicksort (1/9)
 The running time of Quicksort depends on the partitioning of the subarrays:
 If the subarrays are unbalanced, then quicksort can run as
slowly as insertion sort (worst case)
 If the subarrays are balanced, then quicksort can run as fast as mergesort (best case)
Intelligent Networking Laboratory DANG THIEN BINH 16/44 Performance of Quicksort (2/9)  Worst case
 Occurs when the subarrays are completely unbalanced
 Has 0 elements in one subarray and (n-1) elements in the other subarray  Get the recurrence:
 𝑇(𝑛) = 𝑇(𝑛 − 1) + 𝑇(0) + (𝑛)
= 𝑇(𝑛 − 1) + (𝑛) = (𝑛²)
 Same running time as insertion sort
 In fact, the worst-case running time occurs when quicksort
takes a sorted array as input, but insertion sort runs in 𝑂(𝑛) time in this case
Intelligent Networking Laboratory DANG THIEN BINH 17/44 Performance of Quicksort (3/9)  Best case
 Occurs when the subarrays are completely balanced every time.
 Each subarray has  𝑛/2 elements: 𝑛Τ2 and 𝑛Τ2 −1  Get the recurrence:
 𝑇(𝑛) = 2𝑇(𝑛/2) + (𝑛) = (𝑛 lg 𝑛)
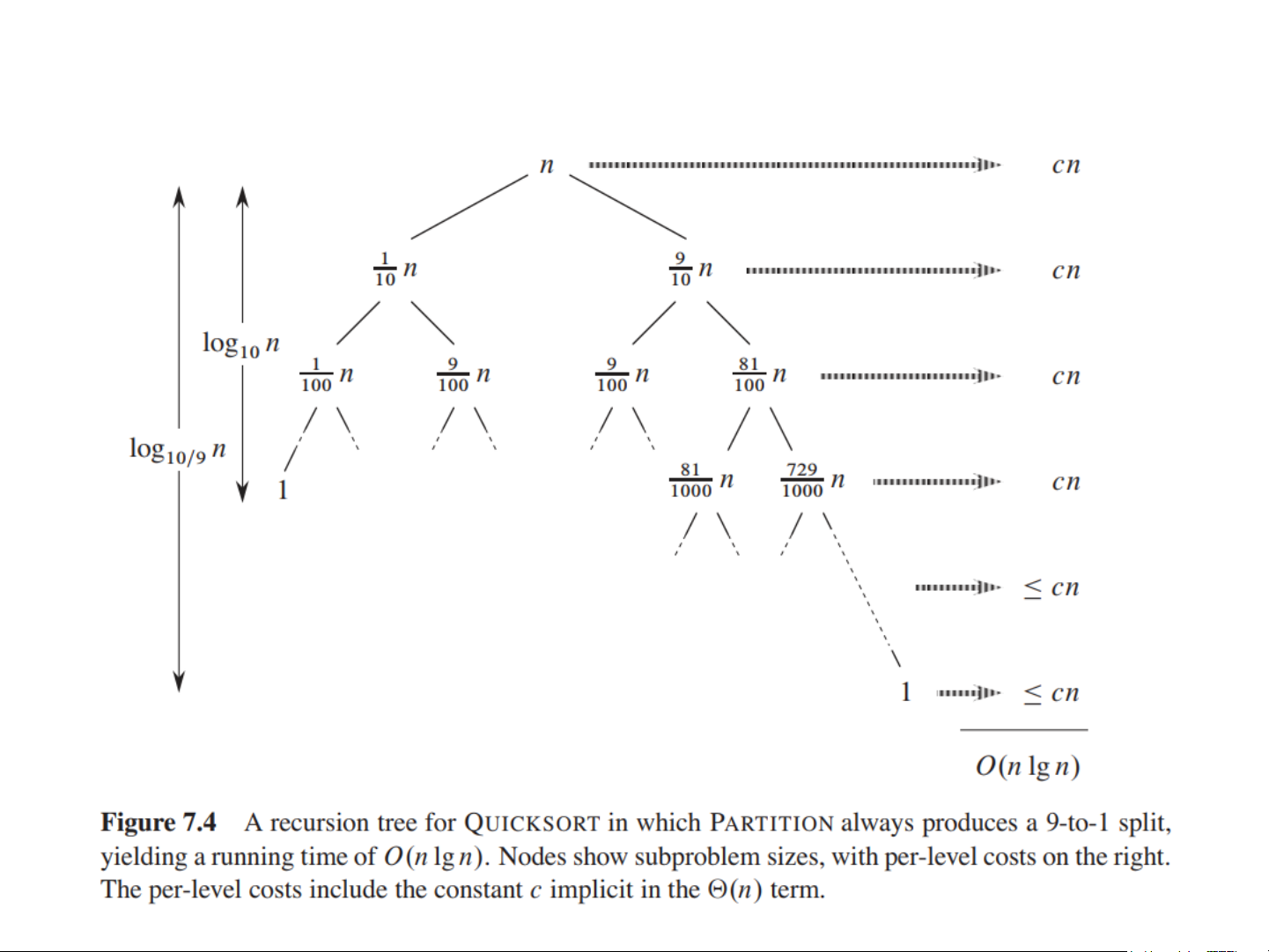
Intelligent Networking Laboratory DANG THIEN BINH 18/44 Performance of Quicksort (4/9)  Balanced partitioning
 Quicksort’s average running time is much closer to the best case than to the worst case.
 Imagine that PARTITION always produces a 9-to-1 split.  Get the recurrence:
 𝑇(𝑛) ≤ 𝑇(9𝑛/10) + 𝑇(𝑛/10) + (𝑛)  𝑂(𝑛 lg 𝑛)
Intelligent Networking Laboratory DANG THIEN BINH 19/44 Performance of Quicksort (5/9)
Intelligent Networking Laboratory DANG THIEN BINH 20/44