44 trang 4 lượt tải

Luyện kỹ năng trắc nghiệm trả lời ngắn nguyên hàm, tích phân và ứng dụng

7

Tài liệu gồm 44 trang, được biên soạn bởi thầy giáo Đặng Công Đức (Giang Sơn), tuyển chọn các bài tập rèn luyện kỹ năng giải toán trắc nghiệm trả lời ngắn chủ đề nguyên hàm, tích phân và ứng dụng trong chương trình môn Toán lớp 12.

Chủ đề: Tài liệu chung 172 tài liệu

Môn: Toán 12 4.3 K tài liệu

Tác giả:

Profile

Linh Đan

2 tuần trước
Danh sách Quiz
/44
1
T
T
À
À
I
I
L
L
I
I
Ệ
Ệ
U
U
T
T
H
H
A
A
M
M
K
K
H
H
Ả
Ả
O
O
T
T
O
O
Á
Á
N
N
H
H
Ọ
Ọ
C
C
P
P
H
H
Ổ
Ổ
T
T
H
H
Ô
Ô
N
N
G
G
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
,
a
V a b
b
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
-
L
L
U
U
Y
Y
Ệ
Ệ
N
N
K
K
Ỹ
Ỹ
N
N
Ă
Ă
N
N
G
G
T
T
O
O
Á
Á
N
N
1
1
2
2
T
T
H
H
P
P
T
T
T
T
R
R
Ắ
Ắ
C
C
N
N
G
G
H
H
I
I
Ệ
Ệ
M
M
T
T
R
R
Ả
Ả
L
L
Ờ
Ờ
I
I
N
N
G
G
Ắ
Ắ
N
N
N
N
G
G
U
U
Y
Y
Ê
Ê
N
N
H
H
À
À
M
M
,
,
T
T
Í
Í
C
C
H
H
P
P
H
H
Â
Â
N
N
V
V
À
À
Ứ
Ứ
N
N
G
G
D
D
Ụ
Ụ
N
N
G
G
(
(
K
K
Ế
Ế
T
T
H
H
Ợ
Ợ
P
P
3
3
B
B
Ộ
Ộ
S
S
Á
Á
C
C
H
H
G
G
I
I
Á
Á
O
O
K
K
H
H
O
O
A
A
)
)
T
T
H
H
Â
Â
N
N
T
T
Ặ
Ặ
N
N
G
G
T
T
O
O
À
À
N
N
T
T
H
H
Ể
Ể
Q
Q
U
U
Ý
Ý
T
T
H
H
Ầ
Ầ
Y
Y
C
C
Ô
Ô
V
V
À
À
C
C
Á
Á
C
C
E
E
M
M
H
H
Ọ
Ọ
C
C
S
S
I
I
N
N
H
H
T
T
R
R
Ê
Ê
N
N
T
T
O
O
À
À
N
N
Q
Q
U
U
Ố
Ố
C
C
C
C
R
R
E
E
A
A
T
T
E
E
D
D
B
B
Y
Y
G
G
I
I
A
A
N
N
G
G
S
S
Ơ
Ơ
N
N
(
(
F
F
A
A
C
C
E
E
B
B
O
O
O
O
K
K
)
)
Đ
Đ
Á
Á
P
P
Á
Á
N
N
C
C
H
H
I
I
T
T
I
I
Ế
Ế
T
T
P
P
D
D
F
F
B
B
Ạ
Ạ
N
N
Đ
Đ
Ọ
Ọ
C
C
V
V
U
U
I
I
L
L
Ò
Ò
N
N
G
G
L
L
I
I
Ê
Ê
N
N
H
H
Ệ
Ệ
T
T
Á
Á
C
C
G
G
I
I
Ả
Ả
G
G
A
A
C
C
M
M
A
A
1
1
4
4
3
3
1
1
9
9
8
8
8
8
@
@
G
G
M
M
A
A
I
I
L
L
.
.
C
C
O
O
M
M
(
(
G
G
M
M
A
A
I
I
L
L
)
)
;
;
T
T
E
E
L
L
0
0
3
3
9
9
8
8
0
0
2
2
1
1
9
9
2
2
0
0
T
T
H
H
À
À
N
N
H
H
P
P
H
H
Ố
Ố
T
T
H
H
Á
Á
I
I
B
B
Ì
Ì
N
N
H
H
–
–
T
T
H
H
Á
Á
N
N
G
G
1
1
2
2
/
/
2
2
0
0
2
2
4
4
2
L
L
U
U
Y
Y
Ệ
Ệ
N
N
K
K
Ỹ
Ỹ
N
N
Ă
Ă
N
N
G
G
T
T
O
O
Á
Á
N
N
1
1
2
2
T
T
H
H
P
P
T
T
T
T
R
R
Ắ
Ắ
C
C
N
N
G
G
H
H
I
I
Ệ
Ệ
M
M
T
T
R
R
Ả
Ả
L
L
Ờ
Ờ
I
I
N
N
G
G
Ắ
Ắ
N
N
N
N
G
G
U
U
Y
Y
Ê
Ê
N
N
H
H
À
À
M
M
,
,
T
T
Í
Í
C
C
H
H
P
P
H
H
Â
Â
N
N
V
V
À
À
Ứ
Ứ
N
N
G
G
D
D
Ụ
Ụ
N
N
G
G
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
_
DUNG
LƯỢNG
NỘI DUNG
1 FILE
10 trang
TRẮC NGHIỆM TRẢ LỜI NGẮN
NGUYÊN HÀM, TÍCH PHÂN THUẦN TÚY
1 FILE
10 trang
TRẮC NGHIỆM TRẢ LỜI NGẮN
ỨNG DỤNG TÍNH DIỆN TÍCH HÌNH PHẲNG, THỂ TÍCH VẬT THỂ
1 FILE
22 trang
TRẮC NGHIỆM TRẢ LỜI NGẮN
ỨNG DỤNG THỰC TẾ NGUYÊN HÀM, TÍCH PHÂN
3
NGUYÊN HÀM VÀ TÍCH PHÂN LỚP 12 THPT
NGUYÊN HÀM VÀ TÍCH PHÂN THUẦN TÚY
LỚP BÀI TOÁN TRẮC NGHIỆM TRẢ LỜI NGẮN
________________________________________
Câu 1. Gọi
F x
là họ các nguyên hàm của hàm số
8sin 3 cosf x x x
. Biết rằng
F x
có dạng
cos 4 cos 2
F x a x b x C
. Khi đó
bằng bao nhiêu?
Trả lời:……………………………………..
Câu 2. Cho
cos 2F x x
là một nguyên hàm của hàm số
.tanf x x
. Biết nguyên hàm của hàm số
tan x
f x
có
dạng
tan
a
x C
b
với
a
,
b
là các số nguyên dương,
a
b
là phân số tối giản và
C
. Tính
2a b
.
Trả lời:……………………………………..
Câu 3. Cho hàm số
y f x
có đạo hàm là
4sin 2 cos ,f x x x x
và
0 2
f
. Biết
F x
là
nguyên hàm của
f x
thỏa mãn
3
F
, khi đó
2
F
bằng bao nhiêu?
Trả lời:……………………………………..
Câu 4. Cho hàm số
y f x
có đạo hàm trên
0;
thỏa mãn
2 2xf x f x x
0;x
,
1 1
f
. Giá trị của biểu thức
6 4
f
là bao nhiêu ?
Trả lời:……………………………………..
Câu 5. (Cho hàm số
y f x
có đạo hàm liên tục trên
và thỏa mãn điều kiện
3 4
6
27 1 0,x f x f x x
và
1 0
f
. Giá trị của
2
f
bằng bao nhiêu ?
Trả lời:……………………………………..
Câu 6. Cho hàm số
f x
thỏa mãn:
2
4
. 15 12f x f x f x x x
,
x
và
0 0 1
f f
. Giá trị
của
2
1
f
bằng bao nhiêu ?
Trả lời:……………………………………..
Câu 7. Cho hàm số
y f x
có đạo hàm là
sin 2 ,f x x x
và
0
4
f
. Biết
F x
là nguyên hàm
của
f x
thỏa mãn
2
2
F
, khi đó
4
F
bằng bao nhiêu ?
Trả lời:……………………………………..
Câu 8. Cho
2 2 x
F x ax bx c e
là một nguyên hàm của hàm số
2 2
2 .
x
f x x e
. Tính tổng
2a b c
(kết
quả là số nguyên).
Trả lời:……………………………………..
Câu 9. Biết
2 2
2
x
F x e x
là một nguyên hàm của hàm số
f x
trên
. Giả sử
G x
là một nguyên hàm
của hàm số
2 cosf x x
. Khi đó
2 0 .
b
G G a e c
,
, ,a b c
. Tính
. .a b c
.
Trả lời:……………………………………..
Câu 10. Cho hàm số
2 2
( ) ( )
x
F x ax bx c e
là một nguyên hàm của hàm số
2 2
( ) (2 8 7)
x
f x x x e
. Tính
tổng
a b c
(kết quả là số nguyên).
Trả lời:……………………………………..
Câu 11. Cho
F x
là một nguyên hàm của hàm số
e 2
x
f x x
thỏa mãn
3
0
2
F
. Tìm
2
F
(làm tròn
đến hàng phần chục).
Trả lời:……………………………………..
Câu 12. Cho hàm số
f x
thỏa mãn
1
2
5
f
và
2
3
f x x f x
với mọi
x
. Giá trị của
1f
bằng
bao nhiêu ?
Trả lời:……………………………………..
Câu 13. Hàm số
f x
có đạo hàm đến cấp hai trên
thỏa mãn:
2 2
1 3 1
f x x f x
. Biết rằng
4
0,f x x
, giá trị tích phân
2
0
2 1 "
I x f x dx
bằng bao nhiêu ?
Trả lời:……………………………………..
Câu 14. Cho hàm số
( )y f x
xác định và có đạo hàm
f x
liên tục trên
[1;3]
;
0, 1;3 ;
f x x
2 4
2
1 1
f x f x x f x
và
1 1
f
. Biết rằng
3
d ln 3 ,
e
f x x a b a b
, giá trị của
2
a b
bằng bao nhiêu ?
Trả lời:……………………………………..
Câu 15. Cho hàm số
f x
thỏa mãn
1 4
f
và
3 2
2 3f x xf x x x
với mọi
0.
x
Giá trị của
2
f
bằng bao nhiêu ?
Trả lời:……………………………………..
Câu 16. Cho hàm số
( )y f x
liên tục trên
và thoả mãn
2
0
f x x f x x dx
, với mọi
x
. Xác định
tổng các giá trị
m
để
2
0
0
mx f x dx
.
Trả lời:……………………………………..
Câu 17. Cho hàm số
y f x
thỏa mãn
4
2
19
f
và
3 2
f x x f x x
. Giá trị của
1f
bằng bao
nhiêu ?
Câu 18. Cho hàm số
y f x
liên tục, nhận giá trị dương trên
0;

và thỏa mãn
1 2
f
;
2
2
x
f x
f x
với mọi
0;x

. Giá trị
3
3
f
bằng bao nhiêu ?
Trả lời:……………………………………..
Câu 19. Cho hàm số
y f x
có đạo hàm liên tục trên
thỏa mãn
1
f e
và
,f x f x x x
. Giá
trị
2
f
bằng bao nhiêu ?
Trả lời:……………………………………..
Câu 20. Cho hàm số
f x
có đạo hàm trên
, thoả mãn
1
f x
và
2
' 1 2 1,f x x x f x x
.
Biết rằng
0 0
f
, khi đó
2
f
có giá trị bằng bao nhiêu ?
Trả lời:……………………………………..
Câu 21. Cho hàm số
( ) | 2 | | 2 |
f x x x
, biết
6
5
( ) ( )
f x dx a b c
, với
a
là số nguyên dương. Giá trị
biểu thức
T a b c
là bao nhiêu ?.
Trả lời:……………………………………..
Câu 22. Cho hàm số
y f x
liên tục trên
0;
thỏa mãn
2 2
3 . . 2
x f x x f x f x
, với
0, 0;f x x
và
1
1
3
f
. Gọi
,M m
lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số
y f x
trên đoạn
1;2
. Tính
2
M m
.
Trả lời:……………………………………..
Câu 23. Cho hàm số
f x
liên tục trên
và thỏa mãn
1
x
xf x x f x e
với mọi
x
. Tính
0
f
.
Trả lời:……………………………………..
Câu 24. Cho
F x
là một nguyên hàm của hàm số
2
3
4x
x
f x e x
. Hàm số
2
F x x
có bao nhiêu
điểm cực trị?
Trả lời:……………………………………..
Câu 25. Cho hàm số
2
2 5 khi 1
3 4 khi 1
x x
f x
x x
. Giả sử
F
là nguyên hàm của
f
trên
thỏa mãn
0 2
F
.
Giá trị của
1 2 2
F F
bằng
Trả lời:……………………………………..
5
Câu 26. Cho hàm số
y f x
liên tục trên đoạn
1;6
và có đồ thị là đường gấp khúc
ABC
trong hình bên.
Biết
F
là nguyên hàm của
f
thỏa mãn
1 2
F
.
Giá trị của
5 6
F F
bằng bao nhiêu
Trả lời:……………………………………..
Câu 27. Cho hàm số
f x
có đạo hàm liên tục trên đoạn
0 1;
thỏa mãn
1 0
f
,
1
2
0
1
3
x f x dx
. Giá trị tích
phân
1
3
0
' .x f x dx
bằng bao nhiêu ?
Trả lời:……………………………………..
Câu 28. Cho hàm số
2
2 3 khi 1
3 2 khi 1
x x
f x
x x
. Giả sử
F
là nguyên hàm của hàm số
f
trên
thỏa mãn
0 2
F
. Giá trị của
1 2 2
F F
bằng
Trả lời:……………………………………..
Câu 29. Cho hàm số
f x
thỏa mãn
1 2
f
và
2
2
2 2
1 1
x f x f x x
với mọi
x
. Giá trị của
2
f
bằng bao nhiêu ?
Trả lời:……………………………………..
Câu 30. Cho hàm số
( )f x
thỏa mãn
(1) 4
f
và
3 2
( ) ( ) 2 3f x xf x x x
với mọi
0
x
. Giá trị của
(2)f
bằng bao nhiêu ?
Trả lời:……………………………………..
Câu 31. Cho hàm số
f x
thỏa mãn
2
2
. 2 1f x f x f x x x

,
x
và
0 0 3
f f
. Giá trị
của
2
1
f
bằng bao nhiêu ?
Trả lời:……………………………………..
Câu 32. Giả sử hàm số
y f x
liên tục, nhận giá trị dương trên
0;

và thỏa mãn
1 1
f
,
. 3 1f x f x x
, với mọi
0
x
. Giá trị
5f
gần nhất với số tự nhiên nào
Trả lời:……………………………………..
Câu 33. Cho hàm số
2
2 7 khi 2
3 1 khi 2
x x
f x
x x
. Giả sử
F
là nguyên hàm của
f
trên
thỏa mãn
0 4
F
.
Giá trị của
2 3 4
F F
bằng bao nhiêu ?
Trả lời:……………………………………..
Câu 34. Cho
F x
là một nguyên hàm của hàm số
1 1
f x x x
trên tập
và thỏa mãn
1 3
F
.
Tính tổng
0 2 3
F F F
.
Trả lời:……………………………………..
Câu 35. Cho hàm số
sin khi
4
cos khi
4
x x
f x
x x
. Giả sử
F
là nguyên hàm của
f
trên
thỏa mãn
6
3
6 2
F
. Giá trị của
0 2
2
F F
bằng bao nhiêu ?
Trả lời:……………………………………..
Câu 36. Cho hàm số
y f x
liên tục trên đoạn
5;6
có đồ thị như hình vẽ. Giá trị của
0
5
f x dx
bằng bao
nhiêu ?
x
y
-1
-1
4
6
2
-2
6
-2
-5
O
1
Trả lời:……………………………………..
Câu 37. Cho với
m
,
p
,
q
và là các phân số tối giản. Giá trị
3
m p q
bằng
bao nhiêu
Trả lời:……………………………………..
Câu 38. Biết rằng
2
1
2
0
d
2
x b c
a
xe x e e
với
, ,a b c
. Giá trị của
a b c
bằng bao nhiêu
Trả lời:……………………………………..
Câu 39. Biết
2
1
1
ln
ln
e
x
dx ae b
x x x
với
,a b
là các số nguyên dương. Tính giá trị của biểu thức
2 2
.T a ab b
Trả lời:……………………………………..
Câu 40. Biết
2
1
1
2
1
p
x
q
x
x e dx me n
, trong đó
, , ,m n p q
là các số nguyên dương và
p
q
là phân số tối giản.
Tính
T m n p q
.
Trả lời:……………………………………..
Câu 41. Số điểm cực trị của hàm số
2
2
2
2 d
1
x
x
t t
f x
t
là
Trả lời:……………………………………..
Câu 42. Cho hàm số
y f x
có đạo hàm trên
đồng thời thỏa mãn
0 1 5
f f
. Tính tích phân
1
0
d
f x
I f x e x
.
Trả lời:……………………………………..
Câu 43. Cho hàm số
f x
có
3 3
f
và
1 1
x
f x
x x
,
0
x
. Khi đó
8
3
6 df x x
bằng
Câu 44. Cho
21
5
ln 3 ln 5 ln 7
4
dx
a b c
x x
, với
, ,a b c
là các số hữu tỉ. Tính giá trị
a b
c
.
Trả lời:……………………………………..
Câu 45. Cho
55
16
d
ln 2 ln 5 ln11
9
x
a b c
x x
, với
, ,a b c
là các số hữu tỉ. Tính
a b
c
.
Trả lời:……………………………………..
Câu 46. Giả sử tích phân
5
1
1
ln 3 ln 5
1 3 1
I dx a b c
x
. Lúc đó giá trị
3
a b c
bằng bao nhiêu
7
Trả lời:……………………………………..
Câu 47. Cho hàm số
f x
có
2 0
f
và
7 3
, ;
2
2 3
x
f x x
x

. Biết rằng
7
4
d
2
x a
f x
b
(
, , 0,
a
a b b
b
là phân số tối giản). Khi đó
a b
bằng
Trả lời:……………………………………..Câu 48. Biết tích phân
ln 6
0
e
d ln 2 ln 3
1 e 3
x
x
x a b c
, với
a
,
b
,
c
là các số nguyên. Tính
P a b c
.
Câu 49. Biết
2
1
( 1) 1
dx
dx a b c
x x x x
với
, ,a b c
là các số nguyên dương. Tính
P a b c
Trả lời:……………………………………..
Câu 50. Biết
1
ln
2
1 ln
e
x
dx a b
x x
với
,a b
là các số hữu tỷ. Tính
3 3S a b
.
Câu 51. Có bao nhiêu giá trị nguyên dương của tham số
m
để
3
0
(10 2 ) 0
x m dx
?
Trả lời:……………………………………..
Câu 52. Giả sử
7 8 8
, , 0 , | |
b
a
a b a b x dx ma nb
trong đó
,m n
là các hằng số thực (không phụ thuộc vào
a
và
b
). Giá trị của biểu thức
5P m n
là bao nhiêu?
Trả lời:……………………………………..
Câu 53. Cho
0
, 0 7
x
g x f t dt x
trong đó
f t
là hàm số có đồ thị như hình. Tính
3
g
.
Trả lời:……………………………………..
Câu 54. Giá trị tích phân
3
1
2
ln ,
x
dx a b c
x
với
, , , 9.
a b c c
Tính tổng
.S a b c
Trả lời:……………………………………..
Câu 55. Cho
2 2
| |
b
a
x dx ma nb
với
, , ,m n a b
là các hằng số thực và
0
a b
. Giá trị của biểu thức
m n
bằng bao nhiêu?
Trả lời:……………………………………..
Câu 56. Cho hàm số
f x
liên tục trên
và
9
2
1 0
d 4, sin cos d 2
f x
x f x x x
x
. Tính tích phân
3
0
dI f x x
.
Trả lời:……………………………………..
Câu 57. Cho
f x
liên tục trên
thỏa mãn
2020
f x f x
và
2017
3
x 4.
f x d
Khi đó
2017
3
xxf x d
bằng
8
Trả lời:……………………………………..
Câu 58. Biết rằng hàm số
f x mx n
thỏa mãn
1
0
d 3
f x x
,
2
0
d 8
f x x
. Tính giá trị
m n
.
Trả lời:……………………………………..
Câu 59. Có hai giá trị của số thực
a
là
1
a
,
2
a
(
1 2
0
a a
) thỏa mãn
1
2 3 d 0
a
x x
. Hãy tính
1 2
2
2
1
3 3 log
a a
a
T
a
.
Câu 60. Có bao nhiêu giá trị nguyên dương của
a
để
0
2 3 d 4
a
x x
?
Trả lời:……………………………………..
Câu 61. Biết
4
2
1
1 e
d e e
4
e
x
b c
x
x
x a
x
x
với
a
,
b
,
c
là các số nguyên. Tính giá trị
T a b c
.
Trả lời:……………………………………..
Câu 62. Cho hàm số
y f x
có đạo hàm liên tục trên
0;1
thỏa mãn
1
2
0
1 0, ( ) d 7
f f x x
và
1
2
0
1
( )d
3
x f x x
. Giá trị tích phân
1
0
( )df x x
bằng bao nhiêu ?
Trả lời:……………………………………..
Câu 63. Cho hàm số
f x
có đạo hàm liên tục trên đoạn
0;1
thỏa mãn
1 4
f
,
1
2
0
d 36
f x x
và
1
0
1
. d
5
x f x x
. Tích phân
1
0
df x x
bằng
Trả lời:……………………………………..
Câu 64. Cho hàm số
f x
có đạo hàm liên tục trên đoạn
0;1
thỏa mãn
1 4
f
,
1
2
0
d 5
f x x
và
1
0
1
. d
2
x f x x
. Tích phân
1
0
df x x
bằng bao nhiêu ?
Trả lời:……………………………………..
Câu 65. Cho
2 5
2
2
2 1
( )
5 1, 3
f x
f x x dx dx
x
. Giá trị của
5
1
( )f x dx
bằng:
Trả lời:……………………………………..
Câu 66. Cho hàm số
f x
xác định trên
\ 0
thỏa mãn
2
1x
f x
x
,
3
2
2
f
và
3
2 2ln 2
2
f
. Giá
trị của biểu thức
1 4
f f
bằng (viết kết quả dưới dạng số thập phân và làm tròn đến hàng phần mười).
Trả lời:……………………………………..
Câu 67. Cho hàm số
f x
liên tục trên
0;1
thỏa mãn
2 3
6
1 6
3 1
f x x f x
x
. Khi đó
1
0
df x x
bằng
Trả lời:……………………………………..
Câu 68. Cho hàm số
( )y f x
liên tục trên thỏa mãn
2
2 1
3 2 2 1 e 4
x x
f x f x x
. Tính tích phân
2
0
dI f x x
ta được kết quả bằng bao nhiêu
Trả lời:……………………………………..
Câu 69. Cho hàm số
f x
liên tục trên
thỏa mãn
5 4 11 8 6 4
1 3 3,xf x f x x x x x x x
. Khi
đó giá trị tích phân
0
1
6 df x x
bằng bao nhiêu ?
Trả lời:……………………………………..
9
Câu 70. Cho hàm số
f x
liên tục trên
và thỏa mãn
2 7 3
2 2 3 1f x xf x x x x
với
x
. Tính tích
phân
1
0
dxf x x
.
Trả lời:……………………………………..
Câu 71. Cho
f x
là hàm số liên tục trên tập xác đinh
và thỏa mãn
2
3 1 2
f x x x
. Giá trị tích
phân
5
1
6 dI f x x
bằng bao nhiêu
Trả lời:……………………………………..
Câu 72. Cho hàm số
f x
thỏa mãn
2
0
3
f
và
1 ' 1, 1.
x x f x x
Biết rằng
1
0
2
15
a b
f x dx
với
, .
a b
Tính giá trị biểu thức
.T a b
Câu 72. Biết rằng hàm số
3 2
f x ax bx cx d
, , ,a b c d
thỏa mãn
1
0
d 4;
f x x
2 3 4
0 0 0
d 2; d 18; d 80
f x x f x x f x x
Tính giá trị của biểu thức
2 3 4 5P a b c d
.
Câu 73. Biết
1
3
2
0
3
d ln 2 ln 3
3 2
x x
x a b c
x x
với
a
,
b
,
c
là các số hữu tỉ, tính giá trị của
2
S a b c
Trả lời:……………………………………..
Câu 74. Cho hàm số
f x
liên tục trên
0;3
và
1 3
0 0
d 2; d 8.
f x x f x x
Giá trị của tích phân
1
1
2 1 d ?
f x x
Trả lời:……………………………………..
Câu 75. Cho hàm số
( )f x
liên tục trên
và có
3
0
( ) 8
f x dx
và
5
0
( ) 4
f x dx
. Tính
1
1
( 4 1)f x dx
Trả lời:……………………………………..
Câu 76. Cho hàm số
3
2 3, khi 2
4 1, khi 2
x x
f x
x x
. Giả sử
F x
là nguyên hàm của
f x
trên
và thỏa mãn
0 3
F
. Giá trị
3 5 5
F F
bằng
Trả lời:……………………………………..
Câu 77. Cho hàm số
3
2 3
khi 0
( )
1 khi 0
x
e m x
f x
x x x
(với m là tham số). Biết hàm số
( )f x
liên tục trên
và
1
1
( )
b
f x dx a e
c
với
*
, , ;
b
a b c
c
tối giản
( 2, 718281828)
e
. Biểu thức
a b c m
bằng
Trả lời:……………………………………..
Câu 78. Cho hàm số
2
1 khi 0
2 2 khi 0
x
e x
y f x
x x x
. Tích phân
2
1
ln 1
d
e
e
f x
a
I x ce
x b
biết
, ,a b c
và
a
b
tối giản. Tính
?a b c
Trả lời:……………………………………..
Câu 79. Cho hàm số
2
2
3 ln 1 khi 0
2 3 1 khi 0
x x x
f x
x x x
. Biết
1
ln
d 3 ln 2
e
e
f x
x a b c
x
với
, ,a b c
. Giá trị
của
6a b c
bằng
Trả lời:……………………………………..
10
Câu 80. Cho hàm số
f x
liên tục trên
. Gọi
, ,
F x G x H x
là ba nguyên hàm của
f x
trên
thỏa
mãn
4
3 33F G H
và
0 0 0 1
F G H
. Tính
1
0
d
3. 3
f x x
Trả lời:……………………………………..
Câu 81. Cho biết
5
3
2
1
ln
1 1
x a
I dx c d
b
x
với
, , ,a b c d
,
a
b
tối giản,
9
d
. Tính giá trị của
T a b c d
.
Trả lời:……………………………………..
Câu 82. Cho
12
5
1
ln
4
dx b
I
a c
x x
với
, ,a b c
là các số nguyên dương và
b
c
là phân số tối giản. Tính
Trả lời:……………………………………..
Câu 83. Biết rằng
2
0
4sin 7 cos
2 ln
2sin 3cos
x x b
I dx
x x a c
với
*
0; , ;
b
a b c
c
tối giản. Hãy tính giá trị biểu thức
.P a b c
Trả lời:……………………………………..
Câu 84. Cho hàm số
f x
liên tục trên
và
9
2
1 0
d 4, sin cos d 2
f x
x f x x x
x
. Giá trị của tích phân
3
0
dI f x x
bằng bao nhiêu ?
Trả lời:……………………………………..
Câu 85. Cho
f x
liên tục trên
thỏa mãn
2020
f x f x
và
2017
3
x 4.
f x d
Khi đó
2017
3
xxf x d
bằng
bao nhiêu
Trả lời:……………………………………..
Câu 86. Cho hàm số
f x
có đạo hàm và xác định trên
.
Biết
1 2
f
và
1 4
2
0 1
1 3
d 2 d 4
2
x
x f x x f x x
x
. Giá trị của
1
0
7 df x x
bằng
Trả lời:……………………………………..
Câu 87. Cho hàm số
( )y f x
liên tục trên
và thỏa mãn
2 3
3
4 ( ) 6 (2 ) 4
5
xf x f x x
. Giá trị tích
4
0
( )df x x
bằng bao nhiêu ?
Trả lời:……………………………………..
Câu 88. Cho
f x
liên tục trên
và thỏa mãn
1
0
2 16, 2 d 2
f f x x
. Tích phân
2
0
dxf x x
bằng bao nhiêu
Trả lời:……………………………………..
Câu 89. Cho hàm số
f x
liên tục trên
, thỏa mãn
2
4
0
tan . cos d 2
x f x x
và
2
2
e
e
ln
d 2
ln
f x
x
x x
. Giá trị
tích phân
2
1
4
2
d
f x
x
x
bằng bao nhiêu ?
Trả lời:……………………………………..
Câu 90. Có bao nhiêu giá trị thực của tham số
m
thỏa mãn:
2
0
3 2 10
m
x x dx m
?
Trả lời:……………………………………..
11
Câu 91. Cho
F x
là nguyên hàm của hàm số
2
sinf x x
trên
thỏa mãn
0
4
F
. Tính giá trị của biểu
thức
2
2
S F F
(Kết quả làm tròn đến hai chữ số thập phân sau dấu phẩy)
Trả lời:……………………………………..
Câu 92. Biết nguyên hàm
d
2tan 1
x
I
x
bằng
ln 2sin cos
a c
x x x C
b b
với (
a
b
,
c
b
là các phân số tối giản
và
*
, ,a c b
). Tính
a b c
.
Trả lời:……………………………………..
Câu 93. Cho
F x
là một nguyên hàm của hàm số
2
1
cos
f x
x
. Biết
4
F k k
với mọi
k
. Tính
0 ... 10
F F F F
.
Trả lời:……………………………………..
Câu 94. Cho hàm số
y f x
với
1 4
x
có đồ thị các đoạn thẳng như hình bên.
Tích phân
4
1
dI f x x
bằng bao nhiêu ?
Trả lời:……………………………………..
Câu 95. Cho hàm số
2
2 1
( )
3 1
x a khi x
f x
x b khi x
thoả mãn
2
0
( ) 13
f x dx
. Giá trị biểu thức
T a b ab
bằng
bao nhiêu ?
Câu 96. Cho hàm số
( )y f x
có đồ thị là đường gấp khúc như hình vẽ bên dưới.
Giá trị của tích phân
4
1
2 3
I f x dx
bằng bao nhiêu ?
Trả lời:……………………………………..
Câu 97. Cho hàm số
y f x
có đạo hàm trên
thỏa mãn
1 1
f
và
2 3
2 5 2 1
f x xf x x x
với mọi
x
. Tính
2
1
'
I xf x dx
.
Trả lời:……………………………………..
Câu 98. Cho hàm số
f x
có đạo hàm liên tục trên đoạn
0;2
thỏa mãn
2 6
f
,
2
2
0
d 7
f x x
và
2
0
17
. d
2
x f x x
. Tích phân
2
0
df x x
bằng
Trả lời:……………………………………..
12
Câu 99. Cho hàm số
f x
liên tục trên
và
2
0
2 16, d 4
f f x x
. Tính
1
0
. 2 dI x f x x
.
Trả lời:……………………………………..
Câu 100. Cho hàm số
f x
có đạo hàm liên tục trên
và thỏa mãn
1
0
d 10
f x x
,
1 cot1
f
. Tính tích phân
1
2
0
tan tan dI f x x f x x x
.
Trả lời:……………………………………..
Câu 101. Cho hàm số
có đạo hàm liên tục trên
. Biết
(5) 1
f
và
1
0
(5 ) 1x f x dx
, khi đó tích phân
5
2
0
( )x f x dx
bằng bao nhiêu
Trả lời:……………………………………..
Câu 102. Cho hàm số
f x
có đạo hàm liên tục trên
0; 2
và thỏa mãn
1 0
f
,
2
2
4 8 32 28
f x f x x x
với mọi
x
thuộc
0; 2
.
Giá trị của
1
0
3 df x x
bằng bao nhiêu
Trả lời:……………………………………..
Câu 103. Cho hàm số
f x
liên tục trên
và thỏa mãn
2 7 3
2 2 3 1f x xf x x x x
với
x
. Tính
tích phân
1
0
dxf x x
(kết quả là số thập phân hữu hạn).
Trả lời:……………………………………..
Câu 104. Cho hàm số
( )y f x
có đạo hàm liên tục trên
thỏa mãn
2
. ( ). '( ) ( ) ,x f x f x f x x x
và có
(2) 1
f
. Tích phân
2
2
0
( )f x dx
(kết quả là số nguyên) có giá trị bằng
Trả lời:……………………………………..
Câu 105. Biết
1
2
0
1 , ,
f x
x e dx ae b a b
.Giá trị của
a b
bằng
Trả lời:……………………………………..
Câu 106. Xét hàm số
f x
liên tục trên đoạn
0;1
và thỏa mãn
2 3 1 1
f x f x x
. Tích phân
1
0
df x x
bằng phân số tối giản
,
a
a b
b
.Tính
2 3a b
.
Trả lời:……………………………………..
Câu 107. Cho hàm số
f x
nhận giá trị dương thỏa mãn
3
2
2
f x
f x x
x
,
0;x
và
3
5
2
2
1
d
20
x
x
f x
.
Giá trị của biểu thức
2 3
f f
bằng bao nhiêu ?
Trả lời:……………………………………..
Câu 108. Cho hàm số
( )y f x
liên tục trên
thỏa mãn:
2
2 1
3 ( ) (2 ) 2( 1) 4,
x x
f x f x x e x
. Tính
giá trị của tích phân
2
0
( )I f x dx
.
Trả lời:……………………………………..
Câu 109. Cho hàm số
y f x
liên tục trên
\ 0; 1
thỏa mãn điều kiện
1 2ln 2
f
và
2
1 . 3 2
x x f x f x x x
.
Giá trị
2 ln 3
f a b
, với
,a b
. Tính
2 2
a b
.
Trả lời:……………………………………..
______________________________
13
NGUYÊN HÀM VÀ TÍCH PHÂN THPT
ỨNG DỤNG TÍNH DIỆN TÍCH HÌNH PHẲNG, THỂ TÍCH VẬT THỂ CỦA TÍCH PHÂN
LỚP BÀI TOÁN TRẮC NGHIỆM TRẢ LỜI NGẮN
_________________________________
Câu 1. Khi cắt một vật thể bởi mặt phẳng vuông góc với trục
Ox
tại điểm có hoành độ
x
(
5
1
2
x
), mặt cắt là
tam giác vuông cân và độ dài một cạnh góc vuông là
2
1
4
2
x
. Tính thể tích vật thể trên (làm tròn kết quả đến
hàng phần trăm).
Trả lời:………………………………….
Câu 2. Cắt một vật thể bởi hai mặt phẳng vuông góc với trục
Ox
tại
1x
và
3
x
. Một mặt phẳng tùy ý vuông
góc với trục
Ox
tại điểm có hoành độ
x
(
1 3
x
) cắt vật thể đó theo thiết diện là một hình chữ nhật có độ dài
hai cạnh là
3x
và
2
3 2
x
. Tính thể tích của phần vật thể giới hạn bởi hai mặt phẳng trên.
Trả lời:………………………………….
Câu 3. Tính thể tích của vật thể nằm giữa hai mặt phẳng
1x
và
4
x
, biết rằng mặt phẳng vuông góc với trục
Ox
tại điểm có hoành độ
1 4
x x
cắt vật thể theo thiết diện là một hình lục giác đều cạnh bằng
2x
(làm
tròn kết quả đến hàng đơn vị).
Câu 4. Cho vật thể (như hình vẽ) có đáy là một đường tròn có bán kính bằng
2
. Khi cắt vật thể bằng mặt phẳng
vuông góc với trục
Ox
tại điểm có hoành độ
2 2
x x
thì được thiết diện là một tam giác đều. Tính thể tích
V
của vật thể đó (làm tròn kết quả đến hàng phần chục).
Trả lời:………………………………….
Câu 5. Một vật thể trong không gian được giới hạn bởi hai mặt phẳng
1, 2
x x
. Một mặt phẳng tùy ý vuông
góc với trục
Ox
tại điểm có hoành độ
1 2
x x
cắt vật thể theo thiết diện là một hình tam giác đều có cạnh
bằng
3 x
. Tính thể tích
V
của vật thể đó (kết quả làm tròn đến hàng phần chục).
Trả lời:………………………………….
Câu 6. Tính thể tích
V
của phần vật thể giới hạn bởi hai mặt phẳng
1x
và
3,x
biết rằng khi cắt vật thể bởi
mặt phẳng tùy ý vuông góc với trục
Ox
tại điểm có hoành độ
x
(1 3)
x
thì được thiết diện là một hình chữ
nhật có hai cạnh là
3x
và
2
x
Trả lời:………………………………….
Câu 7. Cắt một vật thể trong hệ trục toạ độ
Oxyz
, giới hạn bởi hai mặt phẳng vuông góc với trục
Ox
tại
1, 4
x x
, Một mặt phẳng cắt vật thể theo mặt phẳng vuông góc với
Ox
tại
x
1 4
x
được thiết diện là
một hình thoi có hai đường chéo lần lượt là
x
và
2
3 1
x
. Tính thể tích của phần vật thể giới hạn bởi hai mặt
phẳng trên (làm tròn kết quả đến hàng phần trăm).
Trả lời:………………………………….
Câu 8. Một vật thể nằm trong hệ trục toạ độ
Oxyz
, giới hạn bởi hai mặt phẳng vuông góc với trục
Ox
tại
0, 2
x x
, Một mặt phẳng cắt vật thể theo mặt phẳng vuông góc với
Ox
tại
x
0 2
x
được thiết diện là
một hình tròn có bán kính là
2
R x
. Tính thể tích của phần vật thể giới hạn bởi hai mặt phẳng trên (làm
tròn kết quả đến hàng phần trăm).
Trả lời:………………………………….
Câu 9. Một vật thể trong hệ trục toạ độ
Oxyz
, giới hạn bởi hai mặt phẳng vuông góc với trục
Ox
tại
0, 2
x x
,
cắt vật thể theo mặt phẳng vuông góc với
Ox
tại
x
được một hình tam giác đều có cạnh
bằng
2
4 , 0 2
x x
. Tính thể tích vật thể đã cho (làm tròn kết quả đến hàng phần trăm).
14
Câu 10. Cho phần vật thể giới hạn bởi hai mặt phẳng
1x
và
7
x
, biết rằng khi cắt vật thể bởi mặt phẳng
vuông góc với trục
Ox
tại điểm có hoành độ
x
(
1 7
x
) thì được thiết diện là một hình chữ nhật có độ dài
hai cạnh là
2x
và
2
1
x
. Thể tích của phần vật thể đã cho bằng
(
a b
c
c
là số nguyên tố,
6; , , )
b a b c
.
Tính
. .a b c
?
Trả lời:………………………………….
Câu 11. Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường
2 0
x y
;
2 1y x
;
0
y
quay
quanh trục
Ox
bằng
( ,
a
a b
b
,
a
b
tối giản). Tính
bằng bao nhiêu?
Trả lời:………………………………….
Câu 12. Một vật thể hình khối như hình vẽ. Các tứ giác
,
ABCD CDPQ
là các hình vuông cạnh
2,5cm
. Tứ giác
ABEF
là hình chữ nhật cạnh
3,5AF cm
. Mặt
PQFE
được mài nhẵn theo đường parabol
P
có đinh nằm
trên cạnh
EF
. Tính thể tích của vật thể trên (đơn vị:
3
cm
) (làm tròn kết quả đến hàng phần chục).
Trả lời:………………………………….
Câu 13. Cho hình phẳng
H
được giới hạn bởi đường cong
2 2
y m x
(
m
là tham số khác
0
) và trục
hoành. Khi
H
quay xung quanh trục hoành được khối tròn xoay có thể tích
V
. Có bao nhiêu giá trị nguyên
của
m
để
1000
V
.
Trả lời:………………………………….
Câu 14. Tìm
a
để diện tích
S
của hình phẳng giới hạn bởi
2
2
: ,
1
x x
P y
x
đường thẳng
: 1d y x
và
,x a
2x a
( 1)
a
bằng
ln3
?
Trả lời:………………………………….
Câu 15. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số
2
2 3
1
x x
y
x
;
y x
và hai đường thẳng
2; 3
x x
bằng
ln 2
S a b
. Giá trị của
a b
bằng bao nhiêu?
Trả lời:………………………………….
Câu 16. Cho hàm số
y f x
. Đồ thị hàm số
y f x
là đường cong trong hình dưới. Biết rằng diện tích của
các phần hình phẳng
A
và
B
lần lượt là
4
A
S
và
10
B
S
. Tính giá trị của
3f
, biết giá trị của
0 2
f
.
15
Trả lời:………………………………….
Câu 17. Cho hàm số
3
2
7 4 khi 0 1
4 khi 1
x x
f x
x x
. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số
f x
và các đường thẳng
0, 3, 0
x x y
.
Trả lời:………………………………….
Câu 18. Cho
H
là hình phẳng được tô đậm trong hình vẽ và được giới hạn bởi các đường có phương trình
2
10
3
y x x
,
khi 1
2 khi 1
x x
y
x x
. Diện tích của
H
bằng bao nhiêu?
Trả lời:………………………………….
Câu 19. Biết
F x
và
G x
là hai nguyên hàm của hàm số
f x
trên
và
5
0
d 5 0 , 0
f x x F G a a
. Gọi
S
là diện tích hình phẳng giới hạn bỡi các đường
y F x
,
y G x
,
0
x
và
x
. Khi
20
S
thì
a
bằng?
Trả lời:………………………………….
Câu 20. Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường
4
, 0, 1, 4
y y x x
x
quanh
trục
Ox
là bao nhiêu?
Trả lời:………………………………….
Câu 21. Biết thể tích khối tròn xoay tạo nên khi quay xung quanh trục
Ox
hình phẳng giới hạn bởi các đường
2
1
y x
,
0
y
,
0
x
,
2
x
có dạng
a
b
với
a
b
là phân số tối giản. Tính giá trị biểu thức
24 12S a b
.
16
Trả lời:………………………………….
Câu 22. Cho hình phẳng giới hạn bởi các đường
ln , 0,
y x x y x e
quay xung quanh trục
Ox
tạo thành
khối tròn xoay có thể tích bằng
3
2
be
a
với
,a b
. Tính
2 2
P a b
, biết một nguyên hàm của hàm số
2
ln
f x x x
là
3
2
9ln 6ln 2
27
x
F x x x
.
Trả lời:………………………………….
Câu 23. Gọi
V
là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường
,y x
0
y
và
4
x
quanh trục
Ox
. Đường thẳng
0 4
x a a
cắt đồ thị hàm số
y x
tại
M
(xem hình vẽ sau).
Gọi
1
V
là thể tích khối tròn xoay tạo thành khi quay tam giác
OMH
quanh trục
Ox
. Biết rằng
1
2V V
. Khi đó
tổng các giá trị của
a
là bao nhiêu?
Trả lời:………………………………….
Câu 24. Cho các nửa đường tròn như hình vẽ sau, trong đó đường kính của nửa đường tròn lớn gấp đôi đường
kính của nửa đường tròn nhỏ. Biết rằng nửa hình tròn đường kính
AB
có diện tích là
32
và góc
30
BAC
.
Tính thể tích vật thể tròn xoay (làm tròn đến số nguyên) được tạo thành khi quay hình phẳng
H
(phần tô
đậm) xung quanh đường thẳng
AB
.
Câu 25. Gọi
S
là diện tích hình phẳng giới hạn bởi các đường
2 2
, 0
my x mx y m
. Tìm tổng các giá trị
của
m
để
3
S
.
Trả lời:………………………………….
Câu 26. Cho hình thang cong
H
giới hạn bởi các đường
e
x
y
,
0
y
,
0
x
,
ln 4
x
. Đường thẳng
x k
0 ln 4
k
chia
H
thành hai phần có diện tích là
1
S
và
2
S
như hình vẽ bên. Khi
1 2
2S S
thì giá trị
k
e
bằng bao nhiêu
17
Câu 27. Cho parabol
2
:
P y x
và hai điểm
,A B
thuộc
P
sao cho
2AB
. Khi hình phẳng giới hạn bởi
P
và đường thẳng
AB
đạt giá trị lớn nhất thì
2 2
OA OB
bằng bao nhiêu
Trả lời:………………………………….
Câu 28. Cho Parabol
2
: 1
P y x
và đường thẳng
: 2
d y mx
với
m
là tham số. Gọi
0
m
là giá trị của
m
để diện tích hình phẳng giới hạn bởi
P
và
d
là nhỏ nhất. Hỏi tổng các giá trị
0
m
bằng bao nhiêu
Trả lời:………………………………….
Câu 29. Tìm tổng các số thực
a
để hình phẳng giới hạn bởi hai đồ thị hàm
2 2
6
2 3
1
x ax a
y
a
và
2
6
1
a ax
y
a
có diện tích lớn nhất.
Trả lời:………………………………….
Câu 30. Cho hàm số
4 2
6
y x x m
có đồ thị
m
C
. Giả sử
m
C
cắt trục hoành tại bốn điểm phân biệt sao
cho hình phẳng giới hạn bởi
m
C
và trục hoành có phần phía trên trục hoành và phần phía dưới trục hoành có
diện tích bằng nhau. Khi đó
a
m
b
(với
a
,
b
là các số nguyên,
b
,
a
b
là phân số tối giản). Giá trị của biểu
thức
S a b
là:
Trả lời:………………………………….
Câu 31. Tính thể tích khối tròn xoay khi quay hình phẳng
H
giới hạn bởi các đường
2
x
e
y
,
0
y
và
1, 1x x
quanh trục hoành.
Trả lời:………………………………….
Câu 32. Cho parabol
2
1
: 2 3P y x x
cắt trục hoành tại hai điểm
,A B
và đường thẳng
:
d y a
0 4
a
. Xét parabol
2
P
đi qua
,A B
và có đỉnh thuộc đường thẳng
y a
. Gọi
1
S
là diện tích hình phẳng
giới hạn bởi
1
P
và
d
.Gọi
2
S
là diện tích hình phẳng giới hạn bởi
2
P
và trục hoành. Biết
1 2
S S
, tính giá trị
biểu thức
3 2
8 48T a a a
.
Trả lời:………………………………….
Câu 33. Trong mặt phẳng
Oxy
cho là hình phẳng
H
giới hạn bởi parabol
2
4
y x
và trục hoành. Đường
thẳng
, 2 2
x k k
chia
H
thành hai phần
1 2
,
H H
như hình vẽ.
18
Biết rằng diện tích
1
H
gấp
20
7
lần diện tích
2
H
, tính giá trị biểu thức
2
9 6 10
k k
.
Trả lời:………………………………….
Câu 34. Cho hàm số
y f x
có đồ thị như hình vẽ và diện tích hai phần
,A B
lần lượt bằng
11
và
2.
Giá trị của
0
1
3 1 dI f x x
bằng
Trả lời:………………………………….
Câu 35. Cho hàm số
y f x
có đồ thị như hình vẽ và diện tích hai phần
,A B
lần lượt bằng
11
và
2
.
Giá trị của
0
1
3 1 dI f x x
bằng bao nhiêu
Trả lời:………………………………….
Câu 36. Biết
;
F x G x
là hai nguyên hàm của hàm số
f x
trên
và
4
0
4 0 0
f x dx F G a a
.
Gọi
S
là diện tích hình phẳng giới hạn bởi các đường
; ; 0; 4.
y F x y G x x x
Khi
8S
thì
a
bằng
Trả lời:………………………………….
Câu 37. Cho hàm số
4 2
4
y x x m
. Tìm
m
để đồ thị hàm số cắt trục
Ox
tại bốn điểm phân biệt sao cho
hình phẳng giới hạn bởi đồ thị hàm số và Ox có phần phía trên trục hoành là
1
S
, phần dưới trục hoành x là
2
S
19
và
3
S
thỏa
1 2 3
S S S
. Khi đó
a
m
b
(
,a b
là các số nguyên,
b
,
a
b
tối giản). Giá trị của biểu thức
S a b
là
Trả lời:………………………………….
Câu 38. Cho đường cong
3
( ) : 2C y x kx
và parabol
2
: 2
P y x
tạo thành hai miền phẳng có diện tích
1 2
,S S
như hình vẽ bên.
Biết rằng
1
8
3
S
, giá trị của
2
S
bằng phân số tối giản
,
a
a b
b
. Tính
2 3a b
.
Trả lời:………………………………….
Câu 39. Diện tích hình phẳng giới hạn bởi parabol
2
2 1y x x
và đường thẳng
y
( 1) 5m x
có giá trị
nhỏ nhất bằng phân số tối giản
,
a
a b
b
. Tính
2 3a b
.
Trả lời:………………………………….
Câu 40. Gọi
X
là tập hợp tất cả các giá trị của tham số
m
để đường thẳng
d
:
45 2
y m
cùng với đồ thị
( )C
của hàm số
3 2
1
2 1
3
y x mx x
tạo thành hai miền kín có diện tích lần lượt là
1 2
,S S
thỏa mãn
1 2
S S
(xem hình vẽ). Số phần tử của tập
X
là
Trả lời:………………………………….
Câu 41. Gọi
S
là diện tích hình phẳng giới hạn bởi parabol
2
2 1y x x
và các đường thẳng
y m
,
0
x
,
1x
. Có bao nhiêu giá trị nguyên của tham số
4040; 3
m
để
2021
S
?
Câu 42. Cho hình phẳng
( )H
được giới hạn bởi đường cong
2 2
y m x
(
m
là tham số khác
0
) và trục
hoành. Khi
( )H
quay xung quanh trục hoành được khối tròn xoay có thể tích
V
. Có bao nhiêu giá trị nguyên
của
m
để
1000
V
.
Trả lời:………………………………….
O
x
y
3
S
1
S
2
S
20
Câu 43. Gọi
V
là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường
y x
,
0
y
và
4
x
quanh trục
Ox
. Đường thẳng
0 4
x a a
cắt đồ thị hàm số
y x
tại
M
(hình vẽ). Gọi
1
V
là
thể tích khối tròn xoay tạo thành khi quay tam giác
OMH
quanh trục
Ox
. Biết rằng
1
2V V
. Khi đó tổng các giá
trị
a
thu được bằng bao nhiêu
Trả lời:………………………………….
Câu 44. Cho đồ thị
:
C y f x x
. Gọi
H
là hình phẳng giới hạn bởi đồ thị
C
, đường thẳng
9
x
và trục
Ox
. Cho điểm
M
thuộc đồ thị
C
và điểm
9; 0
A
. Gọi
1
V
là thể tích khối tròn xoay khi cho
H
quay
quanh trục
Ox
,
2
V
là thể tích khối tròn xoay khi cho tam giác
AOM
quay quanh trục
Ox
. Biết rằng
1 2
2V V
.
Tính diện tích
S
phần hình phẳng giới hạn bởi đồ thị
C
và đường thẳng
OM
thu được kết quả
3
,
a
a b
b
trong đó phân số
a
b
tối giản. Tính
2 3a b
.
Trả lời:………………………………….
Câu 45. Cho đường thẳng
y x a
(
a
là tham số thực dương) và đồ thị hàm số
y x
. Gọi
1 2
,S S
lần lượt là
diện tích hai hình phẳng được gạch chéo trong hình vẽ bên dưới. Khi
1 2
5
3
S S
thì tổng các giá trị
a
thu được
bằng bao nhiêu ?
Trả lời:………………………………….
Câu 46. Diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số
3 2
2 2 1(y x x mx m
là tham số) và
3 2
3
y x x
đạt giá trị nhỏ nhất bằng bằng M, M gần nhất số nguyên nào ?
Trả lời:………………………………….
Câu 47. Cho hàm số
3 2
, , , , , 0
y f x ax bx cx d a b c d a
có đồ thị
C
. Biết rằng đồ thị
C
tiếp
xúc với đường thẳng
4
y
tại điểm có hoành độ âm và đồ thị của hàm số
'y f x
cho bởi hình vẽ dưới đây.
Tính thể tích vật thể tròn xoay được tạo thành khi quay hình phẳng H giới hạn bởi đồ thị
C
và trục hoành khi
quay xung quanh trục
Ox
là
a
b
(phân số
a
b
tối giản). Tính
2 3a b
.

Tài liệu khác của Toán 12

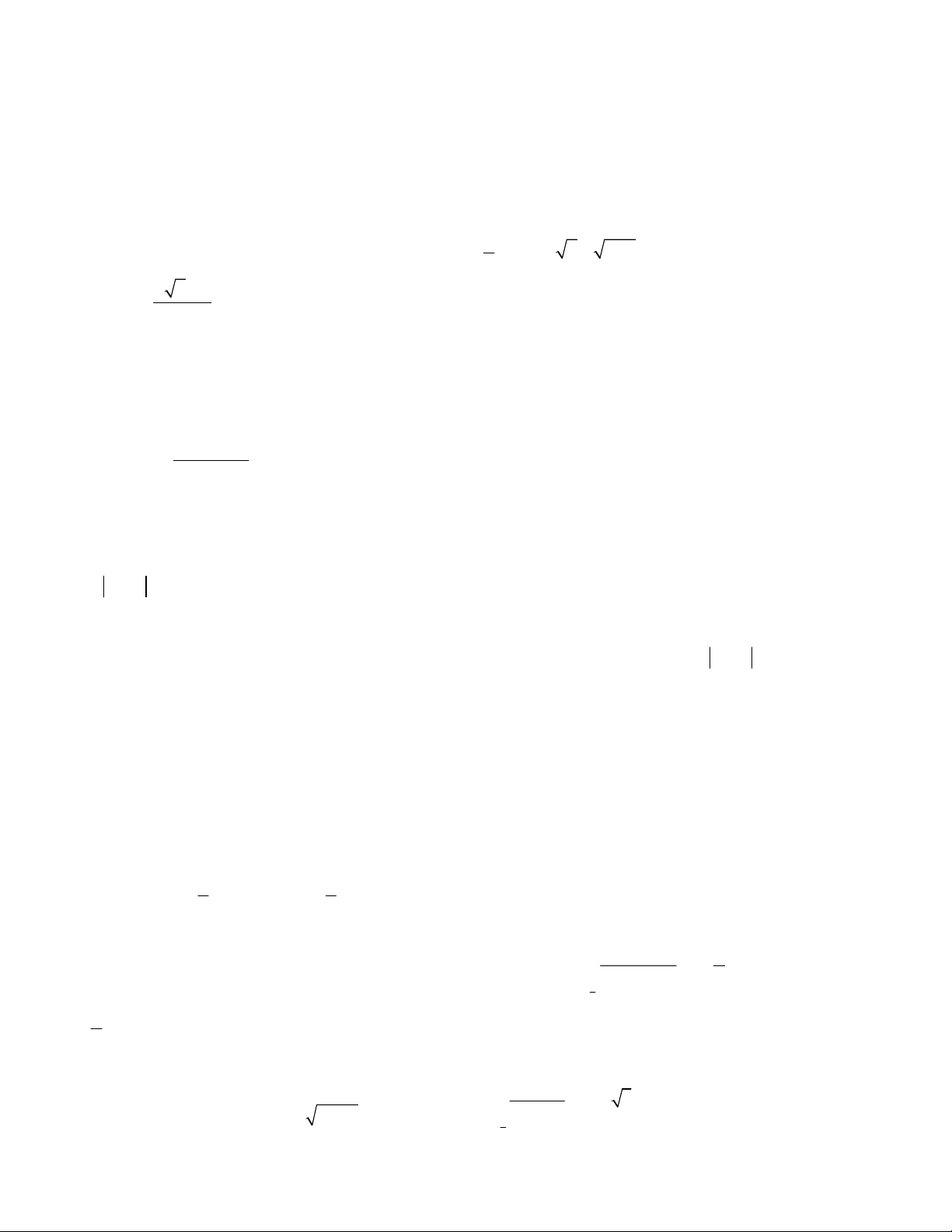
Preview text:


TÀI LIỆU THAM KHẢO TOÁN HỌC PHỔ THÔNG
______________________________________________________________ aV  a,b  b
------------------------------------------------------------------------------------------
LUYỆN KỸ NĂNG TOÁN 12 THPT
TRẮC NGHIỆM TRẢ LỜI NGẮN
NGUYÊN HÀM, TÍCH PHÂN VÀ ỨNG DỤNG
(KẾT HỢP 3 BỘ SÁCH GIÁO KHOA)
THÂN TẶNG TOÀN THỂ QUÝ THẦY CÔ VÀ CÁC EM HỌC SINH TRÊN TOÀN QUỐC
CREATED BY GIANG SƠN (FACEBOOK)
ĐÁP ÁN CHI TIẾT PDF BẠN ĐỌC VUI LÒNG LIÊN HỆ TÁC GIẢ
GACMA1431988@GMAIL.COM (GMAIL); TEL 0398021920
THÀNH PHỐ THÁI BÌNH – THÁNG 12/2024 1
LUYỆN KỸ NĂNG TOÁN 12 THPT
TRẮC NGHIỆM TRẢ LỜI NGẮN
NGUYÊN HÀM, TÍCH PHÂN VÀ ỨNG DỤNG
__________________________ DUNG NỘI DUNG LƯỢNG 1 FILE
TRẮC NGHIỆM TRẢ LỜI NGẮN 10 trang
NGUYÊN HÀM, TÍCH PHÂN THUẦN TÚY 1 FILE
TRẮC NGHIỆM TRẢ LỜI NGẮN 10 trang
ỨNG DỤNG TÍNH DIỆN TÍCH HÌNH PHẲNG, THỂ TÍCH VẬT THỂ 1 FILE
TRẮC NGHIỆM TRẢ LỜI NGẮN 22 trang
ỨNG DỤNG THỰC TẾ NGUYÊN HÀM, TÍCH PHÂN 2
NGUYÊN HÀM VÀ TÍCH PHÂN LỚP 12 THPT
NGUYÊN HÀM VÀ TÍCH PHÂN THUẦN TÚY
LỚP BÀI TOÁN TRẮC NGHIỆM TRẢ LỜI NGẮN
________________________________________
Câu 1. Gọi F x là họ các nguyên hàm của hàm số f x  8sin 3x cos x . Biết rằng F x có dạng
F x  a cos 4x b cos 2x C . Khi đó a b bằng bao nhiêu?
Trả lời:…………………………………….. tan x
Câu 2. Cho F x  cos 2x là một nguyên hàm của hàm số f x.tan x . Biết nguyên hàm của hàm số có f  xa a dạng
tan x C với a , b là các số nguyên dương,
là phân số tối giản và C   . Tính a  2b . b b
Trả lời:……………………………………..
Câu 3. Cho hàm số y f x có đạo hàm là f  x  4sin 2x  cos x, x
   và f 0  2
 . Biết F x là   
nguyên hàm của f x thỏa mãn F    3, khi đó F   bằng bao nhiêu?  2 
Trả lời:……………………………………..
Câu 4. Cho hàm số y f x có đạo hàm trên 0;   thỏa mãn 2xf  x  f x  2x x  0;   , f  
1  1. Giá trị của biểu thức 6 f 4 là bao nhiêu ?
Trả lời:…………………………………….. Câu 5. (Cho hàm số
y f x có đạo hàm liên tục trên  và thỏa mãn điều kiện
x f  x 3    f x 4 6 27 1  0 , x        và f  
1  0 . Giá trị của f 2 bằng bao nhiêu ?
Trả lời:…………………………………….. 2
Câu 6. Cho hàm số f x thỏa mãn:  f  x  f xf  x 4 .
 15x 12x , x
   và f 0  f 0  1. Giá trị của 2 f   1 bằng bao nhiêu ?
Trả lời:……………………………………..   
Câu 7. Cho hàm số y f x có đạo hàm là f  x  sin 2x, x    và f  0  
. Biết F x là nguyên hàm  4       
của f x thỏa mãn F  2  
, khi đó F   bằng bao nhiêu ?  2   4 
Trả lời:…………………………………….. Câu 8. Cho     2    2x F x ax bx
c e là một nguyên hàm của hàm số   2 2  2 . x f x
x e . Tính tổng a b  2c (kết quả là số nguyên).
Trả lời:……………………………………..
Câu 9. Biết F x 2 x 2
e  2x là một nguyên hàm của hàm số f x trên  . Giả sử G x là một nguyên hàm
của hàm số f 2x  cos x . Khi đó 2  0  . b G G
a e c , a, b, c   . Tính . a . b c .
Trả lời:…………………………………….. Câu 10. Cho hàm số 2 2 ( ) ( ) x F x ax bx c e   
là một nguyên hàm của hàm số 2 2 ( ) (2 8 7) x f x x x e     . Tính
tổng a b c (kết quả là số nguyên).
Trả lời:…………………………………….. 3
Câu 11. Cho F x là một nguyên hàm của hàm số    ex f x
 2x thỏa mãn F 0  . Tìm F 2 (làm tròn 2 đến hàng phần chục).
Trả lời:…………………………………….. 1
Câu 12. Cho hàm số f x thỏa mãn f 2   và       2 3 f x x f x f bằng 5 
 với mọi x   . Giá trị của   1 bao nhiêu ?
Trả lời:……………………………………..
Câu 13. Hàm số f x có đạo hàm đến cấp hai trên  thỏa mãn: 2
f   x   2 1
x  3 f x   1 . Biết rằng 3 2
f x  0, x
  , giá trị tích phân I  2x  
1 f " xdx  bằng bao nhiêu ? 0
Trả lời:……………………………………..
Câu 14. Cho hàm số y f (x) xác định và có đạo hàm f   x liên tục trên [1;3] ; f x  0,x 1;3; 3
f  x   f x 2    x  2 1
1  f x 4      và f   1  1. Biết rằng
f x dx a ln 3  b a,b     , giá trị của 2 a b e bằng bao nhiêu ?
Trả lời:……………………………………..
Câu 15. Cho hàm số f x  thỏa mãn f  
1  4 và f x  xf  x 3 2
 2x  3x với mọi x  0. Giá trị của f 2 bằng bao nhiêu ?
Trả lời:…………………………………….. 2
Câu 16. Cho hàm số y f ( x) liên tục trên  và thoả mãn f x  x   f x  x 
dx , với mọi x   . Xác định 0 2
tổng các giá trị m để mx f x dx  0    . 0
Trả lời:…………………………………….. 4
Câu 17. Cho hàm số y f x thỏa mãn f 2   và   3 2 f
x x f xx
   . Giá trị của f   1 bằng bao 19 nhiêu ?
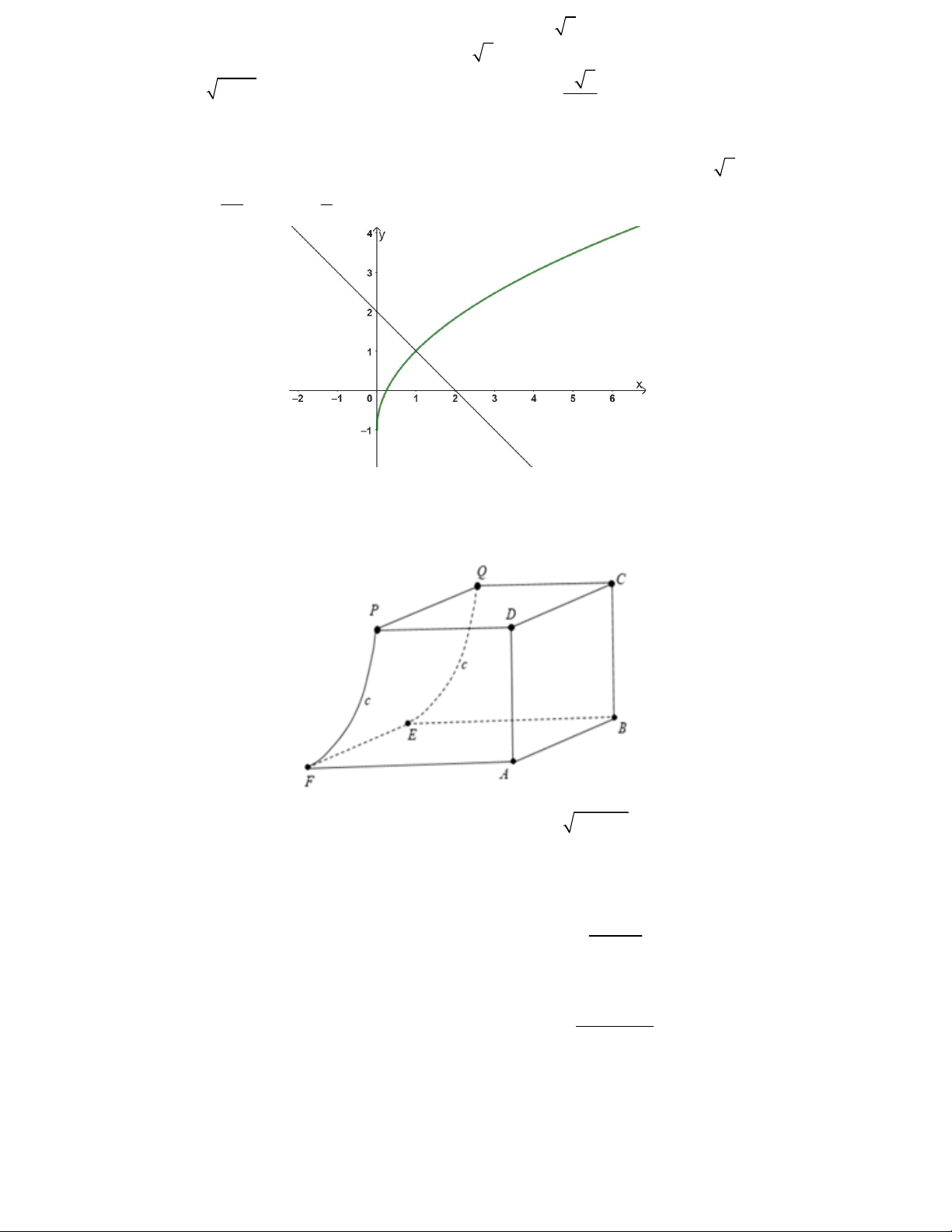
Câu 18. Cho hàm số y f x liên tục, nhận giá trị dương trên 0;  và thỏa mãn f   1  2 ; 2 x
f  x 
với mọi x 0;  . Giá trị 3
f 3 bằng bao nhiêu ?  f x 2   
Trả lời:……………………………………..
Câu 19. Cho hàm số y f x có đạo hàm liên tục trên  thỏa mãn f  
1  e và f  x  f x  , x x   . Giá
trị f 2 bằng bao nhiêu ?
Trả lời:……………………………………..
Câu 20. Cho hàm số f x có đạo hàm trên  , thoả mãn f x  1
 và f x 2 '
x 1  2x f x 1, x    .
Biết rằng f 0  0, khi đó f 2 có giá trị bằng bao nhiêu ?
Trả lời:…………………………………….. 5
Câu 21. Cho hàm số f (x) |
x  2 |  | x  2 | , biết ( )  (  )  f x dx a b
c , với a là số nguyên dương. Giá trị  6
biểu thức T a b c là bao nhiêu ?.
Trả lời:……………………………………..
Câu 22. Cho hàm số y f x liên tục trên 0;   2 2 thỏa mãn 3 .
x f x  x . f  x  2 f x , với 1
f x  0, x
  0;   và f   1 
. Gọi M , m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của hàm số 3
y f x trên đoạn 1; 2 . Tính 2M m .
Trả lời:……………………………………..
Câu 23. Cho hàm số f x liên tục trên  và thỏa mãn     1   x xf x x f x e    
với mọi x . Tính f 0 .
Trả lời:…………………………………….. 2
Câu 24. Cho F x là một nguyên hàm của hàm số    x f x e  3
x  4x  . Hàm số F  2
x x có bao nhiêu điểm cực trị?
Trả lời:…………………………………….. 2x  5 khi x  1
Câu 25. Cho hàm số f x  
. Giả sử F là nguyên hàm của f trên  thỏa mãn F 0  2 . 2
3x  4 khi x  1 
Giá trị của F  
1  2F 2 bằng
Trả lời:…………………………………….. 4
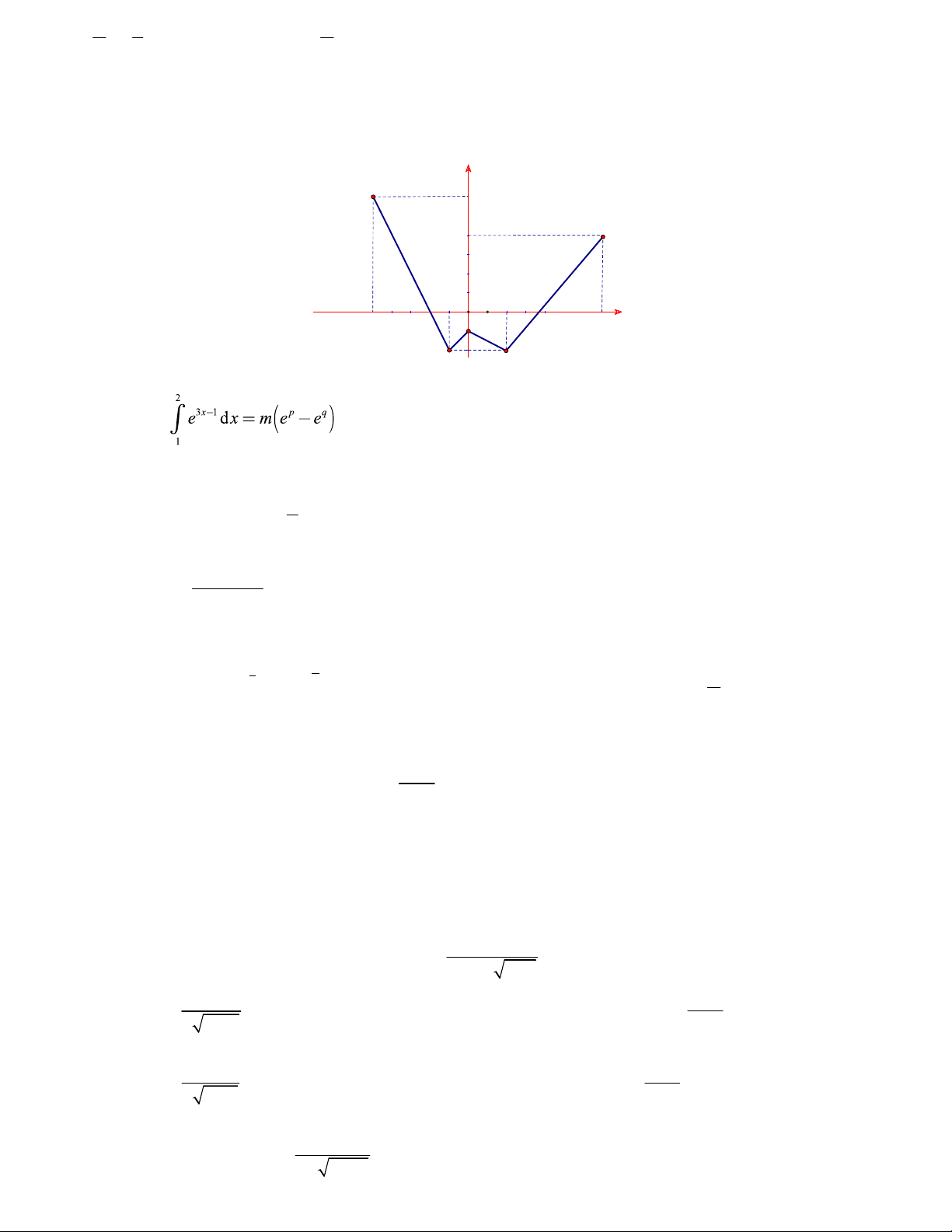
Câu 26. Cho hàm số y f x liên tục trên đoạn  1  ; 
6 và có đồ thị là đường gấp khúc ABC trong hình bên.
Biết F là nguyên hàm của f thỏa mãn F   1  2  .
Giá trị của F 5  F 6 bằng bao nhiêu
Trả lời:…………………………………….. 1 1
Câu 27. Cho hàm số f x có đạo hàm liên tục trên đoạn 0;  1 thỏa mãn f   1  0 , 2
x f xdx   . Giá trị tích 3 0 1 phân 3
x f ' xdx .  bằng bao nhiêu ? 0
Trả lời:……………………………………..  2x  3 khi x  1
Câu 28. Cho hàm số f x  
. Giả sử F là nguyên hàm của hàm số f trên  thỏa mãn 2 3x  2 khi x  1 
F 0  2 . Giá trị của F  
1  2F 2 bằng
Trả lời:…………………………………….. 2 2
Câu 29. Cho hàm số f x thỏa mãn f   1  2 và  2
x   f  x   f x  2 1 x    
1 với mọi x   . Giá trị của
f 2 bằng bao nhiêu ?
Trả lời:……………………………………..
Câu 30. Cho hàm số f (x) thỏa mãn f (1)  4 và 3 2
f (x)  xf (
x)  2x  3x với mọi x  0 . Giá trị của f (2) bằng bao nhiêu ?
Trả lời:…………………………………….. 2
Câu 31. Cho hàm số f x thỏa mãn  f  x  f xf  x 2 .
 2x x  1  
, x   và f 0  f 0  3 . Giá trị của  f   2 1    bằng bao nhiêu ?
Trả lời:……………………………………..
Câu 32. Giả sử hàm số y f x liên tục, nhận giá trị dương trên 0;  và thỏa mãn f   1  1,
f x  f  x. 3x 1, với mọi x  0 . Giá trị f 5 gần nhất với số tự nhiên nào
Trả lời:…………………………………….. 2x  7 khi x  2
Câu 33. Cho hàm số f x  
. Giả sử F là nguyên hàm của f trên  thỏa mãn F 0  4. 2 3x 1 khi x  2 
Giá trị của F  2
   3F 4 bằng bao nhiêu ?
Trả lời:……………………………………..
Câu 34. Cho F x là một nguyên hàm của hàm số f x  1 x  1 x trên tập  và thỏa mãn F   1  3.
Tính tổng F 0  F 2  F   3 .
Trả lời:……………………………………..   sin x khi x    4
Câu 35. Cho hàm số f x  
. Giả sử F là nguyên hàm của f trên  thỏa mãn  cos x khi x    4 5    3    F   
. Giá trị của F 0  2F   bằng bao nhiêu ?  6  2  2 
Trả lời:…………………………………….. 0
Câu 36. Cho hàm số y f x liên tục trên đoạn  5
 ;6có đồ thị như hình vẽ. Giá trị của
f xdx  bằng bao 5 nhiêu ? y 6 4 -1 O 1 2 x -5 -2 -1 6 -2
Trả lời:…………………………………….. Câu 37. Cho
với m , p , q   và là các phân số tối giản. Giá trị 3m p q bằng bao nhiêu
Trả lời:…………………………………….. 1 2  a Câu 38. Biết rằng x 2 xe dx    b c
e e  với a,b,c  . Giá trị của a b c bằng bao nhiêu 2 0
Trả lời:…………………………………….. e x 1 Câu 39. Biết
dx  ln ae b 
với a,b là các số nguyên dương. Tính giá trị của biểu thức 2
x x ln x 1 2 2
T a ab b .
Trả lời:…………………………………….. 2 1 p 2 xp
Câu 40. Biết    1 q x x e
dx me n
, trong đó m, n, p, q là các số nguyên dương và là phân số tối giản. q 1
Tính T m n p q .
Trả lời:…………………………………….. 2 x 2tdt
Câu 41. Số điểm cực trị của hàm số f x   là 2 1 t 2 x
Trả lời:……………………………………..
Câu 42. Cho hàm số y f x có đạo hàm trên  đồng thời thỏa mãn f 0  f   1  5 . Tính tích phân 1 I
f  xf xe dx  . 0
Trả lời:…………………………………….. x 8
Câu 43. Cho hàm số f x có f 3  3 và f  x 
, x  0 . Khi đó 6 f x dx  bằng x 1 x 1 3 21 dx a b Câu 44. Cho
a ln 3  b ln 5  c ln 7 
, với a, b, c là các số hữu tỉ. Tính giá trị . x x  4 c 5
Trả lời:…………………………………….. 55 dx a b Câu 45. Cho
a ln 2  b ln 5  c ln11 
, với a, b, c là các số hữu tỉ. Tính . x x  9 c 16
Trả lời:…………………………………….. 5 1
Câu 46. Giả sử tích phân I
dx a b ln 3  c ln 5 
. Lúc đó giá trị 3a b c bằng bao nhiêu 1 3x 1 1 6
Trả lời:…………………………………….. x  7  3  7  x a
Câu 47. Cho hàm số f x có f 2  0 và f  x  , x   ;    . Biết rằng f dx     2x  3  2   2  b 4 a
( a, b  , b  0,
là phân số tối giản). Khi đó a b bằng b ln 6 ex
Trả lời:……………………………………..Câu 48. Biết tích phân
dx a b ln 2  c ln 3 
, với a , b , c x 0 1  e  3
là các số nguyên. Tính P a b c . 2 dx Câu 49. Biết dx
a b c
với a, b, c là các số nguyên dương. Tính P a b c
(x 1) x x x  1 1
Trả lời:…………………………………….. e ln x Câu 50. Biết
dx a b 2 
với a, b là các số hữu tỷ. Tính S  3a  3b . x 1 ln x 1 3
Câu 51. Có bao nhiêu giá trị nguyên dương của tham số m để (10x  2m)dx  0  ? 0
Trả lời:…………………………………….. b Câu 52. Giả sử 7 8 8 a
 ,b  , a  0  ,
b |x | dx ma nb  trong đó ,
m n là các hằng số thực (không phụ thuộc vào a
a và b ). Giá trị của biểu thức P m  5n là bao nhiêu?
Trả lời:…………………………………….. x
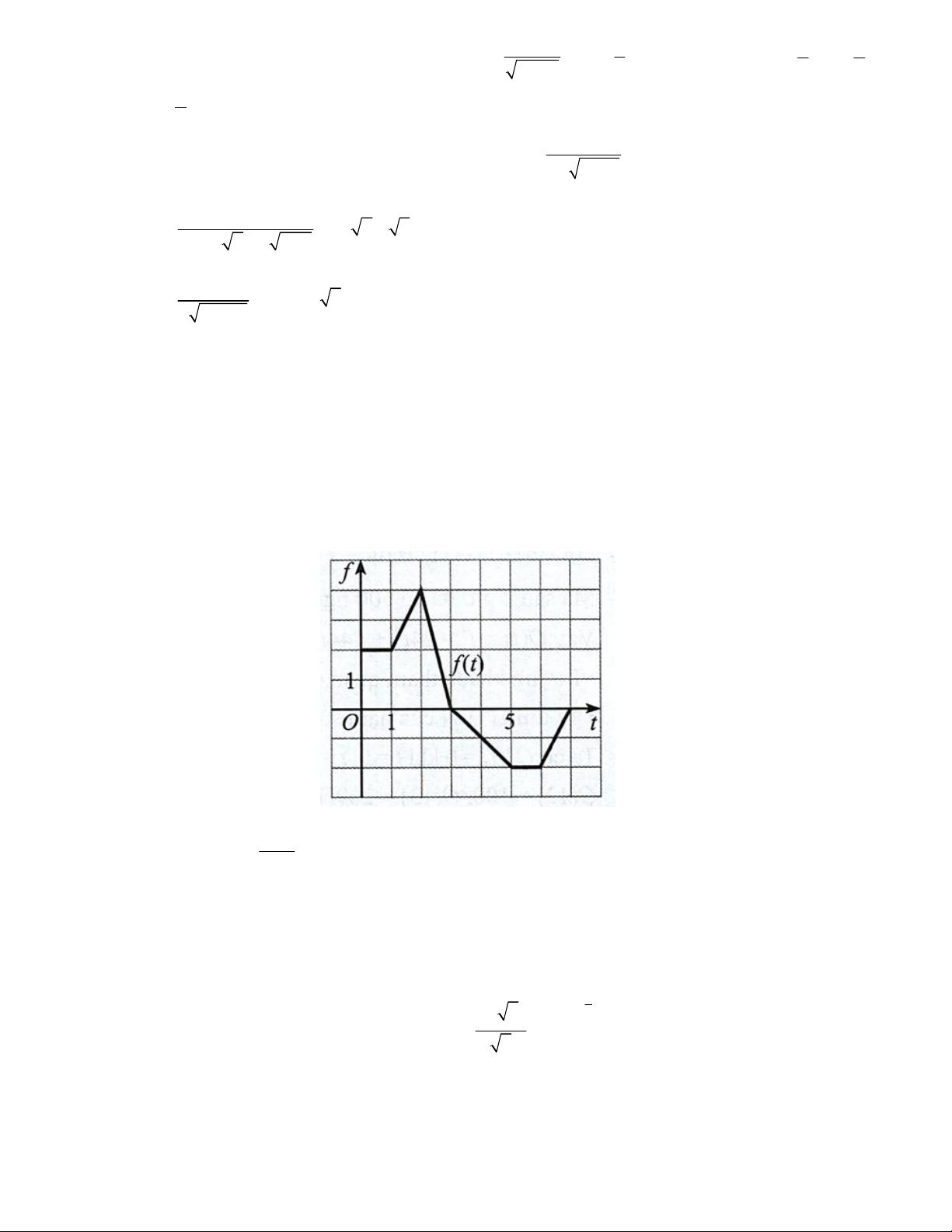
Câu 53. Cho g x  f t dt,0  x  7 
trong đó f t là hàm số có đồ thị như hình. Tính g 3 . 0
Trả lời:…………………………………….. 3 x  2
Câu 54. Giá trị tích phân
dx a b ln c, 
với a, b, c  , c  9. Tính tổng S a b  . c x 1
Trả lời:…………………………………….. b Câu 55. Cho 2 2
|x | dx ma nb  với , m , n ,
a b là các hằng số thực và a  0  b . Giá trị của biểu thức m n a bằng bao nhiêu?
Trả lời:…………………………………….. 9 f x 2
Câu 56. Cho hàm số f x liên tục trên  và dx  4,
f sin xcos d x x  2   . Tính tích phân x 1 0 3 I
f xdx  . 0
Trả lời:…………………………………….. 2017 2017
Câu 57. Cho f x liên tục trên  thỏa mãn f x  f 2020  x và
f xdx  4.  Khi đó
xf xdx  bằng 3 3 7
Trả lời:…………………………………….. 1 2
Câu 58. Biết rằng hàm số f x  mx n thỏa mãn f x dx  3  ,
f x dx  8 
. Tính giá trị m n . 0 0
Trả lời:…………………………………….. a
Câu 59. Có hai giá trị của số thực a là a , a ( 0  a a ) thỏa mãn
2x  3dx  0 1 2 1 2  . Hãy tính 1  a a a 1 2 2 T  3  3  log . 2   a  1  a
Câu 60. Có bao nhiêu giá trị nguyên dương của a để 2x  3 dx  4  ? 0
Trả lời:…………………………………….. 4 1 x  ex Câu 61. Biết 
dx a  eb  ec
với a , b , c là các số nguyên. Tính giá trị T a b c . 2 4x xe x 1
Trả lời:…………………………………….. 1 2
Câu 62. Cho hàm số y f x có đạo hàm liên tục trên 0;  1 thỏa mãn f   1  0,  f (
x) dx  7  và 0 1 1 1 2
x f (x)dx   . Giá trị tích phân f (x)dx  bằng bao nhiêu ? 3 0 0
Trả lời:…………………………………….. 1 2
Câu 63. Cho hàm số f x có đạo hàm liên tục trên đoạn 0;  1 thỏa mãn f   1  4 ,
f  x dx  36    và 0 1 1 1 .   d   x f x x . Tích phân
f x dx  bằng 5 0 0
Trả lời:…………………………………….. 1 2
Câu 64. Cho hàm số f x có đạo hàm liên tục trên đoạn 0;  1 thỏa mãn f   1  4 ,
f  x dx  5    và 0 1 1 1 .
x f x dx    . Tích phân
f x dx  bằng bao nhiêu ? 2 0 0
Trả lời:…………………………………….. 2 5 f (x) 5 Câu 65. Cho f       . Giá trị của f (x)dx  bằng: 
 2x 5 xdx 1, dx 3 2 2 1 x 1
Trả lời:…………………………………….. x 1 3 3
Câu 66. Cho hàm số f x xác định trên  \ 
0 thỏa mãn f  x  , f  2
   và f 2  2ln 2  . Giá 2 x 2 2
trị của biểu thức f  
1  f 4 bằng (viết kết quả dưới dạng số thập phân và làm tròn đến hàng phần mười).
Trả lời:…………………………………….. 6 1
Câu 67. Cho hàm số f x liên tục trên 0 
;1 thỏa mãn f 1 x 2  6x f  3 x   . Khi đó
f xdx  bằng 3x 1 0
Trả lời:……………………………………..
Câu 68. Cho hàm số y f (x) liên tục trên  thỏa mãn f xf x  x  2x2x 1 3 2 2 1 e       4 . Tính tích phân 2 I
f x dx
ta được kết quả bằng bao nhiêu 0
Trả lời:……………………………………..
Câu 69. Cho hàm số f x liên tục trên  thỏa mãn xf  5 x   f  4  x  11 8 6 4 1
x x x  3x x  3, x    . Khi 0 đó giá trị tích phân 6
f x dx  bằng bao nhiêu ? 1 
Trả lời:…………………………………….. 8
Câu 70. Cho hàm số f x liên tục trên  và thỏa mãn f x  xf  2 x  7 3 2
 2x  3x x 1 với x   . Tính tích 1
phân xf  xdx  . 0
Trả lời:…………………………………….. 
Câu 71. Cho f x là hàm số liên tục trên tập xác đinh  và thỏa mãn f  2 x  3x  
1  x  2 . Giá trị tích 5 phân I  6 f
 xdxbằng bao nhiêu 1
Trả lời:…………………………………….. 2 Câu 72. Cho hàm số
f x thỏa mãn f 0  và  x x 1 f ' x 1, x   1  . Biết rằng 3 1 a 2  b
f xdx   với a,b  .
Tính giá trị biểu thức T a  . b 15 0
Câu 72. Biết rằng hàm số   3 2
f x ax bx cx d a, , b ,
c d   thỏa mãn 1 2 3 4
f xdx  4  ; 
f xdx  2;
f xdx  18; f xdx  80    0 0 0 0
Tính giá trị của biểu thức P  2a  3b  4c  5d . 1 3 x  3x Câu 73. Biết
dx a b ln 2  c ln 3 
với a , b , c là các số hữu tỉ, tính giá trị của S  2a b c 2 x  3x  2 0
Trả lời:…………………………………….. 1 3
Câu 74. Cho hàm số f x liên tục trên 0;3 và
f x dx  2; f x dx  8.   Giá trị của tích phân 0 0 1 f
  2x 1 dx  ? 1
Trả lời:…………………………………….. 3 5 1
Câu 75. Cho hàm số f (x) liên tục trên  và có
f (x)dx  8  và
f (x)dx  4  . Tính
f ( 4x 1)dx  0 0 1 
Trả lời:……………………………………..
2x  3, khi x  2
Câu 76. Cho hàm số f x  
. Giả sử F x là nguyên hàm của f x trên  và thỏa mãn 3
4x 1, khi x  2 
F 0  3 . Giá trị F 3  5F 5 bằng
Trả lời:…………………………………….. xe m khi x  0 
Câu 77. Cho hàm số f (x)  
(với m là tham số). Biết hàm số f (x) liên tục trên  và x  x  3 2 3 1 khi x  0  1 b b
f (x)dx a e   với *
a, b, c   ;
tối giản (e  2, 718281828) . Biểu thức a b c m bằng 1 c c
Trả lời:…………………………………….. x 2  ee 1 khi x  0
f ln x   1 a
Câu 78. Cho hàm số y f x   . Tích phân I  dx   ce
biết a, b, c   2
x  2x  2 khi x  0  x b 1 e a và
tối giản. Tính a b c ? b
Trả lời:…………………………………….. 2 3  x ln   x   1 khi x  0 e f ln x
Câu 79. Cho hàm số f x   . Biết
dx a 3  b ln 2  c  với a, ,
b c   . Giá trị 2
2x x  3 1 khi x  0 x  1 e
của a b  6c bằng
Trả lời:…………………………………….. 9
Câu 80. Cho hàm số f x liên tục trên  . Gọi F x, G x, H x là ba nguyên hàm của f x trên  thỏa 1
mãn F 3  G 3  H  
3  4 và F 0  G 0  H 0  1. Tính 3. f 3x dx  0
Trả lời:…………………………………….. 5 3 x a a
Câu 81. Cho biết I dx   c ln d  với a, , b c, d    ,
tối giản, d  9. Tính giá trị của 2 b b 1 x 1 1
T a b c d .
Trả lời:…………………………………….. 12 dx 1 b b
Câu 82. Cho I   ln 
với a, b, c là các số nguyên dương và
là phân số tối giản. Tính x x  4 a c c 5
Trả lời:……………………………………..  2 4
 sin x  7 cos xb b
Câu 83. Biết rằng I dx   2 ln  với *
a  0; b, c   ;
tối giản. Hãy tính giá trị biểu thức
2sin x  3cos x a c c 0
P a b  . c
Trả lời:…………………………………….. 9 f x 2
Câu 84. Cho hàm số f x liên tục trên  và dx  4,
f sin xcos d x x  2  
. Giá trị của tích phân x 1 0 3 I
f xdx  bằng bao nhiêu ? 0
Trả lời:…………………………………….. 2017 2017
Câu 85. Cho f x liên tục trên  thỏa mãn f x  f 2020  x và
f xdx  4.  Khi đó
xf xdx  bằng 3 3 bao nhiêu
Trả lời:……………………………………..
Câu 86. Cho hàm số f x có đạo hàm và xác định trên  . 1 4 1 3 x 1 Biết f   1  2 và 2
x f  x dx
f 2  x dx  4   . Giá trị của 7
f x dx  bằng 0 1   2 x 0
Trả lời:…………………………………….. 3
Câu 87. Cho hàm số y f (x) liên tục trên  và thỏa mãn 2 3
4xf (x )  6 f (2x) 
x  4. Giá trị tích 5 4 f (x)dx  bằng bao nhiêu ? 0
Trả lời:…………………………………….. 1 2
Câu 88. Cho f x liên tục trên  và thỏa mãn f 2  16, f 2x dx  2 
. Tích phân xf  xdx  bằng bao nhiêu 0 0
Trả lời:……………………………………..  2 2 e f ln x
Câu 89. Cho hàm số f x liên tục trên  , thỏa mãn tan . x f   2 4
cos xd x  2 và d x  2  . Giá trị 0 e x ln x 2 f  2x tích phân d x 1  bằng bao nhiêu ? x 4
Trả lời:…………………………………….. m
Câu 90. Có bao nhiêu giá trị thực của tham số m thỏa mãn: 2
3x  2x dx m 10  ? 0
Trả lời:…………………………………….. 10   
Câu 91. Cho F x là nguyên hàm của hàm số f x 2
 sin x trên  thỏa mãn F  0  
. Tính giá trị của biểu  4    
thức S F  
   2F   (Kết quả làm tròn đến hai chữ số thập phân sau dấu phẩy)  2 
Trả lời:…………………………………….. dx a c a c
Câu 92. Biết nguyên hàm I   bằng
ln 2sin x  cos x x C với ( ,
là các phân số tối giản 2 tan x  1 b b b b và *
a  ,c  ,b   ). Tính a b c .
Trả lời:…………………………………….. 1   
Câu 93. Cho F x là một nguyên hàm của hàm số f x  . Biết F
k  k với mọi k   . Tính 2   cos x  4 
F 0  F    F  
   ...  F 10  .
Trả lời:……………………………………..
Câu 94. Cho hàm số y f x với 1  x  4 có đồ thị các đoạn thẳng như hình bên. 4 Tích phân I
f x dx  bằng bao nhiêu ? 1 
Trả lời:……………………………………..  2x a khi x  1 2
Câu 95. Cho hàm số f (x)   thoả mãn
f (x) dx  13    bằng 2 
. Giá trị biểu thức T a b ab 3x b khi x  1  0 bao nhiêu ?
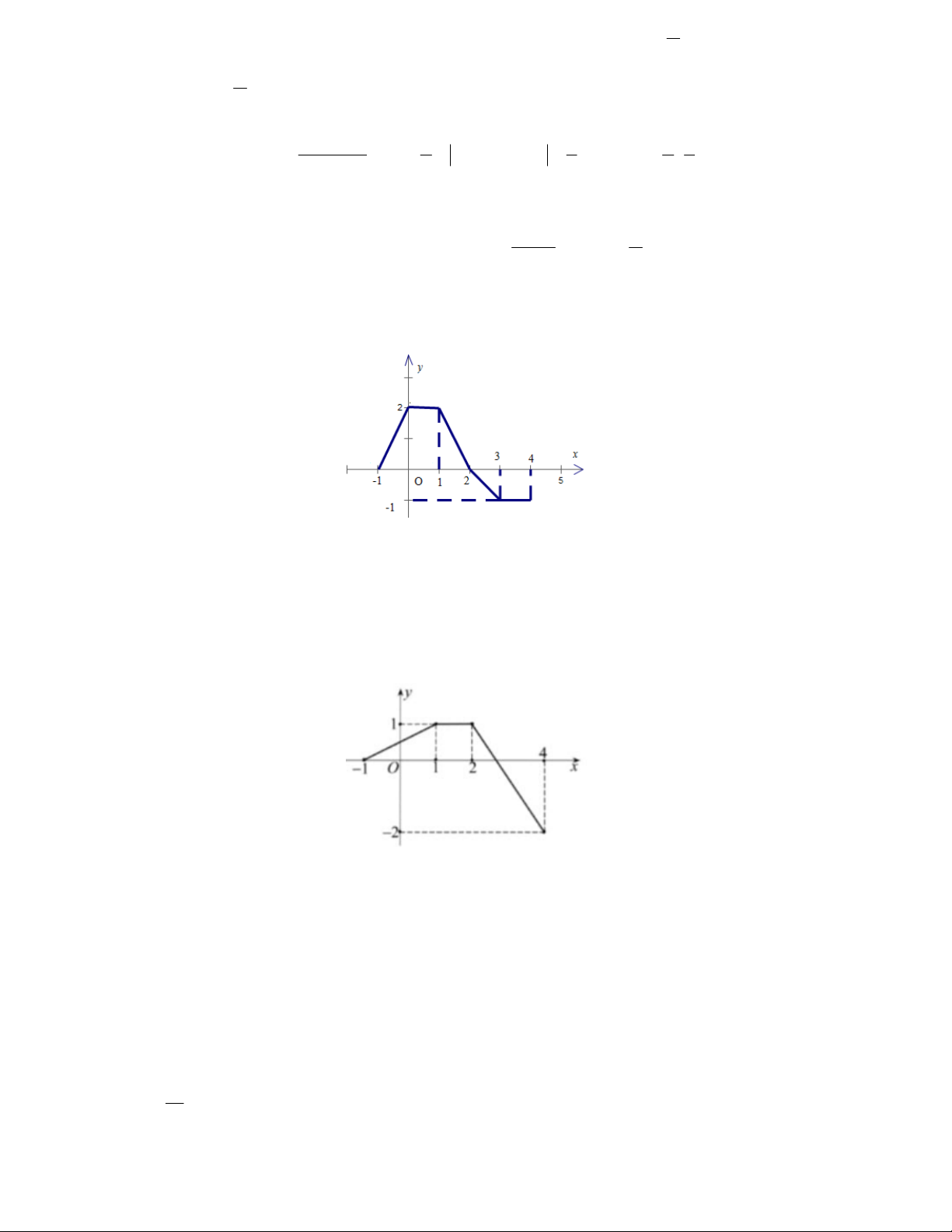
Câu 96. Cho hàm số y f ( x) có đồ thị là đường gấp khúc như hình vẽ bên dưới. 4
Giá trị của tích phân I
2 f x  3 dx    bằng bao nhiêu ? 1 
Trả lời:……………………………………..
Câu 97. Cho hàm số y f x có đạo hàm trên  thỏa mãn f  
1  1và f x  xf  2 x  3 2
 5x  2x 1 với mọi 2
x   . Tính I xf ' xdx  . 1
Trả lời:…………………………………….. 2 2
Câu 98. Cho hàm số f x có đạo hàm liên tục trên đoạn 0; 2 thỏa mãn f 2  6 ,  f  x dx  7    và 0 2 17 2 .
x f x dx   . Tích phân
f x dx  bằng 2 0 0
Trả lời:…………………………………….. 11 2 1
Câu 99. Cho hàm số f x liên tục trên  và f 2  16, f x dx  4  . Tính I  .
x f 2x dx  . 0 0
Trả lời:…………………………………….. 1
Câu 100. Cho hàm số f x có đạo hàm liên tục trên  và thỏa mãn f xdx  10  , f   1  cot1. Tính tích phân 0 1
I   f x 2
tan x f  x tan x d  x    . 0
Trả lời:…………………………………….. 1
Câu 101. Cho hàm số f (x) có đạo hàm liên tục trên  . Biết f (5)  1 và
x f (5x)dx  1  , khi đó tích phân 0 5 2 x f (  x)dx  bằng bao nhiêu 0
Trả lời:……………………………………..
Câu 102. Cho hàm số f x có đạo hàm liên tục trên 0; 2 và thỏa mãn 2 f  
1  0 ,  f  x  f x 2 4
 8x  32x  28 với mọi x thuộc 0; 2 . 1
Giá trị của 3 f x dx  bằng bao nhiêu 0
Trả lời:……………………………………..
Câu 103. Cho hàm số f x liên tục trên  và thỏa mãn f x  xf  2 x  7 3 2
 2x  3x x 1 với x   . Tính 1
tích phân xf  xdx
(kết quả là số thập phân hữu hạn). 0
Trả lời:……………………………………..
Câu 104. Cho hàm số y f (x) có đạo hàm liên tục trên  thỏa mãn 2 .
x f (x). f '(x)  f (x)  x, x    và có 2
f (2)  1. Tích phân 2 f (x)dx
(kết quả là số nguyên) có giá trị bằng 0
Trả lời:…………………………………….. 1
Câu 105. Biết  x   f x 2 1 e dx ae  ,
b a,b   
 .Giá trị của a b bằng 0
Trả lời:……………………………………..
Câu 106. Xét hàm số f x liên tục trên đoạn 0; 
1 và thỏa mãn 2 f x  3 f 1 x  1 x . Tích phân 1 a
f x dx
bằng phân số tối giản
a,b   . Tính 2a  3b . b 0
Trả lời:…………………………………….. 2 f x 3 5 x 1
Câu 107. Cho hàm số f x nhận giá trị dương thỏa mãn f  x 3 
 2x , x  0;  và dx   . x 2 f x 20 2  
Giá trị của biểu thức f 2  f 3 bằng bao nhiêu ?
Trả lời:…………………………………….. 2
Câu 108. Cho hàm số y f (x) x 2 x 1 
liên tục trên  thỏa mãn: 3 f (x)  f (2  x)  2(x 1)e  4, x    . Tính 2
giá trị của tích phân I f (x)dx  . 0
Trả lời:……………………………………..
Câu 109. Cho hàm số y f x liên tục trên  \ 0;   1 thỏa mãn điều kiện f  
1  2 ln 2 và x x   f  x  f x 2 1 .
x  3x  2 .
Giá trị f 2  a b ln 3, với a, b   . Tính 2 2 a b .
Trả lời:……………………………………..
______________________________ 12
NGUYÊN HÀM VÀ TÍCH PHÂN THPT
ỨNG DỤNG TÍNH DIỆN TÍCH HÌNH PHẲNG, THỂ TÍCH VẬT THỂ CỦA TÍCH PHÂN
LỚP BÀI TOÁN TRẮC NGHIỆM TRẢ LỜI NGẮN
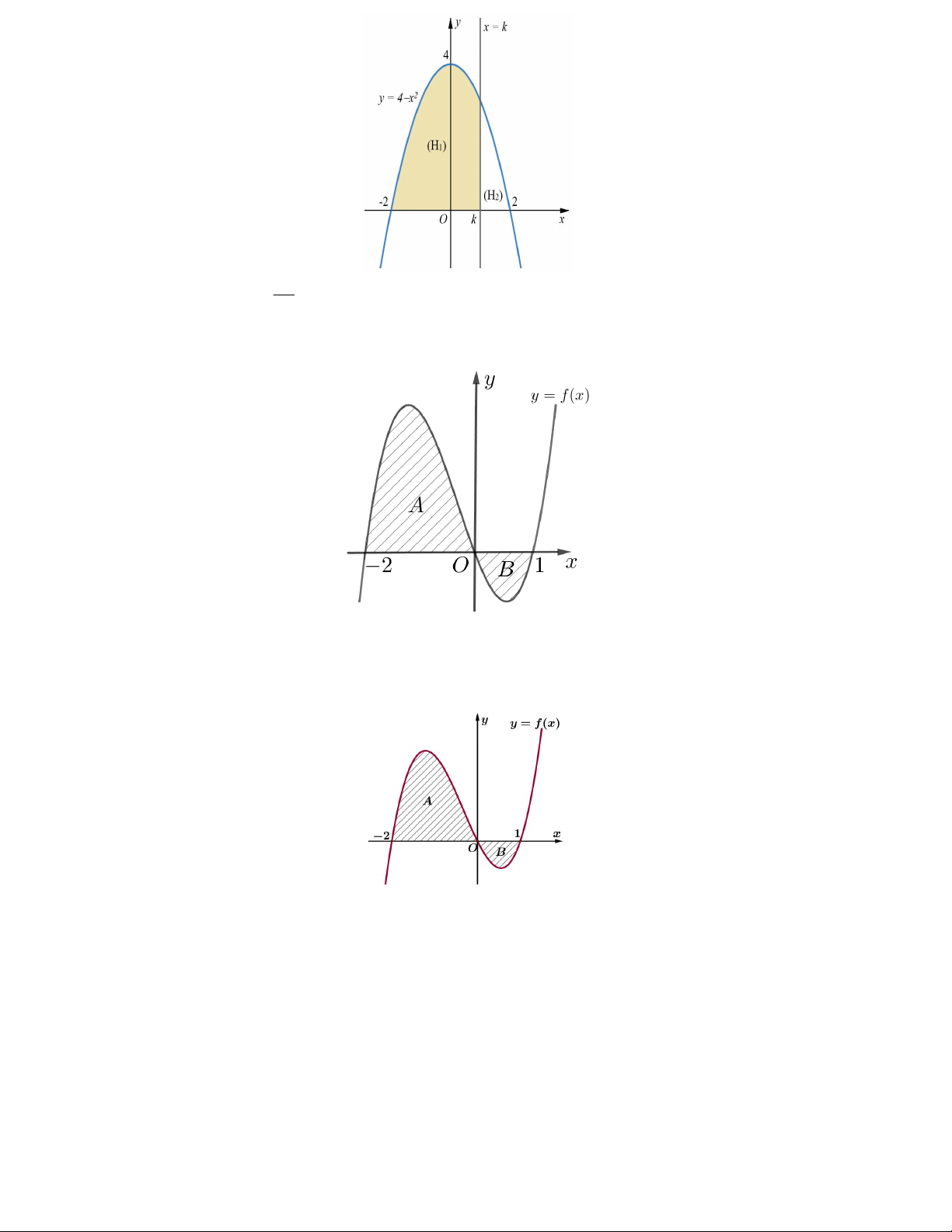
_________________________________ 5
Câu 1. Khi cắt một vật thể bởi mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (1  x  ), mặt cắt là 2 1
tam giác vuông cân và độ dài một cạnh góc vuông là 2 4 
x . Tính thể tích vật thể trên (làm tròn kết quả đến 2 hàng phần trăm).
Trả lời:………………………………….
Câu 2. Cắt một vật thể bởi hai mặt phẳng vuông góc với trục Ox tại x  1 và x  3. Một mặt phẳng tùy ý vuông
góc với trục Ox tại điểm có hoành độ x (1  x  3 ) cắt vật thể đó theo thiết diện là một hình chữ nhật có độ dài hai cạnh là 3x và 2
3x  2 . Tính thể tích của phần vật thể giới hạn bởi hai mặt phẳng trên.
Trả lời:………………………………….
Câu 3. Tính thể tích của vật thể nằm giữa hai mặt phẳng x  1 và x  4 , biết rằng mặt phẳng vuông góc với trục
Ox tại điểm có hoành độ x 1  x  4 cắt vật thể theo thiết diện là một hình lục giác đều cạnh bằng 2x (làm
tròn kết quả đến hàng đơn vị).
Câu 4. Cho vật thể (như hình vẽ) có đáy là một đường tròn có bán kính bằng 2 . Khi cắt vật thể bằng mặt phẳng
vuông góc với trục Ox tại điểm có hoành độ x 2  x  2 thì được thiết diện là một tam giác đều. Tính thể tích
V của vật thể đó (làm tròn kết quả đến hàng phần chục).
Trả lời:………………………………….
Câu 5. Một vật thể trong không gian được giới hạn bởi hai mặt phẳng x  1, x  2 . Một mặt phẳng tùy ý vuông
góc với trục Ox tại điểm có hoành độ x 1  x  2 cắt vật thể theo thiết diện là một hình tam giác đều có cạnh
bằng 3 x . Tính thể tích V của vật thể đó (kết quả làm tròn đến hàng phần chục).
Trả lời:………………………………….
Câu 6. Tính thể tích V của phần vật thể giới hạn bởi hai mặt phẳng x  1 và x  3, biết rằng khi cắt vật thể bởi
mặt phẳng tùy ý vuông góc với trục Ox tại điểm có hoành độ x (1  x  3) thì được thiết diện là một hình chữ
nhật có hai cạnh là 3x và 2 x
Trả lời:………………………………….
Câu 7. Cắt một vật thể trong hệ trục toạ độ Oxyz , giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại
x  1, x  4 , Một mặt phẳng cắt vật thể theo mặt phẳng vuông góc với Ox tại x 1  x  4 được thiết diện là
một hình thoi có hai đường chéo lần lượt là x và 2
3x 1. Tính thể tích của phần vật thể giới hạn bởi hai mặt
phẳng trên (làm tròn kết quả đến hàng phần trăm).
Trả lời:………………………………….
Câu 8. Một vật thể nằm trong hệ trục toạ độ Oxyz , giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại
x  0, x  2 , Một mặt phẳng cắt vật thể theo mặt phẳng vuông góc với Ox tại x 0  x  2 được thiết diện là
một hình tròn có bán kính là R
2  x . Tính thể tích của phần vật thể giới hạn bởi hai mặt phẳng trên (làm
tròn kết quả đến hàng phần trăm).
Trả lời:………………………………….
Câu 9. Một vật thể trong hệ trục toạ độ Oxyz , giới hạn bởi hai mặt phẳng vuông góc với trục Ox tại x  0, x  2 ,
cắt vật thể theo mặt phẳng vuông góc với Ox tại x
được một hình tam giác đều có cạnh bằng 2
4  x ,0  x  2 . Tính thể tích vật thể đã cho (làm tròn kết quả đến hàng phần trăm). 13
Câu 10. Cho phần vật thể giới hạn bởi hai mặt phẳng x  1 và x  7 , biết rằng khi cắt vật thể bởi mặt phẳng
vuông góc với trục Ox tại điểm có hoành độ x (1  x  7 ) thì được thiết diện là một hình chữ nhật có độ dài a b hai cạnh là 2x và 2
x 1 . Thể tích của phần vật thể đã cho bằng
(c là số nguyên tố, b  6; a, b, c ) . c Tính . a . b c ?
Trả lời:………………………………….
Câu 11. Thể tích khối tròn xoay do hình phẳng giới hạn bởi các đường x y  2  0 ; y  2 x 1; y  0 quay aa
quanh trục Ox bằng
(a, b ,
tối giản). Tính a b bằng bao nhiêu? b b
Trả lời:………………………………….
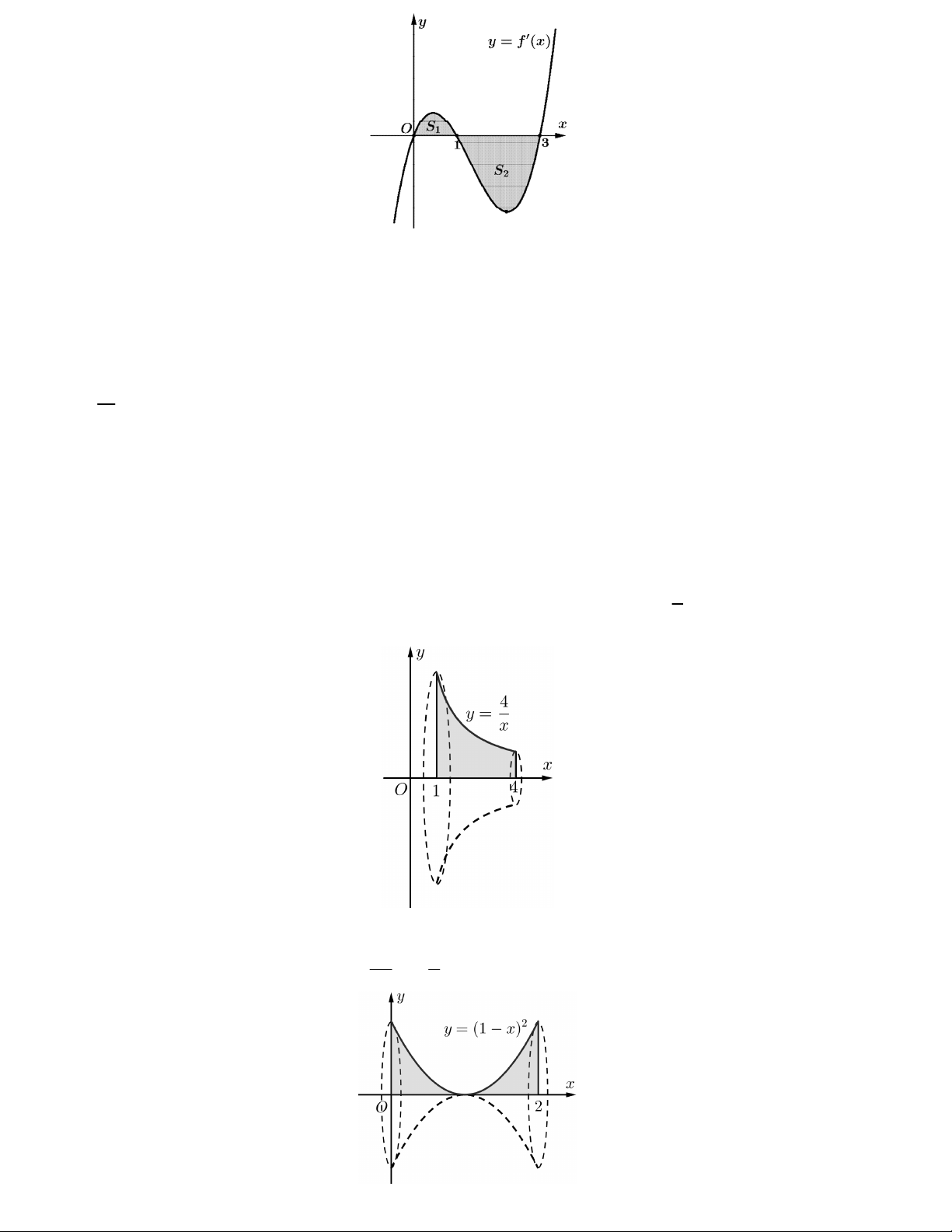
Câu 12. Một vật thể hình khối như hình vẽ. Các tứ giác ABCD, CDPQ là các hình vuông cạnh 2, 5cm . Tứ giác
ABEF là hình chữ nhật cạnh AF  3, 5cm . Mặt PQFE được mài nhẵn theo đường parabol  P có đinh nằm
trên cạnh EF . Tính thể tích của vật thể trên (đơn vị: 3
cm ) (làm tròn kết quả đến hàng phần chục).
Trả lời:………………………………….
Câu 13. Cho hình phẳng  H  được giới hạn bởi đường cong 2 2 y
m x ( m là tham số khác 0 ) và trục
hoành. Khi  H  quay xung quanh trục hoành được khối tròn xoay có thể tích V . Có bao nhiêu giá trị nguyên
của m để V  1000 .
Trả lời:…………………………………. 2 x  2x
Câu 14. Tìm a để diện tích S của hình phẳng giới hạn bởi  P : y
, đường thẳng d : y x 1 và x 1
x a, x  2a (a  1) bằng ln 3 ?
Trả lời:…………………………………. 2 x  2x  3
Câu 15. Diện tích hình phẳng giới hạn bởi hai đồ thị hàm số y
; y x và hai đường thẳng x  1
x  2; x  3 bằng S a ln 2  b . Giá trị của a b bằng bao nhiêu?
Trả lời:………………………………….
Câu 16. Cho hàm số y f x . Đồ thị hàm số y f  x là đường cong trong hình dưới. Biết rằng diện tích của
các phần hình phẳng A và B lần lượt là S  4 và S  10 . Tính giá trị của f 3 , biết giá trị của f 0  2 . A B 14
Trả lời:…………………………………. 3 7  4x khi 0  x  1
Câu 17. Cho hàm số f x  
. Tính diện tích hình phẳng giới hạn bởi đồ thị hàm số 2 4  x khi x  1 
f x và các đường thẳng x  0, x  3, y  0 .
Trả lời:………………………………….
Câu 18. Cho  H  là hình phẳng được tô đậm trong hình vẽ và được giới hạn bởi các đường có phương trình 10 x khi x  1 2 y
x x , y  
. Diện tích của  H  bằng bao nhiêu? 3
x  2 khi x  1 
Trả lời:…………………………………. Câu 19. Biết
F x và G x là hai nguyên hàm của hàm số
f x trên  và 5
f x dx F 5  G 0  a, a  0 
. Gọi S là diện tích hình phẳng giới hạn bỡi các đường y F x , 0
y G x , x  0 và x  5 . Khi S  20 thì a bằng?
Trả lời:…………………………………. 4
Câu 20. Thể tích vật thể tròn xoay khi quay hình phẳng giới hạn bởi các đường y
, y  0, x  1, x  4 quanh x
trục Ox là bao nhiêu?
Trả lời:………………………………….
Câu 21. Biết thể tích khối tròn xoay tạo nên khi quay xung quanh trục Ox hình phẳng giới hạn bởi các đường aa
y    x2 1
, y  0 , x  0 , x  2 có dạng với
là phân số tối giản. Tính giá trị biểu thức S  24a  12b . b b 15
Trả lời:………………………………….
Câu 22. Cho hình phẳng giới hạn bởi các đường y x ln x, y  0, x e quay xung quanh trục Ox tạo thành 
khối tròn xoay có thể tích bằng  3
be  2 với a, b   . Tính 2 2
P a b , biết một nguyên hàm của hàm số a 3 x
f x   x x2 ln
là F x   2
9ln x  6ln x  2 . 27
Trả lời:………………………………….
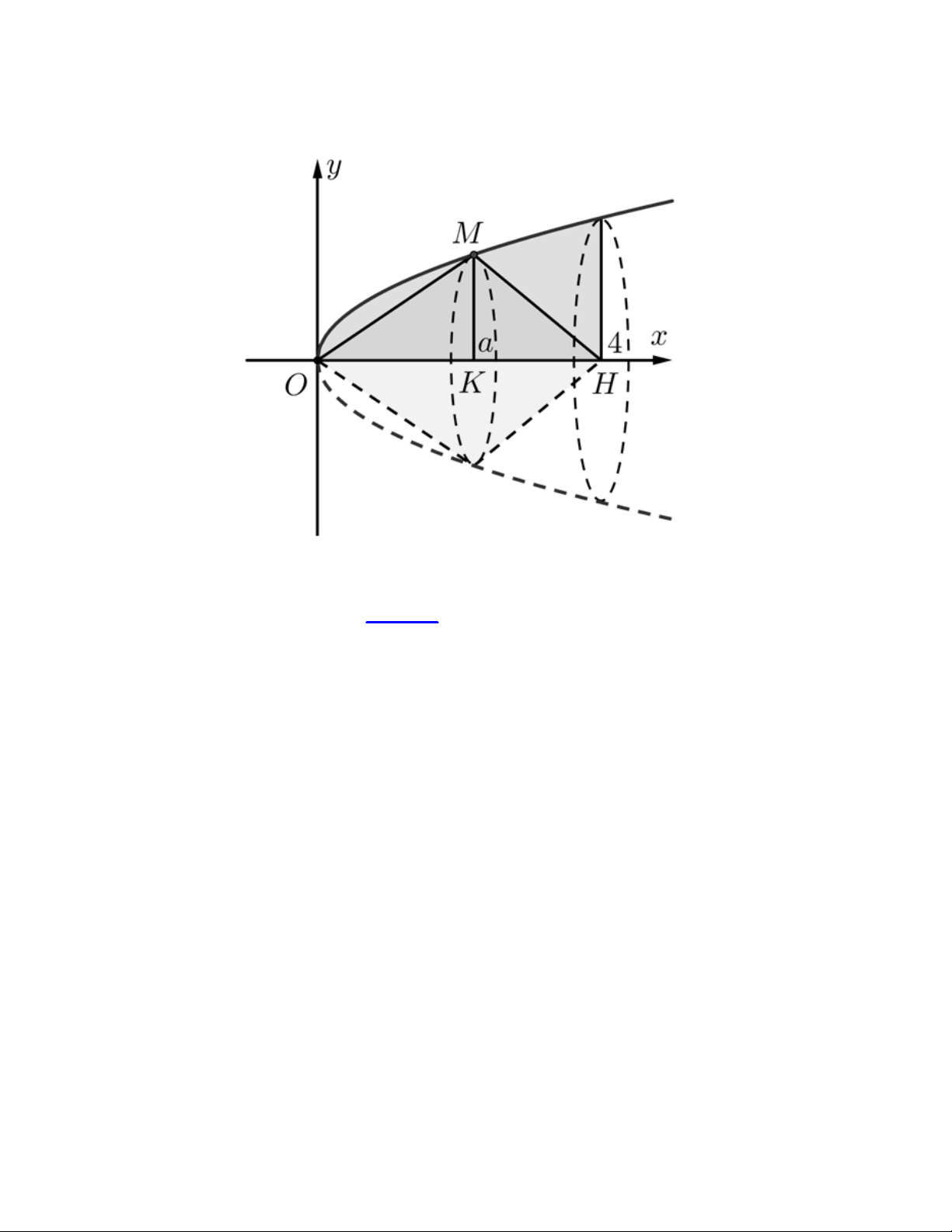
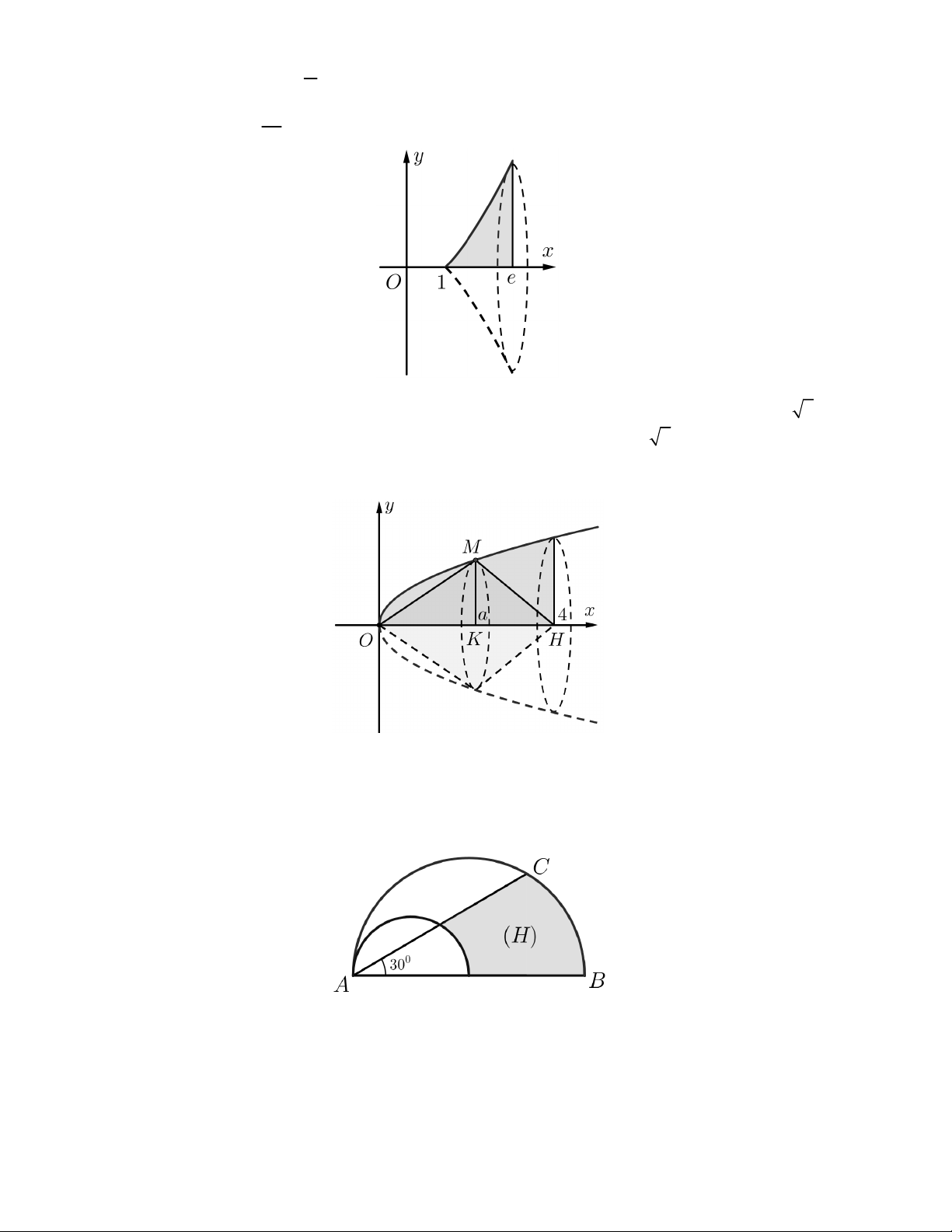
Câu 23. Gọi V là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường y x, y  0
và x  4 quanh trục Ox . Đường thẳng x a 0  a  4 cắt đồ thị hàm số y x tại M (xem hình vẽ sau).
Gọi V là thể tích khối tròn xoay tạo thành khi quay tam giác OMH quanh trục Ox . Biết rằng V  2V . Khi đó 1 1
tổng các giá trị của a là bao nhiêu?
Trả lời:………………………………….
Câu 24. Cho các nửa đường tròn như hình vẽ sau, trong đó đường kính của nửa đường tròn lớn gấp đôi đường 
kính của nửa đường tròn nhỏ. Biết rằng nửa hình tròn đường kính AB có diện tích là 32 và góc BAC  30 .
Tính thể tích vật thể tròn xoay (làm tròn đến số nguyên) được tạo thành khi quay hình phẳng  H  (phần tô
đậm) xung quanh đường thẳng AB .
Câu 25. Gọi S là diện tích hình phẳng giới hạn bởi các đường 2 2
my x , mx y m  0 . Tìm tổng các giá trị
của m để S  3.
Trả lời:………………………………….
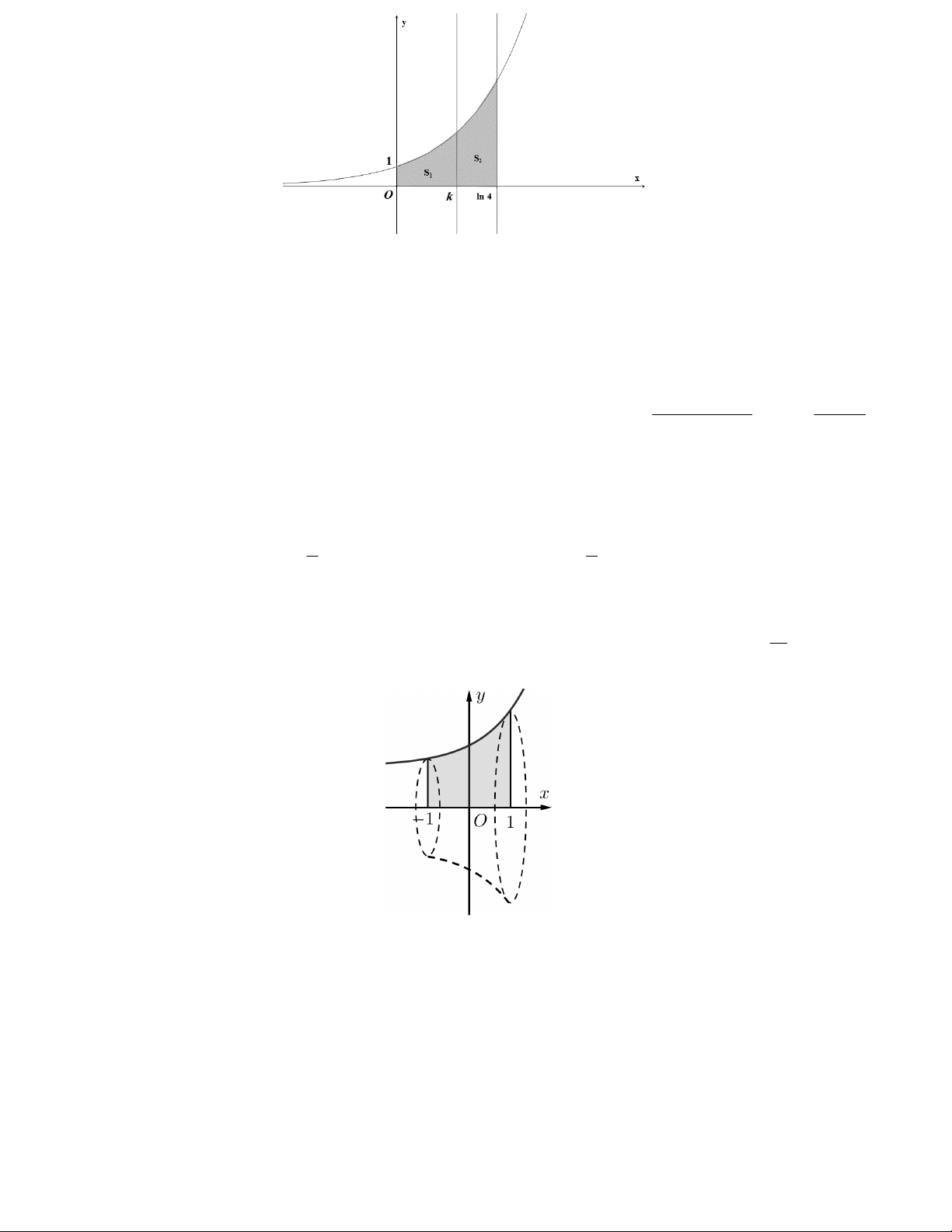
Câu 26. Cho hình thang cong  H  giới hạn bởi các đường ex y
, y  0 , x  0 , x  ln 4 . Đường thẳng x k
0  k  ln 4 chia H  thành hai phần có diện tích là S và S như hình vẽ bên. Khi S  2S thì giá trị 1 2 1 2 k e bằng bao nhiêu 16
Câu 27. Cho parabol  P 2
: y x và hai điểm ,
A B thuộc  P sao cho AB  2 . Khi hình phẳng giới hạn bởi
P và đường thẳng AB đạt giá trị lớn nhất thì 2 2
OA OB bằng bao nhiêu
Trả lời:………………………………….
Câu 28. Cho Parabol  P 2
: y x 1 và đường thẳng d : y mx  2 với m là tham số. Gọi m là giá trị của m 0
để diện tích hình phẳng giới hạn bởi  P và d là nhỏ nhất. Hỏi tổng các giá trị m bằng bao nhiêu 0
Trả lời:…………………………………. 2 2
x  2ax  3a 2 a ax
Câu 29. Tìm tổng các số thực a để hình phẳng giới hạn bởi hai đồ thị hàm y  và y  6 1 a 6 1 a
có diện tích lớn nhất.
Trả lời:…………………………………. Câu 30. Cho hàm số 4 2
y x  6x m có đồ thị C . Giả sử C cắt trục hoành tại bốn điểm phân biệt sao m m
cho hình phẳng giới hạn bởi C
và trục hoành có phần phía trên trục hoành và phần phía dưới trục hoành có m a a
diện tích bằng nhau. Khi đó m
(với a , b là các số nguyên, b  0 ,
là phân số tối giản). Giá trị của biểu b b
thức S a b là:
Trả lời:…………………………………. x e
Câu 31. Tính thể tích khối tròn xoay khi quay hình phẳng  H  giới hạn bởi các đường y  , y  0 và 2 x  1
 , x  1 quanh trục hoành.
Trả lời:………………………………….
Câu 32. Cho parabol  P  2
: y  x  2x  3 cắt trục hoành tại hai điểm ,
A B và đường thẳng d : y a 1
0  a  4 . Xét parabol P đi qua , A B
 . Gọi S là diện tích hình phẳng 2 
và có đỉnh thuộc đường thẳng y a 1
giới hạn bởi  P và d .Gọi S là diện tích hình phẳng giới hạn bởi  P và trục hoành. Biết S S , tính giá trị 2  1  2 1 2 biểu thức 3 2
T a  8a  48a .
Trả lời:………………………………….
Câu 33. Trong mặt phẳng Oxy cho là hình phẳng  H  giới hạn bởi parabol 2
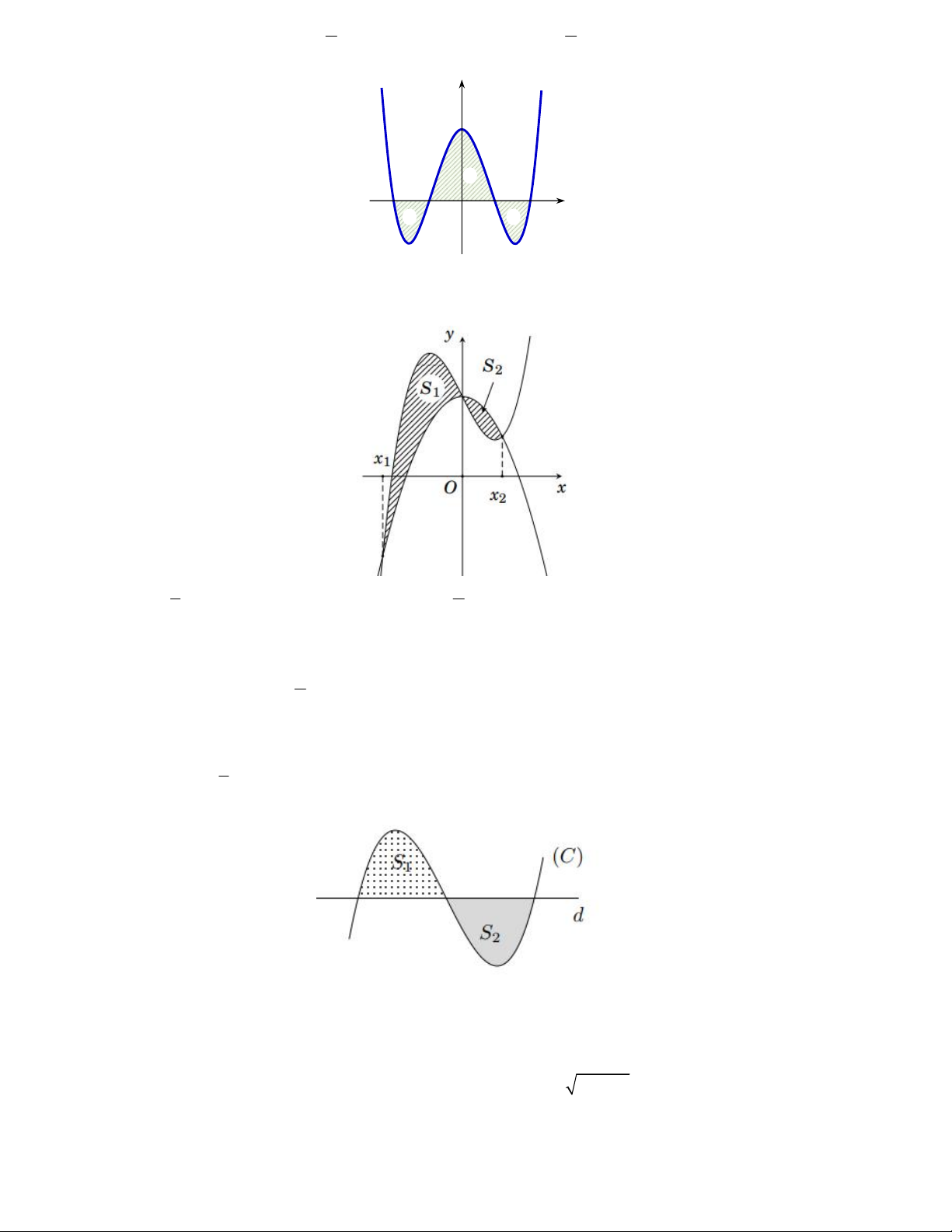
y  4  x và trục hoành. Đường
thẳng x k, 2  k  2 chia  H  thành hai phần  H , H như hình vẽ. 1   2  17 20
Biết rằng diện tích  H gấp
lần diện tích  H
, tính giá trị biểu thức 2
9k  6k 10 . 2  1  7
Trả lời:………………………………….
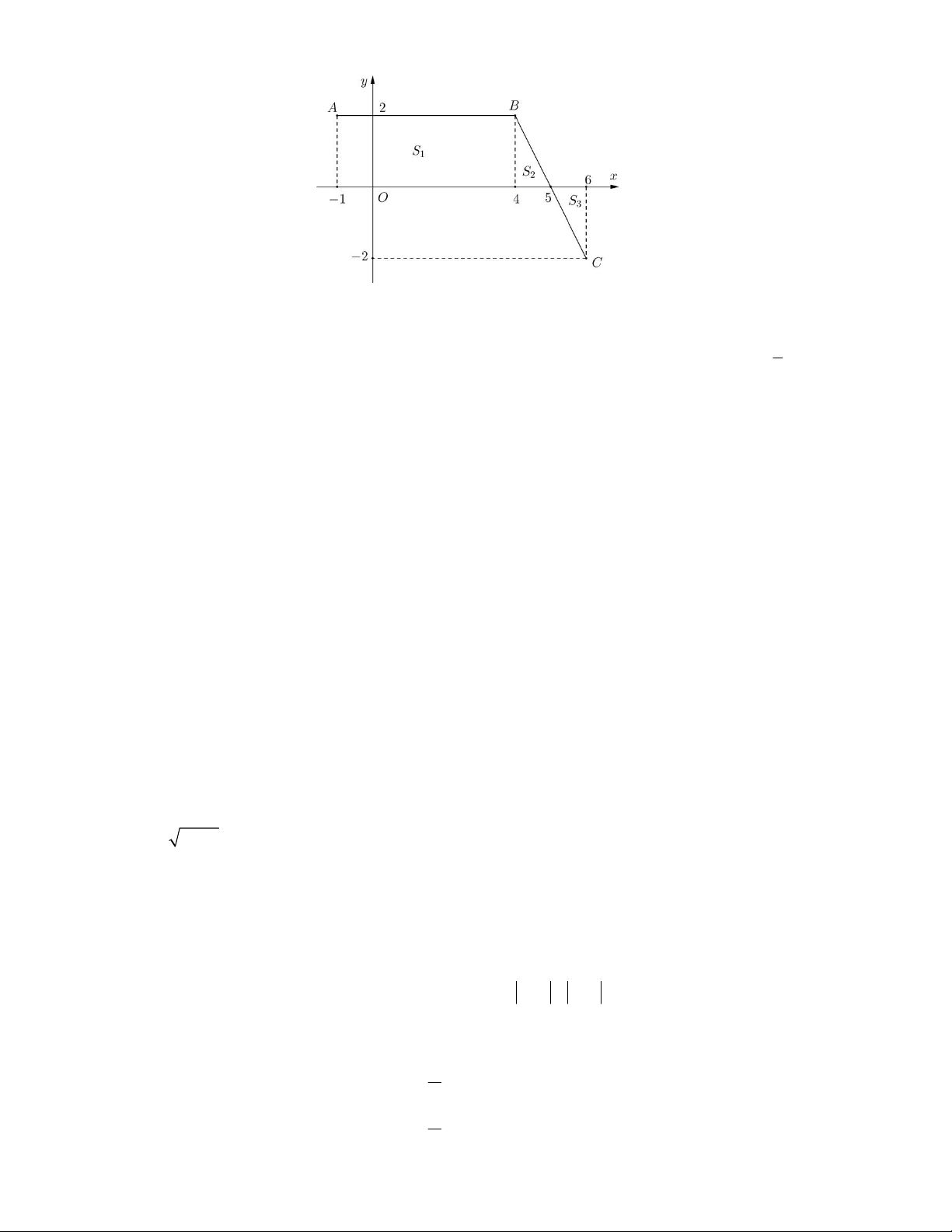
Câu 34. Cho hàm số y f x có đồ thị như hình vẽ và diện tích hai phần ,
A B lần lượt bằng 11 và 2. 0 Giá trị của I f 3x   1 dx  bằng 1 
Trả lời:………………………………….
Câu 35. Cho hàm số y f x có đồ thị như hình vẽ và diện tích hai phần ,
A B lần lượt bằng 11 và 2 . 0 Giá trị của I f 3x   1 dx  bằng bao nhiêu 1
Trả lời:………………………………….
Câu 36. Biết F x; Gx là hai nguyên hàm của hàm số f x trên  và 4
f xdx F 4 G0  a a  0  . 0
Gọi S là diện tích hình phẳng giới hạn bởi các đường y F x; y Gx; x  0; x  4. Khi S  8 thì a bằng
Trả lời:………………………………….
Câu 37. Cho hàm số 4 2
y x  4x m . Tìm m để đồ thị hàm số cắt trục Ox tại bốn điểm phân biệt sao cho
hình phẳng giới hạn bởi đồ thị hàm số và Ox có phần phía trên trục hoành là S , phần dưới trục hoành x là S 1 2 18 a a
và S thỏa S S S . Khi đó m
( a, b là các số nguyên, b  0 ,
tối giản). Giá trị của biểu thức S a b 3 1 2 3 b b là y S3 O x S S 1 2
Trả lời:………………………………….
Câu 38. Cho đường cong 3
(C) : y x kx  2 và parabol 2
P : y  x  2 tạo thành hai miền phẳng có diện tích
S , S như hình vẽ bên. 1 2 8 a Biết rằng S
, giá trị của S bằng phân số tối giản
a,b   . Tính 2a  3b . 1 3 2 b
Trả lời:………………………………….
Câu 39. Diện tích hình phẳng giới hạn bởi parabol 2
y x  2x 1 và đường thẳng y  (m 1)x  5 có giá trị a
nhỏ nhất bằng phân số tối giản
a,b   . Tính 2a  3b . b
Trả lời:………………………………….
Câu 40. Gọi X là tập hợp tất cả các giá trị của tham số m để đường thẳng d : y  45m  2 cùng với đồ thị 1 (C) của hàm số 3 2 y
x  2mx x 1 tạo thành hai miền kín có diện tích lần lượt là S , S thỏa mãn S S 3 1 2 1 2
(xem hình vẽ). Số phần tử của tập X là
Trả lời:………………………………….
Câu 41. Gọi S là diện tích hình phẳng giới hạn bởi parabol 2
y x  2x 1 và các đường thẳng y m , x  0 ,
x  1 . Có bao nhiêu giá trị nguyên của tham số m  4  040;   3 để S  2021?
Câu 42. Cho hình phẳng (H ) được giới hạn bởi đường cong 2 2
y m x ( m là tham số khác 0 ) và trục
hoành. Khi (H ) quay xung quanh trục hoành được khối tròn xoay có thể tích V . Có bao nhiêu giá trị nguyên
của m để V  1000 .
Trả lời:…………………………………. 19
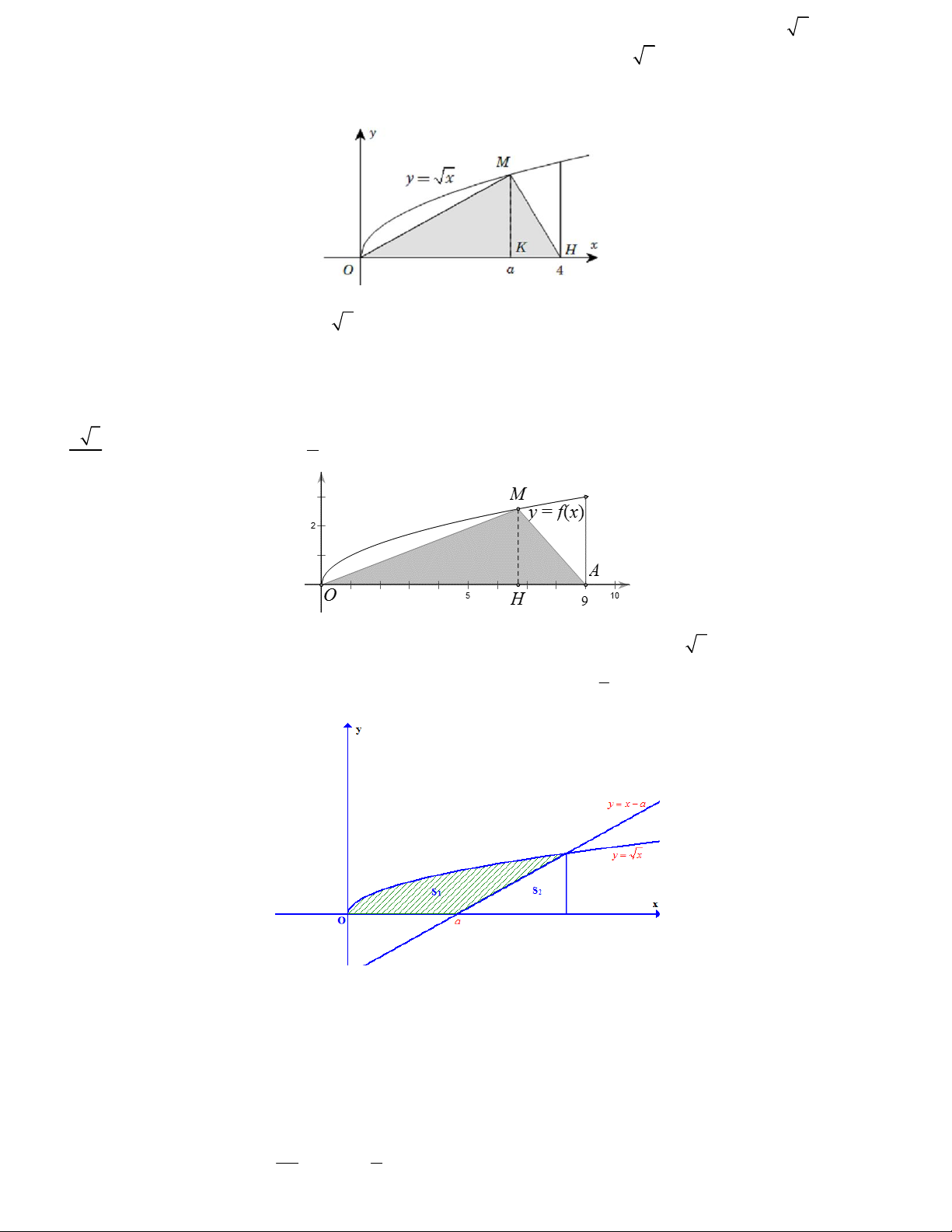
Câu 43. Gọi V là thể tích khối tròn xoay tạo thành khi quay hình phẳng giới hạn bởi các đường y x , y  0
và x  4 quanh trục Ox . Đường thẳng x a 0  a  4 cắt đồ thị hàm số y x tại M (hình vẽ). Gọi V là 1
thể tích khối tròn xoay tạo thành khi quay tam giác OMH quanh trục Ox . Biết rằng V  2V . Khi đó tổng các giá 1
trị a thu được bằng bao nhiêu
Trả lời:………………………………….
Câu 44. Cho đồ thị C  : y f x  x . Gọi  H  là hình phẳng giới hạn bởi đồ thị C  , đường thẳng x  9
và trục Ox . Cho điểm M thuộc đồ thị C  và điểm A9;0 . Gọi V là thể tích khối tròn xoay khi cho  H  quay 1
quanh trục Ox , V là thể tích khối tròn xoay khi cho tam giác AOM quay quanh trục Ox . Biết rằng V  2V . 2 1 2
Tính diện tích S phần hình phẳng giới hạn bởi đồ thị C  và đường thẳng OM thu được kết quả a 3 a
a,b   trong đó phân số tối giản. Tính 2a  3b . b b
Trả lời:………………………………….
Câu 45. Cho đường thẳng y x a ( a là tham số thực dương) và đồ thị hàm số y
x . Gọi S , S lần lượt là 1 2 5
diện tích hai hình phẳng được gạch chéo trong hình vẽ bên dưới. Khi S
S thì tổng các giá trị a thu được 1 2 3 bằng bao nhiêu ?
Trả lời:………………………………….
Câu 46. Diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số 3 2
y x  2x  2mx 1(m là tham số) và 3 2
y x x  3 đạt giá trị nhỏ nhất bằng bằng M, M gần nhất số nguyên nào ?
Trả lời:………………………………….
Câu 47. Cho hàm số y f x 3 2
ax bx cx d , a,b, c, d  , a  0 có đồ thị C  . Biết rằng đồ thị C  tiếp
xúc với đường thẳng y  4 tại điểm có hoành độ âm và đồ thị của hàm số y f ' x cho bởi hình vẽ dưới đây.
Tính thể tích vật thể tròn xoay được tạo thành khi quay hình phẳng H giới hạn bởi đồ thị C  và trục hoành khi aa
quay xung quanh trục Ox là (phân số
tối giản). Tính 2a  3b . b b 20

Tài liệu liên quan: