
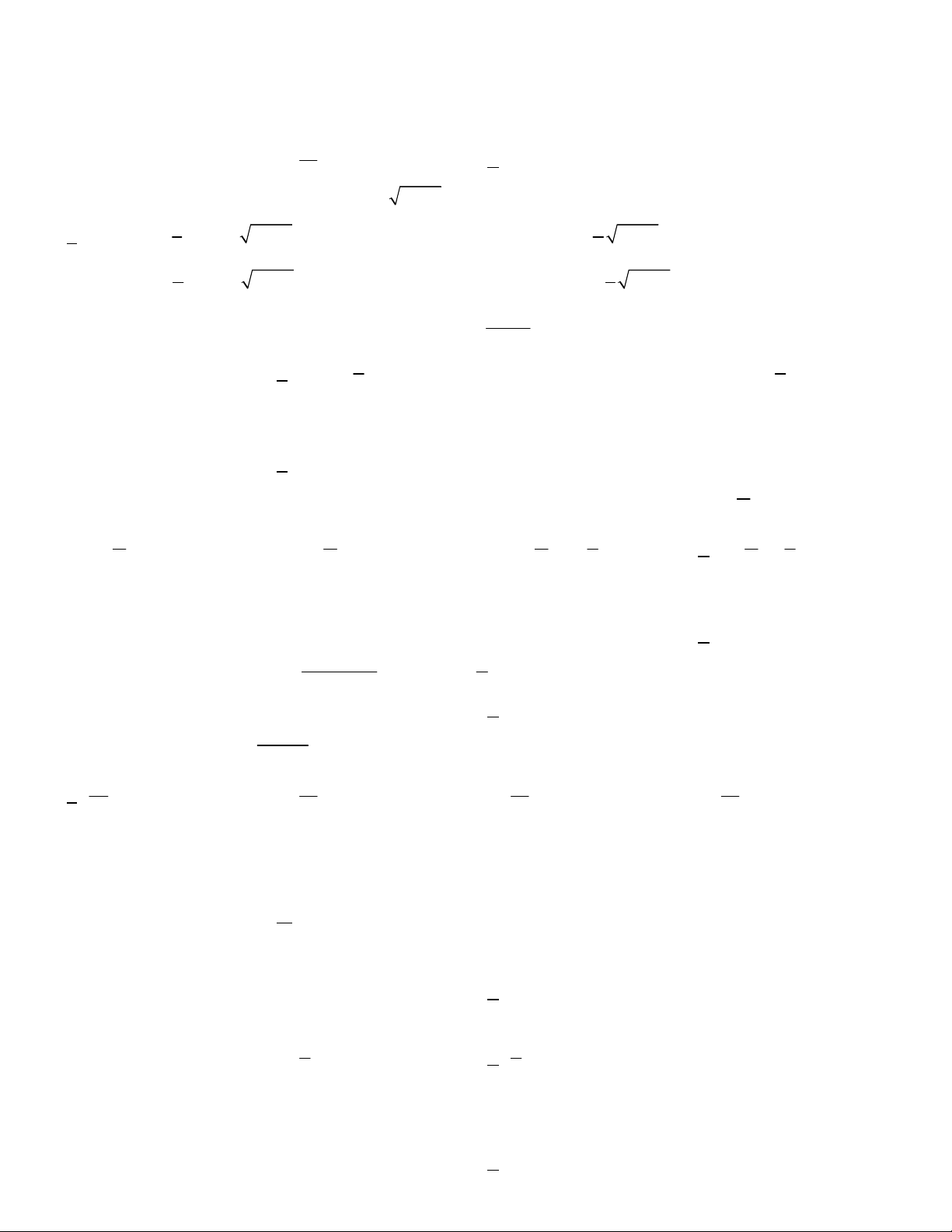


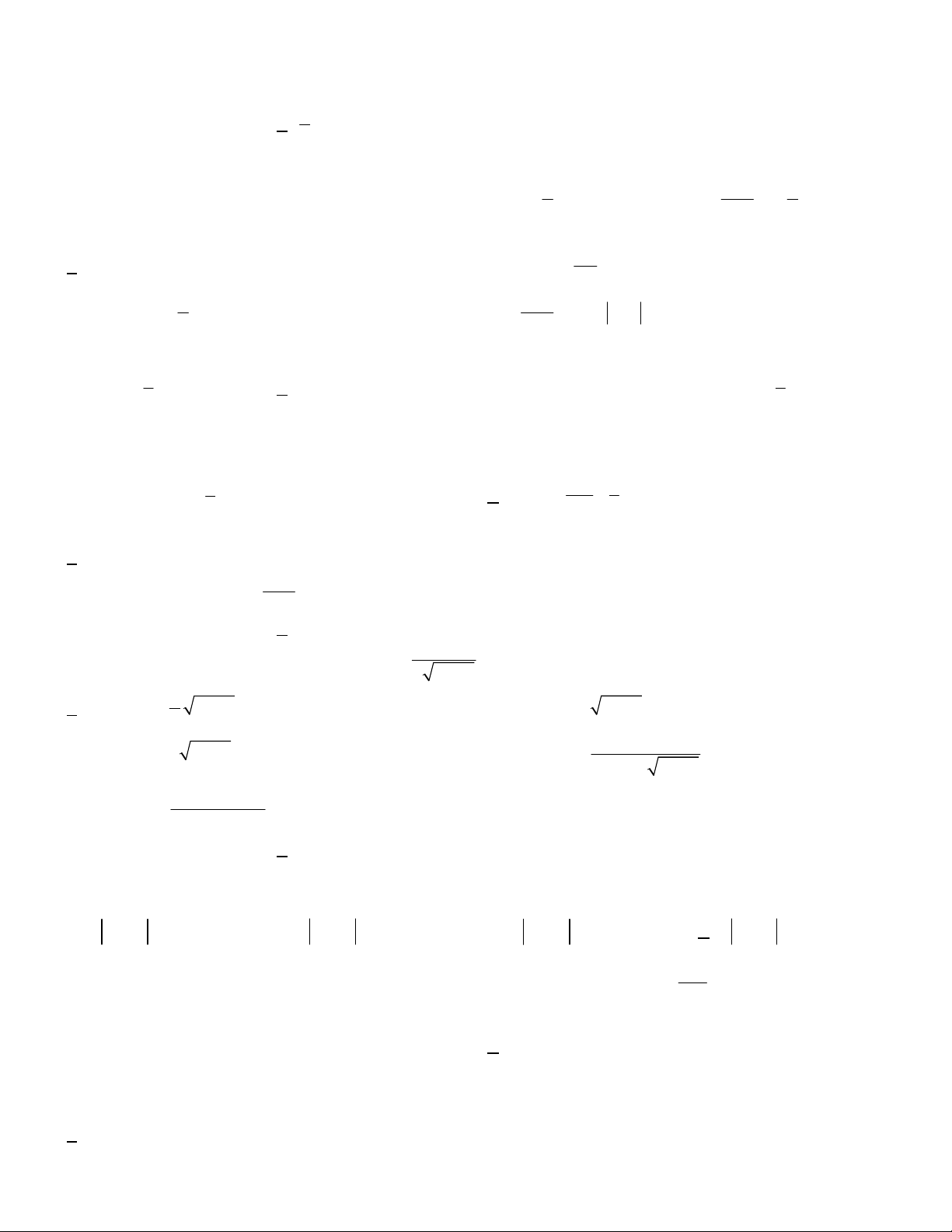




Preview text:
TÀI LIỆU THAM KHẢO TOÁN HỌC PHỔ THÔNG
______________________________________________________________ b f x dx a
------------------------------------------------------------------------------------------
LUYỆN TẬP CHUNG TOÁN 12 THPT
NGUYÊN HÀM, TÍCH PHÂN VÀ ỨNG DỤNG
(KẾT HỢP 3 BỘ SÁCH GIÁO KHOA)
THÂN TẶNG TOÀN THỂ QUÝ THẦY CÔ VÀ CÁC EM HỌC SINH TRÊN TOÀN QUỐC
CREATED BY GIANG SƠN (FACEBOOK)
ĐÁP ÁN CHI TIẾT PDF BẠN ĐỌC VUI LÒNG LIÊN HỆ TÁC GIẢ
GACMA1431988@GMAIL.COM (GMAIL); TEL 0398021920
THÀNH PHỐ THÁI BÌNH – THÁNG 2/2025 1
LUYỆN TẬP CHUNG TOÁN 12 THPT
NGUYÊN HÀM, TÍCH PHÂN VÀ ỨNG DỤNG
__________________________ DUNG NỘI DUNG LƯỢNG 10 FILE LUYỆN TẬP CHUNG 1 file 3 trang
NGUYÊN HÀM, TÍCH PHÂN VÀ ỨNG DỤNG 2
NGUYÊN HÀM VÀ TÍCH PHÂN LỚP 12 THPT
LỚP BÀI TOÁN LUYỆN TẬP CHUNG P1
______________________________________ TRẮC NGHIỆM ABCD
Câu 1. Họ các nguyên hàm của hàm số f x 2 3x 1 là 3 x A. 3 x C . B. x C . C. 3
x x C . D. 6x C . 3
Câu 2. Tìm nguyên hàm của hàm số f x 2x 1 . 1 1 A.
f xdx 2x 1 2x 1 C . B.
f xdx 2x 1 C . 3 2 2 1 C.
f xdx 2x 1 2x 1 C . D.
f xdx 2x 1 C . 3 3 1
Câu 3. Cho F x là một nguyên hàm của hàm số f x
; biết F 2 1. Giá trị F 3 bằng 2x 3 1 1
A. F 3 2ln3 1.
B. F 3 ln3 1.
C. F 3 ln3 1.
D. F 3 ln3 1. 2 2
Câu 4. Với giá trị thực nào của tham số m để hàm số F x 3
mx m 2 3
2 x 4x 3 là một nguyên hàm của
hàm số f x 2
3x 10x 4 ? A. m 0 . B. m 1 . C. m 1. D. m 2 .
Câu 5. Biết F x là một nguyên hàm của hàm số f x 3 sin .
x cos x và F 0 . Tính F . 2 1 1 A. F . B. F . C. F . D. F . 2 2 2 4 2 4 1
Câu 6. Cho I 2
4 x 2m dx . Có bao nhiêu giá trị nguyên của m để I 6 0 ? 0 A. 1. B. 5. C. 2. D. 3. 3 2
x 2x 3 a
Câu 7. Kết quả của tích phân dx có dạng
c ln 2 với a, ,
b c . Tính a b c . x 1 b 2 A.6 B. 5 C. 7 D. 10 2 4 2x 3
Câu 8. Tính tích phân d . x 2 x 1 37 6 19 19 A. . B. . C. . D. . 6 19 3 6 Câu 9. Cho
f ( x ) liên tục trên 1; 2 . Biết F ( x ) là nguyên hàm của f ( x ) trên 1; 2 thoả 2 F 1 2
, F 2 4 . Khi đó f (x)dx bằng 1 A. 2. B 6. C. 2 . D. 6 . 4 4 2 Câu 10. Nếu
f x dx 5 và
f x x d 1 thì
f x dx bằng. 0 2 0 A. 4 . B. 6 . C. 6. D. 4.
Câu 11. Biết F x x 2
e x là một nguyên hàm của hàm số f x trên . Khi đó f 2x dx bằng 1 1 A. x 2
2e 2x C. B. 2 x 2 e x C. C. 2 x 2
e 2x C. D. 2x 2
e 4x C. 2 2
Câu 12. Một ô tô đang chạy với vận tốc 10 m/s thì người lái xe đạp phanh, thời điểm đó ô tô chuyển động chậm
dần đều với vận tốc v t 5t 10 m/s , trong đó t là khoảng thời gian tính băng giây kể từ lúc đạp phanh.
Hỏi từ lúc đạp phanh đến khi dừng hẳn ô tô còn di chuyển được bao nhiêu mét? A. 0, 2m . B. 2m . C. 10m . D. 20m . 3
TRẮC NGHIỆM ĐÚNG, SAI x
Câu 1. Cho hàm số y e có đồ thị C . Các khẳng định sau đúng hay sai?
a) Diện tích hình phẳng giới hạn bởi đồ thị C , O x và 2 đường thẳng x 0, x 1 bằng 1.
b) Diện tích hình phẳng giới hạn bởi đồ thị C , đường thẳng : y 2 x và 2 đường thẳng x 0, x 1 bằng 3.
c) Diện tích hình phẳng giới hạn bởi đồ thị C , đường thẳng d : y x 1, đường thẳng x 2 bằng 4.
d) Cho hình thang cong H giới hạn bởi các đường ex
y , y 0 , x 0 , x ln4. Đường thẳng x k
0 k ln4 chia H thành hai phần có diện tích là S S S 2S 1 và
2 như hình vẽ bên. Khi k ln 3 thì 1 2 .
Câu 2. Khối chỏm cầu có bán kính R 5 và chiều cao h 1 sinh ra khi quay hình phẳng giới hạn bởi cung tròn có phương trình 2
y 25 x , trục hoành và hai đường thẳng x 4 , x 5 xung quanh trục O x .
a) Khoảng cách từ tâm của khối cầu đến khối chỏm cầu bằng 3. 5
b) Thể tích của khối chỏm cầu V 2
1 được tính theo công thức V 25 x dx . 1 4 14
c) Thể tích của khối chỏm cầu V . 1 3 V 7 d) Gọi V
2 là thể tích của nửa khối cầu có bán kính bằng 5. Tỉ số thể tích 1 . V 125 2
Câu 3. Một chất điểm bắt đầu chuyển động thẳng đều với vận tốc v0 , sau 4 giây chuyển động thì gặp chướng 5
ngại vật nên bắt đầu giảm tốc độ với vận tốc chuyển động v(t) t a (m / s), (t 4) cho đến khi dừng hẳn. 2
Quãng đường chất điểm đi được kể từ lúc chuyển động đến khi dừng hẳn là. 80m. Các khẳng định sau đúng hay sai ?
a) Quãng đường chất điểm di chuyển được sau 4(giây) bằng : S 4 4v m . o 5
b) Quãng đường chất điểm di chuyển được sau 5(giây) bằng : S 5 v t dt m 0
c) v 8m / s . o
d) Vận tốc trung bình vtb của chất điểm trong khoảng thời gian từ 3giây đến 7 giây kể từ lúc bắt đầu thỏa mãn
v 8m / s tb Câu 4. Cho hàm số ex y F x
x là một nguyên hàm của hàm số f x . Xét tính đúng sai của các mệnh đề sau? 2 x
a) Hàm số f x ex C . 2 x 1 b) Hàm số y .
x F x có nguyên hàm là H x x 3 1 e x C . 3 1
c) Gọi G x là một nguyên hàm của hàm F x và F 1 G 1
, khi đó F 0 G 0 2. 2
d) Một nguyên hàm của hàm số 2F x f x là R x x 2
e x x 1. 4
TRẮC NGHIỆM TRẢ LỜI NGẮN 1 1 a e b Câu 1. Cho
f x dx 2
. Giá trị của 2 2x
f x e dx bằng
. Khi đó a b c bằng bao nhiêu? c 0 0 3 Câu 2. Cho hàm số 3 2
f (x) ax bx cx thỏa mãn f (1 x) f (1 x) 0 với mọi x và
f (x)dx 9 . Giá trị 0 của f (4) bằng x 2 1
Câu 3. Cho hình phẳng H giới hạn bởi các đồ thị hàm số y 2 ; y
; x ; x 4 . Khi đó, diện tích hình x 2
a b ln 2 c
phẳng H bằng
. Tính a b c ? ln 2 2
Câu 4. Tổng các giá trị của tham số msao cho đường thẳng d : y x m cắt parabol ( )
P : y x 5x4 tại hai 4
điểm phân biệt và diện tích hình phẳng giới hạn bởi d và ( P ) bằng bằng bao nhiêu? 3
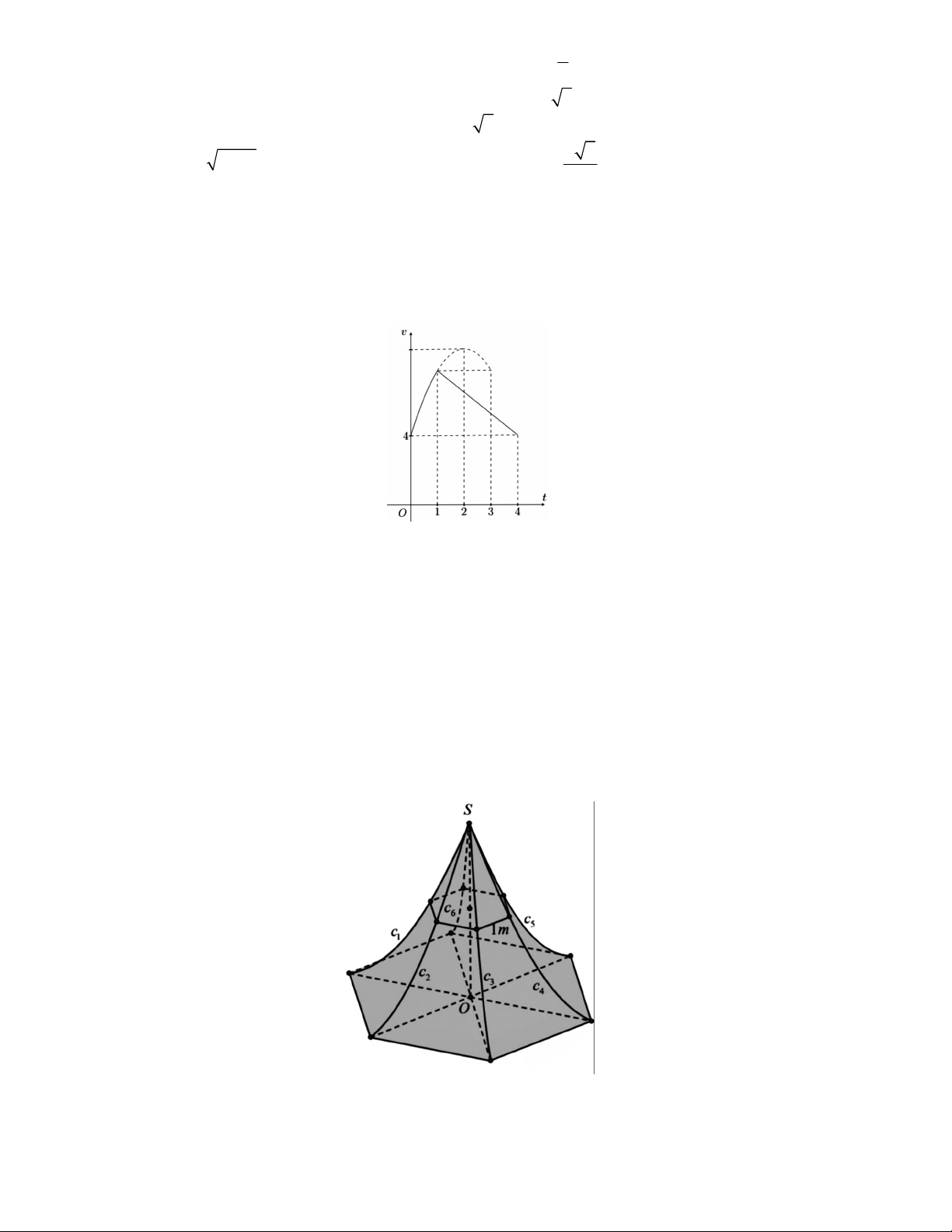
Câu 5. Một vật chuyển động trong 3 giờ với vận tốc v km/h phụ thuộc thời gian t h có đồ thị là một phần
của đường parabol có đỉnh I 2;9 và trục đối xứng song song với trục tung như hình bên. Tính quãng đường
s mà vật di chuyển được trong 3 giờ đó.
Câu 6. Một vật trang trí có dạng khối tròn xoay tạo thành khi quay miền (R) (phần gạch chéo trong hình vẽ)
quay xung quanh trục AB . Biết ABCD là hình chữ nhật cạnh AB 3cm , AD 2cm ; F là trung điểm của BC ;
điểm E cách AD một đoạn bằng 1cm .
Thể tích của vật thể trang trí trên là 3
a cm (quy tròn đến hàng phần chục). Khi đó a bằng 5
NGUYÊN HÀM VÀ TÍCH PHÂN LỚP 12 THPT
LỚP BÀI TOÁN LUYỆN TẬP CHUNG P2
______________________________________ TRẮC NGHIỆM ABCD
Câu 1. Họ nguyên hàm của hàm số 3 f x x là 1 A. 4 4x C . B. 2 3x C . C. 4 x C . D. 4 x C . 4 Câu 2. Cho hàm số x
f x e 2 . Khẳng định nào dưới đây là đúng? A. 2 d x f x x e C . B. d x
f x x e 2x C . C. d x
f x x e C . D. d x
f x x e 2x C . Câu 3. Nguyên hàm 4 x dx bằng 1 A. 5 x C B. 3 4x C C. 5 x C D. 5 5x C 5 4 4 1 Câu 4. Nếu
f x dx 3 thì
f x 5 dx bằng 3 1 1 A. 1 5 . B. 12 . C. 14 . D. 4 . 3 3 3 Câu 5. Biết
f x dx 5
và g x dx 7
. Giá trị của 3 f x 2g x dx bằng 1 1 1 A. 2 9 . B. 3 1. C. 1. D. 29 . 3 Câu 6. Biết 2
F (x) x là một nguyên hàm của hàm số f (x) trên . Giá trị của f (x)dx bằng: 1 26 A. 8 . B. 10 . C. 9 . D. . 3 5 5 3
Câu 7. Cho hàm số y f x liên tục trên và f x dx 10 ,
f x dx 1 . Khi đó
f x dx bằng 1 3 1 A. 11. B. 9 . C. 10 . D. 9 .
Câu 8. Biết F x x 2
e 2x là một nguyên hàm của hàm số f x trên . Khi đó f 2x dx bằng 1 1 A. 2x 2 e 8x C . B. x 2
2e 4x C . C. 2 x 2 e 2x C . D. 2 x 2 e 4x C . 2 2 x 2
Câu 9. Diện tích hình phẳng giới hạn bởi các đường y
và các đường thẳng x 2 và x 6 bằng x 1
A. ln 6 ln 2 4 (đvdt). B. ln 3 4 (đvdt). C. ln 5 4 (đvdt).
D. ln 6 ln 2 4 (đvdt). x ln 2
Câu 10. Cho hàm số f x 2 .
. Hàm số nào dưới đây không là nguyên hàm của hàm số f x ? x A. 2 x F x C B. 22 x F x 1 C C. 22 x F x 1 C D. 1 2 x F x C
Câu 11. Một ô tô đang chạy với vận tốc 10m / s thì người lái xe đạp phanh. Từ thời điểm đó, ô tô chuyển động
chậm dần đều với vận tốc v t 2
t 10m / s , trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu
đạp phanh. Tính quãng đường ô tô di chuyển được trong 8 giây cuối cùng. A. 55m . B. 25m . C. 50m . D. 16m . 1 1
Câu 12. Cho F x là một nguyên hàm của hàm số f x thỏa mãn F 2
và F e ln 2. Giá trị x ln x e 1 của biểu thức F F 2 e bằng 2 e A. 3ln 2 2 . B. ln 2 2 . C. ln 2 1. D. 2 ln 2 1.
TRẮC NGHIỆM ĐÚNG, SAI 6
Câu 1. Cho parabol P 2 : y x .
a) Diện tích hình phẳng giới hạn bởi đồ thị P , Ox và 2 đường thẳng x 0, x 1 bằng 1.
b) Diện tích hình phẳng giới hạn bởi đồ thị P , đường thẳng : y 2x và 2 đường thẳng x 0, x 2 bằng 3.
c) Diện tích hình phẳng giới hạn bởi đồ thị P , đường thẳng d : y 3x 2 bằng 4. d) Cho parabol P 2
: y x và hai điểm ,
A B thuộc P sao cho AB 2 . Diện tích lớn 4
nhất của hình phẳng giới hạn bởi P và đường thẳng AB là . 3
Câu 2. Cho các hàm số 2x y
, y 0 , x 0 , x 2 có đồ thị lần lượt là (C );(C );(C );(C ) Các mệnh đề sau 1 2 3 4 đây đúng hay sai?
a) Đồ thị (C ) và (C ) không có điểm chung. 1 2
b) Gọi M , N , P lần lượt là giao điểm của (C ) và (C );(C ); (C ) . Khi đó M , N, P thẳng hàng. 1 2 3 4 2
c) Gọi S là diện tích của hình phẳng giới hạn bởi các đồ thị trên. Khi đó 2x S dx . 0
d) Gọi V là thể tích khối tròn xoay được tạo bởi phép quay quanh trục Ox hình phẳng giới hạn bởi các đồ thị 2 trên. Khi đó 2x V dx 0
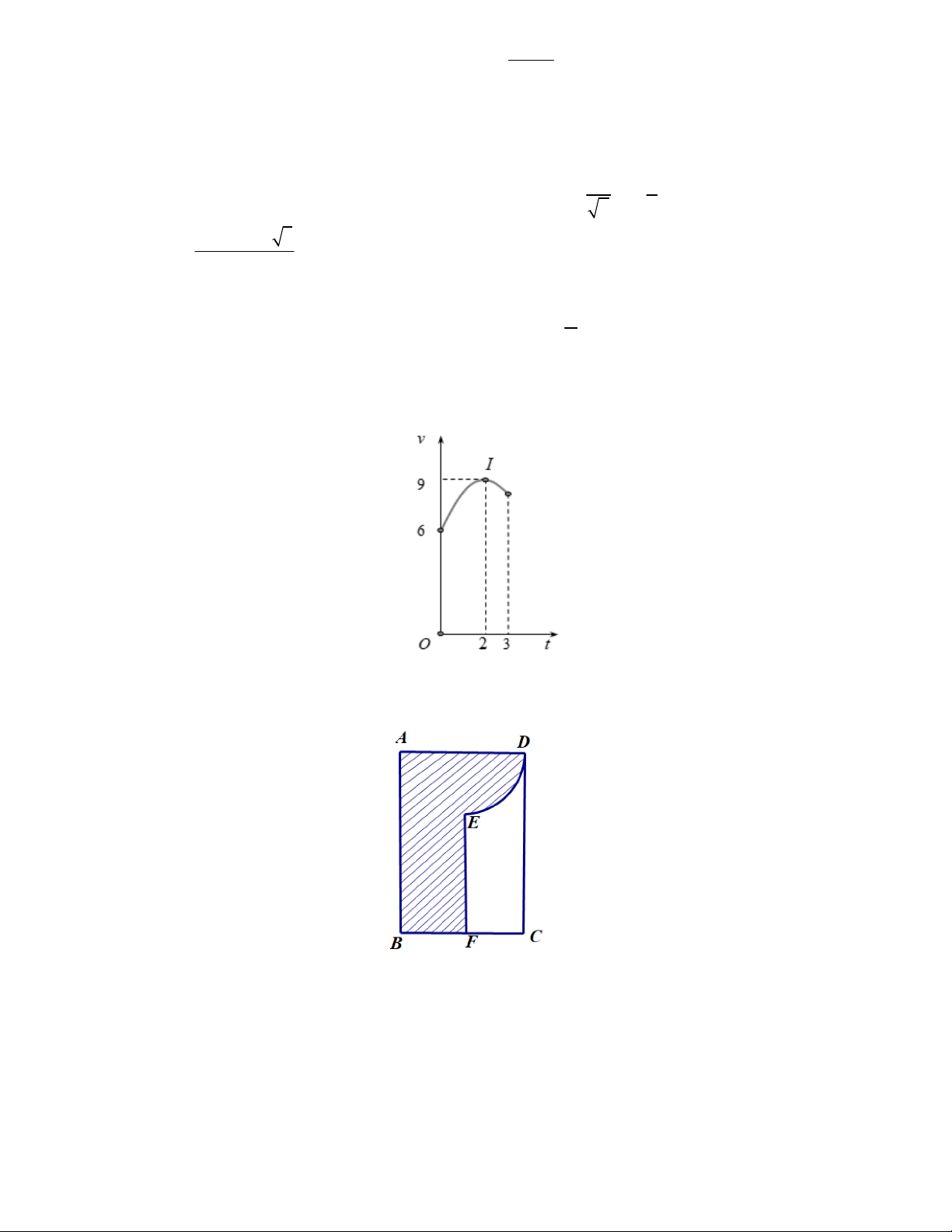
Câu 3. Chất điểm chuyển động theo quy luật vận tốc v t m / s có dạng đường thẳng khi 0 t 3 s và
8 t 15 s và v t có dạng đường Parabol khi 3 t 8s (như hình vẽ)
a) Vận tốc của chất điểm tại thời điểm t 3 là v 3 11m / s . 3
b) Quãng đường chất điểm di chuyển được trong 3 giây đầu tiên là: S 11dt m 1 0
c) Quãng đường chất điểm đi được trong khoảng thời gian từ 8 giây đến 15 giây bằng 73,5m .
d) Vận tốc trung bình v của chất điểm trong khoảng thời gian từ 3 đến 8 giây thỏa mãn v 7 m / s tb tb
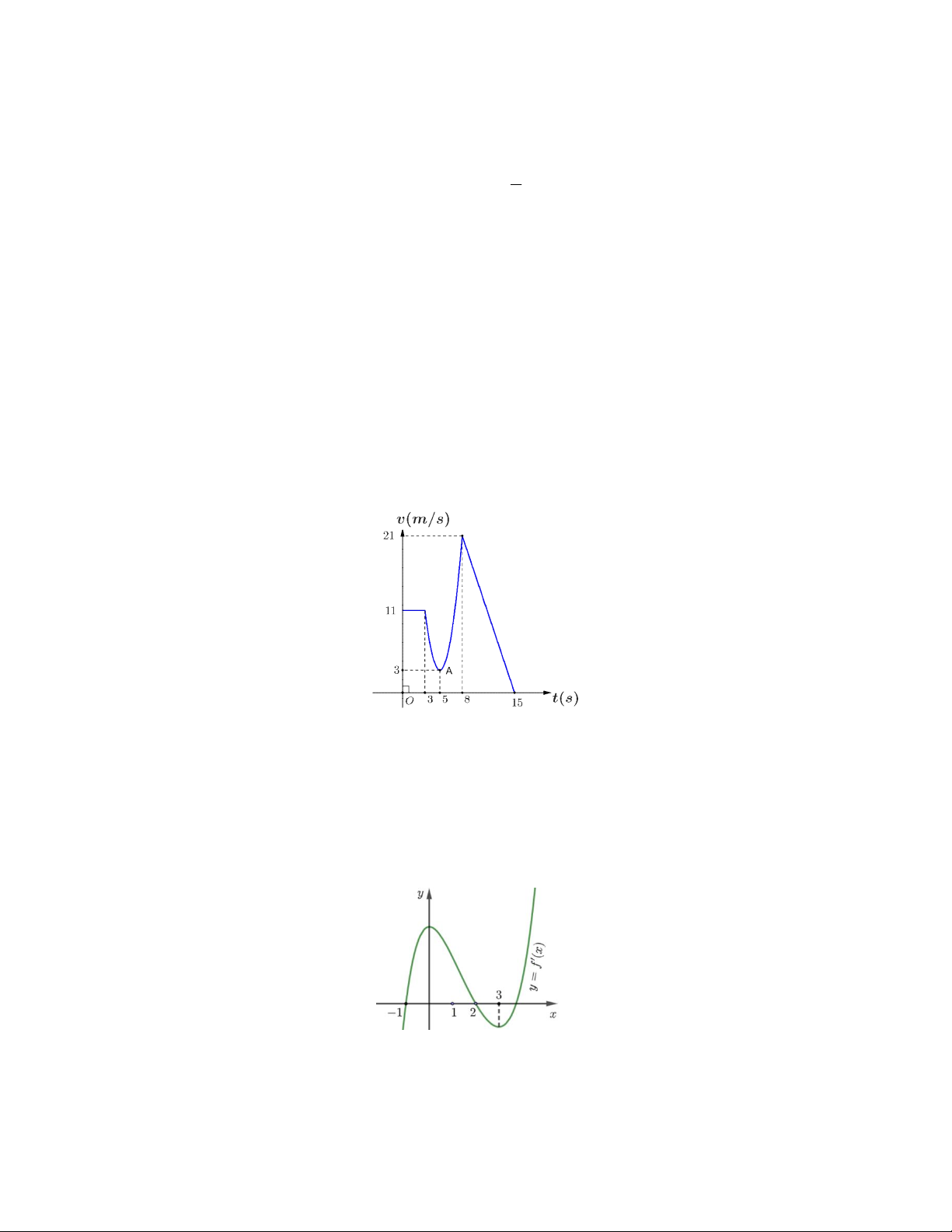
Câu 4. Cho y f ' x là hàm số bậc 3 có đồ thị như hình vẽ bên, biết f 2 3, f 1 1. 2 a)
f ' x dx 2 . 1 m
b) Tồn tại m 0; 2 sao cho
f ' x dx 0 . 0 c) Hàm số y
f ' x dx
có đúng 3 điểm cực trị. d) f 1 f 3 .
TRẮC NGHIỆM TRẢ LỜI NGẮN 7
Câu 1. Tổng các giá trị của tham số m sao cho đường thẳng d : y x m cắt parabol 2
(P) : y x 5x 4 tại hai 4
điểm phân biệt và diện tích hình phẳng giới hạn bởi d và (P) bằng bằng bao nhiêu? 3
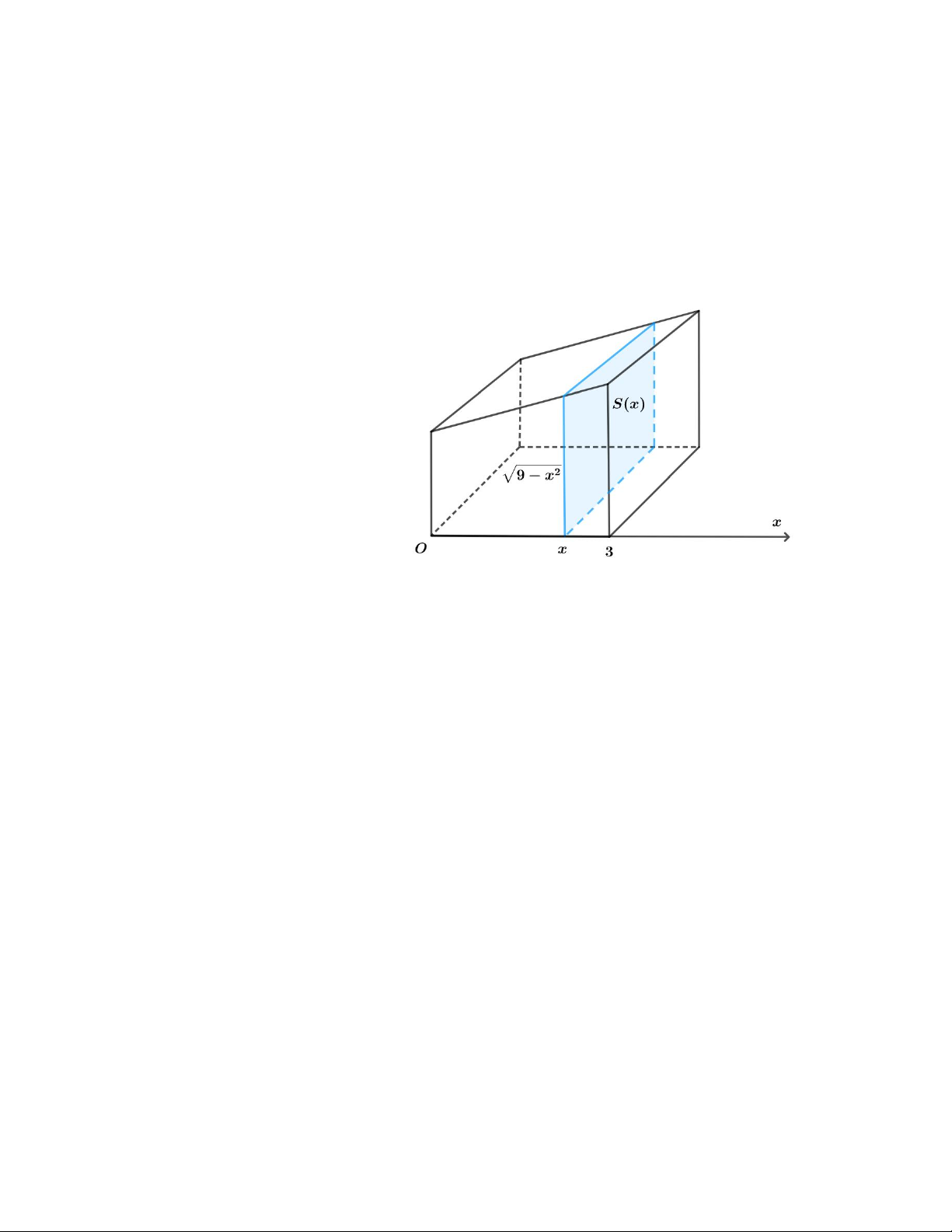
Câu 2. Cho phần vật thể giới hạn bởi hai mặt phẳng x 1 và x 7 , biết rằng khi cắt vật thể bởi mặt phẳng
vuông góc với trục Ox tại điểm có hoành độ x (1 x 7 ) thì được thiết diện là một hình chữ nhật có độ dài a b hai cạnh là 2x và 2
x 1 . Thể tích của phần vật thể đã cho bằng
(c là số nguyên tố, b 6; a, b, c ) . c Tính . a . b c ?
Câu 3. Cho hàm số f x liên tục trên và thỏa mãn 1 x xf x x f x e
với mọi x . Tính f 0 .
Câu 4. Một vật chuyển động trong 4 giờ với vận tốc phụ thuộc vào thời gian t(h) có đồ thị vận tốc như hình vẽ
bên.Trong khoảng thời gian 1 giờ kể từ khi bắt đầu chuyển động, đồ thị đó là một phần của đường parabol có
đỉnh I (2;10) và trục đối xứng song song với trục tung. Khoảng thời gian còn lại vật chuyển động chậm dần đều.
Tính quãng đường S mà vật đi được trong 4 giờ đó.
Câu 5. Chi phí nhiên liệu dự kiến C (tính bằng triệu đô la mỗi năm) khi sử dụng một loại xe tải của một công ty
vận tải từ năm 2020 đến năm 2030 là C 5, 6 2, 2t, 0 t 10 , trong đó t 0 tương ứng với năm 2020. Nếu 1
công ty sử dụng một loại xe tải khác có động cơ hiệu quả hơn thì chi phí nhiên liệu dự kiến sẽ giảm và tuân theo
mô hình C 4, 7 2, 04t, 0 t 10 . Công ty có thể tiết kiệm được bao nhiêu khi sử dụng loại xe tải với động cơ 2 hiệu quả hơn?
Câu 6. Gia đình ông An xây một cái chòi hình lục giác, trong đó mái chòi H có dạng hình “chóp lục giác cong
đều” có trần bằng gỗ như hình vẽ bên. Đáy của H là một hình lục giác đều có đường chéo chính là 6m
Chiều cao SO 6m ( SO vuông góc với mặt phẳng đáy). Các cạnh bên của H là các sợi dây thép
c ; c ; c ; c ; c ; c ; c ; c nằm trên các đường parabol có trục đối xứng song song với SO . Giả sử giao tuyến (nếu 1 2 3 4 5 6 7 8
có) của H với mặt phẳng () vuông góc với SO là một lục giác đều và khi () khi qua trung điểm của SO
thì bát giác đều có cạnh 1m . Tính thể tích phần không gian nằm bên trong mái chòi H đó. 8
NGUYÊN HÀM VÀ TÍCH PHÂN LỚP 12 THPT
LỚP BÀI TOÁN LUYỆN TẬP CHUNG P3
_____________________________________ Câu 1. Nguyên hàm 5 x dx bằng 1 A. 4 5x C . B. 6 x C . C. 6 x C . D. 6 6x C . 6
Câu 2. Họ nguyên hàm của hàm số x
f x e x là 1 x 1 x 1 A. x e 1 C B. x 2
e x C C. 2 e x C D. 2 e x C 2 x 1 2
Câu 3. Trong các khẳng định sau, khẳng định nào sai? 2 x e x A. 2x d 2x x ln 2 C . B. 2 e dx C . 2 1 1 C. cos 2 d x x sin 2x C . D.
dx ln x 1 C x 1 . 2 x 1
Câu 4. Hàm số F x 2
x 1 là một nguyên hàm của hàm số nào sau đây? 1 1 A. f x 3 x x .
B. f x 2x .
C. f x 2x 1. D. f x 3 x 1. 3 3
Câu 5. Câu 2: Họ nguyên hàm của hàm số 2x f x cos 3x là: A. 2x F x
sin 3x C . B. 2x F x
sin 3x C . 2x 1 x 1
C. F x 2 .ln 2 sin 3x C .
D. F x
sin 3x C . 3 ln 2 3
Câu 6. Biết F x là môt nguyên hàm của hàm số 2 x
f x e và F 0 0 . Giá trị của F ln 3 bằng A.4 B. 3 C. 2 D. 1 2 x 1
Câu 7. Cho tích phân I
dx a ln b . Tính giá trị 2 2 a b . x 1 A.6 B. 5 C. 4 D. 3 1
Câu 8. Tìm họ nguyên hàm của hàm số f x . 2 2x 1 1 A.
f xdx 2x 1 C . B.
f xdx 2x 1 C . 2 1 C.
f xdx 2 2x 1 C . D.
f xdx C . 2x 1 2x 1 3 dx Câu 9. Cho
a ln 2 b ln 3 c ln 5
với a, b, c là các số hữu tỉ. Giá trị của 2 3
a b c bằng x 1 x 2 2 A. 3 . B. 6 . C. 5 . D. 4 .
Câu 10. Diện tích hình phẳng giới hạn bởi đồ thị của các hàm số 2
y x , y x và các đường thẳng x 0 , x 1 bằng 0 1 0 1 A. 2
x x dx . B. 2
x x dx . C. 2
x x dx . D. 2
x x dx . 1 0 1 0 3
Câu 11. Một chiếc ô tô chuyển động với vận tốc v t m/s , có gia tốc a t vt 2 m/s . Biết vận tốc t 1
của ô tô tại giây thứ 6 bằng 6 m/s . Tính vận tốc của ô tô tại giây thứ 20 . A. v 3ln 3. B. v 14 . C. v 3ln 3 6 . D. v 26 .
Câu 12. Trong một đợt xả lũ, nhà máy thủy điện Hố Hô đã xả lũ trong 40 phút với tốc độ lưu lượng nước tại thời
điểm t giây là v t t 3 ( ) 10
500 m / s . Hỏi sau thời gian xả lũ trên thì hồ chứa nước của nhà máy đã xả thoát đi
bao nhiêu triệu khối nước? A.30 B. 18 C. 20 D. 16 9
TRẮC NGHIỆM ĐÚNG, SAI Câu 1. Giả sử
2 x F x ax
bx c e là một nguyên hàm của hàm số 2 ( ) x
f x x e . Các khẳng định sau đúng hay sai? a) 2 '( ) 2 2 x F x ax ax bx c e .
b) a b c 0 . c) F (0) 2 . 3 2 3 2 d)
x 3 x 5 x x 3 x 6 ( ). 2 x F x e dx e C . 5 5
Câu 2. Cho hai hàm số f x và g x , biết f x dx 5 và
g x dx 8
. Xét tính đúng sai của các khẳng 1 1 định sau: 5
a) 2 f x dx 10 . 1 5
b) f x g x dx 3 . 1 5
c) f x g x dx 13 . 1 5
d) 3 f x 2g x 2
x dx 10 . 1
Câu 3. Một vật chuyển động trong 3 giờ với vận tốc v (km/h) phụ thuộc thời gian t (h). Trong khoảng thời gian 5
1giờ kể từ khi bắt đầu chuyển động, vận tốc của nó là 2
v t 5t 4 ; trong khoảng thời gian còn lại vật 4 chuyển động đều.
a) Gia tốc của vật trong khoảng thời gian 1 giờ kể từ khi bắt đầu chuyển động bằng 0 .
b) Gia tốc của vật trong khoảng thời gian từ 1 giờ đến 3 giờ bằng 0 .
c) Vận tốc của vật trong khoảng thời gian từ 1 giờ đến 3 giờ bằng 7, 75 (km/h).
d) Quãng đường mà vật chuyển động trong khoảng thời gian 1 giờ kể từ khi bắt đầu chuyển động bằng 4 (km). 1 4
Câu 4. Cho f (x) . Đặt I f (x)dx 2
. Các mệnh đề sau đây đúng hay sai? x x 1 1
a) Ta có I 3 0 . 5 du
b) Đặt u x 1 . Khi đó I . 3 2 u 2u 1 2 x 1 c) F (x) ln
1 là một nguyên hàm của f (x) . x 4 dx 1 d) I a ln b . Khi đó a b 1 . 2 x x 1 2 1 10
TRẮC NGHIỆM TRẢ LỜI NGẮN
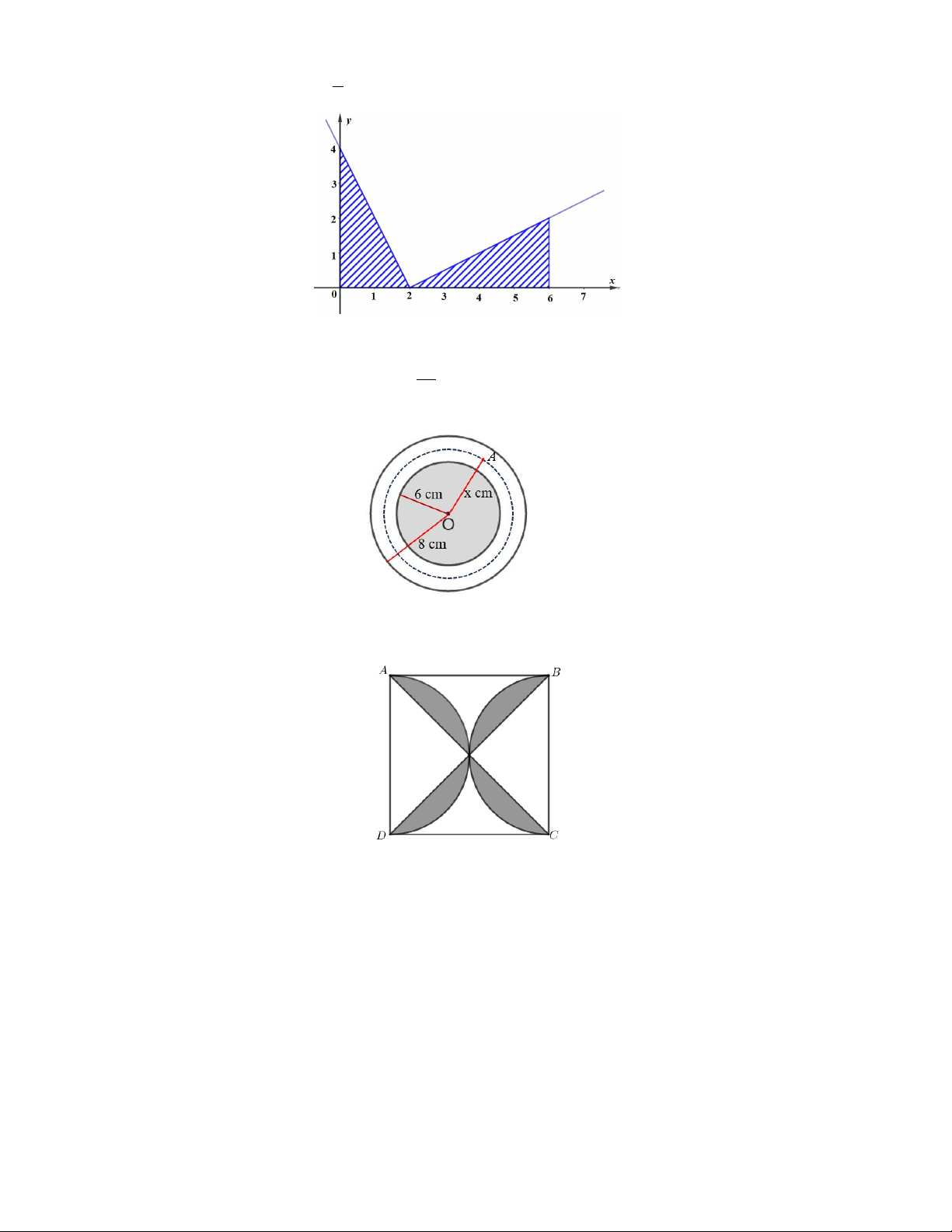
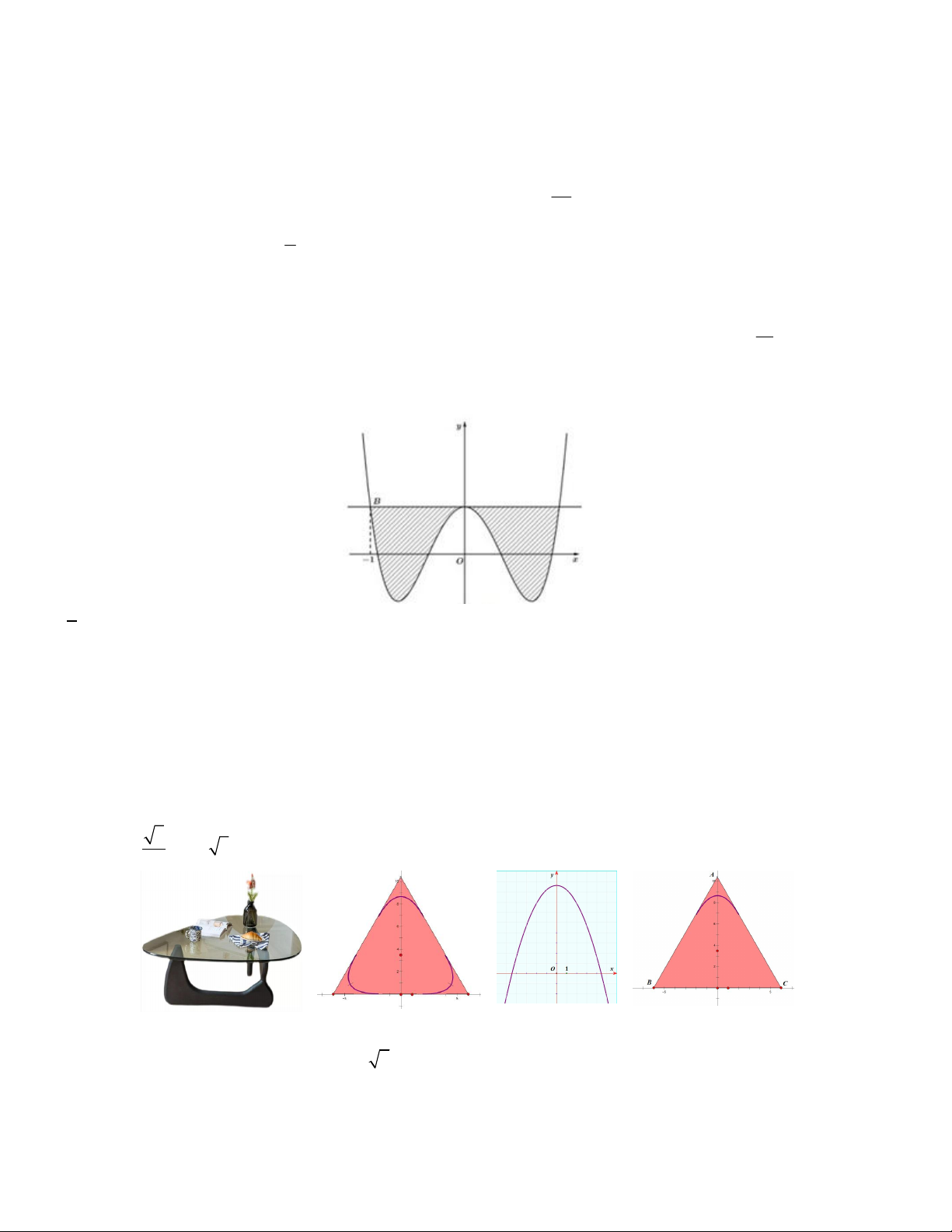
2x 4 x 2
Câu 1. Cho đồ thị hàm số f x 1
. Hình phẳng S (phần gạch sọc) dưới đây có diện tích bằng x 1 x 2 2
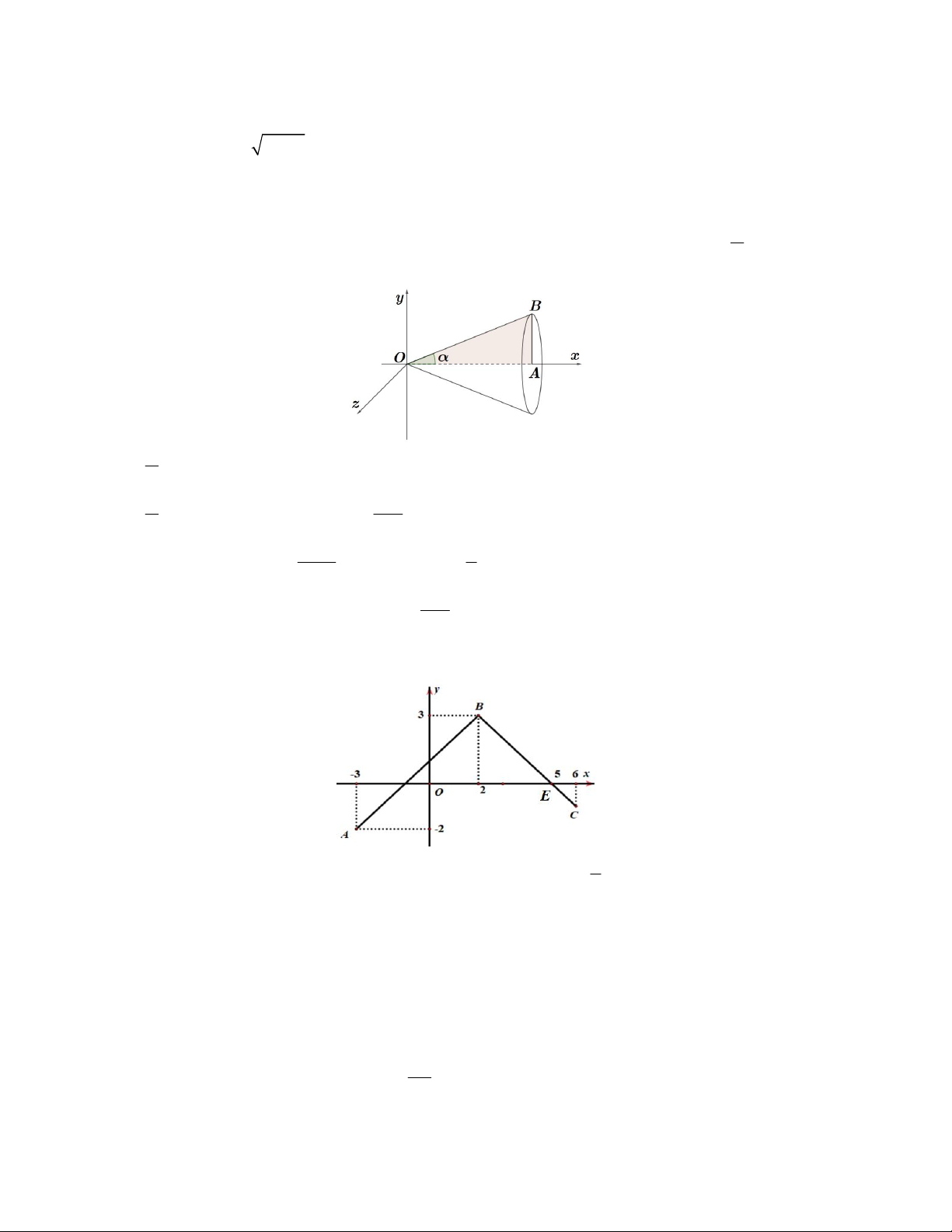
Câu 2. Mặt cắt ngang của một ống dẫn khí nóng là hình vành khuyên như hình vẽ bên. Khí bên trong ống được
duy trì ở 150 oC. Biết rằng nhiệt độ T (oC) tại điểm tại điểm A trên thành ống là hàm số T (x) với x là khoảng 30
cách (cm) từ A đến tâm mặt cắt và
T x
(6 x 8). Nhiệt độ mặt ngoài của ống (theo độ C) gần x
nhất với số nào sau đây
Câu 3. Từ một tấm bìa hình vuông ABCD cạnh 4cm vẽ hai đường chéo và hai nửa đường tròn đường kính là
hai cạnh AD, BC cắt nhau tạo thành 4 hình cánh quạt như hình vẽ. Tính thể tích khối tròn theo 3 cm xoay sinh ra
khi quay 4 cánh quạt này quanh cạnh CD (kết quả làm tròn đến hai chữ số sau dấu phẩy).
Câu 4. Hàm cầu và hàm cung của một sản phẩm được mô hình hoá bởi: Hàm cầu: p 0
, 2x 8 và hàm cung:
p 0,1x 2 , trong đó x là số đơn vị sản phẩm, p là giá của mỗi đơn vị sản phẩm (tính bằng triệu đồng). Tính
tổng thặng dư tiêu dùng và thặng dư sản xuất đối với sản phẩm này
Câu 5. Trong bài này, ta xét một hình huống giả định có một học sinh sau kì nghỉ đã mang virus cúm quay trở lại
khuôn viên trường học biệt lập với 1000 học sinh. Sau khi có sự tiếp xúc giữa các học sinh, virus cúm lây lan
trong khuôn viên trường. Giả thiết hệ thống chống dịch chưa được khởi động và virus cúm được lây lan tự
nhiên. Gọi P t là số học sinh bị nhiễm virus cúm ở ngày thứ t tính từ ngày học sinh mang virus cúm quay trở
lại khuôn viên trường. Biết tốc độ lây lan của virus cúm tỉ lệ thuận với số học sinh không bị nhiễm virus cúm theo
hệ số tỉ lệ là hằng số k 0 . Số học sinh bị nhiễm virus cúm sau 4 ngày là 52 học sinh. Xác định số học sinh bị
nhiễm virus cúm sau 10 ngày. 2
Câu 6. Cho hàm số f x thỏa mãn f x f x f x 2 .
2x x 1 , x
và f 0 f 0 3. Giá trị của f 2 1 bằng bao nhiêu ? 11
NGUYÊN HÀM VÀ TÍCH PHÂN LỚP 12 THPT
LỚP BÀI TOÁN LUYỆN TẬP CHUNG P4
_______________________________________ TRẮC NGHIỆM ABCD 2024
Câu 11. Tích phân 3x I dx bằng 0 2024 3 2024 3 1 A. 2024 3 1 ln 3 . B. . C. 2024 3 1 . D. . ln 3 ln 3
Câu 2. Họ tất cả các nguyên hàm của hàm số f x 2x 5 là: A. 2 x C . B. 2 x 5x . C. 2
x 5x C . D. 2
2x 5x C . 2 2 2 Câu 3. Cho
f x dx 3 và
g x dx 7 , khi đó
f x 3g x d x bằng 0 0 0 A. 16 . B. 18 . C. 24 . D. 10 . 3
Câu 4. Cho F x là một nguyên hàm của hàm số ( ) x
f x e 2x thỏa mãn F 0
. Tìm F x ? 2 x 1 x 3 x 5 x 1 A. F x 2 e x . B. F x 2 e x . C. F x 2 e x . D. F x 2 2e x . 2 2 2 2 3 Câu 5. Biết 2
F x x là một nguyên hàm của hàm số f (x) trên . Giá trị của 1 f (x)dx bằng 1 26 32 A. 10 . B. 8 . C. . D. . 3 3
Câu 6. Tìm họ nguyên hàm của hàm số : 2 (1 tan x)dx A. tan x
B. x tan x C C. cot x C D. tan x C
Câu 7. Tìm nguyên hàm F x x sin x dx
biết F 0 19 . A. F x 2
x cos x 20 . B. F x 2
x cos x 20 . 1 1 C. F x 2
x cos x 20 . D. F x 2
x cos x 20 . 2 2 1
Câu 8. Cho hàm số f x x
. Trong các hàm số dưới đây, hàm số nào là một nguyên hàm của f x x trên 0; ? 2 x 2 x A. F x x . B. F x x . 2 1 2 2 2 x 2 x C. F x 2 x . D. F x 2 x . 4 3 2 2
Câu 9. Tính thể tích V của vật thể giới hạn bởi hai mặt thẳng x 1 và x 4 biết rằng thiết diện của vật thể cắt
bới mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x là 1 x 4 hình vuông có cạnh 4 x . A. 7 . B. 8 . C. 9 . D. 10 . 4 3 2
x x 7x 3 a a Câu 10. Biết dx c ln 5
với a, b, c là các số nguyên dương và
là phân số tối giản. Tính 2 x x 3 b b 1 giá trị của 2 3
P a b c . A. 5 . B. 3 . C. 6 . D. 4 .
Câu 11. Một ô tô đang chuyển động trên đường với vận tốc v t 4t 3 m / s , với t là thời gian tính bằng
giây. Quãng đường ô tô đi được trong khoảng từ 3 đến 5 giây là bao nhiêu?
1 2 khi x 1 16 a a Câu 12. Cho hàm số 4 3
f (x) x . Biết tích phân
f (x) dx
là phân số tối giản, b 0 . b b 2
x x 1 khi x 1 1
Tính tổng a b . A.120 B. 113 C. 90 D. 80
TRẮC NGHIỆM ĐÚNG, SAI 12
Câu 1. Giả sử F x là một nguyên hàm của hàm số f x 2x 1 trên thỏa mãn F 0 2 . Khi đó:
a) F x 2x 1, x . b) F x 2 x 2 , x . c) F 1 0 .
d) Phương trình F x 2
3 x x có 4 nghiệm phân biệt, tổng và tích các nghiệm lần lượt bằng a,b . Khi đó ta b
có khẳng định F x dx 41 . a
Câu 2. Cho tam giác vuông OAB có cạnh OA a nằm trên tục Ox và AOB 0 . Gọi là khối 2
tròn xoay sinh ra khi quay miền tam giác OAB xung quanh trục Ox . a) Khi
thì OB x . 4 3 a b) Khi
thì thể tích V của khối là (đvtt). 6 9 3 4 a 1
c) Khi thể tích V của khối là thì giá trị cos . 3 2 3 a
d) Khi tan cot thì thể tích V của khối là . 3
Câu 3. Cho hàm số y f (x) liên tục trên , đồ thị hàm số C : y f (
x) trên đoạn 3;6 là đường gấp
khúc như hình vẽ. Xét tính đúng sai của các mệnh đề sau? 1 1 1 a) f ( x)dx 2 . b) f ( x)dx . 2 3 0
c) f 2 f 6 4 .
d) f 5 f 3
2 f 2 2 .
Câu 4. Một ô tô đang chạy với vận tốc 16 m / s thì người lái xe bất ngờ phát hiện chường ngại vật trên đường
cách đó 50m . Người lái xe phản ứng một giây sau đó đạp phanh khẩn cấp. Từ thời điểm đó, ô tô chuyển động
chậm dần đều với vận tốc v t 5
t 15 , trong đó t là khoảng thời gian tính bằng giây, kể từ lúc bắt đầu đạp
phanh. Gọi s t là quãng đường ô tô đi được trong t giây kể từ lúc đạp phanh.
Trong các mệnh đề sau mệnh đề nào đúng, mệnh đề nào sai? 2 5t
a) Công thức biểu diễn hàm số s t là s t 15t 16 2
b) Thời gian kể từ khi ô tô đạp phanh đến khi dừng hẳn bằng 3 giây.
c) Kể từ lúc đạp phanh đến khi dừng hẳn, ô tô còn di chuyển được quãng đường là 38,5 m .
d) Xe ô tô không va chạm với chướng ngại. 13
TRẮC NGHIỆM TRẢ LỜI NGẮN 1 2
Câu 1. Cho hàm số f x liên tục trên và thỏa mãn
f x dx 9
. Tích phân f 1 3x 9 dx bằng 5 0
Câu 2. Cho hàm số y f x liên tục và có đạo hàm trên thỏa mãn 2 3 f
x x x 1
f x. f x 2 2 2 3x e
, f 0 2 . 2 1 2
Tính I f x dx . 0
Câu 3. Cho hàm số bậc ba y f (x). Đường thẳng y ax b tạo với đường y f (x) hai miền
phẳng có diện tích là S , S (hình vẽ bên). 1 2 5 1 1 Biết S
và 1 2x f 3x dx
S bằng bao nhiêu? (làm tròn đến hàng phần 1 , giá trị của 12 2 2 0 mười)
Câu 4. Một ô tô đang chạy với vận tốc 20 m/s thì tài xế đạp phanh. Sau khi đạp phanh, ô tô chuyển động chậm
dần đều với vận tốc v t 40t 20 (m/s), trong đó t là khoảng thời gian tính bằng giây kể từ lúc bắt đầu đạp
phanh. Gọi s t là quãng đường xe ô tô đi được trong thời gian t giây kể từ lúc đạp phanh. Hỏi từ lúc đạp
phanh đến khi dừng hẳn, ô tô còn di chuyển bao nhiêu mét?
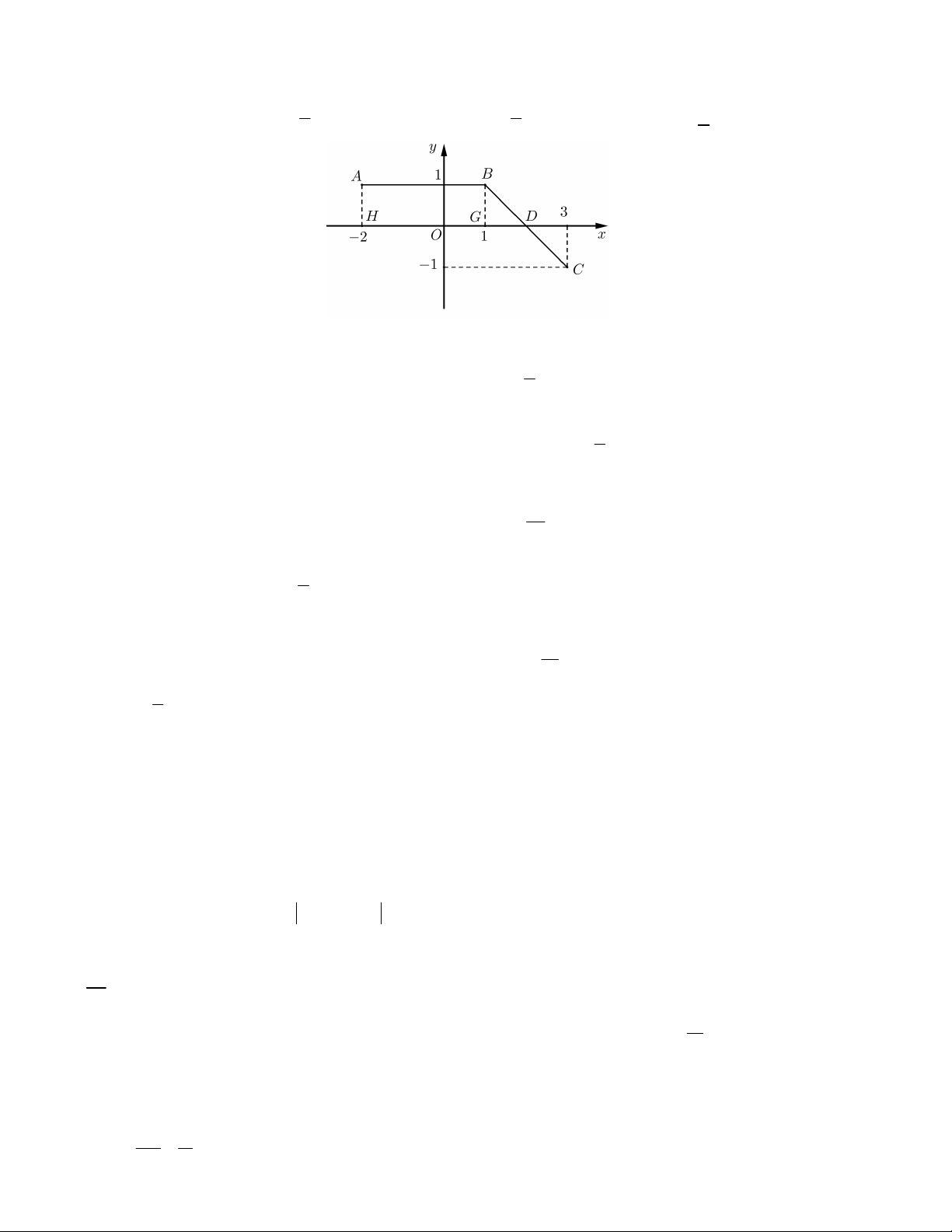
Câu 5. Hình 38 minh họa mặt cắt đứng của một bức tường cũ có dạng hình chữ nhật với một cổng ra vào có
dạng hình parabol với các kích thước được cho như trong hình đó. Người ta dự định sơn lại mặt ngoài của bức
tường đó. Chi phí để sơn bức tường là 15 000 đồng/1 m2. Tổng chi phí để sơn lại toàn bộ mặt ngoài của bức
tường đó sẽ là bao nhiêu đồng? 2 3 x ln x 1 khi x 0 e f ln x
Câu 6. Cho hàm số f x . Biết
dx a 3 b ln 2 c với a, ,
b c . Giá trị 2
2x x 3 1 khi x 0 x 1 e
của a b 6c bằng 14
NGUYÊN HÀM VÀ TÍCH PHÂN LỚP 12 THPT
LỚP BÀI TOÁN LUYỆN TẬP CHUNG P5
______________________________________ TRẮC NGHIỆM ABCD
Câu 1. Cho hai hàm số f (x) và g(x) liên tục trên a ;b. Diện tích hình phẳng giới hạn bởi đồ thị của các hàm
số y f (x) , y g(x) và các đường thẳng x a , x b bằng b b b b
A. f (x) g(x)dx . B.
f (x) g(x) dx . C.
f (x) g(x) dx .
D. f (x) g(x)dx . a a a a
Câu 2. Hàm số F x 4
x 6x là nguyên hàm của hàm số 5 x A. f x 2 3x . B. f x 3 4x 6x . 5 5 x C. f x 3 4x 6 . D. f x 2 3x C . 5
Câu 3. Cho hàm số f x os
c x . Nguyên hàm F x cuả hàm số f x trên sao cho F 0 5 là: A. s inx 5 . B. s inx .
C. s inx C . D. s inx 5 .
Câu 4. Diện tích S của hình phẳng giới hạn bởi các đường 2
y 2 x , y 1
, x 0 và x 1 được tính bởi công thức nào sau đây? 1 1 1 1 2 A. S 2 2x 1 dx . B. S 2 2x 1 dx . C. S 2 2x 1 dx . D. S 2 2x 1 dx . 0 0 0 0 4000
Câu 5. Một đám vi trùng tại ngày thứ t có số lượng là N t con. Biết rằng Nt và lúc đầu đám vi 1 0, 5t
trùng có 250000 con. Hỏi sau 10 ngày số lượng vi trùng gần với số nào sau đây nhất. A. 251000 con. B. 261000 con. C. 264334 con. D. 274334 con. 2 4 4
Câu 6. Cho hàm số f x liên tục trên R và có f (x)dx 9; f (x)dx 4. Tính I f (x)d . x 0 2 0 9 A. I 5 . B. I 36 . C. I . D. I 13 . 4 e x 1
Câu 7. Tính tích phân I dx 2 x 1 1 1 A. I . B. I 1. C. I 1. D. I . e e e
Câu 8. Thể tích khối tròn xoay tạo thành khi cho hình phẳng giới hạn bởi đồ thị hàm số f x x , trục hoành
và hai đường thẳng x 0; x 4 quay quanh trục Ox là 4 4 4 4 A. x . dx B. x . dx C. x . dx D. x . dx 0 0 0 0
Câu 9. Cho F x là một nguyên hàm của hàm số f x x ln x . Tính F x . 1
A. F x x ln x .
B. F x 1 ln x .
C. F x .
D. F x 1 ln x . x 2 2 Câu 10. Cho
f x dx 5
. Tính I f x 2sin x dx . 0 0 A. I 5 . B. I 7 . C. I 5 . D. I 3 . 2
Câu 11. Hàm số nào dưới đây là một nguyên hàm của hàm số f x x sin 2x 1 ? 1 1 A. F x 2
x cos2x 1 . B. F x 2
x 2cos2x 1 . 2 2 1 1 1 1 C. F x 2 x cos2x 1 . D. F x 2 x cos2x 1 . 2 2 2 2 15
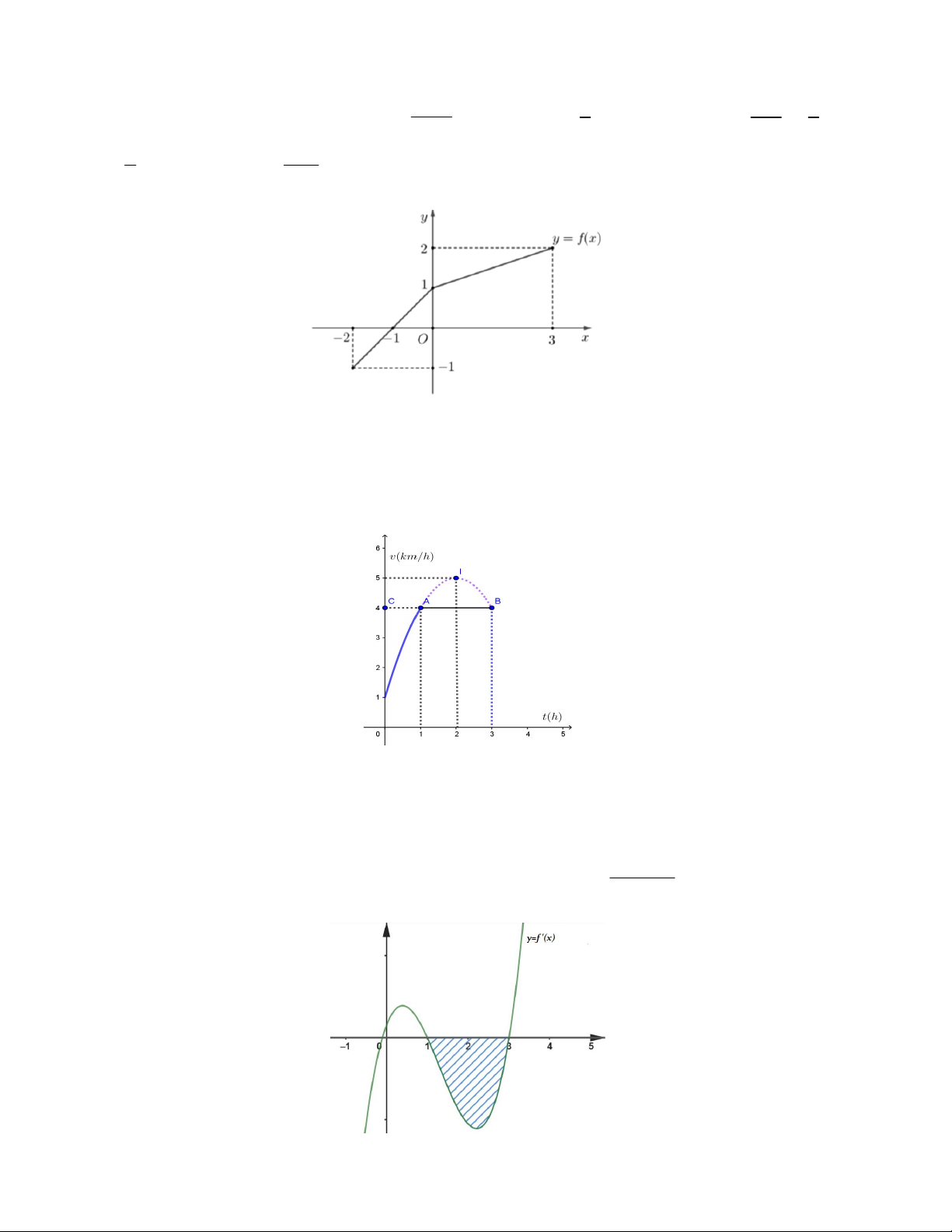
Câu 12. Đường gấp khúc ABC trong hình vẽ bên là đồ thị của hàm số y f x trên đoạn 2; 3 .Tích phân 3
f xdx bằng 2 9 7 A. 4 . B. . C. . D. 3 . 2 2
TRẮC NGHIỆM ĐÚNG, SAI 1
Câu 1. Hàm số F (x) là một nguyên hàm của hàm số f (x) trên ( ;
0) thỏa mãn F (2) 0 , (với C là x
một số thực bất kì). Các mệnh đề sau đúng hay sai? 3
a) F (2e) 1.
b) F (3) ln . 2
c) f (4) ln 2 . d) F ( 1) 1. 1
Câu 2. Biết F x là một nguyên hàm của hàm số f x 2x
trên khoảng 0; . Xét tính đúng sai của 2 x các mệnh đề sau? 1 a) F
1 3 . Khi đó F x 2 x 3. x b) F
1 0 . Phương trình F x 0 có hai nghiệm. 13
c) Đồ thị hàm số y F x đi qua điểm M 1; 2 . Khi đó F 2 2 1 d) F 2
. Hàm số g x xF x có 3 điểm cực trị. 4
Câu 3. Cho các hàm số f x 2 x 2 ;
x g x x 2 . Trong các mệnh đề sau mệnh đề nào đúng, mệnh đề nào sai?
a) Hình phẳng giới hạn bởi đồ thị của hàm số y f (x) , trục hoành và hai đường thẳng x a, x b , a b có b
diện tích được tính theo công thức f (x)d . x a
b) Hình phẳng giới hạn bởi đồ thị hàm số y f (x) , y g(x) và hai đường thẳng x a, x b , a b có diện b
tích được tính theo công thức
f (x) g(x) d . x a
c) Hình phẳng giới hạn bởi đồ thị của hàm số y f (x) , trục hoành và hai đường thẳng x 0, x 2 có diện tích 20 là . 3 11
d) Diện tích hình phẳng giới hạn bởi hai đồ thị của các hàm số y f x , y g x là . 2
Câu 4. Cây cà chua khi trồng có chiều cao 5cm. Tốc độ tăng chiều cao của cây cà chua sau khi trồng được cho
bởi hàm số v t 3 2 0
,1t t , trong đó t tính theo tuần, v t tính bằng cm/tuần. Gọi ht (tính bằng cm) là độ
cao của cây cà chua ở tuần thứ t . Xét tính đúng sai của các khẳng định sau: 4 3 t t
a) h t , với t 0 . 40 3
b) Chiều cao tối đa của cây cà chua đó là 88, 4 cm (Làm tròn kết quả đến hàng phần mười). 16
c) Giai đoạn tăng trưởng của cây cà chua đó kéo dài trong 9 tuần.
d) Vào thời điểm cây cà chua đó phát triển nhanh nhất thì chiều cao cây cà chua đạt 54, 4 cm (kết quả được
làm tròn đến hàng phần mười).
TRẮC NGHIỆM TRẢ LỜI NGẮN 1 1 e 1 3
Câu 1. Biết một nguyên hàm của f x trên khoảng ; thỏa mãn F là 2x 1 2 2 2 1 a c
F x ln bx 1 c .Tính . a b
Câu 2. Cho hàm số y f (x) đồ thị như hình vẽ bên dưới. 1
Câu 3. Cho hàm số f x thoả mãn f x 2
x f x 3 2 1
5x 3x 3x với mọi x . Tích phân f xdx 0 bằng
Câu 4. Một vật chuyển động trong 3 giờ với vận tốc v km / h phụ thuộc vào thời gian t h có đồ thị vận tốc
như hình bên. Tính quãng đường mà vật di chuyển được trong 3 giờ(làm tròn đến hàng phần chục)
Câu 5. Cho hàm số f x liên tục trên . Gọi F x, G x, H x là ba nguyên hàm của f x trên thỏa 1
mãn F 3 G 3 H 3 4 và F 0 G 0 H 0 1. Tính 3. f 3x dx 0
Câu 6. Cho hàm số y f (x) liên tục và có đạo hàm trên với đồ thị hàm số y f '(x) như hình vẽ. Biết diện 3 1
tích phần gạch chéo bằng 2 và f (3) 7 . Khi đó, giá trị biểu thức I 2 f '(x)dx bằng bao nhiêu? f (x).ln 3 1
(Làm tròn đến hàng phần chục). 17
NGUYÊN HÀM VÀ TÍCH PHÂN LỚP 12 THPT
LỚP BÀI TOÁN LUYỆN TẬP CHUNG P6
________________________________________________________ TRẮC NGHIỆM ABCD 1 1
Câu 1. Cho hàm số f x
. Chọn khẳng định đúng: 2 x cos x A.
f xdx ln x tan x C . B.
f xdx ln x tan x C . C.
f xdx ln x tan x C . D.
f xdx ln x tan x . 4 4 3
Câu 2. Cho hàm số f x liên tục trên và f x dx 10 ,
f x dx 4 . Tích phân
f x dx bằng 0 3 0 A. 4 . B. 7 . C. 3 . D. 6 . 1
Câu 3. Nếu F x và F
1 1 thì giá trị của F 4 bằng 2x 1 1 A. ln 7. B. 1 ln 7. C. ln 3. D. 1 ln 7. 2 2 2 2 Câu 4. Cho
f x dx 3
, g x dx 1
thì f x 5g x x dx bằng: 0 0 0 A. 12 . B. 0 . C. 8 . D. 10 m Câu 5. Cho 2
3x 2x
1 dx 6 . Giá trị của tham số m thuộc khoảng nào sau đây? 0 A. 1 ; 2 . B. ; 0 . C. 0; 4 . D. 3; 1 . 6 2 Câu 6. Cho
f (x)dx 12 . Tính I f (3x) . dx 0 0 A. I 5 B. I 36 C. I 4 D. I 6 a
Câu 7. Cho a là số thực dương, tính tích phân I x dx theo a . 1 2 2 a 1 2 a 2 2 2 a 1 3a 1 A. I . B. I . C. I . D. I . 2 2 2 2 Câu 8. Biết x x2 2sin cos
dx asin2x cos2x bx C
, với a,b . Tính 2 2 a b . 17 109 17 109 A. . B. . C. . D. . 2 4 16 16
Câu 9. Cho hình phẳng H giới hạn bởi parapol P 2
: y x và đường thẳng d : y 2x . Thể tích khối tròn
xoay sinh bởi H khi quay quanh trục Ox bằng 64 16 256 4 A. . B. . C. . D. . 15 15 15 3
Câu 10. Thể tích khối tròn xoay giới hạn bởi các đường 2
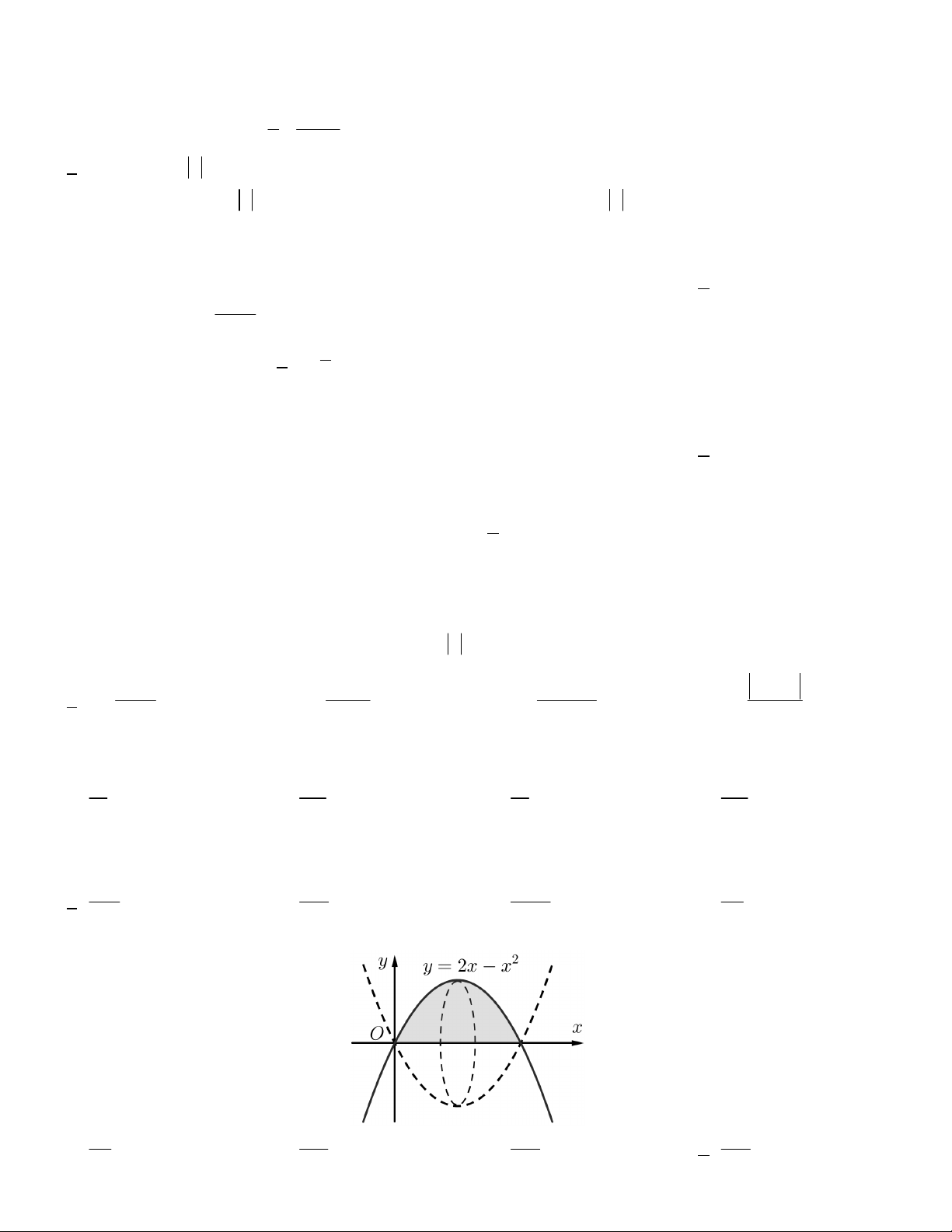
y 2x x , y 0 khi quay quanh trục Ox là: 4 13 14 16 A. . B. . C. . D. . 3 15 15 15 Lời giải 18
Câu 11. Biết F x là một nguyên hàm của hàm số 5 x
f x e 2 thoả mãn F 0 1. Khẳng định nào sau đây đúng? 1 x 4 A. F x 5 e 2x . B. 5x F x e . 5 5 1 1 x 4 C. F x 5 e . D. 5 x F x
e 2x C với C là một số thực bất kì. 5 5 5
Câu 12. Một xe chuyển động với vận tốc thay đổi là 2
v(t) 3at bt . Gọi S(t) là quãng đường đi được sau t
giây. Biết rằng sau 5 giây thì quãng đường đi được là 150m , sau 10 giây thì quãng đường đi được là 1100m .
Tính quãng đường xe đi được sau 20 giây. A. 8400m B. 8000m C. 7600m D. 7200m
TRẮC NGHIỆM ĐÚNG, SAI
Câu 1. Cho hàm số f x 2 2
3x 2 sin x sin x 1. Gọi F x là nguyên hàm của hàm số f x . Các khẳng định sau đúng hay sai? a) f x 2
3x sin x cos 2 . x . b) F x 3
ax b cos x c sin 2x m thì a b c 5 . 3
c) Nếu F 0 2 thì F . 2 8
d) Hàm số g x F x 3 x sin . x cos x chẵn.
Câu 2. Vào năm 2014 , dân số nước ta khoảng 90,7 triệu người. Giả sử, dân số nước ta sau t năm được xác
định bởi hàm số S t (đơn vị: triệu người), trong đó tốc độ gia tăng dân số được cho bởi 0,014 1, 2698.e t S t ,
với t là số năm kể từ năm 2014 , S t tính bằng triệu người/ năm. Xét tính đúng, sai của các khẳng định sau
a) S t là một nguyên hàm của St . b) 0,014 90, 7.e t S t 90, 7.
c) Theo công thức trên, tốc độ tăng dân số nước ta năm 2034 (làm tròn đến hàng phần mười của triệu người/
năm) khoảng 1,7 triệu người/ năm.
d) Theo công thức trên, dân số nước ta năm 2034 (làm tròn đến hàng đơn vị của triệu người) là khoảng 120 triệu người/ năm.
Câu 3. Một vật chuyển động với gia tốc a t t 2
4cos m/s . Tại thời điểm bắt đầu chuyển động vật có
vận tốc bằng 0. Xét tính đúng sai của các khẳng đính sau:
a) Vận tốc của vật được biểu diễn bởi hàm số v t 4cost m/s.
b) Vận tốc của vật tại thời điểm t là 2 m/s 6
c) Tại thời điểm t
s sau khi xuất phát thì vận tốc của vật là 2m/s 4
d) Gia tốc của vật tại thời điểm t (s) là 2 2 2 m/s 4
Câu 4. Cây KEO LAI là một trong các loài cây không chỉ là nguyên liệu giấy quan trọng mà còn là loài cây cung
cấp gỗ nguyên liệu cho các ngành khác như chế biến ván nhân tạo, chế biến đồ mộc xuất khẩu, gỗ bao bì, gỗ
xây dựng. Cây phát triển với tốc độ nhanh. Kí hiệu h(x) là chiều cao của một cây (tính theo mét) sau khi trồng 9
x năm. Biết rằng sau năm đầu tiên cây cao 8m .Trong 10 năm tiếp theo cây phát triển với tốc độ h x x
(m/năm). Xét tính đúng sai của các khẳng đính sau:
a) Biểu thức của h x là: h x 9 ln x C .
b) Sau 3 năm cây cao 20m .
c) Tốc độ phát triển của cây trong 10 năm đầu sẽ giảm dần.
d). Người ta thường thu hoạch cây KEO LAI khi nó có độ cao trong khoảng từ 26 đến 28 mét. Vậy đó là 8 hoặc 9 năm sau khi trồng. 19
TRẮC NGHIỆM TRẢ LỜI NGẮN Câu 1. Biết
F x và G x là hai nguyên hàm của hàm số
f x trên và 2
f x dx F 2 G 0 a a 0
. Gọi S là diện tích hình phẳng giới hạn bởi các đường y F x , 0
y G x , x 0 và x 2 , Khi S 6 thì a bằng
Câu 2. Đặt S là diện tích của hình phẳng giới hạn bởi đồ thị của hàm số 2
y 4 x , trục hoành và đường thẳng 25
x 2 , x m , 2 m 2 . Tìm số giá trị của tham số m để S . 3 1 0 khi x 1
Câu 3. Cho hàm số f x 2 x . Tích phân I 3
t f t dt
bằng bao nhiêu? Làm tròn kết quả
x 1 khi x 1 2
đến chữ số thập phân thứ 2 4 Câu 4. Cho hàm số 4 2
y ax bx c có đồ thị như hình vẽ. Biết miền tô đậm có diện tích bằng và điểm B 15
có hoành độ bằng 1. Số giá trị nguyên của tham số m thuộc đoạn [3;3] để hàm số 3x y f m có đúng một điểm cực trị là A. 1. B. 6. C. 2. D. 0.
Câu 5. Cho hàm số f x có đạo hàm liên tục trên , f 0 0, f 0 0 và thỏa mãn hệ thức
f x f x 2 x 2 . 18
3x x f x 6x
1 f x, x . 1 Biết f x 2 e dx . a e b
, với a;b . Tính giá trị của T a b . 0
Câu 6. Một tấm kính làm mặt bàn (H1) có hình dáng tam giác đều với 3 đỉnh được làm cong (H2). Biết
cạnh tấm kính tam giác ban đầu bằng 12 (dm). Để cắt góc được đẹp thì người ta dùng đường Parabol 3 (P): 2 y
x 5 3 (H3) có hai nhánh tiếp giáp với hai cạnh của tam giác (H4) 4 H1 H2 H3 H4
Diện tích mặt kính là một số có dạng a b . Tính tổng a b . 20

