Lý thuyết Chương 4 - Xác suất thống kê | Trường Đại học Khoa học Tự nhiên, Đại học Quốc gia HCM
Lý thuyết Chương 4 - Xác suất thống kê | Trường Đại học Khoa học Tự nhiên, Đại học Quốc gia HCM được sưu tầm và soạn thảo dưới dạng file PDF để gửi tới các bạn sinh viên cùng tham khảo, ôn tập đầy đủ kiến thức, chuẩn bị cho các buổi học thật tốt. Mời bạn đọc đón xem!
Trường: Trường Đại học Khoa học tự nhiên, Đại học Quốc gia Thành phố Hồ Chí Minh
Thông tin:
Tác giả:
Thông tin :
Môn:
Trường:
Trường Đại học Khoa học tự nhiên, Đại học Quốc gia Thành phố Hồ Chí Minh
Tác giả:
Tài liệu liên quan:
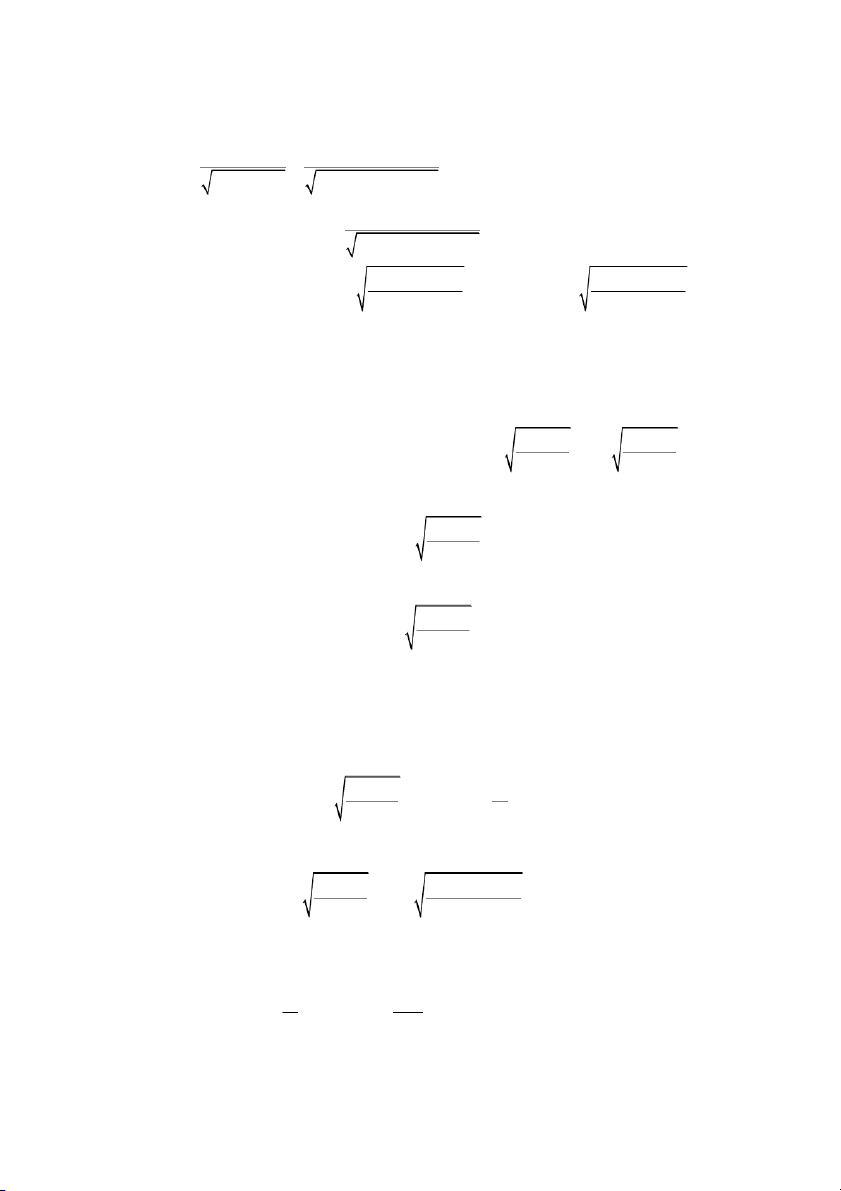
Preview text:
5 Chương 4
LÝ THUYẾT MẪU & THỐNG KÊ SUY DIỂN
Giả sử muốn nghiên cứu về trọng lượng người Việt Nam. Phương pháp chính xác nhất là đo
trọng lượng tất cả mọi người, ghi lại số liệu, và từ đó có thể tính được trọng lượng trung bình, độ
phân tán, tỷ lệ người có trọng lượng trong khoảng a, b , v.v... Điều này không thực tế, vì như vậy
thì số liệu thống kê quá nhiều, rất tốn kém. Ngoài ra, trong bài toán chất lượng sản phẩm, chẳng hạn
bài toán kiểm tra hàm lượng chất béo trong một loại thực phẩm, người ta không thể phá hủy toàn bộ
sản phẩm để thu thập số liệu... Thống kê học đề nghị một phương pháp là quan sát một số trường
hợp được gọi là mẫu và trên cơ sở các số liệu quan sát này, ta suy rộng ra cho tổng thể. Muốn cho
sự suy rộng ít bị sai lầm thì mẫu phải đại diện cho tổng thể, và do đó, việc lấy mẫu phải được thực
hiện sao cho mọi cá thể có cơ hội được quan sát đồng đều như nhau mà ta gọi là mẫu ngẫu nhiên.
Trong chương này, ta khảo sát các đặc trưng quan trọng của một biến số ngẫu nhiên X xác
định trên một tổng thể, gồm trung bình tổng thể , phương sai tổng thể 2
, cũng như tỷ lệ tổng X X
thể p, bằng cách thu thập số liệu của X trên một mẫu ngẫu nhiên, x , x ,
, lấy từ tổng thể. Các 1 2
đặc trưng trên mẫu, gồm trung bình mẫu X , phương sai mẫu 2
S , cũng như tỷ lệ mẫu f, được dùng X
để ước lượng cũng như kiểm định các giả thuyết liên quan đến , 2 , và p. X X 1. LÝ THUYẾT MẪU
Ứng với mỗi một mẫu ngẫu nhiên gồm n phần tử lấy từ tổng thể, ta nhận được một bộ số liệu quan sát x , x ,
của một biến số ngẫu nhiên X. Gọi X , i 1, 2,
, là biến ngẫu nhiên nhận 1 2 i
giá trị x từ mẫu ngẫu nhiên được chọn. Do các phần tử của tổng thể được giả định là có cơ may i
được chọn như nhau trong các mẫu ngẫu nhiên nên X , X ,
được coi là các biến ngẫu nhiên 1 2
độc lập và có cùng phân phối (với phân phối của X xác định trên tổng thể). 1.1. Thống Kê
Thống kê là một biểu thức theo mẫu X , X ,
, ký hiệu T T X , X , . Ứng với 1 2 1 2
mỗi bộ số liệu quan sát x , x , nhận
được, ta được một giá trị của thống kê T, 1 2 T T x , x ,
, và do đó, thống kê T là một biến số ngẫu nhiên. 1 2
Tùy theo từng vấn đề nghiên cứu, ta có thể đặt ra một hay nhiều thống kê khác nhau. Các
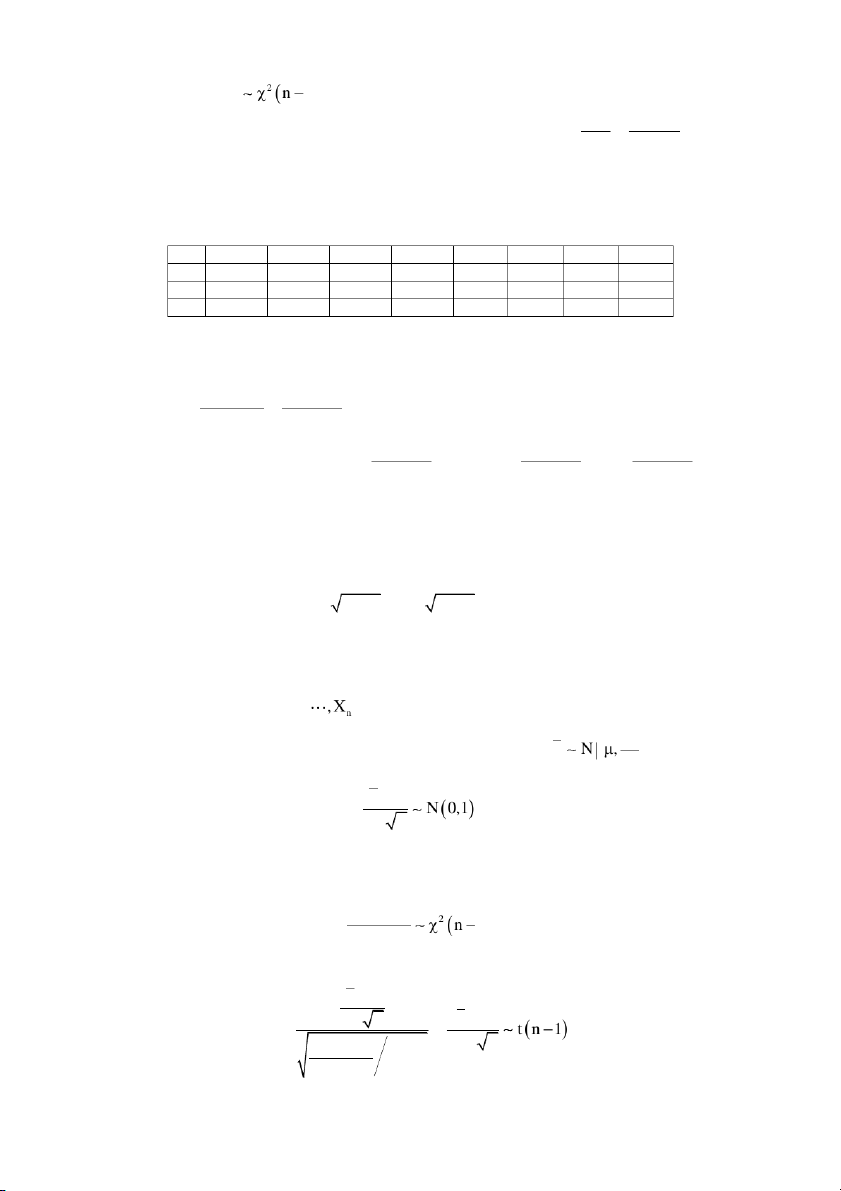
thống kê quan trọng thường dùng là 1. Trung bình mẫu X X : 1 2 X , n X X X X X 2 1 2 2 2 2 2. Phương sai mẫu : S , X n 1
3. Tỷ lệ mẫu : tỷ lệ cho các giá trị của X lấy trong vùng a, b, a b , được xác định bởi #X : a X b i i f , n trong đó
# X : a X b chỉ số số liệu nằm trong vùng a, b . i i 6
Trong thống kê suy diễn, trung bình mẫu, phương sai mẫu, và tỷ lệ mẫu được sử dụng trong
các bài toán ước lượng và kiểm định liên quan đến trung bình, phương sai, và tỷ lệ tổn g thể. Ví dụ 1.
Quan sát chiều cao X (cm) của 10 người, ta ghi được
158, 163, 157, 162, 154, 152, 160, 159, 165, 156.
Với mẫu trên, ta tính được
Chiều cao trung bình mẫu : X 158.60cm , Phương sai của mẫu : 2 2 S 16.49cm , X
Tỷ lệ mẫu trong vùng 3 158,160 : f
do tập các số liệu trong vùng 158,160 , 10 X :158 X 16
0 , chứa 3 số liệu : 158, 160, 159. i i
Tương tự như các tham số đặc trưng cho một biến ngẫu nhiên, trung bình mẫu là giá trị mà ta
hy vọng nhận được khi xem xét một phần tử của mẫu, phương sai mẫu cho ta biết mức độ phân tán
của số liệu mẫu. Phương sai càng nhỏ, số liệu càng ít phân tán.
Lưu ý rằng trong trường hợp số liệu mẫu có lặp lại và ta ghi nhận các tần số xuất hiện của số
liệu trong bảng tần số sau X x x x 1 2 k Tần số n n n 1 2 k
thì cỡ mẫu là n n n
và các công thức tính trung bình cũng như phương sai trở thành 1 2 k n x n x 1 1 2 2 X n x , i i n i1 k 1 S n x X2 2 . X i i n 1 i 1
Ví dụ 2. Để khảo sát trọng lượng X (kg) của dân cư một vùng, người ta thu thập số liệu của X trên
một nhóm người chọn ngẫu nhiên ở vùng này, X 40-45 45-50 50-55 55-60 60-65 65-70 Số người 4 9 17 14 10 2
Điều này có nghĩa là : ta có cả thảy 4 9 17 1410 2 56 số liệu (cỡ mẫu n 56 ), trong đó có
4 số liệu trong khoảng 40,45 , 9 số liệu trong khoảng 45,50 , v.v… Để ước lượng X và 2
S , ta thay thế mỗi khoảng dữ liệu bằng điểm giữa và được bảng tần số X X 42.5 47.5 52.5 57.5 62.5 67.5 Số người 4 9 17 14 10 2
Bấy giờ, ta có trung bình mẫu 42.5 4 47.5 9 1 0 67.5 2 X 54.55 , 56 phương sai mẫu
42.5 54.552 4 47.5 54.552 9 54.552 1
0 67.5 54.552 2 2 S 39.8 , X 56 1
và độ lệch chuẩn mẫu 7 S 34.9 6.31 . X
Ngoài ra, nếu ta quan tâm đến tỷ lệ người “bình thường”, có trọng lượng từ 50 đến 60 kg, ta có tỷ lệ
người “bình thường” trên mẫu là 17 14 f 0.55 55% . 56
1.2. Phân Phối Xác Suất Các Thống Kê Quan Trọng
Như ta đã khảo sát trong các chương trước, các biến số ngẫu nhiên X nhận được từ việc quan
sát các phép thử có phân phối gần đúng với phân phối chuẩn 2
N , . Do đó, bằng số liệu thống
kê trên mẫu lấy từ tổng thể có phân phối chuẩn, ta cần khảo sát các phân phối của thống kê nhận
được từ mẫu, đặc biệt là phân phối của trung bình mẫu và phương sai mẫu. Ta có
1.2.1. Định lý. Nếu mẫu X , X ,
lấy từ tổng thể có phân phối chuẩn 2 N , , nghĩa là 1 2 X , với mọi i, thì i 2 X (1) n và n 2 1 S X 1 . (2) 2
Định lý trên cho thấy thống kê X có kỳ vọng là tham số , trung bình tổng thể, và thống kê 2
S có kỳ vọng là tham số 2
, phương sai tổng thể. Nói cách khác, với mẫu ngẫu nhiên lấy từ tổng X
thể có phân phối chuẩn 2 N ,
, trung bình mẫu X sẽ dao động xung quanh và phương sai mẫu 2
S sẽ dao động xung quanh 2
. Đó là lý do ta dùng trung bình mẫu để suy diễn cho trung bình X
tổng thể, dùng phương sai mẫu để suy diễn cho phương sai tổng thể.
Để có thể suy diễn cho tỷ lệ tổng thể p, ta dùng kết quả sau
1.2.2. Định lý giới hạn trung tâm. Với mẫu ngẫu nhiên Y , Y ,
có cùng một phân phối với 1 2
trung bình và phương sai 2
, trung bình mẫu Y Y 1 2 Y , n
có phân phối gần đúng với phân phối chuẩn trung bình , phương sai 2
/ n , khi n lớn, 2 Y . n
Xuất phát từ mẫu ngẫu nhiên X , X ,
lấy từ phân phối chuẩn 2
N , , để ước lượng 1 2
tỷ lệ p các giá trị X nằm trong vùng a, b , ta đặt 1 , X a,b , i Y i 0, X a, b . i với i 1,2,
, và được mẫu ngẫu nhiên Y , Y ,
có phân phối Bernoulli B 1, p , với trung 1 2
bình 1 p p , và phương sai 2 1 p1 p p 1
p . Do định lý giới hạn trung tâm, ta có 8 p 1 p Y . (a) n
Mặt khác, số các X nằm trong vùng a, b chính là số các Y
lấy giá trị 1, ta được i i #X : a X b Y Y , i i 1 2 và do đó, #X : a X b Y Y i i 1 2 f Y . (b) n n Từ (a, b), ta suy ra p1 p f . (3) n
khi n lớn. Điều này cho thấy tỷ lệ mẫu f có kỳ vọng là tỷ lệ tổng thể p và do đó ta dùng tỷ lệ mẫu f
để suy diễn cho tỷ lệ tổng thể p.
2. ƯỚC LƯỢNG KHOẢNG
Để ước lượng các tham số quan trọng cho một biến số ngẫu nhiên X, gồm trung bình tổng thể
, phương sai tổng thể 2
và tỷ lệ tổng thể p, người ta thu thập một mẫu ngẫu nhiên X , X , 1 2
lấy từ tổng thể và trong phần trên, với các phân phối xác suất (1), (2), và (3), ta thấy trung bình mẫu X , phương sai mẫu 2
S , và tỷ lệ mẫu f, có thể dùng làm các ước lượng (điểm) cho , 2 và p. X
Để đánh giá độ chính xác của các ước lượng (điểm) này, người ta dùng khái niệm “ước lượng khoảng” như sau.
2.1. Định nghĩa. Ứng với một mức xác suất cho trước, khoảng a, b được gọi là một khoảng tin
cậy của tham số ở độ tin cậy khi
P a b .
Các độ tin cậy thông dụng là 0.9 , 0.95, và 0.99, trong đó giá trị 0.95 thường được dùng làm
độ tin cậy mặc nhiên trong các phần mềm thống kê.
Để tìm một khoảng tin cậy cho tham số , ta có
2.2. Định nghĩa. Với mẫu ngẫu nhiên X , X ,
lấy từ tổng thể có tham số , một thống kê T 1 2
xác định trên mẫu ngẩu nhiên này được gọi là một thống kê trục xoay cho khi T lệ thuộc vào ,
T T , nhưng có phân phối hoàn toàn xác định, không phụ thuộc vào .
Ví dụ 3. Xét mẫu ngẫu nhiên X , X ,
lấy từ phân phối chuẩn 2
N , . Với kết quả (2) của 1 2 định lý 1.2.1, n 2 1 S X 1 , 2 ta có thống kê n 2 1 SX T 2 phụ thuộc vào tham số 2
nhưng có phân phối hoàn toàn xác định, 2
n 1 , nên 2 T T là
một thống kê trục xoay cho tham số 2 . 9
Ứng với thống kê trục xoay T T cho tham số , ta có
2.3. Giải thuật tìm một khoảng tin cậy cho tham số
Input : Thống kê trục xoay T T cho tham số và độ tin cậy .
Bước 1. Từ phân phối xác suất của thống kê T, xác định khoảng ước lượng hai bên, a, b , của T ở mức xác suất ,
P a T b .
Bước 2. Giải các bất phương trình a T b theo ẩn , ta được c d . Suy ra
P c d P a T b .
Output. c,d là một khoảng tin cậy của và độ tin cậy . n 2
Áp dụng giải thuật này với thống kê trục xoay 1 SX T 1 cho tham số phương 2 sai tổng thể 2 , ta có 2.4. Ước lượng 2
trong phân phối 2 N ,
Từ mẫu ngẫu nhiên X , X ,
lấy từ tổng thể có phân phối chuẩn 2
N , , ta thành lập 1 2 n 2 thống kê trục xoay cho 1 S 2 , X T
1 . Áp dụng giải thuật 2.3, 2 Bước 1. Với T
1 và độ tin cậy cho trước, tìm khoảng ước lượng hai bên a, b cho T,
P a T b . n 2
Bước 2. Với biểu thức 1 SX T
, giải các bất phương trình a T b , 2 n 2 1 S n 2 1 S n 2 1 S X X 2 X a T b a b . 2 b a Kết luận. Do n 2 1 S n 1 S 2 2 X X P
P a T b , b a n 2 1 S n 1 S X 2 ta suy ra X ,
là một khoảng tin cậy cho 2 ở độ tin cậy . b a
Ví dụ 4. Với số liệu nhận được trong ví dụ 2, ta có cỡ mẫu n 56 , trung bình mẫu X 54.55 , phương sai mẫu 2
S 39.8 và độ lệch chuẩn mẫu S 6.31 . Để ước lượng phương sai 2 ở độ tin X X
cậy 0.95 , ta dùng thống kê trục xoay n 2 1 SX T 1 , 2
và áp dụng giải thuật 2.3, 10 Bước 1. Do n 56 , 2 T 1 5
5 , nên với 0.95 , ta tìm được khoảng ước lượng hai
bên a, b cho T ở mức xác suất 0.95 : Do 1 1 0.95 P T b P T a 0.025 , ta 2 2 được
P T a 1 P T a 0.975 và P T b 0.025 ,
và từ bảng phân phối chi-bình phương, 0.025 0.975 55 77.380 36.398
ta được a 36.398 , b 77.380 , nghĩa là
P 36.398 T 77.380 0.95 . n 2 1 S Bước 2. Với 55 39.8 X T , ta có 2 2 55 39.8 55 39.8 55 39.8 2
36.398 T 77.380 36.398 77.380 2 77.380 36.398 2 28.29 60.14. Kết luận. Do 2
P 28.29 60.14 0.95 , ta được khoảng tin cậy của 2
ở độ tin cậy 0.95 là 28.29,60.1 4 . Ghi chú. Do 2
28.29 60.14 28.29
60.14 5.32 7.75 , ta còn suy ra khoảng
tin cậy cho độ lệch chuẩn ở độ tin cậy 0.95 là 5.32,7.75 .
2.5. Ước lượng trong phân phối 2 N ,
Từ mẫu ngẫu nhiên X , X ,
lấy từ tổng thể có phân phối chuẩn 2
N , , ta cần thành 1 2 2
lập thống kê trục xoay cho . Do kết quả (1) của định lý 1.2.1, ta có X và do đó, n X . / n
Tuy nhiên do thống kê nêu trên lệ thuộc vào hai tham số chưa biết, và 2
, nên ta chưa thể dùng
làm thống kê trục xoay cho . Bằng cách kết hợp với kết quả (2) của định lý 1.2.1, n 2 1 S X 1 , 2
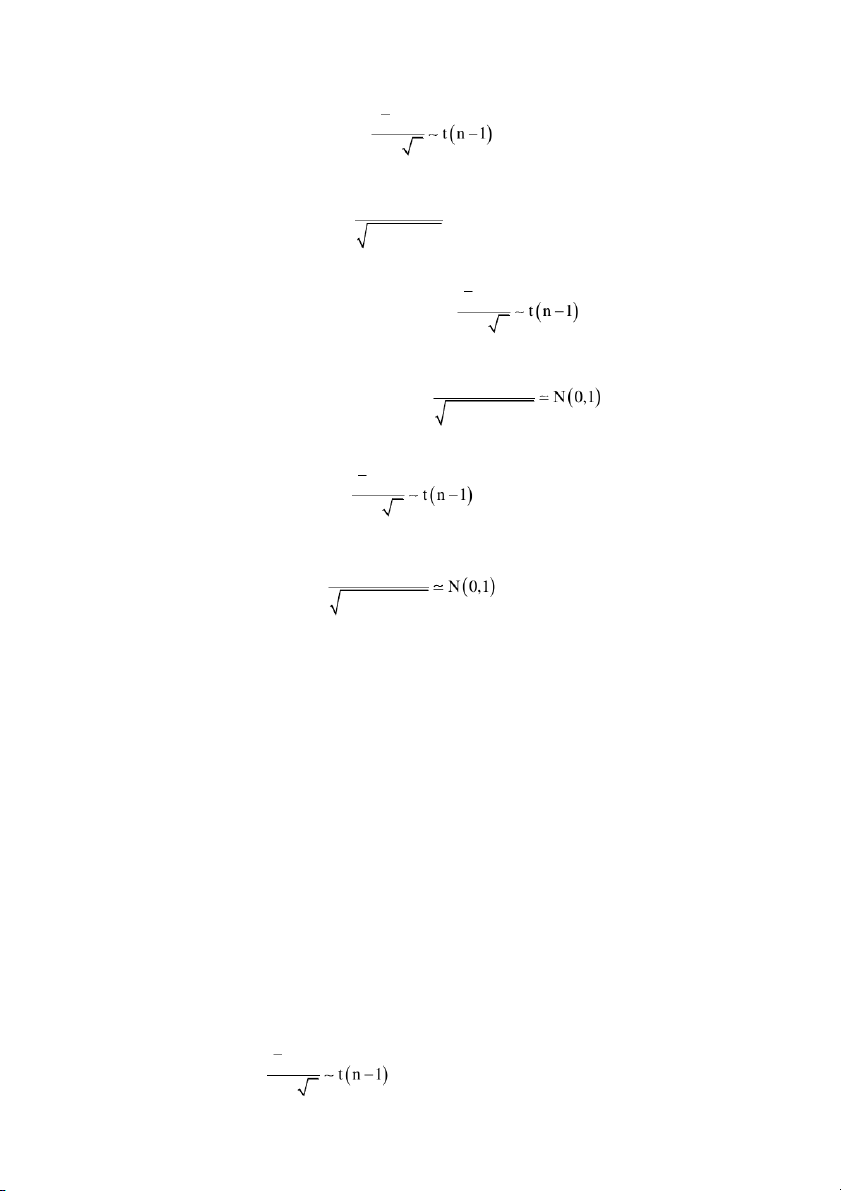
với tính chất của phân phối Student, ta được X / n X T . n 2 1 S n S / n X X 1 2
Do T chỉ còn lệ thuộc vào tham số
nhưng có phân phối hoàn toán xác định nên ta được 11 Thống kê trục xoay X cho : T . (4) S / n X
Áp dụng giải thuật 2.3, Bước 1. Với T
và độ tin cậy cho trước, tìm khoảng ước lượng hai bên C,C cho T,
P C T C .
Bước 2. Với biểu thức X T
, giải các bất phương trình C T C , S / n X X S S X X C T C C C X C X C . S / n n n X Kết luận. Do S S X X P X C X C P C T C , n n S S ta suy ra X X X C , X C
là một khoảng tin cậy cho ở độ tin cậy . n n
Ví dụ 5. Cũng với số liệu nhận được trong ví dụ 2 : cỡ mẫu n 56 , trung bình mẫu X 54.55 , phương sai mẫu 2
S 39.8 và độ lệch chuẩn mẫu S 6.31. Để ước lượng trung bình ở độ tin X X
cậy 0.95 , ta dùng thống kê trục xoay X T . S / n X
Áp dụng giải thuật 2.3, Bước 1. Do n 56 , T 1 t5
5 , nên với 0.95 , ta tìm được khoảng ước lượng hai bên
C,C cho T ở mức xác suất 0.95 : Do P T C 1 P C T C1 1 0.95 0.05 ,
ta được từ bảng phân phối Student, 0.05 1.960
ta được C 1.96 , nghĩa là P 1
.96 T 1.96 0.95. Bước 2. Với X 54.55 T , ta có S / n 6.31/ 56 X 54.55 6.31 6.31 1 .96 T 1.96 1 .96 1.96 54.55 1.96 54.55 1.96 6.31/ 56 56 56 52.9 56.2.
Kết luận. Do P 52.9 56.2 0.95 , ta được khoảng tin cậy của ở độ tin cậy 0.95 là 52.9,56.2 . 12 S S
Ghi chú. Khoảng tin cậy X X X C , X C
cho còn được viết dưới dạng n n SX X C , n trong đó, đại lượng SX C n
được gọi là sai số ước lượng cho ở độ tin cậy . Do sai số ước lượng này sẽ nhỏ khi cỡ mẫu n
lớn, ta có bài toán xác định cỡ mẫu ứng với một sai số ước lượng cho trước: 0
Bài toán cỡ mẫu : Nếu muốn sai số ước lượng cho ở độ tin cậy không quá mức cho trước, 0 cỡ mẫu thỏa 2 S S X X C n C . 0 0 n 0
Ví dụ 6. Tiếp theo ví dụ 5, ta có sai số ước lượng cho ở độ tin cậy 0.95 là S 6.31 X C 1.96 1.65 . n 56
Do vậy, nếu ta muốn sai số ước lượng nhỏ hơn, chẳng hạn nếu muốn sai số ước lượng không quá mức 1.5 , ta cần 0 2 2 S 6.31 X n C 1.96 67.98 , 1.5 0
nghĩa là ta cần ít nhất n 68 số liệu. Chú ý rằng do ta đã có 56 số liệu nên ta chỉ cần thu thập thêm 68 56 12 số liệu.
2.6. Ước lượng tỷ lệ tổng thể p
Từ mẫu ngẫu nhiên X , X ,
lấy từ tổng thể có phân phối chuẩn 2 N ,
, để ước lượng 1 2
tỷ lệ p P a X b , do định lý giới hạn trung tâm, từ (3) ta có p1 p f , (3 ) ’ n #X : a X b i i
khi n lớn, chẳng hạn n 30 , với f )
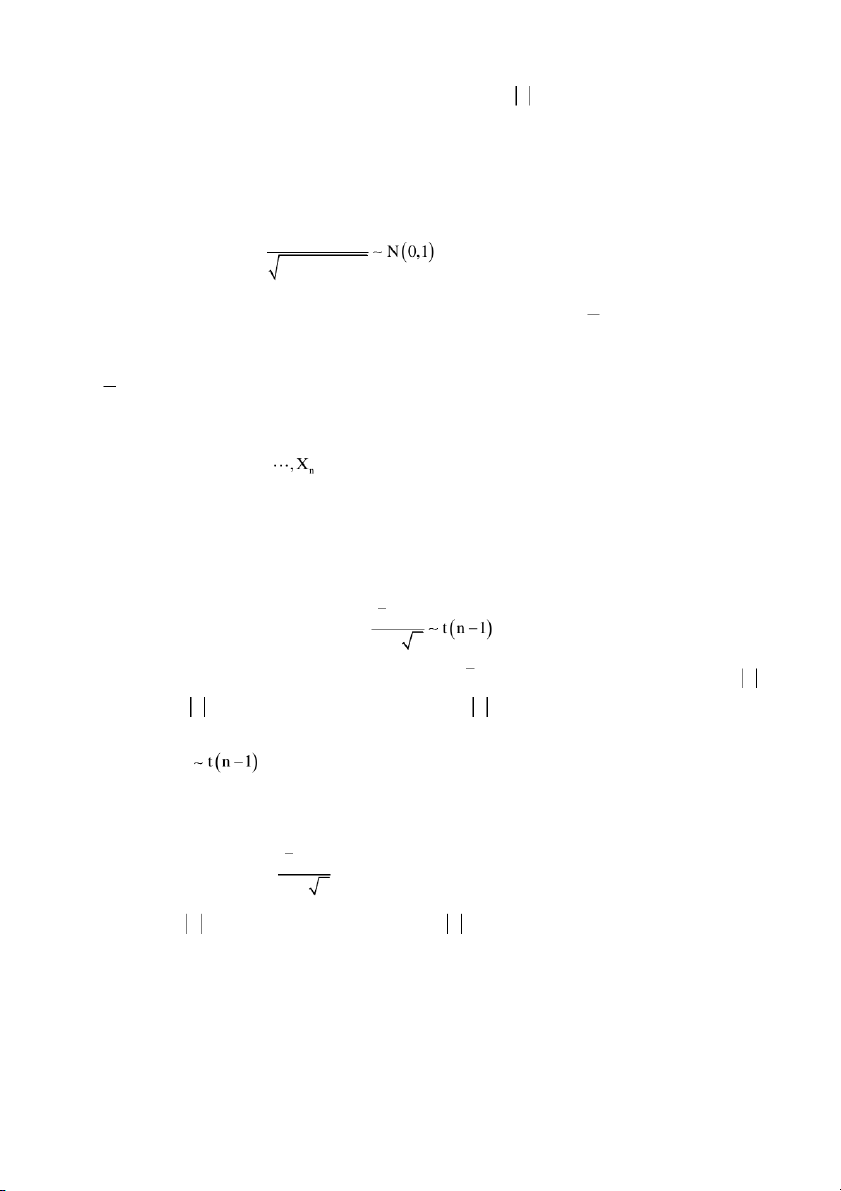
là tỷ lệ mẫu. Từ (3’ , ta suy ra n f p T . (5) p1 p / n
Do T lệ thuộc vào tham số p chưa biết nhưng có phân phối hoàn toàn xác định nên ta có thể dùng T
làm thống kê trục xoay cho p. Tuy nhiên, với thống kê trục xoay này, trong bước 2 của giải thuật
2.3, ta phải giải hệ bất phương trình f p a T b a b p 1 p / n 13
gồm hai bất phương trình bậc hai theo ẩn số p. Do đó, người ta thay mẫu số p1 p / n trong
thống kê T ở (5) bằng một xấp xỉ của nó, f 1 f / n , để nhận được Thống kê trục xoay f p cho p : T , với n 30 . ( ) 6 f 1 f / n
Áp dụng giải thuật 2.3, Bước 1. Với T
và độ tin cậy cho trước, tìm khoảng ước lượng hai bên C,C cho T,
P C T C .
Bước 2. Với biểu thức f p T
, giải các bất phương trình C T C , f 1 f / n f p f 1 f f 1 f C T C C C f C p f C . f 1 f / n n n Kết luận. Do f 1 f f 1 f P f C p f C P C T C , n n f 1 f f 1 f ta suy ra f C , f C
là một khoảng tin cậy cho p ở độ tin cậy . n n
Ví dụ 7. Với số liệu nhận được trong ví dụ 2, ta tìm khoảng tin cậy cho tỷ lệ người “bình thường”,
có trọng lượng từ 50 đến 60 kg,
p P 50 X 60 ,
ở độ tin cậy 0.95 .
Với số liệu nhận được, ta có cỡ mẫu n 56 , và tỷ lệ người “bình thường” trên mẫu là 17 14 f 0.55 55% . 56
ta dùng thống kê trục xoay (6), f p T . f 1 f / n
Áp dụng giải thuật 2.3,
Bước 1. Do T N 0,1 , nên với 0.95 , ta tìm được khoảng ước lượng hai bên C,C cho T ở
mức xác suất 0.95 : Do P C T C C C 2 C 1, ta được 1 10.95 C
0.975 , và từ bảng phân phối Gauss, 2 2 0.05 0.06 0.07 1.9 0.9744 0.9750 0.9756 14
ta được C 1.96 , nghĩa là P 1
.96 T 1.96 0.95. Bước 2. Với f p 0.55 p T , ta có f 1 f / n 0.55 1 0.55 / 56 0.55 p 1 .96 T 1.96 1 .96 1.96 0.551 0.55 / 56 0.55 10.55 0.55 1 0.55 0.55 1.96 p 0.55 1.96 56 56 0.42 p 0.68.
Kết luận. Do P 0.42 p 0.68 0.95 , ta được khoảng tin cậy của ở độ tin cậy p 0.95 là 0.42,0.6 8 . f 1 f f 1 f
Ghi chú. Tương tự như trong phần 2.5, khoảng tin cậy f C , f C cho p còn n n
được viết dưới dạng f 1 f p f C , n trong đó, đại lượng f 1 f C n
được gọi là sai số ước lượng cho p ở độ tin cậy . Do sai số ước lượng này sẽ nhỏ khi cỡ mẫu n
lớn, ta cũng có bài toán xác định cỡ mẫu ứng với một sai số ước lượng cho trước: 0
Bài toán cỡ mẫu : Nếu muốn sai số ước lượng cho p ở độ tin cậy không quá mức cho trước, 0 cỡ mẫu thỏa f 1f 2 C C n f 1 f . 0 0 n 0
Ví dụ 8. Tiếp theo ví dụ , ta có sai số ước lượng cho 7 ở độ tin cậy p 0.95 là f 1 f 0.55 1 0.55 C 1.96 0.13 . n 56
Do vậy, nếu ta muốn sai số ước lượng nhỏ hơn, chẳng hạn nếu muốn sai số ước lượng không quá mức 0.1, ta cần 0 2 2 C
1.96 n f 1 f 0.55 10.5 5 95.08 , 0.1 0
nghĩa là ta cần ít nhất n 96 số liệu. Chú ý rằng do ta đã có 56 số liệu nên ta chỉ cần thu thập thêm 96 56 40 số liệu. 15 3. KIỂM ĐỊNH THAM SỐ
Giả sử ta đi tiếp nhận một lô hàng (rất nhiều) và ta chỉ bằng lòng nhận nếu tỷ lệ hỏng p 0.05
và từ chối nếu p 0.05 .
Vậy ta có bài toán kiểm định H : p 0.05 0 H : p 0.05 A
Mô hình tổng quát của bài toán kiểm định là : ta nêu lên hai mệnh đề khác nhau, một mệnh đề
được gọi là giả thuyết H và mệnh đề còn lại được gọi là đối thuyết H . Giải quyết một bài toán 0 A
kiểm định là nêu lên một quy tắc hành động (chấp nhận giả thuyết H hoặc bác bỏ giả thuyết H ) 0 0
bằng cách dựa vào số liệu thống kê thu thập trên một mẫu ngẫu nhiên lấy từ tổng thể .
Ta nói rằng : chấp nhận giả thuyết H , có nghĩa là ta tin rằng H đúng; từ chối H có nghĩa 0 0 0 là ta tin rằng H sai. 0 3.1. C S
ác Loại ai Lầm
Quan sát ngẫu nhiên một số trường hợp rồi suy rộng ra cho tổng thể, sự suy rộng này có khi
đúng, có khi không đúng. Thống kê học phân biệt hai loại sai lầm :
a. Sai lầm loại 1 : từ chối H , khi H đúng, 0 0
b. Sai lầm loại 2 : chấp nhận H , khi H sai. 0 0
Quyết định Chấp nhận H Từ chối H 0 0 Thực tế H đúng Đúng Sai lầm loại 1 0 H sai Sai lầm loại 2 Đúng 0
Đặt P(Sai lầm loại 1), P(Sai lầm loại 2). Ta muốn các cơ hội sai lầm xảy ra càng ít
càng tốt. Tuy nhiên, nếu hạ thấp thì sẽ tăng và ngược lại. Do đó, trên thực tế thì ta xem giữa
hai loại sai lầm này, sai lầm nào tác hại nhiều hơn thì cần tránh. Trong thống kê, ta quy ước rằng sai
lầm loại 1 tác hại hơn và cần tránh hơn. Do đó, ta chỉ xét các phép kiểm định có cơ hội sai lầm loại
1 ( ) không vượt quá một giá trị ấn định trước, thông thường là 1%; 5% hoặc 10%. Giá trị còn
được gọi là mức ý nghĩa của kiểm định.
3.2. Thống Kê Kiểm Định
Xét một giả thuyết H trên tham số của một biến số ngẫu nhiên X xác định trên một tổng 0
thể. Tương tự như trong lý thuyết về ước lượng khoảng, ta thu thập số liệu của X trên một mẫu ngẫu nhiên X , X ,
lấy từ tổng thể và thành lập một thống kê T. Ta có 1 2
3.2.1. Định nghĩa. Thống kê T xác định trên mẫu X , X ,
được gọi là một thống kê kiểm 1 2
định cho giả thuyết H khi 0
“Nếu H đúng thì phân phối xác suất cho T
được hoàn toàn xác định”. 0
Trong phần kế tiếp, ta kiểm định các giả thuyết liên quan đến tham số trung bình tồng thể
và tỷ lệ tổng thể p :
H : và H : p p , 0 0 0 0
trong đó và p là các hằng số cho trước. 0 0 16
Với thống kê (4) cho , X T , S / n X và thống kê (5) cho p, f p T N0, , 1 p 1 p / n ta có : “Nếu X
H : đúng thì 0 T ”, 0 0 S / n X và “Nếu f p
H : p p đúng thì 0 T ”. 0 0 p 1 p / n 0 0
Do đó, ta nhận được thống kê kiểm định cho H : , 0 0 X 0 T , (4’) S / n X
và thống kê kiểm định cho H : p p , 0 0 f p 0 T . (5’) p 1 p / n 0 0
3.3. Giải thuật kiểm định giả thuyết H 0
Input : Thống kê kiểm định T cho giả thuyết H và
nguy cơ sai lầm (mức ý nghĩa) . 0
Bước 1. Từ phân phối xác suất của thống kê T, xác định khoảng ước lượng, a, b , của T ở mức xác suất 1 ,
P a T b 1 .
Bước 2. Tính giá trị của T theo số liệu nhận được từ mẫu.
Output. (i) T a, b : Bác bỏ giả thuyết H (với nguy cơ sai lầm ). 0
(ii) T a, b : Chấp nhận giả thuyết H . 0
Ghi chú. a) Thực ra, khi T a, b , kết luận đúng phải là “chưa đủ dữ kiện để bác bỏ H ”. 0
b) Loại khoảng ước lượng a, b trong bước
1 tùy thuộc vào đối thuyết H . Với bài toán A
kiểm định trên trung bình tổng thể , H : , 0 0 H : , A 0 khoảng ước lượng cho X 0 T
là khoảng ước lượng hai bên C,C , với S / n X 17 P C T
C 1 và do đó, P T C ,
và giá trị C được tìm thấy trong bảng phân phối Student, dòng ứng với độ tự do n 1 , cột ứng với
giá trị của . Tương tự, với bài toán kiểm định trên trên tỷ lệ tổng thể p, H : p p , 0 0 H : p p , A 0 khoảng ước lượng cho f p 0 T
là khoảng ước lượng hai bên C,C , với p 1 p / n 0 0
P C T C 1 và do đó P T C 1 , 2
và giá trị C được tìm thấy trong bảng phân phối Gauss bằng cách xác định vị trí dòng, cột của giá trị 1 trong bảng. 2
3.4. So sánh trung bình với một số 0 Quan sát mẫu X , X , có phân phối 2
N , . Ta sẽ dùng mẫu trên để kiểm định giả 1 2
thuyết hay không với là một trị số cho trước. Ta xét bài toán kiểm định 0 0 H : 0 0 H : A 0
Ta có thống kê kiểm định cho bởi (4’), X 0 T . S / n X
Giá trị của thống kê T đo lường mức độ khác biệt giữa X và (và do đó giữa và ). Khi T 0 0
nhỏ, chẳng hạn T C , ta chấp nhận H . Ngược lại, khi T C , ta bác bỏ H . Dùng giải thuật 3.3, 0 0 ta có Bước 1. Với T
và nguy cơ sai lầm (mức ý nghĩa) , tìm khoảng ước lượng hai bên
C,C cho T ở mức xác suất 1 ,
P C T C .
Bước 2. Tính giá trị của X 0 T
từ số liệu nhận được trên mẫu. S / n X
Kết luận. Nếu T C , ta bác bỏ H . Ngược lại, nếu T C, ta chấp nhận H . 0 0 Ví dụ 9. c
Giả sử ó tài liệu liên quan đến cư dân trong vùng khảo sát ở ví dụ 2 khẳng định rằng trọng
lượng trung bình dân cư vùng này là 55 (kg). Hỏi rằng số liệu thống kê nhận được trong ví dụ 0
2 có phù hợp với tài liệu trên không? Kết luận với 0.05.
Ta có bài toán kiểm định : H : 55 0 H : 55 A 18
Với thống kê kiểm định X 0 T
, cùng dữ liệu từ ví dụ 2, n 56 , X 54.55 , S / n X
S 6.31, và 55 , ta dùng giải thuật 3.3, X 0 Bước 1. Với T
và 0.05, ta được C 1.96 , với P 1
.96 T 1.96 0.95 1 .
Bước 2. Từ số liệu nhận được, ta có X 54.55 55 0 T 0 .53 . S / n 6.31/ 56 X
Kết luận. Do T C nên ta chấp nhận H , nghĩa là số liệu thống kê phù hợp với tài liệu. 0
Ghi chú. Giả sử trọng lượng trung bình ghi nhận trong tài liệu là 52 (thay vì 55 kg), ta có bài 0 toán kiểm định H : 52 0 H : 52 A
Giá trị thống kê kiểm định T bây giờ là X 54.55 52 0 T 3.02 S / n 6.31/ 56 X
và vì T C nên ta bác bỏ H , nghĩa là số liệu thống kê không phù hợp với tài liệu. 0
3.5. So sánh tỷ lệ tổng thể p với một số p 0
Tương tự như bài toán ước lượng tỷ lệ, với một mẫu ngẫu nhiên X , X , lấy từ tổng thể 1 2 có phân phối chuẩn 2 N ,
, để so sánh tỷ lệ p P a X b với một số p cho trước, ta xét bài 0 toán kiểm định H : p p 0 0 H : p p A 0
Dùng thống kê kiểm định cho bởi (5’) , f p0 T . p 1 p / n 0 0
Giá trị của thống kê T đo lường mức độ khác biệt giữa f và p (và do đó giữa p và p ). Khi T 0 0
nhỏ, chẳng hạn T C , ta chấp nhận H . Ngược lại, khi T C , ta bác bỏ H . Dùng giải thuật 3.3, 0 0 ta có Bước 1. Với T
và nguy cơ sai lầm (mức ý nghĩa) , tìm khoảng ước lượng hai bên
C,C cho T ở mức xác suất 1 ,
P C T C .
Bước 2. Tính giá trị của f p0 T
từ số liệu nhận được trên mẫu. p 1 p / n 0 0
Kết luận. Nếu T C , ta bác bỏ H . Ngược lại, nếu T C, ta chấp nhận H . 0 0 19
Ví dụ 10. Tương tự như ví dụ 9, giả sử tài liệu liên quan đến cư dân trong vùng khảo sát ở ví dụ 2
khẳng định rằng tỷ lệ người “bình thường” (có trọng lượng từ 50 đến 60 kg) là p 60% . Hỏi rằng 0
số liệu thống kê nhận được trong ví dụ 2 có phù hợp với tài liệu trên không? Kết luận với 0.1.
Ta có bài toán kiểm định : H : p 0.6 0 H : p 0.6 A
Với thống kê kiểm định f p0 T
, cùng dữ liệu từ ví dụ 2, n 56 , và tỷ lệ p 1 p n 0 0
người “bình thường” trên mẫu là 17 14 f 0.55 55% , 56 ta dùng giải thuật 3.3, Bước 1. Với T
và 0.1, ta được C 1.645 , với P 1
.645 T 1.645 0.9 1 .
Bước 2. Từ số liệu nhận được, ta có f p 0.55 0.6 0 T 0 .76 . p 1 p n 0.6 1 0.6 / 56 0 0
Kết luận. Do T C nên ta chấp nhận H , nghĩa là số liệu thống kê phù hợp với tài liệu. 0
Ghi chú. Giả sử tỷ lệ người “bình thường” ghi nhận trong tài liệu là p 40% (thay vì 60%), ta có 0 bài toán kiểm định H : p 0.4 0 H : p 0.4 A
Giá trị thống kê kiểm định T bây giờ là f p 0.55 0.4 0 T 2.29 p 1 p n 0.4 1 0.4 / 56 0 0
và vì T C nên ta bác bỏ H , nghĩa là số liệu thống kê không phù hợp với tài liệu. 0 Bài tập
1. Sau khi áp dụng một chế độ dinh dưỡng mới cho dân cư một vùng, người ta đo hàm lượng
cholesterol X (đơn vị mg%) cho một nhóm người trong vùng, với số liệu nhận được như sau X 150-160 160-170 170-180 180-190 190-200 200-210 Số người 3 9 11 6 4 3
Già sử X có phân phối chuẩn.
a) Tìm khoảng tin cậy cho phương sai tổng thể 2
và độ lệch chuẩn tổng thể ở độ tin cậy X X 0.95 .
b) Tìm khoảng ước lượng cho trung bình tổng thể, , ở độ tin cậy 0.95 . X
c) Nếu muốn sai số ước lượng cho trung bình tổng thể, , không quá 4 mg%, ở độ tin cậy X 0
0.95 , thì phải thu thập thêm ít nhất bao nhiêu số liệu ? 20
d) Trước đây, lượng cholesterol trung bình của dân cư vùng này là 180 mg%. Hỏi rằng chế độ 0
dinh dưỡng mới có làm thay đổi hàm lượng cholesterol trung bình không ? (kết luận với 0.1).
e) Người có hàm lượng cholesterol từ 180 mg% trở lên được gọi là có hàm lượng cholesterol cao.
Tìm khoảng ước lượng tỷ lệ người có hàm lượng cholesterol cao tổng th ể , ở độ tin cậy , p 0.95 .
f) Nếu muốn sai số ước lượng cho tỷ lệ người có hàm lượng cholesterol cao, p, không quá
15% , ở độ tin cậy 0.95 , thì phải thu thập thêm ít nhất bao nhiêu số liệu ? 0
g) Trước đây, tỷ lệ người có hàm lượng cholesterol cao của dân cư vùng này là p 55% . Hỏi rằng 0
chế độ dinh dưỡng mới có làm thay đổi tỷ lệ người có hàm lượng cholesterol cao không ? (kết luận với 0.1).
2. Một máy đóng gói các sản phẩm được thiết kế cho ra sản phẩm có khối lượng trung bình
2kg . Sau một thời gian sử dụng, nghi ngờ máy hoạt động không bình thường, người ta tiến 0
hành thu thập số liệu trên một mẫu ngẫu nhiên các sản phẩm và nhận được kết quả như sau : Khối lượng X (kg) 1.5 1.7 1.9 2.1 2.3 2.5 Số sản phẩm 6 30 40 15 3 2
Già sử X có phân phối chuẩn.
a) Tìm khoảng tin cậy cho phương sai tổng thể 2
và độ lệch chuẩn tổng thể ở độ tin cậy X X 0.95 .
b) Tìm khoảng ước lượng cho trung bình tổng thể, , ở độ tin cậy 0.95 . X
c) Nếu muốn sai số ước lượng cho trung bình tổng thể, , không quá 0.03 kg, ở độ tin cậy X 0
0.95 , thì phải thu thập thêm ít nhất bao nhiêu số liệu ?
d) Tham số thiết kế máy đóng gói cho biết khối lượng trung bình sản phẩm là 2kg . Hỏi rằng số 0
liệu thu thập nêu trên có còn phù hợp với tham số trung bình này không ? (kết luận với 0.1).
e) Sản phẩm đạt chuẩn phải có khối lượng từ 1.9 kg đến 2.1 kg. Tìm khoảng ước lượng tỷ lệ sản
phẩm đạt chuẩn tổng thể , , ở độ tin cậy p 0.95 .
f) Nếu muốn sai số ước lượng cho tỷ lệ sản phẩm đạt chuẩn, p, không quá 9% , ở độ tin cậy 0
0.95 , thì phải thu thập thêm ít nhất bao nhiêu số liệu ?
g) Tỷ lệ sản phẩm đạt chuẩn theo thiết kế là p 80% . Hỏi rằng số liệu thu thập nêu trên có còn phù 0
hợp với tham số thiết kế này không ? (kết luận với 0.1).