19 trang 8 lượt tải

Lý thuyết Chương 6: Sự chéo hóa của ma trận vuông môn Đại số tuyến tính | Trường Đại học Khoa học tự nhiên, Đại học Quốc gia Thành phố Hồ Chí Minh

16

Lý thuyết Chương 6: Sự chéo hóa của ma trận vuông môn Đại số tuyến tính | Trường Đại học Khoa học tự nhiên, Đại học Quốc gia Thành phố Hồ Chí Minh. Tài liệu được sưu tầm giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem.

Môn: Đại số tuyến tính (HCMUS) 24 tài liệu

Trường: Trường Đại học Khoa học tự nhiên, Đại học Quốc gia Thành phố Hồ Chí Minh 1.1 K tài liệu

Tác giả:

Profile

lulu

2 tuần trước
Tải xuống
Báo cáo
Danh sách Quiz
Tải xuống
/19
1
GV LÊ VĂN HỢP ĐẠI SỐ TUYẾN TÍNH
CHƯƠNG 6 : SỰ CHÉO HÓA CỦA MA TRẬN VUÔNG
I. TỔNG TRỰC TIẾP CÁC KHÔNG GIAN CON:
1.1/ ĐỊNH NGHĨA: Giả sử R
n
có các không gian con H
1
, H
2
, …, H
k
( k 2 ).
Ta nói R
n
là tổng trực tiếp của các không gian con H
1
, H
2
, …, H
k
(ký hiệu R
n
= H
1
H
2
H
k
hay R
n
=
1
k
j
H
j
) nếu:
a) R
n
= H
1
+ H
2
+
+ H
k
= { =
1
k
j
j
|
j
H
j
(1 ≤ j ≤ k) } (tổng thường).
b) j { 1, 2, …, k }, [ H
j
1
t
tj
k
H
]
= { O }.
Ví dụ:
a) H và K là các không gian con kiểu đường thẳng trong R
2
sao cho các
đường thẳng tương ứng với H và K cắt nhau. Khi đó R
2
= H + K và
H K = { O } nên R
2
= H K.
b) H và K lần lượt là các không gian con kiểu đường thẳng và mặt phẳng
trong R
3
sao cho đường thẳng tương ứng với H cắt mặt phẳng tương ứng
với K. Khi đó R
3
= H + K và H K = { O } nên R
3
= H K.
R
2
= H + K và H K = { O } R
3
= H + K và H K = { O }
nên có tổng trực tiếp R
2
= H K. nên có tổng trực tiếp R
3
= H K.
c) H, K và L là các không gian con kiểu đường thẳng trong R
3
sao cho các
đường thẳng tương ứng với H, K và L không đồng phẳng. Để ý H + K,
2
H + L và K + L là các không gian con kiểu mặt phẳng trong R
3
. Ta có
R
3
= H + K + L, H (K + L) = K (H + L) = L (H + K) = { O } nên
R
3
= H K L.
d) H và K là các không gian con kiểu mặt phẳng trong R
3
và các mặt phẳng
tương ứng với H và K cắt nhau theo không gian con kiểu đường thẳng L.
Khi đó R
3
= H + K [ tổng thường mà không phải là tổng trực tiếp ] vì
H K = L { O } và dim (H K) = dimL = 1 ].
R
3
= H + K+ L, H (K + L) = { O }, R
3
= H + K và H K = L {O} nên
K (H + L) = { O }, L (H + K) = { O }, không có tổng trực tiếp.
nên có tổng trực tiếp R
3
= H K L. R
3
chỉ là tổng thường của H và K.
1.2/ MỆNH ĐỀ: R
n
có các không gian con H
1
, H
2
, …, H
k
( k 2 ).
Các phát biểu sau là tương đương với nhau:
a) R
n
= H
1
H
2
H
k
( V
n
là tổng trực tiếp của H
1
, H
2
, …, H
k
).
b)  R
n
, !
j
H
j
( j { 1, 2, …, k } ), =
1
k
j
j
(viết =
1
k
j
j
).
c) cơ sở B
j
của H
j
( j { 1, 2, …, k } ) , B =
1
k
j
j
B
là một cơ sở của R
n
.
d) cơ sở B
j
của H
j
( j { 1, 2, …, k } ), B =
1
k
j
j
B
là một cơ sở của R
n
n
.
Lưu ý: Nếu R
n
= H
1
+ H
2
+
+ H
k
không phải là tổng trực tiếp thì các kết
quả trên không đúng.  R
n
, 
j
H
j
(j {1, 2, …, k}), =
1
k
j
j
: sự tồn
3
tại của các
j
H
j
không nhất thiết là duy nhất. cơ sở B
j
của H
j
( j {1, 2, …, k}), B =
1
k
j
j
B
là một tập sinh (không chắc là một cơ sở) của R
n
.
OM OA OB
và
ON OC OD
(duy nhất)
OM OA OB
và
ON OC OD
(duy nhất)
R
2
= K H. R
3
= H K.
OM OA OD OA OB OC
(duy nhất)
OM OA OB OC OD
(không duy nhất)
R
3
= H K L. R
3
= H + K (không là tổng trực tiếp).
Ví dụ:
a) H = < A
1
= {
1
= (1, 2, 0, 3),
2
= (0, 1, 1, 1) }> ≤ R
4
và A
1
là một cơ sở
của H vì H = < A
1
> và A
1
độc lập tuyến tính (để ý
1
không tỉ lệ với
2
)
K = < A
2
= {
3
= (3, 2, 1, 0),
4
= (0, 2, 0, 1) }> ≤ R
4
và A
2
là một cơ sở
của K vì K = < A
2
> và A
2
độc lập tuyến tính (để ý
3
không tỉ lệ với
4
).
Ta có A = A
1
A
2
= {
1
,
2
,
3
,
4
} là một cơ sở của R
4
vì
1
2
3
4
=
*
1 2 3
0 1 1
3
1
0
1
2 0
0
1
0 2
=
*
1 2 3
3 1 1
3
1
0
0
2 0
0
1
0 2
=
*
1 2 3
3 1 1
0 2 1
=
*
1 4 3
3 3
1
1
0 0
=
1 4
3 3
= 9 0.
4
Suy ra R
4
= H K.
Xét = (5,9,4,1) R
4
= H K. Ta muốn phân tích = với H
và K. Ta tìm được [ ]
A
=
3
1
4
2
c
c
c
c
=
1
2
3
4
( bằng cách giải phương trình
vector c
1
1
+ c
2
2
+ c
3
3
+ c
4
4
= với các ẩn số thực c
1
, c
2
, c
3
và c
4
).
Khi đó = c
1
1
+ c
2
2
= 2(1, 2, 0, 3) + 3(0, 1, 1, 1) = (2, 1, 3, 3) H
và = c
3
3
+ c
4
4
= (3, 2, 1, 0) + 4(0, 2, 0, 1) = ( 3, 10, 1, 4) K.
b) M = < B
1
= {
1
= (1, 4, 2, 3),
2
= (0, 3, 1, 2)}> ≤ R
4
và B
1
là một cơ sở của
M vì M = < B
1
> và B
1
độc lập tuyến tính ( để ý
1
không tỉ lệ với
2
).
N = < B
2
= {
3
= (2, 0, 1, 0) }> ≤ R
4
và B
2
là một cơ sở của N vì
N = < B
2
> và B
2
độc lập tuyến tính ( để ý
3
O ).
L = < B
3
= {
4
= (0, 3, 0, 1) } > ≤ R
4
và B
3
là một cơ sở của L vì
L = < B
3
> và B
3
độc lập tuyến tính ( để ý
4
O ).
Ta có B = B
1
B
2
B
3
= {
1
,
2
,
3
,
4
} là một cơ sở của R
4
vì
1
2
3
4
=
1 4 2 3
0 3 1 2
2 0 1 0
0 3 0 1
=
*
1
1
4 2 3
3 1 2
8 3 6
3
0
0
0
0
=
*
3 1 2
8 3 6
03
1
=
26 3
0
0
=
9 1
26 3
= 1 0
Suy ra R
4
= M N L.
Xét = ( 5, 14, 5, 3) R
4
= M N L.
Ta muốn phân tích = với M, N và L.
Ta tìm được [ ]
B
=
3
1
4
2
c
c
c
c
=
3
1
4
2
( bằng cách giải phương trình vector
c
1
1
+ c
2
2
+ c
3
3
+ c
4
4
= với các ẩn số thực c
1
, c
2
, c
3
và c
4
).
5
Khi đó = c
1
1
+ c
2
2
= (1, 4, 2, 3) – 4(0, 3, 1, 2) = (1, 8, 2, 5) M,
= c
3
3
= 3(2, 0, 1, 0) = ( 6, 0, 3, 0) N và
= c
4
4
= 2(0, 3, 0, 1) = (0, 6, 0, 2) L.
c) P = < D
1
= {
1
= ( 3, 0, 2) }> ≤ R
3
và D
1
là một cơ sở của P vì
P = < D
1
> và D
1
độc lập tuyến tính ( để ý
1
O ).
Q = < D
2
= {
2
= (4, 1, 3) }> ≤ R
3
và D
2
là một cơ sở của Q vì
Q = < D
2
> và D
2
độc lập tuyến tính ( để ý
2
O ).
U = < D
3
= {
3
= (6, 1, 4) } > ≤ R
3
và D
3
là một cơ sở của U vì
U = < D
3
> và D
3
độc lập tuyến tính ( để ý
3
O ).
D = D
1
D
2
D
3
= {
1
,
2
,
3
} là một cơ sở của R
3
vì
1
2
3
=
3 0 2
4 1 3
6 1 4
=
*
4
0
0
3 2
2 1
6 1
=
3 2
2 1
= 1 0. Do đó R
3
= P Q U.
Xét = (25, 1, 16) R
3
= P Q U.
Ta muốn phân tích = với P, Q và U.
Ta tìm được [ ]
D
=
2
1
3
c
c
c
=
2
5
3
( bằng cách giải phương trình vector
c
1
1
+ c
2
2
+ c
3
3
= với các ẩn số thực c
1
, c
2
và c
3
).
Khi đó = c
1
1
= 5( 3, 0, 2) = (15, 0, 10) P,
= c
2
2
= 2(4, 1, 3) = ( 8, 2, 6) Q và
= c
3
3
= 3(6, 1, 4) = (18, 3, 12) U.
d) V = < C
1
= {
1
= (1, 2, 2),
2
= (4, 7, 1) } > ≤ R
3
và C
1
là một cơ sở của V
vì V = < C
1
> và C
1
độc lập tuyến tính ( vì
1
không tỉ lệ với
2
).
W = < C
2
= {
3
= (2,3, 4),
4
= (3, 7, 15) }> ≤ R
3
và C
2
là một cơ sở của
6
W vì W = < C
2
> và C
2
độc lập tuyến tính ( vì
3
không tỉ lệ với
4
).
Ta có V + W = < C = C
1
C
2
> = < {
1
,
2
,
3
,
4
} >.
Lập ma trận và biến đổi về dạng bậc thang rút gọn:
1
2
3
4
=
1 2 2
4 7 1
2 3 4
3 7 15
*
2 2
1 9
1 8
1 9
0
0
0
1
*
*
0
1 0
0
0
1
0
6
9
1
1
0
0
*
*
*
0
1
0
1
0
0 0
0 0
0 0
1
=
1
2
3
O
.
Ta thấy V + W có một cơ sở là B
o
= {
1
,
2
,
3
}, nghĩa là V + W = R
3
và
dim(V + W) = | B
o
| = 3. Như vậy C = C
1
C
2
= {
1
,
2
,
3
,
4
} không phải
là một cơ sở của R
3
= V + W ( do | C | = 4 3 = dimR
3
). Như vậy
R
3
= V + W là tổng thường mà không phải là tổng trực tiếp.
Xét = (1, 2, 3) R
3
. Ta có sự phân tích không duy nhất = + = +
với = 8
1
6
2
= ( 16, 26, 10) V, = 7
3
+
4
= (17, 28, 13) W,
= 17
1
3
2
= (5, 13, 31) V và =
3
2
4
= ( 4, 11, 34) W.
1.3/ MỆNH ĐỀ: Giả sử R
n
có các không gian con H
1
, H
2
, …, H
k
( k 2 ).
Các phát biểu sau là tương đương với nhau:
a) R
n
= H
1
H
2
H
k
.
b) R
n
= H
1
+ H
2
+
+ H
k
và dim R
n
= dimH
1
+ dimH
2
+
+ dimH
k
.
(nếu R
n
= H
1
+ H
2
+
+ H
k
thì dim R
n
≤ dimH
1
+ dimH
2
+
+ dimH
k
).
Ví dụ: Xét các Ví dụ trong (1.2).
a) R
4
= H K, dimH = | A
1
| = 2, dimK = | A
2
| = 2 và 4 = dimR
4
= dimH + dimK
b) R
4
= M N L, dimM = | B
1
| = 2, dimN = | B
2
| = 1, dimL = | B
3
| = 1 và
4 = dimR
4
= dimM + dimN + dimL.
c) R
3
= P Q U, dimP = | D
1
| = 1, dimQ = | D
2
| = 1, dimU = | D
3
| = 1 và
3 = dimR
3
= dimP + dimQ + dimU.
d) R
3
= V + W (không trực tiếp) nên 3 = dimR
3
< dimV + dimW = 2 + 2 = 4.
7
II.
TRỊ RIÊNG, KHÔNG GIAN RIÊNG, VECTOR RIÊNG VÀ ĐA
THỨC ĐẶC TRƯNG CỦA MA TRẬN VUÔNG:
2.1/ ĐỊNH NGHĨA: Cho A M
n
(R) và c R.
a) Đặt
A
c
E
= {
R
n
| A.
= c.
} = {
R
n
| A.
c.I
n
.
= O }
= {
R
n
| (A
c.I
n
).
= O } thì
A
c
E
R
n
. Hơn nữa
[ A.
A
c
E
=
A
c
E
khi c 0 ] và [ A.
A
c
E
= {O} khi c = 0 ]. Suy ra A.
A
c
E
A
c
E
.
Ký hiệu A.
A
c
E
= { A. |
A
c
E
} ( A. là dạng viết gọn của A.
t
).
b) Nếu
A
c
E
{ O } thì ta nói c là một trị riêng thực của A và
A
c
E
là không
gian riêng của A ứng với trị riêng c. Lúc đó,
A
c
E
\
{ O },
A. = c. và được gọi là một vector riêng của A ứng với trị riêng c.
Ví dụ:
Cho A =
7 6 10
12 17 24
12 15 22
M
3
(R). Xét c = 0 và d = 1 R.
A
o
E
= { = (u, v, w) R
3
| A = O } = { O = (0, 0, 0) } do các phép biến
đổi đưa về dạng bậc thang rút gọn cho ta ( u = v = w = 0 ).
u v w u v w
7 6 10 0
12 17 24 0
12 15 22 0
1 15 16 0
0 2 2 0
2 3 2 0
*
4
1 0
0
0
0 1
1 1 0
33 3 0
*
*
*
01
0
1
0 0
0 0
0 0
0
1
.
8
Suy ra c = 0 không phải là một trị riêng thực của A.
Ta có (A + I
3
) =
7 6 10
12 17 24
12 15 22
+
1
1
0 0
0 0
0 0
1
=
1
8
6 10
12 24
2
18
2
15
1
và
1
A
E
= { = (u,v,w) R
3
| (A + I
3
) = O} ={ = (a, 2a, 2a) | a R} { O }
do các phép biến đổi về dạng bậc thang rút gọn cho ta
w = 2a ( a R ), u = a, v = 2a :
u v w u v w
8 6 10 0
12 18 24 0
12 15 21 0
0
4
0
0
0
3 5
3 3
6 6 0
*
0
4
0
0
1
2 0
1
0 0
0
0
*
*
0
1
0
0
0
0
0
1/ 2
1
0
0
1
Suy ra d = 1 là một trị riêng thực của A và
1
A
E
là không gian riêng của A
ứng với trị riêng ( 1). 
1
A
E
\ {O}, A() = và được gọi là một
vector riêng của A ứng với trị riêng ( 1).
2.2/ ĐỊNH NGHĨA: Cho A M
n
(R).
Cho biến số x lấy giá trị thực . Đặt p
A
(x) = det (x.I
n
A) thì p
A
(x) là
một đa thức đơn khởi bậc n trên R có dạng
p
A
(x) = x
n
+ a
n 1
x
n 1
+
+ a
1
x + a
o
với a
n 1
, … , a
1
, a
o
R.
Ta nói p
A
(x) là đa thức đặc trưng của ma trận vuông thực A.
Ví dụ:
A =
3 4 7
0 2 0
0 0 9
M
3
(R) có xI
3
A =
3 4 7
0 2 0
0 0 9
x
x
x
( x là biến thực )
Ta có p
A
(x) = | xI
3
A | = (x + 3)(x 2)(x 9) = x
3
8x
2
15x + 54.
2.3/ MỆNH ĐỀ: Cho A M
n
(R) và c R. Khi đó
a) c là một trị riêng thực của A
p
A
(c) = 0.
b) Suy ra: tập hợp các trị riêng thực của A chính là tập hợp các nghiệm
thực của đa thức đặc trưng p
A
(x) .
9
Ví dụ:
a) A =
6 3
7 2
M
2
(R) có p
A
(x) = | xI
2
A | =
6 3
7 2
x
x
= x
2
– 4x + 9.
p
A
(x) vô nghiệm trên R (vì ’ = 5 < 0) nên A không có trị riêng thực.
b) B =
6 3 1
12 7 3
16 12 6
M
3
(R) có p
B
(x) = | xI
3
B | =
6 3 1
12 7 3
16 12 6
x
x
x
=
3 6 2
6 3 1
16 12 6
0
x x
x
x
=
6
0 0
1
2
3 3 1
20 2
x
x
x
= (x + 2)
3 1
20 6
x
x
= (x + 1)(x + 2)
2
.
Ta nói B có hai trị riêng thực là c
1
= 1 và c
2
= 2.
III. SỰ CHÉO HÓA CỦA MA TRẬN VUÔNG:
3.1/ MỆNH ĐỀ:
a) Cho c
1
, c
2
, …, c
m
là các trị riêng thực khác nhau của A M
n
(R) ( m 2 )
và W = (
1
A
c
E
+
2
A
c
E
+
+
m
A
c
E
) R
n
. Khi đó ta có W =
1
A
c
E
2
A
c
E
m
A
c
E
.
c) Như vậy tổng của các không gian riêng ứng với các trị riêng thực khác
nhau của ma trận vuông là tổng trực tiếp.
3.2/ ĐỊNH NGHĨA: Cho A, H, K M
n
(R).
a) Ta nói H và K đồng dạng với nhau nếu có P khả nghịch M
n
(R) thỏa
P
1
HP = K (lúc đó ta cũng có Q
1
KQ = H với Q = P
1
). Quan hệ đồng
dạng trên M
n
(R) là một quan hệ tương đương.
b) A chéo hóa được trên R nếu A đồng dạng với một ma trận đường chéo,
nghĩa là có P khả nghịch M
n
(R) thỏa P
1
AP =
1
2
n
.
( P
1
AP là một ma trận đường chéo ).
10
Ví dụ:
A =
7 12 12
6 17 15
10 24 22
M
3
(R). Ta có P =
3 0 2
4 1 3
6 1 4
khả nghịch M
3
(R)
với P
1
=
1 2 2
2 0 1
2 3 3
và P
1
AP =
1
2
1
0 0
0 0
0 0
nên A chéo hóa được trên R.
3.3/ ĐỊNH LÝ: Cho A M
n
(R). Khi đó
a) A chéo hóa được trên R
1 2
1 2 1 2 1 2
(*
,(
*)dim
*) ( ) ( ) ( ) ...( ) , , ,..., , , ..., \{0}
(1 )
j
k
rr r
A k k
A
c j
k
p x x c x c x c c c c r r
E
r
r j k
.
b) Khi xảy ra (*) thì ta nói đa thức p
A
(x) tách được trên R.
3.4/ MỆNH ĐỀ: Cho A M
n
(R). Nếu p
A
(x) có n nghiệm thực khác nhau thì
A chéo hóa được trên R.
3.5/ HỆ QUẢ: Cho A M
n
(R). Khi đó:
a) Để ý
( )
q
q
p p
[ nếu p và q có nội dung độc lập với nhau ].
[ ( )]
p
p q
q p
( nếu có p thì mới hiểu được q ).
b) A không chéo hóa được trên R
( p
A
(x) không tách được trên R ) hoặc
1 2
1 2 1 2 1 2
* ( ) ( ) ( ) ...( )
m
, , ,..., , , ,...,
(**) {1,2,.
}
.., },d
0
i
\{
k
j
A
rr r
A k
c j
k k
p x x c x c x c c
j k E r
c c r r r
.
Ví dụ:
a) A =
3 1 3
3 1 1
2 2 0
M
3
(R) có p
A
(x) = | xI
3
A | =
3 1 3
3 1 1
2 2
x
x
x
=
=
3
4
4
0
1
1 1
2
x
x
x
x
=
1 3
2
0
4
2
0 x
x
x
= (x 4)
2
2
x
x
= (x 4)(x
2
+ 4).
11
Do p
A
(x) không tách được trên R nên A không chéo hóa được trên R.
b) H =
10 13 4
13 16 4
12 12 1
M
3
(R) có p
H
(x) = | xI
3
H | =
10 13 4
13 16 4
12 12 1
x
x
x
=
13 4
16 4
10 2
3
3
1
x
x
x
x
=
13 4
3 0
1
3
0
0
2 1
x
x
x
= (x 3)
3 0
12 1
x
x
= (x 3)
2
(x + 1).
3
H
E
= { R
3
| (H 3I
3
) = O} = { = (v, v, 0) = v(1, 1, 0) | v R}
có cơ sở C = { = (1, 1, 0) } do các phép biến đổi đưa về dạng bậc thang
rút gọn cho ta ( v R , u = v, w = 0 ) :
u v w u v w
( H 3I
3
| O ) =
13 13 4 0
13 13 4 0
12 12 4 0
1 3 0
0 0 0
0 4 0
0
0 0
1
*
*
0
1
0
0
0
1
0
0
1
0
0 0
.
Do dim
3
H
E
= | C | = 1 < 2 nên H không chéo hóa được trên R.
3.6/ CHÉO HÓA MA TRẬN: Cho A M
n
(R) và A chéo hóa được trên R,
nghĩa là
1 2
1 2 1 2 1 2
(*
,(
*)dim
*) ( ) ( ) ( ) ...( ) , , ,..., , , ..., \{0}
(1 )
j
k
rr r
A k k
A
c j
k
p x x c x c x c c c c r r
E
r
r j k
.
* j { 1, 2,…, k }, tìm một cơ sở B
j
cho
j
A
c
E
= { R
n
| (A c
j
I
n
) = O}.
( cơ sở B
j
không duy nhất ).
* Đặt B = B
1
B
2
… B
k
thì B là một cơ sở của R
n
=
1
A
c
E
2
A
c
E
k
A
c
E
( cơ sở B không duy nhất ).
* Đặt P = (C B) với C là cơ sở chính tắc của R
n
thì P khả nghịch M
n
(R)
P không duy nhất và
P
1
AP =
1
1
k
k
c
c
c
c
(j {1, 2,…, k}, c
j
xuất hiện r
j
lần).
12
R
n
=
1
A
c
E
2
A
c
E
k
A
c
E
và A.
j
A
c
E
j
A
c
E
( 1 j k ).
Ví dụ:
a) A =
7 12 2
3 4 0
2 0 2
M
3
(R) có p
A
(x) = | xI
3
A | =
7 12 2
3 4 0
2 0 2
x
x
x
=
= (x 7)(x + 4)(x + 2) 4(x + 4) + 36(x + 2) = x(x + 1)(x 2).
p
A
(x) có 3 nghiệm thực đơn là 0, 1 và 2 nên A chéo hóa được trên R.
A + I
3
=
0
8 12 2
3 0
2
3
1
và A 2I
3
=
0
5 12 2
3 0
2
6
4
.
0
A
E
= { R
3
| A = O } = { = ( 4a, 3a, 4a) = a( 4, 3, 4) | a R }
có một cơ sở là B
1
= {
1
= ( 4, 3, 4) } do các phép biến đổi đưa về
dạng bậc thang rút gọn cho ta [ w = 4a ( a R ), u = 4a, v = 3a ].
u v w u v w
(A | O) =
7 12 2 0
3 4 0 0
2 0 2 0
*
6
1
00
0
4 2 0
8 6
8 0
*
*
01
0
0
1
1
3 / 4
0 0
0 0
0
.
1
A
E
= { R
3
| (A + I
3
) = O} = { = ( a, a, 2a) = a( 1, 1, 2) | a R}
có một cơ sở là B
2
= {
2
= ( 1, 1, 2) } do các phép biến đổi đưa về
dạng bậc thang rút gọn cho ta [ w = 2a ( a R ), u = a, v = a ].
13
u v w u v w
(A + I
3
| O) =
8 12 2 0
3 3 0 0
2 0 1 0
0
1
0
0
0
3 1
6 3
6 3 0
0
1
0
0
0
0
1/ 2
1/ 2
00
1
0
.
2
A
E
= { R
3
| (A 2I
3
) = O} = { = ( 2w, w, w) = w( 2, 1, 1) | w R}
có một cơ sở là B
3
= {
3
= ( 2, 1, 1) } do các phép biến đổi đưa về
dạng bậc thang rút gọn cho ta (w R , u = 2w, v = w ).
u v w u v w
(A 2I
3
| O) =
5 12 2 0
3 6 0 0
2 0 4 0
3
1
00
0
12 10 0
30 0
24 24 0
0
1
0
2 0
1
0
1
0
0
0
0
.
R
3
=
0
A
E
1
A
E
2
A
E
có một cơ sở là B = B
1
B
2
B
3
= {
1
,
2
,
3
} với
A
1
= 0.
1
= O, A
2
=
2
và A
3
= 2
3
.
Đặt P = (C B) = ( [
1
]
C
[
2
]
C
[
3
]
C
) =
4 1 2
3 1 1
4 2 1
với C là cơ sở
chính tắc của R
3
thì P khả nghịch, P
1
=
1 3 1
1 4 2
2 4 1
và P
1
AP =
0
1
0
0
2
0
0
0 0
b) H
=
1 3 1
3 5 1
3 3 1
M
3
(R) có p
H
(x) = | xI
3
H | =
1 3 1
3 5 1
3 3 1
x
x
x
=
=
3 5 1
3
2 2
0
3 1
x
x
x
x
=
3 2 1
0 0
2
3 0 1
x
x
x
= (x 2)
2 1
0 1
x
x
= (x 1)(x 2)
2
.
H I
3
=
3 1
3 1
3 3
2
4
0
và H 2I
3
=
3 1
3 1
3 3
3
3
1
.
1
H
E
= { R
3
| (H I
3
) = O} = { = (w, w, w) = w(1, 1, 1) | w R } có
một cơ sở là B
1
= {
1
= (1, 1, 1) } và dim
1
H
E
= | B
1
| = 1 do các phép biến
đổi đưa về dạng bậc thang rút gọn cho ta ( w R, u = w, v = w ).
14
u v w u v w
( H I
3
| O ) =
2 3 1 0
3 4 1 0
3 3 0 0
*
0
1
0
0
0
0 1
1 1
3 3 0
*
*
0
1
0
0
0
1
0
1
0
1
0
0
.
2
H
E
= { R
3
| (H 2I
3
) = O} = { = (u, v, w) R
3
| 3u + 3v w = 0}
= { = (u, v, 3v 3u) = u(1, 0, 3) + v(0, 1, 3) | u, v R } có một cơ
sở là B
2
= {
2
= (1, 0, 3),
3
= (0, 1, 3) } và dim
2
H
E
= | B
2
| = 2.
Ta có p
H
(x) = (x 1)(x 2)
2
tách được trên R, dim
1
H
E
= 1 và dim
2
H
E
= 2
nên H chéo hóa được trên R. R
3
=
1
H
E
2
H
E
có một cơ sở là B = B
1
B
2
=
= {
1
,
2
,
3
} với H
1
=
1
, H
2
= 2
2
và H
3
= 2
3
.
Đặt P = (C B) = ( [
1
]
C
[
2
]
C
[
3
]
C
) =
1 1 0
1 0 1
1 3 3
với C là cơ sở
chính tắc của R
3
thì P khả nghịch, P
1
=
3 3 1
2 3 1
3 4 1
và P
1
HP =
1
2
0 0
0 0
0 0
2
.
IV. ÁP DỤNG:
4.1/ LŨY THỪA VÀ CĂN THỨC CỦA MA TRẬN CHÉO HÓA ĐƯỢC:
Cho A M
n
(R) và A chéo hóa được trên R. Xét số nguyên k 1.
Tìm ma trận P khả nghịch M
n
(R) thỏa P
1
AP =
1
2
n
.
Suy ra A = P
1
2
n
P
1
và A
k
= P
1
2
k
k
k
n
P
1
.
Nếu có
1
,
2
, … ,
n
R thỏa
k
j
=
j
( 1 j n ), ta chọn
H = P
1
2
n
P
1
M
n
(R) thì H
k
= P
1
2
n
P
1
= A.
Ta nói H là một căn bậc k (không nhất thiết duy nhất) của A trong M
n
(R).
15
Ví dụ:
a) Cho A M
3
(R) trong Ví dụ (3.6) và k là số nguyên 1. Ta có
P
1
AP =
0
1
0
0
2
0
0
0 0
với P =
4 1 2
3 1 1
4 2 1
và P
1
=
1 3 1
1 4 2
2 4 1
M
3
(R).
Suy ra A = P
0
1
0
0
2
0
0
0 0
P
1
và A
k
= P
0
1
0
0
2
0
0
0 0
k
P
1
= P
0
1
2
0 0
0 ( ) 0
0 0
k
k
P
1
= ( 1)
k
S + 2
k
T với S =
1 4 2
1 4 2
2 8 4
và T =
4 8 2
2 4 1
2 4 1
M
3
(R).
Cho số nguyên lẻ r 3.
Chọn D = P
0
1
0
0
2
0
0
0 0
r
P
1
M
3
(R) thì D
r
= P
0
1
0
0
2
0
0
0 0
P
1
= A. Ta có
D = ( 1)S +
2
r
T với S =
1 4 2
1 4 2
2 8 4
và T =
4 8 2
2 4 1
2 4 1
M
3
(R).
b) Cho H M
3
(R) trong Ví dụ (3.6) và k là số nguyên 1. Ta có
P
1
HP =
1
2
0 0
0 0
0 0
2
với P =
1 1 0
1 0 1
1 3 3
và P
1
=
3 3 1
2 3 1
3 4 1
M
3
(R).
Suy ra H = P
1
2
0 0
0 0
0 0
2
P
1
và H
k
= P
1
2
0 0
0 0
0 0
2
k
P
1
= P
1
2
2
0 0
0 0
0 0
k
k
P
1
= S + 2
k
T với S =
3 3 1
3 3 1
3 3 1
và T =
2 3 1
3 4 1
3 3 0
M
3
(R).
Chọn D = P
1 0 0
0 2 0
0 0 2
k
k
P
1
M
3
(R) thì D
k
= P
1
2
0 0
0 0
0 0
2
P
1
= H. Ta có
16
D = S +
2
k
T với S =
3 3 1
3 3 1
3 3 1
và T =
2 3 1
3 4 1
3 3 0
M
3
(R).
5.2/ GIẢI MỘT SỐ HỆ THỨC ĐỆ QUI DỰA THEO SỰ CHÉO HÓA CỦA
MA TRẬN VUÔNG:
a) Tìm u
n
theo n ( n nguyên ≥ 0 ) nếu
u
o
= 1, u
1
= 2 và u
n
+ 2
= u
n
+ 1
+ 6u
n
, n ≥ 0.
k 0, đặt t
k
=
1
k
k
u
u
thì t
o
=
2
1
và t
k + 1
=
2
1
k
k
u
u
=
1
1
6
k k
k
u u
u
=
1 6
1 0
1
k
k
u
u
=
1 6
1 0
t
k
. Vậy k 0, t
k + 1
= At
k
với A =
1 6
1 0
=
= P
3
0
0
2
P
−1
và P =
3 2
1 1
, P
−1
=
1
5
1 2
1 3
(A chéo hóa được trên R).
Do đó, n 0, t
n
=
1
n
n
u
u
= At
n 1
= A
2
t
n 2
=
= A
n 1
t
1
= A
n
t
o
=
= P
3
0
0
2
n
P
−1
2
1
=
1
5
3 2
1 1
3
( 2)
0
0
n
n
1 2
1 3
2
1
=
1
5
1
1
( 2)
3
3
( 2)
n
n
n
n
4
1
=
1
5
1 1
4 3 ( 2)
4 3 ( 2)
n n
n n
. Suy ra n ≥ 0, u
n
=
1
5
[ 4.3
n
+ (
− 2)
n
].
Giải thích tính chéo hóa được trên R của A:
p
A
(x) = | xI
2
A | =
1 6
1
x
x
= x
2
– x + 6 = (x – 3)(x + 2) có 2 nghiệm
thực đơn ( c
1
= 3 c
2
= 2 ) nên A chéo hóa được trên R.
A – 3I
2
=
2 6
1 3
và A + 2I
2
=
3 6
1 2
.
3
A
E
= { R
2
| (A – 3I
2
) = O } = { = (a, b) R
2
| a 3b = 0 }
= { = (3b, b) = b(3,1) | b R } có cơ sở C
1
= {
1
= (3, 1) }.
2
A
E
= { R
2
| (A + 2I
2
) = O } = { = (a, b) R
2
| a + 2b = 0 }
17
= { = ( 2b, b) = b( 2,1) | b R } có cơ sở C
2
= {
2
= ( 2, 1) }.
R
2
=
3
A
E
2
A
E
có cơ sở C = C
1
C
2
= {
1
= (3, 1),
2
= ( 2, 1) }.
Đặt P = ( B C ) = ( [
1
]
B
[
2
]
B
) =
3 2
1 1
với B là cơ sở chính tắc
của R
2
thì P khả nghịch, P
1
=
1
5
1 2
1 3
và P
1
AP =
3
0
0
2
.
b) Tìm u
n
và v
n
theo n ( n nguyên ≥ 0 ) nếu
u
o
= 2, v
o
= 5, u
n + 1
= u
n
4v
n
và v
n + 1
= u
n
+ v
n
, n ≥ 0.
k 0, đặt t
k
=
k
k
u
v
thì t
o
=
2
5
và t
k + 1
=
1
1
k
k
u
v
=
4
k k
k k
u v
u v
=
1 4
1 1
k
k
u
v
=
1 4
1 1
t
k
. Vậy k 0, t
k + 1
= At
k
với A =
1 4
1 1
=
= P
3
0
0
1
P
− 1
và P =
2 2
1 1
, P
− 1
=
1
4
1 2
1 2
(A chéo hóa được trên R).
Do đó n 0, t
n
=
n
n
u
v
= At
n 1
= A
2
t
n 2
=
= A
n 1
t
1
= A
n
t
o
= P
3
0
0
1
n
P
− 1
2
5
=
1
4
2 2
1 1
3
( 1)
0
0
n
n
1 2
1 2
2
5
=
1
4
(
2( 1
2.3
1)
)
3
n
n
n
n
8
12
=
6( 1) 4.3
3( 1) 2.3
n n
n n
.
Suy ra n ≥ 0, u
n
= 6(− 1)
n
4.3
n
và v
n
= 3(− 1)
n
+ 2.3
n
.
Giải thích tính chéo hóa được trên R của A:
p
A
(x) = | xI
2
A | =
1 4
1 1
x
x
= x
2
– 2x – 3 = (x – 3)(x + 1) có 2 nghiệm
thực đơn ( c
1
= 3 c
2
= 1 ) nên A chéo hóa được trên R.
A – 3I
2
=
2 4
1 2
và A + I
2
=
2 4
1 2
.
3
A
E
= { R
2
| (A – 3I
2
) = O } = { = (a, b) R
2
| a 2b = 0 }
= { = ( 2b, b) = b( 2, 1) | b R } có cơ sở C
1
= {
1
= ( 2, 1) }.
18
1
A
E
= { R
2
| (A + I
2
) = O } = { = (a, b) R
2
| a + 2b = 0 }
= { = (2b, b) = b(2, 1) | b R } có cơ sở C
2
= {
2
= (2, 1) }.
R
2
=
3
A
E
1
A
E
có cơ sở C = C
1
C
2
= {
1
= ( 2, 1),
2
= (2, 1) }.
Đặt P = (B C) = ( [
1
]
B
[
2
]
B
) =
2 2
1 1
với B là cơ sở chính tắc
của R
2
thì P khả nghịch, P
1
=
1
4
1 2
1 2
và P
1
AP =
3
0
0
1
.
c) Tìm u
n
, v
n
và w
n
theo n ( n nguyên ≥ 0 ) nếu u
o
= 2, v
o
= 3, w
o
= 1,
u
n + 1
= 6u
n
+ 12v
n
+ 16w
n
, v
n + 1
= 3u
n
– 7v
n
12w
n
và
w
n + 1
= u
n
+ 3v
n
+ 6w
n
, n ≥ 0.
k 0, đặt t
k
=
k
k
k
u
v
w
thì t
o
=
2
3
1
và t
k + 1
=
1
1
1
k
k
k
u
v
w
=
6 12 16
3 7 12
3 6
k k k
k k k
k k k
u v w
u v w
u v w
=
6 12 16
3 7 12
1 3 6
k
k
k
u
v
w
=
6 12 16
3 7 12
1 3 6
t
k
. Vậy k 0, t
k + 1
= At
k
với
A =
6 12 16
3 7 12
1 3 6
= P
1
2
0 0
0 0
0 0
2
P
−1
và P =
4 3 4
3 1 0
1 0 1
, P
−1
=
1 3 4
3 8 12
1 3 5
( A chéo hóa được trên R ).
Do đó n 0, t
n
=
n
n
n
u
v
w
= At
n 1
= A
2
t
n 2
=
= A
n 1
t
1
= A
n
t
o
= P
1
2
0 0
0 0
0 0
2
n
P
− 1
2
3
1
=
4 3 4
3 1 0
1 0 1
1
2
2
0 0
0 0
0 0
n
n
1 3 4
3 8 12
1 3 5
2
3
1
=
=
0
4
3.2 4.2
3
1
2
0 2
n
n
n
n
3
6
2
=
10.2 12
9 6.2
2.2 3
n
n
n
=
1
1
1
5.2 12
9 3.2
2 3
n
n
n
.
Suy ra n ≥ 0, u
n
= 5.2
n +1
− 12 , v
n
= 9 – 2
n + 1
và w
n
= 2
n + 1
− 3.
19
Giải thích tính chéo hóa được trên R của A:
A =
6 12 16
3 7 12
1 3 6
M
3
(R) có p
A
(x) = | xI
3
A | =
6 12 16
3 7 12
1 3 6
x
x
x
=
=
6 12 16
0 2 3 6
1 3 6
x
x x
x
=
6 12 20
0 2 0
1 3 3
x
x
x
= (x 2)
6 20
1 3
x
x
= (x 1)(x 2)
2
.
E
1
= { X R
3
/ (A I
3
)X = O }.
X = (u, v, w) E
1
5 12 16 0
3 8 12 0
1 3 5 0
1 0 4 0
0 1 3 0
0 3 9 0
1 0 4 0
0 1 3 0
0 0 0 0
E
1
= { X = (4w, 3w, w) = w(4, 3, 1) / w R } có cơ sở
C
1
= { X
1
= (4, 3, 1) } và dimE
1
= | C
1
| = 1.
E
2
={ X R
3
/ (A 2I
3
)X = O }.
X = (u, v, w) E
2
4 12 16 0
3 9 12 0
1 3 4 0
1 3 4 0
.
E
2
= { X = ( 3v 4w, v, w) = v( 3, 1, 0) + w( 4, 0, 1) / v, w R } có cơ
sở C
2
= { X
2
= ( 3, 1, 0), X
3
= ( 4, 0, 1) } và dimE
2
= | C
2
| = 2 . Suy ra
A chéo hóa được trên R.
Đặt C = C
1
C
2
= { X
1
, X
2
, X
3
} thì C là một cơ sở của R
3
vì R
3
= E
1
E
2
.
Gọi B = {
1
,
2
,
3
} là cơ sở chính tắc của R
3
.
Xét P = (B C) = ( [ X
1
]
B
[ X
2
]
B
[ X
3
]
B
) =
4 3 4
3 1 0
1 0 1
thì P khà
nghịch , P
1
=
1 3 4
3 8 12
1 3 5
và P
1
AP =
1 0 0
0 2 0
0 0 2
.
---------------------------------------------------------------------------------------------------------

Tài liệu khác của Trường Đại học Khoa học tự nhiên, Đại học Quốc gia Thành phố Hồ Chí Minh

Preview text:

GV LÊ VĂN HỢP ĐẠI SỐ TUYẾN TÍNH
CHƯƠNG 6 : SỰ CHÉO HÓA CỦA MA TRẬN VUÔNG
I. TỔNG TRỰC TIẾP CÁC KHÔNG GIAN CON:
1.1/ ĐỊNH NGHĨA: Giả sử Rn có các không gian con H1, H2 , …, Hk ( k  2 ).
Ta nói Rn là tổng trực tiếp của các không gian con H1, H2 , …, Hk (ký hiệu Rn = H k
1  H2    Hk hay Rn =  H j 1  j ) nếu: k
a) Rn = H1 + H2 +  + Hk = {  =   |  j
j  Hj (1 ≤ j ≤ k) } (tổng thường). j 1  k
b) j  { 1, 2, …, k }, [ H j  H  ] = { O }. t jt 1  Ví dụ:
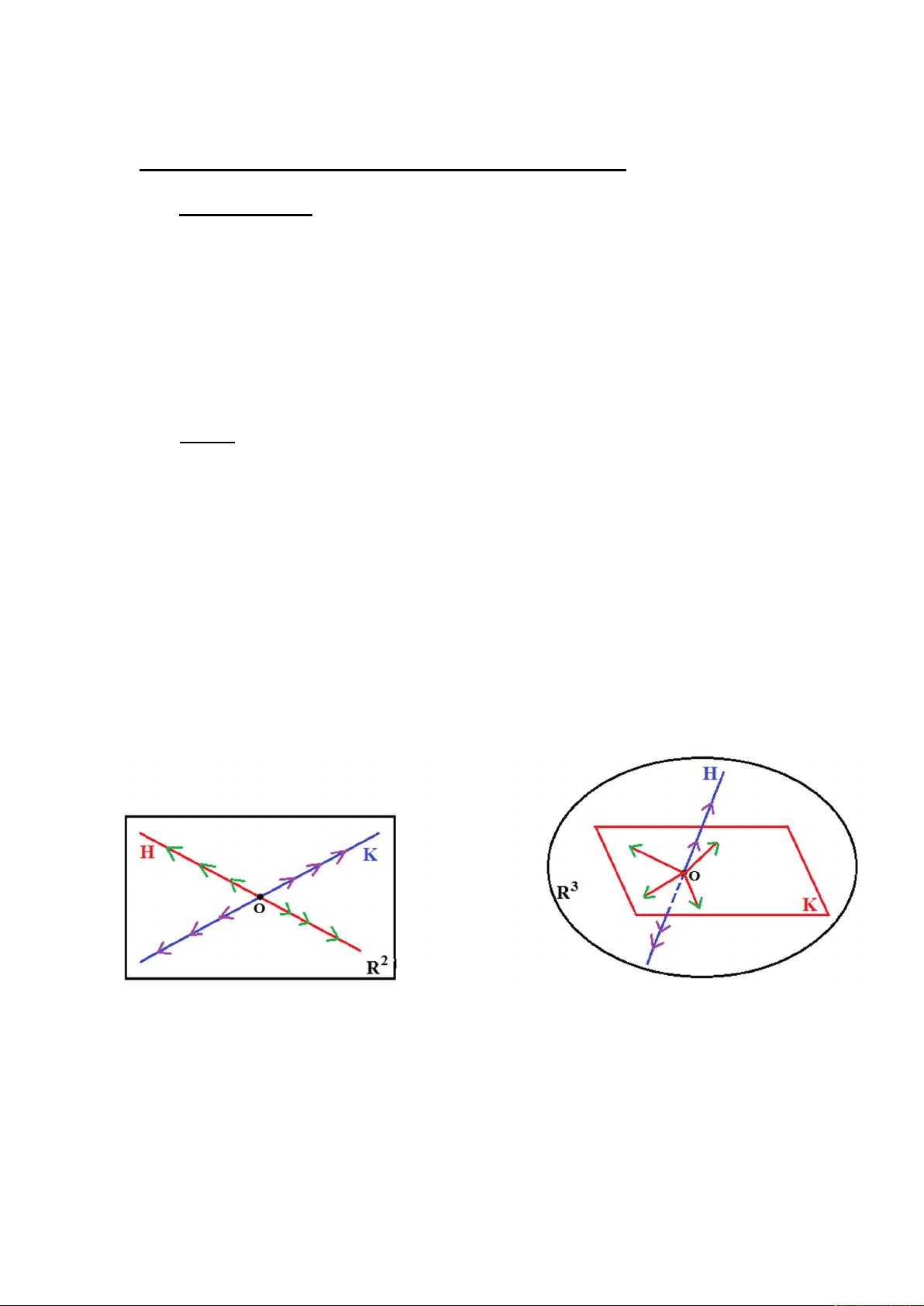
a) H và K là các không gian con kiểu đường thẳng trong R2 sao cho các
đường thẳng tương ứng với H và K cắt nhau. Khi đó R2 = H + K và
H  K = { O } nên R2 = H  K.
b) H và K lần lượt là các không gian con kiểu đường thẳng và mặt phẳng
trong R3 sao cho đường thẳng tương ứng với H cắt mặt phẳng tương ứng
với K. Khi đó R3 = H + K và H  K = { O } nên R3 = H  K.
R2 = H + K và H  K = { O } R3 = H + K và H  K = { O }
nên có tổng trực tiếp R2 = H  K. nên có tổng trực tiếp R3 = H  K.
c) H, K và L là các không gian con kiểu đường thẳng trong R3 sao cho các
đường thẳng tương ứng với H, K và L không đồng phẳng. Để ý H + K, 1
H + L và K + L là các không gian con kiểu mặt phẳng trong R3. Ta có
R3 = H + K + L, H  (K + L) = K  (H + L) = L  (H + K) = { O } nên R3 = H  K  L.
d) H và K là các không gian con kiểu mặt phẳng trong R3 và các mặt phẳng
tương ứng với H và K cắt nhau theo không gian con kiểu đường thẳng L.
Khi đó R3 = H + K [ tổng thường mà không phải là tổng trực tiếp ] vì
H  K = L  { O } và dim (H  K) = dimL = 1 ].
R3 = H + K+ L, H  (K + L) = { O }, R3 = H + K và H  K = L  {O} nên
K  (H + L) = { O }, L  (H + K) = { O }, không có tổng trực tiếp.
nên có tổng trực tiếp R3 = H  K  L. R3 chỉ là tổng thường của H và K.
1.2/ MỆNH ĐỀ: Rn có các không gian con H1, H2 , …, Hk ( k  2 ).
Các phát biểu sau là tương đương với nhau:
a) Rn = H1  H2    Hk ( Vn là tổng trực tiếp của H1, H2 , …, Hk ). k
b)   Rn, !  k
j  Hj ( j  { 1, 2, …, k } ),  =   (viết  =   j j 1  j ). j 1  k
c) cơ sở Bj của Hj ( j  { 1, 2, …, k } ) , B =  B là một cơ sở của Rn j . j 1  k
d)  cơ sở Bj của Hj ( j  { 1, 2, …, k } ), B =  B là một cơ sở của Rn j n . j 1 
Lưu ý: Nếu Rn = H1 + H2 +  + Hk không phải là tổng trực tiếp thì các kết k
quả trên không đúng.   Rn , j  Hj (j  {1, 2, …, k}),  =   : sự tồn j j 1  2
tại của các j  Hj không nhất thiết là duy nhất. cơ sở Bj của Hj k
( j  {1, 2, …, k}), B =  B là một tập sinh (không chắc là một cơ sở) của Rn. j j 1 
  
  
  
  
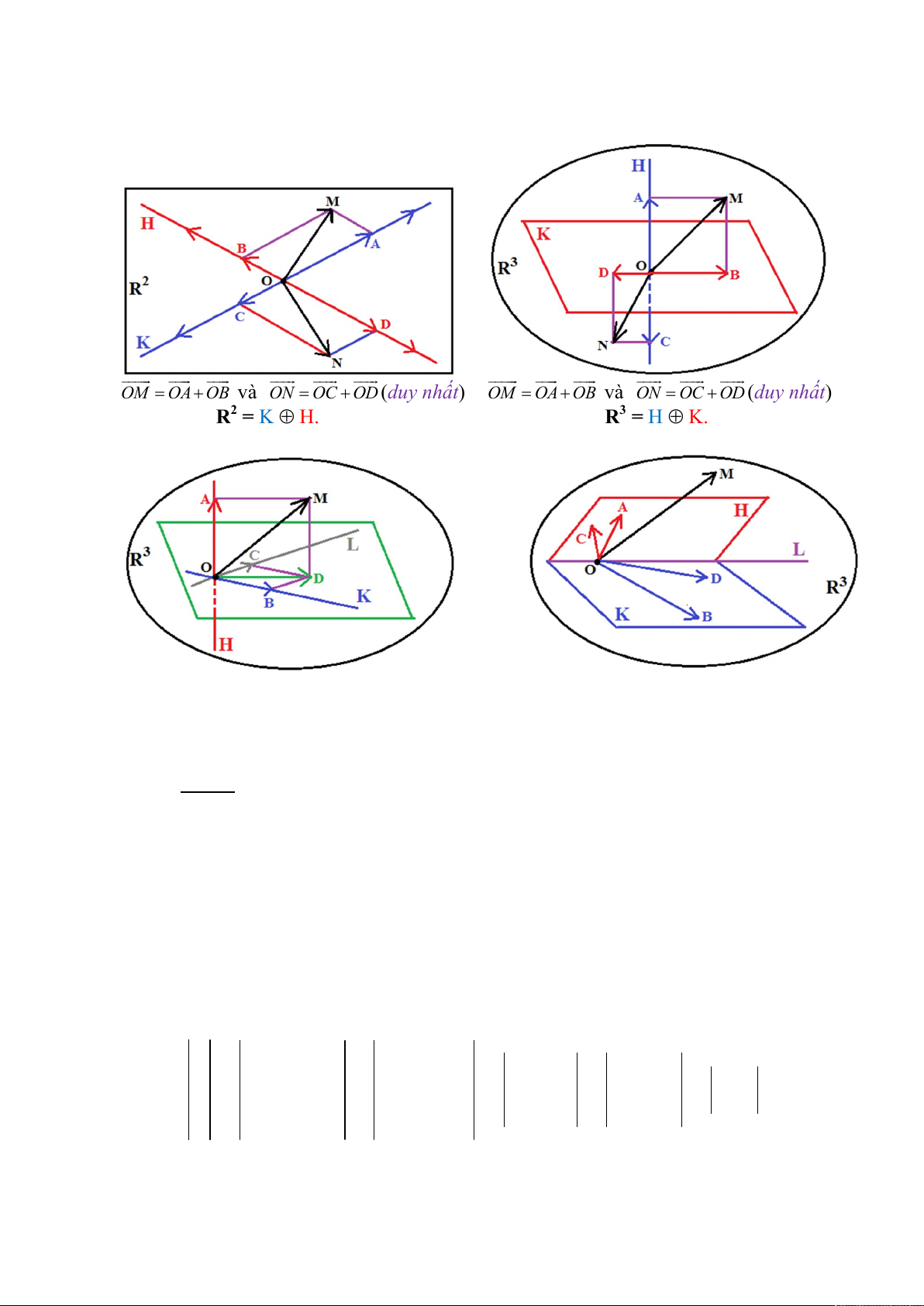
OM OA OB và ON OC OD (duy nhất) OM OA OB và ON OC OD (duy nhất)
R2 = K  H. R3 = H  K.
     
    
OM OA OD OA OB OC (duy nhất) OM OA OB OC OD (không duy nhất)
R3 = H  K  L. R3 = H + K (không là tổng trực tiếp). Ví dụ:
a) H = < A1 = { 1 = (1, 2, 0, 3), 2 = (0, 1,  1, 1) }> ≤ R4 và A1 là một cơ sở
của H vì H = < A1 > và A1 độc lập tuyến tính (để ý 1 không tỉ lệ với 2)
K = < A2 = { 3 = (3,  2, 1, 0), 4 = (0, 2, 0, 1) }> ≤ R4 và A2 là một cơ sở
của K vì K = < A2 > và A2 độc lập tuyến tính (để ý 3 không tỉ lệ với 4).
Ta có A = A1  A2 = { 1 , 2 , 3 , 4 } là một cơ sở của R4 vì  1 2 0 3 1 2 0 3 1 1 2 3 1 4  3  0 1 1  1 3 1 0 1 1 4 2 = = = 3 1  1 = 3 3 1 = = 9  0.  * 3 2 1 0 * 3 2 1 0 3 3 3 * 0 2 1 * 0 0 1  0 2 0 1 0 2 0 1 4 3 Suy ra R4 = H  K.
Xét  = (5,9,4,1)  R4 = H  K. Ta muốn phân tích  =    với   H  c   2  1      c 3
và   K. Ta tìm được [  ] 2     A = =
( bằng cách giải phương trìnhc   1   3     c  4 4   
vector c11 + c22 + c33 + c44 =  với các ẩn số thực c1, c2, c3 và c4 ).
Khi đó  = c11 + c22 =  2(1, 2, 0, 3) + 3(0, 1, 1, 1) = (2, 1, 3, 3)  H
và  = c33 + c44 =  (3,  2, 1, 0) + 4(0, 2, 0, 1) = ( 3, 10,  1, 4)  K.
b) M = < B1 = {1 = (1, 4, 2, 3), 2 = (0, 3, 1, 2)}> ≤ R4 và B1 là một cơ sở của
M vì M = < B1 > và B1 độc lập tuyến tính ( để ý 1 không tỉ lệ với 2 ).
N = < B2 = { 3 = (2, 0, 1, 0) }> ≤ R4 và B2 là một cơ sở của N vì
N = < B2 > và B2 độc lập tuyến tính ( để ý 3  O ).
L = < B3 = { 4 = (0,  3, 0, 1) } > ≤ R4 và B3 là một cơ sở của L vì
L = < B3 > và B3 độc lập tuyến tính ( để ý 4  O ).
Ta có B = B1  B2  B3 = { 1 , 2 , 3 , 4 } là một cơ sở của R4 vì  1 4 2 3 * 1 4 2 3 1 3 1 2 9 1 2  0 3 1 2 0 3 1 2 9 1 2 = = = 8  3  6  = 26 3  6  = =  1  0  2 0 1 0 0 8 3 6  2  6 3  3 * 3  0 1 * 0 0 1  0 3  0 1 0 3  0 1 4
Suy ra R4 = M  N  L.
Xét  = ( 5, 14,  5,  3)  R4 = M  N  L.
Ta muốn phân tích  =      với   M,   N và   L.  c   1 1      c 4  Ta tìm được [  ] 2     B = =
( bằng cách giải phương trình vectorc   3   3     c  2 4   
c11 + c22 + c33 + c44 =  với các ẩn số thực c1, c2, c3 và c4 ). 4
Khi đó  = c11 + c22 = (1, 4, 2, 3) – 4(0, 3, 1, 2) = (1,  8,  2,  5)  M,
 = c33 =  3(2, 0, 1, 0) = ( 6, 0,  3, 0)  N và
 = c44 = 2(0,  3, 0, 1) = (0,  6, 0, 2)  L.
c) P = < D1 = { 1 = ( 3, 0, 2) }> ≤ R3 và D1 là một cơ sở của P vì
P = < D1 > và D1 độc lập tuyến tính ( để ý 1  O ).
Q = < D2 = { 2 = (4, 1,  3) }> ≤ R3 và D2 là một cơ sở của Q vì
Q = < D2 > và D2 độc lập tuyến tính ( để ý 2  O ).
U = < D3 = { 3 = (6, 1,  4) } > ≤ R3 và D3 là một cơ sở của U vì
U = < D3 > và D3 độc lập tuyến tính ( để ý 3  O ).
D = D1  D2  D3 = { 1 , 2 , 3 } là một cơ sở của R3 vì  3 0 2 3  0 2 1 3  2  = 4 1 3  = 2 0 1 = 
=  1  0. Do đó R3 = P  Q  U. 2 2  1  6 1 4 * 6 1 4  3
Xét  = (25, 1,  16)  R3 = P  Q  U.
Ta muốn phân tích  =      với   P,   Q và   U.  c   5   1 Ta tìm được [  ]     D = c = 2 
( bằng cách giải phương trình vector 2      c     3 3   
c11 + c22 + c33 =  với các ẩn số thực c1, c2 và c3 ).
Khi đó  = c11 =  5( 3, 0, 2) = (15, 0,  10)  P,
 = c22 =  2(4, 1,  3) = ( 8,  2, 6)  Q và
 = c33 = 3(6, 1,  4) = (18, 3,  12)  U.
d) V = < C1 = { 1 = (1, 2, 2), 2 = (4, 7, 1) } > ≤ R3 và C1 là một cơ sở của V
vì V = < C1 > và C1 độc lập tuyến tính ( vì 1 không tỉ lệ với 2 ).
W = < C2 = { 3 = (2,3, 4), 4 = (3, 7, 15) }> ≤ R3 và C2 là một cơ sở của 5
W vì W = < C2 > và C2 độc lập tuyến tính ( vì 3 không tỉ lệ với 4 ).
Ta có V + W = < C = C1  C2 > = < { 1 , 2 , 3 , 4 } >.
Lập ma trận và biến đổi về dạng bậc thang rút gọn:     1 2 2 * 1 2 2  * 1 0 16  * 1 0 0    1   1              4 7 1 0 1 9 * 0 1 9 * 0 1 0  2   =            = 2   .     2  3  4   0 1 8   0 0 1   *  0 0 1     3 3                     3 7 15 0 1 9 0 0 0 0 0 0 O 4           
Ta thấy V + W có một cơ sở là Bo = { 1 , 2 , 3 }, nghĩa là V + W = R3 và
dim(V + W) = | Bo | = 3. Như vậy C = C1  C2 = { 1 , 2 , 3 , 4 } không phải
là một cơ sở của R3 = V + W ( do | C | = 4  3 = dimR3 ). Như vậy
R3 = V + W là tổng thường mà không phải là tổng trực tiếp.
Xét  = (1, 2,  3)  R3. Ta có sự phân tích không duy nhất  =  +  =  + 
với  = 81  62 = ( 16,  26, 10)  V,  =  73 + 4 = (17, 28,  13)  W,
 = 171  32 = (5, 13, 31)  V và  =  3  24 = ( 4, 11,  34)  W.
1.3/ MỆNH ĐỀ: Giả sử Rn có các không gian con H1 , H2 , …, Hk ( k  2 ).
Các phát biểu sau là tương đương với nhau:
a) Rn = H1  H2    Hk .
b) Rn = H1 + H2 +  + Hk và dim Rn = dimH1 + dimH2 +  + dimHk .
(nếu Rn = H1 + H2 +  + Hk thì dim Rn ≤ dimH1 + dimH2 +  + dimHk ).
Ví dụ: Xét các Ví dụ trong (1.2).
a) R4 = H  K, dimH = | A1 | = 2, dimK = | A2 | = 2 và 4 = dimR4 = dimH + dimK
b) R4 = M  N  L, dimM = | B1 | = 2, dimN = | B2 | = 1, dimL = | B3 | = 1 và
4 = dimR4 = dimM + dimN + dimL.
c) R3 = P  Q  U, dimP = | D1 | = 1, dimQ = | D2 | = 1, dimU = | D3 | = 1 và
3 = dimR3 = dimP + dimQ + dimU.
d) R3 = V + W (không trực tiếp) nên 3 = dimR3 < dimV + dimW = 2 + 2 = 4. 6
II. TRỊ RIÊNG, KHÔNG GIAN RIÊNG, VECTOR RIÊNG VÀ ĐA
THỨC ĐẶC TRƯNG CỦA MA TRẬN VUÔNG:
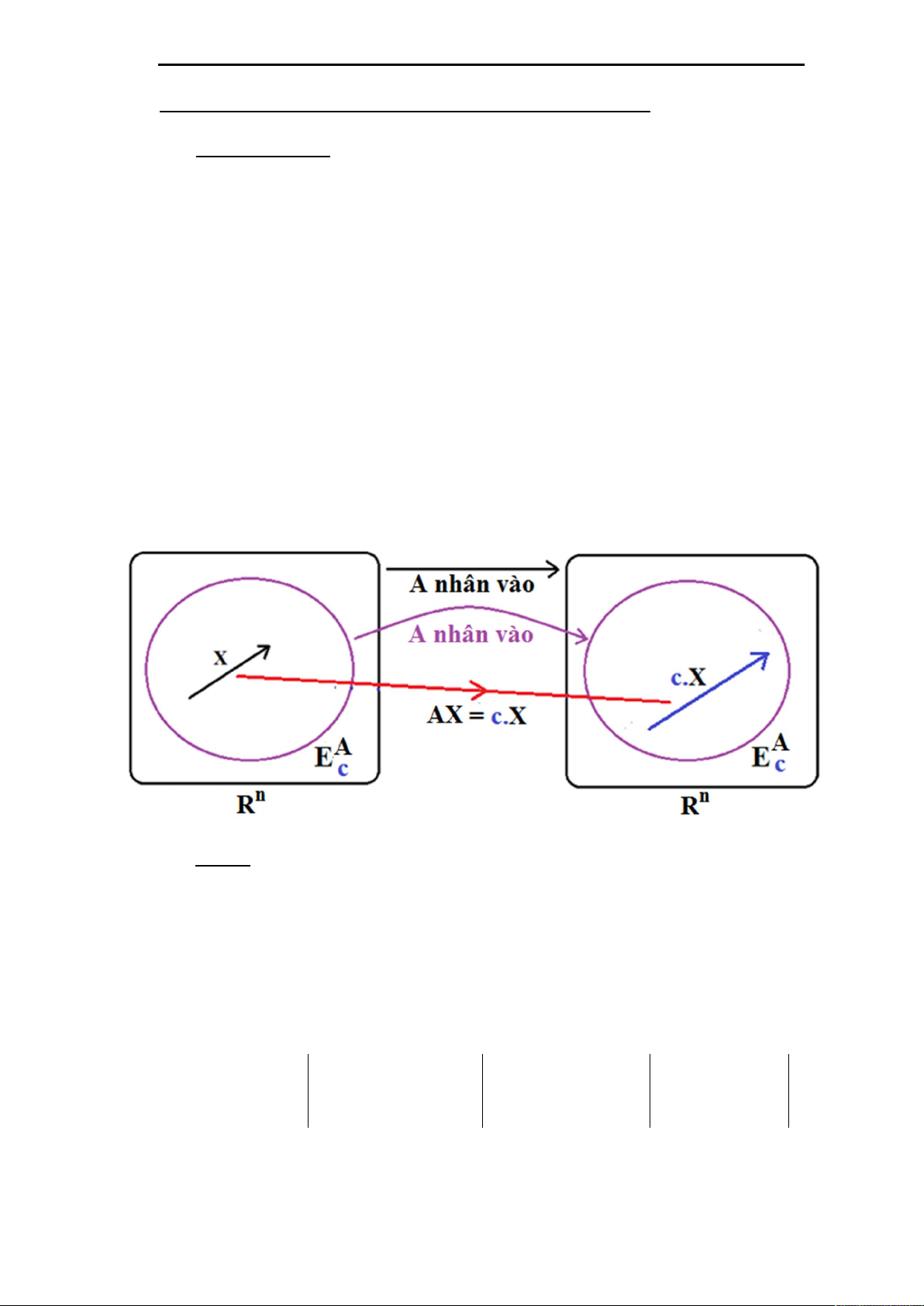
2.1/ ĐỊNH NGHĨA: Cho A  Mn(R) và c  R. a) Đặt A E
= {   Rn | A. = c. } = {   Rn | A.  c.I c n. = O }
= {   Rn | (A  c.In). = O } thì A
E Rn. Hơn nữa c [ A. A E = A
E khi c  0 ] và [ A. A
E = {O} khi c = 0 ]. Suy ra A. A E A E . c c c c c Ký hiệu A. A E = { A. |   A
E } ( A. là dạng viết gọn của A.t ). c c b) Nếu A
E  { O } thì ta nói c là một trị riêng thực của A và A E là không c c
gian riêng của A ứng với trị riêng c. Lúc đó,   A Ec \ { O },
A. = c. và  được gọi là một vector riêng của A ứng với trị riêng c. Ví dụ:  7 6  1  0  Cho A =   12 17 24  M  
3(R). Xét c = 0 và d =  1  R.  12 15 22      A
E = {  = (u, v, w)  R3 | A = O } = { O = (0, 0, 0) } do các phép biến o
đổi đưa về dạng bậc thang rút gọn cho ta ( u = v = w = 0 ). u v w u v w  7 6  1  0 0   1 1  5 1  6 0  * 1 0 1 0  * 1 0 0 0          12 17 24 0 *    0 2 2 0    0 1 1 0    0 1 0 0   .  12 15 22 0     2 3 2 0      0 33 34 0    *  0 0 1 0          7
Suy ra c = 0 không phải là một trị riêng thực của A.  7 6 10   1 0 0   8 6 10  Ta có (A + I       3) = 12 17 24 + 0 1 0 = 12 18 24 và        12 15 22          0 0 1 12 1  5 21     A
E = { = (u,v,w)  R3 | (A + I 1
3) = O} ={ = (a,  2a, 2a) | a  R}  { O }
do các phép biến đổi về dạng bậc thang rút gọn cho ta
w = 2a ( a  R ), u = a, v =  2a : u v w u v w  8 6  10 0   4 3  5 0   4 0 2  0  * 1 0 1 / 2 0          1  2 18 24 0 *    0 3 3 0    * 0 1 1 0    0 1 1 0    12 15 21 0     0 6 6 0     0 0 0 0   0 0 0 0         
Suy ra d =  1 là một trị riêng thực của A và A
E là không gian riêng của A 1
ứng với trị riêng ( 1).   A
E1 \ {O}, A() =   và  được gọi là một
vector riêng của A ứng với trị riêng ( 1).
2.2/ ĐỊNH NGHĨA: Cho A  Mn(R).
Cho biến số x lấy giá trị thực . Đặt pA(x) = det (x.In  A) thì pA(x) là
một đa thức đơn khởi bậc n trên R có dạng
pA(x) = xn + an  1 xn  1 +  + a1x + ao với an  1 , … , a1 , ao  R.
Ta nói pA(x) là đa thức đặc trưng của ma trận vuông thực A. Ví dụ:  3 4 7    x  3 4  7  A =     0 2 0  M 0 x  2 0
( x là biến thực )  
3(R) có xI3  A =    0 0 9      0 0 x  9  
Ta có pA(x) = | xI3  A | = (x + 3)(x  2)(x  9) = x3  8x2  15x + 54.
2.3/ MỆNH ĐỀ: Cho A  Mn(R) và c  R. Khi đó
a) c là một trị riêng thực của A  pA(c) = 0.
b) Suy ra: tập hợp các trị riêng thực của A chính là tập hợp các nghiệm
thực của đa thức đặc trưng pA(x) . 8 Ví dụ:  6 3  x  6 3 a) A = 
  M2(R) có pA(x) = | xI2  A | = = x2 – 4x + 9. 7  2   7 x  2
pA(x) vô nghiệm trên R (vì ’ =  5 < 0) nên A không có trị riêng thực.  6 3 1 x  6 3 1 b) B =   12 7 3   M 12 x  7 3  
3(R) có pB(x) = | xI3  B | =  16 12 6      16 12 x  6 x  6 3  1 x  3 3 1 x  3 1
= 3x  6 x  2 0 = 0 x  2 0 = (x + 2) = (x + 1)(x + 2)2. 2  0 x  6 16 1  2 x  6 2  0 12 x  6
Ta nói B có hai trị riêng thực là c1 =  1 và c2 =  2.
III. SỰ CHÉO HÓA CỦA MA TRẬN VUÔNG: 3.1/ MỆNH ĐỀ:
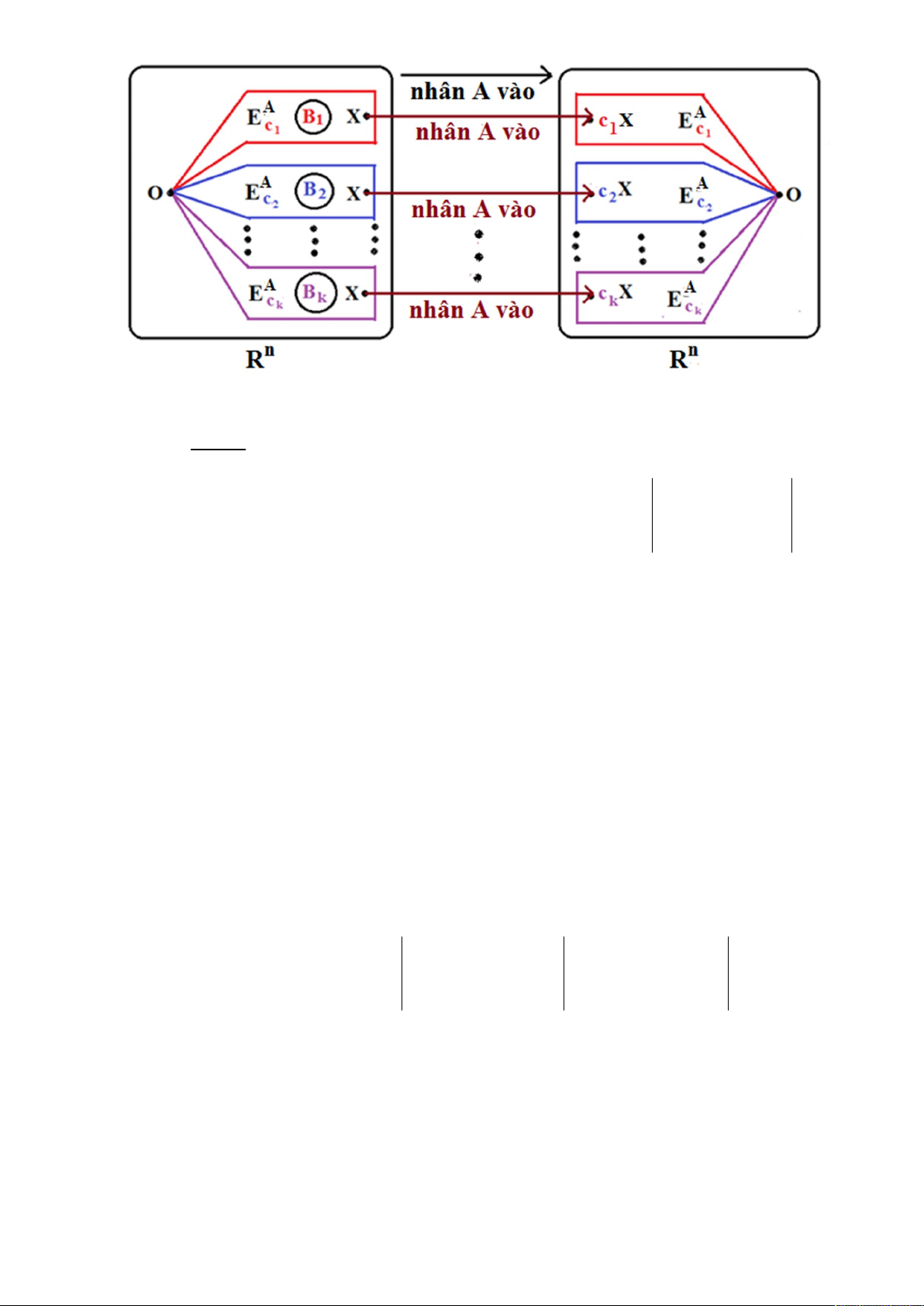
a) Cho c1, c2, …, cm là các trị riêng thực khác nhau của A  Mn(R) ( m  2 ) và W = ( A E + A E +  + A
E )  Rn. Khi đó ta có W = A E A E    A E . 1 c 2 c m c 1 c 2 c m c
c) Như vậy tổng của các không gian riêng ứng với các trị riêng thực khác
nhau của ma trận vuông là tổng trực tiếp.
3.2/ ĐỊNH NGHĨA: Cho A, H, K  Mn(R).
a) Ta nói H và K đồng dạng với nhau nếu có P khả nghịch  Mn(R) thỏa
P  1HP = K (lúc đó ta cũng có Q  1KQ = H với Q = P  1). Quan hệ đồng
dạng trên Mn(R) là một quan hệ tương đương.
b) A chéo hóa được trên R nếu A đồng dạng với một ma trận đường chéo,    1   
nghĩa là có P khả nghịch  M 2  
n(R) thỏa P  1AP = .        n
( P  1AP là một ma trận đường chéo ). 9 Ví dụ:  7 1  2 12   3 0 2  A =     6 17 15  M 4 1
3 khả nghịch  M   3(R). Ta có P =   3(R)  10 24 22        6 1 4     1 2 2   1  0 0  với P 1 =     2 0 1 và P 1AP =
nên A chéo hóa được trên R.   0 2 0    2 3 3       0 0 1  
3.3/ ĐỊNH LÝ: Cho A  Mn(R). Khi đó
a) A chéo hóa được trên R  1 r 2
(*) p (x)  (x c ) (x c )r ...(x c ) kr , c , c ,..., c  , r , r ,..., r   \{0}   A 1 2 k 1 2 k 1 2 k  . (**) dim A E r (1 j k) c    j j
b) Khi xảy ra (*) thì ta nói đa thức pA(x) tách được trên R.
3.4/ MỆNH ĐỀ: Cho A  Mn(R). Nếu pA(x) có n nghiệm thực khác nhau thì
A chéo hóa được trên R.
3.5/ HỆ QUẢ: Cho A  Mn(R). Khi đó:
a) Để ý p q  ( p q) [ nếu p và q có nội dung độc lập với nhau ].
p q  [ p  ( p q )] ( nếu có p thì mới hiểu được q ).
b) A không chéo hóa được trên R
 ( pA(x) không tách được trên R ) hoặc   *   1 r 2
p (x)  (x c ) (x c )r ...(x c ) kr , c , c ,..., c  , r , r ,..., r   \ { } 0 A 1 2 k 1 2 k 1 2 k  . (**) j
 {1, 2,..., k}, dim A E r cj jVí dụ:  3 1 3 x  3 1 3 a) A =   3 1 1 = 
  M3(R) có pA(x) = | xI3  A | = 3  x 1 1  2 2 0     2  2 x x  4 1  3 x  4 1 3 x 2
= x  4 x 1 1 = 0 x 2  = (x  4) = (x  4)(x2 + 4). 2 x 0 2 x 0 2 x 10
Do pA(x) không tách được trên R nên A không chéo hóa được trên R.  10 13 4  x 10 1  3 4 b) H =   13 16 4  13 x 16 4 
  M3(R) có pH(x) = | xI3  H | =  12 12 1     12 12 x 1 x  3 1  3 4 x  3 1  3 4 x  3 0
= x  3 x 16 4 = 0 x  3 0 = (x  3) = (x  3)2(x + 1). 12 x 1 0 12 x 1 0 1  2 x 1 H
E = {  R3 | (H  3I 3
3) = O} = { = (v, v, 0) = v(1, 1, 0) | v  R}
có cơ sở C = {  = (1, 1, 0) } do các phép biến đổi đưa về dạng bậc thang
rút gọn cho ta ( v  R , u = v, w = 0 ) : u v w u v w  1  3 13 4 0   1 1 3 0  * 1 1 0 0    ( H  3I     * 3 | O ) = 1  3 13 4 0    0 0 0 0    0 0 1 0   .  12 12 4 0          0 0 4  0 0   0 0 0 0   Do dim H
E = | C | = 1 < 2 nên H không chéo hóa được trên R. 3
3.6/ CHÉO HÓA MA TRẬN: Cho A  Mn(R) và A chéo hóa được trên R, 1 r 2
(*) p (x)  (x c ) (x c )r ...(x c ) kr , c , c ,..., c  , r , r ,..., r   \{0}  nghĩa là A 1 2 k 1 2 k 1 2 k  . (**) dim A E r (1 j k) c    j j
* j  { 1, 2,…, k }, tìm một cơ sở B A j cho E
= {  Rn | (A  c c jIn) = O}. j
( cơ sở Bj không duy nhất ). * Đặt B = B A A A
1  B2  …  Bk thì B là một cơ sở của Rn = E E    E 1 c 2 c k c
( cơ sở B không duy nhất ).
* Đặt P = (C  B) với C là cơ sở chính tắc của Rn thì P khả nghịch  Mn(R)
P không duy nhất và  c  1       c  1   P  1AP =  
 (j  {1, 2,…, k}, cj xuất hiện rj lần).  ck       c   k  11 Rn = A E A E    A E và A. A E A E ( 1  j  k ). c c c 1 2 k c c j j Ví dụ:  7 1  2 2  x  7 12 2 a) A =   3 4  0  M 3  x  4 0 =  
3(R) có pA(x) = | xI3  A | =  2 0 2      2 0 x  2
= (x  7)(x + 4)(x + 2)  4(x + 4) + 36(x + 2) = x(x + 1)(x  2).
pA(x) có 3 nghiệm thực đơn là 0,  1 và 2 nên A chéo hóa được trên R.  8 12 2    5 12 2   A + I     3 = 3 3  0 và A  2I 3 6  0 .   3 =    2 0 1       2 0 4    A
E = {   R3 | A = O } = {  = ( 4a,  3a, 4a) = a( 4,  3, 4) | a  R } 0
có một cơ sở là B1 = { 1 = ( 4,  3, 4) } do các phép biến đổi đưa về
dạng bậc thang rút gọn cho ta [ w = 4a ( a  R ), u =  4a, v =  3a ]. u v w u v w  7 1  2 2 0  * 1 4  2  0  * 1 0 1 0        (A | O) = 3 4 0 0 *    0 8 6 0    0 1 3 / 4 0   .  2 0 2 0          0 8  6  0   0 0 0 0   A
E = {  R3 | (A + I 1 
3) = O} = { = ( a,  a, 2a) = a( 1,  1, 2) | a  R}
có một cơ sở là B2 = { 2 = ( 1,  1, 2) } do các phép biến đổi đưa về
dạng bậc thang rút gọn cho ta [ w = 2a ( a  R ), u =  a, v =  a ]. 12 u v w u v w  8 12 2  0   1 3 1  0   1 0 1 / 2 0  (A + I       3 | O) = 3 3  0 0    0 6 3 0    0 1 1 / 2 0   .  2 0 1 0          0 6 3 0   0 0 0 0   A
E = {  R3 | (A  2I 2
3) = O} = { = ( 2w, w, w) = w( 2, 1, 1) | w  R}
có một cơ sở là B3 = { 3 = ( 2,  1, 1) } do các phép biến đổi đưa về
dạng bậc thang rút gọn cho ta (w  R , u =  2w, v =  w ). u v w u v w  5 1  2 2  0   1 1  2 1  0 0   1 0 2 0  (A  2I       3 | O) = 3 6  0 0    0 30 30 0    0 1 1 0   .  2 0 4 0          0 2  4 2  4 0   0 0 0 0   R3 = A E A E A
E có một cơ sở là B = B 0 1 2
1  B2  B3 = { 1, 2 , 3 } với
A1 = 0.1 = O, A2 =  2 và A3 = 23 .  4 1  2  
Đặt P = (C  B) = ( [    1 ]C [ 2 ]C [ 3 ]C ) = 3  1 
1 với C là cơ sở    4 2 1     1 3  1  0 0 0 
chính tắc của R3 thì P khả nghịch, P  1 =    1 4 2 và P  1AP = 0 1  0      2 4 1       0 0 2    1  3 1   x  1 3  1 b) H =   3  5 1   M =  
3(R) có pH(x) = | xI3  H | = 3 x  5 1  3 3 1   3 3  x  1   x  2 2  x 0 x  2 0 0 x  2 1 = 3 x  5 1 = 3 x  2 1 = (x  2) = (x  1)(x  2)2. 0 x 1 3 3 x 1 3 0 x 1  2  3 1    3  3 1   H  I     3 = 3  4 1  và H  2I 3  3 1  .   3 =    3 3 0       3  3 1    H
E = {  R3 | (H  I 1
3) = O} = {  = (w, w, w) = w(1, 1, 1) | w  R } có một cơ sở là B H
1 = { 1 = (1, 1, 1) } và dim E1 = | B1 | = 1 do các phép biến
đổi đưa về dạng bậc thang rút gọn cho ta ( w  R, u = w, v = w ). 13 u v w u v w  2 3 1 0  * 1 0 1  0  * 1 0 1  0      ( H  I   * 3 | O ) = 3  4 1 0    0 1 1  0    0 1 1  0   .  3 3 0 0         0 3 3 0   0 0 0 0   H
E = {  R3 | (H  2I 2
3) = O} = { = (u, v, w)  R3 |  3u + 3v  w = 0}
= {  = (u, v, 3v  3u) = u(1, 0,  3) + v(0, 1, 3) | u, v  R } có một cơ sở là B H
2 = { 2 = (1, 0,  3), 3 = (0, 1, 3) } và dim E = | B 2 2 | = 2. Ta có p H H
H (x) = (x  1)(x  2)2 tách được trên R, dim E = 1 và dim E = 2 1 2
nên H chéo hóa được trên R. R3 = H E H
E có một cơ sở là B = B 1 2 1  B2 =
= { 1, 2 , 3 } với H1 = 1 , H2 = 22 và H3 = 23. 1 1 0  Đặt P = (C  B) = ( [    1 ]C [ 2 ]C [ 3 ]C ) = 1 0 1 với C là cơ sở   1 3 3     3 3  1   1 0 0 
chính tắc của R3 thì P khả nghịch, P  1 =    2 3 1 và P  1HP = 0 2 0 .      3 4 1       0 0 2   IV. ÁP DỤNG:
4.1/ LŨY THỪA VÀ CĂN THỨC CỦA MA TRẬN CHÉO HÓA ĐƯỢC:
Cho A  Mn(R) và A chéo hóa được trên R. Xét số nguyên k  1.    1   
Tìm ma trận P khả nghịch  M 2  
n(R) thỏa P  1AP = .        n     k    1 1      k  Suy ra A = P 2   P  1 và Ak = P 2  P 1 .             k    n   n
Nếu có 1, 2, … , n  R thỏa k
 =  ( 1  j  n ), ta chọn j j       1 1       H = P 2   P 1  M 2   P 1 = A.    n(R) thì Hk = P           n   n
Ta nói H là một căn bậc k (không nhất thiết duy nhất) của A trong Mn(R). 14 Ví dụ:
a) Cho A  M3(R) trong Ví dụ (3.6) và k là số nguyên  1. Ta có  0 0 0   4 1  2    1 3  1 P 1AP =       0 1  0 với P = 3  1  1 và P  1 = 1 4 2  M       3(R).  0 0 2       4 2 1   2 4 1   k  0 0 0   0 0 0   0 0 0  Suy ra A = P       0 1  0 P  1 và Ak = P P 1 = P k P  1   0 1  0 0 (1) 0      0 0 2    k    0 0 2   0 0 2    1 4  2    4 8  2  
= ( 1)kS + 2kT với S =     1 4  2  và T = 2 4  1   M     3(R).  2 8 4       2  4 1  
Cho số nguyên lẻ r  3.  0 0 0   0 0 0    Chọn D = P   0 1  0 
 P 1  M3(R) thì Dr = P 0 1  0 P 1 = A. Ta có       0 0 r 2 0 0 2      1 4  2    4 8  2   D = ( 1)S + r     2 T với S = 1 4  2  và T = 2 4  1   M     3(R).  2 8 4       2  4 1  
b) Cho H  M3(R) trong Ví dụ (3.6) và k là số nguyên  1. Ta có  1 0 0  1 1 0   3 3  1  P 1HP =       0 2 0 với P = 1 0 1 và P  1 = 2 3 1  M       3(R).  0 0 2       1 3  3   3 4 1   k  1 0 0   1 0 0   1 0 0  Suy ra H = P       0 2 0 P  1 và Hk = P P 1 = P 0 2k 0 P  1   0 2 0      0 0 2    k    0 0 2   0 0 2    3 3  1  2  3 1   = S + 2kT với S =     3 3  1 và T = 3 4 1   M     3(R).  3 3 1      3 3 0    1 0 0   1 0 0    Chọn D = P   0 k 2 0 
 P 1  M3(R) thì Dk = P 0 2 0 P 1 = H. Ta có       0 0 k 2 0 0 2     15  3 3 1  2  3 1   D = S + k    
2 T với S = 3 3 1 và T = 3 4 1   M     3(R).  3 3 1      3 3 0  
5.2/ GIẢI MỘT SỐ HỆ THỨC ĐỆ QUI DỰA THEO SỰ CHÉO HÓA CỦA MA TRẬN VUÔNG:
a) Tìm un theo n ( n nguyên ≥ 0 ) nếu
uo = 1, u1 = 2 và un + 2 = un + 1 + 6un , n ≥ 0.  u   2   u   u  6u  k  0, đặt t k k k k k = 1 
 thì to =   và tk + 1 = 2   = 1   u  1 u u k     k 1    k 1   1 6   u  1 6  1 6  = k 1      = 
 tk . Vậy k  0, tk + 1 = Atk với A =   = 1 0   u  1 0 1 0 k       3 0   3 2  1  1 2  = P   P −1 và P =   , P −1 = 
 (A chéo hóa được trên R). 0 2   1 1   5 1  3    u  Do đó, n  0, t n n = 1 
 = Atn 1 = A2tn 2 =  = An  1t1 = An to = un n  3 0    1  3 2    3n 0   1 2   2  1 n 1  n 1  3 ( 2  )    4  = P   P −1 2   =         =     0 2  n n n   1   5 1 1   0 (2)   1  3   1   5 3 ( 2  )   1   1 n 1  n 1 4 3  ( 2  )    1 =   . Suy ra n ≥ 0, un = [ 4.3n + (− 2)n ]. 5 4  3n  ( 2  )n   5
Giải thích tính chéo hóa được trên R của A: x 1 6  pA(x) = | xI2  A | =
= x2 – x + 6 = (x – 3)(x + 2) có 2 nghiệm 1  x
thực đơn ( c1 = 3  c2 =  2 ) nên A chéo hóa được trên R.  2 6   3 6  A – 3I2 =   và A + 2I2 =   . 1 3   1 2   A
E = {   R2 | (A – 3I 3
2) = O } = {  = (a, b)  R2 | a  3b = 0 }
= {  = (3b, b) = b(3,1) | b  R } có cơ sở C1 = { 1 = (3, 1) }. A
E = {   R2 | (A + 2I 2
2) = O } = {  = (a, b)  R2 | a + 2b = 0 } 16
= {  = ( 2b, b) = b( 2,1) | b  R } có cơ sở C2 = { 2 = ( 2, 1) }. R2 = A E A
E có cơ sở C = C 3 2 
1  C2 = { 1 = (3, 1), 2 = ( 2, 1) }.  3 2  
Đặt P = ( B  C ) = ( [ 1 ]B [ 2 ]B ) = 
 với B là cơ sở chính tắc 1 1   1  1 2   3 0 
của R2 thì P khả nghịch, P  1 =   và P  1AP =   . 5 1  3   0 2   
b) Tìm un và vn theo n ( n nguyên ≥ 0 ) nếu
uo = 2, vo = 5, un + 1 = un  4vn và vn + 1 =  un + vn , n ≥ 0.  u   2   u   u  4v  k  0, đặt t k k k k = k
 thì to =   và tk + 1 = 1   =   v  5 vu v k     k 1    k k   1 4    u   1 4    1 4   = k     = 
 tk . Vậy k  0, tk + 1 = Atk với A =   = v 1 1    1 1 1 1 k       3 0   2 2  1  1  2  = P   P − 1 và P =   , P − 1 = 
 (A chéo hóa được trên R). 0 1   1 1   4 1 2    u
Do đó n  0, tn = n
 = Atn 1 = A2 tn 2 =  = An  1t1 = An to vn n  3 0    1  2 2   3n 0   1  2   2  = P   P − 1 2   =         0 1  n   5   4 1 1   0 ( 1  )   1 2   5   1  2.3n 2( 1  )n   8   6( 1
 )n  4.3n  =   =   . n n   n n 4 3 ( 1)    12   3( 1  )  2.3  
Suy ra n ≥ 0, un = 6(− 1)n  4.3n và vn = 3(− 1)n + 2.3n .
Giải thích tính chéo hóa được trên R của A: x 1 4 pA(x) = | xI2  A | =
= x2 – 2x – 3 = (x – 3)(x + 1) có 2 nghiệm 1 x 1
thực đơn ( c1 = 3  c2 =  1 ) nên A chéo hóa được trên R.  2  4    2 4   A – 3I2 =   và A + I2 =   . 1  2    1 2   A
E = {   R2 | (A – 3I 3
2) = O } = {  = (a, b)  R2 |  a  2b = 0 }
= {  = ( 2b, b) = b( 2, 1) | b  R } có cơ sở C1 = { 1 = ( 2, 1) }. 17 A
E = {   R2 | (A + I 1
2) = O } = {  = (a, b)  R2 |  a + 2b = 0 }
= {  = (2b, b) = b(2, 1) | b  R } có cơ sở C2 = { 2 = (2, 1) }. R2 = A E A
E có cơ sở C = C 3 1
1  C2 = { 1 = ( 2, 1), 2 = (2, 1) }.  2  2 
Đặt P = (B  C) = ( [ 1 ]B [ 2 ]B ) = 
 với B là cơ sở chính tắc 1 1   1  1  2   3 0 
của R2 thì P khả nghịch, P  1 =   và P  1AP =   . 4 1 2   0 1  
c) Tìm un , vn và wn theo n ( n nguyên ≥ 0 ) nếu uo =  2, vo = 3, wo =  1,
un + 1 = 6un + 12vn + 16wn , vn + 1 =  3un – 7vn  12wn và
wn + 1 = un + 3vn + 6wn, n ≥ 0.  u   2    u
 6u 12v 16w k k 1  k k k k  0, đặt t         k = v thì t 3 và t v
= 3u  7v 12w k   o =   k + 1 = k 1    k k k    w         1  w
u  3v  6w k     k 1    k k k   6 12 16   u   6 12 16  k =       3 7  1  2 v = 3 7  12 t   k   
 k . Vậy k  0, tk + 1 = Atk với  1 3 6   w   1 3 6     k     6 12 16   1 0 0   4 3  4    1 3 4   A =         3 7 
12 = P 0 2 0 P −1 và P = 3 1 0 , P −1 = 3 8  1  2          1 3 6          0 0 2 1 0 1 1 3 5      
( A chéo hóa được trên R ).  u n Do đó n  0, t   n = v = At n  
n 1 = A2 tn 2 =  = An  1t1 = An to  w   n n  1 0 0   2    4 3  4    1 0 0   1  3  4    2   = P             0 2 0 P − 1 3 = 3 1 0 n 3 8  12 3 =       0 2 0        0 0 2  1   1 0 1   n   1 3 5   1        0 0 2       4 3  .2n  4.2n   3   10.2n 12  n 1  5.2  12        =   3 2n 0 n n 1    6  = = .   9  6.2   9  3.2    1 0 2n    n   n 1      2   2.2  3 2  3    
Suy ra n ≥ 0, un = 5.2n +1 − 12 , vn = 9 – 2n + 1 và wn = 2n + 1 − 3. 18
Giải thích tính chéo hóa được trên R của A:  6 12 16  x  6 1  2 16 A =   3 7  1  2  M 3 x  7 12 =  
3(R) có pA(x) = | xI3  A | =  1 3 6    1 3  x  6 x  6 1  2 1  6 x  6 1  2 20 x  6 20 = 0
x  2 3x  6 = 0 x  2 0 = (x  2) = (x  1)(x  2)2. 1 x  3 1  3  x  6 1  3  x  3
E1 = { X  R3 / (A  I3)X = O }.  5 12 16 0   1 0 4 0   1 0 4 0  X = (u, v, w)  E       1  3  8 1  2 0    0 1 3 0    0 1 3 0    1 3 5 0        0 3 9 0   0 0 0 0  
E1 = { X = (4w,  3w, w) = w(4,  3, 1) / w  R } có cơ sở
C1 = { X1 = (4,  3, 1) } và dimE1 = | C1 | = 1.
E2 ={ X  R3 / (A  2I3)X = O }.  4 12 16 0  X = (u, v, w)  E   2  3  9 1  2 0    1 3 4 0 .  1 3 4 0   
E2 = { X = ( 3v  4w, v, w) = v( 3, 1, 0) + w( 4, 0, 1) / v, w  R } có cơ
sở C2 = { X2 = ( 3, 1, 0), X3 = ( 4, 0, 1) } và dimE2 = | C2 | = 2 . Suy ra
A chéo hóa được trên R.
Đặt C = C1  C2 = { X1, X2, X3 } thì C là một cơ sở của R3 vì R3 = E1  E2.
Gọi B = { 1, 2, 3 } là cơ sở chính tắc của R3.  4 3  4   Xét P = (B  C) = ( [ X   1 ]B [ X2 ]B [ X3 ]B ) = 3 1 0 thì P khà    1 0 1     1 3 4    1 0 0  nghịch , P  1 =     3 8  1  2 và P  1AP = 0 2 0 .      1 3 5      0 0 2  
--------------------------------------------------------------------------------------------------------- 19

Tài liệu liên quan: