






































Preview text:
TRNG I HC IN LC
KHOA CÔNG NGH T NG GIÁO TRÌNH
LÝ THUYT IU KHIN T NG (Lu hành ni b)
Biên son: Phm Th Hng Sen Lê Th Vân Anh HÀ NI - 2011 LI NÓI U
Công ngh t ng là mt trong nhng hng phát trin công ngh mi nhn ca t nc
trong th k 21. Vi nn công nghip hin i ngày nay, mc t ng hóa ngày càng c
nâng cao nhm mc ích nâng cao nng sut lao ng, gim chi phí sn xut, gii phóng sc
lao ng cho con ngi,… tip cn vi nn công nghip có mc t ng hóa cao chúng
ta cn trang b nhng kin thc cơ bn v lý thuyt iu khin t ng bên cnh kin thc chuyên môn ca mình.
Lý thuyt iu khin t ng là cơ s lý thuyt thit k, phân tích các h thng t ng
trong các lnh vc khác nhau ca ngành k thut. Nhim v ca lý thuyt iu khin t ng là
kho sát các !c tính ng hc ca các h nhm mc ích thit k h thng th"a mãn các yêu cu cho trc.
Giáo trình Lý thuyt iu khin t ng trình bày nhng kin thc ct lõi ca lý thuyt iu
khin t ng tuyn tính liên tc. Ni dung ca giáo trình c biên son g#m 7 chơng trong
ó: chơng 1, 3, 5 do Ths. Lê Th Vân Anh biên son; chơng 2, 4, 6, 7 do Ths. Phm Th Hơng Sen biên son.
Chơng 1: T$ng quan v iu khin t ng.
Chơng 2: Mô t toán hc h iu khin t ng.
Chơng 3: Kho sát ng hc h thng iu khin tuyn tính liên tc.
Chơng 4: Phân tích tính $n nh và cht lng h thng iu khin.
Chơng 5: Thit k h thng iu khin.
Chơng 6: Nâng cao cht lng h iu khin.
Chơng 7: %ng dng Matlab kho sát h thng iu khin t ng.
Các tác gi xin chân thành cm ơn PGS.TS Phan Xuân Minh, Vin in, i hc Bách
Khoa Hà Ni ã ch& d'n, góp ý trong sut quá trình biên son giáo trình.
Do kh nng và kinh nghim biên son còn nhiu hn ch nên tài liu không th tránh kh"i
nhng thiu sót v m!t ni dung và b cc, chúng tôi rt mong nhn c s góp ý ca các bn
c ln tái bn sau này có cht lng tt hơn. Các tác gi ii MC LC
L(I NÓI )U ........................................................................................................................................... ii
CHƯƠNG 1: T,NG QUAN V- I-U KHI.N T/ 0NG ...........................................................................1
1.1 Gii thiu ............................................................................................................................................1 1.2 H th ng
iu khin t ng...............................................................................................................2
1.2.1 Khái nim và nh ngha ..................................................................................................................2
1.2.2 Nguyên t1c iu khin......................................................................................................................4
1.2.3 Tín hiu ............................................................................................................................................6 1.3 Phân loi h th ng iu khin t ng
................................................................................................7
1.3.1 Phân loi theo mch phn h i
# ..........................................................................................................7
1.3.2 Phân loi theo !c im mô t toán h c
...........................................................................................8
1.3.4 Phân loi mc tiêu iu khin..........................................................................................................8
1.3.4 Phân loi theo dng nng lng s2 d ng
.........................................................................................9 1.3.5 Phân loi theo s l
ng u vào, u ra ..........................................................................................9 1.4 Ví d v
h thng iu khin ..............................................................................................................9
CHƯƠNG 2: MÔ T3 TOÁN H4C H5 TH6NG I-U KHI.N ...................................................................13
2.1. Khái nim.........................................................................................................................................13
2.2. Mô t h thng min thi gian......................................................................................................13
2.2.1 Mô hình phơng trình vi phân .......................................................................................................13
2.2.2 Mô hình trng thái..........................................................................................................................15
2.3. Mô t h thng trong min tn s ....................................................................................................21
2.3.1 Mô hình hàm truyn.......................................................................................................................21 2.3.2 i s sơ kh # i
............................................................................................................................25
2.3.3 Công thc Mason ...........................................................................................................................30 2.4 Mi quan h gi a
các dng mô t toán h c
.......................................................................................33
BÀI T7P CHƯƠNG 2...............................................................................................................................35
CHƯƠNG 3: KH3O SÁT 0NG H4C H5 TH6NG I-U KHI.N TUY8N TÍNH LIÊN T9C ...................37
3.1 Tín hiu cơ bn và áp ng
...............................................................................................................37
3.1.1 Tín hiu xung ơn v và hàm tr ng l
ng .....................................................................................37
3.1.2 Tín hiu bc thang ơn v và hàm quá ......................................................................................38
3.1.3 Tín hiu iu hòa và hàm !c tính tn ...........................................................................................40 3.2 c ! tính ng h
c ca mt s khâu cơ bn ......................................................................................43
3.2.1 Khâu t& l (khâu P) .........................................................................................................................43
3.2.2 Khâu tích phân (khâu I) .................................................................................................................45
3.2.3 Khâu vi phân (khâu D)...................................................................................................................46
3.2.4 Khâu quán tính bc nht (khâu PT1) ..............................................................................................48
3.2.5 Khâu vi phân bc nht....................................................................................................................51
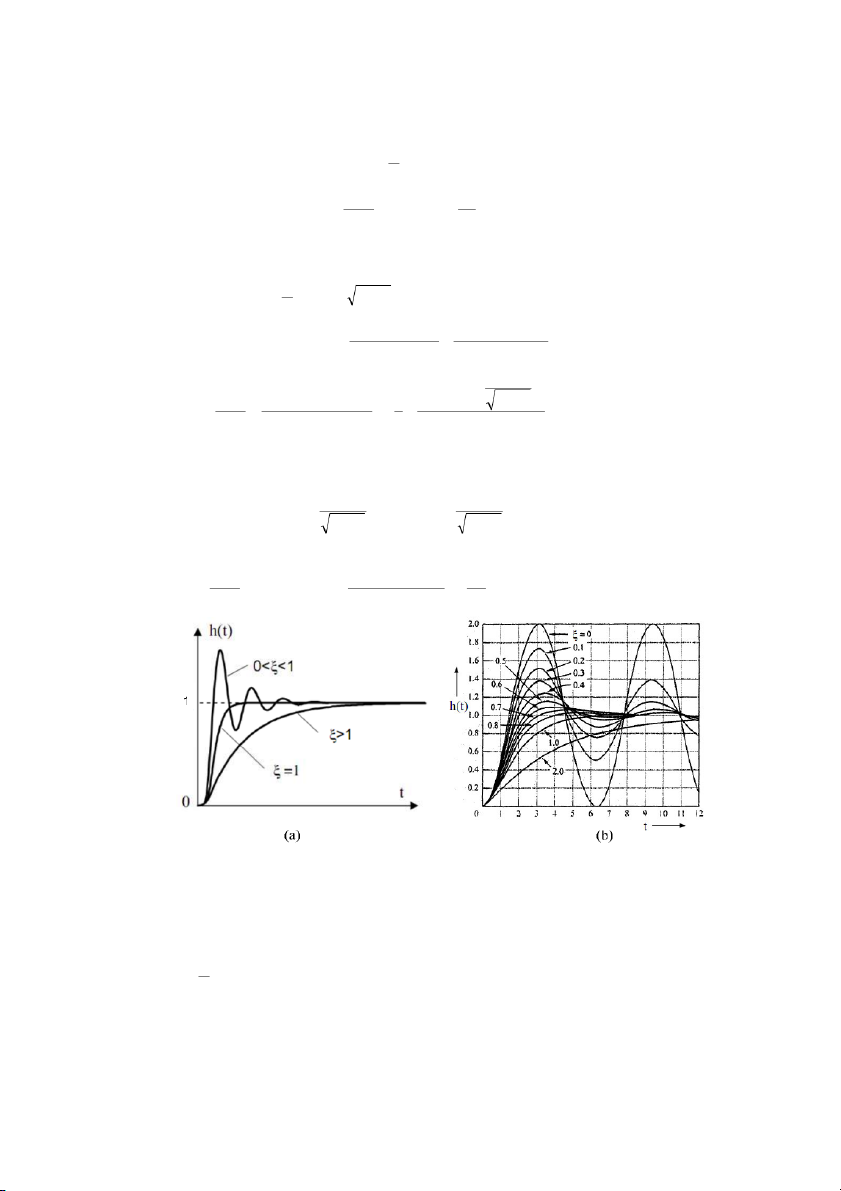
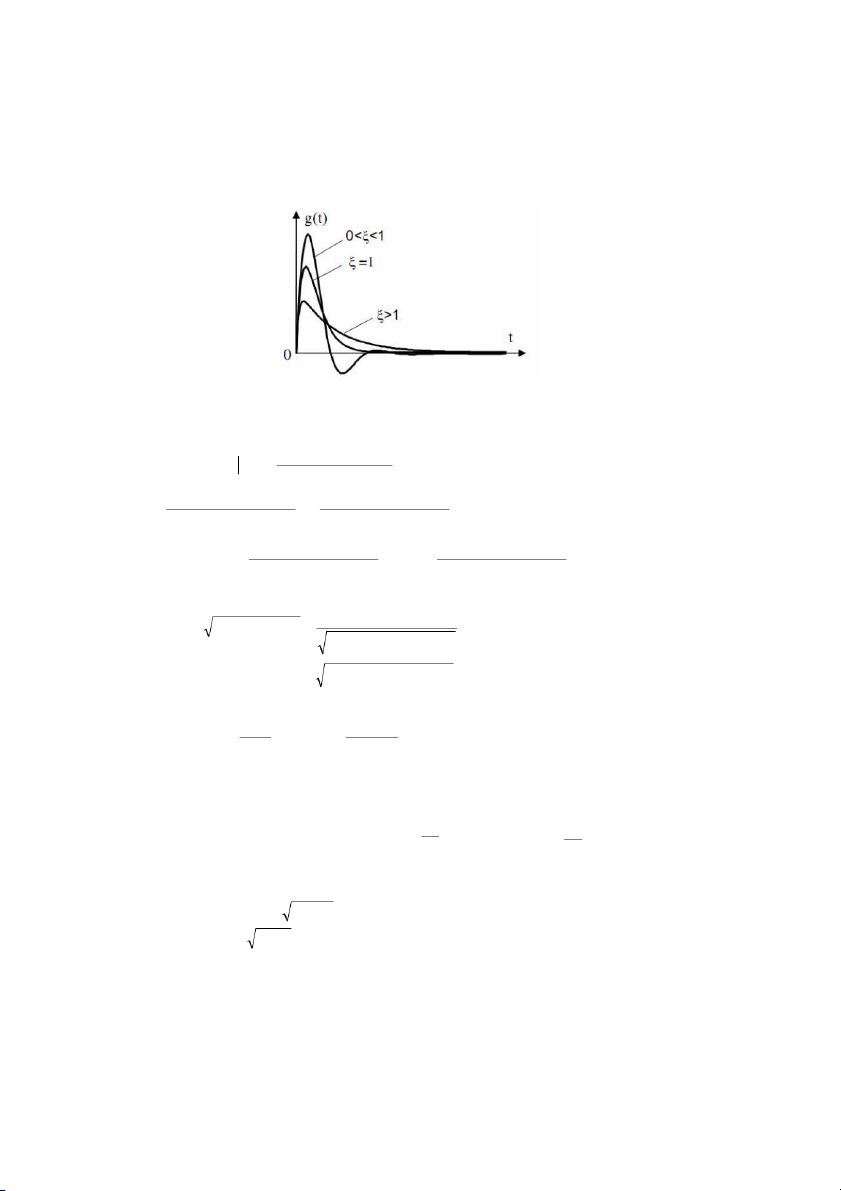
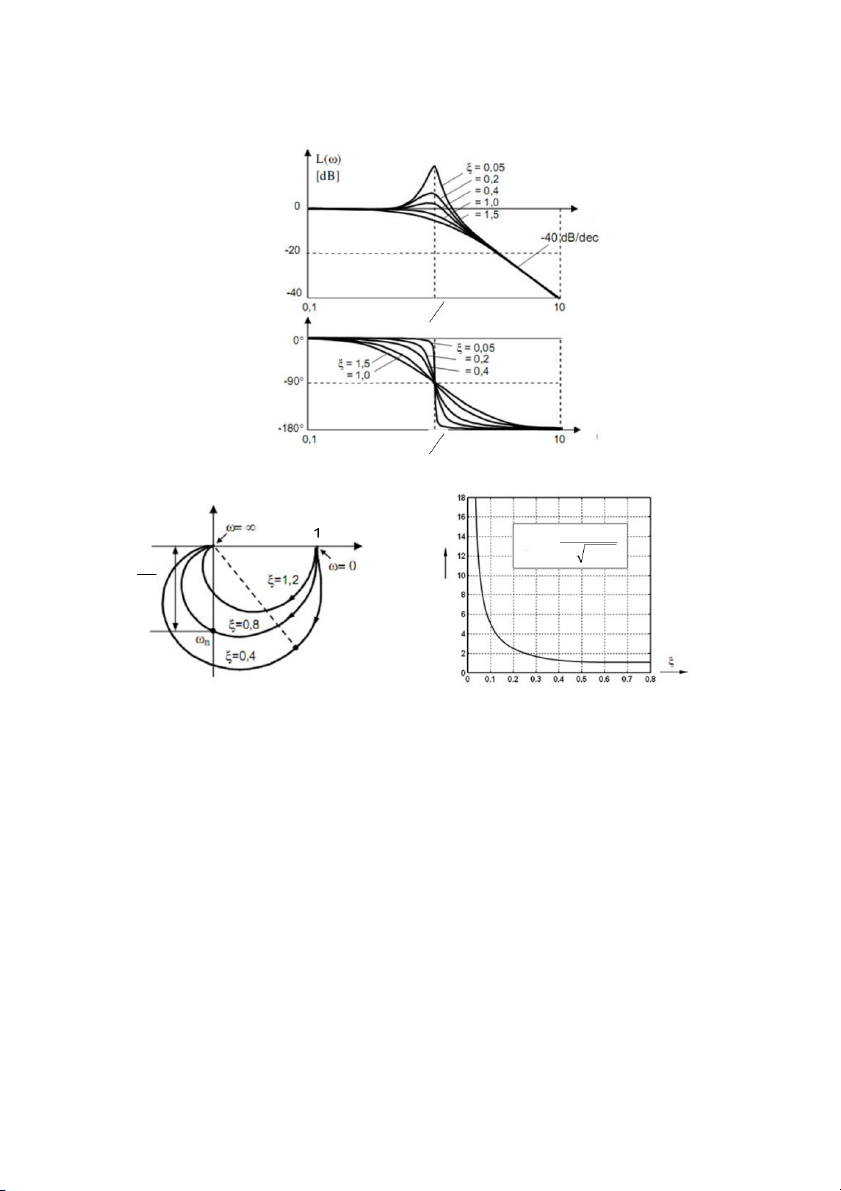
3.2.6 Khâu $n nh bc hai (khâu PT2)...................................................................................................52
3.2.7 Khâu chm tr: ................................................................................................................................58
3.3 Kho sát !c tính ng h c c a
h thng iu khin........................................................................59 3.3.1 c
! tính thi gian ca h th ng
.....................................................................................................60 3.3.2 c ! tính tn s c a h th ng
..........................................................................................................61
BÀI T7P CHƯƠNG 3...............................................................................................................................64 iii
CHƯƠNG 4: PHÂN TÍCH TÍNH ,N ;NH VÀ CH4.1 Khái nim v tính $n nh ................................................................................................................66 4.2 Các tiêu chu>n n
$ nh i s ...........................................................................................................68
4.2.1 iu khin $n nh cn thit..........................................................................................................68 4.2.2 Tiêu chu>n n
$ nh Hurwitz ..........................................................................................................69 4.2.3 Tiêu chu>n n
$ nh Routh..............................................................................................................71 4.3 Các tiêu chu>n n
$ nh tn s ...........................................................................................................74
4.3.1 Nguyên lý góc quay.......................................................................................................................74 4.3.2 Tiêu chu>n n
$ nh tn s Mikhailov ............................................................................................76 4.3.3 Tiêu chu>n n
$ nh tn s Nyquist ................................................................................................77 4.4 d t r n
$ nh..............................................................................................................................80 4.5 Phơng pháp qu
o nghim s......................................................................................................81
4.5.1 Khái nim.......................................................................................................................................81
4.5.2 Quy t1c v? qu o nghim s.......................................................................................................82
4.6 Kho sát cht lng h th ng
iu khin .........................................................................................84
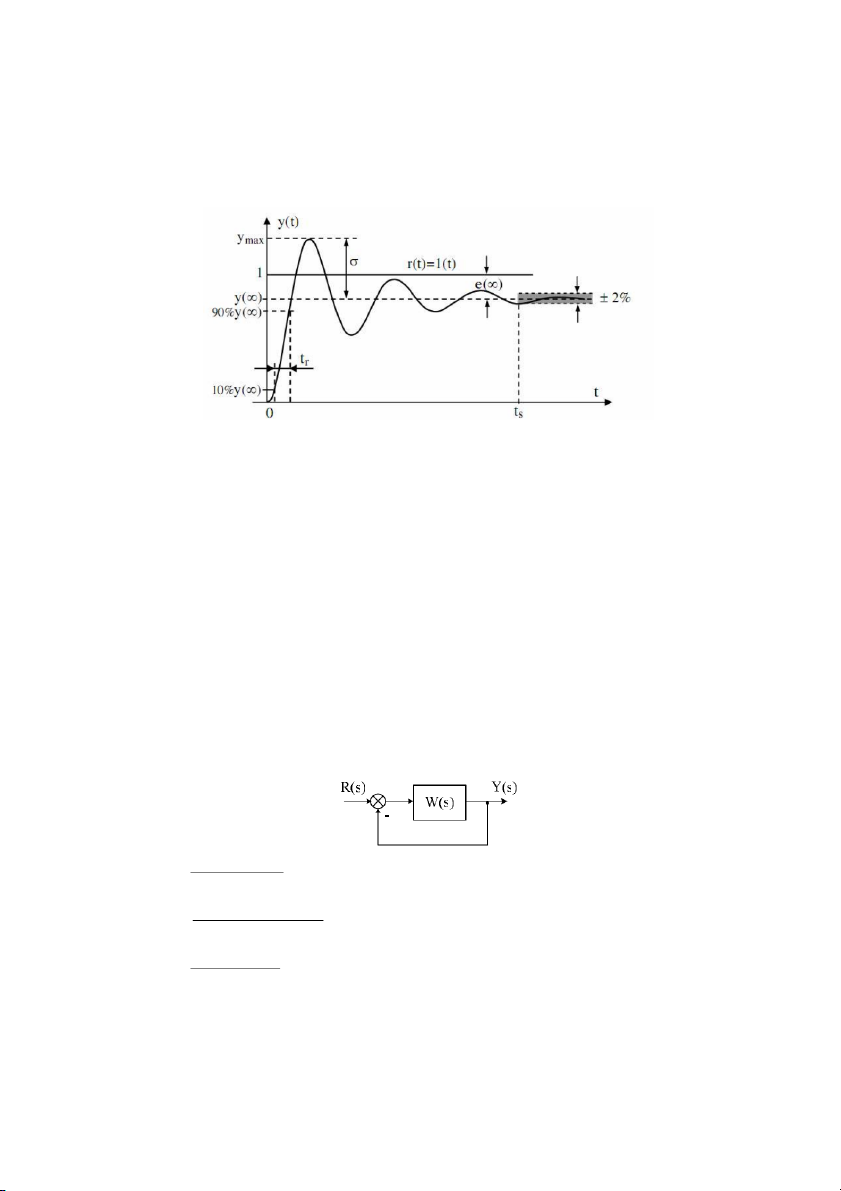
4.6.1 Ch& tiêu cht lng trng thái xác lp.........................................................................................84
4.6.2 Ch& tiêu cht lng trng thái quá .........................................................................................86
BÀI T7P CHƯƠNG 4...............................................................................................................................87
CHƯƠNG 5: THI8T K8 B0 I-U KHI.N ...............................................................................................89 5.1 Mc í
ch iu khin .........................................................................................................................89 5.2 Bài toán t ng h $
p h thng...............................................................................................................91
5.3 Các quy lut iu khin cơ bn.........................................................................................................92
5.3.1 Lut iu khin t& l (lut P) ..........................................................................................................93
5.3.2 Lut iu khin tích phân (lut I) ..................................................................................................94
5.3.3 Lut iu khin t& l - tích phân (lut PI).......................................................................................95
5.3.4 Lut iu khin t& l - vi phân (lut PD) ........................................................................................97
5.3.5 Lut iu khin t& l - vi tích phân (lut PID)................................................................................99 5.4 Mt s ph ơng pháp t ng h $ p b
iu khin PID..........................................................................103
5.4.1 Phơng pháp lý thuyt.................................................................................................................104
5.4.2 Phơng pháp thc nghim...........................................................................................................115 5.5 T ng h $ p b
iu khin trong không gian trng thái .....................................................................119
5.5.1 Tính iu khin c (Controllability)........................................................................................120
5.5.2 Tính quan sát c (Observability) .............................................................................................122
5.5.3 Phơng pháp gán im c c
..........................................................................................................123
BÀI T7P CHƯƠNG 5.............................................................................................................................124
CHƯƠNG 6: NÂNG CAO CH6.1 Phơng pháp bù tác ng nhi
:u .....................................................................................................126 6.1.1 Bù nhi:u ph t
i...........................................................................................................................126
6.1.2 Bù nhi:u !t trc .......................................................................................................................127
6.2 iu khin tng...............................................................................................................................127
CHƯƠNG 7: %NG D9NG MATLAB KH3O SÁT H5 TH6NG I-U KHI.N T/ 0NG .......................130
TÀI LI5U THAM KH3O........................................................................................................................134 iv
CHƠNG 1: TNG QUAN V IU KHIN T NG 1.1 Gii thiu
iu khin t ng ã và ang óng mt vai trò quan trng trong s phát trin khoa hc k
thut, !c bit là các lnh vc nh hàng không, robot và sn xut hin i. Ch@ng hn có th
thy iu khin t ng xut hin các máy công c s, h thng lái t ng và d'n ng
máy bay, tàu v tr trong công nghip hàng không v tr, trong công nghip xe hơi,… Ngoài
ra iu khin t ng cng rt cn thit trong lnh vc iu khin quá trình, nh iu khin áp
sut, >m, nhit , nht, và dòng chy,...
Lc s phát trin iu khin t ng
Lch s2 phát trin ca iu khin t ng c ghi nhn tA trc công nguyên, b1t u tA
#ng h# nc có phao iu ch&nh Ktesibios Hy Lp. H iu ch&nh nhit u tiên do
Cornelis Drebble (1572 - 1633) ngi Hà Lan sáng ch. Nm 1765, Polzunov ch to b iu
ch&nh mc nc n#i hơi. Nm 1784, James Watt ch to b iu tc ly tâm iu ch&nh máy
hơi nc. Các sáng ch này c xem là các cơ cu t ng xut hin u tiên trong công nghip.
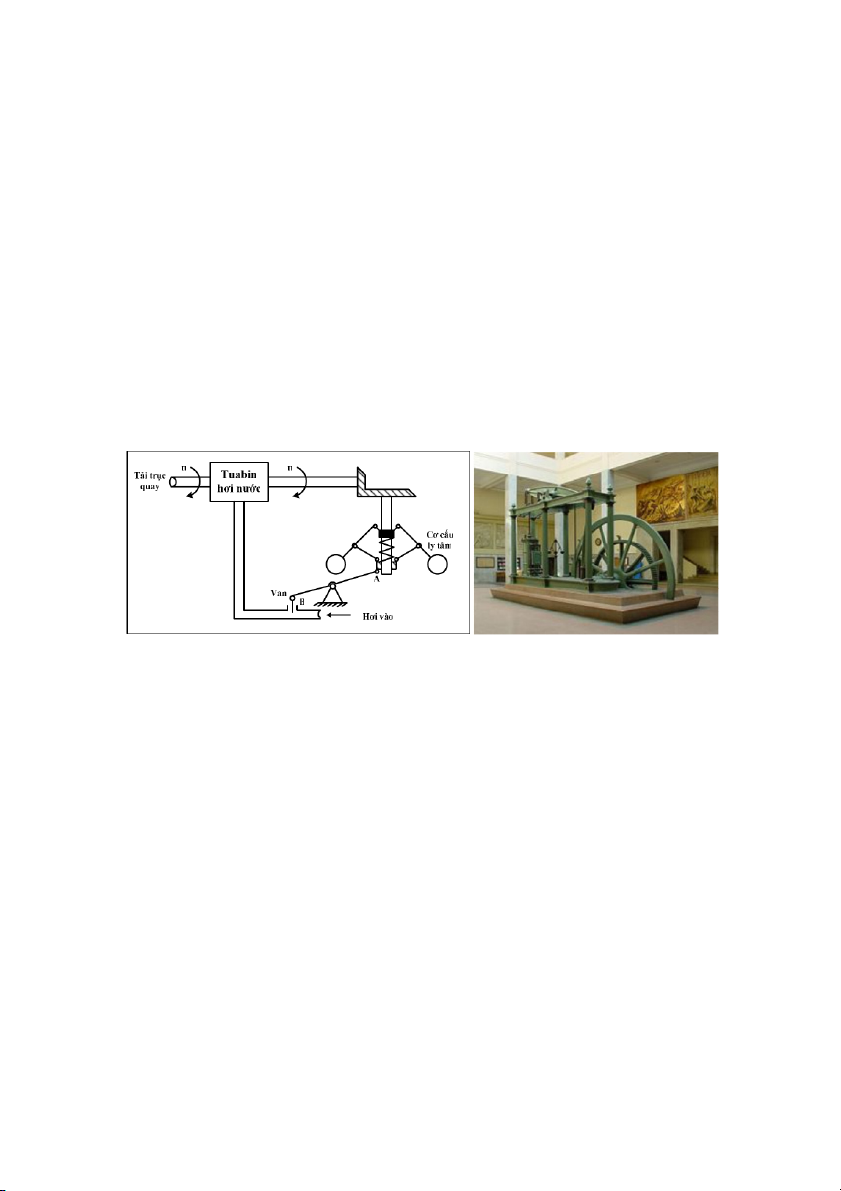
Hình 1.1: H iu tc ca James Watt
Nguyên lý hot ng ca h iu tc ly tâm (hình 1) là duy trì cho tc quay ca tuabin
hơi nc gi $n nh. Nu tc n tng lên, thông qua cơ cu ly tâm, con trt s? kéo lên trên
(kéo c u A ca cánh tay òn AB) và u B b n xung làm cho van óng li, làm gim
lu#ng hơi cp vào tuabin, do ó tc quay ca tuabin gim xung. Tơng t khi tc quay
ca tuabin vì mt nguyên nhân nào ó b gim xung thì cánh tay òn AB thông qua cơ cu ly
tâm s? h u A xung và nâng u B lên m c2a van cho lu#ng hơi vào máy nhiu hơn và
làm tng tc quay ca tuabin hơi nc.
Nhng nghiên cu áng k trong giai on u phát trin ca lý thuyt iu khin t ng
thuc v Minorsky, Hazen và Nyquist. Nm 1922, Minorsky là ngi !t nn móng cho lý
thuyt iu khin tàu thy và ch& ra cách xác nh tính $n nh tA phơng trình vi phân mô t
h thng. Nm 1917, O.Block s2 dng lý thuyt vectơ và hàm bin phc vào vic nghiên cu
lý thuyt iu khin t ng. Trên cơ s ó, nm 1932 Nyquist ã a ra phơng pháp # th
xác nh tính $n nh ca h thng kín tA áp ng tn s ca h h vi tín hiu vào hình sin.
Trong sut thp niên 1940, phơng pháp áp ng tn s, !c bit là phơng pháp biu #
Bode, ã c s2 dng rng rãi phân tích và thit k các h thng iu khin vòng kín
tuyn tính. TA cui thp niên 1940 n u thp niên 1950 Evans phát trin và hoàn ch&nh
phơng pháp qu o nghim. ây là hai phơng pháp ct lõi ca lý thuyt iu khin c$ in,
cho phép thit k c nhng h thng iu khin $n nh và áp ng c các yêu cu iu
khin cơ bn. Các b iu khin c thit k ch yu là b iu khin PID và b iu khin 1
sm tr: pha. Lý thuyt iu khin c$ in (trc 1960) ch yu áp dng cho h tuyn tính bt
bin vi mt u vào-mt u ra.
TA khong 1960, s xut hin ca máy tính s và lý thuyt iu khin s ã to iu kin
cho s ra i lý thuyt iu khin hin i da trên s phân tích và t$ng hp áp ng thi gian
s2 dng bin trng thái. Lý thuyt iu khin hin i rt thích hp thit k các b iu
khin là các chơng trình phn mm chy trên vi x2 lý và máy tính s. iu này cho phép thit
k các h thng phc tp nhiu u vào, nhiu u ra vi cht lng iu khin cao.
Trong nhng thp niên gn ây lý thuyt iu khin hin i phát trin theo các hng:
iu khin ti u các h tin nh và ng'u nhiên, iu khin thích nghi và iu khin thông
minh. Các phơng pháp iu khin thông minh nh iu khin m, mng thn kinh nhân to,
thut toán di truyn b1t chc các h thng thông minh sinh hc, v nguyên t1c không cn
dùng mô hình toán hc thit k h thng, do ó có kh nng ng dng thc t rt ln. Xu
hng kt hp các phơng pháp iu khin trong mt h thng iu khin cng c phát
trin vi s tr giúp ca máy tính s.
Ngày nay, lý thuyt iu khin c$ in v'n gi vai trò quan trng. Nó cung cp các kin
thc cơ bn làm nn tng cho vic tip cn các h thng iu khin hin i, ngày càng phc tp hơn. Khái nim iu khin
iu khin mt h thng c hiu là quá trình thu thp thông tin, x2 lý thông tin và tác
ng lên h thng bin $i, hiu ch&nh sao cho áp ng ca h t mc ích nh trc. Quá
trình iu khin không cn s tham gia trc tip ca con ngi gi là iu khin t ng.
Ví d: Xét quá trình lái (iu khin) mt xe máy xe luôn chy vi tc $n nh
40km/h. t c mc ích này trc ht m1t ngi lái xe phi quan sát #ng h# tc
bit tc hin ti ca xe (thu thp thông tin). Tip theo, b não s? so sánh tc hin ti vi
tc mong mun và ra quyt nh tng ga nu tc <40km/h và gim ga nu tc
>40km/h (x2 lý thông tin). Cui cùng tay ngi lái xe phi v!n tay ga thc hin vic tng
hay gim ga (tác ng vào h thng). Kt qu là tc xe c hiu ch&nh li và gi $n nh
nh mong mun. Trong các h thng iu khin t ng, quá trình iu khin cng di:n ra
tơng t nhng các b phn: m1t, b não, tay ca con ngi c thay th bng các thit b k
thut có chc nng tơng ng.
1.2 H thng iu khin t ng
1.2.1 Khái nim và nh ngha
Mt h thng iu khin t ng t$ng quát c minh ho hình 1.2.
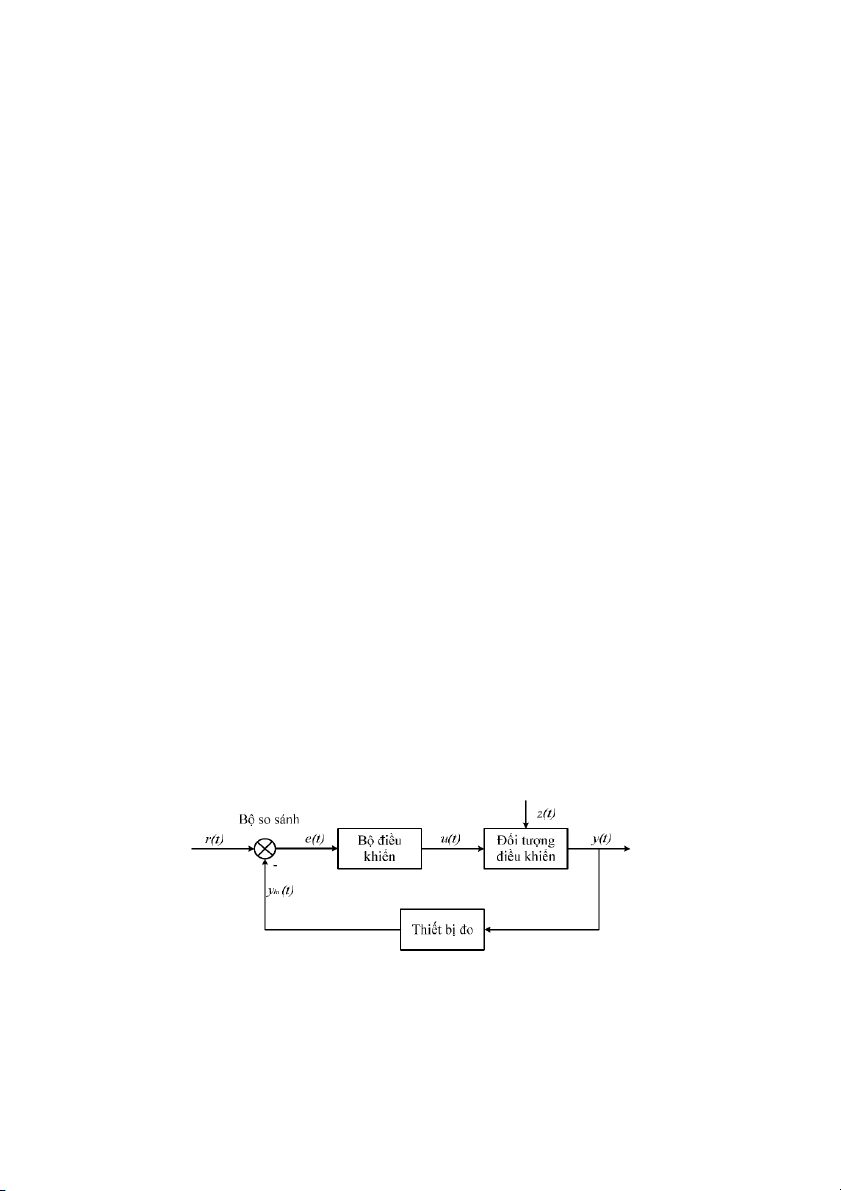
Hình 1.2: Cu trúc c bn ca h thng iu khin
H thng g#m ba thành phn cơ bn là i tng iu khin, thit b o và b iu khin. 2 Trong ó:
r(t): tín hiu vào, chu>n tham chiu (reference input), giá tr !t trc.
y(t): tín hiu ra (output), bin/i lng cn iu khin. y #
ht(t): tín hi u h i ti p.
e(t): tín hiu sai lch. Sai lch gia tín hiu !t và tín hiu ra
u(t): tín hiu iu khin.
z(t): tín hiu nhi:u.
i tng iu khin (TK): là h thng vt lý cn iu khin có áp ng mong
mun. TK bao g#m a dng các loi máy, thit b k thut, quá trình công ngh. TK là
máy, thit b thng c !c trng bng các cơ cu chp hành nh ng cơ, xi lanh, h bàn
trt vi tín hiu ra là chuyn ng vt lý nh vn tc, v trí, góc quay, gia tc, lc. Các quá
trình công ngh thng có tín hiu ra là nhit , áp sut, lu lng, mc. i tng Tín hiu vào Tín hiu ra ng cơ in in áp Vn tc, góc quay Van V trí nòng van Lu lng Xylanh lc Lu lng, áp sut Vn tc, v trí, lc piston Lò nhit Công sut cp nhit Nhit Chit áp V trí con trt in áp
Bng 1.1: Mt s i tưng thưng gp trong k thut và tín hiu vào ra tưng ng.
Thit b o (c m bin): Thc hin chc nng o và chuyn $i i lng ra ca h thng
thành dng tín hiu phù hp thun tin so sánh, x2 lý, hin th. S chuyn $i là cn thit
khi các tín hiu vào, ra không cùng bn cht vt lý: tín hiu ra có th là vn tc, v trí, nhit ,
lc,… trong khi tín hiu vào a phn là tín hiu in. Nguyên t1c chung o các i lng
không in bng phơng pháp in là bin $i chúng thành tín hiu in (in áp ho!c dòng in).
Mt s thit b o in hình là:
- o vn tc: b phát tc (DC tachometer, AC tachometer, optical tacho).
- o lng dch chuyn: chit áp (potentiometer), thc mã hóa.
- o góc quay: chit áp xoay, b mã hóa góc quay (rotary encoder).
- o nhit : c!p nhit ng'u (thermocouple), in tr nhit (thermistor, RTD).
- o lu lng, áp sut: Các b chuyn $i, lu lng, áp sut.
- o lc: cm bin lc (loadcell,…).
B so sánh: so sánh và phát hin sai lch e gia tín hiu vào chu>n và tín hiu h#i tip
(hay giá tr o c ca tín hiu ra).
Thông thng, các thit b o thc hin chuyn $i t& l nên: y s chuyn $i. ht = K.y v i K là h
Nu K = 1 thì e = r - yht = r – y
Trong h thng thc t b so sánh thng c ghép chung vào b iu khin. 3
B iu khin: dùng thông tin v sai lch e to tín hiu iu khin u thích hp, tA ó
tác ng lên i tng. Thut toán xác nh hàm u(t) gi là thut toán iu khin hay lut iu
khin. B iu khin liên tc có th thc hin bng cơ cu cơ khí, thit b khí nén, mch in
RLC, mch khuch i thut toán. B iu khin s thc cht là các chơng trình phn mm
chy trên vi x2 lý hay máy tính.
Nhi!u: các tác ng lên h thng gây nên các nh hng không mong mun c gi
chung là nhi:u. Nhi:u luôn t#n ti và có th tác ng vào bt c phn t2 nào trong h thng,
nhng thng c quan tâm nhiu nht là các nhi:u tác ng lên i tng iu khin, loi
này gi là nhi:u u ra hay nhi:u ph ti.
Trên ây chúng ta ch& mi cp n các thành phn cơ bn ca h thng iu khin. Trong
thc t, cu trúc hoàn ch&nh ca h thng iu khin thng a dng và phc tp hơn. Ví d,
trong h còn có cơ cu thit !t tín hiu vào chu>n, các cơ cu tác ng có vai trò trung gian
gia b iu khin và i tng nh van iu khin, b khuch i công sut, mch cách ly,
ng cơ, các b truyn ng. Trong h thng iu khin s còn có các b chuyn $i A/D, D/A, card giao tip,…
1.2.2 Nguyên t"c iu khin
Nguyên t1c iu khin th hin !c im lng thông tin và phơng thc hình hành tác
ng iu khin trong h thng. Các nguyên t1c iu khin có th xem là kim ch& nam thit
k h thng iu khin t cht lng cao và có hiu qu kinh t nht.
Nguyên t"c 1: Nguyên t1c thông tin phn h#i
Mun quá trình iu khin t cht lng cao, trong h thng phi t#n ti hai dòng thông
tin: mt tA b iu khin n i tng và mt tA i tng ngc v b iu khin (dòng
thông tin ngc gi là h#i tip). iu khin không h#i tip (iu khin vòng h) không th t
cht lng cao nht là khi có nhi:u. Các sơ # iu khin da trên nguyên t1c thông tin phn h#i là:
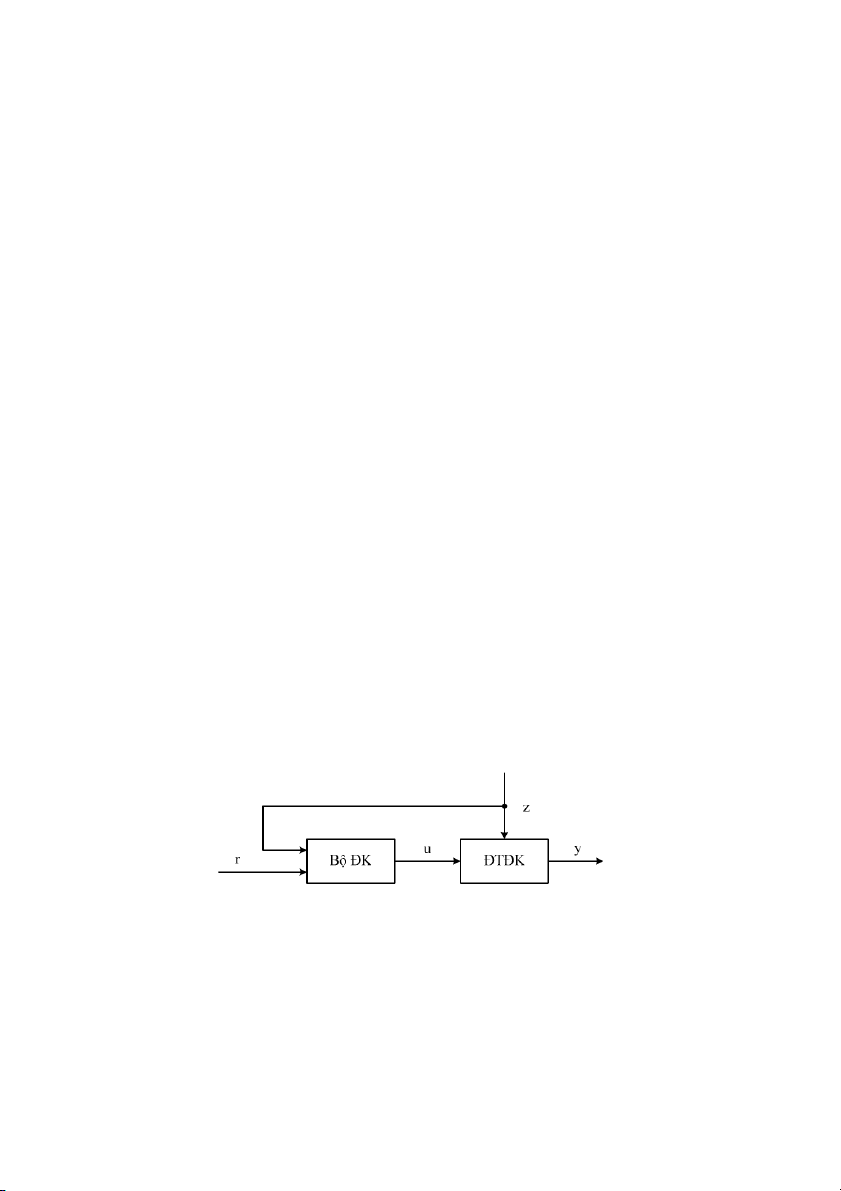
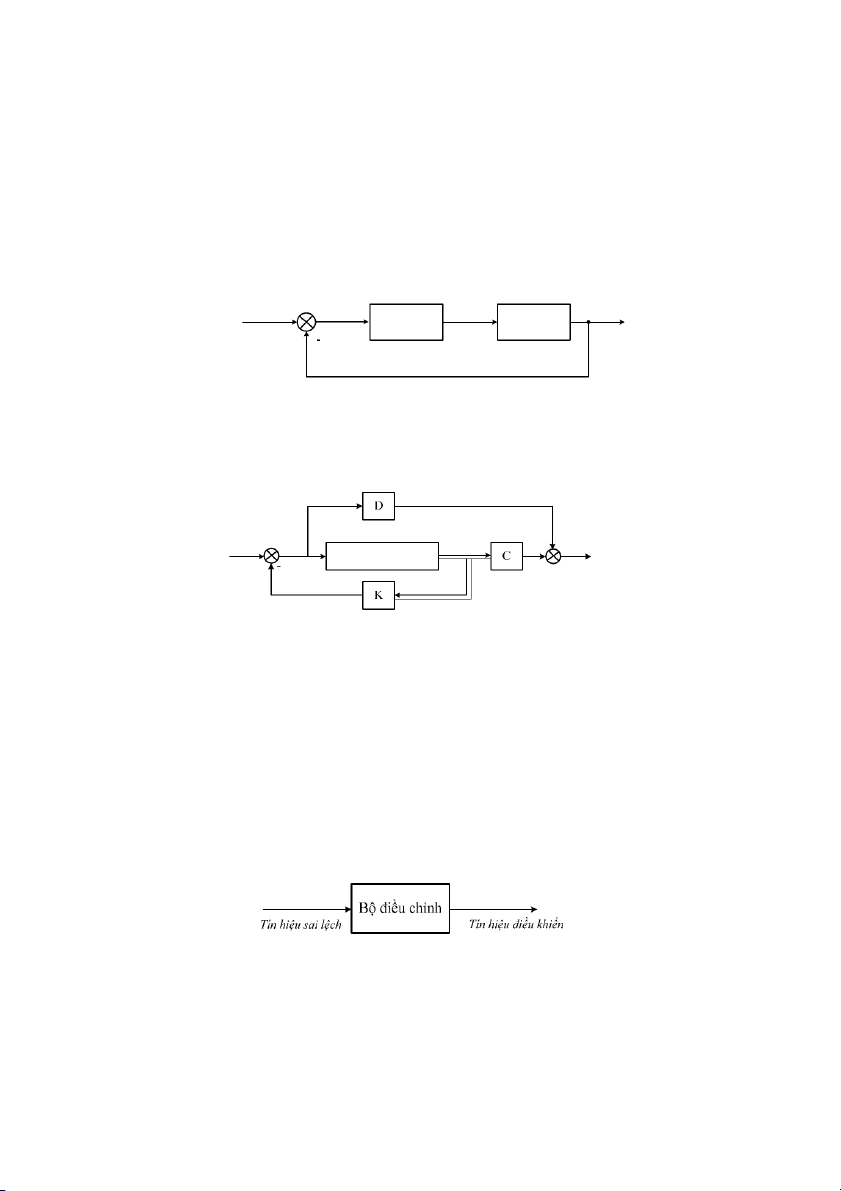
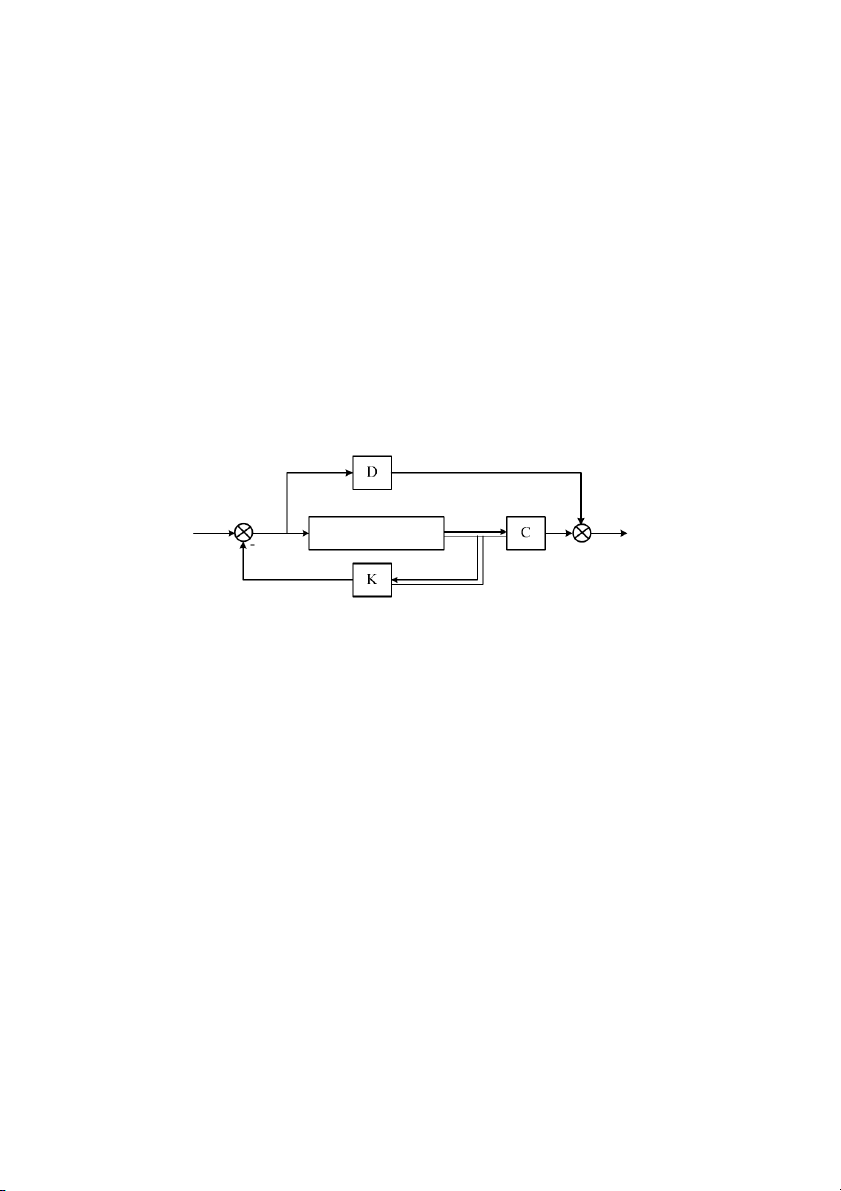
iu khin bù nhiu (Hình 1.3): Nguyên t1c này c dùng khi các tác ng bên ngoài lên
TK có th kim tra và o lng c, còn !c tính ca TK ã c xác nh y . B
iu khin s2 dng giá tr o c ca nhi:u tính toán tín hiu iu khin u(t). Nguyên t1c
iu khin này có ý ngha phòng ngAa, ngn ch!n trc. H thng có kh nng bù trA sai s
trc khi nhi:u thc s gây nh hng n tín hiu ra. Tuy nhiên, vì trong thc t không th
d oán và kim tra ht mi loi nhi:u nên vi các h phc tp thì iu khin bù nhi:u không
th cho cht lng cao.
Hình 1.3: S iu khin bù nhiu
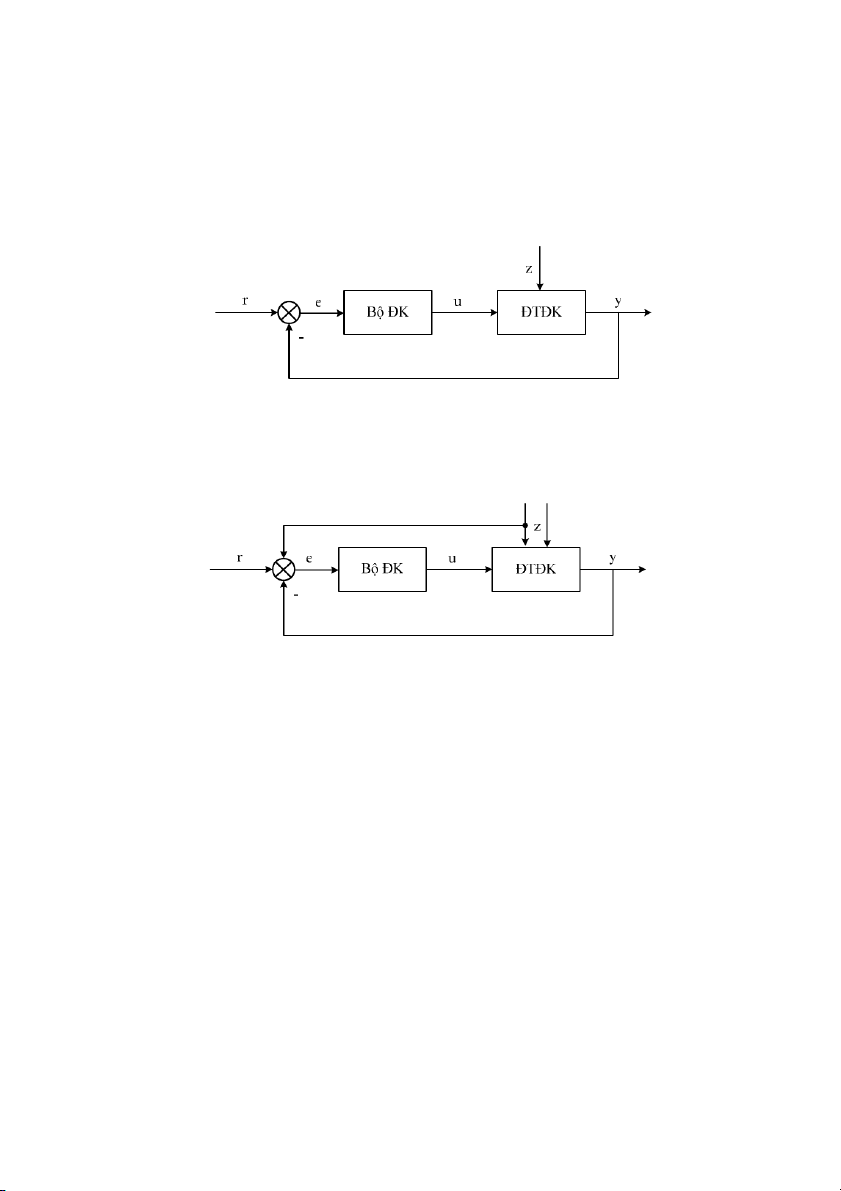
iu khin san bng sai lch (Hình 1.4): Nguyên t1c này c dùng khi các tác ng bên
ngoài không kim tra và o lng c, còn !c tính ca TK thì cha c xác nh y
. Tín hiu ra y(t) c o và phn h#i v so sánh vi tín hiu vào r(t). B iu khin s2 dng
sai lch vào-ra tính toán tín hiu iu khin u(t), iu ch&nh li tín hiu ra theo hng
làm trit tiêu sai lch. Nguyên t1c iu khin này có tính linh hot, th2 nghim và s2a sai. H 4
thng có kh nng làm trit tiêu nh hng ca các nhi:u không bit trc và/ho!c không o
c. Nhc im ca nó là tác ng hiu ch&nh ch& hình thành sau khi sai lch ã t#n ti
và c phát hin, tc là sau khi tín hiu ra ã thc s b nh hng. Các quá trình tr: trong h
làm cho tín hiu ra không gi c $n nh mt cách tuyt i mà thng có dao ng nh" quanh giá tr xác lp.
Hình 1.4: S iu khin san bng sai lch
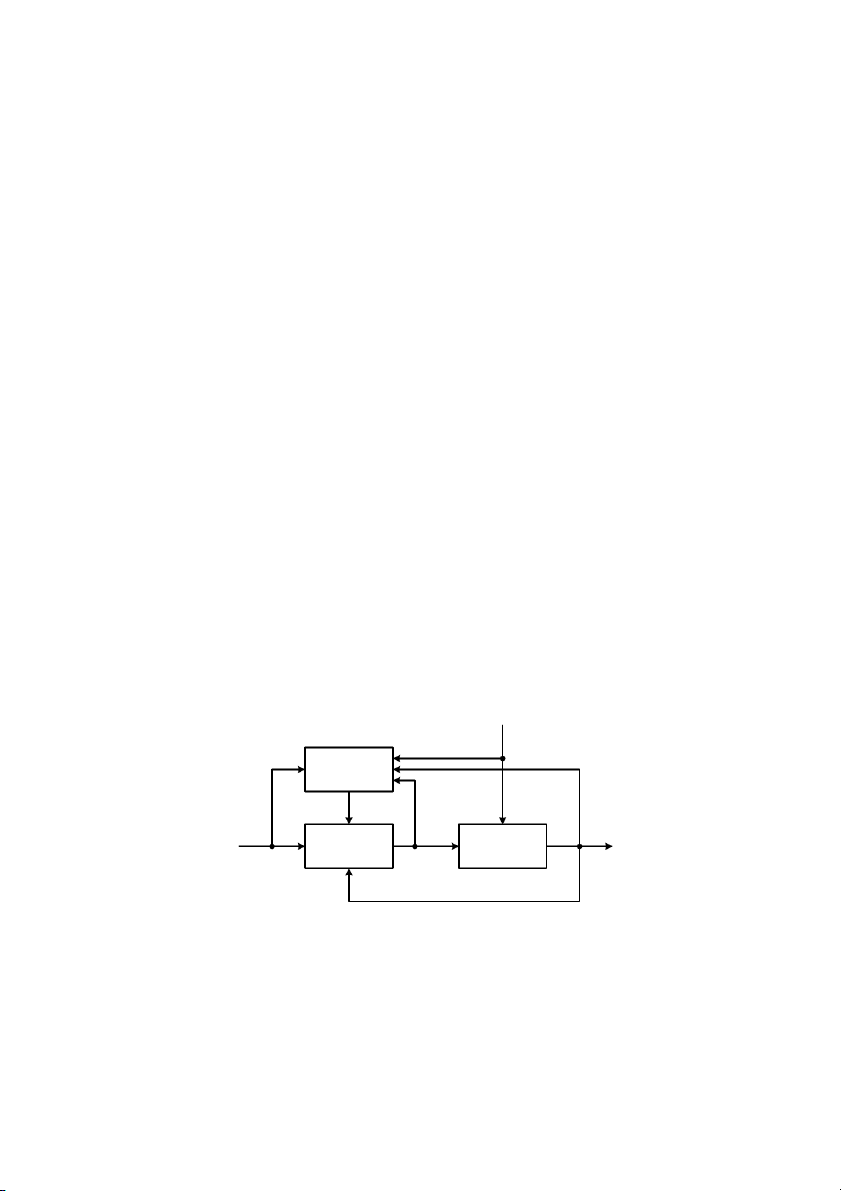
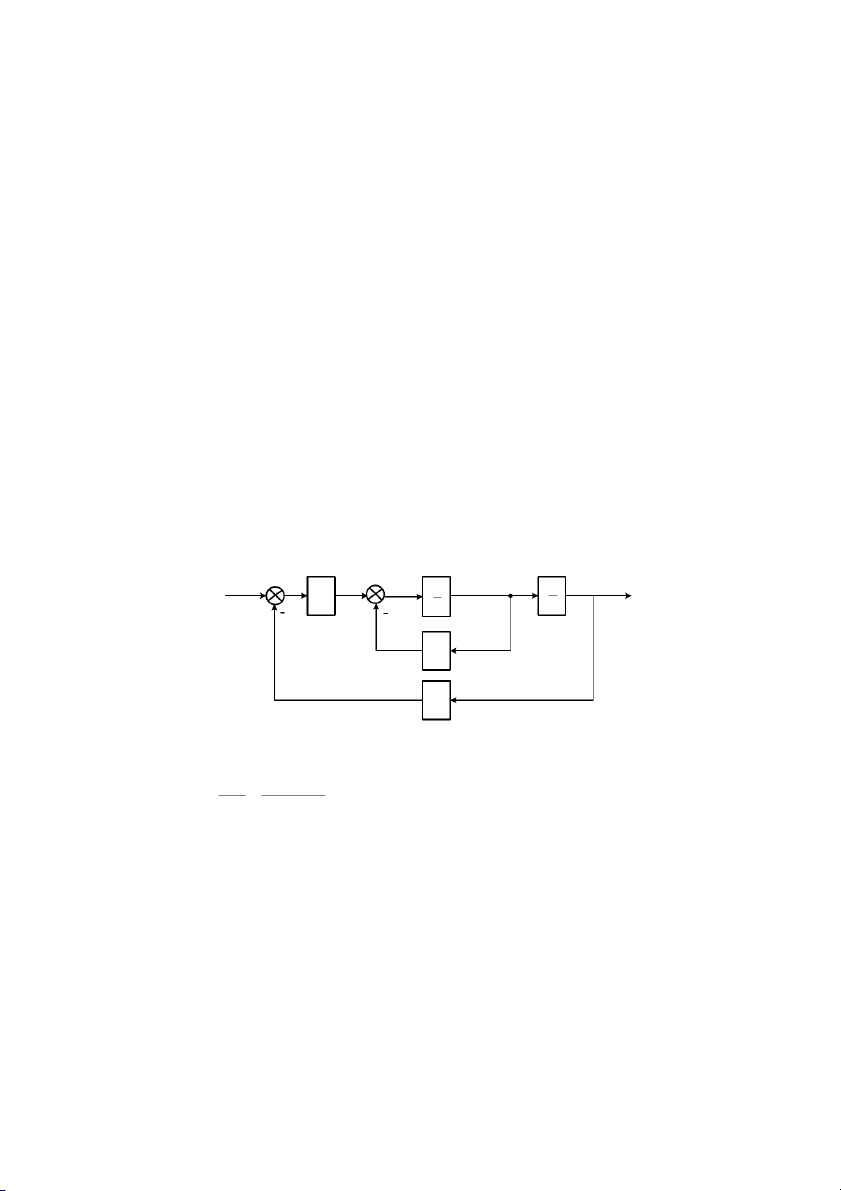
iu khin phi hp (Hình 1.5): nâng cao cht lng iu khin, có th kt hp nguyên
t1c bù nhi:u nguyên t1c san bng sai lch. Mch bù nhi:u s? tác ng nhanh bù trA sai s
to ra bi các nhi:u o c, còn mch iu khin phn h#i s? hiu ch&nh tip các sai s to ra
bi các nhi:u không o c.
Hình 1.5: S iu khin phi hp
Nguyên t"c 2: Nguyên t1c a dng tơng xng
Mun quá trình iu khin có cht lng thì s a dng ca b iu khin phi tơng xng
vi s a dng ca i tng.Tính a dng ca b iu khin th hin kh nng thu thp
thông tin, truyn tin, phân tích x2 lý, chn quyt nh,…Ý ngha ca nguyên t1c này là cn
thit k b iu khin phù hp vi i tng. Hãy so sánh yêu cu cht lng iu khin và b
iu khin s2 dng trong h thng:
- iu khin nhit bàn i (chp nhn sai s ln) vi iu khin nhit lò sy (không
chp nhn sai s ln).
- iu khin mc nc trong b#n cha ca khách sn (ch& cn m bo luôn có nc
trong b#n) vi iu khin mc cht l"ng trong các dây chuyn sn xut (mc cht l"ng cn gi không $i).
Nguyên t"c 3: Nguyên t1c b$ sung ngoài
Mt h thng luôn t#n ti và hot ng trong môi trng c th và có tác ng qua li ch!t
ch? vi môi trng ó. Nguyên t1c b$ sung ngoài thAa nhn có mt i tng cha bit (hp
en) tác ng vào h thng và ta phi iu khin c h thng l'n hp en. Ý ngha ca nguyên
t1c này là khi thit k h thng t ng, mun h thng có cht lng cao thì không th b" qua
nhi:u ca môi trng tác ng vào h thng. 5
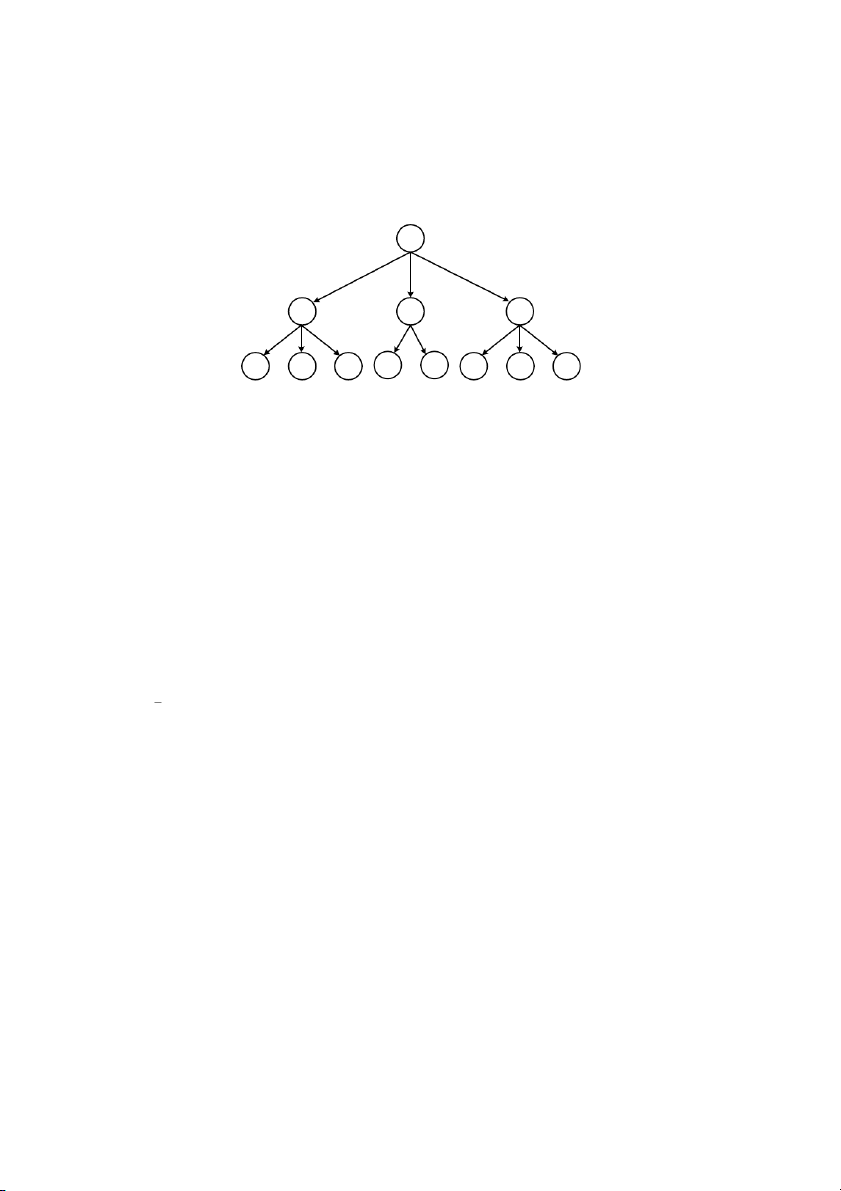
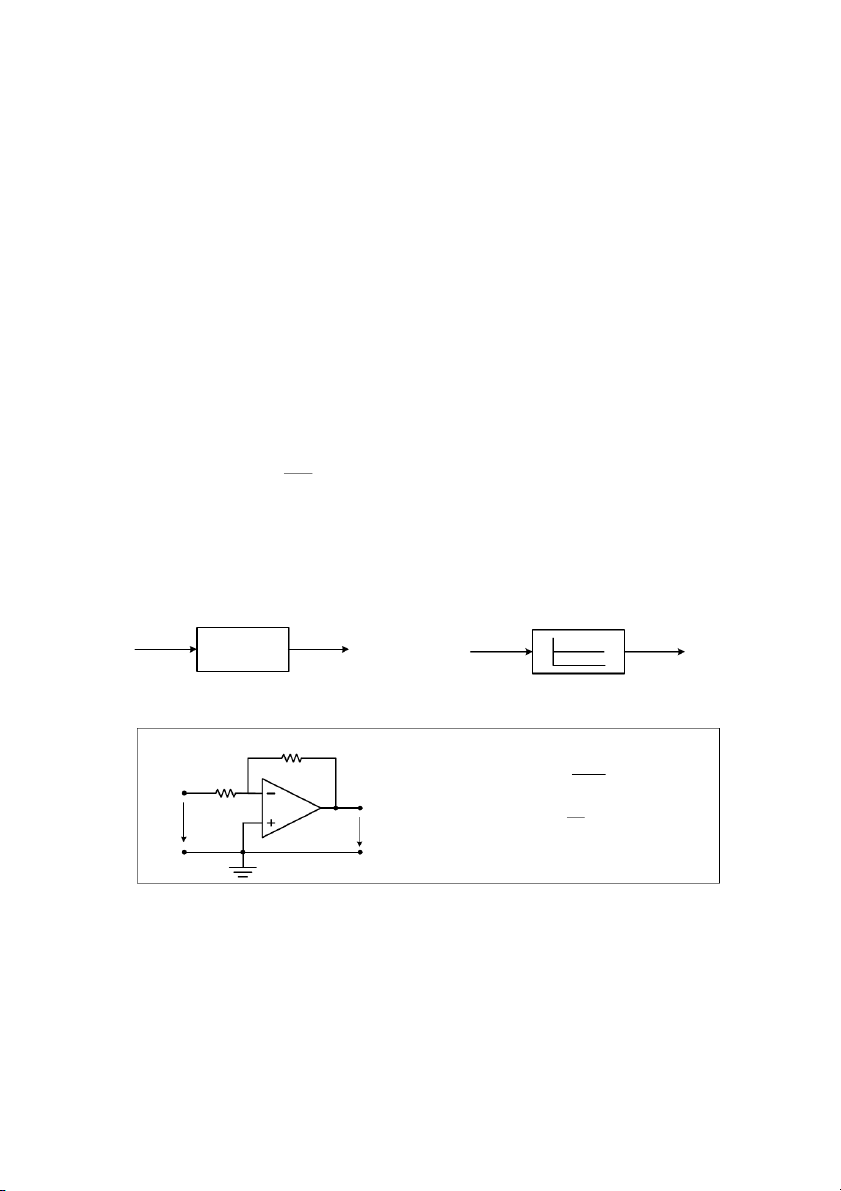
Nguyên t"c 4: Nguyên t1c phân cp (Hình 1.6)
i vi h thng iu khin phc tp cn xây dng nhiu lp iu khin b$ sung cho trung
tâm. Cu trúc phân cp thng s2 dng là cu trúc hình cây, ví d nh h thng iu khin
giao thông ô th hin i, h thng iu khin dây chuyn sn xut.
Hình 1.6: S iu khin phân cp 1.2.3 Tín hiu Tín hiu (
x t) c nh ngha nh là mt hàm s ph thuc thi gian mang thông tin v
các thông s k thut c quan tâm trong h thng và c truyn ti bi nhng i lng
vt lý, nói cách khác tín hiu là mt hình thc biu di:n thông tin.
Ví d : iu khin nhit thì nhit hin thi là mt thông s k thut ca h thng
cn c quan tâm. Giá tr nhit o c bng cm bin ti thi im t c th hin di
dng giá tr ca hàm s ph thuc thi gian u(t ) và là mt i lng in áp có ơn v là Volt.
Nh vy, tín hiu u(t ) là mt hàm thi gian mang thông tin v nhit trong phòng ti thi
im t và c truyn ti bi i lng vt lý là in áp…
Trong mt h thng có nhiu tín hiu x
c quan tâm cùng mt lúc. Tt c
1 (t ), x2 (t ),...xn (t )
các tín hiu c quan tâm ó s? c ghép chung li thành mt vector tín hiu ký hiu bi: x1(t ) x(t )= xn(t) Phân loi tín hiu Do tín hiu trong (
x t) có mô hình là hàm thi gian nh ã nh ngha vAa nêu trên nên ph
thuc vào min xác nh cng nh min giá tr ca hàm s (
x t) là liên tc hay ri rc mà tín hiu (
x t) có th phân thành bn loi sau:
- Tín hiu liên tc: Nu (
x t) là hàm liên tc tAng on theo thi gian, tc là lim x(t ) = x(t k ) t t → k
vi mi t trong tAng khong thi gian. k
- Tín hiu không liên tc: Nu (
x t) là hàm không liên tc theo thi gian. Thng các tín
hiu này ch& c xác nh ti hu hn các im t ,t ,t . 1 2 n
- Tín hiu tơng t: Nu x (t ) là hàm liên tc theo min giá tr.
- Tín hiu ri rc: Nu x(t) là hàm không liên tc theo min giá tr. 6
Bn kiu tín hiu trên ch& là s phân loi cơ bn theo min xác nh ho!c theo min giá tr ca
x(t) . Trên cơ s bn kiu phân loi cơ bn ó mà mt tín hiu x(t ) khi c ý chung #ng
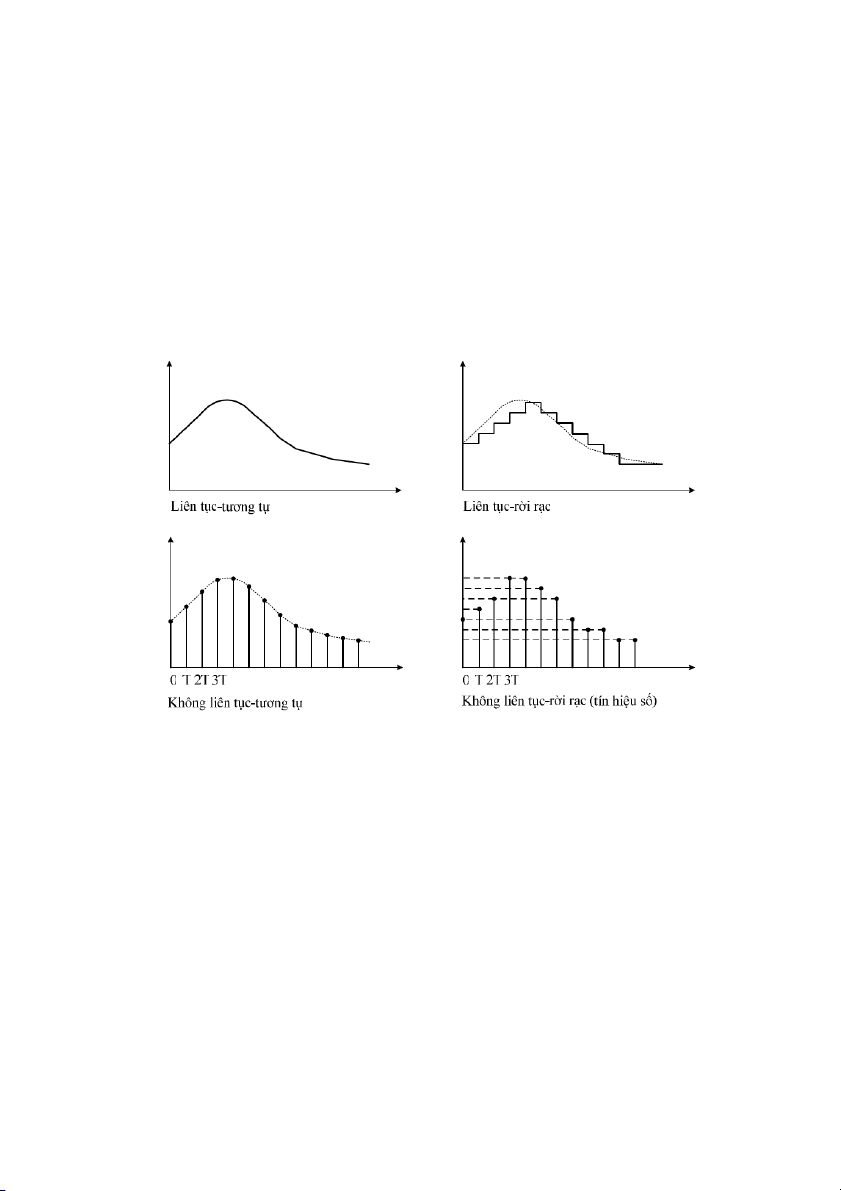
thi ti c min xác nh và min giá tr có th là:
- Dng tín hiu liên tc-tơng t
- Dng tín hiu không liên tc-tơng t
- Dng tín hiu liên tc-ri rc
- Dng tín hiu không liên tc-ri rc
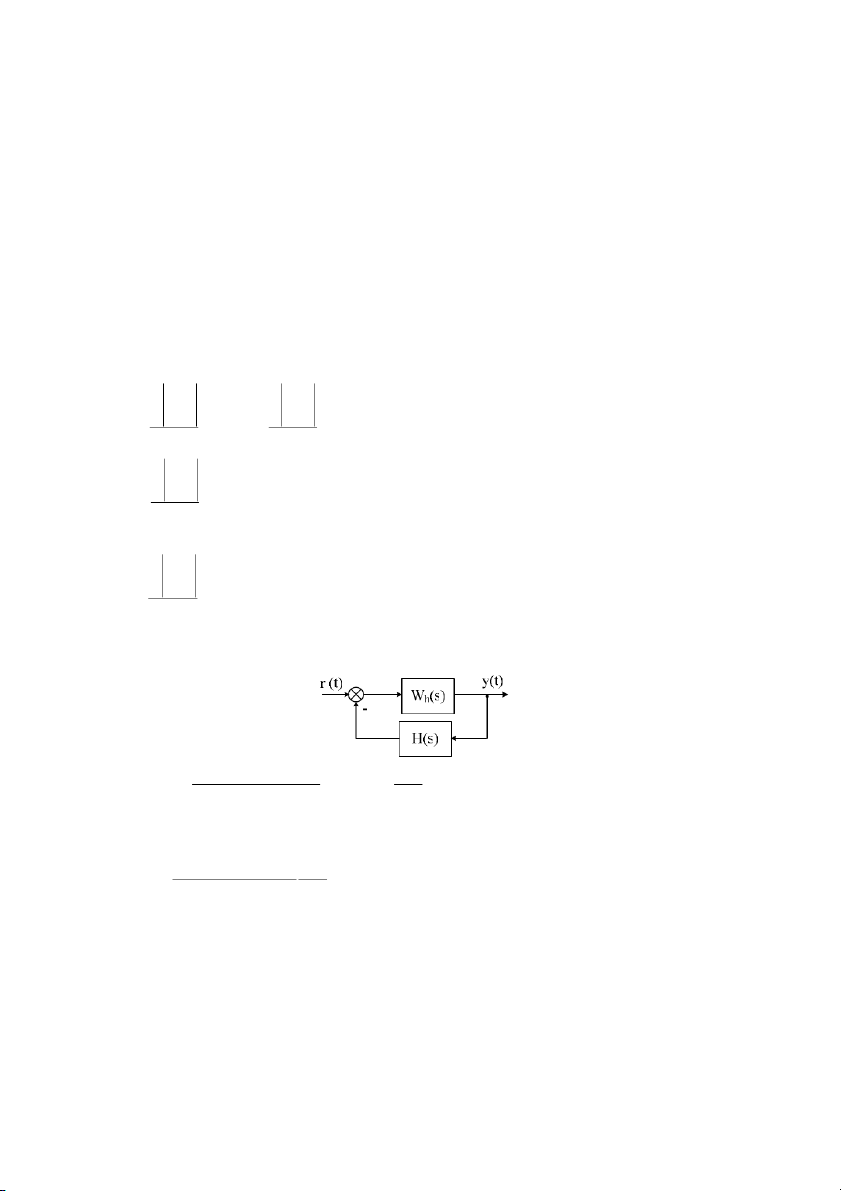
Trong ó dng tín hiu không liên tc - ri rc còn có tên gi là tín hiu s. Hình 1.7 minh
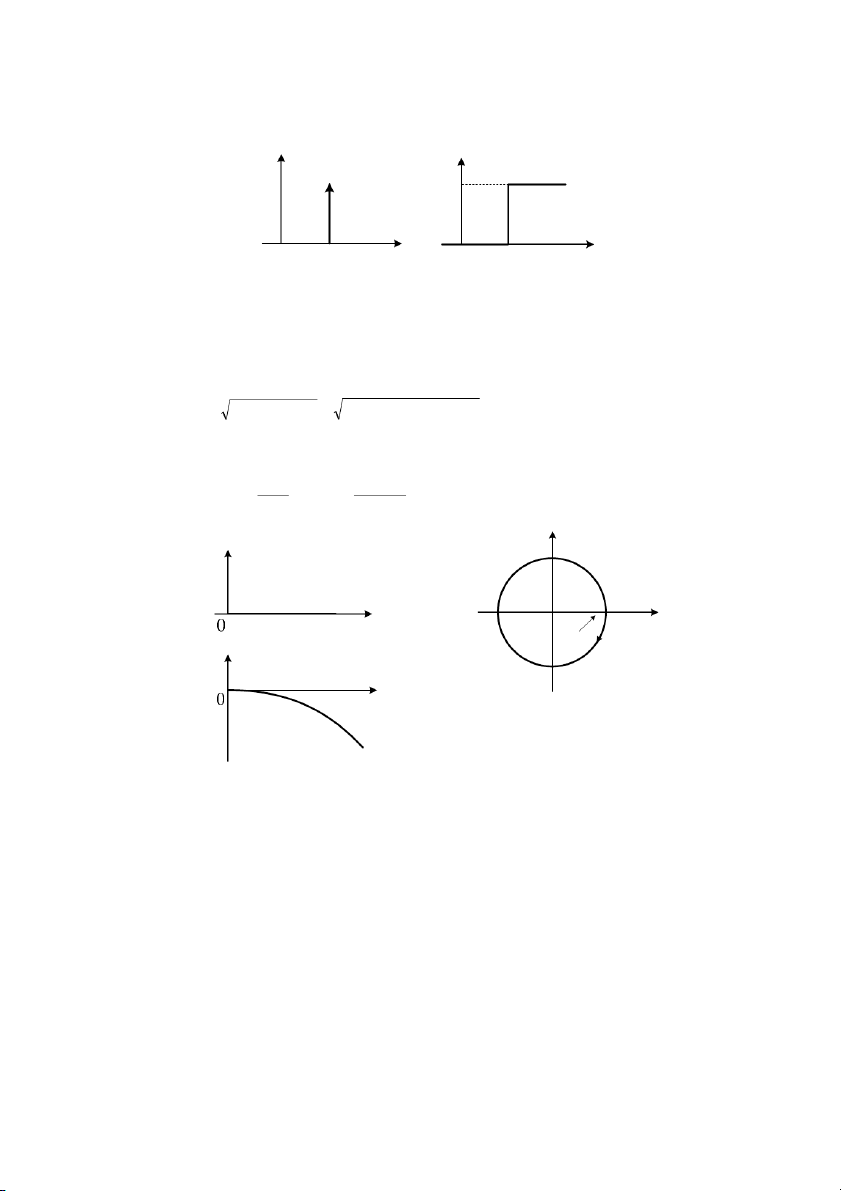
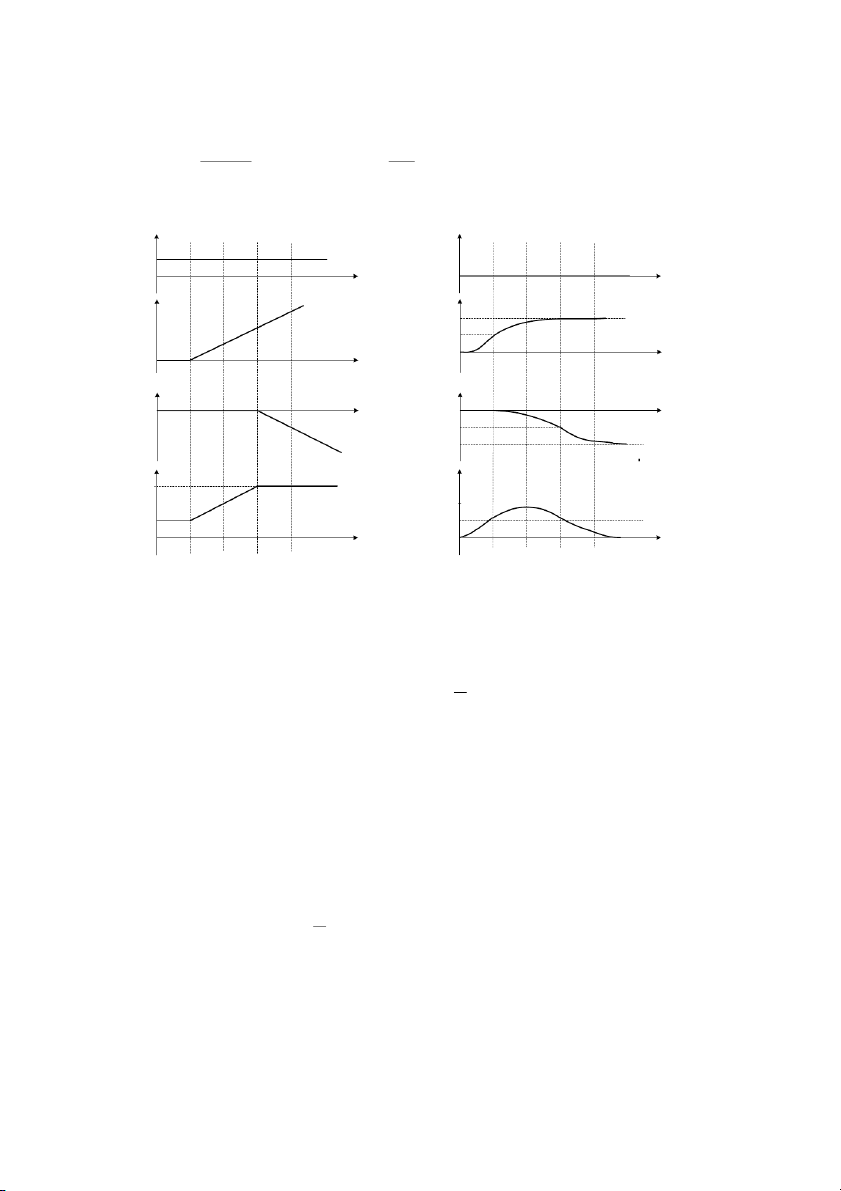
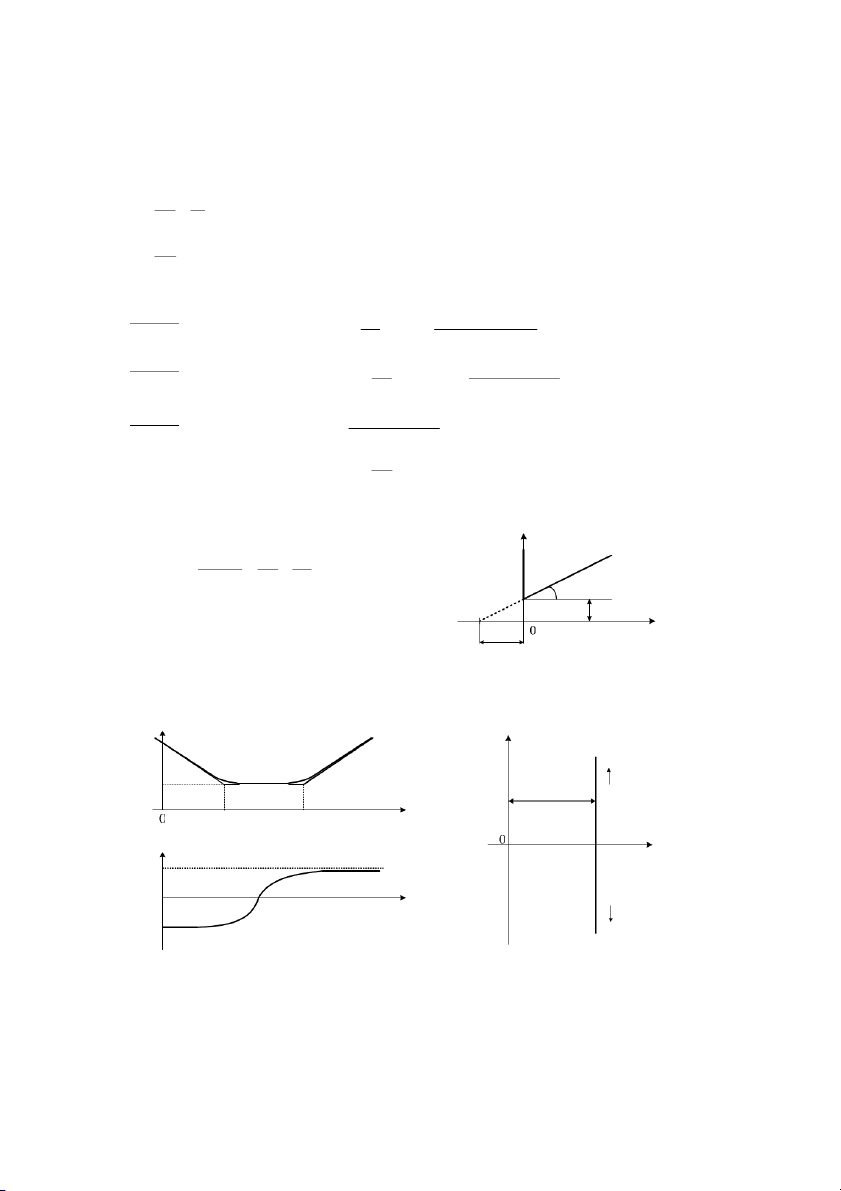
ha trc quan cho bn dng tín hiu vAa trình bày. x (t ) x(t ) t x(t) x (t ) t t
Hình 1.7: Các dng tín hiu khác nhau
1.3 Phân loi h thng iu khin t ng
1.3.1 Phân loi theo mch ph n h#i
- H thng kín: là h thng iu khin có phn h#i, tc là tín hiu ra c o và h#i tip v
so sánh vi tín hiu vào. B iu khin s2 dng sai lch vào-ra tính toán tín hiu iu
khin u(t), hiu ch&nh li tín hiu ra theo hng làm trit tiêu sai lch. Cu trúc h kín có th có
mt ho!c nhiu vòng h#i tip. Sơ # khi ca h kín mt vòng h#i tip c mô t trên Hình 1.2.
- H thng h: không dùng mch phn h#i, tc là không có s so sánh kt qu thc t vi
tr s mong mun sau tác ng iu khin. Các h thng iu khin da trên cơ s thi gian
u là h h. Mt ví d là máy gi!t trong ó các thao tác gi!t, x, v1t c tác ng tun t
bng rơle thi gian, kt qu u ra là sch ca qun áo không c máy kim tra (o) li.
H h có cu trúc ơn gin và thích hp vi các ng dng không òi h"i cao v cht lng áp ng. 7
1.3.2 Phân loi theo $c im mô t toán h%c
- H tuyn tính: Mi phn t2 ca h u có quan h vào-ra là hàm tuyn tính. H tuyn tính
c mô t bng phơng trình vi phân (ho!c sai phân) tuyn tính. !c trng cơ bn ca h
tuyn tính là áp dng c nguyên lý xp ch#ng, tc là nu h có nhiu tác ng vào #ng thi
thì áp ng u ra có th xác nh bng cách ly t$ng các áp ng do tAng tác ng riêng r? to nên.
- H phi tuyn: H có ít nht mt phn t2 có quan h vào-ra là hàm phi tuyn. H phi tuyn
không áp dng c nguyên lý xp ch#ng. H tuyn tính ch& là mô hình lý tng. Các h
thng iu khin thc t u có tính phi tuyn. Ví d trong các b khuch i in, in tA,
thy lc, khí nén luôn có s bão hòa tín hiu ra khi có tín hiu vào ln; trong truyn ng
cơ khí, thy lc, khí nén luôn t#n ti các khâu khe h, vùng không nhy vi tín hiu vào nh";
các h thng iu khin ON/OFF là phi tuyn vi mi giá tr tín hiu vào. ơn gin hóa quá
trình phân tích và thit k, h phi tuyn có phm vi bin thiên ca các bin tơng i nh"
thng c tuyn tính hóa a gn úng v h tuyn tính.
1.3.3 Phân loi theo loi tín hiu trong h thng
- H liên tc: Các tín hiu truyn trong h u là hàm liên tc theo thi gian. H liên tc
c mô t bng phơng trình vi phân.
- H ri rc: Tín hiu mt hay nhiu im ca h là dng chuBi xung hay mã s. H ri
rc c mô t bng phơng trình sai phân.
1.3.4 Phân loi m&c tiêu iu khin
- H thng $n nh hóa: Khi tín hiu vào r(t) không thay $i theo thi gian ta có h thng
$n nh hóa hay h thng iu ch&nh. Mc tiêu iu khin ca h này là gi cho sai s gia tín
hiu vào và tín hiu ra càng nh" càng tt. H thng iu khin $n nh hóa c ng dng
rng rãi trong dân dng và công nghip, in hình là các h thng iu ch&nh nhit , in áp,
tc , áp sut, lu lng, mc nc, n#ng , pH…
- H thng iu khin theo chơng trình: Nu tín hiu vào r(t) là mt hàm nh trc theo
thi gian, yêu cu áp ng ra ca h thng sao chép li các giá tr tín hiu vào r(t) thì ta có h
thng iu khin theo chơng trình. %ng dng in hình ca loi này là các h thng iu
khin máy CNC, robot công nghip. M GH&IHDIH K J L N CDE FE
Hình 1.8: S h thng iu khin thích nghi
- H thng theo dõi: Nu tín hiu vào r(t) là mt hàm không bit trc theo thi gian, yêu
cu iu khin áp ng y(t) luôn bám sát c r(t), ta có h thng theo dõi. iu khin theo
dõi thng c s2 dng trong các h thng iu khin pháo phòng không, rada, tên l2a, tàu ngm… 8
- H thng iu khin thích nghi: Khi cn iu khin các i tng phc tp, có thông s
d: b thay $i do nh hng ca môi trng, ho!c nhiu i tng #ng thi mà phi m bo
cho mt tín hiu có giá tr cc tr, hay mt ch& tiêu ti u nào ó,… thì các b iu khin vi
thông s c nh không th áp ng c, khi ó ta phi dùng nguyên t1c thích nghi. Sơ # h
thng thích nghi nh Hình 1.8. Tín hiu v(t) ch&nh nh li thông s ca b iu khin sao cho
h thích ng vi mi bin ng ca môi trng.
- H thng iu khin ti u: Khi cn to lp nhng lut iu khin cho h thng t ch&
tiêu v tính hiu qu ã c nh trc di dng hàm mc tiêu Q.
1.3.4 Phân loi theo dng n'ng lng s d&ng
- H thng iu khin cơ khí
- H thng iu khin in
- H thng iu khin khí nén
- H thng iu khin thy lc
- H thng iu khin in-khí nén, in-thy lc,…
1.3.5 Phân loi theo s lng (u vào, (u ra
- H SISO (Single Input - Single Output: mt u vào - mt u ra)
- H MIMO (Multi Input - Multi Output: nhiu u vào - nhiu u ra)
Trong khuôn kh$ ca chơng trình môn hc, tài liu này ch& tp trung cp n các vn
ca h thng iu khin tuyn tính bt bin mt u vào - mt u ra.
1.3.6 H b)t bin và h bin *i
- H bt bin theo thi gian (h dAng): Các thông s ca h không thay $i trong sut thi
gian hot ng ca h thng. H bt bin c mô t bng phơng trình vi phân/sai phân h s
hng. áp ng ca h này không ph thuc vào thi im mà tín hiu vào c !t vào h thng.
- H bin $i theo thi gian (h không dAng): Các thông s ca h là tham s ph thuc
vào thi gian, ví d h thng iu khin tên l2a vi khi lng ca tên l2a gim dn do s tiêu
th nhiên liu trong quá trình bay. Phơng trình mô t h bin $i theo thi gian là phơng
trình vi phân/sai phân h s hàm. áp ng ca h này ph thuc vào thi im mà tín hiu vào
c !t vào h thng.
1.4 Ví d& v h thng iu khin
H thng iu khin m+c nc
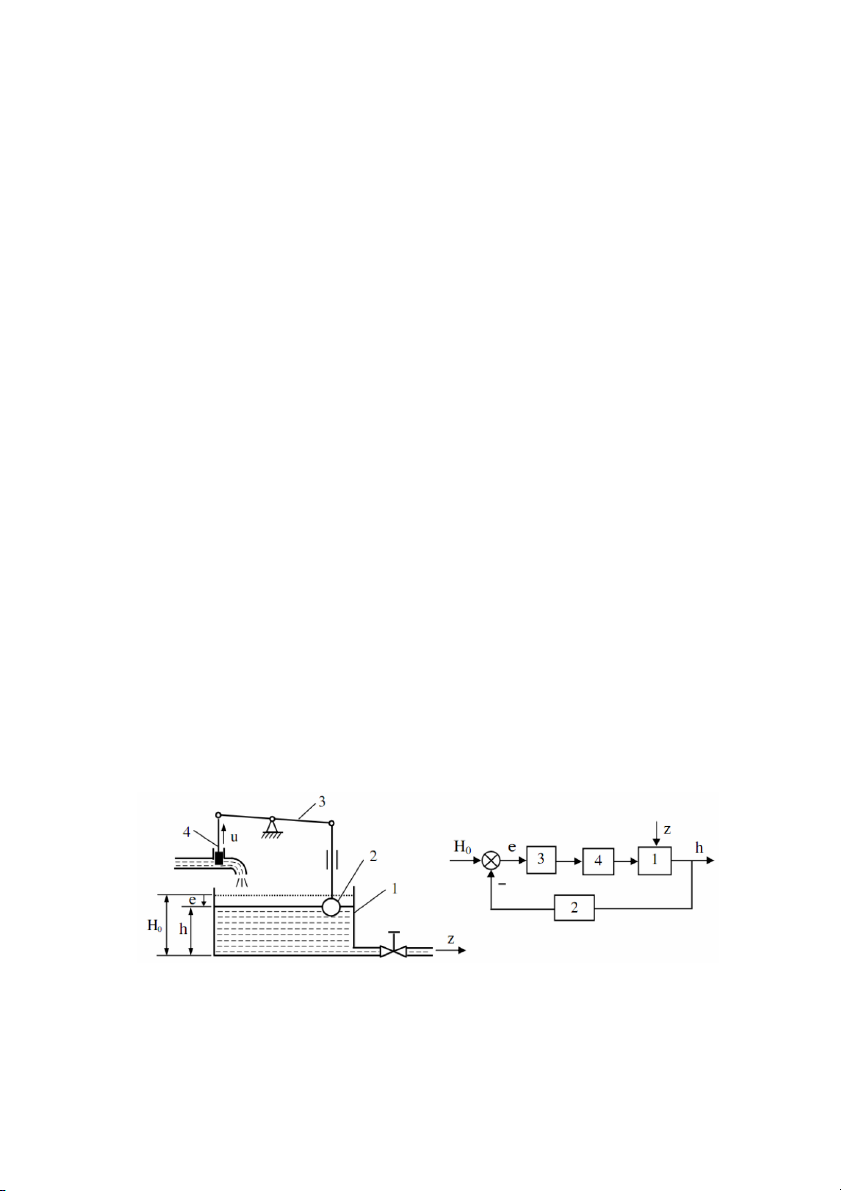
Hình 1.9: H thng iu khin mc nưc n gin 9
Trong h thng iu khin t ng hình 1.9, i tng iu khin là b#n nc (1). Mc
tiêu iu khin là gi mc nc trong b#n luôn $n nh và bng tr s H0 !t trc cho dù
lng nc tiêu th thay $i nh th nào.
Tín hiu ra y = h: mc nc thc t. Tín hiu vào r = H 0: m c n c yêu c u.
Nhi:u z: s thay $i lng nc tiêu th.
Thit b o là phao (2); b iu khin là h thng òn b>y (3) có chc nng khuch i sai lch
và iu khin óng m van; cơ cu tác ng là van (4).
Tín hiu iu khin u: nâng ca van (4).
Tín hiu sai lch: e = r – y = H0 – h
Mc nc yêu cu có th thay $i bng cách iu ch&nh dài on ni tA phao ti òn b>y. Ka E E0 n M2 M1 V1
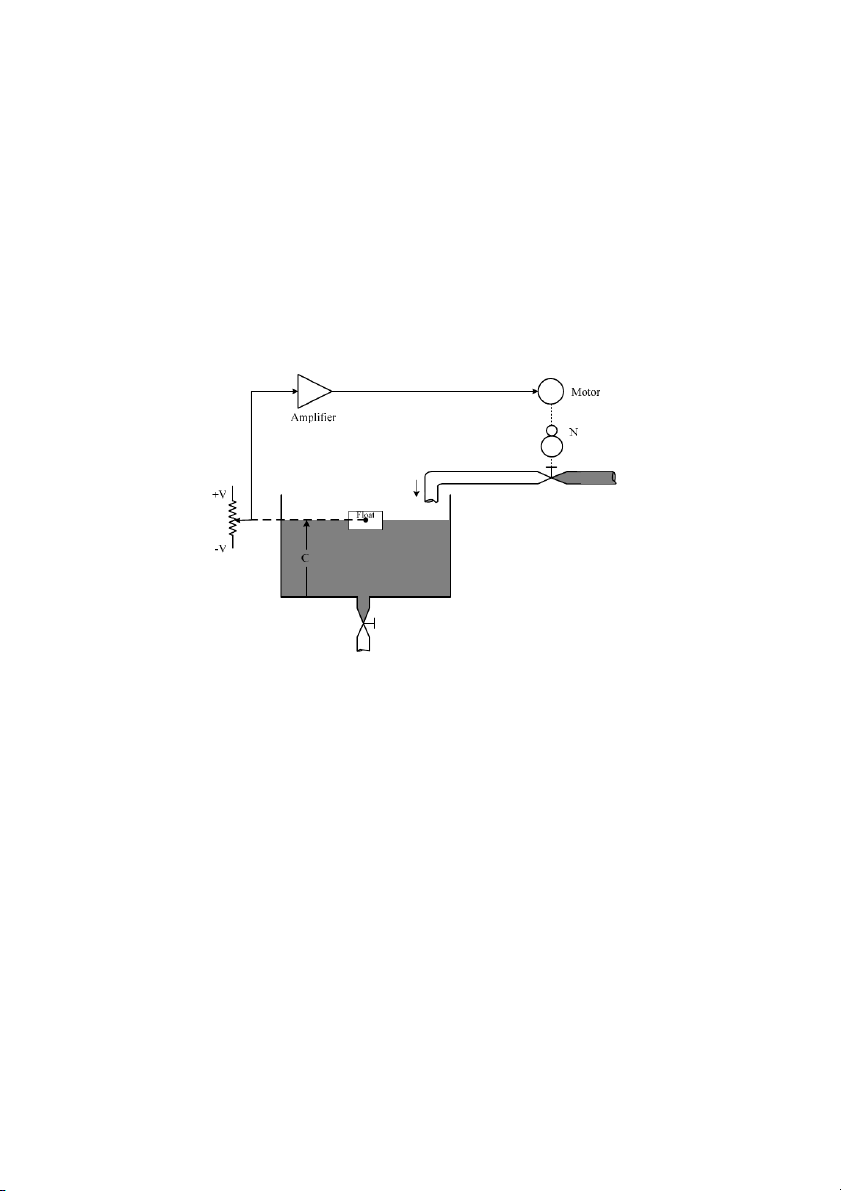
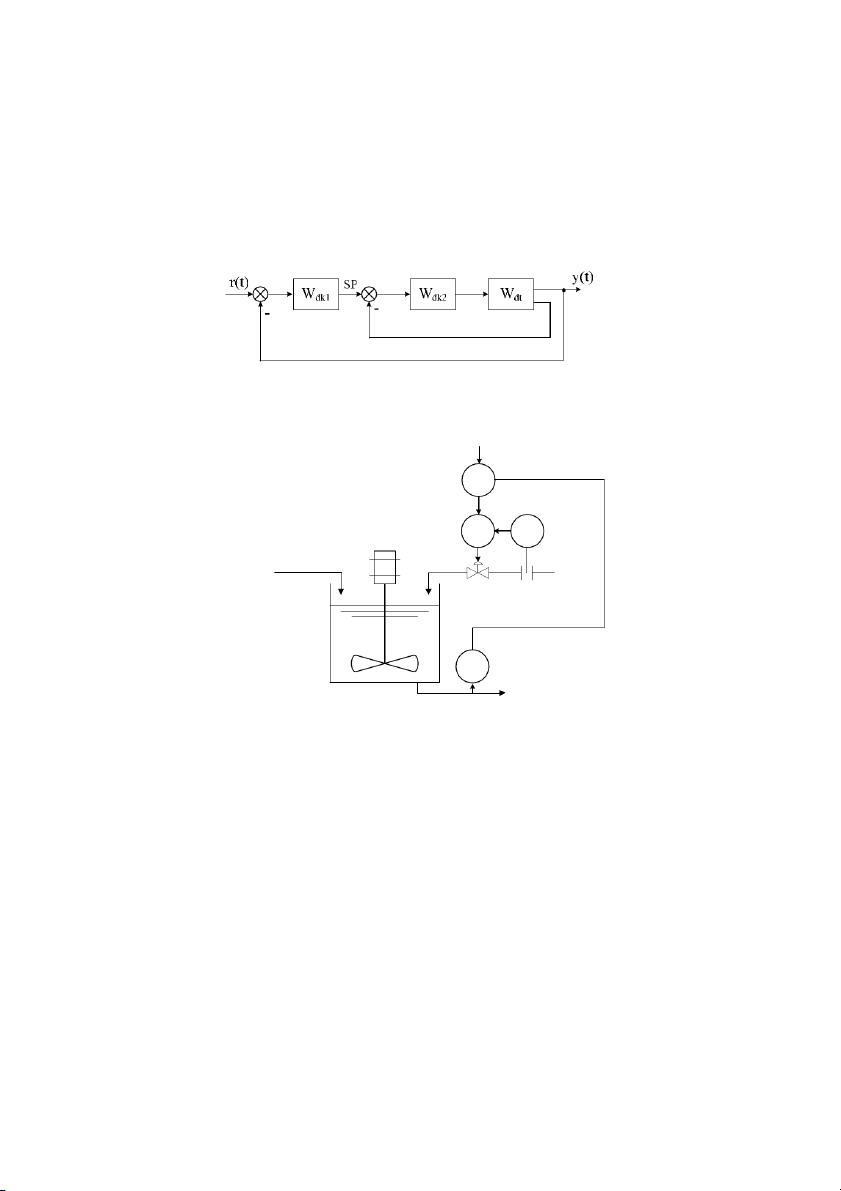
Hình 1.10: H thng iu khin mc nưc
Nguyên lý hot ng ca h thng iu khin mc nc hình 1.10 nh sau: Mc nc
cn gi luôn $n nh là C trong trng hp van V 2
1 m tùy theo nhu c u s d ng ( c coi là
nhi:u). Khi mc nc trong bình khác C, mt in áp chênh lch E
n c t o ra, qua b
khuch i công sut cung cp cho ng cơ. ng cơ này khi quay s? iu ch&nh m M1 ca
van qua ó iu ch&nh dòng M2.
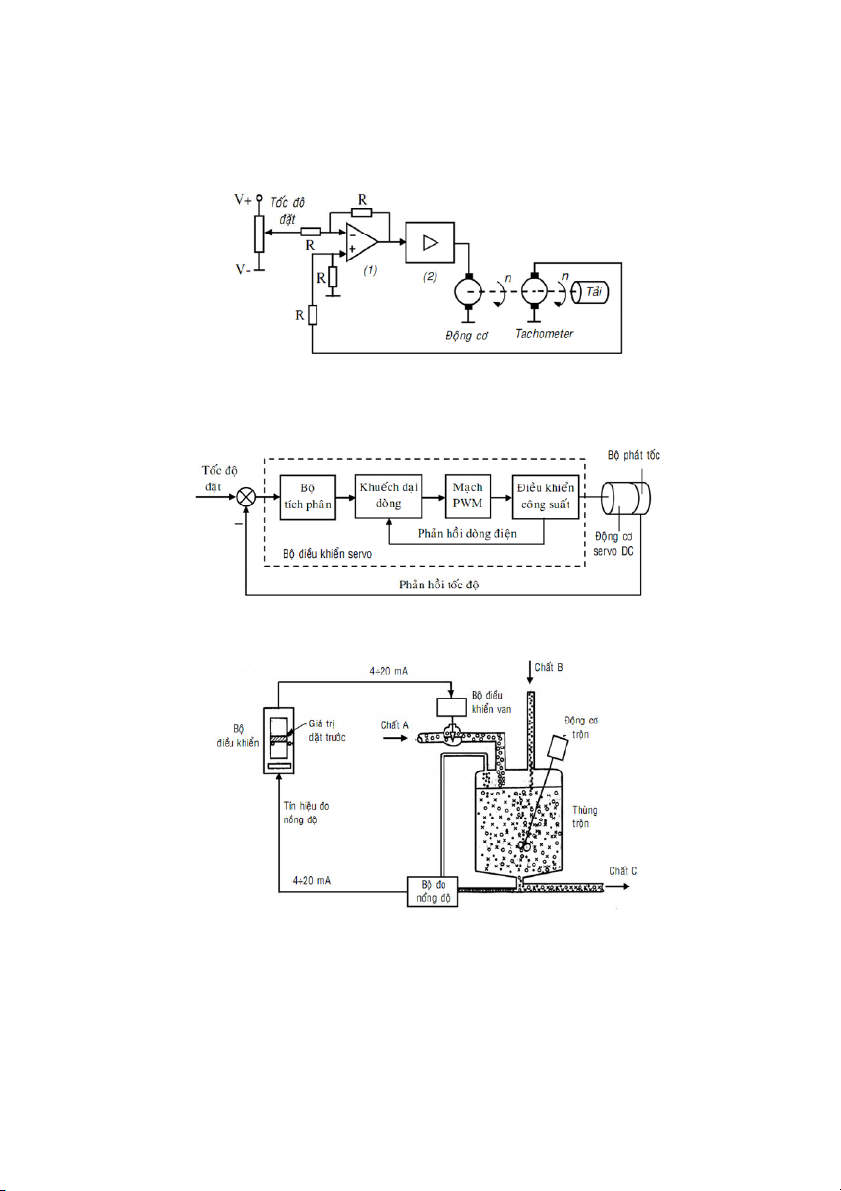
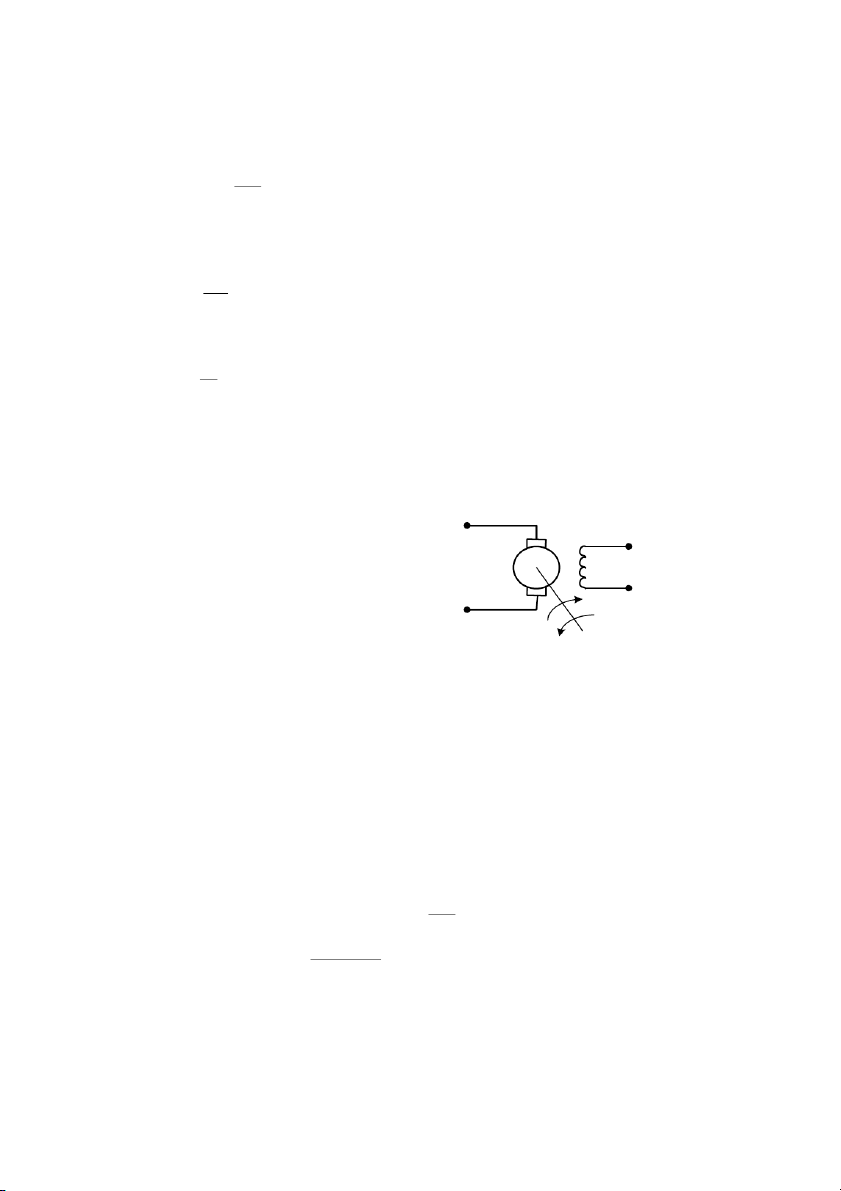
H iu khin tc ng c DC
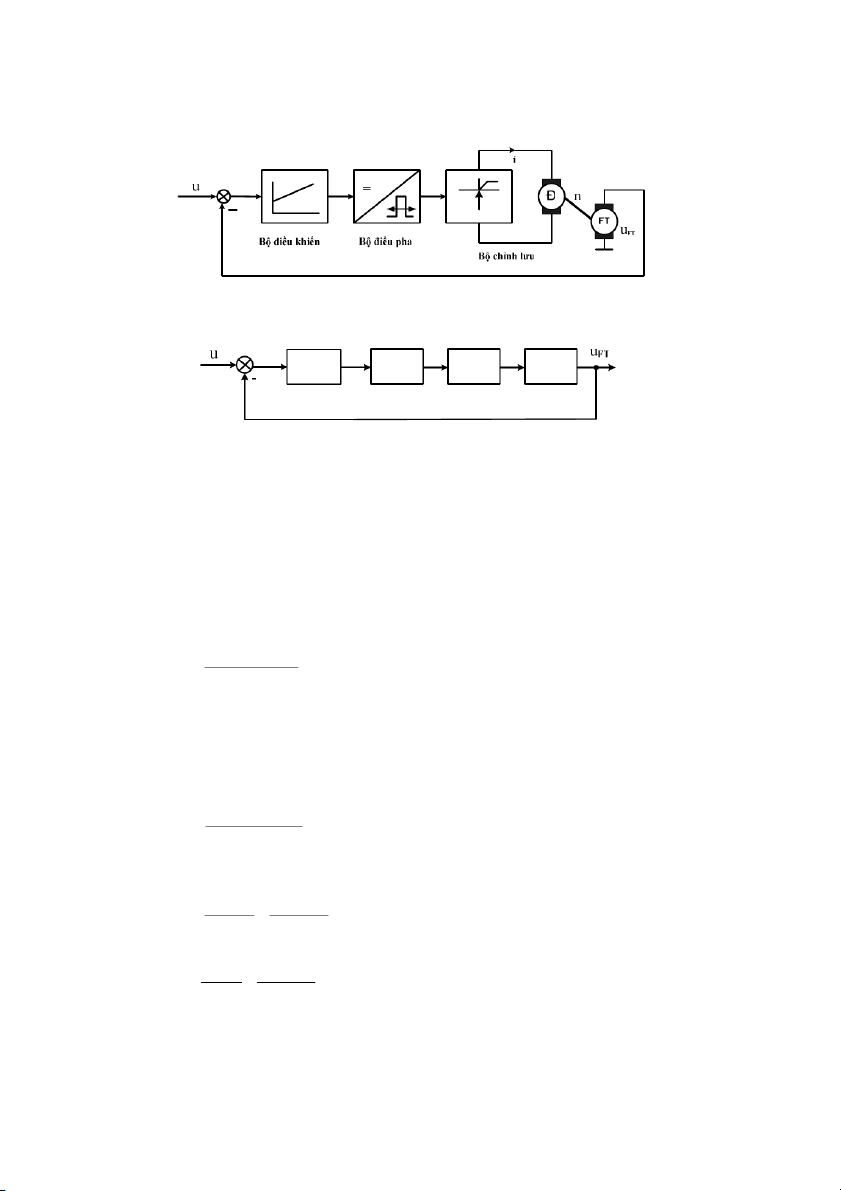
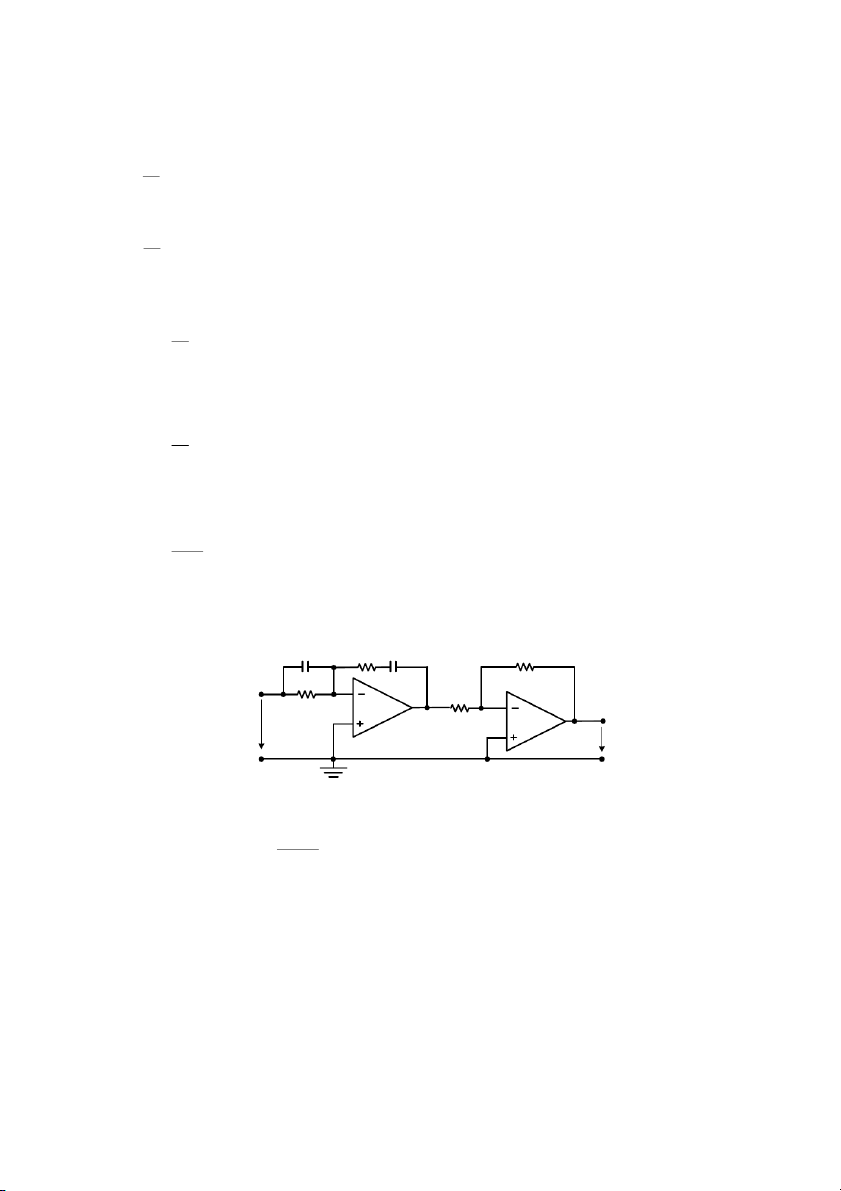
Hình 1.11 gii thiu mt phiên bn ơn gin ca h thng iu khin tc ng cơ DC.
Tc yêu cu c !t ch&nh bng chit áp và có giá tr trong khong 0 ÷ V 10 . B phát tc
(tachometer) o s vòng quay ca ng cơ và chuyn thành tín hiu in áp 0÷ V 10 . B
khuch i vi sai (1) so sánh giá tr !t vi tc thc t, sau ó tín hiu sai lch c chuyn
n b khuch i công sut (2) thành tín hiu iu khin ng cơ. có sai s xác lp
bng 0 và ci thin !c tính ng hc ca ng cơ tt hơn, ngi ta thay b khuch i vi sai
bng b iu khin PID và mch ch&nh lu in t2.
Trong các ng dng iu khin tc và nh v chính xác, hin nay ngi ta thng dùng
ng cơ servo DC và AC. ng cơ servo có quán tính nh", kh nng gia tc tt, làm vic tin
cy, hu nh không cn bo dOng. ng cơ servo DC công sut nh" c s2 dng trong các
thit b vn phòng nh ng cơ quay $ a máy tính, ng cơ quay rulo máy in, … ng cơ 10
servo DC công sut trung bình và ln c s2 dng trong các h thng robot, h thng iu khin máy CNC,…
Hình 1.11: S h thng iu khin tc ng c DC
Hình 1.12 gii thiu h thng iu khin ng cơ servo DC dùng b iu khin in t2
theo nguyên t1c iu bin rng xung (PWM). Tín hiu phn h#i c ly tA b phát tc
ho!c b mã hóa góc quay (encoder) l1p !t sPn trên ng cơ.
Hình 1.12: S h thng iu khin tc ng c servo DC
H thng iu khin máy trn
Hình 1.13: S h thng iu khin máy trn
iu khin mt máy trn (Hình 1.13) là duy trì hBn hp ca hai cht A và B sao cho n#ng
ca chúng không $i. Hai cht A và B c a vào thùng trn và c máy trn khuy
u cho ra mt hBn hp C có t& l % thành phn A úng theo giá tr !t trc. B o n#ng
là mt máy phân tích xác nh t& l phn trm ca thành phn A trong hBn hp C và cho 11
ra tín hiu dòng in tơng ng tA 4÷ 20mA. Tín hiu này d'n v b iu khin bng in t2
to lên mt tín hiu iu khin tác ng vào van (thông qua b iu khin van). khng ch
lu lng cht A chy vào thùng trn.
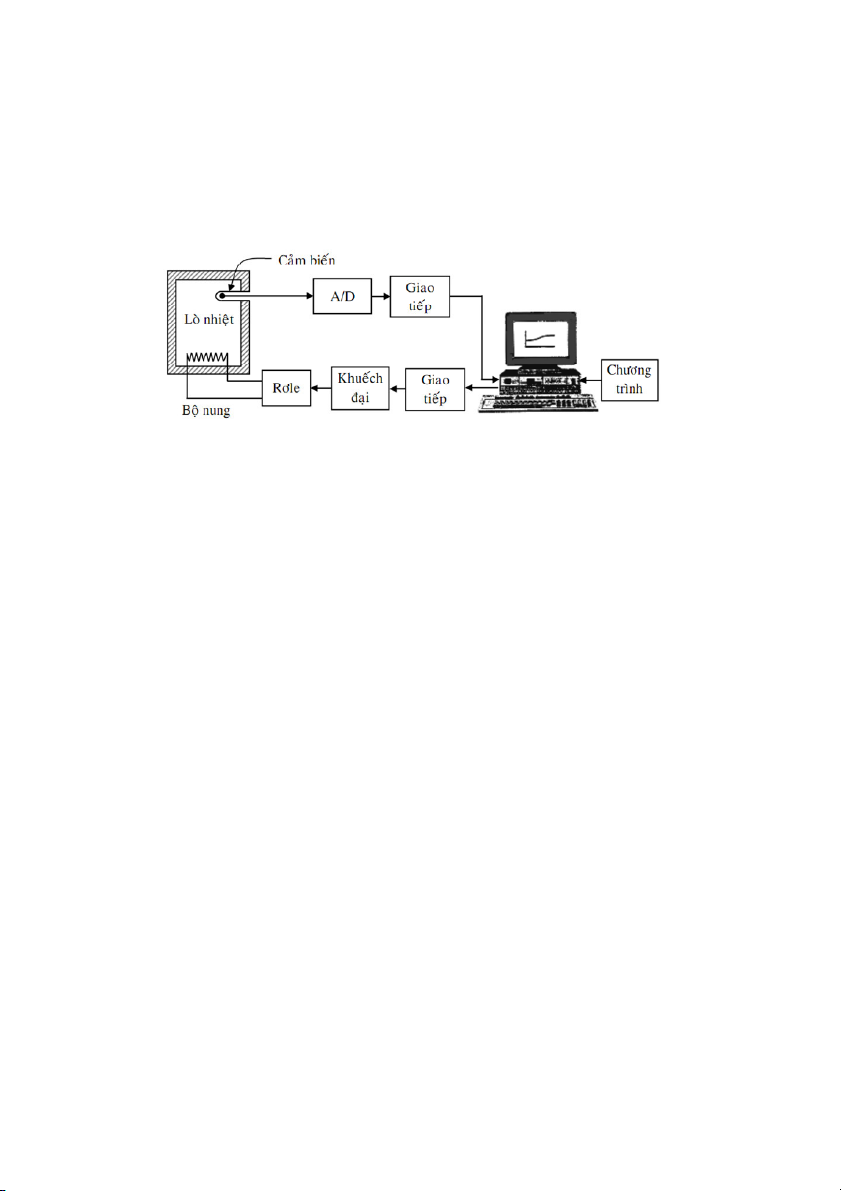
H thng iu khin nhit
Hình 1.14: S h thng iu khin lò nhit
Hình 1.14 gii thiu mt h thng iu khin nhit lò nung in. Nhit trong lò là i
lng liên tc. Nhit này c o bng cm bin, sau ó chuyn thành tín hiu s nh b
chuyn $i liên tc/s (A/D – Analog/Digital) và a vào máy tính thông qua mch giao tip.
Nhit yêu cu cng là dng tín hiu s và c !t ch&nh bng chơng trình phn mm.
Máy tính so sánh nhit h#i tip vi nhit !t và nu có sai lch thì máy tính s? xut hin
tín hiu iu khin mch nung thông qua giao tip, khuch i, rơle cp in cho in tr nung
ho!c qut làm mát trong lò. 12
CHƠNG 2: MÔ T, TOÁN HC H TH-NG IU KHIN 2.1. Khái nim
i tng nghiên cu trong thc t ca h thng iu khin rt a dng và có bn cht vt
lý khác nhau. Các phn t2 trong h thng có th là cơ, in, nhit, thy lc, khí nén, … Do
vy, cn có cơ s chung phân tích, thit k các h thng iu khin có bn cht vt lý khác
nhau và cơ s ó là toán hc.
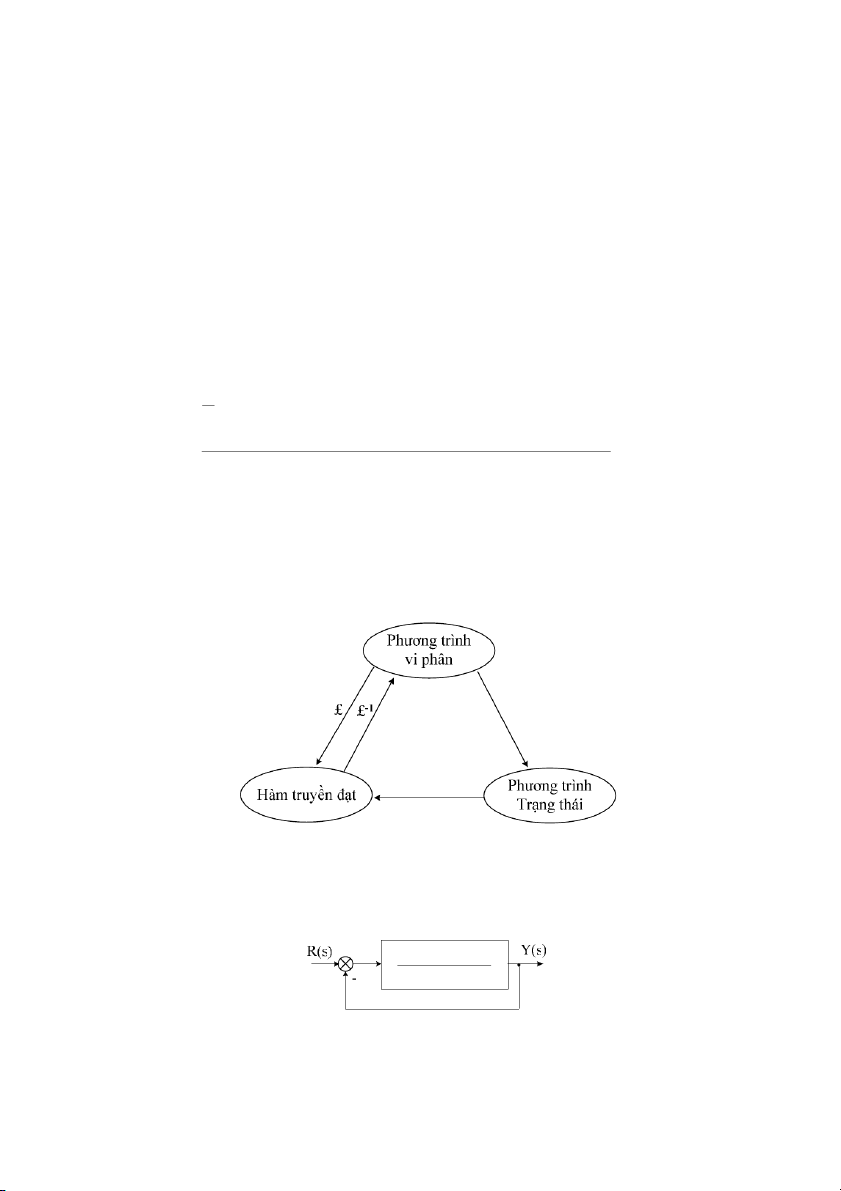
mô t h thng tuyn tính liên tc ngi ta thng s2 dng ba dng mô hình toán hc cơ bn sau:
- Phơng trình vi phân tuyn tính; - Hàm truyn t;
- Phơng trình trng thái.
MBi phơng pháp mô t h thng u có nhng u im riêng, trong tài liu này s? xét c
ba phơng pháp mô t trên.
2.2. Mô t h thng . min th/i gian
2.2.1 Mô hình phng trình vi phân
Mt h thng tuyn tính liên tc có tín hiu vào là r(t) và tín hiu ra là y(t) có th c mô
t bng phơng trình vi phân tuyn tính h s hng có dng t$ng quát: n n−1 m m−1 d y d y dy d r d r dr a +a +... + a + a y t = b + b + + b + (2.1) 0 n 1 n n − − n m b − − m r t 1 1 ( ) 0 m 1 ... ( ) m 1 1 dt dt dt dt dt dt Trong ó: a
là nhng hng s, c xác nh tA tham s ca các phn t2; 0, …, an; b0, …,bm
n là bc ca phơng trình vi phân, m n.
Phơng trình vi phân mô t cho mt h thng bt kQ c xây dng theo phơng pháp gii
tích, tc là da trên các nh lut vt lý biu di:n các quá trình ng hc ca h thng thành
lp phơng trình vi phân. C th là:
- i vi các phn t2 in: áp dng các nh lut Kirchoff dòng in, in áp tìm mi quan
h dòng - áp trên in tr, cun cm, t in,…
- i vi các phn t2 cơ khí: áp dng nh lut II Newton tìm quan h gia lc ma sát và
vn tc, quan h gia lc và bin dng ca lò xo, …
- i vi các phn t2 nhit: thng áp dng nh lut truyn nhit, nh lut bo toàn nng lng, …
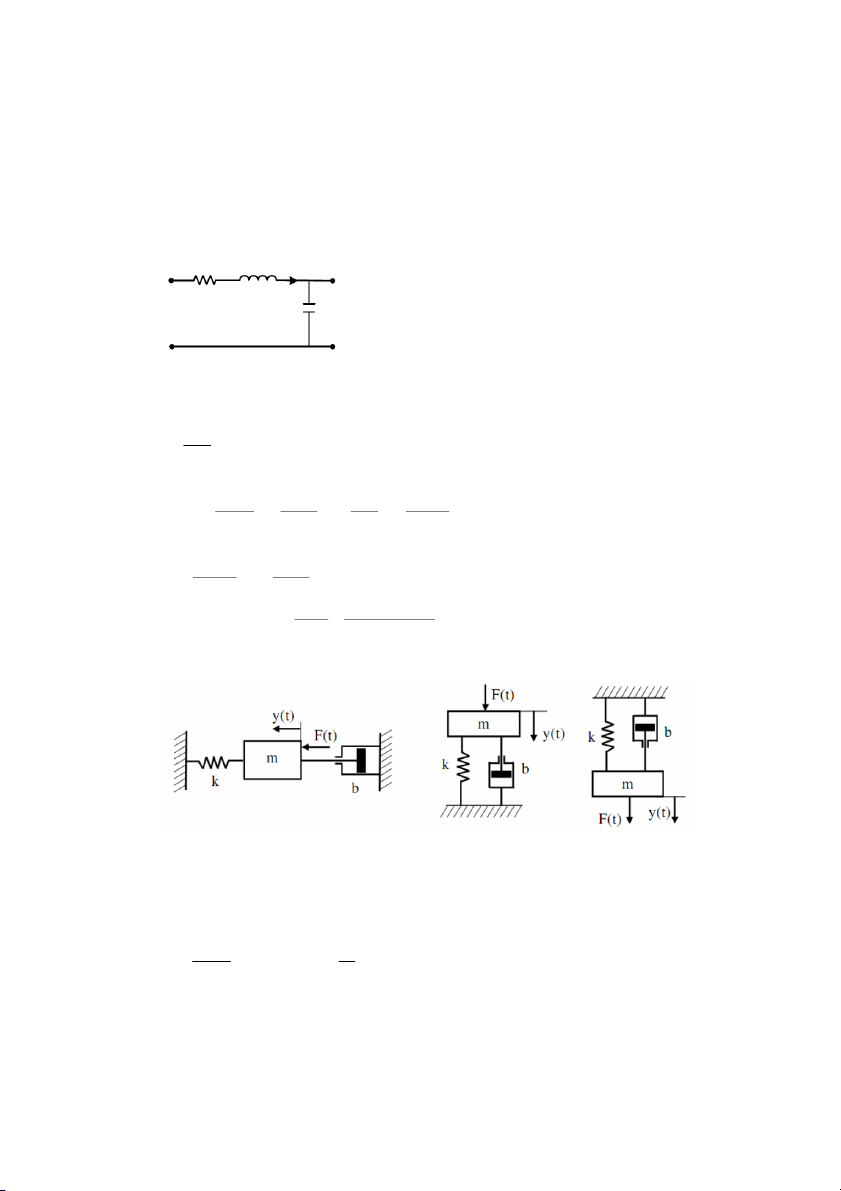
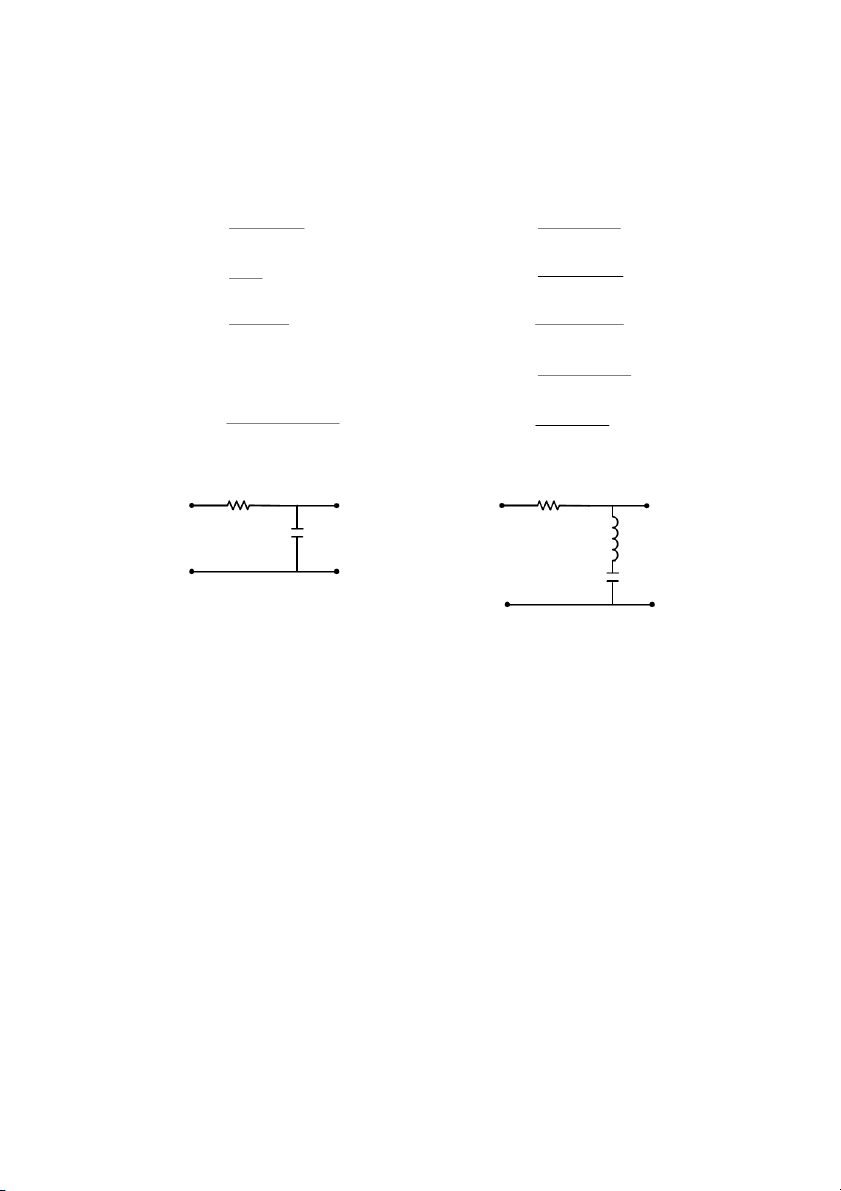
Ví d& 2.1: Cho mch in RC trên hình 2.1. Bit trc giá tr ca in tr R, ca t in C
trong mch. Hãy xác nh mô hình mch in di dng phơng trình vi phân mô t quan h
gia tín hiu vào là in áp u
và tín hiu ra là in áp trên t in. i(t) u0(t)
Theo nh lut Kirchoff ta có: u
R (t) + uC(t) = ui(t) (2.2) G i (2.3) R(t) = iC(t) u (2.4) C(t) = u0(t)
Hình 2.1: Mch in RC 13 M!t khác: du i t ( ) = C C . (2.5) C dt u (2.6) R(t) = R.iR(t)
Thay tr li phơng trình (2.2) ta có c mi quan h gia in áp vào và in áp ra ca mch in: . R . du0 C
+ u (t) = u (t) (2.7) 0 dt i
Vi tín hiu vào r(t) = u ơ
i(t); tín hi u ra y(t) = u0(t) ta có ph
ng trình vi phân mô t cho m ch
in RC chính là phơng trình vi phân cp 1: .dy RC
+ y(t) = r(t) (2.8) dt
Ví d& 2.2: Xác nh phơng trình vi phân mô t cho ng cơ in mt chiu kích tA c lp.
ng cơ là phi tuyn nhng ta xem gn úng là phn t2 tuyn tính. Sơ # cu trúc c mô t
trên hình 2.2. Tín hiu vào là in áp U !t vào phn ng, in áp cun kích tA Ukt, mô men
cn M ; tín hiu ra là tc quay ơ R c n c a ng c .
ây ta xét bài toán có: Ukt = const, Mc =
const, khi ó mô hình ng cơ mt chiu kích thích c lp c xem là mô hình có 1 tín hiu
vào là in áp phn ng U, mt tín hiu ra là tc n.
Quá trình xy ra trong ng cơ là s chuyn
$i in nng sang cơ nng, còn tín hiu ra là
tc ca ng cơ và quá trình ng hc ca U Ukt
chuyn ng quay di tác ng ca momen in nng. n
Trng thái xác lp ca ng cơ ta có các phơng M C
trình cân bng in và cơ: U
Hình 2.2: S cu trúc ng c in
0 = I0R + E = I0R + k1n0 (2.9) trong ó: U i ! ơ 0 -
n áp ban u t vào ph n ng c a ng c I i i i 0, E: n áp, dòng n, s c
n ng ph n ng tr ng thái xác l p và E = kư!n A S = const) 0 = k1n0 (t thông M Mc = M ! A ! d0 = km
I0 = k2I0 (t thông = const) d0 = Mc k & 1, k2 - các h s t l M ' ơ d0 - mô men d n ng c a ng c tr ng thái t nh M ơ c - mô men c n c h c
Khi in áp !t vào phn ng ca ng cơ thay $i bng U i
0 + "U thì dòng n trong ph n ng I c ng cơ
c xy ra trong ng cơ c mô t bng 0 + "I, t
n0 + "n. Quá trình ng h phơng trình vi phân: d∆I U + U ∆ = k n ( + n ∆ ) + R I ( + ∆I )+ L (2.10) 0 1 0 0 dt
d (n0 + ∆n) k (I + I ∆ ) = M + J (2.11) 2 0 c dt
vi J là mô men quán tính ca tt c các phn quay !t lên roto 14
Thay li và rút gn ta c phơng trình vi phân mô t mi liên h gia tín hiu ra là s
thay $i tc ca ng cơ và tín hiu vào là s thay $i in áp !t vào phn ng ng cơ dng: 2 J.R d∆n J. ∆ U ∆ = k . L d n ∆ + + (2.12) 1 n 2 k dt k dt 2 2 J L . d 2∆n J R . d n ∆ 1 + + ∆n = ∆ . U (2.13) k k dt2 k k dt k 1 2 1 2 1
Vy ta có phơng trình vi phân mô t quá trình ng hc ca ng cơ in mt chiu kích tA c lp: d 2 ∆n d∆ n T T . . + T . + n ∆ = K ∆ . U (2.14) t c dt 2 c dt d 1 trong ó: K =
- là h s truyn ng ca ng cơ d k 2 L T =
- là hng s thi gian in tA ca ng cơ t R J . R T =
- là hng s thi gian in cơ ca ng cơ c k .k 1 2
!t: r(t) = #U, y(t) = #n, ta thy mô t cho ng cơ in mt chiu kích tA c lp là
phơng trình vi phân bc hai có dng t$ng quát: 2
T .T .d y + . dy T
+ y(t ) = K .r (t) (2.15) t c 2 c d dt dt 2.2.2 Mô hình trng thái
R phn trc ta ã bit, mt h thng liên tc bt kQ có th mô t quan h gia tín hiu vào
và tín hiu ra bng phơng trình vi phân bc n. i vi các h thng hin i chúng ta thng
cn mt h phơng trình phn ánh không nhng mi quan h gia tín hiu vào và tín hiu ra
mà còn c các mi quan h ràng buc gia các bin trng thái bên trong i tng na. Chính
vì th mt phơng pháp khác cng thng c s2 dng kho sát h thng iu khin t
ng là phơng pháp mô t h thng trong không gian trng thái. Phơng pháp biu di:n trong
không gian trng thái rt thích hp cho vic thit k trên máy tính nên c s2 dng ngày càng
nhiu. H thng mô t trong không gian trng thái chính là chuyn phơng trình vi phân bc n
thành n phơng trình vi phân bc mt bng cách !t n bin trng thái.
Tr ng thái ca mt h thng là tp hp nh" nht các bin (gi là bin trng thái) mà nu
bit giá tr ca các bin này ti thi im t0 và bit tín hiu vào thi im t $ t0, ta hoàn toàn
có th xác nh c áp ng ca h ti mi thi im t $ t0.
H thng bc n có n bin trng thái, n bin trng thái hp li thành véctơ ct gi là véct tr ng thái. Ký hiu: x = [x1 x2 ….. xn]T
Bng cách s2 dng các bin trng thái ta có th chuyn phơng trình vi phân bc n mô t
h thng thành h n phơng trình vi phân bc mt vit di dng ma trn: 15 (
x t) = Ax(t) + Br(t) (2.16) (
y t) = Cx(t) + Dr(t)
Trong ó: A, B, C, D là các ma trn hng s. a a a 11 12 1 n b a a a 1 21 22 2 n b A =
; B = 2 ; C = [c c
c ; D = [d] 1 2 n ] b a a a n n1 n2 nn
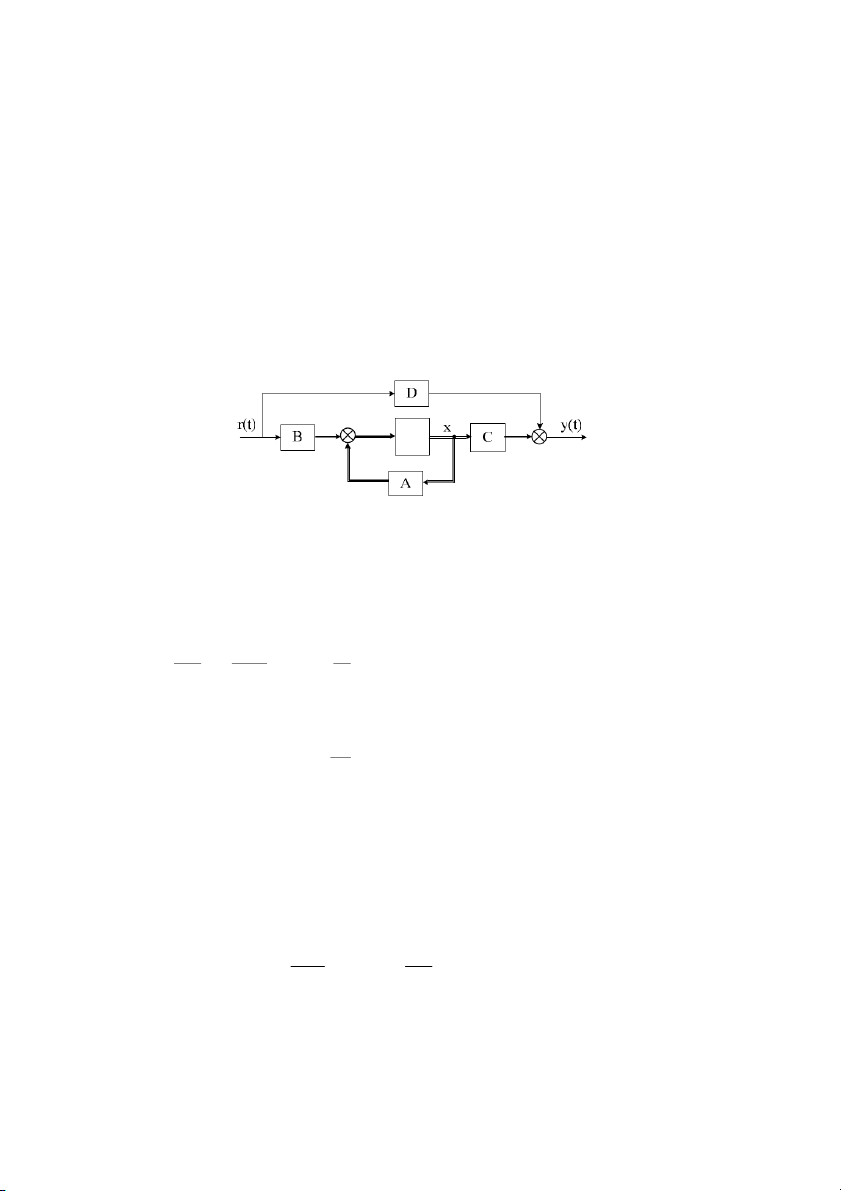
Phơng trình 2.16 c gi là phơng trình trng thái ca h thng, và có th biu di:n
di dng sơ # trng thái nh sau: x
Hình 2.3: S trng thái ca h thng
Phơng pháp thành lp phơng trình trng thái ca h thng có th da trên phơng trình
vi phân. Tùy theo cách !t bin trng thái mà mt h thng có th c mô t bng nhiu dng
phơng trình trng thái khác nhau. Ta xét hai trng hp nh sau:
a. Trưng hp v phi ca phưng trình vi phân mô t h thng không cha o hàm ca tín hiu vào (m = 0)
Phơng trình vi phân mô t h thng có dng: n n −1 d y d y dy a + a +... + a + = (2.17) n a − − n y(t) b r(t) 0 n 1 n 1 1 0 dt dt dt
Quy t1c !t bin trng thái:
- Bin trng thái th nht !t bng tín hiu u ra: x 1(t) = y(t)
- Các bin trng thái th i ( i = ,
2 n ) c !t theo quy t1c: bin trng thái sau !t bng o
hàm ca bin trng thái trc:
x (t) = x ( ) i i 1 t −
Áp dng cách !t bin trng thái nh trên ta có: x1 = y x = 2 1 x x2 = y x 3 = 2 x x3 = y − n 1 n d y d y x x x x = n = n = n 1 − 1 n − dt n n dt
Thay các bin trng thái vAa !t vào phơng trình (2.17) ta c: 16
a x (t) + a x (t) + a x − (t) +
+ a − x (t) + a x (t) = b r(t) 0 n 1 n 2 n 1 n 1 2 n 1 0
Kt hp quan h gia các bin trng thái vi phơng trình trên ta có h phơng trình: x = x 1 2 x x 2 = 3 . x x n −1 = n . a a a a b
xn = − 1 x n(t) − 2 x (t ) n x t n x t r t n 1 − − −1 ( ) ( ) 0 ( ) − 2 − 1 + a a a a a 0 0 0 0 0
Vit li di dng ma trn: x 0 1 0 0 x 0 1 1 x2 0 0 1 0 x 0 2 = + r(t ) (2.18) x 0 0 0 1 x 0 n−1 n− 1 x − a a − a a − a a − a a x b a n 1 0 2 0 3 0 n 0 n 0 0
Tín hiu u ra ca h thng: x1 x2 y t ( ) = x 1 0 0 0 1 = [ ] x n−1 xn
Vy h phơng trình trng thái ca h thng vit li di dng t$ng quát: ( x t) = (
Ax t) + Br(t) ( y ) t = C ( x ) t + D ( r ) t Trong ó: x 0 1 0 0 0 1 x 0 0 1 0 0 2 x = ; A = ; B = x 0 0 0 1 0 − n 1 x − a a a a a a a a b a 1 0 − 2 0 − 3 0 − n n 0 0 0 C = [1 0 0 ] 0 ; D = 0 17
Ngoài ra ta có th !t bin trng thái theo phơng pháp t$ng quát nh sau: a
x1 = x2 − 1 x1 a0 a
x2 = x3 − 2 x1 a 0 a x 1 n 1 = xn − n− x − 1 a0 a b x 0 n = − n x1 + r a a 0 0
Biu di:n di dng véc tơ: x − a a x 1 1 0 1 0 0 1 0 x2 − a a 0 1 0 x 0 2 0 2 = + r(t) (2.19) x − − a a 0 0 1 x 0 n 1 n−1 0 n− 1 x − a a x b a n n 0 0 0 0 n 0 0
Tín hiu u ra ca h thng: x 1 x 2 y(t) = x 1 0 0 0 1 = [ ] x −n1 x n
H phơng trình trng thái ca h thng v'n có dng t$ng quát là:
x(t ) = Ax(t ) + Br(t )
y(t ) = Cx(t) + Dr(t ) Trong ó: x − a a 1 0 0 0 1 1 0 x − a a 0 2 0 0 1 0 2 x = ; A = ; B = x − a a 0 n 1 0 0 0 1 n −1 − x − a a 0 0 0 b a n n 0 0 0 C = [1 0 0 ] 0 ; D = 0 18
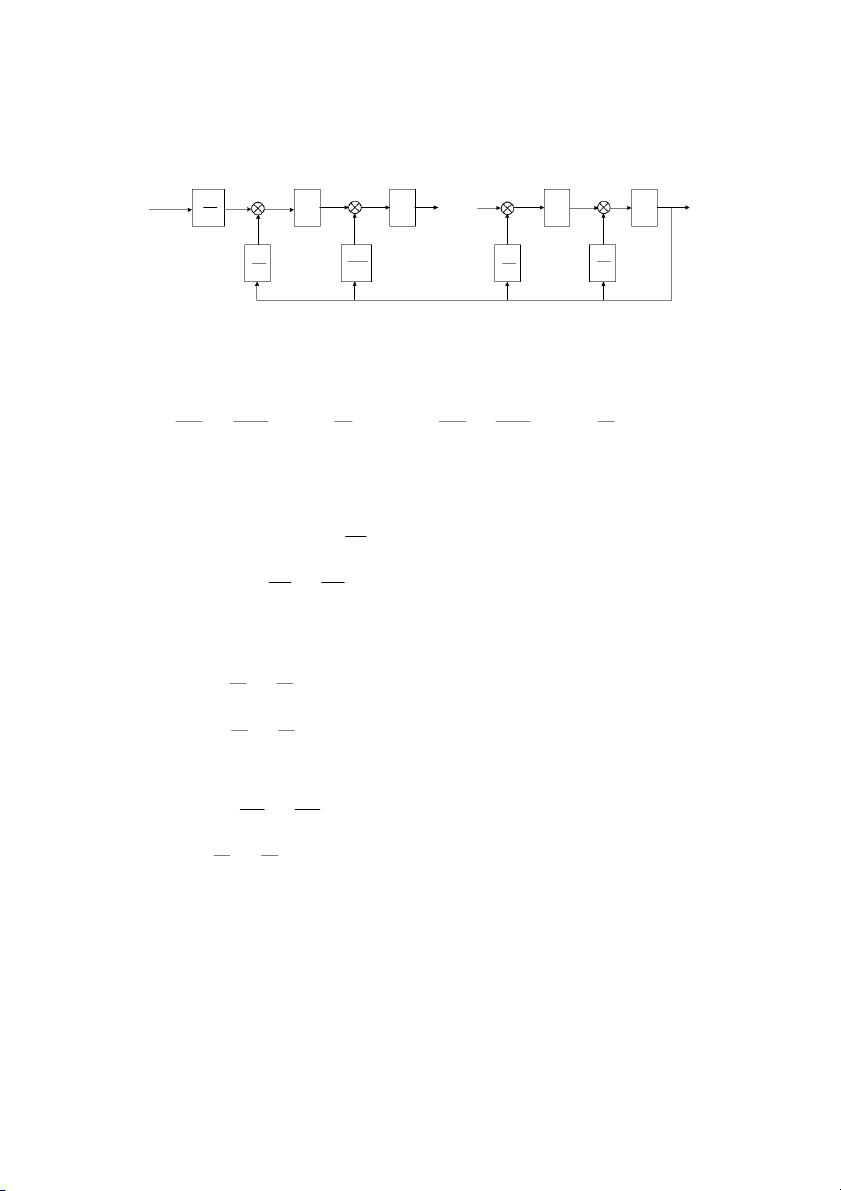
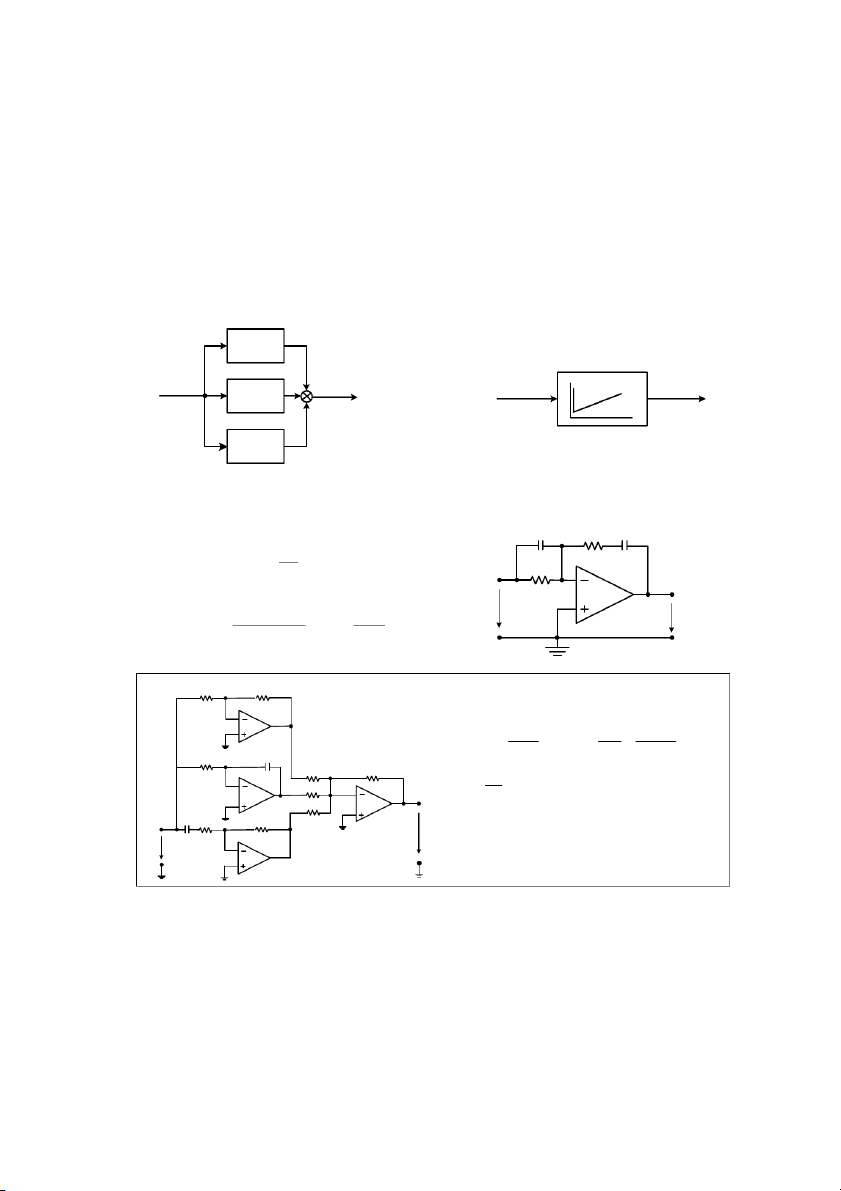
Sơ # cu trúc trng thái tơng ng nh hình 2.4. r(t) K x x x x x x x = y(t) n n n 1 − n 1 − x3 2 2 x1 1 a0 − − − − a a a a n n− 1 2 1 a a a a 0 0 0 0
Hình 2.4: S cu trúc trng thái
2. Trưng hp v phi ca phưng trình vi phân mô t h thng cha o hàm ca tín hiu vào (0
Phơng trình vi phân mô t h thng: n n 1 − m m −1 d y d y dy d r d r dr a + a +... +a
+a y (t ) =b + b + ... + b + b r(t) (2.20) 0 n 1 n 1 n − 1 − n 0 m 1 m − m 1 1 − dt dt dt dt dt dt m
Trc ht ta xét trng hp: m = n-1
Quy t1c !t bin trng thái nh sau:
- Bin trng thái th nht !t bng tín hiu u ra: x1(t) = y(t)
- Các bin trng thái th i (i = ,
2 n ) c !t theo quy t1c: a b
x (t ) = x + + − (t ) i 1 − i −2 x r( ) i i 1 t 1 a a 0 0
Theo cách !t bin trng thái nh trên ta có h phơng trình trng thái: x1 = y a b x x x r 1 = − 1 2 + 0 1 a a 0 0 a b x x x r 2 = − 2 3 + 1 1 a a 0 0 . a b xn =xn − − n 1 x m r m n 1 + −1 1 ; −1 = −2 − a a 0 0 a b xn = − n x m r m n 1 + ; = − 1 a a 0 0
H phơng trình trng thái trên hoàn toàn tơng ơng vi phơng trình vi phân 2.20. Ta
vit li di dng vec tơ nh sau: 19 x − a a x b a 1 1 0 1 0 0 1 0 0 x − a a 0 1 0 x b a 2 2 0 2 1 0 = + r(t) (2.21) x − − a a 0 0 1 x b a n 1 n 1 − 0 n−1 m 1 − 0 x −a a x b a n n 0 0 0 0 n m 0 x1 x2 y t ( ) = [1 0 0 ] 0 xn −1 xn
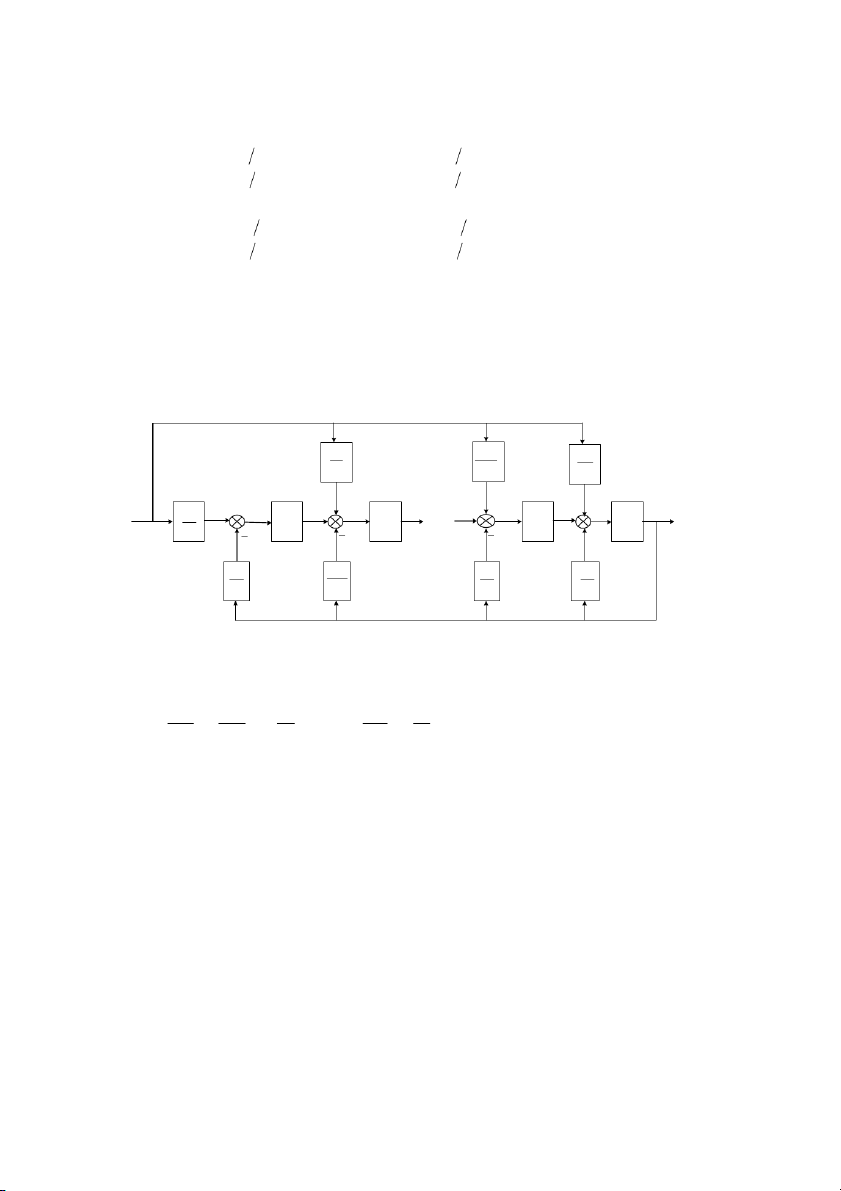
Sơ # cu trúc trng thái ca h thng trong trng hp t$ng quát nh hình 2.5. b b b 1 m− 1 m a a a 0 0 0 r(t) b x x x x x x x x = y(t) n n n 1 − n 1 − 3 2 2 x 0 1 1 a0 − − − − a a a a n n 1 − 2 1 a a a a 0 0 0 0
Hình 2.5: S cu trúc trng thái cho trưng hp m = n-1 Ví d& 2.3:
Cho h thng có phơng trình vi phân: 3 2 2 d y d y dy d r dr 2 +5 1 + 0 + ( y ) t = 2 + 7 +15r(t) (2.22) 3 2 2 dt dt dt dt dt Gi i - !t: x1 = y x 1 ( ) 1 = x 2 − . 2 5x1 + r x ( ) 2 (2.23) 2 = x 3 − x 5 1 + 3. r 5 x ) 3 ( 3 = − . 0 5x1 + 7. r 5
H phơng trình trng thái là: x −2.5 1 0 x 1 1 1 x 2 = − 5 0 1 x2 + . 3 5 r x −0 5 . 0 0 x . 7 5 3 3 20 x1 y = [1 0 ]0 x 2 x3
Vic chng minh h phơng trình trng thái (2.23) tơng ơng vi phơng trình vi phân
(2.22) cng ơn gin nh sau: o hàm hai v phơng trình (1), sau ó thay phơng trình (2)
vào c phơng trình mi, li o hàm thêm mt ln na, r#i thay phơng trình (3) vào, thay tr li x
c ph ng trình vi phân (2.22)
1 = y ta s? có ơ
Trng hp 0 < m < n 1
− chúng ta có th t suy ra cách !t bin trng thái tơng t.
2.3. Mô t h thng trong min t(n s 2.3.1 Mô hình hàm truyn
Mc 2.1.1 ta ã bit mt h thng iu khin có th c mô t bi mt phơng trình vi
phân, nh vy xác nh tín hiu ra khi bit tín hiu vào thì ta cn phi gii phơng trình vi
phân mô t h thng, nhng vi phơng trình vi phân bc cao (n > 2) thì vic gii phơng
trình vi phân tr nên phc tp. Phép bin $i Laplace s? giúp ta gii phơng trình vi phân ơn gin hơn rt nhiu. Phép bin *i Laplace:
Cho f(t) là hàm thi gian, xác nh vi mi t $ 0, bin $i Laplace ca f(t) là: ∞ −
F (s) = £[f(t)] = f (t)e st dt (2.24) 0 Trong ó:
£ -ký hiu phép bin $i Laplace;
F(s) -là nh Laplace ca f(t);
s -s phc, gi là bin Laplace.
Vi mBi hàm f(t) cho trc ch& có duy nht mt ánh x F(s) và ngc li. iu kin hàm
f(t) có bin $i Laplace là tích phân công thc (2.24) hi t.
Quá trình tìm hàm gc f(t) tA hàm nh F(s) c gi là phép bin $i Laplace ngc và ký
hiu là £-1, c tính theo công thc sau: 1 f(t) = £-1[F(s)] = ts F (s e ) ds (s $ 0) (2.25) 2 j π C
vi C là ng cong kín c chn trong min s.
Mt s tính ch)t c0a phép bin *i Laplace:
1. Tính tuyn tính: nu hàm f $ F s = và hàm có bin 1(t) có bi n i Laplace là ( ) £[f (t)] 1 1 f2(t)
$i Laplace là F (s ) = £[f (t)] thì: 2 2
£{a1f1(t) + a2f2(t)} = a1F1(s) + a2F2(s)
2. 3nh ca o hàm: nu hàm f(t) có bin $i Laplace là F (s) = £[f(t)] thì: df (t) £ = ( sF ) s f 0 ( + − ) dt
Trong ó f(0+) là iu kin u, nu iu kin u bng 0 thì: 21 df (t ) £ = sF (s) dt
Và t$ng quát cho trng hp o hàm cp n: n d f (t) £ = n s F(s) 1 − − n s f 0 ( + ) n2 − , − s f 0 ( + ) ( −n ) 1 − − f 0 ( + ) n dt d n f (t) £
= s nF (s ) , nu các iu kin u trit tiêu. dt n
3. 3nh ca tích phân: nu hàm f(t) có bin $i Laplace là F (s) = £[f(t)] thì: t F (s) £ f (τ d ) τ = 0 s
4. nh lý chm tr:: nu f(t) c làm tr: mt khong thi gian % thì ta có hàm f(t-%), khi ó:
£ {f (t −τ }
) = e τ−s.£{f(t)}=e τ−s.F(s)
5. nh lý giá tr cui: nu hàm f(t) có bin $i Laplace là F(s) =£[f(t)] thì:
lim f (t) = lim sF (s) t →∞ s→0
Bng 2.1: Bng bin &i Laplace ca mt s hàm c bn STT f(t) F(s) 1 1 1(t) s 2 T(t) 1 1 3 − t e α ( > 0) s + α α 4 − α t 1 − e s(s+ α ) t K 5 − K 1 ( T −e ) s(Ts + ) 1 1 6 t 2 s ! n 7 tn n+ 1 s 1 8 − αt t e. 2 (s + α) n−1 t 1 9 − α t e (n − ) 1 ! n (s + α) 22 1 1 10 (e−at − e−bt ) b − a s ( +a)(s + b) t t T − T − 1 11 1 1 T 2 2 T 1− e + e T − T T − T s(T s + ) 1 (T s + ) 1 1 2 1 2 1 2 1 e a−t e b−t 1 12 + + ab a(a − b) b(b− a) s(s +a) s ( + b) 1 1 13 1 ( − e a−t − at e . a−t ) a2 2 s(s + a) 1 1 14 (at −1+ e− at ) a2 s2 s ( + a) s 15 cosωt 2 2 s + ω 16 ω sin ωt 2 2 s + ω s + α 17 e−αt cos t ω 2 2 (s + α ) + ω ω 18 e−αt sin t ω 2 2 (s+ α ) + ω Hàm truyn
Mt h thng tuyn tính liên tc có tín hiu vào r(t), tín hiu ra y(t), hàm truyn t W(s)
c nh ngha là t s nh Laplace Y(s) ca áp ng u ra y(t) và nh Laplace R(s) ca tín
hiu kích thích r(t) khi h c kích thích tA trng thái 0. Tc là khi có các iu kin u y(0), dy(0) n 1 − d ( y 0) ,…,
u bng không. Nh vy: dt n 1 − dt Y ( ) s W (s) = R(s )
Khi h thng c mô t bi phơng trình vi phân (2.1), thì có th áp dng các tính cht v
phép bin $i Laplace chuyn tA min gc thi gian sang min nh xác nh hàm truyn t, ta có: ( n n− 1 a s + a s
+ ....... + a s + a )Y(s) = ( m m 1
b s + b s − + .......+ b
s + b )R(s) 0 1 n 1 − n 0 1 m 1 − m m m−1 ( ) ....... Y s b0s + b s 1 + + b s −1 + b m m W (s) = = n n R( s)
a s + a s −1 + .......+ a s + a 0 1 n−1 n
a thc m'u s ca hàm truyn c gi là a thc !c tính (ho!c a thc !c trng): n n A(s) = a ....... 0 s + a s −1 1 + + a s + a n−1 n
Cho m'u s ca hàm truyn bng 0 ta có phơng trình !c tính ca h thng: 23 n n 1 a s + − a s
+....... +a s +a = 0 0 1 n 1 − n
Tính $n nh ca h thng ph thuc vào các nghim ca phơng trình !c tính, s? c xét riêng chơng 4.
Hàm truyn W(s) có th c vit di dng zero-cc nh sau: m ∏(s − z ) Y( ) j s = − − − j 1
(s z )(s z )...(s z ) W ( ) 1 2 m s = = K = K R( ) n s
(s − s )(s − s )...(s − s ) (s − s ) 1 2 n ∏ i i= 1 Trong ó:
z (j = 1…m) - là nghim ca a thc t2 s, gi là im không (zero); j
s (i = 1…n) - là nghim ca a thc m'u s, gi là im cc (pole); i bm K = - là h s truyn. an
Mt h thng hay mt phn t2 tuyn tính có tín hiu vào r(t), tín hiu ra là y(t), sau khi ã
c mô hình hóa và xác nh c hàm truyn W(s) thng c biu di:n ơn gin di dng khi nh sau:
Ngoài ra hàm truyn ca mt s phn t2 trong h thng còn c ký hiu là G(s) , H (s) .
Ví d& 2.4: TA phơng trình vi phân mô t mch in RC ví d 2.1, xác nh hàm truyn t? .dy RC
+ y(t) = r(t) dt Chuyn sang min Laplace:
RCsY (s) + Y (s) = R(s) (RCs + )
1 Y (s) = R(s) Y (s) 1 W (s) = = R (s ) RCs + 1
Ví d& 2.5: Tìm hàm truyn t ca h c mô t bi phơng trình vi phân nh sau: 4 3 2
5 d y + 2d y +15dy dy +
= 10 dr + r(t) 4 3 2 dt dt dt dt dt Chuyn sang min Laplace: 5 4 s Y (s) + 2 3 s Y (s) +15 2
s Y (s) + sY (s) = 10sR(s) + R(s) (5 4 s + 2 3 s +15 2
s + s)Y (s) = 1 ( 0s + ) 1 R(s) ( ) 10 1 Y s s + W (s) = = 4 3 2 R(s)
5 s +2 s +15 s + s
Di ây là hàm truyn t ca mt s thit b in hình trong thc t:
- Các thit b o lng, thit b bin $i tín hiu: W(s) = K
- ng cơ in mt chiu: W ( ) K s = 2 T T s + T s + 1 1 2 2 24 K
- Lò nhit: W (s ) = Ts + 1 - Bng ti: τ − s
W (s) = K e . M t s nh n xét:
- Hàm truyn là mt cách mô t ca phơng trình vi phân;
- Mô t hàm truyn ch& dùng cho phn t2 và h thng tuyn tính bt bin (các h s là hng s);
- Hàm truyn ch& ph thuc vào các thông s a
i, bi và b c n c a h th ng, không ph thu c
vào tín hiu vào và tín hiu ra;
- Vic xác nh tín hiu ra ca h thng khi bit trc tín hiu vào ơn gin hơn nhiu da trên phơng trình: Y(s) = W(s)R(s)
2.3.2 i s s # khi
Các h thng trong thc t thng g#m nhiu phn t2 cơ bn kt ni vi nhau. biu
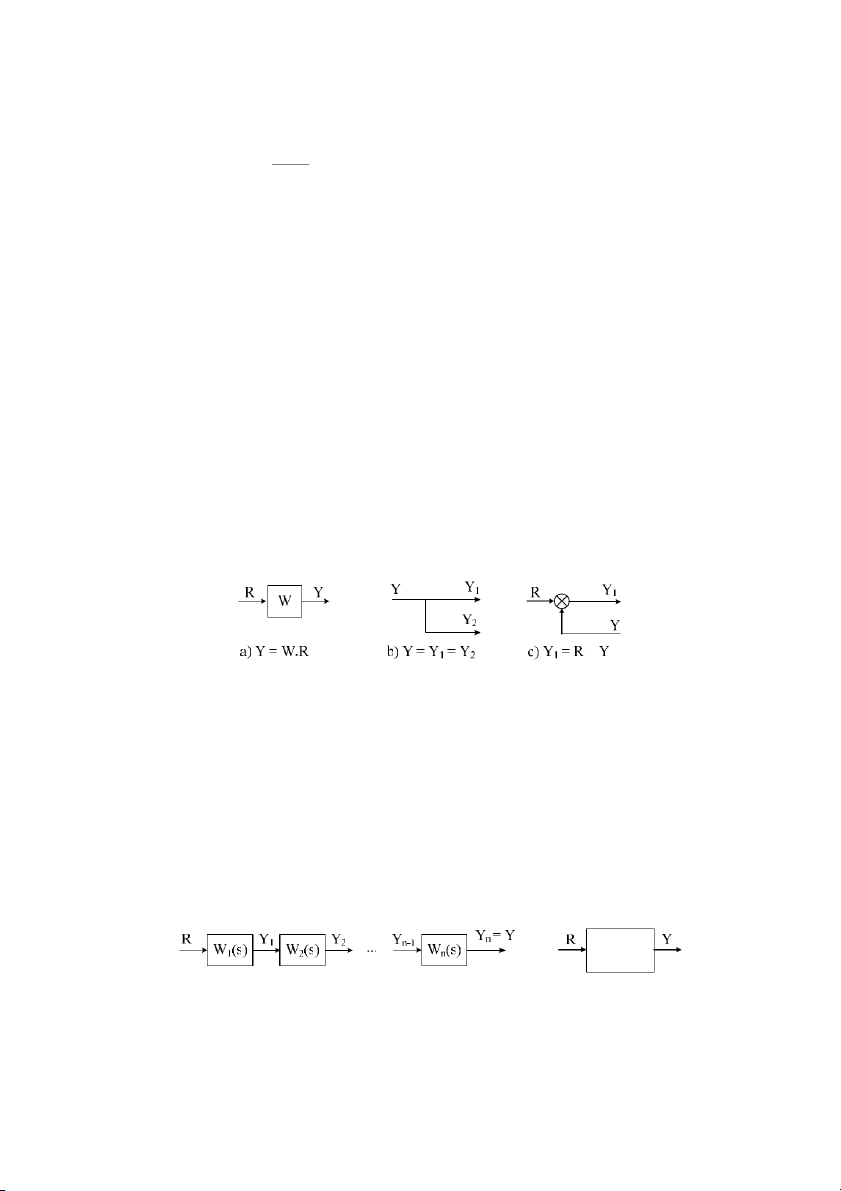
di:n các h thng phc tp ngi ta có th dùng sơ # khi. Sơ # khi ca mt h thng là
hình v? mô t chc nng ca các phn t2 và s tác ng qua li gia các phn t2 trong h
thng. Sơ # khi g#m có ba thành phn cơ bn là khi chc nng, b cng và im r? nhánh.
- Khi chc nng: tín hiu ra ca khi chc nng bng tích tín hiu vào và hàm truyn;
- B cng: tín hiu ra ca b cng bng t$ng i s ca các tín hiu vào;
- im r? nhánh: ti im r? nhánh mi tín hiu u bng nhau. ± ±
Hình 2.6: Các thành ph'n c bn ca s khi
i s sơ # khi là thut toán bin $i tơng ơng các sơ # khi. Hai sơ # c gi là
tơng ơng nu chúng có quan h gia tín hiu vào, tín hiu ra là nh nhau.
tìm hàm truyn ca h thng có sơ # khi phc tp, ta thng tìm cách bin $i sơ #
khi làm xut hin các dng kt ni ơn gin r#i ln lt tính các hàm truyn tơng ơng
theo nguyên t1c: rút gn dn tA trong ra ngoài.
Các phn t2 trong sơ # khi có th m1c ni tip, song song ho!c phn h#i. Di ây là
mt s quy t1c bin $i sơ # khi thng dùng:
a. H thng g#m các ph(n t m"c ni tip
Các phn t2 c gi là m1c ni tip nu tín hiu ra ca phn t2 trc là tín hiu vào ca
phn t2 sau. Tín hiu ra ca phn t2 cui cùng là tín hiu ra ca h thng. Sơ # các phn t2
m1c ni tip c mô t trên hình 2.7. n ⇔ ∏W (s) i = i 1
Hình 2.7: S h thng các ph'n t( m)c ni tip 25 TA sơ # ta có:
Yn = Wn Yn-1 = WnWn-1 Yn-2 = ... = WnWn-1…W2 Y1 = WnWn-1…W2W1R n n Y(s) Y = Y W R W (s )= = W s ( ) n = ∏ i ∏ i R(s) i =1 = i 1
Nh vy hàm truyn t ca h thng các phn t2 m1c ni tip bng tích s hàm truyn t
ca các phn t2 thành phn.
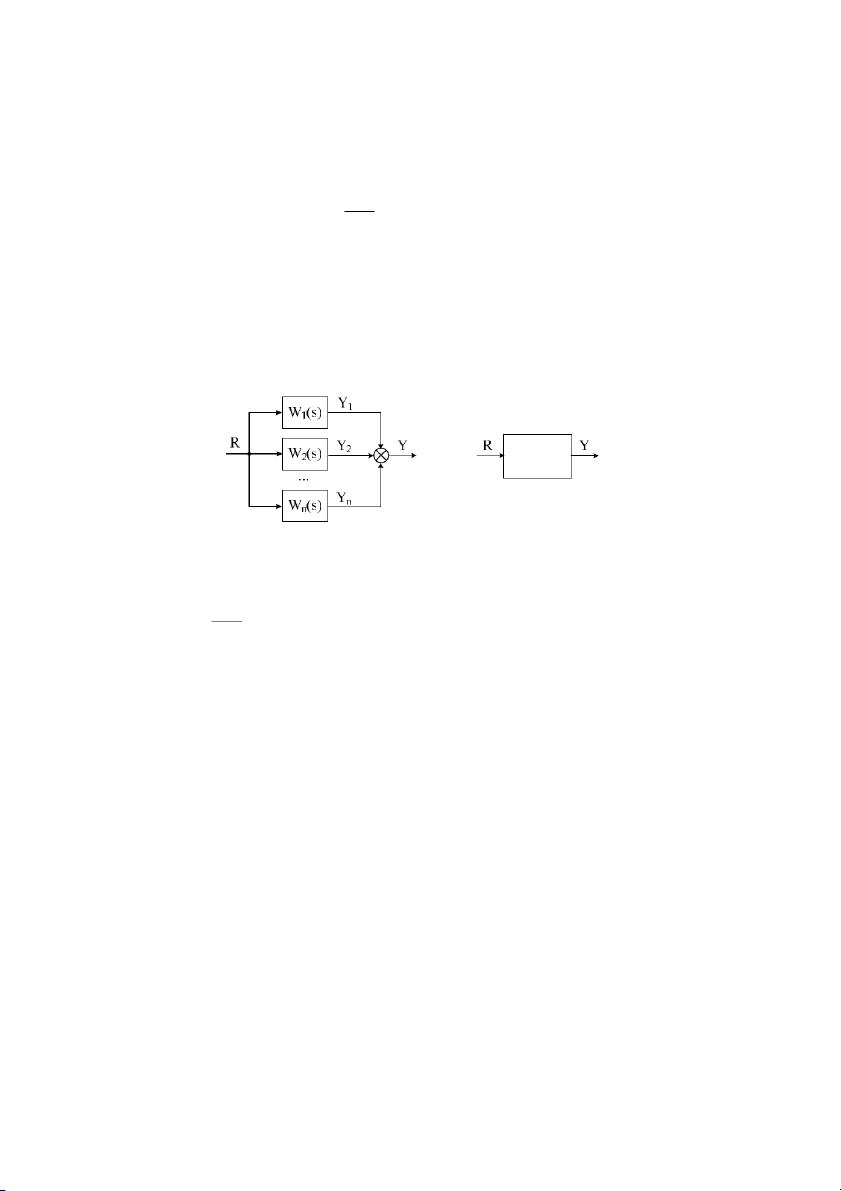
b. H thng g#m các ph(n t m"c song song
H thng c xem là g#m các phn t2 m1c song song nu tín hiu vào ca h thng là tín
hiu vào ca các phn t2 thành phn, còn tín hiu ra ca h thng bng t$ng i s tín hiu ra
ca các phn t2 thành phn. Sơ # h thng các phn t2 m1c song song c mô t trên hình 2.8. n ⇔ W (s) i i =1
Hình 2.8: S h thng các ph'n t( m)c song song
Ta có: Y = Y + Y + ...+ Y = W (s)R + W (s)R + ...+ W (n)R 1 2 n 1 2 n = W
( (s) + W (s) + ... + W (s))R 1 2 n Y ( ) s W (s) =
=W (s) +W (s) + ... + W n ( s) R(s) 1 2
Nh vy hàm truyn ca h thng các phn t2 m1c song song bng t$ng i s hàm truyn
ca các phn t2 thành phn.
c. H thng có mch ph n h#i
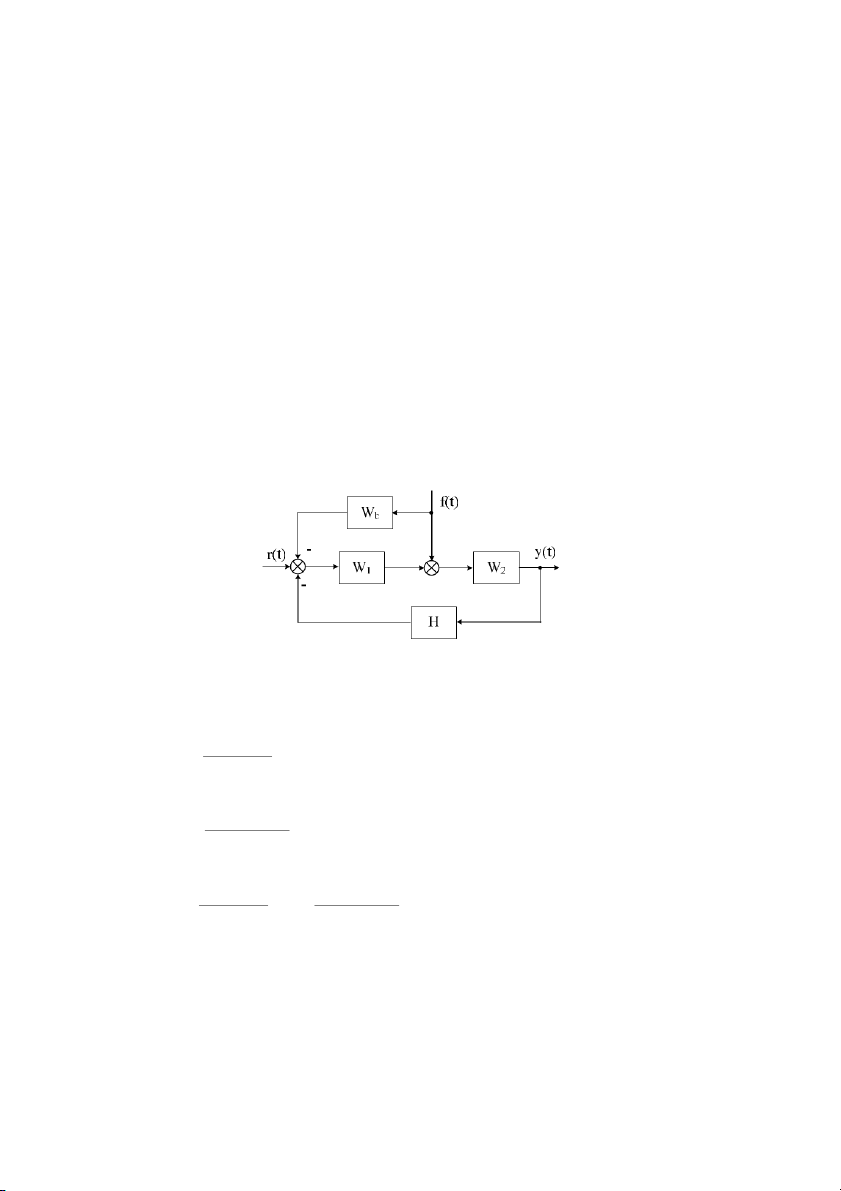
Mch phn h#i là mch a tín hiu tA u ra ca mt phn t2 quay tr li u vào ca nó.
H thng có mch m1c phn h#i g#m hai mch: Mch truyn th@ng W và mch phn h#i t(s)
H(s). Mch phn h#i còn c gi là mch h#i tip.
Tín hiu ra ca mch truyn th@ng là tín hiu ra ca h thng và là tín hiu vào ca mch
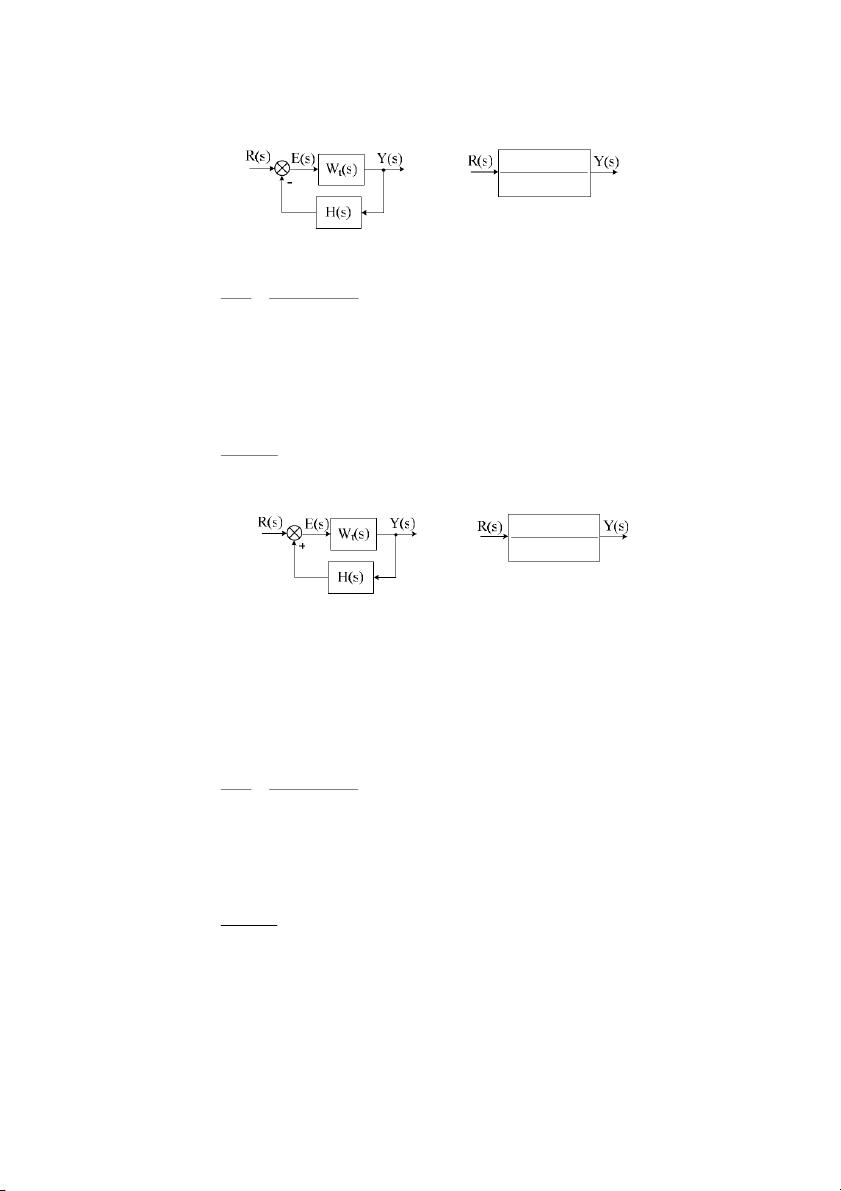
phn h#i. Có hai dng phn h#i: mch phn h#i âm và mch phn h#i dơng. Phn h#i âm:
TA sơ # khi ta có các phơng trình:
E(s) = R(s) −Y (s)H (s) Y( ) s = E( ) s W ( ) s t
Y (s) = [R(s) − Y (s)H (s)]W (s) = R(s)W (s) − Y (s)W (s)H (s) t t t Y (s) 1
[ +W (s)H (s)] = R(s)W (s) t t 26 Wt (s) ⇔ 1 + W (s)H(s) t
Hình 2.9: S h thng có mch m)c phn hi âm
Ta rút ra hàm truyn ca h thng kín có h#i tip âm là: Y( ) s W (s) W (s) t = = ( R ) s
1+ W (s)H (s) t
Nh vy hàm truyn ca h thng vi mch phn h#i âm bng hàm truyn ca mch truyn
th@ng chia cho 1 cng vi tích hàm truyn ca mch truyn th@ng nhân vi hàm truyn ca mch phn h#i.
Trng hp khi hàm truyn mch phn h#i H(s) = 1, gi là h thng có phn h#i âm ơn
v, hàm truyn t ca h là: W (s ) W (s) t = 1+ W (s) t Phn h#i dơng: Wt(s) ⇔ 1− Wt (s)H(s)
Hình 2.10: S h thng có mch m)c phn hi dưng
Tơng t, tA sơ # khi ta có: E( ) s = ( R ) s +Y( ) s H ( ) s
Y (s ) = E (s )W (s ) t Y (s) = [ (
R s) + Y (s)H (s)]W (s) = R(s)W (s)+ Y (s)W (s)H (s) t t t Y (s) 1
[ −W (s)H (s)] = R(s)W (s) t t
Hàm truyn ca h thng kín có h#i tip dơng là: Y( ) s W (s) W (s) t = = ( R ) s
1− W (s)H (s) t
Nh vy hàm truyn ca h thng vi mch phn h#i âm bng hàm truyn ca mch truyn
th@ng chia cho 1 trA i tích hàm truyn ca mch truyn th@ng nhân vi hàm truyn ca mch phn h#i.
Khi H(s) = 1: h thng có phn h#i dơng ơn v, hàm truyn t ca h là: W ( ) s W (s) t = 1−W (s) t
d. Chuyn v trí tín hiu 27
Khi xác nh hàm truyn t ca h thng có nhiu vòng phn h#i, trong nhiu trng hp
phi chuyn v trí các tín hiu. Mc ích ca chuyn v trí tín hiu là a mt h thng có
ng truyn tín hiu phc tp thành mt h thng tơng ơng có ng truyn tín hiu ơn
gin hơn, có dng ni tip, song song ho!c h#i tip. Phép chuyn $i này còn c gi là
chuyn $i sơ # khi. Tín hiu có hai loi: Tín hiu vào (tín hiu có mi tên i vào) và tín
hiu ra (tín hiu có mi tên i ra). Ta có các trng hp chuyn $i tín hiu nh sau:
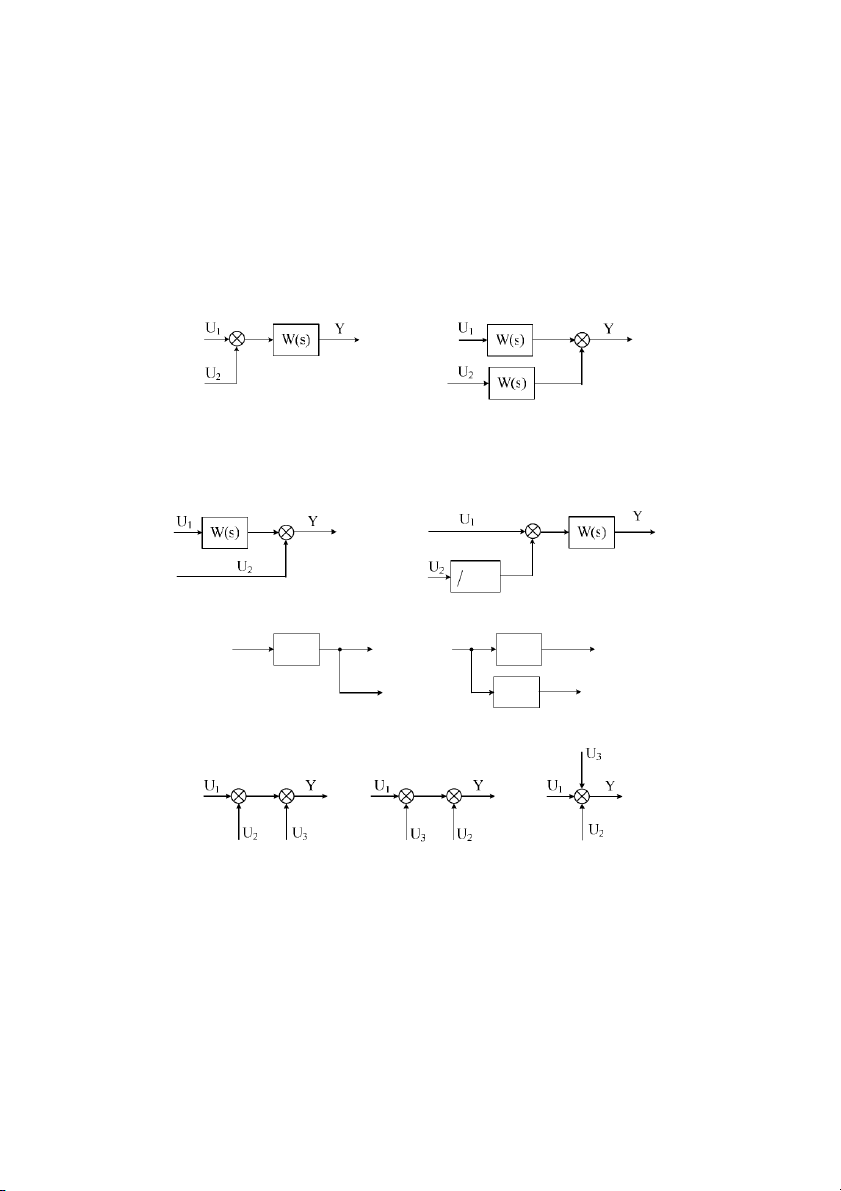
Chuyn v* trí tín hiu vào:
- TA trc ra sau mt khi: ⇔
- TA sau ra trc mt khi:
Chuyn v* trí tín hiu ra:
- TA trc ra sau mt khi: ⇔ 1 W(s)
- TA sau ra trc mt khi: Y Z Y Z UVWX [ [ ⇔ UVWX Z\ Z\ UVWX
Chuyn v* trí, tách hai b cng ± ⇔ ⇔ ± ± ± ± ± Chú ý:
Vic chuyn v trí tín hiu có th t suy lun da trên nguyên t1c khi chuyn v trí tín
hiu không c làm thay $i tính cht truyn tín hiu trong h thng, #ng thi tín
hiu ch& c chuyn qua khi.
Các bin $i sau ây là không tơng ơng:
- Chuyn im r? nhánh tA trc ho!c sau b cng ho!c ngc li: 28 ≠
- Chuyn v trí hai b cng khi gia hai b cng ó có im r? nhánh: ≠
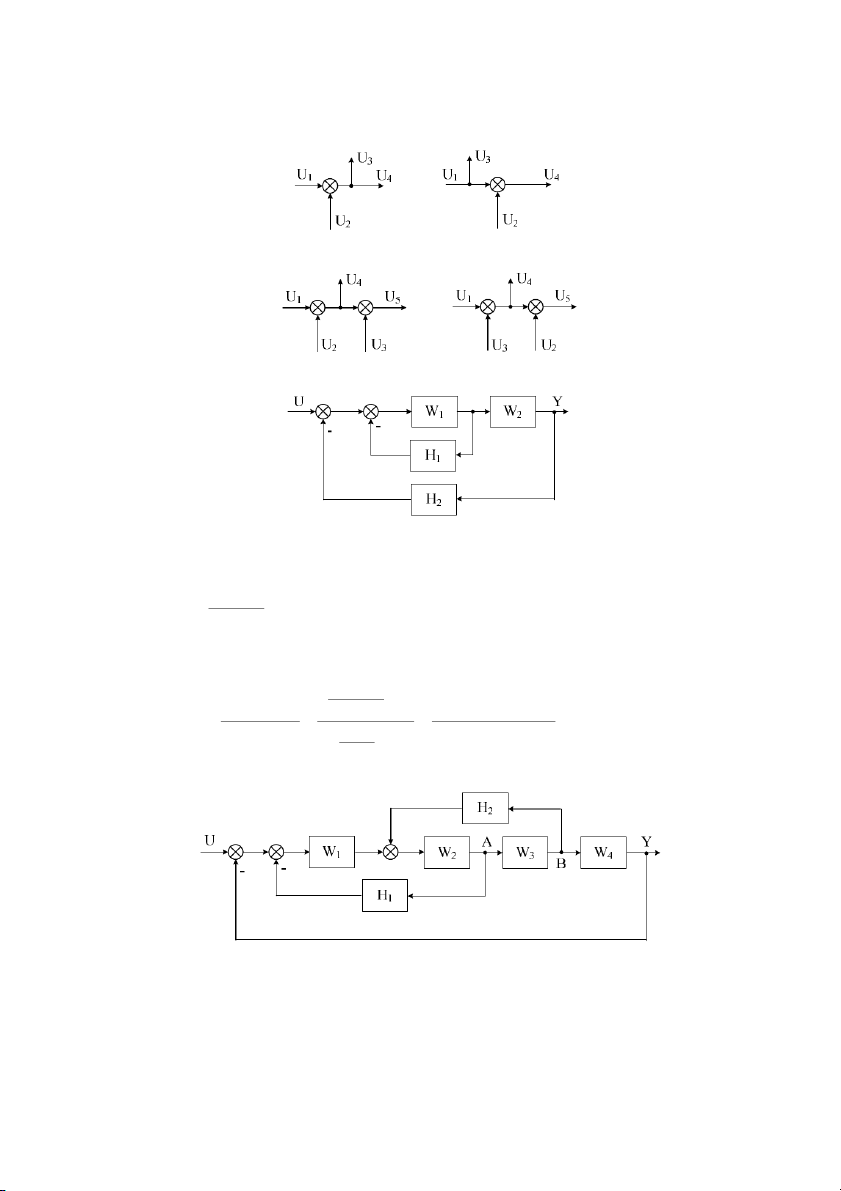
Ví d& 2.6: Tính hàm truyn tơng ơng ca h thng có sơ # khi nh sau:
Gi i: Ln lt rút gn sơ # khi tA trong ra ngoài ta c: Hàm truyn W #
11 ca h kín ph n h i âm W1-H1 là: W1 W = 11 1 + 1 W H1
Hàm truyn kín W (s) ca h thng chính là hàm truyn ca khi (W ni tip ), phn 11 W2 h#i âm H : 2 W1 W2 W W 1 + W H W W 11 2 1 1 1 2 W (s) = = = 1+ W W H W1 1 + W H + W W H 11 2 2 1 1 1 2 2 1 + W H 2 2 W H 1 1
Ví d& 2.7: Xác nh hàm truyn ca h thng có sơ # khi sau:
Gi i: R sơ # khi này tính c hàm truyn ta phi tin hành chuyn $i tín hiu trc.
Bài này có 2 cách chuyn: th nht là có th chuyn tín hiu ra tA trc khi W i 3 ( m A) ra 29 sau khi W i A 3 (ra sau
m B). Cách th 2 là chuy n tín hi u vào t sau kh i W1 ra tr c kh i
W . Di ây ta s? trình bày theo cách làm th nht. 1
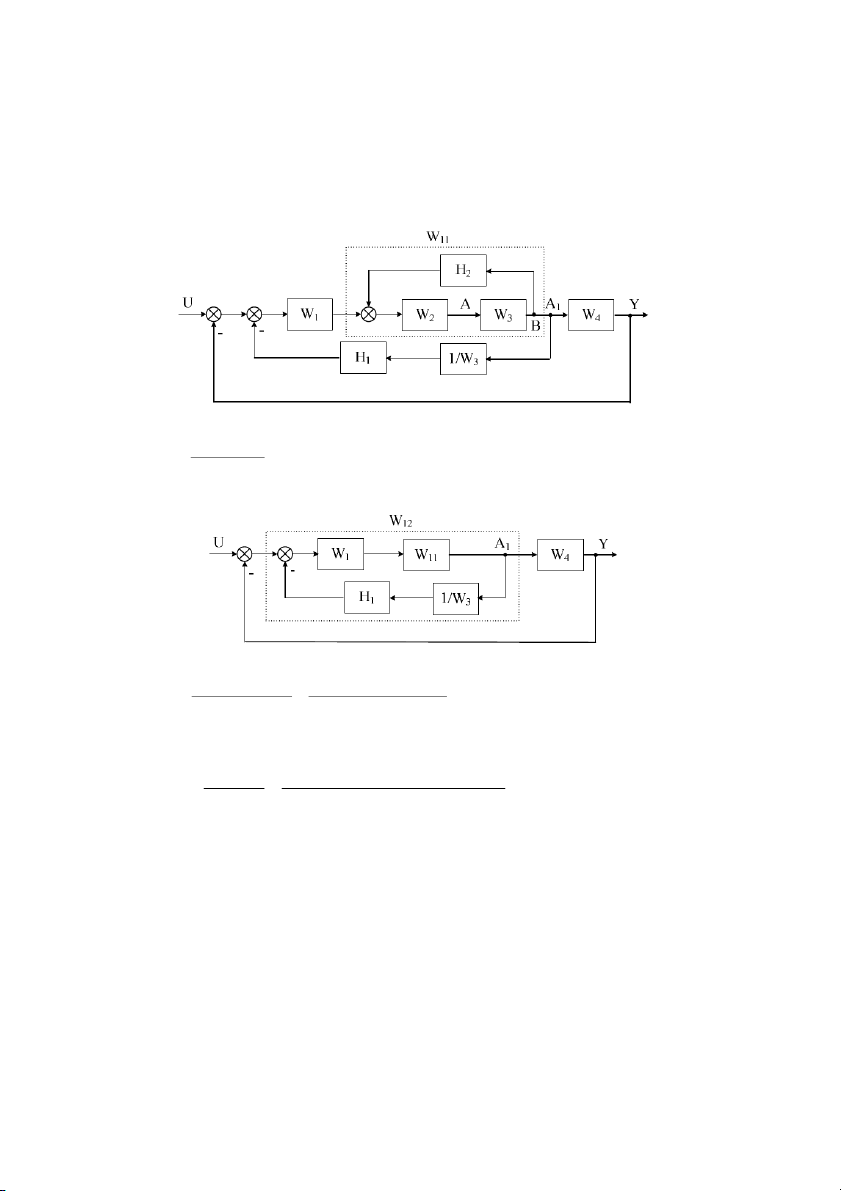
Chn cách chuyn tín hiu ra tA trc ra sau khi W
im A sang im A1), ta có sơ # 3 (tA tơng ơng:
Hàm truyn ca khi W11: W W 2 3 W = 11 1 − 2 W W3H2 Sơ # thay th:
Hàm truyn ca khi W12: W W WW W 1 11 1 2 3 W = = 12 1−W W H /W 1 − + 1 11 1 3 2 W 3 W H2 1 W 2 W 1 H
Hàm truyn ca h thng g#m khi W # ơ
12 n i ti p W4 - ph n h i âm n v , c ng chính là
hàm truyn W (s) ca h thng ang cn tìm, là: W W W W W W 12 4 1 2 3 4 W (s) = = 1+W W 1− + + 12 4 2 W 3 W H2 1 W 2 W 1 H 1 W 2 W 3 W 4 W 2.3.3 Công th+c Mason
biu di:n h thng iu khin t ng, ngoài phơng pháp s2 dng sơ # khi, ta còn
có th s2 dng phơng pháp sơ # dòng tín hiu. S2 dng sơ # dòng tín hiu ta có mt s nh ngha sau ây:
Sơ # dòng tín hiu là mt mng g#m các nút và nhánh.
- Nút: là mt im biu di:n mt bin hay mt tín hiu trong h thng.
- Nhánh: là ng ni trc tip hai nút, trên mBi nhánh có mi tên ch& chiu truyn ca tín
hiu và có ghi hàm truyn cho bit mi quan h gia tín hiu hai nút. 30
- Nút ngu n: là nút ch& có các nhánh hng ra.
- Nút ích: là nút ch& có các nhánh hng vào.
- Nút h n h p: nút có c các nhánh hng ra và các nhánh hng vào. Ti nút hBn hp, tt
c các tín hiu ra u bng nhau và bng t$ng i s ca các tín hiu vào. -
ng ti n: là ng g#m các nhánh liên tip có cùng hng tín hiu i tA nút ngu#n
n nút ích và ch& qua mBi nút mt ln. Hàm truyn ca mt ng tin bng tích các hàm
truyn ca các nhánh trên ng tin ó.
- Vòng kín: là ng khép kín bao g#m các nhánh liên tip có cùng mt hng tín hiu và
ch& i qua mBi nút mt ln. Hàm truyn ca mt vòng kín bng tích các hàm truyn ca các
nhánh trên vòng kín ó.
Nu h thng cho dng sơ # khi mà ta mun áp dng công thc Mason tính hàm
truyn, thì trc ht ta phi chuyn sơ # khi thành sơ # graph. Mi tơng quan gia sơ #
khi và graph tín hiu c trình bày trong bng 2.2.
Mt s lu ý khi chuyn tA sơ # khi sang graph:
- Có th gp hai b cng (ho!c hai im r? nhánh) lin nhau thành mt nút;
- Có th gp mt b cng và mt im r? nhánh lin sau nó thành mt nút;
- Không th gp mt im r? nhánh và mt b cng lin sau nó thành mt nút.
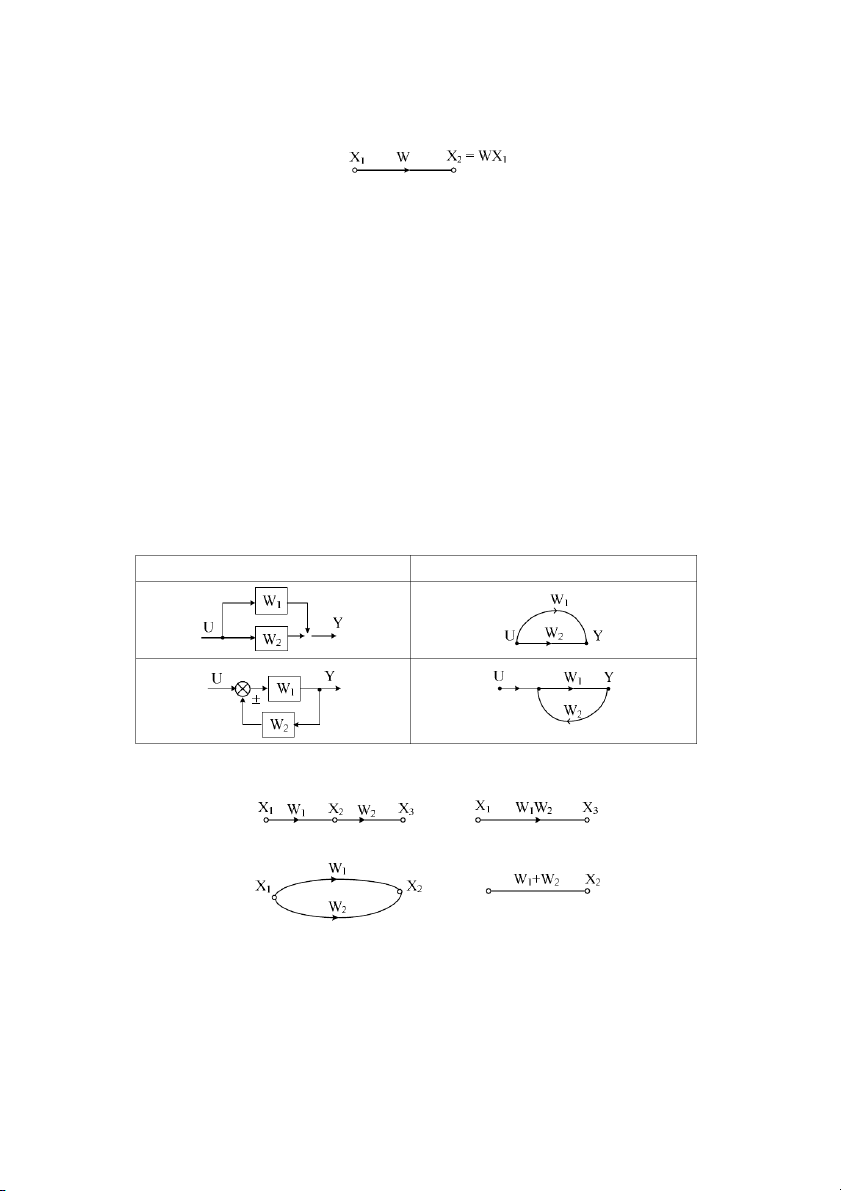
Bng 2.2: Mi tưng quan gi+a s khi và graph tín hiu
Biu di:n dng sơ # khi
Biu di:n bng sơ # graph ± ± ° ±
i s graph tín hiu - Các nhánh ni tip: ⇔ - Các nhánh song song: ⇔ - Nút hBn hp: 31 ⇔ - Vòng phn h#i: w w 1 2 1− w w ⇔ ⇔ 2 3 Công th+c Mason
H thng iu khin t ng biu di:n bng graph tín hiu có hàm truyn tơng ơng tính theo công thc: 1 W = P ∆ ∆ k k k Trong ó: P
ng tin th k; k - hàm truy n c a
∆ - nh thc con th k suy ra tA # bng cách b" i các vòng kín có dính k
vi ng tin th k.
và # - nh thc ca graph tín hiu ∆ = − 1 L + L L − L L L + i i j i j m i i, j i , j ,m Vi:
L : t$ng các hàm truyn ca các vòng kín có trong sơ # graph; i i
L L : t$ng các tích hàm truyn ca hai vòng không dính nhau; i j i, j
(không dính có ngha là không có nút nào chung, nu có ít nht mt nút chung thì gi là dính).
L L L : t$ng các tích hàm truyn ca ba vòng không dính nhau; i j m i , j m ,
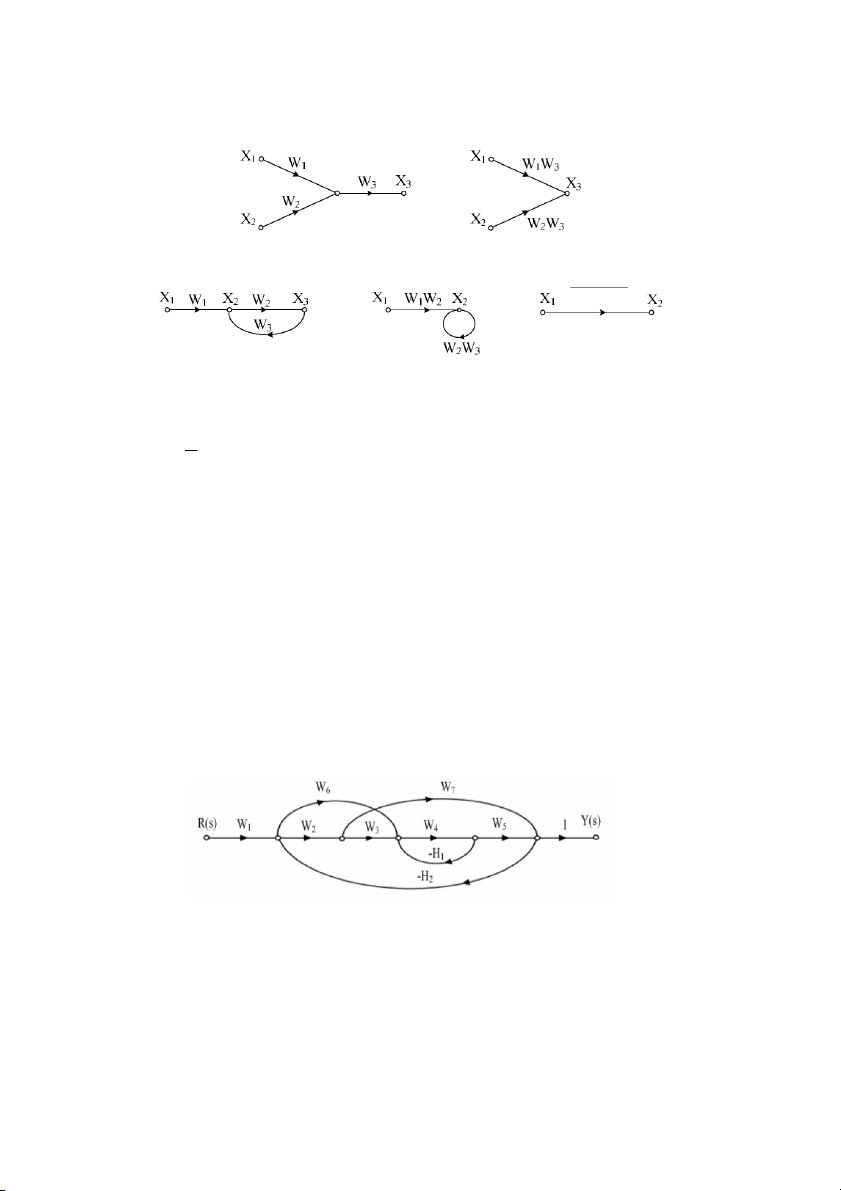
Ví d& 2.8: Tính hàm truyn tơng ơng ca h thng mô t bi sơ # Graph sau ây:
- Xác nh hàm truyn ca các ng tin Pk: 1 P = 1 W 2 W 3 W W4 5 W 2 P = 1 W 6 W W4 5 W 3 P = 1 WW2 7 W 32
- Xác nh các vòng l!p Lk: = 1 L − 4 W H1 L = − 2 2 W 7 W H2 = 3 L − 6 W 4 W 5 W H 2 = 4 L − 2 W 3 W 4 W 5 W H 2
- Tính nh thc ca Graph:
∆ = 1− (L + L + L ) + 1 2 3 1 L 2 L
- Tính các nh thc con: ∆ = ∆ = ∆ =1 − L 1 1 ; 2 1 ; 3 1
Hàm truyn tơng ơng ca h thng là: 1 W =
(P ∆ + P ∆ + P ∆ ) 1 1 2 2 3 3 ∆
W W W W W + WW W W +W W W 1 ( + W H ) 1 2 3 4 5 1 6 4 5 1 2 7 4 1 W = 1 W + H W
+ W H +W W W H +W W W W H +W W W H H 4 1 2 7 2 6 4 5 2 2 3 4 5 2 2 4 7 1 2
2.4 Mi quan h gi1a các dng mô t toán h%c
Mt h thng iu khin t ng có th mô t dng phơng trình vi phân, hàm truyn
t, sơ # khi, ho!c trong không gian trng thái. Tùy theo h thng và bài toán iu khin cn
gii quyt mà chúng ta chn phơng pháp mô t toán hc cho phù hp. Nu là bài toán phân
tích h thng có mt u vào mt u ra thì ta có th chn mt trong ba phơng pháp u
c. Nu h thng là phi tuyn ho!c có thông s bin $i theo thi gian, ho!c h có nhiu u
vào ra thì thng s2 dng mô hình trng thái. !]D^_ID]JI`D]Ha_ W(s) = . C s ( I −A) 1− B . + D
Hình 2.11: Quan h gi+a các dng mô t toán h,c h thng iu khin t ng
Trong mt s trng hp h thng cho di dng sơ # khi ta có th thành lp phơng
trình trng thái bng cách !t bin trng thái trc tip tA sơ # khi.
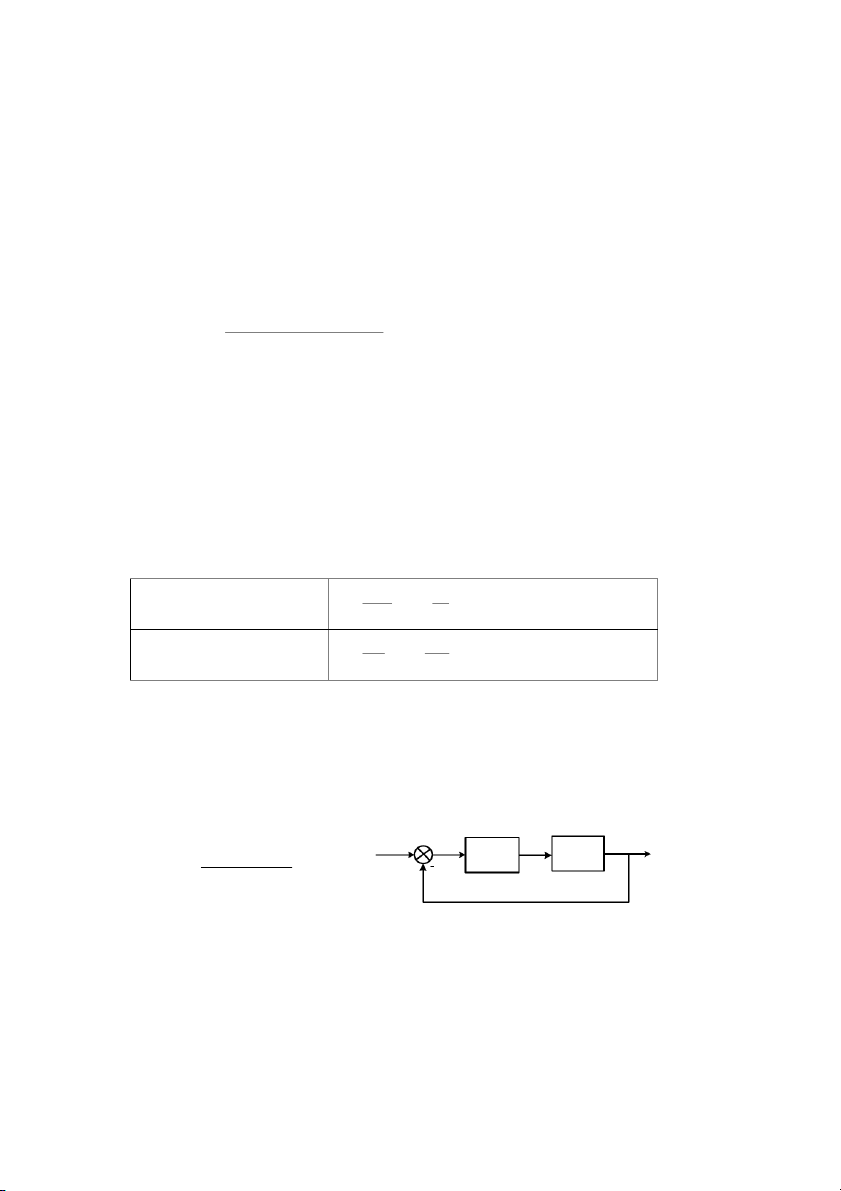
Ví d& 2.9: Thành lp phơng trình trng thái ca h có sơ # khi nh sau: 15 s s ( + ) 4 ( s 3 + 2) 33
Gi i: Sơ # khi tơng ơng: bVWX 1 ceVWX 1 c\VWX 15 c[VWXDdDZVWX s s + 4 s 3 + 2
!t bin trng thái X ơ # ?
1(s), X2(s), X3(s) nh trên s
hình v , ta có các quan h : 15 • X ( ) s = X ( ) 1 s 3s + 2 2
3sX (s) + 2X (s) = 15X (s) 1 1 2 2 x = − x + 5 (1) 1 1 x2 3 1 • X ( ) s = X ( ) (2) 2 s s + 4 3
sX (s) + 4 X (s) = X (s) 2 2 3 x = −4 + (3) 2 x2 3 x 1 • X (s) = − 3 (R(s) X ( 1 s ) ) s
sX (s) = R(s) − X (s) 3 1 x 3 = −x1 + r
Kt hp các phơng trình trng thái (1), (2), (3) thành lp trên ta có h phơng trình
trng thái vit di dng vectơ: x1 − 2/3 5 0 x 0 1 x 2 = 0 − 4 1 x2 + 0 r x3 −1 0 0 x 1 3 x1 y = x 1 0 0 x 1 = [ ] 2 x3
Tìm hàm truyn t ca h tA phơng trình trng thái:
Cho h tuyn tính có mô hình trng thái:
x(t ) = Ax(t ) + Br (t )
y(t ) = Cx(t) + Dr(t )
Bin $i Laplace 2 v ca h phơng trình vi iu kin u bng 0 ta c: sX ( )
s = AX (s) + BR( ) s
(sI − A)X (s) = BR(s)
Y(s) = CX (s) + DR( ) s
Y (s ) = CX (s ) + DR (s )
Y (s) = [C(sI − ) 1
A − B + D]R(s)
vi I là ma trn ơn v.
Hàm truyn t ca h thng tính theo phơng trình trng thái là: 34 Y( s) W s ( ) =
= C(sI − A −1 ) B + D R( s)
Ví d& 2.10: Cho h có phơng trình trng thái: x − 1 3 −1 x1 10 = + r x 1 0 x 0 2 2 x y = [1 ] 1 2 x2
Hãy xác nh hàm truyn t ca h thng. Gi i:
W (s) = C(sI − A −1 ) B ; D = 0 1 0 −3 −1 s +3 1 Ta có: s
( I − A) = s − = 0 1 1 0 −1 s 1 1 1 s − 1 (sI − − A) = Ad ( j sI − ) A = det(sI − ) A ( s s + ) 3 + 1 1 s + 3 s s 1 1 −1 10 1 10 (sI − −) A B = = s(s + ) 3 +1 1 s + 3 0 s (s + ) 3 +1 10 s − 1 1 10 10s + 20 ( C sI − ) A B = [1 2] = ( s s + ) 3 +1 10 s (s + ) 3 + 1 10s + 20 Vy: W (s) = 2 s + 3s + 1 BÀI T2P CHƠNG 2
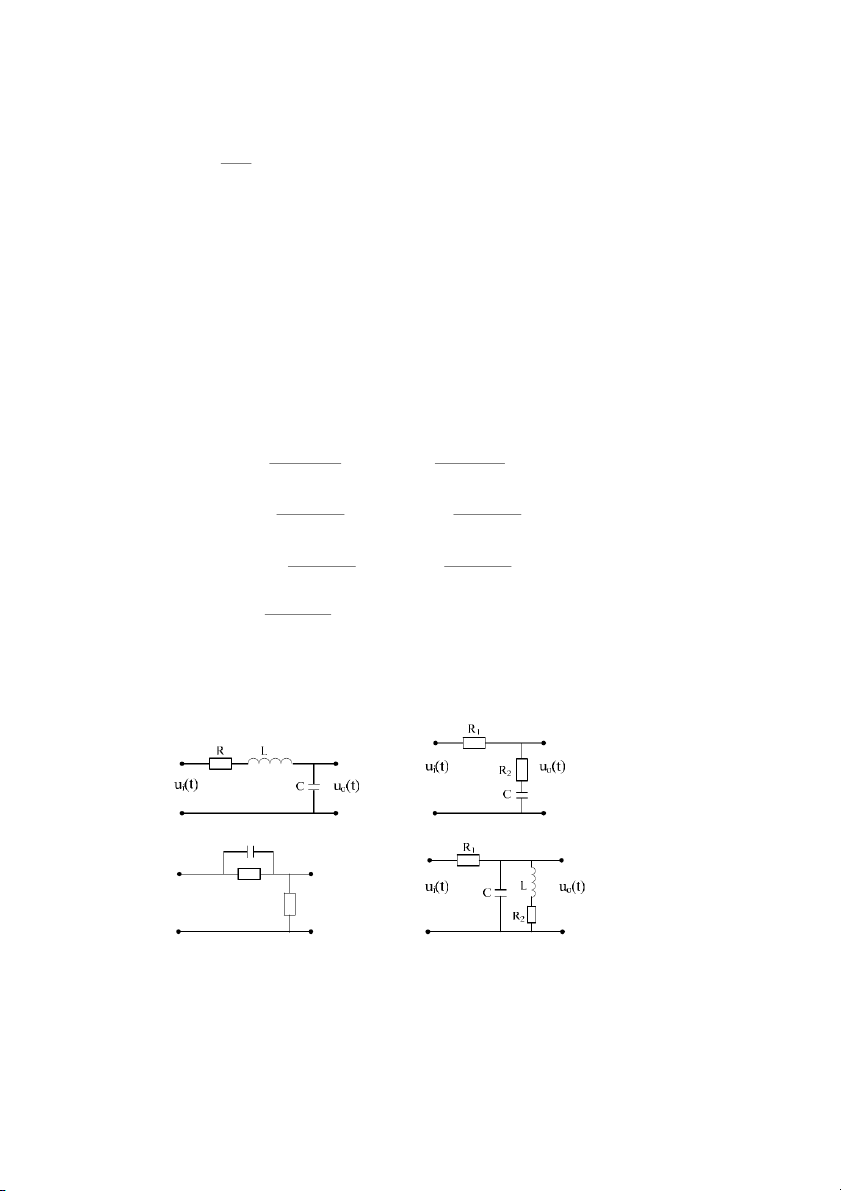
1. Cho các sơ # mch in sau: G b[ L_V]X LfV]X b\
a. Hãy vit phơng trình vi phân mô t các mch in trên.
b. Xác nh hàm truyn t. 35
c. Vit phơng trình trng thái mô t các mch in.
2. Cho h thng có hàm truyn t: 10 a. W ( ) s = 6 3 s + 4 2 s + 3s + 1 4 b. W (s ) = 7 4 s +3 3 s +5 2 s + 2s +1 3s + 1 c. W ( ) s = 2 4 s + 3 3 s + 8 2 s + 5 s +1 5 3 s +11 2 s + 4s +1 d. W (s ) = 4 s + 3 3 s + 10 2 s + 7s + 1
- Vit phơng trình trng thái mô t h thng
- V? sơ # cu trúc mô t h thng.
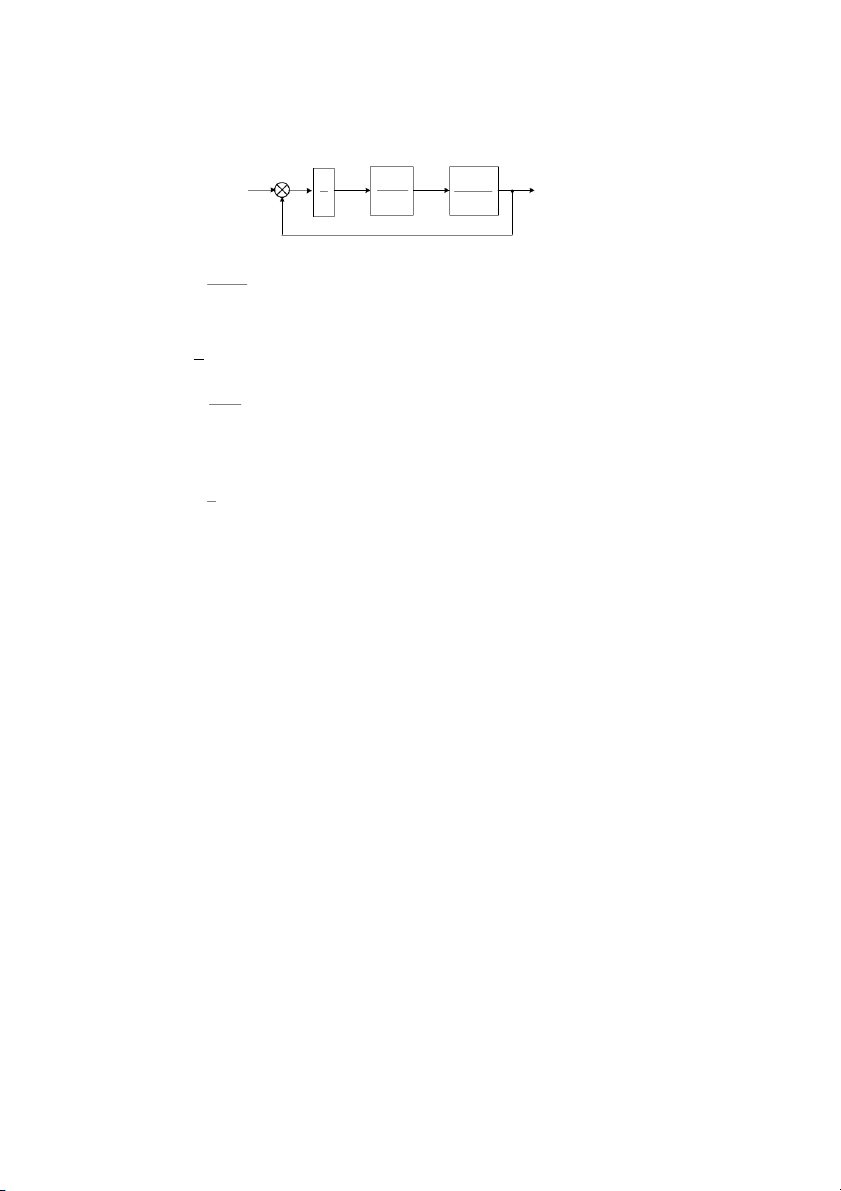
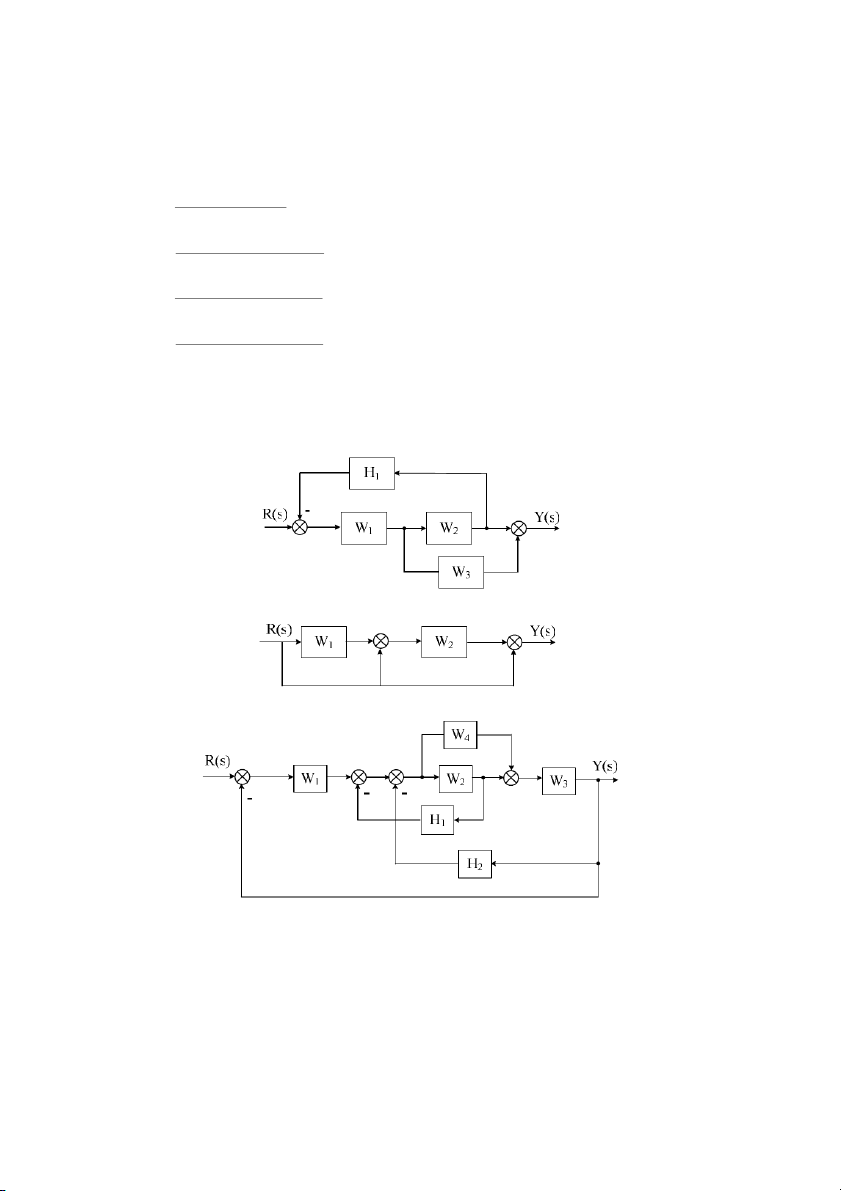
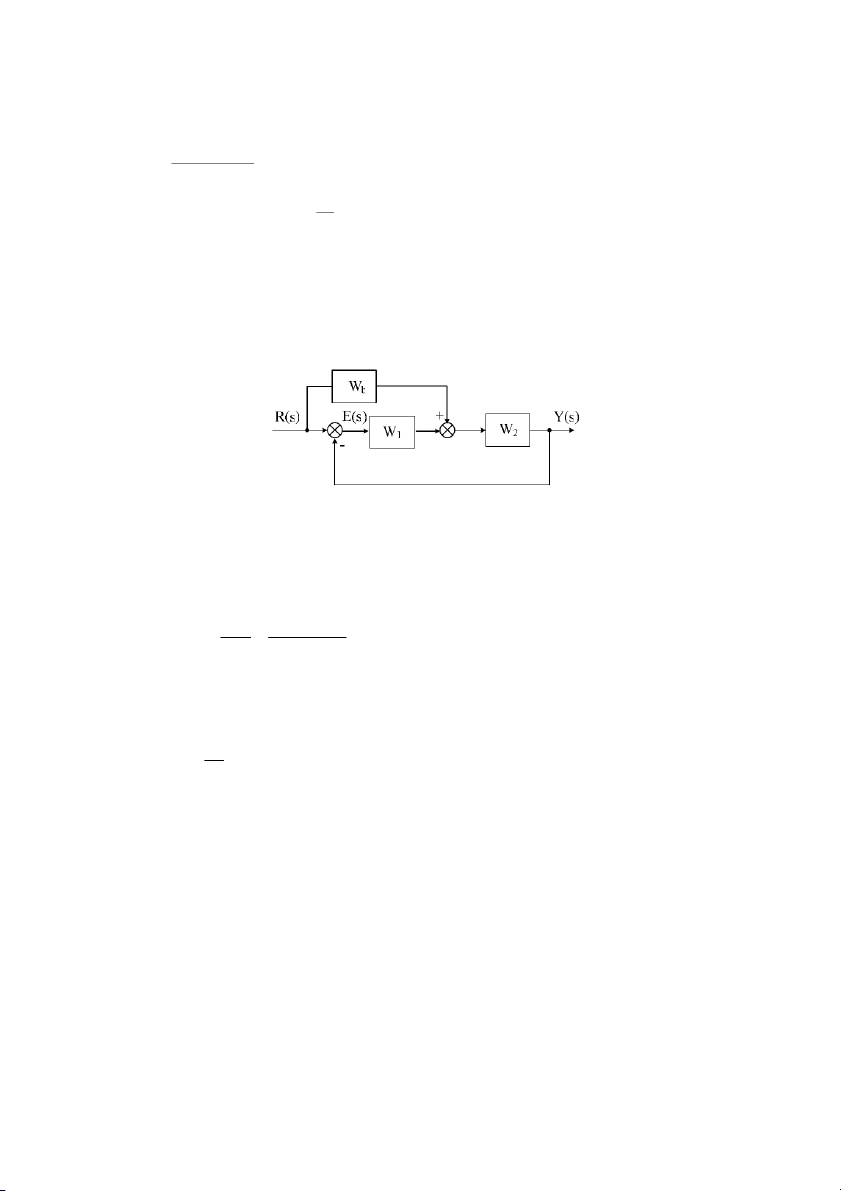
3. Xác nh hàm truyn t ca h có sơ # khi nh sau: a. b. c. 36
CHƠNG 3: KH,O SÁT NG HC
H TH-NG IU KHIN TUYN TÍNH LIÊN TC
R chơng 2, khi xây dng mô t toán cho các phn t2 iu khin chúng ta nhn thy có
nhng phn t2 m!c dù khác nhau v bn cht vt lý nhng li có dng mô hình toán hc ging
nhau. thun tin cho vic kho sát ngi ta chia chúng thành tAng nhóm và gi là khâu
ng hc, ví d khâu t& l, khâu quán tính bc nht, khâu bc hai…Mt i tng iu khin,
b iu khin, hay toàn b h thng cng có th là mt khâu ng hc duy nht ho!c bao g#m
nhiu khâu ng hc cơ bn ghép ni t$ hp vi nhau.
!c tính ng hc ca khâu hay h thng chính là s thay $i tín hiu ra theo thi gian hay
tn s khi có tín hiu tác ng u vào. !c tính ng hc xét trong min thi gian và min
tn s c gi tơng ng là !c tính thi gian và !c tính tn s. Trong thc t các tín hiu
tác ng vào h thng iu khin thng không c bit trc. Do ó, kho sát các !c
trng ca áp ng ng hc ngi ta dùng mt s tín hiu vào chu>n, nh trc, nh tín hiu
bc thang ơn v, tín hiu xung ơn v, tín hiu dc ơn v, tín hiu hình sin. Các tín hiu này
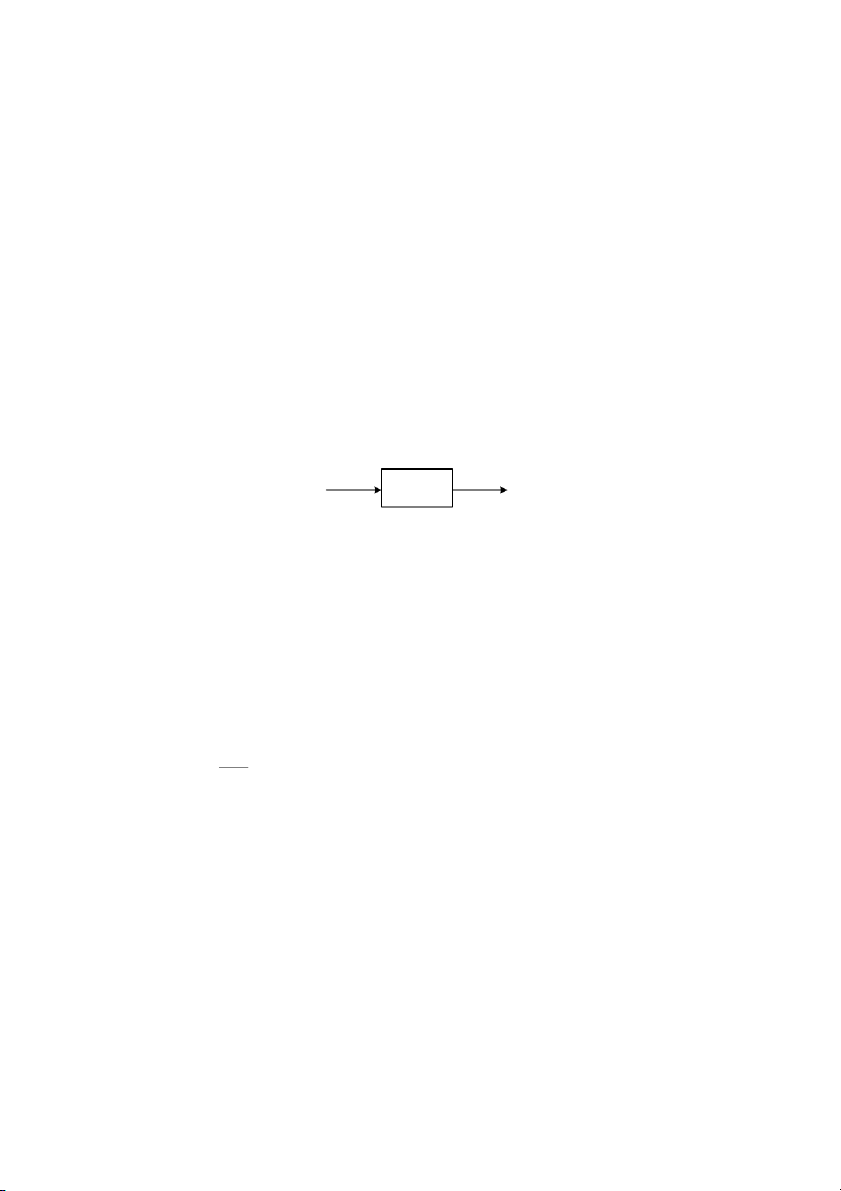
gi là tín hiu th2 hay hàm th2. δ (t ) ( g t ) ( 1 t) W (s ) ( h t) r(t) ( y t)
Hình 3.1: áp ng trên min thi gian ca mt h thng
Vic xác nh !c tính ng hc ca mt i tng iu khin hay mt h thng iu khin
cho phép ánh giá cht lng, $n nh hay t$ng hp b iu khin cho mt h thng. Và trong
mt s trng hp, bng thc nghim, ta thu c !c tính ng hc ca mt i tng iu
khin khi cha có mô hình toán hc ca i tng ó, bng kinh nghim và cơ s toán hc v
!c tính ng hc ca mt s khâu cơ bn s? c trình bày trong phn này ta có th xây dng
li c mô hình toán hc ca i tng ó (phơng pháp nhn dng bng thc nghim).
3.1 Tín hiu c b n và áp +ng
3.1.1 Tín hiu xung n v và hàm tr%ng lng
Tín hiu xung n v hay còn gi là hàm Dirac (ký hiu δ (t )) khi t ≠ 0 (3.1) δ (t) d ( 1 t ) 0 = = dt ∞ khi t = 0 +∞ 0 +
Hàm δ ( )t có tính cht: δ(t )dt = δ(t )dt =1 −∞ 0 ∞ 0+ 0 +
3nh Laplace: F(s) = {
L δ (t)}= δ (t) −
e st dt = δ (t) 0 −
e dt = δ (t)dt = 1 0 0 0
Hàm xung Dirac có rng bng 0 và ln vô cùng ln nên ch& là hàm toán hc thun
túy, trong thc t ch& t#n ti các tín hiu gn úng vi xung Dirac.
Hàm xung Dirac thng c dùng mô t các nhi:u tác ng trong khong thi gian rt
ng1n (tc thi). Ngoài ra, khái nim xung Dirac cng rt hu ích mô t quá trình ri rc hóa
mt tín hiu liên tc bt kQ. 37
Hàm tr%ng lng (ký hiu g(t )) là áp ng ca h thng khi h ang trng thái 0 (có n 1 dy 0 − d y 0 các giá tr ban u ( y ) ( ) ( ) 0 , , ,
bng 0) và c kích thích bi tín hiu dirac δ (t ) n 1 − dt dt u vào.
Do bin $i Laplace ca (r )t = δ (t) là R(s) = L[δ (t)] =1 nên
Y(s) =W(s)R( ) s = W( ) s
tA ó hàm trng lng c xác nh nh sau: ( y )
t = g(t) L− = [1W( )s] (3.2)
Ngc li, khi bit hàm trng lng thì suy ra c hàm truyn bng công thc sau:
W (s) = L[g (t )] (3.3) δ (t )
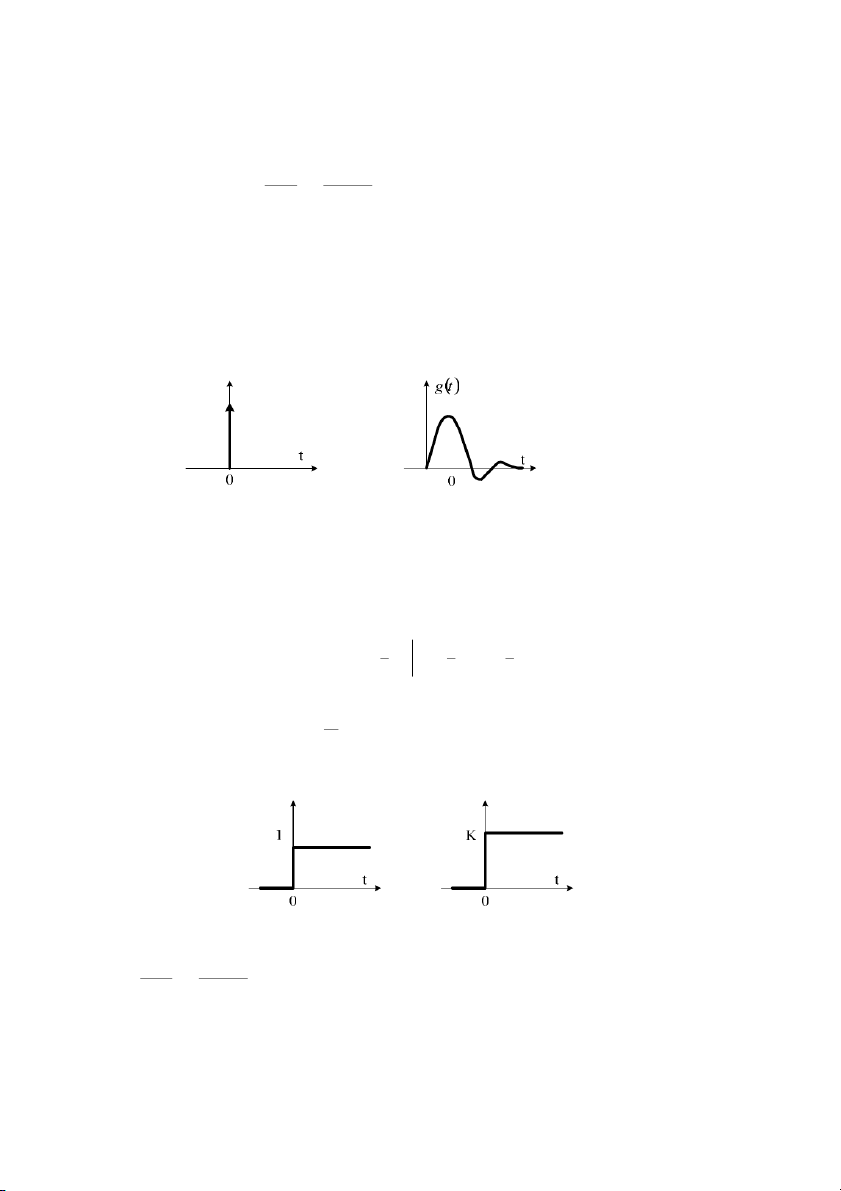
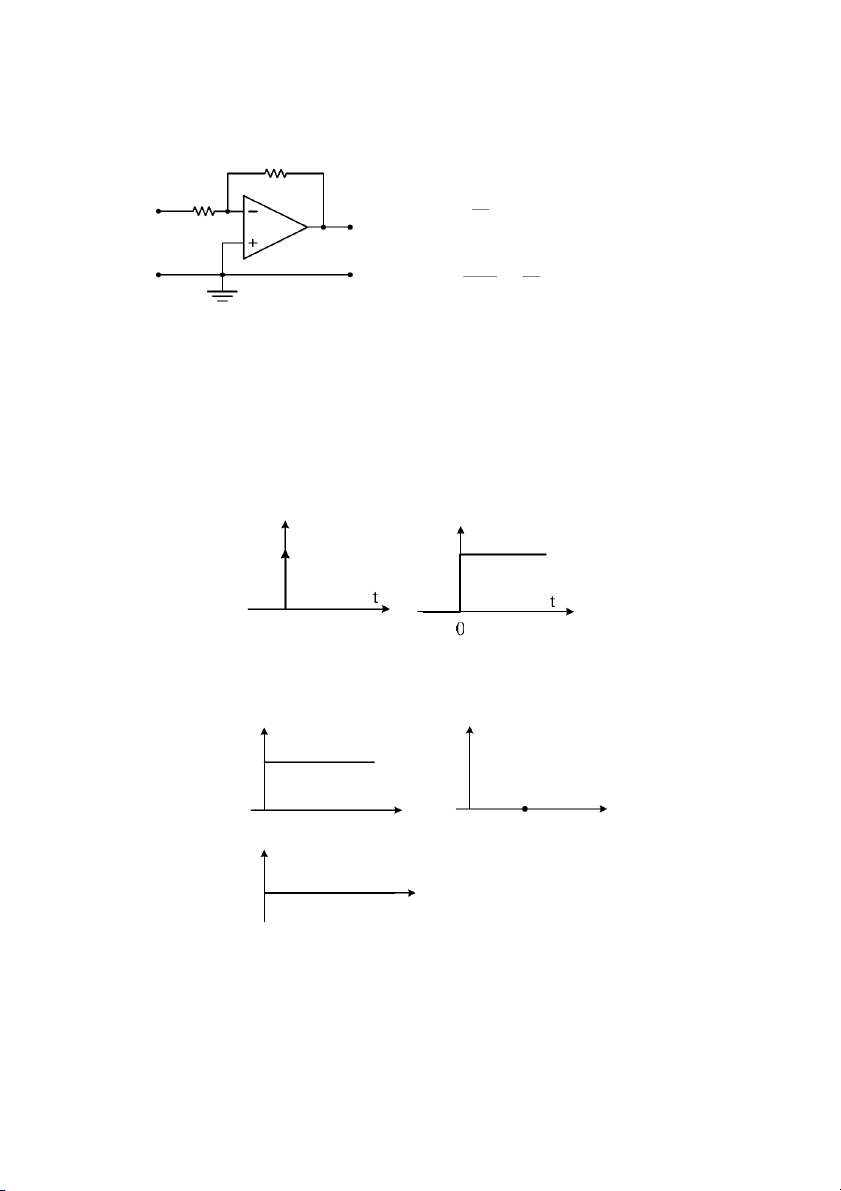
Hình 3.2: Tín hiu xung n v* và hàm tr,ng lưng
3.1.2 Tín hiu b3c thang n v và hàm quá
Tín hiu bc thang ơn v c nh ngha nh sau: khi t ≥ 0 (3.4) ( ) 1 1 t = 0 khi t < 0 ∞ − 1 ∞ − 1 1
3nh Laplace: F(s) = [ L (
1 t)] = e stdt = − e st = − (0 1 − ) = s s s 0 0
Xét trng hp tín hiu bc thang K (t )= K.1(t ), ta có: F(s) = [ L K . ( 1 t)] = K. [ L ( 1 )] K t = s
Tín hiu bc thang ơn v tác ng ti t = 0 tơng ng vi mt tín hiu hng s a t
ngt vào h thng ti thi im t = 0. (1t) K ( ) t K.1(t )
Hình 3.3: Tín hiu bưc nhy
Hàm quá là áp ng ca h thng khi h ang trng thái 0 (có các giá tr ban u n−1 ( y ) d ( y 0 ) d (y ) 0 0 , , ,
bng 0) và c kích thích bi tín hiu bc thang ơn v 1(t) u vào. n 1 − dt dt 38 1
Bin $i Laplace ca r(t) = (
1 t) là R(s )= L[1(t )]= nên: s
Y(s) = H(s) =W(s)R(s) W (s) = s
Suy ra hàm quá c xác nh nh sau: y (t ) 1 W s = h(t ) − ( ) = L (3.5) s
Ho!c áp dng tính cht nh ca tích phân ca phép bin $i Laplace: t
y(t ) = h(t ) = g (τ )dτ (3.6) 0
Khi bit hàm quá có th tìm c hàm truyn bng công thc sau: W (s) dh(t ) = L (3.7) dt h (t )
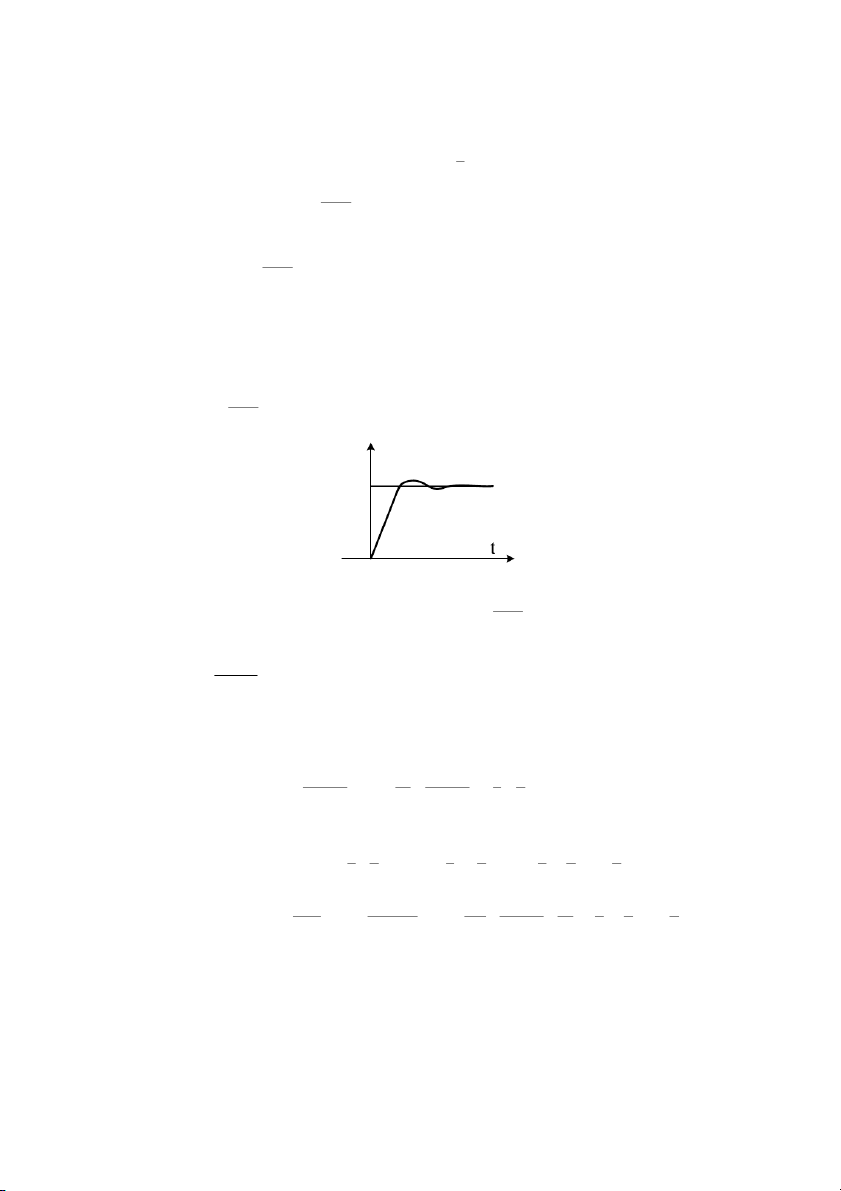
Hình 3.4: Hàm quá
Mi quan h gia hàm trng lng và hàm quá : g(t) d ( h t) = (3.8) dt
Ví d& 3.1: Cho h thng có hàm truyn là W (s) s +1 = ( s s+ ) 3
Xác nh hàm trng lng và hàm quá ca h thng. Gi i: Hàm trng lng: − − + 1 − 1 2 1 2
g (t ) = L 1 [W (s )] 1 s 1 3 − t = L = + = + (s + ) L s 3 s 3 ( 3 + ) e s 3 3 3 Hàm quá : t t t Cách 1: ( h t) = ( g τ ) 1 2 3−τ 1 2 3−τ 1 2 3− t 2 dτ = + e dτ = τ − e = t − e + 3 3 3 9 0 0 0 3 9 9 Cách 2: (h ) 1 − G(s ) 1 − s + 1 1 − 1 2 2 1 2 3−t 2 t = L = L = L − + = t − e + 2 s s (s 3 + ) 3 2 s (9s+ )3 9s 3 9 9
Ví d& 3.2: Cho h thng có áp ng quá là: ( h t ) 2 − t 3 − t =1 − e 3 + 2e
Xác nh hàm truyn ca h thng 39
Gi i: Theo bài ta có: dh t d 1 3 −2 − e t 2 −3 + e t 2 − t 3 6 6 6 W (s ) ( ) ( ) = L = L = { L 6e − 6 − e t }= − = dt dt s + 2 s + 3 (s + ) 2 (s + ) 3
3.1.3 Tín hiu iu hòa và hàm $c tính t(n
Gi s2 tín hiu vào h tuyn tính liên tc có hàm truyn ( W )
s là mt tín hiu iu hòa hình sin:
r (t) = R si ω n t m 3nh Laplace: ω R(s) R
= L[R sin ωt] = m m 2 2 s ω +
Tín hiu ra ca h thng là: ω Y (s) = ( R s)W ( ) R s m = W (s) s2 + 2 ω
Gi s2 W (s) có n im cc p phân bit th"a mãn p ≠ j , ta có th phân tích Y (s) di dng: i ω i n α α β Y(s) = + + i s + jω s − jω 1 s p i = − i
Bin $i Laplace ngc biu thc trên, ta c: n ( y t) − = j t α e ω + j t α e ω + p t i β e i i =1
Nu h thng $n nh thì tt c các im cc p u có phn thc âm (khái nim $n nh s? i
nói rõ chơng sau). Khi ó: n p ti lim β e = 0 →+∞ i t i =1 Do ó: y
t = lim y t =α e− ω + α e ω (3.9) xl ( ) ( ) j t j t t→∞
Nu W (s) có im cc bi thì ta cng có th chng minh c áp ng xác lp ca h thng
có dng nh trên (3.9). Các h s α và α xác nh bi công thc: ω − ω α = W( ) R s m + ω = − (3.10) 2 2 (s j ) R W m ( j ) s +ω 2 j s =−j ω ω ω α = W ( ) R s m − ω = (3.11) 2 2 (s j ) R W m (j ) s +ω 2j s = jω
Thay (3.10) và (3.11) vào (3.9), rút gn biu thc ta c: y = sin + ∠ (3.12) xl (t ) R W m ( ω j ) (ωt W ( ω j ))
Biu thc (3.12) cho thy trng thái xác lp tín hiu ra ca h thng là tín hiu hình sin, cùng
tn s vi tín hiu vào, biên t& l vi biên tín hiu vào (h s t& l là W (jω )) và lch pha
so vi tín hiu vào ( lch pha là ∠W ( ω j ) .
Hàm !c tính tn s ca h thng c hiu là : 40
W (jω )=W (s ) (3.14) s= ω j Ví d& 3.3: 10 s +5
Nu h thng có hàm truyn là W (s) ( ) = (
thì !c tính tn s ca h thng là: s s+ ) 2 W ( j jω ) 10( ω + ) 5 = . ω j ( ω j + 2)
T$ng quát !c tính tn s W (jω) là mt hàm phc nên có th biu di:n di dng biên -
góc pha, và dng phn thc - phn o nh sau: W ( ω j
)= P(ω ) + jQ(ω ) = M(ω) ϕj (ω) e . (3.15) trong ó:
P(ω ) là phn thc
M(ω) là áp ng biên
Q(ω ) là phn o ca !c tính tn s ϕ (ω ) là áp ng pha
Quan h gia hai cách biu di:n W ( jω ) nh sau: M (ω ) = W ( ω j ) 2 = P (ω ) 2 + Q (ω ) (3.16) ϕ (ω) 1 Q ω = ∠ W ( jω) − ( ) = tan (3.17) P (ω ) P(ω ) = M (ω ) [ cos ϕ (ω)] (3.18)
Q(ω )= M (ω )si [ n ϕ (ω )] (3.19)
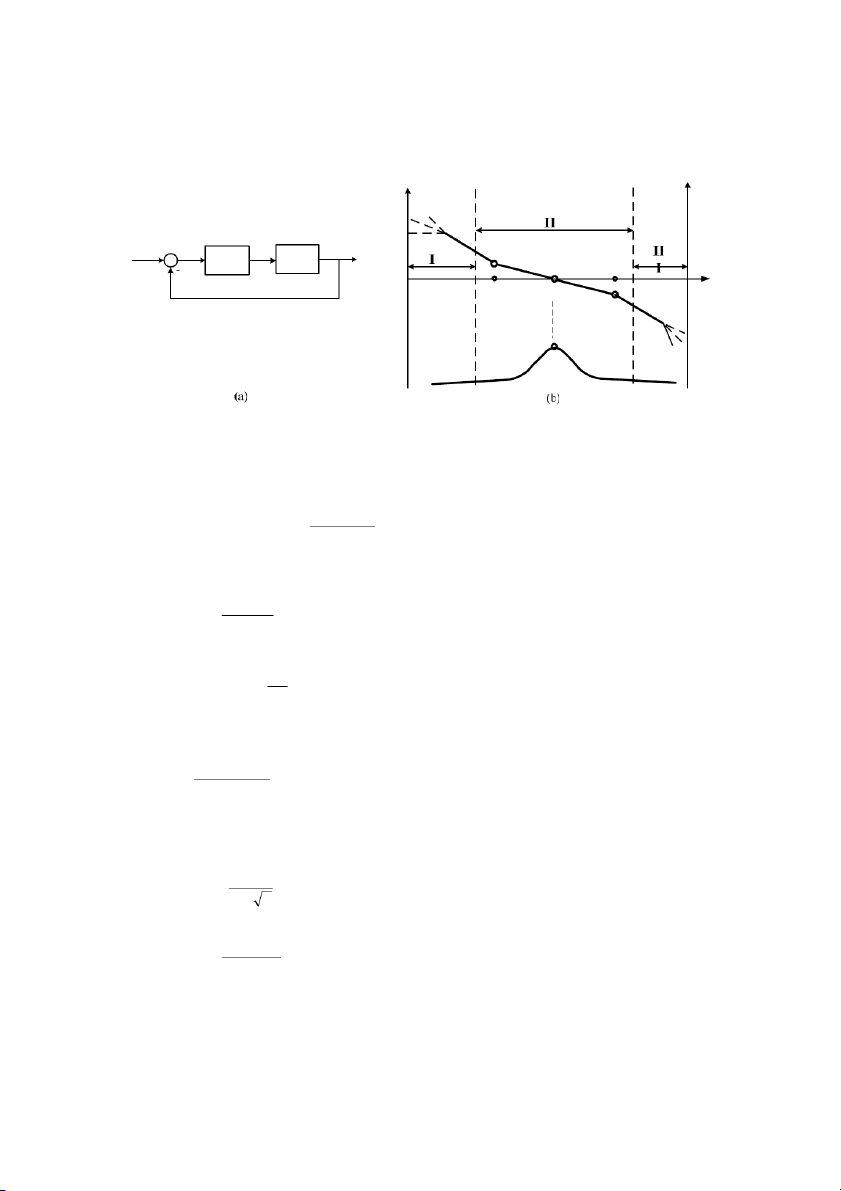
biu di:n !c tính tn s mt cách trc quan, ta có th dùng # th. Có hai dng # th thng s2 dng: 1. Bi u
Nyquist: (ng cong Nyquist) là # th biu di:n !c tính tn s
W ( jω ) trong h
ta cc (phn thc P(ω ), phn o Q(ω)) khi ω thay $i tA −∞ → ∞ .
Xét h tuyn tính nhân qu, tham s hng, có hàm truyn t dng thc-hu t, hp thc. Nói cách khác m m 0 + − 1 1 + + 1 +
W (s ) b s b s b s b m − m = , (m ≤ n) n n a s 0 + a s −1 1 + + a s 1 + a n− n có các h s ? 0 b , 1 b , …, 0
a , a , … là nh ng s th c cho nó s có giá tr th c n u s là s 1 thc. |Do ó W ( ω
j ) =W(− jω) suy ra 1 1 P(ω ) =
[W( ωj)+W(− jω)], ( Q ω ) =
[W( jω)−W(− jω)] 2 2j
TA công thc trên có th thy phn thc P(ω) ca hàm !c tính tn là mt hàm chPn, và phn o Q( )
ω là mt hàm lg. Chính vì vy ng cong Nyquist chính là tp hp tt c các im
ngn ca vector biu di:n s phc W( ω
j ) có dng i xng qua trc thc khi ω thay $i tA
− ∞ → ∞ . K tA ây tr i khi v? biu # Nyquist chúng ta ch& cn kho sát vi ω thay $i tA 0 → ∞ . 41 2. Bi u
Bode là # th g#m hai thành phn:
Biu # Bode biên : # th biu di:n mi quan h gia logarith ca áp ng biên
L(ω ) theo tn s ω . ( L ω ) = 20 lg ( M ω ) (3.20)
L(ω ) là áp ng biên tính theo ơn v dB (decibel).
Biu # Bode pha: # th biu di:n mi quan h gia áp ng pha ϕ (ω) theo tn s ω .
C hai # th trên u c v? trong h ta vuông góc vi trc hoành ω chia theo thang
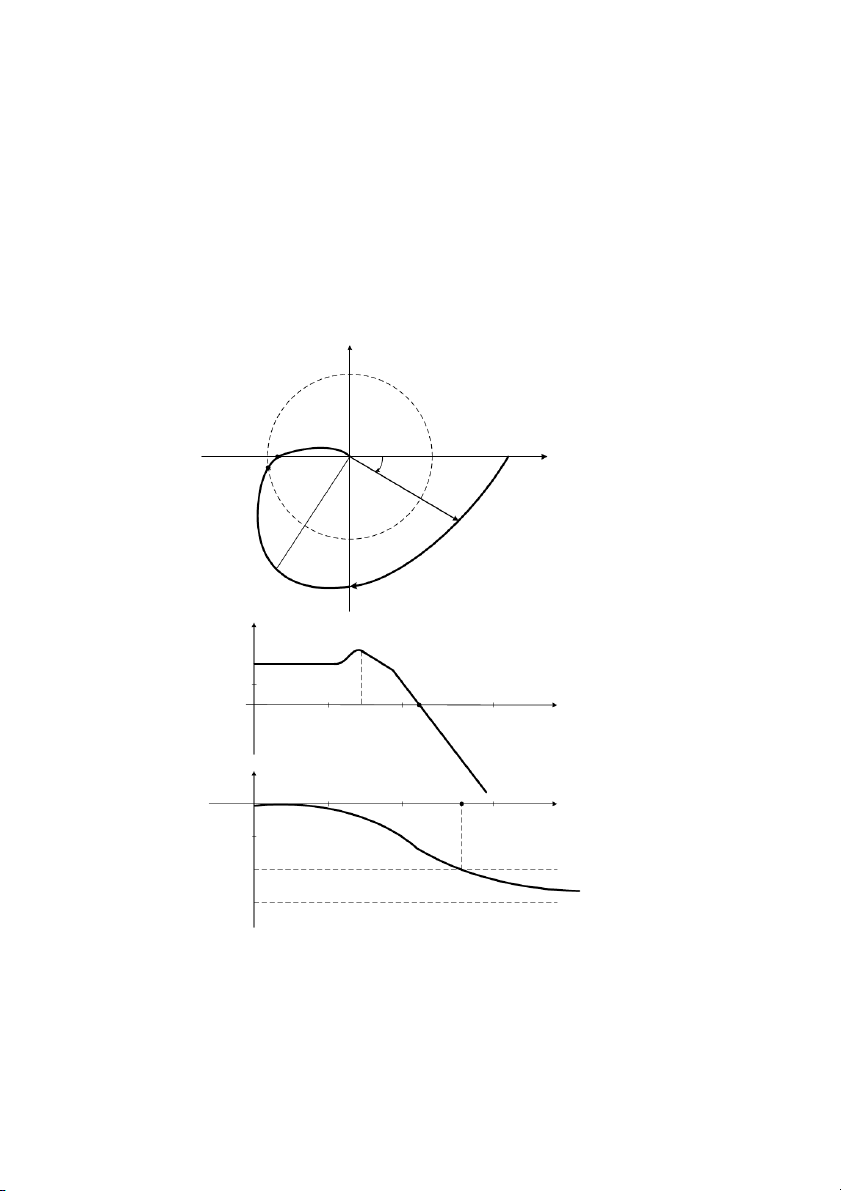
logarith cơ s 10 (Hình 3.5b). Khong cách gia hai tn s hơn kém nhau 10 ln gi là mt decade. jQ (ω ) j[ ω−Π ω → ∞ ω =0 ( P ω ) ϕ (ω) ω c M (ω) MP ωP L (ω)[dB ] ih L \h p j[ h [ ωc \ lg(ω)[dec ] h ωp ω hn[ [ [h [hh j\h ϕ(ω)[ ] j[ h [ ω \ lg −Π (ω)[dec ] [ ω [h hn[ [hh jkh j[lh j\mh
Hình 3.5: Biu din c tính t'n s dùng th*
!c tính tn s ca h thng có các thông s quan trng sau ây: nh c ng h ng
( M : là giá tr cc i ca M (ω ). p ) 42 T n s c ng h ng
( ω : là tn s ti ó có &nh cng hng. p )
T n s c t biên( ω : là tn s ti ó biên ca !c tính tn s bng 1 (hay bng 0dB). c ) M (ω (3.21) c ) = 1 hay L(ω (3.22) c ) = 0 T n s c t pha (ω
: là tn s ti ó pha ca !c tính tn s bng −π (hay o −180 ) −Π ) ϕ (ω (3.23) −π ) o = 1 − 80
M!c dù biu di:n di hai dng # th khác nhau nhng thông tin có c v h thng tA
biu # Bode và biu # Nyquist là nh nhau. TA biu # Bode ta có th suy c biu # Nyquist và ngc li.
3.2 $c tính ng h%c c0a mt s khâu c b n
Mt h thng g#m các phn t2 ni tip vi nhau theo các phơng thc chung nh ni tip,
song song, h#i tip. Tính cht ca quá trình quá toàn h thng ph thuc vào tính cht ng
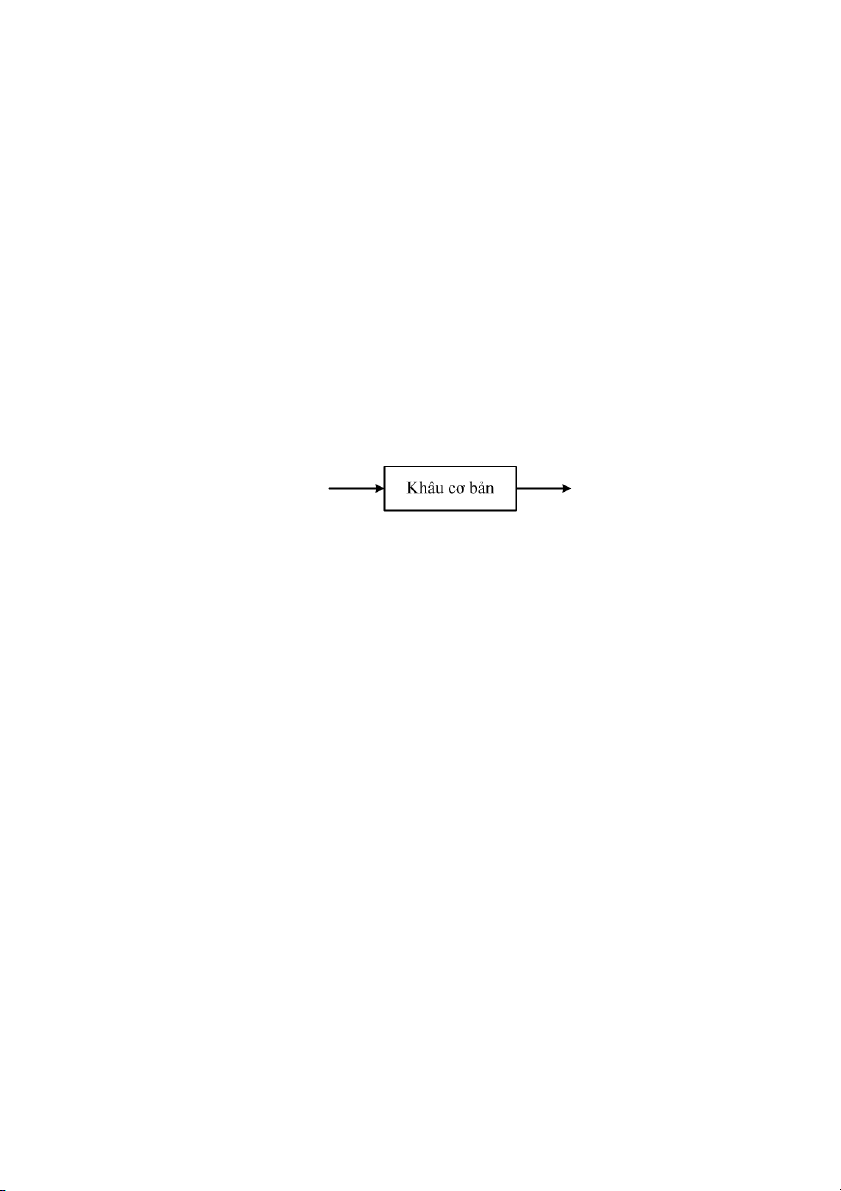
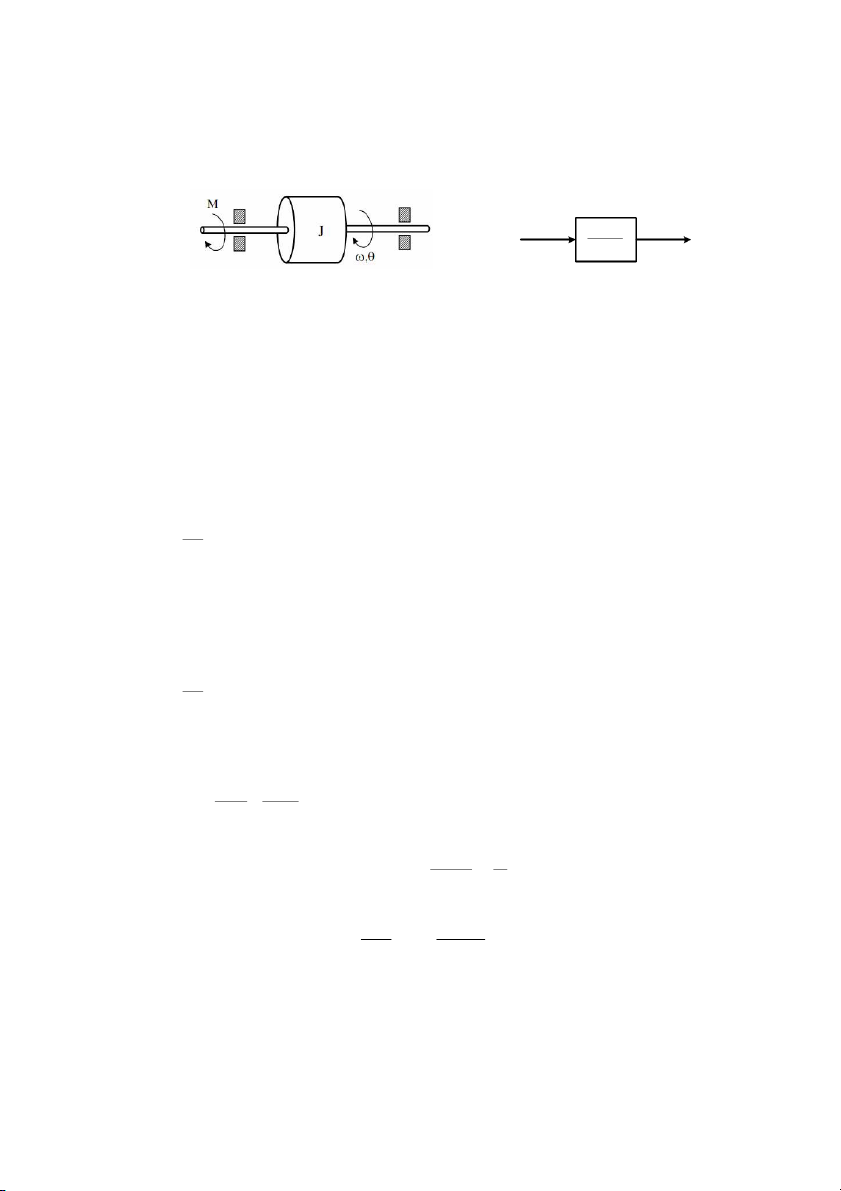
hc ca các phn t2 hp thành. Các phn t2 hp thành ó thng c phân tích thành nhng khâu cơ bn. u (t ) ( y t )
Hình 3.6: Khâu c bn
Các khâu ng hc cơ bn là thành phn ti gin nht ca h thng iu khin t ng.
Mt phn t2 c gi là khâu ng hc cơ bn nu có y các tính cht sau:
- Ch& có mt tín hiu vào và mt tín hiu ra.
- Tín hiu ch& truyn i mt chiu, ngha là khi có tín hiu vào thì có tín hiu ra, tín hiu ra
không nh hng n tín hiu vào.
- Quá trình ng hc ca phn t2 c biu di:n bng phơng trình vi phân không quá bc hai.
Trên cơ s !c tính ng hc ca các khâu cơ bn, mc 3.3 s? trình bày cách xây dng !c
tính ng hc ca h thng t ng. 3.2.1 Khâu t4 l (khâu P)
Khâu t& l còn gi là khâu khuch i, khâu $n nh bc 0, hay khâu P.
Phơng trình vi phân: y(t)= Ku(t) (3.24)
Hàm truyn: W (s )= K (3.25)
Thông s !c trng K gi là h s khuch i.
Mt s phn t2 có quan h t& l nh: lò xo, òn b>y, b truyn bánh rng, bin tr, van
tuyn tính; cm bin, chit áp, mch khuch i công sut, b khuch i cách ly.
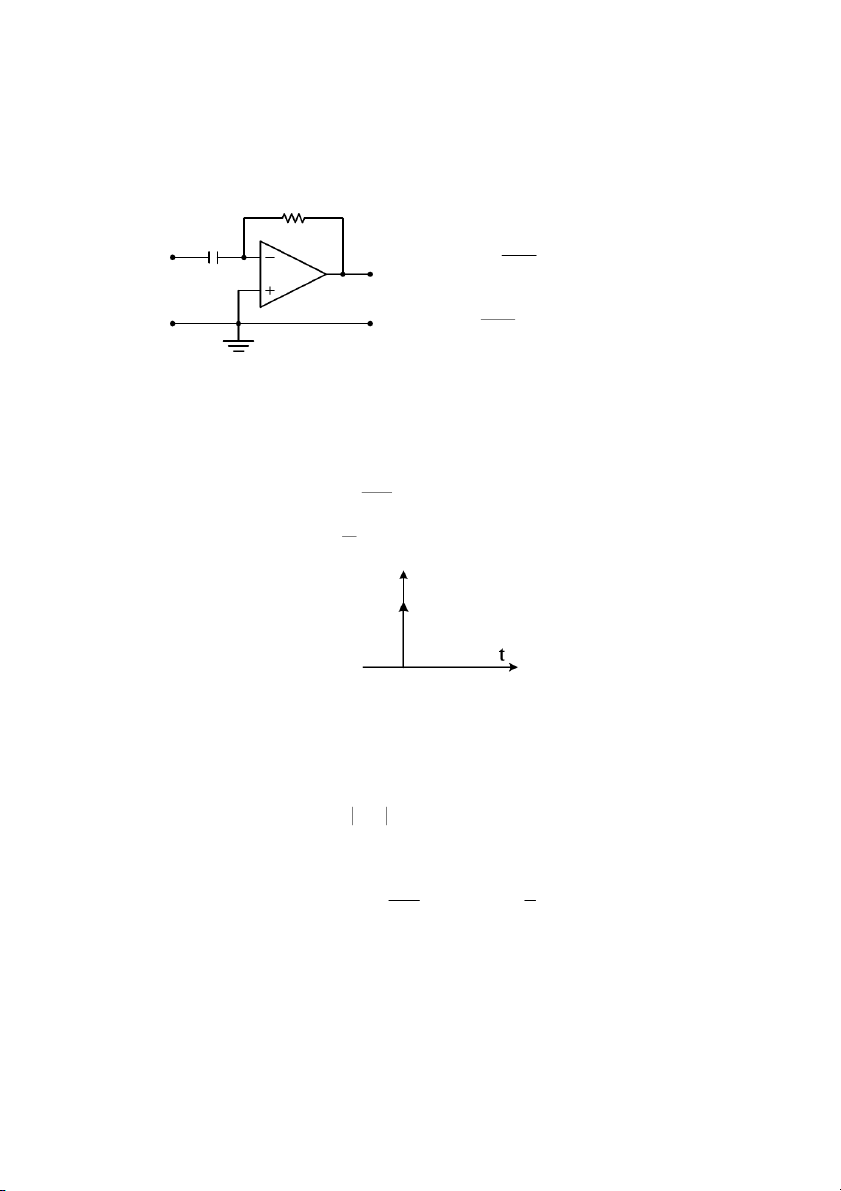
Ví d& 3.4: Mch khuch i o dùng op-amp hình 3.7: 43 2 R
Quan h gia in áp vào và ra là: 1 R u 2 = − o ( ) R t ui (t ) R1 ui( ) t u
Do vy hàm truyn t là: o (t )
W (s) U o( ) s R2 = = − Ui( ) s R 1
Hình 3.7: Mch khuch i o
Các cm bin thng có tín hiu ra ( y )
t t& l vi tín hiu vào u(t ). Ch@ng hn mt cm
bin o áp sut trong tm 0÷10 bar và chuyn thành in áp trong tm 0÷10 V s? có hàm truyn o
W(s) = 1; Mt cm bin nhit o nhit trong tm 0÷500 C và chuyn thành in áp
0÷10 V s? có hàm truyn là W (s )= . 0 02 . !c tính thi gian
- Hàm trng lng: g(t) = Kδ (t) (3.26)
- Hàm quá : h( )t = K ( 1 t) = K (3.27)
Vy tín hiu ra ca khâu t& l bng tín hiu vào khuch i lên K ln (hình 3.8). g (t ) h(t ) K δ . (t ) K
Hình 3.8: Hàm tr,ng lưng và hàm quá ca khâu t- l !c tính tn s
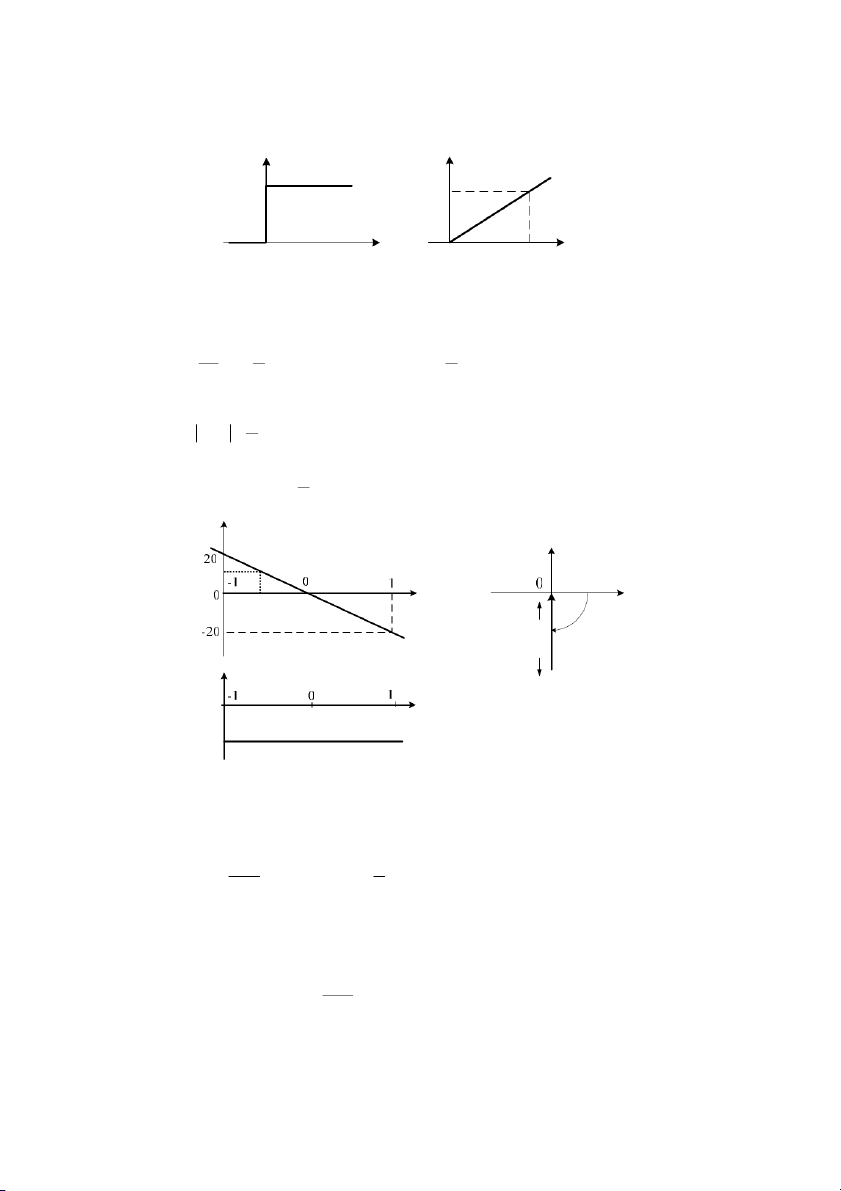
- Hàm !c tính tn: W (jω)= K (3.28) L( ) ω [dB] j ( Q ω ) 20lg K P l ( g ω )[dec] (ω) 0 ω 0 K ϕ (ω )[ ] l ( g ω )[dec ] o 0 ω
Hình 3.9: Biu Bode và biu Nyquist ca khâu t- l
- Biên : M (ω)= K (3.29)
L(ω ) = 20 lg K (3.30) 44 - Góc pha Q ϕ (ω ) (ω ) = arctan = 0 (3.31) P(ω )
Nh3n xét: Khâu t& l có !c tính tn s là hng s vi mi ω
- Biu # Bode biên là ng th@ng song song vi trc hoành, cách trc hoành 20lg K .
- Biu # Bode pha là mt ng nm ngang trùng vi trc hoành.
- Biu # Nyquist là mt im trên trc hoành có ta (K, j0).
3.2.2 Khâu tích phân (khâu I) t Phơng trình vi phân: ( y t) = ( u t)dt (3.32) 0 Hàm truyn: 1 W (s ) = (3.33) s
Mt s phn t2 có quan h tích phân nh: h van nc - b cha, phn t2 gim chn (ma
sát nht), b truyn vitme - ai c, b servo thy lc vi ph ti nh",…
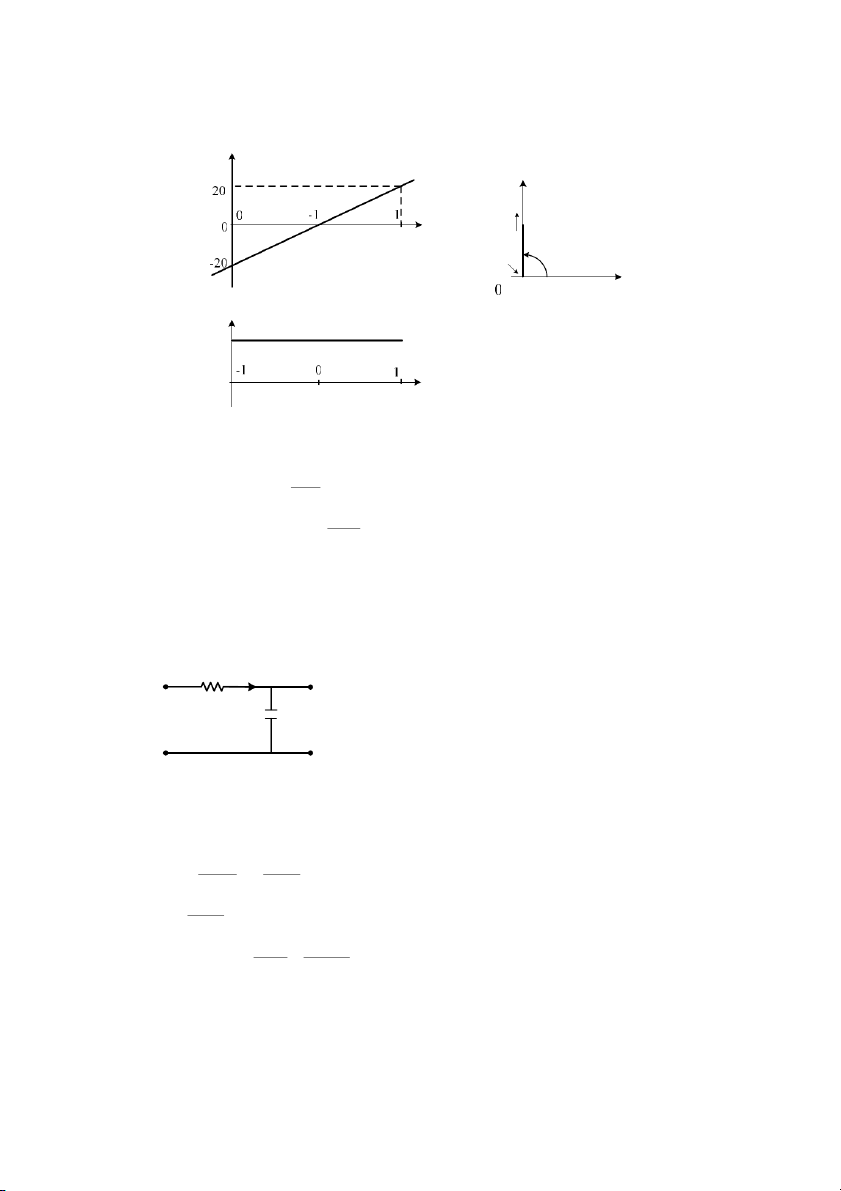
Ví d& 3.5: Xét b truyn vitme – ai c nh hình v?:
Hình 3.10: B truyn vitme – ai c
Tín hiu vào: vn tc góc ω(t) ca vitme [rad/s].
Tín hiu ra: lng di ng (
y t) bàn máy g1n lin vi ai c [m].
Gi P[m] là bc ca vitme, ta có phơng trình quan h: t y( ) = P t ω (t )dt 2π 0
Bin $i Laplace hai v vi iu khin u bng 0 ta c: P ω s Y(s) ( ) = 2π s
Lp t& s tín hiu ra trên tín hiu vào ta c hàm truyn tích phân: P
W (s) Y (s ) P K = vi K = : h s tích phân ω ( = = s ) π 2 s s π 2 !c tính thi gian
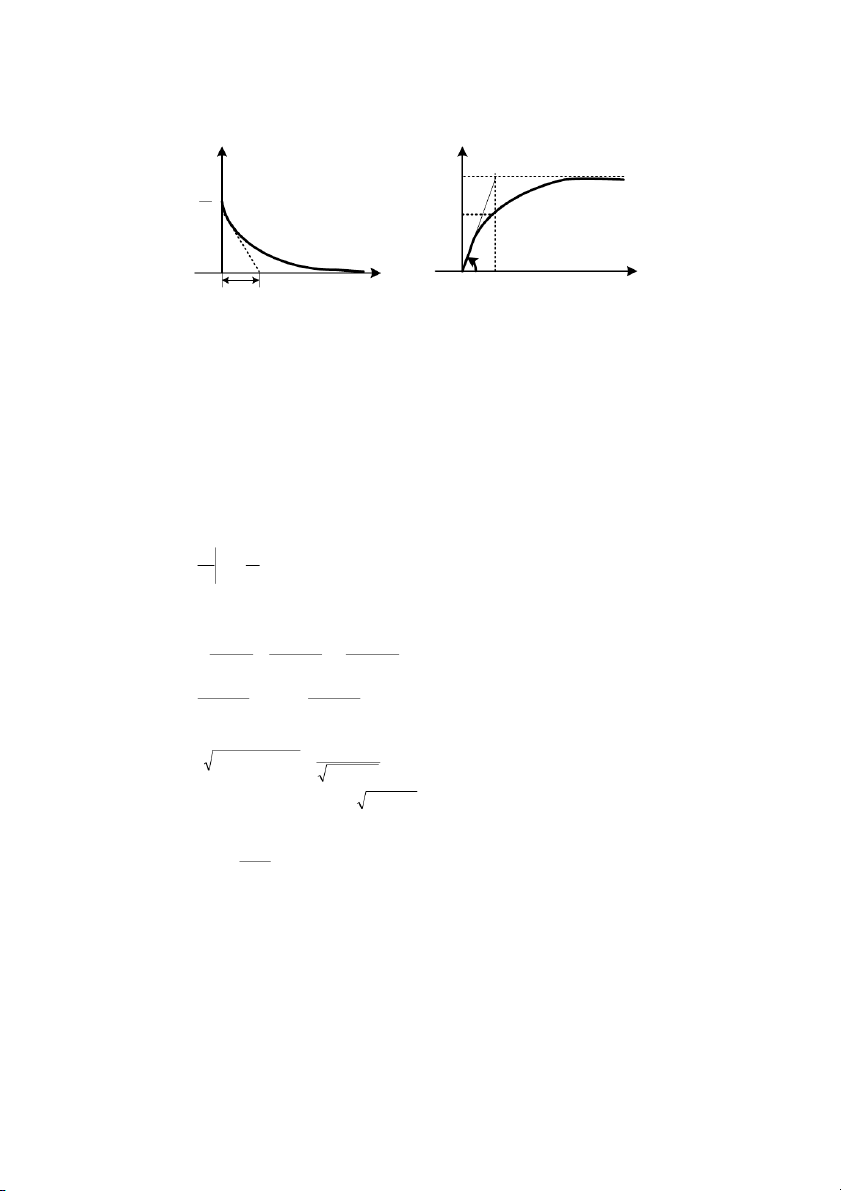
- Hàm trng lng: g(t) = L− [1W (s)] = ( 1 t) (3.34) - Hàm quá : −1 1 1 h(t ) W (s) = − L = L (3.35) 2 = t s s 45 g(t) ( h t ) 1 1 t t 0 0 1
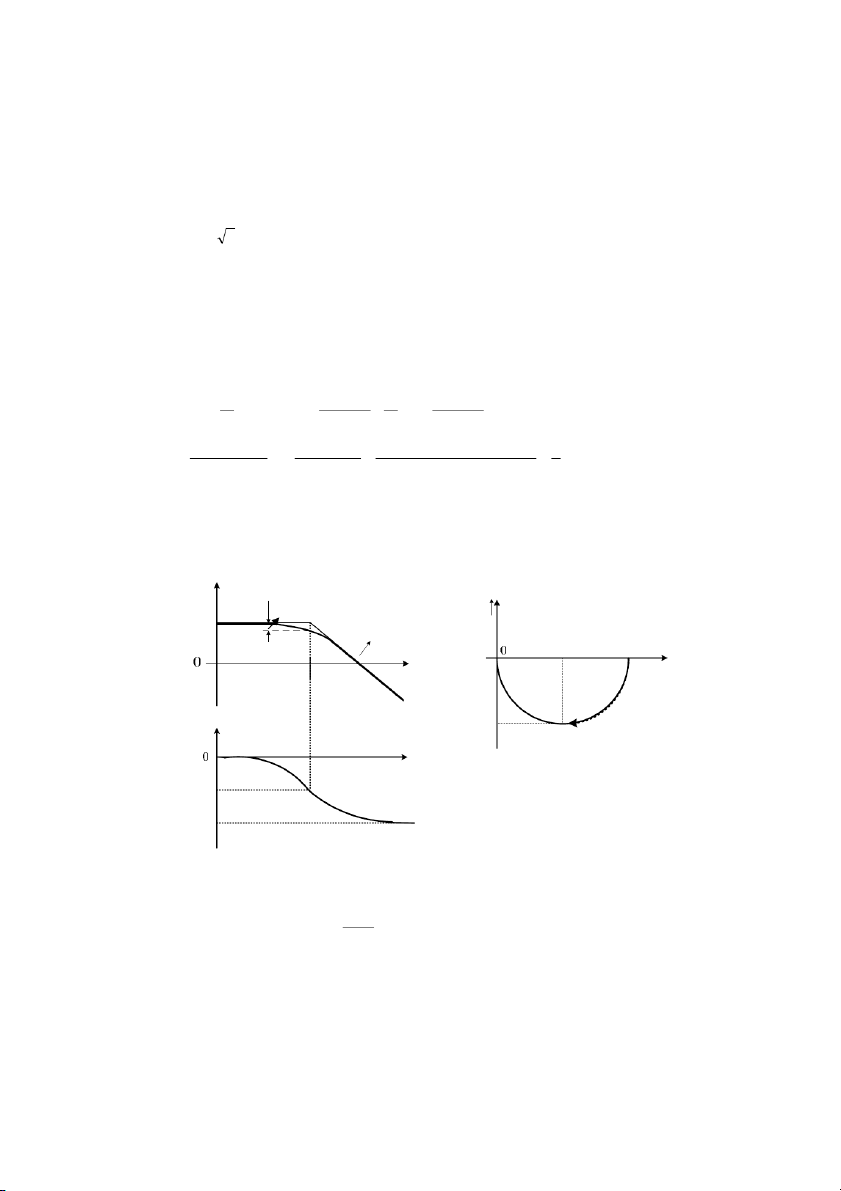
Hình 3.11: Hàm tr,ng lưng và hàm quá ca khâu tích phân !c tính tn s - Hàm !c tính tn W( 1 1 1 jω)= = − j P (ω) = ; 0 Q (ω) = − (3.36) jω ω ω - Biên
ω = biên M (ω ) = ∞ (3.37) M ( 1 ω ) = W(ω ) = => Khi 0 ω
Khi ω = ∞ biên M (ω ) = 0 ( 1 L ω ) = 20 lg ( M ω) = 20lg = 2 − 0lgω (3.38) ω L (ω ) [dB] j ( Q ω) −20dB / dec lg (ω)[de ] c ( P ω ) 1 ω 10− 0 10 1 10 ω = ∞ −π / 2 ϕ (ω) [ ] ω = 0 lg(ω)[dec] o 0 1 10− 0 10 1 ω 10 o − 90
Hình 3.12: Biu Bode và biu Nyquist ca khâu tích phân
Do trc hoành c chia theo thang lgω nên biu # Bode biên là ng th@ng có
dc -20dB/dec và i qua im có ta ( 0 ; 1 ). - Góc pha Q ϕ (ω ) (ω) π = arctan = ar ( ctan − ∞) (3.39) P( = − ω) 2
Tín hiu ra ca khâu tích phân luôn chm pha so vi tín hiu vào mt góc bng π / 2. Biu
# Nyquist là n2a trc o âm.
3.2.3 Khâu vi phân (khâu D)
Phơng trình vi phân: y(t) du(t ) = (3.40) dt 46 Hàm truyn: W( ) s = s (3.41)
Ví d& 3.6: xét mch khuch i thut toán có sơ # nh sau: R
Quan h gia in áp vào và ra là: C u = o (t ) dui (t ) RC dt u
Do vy hàm truyn t là: i (t ) u (t o ) W( ) U o ( ) s s = = = U i(s) RCs Ks
K = RC là h s vi phân.
Hình 3.13: Mch vi phân !c tính thi gian
- Hàm trng lng: g(t) = L− [1W (s)] =δ (t ) (3.42)
- Hàm quá : h(t) −1 W (s ) = L = L− [1 ] 1 = δ (t ) (3.43) s ho!c g( ) d t =
h (t )= δ (t ) (3.44) dt ( h t) δ (t )
Hình 3.14: Hàm quá ca khâu vi phân
Nh3n xét: Hàm quá ca khâu vi phân là hàm xung ơn v, hàm trng lng là o hàm
ca hàm quá , ch& có th mô t bng biu thc toán hc, không biu di:n bng # th c. !c tính tn s
- Hàm !c tính tn: W (jω )= jω P (ω ) = ; 0 Q (ω ) = ω (3.45)
- Biên : M (ω)= W (ω) = ω khi ω → ∞ thì M (ω) → ∞ (3.46)
L (ω )= 20 lg M (ω )= 20lg(ω ) (3.47)
Biu # Bode ng trên Hình 3.11. - Góc pha: ϕ( ) ( Q ω ) π ω = arctan = ar ( ctan + ∞) ( = (3.48) P ω ) 2
Tín hiu ra ca khâu vi phân luôn sm pha hơn tín hiu vào mt góc bng π / 2 .Biu #
Nyquist là n2a trc o dơng do W ( jω) có phn thc bng 0, phn o luôn dơng. 47 L (ω ) [dB ] 20dB / dec jQ(ω ) l ( g ω )[dec] ω = ∞ 1 ω 10− 0 10 1 10 π / 2 ω = 0 P(ω ) ϕ (ω )[ ] o 90 lg(ω )[de ] c o 0 1 10 − 0 ω 10 1 10
Hình 3.15: Biu Bode và biu Nyquist ca khâu vi phân
3.2.4 Khâu quán tính b3c nh)t (khâu PT1) dy(t )
Phơng trình vi phân: T. + ( y t) = K. ( u t) (3.49) dt Hàm tuyn: W( ) K s = (3.50) Ts +1
T là hng s thi gian ca khâu.
K là h s khuch i.
Mt s phn t2 có quan h quán tính bc nht nh: lò nhit, mch RL, RC, tuabin, máy
phát in mt chiu, ng cơ in không #ng b hai pha vi u ra là tc quay…
Ví d& 3.7: Xét mch RC sau: R i(t)
Tín hiu vào: in áp u i (t ) u C u
Tín hiu ra: in áp u trên t C o (t ) o (t ) i(t )
Hình 3.16: Mch RC
Theo nh lut Kirchoff ta có: u + = R (t )
uC (t ) ui (t )
M!t khác quan h gia dòng in và in áp trên t C cho ta: i(t ) duC (t ) duo(t) = C = C dt dt duo(t) Do vy: RC + u = o (t ) ui (t ) dt
Hàm truyn là: W( ) Uo(s) 1 s =
vi hng s thi gian T = RC Ui ( ) = s RCs + 1 48
Ví d& 3.8: Xét mt trc mang ti quay có mô men quán tính J nh hình sau: M 1 ω Js + b
Hình 3.17: Ph'n t( quay
Ti các b m!t tip xúc khi quay ($ O, phanh hãm,…) s? xut hin mô men ma sát M ngc ms
chiu chuyn ng và t& l vi vn tc góc ω . M =
vi b: h s ma sát nht ms ω b
Trc quay cng chu bin dng àn h#i tơng t nh mt lò xo xo1n. Mô men àn h#i xo1n
M ngc chiu chuyn ng và t& l vi góc quay θ ca trc. x M = kθ ω
vi k : cng lò xo xo1n x (t) = k dt
Trong thc t nh hng ca àn h#i xo1n trên trc ng cơ và các ti quay thng c b"
qua (nói cách khác coi trc là cng tuyt i). Áp dng nh lut II Newton cho chuyn ng
quay, ta có phơng trình cân bng mô men: ω d J = M − bω dt
trong ó: M : mô men tác ng, [Nm] 2
J : mô men quán tính ca vt quay, [kg.m ]
ω : vn tc góc, [rad/s]
b: h s ma sát nht (gim chn quay), [Nm.s/rad]
Xét M là tín hiu vào, ω là tín hiu ra, ta có: dω J + bω = M dt
Bin $i Laplace hai v vi iu kin u bng 0, ta c:
Jsω (s) + bω(s) = M (s)
TA ó suy ra hàm truyn t là: ω 1 W (s) (s) = = M( ) s Js + b !c tính thi gian
- Hàm trng lng: g(t) = L 1−[W(s)] −1 K K t − /T = L (3.51) ( = Ts + ) e 1 T
Hàm trng lng ca khâu quán tính bc nht là hàm m suy gim v 0.
- Hàm quá : h(t) 1 W − (s) 1 K = L = L− = K ( t − /T 1− e ) (3.52) s s (Ts + ) 1
Hàm quá ca khâu quán tính bc nht tng theo quy lut hàm m n giá tr xác lp bng K. 49 g(t ) ( h t ) K K T . 0 632K θ 0 t 0 t T T
Hình 3.18: Hàm tr,ng lưng và hàm quá ca khâu quán tính bc nht Nh3n xét:
- Nu gi giá tr xác lp ca h(t) là h(∞) thì: (
h ∞) = lim h(t) = K t →∞
- Ti t = T ta có h(T )= K(1− −
e 1) ≈ 0.632K = (63 2 . %) ( h ∞)
Tc là ti thi im t = T , tín hiu ra c 63.2% giá tr xác lp ($n nh).
Tơng t ta có (h T 2 ) = 86 5 . % (
h ∞) ; h( T 3 ) = 9 % 5 ( h ∞); ( h T 4 ) = 9 . 8 2 h % ( ) ∞ ; ( h T 5 )= 9 . 9 3%h(∞).
Ta thy hng s thi gian T !c trng cho mc áp ng nhanh hay chm ca khâu.
Khâu có T nh" s? nhanh chóng t n trng thái $n nh, ngc li T ln thì khâu cn nhiu
thi gian mi t ti trng thái $n nh.
- Nu kg tip tuyn vi (
h t) ti im 0 và gi góc ca tip tuyn ó là θ thì: dh K tanθ = = dt T t =0 !c tính tn s - Hàm !c tính tn: W ( K K KT ω j ) − ω = = + j (3.53) T ω j +1 2 2 T ω +1 2 2 T ω +1 ( K − KTω P ω) = ; ( Q ω) = (3.54) 2 2 T ω +1 2 2 T ω +1 - Biên : M ( K ω ) 2 = P (ω ) 2 + Q (ω ) = (3.55) 2 2 T ω + 1
L(ω ) = 20lg M (ω ) = 20lg K − 20lg 2 2 T ω +1 (3.56) - Góc pha: ϕ (ω ) Q(ω ) = arctan
= arctan(−Tω ) = −arctan(Tω) (3.57) P(ω ) Nh3n xét:
- v? biu # Bode ta cho ω bin thiên tA 0→ +∞ , tính các giá tr L(ω) và ϕ (ω) tơng
ng r#i th hin trên # th.
- Ho!c biu # Bode biên có th v? gn úng bng 2 ng tim cn sau: • Khi ω < 1
< / T thì L(ω) ≈ 20lg K => ng tim cn nm ngang. 50 • Khi ω > 1
> / T thì L (ω ) ≈ 20lg K − 20lg(ωT ) => ng tim cn nghiêng có dc - 20dB/dec.
im tn s ω = 1/ T ti giao im ca hai tim cn gi là tn s gãy. Ti tn s gãy, sai s
gia ng cong L(ω ) chính xác và các ng tim cn có giá tr ln nht L ∆ (ω) = 2 − 0 lg 2 ≈ − d 3 B
Mt s im !c bit: ω = 0 P(ω ) = K Q(ω ) = 0
L(ω ) = 20 lg K ϕ (ω) = 0 ω = 1/ T ( P ω ) = K / 2
Q(ω ) = −K / 2
L(ω ) = 20 lg K − d 3 B ϕ (ω) o = −45 ω = +∞ ( P ω ) = 0 Q(ω ) = 0 L(ω )= −∞ ϕ (ω) o = −90
- v? biu # Nyquist ta có nhn xét sau: 2 2 2 P (ω ) −K K K K ω + Q (ω )2 − = − + T 2 2 2 T ω 1 + 2 2 2 T ω + 1 ( 2 2 K − KT ω ) 2 2 2 2 K T ω ([ 2 K − KT ω )2 2 + 4 2 2 2 K T ω ] 1 = + = = 2( 2 2 T ω + 1) ( 2 T ω + ) 1 2 2 (4 2 T ω + )2 2 4 1
M!t khác, khi ω = 0 → +∞ thì góc pha ϕ (ω ) = −arctan(Tω )< 0. Do ó biu # Nyquist ca
khâu PT1 là n2a di ca ng tròn tâm (K/2, j0), bán kính K/2. ( L ω ) [dB] jQ(ω ) d 3 B 20lg K − 2 d 0 B / dec P (ω) 1/ K T lg(ω )[dec] K / 2 ω = ∞ ω = 0 ϕ (ω )[ ] − K / 2 ω = / 1 T lg(ω )[dec] 1/ T ω o −45 o − 90
Hình 3.19: Biu Bode và biu Nyquist ca khâu quán tính bc nht 3.2.5 Khâu vi phân b3c nh)t
Phơng trình vi phân: y(t) du(t ) = T + ( u t) (3.58) dt
Hàm truyn: W (s) = Ts +1 (3.59) !c tính thi gian 51
- Hàm trng lng: g(t ) = L−1[W (s)] = L−1[Ts + ]1 =Tδ (t)+δ(t ) (3.60) + - Hàm quá : ( 1 − 1 − 1 h ) W (s ) Ts t = L = L = tδ (t) + ( 1 t) (3.61) s s
Hàm quá ca khâu vi phân bc nht là t$ hp tuyn tính ca hàm xung ơn v và hàm
bc nhy ơn v. Ta thy rng khâu vi phân lý tng và vi phân bc nht có !c im chung
là giá tr hàm quá vô cùng ln ti t = 0. Hàm trng lng ch& có th mô t bng biu thc
toán hc (3.58), không th biu di:n bng # th c.
!c tính tn s: W ( ω j ) = T ω j +1 (3.62) ( P ω) = 1; ( Q ω ) = ω T (3.63) - Biên : M (ω ) 2 = P (ω ) 2 + Q (ω ) 2 2 = 1 + T ω (3.64)
L(ω ) = 20 lg M (ω ) = 20 lg 2 2 T ω +1 (3.65) - Góc pha: ϕ (ω ) Q (ω ) = arctan = arctan (Tω ) (3.66) P (ω )
So sánh biu thc (3.63) và (3.54) vi (3.55) và (3.56) ta rút ra c kt lun: biu #
Bode ca khâu vi phân bc nht và khâu quán tính bc nht i xng nhau qua trc hoành. Do W ( ω
j ) có phn thc P(ω ) luôn luôn bng 1, phn o (
Q ω ) có giá tr dơng tng dn tA
0 n + ∞ khi ω thay $i tA 0 n + ∞ nên biu # Nyquist ca khâu vi phân bc nht là n2a
ng th@ng qua im có hoành bng 1 và song song vi trc tung nh hình 3.14. ( L ω ) [d ] B jQ(ω) ω =∞ 20dB / dec 3dB lg (ω)[dec] 1/ T ω P ω = 0 (ω ) 1/T 1 ϕ(ω)[ ] o 90 o 45 lg(ω) 1/ [dec] T o 0 ω
Hình 3.20: Biu Bode và biu Nyquist ca khâu vi phân bc nht
3.2.6 Khâu *n nh b3c hai (khâu PT2) 2 d ( y ) t dy(t)
Phơng trình vi phân: T + ζ 2 T + ( y t) = ( u ) t (3.67) dt dt
Hàm truyn: W (s) 1 = (3.68) 2 2 T s + 2ξ Ts +1 52 Trong ó:
T: hng s thi gian (chu kQ dao ng riêng)
ξ : h s t1t dn (h s suy gim)
Mt s phn t2 có quan h là khâu bc hai nh: Các h cơ khí g#m lò xo – khi lng –
gim chn, mch in RLC, ng cơ in DC iu khin tc bng in áp phn ng,...
Ví d& 3.9: Xét mch RLC ni tip: R L i(t)
Tín hiu vào: in áp u i (t ) u C u o(t ) i (t )
Tín hiu ra: in áp u trên t C o (t )
Hình 3.21: Mch RLC
Theo nh lut Kirchoff ta có: u + + = R (t )
uL (t ) uC (t ) ui(t ) d ( i t ) L
+ R (it) + u = C( t) ui( ) t dt
M!t khác quan h gia dòng in và in áp trên t C cho ta: d ( i t) 2 d uo(t) (i ) duC (t ) duo(t) t = C =C o = C dt dt 2 dt dt Do vy: 2 d uo(t ) du o(t ) LC + RC +u = 2 o (t ) ui (t ) dt dt
Hàm truyn là: W (s ) Uo (s) 1 = Ui ( ) = 2 s LCs + RCs + 1
Ví d& 3.10: nghiên cu các b gim chn ô tô, thit b máy móc, ngi ta cn phi mô
hình hóa chúng. Sơ # nguyên lý ca b gim chn c cho trong hình:
Hình 3.21: B gim chn
Tín hiu vào: lc F ( )t tác dng tA bên ngoài, [N]
Tín hiu ra: lng di ng y(t ) ca khi lng m, [m]
Gi s2 ti t = 0 h ang trng thái cân bng và không tính n lc trng trng. Theo
nh lut II Newton ta có phơng trình cân bng lc: 2 d (yt) m = F = − − i F 2 (t ) dy b ky (t ) dt dt trong ó:
m: khi lng, [kg] 53
b: h s ma sát nht (gim chn), [N.s/m]
k: cng lò xo, [N/m] 2 d y(t ) m : lc quán tính, [N] 2 dt dy b : lc gim chn, [N] dt
ky(t ): lc lò xo, [N]
Phơng trình vi phân mô t quan h vào ra là: d 2 ( y t) dy m + b
+ ky(t) = F(t) dt2 dt
Bin $i Laplace vi iu kin u bng 0 và lp t& s tín hiu ra trên tín hiu vào ta có hàm truyn t: ( 2
ms + bs + k)Y(s) = F(s ) 1
W (s ) Y (s ) = = F (s )
ms 2 + bs + k !c tính thi gian:
Xét nghim ca phơng trình !c tính: 2 2
T s + 2ξTs + 1= 0
Bit s: ∆′ = (ξ T)2 2 2 − T = T ( 2 ξ − ) 1
Ta phân bit hai trng hp: Khi ξ ≥ 1, khâu PT2 c gi là khâu quán tính bc hai; Khi
0 ≤ξ <1, khâu PT2 c gi là khâu dao ng bc hai .
Khâu quán tính bc hai &n *nh (0 < ξ <1)
- Khi ξ > 1 , phơng trình !c tính có hai nghim thc riêng bit. Nu ký hiu hai
nghim này là s = − 1/ và s = − 1/ ta s? có: 2 ( 2 T ) 1 ( 1 T ) 2 + = 1 2 ξ 2 1 T = và 2 T T T T T W (s ) 1 1 1 = = = (3.69) 2 2 T s + 2ξ Ts + 1 2
T (s − s s − s T s + T s + 1 )( 2 ) ( 1 ) 1 ( 2 ) 1
Do ó khâu quán tính bc hai tơng ơng vi hai khâu quán tính bc nht ghép ni
tip có các hng s thi gian 1
T và T . Ta có: 2 1
H (s ) W (s ) T T 1 T 1 T 1 = = 1 2 = − 1 . + 2 . (3.70) s s T T 1 T T 1 1 1 1 − 2 1 − s s + s + s + 2 s + T T 1 T T2 1 2 Hàm quá : ( h ) t = 1 − 1 T − T t / 1 . T e + 2 −t /T2 .e (3.71) 1 T − 2 T 1 T − 2 T
Hàm trng lng: g(t) dh(t) 1 =
= L− [W (s )] 1 =
( t−/ 1T −t/ 2T e − e ) (3.72) dt − 1 T 2 T
- Khi ξ =1 , phơng trình !c tính có nghim kép s = = − 1 s2 (1/T ) 54
Hàm quá : h(t ) = 1 − 1 +t −t/ T e (3.73) T Hàm trng lng: − 1 g(t) dh(t ) = = L 1 [W( ) s ] − t / T = te (3.74) dt T 2
Khâu dao ng bc hai
- Khi 0 ≤ξ < 1, phơng trình !c tính có hai nghim phc. Vi ký hiu 1 ω = ; 2
ω = ω 1− ξ ; ϕ = arcco ξ s ; ta có: n T n 2 ω
Hàm truyn: W (s ) 1 n = = (3.75) 2 2 2 2 T s + 2ξTs +1 s +2ξω s ω + n n ( ξ s +ξω n ) + ω 2 2
H (s) W (s) ωn 1 1 −ξ = = (3.76) s s ( 2 s +2ξω s + 2 ω s s n n ) = − ( + ξωn)2 + 2 ω
Suy ra hàm quá là : − ξω t n h(t) ξω t ξ e = 1− − e n co ω s t + sin ωt = 1 − sin(ωt + ϕ) (3.77) 1 −ξ 2 1 − ξ 2 Hàm trng lng: 1 − − ω 2 1 ω 2
g (t ) dh (t ) =
= L [W (s)] = L n n = e ξ
− ω tn sinωt (3.75) dt s2 + ξω 2 s + ω 2 ω n n
Hình 3.22: Hàm quá ca khâu bc hai: (a) T&ng quát; (b) Chi tit
Các biu thc trên cho thy !c tính thi gian ca khâu dao ng bc hai có dng dao ng
t1t n. Hàm quá suy gim v giá tr xác lp 1 và hàm trng lng suy gim v 0. Giá tr ξ
càng ln, dao ng suy gim càng nhanh, do ó ξ gi là h s suy gim hay h s t1t dn. Khi ξ = 0 thì ( h )
t = [1 −sin(ω t + π
, áp ng ca khâu là dao ng không $i vi tn n / 2 )] s 1
ω = . Do ó ω gi là tn s riêng ca khâu dao ng bc hai. n T n 55
- Nu kho sát m rng vi ξ < 0 thì áp ng s? là dao ng tng dn ho!c chuyn ng
tng dn, h(∞) = ∞ nên khi ξ < 0 khâu bc hai không $n nh.
Hình 3.23: Hàm tr,ng lưng ca khâu bc hai !c tính tn s:
- Hàm !c tính tn: W ( ω
j )= W (s) 1 = s= ω j 2 2
−T ω + 2ξTjω +1 ( (3.76) 2 2 1 − T ω ) −2ξ ω T = ( + j 2 1 −T ω )2 2 + 4(ξTω )2 ( 2 1 −T ω )2 2 + ( 4 ξTω)2 2 2 1 −T ω − 2ξTω Suy ra: ( P ω) ( ) = ( ; Q (ω )= 2 1 2 −T ω )2 2 + ( 4ξTω )2 ( 2 2 1 − T ω ) + ( 4 ξ ω T )2 - Biên : M (ω ) 2 = P (ω ) 2 + Q (ω ) 1 = (3.77) ( 2 1−T ω )2 2 + ( 4 ξTω)2
L(ω ) =20 lg M (ω ) = 2 − 0 lg ( 2 1 −T ω )2 2 + 4(ξ ω T )2 (3.78) - Góc pha: ϕ (ω ) Q (ω ) 2ξTω = arctan arctan (3.79) P(ω ) = − 1− 2 2 T ω
Mt s im !c bit: ω =0 ( P ω ) = 1 ( Q ω ) = 0 L(ω ) = 0 ϕ (ω)= 0 ω =ω =1/T ( P ω ) = 0 1 1 ϕ (ω) o = 9 − 0 n Q(ω ) = − L (ω ) 20 lg ξ = 2 ξ 2 ω =+∞ ( P ω ) = 0 ( Q ω ) = 0 L(ω ) = −∞ ϕ (ω) o = 1 − 80 Ti tn s 2
ω = ω 1− 2ξ thì o hàm dM / dω = 0 nên biên cc i ch n M = M(ω
. Tn s ω c gi là tn s c$ng hng và ch& t#n ti khi ch ) = 1 /( 2 2ξ 1−ξ max ) ch 1 − 2 2 ξ > 0 hay 0 ≤ ξ < .
0 707 . Nu D càng nh" thì &nh cng hng M và L(ω càng cao. ch ) max
Khi ξ → 0 thì ω → ω và M → ∞ , L(ω
. Mi quan h gia M
và ξ c th hin ch ) → ∞ ch n max max trên Hình 3.26. 56 lg ω 1 ϕ (ω) T l ω g 1 T
Hình 3.24 Biu Bode ca khâu bc hai jQ(ω ) ( P ω ) 1 M = ; max 2ξ 1 2 1 − ξ ξ 2 Mmax M max
Hình 3.25: Biu Nyquist ca khâu bc hai
Hình 3.26: Mi quan h gi+a M
max và ξ c a khâu b c hai 0< ξ < . 0 707 M > 1 max ξ ≥ . 0 707 M = 1 max
Biu # Bode và biu # Nyquist ca khâu bc hai ng vi các giá tr ξ khác nhau c
biu di:n trên Hình 3.24 và Hình 3.25. Vi 0 3
. 8 ≤ ξ ≤ 0.707, biu # Bode ca khâu bc hai có th v? gn úng bng hai ng tim cn:
- Khi ω << 1/ T ⇔ω T << 1 thì L(ω)≈ 0 => ng tim cn nm ngang.
- Khi ω >>1/ T ⇔ω T >> 1 thì L(ω) ≈ −40lg(ωT) => ng tim cn có dc - 40dB/dec.
Hai ng tim cn giao nhau ti tn s ω =1/T nên vi khâu bc hai, tn s dao ng n
riêng ω cng là tn s gãy. n 57
Nh3n xét: H s t1t dn ξ càng bé thì mc dao ng trên biu # hàm quá càng ln, giá
tr biên cng hng M
trên biu # Nyquist và L(ω trên biu # Bode càng cao. ch ) max 3.2.7 Khâu ch3m tr!
Khâu tr: là phn t2 có tín hiu ra l!p li hoàn toàn tín hiu vào sau mt khong thi gian τ
c gi là thi gian tr:. Ví d khâu tr: là s vn chuyn vt liu trên bng ti (Hình 3.27). Tín
hiu vào là lng liu $ lên u bng ti qv, còn tín hiu ra là lng liu c vn chuyn n
u ra ca bng ti pr. Nh vy khi lng liu $ lên u vào thay $i thì sau khong thi gian
vn chuyn cn thit u ra mi nhn bit c s thay $i này. Thi gian tr: s? bng chiu
dài bng ti chia cho tc chuyn dch ca bng ti. qv pr
Hình 3.27: Ví d. v khâu tr q ư & ' / v – L ng li u lên u b ng t i. p ư t 0 ' r – L ng li u xu u ra b/ng t i
Khâu tr: t#n ti trong hu ht các i tng iu ch&nh, nó là s chm tr: truyn tín hiu tA
u vào cho n u ra do quá trình ng hc trong i tng gây lên. Ly ví d lò in tr
vi tín hiu vào in áp cp cho lò còn tín hiu ra là nhit c o bng cm bin o nhit
. Khi in áp cp cho lò thay $i nhng nhit mà cm bin nhn bit c không thay $i
ngay. Nó òi h"i cn phi mt mt khong thi gian nht nh lò tích ly nng lng và
truyn nhit n cm bin o, thi gian ó gi là thi gian tr: và to nên khâu tr: trong thành
phn ca lò. Nh vy, trong lò, ngoài quá trình chuyn $i nng in sang nng lng nhit
t nóng lò còn có quá trình truyn nhit tA si t n cm bin o. Hai quá trình vt lý này
hình thành #ng thi vi nhau, nhng khi mô t !c tính ng hc thì c tách làm hai thành
phn: Thành phn th nht là quá trình chuyn $i và tích ly nng lng, thành phn th hai
là s chm tr: truyn nhit tA si t n cm bin o. Mô t toán hc
Hàm tr: là hàm tín hiu vào r(t ) mt khong thi gian T ta c tín hiu ra: y( )
t = r(t −T ) (3.80)
Bin $i Laplace hàm tr: ta c:
Y (s) = L[r(t −T )]= e−TsR(s) (3.81)
Hàm truyn: W( ) Y( ) s T − s s = = (3.82) R( ) e s !c tính thi gian
- Hàm trng lng: g(t) = L−1[W(s )] =δ (t − T ) (3.83) −Ts - Hàm quá : 1 1 h(t ) W − (s) e = L = L− = ( 1 t −T ) (3.84) s s 58 g(t) h(t) δ(t − T) 1 t t 0 T 0 T
Hình 3.28: Hàm tr,ng lưng và hàm quá ca khâu chm tr !c tính tn s
- Hàm !c tính tn: W ( jω )= e− jωT = cosωT − jsin ωT (3.85) P(ω ) = co ω
s T ; Q (ω) = − sin T ω - Biên : M(ω ) 2 = P (ω ) 2
+ Q (ω ) = (cosω T)2 +(−sinω )2 T =1 (3.86)
L (ω ) = 20 lg M (ω) = 20 lg1 = 0dB (3.87) - Góc pha: −sin ϕ (ω ) Q (ω ) ωT = arctan ( = arctan = ω − (3.88) P ω ) T co ω s T jQ(ω ) ( L ω )[dec] lg(ω )[de ] c 1 P (ω ) ω 0 ω = 0 ϕ (ω)[ ] lg(ω)[de ] c ω
Hình 3.29 Biu Bode và biu Nyquist ca khâu chm tr Nh3n xét: - (
L ω ) luôn bng 0 nên biu # Bode biên trùng vi trc hoành. Hàm góc pha ϕ (ω ) t& l
vi ω nhng do trc hoành ω chia theo thang logarith nên biu # Bode pha ϕ (ω ) = ω − T là
ng cong. Các giá tr !c bit: lim (
P ω )=1 ; lim Q(ω) = 0 ; ϕ(0 )= 0 ω→0 ω→0
lim P(ω) và limQ(ω ) không t#n ti ω→∞ ω→∞
- Biên luôn bng 1 và góc pha thay $i tuyn theo ω nên biu # Nyquist là ng tròn ơn v.
3.3 Kh o sát $c tính ng h%c c0a h thng iu khin 59
3.3.1 $c tính th/i gian c0a h thng
Xét h thng có hàm truyn: m m + −1 ... 1 + + 1 +
W (s ) b s b s b s b o m − m = (3.89) n n a s + a s −1 ... 1 + + a s 1 + a o n− n
Bin $i Laplace ca hàm quá là: m m −1 1 ...
H (s ) W (s ) b s b s b s b o + 1 + + m 1 + = = − m (3.90) n s s a s a s 1 ... a s a o + n − 1 + + n 1 + − n
Tùy theo !c im ca h thng mà !c tính thi gian ca h thng có th có các dng khác
nhau. Tuy vy chúng ta có th rút ra mt s kt lun quan trng sau ây:
- Nu W (s ) không có khâu tích phân, vi phân thì hàm trng lng suy gim v 0, hàm quá
có giá tr xác lp khác 0. m m 1 − g( b s b s b s b ∞ ) o + + + m + = lim sW (s) ... = lim 1 1 − m s = 0 (3.91) n n 1 → s 0 → s 0 a s a s a s a o + − . + .. + + 1 n 1 − n m m 1 − h( b s b s b s b b ∞) o + + + m + = lim sH (s ) 1 ... = lim s . 1 1 − m (3.92) n n = m ≠ 0 1 → s 0 → s 0 s a s a s a s a a o + − + ... + n− + 1 1 n n
- Nu W (s) có khâu tích phân (a = 0 thì hàm trng lng có giá tr xác lp khác 0, hàm n )
quá tng n vô cùng. m − m 1 g( b s b s b s b b ∞) o + + + m + = lim sW (s) ... = lim 1 −1 m s = m ≠ 0 (3.93) n n 1 s 0 → s 0 → a s a s a s a o + − +... + 1 n 1 − n 1 − m m −1 1 ... h ( b s b s b s b ∞) =limsH (s ) o + 1 + + m 1 + = − lims m . = ∞ (3.94) 1 s →0 s →0 s a sn ... o + − a sn 1 + + a s n−1
- Nu W (s) có khâu vi phân (b = thì hàm quá suy gim v 0. m ) 0 m − m 1 h ( b s b s b s ∞) o + + + =limsH (s ) 1 ... =lims . 1 m 1 − = 0 (3.95) n n−1 s 0 → s 0 → s a s a s a s a o + + + + 1 ... n 1 − n
- Nu W (s) là h thng hp thc (m ≤ ) n thì ( h 0) = 0 . m − m 1 h (0) b s b s b s b = lim H (s ) 1 o + 1 +... = lim . + m−1 + m = 0 (3.96) n − n 1 s + → ∞ s→+∞ s a s a s a s a o + . + .. + n− + 1 1 n
- Nu W (s) là h thng hp thc ch!t (m < n) thì g(0)= 0 m − m 1 g(0) b s b s b s b = lim W(s) o + 1 +... = lim + m−1 + m = 0 (3.97) n n−1 s + → ∞ → s +∞ a s a s a s a o + +... + n− + 1 1 n
- Nu W (s) không có khâu tích phân, vi phân và có n im cc phân bit, ( H ) s có th phân tích di dng: n H ( )= o h s + i h (3.98) s
i =1 s − pi
Bin $i Laplace ngc biu thc (3.90) ta c hàm quá ca h thng là: n h (t ) =h (3.99) 0 + p t i h e i i=1 60
Do ó hàm quá là t$ hp tuyn tính ca các hàm m cơ s t nhiên. Nu tt c các im cc
p u là cc thc thì hàm quá không có dao ng; ngc li nu có ít nht mt c!p cc i
phc thì hàm quá có dao ng.
Trên ây vAa trình bày mt vài nhn xét v !c tính thi gian ca h thng t ng. Thông
qua !c tính thi gian chúng ta có th bit c h thng có khâu tích phân, vi phân hay
không? H thng ch& g#m toàn cc thc hay có cc phc?... Nhng nhn xét này giúp chúng ta
có c hình dung ban u v nhng !c im cơ bn nht ca h thng, tA ó chúng ta có th
chn c phơng pháp phân tích, thit k h thng phù hp.
3.3.2 $c tính t(n s c0a h thng
Xét h thng t ng có hàm truyn W (s). Gi s2 W (s) có th phân tích thành tích ca các
hàm truyn cơ bn nh sau: l W (s) = W s (3.100) i ( ) ∏ i =1
!c tính tn s ca h thng là: l W ( jω ) = W jω (3.101) i ( ) ∏ i =1 Biên : l l l
M (ω ) = W ( jω ) = ∏W jω
W jω => M (ω ) = M ω (3.102) i ( ) ∏ i ( ) = ∏ i ( ) i =1 i =1 = i 1 l l l
L(ω )= 20 lg M (ω )= 20 lg M = 20 lgM => ( L ω ) = L ω (3.103) i ( ) i ∏ (ω ) i (ω ) i=1 i=1 i=1
Biu thc (3.103) cho thy biu # Bode biên ca h thng bng t$ng các biu # Bode
biên ca các khâu cơ bn thành phn. Góc pha: l l l ϕ (ω )= ∠W ( ω j ) = arg W => ϕ (ω )= ϕ ω (3.104) i ( ) i
∏ (jω) = ∠Wi( jω) i =1 i=1 i =1
Biu thc (3.104) chng t" biu # Bode pha ca h thng bng t$ng các biu # Bode pha
ca các khâu cơ bn thành phn.
TA hai nhn xét trên ta thy rng v? c biu # Bode ca h thng, ta v? biu #
Bode ca các khâu thành phn, sau ó cng # th li. Da trên nguyên t1c cng # th, ta có
phơng pháp v? biu # Bode biên gn úng ca h thng bng các ng tim cn nh sau:
Ví d& 3.11: V? biu # Bode ca h thng có hàm truyn:
W (s) 10(s + ) 1 = (0 0 . 1s + ) 1
Gi i: Hàm truyn ca h có th tách thành các khâu cơ bn sau
W (s) = 10(s + ) 1 1 ( 0 0 . 1s +1) vi W (s)=10 1
W ( )s = s +1 có tn s gãy là ω = ( 1 rad / sec) 2 61 1 W (s) 1 = có tn s gãy là ω = = 100(rad / sec) 3 0 0 . 1s + 1 0.01 L1 (ω )[dB] ϕ (1ω )[ ] 20 0 lg(ω )[dec] 0 l ( gω )[dec] − 1 0 1 2 3 − 1 0 1 2 3 L2 (ω )[d ] B ϕ (ω 2 )[ ] +20dB / dec 90 45 0 lg(ω)[de ] c 0 l ( g ω)[d ] ec − 1 0 1 2 3 − 1 0 1 2 3 ϕ 3(ω)[ ] L3 (ω )[dB] 0 l ( g ω)[dec] 0 lg(ω )[d ] ec − 1 0 1 2 3 1 − 0 1 2 3 − 45 −20dB / dec − 90 ( Lω ) [d ] B ϕ (ω )[ ] 60 2 + d 0 B / dec 90 20 45 0 lg (ω )[d ] ec 0 lg(ω )[dec ] − 1 0 1 2 3 − 1 0 1 2 3
Hình 3.30: Biu Bode ca h thng 0 ví d. 3.11
Phng pháp v5 biu # Bode biên b6ng các /ng tim c3n:
Gi s2 hàm truyn ca h thng có dng l W (s )= W s i ( ) ∏ i =1
Bc 1: Xác nh tt c các tn s gãy 1 ω =
, và s1p xp theo th t tng dn: i Ti ω < ω < ω ... 1 2 3
Bc 2: Nu tt c các tn s ω ≥1 thì biu # Bode gn úng phi qua im A có ta : i ω =1 ( L ω ) = 20lg K
Bc 3: Qua im A, v? ng th@ng có dc: - (− 2 d 0 B / dec α
× ) nu W (s) có α khâu tích phân. - (+ 2 d
0 B / dec× α ) W(s) có α khâu vi phân.
ng th@ng này kéo dài n tn s gãy k tip. 1
Bc 4: Ti tn s gãy ω =
, dc ca ng tim cn c cng thêm: i Ti - (− 2 d
0 B / dec× β ) nu ω là tn s gãy ca khâu quán tính bc nht. i
- (+ 20dB /dec× β ) nu ω là tn s gãy ca khâu vi phân bc nht. i 62 - (− 4 d
0 B / dec×β ) nu ω là tn s gãy ca khâu dao ng bc hai. i
- (+ 40dB /dec×β ) nu ω là tn s gãy ca khâu vi phân bc hai, ( 2 2 T s + 2ξTs + ) 1 . i
(β là s nghim bi ti ω ) i
ng th@ng này kéo dài n tn s gãy k tip.
Bc 5: L!p li bc 4 cho n khi v? xong ng tim cn ti tn s gãy cui cùng.
Ví d& 3.12: V? biu # Bode biên gn úng ca h thng có hàm truyn: W (s) 10 ( 0 0 1 . s+ ) 1 = (s . 0 01s+ ) 1
Da vào biu # Bode gn úng, hãy xác nh tn s c1t biên ca h thng. Gi i: Các tn s gãy: 1 1 ω = = = 10 1 (rad /sec) T . 0 1 1 1 1 ω = = =100 2 (rad /sec) T . 0 01 2 L (ω )[dB] lgω [dec ] 1 10− 0 10 1 10 2 10 ωc ω
Hình 3.31: Biu Bode biên ca h thng 0 ví d. 3.12
Biu # Bode qua im A có ta : ω =1 (
L ω ) = 20lg K = 20lg100= 40dB
Biu # Bode biên gn úng có dng nh Hình 3.31. Theo hình v?, tn s c1t biên ca h thng là 103rad/sec.
Ví d& 3.13: Hãy xác nh hàm truyn ca h thng, bit rng biu # Bode biên gn úng
ca h thng có dng nh hình 3.32. 63 L(ω)[dB ] lgω [ de ]c ω ω ω ω ω 1 2 3 4
Hình 3.32: Biu Bode biên ca h thng 0 ví d. 3.13
Gi i: H thng có bn tn s gãy ω , ω , ω , ω . Da vào s thay $i dc ca biu # 1 2 3 4
Bode, ta thy hàm truyn ca h thng phi có dng: 2
W (s ) K(T s +1 T s +1 2 )( 3 ) = (T s+1 T s+1 1 )( )2 4
Vn còn li là xác nh thông s ca h thng. Theo hình v?: 20lgK = 34 => K = 50 lgω = 1 − => ω = 0.1 => T =10 1 1 1
dc on BC là -20dB/dec, mà tA im B n im C biên ca biu # Bode gim
40dB (tA 34dB gim xung -6dB), do ó tA B n C tn s phi thay $i là 2 decade. Suy ra: lgω = lgω + 2 =1 => ω = 10 => T = . 0 1 2 1 2 2 lgω = 2 => ω =100 => T = . 0 01 3 3 3
dc on DE là +40dB/dec, mà tA im D n im E biên ca biu # Bode tng
60dB (tA -6dB tng lên +54dB), do ó tA D n E tn s phi thay $i là 1.5 decade. Suy ra: lgω = lgω +1.5 = . 3 5 => ω = 3162 => T = 0 0 . 003 4 3 4 4
Do ó hàm truyn ca h thng là: 2 W (s ) 5 ( 0 . 0 1s +1)( . 0 01s +1) =
(10s+1)(0.003s+1)2 BÀI T2P CHƠNG 3
1. Hãy xác nh hàm trng lng g(t ) và hàm quá h(t ) ca nhng h tuyn tính có hàm
truyn t W (s) nh sau: a. 2s +1 1+ 2 1 b. s c. 2 s + 2s + 1 (1 +3 )s(1 +5 )s 2 . 0
(s1+s)(1+ s 3 )
2. Xác nh hàm truyn t ca h thng có sơ # im
cc (c ánh du bi ×) và im không (c ánh
du bi O ) cho trong Hình 3.33, bit rng W (0)= 2 . Tìm
và v? # th hàm trng lng, hàm quá . Có nhn xét
gì v h thng qua các # th ó. 64
Hình 3.33: Cho bài tp 2
3. Hãy xây dng !c tính tn logarith (biu # Bode) ca nhng h thng có hàm truyn t cho nh sau: a. 10s 0 2 . 2s + 4 W (s ) 2 ( 0 . 0 02s+ ) 1 = b. ( W ) ( ) s = s(0.3s + ) 1 (0 0 . 3s + ) 1 10 2 s 0 0 . 4s +1 c. W ( ) s s = d. ( W ) ( ) s = 2s+1 (s 1 + )(0.3s +1) e. 0 4 . s+ 4 W (s ) 9s +18 = f. W (s ) ( = 0.2s + )2 1 (s + ) 4 ( . 0 2s + ) 1
g. W (s)= 5(20s + 5) 2 h. ( W ) s ( . 0 1s 1 + ) s = ( . 0 02s +1)(s +1) 2 i. s +3 s +1 W( ) 50 s = ( j. W (s) 0 0 . 1 = s + ) 1 ( . 0 2s + ) 2 s( . 0 01s +1)2
4. V? biu # Bode và Nyquist cho các h hình v? sau: R =10kΩ R =10 Ω k u C = F µ 1 u L = H 1 o (t ) i (t ) u uo (t) i (t ) C = F µ 1 (a) (b) 65
CHƠNG 4: PHÂN TÍCH TÍNH N 7NH
VÀ CH8T L9NG H TH-NG IU KHIN
4.1 Khái nim v tính *n nh
,n nh là ch& tiêu cht lng cơ bn, cn thit ca h thng iu khin t ng. Mt h
thng mun s2 dng c thì trc ht phi t yêu cu v $n nh. Tính $n nh !c trng
cho kh nng duy trì c trng thái cân bng ca h khi chu tác ng tA bên ngoài. Hay nói
cách khác h thng iu khin c gi là $n nh nu sau khi có nhi:u tác ng phá vO trng
thái cân bng, nó s? t iu ch&nh tr li trng thái cân bng. Nu trng thái ca nó không
tr v cân bng mà tín hiu ra tin ti vô cùng thì h thng c gi là không $n nh. Trng
hp tín hiu ra ca h thng dao ng vi biên không $i gi là h thng s? biên gii $n nh.
Phơng trình vi phân dng t$ng quát ca h thng tuyn tính có tín hiu vào r(t), tín hiu ra y(t) là: n n−1 m m −1 d y d y dy d r d r dr a (4.1) 0 +a1 . + .. a + + a y t = b + b + +b + b r t n n−1 n 1 ( ) − n 0 m 1 ... m − − m ( ) m 1 1 dt dt dt dt dt dt
Tín hiu ra ca h thng y(t) chính là nghim ca phơng trình vi phân, bao g#m hai thành phn:
y(t) = y0(t) + yq(t) (4.2) trong ó: - y ơ !
0(t) là nghi m riêng c a ph
ng trình vi phân khi có v ph i, c tr ng cho quá trình xác lp; - y $ ơ !
q(t) là nghi m t ng quát c a ph
ng trình khi v ph i b ng 0, c tr ng cho quá
trình quá , chính là nghim ca phơng trình: n n−1 d y d y dy a (4.3) n + a n + ...+ an + a y (t ) n = 0 0 1 − −1 1 dt dt dt Nghim riêng y
ph thuc vào giá tr tác ng u vào và nó !c trng cho tính cht xác 0(t)
lp ca h thng. Nu tác ng u vào là c nh thì y
c nh. Nh vy nghim riêng 0(t)
hoàn toàn không nh hng n tính cht $n nh ca h thng, xét $n nh ta ch& cn xét nghim y
. Nu lim y (t) → 0 thì h thng s? $n nh. q(t) →∞ qd t
Hình 4.1: Các dng quá trình quá
Ta có khái nim khác v tính $n nh: 66
Mt h thng tuyn tính ưc g,i là &n *nh nu quá trình quá t)t d'n theo thi gian.
H thng không &n *nh nu quá trình quá t/ng d'n. H thng 0 biên gii &n *nh nu quá
trình quá không &i, hoc dao ng vi biên không thay &i. Nghim y có dng t$ng quát: q(t) n y s t i (4.4) q(t) = C e i i =1 trong ó:
C - là hng s ph thuc vào thông s ca h và iu kin u (trng thái ban u) i s ơ !
i - (i = 1,2,….,n) là các nghi m c c, chính là nghi m c a ph ng trình c tính: n n 1 a s + − a s + ... +a s a n + n = 0 0 0 1 − Nghim s !
i có th là nghi m th c, nghi m o ho c nghi m ph c: - Nghim thc: s i = α i - Nghim phc: s ±
i = α i jωi
- Nghim o: si = ± jωi
Xét nh hng ca các loi nghim lên tính cht $n nh ca h thng:
- Khi nghim ca phơng trình !c tính là nghim thc si = αi thì: → 0 α → H thng $n nh i < 0 α khi t i limC e = i t →∞ → ∞ khi α → i > 0
H thng không $n nh
- Khi nghim ca phơng trình !c tính là nghim phc s :
i = α ± jωi → 0 khi α → H thng $n nh i < 0 (α ±jω )t i i lim C e = i t →∞ → ∞ khi α
→ H thng không $n nh i > 0
- Khi nghim ca phơng trình !c tính là nghim thun o: s thì:
i = ±jωi s t jω t i i e = e
= acosωit + jbsinωit = Asin(ωit + ϕ )
limC e± jω ti → const : h dao ng vi biên không $i i t→∞
Nh vy tA nhng phân tích trên ta có th rút ra kt lun:
- H thng iu khin t ng s? $n nh khi phơng trình !c tính có tt c các nghim
thc âm ho!c nghim phc có phn thc âm.
- H thng iu khin không $n nh khi phơng trình !c tính t#n ti nghim thc dơng
ho!c nghim phc có phn thc dơng.
- H thng iu khin t ng s? biên gii $n nh nu phơng trình !c tính có nghim
thun o còn tt c các nghim khác là nghim thc âm ho!c nghim phc có phn thc âm.
Nu xét trên m!t ph@ng phân b nghim (hình 4.2) thì khi tt c các nghim ca phơng
trình !c tính phân b bên trái trc o thì h thng $n nh. Ch& cn t#n ti mt nghim bên 67
phi trc o thì h thng s? không $n nh. Còn nu có nghim nm trên trc o, các nghim
khác u nm bên trái trc o thì h thng s? biên gii $n nh. α < α i 0 i
Hình 4.2: Phân vùng nghim trong mt ph1ng phc
Nh vy ánh giá tính $n nh ca h thng ta phi i tìm nghim ca phơng trình vi
phân, sau ó xét du phn thc ca nghim. Vn !t ra là vic gii các phơng trình vi phân
bc cao là tơng i phc tp.Vì vy tính $n nh có th c ánh giá thông qua các phơng
pháp khác ó là qua các tiêu chu>n $n nh. T$ng quát có ba cách ánh giá tính $n nh sau ây:
- Tiêu chu>n $n nh i s: tiêu chu>n Hurwitz, Routh;
- Tiêu chu>n $n nh tn s: tiêu chu>n Mikhailov, Nyquist;
- Phơng pháp chia min $n nh và phơng pháp qu o nghim s, thng c s2
dng xét tính $n nh ca h thng khi có mt thông s ca h bin $i trong mt phm vi nào ó.
Các phơng pháp kho sát tính $n nh u da trên phơng trình !c tính, sau ây s? xét
c th tAng phơng pháp.
4.2 Các tiêu chu:n *n nh i s
4.2.1 iu khin *n nh c(n thit
Xét h thng iu khin t ng $n nh và có phơng trình !c tính: n n 1 a s + − a s +... +a s a n + n = 0 0 1 1 −
Phơng trình !c tính bc n có n nghim và ch& có th có hai loi nghim: - Nghim thc: s 2
i = -α i ; - gi s có m nghi m th c;
- Nghim phc liên hp: s
; - có (n-m)/2 c!p nghim phc liên hp.
k = -α k ± jωk Vi α và u dơng. i; α k ωk
Khi ó có th chuyn phơng trình !c tính sang dng tơng ơng: m ( − n m ) / 2 a ( ∏ s +α s α jω s α jω (4.5) i ) ∏( + k − ).( k + k + ) k = 0 0 i 1 = k 1 = m ( n − ) m / 2 a ( ∏ s +α ) s α ω (4.6) i ∏ + k + k = 0 [( )2 2 ] 0 i 1 = k 1 = 68
Khai trin v trái ca phơng trình (4.6) ta s? c mt a thc g#m tt c các h s
dơng, mà trong h thng iu khin h s a0 luôn luôn dơng. Nh vy có th suy ra: iu
kin c'n thit h thng &n *nh là tt c các h s ca phưng trình c tính dưng.
Ví d& 4.1: Xét các trng hp h thng có phơng trình !c tính nh sau: 4 3 2 s +3s 1
+ 0 s −5s +1= 0
h không $n nh vì có h s âm 5 4 3 s 6
+ s +4s +7s 1 + =0
h không $n nh vì có h s bng không 4 3 2
3s + 4 s + 2 s + 9s + 1= 0
th"a mãn iu kin cn nhng cha kt lun c.
4.2.2 Tiêu chu:n *n nh Hurwitz
Xét h thng có phơng trình !c tính: n n−1 a s + a s + ... + a s a n + n = 0 0 1 1 −
xét tính $n nh ca h thng theo tiêu chu>n Hurwitz, u tiên ta i lp *nh thc
Hurwitz theo quy t1c nh sau:
- nh thc Hurwitz là nh thc vuông cp n × n;
- Trên ng chéo chính ca nh thc Hurwitz ta in các h s tA a 1 n an;
- Hàng lg ca nh thc Hurwitz ta in các h s có ch& s lg theo th t tng dn nu
bên phi ng chéo và gim dn nu bên trái ng chéo. Các v trí trng ta in s 0;
- Hàng chPn ca nh thc Hurwitz ta in các h s có ch& s chPn theo th t tng dn
nu bên phi ng chéo và gim dn nu bên trái ng chéo. Các v trí trng ta in s 0. a a a a 0 1 3 5 7 a a a a 0 2 4 6 0 0 a a a 0 1 3 5 ∆ = n 0 a a a 0 2 4 0 0 an
Phát biu tiêu chu2n Hurwitz:
- iu kin cn và h thng $n nh là tt c các nh thc con dc theo ng chéo
chính ca nh thc Hurwitz u dơng. ∆ ∆ ∆
- S ln $i du trong dãy 2 3 ∆ ,∆ , , ,..., n
bng s nghim nm bên trái trc o ca 1 2 ∆ ∆ ∆ 1 2 n 1 − phơng trình !c tính.
Nh vy iu kin $n nh: ∆ > 0 ; ∆ > 0 ; ∆ > 0 ; ….; ∆ > 0 : 1 2 3 n a a a 1 3 5 a a ∆ = a > 0 ; 1 3 ∆ = > 0 ; ∆ = a a a > 0 ….. 1 1 2 3 0 2 4 a0 a 2 0 1 a 3 a
Ví d& 4.2: Xét tính $n nh ca h bc 3 có phơng trình !c trng: D(s) 3 2
= a s + a s + a s + a = 0 1 0 2 3
- Lp nh thc Hurwitz: 69 a a a 1 3 5 ∆ = a a a 3 0 2 4 0 a a 1 3
Tính các nh thc con: ∆ = a > 1 1 0 a a 1 3 ∆ =
= a a − a a > 2 1 2 0 3 0 a a 0 2 a a a 1 3 5 ∆ = a a
a = a ∆ = a (a a − a a ) > 0 3 0 2 4 3 2 3 1 2 0 3 0 a a 1 3
Nh vy h bc 3 $n nh thì:
a , a ; a ; a 0 0 1 2 3 > a a a a 1 2 > 0 3
Ví d& 4.3: Cho h thng có sơ # khi: 10 s2 (s +4) s ( + ) 1
Tìm iu kin ca K h thng $n nh?
Gi i: Hàm truyn ca h thng kín: K s (s + ) 1 s ( 2 + s + ) 2 K W (s) = = K s(s + ) 1 (s2 + s + ) 2 + K
1+ s(s+ )1(s2+ s+ )2 Phơng trình !c tính: D(s) = ( s s + ) 1 ( 2 s + s + ) 2 + K = 0 4 s + 2 3 s +3 2
s +2 s +K = 0
Các h s ca phơng trình !c tính: a0 = 1; a1 = 2; a2 = 3; a3 = 2; a4 = K.
- Lp nh thc Hurwitz cp 4: 2 2 0 0 1 3 K 0 ∆ = 4 0 2 2 0 0 1 3 K
- Tính các nh thc con dc theo ng chéo chính: ∆ = > 1 2 0 2 2 ∆ = = × − × = > 2 2 3 1 2 4 0 1 3 70 2 2 0 3 K 1 K ∆ = 1 3 K =2 −2 = 2× 6 ( − 2 K) − 2× 2 3 2 2 0 2 0 2 2 ∆ = − K > K < 3 8 4 0 2
∆ = K × ∆ = K − K > < K < 4 3 8 ( 4 ) 0 0 2
Kt lun: iu kin h thng $n nh là : 0 < K < 2
Lu ý: ta luôn có ∆ = ; ∆ a n = n ∆ 1 1 a n 1 −
4.2.3 Tiêu chu:n *n nh Routh
Xét h thng có phơng trình !c tính: n n−1 a s + a s
+ ... + a s + a = 0 0 1 n 1 − n
Mun xét tính $n nh ca h thng theo tiêu chu>n Routh, trc tiên ta thành lp bng
Routh theo quy t1c lp theo tAng hàng:
- Hàng u tiên ca bng Routh in các h s có ch& s chPn ca phơng trình !c tính,
th t tng dn tA trái sang phi.
- Hàng th 2 in các h s có ch& s lg, th t tng dn tA trái sang phi.
- TA hàng th 3 tr i phi tính theo các công thc.
- Bng Routh g#m có n+1 hàng (vi n là bc ca phơng trình !c tính), hàng cui cùng
ch& có mt phn t2 duy nht. Lp bng Routh:
a0 a2 a4 a6 a8 a10 . . . a1 a3 a5 a7 a9 . . . b0 b2 b4 b6 . . . b1 b3 b5 . . . . . . . . . .
z (s hng duy nht ca dòng cui cùng) vi: a a a a a a 0 2 − 0 4 − 0 6 − a a a a a a 1 3 b = ; 1 5 b = ; 1 7 b = …… 0 2 4 a a a 1 1 1 a a a a a a 1 3 − 1 5 − 1 7 − b b b b b b 0 2 b = ; 0 4 b = ; 0 6 b = …… 1 3 5 0 b 0 b 0 b ……………………….
Phát biu tiêu chu>n Routh: H thng iu khin t ng có phưng trình c tính vi các
h s dưng s3 &n *nh nu tt c các h s trong ct 'u tiên ca bng Routh dưng. S ln 71
$i du ca các phn t2 ct u tiên ca bng Routh bng s nghim ca phơng trình !c
tính có phn thc dơng (nm bên phi trc o).
Ví d& 4.4: Xét tính $n nh ca h thng có phơng trình !c tính: 4 s + 2 3 s + 5 2 s + 6s + 4 = 0 Gi i: iu kin cn: Ta có: a .
0 = 1; a1 = 2; a2 = 5; a3 = 6; a4 = 4
Các h s ca phơng trình !c trng dơng: th"a mãn iu kin cn.
Lp bng Routh: 1 5 4 2 6 1 5 1 4 − − 2 6 2 0 = 2 = 4 2 2 2 6 − 2 4 =2 2 2 4 − 2 0 =4 2
Ta thy các h s trên ct u tiên ca bng Routh dơng nên h thng $n nh.
Ví d& 4.5: Xét tính $n nh ca h thng có sơ # khi nh sau: 20 1 Vi W (s) ; H( ) s = h
= s(s + 2)( 2s + 3s + )5 s + 1
Gi i: Ta có phơng trình !c trng ca h thng:
1+ W (s)H (s) h = 0 20 1 1 + = 0 s (s + 2)( 2 s + 3s + ) 5 s +1 s (s + ) 2 ( 2 s +3s + ) 5 (s + ) 1 + 20 = 0 5 s +6 4 s +16 3 s + 21 2 s 1 + 0 s + 20 = 0 iu kin cn:
a0 = 1 ; a1 = 6 ; a2 = 16 ; a3 = 21 ; a4 = 10 ; a5 = 20. 72
Các h s ca phơng trình !c trng dơng: th"a mãn iu kin cn. Lp bng Routh: 1 16 10 6 21 20 1 16 1 10 − − 6 21 6 20 20 = 1 . 2 5 = 6 6 3 6 21 6 20 − − 1 . 2 5 20 / 3 12 5 . 0 = 17.8 = 20 12 5 . 12.5 12.5 20 / 3 − 17.8 20 = .738 17.8 17 8 . 20 − .738 0 =20 . 7 38
Nhn xét: các h s trên ct u tiên ca bng Routh dơng nên h thng $n nh.
Các tr/ng hp $c bit
Trưng hp 1: nu có h s ct 1 ca hàng nào ó bng 0, các h s còn li ca hàng ó khác
0, thì ta thay h s bng 0 ct 1 bng s p dơng, nh" tùy ý, sau ó quá trình tính toán c tip tc.
Ví d& 4.6: Xét tính $n nh ca h có phơng trình !c trng: 4 s + 2 3 s +4 2 s 8 + s +4 =0
H s ca phơng trình !c trng: a0 = 1; a1 = 2; a2 = 4; a3 = 8; a4 = 4.
Các h s ca phơng trình !c trng u dơng: th"a mãn iu kin cn.
Lp bng Routh: 1 4 4 2 8 0→ ε 4 8 8 − < 0 ε 4 8
Ta thy p dơng nh" nên (8 − ) < 0
h thng không $n nh. ε
Trưng hp 2: nu tt c các h s ca hàng nào ó bng 0. Ta xét tính $n nh ca h nh sau:
- Thành lp a thc ph Dp(s) tA các h s ca hàng trc hàng có tt c các h s bng 0. 73
- Thay hàng có tt c các h s bng 0 bi mt hàng khác có các h s chính là các h s dD (s) ca P
. Sau ó quá trình tip tc tính toán. ds
- Nghim ca a thc ph cng chính là nghim ca phơng trình !c trng.
Ví d& 4.7: Xét tính $n nh ca h có phơng trình !c trng: 5 s + 4 4 s + 8 3 s +8 2 s + 7 s + 4 = 0
H s ca phơng trình !c trng: a0 = 1; a1 = 4; a2 = 8; a3 = 8; a4 = 7 ; a5 = 4
Các h s ca phơng trình !c trng u dơng: th"a mãn iu kin cn.
Lp bng Routh: 1 8 7 4 8 4 1 8 1 7 − − 4 8 4 4 = 6 = 6 4 4 4 8 4 4 − − 6 6 6 0 = 4 = 4 6 6 6 6 6 0 − − 4 4 4 0 = 0 = 0 4 4 8 0 dD (s)
a thc ph: D (s)= 4s2 p + 4 = 8s p ds
M!t khác nghim ca a thc ph cng chính là nghim ca phơng trình !c tính:
D ( s) = 4 s2 + 4 s = ± j p
Ta thy các h s ct u tiên ca Routh không âm, phơng trình !c tính có 2 nghim
nm trên trc o nên h thng biên gii $n nh.
Nh n xét: Ta có th s2 dng tiêu chu>n Routh ho!c tiêu chu>n Hurwitz xét $n nh cho tt
c h thng h và h thng kín. Tuy nhiên xét v mc phc tp thì vic tính toán các nh
thc Hurwitz phc tp hơn vic lp bng Routh, nht là i vi h thng có phơng trình !c
tính bc cao. Vì vy trong thc t ngi ta thng lp bng và tính toán theo tiêu chu>n Routh.
4.3 Các tiêu chu:n *n nh t(n s
Các tiêu chu>n $n nh tn s phân tích tính $n nh ca h thng da trên các biu # !c tính tn s. 4.3.1 Nguyên lý góc quay
Xét h thng bc n có phơng trình !c tính:
D(s) = a0sn + a1sn-1+… +an-1s + an = 0 74
Phơng trình bc n có n nghim, gi các nghim ó là s ơ !
1, s2,…, sn. Khi ó ph ng trình c
tính có th vit di dng:
D(s) = a (s −s )(s − s )...(s − s ) n = 0 0 1 2 Thay s = ω
j , ta c a thc !c tính tn s:
D (jω ) = a (jω − s )(jω − s )...(jω −s ) 0 1 2 n
MBi nghim ca phơng trình !c tính s : ! @
i có th bi u di n trên m t ph ng ph c b ng m t
vec tơ có gc trùng vi gc ta , ngn trùng vi im s ω biu di:n
i. Thành ph n ( j −s ) i
bng vec tơ có gc im s
ω thay $i thì dài và
i, ng n n m trên tr c o nh hình 4.3a. Khi
góc ca vec tơ (jω − s ) cng thay $i theo. Quy c chiu quay dơng là chiu ngc chiu i
kim #ng h# thì khi ω bin thiên tA − ∞ n + ∞ thì mBi vec tơ thành phn ( jω − s ) s? quay i
mt góc: là +π nu nghim s −π nu nghim s
i nm bên ph i tr c o;
i nm bên trái tr c o; là là 0 nu s i nm trên tr c o.
Dùng ký hiu ∆ arg ch& góc quay, ta có: +π
nu si nm bên trái trc o
∆arg( jω − s ) = −π nu si nm bên phi trc o i −∞<ω <∞ 0
nu si nm trên trc o jω jω jω s − jω − s i i +π −π ω
Hình 4.3: Minh h,a cho nguyên lý góc quay
Gi s2 phơng trình !c tính ca h có m nghim nm bên phi trc o và (n-m) nghim
nm bên trái trc o. Khi ó: m
∆arg( jω − s ) mπ i = −
i =1 −∞<ω<∞ − n m
∆ arg( jω − s ) (n m)π i = −
i =1 −∞<ω<∞ n −m m arg D( jω ) =
∆arg( jω − s )
arg ( jω s ) (n 2m)π i + ∆ − i = − ∞ − <ω <∞
i =1 −∞<ω <∞
i =1 −∞<ω <∞
Khi xét ω bin thiên tA 0 → +∞ thì: - Nu s ω quay mt góc là +π / 2.
i là nghi m th c n m bên trái tr c o thì ( j − s ) i - Nu s ω quay mt góc là −π /2.
i là nghi m th c n m bên ph i tr c o thì ( j − s ) i
- Nu phơng trình !c tính ca h có m nghim nm bên phi trc o và (n-m) nghim
nm bên trái trc o thì: 75 m π
∆arg( jω − s ) m i = − ω 2 i =1 < 0 <∞ n −m π
∆ arg( jω − s ) n ( m) i = − ω 2 = i 1 < 0 <∞ − n m m π arg D ( jω ) =
∆arg(jω −s )
arg(jω s ) n ( m 2 ) i + ∆ − i = − 0<ω <∞ ω ω 2 i =1 0< <∞ i =1 < 0 <∞
4.3.2 Tiêu chu:n *n nh t(n s Mikhailov
Tiêu chu>n $n nh Mikhailov ã phát biu da vào nguyên lý góc quay nh sau:
iu kin c'n và h tuyn tính &n *nh là biu vect a thc c tính D(j4) xut
phát t5 tr.c thc dưng ti 4 bng không, tu'n t quay n góc ph'n tư theo chiu ngưc chiu
kim ng h khi 4 bin thiên t5 0 n +6; vi n là bc ca phưng trình c tính ca h thng. Ch+ng minh:
Xét h thng có phơng trình !c tính:
D(s) = a0sn + a1sn-1+… +an-1s + an = 0
a thc !c tính tn s: n n
D( jω ) = a ( jω ) + a ( j −
ω ) 1 + ... + a ( jω ) + a 0 1 n −1 n
Ta ã bit iu kin cn h $n nh là các h s ca phơng trình !c tính phi dơng.
Do vy, khi ω = 0 thì D(jω) = a
, tc là ng !c tính D( ω
j ) phi xut phát tA im 0 > 0 (a
) nm trên trc thc dơng. 0,j0
R mc 4.1 ta ã bit, h thng bc n s? $n nh nu tt c n nghim cc u nm bên trái
trc o. Khi ó, theo nguyên lý góc quay ta có: π
arg D( jω ) = n 0 ω < <∞ 2
Nh vy h thng $n nh thì vec tơ D ( jω )phi quay qua n góc phn t khi ω bin thiên tA 0 → ∞ . n = 2 n =1 n = 5 n = 5 n =3 n = 4 n = 4 n = 3
Hình 4.4: Minh h,a tiêu chu2n Mikhailov 76
Hình 4.4 minh ha biu # vectơ a thc !c tính cho trng hp h thng $n nh a) và không $n nh b). Nh3n xét:
- Tiêu chu>n $n nh Mikhailov có th dùng xét $n nh cho c h thng h và h thng kín.
- xây dng ng !c tính ca D (jω) ta thay s = jω vào phơng trình !c tính r#i
tách riêng phn thc và phn o: n n
D( jω ) = a ( jω ) ω ω 0 + a ( j − ) 1 1 +... + a ( 1 j ) + a n − n = Re(ω ) + j Im(ω )
Sau ó xét s phân b nghim s ca phơng trình phn thc Re(ω) = 0 và phn o Im(ω)
= 0. H thng $n nh nu nghim s ca các phơng trình này phân b xen k? nhau. #ng
thi ω = 0 phi là nghim ca phn o.
Ví d& 4.8: Kho sát $n nh theo tiêu chu>n Mikhailov cho h thng có phơng trình !c tính bc ba dng: D(s) 3 2
= a s + a s + a s + a = 0 1 0 2 3
vi: a0, a1, a2 và a3 > 0
Gi i: Thay s = jω vào phơng trình !c tính r#i tách phn thc và phn o: D ( ω j ) = a ( ω j )3 +a ( ω j )2 + a ( ω j ) 2
+a = a − a ω + j ( 3 a ω − a ω ) 0 1 2 3 3 1 2 0 Re(ω ) = a ω2 3 - a1
Im(ω ) = a ω ω3 2 - a0 a Re(4) = 0 3 ω = (ta ly nghim dơng) t 1 1 a a Im(4) = 0 ω ; 2 ω = a = 0 1 a2 0 a
a ,a ,a ,a 0 0 1 2 3 >
H $n nh khi: ω < ω < ω a1 t1 a 2 a a a a 3 0 < 1 2
4.3.3 Tiêu chu:n *n nh t(n s Nyquist
Tiêu chu>n $n nh Nyquist ch& s2 dng xét $n nh cho h thng kín phn h#i ơn v
da vào !c tính tn biên pha (!c tính Nyquist) và tính cht $n nh ca h h. Phát biu:
a) Nu h thng h0 &n *nh:
- H thng kín s3 &n *nh nu ưng c tính t'n biên pha ca h thng h0 không bao
im Nyquist (-1,j0).
- H thng kín 0 biên gii &n *nh nu ưng c tính t'n biên pha ca h thng h0 i qua
im Nyquist (-1,j0).
- H thng kín không &n *nh nu ưng c tính t'n biên pha ca h thng h0 bao im Nyquist (-1,j0). 77
b) Nu h thng h0 không &n *nh: H thng kín s3 &n *nh nu ưng c tính t'n biên pha
ca h thng h0 bao im Nyquist (-1,j0) m l'n theo chiu ngưc chiu kim ng h khi ω thay
&i t5 0 n ∞; vi m là s nghim nm bên phi tr.c o ca phưng trình c tính h h0.
Hình 4.5: Minh h,a tiêu chu2n Nyquist cho ba
trưng hp h h0 &n *nh:
(1) H kín &n *nh
(2) H kín 0 biên gii &n *nh
(3) H kín không &n *nh
Ch+ng minh tiêu chu:n Nyquist: a) Khi h h $n nh:
Hàm truyn t ca h thng h có th biu di:n di dng: N( ) W (s) s = h D(s)
Trong ó N(s) và D(s) là các a thc theo s. h thng t#n ti và kh thi thì bc ca N(s) q bc ca D(s).
Hàm truyn t ca h thng kín: W (s ) W (s) h = k 1+ W (s) h
Phơng trình !c tính ca h h: D(s) = 0.
Phơng trình !c tính ca h kín: N( ) s ( D ) s + N( ) s D (s) 1 W + (s) =1 k + = = h D (s ) ( D ) s D (s)
Nghim ca phơng trình h kín chính là nghim ca phơng trình: D (s) k
= D(s )+ N (s ) = 0
Do bc ca N(s) q bc ca D(s) nên nu phơng trình !c tính h h có bao nhiêu nghim
thì phơng trình !c tính ca h kín cng có by nhiêu nghim. Gi s ơ !
là nghim ca phơng trình !c tính i là nghi m c a ph
ng trình c tính h h , s 'i
h kín, vi i=1,2,.., n. Khi ó: D (s) (s − s s − s s − s k 1' )( 2 ' )...( ') 1 +W ( ) s = = K. n
; K - là hng s. h ( D ) s (s − − − 1 s )(s 2 s )...(s s ) n
Thay s = jω ta có phơng trình !c tính tn s: D ( jω) ( jω − s jω − s jω − s k 1 ')( 2 ' )...( ') 1+ W ( jω ) = = K. n h D( jω )
( jω − s )( jω − s )...( jω − s ) 1 2 n Ta thy vectơ 1+ W (
!c trng cho mi quan h gia h h và h kín. Hàm W 4 h(j ) là h ω j )
hàm truyn tn s ca h h. ng cong W 4 ! h(j ) chính là
ng c tính t n biên pha c a h
h. Vectơ 1+W (j
ni tA im Nyquist (-1,j0) ti ng cong W 4 , góc bao im h ω ) h(j )
Nyquist (-1,j0) ca ng W 4 ơ + W . h ω h(j
) c ng chính là góc quay c a vect 1 ( j ) 78
Nu h h $n nh thì phơng trình !c tính D(s) = 0 có n nghim u nm bên trái trc
o. Theo nguyên lý góc quay: π n ∆arg ( D ω j ) = 0 ω < <∞ 2
H thng kín mun $n nh thì phơng trình !c tính W
k(s) = 0 c ng ph i có n nghi m
bên trái trc o, tc là: nπ ∆arg D ( ω j ) = k 0< ω<∞ 2
Khi ó góc quay ca vectơ 1 +W là: h ( j ω ) D ( j k ω ) π n π n ∆arg 1 [ +W ( j h ω)] = ∆arg = ∆ arg Dk ( ω
j ) − ∆ arg D( jω ) = − = 0 0 <ω <∞ 0<ω <∞ ( D ω j ) 0 <ω<∞ 0<ω<∞ 2 2
iu này xy ra khi ng !c tính tn biên pha ca h h không bao im Nyquist (-1,j0).
b) Khi h h không $n nh:
Trng hp h h không $n nh thì phơng trình !c tính D(s) = 0 có ít nht mt nghim
nm bên phi trc o. Gi s2 có m nghim nm bên phi trc o, còn (n-m) nghim còn li
nm bên trái trc o. Theo nguyên lý góc quay ta có: π π π ∆arg D( ω j ) = m − + (n − m) = (n − 2m) 0 ω < <∞ 2 2 2
H kín mun $n nh thì: nπ ∆arg D ( ω j ) = k 0< ω<∞ 2
Khi ó góc quay 1 +W ( j là: h ω ) nπ π ∆arg 1 [ W +
( jω)] = ∆argD ( jω) − ∆argD( jω) = − n ( − m 2 ) = mπ h k 0 ω < <∞ 0 ω < <∞ 0 ω < <∞ 2 2
Hình 4.6: Minh h,a tiêu chu2n Nyquist cho trưng hp h &n *nh
iu này #ng ngha vi ng !c tính tn biên pha W 4 phi bao m Nyquist (-1,j0) h(j ) i
mt góc úng bng m7 khi 4 bin thiên tA 0 n +6. Lu ý:
- Trc khi xét tính $n nh ca h thng kín thì phi kim tra xem h h có $n nh hay
không, bng cách gii phơng trình !c tính ca h h ho!c áp dng các tiêu chu>n $n nh i s. 79
- i vi các h thng có khâu tích phân lý tng thì h h có nghim cc nm trên trc π
o. áp dng tiêu chu>n Nyquist ta v? thêm mt cung tròn − γ
có bán kính vô cùng ln , 2
vi γ là s khâu tích phân lý tng trong hàm truyn t ca h h.
Ví d& 4.9: Cho h thng iu khin t ng có hàm truyn h h: 100 W (s) = (s + 2)(s + ) 3 (s + ) 5
!c tính tn biên pha ca h thng h nh sau:
Hãy xét tính $n nh ca h kín theo tiêu chu>n Nyquist. Gi i:
Phơng trình !c trng ca h h: (s + 2)(s + ) 3 (s + 5) = 0
Phơng trình có 3 nghim: s = −2 s = −
s = − ; u là các nghim thc âm nên h 1 ; 3 2 ; 5 3 thng h $n nh.
Ta thy h h $n nh và ng !c tính tn biên pha ca h h không bao im Nyquist (-
1,j0) nên theo tiêu chu>n Nyquist h thng kín tơng ng cng $n nh.
4.4 d tr1 *n nh
Mt h thng trên thc t không nhng cn phi $n nh mà còn phi t mc $n nh
cn thit. ánh giá mc $n nh ca h thng ngi ta a ra khái nim d tr biên
và d tr pha. Di ây là mt s khái nim: - Tn s c1t biên 4 4 4
c: là t n s t i ó biên
A( ) = 1, t c là L( ) = 0dB. - Tn s c1t pha 4 8 r
-7: là t n s t i ó góc pha (4) = - .
- d tr biên GM (Gain Margin) !c trng cho mc tip cn gii hn $n nh v
phơng din biên . 1 GM = ( A ω ) π − Hay GM = − ( L ω ) [dB] π − Ta thy khi (
A ω ) tng thì GM gim. Giá tr GM = 1 !c trng cho gii hn $n nh. M!t π −
khác biên A (ω ) chính là t s gia biên ca tín hiu ra và tín hiu vào hình sin, do ó
d tr biên cng biu th mc cho phép tng h s khuch i K ca h h mà v'n m bo cho h kín $n nh. 80
- d tr pha PM (Phase Margin) !c trng cho mc tip cn gii hn $n nh v phơng din góc pha. PM = 1800 + ϕ (ω ) c
d tr $n nh biên và pha ta có th xác nh tA ng !c tính Nyquist ho!c tA # th Bode.
Da vào c tính Nyquist:
TA giao im gia ng Nyquist và trc thc âm ta xác nh c biên 1 A(ω ) =
. Ta xác nh góc γ = PM tA giao im gia ng Nyquist và ng tròn ơn −π GM
v. Nu ng Nyquist nm hoàn toàn bên trong ng tròn ơn v thì PM = s. Nu ng
Nyquist không c1t trc thc âm thì GM = 1/0 = s.
Hình 4.7: Xác *nh d tr+ biên và góc pha t5 c tính Nyquist
Da vào th* Bode:
d tr biên GM c tính tA ng L(4) n trc hoành 4. d tr pha PM c
tính tA ng th@ng −π n ng cong ϕ (ω ) .
Hình 4.8: Xác *nh d tr+ biên và góc pha t5 th* Bode
Sau khi xác nh c d tr biên GM và d tr pha PM ca h h ta có th xét
$n nh ca h kín nh sau: h kín $n nh nu h h có d tr biên và d tr pha u dơng.
Trong thc t, m bo h thng hot ng $n nh thì:
- d tr biên: GM = 10 ÷ 15 dB.
- d tr pha: PM = 30 ÷ 600.
4.5 Phng pháp qu; o nghim s 4.5.1 Khái nim
Qu o nghim s là tp hp tt c các nghim ca phơng trình !c tính ca h thng
khi có mt thông s nào ó trong h thay $i tA 0 s. Phơng pháp qu o nghim s 81
thng c s2 dng khi h thng có mt thông s K ca phơng trình !c tính thay $i tA 0
n ∞. Khi thông s K thay $i, các nghim cc s? chuyn dch trên m!t ph@ng nghim s to
nên nhng qu o nghim, nu qu o nghim nm bên trái trc o thì h thng iu khin t ng s? $n nh.
Qu o nghim s c s2 dng kho sát s nh hng n cht lng h thng khi
thay $i thông s trong h. Ví d kho sát tính $n nh ca h thng khi h s khuch i hay
hng s thi gian thay $i tA 0 s.
4.5.2 Quy t"c v5 qu; o nghim s
Xét h thng có sơ # khi t$ng quát nh hình 4.9:
Hình 4.9: S khi t&ng quát
Phơng trình !c tính ca h: 1+ W ( ) s H (s) = 0
Mun v? qu o nghim s, trc tiên ta phi bin $i tơng ơng phơng trình !c tính v dng: M (s) 1+K
= 0 ; trong ó K là thông s thay $i. ( N ) s
N (s) + KM (s) = 0
Trong ó: M(s) là a thc bc m, có m nghim gi là nghim zero zj;
N(s) là a thc bc n, có n nghim gi là nghim cc s $ i, thông th ng n m.
Xây dng qu; o nghim s theo 8 quy t"c c0a Evans:
Quy t)c 1: Qu o nghim s i xng qua trc thc (vì các nghim phc luôn có tAng c!p liên hp).
Quy t)c 2: S nhánh ca qu o nghim s bng s bc ca phơng trình !c tính (bng n).
Các nhánh này b1t u khi K = 0 im s =
) là im cc ca phơng trình N(s) = 0. i ( i , 1 n
Trong ó có m nhánh kt thúc khi K s ti z =
)là nghim ca phơng trình M(s) = 0. j ( j , 1 m
Quy t)c 3: Qu o nghim s có n-m nhánh còn li kéo ra xa tn vô cùng khi K s.
Quy t)c 4: Góc xut phát ca các nhánh ti các im cc s = ) là: i ( i , 1 n m n θ = 0 180 +
arg(s − z ) − arg s ( − s ) i i j i j j =1 j=1 j ≠i
Quy t)c 5: Tim cn ca n-m nhánh kéo kéo ra vô cùng cùng c1t trc thc ti mt im: 1 n m 0 r = ( s − z ) n − i j m i 1 = j =1
Và hp vi trc thc mt góc: 82 2l +1 α = π ; l = , 0 ± , 1 2 ± n − m
Quy t)c 6: Các im trên trc thc s? thuc qu o nghim s nu t$ng s cc và zero bên phi nó là mt s lg.
Quy t)c 7: Các nhánh ca qu o nghim s c1t nhau ti nhng im th"a mãn: n m 1 1 =
i =1 s − s
j =1 s − z i j
Quy t)c 8: Giao im ca qu o nghim s vi trc o là nghim ca phơng trình: N ( jω K M jω c ) + c ( c ) = 0
Ví d& 4.10: Cho h h#i tip âm ơn v có hàm truyn h h: K W (s) = h s(s + 1)(s + 3)
Hãy v? qu o nghim s ca h kín vi 0 < K < ∞ Gi i
Phơng trình !c tính ca h thng: 1 + Wh(s) = 0 K 1+ = 0 s(s + 1)s + 3) s (s + ) 1 (s + ) 3 + K = 0
N (s) = s(s + ) 1 (s + ) 3 M(s) = 1 im cc: s
1 = 0, s2 = -1 , s3 = -3 im zero: không có.
Vy qu o nghim s có 3 nhánh xut phát tA s 1, s2, s3 và u kéo ra vô cùng.
on trên trc thc: ba nhánh ca qu o nghim s u cha nhng on trên trc thc
g#m on th@ng gia các im s = 0, = -1; và n2a ng th@ng bên trái m = -3. 1 s2 i s3
Góc gia tim cn và trc thc: (2l − ) 1 π (2l − ) 1 π (2 − ) 1 π − π π α = l = = α = ; ;π n −m 3 − 0 3 3 3
ng tim cn ca các nhánh #ng quy ti: 1 4 r = (0 1 − − ) 3 = − 0 3 − 0 3
Các nhánh ca qu o giao nhau trên trc thc (chính là im tách kh"i trc thc) là
nghim ca phơng trình: 1 1 1 + + = 0 s s +1 s + 3 3 2 s + 8s +3 =0 83 − 4 + 7 s =
: b loi vì không thuc on trên trc thc nào. 1 3 − 4 − 7 s = 2 3
Giao im ca qu o nghim s vi trc o: jω jω jω K c ( c + ) 1 ( c + ) 3 + c = 0 4 2 − ω + j (3 3 ω −ω ) +K = 0 c c c c − 4 2 ω + K = 0 ω = 0 ω c = ± 3 c c c ; 3ω − 3 ω = 0 K =0 K c = 36 c c c
Hình 4.10: Qu o nghim s ca ví d. 4.10
Qu o nghim s giao vi trc o ti 3 im: s = 0 (gc ta , tơng ng vi K = 1 c
0); và s = ± j 3 (tơng ng vi Kc = 36). 2,3
Qu o nghim s ca h thng nh hình 4.8. Nhìn vào qu o nghim s ta thy:
- Vi 0 < K < 36: qu o nghim s nm hoàn toàn bên trái trc o, h thng $n nh.
- Vi K = 0, ho!c K = 36: các nghim cc nm trên trc o, h thng biên gii $n nh.
- K > 36: qu o nghim s nm bên phi trc o, h thng không $n nh.
4.6 Kh o sát ch)t lng h thng iu khin
,n nh là iu kin cn i vi mt h thng iu khin t ng, nhng cha phi là iu
kin mt h thng c a vào s2 dng. Trong thc t, h thng còn phi #ng thi
th"a mãn nhiu yêu cu khác, bao g#m các ch& tiêu cht lng trng thái xác lp và trng thái
quá . Sau ây là mt s tiêu chu>n thng dùng ánh giá cht lng h thng iu khin
4.6.1 Ch4 tiêu ch)t lng . trng thái xác l3p
Trng thái xác lp ca h thng c ánh giá bng sai lch tnh (còn gi là sai s xác lp)
ca h iu khin. ó là giá tr sai lch còn t#n ti sau khi quá trình iu khin ã kt thúc. Ch&
tiêu v chính xác ca iu khin này do yêu cu ca quy trình công ngh !t ra mà h thng
iu khin nht thit phi áp ng c. Giá tr sai lch tnh theo lý thuyt c ký hiu là δ
và c tính theo công thc: 84 δ =lim ( e t) (4.7) t→∞
Trong ó: e(t) là sai lch ng t#n ti trong quá trình iu khin.
xác nh sai s xác lp ca h thng có th s2 dng nh lý mi liên h gia gii hn
ca hàm gc và hàm nh trong chuyn $i Laplace. Mi liên h ó c bi:u di:n qua công thc:
δ = lime(t) = lim sE(s) (4.8) t→∞ s 0 → Y ( ) s W (s) W ( ) s Ta có: W (s) h = = Y ( ) s h = R(s) R(s)
1+ W (s)H (s )
1+W (s)H (s) h h M!t khác: W ( ) s
E(s) = R( ) s − H ( ) s Y (s) = ( R ) s − H ( ) s h R (s ) 1 W + (s)H( ) s h R( ) s E( ) s = 1+ W ( ) s H ( ) s h R( ) s Do ó: δ = lims (4.9) s 0 →
1+W (s)H (s) h Nh3n xét
- Sai lch tnh xác nh chính xác tnh ca h.
- Sai lch tnh ca h ph thuc vào cu trúc, thông s ca h, và ph thuc vào tín hiu u vào.
- Nu h thng có phn h#i âm ơn v thì: R(s) δ = lim s (4.10) s 0 → 1 +W (s) h
Ví d& 4.11: Cho h thng iu khin có sơ #: s 2 + 10 s s ( + ) 5 0 ( s 1 . + ) 1
Hãy tính sai s xác lp ca h khi bit: a. r(t) = 1(t) b. r(t) = t c. 2 r(t) = t Gi i: 85 1 a. r(t) = ( 1 t) R(s) = s
Áp dng công thc (4.10) cho h có phn h#i âm ơn v, ta có: R( ) s 1 1 δ = lim s = lims s 0 → 1 + W ( ) s 0 → s s 2s + 10 h 1+ s(s + )( 5 0 1 . s + ) 1 1 δ = = ∞ 10 1 + 0 1
b. r(t) = t ( R ) s = 2 s R( ) s 1 1 δ = lim s = lims s 0 → 1 + W ( ) 2 s 0 → s s 2s + 10 h
1 + s(s +5)( .01s + )1 1 1 1 δ = lim = = → s 0 2s +10 10 2 s + 0 + (s + ) 5 (0 1 . s + ) 1 5 2 c. 2
r(t) = t ( R ) s = 3 t R( ) s 2 1 δ = lim s = lims s 0 → 1 + W ( ) 3 s 0 → s s 2s + 10 h
1 + s(s + )5(0 1.s + )1 2 2 2 δ = lim = = = ∞ → s 0 s s 2 (2 +10) 0 s + 0 + 0 ( s + ) 5 (0 1 . s + ) 1 5
4.6.2 Ch4 tiêu ch)t lng . trng thái quá
Trng thái quá ca h thng c ánh giá bng mc dao ng và thi gian quá .
Có rt nhiu phơng pháp ánh giá cht lng trng thái quá nhng ây ch& phân tích tính
$n nh ca h thng da trên !c tính hàm quá .
Xét !c tính hàm quá bt kQ xác nh các ch& tiêu cht lng trng thái quá nh hình 4.9 - quá i u ch nh
Hin tng quá iu ch&nh là hin tng áp ng ca h thng trong quá trình quá vt
quá giá tr xác lp ca nó. quá iu ch&nh (Percent of Overshoot - POT) c xác nh bi
tr s cc i ca hàm quá so vi tr s xác lp ca nó: y − y σ % max ∞ = .10 % 0 (4.11) y ∞ - Th i gian quá (Settling Time) 86
Thi gian quá t A i $ s là kho ng th i gian c xác nh t th i m có s thay i u
vào n khi áp ng u ra lt hoàn toàn vào hành lang gii hn sai s cho phép ∆
Ví d: ∆ có th là ± % 2 y , ± 5% …` ∞ y∞
Hình 4.11: Các ch- tiêu cht lưng ca h thng
- Th i gian t ng t c: (Rise Time)
Thi gian lên t = t là thi gian áp ng ca h thng tng tA 10% n 90% giá tr xác r rise lp ca nó. - Th i gian lên nh:
Thi gian lên &nh t = t
là thi gian áp ng ra t giá tr cc i. p peak
Thông thng h thng iu khin cn phi áp ng càng nhanh càng tt. Tuy nhiên, i
vi các h thng có quán tính ln, áp ng nhanh thng d'n n quá iu ch&nh cao. Do
ó, dung hòa gia thi gian áp ng và quá iu ch&nh là vn phi quan tâm khi thit k
h thng iu khin t ng. Quy nh cho cht lng mt h thng iu khin thng là:
σ % =10 ÷ 20% và t = 2 ÷ 3 chu kQ dao ng quanh giá tr xác lp. s BÀI T2P CHƠNG 4
1. S2 dng tiêu chu>n Routh, Hurwitz kim tra tính $n nh ca h thng có sơ # khi sau: 50 a. W ( ) s = s( 2 s + 8s + 24) 3s + 1 b. W ( ) s = 2 s 1 ( 00 2 s + 200s + ) 1 18 c. W ( ) s =
s(s + 2)(s + 4) 87 0 5 . (s + 2) d. W (s ) = s(s + . 0 2)(s + 0 ) 5 . (s + ) 3
2. S2 dng tiêu chu>n Mikhailov kim tra tính $n nh ca h có a thc !c trng sau: a. ( D ) 3 s = s + 5 2 s + 8s +1 b. ( D ) s =12 4 s +5 3 s + 3 2 s + 8s +1 c. ( D ) 4 s = s 1 + 0 3 s + 7 2 s + 2 s +1
3. Cho h thng có sơ #:
V? qu o nghim ca h khi K bin thiên tA 0 → ∞ a. W ( ) K s = ; H(s) = 1 s( 2 s + 4s + 1 ) 1 K (s + 9) b. W (s ) = ; H(s) = 1 s( 2 s + 4s + 1 ) 1 K (s + 0 2 . ) c. W (s ) = ; H(s) = 1 2 s (s + . 3 6)
4. Cho h thng có sơ # nh sau: K 1 s ( + ) 1 (s + 2) s
Hãy tìm K h thng kín $n nh. 88
CHƠNG 5: THIT K B IU KHIN
5.1 M&c ích iu khin
Nh trong chơng 4 ta ã xét n tính $n nh ca mt h thng iu khin t ng, $n nh là
iu kin cn i vi mt h iu khin t ng. Tuy nhiên, mt h iu khin t ng $n nh
có th cha chính xác, sai lch iu khin ln, hay nói cách khác là chính xác iu khin
kém, quá trình quá có th quá dài, thi gian quá có th kéo dài gây ra tác ng chm,
dao ng ca h khi tin n trng thái xác lp ln d'n n t$n tht nng lng ca h
thng. Vì vy có th có nhiu yêu cu cùng mt lúc c !t ra khi h thng làm vic vi mt
tín hiu nht nh nào ó, vic kho sát và ánh giá cht lng và ci thin cht lng ca h
thng iu khin là ni dung chính ca chơng này.
Khi kho sát quá trình iu khin ca các h $n nh, ngi ta dùng tín hiu vào có dng
thng g!p hay mt dng tác ng. Cht lng ca h thng iu khin t ng c ánh giá
qua ch& tiêu tính $n nh và các ch& tiêu cht lng khác nhau ca quá trình xác lp và quá
trình quá . Sau ây, ta phân tích mt h h#i tip iu khin cơ bn. Hình 5.1a biu di:n cu
trúc mt h h#i tip, trong ó: (
u t) là tín hiu u vào.
y(t ) là tín hiu u ra. (
e t ) là sai lch u vào. W
là hàm truyn t ca b iu khin. k ( s ) W
là hàm truyn t ca i tng iu khin. t (s ) W
là hàm truyn t mô t thit b o tín hiu (cm bin-sensors). s (s )
n , n , n là các tín hiu nhi:u (không mong mun) tác ng vào h. v r d
Trong trng hp ơn gin hơn, khi tín hiu nhi:u u vào i tng n có th b" qua, v
cng nh các thit b o tín hiu là lý tng W
thì cu trúc h h#i tip s? c rút gn s (s ) = 1 nh Hình 5.1.b mô t. n n v r (rt) (e )t y(t) W W ( s t ) k (s) yht (t) nd Ws (s) nr (rt) (e )t y(t) W Wt( s) k (s)
Hình 5.1: S cu trúc h hi tip vi mt mch vòng 89
H h#i tip vAa trình bày trên là h có cu trúc mt mch vòng iu khin ơn gin nht.
Vy mt mch vòng iu khin cn phi m bo nhng yêu cu gì? 1. Th nh t là n
nh: Tín hiu u vào
u (t) là tín hiu !t trc. Ngi s2 dng !t
trc giá tr mong mun ó di dng giá tr ca tín hiu vào u(t) = a . H làm vic t yêu cu
phi là h mà sau mt khong thi gian cn thit có c tín hiu ra (
y t) ging nh giá tr !t trc:
lim y (t )= a (5.1) t→∞
Rõ ràng là có c (5.1) thì tín hiu ra y (t ) trc ht phi tin n mt hng s (có ch
xác lp), nói cách khác quá trình quá ca h phi t1t dn, hay h phi $n nh. Tuy nhiên
cn phi chú ý rng khi h $n nh thì có th y(t ) tin n mt hng s không mong mun. 2. Th hai là sai l ch t nh ( e t) b ng 0 ho c bám c theo tín hi u t: Yêu cu h $n
nh mi ch& xác nh c là y(t ) s? tin n mt hng s. Song vic hng s ó có bng giá
tr mong mun a y hay không thì cha c m bo. ch1c ch1n có c giá tr mong
mun a u ra thì h phi th"a mãn: lim e(t) = 0 (5.2) t→∞
Trong khi yêu cu (5.1) mi ch& có th có c nu nh tín hiu u vào u(t) = a là hng
s thì ngi ta thng mong mun (5.2) luôn luôn c th"a mãn vi mi tín hiu vào khác
nhau. Hai dng tín hiu lnh thng c quan tâm là:
u (t ) = 1(t ) và ( u t ) = t
Nhng cng phi nói thêm là ngoài hai dng tín hiu trên, khó mà có th áp ng c yêu
cu (5.2) cho mt tín hiu vào u(t) bt kQ. R nhng trng hp rng m hơn, ta có th tìm
c b iu khin W
sao cho vi nó h kín có tín hiu ra gn ging tín hiu vào theo nh k (s ) ngha. y( )
t − u(t) < ε (5.3)
Trong ó, ε là mt hng s dơng nh". Bài toán mang n cho h thng kh nng tín
hiu ra y (t ) bám c theo tín hiu lnh u vào (
u t) nh (5.3) mô t có tên gi là iu khin
bám (tracking control). Ý ngha chu>n sai lch trong (5.3) có th là chu>n bc hai ho!c chu>n
vô cùng tùy theo tAng yêu cu c th ca tAng bài toán. 3. Th ba là tính
ng h c ph i t t: Yêu cu (5.2) mi ch& gii quyt v tính cht tnh ca
h thng. Nhng yêu cu chi tit hơn ca h th hin qua quá trình (
y t) tin ti giá tr mong mun a hay sai lch (
e t) tin v 0 nh th nào c gi là các yêu cu v tính ng hc. Chúng có th là:
- Yêu cu quán tính cn có ca h thng, v thi gian quá trình quá .
- Yu cu có hay không quá iu ch&nh, v min dao ng cho phép ca các giá tr trng thái, các tín hiu…
4. Th t là b n v ng: H phi làm vic không nhng t cht lng ã ra mà còn phi
gi c cht lng ó cho dù:
- Có bt c mt s thay $i nào không lng c trc xy ra bên trong h thng (mô hình tham s thay $i).
- Có s tác ng ca nhng tín hiu nhi:u không mong mun. 90
5. Cu i cùng là t i u: ây là mt trong các yêu cu nâng cao, òi h"i rng h không nhng
t c ch& tiêu cht lng ra mà còn phi t c mt cách tt nht. Ch@ng hn nh
công sut t$n hao cho quá trình quá là ít nht, thi gian xy ra quá trình quá là ng1n nht…
Nhng tiêu chu>n trên là các chi phí cn phi t c ca mt h thng iu khin. Phân
tích h h#i tip có nhim v kim tra xem nhng tiêu chu>n gì h ã có, nhng gì cha t
c còn b$ sung. Mun b$ sung hay mang n thêm cho h thng cht lng mi thì phi
xác nh c nhng tham s gì, các khâu cơ bn nào nh hng trc tip n nhng tiêu
chu>n ã nêu, tA ó bit c phi b$ sung nh th nào thông qua b iu khin W . k ( ) s
5.2 Bài toán t*ng hp h thng
Bài toán t$ng hp h thng hay iu khin h thng c hiu là bài toán can thip vào i
tng iu khin hiu ch&nh, bin $i sao cho nó có c cht lng mong mun. ó là
toàn b quá trình phân tích, tính toán, la chn b$ sung các thit b phn cng cng nh thut
toán phn mm vào h thng cho trc h thng ó khi hot ng th"a mãn yêu cu v cht
lng ã ra nh tính $n nh, chính xác, áp ng quá … thc hin c iu này
cn phi n1m vng v thit b iu khin, o lng và thit b chp hành, cng nh phi có
hiu bit v quy trình công ngh, môi trng làm vic, !c trng ca tAng h thng iu khin
mà ta xây dng. Nh vy rõ ràng khi thc hin mt bài toán iu khin, ta cn phi tin hành
các bc sau ây (Hình 5.2):
1. Xác nh kh nng can thip tA bên ngoài vào i tng. Vì
i tng giao tip vi môi trng bên ngoài bng tín hiu
vào-ra nên ch& có th thông qua tín hiu vào-ra này mi có th
can thip c vào nó. Nh vy phi hiu rõ bn cht tín hiu
i tng là tin nh, ng'u nhiên hay không liên tc.
2. Sau khi ã hiu rõ bn cht, phơng tin can thip i tng
thì bc tip theo phi xây dng mô hình mô t i tng.
Hình thc mô t c dùng nhiu trong iu khin là mô hình
toán hc biu di:n mi quan h gia tín hiu vào-trng thái-tín hiu ra.
3. Vi mô hình toán hc ã có, tip theo ta phi xác nh xem
i tng hin ã có nhng tính cht gì, các !c tính nào cn
phi s2a $i và s2a $i nh th nào h có c cht lng
nh mong mun. Nói cách khác là phi phân tích h thng và
phi ch& rõ tAng nhim v ca s can thip.
4. Khi ã xác nh c tAng nhim v c th cho vic can thip
ta s? tin hành thc hin vic can thip ó mà c th là phi
xác nh tín hiu kích thích u vào mt cách thích hp, ho!c
phi thit k b iu khin to ra uoc tín hiu u vào thích hp ó.
5. Cui cùng phi ánh giá li cht lng ca kt qu can thip
khi chúng làm vic thc vi i tng. Nu iu ó cng mang Hình 5.2: Trình t các bưc
li cht lng nh mong i thì ta kt thúc bài toán iu khin.
thc hin mt bài toán iu
Ngc li, ta phi quay li tA u. khin 91
Có nhiu cách b$ sung b iu khin vào h thng cho trc, trong khuôn kh$ giáo trình này
chúng ta ch yu xét hai cu trúc sau:
iu khin h#i tip u ra bng cách thêm b iu khin ni tip vi i tng iu khin
và tín hiu ra c phn h#i li. B iu khin c s2 dng có th là b bù sm pha (Phase -
Lead), bù tr: pha (Phase - Leg), bù sm tr: pha (Phase - Lead Leg), iu khin t l (P), iu
khin t l tích phân (PI), iu khin t l vi phân (PD), iu khin t l vi tích phân
(PID)…Trong giáo trình này s? ch& i sâu vào b iu khin PID, mt b iu khin cơ bn và
c ng dng rng rãi hin nay. r (t) e(t ) u(t ) ( y t) W Wt (s) k(s)
Hình 5.3: iu khin hi tip 'u ra
iu khin h#i tip trng thái, theo phơng pháp này tt c các trng thái ca h thng
c phn h#i tr v u vào và tín hiu iu khin có dng u(t) = ( r ) t − K ( x t ). Tùy theo cách
tính vector h#i tip trng thái K mà ta có phơng pháp iu khin gán im cc, iu khin ti u LQR… y r t u(t) x t (t) ( ) ( ) x(t) = ( Ax t )+ Bu( ) t
Hình 5.4: iu khin hi tip trng thái
Quá trình thit k h thng là quá trình òi h"i tính sáng to do trong quá trình thit k
thng có nhiu thng s phi la chn. Ngi thit k cn phi hiu c nh hng ca các
khâu hiu ch&nh n cht lng ca h thng và bn cht ca tAng phơng pháp thit k thì
mi có th thit k c h thng có cht lng tt. Do ó các phơng pháp thit k trình bày
trong chơng này ch& mang tính gi ý, ó là nhng cách thng c s2 dng ch không phi
phơng pháp b1t buc phi tuân theo. Vic áp dng mt cách máy móc thng không t c
kt qu mong mun trong thc t. Dù thit k theo phơng pháp nào yêu cu cui cùng v'n là
th"a mãn cht lng mong mun; các thit k, cách la chn thông s không quan trng.
5.3 Các quy lu3t iu khin c b n
B iu ch&nh (hay khâu hiu ch&nh) chính là các b iu khin ơn gin c s2 dng
bin $i hàm truyn ca h thng nhm ci thin !c tính ng hc ca h, làm cho h thng
có áp ng th"a mãn các yêu cu cht lng nh trc. ( e t ) u(t )
Tín hiu vào ca b iu ch&nh là tín hiu sai lch (et) và tín hiu ra ca b iu ch&nh là tín hiu iu khin (
u t) . Sơ # t$ng quát ca các b iu ch&nh có th biu di:n ơn gin nh hình v? trên. 92
Theo loi tín hiu làm vic ngi ta chia thành ba loi chính là b iu ch&nh liên tc, b
iu ch&nh on-off (hai v trí, ba v trí…), và b iu ch&nh s. B iu ch&nh liên tc có th thc
hin bng các cơ cu cơ khí, thit b khí nén, mch in RC, mch khuch i thut toán. B
iu ch&nh on-off thng c thc hin bng các mch rơle in tA, rơle khí nén, chơng
trình PLC. B iu ch&nh s c thc hin bng các chơng trình phn mm chy trên vi x2 lý hay máy tính PC.
Ni dung phn này gii thiu các lut iu khin liên tc in hình bao g#m b P, I, D, PI,
PD, PID. Trong thc t, các hãng sn xut thit b t ng thng cung cp các b iu ch&nh
PID thơng mi ch to bng mch khuch i thut toán. Các b PID c thit k to sPn
này rt tin dng. Ngi s2 dng có th chn các ch iu khin P, I, D, PI, PD, PID tùy
theo yêu cu bng cách t1t m các thành phn chc nng tơng ng.
5.3.1 Lu3t iu khin t4 l (lu3t P)
Lut iu khin t& l to ra tín hiu iu khin u(t) t& l vi tín hiu sai lch e(t).
Phơng trình vi phân: u(t) = K e. P (t)
K : gi là h s khuch i. P Hàm truyn: U s W s = = K P ( ) ( ) E (s ) P
Hàm !c tính tn: W jω = K P ( ) P
!c tính thi gian và !c tính tn s tơng t nh khâu t& l trong chơng 3.
Biu di:n b iu ch&nh P: Bên cnh cách ghi hàm truyn, ngi ta còn dùng cách !t #
th hàm quá , vào trong sơ # khi th hin trc quan !c tính ng hc nh các hình v? di ây: KP e(t ) u (t ) e (t ) u(t ) K P Ho!c
B P bng khuch i thut toán: R B P kiu o 2 W = = P (s )
U 0 (s ) K 1 R U (s) P i R u 2 K = − i u P o 1 R 93 B P kiu không o 2 R W = = P (s ) U 0 (s ) U ( ) K s P i R u 2 K = 1+ i u P R o 1 1 R R
B P kt hp b so in áp R R 2 W = = P (s ) U u (s ) R K 1 U − r ( ) s U ( ) s P y u R r 2 R K = u u P y R u 1 R
B P kt hp b so dòng in 1 R 2 R W = = P (s ) U u (s ) U − r (s ) U ( ) K s P y u r 1 R u 2 R y u K = − u P 1 R
5.3.2 Lu3t iu khin tích phân (lu3t I)
Lut iu ch&nh tích phân to ra tín hiu iu khin u(t) t& l vi tích phân ca tín hiu sai lch e(t).
Phơng trình vi phân: u(t) = K e I (t)dt Hàm truyn: 1
W (s) U (s ) KI = = = I E(s) s T s .I
K : Hng s tích phân I 1 T =
: Hng s thi gian tích phân I KI
!c tính thi gian và !c tính tn s tơng t nh khâu tích phân trong chơng 3.
Biu di:n b iu ch&nh I: KI e(t ) K u ( e t) ( u t) I (t) s Ho!c 94
B I bng khuch i thut toán: C B I kiu o V s K 0 I R W = = I ( ) ( ) s Vi( ) s s u 1 i u K = − o I RC R B I kiu không o 1 W 0 = = I ( ) U (s) K s I U i (s ) R s R 2 1 2 K = I u R C 1 i uo C R2
5.3.3 Lu3t iu khin t4 l - tích phân (lu3t PI)
Lut iu khin PI là cu trúc ghép song song ca khâu P và khâu I. Tín hiu ra ca b PI
là t$ng tín hiu ra ca hai khâu thành phn.
Phơng trình vi phân: u(t)= K . + P
(et ) KI (et)dt Hàm truyn: + W = = + = PI (s ) U (s) K K s K I P I E( ) K s P s s Ho!c 1 . 1 U s T s W s K K 1 PI ( ) ( ) + = = I = + E(s) P P T s . sT I I KP T =
: Thi gian hiu ch&nh hay thi gian tác ng tr: I K I !c tính thi gian: - Hàm quá : h(t ) 1 1 H (s) W s K K PI ( ) =
= p + I =K + 2 P s s s s s T 2 I KI ( KP t h t) =K +K t. = 1 +t K P I P T − T h I I
Hình 5.5: Hàm quá ca b PI !c tính tn s: - Hàm !c tính tn: 95 1 K W j K j K 1 j PI ( ω ) = − I = − P ω P T ω I => ( K
P ω ) = K ; Q(ω ) P = − p T ω I - Biên : M(ω ) 2 = P (ω ) 2 + Q (ω ) KP = 1 + (ω T )2 ω. I TI (
Lω ) = 20 lg M(ω ) = 20 lg K − 20 lgω T + 20lg + ω T P I ( I )2 1 - Góc pha: Q ω 1 K ϕ (ω ) ( ) = I arctan arctan arctan P (ω ) = − = − K ω T ω P I Khi ω π = 0 thì ϕ (ω )= − 2
Khi ω = ∞ thì ϕ (ω ) = 0
Tín hiu ra luôn tr: pha so vi tín hiu vào mt góc tA 0 n π / 2 tùy thuc vào giá tr
ca các tham s K , K và tn s ω ca tín hiu vào. Do ó b PI c xp vào loi iu P I
ch&nh tr: pha. M!t khác, b PI còn có tính cht ca mt b lc thông thp: ch& cho tín hiu vào
tn s thp i qua, tín hiu tn s cao nhanh chóng b suy gim. L (ω ) [dB] j ( Q ) ω − 2 d 0 B / dec K P ( ) ω P 20lg K l ( g ω )[de ] c o ω → ∞ − 45 / 1 T ω I GPI ( ω j ) ϕ (ω) [o] l ( g ω )[de ] c ω o − 45 − KP o − 90 ω = 0
Hình 5.6: Biu Bode ca b PI
Hình 5.7: Biu Nyquist ca b PI Biu di:n b PI KP e( ) t u (t) (et ) ( u ) t Ho!c K / s I
B PI bng khuch i thut toán 96
B PI kiu o, loi 1 1 R 2 R C 1 + W 0 = = + = PI ( ) U (s ) K sT s I I Ui (s) K K P s P sTI u i 1 u R2 o K = − ; K = − T ; = R C P 2 R I R C I 1 1
B I kiu không o, loi 2 2 R C 1 + W 0 = = + = PI ( ) U (s ) K sT s I I Ui (s) K K P s P sTI u R 1 i uo K 2 =1+ ; K = T ; = + P I I (R R 1 2 )C 1 R R R C 1 1 R
B PI kiu o, các thông s iu 2 C ch&nh c lp 1 R +1 W 0 = = + = PI ( ) U (s) K sT s I I U i(s) K K P s P sT u I i uo R R K 2 = − ; K 2 = − ;T = R C 3 R P R I R R C I 3 1 1 3
5.3.4 Lu3t iu khin t4 l - vi phân (lu3t PD)
Lut iu khin t& l - vi phân c to ra bng cách ghép song song khâu P và D. Tín hiu
ra ca b PD là t$ng tín hiu ca hai khâu thành phn.
Phơng trình vi phân: u (t ) =K e. . . . P (t ) d ( e t) +K =K D P ( e t) de (t ) +T dt D dt KD T =
: gi là thi gian tác ng sm (vt sm). D K P Hàm truyn: W = = + PD (s ) U (s) P D E (s ) K K s Ho!c: W = 1+ PD (s) KP ( T s D ) !c tính thi gian: - Hàm quá : ( h t ) 1
H (s) W (s ) K = = p PD +K =K + D P T D s s s ( h t ) = K 1 + δ P (t ) K D (t ) KP t
Hình 5.8: Hàm quá ca b PD 97
Ta thy, trng thái xác lp, b PD làm vic nh b P. R trng thái chuyn tip, nó làm
vic nh b D, tc là tín hiu ra u(t) t& l vi o hàm ca tín hiu vào e(t). !c tính tn s - Hàm !c tính tn: W = 1+ . PD ( jω ) KP ( T jω D ) => ( P ω ) = K ; ( Q ω) = K T ω p P D - Biên : M (ω) 2 = P (ω) 2
+ Q (ω) = K 1+ T ω P ( D )2
Khi ω = 0 thì M (ω) = K P
Khi ω = ∞ thì M (ω )= ∞
L (ω ) =20lg M (ω ) = 20lg K +20lg + T ω P ( D )2 1 Khi 2 2 1
ω T << 1, tc là ω << thì (
L ω ) = 20lg K là tim cn ngang. D T P D Khi 2 2 1
ω T >> 1, tc là ω >> thì (
L ω ) = 20 lg K + 20 lgωT là tim cn xiên có dc D T P D D +20dB/dec. - Góc pha: ϕ (ω ) Q (ω ) K T P D ω = arctan = arctan = arctan (T ω D ) P (ω ) K P Khi ω = 0 thì ϕ (ω )= 0
Khi ω = ∞ thì ϕ (ω ) =π / 2 ( L ω ) [d ] B jQ(ω ) ω =∞ K P + 20dB / dec 20lg K lg(ω)[dec] G PD ( jω ) P (ω ) ω =1/T ω h D ω = 0 ϕ (ω ) [ ]
Hình 5.10: Biu Nyquist ca b PD o 90 o 45 lg(ω )[dec] ω
Hình 5.9: Biu Bode ca b PD
Tín hiu ra ca b PD luôn sm pha hơn so vi tín hiu vào mt góc tA 0 n π / 2 tùy
thuc vào giá tr các tham s K , K và tn s ω ca tín hiu vào. Do ó b PD c xp vào P D 98
loi iu ch&nh sm pha. M!t khác, b PD còn có tính cht ca mt b lc thông cao: ch& cho
tín hiu vào tn s cao i qua, tín hiu tn s thp nhanh chóng b suy gim. Biu di:n b PD K P K P e(t) u( ) t Ho!c (et ) (ut) KD K s . D
B PD bng khuch i thut toán B PD kiu o 2 R W 0 = = + PD (s ) U (s ) K K s 1 R U i(s) P D R2 u K = − ; K = −R C i C P D 2 u R o 1 C
B PD/PDT1 kiu o (khâu sm pha, 0 1 C T >
). B PDT1 kiu o (khâu tr: pha, D 1 T ) R T1 > T 1 R D 0 U s 1 + . s T u W = = PDT ( ) 0 ( ) s K D i 1 U + i (s ) P 1 . s T u 1 o 1 R K = ;T = R C P D 0 0 0 R
B PD/PDT1 kiu không o (khâu sm R1 pha) + W = = PDT ( ) U0 (s) 1 . s T s K D 1 U + i (s ) P u C 1 . s 1 T i 0 uo K = ; 1 T = + = P D ( 0 R 1 R )C ; T R C R 0 1 0 0 0
5.3.5 Lu3t iu khin t4 l - vi tích phân (lu3t PID)
Lut PID c to bng cách ghép song song ba khâu: P, I và D.
Phơng trình vi phân: u(t) = K e. + + . P (t) K e I (t) de(t) dt K D dt
Hay u (t ) =K e P ( ) +K t I e (t ) KD de(t) dt + K K dt P P
K : h s khuch i ca b iu ch&nh PID P 99 -1
K : tc tích phân hay h s tích phân (s ) I
K : h s vi phân hay h s thi gian vi phân (s) D K 1 I =
vi T gi là thi gian hiu ch&nh hay thi gian tác ng tr: K T I P I
KD = T : thi gian tác ng sm D K P
Hàm truyn ca b PID có th biu di:n theo nhiu cách: Cách 1: 2 + + W = + + = PID (s ) K K s K s K K I K s D P I P D s s Cách 2: 2 1 1+ + W = 1 + + = PID (s ) TI s TITDs K T s K P T s D P T s I I Cách 3: 1 + 1+ W 1 2 = PID (s ) ( T s)( T s) KR s Trong ó: K P K =
; T = T + T ; T .T = T .T R I 1 2 I D 1 2 TI !c tính thi gian - Hàm quá : h(t ) H (s ) W s K K PID ( ) p I = = + + K 2 D s s s K I
h (t ) = K .1 + . + δ. P (t ) K t K I D (t) K P t TI
Hình 5.11: Hàm quá ca b PID !c tính tn s
Biu # Bode và biu # Nyquist ca b PID c th hin trên hình 5.12 và hình 5.13. ( L ω)[dB] j ( Q ω ) − d 20 B / dec ω = ∞ 20 lg KR K lg(ω)[ P de ] c 1/ 1/T ω 1 T 2 P(ω ) ϕ (ω )[o ] o + 90 lg(ω)[de ] c ω o − 90 ω = 0
Hình 5.12: Biu Bode ca b PID Hình 5.13: Bi u Nyquist c a b PID 100 Ưu im ca b PID
- Nu sai lch e(t) càng ln thì thông qua thành phn u
, tín hiu iu khin u(t ) càng P (t )
ln (vai trò ca khuch i K ). P - Nu sai lch (
e t) cha bng 0 thì thông qua thành phn u
, PID v'n còn to tín hiu I (t )
iu khin (vai trò ca tích phân K ). I
- Nu tc thay $i ca sai lch e(t) càng ln thì thông qua thành phn u , phn ng D (t)
thích hp ca u(t) s? càng nhanh (vai trò ca vi phân K ). D Biu di:n b PID K P K T ,T P I D ( e t) u (t) e(t ) u(t ) K / s I Ho!c K .s D
B PID thc hin bng khuch i thut toán - Hàm truyn: C C 1 R2 2 W = + + PID (s ) K K I K s P R s D 1 Trong ó: ui R C + R C 1 1 1 2 2 u K = − ; K = − o P I 1 R C2 R1C2 K = R − C D 2 1 R R
B PID/PIDT1 kiu song song, không o, 1 1
các thông s iu ch&nh c lp W = = + + PID (s ) V s 1 . 0 ( ) K 1 s TD V (s) P + i . s TI 1 . R s T 2 C2 1 R R 5 6 6 R R K = ;T = R C 5 P I 2 2 5 R R5 C R T = = D R C ; 3 R T R C 4 3 3 3 1 4 3 u o u i
Di ây là hình dáng ngoài và sơ # cu trúc mt b iu ch&nh PID thc t, c ch to
bng các mch khuch i thut toán. Cu trúc b PID g#m bn nhóm phn t2: nhóm phn t2
so sánh tín hiu vào/ra, nhóm phn t2 !t ch&nh h s khuch i, nhóm phn t2 P-I-D, cui
cùng là nhóm mch cng tín hiu và khâu bão hòa gii hn gii giá tr tín hiu iu khin
u(t) xut ra (0…10V ho!c -10…10V). Cu trúc này cho phép iu ch&nh tAng thông s K , P
K , K ca b PID mt cách riêng bit, c lp. I D 101
Hình 5.14: Cu trúc mt b iu ch-nh PID 102 1 Ngu#n 24V 2 Mass ngu#n (0V) 3
Ngu#n cp cho cm bin 15V 4
Mass ngu#n ca cm bin (0V- analogue ground) 5
u vào tín hiu vào chu>n (giá tr !t-set point) 6
u vào tín hiu h#i tip (giá tr thc qua o lng) 7
im so sánh (im t$ng hp các tín hiu u vào) 8
èn báo tín hiu vào vt mc gii hn 9
im o kim tín hiu vào chu>n 10
im o kim tín hiu h#i tip 11
im o kim tín hiu sai lch 12
im o kim u ra t& l (P) 13
im o kim u ra tích phân (I) 14
im o kim u ra vi phân (D) 15 Nút xoay ch&nh tinh KP 16 Nút xoay chn thô KP 17
èn ch& báo có tín hiu u ra P 18 Nút xoay ch&nh tinh KI 19 Nút xoay chn thô KI 20
èn ch& báo có tín hiu u ra I 21 Nút xoay ch&nh tinh KD 22 Nút xoay chn thô KD 23
èn ch& báo có tín hiu u ra D 24
im t$ng hp tín hiu ra 25
Nút offset tín hiu ra (tín hiu iu khin u) 26
Nút chn khong gii hn bão hòa tín hiu ra. 27
u ra ca b iu ch&nh (tín hiu iu khin u)
5.4 Mt s phng pháp t*ng hp b iu khin PID
B iu khin PID c s2 dng rt rng rãi trong thc t iu khin nhiu loi i
tng khác nhau nh nhit lò nhit, tc ng cơ, mc cht l"ng trong b#n cha…do nó
có kh nng làm trit tiêu sai s xác lp, tng tc áp ng quá , gim quá iu ch&nh
nu các thông s ca b iu khin c la chn thích hp. Do tính thông dng ca nó nên
nhiu hãng sn xut thit b iu khin ã cho ra i các b iu khin PID thơng mi rt tin
dng. Các phơng pháp iu ch&nh thông s b iu khin PID c xp vào hai nhóm
chính: nhóm các phơng pháp lý thuyt, và nhóm các phơng pháp thc nghim. Trong s các
phơng pháp ó thì cha có phơng pháp nào c coi là hoàn ho và tin li. Tuy vy trong 103
thc t nhóm phơng pháp lý thuyt rt ít c s2 dng do s khó khn trong vic xây dng
hàm truyn i tng. Phơng pháp ph$ bin nht chn thông s cho các b iu khin PID
thơng mi hin nay là phơng pháp Zeigler-Nichols thuc nhóm thc nghim.
5.4.1 Phng pháp lý thuyt
1. Phng pháp h6ng s th/i gian t*ng c0a Kuhn
Phơng pháp thi gian t$ng ca Kuhn c ng dng thit k lut iu khin cho lp
i tng có im không và im cc nm trên trc thc v bên trái trc o. i tng vi mô
hình toán hc dng t$ng quát: t t t 1+ T s 1 1 + T s ... 2 + 1 T s − (5.4) W s = K e t ( ) ( )( ) ( m ) sT dt ( m 1 + T s 1 )( m 1+ T s 2 ).. ( m . 1+ T s n ) t
và các hng s thi gian t2 s t
T phi nh" hơn so vi hng s thi gian tơng ng m'u s i m
T , nói cách khác nu ta có: i t t t T và m m m 1 ≥ 2 ≥ ≥ 1 ≥ T2 ≥ ≥ T T T T m n thì phi có: t m
T < T , t m < ,…, t m 1 1 T T T < T 2 2 m m
thì có th nh ngha mt hng s thi gian t$ng T theo công thc: n m m t T = T − T + T (5.5) j i t j =1 i=1
Khi ó các tham s ca lut PID c chn theo Kuhn có dng: 1 T - B iu khin PI K , T = p= K 2 I 2 dt 1 2T - B iu khin PID K , T = , T = 0 1 . 6 T 7 p= K I 3 D dt
Cht lng h thng t c là:
- quá iu chình cc i (POT): σ = 3 . 4 2% . max
- Thi gian t c giá tr xác lp u tiên: T = 1 5 . 7 T 1 .
2. Phng pháp ti u hóa ln (ti tu hóa module)
Mt trong nhng yêu cu cht lng i vi h thng iu khin kín hình 5.15 mô t bi
hàm truyn t W( ) s r (t) e(t) y(t) W Wt (s) k (s) W = k (s )
Wk (s )Wt (s) 1 W
+ k (s)Wt(s)
Hình 5.15: H thng iu khin kín
là h thng luôn có c áp ng y(t ) ging nh tín hiu lnh c c u vào r(t ) ti
mi im tn s ho!c ít ra thi gian quá y(t) bám c vào r(t ) càng ng1n càng tt. Nói
cách khác, b iu khin lý tng W
cn phi mang n cho h thng kh nng k ( s) 104 W vi mi ω (5.6) k ( ω j ) = 1
Nhng trong thc t, vì nhiu lý do mà yêu cu W
th"a mãn (5.3) khó c áp ng, k (s )
ch@ng hn nhu vì h thng thc luôn cha trong nó bn cht quán tính, tính “cOng li lnh”
tác ng tA ngoài vào. Song “tính xu” ó ca h thng li c gim bt mt cách t nhiên
ch làm vic có tn s ln, nên ngi ta thng ã th"a mãn vi b iu khin W khí k ( s)
nó mang li c cho h thng tính cht (5.3) trong mt di tn s rng lân cn thuc 0 hình 5.16. L(ω ) . 0 ω 1 ω 1 ω 0 ω c c c
Hình 5.16: Di t'n s mà 0 ó có biên hàm c tính t'n bng 2, càng rng càng tt B iu khin W th"a mãn k (s ) W (5.7) k ( jω ) ≈ 1
trong di tn s thp có rng ln c gi là b iu khin ti u ln. Hình 5.16 là ví d
minh ha cho nguyên t1c iu khin ti u ln. B iu khin W
cn phi c la k (s )
chn sao cho min tn s ca biu # Bode hàm truyn h kín W th"a mãn k (s ) L(ω ) = 20lgW (5.8) k ( ω j ) ≈ 0
là ln nht. Di tn s này càng ln, cht lng h kín theo ngha (5.8) càng cao.
Phơng pháp ti u ln c xây dng ch yu ch& phc v vic chn tham s b iu
khin PID iu khin các i tng W
có hàm truyn t dng t (s )
- Quán tính bc nht: W = t ( ) K s 1 +Ts
- Quán tính bc hai: W = t ( ) K s (1+ T 1+ 1 ) s ( T2 ) s
- Quán tính bc ba: W = t ( ) K s (1+T s 1+ 1 + 1 )( T s 2 )( T s 3 )
Tuy nhiên, cho lp các i tng có dng hàm truyn t phc tp hơn, ch@ng hn nh: t t t
1 + T1 s 1 + T2 s...1 + T s − W s = K e t ( ) ( )( ) ( m ) sT dt ( m 1 + T1 ) s ( m 1+ T s 2 )..( m . 1+ T s n ) t
ta v'n có th s2 dng c phơng pháp chn tham s PID theo ti u ln bng cách xp x&
chúng v mt trong ba dng cơ bn trên nh phơng pháp t$ng T ca Kuln ho!c phơng pháp
t$ng các hng s thi gian nh" s? c trình bày di ây. 105 1. i u khi n i t ng quán tính b c nh t L(ω ) r(t ) e(t) y(t) W Wt( ) s k(s) ω
Hình 5.17: iu khin i tưng quán tính bc nht
Cho h kín có sơ # khi cho trong hình 5.17, trong ó
- B iu khin là khâu tích phân W ( ) K s P = (5.9) k T s I
- i tng là khâu quán tính bc nht: W = (5.10) t( ) K s 1 +Ts Nh vy s? có
- Hàm truyn t h kín: T W = vi I T = (5.11) k ( ) K s R T s 1 + + K R ( Ts ) K P
- Hàm truyn t h h: W = = (5.12) h ( ) s Wk ( ) s Wt ( ) K s T s + 1 R ( Ts) Suy ra K W jω = k ( )
(K −T Tω + ωT R )22 ( R)2 2 W = k ( K ω j ) 2 2 K + ( 2 T − + R 2KT T R ) 2 2 2 4 ω T T R ω
Và iu kin (5.8) c th"a mãn trong mt di tn s thp có rng ln, tt nhiên
ngi ta phi chn T sao cho R 2 T
T − 2 KT T = 0 T I = = K 2 T R R R KP
Khi ó h kín có biu # Bode cho Hình 5.17 vi hàm truyn t 2 ω 1 1 W (s) K n = = vi ω = và D = k 2KT ( s 1 + T ) 2 2 s + K
s + 2 Dω s + ω n 2T 2 n n
K t lu n 5.1: Nu i tng iu khin là khâu quán tính bc nht (5.10), thì b iu khin
tích phân (5.9) vi tham s TI = 2KT s? là b iu khin ti u ln. KP
Tip theo ta bàn v trng hp i tng W có dng: t (s) W (5.13) = t ( ) K s
(1+T s1)(1+T s2).. (.1+T sn)
Tt nhiên áp dng c kt lun trên vi b iu khin ti u ln là khâu tích phân (5.9)
thì trc tiên ta phi tìm cách chuyn mô hình (5.13) v dng xp x& khâu quán tính bc nht (5.10). 106
Phơng pháp xp x& mô hình (5.13) thành (5.10) sau ây là phưng pháp t&ng các hng s
thi gian nh9. Nó c s2 dng ch yu cho các hàm truyn W kiu (5.13) có , ,..., T T T t (s ) 1 2 n rt nh".
S2 dng công thc khai trin Vieta cho a thc m'u s trong (5.13) c W t ( ) = K s 1 +(T +T .
+ .. +T s + TT +T T + s + 1 2 n ) ( ... 1 2 1 3 ) 2 ...
Do ó, nhng im tn s thp, tc là khi s nh", ta có th b" qua nhng thành phn bc cao
ca s và thu c công thc xp x& (5.10) có n T = T i i= 1 Ta i n:
K t lu n 5.2: Nu i tng iu khin (5.13) có các hng s thi gian T ,T ,...,T rt nh", 1 2 n n
thì b iu khin tích phân (5.6) vi tham s TI = K 2
T s? là b iu khin ti u ln. i KP i =1
Ví d& 5.1: Minh ha kt lun 5.2
Gi s2 i tng iu khin có dng h(t) W = t (s) 2 (1 + . 0 s)6 1 Vy thì
k = 2 và T = 0 6 .
Do ó b iu khin I c s2 dng s? có 1 T = . 2 4 W = k( ) s I 2.4s t(s)
Hình 5.18: Minh h,a cho ví d. 5.1
Hình 5.18 là # th hàm quá ca h kín g#m b iu khin I thit k c và i tng quán tính bc cao ã cho. 2. i u khi n i t ng quán tính b c hai
Xét bài toán chn tham s b iu khin PID cho i tng quán tính bc hai: W = (5.14) t ( ) K s (1+T s 1+ 1 )( T s 2 )
Khi ó, hàm truyn t h h li có dng (5.12), ta chn b iu khin PI thay vì b iu
khin I nh ã làm vi i tng quán tính bc nht: 1 + 1 + 1 T W = 1 + = = , I T = (5.15) k (s ) KP ( T s I ) ( T sI) KP R T s T s T s K I I R P 1 + W = = (5.16) h (s )
Wk (s)Wt (s) K ( T s I ) T 1+ 1+ R
(s T1 )s( T2 )s
nhm thc hin vic bù hng s thi gian 1
T c a (5.14), theo ngh a T = I 1 T 107
Vi cách chn tham s T này, hàm truyn t h h (5.16) tr thành I W = h ( ) K s T s 1+ R ( T s2)
và nó hoàn toàn ging nh (5.12), tc là ta li có c T theo kt lun 5.1: R T T T T I = = 2K ⇔ 1 K I = = R 2 T K P 2KT 2KT P 2 2 Vy:
K t lu n 5.3: Nu i tng iu khin là khâu quán tính bc hai (5.14), thì b iu khin
PI (5.15) vi các tham s T T = , 1 K =
s? là b iu khin ti u ln. I 1 T P 2K 2 T
M rng ra, nu i tng không phi là khâu quán tính bc hai mà li có hàm truyn t W
dng (5.13) vi các hng s thi gian , ,..., rt nh" so vi T T T t (s ) 2 3 n 1
T , thì do nó có th x p x& bng n W = , trong ó T = T t ( ) K s (1+T s i 1 )(1 + Ts ) i= 2
nh phơng pháp t$ng các hng s thi gian nh", ta còn có:
K t lu n 5.4: Nu i tng iu khin (5.13) có mt hng s thi gian T ln vt tri và 1
các hng s thi gian còn li T ,T ,...,T rt nh" so vi i 2 3 n 1 T , thì b u khi n PI (5.15) có các tham s T T = , K 1
s? là b iu khin ti u ln. P = I 1 T n 2K Ti i = 2
Ví d& 5.2: Minh ha kt lun 5.4
Gi s2 i tng iu khin có dng h(t ) W = t (s) 3 (1+ 2s)(1 + . 0 s)5 1
Có k = 3, T = 2 và T = 0 5 . 1 Chn các tham s cho PI 1 W 0 6 . 7 1 k ( ) s = +2 s
là T = 2 và K = 6 . 0 7 I P t(s)
Ta s? c cht lng h kín mô t bi
hàm quá ca nó hình 5.19.
Hình 5.19: Minh h,a cho ví d. 5.2 3. i u khi n i t ng quán tính b c ba
Tơng t nh ã làm vi i tng là quán tính bc hai, nu i tng là quán tính bc ba có hàm truyn t: W = (5.17) t ( ) K s (1+ T s 1+ 1 + 1 )( T s 2 )( T s 3 )
ta s? s2 dng b iu khin PID 108 + + T W = + + = I T = (5.18) k (s ) 1
(1 TA )s(1 T s B ) K 1 T s , P T s D T s R K I R P vi
T + T = T và T T = T T A B I A B I D
Khi ó, hàm truyn t h h s? li tr v dng (5.12), nu ta chn T T T =
, T = T ⇔ T = T + T , 1 2 T = A 1 T B 2 I 1 2 D + 1 T T2 Suy ra T T T +T T I = = 3KT ⇔ 1 2 K I = = R 3 K P 2KT 2KT P 3 3
K t lu n 5.5: Nu i tng là khâu quán tính bc ba, thì b iu khin PID (5.18) vi các tham s T T T +T T = + , 1 2 T = , 1 2 K =
s? là b iu khin ti u ln. I 1 T 2 T D + P 2 1 T T2 3 KT
Trong trng hp i tng li có dng hàm truyn t (5.13) nhng các hng s thi gian
T ,T ,...,T rt nh" so vi hai hng s thi gian còn li 2 ơ $ 3 4 n 1 T , 2 T thì s d ng ph ng pháp t ng các
hng s thi gian nh", xp x& nó v dng quán tính bc ba: n W , trong ó = T = T t ( ) K s (1 +T s i 1 )(1 + T s 2 )(1 + Ts ) i =3
Ta s? áp dng c kt lun 5.5 vi T T T1 +T T = + , 1 2 T = , K = 2 I 1 T 2 T D + P n 1 T T2 2K Ti i =3
Ví d& 5.3: Minh ha kt lun 5.5
Gi s2 i tng iu khin có dng (ht) W = t (s) 4
(1+5s)(1+ 2s)(1 + . 0 s)4 1 Vy thì
k = 4 , T = 5 , T = 2 , T = . 0 4 1 2 S2 dng PID vi T = 7 , T = . 1 43 và K = . 2 2 I D P
Ta s? c cht lng h kín mô t bi
hàm quá ca nó hình 5.20. t(s)
Hình 5.20 Minh h,a cho ví d. 5.3
Ví d& 5.4: Thit k h thng $n nh tc ng cơ in mt chiu kích tA c lp theo
phơng pháp ti u hóa ln. Sơ # chc nng ca h thng c biu di:n ti hình 5.21. 109
Hình 5.21: H thng &n *nh tc ng c
Sơ # iu khin tơng ơng: W W Wdc (s ) u (s ) Wn( ) s k (s ) Trong ó: W
: Hàm truyn ca b iu khin. k ( s) W
: Hàm truyn ca b bin $i công sut. u (s ) W
: Hàm truyn ca ng cơ. dc (s ) W
: Hàm truyn ca b phát tc o tc ng cơ. n (s )
Tham s ca ng cơ: U = 22 V 0 ; N=2376; = . 0 6 ; =1500 , W = 4800 vòng; P kW N rpm m m m N =3000rpm ; 2 J = . 0 042 ; = .
4 3 ; pc = 2 ; R=6.75t. max kgm I A m
Vic tin hành trc tiên là xây dng mô hình toán hc cho i tng. ng cơ in mt
chiu kích tA c lp có mô hình toán hc: W ( ) K s d = (5.19) dc 2
1+ T s + T .T .s c u c
Vi K là h s khuch i, T là hng s thi gian in cơ và T là hng s thi gian in d c u
tA ca ng cơ. Gi thit hng s thi gian in cơ T ln hơn hng s thi gian in tA rt c
nhiu ta có th chp nhn:
T ≈ T + T c c u
Nh vy, mô hình toán hc ca ng cơ trong (5.19) hoàn toàn có th biu di:n di dng: W ( ) K s d = dc (1+T s. 1+ . c )( T s u )
Ngha là ng cơ có th coi nh hai khâu quán tính. Khi b" qua hng s thi gian in tA phn ng (T
thì ng cơ là mt khâu quán tính. u ≈ ) 0 . 0 13 W ( ) K s d = = dc (1+T s. 1+ . 0 023 c ) s
Mô t toán hc ca thit b o tc là mt khâu quán tính bc nht có hàm truyn: . 0 93 W = ω = n ( ) K s 1+ sT 1 +0.00 s 1 ω 110
Hàm truyn ca b bin $i công sut ng cơ: 2 . 3 87 W = = u( ) K s 1+ sT + 0 1 . 0 00 s 1 v
Sơ # rút gn ca h thng: u uFT W
Wt (s ) k (s) Trong ó: . 0 13 . 0 93 2 . 3 87 . 2 89 W = . . = t (s) 1+ . 0 023s 1+ . 0 00 s 1 1+ . 0 00 s 1 (1+0.02 s 3 )(1+ 0.002s)
Hình 5.22: S mô ph9ng ví d. 5.4 bng Matlab Simulink h(t) t
Hình 5.23: Kt qu mô ph9ng ví d. 5.4
Áp dng phơng pháp ti u ln ta s? có hàm truyn ca b iu ch&nh: 1 W 1
k (s) =K + P T s I là mt khâu PI, vi: 1 T . 0 023 K = = = 2 P 2KT 2* . 2 89* . 0 002 2 T = T = I 1 . 0 023
Sơ # mô ph"ng ca h thng Hình 5.23. 111
Quá trình quá ca h thng có quá iu ch&nh σ %= 3 . 4 % , thi gian quá t = . 0 015s . s
3. Phng pháp ti u i x+ng
Có th thy ngay c s hn ch ca phơng pháp thit k PID ti u ln là i tng W
phi $n nh, hàm quá (
h t ) ca nó phi i tA 0 và có dng ch S. t (s )
Phơng pháp chn tham s PID theo nguyên t1c ti u i xng c xem nh là mt s
bù 1p cho iu khim khuyt trên ca ti u ln.
Trc tiên, ta xét h kín cho hình 5.24a. Gi W =
là hàm truyn t ca h( ) s Wk( ) s W (t ) s
h h. Khi ó h kín có hàm truyn t: W s W = W = h( ) k ( ) s k (s ) W (s h ) 1 + W 1 −Wk(s) h( ) s
Và ging nh phơng pháp ti u ln, có W
trong di tn s thp thì phi k ( ω j ) ≈ 1 có W trong di tn ω nh" (5.20) h ( ω j ) >> 1
Hình 5.24b là biu # Bode mong mun ca hàm truyn h h W
g#m L (ω và ϕ (ω . h ) h ) h (s)
Di tn s ω trong biu # Bode c chia ra làm ba vùng:
- Vùng I là vùng t'n s thp. iu kin (5.20) th hin rõ nét vùng I là hàm !c tính tn h h W
phi có biên rt ln, hay L
. Vùng này i din cho cht lng h h(ω ) >> 0 h ( ω j )
thng ch xác lp tnh (tn s nh"). S nh hng ca nó ti tính ng hc ca h kín là có th b" qua.
- Vùng II là vùng t'n s trung bình và cao. Vùng này mang thong tin !c trng ca tính
ng hc h kín. S nh hng ca vùng này ti tính cht h kín di tn s thp (tnh) ho!c
rt cao là có th b" qua. Vùng II !c trng bi im tn s c1t L ω hay W jω . h( c ) = 1 h ( c )= 0
Mong mun rng h kín không có cu trúc phc tp nên hàm W
cng c gi thit ch& h ( ω j ) có mt tn s c1t ω . c
ng # th biên Bode L (ω s? thay $i nghiêng mt giá tr 20dB/dec ti im tn s h )
g'y ω ca a thc t2 s và -20dB/dec ti im tn s gãy ω ca a thc m'u s. Nu 1 2
khong cách nghiêng dài thì ng ϕ
s? thay $i mt giá tr là o 90 ti ω và h (ω ) 1 o − 90 ti ω
. Ngoài ra, h kín s? $n nh nu ti tn s c1t ó h h có góc pha ϕ ω ln h ( c ) 2
hơn −π . Bi vy, tính $n nh ca h kín c m bo nu trong vùng I ã có W
h ( jω ) >> 1
và vùng II này, xung quanh im tn s c1t, biu # Bode L
có dc là -20dB/dec h (ω )
cng nh khong cách dc ó là ln.
- Vùng III là vùng t'n s rt cao. Vùng này mang ít, có th b" qua c, nhng thông tin
v cht lng k thut ca h thng. h không b nh hng bi nhi:u tn s rt cao, tc là
khi tn s rt cao W
cn có biên rt nh", thì trong vùng này hàm W nên có giá tr h ( jω) k (s) tin n 0. 112 ϕ h(ω) Lh (ω ) r (t ) e(t ) y (t ) W Wt( ) s k ( s) ω ω 1 ω ω2 c
Hình 5.24: Minh h,a tư tư0ng thit k b iu khin PID ti ưu i xng
Có th thy ngay c rng, nu ký hiu: −1 T , −1 T = ω , − 1 T = ω I = ω1 c c 1 2 thì h h W
mong mun vi biu # Bode cho trong hình 5.24b phi là h (s) + W = = (5.21) h (s )
Wk (s)Wt (s) Kh(1 T s I ) 2 s (1+ s 1 T ) i t
ng là khâu tích phân – quán tính b c nh t
Hàm truyn i tng là : W = (5.22) t ( ) K s (s1+T s1)
Ta chn b iu khin PI 1 W 1 (5.23) k ( ) s =K + P T s I
Vi các tham s c xác nh nh sau:
- Xác nh 4 > a > 1 tA quá iu ch&nh ∆h cn có ca h kín theo công thc sau: 2 4ln ( h ∆ ) a = (5.24) 2 π + 2 ln (∆h)
Giá tr a c chn càng ln thì quá iu ch&nh càng nh". Nu a ≤ 1, h kín s? không $n
nh. Nu a ≥ 4 , h kín không có dao ng. - Tính T = a I 1 T - Tính 1 K = P KT1 a
Ví d& 5.5: Cho i tng tích phân quán tính bc nht mô t bi 2 W = t (s) (s1+ 0.3 )s
Xác nh tham s ti u i xng cho b iu khin PI. 113 Gi i:
TA mô hình i tng: K = 2 ; T = 0 3 . 1
Chn b iu khin PI iu khin theo nguyên t1c ti u i xng 1 + 1 W = 1 + = k (s) K P ( T s I ) KP T s T s I I
Các tham s c chn nh sau: - Khi a = 2 : K = . 1 18 , T = 0 6 . P I - Khi a = 4 : K = . 0 83, T =1.2 P I - Khi a = 9 : K = . 0 56 , T = 2 7 . P I
Hình 5.25 là # th hàm quá h kín ng vi các tham s b iu khin ã c chn cho c
ba trng hp nêu trên. h (t) h(t ) a = 2 a = 4 t (s) t(s)
Hình 5.25: Hàm quá h kín vi b iu khin PI có
các tham s ưc ch,n theo nguyên t)c iu khin ti
ưu i xng. Minh h,a ví d. 5.5 a = 9 t(s) i t
ng là khâu tích phân – quán tính b c hai
Hàm truyn i tng là : W = ( 1 T ≤ (5.25) 2 T ) t ( ) K s s(1 T + s 1 + 1 )( T s 2 )
Ta chn b iu khin PID 1 W 1 (5.26) k (s) =K + + T s P T s D I
Các tham s c chn nh sau:
- Xác nh 4 > a > 1 tA quá iu ch&nh ∆h cn có ca h kín theo công thc sau: 114 2 4ln ( h ∆ ) a = 2 π + 2 ln (∆h)
Giá tr a c chn càng ln thì quá iu ch&nh càng nh". Nu a ≤ 1, h kín s? không $n
nh. Nu a ≥ 4 , h kín không có dao ng. - Tính a 1 T 2 T T = D + 1 T a 2 T - Tính T = + I 1 T a 2 T - Tính 1 T + a 2 T K = P 2 a a K 2 T
Ví d& 5.6: Xét i tng tích phân quán tính bc hai 2 h (t ) W = t (s) s(1 + s 3 )(1 +5s) TA K = ; 2 T =3 ; T = 5 1 2
Ta có vi a = 8 tham s b iu khin PID là: K ; T = 43 ; T = . 2 8 P = . 0 04 I D
Hình 5.26 biu di:n hàm quá h kín. t(s)
Hình 5.26: Minh h,a ví d. 5.6
5.4.2 Phng pháp thc nghim
a. Phng pháp Ziegler-Nichols
Phơng pháp Ziegler-Nichols là phơng pháp thc nghim thit k b iu khin P, PI,
ho!c PID bng cách da vào áp ng quá ca i tng iu khin. B iu khin PID cn
thit k có hàm truyn là: 1 W 1 (5.27) PID (s ) = +K K I +K s =K + + T s P s D P T s D I
Ziegler-Nichols a ra hai cách chn thông s b iu khin PID tùy theo !c im ca i tng.
Cách 1: Da vào áp ng quá ca h h, áp dng cho các i tng có mô hình xp x& bc
nht có tr: nh hình 5.27a ho!c có áp ng i vi tín hiu vào là hàm bc thang có dng ch
S nh hình 5.27b, ví d nh nhit lò nhit, tc ng cơ,… (1t) h(t) t t ( u t) ( y ) t 115 h (t ) h(t ) K K t t 1 T T2 1 T 2 T (a) (b)
Hình 5.27: áp ng quá ca i tưng bc nht có tr (a)
và quán tính bc hai hoc bc n có dng hình ch+ S (b)
- Nhng i tng có dng áp ng quá nh hình 5.27 có th xp x& di bng mô
hình bc nht có tr: vi hàm truyn t nh sau: T − s 1 W ( ) Ke s = (5.28) 1+T s 2
Vi các tham s c xác nh tơng ng tA hình v?:
h(t ) cha có phn ng ngay vi kích thích (
1 t ) ti u vào. 1
T : là kho ng th i gian u ra
K : là giá tr gii hn h(t ).
Gi A là im kt thúc khong thi gian tr:, tc là im trên trc hoành có hoành bng
tai A t c giá tr 1 T . Khi ó 2
T là kho ng th i gian c n thi t sau 1
T tip tuyn ca h(t) K .
- Nhng i tng có dng áp ng quá nh hình (b) tc có dng gn ging nh hình
ch S ca khâu quán tính bc hai ho!c bc n thì các tham s K , 1 T , T c xác nh nh sau: 2
K : là giá tr gii hn h = lim h ∞ (t) t→∞
Kg ng tip tuyn ca h(t ) ti im un ca nó. Khi ó ? i 1 T s là hoành giao m c a
tip tuyn vi trc hoành và T là khong thi gian cn thit ng tip tuyn i c tA 2
giá tr 0 ti giá tr K .
Thông s ca b iu khin P, PI, PID c xác nh theo bng sau sao cho h thng
nhanh chóng tr v ch xác lp và quá iu ch&nh h ∆
không vt quá mt gii hn max
cho phép, khong 40% so vi h = lim . ∞ ( h t) t→∞
Bng 5.1: Các thông s b iu khin PID theo phưng pháp th nht ca Zeigler-Nichols Thông s K T T B iu khin P I D P T / 2 (T .K 1 ) ∞ 0 PI 0 T 9 . / 0 3 . 2 ( / T K . 1 ) 1 T 0 PID . 1 T 2 2 . 0 5 2 ( / T . 1 ) K 1 T 1 T 116
Ví d& 5.7: Hãy thit k b iu khin PID iu khin nhit ca lò sy, bit !c tính quá
ca lò sy thu c tA thc nghim có dng nh sau: ( h t) C ° 150 0 t(min) 8 24
Hình 5.28: Minh h,a ví d. 5.7
Gi i: Da vào áp ng quá thc nghim ta có: T = 8min 480sec 1 = T = 24min 1440sec 2 =
Chn thông s b iu khin PID theo phơng pháp Zeigler-Nichols: 2 T 1440 K = 1 2 . = . 1 2 = . 3 6 P T 480 1
T = 2 T =2 ×480 =960 sec I 1 TD = 0 5 . 1 T = 5 . 0 × 480 = 240sec Do ó: 1 1 W 1 3 6 . 1 240 PID (s ) =K + +T s = + + s P T s D 960 s I
Cách 2: Da vào áp ng quá ca h kín, áp dng cho các i tng có khâu tích phân, ví
d nh mc cht l"ng trong b#n cha, v trí h truyn ng dùng ng cơ…áp ng quá
(h h) ca các i tng có khâu tích phân tng n vô cùng. i vi các i tng thuc loi
này ta chn thông s b iu khin PID da vào áp ng quá ca h kín nh hình 5.29b.
Tng dn h s khuch i K ca h kín hình 5.29a n giá tr gii hn K , khi ó áp ng gh
ra ca h kín trng thái xác lp là dao ng $n nh vi chu kQ T . gh (h )t h( )t t t Tgh 1 (rt) (yt) t (a) (b)
Hình5.29: áp ng quá ca h kín khi K = K gh
Thông s ca b iu khin P, PI, PID c chn nh sau: 117
Bng 5.2: Các thông s b iu khin PID theo phưng pháp th hai ca Zeigler-Nichols Thông s K T T B iu khin P I D P . 0 5K ∞ 0 gh PI 0 4 . 5K 0 8 . T 3 0 gh gh PID 0 6 . K 0 T 5 . 0.12 T 5 gh gh gh
Ví d& 5.8: Hãy thit k b iu khin PID iu khin v trí góc quay ca ng cơ DC, bit rng
nu s2 dng b iu khin t& l thì bng thc nghim ta xác nh c khi K = 30 v trí góc
quay ng cơ trng thái xác lp là dao ng vi chu kQ T = 2 sec.
Gi i: Theo d kin ca bài toán, ta có: K = 30 ; T = 2sec gh gh
Chn thông s b iu khin PID theo phơng pháp Zeigler-Nichols: K = 0 6 . K = 6 . 0 × 30 =18 P gh T T I = . 0 5 gh = 5 . 0 ×2 =1sec T T D = 0 1 . 25 gh = . 0 125 ×2 = . 0 5sec Do ó: 1 1 W 1 18 1 . 0 5 PID (s ) =K + +T s = + + s P T s D s I
b. Phng pháp Chien, Hrones, và Reswick
V m!t nguyên lý phơng pháp Chien, Hrones, và Reswick gn ging vi phơng pháp
th nht ca Ziegler-Nichols, nhng nó không s2 dng mô hình tham s gn úng dng quán
tính bc nht có tr: mà s2 dng trc tip dng hàm quá ca i tng iu khin.
Phơng pháp Chien, Hrones, và Reswick cng gi thit rng i tng là $n nh, hàm quá
không dao ng và có dng hình ch S. Tuy nhiên phơng pháp này thích hp vi các i
tng bc rt cao nh quán tính bc n: W ( ) K s = (5.29) ( +1)n Ts
C th là nhng i tng có hàm quá (
h t) th"a mãn T / T > 3 trong ó T là hoành g u u
giao im tip tuyn ca (
h t) ti im un U vi trc hoành và T là khong thi gian cn thit g
tip tuyn ó i c tA 0 ti giá tr K = lim h(t ). t→∞ h(t) K T U g > 3 Tu t
Hình 5.30: Hàm quá i tưng thích hp cho phưng pháp Chien, Hrones, và Reswick 118
TA dng hàm quá h(t ) ca i tng vi hai tham s T và T th"a mãn, Chien, Hrones, u g
và Reswick ã a ra bn cách xác nh thông s b iu ch&nh cho bn yêu cu cht lng khác nhau nh sau:
1. Yêu cu ti u theo nhi:u (gim nh hng ca nhi:u) và h kín không có vt l.
2. Yêu cu ti u theo nhi:u (gim nh hng ca nhi:u) và h kín có vt l ≤ 2 % 0 .
3. Yêu cu ti u theo tín hiu !t (gim sai lch bám) và h kín không có vt l.
4. Yêu cu ti u theo tín hiu !t (gim sai lch bám) và h kín có vt l ≤ 20% .
Bng 5.3: Thông s b iu ch-nh PID theo phưng pháp Chien, Hrones, và Reswick
áp ng h kín dng ch S,
áp ng h kín dng dao ng không có vt l t1t dn, v t l
B iu ch&nh Thông ≤20% s Ti u theo Ti u theo Ti u theo Ti u theo nhi:u z giá tr !t r nhi:u z giá tr !t r P K T T T T P u . 0 3 K u . 0 3 K u . 0 7 K u . 0 7 K T T T T g g g g K T T T T P u PI . 0 6 K u . 0 35 K u . 0 7 K u . 0 6 K T T T T g g g g T T 4 . 1 T 2 2. T 3 T I u g u g K T T T T P u PID . 0 95 K u . 0 6 K u . 1 2 K u . 0 95 K T T T T g g g g T . 2 T 4 T T 2 1 3 . T 5 I u g u g T 4 . 0 T 2 . 0 T 5 4 . 0 T 2 . 0 4 T 7 D u g u g
TA bng ta xác nh các h s khác ca b iu ch&nh nh sau: - H s tích phân: KP K = I TI
- H s vi phân: K = K T . D P D
5.5 T*ng hp b iu khin trong không gian trng thái
Trong lý thuyt iu khin t ng hin i, vi nhng h thng iu khin có nhiu u
vào – nhiu u ra (MIMO) thì phơng pháp t$ng hp h thng trong không gian trng thái
thng c s2 dng. Phơng pháp không gian trng thái, cho phép xây dng c các h
thng kín có các im cc mong mun (hay các phơng trình !c trng mong mun) ho!c các
h thng iu khin ti u áp ng c các ch& tiêu ã cho. M!t khác, t$ng hp h thng
trong không gian trng thái cho phép ngi ta tính n c các iu kin khi to t$ng hp
h thng khi cn thit. Tuy nhiên, vic t$ng hp h thng bng không gian trng thái òi h"i
mô t toán hc chính xác ng hc ca h thng. iu này ngc vi các phơng pháp kinh
in, vì trong phơng pháp kinh in, các !c tính tn s nhn c bng thc nghim có th
có chính xác không cao nhng v'n có th c s2 dng t$ng hp h thng, mà không
cn mô t toán hc i vi chúng mt cách chính xác. 119
Xut phát tA quan im tính toán, phơng pháp không gian trng thái !c bit thích hp
cho các phép tính trên máy tính s nh phơng pháp nghiên cu trong min thi gian ca nó.
Vic này giúp cho k s không phi thc hin các phép tính nhàm chán và cho phép h dành
công sc vào phân tích các khía cnh ca bài toán. ây là mt im thun li ca phơng pháp
không gian trng thái. Cui cùng, mt im quan trng áng lu ý là không cn các tham bin
trng thái biu di:n các i lng vt lý ca h thng. Các tham bin không biu di:n các i
lng vt lý, không o lng c cng nh không quan sát c, chúng v'n có th chn làm
các tham bin trng thái. Kh nng t do la chn các tham bin trng thái là mt im thun
li na ca phơng pháp không gian trng thái.
Cho i tng iu khin c mô t bi phơng trình trng thái cp n:
x(t )= Ax(t )+ Bu(t) (5.30)
y(t) = Cx(t)+ Du(t)
H thng iu khin h#i tip trng thái nh hình 5.31 là h thng trong ó tín hiu iu khin xác nh bi: u (t) = ( r t )− K ( x t ) (5.31) r t u(t ) x t ( y t) ( ) ( )
x (t ) = Ax(t )+ B ( u t )
Hình 5.31: H thng iu khin hi tip trng thái
Thay (5.31) vào (5.30) ta c:
x(t )= Ax(t )+ [
B r (t )− K ( x t)]
x(t) = [A − BK ]x(t )+ Br (t ) (5.32)
y (t ) = Cx(t )+ D [r (t )− Kx(t )]
y(t )= [C − KD] (
x t)+ Dr(t)
Thit k h#i tip trng thái là chn vector h#i tip trng thái K sao cho h thng kín mô t
bi biu thc (5.32) th"a mãn yêu cu cht lng mong mun.
có th thit k c h thng h#i tip trng thái, iu kin cn là tt c các trng thái
ca h thng phi o lng c, ho!c tính toán (quan sát c) và h sPn sàng nhn tín hiu
iu khin (iu khin c). Mc này s? trình bày c th v khái nim iu khin c và
quan sát c cng nh các kim tra toán hc ánh giá h có th iu khin c và quan sát c hay không.
5.5.1 Tính iu khin c (Controllability)
Mt h thng tuyn tính liên tc c gi là iu khin c (hay iu khin c hoàn
toàn) nu t#n ti ít nht mt tín hiu iu khin (
u t ) có kh nng chuyn h tA trng thái ban
u x(t n trng thái cui x(T ) bt kQ trong khong thi gian hu hn [t . 0, T ] 0 )
Khái nim iu khin c (Controllability) do Kalman nh ngha nm 1960 và cùng vi
nh ngha ó ông ã a ra tiêu chu>n xét tính iu khin c ca h tuyn tính bt bin nh sau:
Lp ma trn Co , gi là ma trn iu khin c 120 Co [B AB A2B An 1 − = B] (5.33)
iu kin cn và h tuyn tính (5.30) iu khin c là: Rank(C ) o = n (5.34)
Vi h thng SISO thì Co là ma trn vuông cp n. Do ó iu kin trên tơng ơng vi: det(Co) ≠ 0 (5.35)
Ví d& 5.9: Cho h thng mô t bi phơng trình trng thái:
(x )t= A (x )t+ B (u )t
y(t ) =Cx(t ) 0 1 5 trong ó: A = B = C = [1 ] 3 − 2 − 3 2
Hãy ánh giá tính iu khin c ca h thng trên.
Gi i: i vi h bc hai, ma trn iu kin c là: Co = [B AB] 5 0 1 5 5 2 Co = = 2 − 2 −3 2 2 −16 det(Co) = 8 − 4 ≠ 0 Rank (Co) = 2
Do ó h thng trên iu khin c hoàn toàn.
Ví d& 5.10: Cho h thng có sơ # cu trúc nh hình v? sau: r(t ) 1 1 y (t ) 30 s s . 0 5 . 0 4
Hình 5.32: Minh h,a cho ví d. 5.10
TA hình v? ta xác nh c hàm truyn t h kín: W k (s ) Y(s) 20 = (R ) = s 2 2 s + s + 4 x = y 1 !t x 1 = x2
x = −2x − 0 5 . x +1 r 0 2 1 2
Phơng trình trng thái tơng ng là 121 x 0 1 x 0 1 = 1 . + r x 2 . 0 5 x 10 2 − − 2 x y = [1 0 ] 1 . x2
Theo công thc (5.36) ta xét tính iu khin c ca h thng: 0 10 0 10 0 10 Co = [B AB]= vì . A B = . = 10 − 5 10 −5 10 − 5
Hng ca ma trn Co : tính det(Co) = 1
− 00 ≠ 0 vy Rank(C ) o = 2
Vì hng ca ma trn bng 2 nên h thng iu khin c hoàn toàn.
5.5.2 Tính quan sát c (Observability)
Quan sát mt tín hiu trong h thng c hiu là xác nh giá tr tín hiu nh o trc tip
tín hiu ó (bng các thit b cm bin) ho!c thông qua các tín hiu o c khác. Ví d vn
tc có th quan sát c (xác nh c) nh o trc tip bng b phát tc, ho!c gián tip bng
vic o lng dch chuyn trong mt khong thi gian, gia tc xác nh c tA vic o vn
tc, công sut chu>n oán c nh vic o dòng in và in áp.
H thng c gi là quan sát c hoàn toàn ti thi im t nu vi mi , ta luôn 0 T > t0
có th xác nh c trng thái u x(t tA các tín hiu vào ra (
u t ), y(t) trong khong thi 0 ) gian [t ,T . o ]
kim tra tính quan sát c ca h thng ta s2 dng tiêu chu>n Kalman sau:
Lp ma trn Ob , gi là ma trn quan sát c: C CA Ob = (5.36) n−1 CA
iu kin cn và h thng quan sát c là:
Rank(Ob) = n (5.37)
Vi h thng SISO thì ma trn Ob là ma trn vuông cp n. Do ó iu kin trên tr thành: det (Ob) ≠ 0 (5.38)
Ví d& 5.11: Cho h thng mô t bi phơng trình trng thái:
(x )t= A (xt)+ B ( u t) ( y t) = C ( x t) 0 5 0 vi A = ; B = ; C = [1 ] 0 2 3 3
Ta có ma trn quan sát c: [1 ] 0 C 1 0 Ob = = CA [1 0] 0 5 = 0 5 2 3
Vì det(Ob)= 5 ≠ 0 nên rank (Ob)= 2 122
Do ó h thng quan sát c hoàn toàn.
Tính iu khin c và quan sát c có ý ngha rt quan trng trong lý thuyt iu khin
hin i, các tính cht này quyt nh s t#n ti ca li gii cho bài toán iu khin ti u.
5.5.3 Phng pháp gán im cc
Nu h thng (5.30) iu khin c và quan sát c thì có th xác nh c lut iu
khin u(t )= r (t )− Kx (t ) phơng trình !c tính ca h h#i tip trng thái (5.32) có nghim cc theo mong mun.
Phơng trình !c tính ca h h#i tip trng thái là:
det[sI − A + BK] = 0 (5.39)
Phơng pháp chn vector h#i tip trng thái K phơng trình !c tính (5.39) có nghim ti v
trí mong mun gi là phơng pháp phân b cc.
Trình t thit k b iu khin h#i tip trng thái:
Bc 1: Kim tra tính iu khin c (và quan sát c)
- Nu h không iu khin c thì kt thúc vì bài toán phân b cc không có li gii.
- Nu h iu khin c thì tip tc bc 2.
Bc 2: Vit phơng trình !c trng ca h thng h#i tip trng thái:
det[sI − A + BK] = 0 (5.40)
Bc 3: Vit phơng trình !c trng mong mun: n ∏(s − s 0 (5.41) i ) = i=1
trong ó s (i =1. n.) là các nghim cc mong mun. i
Bc 4: Cân bng các h s ca hai phơng trình !c trng (5.40) và (5.41) s? tìm c vector h#i tip trng thái K.
Ví d& 5.12 : Cho h thng mô t bi phơng trình trng thái:
(x )t= A (x )t+ B (u ) t
y(t ) =Cx(t ) 0 1 0 Vi A = ; B = ; C = [1 ] 0 − 2 − 3 2
Hãy thit k b iu khin phn h#i trng thái h thng có hai im cc -2 và -5. Gi i:
Kim tra tính iu khin c và quan sát c:
Ma trn iu khin c: 0 2 Co = [B AB]= 2 −6 det(Co) = 4
− nên Rank(C )
o = 2 . Suy ra h thng iu khin c.
Ma trn quan sát c: C 1 0 Ob = = nên Ran ( k )
Ob = 2 . Do ó h thng quan sát c CA 0 1 123
Phơng trình !c trng ca h thng h#i tip trng thái: 1 0 0 1 0 [
det sI − A + B ] K = det s − + [k k = 1 2] 0 0 1 − 2 −3 2 s −1 det
= s(s +3 +2k + + k = s + s + k + + k = 2 ) (2 2 ) 2 1 (3 2 2) (2 2 1) 0 2 +2 k s +3 + 2 1 k2
Phơng trình !c trng mong mun:
(s + 2)(s + 5)= 0 2 s + 7s + 10 = 0
Cân bng h s hai phơng trình trên ta có: 2 + 2 k 4 1 k = 10 1 = 3 + 2 k 2 2 k = 7 2 = Vy K = [4 2] BÀI T2P CHƠNG 5
1. Hãy xác nh tham s b iu khin I ho!c PI ho!c PID nu i tng có hàm truyn t a. 2 2 W (s) = b. W (s) = 1 + 5s (1+ . 0 s 1 )(1+ s 4 ) c. 3 2 W (s) = = ( d. W (s) 1 + s 5 )(1+ s 3 )(1+ s)
(1+ 3s)(1+ 5 )s(1+ . 0 s)5 2 e. 2 1 + 0 2 . 1 + . 0 1 2 1 + . 0 05s 0 − .5 W (s) ( s )( s ) = f. W (s) ( ) s = ( e
1 + 5s)(1 + 3s)(1 + 2 ) s ( 3
1 +5s)(1 +3s)(1 + . 0 1s)
2. V? biu # bode ca b iu kin PI, PD và PID có hàm truyn t ln lt nh sau: 1 W 5 1 C (s ) = +2 s W = 5 1 + . 0 5 C (s ) ( s ) 2 + . 0 65 W = 3 . 0 3215 C (s ) (s ) s
3. Hãy xác nh tham s ti u i xng cho b iu khin PID (ng vi a = 2, a = 4 , và
a =9 ) iu khin các i tng có hàm truyn t nh sau a. 2 3 W (s) = b. W (s) = s(1+ s 3 )
s(1+ s )(1+ s 5 ) c. 2 1 + 0 2 . 1+ . 0 1 2 1 + 2 . 0 s 1 + . 0 1s −0.5 W (s) ( s )( s) = d. W (s) ( )( ) s = e s(1+ 5s)(1+ 0 25 . s)(1+ 0 15 . s) ( 4 s 1+ 5s)(1+ . 0 3s)
4. Hãy kim tra tính iu khin c và quan sát c ca i tng mô t bi mô hình trng thái nh sau: 124 −40 −25 0 0 a. dx = 16 10 0 x + 3
u và y = (0 2 − ) 1 x dt 3 4 1 − 1 0 0 −2 0 1 1 0 −2
b. dx = 1 0 −3 x + 1 2 u và y = x dt 0 2 2 0 0 −4 −1 1
5. Hãy xác nh iu kin cho tham s a h sau iu khin c: 1 3 0 0 1
dx = a −1 0 x + 2 0 u dt 0 0 a 1 1
6. Thit k b iu khin phn h#i trng thái:
a. Cho i tng có mô hình: dx 0 3 1 = x +
u và y = (0 2)x dt 2 0 1
Sao cho h thng kín có hai im cc mi là s = −1 và s = −2 1 2
b. Cho i tng có mô hình 3 2 1 1
dx(t) = − 2 − 1 4 x(t) + −1 u(t) ; y(t)= (1 2 )1 (xt) dt − 2 − 2 − 4 2
Sao cho h thng kín có ba im cc mong muns = −2, s = 3 − và s = − 3 4 1 2
7. Cho b iu khin PID thc hin bng khuch i thut toán nh hình v? sau: C1 R C 2 2 4 R 1 R 3 R ui uo
Hình 5.33: B iu khin PID
Hãy xác nh các giá tr 1 R , 2 R , 3 R , R , 4 1 C , và 2
C sao cho hàm truy n c a b PID là: 1 W 39 4 . 2 1 . 0 7692 C (s ) = + + s . 3 07 s 7 125
CHƠNG 6: NÂNG CAO CH8T L9NG H IU KHIN
Khi thit k h thng iu khin t ng, mc tiêu trên ht là phi m bo c cht
lng ca quá trình iu khin theo yêu cu ca quy trình công ngh. Mun t c iu ó
ta phi xác nh c tham s ti u ca thit b iu khin. Tuy nhiên trong nhiu trng hp
ta tìm c b thông s ti u ca b iu khin nhng cht lng ca quá trình iu khin
v'n không áp ng c yêu cu ra. Do vy, ngi ta phi tìm ra các bin pháp nâng cao
cht lng h thng bng cách thay $i cu trúc ca h thng iu khin t ng. Di ây là
mt s phơng pháp nâng cao cht lng h thng iu khin.
6.1 Phng pháp bù tác ng nhi!u
Các h thng iu khin thng b nhng tác ng ca nhi:u làm nh hng ti cht lng
ca quá trình iu khin. Nu các nhi:u này mà o c thì ta có th a ra phơng pháp bù
tác ng ca nhi:u nâng cao cht lng iu khin. Nhi:u tác ng lên h thng có hai loi:
nhi:u ph ti và nhi:u !t trc; ta s? xét phơng pháp bù cho tAng loi nhi:u này. 6.1.1 Bù nhi!u ph& t i
Xét h thng b nh hng ca nhi:u f(t), ta mong mun tín hiu ra y(t) b nh hng ca
f(t) là ít nht, nu y(t) không ph thuc vào f(t) ta nói h thng bt bin vi nhi:u.
Hình 6.1: S h thng iu khin bù nhiu ph. ti
H thng có hai tín hiu vào là: tín hiu !t r(t), tín hiu nhi:u f(t). ây là h thng tuyn
tính nên xác nh tín hiu ra y(t) ta áp dng nguyên lý xp ch#ng:
- Xét r(t) ≠ 0 và f (t) = 0, tín hiu ra: W W Y = r (s ) 1 2 R(s) 1 + 1 W W2H
- Xét r(t) = 0 và f (t) ≠ 0, tín hiu ra: 1 ( − 1 W W )W Y (s) b 2 = F (s ) f 1 +W W H 1 2
Y (s) = Y (s) + Y (s) r f W − 1W 2 1 ( 1 W W )W Y (s) = R( ) b 2 s + F (s) 1 + W W H 1 +W W H 1 2 1 2
Ta thy mun y(t) ch& ph thuc r(t) không ph thuc f(t) thì h s ca s hng th hai phi bng không, tc là: 126 1 ( − 1 W Wb)W 2 = 0 1 + 1 W 2 W H 1 1−W W W = b = 0 1 b 1 W
Nh vy, nu ta m1c thêm vào h thng khâu bù có hàm truyn là nghch o ca W k v i
cu trúc nh hình 6.1 thì tín hiu ra y(t) hoàn toàn không b nh hng bi nhi:u f(t).
6.1.2 Bù nhi!u $t trc
H thng có tín hiu !t thng xuyên thay $i, mà h li có quán tính ln thì m bo
c tác ng nhanh thì ta phi có phơng pháp bù trc cho tín hiu !t. Sơ # cu trúc
c mô t trong hình 6.2
Hình 6.2: S h thng iu khin bù nhiu t trưc
Mc ích ca quá trình iu khin bù ây là m bo cho sai lch e(t) = 0, tc là tín hiu
ra y(t) ca h thng luôn luôn bng tín hiu !t r(t). Khi ó ngi ta m1c thêm khi W b(s) nh sơ # 6.2.
Vn dng kin thc phn i s sơ # khi ta tìm c hàm truyn ca h thng có cu trúc bù: Y ( ) s ( + 1 W Wb ) W2 W (s) = = R(s) 1 +W W 1 2
Mun y(t) = r(t) thì Y(s) = R(s) W(s) = 1 (W +W W =1+ 1 b ) 2 1 WW2 W W b = 2 1 1 W = b W2
Nh vy hàm truyn t ca khâu bù là bng nghch o hàm truyn ca i tng. Mun
xây dng c khâu bù thì ta phi xác nh c hàm truyn t ca i tng. 6.2 iu khin t(ng
iu khin tng là h thng iu khin có nhiu hơn mt vòng iu khin (có hai ho!c
nhiu vòng iu khin). H thng có mt vòng iu khin trong nhiu trng hp b iu
khin có tác ng chm, d'n n làm gim chính xác ca quá trình iu khin, không
áp ng c các ch& tiêu cht lng ra. Khi ó ngi ta s2 dng cu trúc iu khin tng.
Hình 6.3 mô t cu trúc iu khin tng có hai mch vòng iu khin m1c ni tip nhau.
Mch vòng iu khin ngoài (mch vòng iu khin sơ cp): s2 dng b iu khin Wk1,
tín hiu ra ca b iu khin mch vòng ngoài s? là giá tr !t cho mch vòng iu khin bên trong. 127
Mch vòng iu khin trong (mch vòng iu khin th cp): s2 dng b iu khin Wk2,
tín hiu ra ca b iu khin mch trong s? tác ng trc tip lên cơ cu chp hành ca i tng.
iu kin thc hin c cu trúc iu khin tng là quá trình quá ca mch vòng
iu khin trong phi nhanh hơn mch vòng bên ngoài.
Hình 6.3: S h thng iu khin t'ng
Ví d: H thng iu khin n#ng sn ph>m ra ca mt thit b pha trn hóa cht, s2 dng
cu trúc iu khin tng có hai mch vòng iu khin. IWy }G ~• uG uF u[ vDI[ u\ vDI\ GH]DyHzD{f|I` GH]DwD!x }F uevDIe
Hình 6.4: S h thng iu khin t'ng cho bình trn Trong ó:
- F1, F2: lu lng cht m !c, cht pha loãng.
- n1, n2: n#ng cht m !c, cht pha loãng.
- F3, n3: lu lng, n#ng sn ph>m ra.
- AT: thit b o n#ng sn ph>m ra.
- AC: b iu khin n#ng sn ph>m ra.
- FT: thit b o lu lng cht m !c.
- FC: b iu khin lu lng cht m !c.
Mch vòng iu khin ngoài: mch vòng iu khin n#ng sn ph>m ra. Thit b AT o
n#ng sn ph>m ra, phn h#i a v b iu khin n#ng AC, so sánh vi giá tr n#ng
!t trc nsp. Tín hiu ra b iu khin n#ng AC s? là giá tr !t SP cho b iu khin lu lng FC. 128
Mch vòng iu khin trong: mch vòng iu khin lu lng cht m !c. Thit b FT
o lu lng cht m !c a v b iu khin lu lng FC, so sánh vi giá tr !t SP
tính toán giá tr iu khin làm thay $i m van cp lu lng cht m !c.
Gi s2 áp sut trên ng ng d'n cht m !c thay $i làm lu lng F2 thay $i, khi ó
b iu khin FC s? ra tín hiu iu khin làm thay $i m van lu lng cht m
!c i vào bình là không thay $i, không làm nh hng ti n#ng sn ph>m ra. 129
CHƠNG 7: KH,O SÁT H TH-NG IU KHIN T NG
MATLAB, tên vit t1t ca cm tA ting Anh: MATrix LABoratory, là mt môi trng
mnh dành cho các tính toán khoa hc. Phn mm Matlab tích hp các phép tính vector, ma
trn và phân tích s da trên các hàm cơ bn. V m!t cu trúc, Matlab g#m mt c2a s$ chính
và nhiu th vin khác nhau:
- Control System Toolbox (dành phân tích, thit k mô ph"ng h thng iu khin)
- System Identification (nhn dng)
- Fuzzy Logic (iu khin m)
- Signal Processing (x2 lý tín hiu s)
- Statistics (toán hc và thng kê)
- Finacial Toolbox (lnh vc kinh t)….
Phn ph lc này s? gii thiu v phn Control System Toolbox, là mt th vin ca
Matlab dùng trong lnh vc iu khin t ng. Sau khi khi ng Matlab, c2a s$ Command
window s? xut hin cùng du nh1c >>. Ti c2a s$ Command window chúng ta có th thc
hin nhp trc tip tAng câu lnh và nhn kt qu tính toán. Sau khi nhp câu lnh và kt thúc
bng ng tác nhn phím Enter, Matlab thc hin lnh và tr v kt qu ngay di dòng lnh.
Ngoài ra, ta có th gõ lnh >>edit vào c2a s$ Editor, ti ây ta có th vit, lu và chy toàn
b chơng trình cùng lúc. Mt s lu ý khi mi s2 dng Matlab:
- Matlab phân bit ch hoa và ch thng. Các bin do ngi dùng t !t có th là ch hoa
ho!c ch thng. Các câu lnh thng vit bng ch thng.
- Du % dùng ghi chú thích, dòng ký t sau sau du % s? không c x2 lý.
- Khi nhp câu lnh trong Command window, kt qu thng hin lên ngay di mBi câu
lnh. Nu không mun hin th ta gõ thêm du ch>m ph>y (;) vào cui mBi câu lnh.
- MBi lnh có th có nhiu chc nng và a dng v cú pháp. Trong tài liu này ch& gii
thiu cách dùng cơ bn mô ph"ng h thng tuyn tính liên tc có mt u vào, mt u ra.
Khi cn thêm tr giúp ta gõ >>help tênlnh
1. nh ngha hàm truyn trong Matlab:
- Cho h có hàm truyn t$ng quát: m m b s ....... 0 +b s −1 1 + + b s −1 + b m m W (s) = n n
a s + a s −1 + ....... + a s + a 0 1 n−1 n
Cách nhp hàm truyn nh sau: >> num = [b0 b1 … bm] >> den = [a0 a1 … an] >> W = tf(num,den)
- Nu hàm truyn mô t di dng các nghim cc và zero:
(s − z )(s − z )...(s − z ) W (s ) 1 2 m = K
(s − s )(s − s )...(s − s ) 1 2 n
Cách khai báo hàm truyn: >> Z = [z1 z2 … zm]; >> P = [s1 s2 … sn]; 130 >> W = zpk(Z,P,K)
Ví d nu ta khai báo dòng lnh:
>> W = zpk([ ], [-1 -3 -4],10)
Khi ó có kt qu hin ra là: 10 W = (s + ) 1 (s + ) 3 (s + 4)
- Hàm truyn có khâu tr:: Ví d cho hàm truyn: −5s 15 W = e s2 + s 7 + 3
>> W = tf(15,[1 7 3],’inputdelay’,5)
2. nh ngha phng trình trng thái >> W= ss(A,B,C,D)
trong ó A,B,C,D là các ma trn trng thái nh ngha h thng ta cn khai báo trc.
Cách chuyn $i gia các dng biu di:n:
- Chuyn tA phơng trình trng thái sang hàm truyn:
>> [num,den] = ss2tf(A,B,C,D)
- Chuyn tA dng zero/cc sang hàm truyn:
>> [num,den] = zp2tf(Z,P,K)
- Chuyn tA hàm truyn sang phơng trình trng thái:
>> [A,B,C,D] = tf2ss(num,den) 3. Kt ni các ph(n t
- Ghép ni tip hai phn t2 W1 và W2: >> W = series(W1,W2)
- Ghép song song hai phn t2 W1 và W2: >> W = parallel(W1,W2)
- ơn gin hàm truyn: >> W = minreal(W1,W2) - H m1c phn h#i:
>> W = feedback(W1,W2) % vi mch phn h#i âm
>> W = feedback(W1,W2,1) % vi mch phn h#i dơng 4. Phân tích h thng: 4.1 Trong min th/i gian - V? hàm quá h(t):
>> step(W): v? hàm quá cho h có hàm truyn W, khong thi gian và bc v? theo m!c nh. 131
>> step(W,t): v? hàm quá tA thi im t = 0 n thi im t cho trc
>> step(W1,W2,...,Wn): v? hàm quá #ng thi cho nhiu h thng.
- V? hàm trng lng g(t):
>> impulse(W): v? hàm trng lng cho h có hàm truyn W, khong thi gian và bc v? theo m!c nh.
- ánh giá các ch& tiêu cht lng:
Kích chut phi vào vùng trng trên # th, ln lt chn Characteristics o Setting Time
(thi gian quá ), Peak Response ( quá iu ch&nh), Steady State (giá tr xác lp), Rise
Time (thi gian tng tc). 4.2 Trong min t(n s
- !c tính tn biên, tn pha:
>> ffplot(W): v? !c tính biên tn s, pha tn s ca h có hàm truyn W.
- !c tính tn biên pha (!c tính Nyquist):
>> nyquist(W): v? !c tính Nyquist ca h có hàm truyn W.
>> nyquist(W,w1,w2): v? !c tính Nyquist tA im có tn s w1 n im có tn s w2. - # th Bode:
>> bode(W): v? # th Bode ca h có hàm truyn W. 5. SIMULINK
Simulink là th vin # ha, mô t h thng di dng sơ # khi; là công c mô ph"ng
h thng, giúp ngi s2 dng phân tích và t$ng hp h thng mt cách trc quan.
khi ng simulink tA Command window ta có th kích vào biu tng trên thanh công
c ho!c gõ dòng lnh >>simulink.
Khi ó s? xut hin c2a s$ th vin chính ca simulink nh hình 7.1
b1t u làm vic, to mt trang ng dng mi bng cách vào File o chn New.
Simulink có các th vin chính nh sau:
- Continuous: h tuyn tính liên tc
- Discrete: h tuyn tính gián on - Nonliear: h phi tuyn
- Source: khi ngu#n tín hiu
- Sinks: khi thu nhn tín hiu - Math: ….
5.1 Mt s khi th/ng dùng - Th vin Source:
Step: to tín hiu bc thang (r(t) = 1(t))
Ramp: to tín hiu dc tuyn tính (r(t) = t)
Sine Wave: to tín hiu hàm sin
Contans: to tín hiu không $i theo thi gian - Th vin Sinks:
Scope: hin th các tín hiu c to ra khi mô ph"ng 132
XY Graph: v? quan h gia 2 tín hiu vào theo trc hoành X và trc tung Y.
To Workspace: tt c các tín hiu ni vào khi này s? c chuyn sang không gian tham
s ca Matlab khi thc hin mô ph"ng - Th vin Continuous:
Transfer Fcn: mô t hàm truyn ca mt h thng liên tc di dng a thc t( s/a
thc m:u s. Các h s ca a thc t2 s và m'u s do ngi s2 dng nhp vào.
State Space: mô t hàm truyn ca h thng liên tc di dng phơng trình trng thái
Integrator: khâu tích phân
sDerivative: khâu vi phân
Transport Delay: khâu to tr: - Th vin Math:
Abs: tín hiu ra là giá tr tuyt i ca tín hiu vào
Gain: tín hiu ra bng tín hiu vào nhân h s t l Gain Sign: hàm du
Sum: b cng, tín hiu ra bng t$ng các tín hiu vào 5.2 Ví d&
Mô ph"ng h thng iu khin có sơ #: 10s+1 4s + 2 2s+1 Step Transfer Fcn Scope
- Khi ng Simulink tA Matlab bng dòng lnh >>simulink
- Trong c2a s$ chính ca Simulink chn biu tng New to c2a s$ ng dng.
- Mun to mt khi trong c2a s$ ng dng, ta tìm khi ó trong các th vin ca
Simulink, kích chn và kéo nó vào c2a s$ ng dng.
Vào khi Continuous -> Sources -> Step
Vào khi Continuous -> Transfer Fcn
Vào khi Continuous -> Scope
- !t thông s cho tAng khi, ta m khi ó ra bng cách double-click chut vào nó, sau
ó !t các thông s theo hng d'n trên màn hình
Ví d khi Transfer Fcn: Double-click chut vào nó, nhp thông s nh sau: Numerator
[10 1], Denomirator [4 2 1].
- ng ni gia các khi c thc hin bng cách dùng chut kéo các mi tên u
(ho!c cui) mBi khi n v tr cn ni.
Sau khi to sơ # khi xong, ta tin hành mô ph"ng bng cách chn Simulation -> Start.
Xem kt qu mô ph"ng bng cách double-click chut vào khi Scope. 133 TÀI LIU THAM KH,O
[1]. Nguy:n Doãn Phc, Lý thuyt iu khin tuyn tính, Nhà xut bn khoa hc và k thut, 2009.
[2]. Nguy:n Vn Hòa, C s0 lý thuyt iu khin t ng, Nhà xut bn khoa hc và k thut, 2001.
[3]. Nguy:n Th Phơng Hà, HuQnh Thái Hoàng, Lý thuyt iu khin t ng, Nhà xut bn
i hc quc gia TP. H# Chí Minh, 2008.
[4]. Nguy:n Th Hùng, Giáo trình iu khin t ng, 2006.
[5]. Katsuhiko.Ogata, Modern Control Engineering, Prentice Hall, 1997.
[6]. Stanley M. Shinners, Modern Control System Theory and Design, A Wiley- Interscience Publication, 1998.
[7]. Phan Xuân Minh, Hà Th Kim Duyên, Phm Xuân Khánh, Lý thuyt iu khin t ng,
Nhà xut bn giáo dc. 134



