Lý thuyết giải tích - Giải Tích | Trường Đại học CNTT Thành Phố Hồ Chí Minh

lOMoAR cPSD| 40551442
* Vô cùng bé (VCB) và vô cùng lớn (VCL):
Cho hàm số f x( ) có TXĐ là D và cho x0 (thường là D ) Ta nói lim f x( ) 0 1
f x( ) là VCB khi x x0 nếu x x . Khi đó, 0
f x ( ) là VCL khi x x0
(Ví du: Cho f x( ) x3 10x5 và x0 0 .
Thì khi x 0 thì f x(
) x3 10x5 0 nên f x( ) là VCB khi x 0 )
Khi x 1 thì f x(
) 13 10.15 11 0 nên f x( ) không phải là VCB khi x 1 ).
Ta nói f x( ) là VCL khi x x0 nếu x xlim 0 f x( )
hoăc ̣ x xlim 0 f x( ) . 1 Khi đó,
là VCB khi x x0 f x( ) 1
Ví du: Cho hàm số f x( )
(x 2)2 và x0 2 1 1
Thì khi x 2 thì f x( ) (x 2 0
nên f x( ) là VCL khi x 2 ) 2)
* So sánh giữa các VCB (và các VCL): lim f x( ) 0 x x 0
Cho f x( ) và g x( ) là các VCB khi x x0 , nghĩa là
x xlim 0 g x( ) 0 Ta xét biểu thức: f x( ) k lim x x 0 g x( )
TH1: k 0,k (nghĩa là k hữu hạn)
Ta nói f x( ) và g x( ) là cùng bâc.̣ TH2: k 0 .
Ta nói f x( ) là VCB cấp cao hơn g x( ) và ta kí hiêu là ̣ f x( ) g x( ) hay
là f x( ) O g x( ( )) khi x x0 (ở đây O Over) TH3: k hoăc ̣ k lOMoAR cPSD| 40551442
Ta nói g x( ) là VCB cấp cao hơn f x( ) và ta kí hiêu là ̣ g x( ) f x( ) hay
là g x( ) O f x( ( )) khi x x0
Ví du: Cho f x( ) x2 và g x( ) x8 và x0 0
Thì khi x 0 ta có f x( ) 0 và g x( ) 0 , mà ta thấy tốc đô tiến về 0 của ̣ g x( ) là nhanh hơn
của hàm f x( ) nên ta nói g x( ) là VCB cấp cao hơn hàm f x( ) và kí hiêu là ̣ g x( ) O f x( ( )) khi x
0 hay là x8 O x( 2) khi x 0
TH4: k 1. Ta nói f x( ) là tương đương với g x( ) và ta kí hiêu là ̣
f x( ) ~ g x( ) khi x x0
Ta có môt số VCB tương đương
sau:̣ sin x ~ x khi x 0 sin
~ khi 0 ln(1 x) ~ x khi x 0 ln(1 ) ~ khi 0 x2 1 cos x ~ khi x 0 2 x2 cos x ~1 khi x 0 2 2 1 cos ~ khi 0 2 2 cos ~1 khi 0 2
tan x ~ x khi x 0 tan ~ khi 0 arcsin x ~ x khi x 0 arcsin ~ khi 0 x
arctan x ~ x khi 0
arctan ~ khi 0 x 0 sin2 x ~ x2 khi sin(x2) ~ x2 khi x 0 ex 1~ x khi
x 0 e 1~ khi
0 ax 1~ xlna khi x 0,a 0 a 1~ ln a khi 0,a 0 lOMoAR cPSD| 40551442
* Áp dụng vào quá trình tính giới hạn hàm sô:
+ Ta có thể cắt bỏ đi các VCB cấp cao (chỉ giữ lại các VCB cấp thấp nhất) (cắt bỏ đi các VCL
cấp thấp và giữ lại các VCL cấp cao nhất) khi tính giới hạn.
+ Ta được thay tùy ý các VCB tương đương vào các biểu thức dạng tích/thương của các hàm.
Còn đối với các biểu thức dạng tổng hoăc hiệ u ta hạn chế thay vào, và chỉ được thay vào khị
hàm số không bị triêt tiêu.̣ Ví du mẫu 1: Tính giới hạn: lim
2xsin x tan x 6 x 0 ln(cos(4 ))x
Ví du mẫu 2: Tính giới hạn lim 1 1 x 0 x 2 sin 2 x Giải:
2xsin x tan6 x 2 .x x x6 2x2 x6 2x2 1
lim lim ln 1 2 2 limx 0 ln 1 8 x2 limx 0 8x2 4 Ví du mẫu
1: x 0 ln(cos(4 ))x x 0 (4 )x Ví du mẫu 2: Cách 1: limx 0 x12 sin12 x limx 0 x12 x12 lim 0x 0 0 Cách 2: 1 1 1 1 cos2 x 1 cos2 x 1 sin2 x
lim x2 sin2 x limx 0 tan2 x sin2 x limx 0 sin2 x sin2 x limx 0 sin2 x limx 0 sin2 x 1 x 0 (sai) Cách 3: lim x12 sin12 x limx 0
sinx22sinx 2 xx2 limx 0
sinx x22x. 2 x2 limx 0 sin2xx4 x2 (*) x 0
Dùng quy tắc L’Hospitale (đạo hàm tử chia đạo hàm mẫu), ta có: (sin2 x x2 )'
2sin x cos x 2x (*) lim 0 x x4 )' limx 0 4x3 (**) lOMoAR cPSD| 40551442 ( Cách 3.1: (**) limx 0
2x cos4xx3 2x limx 0 cos2xx2 1
Dùng quy tắc L’Hospitale (đạo hàm tử chia đạo hàm mẫu), ta có: limx 0 sin4x x limx 0 cos4 x 41 (sai) Cách 3.2: (**) limx 0 sin(2 )4xx3 2x
Dùng quy tắc L’Hospitale (đạo hàm tử chia đạo hàm mẫu), ta có: limx 0
2cos12(2 )xx2 2 limx 0
cos(2 )6xx2 1 limx 0
2sin12x(2 )x limx 0
sin(2 )6x x limx 0 2cos6(2 )x 13 (đúng).
Bài tâp tương tự : a/ limx 0 sin12 x tan12 x b/ lim x12 tan12 x x 0 c/ xlim 1 ln1x ex 11 1
ln(cos )x xsin5 x d/ lim x 0 ln(1 2xsin x) e/ limx 0 lOMoAR cPSD| 40551442 f/ lim x 0 g/ limx 0 1 1 x2 cos1x x2
h/ lim 1 x 1 x x 0 2sin x i/ lim1 3 cos(2 )x x 0 2xsin x
3 cos(3 )x cos(2 )x j/ lim x 0 ln(cos )x
2/ ĐẠO HÀM VÀ ĐẠO HÀM CẤP CAO CỦA HÀM SỐ MÔT BIẾṆ :
Cho hàm số f x( ) có TXĐ là D và cho trước số x0 (thường là D ). Ta xét k x xlim 0
f x( )x xf x0( 0) .
Nếu tồn tại k thì ta gọi đây là giá trị đạo hàm của hàm f x( ) tại x0 và kí hiêu là ̣ f '(x0) lim f x( ) f x( 0) x x x 0 x 0
Ngược lại, nếu không tồn tại k thì ta nói hàm f x(
) không có đạo hàm tại x0 và kí hiêu là ̣ f '(x0)
Nếu f x( ) có đạo hàm tại mọi điểm x0 D thì ta nói f x( ) có đạo hàm tổng quát trên D và kí hiêu là:̣ f 'x hay f x hay dfdx hay fx (d = derivative)
* Nhắc lại môt sô quy tắc tính đạo hàm thông dụng ̣ :
(C) ' 0 , với C hằng số = constant
(ex )' ex ; (eu )' u e' u lOMoAR cPSD| 40551442
(ax )' ax ln a; (au ) ' u a' u ln a , với a 0 2 1 ' 1 , với x 0 ; u1
' uu2' , với u x x 0 1 x ' 2 x 1 ( ln| x |)' u' x
, với x 0 ; u ' 2 u , với u 0 u'
, với x 0 ; (ln |u |)' , với u 0 u 1 u' (log |a x|)'
, với a 0, x 0 ; (log |a u |)'
, với a 0,u 0 xlna uln a
(x )' x 1 , với ; 1;
; (u )' u u' 1 , với ; 1; sin
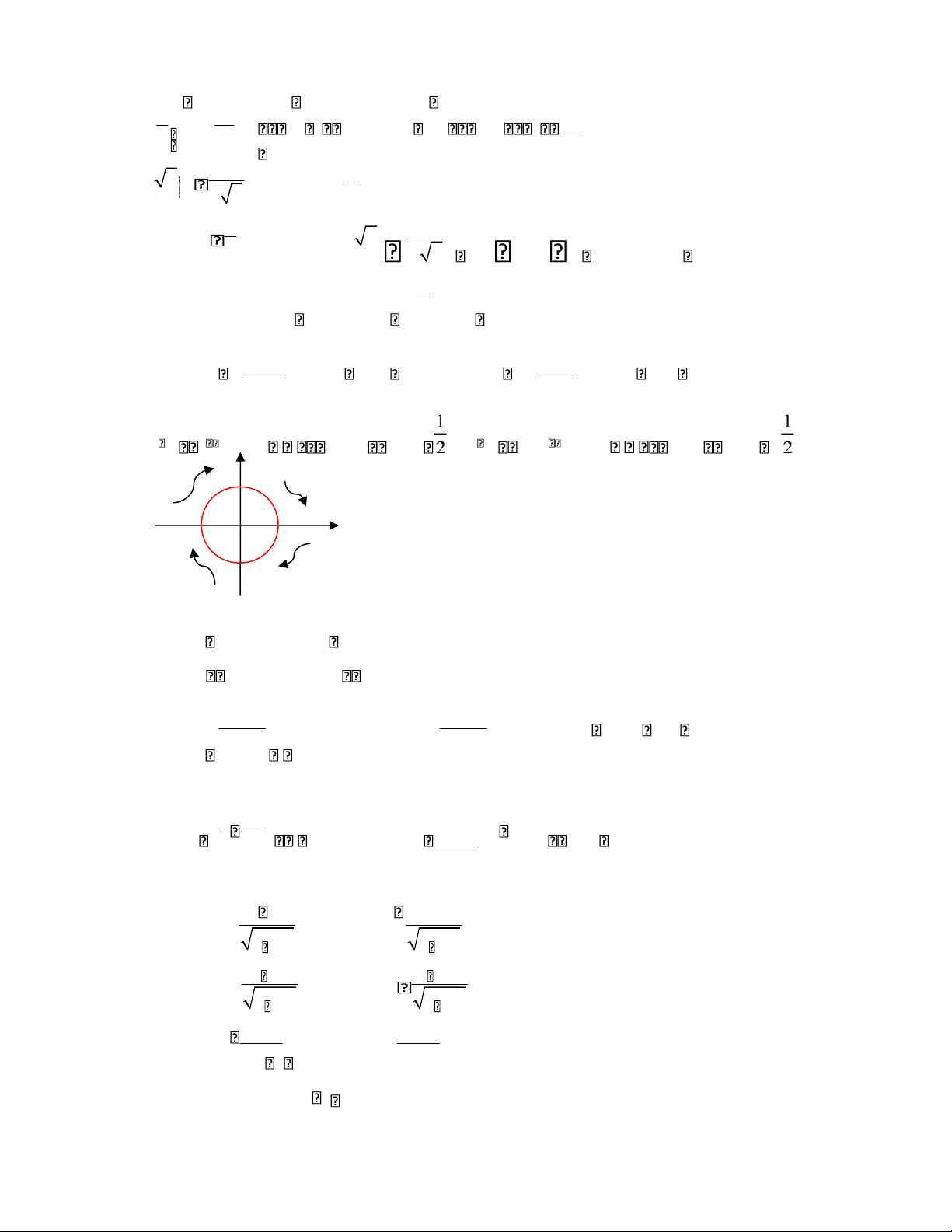
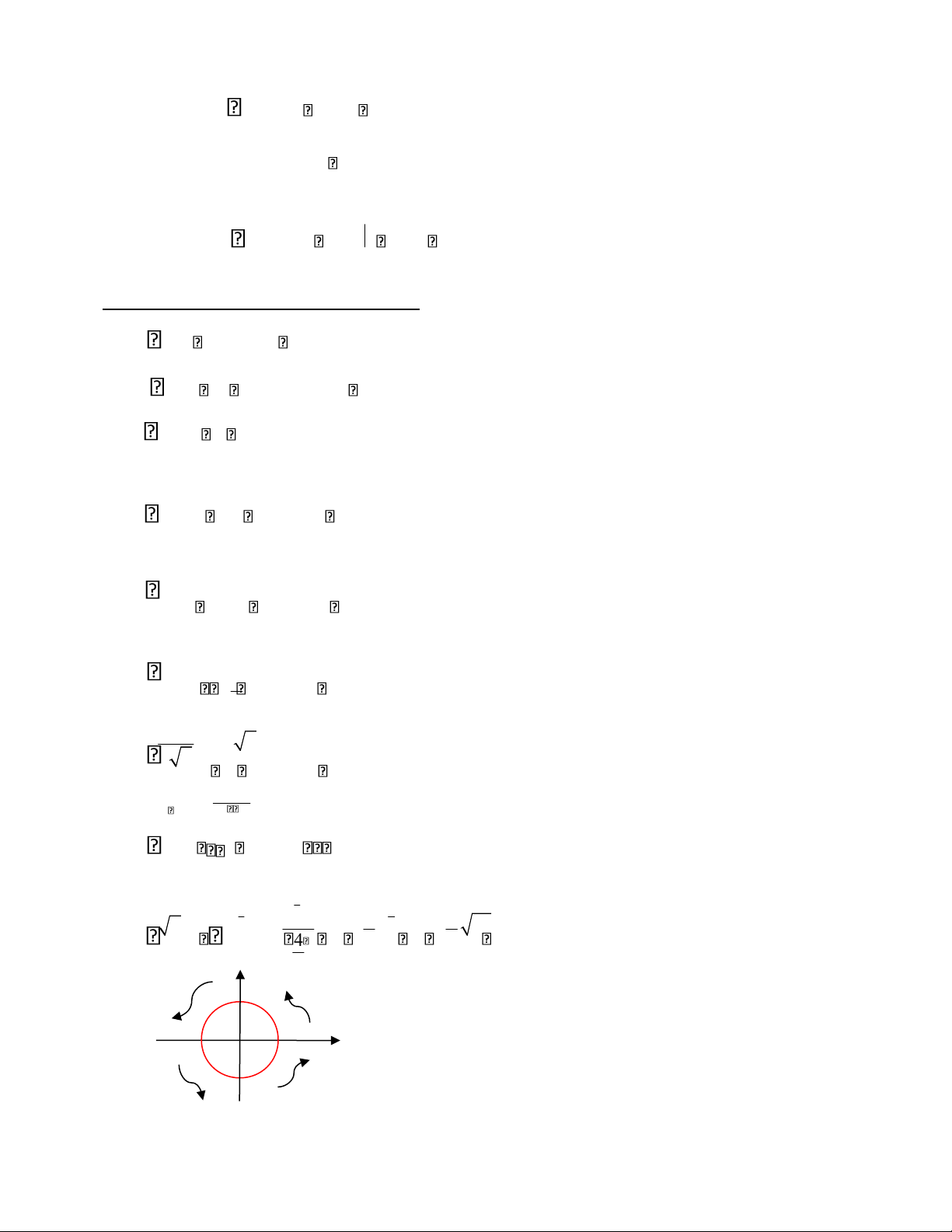
- cos cos chiều quay của đạo hàm là cùng chiều kim đồng hồ (clockwise) - sin
(sin x) ' cos x ; (sin u) ' u 'cosu
(cos x)' sin x; (cosu) ' u 'sin u 2 cos1
x; (tan )'u u2' u u'(1 tan2 u) (tan )'x 2 x 1 tan cos '
(cot )'x sin 12 x 1 cot2 x; (cot )'u
sin u2 u u'(1 cot2 u) 1 u'
(arcsin )'x ; (arcsin )'u 2 1 x 2 1 u 1 u ' 2 1 x 2 1 u (arccos )'x 1 ; (arccos )'u u ' (arctan )'x 1 2 ; (arctan )'u 1 u2 x lOMoAR cPSD| 40551442
(arccot )'x 1 1x2 ; (arccot )'u 1 uu'2 uv
' u v' v 2v u' ;
( . )u v ' u v' v u'
( . .u v w) ' u v w'. . u v w.'. u v w. . ' uv ' ? (uv)'
ev uln ' (vln )'u ev uln
v'lnu v. uu' uv
* Áp dụng đạo hàm để tính giới hạn (quy tắc L’Hospitale): 0 f x( ) có dạng
Cho các hàm số f x() và g x( ) là các hàm số thỏa x xlim 0 g x( ) 0 hoăc ̣ f x( ) f '( )x 0 Ta có x xlim 0 g x( ) x xlim 0
g x'( ) (ta thay x x0 vào để xem còn dạng 0 hoăc ̣ hay không?) f "( )x 0
Nếu còn thì lim x x 0
g"( )x (ta thay x x0 vào để xem còn dạng 0 hoăc ̣ hay không?) f "'( )x
Nếu còn thì lim x x 0 g"'( )x …. 0
(cứ tiếp tuc như vây đến khi biểu thức không còn dạng ̣ hoăc ̣
thì ta dừng bài toán) 0 xx x 0
Ví du mẫu: Tính giới hạn sau: lim (dạng )
x 1 ln x x 1 0
Giải: Dùng quy tắc L’Hospitale ta có lOMoAR cPSD| 40551442 xx x xx ln x x.1 1 x x. x x 1 ln x 1 x lim 1 lim x lim
x 1 ln x x 1 x 1x 1 1 x
lim xx ln x 1 x x. x ln x 1 2 x x. x 1x 1 1 1 0 2 x 1 1 1
Bài tâp tương tự :
Bài 1: Tính các giới hạn sau: a/ lim sin(x x 2)tan 4x limx 2 sin(cotx x2) 2 4 b/ limx 3
xx 33 sin(2sin(3xx 9)6)
ex e x 2x c/ lim x 0 x sin x
ex2 e x2 2x2 d/ limx 0 xsin5 x
etanx ex e/ lim
x 0 tan x x lim 2arctan x f/ 1 x ln 1 x x lOMoAR cPSD| 40551442
g/ xlim xxe e2 x ea x 1 h/ lim với b 0
x 0 sinbx tan x i/ lim x 1
j/ lim ln(1 x) tan 2x x 1 cot x
Bài 2: Tính giới hạn các hàm số sau bằng quy tắc L’Hospitale:
3/ TÍCH PHÂN XÁC ĐỊNH VÀ TÍCH PHÂN BẤT ĐỊNH Cho hàm số f x(
) có TXĐ là D và gọi [a b, ] D.
Ta nói F x( ) là nguyên hàm của f x( ) trên [a b, ] nếu F x'( ) f x( ), x [a b,] lOMoAR cPSD| 40551442
Khi đó, ta viết f x dx( ) F x( ) C và gọi đây là tích phân bất định của f x( ) trên [a b, ], với C hằng số b
Ngoài ra, ta có f x dx( ) F x( )ba F b( ) F(a) là tích phân xác định của f x( ) trên [a b, ]. a
* Môt sô tích phân bất định thông dụng ̣ :
0dx C , với C hằng số = constant
Cdx Cx C1 , với C C, 1 hằng số = constant e dxx ex C ax
a dxx lna C , với a 0 1
x dx ln | x| C , với x 0 1 1
x2 dx x C , với x 0 1
2 x dx x C , với x 0 x 1 x dx 1 C , với 1 1 x 3 xdx x dx 3 1
4 31 C 34 x34 C 43 3 x4 C 3 sin - cos cos
chiều quay của nguyên hàm là ngược chiều kim đồng hồ lOMoAR cPSD| 40551442 - sin (counter-clockwise)
sin xdx cos x C cos xdx sin x C 1
cos2 x dx tan x C 1
sin2 x dx cot x C tan xdx cossin xx dx
cossinxx dx ln |cosx | C cos x cot xdx
sin x dx ln |sin x| C x 2 xdx cossin22 xx dx 1 coscos2 x2 dx cos12 x 1
dx tan x x C tan cot2 xdx sin2 x dx
sinsin2 x2 x dx sin12 x 1 dx cot
x x C cos2 x 1 tan3 xdx ? cot3 xdx ? tan4 xdx ? cot4 xdx ? sin2 xdx 1 cos(2 )2x dx 12 x sin(2 )2 x C 2x sin(2 )4 x C cos2 xdx 1 cos(2 )2x dx 12 x sin(2 )2 x C 2x sin(2 )4 x C lOMoAR cPSD| 40551442 sin3 xdx ? sin4 xdx ? cos3 xdx ? cos4 xdx ?
dx arcsin x C arccos x C 1 1 2 1 x
1 x2 dx arctan x C arccot x C dx x
sin x ln tan 2 C cosdxx ln tan 2x 4 C dx 1 x
Lưu y: Môt số hàm số sau không có tích phân bất định ở dạng hàm sơ cấp, nghĩa là không co ̣
công thức biểu diễn cho nguyên hàm: x2
; e x2dx; cos(x dx2) ; sin(x dx2) ; sinx x dx,… e dx
+ Hàm mũ lẻ đối với sin thì đăt ẩn phu bằng cos (khi xuất hiệ n đồng thời cả sin và cos)̣
Ví du: sin5 x cos6 xdx đăt ̣ t cos x dt sin xdx sin xdx dt
+ Hàm mũ lẻ đối với cos thì đăt ẩn phu bằng sin (khi xuất hiệ n đồng thời cả sin và cos)̣ lOMoAR cPSD| 40551442
Ví du: sin10 x cos7 xdx đăt ̣ t sin x dt cos xdx
+ Hàm mũ lẻ/ mũ chẵn đối với cả sin và cos thì
đăt ẩn phu bằng sin nếu số mũ của sin > số mũ của coṣ
Ví du sin12 x cos8 xdx đăt ̣ t sin x dt cos xdx
đăt ẩn phu bằng cos nếu số mũ của cos > số mũ của siṇ
Ví du sin9 x cos15 xdx đăt ̣ t cos x dt sin xdx sin xdx dt
+ Hàm mũ lẻ/ mũ chẵn đối với cả sin và cos mà có số mũ ngang bằng nhau thì
ta đăt ẩn phu bằng sin hoặ c cos đều được.̣
+ Ta thường dùng công thức hạ bâc nếu trong biểu thức chỉ có sin hoặ c cos (thiếu 1 trong 2) và ̣
tồn tại ở dạng mũ chẵn. x x 2dt
+ Ta có thể đăt ̣ t tan 2 2 arctant x 2arctant dx 1 t2 2t 1 t2
Và ta có sin x 1 2 ;cos x 1
t2 cho hầu như tất cả các bài toán dạng hàm lượng giác. t
* Nhắc lại phương pháp tính tích phân:
a/ Phương pháp đổi biến: b Xét I f x dx( ) và J f x dx( ) a
Đăt ̣ t g x( ) ... dt g x dx'( ) I f x dx( )
....dt thay hàm t g x( ) để biểu diễn tích phân theo biến x , kết hợp với hằng số C a g a( ) b g b( )
Khi tính J thì ta phải đổi cân ̣ J
f x dx( ) ...dt b g b( ) a g a( )
b/ Phương pháp tích phân từng phần: b Xét I f x dx( ) và J f x dx( ) a u g x( ) du g x dx'( ) Đăt ̣ lOMoAR cPSD| 40551442 dv dx v dx I uv vdu g x( ) g x dx'( ) ... b b
Và J uvba vdu ( g x( ))ba g x dx'( ) ... a a
Ví du mẫu: Tính tích phân a/ I 5 (4x 3)2 dx 1 b/ J x e dx2 x 0 Giải: dt
a/ Đăt ̣ t 4x 3
dt 4dx dx 4 2 dt 1 2 1 t 5 1 5 7 5 I 5 (4x 3)2 dx 5 t2 4 4 t dt5 4.
C 28t 5 C 28 5 (4x 3)7 C Với C hằng số.
b/ Dùng pp tích phân từng phần ta đăt ̣ u x2 du 2xdx dv e dxx v e dxx ex 1 1 1 J uv10 vdu x e2x 10
2xe dxx 12e1 02e0 2xe dxx 0 0 0 u1 2x du1 2dx Đăt ̣ dv1 x v1 e dxx ex e dx 1 x1
2e dxx e (2e 0
(2ex)10 e (2e 2.1) e
2 Nên J e 2xe0 0 lOMoAR cPSD| 40551442
Bài tâp tương tự : Tính các tích phân sau: (2x 3)3 a/ 4x2 dx e dx2x b/ ex 1 1 c/ x e dx3 x 0 4 d/ e dxx 0
e/ e2x sin(3 )x dx f/ x arctan
xdx g/ x e3 x2dx
h/ x cos(2 )x dx
i/ x e dx2 4x j/ arccos xdx k/ 54xdx sin xdx l/ 4 cos2 x xe dxx m/ (x 1)2 dx n/ x2 4
dx t tan x , ta có: dx 2dt2 và sin x
2t 2 ;cos x 11 tt22 )
o/ 5 4sin x 3cos x (gợi ý: đăt ̣ 2 1 t 1 t dx x 2dt lOMoAR cPSD| 40551442
p/ sin x 2cos x 3 (gợi ý: đăt ̣ t tan 2 , ta có: dx 1
t2 và sin x 1 2tt2 ;cos x 11 tt22 ) sin3 x q/ cos8 x dx dx
r/ (sin x 4)(sin x 1) 1 t 2 dx x 2dt 2
s/ 3 2cos x (gợi ý: đăt ̣ t tan 2 , ta có: dx 1 t2 và cos x 1 t2 ) 0 e t/ ln2 xdx 1