Lý thuyết Hồi quy tuyến tính | Xác suất thống kế

1. Hồi quy tuyến tính
1.1. Mô hình hồi quy tuyến tính đơn biến (Simple linear regression) 1.1.1. Định nghĩa
Cho 2 biến X và Y, trong đó Y phụ thuộc tuyến tính vào X. Với một giá trị Xi nào
đó của biến X, giá trị tương ứng Yi của biến Y được tình bằng công thức: ! " a # b$ # e
Với a và b là hai thông số (paramater, còn gọi là regression coefficient hay hệ số hồi quy) Trong đó:
a: Hệ số chặn (intercept, tức giá trị lúc Xi = 0)
b: Độ dốc hây hế số góc (slope hay gradient)
ei: Sai số tuân theo luật phân phối chuẩn
Hệ số a thể hiện giá trị ước lượng Y khi giá trị X bằng không. b thể hiện mức thay
đổi của Y khi X thay đổi 1 đơn vị. ei là sai số phần dư biểu diễn ảnh hưởng của các yếu tố
khác ( các yếu tố không được nghiên cứu) đến Y. Một mô hình hồi quy có ý nghĩa khi ei
biên thiên ngẫu nhiên, phân phối chuẩn với trung bình bằng không, phương sai không thay
đổi theo các giá trị X và độc lập tuyến tính (không tự tương quan với nhau). ei là sai lệch
giữa giá trị ước lượng với giá trị thực.
Mô hình hồi quy tổng thể hiện mối liên hệ tuyến tính giữa X và Y được biểu diễn như sau: ! " a # b% # e
1.1.2. Phương pháp bình phương cực tiểu (Ordinary least squares method)
Trong thực tế không thể xác định chính xác giá trị của tham số a và b mà chỉ có thể
ước lượng chúng từ dữ liệu của mẫu thu thập được. Phương pháp ước tình các thông số
này là phương pháp bình phương cực tiểu (Ordinary least squares method).
Ta có: &! " a # b$ # e &
Downloaded by VietJack TV Official (vietjackvideos@gmail.com)
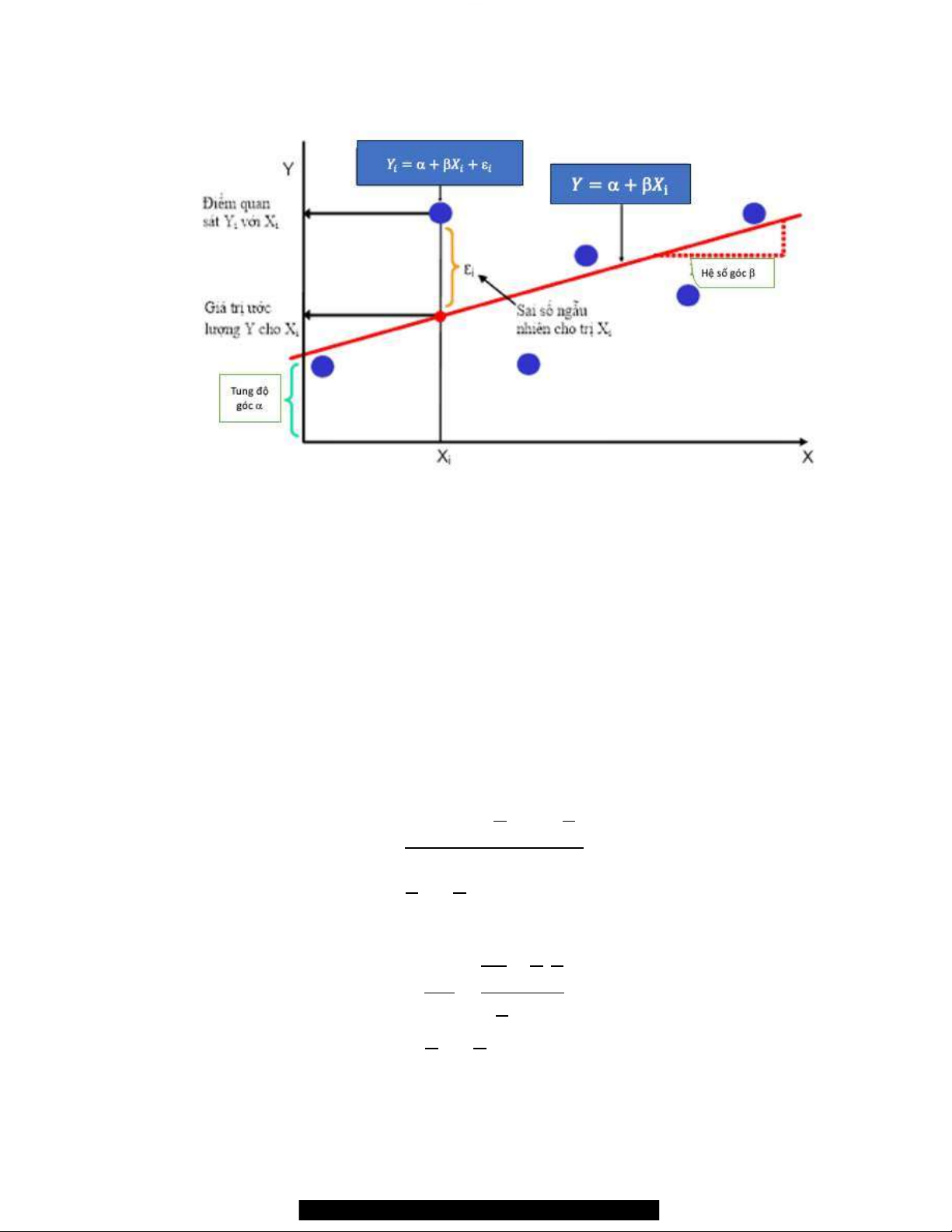
Hình 1 Biểu đồ mô tả điểm quan sát Yi, hàm hồi quy tuyến tính đơn biến Y và sai lệch ei
Cho n mẫu (X1, Y1), (X2, Y2), …, (Xn, Yn). Tìm các giá trị a' và b( để ước lượng cho
các tham số a và b. Thường thì các điểm quan sát không nằm trên cùng một đường thẳng.
Tuy nhiên, phương pháp bình phương cực tiểu sẽ vẽ đường thẳng !) " a' # b($ đi giữa
các điểm quan sát sao cho sai lệch phần dư bình phương ei (RRS) là cực tiểu, tức là
* e " * +, - !). " * /! - 0a' # b($ 12 &đạt giá trị nhỏ nhất. Trong thực tế
người ta sử dụng tham số sai lệch bình phương để tránh trường hợp tổng sai lệch phần dư bằng 0.
Từ đó ta có các ước lượng của a và b là a' và b( được tính theo công thức sau: * +$ - $.+! - !. b( " * +$ - $. Và a' " ! - b($ Mặc khác ta có: 3 $! - $4 ! b( " 3 " 5643 Và a' " ! - b($ Trong đó:
Downloaded by VietJack TV Official (vietjackvideos@gmail.com)
$: Giá trị trung bình của biến độc lập Xi.
!: Giá trị trung bình của biến phụ thuộc Yi.
1.1.3. Đánh giá sự phù hợp
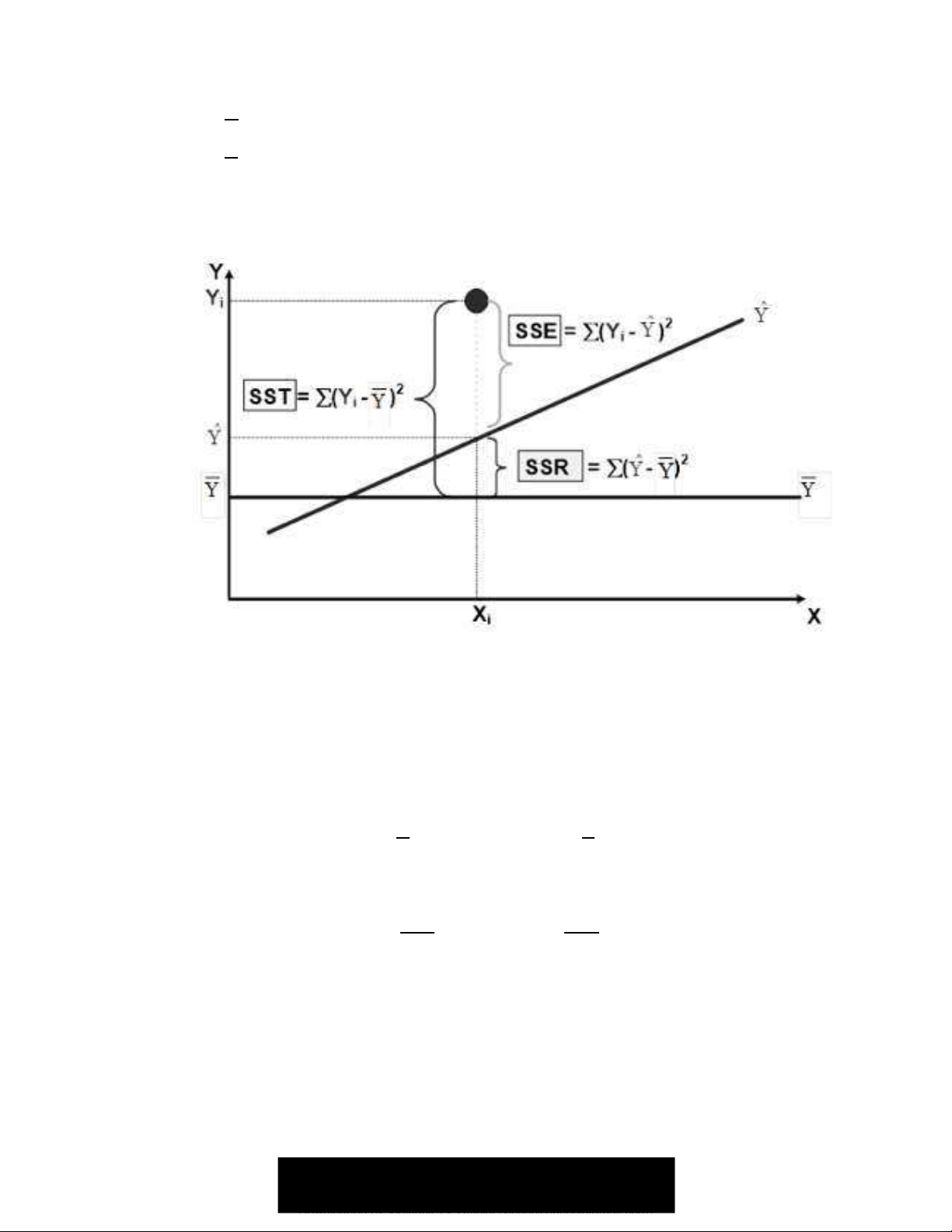
Hình 2: Sai số (phần dư) trong hồi quy
Sau khi xác định được giá trị hệ số hồi quy, cần đánh giá mức độ phù hợp của mô
hình dựa vào hệ số xác định R2 (coefficient of determination) và phương sai của phép hồi
quy. Quan sát hình trên có thể nhận thấy một điểm quan sát bất kỳ nào cũng có thể mô tả bằng biểu thức sau: +, - !. " +, - !(. # +!( - !.
Hệ số xác định R2 là tỉ lệ giữa SSE và SST: 338 337 7 "
339 &:;<&7 " 5 - 339
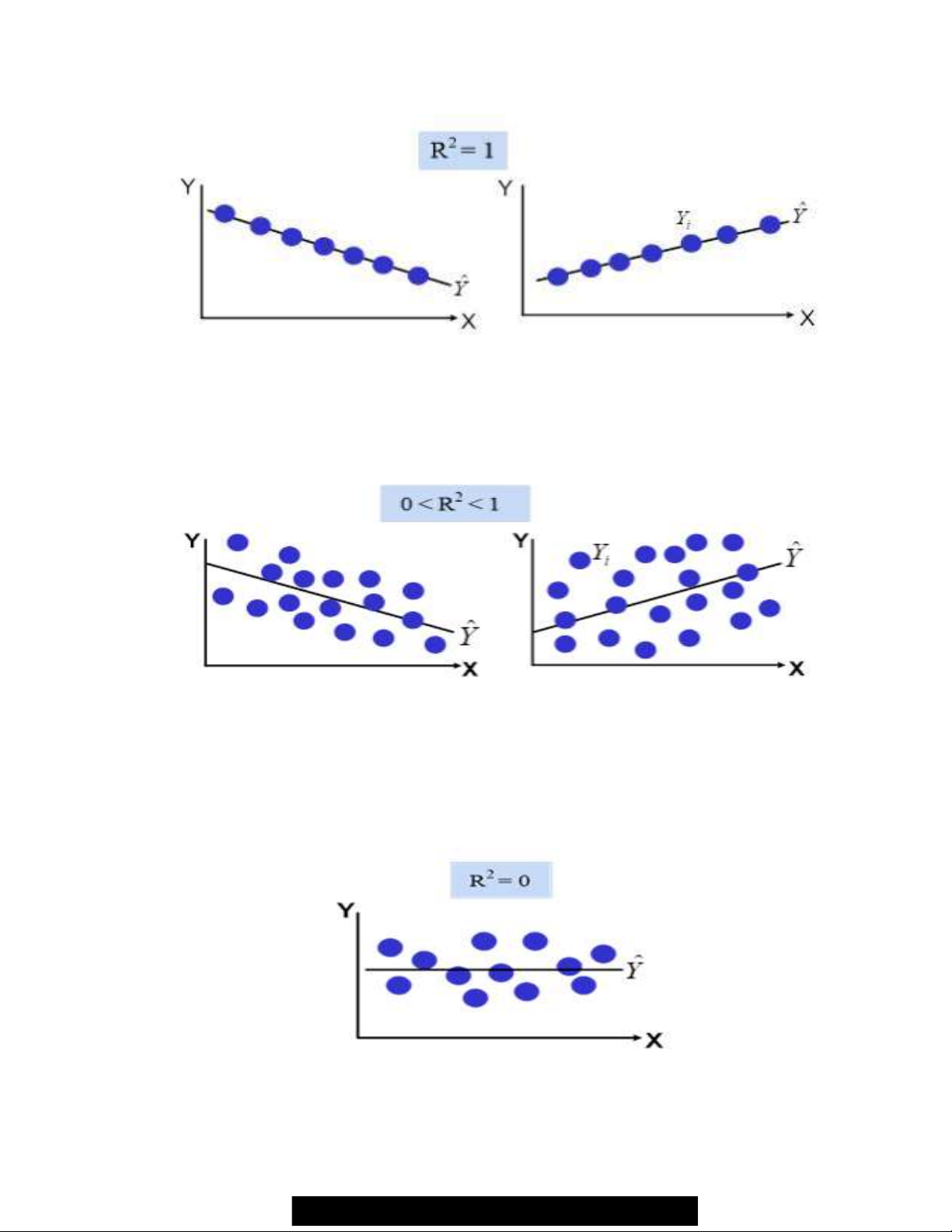
Khi R2 = 1: Mô hình hồi quy không tồn tại sai số, có tương quan hoàn hảo giữa X
và Y, mô hình hồi quy mô tả 100% sự biến đổi của dữ liệu.
Downloaded by VietJack TV Official (vietjackvideos@gmail.com)
Hình 3: Tương quan giữa điểm quan sát Yi với giá trị ước lượng hồi quy !( khi R2 = 1
Khi 0 < R2 < 1: Có tương quan giữa X và Y, mô hình hồi quy tồn tại sai số ở mức
độ phụ thuộc vào giá trị R2. Càng tiến về 1 sai số càng thấp.
Hình 4: Tương quan giữa điểm quan sát Yi với giá trị ước lượng hồi quy !( khi 0 < R2 < 1
Khi R2 = 0: Không có liên hệ giữa biến X và Y. Biến Y không phụ thuộc biến X tức
mô hình hồi quy không mô tả được chuyển vận của dữ liệu. Và dĩ nhiên, không thể sử dụng
mô hình hồi quy hệ số xác định R2 = 0 để mô tả dữ liệu.
Hình 5: Tương quan giữa điểm quan sát Yi với giá trị ước lượng hồi quy !( khi R2 = 0
Downloaded by VietJack TV Official (vietjackvideos@gmail.com)
Phương sai ước lượng S2: giả sử biến phụ thuộc Y phân phối chuẩn, tức tham số ước
lượng a' và b( cũng phân phối chuẩn thì phương sai ước lượng S2 được tính bằng công thức sau: * e 338 3 " 6 - = " 6 - =
Độ lệch chuẩn ước lượng S thể hiện mức độ sai lệch trung bình của trị quan sát Yi
so với đường hồi quy !( (xem đường hồi quy là đường trung bình). 3 " >3
Một cách tổng quát, sai số tổng: SST = SSR + SSE ( Đẳng thức cở bản của phân tích hồi quy)
Chú ý: Ta có thể tính SSR, SSE theo công thức sau:
SSE = SXY - b(.SXY và SSR = b(.SXY
Với: SST: Sai số tổng, bình phương sai lệch của trị Yi quanh trị trung bình Y trung bình. 339 " 3 ?+, - !.
SSR: Sai số hồi quy, bình phương sai lệch giữa giá trị hồi quy Y mũ so với Y trung bình. 337 " ?+!( - !.
SSE: Sai số ước lượng, bình phương sai lệch giữa Yi và Y mũ 338 " ?+, - !(. Trong đó:
!: Giá trị trung bình của biến phụ thuộc Yi. , @ Giá trị quan sát.
!(@ Giá trị ước lượng ứng với một trị Xi (thế Xi vào phương trình hồi quy).
1.1.4. Kiểm định hệ số góc b và AB&CD&EAFG&a
¨ Ước lượng khoảng của hệ số góc và hệ số chặn
Downloaded by VietJack TV Official (vietjackvideos@gmail.com)
- Khoảng tin cậy với độ tin cậy g&EAH&AB&CD&IJE&b là: 3 3 b( K 9( ) " b( K 3 ( ) "L &3 & >3 g b4 9 g b " >3
- Khoảng tin cậy với độ tin cậy g&EAH&AB&CD&EAFG&a là: 3M5 3M5 a' K 6 * $ 9( ) " a' K 3 ( ) 6 * $ a4 9 "L & 3a " >3 g g >3
Chú ý: 3b và 3a được gọi là sai số chuẩn cho hệ số góc
¨ Kiểm định hệ số góc - Giả thuyết Giả thuyết kiểm định H0: b = b0 Giả thuyết đối lập H1: b N b0 - Trị kiểm định b( - b 9 " 3b - Miền bác bỏ
Bác bỏ H0 nếu Tqs thuộc:
Miền bác bỏ đối xứng O ( ) ( ) a " 0-¥P 9 g 1È&+9 g P #¥.& & Miền bác bỏ bên trái O ( ) a " 0-¥P 9 g 1 Miền bác bỏ bên phải O ( ) a " +9 g P #¥.&
Chú ý: Giả thuyết H0: b = 0 nói rằng mô hình hồi qu đơn biến không có ý nghĩa
thông kê. Nếu H0 bị bác bỏ, ta kết luận mô hình hồi quy hữu ích cho việc ước đoán giá trị biến phụ thuộc Y.
¨ Kiểm định hệ số chặn - Giả thuyết
Downloaded by VietJack TV Official (vietjackvideos@gmail.com) Giả thuyết kiểm định H0: a = a0 Giả thuyết đối lập H1: a N a0 - Trị kiểm định a' - a 9 " 3a - Miền bác bỏ
Tương tự kiểm định hệ số góc
1.2. Mô hình hồi quy tuyến tính đa biến (Multiple linear regression) 1.2.1. Định nghĩa
Mô hình diễn đạt qua phương trình ! " a # b$ # e có một yếu tố duy nhất (đó là
X) và vì thế thường được gọi là mô hình hồi quy tuyến tính đơn giản (Simple linear
regression model). Trong thực tế, chúng ta có thể phát triển mô hình này thành nhiều biến
chứ không chỉ giới hạn một biến như trên, chẳng hạn như:
! " a # b $ # b $ # Q# b $ # e Trong đó: a: Hệ số chặn
b1: Hệ số dốc của Y theo biến X1 và giữa các biến X2, X3, …, Xk không đổi
b2: Hệ số dốc của Y theo biến X2 và giữa các biến X2, X3, …, Xk không đổi …
bk: Hệ số dốc của Y theo biến Xk và giữa các biến X2, X3, …, Xk không đổi
ei: Số hạng sai số (Biến ngẫu nhiên)
k: Biến số độc lập trong mô hình
Chú ý trong phương trình trên, chúng ta có nhiều biến X (X1, X2, … dến Xk) mỗi
biến có một thông số bj (j = 1, 2, …, k) cần phải ước tính. Vì thế mô hình này còn được gọi
là mô hình hồi quy tuyến tính đa biến (Multiple linear regression).
1.2.2. Phương pháp bình phương cực tiểu (Ordinary least squares method)
Downloaded by VietJack TV Official (vietjackvideos@gmail.com)
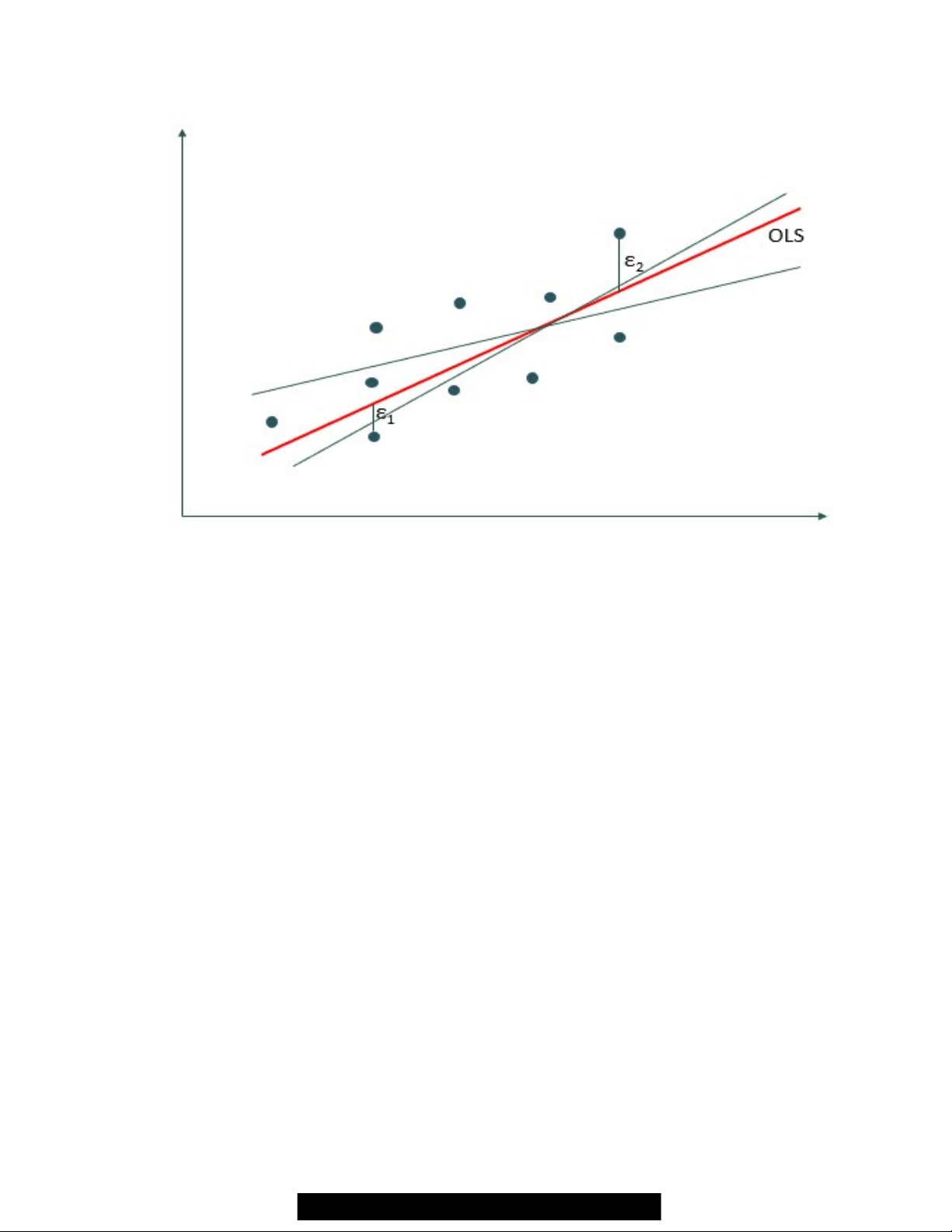
Hình 6: Biểu đồ mô tả hàm hồi quy tuyến tính đa biến Y và sai lệch ei
Khi biểu diễn trên mặt phẳng Oxy, đường hồi quy OLS là một đường thẳng đi qua
đám đông các điểm dữ diệu mà ở đó, khoẳng cách từ các điểm dữ liệu (trị tuyệt đối e) đến
đương hồi quy là ngắn nhất.
Từ đồ thị scatter biểu diễn mối quan hệ giữa biến độc lập và biến phụ thuộc, các
điểm dữ liệu sẽ phân tán nhưng có xu hướng chung tạo thành dạng môt đường thẳng. Chúng
ta có thể có rất nhiều đường hồi quy đi qua đám đông các dữ liệu này chứ không phải chỉ
một đường duy nhất, vấn đề là ta phải chọn ra đường nào là mô tả sát nhất xu hướng dữ
liệu. Phương pháp bình phương cực tiểu OLS sẽ tìm ra đường thẳng đó dựa trên nguyên
tắc cực tiểu hoá khoẳng cách từu các điểm dữ liệu đến đường thẳng. Trên hình ở trên đường
màu đỏ là đường hồi quy OLS. Ta có:
! " a # b $ # b $ # Q# b $ # e
Ta có hàm hồi quy như sau:
!) " a' # bR$ # bR$ # Q# bR$ # e
Downloaded by VietJack TV Official (vietjackvideos@gmail.com)
Theo phương pháp OLS, ta cần tòm các giá trị a' và b) &(j = 1, 2, …, k) sao cho sai
lệch phần dư bình phương (RRS) ei là cực tiểu.
* e " * +, - !). " * /! - 0a' # bR$ # bR$ # Q# bR$ 12 &
Để tối thiểu hoá RSS, ta lấy đạo hàm của RSS theo a' và b) &(j = 1, 2, …, k) rồi cho
các đạo hàm này bằng không. Ta được các hệ phương trình: V 6a' # bR * $ # bR * $ # Q # bR * $ " * ,
Ta' * $ # bR * $ #& & bR * $ $ # Q# &bR * $ $ " * $ , U
W& & & & & & & & & & & & W& & & & & & & & & & & & & & & W& & & & & & & & & & & & & & & & & & & & &W& & & & & & & & & & & &W& & & & & & T
Sa' * $ # bR * $ $ # bR * $ $ # Q # bR * $ " & &* $ ,
Giải hệ phương trình trên ta được các giá trị trị a' và b) &(j = 1, 2, …, k).
1.2.3. Đánh giá sự phù hợp
Trong mô hình hồi quy tuyến tính đơn biến ta đã đưa ra hệ số xác định 338 337 7 "
339 &:;<&7 " 5 - 339
Từ công thức trên tra thấy khi R2 càng lớn thì bình phương sai số dự báo càng nhỏ,
do đó mô hình hồi quy càng phù hợp.
Hệ số xác định R2 có tính chất sau:
¥ Khi R2 = 1: Mô hình hồi quy không tồn tại sai số, có tương quan hoàn hảo giữa
X và Y, mô hình hồi quy mô tả 100% sự biến đổi của dữ liệu.
¥ Khi 0 < R2 < 1: Có tương quan giữa X và Y, mô hình hồi quy tồn tại sai số ở mức
độ phụ thuộc vào giá trị R2.
¥ Khi R2 = 0: Không có liên hệ giữa biến X và Y. Biến Y không phụ thuộc biến X
tức mô hình hồi quy không mô tả được chuyển vận của dữ liệu.
Tính phù hợp của mô hình hồi quy tăng lên khi có nhiều biến giải thích trong mô
hình hơn. Tuy nhiên, người ta luôn muốn dùng một số lượng biến giair thích vừa đủ sao
cho vẫn có được mô hình phù hợp mà không phải tốn kém quá nhiều biến giải thích. Hơn
nữa, nhiều khi đưa thêm một số biến độc lập vào mô hình thì tác động riêng phần của biến
Downloaded by VietJack TV Official (vietjackvideos@gmail.com)
độc lập đó tới biến phụ thuộc lại không thực sự có ý nghĩa thống kê. Vậy vần có tiêu chuẩn
đánh giá sự phù hợp của mô hình, trong đó có cân nhắc đến số lượng biến giải thích cho
mô hình. Một trong số tiêu chuẩn như cậy là hệ số xác định hiểu chỉnh 7XX của R2. 6 - 5
7XX " 5 - +5 - 7 . Y6 - Z - 5[ Trong đó: n: Cỡ mẫu
k: Số biến độc lập trong mô hình
Từ đó 7XX có các tính chất sau:
¥ Nếu k > 1 thì 7XX \ 7 \ 5
¥ Khi số biến độc lập k tăng lên thì 7XX cũng tăng tên theo nhưng chậm hơn so với 7
¥ 7 ] ^, nhưng 7XX có thể âm khi 7XX nhận giá trị âm thì để cho tiện người ta gám
lại cho nó giá trị bằng 0.
Giá trị ước lượng của phương sai S2: * e 338 3 " 6 - Z - 5 " 6 - Z - 5
Ước lượng của phương sai đo lường sự phân tán của các giá trị thực tế đo lường
được của biến phụ thuộc quanh những giá trị của biến phụ thuộc được dự đoán bằng đường hồi quy. 1.2.4. Kiểm định
Mô hình hồi quy mà chúng ta xây dựng là dựa trên dữ liệu một mẫu từ tổng thể vì
vậy nó có thể bị ảnh hưởng của sai số lấy mẫu, vì thế chúng ta cần kiểm định ý nghĩa của toàn bộ mô hình. ¨ Kiểm định F: - Giả thuyết
H0: b1 = b2 = … = bk (hay R2 = 0)
Downloaded by VietJack TV Official (vietjackvideos@gmail.com) H1: _bj N 0 (hay R2 N 0)
Chú ý: Nếu giả thuyết H0 trên đúng nghĩa là tất cả các hệ số độ dốc đồng thời
bằng 0 thì mô hình hồi quy đã xây dựng không hề có tác dụng trong việc dự đoán
hay mô tả về biến phụ thuộc. - Trị kiểm định 337 ` " Z 338 6 - Z - 5 - Qui tắc bác bỏ
Bác bỏ H0 nếu P(F > F1-g) \ 1-g hay nếu F > F1-g&abc&F1-g&def&gh&ijGI&kAlG&
iDc&m&EJ&inE&go&pH&gqrG&gs&CD&dt&u&at&inE&go&pH&pvbc&wxy&CD&dt&6 - Z - 5& ¨ zc{w&|}GA&~@& - Giả thuyết
H0: b1 = b2 = … = bk (hay R2 = 0) H1: _bj N 0 (hay R2 N 0) - Trị kiểm định b•& R 9 " 3b - Miền bác bỏ
Bác bỏ H0 nếu Tqs thuộc:
Miền bác bỏ đối xứng O ( ) ( ) a " 0-¥P 9 g 1È&+9 g P #¥. Miền bác bỏ bên trái O ( ) a " 0-¥P 9 g 1 Miền bác bỏ bên phải O ( ) a " +9 g P #¥.
Downloaded by VietJack TV Official (vietjackvideos@gmail.com) TÀI LIỆU THAM KHẢO
https://nghiencuukhoahoc.edu.vn/bai-viet/hoi-quy-don.html
https://www.phamlocblog.com/2016/11/cach-chay-hoi-quy-trong-spss.html
https://maths.uel.edu.vn/Resources/Docs/SubDomain/maths/TaiLieuHocTap/ToanUngDu ng/m_hnh_hi_quy_a_bin.html
https://eldata11.topica.edu.vn/HocLieu/v1.0/STA301/Giao%20trinh/06_TVU_STA301_B ai4_v1.00131012140.pdf
https://fsppm.fulbright.edu.vn/cache/FSLM-10-MultipleRegressionV-2021-03-01- 16463454.pdf
Downloaded by VietJack TV Official (vietjackvideos@gmail.com)