lOMoAR cPSD| 48541417
TỔNG LÝ THUYẾẾT KYỸ THUẬT ĐỒỒ HOẠ
Chương 2: Đồồ Họa 2 chiềuồ Lý thuyềết: DDA m < 1 : m > 1 :
Lý thuyềết: Bresenham m < 1 : p0 = 2Dy – Dx + xi+1 = xi + 1
+ yi+1 = yi + 1,pi+1 = pi + 2Dy - 2Dx khi pi >= 0 + yi+1 = yi , pi+1 = pi + 2Dy khi pi < 0
Lý thuyềết: Midpoint Đường Tròn p0 = 1 - R xi+1 = xi + 1 + yi+1 = yi - 1, pi+1 = pi + 2xi – 2yi + 5 khi pi >= 0 + yi+1 = yi , pi+1 = pi + 2xi + 3 khi pi < 0 lOMoAR cPSD| 48541417
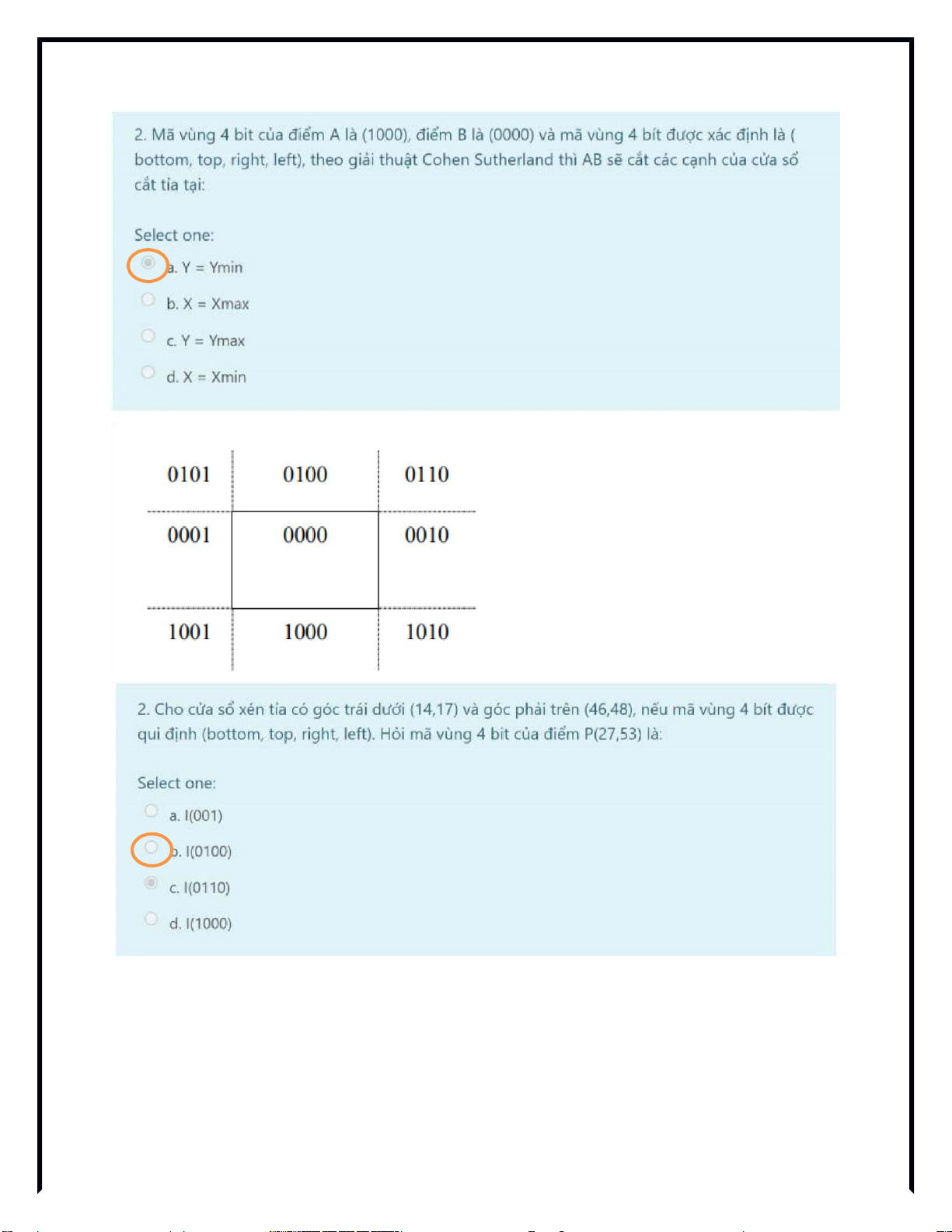
Lý thuyềết: Cohen - Sutherland
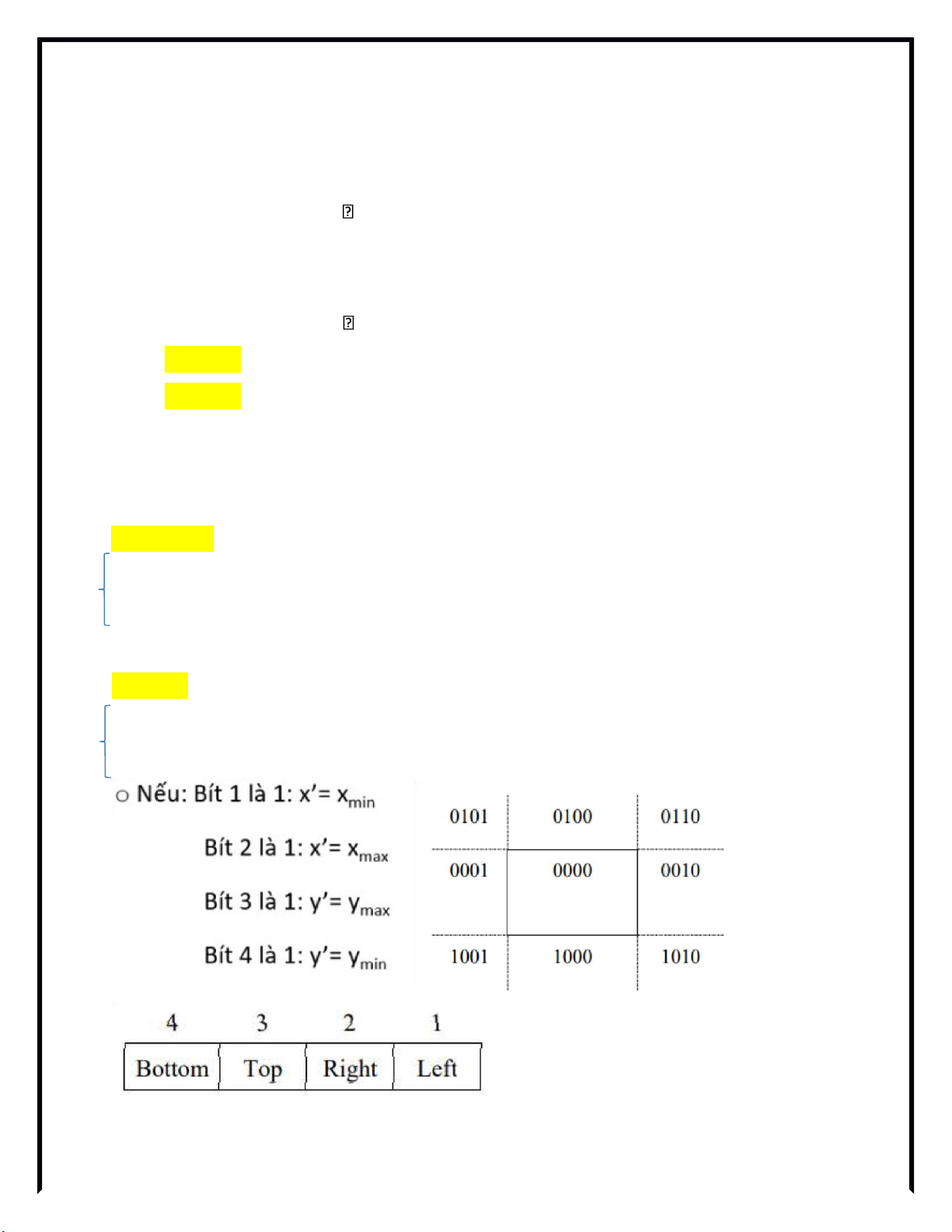
Tìm giao điểm P’(x’,y’) của P1P2 với biên của cửa sổ:
Bit 1 được đặt là 1 nêếu x xmin, khi đó bit 2 được đặt bằằng 0.
Bit 2 được đặt là 1 nêếu x > xmax, khi đó bit 1 được đặt bằằng 0
Bit 3 được đặt là 1 nêếu y > ymax, khi đó bit 4 được đặt bằằng 0.
Bit 4 được đặt là 1 nêếu y ymin , khi đó bit 3 được đặt bằnằg 0
- Nêuế bit 1 là 1 ta có x’= xmin , bit 2 là 1: x’= xmax P1P2 cằết cửa sổ tại biên dọc.
- Nêuế bit 3 là 1 ta có y’= ymax, bit 4 là 1: y’= ymin P1P2 cằết cửa sổ tại biên ngang. Biên ngang y’= y min
hoặc y’ = y max x’ = x 1 + (y’ – y 1 )/m Biên d c ọ x’ = x min ho c ặ x’ = x max y’ = y 1 + m(x’ – x 1 ) lOMoAR cPSD| 48541417
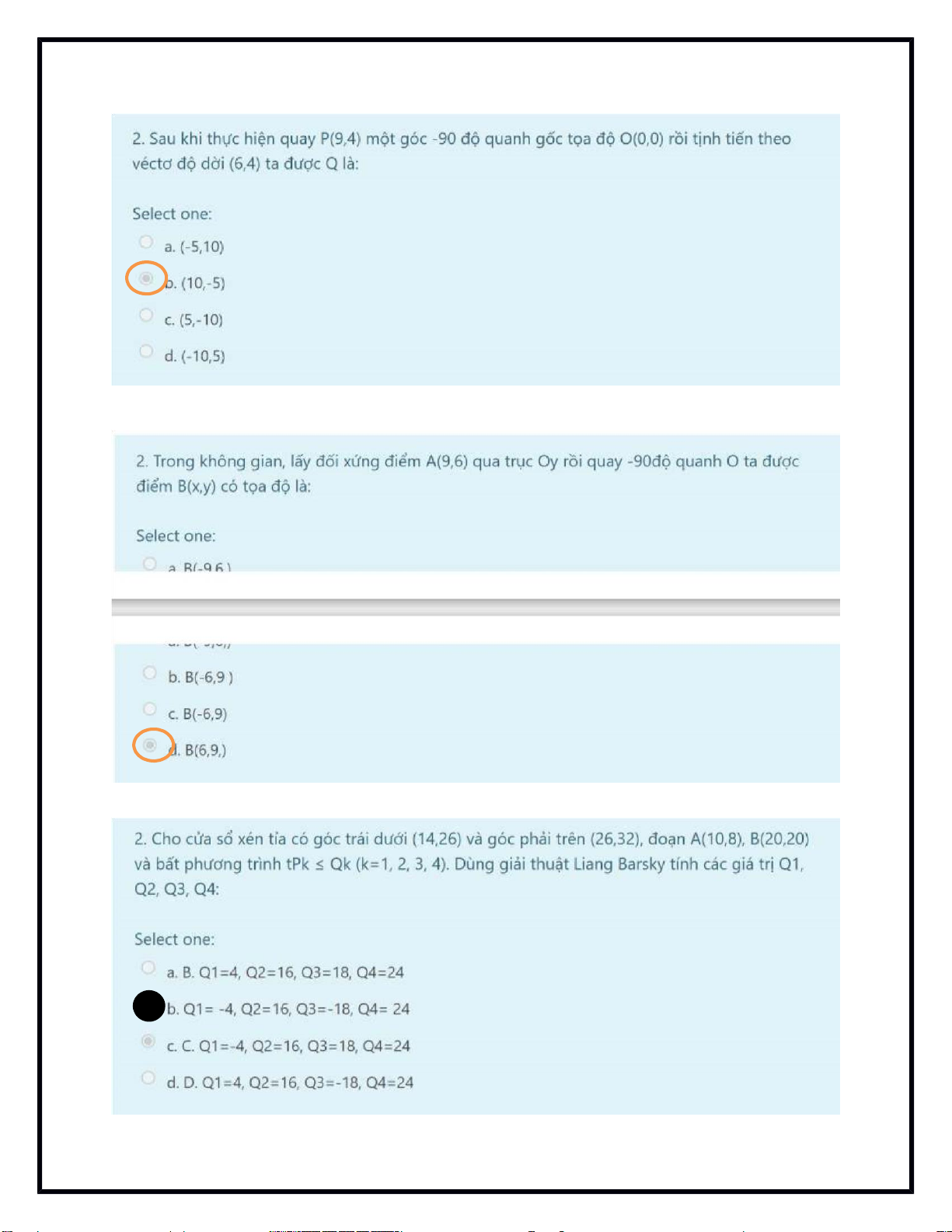
Lý thuyềết: Liang Barsky
Cho 2 điểm P1(x1,y1), P2(x2,y2).
Phương trình tham sốế của đoạn thẳng có 2 điểm đầằu cuốếi P1, P2 là: x = x1 + (x2-x1)t y = y1 + (y2-y1)t x = x1 + tDx y=y1 + tDy
Với t [0,1] ta có phương trình tham sốế của đoạn P1P2
Với t (-∞, +∞) ta có phương trình tham sốế của đường thằằng đi qua P1, P2.
Ứng với mốỗi giá trị t, ta sẽỗ có một điểm P(x,y) tương ứng thuộc đường thẳng:
- Các điểm ứng với t 1sẽỗ thuộc vêằ ta P2x.
- Các điểm ứng với t 0 sẽ ỗthuộc vêằ ta P1x’.
- Các điểm ứng với 0 t 1 sẽ ỗthuộc vêằ đoạn thẳng P1P2 .
Một điểm P(x,y) là giao điểm của đoạn thẳng và cửa sổ ứng với các giá trị t thỏa
hệ bầết phương trình:
xmin ≤ x ≤ xmax xmin ≤ x1 + t Dx ≤
xmax ymin ≤ y ≤ ymax => ymin ≤ y1 + t Dy ≤ ymax 0 ≤ t ≤ 10 ≤ t ≤ 1 Đặt: p1 = -Dx q1 = x1 - xmin p2 = Dx q2 = xmax – x1 p3 = -Dy q3 lOMoAR cPSD| 48541417 = y1 - ymin p4 = Dy q4 = ymax - y1 Phép quay tâm
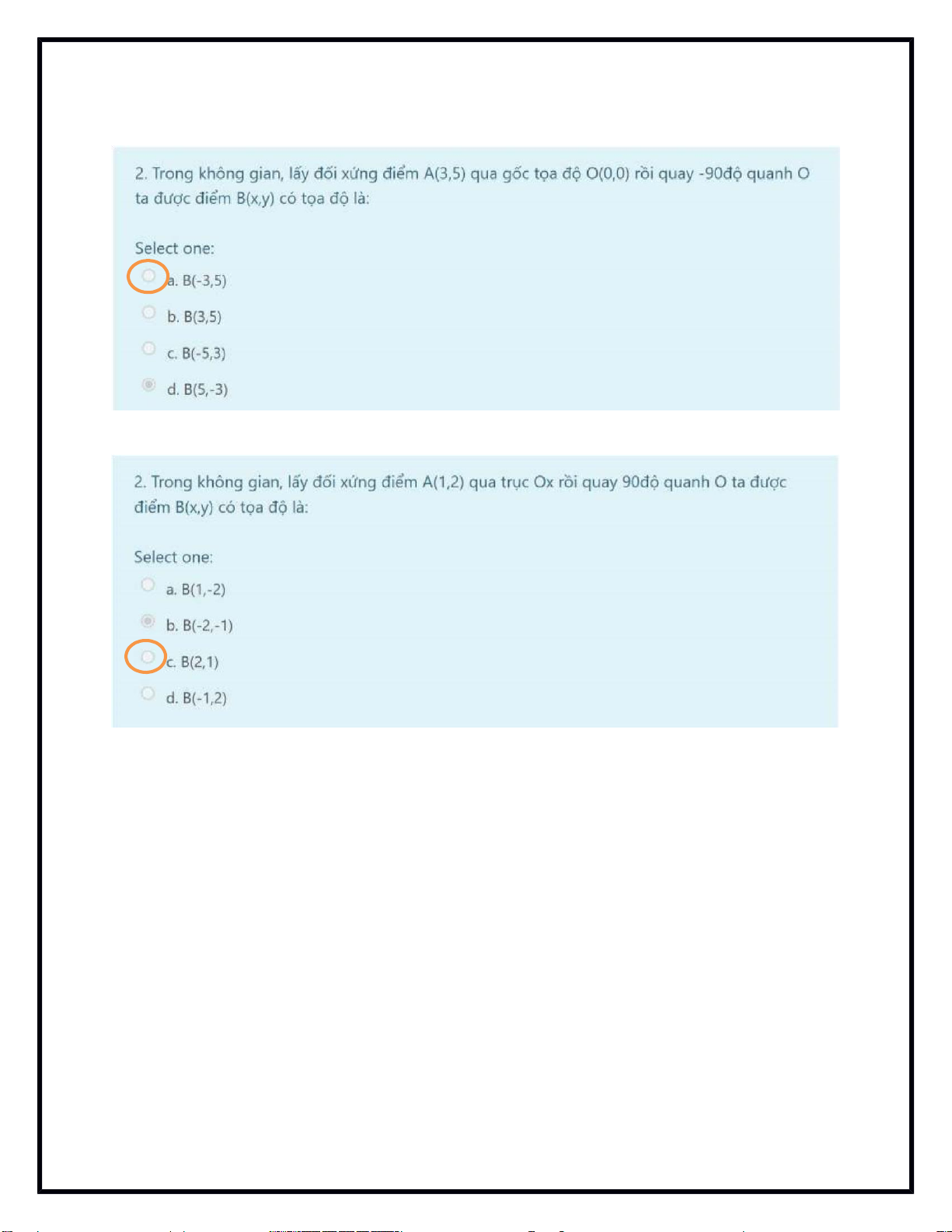
Phép quay làm thay đổi hướng của đốếi tượng. Một phép quay cầằn có tầm quay
và góc quay. Góc quay dương được quy ước là chiêằu ngược chiêuằ kim đốằng
hốằ. Ta có cống thức biêến đổi của phép quay điểm P x, y quanh tầm O(0,0) một góc : x’= x.cosα – y. sinα y’=x. sinα + y. cosα Phép tịnh tềến
Phép tịnh tênế thực hiện di chuyển vị trí của một điểm P(x,y) tới vị trí Q(x’,y’) thẽo
vẽctor độ dời (dx,dy), ta có: lOMoAR cPSD| 48541417 x’= x+dx y’=y+dy Phép
biềến đổi tỉ lệ
Phép biênế đổi tỉ lệ làm thay đổi kích thước, hình dạng của đốếi tượng. Co hay
giãn tọa độ của một điểm P x, y thẽo trục hoành và trục tung với tỷ lệ lầằn lượt
là Sx và Sy được điểm Q(x’,y’): x’= x.Sx y’=y.Sy
Chương 3: Đồồ Họa 3 chiềuồ
1. Phép tịnh tềến X’ = x + dx Y’ = y + dy Z’ = z + dz
2. Phép biềến đổi tỉ lệ
+ Tâm bâết kì I (xi , yi, zi) :
Cho tỉ lệ (Sx, Sy, Sz) , vẽctor (xi, yi, zi)
X’ = xp * Sx + ( 1 – Sx )xi xi + Sx( xp – xi )
Y’ = yp * Sy + ( 1 – Sy )yi
Z’ = zp * Sz + ( 1 – Sz )zi + Tâm O(0, 0,0): X’ = x.Sx lOMoAR cPSD| 48541417 Y’ = y.Sy Z’ = z.Sz 3. Phép quay + Quay trục Ox
P( x, y, z ) -> 90o Q( x, -z, y ) -90o Q( x, z, -y ) + Quay trục Oy
P( x, y, z ) -> 90o Q( z, y, -x ) -90o Q( -z, y, x ) + Quay trục Oz
P( x, y, z ) -> 90o Q( -y, x, z ) -90o Q( y, -x, z )
4. Phép đồếi xứng Cho P( x, y, z )
+ Đốếi xứng qua mặt phẳng xOy Q( x, y, -z)
+ Đốếi xứng qua mặt phẳng xOz Q( x, -y, z)
+ Đốếi xứng qua mặt phẳng yOz Q( -x, y, z)
+ Đốếi xứng qua gốếc tọa độ Q( -x, -y, -z) lOMoAR cPSD| 48541417 m = 0.75 < 1 x 6 7 8 9 10 11 12 13 14 10.7 12.2 y 7 7.75 8.5 9.25 10 5 11.5 5 13 ry 7 8 9 9 10 11 12 12 13 R=6, Tính y t i ạ x = 3 p0 -5 -2 3 0 x 0 1 2 3 y 6 6 6 5 lOMoAR cPSD| 48541417 (26,29) + - 90 o =(29,-26) lOMoAR cPSD| 48541417 12 / 18 lOMoAR cPSD| 48541417 Tính ra đáp án y = 16 lOMoAR cPSD| 48541417 Đi qua A,B y= 2x Đi qua C y= 2x + b Đi qua C,D y= 2x + 1 lOMoAR cPSD| 48541417 Y = ax + b Đi qua A,B y= -1/2x + 15 Đi qua C y= -1/2x + b Đi qua C,D y= -1/2x + 60 m=1/2 p 0 -6 0 x 4 5 6 y 5 6 6 lOMoAR cPSD| 48541417 Bài ktra sốế 2 (-5,-3)->(-3,5) A(1,-2) -> (2,1) lOMoAR cPSD| 48541417 lOMoAR cPSD| 48541417 (4,-9)->(10,-5) -9 ,6 -> 6, 9 lOMoAR cPSD| 48541417 Q1= x1 - xmin = -4 Q2= xmax – x1 = 16 Q3= y1 – ymin = -18 Q4= ymax – y1 = 24 lOMoAR cPSD| 48541417 Cp= 1001 cq= 0000 X’=10 Y’=13 lOMoAR cPSD| 48541417