












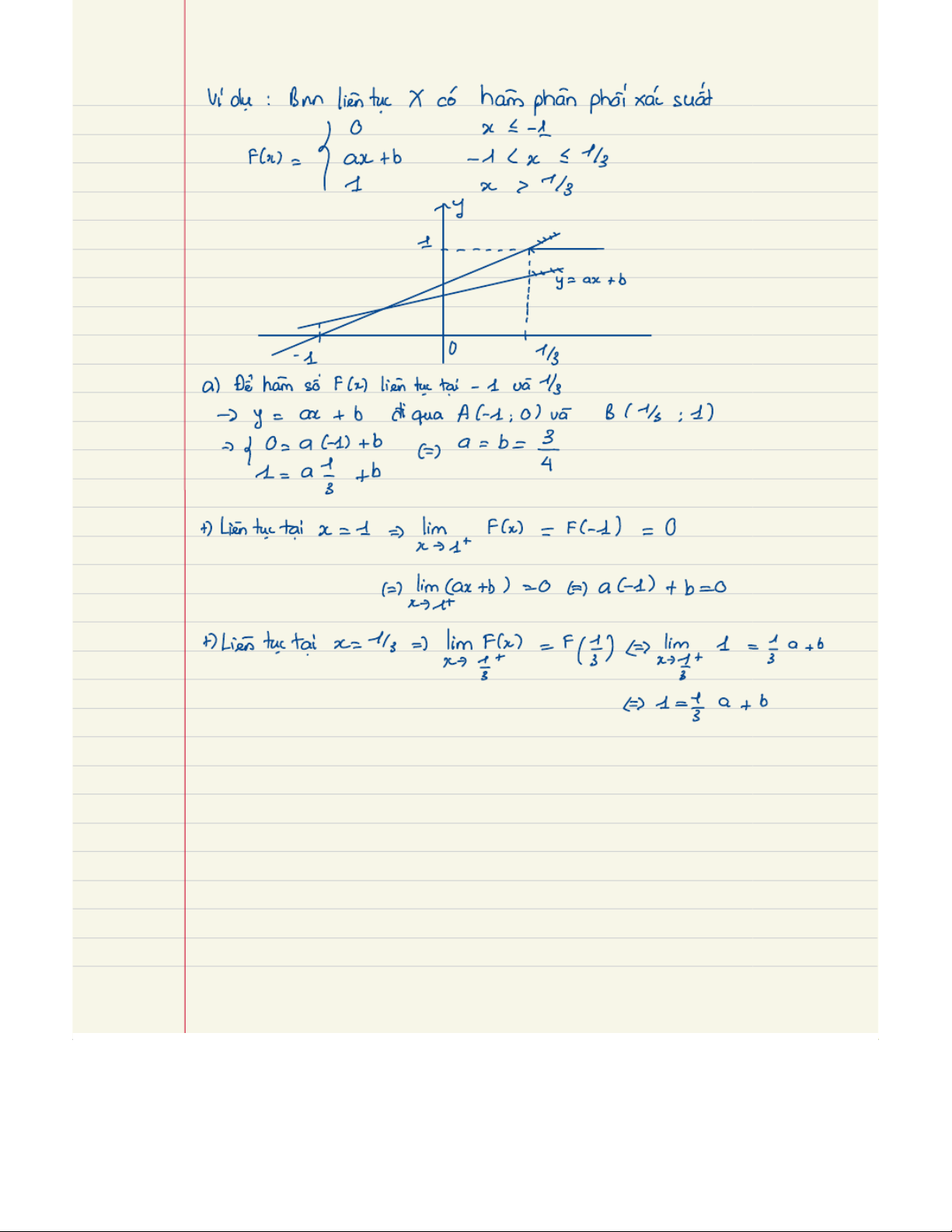






Preview text:
Một xí nghiệp có 3 máy nổ hoạt động độc lập nhau. Xác suất để
trong một ngày máy nổ thứ nhất, thứ hai, thứ ba bị hỏng tương
ứng là 0,2; 0,1; 0,15. Tính xác suất để trong một ngày:
a) Có đúng một máy nổ bị hỏng.
b) Có đúng hai máy bị hỏng.
c) Cả ba máy đều không bị hỏng.
Xác suất để động cơ thứ nhất của máy bay bị trúng đạn là
0,2; để động cơ thứ hai của máy bay bị trúng đạn là 0,3.
Xác suất trúng đạn của phi công là 0,1. Tính xác suất để
máy bay rơi, biết rằng máy bay rơi khi phi công bị trúng đạn
hoặc cả hai động cơ bị trúng đạn.
Có ba hộp đựng sản phẩm. Hộp một có 7 chính phẩm và 3 phế
phẩm. Hộp hai có 8 chính phẩm và 2 phế phẩm. Hộp ba có 10
chính phẩm và 4 phế phẩm.
a. Lấy ngẫu nhiên một hộp, từ đó lấy ngẫu nhiên một sản
phẩm. Tính xác suất để sản phẩm được lấy ra là chính phẩm.
Có ba hộp đựng sản phẩm. Hộp một có 7 chính phẩm và 3 phế
phẩm. Hộp hai có 8 chính phẩm và 2 phế phẩm. Hộp ba có 10
chính phẩm và 4 phế phẩm.
a) Lấy ngẫu nhiên một hộp, từ đó lấy ngẫu nhiên một sản phẩm.
Tính xác suất để sản phẩm được lấy ra là chính phẩm.
b) Lấy ngẫu nhiên một hộp, từ đó lấy ngẫu nhiênmột sản phẩm
thì được 1 chính phẩm. Theo bạn sản phẩm lấy ra có khả năng thuộc hộp nào nhất?
Dây chuyền lắp ráp nhận được các chi tiết do hai máy sản
xuất. Trung bình máy thứ nhất cung cấp 70% chi tiết, máy
thứhai cung cấp 30% chi tiết. Khoảng 90% chi tiết do máy thứ
nhất sản xuất ra đạt tiêu chuẩn, 85% chi tiết do máy thứhai sản
xuất ra đạt tiêu chuẩn.
a) Lấy ngẫu nhiên từdây chuyền ra một sản phẩm. Tính xác
suất để sản phẩm đó đạt tiêu chuẩn.
b) Lấy ngẫu nhiên từdây chuyền ra một sản phẩm thì được
một sản phẩm đạt tiêu chuẩn. Tính xác suất để sản phẩm đó do máy thứhai sản xuất.
Một phân xưởng có 5 máy hoạt động độc lập nhau. Xác
suất để trong mỗi ca làm việc mỗi máy bị hỏng đều bằng 0,1.
a) Tính xác suất để trong một ca làm việc có đúng hai máy bị hỏng.
b) Tính xác suất để trong một ca làm việc có ít nhất hai máy bị hỏng.
Ví dụ 3: Xác suất để xạ thủ bắn trúng bia là 0,8. Xạ thủ
được phát từng viên đạn để bắn cho đến khi trúng bia thì
dừng bắn. Hãy xây dựng quy luật phân phối xác xuất của số viên đạn bắn ra.
Tại một thành phố, tỷ lệ dân chúng thích xem bóng đá là 80%. Chọn ngẫu nhiên 10
người dân của thành phố đó. Gọi X là số người thích xem bóng đá trong số 10 người được chọn.
a. Gọi tên phân phối xác suất của X.
b. Tính xác suất để có đúng 5 người thích xem bóng đá.
c. Tính xác suất để có ít nhất một người thích xem bóng đá.




