
























Preview text:
CHƯƠNG 8
KIỂM ĐỊNH GIẢ THUYẾT HAI MẪU
1. KIỂM ĐỊNH GIẢ THUYẾT SO SÁNH HAI TRUNG BÌNH (HAI MẪU ĐỘC LẬP)
Các giả định chung cho bài toán kiểm định hai mẫu độc lập: X , ,
là mẫu ngẫu nhiên được chọn từ tổng thể 11 X12 . . . , X1n
1 có phân phối chuẩn với trung bình µ và phương sai . 1 σ21 X , ,
là mẫu ngẫu nhiên được chọn từ tổng thể 21 X22 . . . , X2m
2 có phân phối chuẩn với trung bình µ và phương sai . 2 σ22
Tổng thể 1 và 2 (đại diện bởi X và ) độc lập với nhau. 1 X2
1.1. SO SÁNH HAI TRUNG BÌNH, TRƯỜNG HỢP BIẾT PHƯƠNG SAI 1.1.1. Bài toán Cho biến ngẫu nhiên X ,
có trung bình lần lượt là ,
chưa biết và phương sai , 1 X2 µ1 µ2 σ2 σ2 đã 1 2
biết. Một mẫu dữ liệu x , , . . . , của và một mẫu dữ liệu , , . . . , của 11 x12 x1n X1 x21 x22 x2m X2
được thu thập. Hãy kiểm định giả thuyết so sánh hai trung bình ®H ® ® 0 : µ1 − µ2 = µ0 H0 : µ1 − µ2 = µ0 H0 : µ1 − µ2 = µ0 (1) (2) (3) H1 : µ1 − µ2 6= µ0 H1 : µ1 − µ2 < µ0 H1 : µ1 − µ2 > µ0
với mức ý nghĩa α cho trước.
1.1.2. Các bước thực hiện 1
Phát biểu giả thuyết kiểm định. 2
Xác định mức ý nghĩa α. 3
Tính giá trị thống kê kiểm định (TKKĐ) ¯ X Z 1 − ¯ X2 − (µ1 − µ2) 0 = σ2 σ2 1 + 2 n1 n2 4 Xác định miền bác bỏ
Miền bác bỏ và p− giá trị tương ứng Đối thuyết
Miền bác bỏ p−giá trị
H1 : µ1 − µ2 6= µ0 |z0| > z1 z −α/2
p−giá trị = 2 [1 − Φ(| 0|)]
H1 : µ1 − µ2 < µ0 z0 < −z1−α p−giá trị = Φ(z0)
H1 : µ1 − µ2 > µ0 z0 > z1−α p−giá trị = 1 − Φ(z0)
CHƯƠNG 8. KIỂM ĐỊNH GIẢ THUYẾT HAI MẪU | 29
Ngược lại, chưa đủ cơ sở bác bỏ H0. 5 Kết luận.
VÍ DỤ 1.1. Tốc độ cháy của hai loại nguyên liệu rắn sử dụng trong động cơ tên lửa được nghiên
cứu. Được biết tốc độ cháy của hai loại này có xấp xỉ phân phối chuẩn với σ1 = σ2 = 3 cm/s. Hai
mẫu ngẫu nhiên với cỡ mẫu n1 = n2 = 20 được xem xét có tốc độ cháy trung bình ¯x1 = 18 cm/s
và ¯x2 = 24 cm/s. Kiểm định xem hai loại này có cùng trung bình hay không? Với α = 0.05, hãy tìm p−value. ✍ LỜI GIẢI.
Gọi X (cm/s) là tốc độ cháy của loại nguyên liệu rắn thứ nhất, 1
X (cm/s) là tốc độ cháy của loại nguyên liệu rắn thứ hai 2 .
Theo đề bài: X1 ∼ N(µ1; σ2), X ) 1 2 ∼ N (µ2; σ2 2 σ1 = σ2 = 3: đã biết. Mẫu 1: n1 = 20; ¯x1 = 18. Mẫu 2: n2 = 20; ¯x2 = 24. ®
1) Giả thuyết kiểm định: H0 : µ1 = µ2 kiểm định 2 phía. H1 : µ1 6= µ2 2) Mức ý nghĩa: α = 0.05.
3) Giá trị thống kê kiểm định ¯ x 18 − 24 − 0 z 1 − ¯ x2 − (µ1 − µ2) 0 = = ≈ −6.32456. … σ2 σ2 32 32 1 + 2 + n 20 20 1 n2
4) Miền bác bỏ: bác bỏ H khi z0 > z1 . 0 −α/2 Ta có α = 0.05 ⇒ z1 = 1 . −α/2 = z0.975 .96 5) Ta có |z0| > z1−α/2 ⇔ | − 6.32456| > 1.96 ⇔ 6.32456 > 1.96 (đúng) ⇒bác bỏ H0.
Kết luận: Với 95% độ tin cậy, hai loại nguyên liệu rắn không có cùng trung bình. Tính p−giá trị:
p-giá trị = 2 [1 − Φ(|z0|)] = 2 [1 − Φ(| − 6.32456|)] = 2 [1 − Φ(6.32456)] ≈ 0.
BÀI 8.1. Một công ty sản xuất sơn nghiên cứu về 1 loại phụ gia làm giảm thời gian khô của sơn. Thực
hiện thí nghiệm trên 2 mẫu: mẫu thứ nhất gồm 10 mẫu vật được sơn bằng loại sơn bình thường; mẫu
thứ hai gồm 10 mẫu vật được sơn với sơn có chất phụ gia mới. Trong những nghiên cứu trước, biết
rằng độ lệch tiêu chuẩn của thời gian khô sau khi quét sơn là 8 phút và không thay đổi khi thêm phụ
gia vào. Trung bình của mẫu 1 và 2 lần lượt là ¯x1 = 121 phút và ¯x2 = 112 phút. Với mức ý nghĩa 5%,
hãy cho kết luận về loại sơn với chất phụ gia mới. ✍ LỜI GIẢI.
30 | Lý thuyết Xác suất và Thống kê
CHƯƠNG 8. KIỂM ĐỊNH GIẢ THUYẾT HAI MẪU
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
BÀI 8.2. Hai máy được sử dụng để làm đầy các chai nhựa với khối lượng tịnh là 16.0 ounce. Khối lượng
làm đầy có thể được giả định có phân phối chuẩn, với độ lệch chuẩn σ1 = 0.020 và σ2 = 0.025 ounce.
Một thành viên của đội ngũ nhân viên kỹ thuật chất lượng nghi ngờ rằng cả hai máy đều có cùng khối
lượng trung bình, dù khối lượng này có là 16.0 ounce hay không. Một mẫu ngẫu nhiên gồm 10 chai
được lấy từ đầu ra của mỗi máy
Máy 1 16.03 16.01 16.04 15.96 16.05 15.98 16.05 16.02 16.02 15.99
Máy 2 16.02 16.03 15.97 16.04 15.96 16.02 16.01 16.01 15.99 16.00
Suy nghĩ của đội ngũ kỹ sư đúng không? Sử dụng α = 0.05. Tìm p−value.
BÀI 8.3. Hai loại nhựa phù hợp để sử dụng cho một nhà sản xuất linh kiện điện tử. Sức mạnh chịu sự
phá hủy của loại nhựa này là quan trọng. Được biết, σ1 = σ2 = 1 psi. Từ một mẫu ngẫu nhiên có kích
thước n1 = 10 và n2 = 12, ta có được ¯x1 = 162.5 và ¯x2 = 155.0. Công ty sẽ không áp dụng nhựa loại 1
trừ khi sức chịu phá vỡ trung bình của nó vượt quá nhựa loại 2 ít nhất 10 psi.
BÀI 8.4. Hai công thức khác nhau của nhiên liệu động cơ ôxy hóa đang được thử nghiệm để nghiên
cứu số octane của chúng. Phương sai chỉ số octane của công thức thứ nhất σ2 = 1.5 và công thức thứ 1
hai σ2 = 1.2. Hai mẫu ngẫu nhiên có cỡ mẫu n 2
1 = 15 và n2 = 20 được nghiên cứu có chỉ số octane
trung bình lần lượt là ¯x1 = 89.6 và ¯x2 = 92.5. Với giả sử có phân phối chuẩn. Nếu công thức 2 tạo ra
một số octane cao hơn so với công thức 1, nhà sản xuất muốn phát hiện nó. Xây dựng và kiểm định
giả thuyết thích hợp sử dụng α = 0.05 và tính p−value.
1.2. SO SÁNH HAI TRUNG BÌNH, TRƯỜNG HỢP PHƯƠNG SAI BẰNG NHAU CHƯA BIẾT CHƯƠNG 8. KIỂM Đ 1.ỊNH Ki GI ểm Ảđ T ị H nhUY gi Ế ả T H thuA y I ế M t sẪ
o Usánh hai trung bình (hai mẫu độc lập) | 31 1.2.1. Bài toán Cho biến ngẫu nhiên X ,
có trung bình lần lượt là , chưa biết và phương sai , 1 X2 µ1 µ2 σ2 σ2 chưa 1 2
biết, nhưng biết bằng nhau. Một mẫu dữ liệu x , , . . . , của và một mẫu dữ liệu 11 x12 x1n X1 x , , . . . , của
được thu thập. Hãy kiểm định giả thuyết so sánh hai trung bình 21 x22 x2m X2 ®H ® ® 0 : µ1 − µ2 = µ0 H0 : µ1 − µ2 = µ0 H0 : µ1 − µ2 = µ0 (1) (2) (3) H1 : µ1 − µ2 6= µ0 H1 : µ1 − µ2 < µ0 H1 : µ1 − µ2 > µ0
với mức ý nghĩa α cho trước.
1.2.2. Các bước thực hiện 1
Phát biểu giả thuyết kiểm định. 2
Xác định mức ý nghĩa α. 3
Tính giá trị thống kê kiểm định (TKKĐ) ¯ X T 1 − ¯ X2 − (µ1 − µ2) 0 = . S2 S2 p + p n1 n2 trong đó (n + (n S2 1 − 1)S2 1 2 − 1)S2 2 . p = n1 + n2 − 2
Khi H đúng thì T0 ∼ t(n1 + n2 − 2). 0 4 Xác định miền bác bỏ
Miền bác bỏ và p− giá trị tương ứng Đối thuyết
Miền bác bỏ p−giá trị
H1 : µ1 − µ2 6= µ0 |t0| > tα/2,df
p−giá trị = 2P(T ≥ |t0|)
H1 : µ1 − µ2 < µ0 t0 < −tα,df p−giá trị = P(T ≤ t0)
H1 : µ1 − µ2 > µ0 t0 > tα,df p−giá trị = P(T ≥ t0) (df = n + m − 2)
Ngược lại, chưa đủ cơ sở bác bỏ H0. 5 Kết luận.
VÍ DỤ 1.2. Tại một thành phố, ở khu vực A, người ta chọn ngẫu nhiên 17 sinh viên và cho làm
1 bài kiểm tra để đo chỉ số IQs, thu được trung bình mẫu là 106 và độ lệch tiêu chuẩn bằng 10;
tại khu vực B, chỉ số IQs trung bình của một mẫu gồm 14 sinh viên bằng 109 với độ lệch tiêu
chuẩn là 7. Giả sử rằng σ2 = σ2 và quan trắc lấy có phân phối chuẩn. Có sự khác biệt về chỉ số 1 2
IQs của sinh viên ở hai khu vực A và B hay không? α = 0.02. ✍ LỜI GIẢI.
32 | Lý thuyết Xác suất và Thống kê
CHƯƠNG 8. KIỂM ĐỊNH GIẢ THUYẾT HAI MẪU
Gọi X là chỉ số IQs của sinh viên ở khu vực A, 1
X là chỉ số IQs của sinh viên ở khu vực B. 2 Theo đề bài: X ) 1 ∼ N (µ1; σ2), X 1 2 ∼ N (µ2; σ22 σ2 = σ2: chưa biết. 1 2
Mẫu 1: n1 = 17; ¯x1 = 106; s1 = 10.
Mẫu 2: n2 = 14; ¯x2 = 109; s2 = 7. ®
1) Giả thuyết kiểm định: H0 : µ1 = µ2 kiểm định 2 phía. H1 : µ1 6= µ2 2) Mức ý nghĩa: α = 0.02.
3) Giá trị thống kê kiểm định (n1 − 1)s2 + (n
(17 − 1) · 102 + (14 − 1) · 72 2237 s2 1 2 − 1)s2 2 p = = = n1 + n2 − 2 17 + 14 − 2 29 ¯ x 106 − 109 − 0 ⇒ t 1 − ¯ x2 − (µ1 − µ2) 0 = = ≈ −0.94644. s2 s2 2237 2237 p + p 29 + 29 n1 n2 17 14
4) Miền bác bỏ: bác bỏ H khi |t0| > tα/2,n1+n2 . 0 −2
Ta có α = 0.02 ⇒ tα/2,n1+n2−2 = t0.01,29 = 2.462. 5) Ta có |t0| > tα/2,n1+n2−2 ⇔ | − 0.94644| > 2.462 ⇔ 0.94644 > 2.462 (sai)
⇒ chưa đủ cở sở để bác bỏ H0.
Kết luận: Với mức ý nghĩa 2%, không có sự khác biệt về chỉ số IQs của sinh viên ở hai khu vực A và B.
BÀI 8.5. Đường kính của các thanh thép được sản xuất trên hai máy đúc khác nhau đang được nghiên
cứu. Hai mẫu ngẫu nhiên có cỡ mẫu n1 = 15, n2 = 17 được chọn có trung bình và phương sai mẫu ¯ x
và quan trắc lấy có phân phối chuẩn. 1 = 8.73, s2 = 0.35 và ¯ x
= 0.40. Giả sử rằng σ2 = σ2 1 2 = 8.68, s2 2 1 2
Có bằng chứng để khẳng định rằng hai máy sản xuất thanh thép có đường kính trung bình khác nhau?
Sử dụng α = 0.05 khi đưa ra kết luận này. Tìm p−giá trị.
BÀI 8.6. Hai chất xúc tác có thể được sử dụng trong một phản ứng hóa học hàng loạt. Mười hai lô
được sử dụng chất xúc tác 1, dẫn đến năng suất trung bình là 86 và độ lệch chuẩn mẫu là 3. Mười lăm
lô được sử dụng chất xúc tác 2 và kết quả là năng suất trung bình 89 với độ lệch chuẩn là 2. Giả sử
năng suất các phép đo xấp xỉ thường được phân phối với cùng độ lệch chuẩn. Có bằng chứng để khẳng
định rằng chất xúc tác 2 tạo ra năng suất trung bình cao hơn chất xúc tác 1? Sử dụng α = 0.01.
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
................................................................................................................................................................... CHƯƠNG 8. KIỂM Đ 1.ỊNH Ki GI ểm Ảđ T ị H nhUY gi Ế ả T H thuA y I ế M t sẪ
o Usánh hai trung bình (hai mẫu độc lập) | 33
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
BÀI 8.7. Các điểm nóng chảy của hai hợp kim được sử dụng trong công thức hàn được điều tra bằng
cách làm tan chảy 21 mẫu của mỗi vật liệu. Trung bình mẫu và độ lệch chuẩn mẫu của hợp kim thứ
nhất là ¯x1 = 420◦F, s1 = 4◦F và của hợp kim thứ hai là ¯x2 = 426◦F, s2 = 3◦F. Dữ liệu mẫu có hỗ trợ
cho rằng cả hai hợp kim có cùng điểm nóng chảy không? Sử dụng α = 0.05 và giả định rằng cả hai tổng
thể thường có phân phối chuẩn và có cùng độ lệch chuẩn. Tìm p−giá trị cho kiểm định.
BÀI 8.8. Một bài báo về Kỹ thuật Radio và Vật lý điện tử [1984, Vol. 29 No.(3), pp. 63-66] đã nghiên
cứu hành vi của một máy phát ngẫu nhiên khi có tiếng ồn bên ngoài. Số chu kỳ được đo trong một
mẫu là 100 lần với hai mức điện áp nhiễu khác nhau, 100 và 150 mV. Với 100 mV, số chu kì trung bình
là 7.9 với s1 = 2.6. Với 150 mV, giá trị trung bình là 6.9 với s2 = 2.4.
Ban đầu, người ta nghi ngờ rằng việc tăng điện áp tiếng ồn sẽ làm giảm số chu kỳ trung bình. Dữ liệu
có hỗ trợ xác nhận này không? Sử dụng α = 0.01 và giả định rằng hai tổng thể có phân phối chuẩn
cùng phương sai. Tính p−giá trị của kiểm định? (Đs: 2.82 > 2.326, p−giá trị ≈ 0.025)
1.3. SO SÁNH HAI TRUNG BÌNH, TRƯỜNG HỢP PHƯƠNG SAI KHÁC NHAU CHƯA BIẾT 1.3.1. Bài toán Cho biến ngẫu nhiên X ,
có trung bình lần lượt là , chưa biết và phương sai , 1 X2 µ1 µ2 σ2 σ2 chưa 1 2
biết, nhưng biết khác nhau. Một mẫu dữ liệu x , , . . . , của và một mẫu dữ liệu 11 x12 x1n X1 x , , . . . , của
được thu thập. Hãy kiểm định giả thuyết so sánh hai trung bình 21 x22 x2m X2 ®H ® ® 0 : µ1 − µ2 = µ0 H0 : µ1 − µ2 = µ0 H0 : µ1 − µ2 = µ0 (1) (2) (3) H1 : µ1 − µ2 6= µ0 H1 : µ1 − µ2 < µ0 H1 : µ1 − µ2 > µ0
với mức ý nghĩa α cho trước.
1.3.2. Các bước thực hiện 1
Phát biểu giả thuyết kiểm định. 2
Xác định mức ý nghĩa α. 3
Tính giá trị thống kê kiểm định (TKKĐ) ¯ X 1 − 2) T 1 − ¯ X2 − (µ µ 0 = S2 S2 1 + 2 n1 n2
34 | Lý thuyết Xác suất và Thống kê
CHƯƠNG 8. KIỂM ĐỊNH GIẢ THUYẾT HAI MẪU trong đó [(S2 /n /n v = 1 1) + (S 2 2 2)]2 (S2/n (S2/n 1 1)2 + 2 2)2 n1 − 1 n2 − 1 Khi H đúng thì T0 ∼ t(v). 0
Lưu ý: ⌊a⌋ là phép lấy phần nguyên gần nhất và nhỏ hơn a. Ví dụ: ⌊35.8919⌋ = 35. 4 Xác định miền bác bỏ
Miền bác bỏ và p− giá trị tương ứng Đối thuyết
Miền bác bỏ p−giá trị
H1 : µ1 − µ2 6= µ0 |t0| > tα/2,df
p−giá trị = 2P(T ≥ |t0|)
H1 : µ1 − µ2 < µ0 t0 < −tα,df p−giá trị = P(T ≤ t0)
H1 : µ1 − µ2 > µ0 t0 > tα,df p−giá trị = P(T ≥ t0) (df = v)
Ngược lại, chưa đủ cơ sở bác bỏ H0. 5 Kết luận.
BÀI 8.9. Dữ liệu sau thể hiện thời lượng của các bộ phim được sản xuất bởi hai công ty điện ảnh Công ty Thời lượng (phút) 1 102 86 98 109 92 2 81 165 97 134 92 87 114
Kiểm định giả thuyết rằng thời lượng trung bình của các bộ phim được sản xuất bởi công ty 2 dài hơn
thời lượng trung bình của các bộ phim được sản xuất bởi công ty 1 là 10 phút với đối thuyết là nhỏ
hơn 10 phút. Sử dụng mức ý nghĩa 0.1 và giả sử các phân phối của thời lượng là xấp xỉ chuẩn với các phương sai khác nhau.
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
................................................................................................................................................................... CHƯƠNG 8. KIỂM Đ 1.ỊNH Ki GI ểm Ảđ T ị H nhUY gi Ế ả T H thuA y I ế M t sẪ
o Usánh hai trung bình (hai mẫu độc lập) | 35
...................................................................................................................................................................
...................................................................................................................................................................
BÀI 8.10. Trong một nghiên cứu được thực hiện tại Học Viện Kỹ Thuật Virginia, mức axit ascobic
plasma của phụ nữ có thai được so sánh ở những người hút thuốc với những người không hút thuốc. Ba
mươi hai phụ nữ trong ba tháng cuối của thai kỳ, không bị rối loạn sức khỏe nghiêm trọng và có tuổi từ
15 đến 32 được chọn cho nghiên cứu. Trước khi thu thập 20 ml máu, những người tham gia được yêu
cầu không ăn sáng, không dùng thuốc bổ sung vitamin và hạn chế các thực phẩm có hàm lượng axit
ascobic cao. Từ các mẫu máu, các giá trị axit ascobic plasma sau được xác định, theo mg mỗi 100 ml
Các giá trị Axit acobic plasma
Những người không hút thuốc Những người có hút thuốc 0.97 1.16 0.48 0.72 0.86 0.71 1.00 0.85 0.98 0.81 0.58 0.68 0.62 0.57 1.18 1.32 0.64 1.36 1.24 0.98 0.78 0.99 1.09 1.64 0.90 0.92 0.74 0.78 0.88 1.24 0.94 1.18
Hỏi có đủ bằng chứng để kết luận rằng có sự khác nhau giữa mức axit ascobic plasma của những người
hút thuốc và không hút thuốc hay không? Giả sử rằng hai tập dữ liệu từ các tổng thể chuẩn với các
phương sai khác nhau. Sử dụng p−giá trị.
2. KIỂM ĐỊNH GIẢ THUYẾT SO SÁNH HAI PHƯƠNG SAI 2.1. BÀI TOÁN
Cho biến ngẫu nhiên độc lập X , và phương 1 ∼ N (µ1; σ2), X ) có trung bình µ µ 1 2 ∼ N (µ2; σ22 1 2
sai σ2, σ2 đều chưa biết. Một mẫu dữ liệu x , x , . . . , x
của X và một mẫu dữ liệu x21, 1 2 11 12 1n 1 x , . . . , của
được thu thập. Hãy kiểm định giả thuyết so sánh hai phương sai 22 x2m X2 ®H0 : σ2 = σ2 (1) 1 2 H1 : σ21 6= σ22
với mức ý nghĩa α cho trước.
36 | Lý thuyết Xác suất và Thống kê
CHƯƠNG 8. KIỂM ĐỊNH GIẢ THUYẾT HAI MẪU
2.2. CÁC BƯỚC THỰC HIỆN ®H0 : σ2 = σ2 1 2 1
Phát biểu giả thuyết kiểm định H . 1 : σ2 1 6= σ2 2 2
Xác định mức ý nghĩa α. 3
Tính giá trị thống kê kiểm định (TKKĐ) S2 F 1 0 = S22
khi H đúng F0 ∼ F(n1 − 1, n2 − 1). 0 4
Xác định miền bác bỏ: bác bỏ H khi hoặc 0 f0 > fα/2,n f 1−1,n2−1 0 < f1−α/2,n1−1,n2−1 1 Chú ý: f . 1−α,n,m = fα,m,n 5 Kết luận.
VÍ DỤ 2.1. Hàm lượng thạch tín (Asen) (Đv: ppb) trong nước càng cao càng có hại cho
sức khỏe. Người ta kiểm tra hàm lượng thạch tín ở hai khu vực là trung tâm thành phố
Biên Hòa và khu vực gần sân bay Biên Hòa. Tại mỗi khu vực, người ta đo ngẫu nhiên hàm
lượng thạch tín trong nước ứng với 10 địa điểm khác nhau. Số liệu cho bởi bảng thống kê bên dưới Trung tâm TP 3 7 25 10 15 6 12 25 15 7
Khu vực gần sân bay 48 44 40 38 33 21 20 12 1 18
Với α = 0.05, hãy kiểm tra xem có sự khác biệt về hàm lượng thạch tín ở hai khu vực này. ✍ LỜI GIẢI.
Gọi X (ppb) là hàm lượng thạch tín trong nước ở khu vực trung tâm thành phố Biên Hòa, 1
X (ppb) là hàm lượng thạch tín trong nước ở khu vực gần sân bay Biên Hòa. 2 Theo đề bài: X ) 1 ∼ N (µ1; σ2), X 1 2 ∼ N (µ2; σ22
σ2; σ2: chưa có thông tin. 1 2
Mẫu 1: n1 = 10; ¯x1 = 12.5; s1 ≈ 7.63.
Mẫu 2: n2 = 10; ¯x2 = 27.5; s2 ≈ 15.35.
> Kiểm định phương sai ®H0 : σ2 = σ2
• Giả thuyết kiểm định 1 2 H1 : σ2 . 1 6= σ2 2 • Mức ý nghĩa α = 0.05.
• Giá trị thống kê kiểm định s2 7.632 f 1 0 = = ≈ 0.2471. s2 15.352 2 1
• Miền bác bỏ: bác bỏ H khi hoặc 0 f0 > fα/2,n f 1−1,n2−1 0 < fα/2,n2−1,n1−1 Ta có α = 0.05 ⇒ fα/2,n .03 1−1,n2 2 2 1 025 9,9 = 4 .
−1 = fα/ ,n −1,n −1 = f0. ,
CHƯƠNG 8. KIỂM ĐỊNH GIẢ THUYẾT H 2. AI Ki M ể Ẫ m U
định giả thuyết so sánh hai phương sai | 37 Khi đó 1 f hoặc 0 > fα/2,n f 1−1,n2−1 0 < f 2 ⇔ 0.2471 > 4.03 (sai) α/ ,n2−1,n1−1 1 ⇔ 0.2471 < 4.03
⇔ 0.2471 < 0.2481 (đúng) ⇒ bác bỏ H0 ⇒ σ2 . 1 6= σ22
> Kiểm định hai trung bình khi σ21 6= σ22 ®
1) Giả thuyết kiểm định: H0 : µ1 = µ2 kiểm định 2 phía. H1 : µ1 6= µ2 2) Mức ý nghĩa: α = 0.05.
3) Giá trị thống kê kiểm định ¯ x 12.5 − 27.5 − 0 ⇒ t 1 − ¯ x2 − (µ1 − µ2) 0 = = ≈ −2.7672. … 2 s2 s2 7.632 15.35 1 + 2 + n 10 10 1 n2
4) Miền bác bỏ: bác bỏ H khi 0 |t0| > tα/2,v trong đó [(S2 /n /n v = 1 1) + (S 2 2 2)]2 (S2/n (S2/n ≈ ⌊13.1915⌋ = 13. 1 1)2 + 2 2)2 n1 − 1 n2 − 1
Ta có α = 0.05 ⇒ tα/2,v = t0.025,13 = 2.160. 5) Ta có |t0| > tα/2,n1+n2−2 ⇔ | − 2.7672| > 2.160 ⇔ 2.7672 > 2.160 (đúng) ⇒ bác bỏ H0.
Kết luận: Với mức ý nghĩa 5%, có sự khác biệt về hàm lượng thạch tín ở khu vực trung tâm thành
phố và khu vực gần sân bay.
BÀI 8.11. Một nhà sản xuất công bố rằng độ bền kéo trung bình của sợi A vượt quá đồ bền kéo trung
bình của sợi B ít nhất 12 kg. Để kiểm định công bố này, 50 mẫu của mỗi loại sợi được kiểm tra dưới
các điều kiện tương tự. Loại sợi A có độ bền kéo trung bình là 86.7 kg với độ lệch chuẩn 6.28 kg, trong
khi loại sợi B có độ bền kéo trung bình là 77.8 kg với độ lệch chuẩn là 5.61 kg. Kiểm định công bố của
nhà sản xuất bằng cách sử dụng mức ý nghĩa 0.05.
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
38 | Lý thuyết Xác suất và Thống kê
CHƯƠNG 8. KIỂM ĐỊNH GIẢ THUYẾT HAI MẪU
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
BÀI 8.12. Amstat News (Tháng 12/2004) liệt kê tiền lương trung vị cho các chức danh phó giáo sư về
thống kê ở các viện nghiên cứu và ở trường giáo dục đại cương và các viện khác ở Hoa Kỳ. Giả sử rằng
một mẫu 200 phó giáo sư từ các viện nghiên cứu có mức lương trung bình $70 750 mỗi năm với độ lệch
chuẩn $6000. Cũng giả sử rằng một mẫu 200 phó giáo sư từ các viện khác có lương trung bình $65 200
với độ lệch chuẩn $5000. Hãy kiểm định giả thuyết rằng lương trung bình cho các phó giáo sư ở các
viện nghiên cứu là cao hơn $2000 so với ở các viện khác. Sử dụng mức ý nghĩa 0.01.
BÀI 8.13. Một bài báo về Suy thoái và Ổn định Polymer (2006, Tập 91) trình bày dữ liệu từ một
nghiên cứu chín năm về bọt S537. Các mẫu bọt được nén tới 50% độ dày ban đầu của chúng và được
bảo quản ở các nhiệt độ khác nhau trong chín năm. Khi bắt đầu thử nghiệm cũng như trong mỗi năm,
độ dày mẫu được đo và độ dày của tám mẫu tại từng điều kiện lưu trữ được ghi lại. Dữ liệu cho hai điều kiện lưu trữ:
50◦C 0.047 0.060 0.061 0.064 0.080 0.090 0.118 0.165 0.183
50◦C 0.062 0.105 0.118 0.137 0.153 0.197 0.210 0.250 0.375
Có bằng chứng nào để hỗ trợ cho khẳng định rằng trung bình nén có tăng theo nhiệt độ ở điều kiện
bảo quản không? (Đs: −2.349, bác bỏ)
BÀI 8.14. Một quản lý công ty taxi đang cố gắng quyết định xem việc sử dụng vỏ xe radial thay vì vỏ
có lớp bố xiên thông thường có tiết kiệm nhiên liệu hơn không. Mười hai xe hơi được trang bị các vỏ
xe radial và được lái theo một bài kiểm tra quy chuẩn. Không thay đổi tài xế, các xe trên sau đó được
trang bị vỏ có lớp bố xiên thông thường và được lái một lần nữa theo bài kiểm tra trên. Nhiên liệu tiêu
thụ, theo kilomet trên mỗi lít, được ghi lại như sau Vỏ radial
4.2 4.7 6.6 7.0 6.7 4.5 5.7 6.0 7.4 4.9 6.1 5.2
Vỏ bố xiên 4.1 4.9 6.2 6.9 6.8 4.4 5.7 5.8 6.9 4.7 6.0 4.9
Ta có thể kết luận rằng các xe hơi được trang bị vỏ xe radial có mức tiêu hao nhiên liệu tốt hơn những
xe được trang bị vỏ bố xiên không? Giả sử các tổng thể có phân phối chuẩn. Sử dụng p−value trong kết luận của bạn.
3. SO SÁNH HAI TỶ LỆ
CHƯƠNG 8. KIỂM ĐỊNH GIẢ THUYẾT HAI MẪU 3. So sánh hai tỷ lệ | 39 3.1. BÀI TOÁN
Khảo sát những phần tử thỏa một tính chất A nào đó trên hai tổng thể độc lập với tỷ lệ tương
ứng là p và ; từ hai tổng thể chọn ra hai mẫu với cỡ lần lượt là và n . Gọi là số 2 Y1 và 1 p2 n1 Y2
phần tử thỏa tính chất A trong mẫu 1 và mẫu 2. Khi đó, ta có Y1 ∼ B(n1, p1) và Y2 ∼ B(n2, p2).
Bài toán kiểm định giả thuyết gồm các trường hợp sau ®H ® ® 0 : p1 − p2 = p0 H0 : p1 − p2 = p0 H0 : p1 − p2 = p0 (1) (2) (3) H1 : p1 − p2 6= p0 H1 : p1 − p2 < p0 H1 : µ1 − µ2 > p0
với mức ý nghĩa α cho trước. Các giả định Hai mẫu độc lập;
Cỡ mẫu lớn và n1p1 > 5; n1(1 − p1) > 5 và n2p2 > 5; n2(1 − p2) > 5.
3.2. CÁC BƯỚC THỰC HIỆN 1
Phát biểu giả thuyết kiểm định. 2
Xác định mức ý nghĩa α. 3
Tính giá trị thống kê kiểm định (TKKĐ) ˆ P Z 1 − ˆ P2 − (p1 − p2) 0 = Å ã ˆ 1 1 P (1 − ˆ P ) + n1 n2 với ˆ Y Y Y P 1 2 1 + Y2 1 = ; ˆ P2 = ; ˆ P = n1 n2 n1 + n2
nếu H đúng thì Z0 ∼ N(0; 1). 0 4 Xác định miền bác bỏ
Miền bác bỏ và p− giá trị tương ứng Đối thuyết
Miền bác bỏ p−giá trị
H1 : p1 − p2 6= p0 |z0| > z1 p −α/2
−giá trị = 2 [1 − Φ(|z0|)]
H1 : p1 − p2 < p0 z0 < −z1 p −α −giá trị = Φ(z0)
H1 : p1 − p2 > p0 z0 > z1 p −α −giá trị = 1 − Φ(z0)
Ngược lại, chưa đủ cơ sở bác bỏ H0. 5 Kết luận.
VÍ DỤ 3.1. Một công ty sản xuất thuốc cần kiểm tra một loại thuốc có tác dụng là giảm việc
xuất hiện cơn đau ngực ở các bệnh nhân. Công ty thực hiện thí nghiệm trên 400 người, chia làm
40 | Lý thuyết Xác suất và Thống kê
CHƯƠNG 8. KIỂM ĐỊNH GIẢ THUYẾT HAI MẪU
hai nhóm: nhóm 1 gồm 200 được uống thuốc và nhóm 2 gồm 200 người được uống giả dược. Theo
dõi thấy ở nhóm 1 có 8 người lên cơn đau ngực và nhóm 2 có 25 người lên cơn đau ngực. Với
α = 0.05, hãy cho kết luận về hiệu quả của thuốc mới sản xuất. ✍ LỜI GIẢI.
Gọi Y là số người tham gia thí nghiệm lên cơn đau tim khi uống thuốc 1 ;
Y là số người tham gia thí nghiệm lên cơn đau tim khi uống giả dược 2 . Mẫu y 8 1: y 1 1 = 8; n1 = 200; ⇒ ˆ p1 = = = 0.04. n1 200 Mẫu y 25 2: y 2 2 = 25; n2 = 200; ⇒ ˆ p2 = = = 0.125. n 200 2 y 8 + 25 ⇒ ˆp = 1 + y2 = = 0.0825. n1 + n2 200 + 200 ®
1) Giả thuyết kiểm định: H0 : p1 = p2 kiểm định 1 phía. H1 : p1 < p2 2) Mức ý nghĩa: α = 0.05.
3) Giá trị thống kê kiểm định ˆ p 0.04 − 0.125 − 0 z 1 − ˆ p2 − (p1 − p2) 0 = = ≈ −3.08951. Å 1 1 ã Å 1 1 ã ˆ p (1 − ˆp) + 0.0825(1 − 0.0825) + n1 n2 200 200
4) Miền bác bỏ: bác bỏ H khi z0 < −z1 . 0 −α Ta có α = 0.05 ⇒ −z1 −z0.95 −1.645. −α = = 5) Ta có z0 < −z1−α
⇔ −3.08951 < −1.645 (đúng) ⇒bác bỏ H0.
Kết luận: Với mức ý nghĩa 5%, thuốc mới có tác dụng làm giảm xuất hiện cơn đau tim hay thuốc mới có hiệu quả.
BÀI 8.15. Hai loại máy ép phun khác nhau được sử dụng để tạo thành các bộ phân bằng nhựa. Một
phần được coi là khiểm khuyết nếu nó bị co rút quá mức hoặc bị đổi màu. Hai mẫu ngẫu nhiên, mỗi
mẫu có kích thước 300, được chọn thì có 15 bộ phân bị lỗi được tìm thấy trong mẫu từ máy 1 và 8 bộ
phận bị lỗi được tìm thấy trong mẫu từ máy 2. Có hợp lý để kết luận rằng cả hai máy sản xuất cùng
một tỉ lệ các bộ phận lỗi, sử dụng α = 0.05? Tìm p−giá trị cho kiểm định này.
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
CHƯƠNG 8. KIỂM ĐỊNH GIẢ THUYẾT HAI MẪU 3. So sánh hai tỷ lệ | 41
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
BÀI 8.16. Hai loại giải pháp khác nhau về cách đánh bóng đang được đánh giá để sử dụng trong một
hoạt động đánh bóng sản xuất ống kính interocular được dùng trong mắt người sau khi phẫu thuật đục
thủy tinh thể. Ba trăm thấu kính đã được đánh bóng bằng cách sử dụng giải pháp đánh bóng thứ nhất
và 253 sản phẩm không có khuyết tật do đánh bóng. 300 ống kính khác được đánh bóng bằng cách sử
dụng cách đánh bóng thứ hai và 196 ống kính đã đạt yêu cầu sau khi hoàn thành. Có lý do nào để tin
rằng hai giải pháp đánh bóng khác nhau không? Sử dụng α = 0.05. p−giá trị cho kiểm định này là bao nhiêu?
BÀI 8.17. Một mẫu ngẫu nhiên 500 cư dân trưởng thành của Quận Maricopa chỉ ra rằng 385 ủng hộ
việc tăng giới hạn tốc độ đường cao tốc lên 75 dặm một giờ, và một mẫu khác gồm 400 cư dân trưởng
thành của Quận Pima đã chỉ ra rằng 267 đã ủng hộ giới hạn tốc độ tăng lên. Những dữ liệu này cho
thấy có sự khác biệt trong việc hỗ trợ tăng giới hạn tốc độ cho cư dân của hai quận? Sử dụng α = 0.05.
Giá trị p cho kiểm định này là bao nhiêu?
BÀI 8.18. Ô nhiễm không khí có liên quan đến việc giảm cân ở trẻ sơ sinh. Trong một nghiên cứu được
công bố trên Tạp chí của Hiệp hội Y khoa Hoa Kỳ, các nhà nghiên cứu đã kiểm tra tỷ lệ trẻ sơ sinh nhẹ
cân được sinh ra từ các bà mẹ tiếp xúc với liều lượng bồ hóng và tro nặng trong vụ tấn công của Trung
tâm Thương mại Thế giới ngày 11/9/2001. Có 182 đứa bé sinh ra từ những bà mẹ này, 15 đứa được
xếp loại có trọng lượng thấp. Trong số 2300 trẻ sinh ra trong cùng một khoảng thời gian ở New York ở
một bệnh viện khác, 92 đứa được phân loại là có trọng lượng thấp. Có bằng chứng cho thấy rằng các
bà mẹ tiếp xúc ô nhiễm có tỷ lệ trẻ sơ sinh nhẹ cân cao hơn không? (Đs: z0 = 2.712, p−giá trị = 0.003)
BÀI 8.19. Tạp chí Y học New England đã báo cáo một thử nghiệm để đánh giá hiệu quả của phẫu
thuật trên những người đàn ông được chẩn đoán mắc bệnh ung thư tuyến tiền liệt. Một mẫu gồm 347
nam giới trong nghiên cứu đã phẫu thuật và 18 người trong số họ cuối cùng đã chết vì ung thư tuyến
tiền liệt so với 31 trong số 348 người không phẫu thuật. Có bằng chứng nào cho thấy rằng phẫu thuật
giảm tỷ lệ những người chết vì ung thư tuyến tiền liệt?
BÀI 8.20. Vào mùa đông của đại dịch cúm, bố mẹ của 2000 bé đã được các nhà nghiên cứu khảo sát
tại một công ty dược phẩm nổi tiếng để xác định liệu thuốc mới của công ty có hiệu quả sau hai ngày
hay không. Trong số 120 bé bị cúm và được cho dùng thuốc, 29 bé khỏi bệnh trong hai ngày. Trong
280 bé bị cúm nhưng không được cho dùng thuốc mới, có 56 bé phục hồi trong hai ngày. Hỏi có dấu
hiệu có ý nghĩa nào ủng hộ lời tuyên bố của công ty về hiệu quả của thuốc hay không?
BÀI 8.21. Trong một nghiên cứu để ước tính tỷ lệ cư dân trong một thành phố nào đó và các vùng
ngoại ô của nó ủng hộ việc xây dựng nhà máy năng lượng hạt nhân, người ta thấy rằng 63 trong 100
cư dân thành thị ủng hộ việc xây dựng trong khi chỉ 59 trong 125 cư dân ngoại ô là ủng hộ. Có sự khác
biệt có ý nghĩa nào giữa tỷ lệ cư dân thành thị và ngoại ô ủng hộ việc xây dựng nhà máy hạt nhân hay
không? Sử dụng p−giá trị.
42 | Lý thuyết Xác suất và Thống kê
CHƯƠNG 8. KIỂM ĐỊNH GIẢ THUYẾT HAI MẪU
BÀI 8.22. Trong một nghiên cứu về khả năng sinh con của những phụ nữ đã kết hôn được thực hiện
bởi Martin O’Connell và Carolyn C.Rogers cho Cục Điều Tra Dân Số vào năm 1979, hai nhóm phụ nữ
không con tuổi từ 25 đến 29 được chọn ngẫu nhiên và mỗi người được hỏi xem cô ấy cuối cùng đã lên
kế hoạch có em bé hay không. Một nhóm được chọn từ những người vợ đã kết hôn trong vòng hai năm
và nhóm kia từ những người vợ đã kết hôn năm năm. Giả sử rằng 240 trong 300 người vợ đã kết hôn
trong vòng hai năm đã lên kế hoạch có em bé so với 288 trong 400 người vợ đã kết hôn trong vòng năm
năm. Ta có thể kết luận rằng tỷ lệ người vợ đã kết hôn trong vòng hai năm đã lên kế hoạch có em bé
là cao hơn một cách có ý nghĩa so với tỷ lệ người vợ đã kết hôn năm năm không? Sử dụng p−giá trị.
BÀI 8.23. Một cộng đồng đô thị muốn chỉ ra rằng tỷ lệ bị ung thư vú cao hơn ở khu vực nông thôn
(mức PCB tìm thấy cao hơn trong đất của cộng đồng đô thị). Nếu người ta thấy có 20 trong 200 phụ
nữ trưởng thành ở cộng đồng đô thị bị ung thư vú và 10 trong 150 phụ nữ trưởng thành ở cộng đồng
nông thôn bị ung thư vú, thì ta có thể kết luận tại mức ý nghĩa 0.05 rằng ung thư vú là phổ biến hơn
trong cộng đồng đô thị hay không?
CHƯƠNG 8. KIỂM ĐỊNH GIẢ THUYẾT HAI MẪU 3. So sánh hai tỷ lệ | 43 CHƯƠNG 9
HỒI QUY - TƯƠNG QUAN 1. GIỚI THIỆU
Bài toán: trong các hoạt động về khoa học - kỹ thuật, kinh tế, xã hội, . . . ta có nhu cầu xác
định mối liên giữa hai hay nhiều biến ngẫu nhiên với nhau. Ví dụ
Mối liên hệ giữa chiều cao và cỡ giầy của một người, từ đó một cửa hàng bán giầy dép có
thể xác định chính xác cỡ giầy của một khách hàng khi biết chiều cao;
Độ giãn nở của một loại vật liệu theo nhiệt độ môi trường;
Doanh thu khi bán 1 loại sản phẩm và số tiền chi cho quảng cáo và khuyến mãi; . . .
Để giải quyết các vấn đề trên, ta sử dụng kỹ thuật phân tích hồi quy (Regression Analysis).
Phân tích hồi quy được sử dụng để xác định mối liên hệ giữa
một biến phụ thuộc Y (biến đáp ứng) và một hay nhiều biến độc lập X , , . . . , , các biến 1 X2 Xp
này còn được gọi là biến giải thích.
• Biến phụ thuộc Y phải là biến liên tục;
• Các biến độc lập X ,
, . . . , Xp, có thể là biến liên tục, rời rạc hoặc phân loại. 1 X2
Mối liên hệ giữa X , , . . . , và 1 X2 Xp
Y được biểu diễn bởi một hàm tuyến tính.
Sự thay đổi trong Y được giả sử do những thay đổi trong X , , . . . , gây ra. 1 X2 Xp
Trên cơ sở xác định mối liên hệ giữa biến phụ thuộc Y và các biến giải thích X , , . . . , , ta có thể 1 X2 Xp
dự đoán, dự báo giá trị của Y ,
giải thích tác động của sự thay đổi trong các biến giải thích lên biến phụ thuộc.
2. MÔ HÌNH HỒI QUY TUYẾN TÍNH ĐƠN 2.1. ĐỊNH NGHĨA
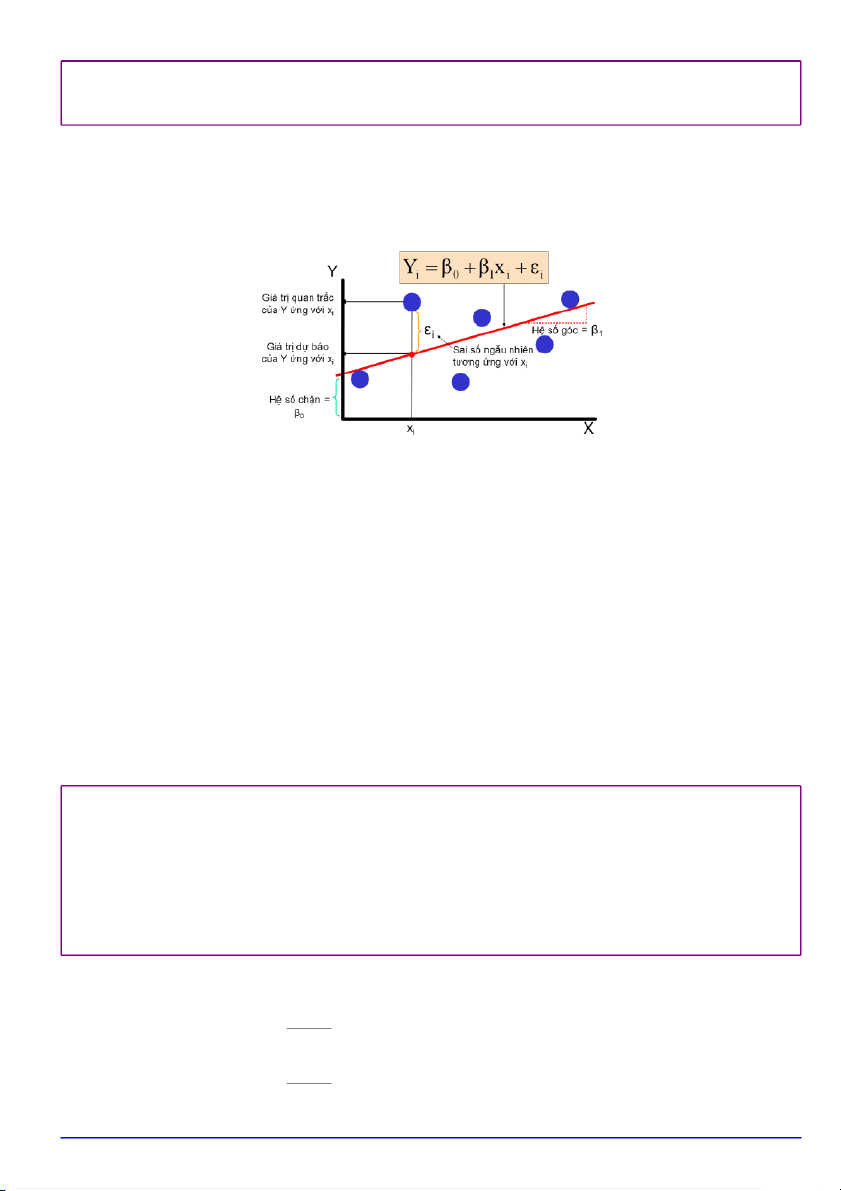
Định nghĩa 1. Một mô hình hồi quy tuyến tính đơn liên quan đến một biến ngẫu nhiên
Y và một biến giải thích x là phương trình có dạng Y = β0 + β1x + ǫ với
β là hệ số chặn của đường thẳng hồi quy. 0
β là hệ số góc của đường thẳng hồi quy. 1
ǫ là thành phần sai số, ǫ được giả sử có phân phối chuẩn với E(ǫ) = 0 và V ar(ǫ) = σ2.
44 | Lý thuyết Xác suất và Thống kê
CHƯƠNG 9. HỒI QUY - TƯƠNG QUAN
Đường thẳng hồi quy thực sự Y = β0 + β1x
Với (x1, y1), . . . , (xn, yn) là n cặp giá trị quan trắc của một mẫu ngẫu nhiên cỡ n, ta có
Yi = β0 + β1xi + ǫi i = 1, . . . , n
Sử dụng đồ thị phân tán để biểu diễn các cặp giá trị quan trắc (xi, yi) trên hệ trục tọa độ Oxy
2.2. ƯỚC LƯỢNG CÁC HỆ SỐ HỒI QUY
Gọi ˆβ và ˆ là các ước lượng của
và . Khi đó, đường thẳng hồi quy với các hệ số ước lượng 0 β1 β0 β1 ˆY = ˆ β0 + ˆ β1x.
Một đường thẳng ước lượng tốt phải “gần với các điểm dữ liệu”. Đề tìm ˆ
β và ˆ , ta dùng phương pháp bình phương bé nhất (PPBPBN). 0 β1 Với dữ liệu (x ,
i, yi) i = 1, . . . , n, ta có ˆ y = ˆ β0 + ˆ β1xi.
Độ lệch giữa giá trị quan trắc y và giá trị dự đoán gọi là i ˆ yi
giá trị thặng dư thứ i, xác định như sau Ä ä e ˆ i = yi − ˆ yi = yi − β0 + ˆ β1xi
Định nghĩa 2. Tổng bình phương sai số (Sum of Squares for Errors - SSE) hay tổng bình
phương thặng dư cho n điểm dữ liệu được định nghĩa như sau n n î Ä äó2 SSE = X e2 ˆ β i = X yi − 0 + ˆ β1xi i=1 i=1
Nội dung của PPBPBN là tìm các ước lượng ˆ β và ˆ sao cho 0 β1
SSE đạt giá trị bé nhất. Lấy đạo hàm theo β và 0 β1 ∂SSE n = −2 X [y ∂β i − (β0 + β1xi)] = 0 0 i=1 ∂SSE n
= −2 X [yi − (β0 + β1xi)] xi = 0 ∂β1 i=1
CHƯƠNG 9. HỒI QUY - TƯƠNG QUAN
2. Mô hình hồi quy tuyến tính đơn | 45
ta thu được hệ phương trình n n nβ0 + β1 X xi = X yi i=1 i=1 n n n β0 X xi + β1 X x2i = X xiyi i=1 i=1 i=1
Giải hệ trên, ta tìm được các ước lượng BPBN của β và là 0 β1 P P yi) P n x n i=1 ˆ n ( S x i=1 i) ( n xy i=1 iyi − = β x Sxx 1 = P i)2 P x2 ni=1 n i=1 ( n i − ˆ β0 = ¯ y − ˆ β1 ¯ x với S và xác định bởi xy Sxx n n P P yi)
Sxy = X (xi − ¯x)(yi − ¯y) = X ( n x ni=1 i=1 i) ( n i=1 i=1 xiyi − n n P x S n i=1 i)2 xx = X (xi − ¯ x)2 = X x2 ( n i=1 i=1 i − n n trong đó 1 1 ¯ x = X x và ¯ y = X y . n i n i i=1 i=1 Các ước lượng ˆ
β và ˆ tìm được gọi là các ước lượng BPBN. 0 β1 Đường thẳng ˆy = ˆ
β0 + ˆβ1x gọi là đường thẳng BPBN, thỏa các tính chất sau n
i) SSE = X (yi − ˆyi)2 đạt giá trị bé nhất. i=1 n n
ii) SE = X (yi − ˆyi) = X ei = 0 với SE là tổng các thăng dư (Sum of Errors). i=1 i=1
2.3. DỰ ĐOÁN GIÁ TRỊ QUAN TRẮC MỚI
Giả sử với giá trị x , ta cần dự đoán giá trị quan trắc
trong tương lai tương ứng với bằng 0 Y0 x0
bao nhiêu. Từ mô hình hồi quy, ta có ˆ Y0 = ˆ β0 + ˆ β1x0 ˆ
Y là một ước lượng điểm của giá trị quan trắc mới 0 Y .
46 | Lý thuyết Xác suất và Thống kê
CHƯƠNG 9. HỒI QUY - TƯƠNG QUAN
2.4. Ý NGHĨA CỦA CÁC HỆ SỐ HỒI QUY
Từ mô hình hồi quy, ta có ˆ Y = ˆ β0 + ˆ β1x.
Ý nghĩa của các hệ số hồi quy ˆβ .
0 : Khi các yếu tố bị loại khỏi mô hình (x = 0), thì trung bình của Y là ˆ β0 ˆβ đơn vị.
1 : khi x thay đổi 1 đơn vị, các yếu tố khác không đổi thì Y thay đổi ˆ β1
VÍ DỤ 2.1. Một công ty sản xuất ô tô muốn điều tra giá của một dòng xe của họ giảm giá thế
nào theo số năm sử dụng. Bộ phận nghiên cứu của công ty đã lấy mẫu gồm 8 chiếc của dòng xe
này và thu thập thông tin về số năm sử dụng (X - năm) và giá của xe (Y - triệu $) được mô tả như sau n n n X xi = 41; X x2i = 259; X yi = 1144; i=1 i=1 i=1 n n X y2i = 221772; X xiyi = 4197. i=1 i=1
a) Tìm đường thẳng hồi quy biểu diễn mối liên hệ giữa giá của xe Y theo số năm sử dụng X.
b) Dựa vào đường thẳng hồi quy vừa ước lượng, hãy cho biết giá của chiếc xe sau 3 năm sử dụng?
c) Dựa vào đường thẳng hồi quy vừa ước lượng, giả sử các yếu tố khác không đổi thì giá của
xe sẽ thay đổi như thế nào? ✍ LỜI GIẢI. a) Ta có n P P yi) • Sxy = X ( n x n i=1 i=1 i) ( n i=1 xiyi − 41 · 1144 = 4197 − 8 = −1666. n P x • S i)2 n i=1 xx = X x2 ( n i=1 i − 412 = 259 − 8 = 48.875. S −1666 • ˆ β xy 1 = = = −34.08696. Sxx 48.875 1 n 1 • ¯x = X x · 41 = 5.125. n i = 8 i=1 n 1 1 • ¯y = y · 1144 = 143 n X i = 8 i=1
CHƯƠNG 9. HỒI QUY - TƯƠNG QUAN
2. Mô hình hồi quy tuyến tính đơn | 47 ⇒ ˆ β0 = ¯ y − ˆ β1 ¯ x
= 143 − (−34.08696) · 5.125 = 317.69567. ⇒ ˆy = ˆ β0 + ˆ β1x
⇒ ˆy = 317.69567 − 34.08696x.
3. HỆ SỐ XÁC ĐỊNH VÀ HỆ SỐ TƯƠNG QUAN
3.1. ĐO SỰ BIẾN THIÊN CỦA DỮ LIỆU Gọi
SST : Tổng bình phương toàn phần (Total Sum of Squares) n SST = X (yi − ¯y)2 i=1
SSR: Tổng bình phương hồi quy (Regression Sum of Squares) n SSR = X (ˆyi − ¯y)2 i=1
SSE: Tổng bình phương sai số (Error Sum of Squares) n SSE = X (yi − ˆyi)2 i=1 trong đó
SST : đo sự biến thiên của các giá trị yi xung quanh giá trị trung tâm của dữ liệu ¯y.
SSR: giải thích sự biến thiên liên quan đến mối quan hệ tuyến tính của X và Y .
SSE: giải thích sự biến thiên của các nhân tố khác (không liên quan đến mối quan hệ tuyến tính của X và Y ). Ta có n n n X (yi − ¯
y)2 = X (ˆyi − ¯y)2 + X (yi − ˆyi)2 i=1 i=1 i=1 SST = SSR + SSE.
48 | Lý thuyết Xác suất và Thống kê
CHƯƠNG 9. HỒI QUY - TƯƠNG QUAN
3.2. HỆ SỐ XÁC ĐỊNH
Định nghĩa 3. Hệ số xác định (Coefficient of Determination) là tỷ lệ của tổng sự biến thiên
trong biến phụ thuộc gây ra bởi sự biến thiên của các biến độc lập (biến giải thích) so với tổng sự
biến thiên toàn phần. Hệ số xác định thường được gọi là R−bình phương (R−squared), ký hiệu là R2. Công thức tính: SSR R2 = . SST Chú ý: 0 ≤ R2 ≤ 1.
Hệ số xác định của một mô hình hồi quy cho phép ta đánh giá mô hình tìm được có giải thích tốt cho
mối liên hệ giữa biến phụ thuộc Y và biến phụ thuộc X hay không.
3.3. HỆ SỐ TƯƠNG QUAN MẪU
Định nghĩa 4. Với mẫu ngẫu nhiên cỡ n: (xi, yi), i = 1, . . . , n. Hệ số tượng quan mẫu, ký
hiệu r , được xác định như sau xy P (xi − ¯x) (yi − ¯y) Sxy n i=1 = √ r S xy = xxSST »P (y n P i − ¯ y)2 (x n i=1 i=1 i − ¯ x)2 n n trong đó y SST = P i)2 X (yi − ¯ y)2 = X y2 ( n i=1 . n i=1 i=1 i −
Hệ số xác định R2 của mô hình hồi quy tuyến tính đơn bằng với bình phương của hệ số tương quan mẫu R2 = r2xy
Đánh giá hệ số tương quan:
Miền giá trị: −1 ≤ rxy ≤ 1. −1 ≤ r càng gần
xy < 0 : tương quan âm. rxy
−1 biểu thị mối liên hệ tuyến tính nghịch giữa X và Y càng mạnh. 0 < r càng gần
xy ≤ 1 : tương quan dương. rxy
1 biểu thị mối liên hệ tuyến tính thuận giữa X và Y càng mạnh. r càng gần xy
0 biểu thị mối liên hệ tuyến tính yếu. rxy = 0 : không có mối liên hệ tuyến tính giữa X và Y .
CHƯƠNG 9. HỒI QUY - TƯƠNG QUAN
3. Hệ số xác định và Hệ số tương quan | 49
VÍ DỤ 3.1. Một công ty sản xuất ô tô muốn điều tra giá của một dòng xe của họ giảm giá thế
nào theo số năm sử dụng. Bộ phận nghiên cứu của công ty đã lấy mẫu gồm 8 chiếc của dòng xe
này và thu thập thông tin về số năm sử dụng (X - năm) và giá của xe (Y - triệu $) được mô tả như sau n n n X xi = 41; X x2 y i = 259; X i = 1144; i=1 i=1 i=1 n n X y2 x i = 221772; X iyi = 4197. i=1 i=1
Tiếp tục với ví dụ 2.1, giả sử ta cần tính hệ số xác định R2 và hệ số tương quan r2 , ta tiến hành xy như sau ✍ LỜI GIẢI. • Tính tổng các sai số n y 11442 SST = P i)2 X y2 ( n i=1 = 221772 − = 58180. n 8 i=1 i − Å −1666ã SSE = SST − ˆ β . 1Sxy = 58180 − − · (−1666) ≈ 1391.13 48.875
SSR = SST − SSE = 58180 − 1391.130435 ≈ 56788.87. SSR 56788.87
⇒ Hệ số xác định R2 = ≈ ≈ 0.98. SST 58180 S −1666
⇒ Hệ số tương quan mẫu r xy xy = √ = √ ≈ −0.99. Sxx · SST 48.875 · 58180
BÀI 9.1. Dữ liệu sau đây cung cấp thông tin về kinh nghiệm (X - năm) và lương hàng tháng (Y - trăm
$) của 9 thư ký được chọn ngẫu nhiên. n n n X xi = 80; X x2i = 968; X yi = 425; i=1 i=1 i=1 n n X y2 x i = 21841; X iyi = 4404. i=1 i=1
a) Tính những ước lượng bình phương tối thiểu cho hệ số góc và tung độ góc.
b) Sử dụng đường thẳng hồi quy vừa ước lượng, hãy dự đoán mức lương hàng tháng của một thư ký có 4 năm kinh nghiệm?
c) Dựa vào đường thẳng hồi quy vừa ước lượng, giả sử các yếu tố khác không đổi thì mức lương
hàng tháng của một thư ký sẽ thay đổi như thế nào?
50 | Lý thuyết Xác suất và Thống kê
CHƯƠNG 9. HỒI QUY - TƯƠNG QUAN
d) Tính hệ số xác định và hệ số tương quan mẫu.
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
VÍ DỤ 3.2. Một công ty sản xuất ô tô muốn điều tra giá của một dòng xe của họ giảm giá thế
nào theo số năm sử dụng. Bộ phận nghiên cứu của công ty đã lấy mẫu gồm 8 chiếc của dòng xe
này và thu thập thông tin về số năm sử dụng (X - năm) và giá của xe (Y - triệu $) được mô tả ở bảng dưới đây Số năm sử dụng 6 3 8 9 2 5 6 2 Giá xe 112 220 38 33 267 134 95 245
a) Tìm đường thẳng hồi quy biểu diễn mối liên hệ giữa giá của xe Y theo số năm sử dụng X.
b) Dựa vào đường thẳng hồi quy vừa ước lượng, hãy cho biết giá của chiếc xe sau 2 năm sử dụng?
c) Dựa vào đường thẳng hồi quy vừa ước lượng, giả sử các yếu tố khác không đổi thì giá của
xe sẽ thay đổi như thế nào?
d) Tính hệ số xác định và hệ số tương quan mẫu.
CHƯƠNG 9. HỒI QUY - TƯƠNG QUAN
3. Hệ số xác định và Hệ số tương quan | 51
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
BÀI 9.2. Để thực hiện một công trình nghiên cứu về mối quan hệ giữa chiều cao (Y - mét) và đường
kính (X - cm) của một loại cây, người ta quan sát trên một mẫu ngẫu nhiên và có kết quả sau: X 26 28 23 25 31 37 29 42 Y 4 5 4 4 7 8 6 9
a) Tìm đường thẳng hồi quy biểu diễn mối liên hệ giữa chiều cao Y theo đường kính X.
b) Dựa vào đường thẳng hồi quy vừa ước lượng, hãy cho biết chiều cao của cây nếu có đường kính 30 cm?
c) Dựa vào đường thẳng hồi quy vừa ước lượng, giả sử các yếu tố khác không đổi thì chiều cao của
cây sẽ thay đổi như thế nào?
52 | Lý thuyết Xác suất và Thống kê
CHƯƠNG 9. HỒI QUY - TƯƠNG QUAN
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
...................................................................................................................................................................
BÀI 9.3. Bệnh tiểu đường và béo phì là những vấn đề sức khỏe nghiêm trọng ở Hoa Kỳ và phần lớn
các nước phát triển. Đo lượng mỡ cơ thể của một người là một cách để theo dõi tiến độ kiểm soát cân
nặng, nhưng đo chính xác nó phải sử dụng đến thiết bị X-quang đắt tiền hoặc nhúng cơ thể xuống
một hồ bơi. Thay vào đó, chỉ số khối cơ thể (BMI) thường được sử dụng làm đại diện cho mỡ cơ thể vì
nó dễ đo: BMI = khối lượng (kg)/(chiều cao (m))2 = 703 khối lượng (lb)/(chiều cao (in))2. Trong một
nghiên cứu của 250 người đàn ông tại Đại học Bingham Young, cả BMI (X) và mỡ cơ thể (Y ) được đo
lường. Các nhà nghiên cứu đã tìm thấy các thống kê tóm tắt sau: n n n
X xi = 6322.28; X x2i = 162674.18; X yi = 4757.90; i=1 i=1 i=1 n n X y2i = 107679.27; X xiyi = 125471.10 i=1 i=1
a) Tính những ước lượng bình phương tối thiểu cho hệ số góc và tung độ góc.
b) Sử dụng đường thẳng hồi quy, hãy tiên đoán lượng mỡ cơ thể của một người đàn ông sẽ được
quan trắc nếu có chỉ số BMI là 30?
c) Xác định hệ số tương quan mẫu rxy.
d) Tính hệ số xác định R2.
BÀI 9.4. Một bài báo trong Nghiên cứu Bê tông “Đặc tính bề mặt gần bê tông: Tính thấm nội tại”
(1989, Tập 41) trình bày dữ liệu về cường độ nén x và độ thấm nội tại y của các hỗn hợp bê tông và
phương pháp xử lý khác nhau. Số liệu được tóm tắt như sau: n n n n = 14; X yi = 572; X y2i = 23530; X xi = 43; i=1 i=1 i=1 n n X x2i = 157.42; X xiyi = 1697.80 i=1 i=1
a) Tính những ước lượng bình phương tối thiểu cho hệ số góc và tung độ góc.
b) Sử dụng đường thẳng hồi quy, hãy tiên đoán lượng độ thấm nội sẽ quan trắc được khi cường độ nén là x = 4.3?
CHƯƠNG 9. HỒI QUY - TƯƠNG QUAN
3. Hệ số xác định và Hệ số tương quan | 53
c) Xác định hệ số tương quan mẫu rxy.
d) Tính hệ số xác định R2.
BÀI 9.5. Các phương pháp hồi quy đã được sử dụng để phân tích dữ liệu từ một nghiên cứu điều tra
mối quan hệ giữa nhiệt độ bề mặt đường (x) và độ lún mặt đường (y). Số liệu được tóm tắt như sau n n n n = 20; X yi = 12.75; X y2i = 8.86; X xi = 1478; i=1 i=1 i=1 n n X x2 x i = 143215.8; X iyi = 1083.67 i=1 i=1
a) Tính những ước lượng bình phương tối thiểu cho hệ số góc và tung độ góc.
b) Sử dụng đường thẳng hồi quy, hãy tiên đoán lượng độ lún mặt đường sẽ quan trắc được khi nhiệt
độ bề mặt đường là 85◦F?
c) Xác định hệ số tương quan mẫu rxy.
d) Tính hệ số xác định R2.
BÀI 9.6. Điểm thi giữa kỳ (x) và cuối kỳ (y) của một lớp có 9 sinh viên là như sau x 77 50 71 72 81 94 96 99 67 y 82 66 78 34 47 85 99 99 68
a) Ước lượng đường hồi quy tuyến tính.
b) Ước lượng điểm bài thi cuối kỳ của một sinh viên có điểm giữa kỳ là 85.
c) Xác định hệ số tương quan mẫu rxy.
d) Tính hệ số xác định R2.
BÀI 9.7. Một nghiên cứu về khối lượng đường bị biến đổi trong một quá trình nào đó ở các nhiệt độ
khác nhau. Dữ liệu được mã hóa và ghi lại như sau
Nhiệt độ (x) Đường bị biến đổi (y) 1.0 8.1 1.1 7.8 1.2 8.5 1.3 9.8 1.4 9.5 1.5 8.9 1.6 8.6 1.7 10.2 1.8 9.3 1.9 9.2 2.0 10.5
54 | Lý thuyết Xác suất và Thống kê
CHƯƠNG 9. HỒI QUY - TƯƠNG QUAN
a) Ước lượng đường hồi quy tuyến tính.
b) Ước lượng khối lượng trung bình của đường bị biến đổi được tạo ra khi nhiệt độ được mã hóa là 1.75.
c) Xác định hệ số tương quan mẫu rxy.
d) Tính hệ số xác định R2.
BÀI 9.8. Khối lượng của một hợp chất hóa học y hòa tan trong 100 gram nước ở các nhiệt độ khác
nhau x được ghi lại như sau x (◦C) y (gram) 0 8 6 8 15 12 10 14 30 25 21 24 45 31 33 28 60 44 39 42 75 48 51 44
a) Tìm phương trình của đường thẳng hồi quy.
b) Ước lượng khối lượng của hợp chất hóa học sẽ hòa tan trong 100 gram nước ở 50◦.
c) Xác định hệ số tương quan mẫu rxy.
d) Tính hệ số xác định R2.
CHƯƠNG 9. HỒI QUY - TƯƠNG QUAN
3. Hệ số xác định và Hệ số tương quan | 55




