















Preview text:
PHẦN I: XAÙC SUAÁT
1. Bieán coá ngaãu nhieân & xaùc suaát cuûa bieán coá:
1.1. Coâng thöùc coäng xaùc suaát:
1.1.1. p(A+B)=p(A)+p(B) (2 bieán coá xung khaéc)
1.1.2. p(A+B)=p(A)+p(B)-p(A.B) p(A+B+C)=p(A)+p(B)+p(C)- [p(AB)+p(AC)+p(BC)]+p(ABC)
1.2. Coâng thöùc nhaân xaùc suaát:
1.2.1. p(A.B)=p(A).p(B) (2 bieán coá ñoäc laäp)
1.2.2. p(A.B)=p(A).p(B/A) p(A A ...A ) p (A ).p (A /A )...p(A /A A ..A ) 1 2 n 1 2 1 n n 1 2 1
1.3. Coâng thöùc Bernoulli: cho 2 bieán coá A vaø A 1.3.1. () x x n x p x C p q , p=p(A), q=1-p nn
1.4. Coâng thöùc xaùc suaát ñaày ñuû: p (F ) p (A ). ( p F / A ) p ( A ). (p F / A ) ... ( p A ) . (p / F ) A 1 1 2 2 nn 1.5. Coâng thöùc Bayes: p (A .F ) p ( A ) . p (F / A ) p (A / ) i i i F i p ( ) F ( p )F
2. Bieán ngaãu nhieân:
2.1. Baûng phaân phoái xaùc suaát (bieán ngaãu nhieân rôøi raïc)
2.2. Haøm maät ñoä xaùc suaátf (x () ) (bieãn ngaãu nhieân lieân tuïc) 2.2.1.f x () 0
2.2.2. f (x) d x 1 2.2.3. b p( a x ) b f ( )x d x a
2.3. Haøm phaân phoái xaùc suaát ( Fx ()
) (duøng cho caû 2 loaïi bieán-thöôøng laø bieán ngaãu nhieân lieân tuïc) 2.3.1.F x () =p( F 2.3.2. F 'x( ) f x( ) 2.3.3. x F ( x) f ( )t d t
2.4. Kyø voïng
2.4.1. E( )x x p x p ... nnx p (töø baûng phaân phoái xaùc suaát) 1 1 2 2 2.4.2. E x( ) x f ( ) x d x
2.5. Phöông sai: 2.5.1. 22 V x( ) E ( x ) [ E x ( ) ] s://fb.com/tailieudientucntt
CuuDuongThanCong.com https://fb.com/tailieudientucntt 2.5.2V. 22 x ( ) x f x( )d x [ x f ( ) x d ]x
3. Moät soá phaân phoái xaùc suaát thoâng duïng:
3.1. Phaân phoái chuaån toång quaùt: 2 XN ~ ( ; ) 2 () 1 x 3.1.1. 2 2 f () x e 2
3.1.2. f (x) d x 1 3.1.3. M o d X M e d X ; 2 E x ( ) , V ( x ) 3.1.4. ba p (a x b ) ( ) ( )
3.1.5. Phaân phoái chuaån taéc 2 0 , 1 3.1.5.1. ~ TN ( 0 , 1) 2 3.1.5.2. t 1 2 f (t) e 2 3.1.5.3. Ñoåi bieán X T 3.1.5.4. p (a x b ) ( b ) (a )
3.2. Phaân phoái Poisson: XP ~ ( ) ,>0 3.2.1. k p() k e k ! 3.2.2. Ex ( ) V (x )
3.3. Phaân phoái nhò thöùc:X ~B (n ,p ) 3.3.1. p( X k) p ( ) k k n k C p q ,k p q 1 nn 3.3.2. n p(X k ) 1 k 0
3.3.3.E x () n p , M o d X x, n p q x n p q 00
3.3.4. Khi n=1: X ~B p(1, ) :phaân phoái khoâng-moät 3.3.4.1. 2 E x ( ) p , E x ( ) p V , x ( ) p q
3.3.5. Xấp xỉ phaân phoái nhò thöùc:
3.3.5.1. Baèng phaân phoái Poisson: n >50, p <0.1; X B n ~p( , ) X P ~ ( ) , np . k p () k k n k x k C p q e n k ! s://fb.com/tailieudientucntt
CuuDuongThanCong.com https://fb.com/tailieudientucntt
3.3.5.2. Baèng phaân phoái chuaån: np 0 n . q 5 , 0 . 5n ,p ,npq .X ~B ( ,n )p X ~ ( N n ,p n p)q 1 k kk p (x) k ( f ) ; p(k 21 k 2) ( ) ( ) 1
3.4. Phaân phoái sieâu boäi: X ~ H (N ,N ,n) [N:toång soá phaàn töû, N :Soá phaàn töû coù tính chaát A A
A trong N, n: soá phaàn töû laáy ngaãu nhieân].Goïi X laø soá phaàn töû coù tính chaát A trong n. k CC . n k p () N N N AA X k n C N 3.4.1. N Nn ( ) , A E X n p p ;V ( )X n .p q , 1 q p N N 1
3.4.2. Xaáp xæ phaân phoái sieâu boäi baèng phaân phoái nhò thöùc: N n 0 .0 5 N X ~ ( B n , p ) ; p ( ) k X k C , k n k A p q p n N
3.5. Bieán ngaãu nhieân 2 chieàu: X vaø Y ñoäc laäp P
p (x ) .q ( y ) vôùi moïi i,j ij i j
3.6. Hieäp phöông sai vaø heä soá töông quan:
3.6.1. Hieäp phöông sai(cov): c o v( X , Y) E(X Y ) E (X )E (Y )
3.6.2. Heä soá töông quan : c o v (XY, ) X , Y X , Y ( X ) Y ( ) PHAÀN 2: THOÁNG KEÂ 1. Toång theå vaø maãu
1.1.Thöïc haønh tính toaùn treân maãu: 1.1.1. Tính trung bình ( 1n X ): Xx n ni n i 1
1.1.2. Tính tyû leä maãu: ( m f ); A f
(m :soá phaàn töû mang tính chaát A; n: kích thöôùc maãu) n n n A 1.1.3. k Tính phöông sai maãu: 1[ ( ) ] 2 2 2 S n x n X n 1 ii 1
1.2.Öôùc löôïng tham soá cuûa toång theå:
1.2.1. Öôùc löôïng ñieåm: 22 E ( X ) , (E )f , (p E )S nn
1.2.2. Öôùc löôïng khoaûng:
1.2.2.1. Öôùc löôïng khoaûng cho trung bình: Vôùi ñoä tin caäy 1- cho tröôùc, 1 maãu kích thöôùc n. n 30 , 2 bieát n 30 , 2 chöa bieát X , X ,s XX , XX , 12 12 s://fb.com/tailieudientucntt
CuuDuongThanCong.com https://fb.com/tailieudientucntt .s u . u n n 2 2 (1 0.5- u ) (1 0.5- u ) 2 2 2 2 n <30, 2 bieát n <30, 2 chöa bieát Nhö TH1 X ,s XX , 12 s t . ( n 1 , ) n 2
1.2.2.2. Öôùc löôïng khoaûng cho tyû leä: toång theå coù tyû leä p chöa bieát, vôùi ñoä tin caäy 1
cho tröôùc, vôùi 1 maãu kích thöôùc n, tyû leä maãu f . Tìm 2 soá p ,p thoaû: n 12 ff (1 ) p p ( p p ) 1 , Coâng thöùc: pf u 12 1 , 2 n n 2
1.2.2.3. Öôùc löôïng khoaûng cho phöông sai:Giaû söû toång theå coù 2 chöa bieát. Döïa
vaøo 1 maãu kích thöôùc n, vôùi ñoä tin caäy 1- cho tröôùc. 22 TH1: chöa bieát, bieát ( 1 n )S ( 1 n )S 2 S . Khi ñoù ta coù 2 [ , ] trong ñoù 22 12 22 1( 1, ) n , 222(1,1 n) 2 2 TH2: bieát. Khi ñoù n (x ) ( ) n x 2 [ , ] i i i i , trong ñoù 22 12 22 1( , ) n , 222(,1 )n 2 2
1.2.3. Kieåm ñònh giaû thuyeát thoáng keâ:
1.2.3.1. Kieåm ñònh giaû thuyeát thoáng keâ cho
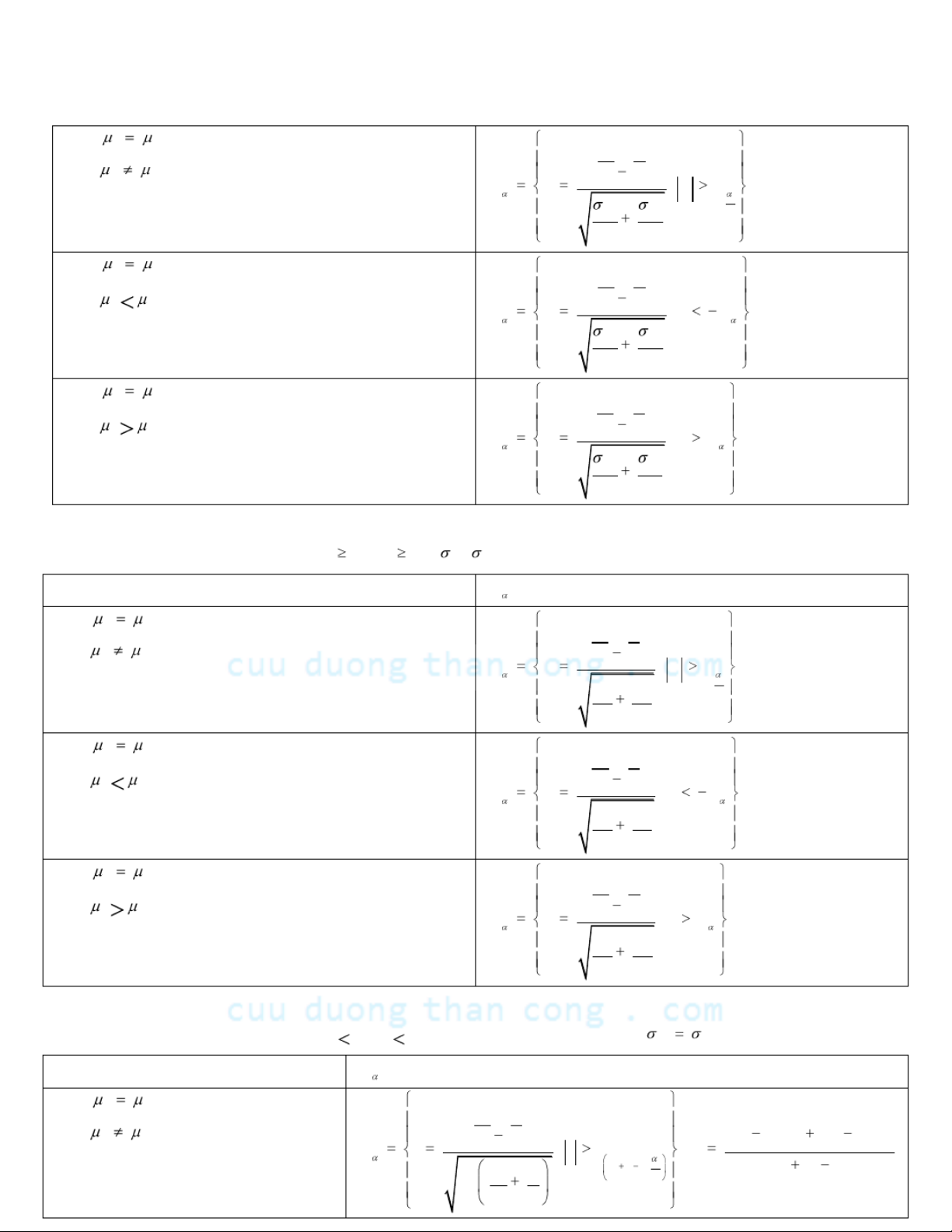
1.2.3.1.1. TH1: 2 bieát
Giaû thuyeát thoáng keâ W : 2 bieát (mieàn baùc boû H ) 0 H : X 00 W u n u > u } H ≠ 0 {, 1: 0 2 H : {X 00 W u n ,u<-u } H < 0 1: 0 H : {X 00 W u n ,u>u } H > 0 1: 0 2 2
1.2.3.1.2. TH2: n 30 , khoâng bieát s://fb.com/tailieudientucntt
CuuDuongThanCong.com https://fb.com/tailieudientucntt
Giaû thuyeát thoáng keâ W (mieàn baùc boû H ) 0 H : X 00 W u n u > u } H ≠ 0 {, 1: s 0 2 H : {X 00 W u n ,u<-u } H < 0 1: s 0 H : {X 00 W u n ,u>u } H > 0 1: s 0
1.2.3.1.3. TH3: n <30, 2 khoâng bieát
Giaû thuyeát thoáng keâ
W (mieàn baùc boû H ) 0 H : X 00 W t n t >t } H ≠ 0 {, 1: s ( n 1 , ) 0 2 H : {X 00 W t n ,t <- t } H < 0 1: s ( n 1 , ) 0 2 H : X 00 W t n t > t } H > 0 {, 1: s ( n 1 , ) 0 2
1.2.3.2. Kieåm ñònh giaû thuyeát thoáng keâ cho tyû leä:
Giaû thuyeát thoáng keâ
W (mieàn baùc boû H ) 0 H p p fp 0 : 0 0 W u {, u > u } Hp ≠ p pp (1 ) 1: 0 00 2 n H p p fp 0 : 0 0 Wu { ,u <-u } Hp < p pp (1 ) 1: 0 00 n H p p fp 0 : 0 0 Wu { ,u > u } Hp > p pp (1 ) 1: 0 00 n
1.2.3.3. Kieåm ñònh giaû thuyeát thoáng keâ cho phöông sai: 1.2.3.3.1. TH1: chöa bieát
Giaû thuyeát thoáng keâ
W (mieàn baùc boû H ) 0 22 H : 2 {ns ( 1) 00 2 W , 2 < 2 hoaëc 2 > 2 2 2 1 2 H ≠ 2 1: 0 0 2 2 2 2 , 12 ( nn 1 ,1 ) ( 1 , ) 22 s://fb.com/tailieudientucntt
CuuDuongThanCong.com https://fb.com/tailieudientucntt 22 H : 2 {ns ( 1) 00 2 W , 2 < 2 2 2 ( n 1 ,1 ) H < 2 1: 0 0 22 H : 2 {ns ( 1) 00 2 W , 2 > 2 2 2 ( n 1 , ) H > 2 1: 0 0 1.2.3.3.2. TH2: bieát.
Giaû thuyeát thoáng keâ
W (mieàn baùc boû H ) 0 22 H : 2 nx() 00 {i 2 W , 2 < 2 hoaëc 2 > 2 2 H ≠ 2 2 1 2 1: 0 0 2 2 2 2 , 12 ( ,1 nn ) ( , ) 22 22 H : 2 nx() 00 {i 2 W , 2 < 2 2 H < 2 2 (n,1 ) 1: 0 0 22 H : 2 nx() 00 {i 2 W , 2 > 2 2 H > 2 2 (n , ) 1: 0 0
1.2.4. So sánh 2 tham số của tổng thể:
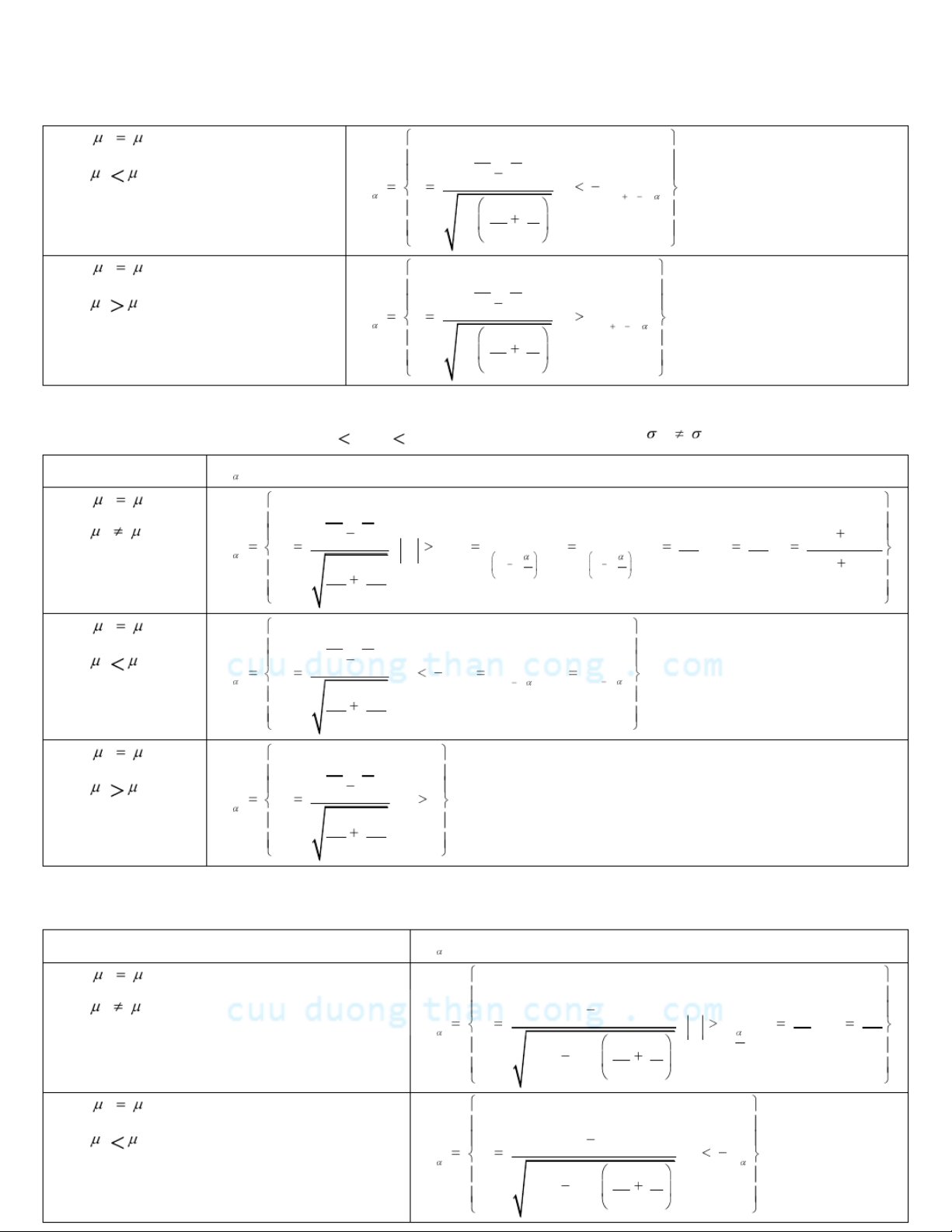
1.2.4.1. So sánh 2 số trung bình: 1.2.4.1.1. TH1: 22 mn 3 0 , 3 0 , , biết 12 GTTK W H : 0 1 2 H : XY 1 1 2 W u ; u u 22 2 12 mn H : 0 1 2 H : XY 11 2 W u ; u u 22 12 mn H : 0 1 2 H : XY 11 2 W u ; u u 22 12 mn
1.2.4.1.2. TH2:m 30,n 30, 22, biết, X,Y có phân phối chuẩn 12 GTTK W s://fb.com/tailieudientucntt
CuuDuongThanCong.com https://fb.com/tailieudientucntt H : 0 1 2 H : XY 1 1 2 W u ; u u 22 2 12 mn H : 0 1 2 H : XY 11 2 W u ; u u 22 12 mn H : 0 1 2 H : XY 11 2 W u ; u u 22 12 mn 1.2.4.1.3. TH3: 22 mn 3 0 , 3 0 , , không biết 12 GTTK W H : 0 1 2 H : XY 1 1 2 W u ; u u 22 ss 2 12 mn H : 0 1 2 H : XY 11 2 W u ; u u 22 ss 12 mn H : 0 1 2 H : XY 11 2 W u ; u u 22 ss 12 mn
1.2.4.1.4. TH4:m 30,n 30, X,Y có phân phối chuẩn, 22 không biết 12 GTTK W H : 0 1 2 H : XY 22 211 m s n s 1 1 2 W t ; t t 12 s 11 mn 2, mn 2 22 s mn s://fb.com/tailieudientucntt
CuuDuongThanCong.com https://fb.com/tailieudientucntt H : 0 1 2 H : XY 11 2 W t ; t t 2, 11 mn 2 s mn H : 0 1 2 H : XY 11 2 W t ; t t mn 2, 11 2 s mn
1.2.4.1.5. TH5:m 30,n 30, X,Y có phân phối chuẩn, 22 chưa biết 12 GTTK W H : 0 1 2 H : 22 XY s s t v t v 1 1 2 1 2 1 1 2 2 W g ; ;g t t t , t t ; v , v ; t 1 2 1 2 22 1 , 1 , mn m n v v ss 22 12 12 mn H : 0 1 2 H : XY 11 2 W g ; g t;t t ,t n t 1 m 1, 2 ( 1 , ) 22 ss 12 mn H : 0 1 2 H : XY 11 2 W g ; g t 22 ss 12 mn
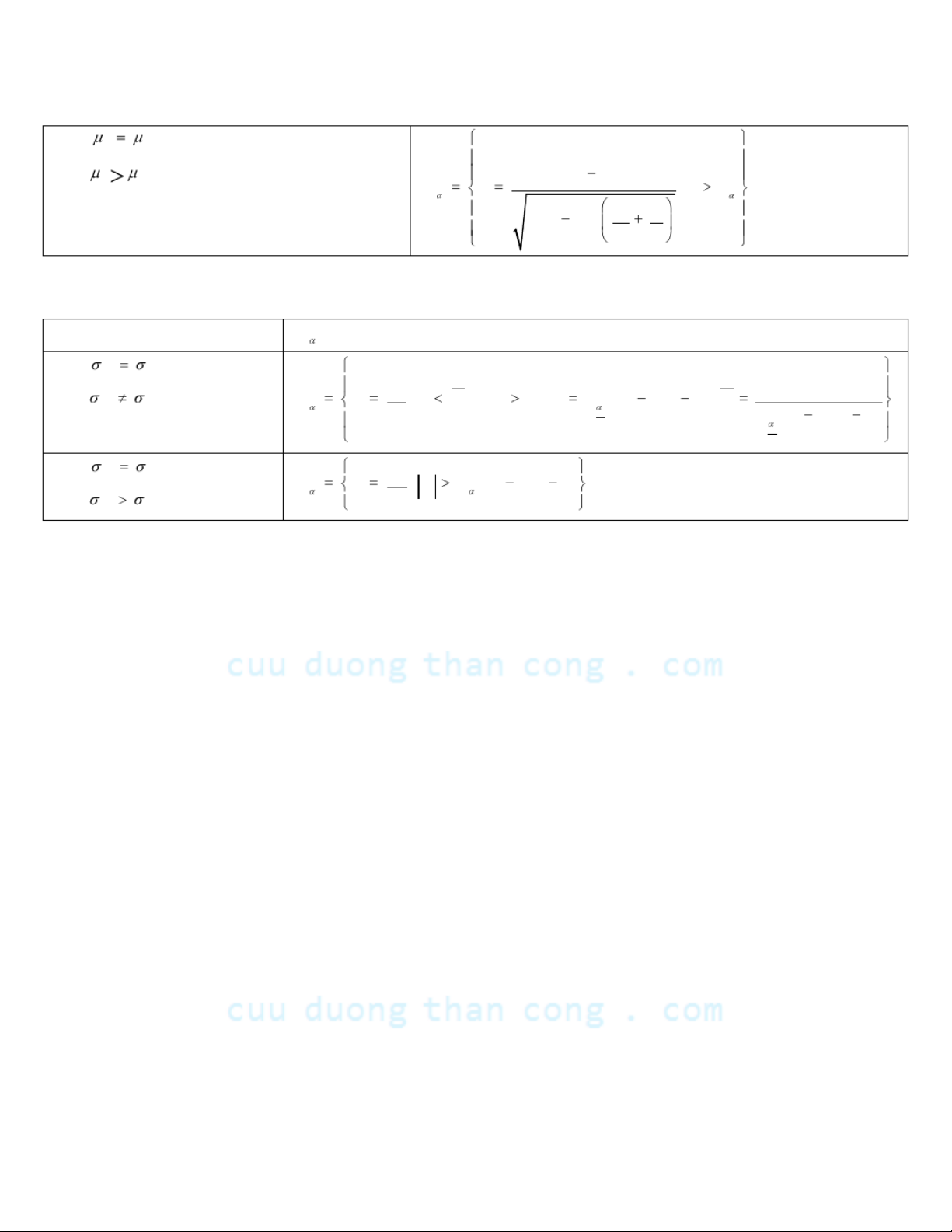
1.2.4.2. So sánh 2 tỷ lệ: GTTK W H : 0 1 2 H : f f k k 1 1 2 1 2 1 2 W u ; u u f ; , f 12 11 mn 2 ff 1 mn H : 0 1 2 H : ff 11 2 12 ; W u u u 11 ff 1 mn s://fb.com/tailieudientucntt
CuuDuongThanCong.com https://fb.com/tailieudientucntt H : 0 1 2 H : ff 11 2 12 ; W u u u 11 ff 1 mn
1.2.4.3. So sánh 2 phương sai: GTTK W 22 H : 0 1 2 s 1 22 H : 2 1 W g , g f h a y g ;f f f m 1, n 1 , f 1 1 2 2 s f n 1 m , 1 22 2 22 H : 2 s 0 1 2 1 W g , g f ( m 1, n 1) 22 H : 2 s 1 1 2 2 s://fb.com/tailieudientucntt
CuuDuongThanCong.com https://fb.com/tailieudientucntt




