PHƯƠNG TRÌNH VI PHÂN
1) Một số khái niệm cơ bản về phương trình vi phân.
2) Phương trình vi phân tách biến được;
3) Phương trình vi phân đẳng cấp.
4) Phương trình vi phân tuyến tính cấp một. 5/19/2020 daothaohus@gmail.com 1
1. Một số khái niệm cơ bản
Cho hàm số y = f(x). Giải phương trình: f(x) = 0
• Tìm giá trị x thỏa mãn phương trình trên. • x – biến số;
• y = f(x) là hàm số theo biến x.
Vấn đề đặt ra: Có tồn tại một dạng phương trình nào đó mà giải ra nghiệm y = f(x)? 5/19/2020 daothaohus@gmail.com 2
1. Một số khái niệm cơ bản
Định nghĩa: Phương trình vi phân là một phương trình
mà đối tượng phải tìm là hàm số, và hàm số phải tìm có
mặt trong phương trình đó dưới dấu đạo hàm hoặc vi phân. • Ví dụ: 2 2 a) y '  y  x 2 b) xdy  y dx  0 2 d y 2 c)  a y 2 dx 5/19/2020 daothaohus@gmail.com 3
1. Một số khái niệm cơ bản
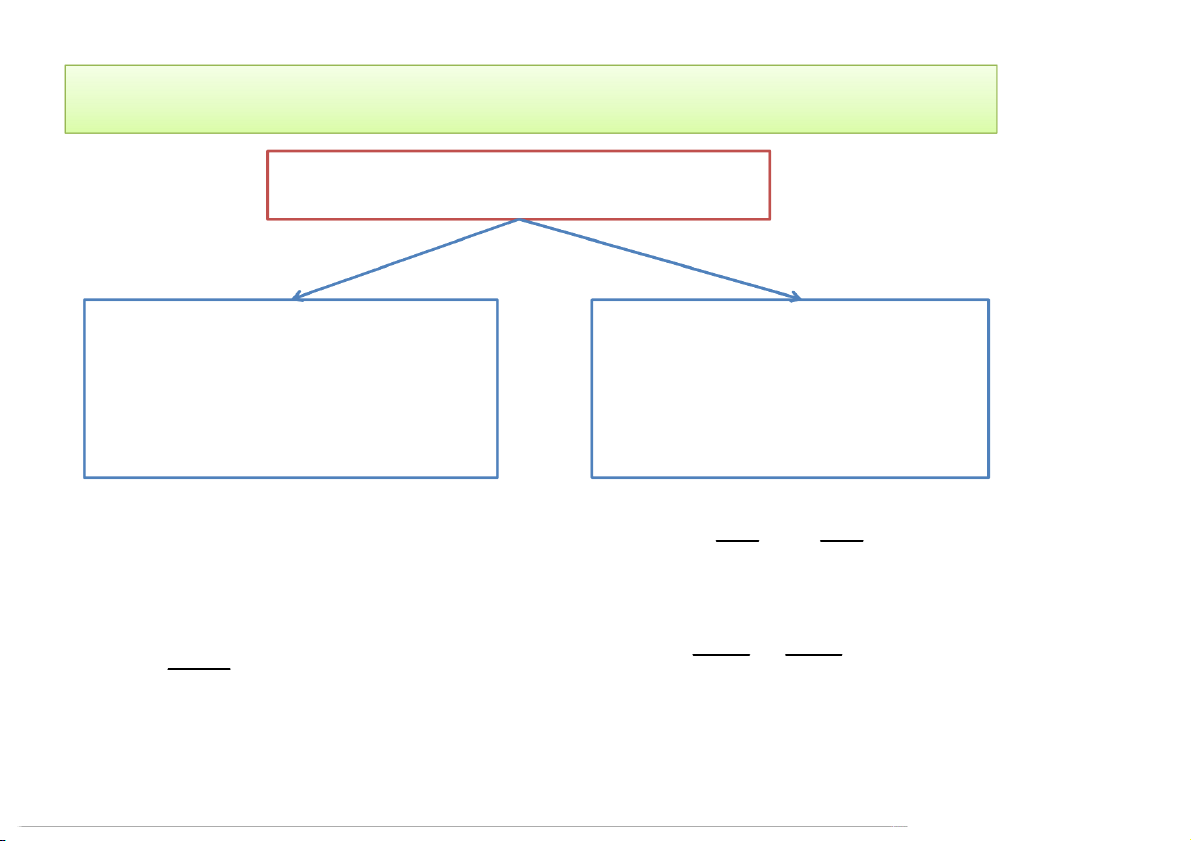
Phân loại phương trình vi phân Hàm phải tìm là hàm Hàm phải tìm là hàm số 1 biến số: - Phương số nhiều biến số: - trình vi phân thường Phương trình vi phân đạo hàm riêng 2 2 a) y'  y  x u  u  a) x  y  u 2 x  y  b) xdy  y dx  0 2 2 2  u  u d y 2 b)   0 ) c  a y 2 2 2 x  y  dx 5/19/2020 daothaohus@gmail.com 4
1. Một số khái niệm cơ bản
Cấp của phương trình vi phân: là cấp cao nhất của đạo
hàm hoặc vi phân của hàm phải tìm có mặt trong phương trình. 2 1) xdy  y dx  0 PTVP thường cấp 1 2 d y 2 2)  a y 2 dx PTVP thường cấp 2 u  u  3) x  y  u x  y 
PTVP đạo hàm riêng cấp 1 2 2  u  u 4)   0
PTVP đạo hàm riêng cấp 2 2 2 x  y  5/19/2020 daothaohus@gmail.com 5
1. Một số khái niệm cơ bản
Dạng tổng quát của phương trình vi phân thường cấp n: n F x, y, y',..., y   0   1
Trong đó, F: hàm n + 2 biến số.
Nếu giải ra được y(n): n n  y    1 x, y, y ',..., y  Ví dụ: 2 y 2x 2 2x 1 y y '  0 y '   .   x, y 2   2 2 1 y 1 x 1 x 2 y 5/19/2020 daothaohus@gmail.com 6
1. Một số khái niệm cơ bản
Nghiệm của phương trình vi phân thường: là một hàm số
y = φ(x) xác định trên (a, b) nào đó thỏa mãn:
F  ,x x,' x n ,...,  x  0
• Đồ thị của nghiệm y = φ(x) được gọi là đường cong tích phân. 5/19/2020 daothaohus@gmail.com 7
1. Một số khái niệm cơ bản
• Ví dụ: Phương trình y’x – y = 0 có nghiệm: y  Cx, C  R
vì thỏa mãn phương trình đã cho. 5/19/2020 daothaohus@gmail.com 8
2. Phương trình vi phân thường cấp 1 Dạng tổng quát F x, y, y'  0 (2) Nếu rút được theo y’: (3) y '  f x, y Hoặc: (4)
M  x, ydx  N x, ydy  0 • Ví dụ: xy ' y  0 xdy  ydx  0 y y '   x 5/19/2020 daothaohus@gmail.com 9
2. Phương trình vi phân thường cấp 1
Nghiệm và tích phân của ptvp cấp 1
• Nghiệm của một phương trình vi phân thường cấp 1 là
một hàm số y = φ(x) xác định trên 1 khoảng (a,b) nào đó thỏa mãn:
F x,  x, ' x  0 (theo 2) Hay:  ' x  f  , x   x   (theo 3)
 Nghiệm có thể viết dưới dạng hàm ẩn:  , x y  0 (5)  
 Phương trình (5) – được gọi là tích phân của PTVP 5/19/2020 daothaohus@gmail.com 10
2. Phương trình vi phân thường cấp 1
Nghiệm và tích phân của ptvp cấp 1 • Ví dụ: Phương trình xdy  ydx  0 có một nghiệm là: 1 y  x Vì:  1  1  1  1 xd  dx  x  dx  dx  0    2 x x x      x c
Nhận thấy y  , c  const Cũng là nghiệm x
 Nghiệm của phương trình vi phân cấp 1 là vô số. 5/19/2020 daothaohus@gmail.com 11
2. Phương trình vi phân thường cấp 1
• Nghiệm của phương trình vi phân cấp 1 là vô số.
• Tập hợp nghiệm của PTVP cấp một phụ thuộc vào một hằng số c tùy ý.
• Trong thực tế, thường quan tâm đến nghiệm của PTVP
cấp 1 thỏa mãn những điều kiện nào đó. • Ví dụ: y(x0) = y0 (6)
Với x0, y0 là các số cho trước.
• Điều kiện cho ở (6) gọi là điều kiện ban đầu
 Bài toán tìm nghiệm PTVP cấp 1 thỏa mãn điều kiện ban
đầu (6) được gọi là bài toán Cauchy. 5/19/2020 daothaohus@gmail.com 12
2. Phương trình vi phân thường cấp 1
• Ý nghĩa hình học của bài toán Cauchy:
Tìm đường cong tích phân của phương trình (3) đi qua điểm (x0, y ) 0 cho trước.
• Ví dụ. Tìm nhiệm của phương trình xdy  ydx  0 Với điều kiện: y(1) = 1. 1  Nghiệm: y  x 5/19/2020 daothaohus@gmail.com 13
2. Phương trình vi phân thường cấp 1
Nghiệm tổng quát, nghiệm riêng • Nghiệm tổng quát
y   x,C , C  const
Hoặc viết dưới dạng hàm ẩn:  , x y,C  0
• Khi gán cho C ở nghiệm tổng quát 1 giá trị bằng số nhất
định, thu được 1 nghiệm riêng của phương trình. 5/19/2020 daothaohus@gmail.com 14
2. Phương trình vi phân thường cấp 1
 Nghiệm tổng quát, nghiệm riêng
• Ví dụ. Phương trình y’ = x2 có nghiệm tổng quát: 1 3 y  x  C, C  const 3 1 Với C = 0: y 
x 3 là một nghiệm riêng của pt. 3 5/19/2020 daothaohus@gmail.com 15
2.1 Phương trình biến số phân ly  Dạng: f xdx  g  ydy
• Lấy tích phân hai vế: f  xdx  g   ydy Hay: F  x  G y  C
Trong đó, F(x) là một nguyên hàm của f(x)
G(y) là một nguyên hàm của g(y) 5/19/2020 daothaohus@gmail.com 16
2.1 Phương trình biến số phân ly
• Ví dụ: Giải phương trình xdx  ydy  0
• Ta có: xdx  ydy  0  xdx   ydy Lấy tích phân 2 vế xdx   ydy   2 2 2 2 Thu được: x y x y    C    C 2 2 2 2 5/19/2020 daothaohus@gmail.com 17
2.1 Phương trình biến số phân ly
• Ví dụ . Giải phương trình 2x 2y dx  dy  0 2 2 1  x 1  y Tích phân tổng quát: 2x 2y d  2 1 x  d  2 1 y  dx  dy  C    C  2  2  2  2 1 x 1 y 1 x 1 y  ln 2 1 x   ln 2 1 y   C   2 1 x  2 1 y   C', C ' C  e  5/19/2020 daothaohus@gmail.com 18
2.1 Phương trình biến số phân ly
 Chú ý: Phương trình có dạng
M x N y dx  M x N y dy  0 (7) 1   1  2   2  M x N y 1 2   Nếu: N y M x  0 : 7    dx  dy  0 1   2  M x N y 2   1   Nếu = 0 tại = , thì = là 1 nghiệm của PTVP. Nếu = 0 tại = , thì = là 1 nghiệm của PTVP.
 Các nghiệm đặc biệt này không chứa trong nghiệm tổng quát của PTVP trên. 5/19/2020 daothaohus@gmail.com 19
2.1 Phương trình biến số phân ly
• Ví dụ. Giải phương trình 2 2
x 1  y dx  y 1  x dy  0 xdx ydy Giả sử: 2 2 1 x 1 y  0    0 2 2 1 x 1 y xdx ydy 1 d  2 1 x  1 d  2 1 y    C     C     2 2 2 2 1 x 1 y 2 1 x 2 1 y 2 2
 1 x  1 y  C ', C '  0 Nghiệm kì dị y 1, y  1  , 1  x 1; 1 2 x  1, x  1  , 1  y  1. 1 2 5/19/2020 daothaohus@gmail.com 20
2.1 Phương trình biến số phân ly  Dạng:
y '  f ax  by  c dz dy  a  b  Đặt: dx dx
z  ax  by  c  dy   f z dx dz      dz a bf z      dx dx a bf z
- Phương trình biến số phân ly 5/19/2020 daothaohus@gmail.com 21
2.1 Phương trình biến số phân ly dy
• Ví dụ. Giải phương trình  2x  y (10) dx dz dy dy Đặt z  2x  y   2  ,  z dx dx dx dz dz Pt (10) trở thành:  2  z   dx dx 2  z Nghiệm ln 2 xC       2   ' x z x C z e z C e  2
2   ' x  2   ' x x y C e y C e  2x   1 5/19/2020 daothaohus@gmail.com 22
2.1 Phương trình biến số phân ly Đường cong tích phân
trong một số trường hợp 5/19/2020 daothaohus@gmail.com 23
2.1 Phương trình biến số phân ly dy 1
• Ví dụ: Giải phương trình   1 dx x  y Đặt z  x  y
Nghiệm  x  y2  2x  C 5/19/2020 daothaohus@gmail.com 24
2.2. Phương trình vi phân thuần nhất dy • Dạng:
 f  x, y, f  x, y  f kx,ky dx y  xz y  Đặt: z    dy dz x  z  x dx dx dz   Suy ra:     y z x
z ,   z  f  x, y  f 1, dx  x    dz dx   Phương trình tách biến   z   z x 5/19/2020 daothaohus@gmail.com 25
2.2. Phương trình vi phân thuần nhất
• Ví dụ. Giải phương trình
x  ydx x  ydy  0 dx 1 d  2 1 2z  z  Tích phân:   C   2 1 x 2 1 2z  z  2ln x  ln  2 1 2z  z   C 2  x  2 1 2z  z   C 2  y y  2 2 2 Nghiệm: x 1 2 
 C  x  2xy  y  C  2 x x    5/19/2020 daothaohus@gmail.com 27
2.2. Phương trình thuần nhất dy  a x  b y  c  • Dạng: 1 1 1  f dx  a x b y c     2 2 2  a b 1 1 a b 1 1 Nếu  0    k a b a b 2 2 2 2  a x  b y  c  k a x  b y  c  1 1 1 2 2  1  f  f  a x b y  c   a x b y  c   2 2 2   2 2 2   g a x  b y  c 2 2  5/19/2020 daothaohus@gmail.com 28
2.2. Phương trình thuần nhất dy  a x  b y  c  • Dạng: 1 1 1  f dx  a x b y c     2 2 2  a b 1 1 a x  b y  c  0 Nếu:  0 Giải hệ: 1 1 1   x , y 0 0  a b 2 2 a x  b y  c  0  2 2 2  x  x  u dx  du Đưa về phương Đặt: 0    trình thuần nhất: y  y  v dy    dv 0 v = zu 5/19/2020 daothaohus@gmail.com 29
2.2. Phương trình thuần nhất dy x  y  1
• Ví dụ. Giải phương trình  dx x  y  3 x  y 1  0 x  1 Giải hệ:    x  y  3  0 y    2 x  1 u dy dv u  v Đặt     y  2  v dx du u  v  dv dz 1 z v  zu   z  u  du du 1 z 2 dz 1 2z  z  u  du 1  z 5/19/2020 daothaohus@gmail.com 30
2.2. Phương trình thuần nhất dy x  y  1
• Ví dụ. Giải phương trình  dx x  y  3 du 1 zdz   2
Phương trình biến số phân ly u 1 2z  z 2 Nghiệm u  2 1 2z  z   C1 2 2  u  2uv  v  C1  x  2 1  2x  
1  y  2  y  22  C1
Nghiệm tổng quát của phương trình ban đầu 2 2
x  2xy  y  2x  6 y  C 5/19/2020 daothaohus@gmail.com 31
2.2. Phương trình thuần nhất
• Ví dụ: Giải phương trình: 2 − 4 + 6 + + − 3 =0.
Ptvp viết lại dưới dạng: 2 − 4 + 6 =− + − 3 Hệ phương trình: 2 − 4 + 6 = 0 + − 3=0 có nghiệm = 1, = 2. = + 1 Đặt: = + 2 5/19/2020 daothaohus@gmail.com 32
2.2. Phương trình thuần nhất • Khi đó: 2 − 4 = − +
Đây là pt đẳng cấp theo và . Đặt v = zu, khi đó: 2 − 4 = + = − 1 + Hay: − + 3 − 2 = 1 + 1 + ⇔ = − + 3 − 2 5/19/2020 daothaohus@gmail.com 33
2.2. Phương trình thuần nhất Tích phân hai vế 1 + = + − + 3 − 2 3 2 ⇔ − + = − 2 − 1 Hay: | − 2| ( − 2) + ln = → = , = ( − 1) ( − 1)
Trở lại biến x, y ban đầu: ( − 2 ) = ( − − 1) 5/19/2020 daothaohus@gmail.com 34
2.3. Phương trình tuyến tính cấp 1
• Dạng tổng quát của phương trình tuyến tính cấp 1: + . = trong đó:
, ( ) là các hàm liên tục cho trước.  Nếu
( )≠0 thì (1) là PTVP tuyến tính cấp 1 không thuần nhất.  Nếu =0,
thì (1) là PTVP tuyến tính cấp 1 thuần nhất (tương ứng).  Nếu , =
, thì (1) là PTVP tuyến tính cấp
1 hệ số hằng số (otonom). 5/19/2020 daothaohus@gmail.com 35
2.3. Phương trình tuyến tính cấp 1
 Cách giải phương trình: + . = ( p( x)dx
Nhân hai vế phương trình (1) với: e p (x )dx p (x )dx p (x )  ( )  ( ) dx y e p x y e q x e        p( x) dx p( x)      ( ) dx y e q x e       p( x) dx p( x)  ( ) dx y e C q x e      dx   p( x) dx p( x)   ( ) dx y e C q x e    dx   Nghiệm tổng quát    5/19/2020 daothaohus@gmail.com 36
2.3. Phương trình tuyến tính cấp 1
Chú ý: Một số PTVP cấp 1 nếu xem = ( ) là nghiệm
phải tìm thì không phải là pt tuyến tính. Nhưng nếu xem
= ( ) thì ta sẽ có pt tuyến tính: + . = .
Khi đó nghiệm tổng quát có dạng: = ∫ + . ∫ , = . 5/19/2020 daothaohus@gmail.com 37
2.3. Phương trình tuyến tính cấp 1
• Ví dụ. Giải phương trình dy y   0 dx x 1 Có: y  y   p x 1 ' 0   x x p  x 1 dx   dx  ln x  x  pxdx  ln x y  C e  y  C e  y  C x 1 1 1 Hay y  Cx 5/19/2020 daothaohus@gmail.com 38
2.3. Phương trình tuyến tính cấp 1
• Ví dụ. Giải phương trình dy  y  2 xe dx '  2 x y y
e  p x 1  p xdx  x   p x dx y e  C q  x pxdx e   dx     x x x x 2 y  e C   2 x e e dx  e C   e d   2x     x y  e  2x C  e  x x  y  e  Ce 5/19/2020 daothaohus@gmail.com 39
2.3. Phương trình tuyến tính cấp 1
• Ví dụ1. Giải phương trình y   y e dx xe   1 dy  0
• Nếu xem y là hàm phải tìm theo biến số x thì pt: − 1 + = 0
 Đây không phải là phương trình tuyến tính cấp 1.
• Nếu xem x là hàm phải tìm theo biến y thì phương trình: 1 + =
 Đây là một phương trình tuyến tính cấp 1 đối với hàm x(y) 5/19/2020 daothaohus@gmail.com 40
2.3. Phương trình tuyến tính cấp 1
• Ví dụ1. Giải phương trình y   y e dx xe   1 dy  0 Giải phương trình: 1 + =
Nghiệm của phương trình:  dy   1 dy x e C e   dy   y  e     y  x  e C  y  y  y  x  Ce  ye 5/19/2020 daothaohus@gmail.com 41
2.3. Phương trình tuyến tính cấp 1
• Ví dụ2: Tìm nghiệm của phương trình vi phân sau đi qua điểm (0, 4): + 3 = Ta có =3 nên∫ = .
Nghiệm tổng quát có dạng: = / + / 1 1 = / / + = + / 3 3 5/19/2020 daothaohus@gmail.com 42
2.3. Phương trình tuyến tính cấp 1
• Ví dụ2: Tìm nghiệm của phương trình vi phân sau đi qua điểm (0, 4): + 3 = Thay: = 0,
= 4 vào đẳng thức trên ta có = 11/3.
Do đó nghiệm riêng cần tìm là: 1 11 = + / 3 3 5/19/2020 daothaohus@gmail.com 43 2.4 Phương trình Bernoulli
• Dạng tổng quát của phương trình: + . = . (2) trong đó:
, ( ) là các hàm liên tục cho trước, ∈ .  Nếu = 0 hoặc
= 1 thì (2) là PTVP tuyến tính cấp 1.  Nếu ≠0, ≠1: Ta thấy = 0 là 1 nghiệm của (2).
( ) ≠ 0: chia cả 2 vế của (2) cho ta có: . + . = ( ) 5/19/2020 daothaohus@gmail.com 44 2.4 Phương trình Bernoulli Đặt : = → = 1 − . . ′
Khi đó ta có PTVP tuyến tính cấp 1 đối với biến : + 1 − . . = 1 − . 5/19/2020 daothaohus@gmail.com 45 2.4 Phương trình Bernoulli
• Ví dụ. Giải phương trình: 2 5 2 2/3
y  9x y  3(x  x ) y , y(0) 1
Phương trình Bernoulli với α = 2/3 1 = / = ⇒ = / ′ 3
Chia 2 vế phương trình cho / ta được phương trình: / − 9 = 3 + Hay: 3 ′ − 9 = 3 + ′ − 3 = + 5/19/2020 daothaohus@gmail.com 46 2.4 Phương trình Bernoulli
• Ví dụ. Giải phương trình: 2 5 2 2/3
y  9x y  3(x  x ) y , y(0) 1 p x 2 2 3
 3x  3 x dx  x    2 3 x dx     5 2   3  x z e C x x e dx   3 x  1 z e C  3x 1d  3 x e      3    3 3     x x 1 z  e C   x 1 x x 2 3 x   3 3 3 1 e  e  Ce    3 3    3 3 5/19/2020 daothaohus@gmail.com 47 2.4 Phương trình Bernoulli 3 3 1/3 x x 2  y  Ce   3 3
Điều kiện đầu: y(0) = 1, suy ra C = 5/3. Nghiệm bài toán Cauchy: 3 3 1/3 5 x x 2 y  e   3 3 3 5/19/2020 daothaohus@gmail.com 48 2.4 Phương trình Bernoulli
• Ví dụ. Giải phương trình: − 4 = . Đây là pt Bernoulli với = 1/2 và = 0 là 1 nghiệm riêng của pt đã cho. Giả sử ≠ 0, chia cả 2 vế cho / ta được: 4 / − = . Đặt: = / → = / ′.
Pt đã cho trở thành ptvp tuyến tính cấp 1 đối với biến : 5/19/2020 daothaohus@gmail.com 49 2.4 Phương trình Bernoulli 2 − = . 2
Giải phương trình này ta tìm được nghiệm: 1 = ln + . 2
Do đó pt đã cho có nghiệm tổng quát: 1 = ln + 2 và nghiệm = 0. 5/19/2020 daothaohus@gmail.com 50 2.4 Phương trình Bernoulli
• Ví dụ. Giải phương trình: + = . Đây là pt Bernoulli với = 3 và =0 là 1 nghiệm riêng của pt đã cho. Giả sử ≠ 0, chia cả 2 vế cho ta được: + = . Đặt: = → = −2
′. Khi đó pt đã cho trở thành
ptvp tuyến tính cấp 1 đối với biến : − 2 = −2 .
Do đó nghiệm tổng quát có dạng: = + + 1.
Đổi lại biến ta có tích phân tổng quát: + + 1 = 1, = . 5/19/2020 daothaohus@gmail.com 51
2.5. Phương trình VP toàn phần (hoàn chỉnh)
 Dạng tổng quát của phương trình: , + , = 0 (3) trong đó ,
, ( , ) là các hàm liên tục cùng với
các đạo hàm riêng cấp 1, và = 5/19/2020 daothaohus@gmail.com 52
2.5. Phương trình VP toàn phần (hoàn chỉnh)  Định lý. PTVP hoàn chỉnh luôn ∃ ( , ) sao cho: = , + , . Hay: = , , = ( , )
Khi đó tích phân tổng quát của PTVP hoàn chỉnh có dạng: , = . 5/19/2020 daothaohus@gmail.com 53
2.5. Phương trình VP toàn phần (hoàn chỉnh)
• Nghiệm có thể xác định theo công thức: F  x y x, y  P  x, ydx  Q  x , y dy 0  0 x 0 y x , y D 0 0  F  x y x, y  P  x, y dx  Q x, y dy 0     0 x 0 y 5/19/2020 daothaohus@gmail.com 54
2.5. Phương trình VP toàn phần (hoàn chỉnh)
• Ví dụ. Giải phương trình: + + + = 0 Ta có: , = + và , = + nên: = = 2
Do đó đây là ptvp hoàn chỉnh, nên tồn tại hàm ( , ) sao cho: = , , = , . Từ phương trình: = , = + . 5/19/2020 daothaohus@gmail.com 55
2.5. Phương trình VP toàn phần (hoàn chỉnh) Suy ra: 1 1 , = + + → = + 4 2 mà: = , = + do đó: = → = . Vậy ta có: 1 1 1 , = + + . 4 2 4 5/19/2020 daothaohus@gmail.com 56
2.5. Phương trình VP toàn phần (hoàn chỉnh)
Do đó tích phân tổng quát của phương trình đã cho là: 1 1 1 + + = . 4 2 4 Hay + = , ≥ 0. 5/19/2020 daothaohus@gmail.com 57
2.5. Phương trình VP toàn phần (hoàn chỉnh)
• Ví dụ. Giải phương trình: 3 1 + − 2 − = 0 Ta có: , =3 1 + và , = −(2 −). Nên 3 = = . 5/19/2020 daothaohus@gmail.com 58
2.5. Phương trình VP toàn phần (hoàn chỉnh)
Do đó đây là ptvp hoàn chỉnh với hàm , có dạng: , = 3 + −(2 − ) = − + 1 + .
Vậy tích phân tổng quát của pt là: − + 1 + = 5/19/2020 daothaohus@gmail.com 59 Bài tập
• Bài 1. Giải các phương trình sau 1. xydx   x  1 dy  0 2 2. y 1dx  xydy 2 2 3. 2 x yy' y  2 2 4. y' xy  2xy 5.  2 x 1 2 y' 2xy  0, y0 1 6. x 2 1 y dx  y 2 1 x dy  0, y  1  1 x  y 7. y'  x 2y 5/19/2020 daothaohus@gmail.com 60 Bài tập
• Bài 1. Giải các phương trình sau 3 8. 2x y '  y  2 2 2x  y 
9. x  2 ydx  xdy  0
10. x x  2ydx   2 2 x  y dy  0
11. 2x  2y 1dx  x  y   1 dy  0
12. 1 x  y dy  1 3x  3y dx 3 3 13. y ' 2xy  2x y 2 14. y ' y  xy 5/19/2020 daothaohus@gmail.com 61 Bài tập
• Bài 1. Giải các phương trình sau dy y 2 15.   xy dx x dy 2 16. 2xy  y  x  0 dx
17.  x  ydx   x  2ydy  0 18.  2 2
x  y  2xdx  2xydy  0 19.  3 2 x  2xy  2dx   2 2 3x y  y dy  0 20.2x  y   1 dx  2y  x   1 dy  0 5/19/2020 daothaohus@gmail.com 62