Lý thuyết tin học ứng dụng -Trường đại học Văn Lang

lOMoARcPSD| 45473628
BI 5 - TRÌNH BÀY BIỂU ĐỒ THỐNG KÊ BIỂU ĐỒ DẠNG PHẢN ÁNH Rẽ quạt Pie
tỷ lệ %, giá trị tuyệt ối Cột/thanh
phân phối các giá trị dữ liệu Column
Trung bình Column/Error Bars ộ chính xác hệ thống sai số chuẩn Phân tán
mối tương quan 2 biến số XY XY (Scatter) Hồi quy
liên quan tuyến tính giữa X,Y Pareto Column kết hợp
các trường hợp cần ưu tiên quan tâm XY (Scatter)
B I 6 - TRẮC NGHIỆM GIẢ THUYẾT BIẾN SỐ THỂ HIỆN THÀNH PHẦN
Định lượng mức ộ, số lượng, ộ lớn… Biến rời rạc
kết quả của sự ếm (vd: 1, 2, 3…)
Biến liên tục
giá trị thực và liên tục
(vd: Khối lượng, hàm lượng…) Định tính tính chất
Biến danh mục
tên gọi, phân loại (vd: Tình trạng hôn nhân
( ộc thân, có gia ình, li dị, goá), nhóm máu (O, A, B, AB) …
Biến thứ hạng (
xếp thứ tự theo quy ước
vd: Tình trạng kinh tế xã hội (giàu, khá
trung bình, nghèo, rất nghèo) … lOMoARcPSD| 45473628
Biến nhị phân
chỉ nhận 1 trong 2 giá trị (vd: Giới tính (nam/nữ) … Biến ịnh lượng Biến ịnh tính
1. Biểu diễn bằng số thực
Không thể hiện bằng số thực 2. Có thể o hoặc ếm Chỉ có thể ếm
3. Có thể rời rạc hoặc liên tục Luôn rời rạc
Không thể tính giá trị trung bình
4. Có thể tính ược giá trị trung bình
Nghiên cứu ịnh lượng trả lời câu hỏi:
Nghiên cứu ịnh tính trả lời câu hỏi: Bao nhiêu?
Như thế nào? Cái gì? Tại sao?
Độ tin cậy (P), mức ý nghĩa (α) và hệ số tin cậy (z)
Độ tin cậy (%) Mức ý nghĩa (α) Hệ số tin cậy (z) 90 0.1 1,650 95 0.05 1,960 99 0.01 2,576
B I 7 – PHÂN TÍCH PHÂN PHỐI CHUẨN Cách ánh giá Điều kiện Yêu cầu Mean và Median
Xem biểu ồ với ường cong chuẩn gần bằng nhau;
tần số cao nhất ở giữa, tần số thấp dần ở 2 bên
(Histograms with normal curve) Skewness gần bằng 0
Vẽ biểu ồ xác suất chuẩn có quan hệ tuyến ường thẳng (normal Q-Q plot) tính
Dùng phép kiểm ịnh Kolmogorov - n > 50 Smirnov p > 0,05
Dùng phép kiểm ịnh Shapiro - Wilk n < 50
B I 8 – LẤY MẪU NGẪU NHIÊN, ƯỚC TÍNH CỠ MẪU
Ước t nh cỡ mẫu
① Cỡ mẫu ước tính số trung bình:
② Cỡ mẫu ước tính tỷ số: Dân số không xác ịnh: Dân số không xác ịnh: lOMoARcPSD| 45473628 z p2 (1 p) z2 2 n 2 n 2 d d Dân số xác ịnh n: Dân số xác ịnh n: Nz 2 2 Nz p2 (1 p) n 2( 1) z2 2 d N
n 2( 1) z p2 (1 p) d N
Lấy mẫu ngẫu nhiŒn (Sampling)
Chọn mẫu ngẫu nhiên
Chọn mẫu phi ngẫu nhiên
(chọn mẫu xác suất)
( chọn mẫu phi xác suất )
Chọn mẫu ngẫu nhiên ơn giản
Chọn mẫu thuận tiện
(simple radom sampling)
( convenience sampling)
• Lập danh sách, ánh stt, rút thăm, dùng
• Dựa trên sự thuận lợi, tính bảng
ngẫu nhiên/máy tính chọn từng dễ tiếp cận ơn vị vào mẫu
• Áp dụng xác ịnh ý nghĩa,
• Vận dụng khi các ơn vị ồng ều, không ước lượng sơ bộ ... phân bố quá rộng
Chọn mẫu phán oán
( judgement sampling)
Chọn mẫu nhiên hệ thống
(systematic sampling) • Tự ưa ra phán oán
• Lập danh sách theo trật tự quy
• Phụ thuộc kinh nghiệm, hiểu
ước, ánh stt, chọn mầm ngẫu biết ...
nhiên Y cách ều k ơn vị
Chọn mẫu ịnh ngạch
( quota sampling)
Chọn mẫu cả khối
(cluster sampling)
• Phân nhóm theo tiêu chuẩn
ược quan tâm, chọn mẫu
• Lập danh sách theo từng khối, chọn
thuận tiện hoặc phán oán ể
ngẫu nhiên 1 khối ể iều tra chọn các ơn vị
• Áp dụng khi không có sẵn danh sách ầy ủ
Chọn mẫu phân tầng (stratified
random sampling)
• Phân chia tổng thể thành các
nhóm, dùng cách chọn mẫu ngẫu
nhiên chọn ra các ơn vị
Chọn mẫu nhiều giai oạn lOMoARcPSD| 45473628
(multi-stage sampling)
• Phân chia tổng thể thành các ơn vị
cấp I --> chọn n cấp I, từ n cấp I
phân chia thành các ơn vị cấp II --> chọn n cấp II...
• Áp dụng tổng thể quá lớn, ịa bàn quá rộng
B I 9 – PHÂN TÍCH THỐNG KÊ MÔ TẢ
Giá trị thống kê mô tả Dân số Mẫu Cỡ N n Giá trị trung bình μ X Độ lệch chuẩn σ S Tỷ số Π P Giá trị Ý nghĩa Hàm tính Excel Mean Trung bình =AVERAGE(…) Standard Error Sai số chuẩn
=STDEV.S(…)/SQRT(COUNT(…)) (SE) Median Số trung vị =MEDIAN(…) Mode Số yếu vị =MODE(…) Standard Deviation Độ lệch chuẩn =STDEV.S(…) Sample Variance Phương sai =VAR.S(…) Kurtosis Độ nhô =KURT(…) Skewness Độ lệch =SKEW(…) Range Khoảng =MAX(…) – MIN(…) Minimum
Giá trị nhỏ nhất =MIN(…) Maximum
Giá trị lớn nhất =MAX(…) Sum Tổng số =SUM(…) Count Cỡ mẫu =COUNT(…) Confidence Level
Giới hạn tin cậy =CONFIDENCE.T(α,STDEV.S(…),COUNT(…)) (95.0%) Coefficient of Hệ số phân tán
=100*STDEV.S(…)/AVERAGE(…) Variation (CV) B i tập Æp dụng
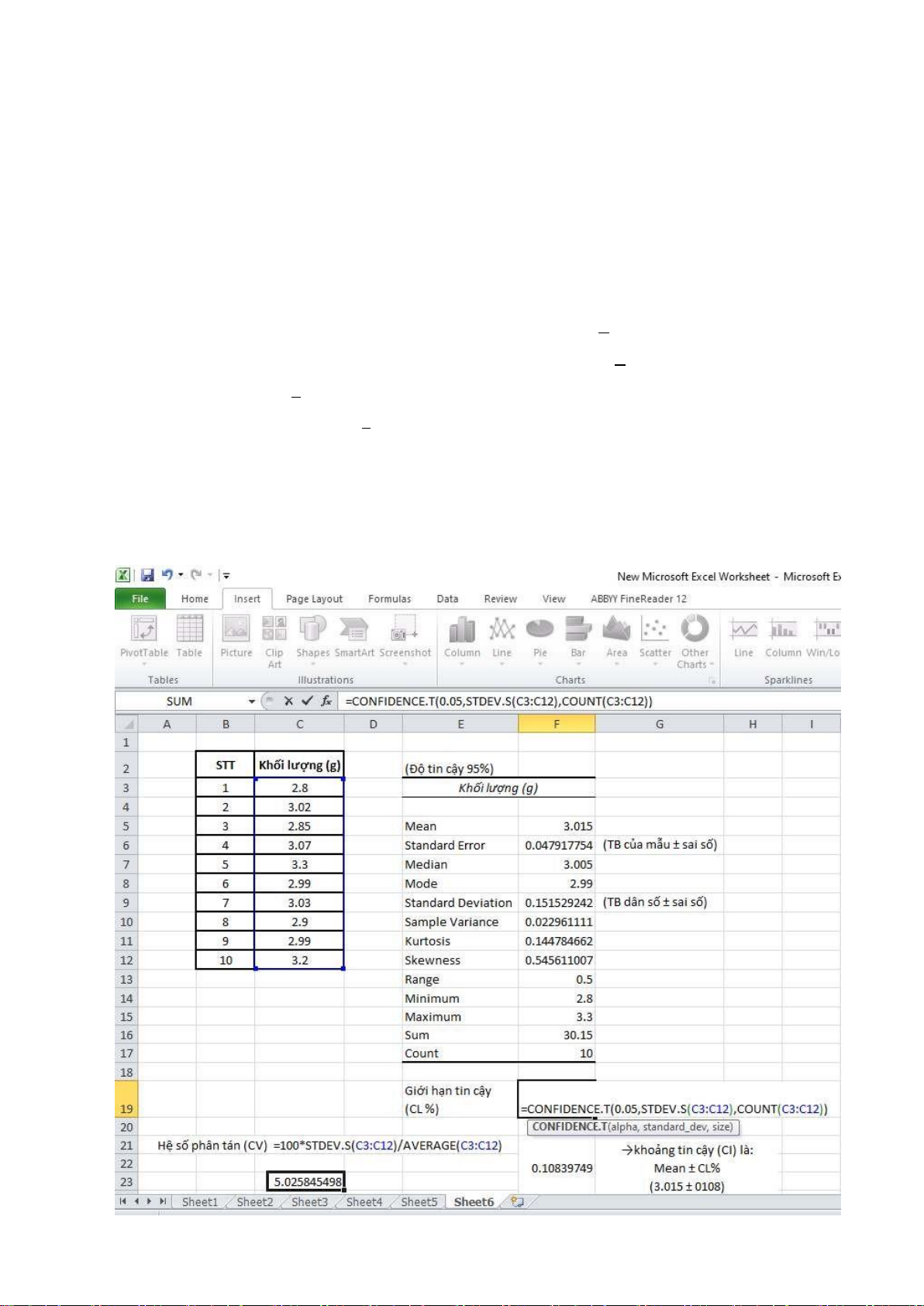
Khối lượng (g) của 10 gói Dobixil trong lô A010307 như sau:
2,80; 3,02; 2,85; 3,07; 3,30; 2,99; 3,03; 2,90; 2,99; 3,20 lOMoARcPSD| 45473628
Hãy tính các giá trị thống kê mô tả (với ộ tin cậy là 95%), và cho biết:
- Trung bình của mẫu ± sai số
- Trung bình dân số ± sai số - Hệ số phân tán - Khoảng tin cậy (CI)
 Nhập dữ liệu, tạo bảng.
 Vào Data → Data analysis → Descriptive Statistics → OK.
 Chọn Input là dữ liệu số cột Khối lượng (g), check vào ô “Labels in first row” nếu có chọn
ô “Khối lượng (g)” (nếu không thì bỏ check), check vào ô “Summary statistics”, kiểm tra
ộ tin cậy ở ô “Confidence Level for Mean” có khớp với ề bài chưa → OK.
(Nếu không check vào ô “Confidence Level for Mean” thì ta phải tự tính giới hạn tin cậy CL bằng
hàm CONFIDENCE.T(alpha, ộ lệch chuẩn,cỡ mẫu) như hình).
 Tính toán khoảng tin cậy CI (= số TB ± giới hạn tin cậy), hệ số phân tán CV (=100* ộ lệch chuẩn/số trung bình). lOMoARcPSD| 45473628
B I 10 – PH´N T˝CH ANOVA MỘT YẾU TỐ
- ANOVA (Analysis of Variance): phân tích phương sai.
- single factor: một yếu tố (yếu tố có thể là biến ộc lập hoặc giải thích).
- Mức: là những “giá trị” của yếu tố.
Anova: single factor – Phân tích phương sai một yếu tố, là phương pháp phân tích dữ liệu dùng ể
so sánh giá trị trung bình hoặc phương sai của dữ liệu, cho phép phân tích k mức ộ (k > 2) trên các giá trị yij:
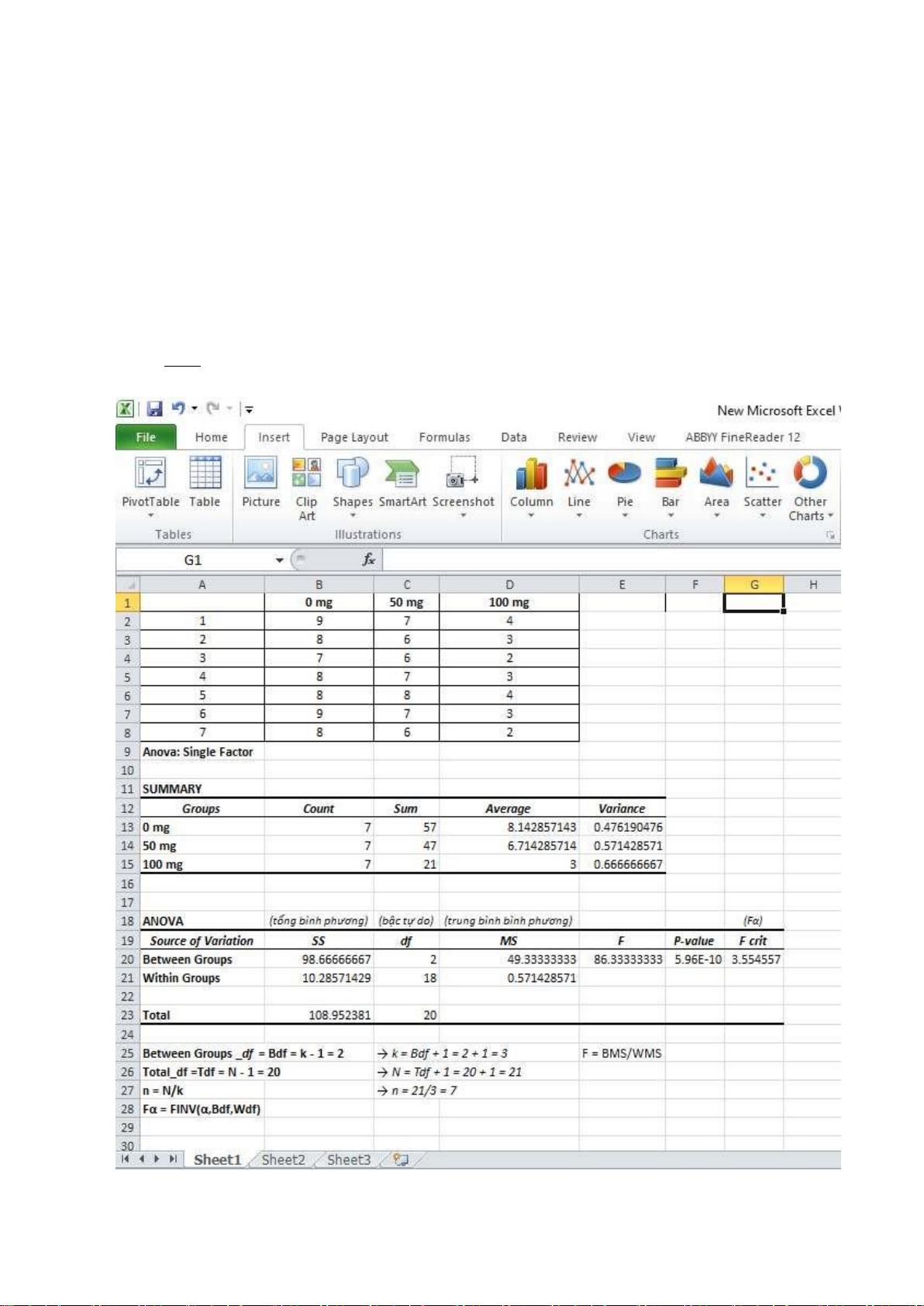
Ví dụ: Thang iểm ánh giá với 3 liều lượng (0 mg, 50 mg, 100 mg) lOMoARcPSD| 45473628
 Nhập dữ liệu, tạo bảng.
 Vào Data → Data analysis → Anova: Single Factor → OK.
(Nếu không nói gì thêm, mặc ịnh α = 0.05)  Biện luận kết quả:
Đặt giả thyết H0: các nhóm 0 mg, 50 mg, 100 mg không khác nhau.
F > Fα (F crit)
→ bác bỏ H0, chọn HA thay thế (và ngược lại). p
< α (p-value < α)
→ bác bỏ H0, chọn HA thay thế (và ngược lại).
B I 12 – PH´N TÍCH TƯƠNG QUAN
- Correlation – Phân tích tương quan.
- Hệ số tương quan rxy (coefficient of correlation – cc): chỉ số thống kê o lường mối liên
hệ giữa 2 dữ liệu khảo sát x, y. - rxy = ryx
- rxy ∈ [−1; 1], rxy < 0: tương quan nghịch, rxy > 0: tương quan thuận
→ r = −1: x, y tương quan nghịch (x tăng y giảm và ngược lại)
→ r = 1: x, y tương quan thuận (x và y cùng tăng hoặc cùng giảm)
→ r = 0: x, y không tương quan (x, y ộc lập với nhau) -
Phương pháp phân tích tương quan: 
Pearson: theo phân phối chuẩn 
Spearman: không theo phân phối chuẩn - Ý
nghĩa thống kê của hệ số tương quan r: Theo Guilford: lOMoARcPSD| 45473628 |r| Mô tả < 0,20 Không áng kể Theo Roundtree: 0,20 – 0,40 Liên quan thấp 0,40 – 0,70 Liên quan khá 0,70 – 0,90 Liên quan cao > 0,90 Liên quan rất cao |r| Mô tả < 0,20 Rất lỏng lẻo 0,20 – 0,40 Lỏng lẻo 0,40 – 0,70 Trung bình 0,70 – 0,90 Chặt chẽ > 0,90 Rất chặt chẽ B i tập Æp dụng:
Dùng phương pháp phân tích tương quan ánh giá mức ộ tương quan giữa liều lượng sử dụng thuốc
ngừa ột quỵ dùng cho 8 bệnh nhân lấy ngẫu nhiên từ các hồ sơ bệnh án trong khoảng thời gian 6 tháng trở lại ây.
Ngày: [3; 2; 4; 3; 2; 4; 4; 3]
Thuốc A (mg/kg): [2,8; 4,0; 1,5; 3,0; 3,7; 2,0; 2,4; 3,5] Thuốc
B (mcg/kg): [275; 225; 250; 225; 300; 225; 275; 275]
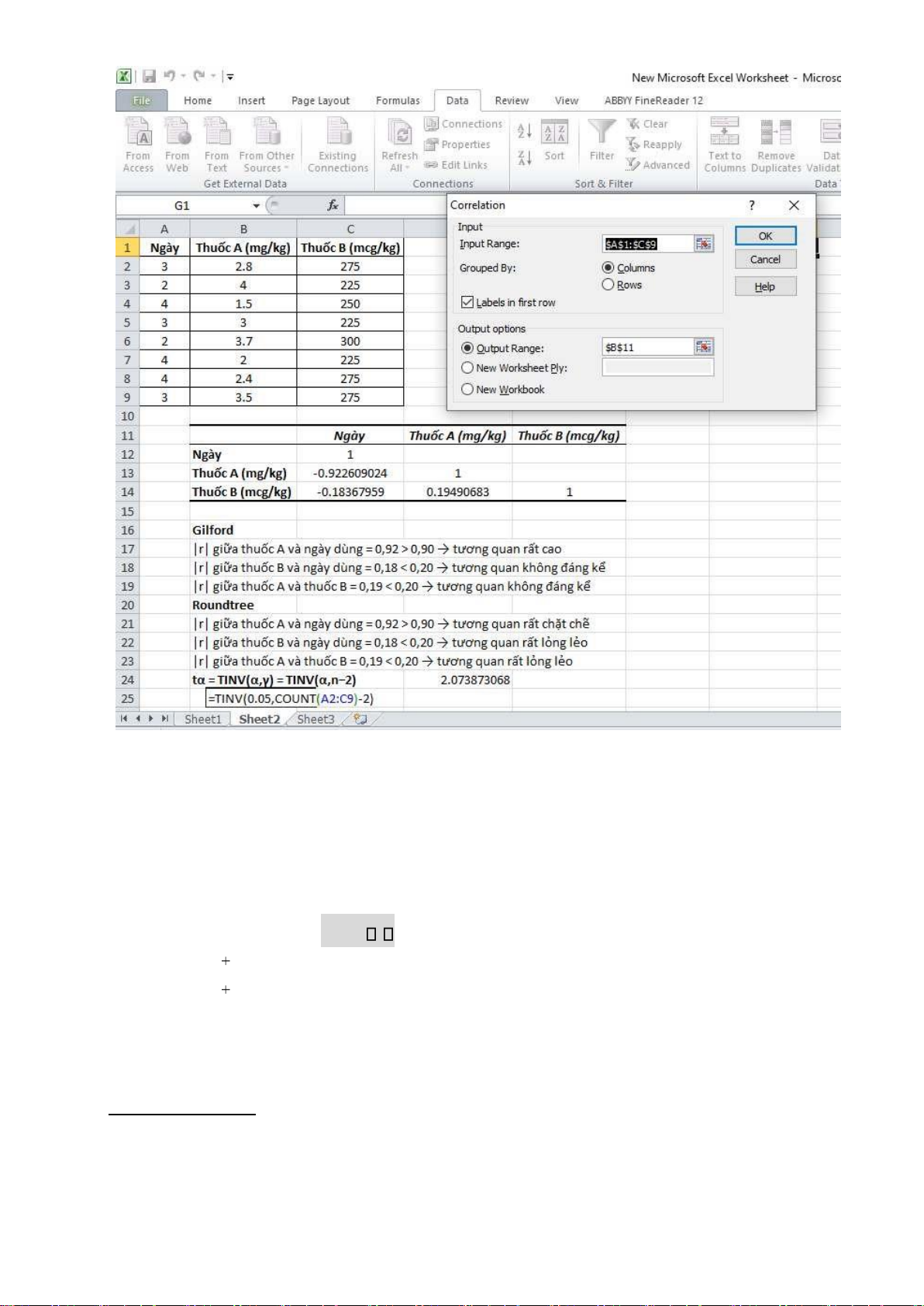
 Nhập dữ liệu, tạo bảng.
 Vào Data → Data analysis → Correlation → OK. lOMoARcPSD| 45473628
B I 13 – PH´N TÍCH HỒI QUY
- Regression – Phân tích hồi quy.
- Khảo sát ảnh hưởng giữa 2 hay nhiều biến số liên tục, các biến số có mối quan hệ phụ thuộc lẫn nhau.
- Thiết lập pt hồi quy: y a bx
a: tung ộ góc (hằng số), ược tính bằng hàm
=INTERCEPT(…) b: ộ dốc (tham số hồi quy), ược tính bằng
hàm =SLOPE(…) - Giá trị R2 (R square) càng gần 1 → sự tuyến tính
càng tốt - R2 = 0 → không có sự tương quan giữa x và y. B i tập Æp dụng:
Hãy thiết lập phương trình hồi quy (với α = 0,05) dữ liệu liên quan giữa chiều cao và trọng lượng cơ thể như sau: lOMoARcPSD| 45473628
Chiều cao (cm): [117; 181; 165; 178; 173; 184; 162; 168; 164; 170] Trọng
lượng (kg): [74; 75; 63; 64; 65; 75; 56; 55; 55; 68]
 Nhập dữ liệu, tạo bảng.
 Vào Data → Data analysis → Regression → OK.
 Biện luận kết quả: Đặt giả thyết H0:
“Chiều cao và trọng lượng không liên quan tuyến tính”.
Phân tích thống kê: F > Fα (=FINV(α,γ1,γ2) → bác bỏ H0, chọn HA thay thế (và ngược lại). Đặt giả thuyết H0:
“Hệ số hồi quy không có ý nghĩa”.
Phân tích thống kê: t > tα → bác bỏ H0, chọn HA thay thế (và ngược lại).