






















































Preview text:
Chương . HÀM SỐ NHIỀU BIẾN 1
1.1. Các khái niệm cơ bản
1.1.1. Không gian Rn
1.1.1.1. Định nghĩa. Không gian Euclide n chiều Rn (nN*) là tập hợp các bộ có thứ tự của n số
thực x1, x2, …, xn tức là
Rn = {(x1,x2, …,xn)| x iR}.
Khi n = 1 thì R1 là tập hợp các số thực R.
Khi n = 2 thì R2 là tập hợp các cặp số thực (x1,x2) hay tập hợp các điểm của mặt phẳng. Theo thói
quen từ trước, các điểm của R2 thường được ký hiệu là (x, y) thay cho (x1,x2) .
Khi n = 3 thì R3 là tập hợp các bộ ba số thực (x1,x2,x3) hay tập hợp các điểm của không gian. Theo
thói quen từ trước, các điểm của
R3 thường được ký hiệu là (x, y,z) thay cho (x1,x2,x3) .
Vì R1 là tập hợp các điểm của trục số, R2 là tập hợp các điểm của mặt phẳng, R3 là tập hợp các
điểm của không gian thực nên R1, R2 và R3 được gọi lần lượt là “không gian Euclide 1 chiều”, “không
gian Euclide 2 chiều” và “không gian Euclide 3 chiều”. Tổng quát, Rn được gọi là “không gian Euclide n
chiều” hay ngắn gọn “không gian Rn” và mỗi phần tử của nó được gọi là một điểm, còn (x1,x2,…,xn)
được gọi là tọa độ của một điểm của không gian Rn.
1.1.1.2. Khoảng cách trong Rn
Khoảng cách giữa hai điểm M1(x1) và M2(x2) trên trục số (R1) được định nghĩa là
d(M , M ) = x − x = (x − x )2 . 1 2 1 2 1 2
Khoảng cách giữa hai điểm M1(x1,y1) và M2(x2,y2) trong mặt phẳng (R2) được định nghĩa là
d(M ,M ) = (x − x )2 + (y − y )2 . 1 2 1 2 1 2
Khoảng cách giữa hai điểm M1(x1,y1,z1) và M2(x2,y2,z2) trong không gian (R3) được định nghĩa là
d(M ,M ) = (x − x )2 + (y − y )2 + (z − z )2 . 1 2 1 2 1 2 1 2
Tổng quát, khoảng cách giữa hai điểm M1(x1,x2,…,xn) và M2(y1,y2,…,yn) trong không gian Rn được n định nghĩa là d(M = − + − + + − = − 1, M2 ) (x1 y )2 1 (x y )2 ... (x y )2 (x y )2 . 2 2 n n i i i=1
Theo định nghĩa, hoảng cách giữa hai điểm trong k Rn là ánh xạ từ
Rn vào R+ (Rn → R+).
Khoảng cách giữa hai điểm được định nghĩa như trên được gọi là khoảng cách Euclide. Cũng như trên trục số, tr mặt phẳng v ong
à trong không gian thực, khoảng cách Euclide trong Rn có các tính chất:
(1) d(M1,M2) 0, d(M1,M2) = 0 M 1 M2 (2) d(M1,M2) = d(M2,M1)
(3) d(M1,M2) d(M1,M3) + d(M3,M2) – c bất đẳng thức tam giá
trong đó M1, M2, M3 là 3 điểm bấ t kỳ của Rn.
1.1.1.3. Lân cận, tập mở, tập đóng t
và tập bị chặn rong Rn
Giả sử Mo là một điểm của không gian Rn, là một số thực dương, khi đó tập hợp tất cả các điểm
MRn sao cho d(M0,M) < được gọi là -lân cận của điểm M0. Mọi tập hợp chứa một -lân cận nào đó
của điểm M0 được gọi là lân cận c ủa điểm M0.
Giả sử tập hợp ERn, điểm M E
được gọi là điểm trong của E nếu tồn tại một -lân cận nào đó
của điểm M nằm hoàn toàn trong E. Tập hợp E được gọi là mở nếu mọi điểm của nó đều là điểm trong.
Giả sử tập hợp ERn, điểm NRn được gọi là điểm biên của tập hợp E nếu mọi -lân cận của điểm
N vừa chứa những điểm thuộc E vừa chứa những điểm không thuộc E. Điểm biên của tập hợp E có thể
thuộc E cũng có thể không thuộc E. Tập hợp tất cả các điểm biên của E được gọi là biên của nó.
Tập hợp ERn được gọi là đóng nếu nó chứa mọi điểm biên của nó. 1
Ví dụ 1.1. Nếu E là tập hợp tất cả các điểm MRn sao cho d(M0,M) < r với M0Rn là một điểm cố
định và r là số thực dương, thì E là tập hợp mở.
Chứng minh. Giả sử M là một điểm bất kỳ của E, do đó d(Mo,M) < r. Đặt = r – d(M0,M), khi đó
-lân cận của M nằm hoàn toàn trong E vì nếu P là một điểm của lân cận ấy thì chúng ta có d(M,P) < ,
do đó theo bất đẳng thức tam giác d(M0,P) d(M0,M) + d(M,P) < d(M0,M) + = r.
Tập hợp E nói trong Ví dụ 1.1. được gọi là quả cầu mở tâm M0 bán kính r. Biên của tập hợp E này
gồm các điểm M sao cho d(M0,M) = r được gọi là mặt cầu tâm M0 bán kính r. Tập hợp các điểm M sao
cho d(M0,M) r là một tập hợp đóng, được gọi là quả cầu đóng tâm M0 bán kính r.
Tập hợp ERn được gọi là bị chặn nếu tồn tại một quả cầu nào đó chứa nó.
Tập hợp ERn được gọi là liên thông nếu có thể nối hai điểm bất kỳ của nó bởi một đường liên tục
nằm hoàn toàn trong E. Tập hợp liên thông được gọi là đơn liên nếu nó bị giới hạn bởi một mặt kín, được
gọi là đa liên nếu nó bị giới hạn bởi nhiều mặt kín rời nhau từng đôi một.
1.1.2. Hàm số nhiều biến, hàm véc tơ
1.1.2.1. Hàm số nhiều biến
Xét không gian Euclide n chiều Rn, giả sử DRn. Khi đó ánh xạ f: D → R được xác định bởi {x =
(x1,x2, …,xn)D} → {y = f(x) f(x1,x2, x
…, n)R} được gọi là hàm số n biến xác định trên D; D được
gọi là tập xác định của hàm số f, ký
hiệu là D(f); còn x1, x2, …, xn được gọi là các biến số độc lập. Tập tất
cả các giá trị của hàm số y = f(x1,x2, …,xn) trên tập xác định D(f) được gọi là tập giá trị của hàm số f, ký hiệu là R(f).
Như vậy, hàm số y = f(x1,x2, …,xn) là ánh xạ f: D(f) → R(f).
Theo thói quen từ trước, với n = 1 chúng ta dùng ký hiệu y = f(x) đối với hàm số 1 biến, với n = 2
chúng ta dùng ký kiệu z = f(x,y) đối với hàm số 2 biến và với n = 3 chúng ta dùng ký hiệu u = f(x,y,z) đối với hàm số 3 biến.
Cũng như đối với hàm số 1 biến, hàm số 2 biến và hàm số 3 biến, tập xác định D(f) của hàm số n
biến là tập hợp tất cả các điểm xRn sao cho biểu thức của hàm số y = f(x) f(x1,x2, …,xn) có hĩa, tức ng
là biểu thức này xác định được.
Từ đây về sau (trong Bài giảng học phần này), các ấn v
đề liên quan đến hàm số nhiều biến được
trình bày cho trường hợp n = 2 (hàm số 2 biến) hoặc n = 3 (hàm số 3 biến). Các vấn đề ấy được mở rộng
hoàn toàn tương tự đối với số nguyên dương
≥ 4 (hàm số n biến) bất kỳ, nếu không lưu ý gì thêm n .
Ví dụ 1.2. Tìm và vẽ tập xác định của các hàm số sau đây x + y + 1 (a) 2 2 z = f (x, y) = 4 − x − y (b) z = f (x, y) = y − 1 x (c) z = f(x,y) = xln(y2 – x) (d) u = f (x, , y z) = 2 2 2 1− x − y − z Bài giải. (a) Đối với hàm số 2 2 f (x, )
y = 4 − x − y xét biểu thức 2 2
4 − x − y , để biểu thức này xác định
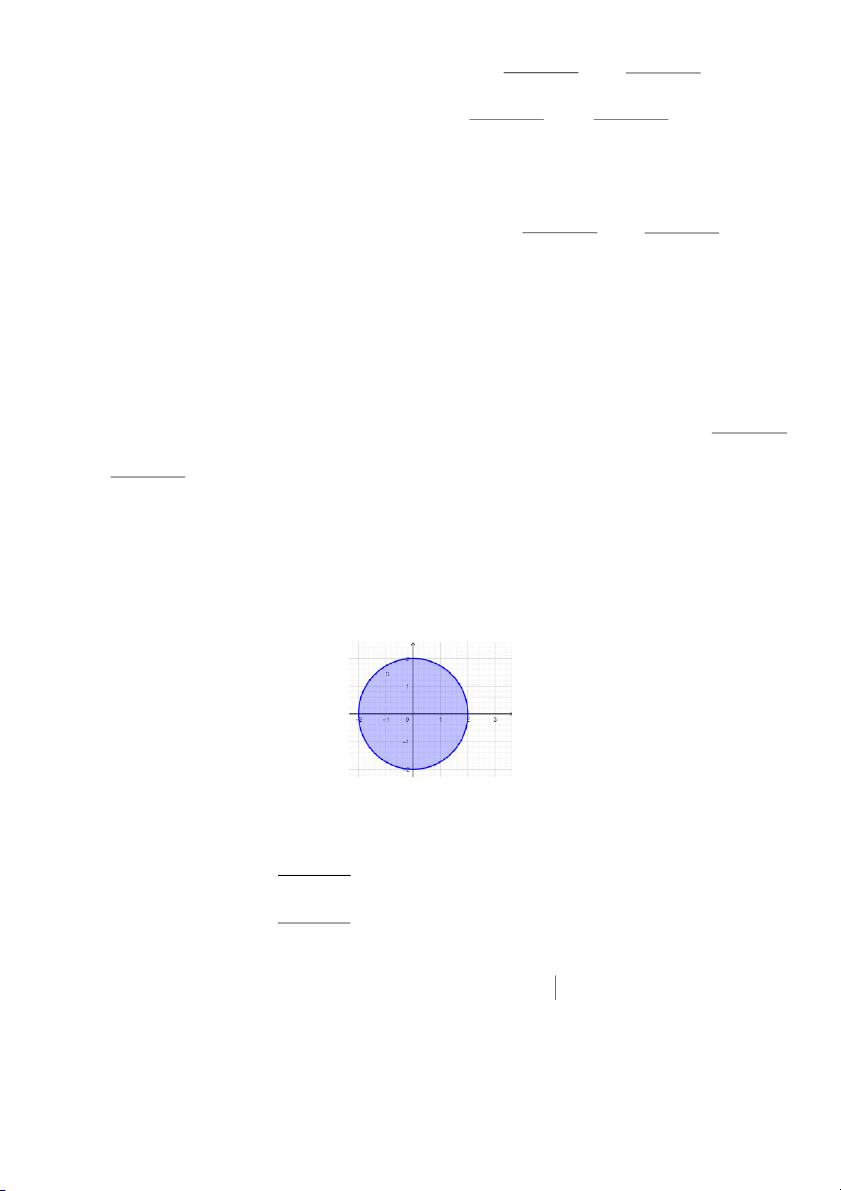
được thì biểu thức dưới căn bậc hai phải không âm, tức là 4 – x2 – y2 0, nên tập xác định D(f) =
{(x,y)R2|x2 + y2 22}. Trên mặt phẳng tọa độ của hệ tọa độ Descartes vuông góc Oxy thì D(f) là các
điểm thuộc hình tròn đóng tâm O(0,0) có bán kính r = 2. 2 x + y + 1 x + y + 1
(b) Đối với hàm số f (x, y) = xét biểu thức
, để biểu thức này xác định được y −1 y − 1
thì biểu thức dưới căn bậc hai ở tử số phải không âm (x + y + 1 ≥ 0) và biểu thức ở mẫu số phải khác
không (y – 1 ≠ 0), nên tập xác định D(f) = {(x,y)R2|x + y +1 ≥ 0 và y – 1 ≠ 0}. Trên mặt phẳng tọa độ
của hệ tọa độ Descartes vuông góc Oxy thì D(f ) là
các điểm thuộc nửa mặt phẳng phía trên đường thẳng y = – x 1 ( –
kể cả các điểm nằm trên đường thẳng này), nhưng không nằm trên đường thẳng y = 1.
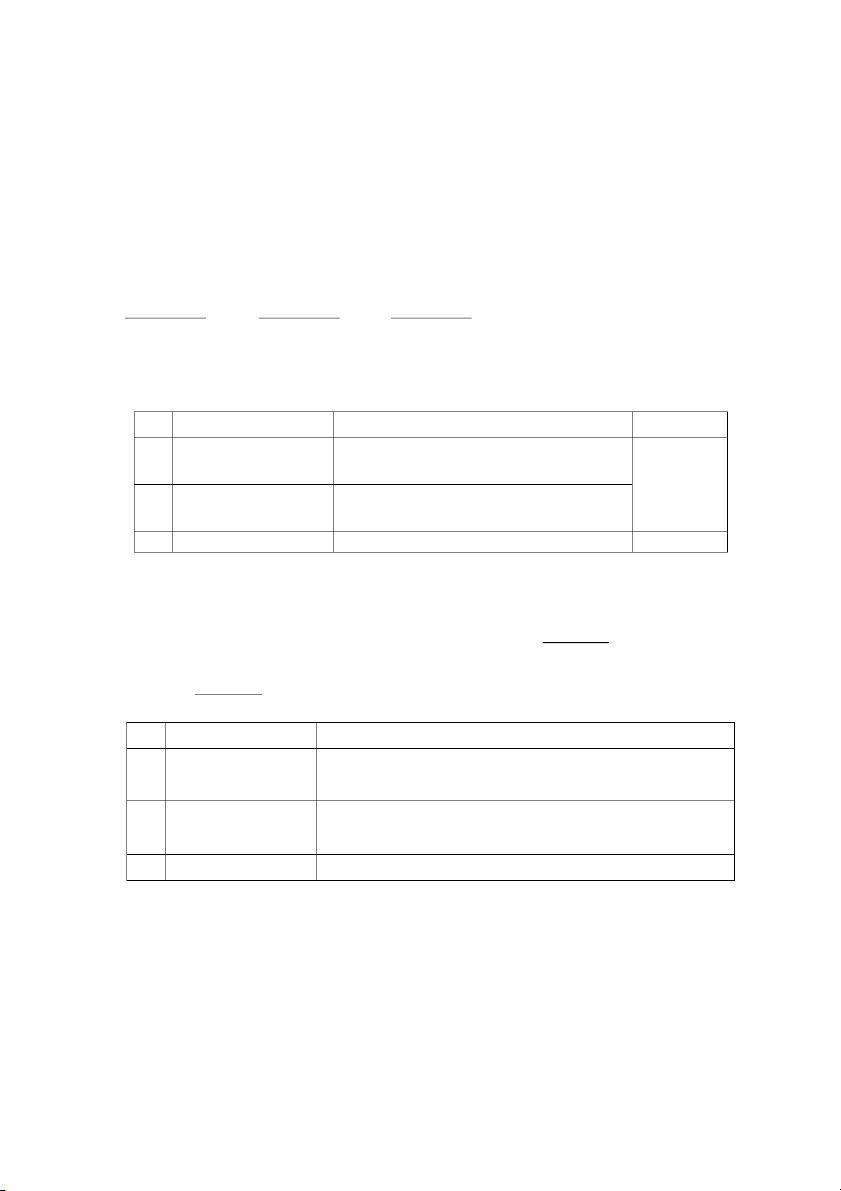
(c) Đối với hàm số f(x,y) = xln(y2 – x), xét biểu th
ức xln(y2 – x), để biểu thức này xác định được thì
đối số của hàm số loga phải dương, tức là y2 – x > 0 hay x < y2, nên tập xác định D(f) = {(x,y)R2|x <
y2}. Trên mặt phẳng tọa độ của hệ tọa độ Descartes vuông góc Oxy thì D(f) là các điểm nằm bên trái đường parabol x = y2 x x
(d) Đối với hàm số f (x, , y z) = , xét biểu thức , để biểu thức 2 2 2 1 − x − y − z 2 2 2 1− x − y − z
này xác định được thì biểu thức trong căn bậc hai ở mẫu số phải dương, tức là 1 – x2 – y2 – z2 > 0, nên
tập xác định D(f) = {(x,y,z)R3|x2 + y2 + z2 < 12}. T ong r
không gian tọa độ của hệ tọa độ Descartes vuông góc Oxyz t
hì D(f) là các điểm thuộc quả cầu mở tâm O(0,0,0) có bán kính r = 1.
Cũng như hàm số 1 biến, một hàm số nhiều biến thường được mô tả bằng 4 cách: (1) bằng công
thức, (2) bằng đồ thị, (3) bằng lời, (4) bằng bảng các giá trị.
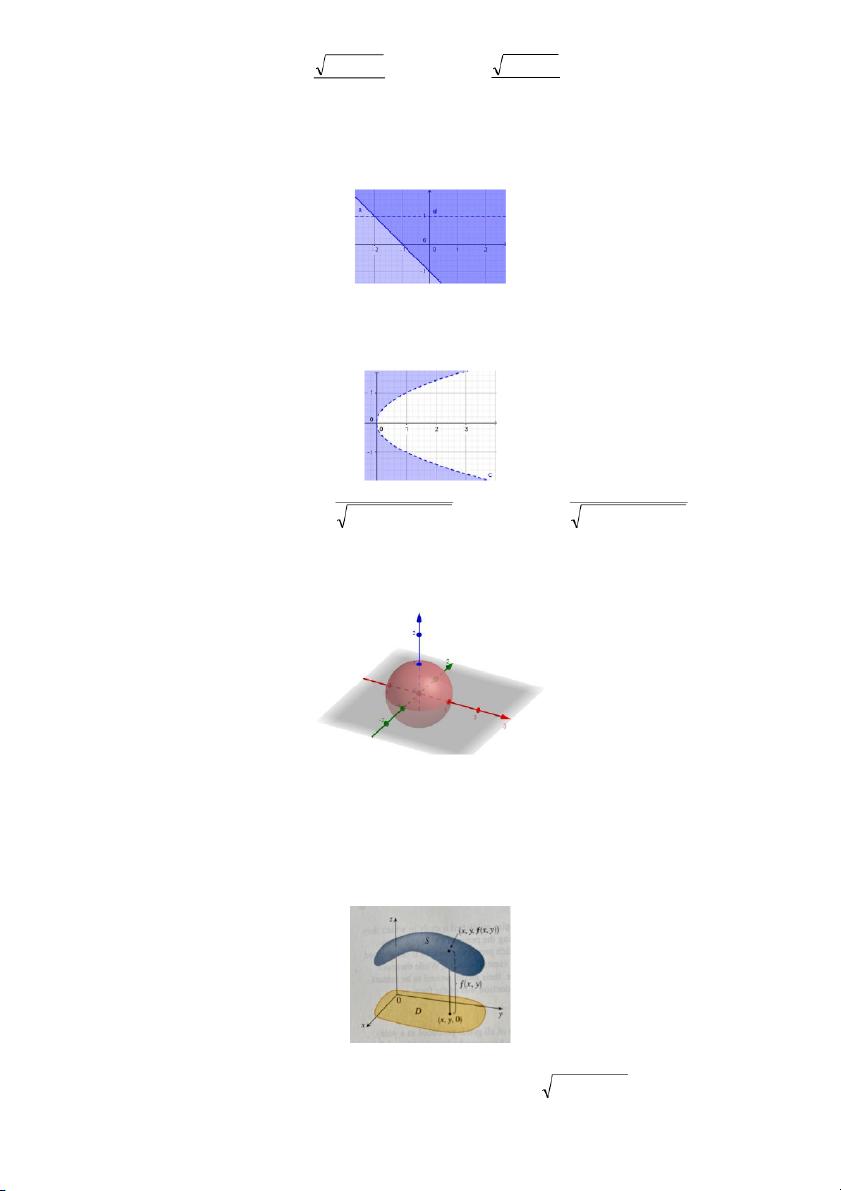
Đồ thị của hàm số 2 biến. Nếu z = f(x,y) là hàm số 2 biến trên tập xác định D(f) thì đồ thị của hàm
số f(x,y) là tập tất cả các điểm (x,y,z)R3 sao cho z = f(x,y) và (x,y) D (f).
Cũng giống như đồ thị của hàm số 1 biến là một đường (thẳng/cong) C có phương trình y = f(x), đồ
thị của hàm số 2 biến là một mặt S
có phương trình z = f(x,y).
Ví dụ 1.3. Vẽ đồ thị của các h àm số sau đây (a) z = f (x, y) = 6 − x 3 − 2y (b) 2 2 z = f (x, y) = 9 − x − y 3 Bài giải.
(a) Tập xác định D(f) = R2.
Đồ thị của hàm số z = f (x, y) = 6 − x 3 − 2y x
3 + 2y + z = 6 là mặt phẳng S giao với các trục tọa
độ Ox, Oy và Oz lần lượt tại các điểm (2,0,0), (0,3,0) và (0,0,6). Nối 3 điểm này với nhau bởi các đường
thẳng, chúng ta nhận được một phần của mặt phẳng S nằm trong góc phần tám thứ nhất của hệ trục tọa độ Descarter vuông góc Oxyz.
(b) Tập xác định D(f) = {(x,y)R2|x2 + y2 32}. Trên mặt phẳng tọa độ Oxy của hệ tọa độ Descartes vuông góc Oxyz t hì D(f
) là các điểm thuộc hình tròn đóng tâm O(0,0) có bán kính r = 3.
Bình phương hai vế của phương trình 2 2
z = 9 − x − y và biến đổi tương đương, chúng ta được 2 2 2 2
x + y + z = 3 , đây là phương trình của mặt cầu có tâm tại gốc tọa độ O(0,0,0) và bán kính r = 3. Vì
z = 9 − x2 − y2 0 nên đồ thị của hàm số 2 2
z = f (x, y) = 9 − x − y là mặt S chỉ có nửa trên (bán cầu trên) của mặt cầu 2 2 2 2 x + y + z = 3 .
Chúng ta nhận thấy rằng, trong hệ tọa độ Descartes vuông góc Oxyz thì toàn bộ mặt cầu không thể
được biểu diễn bởi một hàm số theo x và y. Như chúng ta thấy, trong Ví dụ (b) 1.3. ở trên, bán cầu trên của mặt cầu 2 2 2 2
x + y + z = 3 được biểu diễn bởi hàm số z = f (x, )
y = 9 − x2 − y2 , còn bán cầu dưới của mặt cầu 2 2 2 2
x + y + z = 3 được biểu diễn bởi hàm số z = g(x, y) = − 9 − x2 − y2 . 1.1.2.2. Hàm véc tơ
Giả sử Rn, Rm tương ứng là không gian Euclide n, m chiều. Ánh xạ f: D → Rm, trong đó DRn
được gọi là hàm véc tơ n biến. Giá trị của hàm véc tơ f có m thành phần f = (f
1,f2, …,fm-1,fm)Rm.
Trường hợp riêng, khi n = 1 và m = 1, hàm véc tơ chính là hàm số 1 biến đã được nghiên cứu trong
học phần Giải tích 1; khi n > 1 và m = ,
1 hàm véc tơ chính là hàm số nhiều biến vừa được định nghĩa ở trên và sẽ được ng
hiên cứu trong học phần Giải tích 2 này.
1.2. Giới hạn và tính liên tục 1.2.1. Giới hạn
Chúng ta nói rằng dãy điểm {Mn(xn,yn)} tiến đến điểm M0(x0,y0) trong R2 và viết Mn → M0 khi n lim x = x n 0 →
+ nếu lim d(M , M ) = 0 lim (x , y ) = (x , y ) . 0 n n n 0 0 n→+ n→+ n→+ lim y = y n→+ n 0
Giả sử hàm số z = f(x,y) xác định trong một lân cận V nào đó của điểm M0(x0,y0) (có thể không xác
định tại M0). Chúng ta nói rằng hàm số f(x,y) có giới hạn L (L là số thực hữu hạn) khi điểm M(x,y) tiến
đến điểm M0(x0,y0) (M → M0) và viết lim
f (x, y) = L nếu với mọi dãy điểm Mn(xn,yn) (khác M0) ( x ,y ) ( → x ,y ) 0 0
thuộc lân cận V tiến đến M
0, chúng ta đều có lim f (x , y ) = L . n n n + → 4
Nói cách khác (bằng ngôn ngữ “-”): Giả sử hàm số z = f(x,y) xác định trong một lân cận V nào
đó của điểm M0(x0,y0) (có thể không xác định tại điểm M0). Chúng ta nói rằng hàm số f(x,y) có giới hạn
L khi điểm M(x,y) tiến đến điểm M0(x0,y0) (M → M0) và viết lim
f (x, y) = L nếu với > 0 bé tùy ( x, y) ( → x ,y ) 0 0
ý cho trước, = () > 0 sao cho với (x,y)V thỏa mãn 0 d( , M M ) = (x − 2 x ) + (y − 2 y ) 0 0 0 thì f (x) − L .
Nhận xét. f (x) − L là khoảng cách giữa các số f(x,y) và L, còn 2 2
(x − x ) + (y − y ) là khoảng 0 0
cách giữa điểm (x,y) và điểm (x0,y0); do đó, định nghĩa giới hạn bằng ngôn ngữ “- ” nói lên rằng:
Khoảng cách giữa f(x,y) và L có thể được làm nhỏ tùy ý bằng cách làm cho khoảng cách từ điểm (x,y)
đến điểm (x0,y0) đủ nhỏ (nhưng không bằng không). Lưu ý.
1. Giá trị của x0, y0 có thể nhận các giá trị thuộc tập {– , , + }.
2. Các định lý về giới hạn của tổng/hiệu, tích, thương, lũy thừa, căn đối với hàm số một biến (n = 1)
trong học phần Giải tích 1 vẫn đúng đối với hàm số nhiều biến (n > 1). Cụ thể là: Cho các hàm số ,
f(x,y) g(x,y) và giả sử lim f (x, y) = L , lim g(x, y) = M (các số hữu ( x ,y)→(x ,y ) → 0 0 (x ,y ) ( x ,y ) 0 0
hạn M, LR), khi đó + lim
f(x, y) g(x,y)= L M (x ,y )→(x , y ) 0 0 + lim
cf (x, y) = cL (hằng số cR) ( x,y ) ( → x ,y ) 0 0 + lim f(x,y)g(x, y)= LM ( x,y ) ( → x ,y ) 0 0 f (x, y) L + lim = (M ≠ 0) (x ,y) ( → x ,y ) 0 0 g(x, y) M + lim f ( ,x n n ) y = L (nN*) (x,y) ( → x0 ,y0 ) + n n lim f (x, )
y = L (nN*, nếu n là số chẵn thì thêm giả thuyết lim f (x, y) ) 0 (x,y) ( → x (x ,y) ( → x ,y ) 0 ,y0 ) 0 0
3. Nguyên lý kẹp vẫn
đúng đối với hàm số nhiều biến, cụ thể là:
Cho các hàm số h(x,y), f(x,y), g(x,y); giả sử h(x,y) ≤ f(x,y) ≤ g(x,y) với mọi điểm (x,y) trong một
lân cận nào đó của điểm (x0,y0) và lim h(x, y) = lim
g(x, y) = L (hằng số LR) ( x ,y)→( x , y ) ( x ,y)→( x ,y ) 0 0 0 0 thì lim f (x, ) y = L. (x,y)→(x ,y ) 0 0
4. Tích của một vô cùng bé (VCB) với một hàm số/biểu thức l giới nội à một VCB.
5. Theo định nghĩa giới hạn của hàm số nhiều biến thì giá trị giới hạn L không phụ thuộc vào cách
thức của điểm M tiến đến điểm M0. Do đó, nếu M → M0 theo các cách thức khác nhau mà hàm số tiến
đến các giá trị khác nhau thì hàm số không tồn tại giới hạn tại điểm M 0 khi M → M0.
Do đó, đối với hàm số 2 biến f(x,y), để chứng minh hàm số này không tồn tại giới hạn tại điểm M0
khi M → M0, thường có 4 cách sau đây:
(1) Nếu chỉ ra được hai dãy điểm ( 1() 1 ( ) x , y , ( (2) (2) x , y
cùng tiến đến điểm (x0,y0), cụ thể là n n ) n n ) (x )1(,y )1( → và (x(2) , y(2) →
khi n→+∞, đồng thời khi đó lim f( 1() 1() x , y = L và n n ) n n ) (x ,y ) n n ) (x , y ) 0 0 0 0 1 n + → lim f ( (2) (2) x , y = L mà L1 ≠ L2 thì lim f (x, y) . không tồn tại n n ) 2 n→+ (x,y) ( → x ,y ) 0 0
(2) Nếu chỉ ra được hai đường (thẳng/cong) và nếu M(x,y) → M0(x0,y0) dọc trên hai đường này mà lim
f (x, y) tương ứng nhận hai giá trị khác nhau thì lim
f (x, y) không tồn tại. Cụ thể là, (x,y) ( → x ,y ) → 0 0 (x,y) (x ,y ) 0 0
chỉ ra được hàm số y = g(x) và hàm số y = h(x) thỏa mãn lim g(x) = lim h(x) = y , đồng thời khi đó 0 x→x x→x 0 0 5
lim f (x, g(x)) = L và lim f (x, h(x)) = L mà L1 ≠ L2 thì lim
f (x, y) không tồn tại. Ở đây, x và y 1 2 x x → x→x (x,y) ( → x ,y ) 0 0 0 0 có vai trò như nhau.
(3) Nếu đổi biến từ tọa độ Descarter (x,y) sang tọa độ cực (r,) (thông thường), bằng phép đổi x = x + r cos r 0 biến 0 với và khi đó + (x, )
y → (x , y ) r → 0 , hoặc sang tọa độ cực (r,) y = y + r sin 0 2 0 0 0 x = x + r cos r 0
(mở rộng) bằng phép đổi biến 0
với , là các số thực và và khi đó y = y + r sin 0 2 0 + (x, )
y → (x , y ) r → 0 , mà f(x,y) = g() (chỉ phụ thuộc vào góc ) lim f (x, y) = limg( ) 0 0 (x,y) ( → x ,y ) r 0 → 0 0 = g() thì lim f (x, y) không tồn tại. (x,y) ( → x ,y ) 0 0
Cần lưu ý rằng, khi đổi biến từ tọa độ Descarter (x,y) sang tọa độ cực (r,) (thông thường/mở
rộng), đối với một hàm số f(x,y) cụ thể có tập xác định D(f) ở hệ tọa độ Descarter Oxy thì phải chuyển
D(f) sang hệ tọa độ cực (r, ).
(4) Nếu chỉ ra được dãy điểm (xn,yn) tiến đến điểm (x0,y0) [(xn,yn) → (x0,y0) khi n→+∞] mà f(xn,yn) → –∞/+ t ∞ hì lim f (x, y) không tồn tại. (x,y) ( → x ,y ) 0 0 Ví dụ
Tìm các giới hạn sau đây 1.4. 4 4 2x + x − xy + y 2 2 (a) lim (b) −(x y + ) lim (x + ) y e 2 2 (x,y) → , 1 ( 0) x + y (x ,y) ( → , ) x sin y (c) lim (d) lim e− xy cos x ( + y) ( x,y ) → , 1 ( 6 x2 ) + 1 (x,y)→ ( , 1 −1) Bài giải.
(a) Tập xác định D(f) = R2\{(0,0)}.
Chúng ta có lim (2x4 + x − xy + y4 ) = 3 và lim (x2 + y2 ) =1 (x ,y)→ , 1 ( 0) (x,y) → , 1 ( 0) 4 4 lim (2x4 + x − xy + y4 ) 2x + x − xy + y (x,y)→( , 1 0) 3 lim f (x, y) = lim = = = 3 . (x ,y) ( → , 1 0) (x,y) ( → , 1 0) x 2 + y 2 lim (x2 + y2 ) 1 (x,y) ( → , 1 0)
(b) Tập xác định D(f) = R2. 2 2 x x 0 −(x + xe y ) = → 2 2 2 0 khi x → x + y x Vì e > 1 nên e e 2 2 y y 0 −(x + ye y ) = → 2 2 2 0 khi y → x + e y e y 2 2 2 2 2 2 lim f (x, y) = lim (x + ) y e−(x +y ) = lim xe−(x +y ) + lim ye− (x + y ) = 0 + 0 = 0. (x ,y) ( → , ) (x,y) ( → , ) (x,y) ( → , ) (x,y) ( → , )
(c) Tập xác định là D(f) = R2. 1 1 Chúng ta có lim x sin y = . 1 sin =1. = và lim (x2 + ) 1 = 12 + 1 = 2 (x,y)→ , 1 ( 6) 6 2 2 (x,y) ( → , 1 6) lim x sin y x sin y (x,y)→ , 1 ( 6) 1 2 1 lim f (x, y) = lim = = = . (x,y)→ , 1 ( 6) (x,y)→ , 1 ( 6 x2 ) + 1 lim (x 2 + ) 1 2 4 (x,y) → , 1 ( 6)
(d) Tập xác định D(f) = R2. Chúng ta có lim
e− xy = e−1.(− )1 = e và lim cos x ( + ) y = cos 1 ( − ) 1 = cos0 = 1 (x ,y)→ , 1 ( −1) (x ,y)→ , 1 ( − ) 1 lim f (x, ) y = lim e−xy cos x ( + y) = lim e− xy lim cos x ( + y) = . e 1= e . (x,y)→ , 1 ( − ) 1 (x,y)→ , 1 ( − ) 1 ( x,y)→ ,1 ( − ) 1 (x,y)→ ,1 ( − ) 1
Ví dụ 1.5. Tìm lim f (x, y) của các hàm số sau đây ( x,y ) ( → 0,0) 6 x2 + y2 xy (a) f (x, y) = (b) f (x, y) = x 2 + y2 +1 −1 2 2 x + y x + 2y 3 3 sin x ( ) − sin(y ) (c) f (x, y) = (x + 2y) cos (d) f (x, y) = 2 2 x + 2y 2 2 x + y Bài giải. x2 + y2 0
(a) Tập xác định D(f) = R2\{(0,0)} và lim f (x, y) = lim có dạng vô định . (x,y) ( → 0,0) (x ,y) ( → 0,0) x 2 + y 2 1 + 1 − 0 Theo định nghĩa, khoảng cách từ điểm M(x,y) đến điểm O(0,0) là d( , O ) M = (x − ) 0 2 + (y − ) 0 2 = x2 + y2 d → 0 M (x,y) → O(0,0) ( x,y) → (0,0). x2 + y2 d 2 d2 ( d2 +1 + ) 1 d 2( d 2 +1 + ) 1 f (x, y) = = = = = d 2 +1 +1 2 2 2 2 2 + − + − + − + + d2 x y 1 d 1 1 ( d 1 ) 1 ( d 1 ) 1 lim f (x, ) y = li ( m d2 + 1+ ) 1 = 2 . (x,y) ( → 0,0) d 0 → xy 0
(b) Tập xác định D(f) = R2\{(0,0)} và lim f (x, ) y = lim có dạng vô định . (x,y) ( → 0,0) (x,y) ( → 0,0) 2 2 x + y 0 x x Vì x 2 x 2 + y 2 1 với (x,y) ≠ (0,0) nên f (x, y) = y 1. y = y x2 + y2 x 2 + y 2 0 f (x, )
y y → 0 khi (x,y) → (0,0). Theo nguyên lý kẹp thì lim f (x, y) = 0 . (x ,y) ( → 0,0)
(c) Tập xác định D(f) = R2\{(0,0)}. Chúng ta c ó x + 2y x + 2y 0 f (x, ) y = (x + 2 ) y cos = x + 2y cos x + 2y 1 . = x + 2y ( 2 x + y ) x 2 + 2y 2 x 2 + 2y 2 x + 2y vì cos
1 và x + 2y x + 2y 2 x + 2 y = 2(x + y ) với (x,y) D (f). x 2 + 2y 2 0 f (x, ) y (
2 x + y) → 0 khi (x,y) → (0,0). Theo nguyên lý kẹp thì lim f (x, y) = 0 . (x ,y) ( → 0,0) 3 3 sin x ( ) − sin(y )
(d) Tập xác định D(f) = R2\{(0,0)} và lim f (x, ) y = lim có dạng vô định 2 2 (x,y) ( → 0,0) (x,y) ( → 0,0) x + y 0 . 0 3 3 3 sin(x ) x = x
Vì sin khi α → 0 nên khi (x,y) → (0,0) 3 3 3 sin(y ) y = y 3 3 3 3 3 3 3 3 sin(x ) − sin(y ) sin x ( ) + − sin(y ) sin(x ) + sin(y ) sin(x ) −sin(y ) 0 f (x, y) = = = 2 2 2 2 2 2 2 2 x + y x + y x + y x + y x 3 + y 3 x 3 y 3 x 3 y 3 = + +
= x + y →0 khi (x,y) → (0,0). Theo nguyên lý kẹp x 2 + y2 x 2 + y2 x2 + y2 x2 y2 thì lim f (x, y) = 0 . (x ,y)→(0,0) Cách khác. 3 3 3 sin x ( ) sin(y ) sin x ( ) − 3 3 sin(y ) sin(x ) + − − 3 3 3 sin(y ) sin(x ) sin(y ) 0 f (x, y) = = = + 2 x + 2 2 y x + 2 2 y x + 2 2 y x + 2 2 y x + 2 y 7 sin x ( 3) sin(y3 ) x sin x ( 3) y sin(y3 ) sin x ( 3) sin(y3 ) + = + = x + y → x 1 . + y 1 . = x + y → 0 x 2 y2 x 3 y3 x3 y3 sin(x3 ) sin(y3 ) khi (x,y) → (0,0) vì lim = 1 và lim
= 1 . Theo nguyên lý kẹp thì lim f (x, y) = 0 . x3 0 → x3 y3 0 → y3 (x ,y)→(0,0)
Ví dụ 1.6. Chứng minh rằng, đối với các hàm số f(x,y) sau đây, không tồn tại lim f (x, y) (x,y) ( → 0,0) 2 2 x − y 2 2x y (a) z = f (x, y) = (b) z = f (x, y) = 2 2 x + y 4 2 x + y Bài giải. 2 2 − (a) Tập xác định x y 0 D(f) = R2\{(0,0)} và lim f (x, y) = lim có dạng vô định . 2 2 (x,y) ( → 0,0) (x,y) ( → 0,0) x + y 0 2 1
Cách 1. Xét dãy điểm (x , y ) =
với nN*, khi đó (x , y ) → ) 0 , 0 ( n → n n , n n n n (2 n)2 − 1 ( n)2 3 n 2 3 3 3 f (x = = = = = = n, y n) lim f (x, y) lim f (x 2 2 2 n , y n ) lim (2 n) + 1 ( n) 5 n 5 (x ,y) ( → 0,0) n→ n → 5 5 , , 1 2
Tương tự, xét dãy điểm (x , y ) =
với nN*, khi đó (x, , y, ) → ( 0 , 0 ) n → n n , n n n n − − , 1 ( n)2 , (2 n)2 3 n2 3 3 3 f (x , y ) = =
= − lim f (x, y) = lim f (x , y ) = lim− = − n n 1 ( n)2 + (2 n)2 5 n2 5 n n (x,y)→(0,0) n→ n → 5 5 2 2 x − y
Do đó, theo định nghĩa thì lim . không tồn tại 2 2 (x,y) ( → 0,0) x + y
Nhận xét. Chúng ta có thể thực hiện việc chứng minh trên ngắn gọn hơn, bằng cách xét dãy điểm p q
(x , y ) = , với nN* và p, q là các tham số thực không đồng thời bằng 0, khi đó n n n n (x , y ) → ) 0 , 0 ( n → . n n 2 2 2 2 (p n) − (q n) p − q f (x , y ) = = n n 2 2 2 2 (p n) + (q n) p + q 2 2 2 2 p − q p − q lim f (x, ) y = lim f (x , y ) = lim = n n
, khi cho p hoặc/và q thay đổi thì giá trị 2 2 2 2 (x ,y) ( → 0,0) n → n → p + q p + q 2 2 p − q 2 2 x − y biểu thức
thay đổi, điều này chứng tỏ lim . không tồn tại 2 2 p + q 2 2 (x,y) ( → 0,0) x + y x 2 − 02 x2
Cách 2. Khi (x,y) → (0,0) dọc theo trục hoành Ox (y = 0) thì f (x, ) 0 = = = 1 với x ≠ 0 x 2 + 02 x 2 x 2 − y2 lim = limf (x 0
, ) = 1 , còn khi (x,y) → (0,0) dọc theo trục tung Oy (x = 0) thì (x,y) ( → 0,0) x 2 + y2 x→0 02 − y2 − y 2 x2 − y2 f , 0 ( y) = = = 1 − với y ≠ 0 lim = limf ( , 0 y) = 1
− . Do đó, theo định nghĩa 02 + y2 y2 (x,y) ( → 0,0) x2 + y2 x→0 2 2 − thì không tồn tại x y lim . 2 2 (x,y) ( → 0,0) x + y
x = 0 + r cos = r cos
Cách 3. Đổi tọa độ Descarter (x,y) sang tọa độ cực (r,): với
y = 0 + r sin = r sin r 0 , khi đó f ( D ) = ( , r ) R2 r , 0 0 2 và (x,y) → (0,0) r → 0+. 0 2 8 x = r cos Bây giờ, chúng ta thay
vào biểu thức của hàm số f(x,y) thì được y = r sin 2 x − 2 y (r cos 2 ) −(r sin 2 2 2 ) r (cos − 2 sin f (x, y) = = = ) = 2 cos − 2 sin 2 x + 2 y r ( cos 2 ) +(r sin 2 2 2 ) r (cos + 2 sin ) lim f (x, y) = 2 lim(cos − 2 sin ) = 2 cos − 2
sin , nên khi nhận các giá trị khác nhau + (x ,y)→(0,0) r→0 2 2 x − y thì f(x,y) d t
ần đến các giới hạn khác nhau. Do đó, theo định nghĩa hì lim . không tồn tại 2 2 (x,y) ( → 0,0) x + y 2 2x y 0
(b) Tập xác định D(f) = R2\{(0,0)} và lim f (x, y) = lim có dạng vô định . 4 2 (x,y) ( → 0,0) (x,y) ( → 0,0) x + y 0 p q
Cách 1. Xét dãy điểm (x , y ) = ,
với nN* và p, q là các tham số thực không đồng thời n n 2 n n bằng 0 hi đó , k (x , y ) → ) 0 , 0 ( n → n n p2 q 2 2 2p q . n 2 2 4 f (x n, y n) = n = n = 2p q lim f (x, ) y = lim f (x , y ) = 4 2 4 2 4 2 n n p q p + q p + (x,y) →(0,0) n → q + n n 2 n4 2 2 2p q 2p q 2 2p q lim =
, khi cho p hoặc/và q thay đổi thì giá trị biểu thức thay đổi, điều này 4 2 4 2 n→ p + q p + q 4 2 p + q 2 chứng tỏ 2x y lim . không tồn tại 4 2 (x,y) ( → 0,0) x + y
Cách 2. Nếu cho (x,y) → (0,0) dọc theo đường parabol y = kx2 với tham số k ≠ 0 thì chúng ta nhận 2 2 4 được 2 x 2 (kx ) k 2 x k 2 k 2 k 2 f (x, kx ) = = = lim f (x, ) y = limf (x, kx) = lim = 4 2 2 2 4 2 2 2 (x,y)→(0,0) x 0 → x →0 x + (kx ) 1 ( + k )x 1 + k 1+ k 1+ k
nên giới hạn này sẽ thay đổi khi k thay đổi; chẳng hạn, nếu (x,y) → (0,0) dọc theo đường parabol y = x2 (k = 1) thì lim
f (x, y) =1, còn nếu (x,y) → (0,0) dọc theo đường parabol y = 2x2 (k = 2) ( x, y)→(0,0) 4 2 2x y thì lim f (x, y) = . t
Do đó, theo định nghĩa hì lim . không tồn tại (x , y) ( → 0,0) 5 4 2 (x,y) ( → 0,0) x + y
1.2.2. Tính liên tục
1.2.2.1. Định nghĩa Cho hàm số hai
biến z = f(x,y) có tập xác định D(f)R2, chúng ta nói hàm số f(x,y) liên tục tại điểm M0(x0,y0) D
(f) nếu (1) tồn tại giới hạn lim
f (x, y) và (2) giá trị của giới hạn này bằng giá trị (x ,y)→(x ,y ) 0 0
của hàm số f(x,y) tại điểm (x0,y0), tức là lim
f (x, y) = f (x , y ). Khi đó, điểm M 0 0 0(x0,y0) được gọi là ( x,y) ( → x ,y ) 0 0
điểm liên tục của hàm số f(x,y).
Hàm số f(x,y) được gọi là hàm số liên tục trên tập xác định D(f) nếu nó liên tục tại mọi điểm của tập xác định D(f).
Lưu ý. Các tính chất liên tục đối với hàm số một biến (n = 1) đã học trong học phần Giải tích 1 vẫn
đúng đối với hàm số nhiều biến (n > 1).
Ví dụ 1.7. Xét tính liên tục của các hàm số
f(x,y) sau đây, trên tập xác định D(f) của nó x 2 − 2 y khi (x, ) y ) 0 , 0 ( (a) z = f (x, y) = x2 + y2 0 khi (x, ) y = ( ) 0 , 0 9 xy (b) khi (x, ) y z = f (x, y) = ( 0 , 0 ) x 2 + y2
với tham số R 0 khi (x, y) = ( 0 , 0 ) Bài giải. x 2 − 2 y khi (x, y) ( ) 0 , 0
(a) Tập xác định của hàm số f (x, y) = x2 + y2 là D(f) = R2. 0 khi (x, ) y = ( ) 0 , 0
- Tại điểm O(0,0) có f(0,0) = ,
0 nhưng như chúng ta đã chứng minh ở Ví dụ 1.6.a lim f (x, y) ( x ,y )→(0,0)
không tồn tại, theo định nghĩa, hàm số f(x,y) không liên tục tại điểm O(0,0). x 2 − y2 x 2 − y2 - Tại điểm (x 0 0 0,y0) ≠ (0,0) thì lim f (x, y) = lim = = f (x , y ) nên hàm số (x ,y)→(x ,y ) (x,y) ( → x ,y ) 0 0 0 0 x2 + y2 x 2 + y2 0 0 0 0
f(x,y) liên tục tại mọi điểm (x0,y0) ≠ (0,0). x 2 − 2 y Kết luận: Hàm số khi (x, y) f (x, y) = ( ) 0 , 0 x2 + y2
không liên tục tại điểm O(0,0) và liên tục 0 khi (x, ) y =( ) 0 , 0
tại mọi điểm (x0,y0) (0,0) D(f)\{(0,0)}. xy khi (x, y)
(b) Tập xác định của hàm số f (x, y) = ( , 0 ) 0 x 2 + y2
với R là D(f) = R2. 0 khi (x, ) y = ( 0 , 0 )
- Tại điểm (x0,y0) = (0,0): Theo Bất đẳng thức Cauchy với (x,y)R2, chúng ta có 2 2 x + y 1 xy 2 2 2 2 1 2 2 1 x y xy (x + y )
(x + y ) − với (x,y)R2\{(0,0)} 2 2 2 2 x + y 2 xy 1 + Nếu – 1 > 0 > 1 thì 0 f (x, y =
(x2 + y2 ) 1− → 0 khi (x, y) → ( , 0 0), do đó x 2 + y2 2 theo nguyên lý kẹp lim
f (x, y) = 0 mà f(0,0) = 0 lim f (x, y) = f , 0 ( ) 0 nên t hà heo định nghĩa, m (x ,y)→(0,0) (x ,y) ( → 0,0)
số f(x,y) liên tục tại điểm O(0,0). 1 xy xy + Nếu – 1 = 0 = 1 thì f (x, y) = =
, bây giờ chúng ta cho (x,y) → (0,0) dọc 2 2 2 2 x + y x + y theo đường thẳng y = (với tham số k ≠ 0) kx thì 2 2 xkx k x k x k f (x, ) y = f (x, kx) = = = = 2 2 2 2 2 2 2 2 x + (kx) x + k x 1 ( + k )x 1 + k k lim f (x, y) = limf (x, kx) =
giá trị này thay đổi khi k thay đổi, do đó không tồn 2 (x ,y)→ (0,0) x→ 0 1+ k
tại lim f (x, y) nên theo định nghĩa, hàm số f(x,y) không liên tục tại điểm O(0,0). (x,y) ( → 0,0) + Nếu
– 1 < 0 1 – > 0, bây giờ cho (x,y) → (0,0) dọc theo đường thẳng y = x thì 2 x . x f (x, y) = f (x, x) = = x = 1 1 . lim f (x, y) = limf (x, x) = 1 1 lim = + tức là 2 x + 2 2 2 − 1 ( ) 2 − 1 ( (x,y → ) (0,0) → x 0 → ) x 0 x 2x 2 x 2 x
không tồn tại lim f (x, y) nên theo định nghĩa, hàm số f(x,y) không liên tục tại điểm O(0,0). (x,y) ( → 0,0) xy x y - Tại điểm (x 0 0 0,y0) ≠ (0,0) thì lim f (x, y) = lim = = f (x , y ) nên theo (x ,y) ( → x ,y ) (x ,y) ( → x ,y + + 0 0 0 0 x 2 ) y2 x 2 y 0 0 2 0 0
định nghĩa, hàm số f(x,y) liên tục tại mọi điểm (x0,y0) ≠ (0,0). 10 xy Kết luận khi (x, y) : Khi >
1 thì hàm số f (x, y) = ( , 0 ) 0 x 2 + y2
liên tục trên D(f), còn khi 0 khi (x, ) y = ( 0 , 0 )
1 thì f(x,y) không liên tục tại điểm O(0,0) và liên tục tại mọi điểm (x0,y0) (0,0) D(f)\{(0,0)}.
1.2.2.2. Điểm gián đoạn của hàm số
Hàm số f(x,y) được gọi là gián đoạn tại điểm M0(x0,y0) nếu nó không liên tục tại điểm đó và điểm
M0(x0,y0) được gọi là điểm gián đoạn của hàm số.
Như vậy, khái niệm hàm số gián đoạn tại một điểm là phủ định ái
kh niệm hàm số liên tục tại điểm
đó, tức là hàm số f(x,y) gián đoạn tại điểm M0(x0,y0) nếu:
(1) hoặc nó không xác định tại điểm M0(x0,y0);
(2) hoặc nó xác định tại điểm M0(x0,y0) nhưng không tồn tại giới hạn lim f (x, y) ; (x ,y) ( → x ,y ) 0 0
(3) hoặc nó xác định tại điểm M0(x0,y0) và tồn tại giới hạn lim
f (x, y) nhưng giá trị giới hạn (x ,y)→( x ,y ) 0 0
này khác giá trị của hàm số f(x,y) tại điểm (x0,y0) , tức là lim f (x, y) f (x , y ). 0 0 ( x ,y) ( → x ,y ) 0 0
Ví dụ 1.8. Xác định các điểm gián đoạn và các điểm liên tục của các hàm số sau đây x2 − y2 x 2 + 2xy + 5 khi (x, ) y ( 0 , 0 ) (a) z = f (x, y) = (b) z = f (x, y) = x2 + y2 y 2 − 2x +1 0 khi (x, y) = ( , 0 ) 0 x 2 + y 2 khi (x, y) ( 0 , 0 )
(c) z = f (x, y) = x2 + y2 + 1 −1 0 khi (x, ) y = ( 0 , 0 ) Bài giải. x2 + 2xy + 5 y 2 1 (a) Hàm số f (x, y) = xác định được khi y2 – 2x + 1 ≠ 0 x + nên miền xác y 2 − 2x + 1 2 2 y2 1
định của nó là D(f ) = (x, y) R 2 x
+ . Trên mặt phẳng tọa độ của hệ tọa độ Descartes vuông 2 2 y2 1 góc Oxy thì D(f) là
các điểm trừ các điểm nằm trên đường parabol x = + . 2 2 2
Theo định nghĩa, các điểm (x,y) y 1
R2 nằm trên đường parabol x =
+ là các điểm gián đoạn 2 2 x2 + 2xy + 5 của hàm số f (x, y) = .
Các điểm gián đoạn này thuộc trường hợp (1). y 2 − 2x +1 y2 1
Tại điểm (x0,y0) không nằm trên đường parabol x = + thì 2 2 x 2 +2xy +5 x 2 + + 0 2x0y0 5 lim f (x, ) y = lim = = f (x , y ) . (x,y) ( → x ,y ) (x,y) ( → x ,y ) 0 0 0 0 y2 − 2x + 1 y 2 − 2x + 1 0 0 0 0 x2 + 2xy + 5
Theo định nghĩa, hàm số f (x, y) =
liên tục trên tập xác định D(f) của nó. y 2 − 2x +1 x 2 − 2 y khi (x, y) ( 0 , 0 )
(b) Tập xác định của hàm số f (x, y) = x2 + y2 là D(f ) = R2. 0 khi (x, y) = ( , 0 ) 0 11
Hàm số f(x,y) này xác định tại điểm (0,0), tức là f(0,0) = 0. Tuy nhiên, như chúng ta đã chứng minh
ở Ví dụ 1.6.a, hàm số này không tồn tại giới hạn khi (x,y) → (0,0), nên điểm (0,0) là điểm gián đoạn của nó.
Hơn nữa, như chúng ta đã chứng minh ở Ví dụ 1.7.a, hàm số f(x,y) này liên tục tại mọi điểm (x0,y0) ≠ (0,0). x 2 − 2 y khi (x, y)
Như vậy, đối với hàm số f (x, y) = ( 0 , 0 ) x2 + y2
, điểm gián đoạn duy nhất của nó 0 khi (x, ) y = ( , 0 ) 0
là điểm gốc tọa độ O(0,0). Điểm gián đoạn này thuộc trường hợp (2). x 2 + y 2 khi (x, y) ( , 0 ) 0
(c) Tập xác định của hàm số f (x, y) = x 2 +y2 +1 −1 là D(f) = R2. 0 khi (x, y) = ( 0 , 0 )
Hàm số f(x,y) này xác định tại điểm (0,0), tức là f(0,0) = 0; tuy nhiên, như chúng ta đã chứng minh ở Ví dụ 1. a, hàm 5.
số này có lim f (x, y) = 2 , do đó lim f (x, y) f ( 0 ,
0 ) nên theo định nghĩa, điểm ( x ,y) ( → 0,0) ( x,y) ( → 0,0)
gốc tọa độ O(0,0) là điểm gián đoạn của nó.
Hơn nữa, hàm số f(x,y) đang xét liên tục tại mọi điểm (x0,y0) ≠ (0,0). Thật vậy, chúng ta có x2 + y2 x2 + 0 y2 lim f (x, y) = lim 0 = = f (x , y ) . 0 0 (x,y)→(x ,y ) (x,y)→(x ,y ) 0 0 0 0 x2 + y2 + 1 − 1 x2 + y 2 + 1 − 1 0 0 x 2 + y 2 khi (x, y) ( , 0 ) 0
Như vậy, hàm số f (x, y) = x2 +y2 +1 −1
có điểm gián đoạn duy nhất của 0 khi (x, y) = ( 0 , 0 )
nó là điểm gốc tọa độ O(0,0), điểm gián đoạn này thuộc trường hợp (3).
1.3. Phép tính vi phân
1.3.1. Định nghĩa đạo hàm riêng, đạo hàm riêng của hàm hợp
1.3.1.1. Đạo hàm riêng
Cho hàm số z = f(x,y) xác định trên tập mở D(f)R2, giả sử điểm M0(x0,y0)D(f).
Cho y = y0 thì hàm số hai biến z = f(x,y0) g(x) trở thành hàm số một biến đối với x, khi đó nếu
hàm số g(x) có đạo hàm tại x = x0 thì đạo hàm đó gọi là đạo hàm riêng theo biến x của hàm số f(x,y) tại f (x , y ) điểm M , z , 0 0
0(x0,y0) và ký hiệu là z (x , y ) hoặc
(x , y ) hoặc f (x , y ) hoặc tùy từng x 0 0 x 0 0 x 0 0 x
trường hợp khi sử dụng, nếu không gây ra bất kỳ sự hiểu nhầm nào. − − Như vậy, g(x) g(x ) f (x, y ) f (x , y ) , 0 0 0 0 f (x , y ) = lim = lim nếu ký hiệu – x 0 0 , x = x x0 thì x = x x → x →x − − 0 x x 0 x x 0 0
x0 + x và gọi x là số gia của đối số x thì x → 0 khi x → x0.
Suy ra hiệu g(x) − g(x ) = f (x, y ) − f (x , y ) = f (x + x
, y ) − f (x , y ) được gọi là số gia riêng 0 0 0 0 0 0 0 0
của hàm số f(x,y) theo biến x tại điểm M0(x0,y0) và ký hiệu là xf(x0,y0). + −
Do đó, chúng ta có thể viết , f (x , y ) f (x x, y ) f (x , y ) f (x , y ) = lim x 0 0 = lim 0 0 0 0 . x 0 0 x 0 → x x 0 → x
Tương tự, đạo hàm riêng theo biến y của hàm số f(x,y) tại điểm M 0(x0,y0) là − + − , f (x , y) f (x , y ) f (x , y ) y 0 0 f (x , y y) f (x , y ) f (x , y ) = lim 0 0 0 = lim = lim 0 0 0 0 . y 0 0 y→y − → → 0 y y y 0 0 y y 0 y Nhận xét.
(1) Định nghĩa đạo hàm riêng của hàm số nhiều biến f(x1,x2,…,xn) theo một biến xi (1 ≤ i ≤ n) chính
là định nghĩa đạo hàm của hàm số một biến, khi coi các biến x1,x2,…,xi-1,xi+1,…,xn là các hằng số. Do đó, 12
khi tính đạo hàm riêng của một hàm số nhiều biến theo một biến nào đấy, chúng ta coi các biến còn lại là
hằng số và tính đạo hàm thông thường như đối với hàm số một biến.
(2) Vì (x0,y0) là một điểm bất kỳ thuộc tập xác định D(f) nên ta có thể dùng (x,y) D (f) thay cho
(x0,y0) và để tiện sử dụng, người ta thường ký hiệu đạo hàm riêng của hàm số f(x,y) tại điểm (x,y) bằng
một trong các biểu thức z f (x, y) z, (x, y) hoặc
(x, y) hoặc f , (x, y) hoặc
tùy từng trường hợp khi sử x x x x
dụng, nếu không gây ra bất kỳ sự hiểu nhầm nào. ,f (x , y ) = , f (x, y) x 0 0 x Khi đó (x, y)= (x , y ) 0 0 ,f (x , y ) = , f (x, y) y 0 0 y (x, y) =(x , y ) 0 0
Nếu dùng định nghĩa để tính các đạo hàm riêng f , (x, y), f , (x, y) của hàm số z = f(x,y) xác định x y
trên tập mở D(f)R2 tại một điểm , M0(x0,y0) D
(f) thì chúng ta thực hiện các bước sau đây: x = x − x 0
f (x , y ) = f (x + x, y ) − f (x , y ) Bước 1. Lập các số gia x 0 0 0 0 0 0 y = y − y0
f(x ,y )= f(x ,y + y)− f(x , y ) y 0 0 0 0 0 0 f (x , y ) f (x + x, y ) − lim x 0 0 = f (x , y ) lim 0 0 0 0 f ' (x , y ) x→0 x→ x 0 x x 0 0
Bước 2. Tìm các giới hạn f (x , y ) y 0 0 f (x , y + ) y − lim = f (x , y ) lim 0 0 0 0 f ' (x , y ) y 0 0 y→0 y→ y 0 y
Nếu dùng định nghĩa để tính các đạo hàm riêng f , (x, y), f , (x, y) của hàm số z = f(x,y) xác định x y
trong xác định trên tập mở D(f)R2, tại nhiều điểm (x,y) D
(f) thì chúng ta thực hiện các bước sau đây:
f (x, y) = f (x + x, ) y − f (x, y)
Bước 1. Lập các số gia x
f (x, y) = f (x, y+ ) y − f (x, y) y f (x, y) f (x + x, y) − lim x = f (x, y) lim f, (x, y) x→0 x → x x x 0
Bước 2. Tìm các giới hạn f (x, y) y f (x, y + y)− lim = f (x, y) lim f , (x, y) → y 0 y → y y y 0
Bước 3. Các đạo hàm riêng f , (x, y), f ,
của hàm số f(x,y) tại điểm (x0,y0) D (f) là y (x, y) x , f (x , y ) = , f (x, y) x 0 0 x (x ,y) =(x 0,y0) , f (x , y ) = , f (x, y) y 0 0 x (x ,y) =(x 0,y0)
Ví dụ 1.9. Tính các đạo hàm riêng f , (x, y), f , 2 tại điểm
y (x, y) của hàm số z = f(x,y) = x3 – 2xy + y x
(x0,y0) = (1,2) bằng 2 cách: (1) dùng định nghĩa, (2) dùng các công thức tính đạo hàm đã biết. Bài giải.
- Tập xác định của hàm số f(x,y) = x3 2xy – 2 + y là D(f) = R2.
- Điểm cần tính đạo hàm riêng có hoành độ x0 = 1 và tung độ y0 = 2 và là một điểm thuộc D(f). - Tính bằng định nghĩa
f (x + x, y ) − f (x , y ) , 0 0 0 0 f 1 ( + x, ) 2 − f (x , y ) = lim f, , 1 ( ) 2 = f , 1 ( ) 2 lim x 0 0 x→0 x x x →0 x , f (x , y + ) y − f (x , y ) = f (x , y ) lim 0 0 0 0 , f , 1 ( 2 + y) − f , 1 ( 2) = f , 1 ( ) 2 lim y 0 0 y →0 y y → y 0 y 13 f 1 ( + x, ) 2 = 1 ( + x)3 −2 1 ( + x) 2 . 2 + 2 = −5 −5x + ( 3 x)2 +( x)3 Chúng ta có f , 1 ( 2 + y) =13 − . 1 .
2 (2 + y)2 +(2 + y) = −5 −7 y − ( 2 y)2 3 2 f , 1 ( ) 2 =1 − . 2 2 . 1 +2 = −5 , f 1 ( + x, ) 2 − f , 1 ( ) 2 −5 − 5 x + ( 3 x)2 + (x)3 − (− f , 1 ( ) 2 = lim = ) 5 lim = x → x 0 → x x 0 x 2 , f , 1 ( 2 + y) − f , 1 ( ) 2 −5 −7 y − ( 2 ) y −( − f , 1 ( ) 2 = lim = ) 5 lim = y → y 0 → y y 0 y lim−5 + . 3 x + (x)2 2 = −5 + 0 . 3 + 0 = −5 x →0 lim− 7 − 2 . y = −7 − . 2 0 = −7 y→0 (x 3 , − 2xy 2 + y) f (x, y) = = x 3 2 − y . 1 . 2 2 + 0 = x 3 2 − 2y2 x x - Tính bằng quy tắc 3 2 , (x − 2xy + f (x, y) = y) = 0− 2 .x2y+1= −4xy +1 y y f, , 1 ( ) 2 = f , (x, y) = x x ( x 3 2 − 2y2 ) = 1 . 3 2 − 2 . 2 2 = − 5 (x ,y) = , 1 ( 2) (x ,y) = , 1 ( 2) f , , 1 ( ) 2 = f , (x, y) = y y (− 4xy+ )1(x,y = = − .1 . 4 2+ 1= − 7 (x ,y = ) , 1 ( 2) ) , 1 ( 2) Nhận xét.
(1) Bản chất của việc tính đạo hàm là tính giới hạn, nhưng việc tính giới hạn của một biểu thức toán
học, nói chung là không đơn giản.
(2) Qua Ví dụ 1.9. chúng ta thấy rằng việc tính đạo hàm riêng bằng cách dùng các công thức tính
đạo hàm (quy tắc) đã biết đơn giản hơn rất nhiều so với việc tính nó bằng cách dùng định nghĩa.
(3) Để tính đạo hàm riêng tại điểm của một hàm số, có thể không tính bằng công thức tính đạo hàm
(quy tắc) được, mà chỉ có thể tính bằng định nghĩa. cos y ( 2 )
Ví dụ 1.10. Tính các đạo hàm riêng f , (x, y), f , (x, y) của hàm số z = f (x, y) = tại điểm x y x , 1 ( ). cos y ( 2 )
Bài giải. Hàm số f (x, y) =
xác định được khi x 0 nên tập xác định của nó là x f ( D ) = ( { x, y) R2 x }
0 . Trên mặt phẳng tọa độ của hệ tọa độ Descartes vuông góc Oxy thì D(f ) là các
điểm nằm ngoài trục tung Oy, do đó điểm , 1 ( ) f ( D ).
Chúng ta sẽ tính các đạo hàm riêng f , (x, y), f , (x, y) của hàm số f(x,y) bằng cách dùng các công x y
thức tính đạo hàm (quy tắc) đã biết tại điểm bất kỳ (x,y) D(f),
sau đó thay giá trị cụ thể tại điểm yêu cầu tính đạo hàm riêng. cos y ( 2 ' ) 2 d 1 2 1 cos y ( 2 ) f (x, y) = = cos y ( ) = cos y ( ) − = − x x x dx x x2 x2 2 2 2 f' (x, y) = cos y
( ) = 1 dcos y( ) = 1 2 [y−sin(y2)] = −2ysin(y ) y y x x dy x x cos y ( 2 ) cos f'x ( , 1 )= f ' (x, y) = − = − =1 x 2 2 (x, y)= , 1 ( ) x 1 (x, y)= , 1 ( ) 2 f'y ( , 1 ) ' 2y cos y ( ) 2 sin = f (x, y) = − = − = 0 y (x, y)= , 1 ( ) x 1 (x, y)= , 1 ( ) 14
Ví dụ 1.11. Tính các đạo hàm riêng f , (x, y), f , (x, y) của hàm số 3 3 3 = = + tại điểm x y z f (x, y) x 8y (0,0).
Bài giải. D(f) = R2 (0,0) D (f)
Chúng ta không thể tính các đạo hàm riêng f , 0 , 0 ( ),f , ) 0 , 0 (
của hàm số này bằng cách dùng các x y
công thức tính đạo hàm (quy tắc) đã biết tại điểm bất kỳ (x,y) D(f),
sau đó thay (x,y) = (0,0) vào các
biểu thức của f , (x, y), f ,
vừa tính được; mà phải tính bằng định nghĩa. y (x, y) x
Thật vậy, giả sử chúng ta tính f , (x, y) và f ,y(x, y) bằng công thức tính đạo hàm đã biết tại điểm bất x 1 x , 3 3 1 1− 2 1 f (x, y) = 3 x + 8y = 3 (x + 3 8y ) = 3 3 (x + 3 2 3 8y ) x 3 = x x 3 x 3 (x + 3 2 3 8y ) kỳ (x,y)D(f) , nếu thay 1 8y , 3 1 − 1 2 1 3 3 3 3 3 3 2 3 3 f (x, y) = x + 8y = (x + 8y ) = (x + 8y ) 24y = y y 3 y 3 (x + 3 2 3 8y )
(x,y) = (0,0) vào các biểu thức của f , (x, y), f ,y (x, y) vừa tính được thì không thể xác định được giá trị của x các biểu thức này.
Bây giờ, chúng ta tính f , ) 0 , 0 ( và f , ) 0 , 0 ( bằng định nghĩa x y , f 0 ( + x, ) 0 − f ( , 0 ) 0 3 (0 + x)3 + 8 0 . 3 − 0 x f ( , 0 ) 0 = lim = lim = lim = lim1 =1 x → x 0 → x x 0 → x x 0 → x x 0 , f ( 0 , 0 + y) − f ( 0 , 0 ) 3 03 + ( 8 0 + y)3 − 0 ( 2 y) f ) 0 , 0 ( = lim = lim = lim = lim 2 = 2 y y →0 y → y 0 x → y 0 x → y 0
1.3.1.2. Đạo hàm riêng của hàm hợp x = x(u, v)
Cho z = f(x,y) trong đó x, y là các hàm số của hai biến độc lập u, v: , khi đó y = y(u, v) z = f(x(u, ) v , ( y u, v )
) được gọi là hàm hợp của hai biến độc lập u, v.
Giả sử các hàm số x(u,v), y(u,v) có các đạo hàm riêng x, (u, v), x, (u, v), y, (u, v), y, (u, v) tại điểm u v u v
(u,v) và hàm số f(x,y) có các đạo hàm riêng tương ứng f , (x, y), f , (x, y) tại điểm x y f,u(x(u,v),y(u,v)) , , , ,
= fx(x, y)xu(u,v)+ fy (x, y)yu(u, v) (x, y) = (x(u, v), ( y u, v)) thì f,( x(u,v),y(u,v ) , , , , ) = f (x, y)x (u, v)+ f (x, ) y y (u, v) v x v y v
Ví dụ 1.12. Tính các đạo hàm riêng f ,(x(u, ) v , ( y u, ) ) v , f ,
của hàm hợp z = f(x,y) = v (x (u, v), y(u, v) ) u x = x(u, v) = u 3 − v xlny với . y = ( y u, ) v = ln u ( 2 + v2)
Bài giải. Hàm số f(x,y) = xlny xác định được khi y > 0 nên tập xác định của nó là f ( D ) = ( { x, y) R2 y }
0 . Trên mặt phẳng tọa độ của hệ tọa độ Descartes vuông góc Oxy thì D(f ) là các
điểm thuộc nửa mặt phẳng nằm phía trên trục hoành Ox và không kể các điểm thuộc trục hoành Ox.
Sử dụng công thức trên ta tính được , , , , , (x ln y) u 3 ( − v) (x ln y) ( ln u ( 2 + v2 ) f u (x(u, ) v , y(u, ) v ) = f (x, ) y x (u,v) + f (x, ) y y (u,v) = + ) = x u y u x u y u x 1 x 2u − (ln y 3 ) + 2u = 3ln y + = 3ln(ln(u2 + v2) ) u 3 ( 2 v)u + y u2 + v2 y u2 + v2 (u2 + v2)ln(u2 + v2) 2 2 f , v (x(u, v), y(u, v)) , , , , (x ln y) 3 ( u −v) (x ln y) (ln u ( + v )
= fx (x, y)xv (u, v)+ fy (x, y)y v(u, v) = + ) = x v y v x 1 x 2v − (ln y)(− ) 1 + 2v = − ln y + = −l ( n ln u ( 2 + v2 ) u 3 ( 2 v)v ) + y u 2 + v2 y u 2 + v 2 (u2 + v2) ln u ( 2 + v2 ) 15 z , (e + xy + 2 x + 3 z − ) 1 F (x, , y z) = = 2x + y x , x F (x, , y z) 2x + y , z (x, y) = − x = − x z (e + xy + 2 x + 3 z − ) 1 F (x, , y z) e z 3 , , z + 2 z F (x, , y z) = = x y y , F (x, , y z) , y x z (x, y) z 2 3 = − = − (e +xy +x +z − x ) 1 F (x, , y z) e z 3 , z 2 , z + 2 F (x, , y z) = = e + z z 3 z z vì ez + z 3 2 0 với z .
1.4. Cực trị của hàm nhiều biến 1.4.1. C
ực trị địa phương, phương pháp tìm cực trị địa phương
Định nghĩa. Cho hàm số n biến f (x , x ,..., x ) xác định trên tập mở D(f)Rn. điểm. Chúng ta nói 1 2 n
rằng hàm số f (x , x ,..., x ) có cực trị địa phương tại điểmM (x(0) , x (0 ,)..., x(0)) f ( D ) nếu với mọi điểm 1 2 n 0 1 2 n (
M x , x ,..., x )trong một lân cận nào đó của điểm M 1 2 n 0
nhưng khác M0 và hiệu số
f (x , x ,..., x )− f x , x ,..., x có dấu không đổi. 1 2 n ( (0) (0) (0) 1 2 n )
Nếuf (x , x ,..., x ) − f (x(0), x(0),..., x(0) ) 0thì hàm số f (x , x ,..., x )có cực tiểu địa phương tại 1 2 n 1 2 n 1 2 n điểm M (0) (0) (0) (0) (0) (0) 0, khi đó f
= f (x , x ,..., x ) ; còn nếu f (x ,x ,..., x ) −f (x ,x ,..., x ) 0 thì hàm ct 1 2 n 1 2 n 1 2 n
số f (x , x ,..., x ) có cực đại địa phương tại điểm M (0) (0) (0) 0, do đóf = f (x , x . cđ 1 2 ,..., x n ) 1 2 n
Ví dụ 1.25. Tìm cực trị của các hàm số sau đây (a) z = f(x,y) = –x2 2x + – 14 + 6y y – 2
(b) z = f(x,y) = x2 + xy + y2 3x – 6y –
(c) u = f(x,y,z) = x2 + y2 + z2 + 2x 4z – + 8 y2 z2 2 (d) u = f (x, , y z) = x + +
+ (x > 0, y > 0, z > 0) 4x y z Bài giải.
(a) Tập xác định của hàm số f(x,y) = –x2 – 2x + 14 + 6y – y2 là D(f) = R2.
Vì f(x,y) = –x2 – 2x + 14 + 6y – y2 = – (x + 1)2 – (y
– 3)2 + 24 < 24 = f(–1,3) với (x,y) ≠ (–1,3)
nên theo định nghĩa thì hàm số f(x,y) = –x2 – 2x + 14 + 6y – y2 có cực đại địa phương tại điểm (–1,3)
D(f) và giá trị cực đại này là fcđ = f( 1,3) – = 24.
(b) Tập xác định của hàm số f(x,y) = x2 + xy + y2 – 3x – 6y là D(f) = R2. Vì f (x, ) y = x2 + xy + y2 − x 3 − 6y = (x − 3 ) 2 2 + (y − )
3 2 + xy − 45 4 nên chưa thể xác định được
cực trị của hàm số này bằng cách đơn giản như ở (a).
(c) Tập xác định của hàm số f(x,y,z) = x2 + y2 + z2 + 2x – 4z + 8 là D(f) = R3.
Vì f(x,y,z) = x2 + y2 + z2 + 2x 4z – + 8 = (x + 1)2 + y2 + (z 2) – 2 + 3 > 3 = f( 1,0,2) – với (x,y,z) ≠
(–1,0,2) nên theo định nghĩa thì hàm số f(x,y,z) = x2 + y2 + z2 + 2x – 4z + 8 có cực tiểu địa phương tại
điểm (–1,0,2) D(f) và giá trị cực tiểu này là f ct = f( 1,0,2) – = 3. y2 z2 2
(d) Tập xác định của hàm số f (x, , y z) = x + + + là 4x y z f ( D ) = {(x, , y z) R3 x , 0 y , 0 z } 0
Việc xác định cực trị của hàm số này không thể thực hiện được bằng cách đơn giản như ở (c).
Nhận xét. Không phải bài toán tìm cực trị của hàm số nào cũng giải được đơn giản như đối với các
hàm số (a) và (c) trong Ví dụ 1.25.
Điều kiện cần của cực trị địa phương. Nếu hàm số f (x , x ,..., x ) xác định trên tập mở D(f)Rn, 1 2 n
có cực trị địa phương tại điểm M (x(0), x(0),..., x(0) ) thì tất cả các đạo hàm riêng cấp 1 của nó bằng không 0 1 2 n
tại điểm đó, tức là f , (x(0) ,x(0) ,..., x(0)) = 0 (1 ≤ i ≤ n). xi 1 2 n 30
Điểm mà tại đó, tất cả các đạo hàm riêng cấp 1 của hàm số f (x , x ,..., x ),bằng không được gọi là 1 2 n
điểm tới hạn hay điểm dừng.
- Đối với hàm số 2 biến z = f(x,y) xác định trên tập mở D(f)R2, có cực trị địa phương tại điểm f, (x , y ) = 0 M x 0 0
0(x0,y0)D(f) thì tất cả các đạo hàm riêng cấp 1 của nó bằng không tại điểm đó, tức là . , f (x , y ) = 0 y 0 0
- Đối với hàm số 3 biến u = f(x,y,z) xác định trên tập mở D(f)R3, có cực trị địa phương tại điểm
M0(x0,y0,z0)D(f) thì tất cả các đạo hàm riêng cấp 1 của nó bằng không tại điểm đó, tức là f, (x , y ,z ) = 0 x 0 0 0 f , (x , y ,z ) = 0 . y 0 0 0 f, (x , y ,z ) = 0 z 0 0 0
Trước khi nêu điều kiện đủ của cực trị địa phương, chúng ta định nghĩa Dạng toàn phương và phát
biểu Định lý Sylvester trong Đại số. Dạng toàn phương a a a ... a 11 12 13 1n a a a ... a 21 22 23 2 n Giả sử x = (x
1 x2 … xn) là ma trận cấp (1n), A = a a a ... a là ma trận vuông cấp 31 32 33 3n ... ... ... ... ... a a a a n1 n 2 n 3 nn
(nn) đối xứng (aij = aji với i ,j).
Biểu thức (x1,x2, …,xn) = xAxt (xt là ma trận chuyển vị của ma trận x) được gọi là dạng toàn
phương của n biến x1, x2, …, xn; còn ma trận đối xứng A được gọi là ma trận tương ứng của dạng toàn phương (x1,x2, …,xn).
Vì ma trận A là ma trận đối xứng nên sau khi thực hiện phép nhân 3 ma trận trên chúng ta được n n n (x , x ,..., x ) = a x x a x a 2 x x . 1 2 n = ij i j 2 + ii i ij i j i=1 j =1 = i 1 1 i j n a a a ... a 11 12 13 1n a a a ... a 12 22 23 2 n
Như vậy, nếu cho ma trận A =
là một ma trận vuông đối xứng cấp (n a a a ... a n) 13 23 33 3n ... ... ... ... ... a a a a 1n 2n 3n nn
thì chúng ta xác định được một dạng toàn phương (x1,x2, …,xn) bằng công thức trên; ngược lại, nếu cho
một dạng toàn phương thì chúng ta xác định được một ma trận A tương ứng là ma trận đối xứng cấp (nn).
Ví dụ về việc xác định dạng toàn phương nếu biết ma trận tương ứng của nó 3 6
(a) Xác định dạng toàn phương (x1,x2) có ma trận A = tương ứng. 6 −2 − 2 4 3
(b) Xác định dạng toàn phương (x1,x2,x3) có ma trận A = 4 0 − 5 tương ứng. 3 − 5 1 Bài giải. 31 a = 3 3 6 a a 11 12 11 (a) A = a = 6 12 6 − 2 a a 12 22 a = −2 22 2 2 2 2 2 2 ( x , x ) = a x + a 2 x x = x 3 − 2x + 6 . 2 x x = x 3 − 2x +1 x 2 x . 1 2 ii i ij i j 1 2 1 2 1 2 1 2 i 1 = 1 i j 2 − 2 4 3 a a a a = 4 11 12 13 a = −2 11 12 (b) A = 4 0 − 5 a a a và a = 3 12 22 23 a = 0 22 13 3 − 5 1 a a a a = −5 13 23 33 a = 1 33 23 3 (x , x , x ) = 2 a x + a 2 x x = − 2 2x + 2 x . 0 + 2 x . 1 + . 2 4x x + . 2 x 3 x + . 2 (− ) 5 x x = 1 2 3 ii i ij i j 1 2 3 1 2 1 3 2 3 = i 1 1 i j 3 2 2 − 2x + x + x 8 x + 6x x −1 x 0 x . 1 3 1 2 1 3 2 3
Ví dụ về việc xác định ma trận tương ứng của dạng toàn phương đã biết
(a) Xác định ma trận A tương ứng của dạng toàn phương 2 2 ( x , x ) = x 5 − x x − x . 1 2 1 1 2 2
(b) Xác định ma trận A tương ứng của dạng toàn phương 2 2 (
x , x , x ) = x − 4x + 2x x + x 5 x − x 3 x . 1 2 3 1 2 1 2 1 3 2 3 Bài giải. 2 2 2 1 5 −1 2
(a) (x , x ) =5x −x x − x =5x + 2 1 2 1 1 2 2 1 − x x − x2 A = 1 2 2 2 − 1 2 −1 (b) (x , x , x ) = 2 x − 2 x 4 + 2x x + x 5 x − x 3 x = 1 2 3 1 2 1 2 1 3 2 3 1 1 5 2 2 2 2 5 3 x − 4x + 0 x . + 2 1 . x . x + 2. x x + 2 1 2 3 1 2 1 3 . − x x A = 2 3 1 − 4 − 3 2 2 2 5 2 − 3 2 0
Dạng toàn phương được gọi là :
(1) xác định dương nếu (x1,x2,…,xn) > 0 với (x1,x2,…,xn)Rn và (x1,x2,…,xn) (0,0,…,0);
(2) xác định âm nếu (x1,x2, …,xn) < 0 với (x1,x2,…,xn)Rn và (x1,x2,…,xn) (0,0,…,0) ;
(3) không xác định dấu (không xác định dương cũng không xác định âm) nếu (x1,x2, …,xn) đổi dấu; (4)
suy biến nếu (x1,x2,…,xn) = 0 khi (x1,x2,…,xn) (0,0,…,0). Định lý Sylvester. n
Xét dạng toàn phương (x , x ,..., x ) = a x a 2 x x 1 2 n 2 + ii i ij i j = i 1 1 i j n a a a ... a 11 12 13 1n a a a ... a 12 22 23 2 n có ma trận tương ứng A = a a a ... a là ma trận đối xứng. 13 23 33 3n ... ... ... ... ... a a a a 1n 2n 3n nn a a a ... a 11 12 13 1n a a a ... a 12 22 23 2 n Ký hiệu A = det a a a ... a
với 1 k n là các định thức con chính của ma trận A. k 13 23 33 3n ... ... ... ... ... a a a a k 1 2 k 3k kk 32 Khi đó
(1) (x1,x2, …,xn) xác định dương Ak > 0 với k ( 1 k n),
(2) (x1,x2, …,xn) xác định âm Ak < 0 với k lẻ và A k > 0 với k chẵn (1 k n).
Định lý. Dạng toàn phương xác định dương khi và
chỉ khi các định thức con chính của ma trận của
dạng toàn phương đều dương; dạng toàn phương xác
định âm khi và chỉ khi các định thức con chính của
ma trận của dạng toàn phương: có cấp lẻ đều âm và có cấp chẵn đều dương.
Điều kiện đủ của cực trị địa phương. Nếu hàm số f (x , x ,..., x ) xác định trên tập mở D(f)Rn, 1 2 n
có tất cả các đạo hàm riêng cấp 1 và cấp 2 liên tục trong một lân cận nào đó của điểm dừng
M (x (0),x (0 ,)..., x(0) ) f (
D ) , thì vi phân toàn phần cấp 2 của hàm số f (x , x ,..., x ) tại điểm M0 0 1 2 n 1 2 n 2 2 (0) (0) (0) d f (x , x ,..., x ) = d . x + d . x + ... + d . x f (x (0), x (0 ,)..., x(0)) = 1 2 n 1 2 n 1 2 n x x x 1 2 n n n n ,, (0) (0) (0) f (x , x ,..., x )dx dx = f 2 (x , x ,..., x )dx f 2 (x , x ,..., x d ) x dx x x i j 1 2 n i j ,, (0) (0) (0) 2 + x 1 2 n i i ,, (0) (0) (0) x x 1 2 n i j i j i =1 j=1 i=1 1i j n
là dạng toàn phương của các biến dx1, dx2, ..., dxn. Khi đó:
(1) Nếu d2 f (x(0) , x(0) ,..., x(0) ) xác định âm thì hàm số f (x , x ,..., x ) có cực đại địa phương tại 1 2 n 1 2 n điểm M 2 (0) (0) (0) 0; còn nếu d f (x
, x ,..., x ) xác định dương thì hàm số f (x , x ,..., x ) có cực tiểu địa 1 2 n 1 2 n phương tại điểm M0;
(2) Nếu d2 f (x(0) , x(0) ,..., x(0) ) không xác định dấu thì hàm số f (x , x ,..., x ) không có cực trị tại 1 2 n 1 2 n điểm M0;
(3) Nếu d2 f (x(0) , x(0) ,..., x(0) ) suy biến, tức là tồn tại dx 1 2 n
1, dx2, ..., dxn không đồng thời bằng 0 nhưng d f
2 (x(0), x(0),..., x(0)) = 0 , thì chưa thể kết luận được hàm số f (x , x ,..., x ) có cực trị địa phương 1 2 n 1 2 n
tại điểm M0 hay không, mà phải giải bài toán bằng cách khác.
Đối với các hàm số 2 biến z = f(x,y) xác định trên tập mở D(f)R2 có tất c ,
ả các đạo hàm riêng cấp
1 và cấp 2 liên tục trên D(f), để tìm cực trị địa phương của nó, căn cứ vào điều kiện cần và đủ để hàm số
nhiều biến có cực trị địa phương đã trình bày ở trên, chúng ta thực hiện các bước sau đây:
Bước 1. Tìm tập xác định D(f). f, (x, y)
Bước 2. Tính các đạo hàm riêng cấp 1 của hàm số f(x,y): x
và tìm các điểm dừng (x*,y*) là , f (x, y) y f, (x, y) =0 x
nghiệm của hệ phương trình:f, (x, y) =0 . y (x, y) D f ( ) f,,2 (x, y) x Bước 3. T nh í
các đạo hàm riêng cấp 2 của hàm số f(x,y): f ,, (x, y) và suy ra vi phân toàn phần cấp xy ,, f 2(x, y) y
2 của hàm số f(x,y) tại điểm (x,y): 2 ,, 2 ,, ,, 2 d f (x, ) y = f + + . 2 (x, ) y dx f 2 ( , x ) y dxdy f 2 (x, d ) y y x xy y
Bước 4. Tính vi phân toàn phần cấp 2 của hà
m số f(x,y) tại mỗi điểm (x*,y*): 2 * * ,, * * 2 ,, * * ,, * * 2 d f (x , y ) = f + +
là dạng toàn phương của 2 biến 2 (x , y d ) x f 2 (x , y d ) xdy f 2 (x , y d ) y xy x y dx, dy. Khi đó:
(1) Nếu d2f(x*,y*) xác định dương thì hàm số f(x,y) có cực tiểu địa phương tại điểm (x*,y*) và fct =
f(x*,y*); còn nếu d2f(x*,y*) xác định âm thì hàm số f(x,y) có cực đại địa phương tại điểm (x*,y*) và fcđ = f(x*,y*). 33
(2) Nếu d2f(x*,y*) không xác định dấu thì hàm số f(x,y) không có cực trị tại điểm (x*,y*).
(3) Nếu d2f(x*,y*) suy biến, tức là tồn tại dx và dy không đồng thời bằng không, nhưng d2f(x*,y*) =
0, thì chưa thể kết luận được hàm số f(x,y) có cực trị tại điểm (x*,y*) hay không, mà phải giải bài toán bằng cách khác.
Đối với các hàm số 3 biến z = f(x,y,z) xác định trên tập mở D(f)R3, có tất cả các đạo hàm riêng
cấp 1 và cấp 2 liên tục trên D(f), để tìm cực trị địa phương của nó, căn cứ vào điều kiện cần và đủ để hàm
số nhiều biến có cực trị địa phương đã trình bày ở trên, chúng ta thực hiện các bước sau đây:
Bước 1. Tìm tập xác định D(f). f , (x, , y z) x
Bước 2. Tính các đạo hàm riêng cấp 1 của hàm số f(x,y,z): f , (x, , y z) y và tìm các điểm dừng f ,(x, , y z) z f , (x, , y z) = 0 x f , (x, , y z) = 0
(x*,y*,z*) là nghiệm của hệ phương trình y . f , (x, , y z) = 0 z (x, , y z) D(f ) f ,, f ,, (x, y,z) 2 ( x , y, z ) x xy
Bước 3. Tính các đạo hàm riêng cấp 2 của hàm số f(x,y,z): f ,, , f ,, và suy ra vi yz (x, y, z) 2 (x, y, z) y ,, ,, f f (x, y,z) 2 ( x , y, z ) z zx
phân toàn phần cấp 2 của hàm số f(x,y,z) là 2 d f (x, , y z) = ,, 2 f 2 (x, , y z d ) x + ,, 2 f 2 (x, , y z d ) y + ,, 2 f 2 (x, , y z d ) z + x y z f 2 ,, (x, , y z d ) xdy + f 2 ,, (x, , y z)dydz + f 2 ,, (x, ,
y z)dzdx với (x,y,z)D(f). xy yz zx
Bước 4. Tính vi phân toàn phần cấp 2 của hà
m số f(x,y,z) tại mỗi điểm (x*,y*,z*): 2 * * * d f (x , y ,z ) = ,, * * * 2 f 2 ( x , y , z d ) x + ,, * * * 2 f 2 (x , y , z d ) y + ,, * * * 2 f 2 (x , y , z )dz + x y z f 2 ,, (x* , y* ,z* )dxdy + f 2 ,, (x* , y* ,z* d ) ydz + f 2 ,, (x*, y*,z*)dzdx xy yz zx
là dạng toàn phương của 3 biến dx, dy, dz. Khi đó:
(1) Nếu d2f(x*,y*,z*) xác định dương thì hàm số f(x,y,z) có cực tiểu địa phương tại điểm (x*,y*,z*)
và giá trị cực tiểu của hàm số tại điểm này là f 2 * *
ct = f(x*,y*,z*); còn nếu d f(x*,y ,z ) xác định âm thì hàm số
f(x,y,z) có cực đại địa phương tại điểm (x*,y*,z*) và giá trị cực đại của hàm số tại điểm này là fcđ = f(x*,y*,z*).
(2) Nếu d2f(x*,y*,z*) không xác định dấu thì hàm số f(x,y,z) không có cực trị tại điểm (x*,y*,z*).
(3) Nếu d2f(x*,y*,z*) suy biến, tức là tồn tại dx, dy và dz không đồng thời bằng không, nhưng
d2f(x*,y*,z*) = 0, thì chưa thể kết luận được hàm số f(x,y,z) có cực trị tại điểm (x*,y*,z*) hay không, mà
phải giải bài toán bằng cách khác.
Ví dụ 1.26. Tìm cực trị của các hàm số trong Ví dụ 1.25. bằng cách sử dụng điều kiện cần và đủ vừa trình bày ở trên.
Bài giải. Bây giờ, chúng ta sử dụng điều kiện cần và đủ vừa trình bày ở trên để tìm cực trị của các
hàm số (b) và (d); còn các hàm số (a) và (c) sinh viên tự giải bằng phương pháp này, sau đó so sánh kết
quả với kết quả đã nhận được ở Ví dụ 1.25.
(b) Tìm cực trị của hàm số f(x,y) = x2 + xy + y2 – 3x – 6y
Bước 1. Tập xác định của hàm số f(x,y) = x2 + xy + y2 – 3x – 6y là D(f) = R2. 34 , (x2 + xy + y2 − x 3 −6y) f (x, y) = = 2x + y − 3 x Bước 2. Tính x 2 2 , (x + xy + y − x 3 − f (x, y) = 6y) = x + 2y− 6 y y f ,(x, y) = 0 x 2x + y −3 = 0 x = 0
Điểm dừng là nghiệm của hệ phương trình f (, y x, y) = 0 x+ 2y− 6 = 0 y = 3 (x*,y*) = (0,3)D(f). ,, f , (x, y) (2x + y − f 2 (x, y) = x = ) 3 = 2 x x x ,, f , (x, y) (2x + y − ) 3
Bước 3. Tính f (x, y) = x = = 1 xy y y f , (x, y) ,, y (x + 2y − f 2 (x, y) = = 6) = 2 y y y
Do đó, vi phân toàn phần cấp 2 của hàm số
f(x,y) = x2 + xy + y2 – 3x – tại điểm (x,y) là 6y 2 ,, 2 ,, ,, 2 2 2 d f (x, y) = f + + = + + với (x,y)D(f). 2 ( , x y d ) x f 2 (x, ) y dxdy f 2 (x, y d ) y 2dx d 1 . 2 xdy d 2 y xy x y
Bước 4. Từ kết quả trên, chúng ta có 2 d f ( ) 2 2 3 , 0 = d 2 x + d 1 . 2 xdy + d
2 y là dạng toàn phương của các 2 1
biến dx, dy có ma trận tương ứng là A = . 1 2 2 1
Ma trận A có các định thức con chính A = det = , A = det = 3 0 nên dạng toàn 1 (2) 2 0 2 1 2
phương tương ứng là xác định dương, do đó f(x,y) = x2 + xy + y2 – 3x
– 6y giá trị cực tiểu tại điểm (0,3)
và giá trị cực tiểu của hàm số tại điểm này là f = f ( ) 3 , 0 = (x 2 + xy + y2 − x 3 − 6y) = 02 + 0.3 + 32 − 3.0 − . 6 3 = −9. ct ( x , y) =(0,3) y2 z2 2
(d) Tìm cực trị của hàm số f (x, , y z) = x + + +
(x > 0, y > 0, z > 0) 4x y z y2 z2 2
Bước 1. Tập xác định của hàm số f (x, , y z) = x + + + là 4x y z f ( D ) ={(x, , y z) R3 x , 0 y , 0 z } 0 . 2 2 y z 2 2 y , f (x, y, z) = x + + + = − 1 x 2 x 4x y z 4x 2 2 y z 2 2 Bước 2. Tính y z , f (x, y, z) = x y + + + = − 2 y 4x y z 2x y 2 2 , y z 2 2z 2 f (x, y, z) = x + + + = − z 2 z 4x y z y z 2 y 2 y 1− = 1− = 0 0 , 4x2 2x f (x, , y z) = 0 x 2 2 , y z y z
Điểm dừng là nghiệm của hệ phương trình f (x, , y z) = 0 y − = 0 2 − = 0 2x y 2x y f ,(x, , y z) = 0 z 2z 2 z 1 − = 0 − = 0 y z 2 2 y z 35 x = 1 2 * * * 1 (x , y , z ) = 1 , 1 , D(f ) . y = z = 1 2 , f (x, , y z) 2 y 2 y ,, f 2 (x, , y z) = x = 1− = x 2 3 x x 4x 2x , f (x, , y z) ,, y 2 y z 2 Bước 3. Tính 1 2z f 2 ( x, , y z) = = − = + y 2 3 y y 2x y 2x y ,, , f (x, , y z) 2z 2 f 2 (x, , y z) = 2 4 z = − = + z 2 3 z z y z y z ,, f , (x, , y z) y2 y f (x, , y z) = x = xy − 1 = − 2 2 y y 4x 2x f , (x, , y z) ,, y y z2 2z và f (x, , y z) = = yz − = − 2 2 z z 2x y y , ,, f (x, , y z) 2z 2 f (x, , y z) = z = − = 0 zx 2 x x y z 2 d f (x, , y ) z = ,, 2 f 2 (x, , y d ) z x + ,, 2 f 2 (x, , y d ) z y + ,, 2 f 2 (x, , y z d ) z + x y z f 2 ,, (x, , y z d ) xdy + f 2 ,, (x, , y z)dydz + f 2 ,, (x, ,
y z)dzdx với (x,y,z)D(f). xy yz zx
Bước 4. Tại điểm (x*, y*, z*) = 1 ( 2 ) 1 , 1 , chúng ta có 2 f,, ,, y 2 1 ( 2 = y ) 1 , 1 , = 4 f 1 ( 2 ) 1 , 1 , = − = − x 2 2x3 xy 2x 2 ( x,y,z) = 1 ( ) 1 , 1 , 2 ( x,y,z = ) 1 ( 1 , 1 , 2 ) ,, 1 2z 2 ,, 2z f và f 1 ( 2 ) 1 , 1 , = − = −2 2 1 ( 2 ) 1 , 1 , = + = y 3 3 yz 2 2x y y ( x,y,z) = 1 ( ) 1 , 1 , 2 ( x,y,z = ) 1 ( 1 , 1 , 2 ) ,, f 1 ( 2 ) 1 , 1 , = 0 ,, 2 4 zx f 2 1 ( 2 ) 1 , 1 , = + = z 3 6 y z (x,y,z =) 1( )1, 1 , 2 2 d f(1 2 )1 , 1 , = ,, 2 f 2 1 ( 2 d ) 1 , 1 , x + ,, 2 f 2 1 ( 2 d ) 1 , 1 , y + ,, 2 f 2 1 ( 2 ) 1 , 1 , dz + x y y f 2 ,, xy 1 ( 2 ) 1 , 1 , dxdy + f 2 ,,yz 1 ( 2 d ) 1 , 1 , ydz + f 2 ,,zx 1 ( 2 d ) 1 , 1 , zdx = d 4 x2 + d 3 y2 + 6dz2 + 2.(− d ) 2 xdy + 2.(− ) 2 dydz + . 2 d
0 zdx là dạng toàn phương của các biến dx, 4 − 2 0
dy, dz có ma trận tương ứng là A = −2 3 − 2 . 0 − 2 6
Ma trận A có các định thức con chính 4 − 2 0 4 − 2 A = det( ) 4 = 4 0 , A = det = , A = det − − = nên dạng toàn 3 2 3 2 32 0 2 8 0 1 − 2 3 0 − 2 6
phương tương ứng là xác định dương, do đó hàm số f(x,y,z) có cực tiểu tại điểm 1 ( 2 ) 1 , 1 , và giá trị cực 2 2 2 2
tiểu của hàm số tại điểm này là y z 2 1 1 1 2 f = = + + + = + + + = ct f 1 ( 2 ) 1 , 1 , x . 4 4x y z 2 . 4 1 ( ) 2 1 1 (x,y,z)= 1( 2 )1 , 1 ,
Lưu ý. Chỉ đối với hàm số 2 biến z = f(x,y), về phương diện thực hành, để đơn giản, chúng ta thực
hiện việc tìm cực trị của hàm số f(x,y) như sau. 36 f,,2 (x* , y* ) A x
Giả sử (x*, y*) là điểm dừng của hàm số f(x,y), ký hiệu f,, (x* , y* ) B thì dạng toàn phương xy ,, * * f 2 (x , y ) C y 2 * * ,, * * 2 ,, * * ,, * * 2 2 2 d f (x , y ) = f + + = + + có ma trận 2 (x , y d ) x f 2 (x , y )dxdy f 2 (x , y d ) y Adx 2Bdxdy Bdy xy x y A B tương ứng là . B C A B A B Ma trận 2
có hai định thức con chính là det A ( ) = A và det = AC − B − . B C B C
(1) Khi < 0 thì hàm số f(x,y) có cực tiểu địa phương tại điểm (x*,y*) nếu A > 0, hoặc có cực đại
địa phương tại điểm (x*,y*) nếu A < 0.
(2) Khi > 0 thì hàm số f(x,y) không có cực trị tại điểm (x*,y*).
(3) Khi = 0 thì hàm số f(x,y) có thể có hoặc không có cực trị tại điểm (x*,y*), tức là chưa thể kết
luận được hàm số f(x,y) có cực trị tại điểm (x*,y*) hay không, mà phải giải bài toán bằng cách khác.
Bước 1. Tìm tập xác định D(f). f, (x, ) y = 0 x
Bước 2. Tìm các điểm dừng (x*,y*) là nghiệm của hệ phương trình f, (x, ) y = 0 . y (x, y) D f ( ) f ,, = 2 ( x, y) A(x, y) x Bước 3. Tính f,, (x, ) y = (
B x, y) (x, y) = B2 (x, y) − A(x, y C ) (x, y) với (x,y) D (f). xy f,, = 2 (x, y) C(x, y) y
Bước 4. Tại mỗi điểm (x *,y*) Giá trị * * Kết luận
(x*,y*) A(x ,y ) > 0
(x*,y*) là điểm cực tiểu địa phương và fct = f(x*,y*) < 0
(x*,y*) là điểm cực đại địa phương và f < 0 cđ = f(x*,y*) > 0
(x*,y*) không phải là điểm cực trị = 0
Giải bài toán bằng cách khác
Ví dụ 1.27. Tìm cực trị của hàm số f(x,y) = 8x
2 + 3y2 + 1 – (2x2 + y2 + 1)2.
Bài giải. Chúng ta dùng cách tìm cực trị của hàm số 2 biến f(x,y) vừa trình bày ở trên để giải bài toán này.
Bước 1. Tập xác định của hàm số f(x,y) = 8x2 + 3y2 + 1 – (2x2 + y2 + 1)2 là D(f) = R2. f ' (x, y) =1 x 6 − ( 2 2x2 + y2 + )
1 4x = 8x −16x3 − 8xy2 = 8x 1 ( − 2x2 − y2 ) Bước 2. Chúng ta có x ' 2 2 2 3 2 2 f (x, ) y = 6y− ( 2 2x + y + ) 1 2y = 2y− x 8 y− 4y = 2y 1 ( − 4x − 2y ) y
Nên các điểm dừng (nếu có) là nghiệm của hệ phương trình f ' (x, y) = 0 x 8x 1 ( −2x 2 −y 2) = 0 x 1 ( − 2x2 − y2 ) = 0 f '(x, y) =0 y 2y 1 ( − 4x2 − 2y2 ) = 0 y 1 ( − 4x2 − 2y2 ) = 0 x =0 x 1 ( − 2x 2 − y2) = 0 + Trường hợp 1.
hệ thỏa mãn, hệ có 1 nghiệm là (x , y ) = , 0 ( ) 0 . 1 1 y =0 y 1 ( − 4x2 − 2y2 ) = 0 37 x = 0 x 1 ( − 2x2 − y2 ) = 0 x = 0 + Trường hợp 2. hệ có 2 nghiệm là y 0 1 ( y − 4x2 − 2y2 ) = 0 1− 2y2 = 0 (x , y ) = , 0 ( −1 2), (x , y ) = ( , 0 1 2) . 2 2 3 3 x 0 x 1 ( − 2x2 − y2 ) = 0 1− 2x2 = 0 + Trường hợp 3. hệ có 2 nghiệm là y = 0 y 1 ( − 4x2 − 2y2 ) = 0 y = 0 (x , y ) = (−1 2 ) 0 , , (x , y ) = 1 ( 2 ) 0 , . 4 4 5 5 x 0 x − 1 ( 2x2 − y2 ) = 0 1− 2x2 − y2 = 0 + Trường hợp 4. hệ vô nghiệm. y 0 − 1 ( y 4x2 − 2y2 ) = 0 1− 4x2 − 2y2 = 0
Như vậy, hàm số có 5 điểm dừng (x , y ) = , 0 ( ) 0 , (x , y ) = , 0 ( −1 2), (x , y ) = ( , 0 1 2) , 1 1 2 2 3 3 (x , y ) = (−1 2 ) 0 , , (x , y ) = 1 ( 2 ) 0 , đều thuộc D(f). 4 4 5 5 ,, f, (x, y) 8 ( x −1 x 6 3 − 2 f 2 (x, y) = x = 8xy ) = 8− 4 x 8 2 − 8y2 = A(x, y) x x x ,, f, (x, y) 8 ( x −1 x 6 3 − 2 Bước 3. 8xy ) Tính f (x, y) = x = = −1 x 6 y = ( B x, y) xy y y , 2 3 f (x, y) ,, y (2y− 8x y− f 2 (x, y) = = 4y ) = 2− x 8 2 − 12y2 = ( C x, y) y y y (x, ) y = B2 (x, ) y − A(x, ( C ) y x, y) = (−1 x 6 y)2 − 8 ( − 4 x 8 2 − y 8 2) 2 ( − x 8 2 −1 y 2 2 ) = 16 1 ( −1 x 0 2 − 7y2 + 5 x 6 2y2 + 2 x
4 4 + 6y4 )với (x,y)D(f). Bước 4.
1.Tại điểm dừng (x , y ) = , 0 ( ) 0 1 1 ( 0 , 0 ) = (x, y) =16 0 (x , y ) = ) 0 , 0 (
không phải là điểm cực trị. = 1 1 (x,y) (0,0) 2. Tại điểm (x , y ) = , 0 ( −1 2) 2 2 ( , 0 −1 2) = ( x, y) = 1 − 6 0 ( x,y)=(0, 1 − 2 ) (x , y ) = ( , 0 −1
2) là điểm cực tiểu địa 2 2 A( , 0 − 1 2)= A(x, y) = 4 0 ( x,y)= (0,−1 2 ) phương và f = f (x, ) y = f , 0 ( −1 2) = 1 4 . ct (x,y)=(0, 1 − 2 )
3. Tại điểm dừng (x , y ) = ( , 0 1 2) 3 3 ( 1 , 0 2) = ( x, ) y = 1 − 6 0 (x ,y)=(0 1 , 2 ) (x , y ) = 1 , 0 (
2) là điểm cực tiểu địa phương và 3 3 A 1 , 0 ( 2) = A(x, y) = 4 0 (x ,y) ( = 0 1 , 2 ) f = f (x, y) = f , 0 ( 1 2) = 1 4 . ct (x,y)=(0 1 , 2 )
4. Tại điểm dừng (x , y ) = (−1 2 ) 0 , 4 4 (−1 2 ) 0 , = ( x, ) y
=16 0 (x ,y ) = (−1 2 ) 0 ,
không phải là điểm cực trị. (x,y)=( 1 − 2,0) 4 4
5. Tại điểm dừng (x , y ) = 1 ( 2 ) 0 , 4 4 1 ( 2 ) 0 , = ( x, ) y =16 0 (x , y ) = 1 ( 2 ) 0 ,
không phải là điểm cực trị. (x,y)= 1 ( 2,0) 5 5
1.4.2. Cực trị có điều kiện
Bài toán tìm cực trị của hàm số nhiều biến ở phần trên là tìm cực trị của hàm số không có điều kiện,
tức là không có điều kiện ràng buộc nào giữa các biến của hàm số cần tìm giá trị cực đại hoặc giá trị cực
tiểu hoặc cả giá trị cực đại và giá trị cực tiểu của hàm số. Tuy nhiên, trong ứng dụng thực tế, chúng ta 38
thường gặp các bài toán tìm cực trị của một hàm số với điều kiện ràng buộc nào đó giữa các biến, các bài
toán này được gọi là bài toán tìm cực trị có điều kiện.
Thông thường, có hai cách giải quyết bài toán tìm cực trị có điều kiện. Cách thứ nhất: Nếu từ điều
kiện ràng buộc đã cho giữa các biến mà có thể biểu diễn tường minh và duy nhất một biến qua các biến
còn lại thì có thể đưa bài toán tìm cực trị có điều kiện về bài toán tìm cực trị không có điều kiện với số
biến giảm xuống một. Tuy nhiên, không phải bao giờ cũng làm được như vậy, khi đó chúng ta sử dụng
Cách thứ hai: Sử dụng phương pháp nhân tử Lagrange để đưa bài toán tìm cực trị có điều kiện về bài
toán tìm cực trị không có điều kiện với số biến tăng lên một.
Ví dụ 1.28. Khi sản xuất hộp đựng sữa, để tiết kiệm chi phí bao bì, người ta cần phải giải quyết bài
toán: Tìm hình trụ tròn có thể tích lớn nhất trong các hình trụ tròn có cùng diện tích toàn phần S không đổi.
Bài giải. Gọi chiều cao và bán kính đáy của hình trụ tròn tương ứng là h > 0 và r > 0.
Khi đó, chu vi (Cđ) và diện tích đáy (Sđ) của hình trụ tròn là Cđ = .2r = 2r và Sđ = r2 và diện tích
xung quanh (Sxq) của hình trụ tròn là Sx
q = hCđ = h.2r = 2hr, suy ra diện tích toàn phần (Stp) và thể
tích (V) của hình trụ tròn là Stp = Sx + q
2Sđ = 2hr + 2r2 = 2(h + r)r = S và V = hSđ = h. r2 = hr2.
Như vậy, bài toán cần giải quyết là: Tìm giá trị cực đại của hàm số 2 biến V(h,r) hr2 với điều
kiện ràng buộc giữa các biến h > 0 và r > 0 là 2(h + r)r = S (S là hằng số dương).
Bây giờ chúng ta sử dụng Cách thứ nhất để giải bài toán này. Từ điều kiện 2(h + r)r = S (S là hằng
số) chúng ta biểu diễn tường minh được biến h qua biến r, cụ thể là S h =
−r , tiếp theo, thay giá trị h 2r
này vào biểu thức của V(r,h) chúng ta được S 2 S V(h, r) = − rr = r − r3 f (r) . 2 r 2 d S S Chúng ta có , 3 2 f (r) = r − r
= − 3r nên điểm dừng của hàm số f(r) là nghiệm của phương dr 2 2 , S S S trình f (r) = 0 − 3 r2
= 0 . Phương trình − 3r2 = 0 với điều kiện r > 0 có nghiệm r = là 0 0 2 2 6 S S
điểm dừng của hàm số f(r) h = − = = . 0 r 2 2r 0 2r 0 6 0 0 df , ,, r ( ) d S Chúng ta có f r ( ) = = −3 r 2 = 6 − r f , (,r ) = − 6 r = 6 − r 0 nên hàm số f(r) dr dr 2 0 0 r=r0 S S 3 có cực đại tại r = f = f (r ) = S S . 0 cđ 0 r − r = 6 2 3 6 r =0r
Như vậy, hình trụ tròn có chiều cao bằng đường kính đáy của nó là hình trụ tròn có thể tích lớn nhất
trong các hình trụ tròn có cùng diện tích toàn phần.
Phương pháp nhân tử Lagrange tìm cực trị có điều kiện của hàm số nhiều biến
Bài toán. Tìm cực trị của hàm số n biến f (x , x ,..., x ) xác định trên tập mở D(f)Rn và các biến 1 2 n
x1, x2, …, xn bị ràng buộc bởi điều kiện g(x1,x2,…,xn) = 0.
Nhà toán học Lagrange đã giải bài toán này như sau.
Bước 1. Tìm tập xác định D(f) của hàm số n biến f (x , x ,..., x ) và lập hàm số Lagrange (n + 1) 1 2 n
biến L(x1,x2,…,xn,) = f(x1,x2,…,xn) + g(x1,x2,…,xn), trong đó (được gọi là nhân tử Lagrange) là tham số chưa xác định.
Bước 2. Tìm các điểm(x *,x *,..., x* ) (
D f ) và * tương ứng, là nghiệm (x* , x* ,..., x* , * ) của hệ (n 1 2 n 1 2 n + 1) phương trình: 39
L, (x , x ,..., x ,) = f , (x , x ,..., x ) + g, (x , x ,..., x ) = 0 x 1 2 n x 1 2 n x 1 2 n i i i L,
(x , x ,..., x , ) = g(x , x ,..., x ) = 0 (1 i n) 1 2 n 1 2 n (x , x ,..., x ) D(f ) 1 2 n
Bước 3. Với mỗi * tìm được ở Bước 2 thì hàm số ( L x , x ,..., x , *
) là hàm số n biến (x1,x 1 2 2 2,…,xn)
và tiếp theo, tính vi phân toàn phần cấp 2 của hàm số này tại điểm (x*, x* ,..., x* ) 1 2 n 2 d2 ( L x , * x* ,..., x* , * 1 2 n ) = d . x + d . x +... + 1 2 d
. xn L(x*1, x*2,..., x*n, *) = x x x 1 2 n nn n ,, * * * L (x , x ,..., x ,* d ) x dx = L 2 ( x ,x ,..., x , )dx 2L (x , x ,..., x , )dx dx x x 1 2 n i j i j ,, * * * * 2 + 1 2 n i ,, * * * * x x 1 2 n i j i j i =1 = x j 1 i =1 i 1 i jn
là dạng toàn phương của n biến dx1, dx2, ..., dxn.
Tiếp theo, chúng ta xét dấu của dạng toàn phương d2L(x ,* x ,*..., x*, *
), có hai trường hợp xảy ra: 1 2 n
- Trường hợp thứ nhất. Nếu dạng toàn phương d L 2 (x ,* x ,*..., x*, *
) xác định dương, hoặc xác định 1 2 n
âm thì kết luận: Hàm số f(x ,x ,..., x có cực tiểu địa phương tại điểm (x ,* x*,..., x* ) và 1 2 n ) 1 2 n f = f (x ,
* x*,..., x* ) , hoặc hàm số f(x * * *
1,x2,…,xn) có cực đại địa phương tại điểm (x , x ,..., x ) và ct 1 2 n 1 2 n
f = f (x* , x*,..., x* ) . Bài toán được giải xong. cđ 1 2 n
- Trường hợp thứ hai. Dạng toàn phương d2L(x , * x*,..., x*, *
) không xác định dấu thì thực hiện 1 2 n sang Bước 4.
Bước 4. Tính vi phân toàn phần cấp 1 của hàm số g(x1,x2,…,xn) = 0 n dg(x , x ,..., x ) g, (x , x ,..., x d ) x = 0 với (x1,x2,…,xn) D (f) 1 2 n x 1 2 n i i i 1 = n g, (x*, x *,..., x * d
) x = 0 , vì g, (x*, x* ,..., x* ) (1 ≤ i ≤ n) là các hằng số, nên từ đẳng thức x 1 2 n i i x 1 2 n i i= 1
này có thể biểu diễn tường minh, chẳng hạn biến dxi qua các biến còn lại dx1, dx2,…, dxi-1, dxi+1,…, dxn
là dxi = (dx1,dx2,…,dxi-1,dxi+1,…,dxn) . Bước 5. Thay dx 2 * * * *
i = (dx1,dx2,…,dxi-1,dxi+1,…,dxn) vào d L(x , x ,..., x , ) thì nhận được dạng 1 2 n
toàn phương d2L(x ,* x*,..., x*, *
) của (n–1) biến dx1, dx2,…, dxi-1, dxi+1, …, dxn 1 2 n TT d L 2 (x ,* x ,*..., x*, * ) Kết luận 1 2 n
Hàm số f(x1,x2,…,xn) có cực tiểu địa phương 1 Xác định dương
tại điểm (x ,* x*,..., x* ) và f =f (x ,* x* ,..., x* ) 1 2 n ct 1 2 n
Hàm số f(x1,x2,…,xn) có cực đại địa phương tại 2 Xác định âm
điểm (x*, x* ,..., x* ) và f = f (x*, x*,..., x* ) 1 2 n cđ 1 2 n
Hàm số f(x1,x2,…,xn) không có cực trị tại điểm 3
Không xác định dấu (x*,x* ,...,x* ) 1 2 n
Về mặt thực hành, chúng ta trình bày Phương pháp nhân tử Lagrange tìm cực trị có điều kiện của
hàm số 2 biến f(x,y) như sau.
Bài toán. Tìm cực trị của hàm số z = f(x,y) xác định trên tập mở D(f)R2 và các biến x, y bị ràng
buộc bởi điều kiện g(x,y) = 0.
Bước 1. Tìm tập xác định D(f) của hàm số f(x,y) và lập hàm số Lagrange 3 biến L(x,y,) = f(x,y) + g(x,y), trong đó
(được gọi là nhân tử Lagrange) là tham số chưa xác định. Bước 2 Tìm các điểm . (x*, y*) D f
( ) và * tương ứng, là nghiệm (x*,y*,*) của hệ 3 phương trình 40
L, (x, y, ) =f , (x, y) + g, (x, y) =0 x x x L, (x, ,
y ) = f , (x, y) + g, (x, y) = 0 y y y L, (x, y,) = g(x, y) = 0 (x, y) D f ( )
Hệ phương trình này có thể vô nghiệm, có nghiệm (1 nghiệm hay nhiều nghiệm). Trong trường hợp
hệ vô nghiệm, chúng ta kết luận là hàm số f(x,y) không có cực trị và bài toán giải xong. Trong trường
hợp hệ có nghiệm thì chúng ta thực hiện Bước 3.
Bước 3 Tính vi phân toàn phần cấp 2 của hà .
m số L(x,y,) khi coi là hằng số 2 d ( L x, , y ) = ,, L 2 (x, , y 2 d ) x + ,, 2L (x, , y )dxdy + ,, L 2 (x, , y 2 d ) y = xy x y , , , L (x, , y ) L (x, , y ) L (x, , y ) x 2 y x 2 dx + 2 dxdy + dy x y y
Với mỗi nghiệm (x*,y*,*) chúng ta có 2 * * * ,, * * * 2 ,, * * * ,, * * * 2 d ( L x , y , ) = L + + 2 (x , y , d ) x 2L (x , y , d ) xdy L 2 (x , y , d ) y xy x y TT d2 ( L x*, y*, * ) Kết luận Ghi chú
Hàm số f(x,y) có cực tiểu địa phương 1 Xác định dương
tại điểm (x*, y*) và f =f (x*, y*) ct Bài toán
Hàm số f(x,y) có cực đại địa phương tại giải xong 2 Xác định âm
điểm (x*, y*) và f = f (x*, y*) cđ 3 Không xác định dấu Thực hiện Bước 4
Bước 4. Tính vi phân toàn phần cấp 1 của hàm số g(x,y):dg(x, ) y = g , (x, y d ) x +g, (x, y d ) y = 0 x y
(x,y)D(f) g, (x*, y* d ) x + g, (x*, y* d
) y = 0 . Vì g, (x*, y*) và g, (x*, y*) là các hằng số, nên từ đẳng x y x y g, (x* , y* )
thức này có thể biểu diễn tường minh, chẳng hạn dy qua dx là dy x = − dxnếu g, (x*, y*) 0. g , (x , * y ) * y y g, (x*, y*) Thay dy x = −
dx vào dạng toàn phươngd2L(x*, y*, *
) và xét dấu của biểu thức này g , (x , * y ) * y TT d2L(x*, y*, * ) Kết luận
Hàm số f(x,y) có cực tiểu địa phương tại điểm (x*, y*) 1 Xác định dương và f =f (x*, y*) ct
Hàm số f(x,y) có cực đại địa phương tại điểm (x*, y*) 2 Xác định âm và f = f (x*, y*) cđ 3 Không xác định dấu
Hàm số f(x,y) không có cực trị tại điểm (x*, y*)
Ví dụ 1.29. Tìm cực trị của hàm số f(x,y) = x
2 + y2 – 2x – 2y + 1 với điều kiện x 2 + y2 = 4.
Bài giải. Tập xác định của hàm số f(x,y) = x2 + y2 2x – 2y + – 1 là D(f) = R2.
Điều kiện ràng buộc giữa các biến x, y là g(x,y) = x2 + y2 – 4 = 0.
Bước 1. Lập hàm số Lagrange L(
x,y,) = f(x,y) + g(x,y) = x2 + y2 2x – 2y + – 1 + (x2 + y2 4) –
L, (x,y, ) = f , (x,y) + g, (x, ) y = 2x − 2 + 2x x x x
Bước 2. Chúng ta có L, (x, ,
y ) = f , (x, y)+ g, (x, y) = 2y− 2+ 2 y y y y
L, (x, y,) = g(x, y) = x 2 + y 2 − 4 41 L, (x, y , ) = 0 x 2x − 2 + 2 x = 0 ( + ) 1 x = 1 ,
Hệ phương trình L (x,y , ) = 0 có 2 nghiệm y 2y − 2 + 2 y = 0 ( + ) 1 y = 1 2 2 2 2 L, (x, y , ) = 0 x y 4 0 x y 4 + − = + =
(x*, y*,* ) = (− 2 − , 2 − , − 1 2 ) 2
(x*, y*) = (− 2,− 2) f ( D ) 1 1 1 trong đó 1 1 (x* , y* , * ) = ( 2, 2 − , + 1 2 ) 2 (x*, y* ) = ( 2, 2) f ( D ) 2 2 2 2 2
Bước 3. Tính vi phân toàn phần cấp 2 của hàm số L(x,y,) = x2 + y2 2 2
– 2x – 2y + 1 + (x + y – 4) khi coi là hằng số ,, L, (x, y,) (2x − 2 + 2 L 2(x, y, ) = x = x) = 2+ 2 x x x ,, L, (x, y,) (2x − 2 + 2x)
Chúng ta có L (x, y,) = x = = 0 với (x,y)D(f) xy y y L, (x, y,) ,, y (2y − 2+ L 2(x, y,) = = 2 y) = 2+ 2 y y y 2 d ( L x, , y ) = ,, L 2 ( , x , y 2 d ) x + ,, L 2 (x, , y d ) xdy + ,, L 2 (x, , y 2 d ) y = x xy y 2 2 2 2 (2 + 2 d ) x + d . 0 . 2 xdy + (2 + 2 d ) y = 1 ( 2 + ) dx + 1 ( 2 + )dy với (x,y) D (f) 1. Khi ( , x , y ) =(x ,* y*, * ) =(− 2,− 2, 1 − − 2 ) 2 1 1 1 2 * * * * 2 * 2 2 2 d ( L x , y , ) = 1 ( 2 + d ) x + 1 ( 2 + d ) y = − d 2 x − d
2 y là dạng toàn phương có ma trận 1 1 1 1 1 * − 2 0 tương ứng A( ) = . Ma trận A( *
) có các định thức con chính 1 1 0 − 2 − * 2 0 A ( *
) = det(− 2) = − 2 0 ,A ( ) = det = xác định âm, 2 1 2 0 dL ( 2 x*, y*, * ) 1 1 0 − 2 1 1 1
do đó hàm số f(x,y) = x2 + y2 – 2x – 2y + 1 có cực đại địa phương tại điểm (x,y) =(x*,y*) =(− 2,− 2) 1 1
và f = f (− 2,− 2) = (x2 + y2 − 2x − 2y + ) 1 = 5 + 4 2. cđ (x ,y)=(− 2 ,− 2 ) 2. Khi ( , x , y ) = (x* , y* , * ) = ( 2, 2, 1 − + 2 ) 2 2 2 2 2 * * * * 2 * 2 2 2 d ( L x ,y , ) = 1 ( 2 + d ) x + 1 ( 2 + d ) y = d 2 x + d
2 y là dạng toàn phương có ma trận 2 2 2 2 2 * 2 0 tương ứng A( ) = . Ma trận A( * )
có các định thức con chính 2 2 0 2 * 2 0 A ( *
) =det( 2) = 2 0 , A ( ) = det = xác định dương, do 2 2 2 0 dL2 (x* , y* , * ) 1 2 0 2 2 2 2
đó hàm số f(x,y) = x2 + y2 – 2x – 2y + 1 có cực tiểu địa phương tại điểm (x, y) = (x *,y* ) = ( 2, 2) và 2 2
f = f ( 2, 2) = (x 2 + y 2 − 2x − 2y + ) 1 = 5 − 4 2. ct (x ,y)=( 2 , 2 )
Nhận xét. Ở Ví dụ này, bài toán đã được giải mà chưa cần thực hiện Bước 4.
Ví dụ 1.30. Tìm cực trị của hàm số 2 2 z = f (x, ) y = (x + 2 ) y
− (x − y) với điều kiện (x + 2y)2 + (x − ) y 2 = 9. Bài giải.
Lưu ý. Chúng ta không nên biến đổi biểu thức của hàm số f(x,y) và điều kiện g(x,y) về dạng tổng
của các số hạng vì muốn giữ nguyên các nhóm biến (x + 2y), (x – y) để việc giải hệ phương trình khi xác
định điểm dừng được thuận lợi.
Bước 1. Tập xác định của hàm số 2 2 f (x, y) = (x + 2 ) y
− (x − y) là D(f) = R2. 42
Điều kiện ràng buộc giữa các biến x, y là g(x, ) y = (x + 2 ) y 2 + (x − ) y 2 − 9 = 0 . Lập hàm số Lagrange ( L x, , y ) = f ( , x y) + g (x, )
y = (x + 2y)2 − (x − y)2 + [
(x + 2y)2 + (x − y)2 − ] 9 Bước 2. Chúng ta có L, x (x, , y ) = f ,x (x, ) y + g,x (x, ) y = [ (x + 2 ) y 2 − (x − y)2 ] [ (x + 2 ) y 2 + (x − y)2 − ] 9 + = 2( + ) 1 (x + 2y)+ 2( − ) 1 (x − y) x x L, (x, ,
y ) = f, (x, y) + g, (x, y) = y y y [ (x + 2y)2 − (x − y)2] [ (x + 2 ) y 2 + (x − ) y 2 − ] 9 + = 4( + ) 1 (x + 2y) − ( 2 − ) 1 (x − y) y y L, (x, , y ) = ( g , x ) y = (x + 2 ) y 2 + (x − ) y 2 −9 L, (x, y , ) = 0 x ( 2 + ) 1 (x + 2y) + ( 2 − ) 1 x ( − y) = 0 ,
Hệ phương trình L (x, y , ) = 0 y ( 4 + ) 1 (x + 2 ) y − ( 2 − ) 1 x ( − y) = 0 2 2 L, (x, y, ) 0 (x 2y) (x y) 9 0 = + + − − = ( + ) 1 (x + 2y) + ( − ) 1 (x − y) = 0 ( 2 + ) 1 (x + 2 ) y − ( − ) 1 (x − y) = 0 (x + 2y) 2 +(x − y) 2 = 9 u = x + 2y
Để giải hệ phương trình này, chúng ta đổi biến phụ
, khi đó hệ phương trình này trở v = x − y ( + ) 1 u +( − ) 1 v = 0 ( + ) 1 u = 0 ( + ) 1 u = 0 thành ( 2 + ) 1 u − ( − ) 1 v = 0 ( − )
1 v = 0. Từ hai phương trình suy ra u và v không ( − ) 1 v = 0 2 2 u + v = 9 u2 + v2 = 9
thể đồng thời khác 0, còn từ phương trình u2 + v2 = 9 suy ra u và v không thể đồng thời bằng 0. Do đó,
chỉ xảy ra 2 trường hợp:
Trường hợp 1. u = 0 02 + v2 = 9 v2 = 9 v = 3
0 – 1 = 0 = 1, khi đó hệ ( + ) 1 u = 0 u = 0 x + 2y = 0 x = 2 phương trình ( − )
1 v = 0 v = 3 x − y = 3 y = 1 . 2 2 u + v = 9 = 1 = 1 = 1
Trường hợp 2. v = 0 u2 + 02 = 9 u2 = 9
u = 3 0 + 1 = 0 = –1, khi đó hệ ( + ) 1 u = 0 u = 3 x + 2y = 3 x = 1 phương trình ( − )
1 v = 0 v = 0 x − y = 0 y = 1 . 2 2 u + v = 9 = −1 = − 1 = −1
Như vậy, hệ phương trình trên có 4 nghiệm (x* , y*, * ) = (− , 1 − , 1 − ) 1 (x*, y*) = − ( − , 1 ) 1 1 1 1 1 1 (x* , y* , * ) = − , 1 , 1 ( ) 1 (x*, y* ) = ) 1 , 1 ( 2 2 2
trong đó, cả 4 điểm dừng 2 2 đều thuộc D(f). (x * , y *, * ) = ( − ) 1 , 1 , 2 (x , * y *) = ( − ) 1 , 2 3 3 3 3 3 (x* , y* ,* ) = ( − , 2 ) 1 , 1 (x *, y* ) = ( , 2 − ) 1 4 4 4 4 4
Bước 3. Tính vi phân toàn phần cấp 2 của hà m số ( L x, , y ) = (x + 2 ) y 2 − (x − ) y 2 + [ (x + 2 ) y 2 + (x − ) y 2 − ] 9 khi coi là hằng số Chúng ta có 43 ,, L, (x, y , ) [2 ( + ) 1 x ( + 2y) + ( 2 − ) 1 (x − L 2 (x, y,) = x = y)] =4 x x x ,, L, (x, y, ) [2 ( + ) 1 x ( + 2y) + ( 2 − ) 1 (x − y)] L (x, y , )= x = = 2 ( + ) 3 với (x,y)D(f) xy y y L, (x, y, ) ,, y [ ( 4 + ) 1 (x + 2y) − ( 2 − ) 1 (x − y)] L 2 (x, y , )= = = ( 2 5 + ) 3 y y y 2 dL (x, , y ) = ,, L 2 ( , x , y 2 d ) x + ,, L 2 (x, , y )dxdy + ,, L 2 (x, , y 2 d ) y = xy x y 2 2 4dx + ( 2 . 2 + ) 3 dxdy + 5 ( 2 + ) 3 dy với (x,y)D(f) (1) Khi (x, , y ) = (x* , y* , * ) = (− , 1 − , 1 − ) 1 1 1 1 2 * * * * 2 * * 2 2 2 d ( L x , y , ) = 4 dx + ( 2 . 2 + d ) 3 xdy + 5 ( 2 + d ) 3 y = − d 4 x + . 2 d 4 xdy − d 4 y là dạng toàn 1 1 1 1 1 1 − 4 4
phương có ma trận tương ứng A ( * ) = . Ma trận A( * )
có các định thức con chính 1 1 4 − 4 − 4 4 A ( * ) = det(− ) 4 = 4 − 0 ,A ( * ) = det = 0 dL2 (x* ,y*, *
) không xác định dấu. 1 1 2 1 4 − 4 1 1 1 (2) Khi (x, , y ) = (x* , y *, * ) = , 1 , 1 ( − ) 1 2 2 2 2 * * * * 2 * * 2 2 2 d ( L x , y , ) = 4 dx + ( 2 . 2 + d ) 3 xdy + 5 ( 2 + d ) 3 y = − d 4 x + d 4 . 2 xdy − d 4 y là dạng 2 2 2 2 2 2 − 4 4
toàn phương có ma trận tương ứng A ( * ) = . Ma trận A( * )
có các định thức con chính 2 2 4 −4 − 4 4 A ( * ) = det(− ) 4 = −4 0, A ( * ) = det = 0 dL2 (x* , y* , * ) không xác định dấu. 1 2 2 2 4 − 4 2 2 2 (3) Khi (x, , y ) = (x*, y*, * ) = (− ) 1 , 1 , 2 3 3 3 2 * * * * 2 * * 2 2 2 d ( L x , y , ) = 4 dx + . 2 ( 2 + ) 3 dxdy + 5 ( 2 + d ) 3 y = d 4 x + d 8 . 2 xdy +1 d 6 y là dạng 3 3 3 3 3 3 4 8
toàn phương có ma trận tương ứng A ( * ) = . Ma trận A( * )
có các định thức con chính 3 3 8 16 4 8 A ( * ) = det( ) 4 = 4 0 , A ( * ) = det = 0 dL2(x *, y* , * ) không xác định dấu. 1 3 2 3 8 16 3 3 3 (4) Khi (x, , y ) = (x* , y* , * )= ( , 2 − ) 1 , 1 4 4 4 2 * * * * 2 * * 2 2 2 d L(x , y , ) = 4 dx + ( 2 . 2 + d ) 3 xdy + 5 ( 2 + ) 3 dy = d 4 x + d 8 . 2 xdy +1 d 6 y là dạng toàn 4 4 4 4 4 4 4 8
phương có ma trận tương ứng A(* ) = . Ma trận A( * )
có các định thức con chính 4 4 8 16 4 8 A ( * ) = det( ) 4 = 4 0, A ( * ) = det = 0 dL2 (x* , y* , * ) không xác định dấu. 1 4 2 4 8 16 4 4 4
Cả 4 dạng toàn phương dL2(x*, y*, * ) , dL2(x* , y* , * ) ,dL (2x *, y*, * ) ,dL2(x *, y* , * ) đều không 1 1 1 2 2 2 3 3 3 4 4 4
xác định dấu, do đó chúng ta phải thực hiện Bước 4.
Bước 4. Tính vi phân toàn phần cấp 1 của hàm số g(x,y) = (x + 2y)2 + (x – y)2 – 9 = 0 dg(x, ) y = g, (x, ) y dx + g, (x, ) y dy = 0 x y [ (x + 2 ) y 2 + (x − y)2 − ] 9 [ (x +2y)2 +(x − ) y 2 − ] 9 dx + dy = 0 ( 2 2x + ) y dx + ( 2 x + 5y)dy = 0 x y 2x + y dy = −
dx với x + 5y 0 , cả 4 điểm dừng (x*,y*) tìm được ở trên đều thỏa mãn điều x + 5y kiện này. 44 + Bây giờ, thay 2x y dy = −
dx vào biểu thức của vi phần toàn phần cấp 2 x + 5y 2 2 2 d ( L x, , y ) = 4dx + ( 2 . 2 + d ) 3 xdy + 5 ( 2 + d ) 3 y 2x +y 2x + y 2 2 d L(x, , y ) = 2 4 dx + ( 4 + ) 3 dx − dx + 5 ( 2 + ) 3 − dx = x+ 5y x +5y 2 2x + y 2x + y 2 4 − ( 4 + ) 3 + 5 ( 2 + ) 3 dx x 5 + y x +5y
dL2(x*, y*, * ) = dL2 (− , 1 − , 1 − ) 1 = −9dx2 0
dL2 (x* , y*,* ) = dL2 − ( ) 1 , 1 , 2 = 3 d 6 x 2 0 1 1 1 và 3 3 3
dL2(x* , y* ,* ) = dL2 − , 1 , 1 ( ) 1 = −9dx2 0
dL2(x*, y* , * ) = dL2( , 2 − ) 1 , 1 = 3 d 6 x 2 0 2 2 2 4 4 4 TT (x*, y*, * ) d2 ( L x*, y*, * ) Kết luận
Hàm số f(x,y) có cực đại địa phương tại điểm (− , 1 − ) 1 1 (− ,1− ,1− ) 1 Xác định âm và f = f (− , 1− ) 1 = [−1+ ( 2 − ) 1 2]2 − [−1− (− ) 1 ]2 = 9 cđ
Hàm số f(x,y) có cực đại địa phương tại điểm ) 1 , 1 ( và 2 ( ,1 , 1 − ) 1 Xác định âm f = f ) 1 , 1 ( = 1 ( + ) 1 . 2 2 − 1 ( − ) 1 2 = 9 cđ
Hàm số f(x,y) có cực tiểu địa phương tại điểm (− ) 1 , 2 và 3 (− ) 1 , 1 , 2
Xác định dương f = f(− )1 , 2 = ( 2 − + ) 1 . 2 2 −( 2 − − ) 1 2 = 9 − ct
Hàm số f(x,y) có cực tiểu địa phương tại điểm ( , 2 − ) 1 4 ( ,2− 1, 1 )
Xác định dương và f = f( ,2− )1 =[2+ (2− )1]2 −[2−(− )1]2 = 9 − ct
Nhận xét. Ở Ví dụ này, để giải bài toán, chúng ta thực hiện đủ cả 4 bước.
1.4.3. Giá trị nhỏ nhất và giá trị lớn nhấ t của hàm số
Một số khái niệm về miền đóng trong R2.
(1) Miền liên thông. Miền phẳng đóng DR2 được gọi là miền liên thông nếu chúng ta có thể nối 2
điểm bất kỳ thuộc D bằng một đường thẳng (hoặc/và) cong liên tục nằm hoàn toàn trong D.
(2) Miền đơn liên và miền đa liên. Miền liên thông được gọi là miền đơn liên nếu mọi đường cong
kín nằm hoàn toàn trong D đều bao bọc một miền nằm hoàn toàn trong D. Miền liên thông không đơn
liên được gọi là miền đa liên.
(3) Chiều dương của biên của miền liên thông D (đơn liên/đa liên) là chiều sao cho khi một người
đi trên biên của miền D theo chiều ấy sẽ thấy các điểm trong của miền D luôn luôn ở bên tay trái.
Định nghĩa. Cho hàm số z = f(x,y) xác định và liên tục trên miền đóng D(f)R2. Nếu f(x,y) f(x0,y0) với (
x,y)D(f) thì giá trị f(x0,y0) được gọi là Giá trị nhỏ nhất (GTNN) hay Giá trị cực tiểu toàn
cục của hàm số f(x,y) trên miền đóng D(f) và ký hiệu là GTNN(fD); còn nếu f(x,y) f(x0,y0) với
(x,y)D(f) thì giá trị f(x0,y0) được gọi là Giá trị lớn nhất (GTLN) hay Giá trị cực đại toàn cục của hàm
số f(x,y) trên miền đóng D(f) và ký hiệu là GTLN(fD). 45
Các nhà toán học đã chứng minh rằng: Mọi hàm số f(x1,x2,…,xn) xác định và liên tục trên miền
đóng D(f)Rn (nN*) đều tồn tại GTNN và GTLN trên D(f).
Bài toán. Tìm GTNN(fD) và GTLN(fD) của hàm số f(x1,x2,…,xn) xác định và liên tục trên miền đóng D(f)Rn.
Nếu chúng ta ký hiệu Dt {(x1,x2,…,xn) D(f) là
các điểm trong của D(f)} thì Dt là miền mở trong
Rn, còn ký hiệu Db {(x1,x2,…,xn) D(f)
là các điểm biên của D(f)} thì Db là k đường/mặt liên tục từng
khúc, khép kín tương ứng với k phương trình mô tả trong Rn là g (x , x ,..., x ) = 0(1 i k). i 1 2 n D D = D(f ) Rõ ràng là t b và chúng ta nhận thấy: D D = t b
(1) Nếu hàm số f(x1,x2,…,xn) có GTNN(fD) (và/hoặc) GTLN(fD) tại điểm nào đó thuộc Dt thì điểm
đó phải là điểm cực trị của hàm số f(x1,x2,…,xn) trên Dt, theo điều kiện cần của điểm cực trị, điểm đó phải là điểm dừng.
(2) Xét hàm số f(x1,x2,…,xn), khi đó, các điểm (x1,x2,…,xn) D
b là liên tục và có hai trường hợp xảy ra:
+ Trường hợp 1: Tại các điểm (x1,x2,…,xn) D
b chỉ thuộc một đường/mặt g (x ,x ,..., x ) = 0 (1 i 1 2 n
i k), khi đó, nếu hàm số có GTNN(fD) (và/hoặc) GTLN(fD) tại điểm nào đó thì điểm đó phải là điểm
cực trị của hàm số trên Db, theo điều kiện cần của điểm cực trị, điểm đó phải là điểm dừng.
+ Trường hợp 2: Tại các điểm (x1,x2,…,xn) D
b cùng thuộc ít nhất 2
đường/mặt g (x , x ,..., x ) = 0 , g (x , x ,..., x ) = 0 (1 i j k), khi đó, hàm số f(x i 1 2 n j 1 2 n 1,x2,…,xn) có thể
có GTNN(fD) (và/hoặc) GTLN(fD ) tại các điểm này.
Do đó, Bài toán tìm GTNN(fD) và GTLN(fD) của hàm số f(x1,x2,…,xn) xác định và liên tục trên
miền đóng D(f)Rn được thực hiện như sau:
Bước 1. Tìm các điểm cực trị của hàm số f(x1,x2,…,xn) trên Dt, sau đó tính giá trị của hàm số
f(x1,x2,…,xn) tại các điểm đó. Thực chất, đây là một phần (tìm các điểm cực trị và tính giá trị của hàm số
tại các điểm đó) của bài toán tìm cực trị không có điều kiện.
Bước 2. Tìm các điểm cực trị của hàm số f(x1,x2,…,xn) trên Db thỏa mãn từng điều kiện
g (x , x ,..., x ) = 0 (1 i
k), sau đó tính giá trị của hàm số f(x i 1 2 n
1,x2,…,xn) tại các điểm đó. Thực chất,
đây là một phần (tìm các điểm cực trị và tính giá trị của hàm số tại các điểm đó) của bài toán tìm cực trị có điều kiện.
Bước 3. Tính giá trị của hàm số f(x1,x2,…,xn) tại các điểm (x1,x2,…,xn) D
b cùng thuộc ít nhất 2
đường/mặt g (x , x ,..., x ) = 0 , g (x , x ,..., x ) = 0 (1 i j k). i 1 2 n j 1 2 n
Bước 4. Xác định GTNN(fD) = min{các giá trị của hàm số tìm được ở các Bước 1, 2 và 3} và xác
định GTLN(fD) = max{các giá trị của hàm số tìm được ở các Bước 1, 2 và 3}.
Khi giải Bài toán này trong R2, tức là tìm GTNN(fD) và GTLN(fD) của hàm số f(x,y) xác định và
liên tục trên miền đóng D(f)R2, chúng ta nhận thấy rằng:
(1) Nếu hàm số f(x,y) có GTNN(fD) (và/hoặc) GTLN(fD) tại điểm nào đó thuộc Dt thì điểm đó phải
là điểm cực trị của hàm số f(x,y) trên Dt, theo điều kiện cần của điểm cực trị, điểm đó phải là điểm dừng.
(2) Xét hàm số f(x,y) trên Db, khi đó, các điểm (x,y)Db là liên tục và có hai trường hợp sau đây. df [x, y(x)] df [x(y), y]
+ Trường hợp 1: Tại các điểm (x,y)Db tồn tại hoặc , khi đó Db là một dx dy
(nếu D(f) là đơn liên) hoặc nhiều (nếu D(f) là đa liên) đường cong liền nét, khép kín và trơn toàn bộ hoặc
trơn từng khúc. Khi đó, nếu hàm số có GTNN(fD) (và/hoặc) GTLN(fD) tại điểm nào thì điểm đó phải là
điểm cực trị của hàm số trên Db, theo điều kiện cần của điểm cực trị, điểm đó phải là điểm dừng. 46 df [x, y(x)] df [x(y), y]
+ Trường hợp 2: Nếu ngoài các điểm (x,y)Db tồn tại hoặc , còn có một dx dy df [x, y(x)] df [x(y), y]
số hữu hạn các điểm (x,y)Db mà tại đó, không tồn tại hoặc . Khi đó, hàm số dx dy
f(x,y) có thể có GTNN(fD) (và/hoặc) GTLN(fD) tại các điểm này.
Chú ý. (1) Cần vẽ đồ thị miền đóng D(f); (2) Tại các điểm dừng thuộc Dt hoặc Db, chúng ta không
cần phải xác định rõ điểm nào là điểm cực đại hay là điểm cực tiểu của hàm số, mà chỉ tính giá trị của df [x, y(x)] df [x(y), y]
hàm số; (3) Tại các điểm (x,y) thuộc Db mà tại đó, không tồn tại hoặc , chúng ta dx dy
tính giá trị của hàm số f(x,y).
Như vậy, để tìm GTNN(fD) và GTLN(fD) của hàm số z = f(x,y) xác định và liên tục trên miền đóng
D(f)R2, chúng ta thực hiện các bước sau đây: Bước 1. Vẽ đồ thị miền đóng D(f) = DtDb đã cho.
Bước 2. Tìm các điểm dừng thuộc D
t (nếu có) và tính giá trị của hà
m số f(x,y) tại các điểm này.
Bước 3. Tìm các điểm dừng thuộc D
b (nếu có) và tính giá trị của hà
m số f(x,y) tại các điểm này. Bước 4. df [x, y(x)]
Tính giá trị của hàm số f(x,y) tại các điểm thuộc Db mà tại đó, không tồn tại dx hoặc df [x(y), y] . dy
Bước 5. Xác định GTNN(fD) = min{các giá trị của hàm số tìm được ở các Bước 2, 3, 4} và xác
định GTLN(fD) = max{các giá trị của hàm số tìm được ở các Bước 2, 3, 4}.
Ví dụ 1.31. Tìm GTLN(f 2
D) và GTNN(fD) của hàm số 2
z = f (x, y) = x − y trên miền đóng D(f) là
hình tròn có tâm tại điểm O(0,0) và bán kính r = 2. Bài giải. Chúng ta có D 2 2
t = {(x,y)R2|x2 + y < 4}, Db = {(x,y)R2|x2 + y = 4} và đồ thị của D(f) là Cách 1.
Bước 1. Tìm các điểm cực trị của hàm số 2 2 f (x, y) = x − y trên D 2
t = {(x,y)R2|x2 + y < 4} và tính
giá trị của hàm số f(x,y) tại các điểm này. (x2 , − 2 f (x, y) = y ) =2x x x Chúng ta có
, các điểm cực trị (nếu có) là nghiệm của hệ phương trình 2 2 , (x − f (x, y) = y ) = − 2y y y 2 x = 0 f , (x, y) = 0 x 2 y = 0 (x, y) = ) 0 , 0 ( D f ( ) 0 , 0 = (x2 − y2) = 02 − 02 = 0 . f , (x, ) y = 0 t (x,y)= (0,0) y ( x, y) D t
Bước 2. Tìm các điểm cực trị của hàm số 2 2
f (x, y) = x − y với điều kiện x2 + y2 = 4 và tính giá trị
của hàm số f(x,y) tại các điểm này.
Điều kiện ràng buộc giữa các biến x, y là g(x,y) = x2 + y2 – 4 = 0. 47
Lập hàm số Lagrange L(x,y,) = f(x,y) + g(x,y) = x2 – y2 + (x2 + y2 – 4) L, (x, , y ) = f , (x, ) y + g, (x, y) = 2x + 2 x x x x Chúng ta có L, (x, ,
y ) = f , (x, y) + g, (x, y) = −2y + 2 y y y y L, 2 2 (x, , y ) = g(x, y) = x + y − 4 L, (x, , y ) = 0 x 2x +2x =0 1 ( + )x = 0 Hệ phương trình L, (x, , y ) = 0 2y − 2 y = 0 có 4 nghiệm y 1 ( − )y = 0 2 2 2 2 L, (x, , y ) 0 x y 4 0 x y 4 = + − = + = f(− 0 , 2 ) = (x 2 − y2) = (− ) 2 2 − 02 = 4 (x*, y*, * ) = (− , 2 , 0 − ) 1 (x ,y = ) (−2,0) 1 1 1 2 2 2 2 (x*, y* , * ) = ( , 2 , 0 − ) 1 2 2 2 f ( ) 0 , 2 = (x − y ) = 2 − 0 = 4 (x ,y) =( 2,0) (x*3 , y*3 , *3 ) = , 0 ( − ) 1 , 2 f , 0 ( − ) 2 = (x 2 − y 2) = 02 − (−2)2 = −4 * * * (x ,y = ) (0,−2) (x , y , ) = , 0 ( ) 1 , 2 4 4 4 f , 0 ( ) 2 = (x 2 − y2) = 02 − 22 = − 4 ( x,y) =(0,2) Bước 3. GTNN f ( ) = min{ , 0 , 4 , 4 − , 4 − ) 4 = 4
− tại các điểm (x,y) = (0,2) D và GTLN f ( ) = max{ , 0 , 4 , 4 − , 4 − )
4 = 4 tại các điểm (x,y) = (2,0). D Cách 2.
Bước 1. Miền đóng D(f) là hình tròn có tâm tại điểm O(0,0) và bán kính r = 2 f ' (x, y) = 2x = 0
Bước 2. Chúng ta có hệ phương trình x
để xác định các điểm dừng thuộc các ' f (x, y) = −2y = 0 y
điểm trong của D(f). Hệ phương trình này có nghiệm (x,y) = (0,0), suy ra hàm số f(x,y) có điểm dừng (x , y ) = , 0 ( )
0 thuộc các điểm trong của D(f). Giá trị của hàm số f(x,y) tại điểm dừng này là 1 1 f ( , 0 0) = (x2 − y2 ) = 02 − 02 = 0. (x ,y)= (0,0)
Bây giờ, chúng ta xét các điểm trên biên của D(f), tức là các điểm (x,y) nằm trên đường tròn x2 + y2 = 22 2
y = 4 − x với –2 x 2. Khi đó f (x, )
y = f (x, 4 − x2 ) = x2 − ( 4 − x 2 )2 = 2x 2 − 4 g(x)với –2 x 2 4 khi x = −2
g(x) = 2x 2 −4 khi −2 x 2 4 khi x = 2
Bước 3. Các điểm trong trên biên của D(f) thuộc đường tròn x2 + y2 = 4 (–2 < x < 2)
Chúng ta có g’(x) = 4x g’(x) = 0 4x = 0 x = 0 y = 2, suy ra hàm số f(x,y) có 2 điểm dừng(x , y ) = , 0 ( − ) 2 , (x , y ) = ( , 0 )
2 thuộc các điểm trong trên biên của D(f). Giá trị của hàm số tại các 2 2 3 3 f − , 0 ( ) 2 = (x2 − y2 ) = 02 − − ( ) 2 2 = − 4 điểm dừng này là ( x,y = ) (0,−2) . f ( , 0 ) 2 = (x2 − y2 ) = 02 −22 = − 4 ( x,y) =(0,2) Bước 4. Chúng ta có g(x) − g(−2) (2x2 − ) 4 − 4 x2 − g'(−2 + ) 0 = lim = lim = 4 2 lim = 2 lim (x − ) 2 = −8 x →−2 +0 x− − x →−2 + ( ) 2 0 x + x→− + 2 2 0 x + → x − + 2 2 0 , tuy g(x) − g(2) (2x 2 − ) 4 − 4 x2 − 4 g'(2 − ) 0 = lim = lim = 2 lim = 2 lim (x + ) 2 = 8 x →2−0 x − x →2 − 2 0 x − x →2 − 2 0 x − x →2 − 2 0 nhiên g’(– –0) 2
và g’(2+0) không tồn tại vì –2 x 2, nên tại x = 2 không tồn tại g’(x) vì tại mỗi điểm 48
chỉ có đạo hàm một phía, tức là tại các điểm df [x, y(x)] (x , y ) = (− ) 0 , 2 , (x , y ) = ) 0 , 2 ( không tồn tại 4 4 5 5 dx với 2 y = ( y x) = 4 − x . f − ( ) 0 , 2 = (x2 − y2 ) = − ( ) 2 2 − 02 = 4
Giá trị của hàm số tại các điểm này là (x ,y) =( −2,0) f ( , 2 ) 0 = (x 2 − y2) =2 2 −0 2 = 4 (x ,y = ) (2,0) Bước 5. GTNN f ( ) = min − −
= − tại các điểm(0,2) D ,0 , 4 , 4 , 4 4 4 và GTNN(f ) = ma x , 0 − , 4 − , 4 4 , 4 = 4 tại các điểm ( , 2 0) . D
Ví dụ 1.32. Tìm GTLN(f 2
D) và GTNN(fD) của hàm số z = f(x,y) = x + y2 – xy + x + y trên miền
đóng D(f) là tam giác được tạo bởi các đườn
thẳng x = 0, y = 0 và x + y + g 3 = 0.
Bài giải. Chúng ta có Dt là các điểm trong của AOB các đỉnh A(–3,0), O(0,0) và B(0, 3) – , có
phương trình các cạnh AO, OB và AB tương ứng là y = 0 (–3 x 0), x = 0 (–3 y 0) và y = –x – 3 (–
3 x 0); còn Db là các điểm nằm trên các cạnh AO, OB và AB. Đồ thị của D(f) là Cách 1.
Bước 1. Tìm các điểm cực trị của hàm số f (x, )
y = x2 + y2 − xy + x + y trên miền mở Dt và tính giá
trị của hàm số f(x,y) tại các điểm này. , (x2 + y2 − xy + x + y) f (x, y) = = 2x − y +1 x x Chúng ta có 2 2 , (x + y − xy + x + f (x, y) = y) = 2y − x +1 y y
Điểm cực trị (nếu có) là nghiệm của hệ phương trình − + = , 2x y 1 0 f (x, ) y = 0 x
2y − x + 1= 0 (x, y) = (− ,1− ) 1 D , t f (x, ) y = 0 y ( x, y) Dt f ( − , 1 − ) 1 =(x 2 + y 2 −xy +x +y) =( − ) 1 2 +( − ) 1 2 −( − ) 1 ( − ) 1 1 − 1 − = 1 − . (x,y) ( = − , 1 1 − )
Bước 2. Tìm các điểm cực trị của hàm số f (x, )
y = x2 + y2 − xy + x + y với các điều kiện y = 0 (–3 < x < 0), x = 0 ( 3 – < y < 0) và y = x –
– 3 (–3 < x < 0) trên các cạnh AO, OB và AB tương ứng. Sau đó,
tính giá trị của hàm số f(x,y) tại các điểm này. + Trên cạnh AO:
Điều kiện ràng buộc giữa các biến x, y là g1(x,y) = y = 0 (–3 < x < 0).
Lập hàm số Lagrange L(x, , y ) = f (x, ) y + g (x, )
y = x 2 + y2 − xy + x + y + y 1 , , g (x, y) 1 L (x, , y ) = f (x, y) + = 2x − y + 1 x x x g (x, y)
Chúng ta có L, (x, y, ) = f , (x, y) + 1 = 2y − x +1 + y y y L, (x, , y ) = g (x, y) = y 1 49 L, (x, , y ) = 0 x 2x − y +1 = 0 , x = −1 2 L (x, , y ) = 0 y 2y − x +1 + = 0 Hệ phương trình y = 0 L, (x, , y ) = y 0 0 = = − 3 2 − 3 x 0 − 3 x 0 1 2 2 1 2 2 1 1 1 f− 0 , = (x + y − xy + x + y) = − + − − − + = − 1 0 0 . 0 . 2 ( x,y) = − ,0 2 2 2 2 4 + Trên cạnh OB:
Điều kiện ràng buộc giữa các biến x, y là g2(x,y) = x = 0 (–3 y 0).
Lập hàm số Lagrange L(x, , y ) = f (x, ) y + g (x, )
y = x 2 + y2 − xy + x + y + x 1 , , g (x, y) 2 L (x, , y ) = f (x, y) + = 2x − y +1+ x x x , , g (x, y) Chúng ta có L (x, , y ) = f (x, y) + 2 = 2y − x + 1 y y y
L,(x,y, ) =g (x,y) = x 2 L, (x, , y ) = 0 x 2x − y +1 + = 0 x = , 0 L (x, , y ) = 0 y 2y − x +1 = 0 Hệ phương trình y = −1 2 , x 0 L (x, , y ) = 0 = = − 3 2 − 3 y 0 − 3 y 0 1 2 2 1 2 2 1 1 1 f ,
0 − = (x + y − xy + x + y) =
+ − − − + − = − 1 0 . 0 0 . 2 ( x,y)= 0, − 2 2 2 2 4 + Trên cạnh AB:
Điều kiện ràng buộc giữa các biến x, y là g3(x,y) = x + y + 3 = 0 (–3 x 0 và –3 y 0). Lập hàm số Lagrange ( L , x , y ) = f (x, ) y + g ( , x )
y = x2 + y2 − xy + x + y + (x + y + ) 3 3 g (x, y) , , 3 L (x, , y ) = f (x, y) + = 2x − y +1 + x x x , , g (x, y) Chúng ta có L (x, , y ) = f (x, y) + 3 = 2y − x +1 + y y y
L, (x, y, ) = g (x, y) = x + y + 3 3 L, (x, , y ) = 0 x 2x − y +1 + = 1 0 , x = − L (x, , y ) = 0 y 2y − x +1 + = 0 2 , Hệ phương trình 1 L(x, , y ) = 0 x + y +3 = 0 y = − 2 − 3 x 0 − 3 x 0 1 − 3 y 0 − 3 y 0 = − 2 2 2 1 1 2 2 1 1 1 1 1 1 3
f− ,− = (x + y − xy + x + y) = −
+ − − − − − − = − . 2 2 1 1 (x,y)= − , − 2 2 2 2 2 2 4 2 2
Bước 3. Tính giá trị của hàm số f(x,y) = x2 + y2 – xy + x + y tại các đỉnh A(–3,0), O(0,0) và B(0,–
3) của AOB (tọa độ của mỗi đỉnh đồng thời thỏa mãn phương trình của 2 cạnh liền kề tương ứng). 50 f − ( 0 , 3 ) = (x2 + y2 − xy + x + y) = − ( ) 3 2 + 02 − − ( ) 3 0 . − 3+ 0 = 6 ( x,y) =( −3,0) f 0 , 0 ( ) = (x2 + y2 − xy + x + y) = 02 + 02 − . 0 0+ 0+ 0 = 0 (x ,y) =(0,0) f − , 0 ( ) 3 = (x2 + y2 − xy + x + y) = 02 + − ( ) 3 2 − . 0 − ( ) 3 + 0− 3 = 6 ( x,y = ) (0,−3) Bước 4. GTNN(f ) = mi n − , 1 −1 4, −1 4, − 3 4, , 6 6 , 0 = 1 − tại điểm (− , 1 − ) 1 D và GTLN f ( ) = max− , 1 −1 4 , −1 4, − 3 4, 6 , 0 , 6
= 6 tại các điểm (–3,0), (0,–3). D Cách 2.
Bước 1. Miền đóng D(f) là AOB (miền đơn liên có biên trơn từng khúc) có các đỉnh A(–3,0), O(0,0) và B(0,–3)
f ' (x, y) = 2x − y + 1 = 0
Bước 2. Chúng ta có hệ phương trình x
để xác định các điểm dừng thuộc ' f (x, y) = 2y − x + 1 = 0 y
các điểm trong của D(f). Hệ phương trình này có nghiệm là (− , 1 − )
1 nên hàm số f(x,y) có điểm dừng (x , y ) = (− , 1 − )
1 là điểm trong của D(f). 1 1 f (x , y ) = f (− , 1 − ) 1 = (x2 + y2 − xy + x + y) = (− ) 1 2 + (− ) 1 2 − (− ) 1 (− ) 1 −1−1 = −1. 1 1 (x ,y) ( = − , 1 1 − )
Bước 3. Các điểm trong trên biên của D(f) là các điểm nằm trên các cạnh AO, OB và BA của
AOB, không kể các đỉnh A(–3,0), O(0,0), B(0,–3).
– Các điểm trong trên cạnh AO có phương trình y = 0 với –3 < x < 0 ứng với hàm số f(x,0) = x2 + x
g(x) với –3 < x < 0. Chúng ta có g’(x) = 2x + 1, nên điểm dừng là nghiệm của phương trình g’(x) = 0.
Phương trình g’(x) = 0 2x + 1 = 0 có nghiệm x = −1 2 , trong trường hợp này, hàm số f(x,y) có điểm dừng(x ,y ) = (−1 2, ) 0 . 2 2 1 2 2 1 2 2 1 1 1
f (x , y ) = f− ,0 = (x + y − xy + x + y) = − + − − 1 0 0 . − + 0 = − . 2 2 2 (x ,y) = − ,0 2 2 2 2 4
– Các điểm trong trên cạnh OB có phương trình x = 0 với –3 < y < 0 ứng với hàm số f(0,y) = y2 + y
h(y) với –3 < y < 0. Chúng ta có h’(y) = 2y + 1, nên điểm dừng là nghiệm của phương trình h’(y) = 0.
Phương trình h’(y) = 0 2y + 1 = 0 có nghiệm y = −1 2 , trong trường hợp này, hàm số f(x,y) có điểm dừng(x , y ) = , 0 ( −1 ) 2 . 3 3 1 2 2 1 2 2 1 1 1 f (x , y ) = f ,
0 − = (x + y − xy + x + y) = +
− − − + − = − . 3 3 1 0 0. 0 2 (x,y)= 0, − 2 2 2 2 4
– Các điểm trong trên cạnh BA có phương trình y = – –
x 3 với –3 < x < 0 ứng với hàm số f(x,–x –
3) = 3x2 + 9x + 6 k(x) với –3 < x < 0. Chúng ta có k’(x) = 6x + 9, nên điểm dừng là nghiệm của
phương trình k’(x) = 0. Phương trình k’(x) = 0 6x + 9 = 0 có nghiệm x = − 3 2 , trong trường hợp này,
hàm số f(x,y) có điểm dừng(x , y ) = (−3 2,−3 ) 2 . 4 4 3 3 f (x , y ) = f , (x y xy x y) 4 4 − − = 2 + 2 − + + 3 3 = 2 2 (x ,y) = − , − 2 2 3 2 3 2 3 3 3 3 3
− + − − − − − − = − . 2 2 2 2 2 2 4
Bước 4. Các đỉnh A(–3,0), O(0,0), B(0,–3) của tam giác AOB là các điểm trên biên của D(f) mà tại df [x, y(x)] đấy, không tồn tại
. Tính giá trị của hàm số f(x,y) tại các điểm này, chúng ta được: dx 51 f −( 0, 3 )= (x2 + y2 − xy+ x+ y) = − ( ) 3 2 + 02 − − ( ) 3 . − 0 + 3 0= 6 ( x,y) =( −3,0) f 0 , 0 ( ) = (x2 + y2 − xy + x + y) = 02 + 02 − . 0 0+ 0+ 0 = 0 (x ,y) =(0,0) f − , 0 ( ) 3 = (x2 + y2 − xy+ x+ y) = 02 + − ( ) 3 2 − . 0 − ( + ) 3 − 0 3= 6 ( x,y = ) (0,−3) Bước 5. GTNN(f ) = mi n − , 1 −1 4, −1 4, − 3 4, , 6 6 , 0 = 1 − tại điểm (− , 1 − ) 1 D và GTLN f ( ) = max− , 1 −1 4 , −1 4, − 3 4, 6 , 0 , 6
= 6 tại các điểm (–3,0), (0,–3). D
1.5. Ứng dụng của phép tính vi phân trong hình học
1.5.1. Đường và tiếp tuyến của đường 1.5.1.1.
Đường và tiếp tuyến của đường trong mặt phẳng
Ở Trường THPT chúng ta đã biết rằng, trong hệ tọa độ Descartes vuông góc Oxy, nếu đường L là
đồ thị của hàm số y = f(x) thì phương trình tiếp tuyến tại điểm M0(x0,y0)L là y – y0 = f’(x 0) (x – x0). Tuy
nhiên, không phải khi nào đường L cũng được biểu diễn bằng hàm số y = f(x), mà trong trường hợp tổng
quát, đường L được biểu diễn, nói chung bằng phương trình f(x,y) = 0. Điểm M , , 0(x0,y0) L được gọi
là điểm chính quy nếu f (x , y ) và f (x , y ) không đồng thời bằng x 0 0 y 0 0
không, được gọi là điểm kỳ dị nếu f , (x , y ) và f , (x , y ) đồng thời bằng không. x 0 0 y 0 0
Giả sử điểm M0(x0,y0) là một điểm chính quy của đường L, khi đó phương trình tiếp tuyến của đường L tại điểm M , ,
0 là (x − x )f (x , y ) + (y − y f ) (x , y ) = 0 . 0 x 0 0 0 y 0 0 x = x(t)
Nếu đường L được cho dưới dạng tham số
với t , trong đó x(t), y(t) là các hàm số y = y(t)
liên tục và có các đạo hàm x’(t), y’(t) trên [,] và các đạo hàm này không đồng thời bằng 0 tại mỗi điểm x = x(t ) x − x y − y t[ ,
] thì phương trình tiếp tuyến của đường L tại điểm M 0 0 0 0 0(x0,y0) với là = . y = ( y t ) x'(t 0) y'(t0 ) 0 0 x2 y2
Ví dụ 1.33. Viết phương trình tiếp tuyến với đường ellip +
= 1 (a > 0, b > 0) tại điểm a2 b2
M0(x0,y0) nằm trên đường ellip. Bài giải.
Chúng ta giải bài toán này bằng 2 cách. x2 y2
Cách 1. Viết phương trình biểu diễn đường ellip dưới dạng f (x, y) = + − 1 = 0 a 2 b2 2 2 x y 2x 2x 2x , f (x, y) = 1 f (x , y ) x + − = , 0 2 2 2 = = x 0 0 2 2 x a b a a a (x ,y = ) ( x ,y ) 0 0 x y 2y 2y 2y , 2 2 f (x, y) = + −1 = , f (x , y ) = = 0 y 2 2 2 y 0 0 2 2 y a b b a b (x,y) =( x ,y ) 0 0 x2 y2 Vì điểm M 0 0
0(x0,y0) nằm trên đường ellip nên nó thỏa mãn phương trình + = 1, suy ra x0 và y0 a2 b2
không đồng thời bằng không, tức là , 2x 2y 0 f (x , y ) = , , 0 f (x , y ) =
không đồng thời bằng không, do x 0 0 2 a y 0 0 2 b
đó điểm M0(x0,y0) là điểm chính quy.
Vì M0(x0,y0) là điểm chính quy nên theo định nghĩa, phương trình tiếp tuyến với đường ellip tại
điểm M0(x0,y0) nằm trên đường ellip là 2x 2y
(x − x )f , (x , y ) + (y − y )f , (x , y ) = (x − x ) 0 + (y − y ) 0 = 0 x 0 0 0 y 0 0 0 2 0 0 a b2 52 2 2 2 2 x x y y x y x y x y x2 y2 x y 0 0 0 0 0 0 0 0 2 + − 2 + = 0 x + y = + vì 0 0 + = 1 0 x 0 + y =1 là 2 2 2 2 2 2 2 2 a b a b a b a b a2 b2 a 2 b2
phương trình đường tiếp tuyến cần tìm. x2 y2 x =x( ) =a cos
Cách 2. Phương trình tham số của đường ellip + = 1 là với 0 2, a2 b2 y = y( ) =bsin x = x ( ) x − x y − y
khi đó phương trình tiếp tuyến của đường ellip tại điểm M 0 0 0 0 0(x0,y0) với là = y = y ( ) x'( 0 ) y'( 0 ) 0 0 Chúng ta có d(a cos ) x' ( )= = −a sin x' ( ) = − a sin = −a = − a sin (b sin = − ay ) 0 d 0 = 0 0 0 b b d(b sin ) y'() = = b cos b bx0 y'( ) =b cos =b cos = a ( cos ) = d 0 = 0 0 a 0 a x − x y − y bx ay 0 = 0 0 (x − x ) = −
0 (y− y ) b2x (x− x )= − a2 y (y− y ) 0 0 0 0 0 0 − ay bx 0 0 a b b a 2 b x x − 2 2 b x = − 2 a y y + 2 2 a y 2 b x x + 2 a y y = 2 2 a y + 2 2 b x 0 0 0 0 0 0 0 0 2 2 2 2 2 2 2 2 b x x + a y y a y + b x x y x y x2 y2 x y 0 0 0 0 0 0 0 0 = x + y = + vì 0 0 + = 1 0 x 0 + y =1 là 2 2 2 2 2 2 2 2 a b a b a b a b a2 b2 a 2 b2
phương trình đường tiếp tuyến cần tìm.
1.5.1.2. Đường và tiếp tuyến của đường trong không gian
Trong hệ tọa độ Descartes vuông góc Oxyz, đường L thường được cho dưới dạng tham số x = x(t) y = y(t) với t
, trong đó x(t), y(t), z(t) là các hàm số liên tục và có các đạo hàm x’(t), y’(t), z’(t) z = z(t)
trên [,] và các đạo hàm này không đồng thời bằng 0 tại mỗi điểm t[ ,
] thì phương trình tiếp tuyến x = 0 x(t0 ) − − −
của đường L tại điểm x x y y z z M 0 0 0 0(x0,y0,z0) với y = y(t ) là = = . 0 0 x' (t 0 ) y' (t 0 ) z' (t 0 ) z = z(t ) 0 0
Ví dụ 1.34. Viết phương trình tiếp tuyến của đường L trong không gian R3 được cho dưới dạng x = x(t) = t
tham số y = y(t) = 2t với –3 t 10 tại điểm (x 0,y0,z0) ứng với t0 = 3. z = z(t) = 3 t x = x(t ) = x ) 3 ( = 3 x'(t) = t'= 1 x' ) 3 ( = 0 0 1 2
Bài giải. Chúng ta có y = y(t ) = y ) 3
( = 32 = 9 và y'(t) = (t )'= 2t y' ) 3 ( = 3 . 2 = 6 do đó 0 0 3 2 z = z(t ) = z ) 3 ( = 33 = 27 z'(t) = (t ) = ' 3t z' ) 3 ( = 3 . 3 2 = 27 0 0 x − x y − y z − z x − 3 y − 9 z − 27
phương trình tiếp tuyến của đường L là 0 0 0 = = = = . x' (t ) y' (t ) z' (t ) 1 6 27 0 0 0
1.5.2. Mặt và tiếp tuyến của mặt, mặt phẳng tiếp xúc
Trong hệ tọa độ Descartes vuông góc Oxyz, mặt S được biểu diễn bởi phương trình f(x,y,z) = 0. Giả sử M0(x0,y0,z0) S,
khi đó đường thẳng M0T được gọi là tiếp tuyến của mặt S tại điểm M0 nếu nó là
tiếp tuyến của một đường nào đó trên mặt S tại điểm M0. Tại mỗi điểm M0 trên mặt S, nói chung có vô số
đường thuộc mặt S đi qua, do đó tại điểm M0 có thể có vô số tiếp tuyến của mặt S. 53 Điểm M , , 0(x0,y0,z0) S
được gọi là điểm chính quy nếu f (x , y ,z ) , f (x , y , z ) và x 0 0 0 y 0 0 0
f ,(x , y ,z ) không đồng thời bằng 0, được gọi là điểm kỳ dị nếu f , (x ,y ,z ) , f ,(x , y , z ) và z 0 0 0 x 0 0 0 y 0 0 0
f ,(x , y ,z ) đồng thời bằng 0. z 0 0 0
Định lý. Tập hợp tất cả các tiếp tuyến của mặt S tại một điểm chính quy M0(x0,y0,z0)S là một mặt phẳng đi qua điểm M0.
Định nghĩa. Mặt phẳng chứa mọi tiếp tuyến của mặt S tại điểm M0 S
được gọi là mặt phẳng tiếp
xúc của mặt S tại điểm M0.
Phương trình của mặt phẳng tiếp xúc của mặt S được biểu diễn bởi phương trình f(x,y,z) = 0 tại
điểm chính quy M0(x0,y0,z0)S là f , − + − + − = x (x , y , z )(x
x ) f ,(x , y , z )(y y ) f ,(x , y , z ) z ( z ) 0 0 0 0 0 y 0 0 0 0 z 0 0 0 0
Ví dụ 1.35. Viết phương trình của mặt phẳng tiếp xúc của mặt S được cho bởi phương trình x2 –
4y2 + 2z2 = 6 tại điểm M0(2,2,3).
Bài giải. Viết phương trình của mặt S dưới dạng f (x, , y z) = x 2 − 4y2 + z 2 2 − 6 = 0 . Vì f ( , 2 , 2 ) 3 = (x2 − 4y2 + 2z2 − 6) = 22 − .
4 22 + 2.32 − 6 = 0 nên điểm M0(2,2,3) thuộc (x ,y,z )=(2,2,3) mặt S. , f , ( , 2 ) 3 , 2 = 2x = . 2 2 = f (x, , y z) = 4 2x x x (x ,y,z = ) (22,3) ,
Chúng ta có f (x, y, z) = −8y y f, ( , 2 ) 3 , 2 = −8y = − 2 . 8 = − 16 y (x ,y,z)=(22,3) f ,(x, , y z) = 4z z , f ( , 2 ) 3 , 2 = 4z = 4 3 . = 12 z (x ,y,z)=(22,3) Vì f , ( ) 3 , 2 , 2 = 4 0 , f , ( , 2 ) 3 , 2 = −16 0 và f , ( , 2 ) 3 , 2 = 12 0 nên điểm M x y z 0(2,2,3) là điểm chính quy của mặt f (x, , y z) = x 2 − 4y2 + z
2 2 − 6 = 0 nên theo định nghĩa, phương trình của mặt phẳng tiếp xúc
với mặt S tại điểm M0(2,2,3) là f , ( , 2 ) 3 , 2 (x − ) 2 + f , ( , 2 ) 3 , 2 (y − ) 2 + f , ( , 2 ) 3 , 2 z ( − ) 3 = 0 x y z 4(x − ) 2 − 1 ( 6 y − 2) + 1 ( 2 z − ) 3 = 0 x − 4y + z 3 − 3 = 0. Bài tập
1.1. Tìm và vẽ đồ thị tập xác định của các hàm số sau đây (a) z = f(x,y) = ln(xy) (b) z = f (x, y) = 1 x + y +1 x − y
(c) z = f (x, y) = 4 − x2 − y2 + x2 + y2 −1 (d) z = f ( , x ) y = arcsin ( [ y − ) 1 x] (e) z = f (x, y) = x ln y (f) z = f (x, ) y =1 (y x2 − )
(g) z = f (x, y) = y − x ln(y + x)
(h) z= f(x,y) = lnx + ln(siny) (i) z = f ( , x ) y x cos2 = y 1.2. Tìm lim
f (x, y) của các hàm số sau đây (x,y) ( → 0,0)
(a) z = f (x, y) = x arctan(y x) (b) z = f (x, ) y = (x3 + y3) (x2 + y2 ) 1 + x2 + y2 1 (c) z = f (x, y) = 1 ( − cosy) (d) z = f (x, y) = y cos y2 y − x −1 2 2 2 2 x y + xy (e) 2 2 x + y z = f (x, y) = (cos x + y ) (f) z = f (x, y) = 2 2 x − xy + y
(g) z = f (x, y) = x2 ln(x2 + y2 )
1.3. Chứng minh rằng, đối với các hàm số f(x,y) sau đây, không tồn tại lim f (x, y) (x ,y) ( → 0,0) 54 2 xy x − y +x 2 + y2 (a) z = f (x, y) = (b) z = f (x, y) = 2 4 x + y x + y 1 (x + ) y cos x ( + y) (c) z = f (x, y) = (1+ xy) 2 2 x +y (d) z = f (x, y) = sin x ( − y) x sin y +y sin x y ln x ( + e ) (e) z = f (x, y) = (f) z = f (x, y) = 2 2 x + y 2 2 x + y 2 2 2 2 x + 2x y + x y
1.4. Chứng minh rằng, hàm số f (x, y) =
không có giới hạn tại điểm (0,–1) (đề thi Giải 4 4 x + (y + ) 1
tích 2 năm học 2019-2020). m x y m 1
1.5. Cho hàm số f (x, y) =
với x > 0 và tham số m > 0. Tìm lim f (x, y) khi (đề 2 2 2x + y (x ,y) (0+ → ,0) 0 m 1
thi Giải tích 2 năm học 2020-2021).
1.6. Tìm các giới hạn sau đây 2 sin(xy) (a) 2 lim (b) x + xy lim 1 ( + xy) (x ,y)→(0,3) x (x,y) ( → 0,2) 2 x xy (c) 2 2 − ( x+ y) lim (x + y ) (d) lim 2 2 (x,y)→(+ ,+ ) (x ,y) ( → +, +) x + y x + y (e) lim (f) 2 2 − ( x+ y) lim (x + y e ) 2 2
(x ,y)→(+ ,+ ) x − xy + y (x,y) ( → +, +) 2 2 2 2 x + y + 6 + x + y (g) lim ( x,y)→( , ) 6 4 4 2 2 2 2 x + y + 1 ( 2 + x y ) − x + y
1.7. Chứng minh rằng, các hàm số f(x,y) sau đây, liên tục trên tập xác định D(f) của nó 2 2 1 (x + y )sin khi (x, y) ( , 0 ) 0 (a) z = f (x, y) = x2 + y2 0 khi (x, ) y =( , 0 ) 0 x3 − 3 y khi (x, y) ( , 0 ) 0 (b) z = f (x, y) = x2 + y2 0 khi (x, ) y = ( , 0 ) 0 x arctan (y x) 2 khi (x, ) y ( , 0 ) 0 (c) z = f (x, y) = 0 khi (x, ) y = ( , 0 ) 0 x sin y− ysin x khi (x, y) ( , 0 ) 0 (d) z = f (x, y) = x 2 + y2 0 khi (x, y) = ( , 0 ) 0
1.8. Khảo sát sự liên tục tại điểm gốc tọa độ O(0,0) của các hàm số f(x,y) sau đây x sin 1 ( x) + y khi (x, y) ( , 0 ) 0 (a) z = f (x, y) = x + y 0 khi (x, y) = ( , 0 ) 0 x3 −xy2 khi x 2 +y 2 0 (b) z = f (x, y) = x2 + y2 a khi x 2 + y 2 = 0
1.9. Khảo sát sự liên tục của các hàm số f(x,y) sau đây, trên tập xác định D(f) của nó 55 2 x y khi (x, y) ( , 0 ) 0 (a) z = f (x, y) = x4 + y2 0 khi (x, ) y = ( , 0 ) 0 −1 2 2 x y (b) z = f (x, y) e khi xy = 0 0 khi xy = 0 1.10.
Có thể chọn p để mỗi hàm số sau đây, liên tục tại điểm (0,0) được không? x2 + 2 e y − x2 − xy+ 2 1 y khi (x, ) y khi (x, y) ( , 0 ) 0 (a) f (x, y) = ( , 0 ) 0 x2 + y2 (b) f (x, y) = x2 + xy+ y2 p khi (x, y) = ( , 0 ) 0 p khi (x, y) = ( , 0 ) 0
1.11. Tính các đạo hàm riêng cấp 1 và cấp 2 của hàm số f(x,y) = xxy (x > 0). f
(x(u, v),y(u, v) ) f (x(u, ) v , y(u, v) )
1.12. Tính các đạo hàm riêng ,
của các hàm số sau đây u v x = x(u, ) v = cosu 2 2 (a) x 2 − y z = f (x, y) = e với y = y(u, v) = 2 u + 2 v x = x(u, v) = uv (b) z = f (x, ) y = ln(x2 + y2 ) với y = y(u, ) v = u v x = x(u, ) v = eu (c) y −x z = f (x, y) = xe + ye với y= y(u,v)= u2v x = x(u, v) = u v (d) z = f (x, ) y x2 = ln y với y = ( y u, v) = u 3 − 2v dz 1.13. Tính
của hàm số z = f(x,y) = exlny với y = x2 dx dz x(t) =t2 −3t +1 1.14. Tính
của hàm số z = f(x,y) = x2y với dt y(t) = sin t
1.15. Chứng minh rằng y y
(a) Hàm số z = f (x, y) = y x sin thỏa mãn phương trình x2z, + xyz, = yz . x x y (b) Hàm số 2 z = f (x, y) = y + sin(x2 2 − y2) + cos x
( 2 − y2) + ex −y + ln(x2 − y2)
thỏa mãn phương trình xz, + yz, = x. y x n 2
1.16. Toán tử Laplace trong Rn được ký hiệu và định nghĩa là = . Chứng minh rằng 2 k =1 x k
(a) Hàm số z = f (x, y) = ln( 2 2 1
x + y ) thỏa mãn phương trình Laplace z = 0 trong không gian R2. (b) Hàm số u = f (x, ,
y z) = arctan(x y) + arctan(y z) + arctan z
( x) thỏa mãn phương trình Laplace u
= 0 trong không gian R3. xy khi (x, y) ( , 0 ) 0
1.17. Chứng mỉnh rằng, hàm số f (x, y)= x2 + y2
liên tục tại điểm (0,0) nhưng 0 khi (x, y) =( , 0 ) 0
không khả vi tại điểm này. 56 x3 + 3 y khi (x, y) 0 , 0 ( )
1.18. Chứng mỉnh rằng, hàm số f (x, y) = x2 + y2
có các đạo hàm riêng cấp 1 tại 0 khi (x, ) y = ( , 0 ) 0
điểm (0,0) nhưng không khả vi tại điểm này.
1.19. Tính đạo hàm theo hướng của các hàm số sau đây
(a) u = f(x,y,z) = xy2z3 tại điểm M0(1,2, 1)
– theo hướng của véc tơ M M với M(0,4,–3). 0 (b) u = f (x, , y z) = arcsi ( 2 2 n z
x + y ) tại điểm M0(1,1,1) theo hướng của véc tơ M M với 0 M(3,2,3). → → →
(c) z = f(x,y) = x2 – xy + y2 tại điểm M0(1,1) theo hướng của véc tơ v = 6 i + 8 j .
1.20. (a) Cho hàm số u = f(x,y,z) = xsin(yz), xác định Gradf(x,y,z) và tính đạo hàm theo hướng của véc tơ → → → → → →
e tại điểm M0(1,3,0) nếu e là véc tơ đơn vị của véc tơ v = i + 2 j − k .
(b) Cho hàm số z = f(x,y) = xey, tính vận tốc biến thiên của hàm số f(x,y) theo hướng véc tơ từ
điểm M0(2,0) đến điểm M(5,4). Theo hướng nào thì vận tốc biến thiên đó có giá trị lớn nhất và xác định giá trị ấy?
(c) Tìm độ lớn và hướng của Gradf(x,y,z) của hàm số u = f(x,y,z) = x3 + y3 + z3 – 3xyz tại điểm
M0(1,2,1). Tại các điểm nào thì Gradf(x,y,z) vuông góc với trục Oy? Tại các điểm nào thì Gradf (x,y,z) = 0?
1.21. Tính vi phân toàn phần cấp 1 của các hàm số sau đây (a) z = f(x,y) = sin(x2 + y2)
(b) z = f(x,y) = ex(cosy + xsiny) x + y (c) z = f (x, ) y = arctan (d) x y −y x z = f (x, ) y = e + e x − y
(e) u = f(x,y,z) = xey + yez + zex (f) y2z u = f (x, , y z) = x (x > 0)
1.22. Tính df(1,1) của hàm số 2 f (x, ) y = x y .
1.23. Tính đạo hàm của hàm ẩn y = y(x)
(a) Tính y’(x) nếu x3y – xy3 = a4 (tham số a 0)
(b) Tính y’(x) nếu xey + yex = exy + (c) Tính y’(x) nếu x y y arctan = (tham số a 0) a a
(d) Tính y’(x) và y”(x) nếu ln x2 + y2 = arctan(y x) 1.24.
Tìm cực trị của các hàm số sau đây (a) y z = f (x, ) y = x + y − xe (b) z = f (x, y) = xy 3
( − x − y) (đề thi học phần Giải tích 2 cuối kỳ năm học 2018-2019) (c) 3 2 2 2 z = f (x, y) = x 3
+ xy + 5x + y (x < 0, y < 0) (đề thi học phần Giải tích 2 cuối kỳ năm học 2019-2020) (d) z = f (x, )
y = ey−x (y2 + 2x2 ) (đề thi học phần Giải tích 2 cuối kỳ năm học 2020-2021)
1.25. Giải bài toán ở Ví dụ 1.28. bằng phương pháp nhân tử Lagrange tìm cực trị có điều kiện của hàm số nhiều biến. 1 1 1
1.26. Tìm cực trị của hàm số u = f(x,y,z) = x + y + z với điều kiện + + = 1. x y z
1.27. Tìm tam giác có diện tích lớn nhất trong tất cả các tam giác nội tiếp trong đường tròn bán kính R cho trước. 57
Gợi ý. Ký hiệu các góc của tam giác nội tiếp trong đường tròn bán kính R cho trước là , , và độ
dài các cạnh đối diện với các góc ,
, tương ứng là a, b, c. Sau đó, áp dụng công thức tính diện tích 1 a b c tam giác S= ab sin i và định lý s n = = = 2R. 2 sin sin sin
1.28. Tìm GTNN(fD) và GTLN(fD) của các hàm số sau đây (a) z = f (x, ) y = x2 (
y 4 − x − y) trên miền đóng D(f) giới hạn bởi các đường thẳng x = 0, y = 0 và x + y = 6. (b) z = f (x, )
y = x2 + 2xy − 4x + 8y trên miền đóng D(f) giới hạn bởi các đường thẳng x = 0, x = 1, y = 0 và y = 2. 58




