











Preview text:
5 Chương 1
ĐẠI CƯƠNG VỀ XÁC SUẤT
1. HIỆN TƯỢNG NGẪU NHIÊN
Hiện tượng ngẫu nhiên là đối tượng khảo sát của lý thuyết xác suất. Chúng là những hiện
tượng mà dù được thực hiện trong cùng một điều kiện như nhau vẫn có thể cho ra nhiều kết quả
khác nhau. Chẳng hạn, tung một con xúc xắc, ta không thể chắc chắn rằng mặt nào sẽ xuất hiện; lấy
ra một sản phẩm từ một lô hàng gồm cả hàng chính phẩm lẫn phế phẩm, ta không chắc chắn sẽ
nhận được hàng chính phẩm hay phế phẩm.
Để khảo sát các hiện tượng ngẫu nhiên, người ta cho các hiện tượng này xuất hiện nhiều lần
để quan sát. Mỗi lần cho xuất hiện một hiện tượng ngẫu nhiên được gọi là thực hiện một phép thử.
Khi đó, dù ta không thể dự đoán được kết quả nào sẽ xảy ra nhưng thường ta có thể liệt kê tất cả các
kết quả có thể xảy ra. Tập hợp tất cả các kết quả có thể xảy ra của một phép thử được gọi là không
gian mẫu của phép thử đó. Mỗi phần tử của không gian mẫu được gọi là một biến cố sơ cấp và mỗi
một tập con của không gian mẫu được gọi là một biến cố.
Ta thường ký hiệu cho phép thử, cho không gian mẫu tương ứng, chỉ các biến cố
sơ cấp và các tập con A, B, C, ... của để chỉ các biến cố.
Ví dụ 1. Xét phép thử : "tung con xúc xắc” và quan sát các mặt xuất hiện. Ta có không gian mẫu 1,2,3,4,5, 6 ,
trong đó 1, 2, là các biến cố sơ cấp chỉ việc nhận được mặt 1, 2, ..., tập con A 2,4,6 của chỉ biến cố : , ... "nhận được mặt chẵn"
Ví dụ 2. Lấy ngẫu nhiên một sản phẩm từ một lô hàng là một phép thử mà không gian mẫu
chính là lô hàng đó. Các tập con CP các chính phẩm và PP các phế phẩm là các biến cố mà ta còn
gọi là biến cố “nhận được chính phẩm” và “nhận được phế phẩm”.
Xét không gian mẫu của một phép thử và xét biến cố A . Sau mỗi lần thực hiện
phép thử , ta nhận được một biến cố sơ cấp . Khi đó, nếu A , ta nói : "biến cố A xảy ra";
ngược lại, nếu A , ta nói : "biến cố A . không xảy ra"
Chẳng hạn, với phép thử : "tung con xúc xắc" và biến cố A : "nhận được mặt chẵn". Khi ta
tung con xúc xắc, nếu nhận được mặt 4, ta nói biến cố A xảy ra, nếu nhận được mặt 1, ta nói A không xảy ra, ...
Từ định nghĩa, xét không gian mẫu tương ứng với một phép thử bất kỳ. Ta luôn luôn có hai biến cố đặc biệt
- Biến cố chắc chắn A : là biến cố luôn luôn xảy ra khi thực hiện phép thử,
- Biến cố không thể có A : là biến cố không bao giờ xảy ra khi thực hiện phép thử.
Chẳng hạn, xét phép thử "tung hai con xúc xắc", quan sát tổng số các nút xuất hiện, và xét các biến cố
A : "tổng số nút 13”,
B : "tổng số nút 1".
Ta có A là biến cố chắc chắn và B là biến cố không thể có. 6
Ngoài ra, do mỗi một biến cố là một tập con của không gian mẫu nên bằng các phép toán
tập hợp (xem chương 0), với hai biến cố bất kỳ A, B , ta có thể thành lập các biến cố sau: C A
chỉ biến cố "A và B cùng xảy ra". Khi AB , ta nói A và B là hai biến cố xung khắc
(A và B không bao giờ cùng xảy ra). C A
B chỉ biến cố "A xảy ra hay B xảy ra".
C \ A A chỉ biến cố đối lập của A : A xảy ra nếu và chỉ nếu A không xảy ra.
Chẳng hạn, với không gian mẫu 1,2,3,4,5,
6 của phép thử "tung xúc xắc" và các biến cố A 2,4, 6 , B 1,3, 5 , C
4 , ta có : A B là biến cố chắc chắn, AB là biến cố không thể
có và do đó A, B là hai biến cố đối lập (và đương nhiên là hai biến cố xung khắc), B và C là hai
biến cố xung khắc (nhưng không đối lập). 2. XÁC SUẤT
Quan sát các biến cố đối với một phép thử, mặc dù không thể khẳng định một biến cố có xảy
ra hay không nhưng người ta có thể so sánh cơ may xảy ra của các biến cố này. Chẳng hạn, với
phép thử "tung xúc xắc", người ta nhận thấy biến cố "nhận được mặt 1" ít xảy ra hơn biến cố "nhận
được mặt chẵn". Do đó, người ta tìm cách định lượng khả năng xuất hiện khách quan của một biến
cố mà ta sẽ gọi là xác suất của biến cố đó.
Xác suất của một biến cố là một con số đặc trưng cho khả năng xảy ra khách quan của biến cố đó.
Xác suất của biến cố A, ký hiệu là P A , có thể được định nghĩa bằng nhiều cách.
2.1. Định nghĩa cổ điển
Xét một phép thử với n kết quả có thể xảy ra, nghĩa là không gian mẫu có n biến cố sơ
cấp, và xét biến cố A có k phần tử. Với giả định rằng các biến cố sơ cấp có cùng khả năng xảy
ra thì xác suất của A được định nghĩa là A k P A . n
Ví dụ 3. a) Xét phép thử "tung xúc xắc" với các biến cố
A "nhận được mặt 6", B . "nhận được mặt chẵn"
Với giả định rằng các mặt của con xúc xắc này có cùng khả năng xuất hiện, ta có PA 1 và 6 P B 3 0.5 . 6
b) Xét phép thử "lấy ngẫu nhiên một viên bi trong một hộp đựng 4 bi xanh và 6 bi đỏ" với các biến cố
X "nhận được bi xanh", D . "nhận được bi đỏ"
Với giả định rằng các bi trong hộp có khả năng rút được như nhau, ta có PX 4 0.4 và 10 P D 6 0.6 . 10
Lưu ý rằng, đối với định nghĩa cổ điển, ta cần hai điều kiện :
(i) Số kết quả của phép thử là hữu hạn,
(ii) Các kết quả đồng khả năng xảy ra. 7
Khi một trong hai điều kiện trên không xảy ra, ta không thể dùng định nghĩa cổ điển để xác
định xác suất của một biến cố. Tuy nhiên, bằng cách viết lại định nghĩa cổ điển này,
Số trường hợp thuận lợi cho A P A Số trường hợp xảy ra
ta có thể định nghĩa xác suất bằng phương pháp thống kê như sau
2.2. Định nghĩa xác suất bằng tần suất
Giả sử phép thử có thể lập lại nhiều lần trong điều kiện giống nhau. Nếu trong n lần thực
hiện phép thử mà biến cố A xảy ra k lần thì tỷ số k được gọi là tần suất xuất hiện của A trong n n phép thử.
Người ta chứng minh được rằng, khi n đủ lớn, tần suất của biến cố A sẽ dao động xung quanh
một giá trị nào đó mà ta gọi là xác suất của A, ký hiệu P A. Trong thực tế, với n đủ lớn, người ta
lấy tần suất của A làm giá trị gần đúng cho xác suất của biến cố A, k P A . n
Ví dụ 4. a) Thống kê trên 10.000 người dân thành phố cho thấy có 51 người bị bệnh cao
huyết áp, ta nói xác suất của biến cố "bị bệnh cao huyết áp" là 51 0.005 . 10000
b) Một nhà máy gồm ba phân xưởng A, B, C. Kiểm tra một lô hàng của nhà máy gồm 1000
sản phẩm, người ta thấy có 252 sản phẩm của phân xưởng A, 349 của phân xưởng B và 399 của
phân xưởng C. Ta nói xác suất
nhận được sản phẩm từ phân xưởng A là PA 252 0.25 , 1000
nhận được sản phẩm từ phân xưởng B là PB 349 0.35 , và 1000
nhận được sản phẩm từ phân xưởng C là PC 399 0.4 . 10000
Ta còn nói, các phân xưởng A, B, C tương ứng làm ra 25%, 35% và 40% tổng sản lượng nhà máy.
Tương tự, để tìm xác suất làm ra sản phẩm hỏng của phân xưởng A, người ta thống kê trên
một số sản phẩm của phân xưởng A và quan sát số sản phẩm hỏng. Chẳng hạn, nếu trong 400 sản
phẩm của phân xưởng A nêu trên có 4 sản phẩm hỏng, ta nói xác suất làm ra một sản phẩm hỏng
của phân xưởng A là 4 0.01. 400
Ví dụ 5. Trong phép thử : “thảy đồng xu”, một cách trực giác, ta cho rằng các biến cố sơ
cấp : “nhận được mặt sấp” và : “nhận được mặt ngửa” là đồng khả năng xảy ra, nên do 1 2 định nghĩa cổ điển,
P P 0.5 . 1 2
Khi đó, người ta nói đồng xu này là “công bằng”, “đồng chất đẳng hướng”, ... Bằng thực
nghiệm, Buffon và Pearson đã thảy một đồng xu nhiều lần và nhận được kết quả sau Người thực hiện Số lần thảy Số lần mặt ngửa Tần suất Buffon 4.040 2.048 0.5069 Pearson 12.000 6.019 0.5016 Pearson 24.000 12.012 0.5005 8
và khi đó, ta nói xác suất nhận được mặt ngửa 0.5 .
Tổng quát hơn, độc lập với các quan sát chủ quan, ta có
2.3. Định nghĩa xác suất bằng tiên đề của Kolmogorov
Xác suất là hàm số xác định trên tập hợp các biến cố P , P : P A thỏa các tính chất sau (i) P 1, (ii) P A 0 , A P , và (iii) P A
, với mọi dãy hữu hạn các biến cố 1 A , A ,
xung khắc từng đôi, nghĩa là A khi i j . 1 2 i
Từ định nghĩa, dễ dàng suy ra thêm các tính chất sau (iv) P 0 ,
(v) Nếu A và B xung khắc, AB , thì
P A B P A PB ,
(vi) Công thức cộng :
Với hai biến cố bất kỳ A và B, P A
A PB P AB ,
(vii) P A 1 P A , nghĩa là tổng xác suất hai biến cố đối lập luôn luôn bằng 1.
Ví dụ 6. Qua điều tra trong sinh viên, ta biết 40% học thêm ngoại ngữ, 55% học thêm tin học
và 30% học thêm cả hai môn này. Chọn ngẫu nhiên 1 sinh viên và xét các biến cố
A : “nhận được sinh viên học thêm ngoại ngữ” ,
B : “nhận được sinh viên học thêm tin học”. Khi đó, A
là biến cố “nhận được sinh viên học thêm cả hai môn ngoại ngữ và tin học”, và
P A 0.4 ; P B 0.55 ; P A 3.
Từ đó, ta có thể tính một số xác suất như
P A 1 P A 1 0.4 0.6 ,
nghĩa là có 60% sinh viên không học thêm ngoại ngữ, P A 3 0.65 ,
nghĩa là có 65% sinh viên học thêm (ngoại ngữ hay tin học), PA 0.35,
nghĩa là có 35% sinh viên không học thêm môn nào cả. 9
3. XÁC SUẤT CÓ ĐIỀU KIỆN
Xét phép thử : "tung hai con xúc xắc"
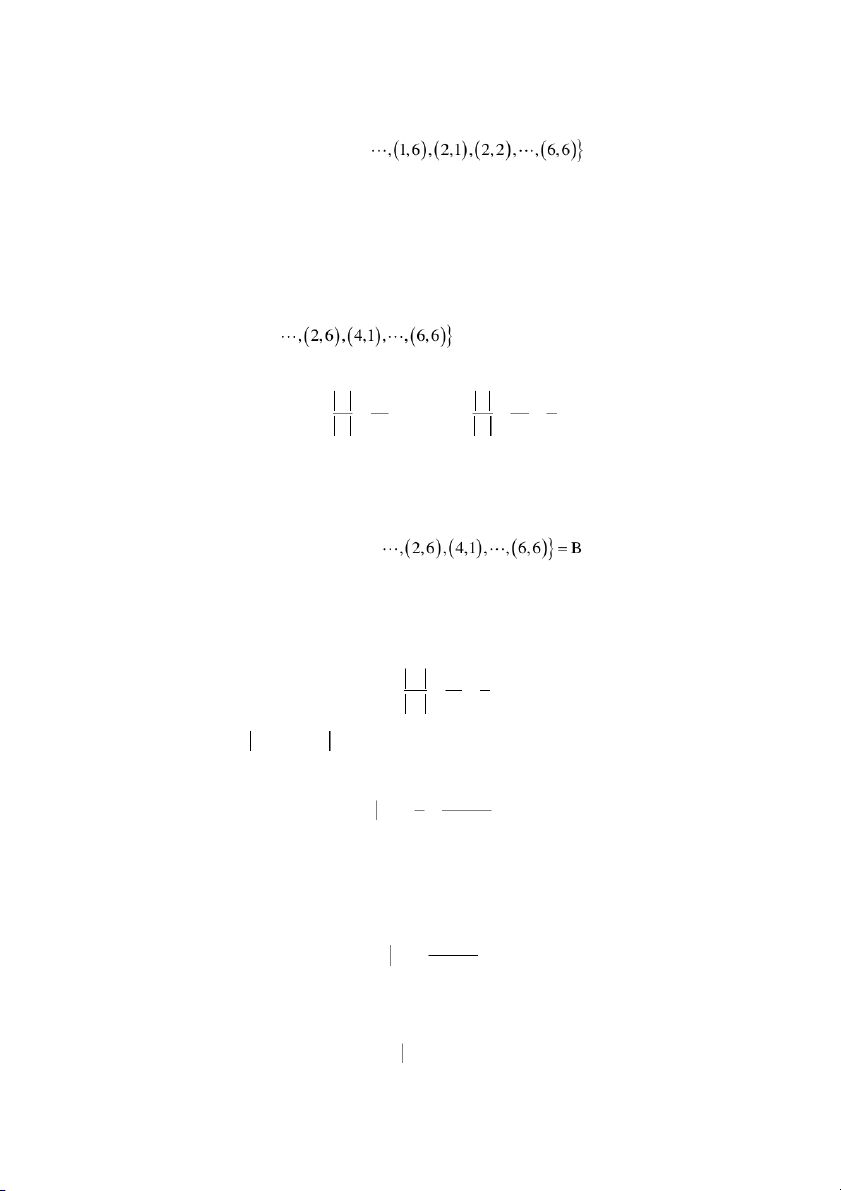
với không gian mẫu tương ứng 1, 1 ,1, 2 ,
(có 36 phần tử) và xét các biến cố
A : "tổng số nút xuất hiện 8 ",
B : "số nút của xúc xắc thứ nhất là số chẵn" . Ta có A
2, 6,3,5,4,4,5,3,6,2 ,
B 2,1, 2, 2, ,
nên từ định nghĩa cổ điển, A 5 P A và B 18 1 P B . 36 36 2
Bây giờ, ta tung hai con xúc xắc và giả sử ta nhận được thông tin thêm là số nút của xúc xắc
thứ nhất đã là số chẵn (nghĩa là biến cố B đã xảy ra). Khi đó, phép thử trở thành phép thử :
"tung hai con xúc xắc khác nhau với số nút của xúc xắc thứ nhất là số chẵn". Do đó, không gian mẫu bị thu hẹp lại là 2, 1 ,2, 2 ,
và hiện tượng biến cố A xảy ra khi biết biến cố B đã xảy ra trở thành hiện tượng biến cố A
2,6,4,4,6,2 AB
xảy ra đối với phép thử
và do đó có xác suất là A 3 1 P A . 18 6
Ta ký hiệu A A B và PA B P A được gọi là xác suất để biến cố A xảy ra khi biết biến cố B đã xảy ra . Từ nhận xét P A B 1 PAB , 6 P B
ta đưa ra định nghĩa tổng quát
3.1. Định nghĩa. Xét biến cố B với PB 0 . Xác suất của biến cố A, khi biết biến cố đã B xảy ra là P A B PAB . P B
Ví dụ 7. Với dữ liệu cho trong ví dụ 4 b), xét biến cố H : "nhận được một sản phẩm hỏng".
Xác suất nhận được sản phẩm hỏng khi biết sản phẩm đó của phân xưởng A là P H A 0.01
và xác suất của biến cố HA : "nhận được một sản phẩm hỏng từ phân xưởng A" là 10
P HA PH A P A 0.01 0.25 0.0025 .
3.2. Định lý (Công thức nhân). Với hai biến cố A và B bất kỳ, ta có
P AB P A BP B .
Tổng quát, với n biến cố bất kỳ A , A , , ta có 1 2 P A A . 1 2
Ví dụ 8. Một thủ quỹ có một chùm chìa khóa gồm 9 chiếc chìa giống hệt nhau trong đó chỉ có
2 chìa có thể mở được tủ sắt. Anh ta thử ngẫu nhiên từng chìa (chìa không trúng được bỏ ra trong
lần thử kế tiếp). Tìm xác suất để anh ta mở được tủ vào đúng lần thứ ba.
Đặt A là biến cố "lần thứ i, mở được tủ". Với quy ước rằng khi biến cố A xảy ra thì các i i biến cố A ,
vẫn có thể đã xảy ra, biến cố "mở được tủ vào đúng lần thứ ba" là A A A và 1 1 2 3
do quy tắc nhân xác suất, ta có
PA A A P A P A A P A A A . 1 2 3
1 2 1 3 1 2 Do 2 7
PA 1 P A 1 , 1 1 9 9 2 6
PA A 1P A A 1 , 2 1 2 1 8 8 2 PA A A , 3 1 2 7 ta suy ra 7 6 2 1 PA A A . 1 2 3 9 8 7 6
Ví dụ 9. Hai sinh viên A và B chơi một trò chơi như sau : Cả hai luân phiên lấy mỗi lần 1 bi
từ một hộp đựng 2 bi trắng và 4 bi đen (bi được rút ra không trả lại vào hộp). Người nào lấy ra được
bi trắng trước thì thắng cuộc. Tính xác suất thắng cuộc của người lấy trước.
Không mất tính tổng quát, giả sử A lấy trước. Xét các biến cố
A : “A lấy được bi trắng ở lần lấy thứ i”, i
B : “B lấy được bi trắng ở lần lấy thứ i”. i
Nếu gọi C là biến cố “A thắng cuộc”, thì C A A . 1 3 Do P A 2 1
và do công thức nhân xác suất 1 6 3 4 3 2 1
PA B A P A P B A P A A B 1 1 2
1 1 1 2 1 1 6 5 4 5
P A B A B P A P B A P A A B P B A B A P A A B A B 1 1 2 2
1 1 1 2 1 1 2 1 1 2 3 1 1 2 2 4 3 2 1 1 1 6 5 4 3 15 11
Vì A , A B A và A B A B A là các biến cố xung khắc từng đôi nên do công thức cộng, 1 1 1 2 1 1 2 2 3 1 1 1 3
PC PA P A B A P A B A B . 1
1 1 2 1 1 2 2 3 5 15 5
3.3. Định lý (công thức xác suất toàn phần). Với hai biến cố A, B bất kỳ, ta có
P A P A BP B PA B PB . Tổng quát, cho B , B ,
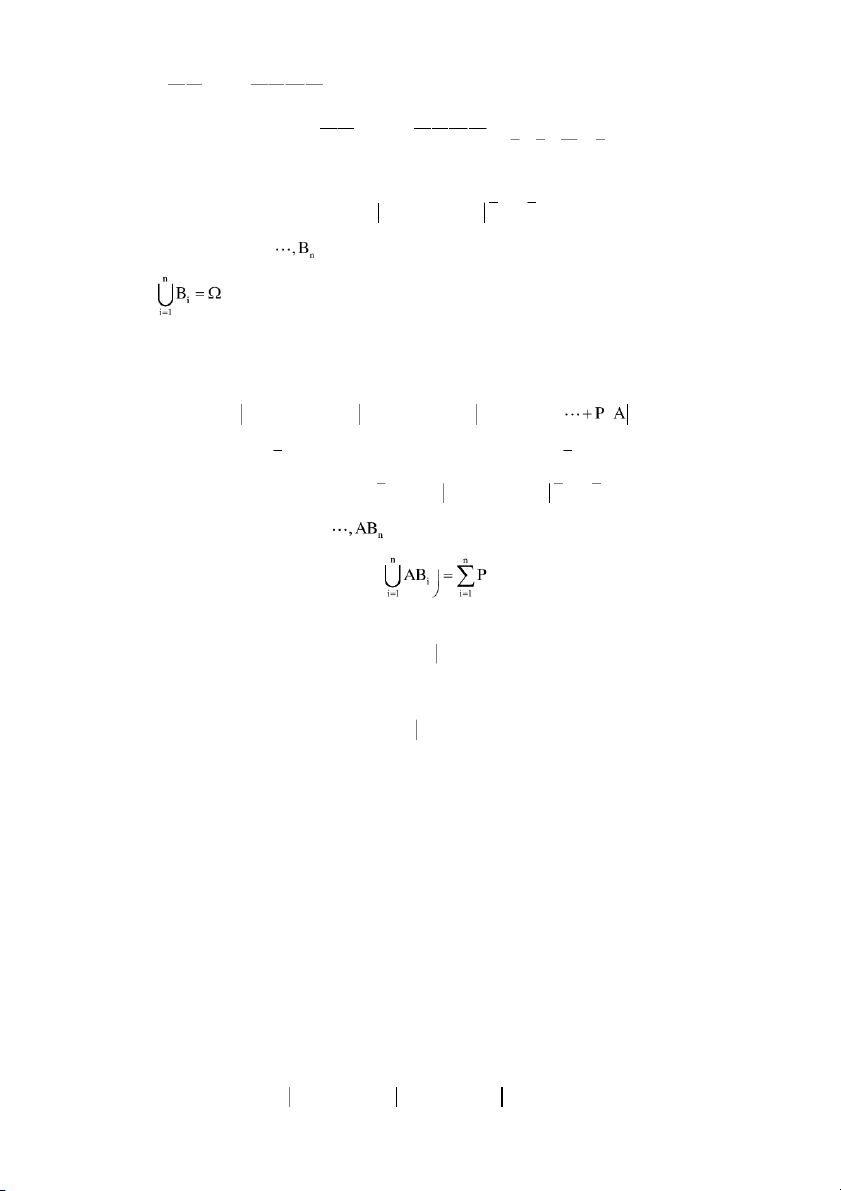
là một họ đầy đủ các biến cố, nghĩa là 1 2 i) v à
ii) B B nếu i j . i j
thì với mọi biến cố A, ta có P A n
PA B P B P A B P B P A B P B B P B . i i 1 1 2 2 n n i 1
Chứng minh. Do AB và AB là hai biến cố xung khắc và A AB AB nên
P A P AB P AB PA B P B P A BP B .
Tổng quát, do các biến cố AB , AB ,
xung khắc từng đôi nên do công thức cộng xác suất 1 2 P A P AB i
và do công thức nhân xác suất, P AB P A B P B i i i với mọi i, ta suy ra n P A P A B P B . i i i 1
Ví dụ 10. Một nhà máy có 3 phân xưởng A, B, C tương ứng làm ra 25%, 35% và 40% tổng
sản phẩm của nhà máy. Giả sử xác suất làm ra một sản phẩm hỏng của các phân xưởng A, B và C
lần lượt là 0,01; 0,02 và 0,025.
Để tính xác suất làm ra một sản phẩm hỏng của nhà máy, ta xét phép thử : "Chọn ngẫu
nhiên một sản phẩm của nhà máy" và xét các biến cố
A : "nhận được sản phẩm của phân xưởng A",
B : "nhận được sản phẩm của phân xưởng B",
C : "nhận được sản phẩm của phân xưởng C", và
H : "nhận được sản phẩm hỏng",
thì A, B, C tạo thành họ đầy đủ các biến cố, với
P A 0.25; PB 0.35; P C 0.4. Ngoài ra,
P H A 0.01; PH B 0.02; P H C 0.025 , 12
nên do công thức xác suất toàn phần,
P H P H APA P H BPB P H C P
C 0.010.25 0.02 0.35 0.0250.4 0.0195.
3.4. Định lý (Công thức Bayès). Cho B , B ,
là một họ đầy đủ các biến cố và xét biến cố A 1 2
với P A 0 . Với mỗi k 1, 2, , ta có P A B P B P B A . k k k n P A B P B i i i 1 Chứng minh.
Áp dụng công thức nhân xác suất
P B A P A P B A P A B P B k k k k
và công thức xác suất toàn phần P A n PA B P B , i i i 1 ta suy ra P A B P B P A B P B k k k k P B A . k P A n P A B P B i i i 1
Ví dụ 11. Với các dữ kiện cho trong ví dụ 10. Giả sử lấy một sản phẩm và thấy rằng đó là sản
phẩm hỏng. Ta có thể tính xác suất để sản phẩm đó do phân xưởng B sản xuất bằng công thức Bayès P H B P B 0.02 0.35 7 P B H . P H 0.195 195
Chú ý. Trong công thức Bayès, xác suất P B , P B ,
để các biến cố B , B , xảy 1 2 1 2
ra được biết trước nên thường được gọi là các xác suất tiên nghiệm. Sau khi thực hiện phép thử,
thấy biến cố A xảy ra, xác suất để các biến cố B , B ,
xảy ra được tính lại với thông tin thêm 1 2
này (nghĩa là các xác suất có điều kiện PB A , P B A ,
A ) nên được gọi là các xác 1 2 suất hậu nghiệm.
Hai biến cố A, B được gọi là độc lập nếu biến cố này xảy ra không ảnh hưởng đến việc xảy ra
hay không xảy ra của biến cố kia. Cụ thể, ta có
3.5. Định nghĩa. Hai biến cố A, B được gọi là độc lập nếu xác suất để biến cố này xảy ra không
phụ thuộc vào việc biến cố kia xảy ra, nghĩa là P A B PA và do đó
P AB P A P B.
Tổng quát, n biến cố A , A , được gọi là
độc lập nếu mỗi biến cố A , với i 1, 2, , 1 2 i
độc lập với tích bất kỳ các biến cố còn lại.
Ví dụ 12. Thảy một đồng xu và một con xúc xắc, ta có không gian mẫu 13 S, 1,S, 2, . Xét các biến cố
A : "nhận được mặt ngửa của đồng xu", và
B : "nhận được nút chẵn của xúc xắc".
Một cách trực giác, đồng xu xuất hiện mặt xấp hay ngửa không ảnh hưởng gì đến số nút xuất
hiện trên con xúc xắc, nghĩa là A, B độc lập nhau. Cụ thể, ta có A
N, 1,N,2,N, 3,N,4,N,5,N,6 ,
B S,2 , S,4 , S,6 , N, 2 , N, 4 , N, 6 , và AB
N, 2,N, 4,N,6. Do đó, 6 1 6 1 3 1 P A ;P B ;P AB . 12 2 12 2 12 4 Vì 1 P AB P A P B
nên A, B độc lập với nhau. 4
Do định nghĩa, nếu ba biến cố A, B, C là độc lập thì A độc lập với B, C và BC nên
P AB P A P B ,
P AC P A P C ,
P ABC P A P BC ,
và vì B, C cũng độc lập với nhau, nên
P BC P B P C và do đó
P ABC P A P B PC.
Tổng quát, n biến cố A , i 1, 2,
là độc lập nếu với bất kỳ k biến cố A , A , khác i 1 i i2 nhau, với k n , P A . ij
Chú ý rằng, nếu từ n biến cố độc lập A , i 1, 2,
, ta thành lập họ biến cố B ,i 1, 2, , i i
với B A hay B A , thì họ biến cố B ,i 1, 2, , cũng độc lập. i i i i i
Ví dụ 13. Từ một hộp đựng 10 viên bi trong đó có 4 bi trắng, lấy lần lượt ra 2 bi. Gọi T , với k
k 1, 2 , là biến cố "nhận được bi trắng ở lần lấy thứ k". Ta có hai trường hợp, tùy thuộc vào lần lấy
thứ nhất có hoàn lại bi vào hộp hay
không hoàn lại bi vào hộp :
i) Trường hợp có hoàn lại : Khi đó, một cách trực giác, ta thấy T , T là hai biến cố độc lập. 1 2 Chính xác hơn, ta có 4 PT , 1 10 14 4 4 4 6 4
PT P T T P T P T T P T , 2
2 1 1 2 1 1 1010 1010 10 4 4 PT T P T T P T P T P T . 1 2 2 1 1 2 1 10 10
ii) Trường hợp không hoàn lại : Trong trường hợp này, ta thấy T , T là hai biến cố không độc 1 2
lập vì ta cảm giác rằng cơ may để lần thứ nhì được bi trắng tùy thuộc vào bi nhận được ở lần thứ
nhất có là bi trắng hay không. Cụ thể, ta có 4 PT , 1 10 3 4 4 6 36 4
PT P T T P T P T T P T . 2
2 1 1 2 1 1 910 910 90 10 nhưng 3 4 P T T P T T P T P TT . 1 2 2 1 1 1 2 9 10
Tổng quát, nếu ta lấy lần lượt ra n bi, với 1 n 10 , thì các T , 1 k n là một họ các biến k
cố độc lập khi mỗi lần lấy bi ra có , nhưn hoàn lại
g không là một họ các biến cố độc lập khi mỗi lần
lấy bi ra không hoàn lại. Tuy nhiên, chú ý rằng trong cả hai trường hợp, ta đều có 4 P T , k 10 với mọi k.
Ví dụ 14. Ba xạ thủ cùng bắn vào một mục tiêu với xác suất bắn trúng mục tiêu của xạ thủ
thứ 1, 2 và 3 lần lượt là 0.4; 0.5 và 0.8. Tính xác suất để
a) có đúng một xạ thủ bắn trúng.
b) có ít nhất một xạ thủ bắn trúng.
Gọi A , với i 1, 2,3 , là biến cố : “xạ thủ i bắn trúng”. Ta có PA 0.4, PA 0.5 và i 1 2
P A 0.8 . Khi đó, 3 A A A A 1 2 3
là biến cố : “có đúng một xạ thủ bắn trúng”, và B A 1
là biến cố : “có ít nhất một xạ thủ bắn trúng”.
Do A A A , A A A , A A A là họ các biến cố xung khắc từng đôi và đồng thời các biến cố 1 2 3 1 2 3 1 2 3
A cũng như các biến cố đối A , với i 1, 2,3 , là các biến cố độc lập nên từ công thức cộng và i i
công thức nhân (cho các biến cố độc lập), ta có
P A P A A A P A A A P A A A 1 2 3 1 2 3 1 2 3
PA P A P A P A P A P A P A P A P A 1
2 3 1 2 3 1 2 3
0.40.50.2 0.6 0.50.2 0.60.50.8 0.34 15
P B P A P A P A P A A P A A P A A P A A A 1 2 3 1 2 1 3 2 3 1 2 3
P A P A P A P A P A P A P A P A P A 1
2 3 1 2 1 3 2 3 P A P A P A 1 2 3 nên
P B 0.4 0.5 0.8 0.4 0.5 0.4 0.8 0.5 0.8 0.4 0.50.8 0.94 .
Chú ý rằng ta còn có thể dùng đẳng thức PB 1 P
B , trong đó B A A A là biến cố : 1 2 3
“cả ba xạ thủ đều không bắn trúng”,
PB 1 PA A A 1 P A P A P A 10.60.50.2 0.94. 1 2 3 1 2 3
4. LƯỢC ĐỒ BERNOULLI
Để khảo sát một biến cố, chẳng hạn như trong định nghĩa xác suất bằng phương pháp thống
kê, người ta phải thực hiện phép thử tương ứng nhiều lần một cách độc lập và quan sát số lần biến
cố đó xảy ra để tính được tần suất của biến cố đó. Phương pháp khảo sát này được gọi là lược đồ Bernoulli.
Xét một phép thử với không gian mẫu và xét biến cố A với xác suất PA p . Ta
thực hiện phép thử này n lần một cách độc lập và quan sát số lần xảy ra biến cố A. Đặt H :
"biến cố A xảy ra đúng k lần", k với 0 k n . Ta có
4.1. Định lý (Công thức Bernoulli).
P H C p 1 pn k k k . k n
Chứng minh. Dùng quy nạp trên n. Hiển nhiên công thức đúng với n 1 vì khi đó H A và 0 H A . Do đó 1
P H 1 p C p 1 p1 0 0 0 0 1 và
P H p C p 1 p1 1 1 1 . 1 1
Giả sử công thức đúng với n 1, nghĩa là khi thực hiện n lần phép thử một cách độc lập thì
xác suất để biến cố A xảy ra đúng k lần là
P H C p 1 pn k k k . k n
Bây giờ, thực hiện phép thử thêm một lần nữa một cách độc lập và gọi X là biến cố : “A
xảy ra trong lần thử thứ n 1 ” thì biến cố : “A xảy ra đúng
k lần trong n 1 phép thử” là H A H A . k k 1
Do các biến cố H A và H A là xung khắc, H và A cũng như H k k 1 k
k và A là các biến cố 1 độc lập nên 16
P H A H A P H A P H A P H P A P H P A k k 1
k k 1 k k 1 n k n k 1 n 1 k k k
C p 1 p 1 p k 1 k 1 C p 1 p p k k 1 C C k p 1 p n n n n C p 1 p n 1 k k k . n 1
Ví dụ 15. Xác suất thành công một thí nghiệm sinh hóa là 40%. Một nhóm gồm 9 sinh viên
cùng tiến hành thí nghiệm này độc lập với nhau. Tìm xác suất để
a) có đúng 6 thí nghiệm thành công,
b) có ít nhất một thí nghiệm thành công,
c) có ít nhất 8 thí nghiệm thành công.
Xét phép thử : "tiến hành thí nghiệm sinh hóa" và biến cố A : " thí nghiệm thành công". Ta
có P A 0.4 và vì thí nghiệm được thực hiện 9 lần độc lập nhau nên nó thỏa lược đồ Bernoulli
với n 9 . Gọi H là biến cố "thí nghiệm thành công đúng k lần" và K là biến cố "thí nghiệm k k
không thành công đúng k lần", ta có
a) Xác suất có đúng 6 thí nghiệm thành công là
P H C 0.46 1 0.49 6 6 . 6 9 0.0743
b) Xác suất có ít nhất một thí nghiệm thành công là
PK 1 PH 1 C 0.601 0.69 0 0 0.9899 . 0 0 9
c) Xác suất có ít nhất 8 lần thành công là
P H H P H PH C 0.48 1 0.49 8 C 0.49 1 0 .49 9 8 9 8 9 8 9 9 9
0.00354 0.00026 0.0038.
Ví dụ 16. Xác suất chữa khỏi bệnh A của một phương pháp điều trị là 95%. Với 10 người bị
bệnh A được điều trị bằng phương pháp này, tính xác suất để
a) có 8 người khỏi bệnh.
b) có nhiều nhất 9 người khỏi bệnh.
Do việc khỏi bệnh của người này và người khác là độc lập nhau nên số người khỏi bệnh trong
10 người điều trị thỏa lược đồ Bernoulli với n 10 và p 0.95. Do đó,
a) Xác suất để có 8 người khỏi bệnh là C 0. 8 95 1 0. 10 8 8 95 0.0746 . 10
b) Biến cố : “có nhiều nhất 9 người khỏi bệnh” là biến cố đối của biến cố : “có 10 người khỏi
bệnh” nên có xác suất là 10 10 10 1 0 1 C 0.95 1 0.95 1 0.5987 0.4013 . 10
5. ĐẠI CƯƠNG VỀ BIẾN SỐ NGẪU NHIÊN VÀ PHƯƠNG PHÁP LẤY MẪU
Trở lại với lược đồ Bernoulli nhưng với phép thử
: "thực hiện phép thử đúng n lần".
Gọi X là số lần biến cố A xảy ra trong n lần thực hiện phép thử . Bấy giờ, ứng với mỗi một
biến cố sơ cấp của phép thử , ta gán với một con số (chỉ số lần biến cố A xuất hiện). Khi đó, ta nói
X là một biến số ngẫu nhiên (ứng với phép thử ) và biến cố 17
H : "biến cố A xảy ra đúng k lần" k
còn được ký hiệu là X k .
Chú ý rằng biến số ngẫu nhiên X chỉ lấy các giá trị là 0,1, 2,
và do định lý Bernoulli, P X k P H k k C p 1 p . k n n k
Bảng các giá trị của k với xác suất P X k tương ứng, X 0 1 2 ... n P p p p ... p 0 1 2 n
trong đó p P X k , được gọi là bảng phân phối xác suất của X. k
Chẳng hạn, với ví dụ 15, ta có bảng phân phối xác suất cho biến số ngẫu nhiên X chỉ số lần thí
nghiệm sinh hóa thành công X 0 1 2 3 4 5 6 7 8 9 P p p p p p p p p p p 0 1 2 3 4 5 6 7 8 9 trong đó
p C 0.4 k 1 0.4 9 k k , k 9
và khi đó, từ bảng phân phối xác suất của X, ta có viết lại
- Xác suất có đúng 6 thí nghiệm thành công là P X 6 p , 6
- Xác suất có ít nhất một thí nghiệm thành công là P X
1 p p p p p p p p p 1 p , 1 2 3 4 5 6 7 8 9 0 9 do p 1, và k k 0
- Xác suất có ít nhất 8 thí nghiệm thành công là
P X 8 P X 8 PX 9 .
Ta xét một ví dụ khác :
i) Một hộp gồm 10 bi trong đó có đúng 4 bi trắng. Thực hiện việc lấy lần lượt 9 bi từ hộp, mỗi
lần lấy ra để quan sát rồi trả lại vào hộp. Gọi X là số bi trắng nhận được. Khi đó, biến cố nhận được
bi trắng ở mỗi lần là độc lập nhau nên ta có thể dùng lược đồ Bernoulli và do đó X là biến ngẫu
nhiên có bảng phân phối xác suất như trong ví dụ trên. Từ đó, ta có thể tính được xác suất để nhận
được : đúng 6 bi trắng, ít nhất một bi trắng, ít nhất 8 bi trắng, ...
ii) Cũng với hộp bi như trên nhưng ta lấy lần lượt ra 9 bi (nhưng không hoàn lại vào hộp sau
mỗi lần lấy). Khi đó số bi trắng X nhận được cũng là một biến số ngẫu nhiên nhưng do mỗi lần lấy
bi ra, ta không trả lại vào hộp nên biến cố nhận được bi trắng ở mỗi lần lấy là không độc lập với nhau.
Để tính PX k , ta xét phép thử : "lấy 9 bi". Bấy giờ, mỗi phần tử của không gian mẫu
chính là một tổ hợp 10 chập 9 nên số phần tử của là 9 C . 10
Mặt khác, mỗi phần tử của biến cố X k được tạo bởi phép chọn k phần tử từ 4 phần tử (bi
trắng) và 9 k phần tử từ 6 phần tử (không là bi trắng) nên số phần tử của biến cố X k là 18 k 9 k C C . 4 6 Do đó, k 9 k P X k C C 4 6 . 9 C10
Chú ý rằng các biến cố X k , với k 2 hay với k 5 là các biến cố không thể có, nên ta có
bảng phân phối xác suất X 0 1 2 3 4 5 6 7 8 9 P 0 0 0 p p 0 0 0 0 0 3 4 trong đó 3 9 3 4 9 4 C C 4 C C 6 4 6 4 6 p ; p . 3 9 4 9 C 10 C 10 10 10 Bài tập
1. Cho A, B, C là ba biến cố. Chứng minh
P A B C P A P B P C P AB P AC P BC P ABC . 2. Cho P A 1 , PB 1 và PA B 3
. Tính PAB, PAB , PA B , P A B , và 3 2 4 P AB .
3. Tỷ lệ người mắc bệnh tim trong một vùng dân cư là 9%, mắc bệnh huyết áp là 12%, mắc cả hai
bệnh này là 7%. Chọn ngẫu nhiên một người trong vùng. Tính xác suất để người đó
a) bị bệnh tim hay bị bệnh huyết áp.
b) không bị bệnh tim cũng không bị bệnh huyết áp.
c) không bị bệnh tim hay không bị bệnh huyết áp.
d) bị bệnh tim nhưng không bị bệnh huyết áp.
e) không bị bệnh tim nhưng bị bệnh huyết áp.
4. Theo dõi dự báo thời tiết trên đài truyền hình (nắng, sương mù, mưa) và so sánh với thời tiết thực
tế xảy ra, ta có bảng thống kê sau dự báo nắng sương mù mưa thực tế nắng 30 5 5 sương mù 4 20 2 mưa 10 4 20
nghĩa là có 30 lần dự báo nắng, trời nắng; 4 lần dự báo nắng, trời sương mù; 10 lần dự báo nắng, trời mưa, v.v...
a) Tính xác suất dự báo trời nắng của đài truyền hình.
b) Tính xác suất dự báo của đài truyền hình là đúng với thực tế.
c) Được tin dự báo là trời nắng. Tính xác suất để thực tế thì trời mưa ? trời sương mù ? trời nắng ?
5. Một hộp đựng 10 phiếu trong đó chỉ có 4 phiếu có trúng thưởng. Hai người A và B lần lượt rút
thăm (không hoàn lại). Tính xác suất đế 19
a) A rút được phiếu trúng thưởng.
b) Cả A lẫn B đều rút được phiếu trúng thưởng.
c) B rút được phiếu trúng thưởng.
d) Các biến cố “A rút được phiếu trúng thưởng” và “B rút được phiếu trúng thưởng” có độc lập không? 6. Có hai hộp đựng bi :
- Hộp H đựng 20 bi trong đó có 5 bi đỏ và 15 bi trắng, 1
- Hộp H đựng 15 bi trong đó có 6 bi đỏ và 9 bi trắng. 2
Lấy một bi ở hộp H , bỏ vào H , trộn đều rồi lấy ra một bi. Tính xác suất nhận được bi đỏ ? bi 1 2 trắng ?
7. Trong một vùng dân cư, cứ 100 người thì có 30 người hút thuốc lá. Biết rằng tỷ lệ người bị viêm
họng trong số người hút thuốc lá là 60%, trong số người không hút thuốc lá là 20%. Khám ngẫu
nhiên một người và thấy người đó bị viêm họng. Tìm xác suất để người đó hút thuốc lá. Nếu người
đó không bị viêm họng thì xác suất để người đó hút thuốc lá là bao nhiêu ?
8. Một dây chuyền lắp ráp nhận các chi tiết từ hai nhà máy khác nhau. Tỷ lệ chi tiết do nhà máy thứ
nhất cung cấp là 60%, của nhà máy thứ hai là 40%. Tỷ lệ chính phẩm của nhà máy thứ nhất là 90%,
của nhà máy thứ hai là 85%. Lấy ngẫu nhiên một chi tiết trên dây chuyền và thấy rằng nó là chính
phẩm. Tìm xác suất để chi tiết đó do nhà máy thứ nhất sản xuất.
9. Một cặp trẻ sinh đôi có thể do cùng một trứng (sinh đôi thật) hay do hai trứng khác nhau sinh ra
(sinh đôi giả). Các cặp sinh đôi thật luôn luôn có cùng giới tính. Các cặp sinh đôi giả thì giới tính
của mỗi đứa độc lập nhau và có xác suất là 0.5. Thống kê cho thấy 34% cặp sinh đôi là trai; 30%
cặp sinh đôi là gái và 36% cặp sinh đôi có giới tính khác nhau.
a) Tính tỷ lệ cặp sinh đôi thật,
b) Tìm tỷ lệ cặp sinh đôi thật trong số các cặp sinh đôi có cùng giới tính.
10. Một trung tâm chẩn đoán bệnh dùng một phép kiểm định T. Xác suất để một người đến trung
tâm mà có bệnh là 0.8. Xác suất để người khám có bệnh khi phép kiểm định dương tính là 0.9 và
xác suất để người khám không có bệnh khi phép kiểm định âm tính là 0.6. Tính các xác suất
a) phép kiểm định là dương tính,
b) phép kiểm định cho kết quả đúng.
11. Một thiết bị gồm 3 cụm chi tiết, mỗi cụm bị hỏng không ảnh hưởng gì đến các cụm khác và chỉ
cần một cụm bị hỏng thì thiết bị ngừng hoạt động. Xác suất để cụm thứ nhất bị hỏng trong ngày là
0.1, cụm thứ hai là 0.05 và cụm thứ ba là 0.15. Tìm xác suất để thiết bị không ngừng hoạt động trong ngày.




