







































Preview text:
Chương TÍCH PHÂN BỘI 2.
2.1. Tích phân hai lớp
2.1.1. Định nghĩa và cách tính tích phân hai lớp
2.1.1.1. Định nghĩa
Bài toán dẫn đến khái niệm tích phân hai lớp
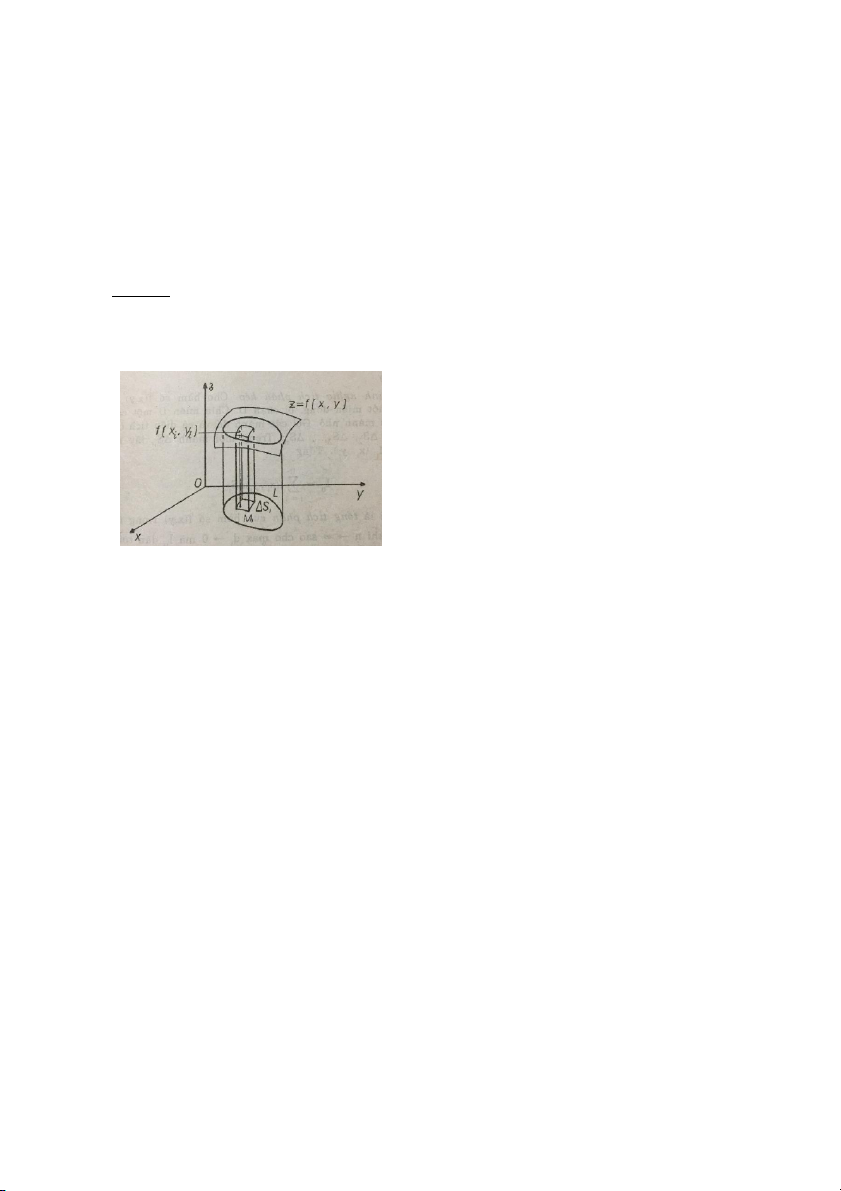
Giả sử có một vật thể hình trụ, phía trên giới hạn bởi mặt cong được biểu diễn bằng phương trình z
= f(x,y), mặt xung quanh là mặt của hình trụ có đường sinh song song với trục Oz, còn phía dưới giới hạn
bởi hình phẳng đóng D nằm trong mặt phẳng tọa độ Oxy và được gọi là đáy của của hình trụ. Yêu cầu
tính thể tích V của vật thể hình trụ này với giả thiết f(x,y) là hàm không âm, xác định và liên tục trên miền đóng D.
Bài giải. Chia D thành n miền nhỏ không dẫm lên nhau (giao của 2 hai miền nhỏ bất kỳ bằng rỗng).
Gọi diện tích của n miền nhỏ đó là S1, S2, …, Sn. Lấy mỗi miền nhỏ là đáy của hình trụ mà mặt xung
quanh có đường sinh song song với trục Oz và phía trên giới hạn bởi mặt cong được biểu diễn bằng phương trình f(x,y).
Như vậy, vật thể hình trụ đã được chia thành n hình
trụ nhỏ. Trong mỗi miền nhỏ Si (1 i n) chúng ta lấy
một điểm tùy ý Mi(xi,yi). Chúng ta có tích zi.Si =
f(xi,yi).Si là thể tích hình trụ có diện tích đáy Si và
chiều cao zi = f(xi,yi). Nếu miền nhỏ Si khá bé, thì do
hàm f(x,y) liên tục trên D nên giá trị của z = f(x,y) xấp xỉ
bằng giá trị của zi = f(xi,yi) nên có thể coi thể tích của
hình trụ nhỏ thứ i là Vi f(xi,yi)Si. Như vậy, nếu mọi
miền nhỏ Si (1 i n) đều khá bé thì có thể coi thể tích n
của hình trụ là V f (x , y ) S . i i i i=1 n Tổng f (x , y . ) S
sẽ có độ chính xác càng cao (tức là giá trị của biểu thức này càng gần thể tích i i i i 1 =
thực V của hình trụ đang xét) nếu n càng lớn và tất cả các Si (1 i n) càng bé. Do đó, thể tích V của n
hình trụ đang xét bằng giới hạn (nếu có) của tổng f (x , y )
S khi n → cùng với đường kính của mỗi i i i i 1 = n miền nhỏ S =
i (1 i n) bé dần về 0, tức là V = lim f (x , y )S với d
max d , trong đó di là đường i i i i d→ 0 1i n i 1 =
kính của mỗi miền nhỏ Si (1 i n) (đường kính của một miền được định nghĩa là khoảng cách lớn
nhất giữa hai điểm trên biên của miền ấy).
Định nghĩa tích phân hai lớp
Cho hàm số f(x,y) xác định trên miền đóng D. Chia miền D một cách tùy ý thành n miền nhỏ không
dẫm lên nhau. Gọi diện tích của n miền nhỏ đó là S1, S2, …, Sn. Trên mỗi miền nhỏ Si (1 i n) n
chúng ta lấy một điểm tùy ý Mi(xi,yi) và lập tổng I = f (x , y ) S . I n i i i
n được gọi là tổng tích phân của i=1
hàm f(x,y) trên miền D nếu khi n → sao cho d = max d →0 (trong đó di là đường kính của miền nhỏ i 1in
Si) mà In dần đến một giá trị hữu hạn không phụ thuộc vào cách chia miền D và cách lấy điểm Mi(xi,yi)
trên mỗi miền nhỏ Si, thì giá trị hữu hạn này được gọi là tích phân hai lớp của hàm số f(x,y) trên miền D
và ký hiệu là f(x,y)dS , khi đó D, f(x,y), dS, x và y lần lượt được gọi là miền tính tích phân, hàm số D
dưới dấu tích phân, vi phân diện tích, các biến tính tích phân. 59 n
Như vậy, chúng ta có f (x, ) y dS = limI = lim f(x ,y ) S
nếu giới hạn này tồn tại và hữu n i i i n → max d 0 → i D 0i n i=1
hạn, khi đó chúng ta nói rằng hàm số f(x,y) khả tích trên miền đóng D . Định lý. D
Nếu hàm số f(x,y) xác định và liên tục trong miền đóng .
thì nó khả tích trên đó
Vì tích phân hai lớp nếu tồn tại thì không phụ thuộc vào cách chia miền D, nên chúng ta có thể chia
D bởi lưới các đường thẳng song song với các trục tọa độ Ox, Oy. Khi đó, mỗi miền nhỏ Si (1 i n)
nói chung là hình chữ nhật, do đó dS = dxdy f (x, y)dS f (x, y)dxdy. = D D
Nhận xét. Bản chất của phép tính tích phân là tính giới hạn, tuy nhiên việc tính tích phân bằng cách
dùng định nghĩa không phải đơn giản, do đó các nhà toán học đã dùng định nghĩa để đưa ra các công thức
tích phân cơ bản để việc tính tích phân đơn giản hơn.
Ý nghĩa hình học của tích phân hai lớp
Nếu hàm số z = f(x,y) > 0, xác định và liên tục với (x,y) D
thì giá trị của tích phân hai lớp
f(x,y)dxdy là thể tích của hình trụ có đáy là miền D thuộc mặt phẳng tọa độ Oxy, mặt xung quanh là D
mặt của hình trụ có đường sinh song song với trục Oz, còn mặt trên của hình trụ là mặt cong được biểu
diễn bằng phương trình z = f(x,y).
Đặc biệt, nếu f(x,y) = 1 với (x,y) D thì giá trị
của tích phân f(x,y)dxdy = d 1 xdy = dxdy là D D D
diện tích S của miền D.
Các tính chất của tích phân hai lớp (1) f(x,y) +g(x,y)
dxdy = f(x,y)dxdy + g(x,y)dxdy D D D
(2) kf (x, y)dxdy = k f (x, y)dxdy (k là hằng số) D D D D =
(3) f(x, y)dxdy = f (x, y d ) xdy + f (x, y d ) xdy với 1 2 D D = D D 1 2 1 D D2
(4) f(x, y)dxdy g(x, y)dxdy nếu f(x,y) g(x,y) với (x,y) D D D
(5) f(x, y)dxdy f(x, y) dxdy D D (6) mS f (x, y)dxdy MS D
với S là diện tích của , m = min f (x, y) và M = max f (x, y) ( x,y) D (x,y) D D
(7) Nếu f(x,y) xác định và liên tục trên D, S là diện tích của D thì ( x, y) D sao cho f (x, y)dxdy = Sf (x, y) D
2.1.1.2.Tích phân lặp
Như đã Nhận xét ở trên, việc tính một tích phân hai lớp trực tiếp từ định nghĩa là điều rất khó, tuy
nhiên, các nhà toán học đã biểu diễn một tích phân hai lớp dưới dạng một tích phân lặp, để sau đó có thể
tính được dễ dàng bằng cách tính 2 tích phân một lớp quen thuộc.
Giả sử hàm số f(x,y) khả tích trên hình chữ nhật D = {(x,y)R2a x b, c y d} [a,b][c,d]. d
Chúng ta sử dụng ký hiệu f (x,y)dy để hàm ý rằng x coi như hằng số và hàm số f(x,y) được lấy tích phân c d
theo y từ y = c đến y = d. Như vậy, sau việc tính tích phân xác định một lớp đối với y thì f (x,y)dy trở c 60
thành một biểu thức của x, vì a x
b nên biểu thức của x là một hàm số của x và chúng ta có thể ký d
hiệu g(x) = f(x,y)dy với a x b. c
Tiếp theo, chúng ta tính tích phân hàm số g(x) theo x từ x = a đến x = b thì b b d
g(x)dx = f(x, )ydydx . Tích phân bên phải của đẳng thức trên được gọi là tích phân lặp. Để đơn a a c
giản, cặp dấu [ ] không viết và dx được viết giữa hai dấu tích phân một lớp, tức là b d b d
dxf(x,y)dy = f(x,y d)ydx . Đẳng thức này có nghĩa là: đầu tiên chúng ta tính tích phân biểu thức a c a c
f(x,y) theo y từ y = c đến y = d khi coi x là hằng số, sau đó tính tích phân biểu thức vừa tính được theo x từ x = a đến x = b. d b d b
Tương tự, tích phân lặp dyf(x,y d
) x = f(x, y)dxdy có nghĩa là: đầu tiên chúng ta tính tích c a c a
phân biểu thức f(x,y) theo x từ x = a đến x = b khi coi y là hằng số, sau đó tính tích phân biểu thức vừa
tính được theo y từ y = c đến y = d. 3 2 2 3
Ví dụ 2.1. Tính các tích phân lặp I = d x f (x, y)dy, J = d
y f (x, y)dx với f(x,y) = x2y 0 1 1 0 Bài giải. y= 2 x=3 3 2 3 2 2 y2 3 3 2 3 x 3 3 27 27 + I = dx x ydy = x dx = x dx = = . = 2 2 2 3 2 3 2 0 1 0 y 1 = 0 x=0 x 3 = y 2 = 2 3 2 2 x3 2 27 27 y y 2 27 3 27 + J = dy x ydx = y d y = ydy = = . = 3 3 3 2 3 2 2 1 0 1 x 0 = 1 y 1 = 27 Nhận xét: I =
= J từ ví dụ trên và nếu thực hiện nhiều ví dụ khác có kết quả tương tự, vậy liệu 2 b d d b
dxf(x,y)dy = dy f(x,y)dx có luôn đúng với cùng f(x,y) không? a c c a
Định lý Fubini. Nếu hàm số f(x,y) xác định và liên tục trên hình chữ nhật D = [a,b][c,d] thì b d d b
f(x,y d)xdy = dx f(x,y d)y = dyf(x,y)dx D a c c a b d
Hệ quả. Nếu f(x,y) = g(x)h(y) thì f (x, y d ) xdy = g(x)h(y)dxdy = g(x)dx h(y)dy D D a c f (x, y) = y sin x ( y)
Ví dụ 2.2. Tính tích phân I = f(x,y)dxdyvới D = , 1 [ ] 2 [ , 0 ] D Bài giải. Hàm số f (x, )
y = y sin(xy) liên tục trên R2 nên liên tục trên DR2, nên theo Định lý 2 2
Fubini thì I = ysin(xy)dxdy = dx ysin(xy)dy = dy ysin(xy)dx . D 1 0 0 1
- Chúng ta tính I theo y trước y= y= y cos x ( y) 1 cos(x) sin(xy) cos(x) sin( x ) y sin(xy)dy = − + cos x ( y)dy = − + = − + 2 2 x y 0 x x x x = = x 0 0 y 0 2 2 = cos(x) sin( x ) sin( x ) x 2 sin 2 I = dx ysin(xy)dy = − + dx = − = − +sin = 0 . x x2 x = 2 1 0 1 x 1
- Bây giờ, chúng ta tính I theo x trước 61 2 2 x 2 ysin(xy)dx = = sin(xy)d(xy) = co − s x ( y) = −cos2y +cosy x 1 = 1 1 y 2 =
I = dy ysin(xy)dx = − cos2y + cos sin 2y sin 2 y dy = − + sin y = − + sin 0 = 0 . 2 2 0 1 0 y= 0
Nhận xét. Ở Ví dụ 2.1. tính tích phân theo biến x hoặc biến y trước đều dễ như nhau, nhưng ở Ví dụ
2.2. việc tính tích phân theo biến x trước dễ hơn nhiều so với việc tính tích phân theo biến y trước. Do đó,
khi tính tích phân hai lớp, chúng ta nên lựa chọn thứ tự tính tích phân sao cho quá trình tính tích phân
theo mỗi lớp đơn giản hơn.
2.1.1.3. Cách tính tích phân hai lớp trong hệ tọa độ Descartes
- Miền tính tích phân là hình chữ nhật D = {(x,y)R2a x b, c y d} = [a,b][c,d] b d d b b
f(x,y)dxdy = dxf(x, y)dy = dyf(x,y)dx (khi tính f(x,y)dx thì coi y là hằng số, khi D a c c a a d
tính f (x,y)dy thì coi x là hằng số). c 0 x 1
Ví dụ 2.3. Tính tích phân I = xydxdy với D= 1 y 2 D
Bài giải. Đồ thị của miền D là Chúng ta 3 c có thể tính I bằng ách: 1 2 1 2 1 y =2 2 1 1 xy x 3 3 Cách 1. I =
xydxdy = xydy dx = dx xydy = dx = dx = xdx = 2 2 2 D 0 1 0 1 0 y =1 0 0 x 1 = 3 x2 3 1 3 = = . 2 2 2 2 4 x=0 2 1 2 1 2 x =1 2 2 2 x y y 1 Cách 2. I =
xydxdy = xydx dy = dy xydx = dy = dy = ydy = 2 2 2 D 1 0 1 0 1 x=0 1 1 2 1 y2 1 4 1 1 3 3 = = − = = . 2 2 2 2 2 2 2 4 1 x 1 = y= 2 1 2 x2 y2 1 4 1 1 3 3 Cách 3. I = xydxdy = xdx ydy = = . − = = . 2 2 2 2 2 2 2 4 D 0 1 x=0 y=1 - Miền tính
tích phân là không phải là hình chữ nhật
+ Trường hợp 1. Trong hệ tọa độ Descartes vuông góc Oxy đồ thị của miền D có dạng 62
Chiếu miền D lên trục Ox thì D = {(x,y)R2a x b, y1(x) y y2(x)} b y2 ( x )
f(x,y)dxdy = dx f(x,y)dy . D a y ( x ) 1
+ Trường hợp 2. Trong hệ tọa độ Descartes vuông góc Oxy đồ thị của miền D có dạng
Chiếu miền D lên trục Oy thì D = {(x,y)R2c y d, x1(y) x x2(y)} d x ( y) 2
f(x,y d)xdy = dy f(x,y)dx . D c x ( y) 1
Ví dụ 2.4. Tính tích phân I = 2
x ydxdy trên miền D xác định bởi tam giác ABC với A(0,0), D B(1,0), C(1,1).
Bài giải. Đồ thị của miền D trong hệ tọa độ Descartes vuông góc Oxy là
Chúng ta có thể tính I bằng 2 cách: 0 x 1
Cách 1. Chiếu miền D lên trục Ox thì D = 0 y x y x = x= 1 1 x 1 2 2 y2 2 1 1 4 1 x5 1 1 1 I = x ydxdy = dx x ydy = x dx = x dx = = = . 2 2 2 5 2 5 10 D 0 0 0 y 0 = 0 x= 0 0 y 1
Cách 2. Chiếu miền D lên trục Oy thì D = y x 1 1 1 1 x =1 3 = x 1 1 x 1 1 2 5 y y 2 2 I = x ydxdy = dy x d y x = y dy = (y− 4 y )dy = − = 3 3 3 2 5 D 0 y 0 x =y 0 = y 0 1 1 1 1 5− 2 1 3 1 − = = = . 3 2 5 3 10 310 10
+ Trường hợp 3. D là miền đóng nội ,
tiếp trong hình chữ nhật {x = a, x = b, y = c, y = d}, trong đó
các điểm tiếp xúc M, Q, P, N có thể là một đoạn thẳng. 63
- Nếu cung MNP được biểu diễn bằng phương trình y = y1(x), còn cung MQP được biểu diễn bằng
phương trình y = y2(x) và chiếu miền D lên trục Ox thì D = {(x,y)R2a x b, y1(x) y y2(x)} b y2 ( x )
f(x,y)dxdy = dx f(x,y)dy . D a y1 ( x )
- Nếu cung QMN được biểu diễn bằng phương trình x = x1(y), còn cung QPN được biểu diễn bằng
phương trình x = x2(y) và chiếu miền D lên trục Oy thì D = {(x,y)R2c y d, x1(y) x x2(y)} d x ( y) 2
f(x,y d)xdy = dy f(x,y)dx . D c x ( y) 1 2 Ví dụ x
2.5. Tính tích phân I =
dxdy trên miền D giới hạn bởi các đường thẳng x = 2, y = x và 2 y D đường hypecbol y =1 x .
Bài giải. Đồ thị của miền D trong hệ tọa độ Descartes vuông góc Oxy là
Chúng ta có thể tính I bằng hai cách: 1 x 2
Cách 1. Chiếu miền D lên trục Ox thì D = 1 ( x) y x = x=2 y x x2 2 x x2 2 2 1 2 3 x 4 x2 9 dxdy = dx dy = − x dx = (x − x)dx = − = . y2 y2 y 4 2 4 D 1 1 x 1 y 1 = x 1 x 1 = 1 y 2 1 ( ) 2 y 1
Cách 2. Chiếu miền D lên trục Oy thì D = D1D2 với D = và D = 1 2 y x 2 1 ( y) x 2 2 2 2 2 2 2 1 2 2 = x I = x dxdy + x dxdy dxdy = x dy dx + x dy dx = 2 2 2 2 2 y y y y y D D D 1 y 1 2 1 y 1 2 64 2 x =2 3 1 x =2 3 2 1 x 1 x 1 8 1 1 8 1 dy + dy = − y dy + − dy = 2 2 2 2 5 y 3 y 3 3 y 3 y y 1 x =y 1 2 = x 1 y 1 1 2 y 2 = y 1 = 1 8 y2 1 8 1 17 5 9 − − + − + = + = . 3 y 2 3 y 4y4 12 6 4 y 1 = y=1 2 d x2 ( y)
Nhận xét. (1) Với miền D ở Ví dụ 2.5. nếu sử dụng công thức f(x, y d
) xdy = dy f(x, y)dx thì D c x1 ( y) b y 2( x )
tính toán cồng kềnh hơn sử dụng công thức f(x, y)dxdy = dx f(x, y)dy . D a y1 ( x )
(2) Nếu biết các cận của tích phân hai lớp, chúng ta có thể suy ra miền tính tích phân D, do đó đổi
được thứ tự tính tích phân. 2 4
Ví dụ 2.6. Đổi thứ tự
tính tích phân của tích phân I = dx f(x, y)dy −2 x2 Bài giải. 2 4 − 2 x 2
Từ các cận của tích phân I = dx f (x, y d ) y D =
nên đồ thị của miền D trong hệ 2 −2 x2 x y 4
tọa độ Descartes vuông góc Oxy là
Đường thẳng y = 4 giao với y = đường parabol
x2 tại 2 điểm (–2,4) và (2,4). 0 y 4 4 y
Nếu chiếu miền D lên trục tung Oy thì miền D=
, khi đó I = dy f (x, ) y dx . − y x y 0 − y xdxdy
Ví dụ 2.7. Tính tích phân
trên miền đóng D = {(x,y)R2|0 ≤ x ≤ 1, x ≤ y ≤ 1} 3 D 1+ y Bài giải.
Đồ thị của miền D trong hệ tọa độ Descartes vuông góc Oxy là 0 x 1 1 1 1 1 xdy dy
Nếu chiếu miền D lên trục Ox thì D = I= dx = xdx 3 x y 1 0 x + 3 1 y 0 x 1+ y 0 y 1 y 1 y 1
Nếu chiếu miền D lên trục Oy thì D = xdx dy I = dy = xdx 3 3 0 x y 0 0 1+ y 0 1 + y 0 65 1 y 1 1 Chúng ta nhận thấy dy dy , tính I =
xdx đơn giản hơn tính I = xdx . 3 3 0 1 + y 0 0 x 1+ y 1 y 1 x =y 2 1 2 1 3 dy 1 x I = xdx = dy = 1 y dy = 1 1 d(y ) = 3 3 2 3 2 2 3 0 1+ y 0 0 1+ 3 y 1 y 1 y x= 0 + 0 + 0 1 1 = − = = ( 1 y 1 y 1 − + − 1+ y3) 3 1 1 3 ( 1 2) 1 1 3 2 1 2 d 1 ( + y ) = 1 ( + y ) = 1+ y = . 6 6 ( 1 − 2) +1 y 0 = 3 y=0 3 0 1 2 Ví dụ 2
2.8. Tính tích phân I = dy x e dx 0 2 y
Bài giải. Các nhà toán học đã chứng minh rằng, biểu thức dưới dấu tích phân trong tích phân 2 2
ex dx không có nguyên hàm sơ cấp, tức là nguyên hàm của tích phânex dx không thể biểu diễn qua 2
các hàm số sơ cấp được, mặc dù về mặt lý thuyết thì tích phân ex dx là khả tích. 1 2 0 y 1
Từ các cận của tích phân 2 I = dy x e dx D =
nên đồ thị của miền D trong hệ tọa độ 2y x 2 0 2 y Descartes vuông góc Oxy là
Bây giờ, chúng ta chiếu miền D lên trục Ox thì miền D được mô tả bằng cách khác là 0 x 2 2 x 2 2 y= x 2 = 2 2 1 2 2 1 2 2 1 x e4 2 − 1 D = I = dx ex 2 dy = ex y dx = xex dx = e x d(x 2) = e x = . 0 y x 2 y= 0 2 4 4 x=0 4 0 0 0 0 0 1 2
Nhận xét. Nếu tính tích phân 2 I = dy x
e dx theo thứ tự đã cho thì không tính được, nhưng nếu đổi 0 2 y 2 x 2
thứ tự tính tích phân thành 2 I = dx x
e dy thì tính được. 0 0 2.1.2.
Phép đổi biến trong tích phân hai lớp
2.1.2.1. Công thức đổi biến trong tích phân hai lớp
Xét tích phân hai lớp f (x, y)dxdy , trong đó hàm số f(x,y) xác định và liên tục trên miền đóng D. D x = x(u, v)
Giả sử chúng ta thực hiện phép đổi biến
thỏa mãn các điều kiện sau đây: y = y(u, v) x = x(u, v) (1) Phép đổi biến
là ánh xạ 1-1 từ miền D lên miền D’ (miền D’ là ảnh của mi qua ền D y = y(u, v) phép đổi biến này);
(2) Các hàm x(u,v), y(u,v) là các hàm số liên tục và có các đạo hàm riêng cấp 1 x , , u ( ) v , x, , u ( ) v , y, , u ( ) v ,
liên tục trên miền đóng D’ = {(u,v)R2} nào đấy; u v u y,v , u ( ) v x, (u, v) x, (u, v)
(3) Định thức Jacobi J = det u v 0 tr ; ong miền D’ y, u (u, ) v y,v (u, v) Khi đó f (x, y dx ) dy f x(u, v), y(u, v)J dudv = . D D' 66 Lưu ý.
(1) Nếu phép đổi biến là ánh xạ 1-1 thì một điểm trong của miền D tương ứng với một điểm trong
của miền D’ và ngược lại, một điểm trên biên của miền D tương ứng với một điểm trên biên của miền D’ và ngược lại.
(2) Nhà toán học Carl Gustav Jacob Jacobi (người Đức) đã chứng minh: Giá trị của định thức x = x(u, v)
Jacobi của phép đổi biến
là nghịch đảo giá trị của định thức Jacobi của phép đổi biến ngược y = y(u, v) u = u(x, y) x, (u,v) x, (u,v ) u v 1
của phép biến đổi trên, tức là J = det = và , , v = v(x, y) y (u, v) y (u, v) u, (x, y) u , (x, y) u v det x y , , v (x, y) v (x, y) x y 1 u, (x, ) y u, (x, y) ngược lại = det x y . , , J vx (x, y) vy (x, y)
Ví dụ 2.9. Tính tích phân I = 2 ( x 3
+ 4xy)dxdy trên miền D là hình bình hành giới hạn bởi các D
đường thẳng {x + 2y = 2, x + 2y = 4, 3x – y = 0, 3x – y = 3}. Bài giải. 2 x + 2y 4
Đồ thị của miền D =
trong hệ tọa độ Descartes vuông góc Oxy là 0 x 3 − y 3 (miền D)
Nếu tính tích phân này trong hệ tọa độ Descartes vuông góc Oxy thì việc chia miền D thành các
miền nhỏ bởi các đường song song với các trục tọa độ là phức tạp (phải tìm tọa độ điểm giao của các
đường thẳng chứa các cạnh của hình bình hành, sau đó chiếu miền D lên trục Ox hoặc trục Oy), dẫn đến
việc tính toán cồng kềnh, do đó chúng ta thực hiện đổi biến sao cho miền D là hình bình hành trong hệ
tọa độ Descartes vuông góc Oxy chuyển thành miền D’ là hình chữ nhật trong hệ tọa độ Descartes vuông u = x +2y u(x, y) x = u 7 + 2v 7 x(u, v) 2 u 4
góc Ouv bằng phép đổi biến D'= vì v = 3x − y v(x, y) y = u 3 7 − v 7 ( y u, v) 0 v 3 2 x + 2y 4 D = . 0 x 3 − y 3 (miền D’) x, (u, v) x, (u,v ) u = x + 2y
Để tìm định thức Jacobi J = det u v từ phép đổi biến chúng ta có thể , , y v = x 3 − y u (u, v) yv (u, v)
thực hiện bằng cách sau đây 2 : u = x + 2y x = u 7 + 2v 7 x , (u, v) x, (u, v) 1 7 2 7 u v 1 - Cách 1. J = det = = − v = x 3 − y y = u 3 7 − v 7 y , (u, v) y, (u, v) 3 7 − 1 7 7 u v 67 u = x + 2y 1 u, (x, y) u , (x, y) 1 2 x y 1 1 - Cách 2. = det = det = 7 − J = = − v = x 3 − y J v, (x, y) v, (x, y) 3 −1 −7 7 x y I = 2 3 ( x + 4xy)dxdy = 2 3
[ x (u, v) + 4x(u, v)y(u, v)]J dudv = D D' 4 3 du ( 3 [ u 7 + 2 2v 7) + ( 4 u 7 + 2v ) 7 ( u 3 7 − v 7)]−1 7 dv = 2 0 v = 4 3 4 3 1 1 2 3 v v 2 du 1 ( u 5 + 3 u 2 v + 2 4v )dv = 2 1 u 5 + v 3 u 2 + 4 du = 3 3 7 7 2 3 2 0 2 v=0 = 4 v 3 1 3 4v 4 2 1 u 5 v + 2 1 u 6 v + du = 1 2 (4 u 5 + 14 u 4 + 3 ) 6 du = 3 7 3 343 2 = 2 v 0 u 4 = 1 u 3 u 2 1 u 4 3 2 1776 45 + = 144 + 3 u 6 = 1 ( u 5 + 7 u 2 + 3 u 6 ) = . 343 3 2 343 u= 2 343 u 2 =
2.1.2.2. Tính tích phân hai lớp trong tọa độ cực Tọa độ cực
Hệ tọa độ cực là một hệ tọa độ hai chiều, trong đó mỗi điểm M bất kỳ trên một mặt phẳng được
biểu diễn duy nhất bằng hai thành phần: Khoảng cách từ
điểm đó tới một điểm gốc O (được gọi là gốc
cực) gọi là bán kính r (0 r < + r
, = 0 khi điểm M trùng với điểm gốc O) và góc (0 2) tạ o bởi
hướng gốc cho trước (được gọi là trục cực) với đường thẳng chứa OM (gọi là đường thẳng OM) theo
chiều dương (trục cực quay quanh gốc cực theo chiều ngược với chiều quay của kim đồng hồ, cho đến
khi trùng với đường thẳng OM), trục cực thường được vẽ theo chiều ngang và hướng về bên phải.
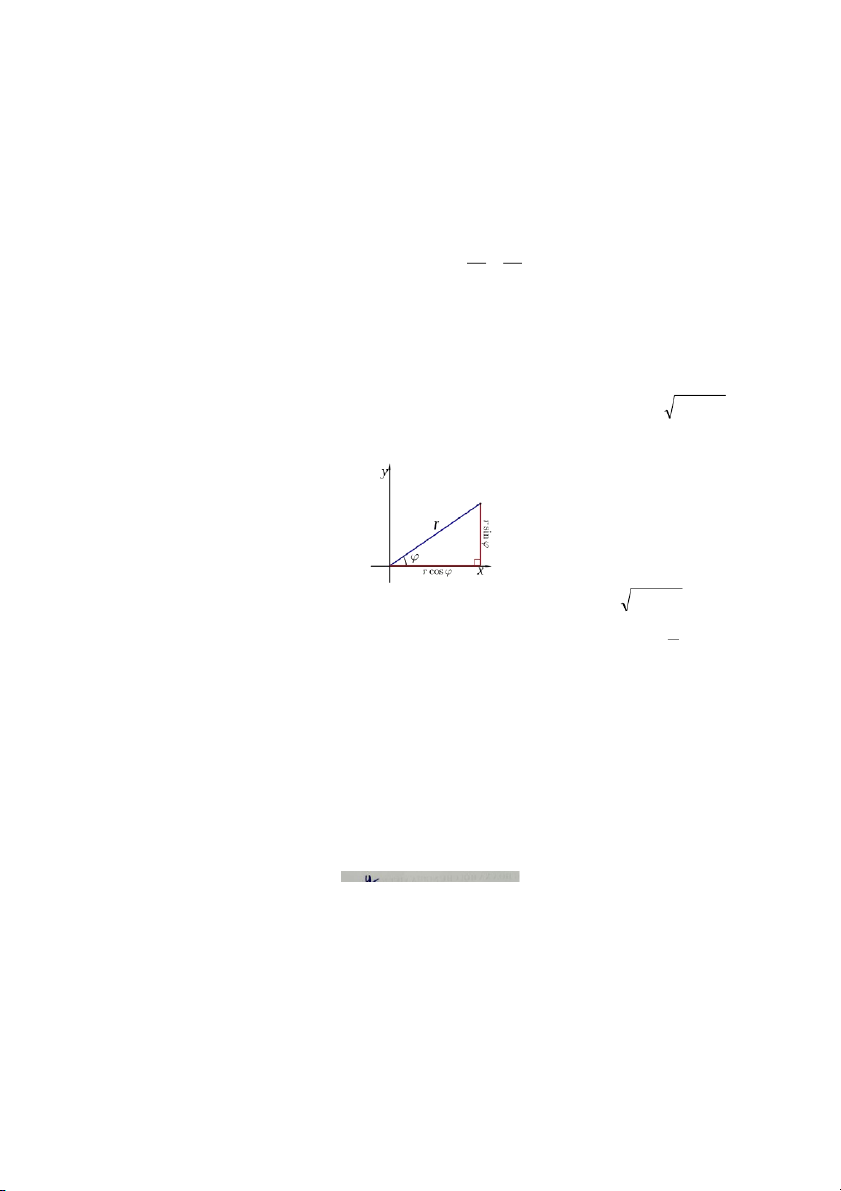
Hình sau đây thể hiện mối quan hệ giữa tọa độ Descartes (x,y) với tọa độ cực (r,) của cùng một
điểm trong mặt phẳng R2 trong trường hợp gốc của hai hệ tọa độ này trùng nhau và trục hoành Ox của hệ
tọa độ Descartes vuông góc Oxy trùng với trục cực của hệ tọa độ cực cả phương và hướng. x = x(r, ) = r cos
Khi đó, phép biến đổi từ tọa độ Descartes ( ) sang tọa x,y độ cực (r,) là , vì các y= y r ( , ) = r si n r 0
hàm số lượng giác cos, sin là các hàm số tuần hoàn có chu kỳ 2 nên với thì phép biến đổi 0 2
này xác định một ánh xạ 1-1 giữa tọa độ Descarter (x,y) và tọa độ cực (r,) của cùng một điểm trong mặt
phẳng R2, riêng điểm gốc tọa độ O(0,0) tương ứng với r = 0 và tùy ý. Còn ép ph
biến đổi từ tọa độ cực r = r(x,y) = x2 + y2
(r,) sang tọa độ Descartes (x,y) là
cũng xác định một ánh xạ 1-1 giữa tọa độ
= (x,y) =arctan(y x)
cực (r,) và tọa độ Descartes (x,y) của cùng một điểm trong mặt phẳng R2. 68
Nhận xét. Hệ tọa độ cực có ích trong những trường hợp mà trong ,
đó quan hệ giữa hai điểm được
mô tả dưới dạng khoảng cách và góc. Trong hệ tọa độ Descartes vuông góc Oxy, quan hệ này được biểu
diễn dưới dạng công thức lượng giác .
Nói chung, có thể đơn giản hơn khi tính tích phân f (x, y)dxdy,
nếu hàm số mô tả biên của miền D D có biểu thức 2 2 x + y hoặc biểu thức 2 2
px + qy (trong các tham số p > 0, q > 0 phải có ít nhất một tham
số có giá trị khác 1, khi p = q = 1 thì 2 2 2 2
px + qy = x + y ) thì nên đổi biến từ tọa độ Descartes (x,y) sang
tọa độ cực (r,) hoặc tọa độ cực (r,) mở rộng.
Đổi biến từ tọa độ Descarter (x,y) sang tọa độ cực (r, )
Nếu hàm số mô tả biên của miền D có biểu thức 2 2
x + y thì đổi tọa độ Descartes (x,y) sang tọa độ x = x(r,) = x + rcos
cực (r,) bằng phép đổi biến 0
, trong đó (x0,y0) là tọa độ (trong hệ tọa độ
y = y(r, ) = y + r sin 0
Descartes vuông góc Oxy) của điểm gốc cực của hệ tọa độ cực. x = x(r,) = x + rcos
r = r(x,y) = (x −x )2 +(y − 2
Phép biến đổi ngược của y ) 0 là 0 0 .
y = y(r, ) = y + r sin 0
= (x,y) =arctan[(y −y ) (x −x )] 0 0 x = x(r,) = x + rcos
Nếu 0 r < + và 0 2 thì phép đổi biến 0
xác định một ánh xạ 1-1 y = y(r, ) = y + 0 r sin
giữa tọa độ Descarter (x,y) và tọa độ cực (r,), riêng điểm gốc cực có tọa độ (x0,y0) trong hệ tọa độ
Descartes vuông góc Oxy, tương ứng với r = 0 và tùy ý. Chúng ta c ó (x + r cos) ( x +r cos ) 0 0 x, (r,) x,(r,) − r r cos r sin J = det = det = det = r 0 y, (r,) y, (r,) ( y + r sin ) (y + r sin ) 0 0 sin r cos r r
trừ điểm gốc cực có tọa độ (x0,y0) trong hệ tọa độ Descartes vuông góc Oxy. Đối với phép đổi biến này,
chúng ta không cần tính J nữa, mà sử dụng |J| = r > 0 luôn.
f(x,y)dxdy = f(x + rcos,y + rsin)Jdr d = rf (x r cos , y r sin )drd 0 0 + + 0 0 , miền D’ D D' D'
trong hệ tọa độ cực (r,) là ảnh của miền D trong hệ tọa độ Descartes vuông góc Oxy. Để đơn giản, nhưng ông kh
mất tính tổng quát, các trình bày sau đây khi đổi biến từ tọa độ
Descartes (x,y) sang tọa độ cực (r,), chúng ta chọn (x0,y0) = (0,0), tức là điểm gốc cực của hệ tọa độ cực
trùng với điểm gốc của hệ tọa độ Descartes vuông góc Oxy.
Có 3 trường hợp xảy ra, khi đổi biến từ tọa độ Descartes (x,y) sang tọa độ cực (r,).
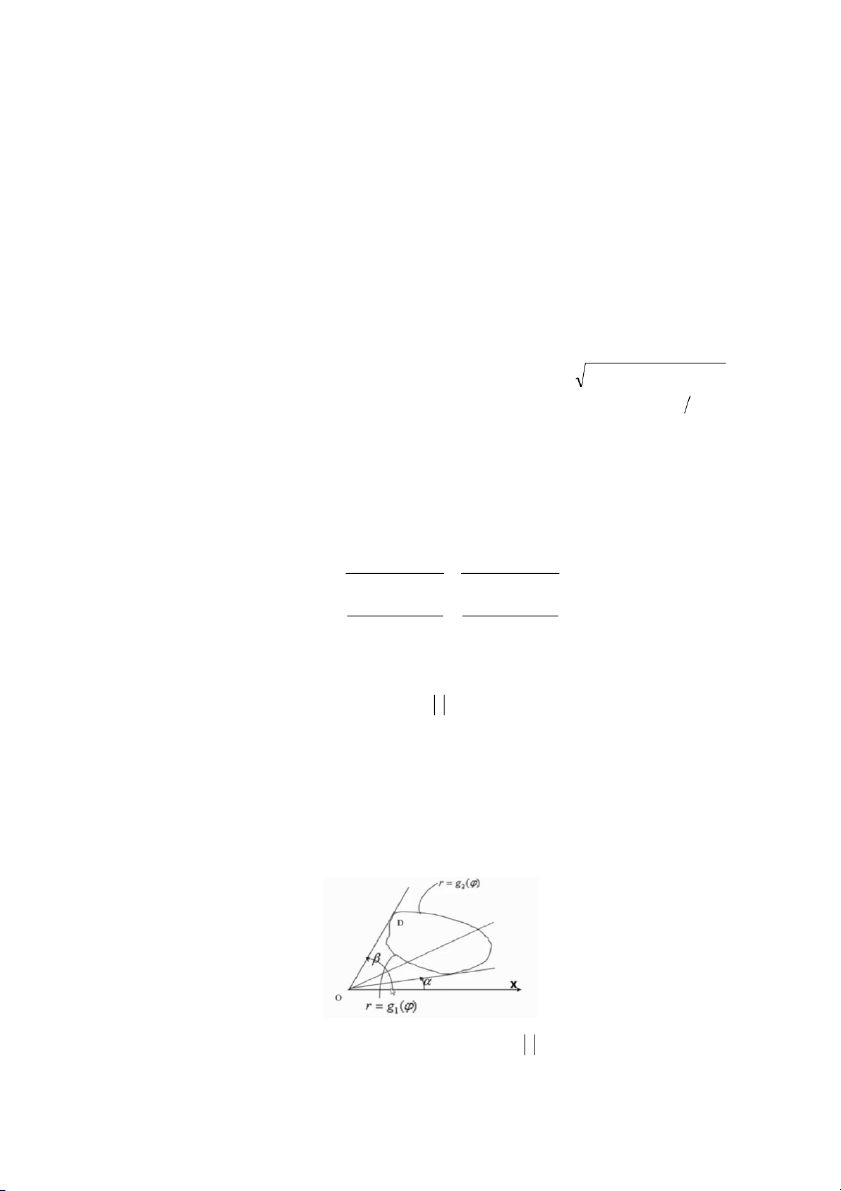
Trường hợp 1. Điểm gốc cực của hệ tọa độ cực nằm ngoài miền D g ( ) 2 D'=
f(x,y)dxdy = f(rco s,rsi n ) J dr d = d rf(rcos,rsi n )dr . g () r g () 1 2 D D' g1 ( ) Trường hợp 2.
Điểm gốc cực của hệ tọa độ cực nằm trên biên của miền D 69 g( ) D'=
f(x,y)dxdy = f(rco s , rsi n ) J drd = d rf(rco s,rsi n )dr . 0 r g() D D' 0 Trường hợp 3.
Điểm gốc cực của hệ tọa độ cực là điểm trong của miền D 2 g 0 ( ) 2 D'=
f(x,y)dxdy = f(rco
s , rsin) J drd = d rf(rco s , rsin)dr . 0 r g() D D' 0 0
Ví dụ 2.10. Tính tích phân I = ydxdy trên miền D = {(x,y)R2|4 ≤ x2 + y2 y ≤ 9,– ≤ x ≤ y} D Bài giải.
Đồ thị của miền D trong hệ tọa độ Descartes vuông góc Oxy là x = r cos
Nếu đổi biến từ tọa độ Descartes (x,y) sang tọa độ cực (r,) theo công thức thì điểm y = r sin
gốc cực của hệ tọa độ cực nằm ngoài miền D (Trường hợp 1), khi đó D'= . g () r g () 1 2
Để xác định các góc , (tạo bởi trục Ox với các đường thẳng y = x, y = –x tương ứng, với chiều
dương là chiều ngược với chiều quay của kim đồng hồ) và các hàm g1(), g2() chúng ta thực hiện như sau x = r cos - Thay
vào các bất đẳng thức –y ≤ x ≤ y –rsin ≤ rcos ≤ rsin –1 ≤ cot ≤ 1 y = r sin
arccot(–1) ≥ ≥ arccot(1) 4
3 4 = 4 và = 3 4 , hoặc bằng cách khác: đường thẳng
y = x có hệ số góc tan = 1 = arctan1 = 4 , còn đường thẳng y = –x có hệ số góc tan = 1 − = arctan(− )
1 = 3 4 4 3 4 . Căn cứ vào đồ thị của miền D, chúng ta cũng có
thể suy ra được 4 3 4. x = r cos - Thay
vào các bất đẳng thức 4 ≤ x2 + y2 ≤ 9 22 ≤ (rcos)2 + (rsin)2 ≤ 3 2 y = r sin
22 ≤ r2 ≤ 32 2 ≤ r ≤ 3 (vì r 0) g1() = 2 và g2() = 3. = 4 g () = 2 1 4 3 4 và ' D = . = 3 4 g () = 3 2 2 r 3 70
Chúng ta có |J| = r và vì f(x,y) = y f(rcos,rsin) = rsin I = ydxdy = (rsin) J dr d = D D' g2 () 3 4 3 3 4 3 2 2 (rsi n r ) drd = d r sindr = sind r dr = sin d 2 r dr = D' g ( ) 4 2 1 4 2 ( r= 3 3 = − cos 3 4 = − − = + − = . = 4 ) r 3 1 3 3 2 2 1 19 2 cos cos (3 2 ) .(27 ) 8 3 4 4 3 2 2 3 3 r= 2
Ví dụ 2.11. Tính tích phân I = ydxdy trên miền D là một phần tư đường tròn có tâm tại gốc tọa D
độ, bán kính R nằm trong góc vuông thứ nhất của hệ tọa độ Descartes vuông góc Oxy. Bài giải.
Đường tròn có tâm tại gốc tọa độ O(0,0) và bán kính R có phương trình x2 + y2 = R2, do đó một
phần tư đường tròn có tâm tại gốc tọa độ, bán kính R nằm trong góc vuông thứ nhất của hệ tọa độ
Descartes vuông góc Oxy là miền D = {(x,y)R2| x2 + y2 ≤ R2, x 0, y 0}
. Đồ thị của miền D trong hệ
tọa độ Descartes vuông góc Oxy là x = r cos
Nếu đổi biến từ tọa độ Descartes (x,y) sang tọa độ cực (r,) theo công thức thì điểm y = r sin
gốc cực của hệ tọa độ cực nằm trên biên của miền D (Trường hợp 2), đồng thời trùng với điểm gốc của
hệ tọa độ Descartes, khi đó D'= . 0 r g ( )
Để xác định các góc , (tạo bởi trục Ox với các đường thẳng y = 0, x = 0 tương ứng, với chiều
dương là chiều ngược với chiều quay của kim đồng hồ) và hàm g() chúng ta thực hiện như sau x = r cos x 0 r cos 0 cos 0 - Thay
vào các bất đẳng thức 0 2 , y = r sin y 0 r sin 0 sin 0
= 0 và = 2 . Căn cứ vào đồ thị của miền D, chúng ta cũng có thể suy ra được 0 2. x = r cos - Thay
vào bất đẳng thức x2 + y2 ≤ R2 (rcos)2 + (rsin)2 ≤ R2 r2 ≤ R2 0 ≤ r ≤ y = r sin
R (vì r 0) g() = R. = 0 0 2 và g ( ) = R D'= . = 2 0 r R
Chúng ta có |J| = r và vì f(x,y) = y nên f(rcos,rsin) = rsin I = ydxdy = (rsin) J dr d = D D' g( ) 2 R 2 R (rsi n ) d r rd = d 2 r sindr = sind 2 r dr = sin d 2 r dr = D' 0 0 0 0 0 ( r= R 3 3 3 − = cos 2 ) r R R = (−0 + ) 1 = . 0 = 3 3 3 r =0
Ví dụ 2.12. Tính tích phân I = (2x + 3y)dxdy trên miền D = {(x,y)R2|x2 + y2 ≤ –2y, x ≤ 0, y ≤ 0} D
Bất đẳng thức x2 + y2 ≤ –2y x2 + y2 + 2y ≤ 0 x2 + y2 + 2y
+ 1 ≤ 1 x2 + (y + 1)2 ≤ 1 2 là hình
tròn có tâm tại điểm (0,–1) và bán kính R = 1, do đó đồ thị của miền D trong hệ tọa độ Descartes vuông góc Oxy là 71 x = r cos
Cách 1. Nếu đổi biến từ tọa độ Descartes (x,y) sang tọa độ cực (r,) theo công thức thì y = r sin
điểm gốc cực của hệ tọa độ cực nằm trên biên của miền D (Trường hợp 2), đồng thời trùng với điểm gốc
của hệ tọa độ Descartes, khi đó D'= . 0 r g()
Để xác định các góc , (tạo bởi trục Ox với các đường thẳng x = 0, y = 0 tương ứng, với chiều
dương là chiều ngược với chiều quay của kim đồng hồ) và hàm g() chúng ta thực hiện như sau x = r cos x 0 r cos 0 c os 0 - Thay
vào các bất đẳng thức
− − 2, y = r sin y 0 r sin 0 s in 0 =
− và = − 2 . Căn cứ vào đồ thị của miền D, chúng ta cũng có thể suy ra
được− − 2. x = r cos - Thay
vào bất đẳng thức x2 + y2 ≤ 2y –
(rcos)2 + (rsin)2 ≤ –2rsin r2 + 2rsin y = r sin
≤ 0 r(r + 2sin) ≤ 0 0 ≤ r ≤ –
2sin (vì r 0) g() = 2s – in. = −
− − 2
và g() = −2sin D'= . = − 2 0 r −2 sin
Chúng ta có |J| = r và vì f(x,y) = 2x + 3y nên f(rcos,rsin) = r(2cos + 3sin) I = (2x +3y)dxdy =
r(2 cos + 3sin ) J drd = (2 cos +3sin 2 )r drd = D D' D' g ( ) − 2 −2sin d (2 cos + 3sin 2 )r dr = (2 co s + 3sin) 2 d r dr = 0 − 0 − r=−2 2 sin − 3 2 r (2 cos +3sin ) d = − 8 3 3 (2co s + 3sin) sin d 3 − = r 0 − 9 sin 2 3cos2 sin 4 3cos4
Hạ bậc biểu thức lượng giác(2 cos + 3sin) sin3 = + − − + 8 2 2 4 8 − 2 8 9 sin 2 3cos 2 sin 4 3cos 4 I = − + − − + d = 3 8 2 2 4 8 − − 2 − 2 − 2 − 2 − 2 − 3 − 4 d sin 2 d + 4 cos 2 + 2 d sin 4 d − cos4 d = 3 3 − − − − − − 2 − 2 − 2 − 2 − − 2 − 4 3
sin 2d(2) + 2 cos2d(2 + 2 ) sin 4 d( 4 − 1 ) cos4d(4 ) = − . 3 2 . 3 4 4 − − − − − 3 + 2 cos − 2 2 + s 2 in − 2 − 1 2 cos − 2 − 1 4 sin 4 − 2 = − − − − 2 3 6 4 3 2 1 1 3 4 − + ( 1 − − ) 1 + ( 2 0 − +0) − 1 ( − ) 1 − ( 0 − +0) = − − . 2 3 6 4 2 3 72
Cách 2. Nếu đổi biến từ tọa độ Descartes (x,y) sang tọa độ cực (r,) theo công thức x = r cos
thì điểm gốc cực của hệ tọa độ cực vẫn nằm trên biên của miền D (Trường hợp 2), y = −1 + r sin
nhưng ở điểm (0,–1) trong hệ tọa độ Descartes, khi đó D'= . 0 r g ( )
Để xác định các góc , (tạo bởi đường thẳng y = 1 với đường thẳng x = 0 tương ứng, với chiều
dương là chiều ngược với chiều quay của kim đồng hồ) và hàm g() chúng ta thực hiện như sau
- Thay x = rcos vào các bất đẳng thức x ≤ 0 rcos ≤ 0 cos ≤ 0 (vì r 0)
2 3 2 = 2 và = 3 2 . Căn cứ vào đồ thị của miền D, chúng ta cũng có thể suy ra
được 2 3 2. x = r cos - Thay
vào bất đẳng thức x2 + y2 ≤ –2y (rcos)2 + (–1 + rsin)2 ≤ –2.(–1 + y = −1 + r sin rsin) r2 – 1 ≤ 0 (
r – 1)(r + 1) ≤ 0 0 ≤ r ≤ 1 (vì r + 1 0) g() = 1. = 2 2 3 2 và g ( ) = 1 D = ' . = 3 2 0 r 1
Chúng ta có |J| = r và f(rcos, 1 + – rsin) = 2rcos + 3( 1 + – rsin) = 3 + – 2rcos + 3rsin I = (2x+ 3y)dxdy = − ( 3+ 2r co s + r 3 sin) J d rd = − ( 3+ 2r co s + r 3 sin)rd rd = D D' D' g ( ) 3 2 1 d ( −3 +2r cos + r 3 sin )rdr = d ( − r 3 + 2 2r cos + 2 r 3 sin )dr = 0 2 0 3 2 2 3 3 r r r =r1 3 2 3 2 − 3 + 2 cos + 3 sin d =
− + cos + sin d = 2 3 3 2 3 2 = 2 r 0 3 2 3 2 3 3 2 3 4
− + sin − cos = − − + (−1− ) 1 − (0 − 0) = − − . 2 3 2 2 2 3 2 3 2
Ví dụ 2.13. Tính tích phânI = 4 − 2 x − 2
y dxdy trên miền D = {(x,y)R2|x2 + y2 ≤ 4} D Bài giải.
Đồ thị của miền D trong hệ tọa độ Descartes vuông góc Oxy là hình tròn x2 + y2 ≤ 22 có tâm tại gốc
tọa độ O(0,0) và bán kính R = 2 73 x = r cos
Nếu đổi biến từ tọa độ Descartes (x,y) sang tọa độ cực (r,) theo công thức thì điểm y = r sin 0 2 gốc cực
của hệ tọa độ cực là điểm trong của miền D (Trường hợp 3), khi đó D'= . 0 r g() x = r cos
Để xác định hàm g() chúng ta thay
vào bất đẳng thức x2 + y2 ≤ 4 (rcos)2 + y = r sin 0 2 (rsin)2 ≤ 22 r
2 ≤ 22 0 ≤ r ≤ 2 (vì r 0) g() = 2 g ( ) = 2 D = ' . 0 r 2 Chúng ta có |J| = r và vì 2 2 f (x, ) y = 4 − x − y nên f r ( co s ,rsin) = 4 − (rcos 2 ) − (rsin 2 ) = 4 − 2 r I = 4 − 2 x − 2 y dxdy = 4 − (r cos 2 ) − (r sin 2 ) J dr d = D D' 2 2 2 2 2 4− 2 r d r r d = d r 4− 2 r dr = d r 4− 2rdr = = 2 1 2 2 ( 4 r d(4 r ) =0 ) − − − = 2 D' 0 0 0 0 0 r= 2 r= 2 1 2 1 1 1 1 + 2 3 2 16 2
− (4− r2 )2 d(4− r2 )= − (4 − r2 )2 = − (4 − r2 )2 = − (− ) 8 = . 2 1 ( ) 2 + 1 3 3 3 0 r 0 = r= 0
Đổi biến từ tọa độ Descartes (x,y) sang tọa độ cực (r, ) mở rộng
Nếu hàm số mô tả biên của miền D có biểu thức 2 2
px + qy (trong các tham số p > 0, q > 0 phải có ít
nhất một tham số có giá trị khác 1) thì đổi tọa độ Descartes (x,y) sang tọa độ cực (r,) bằng phép đổi r x = x(r, ) = x + cos 0 p biến
, trong đó (x0,y0) là tọa độ (trong hệ tọa độ Descartes vuông góc Oxy) y = y(r,) = + r y sin 0 q
của điểm gốc cực của hệ tọa độ cực.
Lưu ý. Căn cứ toán học của phép đổi biến này là: Vì 2 2 2 2
px + qy = ( px) + ( qy) nên nếu đổi biến r x = cos px = r cos p 2 2 2 2 2 ( px) + ( qy) = (r cos ) + (r sin ) = r thì px2 + qy2 = r2. qy = r sin r y = sin q r r x + cos x + co s x, (r,) x, (r,) 0 0 r p p Khi đó r J = det = det = , , y (r,) y (r, r ) r r y + si n y + sin 0 0 r q q 1 r cos − sin p p r det = 0 1 r pq sin cos q q r x = x(r, ) = x + cos 2 2 = = − + − 0 r r(x, y) p(x x ) q(y y ) p 0 0
Phép biến đổi ngược của là . q (y− y ) 0 y = y(r, ) = + r y sin = ( x, y) = arctan 0 p(x − x ) q 0
Đối với phép đổi biến này, chúng ta không cần tính J nữa, mà sử dụng J = r pq 0 luôn. 74 x 2 2 y2
Ví dụ 2.14. Tính tích phânI = 2
x dxdy trên miền D = (x, y) R + 1 9 4 D Bài giải. x 2 y2
Đồ thị của miền D trong hệ tọa độ Descartes vuông góc Oxy là hình ellips + 1 có tâm tại 32 22
gốc tọa độ O(0,0), hai bán trục có độ dài là 3 và 2 x2 y2 p =1 32 1 p = 3 Chúng ta có +
1 px 2 + qy 2 1 với 32 22 q =1 2 2 1 q = 2 x = r 3 co s
Nếu đổi biến từ tọa độ Descartes (x,y) sang tọa độ cực (r,) mở rộng theo công thức y = 2r sin 0 2
thì điểm gốc của hệ tọa độ cực là điểm trong của miền D, khi đó D'= . 0 r g() x = r 3 cos x 2 y2 r 3 ( co s )2 (2r sin ) 2 Thay vào bất đẳng thức + 1 + 1 y = 2r sin 32 22 32 22 0 2
r2 cos2 + r2 sin2 1 r2 1 r 1 0 r 1 (vì r 0) g() = 1 D' = . 0 r 1
Vì |J| =|2.3r| = 6r và f(x,y) = x2 f r 3 ( cos 2 , r sin) = r 3 ( cos 2 ) = 2 2 r 9 cos 2 1 I = 2 x dxdy = 2 2 9r cos J dr d = 2 2 r 9 cos 6rdr d = 5 2 4 cos d 3 r dr = D D' D' 0 0 r 1 = =2 2 1 + cos2 r4 2 1 27 sin 2 27 27 54 d = 27 1 ( + cos2)d = + = 2 = . 2 4 4 4 = 2 4 2 0 r 0 0 = 0
2.1.3. Ứng dụng hình học của tích phân hai lớp
2.1.3.1. Tính diện tích hình phẳng
S = dxdy là diện tích của miền phẳng D . D
Ví dụ 2.15. Tính diện tích S của miền phẳng giới hạn bởi các
đường y = x và y = 2 – x2. Bài giải.
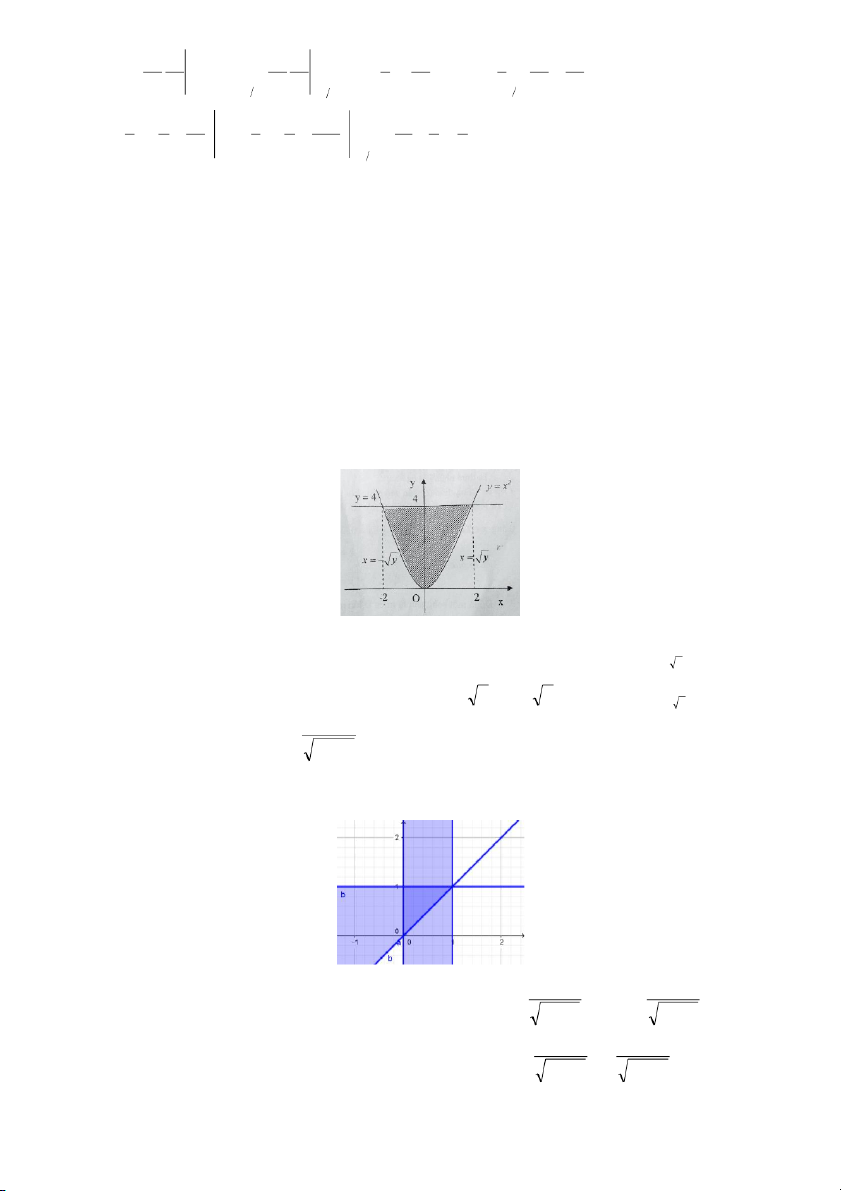
Đồ thị của miền phẳng D là
Đường thẳng y = x giao với đường parabol y = 2 – x2 tại các điểm (1,1); (–2,–2) và khi chiếu miền − 2 x 1
D lên trục Ox chúng ta được D =
nên diện tích S của miền D là x y 2 − 2 x 2 x 1 = 1 2− x 1 1 = − y 2 x2 x3 x 9 S= dxdy = dx dy = y d
x = (2 − x2 − x)dx = 2x − − = . y x = 3 2 2 D 2 − x 2 − − 2 x=−2 75
Lưu ý. Nếu miền phẳng có tính đối xứng thì chỉ cần tính diện tích một phần của nó rồi suy ra diện
tích của cả miền phẳng.
Ví dụ 2.16. Tính diện tích S của miền phẳng D = {y = x2, x = y2}.
Bài giải. Đồ thị của miền D
trong hệ tọa độ Descartes vuông góc Oxy là
Các đường parabol y = x2, x = y2 giao nhau tại các điểm (1,1), (–1,1), (–1,–1), (1,–1).
Ký hiệu D+ là phần của miền D nằm trong góc vuông thứ nhất của hệ tọa độ Descartes vuông góc
Oxy (x 0 và y 0). Do tính đối xứng miền D nên diện tích S của miền D bằng 4 lần diện tích của miền
D+, tức là S = dxdy =4 dxdy . + D D 0 x 1
Chiếu miền D+ lên trục Ox thì + D = x2 y x 1 1 x 1 1 1 1 1 ( 2 + ) 1 3 S = 4 dx dy = y = x x x 4 y 2 dx = 4 ( x − 2 x ) dx = 4 x − 2 2 x dx = 4 − = 2 y x = 1 ( 2) 1 3 0 x 0 0 0 + 0 2 1 1 4 4 − = . 4 = . 3 3 3 3
2.1.3.2. Tính diện tích mặt cong
Nếu mặt cong z = f(x,y) có hình chiếu vuông góc lên mặt phẳng tọa độ Oxy là miền đóng D, còn
hàm số f(x,y) và các đạo hàm riêng f ,
liên tục trên miền D thì diện tích S của mặt cong z = x (x, ) y , f ,y (x, y)
f(x,y) được tính bằng công thức S = 1+ , 2 [f (x, y)] + , 2 [f (x, y)] dxdy . x y D
Vì vai trò của x, y, z là như nhau nên tương tự, với mặt cong x = f(y,z) có hình chiếu vuông góc lên
mặt phẳng tọa độ Oyz là miền đóng D, còn hàm số f(y,z) và các đạo hàm riêng f , ( , y z),f , (y, z) liên tục y z
trên miền D thì diện tích của mặt cong x = f(y,z) được tính bằng công thức S = 1+ , 2 [f ( , y ) z ] + , 2 [f ( , y ) z ] dydz . y z D
Cũng như vậy, với mặt cong y = f(x,z) có hình chiếu vuông góc lên mặt phẳng tọa độ Oxz là miền
đóng D, còn hàm số f(x,z) và các đạo hàm riêng f ,
liên tục trên miền D thì diện tích của mặt x (x, z),f ,z (x, z)
cong y = f(x,z) được tính bằng công thức S = 1+ , 2 [f (x, z)] + , 2 [f (x, ) z ] dxdz . x z D
Ví dụ 2.17. Tính diện tích mặt cầu 2 2 2 2
x + y + z = R bằng tích phân hai lớp
Bài giải. Đồ thị của mặt cầu 2 2 2 2
x + y + z = R bán kính R và tâm tại điểm O(0,0,0) trong hệ tọa độ
Descartes vuông góc Oxyz là 76
Hình chiếu của hai nửa mặt cầu này lên mặt phẳng tọa độ Oxy là D = {(x,y)R2|x2 + y2 ≤ R2} (tương ứng với z = 0). 2 2 2 2 R2 − x2 − y2 khi z 0
Chúng ta có x + y + z = R z = f (x, y) = tương ứng với nửa
− R 2 − x2 − y2 khi z 0
mặt cầu phía trên và nửa mặt cầu phía dưới mặt phẳng tọa độ Oxy.
Hai nửa mặt cầu đối xứng qua mặt phẳng tọa độ Oxy nên diện tích của mặt cầu là S = 2 1+ ' 2 [f (x, y)] + ' 2 [f (x, y)] dxdy với 2 2 2 = − − x y f (x, y) R x y D 2 2 S = 2 1 − 2x 1 − 2y 1+ + dxdy = dxdy 2R 2 2 2 2 2 2 2 2 D R − x − y R − x − 2 2 2 y D R − x − y dxdy x = r cos Để tính tích phân , chúng ta đổi biến
từ tọa độ Descartes (x,y) sang 2 2 2 y = r sin D R − x − y
tọa độ cực (r,) có định thức Jacobi J = r, khi đó miền D là hình tròn x2 + y2 ≤ R2 trong hệ tọa độ 0 r R
Descartes vuông góc Oxy trở thành miền D'=
trong hệ tọa độ cực (r,) . 0 2 J drd rdr d 2 R rdr S = 2R = 2R = R 2 d = 2 2 2 2 2 2 2 D' R − (r co s ) − (r sin) D' R − r 0 0 R − r r= R 1 − + = − − 2 ( 2 1 1 (R r ) R −
(R − r ) d(R − r ) = 2R.2 − = 4 R . = 0 ) 1 R 1 2 2 2 2 2 2 2 2 2 2 2 1 0 − +1 2 r =0
2.1.3.3. Tính thể tích vật thể
Trường hợp 1. Thể tích V của hình trụ có đường sinh song song với trục Oz, có mặt đáy là hình
phẳng D trong mặt phẳng Oxy và mặt trên là mặt cong z = f(x,y) 0 liên tục trên miền D, được tính bằng
công thức V = f(x, y)dxdy . D
Trường hợp 2. Thể tích V của vật thể có đường sinh song song với trục Oz, còn mặt dưới và mặt
trên của vật thể tương ứng là mặt cong z f1(x,y) z1(x,y) và mặt cong z = f2(x,y) z2(x,y), trong đó
f1(x,y) và f2(x,y) là các hàm số liên tục trên miền D, với D là hình chiếu vuông góc của vật thể lên mặt
phẳng Oxy, được tính bằng công thức V = f (x,y) −f (x,y)dxdy z (x, y) z (x, y)dxdy . 2 1 − 2 1 D D Lưu ý.
(1) Nếu vật thể có tính đối xứng thì chỉ cần tính thể tích một phần của nó rồi suy ra thể tích của cả vật thể. 77
(2) Nếu vật thể có dạng không thuộc hai trường hợp cơ bản trên thì chia vật thể thành các phần nhỏ
bằng các mặt phẳng song song với các mặt phẳng tọa độ chứa trục Oz, khi đó các phần nhỏ của vật thể có
dạng thuộc một trong trường hợp cơ bản trên, tính thể tích mỗi phần xong rồi cộng lại.
(3) Vì vai trò của x, y và z là như nhau nên nếu hình trụ có các đường sinh song song với trục Ox
hoặc Oy thì đổi vai trò x với z hoặc y với z trong các công thức trên.
Ví dụ 2.18. Tính thể tích hình cầu 2 2 2 2
x + y + z R bằng tích phân hai lớp. Bài giải.
Đồ thị của hình cầu 2 2 2 2
x + y + z R bán kính R và tâm tại điểm O(0,0,0) trong hệ tọa độ
Descartes vuông góc Oxyz là
Hình chiếu của hình cầu này lên mặt phẳng tọa độ Oxy là D = {(x,y)R2|x2 + y2 ≤ R2} (tương ứng với z = 0). 2 2 2 R2 2 − x2 − y2 khi z 0
Chúng ta có x + y + z = R z = f (x, y) = tương ứng với nửa
− R 2 − x 2 − y2 khi z 0
mặt cầu phía trên và nửa mặt cầu phía dưới mặt phẳng tọa độ Oxy. z (x, )
y f (x, y) = R2 − x2 − y2 khi z 0
Từ đồ thị của hình cầu chúng ta có 2 2 2 2 2 z (x, y) f (x, ) y = − R − x − y khi z 0 1 1
V= f (x,y)− f (x,y)dxdy = 2 R x y dxdy 2 1 2 − 2 − 2 D D x = r cos Để tính tích phân 2 R − 2 x − 2
y dxdy , chúng ta đổi biến
từ tọa độ Descartes (x,y) y = r sin D
sang tọa độ cực (r,) có định thức Jacobi J = r, khi đó miền D là hình tròn x2 + y2 ≤ R2 trong hệ tọa độ 0 r R
Descartes vuông góc Oxy trở thành miền D'=
trong hệ tọa độ cực (r,) . 0 2 2 R V = 2 2 R − (r cos 2 ) − r ( sin 2 ) J drd = 2 2 r R − 2 r drd = 2 d 2 r R − 2 r dr = D' D' 0 0 r =R 1 +1 R 1 2 2 3 2 = − 2( 2 . = − − − = − = 0 ) 1 2 2 2 2 1 (R r ) 4 R (R r )2 d(R r ) 2.2 2 2 1 3 0 +1 2 r =0 Hướng dẫn.
(1) Tính tích phân hai lớp f (x, ) y dxdy D
Bước 1. Vẽ đồ thị của miền D trong hệ tọa độ Descartes vuông góc Oxy.
Bước 2. Căn cứ vào đồ thị của miền D và biểu thức của một/nhiều hàm số biểu diễn biên của miền
D để quyết định tính trực tiếp tích phân này trong hệ tọa độ Descartes vuông góc này, hoặc đổi biến sang
hệ tọa độ Descartes vuông góc khác, hoặc đổi biến sang hệ tọa độ cực/hệ tọa độ cực mở rộng trước khi
tính tích phân. Khi đổi biến cần phải biết giá trị của định thức Jacobi (nếu đã biết giá trị của định thức
Jacobi thì không cần tính mà chỉ việc sử dụng, nếu chưa biết thì phải tính) và xác định miền D’ là ảnh của
miền D qua phép đổi biến. 78
Bước 3. Nếu tính tích phân trong hệ tọa độ Descartes, để xác định các cận của mỗi tích phân một
lớp, chúng ta chiếu miền D lên một trong hai trục tọa độ, sao cho việc tính tích phân đơn giản hơn. Nếu
tính tích phân trong hệ tọa độ cực/hệ tọa độ cực mở rộng, chúng ta thay x và y qua các biến mới vào
một/nhiều hàm số biểu diễn biên của miền D để tìm miền D’. Xác định thứ tự tính tích phân theo nguyên
tắc: Tích phân một lớp nào có cả hai cận là hằng số thì tính sau.
Bước 4. Lần lượt tính các tích phân một lớp từ phải sang trái.
(2) Để đổi thứ tự tính tích phân của tích phân hai lớp khi đã biết trước một thứ tự tính
Bước 1. Từ các cận của tích phân hai lớp theo thứ tự tính đã cho, chúng ta xác định miền tính tích
phân D theo chiều đã được chiếu lên trục tọa độ Ox/Oy của hệ tọa độ Descartes vuông góc Oxy.
Bước 2. Vẽ đồ thị của miền D trong hệ tọa độ Descartes vuông góc Oxy.
Bước 3. Chiếu miền D lên trục tọa độ Oy/Ox của hệ tọa độ Descartes vuông góc Oxy, xác định
miền tính tích phân D theo chiều chiếu này.
Bước 4. Từ miền tính tích phân D được xác định ở Bước 3, chúng ta viết tích phân theo thứ tự
tính còn lại so với thứ tự tính tích phân đã biết.
(3) Tính diện tích của miền phẳng D
Bước 1. S = dxdy là diện tích của miền phẳng D. D
Bước 2. Nếu D có tính đối xứng thì tính diện tích một phần của D rồi suy ra diện tích của D.
Bước 3. Nếu miền D có dạng không thuộc các trường hợp cơ bản thì chia miền này thành các
miền nhỏ bằng các đường thẳng song song với một trong hai trục tọa độ Ox hoặc Oy (sao cho việc tính
tích phân đơn giản hơn), khi đó các miền nhỏ của D có dạng thuộc một trong các trường hợp cơ bản, tính
diện tích của mỗi phần xong rồi cộng lại. 2 16− 2 x
Ví dụ 2.19. Đổi thứ tự tính tích phân của I = dx f (x, )
y dy và tính I với f(x,y) = 3(x + y). 0 8x − 2 x Bài giải.
(1) Đổi thứ tự tính tích phân 2 16 −x 2 0 x 2 Từ I = dx f (x, y d ) y = f (x, y d ) xdy D = 2 2 2 0 x 8 x y 16 x 8 x− D x − − 8x − 2 x y x 8 − 2 x 2 y 2 4 (x − 2 4) + 2 y Chúng ta có nên nửa đường tròn x 8 − x 2 y y 16 − 2 x 2 y 16 − 2 x 2 x + 2 y 2 4
giao với nửa đường tròn 2
y 16 − x tại điểm (2,2 3) .
Đồ thị của miền D trong hệ tọa độ Descartes Oxy là D = D D 0 y 2 3
Chiếu miền D lên trục Oy chúng ta được 1 2 , trong đó D = và 1 D D = 2 1 2
0 x 4 − 16− x 2 3 4− − 2 16 y 4 16− 2 2 3 y y 4 D = I f (x, dx ) y dy f (x, ) y dxdy dy f (x, y)dx dy f (x, ) y dx 2 = 2 + = + 0 x 16− y D 1 D 2 0 0 2 3 0 79
(2) Tính I với f(x,y) = 3(x + y) 2 2 16 −x 2 2 1 − 6 x2 2 2 y = y 1 − 6 x I = dx ( 3 x + y d ) y = 3 dx (x + y)dy = 3 xy + dx = 2 2 2 0 8x− 0 x 8x − 0 x = y 8 − x x2 2 2 2 2 =3 (x 16 − 2 x −x x 8 − 2 x − x 4 + ) 8 dx =3 x 16 − 2 x dx −4 (x − ) 2 dx − x x 8 − 2 x dx = 0 0 0 0 2 2 2 = 3(I 2 2 1 + I2 + I3) với I = x 16 x dx , I = −4 (x ) 2 dx và I = − x 8x x dx 3 − 2 − 1 − 0 0 0 2 2 2 1 2 2 2 1 3 2 64 + I = − = − − − = − − = − 1 x 16 x dx 16 x d 1 ( 6 x ) (16 x )2 8 3 2 3 3 0 0 0 2 2 2 (x − 2)2 + I = −4 (x − ) 2 dx = −4 (x − ) 2 d(x − 2) = − . 4 = 8 2 2 0 0 0 2 2 + I = − x 8x − 2 x dx = − [(x − ) 4 + ] 4 16− (x − 2 4) dx = 3 0 0 2 2 2 2
= − (x − 4) 16 − (x − ) 4 dx − 4 16 − (x − 4) dx = I + I 31 32 0 0 2 2
với I = −(x − 4) 16− (x − 2) 4 dx và I = −4 16 (x 4) dx 32 − − 2 31 0 0 2 2 1
* I = − (x − 4) 16 − (x − 2 4) dx = 16− (x − ) 4 d 16 (x 4) 31 2 − − 2= 2 0 0 2 1 3 3 3 16 − (x − 4 2 1 ) 2 =
16− (2− 4)2 −16− (0− 4)2 2 2 = 8 3 3 3 0 2 * I = − 4 16 − (x − 2 4) dx 32 0 x = 4 + 4sin t x = 0 t = − 2 Đặt x – 4 = 4sint và dx = 4 costdt x = 2 t = − 6 − 6 − 6 − 6 I = −4 16− 2 (4sin t) 4 costdt = −4 4 cost 4 . cos tdt = − 2 64 cos tdt = 32 − 2 − 2 − 2 − 6 − 6 − 6 64 −6 1 − − + 1 ( cos2t d ) t = − 32 dt + cos2tdt = −3 2 t + sin 2t = 6 2 2 2 − 2 2 − 2 − − − 2 3 32 −32 − = − + 8 3 . 3 4 3 I = ( 3 I + I + I + I . 1 2 31 32 ) 64 32 = 3 −8 3 + 8 + 8 3 −
+ 8 3 = 88+ 24 3 − 3 2 3 3 x = r cos
Cách khác: Đổi tọa độ Descartes (x,y) sang tọa độ cực (r,) bằng phép đổi biến y = r sin
J = r và 3(x + y) = 3r(cos + sin) Tìm miền D’: 2 1 − 6 x 2 + Từ I = dx f (x, y)dy x 8 − 2 x y 16− 2 x x 8 − 2 x 2 y 16− 2 x 0 8 x−x 2 80 r 8 cos − 2 2 r cos 2 2 r sin 16 − 2 2 r cos r
8 cos − r 2 cos 2 r 2 sin 2 8cos r 8 cos r 8cos r 4 r2
sin2 16− r2 cos2 r 2 16 r2 16 2 3
+ Từ đồ thị của miền D chúng ta có = và tan =
= 3 = do đó 2 2 1 2 1 3 3 2 8cos r 4 D' = 3 2 2 16 −x2 2 16−x 2 I = dx f (x, y)dy = dx ( 3 x + y)dy = r ( 3 cos + r sin ) J dr d = 0 8x − 2 0 x 8x − 2 D' x 2 4 2 4 2 4 3 (cos + sin) 2 d r dr = d ( 3 r cos + r sin)rdr = 3 d (cos + sin 2 )r dr = 3 8cos 3 8co s 3 8cos 2 = r 4 3 2 r 64 1 ( − 3 8 cos 3 (co s + sin) d = 3 (cos + sin ) ) d = 3 3 3 r =8cos 3 2 64 (co s + sin) 1 ( − 3 8cos ) d 3
Hạ bậc biểu thức lượng giác (cos + sin ) 1
( − 8cos3 ) = −3 + cos + sin − 4 cos 2 − 2sin 2 − cos 4 − sin 4 3
I = 64 (−3 + cos +sin − 4cos2 −2sin 2 −cos4 −sin 4 ) d = 3 2 sin 4 cos 4 6
4 − 3 + sin − cos − 2 sin 2 + cos2 − + = 88+ 24 3 − 3 2 . 4 4 3
2.2. Tích phân ba lớp
2.2.1. Định nghĩa và cách tính tích phân ba lớp
2.2.1.1. Định nghĩa
Cho hàm số f(x,y,z) xác định trong miền hữu hạn V của không gian R3. Chia miền V một cách tùy
ý thành n miền nhỏ không dẫm lên nhau. Gọi thể tích của n miền nhỏ đó là V1, V2, …, Vn. Trong n
mỗi miền nhỏ Vi (1 i n) chúng ta lấy một điểm tùy ý Mi(xi,yi,zi) và lập tổng I = f (x ,y ,z .)V . n i i i i i=1
In được gọi là tổng tích phân của hàm số f(x,y,z) trên miền V nếu khi n → sao cho
d = max d → 0 (trong đó di là đường kính của miền nhỏ Vi) mà In dần đến một giá trị hữu hạn không i 1in
phụ thuộc vào cách chia miền V và cách lấy điểm Mi(xi,yi,zi) trên mỗi miền nhỏ Vi, thì giá trị hữu hạn
này được gọi là tích phân ba lớp của hàm số f(x,y,z) trên miền V và ký hiệu là f(x, ,yz)dV; khi đó V, V
f(x,y,z), dV, x, y và z lần lượt được gọi là miền lấy tích phân, hàm số dưới dấu tích phân, vi phân thể tích,
các biến tính tích phân. n Như vậy, chúng ta có f (x, y, z d ) V = limI = lim
f (x ,y ,z .)Vnếu giới hạn này tồn tại n i i i i n → max di→ 0 V 0 i n i=1
hữu hạn và khi đó chúng ta nói rằng hàm số f(x,y,z) khả tích trên miền V.
Nếu hàm số f(x,y,z) liên tục trong miền V thì nó khả tích trên miền V.
Tích phân ba lớp có đầy đủ các tính chất của tích phân hai lớp. 81
Vì tích phân ba lớp nếu tồn tại thì không phụ thuộc vào cách chia miền V, nên chúng ta có thể chia
V bởi lưới các mặt phẳng song song với các mặt phẳng tọa độ Oxy, Oxz, Oyz. Khi đó, mỗi miền nhỏ Vi
(1 i n) nói chung là hình hộp chữ nhật, do đó dV = dxdydz f(x, , y z)dV = f(x, , y z)dxdydz . V V
2.2.1.2. Cách tính tích phân ba lớp trong hệ tọa độ Descartes
Giả sử miền V giới hạn bởi các mặt có các phương trình z = z1(x,y), z = z2(x,y) tương ứng. Gọi
miền phẳng D là hình chiếu của V lên mặt phẳng tọa độ Oxy (z = 0). Giả sử z1(x,y), z2(x,y) là các hàm số
liên tục và z1(x,y) z2(x,y) với (x,y)D.
Nếu từ một điểm bất kỳ M(x,y) D vẽ
một đường thẳng song song với trục tọa độ Oz, đường thẳng
này sẽ cắt các mặt z = z1(x,y), z = z2(x,y) tại các điểm P1, P2 tương ứng; khi điểm M thay đổi trong miền
D thì các điểm P1, P2 thay đổi tương ứng với độ cao P 1P2 = z
với z1(x,y) z z2(x,y). z ( x, y ) 2
Nếu f(x,y,z) là hàm số liên tục với (x,y,z)V thì f(x, ,yz)dxdydz = dxdy f (x,y,z)dz (khi V D z1 ( x,y) z (x , y) 2
tính f(x, y,z)dz thì coi x, y là các hằng số). z ( 1 x ,y ) z ( x, y) z ( x, y) 2 2 Vì f (x,y, ) z dz = (
F x, y) dxdy f (x,y, ) z dz = (
F x, y)dxdy nên việc tính tích phân ba lớp z ( 1 x, y) D z1( x,y) D
f(x,y,z)dxdydz tiếp tục được về việc tính tích phân hai lớpF(x,y)dxdy đã biết. V D
Ý nghĩa hình học của tích phân ba lớp. Nếu f(x,y,z) = 1 với (x,y,z)V thì dxdydz là thể tích V của miền V.
Định lý Fubini. Nếu hàm số f(x,y,z) xác định và liên tục trên hình hộp chữ nhật V = ( { x, , y z)R3 a x , b c y d, p z } q = a [ , b] , c [ d][ , p q] thì b d q d q b q b d
f(x, y,z)dxdydz = dx dyf(x, ,yz)dz = dydzf(x, ,yz)dx = dzdx f(x, ,yz)dy . V a c p c p a p a c b d q
Hệ quả. Nếu f(x,y,z) = g(x)h(y)k(z) thì
f (x, y, z)dxdydz = g(x)dx h(y)dy k(z)dz . V a c p
Ví dụ 2.20. Tính tích phân I = xyz2dxdydz, V = [0,1][ 1,2] – [0,3] V Bài giải.
Chúng ta có 4 phương án khác nhau khi tính I = xyz2 dxdydz, V = [0,1][ 1,2] – [0,3] bằng cách V
sử dụng 4 công thức tính khác nhau sau đây 1 2 3 2 3 1 3 1 2 I = 2 xyz dxdydz = 2 dx dy xyz dz = 2 dy dz xyz dx = 2 dz dx xyz dy = V 0 −1 0 −1 0 0 0 0 −1 x 1 = y=2 z=3 1 2 3 2 x2 y2 z3 1 3 27 27 xdx ydy z dz = = . . = . 2 2 3 2 2 3 4 0 1− 0 x= 0 y = 1 − z=0 82
Ví dụ 2.21. Tính tích phân I = zdxdydz ,
V = {(x,y,z)R3|x = 0, y = 0, z = 0 và x + y + z = 1}. V Bài giải.
Đồ thị của miền V trong hệ tọa độ Descartes vuông góc Oxyz là
Chúng ta có z = z1(x,y) = 0, z = z2(x,y) = 1 – x – y và nếu gọi D là hình chiếu của mặt phẳng x + y
+ z = 1 xuống mặt phẳng tọa độ Oxy (z = 0) thì D = {(x,y)R20 x 1, 0 y 1 – x}. − 1 x− y z= − 1 x− y 2 z 1 I = zdxdydz = dxdy zdz = dxdy = 1 ( − x − 2 y) dxdy = 2 2 V D 0 D z =0 D 1 − 1 x 1 1−x 1 1 1 1 1 y= − dx − 1 ( x − 2 y) dy = − dx 1 ( − x − 2 y) d 1 ( − x − y) = − 1 ( − x − 1 x 3 y) dx = y =0 2 2 2 3 0 0 0 0 0 1 1 3 1 1 1 4 1 − 1 ( − x) d 1 ( − x) = − . 1 ( − x) = . 6 6 4 0 24 0
2.2.1.3. Công thức đổi biến trong tích phân ba lớp
Xét tích phân ba lớp f(x,y,z)dxdydz, trong đó hàm số f(x,y,z) liên tục trên miền đóng V. V x = x(u, v, w)
Giả sử chúng ta thực hiện phép đổi biến y = y(u,v, w) với các giả thiết z = z(u, v, w)
(1) Các hàm x(u,v,w), y(u,v,w), z(u,v,w) là các hàm số liên tục và có các đạo hàm riêng cấp 1 x, ( , u , v w), x, ( , u , v w), x, ( , u , v w), y, ( , u , v w), y, ( , u , v w), y , ( , u , v w),z, (u, , v w), u v w u v w u z , u ( , , v w),
liên tục trên miền đóng V’ = {(u,v,w)R3 } nào đấy; v z,w , u ( , v w) x = x(u, , v w)
(2) Phép đổi biến y = y(u, , v w) là ánh xạ 1-
1 từ miền V lên miền V’; z = z(u, , v w) x, (u,v, w) x, (u, , v w) x, (u, v, w) u v w
(3) Định thức Jacobi J = det y, (u, v, w) y, (u, v, w) y, (u, v, w) 0 trong miền V’ u v w z , (u, , v w) z, (u, , v w) z, (u, v, w) u v w Khi đó f(x, ,yz d ) xdydz = f[x(u, , v w), y(u, , v w), ( z u, , v w)]J dxdydz V V' Lưu ý.
(1) Nếu phép đổi biến là ánh xạ 1-1 thì một điểm trong của miền V tương ứng với một điểm trong
của miền V’ và ngược lại, một điểm trên biên của miền V tương ứng với một điểm trên biên của miền V’ và ngược lại. 83
(2) Nhà toán học Carl Gustav Jacob Jacobi (người Đức) đã chứng minh: Giá trị của định thức x = x(u, , v w)
Jacobi của phép đổi biến y = y(u, ,
v w) là nghịch đảo giá trị của định thức Jacobi của phép đổi biến z = z(u, , v w) u = u(x, y, w) x, (u, ,
v w) x , (u, v, w) x, (u, v, w) u v w
ngược v = v(x, y, w) của phép biến đổi trên, tức là J = det y, (u, , v w)
y, (u, v, w) y, (u, v, w) = u v w , , , w = w(x, y,z) z (u, v, w) z (u, , v w) z (u, v, w) u v w u, (x, y,z) u, (x, y, ) z u, (x, , y z) 1 x y z 1 hay = det v, (x, , y z) v, (x, , y z) v, (x, , y z) .
u, (x, y,z) u, (x, y,z) u, (x, , y z) J x y z , , , x y z w (x, y,z) w (x, y, ) z w (x, , y z) x y z det v, (x, y, z) v, (x, , y z) v, (x, , y z) x y z , , , w (x, y,z) w (x, , y z) w (x, , y z x y z )
Ví dụ 2.22. T nh thể tích của vật thể V là miền giới hạn bởi các mặt phẳng {x + y + z = í 3, x + 2y – z = 1, x + 4y + z = 2}. Bài giải.
Theo ý nghĩa hình học của tích phân ba lớp thì thể tích của vật thể là V = dxdydz với V là một V
hình hộp xiên giới hạn bởi các mặt phẳng {x + y + z = 3, x + 2y – z = 1, x + 4y + z = 2} trong hệ tọa − 3 x + y + z 3
độ Descartes vuông góc Oxyz V = −1 x + 2y − z 1 nên để tính tích phân ba lớp được dễ dàng, − 2 x + 4y + z 2 u = x + y + z u(x, , y z)
chúng ta dùng phép đổi biến v = x + 2y− z v(x, ,
y z) , do đó ảnh của miền V là miền w = x + 4y + z = w(x, y,z) − 3 u 3
V'= − 1 v 1 là một hình hộp chữ nhật trong hệ tọa độ Descartes vuông góc Ouvw. − 2 w 2 x = x(u,v, w)
Để tính định thức Jacobi, chúng ta không cần phải tìm y = y(u,v, w) từ phép đổi biến trên rồi tính z = z(u,v, w) x, (u, v, w) x , (u, , v w) x , (u, v, w) u = x + y + z u(x, , y z) u v w
ra J = det y, (u, v, w) y , (u, v, w) y, (u, v, w) mà từ v = x + 2y − z v(x, , y z) chúng ta tính được u v w , , , z (u, , v w) z (u, v, w) z (u, v, w) w = x + 4y + z = w(x, y, z) u v w u, (x, y,z) u, (x, , y ) z u, (x, y, z) 1 1 1 1 x y z , , , 1 = det v (x, , y z) v (x, , y z) v (x, y, z) = det 1 2 −1 = 6 J = . J x y z 6 w, (x, y, z) w, (x, , y ) z w, (x, y, z) 1 4 1 x y z 1 1 3 1 2 V= dxdydz = J dudvdw = dudvdw = du dv dw = 6 6 V V' V' − 3 −1 − 2 1 ( u=3 v=1 w 2= u )(v )( ) 1 w = 6 . 4 . 2 . = 8 . 6 u=−3 v=− 1 w=− 2 6
2.2.1.4. Tính tích phân ba lớp trong tọa độ trụ 84
Tọa độ trụ của một điểm M(x,y,z) trong hệ tọa độ Descartes vuông góc Oxyz là bộ ba số (r,,z)
trong đó (r,) là tọa độ cực của điểm M’(x,y) (là hình chiếu của điểm M xuống mặt phẳng tọa độ Oxy).
Khi đó, chúng ta có công thức liên hệ giữa tọa độ Descartes (x,y,z) và tọa độ trụ (r,,z) của cùng một x = r cos 0 r +
điểm M(x,y,z)R3 là y = r sin với 0 2
, còn miền V trong hệ tọa độ Descartes (x,y,z) biến z = z − z +
thành miền V’ trong hệ tọa độ trụ (r,,z). x, x, x, cos − r sin 0 r z
Định thức Jacobi là J = det y, y,
, do đó theo công thức đổi y, = sin r cos 0 = r 0 r z z, z, z , 0 0 1 r z
biến trong tích phân ba lớp từ trường hợp tổng quát áp dụng cho trường hợp này là
f(x, ,y )zdxdydz = f(rco s , r sin, ) z J dr d dz = rf r( co s , r sin, z d ) r d dz . V V' V'
Ví dụ 2.23. Tính I = 2 (x + 2 y d
) xdydz với V là miền giới hạn bởi mặt trụ x2 + y2 = 2x, y 0 và V
các mặt phẳng z = 0, z = 2. Bài giải.
Phương trình của mặt trụ x2 + y2 = 2x
(x – 1)2 + y2 = 12 nên đồ thị của miền V trong hệ tọa độ
Descartes vuông góc Oxyz là x = r cos
Đổi biến y = r sin từ tọa độ Descartes (x,y,z) sang tọa độ trụ (r,,z), định thức Jacobi J = r. z = z
Hình chiếu D của miền V xuống mặt phẳng tọa độ Oxy (z = 0) trong hệ tọa độ Descartes vuông góc
Oxyz là nửa trên của hình tròn (x – 1)2 + y2 1 (y 0) c ó đồ thị là 0 r 2 cos
Ảnh của D là D'= 0 2 trong hệ tọa độ trụ (r,,z), được xác định như sau: z = 0 x = r cos
- Đối với tọa độ r: Thay
vào phương trình hình tròn (x – 1)2 + y2 1 chúng ta được y = r sin r2 – 2rcos 0 r
(r – 2cos) 0 0 r 2cos (vì r 0). 85
- Đối với tọa độ : Từ đồ thị của miền D suy ra 0 /2.
Còn đối với tọa độ z: 0 z 2 0 r 2 cos D'
Do đó, ảnh của V là V' = = 0 2
trong hệ tọa độ trụ (r,,z). 0 z 2 0 z 2
Hàm số dưới dấu tích phân 2 2 2 2 2 f (x, y) = x + y f r ( cos , r sin ) = (r cos ) + r ( sin ) = r 2 2 2 cos 2 2 2 2 2 cos I = drd f r ( cos, r sin ) J dz = drd 2 rr dz = dr d 3 r dz = dz d 3 r dr = D' 0 D' 0 0 0 0 0 0 0 2 2 r= 2 cos 4 2 2 r 1 2 2 dz d = 4 dz 16cos d = 4 dz 4 cos d 4 4 0 0 r= 0 0 0 0 0 1 3 1
Hạ bậc biểu thức lượng giác cos4 = + 2 cos 2 + cos4 4 2 2 2 2 3 1 I = dz +2cos2+ cos 4 d 2 2 0 0 Chúng ta có 2 z= 2 + dz = z = 2 z= 0 0 2 3 1 2 2 2 3 1 + + 2 cos 2 + cos 4 d = d + cos2 d(2 ) + cos4d(4) = 2 2 2 8 0 0 0 0 3 = 2 = 2 1 = 2 3 + sin 2 + sin 4 = 2 =0 =0 8 0 = 4 3 3 I = . 2 = . 4 2
Lưu ý. Nếu miền tính tích phân có dạng hình trụ/hình nón thì đổi tọa độ Descartes (x,y,x) sang tọa
độ trụ (r,,z) thì việc tính tích phân có khả năng dễ tính toán hơn. 2.2.1.5.
Tính tích phân ba lớp trong tọa độ cầu
Tọa độ cầu của một điểm M(x,y,z) trong hệ tọa độ Descartes vuông góc Oxyz là bộ ba số (r, , )
trong đó r = OM, là góc giữa trục Ox và OM' (M’ là hình chiếu của M lên mặt phẳng tọa độ Oxy), là
góc giữa trục Oz và OM . Khi đó, chúng ta có công thức liên hệ giữa tọa độ Descartes (x,y,z) và tọa độ x = r cossin 0 r + cầu (r,
, ) của cùng một điểm M(x,y,z)R3 là y = r sin sin với 0 2 , còn miền V trong hệ tọa z = r cos 0
độ Descartes (x,y,z) biến thành miền V’ trong hệ tọa độ cầu (r,,). 86 x , x , x ,
cos sin r cos cos − r sin s in r
Định thức Jacobi là J = dety , y , y , = sin sin r sincos
r cossin = r 2 sin 0, r z, z, z, cos − r sin 0 r
do đó theo công thức đổi biến trong tích phân ba lớp từ trường hợp tổng quát áp dụng cho trường hợp này là f (x, , y ) z dxdydz = f r
( cossin , r sin sin, r cos) J dr d d = V V'
f (r sin cos, r sinsin , r cos)r2 cosdr d d V'
Ví dụ 2.25. Tính I = 3
z dxdydz với V là miền giới hạn bởi {1 x2 + y2 + z2 4, z 0}. V Bài giải.
12 ≤ x2 + y2 + z2 và x2 + y2 + z2 ≤ 22 là phương trình của hai hình cầu cùng có tâm O(0,0,0) có bán
kính tương ứng bằng R = 1 và R = 2, do đó đồ thị của miền V trong hệ tọa độ Descartes vuông góc Oxyz là x = r cossin
Đổi biến y = r sin sin từ tọa độ Descartes (x,y,z) sang tọa độ cầu (r,,), định thức Jacobi J = z = r cos r2sin.
Hình chiếu D của miền V xuống mặt phẳng tọa độ Oxy (z = 0) trong hệ tọa độ Descartes vuông góc
Oxyz là hình vành khăn {12 x2 + y2 22} có đồ thị là 1 r 2
Ảnh của miền D là D'= 0 2
trong hệ tọa độ cầu (r,,), được xác định như sau: = 2 x = r cossin
- Đối với tọa độ r: Thay y = r sin sin vào các bất đẳng thức 1 x2 + y2 + z2 4 chúng ta được z = r cos
1 r2 4 1 r 2 (vì r 0).
- Đối với tọa độ : 0 2. 1 r 2 D'
Còn đối với tọa độ : 0 /2 (vì z 0) V' = = 0 2 trong hệ tọa độ cầu
0 2 0 2 (r, , ).
Hàm số dưới dấu tích phân f(x,y,z) = z3 f(rsincos,rsincos,rcos) = (rcos)3 = r3cos3. 2 2 I = dr 3 3 d r cos J d = dr 3 3 d r cos 2 r ( sin) d = D' 0 D' 0 87 2 2 2 2 2 2 dr 5 3 d r cos sin d = 5 r dr d 3 cos sin d = 1 0 0 1 0 0 r= 2 = 2 r6 ( = 2 = ) 2 − − 3 2 6 16 cos4 0 1 21 − cos d (cos ) = 2 . − = 21 − = . 6 0 = 6 4 4 4 r 1 0 =0
Lưu ý. Nếu miền tính tích phân có dạng hình cầu hoặc paraboloit thì đổi tọa độ Descartes (x,y,z)
sang tọa độ cầu (r,,) thì việc tính tích phân có khả năng dễ tính toán hơn. 2.2.2.
Ứng dụng của tích phân ba lớp
2.2.2.1. Tính thể tích của vật thể
Theo ý nghĩa hình học của tích phân ba lớp thì dxdydz là thể tích của miền V. V
2.2.2.2. Tính khối lượng của vật thể
Ý nghĩa vật lý của tích phân ba lớp. Nếu hàm số f(x,y,z) > 0 xác định và liên tục với (x,y,z)V, là
khối lượng riêng của miền V tại điểm (x,y,z) thì f(x,y,z)dxdydz là khối lượng của miền V. V
Ví dụ 2.25. Vật thể là hình chóp tam giác giới hạn bởi các mặt phẳng {x = 0, y = 0, z = 0, x + y + z = 1}.
(a) Tính thể tích của vật thể.
(b) Tính khối lượng m của vật thể nếu khối lượng riêng tại điểm (x,y,z) của vật thể là f(x,y,z) = xy. Bài giải.
Đồ thị của vật thể trong hệ tọa độ Descartes vuông góc Oxyz là
Dễ thấy rằng z1(x,y) = 0 và z2(x,y) = 1 – x – y tương ứng là phương trình của mặt dưới và mặt trên
của hình chóp tam giác. Hình chiếu của mặt phẳng x + y + z = 1 lên mặt phẳng tọa độ Oxy (z = 0) là miền
D và nếu chiếu miền D lên trục Ox thì D = {(x,y)R20 x 1, 0 y 1 – x}.
(a) Theo ý nghĩa hình học của tích phân ba lớp thì thể tích của hình chóp tam giác là dxdydz = V z (x ,y ) 2 1−x −y 1 1−x 1−x −y 1 1−x 1 1−x − 1 x− dxdy dz = dxdy dz = dx dy dz = dx ( y z dy dx 1 ( x y)dy 0 ) = − − = D z1 (x,y) D 0 0 0 0 0 0 0 0 1 1 x 1 1− − x 2 1 1 1 ( − x − y) − dx 1 ( − x − y)d 1 ( − x − y) = − = 1 dx 1 ( − 2 x) = − 1 dx 1 ( − 2 x) d 1 ( − x) = 2 2 2 0 0 0 0 0 0 1 1 1 ( − x)3 1 1 1 − . = − .− = . 2 3 2 3 6 0 1−x −y
(b) Theo ý nghĩa vật lý của tích phân ba lớp thì m = xydxdydz = xydxdy dz = V D 0 1 1−x 1 − 1 x xy( 1−x−y z dxdy xy 1 ( x y d ) xdy dx xy 1 ( x y)dy dx (xy x y xy )dy 0 ) = − − = − − = − 2 − 2 = D D 0 0 0 0 − 1 x 1 2 2 3 y 2 y y 1 x 1 ( − 2 2 x) x 1 ( − 2 x) x 1 ( − 3 x) x − x − x dx = − − dx = 2 2 3 2 2 3 0 0 0 88 1 1 1 1 1 x2 x3 x 4 x5 x2 x3 x4 x5 1 (x − 3x2 + x 3 3 − x4 )dx = −3. + 3. − = − + − = . 6 6 2 3 4 5 12 6 8 30 120 0 0 0
Ví dụ 2.26. Tính thể tích của hình cầu 2 2 2 2
x + y + z R bằng tích phân ba lớp. Bài giải
Đồ thị của hình cầu 2 2 2 2
x + y + z R có bán kính R và tâm tại gốc O(0,0,0) của hệ tọa độ
Descartes vuông góc Oxyz là
Hình chiếu của hình cầu lên mặt phẳng tọa độ Oxy (z = 0) là D = {(x,y)R2|x2 + y2 ≤ R 2}. Chúng ta có 2 2 2 2 2 2 2 2 2 2
x + y + z = R z = R − x − y z (x, y) = − R − x − y là phương trình 1 mặt dưới và 2 2 2
z (x, y) = R − x − y là phương trình mặt trên của hình cầu. 2
Theo ý nghĩa hình học của tích phân ba lớp thì thể tích của hình cầu là V = dxdydz = V z (x,y) R 2 −x 2 −y 2 2 2 2 2 dxdy dz = dxdy
dz = z= R −x −y 2 2 2 z 2 2 2 dxdy 2 R x y = z − R − x − = y − − 2 2 2 D z (x,y) D 1 − R −x − D D y x = r cos
Để tính tích phân này, chúng ta đổi biến
từ tọa độ Descartes (x,y) sang tọa độ cực (r,) y = r sin
có định thức Jacobi J = r, khi đó miền D là hình tròn x2 + y2 ≤ R2 trong mặt phẳng tọa độ Oxy có ảnh là 0 r R miền D' = . 0 2 2 2 R − 2 x − 2 y = 2 2 R − (r co 2 s ) − (r sin 2 ) J dr d = 2 2 r R − 2 r dr d = D D' D' 2 R 2 R R 1 2
2 d r R 2 − r 2dr = 2 d r R 2 − r 2dr = 2 ( = ) 1 (R 2 r ) 2 2d(R2 r2) = − − − 0 = 0 0 0 0 2 0 r=R 1 +1 1 (R2 − r2) 2 4 R3 2.2− = . 2 1 3 1 + 2 r=0
Nhận xét. Để tính thể tích V của hình cầu này, chúng ta có thể đổi tọa độ Descartes (x,y,z) sang tọa x = r cossin 0 r R
độ cầu (r,,): y = r sin sin , khi đó ảnh của miền V là miền V' = 0 2 , định thức Jacobi J = z = r cos 0 r2sin. 2 R 2 R V = 2
r sin drdd = d d 2
r sin dr = d sin d 2 r dr = V' 0 0 0 0 0 0 ( = =2 = )( r R 3 3 3 = − cos = ) r R 4 R = 2 2.. = . 0 0 3 3 3 r=0
Ví dụ 2.23. Tính thể tích của vật thể V giới hạn bởi các mặt x2 + y2 = hz, z = h. 89
Vật thể giới hạn dưới bởi paraboloit z 2 2
1(x,y) = (x + y )/h và giới hạn trên bởi mặt phẳng z2(x,y) = h.
Hình chiếu của vật thể lên mặt phẳng tọa độ Oxy là miền D = {x2 + y2 h2} có đồ thị là
Theo ý nghĩa hình học của tích phân ba lớp thì thể tích của vật thể này là z ( x,y) 2 h 2 2
V = dxdydz = dxdy dz = dxdy dz = ( h x y z 2 2 dxdy h dxdy z=( x +y ) h ) = + − 2 2 h V D z1(x,y) D ( x +y ) h D D x = r cos
Để tính tích phân này, chúng ta đổi biến
từ tọa độ Descartes (x,y) sang tọa độ cực (r,) y = r sin
có định thức Jacobi J = r, khi đó miền D là hình tròn x2 + y2 ≤ h2 trong mặt phẳng tọa độ Oxy có ảnh là 0 r h miền D' = . 0 2 (r cos 2 ) + (r sin 2 ) 2 h 3 r 2 h 3 r V = h − rdr d = d hr − dr = d hr − dr = h h h D' 0 0 0 0 ( = = − = = = 0 ) r h hr 2 2 r4 h3 h3 2 . . 2 4h 4 2 r= 0
Nhận xét. Để tính thể tích V của vật thể này, chúng ta có thể đổi tọa độ Descartes (x,y,z) sang tọa x = r cos 0 r h
độ trụ (r,,z):y = r sin , khi đó ảnh của miền V là miền V'= 0 2
, định thức Jacobi J = r2sin. z = z r2 h z h
Miền V’ được xác định như sau: x = r cos
- Đối với tọa độ r: Thay
vào phương trình của hình tròn x2 + y2 h 2 chúng ta được r2 y = r sin h2 0 r h.
- Đối với tọa độ : 0 2. x = r cos
- Đối với tọa độ z: Thay
vào phương trình mặt dưới z = (x2 + y2)/h của vật thể, chúng y = r sin
ta được z = r2/h, còn phương trình mặt trên của vật thể là z = h, do đó r2 h z h . 2 h h 2 h 2 h 2 V = dxdydz =
J drddz = d dr rdz = d ( =zh r rz 2 dr d r h dr = z r h ) = − = 2 h V V' 0 0 r h 0 0 0 0 90 = 2 r h hr2 r4 h3 2 h3 2 = h 3 − d = d = = . 2 4h 4 4 =0 2 0 0 r=0
Hướng dẫn. Để tính tích phân ba lớp I = f (x, , y z d ) xdydz,
chúng ta thực hiện các bước sau đây V
Bước 1. Vẽ đồ thị của miền V trong hệ tọa độ Descartes vuông góc Oxyz.
Bước 2. Xác định phương trình của mặt dưới z1(x,y) và của mặt trên z2(x,y) của miền V.
Bước 3. Chiếu miền V lên mặt phẳng tọa độ Oxy (z = 0) nhận được hình chiếu là một miền phẳng z (x ,y ) 2 D I = f(x, ,
y z)dxdydz = dxdy f(x, y,z)dz . V D z1 (x,y )
Bước 4. Chiếu miền D lên một trong hai trục tọa độ Ox/Oy, sao cho việc tính tích phân đơn giản b y ( x ) d x ( y ) 2 2
hơn, chúng ta sẽ nhận được dxdy = dx dy hoặc dxdy = y d dx D a y ( x ) D c x ( y ) 1 1 b y ( x ) z (x , y) d x ( y) z ( x ,y) 2 2 2 2
I = dx dy f (x,y,z)dz hoặc I = dy dx f(x, ,y )zdz. a y ( x ) z (x ,y ) c x ( y) z ( x ,y) 1 1 1 1
Bước 5. Căn cứ vào đồ thị của miền V, biểu thức của các hàm số y1(x), y2(x), z1(x,y), z2(x,y) hoặc
x1(y), x2(y), z1(x,y), z2(x,y) để quyết định tính trực tiếp tích phân này trong hệ tọa độ Descartes vuông
góc này, hoặc đổi biến sang hệ tọa độ Descartes vuông góc khác, hoặc đổi biến sang hệ tọa độ trụ/hệ tọa
độ cầu trước khi tính tích phân. Khi đổi biến cần phải biết giá trị của định thức Jacobi (nếu đã biết giá trị
của định thức Jacobi thì không cần tính mà chỉ việc sử dụng, nếu chưa biết thì phải tính) và xác định
miền D’ là ảnh của miền D qua phép đổi biến.
Bước 6. Lần lượt tính các tích phân một lớp từ phải sang trái.
Chú ý. Ngoài ứng dụng hình học của tích phân hai lớp/ba lớp như đã trình bày ở các phần ở 2.1. và
2.2., tích phân hai/ba lớp còn dùng để tính khối lượng/trọng tâm của vật thể trong lĩnh vực Cơ học và Vật
lý, hoặc dùng để tính các tích phân trong lĩnh vực Xác suất thống kê, … PHỤ LỤC
1. Phương trình của đường và mặt
1.1. Đường trong mặt phẳng R2
1.1.1. Phương trình tổng quát của đường trong mặt phẳng R2
Hệ tọa độ trực chuẩn Oxy
Trong mặt phẳng tọa độ của hệ tọa độ trực chuẩn Oxy cho một đường (L). Phương trình F(x,y) = 0
được gọi là phương trình của đường (L) nếu điểm M(x,y) nằm trên đường (L) khi và chỉ khi tọa độ (x,y)
của nó thỏa mãn phương trình F(x,y) = 0.
Nếu từ phương trình F(x,y) = 0 giải ra được duy nhất y = f(x) hoặc được cho dưới dạng y = f(x) tức
là F(x,y) = y – f(x) = 0 thì phương trình y = f(x) được gọi là phương trình dạng hiển của đường (L). Còn
nếu từ phương trình F(x,y) = 0 không giải ra được duy nhất y = f(x) thì phương trình F(x,y) = 0 được gọi
là phương trình dạng ẩn của đường (L).
Cần lưu ý rằng, vai trò của các tọa độ x và y là như nhau nên khi hoán đổi x và y cho nhau, chúng
ta cũng có định nghĩa tương tự.
1.1.2. Phương trình tham số của đường trong mặt phẳng R2 91
Trong mặt phẳng tọa độ của hệ tọa độ trực chuẩn Oxy cho một đường (L). Nếu điểm M(x,y) nằm x = f (t) x = f (t)
trên đường (L) khi và chỉ khi có một giá trị t để thì hệ phương trình được gọi là y = g(t) y = g(t)
phương trình tham số của đường (L), t được gọi là tham số, còn f(t) và g(t) là các hàm số của biến t ( t ).
Ví dụ 1. Phương trình tham số của đường tròn 2 2 2 (x − a) + (y − ) b
= R có tâm tại điểm có tọa độ x = a + R cost f (t) = a +R cos t = 0 (a,b) và bán kính R là
(0 t 2), khi đó và . y = b + R sin t g(t) = b + R sin t = 2 2 2 Ví dụ x y
2. Phương trình tham số của đường Ellipse +
= 1 có tâm tại gốc tọa độ (0,0) và các a2 b 2 x = a cost f (t) = a cos t = 0
bán trục a > 0, b > 0 là
(0 t 2), khi đó và . y = b sin t g(t) = b sin t = 2
1.1.3. Phương trình của đường trong hệ tọa độ cực
Trong mặt phẳng tọa độ của hệ tọa độ trực chuẩn Oxy cho một đường (L). Mỗi điểm M(x,y) nằm
trên đường (L) được hoàn toàn xác định bởi bộ hai số (r,) có thứ tự, trong đó 0 r = 2 x + 2 y + và
0 2 ( là góc tạo bởi Ox và OM theo chiều dương). Bộ hai số (r,) được gọi là tọa độ cực của điểm M. r = x2 + 2 x = r cos y
Liên hệ giữa tọa độ (x,y) và tọa cực (r,) là và ngược lại y = r sin y = arctan x
Trong hệ tọa độ cực cho một đường (L). Phương trình (r
, ) = 0 được gọi là phương trình của
đường (L) trong hệ tọa độ cực, nếu điểm M(r,) nằm trên đường (L) khi và chỉ khi tọa độ (r,) của nó
thỏa mãn phương trình (r,) = 0.
Nếu từ phương trình (r
, ) = 0 giải ra được duy nhất r = f() hoặc được cho dưới dạng r = f() tức
là (r,) = r – f() = 0 thì phương trình r = f() được gọi là phương trình dạng hiển của đường (L) trong
hệ tọa độ cực. Còn nếu từ phương trình (r,) = 0 không giải ra được duy nhất r = f() thì phương trình
(r,) = 0 được gọi là phương trình dạng ẩn của đường (L) trong hệ tọa độ cực.
Ví dụ 3. Viết phương trình trong hệ tọa độ cực của đường tròn có tâm tại điểm có tọa độ (a,0) trong
hệ tọa độ trực chuẩn Oxy và có bán kính a > 0, nếu lấy gốc cực là điểm O và trục cực là trục Ox.
Từ hình vẽ trên chúng ta có ngay r = 2acos (–/2 /2). x = r cos Hoặc thay
vào phương trình của đường tròn này 2 2 2
(x − a) + y = a trong hệ tọa độ y = r sin
Descartes Oxy, chúng ta được (r cos − a)2 + (r sin )2 = a2 r = a
2 cos (–/2 /2). 92
Ví dụ 4. Tìm phương trình trong hệ tọa cực (r,) của đường Cacdioit nếu biết phương trình của
đường này trong hệ tọa độ trực chuẩn Oxy là (x2 + y2 − 2ax)2 = a
4 2 (x2 + y2 ) , a > 0 khi lấy gốc cực là
điểm O và trục cực là trục Ox. x = r cos Thay
vào phương trình của đường Cacdioit (x2 + y2 − 2ax)2 = a 4 2 (x2 + y2 ) trong hệ y = r sin
tọa độ Descartes Oxy, chúng ta được (r2 − a 2 r cos )2 = 4a2r2 r = 2a 1 ( + cos ) (0 2) .
Đường Cacdioit tương ứng với a = 1/2 1.2. R Mặt trong không gian 3
1.2.1. Phương trình tổng quát của mặt trong không gian R3
Hệ tọa độ trực chuẩn Oxyz
Cho mặt (S) trong không gian R3 với hệ tọa độ trực chuẩn Oxyz. Phương trình F(x,y,z) = 0 được
gọi là phương trình của mặt (S) nếu điểm M(x,y,z) nằm trên mặt (S) khi và chỉ khi tọa độ (x,y,z) của nó
thỏa mãn phương trình F(x,y,z) = 0.
Nếu từ phương trình F(x,y,z) = 0 giải ra được duy nhất z = f(x,y) hoặc được cho dưới dạng z =
f(x,y) tức là F(x,y,z) = z – f(x,y) = 0 thì phương trình z = f(x,y) được gọi là phương trình dạng hiển của
mặt (S). Còn nếu từ phương trình F(x,y,z) = 0 không giải ra được duy nhất z = f(x,y) thì phương trình
F(x,y,z) = 0 được gọi là phương trình dạng ẩn của mặt (S).
Cần lưu ý rằng, vai trò của các tọa độ x, y và z là như nhau nên khi hoán vị vòng quanh x, y và z
cho nhau, chúng ta cũng có định nghĩa tương tự.
1.2.2. Phương trình tham số của mặt trong không gian R3
Cho mặt (S) trong không gian R3 với hệ tọa độ trực chuẩn Oxyz. Nếu điểm M(x,y,z) nằm trên mặt x = f (u, v) x = f (u, v)
(S) khi và chỉ khi có cặp giá trị (u,v) để y = g(u, v) thì hệ phương trình y = g(u, v) được gọi là z = h(u, v) z = h(u, v)
phương trình tham số của mặt (L), u và v được gọi là các tham số, còn f(u,v), g(u,v) và h(u,v) là các hàm số của hai biến (u,v).
1.2.3. Phương trình của mặt trong hệ tọa độ trụ
Trong hệ tọa độ trực chuẩn Oxyz cho một mặt (S). Hình chiếu của điểm M(x,y,z) nằm trên mặt (S)
chiếu xuống mặt phẳng tọa độ Oxy là điểm M’(x,y,0), khi đó mỗi điểm M(x,y,z) được hoàn toàn xác định
bởi bộ ba số có thứ tự (r,,z), trong đó 0 r = 2 x + 2
y + và 0 2 ( là góc tạo bởi Ox và OM’
theo chiều dương). Bộ ba số (r,,z) được gọi là tọa độ trụ của điểm M 93
Cho mặt (S) trong hệ tọa độ trụ. Phương trình F(r,,z) = 0 được gọi là phương trình của mặt (S) nếu
điểm M(r,,z) nằm trên mặt (S) khi và chỉ khi tọa độ (r,,z) của nó thỏa mãn phương trình F(r,,z) = 0.
Nếu từ phương trình F(r,,z) = 0 giải ra được duy nhất z = f(r,) hoặc được cho dưới dạng z =
f(r,) tức là F(r,,z) = z – f(r,) = 0 thì phương trình z = f(r,) được gọi là phương trình dạng hiển của
mặt (S). Còn nếu từ phương trình F(r,,z) = 0 không giải ra được duy nhất z = f(r,) thì phương trình
F(r,,z) = 0 được gọi là phương trình dạng ẩn của mặt (S).
1.2.4. Phương trình của mặt trong hệ tọa độ cầu
Trong hệ tọa độ trực chuẩn Oxyz cho một mặt (S). Hình chiếu của điểm M(x,y,z) nằm trên mặt (S)
chiếu xuống mặt phẳng tọa độ Oxy là điểm M’(x,y,0), khi đó mỗi điểm M(x,y,z) được hoàn toàn xác định
bởi bộ ba số có thứ tự (r,,), trong đó 0 r = 2 x + 2 y + 2
z +, 0 2 ( là góc tạo bởi Ox và
OM’ theo chiều dương) và 0 ( là óc g
giữa trục Oz và OM). Bộ ba số (r,,) được gọi là tọa độ cầu của điểm M
Cho mặt (S) trong hệ tọa độ cầu. Phương trình F(r,
, ) = 0 được gọi là phương trình của mặt (S) nếu điểm M(r,
, ) nằm trên mặt (S) khi và chỉ khi tọa độ (r,
, ) của nó thỏa mãn phương trình F(r, , ) = 0.
Nếu từ phương trình F(r,
, ) = 0 giải ra được duy nhất r = f(
, ) hoặc được cho dưới dạng r =
f(,) tức là F(r,,) = r – f(,) = 0 thì phương trình r = f(,) được gọi là phương trình dạng hiển của
mặt (S). Còn nếu từ phương trình F(r,,) = 0 không giải ra được duy nhất r = f( , ) thì phương trình
F(r,,) = 0 được gọi là phương trình dạng ẩn của mặt (S).
1.3. Đường trong không gian R3
1.3.1. Phương trình tổng quát của đường trong không gian
Trong hệ tọa độ trực chuẩn Oxyz cho mặt (S1) có phương trình F1(x,y,z) = 0 và mặt (S2) có phương
trình F2(x,y,z) = 0. Giả sử đường (L) là giao của hai mặt (S1), (S2); khi đó điểm M(x,y,z) nằm trên đường
(L) khi và chỉ khi nó đồng thời nằm trên cả hai mặt (S1), (S2) tức là tọa độ của điểm M thỏa mãn hệ F (x, y,z) = 0 phương trình 1
và hệ phương trình này được gọi là phương trình tổng quát của đường (L) F (x, y,z) = 0 2 trong không gian R3. 1.3.2.
Phương trình tham số của đường trong không gian
Cho đường (L) trong không gian R3 với hệ tọa độ trực chuẩn Oxyz. Nếu điểm M(x,y,z) nằm trên x = f (t) x = f (t)
đường (L) khi và chỉ khi có một giá trị t để y = g(t) thì hệ phương trình y = g(t) được gọi là phương z = h(t) z = h(t)
trình tham số của đường (L), t được gọi là tham số, còn f(t), g(t) và h(t) là các hàm số của biến t.
2. Các đường bậc hai trong mặt phẳng R2 94
2.1. Phương trình tổng quát của đường bậc hai
Phương trình tổng quát của đường bậc hai (L) trong hệ tọa độ trực chuẩn Oxy là Ax 2 + B
2 xy + Cy2 + 2Dx + 2Ey + F = 0 trong đó số hạng có tích xy được gọi là số hạng chữ nhật,
còn các hệ số A, B, C không đồng thời bằng không, tức là A2 + B2 + C2 0 A2 + B2 + C2 0
Giả sử B 0, tức là trong phương trình của (L) có số hạng chữ nhật, khi đó chúng ta đổi biến x = x'cos − y'sin
Ax 2 + 2Bxy + Cy2 + 2Dx + 2Ey + F = 0 trở thành y = x'sin + y'cos A'= A cos2 + Bsin 2 + C sin2 ' B = C ( − A) sin 2 + B cos 2
C'= A sin 2 − Bsin 2 + C cos2 A'(x')2 + ' B x' y'+ ' C (y')2 + 2D' x' 2 + E' y'+ ' F = 0 , trong đó ' D = D cos + E sin E'= −Dsin + E cos F' = F
Để phương trình của (L): A'(x')2 + ' B x' y'+ ' C (y')2 + 2D' x' 2 + E' y'+ '
F = 0 trong hệ tọa độ trực chuẩn
O’x’y’ không có số hạng chữ nhật x’y’ thì ta phải tìm góc
sao cho B’ = 0, tức là A − C
(C −A) sin 2 + B cos2 = 0 cot 2 = B 1 A − C x = x'cos −y'sin
Vì B 0 nên nếu lấy = arctan trong phép đổi biến thì phương 2 B y = x'sin +y'cos
trình của (L) trong hệ tọa độ trực chuẩn O’x’y’ trở thành A'(x')2 + ( C y')2 + 2D' x'+2E' ' y + ' F = 0 .
Như vậy, không mất tính tổng quát, đối với đường bậc hai (L), chúng ta coi như phương trình của
nó là Ax 2 + Cy2 + 2Dx + 2Ey + F = 0 . 2.2.
Phương trình chính tắc của đường bậc hai
Giả sử phương trình tổng quát của đường bậc hai (L) là Ax 2 + Cy2 + 2Dx + 2Ey + F = 0 , bây giờ
chúng ta sẽ đơn giản phương trình này trong những trường hợp có thể được. (1) A 0 và C 0:
Trong trường hợp này Ax 2 + Cy2 + D 2 x + 2Ey + F = 0 2 2 2 2 2 D D 2 E E D E Ax + 2x
+ + Cy + 2y + + F − − = 0 A A C C A C 2 2 2 2 D E D E Ax + + C y + = ' F với ' F = + −F A C A C X = x+ D A Đổi biến
Ax 2 + Cy2 + 2Dx + 2Ey + F = 0 trở thành AX 2 + CY2 = ' F Y = y + E C 2 2 A 2 C ' F F'
- Nếu F’ 0: AX + CY = ' F X + Y2 = 1, đặt a2 = và b2 = ' F ' F A C
Tùy theo dấu của A, C và F’ phương trình A 2 C X +
Y 2 =1 có một trong 3 dạng sau ' F ' F X 2 Y 2 + +
=1 (a > 0, b > 0) (L) là đường ellipse, trong trường hợp này, nếu a = b thì đường a2 b2
ellipse suy biến thành đường tròn X2 + Y2 = a2. X2 Y 2 + +
= −1 (L) là đường ellipse ảo. a2 b2 95 X2 Y 2 X2 Y2 + − = 1 hoặc − +
= 1 (L) là đường hypebol. a2 b2 a 2 b2 1 1
- Nếu F’ = 0: AX 2 + CY2 = '
F AX 2 + CY2 = 0, đặt a2 = và b2 = A C
Tùy theo dấu của A và C phương trình AX 2 + CY2 = 0 có một trong 2 dạng sau X2 Y 2 + − = 0 gi
(L) là một cặp đường thẳng ao nhau a2 b2 X2 Y 2 + +
= 0 (L) là một cặp đường thẳng ảo giao nhau a2 b2
(2) Một trong hai số A và C khác không, số còn lại bằng không, chẳng hạn A 0 và C = 0 (thực
hiện tương tự với trường hợp A = 0 và C 0):
Trong trường hợp này Ax 2 + Cy2 + 2Dx + 2Ey + F = 0 Ax 2 + 2Dx + E 2 y + F = 0 2 2 2 D D D 2 - Nếu E 0 thì Ax + D
2 x + 2Ey + F = 0 Ax + 2x
+ + 2Ey+ F− = 0 A A A X = + D x D 2 F D 2 A A x + + 2E y + − = , 0 đổi biến
, khi đó phương trình này trở A 2E 2AE 2 F D Y = y + − 2E 2AE
thànhAX 2 + 2EY = 0 X2 = 2pY (p = − E A) (L) là đường parabol.
- Nếu E = 0 thì Ax 2 + 2Dx + 2Ey + F = 0 Ax 2 + 2Dx + F = 0 D D D 2 X = x + 2 D 2 D 2 D 2 Ax + 2x
+ + F − = 0 Ax + + F− = , 0 đổi biến A , khi A A A A A Y = y 1 D2
đó phương trình này trở thành X2 − ' F = 0 với ' F = − F . 2 A A
+ Nếu F’ > 0, đặt a2 = F’ thì X2 − ' F = 0 X2 − a2 = 0
(L) là cặp đường thẳng song song. + Nếu F’ = 0 thì X2 − '
F = 0 X2 = 0 (L) là cặp đường thẳng trùng nhau.
+ Nếu F’ < 0, đặt a2 = –F’ thì X2 − '
F = 0 X2 + a2 = 0 (L) là cặp đường thẳng ảo song song.
Như vậy, chúng ta luôn tìm được hệ tọa độ trực chuẩn thích hợp sao cho có thể đưa phương trình
đã cho của đường bậc hai về một trong 9 dạng phương trình dưới đây, gọi là các dạng phương trình
chính tắc của đường bậc hai trong hệ tọa độ trực chuẩn. Các nhà toán học đã chứng minh được rằng mỗi
đường bậc hai tồn tại một và chỉ một dạng phương trình chính tắc.
STT Phương trình chính tắc
Tên đường bậc hai Ghi chú X 2 Y 2 a > 0 1 + =1 Đường ellipse a2 b2 b > 0 X 2 Y 2 a > 0 2 + = −1 Đường ellipse ảo a2 b2 b > 0 X 2 Y 2 a > 0 3 − = 1 Đường hypebol a2 b2 b > 0 X 2 Y 2 a > 0 4 − = 0
Cặp đường thẳng giao nhau a2 b2 b > 0 X 2 Y 2 a > 0 5 + = 0
Cặp đường thẳng ảo giao nhau a2 b2 b > 0 6 X2 = 2pY Đường parabol 96
STT Phương trình chính tắc
Tên đường bậc hai Ghi chú 7 X2 − a2 = 0
Cặp đường thẳng song song a > 0 8 X2 = 0
Cặp đường thẳng trùng nhau 9 X2 + a2 = 0
Cặp đường thẳng ảo song song a > 0
2.3. Ba đường conic
Các đường cong bậc hai ellipse, parabol, hyperbol được gọi là các đường conic. Nguồn gốc của từ
“conic” là khi cắt một mặt nón “cone” tròn xoay bởi một mặt phẳng không đi qua đỉnh của mặt nón thì giao tuyến sẽ là:
- Đường ellipse nếu mặt cắt không song song với một đường sinh nào đó của mặt nón (đặc biệt,
ellipse là đường tròn nếu mặt cắt vuông góc với trục của mặt nón).
- Đường parabol nếu mặt cắt song song với một đường sinh của mặt nón.
- Đường hyperbol nếu mặt cắt song song với hai đường sinh của mặt nón.
Định lý. (Dấu hiệu nhận biết các đường conic) Giả sử phương trình tổng quát của đường bậc hai
(L) là Ax 2 + Bxy + Cy2 + Dx + Ey + F = ,
0 trong đó các hệ số A, B, C không đồng thời bằng không. Xét
dấu của biểu thức = B2 − 4AC
- Nếu < 0: (L) là đường ellipse
- Nếu = 0: (L) là đường parabol
- Nếu > 0: (L) là đường hyperbol
3. Các mặt bậc hai trong không gian R3 3.1.
Phương trình tổng quát của mặt bậc hai
Phương trình tổng quát của mặt bậc hai (S) trong hệ tọa độ trực chuẩn Oxyz là a x2 +a y2 +a z2 + a 2 xy + a 2 yz + a 2 zx + a 2 x + a 2 y + a 2 z +a = , 0 trong đó các hệ số 11 22 33 12 23 31 1 2 3 0
của các số hạng bậc hai (a11, a22, a33, a1 , 2 a2 , 3 a3 ) 1
không đồng thời bằng không, tức là
a2 +a2 +a2 +a2 +a2 +a2 0 a2 +a2 +a2 +a2 +a2 +a2 . 0 11 22 33 12 23 31 11 22 33 12 23 31
3.2. Phương trình chính tắc của mặt bậc hai
Chúng ta sẽ đơn giản phương trình a x 2 +a y2 +a z2 + a 2 xy + a 2 yz + a 2 zx + a 2 x + a 2 y + a 2 z +a =0 này trong những 11 22 33 12 23 31 1 2 3 0
trường hợp có thể được.
Đầu tiên, chúng ta chứng minh rằng, có thể tìm được phép đổi biến sao cho phương trình này
không có các số hạng chữ nhật xy, yz, zx.
Trường hợp 1. Một trong các hệ số a11, a22, a33 khác không, chẳng hạn a11, khi đó chúng ta biến đổi 2 2 2 2 2 2 a a a a a 12 12 12 12 12 2 a x + a 2 xy = a x +2x y + y − y = a x + y − y , do đó nếu 11 12 11 11 a a a a a 11 11 11 11 11 ' y = y chúng ta đổi biến a x' = x 12 + y và
thì phương trình của mặt bậc hai (S) trong hệ tọa độ trực a z' = z 11 97
chuẩn O’x’y’z’ sẽ không có số hạng chữ nhật x’y’. Tiếp tục tương tự như vậy, chúng ta sẽ nhận được
phương trình của mặt (S) không có các số hạng chữ nhật trong một hệ tọa độ trực chuẩn mới nào đó.
Trường hợp 2. Các hệ số a11, a2 , a 2
33 đều bằng không, tức là a11 = a22 = a33, khi đó các hệ số a12, a23,
a31 không đồng thời bằng không, chẳng hạn a12 0 (thực hiện tương tự với trường hợp a23 0 và a31 0).
Do đó, nếu chúng ta đổi biến x = x’ + y’, y = x’ – y’ và z = z’ thì 2a12xy = 2a12(x’ + y’)( x’ – y’) =
2a12[(x’)2 – (y’)2] nên phương trình của mặt bậc hai (S) trong hệ tọa độ trực chuẩn O’x’y’z’ có hệ số của (x’)2 là a , =
tức là đã đưa trở về trường hợp 1. 11 2a , 0 12
Như vậy, chúng ta luôn tìm được hệ tọa độ trực chuẩn thích hợp sao cho có thể đưa phương trình đã
cho của mặt bậc hai về dạng không có các số hạng chữ nhật xy, yz, zx. Do đó, không mất tính tổng quát, chúng ta có thể coi như phương trình của mặt bậc hai (S) là a x2 +a y2 +a z2 + a 2 x + a 2 y + a 2 z +a = ,
0 trong đó các hệ số của các số hạng bậc hai (a 11 22 33 1 2 3 0 11, a22, a 2 2 2 2 2 2
33) không đồng thời bằng không, tức là a
+ a + a 0 a + a + a . 0 11 22 33 11 22 33
Bây giờ, chúng ta xét dạng của mặt bậc hai (S) có phương trình trên trong các trường hợp có thể xảy ra.
Trường hợp (a): a11 0, a22 0 và a3 3 0 Khi đó a x2 11 + a y2 22 + a z2 33 + a 2 x + a 2 y + a 2 z + a = 0 1 2 3 0 2 2 2 2 a a 1 1 2 a a 2 2 2 a a a x + 2x + a y + 2y + a z + 2z 3 3 + 11 22 33 a = 0 0 a11 a11 a 22 a22 a33 a 33 2 2 2 a a a a2 a2 a 2 a x 1 + + a y 2 + + a z 3 + +a 1 2 3 − − − = . 0 11 a 22 a 33 a 0 a a a 11 22 33 11 22 33 2 2 2 Đổi biến a a a a a a 1 2 3 x' = x + , ' y = y + , z'= z + và đặt , 1 2 3 a = a − − − , khi đó phương a a a 0 0 a a a 11 22 33 11 22 33
trình của mặt bậc hai (S) trở thành a (x, )2 +a (y,)2 +a z ( , )2 +a, = . 0 11 22 33 0 a a a
- Nếu a , 0 bằng phép đổi biến 11 , 22 , 33 , X = x , Y = y , Z = z thì tùy theo dấu của a 0 , , , 11, a a a 0 0 0 a , 22, a3 và 3
a chúng ta đưa phương trình của mặt bậc hai (S) về một trong bốn dạng sau: 0
+ X2 + Y2 + Z2 = 1 (S) là mặt ellipxoit.
+ X2 + Y2 + Z2 = –1 (S) là mặt ellipxoit ảo.
+ X2 + Y2 – Z2 = 1 (S) là mặt hypeboloit một tầng. + X2 Y – 2 Z
– 2 = 1 (S) là mặt hypeboloit hai tầng.
- Nếu a, = 0 bằng phép đổi biến , , , X = a x , Y = a y , Z =
a z thì tùy theo dấu của a 0 11 22 33 11, a22, a3
3 chúng ta đưa phương trình của mặt bậc hai (S) về một trong hai dạng sau:
+ X2 + Y2 – Z2 = 0 (S) là mặt nón
+ X2 + Y2 + Z2 = 0 (S) là mặt nón ảo
Trường hợp (b): a11 0, a22 0 và a3 = 3 0 Khi đó a x2 + a y2 + a 2 x + a 2 y + a 2 z + a = 0 11 22 1 2 3 0 2 2 2 a a 1 1 2 a a a x + 2x + a y + 2y 2 2 + 2a z + a = 0 11 22 a 3 0 11 a11 a 22 a22 2 2 a a a 2 a2 a x 1 + + + + + − − = 11 a y 2 a 2 z a 1 2 0 a 22 a 3 0 a a 11 22 11 22 2 2 a a Đổi biến a a x'= x 1 + , y'= y 2 + , z'= z và đặt , 1 2 a = a − −
, khi đó phương trình của mặt a a 0 0 a a 11 22 11 22
bậc hai (S) trở thành a (x,)2 +a (y,)2 + a 2 z, +a, = . 0 11 22 3 0 98 , , , a, - Nếu a 0 3 0 thì đổi biến X = a x , Y = a y , Z = a z +
, khi đó tùy theo dấu của a 11 22 3 11, a22, 2
a3 chúng ta đưa phương trình của mặt bậc hai (S) về một trong hai dạng sau:
+ X2 + Y2 + 2Z = 0 (S) là mặt paraboloit elliptic. + X2 Y
– 2 + 2Z = 0 (S) là mặt paraboloit hyperbolic. - Nếu a , 2 , 2 ,
3 = 0 thì phương trình của mặt bậc hai (S) là a (x ) +a (y ) +a = . 0 11 22 0 a a *a , 0 thì đổi biến 11 , 22 , , X = x , Y =
y , Z = z , khi đó tùy theo dấu của a , 11, a22, a chúng 0 , , a a 0 0 0
ta đưa phương trình của mặt bậc hai (S) về một trong ba dạng sau
+ X2 + Y2 = 1 (S) là mặt trụ ellipse. + X2 + Y2 =
–1 (S) là mặt trụ ellipse ảo. + X2 Y
– 2 = 1 (S) là mặt trụ hypebol.
*a, = 0 thì phương trình của mặt bậc hai (S) là a (x, )2 +a (y, )2 = 0, đổi biến 0 11 22 , , , X = a x , Y =
a y , Z = z , khi đó tùy theo dấu của a11, a22 chúng ta đưa phương trình của mặt bậc 11 22
hai (S) về một trong hai dạng sau + X2 Y
– 2 = 0 (S) là cặp mặt phẳng giao nhau.
+ X2 + Y2 = 0 (S) là cặp mặt phẳng ảo.
Trường hợp (c): a11 = 0, a22 0 và a33 = 0 thì phương trình của mặt bậc hai (S) là a y2 22 + a 2 x + a 2 y + a 2 z + a = 0 1 2 3 0 2 2 2 a a a a2 a + + + + = + + + + − = , 22 y 2y 2 2 2a1x 2a 3z a 0 0 a y 2 22 2a x 1 a 2 z 3 a 2 0 0 a a a a 22 22 22 22 a đổi biến x' = x, y' = y 2 +
, z' = z thì phương trình của mặt bậc hai (S) trở thành a22 2 a a ( ' y )2 + a 2 x + + = với , 2 a = a − . 22 1 ' a 2 3 ' z a,0 0 0 0 a22
- Nếu a1 và a3 không đồng thời bằng không, chẳng hạn a1 0 (thực hiện tương tự với trường hợp 2 , a 22 2 a a, a 3 0 3 0) thì a (y') + 2a x'+ a 2 z'+a = 0 (y') + 2 x'+ z'+ = 0 . 22 1 3 0 a a 2a 1 1 1 , Đổi biến a a a 3 0 22 , , X = x'+ z'+ , Y =
y , Z = z thì phương trình của mặt bậc hai (S) trở thành a1 2a 1 a1
Y2 2X = 0 (S) là mặt trụ parabol. a - Nếu a 22 ,
1 = a3 = 0 và a , 0 thì đổi biến , X = x', Y =
y , Z = z thì phương trình của mặt bậc 0 , a0
hai (S) trở thành một trong hai dạng sau + Y2 –
1 = 0 (S) là cặp mặt phẳng song song.
+ Y2 + 1 = 0 (S) là cặp mặt phẳng song song ảo.
- Nếu a = a = a, = 0 thì đổi biến , , X = x', Y =
a y , Z = z thì phương trình của mặt bậc hai 1 3 0 22
(S) trở thành Y2 = 0 (S) là cặp mặt phẳng trùng nhau.
Như vậy, chúng ta luôn tìm được hệ tọa độ trực chuẩn thích hợp sao cho có thể đưa phương trình
đã cho của mặt bậc hai về một trong dạng phương trì 17
nh dưới đây, gọi là các dạng phương trình chính
tắc của mặt bậc hai trong hệ tọa độ trực chuẩn. Các nhà toán học đã chứng minh được rằng mỗi mặt bậc
hai tồn tại một và chỉ một dạng phương trình chính tắc.
STT Phương trình chính tắc Tên mặt bậc hai 1 X2 + Y2 + Z2 = 1 Mặt ellipxoit 99
STT Phương trình chính tắc Tên mặt bậc hai 2 X2 + Y2 + Z2 = –1 Mặt ellipxoit ảo 3 X2 + Y2 – Z2 = 1
Mặt hypeboloit một tầng 4 X2 – Y2 – Z2 = 1
Mặt hypeboloit hai tầng 5 X2 + Y2 – Z2 = 0 Mặt nón 6 X2 + Y2 + Z2 = 0 Mặt nón ảo 7 X2 + Y2 + 2Z = 0
Mặt paraboloit elliptic 8 X2 – Y2 + 2Z = 0
Mặt paraboloit hyperbolic 9 X2 + Y2 = 1 Mặt trụ elliptic 10 X2 + Y2 = –1 Mặt trụ ellipse ảo 11 X2 – Y2 = 1 Mặt trụ hypebolic 12 X2 – Y2 = 0 Cặp mặt phẳng giao nhau 13 X2 + Y2 = 0 Cặp mặt phẳng ảo 14 Y2 2X = 0 Mặt trụ parabolic 15 Y2 – 1 = 0 Cặp mặt phẳng song song 16 Y2 + 1 = 0
Cặp mặt phẳng song song ảo 17 Y2 = 0
Cặp mặt phẳng trùng nhau
3.3. Mặt bậc hai không suy biến
Như đã chỉ ra ở Phần 3.2. Phương trình chính tắc của mặt bậc hai, có những mặt bậc hai là cặp mặt
phẳng, chúng ta gọi chúng là mặt bậc hai suy biến, các mặt bậc hai còn lại và không phải là ảo, được gọi
là mặt bậc hai không suy biến. 3.3.1. Mặt ellipxoit x2 y 2 z2 + +
= 1 (a > 0, b > 0, c > 0) a2 b 2 c2
3.3.2. Mặt hypeboloit một tầng x2 y 2 z2 + −
= 1 (a > 0, b > 0, c > 0) a2 b2 c2
3.3.3. Mặt hypeboloit hai tầng x2 y2 z2 − −
=1 (a > 0, b > 0, c > 0) a2 b2 c2
3.3.4. Mặt paraboloit elliptic x2 y2 +
+ 2kz = 0 (a > 0, b > 0, k 0) a2 b2 3.3.5.
Mặt paraboloit hyperbolic (mặt yên ngựa) x2 y2 −
+ 2kz = 0 (a > 0, b > 0, k 0) a 2 b2 3.3.6. Mặt nón x2 y2 z 2 + −
= 0 (a > 0, b > 0, c > 0) a2 b2 c 2 3.3.7. Mặt trụ x2 y 2 +
= 1 (a > 0, b > 0, – < z < +) – mặt trụ elliptic a2 b 2 x 2 y 2 −
=1 (a > 0, b > 0, – < z < +) – mặt trụ hyperbolic a2 b2
y2 – 2px = 0 (p 0, – < z < +) – mặt trụ parabolic Bài tập 2.1.
Tính các tích phân hai lớp trên miền tương ứng (a) I = xydxdy,
D = {(x,y)R2|y = 1, y = 3, y = x, y = x + 1} D 100 (b) I = (x y)dxdy, +
D = {(x,y)R2|y = 0, y = x2, y + x = 2} D (c) I = xydxdy,
D = {(x,y)R2|xy = 1, xy = 3, y2 = 2x, y2 = 4x} D x −y (d) I = ex y dxdy, +
D = {(x,y)R2|x 0, y 0, x + y 1} D (e) I = (x 2 y 2)dxdy, +
D = {(x,y)R2|x2 + y2 2Rx, R > 0} D x2 y2 x2 2 y2 (f) I = 1 − dxdy, − D = (x, y) R + 2 2 1 a 2 b2 a b D (g) I = (x y)dxdy, − D = ( { x, y) R2 (x − ) 3 2 + (y − ) 2 2 } 1 D (h) I = x y dxdy, + D = {(x,y)R2||x| | ≤ 1, y| ≤ 1} D (i) I = (2x + y)(x 2y)dxdy, −
E là hình vuông ABCD có các đỉnh A(1,0), B(3,1), C(2,3), D(0,2) E
2.2. Đổi thứ tự tính tích phân của các tích phân hai lớp sau đây 3 2y 2 2x 1 + 1 − 2 1 y (a) I = dy f(x,y)dx (b) I = dx f(x, y)dy (c) I = dy f(x, y)dx 1 0 0 2x −x 2 0 − 2 y 1 1− 2 x 2 y 2 − 2 4 y (d) I = dx f(x, y)dy (e) I = dy f(x, y d ) x + dy f(x, y)dx 0 − − 2 1 x 0 0 2 0
2.3. Tính diện tích của các hình phẳng giới hạn bởi các đường bậc nhất/bậc hai sau đây
(a) {(x,y)R2|x = 4y – y2, x + y = 6}
(b) {(x,y)R2|xy = 1, x + y = 5/2}
(c) {(x,y)R2|y2 = 2x, y2 = 3x, x2 = y, x2 = 4y}
2.4. Các đề thi Giải tích 2 về tính tích phân hai lớp x (a) Tính I = y
e dxdy , D là miền giới hạn bởi trục hoành Ox, trục tung Oy, đường thẳng y = 1 và D
đường parabol y2 = x.(năm học 2017 -2018) 1 1 2 (b) Tính I = dy e1− x dx. (năm học 2018-2019) 0 y 2 2 2 2 x (c) Tính I = −x −y e dxdy , D = 1 x + y , 4 y x 3 . (năm học 2019-2020) 3 D dxdy (d) Cho D = x { 2 + y2 a 2 x, a } 0 , xác định a nếu = . 4 (năm học 2020-2021) 2 2 + D x y dxdydz
2.5. (a) Tính I =
, V là miền giới hạn bởi các mặt phẳng tọa độ và mặt phẳng x + y + z 1 ( + x + y + 3 z) V
= 1. Ký hiệu A, B, C tương ứng là các điểm giao của các trục tọa độ Ox, Oy, Oz với mặt phẳng x + y + z
= 1. Tính diện tích S của tam giác ABC và so sánh kết quả tính được với kết quả tính theo công thức sơ
cấp đã biết ở Trường phổ thông. Tính thể tích V của hình chóp OABC và so sánh kết quả tính được với
kết quả tính theo công thức sơ cấp đã biết ở Trường phổ thông. (b) Tính I = 2 (x + 2 y + 2
z )dxdydz , miền V là hình cầu x2 + y2 + z2 x. Tính diện tích mặt cầu và V
thể tích của hình cầu V, so sánh kết quả tính được với kết quả tính theo công thức sơ cấp đã biết ở Trường phổ thông. 101
2.6. Các đề thi Giải tích 2 về tính tích phân ba lớp
(a) Tính thể tích khối vật thể giới hạn bởi mặt paraboloit 2 2
z = 1− x − y và mặt phẳng z = 0.(năm học 2017-2018) dxdydz (b) Tính I =
với V là khối cầu x2 + y2 + z2 . x (năm học 2018-2019) 2 2 2 V x + y + z dxdydz (c) Cho mặt nón 2 2
z = x + y (S) và mặt phẳng z = 2 (P). Tính I = với V là miền giới 2 2 V x + y
hạn bởi (S) và (P).(năm học 2019-2020) 2 a dxdydz (d) Chứng minh = x
y dxdydz với miền V = { x2 + y2 z a, a } 0 . 2 2 2 + 2 6 V x + y V (năm học 2020-2021) z x2 + y2
(e) TínhI = zdxdydz với V là khối nón cụt .(năm học 2021-2022) 1 z V 3
2.7. Tính thể tích miền V bằng tích phân hai lớp
(a) V là miền giới hạn bởi mặt cầu x2 + y2 + z2 =
4 và mặt trụ x2 + y2 = 2y.
(b) V là miền nằm dưới mặt paraboloit z = x2 + y2, bên trên mặt phẳng z = 0 và bên trong mặt trụ x2 + y2 = 2y.
2.8. Tính thể tích miền V bằng tích phân ba lớp
(a) V là miền giới hạn bởi các mặt x = 0, y = 0, z = 0, z = x2 + y2 và nằm trong góc vuông phần tám thứ nhất.
(b) V là miền nằm phía sau mặt phẳng x + y + z = 8, phía trước mặt phẳng x = 0 và bị chặn bởi các 3 3 mặt phẳng z = y, z = . y 2 4
(c) V là miền nằm dưới mặt phẳng z = x + 2, trên mặt phẳng z = 0 và giữa hai hình trụ x2 + y2 = 1, x2 + y2 = 4. x 2 + 3 y 2 z 2 (d) V = (x, y,z) R + 1. a 2 a 3 2 102




