









































Preview text:
Chương TÍCH PHÂN ĐƯỜNG, TÍCH PHÂN MẶT 3.
3.1. Tích phân đường loại một 3.1.1.
Định nghĩa tích phân đường loại một
Bài toán vật lý dẫn đến khái niệm tích phân đường loại một
Giả sử trong mặt phẳng tọa độ Oxy có một sợi dây AB rất mảnh (chỉ có độ dài, còn tiết diện
không đáng kể - coi như không có kích thước) có khối lượng riêng tại điểm (x,y) AB được biểu diễn
bằng hàm số f(x,y) đơn trị, liên tục và không âm. Yêu cầu tìm khối lượng m của sợi dây AB.
Để tính m, chúng ta thực hiện như sau: Chia tùy ý AB thành n
cung nhỏ không dẫm lên nhau bởi
các điểm A A0, A1, A2, …, An-1, An B v
à ký hiệu độ dài của cung nhỏ Ai-1Ai là si (1 i n). Trên
cung Ai-1Ai lấy tùy ý một điểm (xi,yi), nếu cung Ai-1Ai đủ nhỏ thì chúng ta có thể coi giá trị f(xi,yi)
không đổi trên cung Ai-1Ai; khi đó, khối lượng của cung nhỏ Ai-1Ai là mi f(xi,yi).si.
Như vậy, nếu mọi cung Ai-1Ai (1 i n) đủ nhỏ thì có thể c
oi khối lượng của sợi dây AB là n m = m1 + m2 + … + mn
f(x1,y1).s1 + f(x2,y2).s2 + … + f(xn,yn).sn = f (x , y ) . s i i i i=1 n Tổng f (x , y )
. s sẽ có độ chính xác cao (tức là giá trị của biểu thức này càng gần khối lượng i i i i=1
thực m của sợi dây AB) nếu n càng lớn và tất cả các si (1 i n) càng bé. Do đó, khối lượng m của n
sợi dây AB bằng giới hạn của tổng f (x , y )
. s khi n → cùng với độ dài của mỗi cung nhỏ si (1 i i i i=1 n
i n) bé dần về 0, tức là m = lim trong đó = max s . → f (x , y . ) s i i i i 0 1 i n i 1 n = →
Định nghĩa tích phân đường loại một
Cho đường cong phẳng L là cung AB trong mặt phẳng tọa độ Oxy và hàm số f(x,y) xác định,
đơn trị và liên tục với (x,y) AB.
Chia cung AB thành n cung nhỏ tùy ý không dẫm lên nhau bởi các
điểm A A0, A1, A2, …, An-1, An B và ký hiệu độ dài của cung nhỏ Ai-1Ai là si (1 i n). Trên n
cung Ai-1Ai lấy điểm (xi,yi) tùy ý và lập tổng I = f (x , y ). s . n i i i i=1
Nếu khi n → sao cho = max s → 0 mà I → I là một giá trị hữu hạn, không phụ thuộc vào i n 1 i n
cách chia cung AB và cách lấy điểm (xi,yi) trên cung Ai-1Ai thì giá trị hữu hạn I được gọi tích phân
đường loại một của hàm số f(x,y) trên cung AB (hay trên đường cong L) và ký hiệu là n
I = f (x, y)ds = f (x, y)ds = limI = lim f (x , y ) s n → n → i i i 0 i=1 AB L
Khi đó hàm số dưới dấu tích phân f(x,y) được gọi là khả tích trên cung AB (hay trên đường cong
L), còn ds được gọi là vi phân cung.
Nếu hàm số f(x,y) đơn trị và liên tục với (x,y)L thì nó khả tích trên đường cong L.
Hoàn toàn tương tự, chúng ta cũng định nghĩa tích phân đường loại một trên đường cong L trong
không gian 3 chiều, tức là I = f(x, y,z)ds. L
3.1.2. Tính chất của tích phân đường loại một
Đối với tích phân đường loại một trên đường cong phẳng
(1) Tích phân đường loại một không phụ thuộc vào chiều tính tích phân từ A đến B hay ngược
lại, tức là f(x,y)ds = f(x,y)ds. AB BA
Các tính chất khác của tích phân đường loại một giống như các tính chất của tích phân xác định. 103 (2) [f (x, y) + f (x, y) d ] s = f (x, y)ds f (x, y)ds 1 2 + 1 2 L L L
(3) f (x, y)ds = f (x, y)ds (hằng số R) L L L L = L (4) f(x, y d
) s = f (x, y)ds + f(x, y)ds 1 2 L L = L 1 2 1 L L2
Hoàn toàn tương tự đối với tích phân đường loại một trên đường cong trong không gian 3 chiều. 3.1.3.
Cách tính tích phân đường loại một Tính tích p t
hân đường loại một trên đường cong rong R2 (đường cong phẳng) x = x(t)
(1) Nếu đường cong phẳng AB được cho dưới dạng tham số với a t b, y = y(t)
ds = (dx)2 + (dy)2 = [x'(t)dt]2 + [y'(t d ) t]2 = x'(t ) 2 + y'(t)2dt b và f(x, ) y = f (x(t), (
y t)) với a t b, thì f (x, )
y ds = f (x(t),y(t)) x'(t)2 + y'(t)2dt. AB a
(2) Nếu đường cong phẳng AB được cho bởi y = y(x) với a x b, khi đó chúng ta coi x là x = t
tham số t thì đường cong phẳng AB được cho dưới dạng tham số với a t b y = y(t) d t = dx x'(t)= 1 ds = 1 y'(x ) 2 + dx và f (x, y) = f(x, ( y x ) ) với a x b y '(t) = y'(x) b
thì f (x, y)ds = f (x, y(x)) 1+ y'(x)2 dx. AB a
(3) Nếu đường cong phẳng AB được cho bởi x = x(y) với c y d, khi đó chúng ta coi y là x = x(t)
tham số t thì đường cong phẳng AB được cho dưới dạng tham số với c t d y = t d t = dy x
'(t) = x'(y) ds = 1 x'(y ) 2 + dy và f (x, ) y = f(x( ) y , ) y với c y d y'(t)= 1 d
thì f (x, y)ds = f (x(y),y) 1+ x'(y)2 d . y AB c
(4) Nếu đường cong phẳng AB được cho dưới dạng tọa độ cực r = r() với trong hệ
x = r cos = r()cos
tọa độ cực (r,), khi đó
và chúng ta coi là tham số thì đường cong phẳng AB y = rsin = r ( )sin x = x() = r()cos
được cho dưới dạng tham số với y = y() = r()sin ds = d ( x) 2 + (dy) 2 = [x' ( d ) ]2 + [y'( d
) ]2 = x'() 2 + y' ( ) 2 d =
r'()cos − r()sin
2 +r'()sin + r ( ) cos 2 d = [r()]2 + [r'()]2 d và f (x, ) y = f (r cos , rsin ) ( ) thì f (x, y)ds = f (r cos , rsin) r( ) 2 + r'()2 d . AB 104
Tính tích phân đường loại một trên đường cong trong R3 x = x(t)
(1) Nếu đường cong AB trong R3 được cho dưới dạng tham số
y = y(t) với a t b z =z(t) thì f (x, y, ) z ds = f (x(t), y(t), (
z t)) x'(t)2 + y'(t)2 + z'(t) 2 dt AB y = y(x)
(2) Nếu đường cong AB trong R3 được cho bởi các phương trình với a x b z = z(x) b thì f (x, , y z)ds = f (x, y(x), (
z x)) 1 + y'(x)2 + z'(x) 2 dx AB a x = x(y)
tương tự, nếu đường cong AB trong R3 được cho bởi các phương trình với c y d z = ( z y) d thì f (x, , y ) z ds = f (x(y), ,
y z(y)) 1 + x'(y) 2 + z'(y) 2 dy AB c x = x(z)
và tương tự, nếu đường cong AB trong R3 được cho bởi các phương trình với p z q y = y(z) q
thì f (x, y,z)ds = f(x(z),y(z),z) 1 +x'(z)2 +y'(z) 2 dz AB p Lưu ý.
(1) Vì tích phân đường loại một không phụ thuộc vào chiều tính tích phân nên đối với giá trị của
hai cận của tích phân, giá trị nhỏ là cận dưới còn giá trị lớn hơn là cận trên.
(2) Nếu L là đường cong kín thì có thể dùng ký hiệu f (x,y)ds= f (x, y)ds (L là đường cong L L
phẳng) và tương tự f(x, ,yz)ds = f(x, y,z)ds (L là đường cong trong R3) . L L
Ví dụ 3.1. Tính I = xds,
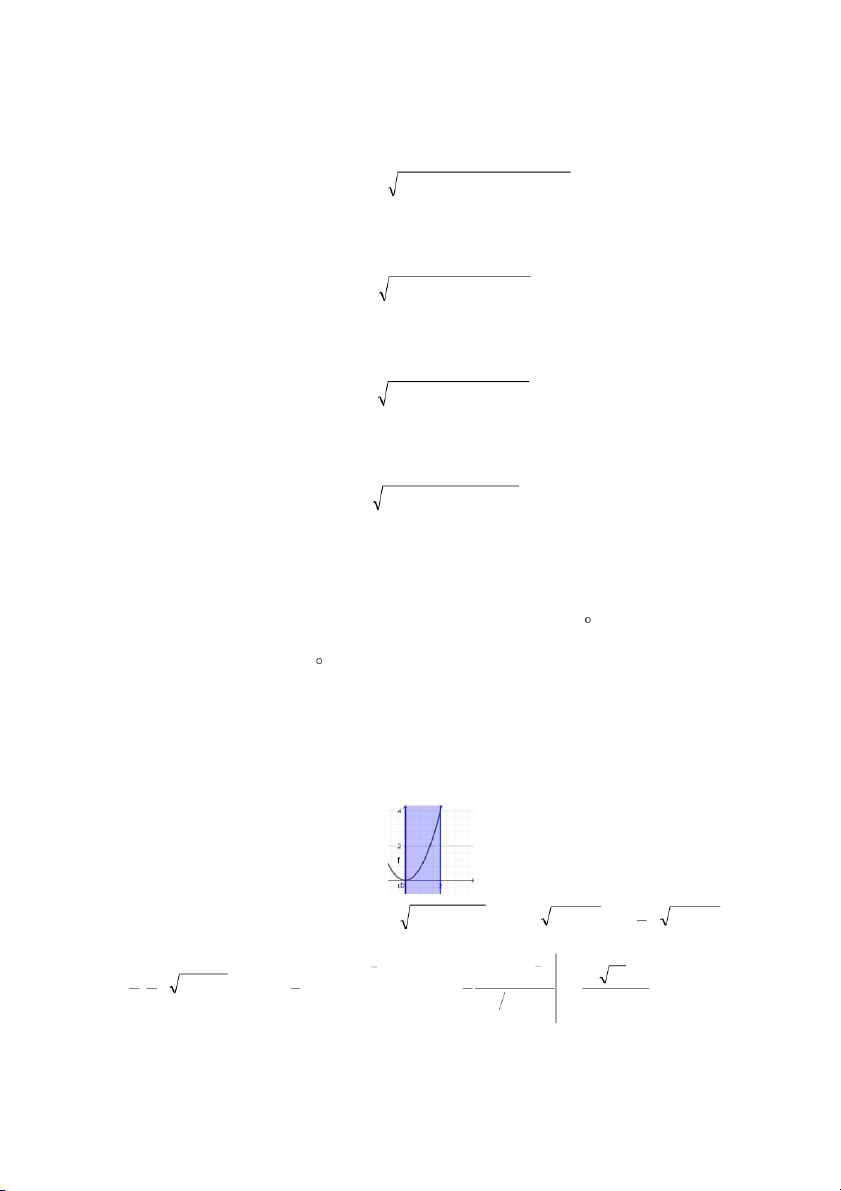
OA là cung của đường parabol y = x2 từ điểm O(0,0) đến điểm A(2,4). OA Bài giải.
Cung OA nằm trên đường parabol y = y(x) = x2 với 0 x 2 nên đồ thị của nó trong hệ tọa độ Descartes vuông góc Oxy là 2 2 2 2 1 2
Chúng ta có y’(x) = 2x I = xds = x 1 +y'(x) dx = x 1 + 4x dx = 1 + 4x2 d(x2 ) = 2 OA 0 0 0 2 1 1 1 + 1 1 2 + − 2 2 1 2 2 2 1 1 ( 4x 2 2 ) 2 17 17 1 . 1 +4x d(4x ) = 1 ( +4x ) d 1 ( + 4x ) = = . 2 4 8 8 1 ( 2) + 1 12 0 0 0
Ví dụ 3.2. Tính I = (x 2 2y)ds, −
L là các cạnh của ABC có tọa độ các đỉnh trong hệ tọa độ L
Descartes vuông góc Oxy là A(1,1), B(3,1) và C(1,5). 105 Bài giải.
Đồ thị của ABC trong hệ tọa độ Descartes vuông góc Oxy là
Chúng ta có L = AB + BC + CA I = 2 (x − 2y d ) s = 2 (x − 2y d ) s + 2 (x − 2y d ) s + 2 (x − 2 ) y ds L AB BC CA - Tính 2
(x − 2y)ds : Lấy x làm tham số, khi (x,y) AB thì y = 1 với 1 ≤ x ≤ 3 AB f (x, y) = f(x, y(x ) ) = x2 − 2y = x2 − . 2 1= x2 − 2 Chúng ta có 2 2
y'(x) = 0 ds = 1 +[y'(x)] dx = 1 + 0 dx = dx 3 3 x3 14 (x2 −2y)ds = (x2 − ) 2 dx = −2x = 3 3 AB 1 1 - Tính 2
(x − 2y)ds : Lấy x làm tham số, khi (x,y) BC
thì phương trình đường thẳng đi qua BC x − x y − y x − 3 y− 1
điểm B(3,1) và điểm C(1,5) là B B = = y = 2 − x + 7 với 1 ≤ x ≤ 3 x − x y − y 1− 3 5 −1 C B C B 2 2
f (x, y) = f [x, y(x)] = x − − ( 2 2x + 7) = x + 4x − 14 Chúng ta có 2 2
y'(x) = − 2 ds = 1+ [y'(x)] dx = + 1 − ( ) 2 dx = 5dx 3 3 x3 x2 10 5 (x2 − 2y d ) s = (x2 + 4x− 1 ) 4 d 5 x = 5 + 4 − 1 x 4 = − 3 2 3 BC 1 1 - Tính 2
(x − 2y)ds : Lấy y làm tham số, khi (x,y) CA thì x = 1 với 1 ≤ y ≤ 5 CA f (x, y) = f (x(y), y ) 2 2 = x − 2y =1 − 2y =1 − 2y Chúng ta có 2 2
x'(y) = 0 ds = 1 + [x'(y)] dy = 1 + 0 dy = dy 5 5 (x 2 − 2y)ds = 1 ( − 2y)dy = (y − y2 ) = 2 − 0 1 CA 1 − − 2 14 10 5 46 10 5
Như vậy, chúng ta được I = (x − 2 ) y ds = − − 20 = . 3 3 3 L
Ví dụ 3.3. Cho L là đường cong có phương trình trong hệ tọa độ cực (r,) là r = cos với 0 2 .
(a) Vẽ đồ thị của L trong hệ tọa độ Descartes vuông góc Oxy.
(b) Tính I = xds trong hệ tọa độ Descartes vuông góc Oxy khi là tham số. L
(c) Tính I = xds trong hệ tọa độ cực (r,) . L Bài giải.
(a) Như chúng ta đã biết, tọa độ Descartes (x,y) biểu diễn qua tọa độ cực (r,) qua công thức x = r co s
x = (cos)cos = cos2 mà r = co s y = r sin
y =(cos ) sin =cos sin 106 x2 + y2 = (cos2 )2 + (cossin )2 = cos2 ( cos2 + sin2 )
= cos2 = x , do đó phương trình 2 2
của đường cong L trong hệ tọa độ Descartes vuông góc Oxy là 2 2 1 2 1
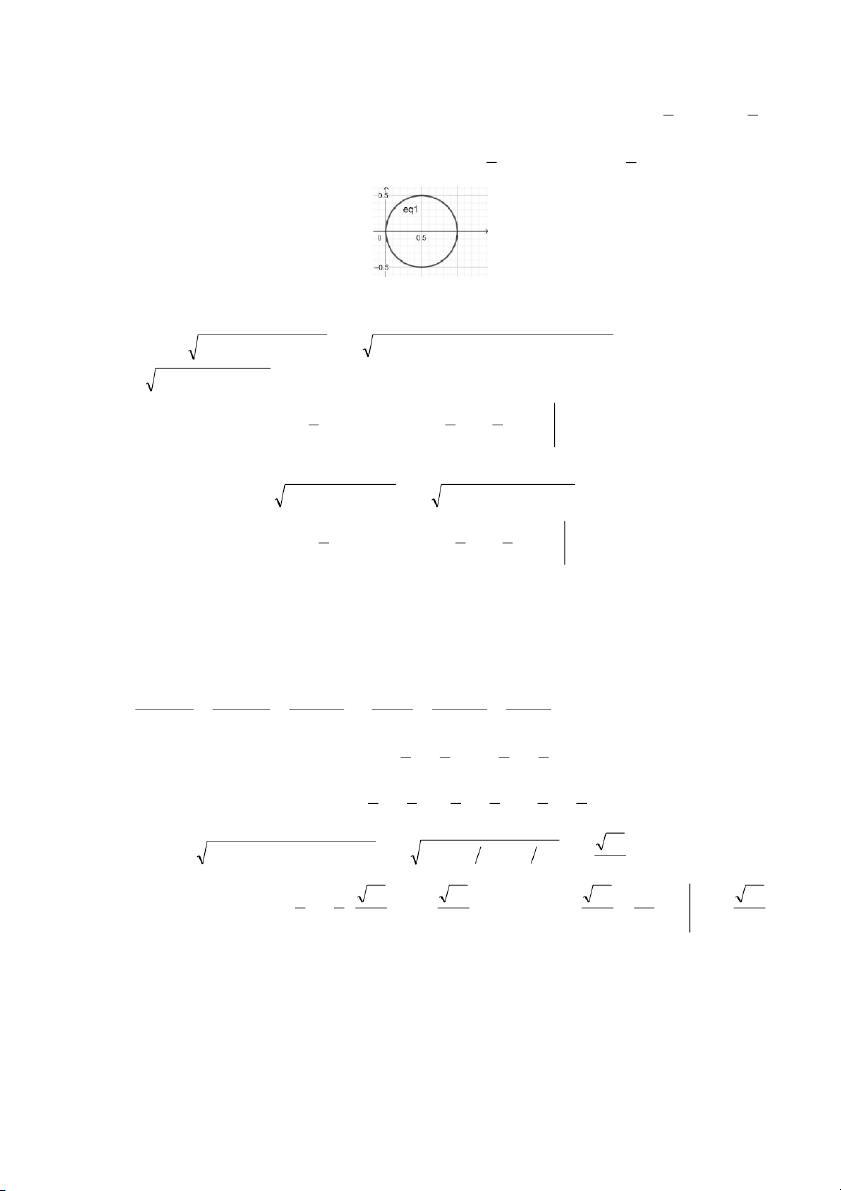
x + y = x x − + y = . 2 2 1
Phương trình này là phương trình của đường tròn có tâm 1 I ,0 , bán kính R = và có đồ thị 2 2 x ( ) = cos2
(b) Biến đổi tương tự như trên, chúng ta có , là tham số y ( ) = cossin
ds = [x, ()]2 + [y, ()]2
d = (2cossin )2 + (−sin2 + cos2 )2 d = sin2 2 + cos2 2 d = d và f (x, ) y = x 2 f (cos , cossin ) = 2 cos 2 2 2 1 2 1 1 I = xds = cos d = 1
( + cos2)d = + sin2 = . 2 2 2 L 0 0 0
f (x, y) = x f (x ( ), y ( ) )= x ( ) = cos2 (c) Chúng ta có ds = [r()]2 +[r'
( )]2 d = (cos)2 + (− sin )2 d = d 2 2 2 1 2 1 1 I = xds = cos d = 1
( + cos2)d = + sin 2 = . 2 2 2 L 0 0 0
Ví dụ 3.4. Tính I = (2x + y − 2z)ds với AB là đoạn thẳng nối điểm A(1,–1,2) với điểm B(– AB
1,2,–1) trong hệ tọa độ Descartes vuông góc Oxyz. Bài giải.
Phương trình đường thẳng đi qua điểm A(1,–1,2) và điểm B(–1,2,–1) là x − x y − y z − z − − − − A A A x 1 y ( ) 1 z 2 = = = = x − x y − y z −z − 1−1 2 − (− ) 1 − 1− 2 B A B A B A
Nếu lấy x làm tham số thì 3 1 3 1 x = x, y = − x + , z = x + với –1 ≤ x ≤ 1 2 2 2 2 3 1 3 1 5 1 f (x, , y ) z = 2x + y − 2z = 2x − x + − 2 x + = − x − 2 2 2 2 2 2
ds = (x')2 +[y'(x)]2 + z['(x)]2dx = 12 + (−3 2)2 + (3 2)2 22 dx = dx 2 1 1 5 1 22 22 1 22 x2 22 I = (2x + y− ) z 2 ds = − x − dx = − 5 ( x + ) 1 dx = − 5 + x = − . − 2 2 2 2 4 2 2 AB 1 −1 −1
3.1.4. Ý nghĩa vật lý và ý nghĩa hình học của tích phân đường loại một
Nếu hàm số dưới dấu tích phân f(x,y) > 0 (đường cong phẳng L) hoặc f(x,y,z) > 0 (đường cong
không gian L) xác định và liên tục với mọi điểm trên đường cong, biểu thị khối lượng riêng của đường
cong tại điểm (x,y) của đường cong phẳng hoặc tại điểm (x,y,z) của đường cong không gian, thì khối
lượng m của đường cong L là m = f (x,y)ds hoặc m = f(x, ,y )zds(ý nghĩa vật lý). Đặc biệt, nếu L L 107
f(x,y) = 1 thì ds (L là đường cong phẳng) hoặc nếu f(x,y,z) = 1 thì ds (L là đường cong không L L
gian) là độ dài của đường cong L (ý nghĩa hình học).
Ví dụ 3.5. Tính chu vi của đường tròn L bán kính R. Bài giải.
Không mất tính tổng quát, có thể coi đường tròn L bán kính R có tâm tại gốc tọa độ O(0,0) của
hệ tọa độ Descartes vuông góc Oxy, khi đó phương trình của đường tròn L trong hệ tọa độ Descartes
vuông góc Oxy là x2 + y2 = R2 và đồ thị của nó là x(t) = R cost
Phương trình tham số của đường tròn x2 + y2 = R2 là
(0 ≤ t ≤ 2), theo ý nghĩa y(t) = R sin t
hình học của tích phân đường loại một thì chu vi của đường tròn L bán kính R là C = ds. L
Đường tròn L là đường cong phẳng khép kín nên bất kỳ điểm nào trên L cũng có thể được chọn
là điểm bắt đầu đồng thời là điểm kết thúc khi tính tích phân C = ds. Để đơn giản, chúng ta chọn L
điểm (x,y) = (R,0) là điểm bắt đầu đồng thời là điểm kết thúc, tương ứng với t = 0 và t = 2. x'(t) = − R sin t Chúng ta có
ds = x'(t) 2 + y'(t) 2dt = (−R sin t)2 + (R cost) d 2 t = Rdt y'(t) = R cost 2 2 2 C = ds = Rdt = R dt = Rt = 2 R . 0 L 0 0
3.2. Tích phân đường loại hai 3.2.1.
Định nghĩa tích phân đường loại hai
Bài toán vật lý dẫn đến khái niệm tích phân đường loại hai → →
Cho một chất điểm M(x,y) di chuyển theo cung phẳng AB dưới tác dụng của lực F = F(x, y)
biến thiên liên tục dọc theo cung AB từ A đến B. Yêu cầu tính công W khi di chuyển chất điểm bằng →
lực F(x, y) từ điểm đầu A đến điểm cuối B của cung AB. →
Giả sử véc tơ F(x, y) có các thành phần P(x,y), Q(x,y) trên các trục tọa độ Ox, Oy. Để tính công
W, chúng ta thực hiện như sau: Chia cung AB thành n cung nhỏ tùy ý không dẫm lên nhau bởi các
điểm A A0, A1, A2, …, An-1, An B. Trên cung Ai-1Ai lấy điểm (x
i,yi) tùy ý và ký hiệu xi , yi là các
thành phần trên các trục tọa độ Ox, Oy của véc tơ A
. Khi đó, nếu cung Ai-1Ai đủ nhỏ thì có thể − A i 1 i → →
coi cung này là thẳng và là véc tơ A , còn lực
có thể coi là không đổi và bằng − A F(x, y) F(x , y ) i 1 i i i
tại mọi điểm của cung Ai-1Ai. →
Do đó, nếu ký hiệu Wi là công của lực F(x , y ) i i
tác dụng tại điểm (xi,yi) làm di chuyển chất →
điểm M trên cung Ai-1Ai thì W F(x , y ) A . . − A = P(x , y ). x + Q(x , y ).y i i i i 1 i i i i i i i
Như vậy, nếu mọi cung Ai-1Ai (1 i n) đều đủ nhỏ thì có thể coi công W khi di chuyển chất → điểm bằng lực F(x, y)
từ điểm đầu A đến điểm cuối B của cung AB là 108 n n W = W + W + ...+ W = w P(x , y ). x Q(x , y ). y . 1 2 n i + i i i i i i = i 1 i=1 n Tổng P(x , y ) . x + Q(x , y )
. y sẽ có độ chính xác cao, tức là giá trị của biểu thức này i i i i i i i =1
càng gần với giá trị chính xác của công W, nếu n càng lớn và tất cả các xi (1 i n) và yi (1 i n
n) càng bé. Do đó, giá trị của công W là giới hạn của tổng P(x , y ).x +Q(x , y ).y khi n → i i i i i i i =1
cùng với maxx → 0và max y →0. i i 1in 1i n
Định nghĩa tích phân đường loại hai
Cho các hàm số P(x,y), Q(x,y) xác định và liên tục trên cung phẳng AB (đường cong phẳng L).
Chia cung AB thành n cung nhỏ tùy ý và không dẫm lên nhau bởi các điểm A A0, A1, A2, …,
An-1, An B. Trên mỗi cung Ai-1Ai lấy điểm (xi,yi) tùy ý, gọi hình chiếu của véc tơ A lên các trục − A i 1 i n
tọa độ Ox, Oy tương ứng là x I = P(x , y ). x
Q(x , y ). y , nếu khi n → n + i, yi. Lập tổng i i i i i i i =1
sao cho max x → 0 và max y
→0 mà tổng In → I là một giá trị hữu hạn, không phụ thuộc vào i i 1in 1i n
cách chia cung AB và cách lấy điểm (xi,yi) trên cung Ai-1Ai thì giá trị hữu hạn I được gọi tích phân
đường loại hai của các hàm số P(x,y), Q(x,y) trên cung AB (hay trên đường cong L) và ký hiệu là
I = P(x, y)dx + Q(x, y)dy = P(x, y)dx + Q(x, y)dy AB L
Khi đó các hàm số P(x,y), Q(x,y) được gọi là khả tích trên cung AB (hay trên đường cong L).
Nếu các hàm số P(x,y), Q(x,y) đơn trị và liên tục với (x,y) L
thì chúng khả tích trên đường cong L.
Hoàn toàn tương tự, chúng ta cũng định nghĩa tích phân đường loại hai trên đường cong L trong
không gian 3 chiều, tức là nếu các hàm số P(x,y,z), Q(x,y,z), R(x,y,z) đơn trị và liên tục với (x,y,z)L thì chúng khả tích trên đường cong L, tức là I = P(x, y,z d ) x + Q(x, y, z)dy + R(x, , y z)dz . L
3.2.2. Tính chất của tích phân đường loại hai
Ngay sau đây, chúng ta nêu các tích chất của tích phân đường loại hai đối với cung phẳng AB
hay đường cong phẳng L, đối với tích phân đường loại hai đối với cung AB hay đường cong L trong
không gian 3 chiều cũng có các tính chất hoàn toàn tương tự.
(1) Tích phân đường loại hai phụ thuộc vào chiều lấy tích phân từ điểm A đến điểm B hay từ
điểm B đến điểm A vì hình chiếu của véc tơ A
lên các trục tọa độ đổi dấu khi véc tơ này đổi − A i 1 i
chiều, tức là P(x, y)dx +Q(x, y)dy = − P(x, y)dx +Q(x, y)dy AB BA
Quy ước. Nếu đường lấy tích phân đường loại hai là đường cong kín L (điểm đầu A trùng với
điểm cuối B), thì chúng ta quy ước chiều dương trên đường L là chiều sao cho khi một người đi trên
đường L theo chiều ấy sẽ thấy miền giới hạn bởi đường L luôn luôn ở bên tay trái. Ký hiệu tích phân
đường loại hai dọc theo đường cong kín L theo chiều dương là P(x,y)dx + ( Q x, y)dy và theo chiều + L
âm là P(x,y)dx +Q(x,y)dy . − L
Các tính chất khác của tích phân đường loại hai giống như các tính chất của tích phân xác định. (2) P (x, y d ) x + Q (x, y)dy P (x, y d ) x Q (x, y)dy 1 1 + + 2 2 = L 109
P (x,y)dx + Q (x,y)dy+ P (x,y)dx Q (x,y)dy 1 1 2 + 2 L L (3) P(x, ) y dx +Q(x, y)dy = P(x, y)dx +Q(x, )
y dy (hằng số R) L L L L = L (4) P(x, y d ) x + Q(x, y d ) y = P(x, y d ) x + Q(x, y d ) y + P(x, y d ) x + Q(x, y)dy 1 2 L L = L 1 2 1 L L2 3.2.3.
Cách tính tích phân đường loại hai x = x(t)
(1) Nếu cung phẳng AB hoặc đường cong phẳng L được cho dưới dạng tham số ( y = y(t) dx = x'(t)dt t )
thì P(x, y)dx + Q(x, y)dy = ( P x(t), ( y t ) ) x'(t) + ( Q x(t), y(t ) ) y'(t) dt . dy = y'(t)dt L
(2) Nếu cung phẳng AB hoặc đường cong phẳng L được cho bởi phương trình y = y(x) (a x b
b) thì dy = y’(x)dx P(x, y)dx + Q(x, y)dy = P(x, y(x)) + Q(x, y(x))y'(x) dx . Hoặc, nếu cung L a
phẳng AB hoặc đường cong phẳng L được cho bởi phương trình x = x(y) (c y d) thì dx = x’(y)dy b
P(x, y)dx + Q(x, y)dy = ( P x(y), y)x'( ) y + ( Q x(y), y) dy . L a x = x(t)
(3) Nếu đường cong không gian L được cho dưới dạng tham số y = y(t) ( t ) z = z(t) dx = x'(t)dt
dy = y'(t)dt thì P(x, y,z d ) x + Q(x, , y z)dy + R(x, , y z)dz = dz = z'(t)dt L
(Px(t),y(t),z(t ))x'(t) + ( Q x(t), y(t), ( z t ) ) ' y (t) + ( R x(t), y(t), ( z t ) ) z'(t ) dt . x2 y2
Ví dụ 3.6. Tính I = xdy − ydx trên đường ellipse L = + = . 2 2 1 + a b L Bài giải. x(t) = a cost
dx = x'(t)dt = (−a sin t)dt
Phương trình tham số của đường L là (0 t 2) . y(t) = b sin t dy = y'(t)dt = (b cost)dt
L là đường cong phẳng khép kín nên bất kỳ điểm nào trên L cũng có thể được chọn là điểm bắt
đầu đồng thời là điểm kết thúc khi tính tích phân I = xdy − ydx . Để đơn giản, chúng ta chọn điểm + L
(x,y) = (a,0) là điểm bắt đầu đồng thời là điểm kết thúc, tương ứng với tham số = 0 và = 2. 2 2 I = xdy − ydx = a ( cost) b ( cost)dt − (b sin t) − ( a sin t)dt = 2 (ab cos t + 2 ab sin t)dt = + L 0 0 2 2 ab dt = abt = 2ab . 0 0
Ví dụ 3.7. Tính I = xydx + (y − x)dy trên L là đường cong từ điểm O(0,0) đến điểm A(1,1) có L
phương trình là (a) y = x3, (b) x = y2. Bài giải. 110
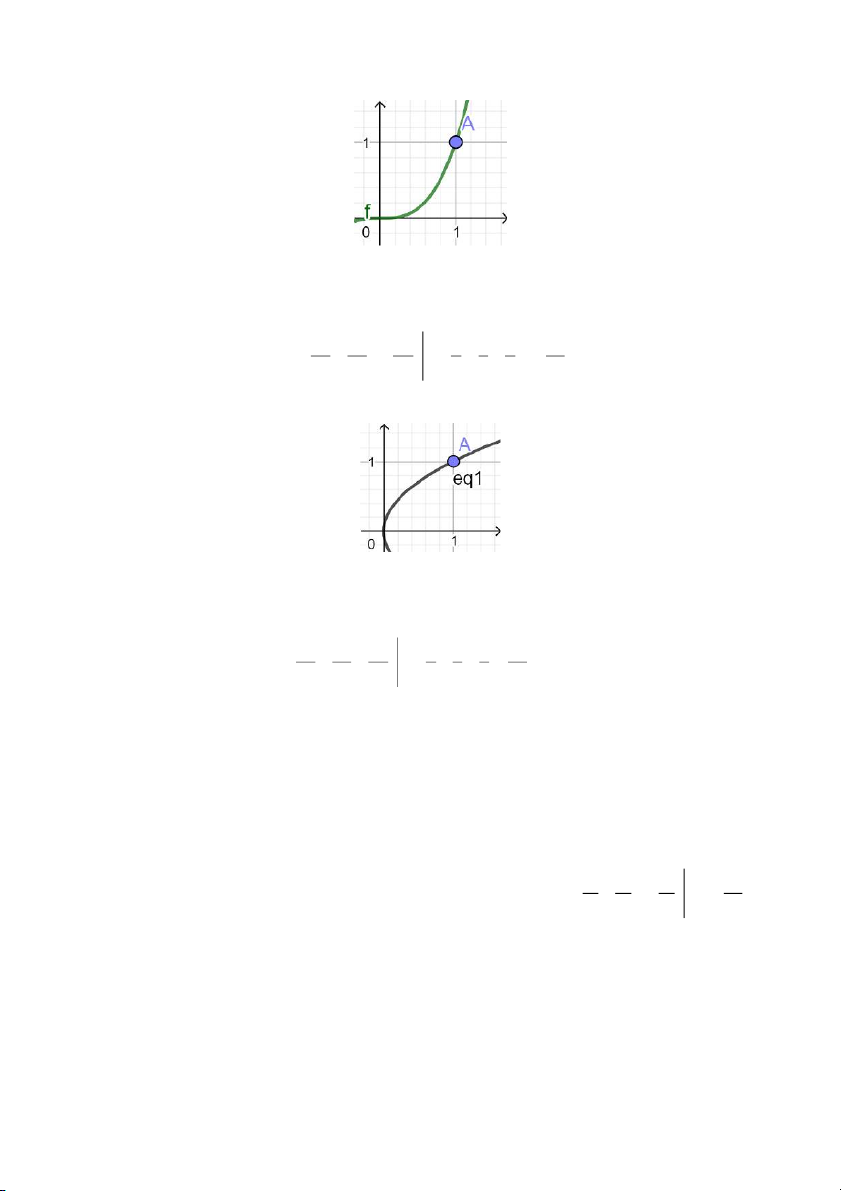
(a) Đồ thị của cung OA thuộc đường cong bậc ba y = x3 từ điểm O(0,0) đến điểm A(1,1) trong
hệ tọa độ Descartes Oxy là Ta có 3
y = x (0 ≤ x ≤ 1) dy = y'(x)dx x 3 2 = dx 1 I = xydx + (y − x d ) y = xydx + (y − x)dy = 3 xx dx + 3 (x − 2 x 3 ) x dx = L OA 0 1 1 x6 x5 x 4 1 1 3 1 x 3 ( 5 + x 4 − x 3 ) 3 dx = 3 + − 3 = + − = − . 6 5 4 2 5 4 20 0 0
(b) Đồ thị của cung OA thuộc đường parabol x = y2 từ điểm O(0,0) đến điể m A(1,1) trong hệ tọa độ Descartes Oxy là Ta có 2
x = y (0 ≤ y ≤ 1) dx = x'(y d ) y = 2ydy 1
I = xydx + (y − x)dy = xydx + (y − x)dy = 2 y y2ydy + (y − 2 y )dy = L OA 0 1 1 4 2 y5 y3 y2 2 1 1 17 (2y − y + y)dy = 2 − + = − + = . 5 3 2 5 3 2 30 0 0
Ví dụ 3.8. Tính I = 2 (y − 2 z d ) x + 2xyzdy − 2
x dz trên đường L là đường cong không gian có L
phương trình tham số là {x = t, y = t2, z = t3 với 0 t 1} theo chiều tăng của tham số t. Bài giải dx = x'(t)dt = d 1 t = dt Ta có dy = y'(t)dt = 2tdt I = 2 (y − 2 z )dx + 2xyzdy − 2 x dz = 2 L dz = z'(t)dt = t 3 dt 1 1 1 8 7 5 (t2 )2 − (t3 )2 2 3 2 2 7 6 4 t t t 3 dt + 2tt t 2tdt − t t 3 dt = (4t − t − 2t d ) t = 4 − − 2 = − . 8 7 5 70 0 0 0 3.2.4.
Ý nghĩa vật lý của tích phân đường loại hai → → →
Tích phân đường loại hai là công do lực F(x, y) = P(x, y) i + Q(x, y) j (trong mặt phẳng) hoặc → → → →
F(x, y,z) = P(x, y,z) i + Q(x, ,
y z) j+ R(x, y, z) k (trong không gian 3 chiều) sản ra khi lực này di
chuyển chất điểm M từ điểm A đến điểm B trên đường cong AB (trong mặt phẳng hoặc trong không gian 3 chiều).
3.3. Công thức Green
3.3.1. Công thức Green 111 Một số khái niệm
(1) Miền liên thông. Miền phẳng DR2 được gọi là miền liên thông nếu chúng ta có thể nối 2
điểm bất kỳ thuộc D bằng một đường liên tục nằm hoàn toàn trong D.
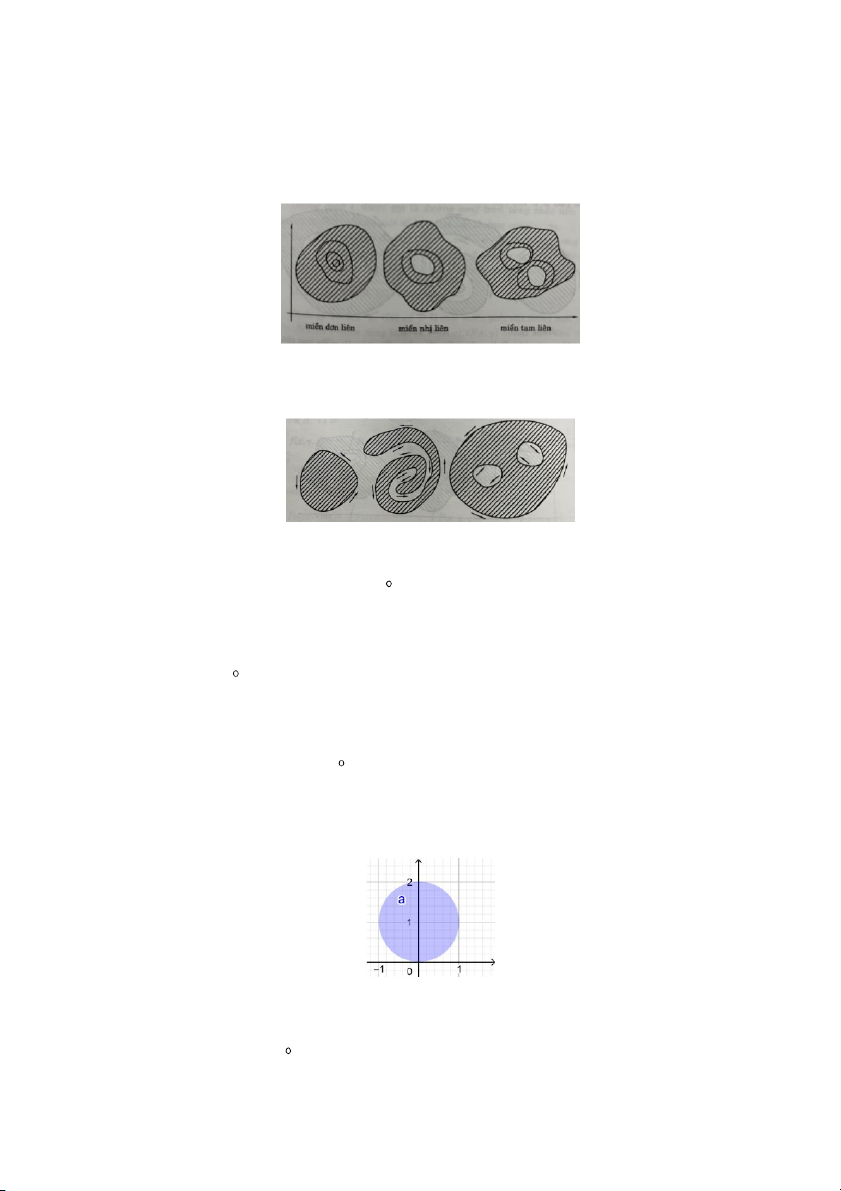
(2) Miền đơn liên và miền đa liên. Miền liên thông được gọi là miền đơn liên nếu mọi đường
cong kín nằm hoàn toàn trong D đều bao bọc một miền nằm hoàn toàn trong D. Miền liên thông không
đơn liên được gọi là miền đa liên.
(3) Chiều dương của biên của miền liên thông D (đơn liên/đa liên) là chiều sao cho khi một
người đi trên biên của miền D theo chiều ấy sẽ thấy các điểm trong của miền D luôn luôn ở bên tay trái.
Nếu các hàm số P(x,y), Q(x,y) xác định, liên tục và các đạo hàm riêng cấp 1 của chúng liên tục
trên miền phẳng D là một miền liên thông, bị chặn và có biên L gồm một hay nhiều đường cong kín
rời nhau từng đôi một. Khi đó chúng ta có P(x, ) y dx+ Q(x, ) y dy =
,Q (x,y)− ,P (x, )y dxdyđược x y + L D
gọi là công thức Green. Công thức Green là công thức liên hệ giữa tích phân đường loại hai và tích phân hai lớp. Ví dụ 3.9. Tính 2 2 − (x arctan x + y )dx +(x +2xy + y
y e )dy trên đường tròn L có phương trình là + L x2 + y2 = 2y. Bài giải.
Việc tính trực tiếp tích phân 2 2 −
(x arctan x + y )dx + (x + 2xy + y y e d
) y trên đường tròn L là + L
không đơn giản, tuy nhiên nếu sử dụng công thức Green thì việc tính tích phân này qua tích phân hai
lớp trên hình tròn D = {x2 + y2 ≤ 2y x2 + (y – 1)2 ≤ 12} là miền có biên là đường tròn L thì việc tính
tích phân này sẽ dễ dàng hơn rất nhiều. P(x, ) y = x arctan x+ y2 P, (x, y) = 2y Đặt y Q , (x, )
y − P ,(x, y) = 1 , mặt khác, theo x y ( Q x, y) = x + 2xy + y 2e−y Q, (x, y) =1 + 2y x
công thức Green chúng ta có P(x,y)dx + ( Q x, y)dy = , Q (x, y) − , P (x, y) dxdy dxdy . x y = + L D D 112 (x arctanx + 2 y d ) x + (x + 2xy + 2 −y y e )dy = dxdy . + L D
Theo ý nghĩa hình học của tích phân hai lớp thì
dxdy chính là diện tích hình tròn D. Hình tròn D
D có bán kính bằng R = 1 nên diện tích của nó là R2 = .12 = . (x arctan x + 2 y )dx + (x + 2xy + 2 − y y e )dy = dxdy = . + L D
Hệ quả của công thức Green (1) P(x, y)dx + Q(x, y d ) y = − , Q (x, y) − , P (x, y) dxdy P (x, ) y Q (x, y) dxdy x y = , − , y x − L D D
(2) Nếu đường cong kín L là biên của miền phẳng D thì diện tích S của miền D được tính bởi công thức = 1 S xdy− ydx . 2 + L Chứng minh P(x, y)dx + ( Q x, y d ) y = − P(x, y d ) x + Q(x, y)dy + − (1) Chúng ta có L L P(x, y)dx +Q(x, y d ) y = ,Q (x,y) − ,P(x,y) dxdy x y +L D P(x, ) y dx + Q(x, ) y dy = ,P(x,y)− ,Q (x, )y dxdy y x − L D P(x, y) = −y P , (x, y) = 1 − (2) Chúng ta lấy y Q, (x, ) y − P, (x, ) y = 2 và thay vào công Q(x, y) = x x y Q, (x, y) = 1 x
thức Green, chúng ta được xdy − ydx = , Q (x, y) − , 1 P (x, y) dxdy d 2 xdy 2 dxdy S 2 S xdy ydx . x y = = = = − + 2 + D D D L L
Ví dụ 3.10. Tính I = 3 (x − 3 y d ) x + 3 (x + 3
y )dy trên đường tròn L có phương trình là x2 + y2 = + L 1. Bài giải.
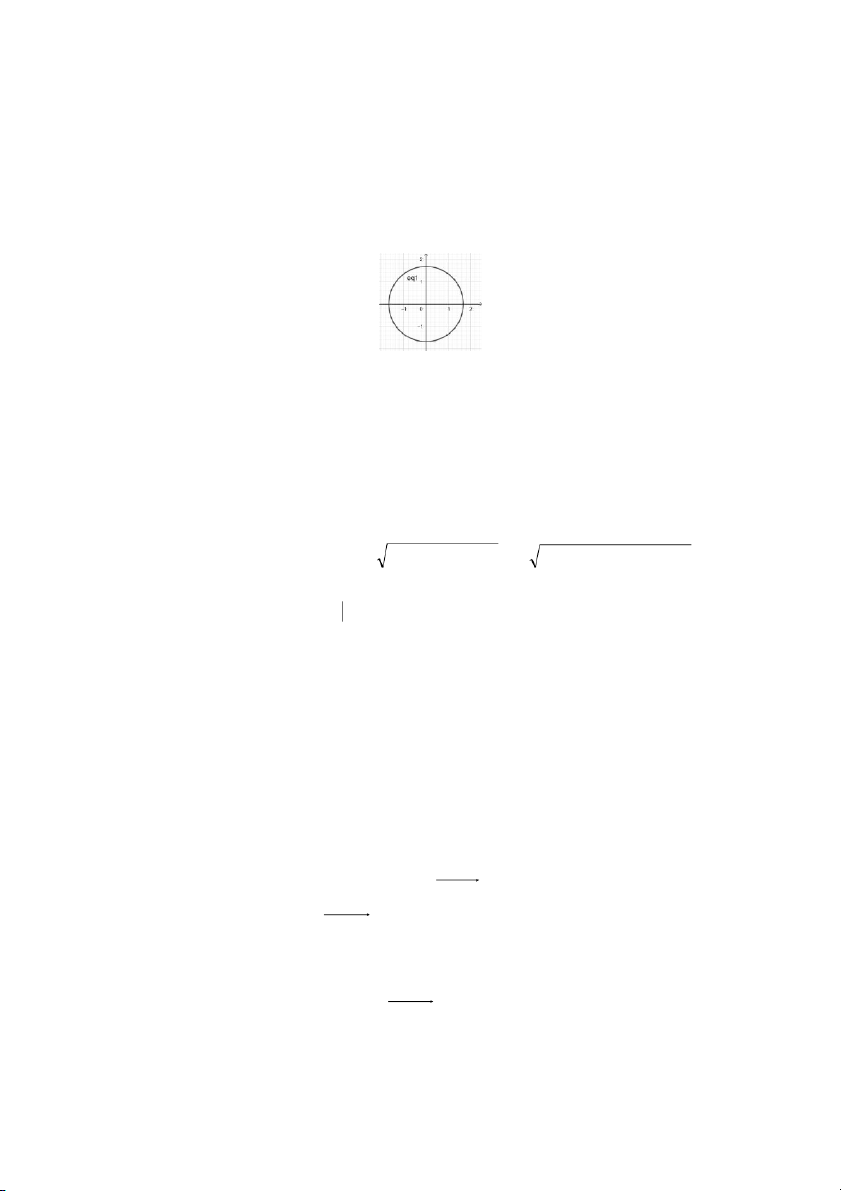
Đồ thị của đường tròn L trong hệ tọa độ Descartes vuông góc Oxy là
Gọi D là miền giới hạn bởi đường tròn L D = {(x, y) R2 x2 + y2 } 1 .
Cũng như ở Ví dụ 3.9, chúng ta sẽ sử dụng công thức Green để tính tích phân I = 3 (x − 3 y d ) x + 3 (x + 3 y )dy . + L P (x, ) y = x 3 − y3 P, (x, y) = 3 − y2 Đặt y
Q, (x, y) − P, (x, y) = x 3 2 + 3y2 = ( 3 x2 + y2 ) và x y Q (x, y) = x3 + y3 Q, (x, ) y = x 3 2 x
thay vào công thức Green, chúng ta được I = 3 (x − 3 y )dx + 3 (x + 3 y d ) y = 2 ( 3 x + 2 y )dxdy = 3 2 (x + 2 y )dxdy . + L D D 113 x = r cos
Đổi tọa độ Descartes (x,y) sang tọa độ cực (r,) bằng phép đổi biến thì định thức y = r sin 0 r 1
Jacobi J = r, x2 + y2 = r2 và ' D = 0 2 r 1 2 1 = 4 =
I = 3 (x2 + y2 )dxdy = 3 r2 J drd = 3 r2rdrd = 3 d r3dr = 3 ( 2 = ) r 3 = . 0 4 2 D D' D' 0 0 r 0 =
Ví dụ 3.11. Tính I = 2 (x + 2 y )dx + 2 (x − 2 y d
) y (trên đường L theo chiều âm), là các cạnh của − L
OAB có tọa độ các đỉnh trong hệ tọa độ Descartes vuông góc Oxy là O(0,0), A(0,1) và B(1,0). Bài giải.
Đồ thị của OAB trong hệ tọa độ Descartes vuông góc Oxy là P(x, y) = x2 + y2 P , (x, y) = 2y Đặt y Q, (x, ) y − P, (x, y) = 2x− 2y = ( 2 x − y) và thay vào Q(x, y) = x2 − y x y 2 Q, (x, y) = 2x x
công thức Green, chúng ta được I= 2 (x + 2 y d ) x + 2 (x − 2 y )dy = − , Q (x, ) y − , P (x, y) dxdy x y = − L D − ( 2 x − y d
) xdy = 2 (y − x)dxdy trên miền D là OAB có cạnh OA nằm trên đường thẳng x = 0, D D
cạnh AB nằm trên đường thẳng x + y = 1 và cạnh BO nằm trên đường thẳng y = 0. 0 x 1 − 1 x 1
Chiếu miền D lên trục Ox thì D =
I = 2 (y − x)dxdy = 2 dx (y − x)dy = 0 y 1− x D 0 0 1 1 x − 1 y 1 = −x (y − x) 2 1 x= 1 2 dx (y− x)d(y− x) = 2 dx = 3 ( x2 − 4x + ) 1 dx = (x 3 − 2x 2 + x) = 0. 2 x= 0 = 0 0 0 y 0 0 2 2 Ví dụ x y
3.12. Tính diện tích của hình ellipse + 1 (a > 0, b > 0). a2 b2 Bài giải. 2 2 2 2 Biên L của hình ellipse x y + x y
1 là đường cong kín ellipse +
= 1 (a > 0, b > 0), nên a 2 b2 a2 b2
diện tích S của hình ellipse được tính bằng công thức = 1 S xdy −ydx . 2 + L x(t) = a cost
Phương trình tham số của đường ellipse là (0 t 2) ( y t) = b sin t d x = x'(t d ) t = a − sin tdt xdy − ydx = (a cost) b ( costdt) − (b sin t)( a − sin tdt) = abdt dy = y'(t)dt = b costdt 1 1 2 ab 2 ab t 2 = S = xdy − ydx = abdt = dt = t = ab . 2 + 2 2 2 t 0 = 0 0 L
Tính diện tích hình quạt 114
Giả sử cung C có phương trình r = r() với trong hệ tọa độ cực (r,), ký hiệu D là
hình quạt giới hạn bởi cung C và hai tia = , = . Chúng ta sẽ đưa ra công thức tính diện tích hình quạt D như sau
Ký hiệu L+ là biên định hướng dương của hình quạt D, khi đó đường cong kín L+ = OACBO
là biên của hình quạt D nên diện tích S(D) của hình quạt D được tính bằng công thức ( S D = 1 ) xdy − = 1 ydx
xdy − ydx + xdy − ydx + xdy − ydx 2 + 2 L + OA C BO x = r co s
- Tính xdy− ydx: Phương trình tham số của đoạn thẳng OA theo tham số r là với y= r si n OA dx = cosdr r( ) r( ) 0 r r()
, do đó xdy − ydx = (r cossin − r sin cos ) dr = 0dr = 0 . dy = sindr OA 0 0
- Tính xdy − ydx : Phương trình tham số của cung C định hướng dương theo tham số là + C x = r co s với ( ) y = r sin x = x() = r() cos dx = x'( d
) = [r'() cos − r() sin d ] ( ) y = ( y ) = r ( ) sin dy = y' ( d ) = [r' ( ) si n + r ( ) co s d ]
xdy − ydx = r() cos[r'()sin + r() cos d ] − r
( ) sin [r'() cos − r() sin d ] = r2 () d
xdy −ydx = r2()d. + C x = r co s
- Tính xdy − ydx: Phương trình tham số của đoạn thẳng BO theo tham số r là với y = r si n BO dx = cosdr 0 0 r() r 0
, do đó xdy − ydx = (r cossin − r sin cos ) dr = 0dr = 0 . dy = sin dr BO r() r( ) 1 ( S D) = 2 1 2 0+ r ( ) d + 0 = r ()d. A b – 2 2 Ví dụ 3.13.
(a) Tìm phương trình trong hệ tọa độ Descartes (x,y) của đường cong có phương trình trong hệ
tọa độ cực là r = 2sin (– ) .
(b) Tính diện tích S của miền phẳng mà biên của nó là đường cong đã cho. Bài giải. x = r co s
(a) Công thức biến đổi từ tọa độ cực (r,) sang tọa độ Descartes (x,y) là (– ) y= r si n
x() = r( ) cos =(2sin ) cos = 2sin cos
(– ) là phương trình tham số của đường
y() = r()sin = (2sin )sin = 2 2 sin cong theo tham số . 115 2 x () = (2 sin cos 2 ) = 2 4 sin 2 cos Chúng ta có 2 y ( ) = 2 (2 sin 2 ) = 4 4 sin x2 ( ) + y2
( ) = 4sin2 cos2 + 4sin4 = 4sin2 = ( 2 2sin2 ) = 2 ( y ) x2 + y2 = 2y x2 + (y − )
1 2 = 1 là phương trình chính tắc của đường tròn có tâm tại điểm (x , y ) = ( ) 1 , 0 và bán kính R = 1. 0 0 1 1 1− cos 2 (b) S = 2 r ( ) d = (2 sin 2 ) d = 2 2 sin d = 4 d = 2 1 ( −cos2)d = 2 2 − − 2 0 0 sin 2 2 − = 2 . 2 0
3.3.2. Điều kiện để tích phân đường loại hai không ph
ụ thuộc vào đường lấy tích phân
Qua các ví dụ trên, chúng ta thấy tích phân đường loại hai không những phụ thuộc vào điểm đầu
và điểm cuối của của đường cong mà còn phụ thuộc vào chính dạng của đường cong. Tuy nhiên,
chúng ta sẽ thấy rằng, có những trường hợp, tích phân đường loại hai (đối với đường cong phẳng) chỉ
phụ thuộc vào điểm đầu và điểm cuối của đường cong mà không phụ thuộc vào dạng của đường cong
như ở ví dụ ngay sau đây.
Ví dụ 3.14. Tính I = (x + 2
y )dx + 2xydy trên cung AB đi từ điểm A(0,0) đến điểm B(2,2) theo AB
hai cách: (a) đoạn thẳng AB; (b) đoạn thẳng AC với
C(2,0), rồi theo đoạn thẳng CB. Bài giải.
(a) Đoạn thẳng AB nối điểm A(0,0) với điểm B(2,2) có phương trình y = x (0 x 2) dy = y = x dx, do đó sau khi thay
(0 x 2) vào biểu thức dưới dấu tích phân của tích phân I chúng ta dy = dx 2 2 2 được I = (x + x2 d ) x + x 2 xdx = x 3 ( 2 + x d ) x = (x3 + x2 ) 2 = 1 . 0 0 0 0
(b) Chúng ta có I = (x + 2 y )dx + 2xydy = (x + 2 y )dx + 2xydy + (x + 2 y d ) x + 2xydy AB AC CB
Đoạn thẳng AC nối điểm A(0,0) với điểm C(2,0) có phương trình y = 0 (0 x 2) dy = 0, do y = 0 đó sau khi thay
(0 x 2) vào biểu thức dưới dấu tích phân của tích phân dy = 0 2 2 2 2 2 2 x (x + 2
y )dx + 2xydy chúng ta được (x + y )dx + 2xydy = (x + 0 )dx + 2 0 . 0 . x = xdx = = 2 . 2 AC AC 0 0 0
Đoạn thẳng CB nối điểm C(2,0) với điểm B(2,2) có phương trình x = 2 (0 y 2) dx = 0, do x = 2 đó sau khi thay
(0 y 2) vào biểu thức dưới dấu tích phân của tích phân dx = 0 (x + 2y)dx +2xydy chúng ta được CB 116 2 2 2 (x+ y2 )dx + 2xydy= (2+ y2 ) 0 . + . 2 2ydy= 4 ydy= 2y2 = . 8 0 CB 0 0 I = (x + y2 d ) x + 2xydy = (x + y2 d ) x + x 2 ydy + (x + y2 d ) x + 2xydy = 2 + 8 =10 . AB AC CB
Như vậy, mặc dù tích phân I = (x + 2)
y dx + 2xydy được tính từ điểm A đến điểm B trên 2 AB
đường khác nhau nhưng có giá trị tính được bằng nhau.
Kết quả trên dẫn đến việc xuất hiện câu hỏi: Với điều kiện nào thì tích phân đường loại hai
không phụ thuộc vào dạng của đường cong phẳng tính tích phân mà chỉ phụ thuộc vào điểm đầu và
điểm cuối của đường cong? Như chúng ta sẽ thấy trong định lý sau đây, các Nhà toán học đã tìm thấy
điều kiện đó là Q , (x, )
y = P, (x, y) đối với tích phân P(x, y d ) x Q(x, y)d . y + x y L
Định lý. Giả sử các hàm số P(x,y), Q(x,y) liên tục cùng với các đạo hàm riêng cấp một của
chúng trong một miền đơn liên D nào đó, khi đó 4 mệnh đề sau là tương đương: (1) Q , (x, ) y = P, với (x,y)D ; x y (x, y) (2) P(x, y)dx + Q(x, y d ) y = 0
với mọi đường cong kín L nằm trong miền D; L
(3) P(x, y)dx +Q(x, y)dy chỉ phụ thuộc vào điểm đầu A và điểm cuối B của cung AB là một AB
cung nằm trong miền D, mà không phụ thuộc vào dạng của cung AB;
(4) Biểu thức P(x,y)dx + Q(x,y)dy là vi phân toàn phần cấp 1 của một hàm số u(x,y) nào đấy xác định trên miền D. du(x, ) y = u , (x, ) y dx + u, (x, y d ) y P(x, y d ) x + ( Q x, y)dy x y
Hệ quả 1. Nếu biểu thức P(x,y)dx + Q(x,y)dy là vi phân toàn phần cấp 1 của hàm số u(x,y) trong
một miền DR2 thì P(x, y d
) x + Q(x, y)dy = u(x , y ) − u(x , y )
dọc theo mọi đường nối điểm A đến điểm B B B A A AB
nằm trong miền D (tương tự như công thức Newton – Leibnitz).
Hệ quả 2. Nếu D = R2 thì biểu thức P(x,y)dx + Q(x,y)dy là vi phân toàn phần cấp 1 của hàm số
u(x,y) được xác định bởi công thức x y
u(x, y) = P(t, y )dt + Q(x, t)dt với (x ) tùy ý thuộc miền D; 0 0,y0 x y 0 0 x y
hoặc u(x, y) = P(t,y)dt + Q(x , t)dt với (x0,y0) tùy ý thuộc miền D. 0 x y 0 0
Giá trị của x0 và y0 được chọn để việc
tính toán các biểu thức toán học cho đơn giản.
Bây giờ, chúng ta quay lại xét Ví dụ 3.14. Tính I = (x + 2
y )dx + 2xydy trên cung AB đi từ AB P ( , x y) = x + y2 P, (x, y) = 2y
điểm A(0,0) đến điểm B(2,2). Nếu đặt y Q, (x, ) y = P, (x, y) thì ( Q x, y) = 2xy x y Q, (x, y) = 2y x
theo Mệnh đề 4 của định lý trên, biểu thức ( P x, ) y dx + ( Q , x y d ) y = (x + y 2 d
) x + 2xydy là vi phân toàn
phần cấp 1 của một hàm số u(x,y) nào đấy. x y x y
Theo Hệ quả 2 thì u(x, y) = P(t, y d ) t Q(x, t)dt P(t 0 , )dt Q(x, t)dt 0 + = + = x y 0 0 0 0 117 x y x y x y 2 2 2 2 t t x 2
(t + 0 )dt + 2xtdt = tdt + 2x tdt = + 2x = + xy 2 2 2 0 0 0 0 0 0 (x ,y = ) (2,2) B(2,2 2 ) x
Theo Hệ quả 1 thì I= (x+ 2 y )dx + 2xydy = u(x, y) = + 2 xy = A( , 0 0) 2 OA (x,y)=( ,00) u( , 2 ) 2 − u 0 ( 0 , ) = 10 − 0 = 10 . P(x, y) = yexy + my2 + x Ví dụ
3.15. Cho các hàm số với m là một tham số. Q(x, y) = xexy − m 2 2 xy
(a) Tìm giá trị của m để biểu thức P(x,y)dx + Q(x,y)dy là vi phân toàn phần cấp 1 của một hàm số u(x,y) nào đấy;
(b) Với giá trị của m tìm được ở (a), xác định hàm số u(x,y). Bài giải.
(a) Theo định lý trên, để biểu thức P(x,y)dx + Q(x,y)dy là vi phân toàn phần cấp 1 của một hàm
số u(x,y) nào đấy thì các hàm số P(x,y), Q(x,y) phải thỏa mãn điều kiện Q , (x, ) y = P, với x y (x, y)
(x,y)D, cụ thể là Q ,( , x y) =P, (x, )
y exy +xyexy −2m2y =exy +xyexy +2my my + = x y m2y 0 m = 0 m 1 ( + m)y = 0 với (x,y) D m = −1 P(x, y) = xy ye + 2 y . 0 + x = xy ye + x (b) Với m = 0 thì Q(x, y) = xy xe − 2 0 . 2 x . y = xy xe x y x y Khi đó u(x, y) = P(t, y d ) t Q(x, t)dt P(t 0 , )dt Q(x, t)dt 0 + = + = x y 0 0 0 0 x x ( y x y 2 2 y e . 0 t 0. + t) xt xt t xt x dt + xe dt = tdt + e d(xt) = + e = + e xy − 1 . 2 0 2 0 0 0 0 0 Thử lại du(x, ) y = u, (x, y d ) x + u, = + + = + . x y (x, ) y dy
(x yexy)dx xexydy P(x, )ydx Q(x, )ydy P(x, y) = ye xy + (− ) 1 y . 2 + x = ye xy + x − y 2 Với m = –1 thì ( Q x, y) = xe xy − . 2 − ( ) 1 2 x . y = xe xy − 2xy x y x y Khi đó u(x, y) = P(t, y )dt + Q(x, t)dt = P(t 0 , d ) t + Q(x, t)dt = 0 x y 0 0 0 0 x y x y y ( t0. e . 0 + t− 2 0 )dt+ ( xt xe − 2xt)dt = tdt+ xt xe dt − 2x tdt = 0 0 0 0 0 x t2 y x 2 y y x2 + ext d(xt) − xt2 = + ext − xy2 = − xy2 + exy −1 2 0 2 0 2 0 0 Thử lại du(x, y) = u, x (x, y d ) x + u,y ( , x y d
) y = (x − y2 + yexy )dx + (− x 2 y + xexy )dy = P(x, ) y dx + Q(x, ) y dy
Nhận xét. Nếu tích phân đường loại hai không phụ thuộc dạng của đường lấy tích phân thì chúng
ta có thể chọn đường lấy tích phân sao cho việc tính toán trở nên đơn giản. x − y x + Ví dụ y 3.16. Tính I = dx +
dy trên cung AB với A(1,1), B(2,2). 2 x + 2 2 y x + 2 y AB Bài giải. 118 x − y − x 2 − + , 2xy y2 P(x, y) = P = 2 2 y (x, y) x + y (x 2 + y 2)2 Chúng ta có
Q, (x, y) = P, (x, y) nên tích x + y x y − x2 − + , 2xy y2 Q(x, y) = Q (x, y) = x2 + y2 x (x 2 + y 2)2 x − y x + y phân I = dx +
dy không phụ thuộc vào dạng vào dạng của đường nối điểm A với 2 x + 2 2 y x + 2 y AB điểm B.
Để việc tính toán được đơn giản, chúng ta chọn đường lấy tích phân là đoạn thẳng AB có
phương trình x = y (1 y 2) dx = dy. Do đó, nếu thay x = y và dx = dy vào biểu thức dưới dấu y − y y + y 0 2y 2 dy 2
tích phân thì chúng ta được I = dx + dy = d . y + dy = = ln y = ln 2 . y2 + y2 y2 + y2 2y2 2y2 y 1 AB AB 1
Ví dụ 3.17. Tính I = 2 xy dx + 2
x ydy trên cung AB với A(0,1), B(3,4). AB Bài giải. P(x, y) = 2 xy , P (x, y) = 2xy Đặt y , Q (x, y) = , P (x, y) I = xy dx x ydy không phụ x y 2 , 2 + 2 Q(x, y) =x y Q (x, y) = 2xy AB x
thuộc vào dạng của đường nối điểm A với điểm B, do đó để tính toán được đơn giản, chúng ta chọn
đường lấy tích phân là các cạnh AC và CB của ACB với C(3,1). I = 2 xy dx + 2 x ydy = 2 xy dx + 2 x ydy + 2 xy dx + 2 x ydy AB AC CB - =
Phương trình đoạn thẳng AC là y 1 (0 x 3) dy = 0 (0 x 3) 3 3 3 2 2 2 2 x 2 9 xy dx + x ydy = 1 . x dx + x . . 1 0 = xdx = = 2 2 AC 0 0 0
- Phương trình đoạn thẳng CB là x = 3 (1 y 4) dx = 0 (1 y 4) 4 4 4 4 2 2 2 2 y2 9 xy dx + x ydy = 3y 0 . +3 ydy = 9ydy =9 ydy = . 9 =72 − 2 2 CB 1 1 1 1 2 2 9 9
I = xy dx + x ydy = +72 − = 72 . 2 2 AB
Cách khác. Vì Q , (x, y) = P, ( ,
x y) nên biểu thức dưới dấu tích phân x y
xy 2dx + x 2 ydy P(x, y)dx + ( Q x, )
y dy là vi phân toàn phần cấp 1 của hàm số x y x y x y
u(x, y) = P(t, y )dt + Q(x, t)dt = P(t 0 , )dt + Q(x, t)dt = 2 . t 0 dt + 2 x tdt = 0 x 0 y0 0 0 0 0 y y 2 t 2 2 x2 y2 0 +x tdt = x = . 2 2 0 0 119 (x,y) ( = , 3 4) B( , 3 4 2 2 x 2 ) y 2
I = xy dx + x ydy = u(x, y) = = u , 3 ( ) 4 −u( ) 1 , 0 = 72 −0 = 72 . A(0 ) 1 , 2 AB (x,y) ( = 0 ) 1 ,
3.4. Tích phân mặt loại một
3.4.1. Định nghĩa tích phân mặt loại một
Bài toán vật lý dẫn đến khái niệm tích phân mặt loại một
Giả sử trong hệ tọa độ Descartes vuông góc Oxyz có một mặt cong S mỏng (chỉ có kích thước
rộng và dài, độ dày không đáng kể) có khối lượng riêng tại điểm (x,y,z)S được biểu diễn bằng hàm
số f(x,y,z) đơn trị, liên tục và không âm. Yêu cầu tìm khối lượng m của mặt cong S.
Để tính m, chúng ta thực hiện như sau: Chia tùy ý mặt cong S thành n mặt cong nhỏ Si (1 i
n) không dẫm lên nhau và ký hiệu diện tích của mặt cong nhỏ Si là Si (1 i n). Trên mặt cong nhỏ
Si lấy tùy ý một điểm (xi,yi,zi), nếu mặt cong Si đủ nhỏ thì chúng ta có thể coi giá trị f(xi,yi,zi) không
đổi trên mặt cong nhỏ Si; khi đó, khối lượng của mặt cong nhỏ Si là mi f(xi,yi,zi).Si.
Như vậy, nếu mọi mặt cong nhỏ Si (1 i n) đủ nhỏ thì có thể c
oi khối lượng của mặt S là n
m = m1 + m2 + … + mn f(x1,y1,z1).S1 + f(x2 2 ,y ,z2).S2 n + … + f(x n
,y ,zn).Sn = f (x , y ,z ).S i i i i i =1 n
Tổng f (x , y ,z ).S sẽ có độ chính xác cao (tức là giá trị của biểu thức này gần với khối i i i i i =1
lượng thực m của mặt cong S) nếu n càng lớn và tất cả các Si (1 i n) càng bé. Do đó, khối lượng n
m của mặt cong S bằng giới hạn của tổngf (x , y ,z ).S khi n → cùng với diện tích của mỗi i i i i i =1 n
mặt cong nhỏ Si (1 i n) bé dần về
0, tức là m = lim f(x , y ,z .) S . i i i i maxS → 0 i 1 i n i=1 n→
Định nghĩa tích phân mặt loại một
Cho mặt cong SR3 và hàm số f(x,y,z) xác định với (x,y,z) S.
Chia S thành n mặt cong nhỏ
Si (1 i n) không dẫm lên nhau có diện tích tương ứng bằng S1, S2, …, Sn. Trên mỗi mặt cong
Si (1 i n) lấy điểm (xi,yi,zi) tùy ý. n Lập tổng I =
f (x , y , z ). S , nếu khi n → s ao cho max S
→0 mà In → I là một giá trị n i i i i i i =1 1 i n
hữu hạn, không phụ thuộc vào cách chia mặt cong S thành n mặt cong nhỏ và cách chọn điểm (xi,yi.zi)
trên mỗi mặt cong nhỏ Si (1 i n), thì I được gọi là tích phân mặt loại một của hàm số f(x,y,z) trên
mặt cong S và ký hiệu là I = f(x, ,y )zdS, trong đó f(x,y,z) và dS được gọi tương ứng là hàm dưới S
dấu tích phân và vi phân diện tích mặt cong (vi phân mặt).
Nếu S là mặt cong trơn (phương trình của mặt cong S là hàm số z = z(x,y) đơn trị, liên tục cùng
với các đạo hàm riêng của nó) và nếu hàm số f(x,y,z) liên tục với (x,y,z)S thì tích phân mặt loại một tồn tại.
3.4.2. Tính chất của tích phân mặt loại một
Tích phân mặt loại một có các tính chất giống như các tính chất của tích phân xác định.
3.4.3. Cách tính tích phân mặt loại một
Trong không gian R3 cho mặt cong S. Giả sử hình chiếu của S lên mặt phẳng tọa độ Oxy là một
miền đóng D. Giả sử phương trình của mặt cong S là hàm số z = z(x,y) đơn trị, liên tục với (x,y)D
và có các đạo hàm riêng z, (x, ) y ,
liên tục với (x,y)D . x z,y(x, y) 120
Nếu mỗi đường thẳng song song với trục tọa độ Oz cắt mặt cong S không quá một điểm và hàm
số f(x,y,z) liên tục với (x,y,z) S thì
vi phân mặt dS = 1+ [z , (x, y)]2 +[z, (x, ) y ]2 và hàm dưới x dxdy y
dấu tích phân f (x, y, z) = f[x, y, z(x, y)] f (x, , y d ) z S = f[x, , y ( z x, ) y ] 1 + z [ , (x, ) y ]2 [z, (x, ) y ]2dxdy + . x y S D
Như vậy, tích phân mặt loại một được đưa về việc tính tích phân hai lớp và thực hiện các công việc sau đây:
- Sử dụng phương trình của mặt S (đã được cho hoặc giải ra từ phương trình ẩn đối với z) dưới
dạng hiện z = z(x,y) để tìm vi phân mặt dS = 1+ [z , (x, y)]2 +[z, (x, ) y ]2 và hàm dưới dấu tích x dxdy y phân f[x, y, z(x, y)].
- Tìm hình chiếu D của mặt S lên mặt phẳng tọa độ Oxy. - Thay vào công thức f (x, y,z d ) S = f [ , x , y ( z x, y)] 1+ z [ , (x, y)]2 z [ , (x, ) y ]2 dxdy + để tính. x y S D
Ví dụ 3.18. Tính I = zdS trên mặt S S (a) S là nửa mặt cầu 2 2 2 z = R − x − y .
(b) S là paraboloit x2 + y2 = 2z (0 z 1). Bài giải. − 1 z (x, y) x(R x y ) 2 2 2 , = − 2 − 2 − 2 2
(a) Chúng ta có z(x, y) = R − x − y x 1 − , 2 2 2 z (x, y) = −y(R − x − 2 y ) y , 2 , 2 R dS = 1+ z [ (x, y)] + [z (x, y)] dxdy = dxdy x y R2 − x2 − y2
Hàm số dưới dấu tích phân 2 2 2 f[ , x , y ( z x, y)] = z = ( z x, y) = R − x − y
Hình chiếu của mặt S lên mặt phẳng Oxy là hình tròn D = {x2 + y2 ≤ R 2}. I = zdS = 2 R − 2 x − 2 R y dxdy = R dxdy 2 2 2 R x y S D − − D
Theo ý nghĩa hình học của tích phân 2 lớp thì tích phân dxdy là diện tích của hình tròn D có D bán kính R dxdy = R 2 I = R dxdy = R R2 = R3 . D D + 2 x 2 2 y2 (b) x + y = 2z z(x, y) =
là phương trình của mặt cong S. 2 Chúng ta có , x 2 + y2 z (x, ) y = x ( z x, y) x = dS = 1+ z [ , (x, ) y ]2 + z [ , (x, y)] d 2 xdy = 1+ x 2+ y d 2 xdy 2 z, (x, y) = y x y y 121 2 2 +
Hàm số dưới dấu tích phân f (x, , y z(x, y)) x y = z = ( z x, y) = 2
Giao của mặt phẳng z = 1 với paraboloit tròn xoay x2 + y2 = 2z là hình tròn D = {x2 + y2 2}
nên hình chiếu của mặt S lên mặt phẳng Oxy là hình tròn D = {x2 + y2 2}. 2 2 I = zdS x + = y 1 + 2 x + 2 y = 1 dxdy 2 (x + 2 y ) 1 + 2 x + 2 y dxdy 2 2 S D D x = r cos
Đổi tọa độ Descartes (x,y) sang tọa độ cực (r,) bằng phép đổi biến J = r và miền y = r sin 0 r x = r cos D' = 2
vì đối với tọa độ r, chúng ta thay
vào phương trình của hình tròn x2 + y2 0 2 y = r sin 2 r2
2 0 r 2 , còn đối với tọa độ thì 0 2.
Hàm dưới dấu tích phân 2 2 2 2 2 2 f ( , x )
y = (x + y ) 1+ x + y f (r cos , r sin ) = r 1+ r 2 2 I = r 2 1+ r 2 J dr d = r 2 1+ r 2rdr d = r 3 1+ r 2dr d = d 3 2 r 1 + r dr D' D' D' 0 0 2 =2 - Tính d = = 2 =0 0 2 2 1 2 3 1 - Tính r3 1+ r2 dr = 1 ( + r2 − ) 1 1 ( + r2 ) 2d 1 ( + r2 ) =
1(+ r2 )2 − 1(+ r2)2 d 1(+ r2)= 0 0 0 r= 2 3 1 +1 +1 1 ( + r2 )2 1 ( + r2 ) 2 4(6 3+ ) 1 − = (3 2) + 1 1 ( 2) +1 15 r=0 ( 4 6 3 + ) 1 ( 8 6 3 + ) 1 I = 2 . = . 15 15
3.4.4. Ý nghĩa vật lý và ý nghĩa hình học của tích phân mặt loại một
Nếu mặt cong S có khối lượng riêng tại điểm (x,y,z) S
bằng f(x,y,z) > 0 thì khối lượng m của
mặt cong S là m = f(x, ,y )zdS (ý nghĩa vật lý). Đặc biệt, khi f(x,y,z) = 1 thì S = dS là diện tích S S
của mặt cong S (ý nghĩa hình học).
3.5. Tích phân mặt loại hai
3.5.1. Khái niệm mặt định hướng Trong không gian R3 cho mặt cong trơn S.
Mặt S được gọi là mặt hai phía nếu khi đi theo một đường cong đóng bất kỳ nằm trong mặt S
không có điểm chung với biên của S thì hướng của véc tơ pháp tuyến c
ủa mặt S không thay đổi.
Nếu trên mặt S có một đường cong đóng mà đi theo đường cong này hướng của véc tơ pháp
tuyến đổi ngược lại thì mặt S được gọi là mặt một phía.
Một ví dụ điển hình về mặt một phía là dải Mobius: Lấy một băng giấy hình chữ nhật ABCD và
xoắn băng giấy này nửa vòng theo chiều dài rồi gắn điểm C với điểm A, điểm D với điểm B. 122
Khi điểm M di chuyển một vòng trên dải Mobius, xuất phát từ điểm MO thì lúc gặp lại điểm MO →
véc tơ pháp tuyến n đổi hướng ngược lại.
Mặt hai phía được gọi là mặt định hướng được, còn mặt một phía được gọi là mặt không định
hướng được. Ở đây, chúng ta chỉ xét các mặt định hướng được. → →
Giả sử S là mặt định hướng được và gọi n = n(x, y,z) là véc tơ pháp tuyến của mặt S tại điểm
M(x,y,z)S (véc tơ pháp tuyến là véc tơ vuông góc với mặt phẳng tiếp xúc của mặt S tại điểm M), khi →
đó hướng của mặt S được xác định là hướng của n . Nếu S là mặt kín và định hướng được thì sẽ xác
định được phía trong, phía ngoài; còn nếu S là mặt không kín thì sẽ xác định được phía trên, phía dưới.
Giả sử mặt S trong không gian R3 có phương trình F(x,y,z) = 0, các Nhà toán học đã chứng →
minh rằng véc tơ pháp tuyến n tại điểm (x,y,z) S
chính là véc tơ GradF(x,y,z), tức là → → → → n(x, ,
y z) = Gradf (x, y, z) = F,(x, y, z) i + F,(x, y, z) j + F, (x, y, z) k . x y z →
Chúng ta lưu ý rằng, tại điểm (x,y,z) S
thì véc tơ pháp tuyến n có hai hướng ngược nhau, do
đó nếu chúng ta quy ước một hướng của nó là dương (dấu +) thì hướng ngược lại của nó là âm (dấu –). → →
Nếu ký hiệu N = N(x, y,z) là véc tơ pháp tuyến đơn vị của mặt S tại điểm M(x,y,z)S thì → → → → → →
N = n | n | = (cos) i + (cos) j + (cos) k với cos, cos và cos là các cosin chỉ phương của véc tơ →
pháp tuyến của mặt S tại điểm M(x,y,z) S. Trong
đó , và là các góc tạo bởi véc tơ pháp tuyến n → → → → → →
với các trục tọa độ Ox, Oy và Oz tức là = (n,Ox) , = (n, Oy) và = (n, Oz) .
Do đó, véc tơ pháp tuyến đơn vị của mặt S tại điểm M(x,y,z)S là → → → → , , , → → → Gradf (x, , y z) F (x, , y z) i + F (x, , y z) j+ F (x, , y ) z k N = = x y z = (co s ) i + (co s ) j+ (co s ) k Gradf (x, , y z) [F, (x, , y z)]2 +[F, (x, , y ) z ]2 +[F,(x, y,z)]2 x y z , cos = F (x, y,z) x , 2 [F (x, , y z)] + , 2 [F (x, , y z)] + , 2 [F (x, , y z)] x y z , F (x, y,z) cos = y , 2 [F (x, , y z)] + , 2 [F (x, , y z)] + , 2 [F (x, , y z)] x y z , cos = F (x, y,z) z , 2 , 2 , 2 [F (x, , y z)] + [F (x, , y z)] + [F (x, , y z)] x y z →
Ví dụ 3.19. Xác định véc tơ pháp tuyến đơn vị N tại điểm (x,y,z) S (a) S là mặt cầu 2 2 2 2 x + y + z = R (b) S là mặt nón 2 2 z = x + y
(c) S là mặt phẳng đi qua các điểm A, B và C có tọa độ (a,0,0), (0,b,0) và (0,0,c)
với a > 0, b > 0 và c > 0.
Bài giải. (a) Viết phương trình của mặt cầu S dưới dạng (
F x, y, z) = x2 + y2 + z2 − R 2 = 0 123 F ,(x, , y ) z = 2x x Chúng ta có F, (x, , y ) z = 2y y F,(x, , y ) z = 2z z → → → → → → →
n(x, y, z) = F, (x, y, z) i + F, (x, y, z) j + F, (x, y, z) k = 2x i + 2y j + 2z k x y z → → → → → → → → → → → n 2x i+ 2y + j 2z k 2x i + 2y j+ N(x, , y z) = = = 2z k x y z = i + j+ k → (2x)2 + (2y)2 + (2z)2 ( 4 x 2 + y 2 + z 2) R R R | n |
(b) Viết phương trình của mặt nón S dưới dạng ( F x, , y ) z = z − ( z , x ) y = z − x 2 + y2 = 0 F, (x, , y z) = − x x2 + y2 x Chúng ta có F ,(x, , y ) z = −y x 2 + y 2 y , F (x, , y ) z =1 z → → → → → → → − x −y n(x, , y ) z = F, (x, , y z) i + F, (x, , y z) j+ F,(x, , y ) z k = i + x y z j +k x2 + y2 x2 + y2 − → x − → → y − → x − → → y → i + j + k i + j + k → n x2 + y2 x2 + y2 x 2 + y 2 x 2 + y2 N(x, , y z) = = = = → 2 2 | n | 2 − x − y + + 2 2 2 2 2 1 x + y x + y → → → − x − + y i + 1 j k . ( 2 x2 + y2 ) ( 2 x2 + y2 ) 2
(c) Phương trình mặt phẳng S đi qua 3 điểm A(a,0,0), B(0,b,0) và C(0,0,c) với a > 0, b > 0 và c > x y z 0 là
+ + = 1. Chúng ta viết phương trình của mặt phẳng S dưới dạng a b c x y z ( F x, y, z) = + + 1 − = 0 . a b c F,(x, , y z) = 1 a x Chúng ta có F,(x, , y ) z = 1 b y F,(x, , y z) =1 c z → → → → → → → , , , i j k n(x, , y z) = F (x, , y z) i + F (x, , y z) j + F (x, , y z) k = + + x y z a b c → → → → i + j + k → → → → n 1 1 1 N(x, , y z) = = a b c = i + j + → k 1 | n | + 1 + 1 1 a + 1 + 1 1 b + 1 + 1 1 c + 1 + 1 a2 b2 c2 a2 b2 c2 a2 b2 c2 a 2 b2 c2
3.5.2. Định nghĩa tích phân mặt loại hai
Trong không gian R3 cho mặt (phẳng/cong) S định hướng được và chúng ta xét 3 trường hợp:
(1) Phương trình của mặt cong S là hàm số z = z(x,y), (2) Phương trình của mặt cong S là hàm số x =
x(y,z) và (3) Phương trình của mặt cong S là hàm số y = y(x,z). 124
Trường hợp 1. Giả sử hình chiếu của mặt S lên mặt phẳng tọa độ Oxy là một miền đóng Dxy.
Giả sử phương trình của mặt S là hàm số z = z(x,y) đơn trị, liên tục với (x,y)Dxy và có các đạo hàm riêng z, (x, )
y ,z, (x, y) liên tục với (x,y) D xy. x y
Vì mặt S định hướng được, nên có hai phía và chúng ta ký hiệu S+ là mặt S được định hướng lên → → →
phía trên so với trục Oz, tức là véc tơ pháp tuyến n tạo với trục Oz một góc nhọn (n, Oz) 2 , còn →
S– là mặt S được định hướng xuống phía dưới so với trục Oz, tức là véc tơ pháp tuyến n tạo với trục → →
Oz một góc tù (n, Oz) 2 .
Giả sử hàm số R(x,y,z) được xác định trên mặt S định hướng được, tức là (x,y,z)S → R(x,y,z)R.
Khi đó, chúng ta gọi tích phân của hàm số R(x,y,z) lấy theo phía trên của mặt S và theo vi phân
dxdy là tích phân của hàm hợp R[x,y,z(x,y)] lấy trên miền Dxy và ký hiệu là
R(x, ,y )zdxdy = [ R x, , y ( z x, y) d
] xdy là tích phân mặt loại hai của hàm số R(x,y,z) lấy theo phía + S D xy trên của mặt S.
Tương tự, chúng ta gọi tích phân của hàm số R(x,y,z) lấy theo phía dưới của của mặt S và theo
vi phân dxdy là tích phân của hàm hợp R[x,y,z(z,y)] lấy trên miền Dxy và ký hiệu là
R(x, ,yz d)xdy= − [ R x, , y z(x, y) d
] xdy là tích phân mặt loại hai của hàm số R(x,y,z) lấy theo phía − S Dxy dưới của mặt S.
Như vậy, theo định nghĩa thì chúng ta có R(x, , y z d ) xdy = − R(x, , y z d ) xdy. S+ S− → →
Bây giờ, chúng ta tính tích phân mặt loại một R(x, ,yz)cos n
( , Oz)dS với (1) phương trình của S →
mặt S được cho dưới dạng hiện z = z(x,y) F(x,y,z) = F[x,y,z(x,y)] = z – z(x,y) = 0 và (2) n là véc → →
tơ pháp tuyến của mặt S hướng lên phía trên (theo định nghĩa thì = (n, Oz) là góc nhọn).
+ Hàm dưới dấu tích phân R(x,y,z) = R[x,y,z(x,y)] , → → F (x, , y ) z 1 + z cos n ( ,Oz) = cos = = , 2 , 2 , 2 , 2 , 2 [F (x, ,
y z)] + [F (x, y,z)] + [F (x, y,z)] 1+ [z (x, y)] + [z (x, y)] x y z x y → →
ở đây lấy dấu + vì = (n, Oz) là góc nhọn.
+ Vi phân mặtdS = 1 +[z, (x, y)]2 +[z, (x, y)]2dxdy x y → → R(x, , y ) z cos n ( ,Oz)dS = S 1 R[x, y, z(x, y)] 1 + , 2 [z (x, y)] + , 2 [z (x, y)] dxdy = x y , 2 , 2 D 1 + [z (x, y)] + [z (x, y)] xy x y [ R x, , y ( z x, y) d ] xdy x D y
Mặt khác, theo định nghĩa thì R(x, ,y ) z dxdy = [ R x, , y ( z x, y) d ] xdy + S Dxy → → R(x, , y d ) z xdy = R(x, , y ) z co n s( , O ) z d . S (*) S+ S 125 → →
Hoàn toàn tương tự, chúng ta tính tích phân mặt loại một R(x, , y ) z cos n ( , Oz)dS với (1) S
phương trình của mặt S được cho dưới dạng hiện z = z(x,y) F(x,y,z) = F[x,y,z(x,y)] = z – z(x,y) = 0 → → →
và (2) n là véc tơ pháp tuyến của mặt S hướng xuống phía dưới (theo định nghĩa thì = (n, Oz) là góc tù).
+ Hàm dưới dấu tích phân R(x,y,z) = R[x,y,z(x,y)] , → → F (x, , y ) z −1 + z cos n ( ,Oz) = cos = = , 2 , 2 , 2 , 2 , 2 [F (x, ,
y z)] + [F (x, y,z)] + [F (x, y,z)] 1+ [z (x, y)] + [z (x, y)] x y z x y → →
ở đây lấy dấu – vì = (n, Oz) là góc tù.
+ Vi phân mặtdS = 1 +[z, (x, y)]2 +[z, (x, y)]2 x dxdy y → → R(x, , y ) z cos n ( ,Oz)dS = S −1 R[x, y, z(x, y)] 1 + , 2 [z (x, y)] + , 2 [z (x, y)] dxdy = x y , 2 , 2 D 1 + [z (x, y)] + [z (x, y)] xy x y − [ R x, , y ( z x, ) y d ] xdy D xy
Mặt khác, theo định nghĩa thì R(x, ,yz d ) xdy = − [ R x, , y ( z x, y) d ] xdy − S Dxy → → R(x, , y z d ) xdy = R(x, , y ) z cos n ( , O ) z d . S (**) S− S → →
Các công thức (*), (**) có thể viết chung thành R(x, ,y )zdxdy = R(x, ,yz)cos n(,Oz)dS S S
trong đó, vế phải của công thức này là tích phân mặt loại một mà chúng ta đã biết cách tính. Như vậy,
việc tính tích phân mặt loại hai được đưa về việc tính tích phân mặt loại một theo công thức này.
Nhận xét. Nếu mặt S là mặt trụ có đường sinh song song với trục tọa độ Oz (phương trình của
mặt S không có biến z) thì phương trình của mặt S không thể xác định bởi phương trình z = z(x,y)
được, nên định nghĩa của tích phân mặt loại hai vừa nêu ở trên là
R( ,x ,y )zdxdy = [ R x, , y z( , x y) d ] xdy và R(x, , y z d ) xdy = − [ R x, , y ( z x, y) d ] xdy không có + S D − xy S x D y
nghĩa vì khi đó hình chiếu của mặt S xuống mặt phẳng tọa độ Oxy
là một đường cong (coi như có diện
tích bằng không). Do đó, chúng ta quy ước: khi S là mặt trụ có đường sinh song song với trục tọa độ Oz thì coi như R(x, , y d ) z xdy = . 0
Quy ước này hoàn toàn phù hợp với công thức S → → → → → → R(x, , y d ) z xdy = R(x, , y ) z cos n ( , Oz d ) S =0
vì khi đó (n,Oz) = 2 cos n ( , Oz) = 0 . S S
Như vậy, với quy ước trên, chúng ta luôn luôn có công thức → →
R(x, ,y )zdxdy = R(x, ,yz)cos n(,Oz)dS . S S
Trường hợp 2. Giả sử hình chiếu của mặt S lên mặt phẳng tọa độ Oyz là một miền đóng Dyz.
Giả sử phương trình của mặt S là hàm số x = x(y,z) đơn trị, liên tục với (y,z)Dyz và có các đạo hàm riêng x , ( , y z), liên tục với (y,z) D yz. y x,z( , y ) z
Vì mặt S định hướng được nên có hai phía và chúng ta ký hiệu S+ là mặt S được định hướng lên → → →
phía trên so với trục Ox, tức là véc tơ pháp tuyến n tạo với trục Ox một góc nhọn (n, Ox) 2, còn 126 →
S– là mặt S được định hướng xuống phía dưới so với trục Ox, tức là véc tơ pháp tuyến n tạo với trục → →
Ox một góc tù (n, Ox) 2.
Giả sử hàm số P(x,y,z) được xác định trên mặt S định hướng được, tức là (x,y,z)S → P(x,y,z)R.
Tiếp tục hoàn toàn tương tự như Trường hợp 1, chúng ta nhận được → →
P(x, ,y )zdydz = P(x, ,y )zcos n(,Ox)dS . S S
Trường hợp 3. Giả sử hình chiếu của mặt S lên mặt phẳng tọa độ Oxz là một miền đóng Dxz.
Giả sử phương trình của mặt S là hàm số y = y(x,z) đơn trị, liên tục với (x,z) D
xz và có các đạo hàm
riêng y, (x,z),y, (x,z) liên tục với (x,z) D xz. x z
Vì mặt S định hướng được nên có hai phía và chúng ta ký hiệu S+ là mặt S được định hướng lên → → →
phía trên so với trục Oy, tức là véc tơ pháp tuyến n tạo với trục Oy một góc nhọn (n, Oy) 2, còn →
S– là mặt S được định hướng xuống phía dưới so với trục Oy, tức là véc tơ pháp tuyến n tạo với trục → →
Oy một góc tù (n, Oy) 2.
Giả sử hàm số Q(x,y,z) được xác định trên mặt S định hướng được, tức là (x,y,z)S → Q(x,y,z)R.
Tiếp tục hoàn toàn tương tự như Trường hợp 1 và Trường hợp 2, chúng ta cũng nhận được → → Q(x, ,y d) z xdz = Q(x, , y z) cos n ( , O ) y dS . S S
Tóm lại. Nếu phương trình của mặt S có thể viết đồng thời dưới ba dạng z = z(x,y), x = x(y,z), y
= y(x,z) và P(x,y,z), Q(x,y,z), R(x,y,z) là ba hàm số xác định và liên tục trên mặt S thì chúng ta định
nghĩa được tích phân mặt loại hai tổng quát lấy trên mặt S định hướng được theo chiều của véc tơ →
pháp tuyến n là tổng của ba tích phân P(x, , y ) z dydz + ( Q x, , y ) z dzdx + R(x, , y ) z dxdy = S
P(x, ,y )zdydz+ ( Q x, , y ) z dzdx + R(x, , y ) z dxdy S S S
với quy ước: nếu S là mặt trụ có đường sinh song song với trục tọa độ Ox thì tích phân thứ nhất ở vế phải bằng không P(x, , y ) z dydz =
0, nếu S là mặt trụ có đường sinh song song với trục tọa độ Oy S
thì tích phân thứ hai ở vế phải bằng không Q(x, , y ) z dzdx =
0 và nếu S là mặt trụ có đường sinh S
song song với trục tọa độ Oz thì tích phân thứ ba ở vế phải bằng không R(x, , y d ) z xdy = 0 . S
3.5.3. Tính chất của tích phân mặt loại hai
Nếu đổi hướng mặt S thì tích phân mặt loại hai trên mặt S đổi dấu.
Tích phân mặt loại hai có các tính chất giống như các tính chất của tích phân xác định. 3.5.4. ha
Cách tính tích phân mặt loại i
Để tính tích phân mặt loại hai (lấy theo phía trên/dưới đối với mặt không kín hoặc lấy theo phía
ngoài/trong đối với mặt kín) 127 P(x, , y z d ) ydz + Q(x, , y d ) z zdx + R(x, , y ) z dxdy = S
P(x, ,y )zdydz+ ( Q x, , y ) z dzdx + R(x, , y )
z dxdy được định nghĩa ở trên, chúng ta ký S S S I = P(x, , y z)dydz x S
hiệu I = P(x, ,y )zdydz + ( Q x, , y d ) z zdx + R(x, , y ) z dxdy và I = Q(x, , y z)dzdx y S S I = R(x, , y ) z dxdy z S
Chúng ta tính từng tích phân Ix, Iy, Iz và suy ra I = Ix + Iy + Iz. - Tính I = R(x, , y )
z dxdy : Sử dụng phương trình của mặt S (đã được cho hoặc giải ra từ z S
phương trình ẩn đối với z) dưới dạng hiện z = z(x,y) – là hàm số có các đạo hàm riêng liên tục với (x,y)Dxy.
+ Nếu véc tơ pháp tuyến của mặt S (lấy theo phía trên/dưới đối với mặt không kín hoặc lấy
theo phía ngoài/trong đối với mặt kín) tạo thành với trục Oz một góc nhọn thì I = [ R x, , y ( z x, y) d ] xdy . z D xy
+ Nếu véc tơ pháp tuyến của mặt S (lấy theo phía trên/dưới đối với mặt không kín hoặc lấy
theo phía ngoài/trong đối với mặt kín) tạo thành với trục Oz một góc tù thì I = − [ R x, , y ( z x, y) d ] xdy . z Dxy
+ Nếu véc tơ pháp tuyến của mặt S (lấy theo phía trên/dưới đối với mặt không kín hoặc lấy
theo phía ngoài/trong đối với mặt kín) tạo thành với trục Oz một góc vuông thì I = 0 . z
- Các tích phân Ix, Iy được tính tương tự.
Ví dụ 3.20. Tính I = xdydz + ydzdx + zdxdy S
(a) S là mặt định hướng theo pháp tuyến phía ngoài mặt cầu x2 + y2 + z2 = R2. x2 y2 z 2
(b) S là mặt định hướng theo pháp tuyến phía ngoài mặt ellipsoit + + =1 (a a 2 b2 c 2
> 0, b > 0 và c > 0).
Bài giải. (a) Đồ thị của mặt cầu x2 + y2 + z2 = R2
Vì phương trình của mặt cầu và biểu thức dưới dấu tích phân không đổi khi hoán vị vòng quanh
x, y, z nên chúng ta có xdydz = ydzdx = zdxdy I =3zdxdy , do đó chúng ta chỉ phải tính S S S S tích phân zdxdy . S 128
Từ phương trình x2 + y2 + z2 = R2 2 2
của mặt cầu chúng ta giải ra được 2
z = R − x − y , khi đó S = S 2 2 2
tSd với St và Sd là nửa mặt cầu trên và nửa mặt cầu dưới của mặt cầu x2 + y + z = R , có
phương trình tương ứng là 2 2 2 z ( , x )
y = R − x − y (z 0) và 2 2 2 z ( , x )
y = − R − x − y (z 0). t d
Do đó zdxdy = z (x, ) y dxdy + z (x, y d ) xdy t d S St Sd Suy ra I = 3 z (x, y d ) xdy + z (x, y d ) xdy = t d St Sd 2 2 2 2 2 2 3 R − x − y dxdy + − R − x − y dxdy = St Sd 2 2 2 2 2 2 3 R − x − y dxdy − R − x − y dxdy tS Sd Hình chiếu của S 2 2 2
t và Sd lên mặt phẳng tọa độ Oxy là hình tròn Dxy = {x + y R }.
Vì véc tơ pháp tuyến hướng ra phía ngoài của nửa mặt cầu trên (S1) tạo thành với trục tọa độ Oz
một góc nhọn nên theo định nghĩa thì 2 R − 2 x − 2 y dxdy = 2 R − 2 x − 2 y dxdy , còn véc tơ pháp S t D xy
tuyến hướng ra phía ngoài của nửa mặt cầu dưới (S2) tạo thành với trục tọa độ Oz một góc tù nên theo định nghĩa thì 2 R − 2 x − 2 y dxdy = − 2 R − 2 x − 2 y dxdy Sd D xy I = 3 2 2 2 R − x − y − − 2 R − 2 x − 2 2 2 2 y = 6 R − x − y dxdy . D D xy xy Dxy Để tính tích phân 2 R − 2 x − 2
y dxdy chúng ta đổi tọa độ Descartes (x,y) sang tọa độ cực D xy x = r cos 0 r R
(r,) bằng phép đổi biến J = r và miền D, = xy
vì đối với tọa độ r, chúng ta y = r sin 0 2 x = r cos thay
vào phương trình của hình tròn x2 + y2 R2 r2 R2 0 r R , còn đối với tọa y = r sin
độ thì 0 2.
Biểu thức dưới dấu tích phân 2 2 2 2 2 f ( , x )
y = R − x − y f (r cos , r sin ) = R − r 2 R I = 2 6 R − 2 r J dr d = 2 6 R − 2 r rdr d = 2 6 r R − 2 r dr d = 6 d 2 r R − 2 r dr D' D' D' 0 0 2 = d 2 = = 2 = 0 0 r= R R3 Vì 1 + I = 2 . 6 . = 4R3 . 1 R R 1 2 2 3 2 3 − 2 2 1 2 2 2 2 1 (R r ) R r R − r dr = − (R −r ) 2d(R −r ) = − = 2 2 1 3 0 0 +1 2 r= 0 x2 y2 z 2
(b) Đồ thị của mặt ellipsoit + + = 1 a 2 b2 c 2 129 I = P(x, , y ) z dydz x S P(x, , y z) = x
Chúng ta có I = Ix + Iy + Iz với I = Q(x, , y ) z = y và các tích phân y
Q(x, ,y )zdzdx trong đó S R(x, , y z) = z I = z R(x, ,y )zdxdy S
được lấy theo mặt ngoài của ellipsoit. - Tính I = xdydz x S 2 2 2 Từ phương trình x y z + +
= 1 của mặt ellipsoit chúng ta giải ra được a 2 b2 c 2 2 2 y z x = x( , y z) = a 1− − , khi đó x x S = S S với x S và x
S là nửa mặt ellipsoit trên và nửa 2 2 b c t d t d x2 y2 z 2
mặt ellipsoit dưới của mặt ellipsoit + +
=1, có phương trình tương ứng là a2 b2 c 2 2 2 y z 2 2 y z x (y, z) = a 1− −
(x 0) và x (y, z) = −a 1− − (x 0). t 2 2 b c d 2 2 b c Do đó I = xdydz = xdydz + xdydz = x ( , y ) z dydz + x ( , y ) z dydz = x t d x x x x S S S S t d t Sd 2 2 2 2 a − y 1 − z dydz + − a − y 1 − z dydz = 2 2 2 2 b c b c x x St S d 2 2 2 2 a − y 1 − z dydz − a − y 1 − z dydz = 2 2 2 2 b c b c x x St Sd 2 2 2 2 y z y z a 1 − − dydz − 1− − dydz 2 2 2 2 b c b c x x St S d y2 z 2 Hình chiếu của x S và x
S lên mặt phẳng tọa độ Oyz là ellipse D . yz = + 1 2 2 t d b c
Vì véc tơ pháp tuyến hướng ra phía ngoài của nửa mặt ellipsoit trên ( x
S ) tạo thành với trục tọa t 2 2 2 2 y z y z
độ Ox một góc nhọn nên theo định nghĩa thì − 1 − dydz = 1 dydz , còn véc tơ 2 2 − − 2 2 b c b c x S Dyz t
pháp tuyến hướng ra phía ngoài của nửa mặt ellipsoit dưới ( x
S ) tạo thành với trục tọa độ Oz một góc d 2 2 2 2 y z y z
tù nên theo định nghĩa thì 1− − dydz = − 1 dydz 2 2 − − 2 2 b c b c x S D yz d 130 2 2 2 2 y z y z I = a 1 − − dydz − 1− − dydz = x 2 2 2 2 b c b c x x St S d 2 2 2 2 a y z y z 1 − − dydz − − 1− − dydz = 2 2 b c 2 2 b c Dyz Dyz 2 2 2 2 2 2 y z y z y z a 1− − dydz + 1 − − dydz 2a 1 dydz 2 2 = 2 2 b c b c − − 2 2 b c Dyz y D z D yz 2 2 y z
Để tính tích phân 1− − dydz chúng ta đổi tọa độ Descartes (x,y) sang tọa độ cực (r,) 2 2 b c D yz y = br cos 0 r 1
mở rộng bằng phép đổi biến J = bcr và miền D, = yz z = cr sin 0 2 2 2
Biểu thức dưới dấu tích phân y z 2 f (y, ) z = 1− − f (br cos , crsin ) = 1− r 2 2 b c 2 1 2 1 I = a 2 bcr 1 − 2 r drd = a 2 bc d r 1 − 2 r dr =2abc d r 1 r dr x − 2 D, 0 0 0 0 yz 2 = d 2 = = 2 = 0 0 r 1 = 1 4 1 + I = 2abc 2 . . = abc. 1 x 1 1 1 2 2 3 3 − 2 1 2 2 1 1 ( r ) 1 r 1 − r dr = − 1 ( − r )2 d 1 ( − r ) = − = 2 2 1 3 0 0 + 1 2 r 0 = 4 I = abc y 3 - Tính I = ydzdx và I =
zdxdy hoàn toàn tương tự như trên, chúng ta được z y 4 S S I = z ab c 3 4 4 4 I = I + I + I = + + = x y z abc abc abc a 4 bc . 3 3 3 x2 y2 z 2
Nhận xét. Từ kết quả của (b), nếu cho a = b = c = R thì mặt ellipsoit + + = 1 suy biến a2 b2 c 2 thành mặt cầu 2 2 2 2
x + y + z = R và I = 4R3 trùng với kết quả của (a).
Ngoài ra, để tính tích phân mặt loại hai, chúng ta có thể sử dụng công thức P(x, , y ) z dydz + ( Q x, , y ) z dzdx + R(x, , y ) z dxdy = S → → → → → → [P(x, ,y )zco n s( , Ox) + Q(x, , y ) z cos n ( , Oy) + R(x, , y ) z cos n ( , O ) z d ] S S
mà vế phải của công thức này là tích phân mặt loại một.
Khi tính tích phân mặt loại hai mà mặt S là mặt phẳng thì người ta hay sử dụng công thức này vì
đối với một mặt phẳng xác định, véc tơ pháp tuyến không thay đổi tại mọi điểm của mặt phẳng này.
Ví dụ 3.21. Tính I = (x + 2y − d ) z ydz + (−2x + y + ) z 3 dzdx + (4x − y + 2 ) z dxdy , S là mặt định S
hướng theo pháp tuyến mặt ngoài của tứ diện OABC với O(0,0,0), A(2,0,0), B(0,1,0), C(0,0,3). 131 Bài giải.
Cách 1. Chúng ta sẽ tính tích phân đã cho trên từng mặt của tứ diện OABC
I = IABC + IOAB + IOBC + IOCA
Để tính các tích phân IABC, IOA , I B OBC, IOCA, chúng
ta sẽ sử dụng công thức P(x, , y ) z dydz + ( Q x, , y ) z dzdx + R(x, , y ) z dxdy = S → → → → → → [P(x, ,yz)cos n(,Ox)+ ( Q x, , y ) z cos n ( ,Oy) + R(x, , y z)cos n ( ,Oz) d ] S S - Tính IABC: x z
Phương trình của mặt phẳng ABC là + y + =1 (
F x, y, z) = 3x +6y +2z −6 = 0 2 3 → → → → → → → n(x, y, z) = F,
x (x, y, z) i + F ,y(x, y, z) j + F,z (x, y, z) k = 3 i + 6 j + 2 k → → → → → → → → n . i 3 ( i + 6 j + cos n ( ,Ox) = = 2 k). i = 3 → → 32 + 62 + 22 1 . 7 | n | i | → → → → → → → → n . j (3 i + 6 j+ 2 k). j 6 cos n ( ,Oy)= = = → → 32 + 62 + 22 1 . 7 | n | j | → → → → → → → → n.k (3 i + 6 j+ 2 k).k 2 cos n ( ,Oz) = = = → → 2 2 2 3 + 6 + 2 1 . 7 | n | k | → → → → → → I = [(x + 2y − ) z cos n ( ,Ox) + (−2x + y + z 3 ) cos n ( ,Oy) + (4x − y + 2 ) z cos n ( , Oz) d ] S = ABC SABC 3 6 2 (x + 2y− z) + − ( 2x + y+ ) z 3 + (4x − y + z 2 ) dS = 1 − ( x + 1 y 0 +19 ) z dS 7 7 7 7 S ABC SABC
Tích phân (−x +10y +1 z
9 )dS là tích phân mặt loại một với f (x, y,z) = −x + 10y +1 z 9 và SABC 3 z(x, y) = 3 −
x − 3y (giải ra từ phương trình của mặt phẳng ABC: (
F x, y, z) = 3x + 6y + 2z − 6 = 0) 2
nên chúng ta tính như sau: , 2 , 3 2 2 2 7
- Vi phân mặt dS = 1 +[z (x, y)] + z [ ( = + − + − = x y x, y)] dxdy 1 ( ) 3 dxdy dxdy 2 2
- Hàm dưới dấu tích phân f (x, y, z) = −x +10y +1 z 9 3 59 f[x, y, z(x, y)] = x − +1 y
0 +193 − x − 3y = 57 − x − 47y 2 2
- Hình chiếu của mặt SABC lên mặt phẳng tọa độ Oxy là 132 0 x 2 D = xy 0 y 1 − x 2 →
Từ đồ thị của tứ diện OABC, chúng ta thấy rằng, véc tơ pháp tuyến n mặt ngoài của mặt phẳng
ABC là pháp tuyến hướng lên phía trên so với trục Oz nên chúng ta lấy dấu + đối với tích phân hai lớp
lấy trên hình chiếu D của mặt SABC lên mặt phẳng tọa độ Oxy, tức là 1 59 7 1 59 I = + 57 x 47y dxdy 57 x 47y dxdy ABC − − = − − = 7 2 2 2 2 D D 2 1− 1 59 x 2 1 59 57 − x − 47y dxdy = dx 57 − x −47y dy = 2 2 2 2 D 0 0 = y − 1 x 2 2 1 2 5 x 9 y 47y 2 1 2 7 x 1 57y − − dx = − 6 x 9 + 67 dx = 2 2 2 4 4 0 y= 0 0 x=2 1 7 x 1 3 69x2 65 − +67x = . 4 12 2 6 x= 0
- Tính IOAB: Phương trình của mặt phẳng OAB là z = 0 ( F x, y,z) = z = 0 → → → → → → → →
n(x, y,z) = F,(x, y, z) i + F,(x, ,
y z) j + F, (x, y, z) k = 0. i + . 0 j+ 1. k = k x y z → → → → → → cos n ( ,Ox) = cos k ( ,Ox) = k . i = 0 → → | k | i | → → → → → → k . j cos n ( ,Oy) = cos k ( ,Oy) = = → → 0 | k | j | → → → → → → k .k cos n ( , Oz) = cos k ( ,Oz) = = → → 1 | k | k | → → → → → → I = [(x + 2y − z) cos n ( ,Ox) + − ( 2x + y + z 3 ) cos n
( , Oy) + (4x − y + 2z) cos n ( , Oz) d ] S = OAB S OAB
[(x +2y − )0 0. +(−2x +y + .30) 0. +(4x −y +2. )0. d] 1 S = (4x −y)dS O S AB O S AB
Tích phân (4x − y)dS là tích phân mặt loại một với f(x, ,
y z) = 4x − y và z(x, y) = 0 nên SOAB chúng ta tính như sau:
- Vi phân mặt dS = 1 +[z, (x, y)]2 +[z, (x, y)]2dxdy = 1 + 02 + 02 dxdy = dxdy x y
- Hàm dưới dấu tích phân f (x, , y z) = 4x − y
- Hình chiếu của mặt SOAB lên mặt phẳng tọa độ Oxy là 0 x 2 D = xy 0 y 1 − x 2 133 →
Từ đồ thị của tứ diện OABC, chúng ta thấy rằng, véc tơ pháp tuyến n mặt ngoài của mặt phẳng
OAB là pháp tuyến hướng xuống phía dưới so với trục Oz nên chúng ta lấy dấu – đối với tích phân hai
lớp lấy trên hình chiếu Dxy của mặt S
OAB lên mặt phẳng tọa độ Oxy, tức là 2 1− y 1 x 2 x 2 2 2 y = − I = − (4x − y)dxdy = (y − 4x)dxdy = dx (y − 4x d ) y = − 4xy dx = OAB 2 D D 0 0 0 xy xy y =0 x=2 1 2 17x2 1 1 7x 3 9x 2 7 − 9x +1 dx = − + x = − . 2 4 2 12 2 3 0 x= 0
- Tính IOBC: Phương trình của mặt phẳng OBC là x = 0 ( F x, y,z) = x = 0 → → → → → → → → n(x, ,
y z) = F,(x, y, z) i + F ,(x, y, z) j+ F, (x, y,z) k = . 1 i + 0. j+ 0.k = i x y z → → → → → → cos n ( ,Ox) = cos(i ,Ox) = i . i = 1 → → | i | i | → → → → → → i . j cos n ( ,Oy) = cos(i ,Oy) = = → → 0 | i | j | → → → → → → i .k cos n ( ,Oz) = cos(i ,Oz) = = → → 0 | i | k | → → → → → → I = [(x + 2y − z) cos n ( , Ox) + (−2x + y + z 3 ) cos n
( , Oy) + (4x − y + 2z) cos n ( , Oz) d ] S = OBC S OBC
[(0 + 2y −z) 1.+(−2.0 + y + z 3 ) 0 . + (4.0 − y + 2z). d ] 0 S = (2y − z)dS O S BC SOBC
Tích phân (2y − z)dS là tích phân mặt loại một với f (x, , y z) = 2y − z và x( , y z) = 0 nên SOBC chúng ta tính như sau:
- Vi phân mặt dS = 1 +[x , ( ,
y z)]2 +[x, (y,z)]2dydz = 1 + 02 + 02 dydz = dydz y z
- Hàm dưới dấu tích phân f (x, , y z) = 2y − z 0 y 1
- Hình chiếu của mặt SOBC lên mặt phẳng tọa độ Oyz là D = yz 0 z 3 −3y →
Từ đồ thị của tứ diện OABC, chúng ta thấy rằng, véc tơ pháp tuyến n mặt ngoài của mặt phẳng
OBC là pháp tuyến hướng xuống phía dưới so với trục Ox nên chúng ta lấy dấu – đối với tích phân hai
lớp lấy trên hình chiếu Dyz của mặt S
OBC lên mặt phẳng tọa độ Oyz , tức là z =3 − 1 3 −3y 2 2 z 3y I = − (2y− ) z dydz = (z− 2y)dydz = dy z ( − 2y)dz = − 2yz dy = OBC 2 D D 0 0 0 yz yz z =0 y 1 = 1 2 y 1 2 9 7y3 15y2 9y 1 −15y + dy = − + = . 2 2 2 2 2 2 0 y=0
- Tính IOCA: Phương trình của mặt phẳng OCA là y = 0 ( F x, y,z) = y = 0 → → → → → → → →
n(x, y, z) = F, (x, y, z) i + F, (x, y, z) j + F,(x, y,z) k = 0. i +1. j+ 0.k = j x y z 134 → → → → → → cos n ( ,Ox) = cos( j,Ox) = j . i = 0 → → | j | i | → → → → → → j . j cos n ( , O ) y = cos( j,Oy) = = 1 → → | i | j | → → → → → → j .k cos n ( , Oz) = cos( j,Oz) = = 0 → → | j | k | → → → → → → I = [(x + 2y − ) z cos n ( ,Ox) + (−2x + y + ) z 3 cos n ( ,Oy) + (4x − y + 2z) cos n ( , Oz) d ] S = OCA SOCA
[(x +2.0 −z) 0. +( −2x +0 + z 3 ) 1 . +(4x −0 +2z) 0 . d ] S = ( −2x +3z)dS O S CA SOCA Tích phân − ( 2x + z
3 )dS là tích phân mặt loại một với f (x, y,z) = 2 − x + z 3 và ( y x,z) = 0 nên SOCA chúng ta tính như sau:
- Vi phân mặt dS = 1+ [y, (x, ) z ]2 + [y, ( , x )
z ]2 dxdz = 1+ 02 + 02dxdz = dxdz x z
- Hàm dưới dấu tích phân f (x, y,z) = 2 − x + z 3 0 z 3
- Hình chiếu của mặt SOCA lên mặt phẳng tọa độ Oxz là D = xz 0 x 2 − 2z 3 →
Từ đồ thị của tứ diện OABC, chúng ta thấy rằng, véc tơ pháp tuyến n mặt ngoài của mặt phẳng
OCA là pháp tuyến hướng xuống phía dưới so với trục Oy nên chúng ta lấy dấu – đối với tích phân hai
lớp lấy trên hình chiếu Dxz của mặt S OCA lên mặt phẳ ng tọa độ Oxz, tức là 3 2−2z 3 3 x= − I = − (−2x + z 3 d ) xdz = (2x −3z)dxdz = dz (2x −3z)dx = x z 3 x dz OCA ( 2 − ) 2 2z 3 = x= 0 D D 0 0 0 xz xz z 3 = 3 2 z 2 2 2 z 6 2 z 2 3 1 z 3 2 − + 4 dz = − + 4z = − . 5 9 3 27 3 0 z 0 = 65 7 1
I = IABC + IOAB + IOBC + IOCA = − + − 5 = 4. 6 3 2 I = x P(x, ,y )zdydz S P(x, , y ) z = x + 2y − z
Cách 2. Chúng ta có I = Ix + Iy + Iz với I = Q(x, , y ) z = − 2x + y+ y
Q(x, ,y )zdzdx trong đó 3z và S R(x, ,yz) = 4x − y + 2z I = R(x, , y ) z dxdy z S
các tích phân được lấy theo mặt ngoài của tứ diện. x I = (x + 2y − z)dydz ABC ABC xI = (x + 2y− z)dydz OAB - Tính x x x x I = (x + 2y − ) z dydz = I + I + I + I với OAB x ABC OAB OBC OCA x S I = (x + 2y − z)dydz OBC OBC x I = (x + 2y − OCA z)dydz OCA 135 + x I = (x 2y ) z dydz ABC + − ABC
Phương trình của mặt phẳng ABC là x z 2 + y + =1 x = x( , y z) = 2 −2y − z . 2 3 3
Hình chiếu của mặt phẳng ABC lên mặt phẳng tọa độ Oyz (x = 0) là OBC và ký hiệu là 0 y 1 D = . yz 0 z 3 − 3y
Vì véc tơ pháp tuyến hướng ra phía ngoài của mặt phẳng ABC tạo thành với trục tọa độ Ox một
góc nhọn nên theo định nghĩa thì 2 5
(x + 2y − z)dydz = +
2− 2y− z + 2y − z dydz = 2− z dydz 3 3 ABC D yz Dyz z= − 3 3y x 5 1 − 3 3y 5 1 2 z 5 I = 2 − zdydz = dy 2− z dz = 2z − dy = ABC 3 3 6 D 0 0 0 yz z =0 y 1 = 1 15y2 3 5y3 9y2 3y 1 − + 9y − dy = − + − = . 2 2 2 2 2 2 0 y=0 + x I = (x 2y ) z dydz OAB + − OAB
Phương trình của mặt phẳng OAB là z = 0 ình , h
chiếu của mặt phẳng OAB lên mặt phẳng tọa độ
Oyz là đoạn thẳng OB có diện tích bằng không nên Ix = 0. OAB + x I = (x 2y ) z dydz OBC + − OBC
Phương trình của mặt phẳng OBC là x = 0, ình chiếu của mặt phẳng h
OBC lên mặt phẳng tọa độ 0 y 1
Oyz là OBC và ký hiệu là D = . yz 0 z 3 −3y
Vì véc tơ pháp tuyến hướng ra phía ngoài của mặt phẳng OBC tạo thành với trục tọa độ Ox một
góc tù (chính xác là ) nên theo định nghĩa thì (x + 2y− d) z ydz = − 0 ( + 2y − d ) z ydz = z ( − 2 ) y dydz OBC D yz Dyz = z − 1 − 3 3y 1 2 z 3 3y 1 I = z
( − 2y)dydz = dy (z − 2y)dz = − 2yz dy = 3 2 (7y − 1 y 0 + d ) 3 y = OBC 2 2 D 0 0 0 yz z= 0 0 y 1 = 3 7y3 2 1 − 5y + 3y = . 2 3 2 y 0 = + x I = (x 2y d ) z ydz OCA + − OCA
Phương trình của mặt phẳng OCA là y = 0 ình c , h
hiếu của mặt phẳng OCA lên mặt phẳng tọa độ
Oyz là đoạn thẳng OC có diện tích bằng không nên Ix = 0 . OCA x x x x 1 1 I = (x + 2y − ) z dydz = I + I + I + I = + 0 + + 0 = . 1 x ABC OAB OBC OCA 2 2 S 136 y I = − ( 2x + y + z 3 )dxdz ABC ABC y I = ( −2x + y + z 3 )dxdz OAB - Tính y y y y I = ( 2 − x + y + d ) z 3 xdz = I + I + I + I OAB y với ABC OAB OBC OCA y S I = − ( 2x + y + z 3 )dxdz OBC OBC y I = − ( 2x + y + OCA z 3 )dxdz OCA + y I = ( 2x y ) z 3 dxdz ABC − + + ABC
Phương trình của mặt phẳng ABC là x z x z
+ y + =1 y = y(x, z) =1 − − . 2 3 2 3
Hình chiếu của mặt phẳng ABC lên mặt phẳng tọa độ Oxz (y = 0) là OAC và ký hiệu là 0 x 2 D = . xz 0 z 3 − 3x 2
Vì véc tơ pháp tuyến hướng ra phía ngoài của mặt phẳng ABC tạo thành với trục tọa độ O một y
góc nhọn nên theo định nghĩa thì x z 5 8 − ( 2x + y + z 3 )dxdz = + − 2x + 1− − + z 3 dxdz = 1− x + zdxdz 2 3 2 3 ABC D xz Dxz y 5 8 2 − 3 3x 2 5 8 2 5 4 2 = z − 3 3x 2 I = 1 − x + z dxdz = dx
1− x + zdz = z− xz + z dx = ABC 2 3 2 3 2 3 D 0 0 0 z=0 xz x= 2 2 27 2 9x3 2 x 1 2 x − 2 x 1 +15dx = − +1 x 5 = . 6 4 4 2 0 x= 0 + y I = ( 2x y ) z 3 dxdz OAB − + + OAB
Phương trình của mặt phẳng OAB là y = 0 ình c , h
hiếu của mặt phẳng OAB lên mặt phẳng tọa độ
Oxz là đoạn thẳng OA có diện tích bằng không nên Iy = 0 . OAB + y I = ( 2x y ) z 3 dxdz OBC − + + OBC
Phương trình của mặt phẳng OBC là x = 0, ình chiếu của mặt phẳng h
OBC lên mặt phẳng tọa độ
Oxz là đoạn thẳng OC có diện tích bằng không nên Iy = 0 . OBC + y I = ( 2x y ) z 3 dxdz OCA − + + OCA
Phương trình của mặt phẳng OCA là y = 0,
ình chiếu của mặt phẳng OC h
A lên mặt phẳng tọa độ 0 x 2 Oxz (y = 0) là O A C và ký hiệu là D = . xz 0 z 3 − 3x 2
Vì véc tơ pháp tuyến hướng ra phía ngoài của mặt phẳng OCA tạo thành với trục tọa độ Oy một
góc tù (chính xác là ) nên theo định nghĩa thì
(−2x + y+ 3z)dxdz = − (−2x + 0 + 3z)dxdz = (2x −3z)dxdz OCA Dxz Dxz = z − 2 3−3x 2 2 3 3x 2 y 3 2 I = (2x − z 3 )dxdz = dx (2x − 3 ) z dz = 2xz z dx OCA − = 2 D 0 0 0 z=0 xz x =2 1 2 5 x 1 2 1 17x3 3 x 9 2 − + 3 x 9 − 27 dx = − + − 2 x 7 = − . 5 2 4 2 4 2 0 x=0 137 I = ( 2 − x + y + z 3 d ) xdz = I y + + + = + + − = y ABC IyOAB IyOBC IyOCA 6 0 0 5 . 1 S z I = (4x − y + z 2 )dxdy ABC ABC zI = (4x − y + z 2 )dxdy OAB - Tính z z z z I = (4x − y + 2 ) z dxdz = I + I + I + I OAB z với ABC OAB OBC OCA z S I = (4x − y + 2 ) z dxdy OBC OBC z I = (4x − y + OCA z 2 )dxdy OCA + z I = (4x y 2z d ) xdy ABC − + ABC
Phương trình của mặt phẳng ABC là x z 3
+ y + =1 z = z(x, y) = 3 − x − 3y , hình chiếu của 2 3 2 0 x 2
mặt phẳng ABC lên mặt phẳng tọa độ Oxy (z = 0) là OAB và ký hiệu là D = . xy 0 y 1 −x 2
Vì véc tơ pháp tuyến hướng ra phía ngoài của mặt phẳng ABC tạo thành với trục tọa độ Oz một
góc nhọn nên theo định nghĩa thì
(4x− y+ 2z)dxdy = + 3 4x − y+ 2 3− x − 3y dxdy = (6+ x − 7y)dxdy 2 ABC D xy Dxy 2 1−x 2 = y − 2 z 7 2 1 x 2 I = 6 ( + x −7 ) y dxdy = dx 6 ( +x −7y d ) y = 6y + xy − y dx = ABC 2 D 0 0 0 y=0 xy x=2 1 2 1 x 1 2 1 1 x 1 3 x 3 2 13 − + x 3 +5 dx = − + + 5x = . 2 4 2 12 2 3 0 x=0 + z I = (4x y z 2 )dxdy OAB − + OAB
Phương trình của mặt phẳng OAB là z = 0, hình chiếu của mặt phẳng OAB lên mặt phẳng tọa độ 0 x 2
Oxy là OAB và ký hiệu là D = . xy 0 y 1 − x 2
Vì véc tơ pháp tuyến hướng ra phía ngoài của mặt phẳng OAB tạo thành với trục tọa độ Oz một
góc tù (chính xác là ) nên theo định nghĩa thì (4x− y+ )z 2 dxdy = − (4x − y+ d ) 0 . 2 xdy = (y − 4x)dxdy . OAB Dxy Dxy = y − 2 1− 1 x 2 x 2 2 2 y z I = (y− 4x)dxdy = dx (y− 4x)dy = − 4xy dx = OAB 2 D 0 0 0 xy y =0 x=2 1 2 17x2 1 1 7x 3 9x 2 7 − 9x +1 dx = − + x = − . 2 4 2 12 2 3 0 x= 0 + z I = (4x y 2 ) z dxdy OBC − + OBC
Phương trình của mặt phẳng OBC là x = 0, ình chiếu của mặt phẳng h
OBC lên mặt phẳng tọa độ Oxy B
là đoạn thẳng O có diện tích bằng không nên Iz = 0 . OBC + z I = (4x y 2 ) z dxdy OCA − + OCA 138
Phương trình của mặt phẳng OCA là x = 0, hình chiếu của mặt phẳng OCA lên mặt phẳng tọa độ
Oxy là đoạn thẳng OA có diện tích bằng không nên z I = 0. OCA z z z z 13 7 I = (4x − y + 2 d ) z xdy = I + I + I + I = − + 0 + 0 = . 2 z ABC OAB OBC OCA 3 3 S
I = Ix + Iy + Iz = 1 + 1 + 2 = 4.
Nhận xét. Rõ ràng là, đối với tích phân mặt loại hai ở ví dụ này, tính theo Cách 1 đơn giản và
ngắn hơn tính theo Cách 2.
3.6. Mối quan hệ của các tích phân bội, đường và mặt
3.6.1. Công thức Green
Ở mục 3.3. chúng ta đã biết công thức Green là công thức liên hệ giữa tích phân hai lớp và tích
phân đường loại hai. Nếu các hàm số P(x,y), Q(x,y) liên tục và các đạo hàm riêng cấp 1 của chúng liên
tục trên miền phẳng D là một miền liên thông, bị chặn và có biên L gồm một hay nhiều đường cong
kín rời nhau từng đôi một thì P(x, ) y dx + ( Q x, y d ) y = , Q ( , x y) − , . x y P (x, y ) dxdy + L D
Hệ quả. Diện tích S của miền phẳng D có biên là đường cong kín L được tính bởi công thức = 1 S xdy − ydx . 2 + L
3.6.2. Công thức Stokes
Công thức Stokes là công thức liên hệ giữa tích phân đường loại hai trên đường cong kín L trong
không gian với tích phân mặt loại hai trên mặt S định hướng được, giới hạn bởi đường biên L.
Giả sử S là mặt định hướng được và trơn từng mảnh, biên L của nó là một đường cong kín trơn
từng khúc, đồng thời các hàm số P(x,y,z), Q(x,y,z), R(x,y,z) liên tục và có các đạo hàm riêng cấp 1
liên tục trên mặt S thì ( P x, , y ) z dx + ( Q x, , y z d ) y + R(x, , y ) z dz = + L , [R (x, , y z) − , Q (x, , y z) d ] ydz + , [P (x, y, ) z − , R (x, , y ) z d ] zdx + , [Q (x, , y ) z − , P (x, , y ) z d ] xdy y z z x x y S
Công thức Stoker là kết quả mở rộng công thức Green trong không gian R2 sang không gian R3.
Từ công thức Stoker suy ra điều kiện cần và đủ để tích phân đường trong không gian không phụ thuộc
vào đường lấy tích phân là R, (x, , y z) = Q, (x, , y z) y z P,(x, y,z) =R , (x, , y z) z x , , Q (x, , y ) z = P (x, , y z) x y
Điều kiện này cũng là điều kiện cần và đủ để biểu thức
P(x,y,z)dx + Q(x,y,z)dy + R(x,y,z)dz là vi phân toàn phần cấp 1 của một hàm số u(x,y,z) nào đấy.
3.6.3. Công thức Ostrogradsky
Công thức Ostrogradsky là công thức liên hệ giữa tích phân mặt loại hai lấy trên mặt ngoài của
mặt cong kín S với tích phân ba lớp trên miền V có biên là mặt cong kín S.
Giả sử V là miền giới nội và đóng trong không gian R3 có biên là mặt cong kín S, trơn từng
mảnh; các hàm số P(x,y,z), Q(x,y,z), R(x,y,z) liên tục và có các đạo hàm riêng cấp 1 liên tục trong miền V thì ( P x, , y ) z dydz + ( Q x, , y ) z dzdx + R(x, , y ) z dxdy = , [P (x, y, ) z + , Q (x, y, ) z + , R (x, , y ) z d ] xdydz x y z S V
Hệ quả. Thể tích V của vật thể giới hạn bởi mặt cong kín S được tính bằng công thức: 139 = 1 V xdydz + ydzdx + zdxdy 3 S P(x, , y z) = x P, (x,y,z) = 1 x
Chứng minh. Chúng ta lấy Q(x,y,z) = y Q, (x,y,z) = 1 y
và thay vào công thức Ostrogradsky R(x, , y ) z = z R, (x, y,z) = 1 z
thì được xdydz + ydzdx + zdxdy = 1(+1+ )1dxdydz =3dxdydz , theo ý nghĩa hình học của tích S V V 1 phân ba lớp dxdydz = V , do đó xdydz + ydzdx + zdxdy = V 3 V = xdydz + ydzdx + zdxdy. 3 V S S PHỤ LỤC
P1. Tham số hóa phương trình của đường trong mặt phẳng (R2)
Phương trình của đường trong mặt phẳng (gọi ngắn gọn là đường phẳng) thường được tham số
hóa (1) theo tham số tổng quát, (2) theo tọa độ Descartes, (3) theo tọa độ cực tùy thuộc vào từng loại đường phẳng cụ thể.
P1.1. Tham số hóa phương trình của đường thẳng
(1) Theo tham số tổng quát
Véc tơ u được gọi là véc tơ chỉ phương của đường thẳng () nếu | u | 0 và u song song hoặc
nằm trên đường thẳng ().
Như vậy, nếu véc tơ u là một véc tơ chỉ phương của đường thẳng () thì véc tơ u ( 0) cũng
là véc tơ chỉ phương của đường thẳng (), do đó một đường thẳng có vô số véc tơ chỉ phương. Phương trình a
x + by + c = 0 với a và không b đồng thời bằng ,
không được gọi là phương trình
tổng quát của đường thẳng () trong mặt phẳng.
Các trường hợp đặc biệt: + a = 0, b 0 a + x by + c = 0 y = c
– /b: ()//Ox hoặc trùng với Ox (khi c = 0).
+ a 0, b = 0 ax + by + c = 0 x = c
– /a: ()//Oy hoặc trùng với Oy (khi c = 0). + Nếu c = 0 thì a + x by + c = 0 a +
x by = 0: () đi qua gốc tọa độ O(0,0).
+ Nếu đường thẳng () cắt Ox tại điểm A(ax,0) với ax 0 và Oy tại điểm B(0,by) với by 0 thì
phương trình của đường thẳng x y () là + = . 1 a b x y
Véc tơ pháp tuyến và véc tơ chỉ phương của một đường thẳng là vuông góc với nhau nên tích vô
hướng của hai véc tơ này bằng không. Do đó (như chúng ta đã biết), đường thẳng ax + by + c = 0 c ó véc tơ pháp tuyến là n a
( , b) , nên đường thẳng ax + by + c = 0 có hai véc tơ chỉ phương là u(− , b a) , u( , b −a).
Một đường thẳng hoàn toàn được xác định nếu biết một điểm và một véc tơ chỉ phương của
đường thẳng đó. Ví dụ 1.
(a) Tìm phương trình của đường thẳng () đi qua điểm M(xM,yM) và véc tơ chỉ phương của
đường thẳng () là u(u ,u ) . x y
(b) Tham số hóa phương trình đường thẳng (). Bài giải.
(a) Giả sử ax + by + c = 0 (a và b không đồng thời bằng không) là phương trình tổng quát của đường thẳng (). 140
Véc tơ chỉ phương và véc tơ pháp tuyến đường thẳng () là vuông góc với nhau nên tích vô
hướng của hai véc tơ này bằng không, do đó, nếu véc tơ chỉ phương của đường thẳng () là u u ( , u ) x y
thì đường thẳng () có hai véc tơ pháp tuyến là n( u − ,u ) và n u ( ,−u ) . y x y x a = − uy
- Nếu véc tơ pháp tuyến của đường thẳng () là n( u − ,u ) thì
, còn c được xác định y x b = u x
từ phương trình − u x + u y + c = 0 c = u x − u y . Do đó, phương trình đường thẳng () là y M x M y M x M x − x y − y M M
− u x + u y + u x − u y = 0 u
− (x − x ) + u (y − y ) = 0 = . y x y M x M y M x M u u x y a = u y
- Nếu véc tơ pháp tuyến của đường thẳng () là n u ( ,−u ) thì
, còn c được xác định y x b = − ux
từ phương trình u x − u y + c = 0 c = u y − u x . Do đó, phương trình của đường thẳng () y M x M x M y M x − x y − y là M M
u x − u y + u y − u x = 0 u (x − x ) − u (y − y ) = 0 = . y x x M y M y M x M u u x y x − x −
Tóm lại, phương trình đường thẳng () tìm được là y y M M = . u u x y − −
(b) Để tham số hóa phương trình đường thẳng x x y y M M = , chúng ta đặt u u x y x − x − x − x = u t x = x + u t M y yM = = t (tR) M x M x (tR) . u u y − y = u t y = y + u t x y M y M y
Một đường thẳng hoàn toàn được xác định nếu biết hai điểm của đường thẳng đó. Ví dụ 2.
(a) Tìm phương trình của đường thẳng () đi qua điểm A(xA,yA) và điểm B(xB,yB) không trùng với điểm A.
(b) Tham số hóa phương trình đường thẳng () . Bài giải.
(a) Giả sử ax + by + c = 0 (a và b không đồng thời bằng không) là phương trình của đường thẳng ().
Dễ thấy rằng, véc tơ AB(x − x , y −y ) là véc tơ chỉ phương của đường thẳng (). Theo giả A A B B
thiết, điểm A không trùng với điểm B nên các số (x − x ) , (y − y ) không đồng thời bằng không, B A B A
do đó điều kiện đối với véc tơ chỉ phương là | AB | = (x −x ) 2 +(y − được thỏa mãn. B A B y )2 A 0
Bây giờ, nếu chúng ta coi điểm A là điểm M trong Ví dụ 1 và coi véc tơ chỉ phương AB là véc
tơ chỉ phương u trong Ví dụ 1 thì theo cách giải của Ví dụ 1 thì phương trình của đường thẳng () là
(y − y )x + (x − x )y + (y − y )x − (x − x )y = 0 A B B A B A A B A A x − x y − y A A
(y − y )(x − x ) + (x − x )(y − y ) = 0 = A B A B A A x − x y − y B A B A
Mặt khác, nếu chúng ta coi điểm B là điểm M trong Ví dụ 1 và coi véc tơ chỉ phương AB là véc
tơ chỉ phương u trong Ví dụ 1 thì theo cách giải của Ví dụ 1 thì phương trình của đường thẳng () là
(y − y )x + (x − x )y + (y − y )x − (x − x )y = 0 A B B A B A B B A B x − x − B y yB
(y − y )(x − x ) + (x − x )(y − y ) = 0 = A B B B A B x − x y − y B A B A 141 − − − − Phương trình x x y y x x y y A A = hoặc B B =
được gọi là phương trình chính tắc x − x y − y x − x y − y B A B A B A B A
của đường thẳng trong mặt phẳng. − −
(b) Để tham số hóa phương trình đường thẳng x x y y B B = , chúng ta đặt x − − B x A yB yA x − x y − y x −x =(x −x )t B B A x = x + (x − x )t B B = = t (tR) B B A (tR). x − − y − y = (y − y )t B B A y = y + B (y − B x A yB yA B yA )t − −
Để tham số hóa phương trình đường thẳng x x y y A A = , chúng ta đặt x − − B xA y B y A x − x y − y x − x = (x − x )t A B A x = x + (x − x )t A A = = t (tR) A B A (tR) . x − − y − y = (y − y )t A B A y = y + A (y − B x A yB yA B yA )t
(2) Theo tọa độ Descartes
Nếu phương trình của đường thẳng () được cho dưới dạng tổng quát ax + by + c = 0 với a và b
không đồng thời bằng không. a 0 - Trường hợp 1. b 0 x(t) = t a c
+ Cách 1. Đặt x = t at + by + c = 0 y = − t − a c (tR) là phương b b y(t) = − t − b b
trình tham số của đường thẳng () theo tham số t. b c b c x(t) = − t −
+ Cách 2. Đặt y = t ax + bt + c = 0 x = − t − a a (tR) là phương a a y(t) = t
trình tham số của đường thẳng () theo tham số t. a 0 - Trường hợp 2. a + x by + c = 0 x = c
– /a: ()//Oy hoặc trùng với Oy (khi c = 0). b = 0 a = 0 - Trường hợp 3. a + x by + c = 0 y = c
– /b: ()//Ox hoặc trùng với Ox (khi c = 0). b 0
P1.2. Tham số hóa phương trình của đường cong
Nếu đường cong là các đường cong bậc hai: (1) Đường tròn, (2) Ellipse (đường tròn là trường
hợp đặc biệt của đường ellipse khi hai bán trục của đường ellipse bằng nhau), (3) Parabol, (4)
Hypecbol; mà phương trình được cho trong hệ tọa độ Descartes (x,y), thì chúng ta tham số hóa
phương trình của nó như sau: (1) Đường tròn
Nếu phương trình của đường tròn có tâm (x0,y0) và bán kính R > 0, được cho dưới dạng chính tắc 2 2 2
(x − x ) + (y − y ) = R trong hệ tọa độ Descartes Oxy thì phương trình này được tham số h 0 óa 0
về dạng tọa độ cực như sau: 142 − − 2 2 2 x x 2 y y 2
Chúng ta có (x − x ) + (y − y ) = R 0 0 +
= 1, đẳng thức này cho phép 0 0 R R x − x0 = cost x(t) = x + R cost đặt R (0 t 2) 0
(0 t 2) là phương trình tham số của đường y − y y(t) =y + 0 R sin t 0 = sin t R
tròn có tâm (x0,y0) và bán kính R > 0 theo tham số t. (2) Đường ellipse
Nếu phương trình của đường ellipse có tâm (x0,y0) và các bán trục a > 0, b > 0, được cho dưới (x − x ) 2 (y − y )2 dạng chính tắc 0 0 +
= 1 trong hệ tọa độ Descartes Oxy thì phương trình này được a2 b2
tham số hóa về dạng tọa độ cực mở rộng như sau: x − x0 = cost (x − x ) 2 (y − y )2 a Chúng ta có 0 0 +
= 1, đẳng thức này cho phép đặt (0 t 2) a2 b2 y − y0 = sin t b x(t) = x + a cost 0
(0 t 2) là phương trình tham số của ellipse có tâm (x0,y0) và các bán y(t) = y + bsin t 0
trục a > 0, b > 0 theo tham số t. (3) Đường parabol
- Nếu phương trình của đường parabol được cho dưới dạng y = ax2 + bx + c (a 0) trong hệ tọa x(t) = t
độ Descartes Oxy thì phương trình tham số của nó là theo tham số tR. y(t) = at2 + bt + c
- Nếu phương trình của đường parabol được cho dưới dạng x = ay2 + by + c (a 0) trong hệ tọa x(t) = at 2 + bt + c
độ Descartes Oxy thì phương trình tham số của nó là theo tham số tR. y(t) = t (4) Đường hypecbol
Nếu phương trình của đường hypecbol được cho dưới dạng xy = a (a 0) trong hệ tọa độ x(t) = t a x(t) =
Descartes Oxy thì phương trình tham số của nó là a hoặc
t theo tham số tR. y(t) = t y(t) = t 2 2
Nếu phương trình của đường hypecbol được cho dưới dạng chính tắc x y − = 1 (a > 0, b > 0) a 2 b2
trong hệ tọa độ Descartes Oxy thì phương trình tham số của nó được xác định như sau: x 1 2 2 = 2 2 x y x y a cos t Chúng ta có −
= 1 =1 + , đẳng thức này cho phép đặt (0 t 2) 2 2 a b a b y = tan t b a x(t) = 2 1 vì 1 + tan t = , do đó
cost (0 t 2) là phương trình tham số của đường hypecbol cos2 t y(t) = btan t theo tham số t. 143
Nếu đường cong mà phương trình được cho trong hệ tọa độ cực (r,) dưới dạng r = r() (
) thì phương trình của đường cong trong hệ tọa độ Descartes được tham số hóa theo tham số như x = r cos
sau: Công thức biến đổi từ tọa độ cực (r,) sang tọa độ Descartes (x,y) là ( ) y = r sin x() = r() cos
( ) là phương trình tham số của đường cong theo tham số . y ( ) = r ( ) sin
Ví dụ 3. Cho r = 3cos (0 2) là phương trình của đường cong trong hệ tọa độ cực (r,).
(a) Tìm phương trình tham số của đường cong theo tham số trong hệ tọa độ Descartes. (b) Đường
cong này là đường cong gì? Bài giải. x = r co s
(a) Công thức biến đổi từ tọa độ cực (r,) sang tọa độ Descartes (x,y) là (0 y = r sin x() = r() cos = 3 ( cos) cos = 3cos2 2)
(0 2) là phương trình tham số của y ( ) = r ( ) sin = 3 ( co s ) sin = 3co s sin
đường cong theo tham số . 2 x () = 2 3 ( cos 2 ) = 4 9 cos (b) Chúng ta có 2 y () = 3 ( cossin 2 ) = 2 9 cos 2 sin x2
( ) + y2() = 9 cos4 + 9 cos2 sin2 = 9 cos2 = 3 ( 3 cos2 ) = x 3 ( ) 2 2 2 2 3 2 3
x + y = 3x x − + y = là phương trình chính tắc của đường tròn có tâm tại 2 2 3 3 điểm (x , y ) = và bán kính R = . 0 0 ,0 2 2
P2. Tham số hóa phương trình của đường trong không gian (R3)
P2.1. Tham số hóa phương trình của đường thẳng
Một đường thẳng hoàn toàn được xác định nếu biết một điểm và một véc tơ chỉ phương của
đường thẳng đó.
Đường thẳng () trong không gian đi qua điểm M0(x0,y0,z0) và có véc tơ chỉ phương x = x(t) = x + u t 0 x u u (
, u , u ) với điều kiện uxuyuz 0 có phương trình tham số là y = y(t) = y +u t (tR) . x y z 0 y z = ( z t) = z +u t 0 z x − x 0 x = x + u t t = 0 x u x y − y x − x y − y z − z Chúng ta có 0 0 0 0 y= y + u t t = = = 0 y
được gọi là phương trình u u u u y x y z z − z 0 z = z + u t t = 0 z uz
chính tắc của đường thẳng trong không gian.
Một đường thẳng hoàn toàn được xác định nếu biết hai điểm của đường thẳng đó.
Tìm phương trình tham số và phương trình chính tắc của đường thẳng () trong không gian đi
qua điểm A(xA,yA,zA) và điểm B(xB,yB,zB) không trùng với điểm A. Bài giải. 144
Dễ thấy rằng, véc tơ AB(x − x , y −y ,z − z ) là véc tơ chỉ phương của đường thẳng (). A A B B A B
Theo giả thiết, điểm A không trùng với điểm B nên các số x − x 0 , y − y 0, z − z 0 do B A B A B A
đó điều kiện đối với véc tơ chỉ phương là (x − x )(y − y ) z (
− z ) 0 được thỏa mãn. B A B A B A
Bây giờ, nếu chúng ta coi điểm A (hoặc điểm B) là điểm M0 và coi véc tơ chỉ phương AB là véc x = x(t) = x + (x − x )t A B A
tơ chỉ phương u thì phương trình tham số của đường thẳng () là y = y(t) = y + (y − y )t (tR) A B A z = z(t) = z + (z − z )t A B A x = x(t) = x + (x − x )t B B A
hoặc y= y(t)= y + (y − y )t (tR) . B B A z = z(t) = z + z ( − z )t B B A − − − − − −
Chúng ta cũng tìm được x x y y z z x x y y z z A A A = = hoặc B B B = = là x − x y − y z − z x − x y − y z − z B A B A B A B A B A B A
phương trình chính tắc của đường thẳng () trong không gian.
P2.2. Tham số hóa phương trình của đường cong
Đường cong trong không gian thường được cho dưới dạng là giao tuyến của hai mặt trong không
gian, có 3 trường hợp: (1) mặt phẳng giao với mặt phẳng, (2) mặt phẳng giao với mặt cong và (3) mặt cong giao với mặt cong).
Chúng ta lưu ý rằng: (1) Phương trình của giao tuyến L là nghiệm của hệ 2 phương trình, trong
đó mỗi phương trình tương ứng với phương trình của mỗi mặt. (2) Không có một phương pháp chung
nào để tham số hóa phương trình của đường cong được cho dưới dạng là giao tuyến của hai mặt trong
không gian, mà chúng ta chỉ căn cứ vào từng trường hợp cụ thể của các mặt để thực hiện mà thôi.
Ví dụ 4. Tìm phương trình tham số của đường L là giao tuyến của mặt nón 2 2 z = x + y với mặt phẳng z = y + 2. Bài giải. z = x2 + 2
Phương trình của đường L là nghiệm của hệ phương trình y z = y + 2 x(t) = t 2 2 2 x2 2 2 x + y = (y + 2) y = − 1 2 z = x + y = y + 2 t 4 y(t) =
−1 (tR) là phương z = y + 2 0 4 z = y + 2 t 2 ( z t) = +1 4
trình tham số của đường L.
Ví dụ 5. Tìm phương trình tham số của đường L là giao tuyến của mặt paraboloit 2 2 z = x + 4y với mặt trụ y = 2x2. Bài giải. z = 2 x + 2 4y
Phương trình của đường L là nghiệm của hệ phương trình y = 2 2x z = 2 t + 4 1 t 6
Đặt x = t và thay vào hệ phương trình trên chúng ta được y = 2 2t 145 x(t) = t y(t) = 2 2t
(tR) là phương trình tham số của đường L. ( z t) = 2 t + 4 16t
Ví dụ 6. Tìm phương trình tham số của đường L là giao tuyến của mặt cầu x2 + y2 + z2 = 4 với mặt phẳng y = x. Bài giải. x2 + y2 + z2 = 4
Phương trình của đường L là nghiệm của hệ phương trình y = x 2 2 2 2 x 2 2 z 2
Thay y = x vào phương trình của mặt cầu x + y +z = 4 2x +z = 4 + = 1, 2 2 x = cost x = 2 cost
đẳng thức này cho phép đặt 2 (0 t 2) (0 t 2) z z = 2sin t = sin t 2
Thay x = 2 cost vào phương trình y = x chúng ta được y = 2 cos t x(t) = 2 cost
y(t) = 2 cost (0 t 2) là phương trình tham số của đường L. ( z t) = 2sin t
Ví dụ 7. Tìm phương trình tham số của đường L là giao tuyến của mặt trụ x2 + 9y2 = 4 với mặt phẳng x + 2y + 3z = 5. Bài giải. x2 + 9y2 =
Phương trình của đường L là nghiệm của hệ phương trình 4 x + 2y + z 3 = 5 2 x 2 2 3y 2
Chúng ta có x + 9y = 4 + = 1 2 2 x = cost x = 2cost
Đẳng thức trên cho phép đặt 2 (0 t 2) 2 (0 t 2) 3y y = sin t = sin t 3 2 x = 2cost 4 Thay 2
vào phương trình x + 2y + z
3 = 5 chúng ta được 2 cost + sin t + z 3 = 5 y = sin t 3 3 5 2 4 z = − cost − sin t 3 3 9 x(t) = 2cost 2 y(t) = sin t
(0 t 2) là phương trình tham số của đường L. 3 5 2 4 ( z t) = − cost − sin t 3 3 9 146
Ví dụ 8. Tìm phương trình tham số của đường L là giao tuyến của mặt trụ x2 + y2 = 9 với mặt z = xy. Bài giải. x2 + y2 = 9
Phương trình của đường L là nghiệm của hệ phương trình z = xy 2 2 2 2 x y
Chúng ta có x + y = 9 + 1 = 3 3 x = cost x = 3cost
Đẳng thức này cho phép đặt 3 (0 t 2) (0 t 2) y y = 3sin t = sin t 3 x = 3cost Thay
vào phương trình z = xy chúng ta được z = 9 cost sin t y = 3sin t x(t) = 3cost y(t) = 3sin t
(0 t 2) là phương trình tham số của đường L. ( z t) = 9 cost sin t
Ví dụ 9. Tìm phương trình tham số của đường L là giao tuyến của mặt trụ 4x2 + y2 = 4 với mặt trụ z = x2. Bài giải. 2 4x + 2 y = 4
Phương trình của đường L là nghiệm của hệ phương trình z = 2 x 2 2 2 y 2
Chúng ta có 4x + y = 4 x + =1 2 x = cost x = cost
Đẳng thức này cho phép đặt y (0 t 2) (0 t 2) = sin t y = 2sin t 2
Thay x = cost vào phương trình z = x2 chúng ta được z = c os2t x(t) = 2cost
y(t) = 2sin t (0 t 2) là phương trình tham số của đường L. ( z t) = cos2 t Bài tập
3.1. Tính I = xyds L 2 2
(a) L là cung của đường ellipse x y +
= 1 nằm trong góc vuông thứ nhất (x 0, y 0). a2 b2
(b) L là các cạnh của hình chữ nhật OABC có tọa độ các đỉnh là O(0,0), A(4,0), B(4,2) và C(0,2).
(c) L là các cạnh của hình vuông |x| + |y| = a (a > 0). 3.2. Tính I = 2 (x + 2 y )ds L
(a) L là đoạn thẳng nối điểm O(0,0) với điểm A(2,4).
(b) L là các cạnh của OAB có tọa độ các đỉnh là O(0,0), A(1,1) và B(–1,1). 147
(c) L là đường tròn x2 + y2 = ax (a > 0). 3.3. Tính I = 2 x + 2
y ds với C là đường cong có phương trình trong hệ tọa độ cực (r,) là r = 4sin C
(0 ) . Vẽ đồ thị của đường cong C.
3.4. Tính các tích phân sau đây x = t (a) I = 2yds , cung L c
ó phương trình tham số y = t 2 2 với 0 ≤ t ≤ 1. L z = t 3 3 x = a cost (b) I = 2 (x + 2 y + 2
z )ds , cung L là đường xoắn ốc có phương trình tham số y = a sin t với L z = bt a 0 và 0 ≤ t ≤ 2. b 0 (c) I = 2 ( 5 x − 2 y ) + 24xy + (z − 2 ) 1 + d
4 s , L là giao tuyến của mặt trụ x2 + y2 = 4 với mặt L phẳng 2x – 3y + z = 1. (d) I = 2
x ds , L là giao tuyến của mặt cầu x2 + y2 + z2 2
= a (a > 0) với mặt phẳng x + y + z = 0. L
3.5. Tính khối lượng của sợi dây có phương trình a x x −
(a) là đường cong phẳng y = a e + a e
với 0 x a (a > 0), biết rằng khối lượng riêng của 2
đường cong tại điểm (x,y) là f (x,y) =1 y . x = a cost
(b) là đường xoắn ốc y = a sin t với 0 t 2, a = b = 1, biết rằng khối lượng riêng của sợi dây z = bt
tại điểm (x,y,z) là f (x, , y ) z = x2 + y2 + z2 . x2
3.6. Tính độ dài cung có phương trình y = − ln x (1 x e). 4
3.7. Tính các tích phân đường loại hai (a) I = (x − 2 y) dx + (x + 2 )
y dy trên L là các đoạn thẳng từ A đến B và từ B đến C với A(0,0), L B(2,2) và C(4,0). (b) I = ydx − (y + 2
x )dy trên cung phẳng L là cung của đường parabol y = 2x – x2 nằm phía L
trên trục Ox theo chiều kim đồng hồ. (c) I = 2 (x + 2 y )dx + 2 (x − 2
y )dy trên L là đường y = 1 – 1
– x (0 x 2) theo chiều tăng L của x. x(t) = a 1 ( − sin t) (d) I = (2a − y d
) x + xdy trên L là đường
với 0 t 2 và a > 0. y(t) = a 1 ( − cost) L x2 y2 (e) I = (x + y)dx +(x − )
y dy trên L là đường ellipse + =1. a 2 b2 + L 148 2 (x − 2 y )dy − 2xydx (f) I =
trên cung AB là nửa đường tròn x2 + y2 = 2y về phía x 0 nối từ 2 x + 2 y AB
điểm A(0,0) đến điểm B(0,2).
3.8. Tính tích phân đường loại hai I = (xy − d ) 1 x + 2
x ydy trên đường nối từ điểm A(1,0) đến điểm AB 2
B(0,2) theo chiều dương trong 3 trường hợp 2 y
(a) 2x + y = 2; (b) 4x + y2 = 4; (c) x + =1. 4
3.9. Tính trực tiếp các tích phân đường loại hai sau đây, sau đó kiểm tra kết quả bằng cách tính qua công thức Green (a) I = ( x 2 y − 2 x d ) x +(x + 2
y )dy trên L là đường cong kín tạo bởi hai cung parabol y = x2, x = + L y2. (b) I = 3 (2x − 3 y )dx + 3 (x + 3
y )dy trên L là đường tròn x2 + y2 = 1. + L (c) I = 2 (x + 2 y )dx + 2 (x − 2 y d
) y trên cạnh AB (từ điểm A đến điểm B), cạnh BC (từ điểm B ABCA
đến điểm C) và cạnh CA (từ điểm C đến điểm A) của ABC với A(0,0), B(1,0) và C(0,1).
3.10. Tính các tích phân đường loại hai x y
(a) I = xy + ydy − xyx + dx trên L là ba cạnh của ABC với A(-1,0), B(1,-2) và + 2 2 L C(1,2). (b) I = (xy + x + ) y dx + (xy + x − )
y dy trên L là đường tròn x2 + y2 = ax (a > 0). + L (c) I = 2 ( 2 x + 2 y )dx + (4y + )
3 xdy trên cạnh OA (từ điểm O đến điểm A ) và cạnh AB (từ OAB
điểm A đến điểm B) của OAB với O(0,0), A(1,1) và B(0,2). x y 2 x 3 − 2 2 y 3y − 2 x
3.11. Cho tích phân đường loại hai I = + dx + dy y x x y L
(a) Tích phân này có phụ thuộc vào đường lấy tích phân không? x = t + cos2 t
(b) Tính tích phân này trên cung AB được cho dưới dạng tham số 0 t y =1 +sin2 t 2
theo chiều tăng của tham số ứng (t = 0 ứng với điểm đầu A và t =
ứng với điểm cuối B). 2 (mx − y)dx + (nx + y)dy
3.12. Tìm các tham số m, n để tích phân đường loại hai I = không phụ 2 x + 2 y AB
thuộc vào dạng của đường lấy tích phân. 3.13.
Tìm các tham số m, n để tích phân đường loại hai
I = [(x +a)(y + b) 2 +(n −m)by + may d ] x +[(x +a) ( 2 y +b) +2(n − ) 1 ax d ] y = 0 với mọi đường L cong kín L và
với mọi giá trị của a và b. (x− ) y dx + (x+ y)dy
3.14. Tìm tham số m để biểu thức
là vi phân toàn phần cấp 1 của một hàm số 2 2 m (x + y ) u(x,y) nào đấy.
3.15. Chứng minh rằng biểu thức 6xeydx + (3x2 + y + 1)eydy là vi phân toàn phần cấp 1 của một hàm
số u(x,y) nào đó.Tìm hàm số u(x,y).
3.16. Xác định hàm số u(x,y) thỏa mãn du(x,y) = 2xy3dx + (3x2y2 + cosy)dy. 149
3.17. Các đề thi về tích phân đường
(a) Tính tích phân đường (xy + )
y dx + xydy với C là đường tròn x2 + y2 = 1.(năm học 2017- + C 2018)
(b) Cho tích phân đường (y +sin x)dx −(x + y
e )dy : (b1) Tính I nếu L là đoạn thẳng AB với L A(1,1) và B(1, 1) – ; (b 2
2) Sử dụng (b1) và công thức Green để tính I nếu L là nửa đường tròn (C) x2 + y = 2x (x 1), c -
hiều của (C) là ngược chiều kim đồng hồ.(năm học 2018 2019)
(c) Tính tích phân đường 2
y dx + xydy với C là đường biên kín định hướng dương của nửa C
hình khuyên bên trên trục Ox nằm giữa hai đường tròn x2 + y2 = 1, x2 + y2 = 2.(năm học 2019-2020)
(d) Cho C là chu tuyến định hướng dương của ABC với A(0,0), B(a,a) và C(0,2a) (a > 0). Tính tích phân đường ( x 2 y − 3 x d ) x + (x + 3
y )dy theo hai cách: tính trực tiếp và sử dụng công thức C Green.(năm học 2020-2021)
(e) Tính tích phân đường 4 ( x + 1+ y)dx + 4 ( y + 1+ x xe d
) yvới C là biên của tam giác, đi từ C
điểm (0,0) đến điểm (1,1), đi tiếp đến điểm (2,0) và trở về điểm (0,0).(năm học 2021-2022)
3.18. Tính các tích phân mặt loại một (a) I = 2 z(x + 2
y )dS , S là phần của mặt cầu x2 + y2 + z2 = a2 (a
> 0) ứng với x 0 và y 0. S
(b) I = (2x + 2y+ z− )
1 dS , S là phần của mặt phẳng x + y + z = 1 nằm trong góc vuông phần S tám thứ nhất.
(c) I = yzdS, S là phần của mặt phẳng 2x – 2y – z + 2 = 0 thỏa mãn điều kiện 0 x 1 và 0 S y x.
3.19. Tính các tích phân mặt loại hai (a) I = 2 ( z x + 2
y )dxdy , S là mặt phía ngoài của nửa mặt cầu x2 + y2 + z2 = 1 (z 0) có véc tơ S
pháp tuyến hướng lên phía trên. y 2 (b) I = ydxdz + 2
z dxdy , S là mặt phía ngoài của mặt ellipsoit x2 + + z2 = 1 nằm trong góc 4 S
vuông phần tám thứ nhất và có véc tơ pháp tuyến hướng lên phía trên.
(c) I = xdydz +dxdz −dxdy , S là mặt phẳng (ABC) với A(1,0,0), B(0,2,0), C(0,0,3) và có véc S
tơ pháp tuyến hướng lên phía trên.
3.20. Tính diện tích miền phẳng bằng tích phân đường lấy theo chu tuyến kín của miền.
(a) Miền phẳng là tứ giác giới hạn bởi 4 đường thẳng x = y, x = 2y, x + y = 2, x + 3y = 2.
(b) Miền phẳng là tứ giác cong giới hạn bởi 4 đường cong x2 = 2y, x2 = 4y, y2 = x, y2 = 3x. 2 x 3.21. Tính I = dS , S là phần mặt nón 2 2
z = x + y nằm dưới mặt phẳng z = 2.(đề thi năm học 3 z S 2019-2020) 150




