

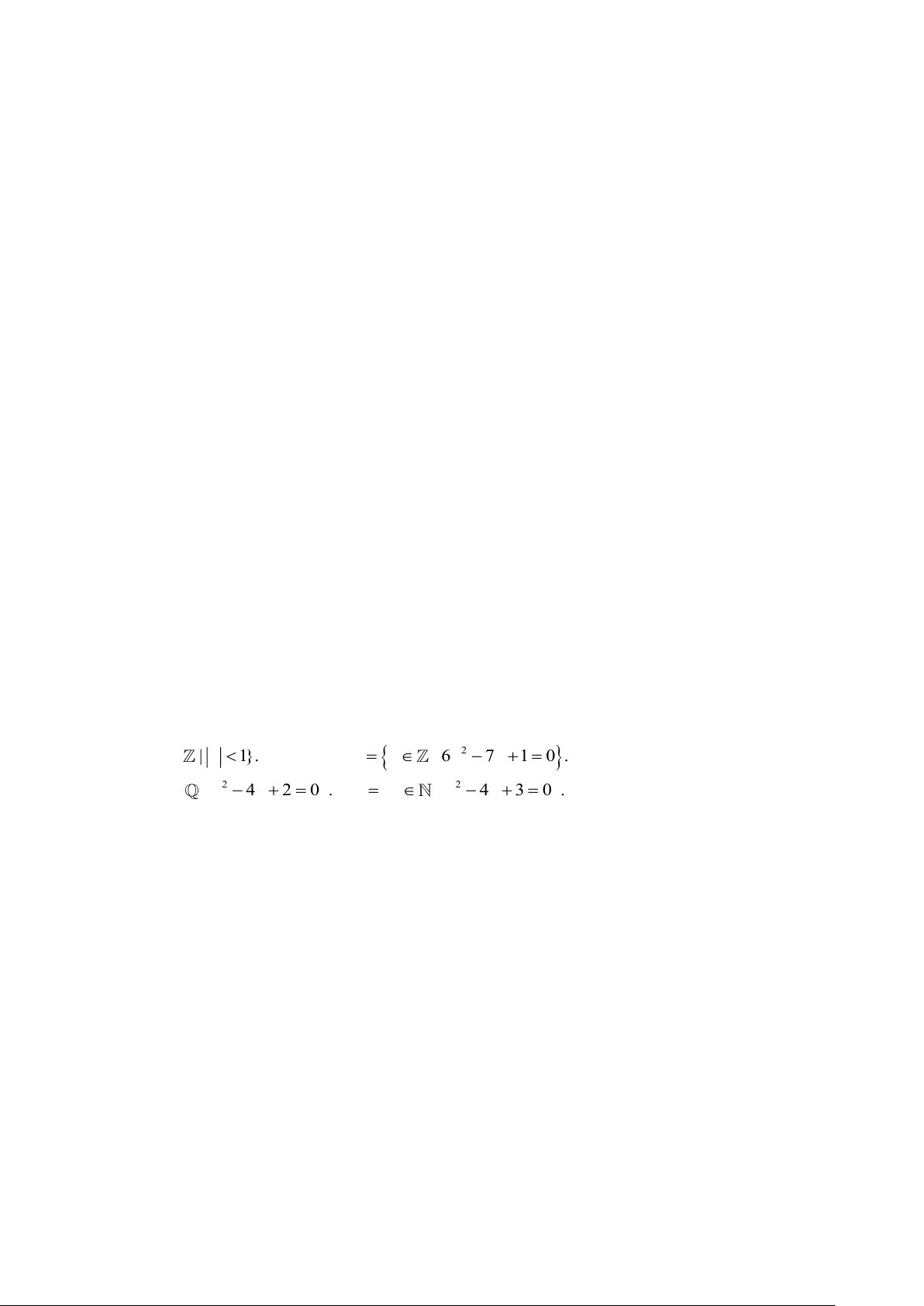












Preview text:
CHUYÊN ĐỀ 1: ĐẠI SỐ TỔ HỢP BÀI 1. TẬP HỢP
YÊU CẦU CẦN ĐẠT
- Nhận biết các khái niệm cơ bản về tập hợp.
- Thực hiện các phép toán trên tập hợp và vận dụng giải một số bài toán có nội dung thực tế. -
Sử dụng biểu đồ Ven để biểu diễn tập hợp và các phép toán trên tập hợp.
I. KHÁI NIỆM TẬP HỢP 1. Tập hợp
Trong toán học, ta thường gặp các cụm từ: Tập hợp các số tự nhiên, tập hợp các điểm…Trong
đời sống sinh hoạt hàng ngày, ta hay nói: Tập hợp các em học sinh trong một lớp, tập hợp các nước
trong một khối liên hiệp, v.v….
Khái niệm tập hợp là một khái niệm cơ bản của toán học, không được định nghĩa mà chỉ
được mô tả để nhằm giải thích nó.
Người ta thường ký hiệu tập hợp bằng các chữ cái in hoa ,
A B,C … Các phần tử của tập hợp
được ký hiệu bởi các chữ cái in thường a, , b c
Nếu a là một phần tử của tập hợp ,
A ta viết a A (đọc là a thuộc A ). Nếu a không phải
là một phần tử của tập hợp ,
A ta viết a A (đọc là a không thuộc A ).
Số phần tử của tập hữu hạn A được kí hiệu là n( A).
* Chúng ta có thể mô tả tập hợp bằng một trong hai cách sau
Cách 1: Liệt kê các phần tử của tập hợp
Cách 2: Chỉ ra tính chất đặc trưng cho các phần tử của tập hợp
Chú ý: a S : Phần tử a thuộc tập hợp S
a S : Phần tử a không thuộc tập hợp S
Tập hợp không chứa phần tử nào được gọi là tập rỗng, kí hiệu
Ví dụ 1. Viết các tập hợp sau dưới dạng liệt kê các phần tử: A = 2
x | 2x − 3x +1 = 0 . B = 2 x x − 3 2 x . . .
C = x | x là ước của 12 .
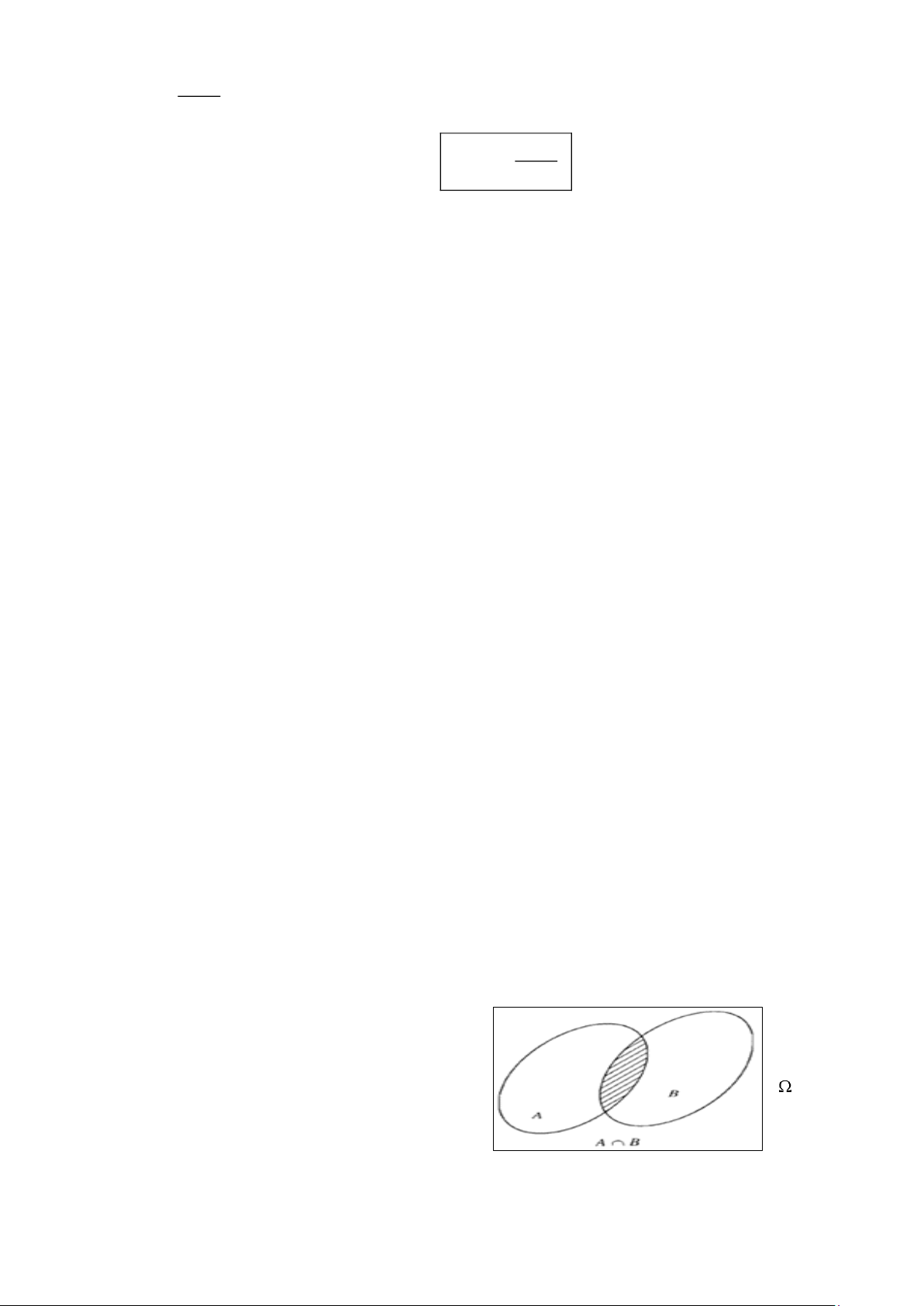
* Biểu đồ Ven: Người ta thường minh họa một tập hợp bằng một hình phẳng được bao quanh bởi
một đường kín gọi là biểu đồ Ven. Mỗi một điểm nằm bên trong đường cong biểu diễn một phần tử
của tập hợp, mỗi điểm nằm bên ngoài đường cong biểu diễn một phần tử không thuộc tập hợp. 2. Tập hợp con 1
Nếu mọi phần tử của tập hợp T đều là phần tử thuộc
tập hợp S thì ta nói T là tập hợp con của tập hợp S .
Kí hiệu: T S xT xS Chú ý:
- Tập rỗng là tập con của mọi tập hợp.
- Trong toán học ta có mối quan hệ giữa các tập hợp số như sau:
Ví dụ 2. Cho tập hợp A = 1;2;
3 . Hãy liệt kê tất cả các tập con của tập hợp A
3. Hai tập hợp bằng nhau
Hai tập hợp T và S được gọi là hai tập hợp bằng nhau nếu mỗi phần tử của T cũng là phần
tử của S và ngược lại. Kí hiệu: T = S . T S
Như vậy ta có T = S S T
Ví dụ 3. Cho hai tập hợp A = x |0 x 3 và B = 2
x | x − 3x + 2 = 0 . Chứng tỏ hai tập
hợp A và tập hợp B bằng nhau
II. CÁC PHÉP TOÁN TRÊN TẬP HỢP
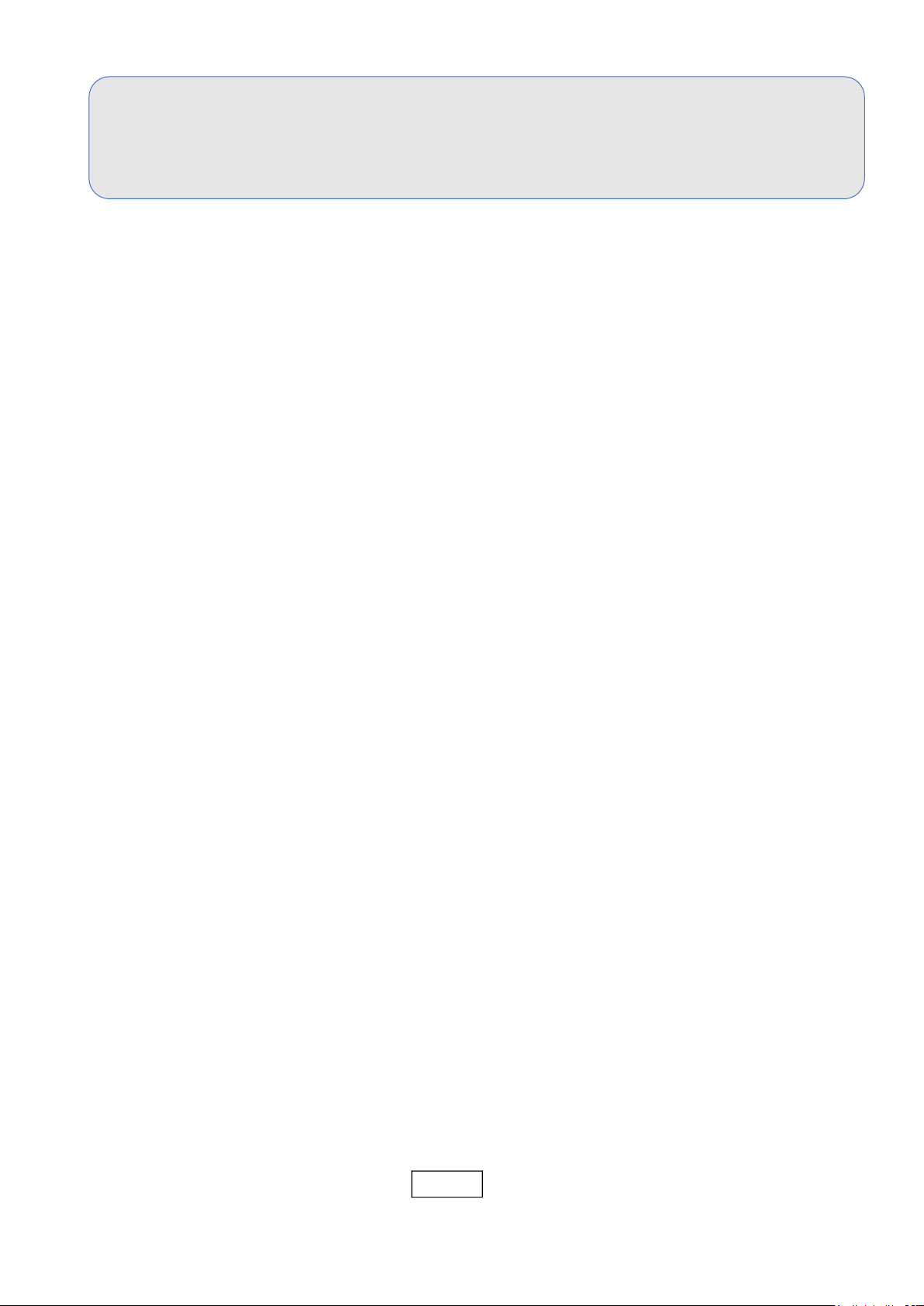
1. Giao của hai tập hợp
Tập hợp gồm các phần tử thuộc cả hai tập hợp T và S gọi là
giao của hai tập hợp T và S
Kí hiệu: T S = x | xS và xT
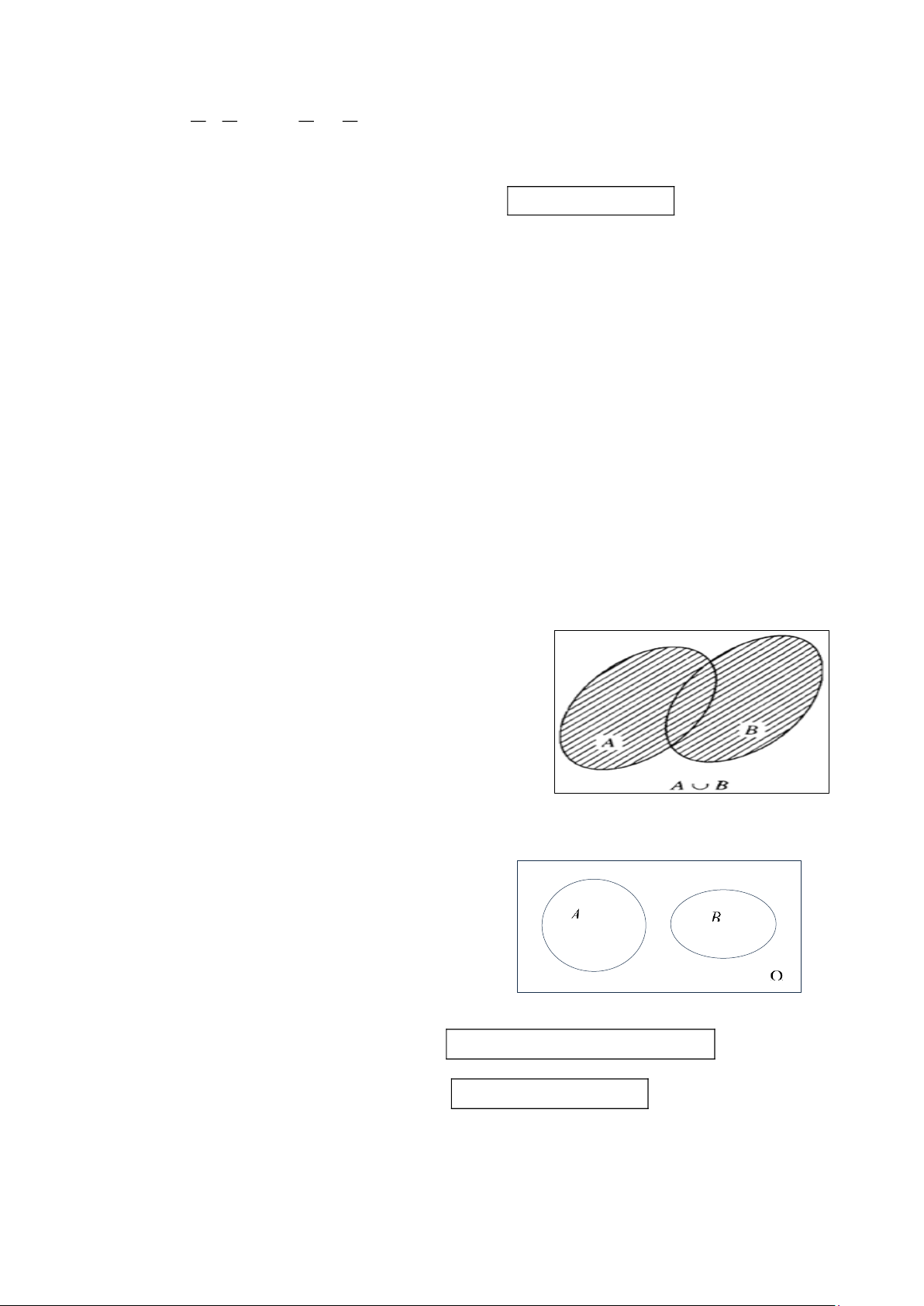
2. Hợp của hai tập hợp
Tập hợp gồm các phần tử thuộc tập hợp S hoặc thuộc tập hợp
T gọi là hợp của hai tập hợp S và T .
Kí hiệu S T = { x | x S hoặc xT }
3. Hiệu của hai tập hợp
Hiệu của hai tập hợp S và T là tập hợp gồm các phần tử
thuộc S nhưng không thuộc T . Kí hiệu S \T
Chú ý: Nếu T S thì S \T được gọi là phần bù của T trong S . Kí hiệu C T S 2
Ví dụ 4. Cho các tập hợp A = 1;2;3;4;5; 6 , B = 3;6; 9 .
Xác định các tập hợp A B, A B, A \ B .
Ví dụ 5. Cho các tập hợp A = ( 2 − ;3), B = 1 − ;+) .
Xác định các tập hợp A B, A B, A \ B,C B .
Ví dụ 6. Cho các tập hợp A = (− ; m − )
1 , B = 1;+) . Tìm tất cả giá trị của m để AB = .
BÀI TẬP THỰC HÀNH
PHẦN 1 . Câu trắc nghiệm nhiều phương án lựa chọn 1
Câu 1. Cho các tập hợp A = 2
x 2x + 3x +1 = 0 ; B = − 1 ;C = 1
− ;− . Khẳng định nào 2 dưới đây đúng?
A. C B .
B. A = B .
C. A = C . D. A =
Câu 2. Cho A = 1;3;
5 . Tập hợp nào sau đây là tập con của tập A ? A. 1; 2 . B. 0;1; 5 . C. 1; 3 . D. 1;3;5; 6 .
Câu 3. Liệt kê các phần tử của tập hợp A = x x 5
A. A = 1;2;3;4; 5 .
B. A = 1;2;3; 4 .
C. A = 0;1;2;3;4; 5 .
D. A = 0;1;2;3; 4
Câu 4. Cho A = a;b;c và B = a;c;d ;
e . Hãy chọn khẳng định đúng?
A. A B = a; c .
B. A B = a;b;c;d ; e .
C. A B = b .
D. A B = d ; e .
Câu 5. Cho hai tập hợp A = 2;4;6;8 , B = 4;8;9;
0 . Xét các khẳng định:
1) A B = 4; 8 .
2) A B = 0;2;4;6;8; 9 .
3) B \ A = 2; 6 .
Có bao nhiêu khẳng định đúng trong ba khẳng định trên? A. 2 . B. 3. C. 0 . D. 1.
Câu 6. Cho tập hợp A = a;b;c;d. Tập A có mấy tập con? A. 16. B. 15. C. 12 . D. 10.
Câu 7. Cho hai tập hợp A = 5;7;
9 và B = 2;3;5;8;
9 . Tìm tâp hợp A B . 3
A. A B = 2;3; 8 .
B. A B = 5; 9 .
C. A B = 5;7;
9 . D. A B = 7 .
Câu 8. Cho hai tập hợp A = (−
;5 và B = (0;+) . Tập hợp A B là A. (0; 5 . B. 0;5) . C. (0;5) . D. (− ; +) .
Câu 9. Cho hai tập hợp A = (−
;5 và B = (0;+) . Tập hợp A B là A. (− ; +) . B. (0; 5 . C. (0;5) . D. 0;5 .
Câu 10. Cho hai tập hợp A = 2 − ;
3 , B = (1;+ ) . Tập hợp A\ B là A. 2 − ; 1 . B. ( 2 − ;1 . C. ( 2 − ;− ) 1 . D. 2 − ) ;1 .
Câu 11. Cho hai tập hợp A = ( 1
− ;+), B = (−
;3 . Hãy chọn khẳng định đúng.
A. A \ B = (3;+) .
B. A \ B = ( 1 − ;3) .
C. A \ B = 3;+) . D. A \ B = (− ; 1 .
Câu 12. Cho hai tập hợp A = ( 4
− ;3) và B = (m−7;m) . Tìm tất cả số thực m để B A ? A. m 3 . B. m 3 . C. m = 3. D. m 3.
PHẦN 2: Câu trắc nghiệm đúng sai
Câu 13. Cho hai tập hợp A = {1;3;5}, B = {1;2;3} .
a) A B = {1}
b) A B = {1;2;3;5} c) A \ B = {5} d) B \ A = {3}
Câu 14. Cho các tập hợp
A = {x | x 1}. B = 2
x ∣ 6x − 7x +1 = 0 . C = 2
x ∣ x − 4x + 2 = 0 . D = 2
x ∣ x − 4x + 3 = 0 .
a) Tập hợp A có 2 phần tử
b) Tập hợp B có 1 phần tử
c) Tập hợp C có 3 phần tử
d) Tập hợp D có 2 phần tử
Câu 15. Một lớp có 7 học sinh giỏi Toán, 5 học sinh giỏi Lý, 6 học sinh giỏi Hóa, 2 học sinh chỉ
giỏi Toán và Lý, 3 học sinh chỉ giỏi Toán và Hóa, 1 học sinh chỉ giỏi cả Lý và Hóa, 1
học sinh giỏi cả 3 môn Toán, Lý, Hóa. Vậy
a) Số học sinh chỉ giỏi môn Toán là 1 học sinh
b) Số học sinh chỉ giỏi môn Lý là 1 học sinh
c) Số học sinh chỉ giỏi môn Hóa là 2 học sinh
d) Số học sinh giỏi ít nhất một môn (Toán, Lý, Hóa) là 10 học sinh.
Câu 16. Xác định tính đúng, sai của các mệnh đề sau a) A = [3;9] \ (− ; 7) = [7;9] b) B = [ 1 − ;+) ( 7 − ;9] = [ 1 − ;9]
c) C = [1;6][4; +) = [1; +) 4 d) D = \ [ 1 − ;+) = (− ; 1 − )
PHẦN 3. Câu trả trắc nghiệm trả lời ngắn
Câu 17. Cho hai tập hợp A = [ 4
− ;1], B = [−3;m] . Có bao nhiêu giá trị nguyên dương của m để
A B = A Đáp số: 1
Câu 18. Cho các tập hợp A = [m −1;2m +1) và B = (−2;3) . Có bao nhiêu giá trị nguyên của m
để A B . Đáp số: 2
Câu 19. Cho hai tập hợp: A = [m − 3;m + 2], B = ( 3
− ;5) với m . Có bao nhiêu giá trị nguyên
của m để A B khác tập rỗng Đáp số: 12
Câu 20. Cho các tập hợp khác rỗng A = (− ;
m) và B = 2m − 2;2m + 2. Tìm giá trị nguyên nhỏ
nhất để C A B R Đáp số: 2 −
Câu 21. Một lớp học có 25 học sinh chơi bóng đá, 23 học sinh chơi bóng bàn, 14 học sinh chơi
cả bóng đá và bóng bàn, 6 học sinh không chơi môn nào. Tìm số học sinh chỉ chơi một môn thể thao Đáp số: 20
Câu 22. Lớp 10A có 10 học sinh giỏi Toán, 10 học sinh giỏi Lý, 11 học sinh giỏi Hóa, 6 học sinh
giỏi cả Toán và Lý, 5 học sinh giỏi cả Hóa và Lý, 4 học sinh giỏi cả Toán và Hóa, 3 học
sinh giỏi cả ba môn Toán, Lý, Hóa. Hỏi số học sinh giỏi ít nhất một trong ba môn (Toán,
Lý, Hóa) của lớp 10A là bao nhiêu? Đáp số: 19 5
BÀI 2. ĐẠI SỐ TỔ HỢP
YÊU CẦU CẦN ĐẠT
- Vận dụng quy tắc cộng, quy tắc nhân để tính số cách thực hiện một công việc hoặc đếm số phần
tử của m .ộ t tập hợp.
- Tính số hoán vị, chỉnh hợp, tổ hợp. I. QUY TẮC ĐẾM
1. Quy tắc cộng
Một công việc được hoàn thành bởi một trong hai hành động. Nếu hành động thứ nhất có m
cách thực hiện, hành động thứ hai có n cách thực hiện không trùng với bất kỳ cách nào của hành
động thứ nhất thì công việc đó có m + n cách thực hiện. Chú ý
- Quy tắc cộng có thể mở rộng cho nhiều hành động.
- Áp dụng quy tắc cộng để đếm số phần tử của hợp các tập hợp hữu hạn không giao nhau như sau: Nếu các tập hợp
A , A ,... A đôi một rời nhau, thì 1 2 n
n( A A ... A = n A + n A + ... + n A 1 2 n ) ( 1) ( 2) ( n) 2. Quy tắc nhân
Một công việc được hoàn thành bởi hai hành động liên tiếp. Nếu có m cách thực hiện hành
động thứ nhất và ứng với mỗi cách đó có n cách thực hiện hành động thứ hai thì có . m n cách hoàn thành công việc đó.
Chú ý: Quy tắc nhân có thể mở rộng cho nhiều hành động liên tiếp.
Ví dụ 1. Từ một hộp có 5 quả cầu màu đỏ, 7 quả cầu màu xanh và 8 quả cầu màu vàng, có bao nhiêu cách chọn ra: a) 1 quả cầu.
b) 3 quả cầu với ba màu khác nhau . c) 2 quả cầu khác màu .
Ví dụ 2. Cho các số 1, 2, 3, 4, 5. Từ các số này có thể lập được bao nhiêu số tự nhiên: a) có 4 chữ số.
b) có 4 chữ số khác nhau.
c) là số chẵn có 4 chữ số khác nhau.
II. HOÁN VỊ – CHỈNH HỢP – TỔ HỢP 1. Hoán vị
a. Định nghĩa
Cho tập A gồm n phần tử (n )
1 . Mỗi kết quả của sự sắp xếp thứ tự n phần tử của tập hợp
A được gọi là một hoán vị của n phần tử đó. b. Công thức
Số các hoán vị của n phần tử được kí hiệu là Pn và ta có
P = n! (n ) 1 n 6
Chú ý: Hai hoán vị của n phần tử chỉ khác nhau ở thứ tự sắp xếp.
Ví dụ 3. Cho 6 học sinh gồm 3 nam và 3 nữ trong đó có 2 bạn ,
A B . Hỏi có bao nhiêu cách xếp 6
học sinh ngồi vào một ghế dài sao cho:
a) Các học sinh ngồi tuỳ ý. b) Hai bạn ,
A B ngồi ở 2 đầu ghế. c) Hai bạn ,
A B ngồi cạnh nhau.
d) Các bạn nam và nữ ngồi xen kẽ. 2. Chỉnh hợp a. Định nghĩa
Cho tập A gồm n phần tử (n )
1 . Kết quả của việc lấy k phần tử khác nhau từ n phần tử
của tập A và sắp xếp chúng theo một thứ tự nào đó được gọi là một chỉnh hợp chập k của n phần tử đã cho. b. Công thức
Số các chỉnh hợp chập k của n phần tử được ký hiệu là k An và ta có k n! A =
k n k n n ( n − k ) (1 ; , ) ! Chú ý:
- Hai chỉnh hợp được gọi là khác nhau nếu có ít nhất 1 phần tử khác nhau hoặc các phần tử
giống nhau nhưng thứ tự khác nhau.
- Hoán vị là sắp xếp tất cả các phần tử của tập hợp, còn chỉnh hợp là chọn ra một số phần tử
và sắp xếp chúng theo thứ tự. Mỗi hoán vị của n phần tử cũng chính là trường hợp chọn ra tất cả n
phần tử và sắp xếp chúng, tức là trong trường hợp này nó là một chỉnh hợp chập n của n phần tử, do đó n P = A n n
Ví dụ 4. Từ các chữ số 0, 1, 2, 3, 4, 5, 6 có thể lập được bao nhiêu số tự nhiên:
a) có 4 chữ số khác nhau.
b) là số chẵn có 4 chữ số khác nhau.
c) chia hết cho 5 và có 4 chữ số khác nhau.
d) có 4 chữ số khác nhau sao cho luôn có mặt chữ số 0 . 3. Tổ hợp
a. Định nghĩa
Cho tập A gồm n phần tử (n )
1 . Một tập con gồm k phần tử của A được gọi là một tổ
hợp chập k của n phần tử đã cho. b. Công thức
Số các tổ hợp chập k của n phần tử được ký hiệu là k Cn và ta có k n! C =
k n k n n k ( ! n − k ) (1 ; , ) ! c. Tính chất +) k n−k C = C k n n n (0 ) 7 k 1 +) − k k C + C =C
1 k n n 1 − n 1 − n ( ) Chú ý
- Hai tổ hợp được gọi là khác nhau nếu chúng có chứa ít nhất 1 phần tử khác nhau.
- Chỉnh hợp và tổ hợp có điểm giống nhau là đều chọn một số phần tử trong một tập hợp,
nhưng khác nhau ở chỗ, chỉnh hợp là chọn có xếp thứ tự, còn tổ hợp là chọn không xếp thứ tự. 0 0!=1; C =1 - Quy ước: n
Ví dụ 5. Một tổ học sinh có 6 bạn nam và 4 bạn nữ, chọn ra đồng thời 4 bạn. Hỏi có bao nhiêu cách để:
a) Chọn được 4 bạn nữ.
b) Chọn được 3 bạn nữ và 1 bạn nam.
c) Chọn được ít nhất 1 bạn nam.
Ví dụ 6. Một hộp có 3 viên bi xanh, 4 viên bi đỏ và 5 viên bi vàng. Hỏi có bao nhiêu cách chọn ra 4 viên bi: a) Có đúng 1 màu. b) Có 2 màu. c) Có đủ cả ba màu.
BÀI TẬP THỰC HÀNH
PHẦN 1. Câu trắc nghiệm nhiều phương án lựa chọn
Câu 1. Với k và n là hai số nguyên dương tùy ý thỏa mãn 1 k n . Mệnh đề nào dưới đây đúng? n k ! A. C = . B. n k ! n C = . k ( ! n − k )! n k ! n k n − k k (! )! k ! C. C = . D. C = . n (n−k)! n n!
Câu 2. Số chỉnh hợp chập 4 của 7 phần tử bằng? A. 24 . B. 720 . C. 840 . D. 35.
Câu 3. Cho tập hợp M có 30 phần tử. Số tập con gồm 5 phần tử của M là A. 5 A C 30 . B. 5 30 . C. 30 5 . D. 530 .
Câu 4. Có bao nhiêu cách chọn hai học sinh từ một nhóm gồm 41 học sinh? A. 2 A C 41 . B. 2 41 . C. 41 2 . D. 241 .
Câu 5. Số cách sắp xếp 4 bạn học sinh vào 4 ghế xếp thành một hàng ngang là A. 4 4 . B. 4!. C. 1. D. 4
Câu 6. Một đoàn công tác gồm có 5 người. Có bao nhiêu cách chọn ra 2 trong số 5 người này
để phân công làm trưởng đoàn và phó đoàn công tác? A. 16. B. 25 . C. 10. D. 20 .
Câu 7. Từ một nhóm có 10 học sinh nam và 8 học sinh nữ, có bao nhiêu cách chọn ra 5 học sinh
trong đó có đúng 3 học sinh nam? 8 A. 3 2 C C . B. 3 2 A A . C. 3 2 C + C . D. 3 C . 10 8 10 8 10 8 10
Câu 8. Một nhóm có 6 học sinh gồm 4 nam và 2 nữ. Hỏi có bao nhiêu cách chọn ra 3 học sinh
trong đó có cả nam và nữ? A. 6 . B. 16. C. 20 . D. 32.
Câu 9. Một hộp chứa 20 quả cầu khác nhau trong đó có 12 quả đỏ, 8 quả xanh. Hỏi có bao nhiêu
cách lấy được 3 quả trong đó có ít nhất 1 quả xanh? A. 600 . B. 220 . C. 900. D. 920.
Câu 10. Cho tập hợp A = 0,1,2,3,
4 . Có thể lập được bao nhiêu số tự nhiên có 5 chữ số khác nhau và là số chẵn? A. 60 . B. 96. C. 120. D. 72 .
Câu 11. Số véctơ khác 0 có điểm đầu, điểm cuối là 2 trong 6 đỉnh của lục giác ABCDEF là A. P C A 6 B. 26 C. 26 D. 36
Câu 12. Nếu tất cả các đường chéo của đa giác đều 12 cạnh được vẽ thì số đường chéo là A. 121 B. 66 C. 132 D. 54
PHẦN 2: Câu trắc nghiệm đúng sai
Câu 13. Trên bàn có 8 chiếc bút chì khác nhau, 6 chiếc bút bi khác nhau và 10 quyển vở khác nhau. Khi đó:
a) Nếu chọn một cây bút chì có: 8 cách.
b) Có 16 cách chọn ra một cây bút bi và một quyển vở
c) Nếu chọn một quyển vở và 2 chiếc bút chì có 80 cách.
d) Có 480 cách chọn một đồ vật duy nhất hoặc một cây bút chì hoặc một cây bút bi hoặc một quyển vở.
Câu 14. Một hộp có 6 viên bi xanh, 5 viên bi đỏ và 4 viên bi vàng, chọn ngẫu nhiên 4 viên bi, khi đó:
a) Chọn 2 bi xanh, 1 bi đỏ và 1 bi vàng có: 300 cách.
b) Chọn 1 bi xanh, 2 bi đỏ và 1 bi vàng có: 120 cách.
c) Chọn 1 bi xanh, 1 bi đỏ và 2 bi vàng có: 180 cách.
d) Có 600 cách chọn ra 4 viên bi từ hộp sao cho có đủ cả ba màu
Câu 15. Cho tập hợp A gồm 20 số nguyên dương không vượt quá 20.
a) Số cách chọn 4 số nguyên dương từ tập A là 420 A .
b) Tích của 4 số nguyên dương là số lẻ khi và chỉ khi cả 4 số là số lẻ.
c) Tập hợp A có 10 số lẻ.
d) Số cách chọn ra 4 số từ tập A sao cho tích của 4 số đó là số chẵn là 4 4 − 2 A 0 1 A 0.
Câu 16. Cho tập hợp A gồm tất cả các chữ số là 0,1,2,3,4,5,6,7,8,9.
a) Tập hợp A có 10 phần tử .
b) Số tập con gồm 6 phần tử của A là 6 10 A . 9
c) Với mỗi tập con gồm 6 phần tử của A thì có đúng một cách sắp xếp các phần tử theo thứ tự giảm dần. d) Có 6
A số gồm 6 chữ số có dạng abc deg thoã mãn a b c d e g . 10
PHẦN 3. Câu trắc nghiệm trả lời ngắn.
Câu 17. Một người gieo đồng xu hai mặt, sau mỗi lần gieo thì kết quả nhận được luôn là sấp hoặc
ngửa. Hỏi nếu người đó gieo 10 lần thì có bao nhiêu khả năng xảy ra? Đáp số: 1024
Câu 18. Có 6 học sinh lớp 12, 5 học sinh lớp 11 và 4 học sinh lớp 10. Có bao nhiêu cách chọn ra 4
học sinh có đủ cả ba khối? Đáp số: 720
Câu 19. Từ các chữ số 0, 4, 5,6, 7, 9 có thể lập được bao nhiêu số tự nhiên có 4 chữ số khác nhau chia hết cho 5? Đáp số: 108
Câu 20. Từ các chữ số 0, 1, 2, 3, 4, 5, 6, 7 có thể lập được bao nhiêu số tự nhiên có 5 chữ số đôi
một khác nhau sao cho có đúng 3 chữ số chẵn và 2 chữ số lẻ? Đáp số: 2448
Câu 21. Có bao nhiêu cách xếp 4 bạn nam và 4 bạn nữ vào một hàng dọc sao cho 2 bạn nam bất kì
không đứng liền nhau và 2 bạn nữ bất kì không đứng liền nhau? Đáp số: 1152
Câu 22. Có bao nhiêu cách lập một mật khẩu là một dãy 8 kí tự, mỗi kí tự là một chữ số mà số 1
xuất hiện 3 lần, số 2 xuất hiện 3 lần, số 3 xuất hiện 2 lần? Đáp số: 560 10
BÀI 3. NHỊ THỨC NEWTON
YÊU CẦU CẦN ĐẠT
- Giải thích được khai triển tổng quát của Nhị thức Newton .
- Khai triển nhị thức newton ( + )n
a b vận dụng với số mũ thấp ( n = 4 hoặc n = 5).
- Vận dụng khai triển Nhị thức Newton trong tìm hệ số, số hạng…trong khai triển nhị thức với số
mũ thấp n = 4 hoặc n = 5.
1. Công thức nhị thức Newton n
Xét khai triển tổng quát n 0 n 1 n 1 a b C a C a b ... n n k n k k C b C a
b (với n ) n n n n k 0 2. Nhận xét
Trong khai triển Nhị thức Newton ( + )n
a b ta có các tính chất sau
- Có tất cả n +1 số hạng;
- Số mũ của a giảm từ n về 0 và số mũ của b tăng từ 0 đến n ;
- Tổng các số mũ của a và b trong mỗi số hạng đều bằng n ;
- Các hệ số có tính đối xứng k n k C C − = n n ;
- Số hạng tổng quát (số hạng thứ k +1) trong khai triển là k n−k k T = C a b . k 1 + n 3. Đặc biệt
+ Với n = 4 ta có (a +b)4 0 4 1 3 2 2 2 1 3 4 4
= C a + C a b + C a b + C ab + C b 4 4 4 4 4
+ Với n = 5 ta có (a + b)5 0 5 1 4 2 3 2 3 2 3 4 4 5 5
= C a + C a b + C a b + C a b +C ab +C b 5 5 5 5 5 5
Ví dụ 1. Áp dụng công thức khai triển nhị thức Newton, hãy khai triển các biểu thức sau:
a) P( x) = (x + )4 2
b) P(x) = ( − x)5 1 3
Ví dụ 2. Xét khai triển ( + )5 2 3x
a) Có bao nhiêu số hạng trong khai triển.
b) Tìm hệ số của số hạng chứa 4 x trong khai triển. 5 1
Ví dụ 3. Xét khai triển: 2x − x
a) Tìm số hạng không chứa x trong khai triển. b) Tìm số hạng chứa 2 x trong khai triển.
BÀI TẬP THỰC HÀNH
PHẦN 1. Câu trắc nghiệm nhiều phương án lựa chọn
Câu 1. Trong khai triển nhị thức Newton của ( x − )4 2 3 có bao nhiêu số hạng? A. 6. B. 3. C. 5. D. 4. 11
Câu 2. Trong khai triển nhị thức Newton của ( )1n x +
có 6 số hạng. Khi đó n bằng A. 6. B. 3. C. 5. D. 4.
Câu 3. Trong khai triển nhị thức Newton của (x − )5
1 số hạng không chứa x là A. 5 − . B. −1. C. 5. D. 1.
Câu 4. Cho tập A có 5 phần tử. Số tập con của tập A là A. 5. B. 32. C. 10. D. 16.
Câu 5. Trong khai triển nhị thức Newton của (x + )5
2024 hệ số của số hạng chứa x với bậc cao nhất là A. −1. B. 2024. C. 5. D. 1.
Câu 6. Khai triển của nhị thức Newton ( − )4 a b bằng A. ( − )4 4 4
a b = a − b .
B. (a −b)4 4 2 2 4
= a − 2a b +b .
C. (a −b)4 4 3 2 2 3 4
= a − 4a b + 6a b − 4ab + b . D. ( − )4 = ( 2 2 − )( 2 2 a b a b a + b ) .
Câu 7. Khai triển theo công thức nhị thức newton 5 x 1 là A. 5 4 3 2
x + 5x +10x +10x + 5x +1. B. 5 4 3 2
x − 5x −10x +10x − 5x +1. C. 5 4 3 2
x − 5x +10x −10x + 5x −1. D. 5 4 3 2
5x +10x +10x + 5x + 5x +1.
Câu 8. Khai triển nhị thức Newton ( x − )5 2 1 là A. 5 4 3 2
32x − 80x + 80x − 40x +10x −1. B. 5 4 3 2
2x − 80x + 80x − 40x +10x −1 C. 5 4 3 2
32x + 80x − 80x + 40x −10x +1. D. 5 4 3 2
32x + 80x + 80x + 40x +10x +1
Câu 9. Hệ số của 3
x trong khai triển Newton biểu thức ( x + )5 2 1 là A. 80 − . B. 10. C. 40 . D. 80 .
Câu 10. Hệ số của 4
x trong khai triển Newton biểu thức ( x − )5 2 3 là A. 270 − . B. 80 − . C. 240 . D. 240 − . Câu 11. Khai triển 5 (x + 2) . Hệ số 4
x trong khai triển là A. 20 B. 40 C. 30 D. 10 Câu 12. Tổng 0 5 1 4 2 3 3 2 4 1 5
S = C 2 + C 2 + C 2 + C 2 + C 2 + C 5 5 5 5 5 5
A. 243. B. 461. C. 631. D. 362.
PHẦN 2: Câu trắc nghiệm đúng sai
Câu 13. Xét tính đúng, sai của các khai triển dưới đây a) (a + b)5 5 4 3 2 2 3 4 5
= a + 5a b +10a b +10a b + 5ab + b b) (a −b)5 5 4 3 2 2 3 4 5
= a −5a b +10a b +10a b −5ab + b c) ( + )5 5 5
a b = a + b 12 d) ( − )5 5 5
a b = a − b 4 2
Câu 14. Xét khai triển nhị thức P = x + (x 0) x
a) Trong khai triển trên có 4 số hạng
b) Khi x =1 thì P = 81
c) Số hạng không chứa x là 96 32
d) Số hạng thứ 4 trong khai triển là − 2 x
Câu 15. Xét khai triển nhị thức P = ( + x)5 1
a) Khai triển nhị thức trên có 6 số hạng
b) Tổng các hệ số của các số hạng trong khai triển bằng 32
c) Hệ số lớn nhất trong các đơn thức bằng 10
d) Hệ số của số hạng chứa 5 x bằng 5 5 r
Câu 16. Xét khai triển 2 P = x + (r
); biết hệ số của số hạng chứa x trong khai triển bằng x 640.
a) Số hạng tổng quát trong khai triển có dạng k 10 3 − k k C x r 5
b) Số hạng chứa x tương ứng với k = 2
c) Hệ số của số hạng chứa x là 3 3 C r 5
d) Giá trị của r = 4
PHẦN 3. Câu trắc nghiệm trả lời ngắn
Câu 17. Tìm hệ số của số hạng chứa 2
x trong khai triển nhị thức Newton của
P( x) = x + x(x − )4 2 4 2 Đáp số: 28 − 4 1
Câu 18. Tìm số hạng không chứa x trong khai triển nhị thức Newton của + x 3 x Đáp số: 4
Câu 19. Tìm hệ số của 2
x trong khai triển Newton biểu thức ( x − )4 4 3 Đáp số: 864 4 1 Câu 20. Cho 2 3 4 2x −
= a + a x + a x + a x + a x m
.Tổng S = a + a + a + a + a = . Tìm giá 0 1 2 3 4 3 0 1 2 3 4 81 trị của m Đáp số: 625 13 5 2 1 a
Câu 21. Hệ số của 3
x trong khai triển Newton biểu thức x + có dạng
. Tìm giá trị của a 3 4 27 Đáp số: 5 5 3 1 Câu 22. Cho 2 3 4 5 x +
= a + a x + a x + a x + a x + a x m . Biết a =
( m là phân số tối giản), 0 1 2 3 4 5 5 2 3 n n
Tính tính tổng m + n Đáp số: 77 14
ÔN TẬP CHUYÊN ĐỀ 1
PHẦN 1. Câu trắc nghiệm nhiều phương án lựa chọn
Câu 1: Cho A = ; a ; b ;
c d. Trong các mệnh đề sau, tìm mệnh đề sai:
A. a A . B. ;
a d A. C. ; b
c A .
D. d A .
Câu 2: Cho hai tập hợp A = 2 − ; 1 − ;3;5; 7 , B = 2 − ;5;7;13;2
0 , khi đó tập A B là
A. A B = 2 − ; 1 − ;3;5;7;13;2 0 .
B. A B = 1 − ; 3 .
C. A B = 13;2 0 .
D. A B = 2 − ;5; 7 .
Câu 3: Với k, n là hai số nguyên dương tùy ý k n , mệnh đề nào dưới đây đúng? n n k ! k ! A. A = . B. A = . n k ( ! n − k )! n (n−k)! k n k ! ! C. n k ! A = . D. A = . n k ! n (n−k)!
Câu 4: Số chỉnh hợp chập 4 của 6 là A. 360. B. 6. C. 24. D. 15.
Câu 5: Số cách chọn 3 học sinh từ 6 học sinh là A. 3 C A 6 . B. 3 6 . C. 36 . D. 6 3 .
Câu 6: Có bao nhiêu số tự nhiên có 4 chữ số được lập từ các chữ số 1, 2,3, 4,5? A.120. B. 24 . C. 625. D. 5.
Câu 7: Có bao nhiêu cách xếp khác nhau cho 5 người ngồi vào một bàn dài? A. 5. B. 120. C. 20 . D. 25 .
Câu 8: Số cách chọn 3 học sinh từ một nhóm gồm 18 nam và 17 nữ là A. 3 C . B. 3 C . C. 3 C . D. 3 A . 18 17 35 15
Câu 9: Trong khai triển nhị thức ( x + )15 2 7
có tất cả bao nhiêu số hạng? A. 14. B. 15. C. 16. D. 18.
Câu 10: Từ một hộp kín đựng 7 quả cầu xanh và 5 quả cầu đỏ. Có bao nhiêu cách chọn 3 quả cầu xanh A. 3 A B. 3 C C. 3 C D. 3 A 5 12 7 12
Câu 11: Một tổ có 6 học sinh nam và 9 học sinh nữ. Hỏi có bao nhiêu cách chọn 6 học sinh đi
lao động, trong đó có đúng 2 học sinh nam? A. 2 4 C + C . B. 2 4 C C . C. 2 4 A A . D. 2 4 C C . 6 9 6 13 6 9 6 9
Câu 12: Một hộp chứa 11 quả cầu gồm 5 quả cầu màu xanh và 6 quả cầu màu đỏ. Có bao nhiêu
cách để chọn 2 quả cầu cùng màu. A. 2 2 A + A C .C C + C A A 5 6 . B. 2 2 5 6 . C. 2 2 5 6 . D. 2 2 5 6 .
PHẦN 2: Câu trắc nghiệm đúng sai 5 1 Câu 13. Cho 2 3 4 5 1− x
= a + a x + a x + a x + a x + a x . 0 1 2 3 4 5 2 15 a) 5 a = 3 2 b) 1 a = − 5 32
c) Hệ số lớn nhất trong tất cả hệ số là 5 2 d) Tổng 1
a + a + a + a + a + a = 0 1 2 3 4 5 16
Câu 14. Một tập thể có 14 người trong đó có hai bạn tên A và B . Người ta cần chọn một tổ công
tác gồm 6 người, khi đó:
a) Chọn nhóm 6 bạn bất kỳ ta có 3003 cách
b) Chọn nhóm 6 bạn trong đó có cả A và B , có 1848 cách
c) Chọn nhóm 6 bạn trong đó không có hai bạn A và B , có 924 cách
d) Có 66 cách chọn 6 bạn trong đó luôn A và không có B .
Câu 15. Bạn An có 2 cuốn sách môn Toán, 3 cuốn sách môn Vật lí, 3 cuốn sách môn Hoá học, các
cuốn sách đôi một khác nhau. Giá sách của bạn An chỉ có 1 hàng gồm 3 ngăn liền nhau. Bạn An
xếp các cuốn sách trên vào giá sách sao cho mỗi ngăn chỉ có một môn.
a) Số cách xếp 2 cuốn sách môn Toán trong một ngăn là 2!.
b) Số cách xếp 3 cuốn sách môn Vật lí trong một ngăn là 3.
c) Số cách xếp 3 cuốn sách môn Hoá học trong một ngăn là 3!.
d) Số cách xếp các cuốn sách sao cho mỗi ngăn chỉ có một môn là 432.
Câu 16. Một hộp chứa 18 quả cầu có kích thước và khối lượng như nhau, trong đó có 4 quả cầu
màu xanh được đánh số từ 1 đến 4, có 6 quả cầu màu đỏ đựợc đánh số từ 1 đến 6, có 8 quả cầu màu
vàng được đánh số từ 1 đến 8. Lấy 2 quả cầu từ hộp.
a) Có 20 cách lấy 2 quả cầu khác số, trong đó có 1 quả cầu màu xanh và 1 quả cầu màu đỏ.
b) Có 24 cách lấy 2 quả cầu khác số, trong đó có 1 quả cầu màu xanh và 1 quả cầu màu vàng.
c) Có 42 cách lấy 2 quả cầu khác số, trong đó có 1 quả cầu màu đỏ và 1 quả cầu màu vàng.
d) Số cách để 2 quả cầu được lấy vừa khác màu vừa khác số là 90.
PHẦN 3. Câu trắc nghiệm trả lời ngắn
Câu 17. Một tổ có 4 học sinh nam và 5 học sinh nữ. Hỏi có bao nhiêu cách xếp học sinh trong tổ
thành hàng ngang sao cho nam nữ đứng xen kẽ? Đáp số: 2880 .
Câu 18. Từ các chữ số 1, 2 , 3 , 4 , 5 , 6 có thể lập được bao nhiêu số tự nhiên có 6 chữ số khác
nhau và tổng của ba chữ số đầu nhỏ hơn tổng của ba chữ số cuối một đơn vị. Đáp số: 108.
Câu 19. Có 5 bì thư khác nhau và 6 con tem thư khác nhau. Chọn 3 con tem thư và 3 bì thư, sau
đó dán mỗi tem vào mỗi bì. Hỏi có bao nhiêu cách làm như vậy? Đáp số. 1200.
Câu 20. Từ các chữ số 1, 2,3, 4,5,6 lập được bao nhiêu số tự nhiên có 5 chữ số đôi một khác nhau
trong đó luôn có mặt hai chữ số 1 và 6.
Đáp số. 480. 16
Câu 21. Một đội thanh niên tình nguyện có 15 người gồm 12 nam và 3 nữ. Gọi T là số cách phân
công đội thanh niên tình nguyện thành 3 nhóm, sao cho mỗi nhóm có 4 nam và 1 nữ. Giá trị của T bằng bao nhiêu? 100 Đáp số. 2079
Câu 22 [TN 2025]: Có bốn ngăn (trong một giá để sách) được đánh số thứ tự 1, 2,3, 4 và bảy
quyển sách khác nhau. Bạn An xếp hết bảy quyển sách nói trên vào bốn ngăn đó sao cho mỗi ngăn
có ít nhất một quyển sách và các quyển sách được xếp thẳng đứng thành một hàng ngang với gáy
sách quay ra ngoài ở mỗi ngăn. Khi đã xếp xong bảy quyển sách, hai cách xếp của bạn An được
gọi là giống nhau nếu chúng thoả mãn đồng thời hai điều kiện sau đây:
+ Với từng ngăn, số lượng quyển sách ở ngăn đó là như nhau trong cả hai cách xếp;
+ Với từng ngăn, thứ tự từ trái sang phải của các quyển sách được xếp là như nhau trong cả hai cách xếp. T
Gọi T là số cách xếp đôi một khác nhau của bạn An. Giá trị của bằng bao nhiêu? 100 Đáp số. 1008 17
CHUYÊN ĐỀ 2: XÁC SUẤT BÀI 1. XÁC SUẤT YÊU CẦU CẦN ĐẠT
- Nhận biết một số khái niệm: Phép thử ngẫu nhiên, không gian mẫu, biến cố, biến cố đối, định .
nghĩa cổ điển của xác suất. -
Mô tả không gian mẫu, biến cố trong một phép thử đơn giản, mô tả tính chất cơ bản của xác suất
- Nhận biết các khái niệm biến cố hợp, biến cố giao, biến cố độc lập, biến cố xung khắc
- Tính xác xuất của biến cố hợp của hai biến cố xung khắc, giao của hai biến cố độc lập bằng cách
sử dụng công thức cộng, công thức nhân xác suất.
I. PHÉP THỬ VÀ BIẾN CỐ 1. Phép thử
a) Phép thử ngẫu nhiên
Phép thử ngẫu nhiên (gọi tắt là phép thử) là một thí nghiệm hay một hành động mà:
- Kết quả của nó không đoán trước được;
- Có thể xác định được tập hợp tất cả các kết quả có thể xảy ra của nó.
Phép thử thường được kí hiệu bởi chữ T .
b) Không gian mẫu
Tập hợp tất cả các kết quả có thể xảy ra của phép thử được gọi là không gian mẫu của phép
thử và được kí hiệu bởi chữ . 2. Biến cố
Biến cố là một tập con của không gian mẫu, thường được kí hiệu bằng các chữ cái in hoa , A B,C,...
Ta nói rằng biến cố A xảy ra trong một phép thử nào đó khi và chỉ khi kết quả của phép
thử đó là một phần tử của A (hay gọi thuận lợi cho biến cố A ).
Như vậy biến cố là biến cố không bao giờ xảy ra khi thực hiện phép thử, gọi là biến cố
không thể. Biến cố là biến cố luôn xảy ra khi thực hiện phép thử, gọi là biến cố chắc chắn.
Biến cố đối của biến cố E là biến cố “ E không xảy ra” kí hiệu E
Ví dụ 1. Xác định số phần tử của không gian mẫu trong các phép thử sau:
a) Gieo đồng thời hai con súc sắc.
b) Gieo đồng thời hai đồng xu cân đối đồng chất.
c) Chọn ngẫu nhiên 2 học sinh trong một lớp gồm 24 học sinh nam và 16 học sinh nữ.
Ví dụ 2. Cho phép thử “Chọn ngẫu nhiên một số trong dãy các số tự nhiên từ 1 đến 20”
a) Mô tả không gian mẫu.
b) Hãy xác định tập hợp các kết quả thuận lợi mô tả các biến cố ,
A B,C ; trong đó: A là
biến cố “ Số được chọn là số chẵn”; B là biến cố “ Số được chọn chia hết cho 5”; C là biến cố
“Số được chọn không nhỏ hơn 15 ”.
c) Xác định biến cố đối của các biến cố ,
A B,C ở ý b).
II. XÁC SUẤT CỦA BIẾN CỐ
1. Định nghĩa 18
Giả sử A là biến cố liên quan đến một phép thử có không gian mẫu là tập hữu hạn. Ta n ( A) gọi tỉ số
là xác suất của biến cố A , kí hiệu là P( ) A . n ()
P ( A) n( A) = n()
Trong đó n ( A) là số phần tử của A hay gọi là số các kết quả thuận lợi cho biến cố A ,
n() là số các kết quả có thể xảy ra của phép thử.
Chú ý: +) 0 P( )
A 1, với mọi biến cố A .
+) P() = 1, P() = 0 .
Ví dụ 3. Từ một hộp chứa 6 quả cầu màu đỏ và 4 quả cầu màu xanh, lấy ngẫu nhiên đồng thời 3
quả cầu. Tính xác suất để 3 quả lấy ra a) Đều màu xanh. b) Có đủ hai màu.
c) Có ít nhất 1 quả màu xanh.
Ví dụ 4. Một nhóm có 10 học sinh, trong đó có 3 học sinh lớp A, 4 học sinh lớp B và 3 học sinh lớp
C. Chọn ngẫu nhiên 4 học sinh. Tính xác suất để 4 học sinh được chọn:
a) Không có học sinh lớp C.
b) Có đủ học sinh của 3 lớp.
Ví dụ 5. Có 6 học sinh nam và 4 học sinh nữ được xếp thành 1 hàng ngang. Tính xác suất để:
a) Các học sinh nữ ngồi cạnh nhau.
b) Không có bất kì bạn nữ nào ngồi cạnh nhau.
Ví dụ 6. Chọn ngẫu nhiên đồng thời hai số từ tập hợp 20 số nguyên dương đầu tiên. Tính xác suất để
a) Cả hai số được chọn đều chia hết cho 5.
b) Cả hai số được chọn đều là số lẻ.
Ví dụ 7. Gọi S là tập các số tự nhiên có 4 chữ số khác nhau được tạo thành từ các số 0;1;2;3;4;5 .
Chọn ngẫu nhiên một số từ tập S . Tính xác suất để số được chọn là số chẵn.
III. CÁC QUY TẮC TÍNH XÁC SUẤT
1. Công thức nhân xác suất
a) Giao của hai biến cố
Cho hai biến cố A và B . Biến cố: “Cả A và B đều xảy ra” được gọi là biến cố giao của A và
B , kí hiệu là AB .
Nhận xét: Biến cố giao của của hai biến cố A
và B là tập con A B của không gian mẫu
b) Biến cố độc lập 19
Hai biến cố gọi là độc lập với nhau nếu việc xảy ra hay không xảy ra của biến cố này không
làm ảnh hưởng tới xác suất xảy ra của biến cố kia.
Nhận xét: Nếu hai biến cố A và B độc lập với nhau thì ta cũng có các cặp biến cố sau là độc
lập: A và B ; A và B ; A và B
c) Công thức nhân xác suất cho 2 biến cố độc lập
Nếu hai biến cố A và B độc lập với nhau thì P ( AB) = P ( A).P (B) .
+) Ngược lại: Nếu ta có P( AB) = P( A).P(B) thì hai biến cố A và B là độc lập với nhau
Tổng quát: Nếu k biến cố A , A , ..., A độc lập với nhau thì: 1 2 k
P( A .A ... A
= P A .P A . ... .P A 1 2 k ) ( 1) ( 2) ( k )
Ví dụ 8. Gieo đồng thời một con xúc sắc và một đồng xu cân đối, đồng chất. Tính xác suất
để đồng xu xuất hiện mặt sấp và con xúc sắc xuất hiện mặt 6 chấm.
Ví dụ 9. Cả hai xạ thủ cùng bắn vào một bia. Xác xuất bắn trúng bia của xạ thủ thứ nhất là
0,6, xác suất bắn trúng bia của xạ thủ thứ 2 là 0,9. Tính xác suất để cả hai xạ thủ cùng bắn không trúng bia.
Ví dụ 10. Có hai bình chứa các viên bi chỉ khác nhau về màu. Bình thứ nhất có 3 bi xanh, 4
viên bi đỏ. Bình thứ hai có 2 bi xanh, 5 viên bi đỏ. Lấy ngẫu nhiên từ mỗi bình một viên bi. Tính
xác suất để được 2 viên bi màu xanh.
2. Công thức cộng xác suất
a) Hợp của hai biến cố
Cho hai biến cố A và B . Biến cố “ A hoặc B xảy ra” được gọi là biến cố hợp của các biến
cố A và B , kí hiệu là A B .
Nhận xét: Biến cố hợp của của hai biến cố A và
B là tập con A B của không gian mẫu
b) Biến cố xung khắc
Hai biến cố A và B được gọi là xung khắc nếu hai biến cố không đồng thời xảy ra.
Như vậy hai biến cố A và B là xung
khắc khi và chỉ khi A B = .
c) Quy tắc cộng xác suất
Cho hai biến cố A và B. Khi đó ta có P ( A B) = P ( A) + P (B) − P ( AB)
Nếu hai biến cố A và B xung khắc thì P ( A B) = P ( A) + P (B) .
Tổng quát: Cho k biến cố A , A , ..., A đôi một xung khắc. 1 2 k
Khi đó: P( A A ... A
= P A + P A + ... + P A 1 2 k ) ( 1) ( 2) ( k ) 20



