97 trang 2 lượt tải

Tổng hợp bài tập: Các bài toán bất đẳng thức môn Toán 10

4

Tổng hợp bài tập: Các bài toán bất đẳng thức môn Toán 10. Tài liệu được sưu tầm giúp bạn tham khảo, ôn tập và đạt kết quả cao. Mời bạn đọc đón xem.

Chủ đề: Chuyên đề Toán 10 224 tài liệu

Môn: Toán 10 3.2 K tài liệu

Tác giả:

Profile

THCS Đức Ninh Lý Thị Thanh Vĩnh

7 giờ trước
Tải xuống
Báo cáo
Danh sách Quiz
Tải xuống
/97
Tailieumontoan.com

Điện thoại (Zalo) 039.373.2038
CÁC BÀI TOÁN
BẤT ĐẲNG THỨC HAY
(Liệu hệ tài liệu word môn toán SĐT (zalo) : 039.373.2038)
Tài liệu sưu tầm, ngày 20 tháng 7 năm 2024
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 1
Website: tailieumontoan.com
Bài 1. Cho a, b, c > 0. Chứng minh rằng :

+ + + + +

+ + + + + +

21
2 2 2 2 2 2
a b c b c a
b c c a a b b a c b a c
DAP AN
Bài
Nội dung
Điểm
6
(0,75 điểm)

+ + + + +

+ + + + + +

21
2 2 2 2 2 2
a b c b c a
b c c a a b b a c b a c

+ − + − + −
+ + + + +

+ + + + + +

2 2 2 2 2 2
21
2 2 2 2 2 2
a b c b a a c b b a c c
b c c a a b b a c b a c
+ + + + +
+ + + + + +
1 1 1 1 1 1
2
2 2 2 2 2 2
a b c
b c b a c a c b a b a c
Áp dụng bất đẳng thức :
a b a b
1 1 4
+
+
ta có
+ =
+ + + + + +
1 1 4 2
2 2 2 2 2b c b a a b c a b c
Suy ra

+

+ + + +

1 1 2
22
a
a
b c b a a b c
Tương tự

+

+ + + +

1 1 2
22
b
b
c a c b a b c

+

+ + + +

1 1 2
22
c
c
a b a c a b c
Cộng các bất đẳng thức theo vế ta được:
+ + + + +
+ + + + + +
1 1 1 1 1 1
2
2 2 2 2 2 2
a b c
b c b a c a c b a b a c
(đpcm)
Đẳng thức xảy ra khi a=b=c
0.25
0.25
0.25
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 2
Website: tailieumontoan.com
Bài 2. Cho x, y, z là ba số dương thỏa mãn xyz = 1. Chứng minh rằng:
2 2 2
x y z 3
y 1 z 1 x 1 2
+ +
+ + +
DAP AN
Bài
Nội dung
Điểm
6
(0,75 điểm)
Áp dụng bất đẳng thức Cô si ta có:
22
x y 1 x y 1 x
2 . 2. x
y 1 4 y 1 4 2
++
+ = =
++
(1)
Tương tự:
2
y z 1
y
z 1 4
+
+
+
(2);
2
z x 1
z
x 1 4
+
+
+
(3)
Cộng từng vế các bất đẳng thức (1), (2), (3) ta được:
2 2 2
x y z x 1 y 1 z 1
x y z
y 1 z 1 x 1 4 4 4
+ + +
+ + + + + + +
+ + +
( )
2 2 2
3 x y z 3
x y z
y 1 z 1 x 1 4
+ + −
+ +
+ + +
(4)
Mặt khác cũng theo bất đẳng thức Cô – si ta có :
3
3
x y z 3. xyz 3. 1 3+ + = =
(5)
Từ (4) và (5) suy ra:
2 2 2
x y z 3.3 3 3
y 1 z 1 x 1 4 2
−
+ + =
+ + +
Dấu “=” xảy ra
x = y = z = 1
0,25
0,25
0,25
Bài 3. Cho n > 1; m > 1. Tìm giá trị nhỏ nhất của biểu thức E =
22
nm
m 1 n 1
+
−−
.
DAPAN
Bài
Nội dung
Điểm
6
(0,75 điểm)
* Với n > 1; m > 1 thì
22
;
11
nm
mn−−
là hai số dương
Áp dụng bất đẳng thức Cô si ta có:
E =
2 2 2 2
2 . 2 .
1 1 1 1
11
n m n m n m
m n m n
nm
+ =
− − − −
−−
*Mà
( )
2
11
21
2 0 0
1 1 1
n
n n n
n n n
−−
−−
− − −
(1)
Do bất đẳng thức (1) đúng với mọi n >1 nên bất đẳng thức cần
chứng minh đúng. Dấu ‘=’ xảy ra khi và chỉ khi n = 2.
* Áp dụng kết quả câu trên ta có:
2 . 8
11
nm
nm
−−
=> E
8
Vậy E
min
= 8 khi n = m = 2.
0,25
0,25
0,25
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 3
Website: tailieumontoan.com
Bài 4. Cho các số dương x, y, z thỏa mãn
+ + =
+ + +
1 1 1
12
x y y z z x
. Tìm giá trị lớn nhất
của biểu thức:
111
P
3x 3y 2z 3x 2y 3z 2x 3y 3z
= + +
+ + + + + +
.
DAPAN
Bài
Nội dung
Điểm
6
(0,75 điểm)
Áp dụng bất đẳng thức Cosi cho 2 số a, b dương, ta có
a b 2 ab+
,
1 1 1
2
a b ab
+
.
( )
1 1 1 1 4 1 1 1 1
a b 4
a b a b a b a b 4 a b
+ + + +
++
(*)
Dấu bằng xảy ra khi a = b.
0,25
Áp dụng BĐT (*) ta có:
( ) ( ) ( ) ( ) ( )
( )
( ) ( )
( ) ( )
1 1 1 1 1
3x 3y 2z 4 2 x y
x z y z 2 x y x z y z
1 1 1 1 1 1 1
4 8 x y 16 x z y z 8 x y
x z y z

= +


+ + +
+ + + + + + + +


= + + +

+ + + +

+ + +


Chứng minh tương tự, ta có
( )
( )
1 1 1 1 1
;
3x 2y 3z 16 x y y z 8 x z
1 1 1 1 1
2x 3y 3z 16 x y x z 8 y z

+ +

+ + + + +


+ +

+ + + + +

0,25
Cộng từng vế 3 bất đẳng thức ta được:

= + + + +

+ + + + + + + + +


+ + + = + =

+ + +

1 1 1 1 2 2 2
P
3x 3y 2z 3x 2y 3z 2x 3y 3z 16 x y y z z x
1 1 1 1 1 1
.12 .12 3
8 x y y z z x 8 8
Dấu bằng xảy ra khi x = y = z =
1
8
Vậy GTLN của biểu thức P là 3 khi x = y = z =
1
8
0,25
Bài 5. Cho a > 0, b > 0 thỏa mãn
11
2
ab
+=
. Tìm giá trị lớn nhất của biểu thức
4 2 2 4 2 2
11
22
Q
a b ab b a ba
=+
+ + + +
.
DAPAN
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 4
Website: tailieumontoan.com
Bài
Nội dung
Điểm
6
(0,75 điểm)
Với
0; 0ab
tacó:
2 2 4 2 2 4 2 2
( ) 0 2 0 2a b a a b b a b a b− − + +
4 2 2 2 2
2 2 2a b ab a b ab + + +
( )
4 2 2
11
(1)
22a b ab ab a b

+ + +
Tương tự có
( )
4 2 2
11
(2)
22b a a b ab a b
+ + +
.
Từ (1) và (2)
( )
1
Q
ab a b

+
Vì
11
22a b ab
ab
+ = + =
mà
21a b ab ab+
2
11
2( ) 2
Q
ab
.Khi a = b = 1 thì
1
2
Q=
.
Vậy giá trị lớn nhất của biểu thức là
1
2
0,25
0,25
0,25
Bài 6. Cho a,b,c, là độ dài 3 cạnh của một tam giác. CMR:
1 1 1 1 1 1
a b c b c a c a b a b c
+ + + +
+ − + − + −
DAPAN
Bài
Nội dung
Điểm
Áp dụng BĐT côsi với 2 số dương x, y ;
11
;
xy
ta có:
4)
11
)((
1
.2
11
2
++
+
+
yx
yx
xy
yx
xyyx
hay
yxyx +
+
411
(1)
Dấu “=” xảy ra
x = y
do a, b, c là độ dài ba cạnh của tam giác nên theo bất đẳng thức
tam giác, có: a + b – c > 0.
Áp dụng bất đẳng thức (1) ta có:
cbacabc 2
411
−+
+
−+
tương tự
bcbaabc 2
411
−+
+
−+
0,25
0,25
0,25
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 5
Website: tailieumontoan.com
acbabac 2
411
−+
+
−+
Cộng 3 bất đẳng thức trên và suy ra đpcm
Dấu “=” xảy ra khi và chỉ khi a=b=c
Bài 7. Cho x, y, z là ba số dương thoả mãn x + y + z =3. Chứng minh rằng:
x y z
1
x 3x yz y 3y zx z 3z xy
+ +
+ + + + + +
.
DAPAN
Bài
Nội dung cần đạt
Điểm
Bài 6
(0,75 điểm)
Ta có: 3x + yz = (x + y + z)x + yz = x
2
+ yz + x(y + z)
x(y z) 2x yz + +
Suy ra
3x yz x(y z) 2x yz x( y z)+ + + = +
x 3x yz x( x y z)+ + + +
xx
x 3x yz x y z

+ + + +
(1)
0,25
Tương tự ta có:
y
y
y 3y zx x y z
+ + + +
(2),
zz
z 3z xy x y z
+ + + +
(3)
Từ (1), (2), (3) ta có
x y z
1
x 3x yz y 3y zx z 3z xy
+ +
+ + + + + +
0,25
Dấu “=” xảy ra khi x = y = z = 1
0,25
Bài 8. Cho ba số thực dương thỏa mãn: x + 2y + 3z = 2.
Tìm giá trị lớn nhất của biểu thức: .
x,y,z
xy 3yz 3xz
S
xy 3z 3yz x 3xz 4y
= + +
+ + +
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 6
Website: tailieumontoan.com
DAP AN
Bài
Đp n
Điểm
Bài 6
( 0,75
điểm)
Đặt a = x ; b = 2y ; c = 3z a, b, c > 0 và a + b + c = 2
Khi đó S =
Xét
Đẳng thức xảy ra khi
0,25
Tương tự ta có
;
Đẳng thức xảy ra khi ;
0,25
Cộng các vế ta được
S
Vậy GTLN của S = ; ;
0,25
Bài 9. Cho các số thực dương
,,x y z
. Chứng minh rằng
2 2 2 2 2 2
1 1 1
.
2 2 2
yz zx xy
x y z
x y x z y z y x z x z y
DAPAN
Bài
Nội dung
Điểm
6
(0,75
điểm)
Áp dụng BĐT
AM GM
ta được
22
1
2.
44
( ) ( )
yz y z yz y z
yz yz x
x y z x y z
2
1 1 1 1 1
44
()
yz y z
x yz x y z
x y z
0,25
ab bc ac
ab 2c bc 2a ac 2b
++
+ + +
ab ab ab 1 a b
ab 2c ab (a b c)c (a c)(b c) 2 a c b c

= = +

+ + + + + + + +

ab
a c b c
=
++
bc 1 b c
bc 2a 2 b a c a

+

+ + +

ac 1 a c
ac 2b 2 a b c b

+

+ + +

bc
b a c a
=
++
ac
a b c b
=
++
1 a b b c a c 3
2 a b b c a c 2
+ + +

+ + =

+ + +

32
a b c
23
= = =
2
x
3
=
1
y
3
=
2
z
9
=
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 7
Website: tailieumontoan.com
Tương tự:
22
1 1 1 1 1 1 1 1
;
44
( ) ( )
zx xy
y x z z x y
y z x z x y
0,25
Cộng các BĐT cùng chiều ta được
222
222
222
( ) ( ) ( )
1 1 1 1 1 1 1 1 1 1 1 1
444
1 1 1 1 1 1 1
2
( ) ( ) ( )
1 1 1
22
( ) ( ) ( )
yz zx xy
x y z y z x z x y
x y z y x z z x y
yz zx xy
x y z x y z
x y z y z x z x y
yz zx xy
xy
x y z y z x z x y
2z
Dấu “=” xảy ra khi và chỉ khi
.x y z
0,25
Bài 10. Cho các số x, y, z > 0 thỏa mãn x + y + z =
11
. Tìm giá trị nhỏ nhất của
biểu thức: A =
2 2 2 2 2 2
5x xy 5y 5y yz 5z 5z zx 5x+ + + + + + + +
.
DAPAN
Bài
Nội dung
Điểm
(0,75điểm)
Chứng minh:
( )
2
22
11
5x xy 5y x y
4
+ + +
. (1)
( )
2 2 2 2
20x 4xy 20y 11 x 2xy y + + + +
( )
2
22
9x 18xy 9y 0 9 x y 0 − + −
(2) luôn đúng với mọi
x, y.
Vậy BĐT (1) đúng. Dấu "=" xảy ra khi x = y.
0,25
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 8
Website: tailieumontoan.com
b) Áp dụng bất đẳng thức (1) với x, y > 0 ta có
( )
2
22
11
5x xy 5y x y
4
+ + +
Suy ra
( ) ( )
2
22
11 11 11
5x xy 5y x y x y x y
4 2 2
+ + + = + = +
Lập luận tương tự có
( )
22
11
5y yz 5z y z
2
+ + +
,
( )
22
11
5z zx 5x z x
2
+ + +
Cộng các BĐT cùng chiều ta có
( )
11
A x y y z z x 11. 11 11
2
+ + + + + = =
.
Do đó MinA = 11 khi và chỉ khi
11
x y z
3
= = =
.
0,25
0,25
Bài 11. Cho
,,abc
là các số dương. Chứng minh rằng:
3 3 3
2 2 2 2 2 2
.
3
a b c a b c
a ab b b bc c c ca a
++
+ +
+ + + + + +
DAPAN
Câu
Lời giải sơ lược
Điểm
6
(0,75đ)
Chứng minh bất đẳng thức sau:
3
22
.
2
ab
a
ab
−
+
Ta có
( )
2 2 2
32
2 2 2 2 2 2
aa
.
b ab
a ab
a
a b a b a b
+−
= = −
+ + +
Theo BĐT Cauchy ta có
22
22
.
22
ab ab b
a a a
a b ab
− − = −
+
Tương tự theo câu a) ta có :
3
22
,
2
bc
b
bc
−
+
3
22
.
2
ca
c
ca
−
+
Cộng vế theo vế ba bất đẳng thức trên ta có:
3 3 3
2 2 2 2 2 2
.
2
a b c a b c
a b b c c a
++
+ +
+ + +
0,25
0,25
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 9
Website: tailieumontoan.com
Ta có:
3 3 3
22
2 2 2 2
22
2
..
3
2
a a a
ab
a ab b a b
ab
=
+
+ + +
++
Tương tự ta có
33
2 2 2 2
2
.,
3
bb
b bc c b c
+ + +
33
2 2 2 2
2
..
3
cc
c ca a c a
+ + +
Cộng vế theo vế ba bất đẳng thức trên ta có:
3 3 3
2 2 2 2 2 2
3 3 3
2 2 2 2 2 2
2
.
33
a b c
a ab b b bc c c ca a
a b c a b c
a b b c c a
++
+ + + + + +

++
+ +

+ + +

0,25
Bài 13.
Cho
,ab
là các số thực dương, thỏa mãn
a
ab
b
. Chứng minh:
1 1 1 9ab
a b a b ab a b ab a b ab
. Đẳng thức xảy ra khi nào?
DAPAN
Bài
Nội dung
Điểm
6
(0,75
điểm)
Ta có
2
( 1)
a
a b ab a b ab a b b b
b
Lại có
2
( 1) 0 1
a
a b a b b b
b
. Do đó
0ab a b
Áp dụng bất đẳng thức
1 1 4
x y x y
với
,xy
là các số dương, ta
có:
1 1 4 4
.
ab ab
a b a b ab a b a b a b ab a b a b
0,25
Áp dụng bất đẳng thức Cauchy - Schwarz ta có:
2
21
4 1 9
a b ab a b a b ab a b ab
Vậy
1 1 1 9ab
a b a b ab a b ab a b ab
0,25
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 10
Website: tailieumontoan.com
Dấu đẳng thức xảy ra khi:
2
2
2
2
2
22
21
1
b
a b ab a b
a
bb
b
b
a
b
bb
ab
a
b
b
.
Khi đó
2 2 2a
Vậy đẳng thức xảy ra khi và chỉ khi
2 2 2a
và
22b
.
0,25
Bài 14.
Tìm giá trị lớn nhất của biểu thức:
1 2 3yz x xz y xy z
P
xyz
− + − + −
=
.
DAPAN
Bài 6
( 0,75
điểm)
Điều kiện xác định
1, 2, 3x y z
.
1 2 3 2
13
yz x xz y xy z y
xz
P
xyz x y z
− + − + − −
−−
= = + +
Áp dụng bất đẳng thức Cô-si ta có:
11
1 ( 1) 2 1
2
x
x x x
x
−
= + − −
.
0,25
2
1
2 ( 2) 2 2( 2)
22
y
y y y
y
−
= + − −
31
3 ( 3) 2 3( 3)
23
z
z z z
z
−
= + − −
Suy ra
1 1 1
2
2 2 2 3
P + +
0,25
Dấu “=” xảy ra
1 1 2( )
2 2 4( )
3 3 6( )
x x TM
y y TM
z z TM

− = =

− = =


− = =

Vậy
ax
2
1 1 1
4
2
2 2 2 3
6
m
x
Py
z
=
= + + =
=
0,25
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 11
Website: tailieumontoan.com
Bài 15. Cho a, b, c là các số dương thỏa mãn điều kiện a + b+ c =1. Chứng minh rằng:
2 2 2
1 1 1 1
4

+ + + +

+ + +

a b c
a b b c c a a b c
DAPAN
Bài
Nội dung cần đạt
Điểm
(0,75 điểm)
Với x, y> 0 , ta có:
( ) ( )
22
1 1 4
40x y xy x y
x y x y
+ + −
+
(luôn đúng)
=>
1 1 4
x y x y
+
+
Dấu “=” xảy ra x = y
0,25
Có a +b
2
= a(a +b+c) +b
2
= a
2
+ b
2
+ ab+ ac ≥ 2ab +ab+ac = 3ab
+ac
2
11
3 3 2
= =
+ + + + +
aa
a b ab ac b c b b c
Áp dụng bất đẳng thức
1 1 4
x y x y
+
+
ta có:
1 1 1 1 1 1 1 1 1 1 1 1 3 1
.
2 4 2 8 4 8 16 16
+ = + + + = +
+ + + +
b b c b b c b b c b b c b c
2
1 3 1
16

+

+

a
a b b c
(1)
0,25
Chứng minh tương tự ta có:
( )
( )
2
2
1 3 1
2
16
1 3 1
3
16

+

+


+

+

b
b c c a
c
c a a b
Cộng từng vế của (1), (2) và (3) ta có:
2 2 2
1 1 1 1
4

+ + + +

+ + +

a b c
a b b c c a a b c
Dấu “=” xảy ra khi
1
a b c
3
= = =
0,25
Bài 16. Cho các số dương
,,x y z
. Chứng minh rằng:
( )( ) ( )( ) ( )( )
2 2 2
x y z 3
x y x z y z y x z x z y 4
+ +
+ + + + + +
DAP AN
Bài
Đp n
Điểm
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 12
Website: tailieumontoan.com
Bài 6
(0,75 điểm)
Với hai số a, b và hai số dương x, y ta có:
2 2 2
()
(*)
a b a b
x y x y
+
+
+
Thật vậy:
(*)
( ) ( )
2 2 2
()a y x y b x x y a b xy + + + +
2 2 2 2
2a y b x abxy +
2
( ay bx ) 0 −
(luôn đúng)
Do đó bất đẳng thức (*) đúng.
Dấu "=" xảy ra khi và chỉ khi
ab
xy
=
.
Áp dụng bất đẳng thức (*) ta được với ba số
,,abc
và ba số dương
,,x y z
bất kì:
2 2 2 2 2 2
a b c (a b) c (a b c)
(**)
x y z x y z x y z
+ + +
+ + +
+ + +
0,25
Áp dụng bất đẳng thức (**) ta có:
( )( ) ( )( ) ( )( )
( )( ) ( )( ) ( )( )
2 2 2
2
x y z
++
x + y x +z y +z y + x z + x z + y
(x + y + z)
x + y x +z + y + z y + x + z + x z + y
( ) ( )
22
2 2 2 2
( ) ( )
3 ( )
x y z x y z
x y z xy yz zx x y z xy yz zx
+ + + +
==
+ + + + + + + + + +
Mà
( )
2
1
3
xy yz zx x y z+ + + +
Suy ra:
( )( ) ( )( ) ( )( )
2 2 2
2
2
2
x y z
x y x z y z y x z x z y
( ) 3
()
4
()
3
x y z
x y z
x y z
++
+ + + + + +
++
=
++
+ + +
0,25
( )( ) ( )( ) ( )( )
2 2 2
x y z 3
x y x z y z y x z x z y 4
+ +
+ + + + + +
(đpcm)
Dấu “=” xẩy ra khi và chỉ khi
x y z==
0,25
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 13
Website: tailieumontoan.com
Bài 17. Cho
,xy
là các số dương thỏa mãn
2.xy
Tìm giá trị nhỏ nhất của biểu thức:
22
22
11
2 1 2 1
xy
P
xy
xy
DAPAN
Bài 6
( 0,75
điểm)
Ta có
22
1 1 1 1
2
2 1 2 1
P
xy
xy
Áp dụng BĐT
1 1 4
a b a b
với
,0ab
, ta được:
2 2 2
1 1 2 4 2
3 3 3
1
1
42
53
P
xy xy xy
xy
x y xy
xy xy
0,25
Lại có
2
1
4 1 2 .x y xy x y
xy
Do đó
4 2 4
6 3 3
P
0,25
Dấu “=” xảy ra khi
22
2
2 1.
x y xy
x y x y
xy
Vậy
4
min
3
P
đạt được khi
1.xy
0,25
Bài 18. Cho 3 số dương a, b, c với abc = 1. Tìm giá trị lớn nhất của biểu thức:
2 2 2 2 2 2
1 1 1
P
a 2b 3 b 2c 3 c 2a 3
= + +
+ + + + + +
.
DAPAN
Bài 6
(0,75đ)
Chứng minh bất đẳng thức phụ :
22
21
x 2y 3 xy y 1
+ + + +
(x, y > 0)
Vì x, y > 0 nên
22
x 2y 3 0; xy y 1 0+ + + +
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 14
Website: tailieumontoan.com
Do đó :
22
21
x 2y 3 xy y 1
+ + + +
22
2xy 2y 2 x 2y 3 + + + +
22
(x y) (y 1) 0 − + −
với mọi x, y > 0
Dấu bằng xảy ra khi x = y = 1.
0,25
2)Áp dụng bất đẳng thức ở câu 1) ta có:
2 2 2 2
1 1 2 1 1
2 2 ab b 1
a 2b 3 a 2b 3
=
++
+ + + +
2 2 2 2
1 1 2 1 1
2 2 bc c 1
b 2c 3 b 2c 3
=
++
+ + + +
2 2 2 2
1 1 2 1 1
2 2 ca a 1
c 2a 3 c 2a 3
=
++
+ + + +
Cộng từng vế của các bất đẳng thức cùng chiều ta được:
1 1 1 1
P
2 ab b 1 bc c 1 ca a 1

+ +

+ + + + + +

0,25
Do abc = 1 nên:
1 1 1
ab b 1 bc c 1 ca a 1
++
+ + + + + +
2
ca a 1
abc ac a ca a 1
ca b abc ca
= + +
+ + + +
++
ca a 1
1
ca a 1 ca a 1 ca a 1
= + + =
+ + + + + +
.
Do đó
1
P
2
. Dấu “=” xảy ra khi a = b = c =1.
Vậy
1
max P =
2
đạt được khi a = b = c =1.
0,25
Bài 19.Cho ba số dương
,,abc
có:
1abc+ + =
. Chứng minh rằng:
4 4 4
1
18
a b c
b c c a a b
+ +
+ + +
DAPAN
6
(0,75 điểm)
Áp dụng bất đẳng Cosy ta có
42
36 3
a b c a
bc
+
+
+
;
42
36 3
b c a b
ca
+
+
+
;
42
36 3
c a b c
ab
+
+
+
0,25
( )
4 4 4
2 2 2
1
36 36 36 3
a b c b c c a a b
abc
b c c a a b
+ + +
+ + + + + + +
+ + +
Suy ra:
( )
4 4 4
2 2 2
11
(1)
18 3
a b c
abc
b c c a a b
+ + + + +
+ + +
0,25
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 15
Website: tailieumontoan.com
Mà:
( )
2
2 2 2
11
(2)
33
a b c a b c+ + + + =
Từ (1), (2) Suy ra:
4 4 4
11
18 9
a b c
b c c a a b
+ + +
+ + +
4 4 4
1
18
a b c
b c c a a b
+ +
+ + +
( đpcm)
Dấu “=” xẩy ra khi:
1
3
abc= = =
.
0,25
Bài 20. Cho các số thực
, , a b c
dương thỏa mãn
1abc+ + =
. Tìm giá trị nhỏ nhất
của biểu thức:
2 2 2
3P a abc b abc c abc abc= + + + + + +
.
DAPAN
Bài 6
(0,75
điểm)
Ta có
( )
( )
( )( )
( )
2
a abc abc a a a b c bc bc a a b a c bc+ + = + + + + = + + +
0,25
Theo BĐT cosi cho hai số dương ta có:
1 3 1
3. .
3 2 3
a a a

= +


( )( )
( )
1
22
a b a c b c
a b a c bc
+ + + +
+ + + + =
Từ đó suy ra
2
31
23
a abc abc a

+ + +


Tương tự ta có:
2
31
23
b abc abc b

+ + +


;
2
31
23
c abc abc c

+ + +


0,25
Từ đó
3 1 3 1 3 1
3
2 3 2 3 2 3
P a b c
+ + + + + =
.
Dấu bằng xảy ra
1
3
abc = = =
.
Vậy giá trị nhỏ nhất giá trị nhỏ nhất của P là
3
khi
1
3
abc= = =
0,25
Bài 21.
a) Cho hai số dương a, b . Chứng minh rằng:
1 1 4
a b a b
+
+
.
Đẳng thức xảy ra khi nào?
b) Cho hai số dương a, b thỏa mãn a + b = 1. Tìm giá trị nhỏ nhất của biểu thức:
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 16
Website: tailieumontoan.com
22
11
P
1 3ab a 1 3ab b
=+
+ + + +
Bài
Đáp án
Điểm
Bài 5
(0,75
điểm)
5.a (0,25 điểm)
( ) ( ) ( )
2
1 1 4
a a b b a b 4ab a b 0
a b a b
+ + + + −
+
Luôn đúng vơi mọi a, b dương
Dấu “=” xẩy ra khi a = b
0,25
5.b (0,5 điểm)
Áp dụng phần a ta có:
2 2 2 2
1 1 4
1 3ab a 1 3ab b 1 3ab a 1 3ab b
+
+ + + + + + + + +
( )
2
22
1 1 4
1 3ab a 1 3ab b
2 a b 4ab
+
+ + + +
+ + +
Mà : a + b = 1 nên
2 2 2
1 1 4
(1)
1 3ab a 1 3ab b 2 1 4ab
+
+ + + + + +
0,25
Lại có:
( )
2
2
22
2
ab
a b 0 a,b a b 2ab 4ab a,b ab a,b
2
11
ab ab (2)
24
+

− + +





Từ (1) và (2) Suy ra
P1
Vậy giá trị nhỏ nhất của P = 1 khi a = b = 0,5
0,25
Bài 22.
Chứng minh rằng:
( ) ( )
a + b + c 1
2
a a + 3b b b + 3c ( 3 )c c a
+ + +
với a,b,c là các số dương.
DAPAN
Bài
Đp n
Điểm
Với x, y > 0, ta có:
(1) 2
2
xy
xy xy x y
+
+
20x y xy + −
2
( ) 0xy −
(2).
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 17
Website: tailieumontoan.com
6
(0,75 đ)
Vì (2) luôn đúng với mọi số thực không âm, nên BĐT đã cho đúng.
Dấu “=” xảy ra khi x = y.
Xét
( ) ( ) ( ) ( )
a + b +c 2(a + b + c)
(1)
a a + 3b b b + 3c ( 3 ) 4a a + 3b 4b b + 3c 4 ( 3 )c c a c c a
=
+ + + + + +
Áp dụng bất đẳng thức ở câu a cho các số dương 4a, a + 3b, 4b,
b+3c,4c, c+3a ta được:
( ) ( )
( ) ( )
( ) ( )
4a + (a + 3b) 5a + 3b
4a a + 3b 2
22
4b + (b + 3c) 5b + 3c
4b b + 3c 3
22
4 + (c + 3a) 5c + 3a
4c c + 3a 4
22
c
=
=
=
0,25
Từ (2), (3) và (4) suy ra:
( ) ( )
4a a + 3b 4b b +3c 4 ( 3 ) 4a + 4b + 4c (5)c c a+ + +
Từ (1) và (5) với điều kiện các số a,b,c đều dương ta suy ra:
( ) ( )
a + b + c 2(a + b +c) 1
4a + 4b + 4c 2
a a + 3b b b + 3c ( 3 )c c a
=
+ + +
.
0,25
Dấu “=” xảy ra khi và chỉ khi:
43
43
43
a a b
b b c a b c
c c a
=+
= + = =
=+
.
0,25
Bài 23.Cho 3 số dương a, b, c thỏa mãn abc = 1. Tìm giá trị lớn nhất của biểu thức:
2 2 2 2 2 2
1 1 1
2 3 2 3 2 3
= + +
+ + + + + +
P
a b b c c a
.
DAPAN
Bài 6
Áp dụng bất đẳng thức ở câu a) ta có:
Cộng từng vế của các bất đẳng thức trên ta được:
0,25
2 2 2 2
1 1 2 1 1
..
2 2 ab b 1
a 2b 3 a 2b 3
=
++
+ + + +
2 2 2 2
1 1 2 1 1
..
2 2 bc c 1
b 2c 3 b 2c 3
=
++
+ + + +
2 2 2 2
1 1 2 1 1
..
2 2 ca a 1
c 2a 3 c 2a 3
=
++
+ + + +
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 18
Website: tailieumontoan.com
Có
(do abc = 1)
0,25
Do đó . Dấu “=” xảy ra khi a = b = c =1.
Vậy đạt được khi a = b = c =1.
0,25
Bài 24. Chứng minh với .
DAPAN
Bài
Đp n
Điểm
1 1 1 1
P
2 ab b 1 bc c 1 ca a 1

+ +

+ + + + + +

1 1 1
ab b 1 bc c 1 ca a 1
++
+ + + + + +
2
ca a 1
abc ac a ca a 1
ca b abc ca
= + +
+ + + +
++
ca a 1
1
ca a 1 ca a 1 ca a 1
= + + =
+ + + + + +
1
P
2
1
maxP =
2
( ) ( )
+ + +
a + b + c 1
2
a a + 3b b b + 3c c(c 3a)
( )
a, b, c 0
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 19
Website: tailieumontoan.com
Bài
6(0.75đ)
(0,75 điểm)
Ta có:
( ) ( )
( ) ( )
+ + +
=
+ + +
a + b +c
a a + 3b b b + 3c c(c 3a)
2(a + b + c)
(1)
4a a + 3b 4b b + 3c 4c(c 3a)
Áp dụng bất đẳng thức Cô-si cho các số dương 4a và a + 3b; 4b và
b + 3c; 4c và c+3a ta được:
0.25
Từ (2), (3) và (4) suy ra:
Từ (1) và (5) với điều kiện các số a,b,c đều dương ta suy ra:
.
0.25
Dấu “=” xảy ra khi và chỉ khi: .
Vậy ta có điều phải chứng minh.
0.25
Bài 25. Cho hai số dương a, b thỏa mãn điều kiện: a+ b= 1.
Hãy tìm giá trị nhỏ nhất của biểu thức: B =
2 2 2 2
1 1 4
4 + 4a 10aba b b
++
+
DAPAN
Bài
Nội dung đáp án
Điểm
( ) ( )
( ) ( )
( ) ( )
=
=
=
4a + (a + 3b) 5a + 3b
4a a + 3b 2
22
4b + (b + 3c) 5b + 3c
4b b + 3c 3
22
4c + (c + 3a) 5c + 3a
4c c + 3a 4
22
( ) ( )
+ + + 4a a + 3b 4b b +3c 4c(c 3a) 4a + 4b + 4c (5)
( ) ( )
=
+ + +
a + b + c 2(a + b +c) 1
4a + 4b + 4c 2
a a + 3b b b + 3c c(c 3a)
=+
= + = =
=+
4a a 3b
4b b 3c a b c
4c c 3a

Tài liệu khác của Toán 10

Preview text:

Tailieumontoan.com 
Điện thoại (Zalo) 039.373.2038 CÁC BÀI TOÁN
BẤT ĐẲNG THỨC HAY
(Liệu hệ tài liệu word môn toán SĐT (zalo) : 039.373.2038)
Tài liệu sưu tầm, ngày 20 tháng 7 năm 2024
Website: tailieumontoan.com
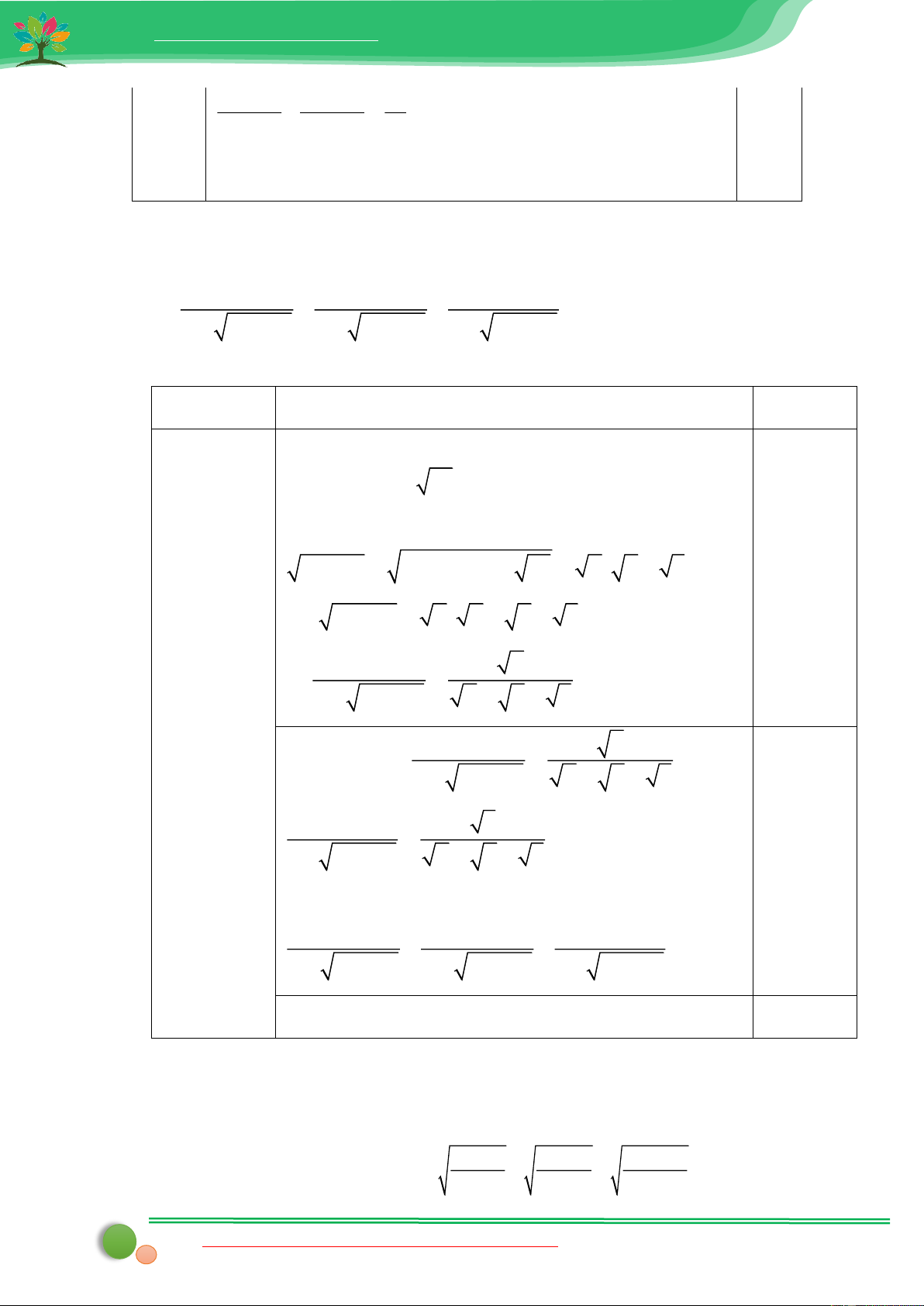
Bài 1. Cho a, b, c > 0. Chứng minh rằng : a b c b c a 2 + +  1+ + +  
b + 2c c + 2a a + 2b
b + 2a c + 2b a + 2c DAP AN Bài Nội dung Điểm 6 a b c b c a (0,75 điể 2 + +  1+ + + m)  
b + 2c c + 2a a + 2b
b + 2a c + 2b a + 2c a b c
b + 2a − 2a c + 2b − 2b a + 2c − 2 2 c + +  1+ + +  
b + 2c c + 2a a + 2b b + 2a c + 2b a + 2c a b c  2a 2b 2c  2 + +  4 − − −  
b + 2c c + 2a a + 2b
b + 2a c + 2b a + 2c 0.25  1 1   1 1   1 1   a + + b + + c +        2
b + 2c b + 2a
c + 2a c + 2b
a + 2b a + 2c  1 1 4 + 
Áp dụng bất đẳng thức : a b a + b ta có 1 1 4 2 +  =
b + 2c b + 2a 2a + 2b + 2c a + b + c  1 1  2a Suy ra a +   
b + 2c b + 2a a + b + c 0.25  1 1  2b Tương tự b +   
c + 2a c + 2b a + b + c  1 1  2c c +   
a + 2b a + 2c a + b + c
Cộng các bất đẳng thức theo vế ta được: 0.25  1 1   1 1   1 1   a + + b + + c +        2
b + 2c b + 2a
c + 2a c + 2b
a + 2b a + 2c  (đpcm)
Đẳng thức xảy ra khi a=b=c
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 1
Website: tailieumontoan.com
Bài 2. Cho x, y, z là ba số dương thỏa mãn xyz = 1. Chứng minh rằng: 2 2 2 x y z 3 + +  y +1 z +1 x +1 2 DAP AN Bài Nội dung Điểm 6
Áp dụng bất đẳng thức Cô si ta có: (0,75 điểm) 2 2 x y +1 x y +1 x +  2 . = 2. = x (1) y +1 4 y +1 4 2 0,25 2 + 2 + Tương tự y z 1 z x 1 : +  y (2); +  z (3) z +1 4 x +1 4
Cộng từng vế các bất đẳng thức (1), (2), (3) ta được: 2 2 2 x y z x +1 y +1 z +1 + + + + +  x + y + z y +1 z +1 x +1 4 4 4 2 2 2 x y z 3(x + y + z) − 3 0,25  + +  (4) y +1 z +1 x +1 4
Mặt khác cũng theo bất đẳng thức Cô – si ta có : 3 3
x + y + z  3. xyz = 3. 1 = 3 (5) 2 2 2 x y z 3.3 − 3 3 0,25 Từ (4) và (5) suy ra: + +  = y +1 z +1 x +1 4 2
Dấu “=” xảy ra  x = y = z = 1 2 2 n m
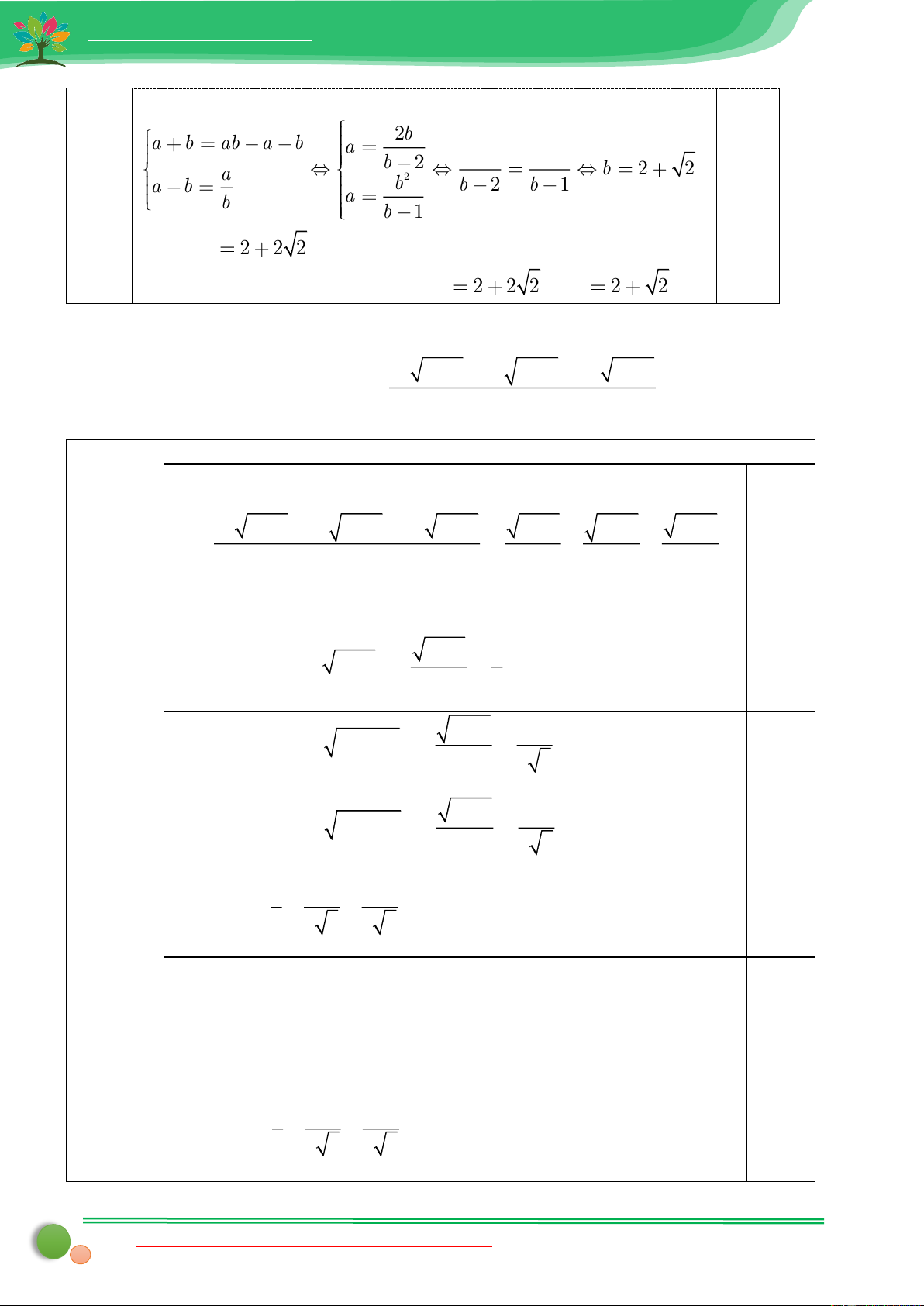
Bài 3. Cho n > 1; m > 1. Tìm giá trị nhỏ nhất của biểu thức E = + m −1 n − . 1 DAPAN Bài Nội dung Điểm 6 2 2 n m
* Với n > 1; m > 1 thì ; là hai số dương (0,75 điểm) m −1 n −1 0,25
Áp dụng bất đẳng thức Cô si ta có: 2 2 2 2 n m n m n m E = +  2 . = 2 . m −1 n −1 m −1 n −1 n −1 m −1 − − ( n− − n n n )2 1 1 2 1 *Mà  2   0   0 (1) n −1 n −1 n −1 0,25
Do bất đẳng thức (1) đúng với mọi n >1 nên bất đẳng thức cần
chứng minh đúng. Dấu ‘=’ xảy ra khi và chỉ khi n = 2. n m
* Áp dụng kết quả câu trên ta có: 2 .  8 => E  8 0,25 n −1 m −1
Vậy Emin = 8 khi n = m = 2.
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 2
Website: tailieumontoan.com 1 1 1
Bài 4. Cho các số dương x, y, z thỏa mãn + +
= 12 . Tìm giá trị lớn nhất x + y y + z z + x 1 1 1 của biểu thức: P = + + . 3x + 3y + 2z 3x + 2y + 3z 2x + 3y + 3z DAPAN Bài Nội dung Điểm 6
Áp dụng bất đẳng thức Cosi cho 2 số a, b dương, ta có (0,75 điểm) 1 1 1 a + b  2 ab , +  2 . a b ab 0,25      ( + ) 1 1 1 1 4 1 1 1 1 a b +  4  +    +     (*)  a b  a b a + b a + b 4  a b 
Dấu bằng xảy ra khi a = b. Áp dụng BĐT (*) ta có: 1 1 1  1 1  =   +  3x + 3y + 2z (x + z)+(y + z) + 2  (x + y) 4    (x + z) + (y + z) 2  (x + y)  1 1 1 1  1 1  1 = +  + +   4 (x + z) + (y + z) 8 
(x + y) 16  x + z y + z  8(x +y) 0,25
Chứng minh tương tự, ta có 1 1  1 1  1  + +   + +  + + z  8(x + z) ; 3x 2y 3z 16 x y y 1 1  1 1  1  + +   2x + 3y + 3z
16  x + y x + z  8(y + z)
Cộng từng vế 3 bất đẳng thức ta được: 1 1 1 1  2 2 2  P = + +  + +   3x + 3y + 2z 3x + 2y + 3z 2x + 3y + 3z
16  x + y y + z z + x  0,25 1  1 1 1  + + + = 1 + 1 .12 .12 =   3 8  x + y y + z z + x  8 8 1
Dấu bằng xảy ra khi x = y = z = 8 1
Vậy GTLN của biểu thức P là 3 khi x = y = z = 8
Bài 5. Cho a > 0, b > 0 thỏa mãn 1 1
+ = 2 . Tìm giá trị lớn nhất của biểu thức a b 1 1 Q = + . 4 2 2 4 2 2
a + b + 2ab
b + a + 2ba DAPAN
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 3
Website: tailieumontoan.com Bài Nội dung Điểm 6
Với a  0;b  0 tacó: 2 2 4 2 2 4 2 2 (a − ) b
 0  a − 2a b +b  0  a +b  2a b (0,75 điểm) 1 1 4 2 2 2 2
a +b + 2ab  2a b + 2ab   (1) 4 2 2
a + b + 2ab
2ab (a + b) 0,25 Tương tự có 1 1  (2) . 4 2 2
b + a + 2a b
2ab (a + b) 1
Từ (1) và (2)  Q
ab (a + b) 0,25 1 1 Vì
+ = 2  a + b = 2ab mà a + b  2 ab ab 1 a b 1 1  1 Q
 .Khi a = b = 1 thì  Q = . 2 2(ab) 2 2 0,25
Vậy giá trị lớn nhất của biểu thức là 1 2 Bài 6.
Cho a,b,c, là độ dài 3 cạnh của một tam giác. CMR: 1 1 1 1 1 1 + +  + +
a + b − c
b + c − a c + a − b a b c DAPAN Bài Nội dung Điểm
Áp dụng BĐT côsi với 2 số dương x, y 1 1 ; ; ta có: x y
x + y  2 xy  1 1 1 1 4 1 1 1
 (x + y)( + )  4 +  +  hay (1) . 2  x y x y x + yx y xy
Dấu “=” xảy ra  x = y
do a, b, c là độ dài ba cạnh của tam giác nên theo bất đẳng thức
tam giác, có: a + b – c > 0. 0,25
Áp dụng bất đẳng thức (1) ta có: 1 1 4 0,25 + 
c + b − a
c + a − b c 2 tương tự 1 1 4 +  0,25
c + b − a
a + b − c b 2
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 4
Website: tailieumontoan.com 1 1 4 + 
c + a − b
a + b − c 2a
Cộng 3 bất đẳng thức trên và suy ra đpcm
Dấu “=” xảy ra khi và chỉ khi a=b=c
Bài 7. Cho x, y, z là ba số dương thoả mãn x + y + z =3. Chứng minh rằng: x y z + +  1. x + 3x + yz y + 3y + zx z + 3z + xy DAPAN Bài
Nội dung cần đạt Điểm
Ta có: 3x + yz = (x + y + z)x + yz = x2 + yz + x(y + z)  x(y + z) + 2x yz Suy ra 0,25
3x + yz  x(y + z) + 2x yz = x ( y + z ) x + 3x + yz  x ( x + y + z ) x x   (1) x + 3x + yz x + y + z Bài 6 y y Tương tự ta có:  (2), (0,75 điểm) y + 3y + zx x + y + z z z  (3) z + 3z + xy x + y + z Từ (1), (2), (3) ta có 0,25 x y z + +  1 x + 3x + yz y + 3y + zx z + 3z + xy
Dấu “=” xảy ra khi x = y = z = 1 0,25
Bài 8. Cho ba số thực dương x, y, z thỏa mãn: x + 2y + 3z = 2. xy 3yz 3xz
Tìm giá trị lớn nhất của biểu thức:S = + + . xy + 3z 3yz + x 3xz + 4y
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 5
Website: tailieumontoan.com DAP AN Bài Đáp án Điểm
Đặt a = x ; b = 2y ; c = 3z  a, b, c > 0 và a + b + c = 2 Khi đó S = ab bc ac + + ab + 2c bc + 2a ac + 2b 0,25 ab ab ab 1  a b  Xét = =  +   ab + 2c ab + (a + b + c)c (a + c)(b + c) 2  a + c b + c  Đẳ a b = ng thức xảy ra khi a + c b + c Tương tự ta có bc 1  b c   + ac 1  a c  ;  +     bc + 2a 2  b + a c + a  ac + 2b 2  a + b c + b  0,25 Bài 6 Đẳ b c a c ng thức xảy ra khi = ; = b + a c + a a + b c + b ( 0,75 điểm) Cộng các vế ta được 1  a + b b + c a + c  3 S  + + =   2  a + b b + c a + c  2 0,25 3 2 Vậy GTLN của S =  a = b = c = 2  x = 1 ; y = 2 ; z = 2 3 3 3 9
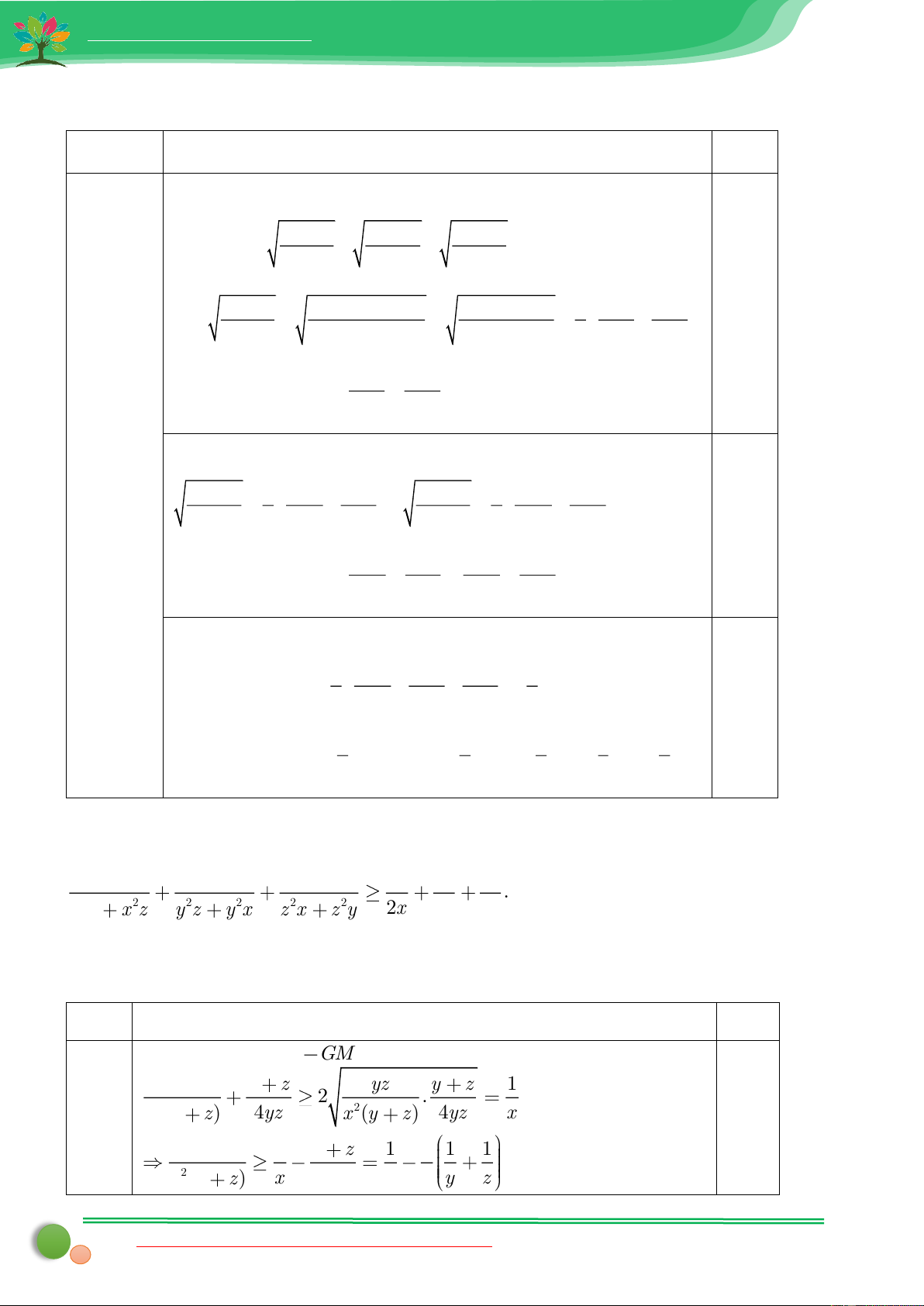
Bài 9. Cho các số thực dương x, ,
y z . Chứng minh rằng yz zx xy 1 1 1 . 2 2 2 2 2 2 x y x z y z y x z x z y 2x 2y 2z DAPAN Bài Nội dung Điểm Áp dụng BĐT AM GM ta được 6 yz y z yz y z 1 2 . 2 2 (0,75 x (y z) 4yz x (y z) 4yz x 0,25 điểm) yz 1 y z 1 1 1 1 2 x (y z) x 4yz x 4 y z
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 6
Website: tailieumontoan.com zx 1 1 1 1 xy 1 1 1 1 Tương tự: ; 0,25 2 2 y (z x) y 4 x z z (x y) z 4 x y
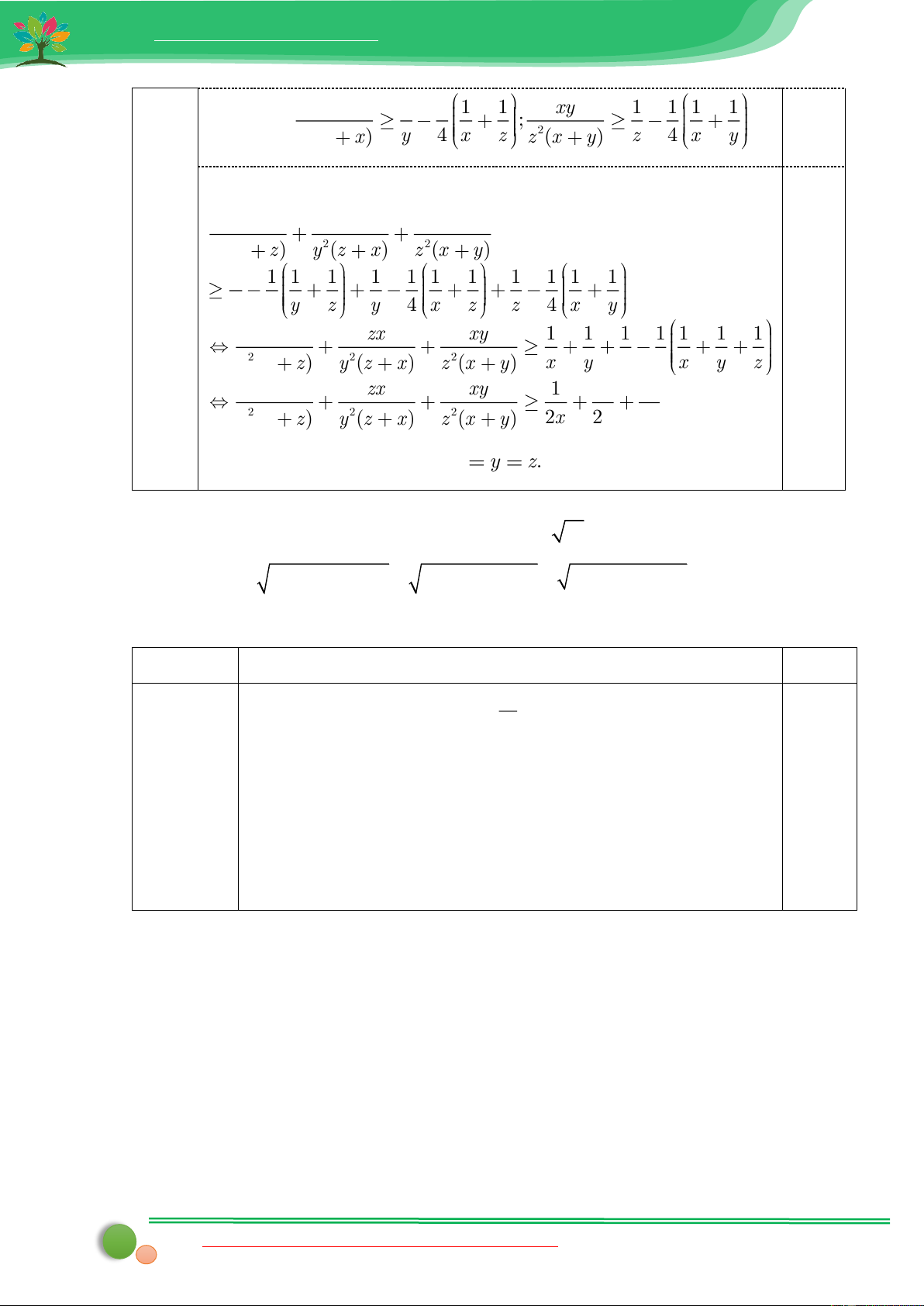
Cộng các BĐT cùng chiều ta được yz zx xy 2 2 2 x (y z) y (z x) z (x y) 1 1 1 1 1 1 1 1 1 1 1 1 x 4 y z y 4 x z z 4 x y yz zx xy 1 1 1 1 1 1 1 0,25 2 2 2 x (y z) y (z x) z (x y) x y z 2 x y z yz zx xy 1 1 1 2 2 2 x (y z) y (z x) z (x y) 2x 2y 2z
Dấu “=” xảy ra khi và chỉ khi x y z.
Bài 10. Cho các số x, y, z > 0 thỏa mãn x + y + z = 11 . Tìm giá trị nhỏ nhất của biểu thức: A = 2 2 2 2 2 2
5x + xy + 5y + 5y + yz + 5z + 5z + zx + 5x . DAPAN Bài Nội dung Điểm (0,75điểm) Chứng minh: 2 2 11 5x + xy + 5y  (x + y)2 . (1) 4 2 2  + +  ( 2 2 20x 4xy 20y 11 x + 2xy + y ) 2 2
 9x −18xy + 9y  0  9(x − y)2  0 (2) luôn đúng với mọi x, y. 0,25
Vậy BĐT (1) đúng. Dấu "=" xảy ra khi x = y.
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 7
Website: tailieumontoan.com
b) Áp dụng bất đẳng thức (1) với x, y > 0 ta có 2 2 11 5x + xy + 5y  (x + y)2 4 Suy ra 2 2 11 + +  ( + )2 11 11 5x xy 5y x y = x + y = (x + y) 4 2 2 Lập luận tương tự có 2 2 11 5y + yz + 5z  (y + z), 2 2 2 11 5z + zx + 5x  (z + x) 0,25 2
Cộng các BĐT cùng chiều ta có 11 A 
(x + y + y + z + z + x) = 11. 11 =11. 2 0,25
Do đó MinA = 11 khi và chỉ 11 khi x = y = z = . 3 Bài 11. Cho , a ,
b c là các số dương. Chứng minh rằng: 3 3 3 a b c a + b + c + +  . 2 2 2 2 2 2
a + ab + b
b + bc + c
c + ca + a 3 DAPAN Câu
Lời giải sơ lược Điểm 6 3 a b
(0,75đ) Chứng minh bất đẳng thức sau:  a − . 2 2 a + b 2 a ( 2 2 a + b ) 2 3 2 − ab a ab Ta có = = a − . 2 2 2 2 2 2 a + b a + b a + b 2 2 Theo BĐT Cauchy ta có ab ab b a −  a − = a − . 0,25 2 2 a + b 2ab 2 3 3 Tương tự b c c a theo câu a) ta có :  b − ,  c − . 2 2 b + c 2 2 2 c + a 2
Cộng vế theo vế ba bất đẳng thức trên ta có: 3 3 3 a b c a + b + c + +  . 2 2 2 2 2 2 a + b b + c c + a 2 0,25
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 8
Website: tailieumontoan.com 3 3 3 a a 2 a Ta có:  = . . 2 2 2 2 2 2
a + ab + b a + b + 2 2 3 a b a + + b 2 3 3 3 3 Tương tự b 2 b c 2 c ta có  . ,  . . 2 2 2 2
b + bc + c 3 b + c 2 2 2 2
c + ca + a 3 c + a
Cộng vế theo vế ba bất đẳng thức trên ta có: 3 3 3 a b c + + 0,25 2 2 2 2 2 2
a + ab + b
b + bc + c
c + ca + a 3 3 3 2  a b c
a + b + c   + +   . 2 2 2 2 2 2 3  a + b b + c c + a  3 Bài 13. a
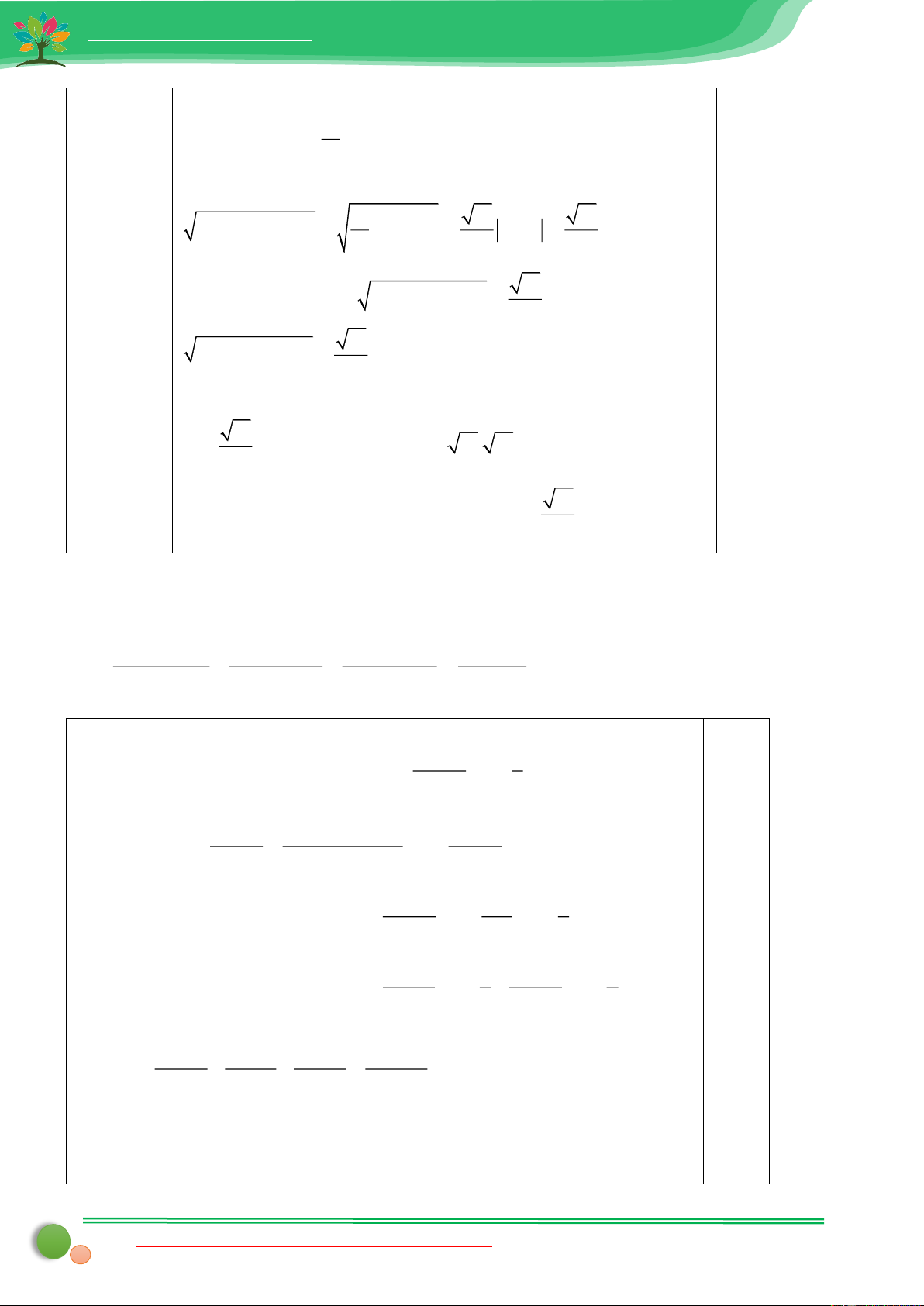
Cho a,b là các số thực dương, thỏa mãn a b . Chứng minh: b ab 1 1 1
9 . Đẳng thức xảy ra khi nào? a b a b ab a b ab a b ab DAPAN Bài Nội dung Điểm a Ta có 2 a b ab a b ab a b ( b b 1) b a Lại có 2 a b a(b 1) b 0 b 1 . Do đó b ab a b 0 1 1 4 0,25
Áp dụng bất đẳng thức
với x,y là các số dương, ta x y x y 6 có: (0,75 điể ab 1 1 ab 4 4 m) . a b a b ab a b a b a b ab a b a b
Áp dụng bất đẳng thức Cauchy - Schwarz ta có: 2 2 1 4 1 9 a b ab a b a b ab a b ab 0,25 ab 1 1 1 9 Vậy a b a b ab a b ab a b ab
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 9
Website: tailieumontoan.com
Dấu đẳng thức xảy ra khi: 2b a b ab a b a 2 2 2 b b b b 2 2 a 2 . a b b b 2 b 1 a b 0,25 b 1 Khi đó a 2 2 2
Vậy đẳng thức xảy ra khi và chỉ khi a 2 2 2 và b 2 2 . Bài 14.
yz x − 1 + xz y − 2 + xy z − 3
Tìm giá trị lớn nhất của biểu thức: P = . xyz DAPAN Bài 6
Điều kiện xác định x  1,y  2,z  3. ( 0,75 điểm)
yz x − 1 + xz y − 2 + xy z − 3 x − 1 y − 2 z − 3 P = = + + xyz x y z 0,25
Áp dụng bất đẳng thức Cô-si ta có: x − 1 1
x = 1 + (x − 1)  2 x − 1   . x 2 y − 2 1
y = 2 + (y − 2)  2 2(y − 2)   y 2 2 z − 3 1
z = 3 + (z − 3)  2 3(z − 3)   z 2 3 0,25 1 1 1 Suy ra P  + + 2 2 2 2 3 x  − 1 = 1 x  = 2(TM)  
Dấu “=” xảy ra  y  − 2 = 2  y  = 4(TM) z  3 3 z  − = = 6(TM)   0,25 x  = 2 1 1 1  Vậy P = + +  y  = 4 max 2 2 2 2 3 z  = 6 
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 10
Website: tailieumontoan.com
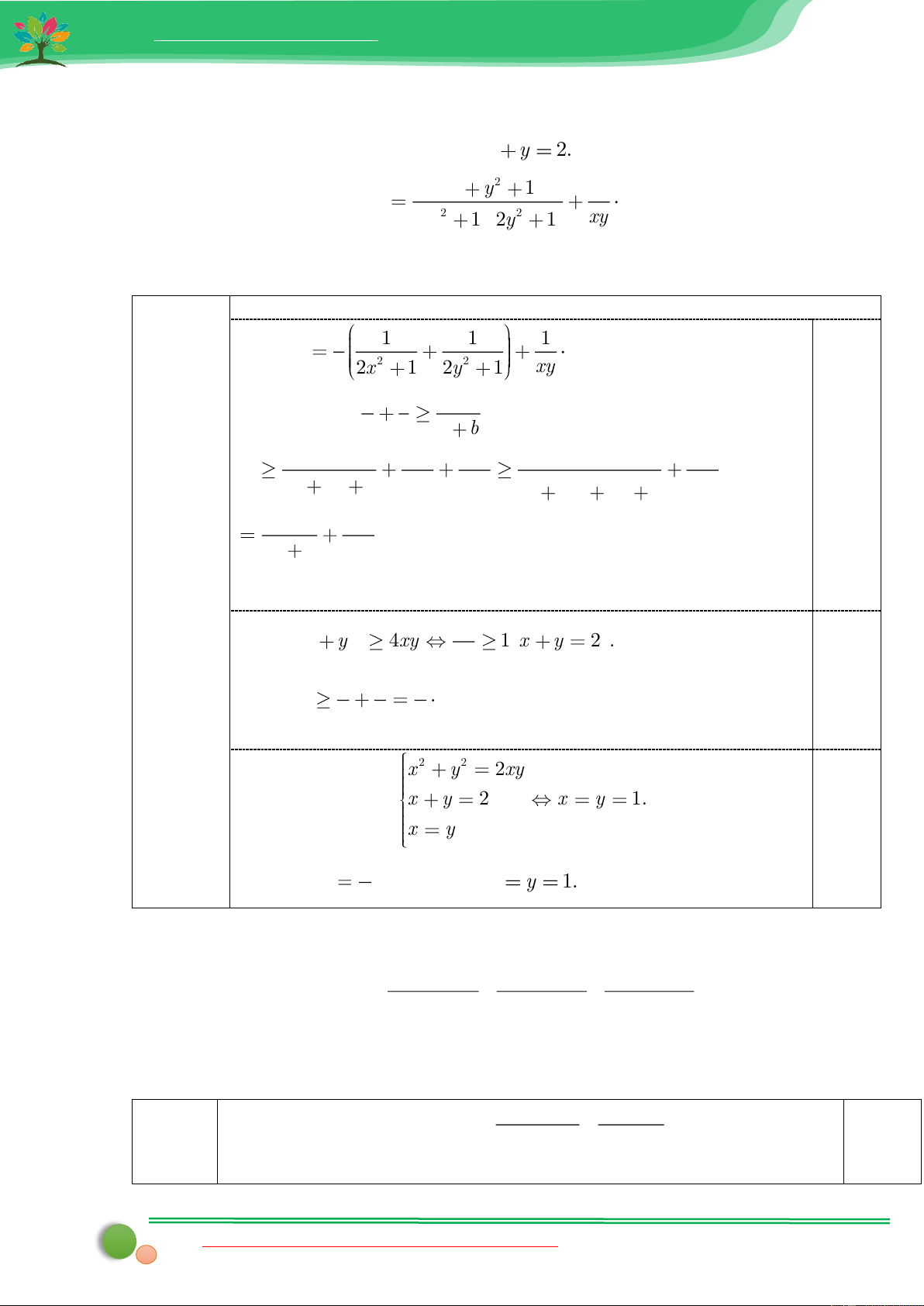
Bài 15. Cho a, b, c là các số dương thỏa mãn điều kiện a + b+ c =1. Chứng minh rằng: a b c 1  1 1 1  + +  + +   2 2 2 a + b b + c c + a 4  a b c  DAPAN Bài
Nội dung cần đạt Điểm
Với x, y> 0 , ta có: 1 1 4 + 
 (x + y)2  4xy  (x − y)2  0(luôn đúng) + 0,25 x y x y 1 1 4 => +  x y x +
Dấu “=” xảy ra  x = y y
Có a +b2 = a(a +b+c) +b2 = a2 + b2 + ab+ ac ≥ 2ab +ab+ac = 3ab +ac a a 1 1   = = 2 a + b 3ab + ac 3b + c
2b + b + c 0,25 1 1 4
Áp dụng bất đẳng thức +  x y x + ta có: y (0,75 điểm) 1 1  1 1  1 1 1 1 1  1 1  1  3 1   + = + .  + + = +      
2b + b + c 4  2b b + c  8b 4 b + c 8b 16  b c  16  b c   a 1  3 1   +   (1) 2 a + b 16  b c
Chứng minh tương tự ta có: b 1  3 1   + 2   2 ( ) b + c 16  c a  0,25 c 1  3 1   + 3   2 ( ) c + a 16  a b
Cộng từng vế của (1), (2) và (3) ta có: a b c 1  1 1 1  + +  + +   2 2 2 a + b b + c c + a 4  a b c  1
Dấu “=” xảy ra khi a = b = c = 3
Bài 16. Cho các số dương ,
x y, z . Chứng minh rằng: 2 2 2 x y z 3 ( + + 
x + y)(x + z) ( y + z)( y + x) (z + x)(z + y) 4 DAP AN Bài Đáp án Điểm
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 11
Website: tailieumontoan.com 2 2 2 a b (a + b)
Với hai số a, b và hai số dương x, y ta có: +  (*) x y x + y Thật vậy: (*) 2
a y (x + y) 2
+ b x (x + y) 2
 (a + b) xy 2 2 2 2
a y +b x  2abxy 2
 ( ay − bx )  0 (luôn đúng) Do đó bất đẳ ng thức (*) đúng. 0,25 a b
Dấu "=" xảy ra khi và chỉ khi = . x y
Áp dụng bất đẳng thức (*) ta được với ba số , a ,
b c và ba số dương 2 2 2 2 2 2 a b c (a + b) c (a + b + c) + +  +  ,
x y, z bất kì: (**) x y z x + y z x + y + z
Áp dụng bất đẳng thức (**) ta có: 2 2 2 x y z + +
(x + y)(x + z) (y + z)(y + x) (z + x)(z + y) 2 (x + y + z)
 (x+y)(x+z)+(y+z)(y+x)+(z+x)(z+y) Bài 6 2 2
(x + y + z)
(x + y + z) = = (0,75 điể m) 2 2 2
x + y + z + 3( xy + yz + zx) 2
(x + y + z) + ( xy + yz + zx) 0,25 1
Mà xy + yz + zx  ( x + y + z)2 3 Suy ra: 2 2 2 x y z ( + +
x + y)(x + z) ( y + z)(y + x) (z + x)(z + y) 2
(x + y + z) 3  = 2
(x + y + z) 2 4
(x + y + z) + 3 2 2 2 x y z 3  ( + +  (đpcm)
x + y)(x + z) ( y + z)(y + x) (z + x)(z + y) 4 0,25
Dấu “=” xẩy ra khi và chỉ khi x = y = z
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 12
Website: tailieumontoan.com
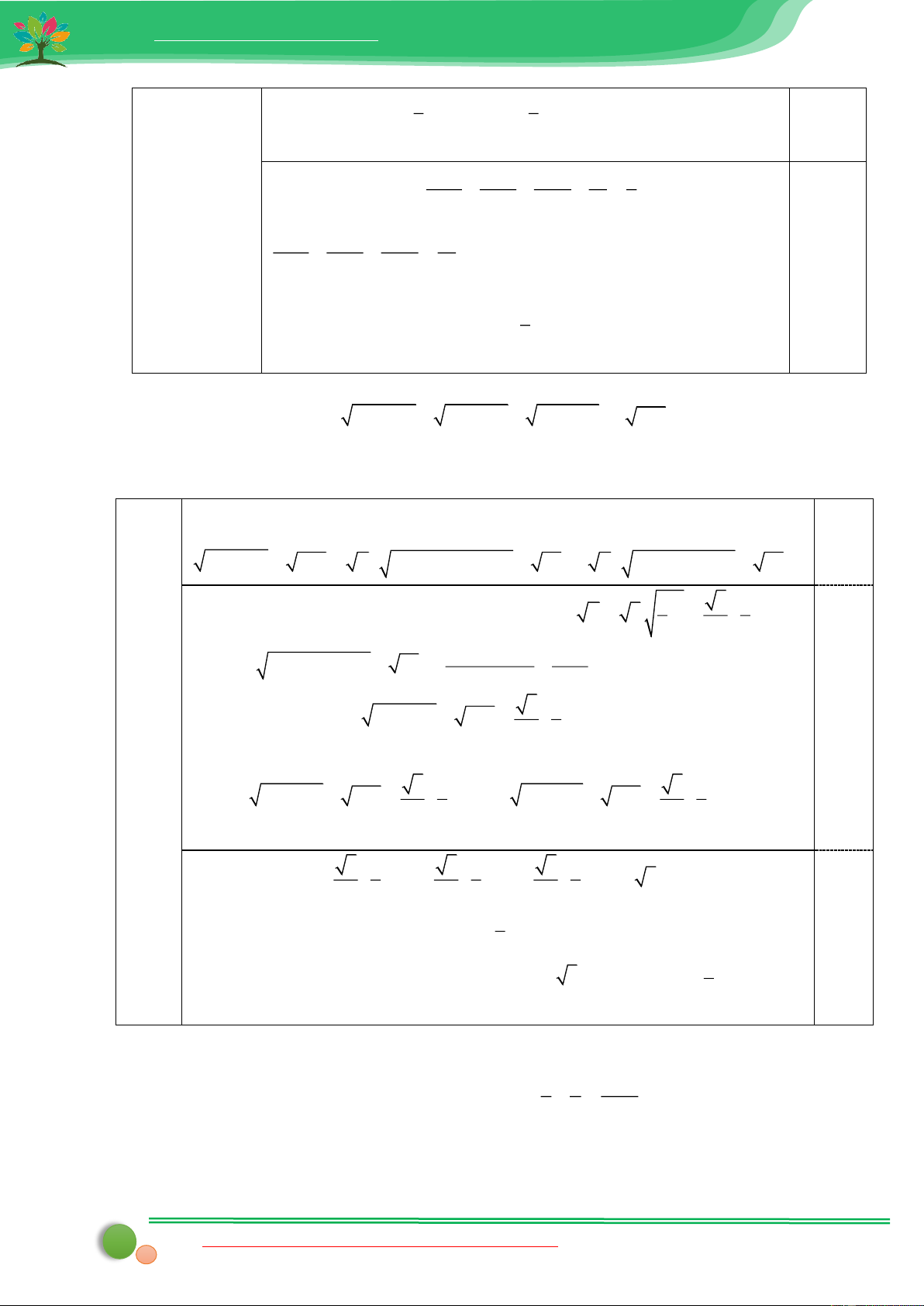
Bài 17. Cho x,y là các số dương thỏa mãn x y
2. Tìm giá trị nhỏ nhất của biểu thức: 2 2 x y 1 1 P 2 2 2x 1 2y 1 xy DAPAN Bài 6 1 1 1 1 ( 0,75 Ta có P 2 2 2 x y xy điểm) 2 1 2 1 1 1 4 Áp dụng BĐT với ,
a b  0 , ta được: a b a b 1 1 2 4 2 P 0,25 2 2 2 x y 1 3xy 3xy 3 x y xy 1 xy 4 2 xy 5 3xy 2 1 Lại có x y 4xy 1 x y 2 . xy 4 2 4 0,25 Do đó P 6 3 3 2 2 x y 2xy
Dấu “=” xảy ra khi x y 2 x y 1. x y 0,25 4 Vậy min P đạt được khi x y 1. 3
Bài 18. Cho 3 số dương a, b, c với abc = 1. Tìm giá trị lớn nhất của biểu thức: 1 1 1 P = + + . 2 2 2 2 2 2 a + 2b + 3 b + 2c + 3 c + 2a + 3 DAPAN Bài 6
Chứng minh bất đẳng thức phụ : 2 1  (x, y > 0) 2 2 x + 2y + 3 xy + y +1 (0,75đ) Vì x, y > 0 nên 2 2
x + 2y + 3  0; xy + y +1  0
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 13
Website: tailieumontoan.com Do đó : 2 1  2 2
 2xy + 2y + 2  x + 2y +3 2 2 x + 2y + 3 xy + y +1 0,25 2 2
 (x − y) + (y −1)  0 với mọi x, y > 0
Dấu bằng xảy ra khi x = y = 1.
2)Áp dụng bất đẳng thức ở câu 1) ta có: 1 1 2 1 1 =  2 2 2 2 a + 2b + 3 2 a + 2b + 3 2 ab + b +1 1 1 2 1 1 =  2 2 2 2 b + 2c + 3 2 b + 2c + 3 2 bc + c +1 1 1 2 1 1 =  2 2 2 2 c + 2a + 3 2 c + 2a + 3 2 ca + a +1
Cộng từng vế của các bất đẳng thức cùng chiều ta được: 0,25 1  1 1 1  P  + +  
2  ab + b +1 bc + c +1 ca + a +1  Do abc = 1 nên: 1 1 1 + + ca a 1 = + + ab + b +1 bc + c +1 ca + a +1 2 ca b + abc + ca abc + ac + a ca + a +1 ca a 1 = + + =1. ca + a +1 ca + a +1 ca + a +1 Do đó 1 P 
. Dấu “=” xảy ra khi a = b = c =1. 2 Vậy 1 0,25 max P =
đạt được khi a = b = c =1. 2 4 4 4 a b c 1
Bài 19.Cho ba số dương , a ,
b c có: a + b + c =1. Chứng minh rằng: + +  b + c c + a a + b 18 DAPAN
Áp dụng bất đẳng Cosy ta có 4 2 a b + c a 4 2 + 4 2 + 0,25 +  b c a b c a b c ; +  ; +  b + c 36 3 c + a 36 3 a + b 36 3 4 4 4 a b c b + c c + a a + b 1 2 2 2 6 + + + + +
 (a + b + c ) + + + (0,75 điểm) b c c a a b 36 36 36 3 0,25 4 4 4 a b c 1 1 Suy ra: + + +  ( 2 2 2
a + b + c )(1) b + c c + a a + b 18 3
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 14
Website: tailieumontoan.com 1 1
Mà: a + b + c  (a + b + c)2 2 2 2 = (2) 3 3 4 4 4 a b c 1 1 Từ (1), (2) Suy ra: + + +  b + c c + a a + b 18 9 4 4 4 a b c 1 + +  ( đpcm) b + c c + a a + b 18 0,25 1
Dấu “=” xẩy ra khi: a = b = c = . 3
Bài 20. Cho các số thực , a ,
b c dương thỏa mãn a + b + c =1. Tìm giá trị nhỏ nhất của biểu thức: 2 2 2 P =
a + abc + b + abc + c + abc + 3 abc . DAPAN Ta có 0,25 2
a + abc + abc =
a ( a(a + b + c) + bc + bc ) = a ( (a + b)(a + c) + bc )  
Theo BĐT cosi cho hai số dương ta có: 1 3 1 a = 3. .a  + a   3 2  3 
( ( + )( + )+ ) a+b+a+c b+c a b a c bc  + = 1 2 2 3  1  Từ đó suy ra 2
a + abc + abc  + a   0,25 Bài 6 2  3  (0,75 Tương tự ta có: điểm) 3  1  3  1  2
b + abc + abc  + b   ; 2
c + abc + abc  + c   2  3  2  3        Từ đó 3 1 3 1 3 1 P  + a + + b + + c = 3       . 2  3  2  3  2  3  1
Dấu bằng xảy ra  a = b = c = . 3 0,25 1
Vậy giá trị nhỏ nhất giá trị nhỏ nhất của P là 3 khi a = b = c = 3 Bài 21. 1 1 4
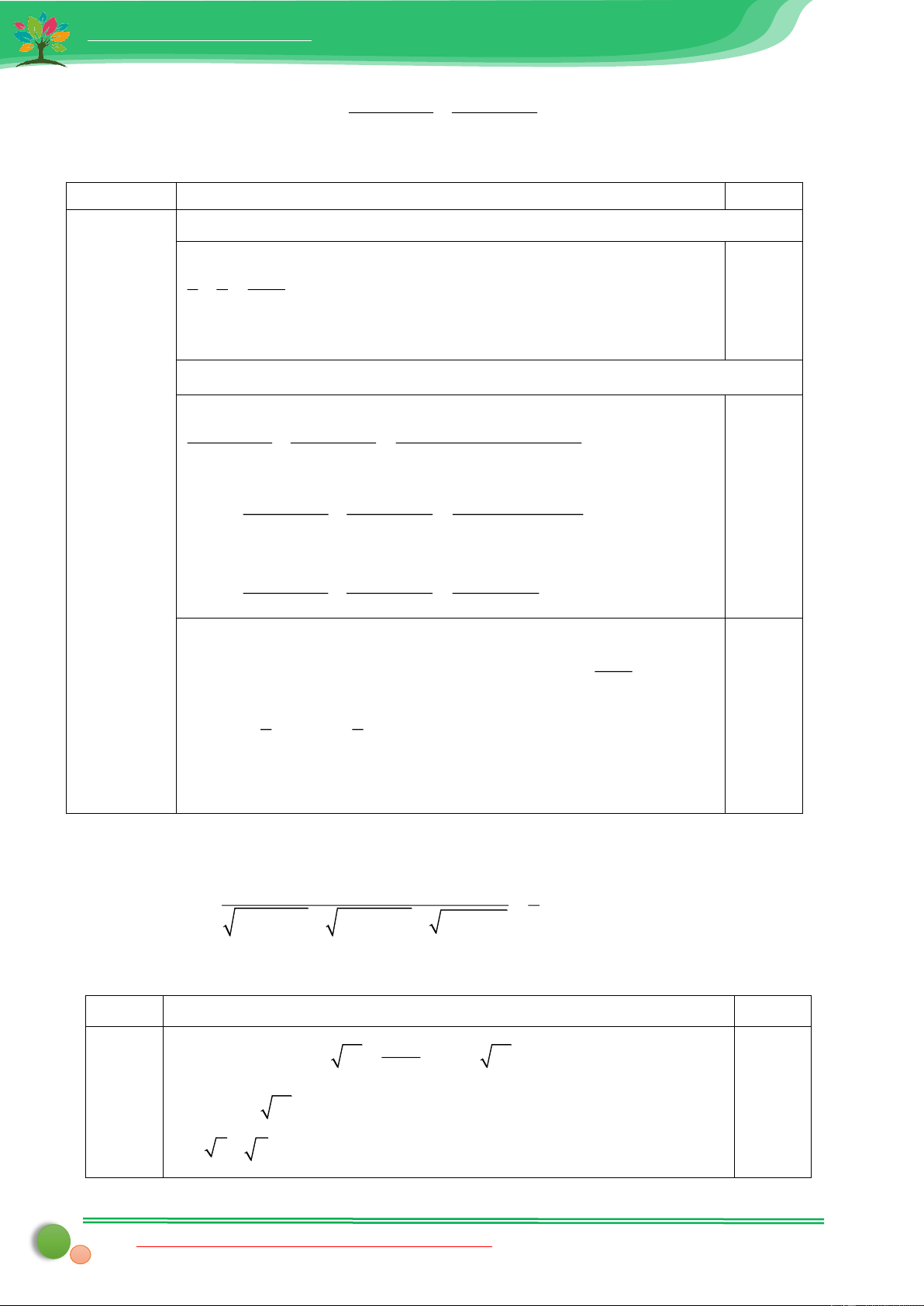
a) Cho hai số dương a, b . Chứng minh rằng: +  . a b a + b
Đẳng thức xảy ra khi nào?
b) Cho hai số dương a, b thỏa mãn a + b = 1. Tìm giá trị nhỏ nhất của biểu thức:
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 15
Website: tailieumontoan.com 1 1 P = + 2 2 1 + 3ab + a 1 + 3ab + b Bài Đáp án Điểm 5.a (0,25 điểm) 1 1 4 +  
a (a + b) + b(a + b)  4ab  (a − b)2  0 a b a + b
Luôn đúng vơi mọi a, b dương
Dấu “=” xẩy ra khi a = b 0,25 5.b (0,5 điểm) Áp dụng phần a ta có: 1 1 4 +  2 2 2 2 1 + 3ab + a 1 + 3ab + b 1 + 3ab + a + 1 + 3ab + b Bài 5 1 1 4 (0,75 +  2 2 điể 1 + 3ab + a 1 + 3ab + b 2 + (a + b)2 m) + 4ab Mà : a + b = 1 nên 1 1 4 +  (1) 0,25 2 2 2 1 + 3ab + a 1 + 3ab + b 2 + 1 + 4ab Lại có: 2 (  +  a − b)2 a b 2 2  0 a
 ,b  a + b + 2ab  4ab a  ,b  ab  a  ,b    2  2  1  1  ab   ab  (2)    2  4
Từ (1) và (2) Suy ra P  1
Vậy giá trị nhỏ nhất của P = 1 khi a = b = 0,5 0,25 Bài 22. a + b + c 1 Chứng minh rằng:
 với a,b,c là các số dương.
a (a + 3b) + b(b + 3c) + c(c + 3a) 2 DAPAN Bài Đáp án Điểm x + y
Với x, y > 0, ta có: xy
(1)  2 xy x + y 2
x + y − 2 xy  0 2
 ( x − y )  0 (2).
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 16
Website: tailieumontoan.com 6
Vì (2) luôn đúng với mọi số thực không âm, nên BĐT đã cho đúng.
(0,75 đ) Dấu “=” xảy ra khi x = y. Xét a + b +c 2(a + b + c) = ( ) + ( ) + c c+ a ( ) + ( ) (1) a a + 3b b b + 3c ( 3 ) 4a a + 3b 4b b + 3c + 4 ( c c + 3a) 0,25
Áp dụng bất đẳng thức ở câu a cho các số dương 4a, a + 3b, 4b, b+3c,4c, c+3a ta được: ( ) 4a + (a + 3b) 5a + 3b 4a a + 3b  = (2) 2 2 ( ) 4b + (b + 3c) 5b + 3c 4b b + 3c  = (3) 2 2 ( ) 4c + (c + 3a) 5c + 3a 4c c + 3a  = (4) 2 2 Từ (2), (3) và (4) suy ra:
4a (a + 3b) + 4b (b +3c) + 4c(c + 3a)  4a + 4b + 4c (5)
Từ (1) và (5) với điều kiện các số a,b,c đều dương ta suy ra: 0,25 a + b + c 2(a + b +c) 1  = .
a (a + 3b) + b (b + 3c) + c(c + 3a) 4a + 4b + 4c 2
4a = a + 3b
Dấu “=” xảy ra khi và chỉ khi: 4b = b + 3c a = b = c . 0,25
4c = c +3a
Bài 23.Cho 3 số dương a, b, c thỏa mãn abc = 1. Tìm giá trị lớn nhất của biểu thức: 1 1 1 P = + + . 2 2 2 2 2 2 a + 2b + 3 b + 2c + 3 c + 2a + 3 DAPAN
Bài 6 Áp dụng bất đẳng thức ở câu a) ta có: 1 1 2 1 1 = .  . 2 2 2 2 a + 2b + 3 2 a + 2b + 3 2 ab + b +1 1 1 2 1 1 = .  . 0,25 2 2 2 2 b + 2c + 3 2 b + 2c + 3 2 bc + c +1 1 1 2 1 1 = .  . 2 2 2 2 c + 2a + 3 2 c + 2a + 3 2 ca + a +1
Cộng từng vế của các bất đẳng thức trên ta được:
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 17
Website: tailieumontoan.com 1  1 1 1  P  + +  
2  ab + b +1 bc + c +1 ca + a +1  1 1 1 ca a 1 Có + + = + + ab + b +1 bc + c +1 ca + a +1 2 ca b + abc + ca abc + ac + a ca + a +1 0,25 ca a 1 = + + =1 (do abc = 1) ca + a +1 ca + a +1 ca + a +1 Do đó 1 P 
. Dấu “=” xảy ra khi a = b = c =1. 2 Vậy 1 max P =
đạt được khi a = b = c =1. 0,25 2 a + b + c 1 Bài 24. Chứng minh
 với (a,b,c  0) .
a (a + 3b) + b(b + 3c) + c(c + 3a) 2 DAPAN Bài Đáp án Điểm
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 18
Website: tailieumontoan.com (0,75 điểm) Ta có: a + b +c
a (a + 3b) + b (b + 3c) + c(c + 3a) 2(a + b + c) = (1)
4a (a + 3b) + 4b (b + 3c) + 4c(c + 3a) Bài
Áp dụng bất đẳng thức Cô 6(0.75đ)
-si cho các số dương 4a và a + 3b; 4b và
b + 3c; 4c và c+3a ta được: ( )  4a + (a + 3b) = 5a + 3b 4a a + 3b (2) 2 2 4b + (b + 3c) 5b + 3c 4b (b + 3c)  = (3) 2 2 0.25 ( )  4c + (c + 3a) = 5c + 3a 4c c + 3a (4) 2 2 Từ (2), (3) và (4) suy ra:
4a (a + 3b) + 4b (b +3c) + 4c(c + 3a)  4a + 4b + 4c (5) 0.25
Từ (1) và (5) với điều kiện các số a,b,c đều dương ta suy ra: a + b + c  2(a + b +c) = 1 .
a (a + 3b) + b (b + 3c) + c(c + 3a) 4a + 4b + 4c 2 4a = a + 3b 
Dấu “=” xảy ra khi và chỉ khi:4b = b + 3c  a = b = c . 0.25 4c = c +  3a
Vậy ta có điều phải chứng minh.
Bài 25. Cho hai số dương a, b thỏa mãn điều kiện: a+ b= 1.
Hãy tìm giá trị nhỏ nhất của biểu thức: 1 1 4 B = + + 2 2 2 2 a + 4b b + 4a 10ab DAPAN Bài Nội dung đáp án Điểm
Liên hệ tài liệu word toán SĐT (zalo): 039.373.2038 19

Tài liệu liên quan: