3/24/2022 TÍCH PHÂN KÉP
1) Khái niệm tích phân kép, tính chất 2) Cách tính 3) Ứng dụng
4) Tài liệu: TCC: 81-117, Calculus: 951-989 3/24/2022
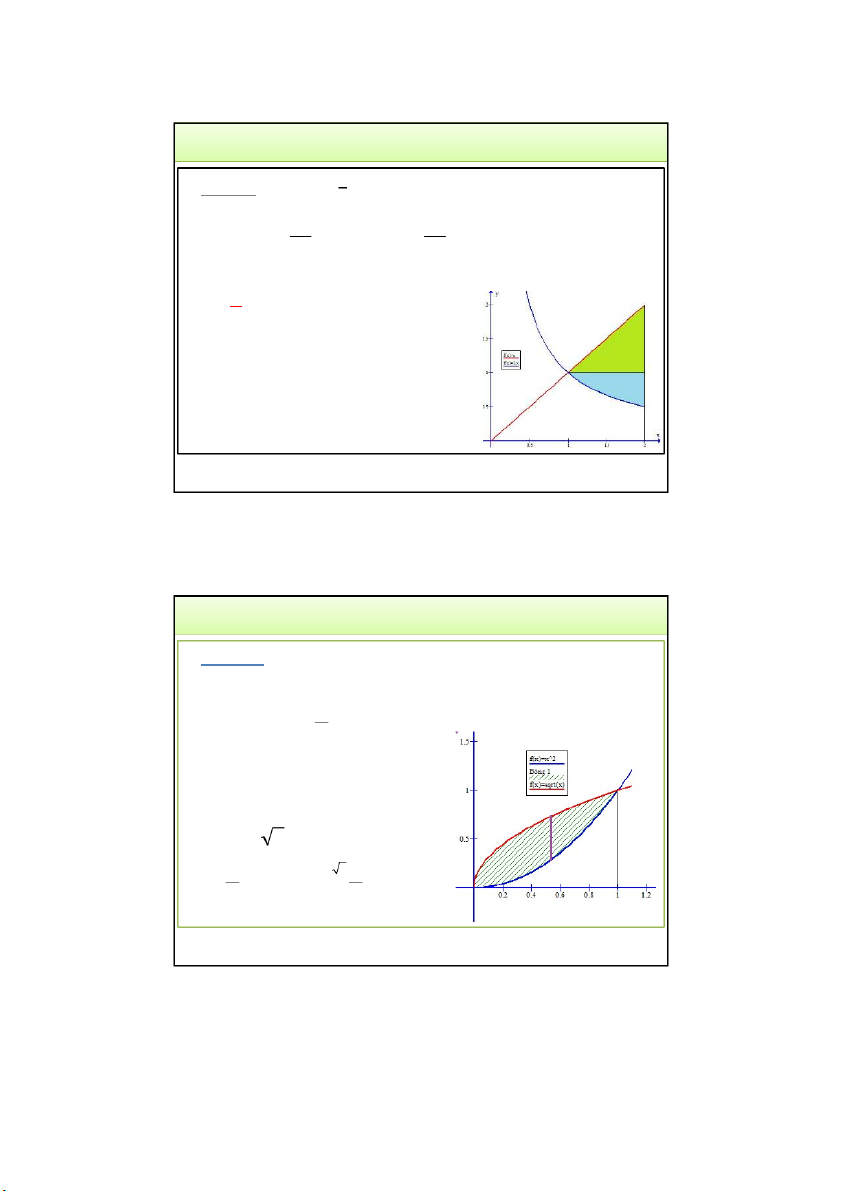
Tích phân kép và ứng dụng 1 1 1. Tích phân kép
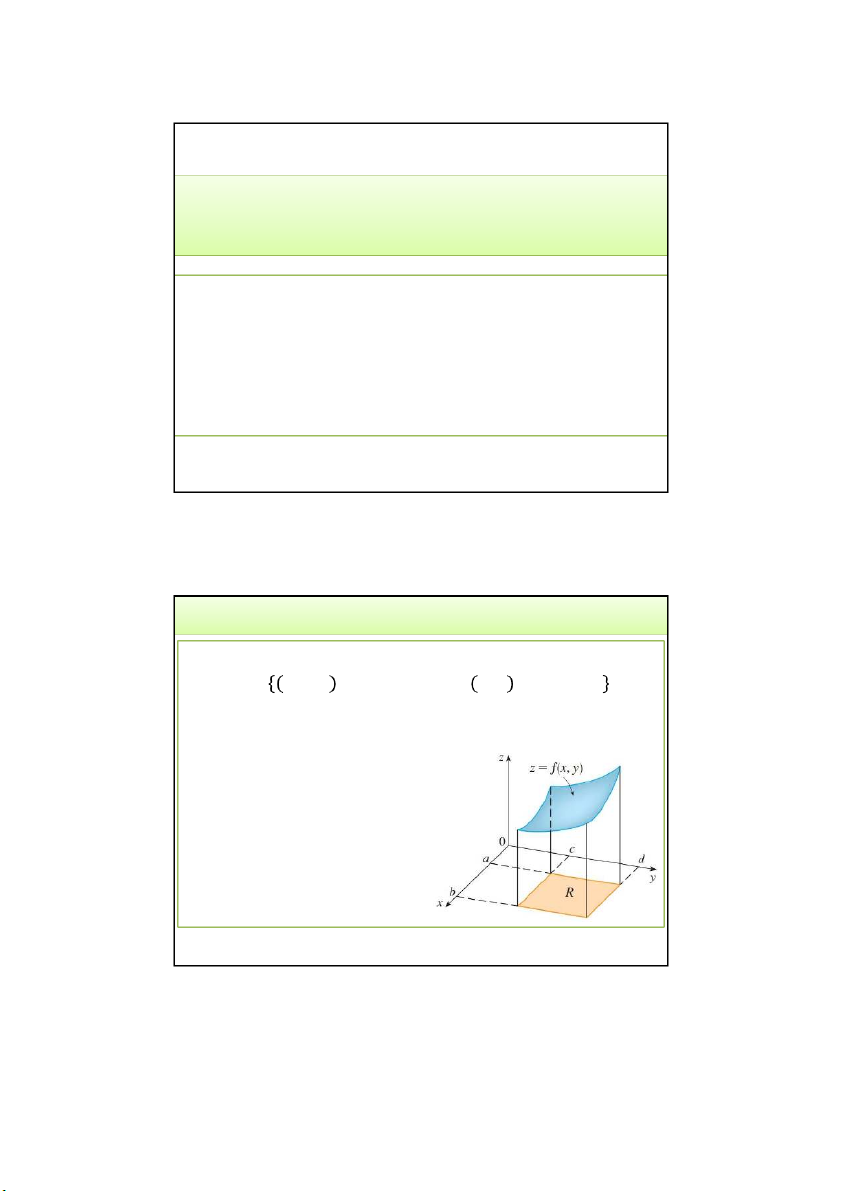
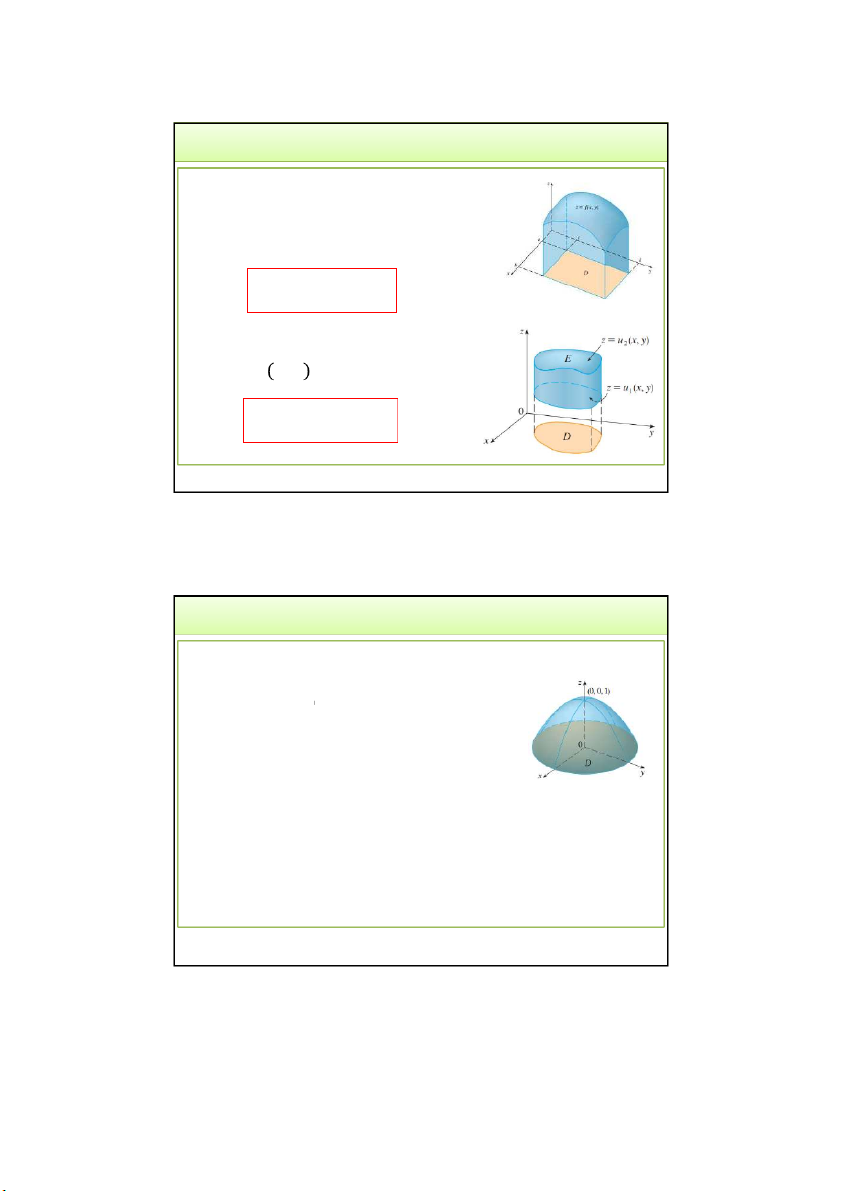
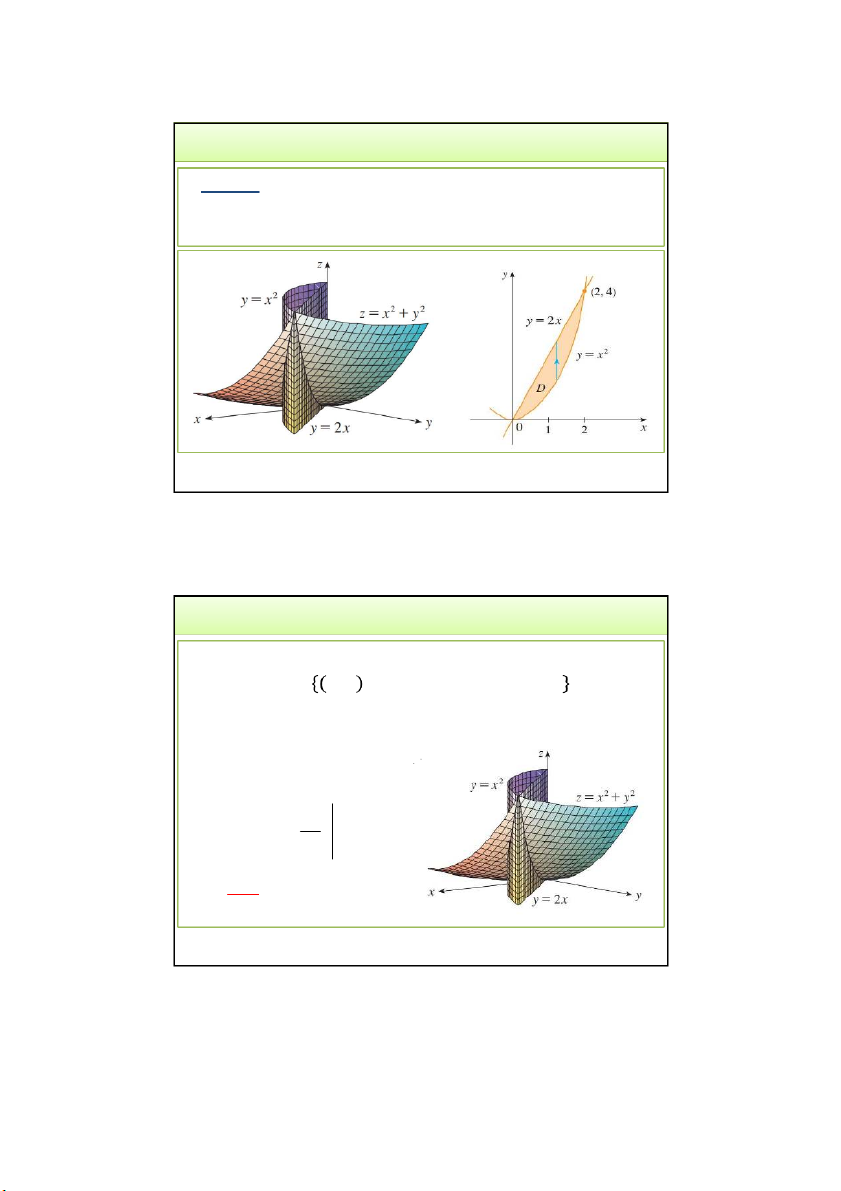
 Cho vật thể S xác định bởi:
𝑆 = 𝑥, 𝑦, 𝑧 ∈ 𝑹|0 ≤ 𝑧 = 𝑓 𝑥, 𝑦 , (𝑥, 𝑦) ∈ 𝑅
Tính thể tích vật thể S? 3/24/2022
Tích phân kép và ứng dụng 2 2 1 3/24/2022 1. Tích phân kép
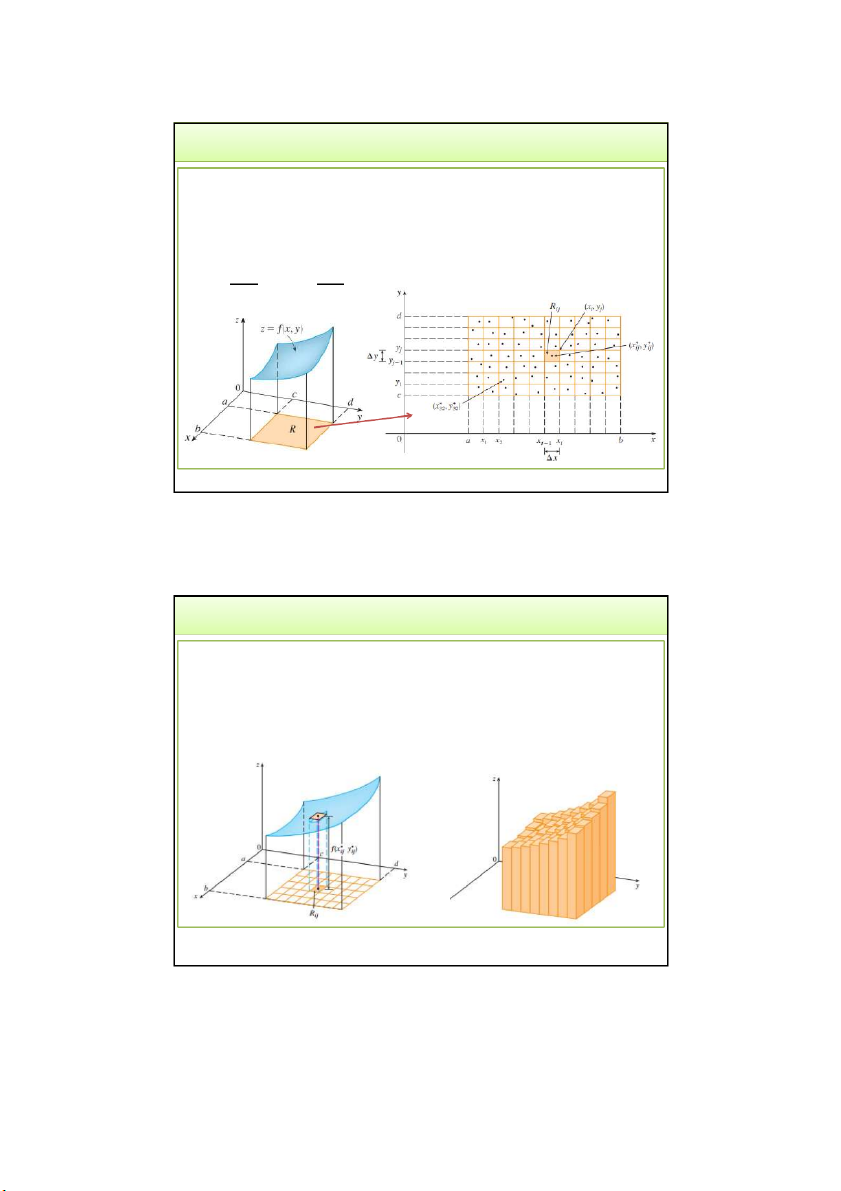
• Chia miền R thành các hình chữ nhật con 𝑅,:
R  x , x  y , y   , x y | x  x  x , y  y  y ij i 1  i   j 1  j     i 1 i j 1  j
Diện tích của các hcn con: ∆𝐴 = ∆𝑥 × ∆𝑦, Trong đó:
∆𝑥 = ; ∆𝑦 =  .   3/24/2022
Tích phân kép và ứng dụng 3 3 1. Tích phân kép
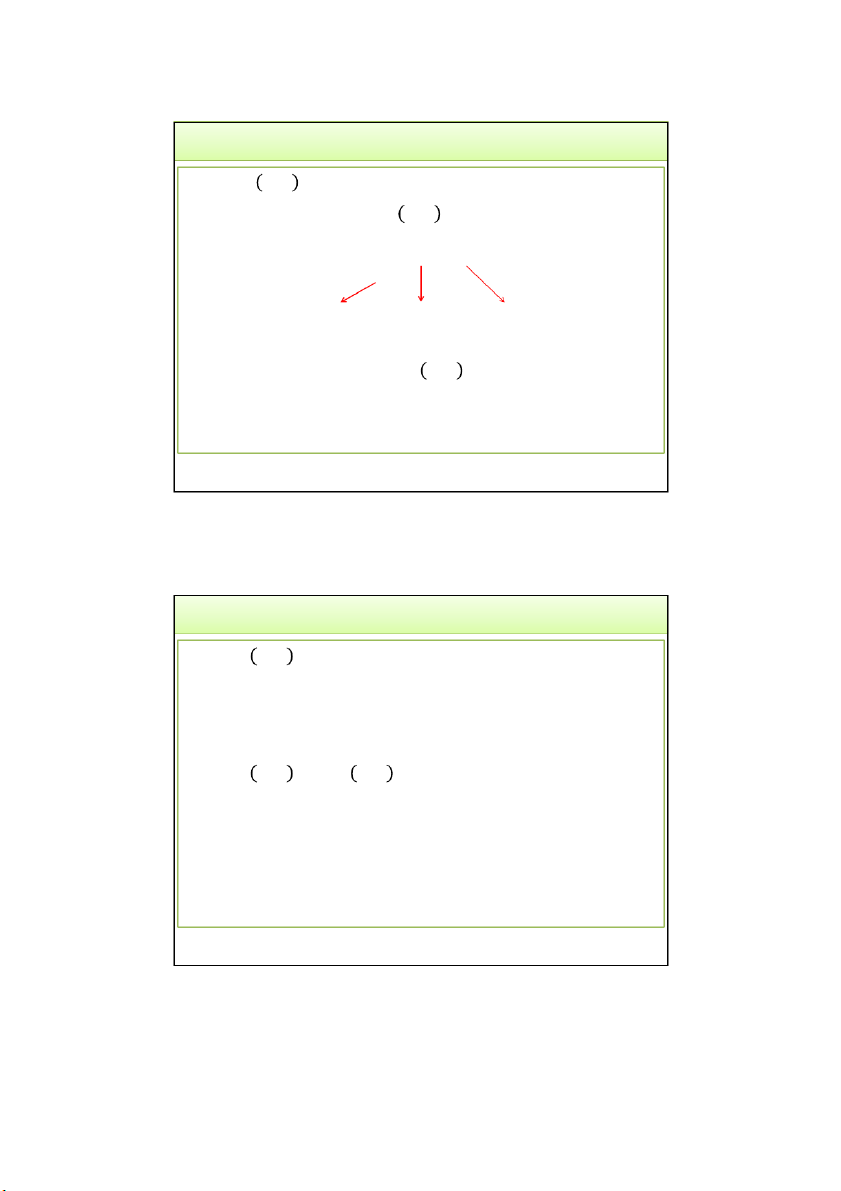
• Khi đó vật thể S ban đầu được chia thành mxn vật thể con 𝑆 hình trụ: V  f x y A S  * * , ij ij  . ij m n
• Thể tích của S được xấp xỉ bằng: V  f x y A  S  * * , ij ij  . i1 j1 3/24/2022
Tích phân kép và ứng dụng 4 4 2 3/24/2022 1. Tích phân kép
Khi m, n càng lớn. Độ chính xác của V càng cao. Do đó: m n V  lim f   * * x , y A ij ij . m ,n i1 j1 3/24/2022
Tích phân kép và ứng dụng 5 5 1. Tích phân kép
Định nghĩa: Tích phân hai lớp của 𝑓 trên một miền hình chữ nhật R là: m n f
 x, ydA  lim  f  * * x , y A ij ij . m,n R i1 j 1 
nếu giới hạn trên tồn tại. 3/24/2022
Tích phân kép và ứng dụng 6 6 3 3/24/2022 1. Tích phân kép
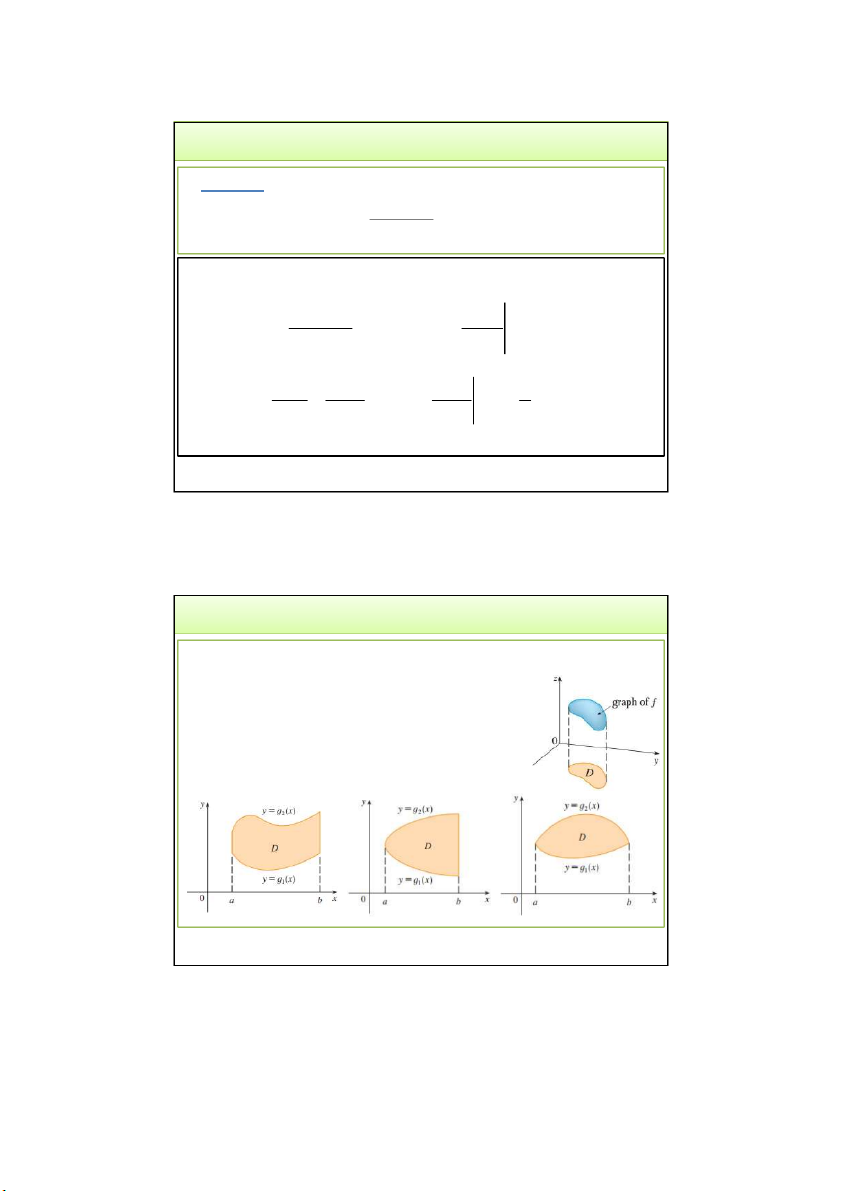
• Hàm 𝑓 𝑥, 𝑦 xác định trong một miền đóng, bị chặn D.
Tích phân kép của hàm 𝑓 𝑥, 𝑦 trong miền D: f  x, y dxdy D Miền lấy Hàm dưới dấu Yếu tố tích phân tích phân diện tích
Nếu tích phân trên tồn tại: 𝑓 𝑥, 𝑦 khả tích trong miền D
 Nếu hs liên tục trong miền bị chặn, đóng D thì nó khả tích trong miền đấy. 3/24/2022
Tích phân kép và ứng dụng 7 7 1. Tích phân kép
• Nếu 𝑓 𝑥, 𝑦 liên tục, không âm trên D, tích phân kép bằng
thể tích vật thể hình trụ: V  f   ,x ydS  f   ,x ydxdy D D
• Nếu 𝑓 𝑥, 𝑦 = 1, ∀ 𝑥, 𝑦 ∈ 𝐷, tích phân kép bằng diện tích của miền D: S  dS  d dx y   D D 3/24/2022
Tích phân kép và ứng dụng 8 8 4 3/24/2022 1. Tích phân kép 1)  f
  x,y g x,y dxdy f   x,ydxdy g  x,ydxdy   D D D 2) kf  x, ydxdy  k f
 x,ydxdy k  const D D 3) f  x,ydxdy  f  x,ydxdy  f  x,ydxdy D D D 1 2 4) f  , x y  g , x y,  , x y D: f   ,x y dxdy  g   ,x ydxdy D D
5) m  f  x, y  M , x, y  D : mS  f  x,ydxdy  MS D 6) x, y  : D f
  ,x y dxdy  f  ,x y S D 3/24/2022
Tích phân kép và ứng dụng 9 9 2. Cách tính 2.1. Trong hệ Đề các
 TH1. 𝐷 = 𝑎, 𝑏 × 𝑐, 𝑑
Nếu 𝑓 𝑥, 𝑦 liên tục trên D thì: f  b d d b , x y dxdy  f x y dy dx  f x y dx dy      a   ,  c  c   ,  a  D (Định lý Fubini) 3/24/2022
Tích phân kép và ứng dụng 10 10 5 3/24/2022
2. Cách tính tích phân trong hệ Đề các
• Ví dụ: tính các tích phân sau:    
𝑎)   𝑥𝑦𝑑𝑦 𝑑𝑥 ; 𝑏)   𝑥𝑦𝑑𝑥 𝑑𝑦 .    
HD: a) Coi x như một hằng số, ta có: y2 2 2 2 2       2 2 y 2 2 2 1 3 2 x ydy  x  x  x  x        1 2 2 2 2       y 1  3 3 3 2 3 2 3 2  2  3 2 x 27  x ydydx  x ydy dx  x dx        0 1 0  1   0  2 2 2 0 3/24/2022
Tích phân kép và ứng dụng 11 11
2. Cách tính tích phân trong hệ Đề các  
𝑏)   𝑥𝑦𝑑𝑥𝑑𝑦  
Tính theo biến x trước, coi như y là hằng số, ta có: x 3 3  3 2 x x ydx  y  9 y 0 3 x 0  2 2 3 2 3 2 9 27 2  2  2  x ydxdy  x ydx dy  9ydy  y       1 0 1  0   1  2 2 1 3/24/2022
Tích phân kép và ứng dụng 12 12 6 3/24/2022
2. Cách tính tích phân trong hệ Đề các
• Nếu 𝑓 𝑥, 𝑦 = 𝑓 𝑥 . 𝑓 𝑦 : f   b d , x ydxdy  f x d . x f y dy  1    2   a c D • Ví dụ:    
 (𝑥 + 1)𝑦 𝑑𝑦𝑑𝑥 =  𝑥 + 1 𝑑𝑥 .  𝑦𝑑𝑦     5 37 185 = 2. 3 = 6 3/24/2022
Tích phân kép và ứng dụng 13 13 2. Cách tính
 Ví dụ. Tính tích phân trong miền 𝐷 = { 𝑥, 𝑦 |0 ≤ 𝑥 ≤ 2, 1 ≤ 𝑦 ≤ 2}:  2 x  3y dS D I  x  3y  2 2 2 dS     2 x  3y dxdy 1 0 D x2  2  2  x  2 I    3xy d  y    1  2    x0   2 I    2 2  6y dy  1  2 1 3/24/2022
Tích phân kép và ứng dụng 14 14 7 3/24/2022 2. Cách tính  Ví dụ 1. Tính dxdy I  , D  1,2  2  2 x  y D  
Vì 𝑓(𝑥, 𝑦) liên tục trên D nên: 2     2 2 1 2 1 I   dy dx   dx     x  y 2 1 1 1 x  y   1   2 2  1 1  x 1 9 I     dx  ln  ln 1  x 1 x  2  x  2 8 1 3/24/2022
Tích phân kép và ứng dụng 15 15 2. Cách tính
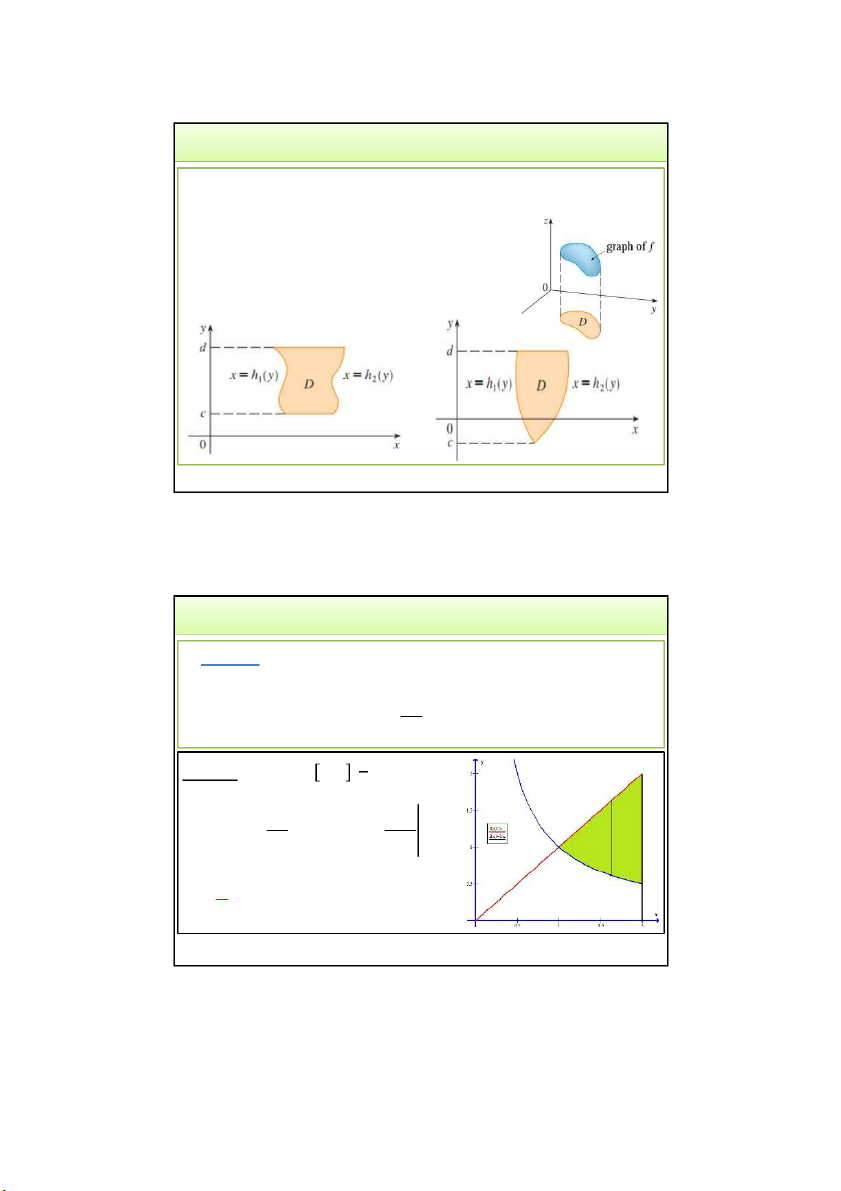
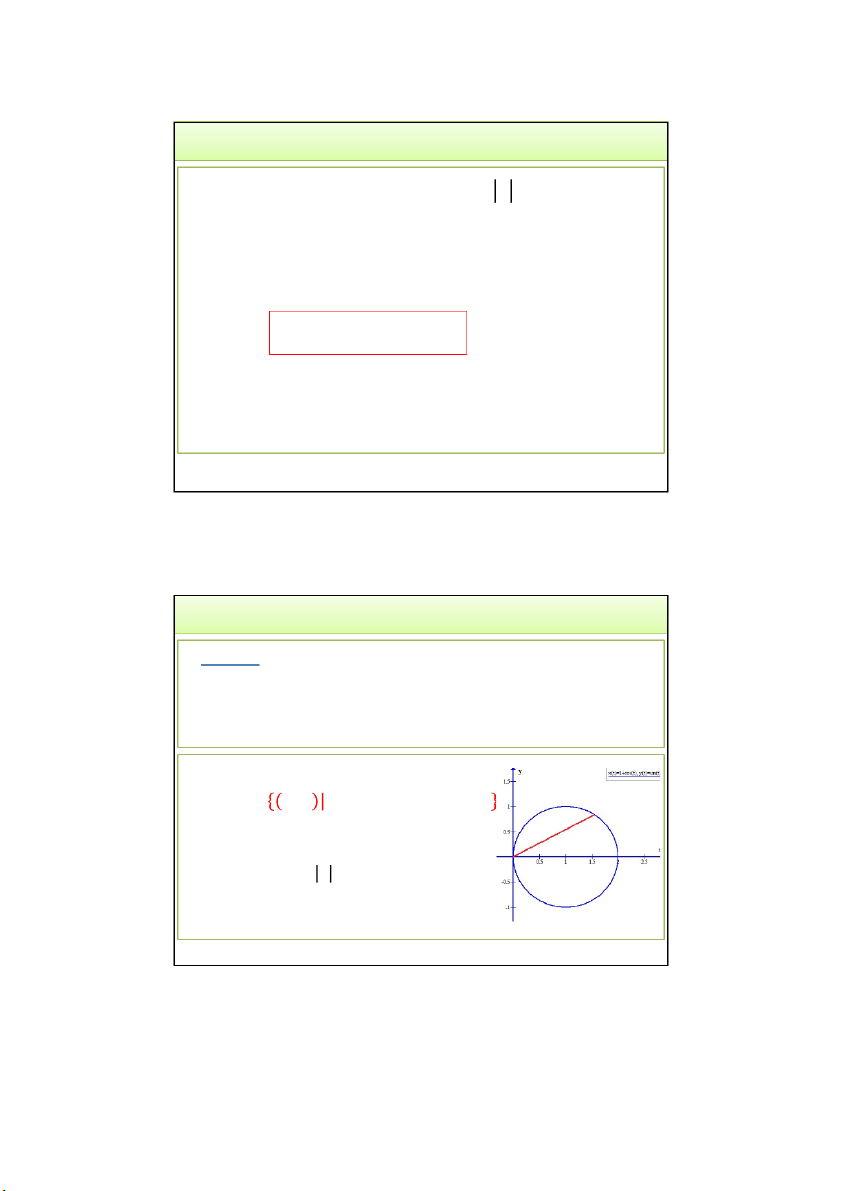
 TH2. Miền lấy tích phân là miền bị chặn bất kỳ: D  
 ,x y: a  x  ,b y x  y  y x 1   2   f   b y x , x  2   y dxdy  f x y dy dx   a   ,  y x 1    D 3/24/2022
Tích phân kép và ứng dụng 16 16 8 3/24/2022 2. Cách tính Nếu D  
 ,x y: x y  x  x y ,c  y  d 1   2    f  d x y x, y  2   dxdy  f x y dx dy    c   ,  1 x y    D 3/24/2022
Tích phân kép và ứng dụng 17 17 2. Cách tính
• Ví dụ 2. Tính tích phân trong miền D giới hạn bởi các
đường 𝑥 = 2, 𝑦 = 𝑥, 𝑥𝑦 = 1: 2 x I  dxdy 2  2y D
Cách 1. Coi 𝑥 ∈ 1,2 ,  ≤ 𝑦 ≤ 𝑥  2 2 x 2  x  2 x  x  I  dy dx    dx 2   2   1 1/ x 1  y   y   1/ x  9 I  2 4 3/24/2022
Tích phân kép và ứng dụng 18 18 9 3/24/2022 2. Cách tính
• Cách 2. Coi 𝑦 ∈ [ , 2]  2 2 1  2  2  2 x x  I  dx dy  dx dy 2   2    2  1/2 1/y 1 y y y     9 I  2 4 3/24/2022
Tích phân kép và ứng dụng 19 19 2. Cách tính
 Ví dụ 3. Tính tích phân trong miền D giới hạn bởi các
parabol 𝑦 = 𝑥, 𝑥 = 𝑦: x I  dxdy 3  y D Hướng dẫn:
Khi 𝑥 ∈ [0,1] thì y thay đổi từ 𝑥 đến 𝑥: 1 x x  x  dxdy  dy dx    2  0 x y  y D  3/24/2022
Tích phân kép và ứng dụng 20 20 10 3/24/2022 2. Cách tính 1 1 x 3 I  x ln y dx   x ln xdx 2 3   TPSR loại II 0 x 0 2 1 3 1 3  1 1   2 2 I lim x ln xdx lim  x ln x x           3 a0 a a0 2 2  2 4   a   3 2 3 3 I   lima lna   3 a0 4 8 8 ln L a 1 / a 1 Do: 2 lim a ln a 0. 2  lim lim  lim a  0 3 a 0  a 0  1 a 0  a 0 2 / a 2  2 a 3/24/2022
Tích phân kép và ứng dụng 21 21 2. Cách tính
• 2.2. Đổi biến số trong tích phân kép
• Xét tích phân kép ∬ 𝑓 𝑥, 𝑦 𝑑𝑥𝑑𝑦  , f(x,y) liên tục trên D.
Thực hiện phép đổi biến số 𝑥 = 𝑥 𝑢, 𝑣 , 𝑦 = 𝑦 𝑢, 𝑣 . f   ,x ydxdy  f
 x ,uv, y ,uv J dudv D D' D x, y ' ' x x 1 D u,v ' ' u u u v J    J  : x y K   Du,v 0; ' ' y y K D , x y ' ' v v u v x y 3/24/2022
Tích phân kép và ứng dụng 22 22 11 3/24/2022 2. Cách tính
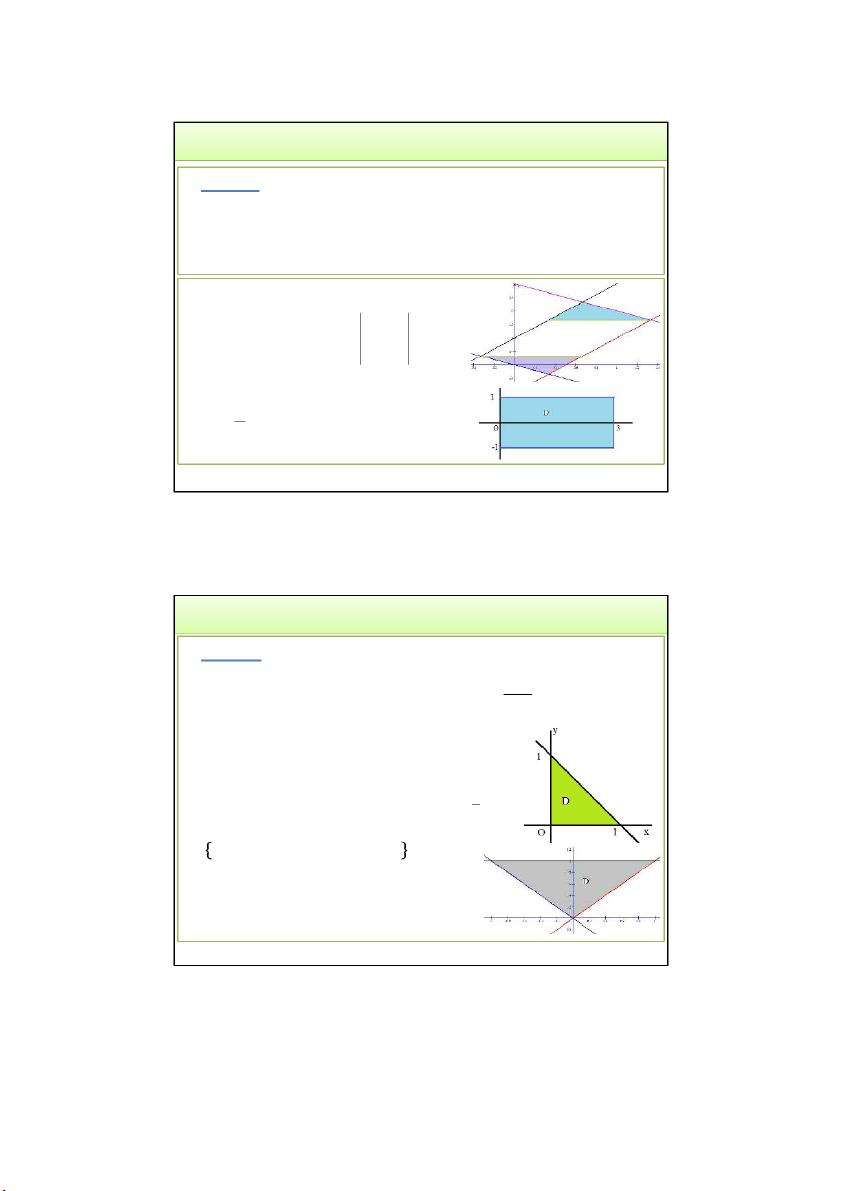
• Ví dụ 4. Tính tích phân trong miền D giới hạn bởi các
đường 𝑦 = −𝑥, 𝑦 = −𝑥 + 3, 𝑦 = 2𝑥 − 1, 𝑦 = 2𝑥 + 1: I  x  y dxdy 4   D • Đổi biến số: u  x  y 1 1   K   3 v  2  x  y 2 1  J 1/ 3 3 1 1 I  ududv  3 4   0 1 3  3/24/2022
Tích phân kép và ứng dụng 23 23 2. Cách tính
• Ví dụ 5: Tính tích phân sau trên miền D xác định bởi: 
𝑥 ≥ 0, 𝑦 ≥ 0, 𝑥 + 𝑦 ≤ 1:  𝑒𝑑𝑥𝑑𝑦 
Giải: Thực hiện phép đổi biến: 𝑥 − 𝑦 = 𝑢
󰇫𝑥 + 𝑦 = 𝑣 → 󰇫𝑥 = (𝑢 + 𝑣)/2
𝑦 = (𝑣 − 𝑢)/2 ; 𝐽 = 
𝐷: 𝑥 ≥ 0, 𝑦 ≥ 0, 𝑥 + 𝑦 ≤ 1
→ 𝐷󰆒: {𝑢 + 𝑣 ≥ 0, 𝑣 − 𝑢 ≥ 0, 𝑣 ≤ 1. 3/24/2022
Tích phân kép và ứng dụng 24 24 12 3/24/2022 2. Cách tính Vậy: v 1 u 1 u v 1 1 1 1 1 v v e dudv  ve dv  e  vdv       0  v 2 2 0 2 e 0   v 1  1   e   4   e  3/24/2022
Tích phân kép và ứng dụng 25 25
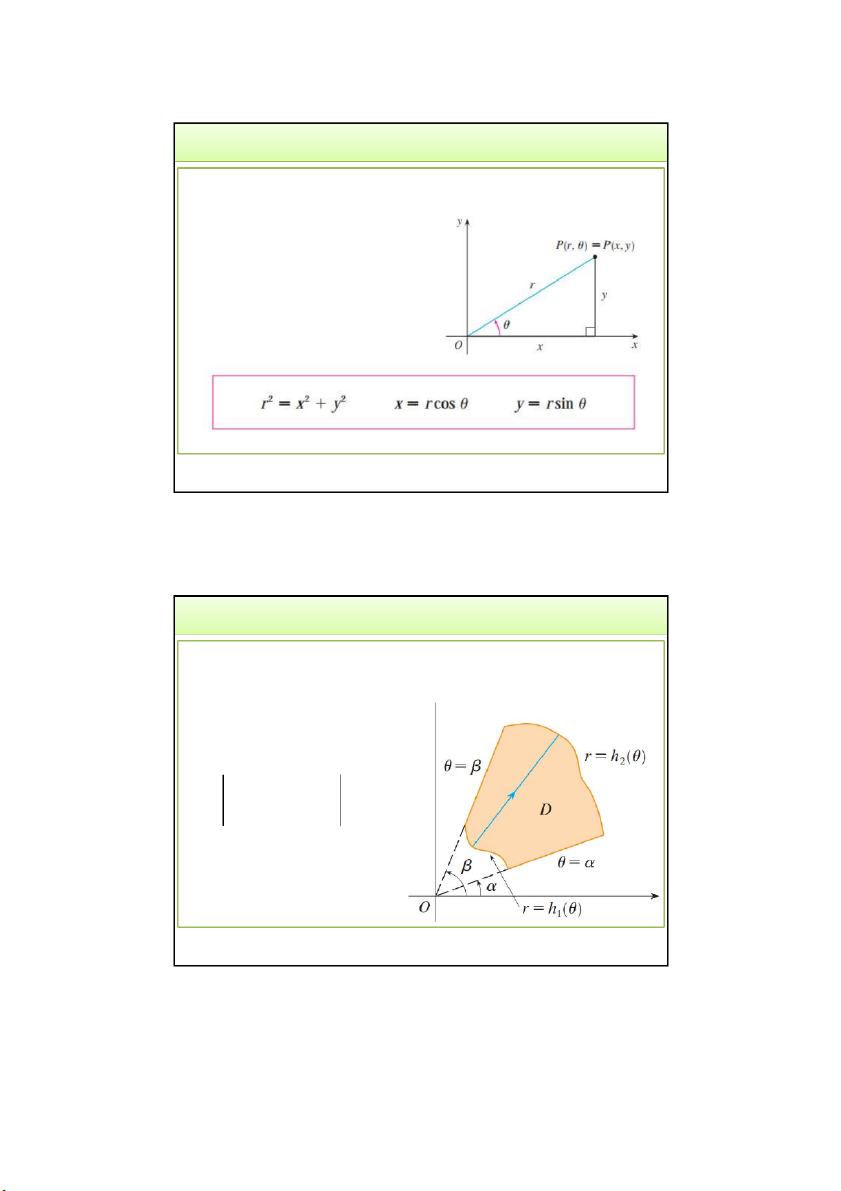
2.2. Đổi biến số trong tích phân kép • Hệ tọa độ cực:
• Là hệ tọa độ bao gồm một điểm cực và một trục cực
• Điểm M bất kỳ trong hệ tọa độ cực: 𝑀(𝑟, 𝜑)
- 𝑟: khoảng cách từ M đến điểm cực (r>=0) M r
- 𝜑: góc gữa véc-tơ OM và trục cực 𝜑 Phương trình đường cong trong hệ tọa độ cực: O P 𝑟 = 𝑟 𝜑 3/24/2022
Tích phân kép và ứng dụng 26 26 13 3/24/2022
2.2. Đổi biến số trong tích phân kép
• Phép biến đổi giữa hệ tọa độ cực và hệ Đề các 3/24/2022
Tích phân kép và ứng dụng 27 27
2.2. Đổi biến số trong tích phân kép
Trong phép biến đổi từ tọa độ x,y sang tọa độ cực: x  r cos y  r sin  • Khi đó: cos r  sin   r  0 sin  rcos (trừ điểm (0,0)). Với 0 ≤ 𝜃 ≤ 2π 3/24/2022
Tích phân kép và ứng dụng 28 28 14 3/24/2022
2.2. Đổi biến số trong tích phân kép  I  f  x, ydxdy  f  r,  J drd D ' D Nếu:
D '      ,h   r  h  1   2    2 r I  f    r, rdr  d     1 r  3/24/2022
Tích phân kép và ứng dụng 29 29 2. Cách tính
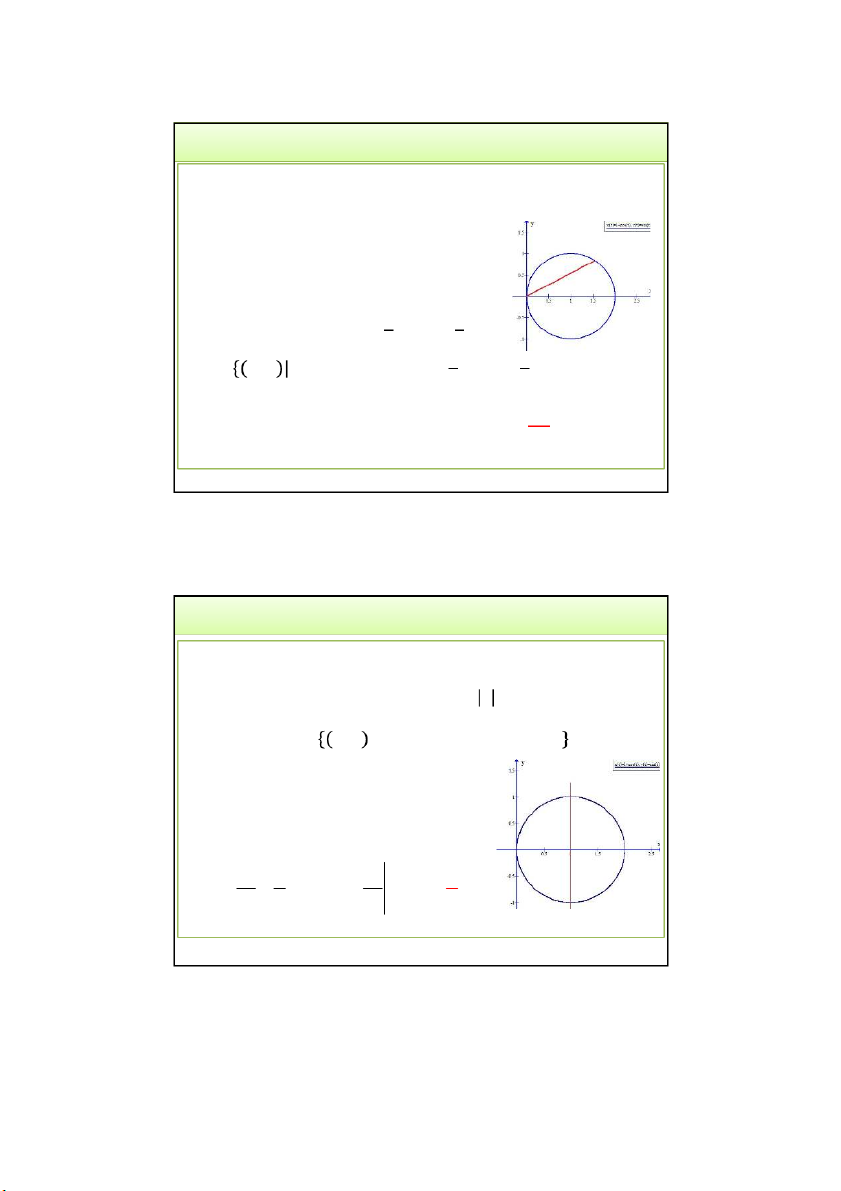
• Ví dụ 6. Tính tích phân trong miền D giới hạn bởi đường
tròn 𝑥 + 𝑦 = 2𝑥: I   2 2 x  y dxdy 5  D • Phân tích:
Miền 𝐷 = 𝑥, 𝑦 𝑥 + 𝑦 ≤ 2𝑥; 𝑥 ≥ 0
Khi đổi sang tọa độ cực: 𝑥 = 𝑟. cos 𝜃
𝑦 = 𝑟. sin 𝜃 ⇒ 𝐽 = 𝑟 , 3/24/2022
Tích phân kép và ứng dụng 30 30 15 3/24/2022 2. Cách tính
Phương trình đường tròn trong hệ tọa độ cực:
𝑟. cos 𝜃 + 𝑟. sin 𝜃 = 2. 𝑟. cos 𝜃 ↔ 𝑟 = 2. cos 𝜃 Xác định miền D’:
Từ: 𝑥 + 𝑦 ≤ 2𝑥 ⇒ 𝑟 ≤ 2 cos 𝜃
𝑥 ≥ 0 ⇒ cos 𝜃 ≥ 0 ⇒ −  ≤ 𝜃 ≤   
𝐷󰆒 = 𝑟, 𝜃 0 ≤ 𝑟 ≤ 2. cos 𝜃 ; −  ≤ 𝜃 ≤ }   / . 3π
𝐼 =   𝑟. 𝑟 𝑑𝑟𝑑𝜃 = 2 /  3/24/2022
Tích phân kép và ứng dụng 31 31 2. Cách tính
• Cách 2. Sử dụng tọa độ cực suy rộng
󰇫𝑥 − 1 = 𝑟. cos 𝜃
𝑦 = 𝑟. sin 𝜃 ⇒ 𝐽 = 𝑟
𝐷󰆒 = 𝑟, 𝜃 : 0 ≤ 𝑟 ≤ 1; 0 ≤ 𝜃 ≤ 2𝜋 I   2 2 x  y dxdy 5  D 2  1
    2r  2r cos 1.rdrd 0 0 1 4 2 2 r 2  3 r 3    cos .  r   d   0  4 3 2  2  0  3/24/2022
Tích phân kép và ứng dụng 32 32 16 3/24/2022 2. Cách tính Nhận xét:
 Cách 1: cận phức tạp nhưng hàm dưới dấu tích phân đơn giản
 Cách 2: cận đơn giản nhưng hàm dưới dấu tích phân phức tạp
 Tùy từng bài nên có cách chọn phù hợp. 3/24/2022
Tích phân kép và ứng dụng 33 33 3. Ứng dụng
 3.1. Tính diện tích của miền phẳng D trong Oxy S  dxdy D 3/24/2022
Tích phân kép và ứng dụng 34 34 17 3/24/2022 3. Ứng dụng
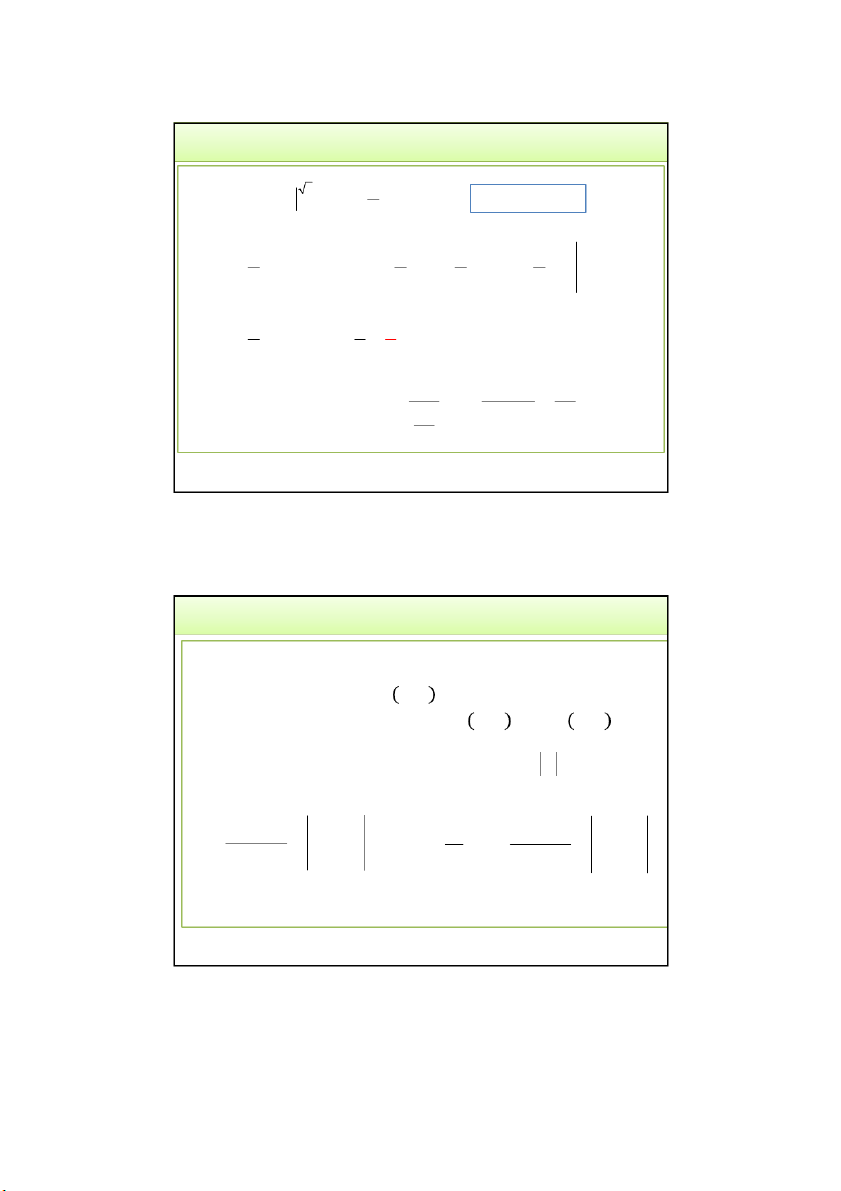
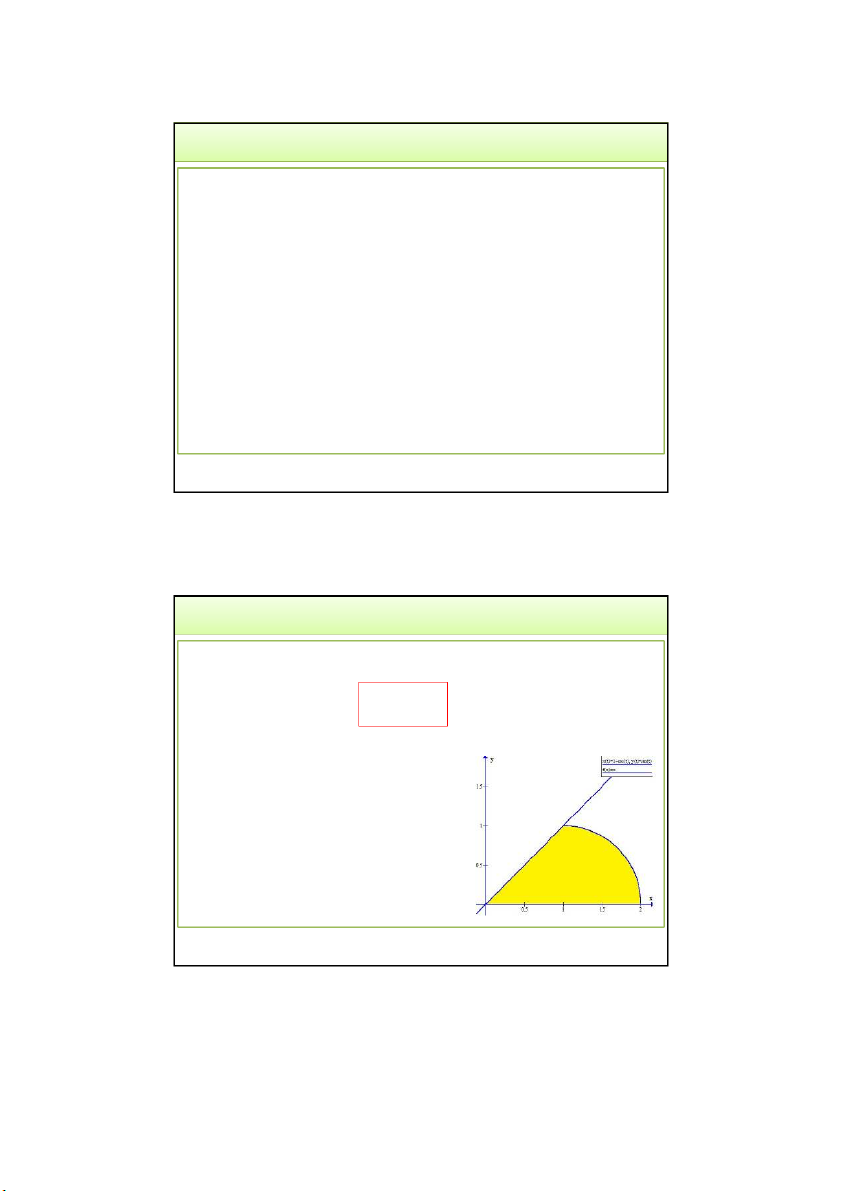
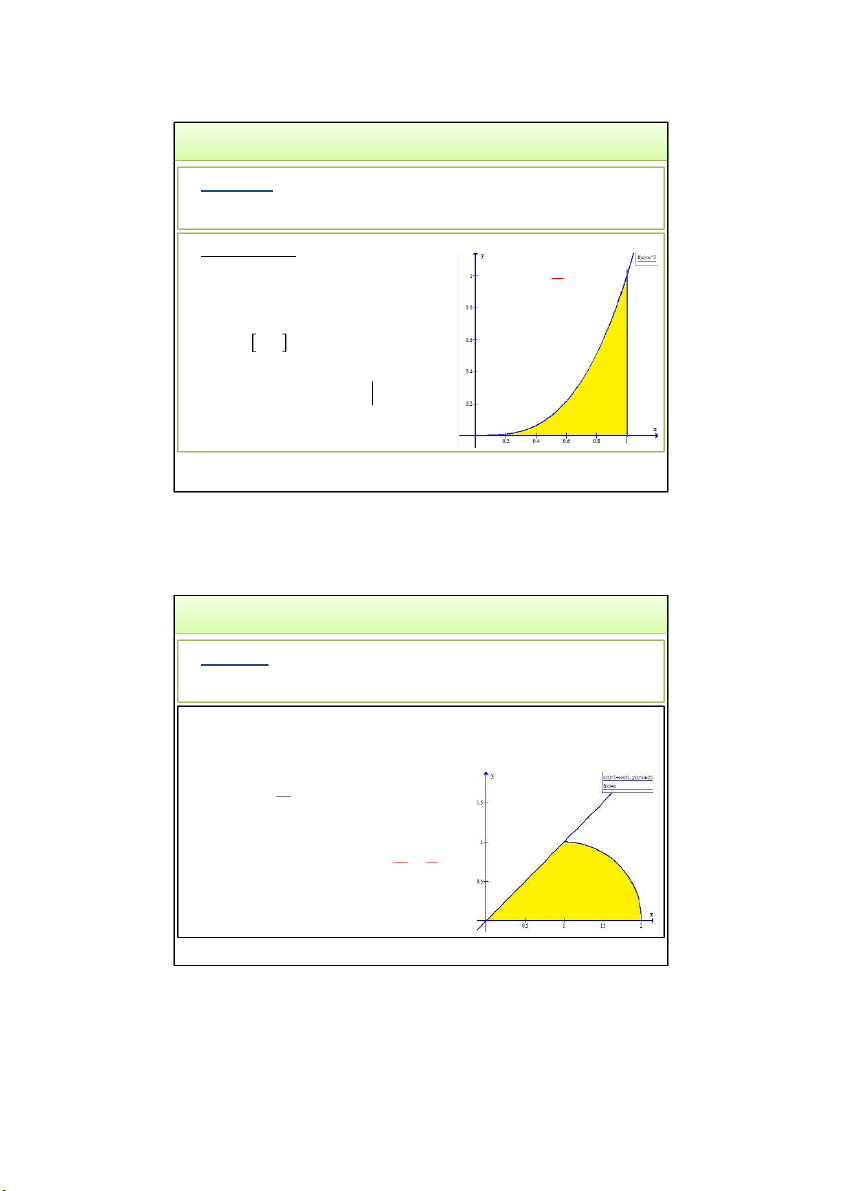
 Ví dụ 6. Tính diện tích của miền phẳng D giới hạn bởi các
đường thẳng 𝑥 = 1, 𝑦 = 0 và đường cong 𝑦 = 𝑥. Hướng dẫn: 1
Chiếu miền D lên trục Ox được I  6 4
đoạn [0,1]: biên dưới của D.
Khi 𝑥 ∈ 0,1 , y biến thiên: 0 → 𝑥 3 1 x 1   x I  dy dx  y dx 6    0  0  0  3 0    3/24/2022
Tích phân kép và ứng dụng 35 35 3. Ứng dụng
Ví dụ 7. Tính diện tích của miền phẳng D giới hạn bởi các
đường thẳng 𝑦 = 0, 𝑦 = 𝑥 và đường tròn 𝑥 + 𝑦 = 2𝑥
• Chuyển sang tọa độ cực
Phương trình đường tròn: 2
r  2r cos  r  2cos   0   ; 0     r  2cos 4    /4 2cos   1 S  rdr  d     0  0   4 2 3/24/2022
Tích phân kép và ứng dụng 36 36 18 3/24/2022 3. Ứng dụng
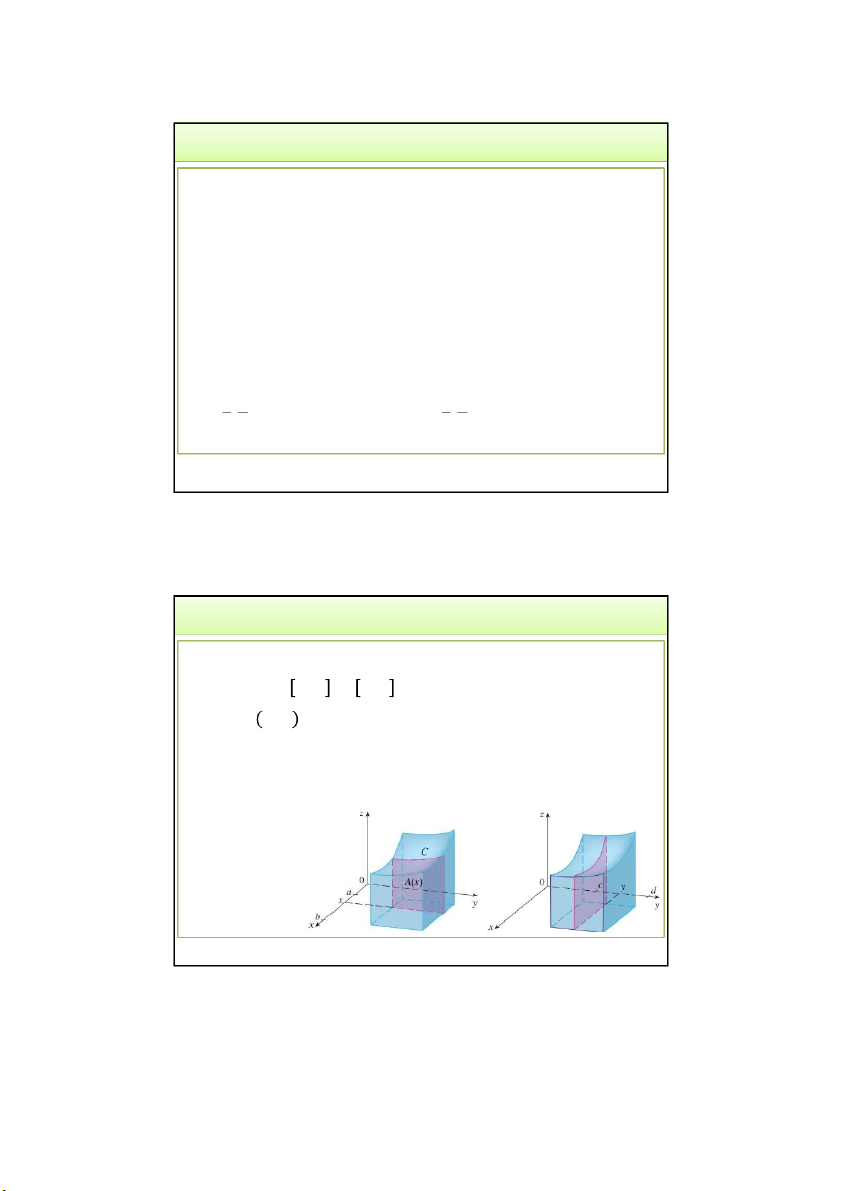
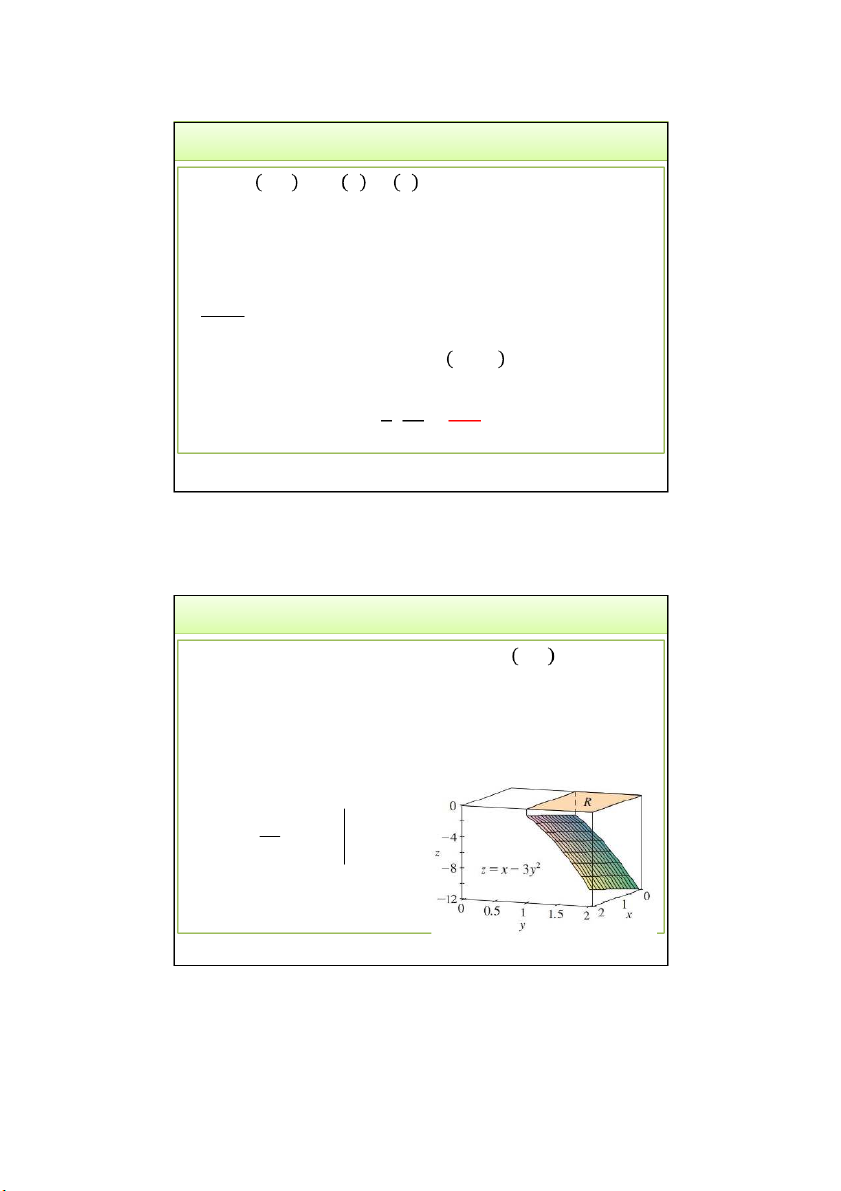
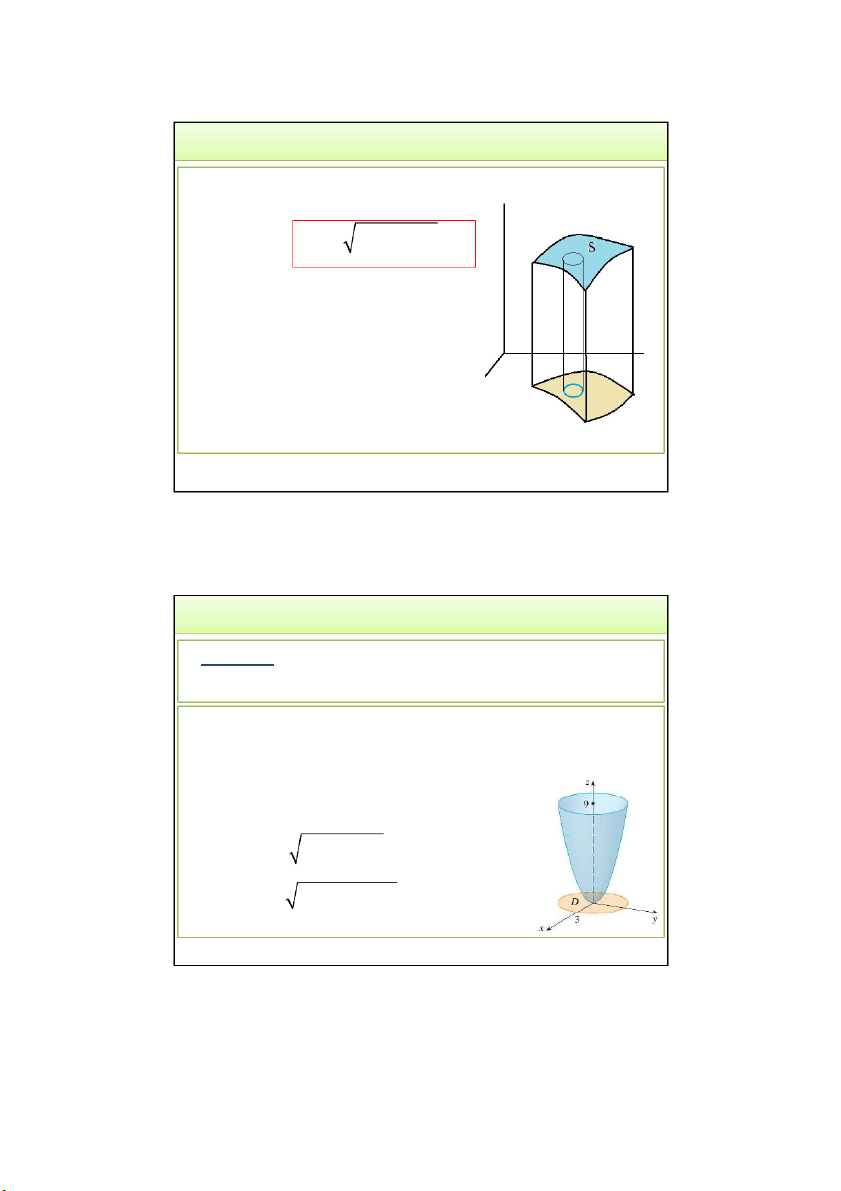
3.2. Tính thể tích của vật thể hình trụ:
Phía trên: mặt 𝑧 = 𝑓(𝑥, 𝑦),
Phía dưới: miền D trong Oxy V  f  , x y dxdy D
 TH vật thể giới hạn bởi 2 mặt:
𝑆1: 𝑧 = 𝑢 𝑥, 𝑦 ; 𝑆2:𝑧 = 𝑢(𝑥, 𝑦) V  u u dxdy 2 1  D 3/24/2022
Tích phân kép và ứng dụng 37 37 3. Ứng dụng
• Ví dụ. Tính thể tích vật thể giới hạn bởi mặt phẳng 𝑧 = 0
và mặt S: 𝑧 = 1 − 𝑥 − 𝑦 3/24/2022
Tích phân kép và ứng dụng 38 38 19 3/24/2022 3. Ứng dụng
• Ví dụ. Tính thể tích vật thể giới hạn bởi mặt phẳng 𝑧 = 0
và mặt S: 𝑧 = 1 − 𝑥 − 𝑦
• HD: Giao của mặt S và mặt phẳng 𝑧 = 0: 𝑥 + 𝑦 = 1
Suy ra: 𝐷 = 𝑥, 𝑦 𝑥 + 𝑦 ≤ 1
𝑉 =  1 − 𝑥 − 𝑦 𝑑𝑥𝑑𝑦 
Chuyển sang tọa độ cực:
𝑥 = 𝑟. cos 𝜑 ; 𝑦 = 𝑟. sin 𝜑 ; 𝐽 = 𝑟 3/24/2022
Tích phân kép và ứng dụng 39 39 3. Ứng dụng
𝐷 → 𝐷󰆒 = { 𝑟, 𝜑 |0 ≤ 𝜑 ≤ 2𝜋, 0 ≤ 𝑟 ≤ 1
𝑉 =  1 − 𝑟 𝑟𝑑𝑟𝑑𝜑 󰆒
𝑉 = ∫ ∫ 𝑟 − 𝑟 𝑑𝑟 (đ𝑣𝑡𝑡)   𝑑𝜑 =  3/24/2022
Tích phân kép và ứng dụng 40 40 20 3/24/2022 3. Ứng dụng
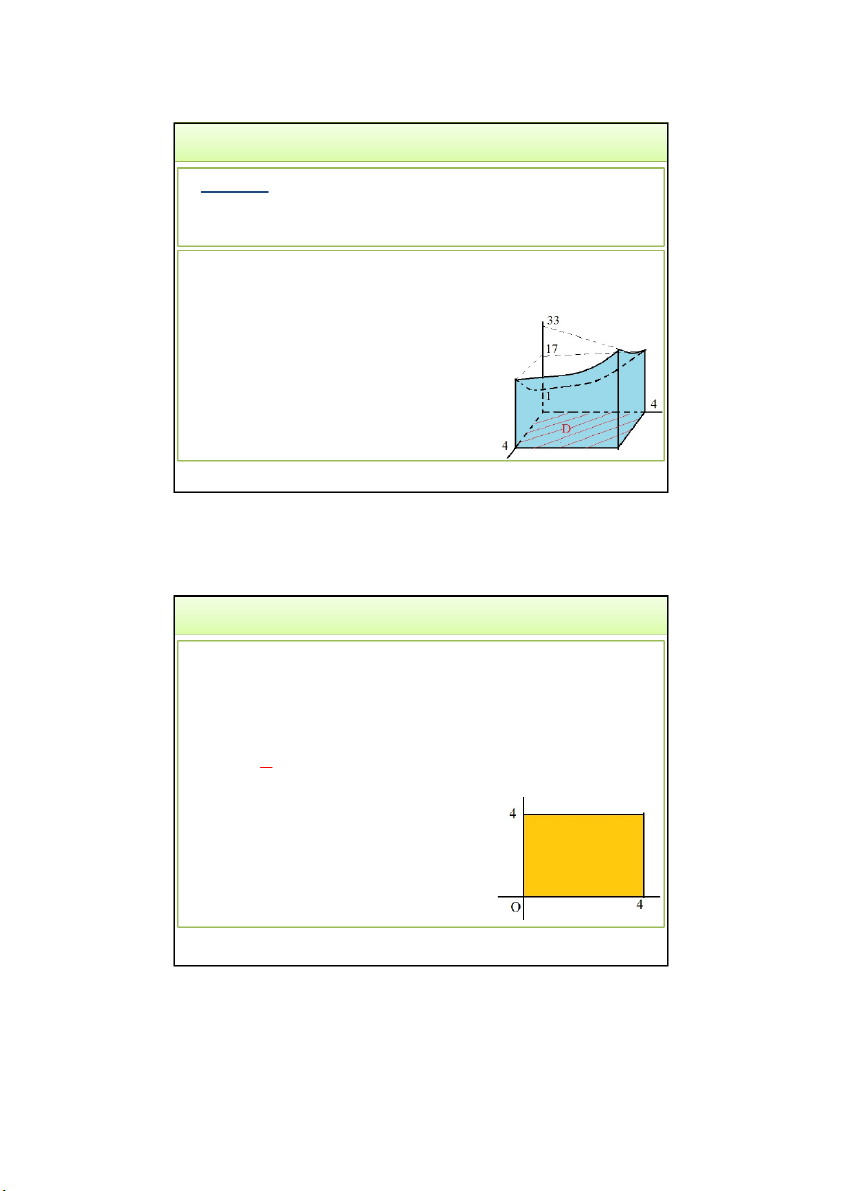
Ví dụ 8. Tính thể tích vật thể V giới hạn bởi các mặt 𝑥 =
0, 𝑦 = 0, 𝑧 = 0, 𝑥 = 4, 𝑦 = 4 và mặt parabolid (S): 𝑧 = 𝑥 + 𝑦 + 1. Hướng dẫn:
Ta có: (S): 𝑧 = 𝑥 + 𝑦 + 1 ≥ 1, ∀(𝑥, 𝑦)
Mặt (S) không giao với mp 𝑧 = 0
Miền D – hình chiếu của V lên (Oxy)
là hình vuông giới hạn bởi các đường:
𝑥 = 0, 𝑦 = 0, 𝑧 = 0, 𝑥 = 4, 𝑦 = 4 . 3/24/2022
Tích phân kép và ứng dụng 41 41 3. Ứng dụng • Thể tích vật thể V: V x y 1 4 4 2 2 dxdy     2 2 x y 1dx        dy 0  0   D 2 V 186 3 3/24/2022
Tích phân kép và ứng dụng 42 42 21 3/24/2022 3. Ứng dụng
Ví dụ 9. Tìm thể tích vật thể T ở bên dưới mặt 𝑧 = 𝑥 + 𝑦
và bên trên miền D trong mặt phẳng xy giới hạn bởi các
đường 𝑦 = 2𝑥, 𝑦 = 𝑥 3/24/2022
Tích phân kép và ứng dụng 43 43 3. Ứng dụng
Hình chiếu của vật thể T lên mặt phẳng Oxy là miền D:
𝐷 = 𝑥, 𝑦 |0 ≤ 𝑥 ≤ 2, 𝑥 ≤ 𝑦 ≤ 2𝑥
Thể tích vật thể T bằng: 2 2 x 2 2 V  x  y dydx   2   0 x 2x 3 2   2 y V  x y  dx    0  3  2x 216 V  35 3/24/2022
Tích phân kép và ứng dụng 44 44 22 3/24/2022 3. Ứng dụng
3.3. Diện tích mặt S: 𝑧 = 𝑓(𝑥, 𝑦) chiếu lên miền D của Oxy: '2 '2 S  1 z  z dxdy  x y D 3/24/2022
Tích phân kép và ứng dụng 45 45 3. Ứng dụng
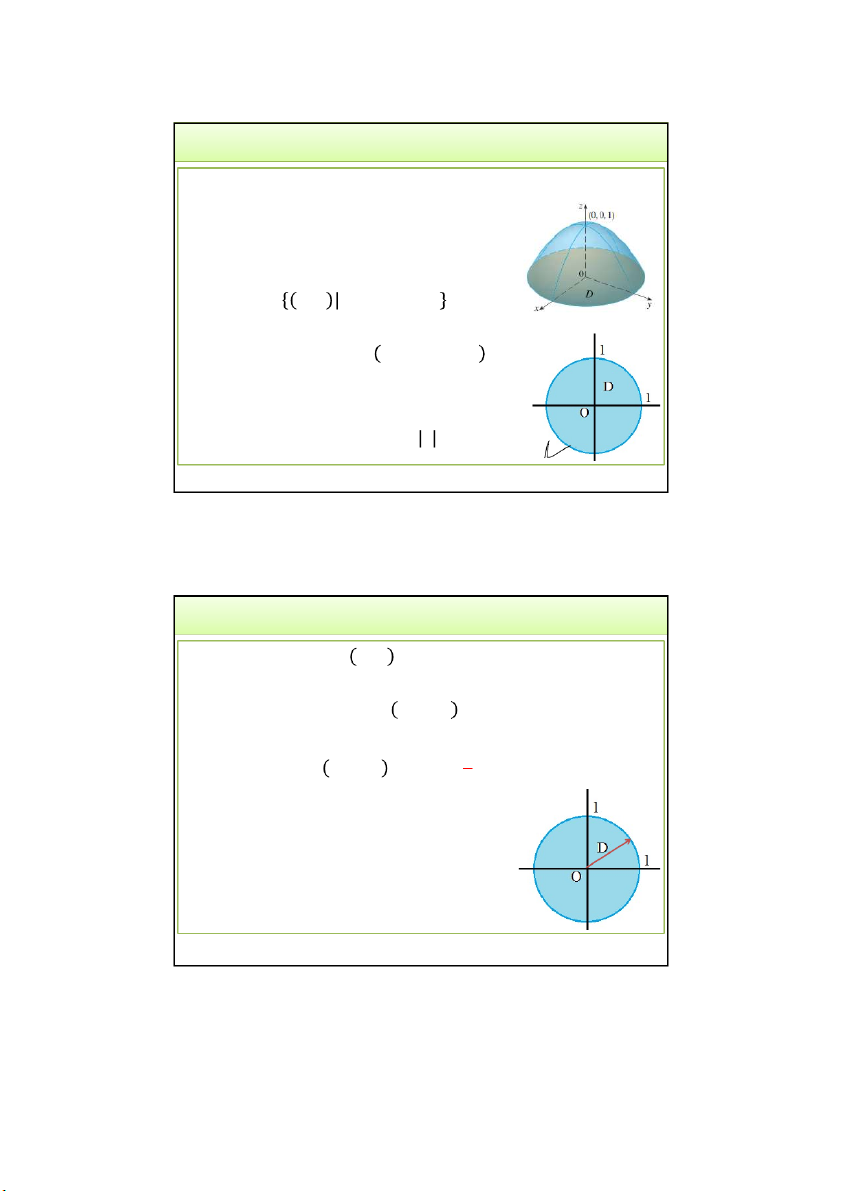
 Ví dụ 10. Tính diện tích mặt Paraboloid 𝑧 = 𝑥 + 𝑦 nằm bên dưới mặt 𝑧 = 9?
• Giao của mặt paraboid với mặt 𝑧 = 9 là đường tròn: 𝑥 + 𝑦 = 9
Hình chiếu của paraboid cần tính lên Oxy
là D: hình tròn 𝑥 + 𝑦 ≤ 9 '2 '2 S  1 z  z dxdy x y D 2 2 S  1 4x  4y dxdy D 3/24/2022
Tích phân kép và ứng dụng 46 46 23 3/24/2022 3. Ứng dụng
• Chuyển sang tọa độ cực: x  r cos 
,0   2 ,0  r  3,J  r y  r sin  2 3 2 S  1 4r rdrd   0 0 3 1
 2 .  1 4r 1/2 2 d  2 1 4r  0 8 1 2   2 . . .1 4r  3 3/2 2  37 37 1 8 3 0 6 3/24/2022
Tích phân kép và ứng dụng 47 47 3. Ứng dụng
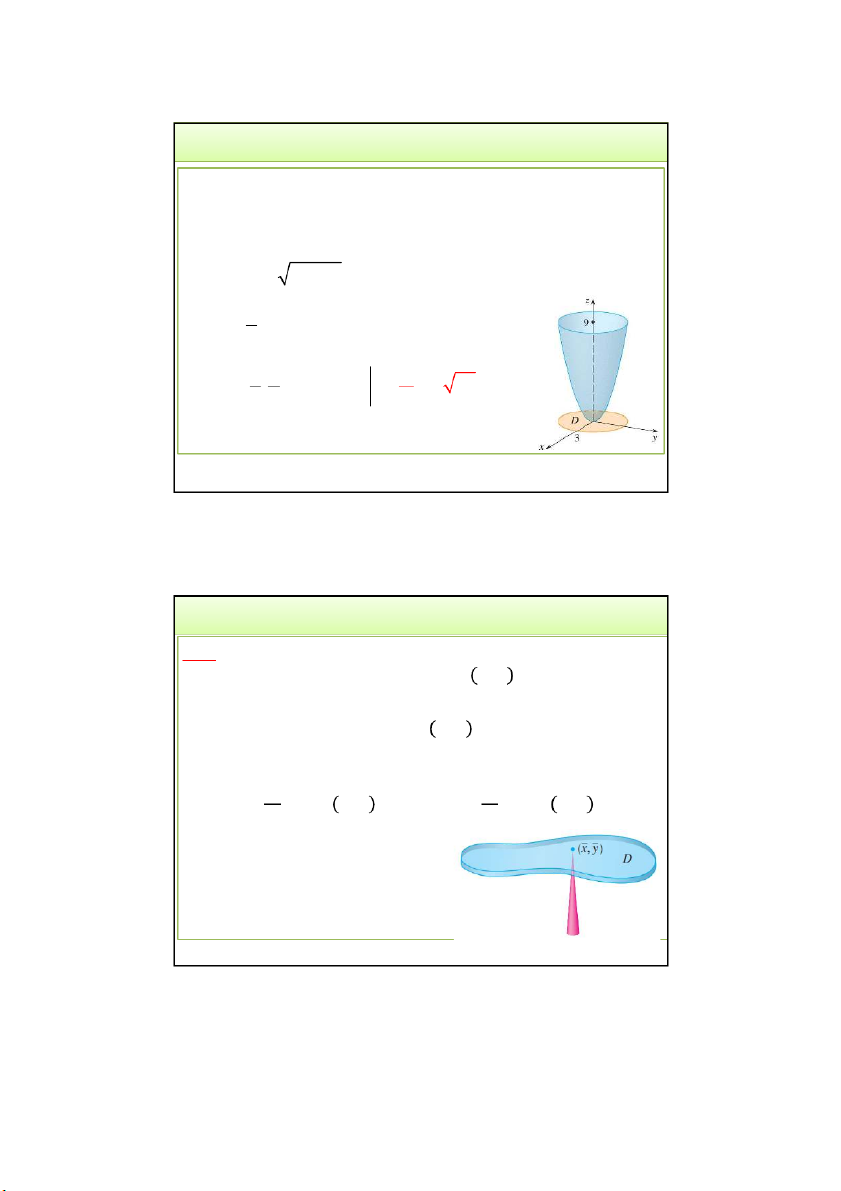
3.4. Khối lượng, Tọa độ khối tâm của một bản mỏng nằm
trong và có hàm mật độ khối lượng 𝜌 𝑥, 𝑦 :
𝑚 =  𝜌 𝑥, 𝑦 𝑑𝐴  1 1
𝑥 = 𝑚𝑥𝜌 𝑥,𝑦 𝑑𝐴 , 𝑦 = 𝑚𝑦𝜌 𝑥,𝑦 𝑑𝐴   3/24/2022
Tích phân kép và ứng dụng 48 48 24 3/24/2022 3. Ứng dụng
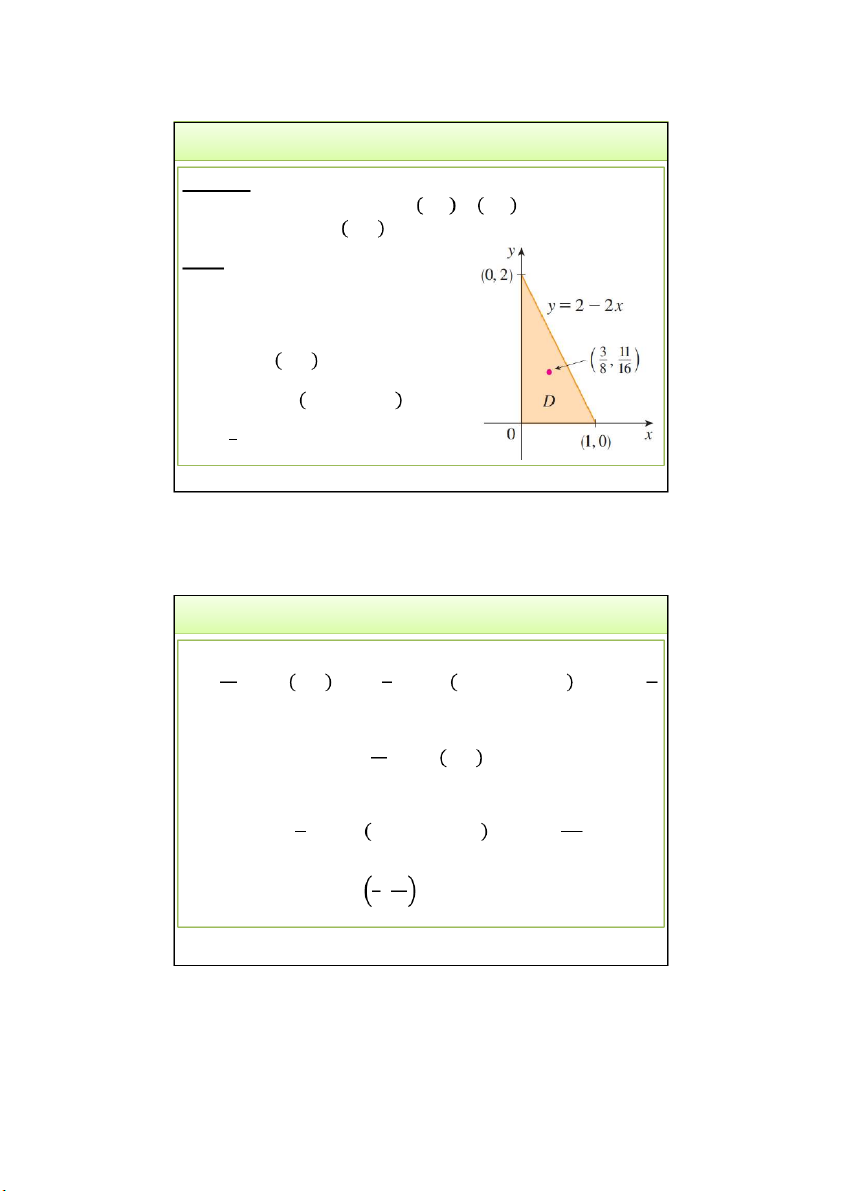
Ví dụ 12. Tính khối lượng và tọa độ khối tâm của bản mỏng
hình tam giác có các đỉnh là O 0,0 , 𝐴 1,0 , 𝐵(0, 2) và hàm
mật độ khối lượng 𝜌 𝑥, 𝑦 = 1 + 3𝑥 + 𝑦. Giải:
Pt đường thẳng đi qua AB: 𝑦 = 2 − 2𝑥
𝑚 = ∬ 𝜌 𝑥, 𝑦 𝑑𝐴 
𝑚 = ∫∫ 1 + 3𝑥 + 𝑦 𝑑𝑦   𝑑𝑥 𝑚 = . 3/24/2022
Tích phân kép và ứng dụng 49 49 3. Ứng dụng   1 3 3
𝑥 = 𝑚𝑥𝜌 𝑥,𝑦 𝑑𝐴= 8  𝑥 + 3𝑥 + 𝑥𝑦 𝑑𝑦 𝑑𝑥 = 8    1
𝑦 = 𝑚𝑦𝜌 𝑥,𝑦 𝑑𝐴    3 11
𝑦 = 8  𝑦 +3𝑥𝑦+ 𝑦 𝑑𝑦 𝑑𝑥 = 16  
Vậy tọa độ khối tâm là ,  .   3/24/2022
Tích phân kép và ứng dụng 50 50 25 3/24/2022 Bài tập
• Đổi thứ tự lấy tích phân trong các tích phân sau 2 4 2 1 1 1y 1) dx f x, y dy   4) dy f   x, y dx 2   2 x 0 2y 3 2 y 2) dy f x ,y dx   2 x2 5) dx f x ,y dy  2   0 0 1 x e ln x 3) dx f   x,y dy 2 a 2 ax 6) dx f x, y dy   2   1 0 0 2axx 3/24/2022
Tích phân kép và ứng dụng 51 51 Bài tập
• Tính các tích phân sau: 2  /2 3) x sin ydydx 2   0 0 3 1 1) 1 4xydxdy 10    /2 5 1 0 4) cos ydxdy 4    /6 1  1 2 2)    3 2 2 4x  9x y dydx 6  2 1 8 0 1 5) 2x  y dxdy   0 0 6)  2 3 4
6x y  5y dS, D x, y| 0  x  3,0  y   1 D 7) cos
 x  2ydS , D  x,y | 0  x  ,0  y  /  2 D 2 xy 8)
dS, D  x, y | 0  x 1, 3   y 3  2     x 1 D 3/24/2022
Tích phân kép và ứng dụng 52 52 26 3/24/2022 Bai tập
• Tính các tích phân sau: 3 4y 1)    x  ydxdy y 0  x 1    2)  2 2
cos x  sin y dxdy, D : 0  x  , 0  y  4 4 D dxdy 3)
, D : x  1, y  1, x  y  3  x y D  3 2 2 2 2 2 4) x  y dxdy, D :x  y  a D  2 2  x y  2 2 2 5) e dxdy, D :x  y  a . D 3/24/2022
Tích phân kép và ứng dụng 53 53 Bài tập
6) x  y dxdy, D : A
 BC |A 1,1, B 4,  1 , C 4,4  D 2 7)
xdxdy, D :y  3x , y  6  3x D  1 2 2 8)
x y dxdy, D :x  2, y  x, y   x D 9) x
e dxdy, D :x  0, y 1, y  2, x  ln y D 2 2
10) xdxdy , D :x  y  4x  2y  4.  . D 3/24/2022
Tích phân kép và ứng dụng 54 54 27 3/24/2022 Bài tập
• Tính thể tích các vật thể giới hạn bởi các mặt:
1) 3x  2y  z  12,x  0,x  1, y  2, y  3 95 / 2 2 2
2) z  4  x  y ,z  0,x  1
 ,x 1, y  0, y  2 12 2 2 x y 166 3) 
 z  1,z  0,x  1, x  1, y  2, y  2 4 9 27 2 2   216 z  x  y , D    x, y 1 4)
| 0  y  4, y  x  y   2  35 5) z  xy, x,y  2
 D gh:y  x -1, y  2x  6;36   2 2 
6) z  1 x  y , y  x,y  3x,z  0,x  0, y  0,z  0 48    3/24/2022
Tích phân kép và ứng dụng 55 55 Bài tập
• Tính diện tích của các miền giới hạn bởi các đường sau: 1)
 0;  0; x  2; y  ex x y 2 2 2) y  1  ; y   ; x x  y  2  y 2 3) x  2; y  x  2 4)  x  y 2 2 2 2  2.a  2 2 x  y  5)  x  y 3 2 2 4 4  x  y 6)  x  y 2 2 2 3  2 y 3/24/2022
Tích phân kép và ứng dụng 56 56 28 3/24/2022 Bài tập
• Tính thể tích vật thể giới hạn bởi các mặt sau: 2 1) y  x ; y  1; x  y  z  4; z  4; 4 / 5 2 2
2) z  y  x ; z  0; y  2  ; 32 / 3
3) x  2y  z  2, x  2 y, x  0,z  0; 1/ 3 2 2 4) z  x  3y ,
x  0, y  1, y  x, z  0; 5 / 6 2 2 2 2
5) z  4 x  y ; 2z  2  x  y 3 2 6) y  x ; z  0; y  z  2; 32 5 /15 2 2 2 2 2 2 3
7) x  y  z  R ; x  y  R ; x R 3  4 /18 2 2 2
8) 2z  x  y ;x  y2 1; 2 2 2   1 / 3 3/24/2022
Tích phân kép và ứng dụng 57 57 Bài tập
• Tính diện tích của các phần mặt cong sau:
1. Tính diện tích của phần mặt cầu 𝑥 + 𝑦 + 𝑧 = 𝑅 nằm
trong hình trụ 𝑥 + 𝑦 = 𝑅𝑦. 4𝑅  − 1 
2. Tính diện tích của phần mặt cầu 𝑥 + 𝑦 + 𝑧 = 𝑅 nằm
trong hình trụ 𝑧 + 𝑦 = 𝑅𝑦 + 𝑅𝑧
3. Tính diện tích phần mặt nón 𝑧 = 𝑥 + 𝑦 nằm bên
trong hình trụ 𝑥 + 𝑦 = 2𝑥. 𝜋 2
4. Tính diện tích mặt trụ 𝑥 = 2𝑧 bị cắt bởi các mặt phẳng
𝑥 − 2𝑦 = 0, 𝑦 = 2𝑥, 𝑥 = 2 2. 13 3/24/2022
Tích phân kép và ứng dụng 58 58 29 3/24/2022 Bài tập 3/24/2022
Tích phân kép và ứng dụng 59 59 Bài tập 3/24/2022
Tích phân kép và ứng dụng 60 60 30 3/24/2022 Bài tập 3/24/2022
Tích phân kép và ứng dụng 61 61 Bài tập
In the first octant: góc phần tám thứ nhất. 3/24/2022
Tích phân kép và ứng dụng 62 62 31