Lý thuyết Vi phân, Cực trị - Giải tích 2 | Trường Đại học Công nghệ, Đại học Quốc gia Hà Nội

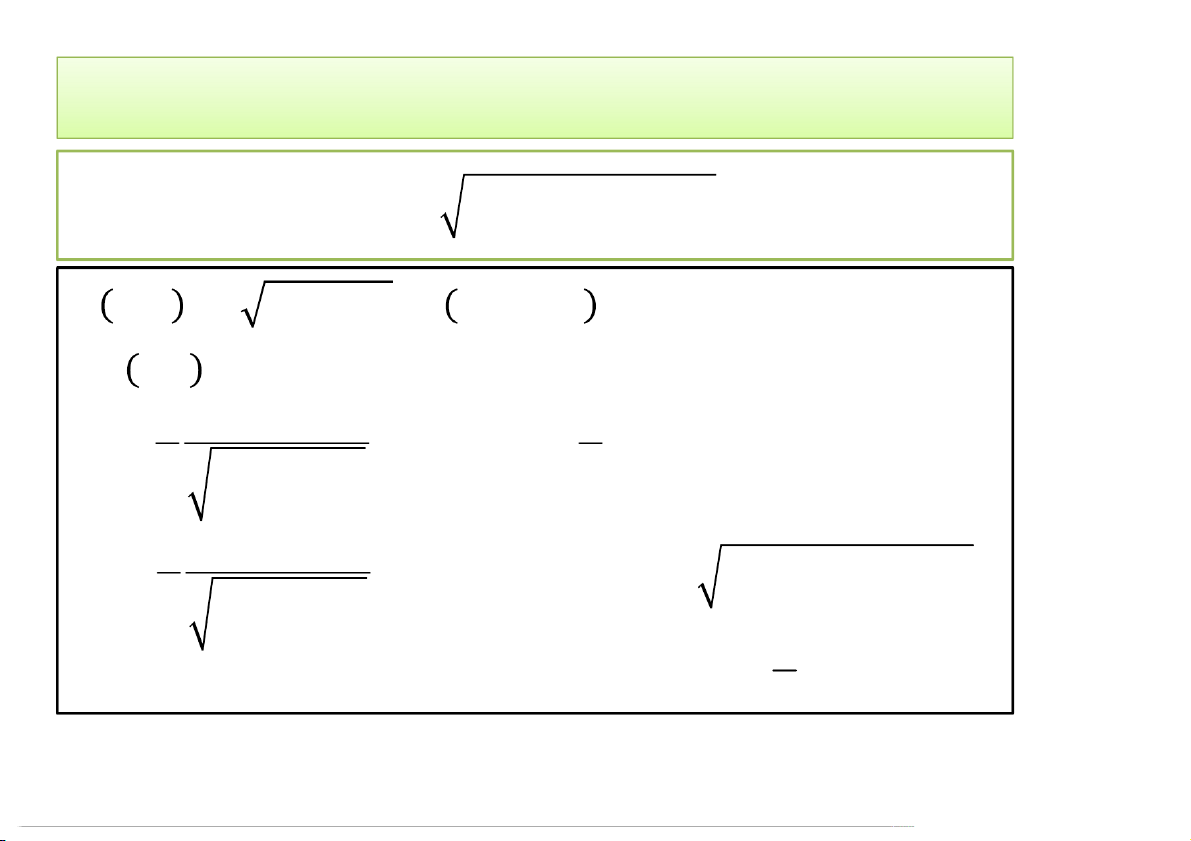
VI PHÂN, CỰC TRỊ 1) Vi phân;
2) Cực trị không điều kiện hàm nhiều biến;
3) Cực trị có điều kiện;
4) Giá trị lớn nhất, giá trị nhỏ nhất của hàm số
Tài liệu: Toán cao cấp tập 3, trang 10 – 29. Calculus, page 922 – 941. 3/24/2020
Đạo hàm, vi phân cấp cao 1 1. Vi phân (Differential)
• Nhắc lại: Đối với hàm 1 biến
• Xét hàm  = (), khi đó  =   . 
• Với  – số gia của biến số (là 1 biến độc lập) – có thể là một số thực tùy ý.
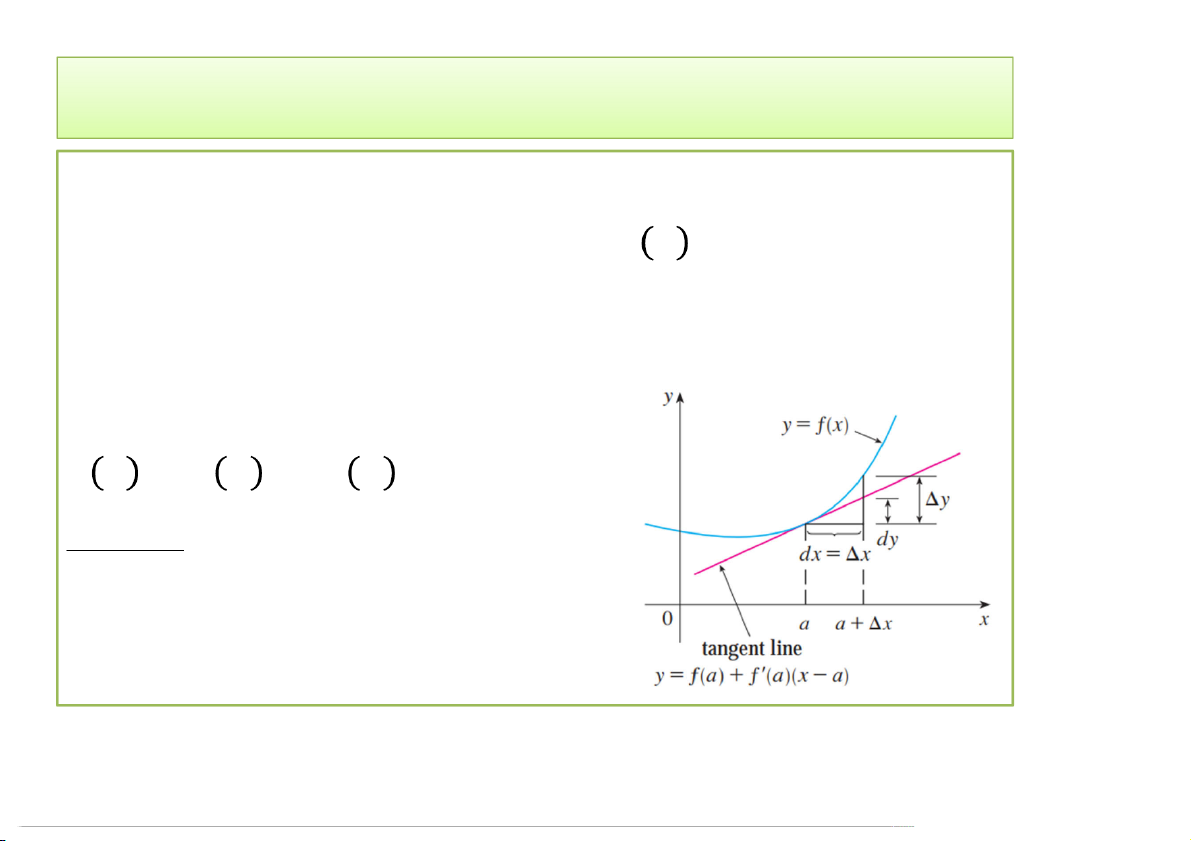
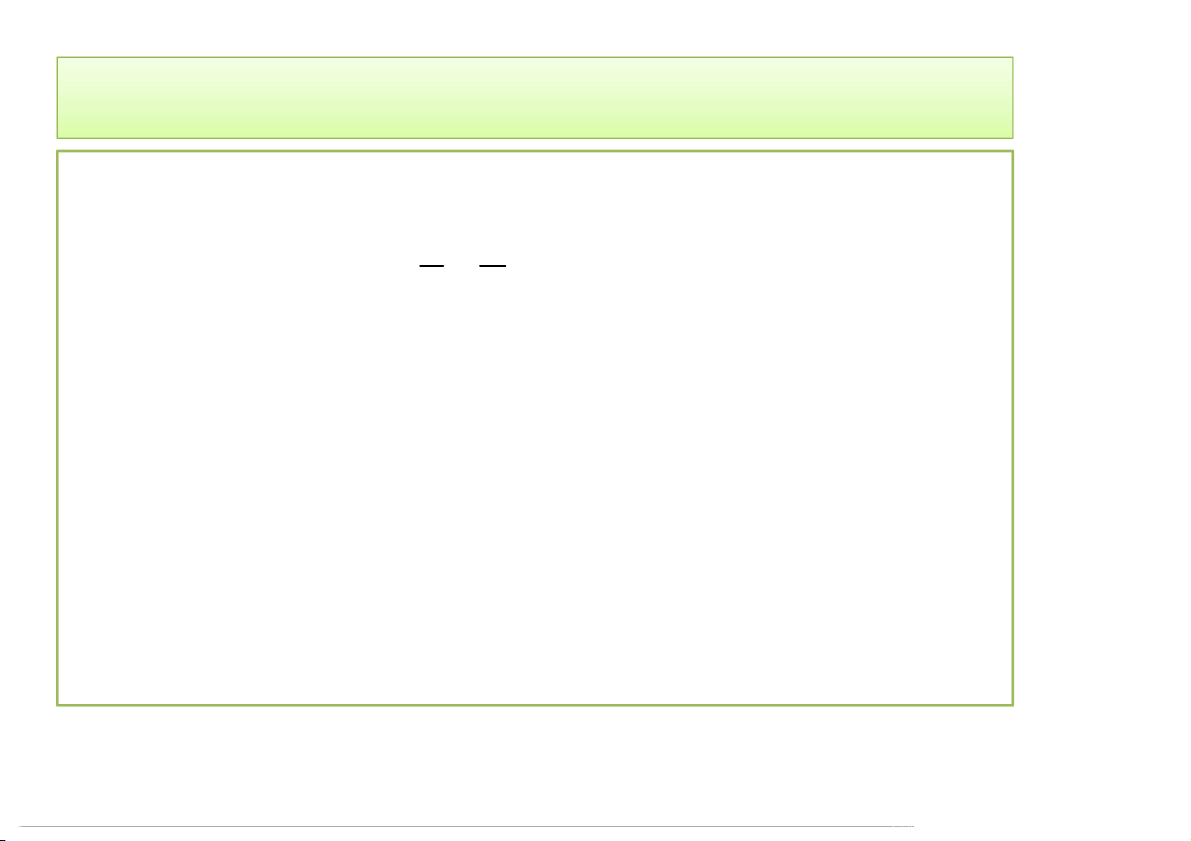
• Công thức tính gần đúng:
  ≈   +   . ( − )
Ý nghĩa: Tại lân cận điểm a,
() ≈ giá trị nằm trên đường tiếp
tuyến tại a. Suy ra ∆ lớn sẽ k đúng 3/24/2020
Đạo hàm, vi phân cấp cao 2 1. Vi phân (Differential)
• Đối với hàm 2 biến:  = (, ), coi ,  – biến độc lập,
do đó có thể là một số thực tùy ý.
• Khi đó vi phân (): vi phân toàn phần bằng:  
 =  ,  .  +  ,  .  =  + 
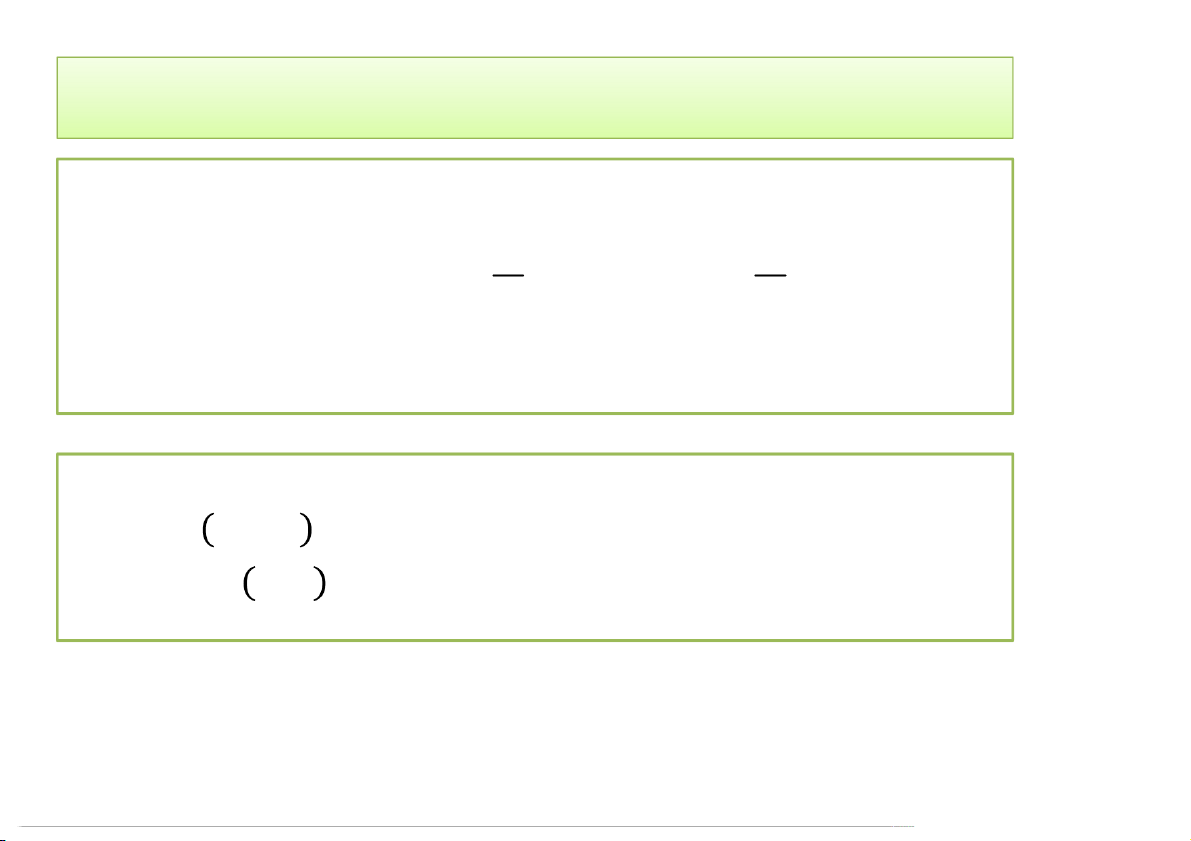
Nếu lấy  = ∆ =  − ;   = ∆ =  −  thì:
 =  ,  .  −  +  ,  . ( − ) 3/24/2020
Đạo hàm, vi phân cấp cao 3 1. Vi phân (Differential)
• Ví dụ. Tìm vi phân toàn phần của hàm số: 
 ,  = ln   • Hướng dẫn: ' 2y ' 2 f  ; f  x y 2 2 y 2 y x sin xsin x x 2  y 2dy 2 xdy  ydx ' '    df  f dx  f dy  dx   x y 2 2y 2y 2 2y x sin xsin x sin x x x 3/24/2020 4 1. Vi phân (Differential)
 Áp dụng vi phân toàn phần để tính gần đúng:
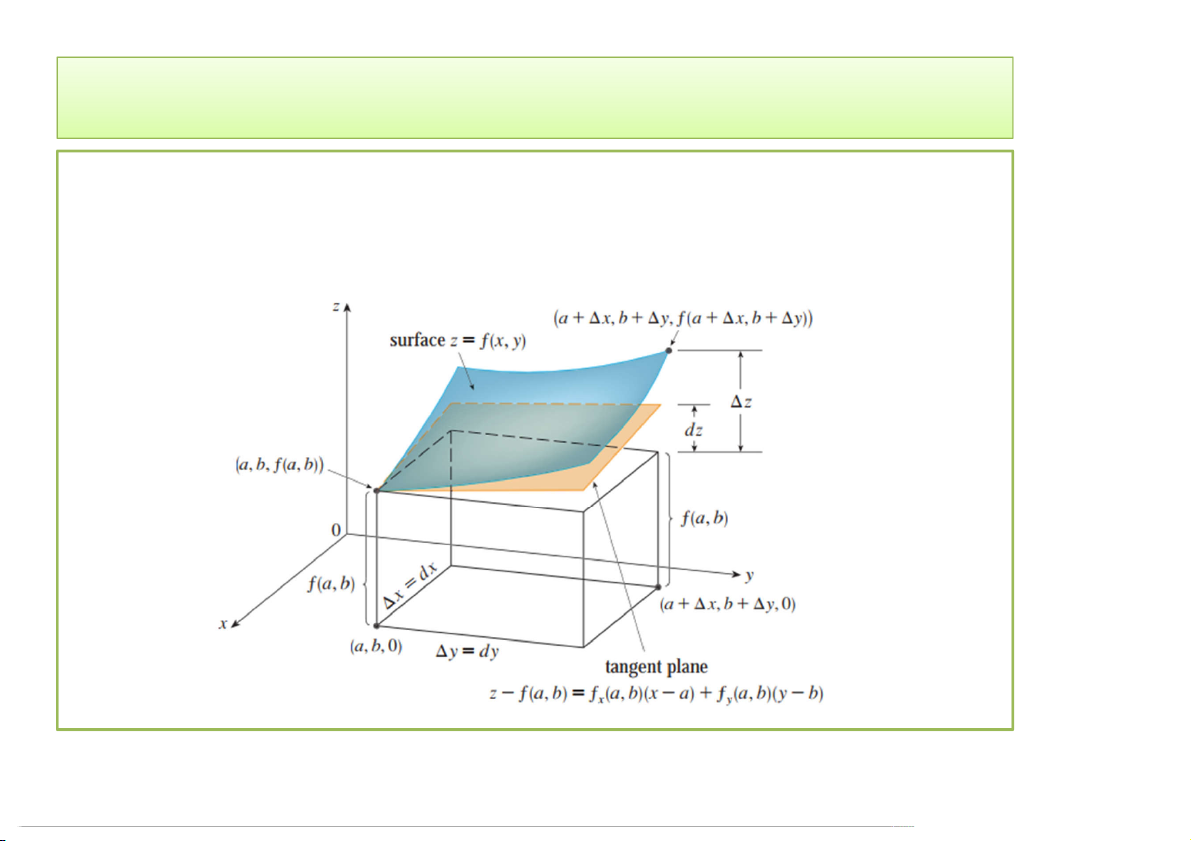
Để tính gần đúng giá trị  ,  ở lân cận tiếp điểm
M(, ), ta tính thông qua (, ) – phương trình mặt tiếp diện của S tại M. Pt mặt tiếp diện:
 =  ,  =  +  ,  .  −  +  ,  .  −  , Hay:
  + ∆,  + ∆ =  +  ,  . ∆ +  ,  . ∆ Với  = (, ) 3/24/2020 5 1. Vi phân (Differential)
• Vậy công thức tính gần đúng đối với hàm 2 biến: f a  x b  y   f   '  f   ' ( , ) a,b a,b . x   f a,b. y  x y 3/24/2020
Đạo hàm, vi phân cấp cao 6 1. Vi phân (Differential)
 Các bước để tính gần đúng:
 Xác định hàm , ∆, ∆, ∆, …
 Tính các đạo hàm riêng ′, ′, ′,…
 Thay vào công thức tính gần đúng
Ví dụ: Cho hàm số  =  ,  =  + 3 − . a) Tính ?
b) Nếu x thay đổi từ 2 tới 2.05, y thay đổi từ 3 tới 2.96, so
sánh giá trị của ∆ và ? 3/24/2020
Đạo hàm, vi phân cấp cao 7 1. Vi phân (Differential)
 =  ,  =  + 3 − 
a) Tính được:  = 2 + 3;  = 3 − 2
⇒  = 2 + 3  + 3 − 2 
b) Thay  = 2,  = 3, ∆ = 0.05, ∆ = −0.04 vào :
 = 13 × 0.05 + 5 × −0.04 = 0.65 Số gia của z bằng:
∆ =  2.05,2.96 −  2,3
= 2.05  + 3 × 2.05 × 2.96 − 2.96  − 4 − 18 + 9 = 0.6449
Nhận thấy ∆ ≈ , nhưng  dễ tính hơn. 3/24/2020
Đạo hàm, vi phân cấp cao 8 1. Vi phân (Differential) 2 2
• Ví dụ. Tính gần đúng 3 1,0  1  0,05
 ,  =   +  =  +  /,
 1,0 , ∆ = 0,01, ∆ = 0,05 ' 2 x ' f   f M  x x  2 0  3 x  y 2 2 2 3 3 2 y ' ' f   f M  2 2 y y  0 0  3 1,01  0,05 3 x  y 2 2 2 3 2 1  .0,01 1,0067 f 1,0 1 3 3/24/2020 9 1.2. Vi phân cấp 2
• Vi phân của vi phân toàn phần cấp 1 tại điểm M(x,y) được
gọi là vi phân cấp 2 của hàm f(x,y) tại điểm M(x,y).
• Kí hiệu:  ,  =   ,  .
• Nếu hàm f(x,y) có các đạo hàm riêng liên tục cấp 2 và là biến độc lập thì 2 2 2 2        2 f 2 f f 2 d f  dx  2 dxdy  dy  dx  dy f 2 2 x x y y  x y          3/24/2020
Đạo hàm, vi phân cấp cao 10 1.2. Vi phân cấp 2
• Ví dụ. Xác định vi phân cấp 2 của hàm số:
 ,  = 2 −  −  − 6 − 3 + 5 Theo bài cho ta có: ' '
f  4x  y  6; f  x  2y  3 x y " " " f  4; f  1; f  2 xx xy yy 2  d f x y  2 2 ,  4dx  2dxdy  2dy 3/24/2020
Đạo hàm, vi phân cấp cao 11 1.3. Khai triển Taylor
 Công thức khai triển Taylor:
f  M   f M  df M  1 1 2  d f M  ... n  d f M  R 0 0  0   0  2! ! n n Trong đó, Rn là phần dư.
Ví dụ. Khai triển hàm số sau theo công thức Taylor ở lân cận điểm  1, −2
 ,  = 2 −  −  − 6 − 3 + 5 3/24/2020
Đạo hàm, vi phân cấp cao 12 1.3. Khai triển Taylor
 ,  = 2 −  −  − 6 − 3 + 5;  1, −2 Ta có: f M  5 0  ' '
f  4x  y  6; f  x  2y  3 x y " " " f  4; f  1  ; f  2  xx xy yy '  f M  f M   x   ' 0; 0 0 y  0    " f M  f M   f M    xx   " 4; xy   " 1; 2 0 0 yy  0  
Thay vào công thức khai triển Taylor, suy ra:
f x y   x  2  x   y     y  2 , 5 2 1 1 2 2 3/24/2020
Đạo hàm, vi phân cấp cao 13
2. Cực trị không có điều kiện hàm 2 biến • Định nghĩa
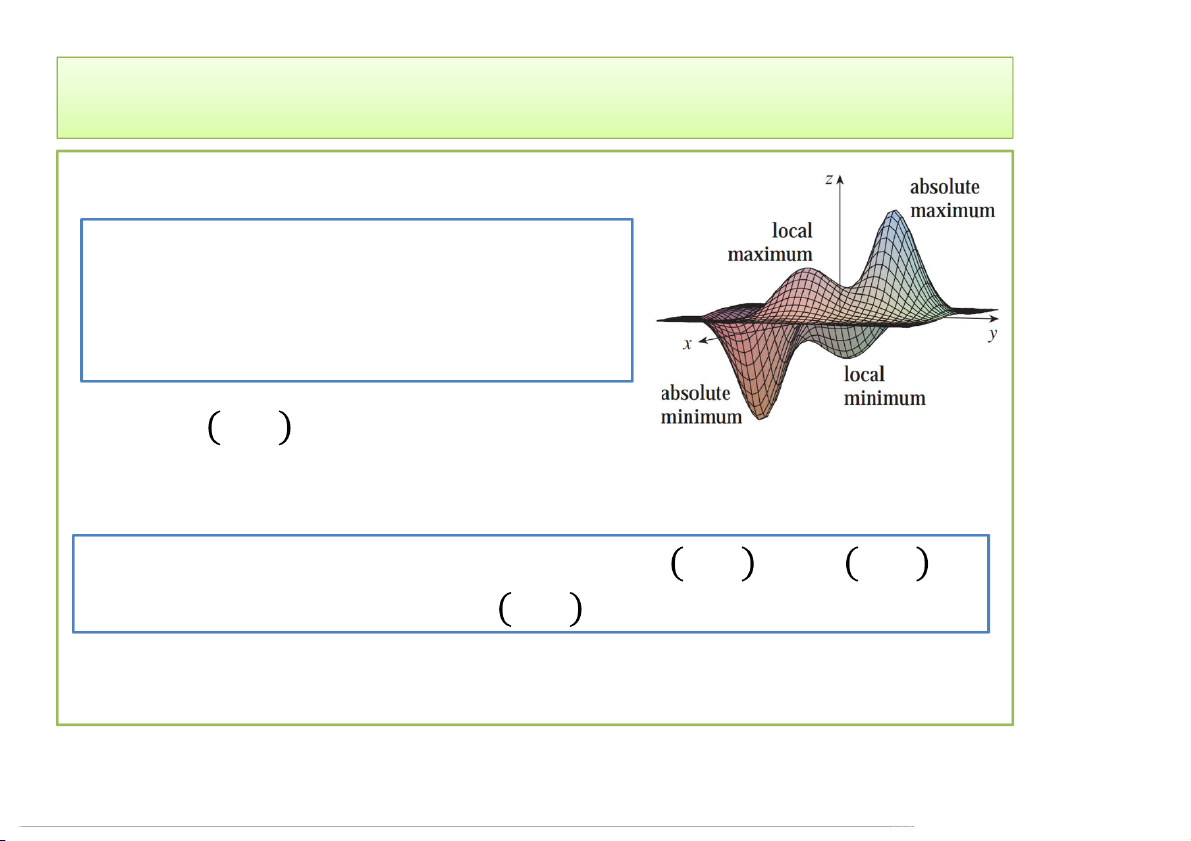
Một hàm hai biến có cực đại tại
(a,b) nếu (, ) ≤ (, ) khi (, ) gần (, ).
Giá trị  ,  : giá trị cực đại. Cực tiểu:
Nếu (, ) ≥ (, ) khi (, ) gần ,  thì  ,  có
cực tiểu tại (, ). Giá trị  ,  là giá trị cực tiểu.
 Điểm cực đại, cực tiểu: điểm cực trị 3/24/2020
Đạo hàm, vi phân cấp cao 14
2. Cực trị không có điều kiện của hàm 2 biến • Định lý:
Nếu hàm f có cực đại hoặc cực tiểu tại (, ) và các đạo
hàm riêng cấp một của f tồn tại thì:
 ,  = 0à ,  = 0 • Điểm tới hạn:
Điểm (, ) được gọi là điểm tới hạn (hoặc điểm dừng) của
f nếu  ,  = 0à ,  = 0, hoặc 1 trong các đạo
hàm riêng đó không tồn tại.
Nếu (, ) là điểm cực trị ⇒  (, ) là điểm tới hạn.
Nếu (, ) là điểm tới hạn ⇏ (, ) là điểm cực trị. 3/24/2020
Đạo hàm, vi phân cấp cao 15
2. Cực trị không có điều kiện của hàm 2 biến
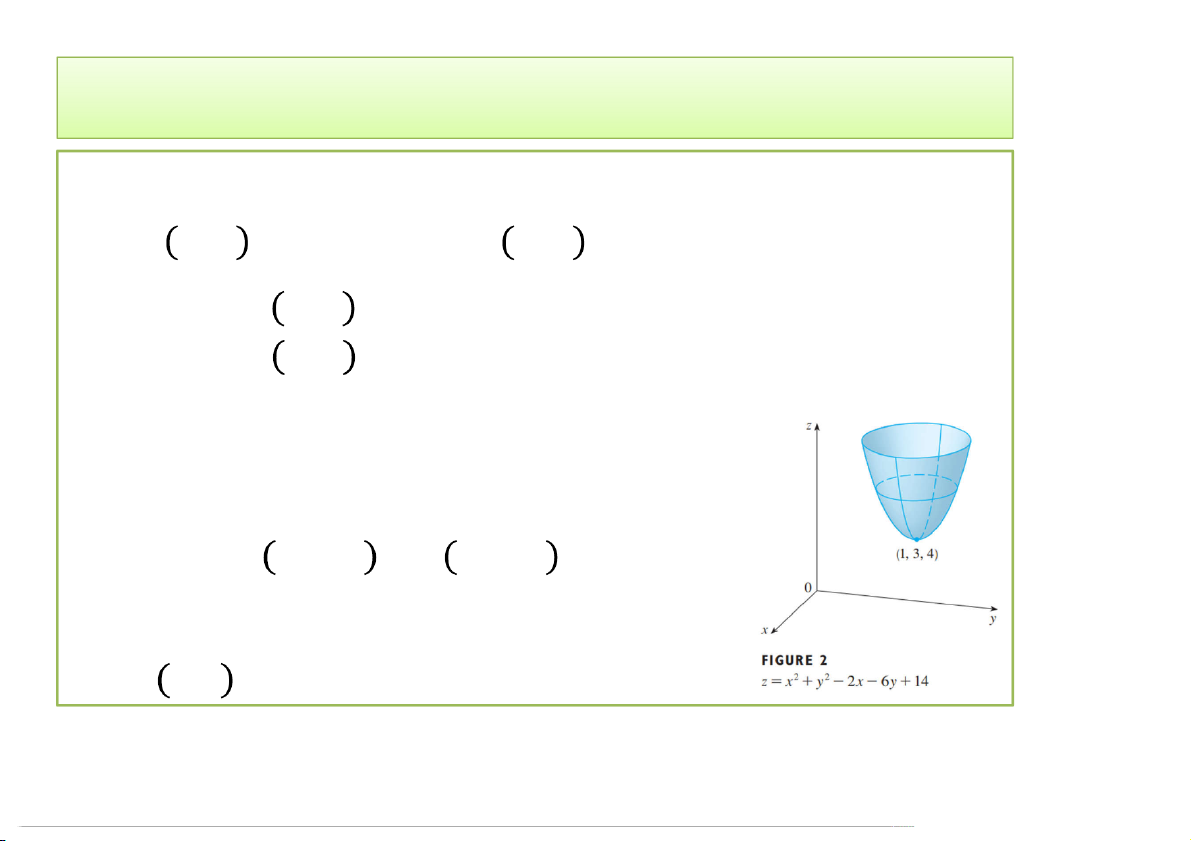
• Ví dụ. Xét hàm  =  +  − 2 − 6 + 14.
Có:  ,  = 2 − 2;   ,  = 2 − 6    ,  = 0
 ,  = 0 ⇔ 2 − 2 = 0 2 − 6 = 0 ⇔  = 1  = 3
Vậy điểm dừng: (1,3).
Lại có:  =  +  − 2 − 6 + 14
   =  − 1  +  − 3  + 4 ≥ 4.
Vậy (1,3): điểm cực tiểu của f,
 1,3 = 4: giá trị cực tiểu của f. 3/24/2020
Đạo hàm, vi phân cấp cao 16
2. Cực trị không có điều kiện của hàm 2 biến
• Ví dụ: Tìm giá trị cực trị của  =  − .
Ta có:  ,  = −2;   ,  = 2;    ,  = 0
 ,  = 0 ⇔ −2 = 0 2 = 0 ⇔  = 0  = 0 Điểm dừng: (0,0);
Các điểm trên :  = − < 0,  ≠ 0;
Các điểm trên : =  > 0,  ≠ 0;
Lân cận (0,0), f lấy giá trị dương và âm.
 Hàm f không có cực trị tại (0,0). M(0,0): điểm yên ngựa. 3/24/2020
Đạo hàm, vi phân cấp cao 17
2. Cực trị không có điều kiện của hàm 2 biến
• Dấu hiệu sử dụng đạo hàm riêng cấp 2
Giả sử các đạo hàm riêng cấp 2 của f liên tục tại lân cận (a,b) và
(a,b) là một điểm tới hạn của f.
Xét  =  ,  .  ,  − (, ) 
 Nếu  > 0à ,  > 0 thì (, ): điểm cực tiểu;
 Nếu  > 0à ,  < 0 thì (, ): điểm cực đại;
 Nếu  < 0thì (, ): không là điểm cực trị. 3/24/2020
Đạo hàm, vi phân cấp cao 18
2. Cực trị không có điều kiện của hàm 2 biến
• Ví dụ. Tìm cực trị của hàm  ,  =  +  − 4 + 1.
• Giải: Ta có  = 4 − 4;  = 4 − 4  Giải hệ:  = 0  ;
 = 0 ⇔ 4 − 4 = 0 4 − 4 = 0
Các điểm tới hạn:  0,0 ;  1,1 ;  −1, −1 ;
Đạo hàm riêng cấp 2:  = 12;  = 12;  = −4
 ,  = 144 − 16
 0,0 = −16 ⇒ (0,0): không là cực trị;
 1,1 = 128;  = 12 ⇒ (1,1): điểm cực tiểu;
 −1, −1 = 128;  = 12 ⇒ (−1, −1): điểm cực tiểu. 3/24/2020
Đạo hàm, vi phân cấp cao 19
2. Cực trị không có điều kiện của hàm 2 biến
• Tóm tắt: Các bước làm bài toán tìm cực trị không điều kiện Tính  Tính Kiểm tra D (, ) , , tại điểm tìm điểm , , dừng rồi dừng ; Lập D KL 3/24/2020
Đạo hàm, vi phân cấp cao 20
2. Cực trị không có điều kiện của hàm 2 biến
• Ví dụ. Tìm các điểm cực trị của hàm số: 3 2 2 z  8x  2xy  3x  y ' 2 ' z  24x  2y  6x; z  2x  2y x y " " " " z  48x  6; z  z  2; z  2 xx xy yx yy
Điểm dừng hàm số được xác định từ hệ: ' x  y  0 2 z  0   x 12x  y 3x  0       1 1 ' z  0 x  y  0 x  , y    y    3 3  1 1  M 0,0 ; M , 1   2  3 3   3/24/2020
2. Cực trị không có điều kiện của hàm 2 biến
• Xét tại điểm M1 ta có: A0,0  6;
B0,0  2; C0,0  2 2
 D  AC  B  12  4  16  0
Vậy M1 không phải là điểm cực trị của hàm đã cho
• Xét tại điểm M2 ta có:  1 1   1 1   1 1 A , 10; B , 2; C ,        2  3 3  3 3   3 3        2
 D  AC  B  20  4  16  0
Vậy M2 là điểm cực tiểu của hàm đã cho. 3/24/2020
2. Cực trị không có điều kiện của hàm 2 biến
• Ví dụ: Tìm các điểm cực trị của hàm số: 2   2 . x y z x e y  e  e ' x ' x x  0 z 1  e z  0     e  x x 1 0         y 1 ' 2 ' 2 z  2e  2e z  0   2e  2 y e  y  y y 0    2 1 M 0,   0  2    " x " z  e  z M   xx xx  1 0  1 0 " 2y " z  4  e  z M   e  D   4e  0 yy yy  4 0  0 4  e " " z  0  z M  xy xy  0 0  : điểm cực đại.
2.2. Cực trị hàm nhiều biến
Cực trị của hàm nhiều biến số.
• Xét hàm n biến ( n > 2): f(x1, x ,…, x ) 2 n có tập xác định A trong Rn. '  f  0 1 x  '  f  0 x
• Điểm dừng của hàm f thỏa mãn hệ: 2 ..........  ' f  0  nx • Gọi M(x10, x ,…, x ) 20
n0 là một điểm dừng của hàm f. 2 n  f M 2   d f   a dx dx ; a  • Xét: ij i j ij i, j 1  x x i j
2.2. Cực trị hàm nhiều biến • Lập ma trận H = (a (Hess) ij)n.n
• Kí hiệu Hk: định thức con chính cấp k (tạo từ k hàng đầu và k cột đầu của H). Khi đó:
 Nếu Hk > 0 với mọi k = 1, 2,.., n thì M là điểm cực tiểu;  Nếu (-1)k H đại
k > 0 với mọi k thì M là điểm cực . •
2.2. Cực trị hàm nhiều biến
• Ví dụ: Tìm cực trị hàm: 2 2 f  x y z y z 2 , ,  x    ,  ,x , y z  0 4x y z • Hướng dẫn: 2  y 1  0 Xác định điểm dừng:  2 ' 4   0 x fx  2  '  y z  f  0     0 y 2 2x y  '  x  1/ 2 f  0  z    1 2z 2 y 1 M ,1,1       0   2  2   y z z 1 
2.2. Cực trị hàm nhiều biến • Lập ma trận Hess: " a  f M  a  f M  a  f M  xx   " 4; yy   " 3; 6 11 22 zz   33 " a  a  f M   a  a  f M  xy   " 2; 0 12 21 13 31 xz   " a  a  f M  2 23 32 yz    4 2  0  H  4  0 1  H  2 3 2     H  8  0   2  0 2 6      H  32  0  3
• Vậy M (1/2, 1, 1) là điểm cực tiểu.
3. Cực trị có điều kiện của hàm 2 biến • Định nghĩa:
Cực trị của hàm f(x,y) trong đó x, y bị rằng buộc bởi hệ
thức g(x,y) = 0 được gọi là cực trị có điều kiện trong miền xác định D.
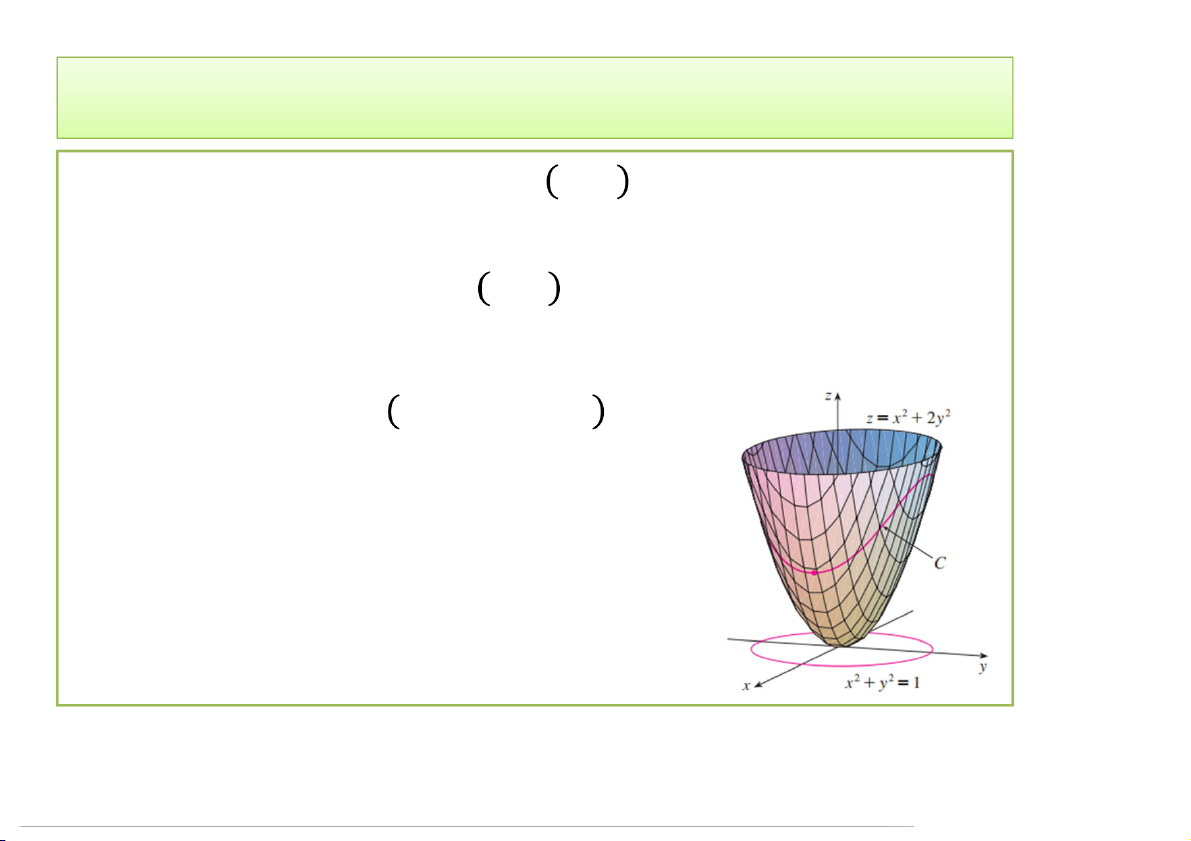
Ví dụ: Tìm cực trị của hàm  ,  =  + 2 trên đường tròn  +  = 1. 3/24/2020 Cực trị, min, max 28
3. Cực trị có điều kiện của hàm 2 biến
Cách tìm: Phương pháp nhân tử Lagrange
• Lập hàm Lagrange:  =  ,  +  , 
Với λ : hằng số nhân chưa xác định (nhân tử Lagrange)
• Tính: ′; ′; • Tìm điểm dừng: ' L  0 x  Giải hệ ' L  0  x, y, y g   x, y  0 3/24/2020 Cực trị, min, max 29
3. Cực trị có điều kiện của hàm 2 biến
• Xét dấu của : 2 2 2  L  L  L 2 2 2 d L  dx  2 dxdy  dy 2 2 x xy y Với điều kiện: g g dx  dy   2 2 0 dx  dy  0 x  y 
 Nếu  < 0: f(x,y) có cực đại có điều kiện
 Nếu  > 0: f(x,y) có cực tiểu có điều kiện
 Nếu  = 0: chưa nhận xét được gì 3/24/2020 Cực trị, min, max 30
3. Cực trị có điều kiện của hàm 2 biến
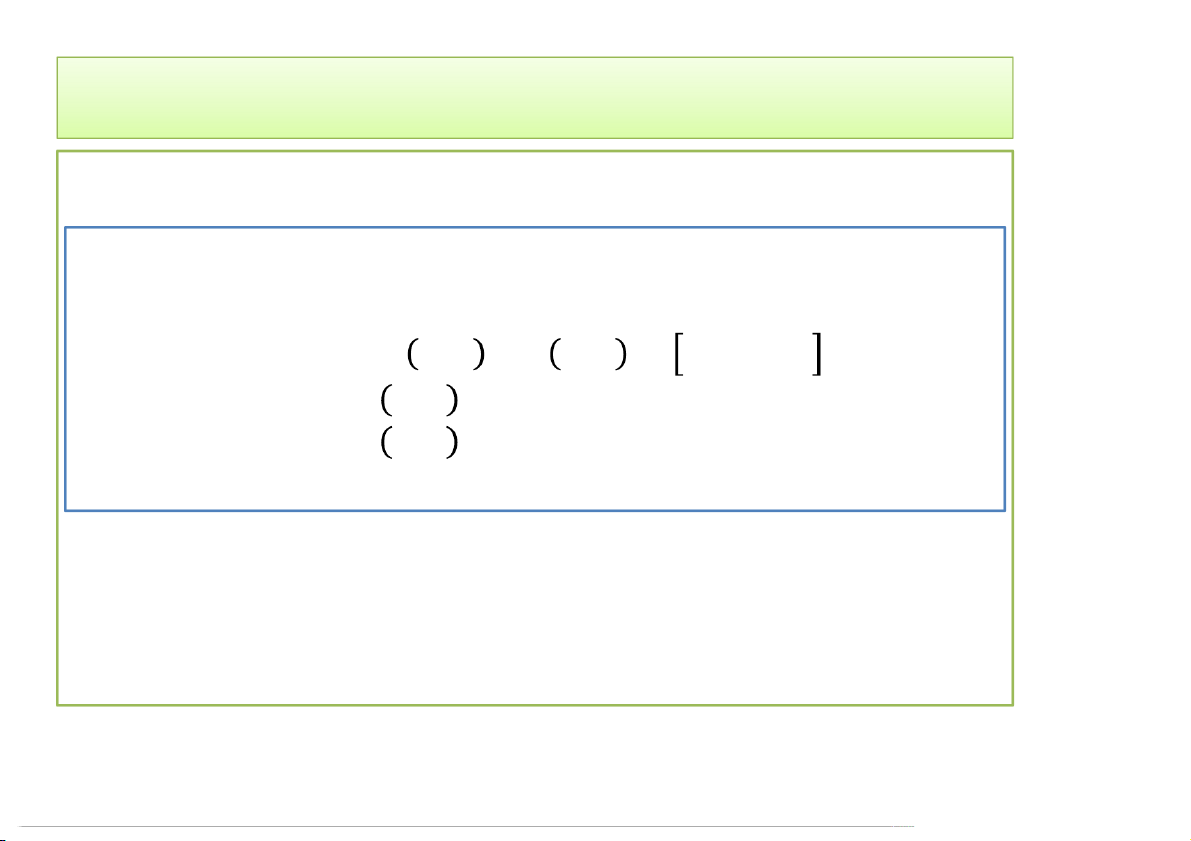
• Ví dụ. Tìm cực trị của hàm  ,  =  + 2 trên đường tròn  +  = 1.
• Giải. Từ bài cho ta có:  ,  =  +  − 1 • Hàm Lagrange:
•  =  + 2 +   +  − 1
•  = 2 + 2;  = 4 + 2 2 + 2 = 0 •  4 + 2=0  +  = 1 3/24/2020
Đạo hàm, vi phân cấp cao 31
3. Cực trị có điều kiện của hàm 2 biến
• Có 4 điểm dừng: λ = −2:  0,1 ;  0, −1 ;
λ = −1:  −1,0 ; (1,0)
 = 2 + 2;  = 0;  = 4 + 2 Xét:  =   
 + 2 + 
 0,1 =  0, −1 = −2> 0
 1,0 =  −1,0 = 2 < 0
Vậy  0,1 ;  0, −1 : điểm cực đại
 −1,0 ; (1,0): điểm cực tiểu. 3/24/2020
Đạo hàm, vi phân cấp cao 32
3. Cực trị có điều kiện của hàm 2 biến
Ví dụ: Tìm cực trị của hàm số:  ,  =  +  với điều
kiện g(x, y) = 2x + 2y – 1.  Hướng dẫn:
– Lập hàm Lagrange:  =  +  +  2 + 2 − 1
– Xác định điểm dừng: Giải hệ ' L  0 x 2x  2  0 x    '   L  0  2 y  2  0  y   y    g  x y 2x  2 y 1  0 2  2 1  0 ,  0    3/24/2020 Cực trị, min, max 33
3. Cực trị có điều kiện của hàm 2 biến x 1/ 4   1 1    y 1/ 4 Điểm dừng M , 0   4 4     1/ 4  " " " Mà L  2; L  2; L  0 2 2 x y xy 2 2 2
 d L  dx  dy   2 2 2 2 2 dx  dy   0
Suy ra M0 là điểm cực tiểu của hàm số với điều kiện đã cho. 3/24/2020 Cực trị, min, max 34
3. Cực trị có điều kiện của hàm 2 biến
• Ví dụ 2. Tìm cực trị có điều kiện của hàm: f x y  2 2 ,
 x  y  xy  5x  4y 10, x  y  4 • Hướng dẫn: Hàm Lagrange:
 =  +  +  − 5 − 4 + 10 +   +  − 4
Tìm điểm dừng: Giải hệ ' L  0 x 2x  y  5  0  x  y  1 0  '   L  0
 2 y  x  4   0  x  y  4  0 y    g  x y x  y  4  0 2x  y  5    0 , 0    3/24/2020 Cực trị, min, max 35
3. Cực trị có điều kiện của hàm 2 biến 5 3 3  5 3   x  , y  ,    M , 0 2 2 2  2 2    Vì " " " L  2; L  1; L  2 2 xy 2 x y Suy ra: 2 2 d L  2 2 2 dx  dxdy  dy   1  3 2  2 dx  dy  dy  0  2    4
Vậy điểm M0 là điểm cực tiểu của hàm với điều kiện đã cho.   f  x y 5 3 15 min ,  f ,   2 2    4 3/24/2020 Cực trị, min, max 36
3. Cực trị có điều kiện của hàm 2 biến
• Cách 2. Phương pháp khử biến số
• Từ điều kiện ta có: y = 4 – x , thế vào f(x,y) ta được:
h x  x    x2 2 4
 x4  x  5x  44  x 10 h x 2  x  5x 10 Hàm một biến số
• Khảo sát cực trị hàm h(x): h 'x  2x  5  5  h"  2  0   h x 5 '  0  x   2 2 3/24/2020 Cực trị, min, max 37
3. Cực trị có điều kiện của hàm 2 biến
Suy ra: x = 5/2 là điểm cực tiểu của h(x) 5 3 x   y  4  x  2 2 Vậy:   f  x y 5 3 15 min ,  f ,   2 2    4 3/24/2020 Cực trị, min, max 38
4. Giá trị lớn nhất và nhỏ nhất của hàm số
 Nhận xét: Mọi hàm số nhiều biến số liên tục trong một
miền đóng bị chặn D đều đạt giá trị lớn nhất và nhỏ nhất của nó trong miền đó.
Cách tìm: Hàm số f(x,y) xác định trên miền D. So sánh các giá Tìm các điểm Tính các giá trị trị cực trị và giá tới hạn cực trị trị trên biên rồi KL 3/24/2020 Cực trị, min, max 39
4. Giá trị lớn nhất và nhỏ nhất của hàm số
 Ví dụ. Tìm giá trị lớn nhất và nhỏ nhất của hàm số
 ,  =  +  −  +  + 
Trong miền  =  ≤ 0,  ≤ 0,  +  ≥ −3 .  Hướng dẫn:
• Xác định điểm dừng: giải hệ '  f  0  x 2x  y 1  0 x  1       '  f  0 2y    x 1  0 y   1  y
Suy ra điểm dừng:  −1, −1 . 3/24/2020 Cực trị, min, max 40
4. Giá trị lớn nhất và nhỏ nhất của hàm số Xét tại điểm M:
  =  −1, −1 = −1 Khảo sát trên biên: Biên  = 0
⇒  =  + : hàm một biến đối với , −3 ≤  ≤ 0  = 0 ⇔  = −1/21
 −1/2 = − 4;  0 = 0; −3 = 6 3/24/2020 Cực trị, min, max 41
4. Giá trị lớn nhất và nhỏ nhất của hàm số Biên  = 0
 ⇒  =  + : hàm một biến đối với x, −3 ≤  ≤0  = 0 ⇔  = −1/2 1
 −1/2 = − 4;  0 = 0; −3 = 6
Biên  +  = −3 ⇒  = −3 − 
⇒  = 3 + 9 + 6: hàm 1 biến đối với x, −3 ≤  ≤ 0
 = 0 ⇔  = −3/23
 −3/2 = − 4;  0 = 6; −3 = 6 3/24/2020 Cực trị, min, max 42
4. Giá trị lớn nhất và nhỏ nhất của hàm số
So sánh các giá trị của f(x,y) kết luận:   ,  = 6
tại ,  = 0, −3 , −3,0
  ,  = −1 tại ,  = −1, −1 3/24/2020 Cực trị, min, max 43
4. Giá trị lớn nhất và nhỏ nhất của hàm số
• Ví dụ. Tìm giá trị lớn nhất, giá trị nhỏ nhất của hàm số:
 = 8 + 3 + 1 − 2 +  + 1 
Trong miền tròn đóng D xác định bởi  +  ≤ 1. • Hướng dẫn:
z  x  y    x  y  2 2 2 2 2 8 3 1 2 1
• Điểm tới hạn: giải hệ phương trình x  0, y  0 z   0 8  x  x  y  x   2 2 ' 1 2  0      x  0, y  1  / 2 ' z  0  y 2   y   2 2 1 4x  2 y   0 x  1/ 2, y  0  3/24/2020 Cực trị, min, max 44
4. Giá trị lớn nhất và nhỏ nhất của hàm số Các điểm tới hạn:  1    1   1    1  M 0,0 ; M 0, ; M 0, ; M ,0 ; M ,0 1   2   3   4   5 2 2 2  2          Ta có: z  1
M  0; z M  z M  ; z M  z M  1 1   2  3  4  5 4
Xét trên biên:  +  = 1 ⇒  = 1 − ; −1 ≤  ≤ 1
⇒  = 8 + 3 1 −  + 1 − 2 + 1 −  + 1 
 = − +  =  1 −  : hàm 1 biến đối với x
 = −4 + 2 = 2 1 − 2 3/24/2020 Cực trị, min, max 45
4. Giá trị lớn nhất và nhỏ nhất của hàm số  = 0    = 0 ⇔  1  = ± 2      z   1 1 1 0  0; z  z   2   2      4 min z  0; max z  1 Vậy: D D 3/24/2020 Cực trị, min, max 46 Bài tập
• Bài 1. (Kết thúc môn HKI-19-20) • Cho hàm số hợp    =   = 
 =  ,  = 2 +  ; Tính  .
• Bài 2. Dùng vi phân, tính gần đúng các hàm số sau: 1) 1,022 0,0 2 3 5 3) 9.1,952 8, 2 1 2) ln  3 1,03 4  0,98 1 2 0,015 4) sin 1,55  8.e 3/24/2020
Đạo hàm, vi phân cấp cao 47 Bài tập
• Bài 2. Tìm  nếu: 1) xy u  e 2) u  xyz 3) u  t  2 2 , t  x  y 4) u  f  , v w , v  ax, w  by x 5) w u  v , v  , w  xy y 2 2 2
6) u  x  xy  y  4ln x 10ln y; d u1,2  ? 3/24/2020
Đạo hàm, vi phân cấp cao 48 Bài tập
Bài 3. a) Chứng minh rằng hàm số: 1  = ln  + 2 2   Thỏa mãn phương trình: u u   0 2 2 x  y  1
b) Chứng minh rằng hàm số: u  thỏa mãn: 2 2 2 x  y  z 2 2 2  u  u  u    0 2 2 2 x  y  z  3/24/2020
Đạo hàm, vi phân cấp cao 49 Bài tập
• Bài 4. Tìm cực trị các hàm số
1) f x, y   4 x  y  2 2  x  y 2) f x, y 3 2  x  3xy 15x  12y 3) f x, y y  x  y  xe
4) f x, y  xy lnx  2y, x  0, y  0 (HKI, 19-20) 5) f x, y 2  x x   3 1  y 6) f x, y 4 4 2 2  2x  y  x  2y 7) f x, y 2 2  1 6x  x  xy  y 3/24/2020
Đạo hàm, vi phân cấp cao 50 Bài tập Tiếp bài 4:
8) f x, y   x 12 2  2y 9) f x, y 2 2
 x  xy  y  2x  y 10) f x, y 3 2
 x y 6  x  y x  0, y  0 3/24/2020
Đạo hàm, vi phân cấp cao 51 Bài tập
• Bài 5. Tìm cực trị của các hàm số sau với các điều kiện kèm theo: 1) f x, y 2 2  x  2 ; y x  y  5 2) f x, y 2 2  x  y ; xy  1 3) f  , x y 2 2  4x  6 ; y x  y 13 4) f  , x y 2 2 2  x ; y x  2 y  6 5) f x, y xy 3 3  e ; x  y  16 3/24/2020 Cực trị, min, max 52 Bài tập • Tiếp bài 5: x y 6) f x, y 2 2  x  y ;  1 2 3 7) f x, y 2 2
 x  y  xy  5x  4y 10; x  y  4 z  x  8) f x, y,z  1 2
 x  y  z ; y xz 1 
9) Một hình hộp chữ nhật không có nắp được tạo ra từ 1 tấm
bìa catton 12. Tìm kích thước của hình hộp có thể tích lớn nhất tạo được. 3/24/2020
Đạo hàm, vi phân cấp cao 53 Bài tập
Bài 6. Tìm giá trị lớn nhất, giá trị nhỏ nhất của các hàm số: 2
1) f  x y2  x  y; D  x  0, y  0, x  y   6 2) f  x  y, D   2 2 x  y   1 3) f   2 2 x  y , D   2 2 x  y   1 3 3
4) f  x  y  3xy, D  0  x  2,1 y   2
5) f  1 x  2 y, D  x  0, y  0, x  y   1
6) f  1 x  2 y, D  x  0, y  0, x  y   1 3 3
7) f  x  y  3xy, D  0  x  2, 1 y   2 3/24/2020 Cực trị, min, max 54