10. Mật mã lOMoARcPSD| 40651217 Playfair lOMoAR cPSD| 40651217 10. Mật mã Playfair lOMoARcPSD| 40651217
1854, phát minh bởi nhà khoa học người Anh - Charles Wheatstone
Được sử dụng rộng rãi trong quân ội Anh, Mỹ và ồng
minh trong chiến tranh thế giới thứ II.
Mật mã Playfair sẽ thay thế từng cặp 2 kí tự trong bản
rõ bởi 2 kí tự tương ứng trong ma trận khoá 5 x 5. Qui trình mã hóa: Tạo bảng Playfair
Chia bản rõ thành các cặp chữ cái 10. Mật mã lOMoARcPSD| 40651217 Playfair
Mã hóa từng cặp chữ cái
Kết hợp các cặp ã mã hóa lại
Qui trình giải mã: thực hiện ngược lại. 10. Mật mã Playfair Qui trình mã hóa: lOMoARcPSD| 40651217 Tạo bảng Playfair
Chia bản rõ thành các cặp chữ cái
Mã hóa từng cặp chữ cái Kết hợp các cặp ã mã hóa lại
Qui trình giải mã: thực hiện ngược lại.
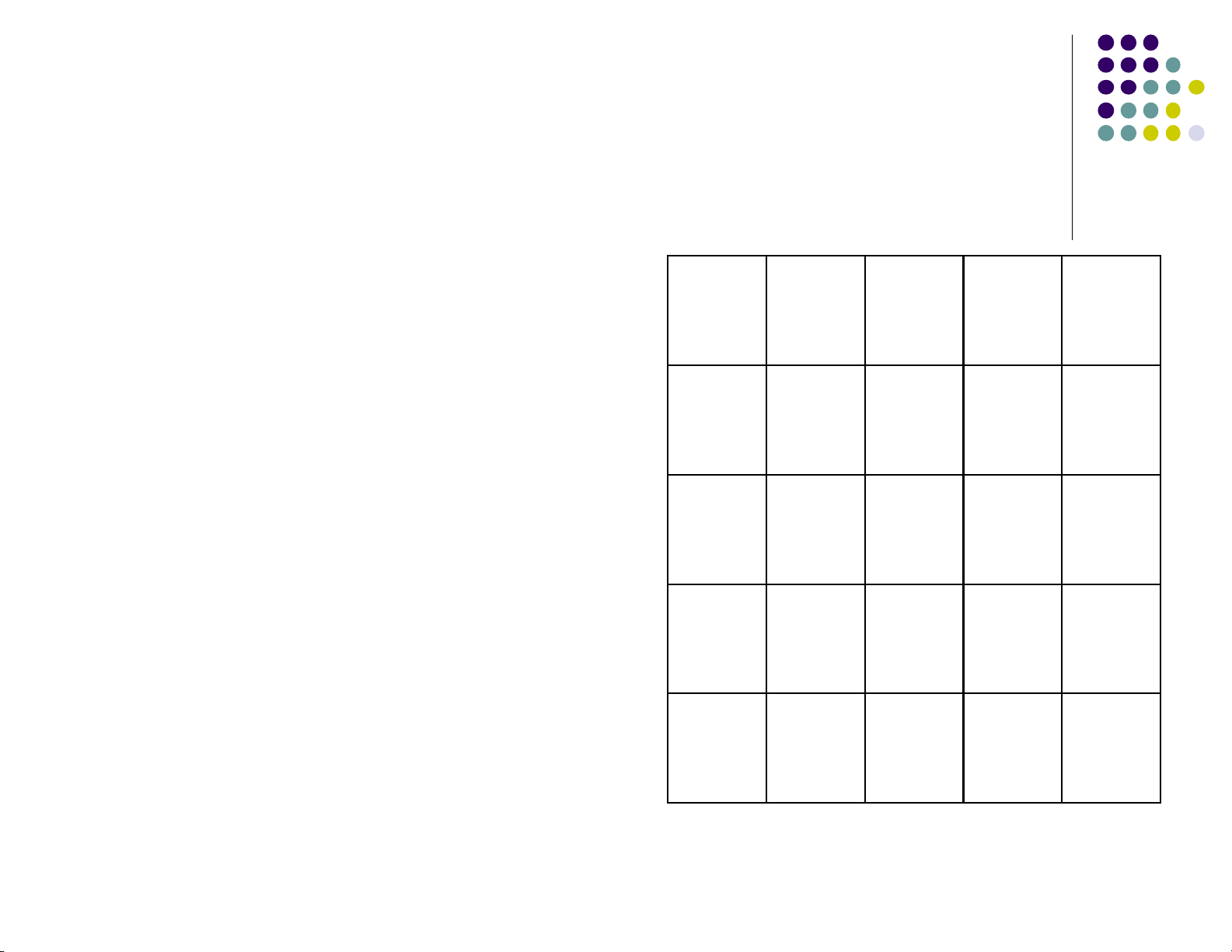
Ví dụ, nếu chọn từ khoá là MONARCHY thì ma trận khoá
(bảng Playfair) sẽ như sau: 10. Mật mã lOMoARcPSD| 40651217 Playfair M O N A R
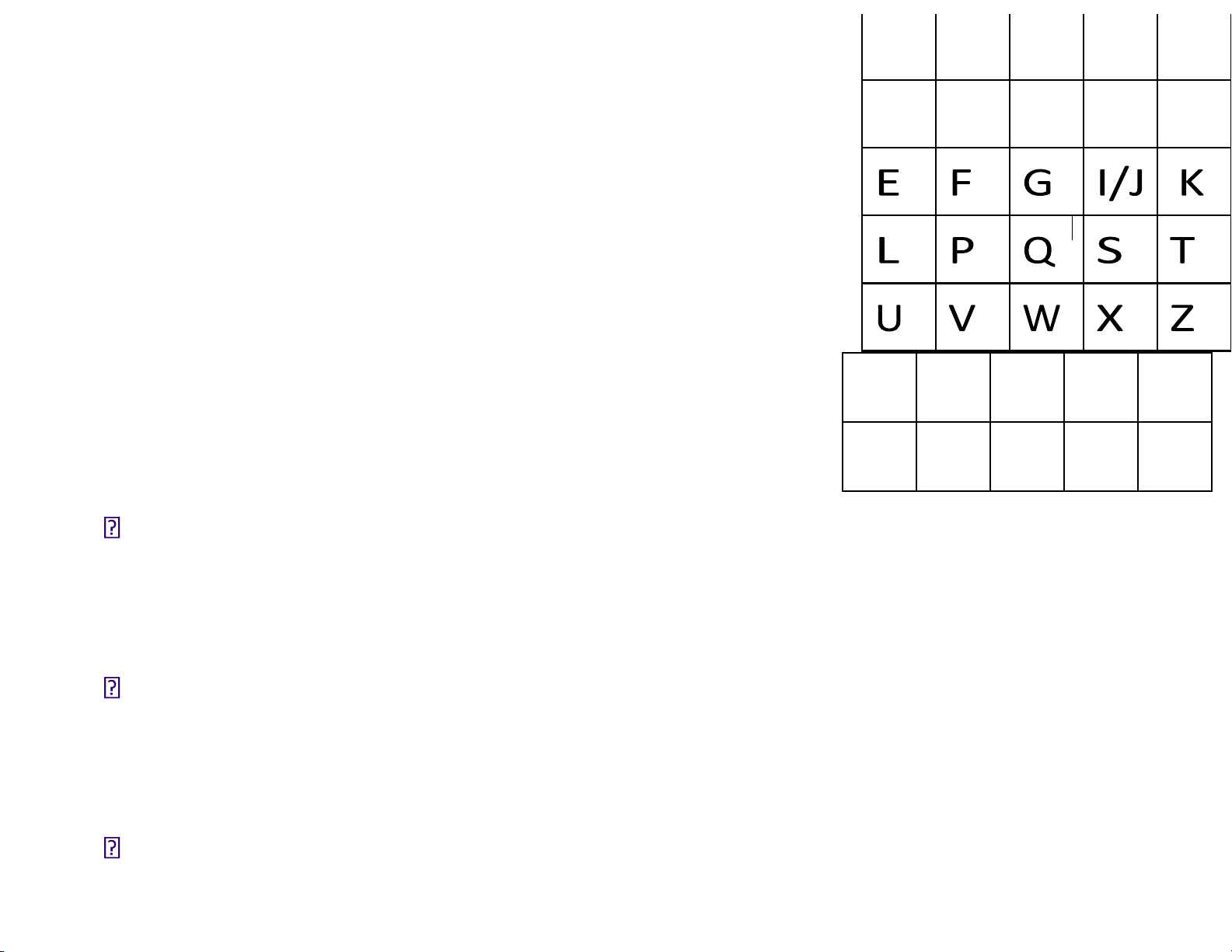
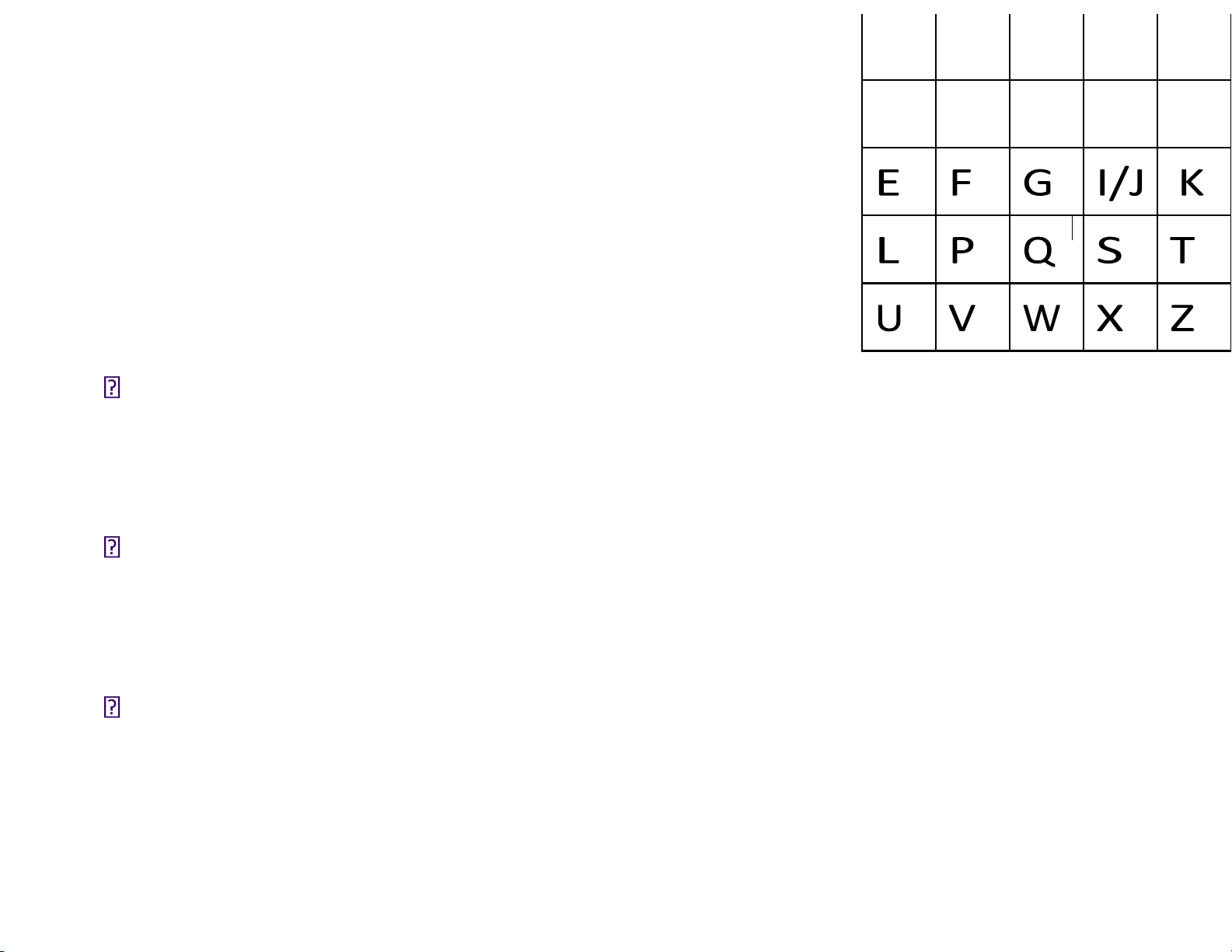
• Lần lượt viết từng kí tự của khóa
vào ma trận, từ trái sang phải, từ C H Y B D
trên xuống dưới, bỏ các kí tự trùng lặp E F G I/J K
• Viết các ký tự còn lại trong bảng
chữ cái vào ma trận theo thứ tự, L P Q S T
I và J ược coi như một ký tự U V W X Z 10. Mật mã lOMoARcPSD| 40651217 Playfair
Mỗi ký tự trong cặp plaintext sẽ ược mã hoá bằng ký tự
nằm cùng hàng với nó, nhưng cùng cột với ký tự kia trong bảng Playfair
Giả sử trong plaintext có cặp kí tự HS, nó sẽ ược thay thế bởi cặp BP M O N A R C H Y B D E F G I/J K 10. M O N A R lOMoARcPSD| 40651217 C H Y B D Mật mã Playfair L P Q S T U V W X Z
Nếu cặp ký tự plaintext rơi vào cùng một hàng của ma
trận thì mỗi ký tự ược thay thế bởi ký tự bên phải nó.
Nếu ký tự plaintext rơi vào cột cuối cùng, thì ciphertext
của nó là ký tự cùng hàng ở cột ầu tiên.
Ví dụ, AR sẽ ược mã hóa thành RM 10. M O N A R lOMoARcPSD| 40651217 C H Y B D Mật mã Playfair
Nếu cặp ký tự plaintext rơi vào chung một cột của ma
trận thì mỗi ký tự ược thay thế bởi ký tự ngay sát dưới.
Nếu ký tự plaintext rơi vào hàng cuối cùng, thì
ciphertext của nó là ký tự cùng cột, ở hàng ầu tiên.
Ví dụ, MU ược mã hóa thành CM 10. M O N A R lOMoARcPSD| 40651217 C H Y B D Mật mã Playfair
Nếu hai kí tự (cùng nhóm) trong plaintext giống nhau thì
chúng sẽ ược ược cách ly bằng một ký tự ại diện, chẳng hạn là X.
Ví dụ, từ BALLOON sẽ ược tách ra thành BA LX LO ON 10. Mật mã lOMoARcPSD| 40651217 Playfair Nhận xét:
Mật mã Playfair có không gian khoá lớn tương tự mật
mã Monoalphabetic nên khó bẻ ược khoá bằng phương pháp Brute - force 10. Mật mã lOMoARcPSD| 40651217 Playfair
Mật mã Playfair có khả năng che giấu một phần thông
tin về tần suất xuất hiện các chữ cái, nhờ thực hiện mã
hoá từng cặp hai kí tự Bài tập 1:
Chọn một từ khoá bất kì rồi xây dựng ma trận khoá Playfair 10. Mật mã lOMoARcPSD| 40651217 Playfair
Chọn một plaintext bất kì ( ộ dài 10 ký tự), áp dụng ma
trận khoá trên ể tạo ra ciphertext.
Thử giải mã ciphertext rồi so sánh với plaintext ban ầu Bài tập 2: 10. Mật mã lOMoARcPSD| 40651217 Playfair a. Cho từ khóa MISSISSIPPI b.
Mã hóa thông iệp sau bằng thuật toán Playfair: BANAMANNHODEN c.
Giải mã chuỗi mã thu ược ở câu b. 10. Mật mã lOMoARcPSD| 40651217 Playfair
Bài tập 3 (Bài tập về nhà):
Viết chương trình mã hoá và giải mã theo thuật toán Playfair, với: P = “HOMNAYLATHUBON” và khóa K = “NGAYTRONGTUAN” lOMoARcPSD| 40651217 11. Các hệ mã dòng Định nghĩa
Mật mã dòng là một bộ (P,C,K,L,F,E,D) thoả mãn ược các iều kiện sau:
1. P: tập hữu hạn các bản rõ có thể.
2. C: tập hữu hạn các bản mã có thể.
3. K: tập hữu hạn các khoá có thể (không gian khoá)
4. L: tập hữu hạn các bộ chữ của dòng khoá.
5. F = (f1, f2...): bộ tạo dòng khoá. Với i 1 fi : K Pi -1 L
6. Với mỗi z L có một quy tắc mã ez E và một quy tắc giải
mã tương ứng dz D. ez : P C và dz : C P lOMoARcPSD| 40651217 11. Các hệ mã dòng
là các hàm thoả mãn dz(ez(x))= x x P.
Các mã dòng thường ược mô tả trong các bộ chữ nhị phân tức là P= C=L= Z2.
Trong trường hợp này, các phép toán mã và giải mã là phép cộng theo modulo 2: Mã hóa (encryption): Giải mã (decryption: lOMoARcPSD| 40651217 11. Các hệ mã dòng zi zi
Sơ ồ quá trình mã hoá và giải mã lOMoARcPSD| 40651217 11. Các hệ mã dòng " bi lOMoARcPSD| 40651217 11. Các hệ mã dòng
Hàm mã hóa và giải mã ược thực hiện bởi cùng một phép toán
là phép cộng theo modulo 2(hay phép XOR) Chứng minh Quá trình giải mã: Trong
ó với zi=0 hoặc zi=1 thì lOMoARcPSD| 40651217 11. Các hệ mã dòng
Dòng khóa (stream key) zi ược sinh ra từ một khóa ban ầu K.
Cần phải tạo dòng khóa zi sao cho các chữ (trong bộ chữ)
của chúng không phụ thuộc lẫn nhau ể tránh bị tìm ra quy luật.
→ các bộ chữ của zi phải ược tạo ra một cách hoàn toàn ngẫu nhiên. lOMoARcPSD| 40651217 11. Các hệ mã dòng
Phương pháp tạo khóa nhị phân: Máy tạo dòng khóa
tuyến tính – LFSR-3, máy chạy và dừng luân phiên, One- time pad(OTP), …
Ví dụ: mã hóa ký tự ‘A’
Ký tự ‘A’ trong bảng mã ASCII
ược tướng ứng với mã
6510=10000012 ược mã hóa bởi hệ khóa z1,…,z7= 0101101 Mã hóa:
Bản rõ xi 1000001 =‘A’ (ký tự ASCII) Dòng khóa zi 0101101 Bản mã yi 1101100 =‘l’(ký tự ASCII) Giải mã: lOMoARcPSD| 40651217 11. Các hệ mã dòng i Dòng khóa z i 0101101 Bản rõ xi 1000001 =‘A’ (ký tự ASCII) Bản mã y 1101100 =‘l’’ (ký tự ASCII) lOMoARcPSD| 40651217
12. Mã hóa One-time Pad(OTP)
Định nghĩa 1: Một hệ mật mã ược coi là an toàn không iều kiện
khi nó không thể bị phá ngay cả với khả năng tính toán không hạn chế.
Frank Miller (1982): bảo mật iện báo - mô hình mã hóa
Vigenère sử dụng phép cộng modulo
Gilbert Vernam (thuộc Tập oàn AT&T, US): phát minh lại
(1917) và ược cấp bằng sáng chế (1919) - sử dụng phép toán
XOR thay vì cộng modulo như thuật toán Vigenère lOMoARcPSD| 40651217
Thuật toán duy nhất chứng minh ược về lý thuyết là
không thể phá ược ngay cả với tài nguyên vô tận (tức
là có thể chống lại kiểu tấn công brute-force).
12. Mã hóa One-time Pad(OTP)
Kiểu tấn công brute force: kiểu tấn công được dùng cho tất cả
các loại mã hóa, hoạt động bằng cách thử tất cả các chuỗi
mật khẩu có thể để tìm ra mật khẩu. thời gian cần rất lâu
(tùy theo độ dài của mật khẩu) nhưng luôn có khả năng để
tìm ra nếu không giới hạn thời gian.
Để có thể ạt ược mức ộ bảo mật của OTP, tất cả những iều
kiện sau phải ược thỏa mãn:
• Khóa có độ dài bằng đúng độ dài của bản rõ
• Khóa được tạo một cách thật sự ngẫu nhiên lOMoARcPSD| 40651217
• Khóa chỉ sử dụng một lần và không sử dụng cho lần mã hóa khác
• Khóa phải được giữ bí mật.
12. Mã hóa One-time Pad(OTP) Định nghĩa 2:
Trong hệ mã hóa OTP ta có |P|=|C|=|K| với Mã hóa (encrypt): lOMoARcPSD| 40651217 Giải mã (decrypt):
12. Mã hóa One-time Pad(OTP)
Qui trình sinh/phá mã của One time pad (OTP)
Chuyển dữ liệu sang dạng nhị phân (plaintext)
Sinh ngẫu nhiên một mảng dữ liệu nhị phân (skey)
với chiều dài của plaintext.
Mã hóa: XOR từng bit trong plaintext với bit ở vị trí
tương ứng trong skey ể ược dữ liệu mã hóa (cipher)
Giải mã: thực hiện XOR cipher với skey lOMoARcPSD| 40651217
12. Mã hóa One-time Pad(OTP)
Thực tế những iều kiện bảo mật của OTP khó có thể thỏa mãn ược.
Ví dụ: Giả sử A muốn mã hóa chỉ 10MB dữ liệu bằng
OTP A phải cần một chìa khóa (ngẫu nhiên) có ộ dài 10MB.
Để tạo ra một số ngẫu nhiên lớn như vậy A cần một bộ
tạo số ngẫu nhiên thực (TRNG - True Random Number Generator).
Các thiết bị này sử dụng nguồn ngẫu nhiên vật lý như sự
phân rã hạt nhân hay bức xạ trên vũ trụ.
Hơn nữa việc lưu trữ, chuyển giao và bảo vệ một chìa
khóa như vậy cũng hết sức khó khăn. lOMoARcPSD| 40651217
12. Mã hóa One-time Pad(OTP)
Phương án dễ hơn: dùng một bộ tạo số ngẫu nhiên ảo
(PRNG - Pseudo Random Number Generator)
khi ó mức ộ bảo mật giảm xuống gần bằng 0 hay cùng
lắm chỉ tương ương với một thuật toán dòng như RC4 mà thôi.
Do có những khó khăn như vậy nên việc sử dụng
OTP trong thực tế là không khả thi.
12. Mã hóa One-time Pad(OTP) lOMoARcPSD| 40651217 Bài tập:
1. Mã hóa chuỗi ký tự sau bằng OTP: P = KHONGKHATHI
Đặt tên khóa ngẫu nhiên là K, chuỗi mã là C
2. Giải mã chuỗi C bằng OTP. 13. Lý thuyết thông tin
Kỹ thuật nhầm lẫn/ hỗn loạn và khuếch tán (Confusion and Diffusion) lOMoARcPSD| 40651217
Theo Claude Shannon, có hai phép toán nguyên
thủy nhờ ó các thuật toán mã hóa mạnh có thể
ược xây dựng: nhầm lẫn/ hỗn loạn và khuếch tán. lOMoARcPSD| 40651217 13. Lý thuyết thông tin
Kỹ thuật nhầm lẫn/ hỗn loạn (Confusion):
Sự phụ thuộc của bản mã ối với bản rõ phải thực phức
tạp ể gây rắc rối, tạo cảm giác hỗn loạn, từ ó gây khó
khăn cho việc phân tích tìm qui luật ể phá mã.
Kỹ thuật nhầm lẫn/hỗn loạn (Confusion):
Phương pháp dê ̃ nhất ể thực hiện iều này là thông qua kỹ thuật thay thế.
Một hệ mã hóa thay thế ơn giản, chẳng hạn hệ mã dịch
vòng Caesar, dựa trên nền tảng của sư ̣ thay thế các chữ lOMoARcPSD| 40651217 13. Lý thuyết thông tin
cái của bản rõ, nghĩa là chữ cái này ược thay thế bằng chữ cái khác.
Kỹ thuật khuếch tán (Diffusion): ảnh hưởng của một
ký hiệu bản rõ ược trải rộng trên nhiều ký hiệu
bản mã với mục ích che giấu các thuộc tính thống kê của bản rõ.
Công việc dò tìm qui luật của người thám mã sẽ rất mất thời gian và phức tạp.
Cách ơn giản nhất tạo ra tính khuếch tán là thông qua kỹ
thuật hoán vị (sử dụng thường xuyên trong DES)
Kỹ thuật khuếch tán (Diffusion): lOMoARcPSD| 40651217 13. Lý thuyết thông tin
Ví dụ: Phép hoán vị cột.
P = “viec giai ma that phuc tap” Ma hoa: v i e c g i a i m a t h a t p h u c t a p x x x Viết lại theo cột:
C = v g m a u p i i a t c x e a t p t x c i h h a x
Thông thường các hệ mã hiện ại thường kết hợp cả
hai kỹ thuật thay thê ́ và hoán vị ể tạo ra các thuật
toán mã hóa có ộ an toàn cao hơn. lOMoARcPSD| 40651217
14. Lý thuyết ộ phức tạp
Lý thuyết thông tin ã cho chúng ta biết rằng một thuật
toán mã hoá có thể bị bại lộ. lOMoARcPSD| 40651217
14. Lý thuyết ộ phức tạp
Lý thuyết ộ phức tạp cho biết khả năng bị thám mã của một hệ mã mật.
a) Độ an toàn tính toán : lOMoARcPSD| 40651217
14. Lý thuyết ộ phức tạp
Định nghĩa: Một hệ mật ược gọi là an toàn về mặt tính
toán nếu có một thuật toán tốt nhất ể phá nó thì cần
ít nhất N phép toán, với N là một số rất lớn nào ó.
b) Đô ̣ an toàn không iều kiện lOMoARcPSD| 40651217
14. Lý thuyết ộ phức tạp
Định nghĩa: Một hệ mật ược coi là an toàn không iều
kiện khi nó không thể bị phá ngay cả với khả năng tính toán không hạn chế.