Một số Cấu trúc dữ liệu và thuật toán cơ bản | Môn Cấu trúc dữ liệu và thuật toán - Trường Đại học Khoa học, Đại học Huế

lOMoAR cPSD| 58702377 Mục lục 7.3
Xóa nút ............................................................... 1 Tổ hợp 8
........................................................................ 3 7.4
Locate ................................................................. 2 Tháp Hà Nội 8
............................................................... 3 7.5
Hiển thị ds .......................................................... 3 Quay lui hoán vị 8
......................................................... 3 8 Stack – ds móc nối đơn 4 Hiển thị ngoặc đúng
.............................................. 8
................................................... 3 8.1
Tạo mới một stack ............................................. 5 Xếp hậu 8
...................................................................... 4 8.2
Ds rỗng trả về true ............................................. 6 Danh sách móc nối đơn 9
............................................. 4 8.3
Push ................................................................... 6.1
Xóa phần tử cuối ................................................ 9 5 8.4
Pop ..................................................................... 6.2
Xóa phần tử đầu ................................................ 9 5 8.5
Lấy ra các phần tử trong stack ........................... 6.3
Chèn vào giữa .................................................... 9 5 9 Stack – mảng 6.4
Chèn vào cuối .....................................................
.............................................................. 9 5 9.1
Tạo mới một stack ............................................. 6.5
Chèn vào đầu ..................................................... 9 5 9.2
Nếu stack rỗng trả về true ................................. 6.6
Hiển thị danh sách ............................................. 9 6 9.3
Push ................................................................... 6.7
Tạo mới một nút ................................................ 9 6 9.4
Pop ..................................................................... 6.8
Đảo chiều danh sách .......................................... 9 6 9.5
Lấy ra các phần tử trong stack ........................... 9 6.9
Trộn 2 ds sx tăng dần thành 1 ds giảm dần ....... 6 10
Queue – ds móc nối đôi .........................................
6.10 Trộn 2 ds sx giảm dần thành 1 ds giảm dần ....... 9 7
10.1 Tạo mới một queue ......................................... 7 Danh sách dùng mảng 10
................................................ 7
10.2 Nếu queue rỗng trả về true ............................. 7.1
Tạo mới một nút ................................................ 10 7
10.3 Thêm một phần tử vào queue ......................... 7.2
Thêm nút mới .................................................... 10 8 lOMoAR cPSD| 58702377
10.4 Lấy ra một phần tử của queue ......................... 15
Số nút có info lớn hơn k ....................................... 10 13
10.5 Lấy hết các phần tử trong queue ..................... 16
Kiểm tra đẳng cấu hai cây .................................... 10 13 11
Cây ....................................................................... 17
Sắp xếp ................................................................. 10 13
11.1 Tạo mới một nút ..............................................
17.1 Hiển thị ds ........................................................ 10 13
11.2 Duyệt cây theo thứ tự trước ...........................
17.2 Swap ................................................................ 11 13
11.3 Duyệt cây theo thứ tự sau ...............................
17.3 SelectionSort .................................................... 11 14
11.4 Duyệt cây theo thứ tự giữa .............................
17.4 InsertionSort .................................................... 11 14
11.5 Đếm số nút cây ................................................
17.5 BubleSort ......................................................... 11 14
11.6 Chiều sâu cây ...................................................
17.6 MergSort .......................................................... 11 14
11.7 Cây nhị phân đầy đủ ........................................
17.7 QuickSort ......................................................... 12 15
17.8 HeapSort .......................................................... 11.7.1
Tạo cây nhị phân đầy đủ .......................... 15 12 17.8.1
Max-heap ................................................. 11.7.2
Kiểm tra cây nhị phân đầy đủ .................. 15 12
11.8 Cây nhị phân hoàn chỉnh ................................. 17.8.2
Min-heap .................................................. 16 12 17.8.3
Khôi phục tính chất đống ......................... 11.8.1
Tạo cây nhị phân hoàn chỉnh ................... 16 12 11.8.2
Số nút của cây hoàn chỉnh ....................... 17.8.4
Xây dựng đống ......................................... 12 16
11.9 Cây nhị phân cân bằng ..................................... 17.8.5
Sắp xếp đống ............................................ 13 16 12
Kiểm tra cây nhị phân đầy đủ .............................. 18
Tìm kiếm nhị phân ............................................... 13 16 13
Phản xạ gương cây ...............................................
18.1 Tìm kiếm nhị phân ........................................... 13 16 14
Số lá chẵn của cây ................................................
18.2 Cây nhị phân tìm kiếm (BST) ............................ 16 13 lOMoAR cPSD| 58702377 18.2.1
Thuật toán tìm kiếm (Search) .................. 18.3.2
Cây con phải cao hơn cây con trái do cây 17
con phải của con phải .............................................. 18 18.2.2
Thuật toán bổ sung (Insertion) ................ 17 18.3.3
Cây con trái co hơn cây con phải do cây
con phải của con trái ................................................ 18.2.3
Thuật toán loại bỏ (delete) ...................... 18 17 18.3.4
Cây con phải cao hơn cây con trái do cây
18.3 Cây AVL ............................................................ 17
con trái của con phải ................................................ 19 18.3.1
Cây con trái cao hơn cây con phải do cây
con trái của con trái ................................................. 18 1 Tổ hợp 3 Quay lui hoán vị int C(int n, int k){ if int n, ((k==0)||(k==n)) return 1; count; int else return C(n-1,k- a[20]; int 1)+C(n-1,k); m[5]; void } Ghinhan() { C(9, 5) = 126 int i; 2 Tháp Hà Nội
count++; printf("%i. ",count);
int solanchuyen = 0; void thapHN(int n,
for (i=1; i<=n;i++) printf("%i
char a, char b, char c){ if (n==1) ",a[i]); printf("\n");
printf("%d:Chuyen 1 dia tu %c sang } %c\n",++solanchuyen,a,c); int UCV(int i, int k){ else { thapHN(n- int j; 1,a,c,b); for(j=1;jthapHN(1,a,b,c); if(m[i]==a[j]) thapHN(n-1,b,a,c); return 0; return 1; } } } void hienhoanvi(int k){
int i; for(i=1;i<=n;i++) { if(UCV(i,k)==1) { a[k] = m[i]; if(k==n) lOMoAR cPSD| 58702377 Ghinhan(); else int i; hienhoanvi(k+1);
count++; printf("%i. ",count); for }
(i=1; i<=n;i++) printf("%c ",a[i]); } printf("\n"); } }
4 Hiển thị ngoặc đúng int UCV(char c, int k){ int n, count; char int t=0; int i; a[20]; int for(i=1;iGhinhan() { if(a[i]=='(') t++; lOMoAR cPSD| 58702377 else t--; int i; if(t<0) return 0;
count++; printf("%i. ",count); for }
(i=1; i<=n;i++) printf("%i ",a[i]); if(c=='(') t++; printf("\n"); else t--; if(k} if(t<0) return 0; int abs(int x){ else return 1; if(x<0) return -x; } return x; else if(k==n) { } if(t!=0) return 0; int UCV(int i, int k){ else return 1; int j; for(j=1;j }
if((a[j]==i)||(abs(a[j]-i)==abs(j-k))) } return 0; void hienthingoacdung(int k){ } if(UCV('(',k)==1) { a[k] = return 1; '('; if(k==n) Ghinhan(); } else hienthingoacdung(k+1); void xephau(int k){ } int i; for(i=1;i<=8;i++) if(UCV(')',k)==1) { a[k] = { if(UCV(i,k)==1) { ')'; if(k==n) Ghinhan(); a[k] = i; if(k==n) else hienthingoacdung(k+1); Ghinhan(); else } xephau(k+1); } } 5 Xếp hậu } int n, count; int } a[20]; int Ghinhan() {
6 Danh sách móc nối đơn
typedef int elementtype; typedef struct _newNodeType { lOMoAR cPSD| 58702377 elementtype Inf; 6.3 Chèn vào giữa
void insertToMiddle(NodeType *pred, elementtype struct _newNodeType datum) { *Next;
NodeType *newNode = (NodeType *) } NodeType;
malloc(sizeof(NodeType)); if(newNode
== NULL) { printf("Khong the cap phat
6.1 Xóa phần tử cuối bo nho\n");
NodeType *delete_Last(NodeType *First){ return;
if(First==NULL) return NULL; NodeType }
*t2 = First; NodeType *t1 = NULL;
newNode->Inf = datum; newNode- if(t2->Next==NULL) {
>Next = pred->Next; pred->Next = free(t2); newNode; return NULL; return; } } while(t2->Next!=NULL) { t1 = t2; 6.4 Chèn vào cuối
void insertToLast(NodeType *head, elementtype datum) { t2 = t2->Next;
NodeType *newNode = (NodeType *) }
malloc(sizeof(NodeType)); if(newNode t1->Next =
== NULL) { printf("Khong the cap phat NULL; free(t2); bo nho\n"); return NULL; return First; } } newNode->Inf = datum;
6.2 Xóa phần tử đầu newNode->Next = NULL;
NodeType *delete_Head(NodeType *First){ while(head->Next != NULL) if(First==NULL) return NULL;
head = head->Next; head->Next NodeType *p = = newNode; First; First = First- return; >Next; free(p); } return First; 6.5 Chèn vào đầu }
NodeType *insertToHead(NodeType *head, elementtype datum) { lOMoAR cPSD| 58702377 NodeType *newNode =
6.8 Đảo chiều danh sách (NodeType *)
NodeType *daoChieuDS_pp1(NodeType *header){ malloc(sizeof(NodeType)); if(header==NULL) return NULL; if(newNode == NULL) {
NodeType *dsmoi = NULL; NodeType
printf("Khong the cap phat bo nho\n"); *p = header; while(p!=NULL) { return NULL;
dsmoi = Insert_ToHead(dsmoi,p->Inf); } p = p->Next; newNode->Inf = datum; }
newNode->Next = head; return return dsmoi; newNode; } }
6.9 Trộn 2 ds sx tăng dần thành 1 ds giảm
6.6 Hiển thị danh sách dần
void printList(NodeType *head) {
ListNode *sortInsert(ListNode *head1, ListNode *head2) { while(head != NULL) {
if(head1 == NULL || head2 == NULL) return NULL;
printf("%d\t", head->Inf); head
ListNode *head = NULL, *compare = NULL; = head->Next; } do { compare = head; printf("\n");
if(head1->Inf > head2->Inf) { return; head = head2; head2 = } head2->next; head->next
6.7 Tạo mới một nút = compare;
NodeType *createNewNode(elementtype datum) { } else { head =
NodeType *newNode = (NodeType *) head1; head1 = head1-
malloc(sizeof(NodeType)); if(newNode >next; head->next =
== NULL) { printf("Khong the cap phat compare; bo nho\n"); return NULL; } }
} while(head1 != NULL && head2 != NULL); newNode->Inf = datum;
while(head1 != NULL) { compare = head;
newNode->Next = NULL; return head = head1; newNode; } lOMoAR cPSD| 58702377 head1 = head1->next; insertNode->next = head2; head->next = compare; head2 = head2->next; }
insertNode = insertNode->next; while(head2 !=
insertNode->next = compare; NULL) { } else { compare = head; insertNode = compare; head = head2; compare = compare->next; head2 = head2- } >next; head-
}while(head2 != NULL && compare != NULL); >next = compare; }
if(head2 != NULL) insertNode->next = return head; head2; return head1; } }
6.10 Trộn 2 ds sx giảm dần thành 1 ds
7 Danh sách dùng mảng giảm dần
# define maxlength 1000 typedef int elementtype; /*
ListNode *sortInsert2(ListNode *head1, ListNode
elements are integers */ typedef struct list_tag { *head2) {
elementtype elements [maxlength]; // khai báo mảng
if(head1 == NULL || head2 == NULL) 1000 phần tử return NULL; int last;
ListNode *compare = NULL, *insertNode } list_type;
= NULL; if(head2->Inf > head1->Inf) {
7.1 Tạo mới một nút
compare = head1; head1 = head2;
list_type *create() { list_type* lp =
head2 = head2->next; head1->next =
(list_type*)malloc(sizeof(list_type)); lp->last = -1; return lp; compare; } } int end (list_type *lp){ insertNode = head1; return (lp->last +1); compare = head1->next; } do { if(head2->Inf > compare->Inf) { lOMoAR cPSD| 58702377 7.2 Thêm nút mới 7.4 Locate
void insert (elementtype x , int p , list_type * lp){
int locate (elementtype x , list_type * lp){
int v; // running position if (lp -> last >=
int q; for (q = 0; q <= lp ->last; q++)
maxlength - 1) { printf("\n%s ","list is full");
if (lp -> elements [q] == x) return (q); return;
return (lp -> last + 1); /* if not found */ } }
if ((p < 0) || (p > lp -> last + 1)) { printf("\n%s 7.5 Hiển thị ds ","position does not exist"); void hienthi(list_type *lp){ return; int i;
} else { int q; for (q = lp -> last; q >=
if(lp==NULL) return; printf("Cac ptu co
p; q--) lp -> elements [q+1] = lp ->
trong danh sach: \n"); for(i=0;ielements [q]; lp -> last = lp -> last +1 ;
>last+1;i++) printf("%d ",lp- lp -> elements[p] = x;
>elements[i]); printf("\n"); } } }
8 Stack – ds móc nối đơn 7.3 Xóa nút typedef int Item; typedef
void deleteL(int p , list_type * lp){ int q; /* struct _StackNode { Item
running position */ if ((p > lp-> last) || (p < 0)) { item; struct _StackNode
printf("\n%s ","position does not exist"); *next; } StackNode; typedef return; struct _Stack { } StackNode *top; else /* shift elements */ { } Stack;
lp -> last --; int q; for (q
8.1 Tạo mới một stack
= p; q <= lp ->last; q++) lp -> Stack *StackInit(){
Stack *s = (Stack*)malloc(sizeof(Stack));
elements [q] = lp -> elements
if(s==NULL) return NULL; s->top = NULL; return [q+1]; s; } } } lOMoAR cPSD| 58702377
8.2 Ds rỗng trả về true N = 0;
int StackEmpty(Stack *s){ return } (s->top==NULL);
9.2 Nếu stack rỗng trả về true } int STACKempty() { return 8.3 Push N==0;
void StackPush(Stack *s, Item x){ } StackNode *newnode = 9.3 Push
(StackNode*)malloc(sizeof(StackNode));
void STACKpush(Item item) { s[N++]
if(newnode==NULL) return; newnode- = item;
>item = x; newnode->next = s->top; s- } >top = newnode; 9.4 Pop } Item STACKpop() { return 8.4 Pop s[--N];
Item StackPop(Stack *s){ if(s->top }
== NULL) return NULL; Item X = s-
9.5 Lấy ra các phần tử trong stack
>top->item; StackNode *t = s->top; while(!STACKempty())
s->top = s->top->next; printf("%d\n",STACKpop()); free(t); return X;
10 Queue – ds móc nối đôi } typedef int Item; typedef
8.5 Lấy ra các phần tử trong stack struct _QueueNode { while(!StackEmpty(st)) Item item; struct printf("%d\t",StackPop(st)); _QueueNode *next; } 9 Stack – mảng QueueNode; typedef struct typedef int Item; static Item _Queue { QueueNode *s; static int *front; N; QueueNode *back;
9.1 Tạo mới một stack } Queue;
10.1 Tạo mới một queue void STACKinit(int maxN){ s = Queue *QueueInit() { (Item *) malloc(maxN*sizeof(Item)); lOMoAR cPSD| 58702377
Queue *q = (Queue*)malloc(sizeof(Queue)); >front = NULL; q-
if(q==NULL) return NULL; q->front = NULL; q- >back = NULL; return >back = NULL; return q; X; } } else { temp = q-
10.2 Nếu queue rỗng trả về true >front; X = temp->item;
int QueueEmpty(Queue *q) { return
q->front = q->front->next; (q->front==NULL); free(temp); return X; } }
10.3 Thêm một phần tử vào queue }
void enqueue(Queue *q, Item x){
10.5 Lấy hết các phần tử trong queue QueueNode *newnode = while(!QueueEmpty(q)) {
(QueueNode*)malloc(sizeof(QueueNode)); printf("%d\n",dequeue(q));
if(newnode==NULL) return; newnode->item = x; 11 Cây
newnode->next = NULL; if((q-
typedef struct _Tnode{ char word; // Dữ
>front==NULL)&&(q->back==NULL)) { q- liệu cất giữ ở nút struct _Tnode
>front = newnode; q->back = newnode; *leftmost_child; struct _Tnode } else { *right_sibling;
q->back->next = newnode; q->back } treeNode; = newnode;
11.1 Tạo mới một nút }
treeNode *maketreenode(char w){ } treeNode *temp =
10.4 Lấy ra một phần tử của queue
(treeNode*)malloc(sizeof(treeNode));
Item dequeue(Queue *q){ if(QueueEmpty(q))
if(temp==NULL) return NULL; temp->leftmost_child return NULL;
= NULL; temp->right_sibling = NULL; temp->word = w; return temp; QueueNode *temp; Item X; if(q- } >front==q->back) {
11.2 Duyệt cây theo thứ tự trước
void preOrder(treeNode *r){ if(r==NULL) temp = q->front;
return; printf("%c ",r->word); treeNode *p = X = temp->item;
r->leftmost_child; while(p!=NULL) { free(temp); q-
preOrder(p); p = p->right_sibling; lOMoAR cPSD| 58702377 } } } 11.6 Chiều sâu cây
11.3 Duyệt cây theo thứ tự sau int depth(treeNode *tree){ void postOrder(treeNode *r){
if(tree==NULL) return 0; treeNode *p if(r==NULL) return;
= tree->leftmost_child; int
treeNode *p = r->leftmost_child;
k,dosaumax = 0; while(p!=NULL) {
while(p!=NULL) { postOrder(p);
k = depth(p); if(k>dosaumax) p = p->right_sibling;
dosaumax = k; p = p->right_sibling; } } return dosaumax + 1; printf("%c ",r->word); } }
11.7 Cây nhị phân đầy đủ
11.4 Duyệt cây theo thứ tự giữa
Cây nhị phân đầy đủ là cây nhị phân:
void inOrder(treeNode *r) { if(r==NULL) •
return; treeNode *p = r->leftmost_child;
Mỗi nút lá đều có cùng độ sâu
• Các nút trong có đúng hai con
inOrder(p); printf("%c ",r->word);
if(p!=NULL) p = p->right_sibling;
while(p!=NULL) { inOrder(p); p = p->right_sibling; } }
11.5 Đếm số nút cây
11.7.1 Tạo cây nhị phân đầy đủ treeNode int CountNodes(treeNode
*taocaynhiphandaydu(int n, char X)
*tree) { if(tree==NULL) return { 0; int sonut = 1; treeNode
if(n==0) return NULL; treeNode *r = *p = tree->leftmost_child;
maketreenode(X); treeNode *left = while(p!=NULL) { sonut
taocaynhiphandaydu(n-1,X); treeNode *right = += CountNodes(p); p = p- taocaynhiphandaydu(n-1,X); >right_sibling;
r->left = left; r->right = } right; return r; return sonut; lOMoAR cPSD| 58702377 }
char X) { int k = somuccuacayhc(n); treeNode
11.7.2 Kiểm tra cây nhị phân đầy đủ int *r = taocaynhiphandaydu(k);
kiemtramotcaynhiphandaydu(treeNode *tree) } {
11.8.2 Số nút của cây hoàn chỉnh
if(tree==NULL) return 0; if((tree- int somuccuacayhc(int n) {
>left==NULL)&&(tree->right==NULL)) int k=0; while(power(2,k)- return 1; 1<=n)
int i = kiemtramotcaynhiphandaydu(tree->left); int j k++;
= kiemtramotcaynhiphandaydu(tree->right); int hi = return k-1; }
depth(tree->left); int hj = depth(tree->right);
if((i==1)&&(j==1)&&(hi==hj))
11.9 Cây nhị phân cân bằng
Cây nhị phân cân bằng là cây có chiều cao cây con trái và return
chiều cao cây con phải của mọi nút chênh lệch nhau không quá 1 đơn vị 1; else return 0; }
11.8 Cây nhị phân hoàn chỉnh
Cây nhị phân hoàn chỉnh là cây nhị phân độ sâu n thỏa mãn:
• Là cây nhị phân đầy đủ nếu không tính đến các nút ở độ sâu n
12 Kiểm tra cây nhị phân đầy đủ
• Tất cả các nút ở độ sâu n lệch sang trái nhất
int kiemtramotcaynhiphandaydu(treeNode *tree){ có thể được
if(tree==NULL) return 0; if((tree->left==NULL)&&(tree- >right==NULL)) return 1;
int i = kiemtramotcaynhiphandaydu(tree->left);
int j = kiemtramotcaynhiphandaydu(tree->right);
int hi = depth(tree->left); int hj = depth(tree-
11.8.1 Tạo cây nhị phân hoàn chỉnh
>right); if((i==1)&&(j==1)&&(hi==hj))
treeNode *taocaynhiphanhoanchinh(int n, lOMoAR cPSD| 58702377 return 17 Sắp xếp 1; else 17.1 Hiển thị ds return 0;
void Print(int p[], int len) { }
int i; for(i = 0; i < len;)
13 Phản xạ gương cây printf("%d\t", p[i++]); treeNode *mirror(treeNode printf("\n");
*nodePrt) { if (nodePrt == NULL) } return NULL; treeNode *tmp = 17.2 Swap
mirror(nodePrt->left); nodePrt- void Swap(int *a, int *b) {
>left = mirror(nodePrt->right); int tmp = *a; *a = *b; nodePrt->right = tmp; *b = tmp; return nodePrt; } } 17.3 SelectionSort
14 Số lá chẵn của cây
void SelectionSort(int p[], int len) {
Int EvenLeaf(treeNode *RootTree) {
int i, j, jmin; for(i = 0; i < len - 1; ++i) { If(RootTree == null) Return 0;
jmin = i; for(j=i+1; j < len; ++ j) if(p[j] <
If(RootTree-left==null && RootTree->right ==null)
p[jmin]) jmin = j; if(jmin != i) {
Swap(&p[jmin], &p[i]); If(RootTree->key % 2) } Return 0; } Return 1; 17.4 InsertionSort }
void InsertionSort(int a[], int len) { int i, j, tmp; for(i =
Return EvenLeaf(RootTree->left) + EvenLeaf(RootTree>right);
0; i < len-1; ++i) { tmp = a[i]; j = i - 1; }
while(j > 0 && tmp < a[j]) { a[j+1] = a[j];
15 Số nút có info lớn hơn k --j; Giống bài duyệt cây }
16 Kiểm tra đẳng cấu hai cây a[j+1] = tmp; } lOMoAR cPSD| 58702377 return;
int first1 = first; int last1 = mid; int first2 = mid + }
1; int last2 = last; int index = first1; for(; (first1 <= 17.5 BubleSort
last1) && (first2 <= last2); ++index) { if(a[first1] <
void BubbleSort(int a[], int len) {
a[first2]) { tmpA[index] = a[first1]; int i, j, tmp; ++first1; } else { for(i = 0; i < len - 1; tmpA[index] = a[first2]; ++i) for(j = i; j ++first2; < len; ++j) } if(a[i] > a[j]) { } tmp = a[i];
for(; first1 <= last1; ++first1, ++index) tmpA[index] a[i] = a[j];
= a[first1]; // sao not day con 1 for(; first2 <= last2; a[j] = tmp; } } 17.6 MergSort
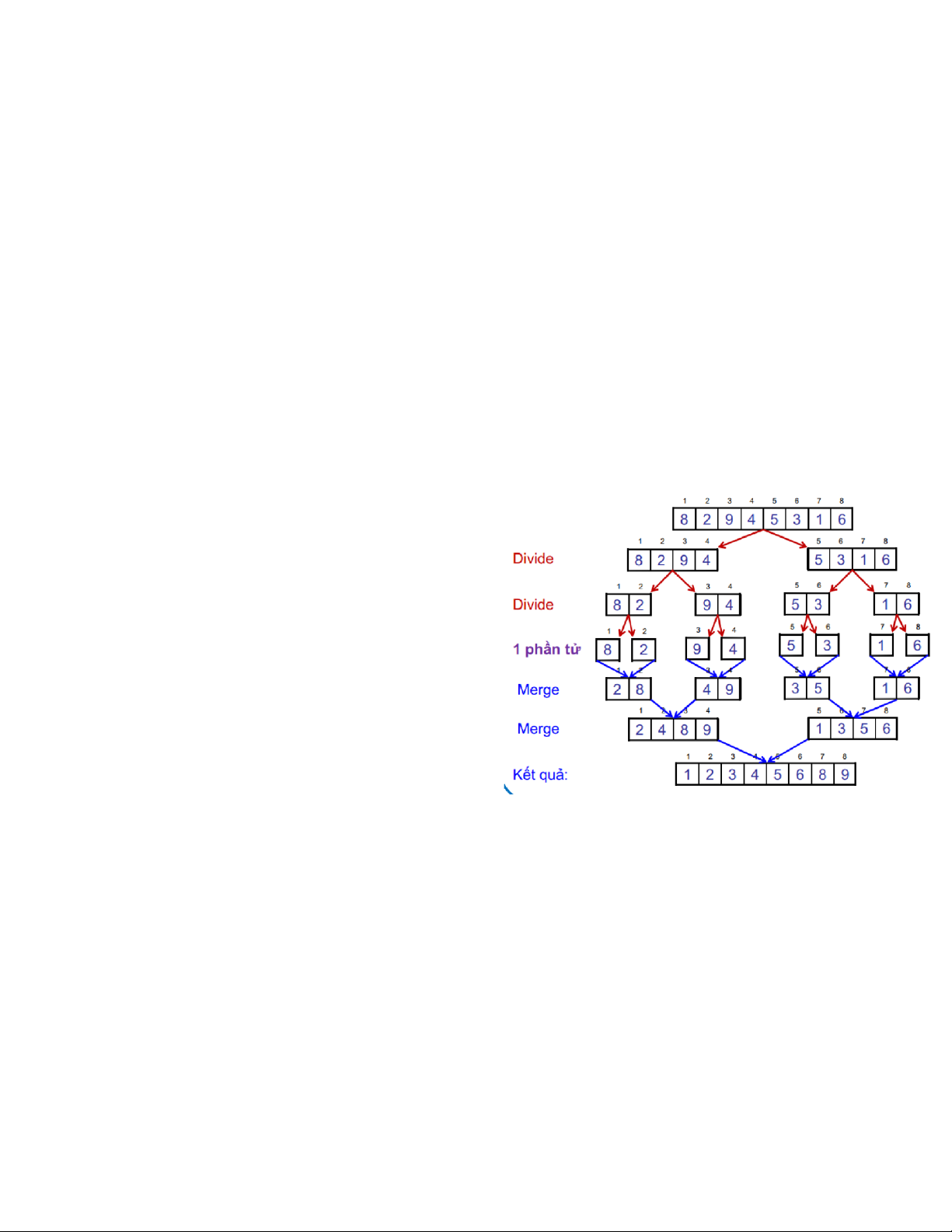
void MergeSort(int a[], int first, int
last) { if(first < last) { int mid = (first + last)/2; MergeSort(a, first, mid); MergeSort(a, mid+1, last);
++first2, ++index) tmpA[index] = a[first2]; // sao Merge(a, first, mid, last);
not day con 2 for(index = first; index <= last; ++index) } else
a[index] = tmpA[index]; // sao tra mang ket qua return; } return; }
void Merge(int a[], int first, int mid, int 17.7 QuickSort
last) { int tmpA[MAX_SIZE]; // mang
void QuickSort(int a[], int first, int last) { phu
if(first < last) { int pivot = Partition(a,
first, last); if(first < pivot) lOMoAR cPSD| 58702377 QuickSort(a, first, pivot - Swap(&a[i], &a[j]); 1); else }
QuickSort(a, pivot + 1, last); Swap(&a[i], &a[j]); }
Swap(&a[j], &a[first]); return return; j;
} int Partition(int a[], int first, }
int last) { int i = first, j = last 17.8 HeapSort
+ 1, p = a[first]; while(i < j) {
Đống là cây nhị phân gần hoàn chỉnh có 2 tính chất: ++i; while((i <=
• Tính cấu trúc: tất cả các mức đều là đầy trừ mức
cuối cùng. Mức cuối được điền đầy từ trái sang
last) && (a[i] < p)) phải
• Tính chất đống: với mỗi nút ta luôn có con ≥ hoặc ++i; ≤ cha. --j; 17.8.1 Max-heap
while((j >= first) && (a[j] > p))
Với mọi nút I ta luôn có A[parent(i)] ≥ A[ i] --j;
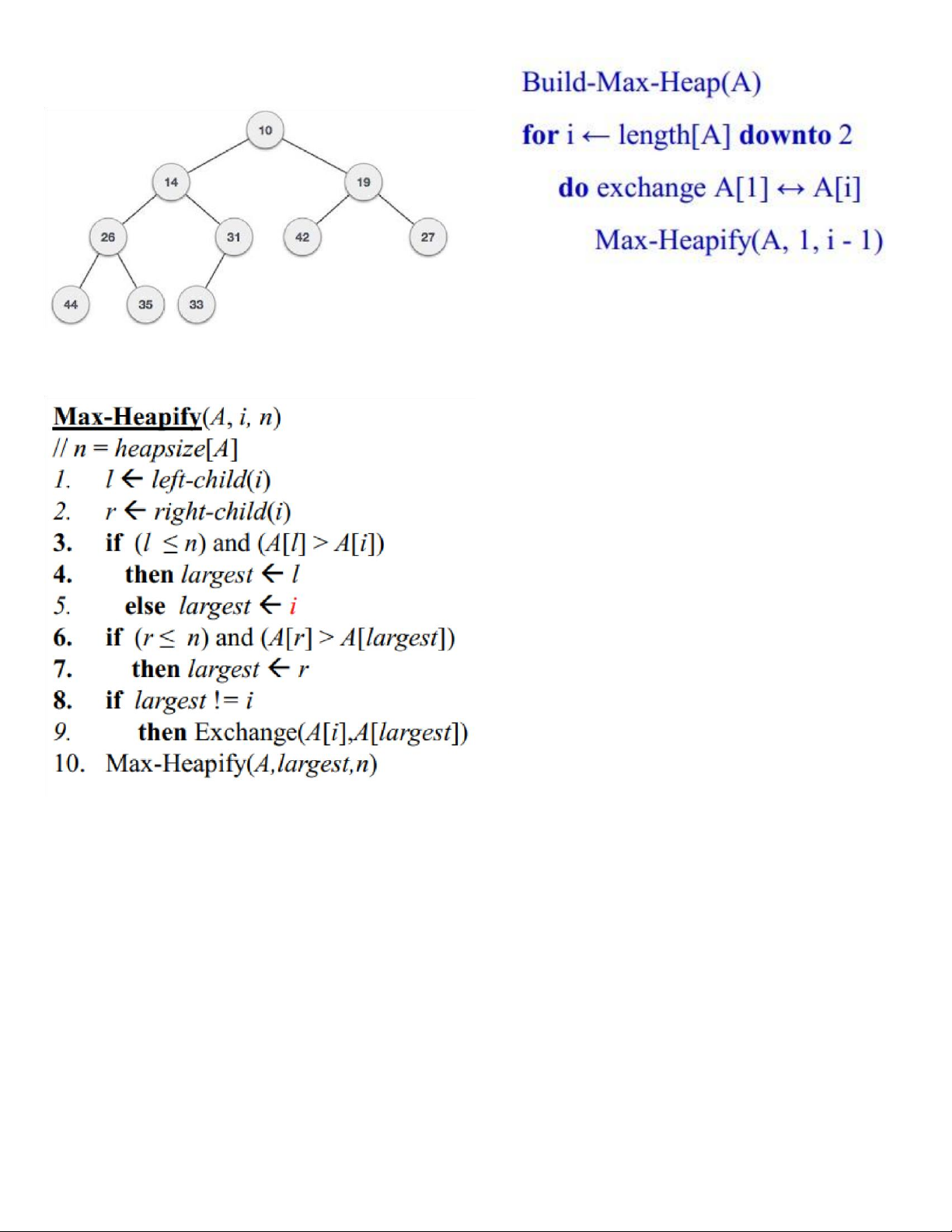
17.8.4 Xây dựng đống 17.8.2 Min-heap
17.8.5 Sắp xếp đống lOMoAR cPSD| 58702377 18
V ớ i m ọ i nút I ta luôn có A[parent(i)] ≤ A[ i]
Tìm kiếm nhị phân
17.8.3 Khôi phục tính chất đống
18.1 Tìm kiếm nhị phân
Điều kiện để tìm kiếm nhị phân là: •
Ds phải được sắp xếp theo thứ tự không giảm •
Phải cho phép trực truy (tức là không áp dụng được với ds móc nối)
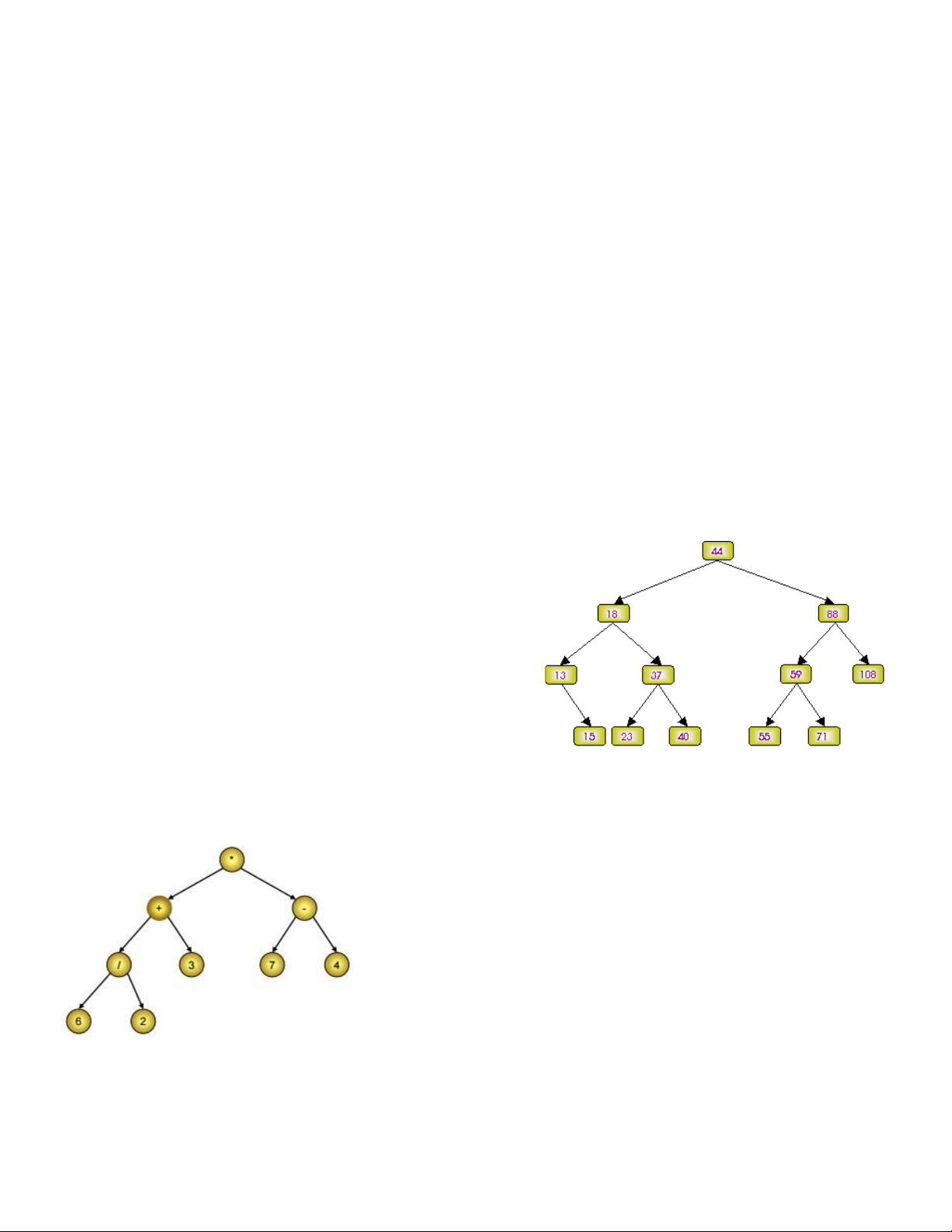
18.2 Cây nhị phân tìm kiếm (BST)
Cây nhị phân tìm kiếm là cây nhị phân: • Left trỏ đến con trái • Right trỏ đến con phải • Parent trỏ đến cha • Info • Tính chất
BST: mọi nút thuộc cây con trái có giá
trị nhỏ hơn cha. Mọi nút thuộc cây con
phải có giá trị lớn hơn cha. lOMoAR cPSD| 58702377
N ế u nút c ầ n xóa ch ỉ có con trái
N ế u nút c ầ n xóa ch ỉ có con p h ả i
Duyệt cây theo thứ tự giữa sẽ được dãy sắp xếp
18.2.1 Thuật toán tìm kiếm (Search)
• Nếu khóa cần tìm nhỏ hơn khóa của nút hiện tại thì tiếp
tục tìm kiếm ở cây con trái.
• Nếu khóa cần tìm lớn hơn khóa của nút hiện tại thì tiếp
tục tim kiếm ở cây con phải.
• Nếu tìm thấy thì trả lại con trở đên nút chứa khóa
cần tìm, ngược lại trả về Null.
• Nếu nút cần xóa có hai con:
18.2.2 Thuật toán bổ sung (Insertion)
• Tạo nút mới chứa phần tử chèn
• Di chuyển trên cây để tìm cha của nút mới: so sách khóa
của phần tử cần chèn với khóa của nút đang xét, nếu
khóa của phần tử cần chèn lớn hơn (nhỏ hơn) khóa của
nút đang xét thì rẽ theo con phải ( con trái) của nút
đang xét. Nếu gặp Null thì dừng, nút đang xét là cha cần tìm.
• Gắn nút mới vào cha vừa tìm được.
18.2.3 Thuật toán loại bỏ (delete)
• Nếu nút cần xóa là lá lOMoAR cPSD| 58702377 18.3 Cây AVL
Là cây nhị phân tìm kiếm thỏa mãn tính chất AVL: chiều cao của cây con
trái và cây con phải của một gốc chỉ sai khác nhau không quá 1 và cả cây
con trái và cây con phải đều là cây AVL.
Có 4 trường hợp khôi phục tính cân bằng của cây: 18.3.1 Cây
phải của con phải
con trái cao hơn cây con phải do cây con trái của con trái Thực hiện cân bằng: Thực hiện cân bằng:
18.3.3 Cây con trái co hơn cây con phải do cây con
18.3.2 Cây con phải cao hơn cây con trái do cây con lOMoAR cPSD| 58702377 phải của con trái Thực hiện cân bằng:
18.3.4 Cây con phải cao hơn cây con trái do cây con trái của con phải Thực hiện cân bằng: