Motion in two or three dimesions | Bài tập môn Vật lý đại cương 1 CTTT | Trường Đại học Bách Khoa Hà Nội

02/07/2021 Projectile motion
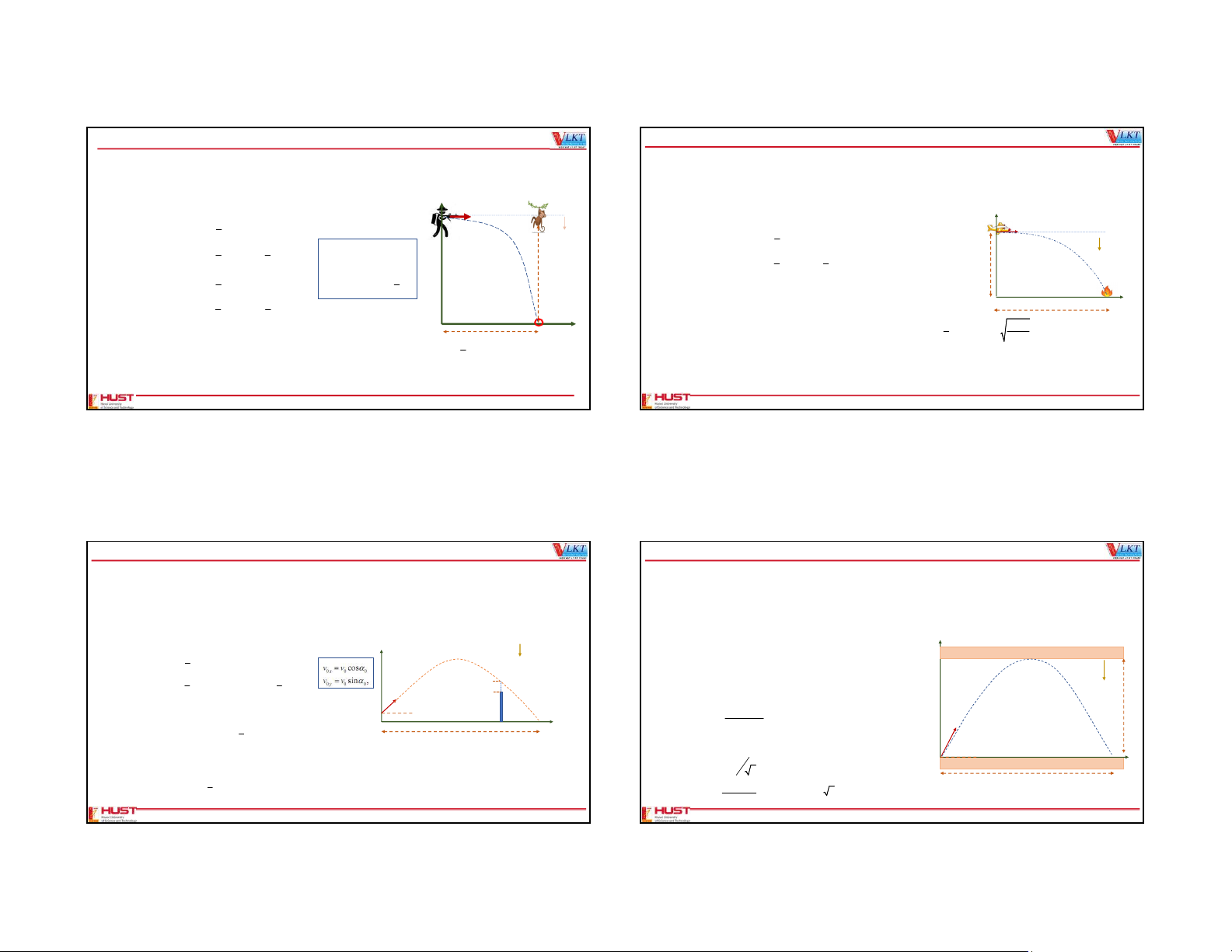
We can then analyze the motion in the x and y direction separately using the equations of motion v  v  a t x 0 x x y x x 0  g 0  1 2
horizontal x  x  v t  a t 0 0 x x g
Chapter 3: MOTION IN TWO OR THREE DIMENSIONS motion 2  2 2 v  v  2a (x  x )  x 0 x x 0 v v y0 0 v v y0 0 v  v  a t y 0 y y y ay= -g  0 v y  v x0 = v0cos 0 x 0 v
Exercises: 1, 3, 5, 7, 9, 11, 19, 21, 23, 25, 33, 37, 41, 43  x 0 a vertical v y= g  1 y0= v0sin 2 y  y  v t  a t vx0 = v0cos 0 0 y y motion
Problems: 45, 51, 53, 55, 57, 61, 63, 65, 69, 71, 73, 75, 79, 81, 85, 50, 77 2 0  x y vy0= -v0sin x 2 2 0 v  v  2a (y  y ) y 0 y y 0  Dang Duc Vuong
Value of ay depends on your choice of orientation for the axis y; ay=-g if you decide to choose +y pointing upward and ay=-g if +y pointing downward
Email: vuong.dangduc@hust.edu.vn
Note: You might consider a problem where an object is subject to an acceleration other than that of gravity 
The resultant acceleration is the addition of a & g : A  a  g One Love. One Future. 7/2/2021 Dang Duc Vuong –SEP-HUST 1 7/2/2021 Dang Duc Vuong –SEP-HUST 2 1 2
Linear motion and Circular motion Linear motion Circular motion
3.45 A student is moving in a dark room try to find out a 20$ bill. The student’s coordinate is given as a function of time by
Linear motion involves an object moving from Rotational motion involves an
x(t) = αt and y(t) = 15.0m - βt2, where α = 1.20 m/s and β = 0.500 m/s2. Unknown to the student, the 20$ bill is at the origin.
one point to another in a straight line. object rotating about an axis.
a) at which time(s) the student’s velocity is perpendicular to his acceleration? b) at which time(s) the student’s speed
instantaneously not changing? c) At which time(s) the student’s velocity is perpendicular to his position vector? What is x
location of the student at these times? d) What is minimum distance from the student to the bill? At what time it occurs? v
e) Sketch the path of hapless student.   dr dx(t)  dy(t)     a at Analyze v   i  j  v i  v j x y dt dt dt Position x(t) a (a) a ⊥ v  a. v = 0  n dv dv (t)  dv (t)     dx Angular position  (t) (b) v(t)=const  dv/dt=0; x y a   i  j  a i  a j Velocity v   x  x y dt dt dt dt d (c) Angular velocity    
v ⊥ r⃗  v. r⃗ = 0 solve this equation to find t  location   2 dv d x
(d) d(t)=[x2(t) + y2(t)]1/2; r(t) get the critical point when dr(t)/dt=0; Acceleration a    x dt     A.B A .B A .B A .B 2 d d 
(e) Sketch the path of student: draw (x,y) at different time; x x y y z z 2 dt dt Angular acceleration      2 v  v  at dt dt Solution 0     t 1 0 (a) a ⊥ v  a. v = 0 v . a = v a + v a = 0  .
 0  2t.(2 )   0  t  0 2 x  x  v t  at    0 0 2 1 2  dv d(R) d      t  t 2 2 2 2 a    R  a  R
(b) v  v  v    (2t)  dv/dt=0 only at t = 0 0 0 x y 2 2 v  v  2a(x  x ) t t 2 dt dt dt 0 0 2  v .x(t)  v .y(t)  .  t
  2t .(15  t )  0  t  0;t  5.208 s 2 2 2 v     2 (     ) (c) v ⊥ r⃗  v. r⃗ = 0 x y   1 2   2 0 0 a  a   R  radial n R
location of the student: (0m, 15.0m) and (6.25m, 1.44m)     dv d(R) d d Orbit a    R  a  R d) What is minimum distance
d(t)  0  t  5.208s;d(5.208)  6.41m t t dt dt dt dt 7/2/2021 Dang Duc Vuong –SEP-HUST 3 7/2/2021 Dang Duc Vuong –SEP-HUST 4 3 4 1 02/07/2021
3.51 A jungle veterinarian with a blow-gun loaded with a tranquilizer dart and a sly 1.5 kg monkey are each 25 m above the
3.53. In fighting forest fires, airplanes work in support of ground crews by dropping water on the fires. A pilot is practicing by
ground in trees 90 m apart. Just as the hunter shoots horizontally at the monkey, the monkey drops from the tree in a vain
dropping a canister of red dye, hoping to hit a target on the ground below. If the plane is flying in a horizontal path 90.0 m
attempt to escape being hit. What must the minimum muzzle velocity of the dart have been for the hunter to hit the monkey
above the ground and with a speed of 64.0 m/s (143 mi/h), at what horizontal distance from the target should the pilot release before it reached the ground? y-axis
the canister? Ignore air resistance. Motion equations y v0 y 0 A  1 g Motion equations  2
x (t)  x  v t  a t  v t  1 y V0 1 10 10 x 1x 0  tranquilizer 2 2 0 
x (t)  x  v t  a t  v t 1 10 10 x 1x 0  dart 1 1 Canister 2 g x (t)  v t 2 2
y (t)  y  v t  a t  25  gt  1 0 1 10 10 y 1y  2 2 1 1 x (t)  90 2 2  90.0 m
y (t)  y  v t  a t  90  gt 2 1 10 10 y 1y  2 2  1 1 2
x (t)  x  v t  a t  x  90 2 y (t)  y (t)  25  gt 2 20 20x 2 x 20  2   1 2 2 x (t) x 2 0 fire x monkey   1 1 y (t)  0 2 O x 2 2
y (t)  y  v t  a t  25  gt ? 0 2 20 20 y 2 y  2 2 B X O 1 2  90 2
* Both objects always have the same vertical component y
Canister of red dye hit a target on the ground (fire) y (t)  y (t)  0  90  gt  0  t   4.284 s 1 2   1(t) = y2(t) d = 90 m x-axis 2 9.81 1
* In the case the dart hit the monkey at time monkey just reach the ground: 2
y (t)  y (t)  25  gt  0  t  2.259s
x (t)  x (t)  v t  x  x  64.0 4.284  274.1 m 1 2 2 1 2 0 0 0
During this time the dart must travel 90 m, so the horizontal component of its velocity must be
x (t)  x (t)  v t  90  v  40 m / s
The dart hits the monkey for any muzzle velocity greater than 40 m/s. 1 2 0 0   7/2/2021 Dang Duc Vuong –SEP-HUST 5 7/2/2021 Dang Duc Vuong –SEP-HUST 6 5 6
3.55: The longest home run. According to the Guinness Book of World Records, the longest home run ever measured was hit by Roy
3.57(B): Hallway Catch. You are playing catch with a friend in the hallway of your dormitory. The distance from floor to
"Dizzy" Carlyle in a minor league game. The ball traveled 188 m (618 ft) before landing on the ground outside the ballpark. (a) Assuming
ceiling is D, and you throw the ball with an initial speed v0 =(6gD)1/2. What is the maximum horizontal distance (in term of D)
the ball’s initial velocity was 45° above the horizontal and ignoring air resistance, what did the initial speed of the ball need to be to produce
that the ball can travel without bouncing? (Assume that the ball is launched from the floor).
such a home run if the ball was hit at a point 0.9 m (3.0 ft) above ground level? Assume that the ground was perfectly flat. (b) How far would
the ball be above a fence 3.0 m (10 ft) high if the fence was 116 m (380 ft) from home plate? Analyze Projectile motion;
(a) Take the origin of coordinates at the point where the ball leaves the y-axis
bat, and take y + to be upward.
The ball travel without bouncing  h  max
D  condition for throwing angle y-axis g  1
 The distance in relationship with throwing angle 2
x(t)  x  v t  a t  v cos  t 0 0 x x  0 0   2  maximum distance ball  g 1 1 2
y(t)  y  v t  a t  0.9  v sin  2 t  gt Solution 0 0 y y 0 0 ?  2 2 v0 ? The highest coordinate: 3 m
The ball traveled 188 m before landing on the ground: D α 2 2 0 = 45o    v cos  t  188 v sin 0 0 2    0 0  A x(t)  188  h 3D sin max 0     v  42.8 m / s 1 2g 0   O X s = 116m y(t)  0 0.9   v sin  2 t  gt  0 v=(6gD)1/2 0 0 d = 188 m  2 h  D A max
(b) How far would the ball be above a fence α0 1 o O x        x(t)  v cos t sin 35.36 0 0   3 
When x(t) = 116 m  y(t) = 45.0 m R y(t)  0.9  2  v sin   1 2 t  gt
 the height of the ball above the fence: 42.0 m v sin 2 0 0  2 0 0  R   6Dsin 70.72  4 2D g 7/2/2021 Dang Duc Vuong –SEP-HUST 7 7/2/2021 Dang Duc Vuong –SEP-HUST 8 7 8 2 02/07/2021
3.61(E) (a) Prove that a projectile launched at angle αo has the same horizontal range as one launched with the same speed at
3.63(E) Leaping the River II. A physics professor did daredevil stunts in his spare time. His
angle (90o- αo ). (b) A frog jumps at a speed of 2.2 m/s and lands 25 cm from its starting point. At which angles above the
last stunt was an attempt to jump across a river on a motorcycle (Fig.). The takeoff ramp was
horizontal could it have jumped?
inclined at 53.0o, the river was 40.0 m wide, and the far bank was 15.0 m lower than the top of Analyze
the ramp. The river itself was 100 m below the ramp. You can ignore air resistance. (a) What
should his speed have been at the top of the ramp to have just made it to the edge of the far
(a) Using the formula of range in projectile motion;
bank? (b) If his speed was only half the value found in (a), where did he land?
(b) α=? v0 = 2.2 m/s; R=0.25 m; Calculate α from R;
a) Take the origin of coordinates at the top of the ramp and take y + to be upward. y-axis  1 2 g (a) Proving:
x(t)  x  v t  a t  v cos .t 0 0 x x 0 0  2 2 v sin 2 Motorcycle  With initial angle α: 0 R  1 1  g 2 2
y(t)  y  v t  a t 15  v sin  .t  gt 0 0 y y 0 0  2 2 O α 2 0 =53o v sin 290   2 v sin 180  2  2 v sin 2 0 0 0
With initial angle (90o- α): R     R x(t)  40.0m x-axis 90  
he lands in the edge of the far bank: g g g    v 17.8 m / s 0   y(t)  1  5.0m (b) We have: 2 v sin 2
b) his speed was only half the value found in (a):  v1 = 8.9 m/s 0 R   2  gR arcsin    α = 15.2o or 74.8o; g 2 v x(t)  v cos .t 0 1 0 
He reach the water: y(t) = -100 m  t = 5.30 s  1 2
y(t) 15  v sin  .t  gt 
t = 5.30 s  x(5.30s) = 28.4 m 1 0  2 7/2/2021 Dang Duc Vuong –SEP-HUST 9 7/2/2021 Dang Duc Vuong –SEP-HUST 10 9 10
3.65(E). A 5500-kg cart carrying a vertical rocket launcher moves to the right at a constant speed of 30.0 m/s along a  1
horizontal track. It launches a 45.0-kg rocket vertically upward with an initial speed of 40.0 m/s relative to the cart. (a) How 2
x (t)  x  v t  a t  v t 1 10 10x 1x 0 x  2
high will the rocket go? (b) Where, relative to the cart, will the rocket land? (c) How far does the cart move while the rocket Rocket  1 1 2 2 
is in the air? (d) At what angle, relative to the horizontal, is the rocket traveling just as it leaves the cart, as measured by an
y (t)  y  v t  a t  v t  gt 1 10 10 y 1y 10 y  2 2
observer at rest on the ground? (e) Sketch the rocket’s trajectory as seen by an observer (i) stationary on the cart and (ii)  1 2
x (t)  x  v t  a t  v t stationary on the ground. 2 20 20 x 2 x 0 x  2 Cart  1 y-axis g 2
y (t)  y  v t  a t  0 2 20 20 y 2 y  2
Cart : v1 = v cart/ground = 30.0 m/s v  v  v
Rocket : v2 = vrocket/cart = 40.0 m/s rocket /ground rocket/cart cart /ground 2 2        v
(a) How high will the rocket go? v 0 v v 2g(y y ) y 81.6m y y 0 y 0 0 v2 v  v  30.0 m / s
(b) Where, relative to the cart, will the rocket land? Both the cart and the rocket have the same constant horizontal velocity,   ox 1   α0 v  O
so both travel the same horizontal distance while the rocket is in the air and the rocket lands in the cart. 0 v1 v  v  40.0 m / s  oy 2   1
(c) How far does the cart move while the rocket is in the air? 2
y (t)  0  v t  gt  0  t  8.164s  x (t)  245m 1 10 y 2 2  1
(d) At what angle the rocket traveling just as it leaves the cart, as measured by an observer at rest on the ground? 2
x (t)  x  v t  a t  v t  1 2     1 10 10x 1x 0 x  2 x (t) x v t a t v t 2 20 20 x 2 x 0 x  v 40 Rocket   2 0 y o tan       53.1 1 1 Cart  0 0 v 30 2 2
y (t)  y  v t  a t  v t  gt 1 2      0 x 1 10 10 y 1y 10 y  2 2 y (t) y v t a t 0 2 20 20 y 2 y  2
(e) Sketch the rocket’s trajectory (i) the observer stationary on the cart
(ii) the observer stationary on the ground 7/2/2021 Dang Duc Vuong –SEP-HUST 11 7/2/2021 Dang Duc Vuong –SEP-HUST 12 11 12 3 02/07/2021
3.69. Two tanks are engaged in a training exercise on level ground. The first tank fires a paint-filled training round with a
Note: Tank 1 (symbol 1); Tank 2 (symbol 2)   
muzzle speed of 250 m/s at 10.0o above the horizontal while advancing toward the second tank with a speed of 15.0 m/s y-axis g Shell (symbol 0) v  v  v shell/ground shell/ tank1 tank1/ground
relative to the ground The second tank is retreating at 35.0 m/s relative to the ground, but is hit by the shell. You can ignore v  v  15 m / s 1 tan k1/ground   vshel /tank
air resistance and assume the shell hits at the same height above ground from which it was fired. Find the distance between v  v  35 m / s 2 tan k 2/ground   vtank2/ground 0 x-axis
the tanks (a) when the round was first fired and (b) at the time of impact. α =10o v  v  250 1  0 O 0 shell/ tan k1 v 1st tank tank1/ground 2nd tank   v  v  v cos s 0 x 1 0 d=? v  v  s 0 shell/ground y-axis g    v  v sin  v  v  v  s0y 0 shell/ground shell/tank1 tank1/ground  1  1 2  1 2
x (t)  x  v t  a t  v t
x (t)  x  v t  a t  d  v t 2
x (t)  x  v t  a t  v  v cos  t s s 0 s 0 x sx  1 0  2 20 20 x 2 x 2  1 10 10 x 1x 1  2  v  2 Tan k2  2 shel /tank Tan k1   Shell  1 1 2  1 1 2
y (t)  y  v t  a t  0
y (t)  y  v t  a t  0 2
y (t)  y  v t  a t  v sin t  gt s s 0 s 0 y sy  0  2 2 20 20 y 2 y  1 10 10 y 1y  2  2  2 2 α =10o v O tank2/ground x-axis v 
 v  v cost  d  v t  0
 15  250cos10 t  d  35t 1 0 2  tank1/ground x (t)  x (t)   1st tank 2nd tank a) Tank 2 is hit by the shell s 2     
 t  8.86s  d  2624m 1 1 y (t)  y (t) v sin  t  gt  0 250sin10 t  9.81 t  0 s 2    0  2  0  2 d=?  2  2
b) the distance between the tanks at the time of impact.
s  x (8.86s)  x (8.86s)  ? 2 1 7/2/2021 Dang Duc Vuong –SEP-HUST 13 7/2/2021 Dang Duc Vuong –SEP-HUST 14 13 14
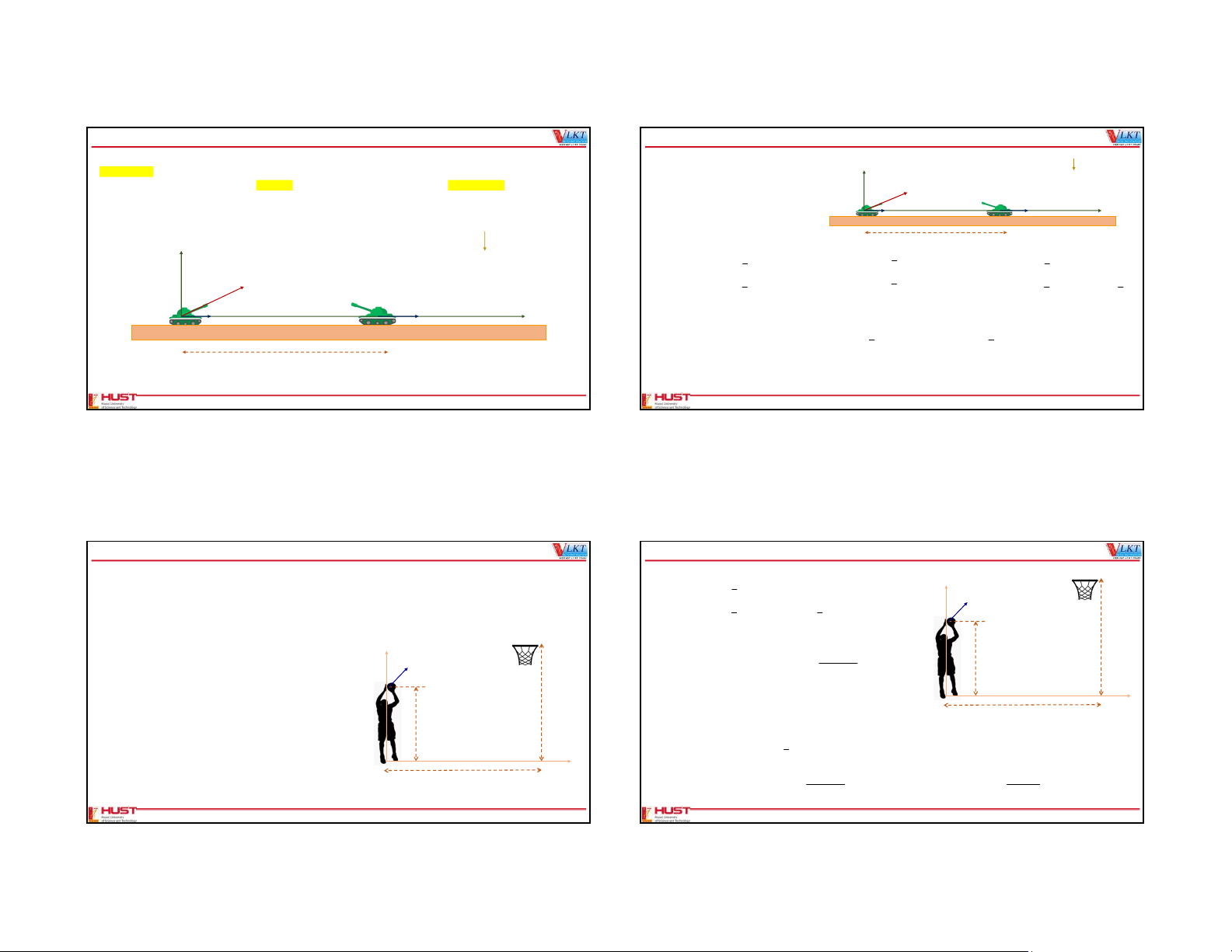
3.71 (O). A basket player is fouled and knocked to the floor during a layup attempt. The player is awarded two free throws. Motion equations of ball y-axis
The center of the basket is a horizontal distance of 4.21 m from the foul line and it is a height of 3.05 m above the floor. On  1 2
x(t)  x  v t  a t  v cos .  t 0 0 x x 0 
the first attempt he shoots the ball at an angel 35.0o above the horizontal and with the speed of v 2 v0 0 = 4.88 m/s. The ball is ball  1 1
released 1.83 m above the floor. This shot missed badly. You can ignore air resistance. 2 2         α=35o y(t) y v t a t 1.83 v sin .t gt 0 0 y y 0  2 2
(a) What is the maximum height reached by the ball? The 1st throw 3.05 m y-axis
(b) At what distance along the floor from the free throw line
(a) What is the maximum height reached by the ball? 1.83 m does the ball land? v sin  2 2  0 2 v0
v  v  2a (y  y )  y  y   2.23m y 0 y y max 0 max 0
(c) For the second throw, the ball is thrown into the center of 2g α=35o
(b) The distance of landing position:
basket. For this second throw, the player again shoots the ball at 3.05 m
y(t)  0  t*   x(t*)  3.84m
35.0o above the horizontal and releases it 1.83 m above the 4.21 m x-axis O The 2nd throw:
floor. What initial speed does the player give the ball on this 1.83 m
(c) To goes through the basket second attempt?    x(t)  4.21 v cos .t 4.21 0 
(d) For the second throw what is the maximum height reached    1  v  8.65 m / s 0   y(t)  3.05 2 1.83  v sin .  t  gt  3.05
by the ball? At this point, how far horizontally is the ball from  0  2 4.21 m x-axis the basket?
How far horizontally from highest point to basket: O
d) what is the maximum height reached by the ball v sin2 2 v sin 2 2 2 0
v  v  2a (y  y )  y  y   3.09m 0 d  4.21  0.62m y 0 y y max 0 max 0 2g 2g 7/2/2021 Dang Duc Vuong –SEP-HUST 15 7/2/2021 Dang Duc Vuong –SEP-HUST 16 15 16 4 02/07/2021
3.73(O).A rocket is initially at rest on the ground. When its engines fire, the rocket flies off in a straight line at an angle 53.1o Part 2 (t>T) y-axis
above the horizontal with a constant acceleration of magnitude g. The engines stop at a time T after the launch, after which Part 1 Part 2 v  v  g cosT  0.6gT g
the rocket is put in projectile motion. You can ignore air resistance and assume g is independent of altitude. (a) Draw the x2 1 x T vy2_0 v2_0 x-axis:
trajectory of the rocket from when its engines first fire until the rocket hits the ground. Indicate the direction of the velocity 2
x  x  v t  0.3gT  0.6gT t T  gTt  gT T x   2 0.6 0.3 2 1 20
and acceleration vectors at various points along the trajectory. (b) Sketch v α x20 =x1T
x-t and vy-t graphs for the motion of the rocket a  g y2 v
from when its engines first fire until the rocket hits the ground. (c) Find the maximum altitude reached by the rocket (in term x2_0 a y-axis: v  v
 a t  g sinT  t  0.8gT  gt y 2 y1T y2  
of g and T). (d) Find the horizontal distance from the launch point to where the rocket hits the ground (the range) in term of g 1_0=g and T. 2 a y 2 2 y1_0 20 =y1T 1 y  y  v t T  a t T
 0.5gt 1.8gTt  0.9gT 2 1T y 20   y 2   y-axis 2 Part 1 Part 2 Part 1 (0a x-axis The rocket hits the ground y   x1_0 v g    t 3T y2_0 a g cos 0.6g v 2 = 0 land 2_0 1 x v  v
 a t  g cost  0.6gt 1 x 1 x _ 0 1 x x-axis:
(a) the trajectory of the rocket from when its engines first fire α x20 =x1T
until the rocket hits the ground 2 2 2 1 1 x  x  v t  a t  g cost  0.3t vx2_0 1 10 1 x _ 0 1 2 x 2 y a1_0=g a  g sin  0.8g 1 y a y y1_0 20 =y1T v  v
 a t  g sint  0.8gt y-axis: y1 y1_ 0 1 y a x-axis x1_0 2 2 2 1 1 y  y  v t  a t  g sint  0.4gt 1 10 y1_ 0 y1 2 2 x 7/2/2021 Dang Duc Vuong –SEP-HUST 17 7/2/2021 Dang Duc Vuong –SEP-HUST 18 17 18 (b) Sketch v v
3.75(O). A rock tied to a rope moves in the xy-plane. Its coordinates are given as functions of time by x(t) = Rcosωt and x-t and vy-t graphs x
y(t) = Rsinωt, where R and ω are constants. (a) Show that the rock’s distance from the origin is constant and equal to R, that x-axis:  0.6gt 0  t  T  0.6gT
is, the path is a circle of radius R. (b) Show that at every point the rock’s velocity is perpendicular to its position vector. (c) v  x 
Show that the rock’s acceleration is always opposite in direction to its position vector and has magnitude ω 2R. (d) Show 0.6gT  T  t  3T 
that the magnitude of the rock’s velocity is constant and equal to ωR. (e) Combine the results of parts (c) and (d) to show y-axis: 
that the rock’s acceleration has constant magnitude v2/R. 0.8gt 0  t  T  O v  3T t T y 
(a) Find distance from the co-ordinates x and y; 0.8gT  gt  T  t  3T  vy
xt  R cost; yt   Rsint    2    2    2 r t x t y t  R  R (c) The maximum altitude: (b) Show that 0.8gT
𝑟⃗ ⊥ 𝑣⃗  𝑟⃗. 𝑣⃗=0 2 v 0.8gT dxt dy t y 2_ 0 2  2 2 h  y   0.4gT   0.72gT v   R sint   ; v   R cos t x y   max 02 2g 2g dt dt 1.8T   2
 r  v  xv  yv  R  t t  R  t t  x y     2 sin cos sin  cos  0 (d) The horizontal distance: O t T 3T
(c) Show that acceleration vector is opposite in direction with position vector  𝑟⃗. 𝑎⃗ <0 R  x t  3T  2 1.5gT 2 dv t dv t x   2 a   R t a   R t x   y   2 sin ; cos y   dt dt   2 2 2 2 2 2 2 2 -1.2gT
 r  a  xa  ya  R  sin t  R  cos t  R   0 x y 7/2/2021 Dang Duc Vuong –SEP-HUST 19 7/2/2021 Dang Duc Vuong –SEP-HUST 20 19 20 5 02/07/2021 Other dv t dv t
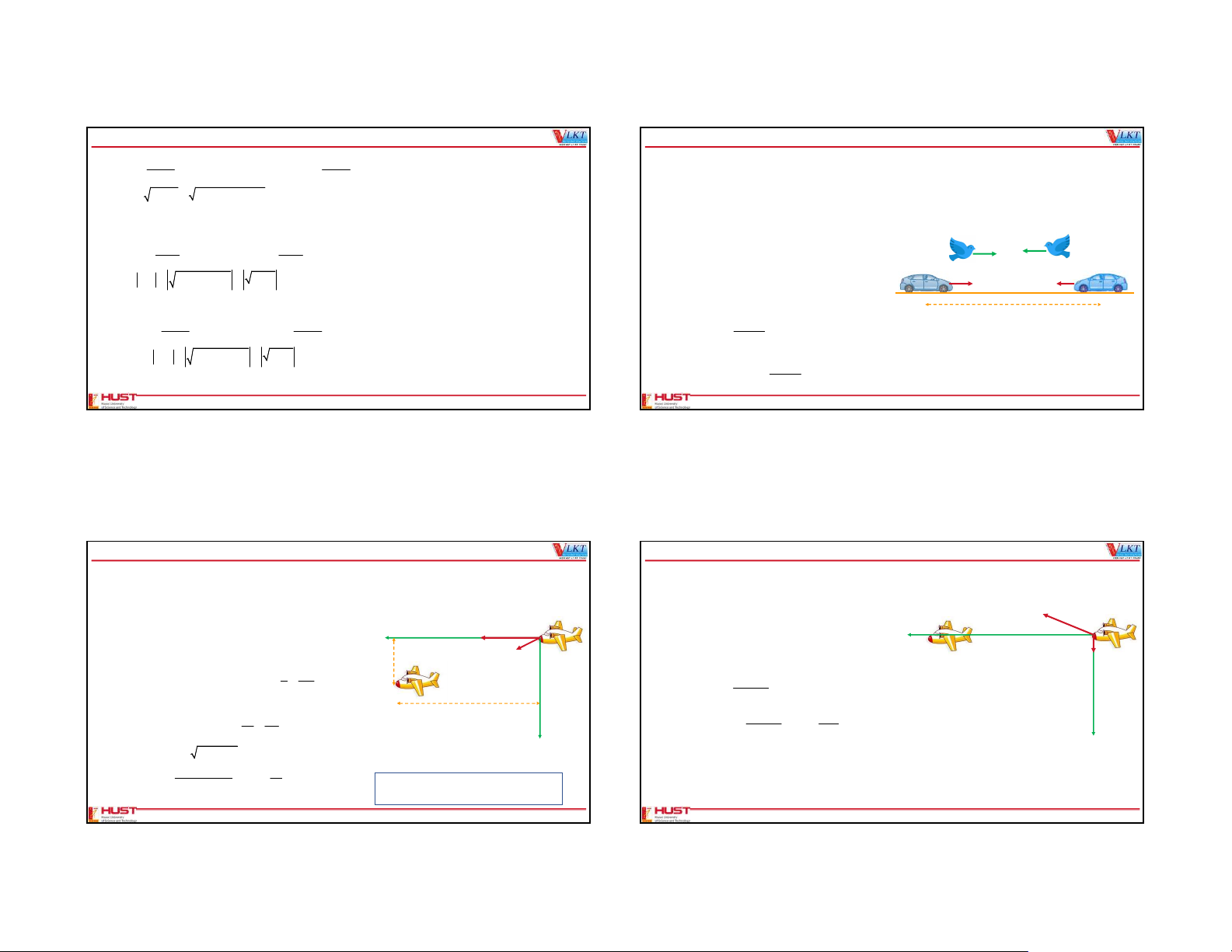
3.79(E): The carrier Pigeon Problem. Larry is driving east at 40 km/h. His twin brother Harry is driving west at 30 km/ h, x   2 a   R t  x t a R t  y t x   2 y   2      y   2 sin ( ); cos   ( ) dt dt
toward Larry in and identical car on the same direction straight road. When they are 42 km apart, Larry sends out a carrier
pigeon, which flies at a constant speed of 50 km/h (all speeds are relative to the earth). The pigeon flies to Harry, becomes 2 2 4 2 4 2 2
a  a  a   x(t)   y(t)  R x y    
confused and immediately returns, becomes more confused and immediately flies back to Harry. This continues until the twin   2 2
a  a i  a j   (x(t).i  y(t). j)   r
meet, at which time the dazed pigeon drops to the ground in exhaustion. Ignoring turnaround time, how far did the pigeon x y
(d) Prove that |v|= ωR = const; fly? 50 km/h Analyze 50 km/h dxt dy t v   R sint   ; v   R cos t x y  
We first think to calculate each parts of the motion dt dt
of pigeon then calculate the sum; Larry Harry 40 km/h 30 km/h vt 2  v t 2  y t 2 2  R   R  const y x
But think out of box – some how: the total distance = total time * velocity; 42 km
(e) Prove that a = v2/R = ωR2 =const;
The time it take to let Harry meet Larry: dv t dv t x   2 d a   R t a   R t t  x   y   2 sin ; cos y   dt dt v  v L H  at 2  a t 2  a t 2 4 2  R   R  const
The total distance the pigeon fly: y x 50 42 s  v t   30 km piegon P   40  30 7/2/2021 Dang Duc Vuong –SEP-HUST 21 7/2/2021 Dang Duc Vuong –SEP-HUST 22 21 22
3.81(B). An airplane pilot sets a compass course due west and maintains an airspeed of 220 km/h. After flying for 0.500 h,
she finds herself over a town 120 km west and 20 km south of her starting point. (a) Find the wind velocity (magnitude and Relative velocity:
direction). (b) If the wind velocity is 40 km/h due south, in what direction should the pilot set her course to travel due west?    v  v  v
Use the same airspeed of 220 km/h. plane/ ground plane/air air/ ground 220 km/h vplane/air v West/+ x-axis
Assume that the airplane has the direction as in the plane/air (a) Relative velocity: θ 220 km/h   
figure. The plane travels due West when v v  v  v θ y_plane/ground=0; plane/ ground plane/air air/ ground 20 km v  v  v sin  0
Define West – positive x; South – positive y. After 0.5h: y _ plane/ ground air / ground plane v v air/ground =? x-axis: air/ground =? West/+ x-axis x 120 v  v  v cos    240 km / h v x _ plane/ ground plane/air air/ ground   t 0.5 /    0.5h sin air ground  v cos  20 km / h v air/ ground   120 km plane/air y-axis: y vair ground 44.7 p 20 v  v sin    40 km / h South/+y-axis / o South/+y-axis    arcsin  arcsin  10.3 y _ plane/ ground air / ground   t 0.5 v 220 plane/air 2 2  v  40  20  44.7 km / h
The direction of the airplane is 10.3o North of West air/ ground      v sin air/ ground 40   arctan  arctan  63.4o  v cos 20 The wind velocity  air/ ground
44.7 km/h and of direction 63.4o South of West 7/2/2021 Dang Duc Vuong –SEP-HUST 23 7/2/2021 Dang Duc Vuong –SEP-HUST 24 23 24 6 02/07/2021
3.85. In a World Cup soccer match, Juan is running due north toward the goal with a speed of 8.00 m/s relative to the
3.50. Spiraling Up. It is common to see birds of prey rising upward on thermals. The paths they take may be spiral-like. You
ground. A teammate passes the ball to him. The ball has a speed of 12.0 m/s and is moving in a direction of 37.0o east of
can model the spiral motion as uniform circular motion combined with a constant upward velocity. Assume a bird completes a
north, relative to the ground. What are the magnitude and direction of the ball’s velocity relative to Juan?
circle of radius 8.00 m every 5.00 s and rises vertically at a rate of 3.00 m/s. Determine: (a) the speed of the bird relative to
• Define North – positive y-axis, East – positive x-axis;
the ground; (b) the bird's acceleration (magnitude and direction); and (c) the angle between the bird's velocity vector and the North/+y-axis
• Velocity of Juan relative to the ground - Juan is running due north: horizontal.      v  8.0 m / s (a) v v v bird / ground up circular Juan/ ground   v  2m / s up 
• Velocity of ball relative to the ground – the ball is moving in a vup vtotal
direction of 37.0o east of north :  v circumference 2 R v    10m / s circular  v 12.0 m / s bal /ground θ ball / ground   period T v 2 2
• Velocity of ball relative to Juan: Juan/ground  v  v  v 10.5 m / s bird / ground up circular        θ -vJuan/ground v v  v  v  v  v circular ball / Juan ball / ground ground / Juan ball / ground Juan/ ground
(b) The acceleration of the bird is the centripetal acceleration in the circular motion; α vbal /Juan 2 v  v cos  7.22 m / s v  7.39 m / s vcircular a  a  a   m s bird centripetal c  2 12.6 /  ball / Juan   ball / Juan _ x ball / ground       R v  v sin  v 1.58 m / s o    77.6 ball / Juan _ y ball/ ground Juan/ ground   East/+ x-axis
(c) The angle between total velocity vector and horizontal direction is: v
The ball is moving with velocity of 7.39 m/s and direction of 77.6o   arctan up  16.6o East of North. vcircular 7/2/2021 Dang Duc Vuong –SEP-HUST 25 Dang Duc Vuong –SEP-HUST 26 25 26
3.77. Cycloid. A particle moves in the xy-plane. Its coordinates are given as functions of time by x(t) = R(ωt - sinωt) and www.hust.edu.vn
y(t) = R(1 - cosωt), where R and ω, are constants. (a) Sketch the trajectory of the particle. (This is the trajectory of a point on
the rim of a wheel that is rolling at a constant speed on a horizontal surface. The curve traced out by such a point as it moves
through space is called a cycloid). (b) Determine the velocity components and the acceleration components of the particle at
any time t. (c) At which times is the particle momentarily at rest? What are the coordinates of the particle at these times?
What are the magnitude and direction of the acceleration at these times? (d) Does the magnitude of the acceleration depend
on time? Compare to uniform circular motion.
(a) Sketch the trajectory of the particle
b) Determine the v, a components 2R  dx  dv v   R  t  x 2 a   R sint x 1 cos    dt x  dt x(t) = R(ωt - sinωt)   dv y(t) = R(1 - cosωt), dy  v   R sint y  2 a   R cost y  dt y  dt
(c) At which times is the particle momentarily at rest (v = 0) πR 2πR k 2 2 v  v  v  0 2 2 2 2
 2R   2R  cost  0  cost  2 1  t  x y 
the coordinates of the particle x(t) = 0, 2R, 4R, … and y(t) = 0.
(d) The magnitude of the acceleration 2 2 2
a  a  a  R  const
Similar to the uniform circular motion; x y Thank you for your attentions! 7/2/2021 Dang Duc Vuong –SEP-HUST 27 28 7/2/2021 Dang Duc Vuong –SEP-HUST 27 28 7