Bµi Gi¶ng - H­íng dÉn gi¶i bµi tËp c¬ kÕt cÊu 2 Lêi Nãi ®Çu
Nh»m h­íng tíi môc tiªu kh«ng cã sinh viªn nµo ph¶i lÊy tiÒn häc bæng
®Ó ®ãng tiÒn häc l¹i C¬ kÕt cÊu f2, m×nh biªn so¹n cuèn bµi gi¶ng “H­íng
dÉn gi¶i bµi tËp c¬ kÕt cÊu f2” míi môc ®Ých ®Ó c¸c b¹n sinh viªn cã tµi
liÖu tham kh¶o, hç trî cho c«ng cuéc häc tËp m«n c¬ kÕt cÊu f2. Tµi liÖu
tr×nh bµy theo h¬i h­íng phôc vô viÖc hoµn thµnh tèt c¸c bµi kiÓm tra vµ
v­ît qua kú thi cuèi kú, do vËy tµi liÖu kh¸i qu¸t s¬ bé lý thuyÕt, cã vÝ dô
®iÓn h×nh hÇu hÕt c¸c d¹ng bµi tËp ®Ó c¸c b¹n tham kh¶o.
Bµi gi¶ng chØ thÝch hîp ®èi víi sinh viªn ®äc v× lèi viÕt mang khuynh
h­íng trÎ trung, ph¸ c¸ch cña mét sinh viªn míi tèt nghiÖp 2015. §«i khi sö
dông tõ ng÷ kh«ng theo v¨n phong chuÈn mùc, bµi gi¶ng cã thùc hiÖn hai
c¸ch tr×nh bµy kh¸c nhau theo tr­êng §H Giao th«ng vËn t¶i Hµ Néi vµ
tr­êng §H X©y dùng Hµ Néi.
Bµi gi¶ng gåm nh÷ng ch­¬ng chñ yÕu sau ®©y:
CH¦¥NG 1 : Ph­¬ng ph¸p lùc
CH¦¥NG 2 : Ph­¬ng ph¸p chuyÓn vÞ
CH¦¥NG 3 : Ph­¬ng ph¸p hçn hîp
Trong ®ã ch­¬ng 1 gåm c¶ ph­¬ng ph¸p ph­¬ng tr×nh 3 m«men, t©m
®µn håi vµ phÇn ®­êng ¶nh h­ëng cña kÕt cÊu siªu tÜnh.
Bµi gi¶ng cã tham kh¶o tµi liÖu cña nhiÒu tr­êng ®¹i häc, cao ®¼ng vµ
nguån ®Ò thi trªn internet ®Ó thùc hiÖn c¸c vÝ dô gÇn gòi nhÊt víi sinh viªn,
®Æc biÖt lµ “Anh X©y” vµ “Anh Th«ng”.
Tuy rÊt cÈn thËn vµ cã nhiÒu cè g¾ng trong qu¸ tr×nh biªn so¹n. Nh­ng v×
lµ sinh viªn nªn kiÕn thøc cßn nhiÒu h¹n chÕ vµ thiÕu sãt, l¹i cßn m¾t kÐm 
nªn t«i mong nhËn ®­îc nh÷ng ý kiÕn ®ãng gãp tõ c¸c b¹n sinh viªn ®Ó
hoµn thiÖn bµi gi¶ng h¬n. “Tµi liÖu chØ dµnh cho sinh viªn”. Grazie. Buona fortuna! T¸c gi¶: NS - 박 1
Bµi Gi¶ng - H­íng dÉn gi¶i bµi tËp c¬ kÕt cÊu 2
CH¦¥NG 1 : Ph­¬ng ph¸p lùc
1.1. HÖ siªu tÜnh (statically indeterminate structure)
1.1.1. Kh¸i niÖm vÒ hÖ siªu tÜnh
HÖ ®­îc gäi lµ siªu tÜnh nÕu trong toµn hÖ hoÆc trong mét vµi phÇn cña hÖ
ta kh«ng thÓ chØ dïng c¸c ph­¬ng tr×nh c©n b»ng tÜnh häc ®Ó x¸c ®Þnh
®­îc tÊt c¶ c¸c ph¶n lùc vµ néi lùc.
VÒ ph­¬ng diÖn cÊu t¹o, h×nh häc hÖ siªu tÜnh lµ hÖ bÊt biÕn h×nh thõa liªn
kÕt. Sè liªn kÕt thõa lµ ®Æc tr­ng cña hÖ siªu tÜnh, song ë ®©y liªn kÕt thõa lµ
nh÷ng liªn kÕt kh«ng cÇn thiÕt cho sù cÊu t¹o h×nh häc cña hÖ nh­ng vÉn
cÇn cho sù lµm viÖc cña c«ng tr×nh.
H×nh 1.1 KÕt cÊu siªu tÜnh
1.1.2. §Æc ®iÓm cña hÖ siªu tÜnh
a. ChuyÓn vÞ, biÕn d¹ng vµ néi lùc trong hÖ siªu tÜnh nãi chung nhá h¬n
trong hÖ tÜnh ®Þnh cã cïng kÝch th­íc vµ t¶i träng.
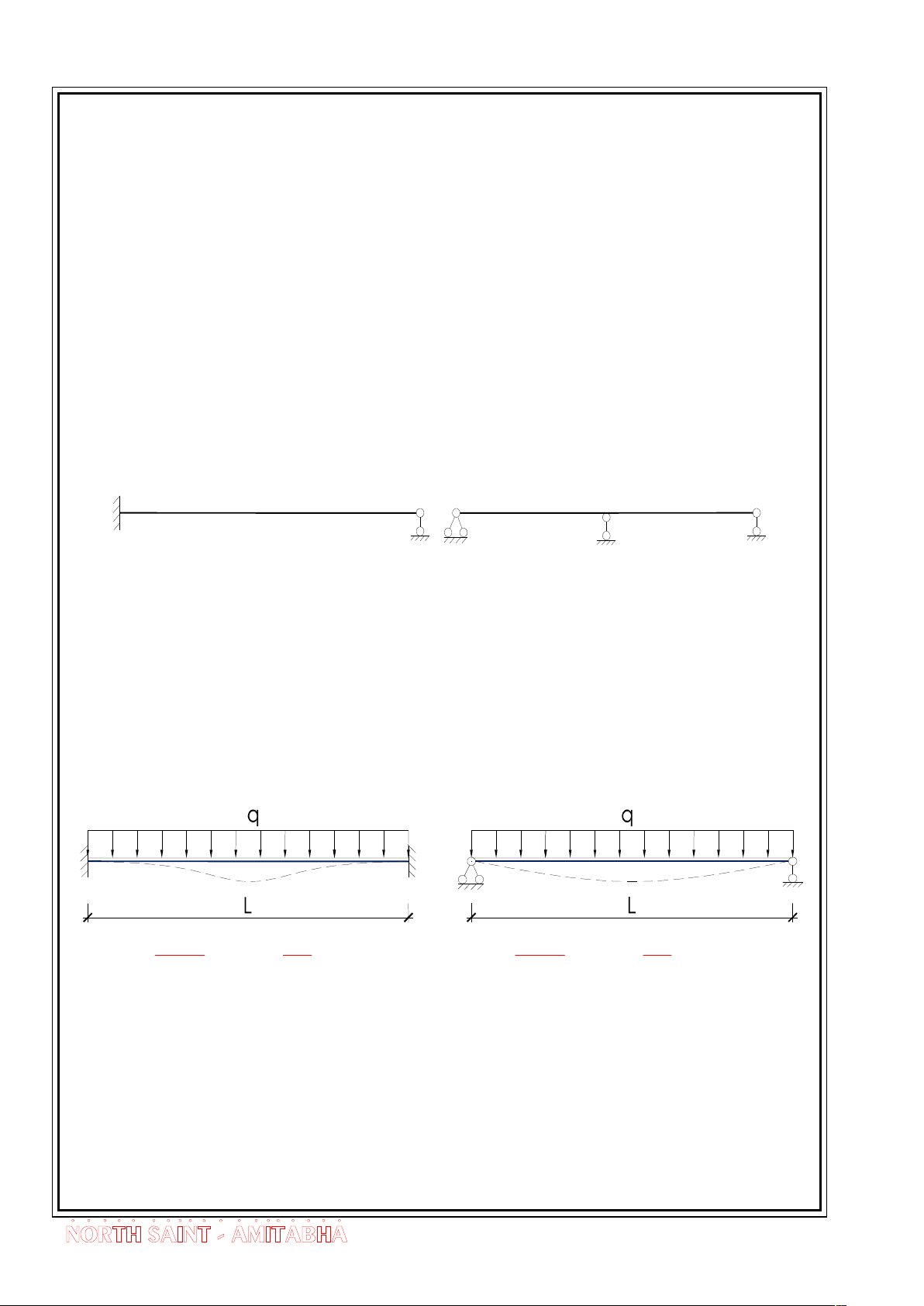
Ta xÐt 2 dÇm cã cïng chiÒu dµi vµ ®é cøng chèng uèn, cïng chÞu t¶i träng
r¶i ®Òu q thÓ hiÖn nh­ h×nh vÏ. 4 2 ql ql 4 2 y  ; M  "in fixed" 5ql ql y  ; M  "in mid span" max max 384EI 12 max max 384EI 8
b. HÖ siªu tÜnh ph¸t sinh néi lùc do sù thay ®æi nhiÖt ®é, sù chuyÓn vÞ c¸c gèi
tùa, sù chÕ t¹o l¾p r¸p kh«ng chÝnh x¸c (Nh÷ng yÕu tè nµy kh«ng g©y ra
néi lùc trong kÕt cÊu tÜnh ®Þnh).
c. Néi lùc trong hÖ siªu tÜnh phô thuéc vµo vËt liÖu, kÝch th­íc vµ h×nh d¹ng cña tiÕt diÖn c¸c thanh. 2
Bµi Gi¶ng - H­íng dÉn gi¶i bµi tËp c¬ kÕt cÊu 2 1.1.3. BËc siªu tÜnh
BËc siªu tÜnh cña hÖ siªu tÜnh b»ng sè liªn kÕt thõa ®· quy ®æi ra liªn kÕt
thanh ngoµi sè liªn kÕt cÇn thiÕt ®ñ ®Ó cho hÖ bÊt biÕn h×nh.
Cã nhiÒu c¸ch ®Ó x¸c ®Þnh bËc siªu tÜnh, nh­ng ta chØ quan t©m c¸c c¸ch
hay ¸p dông vµ dÔ ¸p dông nhÊt.
C¸ch 1: Lo¹i bá dÇn liªn kÕt
Th«ng th­êng ta thÊy 1 kÕt cÊu tÜnh ®Þnh ph¶i cã 3 ph¶n lùc gèi (Trõ hÖ
khung 3 khíp) vËy trªn c¬ së ®ã ta cø lo¹i bá dÇn dÇn liªn kÕt thõa trong
hÖ siªu tÜnh ®Õn khi cßn 3 ph¶n lùc th× ta ®­îc kÕt cÊu c¬ b¶n vµ sè liªn kÕt
lo¹i bá chÝnh lµ bËc siªu tÜnh. Nh­ng cÇn l­u ý viÖc lo¹i bá ph¶i ®¶m b¶o
kÕt cÊu kh«ng biÕn h×nh hay biÕn h×nh tøc thêi. H×nh 1.2 S¬ ®å vÝ dô
Trong s¬ ®å ta thÊy cã tæng thÓ cã 6 ph¶n lùc gèi (Reaction), nÕu ta bá 3
liªn kÕt t¹i B, C, D ta cã s¬ ®å c«ng sol. NÕu bá 1 liªn kÕt t¹i A (Gãc xoay)
vµ 2 liªn kÕt bÊt kú t¹i 3 vÞ trÝ B, C, D ta còng ®­îc c¸c s¬ ®å tÜnh ®Þnh.
H×nh 1.3 Mét sè s¬ ®å lo¹i bá liªn kÕt
C¸ch 2: Sö dông c«ng thøc - C¸ch nµy ta hay sö dông nhÊt.
Nh×n chung th× c«ng thøc ¸p dông ®Ó tÝnh bËc siªu tÜnh lµ kh«ng cã g× qu¸
phøc t¹p, dÔ ¸p dông vµ dÔ hiÓu “§©y chÝnh lµ sù tuyÖt vêi mµ c¸c thÇy c«
viÕt s¸ch mang l¹i cho chóng ta”.
C«ng thøc sè 1 : n = L0 + 2K - 3T (n = C + 2K - 3D) ( 1.1 )
 L0 (C) - Sè liªn kÕt víi ®Êt
 K - Sè liªn kÕt khíp (§· quy ®æi ra liªn kÕt ®¬n gi¶n)
 T (D) - TÊm cøng tÜnh ®Þnh 3
Bµi Gi¶ng - H­íng dÉn gi¶i bµi tËp c¬ kÕt cÊu 2
E.X 1.1 - Ta x¸c ®Þnh bËc siªu tÜnh cho H×nh 1.2 ta cã L0 = 6, K = 0, T = 1 (Coi
AD lµ 1 tÊm cøng) th× n = 6 + 2.0 - 1.3 = 3. NÕu ta coi AB, BC, CD lµ tõng
miÕng cøng th× biÓu thøc (1.1) cÇn céng thªm 3H (Liªn kÕt hµn), lóc nµy n = 6 + 2.0 + 3.2 - 3.3 = 3.
Tõ vÝ dô nµy ta thÊy r»ng viÖc quan niÖm tÊm cøng kh¸c nhau còng ¶nh
h­ëng ®Õn viÖc x¸c ®Þnh bËc siªu tÜnh. Do ®ã, nªn coi lµm sao cho cµng Ýt
th«ng sè trong biÓu thøc cµng khoÎ.
NÕu ta coi thanh cong lµ 1 tÊm cøng th× n = 5 + 2.0 - 3.1 = 2.
NÕu coi thanh th¼ng lµ tÊm cøng th× n = 5 + 2.0 + 3.1 - 3.2 = 2.
C«ng thøc sè 2 : n = 3V - K ( 1.2 )  V - Sè khung kÝn  K - Sè khíp ®¬n gi¶n
C«ng thøc sè 3 : n = D(T) + C(L0) - 2M(K) (Dïng víi hÖ giµn nèi ®Êt) ( 1.3 )  M - M¾t thanh
 C¸c th«ng sè kh¸c nh­ ®· tr×nh bµy ë trªn.
§Ó sö dông (1.2 C«ng thøc sè 2 : n = 3V - K ( 1.2) ta cÇn l­u ý ph¶i quan
niÖm tr¸i ®Êt lµ tÊm cøng hë. n = 3.1 - 0 = 3 n = 3.1 - 1 = 2 n = 3.2 - 3 = 3
Nh×n chung, th× viÖc x¸c ®Þnh bËc siªu tÜnh h·y cø hiÓu mét c¸ch ®¬n gi¶n
nhÊt lµ ta bá liªn kÕt ®i ®Ó kÕt cÊu thµnh tÜnh ®Þnh ®Ó tÝnh to¸n víi yªu cÇu
kÕt cÊu bÊt biÕn h×nh. Nh­ng ®«i khi cÇn ph¶i ph©n râ kÕt cÊu ngo¹i siªu
tÜnh vµ kÕt cÊu néi siªu tÜnh. 4
Bµi Gi¶ng - H­íng dÉn gi¶i bµi tËp c¬ kÕt cÊu 2
VÝ dô c¸c kÕt cÊu trong H×nh 1.3 lµ c¸c kÕt cÊu ngo¹i siªu tÜnh.
ë H×nh 1.4 ta thÊy víi 3 ph­¬ng tr×nh ta ®Òu x¸c ®Þnh ®­îc c¸c ph¶n lùc
nµy, nh­ng víi thanh thanh 2 ®Çu khíp ta vÉn ch­a x¸c ®Þnh ®­îc néi lùc trong nã.
H×nh 1.4 KÕt cÊu néi siªu tÜnh
1.1.4. Chän kÕt cÊu c¬ b¶n
ViÖc lùa chän kÕt cÊu c¬ b¶n lµ c«ng viÖc quan träng trong bµi to¸n siªu
tÜnh gi¶i theo ph­¬ng ph¸p lùc v× nã lµ nh÷ng b­íc c¬ së tiÒn ®Ò ¶nh
h­ëng ®Õn c¶ bµi to¸n. Th«ng th­êng bËc siªu tÜnh chÝnh lµ sè Èn ta bá ®i
trong kÕt cÊu siªu tÜnh ®Ó ®­îc kÕt cÊu tÜnh ®Þnh gäi ®ã lµ kÕt cÊu c¬ b¶n
(KÕt cÊu c¬ b¶n th­êng lµ kÕt cÊu tÜnh ®Þnh, cã nh÷ng tr­êng hîp kÕt cÊu
c¬ b¶n vÉn lµ kÕt cÊu siªu tÜnh).
CÇn lùa chän kÕt cÊu c¬ b¶n thø nhÊt lµ ph¶i ®óng tøc lµ kÕt cÊu kh«ng
biÕn h×nh hay biÕn hµnh tøc thêi. Sau ®ã, khi ®· ®óng ta míi tiÕn ®Õn viÖc
lùa chän kÕt cÊu c¬ b¶n sao cho tÝnh to¸n nhanh vµ ng¾n gän - c¸i nµy cÇn häc nhiÒu.
Víi tÊt c¶ c¸c t¸c ®éng nh­ nhiÖt ®é, t¶i träng th× kÕt cÊu c¬ b¶n chØ cÇn
chän ®Ó kÕt cÊu bÊt biÕn h×nh lµ ®­îc. Cßn víi kÕt cÊu chÞu chuyÓn vÞ gèi
tùa nh­ng kÕt cÊu cã chuyÓn vÞ c­ìng bøc th× nªn lùa chän kÕt cÊu c¬
b¶n hîp lý - Th«ng th­êng th× c¾t liªn kÕt ra chø kh«ng lo¹i bá or cßn gi¶i
ph¸p ®ã lµ sö dông lo¹i bá Èn t¹i vÞ trÝ kh«ng cã chuyÓn vÞ gèi tùa môc ®Ých
chØ ®Ó vÕ ph¶i cña ph­¬ng tr×nh chÝnh t¾c lu«n b»ng 0. Vµ nÕu b¹n lo¹i bá
th× cÇn chó ý ®Õn vÕ ph¶i cña ph­¬ng tr×nh chÝnh t¾c ®Ó tr¸nh dÉn ®Õn
viÖc tÝnh to¸n sai kÕt qu¶. 5
Bµi Gi¶ng - H­íng dÉn gi¶i bµi tËp c¬ kÕt cÊu 2
Tr­êng hîp hÖ giµn hay thanh 2 ®Çu khíp cã EA ≠ ∞ vµ t¶i träng kh«ng t¸c
dông trªn thanh ta quy ®Þnh chØ ®­îc phÐp c¾t vµ thay thÕ b»ng c¸c cÆp
lùc ng­îc chiÒu nhau vµ kh«ng ®­îc phÐp c¾t bá. (a) (b)
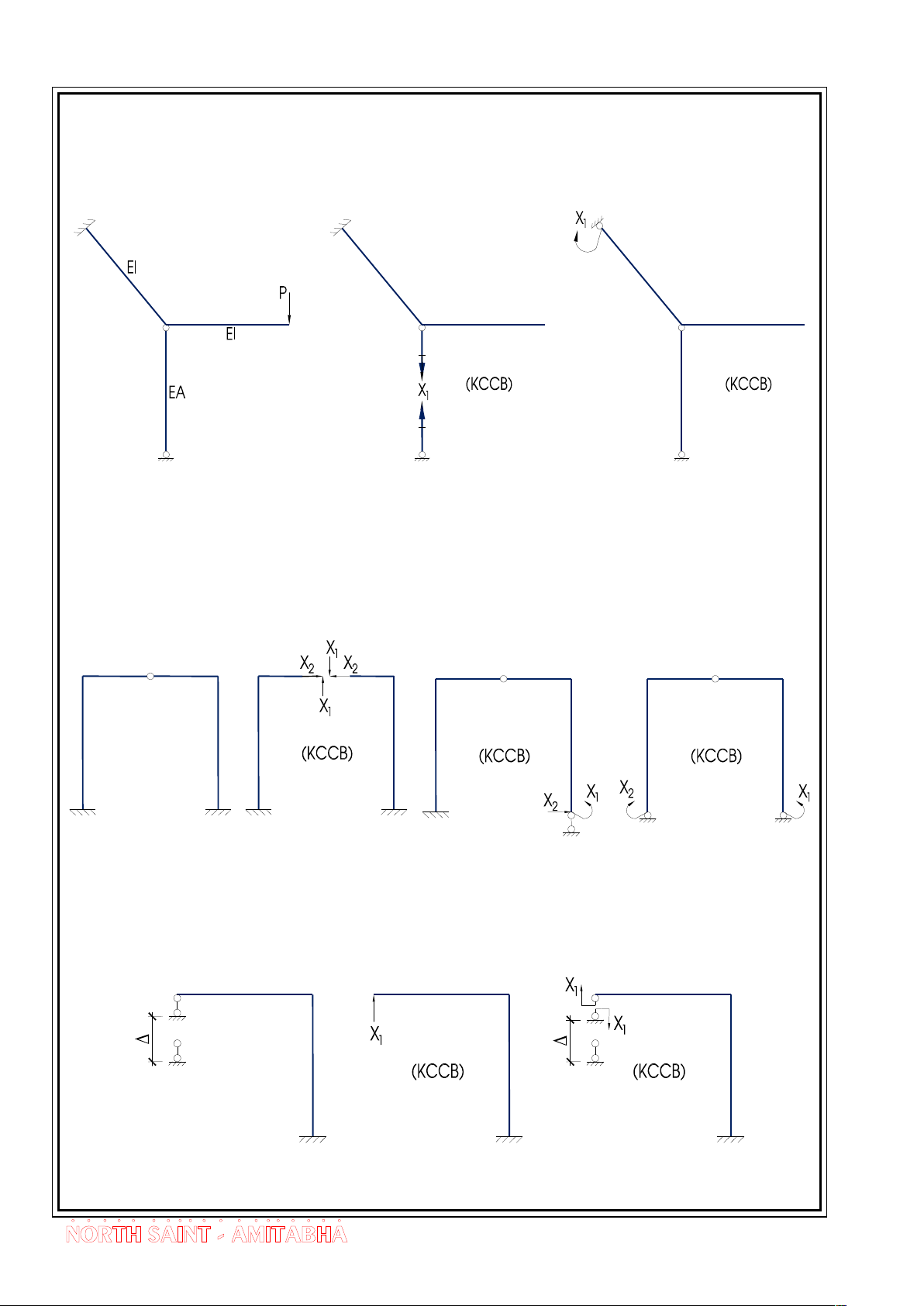
H×nh 1.5 Lùa chän kÕt cÊu c¬ b¶n (n = 1)
ë H×nh 1.5 ta thÊy kÕt cÊu cã bËc siªu tÜnh n = 5 + 2.1 - 3.2 = 1, trªn h×nh lµ 2
c¸ch chän kÕt cÊu c¬ b¶n. Víi bµi to¸n nµy ta nªn chän kÕt cÊu c¬ b¶n theo h×nh a. (a) (b) (c)
H×nh 1.6 Lùa chän kÕt cÊu c¬ b¶n (n = 2)
ë H×nh 1.6 ta nªn chän kÕt cÊu c¬ b¶n theo h×nh a v× kÕt cÊu ®èi xøng nªn c¸c hÖ sè tÝnh to¸n dÔ. (a) (b)
H×nh 1.7 KÕt cÊu c¬ b¶n cho hÖ chÞu chuyÓn vÞ c­ìng bøc t¹i gèi tùa 6
Bµi Gi¶ng - H­íng dÉn gi¶i bµi tËp c¬ kÕt cÊu 2
Ta thÊy nÕu lùa chän KCCB theo h×nh a th× ph­¬ng tr×nh chÝnh t¾c
 X     , nÕu lùa chän kÕt cÊu c¬ b¶n theo h×nh b th× ph­¬ng tr×nh 11 1 1
chÝnh t¾c  X    .  0 11 1 1 1.2. HÖ 1 bËc siªu tÜnh
Ta thùc hiÖn theo c¸c b­íc c¬ b¶n sau:
B­íc 1 - BËc siªu tÝnh n = 1
B­íc 2 - Chän kÕt cÊu c¬ b¶n nh­ h×nh vÏ
Cã rÊt nhiÒu c¸ch chän kÕt cÊu c¬ b¶n, nªn viÖc lùa chän kccb sao cho
viÖc vÏ vµ tÝnh to¸n ®¬n gi¶n nhÊt cã thÓ.
B­íc 3 - Ph­¬ng tr×nh chÝnh t¾c
ViÖc viÕt ph­¬ng tr×nh chÝnh t¾c trªn nguyªn t¾c céng t¸c dông, khi ®Ò bµi
cho kÕt cÊu chÞu t¸c ®éng nµo th× ta thiÕt lËp víi lo¹i t¸c ®éng ®ã. Ph­¬ng
tr×nh chÝnh t¾c d­íi ®©y viÕt víi tr­êng hîp kÕt cÊu chÞu t¶i träng, nhiÖt ®é, chuyÓn vÞ c­ìng bøc.
 X        ( 1.4 )  0 11 1 1P 1t 1
B­íc 4 - VÏ biÓu ®å m«men do t¶i träng ®¬n vÞ, t¶i träng, nhiÖt ®é vµ
chuyÓn vÞ c­ìng bøc g©y ra trªn kÕt cÊu c¬ b¶n
B­íc 5 - TÝnh to¸n c¸c hÖ sè vµ sè h¹ng tù do
Bµi to¸n nh©n biÓu ®å, ta nªn vËn dông linh ho¹t ®Ó viÖc nh©n biÓu ®å
thùc hiÖn ®¬n gi¶n nhÊt. Nguyªn t¾c chung vÉn lµ diÖn tÝch bËc cao nh©n
tung ®é bËc thÊp, khi chóng ®ång bËc nªn lùa chän hîp lý viÖc x¸c ®Þnh
h×nh lÊy diÖn tÝch vµ h×nh lÊy tung ®é. Khi nh©n biÓu ®å cÇn chó ý thí c¨ng
cña nhau ®Ó tr¸nh sai dÊu.
E.X 1.2 - Thùc hiÖn ph©n tÝch 1 h×nh ®Ó hiÓu râ c¸ch nh©n biÓu ®å. 7
Bµi Gi¶ng - H­íng dÉn gi¶i bµi tËp c¬ kÕt cÊu 2 H×nh 1.8 H×nh thùc nghiÖm
ë bµi vÝ dô nµy ta thùc hiÖn lÊy diÖn tÝch cña h×nh 1 nh©n víi tung ®é t­¬ng
øng cña h×nh 2 (ViÖc thùc hiÖn ng­îc l¹i lµ hoµn toµn t­¬ng tù) hay thÓ hiÖn b»ng biÓu thøc (
 1).y(2) viÖc tÝnh to¸n thùc hiÖn nh­ sau.
H×nh 1 - Lµ tam gi¸c nªn ta cã ngay diÖn tÝch tam gi¸c 1   .a.L , sau ®ã (1) 2
ta x¸c ®Þnh ®­îc träng t©m h×nh häc cña h×nh 1, ë ®©y ta chØ quan t©m 1
to¹ ®é cña träng t©m ®ã lµ tung ®é. Sau ®ã, chiÕu to¹ ®é träng t©m nµy
xuèng h×nh 2 th× ta ®­îc 1 ®o¹n tung ®é y(2) t­¬ng øng. XÐt tû sè tam gi¸c y
®ång d¹ng ta cã (2) 2L / 3 2 2b    y(2) 
. Hay biÓu thøc cuèi cïng ta cã b L 3 3 ®­îc lµ 1 2b abL  .y  .a.L.  . (1) (2) 2 3 3
Nh×n chung lµ b­íc nµy yªu cÇu c¸c b¹n tÝnh to¸n cÈn thÈn chót ®Ó h¹n chÕ sai sãt.
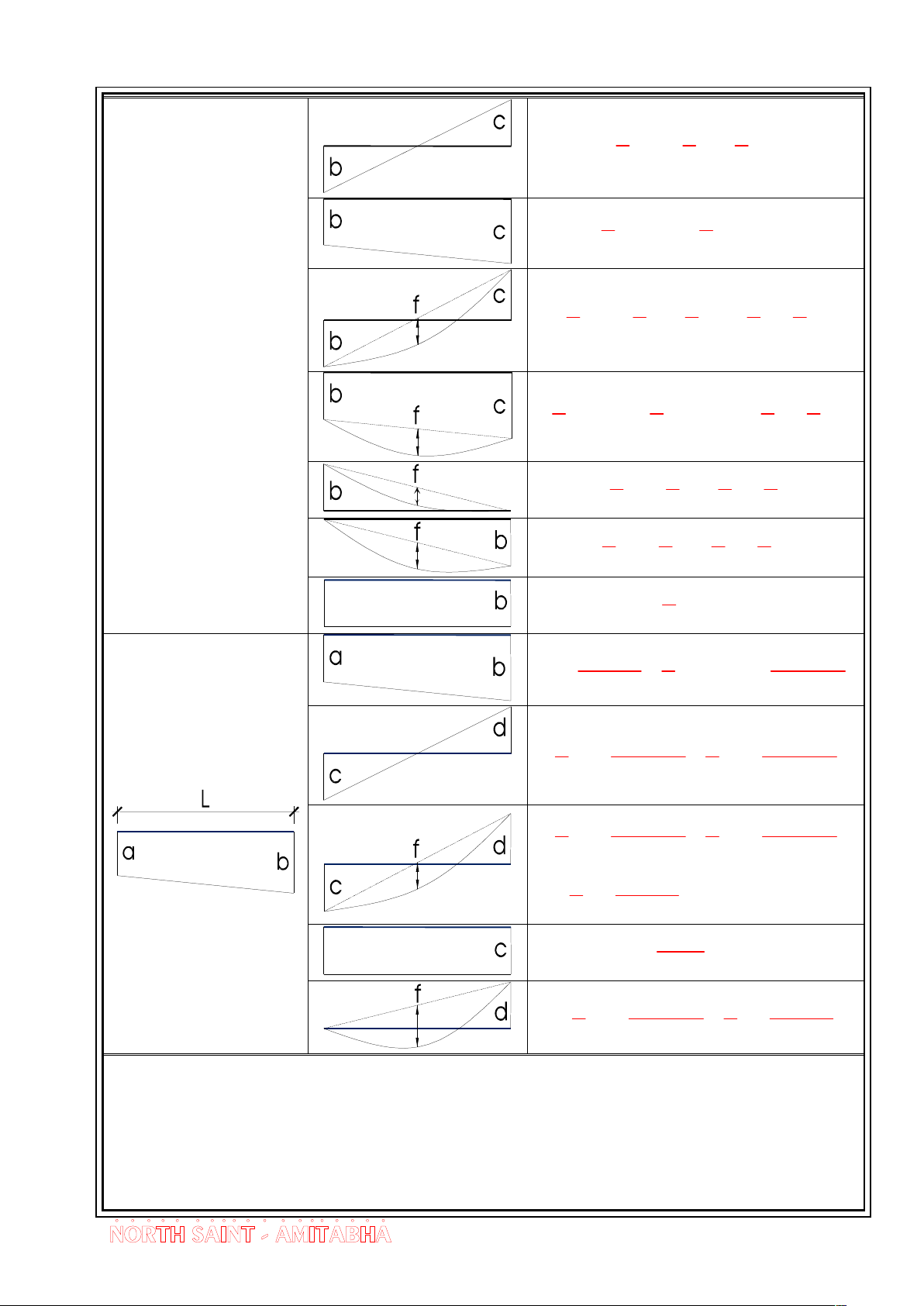
Sau ®©y lµ nh÷ng h×nh ®¬n gi¶n hay gÆp trong qu¸ tr×nh nh©n biÓu ®å. Do
vËy h·y rÌn luyÖn kü n¨ng bÊm m¸y tÝnh ®Ó h¹n chÕ thêi gian tÝnh to¸n, v×
th«ng th­êng bµi to¸n theo ph­¬ng ph¸p lùc lµ tÝnh to¸n kh¸ nhiÒu.
B¶ng 1.1 B¶ng nh©n biÓu ®å H×nh 1 H×nh 2 BiÓu thøc nh©n biÓu ®å 1 2 abL .a.L. .b  2 3 3 1 1 abL .a.L. .b  2 3 6 8
Bµi Gi¶ng - H­íng dÉn gi¶i bµi tËp c¬ kÕt cÊu 2 1  1 2 .a.L. .b .c  2  3 3    1  2 .a.L. b .c b     2  3  1  1 2  2 1 .a.L. .b  .c  .f.L. .a 2  3 3    3 2 1  2      2 1 .a.L. b . c b  .f.L. .a 2 3    3 2 1 1 2 1  .a.L. .b  .f.L. .a 2 3 3 2 1 2 2 1 .a.L. .b  .f.L. .a 2 3 3 2 1 .a.L.b 2 ab 1  a.L.  .b  a a 2b .L. 2 2 3 1 2ab 1 a 2b .c.L.  .d.L. 2 3 2 3 1 2ab 1 a2b .c.L.  .d.L. 2 3 2 3 1 ab  .f.L. 2 2 ab.L.c 2 1 a 2b 2 ab  .d.L.  .f.L. 2 3 3 2
Víi nh÷ng bµi to¸n trong kÕt cÊu cã thanh mµ xÐt ®Õn biÕn d¹ng däc trôc
“Th­êng th× trong ®Ò thanh ®ã sÏ cho cã ®é cøng EA (EF)” th× khi tÝnh to¸n
hÖ sè hay sè h¹ng tù do kh«ng ®­îc bá qua nã.
B­íc 6 - Thay sè vµo gi¶i hÖ ra ta cã X1 = 9
Bµi Gi¶ng - H­íng dÉn gi¶i bµi tËp c¬ kÕt cÊu 2
B­íc 7 - Theo nguyªn t¾c céng t¸c dông ta cã biÓu ®å m«men cuèi cïng ( 1.5 ) M  M X  M 1 1  P 
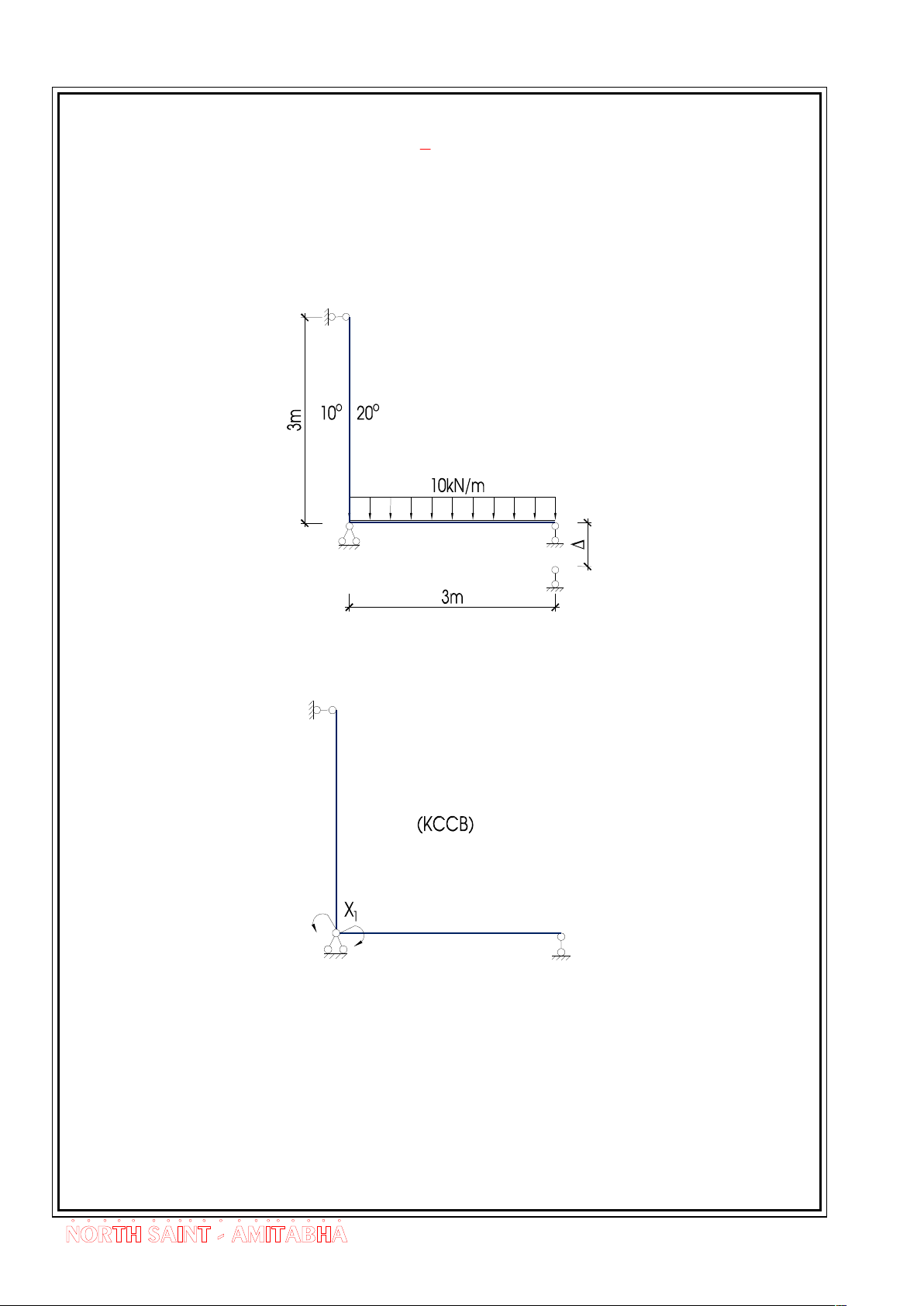
E.X 1.3 - Cho kÕt cÊu nh­ h×nh vÏ sau. TÝnh to¸n vµ vÏ biÓu ®å m«men theo
ph­¬ng ph¸p lùc. Cho biÕt chiÒu cao h cña tiÕt diÖn kh«ng ®æi, EI = Const,
vËt liÖu cã hÖ sè gi·n në v× nhiÖt .”TrÝch ®Ò thi CKC f2 §H X©y Dùng Hµ Néi”.
BËc siªu tÜnh n = L0 + 2K - 3T = 4 + 0 - 3.1 = 1
Chän kÕt cÊu c¬ b¶n nh­ h×nh vÏ sau
Ph­¬ng tr×nh chÝnh t¾c  X         0 11 1 1P 1t 1
VÏ biÓu ®å m«men vµ lùc däc t­¬ng øng do t¶i träng ®¬n vÞ vµ t¶i träng
g©y ra trªn kÕt cÊu c¬ b¶n. 10
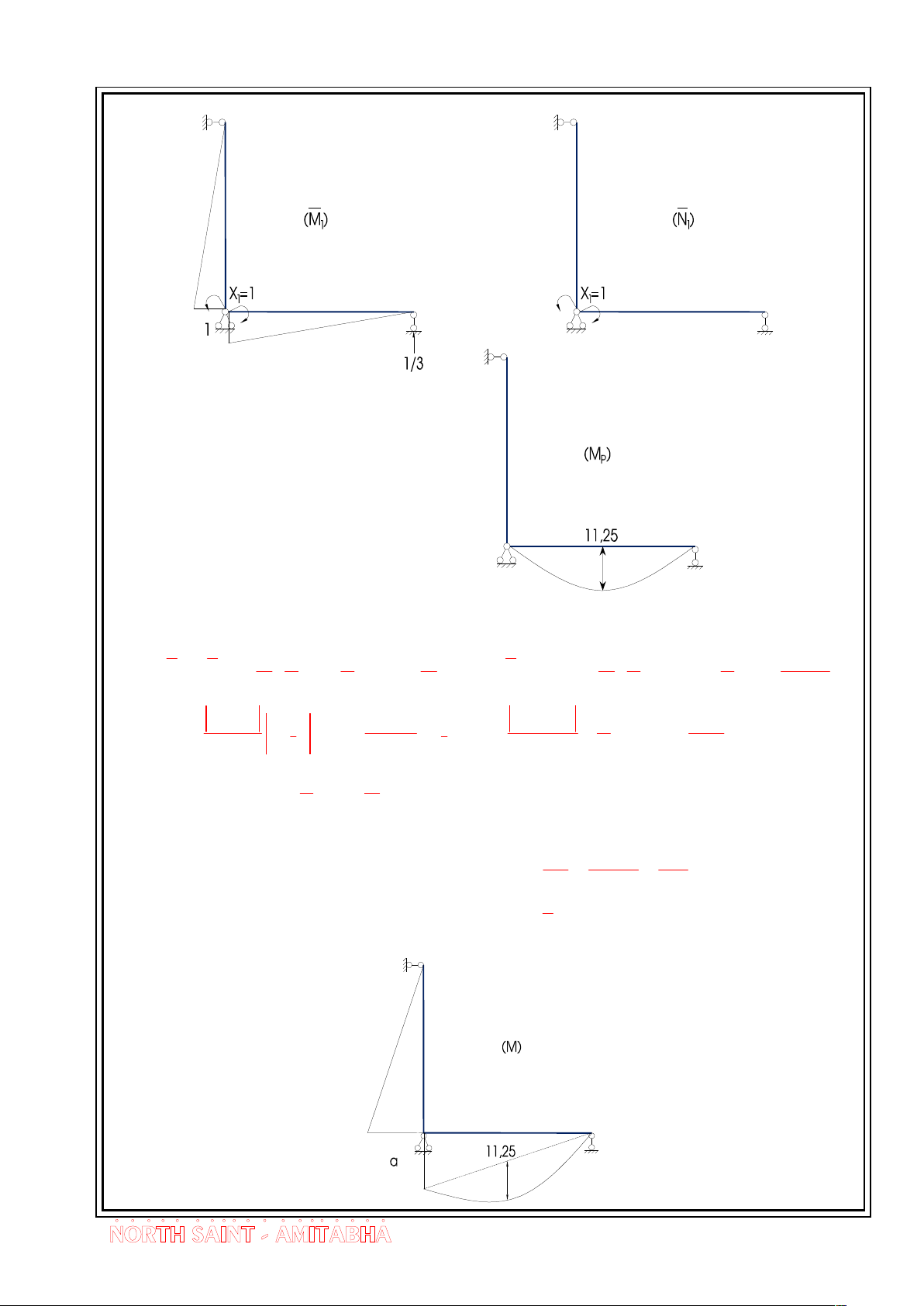
Bµi Gi¶ng - H­íng dÉn gi¶i bµi tËp c¬ kÕt cÊu 2
TÝnh to¸n c¸c hÖ sè vµ sè h¹ng tù do 1 1 2  2 1 2 1  11, 25 1  1   1 M  1 M   .3.1. .1.2  ;   1  P   1 M  P M   .3.11,25. .1  EI 2 3 EI EI 3 2      EI t  t t  t 20 10 2 1 1 2  1  15 1  t          . .3.1     1 M   1N h 2 h  2  h  1  
           R . 1  i i  3    3
Thay sè vµo gi¶i ph­¬ng tr×nh ra ta cã 45 15EI EI X      a  0 "Gi¶ sö" 1 8 2h 6
Theo nguyªn lý céng t¸c dông ta cã M  M X  M 1 1  P  11
Bµi Gi¶ng - H­íng dÉn gi¶i bµi tËp c¬ kÕt cÊu 2
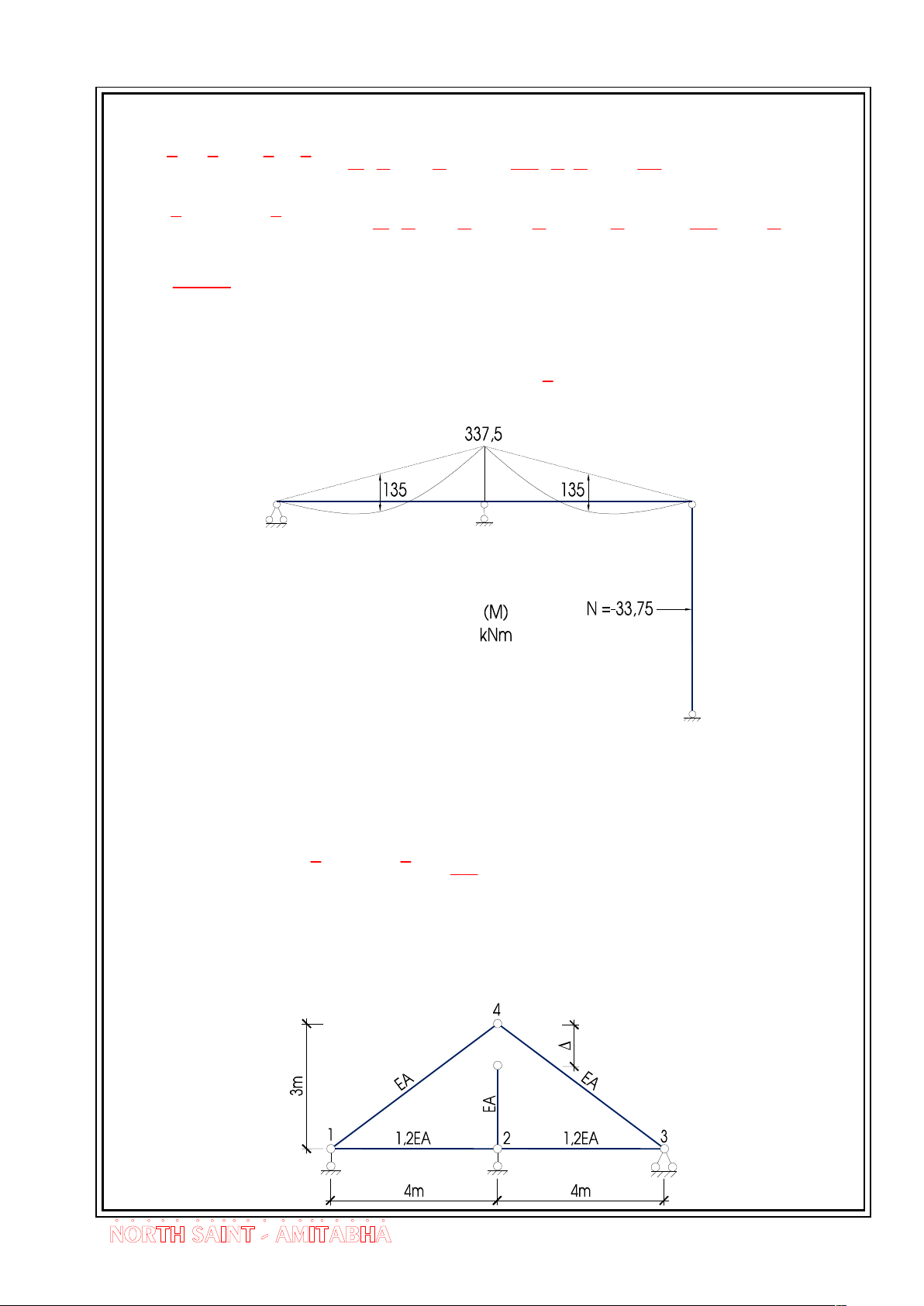
E.X 1.4 - TÝnh to¸n vµ vÏ biÓu ®å m«men cña kÕt sau b»ng ph­¬ng ph¸p
lùc. Gi¶ thiÕt EI = Const, EA = 3EI/72. TÝnh chuyÓn vÞ th¼ng ®øng t¹i K. ”TrÝch
®Ò thi CKC f2 §H X©y Dùng Hµ Néi”.
BËc siªu tÜnh n = L0 + 2K - 3T = 5 + 2.1 - 3.2 = 1
Chän kÕt cÊu c¬ b¶n nh­ h×nh vÏ
Ph­¬ng tr×nh chÝnh t¾c  X    0 11 1 1P
VÏ biÓu ®å m«men do t¶i träng ®¬n vÞ vµ t¶i träng g©y ra trªn KCCB 12
Bµi Gi¶ng - H­íng dÉn gi¶i bµi tËp c¬ kÕt cÊu 2
TÝnh to¸n c¸c hÖ sè vµ sè h¹ng tù do 1 1 2  1 1 1  72   M M  N N  .6.3. .3.2  . .6  11
 1 1  1 1 EI2 3  EA 2 2      EI 1 1 2 2 1  1  1 M M N N .3.6. .540 .6.135. .3 .2 180. .6        1P
 1 P  1 P EI2 3 3 2  EA  2      21060   EI
Thay sè vµo gi¶i ph­¬ng tr×nh ra ta cã X  292, 5kN 1
Theo nguyªn lý céng t¸c dông ta cã M  M X  M 1 1  P 
Ta thiÕt lÊp tr¹ng th¸i “K” b»ng c¸ch ®Æt lùc Pk = 1 t¹i K theo chiÒu h­íng
xuèng vµ vÏ biÓu ®å m«men ®¬n vÞ trªn KCCB. Lóc nµy ta cã trong thanh
th¼ng ®øng cã lùc däc ®¬n vÞ = -1. VËy chuyÓn vÞ th¼ng ®øng t¹i K lµ: 1 y  M M  N N 
 1 . 33,75 .6  4860 "  " K
  k   k     EA 
E.X 1.5 - Ta tÝnh néi lùc trong thanh giµn cã thanh chÕ t¹o chiÒu dµi kh«ng
chÝnh x¸c. “TrÝch ®Ò thi CKC f2 tr­êng §HXD Hµ Néi 12/2015 - M· ®Ò 29”  = 9,0.10-3 13
Bµi Gi¶ng - H­íng dÉn gi¶i bµi tËp c¬ kÕt cÊu 2
BËc siªu tÜnh n = D + C - 2M = 5 + 4 - 2.4 = 1. Anh ®i ®©u rïi!
Chän kÕt cÊu c¬ b¶n nh­ h×nh vÏ sau:
Ph­¬ng tr×nh chÝnh t¾c  X     0 11 1 1
Ta thiÕt lËp tr¹ng th¸i “k” b»ng c¸ch cho X1 = 1 ®Ó x¸c ®Þnh lùc däc trong c¸c thanh.
KÕt qu¶ ®­îc thèng kª trong b¶ng sau:
B¶ng 1.2 - Thèng kª kÕt qu¶ Thanh li (m) EAi 1 N 1 N . 1 N .il /EA N 1 - 2 4 1,2EA -2/3 40/27EA 4 4, 67.10 EA 2 - 3 4 1,2EA -2/3 40/27EA 4 4, 67.10 EA 3 - 4 5 EA 5/6 125/36EA 4 5,83.10  EA 4 - 1 5 EA 5/6 125/36EA 4 5,83.10  EA 2 - 4 3 EA -1 3EA 4 7.10 EA
Ta tÝnh to¸n c¸c hÖ sè vµ sè h¹ng t­ do 40 125 3 697   .2  .2   11 27EA 36EA EA 54EA 3 "k   iNkim " 1   ( 1
 ).()    9.10   Thay sè vµo gi¶i ra ta cã 4  1 X  7  .10 EA
VËy ta cã lùc däc trong c¸c thanh N  N X 1 1 14
Bµi Gi¶ng - H­íng dÉn gi¶i bµi tËp c¬ kÕt cÊu 2
Lùc däc trong c¸c thanh ®­îc thèng kª trong B¶ng 1.2 Over there 
1.3. HÖ cã bËc siªu tÜnh lín h¬n 1 “Th«ng th­êng lµ 2 trong ®Ò”
C¸c vÝ dô ®­îc thùc hiÖn chi tiÕt râ rµng ®Ýnh kÌm trong 3 cuèn h­íng dÉn
gi¶i bµi tËp c¬ kÕt cÊu F2 do KS. NguyÔn V¨n B¾c biªn so¹n n¨m 2015.
 Cuèn 1: H­íng dÉn gi¶i bµi tËp c¬ kÕt cÊu F2 - Uno
 Cuèn 2: H­íng dÉn gi¶i bµi tËp c¬ kÕt cÊu F2 - Due
 Cuèn 3: H­íng dÉn gi¶i bµi tËp c¬ kÕt cÊu F2 - Tre
Uno - Cuèn nµy h­íng dÉn gi¶i bµi tËp trong gi¸o tr×nh bµi tËp c¬ kÕt cÊu
F2 do ThÇy §inh NghÜa Dòng - Gi¶ng viªn §H GTVT Hµ Néi biªn so¹n.
Due - Cuèn nµy h­íng dÉn gi¶i bµi tËp c¬ kÕt cÊu F2, ®Ò bµi do ThÇy T¹
Duy HiÓn - Gi¶ng viªn §H GTVT Hµ Néi biªn so¹n.
Tre - Cuèn nµy h­íng dÉn gi¶i bµi tËp c¬ kÕt cÊu F2, ®Ò bµi do ThÇy
NguyÔn Duy H­ng - Gi¶ng viªn §H GTVT Hµ Néi biªn so¹n.
1.3.1. HÖ kÕt cÊu chÞu t¸c dông cña t¶i träng
Bµi to¸n nµy lµ phæ biÕn nhÊt trong c¸c bµi kiÓm tra hay bµi thi v× nã mang
tÝnh chÊt c¬ së sinh viªn nµo còng ph¶i biÕt lµm nªn ta sÏ ®i t×m hiÓu trong
kh¶ n¨ng cã thÓ tÊt c¶ nh÷ng d¹ng to¸n liªn quan ®Õn t¸c dông cña t¶i träng.
D¹ng 1: Cho 1 kÕt cÊu siªu tÜnh th«ng th­êng chÞu t¸c dông cña t¶i träng.
Yªu cÇu: TÝnh to¸n vµ vÏ biÓu ®å m«men cña kÕt cÊu. VÏ biÓu ®å lùc c¾t
vµ lùc däc. §Ó hiÓu râ ta thùc hiÖn mét vÝ dô kÌm theo c¸c b­íc cô thÓ.
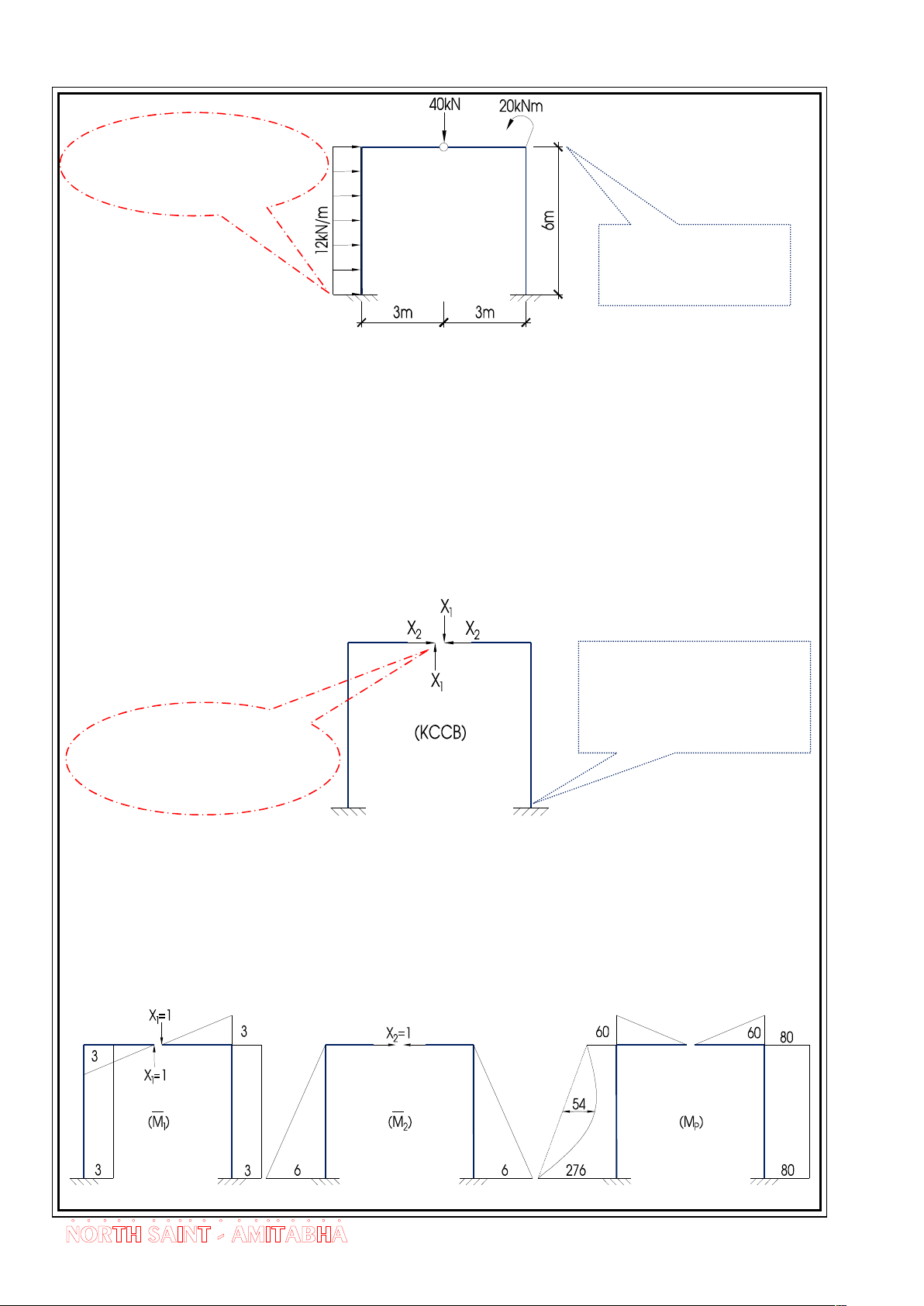
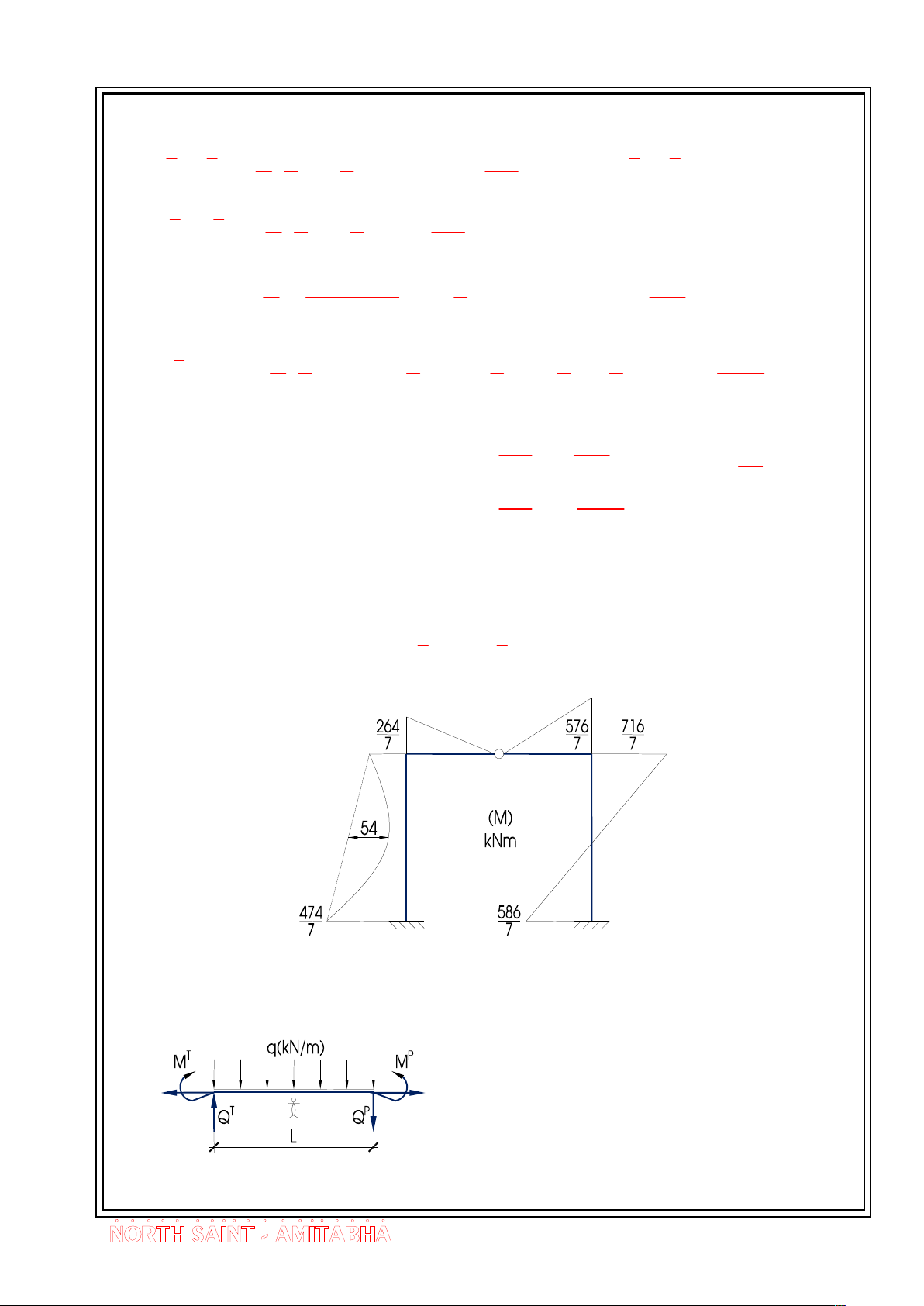
E.X 1.6 - TÝnh to¸n vµ vÏ biÓu ®å m«men cña kÕt cÊu sau b»ng ph­¬ng
ph¸p lùc. Gi¶ thiÕt EI = Const. “TrÝch ®Ò thi CKC f2 §H GTVT Hµ Néi - §Ò sè 3” 15
Bµi Gi¶ng - H­íng dÉn gi¶i bµi tËp c¬ kÕt cÊu 2 Tr­íc em anh ®· yªu ai ch­a vËy? Anh míi yªu cã 2 ng­êi thui ah!
B­íc 8 - X¸c ®Þnh bËc siªu tÜnh: X¸c ®Þnh theo1.1.3 th­êng th× trong bµi thi
tr­êng §H GTVT Hµ Néi th× n = 2 “§Ò 2 tÝn chØ”, b©y giê ®Ò 4 tÝn chØ theo quan
s¸t th× bµi siªu tÜnh ®a phÇn lµ yªu cÇu tÝnh to¸n theo ph­¬ng ph¸p chuyÓn vÞ. n = 3V - K = 3.1 - 1 = 2
B­íc 9 - Chän kÕt cÊu c¬ b¶n. Ko ®©u em, vÞ trÝ ®ã lµm em ®Ñp vµ Anh ah chç nµy quyÕn rò h¬n nhiÒu! cã nh¹y c¶m ko?
 X   X    0
B­íc 10 - HÖ ph­¬ng tr×nh chÝnh t¾c 11 1 12 2 1P   X   X    0  21 1 22 2 2P
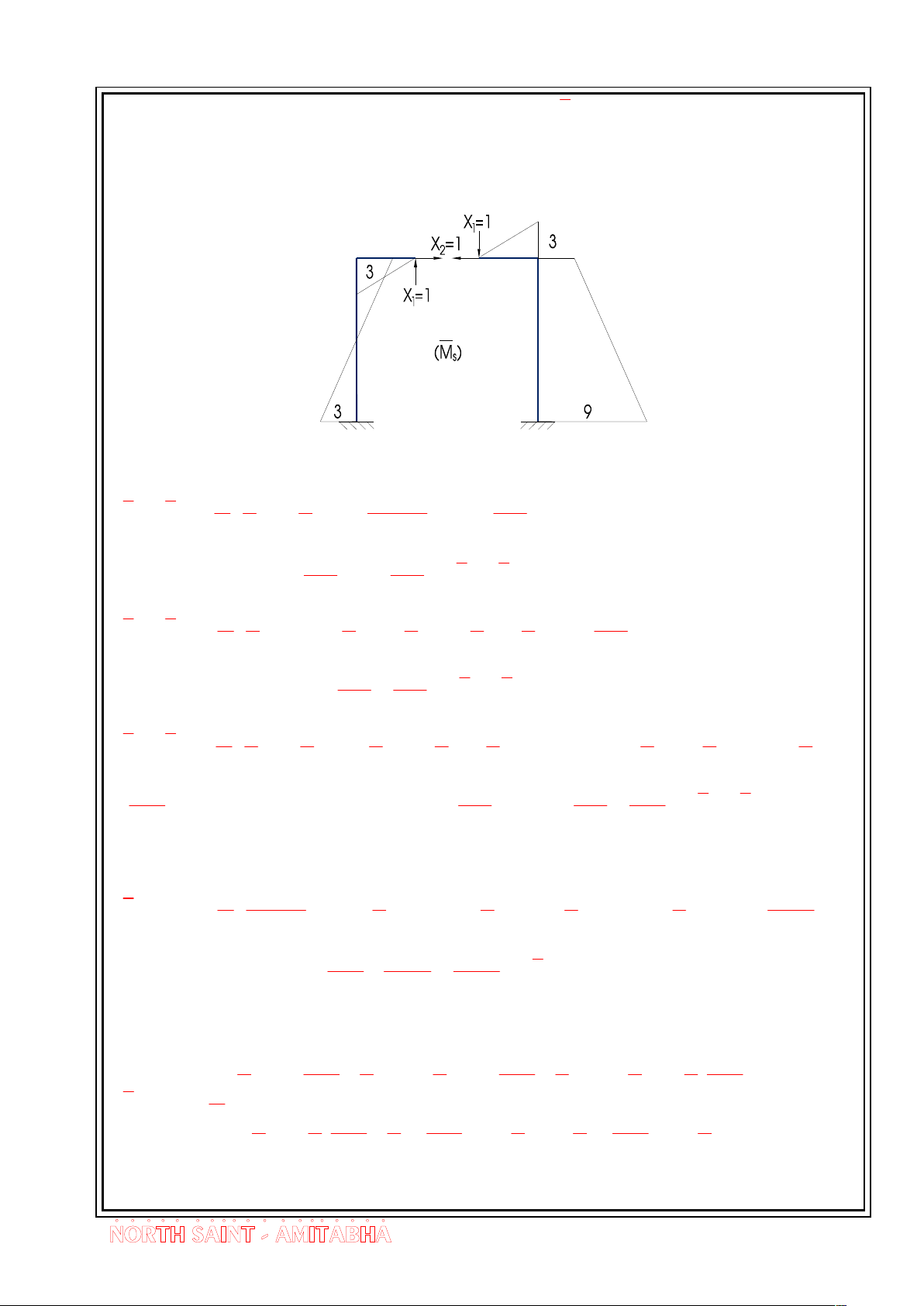
B­íc 11 - VÏ biÓu ®å m«men do t¶i träng ®¬n vÞ vµ t¶i träng g©y ra trªn KCCB. 16
Bµi Gi¶ng - H­íng dÉn gi¶i bµi tËp c¬ kÕt cÊu 2
B­íc 12 - TÝnh to¸n c¸c hÖ sè vµ sè h¹ng tù do 1 1 2  126   M M  .3.3. .3  6.3.3 .2  ;    M M  0 11  1 1   12 21  1 2 EI 2 3  EI 1 1 2  144   M M  .6.6. .6 .2  22  2 2 EI2 3    EI 1  60  276 2  936   M M  
.6.3  .54.6.3  80.6.3   1P  1 P   EI  2 3   EI  1 1  2  2 1 1  4464 2P   2 M  P
M    .6.6. 60  .216  .54.6. .6  .6.6.80     EI 2  3  3 2 2  EI 1  26 936 X   0  52  1 B­íc 13 -  EI EI X  kN
Thay sè vµo gi¶i hÖ ra ta cã 1    7 144 4464  X   0 X  3  1kN 2 2  EI EI
B­íc 14 - Theo nguyªn t¾c céng t¸c dông ta cã biÓu ®å m«men cuèi cïng.
M  M X  M X  M 1  1  2  2  P 
X¸c ®Þnh lùc c¾t: Ta x¸c ®Þnh theo biÓu ®å m«men - Trªn c¬ së ®ã ta cã
biÓu thøc x¸c ®Þnh lùc c¾t nh­ sau:
§Ó cã ®­îc biÓu thøc nµy ta thùc
lÊy tæng m«men t¹i ®iÓm bªn ph¶i NT NP
sÏ cã biÓu thøc QT vµ lÊy tæng
m«men t¹i ®iÓm bªn tr¸i ta ®­îc QT. 17
Bµi Gi¶ng - H­íng dÉn gi¶i bµi tËp c¬ kÕt cÊu 2 P T P T T M  M 1 P M  M 1 Q   qL vµ Q   qL ( 1.6 ) L 2 L 2
Chó ý ta cÇn ®Ó ý vÞ trÝ ®øng ®Ó lÊy dÊu gi¸ trÞ m«men. Dï ®øng ë vÞ trÝ nµo
th× gi¸ trÞ m«men c¨ng trªn lµ ©m (-), c¨ng d­íi lµ d­¬ng (+). Ta cÇn linh
ho¹t vËn dông biÓu thøc ®Ó tr¸nh sai kÕt qu¶ khi thay ®æi vÞ trÝ ®øng.
§Ó hiÓu râ biÓu thøc (1.6) ta thùc hiÖn cho vÝ dô sau:
E.X 1.6 - TÝnh to¸n vµ vÏ biÓu ®å m«men cña kÕt cÊu sau b»ng ph­¬ng
ph¸p lùc. Gi¶ thiÕt EI = Const. Ta ®¸nh dÊu c¸c ®iÓm cô thÓ nh­ h×nh sau.
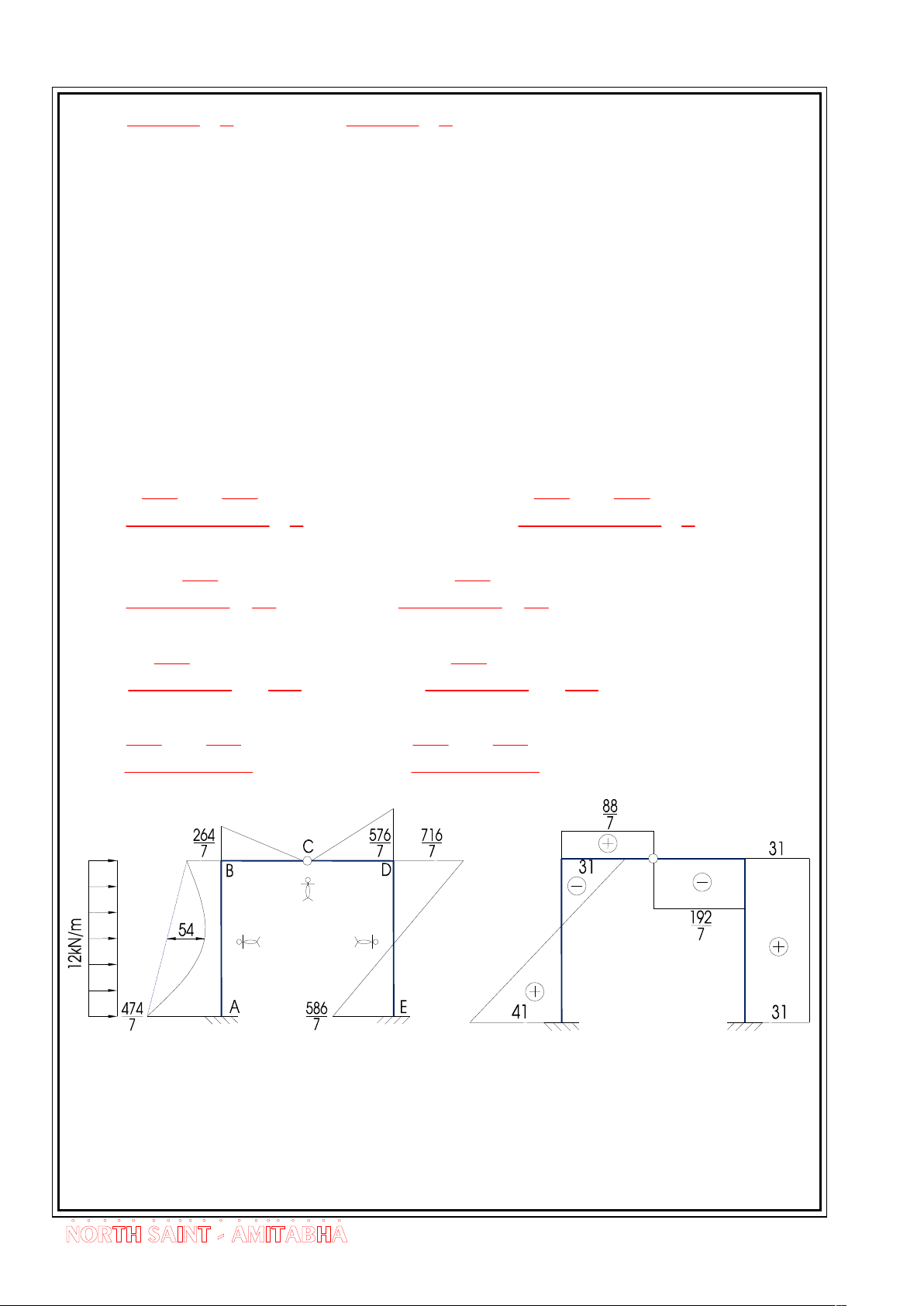
Víi vÞ trÝ ®øng t­¬ng øng cho tõng ®o¹n, ta cã gi¸ trÞ lùc c¾t ®­îc thÓ hiÓn nh­ biÓu thøc sau: 264  474  264  474            T 7  7  1 P 7  7  1 Q   .12.6  41kN vµ Q   .12.6  31kN AB BA 6 2 6 2  264   264 0 0          T  7  88 P  7  88 QBC   kN vµ QCB   kN 3 7 3 7  576   576 0      0     T  7  192 P  7  192 Q    kN vµ Q    kN CD DC 3 7 3 7 586  716  586  716         T 7 Q   7  P 7  7 31kN vµ Q     31kN DE ED 6 6 (Q) kN
B­íc 15 - KiÓm tra biÓu ®å (Khi cã yªu cÇu th× thùc hiÖn b­íc nµy cßn nÕu kh«ng th× thui). 18
Bµi Gi¶ng - H­íng dÉn gi¶i bµi tËp c¬ kÕt cÊu 2
Tr­íc tiªn ta vÏ biÓu ®å m«men tæng céng M do X s 1 =1 vµ X2 =1 t¸c dông
lªn kÕt cÊu c¬ b¶n. Víi biÓu ®å nµy ta cø céng t¸c dông t¹i tõng vÞ trÝ cÇn
thiÕt ®Ó vÏ nhanh biÓu ®å. KiÓm tra c¸c hÖ sè  1 1 2 3  9  126 M M   .3.3. .3.2  .6.3  s   1   EI 2 3 2   EI  126 126 MÆt kh¸c,      0   M M  Ok 11 12  s 1 EI EI  1 1  2  1  2 1  144
M M   .6.6. 3  .6  .6.6. .3  .3      s   2  EI 2  3  2  3 3  EI 144 144
MÆt kh¸c,     0    M M  Ok 21 22  s 2 EI EI  1 1 2 M M   .3.3. 1  2 1   1  1  2
.3.2  .3.6. .3  .3 .2  3.6. 3  .6  .6.6. 3  .6 s   s  EI 2 3 2  3 3     2  2  3  270 126 144 270 
. MÆt kh¸c,          0  0    M M  Ok 11 12 21 22  s s EI EI EI EI
KiÓm tra c¸c sè h¹ng tù do  1  3  9 1  2  1  1  3528 M M  
.6.80  .6.3. 60  .216  .6.3. 60  .216      s   P    EI  2 2   3  2  3  EI  936 4464 3528
MÆt kh¸c,         M M  Ok 1P 2P  s P EI EI EI
KiÓm tra kÕt qu¶ cuèi cïng 1  264 2  1  264 1  1 2 264  .6.3.  .30  .6.3.  .30  .3.3. .   1 2  7 3  2  7 3      2 3 7  M M     0  Ok s   EI  1 2 576 1 716  1  1 586  2    .3.3. .  .6. . 3  .6  .6. . 3  .6  2 3 7 2 7  3  2 7  3    
BiÓu ®å lùc däc. Ta xÐt c©n b»ng c¸c nót tõ biÓu ®å lùc c¾t 19
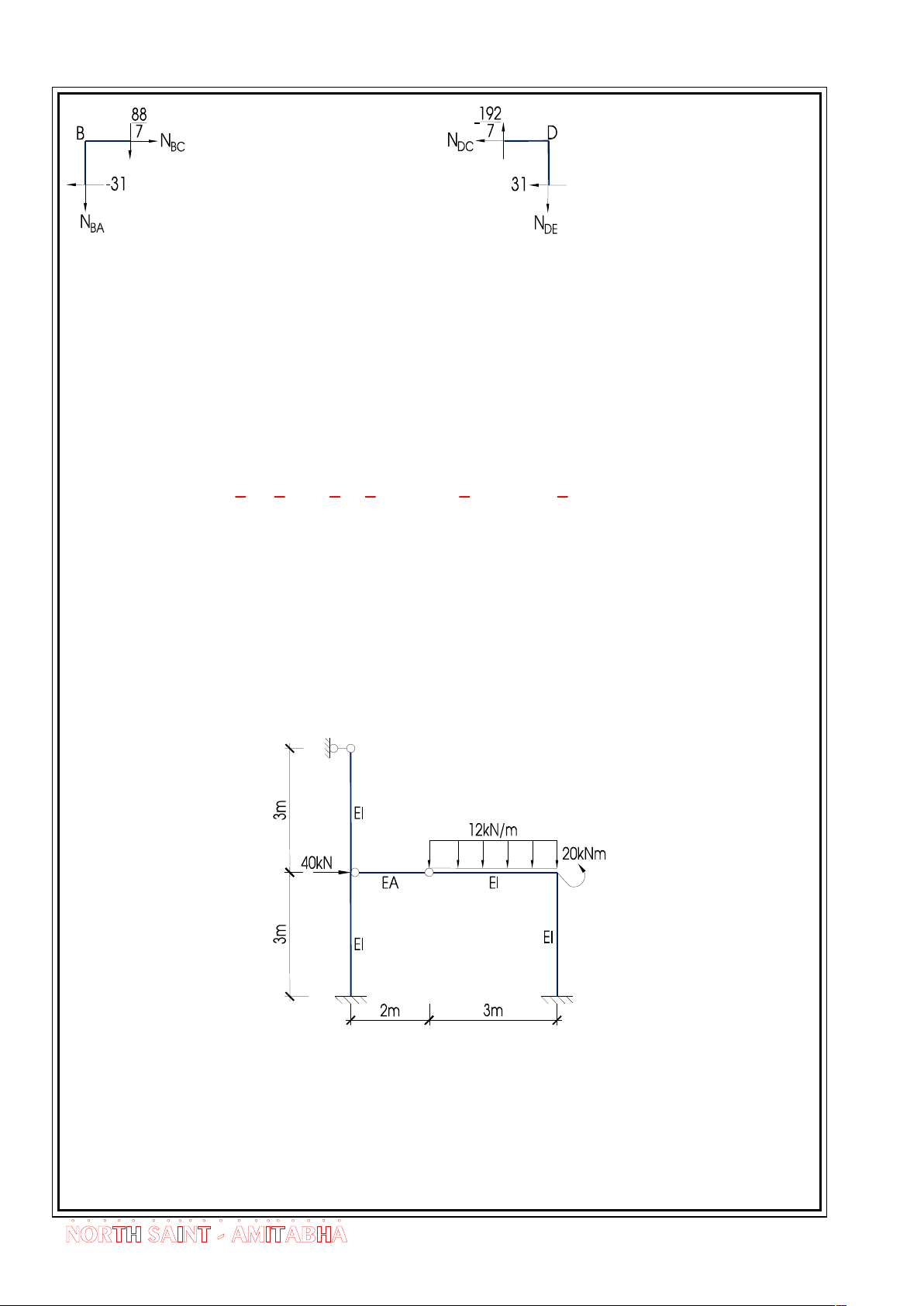
Bµi Gi¶ng - H­íng dÉn gi¶i bµi tËp c¬ kÕt cÊu 2 Tæng h×nh chiÕu theo Tæng h×nh chiÕu theo ph­¬ng ngang ta cã: ph­¬ng ngang ta cã: NBC = -31kN NDC = -31kN Tæng h×nh chiÕu theo Tæng h×nh chiÕu theo ph­¬ng th¼ng ®øng: ph­¬ng th¼ng ®øng: NBA = -88/7kN NDE = -192/7kN
D¹ng 2: Cho 1 kÕt cÊu siªu tÜnh th«ng th­êng chÞu t¸c dông cña t¶i träng.
Nh­ng trong kÕt cÊu cã 1 thanh cã xÐt ®Õn ¶nh h­ëng cña lùc däc or cho
cã cho EA nh­ng EA = ∞. Yªu cÇu: TÝnh to¸n vµ vÏ biÓu ®å m«men cña kÕt
cÊu. VÏ biÓu ®å lùc c¾t vµ lùc däc.
Khi tÝnh to¸n c¸c hÖ sè vµ sè h¹ng tù do th× cÇn xÐt ®Õn ¶nh h­ëng däc
trôc cña c¸c thanh 2 ®Çu khíp hay c¸c hÖ sè ®­îc thÓ hiÖn cô thÓ sau: ( 1.7 )
  M M  N N ;   M M  N N ij
 i j  i j iP  i P  i P
Víi EA = ∞ th× biÓu thøc (1.7) sÏ chØ cã c¸c thµnh phÇn thø nhÊt, c¸c thµnh
phÇn thø hai (hay chuyÓn vÞ däc trôc) = 0. Ta ®i vµo tõng vÝ dô cô thÓ sau
®©y ®Ó hiÓu râ vÊn ®Ò.
E.X 1.7 - VÏ biÓu ®å m«men cña kÕt cÊu b»ng ph­¬ng ph¸p lùc. “TrÝch ®Ò
thi CKC f2, 2 tÝn chØ tr­êng §H GTVT Hµ Néi - M· ®Ò 37”. Gi¶ thiÕt EA = EI.
BËc siªu tÜnh n = L0 + 2K - 3T = 7 + 2.2 - 3.3 = 2
Chän kÕt cÊu c¬ b¶n nh­ h×nh sau: 20