
































































































Preview text:
Xác suất thống kê Bài tập Nguyễn Đăng Minh Copyright c 2019 Nguyễn Đăng Minh LƯU HÀNH NỘI BỘ
HTTPS://SITES.GOOGLE.COM/VIEW/NGUYENDANGMINH1986/HOME
In lần đầu, Ngày 20 tháng 5 năm 2019 3 Mục lục I Phần Một: Xác suất 1
PHÉP ĐẾM . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9 1.1 Lý thuyết 9 1.2 Bài tập 10 2
XÁC SUẤT CƠ BẢN . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 11 2.1 Một số khái niệm 11 2.2 Xác suất có điều kiện 15 2.3 Xác suất toàn phần 17 3
BIẾN NGẪU NHIÊN RỜI RẠC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 21 3.1 Lý thuyết 21 3.2 Phân phối nhị thức 25 3.3 Phân phối siêu bội 28 3.4 Phân phối Poisson 29 4
BIẾN NGẪU NHIÊN LIÊN TỤC . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 31 4.1 Định nghĩa 31 4.2 Phân phối chuẩn 36 4.3 Định lí giới hạn 38 5
PHÂN PHỐI XÁC SUẤT ĐỒNG THỜI . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 41 5.1 Lý thuyết 41 5.2 Bài tập 43 II Phần Hai: Thống Kê 6
THỐNG KÊ MÔ TẢ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 47 6.1 Lý thuyết 47 6.2 Bài tập 50 7
ƯỚC LƯỢNG ĐIỂM . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 51 7.1
Một số khái niệm cơ bản 51 7.2
Khoảng tin cậy cho trung bình của phân phối chuẩn 52 7.2.1
Khoảng tin cậy cho trung bình khi biết phương sai . . . . . . . . . . . . . . . . . . . . . 52 7.2.2
Khoảng tin cậy cho trung bình khi chưa biết phương sai . . . . . . . . . . . . . . . . 53 7.3
Khoảng tin cậy cho phương sai 56 7.4
Khoảng tin cậy cho tỉ lệ của phân phối nhị thức 58 8
KIỂM ĐỊNH MỘT MẪU . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 59 8.1 Một số khái niệm 59 8.2 Kiểm định trung bình 60 8.3 Kiểm định phương sai 68 8.4 Kiểm định tỉ lệ 69 9
KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ HAI MẪU . . . . . . . . . . . . . . . . . . . . . 73 9.1 Lý thuyết 73 9.2 Bài tập 74 10
HỒI QUY – TƯƠNG QUAN . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83 10.1 Lý thuyết 83
10.1.1 Mô hình và ước lượng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 83
10.1.2 Tính chất thống kê . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 84
10.1.3 Kiểm định giả thuyết trong hồi quy tuyến tính . . . . . . . . . . . . . . . . . . . . . . . . . . 85
10.1.4 Khoảng tin cậy . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85
10.1.5 Tiên đoán giá trị quan trắc mới . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 85 10.2 Bài tập 86 III Phần Ba: Đề Thi Mẫu 11
ĐỀ THI GIỮA KÌ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 91 11.1 Đề 2 giữa kì 2018-2019 91 11.2 Đề 1 giữa kì 2018-2019 91 11.3 Đề 2 giữa kì 2018-2019 92 11.4 Đề 1 giữa kì 2017-2018 92 11.5 Đề 2 giữa kì 2017-2018 92 11.6 Đề giữa kì 2016-2017 93 11.7 Đề giữa kì 2015-2016 94 12
ĐỀ THI CUỐI KÌ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 99 12.1
Đề 1 cuối kì I năm 2018-2019 99 12.2
Đề 2 cuối kì I năm 2018-2019 100 12.3 Đề 1 cuối kì 2017-2018 100 12.4 Đề 2 cuối kì 2017-2018 101 12.5 Đề 3 cuối kì 2017-2018 102 12.6
Đề cuối kì 2017-2018 học kì hè 102 IV Phần Bốn: Phụ lục 13
MỞ ĐẦU VỀ CHƯƠNG TRÌNH R . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 107 13.1
Cài đặt và làm việc với các cửa sổ của R 107 13.2 Sử dụng lệnh help 107 13.3 Gói hàm - packages 108 13.4 Những lệnh cơ bản 108
13.4.1 Biến và các phép toán . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 108
13.4.2 Các phép toán . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 108
13.4.3 Vectơ . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 109
13.4.4 Ma trận . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 110
13.4.5 Mảng . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 110
13.4.6 Danh sách . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 110
13.4.7 Data frames . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 110 13.5 Nhập xuất dữ liệu 111
13.5.1 Nhập dữ liệu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 111
13.5.2 Xuất dữ liệu . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 111 13.6
Cấu trúc lập trình cơ bản 112
13.6.1 Cấu trúc điều kiện . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 112
13.6.2 Cấu trúc lặp . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 112
13.6.3 Cấu trúc hàm . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 112 14
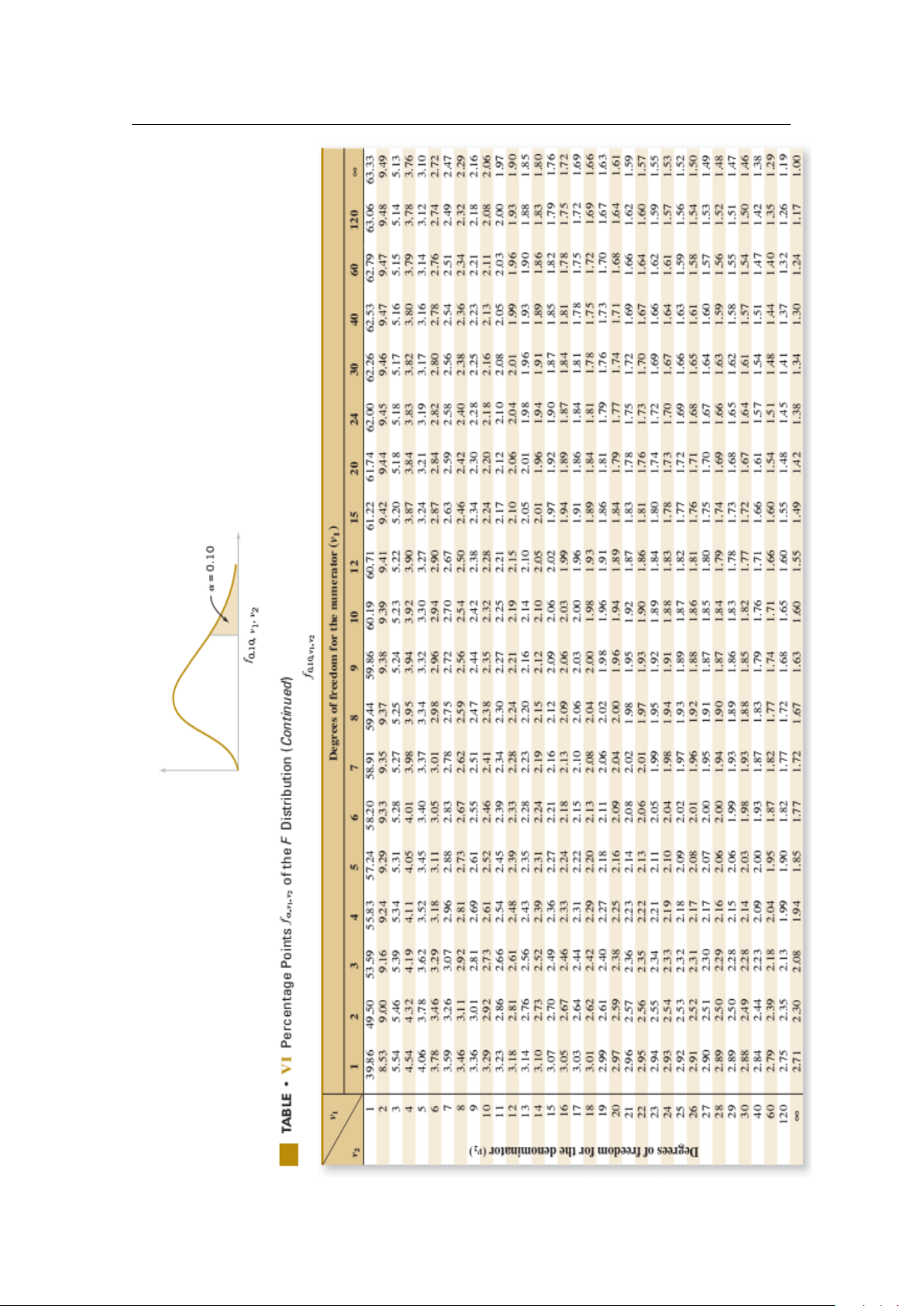
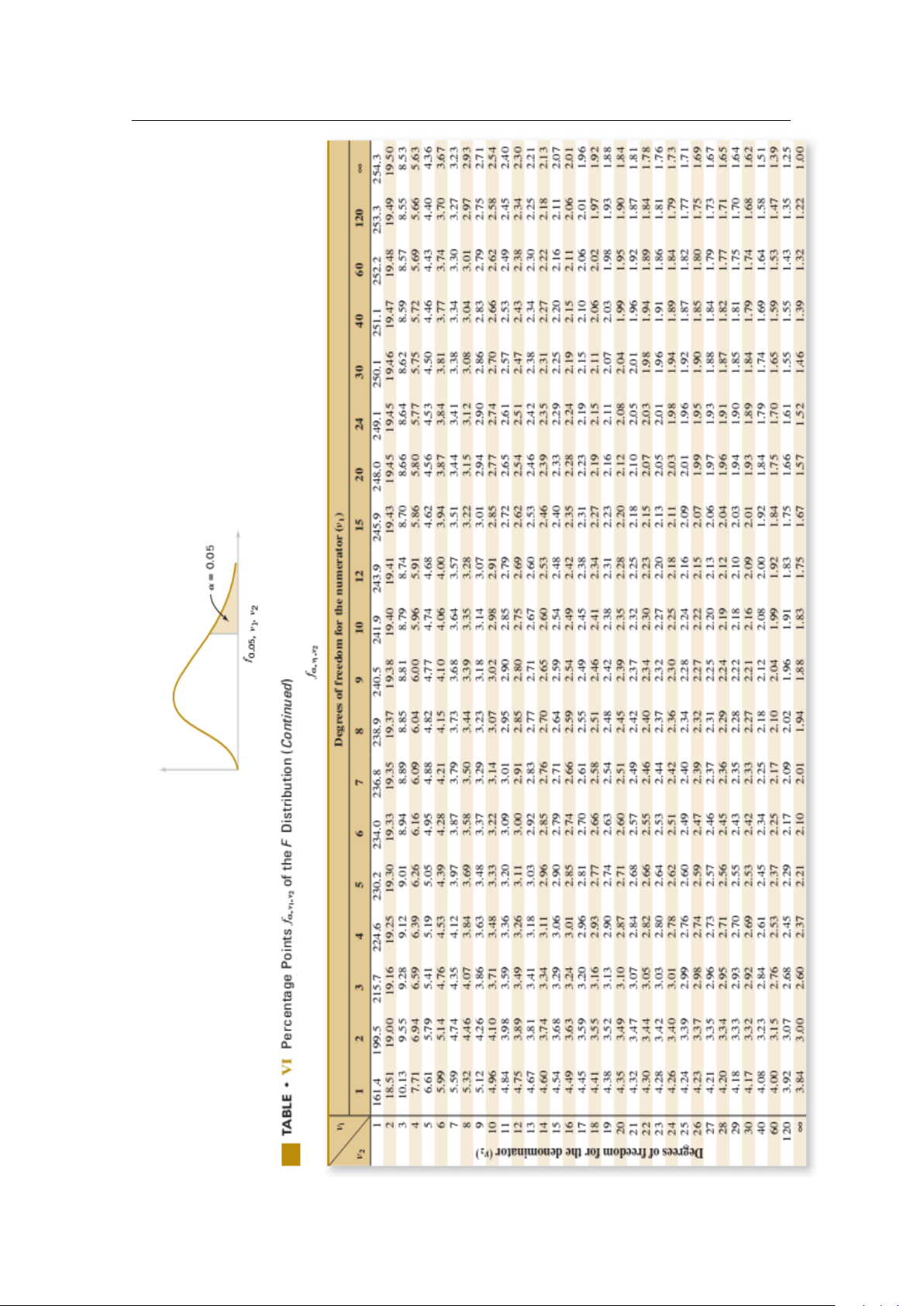
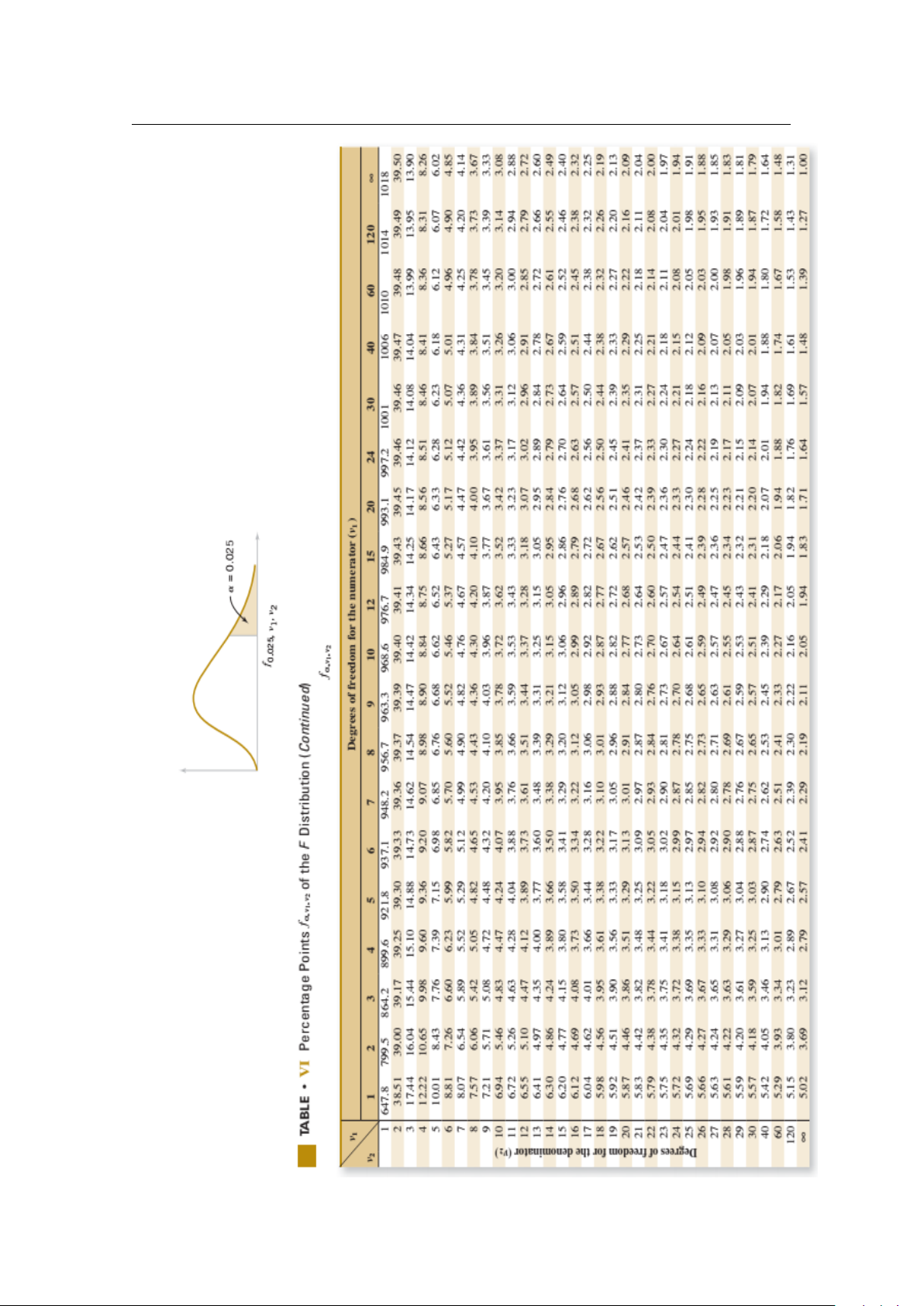
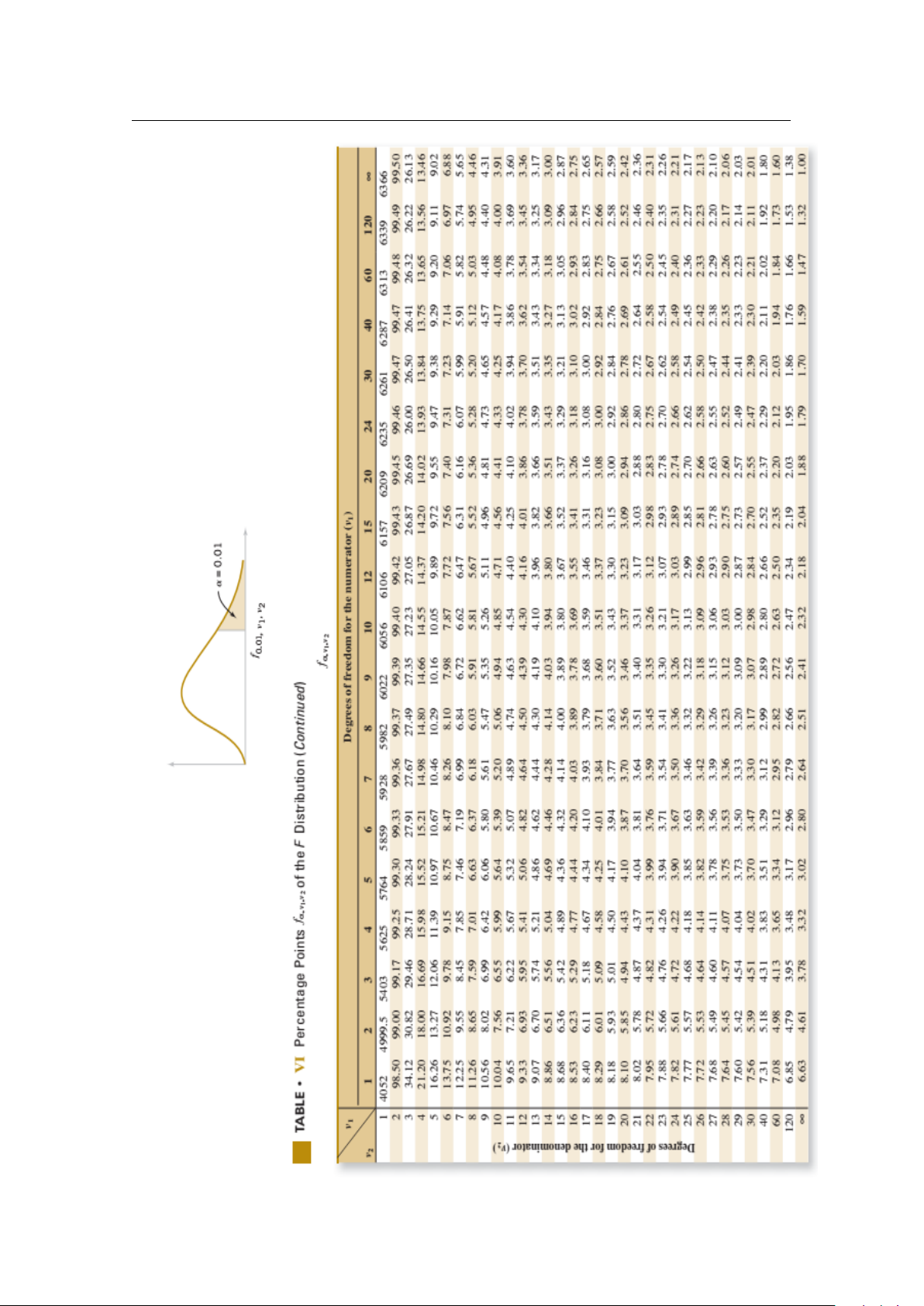
BẢNG GIÁ TRỊ CỦA HÀM PHÂN PHỐI TÍCH LŨY . . . . . . . . . . . . . . . . . 115 Articles 125 Books 125 I PhầnMột:Xácsuất 1
PHÉP ĐẾM . . . . . . . . . . . . . . . . . . . . . . . . . . . . 9 1.1 Lý thuyết 1.2 Bài tập 2
XÁC SUẤT CƠ BẢN . . . . . . . . . . . . . . . . . . . 11 2.1 Một số khái niệm 2.2 Xác suất có điều kiện 2.3 Xác suất toàn phần 3
BIẾN NGẪU NHIÊN RỜI RẠC . . . . . . . . . . . 21 3.1 Lý thuyết 3.2 Phân phối nhị thức 3.3 Phân phối siêu bội 3.4 Phân phối Poisson 4
BIẾN NGẪU NHIÊN LIÊN TỤC . . . . . . . . . . . 31 4.1 Định nghĩa 4.2 Phân phối chuẩn 4.3 Định lí giới hạn 5
PHÂN PHỐI XÁC SUẤT ĐỒNG THỜI . . . . 41 5.1 Lý thuyết 5.2 Bài tập 9 1. PHÉP ĐẾM 1.1 Lý thuyết
Định nghĩa 1.1.1 (Phép nhân)
Giả sử một thao tác có thể được mô tả như một chuỗi gồm k bước và
i. số cách hoàn thành bước 1 là n1 và
ii. số cách hoàn thành bước 2 là n2 cho mỗi cách hoàn thành ở bước 1 và
iii. số cách hoàn thành bước 3 là n3 cho mỗi cách hoàn thành ở bước 1 và ...
Tổng số cách hoàn thành thao tác là n1 × · · · × nk.
Định nghĩa 1.1.2 Số hoán vị của n phần tử khác nhau là n! = n × (n − 1) . . . 2 × 1.
Định nghĩa 1.1.3 Số hoán vị của n = n1 + n2 + · · · + nr phần tử gồm n1 phần tử loại 1, n2 phần
tử loại 2...và nr phần tử loại r được tính n! . n1!n2!n3! . . . nr !
Định nghĩa 1.1.4 (Chỉnh hợp)
Số hoán vị của các tập con gồm r phần tử được chọn từ một tập hợp n phần tử khác nhau là Ar = . n
n × (n − 1) × (n − 2) × · · · × (n − r + 1) = n! (n − r)!
Định nghĩa 1.1.5 Số tổ hợp, tập hợp con gồm r phần tử được chọn từ một tập hợp n phần tử, được tính Cr = n! . n r!(n − r)! 10 Chương 1. PHÉP ĐẾM 1.2 Bài tập
Bài 1.1. Có bao nhiêu cách thiết kế cho một trang web là bao gồm bốn màu, ba phông chữ và ba vị trí cho một hình ảnh.
Bài 1.2. Quảng cáo trên web có thể được thiết kế từ bốn màu khác nhau, ba loại phông chữ, năm
kích thước phông chữ, ba hình ảnh và năm cụm từ văn bản. Có thể thiết kế bao nhiêu mẫu khác nhau? (Đs: 900)
Bài 1.3. Một ổ khóa có ba vòng khóa, mỗi vòng có 10 chữ số: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9. Hỏi có tất cả bao nhiêu mã khóa?
Bài 1.4. Một thiết kế cho một máy tính có thể chỉ định bất kỳ một trong năm kích thước bộ nhớ,
một trong ba loại màn hình, một trong bốn kích cỡ của một đĩa cứng và có thể bao gồm hoặc không
bao gồm một cây bút điện tử. Có bao nhiêu hệ thống máy tính khác nhau có thể được thiết kế? (Đs: 120)
Bài 1.5. Thiết kế mới cho một bể xử lý nước thải đã được đề xuất với ba hình dạng có thể, bốn kích
thước có thể, ba vị trí cho van đầu vào và bốn vị trí cho van đầu ra. Có thể thiết kế bao nhiêu sản phẩm khác nhau? (Đs: 144)
Bài 1.6. Trong một lớp gồm 30 sinh viên, cần chọn ra 3 sinh viên để làm lớp trưởng, lớp phó và
thủ quỹ. Hỏi có bao nhiêu cách bầu chọn?
Bài 1.7. Một hộp đựng 6 bi trắng và 4 bi đen.
a. Có tất cả bao nhiêu cách lấy ra 5 bi?
b. Có bao nhiêu cách lấy ra 5 bi trong đó có 2 bi trắng?
Bài 1.8. Một lô 140 chip bán dẫn được kiểm tra bằng cách chọn một mẫu 5 chip. Giả sử 10 trong
số các chip này không phù hợp với yêu cầu của khách hàng.
a. Có bao nhiêu cách chọn mẫu khác nhau?
b. Có bao nhiêu mẫu trong số năm mẫu chứa chính xác một chip không phù hợp?
c. Có bao nhiêu mẫu trong số năm mẫu chứa ít nhất một chip không phù hợp?
(Đs: 416.965.528; 113.588.800; 130.721.752)
Bài 1.9. Xem xét việc thiết kế của một hệ thống truyền thông.
a. Có bao nhiêu số điện thoại mà ba chữ số đầu tiên được sử dụng để đại diện cho một khu vực
địa lý cụ thể (chẳng hạn như mã vùng) có thể được tạo từ các chữ số từ 0 đến 9?
b. Như một phần (a), có bao nhiêu số điện thoại mà ba chữ số đầu có thể không bắt đầu bằng 0
hoặc 1, nhưng chứa 0 hoặc 1 làm chữ số giữa?
c. Có thể có bao nhiêu số điện thoại mà có ba chữ số đầu trong đó không có chữ số nào xuất
hiện nhiều hơn một lần trong đó? (Đs: 1000; 160; 720)
Bài 1.10. Một thùng chứa 50 phần trong đó 5 phần bị lỗi. Một mẫu 10 phần được chọn ngẫu nhiên,
không hoàn lại. Có bao nhiêu mẫu chứa ít nhất bốn bộ phận bị lỗi? (Đs: 41,947,059)
Bài 1.11. Trong một nhóm ứng viên gồm 7 nam và 3 nữ.
a. Có bao nhiêu cách thành lập một ủy ban bao gồm 3 người?
b. Có bao nhiêu cách thành lập một ủy ban bao gồm 3 người trong đó có đúng 1 nữ?
c. Có bao nhiêu cách thành lập một ủy ban bao gồm 3 người trong đó có ít nhất 1 nữ? 11 2. XÁC SUẤT CƠ BẢN 2.1 Một số khái niệm
Định nghĩa 2.1.1 Một thí nghiệm có thể dẫn đến các kết quả khác nhau, mặc dù nó được lặp
lại theo cùng một cách thức trong mỗi lần thực hiện, được gọi là một thí nghiệm ngẫu nhiên.
Định nghĩa 2.1.2 Không gian mẫu Ω của một hiện tượng ngẫu nhiên là tập hợp tất cả các khả năng có thể xảy ra.
Định nghĩa 2.1.3 Biến cố là một khả năng hay một tập hợp các khả năng của một hiện tượng
ngẫu nhiên. Nói cách khác, biến cố là một tập con A của không gian mẫu Ω và kí hiệu là: A ⊂ Ω.
Định nghĩa 2.1.4 Các quy tắc xác suất:
i. Xác suất P(A) của biến cố A thỏa 0 ≤ P(A) ≤ 1.
ii. Nếu Ω là không gian mẫu của mô hình xác suất thì P(Ω) = 1.
iii. Hai biến cố rời nhau khi chúng không có khả năng chung và không bao giờ xảy ra cùng
nhau. Khi hai biến cố A, B rời nhau thì P(A ∪ B) = P(A) + P(B).
Đây là quy tắc cộng cho hai biến cố rời nhau.
iv. Biến cố đối Ac của biến cố A là những khả năng biến cố A không xảy ra. Quy tắc đối là: P(Ac) = 1 − P(A).
Định lí 2.1.1 Xác suất trong không gian mẫu hữu hạn
Khi ta thực hiện phép gán xác suất cho mỗi khả năng riêng rẽ với một số nằm giữa 0 và 1, đồng
thời có tổng là 1. Xác suất của một biến cố bất kì là tổng các xác suất của mỗi khả năng xảy ra
trong biến cố đó. Khi đó, ta có được một mô hình xác suất trong không gian mẫu hữu hạn.
Chú ý, khi ta gán xác suất cho mỗi khả năng bằng nhau thì ta gọi đó là mô hình xác suất đồng khả 12
Chương 2. XÁC SUẤT CƠ BẢN năng.
Định nghĩa 2.1.5 Hai biến cố độc lập nhau khi biết rằng xác suất xảy ra biến cố này không làm
thay đổi xác suất xảy ra của biến cố kia, khi đó P(A và B) = P(A)P(B).
Đây là quy tắc nhân của hai biến cố độc lập.
Bài 2.1. Hãy chỉ rõ không gian mẫu trong mỗi hiện tượng ngẫu nhiên sau:
a. Thả một đồng xu.
b. Để một cây bút chì rơi tự do vào một tờ giấy có ghi những chữ số một cách ngẫu nhiên, sau
đó ghi lại số có dấu chấm của đầu bút chì.
c. Thảy một đồng xu 4 lần rồi ghi lại chuỗi kết quả. Hãy liệt kê không gian mẫu. Hơn nữa, nếu
ta chỉ quan tâm tới số lượng mặt ngửa trong chuỗi kết quả. Cho biết không gian mẫu lúc này.
d. Bạn là nhà thiết kế trang web và bạn thiết lập một trang với 5 liên kết khác nhau. Người dùng
có thể nhấp vào một trong các liên kết hoặc họ có thể rời khỏi trang đó. Mô tả không gian
cho kết quả của khách truy cập vào trang Web của bạn.
Bài 2.2. Sử dụng dữ liệu từ Bài 2.1 câu 3, hãy mô tả biến cố A là chuỗi kết quả có chính xác 2 mặt ngửa xuất hiện.
Bài 2.3. Nếu ta tung 1 đồng súc sắc cân bằng thì xác suất để được mặt chẵn hoặc lớn hơn 4 chấm là bao nhiêu?
Bài 2.4. Sử dụng biểu đồ Veen, mô tả các khái niệm: hai biến cố rời nhau và hai biến cố đối nhau.
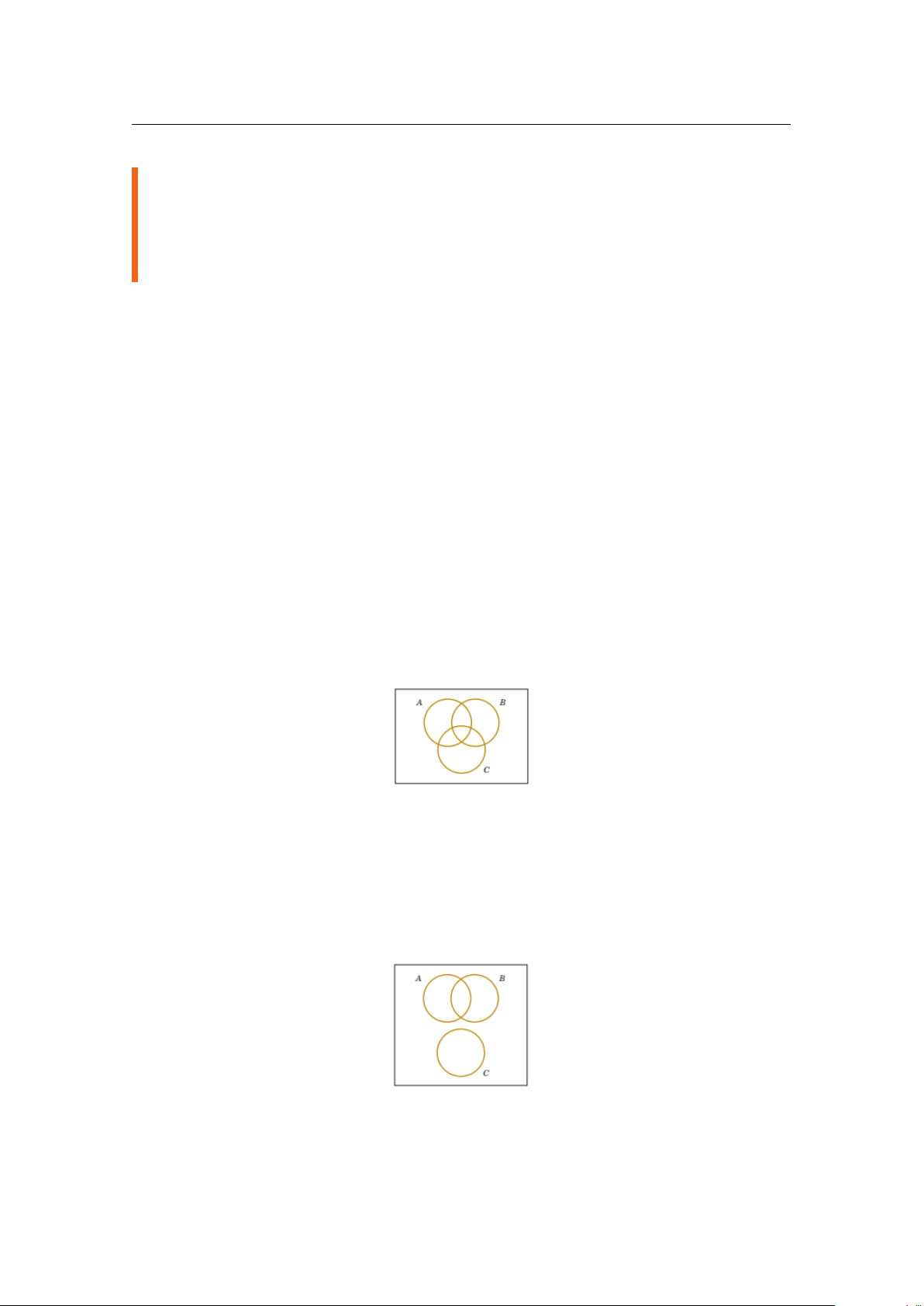
Bài 2.5. Cho ba biến cố được biểu diễn bởi biểu đồ Veen như sau:
Vẽ lại hình trên rồi tô đậm những vùng tương ứng với biến cố sau: a. Ac d. (B ∩ C)c b. A ∪ B e. (A ∪ B)c ∩ C c. (A ∪ B) ∩ C
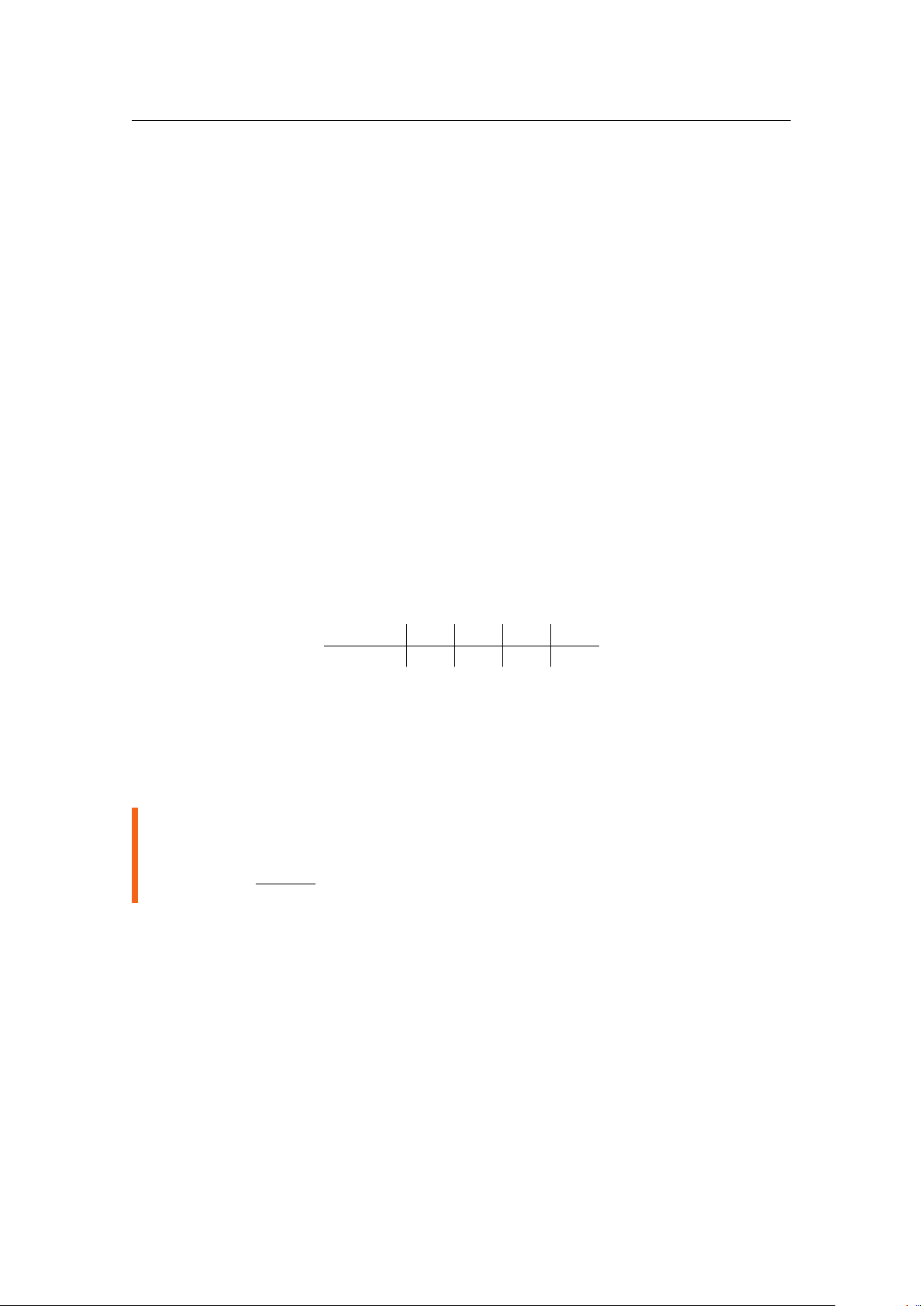
Bài 2.6. Cho ba biến cố được biểu diễn bởi biểu đồ Veen như sau:
Vẽ lại hình trên rồi tô đậm những vùng tương ứng với biến cố sau: 2.1 Một số khái niệm 13 a. Ac d. (B ∩ C)c
b. (A ∪ B) ∩ (A ∪ Bc) e. (A ∪ B)c ∩ C c. (A ∪ B) ∩ C
Bài 2.7. Xác suất xảy ra của 5 khả năng trong một thí nghiệm ngẫu nhiên là như nhau. Không gian
mẫu Ω = {a, b, c, d, e}. Đặt các biến cố A = {a, b} và B = {c, d, e}. Tính: a. P(A) d. P(A ∩ B) b. P(B) e. P(A ∪ B) c. P(Ac)
Bài 2.8. Không gian mẫu của một thí nghiệm ngẫu nhiên là Ω = {a, b, c, d, e} với xác suất tương
ứng 0.1, 0.1, 0.2, 0.4 và 0.2. Đặt các biến cố A = {a, b, c} và B = {c, d, e}. Tính: a. P(A) d. P(A ∩ B) b. P(B) e. P(A ∪ B) c. P(Ac)
Bài 2.9. Ta xem như một hộ gia đình giàu có nếu thu nhập của họ vượt quá 100,000$ và xem hộ
gia đình trí thức nếu chủ nhà hoàn thành bậc đại học. Chọn ngẫu nhiên một hộ gia đình người Mỹ,
và xét A là biến cố mà hộ gia đình được chọn là giàu có và B là biến cố gia đình trí thức. Theo khảo
sát dân số hiện tại, người ta thấy xác suất P(A) = 0.138, P(B) = 0.261 và xác suất một gia đình vừa
giàu có vừa trí thức là P(A và B) = 0.082.
a. Hãy tính xác suất chọn một gia đình hoặc là giàu có hoặc là trí thức.
b. Vẽ biểu đồ Veen biểu diễn mối quan hệ giữa hai biến cố A và B.
c. Biễu diễn và tính những xác suất sau: i. { A và B} iii. { A và Bc } ii. { Ac và B} iv. { Ac và Bc }
Bài 2.10. Cho P(A) = 1/3; P(B) = 1/2 và P(A hoặc B) = 3/4. Tính: a. P(A và B) d. P(Ac và B) b. P(Ac và Bc) e. P(A và Bc) c. P(Ac hoặc Bc)
Bài 2.11. Cho P(A) = 0.3, P(B) = 0.2 và P(A ∩ B) = 0.1. Tính các xác suất sau: a. P(Ac) d. P(A ∩ Bc) b. P(A ∪ B) e. P(A ∪ Bc) c. P(Ac ∩ B) f. P(Ac ∪ B)
Bài 2.12. Cho A, B, C là những biến cố đôi một rời nhau lần lượt có xác suất là: 0.2, 0.3 và 0.4. Tính những xác suất sau: a. P(A ∪ B ∪ C) d. P ((A ∪ B) ∩ C) b. P(A ∩ B ∩ C) e. P(Ac ∩ Bc ∩ Cc) c. P(A ∩ B) (Đs: 0.9; 0; 0; 0; 0.1) 14
Chương 2. XÁC SUẤT CƠ BẢN
Bài 2.13. Tỷ lệ người mắc bệnh tim trong một vùng dân cư là 9%, mắc bệnh huyết áp là 12% và
mắc cả hai bệnh là 7%. Chọn ngẫu nhiên một người trong vùng. Tính xác suất để người đó
a. Bị bệnh tim hay bị bệnh huyết áp.
b. Không bị bệnh tim cũng không bị bệnh huyết áp.
c. Không bị bệnh tim hay không bị bệnh huyết áp.
d. Bị bệnh tim nhưng không bị bệnh huyết áp.
e. Không bị bệnh tim nhưng bị bệnh huyết áp.
(Đs: 0.14; 0.86; 0.93; 0.02; 0.05)
Bài 2.14. Một số tiểu bang đang xem xét luật sẽ cấm sử dụng điện thoại di động trong khi lái xe vì
họ tin rằng lệnh cấm sẽ giảm tai nạn xe hơi liên quan đến điện thoại. Một nghiên cứu phân loại các
loại tai nạn này vào các ngày trong tuần khi chúng xảy ra. Trong ví dụ này, ta sử dụng các giá trị từ
nghiên cứu này làm mô hình xác suất. Dưới đây là xác suất: Thứ Chủ nhật Hai Ba Tư Năm Sáu Bảy Xác suất 0.03 0.19 0.18 0.23 0.19 0.16 0.02
Hãy kiểm tra các quy tắc xác suất của mô hình trên. Sau đó, áp dụng các quy tắc xác suất, tính các trường hợp sau
a. Xác suất xảy ra tai nạn vào ngày nghỉ cuối tuần.
b. Xác suất xảy ra tai nạn vào ngày trong tuần.
Bài 2.15. Phân bố các loại máu
Máu người có thể là một trong các nhóm: O, A, B hoặc AB nhưng phân bố các loại khác nhau giữa
các nhóm ở người. Bảng sau là sự phân bố các loại máu cho một người được chọn ngẫu nhiên tại Hoa Kỳ: Loại máu A B AB O Xác suất 0.40 0.11 0.04 ?
a. Tính xác suất của nhóm máu O ở Hoa Kỳ.
b. Maria có máu loại B. Cô ấy có thể được truyền máu một cách an toàn từ những người có
nhóm máu O và B. Xác suất khi chọn ngẫu nhiên một người Mỹ có thể hiến máu cho Maria?
Bài 2.16. Phân phối Benford
Số giả mạo trong bản khai thuế, hồ sơ thanh toán, hóa đơn, xác nhận quyền sở hữu tài khoản và
nhiều loại giấy tờ khác thường có ở những mẫu không có trong hồ sơ hợp lệ. Một số mẫu qua mặt
quản lí dễ dàng bởi một kẻ lừa đảo thông minh. Tuy nhiên, có một nghiên cứu chuyên sâu đã chỉ ra
rằng các chữ số đầu tiên của các con số trong hồ sơ hợp pháp thường theo một phân phối được gọi là quy luật Benford. Số đầu tiên 1 2 3 4 5 6 7 8 9 Xác suất 0.301 0.176 0.125 0.097 0.079 0.067 0.058 0.051 0.046
Chú ý số 0 không thể đứng đầu tiên.
a. Xét những biến cố: A={chữ số 1 đứng đầu} và B={chữ số đầu là 6 hoặc lớn hơn}. Hãy tính
xác suất của mỗi biến cố.
b. Tính xác suất khi chữ số đầu tiên lớn hơn 1.
2.2 Xác suất có điều kiện 15
c. Sử dụng xác suất biến cố A và B, tính xác suất khi số đầu tiên là 1 hoặc là 6 hoặc lớn hơn.
d. Tính xác suất biến cố C chữ số đầu tiên là số lẻ. Sau đó suy ra xác suất P(B hoặc C) và chứng
minh nhỏ hơn tổng xác suất 2 biến cố B, C. Giải thích.
Bài 2.17. Những kẻ lừa đảo có thể nghĩ rằng chữ số đầu tiên phải được phân phối "ngẫu nhiên"
trong số các chữ số từ 1 đến 9 trong hồ sơ kinh doanh (tức là có xác suất xuất hiện như nhau). Hãy
mô tả không gian mẫu và tính xác suất của biến cố B (phát biểu ở bài trên). So sánh kết quả với Bài
tập 2.16 và rút ra cách nhận biết kẻ lừa đảo làm giả giấy tờ.
Bài 2.18. (Biến cố độc lập) Tính xác suất trong các trường hợp sau:
a. Xác suất có hai mặt ngửa khi tung hai đồng xu đồng chất.
b. Gregor Mendel đã sử dụng đậu Hà Lan trong một số thí nghiệm cho thấy rằng sự di truyền
màu hạt hoạt động một cách ngẫu nhiên. Màu hạt của đậu Hà Lan có thể là màu xanh lá cây
hoặc màu vàng. Hai cây bố mẹ được cho lai tạo (một kiểu thụ phấn) để tạo ra hạt giống. Mỗi
cây bố mẹ mang hai gen cho màu hạt giống, và mỗi gen này có xác xuất 1/2 được truyền cho
một hạt giống. Hai gen mà hạt giống nhận được một từ bố một mẹ xác định màu của nó. Cha
mẹ đóng góp gen độc lập với nhau.
Giả sử cả cha lẫn mẹ đều mang gen G và Y . Hạt mầm sẽ có màu xanh nếu cả hai bố mẹ đóng
góp một gen G; bằng không nó sẽ có màu vàng. Nếu M là biến cố cây bố đóng góp một gen
G và F là biến cố cây mẹ đóng góp một gen G thì xác suất của một hạt màu xanh lá cây là bao nhiêu?
c. Phân phối nhóm máu của người Hoa khác với phân phối của người Hoa Kỳ (xem Bài tập
2.15)và được cho bởi bảng sau Loại máu A B AB O Xác suất 0.27 0.26 0.12 0.35
Chọn một người Mỹ và một người Hoa ngẫu nhiên độc lập với nhau. Xác suất mà cả hai đều
có loại máu O là bao nhiêu? Xác suất mà cả hai đều có cùng một loại máu? 2.2 Xác suất có điều kiện
Định nghĩa 2.2.1 Khi cần tính xác suất của biến cố B mà ta đã biết trước thông tin của biến cố
A, ta sẽ sử dụng khái niệm xác suất có điều kiện P(B| A) theo công thức P(B| A) = P(A ∩ B) . P(A)
Bài 2.19. Đĩa nhựa polycarbonate từ một nhà cung cấp được phân tích về khả năng chống trầy xước
và sốc. Kết quả từ 100 đĩa được tóm tắt như sau: Chống sốc Cao Thấp Cao 70 9 Chống xước Thấp 16 5
Đặt A là biến cố một đĩa có khả năng chống sốc cao, và để B là biến cố đĩa có khả năng chống
xước cao. Xác định xác suất sau: 16
Chương 2. XÁC SUẤT CƠ BẢN a. P(A) b. P(B) c. P(A|B) d. P(B| A)
Bài 2.20. Bảng sau đây tóm tắt phân tích các mẫu thép mạ kẽm cho trọng lượng lớp phủ và độ nhám bề mặt: Trọng lượng lớp phủ Cao Thấp Cao 12 16 Độ nhám bề mặt Thấp 88 34
a. Nếu trọng lượng lớp phủ của mẫu cao, xác suất độ nhám bề mặt cao là bao nhiêu?
b. Nếu độ nhám bề mặt của mẫu cao, xác suất trọng lượng lớp phủ cao là bao nhiêu?
c. Nếu độ nhám bề mặt của mẫu thấp, xác suất trọng lượng lớp phủ thấp là bao nhiêu?
Bài 2.21. Trong kì thi cuối kì của ĐH New Harmony có 10000 kết quả thi của 3 khoa chính: khoa
nghệ thuật, khoa kĩ thuật và vật lí, khoa sức khỏe được thống kê trong bảng sau: Khoa Điểm A Điểm B Điểm dưới B Tổng Nghệ thuật 2142 1890 2268 6300 Kĩ thuật & vật lí 368 432 800 1600 Sức khỏe 882 630 588 2100 Tính xác suất:
a. Lấy ngẫu nhiên được 1 điểm loại dưới B.
b. Lấy ngẫu nhiên được 1 điểm loại dưới B với thông tin điểm đó lấy từ khoa kĩ thuật.
c. Xác suất là bao nhiêu để điểm lấy ra từ khoa sức khỏe.
d. Lấy ngẫu nhiên được 1 điểm A.
e. Lấy ngẫu nhiên được 1 điểm A với thông tin điểm đó lấy từ khoa sức khỏe
f. Hãy tính xác suất lấy được một điểm loại A từ trường ĐH New Harmony khoa nghệ thuật
bằng 2 cách: số lượng trong bảng và công thức xác suất điều kiện. So sánh kết quả.
Hãy giải thích sự khác nhau ở đáp số câu 1 với câu 2; câu 4 với câu 5.
Bài 2.22. Trong một nhóm sinh viên đại học, người ta phân loại theo giới tính và mức độ thường
xuyên uống rượu bia hay không. Dưới đây là xác suất Nam Nữ Thường xuyên 0.11 0.12 Không thường xuyên 0.32 0.45
Kiểm tra xem bảng xác suất trên có tổng là 1 không? Hãy tính xác suất chọn ngẫu nhiên:
a. Một người không thường uống rượu bia.
b. Một người nam sinh viên không thường uống rượu bia. So sánh với kết quả trên.
c. Một người nam sinh viên thường uống rượu bia; một người nữ sinh viên thường uống rượu bia.
d. Xác suất một sinh viên thường uống rươu bia với điều kiện phải là sinh viên nam. Xác suất
chọn một sinh viên thường uống rươu bia với điều kiện phải là sinh viên nữ.
e. Giải thích tại sao lại có kết quả xác suất câu 3 lớn hơn câu 4 ở nữ và nhỏ hơn ở nam. Rút ra nhận xét. 2.3 Xác suất toàn phần 17
Bài 2.23. Sử dụng số liệu của mô hình xác suất trong Bài tập 2.9, hãy tính xác suất chọn ngẫu
nhiên một gia đình giáu có biết trước thông tin là gia đình trí thức?
Bài 2.24. Theo dõi dự báo thời tiết trên đài truyền hình (nắng, sương mù, mưa) và so sánh với thời
tiết thực tế xảy ra, ta có bảng thống kê sau: Thực tế Dự báo nắng sương mù mưa nắng 30 5 5 sương mù 4 20 2 mưa 10 4 20
nghĩa là có 30 lần dự báo nắng, trời nắng, 4 lần dự báo nắng, trời sương mù; 10 lần dự báo nắng, trời mưa,...
a. Tính xác suất dự báo trời nắng của đài truyền hình.
b. Tính xác suất dự báo của đài truyền hình là đúng thực tế.
c. Được tin dự báo là trời nắng. Tính xác suất để thực tế thì trời mưa ? trời sương mù ? trời nắng ?
Bài 2.25. Xác suất của giai đoạn đầu tiên của sản xuất gia công được kiểm soát bằng số vòng của
các piston đáp ứng các thông số kỹ thuật là 0.90. Thất bại xảy ra do các biến thể kim loại, liên kết
cố định, cắt điều kiện lưỡi dao, độ rung và điều kiện môi trường xung quanh. Do giai đoạn đầu đáp
ứng các thông số kỹ thuật, xác suất mà giai đoạn gia công thứ hai đáp ứng các thông số kỹ thuật là
0,95. Xác suất mà cả hai giai đoạn đáp ứng thông số kỹ thuật là gì? Sử dụng công thức xác suất có điều kiện P(A và B). 2.3 Xác suất toàn phần
Định nghĩa 2.3.1 (Công thức xác suất toàn phần) Giả sử E , , . . ., 1 E2
Ek là k tập đôi một rời nhau, khi đó
P(B) = P(B ∩ E1) + P(B ∩ E2) + · · · + P(B ∩ Ek )
= P(B|E1)P(E1) + P(B|E2)P(E2) + · · · + P(B|Ek)P(Ek) R
Biểu đồ cây rất hữu ích để xử lí những bài toán liên quan tới xác suất có điều kiện và công
thức xác suất toàn phần!
Từ hai định nghĩa trên, ta suy ra được công thức:
Mệnh đề 2.3.1 (Công thức Bayes) Giả sử P(A) > 0 và hệ những biến cố đầy đủ {B , , . . ., 1 B2 Bn}
có P(Bk) > 0 với mọi k = 1, n. Khi đó, ta có: P(B , k | A) = P(Bn)P(A| Bk ) k = 1, n.
P(B1)P(A| B1) + P(B2)P(A| B2) + · · · + P(Bn)P(A|Bn)
Bài 2.26. (Sử dụng biểu đồ cây để tính xác suất toàn phần)
Một nhà máy có ba phân xưởng A, B, C tương ứng làm ra 25%, 35% và 40% tổng sản phẩm của
nhà máy. Giả sử xác suất làm ra một sản phẩm hỏng của các phân xưởng A, B và C lần lượt là 0.01,
0.02 và 0.025. Hãy tính xác suất nhận được một sản phẩm hỏng. (Đs: 0.0195) 18
Chương 2. XÁC SUẤT CƠ BẢN
Bài 2.27. Một dây chuyền lắp ráp nhận các chi tiết từ hai nhà máy khác nhau. Tỷ lệ chi tiết do nhà
máy thứ nhất cung cấp là 60%, của nhà máy thứ hai là 40%. Tỷ lệ chính phẩm của nhà máy thứ
nhất là 90%, của nhà máy thứ hai là 85%. Lấy ngẫu nhiên một chi tiết trên dây chuyền và thấy rằng
nó tốt. Tìm xác suất để chi tiết đó do nhà máy thứ nhất sản xuất. (Đs: 0.614)
Bài 2.28. Trong một vùng dân cư, cứ 100 người thì có 30 người hút thuốc lá. Biết tỷ lệ người bị
viêm họng trong số người hút thuốc lá là 60%, trong số người không hút thuốc lá là 30%. Khám
ngẫu nhiên một người và thấy người đó bị viêm họng. Tìm xác suất để người đó hút thuốc lá. Nếu
người đó không bị viêm họng thì xác suất để người đó hút thuốc lá là bao nhiêu? (Đs: 0.4615; 0.1967)
Bài 2.29. Trong một lượng lớn sinh viên đại học quốc gia, 61% tham dự các ĐH 4 năm và các học
viên còn lại theo học các ĐH 2 năm. Nam giới chiếm 44% số học sinh trong các ĐH 4 năm và 41%
học sinh trong các ĐH 2 năm.
a. Hãy lập bảng xác suất cho mô hình trên.
b. Giả sử ta lấy ngẫu nhiên 1 sinh viên nữ từ trường đại học quốc gia, xác suất sinh viên đó học
ĐH 4 năm là bao nhiêu? (Đs: 0.5975)
Bài 2.30. Xe cơ giới được bán cho các cá nhân được phân loại là ô tô hoặc xe tải nhẹ (bao gồm cả
xe SUV) và là xe nội địa hoặc nhập khẩu. Trong một năm gần đây, 69% số xe được bán là xe tải
nhẹ, 78% là trong nước và 55% là xe tải nhẹ nội địa. Hãy để A là biến cố một chiếc xe là ô tô và B
biến cố nó được nhập khẩu. Hãy tính xác suất:
a. Phương tiện cơ giới là một chiếc bán tải.
b. Phương tiện cơ giới là một chiếc ô tô nhập khẩu.
c. Giả sử có thông tin một chiếc xe là nhập khẩu, hãy tính xác suất nó là xe bán tải.
d. Có thể khẳng định hai biến cố: chiếc xe là bán tải và chiếc xe nhập khẩu là độc lập hay không? Giải thích.
Bài 2.31. Phòng chat trực tuyến bị chi phối bởi giới trẻ. Thanh thiếu niên là những người dùng lớn
nhất. Nếu chúng ta chỉ thống kê người trưởng thành (từ 18 tuổi trở lên) dùng Internet, 47% trong
nhóm tuổi từ 18 đến 29, cũng như 21% trong nhóm tuổi 30 đến 49 và chỉ 7% trong số 50 người đó
trở lên. Để tìm hiểu phần trăm của người dùng Internet tham gia trò chuyện, ta cũng cần phân tích
theo độ tuổi người dùng. Ở đây là: 29% người dùng Internet trưởng thành từ 18 đến 29 tuổi (biến cố
A1), 47% khác là 30 đến 49 (biến cố A2) và 24% còn lại là từ 50 trở lên (biến cố A3).
a. Hãy tính xác suất nếu chọn ngẫu nhiên một người sử dụng Internet tham gia trò chuyện.
b∗. Bao nhiêu phần trăm người trưởng thành sử dụng Internet để trò chuyện nằm trong độ tuổi
18 tới 29 tuổi? Tính P(A1|C).
Bài 2.32. Julie vừa tốt nghiệp đại học. Cô đã học sinh học, hóa học, tính toán và hy vọng sẽ làm
việc như một nhà khoa học pháp y áp dụng kiến thức của mình để điều tra tội phạm. Một đêm
khuya, cô nghĩ về một số công việc mà cô đã nộp đơn xin. Gọi A, B và C là các biến cố mà Julie
xin được một công việc bằng cách:
A: văn phòng Giám đốc Y khoa ở Connecticut
B: sở tư pháp hình sự tại New Jersey
C: nhóm hoạt động về thiên tai ở của liên bang
với xác suất được nhận lần lượt là: P(A) = 0.7 P(A và B) = 0.3 P(A và B và C) = 0 P(B) = 0.5 P(A và C) = 0.1 P(C) = 0.3 P(B và C) = 0.1 2.3 Xác suất toàn phần 19
a. Sử dụng biểu đồ Veen mô tả mô hình xác suất trên.
b. Xác suất để Julie có được ít nhất một việc làm trong ba việc trên.
c. Nếu Julie đã được nhận làm việc liên bang thì xác suất có điều kiện để cô ta có việc ở New
Jersey là bao nhiêu? (Đs: 1/3.)
d. Nếu Julie đã được nhận làm việc New Jersey thì xác suất có điều kiện để cô ta có việc ở liên
bang là bao nhiêu? (Đs: 0.2)
Bài 2.33. Một thiết bị gồm 3 cụm chi tiết, mỗi cụm bị hỏng không ảnh hưởng gì đến các cụm khác
và chỉ cần một cụm bị hỏng thì thiết bị ngừng hoạt động. Xác suất để cụm thứ nhất bị hỏng trong
ngày là 0.1, cụm thứ hai là 0.05 và cụm thứ ba là 0.15. Tìm xác suất để thiết bị không ngừng hoạt
động trong ngày. (Đs: 0.7267) 21
3. BIẾN NGẪU NHIÊN RỜI RẠC 3.1 Lý thuyết Định nghĩa 3.1.1
i. Biến ngẫu nhiên là một biến mà mỗi giá trị của nó được gán tương ứng với mỗi khả năng
có thể xảy ra của hiện tượng ngẫu nhiên.
ii. Biến ngẫu nhiên rời rạc X là biến ngẫu nhiên chỉ nhận đếm được những giá trị. Phân phối
xác suất của X là một bảng gồm các giá trị và xác suất tương ứng của chúng. Người ta
cũng có thể mô tả X bằng đồ thị histogram (xem Chương 6) và hàm phân phối tích lũy.
Định nghĩa 3.1.2 Các tham số đặc trưng thống kê
i. Trung bình hay kì vọng của biến ngẫu nhiên rời rạc X nhận giá trị {x , , 1 x2 · · · , xk } tương ứng với xác suất {p , ,
1 p2 · · · , pk } là đại lượng được tính: k Õ EX = µ . X = x = xi pi i=1 Tính chất:
a. Nếu X là biến ngẫu nhiên và a, b là những số cố định thì µa+bX = a + bµX.
b. Nếu X và Y là hai biến ngẫu nhiên thì µX+Y = µX + µY .
ii. Kì vọng (mean, expected value) của một hàm phụ thuộc vào một biến ngẫu nhiên rời rạc X được tính Eh(X) = Õ h(x . i )pi i
Đặc biệt, nếu h(x) = xr ta gọi Eh(X) là moment bậc r. Nếu h(x) = etx thì ta gọi Eh(X)
là hàm gây (sinh) moment. Nếu h(x) = e−itx thì ta gọi Eh(X) là hàm đặc trưng của biến ngẫu nhiên X.
iii. Phương sai (varience) của biến ngẫu nhiên rời rạc X nhận giá trị {x , ,
1 x2 · · · , xk } tương 22
Chương 3. BIẾN NGẪU NHIÊN RỜI RẠC
ứng với xác suất {p , ,
1 p2 · · · , pk } là đại lượng được tính: k k Õ Õ VarX = σ2 = (x x2 p . X i − µX )2 pi = k k − µ2 X i=1 i=1
iv. Độ lệch chuẩn σX của biến ngẫu nhiên rời rạc X là căn bậc 2 của phương sai. Tính chất:
a. Nếu X là biến ngẫu nhiên và a, b là những số cố định thì σ2 = b2σ2 . a+bX X
b. Nếu X và Y là hai biến ngẫu nhiên độc lập thì σ2 = σ2 + σ2. X±Y X Y
c. Nếu X và Y là hai biến ngẫu nhiên có hệ số tương quan ρ thì σ2 = σ2 + σ2 ± ρσ σ . X±Y X Y X Y
v. Trung vị (median) là số x thỏa điều kiện P(X ≤ x) = P(X ≥ x) = 0.5. Trong trường hợp
xác suất đồng khả năng, để tìm trung vị người ta xếp tập X(Ω) tăng dần, sau đó nếu số
phần tử của X(Ω) là số lẻ thì ta lấy số chính giữa. Ngược lại ta sẽ lấy trung bình của hai
số chính giữa nếu số phần tử của X(Ω) là số chẵn.
vi. Yếu vị (mod) là số x ∈ X(Ω) sao cho P(X = x) lớn nhất.
vii. Ngoài ra, người ta còn sử dụng những tham số đặc trưng là các moment bậc cao!!!
Code R 3.1.1 Sử dụng code R để tính trung bình, phương sai, độ lệch chuẩn của biến ngẫu nhiên rời rạc: R > x <- c(0,1,2,3)
R > f <- c(1/8, 3/8, 3/8, 1/8) R > mu <- sum(x * f) R > mu
R > sigma2 <- sum((x-mu)^2 * f) R > sigma2
R > sigma <- sqrt(sigma2) R > sigma R > F = cumsum(f) R > F
hoặc sử dụng thư viên distrEx [74] như sau: R > library(distrEx)
R > X <- DiscreteDistribution(supp = 0:3, prob = c(1,3,3,1)/8) R > E(X); var(X); sd(X)
Bài 3.1. Trong mỗi tình huống dưới đây, biến ngẫu nhiên là liên tục hay rời rạc. Hãy cho biết lí do:
a. Trang web của bạn có năm liên kết khác nhau và người dùng có thể nhấp vào một trong các
liên kết hoặc có thể rời khỏi trang. Bạn ghi lại khoảng thời gian người dùng bỏ ra trên trang
web trước khi nhấp vào một trong các liên kết hoặc rời khỏi trang.
b. Số lần truy cập trên trang web của bạn.
c. Lượng khách truy cập hằng năm của trang web.
Bài 3.2. Trò chơi đánh bài Texas bắt đầu với việc mỗi người chơi nhận được 2 là bài trên tay. Sau
đây là bảng phân phối số lượng con bài át trong hai lá bài đó Số lượng át 0 1 2 Xác suất 0.559 0.382 0.059 3.1 Lý thuyết 23
a. Hãy kiểm tra xem mô hình trên có phải là một biến ngẫu nhiên rời rạc?
b. Vẽ biểu đồ histogram cho phân phối trên.
c. Xác suất mà trong hai lá chứa ít nhất một át? Tính toán bằng hai cách khác nhau.
Bài 3.3. Phần mềm kiểm tra chính tả bắt lỗi “lỗi không phải từ”, là lỗi tạo thành bởi một chuỗi các
chữ cái sắp xếp không tạo thành một từ, ví dụ chữ “the” được nhập là “teh”. Khi sinh viên đại học
được yêu cầu viết một bài luận 250 từ (không được kiểm tra lại lỗi chính tả), và X số lượng từ bị lỗi có phân phối sau: Giá trị của X 0 1 2 3 4 Xác suất 0.1 0.3 0.3 0.2 0.1
a. Vẽ phân phối xác suất của biến ngẫu nhiên X.
b. Viết biến cố “có ít nhất 1 lỗi” theo biến ngẫu nhiên X. Xác suất của biến cố này là bao nhiêu?
c. Phát biểu thành lời biến cố X ≤ 2. Tính xác suất biến cố đó và xác suất của biến cố X < 2.
Bài 3.4. Thả hai con súc sắc cân bằng với xác suất của mỗi mặt chấm xuất hiện là như nhau. Gọi
biến ngẫu nhiên X là tổng số chấm xuất hiện khi thả hai con súc sắc.
a. Hãy viết không gian mẫu những khả năng khi tung 2 súc sắc.
b. Tính xác suất của mỗi khả năng.
c. Sử dụng kết quả câu b để lập bảng phân phối xác suất và vẽ histogram cho phân phối này.
d. Người chơi sẽ thắng cược khi tổng súc sắc là 7 hoặc 11. Tính xác suất để người chơi thắng khi thả súc sắc.
Bài 3.5. Hãy lập bảng phân phối xác suất, vẽ biểu đồ histogram của thí nghiệm đếm số mặt ngửa
trong mỗi chuỗi 2 lần tung đồng xu với giả thiết đồng xu cân bằng và những lần tung là độc lập với
nhau. Suy ra các xác suất: có ít nhất 2 lần mặt ngửa xuất hiện. Làm lại bài trên với chuỗi 4 đồng xu.
Bài 3.6. Đại học bang North Carolina đăng bản phân phối cấp lớp cho các khóa học trực tuyến.
Học sinh trong học phần tiếng Anh 210 của học kỳ mùa xuân 2006 đã nhận được 31% A, 40% B,
20% C, 4% D và 5% F. Chọn ngẫu nhiên một học sinh Anh ngữ 210. "Chọn ngẫu nhiên" có nghĩa
là mọi học sinh cùng một cơ hội được chọn. Điểm của học sinh theo thang điểm bốn điểm (với A =
4) là một biến ngẫu nhiên X.
a. Hãy lập bảng phân phối xác suất, vẽ biểu đồ histogram và tính xác suất học sinh được chọn B hoặc tốt hơn.
b. Giả sử khi đạt điểm D và F trong học phần tiếng Anh 210, học sinh đó bị coi như chưa hoàn
thành chuyên ngành ngôn ngữ học. Hãy tính xác suất để học sinh chọn không thỏa yêu cầu của chuyên ngành.
Bài 3.7. Sử dụng số liệu từ Bài tập 2.16, ta xét biến ngẫu nhiên V chính là giá trị của chữ số đầu
tiên. Hãy tính trung bình của V . Bài 3.8.
a. Cho biến ngẫu nhiên X có kì vọng µX = 10 thì biến ngẫu nhiên Y = 15 + 8X có kì vọng là bao nhiêu?
b. Cho biến ngẫu nhiên U có trung bình µU = 20 và biến ngẫu nhiên V có trung bình µV = 20
thì biến ngẫu nhiên Z = 0.5U + 0.5V có trung bình là bao nhiêu?
Bài 3.9. Linda là một nhân viên bán hàng tại một đại lý ô tô lớn. Với mức hoa hồng 25% lợi nhuận
tính trên mỗi chiếc xe cô bán, Linda dự kiến sẽ kiếm được 350$ cho mỗi chiếc xe hơi bán được và
400$ cho mỗi chiếc xe tải hoặc SUV bán được. Linda thúc đẩy bản thân bằng cách sử dụng ước 24
Chương 3. BIẾN NGẪU NHIÊN RỜI RẠC
lượng xác suất cho doanh thu của mình. Vào một ngày Thứ Bảy của tháng Tư, cô ước tính doanh số
bán xe hơi của mình như sau: Số xe bán 0 1 2 3 Xác suất 0.3 0.4 0.2 0.1
và xe tải hoặc SUV như sau Số xe bán 0 1 2 Xác suất 0.4 0.5 0.1
Đặt X là số xe hơi Linda bán và Y số xe tải hoặc SUV.
a. Hãy tính trung bình lượng xe mỗi loại cô ta bán từ đó suy ra doanh thu trung bình cô ta thu được.
b. Tính phương sai và độ lệch chuẩn cho biến X.
(Đs: 1.1, 0.7, 665; 0.89, 0.943)
Bài 3.10. Điểm số phần Toán trong kỳ thi tuyển sinh đại học SAT của Hoa Kỳ trong một năm gần
đây có trung bình là 519 và độ lệch chuẩn 115. Điểm số phần Verbal của SAT có trung bình là 507
và độ lệch chuẩn 111. Độ lệch chuẩn và trung bình của tổng điểm SAT là bao nhiêu nếu giả sử điểm
hai phần là độc lập nhau? Tuy nhiên, thực tế điểm Verbal và Toán trong SAT không thể độc lập
vì sinh viên luôn có xu hướng đạt điểm cao trong cả hai phần. Hãy tính lại phương sai và độ lệch
chuẩn tổng điểm của 2 phần thi nếu biết hệ số tương quan ρ = 0.71.
Bài 3.11. Một báo cáo của Trung tâm Thống kê Y tế Quốc gia cho biết rằng chiều cao của nam
giới 20 tuổi có nghĩa là 176.8cm và độ lệch chuẩn 7.2cm. Biết 2.54cm tương ứng với 1inch. Độ
lệch trung bình và tiêu chuẩn tính bằng inch là bao nhiêu?
Bài 3.12. ∗ Giả sử biến ngẫu nhiên X có phân phối nhị thức f (x) = Cxn px(1 − p)n−x.
Xác định hàm gây moment và sử dụng nó kiểm chứng lại trung bình và phương sai của biến ngẫu nhiên nhị thức.
Bài 3.13. ∗ Giả sử biến ngẫu nhiên X có phân phối đều rời rạc f (x) = 1 , x = 1, m. m
a. Chứng minh hàm gây moment là M . X (t) = et (1 − etm) m(1 − et )
b. Sử dụng hàm MX (t) tính trung bình và phương sai của biến ngẫu nhiên phân phối đều rời rạc.
Bài 3.14. ∗ Giả sử biến ngẫu nhiên X có phân phối Poisson f (x) = e−λλx , x ∈ N. x! 3.2 Phân phối nhị thức 25
a. Chứng minh hàm gây moment là λ M (et −1). X (t) = e
b. Sử dụng hàm MX (t) tính trung bình và phương sai của biến ngẫu nhiên phân phối Poisson.
Bài 3.15. ∗ Giả sử biến ngẫu nhiên X có phân phối hình học f (x) = (1 − p)x−1p, x ∈ ∗ N .
a. Chứng minh hàm gây moment là M . X (t) = pet 1 − (1 − p)et
b. Sử dụng hàm MX (t) tính trung bình và phương sai của biến ngẫu nhiên X. 3.2 Phân phối nhị thức
Định nghĩa 3.2.1 Phân phối nhị thức X ∼ B(n, p)
i. Phép thử Bernoulli là thí nghiệm (hay phép thử) chỉ có hai kết quả và thường được sử
dụng để xây dựng một chuỗi các phép thử ngẫu nhiên.
ii. Phép thử n Bernoulli là một nhóm các phép thử Bernoulli thỏa 3 điều kiện: các phép thử
trong mỗi chuỗi là độc lập; mỗi phép thử chỉ có 2 kết quả là “thành công” và “thất bại”;
xác suất thành công của mỗi phép thử là p và không đổi.
iii. Biến ngẫu nhiên nhị thức chính là số lần thành công của phép thử n Bernoulli tham số
0 < p < 1 với xác suất tương ứng P(X = x) = Cx n px (1 − p)n−x, x = 0, n.
iv. Các đặc trưng thống kê: trung bình µX = np và phương sai σ2 = np(1 − p). X Code R 3.2.1
R > dbinom (x = 0:4, size = 4, prob = 1/2) # tính xác suất P(X=x)
R > pbinom (q = 3, size = 4, prob = 1/2) # tính phân phối tích lũy
R > pbinom(9, size=12, prob=1/6) - pbinom(6, size=12, prob=1/ên
R > diff(pbinom(c(6,9), size = 12, prob = 1/6)) # tương đương lệnh trên
R > rbinom (x = 3, size = 4, prob = 1/2)
# tạo 3 số ngẫu nhiên có phân phối nhị thức B(4;1/2)
Bài 3.16. Trong mỗi tình huống dưới đây, có hợp lý khi sử dụng phân phối nhị thức cho biến ngẫu
nhiên X không? Đưa ra lý do cho câu trả lời của bạn trong mỗi trường hợp. Nếu là phân phối nhị
thức, hãy cho các giá trị của n và p.
a. Một cuộc thăm dò ý kiến của 200 sinh viên đại học hỏi bạn có thường hay cáu kỉnh vào buổi
sáng hay không. X là số người trả lời rằng chúng thường dễ cáu kỉnh buổi sáng.
b. Bạn ném một đồng xu cân bằng cho đến khi mặt ngửa xuất hiện. X là số lần tung mà bạn thực hiện.
c. Hầu hết các cuộc gọi điện thoại khảo sát được thực hiện ngẫu nhiên và mẫu được coi là không
thành công khi không nói chuyện với trực tiếp một người. Trong số các cuộc gọi đến thành
phố New York, chỉ 1/12 thành công. Cuộc khảo sát cuộc gọi 500 số được chọn ngẫu nhiên ở
thành phố New York. X là số tiếp cận một người trực tiếp. 26
Chương 3. BIẾN NGẪU NHIÊN RỜI RẠC
d. Một quy trình sản xuất ra hàng nghìn đầu dò nhiệt độ. Cho X biểu thị số đầu dò không phù
hợp trong một mẫu có kích thước 30 được chọn ngẫu nhiên từ quá trình sản xuất trên.
e. Xét X biểu thị số vụ tai nạn xảy ra trên đường cao tốc liên bang ở Arizona trong thời gian một tháng.
Bài 3.17. Biến ngẫu nhiên X có phân phối nhị thức với n = 10 và p = 0.5. Xác định xác suất: a. P(X = 5) b. P(X ≤ 2) c. P(X ≥ 9) d. P(3 ≤ X < 5)
Bài 3.18. Biến ngẫu nhiên X có phân phối nhị thức với n = 10 và p = 0.01. Xác định xác suất: a. P(X = 5) b. P(X ≤ 2) c. P(X ≥ 9) d. P(3 ≤ X < 5)
e. Hãy vẽ hàm phân phối tích lũy của mô hình trên.
Bài 3.19. Một phân xưởng có 5 máy. Xác suất để trong một ca, mỗi máy bị hỏng là 0.1. Tìm xác
suất để trong một ca, có đúng 2 máy bị hỏng. (Đs: 0.0729)
Bài 3.20. Tính xác suất để gieo con xúc xắc 10 lần, mặt một nút xuất hiện không quá 3 lần. (Đs: 0.93)
Bài 3.21. Giả sử tỷ lệ sinh con trai và con gái là bằng nhau và bằng 1/2. Một gia đình có 4 người
con. Tính xác suất để 4 đứa con đó gồm a. 2 trai và 2 gái b. 1 trai và 3 gái c. 4 trai (Đs: 3/8; 1/4; 1/16)
Bài 3.22. Tỷ lệ một loại bệnh bẩm sinh trong dân số là p = 0.01. Bệnh này cần sự chăm sóc đặc
biệt lúc mới sinh. Một nhà bảo sinh thường có 20 ca sinh trong một tuần. Tính xác suất để
a. không có trường hợp nào cần chăm sóc đặc biệt;
b. có đúng một trường hợp cần chăm sóc đặc biệt;
c. có nhiều hơn một trường hợp cần chăm sóc đặc biệt. (Đs: 0.8179; 0.1652; 0.0168)
Bài 3.23. Một đèn giao thông trên tuyến đường một người đi làm vào buổi sáng có màu xanh chiếm
20% số lần người ta tới ngã tư đó. Giả sử mỗi buổi sáng đi làm để thu thập số liệu là độc lập
a. Với 5 buổi sáng đi làm, hãy tính xác suất gặp đèn xanh đúng 1 ngày.
b. Với 20 buổi sáng đi làm, hãy tính xác suất gặp đèn xanh đúng 4 ngày.
c. Với 20 buổi sáng đi làm, hãy tính xác suất gặp đèn xanh nhiều hơn 4 ngày. (Đs: 0.410; 0.218; 0.37)
Bài 3.24. Các đường dây (lines) điện thoại đến hệ thống đặt vé máy bay bận chiếm 40% số lần gọi.
Giả sử rằng việc các đường dây bận khi cuộc gọi đến là độc lập. Giả sử rằng 10 cuộc gọi được đặt cho hãng hàng không.
a. Xác suất để có đúng 3 cuộc gọi tới bị bận đường dây.
b. Xác suất để có ít nhất 1 cuộc gọi tới không bị bận.
c. Tính trung bình số cuộc gọi tới bị bận bằng hai cách. (Đs: 0.215; 0.994; 4)
Bài 3.25. Bài kiểm tra trắc nghiệm chứa 25 câu hỏi, mỗi câu hỏi có bốn câu trả lời. Giả sử một học
sinh chỉ đoán ngẫu nhiên để câu hỏi
a. Xác suất để học sinh đó có nhiều hơn 20 câu trả lời đúng. 3.2 Phân phối nhị thức 27
b. Xác suất để học sinh đó có ít hơn 5 câu trả lời đúng.
Bài 3.26. Một bài thi trắc nghiệm gồm 12 câu hỏi, mỗi câu có 5 câu trả lời, trong đó chỉ có một
câu đúng. Giả sử mỗi câu trả lời đúng, thí sinh được 4 điểm, mỗi câu trả lời sai, thí sinh bị trừ 1
điểm. Một thí sinh làm bài bằng cách chọn ngẫu nhiên các câu trả lời. Tìm xác suất để 28
Chương 3. BIẾN NGẪU NHIÊN RỜI RẠC
a. thí sinh được 13 điểm
b. thí sinh bị điểm âm (Đs: 0.0532; 0.558)
Bài 3.27. Một người bắn bia với xác suất bắn trúng là p = 0.7
a. Bắn liên tiếp 3 phát. Tính xác suất có ít nhất 1 lần trúng bia.
b. Hỏi phải bắn ít nhất mấy lần để có xác suất ít nhất một lần trúng bia ≥ 0.9. (Đs: 0.973; ít nhất 2)
Bài 3.28. Một nhà máy sản xuất với tỷ lệ phế phẩm là 7%
a. Quan sát ngẫu nhiên 10 sản phẩm. Tính xác suất để có:
i. đúng một phế phẩm
ii. ít nhất một phế phẩm
iii. nhiều nhất một phế phẩm (Đs: 0.3643; 0.516; 0.8483)
b. Hỏi phải quan sát ít nhất bao nhiêu sản phẩm để xác suất nhận được ít nhất một phế phẩm ≥ 0.9. (Đs: ít nhất 32) 3.3 Phân phối siêu bội
Định nghĩa 3.3.1 Phân phối siêu bội X ∼ H(N, K, n)
i. Biến ngẫu nhiên siêu bội:
Ta xét tập hợp N đối tượng bao gồm: K đối tượng được phân loại là “thành công” và
N − K đối tượng là “thất bại”, lấy một mẫu ngẫu nhiên gồm n đối tượng (không hoàn lại)
từ N đối tượng này (K < N và n < N). Khi đó, biến ngẫu nhiên siêu bội là số đối tượng
thành công trong mẫu với xác suất tương ứng Cx Cn−x K N −K P(X = x) =
, max{0, n + K − N} ≤ x ≤ min{K,n}. Cn N N − n
ii. Các đặc trưng thống kê: trung bình µX = np và phương sai σ2 = np(1 − p) với X N − 1 p = K/N.
iii. Chú ý: đại lượng N−n được gọi là hệ số hiệu chỉnh. Khi n nhỏ hơn N, thì hệ số hiệu N −1
chỉnh nhỏ và phân phối siêu bội X ∼ H(N, K, n) có thể được xấp xỉ bới phân phối nhị thức X ∼ B(n, K/N).
Code R 3.3.1 Thay các lệnh dbinom, pbinom, rbinom bằng lệnh dhyper, phyper, rhyper.
Bài 3.29. Giả sử X có phân phối siêu bội với N = 100, n = 4, và K = 20. Xác định a. P(X = 1) b. P(X = 6) c. P(X = 4) d. P(X ≤ 2)
e. µX và σ2 bằng 2 cách: công thức và bảng phân phối xác suất. X
Bài 3.30. Giả sử biến ngẫu nhiên X có phân phối siêu bội với N = 10, n = 3 và K = 4. Vẽ hàm phân
phối xác suất và phân phối tích lũy của X.
Bài 3.31. Một lô chứa 36 tế bào vi khuẩn và 12 tế bào trong đó không có khả năng sao chép (sinh
sản) tế bào. Giả sử bạn kiểm tra 3 tế bào vi khuẩn được chọn ngẫu nhiên, không cần hoàn lại.
a. Hãy mô tả hàm phân phối ứng với biến ngẫu nhiên X là số tế bào có thể sao chép trong mẫu lấy ra.
b. Tính trung bình và phương sai của X. 3.4 Phân phối Poisson 29
c. Tính xác suất để có ít nhất 1 tế bào trong mẫu không thể sao chép.
Bài 3.32. (Sử dụng phân phối nhị thức xấp xỉ phân phối siêu bội)
Một công ty sử dụng 800 người đàn ông dưới 55 tuổi. Giả sử 30% mang dấu hiệu trên nhiễm sắc
thể nam biểu thị nguy cơ cao huyết áp.
a. Nếu 10 người đàn ông trong công ty được xét nghiệm dấu hiệu của nhiễm sắc thể này, xác
suất có chính xác một người đàn ông mang dấu hiệu đó với nhận xét số người được xét
nghiệm n = 10 nhỏ hơn rất nhiều so với N = 800?
b. Nếu 10 người đàn ông trong công ty được xét nghiệm dấu hiệu của nhiễm sắc thể này, xác
suất có nhiều hơn một người đàn ông mang dấu hiệu đó? (Đs: 0.1201; 0.8523) 3.4 Phân phối Poisson
Định nghĩa 3.4.1 Phân phối Poisson X ∼ P(λ)
i. Biến ngẫu nhiên Poisson: một biến ngẫu nhiên rời rạc được mô hình bằng phân phối
Poisson nếu thỏa các điều kiện
a. Các biến cố xảy ra một cách ngẫu nhiên và độc lập giữa những khoảng thời gian
hoặc không gian nhất định.
b. Số lượng trung bình λ các biến cố xảy ra trong những khoảng là đồng nhất và hữu hạn.
Khi đó, số lượng biến cố xảy ra trong những khoảng thời gian tương ứng với xác suất P(X = x) = e−λλx , x ∈ N. x!
ii. Các đặc trưng thống kê: trung bình µX = λ và phương sai σ2 = λ. X
iii. Chú ý: Khi X ∼ B(n, p) với p nhỏ và n lớn thì ta có thế xấp xỉ bởi phân phối Poisson X ∼ P(np).
Code R 3.4.1 Thay các lệnh dbinom, pbinom, rbinom bằng lệnh dpois, ppois, rpois.
Bài 3.33. Giả sử X có phân phối Poisson với trung bình là 4. Tính xác suất a. P(X = 0) b. P(X ≤ 2) c. P(X = 4) d. P(X = 8)
Bài 3.34. Số lượng các cuộc gọi điện thoại đến trao đổi với một trạm giao dịch thường được mô
hình hóa bằng biến ngẫu nhiên Poisson. Giả sử trung bình có 10 cuộc gọi mỗi giờ. Xác suất có chính xác
a. 5 cuộc gọi trong một giờ.
c. 15 cuộc gọi trong hai giờ.
b. 3 cuộc gọi hoặc ít hơn trong một giờ.
d. 5 cuộc gọi trong 30 phút.
Bài 3.35. Các nhà thiên văn học đếm số lượng các ngôi sao trong một thể tích không gian cho trước
được xem như là biến ngẫu nhiên Poisson. Mật độ trong thiên hà Milky Way trong vùng lân cận với
hệ mặt trời của chúng ta là một ngôi sao trên 16 năm ánh sáng.
a. Xác suất để có từ 2 ngôi sao trở lên trong 16 năm ánh sáng.
b. Cần bao nhiêu năm ánh sáng để xác suất có 1 hoặc nhiều hơn ngôi sao lớn hơn 0.95. (Đs: 0.264; 48)
Bài 3.36. Số lỗ hỏng trên tấm vải của nhà máy dệt được giả định là phân phối Poisson với trung
bình 0.1 lỗ trên một mét vuông vải. Xác suất để có 30
Chương 3. BIẾN NGẪU NHIÊN RỜI RẠC
a. 2 lỗ hỏng trên 1m2 vải.
c. 0 lỗ hỏng trên 20m2 vải.
b. 1 lỗ hỏng trên 10m2 vải.
d. ít nhất 2 lỗ hỏng trên 10m2 vải.
Bài 3.37. Giả sử rằng số lượng khách hàng bước vào ngân hàng trong một giờ là một biến ngẫu
nhiên Poisson và giả sử rằng P(X = 0) = 0.05. Xác định trung bình và phương sai của X.
Bài 3.38. Số lượng danh mục của một trang Web thay đổi tuân theo phân phối Poisson với trung
bình là 0.25 trên 1 ngày. Xác suất có
a. nhiều hơn hay bằng 2 thay đổi trong một ngày.
b. không có thay đổi trong năm ngày.
c. ít hơn hay bằng 2 thay đổi trong năm ngày. (Đs: 0.026; 0.287; 0.868)
Bài 3.39. Một trung tâm bưu điện nhận được trung bình 3 cuộc điện thoại trong mỗi phút. Tính
xác suất để trung tâm này nhận được 1 cuộc, 2 cuộc, 3 cuộc gọi trong 1 phút, biết rằng số cuộc gọi
trong một phút có phân phối Poisson. (Đs: 0.1494; 0.224; 0.224)
Bài 3.40. Khi nhà sản xuất đĩa máy tính kiểm tra đĩa, họ ghi vào đĩa và sau đó kiểm tra nó bằng
cách sử dụng một chương trình xác nhận. Trình xác nhận đến số xung hoặc lỗi bị thiếu. Số lỗi trên
vùng thử của đĩa có phân phối Poisson với λ = 0.2
a. Xác định số lỗi trung bình trên phần diện tích được kiểm tra.
b. Tỉ lệ phần trăm diện tích kiểm tra để có hai lỗi hay ít hơn. (Đs: 99.89%)
Bài 3.41. Số lượng các lỗ hổng bề mặt trong các tấm nhựa được sử dụng làm nội thất của xe ô tô
có phân bố Poisson với giá trị trung bình 0,05 lỗ trên một foot vuông của bảng nhựa. Giả sử một bộ
phận nội thất ô tô chứa 10 feet vuông của bảng nhựa.
a. Xác suất để không có lỗi nào trên bộ phận nội thất đó.
b. Nếu 10 chiếc xe được bán cho một công ty cho thuê, xác suất để không có bất kì chiếc trong
số 10 chiếc xe có bất kỳ sai sót bề mặt nào?
c. Nếu 10 chiếc xe được bán cho một công ty cho thuê, xác suất để nhiều nhất một chiếc trong
số 10 chiếc xe có bất kỳ sai sót bề mặt nào? (Đs: 0.6065; 0.0067; 0.0504)
Bài 3.42. Tỷ lệ một loại bệnh bẩm sinh trong dân số là p = 0.01. Bệnh này cần sự chăm sóc đặc
biệt lúc mới sinh. Một nhà bảo sinh thường có 20 ca sinh trong một tuần. Tính xác suất để
a. Không có trường hợp nào cần chăm sóc đặc biệt.
b. Có đúng một trường hợp cần chăm sóc đặc biệt.
c. Có nhiều hơn một trường hợp cần chăm sóc đặc biệt.
Tính bằng quy luật nhị thức rồi dùng quy luật Poisson để so sánh kết quả khi ta xấp xỉ phân phối
nhị thức bằng phân phối Poisson . 31
4. BIẾN NGẪU NHIÊN LIÊN TỤC 4.1 Định nghĩa Định nghĩa 4.1.1
a. Biến ngẫu nhiên liên tục là biến ngẫu nhiên nhận giá trị trong một khoảng con (hữu hạn
hoặc vô hạn) của tập số thực.
b. Hàm mật độ xác suất của một biến ngẫu nhiên liên tục là hàm số thỏa i. f (x) ≥ 0; ∫ +∞ ii. f (x)dx = 1; −∞ ∫ b iii. P(a ≤ X ≤ b) = f (x)dx. a
c. Hàm phân phối tích lũy của một biến ngẫu nhiên liên tục được định nghĩa ∫ x F(x) = P(X ≤ x) = f (s)ds, x ∈ R. −∞ Định nghĩa 4.1.2
i. Trung bình của một biến ngẫu nhiên liên tục có hàm mật độ f (x) được định nghĩa ∫ +∞ E(X ) = µX = x f (x)dx. −∞
ii. Phương sai của một biến ngẫu nhiên liên tục có hàm mật độ f (x) được định nghĩa ∫ +∞ ∫ +∞ V(X ) = σ2 = (x − µ x2 f (x)dx − µ2 . X X )2 f (x)dx = X −∞ −∞
iii. Kì vọng của một hàm phụ thuộc liên tục vào một biến ngẫu nhiên liên tục X có hàm mật 32
Chương 4. BIẾN NGẪU NHIÊN LIÊN TỤC
độ xác suất f (x) được tính ∫ +∞ Eh(X) = h(x) f (x)dx. −∞
Đặc biệt, nếu h(x) = xr ta gọi Eh(X) là moment bậc r. Nếu h(x) = etx thì ta gọi Eh(X)
là hàm gây (sinh) moment. Nếu h(x) = e−itx thì ta gọi Eh(X) là hàm đặc trưng của biến ngẫu nhiên X.
Code R 4.1.1 Sử dụng hàm tính tích phân để tính xác suất
R > f <- function(x) 3 * x^2
R > integrate(f, lower = 0.14, upper = 0.71) hoặc sử dụng thư viện R > library(distr)
R > f <- function(x) 3 * x^2
R > X <- AbscontDistribution(d = f, low1 = 0, up1 = 1) R > p(X)(0.71) - p(X)(0.14) R > library(distrEx) R > E(X) R > var(X)
Bài 4.1. Dòng điện trong một mạch nhất định được đo bằng một ampe kế là biến ngẫu nhiên liên
tục X với hàm mật độ sau:
0.075x + 0.2 khi 3 ≤ x ≤ 5, f (x) = 0 chỗ khác.
a. Hãy vẽ hàm mật độ của phân phối và kiểm tra phần diện tích phía dưới đường cong của hàm mật độ là 1.
b. Tính P(X ≤ 4) và so sánh với xác suất P(X > 4).
c. Tính xác suất P(3.5 ≤ X ≤ 4.5) và P(X > 4.5).
Bài 4.2. Lỗi liên quan đến việc thực hiện một phép đo nhất định là một biến ngẫu nhiên X liên tục với hàm mật độ:
0.09375(4 − x2) khi − 2 ≤ x ≤ 2, f (x) = 0 chỗ khác.
a. Hãy vẽ hàm mật độ của phân phối. b. Tính P(X > 0).
c. Tính P(−1 < X < 1).
d. Tính P(X < −0.5 hoặc X > 0.5).
Bài 4.3. Một giáo sư đại học không bao giờ kết thúc bài giảng của mình trước khi hết giờ và luôn
hoàn thành bài giảng của mình trong vòng 2 phút sau giờ học. Cho X là thời gian trôi qua giữa thời
điểm hết tiết học và kết thúc bài giảng của giáo sư. Giả sử hàm mật độ của X là: k x2 khi 0 ≤ x ≤ 2, f (x) = 0 chỗ khác.
a. Tìm k và vẽ hàm mật độ tương ứng.
b. Hãy tính xác suất bài giảng kết thúc trong vòng 1 phút sau khi giờ học kết thúc.
c. Hãy tính xác suất bài giảng tiếp tục diễn ra sau khi giờ học kết thúc từ 60s tới 90s. 4.1 Định nghĩa 33
d. Xác suất mà bài giảng tiếp tục trong ít nhất 90s ngoài giờ kết thúc là bao nhiêu?
Bài 4.4. Giả sử nhiệt độ phản ứng X (tính theo oC) trong một quá trình phản ứng hóa học nhất
định có phân phối đều với A = −5 và B = 5. a. Tính P(X < 0).
b. Tính P(−2.5 < X < 2.5).
c. Tính P(−2 ≤ X ≤ 3).
d. Với k thỏa −5 < k < k + 4 < 5, hãy tính P(k < X < k + 4).
Bài 4.5. Một bài báo: “Second Moment Reliability Evaluation vs. Monte Carlo Simulations for
Weld Fatigue Strength (Quality and Reliability Engr. Intl., 2012: 887-896)” xem xét việc sử dụng
phân phối đều với A = 0.20 và B = 4.25 cho đường kính X của những mối hàn (mm).
a. Tìm và vẽ hàm mật độ của X.
b. Xác suất đường kính vượt quá 3mm là bao nhiêu?
c. Xác suất đường kính trong vòng 1 mm của đường kính trung bình là bao nhiêu?
d. Với a thỏa điều kiện 0.2 < a < a + 1 < 4.5 thì xác suất P(a < X < a + 1) bao nhiêu?
Bài 4.6. Khi đi làm, một giáo sư trước tiên phải lên xe buýt gần nhà cô và sau đó chuyển sang tuyến
xe buýt thứ hai. Nếu thời gian chờ đợi (tính bằng phút) tại mỗi điểm dừng có phân bố đều với A = 0
và B = 5, khi đó có thể thấy rằng tổng thời gian chờ đợi Y có hàm mật độ: 1 y khi 0 ≤ y < 5, 25 f (y) = 2 1 − y khi 5 ≤ y ≤ 10, 5 25 0 chỗ khác.
a. Vẽ hàm mật độ của Y . ∫ ∞
b. Kiểm tra tính chất f (y)dy = 1. −∞
c. Xác suất tổng thời gian chờ tối đa 3 phút là bao nhiêu?
d. Xác suất tổng thời gian chờ tối đa 8 phút là bao nhiêu?
e. Xác suất tổng thời gian chờ từ 3 đến 8 phút là bao nhiêu?
f. Xác suất mà tổng thời gian chờ đợi là ít hơn 2 phút hoặc lớn hơn 6 phút?
Bài 4.7. Gọi X biểu thị ứng suất rung (với đơn vị psi) trên lưỡi tuabin gió ở tốc độ gió cụ thể trong
đường hầm gió. Bài báo “Blade Fatigue Life Assessment with Application to VAWTS” (J. of Solar
Energy Engr., 1982: 107–111)” đề xuất phân phối Rayleigh, với hàm mật độ: ( x e−x2/(2θ2) khi x > 0, f (x; θ) = θ2 0 chỗ khác.
là mô hình cho phân phối của X.
a. Kiểm tra tính hợp lí của hàm f (x; θ).
b. Giả sử θ = 100 (một giá trị được đề xuất bằng một đồ thị có trong bài báo). Tính xác suất X
nhiều nhất là 200? Ít hơn 200? Nhiều hơn 200?
c. Tính xác suất X nằm giữa 100 và 200 (vẫn với giả thiết về θ như trên).
d. Tính hàm P(X ≤ x).
Bài 4.8. Dựa trên cơ sở phân tích dữ liệu, một bài báo trên: “Pedestrians’ Crossing Behaviors and
Safety at Unmarked Roadways in China (Accident Analysis and Prevention, 2011: 1927–1936)” đã
đề xuất hàm mật độ f (x) = 0.15e−0.15(x−1) với x ≥ 1 làm mô hình cho phân phối của X = thời gian
(giây) được sử dụng ở dòng trung bình.
a. Xác suất mà thời gian chờ tối đa là 5 giây là bao nhiêu? Hơn 5 giây? 34
Chương 4. BIẾN NGẪU NHIÊN LIÊN TỤC
b. Xác suất mà thời gian chờ đợi là từ 2 đến 5 giây là bao nhiêu?
Bài 4.9. Gọi X là tuổi thọ của con người. Một công trình nghiên cứu cho biết hàm mật độ của X là
cx2(100 − x)2 khi 0 ≤ x ≤ 100, f (x) = 0 khi x < 0 hay x > 100.
a. Xác định hằng số c.
b. Tính trung bình và phương sai của X.
c. Tính xác suất của một người có tuổi thọ ≥ 60.
d. Tính xác suất của một người có tuổi thọ ≥ 60, biết rằng người đó hiện nay đã 50 tuổi.
(Đs: 3.10−9; 50, 2500/7; 0.31744; 0.63548)
Bài 4.10. Cho X là biến ngẫu nhiên liên tục với hàm phân phối tích lũy 0 khi x ≤ 0, x 4 F(x) = 1 + ln khi 0 < x ≤ 4, 4 x 1 khi x ≥ 0.
(Hàm phân phối tích lũy này được đề xuất trong bài báo “Variability in Measured BedloadTransport
Rates (Water Resources Bull., 1985: 39–48)” được xem như mô hình cho biến ngẫu nhiên về thủy văn. Hãy tính a. P(X ≤ 1)? b. P(1 ≤ X ≤ 3)?
c. Hàm mật độ của X?
Bài 4.11. Cho hàm phân phối tích lũy của biến ngẫu nhiên X trong Bài tập 4.2 là: 0 khi x < −2, 1 x3 F(x) = + 3 4x − khi − 2 ≤ x < 2, 2 32 3 1 khi x ≥ 2, a. Tính P(X < 0).
b. Tính P(−1 < X < 1). c. Tính P(X > 0.5).
d. Kiểm tra lại hàm mật độ f (x) là đạo hàm của F 0(x).
e. Chứng minh rằng: µ = 0.
Bài 4.12. Cho X là một biến ngẫu nhiên có hàm phân phối tích lũy như sau: 0 khi x < 0, x2 F(x) = khi 0 ≤ x < 2, 4 1 khi x ≥ 2, a. Tính P(X ≤ 1).
b. Tính P(0.5 ≤ X ≤ 1). c. Tính P(X ≥ 1.5).
d. Tìm giá trị trung vị µ?
e. Tìm hàm mật độ f (x). f. Tính E(X). g. Tính V(X) và σX. 4.1 Định nghĩa 35
h. Tính giá trị kì vọng của biến ngẫu nhiên h(X) = X2.
Bài 4.13. Trong bài báo: “Modeling Sediment and Water Column Interactions for Hydrophobic
Pollutant (Water Research, 1984: 1169–1174)” đề xuất phân bố đồng đều trên khoảng (7.5, 20) làm
mô hình cho độ sâu (cm) của lớp sinh học trong trầm tích ở một khu vực nhất định.
a. Tính trung bình và phương sai của độ sâu.
b. Tính hàm phân phối tích lũy của độ sâu.
c. Xác suất quan sát độ sâu tối đa là 10? Từ 10 đến 15?
d. Xác suất mà độ sâu quan sát được trong phạm vi 1 lần độ lệch chuẩn của giá trị trung bình là
bao nhiêu? Trong vòng 2 lần độ lệch chuẩn?
Bài 4.14. Gọi X là lượng không gian bị chiếm bởi một văn kiện được đặt trong một thùng container
loại 1 f t3. Hàm mật độ xác suất của X là:
90x8(1 − x) khi 0 < x < 1, f (x) = 0 chỗ khác.
a. Vẽ hàm mật độ của X. Tìm hàm phân phối tích lũy của X và vẽ hàm này.
b. Tìm P(X ≤ 0.5)? So sánh với F(0.5).
c. Sử dụng kết quả từ câu a tính xác suất P(0.25 < X ≤ 0.5). Kết quả có khác với P(0.25 ≤ X ≤ 0.5).
d. Hãy tìm vị trí của x khi xác suất đạt 75%. e. Tính E(X) và σX.
f. Hãy tính xác suất khi X lớn hơn một lần độ lệch chuẩn so với giá trị trung bình.
Bài 4.15. Bài viết “A Model of Pedestrians’ Waiting Times for Street Crossings at Signalized
Intersections (Transportation Research, 2013: 17–28)” gợi ý rằng trong một số trường hợp, phân
phối của thời gian chờ X có thể được mô hình hóa bằng hàm mật độ sau: (
θ (1− x/τ)θ−1 khi 0 ≤ x < τ, f (x; θ, τ) = τ 0 chỗ khác.
a. Vẽ hàm mật độ của X khi τ = 80 và θ = 4, 1 và 0.5 và nhận xét đồ thị của chúng.
b. Tìm hàm phân phối tích lũy của X.
c. Tìm giá trị trung vị của thời gian chờ.
d. Với θ = 4 và τ = 80 hãy tính P(50 ≤ X ≤ 70)
Bài 4.16. ∗ Một biến ngẫu nhiên liên tục X có hàm phân phối f (x) = 4xe−2x, x > 0.
a. Tìm hàm gây moment MX (t).
b. Tính trung bình và phương sai của X.
Bài 4.17. ∗ Cho biến ngẫu nhiên đều liên tục X có hàm mật độ f (x) = 1 , α ≤ β x ≤ β. − α
a. Chứng minh hàm gây moment của X là MX (t) = etβ−etα . t(β−α)
b. Sử dụng MX (t) tính trung bình và phương sai của X.
Bài 4.18. ∗ Cho biến ngẫu nhiên có phân phối mũ X có hàm mật độ f (x) = λe−λx, x > 0. 36
Chương 4. BIẾN NGẪU NHIÊN LIÊN TỤC
a. Chứng minh hàm gây moment của X là M −1 X (t) = 1 − tλ .
b. Sử dụng MX (t) tính trung bình và phương sai của X.
Bài 4.19. ∗ Cho biến ngẫu nhiên có phân phối gamma X có hàm mật độ λ f (x) = (λx)r−1e−λx, x > 0, Γ(r) với ∫ +∞ Γ(r) = xr−1e−x dx. 0
a. Chứng minh hàm gây moment của X là M −r X (t) = 1 − tλ .
b. Sử dụng MX (t) tính trung bình và phương sai của X.
Bài 4.20. ∗ Cho biến số ngẫu nhiên X có hàm mật độ 1 f (x) = λ e− xλ khi x > 0, 0 khi x ≤ 0. với λ > 0.
a. Tính trung bình và phương sai.
b. Tìm hàm đặc trưng M(t). Dùng hàm đặc trưng, tính lại trung bình và phương sai σ2.
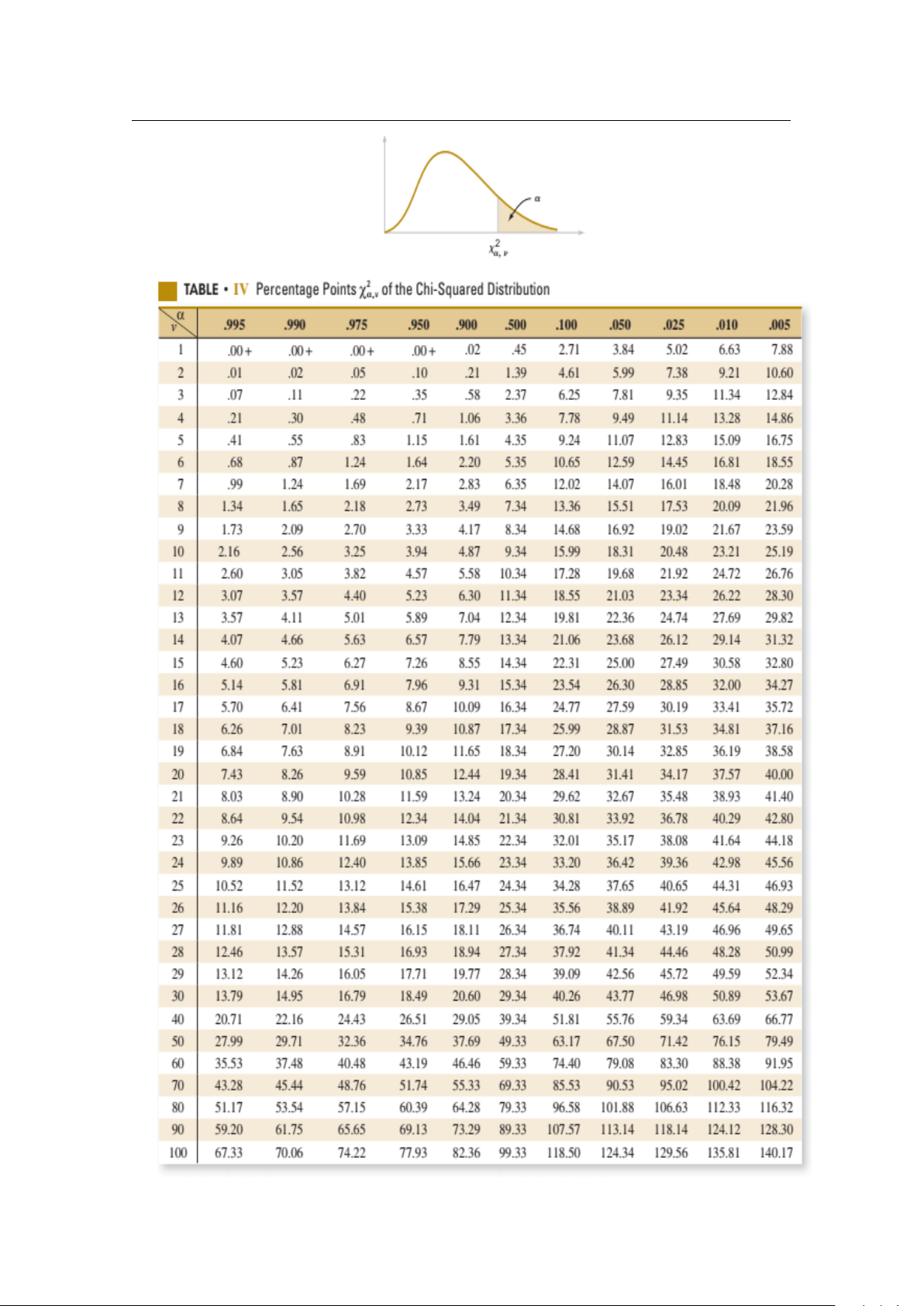
Bài 4.21. Cho biến ngẫu nhiên có phân phối chi bình phương với k bậc tự do có hàm gây moment
M(t) = (1 − 2t) − k/2. Giả sử X và Y là hai biến ngẫu nhiên có phân phối chi bình phương với k1 và
k2 là bậc tự do. Tìm phân phối của Z = X +Y ? 4.2 Phân phối chuẩn
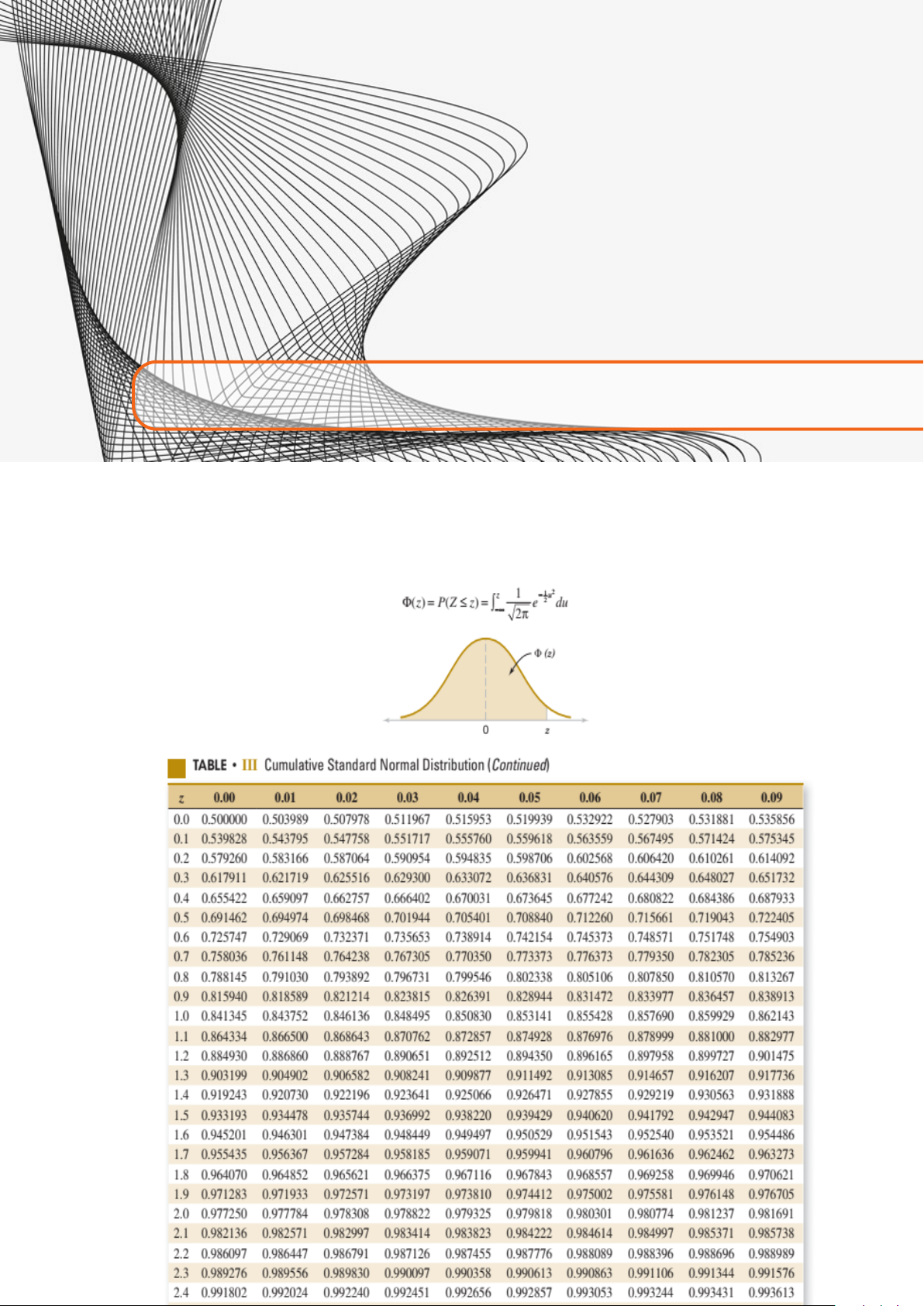
Định nghĩa 4.2.1 Phân phối chuẩn X ∼ N(µ, σ2)
Biến ngẫu nhiên X được gọi là có phân phối chuẩn nếu hàm mật độ xác suất có dạng ( − x−µ)2 f (x) = 1 √ e 2σ2 , σ 2π
trong đó µ = E(X) và σ2 = V(X). Đặc biệt, nếu µ = 0 và σ2 = 1 thì ta gọi Z là biến ngẫu nhiên
có phân phối chuẩn tắc và đặt Φ là hàm phân phối tích lũy có dạng Φ(z) = P(Z ≤ z).
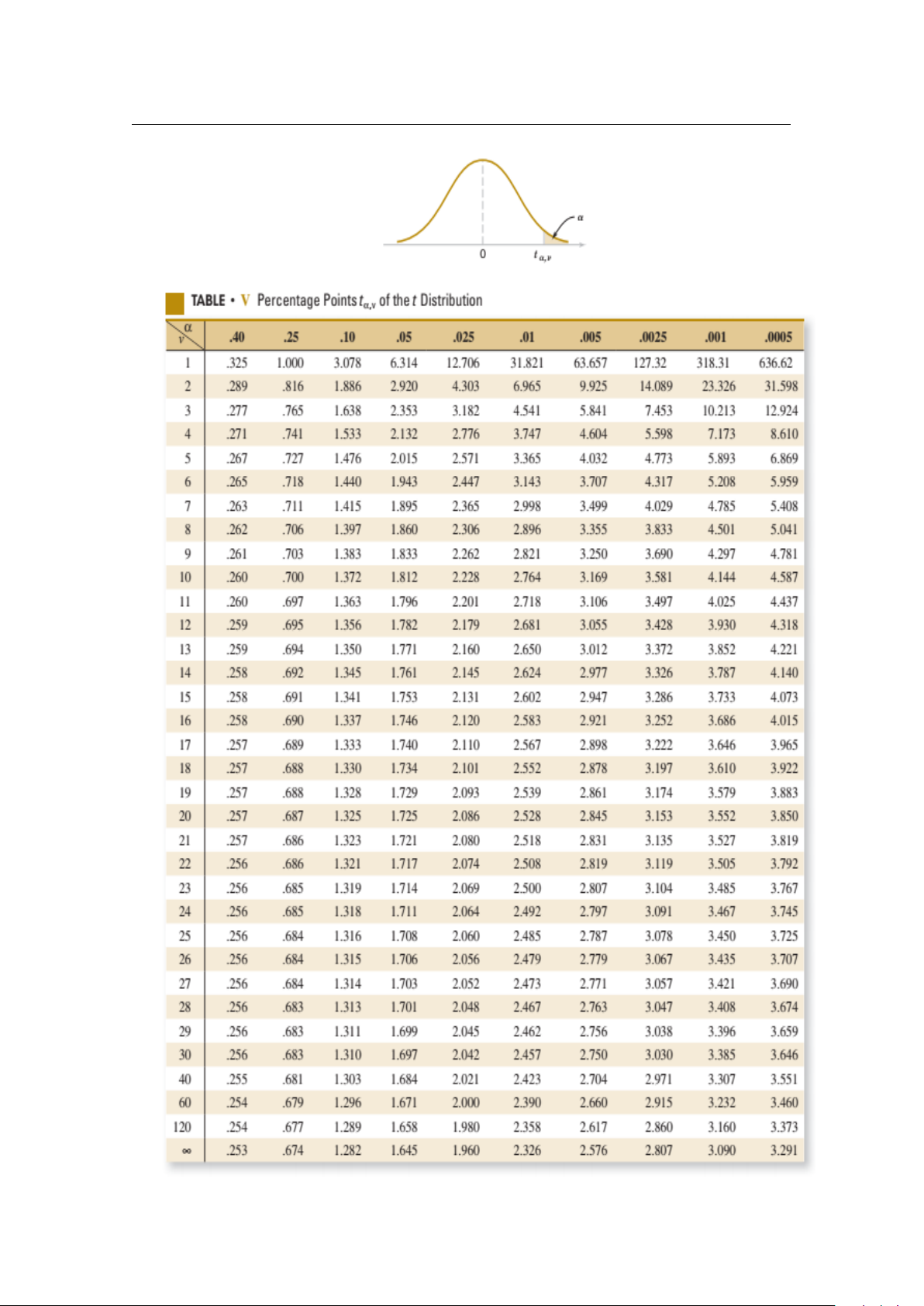
Định lí 4.2.1 (Chuẩn tắc hóa một phân phối chuẩn)
Cho trước X ∼ N(µ, σ2), ta đặt Z = X−µ σ
thì Z ∼ N(0, 1). Khi đó, ta có thể tính xác suất X − µ x − µ P(X ≤ x) = P ≤ = σ σ P(Z ≤ z) = Φ(z),
với z = (x − µ)/σ được gọi là “z-value” (giá trị tới hạn).
Bài 4.22. Sử dụng bảng phân phối chuẩn tắc hoặc máy tính, vẽ và tính các xác suất sau 4.2 Phân phối chuẩn 37 a. P(Z < 1.32) d. P(Z > −2.15) b. P(Z < 3)
e. P(−2.34 < Z < 1.76) c. P(Z > 1.45)
Bài 4.23. Sử dụng bảng phân phối chuẩn tắc hoặc máy tính, vẽ và tính các xác suất sau
a. P(−1 < Z < 1) d. P(Z > 3)
b. P(−2 < Z < 2) e. P(0 < Z < 1)
c. P(−3 < Z < 3)
Bài 4.24. Sử dụng bảng phân phối chuẩn tắc hoặc máy tính, vẽ và tính các z-value nếu biết a. P(Z < z) = 0.9 d. P(Z > z) = 0.9 b. P(Z < z) = 0.5
e. P(−1.24 < Z < z) = 0.8 c. P(Z > z) = 0.1
Bài 4.25. Sử dụng bảng phân phối chuẩn tắc hoặc máy tính, tính các z-value nếu biết
a. P(−z < Z < z) = 0.95
c. P(−z < Z < z) = 0.68
b. P(−z < Z < z) = 0.99
d. P(−z < Z < z) = 0.9973
Bài 4.26. Cho X là biến ngẫu nhiên phân phối chuẩn với trung bình 10 và phương sai 2. Xác định a. P(X < 13) d. P(2 < X < 4) b. P(X > 9)
e. P(−2 < X < 8) c. P(6 < X < 14)
Bài 4.27. Cho X là biến ngẫu nhiên phân phối chuẩn với trung bình 10 và phương sai 2. Xác định giá trị của x thỏa a. P(X > x) = 0.5
d. P(−x < X − 10 < x) = 0.95 b. P(X > x) = 0.95
e. P(−x < X − 10 < x) = 0.99
c. P(x < X < 10) = 0.2
Bài 4.28. Trọng lượng X (tính bằng gam) một loại trái cây có phân phối chuẩn với trung bình
500 gam và phương sai 16 gam2. Trái cây thu hoạch được phân loại theo trọng lượng như sau: . Loại 1: trên 505 gam
. Loại 2: từ 495 gam tới 505 gam . Loại 3: dưới 495 gam
Tính tỷ lệ mỗi loại. (Đs: 0.10565; 0.7887; 0.10565)
Bài 4.29. Cường độ nén của các mẫu xi măng có thể được mô hình hóa bởi một phân bố chuẩn với
giá trị trung bình 6000 kg/cm2 và độ lệch chuẩn là 100 kg/cm2.
a. Xác suất để cường độ nén của mẫu nhỏ hơn 6250 kg/cm2.
b. Xác suất để cường độ nén của mẫu trong khoảng 5800 − 5900 kg/cm2.
c. Độ nén là bao nhiêu để có thể chiếm ít nhất 95% mẫu. (Đs: 0.99379; 0.13591; 5835)
Bài 4.30. Thời gian cho đến khi cần sạc lại pin cho một máy tính xách tay trong điều kiện bình
thường là phân phối chuẩn với trung bình 260 phút và độ lệch chuẩn là 50 phút.
a. Xác suất pin sử dụng kéo dài hơn bốn giờ là bao nhiêu? 38
Chương 4. BIẾN NGẪU NHIÊN LIÊN TỤC
b. Xác định thời gian sử dụng pin tại những giá trị phân vị, là giá trị của z sao cho xác suất
P(Z < z) đạt 25% và 75%?
c. Xác định thời gian sử dụng pin tương ứng với xác suất ít nhất 0.95.
Bài 4.31. Cholesterol (chất béo) là một phần quan trọng của lớp màng ngoài tế bào trong cơ thể của
động vật. Giới hạn bình thường của nó đối với người lớn là 120 − 240mg/dl. Viện Thực phẩm và
Dinh dưỡng của Philippines nhận thấy rằng tổng mức cholesterol ở người trưởng thành Philippines
có trung bình là 159.2mg/dl và 84.1% người trưởng thành có mức cholesterol dưới 200mg/dl
(theo http://www.fnri.dost.gov.ph/). Giả sử tổng mức cholesterol có phân phối chuẩn.
a. Xác định độ lệch chuẩn của phân phối trên (sử dụng dạng chuẩn hóa).
b. Tìm các phân vị của phân phối.
c. Mức cholesterol là bao nhiêu thì chiếm ít nhất 90% dân số.
d. Một người trưởng thành được coi như có nguy cơ mắc bệnh nếu lượng cholesterol cao hơn
hơn mức trung bình một lượng bằng với độ lệch chuẩn hoặc thấp hơn mức trung bình hai lần
độ lệch chuẩn. Xác định tỉ lệ phần trăm dân số mắc nguy cơ này.
e. Một người trưởng thành được coi như có nguy cơ cao mắc bệnh nếu lượng cholesterol cao
hơn mức trung bình hai lần độ lệch chuẩn. Xác định tỉ lệ phần trăm dân số mắc nguy cơ này.
Bài 4.32. Đường kính của một chi tiết máy do một máy tiện tự động sản xuất có phân phối chuẩn
với trung bình 50mm và độ lệch chuẩn 0.05mm. Chi tiết máy được xem là đạt yêu cầu nếu đường kính không sai quá 0.1mm.
a. Tính tỷ lệ sản phẩm đạt yêu cầu.
b. Lấy ngẫu nhiên 3 sản phẩm. Tính xác suất có ít nhất một sản phẩm đạt yêu cầu. (hd:sử dụng
kết quả câu 1 và phân phối nhị thức) (Đs: 0.9544; 0.9999) 4.3 Định lí giới hạn Định lí 4.3.1
Sử dụng phân phối chuẩn để xấp xỉ phân phối nhị thức và phân phối Poisson:
i. Cho X ∼ B(n, p) thì biến ngẫu nhiên Z = X−np √
được bởi xấp xỉ phân phối chuẩn tắc đủ np(1−p)
tốt khi np > 5 và n(1 − p) > 5. Khi đó, ta sử dụng hiệu chỉnh liên tục để tính xác suất ! x + 0.5 − np
P(X ≤ x) = P(X ≤ x + 0.5) P Z ≤ , pnp(1 − p) ! x − 0.5 − np
P(X ≥ x) = P(X ≥ x − 0.5) P Z ≥ . pnp(1 − p)
ii. Cho X ∼ P(λ) thì biến ngẫu nhiên Z = X−λ √
được bởi xấp xỉ phân phối chuẩn tắc đủ tốt khi λ
λ > 5. Khi đó, ta sử dụng công thức hiệu chỉnh liên tục tương tự như trên để tính xác suất.
Bài 4.33. Giả sử X có phân phối nhị thức với n = 200 và p = 0.4. Hãy xấp xỉ xác suất a. P(X ≤ 70) b. P(70 ≤ X ≤ 90) c. P(X = 80)
Hướng dẫn: sử dụng công thức hiệu chỉnh liên tục P(X = 80) = P(80 ≤ X ≤ 80) = P(79.5 ≤ X ≤ 80.5). (Đs: 0.0853; 0.8293; 0.0575)
Bài 4.34. Giả sử X có phân phối Poisson với λ = 6. 4.3 Định lí giới hạn 39
a. Tính chính xác xác suất X nhỏ hơn 4.
b. Sử dụng cách xấp xỉ để tính xác suất trên và so sánh kết quả.
c. Xấp xỉ xác suất để 8 < X < 12. Tính bằng hai cách.
Bài 4.35. Giả sử rằng X có phân bố Poisson với trung bình là 64. Ước tính gần đúng các xác suất sau: a. P(X > 72) b. P(X < 64) c. P(60 < X ≤ 68) (Đs: 0.1446; 0.4761; 0.3823)
Bài 4.36. Trong một kênh truyền thông kỹ thuật số, giả sử rằng số lượng bit nhận được có lỗi được
mô hình hóa bởi một biến ngẫu nhiên nhị thức và giả định rằng xác suất mà một bit được nhận theo
lỗi là 10−5. Nếu 16 triệu bit được truyền đi, xác suất xảy ra là ít hơn hoặc bằng 150 là bao nhiêu?
Nêu khó khăn trong việc tính xác suất bằng cong thức phân phối nhị thức và sử dụng phân phối
chuẩn để tính. (Đs: 0.227)
Bài 4.37. Giả sử rằng số lượng các hạt amiăng trong một mét vuông trên bề mặt tuân theo phân bố
Poisson với giá trị trung bình là 1000. Nếu phân tích một mét bụi bình phương, xác suất nào có
thể tìm thấy ít hơn hoặc bằng 950 hạt bằng công thức phân phối Poisson và phân phối chuẩn? Nêu
thuận lợi và khó khăn. (Đs: 0.058)
Bài 4.38. Có 49,7 triệu người bị một số bệnh khuyết tật sống ở Hoa Kỳ vào năm 2000. Trong đó
chiếm 19.3% từ năm tuổi trở lên (http: // factfinder. Census.gov). Một mẫu 1000 người được chọn ngẫu nhiên.
1. Ước tính xác suất gần đúng để có hơn 200 người trong mẫu có bệnh khuyết tật.
2. Ước tính xác suất gần đúng để có khoảng từ 180 đến 300 người trong mẫu có bệnh khuyết tật.
(Đs: 0.2743; 0.8413. Chú ý: n = 1000, p = 19.3%.)
Bài 4.39. Một sản phẩm điện tử văn phòng chứa 5000 linh kiện điện tử. Giả sử rằng xác suất mà
mỗi thành phần hoạt động mà không có hư hỏng trong thời gian sử dụng hữu ích của sản phẩm
là 0.999 và giả định rằng các thành phần hoạt động một cách độc lập. Xấp xỉ xác suất có nhiều
hơn hoặc bằng 10 trong số 5000 thành phần ban đầu bị hư hỏng thời gian sử dụng hữu ích của sản phẩm. (Đs: 0.022)
Bài 4.40. Giả sử rằng số lượng các hạt amiăng trong một centimet vuông trên bề mặt tuân theo
phân bố Poisson với giá trị trung bình là 1000. Xác suất để trong 10 centimet vuông có nhiều hơn 10000 hạt. (Đs: 0.5)
Bài 4.41. Số lần truy cập vào một trang web được giả định tuân theo phân phối Poisson với giá trị
trung bình là 10.000 mỗi ngày. Xấp xỉ từng điều sau đây:
a. Xác suất để có nhiều hơn 20000 lượt truy cập trong một ngày.
b. Xác suất để có nhỏ hơn 9900 lượt truy cập trong một ngày.
c. Số lượt truy cập để xác suất có ít nhất 0.01.
d. Xấp xỉ số ngày trong năm (365 ngày) có nhiều hơn 10200 lượt truy cập.
(Đs: 0; 0.156; 13300; 8.3 ngày/năm) 41
5. PHÂN PHỐI XÁC SUẤT ĐỒNG THỜI 5.1 Lý thuyết
Định nghĩa 5.1.1 Hàm trọng lượng xác suất đồng thời của hai biến ngẫu nhiên rời rạc X và Y ,
kí hiệu là fXY (x, y), thỏa i. fXY (x, y) ≥ 0, ii. Í Í X Y fXY (x, y) = 1,
iii. fXY (x, y) = P (X = x;Y = y).
Hàm phân phối xác suất đồng thời của hai biến ngẫu nhiên liên tục X và Y , kí hiệu là fXY (x, y), thỏa i. fXY (x, y) ≥ 0, ∫ +∞ ∫ +∞ ii. f −∞ −∞ XY (x, y) = 1, iii. Với R ⊂ 2
R ta có P ((X,Y ) ∈ R) = ∬ f R XY (x, y)dx dy.
Định nghĩa 5.1.2 Nếu hàm phân phối xác suất đồng thời của hai biến ngẫu nhiên liên tục X và
Y là fXY (x, y) thì hàm phân phối xác suất thành phần (phân phối lề) của X và Y được định nghĩa ∫ +∞ ∫ +∞ fX(x) = fXY (x, y)dy và fY (y) = fXY (x, y)dx. −∞ −∞
Định nghĩa 5.1.3 Cho hai biến ngẫu nhiên liên tục X và Y có hàm phân phối xác suất đồng
thời là fXY (x, y), hàm phân phối xác suất có điều kiện của Y với thông tin X = x là fY |x(y) = fXY (x, y) với fX(x) > 0. fX(x)
Tính chất: vì hàm phân phối xác suất có điều kiện fY |x(y) cũng là một hàm phân phối xác suất nên nó cũng thỏa i. fY |x(y) ≥ 0, ∫ ii. fY |x(y)dy = 1,
iii. P (Y ∈ B|X = x) = ∫ f
B Y |x (y)dy với B là tập con bất kì trong tập giá trị của Y . 42
Chương 5. PHÂN PHỐI XÁC SUẤT ĐỒNG THỜI
Định nghĩa 5.1.4 Trung bình có điều kiện và phương sai có điều kiện của Y với thông tin X = x
lần lượt được kí hiệu µ , σ2 Y |x và định nghĩa Y |x ∫ µY |x = y fY |x(y)dy, ∫ ∫ σ2 = (y − µ y2 f . Y |x Y |x )2 fY |x (y)dy = Y |x (y)dy − µ2 Y |x
Định lí 5.1.1 Cho X và Y là hai biến ngẫu nhiên, những phát biểu sau là tương đương:
i. fXY (x, y) = fX(x) fY (y) với mọi x, y.
ii. fY |x(y) = fY (y) với x, y và fX(x) > 0.
iii. fX |y(x) = fX(x) với x, y và fY (y) > 0.
iv. P (X ∈ A,Y ∈ B) = P (X ∈ A) P (Y ∈ B) với A, B lần lượt là các tập con bất kì trong tập giá trị của X,Y .
v. X và Y là hai biến ngẫu nhiên độc lập. Định nghĩa 5.1.5
i. Kì vọng của một hàm phụ thuộc hai biến ngẫu nhiên được định nghĩa Í Í h(x, y) fXY (x, y), X,Y rời rạc, Eh(X,Y ) =
∫ ∫ h(x, y) fXY(x, y)dxdy, X,Y liên tục
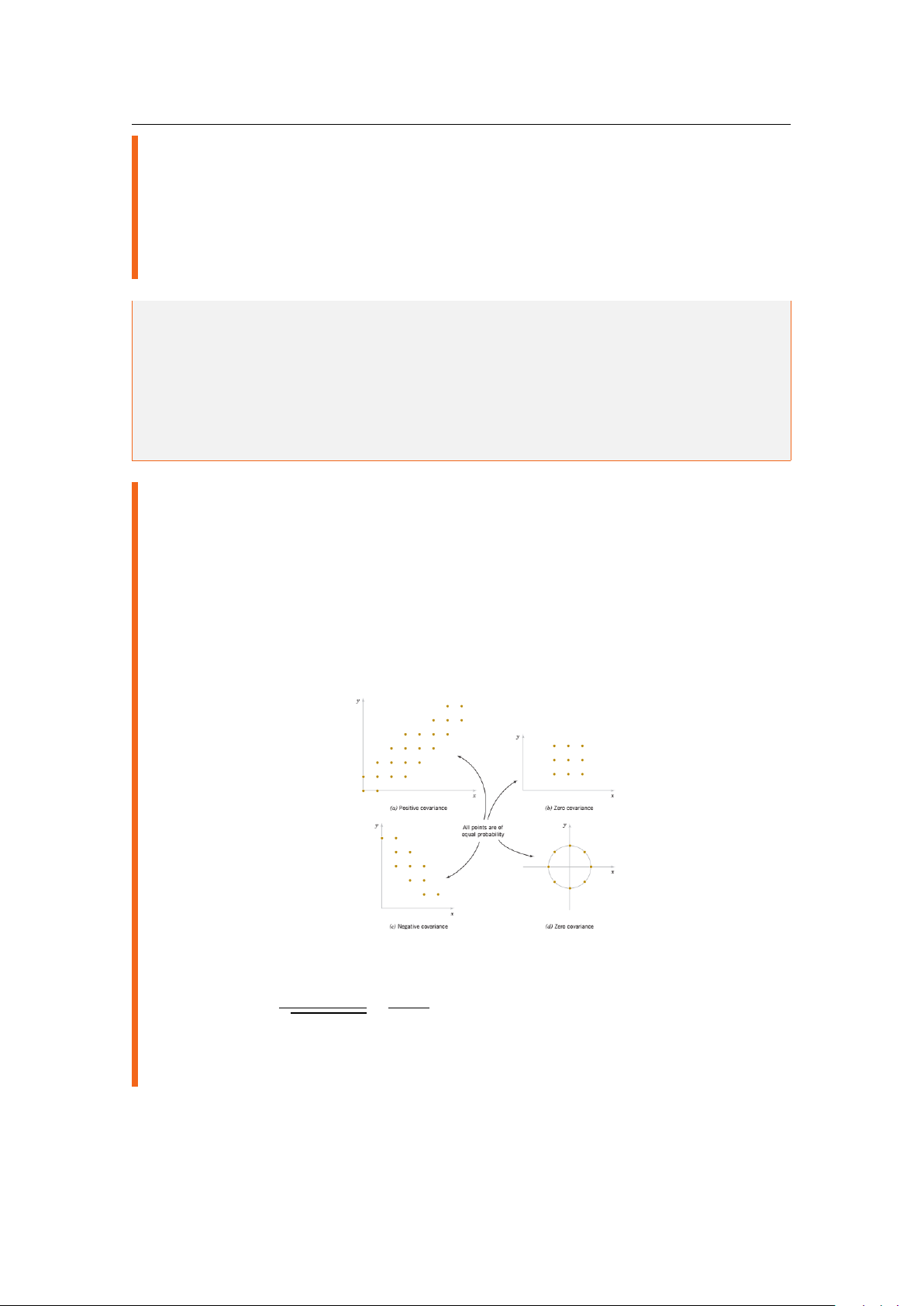
ii. Hiệp phương sai giữa hai biến ngẫu nhiên X và Y , kí hiệu là cov(X,Y ) hay σXY , được định nghĩa σ µ .
XY = E(X − µX )(Y − µY ) = E(XY ) − µX Y
iii. Tương quan giữa hai biến ngẫu nhiên X và Y , kí hiệu là ρXY , được định nghĩa σ ρ XY . XY = cov(X,Y ) √ = VarX .VarY σ σ X Y
Ta dễ thấy −1 ≤ ρXY ≤ 1. Hơn nữa, nếu hai biến ngẫu nhiên X và Y độc lập thì σXY = ρXY = 0. 5.2 Bài tập 43 5.2 Bài tập
Bài 5.1. Cho vectơ ngẫu nhiên có hàm mật độ
c(x + y)2 khi (x, y) ∈ [0, 1] × [0, 1], f (x, y) = 0
khi (x.y) < [0, 1] × [0, 1] .
a. Tìm các hàm mật độ thành phần fX (x), fY (y).
b. Tìm các trung bình µ , µ , σ2 X Y , các phương sai σ2 và hệ số tương quan ρ X Y X,Y .
(Đs: c = 6/7; 9/14, 9/14, 199/2940, 199/2940, -0.127)
Bài 5.2. Tính hiệp phương sai và tương quan nếu biết hàm mật độ xác suất đồng thời như sau x 1 1 2 4 y 3 4 5 6 fXY (x, y) 1/8 1/4 1/2 1/8
Bài 5.3. Tính hiệp phương sai và tương quan nếu biết hàm mật độ xác suất đồng thời như sau x -1 -0.5 0.5 1 y -2 -1 1 2 fXY (x, y) 1/8 1/4 1/2 1/8
Bài 5.4. Xác định hằng số c, hiệp phương sai và tương quan với trọng lượng xác suất đồng thời
fXY (x, y) = c(x + y) với x = 1, 2, 3 và y = 1, 2, 3.
Bài 5.5. Xác định hằng số c, hiệp phương sai và tương quan với trọng lượng xác suất đồng thời
fXY (x, y) = cxy với 0 < x < 3 và 0 < y < x.
Bài 5.6. Xác định hằng số c, hiệp phương sai và tương quan với trọng lượng xác suất đồng thời
fXY (x, y) = c với 0 < x < 5, y > 0 và x − 1 < y < x + 1.
Bài 5.7. Xác định hằng số c, hiệp phương sai và tương quan với trọng lượng xác suất đồng thời
fXY (x, y) = e−x−y với x > 0, y > 0.
Bài 5.8. Xác định hằng số c, hiệp phương sai và tương quan với trọng lượng xác suất đồng thời
fXY (x, y) = 6 × 10−6e−0.001x−0.002y với x > 0, y > x.
Bài 5.9. Cho hàm phân phối xác suất đồng thời như sau x -1 0 0 1 y 0 -1 1 0 fXY (x, y) 1/4 1/4 1/4 1/4
Chứng minh rằng tương quan giữa X và Y bằng 0 nhưng X và Y không độc lập.
Bài 5.10. Giả sử X và Y là hai biến ngẫu nhiên liên tục và độc lập. Chứng minh σXY = 0.
Bài 5.11. Cho X và Y có hệ số tương quan là ρ. Với những hằng số a, b, c và d, hãy tính U = aX + b và V = cY + d. II PhầnHai:ThốngKê 6
THỐNG KÊ MÔ TẢ . . . . . . . . . . . . . . . . . . . . 47 6.1 Lý thuyết 6.2 Bài tập 7
ƯỚC LƯỢNG ĐIỂM . . . . . . . . . . . . . . . . . . 51 7.1
Một số khái niệm cơ bản 7.2
Khoảng tin cậy cho trung bình của phân phối chuẩn 7.3
Khoảng tin cậy cho phương sai 7.4
Khoảng tin cậy cho tỉ lệ của phân phối nhị thức 8
KIỂM ĐỊNH MỘT MẪU . . . . . . . . . . . . . . . . . 59 8.1 Một số khái niệm 8.2 Kiểm định trung bình 8.3 Kiểm định phương sai 8.4 Kiểm định tỉ lệ 9
KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ HAI MẪU 73 9.1 Lý thuyết 9.2 Bài tập 10
HỒI QUY – TƯƠNG QUAN . . . . . . . . . . . . 83 10.1 Lý thuyết 10.2 Bài tập 47 6. THỐNG KÊ MÔ TẢ 6.1 Lý thuyết
Định nghĩa 6.1.1 Tham số đặc trưng thống kê mẫu:
i. Trung bình mẫu: cho n giá trị quan trắc x , 1 · · · , xn ta có n Õ x = 1 x . i n i=1
ii. Phương sai mẫu: cho n giá trị quan trắc x , 1 · · · , xn ta có n Õ s2 = 1 (xi − x)2. n − 1 i=1
iii. Độ lệch chuẩn mẫu: là căn bậc hai của phương sai.
iv. Khoảng mẫu: là độ rộng của dữ liệu và được tính r = max{xi} − min{xi}.
Định nghĩa 6.1.2 Lược đồ Stem-Leaf: giả sử cho trước một bộ dữ liệu x ,
1 · · · , xn trong đó mỗi
số xi gồm ít nhất hai chữ số. Lược đồ được xây dựng theo các bước sau:
i. Chia mỗi giá trị của số xi chia thành hai phần: phần stem bao gồm một hay vài chữ số
đầu, phần leaf bao gồm những chữ số còn lại.
ii. Liệt kê tất cả những giá trị stem thành một cột.
iii. Ghi nhận lại các giá trị leaf trong các giá trị xi bên cạnh giá trị stem của nó.
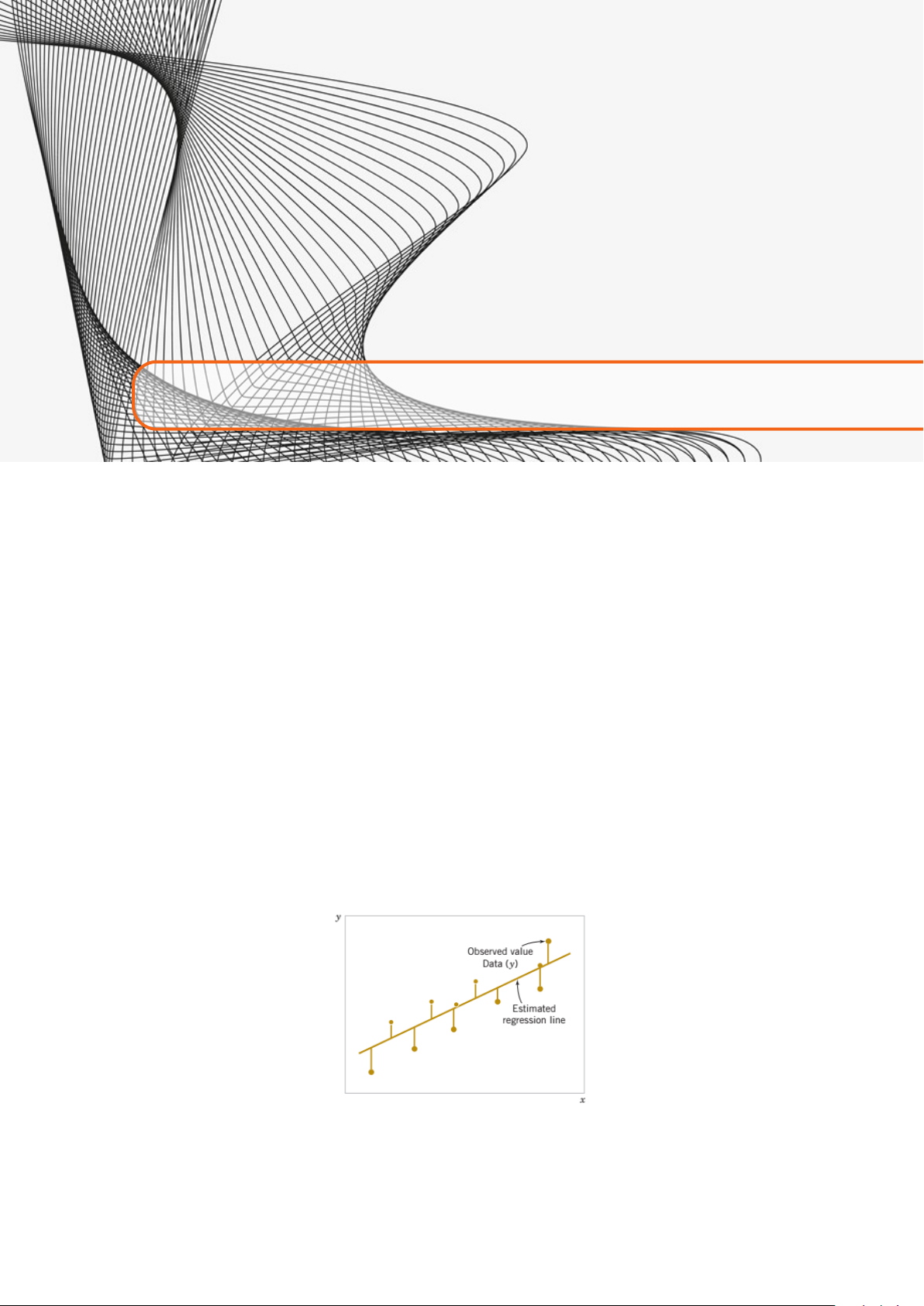
iv. Viết ghi chú giải thích cho stem và leaf
Định nghĩa 6.1.3 Đồ thị histogram được xây dựng theo các bước sau:
i. Ghi nhãn và chia độ lớn bin theo trục hoành theo một tỉ lệ nhất định. 48
Chương 6. THỐNG KÊ MÔ TẢ
ii. Ghi nhãn và chia độ lớn trục tung theo giá trị tần suất của quan trắc.
iii. Trên mỗi bin, ta vẽ hình chữ nhật với qui luật: chiều cao của hình chữ nhật = tần suất quan
trắc của bin : bề rộng của mỗi bin (diện tích của hình chữ nhật chính là xác suất của bin).
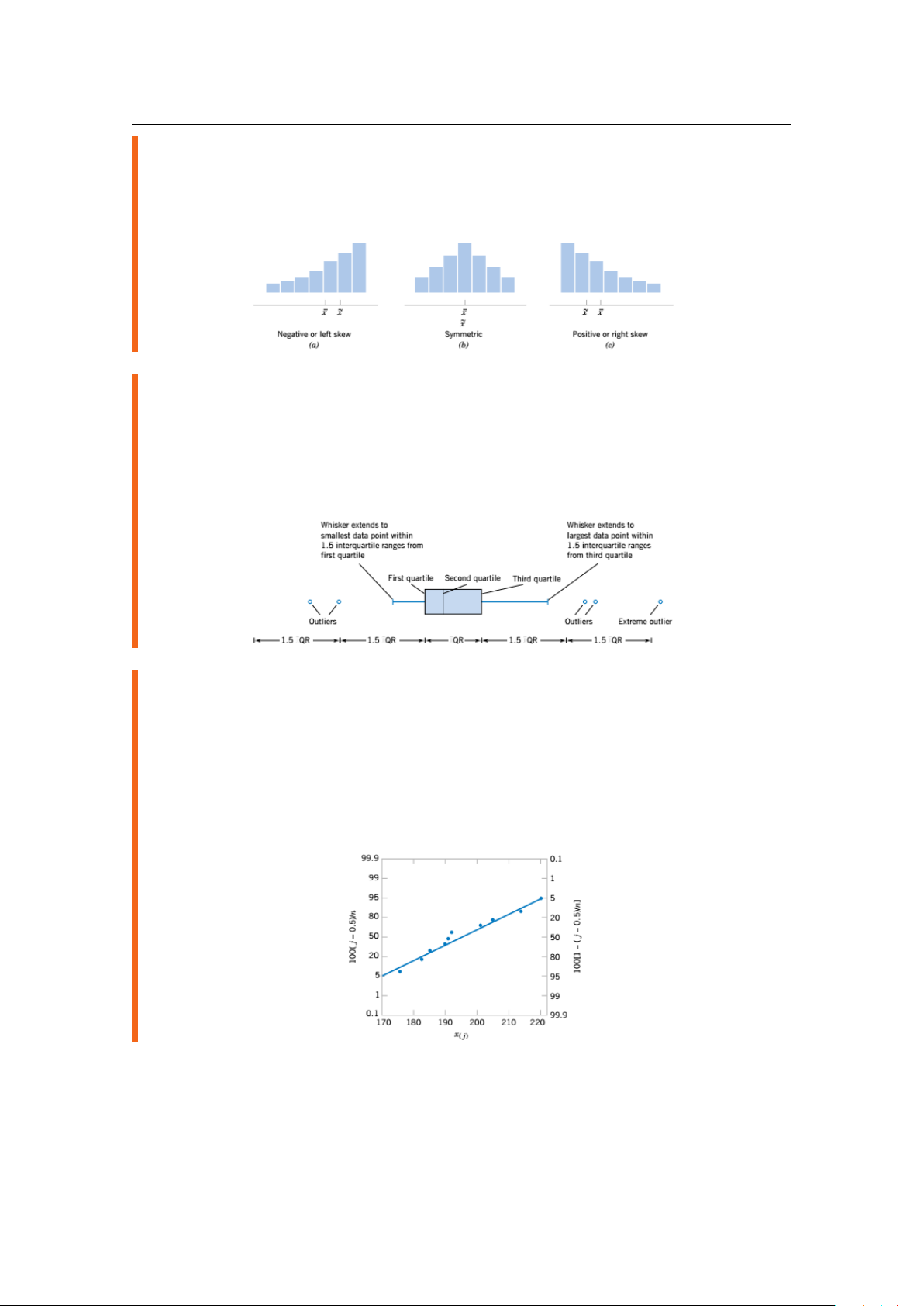
Một số dạng của đồ thị histogram:
Định nghĩa 6.1.4 Đồ thị hộp (box plot) được xây dựng theo các bước sau:
i. Xác định phân vị đầu là giá trị nhỏ nhất của dữ liệu.
ii. Xác định phân vị thứ hai là giá trị trung vị (median) của dữ liệu.
iii. Xác định phân vị cuỗi là giá trị lớn nhất của dữ liệu.
iv. Vẽ hình chữ nhật và đoạn thẳng như hình vẽ sau biết hai đoạn thẳng có độ dài gấp 1.5 lần
chiều dài mỗi hình chữ nhật nhỏ.
Định nghĩa 6.1.5 Đồ thị xác suất giả sử cho trước một bộ dữ liệu x ,
1 · · · , xn, ta thực hiện các bước sau:
i. Sắp xếp lại dữ liệu theo thứ tự tăng dần x , (1) · · · , x(n).
ii. Tại mỗi giá trị x(i) ta tính tần suất tích lũy (i − 0.5)/10.
iii. Nếu phân phối giả định được mô tả đúng bởi dữ liệu thì những điểm xi ta vẽ sẽ giảm xấp
xỉ như đường thẳng. Ngược lại thì ta kết luận phân phối giả định không được mô tả đúng thông qua quan trắc.
Dưới đây là đồ thị xác suất của phân phối chuẩn. Code R 6.1.1
1. Tính những tham số đặc trưng thống kê của số liệu: R > x <- runif(100) R > mean(x); var(x); sd(x);
R > # tính moment cấp 3 và 4 6.1 Lý thuyết 49
R > install.packages("psych") R > library("psych") R > skew(x); kurtosi(x)
R > min(x); max(x); range(x) R > quantile(x); median(x) R > quantile(x, 0.9)
R > summary(x) # tìm hiểu về lệnh này
Hãy tìm hiểu để giải thích
R > dataset <- c( -15,2,3,4,5,6,7,8,9,12 ) R > mean( x = dataset )
R > mean( x = dataset, trim = .1)
R > mean( x = afl.margins, trim = .05)
Đặc biệt, muốn tính (mood ta sử dụng đoạn code sau: R > install.packages("lsr") R > library("lsr") R > print(afl.margins) R > table( afl.finalists )
R > modeOf( x = afl.finalists )
R > maxFreq( x = afl.finalists )
R > modeOf( x = afl.margins )
R > maxFreq( x = afl.margins )
2. Vẽ biểu đồ Stem-Leaf ta sử dụng đoạn code sau:
R > install.packages("aplpack") R > library("aplpack") R > stem.leaf(rivers) R > stem.leaf(precip) 3. Vẽ histogram R > x <- rnorm(50000) R > hist(x) R > hist(rivers)
4. Vẽ box-plot: chạy 2 lệnh sau rồi giải thích kết quả R > boxplot.stats(rivers) R > boxplot(rivers)
R > boxplot.stats(rivers)$out
5. Vẽ đồ thị xác suất theo đoạn code sau R > # Q-Q plots R > par(mfrow=c(1,2))
R > # create sample data - có thể thay bằng dữ liệu người dùng R > x <- rt(100, df=3) R > # normal fit R > qqnorm(x); qqline(x) R > # t(3Df) fit
R > qqplot(rt(1000,df=3), x, main="t(3) Q-Q Plot",
+ > ylab="Sample Quantiles") R > abline(0,1) 50
Chương 6. THỐNG KÊ MÔ TẢ
6. Để xuất ra hình ảnh các đồ thị ta sử dụng:
R > dev.print( device = jpeg,
+ > filename = "thisfile.jpg", + > width = 480, + > height = 300 + > ) 6.2 Bài tập
Bài 6.1. Tám phép đo được thực hiện trên đường kính bên trong của vòng piston rèn được sử dụng
trong một động cơ ô tô. Dữ liệu (tính bằng milimt) là 74.001, 74,003, 74.015, 74.000, 74,005,
74,002, 74,005 và 74,004. Tính trung bình mẫu và độ lệch chuẩn của mẫu, xây dựng một biểu đồ
dấu chấm và nhận xét về dữ liệu
Bài 6.2. Bài báo trong tháng 1 năm 1990 của Arizona Trend có bổ sung mô tả 12 khóa học golf
“tốt nhất” trong tiểu bang. Các yardages (độ dài) của các khóa học này như sau: 6981, 7099, 6930,
6992, 7518, 7100, 6935, 7518, 7013, 6800, 7041 và 6890. Tính giá trị trung bình mẫu và độ lệch chuẩn của mẫu.
Bài 6.3. Một bài báo trong Technometrics (1977, Vol. 19, p. 425) trình bày các dữ liệu sau đây về
xếp hạng octane nhiên liệu động cơ của một số hỗn hợp xăng:
88.5 98.8 89.6 92.2 92.7 88.4 87.5 90.9 94.7 88.3 90.4 83.4 87.9 92.6 87.8 89.9 84.3 90.4 91.6 91.0
93.0 93.7 88.3 91.8 90.1 91.2 90.7 88.2 94.4 96.5 89.2 89.7 89.0 90.6 88.6 88.5 90.4 84.3 92.3 92.2
89.8 92.2 88.3 93.3 91.2 93.2 88.9 91.6 87.7 94.2 87.4 86.7 88.6 89.8 90.3 91.1 85.3 91.1 94.2 88.7
92.7 90.0 86.7 90.1 90.5 90.8 92.7 93.3 91.5 93.4 89.3 100.3 90.1 89.3 86.7 89.9 96.1 91.1 87.6 91.8 91.0 91.0
Xây dựng biểu đồ stem-leaf cho dữ liệu trên. Suy ra median (trung vị) và các phân vị.
Bài 6.4. Các dữ liệu sau thống kê cho sản lượng trên 90 lô các chất nền gốm mà lớp phủ kim loại
đã được áp dụng bởi quá trình lắng đọng hơi. Xây dựng biểu đồ stem-leaf cho những dữ liệu này.
Tính trung bình và phần tư của các dữ liệu này:
94.1 86.1 95.3 84.9 88.8 84.6 94.4 84.1 93.2 90.4 94.1 78.3 86.4 83.6 96.1 83.7 90.6 89.1 97.8 89.6
85.1 85.4 98.0 82.9 91.4 87.3 93.1 90.3 84.0 89.7 85.4 87.3 88.2 84.1 86.4 93.1 93.7 87.6 86.6 86.4
86.1 90.1 87.6 94.6 87.7 85.1 91.7 84.5 95.1 95.2 94.1 96.3 90.6 89.6 87.5 90.0 86.1 92.1 94.7 89.4
90.0 84.2 92.4 94.3 96.4 91.1 88.6 90.1 85.1 87.3 93.2 88.2 92.4 84.1 94.3 90.5 86.6 86.7 86.4 90.6
82.6 97.3 95.6 91.2 83.0 85.0 89.1 83.1 96.8 88.3
Bài 6.5. Xây dựng đồ thị histogram cho Bài tập 6.3-6.4.
Bài 6.6. “Thời gian bắt lửa lạnh” của một động cơ ô tô đang được nhà sản xuất xăng điều tra. Các
quan trắc sau (tính bằng giây) thu được cho một phương tiện thử nghiệm: 1,75, 1,92, 2,62, 2,35, 3,09, 3,15, 2,53, 1,91.
a. Tính trung bình mẫu, phương sai mẫu và độ lệch chuẩn mẫu.
b. Xây dựng biểu đồ box plot.
Bài 6.7. Xây dựng một đồ thị xác suất phân phối chuẩn của dữ liệu đường kính vòng piston trong
Bài tập 6.1. Nó có hợp lý để giả định rằng đường kính vòng piston có phân phối chuẩn? 51 7. ƯỚC LƯỢNG ĐIỂM 7.1
Một số khái niệm cơ bản Định nghĩa 7.1.1 a. Mẫu ngẫu nhiên: Các biến ngẫu nhiên X ,
1 · · · , Xn được gọi là mẫu ngẫu nhiên nếu thỏa 2 điều kiện:
i) các biến ngẫu nhiên là độc lập nhau,
ii) các biến ngẫu nhiên có cùng phân phối xác suất.
b. Thống kê là một hàm số của những quan trắc phụ thuộc vào mẫu ngẫu nhiên.
c. Phân phối mẫu là phân phối xác suất của thống kê.
Định lí 7.1.1 (Định lí giới hạn trung tâm) Cho X ,
1 · · · , Xn là một mẫu ngẫu nhiên của tổng thể (có thể hữu hạn hoặc vô hạn) với trung
bình µ và phương sai σ2. Nếu X = ˆµ là trung bình mẫu thì ta có giới hạn của thống kê Zn = X − µ √ σ/ n
là phân phối chuẩn tắc khi n → ∞.
Chạy code sau sử dụng hai thư viên TeachingDemos, distrTeach và quan sát sự hội tụ của phân phối mẫu. Code R 7.1.1 > library(TeachingDemos) > example(clt.examp) > library(distrTeach) > example(illustrateCLT) 52
Chương 7. ƯỚC LƯỢNG ĐIỂM 7.2
Khoảng tin cậy cho trung bình của phân phối chuẩn 7.2.1
Khoảng tin cậy cho trung bình khi biết phương sai
Định lí 7.2.1 (Khoảng tin cậy cho ước lượng trung bình của phân phối chuẩn biết trước phương sai)
Nếu x là trung bình mẫu được tính từ mẫu ngẫu nhiên với cỡ mẫu n được lấy từ một tổng thể có
phân phối chuẩn với phương sai σ2 đã biết, thì khoảng tin cậy 100(1 − α)% của µ được tính √ √ x − zα σ σ /2 / n ≤ µ ≤ x + zα/2 / n,
với zα/2 thỏa P(Z < zα/2) = 1 − α/2 với Z ∼ N(0, 1).
Chú ý: nếu x là một ước lượng của µ, ta có thể xây dựng khoảng tin cậy 100(1 − α)% với sai số
| x − µ| < E với cỡ mẫu n = (zα σ /2 /E)2. Code R 7.2.1
1. Chạy code và đếm kết quả. Giải thích kết quả vừa chạy R > library(TeachingDemos) R > example(ci.examp)
2. Xem xét đoạn code sau rồi rút ra cấu trúc xây dựng khoảng tin cậy cho trung bình. R > library(TeachingDemos)
R > temp <- with(PlantGrowth, z.test(weight, stdev = 0.7)) R > temp
Bài 7.1. Đo lượng cholesterol (đơn vị mg%) cho một số người, ta được X (mg%) 150–160 160–170 170–180 180–190 190–200 200–210 Số người 2 4 5 6 4 3
a. Tính trung bình mẫu và độ lệch chuẩn mẫu.
b. Một mẫu thứ nhì Y có 30 người cho trung bình 180mg% và độ lệch chuẩn 16mg%. Nhập hai
mẫu lại, tính trung bình và độ lệch chuẩn của mẫu nhập.
(Đs: 181.25, 14.98; 180.55, 15.49)
Bài 7.2. Cho tổng thể có phân phối chuẩn với tham số σ2 đã biết. Xác định √ √
a. Độ tin cậy của ước lượng khoảng x − 2.14σ/ n ≤ µ ≤ x + 2.14σ/ n. √ √
b. Độ tin cậy của ước lượng khoảng x − 2.49σ/ n ≤ µ ≤ x + 2.49σ/ n. √ √
c. Độ tin cậy của ước lượng khoảng x − 1.85σ/ n ≤ µ ≤ x + 1.85σ/ n. (Đs: 96.76%; 98.72%; 93.56%)
Bài 7.3. Cho tổng thể có phân phối chuẩn với tham số σ2 đã biết. Xác định
a. Giá trị của zα/2 ứng với độ tin cậy 98% trong công thức xây dựng khoảng tin cậy.
b. Giá trị của zα/2 ứng với độ tin cậy 80% trong công thức xây dựng khoảng tin cậy.
c. Giá trị của zα/2 ứng với độ tin cậy 75% trong công thức xây dựng khoảng tin cậy. (Đs: 2.33; 1.285; 1.151)
Bài 7.4. Ước lượng khoảng tin cậy cho độ hoàn thiện mạch của một thiết bị bán dẫn. Giả sử mức
độ hoàn thiện tuân theo phân phối chuẩn với độ lệch chuẩn σ = 20. Tính
a. Khoảng tin cậy 95% cho µ khi n = 10 và x = 1000.
b. Khoảng tin cậy 95% cho µ khi n = 25 và x = 1000.
7.2 Khoảng tin cậy cho trung bình của phân phối chuẩn 53
c. Khoảng tin cậy 99% cho µ khi n = 10 và x = 1000.
d. Khoảng tin cậy 99% cho µ khi n = 25 và x = 1000.
e. Nhận xét độ rộng của khoảng tin cậy khi thay đổi cỡ mẫu và độ tin cậy.
(Đs: [987.6;1012.4]; [992.16;1007.84]; [983.71;1016.28]; [989.7;1010.3])
Bài 7.5. Một mẫu ngẫu nhiên đã được lấy từ một tổng thể có phân phối chuẩn và các khoảng tin
cậy sau được xây dựng bằng cách sử dụng cùng một dữ liệu: (38.02, 61.98) và (39.95, 60.05)
a. Xác định trung bình mẫu? (Đs: 50; 50)
b. Giả sử hai khoảng tin cậy tương ứng với độ tin cậy 95% và 90%. Khoảng nào ứng với độ tin cậy 95%? Tại sao?
Bài 7.6. Một mẫu ngẫu nhiên đã được lấy từ một tổng thể có phân phối chuẩn và các khoảng tin
cậy sau được xây dựng bằng cách sử dụng cùng một dữ liệu: (37.53, 49.87) và (35.59, 51.81)
a. Xác định trung bình mẫu? (Đs: 43.7; 43.7)
b. Giả sử hai khoảng tin cậy tương ứng với độ tin cậy 95% và 99%. Khoảng nào ứng với độ tin cậy 95%? Tại sao?
Bài 7.7. Sử dụng lại số liệu của Bài tập 7.4. Tìm cỡ mẫu n để:
a. Độ rộng của khoảng tin cậy 95% là 40.
b. Độ rộng của khoảng tin cậy 99% là 40. (Đs: 4; 7)
Bài 7.8. Giả sử người ta lấy mẫu ngẫu nhiên cỡ n = 100 từ một hồ nước ngọt để đo nồng độ Canxi
(mg/l). Khoảng tin cậy 95% cho nồng độ trung bình của Canxi là 0.49 ≤ µ ≤ 0.82.
a. Khoảng tin cậy 99% được xây dựng từ cùng mẫu ngẫu nhiên trên có độ rộng lớn hơn hay nhỏ hơn trên? (Đs: lớn hơn)
b. Xét phát biểu: “có 95% khả năng tìm thấy µ trong khoảng từ 0.49 tới 0.82”. (Đs: sai)
c. Xét phát biểu: “nếu lấy mẫu ngẫu nhiên với cỡ mẫu n = 100 rồi tính khoảng tin cậy 95% và
cứ lặp lại quá trình này 1000 lần thì có 950 lần khoảng tin cậy này sẽ chứa giá trị µ chính xác”. (Đs: đúng)
Bài 7.9. Đường kính của những cái lỗ trên dây nịt có phân phối chuẩn với độ lệch chuẩn 0.01 inch.
Một mẫu ngẫu nhiên có cỡ là 10 với đường kính trung bình là 1.5054 inch. Tìm khoảng tin cậy
99% cho ước lượng trung bình đường kính lỗ. (Đs: [1.49725;1.51355])
Bài 7.10. Một kỹ sư xây dựng phân tích cường độ nén của bê tông. Cường độ nén thường có phân
phối chuẩn 1000 (psi)2. Một mẫu ngẫu nhiên gồm 12 mẫu có cường độ nén trung bình x = 3250 psi.
a. Xây dựng khoảng tin cậy 95% cho trung bình cường độ nén của bê tông. (Đs: [3232.11;3267.89])
b. Xây dựng khoảng tin cậy 99% cho trung bình cường độ nén của bê tông và so sánh độ rộng
với câu trên. (Đs: [3226.4;3273.6])
c. Để có được ước lượng cho trung bình độ nén với sai số không vượt quá 15 psi ở dộ tin cậy
99% thì cỡ mẫu phải là bao nhiêu? (Đs: 30) 7.2.2
Khoảng tin cậy cho trung bình khi chưa biết phương sai
Định lí 7.2.2 Khoảng tin cậy cho ước lượng trung bình của phân phối chuẩn khi không biết phương sai
Phân phối student T ∼ t(k) là phân phối có hàm mật độ là Γ k+1 2 f (x) = , √π (k +1)/2 k Γ k x2 + 1 2 k 54
Chương 7. ƯỚC LƯỢNG ĐIỂM
với k là bậc tự do. Khi đó, T có trung bình 0 và phương sai k/(k − 2) với k > 2. i.
ii. Định lí: cho X ,
1 · · · , Xn là một mẫu ngẫu nhiên lấy từ phân phối chuẩn với hai tham số
µ, σ2 chưa biết. Khi đó, biến ngẫu nhiên T = X − µ √ S/ n
có phân phối Student t(n − 1) với n − 1 bậc tự do.
iii. Khoảng tin cậy: nếu x, s lần lượt là trung bình và độ lệch chuẩn mẫu của một mẫu ngẫu
nhiên lấy từ phân phối chuẩn với hai tham số µ, σ2 chưa biết thì khoảng tin cậy 100(1 − α)% của µ được tính √ √
x − tα/2,n−1s/ n ≤ µ ≤ x + tα/2,n−1s/ n
với tα/2,n−1 thỏa P(|T | > tα/2,n−1) = α với T ∼ t(n − 1).
Bài 7.11. Hãy tìm những giá trị của t , , ,
0.025,15 t0.05,10 t0.10,20 t0.005,25 và t0.001,20.
Bài 7.12. Xác định giá trị t trong xây dựng khoảng tin cậy tương ứng với:
a. Độ tin cậy 95% với bậc tự do 12.
c. Độ tin cậy 99% với bậc tự do 13.
b. Độ tin cậy 95% với bậc tự do 24.
d. Độ tin cậy 99.9% với bậc tự do 15.
(Đs: 2.179; 2.064; 3.012; 4.073)
Bài 7.13. Một mẫu ngẫu nhiên đã được lấy từ một phân phối chuẩn. Đầu ra từ một gói phần mềm xuất ra dưới đây: Biến N Trung bình SE mean Độ lệch chuẩn Phương sai Tổng x 10 ? 0.507 1.605 ? 251.848 √
với SE mean là độ lệch chuẩn của trung bình σx = σ/ n.
a. Điền cho đầy đủ bảng số liệu trên. (Đs: (a) Mean 25.1848, Variance 2.5760)
b. Tìm khoảng tin cậy 95% cho ước lượng trung bình. (Đs: 24.037 ≤ µ ≤ 26.333)
Bài 7.14. Một mẫu ngẫu nhiên đã được lấy từ một phân phối chuẩn. Đầu ra từ một gói phần mềm xuất ra dưới đây: Biến N Trung bình SE mean Độ lệch chuẩn Phương sai Tổng x ? ? 1.58 6.11 ? 751.40
a. Điền cho đầy đủ bảng số liệu trên.
b. Tìm khoảng tin cậy 95% cho ước lượng trung bình.
Bài 7.15. Kỹ sư nghiên cứu cho một nhà sản xuất lốp xe đang nghiên cứu tuổi thọ lốp làm từ một
hợp chất cao su mới và đã chế tạo 16 lốp xe, thử nghiệm tuổi thọ khi chúng chạy trên đường. Giá trị
trung bình mẫu và độ lệch chuẩn là 60139.7 và 3645.94 km. Tìm khoảng tin cậy 95% cho tuổi thọ
trung bình của lốp. (Đs: [58197.33, 62082.07])
Bài 7.16. Cục Khí tượng của Chính phủ Úc đã cung cấp lượng mưa trung bình hàng năm (milimet)
ở Úc 1983-2002 như sau (http://www.bom.gov.au/climate/change/rain03.txt):
7.2 Khoảng tin cậy cho trung bình của phân phối chuẩn 55
499.2, 555.2, 398.8, 391.9, 453.4, 459.8, 483.7, 417.6, 469.2, 452.4, 499.3, 340.6, 522.8, 469.9,
527.2, 565.5, 584.1, 727.3, 558.6, 338.6
Xây dựng khoảng tin cậy 95% cho lượng mưa trung bình hàng năm. Chú ý: ta có thể phải kiểm tra
giả thiết tổng thể có phân phối chuẩn bằng cách vẽ đồ thị box-plot (xem Định nghĩa 6.1.4) và đồ thị
xác suất của phân phối chuẩn:trục hoành là x, trục tung là xác suất (xem Định nghĩa 6.1.5). (Đs:
x = 485.755, s2 = 1149, 229, [469.89, 501.62])
Bài 7.17. Một bài báo trên Tạp chí Vật liệu tổng hợp (tháng 12 năm 1989, tập 23, trang 1200)
mô tả ảnh hưởng của sự phân tách trên tần số tự nhiên của các chùm được làm từ các loại vật liệu
composite. Năm chùm bị ô nhiễm như vậy đã chịu tải trọng, và kết quả tần số như sau (đơn vị Hert z):
230.66, 233.05, 232.58, 229.48, 232.58
Kiểm tra giả định về phân phối chuẩn của tổng thể. Tính khoảng tin cậy 90% cho trung bình tần số tự nhiên.
Bài 7.18. Độ sáng của ống hình ảnh của tivi có thể được đánh giá bằng cách đo lượng dòng điện
cần thiết để đạt được một mức độ sáng cụ thể. Một mẫu của 10 ống cho kết quả độ lệch chuẩn là
15.7 và trung bình là 317.2. Tìm (trong microamps) khoảng tin cậy 99% cho trung bình thực tế
yêu cầu. Nêu những giả định cần thiết về phân phối của dữ liệu. (Đs: [301.06, 333.34])
Bài 7.19. Một bài báo về Kỹ thuật hạt nhân quốc tế (tháng 2 năm 1988, trang 33) mô tả một số đặc
tính của các thanh nhiên liệu được sử dụng trong lò phản ứng thuộc sở hữu của một công ty điện ở
Na Uy. Các phép đo về tỷ lệ làm giàu của 12 thanh đã được báo cáo như sau:
2.94; 3.00; 2.90; 2.75; 3.00; 2.95; 2.90; 2.75; 2.95; 2.82; 2.81; 3.05
a. Sử dụng đồ thị của xác suất phân phối chuẩn để kiểm tra giả định phân phối chuẩn của số liệu.
b. Tìm khoảng tin cậy 99% cho tỷ lệ phần trăm trung bình của làm giàu. Bạn có đồng ý với
tuyên bố rằng tỷ lệ phần trăm trung bình của làm giàu là 2.95%? Tại sao? (Đs: [2.813, 2.991])
Bài 7.20. Đo đường kính của một chi tiết máy do một máy tiện tự động sản xuất, ta ghi nhận được số liệu như sau: X 12.00 12.05 12.10 12.15 12.20 12.25 12.30 12.35 12.40 N 2 3 7 9 10 8 6 5 3
với N chỉ số trường hợp tính theo từng giá trị của X (mm).
a. Tính trung bình mẫu và độ lệch chuẩn của mẫu. (Đs: 12.21, 0.103)
b. Ước lượng đường kính trung bình µ ở độ tin cậy 0.95. (Đs: [12.18; 12.24])
c. Nếu muốn sai số ước lượng không quá E = 0.02 mm ở độ tin cậy 0.95 thì phải quan sát ít
nhất mấy trường hợp. (Đs: 102)
Bài 7.21. Quan sát chiều cao X (cm) của một số người, ta ghi nhận X 140-145 145-150 150-155 155-160 160-165 165-170 Số người 1 3 7 9 5 2
a. Tính trung bình mẫu và phương sai mẫu.(Đs: 156.2;37.68) 56
Chương 7. ƯỚC LƯỢNG ĐIỂM
b. Ước lượng trung bình và phương sai của tổng thể ở độ tin cậy 0.95.(Đs: [153.77;158.63])
Bài 7.22. Đem cân một số trái cây vừa thu hoạch, ta được kết quả sau X (g) 200–210 210–220 220–230 230–240 240–250 Số trái 12 17 20 18 15
a. Tìm khoảng ước lượng của trọng lượng trung bình của trái cây với độ tin cậy 0.95 và 0.99.
(Đs: [222.98;228.72], [222.08;229.63])
b. Nếu muốn sai số ước lượng không quá E = 2g ở độ tin cậy 99% thì phải quan sát ít nhất bao nhiêu trái? (Đs: 293)
Bài 7.23. Người ta đo ion Na+ trên một số người và ghi nhận lại được kết quả như sau
129, 132, 140, 141, 138, 143, 133, 137, 140, 143, 138, 140
a. Tính trung bình mẫu và phương sai mẫu. (Đs: 137.83; 19.42)
b. Ước lượng trung bình và phương sai của tổng thể ở độ tin cậy 0.95. (Đs: [135.01;140.63]; [9.76;56.1])
c. Nếu muốn sai số ước lượng trung bình không quá E = 1 với độ tin cậy 0.95 thì phải quan sát
mẫu gồm ít nhất mấy người? (Đs: 75)
Bài 7.24. Quan sát tuổi thọ X (giờ) của một số bóng đèn do xí nghiệp A sản xuất, ta ghi nhận X 1000 1100 1200 1300 1400 1500 1600 1700 1800 N 10 14 16 17 18 16 16 12 9
a. Tính trung bình mẫu và độ lệch chuẩn mẫu.(Đs: 1391.41; 234.45)
b. Ước lượng tuổi thọ trung bình của bóng đèn ở độ tin cậy 0.95.(Đs: [1350.79;1432.03])
c. Nếu muốn sai số ước lượng trung bình không quá E = 30 với độ tin cậy 0.95 thì phải quan
sát mẫu gồm ít nhất mấy bóng đèn?(Đs: 235)
Bài 7.25. Có 3 mẫu quan sát sức nặng con người, kết quả ghi nhận Lần quan sát Trung bình Độ lệch chuẩn Mẫu 1 70 55 kg 8.30 kg Mẫu 2 75 57 kg 8.60 kg Mẫu 3 90 54 kg 8.50 kg
Nhập chung 3 mẫu lại, tính trung bình và độ lệch mẫu nhập. Dựa vào mẫu nhập để ước lượng
trung bình của tổng thể ở độ tin cậy 95% và 99%. (Đs: 55.25, 8.56; [54.156; 56.344], [53.81; 56.69]) 7.3
Khoảng tin cậy cho phương sai
Định lí 7.3.1 (Khoảng tin cậy cho ước lượng phương sai của phân phối chuẩn)
Phân phối chi bình phương X ∼ χ2(k − 1) là phân phối có hàm mật độ là f (x) = xk/2−1e−x/2, x > 0, 2k/2Γ k2
7.3 Khoảng tin cậy cho phương sai 57
với k là bậc tự do. Khi đó, X có trung bình k và phương sai 2k. i.
ii. Định lí: cho X ,
1 · · · , Xn là một mẫu ngẫu nhiên lấy từ phân phối chuẩn với hai tham số
µ, σ2. Nếu S2 là phương sai mẫu thì biến ngẫu nhiên (n − 1)S2 ∼ χ2(n−1). σ2
iii. Khoảng tin cậy: nếu s2 là phương sai mẫu của mẫu ngẫu nhiên cỡ n được lấy từ tổng thể
của một phân phối chuẩn với hai tham số µ và σ2 thì khoảng tin cậy 100(1 − α)% của σ2 được tính (n − 1)s2 (n − 1)s2 ≤ σ2 ≤ , χ2 χ2 α/2,n−1 1−α/2,n−1 trong đó χ2 , χ2 α lần lượt thỏa: /2,n−1 1−α/2,n−1 P χ > χ2 χ > χ2 α = α/2, = 1 − α/2. /2,n−1 P 1−α/2,n−1
Bài 7.26. Xác định giá trị χ2α,n trong các trường hợp sau: χ2 , χ2 , χ2 , χ2 , χ2 . 0.05,10 0.025,15 0.01,12 0.99,16 0.005,25
Bài 7.27. Xác định giá trị χ2α
trong trường hợp sau: độ tin cậy 90% với bậc tự do 19. /2,n
Bài 7.28. Tỷ lệ titan trong một hợp kim được sử dụng trong đúc các bộ phận hàng không vũ trụ
được đo bằng 51 mẫu được chọn ngẫu nhiên. Độ lệch chuẩn mẫu là s = 0.37. Xây dựng một khoảng
tin cậy có độ tin cậy 95% cho σ. (Đs: [0.31, 0.46])
Bài 7.29. Hàm lượng đường của xi-rô trong hộp thường có phân phối chuẩn. Một mẫu ngẫu nhiên
với n = 10 lon mang lại độ lệch chuẩn của mẫu là 4.8 miligam. Tính toán khoảng tin cậy 95% cho σ.
Bài 7.30. Một bài báo trong tạp chí “hệ sinh thái đô thị”: Đô thị hóa và sự ấm lên của Phoenix
(Arizona, Mỹ): Tác động, phản hồi và giảm nhẹ (2002, Vol. 6, pp. 183–203), đề cập rằng Phoenix
là lý tưởng để nghiên cứu ảnh hưởng của nhiệt độ của một đô thị hòn đảo vì nó đã phát triển từ dân
số 300.000 đến gần 3 triệu trong 50 năm qua và đây là một khoảng thời gian thay đổi khí hậu liên
tục. Trung bình 50 năm của nhiệt độ trung bình hàng năm tại tám địa điểm ở Phoenix được mô tả
bởi một bảng dưới đây. Kiểm tra giả định về phân phối chuẩn. Xây dựng khoảng tin cậy 95% cho
độ lệch chuẩn dựa trên dữ liệu tại vị trí có nhiệt độ trung bình hàng năm. (Đs: [0.626, 1.926]) Vị trí Trung bình nhiệt độ Sky Harbor Airport 23.3 Phoenix Greenway 21.7 Phoenix Encanto 21.6 Waddell 21.7 Litchfield 21.3 Laveen 20.7 Maricopa 20.9 Harlquahala 20.1 58
Chương 7. ƯỚC LƯỢNG ĐIỂM 7.4
Khoảng tin cậy cho tỉ lệ của phân phối nhị thức
Định lí 7.4.1 (Khoảng tin cậy cho ước lượng tỉ lệ của pp nhị thức B(1, p))
Ta cần đi xây dựng khoảng tin cậy cho ước lượng tỉ số p là xác suất tương ứng với tỉ lệ “thành
công (hoặc thất bại)”. Chú ý trung bình của biến ngẫu nhiên B(1, p) là p nên ta có trung bình mẫu
f = x = số lần thành công hoặc
f = x = số lần thất bại . n n Độ lệch chuẩn mẫu s = pn f (1 − f ).
Khi đó, khoảng tin cậy 100(1 − α)% của σ2 được tính
f − zα/2s/n ≤ p ≤ f + zα/2s/n,
với zα/2 thỏa P(Z < zα/2) = 1 − α/2 với Z ∼ N(0, 1).
Bài 7.31. Phần nhỏ của các mạch tích hợp khiếm khuyết được tạo ra trong quá trình quang khắc được
nghiên cứu. Một mẫu ngẫu nhiên của 300 mạch được kiểm tra đã phát hiện được 13 khiếm khuyết.
Tính khoảng tin cậy 95% trên phần mạch bị lỗi do quá trình trên tạo ra. (Đs: [0.02029, 0.06637])
Bài 7.32. Trong số liệu từ cuộc bầu cử tổng thống năm 2004, một bang quan trọng là bang Ohio
đã cho kết quả sau đây: đã có 2020 người trả lời trong các cuộc thăm dò xuất cảnh và 768 là sinh
viên tốt nghiệp đại học. Trong số các sinh viên tốt nghiệp đại học có 412 bầu cho George Bush.
Xây dựng khoảng tin cậy 95% cho tỉ lệ sinh viên tốt nghiệp đại học bầu cho George Bush.(Đs: [0.501;0.571])
Bài 7.33. Trong số 1000 trường hợp ung thư phổi được chọn ngẫu nhiên, 823 kết quả tử vong trong vòng 10 năm
a. Tính toán khoảng tin cậy 95% về tỷ lệ tử vong do ung thư phổi.
b. Sử dụng ước tính điểm của p tính được từ mẫu sơ bộ, tính kích thước mẫu cần thiết để 95%
tin rằng lỗi trong ước tính giá trị thực của p ít hơn hơn 0.03? (Đs: 622)
Bài 7.34. Một loại thuốc mới đem điều trị cho 50 người bị bệnh B, kết quả có 40 người khỏi bệnh.
a. Ước lượng tỷ lệ khỏi bệnh p nếu dùng thuốc đó điều trị với độ tin cậy 0.95 và 0.99.(Đs: [0.65;0.946])
b. Nếu muốn sai số ước lượng không quá 0.02 ở độ tin cậy 0.95 thì phải quan sát ít nhất mấy trường hợp ?(Đs: 1537)
Bài 7.35. Một loại bệnh có tỷ lệ tử vong là 0.01. Muốn chứng tỏ một loại thuốc có hiệu nghiệm
(nghĩa là hạ thấp được tỷ lệ tử vong nhỏ hơn 0.005) ở độ tin cậy 0.95 thì phải thử thuốc đó trên ít
nhất bao nhiêu người?(Đs: 1522)
Bài 7.36. Ta muốn ước lượng tỷ lệ viên thuốc bị sức mẻ p trong một lô thuốc lớn.
a. Nếu muốn sai số ước lượng không quá 0.01 với độ tin cậy 0.95 thì phải quan sát ít nhất mấy
viên? (Hướng dẫn: tìm giá trị lớn nhất của f (1 − f ). Đs: 9604)
b. Quan sát ngẫu nhiên 200 viên, thấy có 18 viên bị sứt mẻ. Hãy ước lượng p ở độ tin cậy 0.95.
Khi đó, nếu muốn sai số ước lượng không quá 0.01 với độ tin cậy 0.95 thì phải quan sát ít nhất mấy viên?(Đs:3147) 59 8. KIỂM ĐỊNH MỘT MẪU 8.1 Một số khái niệm Định nghĩa 8.1.1
i. Giả thuyết thống kê là một phát biểu về những tham số của một hay nhiều tổng thể.
ii. Giả thuyết H0 là một phát biểu sẽ được kiểm tra thông qua một phép kiểm định có ý nghĩa,
nghĩa là thông qua đó ta có bằng chứng đủ mạnh để bác bỏ H0. Thông thường, giả thuyết
H0 là một phát biểu với cụm từ “không hiệu quả” hoặc “không khác”. Định nghĩa 8.1.2
i. Sai lầm kiểm định:
a. Sai lầm loại I: là sai lầm nếu bác bỏ giả thuyết H0 khi nó đúng.
b. Sai lầm loại II: là sai lầm nếu chấp nhận giả thuyết H0 khi nó sai.
ii. Xác suất của sai lầm loại I
α = P(sai lầm loại I) = P(bác bỏ H0 khi H0 đúng).
Khi đó α được gọi là mức ý nghĩa hay sai số−α.
iii. Xác suất của sai lầm loại II
β = P(sai lầm loại II) = P(chấp nhận H0 khi H0 sai).
iv. Độ mạnh (power) của kiểm định thống kê là xác suất mà ta bác bỏ giả thuyết H0 khi đối
thuyết H1 đúng. Độ mạnh được tính là 1 − β. Ngược lại, ta có đối thuyết H1.
Định nghĩa 8.1.3 Giá trị p−value là mức ý nghĩa nhỏ nhất dẫn tới quyết định bác bỏ giả thuyết
H0 ứng với dữ liệu đã cho.
Định lí 8.1.1 Nếu p − value < α thì bác bỏ giả thuyết H0.
Mệnh đề 8.1.2 Một số nguyên tắc chung áp dụng trong xây dựng và giả quyết bài toán kiểm định: 60
Chương 8. KIỂM ĐỊNH MỘT MẪU
i. Xác định tham số mình quan tâm trong một bài toán cụ thể.
ii. Phát biểu giả thuyết H0 về tham số quan tâm.
iii. Chỉ định đối thuyết H1 sẽ thay thế H0.
iv. Tiến hành kiểm định thống kê với những lưu ý sau:
a. Kiểm định sẽ dựa trên thống kê sử dụng để ước lượng tham số xuất hiện trong giả
thuyết. Thông thường, thống kê này giống như thống kê sử dụng trong xây dựng khoảng
tin cây ở chương trước. Khi H0 đúng, chúng ta mong muốn giá trị ước lượng đủ gần giá
trị tham số do H0 định nghĩa.
b. Giá trị của ước lượng có khoảng cách lớn so với giá trị tham số trong H0 thì đó là bằng
chứng. Khi đó, đối thuyết H1 sẽ cho ta phương án thay thế H0.
c. Để đánh giá khoảng cách trên, người ta thường sử dụng thống kê cho kiểm định sau:
z = giá trị ước lượng − giá trị tham số kiểm định .
độ lệch chuẩn của ước lượng
v. Phát biểu kết quả kiểm định thống kê vào bài toán cụ thể đang xét. 8.2 Kiểm định trung bình
Định lí 8.2.1 (Kiểm định giá trị trung bình của phân phối chuẩn khi biết phương sai)
Xét bài toán kiểm định giá trị trung bình µ của một tổng thể có phân phối chuẩn với phương
sai đã biết từ một bộ dữ liệu (mẫu ngẫu nhiên) X ,
1 · · · , Xn được quan trắc từ tổng thể. Khi đó, ta phát biểu giả thuyết H , 0 : µ = µ0 H , 1 : µ , µ0
với µ0 là giá trị tham số đặc biệt mà ta quan tâm.
Đối tượng ở đây là giá trị trung bình, do đó ta sử dụng ước lượng X cho tham số µ. Chú ý, ước
lượng không chệch X có phân phân phối chuẩn với trung bình µ và phương sai σ2/n. Ta định
nghĩa thống kê cho kiểm định z . 0 = x − µ0 √ σ/ n
Kết luận: bác bỏ H0 nếu |z0| > zα/2 với zα/2 thỏa P(Z < zα/2) = 1 − α/2. Ngược lại thì chấp nhận.
Giá trị p − value = 2 (1 − Φ(|z0|)) với Φ(z0) là hàm phân phối tích lũy của N(0, 1).
Chú ý: giả sử giả thuyết H0 là sai và giá trị trung bình đúng là µ = µ0 + δ với δ > 0 (δ < 0 tương
tự), khi đó xác suất sai lầm loại II được tính theo công thức √ √ δ δ β = n n Φ zα . /2 − − − σ Φ zα/2 − σ Vì √ δ n Φ −zα/2 − ' σ 0
nên người ta có thể suy ra công thức xác định cỡ mẫu để có giá trị β khi biết trước α và δ (zβ + zα/2)2σ2 n ' . δ2 8.2 Kiểm định trung bình 61 R i. Nếu H >
1 : µ > µ0 thì ta sẽ bác bỏ giả thuyết H0 khi z0
zα, p − value = 1 − Φ(z0) và (z n ' β +zα )2σ2 δ . 2 ii. Nếu H <
1 : µ < µ0 thì ta sẽ bác bỏ giả thuyết H0 khi z0
−zα, p − value = Φ(z0) và (z n ' β +zα )2σ2 δ . 2
Bài 8.1. Hãy phát biểu giả thuyết H0 và đối thuyết H1 trong các trường hợp sau:
a. Kiểm định cung cấp bằng chứng cho thấy trung bình của tổng thể lớn hơn 10.
b. Kiểm định cung cấp bằng chứng cho thấy trung bình của tổng thể không bằng 7.
c. Kiểm định cung cấp bằng chứng cho thấy trung bình của tổng thể nhỏ hơn 10.
Bài 8.2. Một giả thuyết sẽ được kiểm định rằng trung bình tổng thể bằng 7 có đối thuyết là trung
bình khác 7 với phương sai đã biết. Hãy tìm giá trị để đưa ra quyết định ứng với mức ý nghĩa: a. 0.01 b. 0.05 c. 0.10
Bài 8.3. Một giả thuyết sẽ được kiểm định rằng trung bình tổng thể bằng 10 có đối thuyết là trung
bình lớn hơn 10 với phương sai đã biết. Hãy tìm giá trị để đưa ra quyết định ứng với mức ý nghĩa: a. 0.01 b. 0.05 c. 0.10
Bài 8.4. Một giả thuyết sẽ được kiểm định rằng trung bình tổng thể bằng 5 có đối thuyết là trung
bình nhỏ hơn 5 với phương sai đã biết. Hãy tìm giá trị để đưa ra quyết định ứng với mức ý nghĩa: a. 0.01 b. 0.05 c. 0.10 (Đs: -2.33; -1.64; -1.29)
Bài 8.5. Cho giả thuyết kiểm định H0 : µ = 7 với đối thuyết H1 : µ , 7 và phương sai đã biết, tính
p−value trong các trường hợp sau: a. z0 = 2.05 b. z0 = −1.84 c. z0 = 0.4
Bài 8.6. Cho giả thuyết kiểm định H0 : µ = 5 với đối thuyết H1 : µ < 5 và phương sai đã biết, tính
p−value trong các trường hợp sau: a. z0 = 2.05 b. z0 = −1.84 c. z0 = 0.4 (Đs: 0.98; 0.03; 0.65)
Bài 8.7. Một phần mềm thống kê cho ra bảng kết quả: One-Sample Z: Test of mu=35 vs not 35
The assumed standard deviation 1.8 Variable N Mean StDev SE Mean Z P-Value x 25 35.710 1.475 ? ? ?
a. Điền vào các mục còn thiếu. Bạn sẽ rút ra kết luận gì?
b. Kiểm định trên là một bên hay hai bên. 62
Chương 8. KIỂM ĐỊNH MỘT MẪU
c. Sử dụng bảng phân phối chuẩn và sử dụng số liệu trên xây dựng khoảng tin cậy 95% cho tham số trung bình.
d. Tính p−value nếu đối thuyết H1 : µ > 35.
Bài 8.8. Một phần mềm thống kê cho ra bảng kết quả: One-Sample Z: Test of mu=20 vs > 20
The assumed standard deviation 0.75 Variable N Mean StDev SE Mean Z P-Value x 10 19.889 ? 0.237 ? ?
a. Điền vào các mục còn thiếu. Bạn sẽ rút ra kết luận gì?
b. Kiểm định trên là một bên hay hai bên.
c. Sử dụng bảng phân phối chuẩn và sử dụng số liệu trên xây dựng khoảng tin cậy 95% cho tham số trung bình.
d. Tính p−value nếu đối thuyết H1 : µ , 20.
Bài 8.9. Một phần mềm thống kê cho ra bảng kết quả: One-Sample Z:
Test of mu=14.5 vs > 14.5
The assumed standard deviation 1.1 Variable N Mean StDev SE Mean Z P-Value x 16 15.016 1.015 ? ? ?
a. Điền vào các mục còn thiếu. Bạn sẽ rút ra kết luận gì?
b. Kiểm định trên là một bên hay hai bên.
c. Sử dụng bảng phân phối chuẩn và sử dụng số liệu trên xây dựng khoảng tin cậy 95% cho tham số trung bình.
d. Tính p−value nếu đối thuyết H1 : µ , 14.5.
Bài 8.10. Một phần mềm thống kê cho ra bảng kết quả: One-Sample Z: Test of mu=99 vs > 99
The assumed standard deviation 2.5 Variable N Mean StDev SE Mean Z P-Value x 12 100.039 2.365 ? 1.44 0.075
a. Điền vào các mục còn thiếu. Bạn sẽ rút ra kết luận gì?
b. Kiểm định trên là một bên hay hai bên.
c. Nếu giả thuyết H0 : µ = 98 với đối thuyết H1 : µ > 98 bạn có bác bỏ giả thuyết H0 với mức ý nghĩa 0.05.
d. Sử dụng bảng phân phối chuẩn và sử dụng số liệu trên xây dựng khoảng tin cậy 95% cho tham số trung bình.
8.2 Kiểm định trung bình 63
e. Tính p−value nếu đối thuyết H1 : µ , 99.
Bài 8.11. Một hệ thống tên lửa phản lực sử dụng động cơ đẩy nhiên liệu rắn. Tốc độ cháy của nhiên
liệu rắn là một đặc trưng quan trọng của động cơ. Thông số kĩ thuật yêu cầu tốc độ cháy trung
bình của thanh nhiên liệu là 50 cm/s. Các kĩ sư biết rằng độ lệch chuẩn của tốc độ cháy là 2 cm/s.
Những kĩ sư kiểm nghiệm xác định xác suất của sai lầm loại I hoặc mức ý nghĩa α = 0.05 và chọn
cỡ mẫu là n = 25 với trung bình mẫu tốc độ cháy là x = 51.3 cm/s. Kết luận rút ra như thế nào? (Đs: bác bỏ)
Bài 8.12. Nhiệt độ nước trung bình hạ lưu từ ống tháp xả giải nhiệt của nhà máy điện không được
lớn hơn 100oF. Kinh nghiệm quá khứ đã chỉ ra rằng độ lệch chuẩn của nhiệt độ là 2oF. Nhiệt độ
nước được đo trên chín ngày được lựa chọn ngẫu nhiên, và nhiệt độ trung bình được tìm thấy là 98oF.
a. Có bằng chứng gì cho ta thấy nhiệt độ nước có thể chấp nhận được hay không với mức ý nghĩa 0.05?
b. Tính p−value của kiểm định.
c. Tính xác suất chấp nhận giả thuyết H0 với α = 0.5 nếu nhiệt độ trung bình thật sự của nước là 104oF.
Bài 8.13. Một nhà sản xuất làm trục khuỷu (crankshafts) cho động cơ ô tô. Mức độ mòn của trục
khuỷu sau 100.000 dặm (0,0001 inch) là quan tâm vì nó có thể có ảnh hưởng đến thời hạn bảo hành.
Một mẫu ngẫu nhiên của n = 15 trục được kiểm tra và x = 2.78. Biết rằng σ = 0.9 và thường được
giả định có phân phối chuẩn.
a. Kiểm định H0 : µ = 3 với đối thuyết H1 : µ , 3 với mức ý nghĩa α = 0.05.
b. Độ mạnh của kiểm định nếu µ = 3.25?
c. Cỡ mẫu phải là bao nhiêu để nhận thấy giá trị trung bình đúng là 3.75 nếu ta muốn độ mạnh
của kiểm định ít nhất 0.9. (Đs: -0.95>-1.96; 0.80939)
Bài 8.14. Một thử nghiệm điểm nóng chảy của n = 10 mẫu của một chất kết dính được sử dụng
trong sản xuất một chất đẩy nhiên liệu tên lửa dẫn với trung bình x = 154.2oF. Giả sử điểm nóng
chảy có phân phối chuẩn với σ = 1.5oF.
a. Kiểm định H0 : µ = 155 với đối thuyết H1 : µ , 155 với α = 0.01. b. Tính p−value.
c. Tính sai số β nếu giá trị đúng µ = 150.
d. Tính cỡ mẫu cần để ta có β < 0.1 khi µ = 150 với α = 0.01. Bài 8.15.
a. Sử dụng số liệu của Bài tập 8.11. Giả sử tốc độ cháy trung bình đúng là 49 cm/s. Hãy tính β
ứng với α = 0.05, σ = 2 và n = 25. (Đs: 0.295)
b. Giả sử người thiết kế thí nghiệm cần kiểm định rằng nếu tốc độ cháy trung bình sai khác với
50 cm/s nhiều nhất khoảng 1 cm/s. Phép kiểm định sẽ phát hiện ra điều này (nghĩa là bác
bỏ H0) với xác suất 0.9 tức là sai số β = 0.1. Với số liệu α = 0.05, σ = 2 và n = 25, hãy tính
cỡ mẫu cần thiết để phục vụ mục đích này. (Đs: 42)
Bài 8.16. Tuổi thọ của pin được xem như có phân phối xấp xỉ phân phối chuẩn với độ lệch chuẩn
σ = 1.25 h. Một mẫu ngẫu nhiên gồm 10 viên pin có tuổi thọ trung bình là x = 40.5 h, α = 0.05.
a. Có thêm bằng chứng gì để hỗ trợ cho tuyên bố rằng tuổi thọ của pin không vượt quá 40h?
b. Tính p−value cho phép kiểm định ở câu trên.
c. Tính xác suất của sai lầm loại II hay sai số β nếu tuổi thọ trung bình đúng của pin là 42 h.
d. Cỡ mẫu phải bao nhiêu để sai số β không vượt quá 0.01 nếu tuổi thọ trung bình đúng của pin là 44 h. 64
Chương 8. KIỂM ĐỊNH MỘT MẪU
(Đs: 1.26<1.65; 0.1038; 0.000325; 1)
Bài 8.17. Các kĩ sư nghiên cứu độ bền sức kéo của một hợp kim được sử dụng làm trục của gậy
đánh golt biết rằng độ bền xấp xỉ phân phối chuẩn với σ = 60 psi. Một mẫu ngẫu nhiên gồm 12
mẫu vật có trung bình độ bền là 3450 psi.
a. Kiểm định giả thuyết rằng trung bình độ bền là 3500 psi với α = 0.01.
b. Tính mức ý nghĩa nhỏ nhất khi bạn đưa ra kết luận bác bỏ giả thuyết H0.
c. Tính xác suất của sai lầm loại II hay sai số β nếu giá trị trung bình thật là 3470.
d. Giả sử ta muốn bác bỏ giả thuyết H0 với xác suất ít nhất 0.8 khi trung bình thật là µ = 3500
thì cỡ mẫu phải là bao nhiêu?
e. Giải thích thêm cho kết luận ở phần trên bằng cách sử dụng khoảng tin cậy của µ.
Bài 8.18. “Supercavitation” là một công nghệ đẩy áp dụng cho các phương tiện dưới biển làm tăng
tốc độ của chúng. Nó xảy ra trên khoảng 50 m/s, khi áp suất giảm đủ để cho phép nước phân ly
thành hơi nước, tạo thành bọt khí phía sau phương tiện. Khi bong bóng khí hoàn toàn bao quanh
phương tiện, hiện tượng supercavitation được cho là xảy ra. Tám thử nghiệm đã được tiến hành trên
một mô hình phương tiện dưới biển cho tốc độ trung bình quan sát được là x = 102.2 m/s. Giả sử
rằng tốc độ thường được phân phối với độ lệch chuẩn đã biết 4 m/s.
a. Kiểm định giả thuyết H0 : µ = 100 với đối thuyết H1 : µ < 100 với α = 0.05.
b. Tính p−value trong phần trên.
c. Tính độ mạnh của kiểm định nếu giá trị trung bình đúng là 95 m/s.
d. Tính cỡ mẫu cần thiết để có thể phát hiện ra vận tốc đúng là 95 m/s nếu ta cần độ mạnh của
kiểm định ít nhất 0.85.
(Đs: 1.56>-1.65; 0.14; 0.97062; 5)
Bài 8.19. Một ổ đỡ được sử dụng trong một công nghiệp ô tô có đường kính bên trong đạt tiêu
chuẩn là 1.5 inches. Một mẫu ngẫu nhiên gồm 25 ổ đỡ được chọn có trung bình đường kính trong là
1.4975 inches. Đường kính ổ đỡ được biết là có phân phối chuẩn với độ lệch chuẩn σ = 0.01 inch.
a. Kiểm định giả thuyết H0 : µ = 1.5 với đối thuyết H1 : µ , 1.5 với α = 0.01.
b. Tính p−value cho phép kiểm định ở câu trên.
c. Tính độ mạnh của phép kiểm định nếu trung bình đúng của đường kính ổ đỡ là 1.495 inches.
d. Giải thích thêm cho kết luận ở phần trên bằng cách sử dụng khoảng tin cậy của µ.
Định lí 8.2.2 (Kiểm định giá trị trung bình của phân phối chuẩn khi chưa phương sai)
Xét bài toán kiểm định giá trị trung bình µ của một tổng thể có phân phối chuẩn với phương sai
chưa biết từ một bộ dữ liệu (mẫu ngẫu nhiên) X ,
1 · · · , Xn được quan trắc từ tổng thể. Khi đó, ta phát biểu giả thuyết H , 0 : µ = µ0 H , 1 : µ , µ0
với µ0 là giá trị tham số đặc biệt mà ta quan tâm.
Đối tượng ở đây là giá trị trung bình, do đó ta sử dụng ước lượng X cho tham số µ. Chú ý, ước
lượng không chệch X có phân phân phối chuẩn với trung bình µ và phương sai σ2/n. Ta định
nghĩa thống kê cho kiểm định có phân phối Student (xem mục 7.2.2) T0 = x − µ0 √ ∼ t(n − 1). S/ n
Kết luận: bác bỏ H0 nếu |T0| > tα/2,n−1 với tα/2,n−1 thỏa P(|T | > tα/2,n−1) = α với T ∼ t(n − 1). 8.2 Kiểm định trung bình 65
Ngược lại thì chấp nhận. Giá trị p − value = 2P(T > |T0|) với T ∼ t(n − 1). R i. Nếu H > ,
1 : µ > µ0 thì ta sẽ bác bỏ giả thuyết H0 khi T0
tα,n−1 p − value = P(T > T0). ii. Nếu H < ,
1 : µ < µ0 thì ta sẽ bác bỏ giả thuyết H0 khi T0
−tα,n−1 p − value = P(T < T0).
Bài 8.20. Một giả thuyết được kiểm định rằng trung bình của tống thể bằng hay khác 7 với phương
sai chưa biết. Hãy tìm giá trị quyết định của thống kê T0 ứng với mức ý nghĩa và cỡ mẫu:
a. α = 0.01 và n = 20.
b. α = 0.05 và n = 12.
c. α = 0.10 và n = 15.
Bài 8.21. Một giả thuyết được kiểm định rằng trung bình của tống thể bằng hay lớn hơn 10 với
phương sai chưa biết. Hãy tìm giá trị quyết định của thống kê Z0 ứng với mức ý nghĩa và cỡ mẫu:
a. α = 0.01 và n = 20.
b. α = 0.05 và n = 12.
c. α = 0.10 và n = 15.
(Đs: >2.539; >1.796; >1.345)
Bài 8.22. Một giả thuyết được kiểm định rằng trung bình của tống thể bằng hay nhỏ hơn 5 với
phương sai chưa biết. Hãy tìm giá trị quyết định của thống kê Z0 ứng với mức ý nghĩa và cỡ mẫu:
a. α = 0.01 và n = 20.
b. α = 0.05 và n = 12.
c. α = 0.10 và n = 15.
Bài 8.23. Kiểm định giả thuyết H0 : µ = 7 với đối thuyết H1 , 7 với phương sai không biết và
n = 20, xấp xỉ p−value cho mỗi thống kê kiểm định sau: a. t0 = 2.05 b. t0 = −1.84 c. t0 = 0.4
Bài 8.24. Kiểm định giả thuyết H >
0 : µ = 10 với đối thuyết H1
10 với phương sai không biết và
n = 15, xấp xỉ p−value cho mỗi thống kê kiểm định sau: a. t0 = 2.05 b. t0 = −1.84 c. t0 = 0.4
Bài 8.25. Kiểm định giả thuyết H <
0 : µ = 5 với đối thuyết H1
5 với phương sai không biết và
n = 15, xấp xỉ p−value cho mỗi thống kê kiểm định sau: a. t0 = 2.05 b. t0 = −1.84 c. t0 = 0.4
Bài 8.26. Một kết quả kiểm định bằng phần mềm cho ra bảng kết quả: One-Sample T: Test of mu = 91 vs >91 Variable N Mean StDev SE Mean 95% Lower bounded T P x 20 92.379 0.717 ? ? ? ?
a. Tìm những thông số chưa có. Tính giá trị p−value và rút ra kết luận.
b. Kiểm định này là một bên hay hai bên?
c. Nếu kiểm định với H0 : µ = 90 với đối thuyết H1 : µ > 90 thì kết luận có thay đổi gì không? 66
Chương 8. KIỂM ĐỊNH MỘT MẪU
Bài 8.27. Một kết quả kiểm định bằng phần mềm cho ra bảng kết quả: One-Sample T:
Test of mu = 12 vs not = 12 Variable N Mean StDev SE Mean T P x 10 12.564 ? 0.296 ? ?
a. Thống kê kiểm định t có bậc tự do là bao nhiêu?
b. Tìm những thông số chưa có.
c. Kiểm định này là một bên hay hai bên?
d. Xây dựng khoảng tin cậy 95% cho trung bình.
e. Nếu kiểm định với H0 : µ = 12 với đối thuyết H1 : µ > 12 thì kết luận có thay đổi gì không?
f. Nếu kiểm định với H0 : µ = 11.5 với đối thuyết H1 : µ , 11.5 thì bạn có bác bỏ H0 hay không
khi mức ý nghĩa α = 0.05. Sử dụng kết quả ở những câu trên giải thích.
Bài 8.28. Một kết quả kiểm định bằng phần mềm cho ra bảng kết quả: One-Sample T:
Test of mu = 34 vs not = 34 Variable N Mean StDev SE Mean 95% CI T P x 16 35.274 1.783 ? (34.324, 36.224) ? 0.012
a. Thống kê kiểm định t có bậc tự do là bao nhiêu?
b. Tìm những thông số chưa có.
c. Nếu kiểm định H0 : µ = 34 với đối thuyết H1 : µ > 34 thì p−value lớn hơn hay nhỏ hơn?
d. Nếu kiểm định với H0 : µ = 34.5 với đối thuyết H1 : µ , 34.5 thì bạn có bác bỏ H0 hay không
khi mức ý nghĩa α = 0.05. Tính giá trị p−value.
Bài 8.29. Một bài viết về Tăng trưởng: tạp chí dành cho các vấn đề về tăng trưởng bình thường và
bất thường: “So sánh tỷ lệ béo và chất béo ước tính được đo lường, chất béo, kali và nitơ của lợn
trồng” (Vol. 46, No. 4, 1982, pp. 306–321)] báo cáo kết quả của một nghiên cứu đo trọng lượng cơ
thể (tính bằng gam) đối với lợn guinea khi sinh. 421.0 452.6 456.1 494.6 373.8 90.5 110.7 96.4 81.7 102.4 241.0 296.0 317.0 290.9 256.5 447.8 687.6 705.7 879.0 88.8 296.0 273.0 268.0 227.5 279.3 258.5 296.0
a. Kiểm tra giả thuyết trọng lượng trung bình là 300 gr am với α = 0.05. Tính giá trị p−value.
b. Giải thích thêm cho kết luận ở phần trên bằng cách sử dụng khoảng tin cậy của µ.
Bài 8.30. Một bài báo năm 1992 trên Tạp chí Hiệp hội Y khoa Hoa Kỳ (“Thẩm định quan trọng
98.6o F, giới hạn trên của nhiệt độ cơ thể bình thường và các di sản khác của Carl Reinhold August
Wunderlich”) đã báo cáo nhiệt độ cơ thể, giới tính và nhịp tim cho một số đối tượng. Nhiệt độ cơ
thể cho 25 đối tượng nữ theo sau: 97.8, 97.2, 97.4, 97.6, 97.8, 97.9, 98.0, 98.0, 98.0, 98.1, 98.2,
98.3, 98.3, 98.4, 98.4, 98.4, 98.5, 98.6, 98.6, 98.7, 98.8 , 98.8, 98.9, 98.9 và 99.0 8.2 Kiểm định trung bình 67
a. Kiểm tra giả thuyết H0 : µ = 98.6 có đối thuyết H1 : µ , 98.6 với α = 0.05. Tính giá trị p−value.
b. Giải thích thêm cho kết luận ở phần trên bằng cách sử dụng khoảng tin cậy của µ.
Bài 8.31. Hàm lượng natri của hai mươi hộp bắp hữu cơ 300 gram được xác định. Dữ liệu (tính
bằng miligam) như sau: 131.15, 130.69, 130.91, 129.54, 129.64, 128.77, 130.72, 128.33, 128.24,
129.65, 130.14, 129.29, 128.71, 129.00, 129.39, 130.42, 129.53, 130.12, 129.78, 130.92.
a. Bạn hãy kiểm định giá trị trung bình có khác 130 milligr am với α = 0.05. Tính giá trị p−value.
b. Giải thích thêm cho kết luận ở phần trên bằng cách sử dụng khoảng tin cậy của µ.
Bài 8.32. Đo cholesterol ( đơn vị mg%) cho một nhóm người, ta ghi nhận lại được Chol. 150 - 160 160 - 170 170 - 180 180 - 190 190 - 200 200 - 210 Số người 3 9 11 3 2 1
a. Tính trung bình và phương sai mẫu.
b. Tìm khoảng ước lượng cho trung bình cholesterol trong dân số với độ tin cậy 0.95.
c. Có tài liệu cho biết lượng cholesterol trung bình là 175 mg%. Giá trị này có phù hợp với mẫu
quan sát không ? ( kết luận với α = 0.05).
Bài 8.33. Một máy đóng gói các sản phẩm có khối lượng 1kg. Nghi ngờ máy hoạt động không
bình thường, người ta chọn ra một mẫu ngẫu nhiên gồm 100 sản phẩm thì thấy như sau: Khối lượng 0.95 0.97 0.99 1.01 1.03 1.05 Số gói 9 31 40 15 3 2
Với mức ý nghĩa 0.05, hãy kết luận về nghi ngờ trên.
Bài 8.34. Quan sát số hoa hồng bán ra trong một ngày của một cửa hàng bán hoa sau một thời gian,
người ta ghi được số liệu sau: Số hoa hồng ( đoá ) 12 13 15 16 17 18 19 Số ngày 3 2 7 7 3 2 1
a. Tìm ướcc lượng điểm của số hoa hồng trung bình bán được trong một ngày.
b. Sau khi tính toán, ông chủ cửa hàng nói rằng nếu trung bình một ngày không bán được 15
đoá hoa thì chẳng thà đóng cửa còn hơn. Dựa vào số liệu trên, anh (chị) hãy kết luận giúp
ông chủ cửa hàng xem có nên tiếp tục bán hay không ở mức ý nghĩa 0.05.
c. Giả sử những ngày bán được từ 13 đến 17 đoá hồng là những ngày “bình thường”. Hãy ước
lượng tỉ lệ của những ngày bình thường của cửa hàng ở độ tin cậy 90%. ( Giả thiết rằng số
hoa bán ra trong ngày có phân phối chuẩn).
Bài 8.35. Một xí nghiệp đúc một số rất lớn các sản phẩm bằng thép với số khuyết tật trung bình ở
mỗi sản phẩm là 3. Người ta cải tiến cách sản xuất và kiểm tra 36 sản phẩm. Kết quả như sau:
Số khuyết tật trên sản phẩm 0 1 2 3 4 5 6
Số sản phẩm tương ứng 7 4 5 7 6 6 1
Giả sử số khuyết tật của các sản phẩm có phân phối chuẩn. 68
Chương 8. KIỂM ĐỊNH MỘT MẪU
a. Hãy ướcc lượng số khuyết tật trung bình ở mỗi sản phẩm sau khi cải tiến, với độ tin cậy 90%.
b. Hãy cho kết luận về hiệu quả của việc cải tiến sản xuất với mức ý nghĩa 0.05.
Bài 8.36. Đối với người Việt Nam, lượng huyết sắc tố trung bình là 138.3g/l. Khám cho 80 công
nhân ở nhà máy có tiếp xúc hoá chất, thấy huyết sắc tố trung bình là 120g/l; s = 15g/l. Từ kết quả
trên, có thể kết luận lượng huyết sắc tố trung bình của công nhân nhà máy hoá chất này thấp hơn
mức chung hay không? Kết luận với 8.3 Kiểm định phương sai
Định lí 8.3.1 (Kiểm định giá trị phương sai và độ lệch chuẩn của phân phối chuẩn)
Xét bài toán kiểm định phương sai của một tổng thể của phân phối chuẩn σ2 có bằng với một giá
trị đặc biệt σ2 (hay tương đương độ lệch chuẩn σ có bằng giá trị đặc biệt σ 0 0) từ một bộ dữ liệu (mẫu ngẫu nhiên) X ,
1 · · · , Xn được quan trắc từ tổng thể. Khi đó, ta phát biểu giả thuyết H , 0 : σ2 = σ2 0 H , 1 : σ2 , σ2 0
với σ0 là giá trị tham số đặc biệt mà ta quan tâm.
Ta định nghĩa thống kê cho kiểm định có phân phối Chi bình phương (xem mục 7.2.2) (n − 1)S2 X2 = ∼ χ2 . 0 σ2 n−1 0 Kết luận: bác bỏ H > χ2 0 nếu X 2 với χ2 thỏa X > χ2 = α/2 với X ∼ χ2 . 0 α/2,n−1 α/2,n−1 P α/2,n−1 n−1
Ngược lại thì chấp nhận. R i. Nếu H > χ2
1 : µ > µ0 thì ta sẽ bác bỏ giả thuyết H0 khi X 2 . 0 α,n−1 ii. Nếu H <
1 : µ < µ0 thì ta sẽ bác bỏ giả thuyết H0 khi X 2 − χ2 . 0 α,n−1
Bài 8.37. Xét kiểm định H0 : σ2 = 5 với H1 : σ2 < 5. Tính giá trị p−value trong mỗi trường hợp
kiểm định thống kê sau:
a. x2 = 25.2 và n = 20. 0
b. x2 = 15.2 và n = 12. 0 c. x2 = 4.2 và n = 15. 0
Bài 8.38. Xét kiểm định H0 : σ2 = 10 với H1 : σ2 > 10. Tính giá trị p−value trong mỗi trường hợp
kiểm định thống kê sau:
a. x2 = 25.2 và n = 20. 0
b. x2 = 15.2 và n = 12. 0 c. x2 = 4.2 và n = 15. 0
Bài 8.39. Một máy làm đầy tự động được sử dụng để đổ đầy chất tẩy lỏng vào chai. Một mẫu ngẫu
nhiên gồm 20 chai có phương sai mẫu của khối lượng đầy s2 = 0.01553 (chất lỏng ounces)2. Nếu
phương sai khối lượng khác 0.01 (chất lỏng ounces)2, thì chai không được chấp nhận vì quá đầy
hoặc quá vơi. Có bằng chứng trong dữ liệu mẫu để cho thấy rằng nhà sản xuất có một sản phẩm quá
đầy hoặc quá vơi? Sử dụng α = 0.05, và giả định rằng khối lượng đổ đầy có phân phối chuẩn. 8.4 Kiểm định tỉ lệ 69
Bài 8.40. Tỷ lệ titan trong một hợp kim được sử dụng trong đúc hàng không vũ trụ được đo đạc
trên 51 mẫu được chọn ngẫu nhiên. Độ lệch chuẩn của mẫu là s = 0.37.
a. Kiểm định giả thuyết H0 : σ = 0.35 với giả thuyết H1 : σ , 0.35 với α = 0.05. Nêu giả thiết
cần thiết về phân phối của dữ liệu để có thể đưa ra kết luận. b. Tính p−value.
c. Tìm khoảng tin cậy 95% cho σ.
d. Sử dụng kết quả ở trên giải thích kết luận kiểm định. 8.4 Kiểm định tỉ lệ
Định lí 8.4.1 (Kiểm định tỉ lệ của phân phối nhị thức)
Ta phát biểu giả thuyết H , 0 : p = p0 H , 1 : p , p0
với p0 là giá trị tham số đặc biệt mà ta quan tâm.
Sử dụng ước lượng trung bình mẫu hay tỉ lệ mẫu f ở chương trước, ta định nghĩa thống kê cho kiểm định z . 0 = n f − np0 pnp0(1 − p0)
Kết luận: bác bỏ H0 nếu |z0| > zα/2 với zα/2 thỏa P(Z < zα/2) = 1 − α/2. Ngược lại thì chấp nhận.
Giá trị p − value = 2 (1 − Φ(|z0|)) với Φ(z0) là hàm phân phối tích lũy của N(0, 1).
Chú ý: xác suất sai lầm loại II được tính theo công thức p ! p ! f − p p f − p p β = 0 + zα/2 0(1 − p0)/n 0 − zα/2 0(1 − p0)/n Φ − Φ p p f (1 − f )/n f (1 − f )/n
Người ta có thể suy ra công thức xác định cỡ mẫu để có sai số β cho trước khi biết α và δ ( p p zβ
f (1 − f ) + zα/2 p0(1 − p0))2 n ' . ( f − p0)2 R i. Nếu H >
1 : p > p0 thì ta sẽ bác bỏ giả thuyết H0 khi z0
zα, p − value = 1 − Φ(z0) và √ √ (zβ f (1− f )+zα p n ' 0 (1−p0 ))2 . ( f −p0)2 ii. Nếu H <
1 : p < p0 thì ta sẽ bác bỏ giả thuyết H0 khi z0
−zα, p − value = Φ(z0) và √ √ (zβ f (1− f )+zα p n ' 0 (1−p0 ))2 . ( f −p0)2
Bài 8.41. Một nhà sản xuất chất bán dẫn sản xuất bộ điều khiển sử dụng trong công nghệ động cơ
ô tô. Khách hàng yêu cầu phần khiếm khuyết ở các bước sản xuất quan trọng không vượt quá 0.05
và nhà sản xuất chứng minh khả năng xử lý ở mức chất lượng này bằng cách sử dụng α = 0.05. Nhà
sản xuất chất bán dẫn lấy mẫu ngẫu nhiên gồm 200 thuyết bị và thấy rằng bốn thuyết bị này bị lỗi.
Nhà sản xuất có thể chứng minh khả năng xử lý cho khách hàng không? (Đs: kết luận rằng quá
trình này là có khả năng) 70
Chương 8. KIỂM ĐỊNH MỘT MẪU
Bài 8.42. Sử dụng số liệu của Bài tập 8.41, giả sử quá trình sản xuất thực tế có p = 0.03. Sai số β
sẽ là bao nhiêu nếu n = 200 và α = 0.05? Giả sử rằng nhà sản xuất chất bán dẫn đã sẵn sàng chấp
nhận một sai số β = 0.1 nếu giá trị thực sự của phần quá trình bị lỗi là p = 0.03 và α = 0.05, kích
thước mẫu nào sẽ được yêu cầu?
Bài 8.43. Một phần mềm thống kê cho ra bảng kết quả:
Test and Cl for One Proportion
Test of p = 0.4 vs p not = 0.4 Variable N Sample p 95% CI Z-Value P-Value 98 275 ? (0.299759, 0.412968) ? ?
Sử dụng xấp xỉ phân phối chuẩn, tính
a. Kết quả này là kiểm định hai bên hay một bên?
b. Tính những chỗ còn thiếu.
c. Tại sao lại xấp xỉ được bằng phân phối chuẩn?
Bài 8.44. Một phần mềm thống kê cho ra bảng kết quả:
Test and Cl for One Proportion
Test of p = 0.6 vs p < 0.6 Variable N Sample p 95% CI Z-Value P-Value 287 500 ? ? ? ?
a. Kết quả này là kiểm định hai bên hay một bên?
b. Tại sao lại xấp xỉ được bằng phân phối chuẩn?
c. Tính những chỗ còn thiếu.
d. Giả sử đối thuyết là kiểm định 2 bên. Hãy tính p−value.
Bài 8.45. Giả sử rằng 1000 khách hàng được khảo sát và 850 người hài lòng hoặc rất hài lòng với
các sản phẩm và dịch vụ của công ty
a. Kiểm định với giả thuyết H0 : p = 0.9 với đối thuyết H1 : p , 0.9 với mức α = 0.05. Tìm p−value.
b. Giải thích thêm cho kết luận trên bằng cách sử dụng khoảng tin cậy cho p.
Bài 8.46. Giả sử người ta kiểm tra 500 thành phần máy móc do một nhà máy sản xuất và thấy có 10
thành phần bị loại bỏ. Kiểm định giả thuyết H0 : p = 0.03 với đối thuyết H1 : p < 0.03 và α = 0.05. Tìm p−value.
Bài 8.47. Một bài báo trên tạp chí y khoa Anh “So sánh điều trị sỏi thận bằng phẫu thuật phẫu
thuật, cắt bỏ sỏi thận, và Lithotrips sóng bổ sung,” (1986, Vol. 292, pp. 879–882)] thấy rằng tác
động qua da (PN) có tỷ lệ thành công trong việc loại bỏ sỏi thận của 289 trong số 350 bệnh nhân.
Phương pháp truyền thống đạt hiệu quả 78%. Có bằng chứng gì cho thấy tỉ lệ thành công của PN
lớn hơn so với truyền thống với mức ý nghĩa α = 1%? Tìm p−value.
Bài 8.48. Một mẫu ngẫu nhiên gồm 300 mạch có 13 khiếm khuyết.
a. Kiểm định với giả thuyết H0 : p = 0.05 với đối thuyết H1 : p , 0.05 với mức α = 0.05. Tìm p−value. 8.4 Kiểm định tỉ lệ 71
b. Giải thích thêm cho kết luận trên bằng cách sử dụng khoảng tin cậy cho p.
Bài 8.49. Một máy nhà sản xuất ống kính interocular có một máy nghiền mới được coi là đủ điều
kiện nếu có bằng chứng cho thấy tỷ lệ phần trăm của các thấu kính được đánh bóng có chứa khuyết
tật bề mặt không vượt quá 2%. Một mẫu ngẫu nhiên gồm 250 thấu kính thì chứa sáu ống kính bị lỗi.
a. Xây dựng và kiểm tra giả thuyết phù hợp để xác định xem máy có đủ điều kiện hay không.
Giả sử α = 0.05, hày tìm p−value.
b. Giải thích thêm cho kết luận trên bằng cách sử dụng khoảng tin cậy cho p.
Bài 8.50. Một bài báo trên tạp chí Fortune (ngày 21 tháng 9 năm 1992) tuyên bố rằng gần một nửa
số kỹ sư tiếp tục học bậc học sau ĐH, cuối cùng nhận được bằng Thạc sĩ hoặc Tiến sĩ. Dữ liệu từ
bài viết trong Horizons Engineering (Mùa xuân 1990) cho thấy rằng 117 trong số 484 sinh viên tốt
nghiệp ngành kỹ thuật có kế hoạch học sau đại học.
a. Dữ liệu từ Engineering Horizons có phù hợp với yêu cầu của Fortune không? Sử dụng
α = 0.05 để đưa ra kết luận của bạn. Tìm p−value cho kiểm định trên.
b. Giải thích thêm kết luận trên bằng khoảng tin cậy cho p.
Bài 8.51. Một nhà nghiên cứu tuyên bố rằng ít nhất 10% của tất cả các mũ bảo hiểm bóng đá có lỗi
sản xuất có khả năng có thể gây thương tích cho người đội. Một mẫu 200 mũ bảo hiểm cho thấy 16
mũ bảo hiểm chứa các khuyết tật như vậy.
a. Phát hiện này có ủng hộ tuyên bố của nhà nghiên cứu không?
b. Giải thích thêm cho kết luận trên bằng cách sử dụng khoảng tin cậy cho p.
Bài 8.52. Quảng cáo pin của một hãng sản xuất điện thoại di động được biết là sẽ hoạt động liên
tục 48 giờ hoạt động, với các một lần sạc pin đúng yêu cầu kĩ thuật. Một nghiên cứu về 5000 pin
được thực hiện và 15 ngừng hoạt động trước 48 giờ. Những kết quả thử nghiệm này có ủng hộ cho
tuyên bố rằng dưới 0.2% pin của công ty sẽ không hoạt động như trong khoảng thời gian được
quảng cáo, với các một lần sạc pin đúng yêu cầu kĩ thuật không? Sử dụng kiểm định giả thuyết trên với α = 0.01.
Bài 8.53. Trong một mẫu ngẫu nhiên gồm 85 vòng bi trục khuỷu động cơ ô tô trong đó có 10 vòng
độ nhám bề mặt hoàn thiện vượt quá các thông số kỹ thuật. Dữ liệu này có cho thấy bằng chứng rõ
ràng rằng tỷ lệ vòng bi trục khuỷu có độ nhám bề mặt vượt quá 0.10?
a. Phát biểu và kiểm định giả thuyết trên với mức α = 0.05.
b. Nếu p thực sự là 0.15, hãy tính xác suất để không bác bỏ giả thuyết H0 (sai số β)?
c. Nếu p = 0.15, cỡ mẫu phải là bao nhiêu để xác suất bác bỏ đúng giả thiết H0 với xác suất 0.9?
Bài 8.54. Trong một vùng dân cư có 18 bé trai và 28 bé gái mắc bệnh B. Hỏi rằng tỷ lệ nhiễm bệnh
của bé trai và bé gái có như nhau không? (Kết luận với α = 0.05 và giả sử rằng số lượng bé trai và
bé gái trong vùng tương đương nhau, và rất nhiều). 72
Chương 8. KIỂM ĐỊNH MỘT MẪU 73
9. KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ HAI MẪU 9.1 Lý thuyết
Giả thiết chung cho chương này là hai mẫu phải thỏa các điều kiện: i. Quan trắc X ,
11 · · · , X1n là một mẫu ngẫu nhiên lấy từ tổng thể thứ nhất. 1 ii. Quan trắc X ,
21 · · · , X2n là một mẫu ngẫu nhiên lấy từ tổng thể thứ hai. 2
iii. Hai tổng thế đại diện bởi X , 1 X2 là độc lập nhau.
iv. Cả hai tổng thể đều có phân phối chuẩn.
Định lí 9.1.1 (Kiểm định sự khác nhau hai giá trị trung bình của hai tổng thể phân phối chuẩn khi biết phương sai)
Ta phát biểu giả thuyết H , 0 : µ1 − µ2 = ∆0 H , 1 : µ1 − µ2 , ∆0
với ∆0 là giá trị đặc biệt mà ta quan tâm. Ta định nghĩa thống kê cho kiểm định có phân phối chuẩn Z0 = X1 − X2 − ∆0 ∼ N(0, 1). qσ2/n /n 1 1 + σ2 2 2 Kết luận: bác bỏ H > < 0 nếu z0 zα/2 hoặc z0
−zα/2 với zα/2 thỏa P(Z < zα/2) = 1 − α/2. Ngược lại
thì chấp nhận. Giá trị p − value = 2 (1 − Φ(|z0|)) với Φ(z0) là hàm phân phối tích lũy của N(0, 1).
Chú ý: giả sử giả thuyết H0 là sai và giá trị trung bình đúng là µ = µ0 + ∆ với ∆ > 0, khi đó xác
suất sai lầm loại II được tính theo công thức β = © ∆ − ∆0 ∆ − ∆ ª © 0 ª Φ . zα/2 − ® − Φ −zα/ ® q 2 − q σ2/ ® ® n /n σ2/n /n 1 1 + σ2 2 2 1 1 + σ2 2 2 « ¬ « ¬ 74
Chương 9. KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ HAI MẪU Vì © ∆ − ∆0 ª Φ −zα/2 − ® ' 0, q σ2/ ® n /n 1 1 + σ2 2 2 « ¬
nên người ta có thể suy ra công thức xác định cỡ mẫu n = n1 = n2 để có giá trị β khi biết trước α và ∆ (zβ + zα/2)2(σ2 + σ2) n ' 1 2 . (∆ − ∆0)2 Đặc biệt: Nếu H > > 1 : µ1 − µ2
∆0 thì ta sẽ bác bỏ giả thuyết H0 khi z0
zα, p − value = 1 − Φ(z0) và (zβ +zα)2(σ2+σ2) n ' 1 2 . (∆−∆0)2 i. ii. Nếu H < < 1 : µ1 − µ2
∆0 thì ta sẽ bác bỏ giả thuyết H0 khi z0
−zα, p − value = Φ(z0) và (zβ +zα)2(σ2+σ2) n ' 1 2 . (∆−∆0)2
Định lí 9.1.2 (Kiểm định sự khác nhau hai giá trị trung bình của hai tổng thể phân phối chuẩn
khi phương sai khác nhau chưa biết)
Ta phát biểu giả thuyết H , 0 : µ1 − µ2 = ∆0 H , 1 : µ1 − µ2 , ∆0
với ∆0 là giá trị đặc biệt mà ta quan tâm. Ta định nghĩa thống kê cho kiểm định có phân phối Student
T0 = X1 − X2 − (µ1 − µ2) ∼ t(ν), q S2/n /n 1 1 + S2 2 2 với bậc tự do S2/n /n 2 ν = 1 1 + S22 2 . (S2 /n /n 1 1)2 2)2 + (S22 n n 1−1 2−1
Tất cả các kết luận giống như mục 9.1.1. 9.2 Bài tập
Bài 9.1. Xét giả thuyết H0 : µ1 = µ2 với đối thuyết H1 : µ1 , µ2 có σ1 = 10 và σ2 = 5. Giả sử cỡ
mẫu n1 = 10, n2 = 15 và x1 = 4.7, x2 = 7.8. Sử dụng α = 0.05
a. Kiểm định giả thuyết trên và tìm p−value.
b. Tính độ mạnh của kiểm định nếu µ1 hơn µ2 đúng ba đơn vị.
c. Giả sử hai mẫu có kích thước bằng nhau, cỡ mẫu đó phải là bao nhiêu để µ1 hơn µ2 đúng ba
đơn vị có sai số β = 0.05 biết α = 0.05.
(Đs: −1.96 < z0 = 0.9 < 1.96, 0.368; 0.14; 180)
Bài 9.2. Xét giả thuyết H < µ
0 : µ1 = µ2 với đối thuyết H1 : µ1
2 có σ1 = 10 và σ2 = 5. Giả sử cỡ
mẫu n1 = 10, n2 = 15 và x1 = 14.2, x2 = 19.7. Sử dụng α = 0.05
a. Kiểm định giả thuyết trên và tìm p−value.
b. Tính độ mạnh của kiểm định nếu µ1 hơn µ2 đúng bốn đơn vị. 9.2 Bài tập 75
c. Giả sử hai mẫu có kích thước bằng nhau, cỡ mẫu đó phải là bao nhiêu để µ1 hơn µ2 đúng
bốn đơn vị có sai số β = 0.05 biết α = 0.05.
Bài 9.3. Xét giả thuyết H > µ
0 : µ1 = µ2 với đối thuyết H1 : µ1
2 có σ1 = 10 và σ2 = 5. Giả sử cỡ
mẫu n1 = 10, n2 = 15 và x1 = 24.5, x2 = 21.3. Sử dụng α = 0.01
a. Kiểm định giả thuyết trên và tìm p−value.
b. Tính độ mạnh của kiểm định nếu µ1 hơn µ2 đúng hai đơn vị.
c. Giả sử hai mẫu có kích thước bằng nhau, cỡ mẫu đó phải là bao nhiêu để µ1 hơn µ2 đúng hai
đơn vị có sai số β = 0.05 biết α = 0.05.
(Đs: z0 = 0.937 < 2.325, 0.174; 0.04; 339)
Bài 9.4. Hai máy được sử dụng để làm đầy các chai nhựa với khối lượng tịnh là 16.0 ounce. Khối
lượng làm đầy có thể được giả định có phân phối chuẩn, với độ lệch chuẩn σ1 = 0.020 và σ2 = 0.025
ounce. Một thành viên của đội ngũ nhân viên kỹ thuật chất lượng nghi ngờ rằng cả hai máy đều có
cùng khối lượng trung bình, dù khối lượng này có là 16.0 ounce hay không. Một mẫu ngẫu nhiên
gồm 10 chai được lấy từ đầu ra của mỗi máy:
Máy 1: 16.03 16.01 16.04 15.96 16.05 15.98 16.05 16.02 16.02 15.99
Máy 2: 16.02 16.03 15.97 16.04 15.96 16.02 16.01 16.01 15.99 16.00
a. Suy nghĩ của đội ngũ kỹ sư đúng? Sử dụng α = 0.05. Tìm p−value.
b. Tính độ mạnh của kiểm định nếu sự khác nhau của 2 trung bình đúng bằng 0.04.
c. Giả sử hai mẫu có kích thước bằng nhau, cỡ mẫu đó phải là bao nhiêu để µ1 khác µ2 đúng
bằng 0.04 có sai số β = 0.05 biết α = 0.05.
Bài 9.5. Hai loại nhựa phù hợp để sử dụng cho một nhà sản xuất linh kiện điện tử. Sức mạnh chịu
sự phá hủy của loại nhựa này là quan trọng. Được biết, σ1 = σ2 = 1 psi. Từ một mẫu ngẫu nhiên
có kích thước n1 = 10 và n2 = 12, ta có được x1 = 162.5 và x1 = 155.0. Công ty sẽ không áp dụng
nhựa loại 1 trừ khi sức chịu phá vỡ trung bình của nó vượt quá nhựa loại 2 ít nhất 10 psi.
a. Trên cơ sở thông tin đó, ta có nên sử dụng nhựa loại 1? Sử dụng α = 0.05 đưa ra câu trả lời. Tìm p−value.
b. Giả sử sự khác nhau giữa chúng đúng là 12 psi. Tính độ mạnh của kiểm định với α = 0.05.
c. Giả sử sự khác nhau giữa chúng đúng là 12 psi. Cỡ mẫu ở câu a có đủ để có khẳng định đúng đắn?
(Đs: z0 = −5.84 < 1.645,1; 0.9988; đủ)
Bài 9.6. Tốc độ cháy của hai loại nguyên liệu rắn sử dụng trong động cơ tên lửa được nghiên cứu.
Được biết tốc độ cháy của hai loại này có xấp xỉ phân phối chuẩn với σ1 = σ2 = 3 cm/s. Hai mẫu
ngẫu nhiên với cỡ mẫu n1 = n2 = 20 được xem xét có tốc độ cháy trung bình x1 = 18 cm/s và x2 = 24 cm/s.
a. Kiểm định xem hai loại này có cùng trung bình hay không? Với α = 0.05, hãy tìm p−value.
b. Hãy tìm sai số β của phần trên nếu biết sự khác nhau của hai trung bình đúng bằng 2.5 cm/s.
c. Giả sử hai mẫu ngẫu nhiên có cùng cỡ, hãy tìm cỡ mẫu để có được độ mạnh kiểm định là 0.9
với sự khác nhau của trung bình đúng bằng 14 cm/s.
Bài 9.7. Hai công thức khác nhau của nhiên liệu động cơ ôxy hóa đang được thử nghiệm để nghiên
cứu số octane của chúng. Phương sai chỉ số octane của công thức thứ nhất σ2 = 1.5 và công thức 1
thứ hai σ2 = 1.2. Hai mẫu ngẫu nhiên có cỡ mẫu n 2
1 = 15 và n2 = 20 được nghiên cứu có chỉ số
octane trung bình lần lượt là x1 = 89.6 và x2 = 92.5. Với giả sử có phân phối chuẩn
a. Nếu công thức 2 tạo ra một số octane cao hơn so với công thức 1, nhà sản xuất muốn phát
hiện nó. Xây dựng và kiểm định giả thuyết thích hợp sử dụng α = 0.05 và tính p−value.
b. Cỡ mẫu bao nhiêu sẽ được yêu cầu trong mỗi tổng thể nếu bạn muốn tin tưởng 95% rằng sai
số trong sự khác biệt trong chỉ số octane trung bình nhỏ hơn 1? 76
Chương 9. KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ HAI MẪU
(Đs: z0 = −7.25 < −1.645, 0; 11)
Bài 9.8. Xét kiểm định giả thuyết H0 : µ1 = µ2 với đối thuyết H1 : µ1 , µ2. Với cỡ mẫu n1 = n2 = 15
có x1 = 4.7, x2 = 7.8 và s2 = 4, s2 = 6.25, giả sử σ2 = σ2 và mẫu lấy từ phân phối chuẩn. Sử dụng 1 2 1 2 α = 0.05, tính
a. Kiểm định giả thuyết trên và tìm p−value.
b. Tính độ mạnh của kiểm định trên nếu hai trung bình thực sự khác nhau 3 đơn vị.
c. Giả sử cỡ mẫu bằng nhau, sử dụng cỡ mẫu bao nhiêu để có được β = 0.05 nếu trung bình
khác nhau bằng -2 với α = 0.05.
Bài 9.9. Xét kiểm định giả thuyết H0 : µ1 = µ2 với đối thuyết H1 : µ1 , µ2. Với cỡ mẫu n1 = n2 = 15
có x1 = 6.2, x2 = 7.8 và s2 = 4, s2 = 6.25, giả sử σ2 = σ2 và mẫu lấy từ phân phối chuẩn. Sử dụng 1 2 1 2 α = 0.05, tính
a. Kiểm định giả thuyết trên và tìm p−value.
b. Tính độ mạnh của kiểm định trên nếu µ1 nhỏ hơn µ2 đúng 3 đơn vị.
c. Giả sử cỡ mẫu bằng nhau, sử dụng cỡ mẫu bao nhiêu để có được β = 0.05 nếu µ1 nhỏ hơn µ2
đúng 2.5 đơn vị với α = 0.05.
(Đs: t0 = −1.94 < −1.70, 0.025 < p < 0.05; 0.95; 21)
Bài 9.10. Xét kiểm định giả thuyết H0 : µ1 = µ2 với đối thuyết H1 : µ1 , µ2. Với cỡ mẫu n1 = n2 = 10
có x1 = 7.8, x2 = 5.6 và s2 = 4, s2 = 9, giả sử σ2 = σ2 và mẫu lấy từ phân phối chuẩn. Sử dụng 1 2 1 2 α = 0.05, tính
a. Kiểm định giả thuyết trên và tìm p−value.
b. Tính độ mạnh của kiểm định trên nếu µ1 lớn hơn µ2 đúng 3 đơn vị.
c. Giả sử cỡ mẫu bằng nhau, sử dụng cỡ mẫu bao nhiêu để có được β = 0.05 nếu µ1 lớn hơn µ2
đúng 3 đơn vị với α = 0.05.
Bài 9.11. Đường kính của các thanh thép được sản xuất trên hai máy đúc khác nhau đang được
nghiên cứu. Hai mẫu ngẫu nhiên có cỡ mẫu n1 = 15, n2 = 17 được chọn có trung bình và phương sai
mẫu x1 = 8.73, s2 = 0.35 và x
= 0.40. Giả sử rằng σ2 = σ2 và quan trắc lấy có phân phối 1 2 = 8.68, s2 1 1 2
chuẩn. Có bằng chứng để khẳng định rằng hai máy sản xuất thanh thép có đường kính trung bình khác
nhau? Sử dụng α = 0.05 khi đưa ra kết luận này. Tìm giá trị p. (Đs: −2.042 < t0 = 0.230 < 2.042; p−value>0.80)
Bài 9.12. Hai chất xúc tác có thể được sử dụng trong một phản ứng hóa học hàng loạt. Mười hai lô
được sử dụng chất xúc tác 1, dẫn đến năng suất trung bình là 86 và độ lệch chuẩn mẫu là 3. Mười
lăm lô được sử dụng chất xúc tác 2, và kết quả là năng suất trung bình 89 với độ lệch chuẩn là 2.
Giả sử năng suất các phép đo xấp xỉ thường được phân phối với cùng độ lệch chuẩn. Có bằng chứng
để khẳng định rằng chất xúc tác 2 tạo ra năng suất trung bình cao hơn chất xúc tác 1? Sử dụng
α = 0.01. (Đs: t0 = −3.11 < −2.485)
Định lí 9.2.1 (Kiểm định sự khác nhau hai giá trị trung bình của hai tổng thể phân phối chuẩn
khi phương sai bằng nhau chưa biết)
Ta phát biểu giả thuyết H , 0 : µ1 − µ2 = ∆0 H , 1 : µ1 − µ2 , ∆0
với ∆0 là giá trị đặc biệt mà ta quan tâm. Ta định nghĩa thống kê cho kiểm định có phân phối Student 9.2 Bài tập 77
T0 = X1 − X2 − (µ1 − µ2) ∼ t(n1 + n2 − 2), p Sp 1/n1 + 1/n2
với một ước lượng gộp của σ1 = σ2 = σ là Sp được định nghĩa (n1 − 1)S2 + (n2 − 1)S2 S2 = 1 2 . p n1 + n2 − 2 Kết luận: bác bỏ H > < 0 nếu T0 tα/2,n −tα 1+n2−2 hoặc T0
/2,n1+n2−2 với tα/2,n1+n2−2 thỏa P(|T | >
tα/2,n1+n2−2) = α với T ∼ t(n1 + n2 − 2). Ngược lại thì chấp nhận. Giá trị p − value = 2P(T > |T0|) với T ∼ t(n1 + n2 − 2). Đặc biệt: Nếu H > > , 1 : µ1 − µ2
∆0 thì ta sẽ bác bỏ giả thuyết H0 khi T0 tα,n p − value = 1+n2−2 P(T > T0). i. ii. Nếu H < < , 1 : µ1 − µ2
∆0 thì ta sẽ bác bỏ giả thuyết H0 khi T0 −tα,n p − value = 1+n2−2 P(T < T0).
Bài 9.13. Trong sản xuất chất bán dẫn, khắc hóa chất ướt thường được sử dụng để loại bỏ silic từ
mặt sau của tấm wafer trước khi kim loại hóa. Tỷ lệ etch là một đặc tính quan trọng trong quá trình
này và được biết là tuân theo sự phân bố chuẩn. Hai giải pháp khắc khác nhau đã được so sánh bằng
cách sử dụng hai mẫu ngẫu nhiên gồm 10 tấm mỏng cho mỗi dung dịch. Tỷ lệ etch quan sát được
như sau (trong mils mỗi phút):
Mẫu 1: 9.9 10.6 9.4 10.3 9.3 10.0 9.6 10.3 10.2 10.1
Mẫu 2: 10.2 10.0 10.6 10.2 10.7 10.7 10.4 10.4 10.5 10.3
a. Xây dựng đồ thị xác suất phân phối chuẩn cho hai mẫu. Từ đó rút ra giả thiết hai mẫu có phân
phối chuẩn và cùng phương sai.
b. Dữ liệu có hỗ trợ tuyên bố rằng tỷ lệ etch trung bình là giống nhau cho cả hai giải pháp? Để
đạt được kết luận của bạn, sử dụng α = 0.05 và giả sử rằng cả hai phương sai giống nhau. Tính giá trị p.
(Đs: Assumptions verifed; t0 = −2.83 < −2.101, 0.010 < p < 0.020)
Bài 9.14. Các điểm nóng chảy của hai hợp kim được sử dụng trong công thức hàn được điều tra
bằng cách làm tan chảy 21 mẫu của mỗi vật liệu. Trung bình mẫu và độ lệch chuẩn mẫu của hợp
kim thứ nhất là x1 = 420oF, s1 = 4oF và của hợp kim thứ hai là x1 = 426oF, s1 = 3oF.
a. Dữ liệu mẫu có hỗ trợ cho rằng cả hai hợp kim có cùng điểm nóng chảy không? Sử dụng
α = 0.05 và giả định rằng cả hai tổng thể thường có phân phối chuẩn và có cùng độ lệch
chuẩn. Tìm giá trị p cho kiểm định.
b. Giả sử rằng sự khác biệt trung bình thực sự ở các điểm nóng chảy là 3o F. Cỡ mẫu sẽ được
yêu cầu để phát hiện sự khác biệt này bằng cách sử dụng kiểm định mức α = 0.05 với xác
suất ít nhất là 0.9? Sử dụng σ1 = σ2 = 4 làm ước lượng ban đầu về độ lệch chuẩn chung.
(Đs: -5.498<-2.021, p < 0.001; 38)
Bài 9.15. Một bài viết trong Hội nghị Công nghệ và Linh kiện Điện tử (2001, Vol. 52, pp.
1167–1171) đã so sánh trục đơn so với trục kép trong quy trình sản xuất các tấm kim loại đồng.
Tổng cộng 15 thiết bị của mỗi loại được đo chiều rộng của chipout mặt sau, xs = 66.385, ss = 7.895 và xd = 45.278, ss = 8.612.
a. Dữ liệu mẫu có hỗ trợ khẳng định rằng cả hai quy trình đều có cùng kết quả đầu ra của chip?
Sử dụng α = 0.05 và giả định rằng cả hai tổng thể có phân phối chuẩn cùng phương sai. Tìm
giá trị p cho kiểm định. 78
Chương 9. KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ HAI MẪU
b. Nếu sai số β của sự khác nhau thực sự của trung bình trong các đầu ra của chip là 15 không
được vượt quá 0.1, thì phải sử dụng cỡ mẫu nào? Sử dụng α = 0.05.
(Đs: 7.0>2.056, p ' 0; >8)
Bài 9.16. Một bài báo về Kỹ thuật Radio và Vật lý điện tử [1984, Vol. 29 No.(3), pp. 63-66] đã
nghiên cứu hành vi của một máy phát ngẫu nhiên khi có tiếng ồn bên ngoài. Số chu kỳ được đo
trong một mẫu là 100 lần với hai mức điện áp nhiễu khác nhau, 100 và 150mV . Với 100mV , số chu
kì trung bình là 7.9 với s = 2.6. Với 150 mV, giá trị trung bình là 6.9 với s = 2.4.
Ban đầu, người ta nghi ngờ rằng việc tăng điện áp tiếng ồn sẽ làm giảm số chu kỳ trung bình. Dữ
liệu có hỗ trợ xác nhận này không? Sử dụng α = 0.01 và giả định rằng hai tổng thể có phân phối
chuẩn cùng phương sai. Giá trị p của kiểm định? (Đs: 2.82>2.326, p ' 0.025)
Bài 9.17. Một bài báo về Suy thoái và Ổn định Polymer (2006, Tập 91) trình bày dữ liệu từ một
nghiên cứu chín năm về bọt S537. Các mẫu bọt được nén tới 50% độ dày ban đầu của chúng và
được bảo quản ở các nhiệt độ khác nhau trong chín năm. Khi bắt đầu thử nghiệm cũng như trong
mỗi năm, độ dày mẫu được đo và độ dày của tám mẫu tại từng điều kiện lưu trữ được ghi lại. Dữ
liệu cho hai điều kiện lưu trữ:
50oC: 0.047, 0.060, 0.061, 0.064, 0.080, 0.090, 0.118, 0.165, 0.183
60oC: 0.062, 0.105, 0.118, 0.137, 0.153, 0.197, 0.210, 0.250, 0.375
Có bằng chứng nào để hỗ trợ cho khẳng định rằng trung bình nén có tăng theo nhiệt độ ở điều kiện
bảo quản không? (Đs: -2.349 bác bỏ)
Định lí 9.2.2 (Kiểm định sự khác nhau hai phương sai của hai tổng thể có phân phối chuẩn)
Ta phát biểu giả thuyết H , 0 : σ2 = σ2 1 2 H , 1 : σ2 1 , σ2 2
Ta định nghĩa thống kê cho kiểm định có phân phối Fisher S2 F 1 0 = ∼ F(n1 − 1; n2 − 1). S22 Kết luận: bác bỏ H > < 0 nếu F0 fα/2,n 1/ fα 1−1, n2−1 hoặc F0
/2,n2−1,n1−1 với fα/2,n1−1,n2−1 thỏa
P(F > fα/2,n1−1,n2−1) = α/2 với F ∼ F(n1 − 1; n2 − 1). Ngược lại thì chấp nhận. Đặc biệt: Nếu H > σ2 > 1 : σ2
thì ta sẽ bác bỏ giả thuyết H f 1 2 0 khi F0 α,n1−1,n2−1. i. ii. Nếu H < σ2 < 1 : σ2
thì ta sẽ bác bỏ giả thuyết H 1/ f 1 2 0 khi F0 α,n2−1,n1−1.
Chú ý: phân phối Fisher có tính chất f . 1−α,u,v = 1 fα,v,u
Bài 9.18. Cho phân phối F, hãy tính: a. f0.25,5,10 c. f0.05,8,15 e. f0.90,24,9 b. f0.10,24,9 d. f0.75,5,10 f. f0.99,8,15
(Đs: 1.59, 2.28, 2.64, 0.529, 0.525, 0.311)
Bài 9.19. Cho phân phối F, hãy tính: 9.2 Bài tập 79 a. f0.25,7,15 c. f0.01,20,10 e. f0.90,10,12 b. f0.10,10,12 d. f0.75,7,15 f. f0.99,20,10
Bài 9.20. Cho giả thuyết H < σ2
0 : σ2 = σ2 với đối thuyết H . Cho trước n 1 2 1 : σ2 1 2 1 = 5, n2 = 10 và
s2 = 23.3, s2 = 28.8. Sử dụng mức α = 0.05, hãy kiểm định giả thuyết trên. (Đs: 0.805>0.166 ) 1 2
Bài 9.21. Cho giả thuyết H > σ2
0 : σ2 = σ2 với đối thuyết H . Cho trước n 1 2 1 : σ2 1 2 1 = 20, n2 = 8 và
s2 = 4.5, s2 = 2.3. Sử dụng mức α = 0.01, hãy kiểm định giả thuyết trên. 1 2
Bài 9.22. Cho giả thuyết H0 : σ2 = σ2 với đối thuyết H . Cho trước n 1 2 1 : σ2 1 , σ2 2 1 = 15, n2 = 15 và
s2 = 2.3, s2 = 1.9. Sử dụng mức α = 0.05, hãy kiểm định giả thuyết trên. (Đs: 1.21>0.333) 1 2
Bài 9.23. Hai công ty hóa chất cùng cung cấp một loại nguyên liệu thô. Nồng độ của một nguyên
tố cụ thể trong vật liệu này là quan trọng. Nồng độ trung bình do cả hai nhà cung cấp là như nhau,
nhưng bạn nghi ngờ rằng sự thay đổi về nồng độ có thể khác nhau đối với hai công ty. Độ lệch
chuẩn của nồng độ trong một mẫu ngẫu nhiên có cỡ mẫu n1 = 10 lô được sản xuất bởi công ty
1 là s1 = 4.7 gam/lít và đối với công ty 2, một mẫu ngẫu nhiên có cỡ mẫu n2 = 16 lô sản lượng
s2 = 5.8 gam/lít. Có bằng chứng đủ để kết luận rằng hai phương sai là khác nhau? Sử dụng α = 0.05.
Bài 9.24. Một nghiên cứu được thực hiện để xác định liệu nam giới và nữ giới có khác nhau về độ
lặp lại trong việc lắp ráp các thành phần trên các bảng mạch in hay không. Các mẫu ngẫu nhiên
gồm 25 người đàn ông và 21 phụ nữ đã được chọn, và mỗi người cùng làm các đơn vị công việc
như nhau. Hai độ lệch chuẩn của thời gian lắp ráp là smen = 0.98 phút và swomen = 1.02 phút. Có
bằng chứng nào để ủng hộ tuyên bố rằng đàn ông và phụ nữ khác nhau về tính lặp lại cho nhiệm vụ
lắp ráp này không? Sử dụng α = 0.02 và nêu rõ bất kỳ giả định cần thiết nào về phân phối dữ liệu
cần. (Đs: 0.923>0.365, không bác bỏ H0)
Bài 9.25. Kiểm định giả thuyết H0 : σ2 = σ2 với đối thuyết H
với số liệu từ Bài tập 9.11 1 2 1 : σ2 1 , σ2 2 - 9.17 với mức α = 0.05.
Bài 9.26. Trong cuộc bầu cử tổng thống năm 2004, các cuộc thăm dò ý kiến từ tiểu bang quan
trọng của Ohio đã cung cấp các kết quả sau: những người được hỏi có trình độ đại học, 53% đã bầu
cho Bush và 46% đã bỏ phiếu cho Kerry. Có 2020 người trả lời. Có sự khác biệt đáng kể trong các
tỷ lệ này không? Sử dụng α = 0.05. Giá trị p? (Đs: 4.45 > 1.96, p − value ' 0)
Bài 9.27. Hai loại máy ép phun khác nhau được sử dụng để tạo thành các bộ phận bằng nhựa. Một
phần được coi là khiếm khuyết nếu nó bị co rút quá mức hoặc bị đổi màu. Hai mẫu ngẫu nhiên, mỗi
mẫu có kích thước 300, được chọn, và 15 bộ phận bị lỗi được tìm thấy trong mẫu từ máy 1, và 8 bộ
phận bị lỗi được tìm thấy trong mẫu từ máy 2. Có hợp lý để kết luận rằng cả hai máy sản xuất cùng
một tỉ lệ các bộ phận lỗi, sử dụng α = 0.05? Tìm giá trị p cho kiểm định này.
Bài 9.28. Hai loại giải pháp khác nhau về cách đánh bóng đang được đánh giá để sử dụng trong
một hoạt động đánh bóng sản xuất ống kính interocular được dùng trong mắt người sau phẫu thuật
đục thủy tinh thể. Ba trăm thấu kính đã được đánh bóng bằng cách sử dụng giải pháp đánh bóng
thứ nhất và 253 sản phẩm không có khuyết tật do đánh bóng. 300 ống kính khác được đánh bóng
bằng cách sử dụng cách đánh bóng thứ hai và 196 ống kính đã đạt yêu cầu sau khi hoàn thành. Có
lý do nào để tin rằng hai giải pháp đánh bóng khác nhau không? Sử dụng α = 0.05. Giá trị p cho
kiểm định này là bao nhiêu? (Đs: 5.36 > 2.58, p ' 0)
Định lí 9.2.3 (Kiểm định sự khác nhau tỉ lệ của hai tổng thể có phân phối nhị thức)
Ta phát biểu giả thuyết H , 0 : p1 = p2 H , 1 : p1 , p2 80
Chương 9. KIỂM ĐỊNH GIẢ THUYẾT THỐNG KÊ HAI MẪU
Ta định nghĩa thống kê cho kiểm định có phân phối chuẩn Z0 = f1 − f2 ∼ N(0; 1), p f (1 − f )(1/n1 + 1/n2)
với ước lượng trung bình gộp f = ( f1n1 + f2n2)/(n1 + n2). Ta có kết luận giống mục 9.1.1.
Bài 9.29. Một mẫu ngẫu nhiên 500 cư dân trưởng thành của Quận Maricopa chỉ ra rằng 385 ủng
hộ việc tăng giới hạn tốc độ đường cao tốc lên 75 dặm một giờ, và một mẫu khác gồm 400 cư dân
trưởng thành của Hạt Pima đã chỉ ra rằng 267 đã ủng hộ giới hạn tốc độ tăng lên. Những dữ liệu
này cho thấy có sự khác biệt trong việc hỗ trợ tăng giới hạn tốc độ cho cư dân của hai quận? Sử
dụng α = 0.05. Giá trị p cho kiểm định này là bao nhiêu?
Bài 9.30. Ô nhiễm không khí có liên quan đến việc giảm cân ở trẻ sơ sinh. Trong một nghiên cứu
được công bố trên Tạp chí của Hiệp hội Y khoa Hoa Kỳ, các nhà nghiên cứu đã kiểm tra tỷ lệ trẻ sơ
sinh nhẹ cân được sinh ra từ các bà mẹ tiếp xúc với liều lượng bồ hóng và tro nặng trong vụ tấn
công của Trung tâm Thương mại Thế giới ngày 11/9/2001. Có 182 đứa bè sinh ra từ những bà mẹ
này, 15 đứa được xếp loại có trọng lượng thấp. Trong số 2300 trẻ sinh ra trong cùng một khoảng
thời gian ở New York ở một bệnh viện khác, 92 đứa được phân loại là có trọng lượng thấp. Có bằng
chứng cho thấy rằng các bà mẹ tiếp xúc ô nhiễm có tỷ lệ trẻ sơ sinh nhẹ cân cao hơn không? (Đs: z0 = 2.712, p = 0.003)
Bài 9.31. Tạp chí Y học New England đã báo cáo một thử nghiệm để đánh giá hiệu quả của phẫu
thuật trên những người đàn ông được chẩn đoán mắc bệnh ung thư tuyến tiền liệt. Một nửa số mẫu
ngẫu nhiên của 695 (là 347) nam giới trong nghiên cứu đã phẫu thuật và 18 người trong số họ cuối
cùng đã chết vì ung thư tuyến tiền liệt so với 31 trong số 348 người không phẫu thuật. Có bằng
chứng nào cho thấy rằng phẫu thuật giảm tỷ lệ những người chết vì ung thư tuyến tiền liệt? 9.2 Bài tập 81 83 10. HỒI QUY – TƯƠNG QUAN 10.1 Lý thuyết 10.1.1 Mô hình và ước lượng
Mô hình hồi quy tuyến tính đơn giản xem xét một biến hồi qui đơn (hoặc biến dự đoán) x và
biến phụ thuộc (hoặc biến đáp ứng) Y . Giả sử rằng mối quan hệ thực sự giữa Y và x là một đường
thẳng và quan trắc Y tại mỗi giá trị của x là một biến ngẫu nhiên thỏa E(Y | x) = β0 + β1 x,
với tung độ gốc β0 và hệ số góc β1 là những hệ số hồi quy chưa biết. Giả sử những giá trị quan trắc
Y được biểu diễn thông qua mô hình Y = β0 + β1x + , (10.1)
với sai số ngẫu nhiên có trung bình 0 và phương sai (không biết) σ2. Sai số của mỗi quan trắc Y
khác nhau được giả sử là những biến ngẫu nhiên không tương quan.
Giả sử ta có n cặp quan trắc (x , , ,
1 y1), (x2 y2), . . . , (xn yn) như hình vẽ và mô hình y , i = β0 + β1 xi + i i = 1, 2, . . ., n. 84
Chương 10. HỒI QUY – TƯƠNG QUAN
Ta định nghĩa hàm tổng bình phương sai số giữa giá trị quan trắc và đường thẳng hồi quy đúng là n n Õ Õ L = 2 = (y i i − β0 − β1 xi )2 . i=1 i=1
Tìm cực tiểu sai số bằng đạo hàm riêng ∂ n L = Õ − ( ∂ β 2 yi − β0 − β1 xi) = 0, 0 i=1 ∂ n L = Õ − ( ∂ β 2 yi − β0 − β1 xi) xi = 0. 1 i=1
Giải hệ ta được kết quả sau
Định lí 10.1.1 Ước lượng bình phương cực tiểu của tung độ gốc và hệ số góc của mô hình hồi quy là ˆ β0 = y − ˆβ1x, Ín y y Ín x S ˆ β i=1 i xi − n−1 Ín i=1 i i=1 i xy , 1 = := Ín x2 − n−1 Ín x 2 Sxx i=1 i i=1 i với x = n−1 Ín x y i=1 i và y = n−1 Ín i=1 i. 10.1.2 Tính chất thống kê
Từ Định lý 10.1.1 trên, ước lượng cho đường thẳng hồi quy có dạng ˆy = ˆβ0 + ˆβ1x.
Chú ý rằng tại những điểm quan trắc ta có biểu thức liên hệ: y , i = ˆ β0 + ˆβ1xi + ei
với ei = yi − ˆyi được gọi là thặng dư (hay phần dư), đại lượng biểu diễn cho sai số giữa mô hình ước
lượng và giá trị quan trắc. Sử dụng khái niệm này, ta có thể xây dựng một ước lượng cho phương sai
của sai số trong mô hình hồi quy (10.1).
Định lí 10.1.2 Ước lượng không chệch của phương sai trong mô hình (10.1) là ˆ σ2 = SSE , n − 2 với SSE = Ín e2 = Ín (y i=1 i i=1 i − ˆ yi)2.
Mệnh đề 10.1.3 Trong mô hình hồi quy tuyến tính, ước lượng cho độ lệch chuẩn cho hệ số góc và
tung độ gốc lần lượt là s v u t ! ˆ σ2 1 se ˆ β ˆ β , 1 = và se 0 = ˆσ2 + x2 Sxx n Sxx với ˆ
σ2 như trong Định lý 10.1.2 và Sxx như trong Định lý 10.1.1. 10.1 Lý thuyết 85 10.1.3
Kiểm định giả thuyết trong hồi quy tuyến tính
Xét bài toán kiểm định hệ số góc của mô hình hồi quy tuyến tính có bằng hằng số β1,0 hay
không? Khi đó, ta phát biểu giả thuyết H , 0 : β1 = β1,0 H , 1 : β1 , β1,0
với β1,0 là giá trị tham số đặc biệt mà ta quan tâm. Ta định nghĩa thống kê cho kiểm định ˆ β1 − β1,0 T0 = ∼ t(n − 2). se ˆ β1
Kết luận: bác bỏ H0 nếu |T0| > tα/2,n−2. Ngược lại thì chấp nhận.
Tương tự cho bài toán kiểm định tung độ gốc H , 0 : β0 = β0,0 H , 1 : β0 , β0,0
với β0,0 là giá trị tham số đặc biệt mà ta quan tâm. Ta định nghĩa thống kê cho kiểm định ˆ β0 − β0,0 T0 = ∼ t(n − 2). se ˆ β0
Kết luận: bác bỏ H0 nếu |T0| > tα/2,n−2. Ngược lại thì chấp nhận. 10.1.4 Khoảng tin cậy
Định lí 10.1.4 Giả sử quan trắc có phân phối chuẩn và độc lập nhau. Khi đó, ta có khoảng tin
cậy 100(1 − α)% cho hệ số góc và tung độ gốc lần lượt là ˆ β ˆ β ˆ β , 1 − tα/2,n−2 se 1 ≤ β1 ≤ ˆ β1 + tα/2,n−2se 1 ˆ β ˆ β ˆ β . 0 − tα/2,n−2 se 0 ≤ β0 ≤ ˆ β0 + tα/2,n−2se 0 10.1.5
Tiên đoán giá trị quan trắc mới
Nếu x0 là giá trị cần tiên đoán trong mô hình hồi quy 10.1, ta có ˆ Y , 0 = ˆ β0 + ˆβ1x0
là một ước lượng cho giá trị đáp ứng tương lai.
Định lí 10.1.5 Khoảng tin cậy 100(1 − α)% cho tiên đoán giá trị đáp ứng Y0 tương lai tại x0 được tính bằng s (x 0 − x)2 ˆy0 − tα/2,n−2 ˆ σ2 1 + 1 + n Sxx s (x ≤ 0 − x)2 Y , 0 ≤ ˆ y0 + tα/2,n−2 ˆ σ2 1 + 1 + n Sxx
với ˆy0 được tính từ ước lượng của mô hình hồi quy ˆy0 = ˆβ0 + ˆβ1x0. 86
Chương 10. HỒI QUY – TƯƠNG QUAN 10.2 Bài tập
Bài 10.1. Bệnh tiểu đường và béo phì là những vấn đề sức khỏe nghiêm trọng ở Hoa Kỳ và phần
lớn các nước phát triển. Đo lượng mỡ cơ thể của một người là một cách để theo dõi tiến độ kiểm
soát cân nặng, nhưng đo chính xác nó phải sử dụng đến thiết bị X-quang đắt tiền hoặc nhúng cơ thể
xuống một hồ bơi. Thay vào đó, chỉ số khối cơ thể (BMI) thường được sử dụng làm đại diện cho
mỡ cơ thể vì nó dễ đo: BMI = khối lượng (kg) / (chiều cao (m))2 = 703 khối lượng (lb) / (chiều cao
(in))2. Trong một nghiên cứu của 250 người đàn ông tại Đại học Bingham Young, cả BMI và mỡ cơ
thể được đo lường. Các nhà nghiên cứu đã tìm thấy các thống kê tóm tắt sau: n n n n n Õ Õ Õ Õ Õ xi = 6322.28, x2 = 162674.18, y y2 = 107679.27, x i i = 4757.90, i i yi = 125471.10 i=1 i=1 i=1 i=1 i=1
a. Tính những ước lượng bình phương tối thiểu cho hệ số góc và tung độ góc. Vẽ đồ thị của đường thẳng hồi quy.
b. Sử dụng đường thẳng hồi quy, hãy tiên đoán lượng mỡ cơ thể của một người đàn ông sẽ được
quan trắc nếu có chỉ số BMI là 30?
c. Giả sử rằng người ta quan trắc lượng mỡ cơ thể của một người đàn ông có chỉ số BMI 25 là
25%. Tìm thặng dư của quan trắc này?
d. Ước lượng tiên đoán của câu c) so với số liệu quan trắc là ước lượng thiếu hay ước lượng thừa. Giải thích?
Bài 10.2. Một bài báo trong Nghiên cứu Bê tông “Đặc tính bề mặt gần bê tông: Tính thấm nội tại”
(1989, Tập 41) trình bày dữ liệu về cường độ nén x và độ thấm nội tại y của các hỗn hợp bê tông và
phương pháp xử lý khác nhau. Số liệu được tóm tắt như sau: Õ Õ Õ Õ Õ n = 14; yi = 572; y2 = 23530; x x2 = 157.42; x i i = 43; i i yi = 1697.80.
a. Tính những ước lượng bình phương tối thiểu cho hệ số góc và tung độ góc. Ước lượng σ2. Vẽ
đồ thị của đường thẳng hồi quy.
b. Sử dụng đường thẳng hồi quy, hãy tiên đoán lượng độ thấm nội sẽ quan trắc được khi cường độ nén là x = 4.3?
c. Giả sử rằng giá trị quan trắc độ thấm nội tại x = 3.7 là y = 46.1. Tính toán thằng dư tương ứng.
Bài 10.3. Các phương pháp hồi quy đã được sử dụng để phân tích dữ liệu từ một nghiên cứu điều
tra mối quan hệ giữa nhiệt độ bề mặt đường (x) và độ lún mặt đường (y). Số liệu được tóm tắt như sau: Õ Õ Õ Õ Õ n = 20; yi = 12.75; y2 = 8.86; x x2 = 143215.8; x i i = 1478; i i yi = 1083.67.
a. Tính những ước lượng bình phương tối thiểu cho hệ số góc và tung độ góc. Ước lượng σ2. Vẽ
đồ thị của đường thẳng hồi quy.
b. Sử dụng đường thẳng hồi quy, hãy tiên đoán lượng độ lún mặt đường sẽ quan trắc được khi
nhiệt độ bề mặt đường là 850F?
Bài 10.4. Xem bảng sau để biết dữ liệu về xếp hạng cầu thủ ném bóng cà na trong mùa giải bóng
quốc gia 2008 (The Sports Network). Người ta nghi ngờ rằng tốc độ (y) có liên quan đến số lượng
trung bình đạt được cho mỗi lần bóng bay (x) 10.2 Bài tập 87
a. Tính những ước lượng bình phương tối thiểu cho hệ số góc và tung độ góc. Ước lượng σ2. Vẽ
đồ thị của đường thẳng hồi quy.
b. Cho x = 7.21 yards, tính giá trị hồi quy và thặng dư tương ứng.
Bài 10.5. Một động cơ tên lửa được sản xuất bằng cách liên kết với nhau hai thành phần: một bộ
đánh lửa và một máy phát điện. Độ bền cắt của liên kết y được cho là một hàm tuyến tính của tuổi
động cơ đẩy x khi động cơ được đúc. Bảng số liệu 20 quan trắc như sau:
a. Vẽ một sơ đồ phân tán dữ liệu. Mô hình hồi quy tuyến tính có hợp lý không?
b. Tính những ước lượng bình phương tối thiểu cho hệ số góc và tung độ góc. Ước lượng σ2. Vẽ
đồ thị của đường thẳng hồi quy.
Bài 10.6. Sử dụng lại số liệu từ Bài tập 10.1. Tính
a. Ước lượng sai số độ lệch chuẩn.
b. Ước lượng độ lệch chuẩn của hệ số góc.
c. Tìm giá trị thống kê t của hệ số góc.
d. Hãy kiểm định giả thuyết β1 = 0 khi α = 0.05. Tìm p-value?
Bài 10.7. Sử dụng lại số liệu từ Bài tập 10.5.
a. Ước lượng sai số chuẩn cho ˆ β0 và ˆβ1.
b. Kiểm định giả thuyết H0 : β1 = −30 với đối thuyết H1 : β1 , −30 sử dụng α = 0.01. Tính p-value?
c. Kiểm định giả thuyết H0 : β0 = 0 với đối thuyết H1 : β0 , 0 sử dụng α = 0.01. Tính p-value?
d. Kiểm định giả thuyết H >
0 : β0 = 2500 với đối thuyết H1 : β0
2500 sử dụng α = 0.01. Tính p-value?
Bài 10.8. Sử dụng lại số liệu từ Bài tập 10.1. Tính 88
Chương 10. HỒI QUY – TƯƠNG QUAN
a. Khoảng tin cậy 95% của hệ số góc.
b. Khoảng tin cậy 95% cho trung bình phần trăm mỡ cơ thể của một người đàn ông có chỉ số BMI là 25.
c. Khoảng tiên đoán 95% cho phần trăm mỡ cơ thể của một người đàn ông có chỉ số BMI là 25.
Bài 10.9. Sử dụng lại số liệu từ Bài tập 10.5.
a. Khoảng tin cậy 95% cho: hệ số góc và tung độ góc.
b. Trung bình độ thấm nội khi x = 2.5.
c. Khoảng tiên đoán 95% cho độ thấm nội khi x = 2.5. III PhầnBa:ĐềThiMẫu 11
ĐỀ THI GIỮA KÌ . . . . . . . . . . . . . . . . . . . . . . . 91 11.1 Đề 2 giữa kì 2018-2019 11.2 Đề 1 giữa kì 2018-2019 11.3 Đề 2 giữa kì 2018-2019 11.4 Đề 1 giữa kì 2017-2018 11.5 Đề 2 giữa kì 2017-2018 11.6 Đề giữa kì 2016-2017 11.7 Đề giữa kì 2015-2016 12
ĐỀ THI CUỐI KÌ . . . . . . . . . . . . . . . . . . . . . . . 99 12.1
Đề 1 cuối kì I năm 2018-2019 12.2
Đề 2 cuối kì I năm 2018-2019 12.3 Đề 1 cuối kì 2017-2018 12.4 Đề 2 cuối kì 2017-2018 12.5 Đề 3 cuối kì 2017-2018 12.6
Đề cuối kì 2017-2018 học kì hè 91 11. ĐỀ THI GIỮA KÌ 11.1 Đề 2 giữa kì 2018-2019
Bài 11.1. Một nghiên cứu về sức khỏe đã theo dõi một nhóm người trong 5 năm. Trong đó có 20%
được xem là người nghiện thuốc lá nặng, 30% là người nghiện thuốc lá nhẹ và 50% không hút
thuốc. Kết quả nghiên cứu cho thấy xác suất tử vong trong 5 năm nghiên cứu ở những người nghiện
thuốc lá nặng, nhẹ và không hút thuốc lần lượt là 0.5; 0.3 và 0.2. Một người tham gia được chọn
ngẫu nhiên từ nghiên cứu.
a. Tính xác suất người này tử vong trong thời gian 5 năm nghiên cứu.
b. Biết rằng người này đã tử vong trong thời gian 5 năm nghiên cứu. Tính xác suất người này nghiện thuốc lá nặng 11.2 Đề 1 giữa kì 2018-2019
Bài 11.2. Một nhà máy có ba loại máy sản xuất một linh kiện. Các xác suất để linh kiện đạt chuẩn
nếu nó được sản xuất bởi máy i được cho trong bảng sau: Máy loại
Xác suất linh kiện đạt chuẩn 1 0.94 2 0.95 3 0.97
Tổng sản lượng được phân phối giữa các máy như sau: 30% được làm bởi các máy loại 1, 50%
bởi loại 2, 20% bởi loại 3. Một linh kiện được chọn ngẫu nhiên từ nhà máy.
a. Hỏi xác suất để nó đạt chuẩn là bao nhiêu?
b. Nếu nó đạt chuẩn, hỏi xác suất để nó được sản xuất bởi máy loại 1 là bao nhiêu?
Bài 11.3. Giả sử rằng thời gian cần thiết để một sinh viên hoàn thành một bài kiểm tra giữa kì môn
XSTK có phân phối chuẩn với trung bình là 40 phút, và độ lệch chuẩn 10 phút. Biết rằng thời gian
làm bài được quy định là 60 phút. Một sinh viên được chọn ngẫu nhiên. Tính xác suất để: 92
Chương 11. ĐỀ THI GIỮA KÌ
a. thời gian làm bài của người ấy không quá 50 phút.
b. người này không hoàn thành bài kiểm tra trong thời gian quy định.
c. lấy ngẫu nhiên 10 sinh viên thì có không quá hai sinh viên không hoàn thành bài kiểm tra trong thời gian quy định. 11.3 Đề 2 giữa kì 2018-2019
Bài 11.4. Một nhà sản xuất máy quay kỹ thuật số sử dụng một vi mạch cho mỗi máy quay mà nó
sản xuất. Các vi mạch được mua từ các nhà cung cấp A, B và C và được chọn ngẫu nhiên để lắp ráp
cho mỗi máy quay. Hai mươi phần trăm số vi mạch đến từ A, 35% đến từ B, và còn lại đến từ C.
Dựa trên kinh nghiệm trong quá khứ, nhà sản xuất tin rằng xác suất mà một vi mạch từ A bị lỗi là
0.03, và xác suất tương ứng với B và C là 0.02 và 0.01. Một máy quay được chọn ngẫu nhiên từ một ngày sản xuất.
a. Tìm xác suất để vi mạch của nó bị lỗi.
b. Nếu vi mạch của nó được phát hiện bị lỗi. Tìm xác suất nó được cung cấp từ A.
Bài 11.5. Giả sử rằng thời gian cần thiết để một sinh viên hoàn thành một bài kiểm tra giữa kì môn
XSTK có phân phối chuẩn với trung bình là 45 phút, và độ lệch chuẩn 10 phút. Biết rằng thời gian
làm bài được quy định là 60 phút. Một sinh viên được chọn ngẫu nhiên. Tính xác suất để:
a. thời gian làm bài của người ấy không quá 40 phút.
b. người này không hoàn thành bài kiểm tra trong thời gian quy định.
c. lấy ngẫu nhiên 10 sinh viên thì có không quá hai sinh viên không hoàn thành bài kiểm tra trong thời gian quy định. 11.4 Đề 1 giữa kì 2017-2018
Bài 11.6. Ba máy tự động sản xuất cùng một loại chi tiết, trong đó máy I sản xuất 20%, máy II
sản xuất 30% và máy III sản xuất 50% tổng sản lượng. Tỷ lệ phế phẩm của các máy lần lượt là
3%;2%;1%. Tìm xác suất để khi chọn ngẫu nhiên ra 1 sản phẩm từ kho thì
a. được chi tiết phế phẩm.
b. chi tiết phế phẩm đó do máy II sản xuất.
Bài 11.7. Tuổi thọ của một loài côn trùng (đv: tháng) là biến ngẫu nhiên có hàm mật độ xác suất
k(4x − 2x2) nếu x ∈ [0, 2] f (x) = 0 nếu x < [0, 6]
a. Tính tuổi thọ trung bình của loài côn trùng trên.
b. Tính tỷ lệ côn trùng có tuổi thọ dưới 1 tháng tuổi. 11.5 Đề 2 giữa kì 2017-2018
Bài 11.8. Một nhà máy có hai phân xưởng. Sản phẩm của phân xưởng II gấp đôi sản phẩm của
phân xưởng I. Tỷ lệ hàng kém chất lượng của hai phân xưởng lần lượt là 10% và 15%. Chọn ngẫu
nhiên một sản phẩm của nhà máy
a. Tính tỷ lệ sản phẩm kém chất lượng của nhà máy.
b. Giả sử chọn được sản phẩm tốt. Tính xác suất sản phẩm này do phân xưởng I làm ra.
Bài 11.9. Giả sử lượng xăng bán ra trong một tuần lễ tại một cây xăng là biến ngẫu nhiên có hàm
mật độ xác suất (đv: 1000 m3)
C(1 − x)2 nếu 0 < x < 1 f (x) = 0 chỗ khác
11.6 Đề giữa kì 2016-2017 93
a. Lượng xăng trung bình bán ra trong một tuần là bao nhiêu?
b. Tính xác suất để lượng xăng bán ra trong một tuần lễ ít hơn 500 m3. 11.6 Đề giữa kì 2016-2017
Bài 11.10. Cho A và B là hai biến cố ngẫu nhiên, B ⊂ A. Điều nào sau đây không đúng A. P(A) = P(BA) + P(A ¯ B)
C. P(A + B) = P(B) + P(A) B. P(A) = P(B) + P(A ¯ B) D. P(A) ≥ P(B)
Bài 11.11. Một tháp điện thoại di động có vùng phủ sóng trong vòng bán kính 10km. Nếu một
cuộc gọi được bắt đầu từ một điểm ngẫu nhiên trong vùng phủ sóng, tìm xác suất mà các cuộc gọi
đến từ bên trong vòng 2km của tháp. A. 0.2 B. 0.1 C. 0.02 D. 0.04
Bài 11.12. Phân tích sự phù hợp với các thông số kỹ thuật của các trục cho máy nén được tóm tắt trong bảng sau Độ tròn phù hợp Độ tròn không phù hợp
Bề mặt hoàn thành phù hợp 345 5
Bề mặt hoàn thành không phù hợp 12 8
Nếu chọn ngẫu nhiên một trục, tính xác suất trục đó có thông số về bề mặt hoàn thành phù hợp với
yêu cầu hoặc trục đó không phù hợp với yêu cầu về thông số độ tròn? A. 362 B. 353 C. 358 D. 348 370 370 370 370
Bài 11.13. Một lô hàng có 500 thùng nước cam, trong đó có 5 thùng bị lỗi. Chọn ngẫu nhiên không
hoàn lại ba thùng. Tính xác suất thùng nước cam lấy ra ở lần thứ 3 bị lỗi nếu thùng nước cam lấy ra
ở lần thứ nhất là thùng bị lỗi và lấy ra ở lần thứ hai là thùng nước không bị lỗi. A. 8 × 10−3 B. 8 × 10−5 C. 0.98 D. 0.992
Bài 11.14. Các cuộc gọi đến Trung tâm dịch vụ khách hàng được phân loại là khiếu nại (75% của
cuộc gọi) hoặc yêu cầu thông tin (25% cuộc gọi). Các khiếu nại, 40% đối phó với các thiết bị máy
tính không đáp ứng và 57% đối phó với cài đặt phần mềm không đầy đủ; và trong 3% còn lại khiếu
nại của người sử dụng đã không đúng theo hướng dẫn cài đặt. yêu cầu đối với thông tin được chia ra
đồng đều trên các câu hỏi kỹ thuật (50%) và các yêu cầu để mua các sản phẩm (50%). Xác suất mà
các cuộc gọi đến Trung tâm dịch vụ khách hàng sẽ từ một khách hàng người đã không theo hướng
dẫn cài đặt đúng cách là A. 0.225 B. 0.4 C. 0.04 D. 0.0225
Từ câu 11.15 – 11.16 sử dụng đề bài sau: Giả sử tỷ lệ sản phẩm bị lỗi tùy thuộc vào mức độ ô
nhiễm trong sản suất: 10% nếu mức độ ô nhiễm cao; 1% nếu mức độ ô nhiễm trung bình; 0.1% nếu
mức độ ô nhiễm thấp. Trong sản suất, 20% các con chip chịu mức độ ô nhiễm cao, 30% các con
chip chịu mức độ ô nhiễm trung bình, 50% các con chip chịu mức độ ô nhiễm thấp.
Bài 11.15. Chọn ngẫu nhiên một con chip, tính xác suất con chip đó là sản phẩm không bị lỗi? 94
Chương 11. ĐỀ THI GIỮA KÌ A. 0.0225 B. 0.9765 C. 0.111 D. 0.889
Bài 11.16. Nếu con chip được chọn là sản phâm không bị lỗi, tính xác suất con chip đó là sản phẩm
chịu ô nhiễm mức độ trung bình. A. 0.1333 B. 0.334 C. 0.027 D. 0.3041
Bài 11.17. Ba người đi săn mỗi người bắn 1 phát đạn vào con mồi. Gọi A , , 1 A2 A3 lần lượt là các
biến cố người thứ 1, thứ 2, thứ 3, bắn trúng mồi. Gọi A là biến cố con mồi trúng đạn, B là biến cố
con mồi chỉ trúng một viên đạn. Điều nào sau đây không đúng A. B = A ¯ ¯ ¯ ¯ 1 A2 A3 + ¯ A1 A2 A3 + ¯ A1 A2 A3 B. ¯ A= ¯ A ¯ ¯ 1 A2 A3 C. A = A1 + A2 + A3 D. ¯ A = ¯ A1 A2 A3
Bài 11.18. Tung một con xúc xắc hai lần. Tính xác suất cả hai lần tung đều được mặt sáu chấm biết
rằng lần tung thứ nhất được mặt một chấm. A. 1 B. 5 C. 1 D. 5 6 6 36 36
Bài 11.19. Có hai hộp đựng các viên bi. Hộp thứ nhất gồm 15 viên bi, trong đó có 3 viên bi trắng
và 12 viên bi xanh. Hộp thứ 2 gồm 20 viên bi, trong đó có 4 viên bi trắng và 16 viên bi xanh. Chọn
ngẫu nhiên một viên bi từ hộp 1 bỏ sang hộp 2. Sau đó chọn ngẫu nhiên một viên bi từ hộp hai .
Tính xác suất viên bi lấy ra từ hộp 2 là viên bi trắng từ hộp 2 ban đầu. A. 0.95 B. 0.86 C. 0.76 D. 1.00 11.7 Đề giữa kì 2015-2016
Bài 11.20. Cho X số sản phẩm bị hỏng trong một dây chuyền sản xuất. Kiểm tra một lô hàng biết
rằng X có phân phối nhị thức với kì vọng bằng bằng 240 và phương sai 48. Số lần kiểm tra ngẫu
nhiên độc lập các sản phẩm và xác suất một sản phẩm bị hỏng lần lượt bằng: A. 192; 0.2 B. 300; 0.8 C. 192; 0.8 D. 300; 0.2
Từ câu 11.21–11.22 sử dụng đề bài sau: Một cuốn sách có 500 trang, trong đó trung bình có
một lỗi in sai trong một trang.
Bài 11.21. Xác suất để một trang chứa ít nhất một lỗi in sai là: A. 0.6321 B. 0.7358 C. 0.2642 D. 0.3679
Bài 11.22. Xác suất ít nhất 3 trang chứa ít nhất một lỗi in sai là: A. 1.0000 B. 0.4232 C. 0.9921 D. 0.5768
Bài 11.23. Tuổi thọ của một thiết bị điện tử có phân phối mũ với trung bình 25 năm. Nếu ba thiết
bị được chọn ngẫu nhiên, vận hành độc lập cùng trong một khoảng thời gian, xác suất ít nhất 2 sẽ vận hành sau 35 năm là: A. 0.2466 B. 0.7534 C. 0.1524 D. 0.8476
Bài 11.24. Giả sử phân phối nhiệt độ T (đơn vị: oF) của một bình ga là chuẩn với kì vọng µ = 400
và phương sai là 1600. P(|T − µ| ≤ 20|T ≥ 300) là:
11.7 Đề giữa kì 2015-2016 95 A. 0.3830 B. 0.9938 C. 0.6170 D. 0.3854
Bài 11.25. Vì sẽ hiệu quả kinh tế hơn khi giới hạn độ dài các cuộc điện thoại trong ba phút hoặc ít
hơn ba phút nên ta có hàm phân phối xác suất của độ dài các cuộc điện thoại X (đơn vị phút) có dạng: 0, x < 0; F(x) = 1 − e−x/3, 0 ≤ x < 3; 1 − e−x/3 , x ≥ 3. 2
Xác suất X nằm trong khoảng từ hai đến sáu phút là: A. 0.4866 B. 0.4457 C. 0.5134 D. 0.9323
Từ câu 11.26–11.27 sử dụng đề bài sau: Một biến ngẫu nhiên X với hàm mật độ xác suất
f (x) = cx + d với 0 ≤ x ≤ 1 và bằng 0 với các trường hợp khác. Giả sử rằng, P(X > 1 ) = 1 2 3
Bài 11.26. Xác định c, d. A. −4, 5 B. 4, 1 C. 1, 4 D. 5, −4 3 3 3 3 3 3 3 3
Bài 11.27. Tính kỳ vọng và độ lệch tiêu chuẩn của X √ A. 11, 2 B. 7 , 23 , 23 D. 11, 4 18 3 18 324 C. 7 18 18 18 9
Bài 11.28. Cho X là biến ngẫu nhiên có E(X) = 100 và V ar(X) = 15. Tính E(X2);V ar(−3X + 50)? A. 10015; 135 B. 9985; 5 C. 10015; 95 D. 9985; 185
Bài 11.29. Một vòng quay số gồm 18 rãnh đen, 18 rãnh đỏ và 2 rãnh xanh, mỗi lần quay sẽ dừng
lại 1 rãnh. Người chơi chỉ cược 10 USD vào rãnh đỏ, nếu thắngsẽ được số tiền cược, nếu thua sẽ
mất số tiền đó, về trung bình người chơi sẽ thắng hay thua? A. Không thể kết luận. C. Người đó thắng. B. Người đó thua. D. Người đó sẽ hòa.
Bài 11.30. Cho A và B là hai biến cố ngẫu nhiên, B ⊂ A. Điều nào sau đây không đúng: A. P(A) = P(BA) + P(A ¯ B)
C. P(A + B) = P(B) + P(A) B. P(A) = P(B) + P(A ¯ B) D. P(A) ≥ P(B)
Bài 11.31. Một tháp điện thoại di động có vùng phủ sóng trong vòng bán kính 10km. Nếu một
cuộc gọi được bắt đầu từ một điểm ngẫu nhiên trong vùng phủ sóng, tìm xác suất mà các cuộc gọi
đến từ bên trong vòng 2km của tháp. A. 0.2 B. 0.1 C. 0.02 D. 0.04
Bài 11.32. Phân tích sự phù hợp với các thông số kỹ thuật của các trục cho máy nén được tóm tắt trong bảng sau Độ tròn phù hợp Độ tròn không phù hợp
Bề mặt hoàn thành phù hợp 345 5
Bề mặt hoàn thành không phù hợp 12 8
Nếu chọn ngẫu nhiên một trục, tính xác suất trục đó có thông số về bề mặt hoàn thành phù hợp với
yêu cầu hoặc trục đó không phù hợp với yêu cầu về thông số độ tròn? 96
Chương 11. ĐỀ THI GIỮA KÌ A. 362 B. 353 C. 358 D. 348 370 370 370 370
Bài 11.33. Một lô hàng có 500 thùng nước cam, trong đó có 5 thùng bị lỗi. Chọn ngẫu nhiên không
hoàn lại ba thùng. Tính xác suất thùng nước cam lấy ra ở lần thứ 3 bị lỗi nếu thùng nước cam lấy ra
ở lần thứ nhất là thùng bị lỗi và lấy ra ở lần thứ hai là thùng nước không bị lỗi. A. 8 × 10−3 B. 8 × 10−5 C. 0.98 D. 0.992
Bài 11.34. Các cuộc gọi đến Trung tâm dịch vụ khách hàng được phân loại là khiếu nại (75% của
cuộc gọi) hoặc yêu cầu thông tin (25% cuộc gọi). Các khiếu nại, 40% đối phó với các thiết bị máy
tính không đáp ứng và 57% đối phó với cài đặt phần mềm không đầy đủ; và trong 3% còn lại khiếu
nại của người sử dụng đã không đúng theo hướng dẫn cài đặt. yêu cầu đối với thông tin được chia ra
đồng đều trên các câu hỏi kỹ thuật (50%) và các yêu cầu để mua các sản phẩm (50%). Xác suất mà
các cuộc gọi đến Trung tâm dịch vụ khách hàng sẽ từ một khách hàng người đã không theo hướng
dẫn cài đặt đúng cách là A. 0.225 B. 0.4 C. 0.04 D. 0.0225
Từ câu 11.35–11.36 sử dụng đề bài sau: Giả sử tỷ lệ sản phẩm bị lỗi tùy thuộc vào mức độ ô
nhiễm trong sản suất: 10% nếu mức độ ô nhiễm cao; 1% nếu mức độ ô nhiễm trung bình; 0.1% nếu
mức độ ô nhiễm thấp. Trong sản suất, 20% các con chip chịu mức độ ô nhiễm cao, 30% các con
chip chịu mức độ ô nhiễm trung bình, 50% các con chip chịu mức độ ô nhiễm thấp.
Bài 11.35. Chọn ngẫu nhiên một con chip, tính xác suất con chip đó là sản phẩm không bị lỗi? A. 0.0225 B. 0.9765 C. 0.111 D. 0.889
Bài 11.36. Nếu con chip được chọn là sản phâm không bị lỗi, tính xác suất con chip đó là sản phẩm
chịu ô nhiễm mức độ trung bình. A. 0.1333 B. 0.334 C. 0.027 D. 0.3041
Bài 11.37. Ba người đi săn mỗi người bắn 1 phát đạn vào con mồi. Gọi A , , 1 A2 A3 lần lượt là các
biến cố người thứ 1, thứ 2, thứ 3, bắn trúng mồi. Gọi A là biến cố con mồi trúng đạn, B là biến cố
con mồi chỉ trúng một viên đạn. Điều nào sau đây không đúng A. B = A ¯ ¯ ¯ ¯ 1 A2 A3 + ¯ A1 A2 A3 + ¯ A1 A2 A3 B. ¯ A= ¯ A ¯ ¯ 1 A2 A3 C. A = A1 + A2 + A3 D. ¯ A = ¯ A1 A2 A3
Bài 11.38. Tung một con xúc xắc hai lần. Tính xác suất cả hai lần tung đều được mặt sáu chấm biết
rằng lần tung thứ nhất được mặt một chấm. A. 1 B. 5 C. 1 D. 5 6 6 36 36
Bài 11.39. Có hai hộp đựng các viên bi. Hộp thứ nhất gồm 15 viên bi, trong đó có 3 viên bi trắng
và 12 viên bi xanh. Hộp thứ 2 gồm 20 viên bi, trong đó có 4 viên bi trắng và 16 viên bi xanh. Chọn
ngẫu nhiên một viên bi từ hộp 1 bỏ sang hộp 2. Sau đó chọn ngẫu nhiên một viên bi từ hộp hai .
Tính xác suất viên bi lấy ra từ hộp 2 là viên bi trắng từ hộp 2 ban đầu.
11.7 Đề giữa kì 2015-2016 97 A. 0.95 B. 0.86 C. 0.76 D. 1.00 99 12. ĐỀ THI CUỐI KÌ 12.1
Đề 1 cuối kì I năm 2018-2019 Bài 12.1. (7 điểm)
Gọi X (giờ) là thời gian tự học hàng ngày của sinh viên, khảo sát 120 sinh viên trường Đại học
KHXHNV. Kết quả cho bởi bảng sau: Thời gian tự học (giờ) 1 2 3 4 5 6 7 8 Số sinh viên 13 18 14 23 15 16 17 4
Giả sử thời gian tự học của sinh viên có phân phối chuẩn.
a. Ước lượng thời gian tự học trung bình của sinh viên trường KHXHNV với độ tin cậy 98%. (1.5đ)
b. Với độ tin cậy 95%, ước lượng tỉ lệ những sinh viên có thời gian tự học trên 5 giờ mỗi ngày. (1.5đ)
c. Khảo sát thời gian tự học của 90 sinh viên trường Đại học Kinh tế Thời gian tự học (giờ) 1 2 3 4 5 6 Số sinh viên 7 8 17 24 20 14
Có ý kiến cho rằng thời gian tự học của sinh viên trường KHXHNV lớn hơn sinh viên trường
Kinh tế. Với mức ý nghĩa 5%, hãy kiểm định ý kiến trên. (2đ)
d. So sánh tỷ lệ những sinh viên có thời gian tự học trên 5 giờ mỗi ngày giữa hai trường
KHXHNV và Kinh tế. (α = 1% (2đ)) Bài 12.2. (3 điểm)
Trong cấu tạo một loại dây thừng, người ta quan tâm đến hàm lượng nylon x (đv: %) ảnh hưởng
như thế nào đến lực căng y (đv: psi) (lực kéo tối đa trước khi sợi dây bị đứt). Số liêu bên dưới cho
kết quả đo tương ứng (x, y) của 8 sợi dây: 100
Chương 12. ĐỀ THI CUỐI KÌ Hàm lượng nylon 0 10 20 20 30 40 50 50 Lực căng 160 240 320 340 395 450 510 520
a. Tìm phương trình hồi quy tuyến tính biểu diễn mối liên hệ của x vào y dưới dạng: ˆy = ˆ β0 + ˆβ1x. (2đ)
b. Giải thích ý nghĩa của hệ số β1 nhận được và dự đoán lực căng của một sợi dây có hàm lượng nylon bằng 45. (1đ) 12.2
Đề 2 cuối kì I năm 2018-2019
Bài 12.3. Thực hiện một khảo sát xã hội về số tiền chi trả cho các hoạt động vui chơi giải trí trong
1 tháng của 400 thanh niên tại TP.HCM người ta thu được bảng sau: Số tiền (USD) 50-80 80-120 120-160 160-200 200-220 220-250 Số người 50 80 100 80 60 30
Giả thiết số tiền phải bỏ ra cho các hoạt động vui chơi giải trí trong một tháng của một thanh
niên tại TP.HCM là một đại lượng ngẫu nhiên phân phối theo qui luật chuẩn.
a. Ước lượng số tiền trung bình một thanh niên phải bỏ ra với độ tin cậy 95%. (1.5đ)
b. Những thanh niên bỏ ra trên 200 USD/tháng cho các hoạt động vui chơi là những thanh niên
khá giả. Hãy ước lượng tỉ lệ những thanh niên khá giả với độ tin cậy 97%. Nếu muốn sai số
≤ 0.1 thì phải khảo sát thêm bao nhiêu thanh niên? (2.5đ)
c. Một nhà nghiên cứu xã hội cho rằng cứ 100 thanh niên ở TP.HCM thì có 30 người thuộc diện
khá giả, trong khi nhà thống kê lại tỏ ra nghi ngờ và họ cho rằng con số này thực sự phải nhỏ
hơn con số thống kê do nhà nghiên cứu ngày đưa ra. Vậy theo các bạn, ý kiến nào đúng đắn
với mức ý nghĩa α = 5%. (1.5đ)
d. Lời khẳng định: “ Tỷ lệ thanh niên có thu nhập hạn chế là 50%” có được chấp nhận hay
không, mức ý nghĩa 1%. Biết rằng một thanh niên được gọi là có thu nhập hạn chế nếu số
tiền bỏ ra cho hoạt động vui chơi dưới 120 USD/tháng. (1.5đ)
Bài 12.4. Bảng số liệu bên dưới mô tả về chỉ số khối cơ thể x (Body Mass Index - BMI) và huyết
áp y của 8 người được chọn ngẫu nhiên. BMI được tính bởi công thức (cân nặng (kg)/chiều cao (m))2. BMI 20.3 22.0 26.4 28.2 31 32.6 17.6 19.4 Huyết áp 116 110 131 136 144 138 122 115
a. Tìm phương trình hồi quy tuyến tính biểu diễn mối liên hệ của x vào y dưới dạng: ˆy = ˆ β0 + ˆβ1x. (2đ)
b. Giải thích ý nghĩa của hệ số β1 nhận được và dự đoán huyết áp của một người có BMI bằng 30. (1đ) 12.3 Đề 1 cuối kì 2017-2018
Bài 12.5. Các sản phẩm được sản xuất trong một dây chuyền. Để thực hiện kiểm tra chất lượng,
mỗi giờ người ta rút ngẫu nhiên không hoàn lại 10 sản phẩm từ một hộp có 25 sản phẩm. Quá trình
sản xuất được báo cáo là đạt yêu cầu nếu có không quá một sản phẩm là thứ phẩm.
12.4 Đề 2 cuối kì 2017-2018 101
a. Nếu tất cả các hộp được kiểm tra đều chứa chính xác hai thứ phẩm, thì xác suất quá trình sản
xuất được báo cáo đạt yêu cầu ít nhất 7 lần trong một ngày làm việc 8 giờ là bao nhiêu?
b. Sử dụng phân phối Poisson để xấp xỉ xác suất được tính trong câu (a).
c. Biết rằng lần kiểm tra chất lượng cuối cùng trong câu (a), quá trình sản xuất được báo cáo
đạt yêu cầu. Hỏi xác suất mẫu 10 sản phẩm tương ứng không chứa thứ phẩm là bao nhiêu?
Bài 12.6. Khảo sát về thu nhập của một số người làm việc ở một công ty, người ta thu được các số liệu cho ở bảng sau:
Thu nhập (triệu đồng/tháng) 5 5.5 6 6.5 7 7.5 8 9 10 Số người 6 12 20 34 30 16 12 10 4
Giả sử thu nhập là đại lượng ngẫu nhiên có phân phối chuẩn.
a. Giả sử thu nhập là đại lượng ngẫu nhiên có phân phối chuẩn 90%.
b. Nếu muốn sai số ước lượng thu nhập trung bình của một người ở công ty không vượt quá
200000 đồng/tháng ở độ tin cậy 99% thì cần khảo sát thêm ít nhất bao nhiêu người nữa?
c. Nếu nói rằng thu nhập trung bình của một người ở công ty là 7 triệu đồng/tháng thì có đáng
tin cậy không? Hãy kết luận với mức ý nghĩa 5%. 12.4 Đề 2 cuối kì 2017-2018
Bài 12.7. Một công ty kỹ thuật thiết lập một bài kiểm tra năng lực khi các ứng viên nộp đơn để
thực tập. Thời gian hoàn thành bài kiểm tra có phân phối chuẩn với trung bình 40,5 phút và độ
lệch chuẩn 7,5 phút. Các ứng viên hoàn thành bài thi ít hơn 30 phút được chấp nhận thực tập ngay.
Những người hoàn thành bài thi từ 30 đến 36 phút được yêu cầu làm thêm một bài kiểm tra khác.
Mọi ứng viên khác sẽ bị từ chối.
a. Với một ứng viên được chọn ngẫu nhiên, tính xác suất để người này được
i. chấp nhận thực tập ngay;
ii. yêu cầu làm thêm một bài kiểm tra khác.
b. Cho biết một ứng viên được chọn ngẫu nhiên không bị từ chối sau bài kiểm tra đầu tiên này,
tính xác suất ứng viên được chấp nhận thực tập ngay.
c. Vào một dịp nào đó có 100 ứng viên. Sử dụng một xấp xỉ phù hợp để tính xác suất có nhiều
hơn 25 ứng viên được yêu cầu làm thêm một bài kiểm tra khác.
Bài 12.8. Điều tra năng suất lúa trên diện tích 100 hecta trồng lúa của một vùng, ta thu được bảng số liệu sau: Năng suất (tạ/ha) 41 44 45 46 48 52 54 Diện tích (ha) 10 20 30 15 10 10 5
Giả sử năng suất lúa có phân phối chuẩn.
a. Hãy ước lượng năng suất lúa trung bình của vùng đó với độ tin cậy 95%.
b. Nếu muốn sai số ước lượng của năng suất lúa trung bình không vượt quá 0.5 tạ/ha, với độ tin
cậy 99% thì cần điều tra thêm ít nhất bao nhiêu hecta lúa nữa?
c. Những thửa ruộng có năng suất từ 48 tạ/ha trở lên được xem là những thửa có năng suất cao.
Hãy ước lượng tỷ lệ diện tích có năng suất cao trong vùng với độ tin cậy 90%.
d. Có tài liệu cho biết năng suất lúa trung bình là 47 tạ/ha. Giá trị này có phù hợp với mẫu quan
sát không? Hãy kết luận với mức ý nghĩa 5%. 102
Chương 12. ĐỀ THI CUỐI KÌ 12.5 Đề 3 cuối kì 2017-2018
Bài 12.9. Trọng lượng A của mỗi con bò trong một đàn bò là biến ngẫu nhiên có phân phối chuẩn
với kỳ vọng 300kg và độ lệch chuẩn 50kg. Chọn ngẫu nhiên một con bò trong chuồng. Tính xác
suất để con bò được chọn:
a. Có trọng lượng trên 500kg.
b. Có trọng lượng từ 250 kg tới 350kg.
c. Chọn ngẫu nhiên 4 con bò trong đàn bò nói trên. Tính xác suất để có 2 trong 4 con bò nói
trên có trọng lượng từ 250kg tới 3050kg.
Bài 12.10. Một khảo sát về chiều cao X(cm) của một giống cây trồng người ta quan sát một mẫu và có kết quả như sau: Chiều cao (cm) 100 110 120 130 140 150 160 Số cây 10 10 15 30 10 10 15
Giả sử chiều cao X có phân phối chuẩn.
a. Ước lượng chiều cao trung bình của giống cây trồng trên với độ tin cậy 95%.
b. Những cây trồng có chiều cao từ 135cm trở lên được gọi là những cây “cao”. Hãy ước lượng
tỉ lệ những cây cao với độ tin cậy 95%.
c. Người ta áp dụng phương pháp mới trong việc trồng và chăm sóc cây. Sau một thời gian,
khảo sát 100 cây trồng theo phương pháp mới được bảng số liệu sau: Chiều cao (cm) 100 110 120 130 140 150 160 Số cây 6 10 20 34 12 7 11
Với mức ý nghĩa 5%, hãy kiểm định xem phương pháp mới có làm tăng chiều cao trung bình của cây hay không?
d. Có ý kiến cho rằng phương pháp mới làm tăng tỉ lệ cây “cao”. Với mức ý nghĩa 5%, hãy kiểm tra ý kiến này. 12.6
Đề cuối kì 2017-2018 học kì hè
Bài 12.11. Cho biến ngẫu nhiên X (phút) thể hiện thời gian chờ mua trà sữa của khách hàng ở một
quán nhỏ ven đường và có hàm mật độ là:
k x2(6 − x) nếu x ∈ [0, 6] fX(x) = 0 nếu x ∈ R[0, 6]
trong đó k là một số thực nào đó. a. Tìm k.
b. Tìm thời gian chờ trung bình của khách.
c. Tìm hàm phân phối tích lũy của biến ngẫu nhiên X.
Bài 12.12. Một nhà nông trồng giống cherry Úc theo phương pháp được các nhà khoa học đề xuất;
chính vì thể đường kính của quả cherry tuân theo phân phối chuẩn với trung bình 28mm và độ
lệch chuẩn 2mm. Một quả cherry được gọi là có size 32 nếu đường kính của quả cherry nằm trong
[30, 32]. Giả sử các quả cherry có size 32 độc lập nhau.
a. Chọn ngẫu nhiên một quả cherry trong vườn, tìm xác suất nhận được quả cherry có size 32.
12.6 Đề cuối kì 2017-2018 học kì hè 103
b. Tìm số tự nhiên n nhỏ nhất sao cho chọn n quả cherry trong vườn thì xác suất nhận được ít
nhất 1 quả cherry size 32 không bé hơn 0.99.
c. Chọn ngẫu nhiên 100 quả cherry trong vườn, hãy chọn mô hình xấp xỉ thích hợp để tìm xác
suất có ít nhất 20 quả cherry size 32.
Bài 12.13. Để xem xét tình hình học tập môn xác suất thống kê (XSTK), một giảng viên (GV) đã
tiến hành lấy mẫu (2 lần). Biết rằng điểm số sinh viên tuân theo phân phối chuẩn. Điểm sinh viên
nam và sinh viên nữ độc lập nhau.
a. Ở lần lấy mẫu thứ nhất, GV này thu thập được thông tin của 20sinh viên với điểm trung bình
5.5 và độ lệch chuẩn 0.75. Sử dụng thông tin này để ước lượng điểm trung bình của sinh viên với độ tin cậy 95%.
GV này tiếp tục thực hiện lấy mẫu lần thứ hai và thu thập được bảng thông tin sau: Điểm [0,1) [1,2) [2,3) [3,4) [4,5) [5,6) [6,7) [7,8) [8,9) [9,10] Nam 4 6 4 6 2 6 5 2 6 4 Nữ 5 10 8 8 5 4 3 2 3 2
(Bảng dữ liệu chứa thông tin: có 4 sinh viên nam và 5 sinh viên nữ có điểm số nằm trong [0, 1),
có 6 sinh viên nam và 10 sinh viên nữ có điểm số nằm trong [1, 2...)
Hãy sử dụng thông tin ở lần lấy mẫu thứ hai để giải các câu hỏi 3(b-c-d)
b. Một sinh viên được gọi là có điểm cao nếu điểm lớn hơn hoặc bằng 7.0. Ước lượng khoảng
tin cậy cho tỉ lệ học sinh có điểm cao với độ tin cậy 99%.
c. Dựa theo số liệu điểm môn SXTK trong học kì trước, điểm trung bình của sinh viên nam là
5.0. Hãy cho biết giá trị trên có phù hợp với dữ liệu quan sát (điểm sinh viên nam đã thu thập
được) hay không với mức ý nghĩa 2%?
d. Có nhiều người cho rằng các bạn nữ chăm học hơn các bạn nam nên điểm trung bình của các
bạn nữ cao hơn điểm trung bình của các bạn nam. Tuy nhiên, GV này cho rằng điểm trung
bình của các bạn nữ không cao hơn điểm trung bình của các bạn nam. Hãy sử dụng dữ liệu
quan sát để kiểm tra nhận định về hai điểm trung bình của GV với mức ý nghĩa 2%. IV PhầnBốn:Phụlục 13
MỞ ĐẦU VỀ CHƯƠNG TRÌNH R . . . . . . . 107 13.1
Cài đặt và làm việc với các cửa sổ của R 13.2 Sử dụng lệnh help 13.3 Gói hàm - packages 13.4 Những lệnh cơ bản 13.5 Nhập xuất dữ liệu 13.6
Cấu trúc lập trình cơ bản 14
BẢNG GIÁ TRỊ CỦA HÀM PHÂN PHỐI TÍCH
LŨY . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . 115 Articles Books 107
13. MỞ ĐẦU VỀ CHƯƠNG TRÌNH R 13.1
Cài đặt và làm việc với các cửa sổ của R
Đường dẫn download chương trình R: https://www.r-project.org/
Nếu người dùng muốn sử dụng R có giao diện thì cài đặt thêm chương trình RStudio sau khi đã cài R: https://www.rstudio.com/
Chú ý, tất cả những ví dụ code R trong mục này đều viết trong của sổ “R prompt”. Chạy thử đoạn code sau: R > help(plot) R > print( + > "Hello word!" + > )
Hãy nhận xét về dòng lệnh: R > và + >? Lệnh help có tác dụng gì? Chạy đoạn code sau:
R > # sử dụng để ghi chú
R > print( # Ghi chú được để ở phần cuối một câu lệnh + > "Hello word!")
R > q # được hiểu như một kí tự code
R > q() # thoát chương trình R 13.2 Sử dụng lệnh help
So sánh kết qả trả ra từ hai đoạn code sau: 1. Code 1: 108
Chương 13. MỞ ĐẦU VỀ CHƯƠNG TRÌNH R R > help(plot)
R > ?plot # trợ giúp nhanh 2. Code 2: R > help.search("plot")
R > ??plot # trợ giúp nhanh
Hơn nữa, bạn có thể tìm hiểu thông tin nhiều hơn về lệnh help và help.search bằng lệnh R > help(help) R > help(help.search) 13.3 Gói hàm - packages
Một packages trong R là tập những hàm (đôi khi là dữ liệu) được phát triển bởi cộng đồng
người sử dụng ngôn ngữ R mà thường là những nhà nghiên cứu thống kê. Để sử dụng một hàm nào
đó cho nhu cầu code, người dùng thực hiện như sau:
1. Tìm tên hàm và package trong đường dẫn sau: https://cran.r-project.org/index.
html bên trái cửa số trang web ở mục Software rồi Packages.
2. Sau khi tìm được package mong muốn, ta dùng lệnh install.packages để cài đặt.
3. Từ sau khi đã cài đặt mỗi lần sử dụng hàm trong package ta phải dùng lệnh library. Chú ý
rằng mỗi lần khởi động ngôn ngữ R muốn sử dụng package ta đều phải chạy lệnh này một lần. Chạy ví dụ sau:
R > install.packages("foreign") # Cài đặt package
R > library(foreign) # Gọi package
R > search() # Kiểm tra những package đã gọi
R > ls(pos=2) # Kiểm tra những mục con trong gói số 2
R > update.packages() # Update các gói đã cài đặt 13.4 Những lệnh cơ bản 13.4.1 Biến và các phép toán Hãy chạy đoạn code
Trả lời các câu hỏi sau:
1. Dấu: =, < −, − > có tác dụng gì? R > a = 17
2. Lệnh: ls và objects có tác dụng gì? R > b <- 8
3. Nêu tác dụng cảu hai dòng lệnh rm(z_42) R > 17 -> c và remove(a)? R > a + b + c R > z_42 <- "Hello" R > z_42 <- a + b + c R > ls() R > objects() R > rm(z_42) R > remove(a) 13.4.2 Các phép toán 13.4 Những lệnh cơ bản 109 Hãy chạy đoạn code
Trả lời các câu hỏi sau:
1. Lệnh typeof được sử dụng làm gì? R > a <- 2 + 2 R > pi R > cos(3*pi/2) R > b <- exp(8.17) R > typeof(a) R > typeof(b) R > typeof(a + b) R > s <- "Hello" R > typeof(s) R > 2 == 3 R > t <- 2 < 3 R > typeof(t) 13.4.3 Vectơ Hãy chạy đoạn code R > length(v2) R > sort(v2)
R > v1 <- c(2, 3, 5, 8, 4, 6); v1
R > typeof(v1) # Loại dữ liệu của các phần tử R > is.vector(v1) R > c(1, 3.14, "Hello") R > 1:10
R > seq(seq(from=1, to=20, by=2) R > seq(1, 20, by=5) R > seq(1, 20, length=5) R > rep(5, times=10) R > rep(c(1, 2), 3) R > rep(c(1, 2), each=3)
R > v1[2]; v1[2:4]; v1[c(1, 4)] R > v1[-3] R > v1[-1:2] # Error, why? R > v1[(1:2)] R > v1[3] <- NA; v1 R > is.na(v1) R > help(NA) R > any(is.na(v1)) R > all(is.na(v1))
R > v2 <- c(a=32, b=26, c=12, d=41) R > v2["b"] <- 22; v2 R > names(v2) R > names(v2) <- c( + > "a1", "a2", "a3", "a4") R > v2 > 30 R > v2[v2 > 30] R > which(v2 > 30) R > v2 + 100 R > v1 + v2 # Error, why? R > 1:4 + v2; 1:8 + v2 R > cos(v2) 110
Chương 13. MỞ ĐẦU VỀ CHƯƠNG TRÌNH R
Trả lời các câu hỏi sau: 13.4.4 Ma trận
R > A <- matrix(1:15, ncol=5) R > A; t(A)
R > B <- matrix(1:15, nc=5, byrow=TRUE)
R > B2 <- B; B2[1, 1] <- "Hello"; B2 R > typeof(B); typeof(B2) R > cbind(A, B) R > rbind(A, B) R > A[1, 3]; A[2,]; A[, 2] R > A[1:3, 2:4]
R > g <- seq(0, 1, length=20)
R > C <- matrix(g, nrow=4)
R > C[C[, 1] > 0.1,] # ***
R > A + B; A * B # Elementwise
R > A %*% t(B) # Matrix product R > cos(A) R > I <- diag(rep(1, 2)) R > diag(A)
R > D <- solve(A[1:2, 1:2])
R > all(A[1:2, 1:2] %*% D == I) # Why? R > apply(A, 2, sum) R > apply(A, 1, max) 13.4.5 Mảng
R > A <- array(1:12, c(2, 3, 2)) R > A R > dim(A); length(A) R > nrow(A); ncol(A) R > apply(A, 1, mean) R > apply(A, 2, mean) R > apply(A, 3, mean) 13.4.6 Danh sách
R > l1 <- list("Bobby", 1:8); l1 R > l1[[1]] R > l1[[2]] + 10 R > l2 <- list( + >
vect=1:5, text="DVORAK", scal=8) R > names(l2) R > l2$text R > l2[c("scal", "vect")]
R > length(l2); length(l2$vect) 13.4.7 Data frames
R > height <- runif(20, 150, 180)
R > mass <- runif(20, 50, 90)
R > sex <- sample(c("M", "F"), 20, 13.5 Nhập xuất dữ liệu 111 + > rep=TRUE)
R > color <- c("Blue", "Green", "Brown")
R > eyes <- sample(color, 20, rep=TRUE) R > table(sex); table(eyes) R > table(sex, eyes) R > H <- data.frame( + > height, mass, sex, eyes) R > H; summary(H) R > head(H) R > tail(H) R > H[1,] R > H$height R > H$sex R > is.data.frame(H) R > is.matrix(H)
R > as.matrix(H) # Cast as a matrix 13.5 Nhập xuất dữ liệu 13.5.1 Nhập dữ liệu
Trong R, ta có thể đọc dữ liệu từ một file .txt theo định dạng sau: f ile1.csv f ile2.t xt f ile3.t xt f ile4.t xt X1;X2;X3 5,2.5,3.8 5 2.5 3.8 5;2.5;3.8 5;2,5;3,8 8,3.2,3.4 8 3.2 3.4 8;3.2;3.4 8;3,2;3,4 12,4.6,5 12 4.6 5 12;4.6;5 12;4,6;5
Hãy tạo file theo định dạng và chạy đoạn code sau
R > f1 <- read.table("file1.csv", sep=",") R > f1
R > f1bis <- read.csv("file1.csv") R > f1bis
R > f1bis <- read.csv("file1.csv", + > header=FALSE) R > f1bis 13.5.2 Xuất dữ liệu
Chạy đoạn code dưới đây và cho biết vai trò của lệnh sink.
R > A <- seq(1, 10, length=50) R > write.table(A, "A.txt") R > sink("A2.txt") R > A R > summary(A) R > sink() R > summary(A) 112
Chương 13. MỞ ĐẦU VỀ CHƯƠNG TRÌNH R 13.6
Cấu trúc lập trình cơ bản 13.6.1 Cấu trúc điều kiện R > x <- rnorm(10)
R > if (is.double(x)) print("OK")
R > if (is.integer(x)) print("KO")
R > if (x[1] > 0) 1 else -1 R > if (x[1] > 0) { + > y <- 1 + > print("Positive") + > } else { + > y <- -1 + > print("Non positive") + > }
R > y <- ifelse(x > 0, 1, -1); y R > z <- "cat" R > switch(z, + > cat=print("Hi Felix!"), + > dog=print("Hi Snowy!"),
+ > print("What is this pet?")) 13.6.2 Cấu trúc lặp R > x <- c(17, 8, 42, 3) R > for (e in x) print(e)
R > for (i in 1:length(x)) print(x[i])
R > for (i in seq_along(x)) print(x[i]) R > for (i in seq_len(5)) { + > fact <- prod(1:i)
+ > cat(i, "! = ", fact, "\n", sep="") + > }
R > for (k in seq_len(10)) { + > if (k %% 2 == 0) next + > print(k) + > } R > i <- 1; s <- 0
R > while (i <= length(x)) { + > s <- s + x[i] + > i <- i + 1 R > } R > s R > x <- 0 R > repeat { + > print(x) + > x <- x + 1 + > if (x == 10) break R > } 13.6.3 Cấu trúc hàm
R > f1 <- function() print("Hello!")
13.6 Cấu trúc lập trình cơ bản 113 R > f1 R > f1()
R > f2 <- function(k) cat(2*k) R > f2(21)
R > f3 <- function(k) return(2*k) R > f3(21) R > y <- f3(21); y R > f3 <- fix(f3)
R > f4 <- function(a, b=0) return(a + 2*b)
R > f4(2, 3); f4(5); f4(b=2, a=1)
R > f5 <- function(a, b=a) return(a + 2*b) R > f5(2, 3); f5(5)
R > my_circle <- function(r) { + > p <- 2*pi*r + > a <- pi*r*r + > return(list(radius=r, + > perimeter=p, + > area=a)) + > } R > y <- my_circle(3) R > y$area == pi*y$radius^2 R > my_var <- 17 R > f6 <- function(x) { + > my_var <- x + > print(my_var) + > }
+ > print(my_var); f6(8); print(my_var) 115 116
Chương 14. BẢNG GIÁ TRỊ CỦA HÀM PHÂN PHỐI TÍCH LŨY
14. BẢNG GIÁ TRỊ CỦA HÀM PHÂN PHỐI TÍCH LŨY 117 118
Chương 14. BẢNG GIÁ TRỊ CỦA HÀM PHÂN PHỐI TÍCH LŨY 119 120
Chương 14. BẢNG GIÁ TRỊ CỦA HÀM PHÂN PHỐI TÍCH LŨY 121 122
Chương 14. BẢNG GIÁ TRỊ CỦA HÀM PHÂN PHỐI TÍCH LŨY 123 TÀI LIỆU THAM KHẢO 125 Tài liệu tham khảo Bài báo Sách
[1] Phạm Hoàng Quân & Đinh Ngọc Thanh, Xác suất thống kê, NXB Giáo Dục Việt Nam, 2011.
[2] Douglas C. Montgomery & George C. Runger, Applied Statistics and Probability for Engi-
neers, Fifth Edition, John Wiley & Sons, Inc., 2011.
[3] David S. Moore, George P. McCabe & Bruce A. Craig, Introduction to the Practice of
Statistics, W. H. Freeman and Company, New York, 2009.
[4] Anthony Eccles, Bob Francis, Alan Graham & Roger Porkess, Statistics 1 & 2, Third Edition,
Hodder Education an Hachette UK Company, 2004.
[5] Bernard Rosner, Fundamentals of Biostatistics, Seventh Edition, Brooks/Cole Cengage Learn- ing, Boston USA, 2011.
[6] Douglas C. Montgomery, George C. Runger & Norma Faris Hubele, Engineering Statistics,
Fifth Edition, John Wiley & Sons, Inc., 2011.
[7] Joy Devore, Probability and Statistics for Engineering and the Sciences, Ninth Edition,
Brooks/Cole Cengage Learning, Boston USA, 2014.
Document Outline
- Phn I — Phn Mt: Xác sut
- 1 PHÉP ÐM
- 1.1 Lý thuyt
- 1.2 Bài tp
- 2 XÁC SUT C BAN
- 2.1 Mt s khái nim
- 2.2 Xác sut có iu kin
- 2.3 Xác sut toàn phn
- 3 BIN NGU NHIÊN RI RAC
- 3.1 Lý thuyt
- 3.2 Phân phi nhi thc
- 3.3 Phân phi siêu bi
- 3.4 Phân phi Poisson
- 4 BIN NGU NHIÊN LIÊN TUC
- 4.1 Ðinh nghıa
- 4.2 Phân phi chun
- 4.3 Ðinh lí gii han
- 5 PHÂN PHI XÁC SUT ÐNG THI
- 5.1 Lý thuyt
- 5.2 Bài tp
- 1 PHÉP ÐM
- Phn II — Phn Hai: Thng Kê
- 6 THNG KÊ MÔ TA
- 6.1 Lý thuyt
- 6.2 Bài tp
- 7 C LNG ÐIM
- 7.1 Mt s khái nim c ban
- 7.2 Khoang tin cy cho trung bình cua phân phi chun
- 7.3 Khoang tin cy cho phng sai
- 7.4 Khoang tin cy cho ti l cua phân phi nhi thc
- 8 KIM ÐINH MT MU
- 8.1 Mt s khái nim
- 8.2 Kim inh trung bình
- 8.3 Kim inh phng sai
- 8.4 Kim inh ti l
- 9 KIM ÐINH GIA THUYT THNG KÊ HAI MU
- 9.1 Lý thuyt
- 9.2 Bài tp
- 10 HI QUY – TNG QUAN
- 10.1 Lý thuyt
- 10.2 Bài tp
- 6 THNG KÊ MÔ TA
- Phn III — Phn Ba: Ð Thi Mu
- 11 Ð THI GIA KÌ
- 11.1 Ð 2 gia kì 2018-2019
- 11.2 Ð 1 gia kì 2018-2019
- 11.3 Ð 2 gia kì 2018-2019
- 11.4 Ð 1 gia kì 2017-2018
- 11.5 Ð 2 gia kì 2017-2018
- 11.6 Ð gia kì 2016-2017
- 11.7 Ð gia kì 2015-2016
- 12 Ð THI CUI KÌ
- 12.1 Ð 1 cui kì I nam 2018-2019
- 12.2 Ð 2 cui kì I nam 2018-2019
- 12.3 Ð 1 cui kì 2017-2018
- 12.4 Ð 2 cui kì 2017-2018
- 12.5 Ð 3 cui kì 2017-2018
- 12.6 Ð cui kì 2017-2018 hoc kì hè
- 11 Ð THI GIA KÌ
- Phn IV — Phn Bn: Phu luc
- 13 M ÐU V CHNG TRÌNH R
- 13.1 Cài t và làm vic vi các ca s cua R
- 13.2 S dung lnh help
- 13.3 Gói hàm - packages
- 13.4 Nhng lnh c ban
- 13.5 Nhp xut d liu
- 13.6 Cu trúc lp trình c ban
- 14 BANG GIÁ TRI CUA HÀM PHÂN PHI TÍCH LUY
- Articles
- Books
- Index
- 13 M ÐU V CHNG TRÌNH R





