3 trang 18 lượt tải

Nhận dạng đồ thị hàm số Toán 12 | Chuyên đề Toán 12

35

Toán 12 Nhận biết dạng đồ thị hàm số vừa được biên soạn và xin gửi tới bạn đọc để bạn đọc cùng tham khảo. Mời các bạn cùng theo dõi bài viết dưới đây nhé.

Chủ đề: Chuyên đề Toán 12 158 tài liệu

Môn: Toán 12 3.9 K tài liệu

Sách: Kết nối tri thức, Cánh diều, Chân trời sáng tạo

Tác giả:

Profile

Linh Đan

2 tháng trước
Danh sách Quiz
/3
Nhận dạng hàm số thường gặp thông qua đồ thị
A. Hàm số bậc ba
y ax bx cx d a
3 2
0
TRƯỜNG HỢP
a 0
0a
Phương trình
y ' 0
có
2 nghiệm phân biệt
Phương trình
y
/
0
có
nghiệm kép
Phương trình
/
0y
vô
nghiệm
B. Hàm số trùng phương
y ax bx c a
4 2
0
a 0
0a
y
/
0
y ' 0
C. Hàm số nhất biến
0, 0
ax b
y c ad bc
cx d
Tập xác định:
\
d
D
c
.
Đạo hàm:
2
,
ad bc d
y x
c
cx d
.
Nếu
0ad bc
: hàm số đồng biến trên từng khoảng xác định.
Nếu
0ad bc
: hàm số nghịch biến trên từng khoảng xác định.
Giới hạn, tiệm cận
lim lim
x x
ax b a
y
cx d c
 
suy ra
a
y
c
là tiệm cận ngang của đồ thị hàm số.
lim lim
d d
x x
c c
ax b
y
cx d
suy ra
d
x
c
là tiệm cận đứng của đồ thị hàm số.
Bảng biến thiên
Đồ thị hàm số
0, 0
ax b
y c ad bc
cx d
0ad bc
0ad bc

Tài liệu khác của Toán 12

Preview text:

Nhận dạng hàm số thường gặp thông qua đồ thị
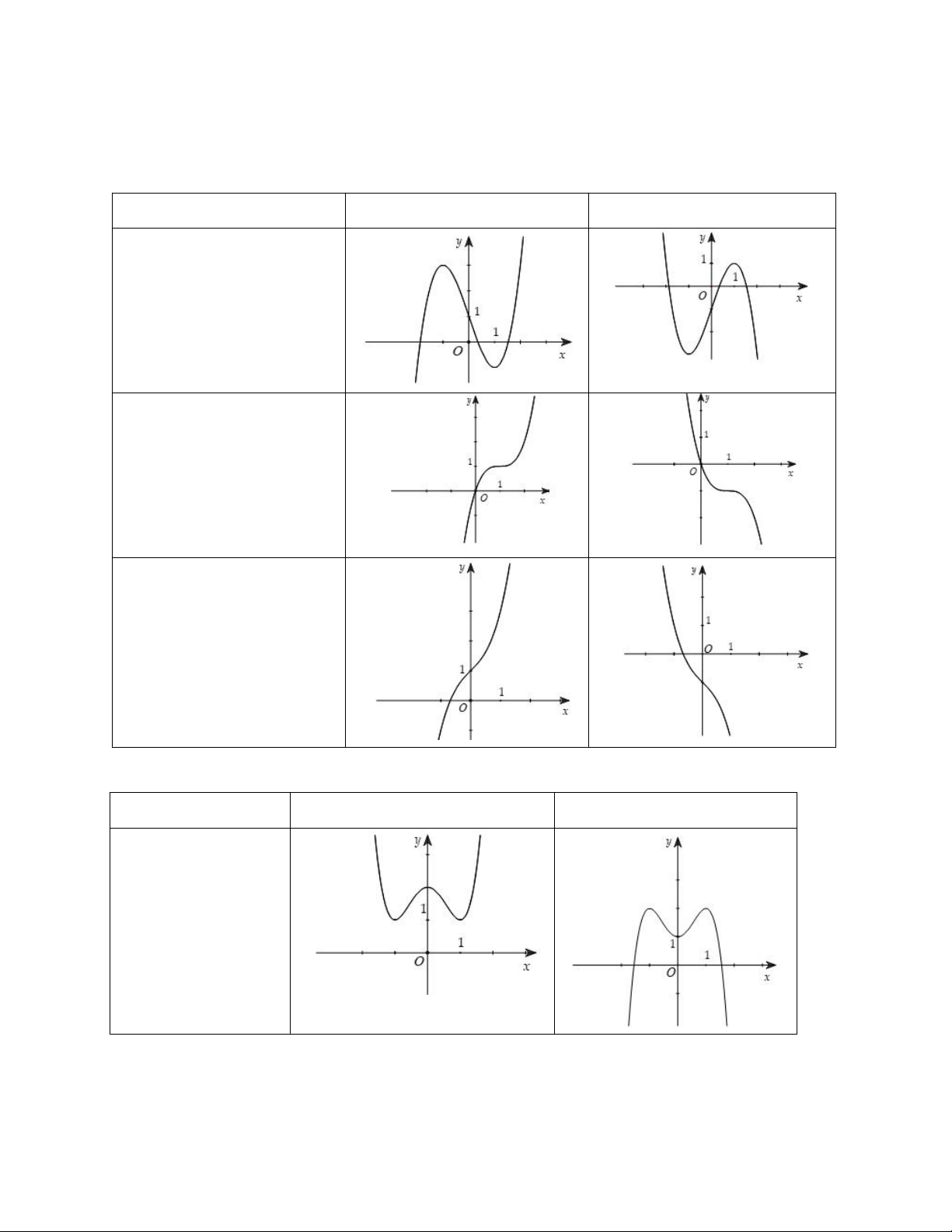
A. Hàm số bậc ba y ax3  bx2  cx d a  0 TRƯỜNG HỢP a  0 a  0
Phương trình y '  0 có 2 nghiệm phân biệt
Phương trình y/  0 có nghiệm kép Phương trình / y  0 vô nghiệm
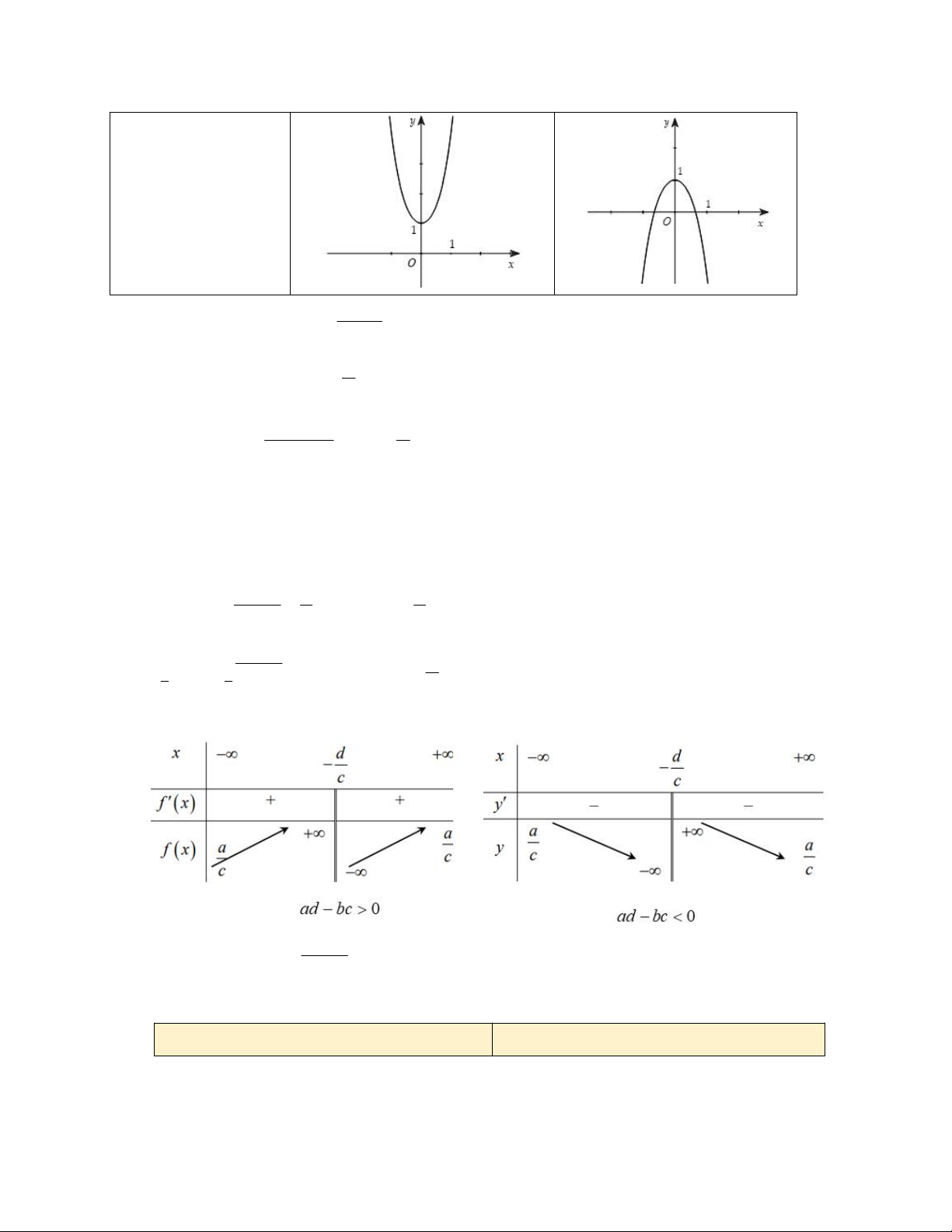
B. Hàm số trùng phương y ax4  bx2  c a  0 TRƯỜNG HỢP a  0 a  0
Phương trình y/  0 có 3 nghiệm phân biệt (a.b < 0)
Phương trình y '  0 có 1 nghiệm.
C. Hàm số nhất biến ax b y
c  0, ad bc  0 cx d \  d D     Tập xác định:c  . ad bc   , d yx   Đạo hàm:cx d 2 c .
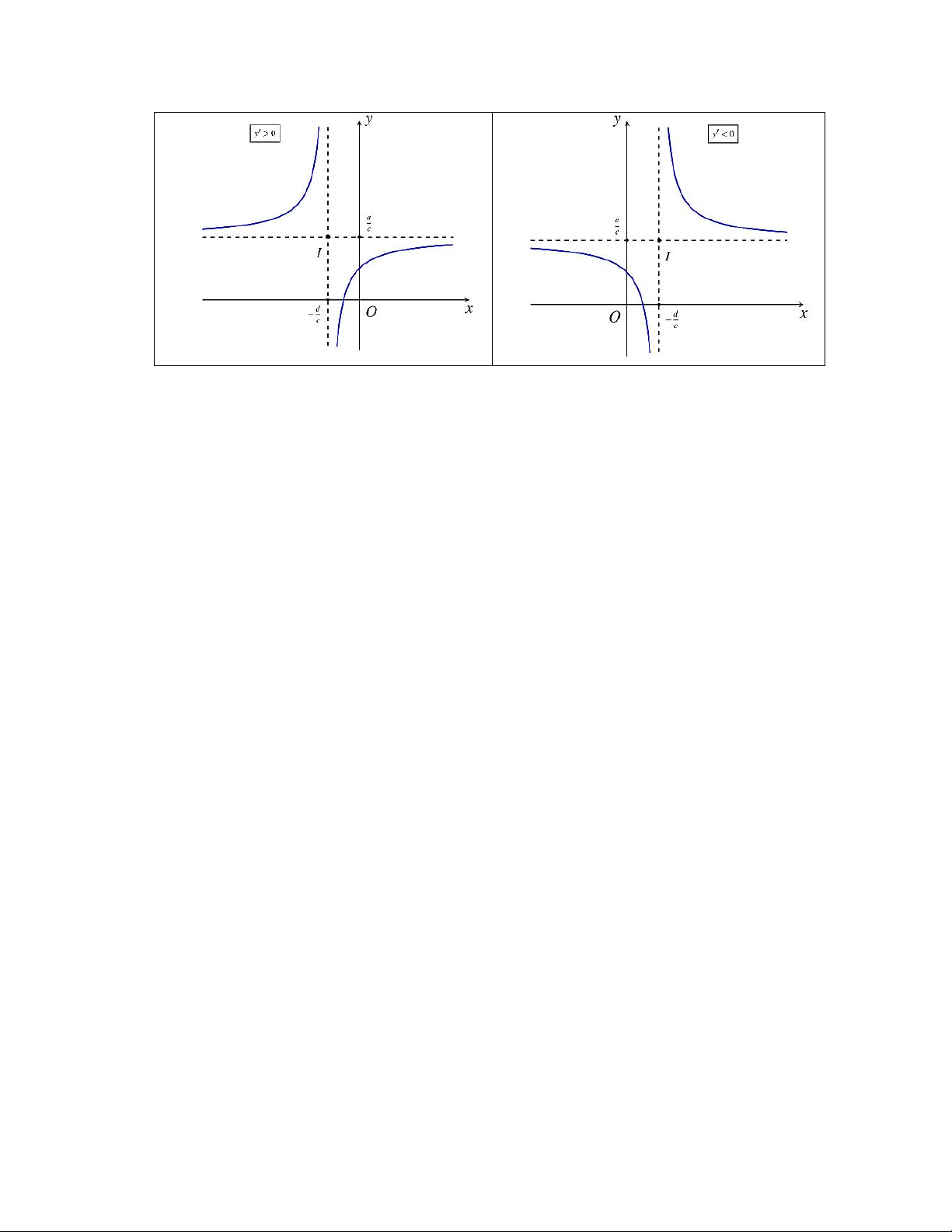
Nếu ad bc  0 : hàm số đồng biến trên từng khoảng xác định.
Nếu ad bc  0 : hàm số nghịch biến trên từng khoảng xác định.
Giới hạn, tiệm cận
lim  lim ax b a ya y x
x cx d c suy ra
c là tiệm cận ngang của đồ thị hàm số.
lim  lim ax b y   d d d x   x
x cx d c c suy ra
c là tiệm cận đứng của đồ thị hàm số. Bảng biến thiên ax b y
c  0,ad bc  0 Đồ thị hàm số cx d ad bc  0 ad bc  0
Document Outline

  • Nhận dạng hàm số thường gặp thông qua đồ thị

Tài liệu liên quan: