Ôn luyện các nhóm câu hỏi vận dụng cao trong đề thi THPTQG môn Toán

Tài liệu gồm 26 trang tuyển chọn 40 câu hỏi vận dụng cao trong đề thi THPT Quốc gia môn Toán giúp học sinh ôn luyện đạt điểm 8 – 9 – 10, tài liệu được biên soạn bởi nhóm Chinh phục Olympic Toán.

37 19 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Tài liệu ôn thi THPTQG môn Toán

Môn: Toán

Thông tin:

26 trang 6 tháng trước

Tác giả:

Profile Nguyễn Vân
Fanpage: Tạp chí và tư liệu toán học Chinh phục olympic toán | 1
ĐỀ ÔN LUYỆN CÁC NHÓM CÂU HỎI
VẬN DỤNG CAO TRONG ĐỀ THI THPT QUỐC GIA
Đề thi gồm 40 câu trắc nghiệm
Thời gian làm bài 180 phút
Good Luck!
Câu 1: Cho tam giác ABC vuông tại A. Gọi
là góc giữa hai đường trung tuyến BD và CK.
Giá trị nhỏ nhất của
cos
bằng?
A.
4
5
B.
5
4
C.
4
3
D.
3
4
Câu 2: Cho hàm số
có đồ thị như hënh vẽ. Hỏi có tất cả bao nhiêu giá trị m
nguyên để phương trënh sau có 8 nghiệm phân biệt:
4 16 4 0m m f x f x
A.
3
B.
2
C.
4
D.
0
Câu 3: Cho hàm số
2 2 2
2 sin 2 cos 3 sin
62
x
y x x a
(với là tham số). Gọi
, mM
lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của hàm số trên đoạn
2
;.
63




Có bao nhiêu
giá trị nguyên của
a
để
2
321
4
mM
?
A.
3.
B.
4.
C.
6.
D.
7.
Câu 4: Cho dãy số
n
u
như sau:
24
1
n
n
u
nn

,
1n
,
2
,
...
Tính giới hạn của tổng
12
lim ...
n
x
u u u

.
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
2 | Chinh phục olympic toán Fanpage: Tạp chí và tư liệu toán học
A.
1
4
B.
1.
C.
1
2
D.
1
3
Câu 5: Cho hàm số
42
2 1 8 4f x ax a b x a b
có
;0
max 3f x f


. Giá trị lớn của
hàm số
fx
trên đoạn
1
;3
2



là?
A. 4
B. 5
C.
4 25a
D.
5 25a
Câu 6: Cho tứ diện vuông O.ABC, gọi R và r lần lượt là bán kính mặt cầu ngoại tiếp và nội
tiếp của tứ diện. Biết rằng
3
13
2
Rr
và
22
2 3 6 10OC OA OB
. Tính
OABC
V
?
A.
2
3
B.
4
3
C.
5
3
D.
1
3
Câu 7: Cho 4 số thực
, , ,a b c d
sao cho
0cd
đồng thời thỏa mãn
22
4
22
log 1 1 log
2 .2 .2 ln 2 4 4 5 16
cd
cd
a b a b
c d cd c d

Gọi M và m lần lượt là GTNN và GTLN của biểu thức
22
P a c b d
. Tính giá trị
của
S M n
?
A.
62
B.
82
C.
10 2
D.
12 2
Câu 8: Gọi
;ab
là tập hợp các giá trị của m để phương trënh
4 1 2 1
1
xx
m
xx


. Với
giá trị nào của m thì bất phương trënh luôn đúng?
A.
33m
B.
25m
C.
5m
D.
4m
Câu 9: Cho tam giác
ABC
đều cạnh
a
,trên đường thẳng
d
vuông góc với mặt phẳng
ABC
tại
A
lấy điểm
M
bất kỳ khác
A
. Gọi
H
là trực tâm tam giác
MBC
, biết rằng
đường thẳng
vuông góc với mặt phẳng
MBC
tại
H
luôn cắt đường thẳng
d
tại
N
Tìm giá trị nhỏ nhất của diện tích toàn phần tứ diện
MNBC
.
A.
2
2 2 5
2
a
B.
2
2 5 2
2
a
C.
2
25
2
a
D.
2
52
2
a
Câu 10: Cho ba số thực dương a,b,c thoả mãn
1
1 1 1 15
abc
a b c
. Gọi
M, N
lần lượt
là giá trị nhỏ nhất và giá trị lớn nhất của
P ab bc ca
. Tính giá trị biểu thức:
A.
1.
B.
41.
C.
15.
D.
65.
Câu 11: Cho hàm số
10 khi 2018
11 khi 2018
xx
fx
f f x x


. Tính giá trị
1 2018ff
.
A.
1999
B.
2009
C.
4018
D.
4036
Câu 12: Một chiếc đồng hồ cát có thiết diện qua trục là 2 parapol đối xứng qua mặt nằm
ngang. Khi để thẳng đứng và cát không chảy thë nó như hënh vẽ ( phần màu xanh là cát),
40 CÂU VẬN DỤNG CAO CÓ GIẢI CHI TIẾT
Fanpage: Tạp chí và tư liệu toán học Chinh phục olympic toán | 3
và mực cát của parapol ở trên là
1
5
chiều cao của parapol ở trên. Khi lật ngược đồng hồ cát
thë lưu lượng cát chảy từ trên xuống dưới không đổi là
3
3cm
/phút. Khi chiều cao ở trên là
6cm thì bề mặt trên tạo thành 1 đường tròn có diện tích
2
9cm
. Biết sau 900s thì cát không
còn chảy nữa. Hỏi khi lượng cát chảy xuống dưới bằng chiều cao của parapol thì thể tích
cát của phần parapol ở trên là bao nhiêu (coi lượng cát đang chảy không đáng kể).
A.
14
B.
13, 05
C.
12,75
D.
13,6
Câu 13: Tìm số hạng tổng quát của dãy số
n
u
biết
1
1
21
31
3
n
n
n
u
u
u
u

A.
tan 1
86
n
un




B.
tan 1
36
n
un




C.
tan 1
23
n
un




D.
tan 1
47
n
un




Câu 14: Cho hai hàm số
fx
và
gx
có đạo hàm liên tục trên
0;2 ,
thỏa mãn
' 0 . ' 2 0ff
và
. ' 2 .
x
g x f x x x e
Tính tích phân
2
0
. ' d .I f x g x x
A.
4.I 
B.
4.I
C.
2.Ie
D.
2.Ie
Câu 15: Cho hàm số
fx
xác định và liên tục trên
0;1 ,
thỏa mãn
' ' 1f x f x
với
mọi
0;1 .x
Biết rằng
0 1, 1 41.ff
Tính tích phân
1
0
d.I f x x
A.
41.I
B.
21.I
C.
41.I
D.
42.I
Câu 16: Với n là số nguyên dương và
0x
, xét khai triển Newton
83
27
11
n
xx
xx



. Hỏi
có bao nhiêu số
2018n
sao cho khai triển của biểu thức trên có số hạng tự do là
0
?
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
4 | Chinh phục olympic toán Fanpage: Tạp chí và tư liệu toán học
A. 1009 B. 403 C. 1615 D. 625
Câu 17: Có bao nhiêu số nguyên dương
m
trong đoạn
2018 ; 2018
sao cho bất phương
trënh sau đúng với mọi
1;100x
:
11
log
log
10
10
10 10
x
x
m
x
.
A.
2018
B.
4026
C.
2013
D.
4036
Câu 18: Một số tự nhiên được gọi là số thú vị nếu số này có 8 chữ số đôi một khác nhau
được lập thành tự tập
1; 2;...;8
và số đó chia hết cho 1111. Hỏi có bao nhiêu số tự nhiên
thú vị như thế?
A.
384
B.
385
C.
386
D.
387
Câu 19: Cho hàm số
32
,x ax b
gọi M là giá trị lớn nhất của hàm số trên đoạn
3; 2
.
Khi M đạt giá trị nhỏ nhất thì
1
log
a
Tb
có giá trị là ?
A.
0
B.
4026
C.
2
D.
1
2
Câu 20 : Cho hình hộp
. ' ' ' 'ABCD A B C D
có cạnh
AB a
và diện tích tứ giác
11
A B CD
là
2
2a
Mặt phẳng
11
A B CD
tạo với mặt phẳng đáy 1 góc
0
60
. Khoảng cách giữa hai đường thẳng
1
AA
và
CD
là P. Khi P max , tìm thể tích của khối hộp biết hình chiếu của đỉnh
1
A
thuộc
miền giữa hai đường thẳng AB và CD
A.
3
43a
B.
3
67a
C.
3
27a
D.
3
37a
Câu 21: Có bao nhiêu giá trị nguyên của tham số
m
để phương trënh:
3 3 3
sin 2 cos2 2 2 cos 1 2 cos 2 3 2 cos 2x x x m x m x m
Có đúng một nghiệm thuộc
2
0;
3


?
A.
1.
B.
2.
C.
3.
D.
4.
Câu 22: Cho tam giác
ABC
có
3AB
,
4AC
. Phân giác trong
AD
của góc
BAC
cắt
trung tuyến
BM
tại
I
. Tính tỉ số
AD
AI
.
A.
13
8
B.
11
6
C.
10
7
D.
10
5
Câu 23: Cho bất phương trënh sau
22
22
11
1 3 1 1 2 1
23
x x m
xx

.
Biết rằng với
; , 0m a b a b

thì bất phương trënh trên luôn đúng với mọi x. Khi
đó tổng
S a b
có giá trị bằng bao nhiêu?
A.
301
B.
302
C.
304
D.
305
40 CÂU VẬN DỤNG CAO CÓ GIẢI CHI TIẾT
Fanpage: Tạp chí và tư liệu toán học Chinh phục olympic toán | 5
Câu 24: Xét các số thực
,,a b c
sao cho phương trënh
2
0ax bx c
có hai nghiệm thuộc
0; 1
. Giá trị lớn nhất của biểu thức
2a b a b
T
a a b c


là
A.
max
3.T
B.
max
3
.
2
T
C.
max
35
.
8
T
D.
max
8
3
T
Câu 25: Gọi
A
là tập hợp tất cả các số tự nhiên có tám chữ số đôi một khác nhau. Chọn
ngẫu nhiên một số thuộc
A
, tính xác suất để số tự nhiên được chọn chia hết cho 45.
A.
53
2268
B.
54
2267
C.
56
2263
D.
1
41
Câu 26: Cho các số thực x,y thỏa mãn
2 2 2
2 2 2 2
log log log 6 log 4 0x y xy xy
. Gọi M,m
lần lượt là max và min của biểu thức
32
8
log
xy
x
P
y
. Tính M.n?
A.
15
23
B.
14
23
C.
16
23
D.
17
23
Câu 27: Cho 2 số thực
1, 0xy
thỏa mãn điều kiện
2
2
22
max 1 ; 2 1
xy
x x y
xy
.
Hỏi biểu thức
2
3 1 2 1P x x y
có tất cả bao nhiêu ước số nguyên dương?
A.
5
B.
6
C.
7
D.
8
Câu 28: Cho các số
1 2 3 4 5
, , , , 0a a a a a
lập thành cấp số cộng với công sai d và
1 2 3 4 5
, , , , 0b b b b b
lập thành cấp số nhân với công bội q . Biết rằng
11
ab
và
55
ab
. Hỏi
có bao nhiêu khẳng định luôn đúng trong các khẳng định sau?
i)
22
ab
ii)
33
ab
iii)
44
ab
iv)
dq
A. 1
B. 2
C. 3
D. 4
Câu 29: Cho hai hình cầu đồng tâm
0,0,0O
, bán kính
12
2, 10RR
. Tứ diện ABCD
có
12
, , ; , ,A B O R C D O R
. Tìm giá trị lớn nhất của thể tích tứ diện ABCD.
A.
63
B.
62
C.
42
D.
43
Câu 30: Cho hình chóp tứ giác đều S.ABCD có cạnh bên bằng 1, các mặt bên là các tam
giác có góc ở đỉnh S bằng
0
45
. Cho A’ là trung điểm SA, C’ thuộc cạnh SC sao cho
3
2
SC
SC
. Mặt phẳng (P) đi qua A’, C’ cắt các cạnh SB, SD lần lượt tại B’, D’. Số nào gần với giá trị
nhỏ nhất của chu vi tứ giác A’B’C’D’ .
A. 1.79
B. 3.3
C. 2.05
D. 1.3
Câu 31: Cho hàm số
32
y ax bx cx d
có đồ thị
C
. Biết rằng
C
cắt trục hoành tại 3
điểm phân biệt có hoành độ
1 2 3
0x x x
và trung điểm nối 2 điểm cực trị của
C
có
hoành độ
0
1
3
x
. Biết rằng
2
1 2 3 1 2 2 3 3 1
3 4 5 44x x x x x x x x x
. Hãy tính tổng
23
1 2 3
S x x x
?
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
6 | Chinh phục olympic toán Fanpage: Tạp chí và tư liệu toán học
A.
137
216
B.
45
157
C.
133
216
D.
1
Câu 32: Cho các Parabol
22
12
1
: , : 4 0
4
P y f x x x P y g x ax ax b a
có các
đỉnh lần lượt là
12
,II
. Gọi
,AB
là giao điểm của
1
P
và
Ox
. Biết rằng 4 điểm
12
, , ,A B I I
tạo thành tứ giác lồi có diện tích bằng
10.
Tính diện tích
S
của tam giác
IAB
với
I
là đỉnh
của Parabol
:.P y h x f x g x
A.
4S
B.
6S
C.
7S
D.
9S
Câu 33: Cho hàm số bậc ba
fx
và
2
,,g x f mx nx p m n p
có đồ thị như hënh
dưới, trong đó đường nét liền là đồ thị hàm
fx
, đồ thị hàm nét đứt là đồ thị hàm
gx
,
đường
1
2
x 
là trục đối xứng hàm
gx
.
Giá trị của biểu thức
2P n m m p p n
bằng bao nhiêu?
A.
6
B.
24
C.
12
D.
16
Câu 34: Có bao nhiêu số nguyên
2018; 2018m
để phương trënh
1
2
3
28
2
x
xm
có
đúng 2 nghiệm thực phân biệt?
A.
2013
B.
2012
C.
4024
D.
2014
Câu 35: Với
1x 
ta có khai triển sau:
40 CÂU VẬN DỤNG CAO CÓ GIẢI CHI TIẾT
Fanpage: Tạp chí và tư liệu toán học Chinh phục olympic toán | 7
2018
2
2 2018
3 2018
12
0 1 2 2018
2 3 2018
22
... ...
11
1 1 1
bb
bb
xx
a a x a x a x
xx
x x x





Tính tổng
2018
1
k
k
Sb
?
A.
2017 1009
2018
1
2.
2
SC
B.
2018 1009
2018
1
2.
2
SC
C.
2018 1009
2018
2.SC
D.
2018 1009
2018
2 2 .SC
Câu 36: Có bao nhiêu hàm số
liên tục trên
0; 1
thỏa mãn điều kiện
1 1 1
2018 2019 2020
0 0 0
f x dx f x dx f x dx
A.
1
B.
2
C.
3
D.
4
Câu 37: Cho các hàm số
,fx
gx
liên tục trên
0;1 ,
thỏa
. . 1m f x n f x g x
với
,mn
là số thực khác
0
và
11
00
d d 1.f x x g x x

Tính
.mn
A.
0.mn
B.
1
.
2
mn
C.
1.mn
D.
2.mn
Câu 38: Có bao nhiêu số tự nhiên có
2018
chữ số sao cho trong mỗi số tổng các chữ số
bằng
5
?
A.
1 2 2 3 2 2 4
2017 2017 2017 2017 2016 2016 2017
1 4 2C C A C A C C
B.
1 2 2 3 2 2 4
2017 2017 2017 2017 2016 2016 2017
1 4 3C C A C A C C
C.
1 2 2 3 2 2 4
2017 2017 2017 2017 2016 2016 2017
1 4 2 4C C A C A C C
D.
1 2 2 3 2 2 4
2017 2017 2017 2017 2016 2016 2017
1 4 2 4 2C C A C A C C
Câu 39: Cho 2 số thực
,1xy
thỏa mãn điều kiện:
2 2 2
9
1 log 3 2 log 3 3 log 3 log 2
2
x
y y xy
.
Đặt
22
P x xy y
. Hỏi mệnh đề nào sau đây đúng?
A.
11;12P
B.
12;13P
C.
10;11P
D.
min 10P
Câu 40: Cho tứ diện đều
ABCD
có cạnh bằng
1
. Gọi
M
,
N
là hai điểm thay đổi lần lượt
thuộc cạnh
BC
,
BD
sao cho
AMN
luôn vuông góc với mặt phẳng
BCD
. Gọi
1
V
,
2
V
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của thể tích khối tứ diện
AB M N
. Tính
12
VV
.
A.
17 2
216
B.
17 2
72
C.
17 2
144
D.
2
12
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
8 | Chinh phục olympic toán Fanpage: Tạp chí và tư liệu toán học
LỜI GIẢI CHI TIẾT ĐỀ VẬN DỤNG CAO
LỜI GIẢI ĐƯỢC THỰC HIỆN BỞI
NHÓM CHINH PHỤC OLYMPIC TOÁN
Câu 1.
Ta có
11
.
.
22
cos
..
BA BC CA CB
BD CK
BD CK BD CK

2
.)
. . . .
4. . 4. .
BA CA BC CA BA BC
BA CA BA CB BC CA BC CB
BD CK BD CK

2
2
2
4. . 2. .
BC
BC
BD CK BDCK

Vì tam giác ABC vuông tại A nên
.0BA CA
Mặt khác
2 2 2 2 2 2
22
2. .
2 4 2 4
AM GM
AB BC AC AC BC AB
BDCK BD CK

2 2 2 2
22
5
4 4 4
AB AC BC BC
BC BC
2
2
4
cos
5
5
4
BC
BC
Dấu “=” xảy ra khi và chỉ khi BD = CK hay
ABC
vuông cân tại A88
Câu 2.
Đặt
,0t f x t
Dựa vào đồ thị ta thấy, với
01t
cho ta 4 giá trị của x.
Phương trënh trở thành:
2
4 16 4 4 16 16m m t t m m t t
Đặt
16 , 0u m t u
, ta có hệ phương trënh:
2
2
4 16 1
16 2
m u t
m t u


Từ (1) và (2) suy ra:
4 4 4 0 4 4 4 0u t u t u t do u t
. Khi đó:
2
4 16 16 16 * 0t m t t t m t
Xét hàm số
2
16 16f t t t
trên
0;
Để phương trënh đã cho có 8 nghiệm phân biệt thë phương trình (*) phải có 2 nghiệm
12
;tt
thỏa mãn:
12
0 1 4 0t t m
. Do m là số nguyên nên
3; 2; 1m
.
Câu 3.
Ta có
2
2 cos 3 sin cos 3 sin 1 1 2 sin .
26
x
x x x x
40 CÂU VẬN DỤNG CAO CÓ GIẢI CHI TIẾT
Fanpage: Tạp chí và tư liệu toán học Chinh phục olympic toán | 9
Do đó
22
2 sin 2sin 1.
66
y x x a

Đặt
sin ,
6
tx




vì
2
; 0;1
63
xt




Hàm số trở thành
2
2 2 2
11
2 2 1 2 .
22
y t t a t a



Vì
2
1 1 1 1 1
0 1 0
2 2 2 2 4
t t t



. Suy ra
2
2 2 2
1 1 1
2 1.
2 2 2
a t a a



2
2
2 2 2
2
1
321 1 321
1 3 3.
2
4 2 4
1
ma
m M a a a
Ma





Suy ra có
7
giá trị nguyên của thỏa.
Câu 4.
Ta có
2
22
22
22
1 1 1
2 1 1
11
1
n
nn
u
n n n n
n n n n
nn




Ta có
12
22
1 1 1 1 1 1 1 1 1 1
... 1 ...
2 3 3 7 7 13 13 21 1 1
n
u u u
n n n n



2
22
1 1 1
1
2 1 2 1
nn
n n n n



12
2
1
1
11
lim ... lim
11
22
1
n
n
u u u
nn

.
Câu 6.
Để đơn giản bài toán ta đặt
,,OA a OB b OC c
.Ta có công thức quen thuộc để tính bán
kính mặt cầu ngoại tiếp của tứ diện vuông là
2 2 2
1
2
R a b c
. Công việc còn lại ta sẽ đi
tính bán kính mặt cầu nội tiếp tứ diện này. Gọi T là tâm mặt cầu nội tiếp tứ diện OABC, ta
có
3
11
( ) .
33
OABC
OABC TOAB TOAC TOBC TABC OAB OAC OBC ABC tp
tp
V
V V V V V r S S S S r S r
S
Vậy tóm lại ta có
2 2 2
1
2
R a b c
và
3
OABC
tp
V
r
S
, do đó:
O
B
C
A
T
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
10 | Chinh phục olympic toán Fanpage: Tạp chí và tư liệu toán học
2 2 2 2 2 2 2 2 2
2 2 2
2 2 2
1
.
.
2
2
3
3
3.
6
tp
OABC
OABC
tp
a b c ab bc ca a b a c b c
S a b c
R a b c
V abc
rV
S


3 3 3
2 2 2 2 2 2 4 4 4
2 2 2 2 2 2 2 2 2
3 3 3
.
2
a b c a b c a b c
a b c ab bc ca a b a c b c
R
r abc abc



3 3 3
3 3 1
abc abc
abc
.
Vậy
2
3 1 3
R
r

. Dấu “=” xảy ra khi
a b c
Thay vào giả thiết thứ 2 ta tëm được
14
2 .2.2.2
63
OABC
a b c V
.
Câu 7.
Biến đổi giả thiết đầu tiên ta có
22
2 2 2 2
log 1 1 log 1 10 5 5 49a b a b a b a b a b
Giả thiết 2 tương đương
44
2
22
2 .2 .2 ln 2 4 4 5 16 2 ln 2 1 16
cd
cd
c d c d
c d cd c d c d


Theo bất đẳng thức AM – GM ta có
4
2 4 4
2 2 2 16
cd
cd
Mặt khác
2
ln 2 1 0 16c d VT
. Dấu “=” xảy ra khi
2cd
Ta sẽ sử dụng phương pháp hënh học cho bài này.
Xét đường tròn tâm
5; 5I
bán kính
7R
, và đường thẳng
: 2 0xy
. Gọi điểm
; , ;A a b B c d
. Ta có hình vẽ dưới đây.
40 CÂU VẬN DỤNG CAO CÓ GIẢI CHI TIẾT
Fanpage: Tạp chí và tư liệu toán học Chinh phục olympic toán | 11
Ta có
22
P a c b d AB
min
max min
0; 6 2 7
2 6 2 7
AB d R
AB AB R
Câu 8.
Đặt
22
21
21
1
ax
ab
bx


. Phương trënh trở thành:
2 2 2
4
33
ab
b a b

Ta có:
4 4 4 2
42
3
2 2 2 4 2
222
27 3 3
1
..
27
27
AM GM
a a a a a
aa
a b b b b
a b b

4 4 4
33
2 2 2 2 2
22222
16 16 16
2
2
2
3
3
AM GM
b b b
b a b a b
b a a b b







2
42
2
22
22
16 4
108 3 3.2
bb
bb
ab
ab
Cộng lại ta được
33VT VP
. Dấu “=” xảy ra khi
32
33
a b x
.
Vậy
33m
Câu 9.
Gọi
I
là trung điểm
BC
ta dễ dàng chứng minh được
BC MAI
MAI

Gọi
O AI
, ta có
O
là trực tâm
MNI
..AM AN AO AI
2.MN AO AI
Ta dễ dàng chứng minh được
O
là trọng tâm tam giác
ABC
2MN a
O
I
A
C
B
M
N
H
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
12 | Chinh phục olympic toán Fanpage: Tạp chí và tư liệu toán học
Vì
33
;
32
aa
AO AI
do tam giác
ABC
đều cạnh
a
.
Rõ ràng
;;MN AB MI BC NI BC
nên
1
. . . .
2
tp
S MN AB MI BC MN AC NI BC
1
2
2
a MN MI NI
vì
ABC
đều cạnh
a
.
Ta có
2
2 2 2
3
4
a
MI AM AI AM
. Nên theo ta có
3
. 2 . 3
2
5
a
AM
MI
Tương tự ta cũng có
3
. 2 . 3
2
5
a
AN
NI
. Do đó
1 2 3
2
25
5
tp
a
S a MN MN




Mà
2MN a
nên
2
2 2 5
2
tp
a
S
. Dấu bằng xảy ra khi
2
2
a
AM AN
Câu 10.
Từ giả thiết suy ra:
13.ab bc ca a b c
Áp dụng bất đẳng thức AM – GM ta có:
22
1
15 1 1 1 1 1 . 1
a
a b c a bc a
a
22
2
3 5 3 5
1 16 1 4 3 1 0
44
a a a a a a a a a

Đặt
22
3 5 3 5
;.
44
ki


Chứng minh tương tự thë ta cũng thu được
;i b c k
Từ đó suy ra:
32
3 2 2
32
2 3 2
2
01
1
1 13 13 5
1 13 .
2
a k b k c k k k a b c k ab bc ca
k k a b c ab bc ca k k ab bc ca
kk
ab bc ca k k k k ab bc ca
kk
Hoàn toàn tương tự với i:
13 5
0.
2
a i b i c i ab bc ca
Vậy
13 5
2
41.
13 5
2
M
Q MN
N
Câu 11.
Ta có
40 CÂU VẬN DỤNG CAO CÓ GIẢI CHI TIẾT
Fanpage: Tạp chí và tư liệu toán học Chinh phục olympic toán | 13
2018 2018 11 2029 2019 10 2009
2017 2017 11 2028 2018 2009
...
2009 2009 11 2020 2010 2009
2008 2008 11 2019 2009 2009
2007 2007 11 2018 2009 2009
2006 2006 11 2017 2009 2
f f f f f
f f f f f f
f f f f f f
f f f f f f
f f f f f f
f f f f f f
009
...
1 1 11 12 2009f f f f f
Do đó ta có
2018 2018 ... 1 2009 1 2018 4018f f f f f
Câu 12.
Gọi chiều cao 1 parapol là h. Ta có
2
93S cm R
. Xét thiết diện qua trục thẳng đứng
thì ta thấy parapol đi qua các điểm
0;0 , 3; 6 , 3;6
Nên
2
2
3
x
y 
Diện tích hình tròn qua thiết diện nằm ngang là
3
2
y
Thể tích phần phìa dưới của đồng hồ cát là
0
3 60
45
2
h
ydy h
Thể tích phần cát cần tìm
3
5
0
3
1,8
2
h
C
V ydy cm
Câu 13.
Ta có
1
tan
8
u
và
1
1
3
1
1
3
n
n
n
u
u
u
=
tan
6
1 tan
6
n
n
u
u
1
. Đặt
tan
nn
uv
khi đó
1
trở thành:
1
tan tan
6
tan tan
6
1 tan tan
6
n
nn
n
v
vv
v



1
6
nn
vv
Mà
1 1 1
tan 2 1 tan
88
u v v

.
Từ đó ta có
11
. . 1
8 6 8 6
nn
v v n d n v n
Hay
tan 1
86
n
un




Câu 14.
Từ giả thiết
' 0 0
' 0 . ' 2 0
' 2 0
f
ff
f

TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
14 | Chinh phục olympic toán Fanpage: Tạp chí và tư liệu toán học
Do đó từ
. ' 2
x
g x f x x x e
2 2 2
20
'2
0 0 2
00
'0
x
x
e
g
f
e
g
f


Tích phân từng phần ta được
2
2
0
0
. . ' dI f x g x g x f x x


22
00
2 . 2 0 . 0 2 d 2 d 4.
xx
f g f g x x e x x x e x

Câu 15.
Ta có
' ' 1 1f x f x f x f x C
0 1 42f f C C
1 42 1 42f x f x f x f x
11
00
1 d 42d 42f x f x x x



1
Vì
11
00
' ' 1 d 1 d .f x f x f x x f x x

2
Từ
1
và
2,
suy ra
11
00
d 1 d 21.f x x f x x

Câu 16.
Ta có
8 3 5 3
2 7 7
1 1 1
1
nn
n
x x x x
x x x
nên số hạng tổng quát của khai triển trên là
5 3 10 3 5 10k k h n h k h n k h
n n n n
T C x C x C C x
.
Số hạng này là số hạng tự do khi
3 5 10 0 3 5(2 )n k h n h k
.
Nếu
n
không chia hết cho
5
thì khai triển sẽ không chứa số hạng tự do, tức là số hạng tự
do là
0
. Còn khi
n
chia hết cho
5
thì khi
2
,
55
nn
hk
, số hạng tự do sẽ là
0
kh
nn
CC
,
không thỏa.
Câu 17.
Biến đổi giả thiết tương đương
log
11
log 1 log log 10 log 1 11log 0
10 10
x
m x x x m x x



2
10 log 1 log 10 log 0m x x x
.
Do
1;100 log 0 ;2xx
. Do đó ta có
2
2
10log log
10 log 1 log 10log 0 10
log 1
xx
m x x x m
x
Đặt
logtx
,
, xét hàm số
2
10
1
tt
ft
t
40 CÂU VẬN DỤNG CAO CÓ GIẢI CHI TIẾT
Fanpage: Tạp chí và tư liệu toán học Chinh phục olympic toán | 15
Ta có:
2
2
10 2
' 0 0 ; 2
1
tt
f t t
t

. Do đó
16
0 2 0
3
f f t f f t
Để
2
10log log
10
log 1
xx
m
x
đúng với mọi
1;100x
thì
16 8
10
3 15
mm
Do đó
8
;2018
15
m



hay có
2018
số thỏa mãn.
Câu 18.
Số cần tìm có dạng
1 2 3 4 1 2 3 4
i a a a a b b b b
. Ta có tổng các chữ số của số cần tìm là tổng các chữ
số từ 1 đến 8 bằng 36 chia hết cho 9 nên số cần tìm chia hết cho 9. Do 9 và 1111 có ước
chung lớn nhất là 1 nên theo giả thiết thì i chia hết cho 9999.
Đặt
1 2 3 4 1 2 3 4
,x a a a a y b b b b
. Ta có
4
.10 9999i x y x x y
chia hết cho 9999 từ đó suy
ra
xy
chia hết cho 9999.
Mặt khác
0 2.9999 9999x y x y
. Do đó
1 1 2 2 3 3 4 4
9a b a b a b a b
Từ các chữ số 1,2,3,4,5,6,7,8 có 4 cặp
1;8 , 2;7 , 3;6 , 4; 5
nên có 8 cách chọn
1
a
; 6 cách
chọn
2
a
; 4 cách chọn
3
a
và 2 cách chọn
1
a
tức chọn
k
a
có luôn
k
b
.
Vậy số các số thú vị là
8.6.4.2 384
số
Câu 19.
Xét hàm số
32
h x x ax b
Gọi m,n lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của
hx
trên đoạn
3; 2
.
Suy ra
48
9 27
m a b
n x b
hoặc
9 27
48
m x b
n a b
max ;
2
4 8 9 27 4 8 9 27
2
max
max
m n m n
y m n
a b a b a b a b
y

Vì
4 8 9 27 0a b a b
;
4 8 9 27 0a b a b
Vậy
0.
max
y
Dấu “=” xảy ra khi
7
0
36
0
mn
a
m
b
n


16
log log 36 2.
a
Tb
Câu 20.
Ta có
11
AB a A B a
. Gọi DK là đường cao của hình hộp
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
16 | Chinh phục olympic toán Fanpage: Tạp chí và tư liệu toán học
DH là đường cao của
11
A B CD
2
2
2.
a
DH a
a
.Khoảng cách giữa hai đường thẳng
1
AA
và CD bằng khoảng cách từ
1
D
đến
11
ABB A
. Từ A để đường cao AQ đến
1 1 1 1
A B C D
,
tách hình ra ta có
1
h
và
2
h
là hình chiếu từ K và Q đến
11
AB
, suy ra
1 2 1
h h D J x
. Đặt
khoảng cách từ Q đến
11
ABB A
là h.
Từ góc giữa
11
A B CD
và
0
1 1 1 1
1
60 ;DK AQ 3 .
2
A B C D KH DH a a
Ta có :
2
2 2 2 2
1
1 1 1 1 1
3h h AQ a
xa
2
2
3
3.
a x a
h
a x a


2
11
2
3
3
;.
3
aa
d K ABB A h
xa
a x a


Ta có
1 1 1
1
2
11
;
;
d D ABB A
DJ
x
ha
d K ABB A

1 1 1
2 2 2
2
33
;
42
3
ax ax
d D ABB A
a ax x
a x a


22
2
2
2
3 3 3 3
2
3
42
4 2 1 3
2 1 3
1
4
4
4
a a a a
a
aa
aa
a
xx
x x x
xa








Dấu bằng “=” xảy ra
21
4
2
ax
xa
x
3
1 1 1
. . 3 .4 . 4 3 .V DK D J A B a a a a
40 CÂU VẬN DỤNG CAO CÓ GIẢI CHI TIẾT
Fanpage: Tạp chí và tư liệu toán học Chinh phục olympic toán | 17
Câu 21.
Phương trënh tương đương với
3 3 3 3
2 sin sin 2 2 cos 2 2 cos 2 2 cos 2.x x x m x m x m
Xét hàm
3
2f t t t
với
0.t
Ta có
2
' 6 1 0f t t
ft
đồng biến.
Mà
3
sin 2 cos 2 ,f x f x m
suy ra
3
23
sin 0
sin 2 cos 2
sin 2 cos 2
x
x x m
x x m
23
sin 2 cos 2x x m
vì
2
sin 0, 0;
3
xx


2 3 3 2
1 cos 2 cos 2 2 cos cos 1.x x m m x x
Đặt
cosux
, vì
21
0; ;1 .
32
xu


Khi đó phương trënh trở thành
32
2 1.m u u
Xét
32
21g u u u
, có
2
1
0 ;1
2
' 6 2 ; ' 0 .
11
;1
32
u
g u u u g u
u




Lập bảng biến thiên suy ra phương trënh có 1 nghiệm khi
28
4
27
m
4; 3; 2 .m
Câu 22.
Theo tính chất đường phân giác ta có
3
2 3 0
2
IB AB
IB IM
IM AM
Và
3
4 3 0
4
DB AB
DB DC
DC AC
Vậy ta có
2 3 0
4 3 0
IB IM
DB D C


2 3 5
4 3 7
AB AM AI
AB AC AD


4 6 10
4 3 7
AB AM AI
AB AC AD


Suy ra
3 6 7 10AC AM AD AI
7 10 0AD AI
10
7
AD
AI

.
Câu 23.
Đặt , ta đi chứng minh
22
a 3 x
a b 1
b x 2


2
1 1 1
1 a 1 1 b 1 VP
2 b a



TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
18 | Chinh phục olympic toán Fanpage: Tạp chí và tư liệu toán học
Câu 24.
Với các số thực
,,a b c
làm cho phương trënh
2
0ax bx c
có hai nghiệm thuộc
0; 1
.
Suy ra
0a
. Gọi hai nghiệm đó là
12
,xx
, theo định lì Viet ta được
12
12
.
b
xx
a
c
xx
a

Ta có
2
1 2 1 2
1 2 1 2
2
12
(2 ) 1 2
( ) 1
1
bb
a b a b
a b a b x x x x
aa
a
T
a b c b c
a a b c x x x x
a a a




22
22
1 2 1 2 1 2 1 2
1 2 1 2
1 2 1 2 1 2 1 2
21
2.
11
x x x x x x x x
x x x x
x x x x x x x x
Không mất tính tổng quát ta có thể giả sử
12
01xx
,
Suy ra
2
1 1 2
2 2 2
1 2 1 2 1 2 1 1 2 1 2
2
2
11
1
x x x
x x x x x x x x x x x
x
Suy ra
2 2 2 2 2 2
1 2 1 2 1 2 1 2 1 2 1 2
2 2 2
1 2 1 2 1 2 1 1 2 1 2
1.
11
x x x x x x x x x x x x
x x x x x x x x x x x
Suy ra
2 1 3T
. Vậy
max
3T
, dấu “=” xảy ra khi
12
1.xx
Nếu hàm số
()y f x
là hàm số lẻ trên đoạn
; , 0a a a
và có giá trị lớn nhất và giá trị
nhỏ nhất thì
; 0; ;a a a a a
max f x max f x min f x


Câu 25.
2
2
22
2
11
1 a 1 1 b 1
ba
1 1 1 1
a b b a
1 1 a b a b
2 2 2 2
22
a b b a ab b a









2
22
33
AM GM
2
2
22
3
2
AM GM
66
22
6
6
ba
3a 3b
ab
44
2
ab b a
ab
6 ab
66
44
4 2 2 2 17 12 2
ab
16 ab
ab
16
2
























40 CÂU VẬN DỤNG CAO CÓ GIẢI CHI TIẾT
Fanpage: Tạp chí và tư liệu toán học Chinh phục olympic toán | 19
Ta có
87
10 9
n A A
.
Gọi
A
là tập hợp các số
a
có 8 chữ số khác nhau chia hết cho
45
.
Khi đó
a
chia hết cho
5
và
9
(tổng các chữ số chia hết cho
9
và số hàng đơn vị bằng
0
hoặc
5
).
Trường hợp 1:
a
có hàng đơn vị bằng
0
;
7
chữ số còn lại có chữ số
9
và
3
trong
4
bộ số
1; 8
,
2;7
,
3;6
,
4;5
, có
4.7!
số.
Trường hợp 2:
a
có hàng đơn vị bằng
5
;
7
chữ số còn lại có chữ số
4
và
3
trong
4
bộ số
0;9
,
1; 8
,
2;7
,
3;6
.
Không có bộ
0;9
, có
7!
số.
Có bộ
0;9
, có
2
3
7! 6!C
số
2
3
4.7! 7! 6!n A C
số
2
3
87
10 9
4.7! 7! 6!
53
2268
C
PA
AA

.
Câu 26.
Đặt
2
22
2
log
2 2 2 6 6 4 0
log
ax
x y xy x y
by
Yêu cầu của bài toán trở thành
2
2
8
log
3
5 3 1 1 5 3
32
4
log
x
y
ab
P P a b a b a P b P P
ab
xy


Đến đây thế a theo b và P thay vào phương trënh trên ta được một phương trënh bậc 2, sử
dụng điều kiện có nghiệm ta sẽ suy ra kết quả của bài toán!
Ta được
27 8 6 27 8 6
minP ,max
23 23
P


.
Câu 27.
Ta có một tính chất cơ bản của hàm trị tuyệt đối
max ;
22
a b a b
ab


Áp dụng ta có
22
2
2 2 2
max 1 ; 2 1
22
x x y x x y
x x y
Sử dụng bất đẳng thức trị tuyệt đối ta có
22
22
2 2 2
2 2 2 2
21
2 2 2 2
x x y x x y
xx
x

Mặt khác theo bất đẳng thức Cauchy – Schwarz ta có
2
22
2
2 2 2 2
2
2
xy
xy
x y x y


Vậy
2VT VP
. Dấu “=” xảy ta khi và chỉ khi
1xy
.
Khi đó
24P
có tất cả 8 ước số nguyên dương.
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
20 | Chinh phục olympic toán Fanpage: Tạp chí và tư liệu toán học
Câu 28.
Đặt
1 1 5 5
,a b x a b y
, mà
51
4a a d
và
21
a a d
nên
41
2
3
3
.
44
xy
aa
a

Tương tự
ta tình được
3
2
xy
a
và
4
3
.
4
xy
a
Lập luận tương tự với CSN, ta cũng có
33
44
2 3 4
,,b x y b xy b xy
. Theo bất đẳng thức
Cô-si thì
33
44
3 3 2 2 4 4
33
, , .
2 4 4
x y x y x y
a xy b a x y b a xy b
Do đó, cả i), ii) va iii) đều đúng. Tuy nhiên, điêu kiên iv) không luôn đúng, chẳng hạn khi
xy
thì
0d
nhưng
1.q
Câu 29.
+ Dựng mặt phẳng (P) chứa AB và song song CD cắt
1
,OR
theo giao tuyến là đường tròn
tâm I.
+ Dựng mặt phẳng (Q) chứa CD và song song AB cắt
2
,OR
theo giao tuyến là đường
tròn tâm J.
+ Lần lượt dựng 2 đường kính
,A B C D
vuông góc nhau.
Khi đó,
,,IJ d AB CD d A B C D

Ta có:
11
. . , .sin , . .
66
ABCD A B C D
V ABCD d AB CD AB CD A B C D IJ V
. Do đó chỉ cần xét
các tứ diện dạng
A B C D
.
Vậy điều kiện cần để
ABCD
V
lớn nhất là
AB CD
. Gọi M, N lần lượt là trung điểm của AB
và CD.
Đặt
, . 0, 10 , 0,2AM x CN y x y
2 2 2 2
10 ; 4 ; , 10 4ON x OM y d AB CD MN OM ON x y
.
Khi đó:
2 2 2 2
1 1 2
. . , 2 .2 10 4 10 4
6 6 3
ABCD
V ABCD d AB CD x y x y xy x y
40 CÂU VẬN DỤNG CAO CÓ GIẢI CHI TIẾT
Fanpage: Tạp chí và tư liệu toán học Chinh phục olympic toán | 21
Ta có:
22
22
2 10 2 10
2 1. 4 2 1 4
3 2 3 2
ABCD
xx
V xy y xy y








22
2 3 2 3 2
18 2 18 2 2 3 9 2
3 2 3 2 3
ABCD
V xy x y xy xy xy xy
3
2
2
92
4 8 8
22
3 9 2 9 2
9 3 3 3
22
ABCD
xy xy
xy
xy xy
V xy xy xy






3
2
89
72 6 2
33
ABCD ABCD
VV



. Vậy
max
6 2.V
Dấu “=” xảy ra khi:
2
2
10
4
2
6
1
2
3
92
2
x
y
x
y
xy
xy



.
Câu 30.
Từ giả thiết của bài toán ta có:
7
'2
SA SC SB SD SB SD
SA SC SB SD SB SD


(1)
Trải phẳng 4 mặt bên của hình chóp và ghép lại sao cho thu được một nủa lục giác đều với
cạnh SA tách thành SA và SA’ và đặt vào hệ Oxy(hình vẽ)
G
A'
E
D
C
B
A
S
B'
C'
D'
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
22 | Chinh phục olympic toán Fanpage: Tạp chí và tư liệu toán học
Khi đó ta có:
'
1
1 1 2
0;0 ; 0;1 ; 0; 1 ; 0; ; 0; ; ;0 ;
2 2 3
S A A A A C



và
2
' ; ; ; ; ; 0;
2
B a a D b b a b




.
1 1 7 7 4 4 2
1
7
22
ab
a b a b
Chu vi cần A’B’C’D’ là
'
1
c A B B C C D D A

2 2 2 2
2 2 2 2
1 2 1 2
2 3 2 3
c a a a a b b b b
2 2 2 2
2 2 2 2
1 1 2 2
2 2 3 3
c a a b b a a b b
2
22
2
4
1 ( ) min 1.79
3
c a b a b a b a b c



Dấu “=” xảy ra khi
22
7
ab
//B D BD

.
Câu 31.
Trung điểm đoạn nối 2 điểm cực trị là điểm uốn của đồ thị hàm số, có tọa độ
;
33
bb
y
aa







. Theo Viet ta có
1 2 3
1 2 3
0
1
1
33
b
x x x
a
x x x
b
x
a
Thế
3 1 2
1x x x
vào giả thiết thứ 2 ta được
2
1 2 1 2 1 2 1 2 1 2
22
1 1 2 2 2
3 4 5 5 5 44 44 1
48 16 3 4 45 54 25 0
x x x x x x x x x x
x x x x x
Ta có
1
2
2
176 3 1 0
x
x
vậy
. Dấu “=” xảy ra khi
1 2 3
1 1 1
;;
2 3 6
x x x
Câu 32.
Dễ dàng tëm được
12
0;0 , 4;0 , 2; 1 , 2; 4A B I I b a
với
40ba
(vì tứ giác
12
I A I B
lồi). Khi đó tứ giác
12
I A I B
có hai đường chéo vuông góc nên
12
12
11
. 4. 1 4 2 1 4 10 4 4.
22
I AI B
S AB I I b a b a b a
Ta có
2
1
4 1 4 4
4
h x f x g x a x a x a



nên tọa độ đỉnh
I
là
41
2
1
1
2
2; 3 .3.4 6.
4
2
2 4 1 8 2 4 4 3
I
IAB
I
a
x
a
IS
y h a a a




Câu 33.
40 CÂU VẬN DỤNG CAO CÓ GIẢI CHI TIẾT
Fanpage: Tạp chí và tư liệu toán học Chinh phục olympic toán | 23
Ta có
3 2 2
' 3 2f x ax bx cx d f x ax bx c
. Hàm số đạt cực trị tại
0; 2xx
và
đồ thị đi qua điểm
1;0 , 0;2
nên ta có
32
' 0 0
1
' 2 0
3
32
0
10
2
02
f
a
f
b
f x x x
c
f
d
f





Ta có
32
22
32g x mx nx p mx nx p
. Hệ số tự do bằng
32
32pp
. Đồ thị
hàm số
gx
đi qua điểm
0;0
nên
32
3 2 0 1p p p
. Đồ thị hàm số
2
g x f mx nx p
có trục đối xứng
1
2
x 
nên đồ thị hàm số
2
y mx nx p
cũng có
trục đối xứng
11
2 2 2
n
x m n
m
.
Đồ thị hàm số
gx
đi qua điểm
2; 2
nên
32
1
2 0 2 1 3 2 1 2 2
1
2
mn
g g x m m
mn

Do đồ thị có hướng quay lên trên nên ta suy ra
01m m n p
Câu 34.
Phương trënh tương đương với
1
2
3
28
2
x
mx
. Hàm số
1
2
3
28
2
x
f x x
là một
hàm số chẵn do đó ta chỉ cần xét trên nửa khoảng
0;
để suy ra bảng biến thiên của
hàm số
fx
trên cả tập số thực.
Xét hàm số
2
1
1
1
2
21
1
3
2 8 2
2 ln 2 3 2
3
2
2 8 '
2
3 2 ln 2 3 0 0 2
2 8 0 2
2
x
x
x
x
x
x
x
g x x x
f x x f x
x x x
x


Ta có
1 2 2
' 2 ln 3 8ln 2 3 0, 2, 2 8ln 2 6 0, 3 16 ln 2 9 0
x
g x x x g g
nên
phương trënh
0gx
có nghiệm
0
2; 3x
.
Vẽ bảng biến thiên cho hàm số
fx
ta suy ra được phương trënh có đúng 2 nghiệm thực
khi và chỉ khi
0
2
1
0
0
6
7,8,..., 2018
3
28
2
x
m
m
x
m f x

Câu 35.
Đặt
2018
2
22
,
1
xx
fx
x




ta có
2018
0 1 2018
0 ... 2 .f a b b
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
24 | Chinh phục olympic toán Fanpage: Tạp chí và tư liệu toán học
Suy ra
2018
0
2aS
1
Lại có
2018
2018
2 2018
2018
0
1
11
1
k
k
k
f x x C x
x



1008 2018
2 2018
2018
2018
2018 2
0 1009
1.
1
k
k
k
k
kk
C
Cx
x


Suy ra
0 1 1007 1008
1 3 2017 2 4 2018 2018 2018 2018 2018
... 0 ... ...b b b S b b b C C C C
1009 1010 2017 2018 1009
0 2018 2018 2018 2018 2018
...a C C C C C S
(vì
k n k
nn
CC
).
2
Từ
1
và
2,
suy ra
2017 1009
2018
1
2.
2
SC
Câu 36.
Từ điều kiện ta suy ra
1
2018 2 2018 2
0
1 0 1 0f x f x dx f x f x
Mà
fx
liên tục trên
0; 1
nên
1
0
fx
fx
. Vậy có 2 hàm thỏa mãn yêu cầu đề bài.
Câu 37.
Từ giả thiết
. . 1m f x n f x g x
, lấy tích phân hai vế ta được :
Do
11
00
d d 1f x x g x x

11
00
. . 1 ( )dm f x n f x dx g x x



1
0
1 d 1 1m n f x x
Xét tích phân
1
0
1 d .f x x
Đặt
1tx
, suy ra
d d .tx
Đổi cận:
01
10
xt
xt
Khi đó
1 0 1 1
0 1 0 0
1 d d d d 1.f x x f t t f t t f x x
2
Từ
1
và
2,
suy ra
1mn
.
Câu 38.
Vì
5 4 1 3 2 2 2 1 3 1 1 2 1 1 1 1 1 1 1 1
nên ta có các trường hợp
sau:
Trường hợp 1: Số tự nhiên có một chữ số
5
đứng đầu và
2017
số
0
đứng sau: Có
1
số.
Trường hợp 2: Số tự nhiên có một chữ số
4
, một chữ số
1
và
2016
số
0
.
+ Khả năng 1: Nếu số
4
đứng đầu thì số
1
đứng ở một trong
2017
vị trí còn lại nên ta có
1
2017
C
số.
+ Khả năng 2: Nếu số
1
đứng đầu thì số
4
đứng ở một trong
2017
vị trí còn lại nên ta có
40 CÂU VẬN DỤNG CAO CÓ GIẢI CHI TIẾT
Fanpage: Tạp chí và tư liệu toán học Chinh phục olympic toán | 25
1
2017
C
số.
Trường hợp 3: Số tự nhiên có một chữ số
3
, một chữ số
2
và
2016
số
0
+ Khả năng 1: Nếu số
3
đứng đầu thì số
2
đứng ở một trong
2017
vị trí còn lại nên ta có
1
2017
C
số.
+ Khả năng 2: Nếu số
2
đứng đầu thì số
3
đứng ở một trong
2017
vị trí còn lại nên ta có
1
2017
C
số.
Trường hợp 4: Số tự nhiên có hai chữ số
2
, một chữ số
1
và
2015
số
0
+ Khả năng 1: Nếu số
2
đứng đầu thì số
1
và số
2
còn lại đứng ở hai trong
2017
vị trí còn
lại nên ta có
2
2017
A
số.
+ Khả năng 2: Nếu số
1
đứng đầu thì hai chữ số
2
đứng ở hai trong
2017
vị trí còn lại nên
ta có
2
2017
C
số.
Trường hợp 5: Số tự nhiên có
2
chữ số
1
, một chữ số
3
thë tương tự như trường
hợp
4
ta có
22
2017 2017
AC
số.
Trường hợp 6: Số tự nhiên có một chữ số
2
, ba chữ số
1
và
2014
số
0
.
+ Khả năng 1: Nếu số
2
đứng đầu thì ba chữ số
1
đứng ở ba trong
2017
vị trí còn lại nên
ta có
3
2017
C
số.
+ Khả năng 2: Nếu số
1
đứng đầu và số
2
đứng ở vị trí mà không có số
1
nào khác đứng
trước nó thì hai số
1
còn lại đứng ở trong
2016
vị trí còn lại nên ta có
2
2016
C
số.
+ Khả năng 3: Nếu số
1
đứng đầu và số
2
đứng ở vị trì mà đứng trước nó có hai số
1
thì
hai số
1
và
2
còn lại đứng ở trong
2016
vị trí còn lại nên ta có
2
2016
A
số.
Trường hợp 7: Số tự nhiên có năm chữ số
1
và
2013
số
0
, vì chữ số
1
đứng đầu
nên bốn chữ số
1
còn lại đứng ở bốn trong
2017
vị trí còn lại nên ta có
4
2017
C
số.
Áp dụng quy tắc cộng ta có
1 2 2 3 2 2 4
2017 2017 2017 2017 2016 2016 2017
1 4 2C C A C A C C
số cần
tìm.
Câu 39. Biến đổi giả thiết ta được:
2 2 2
2 2 2 2 2 2
9
1 log 3 2 log 3 3 log 3 log 2
2
89
log log log 3 2 log 3 log log
32
x
y y xy
x x y y x
xy
Ta nhận thấy rằng
2 2 2
8
log log 3 log 3
3
xy
xy
.
Để đơn giản ta đặt
2
2
2
log
log 3
8
log
3
xa
yb
c
xy
Lúc này ta có 2 giả thiết
3
9
2
2
a b c
a ab abc
.
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
26 | Chinh phục olympic toán Fanpage: Tạp chí và tư liệu toán học
Thế
3b a c
vào giả thiết dưới ta được:
22
9
2 1 2 5 4 0
2
c a c c a
Coi vế trái là tam thức bậc 2 theo biến a với c là tham số ta có:
2
2
22
2 5 4 18 2 1 2 1 4 2c c c c c c
Chú ý với điều kiện
,1xy
ta sẽ có
, , 0a b c
. Mặt khác
33a b c c
Suy ra
0
, điều này đồng nghĩa
0VT
Dấu “=” xảy ra khi và chỉ khi
2
2
2
33
log
22
22
1 log 3 1
2
1 8 1
3
log
2 3 2
ax
x
by
y
c
xy




Từ đây suy ra
76 12 2
9
P
.
Câu 40.
Gọi
H
là tâm tam giác
BCD
, ta có
AH BCD
, mà
AMN BCD
nên
AH AMN
hay
MN
luôn đi qua
H
.
Ta có
3
3
BH
22
AH AB BH
16
1
33
.
Thể tích khối chóp
AB MN
là
1
..
3
BMN
V AH S
1 6 1
. . . .sin 60
332
BM BN
2
.
12
BM BN
.
Do
MN
luôn đi qua
H
và
M
chạy trên
BC
nên
.BM B N
lớn nhất khi
MC
hoặc
ND
khi đó
1
2
24
V
.
.BM B N
nhỏ nhất khi
//MN CD
khi
2
3
BM BN
2
2
27
V
. Vậy
12
17 2
216
VV
.
| 1/26
| | Tải xuống

Có thể bạn quan tâm:

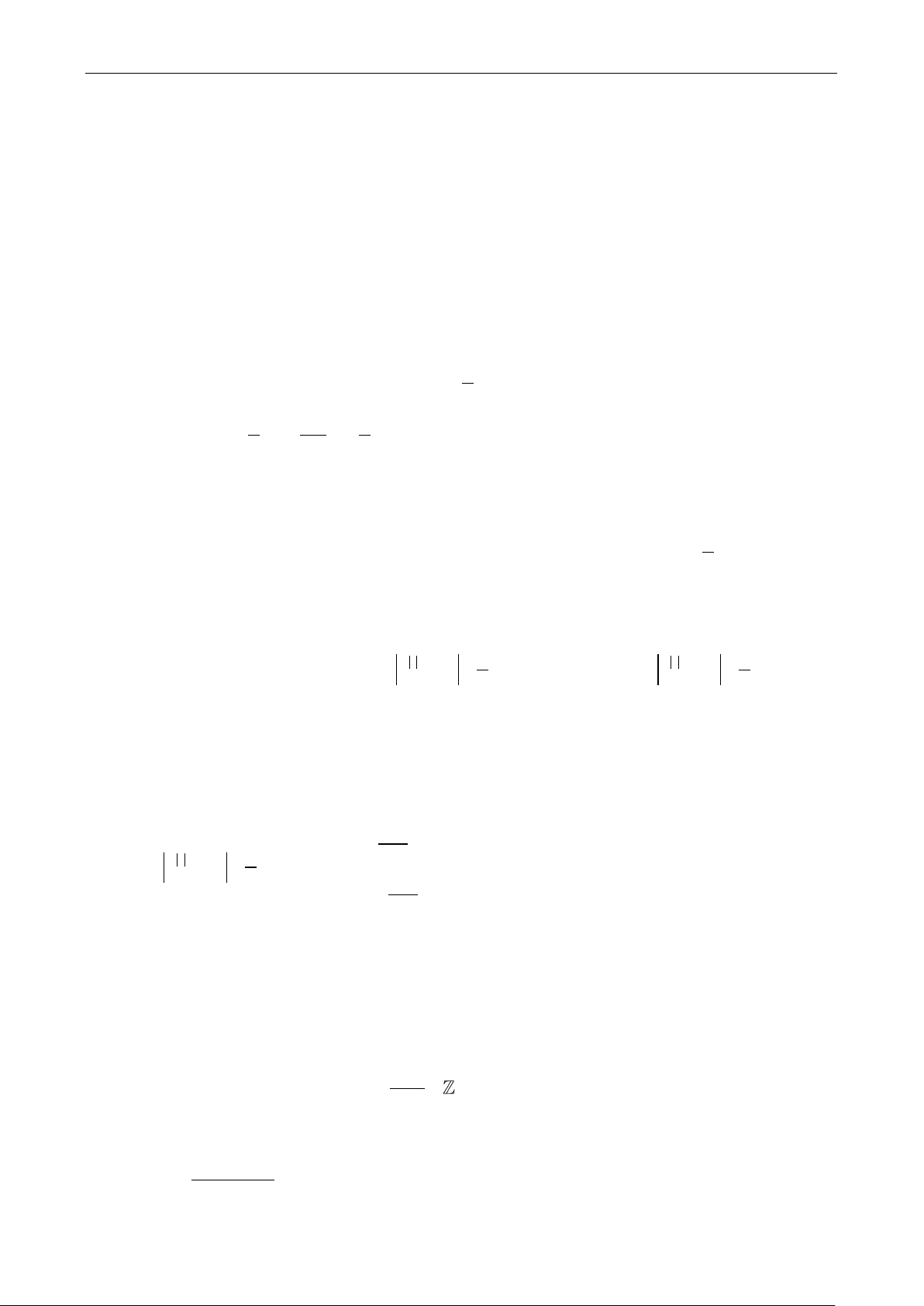
Preview text:


ĐỀ ÔN LUYỆN CÁC NHÓM CÂU HỎI
VẬN DỤNG CAO TRONG ĐỀ THI THPT QUỐC GIA
Đề thi gồm 40 câu trắc nghiệm
Thời gian làm bài 180 phút Good Luck!
Câu 1: Cho tam giác ABC vuông tại A. Gọi  là góc giữa hai đường trung tuyến BD và CK.
Giá trị nhỏ nhất của cos bằng? A. 4 B. 5 C. 4 D. 3 5 4 3 4
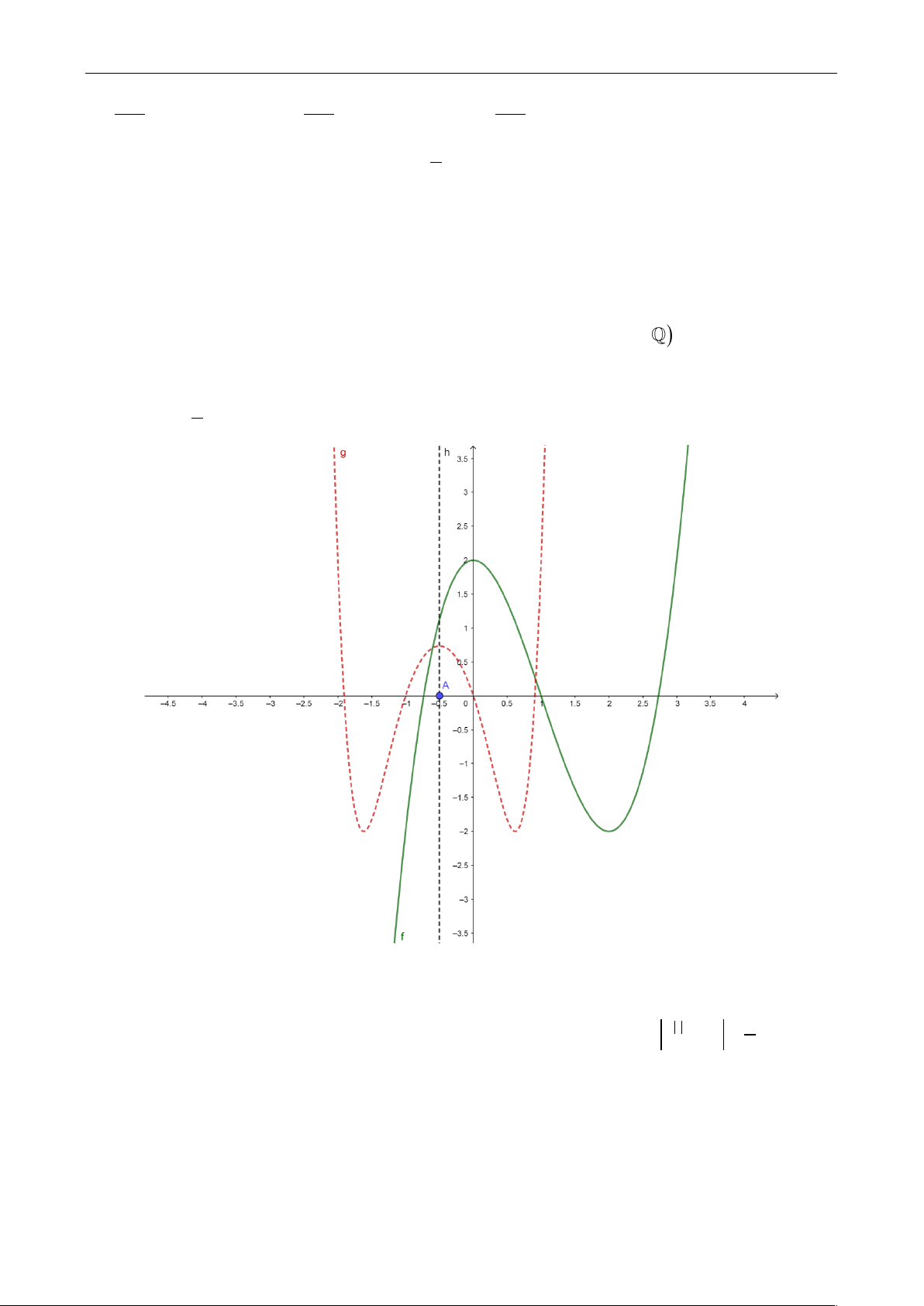
Câu 2: Cho hàm số y f x có đồ thị như hënh vẽ. Hỏi có tất cả bao nhiêu giá trị m
nguyên để phương trënh sau có 8 nghiệm phân biệt: m  4 m  16 f x  4 f x  0 A. 3 B. 2 C. 4 D. 0 Câu 3: Cho hàm số   2  2  x  2
y  2 sin x   2 cos  3 sin x     
a (với là tham số). Gọi m, M  6   2 
lần lượt là giá trị nhỏ nhất, giá trị lớn nhất của hàm số trên đoạn  2 ; .  Có bao nhiêu 6 3   
giá trị nguyên của a để 2 321 m M  ? 4 A. 3. B. 4. C. 6. D. 7.
Câu 4: Cho dãy số  n
u như sau: u
,n  1 , 2 ,... Tính giới hạn của tổng n n 2 4 1  n n
lim u u  ... u . 1 2 n x
Fanpage: Tạp chí và tư liệu toán học
Chinh phục olympic toán | 1
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN A. 1 B. 1. C. 1 D. 1 4 2 3
Câu 5: Cho hàm số f x 4
ax   a b   2 2
1 x  8a  4b có max f x  f  3
  . Giá trị lớn của ;0 hàm số  1 
f x trên đoạn ; 3  là? 2    A. 4 B. 5
C. 4  25a
D. 5  25a
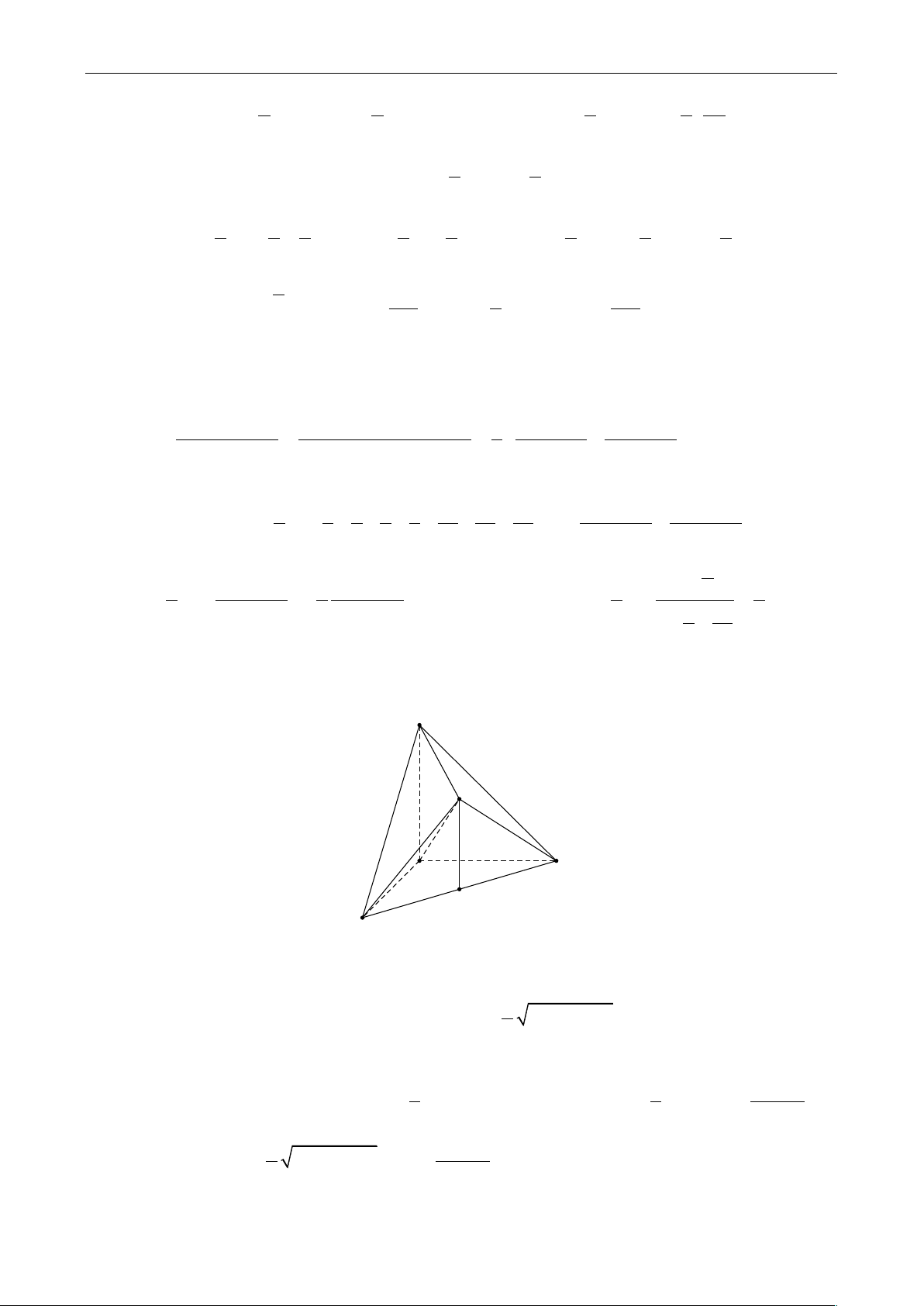
Câu 6: Cho tứ diện vuông O.ABC, gọi R và r lần lượt là bán kính mặt cầu ngoại tiếp và nội
tiếp của tứ diện. Biết rằng 3
R r 1 3 và 2 2
2OC  3OA  6OB  10 . Tính V ? 2 OABC A. 2 B. 4 C. 5 D. 1 3 3 3 3
Câu 7: Cho 4 số thực a,b,c,d sao cho c d  0 đồng thời thỏa mãn log  2 2
1  a b   1 log a b   4 
2c.2d.2cd  ln   2 2
c d  2cd  4c  4d  5  16
Gọi M và m lần lượt là GTNN và GTLN của biểu thức    2    2 P a c b d . Tính giá trị
của S M n ? A. 6 2 B. 8 2 C. 10 2 D. 12 2 4 1  x 2 x  1
Câu 8: Gọi a;b là tập hợp các giá trị của m để phương trënh   m . Với x 1  x
giá trị nào của m thì bất phương trënh luôn đúng?
A. m  3 3
B. m  2 5
C. m  5
D. m  4
Câu 9: Cho tam giác ABC đều cạnh a ,trên đường thẳng d vuông góc với mặt phẳng
ABC tại A lấy điểm M bất kỳ khác A . Gọi H là trực tâm tam giác MBC , biết rằng
đường thẳng  vuông góc với mặt phẳng MBC tại H luôn cắt đường thẳng d tại N
Tìm giá trị nhỏ nhất của diện tích toàn phần tứ diện MNBC . 2 a 2 2  5 2 a 2 5  2  2 a 2  5 2 a 5 2  A. B. C. D. 2 2 2 2  abc  1
Câu 10: Cho ba số thực dương a,b,c thoả mãn  . Gọi M,N lần lượt a  1 
b  1c  1  15
là giá trị nhỏ nhất và giá trị lớn nhất của P ab bc ca . Tính giá trị biểu thức: Q MN A. 1. B. 41. C. 15. D. 65. x  10 khi x  2018 Câu 11: Cho hàm số 
f x  
. Tính giá trị f 1  f 2018 . f
  f x  11 khi x   2018 A. 1999 B. 2009 C. 4018 D. 4036
Câu 12: Một chiếc đồng hồ cát có thiết diện qua trục là 2 parapol đối xứng qua mặt nằm
ngang. Khi để thẳng đứng và cát không chảy thë nó như hënh vẽ ( phần màu xanh là cát),
2 | Chinh phục olympic toán
Fanpage: Tạp chí và tư liệu toán học
40 CÂU VẬN DỤNG CAO CÓ GIẢI CHI TIẾT
và mực cát của parapol ở trên là 1 chiều cao của parapol ở trên. Khi lật ngược đồng hồ cát 5
thë lưu lượng cát chảy từ trên xuống dưới không đổi là 3
3cm /phút. Khi chiều cao ở trên là
6cm thì bề mặt trên tạo thành 1 đường tròn có diện tích 2
9cm . Biết sau 900s thì cát không
còn chảy nữa. Hỏi khi lượng cát chảy xuống dưới bằng chiều cao của parapol thì thể tích
cát của phần parapol ở trên là bao nhiêu (coi lượng cát đang chảy không đáng kể). A. 14 B. 13,05 C. 12,75 D. 13,6 u  2  1 1 
Câu 13: Tìm số hạng tổng quát của dãy số u biết n   3u n 1 u   n1 3   un A.         u  tan   n B. u  tan   n n  1 n  1 8 6      3 6      C.     u  tan   n D. u  tan   n n  1 n  1 2 3      4 7 
Câu 14: Cho hai hàm số f x và gx có đạo hàm liên tục trên 0;2, thỏa mãn 2
f '0. f '2  0 và  . '     2 x g x f x x x
e . Tính tích phân I f
 x.g'xd .x 0
A. I  4.
B. I  4.
C. I e  2.
D. I  2  .e
Câu 15: Cho hàm số f x xác định và liên tục trên 0;1, thỏa mãn f 'x  f '1 x với 1
mọi x 0;1. Biết rằng f 0  1, f 1  41. Tính tích phân I f  xd .x 0
A. I  41.
B. I  21.
C. I  41.
D. I  42.
Câu 16: Với n là số nguyên dương và  1 1 n
x  0 , xét khai triển Newton 8 3 x x    . Hỏi 2 7 x x   
có bao nhiêu số n  2018 sao cho khai triển của biểu thức trên có số hạng tự do là 0 ?
Fanpage: Tạp chí và tư liệu toán học
Chinh phục olympic toán | 3
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN A. 1009 B. 403 C. 1615 D. 625
Câu 17: Có bao nhiêu số nguyên dương m trong đoạn  2018 
; 2018 sao cho bất phương 11 log x trënh sau đúng với mọi  log x
x 1 ;100:  xm 10 10 10  10 . A. 2018 B. 4026 C. 2013 D. 4036
Câu 18: Một số tự nhiên được gọi là số thú vị nếu số này có 8 chữ số đôi một khác nhau
được lập thành tự tập 1;2;...; 
8 và số đó chia hết cho 1111. Hỏi có bao nhiêu số tự nhiên thú vị như thế? A. 384 B. 385 C. 386 D. 387
Câu 19: Cho hàm số 3 2
x ax b , gọi M là giá trị lớn nhất của hàm số trên đoạn 3;2.
Khi M đạt giá trị nhỏ nhất thì T  log có giá trị là ?  b a 1 A. 0 B. 4026 C. 2 D. 1 2
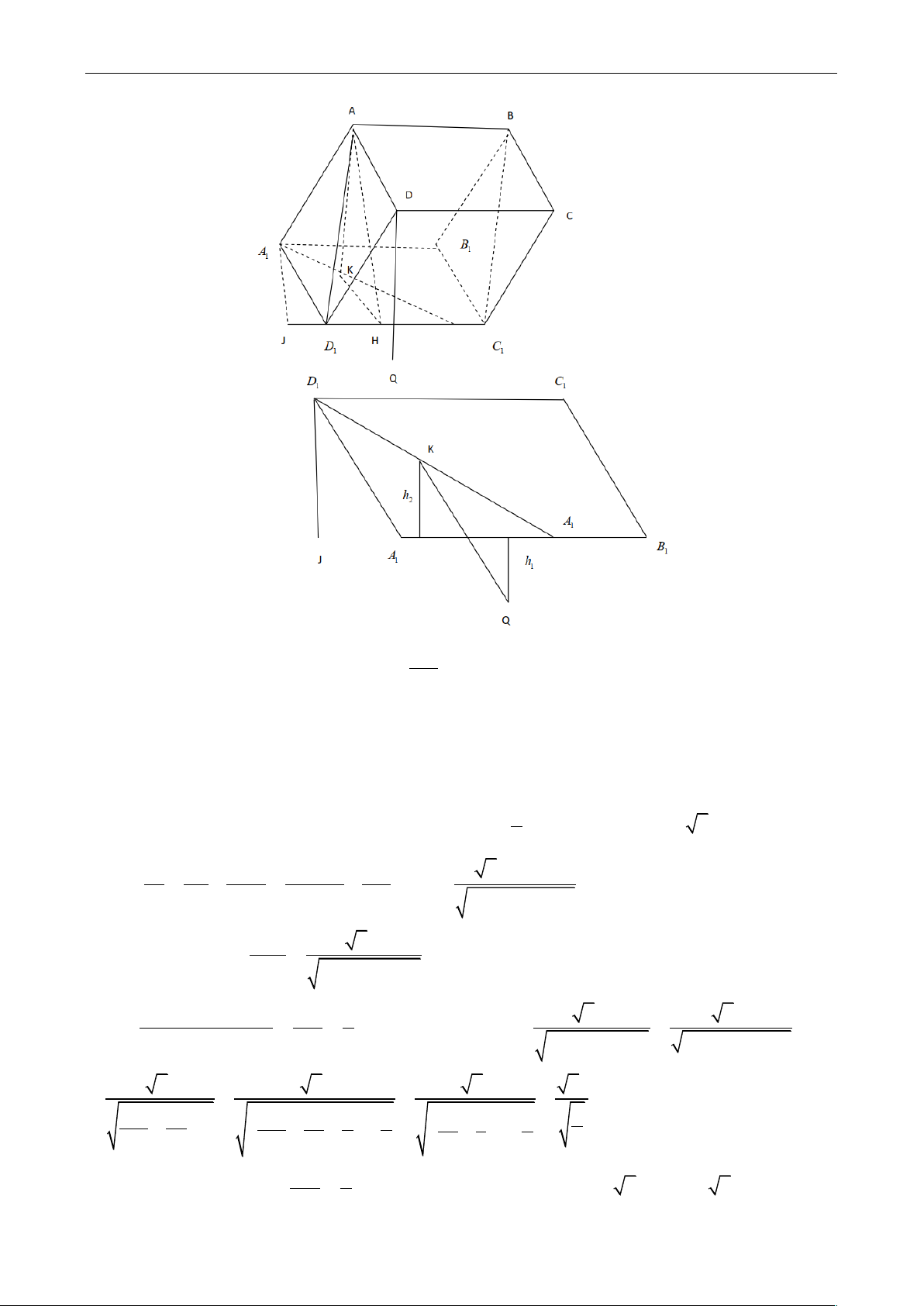
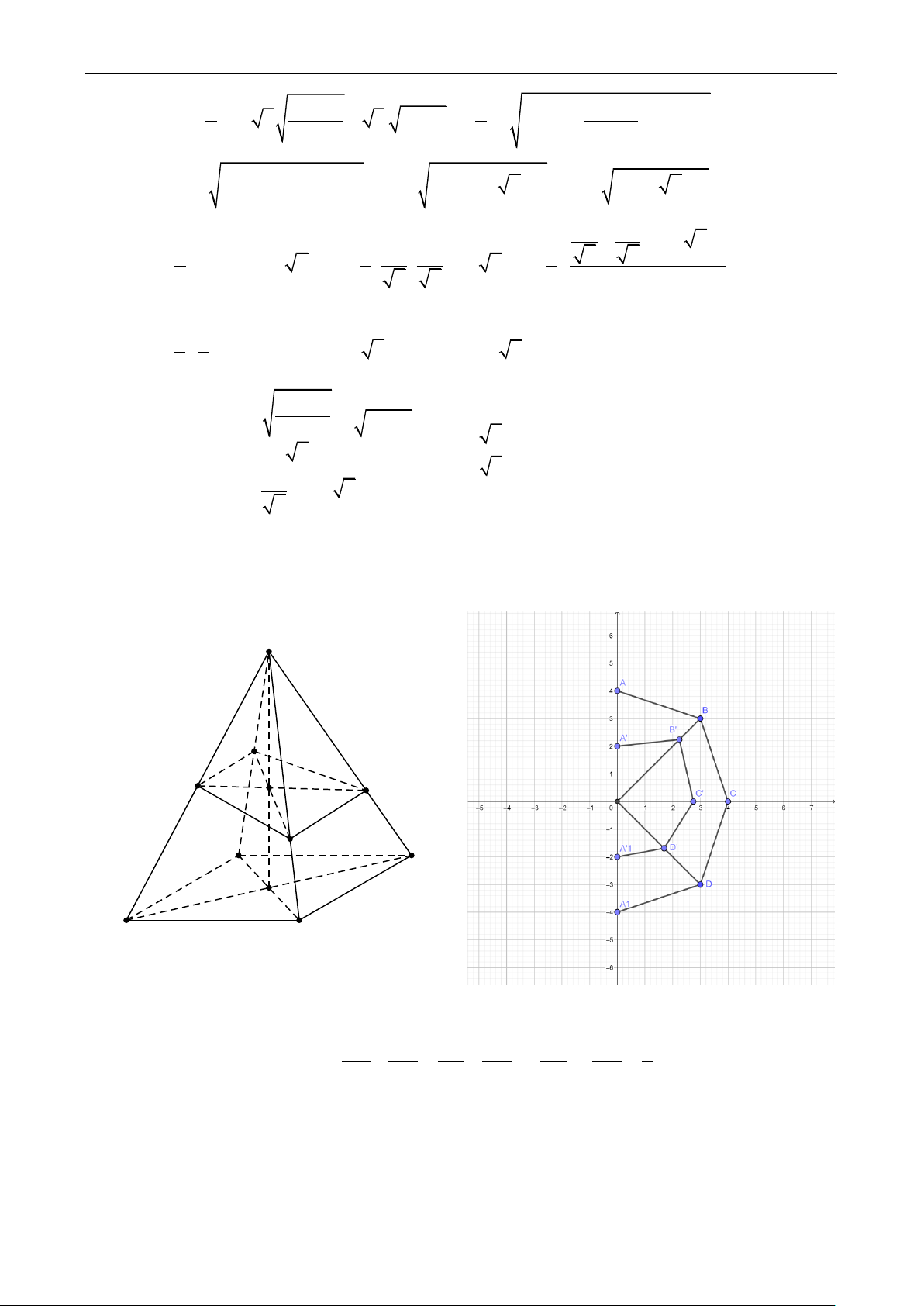
Câu 20 : Cho hình hộp ABC .
D A'B'C 'D' có cạnh AB a và diện tích tứ giác A B CD là 2 2a 1 1
Mặt phẳng A B CD tạo với mặt phẳng đáy 1 góc 0
60 . Khoảng cách giữa hai đường thẳng 1 1
AA và CD là P. Khi P max , tìm thể tích của khối hộp biết hình chiếu của đỉnh A thuộc 1 1
miền giữa hai đường thẳng AB và CD A. 3 4 3a B. 3 6 7a C. 3 2 7a D. 3 3 7a
Câu 21: Có bao nhiêu giá trị nguyên của tham số m để phương trënh: x   x  
3 x m   3 3 sin 2 cos 2 2 2 cos
1 2 cos x m  2  3 2 cos x m  2
Có đúng một nghiệm thuộc  2  0;  ?  3  A. 1. B. 2. C. 3. D. 4.
Câu 22: Cho tam giác ABC có AB  3 , AC  4 . Phân giác trong AD của góc BAC cắt
trung tuyến BM tại I . Tính tỉ số AD . AI A. 13 B. 11 C. 10 D. 10 8 6 7 5
Câu 23: Cho bất phương trënh sau        x  2       x  2 2 2 1 1 1 3 1 1 2 1  m  .  x  2   3  x
Biết rằng với m;aba,b  0 
thì bất phương trënh trên luôn đúng với mọi x. Khi
đó tổng S a b có giá trị bằng bao nhiêu? A. 301 B. 302 C. 304 D. 305
4 | Chinh phục olympic toán
Fanpage: Tạp chí và tư liệu toán học
40 CÂU VẬN DỤNG CAO CÓ GIẢI CHI TIẾT
Câu 24: Xét các số thực a,b,c sao cho phương trënh 2
ax bx c  0 có hai nghiệm thuộc 
ab2a b
0;1 . Giá trị lớn nhất của biểu thức T  là
aa b cA. 3 35 8 T  3. B. T  . C. T  . D. T max max 2 max 8 max 3
Câu 25: Gọi A là tập hợp tất cả các số tự nhiên có tám chữ số đôi một khác nhau. Chọn
ngẫu nhiên một số thuộc A , tính xác suất để số tự nhiên được chọn chia hết cho 45. A. 53 B. 54 C. 56 D. 1 2268 2267 2263 41
Câu 26: Cho các số thực x,y thỏa mãn 2 2 2
log x  log y  log xy  6log xy  4  0 . Gọi M,m 2 2 2 2
lần lượt là max và min của biểu thức 8x P  log . Tính M.n? 32 y xy A. 15 B. 14 C. 16 D. 17 23 23 23 23 
Câu 27: Cho 2 số thực x y
x  1, y  0 thỏa mãn điều kiện max x  1 ; 2x y  1  2 2  . 2 2 x y
Hỏi biểu thức P  x   2 3
1 x  2y  1 có tất cả bao nhiêu ước số nguyên dương? A. 5 B. 6 C. 7 D. 8
Câu 28: Cho các số a , a , a , a , a  0 lập thành cấp số cộng với công sai d và 1 2 3 4 5
b ,b ,b ,b ,b  0 lập thành cấp số nhân với công bội q . Biết rằng a b và a b . Hỏi 1 2 3 4 5 1 1 5 5
có bao nhiêu khẳng định luôn đúng trong các khẳng định sau? i) a b ii) a b iii) a b iv) d q 2 2 3 3 4 4 A. 1 B. 2 C. 3 D. 4
Câu 29: Cho hai hình cầu đồng tâm O0,0,0 , bán kính R  2, R  10 . Tứ diện ABCD 1 2
có A,BO,R ; C,DO,R . Tìm giá trị lớn nhất của thể tích tứ diện ABCD. 1   2  A. 6 3 B. 6 2 C. 4 2 D. 4 3
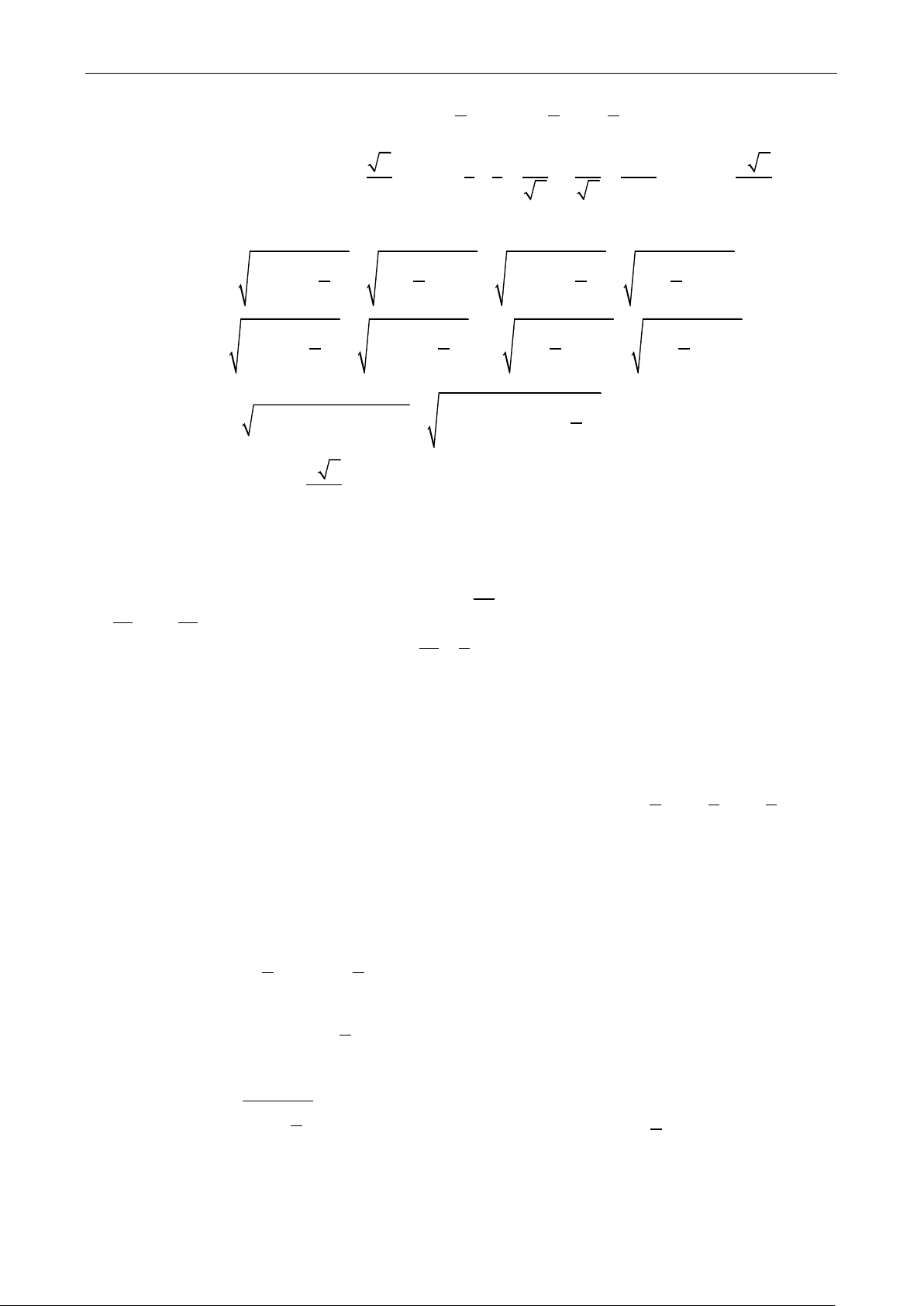
Câu 30: Cho hình chóp tứ giác đều S.ABCD có cạnh bên bằng 1, các mặt bên là các tam
giác có góc ở đỉnh S bằng 0 SC
45 . Cho A’ là trung điểm SA, C’ thuộc cạnh SC sao cho 3  SC 2
. Mặt phẳng (P) đi qua A’, C’ cắt các cạnh SB, SD lần lượt tại B’, D’. Số nào gần với giá trị
nhỏ nhất của chu vi tứ giác A’B’C’D’ . A. 1.79 B. 3.3 C. 2.05 D. 1.3 Câu 31: Cho hàm số 3 2
y ax bx cx d có đồ thị C . Biết rằng C cắt trục hoành tại 3
điểm phân biệt có hoành độ x x x  0 và trung điểm nối 2 điểm cực trị của C có 1 2 3 hoành độ 1
x  . Biết rằng 3x  4x  5x 2  44 x x x x x x . Hãy tính tổng 1 2 3  1 2 2 3 3 1 0 3 2 3
S x x x ? 1 2 3
Fanpage: Tạp chí và tư liệu toán học
Chinh phục olympic toán | 5
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN A. 137 B. 45 C. 133 D. 1 216 157 216
Câu 32: Cho các Parabol P  : y f x 1 2
x x, P  : y gx 2
ax  4ax b a  0 có các 1 2   4
đỉnh lần lượt là I , I . Gọi A, B là giao điểm của P và Ox . Biết rằng 4 điểm A, B, I , I 1  1 2 1 2
tạo thành tứ giác lồi có diện tích bằng 10.Tính diện tích S của tam giác IAB với I là đỉnh
của Parabol P : y hx  f x  gx.
A. S  4
B. S  6
C. S  7
D. S  9
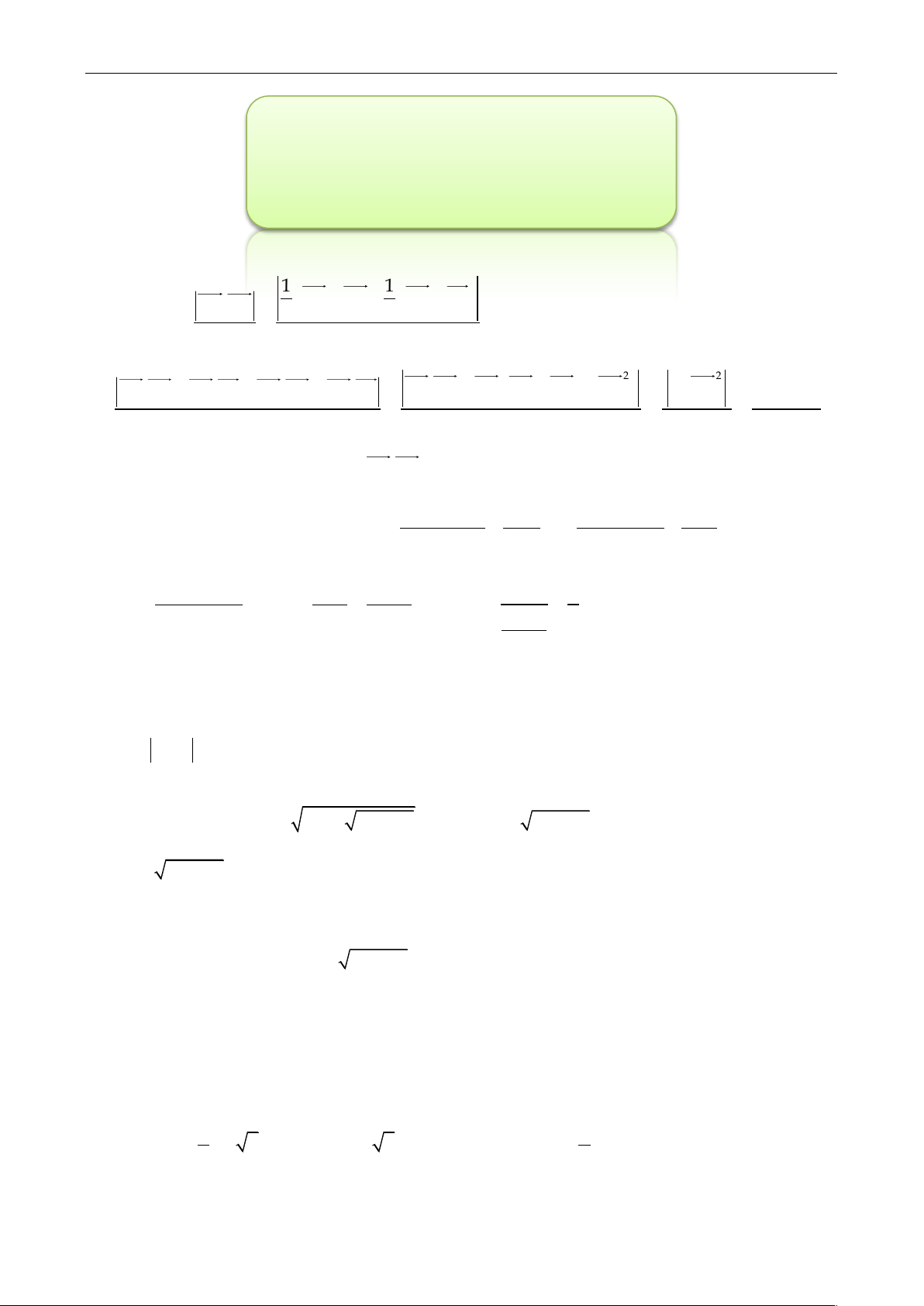
Câu 33: Cho hàm số bậc ba f x và gx  f  2
mx nx pm,n, p  có đồ thị như hënh
dưới, trong đó đường nét liền là đồ thị hàm f x, đồ thị hàm nét đứt là đồ thị hàm gx , đường 1
x   là trục đối xứng hàm g x . 2
Giá trị của biểu thức P  n mm pp  2n bằng bao nhiêu? A. 6 B. 24 C. 12 D. 16
Câu 34: Có bao nhiêu số nguyên x  3 m 20
 18;2018 để phương trënh 1 2 2
 8  x m có 2
đúng 2 nghiệm thực phân biệt? A. 2013 B. 2012 C. 4024 D. 2014
Câu 35: Với x  1 ta có khai triển sau:
6 | Chinh phục olympic toán
Fanpage: Tạp chí và tư liệu toán học
40 CÂU VẬN DỤNG CAO CÓ GIẢI CHI TIẾT 2018 2
x  2x  2  2 2018 b b b b 1 2 3 2018  
a a x a x  ... a x     ... 0 1 2 2018  x  1 
x  1 x  12 x  13 x  12018 2018
Tính tổng S  b ? k k1 A. 2017 1 1009 1 S  2  C . B. 2018 1009 S  2  C . C. 2018 1009 S  2 C . D. 2018 1009 S  2  2C . 2018 2 2018 2 2018 2018
Câu 36: Có bao nhiêu hàm số y f x liên tục trên 0;1 thỏa mãn điều kiện
1  f x2018 1
dx   f x2019 1 dx   
  f x2020 dx 0 0 0 A. 1 B. 2 C. 3 D. 4
Câu 37: Cho các hàm số f x , gx liên tục trên 0;1, thỏa .
m f x  .
n f 1  x  g x 1 1
với m, n là số thực khác 0 và f
 xdx g
 xdx  1. Tính m .n 0 0
A. m n  0. B. 1
m n  .
C. m n  1.
D. m n  2. 2
Câu 38: Có bao nhiêu số tự nhiên có 2018 chữ số sao cho trong mỗi số tổng các chữ số bằng 5 ? A. 1 1  4C  2 2 2 CA    3 2 2 CAC  4  C 2017 2017 2017 2017 2016 2016 2017 B. 1 1  4C  3 2 2 CA    3 2 2 CAC  4  C 2017 2017 2017 2017 2016 2016 2017 C. 1 1  4C  2 2 2 CA   4 3 2 2 CAC  4  C 2017 2017 2017 2017 2016 2016 2017 D. 1 1  4C  2 2 2 CA  4 3 2 2 CAC  4  2C 2017 2017 2017 2017 2016 2016 2017
Câu 39: Cho 2 số thực x, y  1 thỏa mãn điều kiện: 9
1  log 3y  2 log 3y 3  log 3xy  log 2 . 2 2  2  2 x Đặt 2 2
P x xy y . Hỏi mệnh đề nào sau đây đúng?
A. P 11;12
B. P 12;13
C. P 10;11 D. min P  10
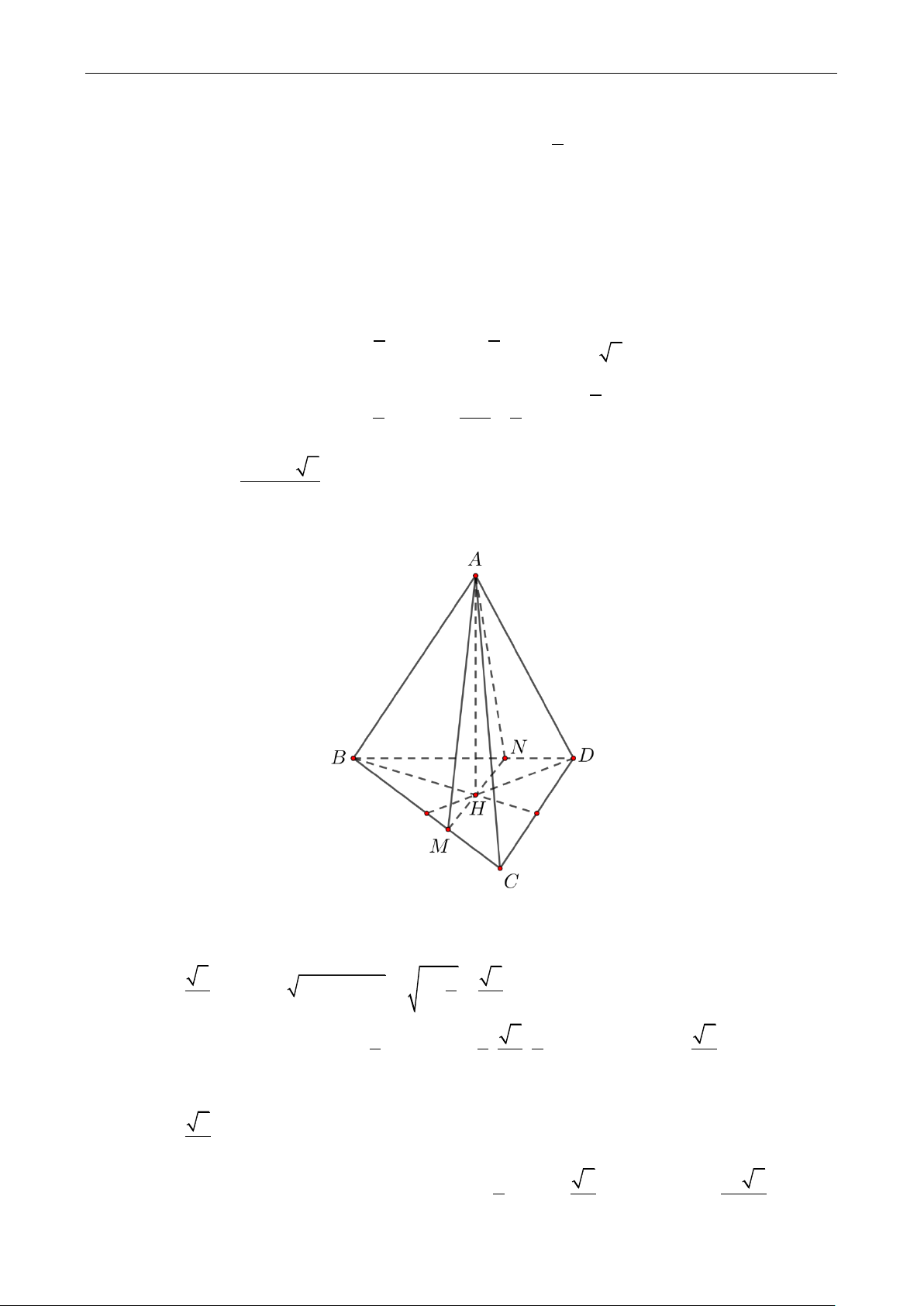
Câu 40: Cho tứ diện đều ABCD có cạnh bằng 1 . Gọi M , N là hai điểm thay đổi lần lượt
thuộc cạnh BC , BD sao cho AMN  luôn vuông góc với mặt phẳng BCD. Gọi V , V 1 2
lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của thể tích khối tứ diện ABMN . Tính V V . 1 2 A. 17 2 B. 17 2 C. 17 2 D. 2 216 72 144 12
Fanpage: Tạp chí và tư liệu toán học
Chinh phục olympic toán | 7
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
LỜI GIẢI CHI TIẾT ĐỀ VẬN DỤNG CAO
LỜI GIẢI ĐƯỢC THỰC HIỆN BỞI
NHÓM CHINH PHỤC OLYMPIC TOÁN Câu 1.
1 BABC 1. . CACB BD CK  Ta có 2 2 cos    . BD CK . BD CK 2 . BA CA  .
BA CB BC.CA BC.CB
BA CA BC CA BA 2 .  BC ) 2  BC 2   BC   4. . BD CK 4. . BD CK 4. . BD CK 2. . BD CK
Vì tam giác ABC vuông tại A nên . BA CA  0 AMGM 2 2 2 2 2 2       Mặt khác 2 2 AB BC AC AC BC AB 2.B .
DCK BD CK          2 4   2 4  2 2 2 2  2 2 AB AC 2 BC 5BCBC 4 BC   BC    cos   4 4 4 2 5BC 5 4
Dấu “=” xảy ra khi và chỉ khi BD = CK hay ABC vuông cân tại A88 Câu 2.
Đặt t f x ,t  0
Dựa vào đồ thị ta thấy, với 0  t  1 cho ta 4 giá trị của x. Phương trënh trở thành: 2
m  4 m  16t  4t m  4 m  16t  16t 2
m  4u  16t 1
Đặt u m  16t ,u  0 , ta có hệ phương trënh:  2
m  16t u  2
Từ (1) và (2) suy ra: u  4t4  u  4t  0  u  4t do 4  u  4t  0 . Khi đó: 2
4t m  16t  16t  16t m*t  0
Xét hàm số f t 2
 16t  16t trên 0;
Để phương trënh đã cho có 8 nghiệm phân biệt thë phương trình (*) phải có 2 nghiệm t ;t 1 2
thỏa mãn: 0  t t  1  4  m  0 . Do m là số nguyên nên m 3  ; 2  ;  1 . 1 2 Câu 3. Ta có     2 x  2 cos
 3 sin x  cos x  3 sin x  1  1  2 sin x     .  2   6 
8 | Chinh phục olympic toán
Fanpage: Tạp chí và tư liệu toán học
40 CÂU VẬN DỤNG CAO CÓ GIẢI CHI TIẾT Do đó          2  2  2 
y  2 sin x   2 sin x   a     
1. Đặt t  sin x    , vì x  ;  t 0;  1  6   6   6  6 3    2 Hàm số trở thành 2 2  1  2 1
y  2t  2t a  1  2 t   a    .  2  2 2 2 Vì 1 1 1  1  1 1  1  1
0  t  1    t    0  t   . Suy ra 2 2 2
a   2 t
a   a    1. 2 2 2 2    4 2  2  2  2 1 2 m a  2 321  2 1   
2  m M   a     2a   321 1   3  a  3. 2 4   2  4 M a   1
Suy ra có 7 giá trị nguyên của thỏa. Câu 4. Ta có n n 1  1 1  u     n   
1  n 2  n
 2n n1 2 2 2 n n  1 2 2
2  n n  1 n n  1  Ta có 1  1 1 1 1 1 1 1 1 1 
u u  ...  u  1        ...  1 2 n 2 2 2  3 3 7 7 13 13 21 n n 1 n n 1       1 2  1  1  1 n n 1  1 n 1 1   
 lim u u ... u   . n lim 1 2  2  2 2 
n n  1  2 n n  1 2 1 1 2 1   2 n n Câu 6. A T C O B
Để đơn giản bài toán ta đặt OA a,OB b,OC c .Ta có công thức quen thuộc để tính bán
kính mặt cầu ngoại tiếp của tứ diện vuông là 1 2 2 2 R
a b c . Công việc còn lại ta sẽ đi 2
tính bán kính mặt cầu nội tiếp tứ diện này. Gọi T là tâm mặt cầu nội tiếp tứ diện OABC, ta có 1 1 3V VVVVVr(SSSS )  r. OABC S r OABC TOAB TOAC TOBC TABC 3 OAB OAC OBC ABC 3 tp Stp Vậy tóm lại ta có 1 2 2 2 V R
a b c và 3 OABC r  , do đó: 2 Stp
Fanpage: Tạp chí và tư liệu toán học
Chinh phục olympic toán | 9
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN 2 2 2 1
a b c . 2
ab bc ca a b a c b c R
a b c S
a b c tp .  2 2 2 2 2 2 2 2 2 2 2 2  2    r 3V V abc OABC 3 OABC 3. S 6 tp  
a b c . ab bc ca a b a c b c a b c a b c a b c 2R   3 2 2 2 3 2 2 2 3 4 4 4 2 2 2 2 2 2 2 2 2 3 3 3       r abc abc 3 3abc  3abc   3 3 1. abc
Vậy 2R  31 3. Dấu “=” xảy ra khi a b c r
Thay vào giả thiết thứ 2 ta tëm được 1 4
a b c  2  V   . OABC .2.2.2 6 3 Câu 7.
Biến đổi giả thiết đầu tiên ta có
  a b    ab  a b   ab  a 2 b 2 2 2 2 2 log 1 1 log 1 10 5 5  49
Giả thiết 2 tương đương 4            4 cd c d c d cd c d cd c d  
  c d  2 2 2 2 .2 .2 ln 2 4 4 5 16 2 ln 2  1  16 4
Theo bất đẳng thức AM – GM ta có cdcd 2 4 4 2  2  2  16
Mặt khác  c d  2 ln
2  1  0 VT  16 . Dấu “=” xảy ra khi c d  2 
Ta sẽ sử dụng phương pháp hënh học cho bài này.
Xét đường tròn tâm I 5;5 bán kính R  7 , và đường thẳng  : x y  2  0 . Gọi điểm
Aa;b ,Bc;d . Ta có hình vẽ dưới đây.
10 | Chinh phục olympic toán
Fanpage: Tạp chí và tư liệu toán học
40 CÂU VẬN DỤNG CAO CÓ GIẢI CHI TIẾT
AB d 0;  R  6 2 7 min  
Ta có    2    2 P a c
b d AB   AB
AB  2R  6 2  7 max min Câu 8.
a  2x  1 Đặt 2 2 a 4b
a  2b  1. Phương trënh trở thành:   3 3  2 2 2 b  1  x b a b Ta có: 4 AMGM 4 4 2 a a a a 4 a 2     27a   3 3a 2 2 2 a .b .b    3 4 2 2 2 2 1 b b a b b 27 27 4 AMGM 4 4 16b 16b 16b   2 2b  2 2 a b  2 2 a b  3 3 2 2 2 2 2
 2b a a b b   2      3  3    2 16b 4 4b 2     108b   3 3.2b 2 2 2 2 2 a   b a b
Cộng lại ta được VT  3 3  VP . Dấu “=” xảy ra khi 3 2 a b   x  . 3 3 Vậy m  3 3 Câu 9. M A C H O I N B
BC  MAI
Gọi I là trung điểm BC ta dễ dàng chứng minh được 
  MAI
Gọi O   AI , ta có O là trực tâm MNI AM.AN AO.AI MN  2 . AO AI
Ta dễ dàng chứng minh được O là trọng tâm tam giác ABC MN a 2
Fanpage: Tạp chí và tư liệu toán học
Chinh phục olympic toán | 11
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN Vì a 3 a 3 AO  ; AI
do tam giác ABC đều cạnh a. 3 2
Rõ ràng MN AB; MI BC;NI BC nên 1 1 S
MN AB MI BC MN AC NI BC a2MN MI NI vì ABC đều cạnh a . tp  . . . .  2 2 a 3 2 AM. 2  . 3 Ta có 2 2 2 3a
MI AM AI AM  . Nên theo ta có 2 MI  4 5 a 3 AN. 2  . 3   Tương tự ta cũng có 2 a NI  . Do đó 1 2 3
S aMN MNtp 2  5 2  5 5    2 a 2 2  5 Mà a
MN a 2 nên S  . Dấu bằng xảy ra khi 2 AM AN tp 2 2 Câu 10.
Từ giả thiết suy ra: ab bc ca a b c  13.
Áp dụng bất đẳng thức AM – GM ta có:
            2 a  a b c a bc   a  2 1 15 1 1 1 1 1 . 1 a 2 2   
a a  12 3 5 3 5
 16a a a  1  4 a a  3 a  1  0   a 4 4   2   2 3 5 3 5 Đặt k  ;i
. Chứng minh tương tự thë ta cũng thu được i b;c k 4 4 Từ đó suy ra:
a kb kc k 3 2
 0  1  k k a b c  k ab bc ca 3 2
 1  k k a b c ab bc ca   2
k k ab bc ca 3 2    
ab bc ca 2 k k  3 2 1 k 13k 13 5
 1  k  13k ab bc ca   . 2 k k 2
Hoàn toàn tương tự với i:  
a ib ic i 13 5
 0  ab bc ca  . 2  13  5 M  Vậy  2 
Q MN  41.  13  5 N   2 Câu 11. Ta có
12 | Chinh phục olympic toán
Fanpage: Tạp chí và tư liệu toán học
40 CÂU VẬN DỤNG CAO CÓ GIẢI CHI TIẾT
f 2018  f f 2018  11  f f 2029  2019  10  2009
f 2017  f f 2017  11  f f 2028  f 2018  2009 ...
f 2009  f f 2009  11  f f 2020  f 2010  2009
f 2008  f f 2008  11  f f 2019  f 2009  2009
f 2007  f f 2007  11  f f 2018  f 2009  2009
f 2006  f f 2006  11  f f 2017  f 2009  2009 ...
f 1  f f 1  11  f f 12  2009
Do đó ta có f 2018  f 2018  ...  f 1  2009  f 1  f 2018  4018 Câu 12.
Gọi chiều cao 1 parapol là h. Ta có 2 S  9 cm
R  3 . Xét thiết diện qua trục thẳng đứng
thì ta thấy parapol đi qua các điểm 0;0,3;6, 3  ;6 2 Nên 2xy
 Diện tích hình tròn qua thiết diện nằm ngang là 3 y 3 2
Thể tích phần phìa dưới của đồng hồ cát là h 3 60 
ydy  45  h  0 2  h
Thể tích phần cát cần tìm 3 V   ydy cm C 1,8   3 5  0 2 Câu 13. 1 u   n u n tan Ta có  u  tan và 3 u  =
6 1 . Đặt u
v khi đó 1 trở thành: n tan 1 8 n1 1  n 1  u 1  tan u 3 n 6 n  tan v n tan 6     tan v     v    v   v n tan 1 n  6   n 1 n 1 tan tan v   6 6 n Mà  
u  tan v  2  1  tan  v  . 1 1 1 8 8 Từ đó ta có     v          v n d n v n n . . n 1 1 1   8 6 8 6 Hay     u  tan   n n  1 8 6    Câu 14.  f '0  0
Từ giả thiết f '0.f '2  0    f '  2  0
Fanpage: Tạp chí và tư liệu toán học
Chinh phục olympic toán | 13
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN x     e g 2 2 2 2    f   0 ' 2
Do đó từ  . '     2 x g x f x x x e   x    e g 0 00 2    f    0 ' 0 2
Tích phân từng phần ta được I   f
 x.g x 2   g
 x.f 'xdx 0 0 2 2
 2. 2  0. 0    2 xd    2 x f g f g x x e x x x e dx  4. 0 0 Câu 15.
Ta có f 'x  f '1 x  f x   f 1 x C f 0   f 1 C C  42 1 1
f x   f 1 x  42  f x  f 1 x  42   f
 x f 1xdx  42dx  42   1 0 0 1 1
Vì f 'x  f '1 x  f
 xdx f
 1xd .x 2 0 0 1 1
Từ 1 và 2 , suy ra f
 xdx f
 1xdx  21. 0 0 Câu 16. n n Ta có  8 3 1 1    x x      5  x n 3 1 1  x  
nên số hạng tổng quát của khai triển trên là 2 7 7 x x x      k 5k
h 3n10h k
h 3n5k10h
T C x C xC C x . n n n n
Số hạng này là số hạng tự do khi 3n  5k  10h  0  3n  5(2h k) .
Nếu n không chia hết cho 5 thì khai triển sẽ không chứa số hạng tự do, tức là số hạng tự do là n n
0 . Còn khi n chia hết cho 5 thì khi 2 h
, k  , số hạng tự do sẽ là k h C C  0 , 5 5 n n không thỏa. Câu 17.
Biến đổi giả thiết tương đương  log x m   x   11 log 1 
log x  log x  10mlog x  1  11log x    0  10  10  mx   2 10 log
1  log x  10log x  0 .
Do x 1;100  log x0 ;2 . Do đó ta có 2  mx   2 10log x log x 10 log
1  log x  10log x  0  10m  log x  1 2 Đặt 10t t
t  log x , t 0 ;2 , xét hàm số f t  t  1
14 | Chinh phục olympic toán
Fanpage: Tạp chí và tư liệu toán học
40 CÂU VẬN DỤNG CAO CÓ GIẢI CHI TIẾT 2 Ta có:    t 10 2t t f '   0 t
  0 ;2 . Do đó f    f t  f     f t 16 0 2 0  2   t 1 3 2 Để
10log x  log x 10m
đúng với mọi x 1;100 thì 16 8 10m   m  log x  1 3 15 Do đó  8  m ;2018 
hay có 2018 số thỏa mãn. 15    Câu 18.
Số cần tìm có dạng i a a a a b b b b . Ta có tổng các chữ số của số cần tìm là tổng các chữ 1 2 3 4 1 2 3 4
số từ 1 đến 8 bằng 36 chia hết cho 9 nên số cần tìm chia hết cho 9. Do 9 và 1111 có ước
chung lớn nhất là 1 nên theo giả thiết thì i chia hết cho 9999.
Đặt x a a a a , y b b b b . Ta có 4
i x.10  y  9999x x y chia hết cho 9999 từ đó suy 1 2 3 4 1 2 3 4
ra x y chia hết cho 9999.
Mặt khác 0  x y  2.9999  x y  9999 . Do đó a b a b a b a b  9 1 1 2 2 3 3 4 4
Từ các chữ số 1,2,3,4,5,6,7,8 có 4 cặp 1;8,2;7,3;6,4;5 nên có 8 cách chọn a ; 6 cách 1
chọn a ; 4 cách chọn a và 2 cách chọn a tức chọn a có luôn b . 2 3 1 k k
Vậy số các số thú vị là 8.6.4.2  384 số Câu 19. Xét hàm số   3 2
h x x ax b
Gọi m,n lần lượt là giá trị nhỏ nhất và giá trị lớn nhất của hx trên đoạn 3;2 .
m  4a b  8
m  9x b  27 Suy ra  hoặc 
n  9x b  27 
n  4a b  8 
m n m n ym n max max ;  2
4a b  8  9a b  27  4a b  8  9a b  27 ymax 2
Vì 4a b  8  9a b  27  0 ; 4a b  8  9a b  27  0 m n  a  7 Vậy y
 Dấu “=” xảy ra khi m  0   T  log    b a log 36 2. max 0.  1 6  b  36  n   0 Câu 20.
Ta có AB a A B a. Gọi DK là đường cao của hình hộp 1 1
Fanpage: Tạp chí và tư liệu toán học
Chinh phục olympic toán | 15
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN 2 DH là đường cao của 2a
A B CD DH   2 .
a .Khoảng cách giữa hai đường thẳng AA 1 1 a 1
và CD bằng khoảng cách từ D đến ABB A . Từ A để đường cao AQ đến A B C D , 1 1 1 1  1 1  1
tách hình ra ta có h và h là hình chiếu từ K và Q đến A B , suy ra h h D J x . Đặt 1 2 1 1 1 2 1
khoảng cách từ Q đến ABB A là h. 1 1  Từ góc giữa  1
A B CD và  A B C D  60  KH DH a;DK  AQ  3 . a 1 1 1 1  0 1 1  2
3ax a Ta có : 1 1 1 1 1      h  2 2 2 h h AQx a2 2 3a 1
3a  x a2 2 .  2  a 3a d K; ABB Ah.  1 1  x a
3a  x a2 3
dD ; ABB A 1  1 1  Ta có D J x     3ax 3ax d D ; ABB A   1  1 1  d 1 K;ABB A h a 2 2 2 2 1 1  2
3a  x a
4a  2ax x 3a 3a 3a 3a      2a 2 2 2 4a 2a  4a 2a 1  3 3  2a 1  3   1        2 2 x xx x x  4   4  x a  4 Dấu bằng “=” xảy ra 2ax 1 
  x  4a 3
V DK.D J.A B  3 .4 a . a a  4 3a . x 2 1 1 1
16 | Chinh phục olympic toán
Fanpage: Tạp chí và tư liệu toán học
40 CÂU VẬN DỤNG CAO CÓ GIẢI CHI TIẾT Câu 21.
Phương trënh tương đương với 3 x x  
3 x m   3 3 2 sin sin 2 2 cos 2
2 cos x m  2  2 cos x m  2.
Xét hàm f t 3
 2t t với t  0. Ta có f t 2 '
 6t  1  0  f t đồng biến. Mà f x  f  3 sin
2 cos x m  2 , suy ra sin x  0 3
sin x  2 cos x m  2   2 3
sin x  2 cos x m   2   2 3  
sin x  2 cos x m  2 vì 2 sin x  0, x   0;   3  2 3 3 2
 1  cos x  2 cos x m  2  m  2
 cos x  cos x  1. Đặt      u  cosx, vì 2 1 x  0;  u    
;1 . Khi đó phương trënh trở thành 3 2      3 2
m  2u u  1.   1  u  0     ;1 Xét  2  g u 3 2  2
u u  1, có g'u 2  6
u  2u; g'u  0   .  1  1  u      ;1  3 2   
Lập bảng biến thiên suy ra phương trënh có 1 nghiệm khi 28 4   m    m 4  ; 3  ;   2 . 27 Câu 22.
Theo tính chất đường phân giác ta có IB AB 3 
  2IB 3IM  0 IM AM 2 Và DB AB 3 
  4DB  3DC  0 DC AC 4
2IB 3IM  0
2AB 3AM  5AI
4AB 6AM  10AI Vậy ta có     
4DB  3DC  0
4AB  3AC  7AD
4AB  3AC  7AD Suy ra AD
3AC  6AM  7AD  10AI  7AD  10AI  10 0   . AI 7 Câu 23. a  3  x 2 Đặt 2 2 1   1   1 
 a  b  1 , ta đi chứng minh 1a 1    1  b 1   VP   b  x  2 2   b  a 
Fanpage: Tạp chí và tư liệu toán học
Chinh phục olympic toán | 17
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN 2    1         1 1 a 1 1 b 1     b    a   2       2 1 1 2 1 1      2 a b b a 1 1 a b   2 2     2 2      a b    2          2  a b b a ab b a        2 2 2  b a  3 3  3a  3b  AMGM 4 4  a b       2 ab b a        2 2  2 2 a b     3 6 ab   2   AMGM  4 4   6  6   4   2    2  2 17  12 2     6 6 2 2   ab  16 ab   a  b  6   6  16     2    Câu 24.
Với các số thực a,b,c làm cho phương trënh 2
ax bx c  0 có hai nghiệm thuộc 0;1 .  b x x   1 2  a
Suy ra a  0 . Gọi hai nghiệm đó là x ,x , theo định lì Viet ta được  1 2 cx .x  1 2  a
a b2a b  b  b     a b 1  2    2 (2a b) a a a
1 x x 2  x     x 1 2   1 2  Ta có T     (
a a b c)
a b c b c
1  x x x x 1 2 1 2 1   a a a
21  x x x x  2 2 2 2
x x x x    1 2 1 2 1 2 1 2 x x x x 1 2 1 2   2  .
1  x x x x
1  x x x x 1 2 1 2 1 2 1 2
Không mất tính tổng quát ta có thể giả sử 0  x x  1 , 1 2 2 x x x Suy ra 1 1 2 2 2 2 
 1  x x x x  1 x x x x x x x 1 2 1 2 1 2 1 1 2 1 2 2 x  1 2 2 2 2 2 2 2
Suy ra x x x x
x x x x
x x x x 1 2 1 2 1 2 1 2 1 2 1 2    1. 2 2 2
1  x x x x
1  x x x
x x x x 1 2 1 2 1 2 1 1 2 1 2
Suy ra T  2  1  3 . Vậy T
 3 , dấu “=” xảy ra khi x x  1. max 1 2
Nếu hàm số y f (x) là hàm số lẻ trên đoạn a;a,a  0 và có giá trị lớn nhất và giá trị
nhỏ nhất thì max f x  max f x  min f x a;a 0;a a;aCâu 25.
18 | Chinh phục olympic toán
Fanpage: Tạp chí và tư liệu toán học
40 CÂU VẬN DỤNG CAO CÓ GIẢI CHI TIẾT Ta có n 8 7  A A . 10 9
Gọi A là tập hợp các số a có 8 chữ số khác nhau chia hết cho 45 .
Khi đó a chia hết cho 5 và 9 (tổng các chữ số chia hết cho 9 và số hàng đơn vị bằng 0 hoặc 5 ).
 Trường hợp 1: a có hàng đơn vị bằng 0 ; 7 chữ số còn lại có chữ số 9 và 3 trong 4 bộ số 1;  8 , 2;  7 , 3;  6 , 4;  5 , có 4.7! số.
 Trường hợp 2: a có hàng đơn vị bằng 5 ; 7 chữ số còn lại có chữ số 4 và 3 trong 4 bộ số 0;  9 , 1;  8 , 2;  7 , 3;  6 . Không có bộ 0;  9 , có 7 ! số. Có bộ 0;  9 , có 2 C 7! 6! số 3   2 4.7!C 7! 6!  53 nA 2
 4.7!C 7! 6! số  PA 3     . 3   8 7 A A 2268 10 9 Câu 26. a  log x Đặt 2 2 2 
 2x  2y  2xy  6x  6y  4  0 b   log y 2
Yêu cầu của bài toán trở thành 8x
log2 y 3ab P  
P5  a b  3  a b aP  1  bP  1  5P  3 32 4 log  a b 2 xy
Đến đây thế a theo b và P thay vào phương trënh trên ta được một phương trënh bậc 2, sử
dụng điều kiện có nghiệm ta sẽ suy ra kết quả của bài toán! Ta được 27  8 6 27  8 6 minP  ,max P  . 23 23 Câu 27.
Ta có một tính chất cơ bản của hàm trị tuyệt đối a b a b
 max a ; b 2 2 Áp dụng ta có       x x y   2 2 2 x 2x y 2 x 2x y max 1 ; 2 1   2 2
Sử dụng bất đẳng thức trị tuyệt đối ta có 2 2 2 2
x  2x y  2
x  2x y 2x  2 2x  2     2x  1 2 2 2 2
    2x y x y 2 2 2 2
Mặt khác theo bất đẳng thức Cauchy – Schwarz ta có   2 2 2 2 2 x y x y
Vậy VT  2  VP . Dấu “=” xảy ta khi và chỉ khi x y  1.
Khi đó P  24 có tất cả 8 ước số nguyên dương.
Fanpage: Tạp chí và tư liệu toán học
Chinh phục olympic toán | 19
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN Câu 28. Đặt a  3a 3x y
a b x, a b y , mà a a  4d và a a d nên 4 1 a   . Tương tự 1 1 5 5 5 1 2 1 2 4 4 ta tình được x y x  3y a  và a  . 3 2 4 4
Lập luận tương tự với CSN, ta cũng có 3 3 4 4
b x y ,b xy ,b xy . Theo bất đẳng thức 2 3 4 Cô-si thì x y 3x y  3 x 3y 3 4 4 a
xy b , a
x y b , a   xy b . 3 3 2 2 4 4 2 4 4
Do đó, cả i), ii) va iii) đều đúng. Tuy nhiên, điê u kiê n iv) không luôn đúng, chẳng hạn khi
x y thì d  0 nhưng q  1. Câu 29.
+ Dựng mặt phẳng (P) chứa AB và song song CD cắt O, R theo giao tuyến là đường tròn 1  tâm I.
+ Dựng mặt phẳng (Q) chứa CD và song song AB cắt O, R theo giao tuyến là đường 2  tròn tâm J.
+ Lần lượt dựng 2 đường kính A B  , C D   vuông góc nhau.
Khi đó, IJ dAB,CD  dA B  ,C D   Ta có: 1 VABCD d AB CD AB CD A B  C D   IJ V . Do đó chỉ cần xét ABCD     1 . . , .sin , . . 6 6 A B  C D  
các tứ diện dạng A B  C D   .
Vậy điều kiện cần để V
lớn nhất là AB CD . Gọi M, N lần lượt là trung điểm của AB ABCD và CD.
Đặt AM x, CN  .
y x0, 10 ,y0,2   2 2  ON   x OM   y d AB CD 2 2 10 ; 4 ; ,
MN OM ON  10  x  4  y . Khi đó: 1 V
ABCD d AB CD   x yx   y xyx   y ABCD   1  2 2  2 . . , 2 .2 10 4  2 2 10 4  6 6 3
20 | Chinh phục olympic toán
Fanpage: Tạp chí và tư liệu toán học
40 CÂU VẬN DỤNG CAO CÓ GIẢI CHI TIẾT  2  2     Ta có: 2 10 x 2 2 x Vxy    y   xy     y ABCD 2 1. 4 2 1 10 2 4  3  2  3    2  2 3 Vxyx yxyxy xyxy ABCD   2 2  2 3   2 18 2 18 2 2 39 2  3 2 3 2 3 3  xy xy    9  2xy 4 xy xy    Vxyxy     xy    ABCD  2 2    8   8 2 2 3 9 2 9 2 9 3 2 2 3  3      3 2 8  9  V      V  . Vậy V  6 2. ABCD 72 ABCD 6 2 3  3  max  2 10  x  2 4  2  y    x  6
Dấu “=” xảy ra khi:  2 1   .  y  3 xy   9  2xy  2 Câu 30. S D' A' C' G D B' C E A B
Từ giả thiết của bài toán ta có: SA SC SB SD SB SD 7       (1)
SASCSBSDSB' SD 2
Trải phẳng 4 mặt bên của hình chóp và ghép lại sao cho thu được một nủa lục giác đều với
cạnh SA tách thành SA và SA’ và đặt vào hệ Oxy(hình vẽ)
Fanpage: Tạp chí và tư liệu toán học
Chinh phục olympic toán | 21
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN Khi đó ta có:       S
A  A   1 ' 1 2 0;0 ; 0;1 ; 0; 1 ; A 0; ; A 0;    
 ;C ;0 ; và 1  2   2   3   
B a aDb b 2 ' ; ; ; ; a;b 0;   .  1 1 7 7 4 4 2 1       a b  2    a b 2 2 a b 7
Chu vi cần A’B’C’D’ là ' c A B
   BC C D    D A  1 2 2 2 2 2  1   2  2 2  1   2  2
c a a   a
a b b   b           b  2   3   2   3   2 2   2 2  2  1  2  1   2  2  2  2
c   a a   b b     a   a b           b    2   2     3   3       2  
c  a b2  a b  2 2 4
1  (a b)  a b   minc    1.79  3  Dấu “=” xảy ra khi 2 2 a b
BD//BD . 7 Câu 31.
Trung điểm đoạn nối 2 điểm cực trị là điểm uốn của đồ thị hàm số, có tọa độ  b     x x x bb   1 2 3   a  ; y  . Theo Viet ta có 
x x x  1  3a  3a   1 2 3 b 1 x    0  3a 3
Thế x  1  x x vào giả thiết thứ 2 ta được 3 1 2
3x  4x  5 5x  5x 2  44x x  44 x x 1 x x 1 2 1 2 1 2  1 2  1 2  2
 48x  16x 3x  4 2
 45x  54x  25  0 1 1 2 2 2 Ta có    1 1 1 x
 vậy VT VP . Dấu “=” xảy ra khi x  ;x  ;x x 1763 1 0 2 2 1 1 2 3 2 3 6 Câu 32.
Dễ dàng tëm được A0;0, B4;0, I 2; 1
 , I 2;b  4a với b  4a  0 (vì tứ giác I AI B 1   2   1 2
lồi). Khi đó tứ giác I AI B có hai đường chéo vuông góc nên 1 2 1 1 SAB I I   b a   b a
b a I AI B . 4.1 4  21 4  10 4 4. 1 2 1 2 2 2 Ta có  
hx  f x  gx 1 2  a
x  4a  1x  4a   
4 nên tọa độ đỉnh I là  4   4a  1 x    I 2   1    a    I   1 2 2; 3  S   IAB .3.4 6.  4  2  y h
a   a   a    I 2 4 1 8 2 4 4 3 Câu 33.
22 | Chinh phục olympic toán
Fanpage: Tạp chí và tư liệu toán học
40 CÂU VẬN DỤNG CAO CÓ GIẢI CHI TIẾT Ta có f x 3 2
ax bx cx d f x 2 '
 3ax  2bx c . Hàm số đạt cực trị tại x  0; x  2 và
đồ thị đi qua điểm 1;0,0;2 nên ta có  f '0  0 a  1   f '2 0   b  3      f x 3 2    f   x x 1 3 2  0 c  0   f  0  2 d  2
Ta có gx  mx nx p3  mx nx p2 2 2 3
 2 . Hệ số tự do bằng 3 2
p  3p  2 . Đồ thị
hàm số gx đi qua điểm 0;0 nên 3 2
p  3p  2  0  p  1 . Đồ thị hàm số     2 g x
f mx nx p có trục đối xứng 1
x   nên đồ thị hàm số 2
y mx nx p cũng có 2 trục đối xứng 1 n 1 x    
   m n. 2 2m 2
Đồ thị hàm số gx đi qua điểm 2;2 nên m n  1 g  2 0
g x 2m 13 32m 12 2 2            1
m n    2
Do đồ thị có hướng quay lên trên nên ta suy ra m  0  m n p  1 Câu 34.
Phương trënh tương đương với x 1 3 2 x  3 m  2
 8  x . Hàm số f x 1 2  2  8  x là một 2 2
hàm số chẵn do đó ta chỉ cần xét trên nửa khoảng 0; để suy ra bảng biến thiên của
hàm số f x trên cả tập số thực. Xét hàm số 2  x1 3x 2  8  x   2   g x    x x x  3   x 1 2 ln 2 3 2 1   f x 2 2  2  8  x  
f 'x   2 x1 2       x1 3x x x 2  8  0  x  2 2 ln 2 3 0  0 2  2 Ta có g xx1 2 2 '
 2 ln x  3  8ln 2  3  0, x
  2, g2  8ln 2  6  0, g3  16ln 2  9  0 nên
phương trënh gx  0 có nghiệm x  2;3 . 0  
Vẽ bảng biến thiên cho hàm số f x ta suy ra được phương trënh có đúng 2 nghiệm thực m  6 khi và chỉ khi  2    x mx 3 7,8,...,201 
m f x  8 0 1 0  2  8   0  2 Câu 35. 2018 2     Đặt f xx 2x 2    , ta có f 0 2018
a b  ... b  2 .  x  1  0 1 2018
Fanpage: Tạp chí và tư liệu toán học
Chinh phục olympic toán | 23
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN Suy ra 2018 a S  2 1 0 2018 2018 Lại có   f x 1  x  1 k
 C x    12k2018 2018  x  1  k0 1008 k 2018 C     C x  1 k k  . 20182k 2018  2 2018 2018
k0 x  1 k1009 Suy ra  0 1 1007 1008
b b  ...  b
 0  S b b  ... bCC  ...CC 1 3 2017 2 4 2018 2018 2018 2018 2018  1009 1010 2017 2018 1009 a CC  ...CCCS (vì k n k C C   ).2 0 2018 2018 2018 2018 2018 n n Từ  1 1 và 2 , suy ra 2017 1009 S  2  C . 2018 2 Câu 36.
Từ điều kiện ta suy ra 1
  f x2018  f x12 dx  0   f x2018  f x12  0 0
f x  1
Mà f x liên tục trên 0;1 nên 
. Vậy có 2 hàm thỏa mãn yêu cầu đề bài.  f  x  0 Câu 37. Từ giả thiết .
m f x  .
n f 1  x  gx , lấy tích phân hai vế ta được : 1 1 1 1 Do f
 xdx g
 xdx  1   . m f
 x .nf 1xdx  (gx)dx   0 0 0 0 1  m n f
 1xdx  11 0 1
x  0  t  1 Xét tích phân f
 1xd .x Đặt t  1 x, suy ra dt  dx. Đổi cận: 
x  1  t   0 0 1 0 1 1 Khi đó f
 1xdx   f
 tdt f
 tdt f
 xdx  1. 2 0 1 0 0
Từ 1 và 2 , suy ra m n  1 . Câu 38.
Vì 5  4  1  3  2  2  2  1  3  1  1  2  1  1  1  1  1  1  1  1 nên ta có các trường hợp sau:
 Trường hợp 1: Số tự nhiên có một chữ số 5 đứng đầu và 2017 số 0 đứng sau: Có 1 số.
 Trường hợp 2: Số tự nhiên có một chữ số 4 , một chữ số 1 và 2016 số 0 .
+ Khả năng 1: Nếu số 4 đứng đầu thì số 1 đứng ở một trong 2017 vị trí còn lại nên ta có 1 C số. 2017
+ Khả năng 2: Nếu số 1 đứng đầu thì số 4 đứng ở một trong 2017 vị trí còn lại nên ta có
24 | Chinh phục olympic toán
Fanpage: Tạp chí và tư liệu toán học
40 CÂU VẬN DỤNG CAO CÓ GIẢI CHI TIẾT 1 C số. 2017
 Trường hợp 3: Số tự nhiên có một chữ số 3 , một chữ số 2 và 2016 số 0
+ Khả năng 1: Nếu số 3 đứng đầu thì số 2 đứng ở một trong 2017 vị trí còn lại nên ta có 1 C số. 2017
+ Khả năng 2: Nếu số 2 đứng đầu thì số 3 đứng ở một trong 2017 vị trí còn lại nên ta có 1 C số. 2017
 Trường hợp 4: Số tự nhiên có hai chữ số 2 , một chữ số 1 và 2015 số 0
+ Khả năng 1: Nếu số 2 đứng đầu thì số 1 và số 2 còn lại đứng ở hai trong 2017 vị trí còn lại nên ta có 2 A số. 2017
+ Khả năng 2: Nếu số 1 đứng đầu thì hai chữ số 2 đứng ở hai trong 2017 vị trí còn lại nên ta có 2 C số. 2017
 Trường hợp 5: Số tự nhiên có 2 chữ số 1 , một chữ số 3 thë tương tự như trường hợp 4 ta có 2 2 AC số. 2017 2017
 Trường hợp 6: Số tự nhiên có một chữ số 2 , ba chữ số 1 và 2014 số 0 .
+ Khả năng 1: Nếu số 2 đứng đầu thì ba chữ số 1 đứng ở ba trong 2017 vị trí còn lại nên ta có 3 C số. 2017
+ Khả năng 2: Nếu số 1 đứng đầu và số 2 đứng ở vị trí mà không có số 1 nào khác đứng
trước nó thì hai số 1 còn lại đứng ở trong 2016 vị trí còn lại nên ta có 2 C số. 2016
+ Khả năng 3: Nếu số 1 đứng đầu và số 2 đứng ở vị trì mà đứng trước nó có hai số 1 thì
hai số 1 và 2 còn lại đứng ở trong 2016 vị trí còn lại nên ta có 2 A số. 2016
 Trường hợp 7: Số tự nhiên có năm chữ số 1 và 2013 số 0 , vì chữ số 1 đứng đầu
nên bốn chữ số 1 còn lại đứng ở bốn trong 2017 vị trí còn lại nên ta có 4 C số. 2017
Áp dụng quy tắc cộng ta có 1 1  4C  2 2 2 CA    3 2 2 CAC  4  C số cần 2017 2017 2017 2017 2016 2016 2017 tìm.
Câu 39. Biến đổi giả thiết ta được: 9
1  log 3y  2 log 3y 3  log 3xy  logx 2 2 2  2  2 8 9
 log x  log x log 3y  2 log 3y log x log  2 2 2 2 2 2 3xy 2 Ta nhận thấy rằng 8
log x  log 3y  log  3 . 2 2 2 3xy  log x a 2 
a b c  3
Để đơn giản ta đặt  
log 3y b Lúc này ta có 2 giả thiết . 2  9 
a ab  2abc  8    log  c 2 2  3xy
Fanpage: Tạp chí và tư liệu toán học
Chinh phục olympic toán | 25
TUYỂN TẬP MỘT SỐ NHÓM CÂU HỎI VẬN DỤNG CAO MÔN TOÁN
Thế b  3  a c vào giả thiết dưới ta được:
c   2a  2c c   9 2 1 2 5 4 a   0 2
Coi vế trái là tam thức bậc 2 theo biến a với c là tham số ta có:
   c c  2   c     c  2 2  2 2 5 4 18 2 1 2 1
c  4c  2
Chú ý với điều kiện x, y  1 ta sẽ có a,b,c  0 . Mặt khác a b c  3  c  3
Suy ra   0 , điều này đồng nghĩa VT  0 3   3 a  log x   2 2 2 x   2 2
Dấu “=” xảy ra khi và chỉ khi   
b  1  log 3y  1  2  2     1 8 1 y  3 c   log  2  2  3xy 2 Từ đây suy ra 76  12 2 P  . 9 Câu 40.
Gọi H là tâm tam giác BCD , ta có AH  BCD, mà AMN  BCD nên AH  AMN
hay MN luôn đi qua H . Ta có 3 1 6 BH  2 2
AH AB BH  1   . 3 3 3
Thể tích khối chóp ABMN là 1 V  1 6 1 .AH.S  .
. BM.BN.sin 60 2  BM.BN . 3 BMN 3 3 2 12
Do MN luôn đi qua H và M chạy trên BC nên BM.BN lớn nhất khi M C hoặc N D khi đó 2 V  . 1 24 2 17 2
BM.BN nhỏ nhất khi MN//CD khi 2
BM BN   V
. Vậy V V  . 3 2 27 1 2 216
26 | Chinh phục olympic toán
Fanpage: Tạp chí và tư liệu toán học