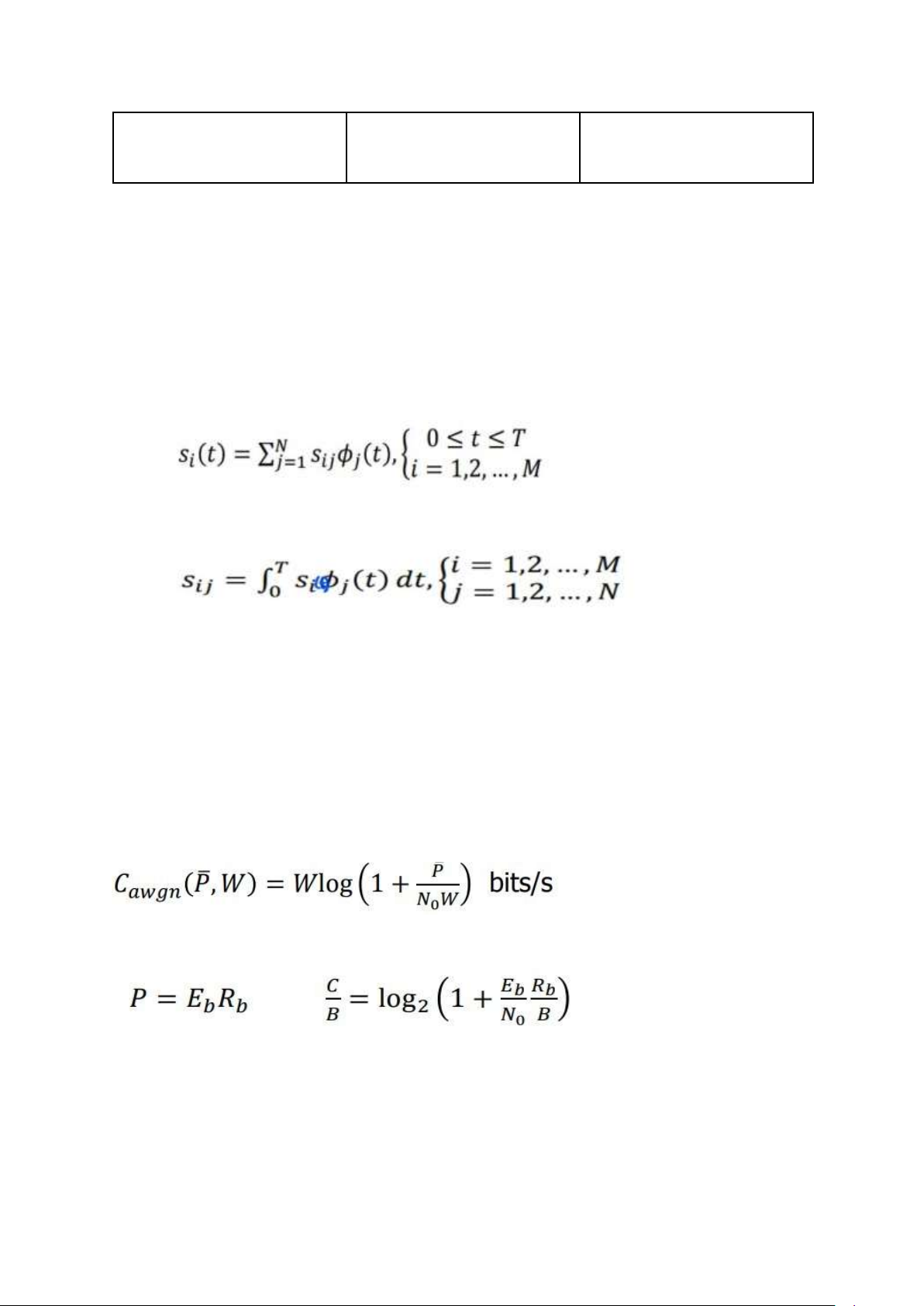






Preview text:
lOMoAR cPSD| 58833082
Ôn tập truyền thông mã hóa Câu 1
1A Nêu khác biệt về cấu trúc hệ thống giữa hệ truyền tin tương tự và hệ truyền tin số.
Giải thích tại sao có sự khác biệt này.
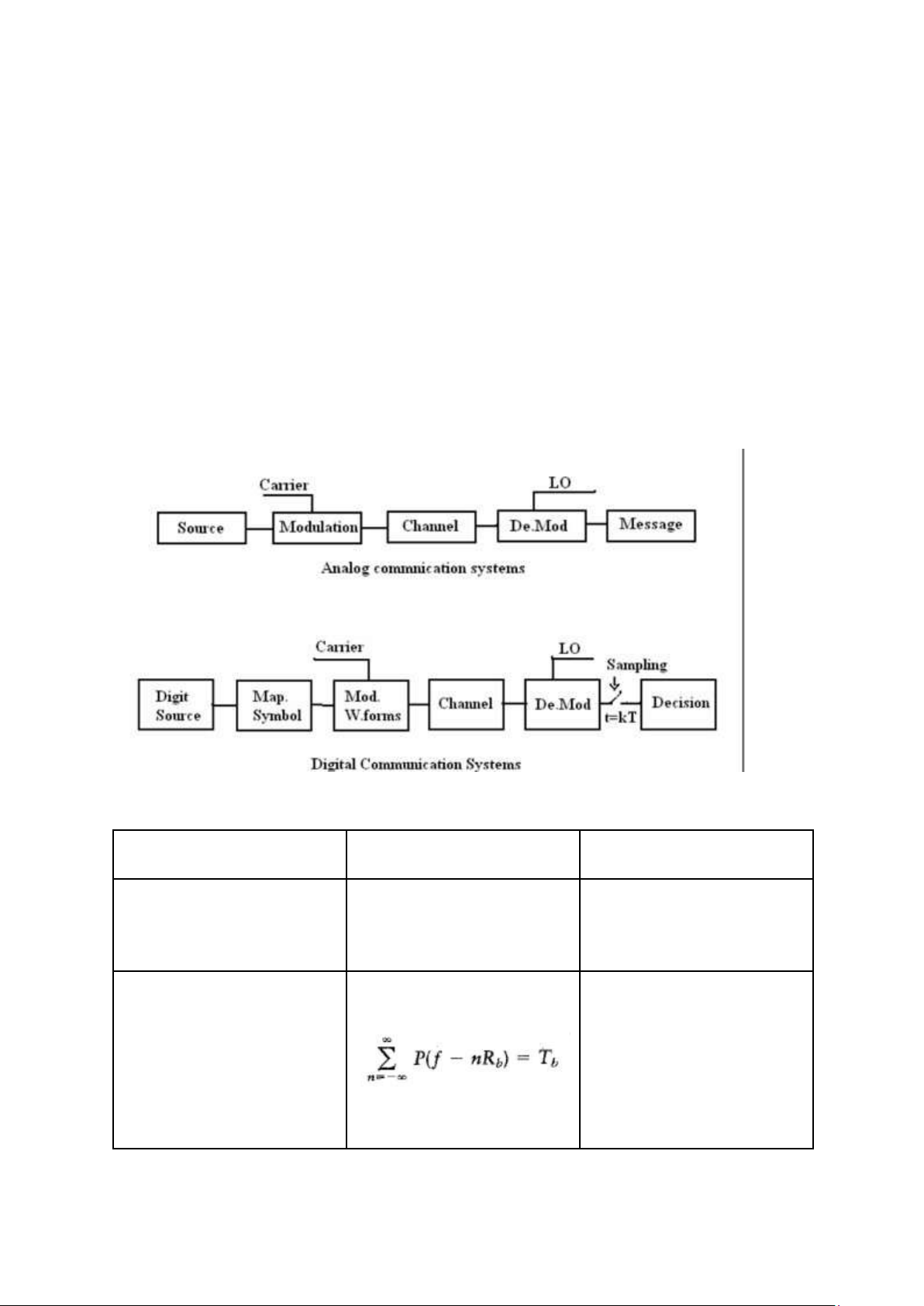
- Cấu trúc của hệ thống truyền tin tương tự đơn giản hơn. Bản tin chỉ cần đặt lên sóng
mang và truyền qua kênh, bên thu tách bản tin ra khỏi sóng mang là nhân được dữ liệu.
- Với truyền tin số , cấu trúc của hệ thống phức tạp hơn vì cần 1 bộ map symbol ánh xạ
dạng sóng, ở bên thu cần thêm 1 bộ sampling lấy mẫu và 1 bộ decision quyết định
dạng sóng. - Có sự khác biệt này do có sự khác nhau về bản tin. Ở truyền tin số thì
bản tin là chuỗi bit -> cần có bộ Map Symbol để ánh xạ dạng sóng đồng thời sau khi
đến bên nhận thì phải có bộ Sampling & Decision để xác định dạng sóng tương ứng với bit nào.
1B Nêu khác biệt giữa bộ lọc Nyquist và bộ lọc phù hợp về: Chức năng nhiệm vụ, cách
thực hiện và vị trí đặt bộ lọc trong hệ thống truyền tin số Lọc Nyquist Lọc phù hợp Chức năng nhiệm vụ
Hạn chế ảnh hưởng của ISI
Khuếch đại tỉ số SNR tại trong truyền thống số
điểm lấy mẫu nhằm giảm
ảnh hưởng của tạp âm Cách thực hiện
Giải bài toán trong miền tần Khuếch đại tín hiệu bằng bộ
số, Nyquist tìm ra chuẩn tạo lọc có tần số trùng với bản tin tạo ra cộng hưởng
dạng phổ trong miền tần số lOMoAR cPSD| 58833082 Vị trí đặt trước bộ lấy mẫu
Tại bên thu,trước bộ lấy mẫu.
1C. Lý thuyết không gian tín hiệu có vai trò gì trong truyền tin số. Giản đồ chòm sao
cho ta biết thống tin gì của hệ truyền tin
- Lý thuyết không gian tín hiệu có vai trò quan trọng trong truyền thông số. Vì nó là coi
một tín hiệu như 1 vector bằng cách biểu diễn tín hiệu thành tổ hợp tuyến tính của N
hàm cơ sở trực chuẩn, một điều vô cùng cần thiết nếu muốn một dạng sóng mang nhiều bit.
- Ví dụ nếu muốn 1 dạng sóng mang n bit, ta cần 2n dạng sóng, từ đó thiết kế bộ thu
phát phù hợp với đúng từng đấy dạng sóng. công thức cơ sở của bên phát - công thức cơ sở của bên phát :
Trong đó là hệ số được xác định bởi :
M là số dạng sóng, N là số hàm cơ sở, với điều kiện các hàm cơ sở phải trực chuẩn
- Từ các hệ số sinh ra bởi các hàm cơ sở và vector, ta có thể vẽ nên giản đồ chòm sao,
từ giản đồ chòm sao, ta có thể xác định đây là kỹ thuật gì, số các sao coi như số dạng
sóng, cho biết biên độ và pha của sóng tỷ lệ lỗi, xây dựng sơ đồ thu, phát và bộ
Decision, biết được có bao nhiêu dạng sóng và số bit trong mỗi dạng sóng.
1D. Nêu các cách viết công thức Shanon về dung năng kênh và ý nghĩa của các cách viết này Công thức 1 :
Thể hiện tốc độ truyền tối đa số bit trên giây có thể truyền mà không có lỗi, đường truyền đáng tin cậy
c/w = log(1+EbRb/NoW) : bit/s/hz
Thể hiện hiệu suất phổ : 1Hz cõng trên lưng bao nhiêu bit/s lOMoAR cPSD| 58833082 bit/ lần truyền 1/2log(1+P/NoW)
Thể hiển số bit cực đại trên 1 lần truyền mà có thể không có lỗi
Trong đó C : dung năng của kênh (bit/s) P
= EbRb : Công suất tín hiệu (W)
W = độ rộng băng tần của kênh (Hz)
No : mật độ phổ công suất (W/Hz) Eb : năng lượng bit (J)
Rb : tốc độ dữ liệu ( bit/s)
→ Shannon chứng minh nếu tốc độ truyền tin R < dung năng kênh C thì có thể truyền kênh không có lỗi
1E Trình bày cơ sở của qui tắc quyết định MAP và ML và sự khác nhau của 2 qui tắc này -
Quyết định MAP ( Xác suất hậu nghiệm):
Xác suất lỗi quyết định được tính là :
Ta biết tiêu chuẩn quyết định là lỗi tối thiểu hay quy tắc quyết định tối ưu là Chọn m = mi nếu k = 1, 2, 3, … M
Quy tắc cực đại sau xác suất ( xác suất hậu nghiệm , MAP) chứa đựng các xác suất
trước( xác suất tiền nghiệm) của tín hiệu phát và hàm hợp lý. - Quyết định ML:
Theo quy tắc Bayes ta có như sau : Quyết định là mi nếu
Trong đó pk là xác suất trước, fx(x|mk) là hàm khả năng (khả năng thu được khi mk
được phát, xác suất do kênh ồn gây nên) và fx(x) là hàm mật độ xác suất liên kết
không điều kiện của vector x. Do mẫu số độc lập với tín hiệu phát nên nếu muốn xác
suất trước là bằng nhau thì:
Quyết định là mi nếu fx(x|mk)là cực đại khi k = i lOMoAR cPSD| 58833082 Câu 2
2A. Một kênh truyền tin có độ rộng băng tần 600 KHz, công suất mật độ tạp âm là N0=
10^-7 W/Hz được yêu cầu truyền dữ liệu nhị phân tốc độ 1.0Mb/s dùng nghiệm Cosin tăng.
a) Xác định nhân tử α của bộ lọc
Do là dữ liệu nhị phân -> mỗi sóng mang 1 bit -> Rs = Rb Tổng
quát Rs = Rb/n với n là số bit sóng mang
B=W(1+alpha) =Rs/2∗(1+alpha) = Rb/2* (1+alpha)
Rb=10^6, B=600.10^3 => alpha = 0.2
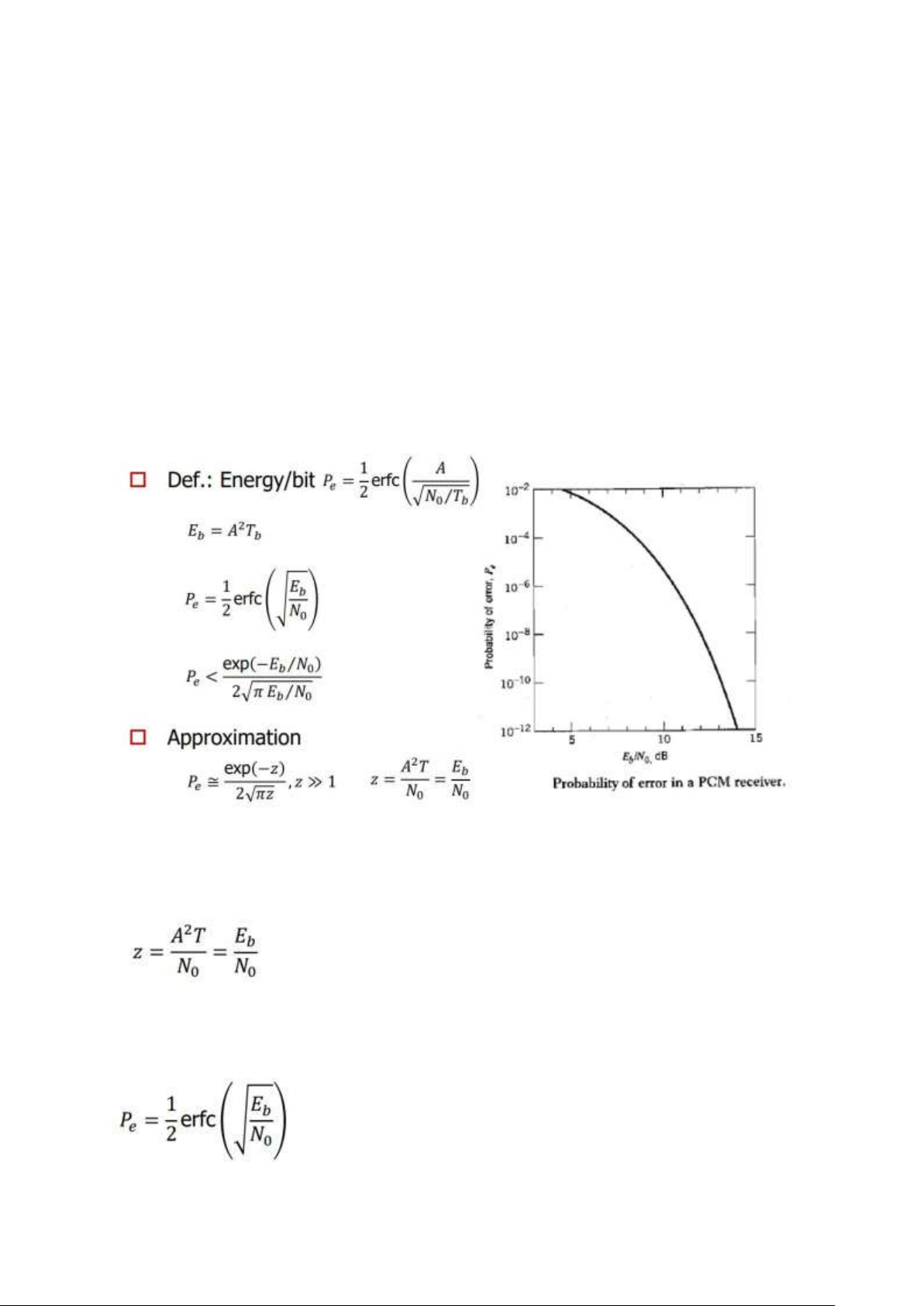
b) Xác định tỷ lệ lỗi tín hiệu nếu biên độ tín hiệu nhận được là 5mV Công thức Rb=10^6 => Tb =10^-6
-> z = 2.5 * 10-4 << 1 -> Áp dụng lOMoAR cPSD| 58833082
Tra bảng erfc để lấy kết quả (“Nếu không có bảng thì ghi vào là phải tra bảng vì tích phân
hàm erfc không tính được, Thầy bảo thế”) Nếu z >1 thì ta dúng CT xấp xỉ cận trên được
2B. Cho dạng sóng s(t)=cosin(t) với 0≤t≤ Tb=2π Nêu cách xây dựng bộ lọc phù hợp với
dạng sóng này và tính giá trị đỉnh tại thời điểm Tb ở lối ra bộ lọc. h(t) = s(T-t) = cos(Tb-t)
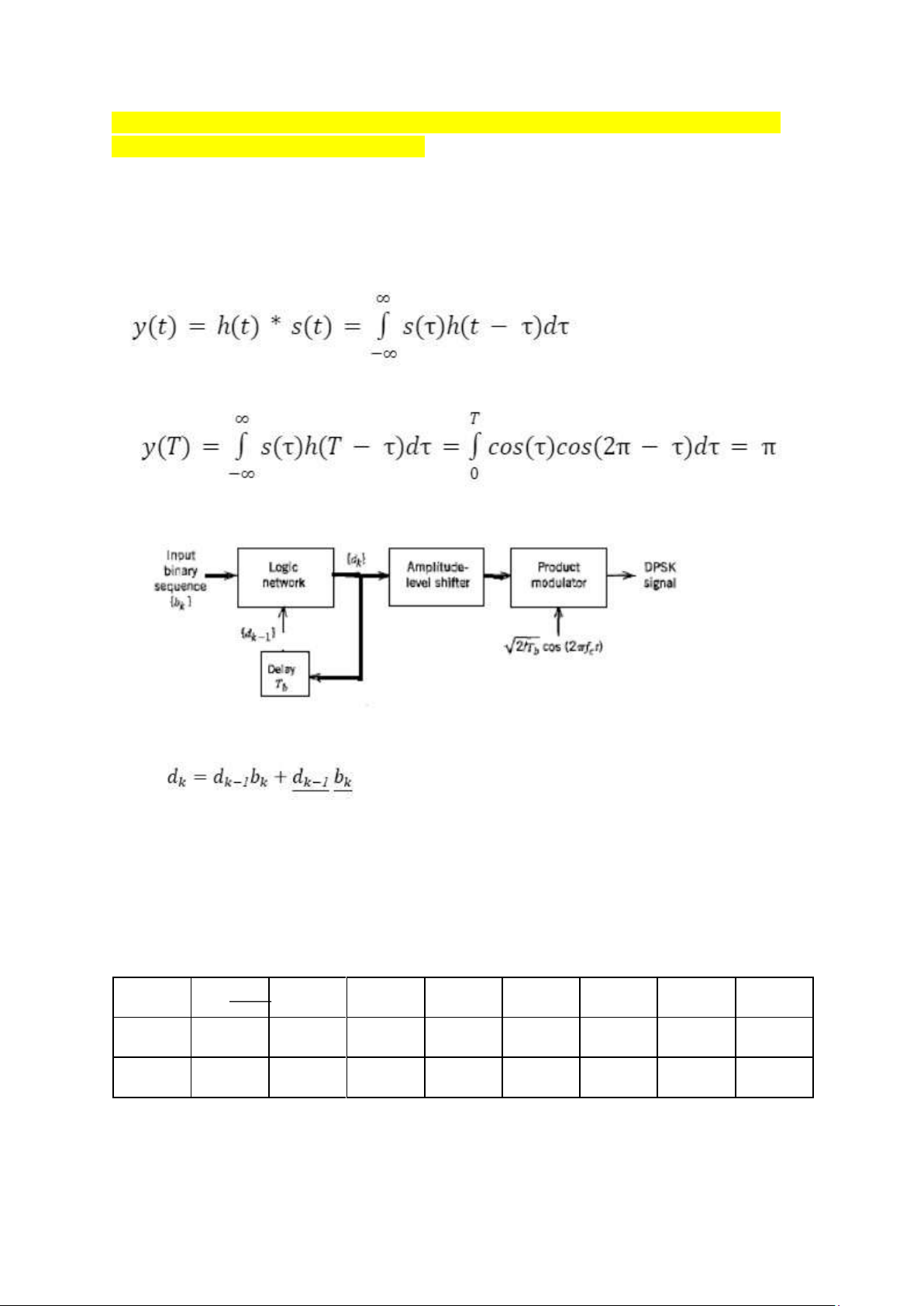
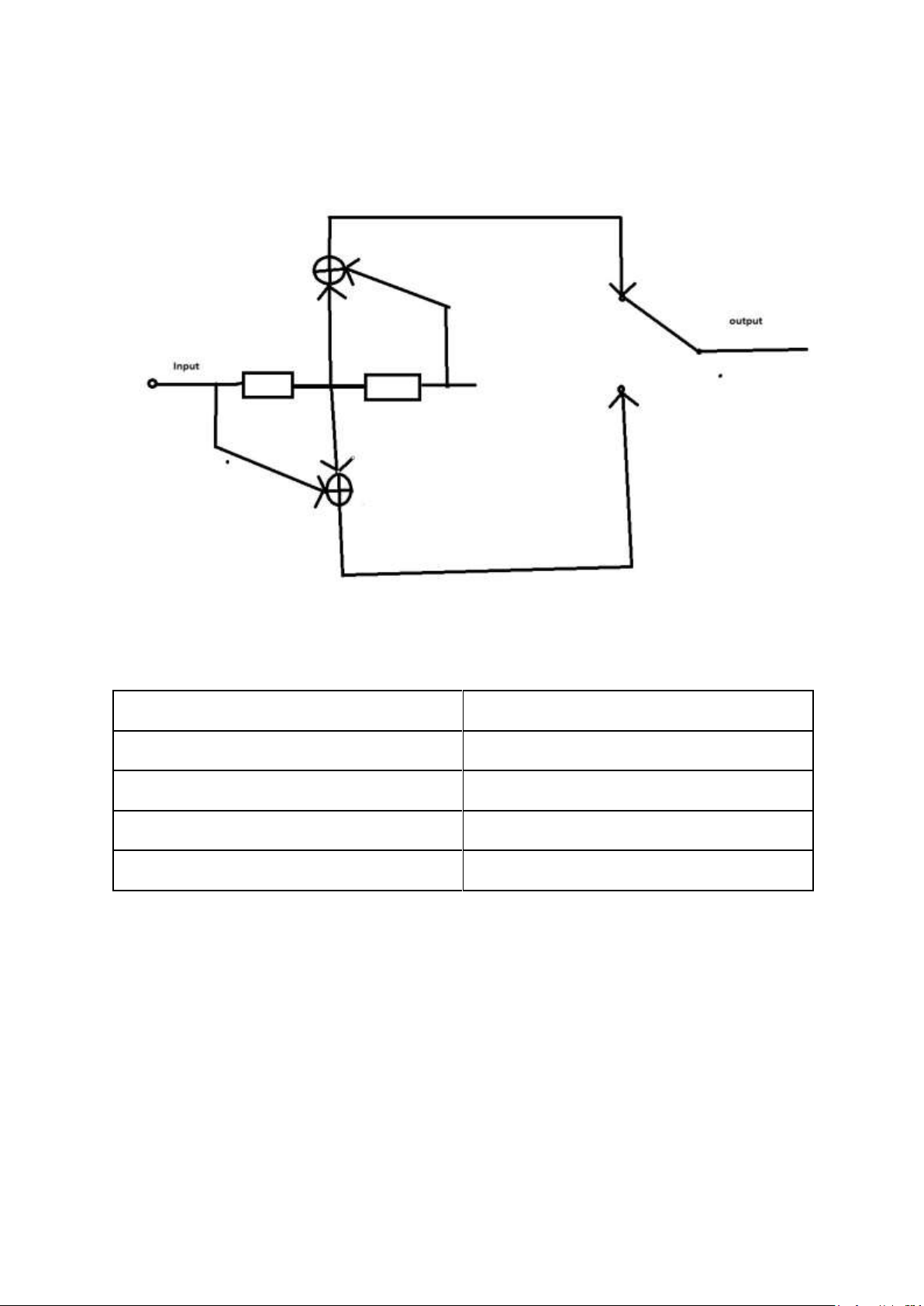
2C. Cho dãy nhị phân 1100111 cấp cho bộ phát theo kỹ thuật DPSK (hình vẽ dưới)
nguyên lý: gồm 2 khối:
- Logic network + delay -> Khối mã vi phân cho ra hàm lối ra
- Nếu bit vào = 1 -> dạng sóng sau giống dạng sóng trước.
- Nếu bit vào = 0 -> dạng sóng sau sẽ là đảo của dạng sóng trước
- Bên thu có thêm bộ nhớ dạng sóng trước để so sánh dạng sóng trước với dạng sóng sau.
- Amplitude-level shifter + product modulator -> Khối BFSK
a) Xác định lối ra của bộ mã vi phân với trạng thái ban đầu thiết lập là 0 với bk
là bit vào bk = 1 -> dk = dk-1 bk = 0 -> dk = dk−1 bk 1 1 0 0 1 1 1 dk 0 0 0 1 0 0 0 0 phase π π π 0 π π π π
b) Vẽ dạng sóng tín hiệu DPSK lối ra lOMoAR cPSD| 58833082 Cách vẽ
2D. a) Giải thích hoạt động của sơ đồ sau
Chuỗi tín hiệu nhị phân sau khi đi qua bộ mã mức NRZ sẽ chuyển thành các xung với mức 0
(- căn Eb) và 1 (căn Eb). Bộ mã mức sẽ giữ biên độ ở mức 0 hoặc 1 đến hết chu kì bit (NRZ). Bộ phân kênh
bit I đưa lên trên điều khiển vector phi 1 quay trái phải bit Q
đưa xuống dưới điều vector phi 2 quay lên hoặc xuống lOMoAR cPSD| 58833082
b). Sơ đồ trên có sự khác biệt gì so với sơ đồ BPSK - Sơ đồ BPSK
điều chế 2 dạng sóng, mỗi dạng sóng mang 1 bit, thông tin ở pha, 1 hàm cơ sở, 2 dạng sóng lệch 180 độ. lOMoAR cPSD| 58833082 - Sơ đồ QPSK
điều chế 4 dạng sóng, mỗi dạng sóng mang 2 bit, thông tin mang ở pha, 2 hàm cơ
sở trực chuẩn (toạ độ đề-các) các dạng sóng (sao) gần nhau cách nhau 1 bit.
Do có 2 hàm cơ sở nên cần 2 hệ số để biểu diễn mỗi dạng sóng, mỗi nửa trên và dưới
sẽ quyết định 1 hệ số bằng việc sử dụng 1 trong 2 bit truyền, gọi là bit I và Q.
Xung của bit I kéo dài cho cả bit Q và xung của bit Q kéo dài cho cả bit I. Và phải
làm trễ một dòng để được I,Q đồng thời.
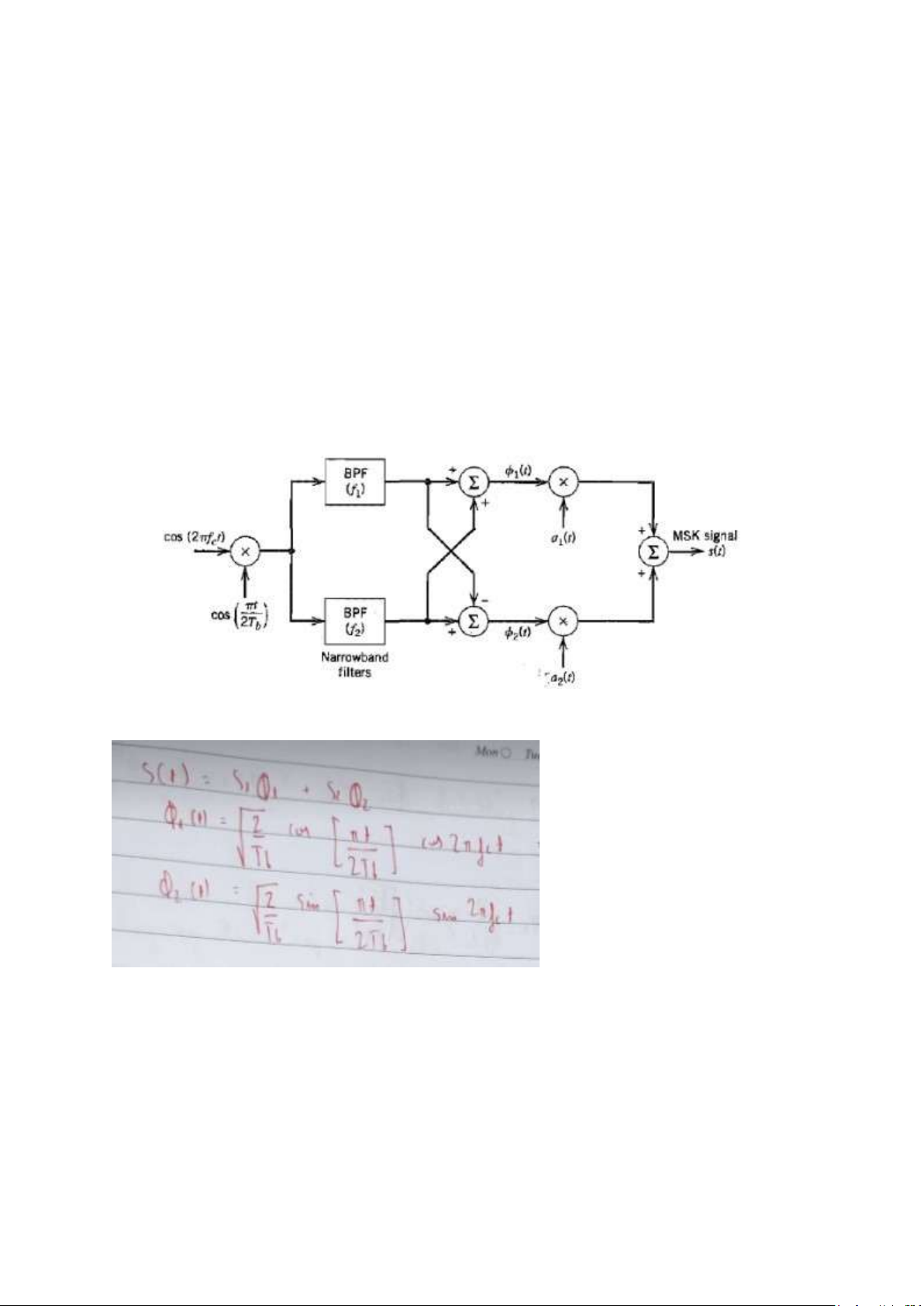
2E. a) Giải thích hoạt động của sơ đồ sau:
Sơ đồ này tạo ra tín hiệu MSK ( minimum shift keying) là tổ hợp tuyến tính của các hàm cơ
sở có hệ số là a1,a2. Hàm cơ sở của MSK
Lối vào = cos(2πfct) * cos (πt/2Tb) = 1/2 * [ cos(2πfct + πt/2Tb) + cos(2πfct - πt/2Tb) ] f1 f2
Thành phần cộng cho tần số f1, thành phần trừ cho tần số f2.Đi qua bộ lọc f1 thu được
cos(f1t) , qua bộ lọc f2 thu đc cos(f2). Sau đó
• cos(f1t) + cos(f2t) -> phi 1
• cos(f1t) – cos(f2t) -> phi 2 lOMoAR cPSD| 58833082
Sau khi có hàm cơ sở thì nhân tương ứng với hệ số a1, a2 rồi cộng lại với nhau ta thu được dạng sóng MSK.
b). Sơ đồ trên có khác biệt gì với điều chế GMSK trong hệ thống 2G GSM Câu 3
3A a) Kênh truyền nhị phân có xác suất lỗi truyền là p=0,5.10^-3 . Tính xác suất lỗi
truyền nếu sử dụng mã lặp lại 3 lần
p là xác xuất bit truyền bị lỗi 1-
p xác xuất bit truyền đúng
Xác suất lỗi khi truyền: Pe = (1-p)*p2 + p*(1-p)p + p2(1-p) + p3
Quyết theo đa số -> 2/3 bit bị lỗi thì quyết sai Pe = 3P^2*(1-P) + P^3
2 bit gây lỗi cả 3 bit đều gây lỗi = 7,49 * 10-7
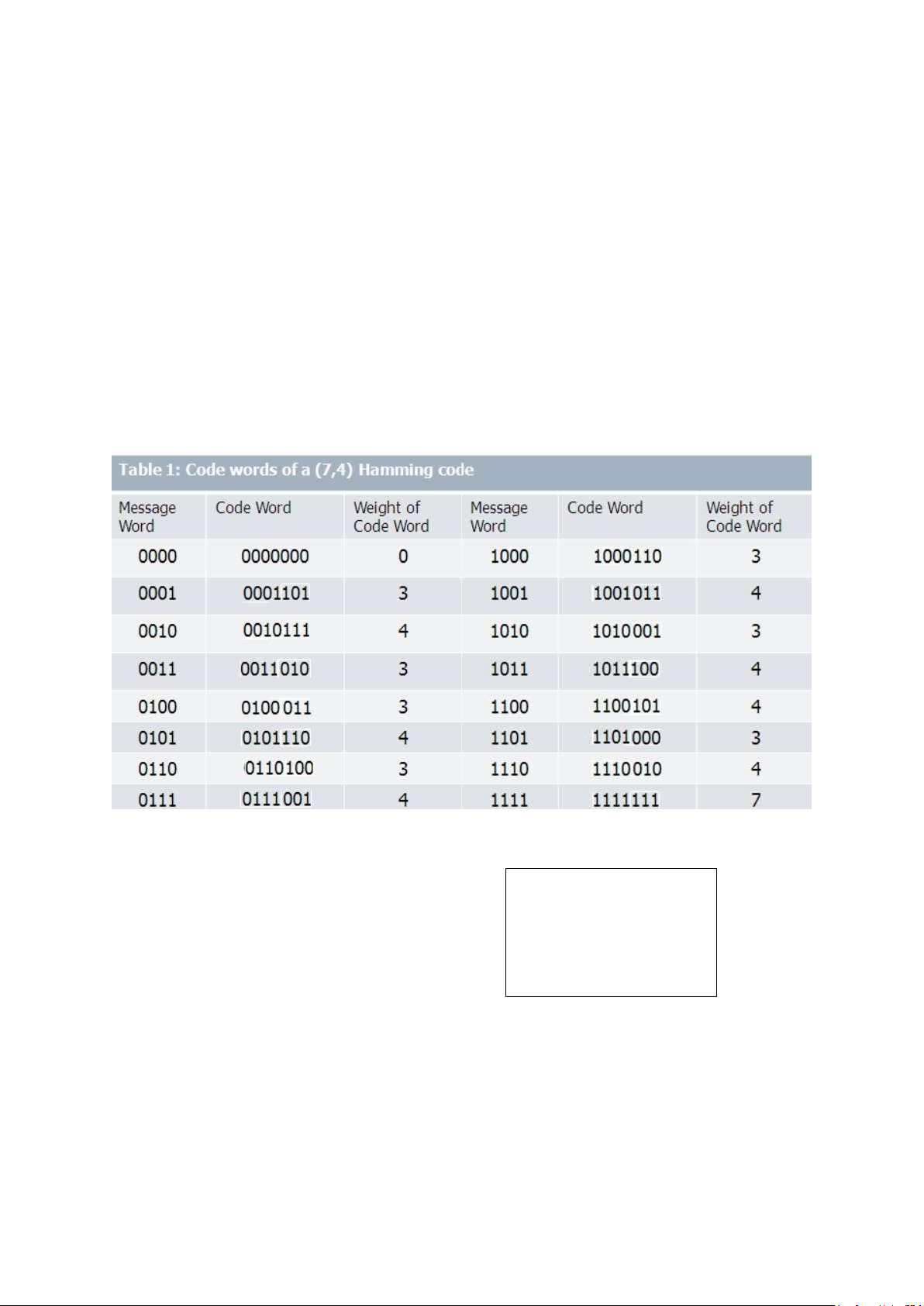
b) Nếu dùng mã Hamming (7,4) có khả năng hiệu chỉnh 1 lỗi, thì lỗi của mã này qua
kênh nói trên là bao nhiêu. So sánh hiệu quả của 2 mã Công thức lOMoAR cPSD| 58833082
Ở đây n = 7, t = 1, p = 0,5 * 10-3 -> Pe = C27 p2 (1−p)5 = 5.23 * 10-6 So sánh :
- Mã lặp lại 3 bit sửa 1 lỗi , tốc độ giảm 1/3
- Mã hamming (7,4) 7 bit sửa 1 lỗi , tốc độ giảm 4/7
3B Một mã chập có 2 tầng ghi dịch đơn. Ba bộ cộng lối ra và 1 bộ ghép kênh. Dãy sinh
cho 3 lối ra là: g(1)=(1,1,0) g (2)=(1,0,1) g (1)=(0,1,1)
a) Vẽ sơ đồ khối của mã
b) Xây dựng giản đồ lưới của mã
c) Xác định từ mã nếu dãy bít thông tin vào là 1011 lOMoAR cPSD| 58833082
3C. Xét mã khối (7,4) với ma trận kiểm tra H là n = 7, k = 4 lOMoAR cPSD| 58833082
a) Cấu tạo từ mã với bản tin m=0110 Có H = [ P , In-k] G = [Ik , P^T]
→ Ma trận chẵn lẻ là G = [ 1 0 0 0 1 1 0 0 1 0 0 0 1 1 0 0 1 0 1 0 1 0 0 0 1 1 1 1 ] c = m.G = 0110110 d5 = d1 + d3 + d4 d6 = d1 + d2 + d4 d7 = d2 + d3 + d4
b) Xác định khả năng sửa lỗi của mã này (thông qua tìm dmin)
Lập bảng và tìm dmin với d = số bit 1 của mã -> dmin trong bài thông qua bảng = 3
Số bit lỗi có khả năng hiệu chỉnh t = (dmin – 1) / 2 = 1
c) Tìm bản tin nếu từ qua kênh nhận được là c’= 1110110
s=c’.HT = 1110110 * [1 1 0 = [1 1 0] = > Lỗi ở bit thứ nhất do s 0 1 1
giống với hàng 1 của 1 0 1 HT 1 1 1 1 0 0 0 1 0 0 0 1]
Hiệu chỉnh từ mã => c = 0110110 => m =0110
3D Một bộ mã chập có 2 thanh ghi dịch đơn nối tiếp, 2 bộ cộng modul-2 cung cấp 2 lối
ra và một bộ ghép kênh sau cùng. Đáp ứng kênh ứng với 2 lối ra (còn gọi là dãy sinh) lần lượt là: lOMoAR cPSD| 58833082 g(1)=(0,1,1); g(2)=(1,1,0)
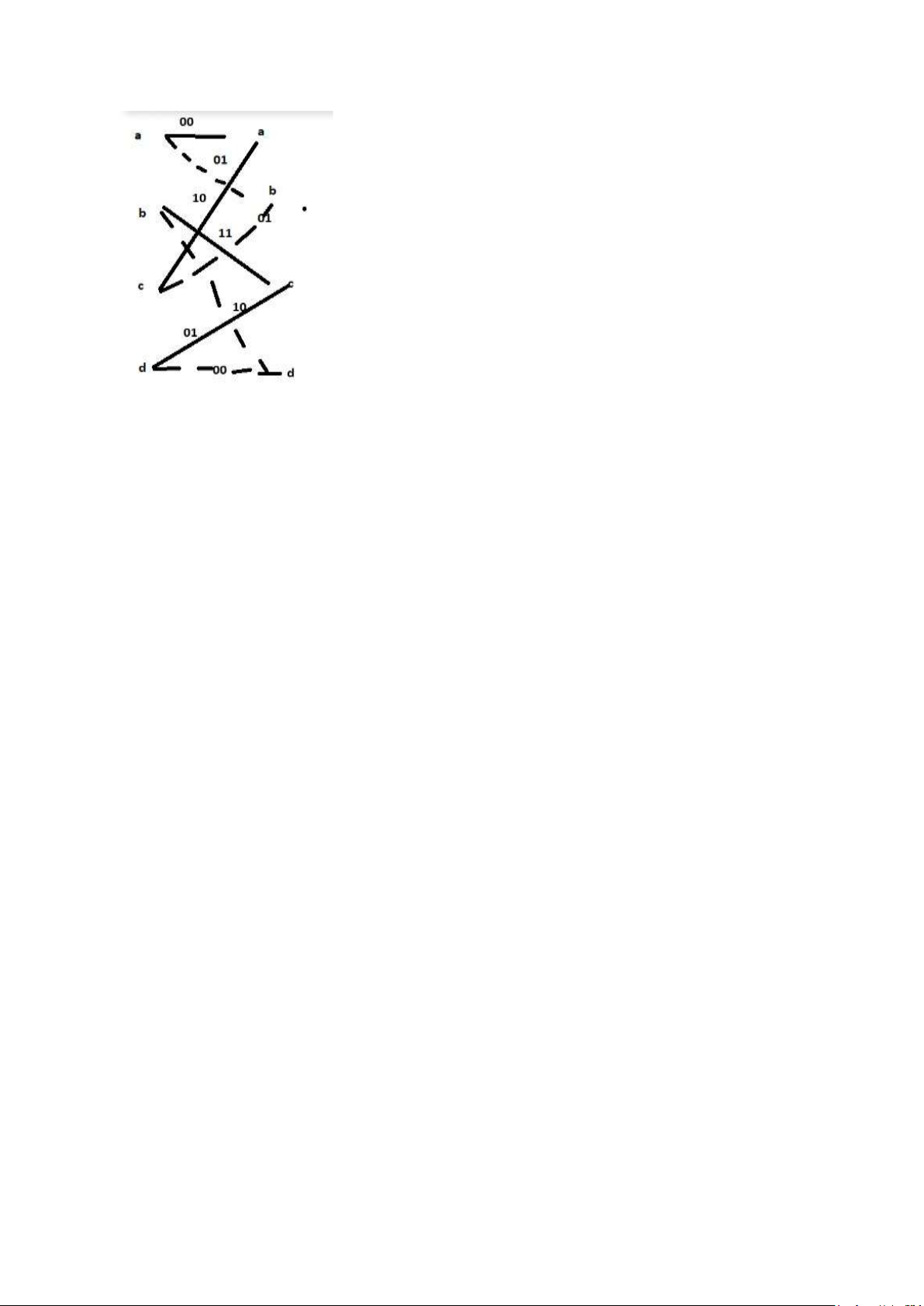
a) Vẽ sơ đồ khối và biểu diễn lưới rút gọn của mã nói trên M =2 , n =2 , k=1, K = 3 Sơ đồ khối :
b) Xác định từ mã nếu bản tin là 10111
g(1)=D+D^2 => c1= (1+D^2+D^3+D^4).(D+D^2) = D+D^3+D^2+D^6 = 0111001
g(2)=1+D => c2= (1+D^2+D^3+D^4)(1+D) = 1+D^2 + D+D^5 = 1110010 c = 01,11,11,10,00 Trạng thái Giá trị a 00 b 10 c 01 d 11 Cây rút gọn : lOMoAR cPSD| 58833082
3E. a) Chứng minh rằng mã lặp lại 3 lần cũng là mã khối. Tìm ma trận sinh và ma trận
kiểm tra của mã này
Vì mã lặp lại tách 1 bit ra và truyền theo từng khối 3 bit -> mã khối với k = 1 và n = 3 1→ 111
0→ 000 c1 = d1 c2 = d1 → P=[ 1 → G = [Ik PT] = [1 1 1] → H^T = [P^t = [ 1 1 c3 = d1 1] In-k] 1 0 0 1 ] dmin = 3 → sửa 1 lỗi
b) So sánh tỷ lệ lỗi trong mã lặp lại 3 lần và mã Hamming (7,4) Làm ở trên r



