Ôn Tập Cuối Kỳ: Đệ Quy, Cây, Danh Sách và Giải Thuật | Môn Cấu trúc dữ liệu và thuật toán - Trường Đại học Khoa học, Đại học Huế

lOMoAR cPSD| 58702377 ÔN TẬP
1. Những khái niệm, quy trình phân tích thiết kế giải thuật, tính độ
phức tạp thuật toán (lưu ý lệnh tích cực, lưu ý bước nhảy của vòng lặp )
2. Các phương pháp để lưu trữ dữ liệu:
- Lưu trữ tuần tự (mảng 1 chiều)
+Cố định,truy nhập qua chỉ số,tốc độ truy cập đồng đều
- Lưu kế móc nối (đơn, đôi, vòng, 1 con trỏ đầu, 2 con trỏ đầu)
+Truy nhập từng phần tử một theo thứ tự, tốc độ truy cập không đồng đều
3. Mảng 1 chiều, 2 chiều, nhiều chiều (lưu trữ tuần tự)
4. Danh sách tuyến tính: Stack, Queue
a. Các biến thể của các cấu trúc trên (hàng đợi ưu tiên, hàng đợi vòng)
b. Ứng dụng của chúng: tính giá trị biểu thức hậu tố, chuyển
đổi cơ số, kiểm tra cặp dấu ngoặc
c. Lưu trữ bằng CTLT tuần tự, CTLT móc nối
5. Đệ quy và khử đệ quy (độ phức tạp tính toán)
6. Cây Nhị phân (đặc biệt lưu ý cây NPTK: có tính chất trái < gốc < phải)
- Các thao tác trên cây NPTK: tạo cây rỗng, bổ sung, loại bỏ,
duyệt cây (hiểu code, mô tả được), tìm kiếm, tính toán
- Heap: tính chất cha >con (Max-Heap)
Tính chất chaCài đặt cây NP: lOMoAR cPSD| 58702377
- Lưu trữ tuần tự (dùng mảng 1 chiều, lưu ý các phần tử bị
khuyết thì để là rỗng (trong trường hợp cây NP không hoàn chỉnh, không đầy đủ)
- Lưu trữ móc nối Cây tổng quát:
- Cài đặt bằng danh sách móc nối (số thành phần phần của một
nút bằng = 1+ cấp của cây hoặc cài đặt gián tiếp thông qua cây NP (code)
- Mô tả cách chuyển một cây tổng quát về cây NP
7. Các giải thuật sắp xếp
- Chèn, chọn, nổi bọt, nổi bọt cải tiến - Nhanh, phân đoạn, vun đống, hòa trộn
8. Các giải thuật tìm kiếm: - Tuần tự - Nhị phân - Trực tiếp 9. Đồ thị - Các khái niệm cơ bản
- Các phép duyệt đồ thị: theo chiều rộng, sâu
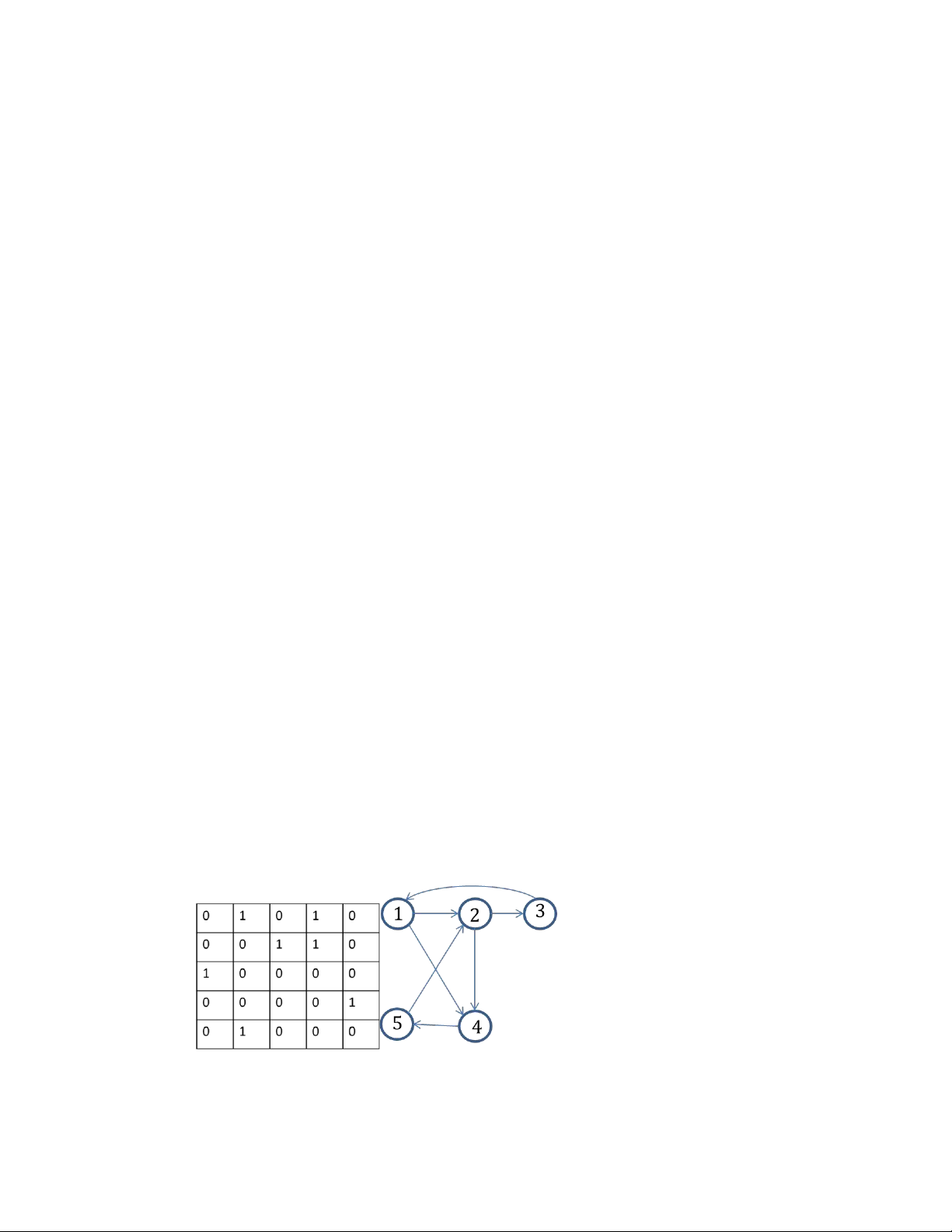
- Cài đặt đồ thị (biểu diễn đồ thị) bằng ma trận kề (ma trận đỉnh
kề, ma trận cạnh kề (đồ thị có trọng số)), bằng danh sách kề
Xây dựng ma trận đỉnh kề
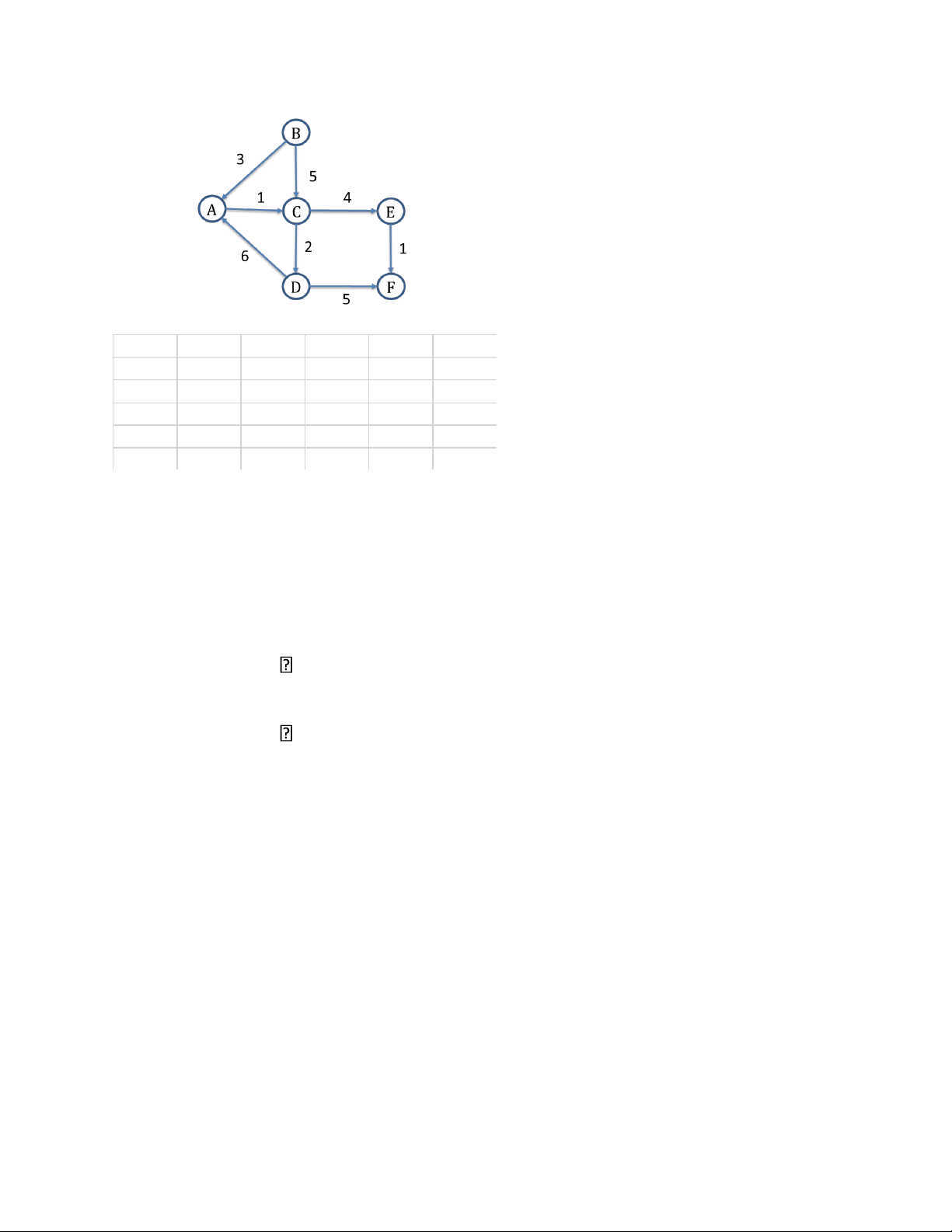
Xây dựng ma trận cạnh kề lOMoAR cPSD| 58702377 0 0 1 0 0 0 3 0 5 0 0 0 0 0 0 2 4 0 6 0 0 0 0 5 0 0 0 0 0 1 0 0 0 0 0 0
- Các bài toán ứng dụng đồ thị: o Dựng cây khung. o Cây khung
cực tiểu o Sắp xếp topo
o Tìm đường đi ngắn nhất từ 1 điểm đến các điểm còn lại (Dijkstra) o Tìm đường đi:
có đường đi từ đỉnh I đến đỉnh j hay không (xác định
dựa vào ma trận đường đi P)
Có đường đi từ I đến j mà có độ dài bằng t hay
không (xác định dựa vào ma trận A(t))
Lưu ý: Bổ sung code cho những thuật toán chưa có code. Danh sách liên kết đơn #include using namespace std; template class LinkedListNode{ public: T value; LinkedListNode* Next; public: lOMoAR cPSD| 58702377
LinkedListNode(T v):value(v){ Next=0; } }; template class LinkedList{ LinkedListNode *head,*tail; int count; public: LinkedList():count(0){ head=tail=0; } void AddFirst(const T&v){
LinkedListNode *p=new LinkedListNode(v); if(count++==0){ tail=p; } else{ p->Next=head; } head=p; } void AddLast(const T&v){
LinkedListNode *p=new LinkedListNode(v); if(count++==0){ head=p; } else{ tail- >Next=p; } tail=p; } void RemoveFirst(){ LinkedListNode *p=head;
head=p->Next; delete p; if(-- count==0){ tail=0; lOMoAR cPSD| 58702377 } } void RemoveLast(){ if(count==1){ RemoveFirst(); return; }
LinkedListNode *p=head; while(p-
>Next->Next!=NULL){ p=p->Next; } tail=p; delete(p->Next); p->Next=NULL; --count; } void RemoveAt(int k){ LinkedListNode *p=head; for(int i=0;i>Next; }
LinkedListNode *temp=p->Next; p->Next=temp->Next; delete temp; } void RemoveAll(){ while(count){ --count;
LinkedListNode *p=head; head=p- >Next; delete p; } } void PrintList(){ lOMoAR cPSD| 58702377 LinkedListNode *p=head;
while(p!=NULL){ cout<>value<<' '; p=p->Next; } } int Count(){ return count; } }; int main(){ LinkedList s; unsigned int x=25; do{ s.AddFirst(x%2); x/=2; } while(x); s.PrintList(); } Ngăn xếp #include using namespace std; template class Stack{ int value; T*data; int top; public: Stack(T v):value(v),top(-1){ data=new T[value]; } lOMoAR cPSD| 58702377 ~Stack(){ delete [] data; } void Push(const T&v){ data[++top]=v; } T &Pop(){ return data[top--]; } int IsEmpty(){ return top==-1; } int IsFull(){ return top==(value-1); } int Count(){ return top+1; } }; int main(){ Stack s(32); unsigned int x=25; do{ s.Push(x%2); x/=2; }while(x); lOMoAR cPSD| 58702377 while(!s.IsEmpty()){ cout< } }