Ôn tập olympic toán giải tích sinh viên môn Giải tích 2 | Đại học Đồng Tháp

ÔN TẬP OLYMPIC TOÁN GIẢI TÍCH SINH VIÊN LỜI GIẢI CỦA GSTSTPT
Câu 1: Cho dãy số xn xác định bởi:
ÔN TẬP OLYMPIC TOÁN GIẢI TÍCH SINH VIÊN LỜI GIẢI CỦA GSTSTPT
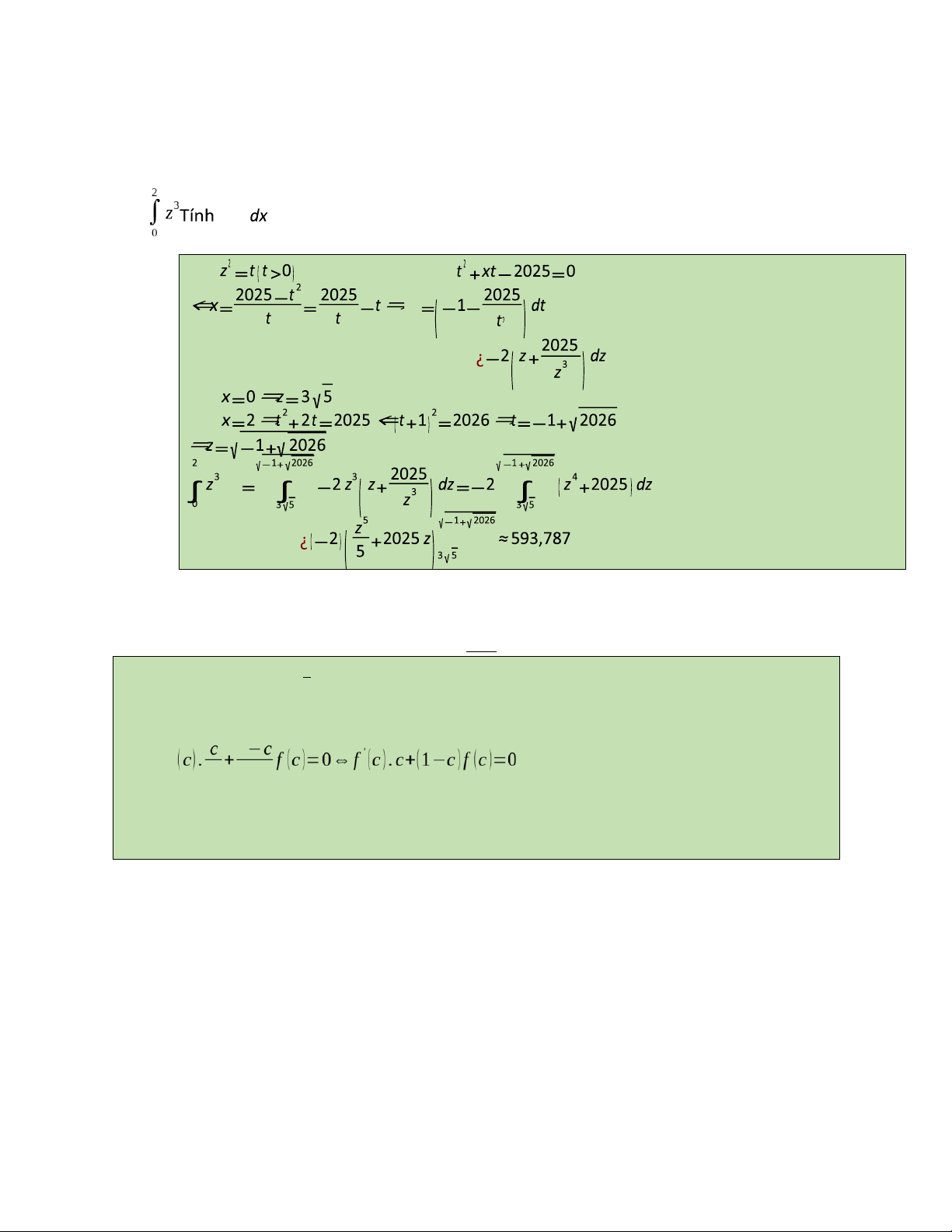
Câu 2: Với mỗi x≥0, gọi z=z ( x ) là nghiệm dương của phương trình:
z4+x z2=2025 (¿ ) Câu 3: Đặt Cho khi đó (*) trở thành: hàm dx số f ( x ) liên Với Với tục trên [ dx 0;1], khả vi
trên khoảng (0;1) và f (1)=0 Chứng minh rằng tồn tại c ∈(0;1) sao cho:
f ' (c )=c−1 f (c) c x
Xét hàm số g ( x )=f ( x ) . x có: f (1)=f (0)=0 e
Theo định lý Rolle thì ∃c∈(0;1) thỏa mãn g' (c )=0 Hay f ' c 1 c e e
ÔN TẬP OLYMPIC TOÁN GIẢI TÍCH SINH VIÊN LỜI GIẢI CỦA GSTSTPT
⇔f ' (c ) c−1 =
f (c )(đcpcm) c Câu 4: Cho hàm số
f ( x )={3 x22 ax2bx khikhixx>≤00 (a,b) ∈R2 +
a) Chứng minh rằng f ( x ) liên tục trên R
Hàm số chỉ có điểm kỳ dị là x=0 nên ta xét hàm số tại đó:
Ta có: ¿ nên hàm số liên tục tại x=0
Đồng nghĩa với hàm số không gãy đoạn tại điểm kỳ dị nên hàm số đã cho liên tục trên R. b) Giả sử , tìm GTNN của:
ÔN TẬP OLYMPIC TOÁN GIẢI TÍCH SINH VIÊN LỜI GIẢI CỦA GSTSTPT Ta có: 1 2 1 1 Vậy GTNN của T là 12,5. c) Giả sử
,tìm a,b để f (x ) có đạo hàm tại0. Từ đó tính I dx