Ôn tập toán rời rạc | Đại học Kinh tế Kỹ thuật Công nghiệp

lOMoAR cPSD| 46884348 PHẦN 2: Câu 1: ∞ 14 10 40 08 ∞ 18 24 30 12 ∞ 24 10 40 34 ∞ Giải:
Cố định thành phố xuất phát là T1
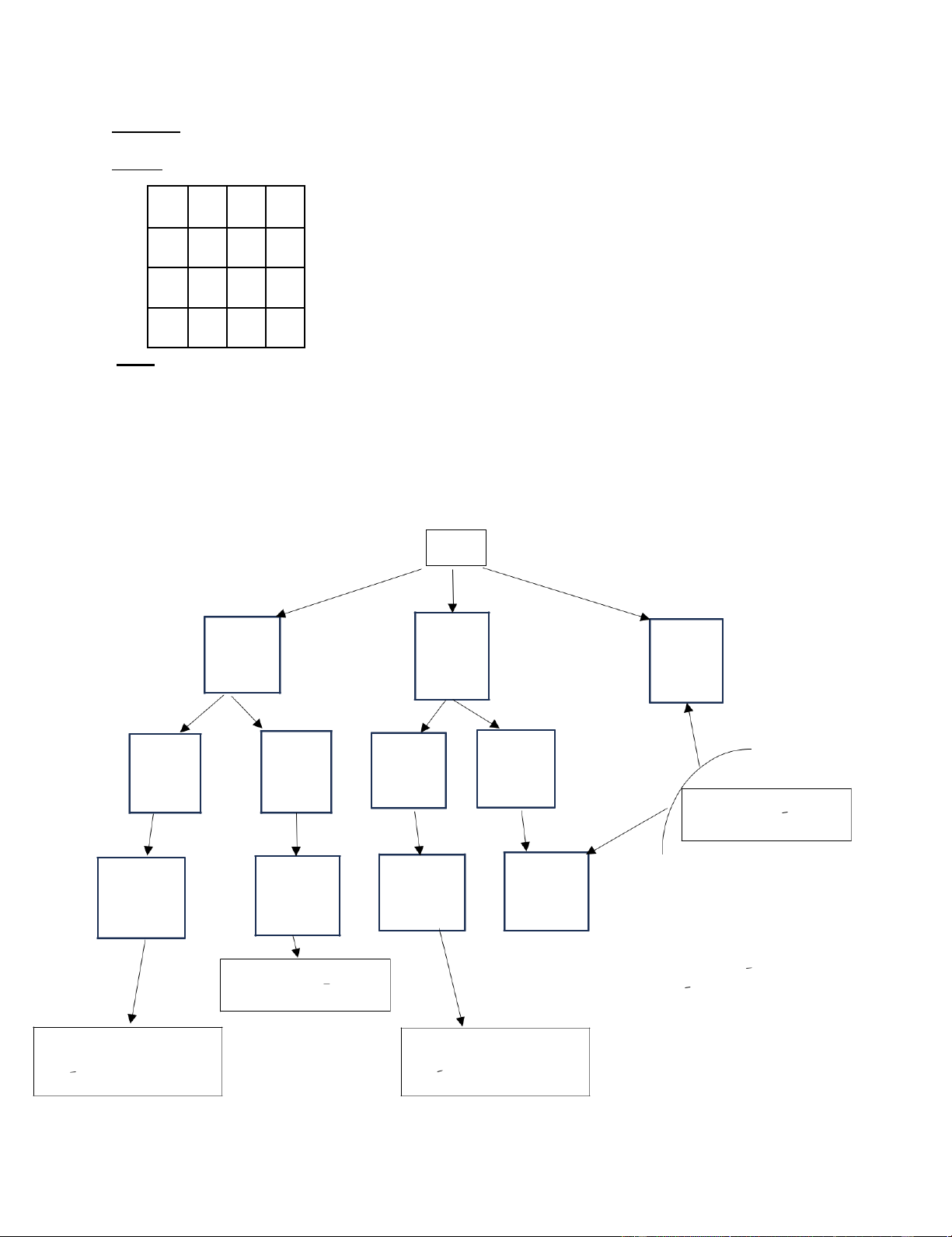
Ta có Cmin=08 là chi phí đi lại nhỏ nhất giữa các thành phố.Qúa trình thực hiện thuật toán được mô tả
bơi cây 琀 m kiếm lời giải.
Thông 琀椀n được ghi trong các ô trên hình vẽ theo thứ tự sau:
- Đầu 琀椀ên là các thành phần của phương án.
- Tiếp đến là chi phí theo hành trình bộ phận
- g là cận dưới: g(u1, u2 , ..., uk ) = + (n-k+1) cmin f=+ ∞ (1,3) (1,2) (1,4) =14 =10 =40 g=38 g=34 g=64 (1,2,3) (1,2,4) (1,3,4) (1,3,2) =32 =38 =22 =34 g=48 g=54 g=38 g=50
Các nhánh này bị loại vì có cận dưới g > f=56 (1,2,3,4) (1,2,4,3) (1,3,2,4) (1,3,4,3) =56 =72 =46 =74 g=64 g=80 g=54 g=82 Nhánh này bị loại vì có cận dưới g > f=66 Hành trình (1,2,3,4,1)
Hành trình mới (1,3,2,4,1) Có chi phí: 66 Có chi phí: 56 Đặt f =66 Đặt f =56
Kết thúc thuật toán, ta thu được phương án tối ưu (1,3,2,4,1) tương ứng với hành trình:
T1 -> T3 -> T2 -> T4 -> T1 Chi phí nhỏ nhất là: 56 lOMoAR cPSD| 46884348 Câu 2: 5x1 + x2 + 9 x3 -> max,
4 x1 + 2 x2 + 6 x3 ≤ 10, Với xj >=0 nguyên, j = 1,2,3 Giải: Ta có :b=10,n=3 c1=5 ; c2=1 ; c3=9 a1=4 ; a2=2 ; a3=6
Ta có: c3/ a3=9/6 > c1/a1=5/4 > c2/a2=1/2
Từ đó ta nhận thấy đề bài chưa thỏa mãn bất đẳng thức:
c1 /a1 ≥ c2 / a2 ≥ . . . ≥ cn / an
(Có nghĩa là các đồ vật được sắp xếp theo thứ tự không tăng của giá trị một đơn vị trọng lượng)
Sắp xếp lại theo chiều giảm dần:
c1/a1=9/6 > c2/a2=5/4 >c3/ a3=1/2
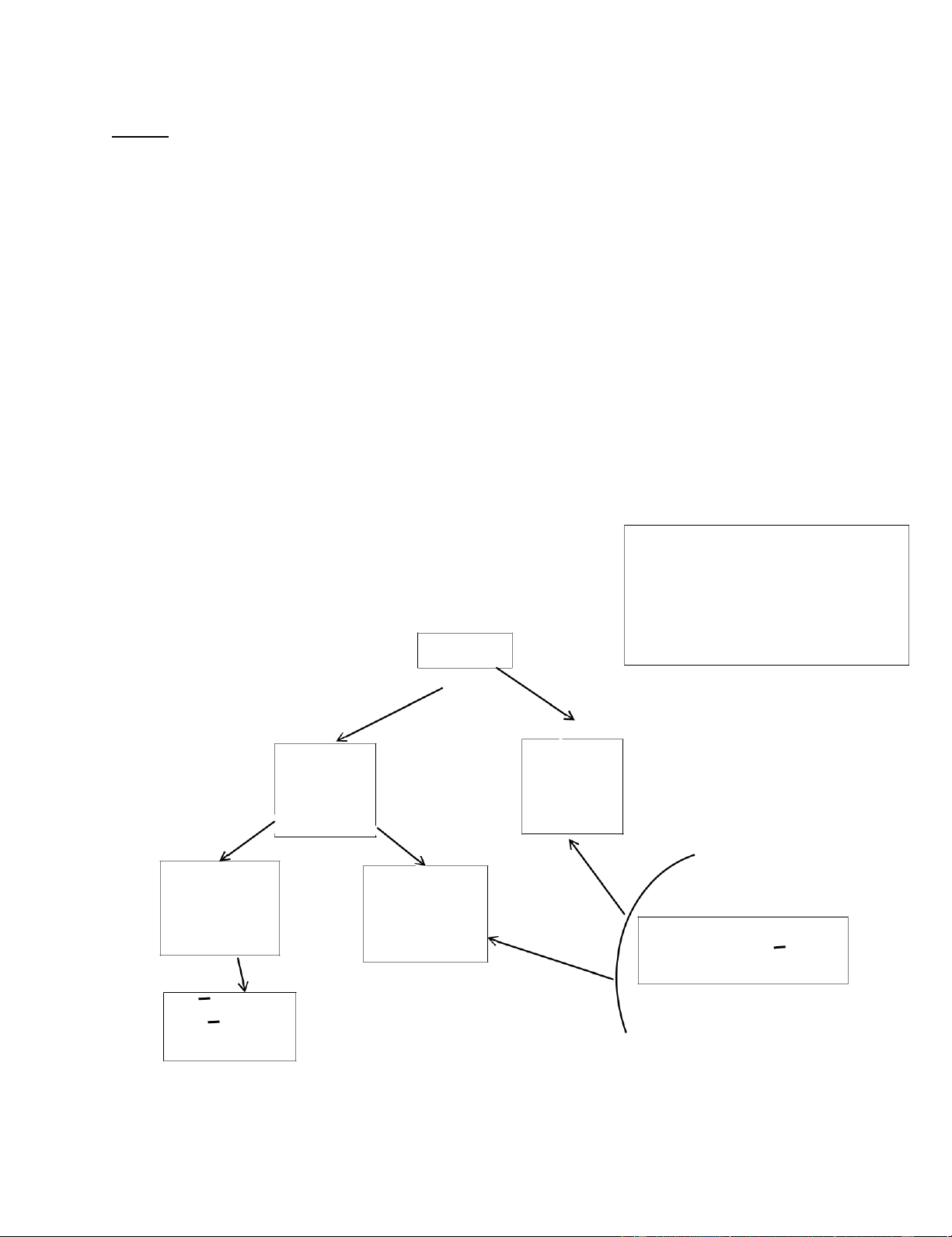
- : giá trị các đồ vật đang chất Sau khi sắp xếp: trong túi f(x)= 9x1 + 5x2 + x3 -> max,
- w: trọng lượng còn lại của túi 6x1 + 4x2 + 2x3 ≤ 10,
- g: cận trên. g Với x k = k + ck+1 /
j >=0 nguyên, j = 1,2,3 f=-∞ ak+1 * wk X1=1 X1=0 (1); (0); =0 =9 w=10 w=4 g=12,5 X2=1 X2=0 g=14 (1,1); =14 (1,0); =9 w=0 w=4 g=14 g=11
Các nhánh này bị loại vì X3=0
cận trên g < kỷ lục f=14
Thu được phương án của bài toán X=(1,1,0) Cập nhật lại kỷ lục f=14 lOMoAR cPSD| 46884348
Kết thúc thuật toán, ta thu được:
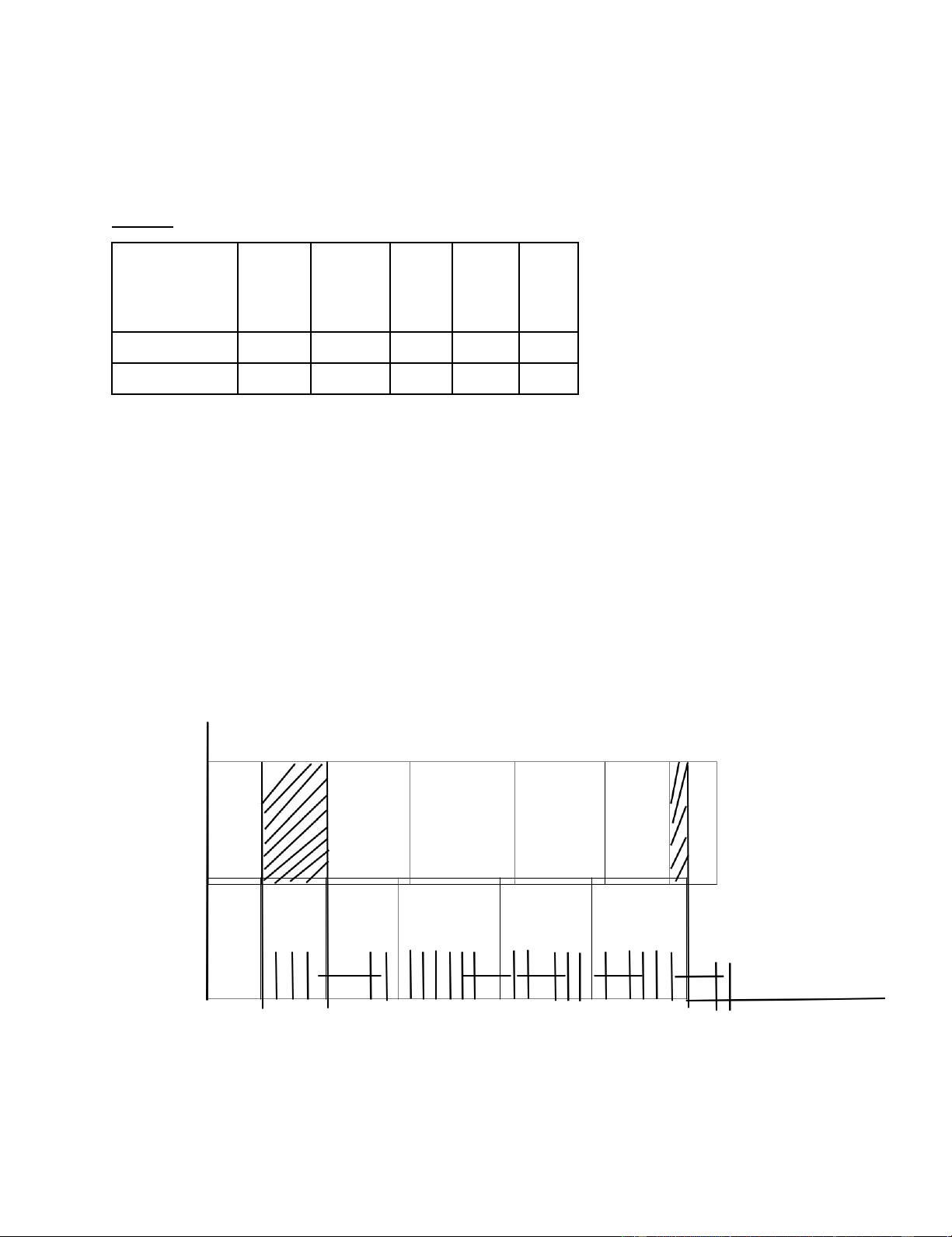
+)Phương án tối ưu: x*=(1,1,0) +)Gía trị tối ưu: f*=14 Câu 3: Máy D1 D2 D3 D4 D5 Chi tiết A 5 7 7 8 4 B 8 5 2 7 6 Giải:
Chia các chi tiết thành 2 nhóm: N1= {D1, D5} N2= {D2, D3, D4} Sắp xếp các chi tiết: N1= {D5, D1} N2= {D4, D2, D3}
Nối N2 vào đuôi N1, ta được lịch gia công tối ưu: Π=(D5, D1, D4, D2, D3) Sơ đồ
Gantt cho lịch gia công chi tiết : B D5 D1 D4 D2 D 3 AD5D1 D4 D2 D3
Vậy thời gian gia công tối ưu T(Π)=33