Ôn tập từ chương 2 đến chương 4 môn Xác suất thống kê| Trường Đại học Ngoại Thương

ÔN TẬP TỔNG HỢP TỪ CHƯƠNG 2 ĐẾN CHƯƠNG 4 I. CHƯƠNG 2
I. Biến Ngẫu Nhiên Rời Rạc
Bài 1. Kiểm tra chất lượng (Dạng Nhị thức)
Một lô hàng linh kiện điện tử có tỷ lệ phế phẩm là 0,1. Lấy ngẫu nhiên 12 linh kiện để
kiểm tra. Gọi X là số linh kiện đạt chuẩn (không phải phế phẩm). a) Tính E(X) và Var(X).
b) Tính xác suất để có đúng 10 linh kiện đạt chuẩn.
Bài 2. Lợi nhuận đầu tư (Biến đổi biến ngẫu nhiên)
Một nhà đầu tư mua một mã cổ phiếu. Xác suất giá tăng là p=0.7. Nếu giá tăng, nhà đầu
tư lãi 5 triệu đồng. Nếu giá không tăng (giảm hoặc đứng yên), nhà đầu tư lỗ 2 triệu đồng.
Gọi X là số trường hợp giá tăng (xét trong 1 lần mua), Y là số tiền lãi/lỗ thu được. a) Lập hàm của Y theo X.
b) Tính E(Y) (Lợi nhuận kỳ vọng).
Bài 3. Gieo xúc xắc (Tổng số chấm)
Gieo 2 con xúc xắc cân đối và đồng chất. Gọi X là tổng số chấm xuất hiện trên hai mặt. a) Tính P(X=7). b) Tính kỳ vọng E(X).
Bài 4. Xạ thủ bắn bia (Bernoulli không đồng nhất)
Có 3 xạ thủ cùng bắn vào một mục tiêu độc lập nhau. Xác suất bắn trúng của từng người lần lượt là p =0,6; 1 p =0,7; 2
p3=0,8. Gọi X là số viên đạn trúng mục tiêu.
Lập bảng phân phối xác suất của X.
Bài 5. Tìm tham số bảng phân phối
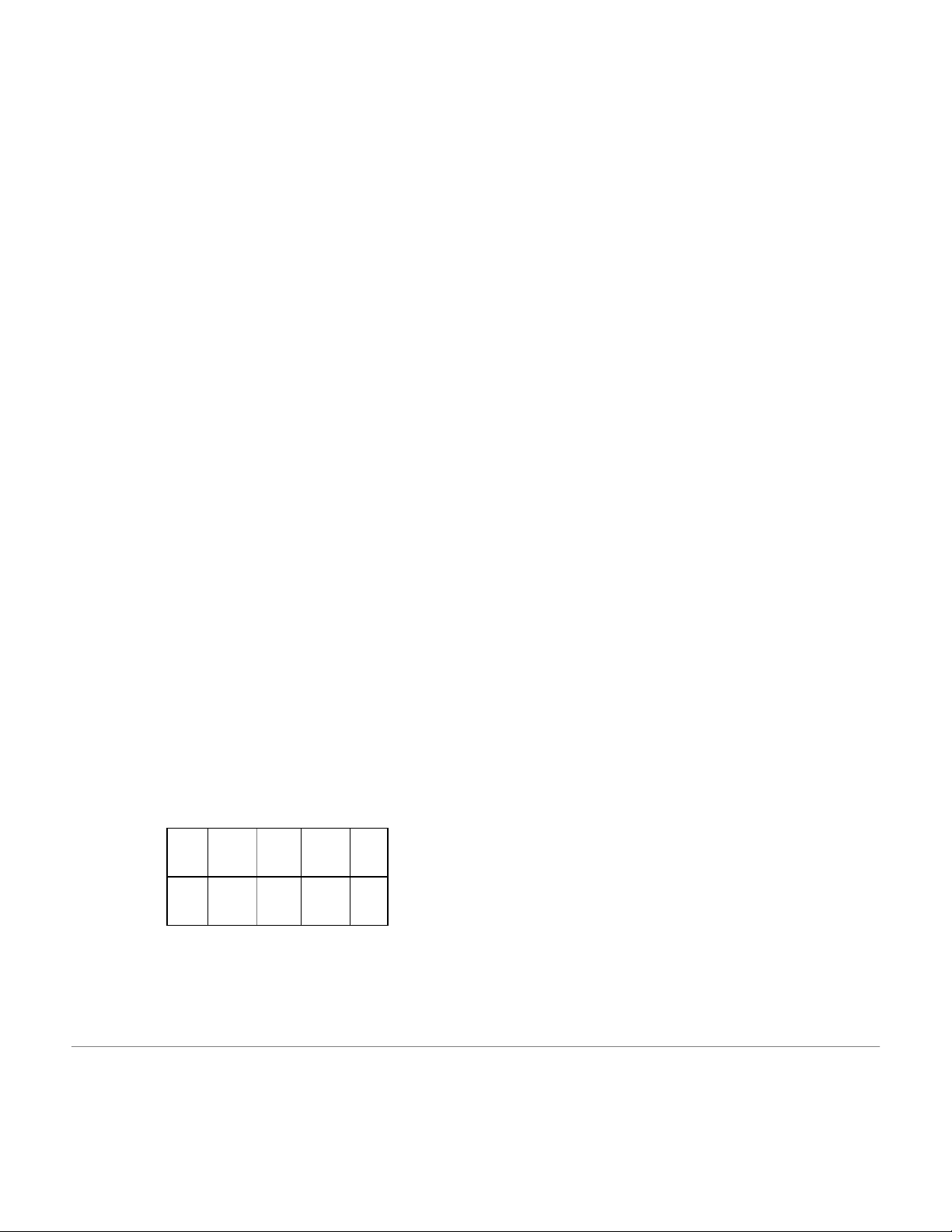
Cho biến ngẫu nhiên rời rạc X có bảng phân phối xác suất như sau: X -1 1 2 5 P0,2 2a 0,3 a a) Tìm giá trị của a. b) Tính E(X) và Var(X).
Bài 6. Chọn nhân sự (Phân phối Siêu bội - Hypergeometric)
Một tổ công tác gồm 5 nam và 4 nữ. Cần chọn ngẫu nhiên 3 người để đi công tác. Gọi X là số nữ được chọn.
a) Lập bảng phân phối xác suất của X.
b) Tính trung bình số nữ được chọn. Bài 7. Xác suất tích lũy
Một bài thi có 10 câu hỏi đúng/sai. Một học sinh chọn ngẫu nhiên đáp án cho cả 10 câu.
Xác suất chọn đúng mỗi câu là 0,5. Gọi X là số câu trả lời đúng.
Tính xác suất để học sinh đó trả lời đúng ít nhất 8 câu.
II. Biến Ngẫu Nhiên Liên Tục
Bài 8. Hàm mật độ lũy thừa
Cho hàm mật độ f(x) = kx 2 với 0 ≤ x ≤ 3 a) Tìm hằng số k. b) Tính E(X).
Bài 9. Phân phối đều (Uniform)
Thời gian chờ xe bus (đơn vị: phút) là biến ngẫu nhiên X có phân phối đều trên đoạn [0, 10].
a) Viết hàm mật độ f(x) và tính phương sai Var(X).
b) Tính xác suất để thời gian chờ nhỏ hơn 3 phút.
Bài 10. Hàm mật độ đối xứng
Cho hàm mật độ f(x) = a(4 – x ) 2 với -2 ≤ x ≤ 2 . a) Tìm a. b) Tính P(-1 < X < 1).
Bài 11. Phân phối Mũ (Exponential)
Tuổi thọ của một loại bóng đèn (đơn vị: nghìn giờ) có hàm mật độ $f(x) = 2e-2x với 0 ≤ x
a) Tính xác suất để bóng đèn hỏng trước 0,5 (nghìn giờ). b) Tính trung vị Med(X).
Bài 12. Kỳ vọng của hàm biến ngẫu nhiên
Cho hàm mật độ f(x) = 3/8 x 2 với 0 ≤ x ≤ 2.
a) Chứng minh đây là hàm mật độ xác suất. b) Tính E(3X - 1).
Bài 13. Xác suất có điều kiện
Cho biến ngẫu nhiên X có hàm mật độ f(x) = 2x với 0 ≤ x ≤ 1.
Tính P(X > 0,6| X > 0,3). II. CHƯƠNG 3
1. Dạng Biến Ngẫu Nhiên Rời Rạc (Kỳ vọng, Phương sai)
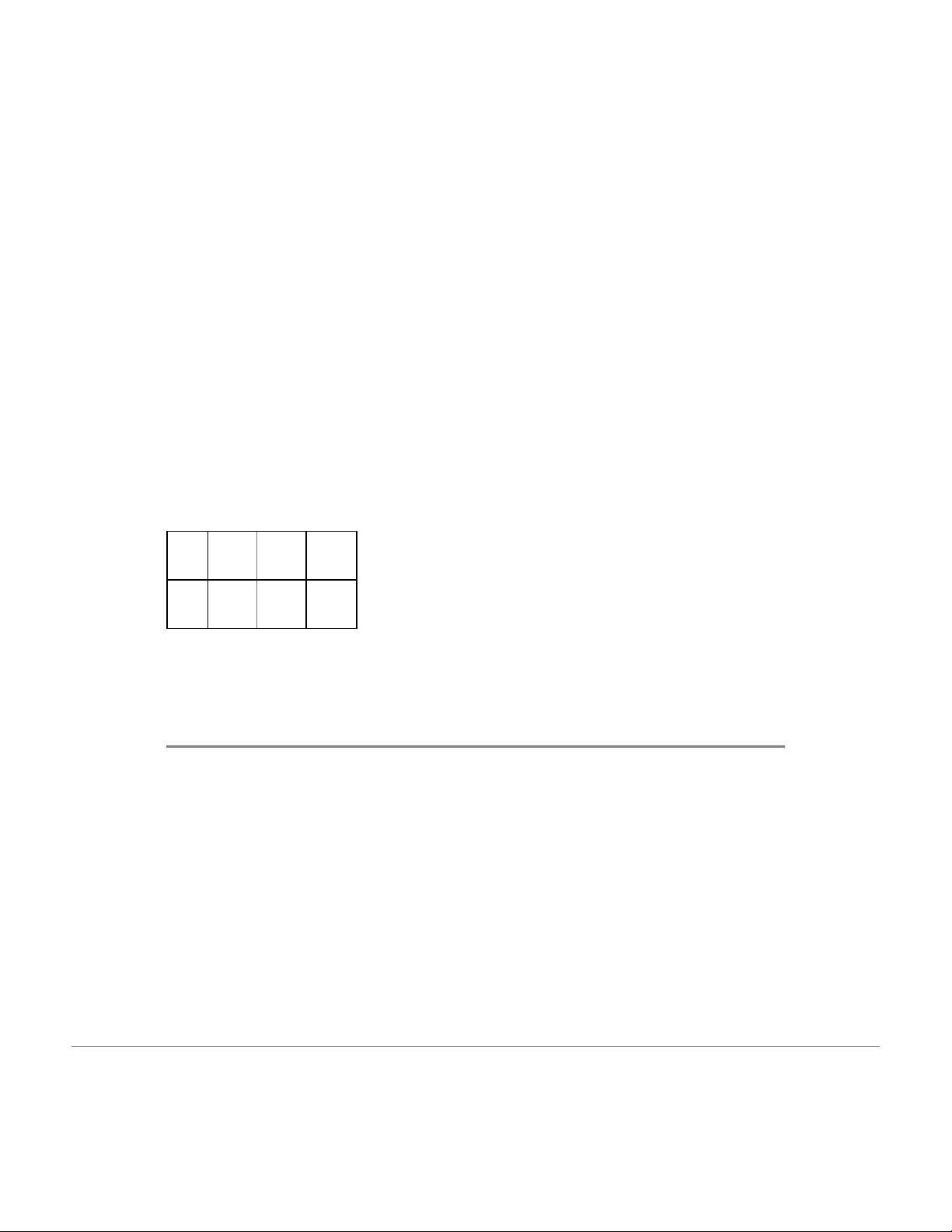
Bài 1.1. Cho bảng phân phối xác suất của biến ngẫu nhiên rời rạc X (số đơn hàng một
nhân viên nhận được trong ngày) như sau: X 2 4 5 P0,3 0,6 0,1
Tính số đơn hàng trung bình mỗi ngày E(X), phương sai V(X) và độ lệch chuẩn của X.
Bài 1.2. Một nhà đầu tư dự định mua cổ phiếu. Nếu thị trường tốt (xác suất 0,6), ông lãi 8
triệu đồng. Nếu thị trường xấu (xác suất 0,4), ông lỗ 2 triệu đồng.
Tính lợi nhuận kỳ vọng của nhà đầu tư này.
2. Dạng Phân Phối Nhị Thức B(n, p)
Bài 2.1. Tỷ lệ nảy mầm của một loại hạt giống là 0,8. Gieo trồng thử nghiệm 10 hạt giống
một cách độc lập. Tính xác suất để:
a) Có đúng 8 hạt nảy mầm.
b) Có ít nhất 9 hạt nảy mầm.
Bài 2.2. Trong một dây chuyền sản xuất, xác suất để một sản phẩm bị lỗi là 5%. Kiểm tra
ngẫu nhiên 20 sản phẩm. Gọi X là số sản phẩm bị lỗi tìm thấy.
Hỏi X tuân theo quy luật phân phối nào? Viết công thức tính xác suất tổng quát P(X=k).
3. Dạng Phân Phối Poisson
Bài 3.1. Số lượng tin nhắn đến tổng đài hỗ trợ khách hàng trong một phút là biến ngẫu
nhiên tuân theo phân phối Poisson với trung bình 4 tin nhắn/phút. Tính xác suất để trong một phút bất kỳ:
a) Nhận được đúng 2 tin nhắn.
b) Nhận được ít hơn 2 tin nhắn
Bài 3.2. Một cuốn sách giáo khoa dày 500 trang. Xác suất để một trang có lỗi in ấn là
0,004. Gọi X là số trang có lỗi in ấn trong cuốn sách.
Sử dụng phân phối Poisson để xấp xỉ, tính xác suất để cuốn sách có đúng 3 trang bị lỗi in.
4. Dạng Phân Phối Siêu Hình Học & Biến Cố
Bài 4.1. Trong một hộp có 15 quả cầu, trong đó có 10 quả màu Đỏ và 5 quả màu Xanh.
Lấy ngẫu nhiên 4 quả cầu từ hộp. Tính xác suất để:
a) Lấy được đúng 2 quả cầu Đỏ.
b) Lấy được ít nhất 1 quả cầu Xanh.
Bài 4.2. Khảo sát một nhóm sinh viên về ngoại ngữ: 60% biết tiếng Anh, 30% biết tiếng
Pháp, và 10% biết cả hai thứ tiếng. Chọn ngẫu nhiên một sinh viên.
a) Tính xác suất sinh viên đó không biết tiếng Anh cũng không biết tiếng Pháp.
b) Tính xác suất sinh viên đó chỉ biết tiếng Anh mà không biết tiếng Pháp.
5. Dạng Phân Phối Chuẩn
Bài 5.1. Chiều cao của nam giới trưởng thành ở một vùng tuân theo phân phối chuẩn với
trung bình170 cm và phương sai 25 cm
2 . Tính xác suất để chọn ngẫu nhiên một người: a) Cao trên 175 cm.
b) Có chiều cao từ 165 cm đến 180 cm.
Bài 5.2. Trọng lượng của các bao xi măng tuân theo phân phối chuẩn với trung bình 50
kg và độ lệch chuẩn 1 kg. Một bao xi măng được coi là "đạt chuẩn" nếu trọng lượng nằm trong khoảng [49, 51] kg.
a) Tính xác suất để một bao xi măng bất kỳ đạt chuẩn.
b) Nếu kiểm tra 100 bao, tính xác suất để có ít nhất 90 bao đạt chuẩn (Gợi ý: Dùng kết
quả câu a làm tham số p cho phân phối nhị thức, hoặc xấp xỉ chuẩn nếu cần).
6. Dạng Bài Toán Kinh Tế / Lợi Nhuận
Bài 6.1. Một công ty tham gia đấu thầu một dự án. Chi phí để chuẩn bị hồ sơ thầu là 50
triệu đồng (khoản này mất đi dù thắng hay thua). Nếu thắng thầu (xác suất 0,2), công ty
sẽ thu về lợi nhuận gộp là 500 triệu đồng (chưa trừ chi phí hồ sơ). Nếu thua, công ty không thu được gì.
Gọi L là lợi nhuận ròng của công ty.
a) Lập bảng phân phối xác suất cho L.
b) Tính lợi nhuận ròng trung bình (kỳ vọng) của công ty khi tham gia đấu thầu. III. CHƯƠNG IV
Dạng 1: Thống kê mô tả (Tính các tham số mẫu)
Bài tập 1: Điều tra năng suất lúa (tạ/ha) của 100 thửa ruộng thí nghiệm, ta thu được bảng số liệu sau:
Năng suất (xi) 50 55 60 65 70 75
Số thửa (ni)10 15 30 25 15 5 a) Tính trung bình mẫu
b) Tính phương sai mẫu và phương sai mẫu hiệu chỉnh
Bài tập 2: Khảo sát chiều cao (cm) của 50 cây giống trong một vườn ươm, kết quả được phân lớp như sau:
Chiều cao (khoảng) 20 – 30 30 – 40 40 – 50 50 – 60 60 – 70 Số cây 5 10 20 10 5
a) Tính chiều cao trung bình của cây giống.
b) Tính độ lệch chuẩn mẫu hiệu chỉnh.
Dạng 2: Véc-tơ ngẫu nhiên rời rạc (Bảng phân phối đồng thời)
Bài tập 3: Cho bảng phân phối xác suất đồng thời của véc-tơ ngẫu nhiên (X, Y), trong đó
X là số lượng sản phẩm A và Y là số lượng sản phẩm B bán được trong ngày: X \ Y 10 20 30 10.10 0.15 0.05 20.15 0.30 0.10 30.05 0.05 0.05
a) Tìm xác suất để bán được đúng 1 sản phẩm A (Tìm phân phối lề của X).
b) Lập bảng phân phối xác suất của Y.
c) Tính kỳ vọng về số lượng sản phẩm B bán được (E(Y)).
d) Lập bảng phân phối xác suất có điều kiện của X khi biết Y = 20.
Bài tập 4: Doanh thu (X - triệu đồng) và Chi phí (Y - triệu đồng) có bảng phân phối xác suất đồng thời: X \ Y 2 4 10 0.2 0.3 20 0.4 0.1
a) Tính hiệp phương sai Cov(X, Y) = E(XY) - E(X)E(Y).
b) Tính hệ số tương quan giữa X và Y.
Dạng 3: Phân phối chuẩn, Phân phối mẫu và Ước lượng.
Bài tập 5: Tuổi thọ của một loại bóng đèn là biến ngẫu nhiên phân phối chuẩn với trung
bình 1000 giờ và độ lệch chuẩn 50 giờ. Lấy mẫu ngẫu nhiên gồm n = 100 bóng đèn.
Tính xác suất để tuổi thọ trung bình của mẫu nằm trong khoảng từ 990 đến 1010 giờ.
Bài tập 6: Tỷ lệ người dân ủng hộ chính sách mới ở một thành phố là p. Muốn ước lượng
tỷ lệ này với độ tin cậy 95% và sai số không quá 3% (0.03), cần điều tra mẫu có kích
thước tối thiểu là bao nhiêu? Biết rằng theo số liệu cũ tỷ lệ này khoảng 60%.
Bài tập 7: Đo đường kính của 20 chi tiết máy, ta tính được trung bình mẫu 15.02 mm.
Biết đường kính chi tiết máy tuân theo phân phối chuẩn với độ lệch chuẩn 0.05 mm.
Hãy ước lượng đường kính trung bình của chi tiết máy với độ tin cậy 95%.