Ôn Thi Cuối Kỳ - CTDLGT: Độ Phức Tạp Thuật Toán, Cây Nhị Phân, Sắp Xếp Môn Câu trúc dữ liệu giải thuật | Trường Đại học Công nghiệp Thành phố Hồ Chí Minh

Nôi dung:
1. Độ phức tạp thuật toán
2. Thuật toán tìm kiếm và sắp xếp
3. Cây nhị phân tìm kiếm
4. Cây cân bằng (ko kiểm tra code) Ví dụ:
Câu 1: ([LO3] – 2.0 điểm) Cho đoạn code dưới đây: 1. float s = 0; 2. int i = n; 3. while(i > 0) 4. { 5. s = s + i; 6. i--; 7. } 8. cout<9. s = 0; 10. int i = n; 11. while(i != 0) 12. { 13. s = s + 1.0 / i; 14. i/= 2; 15. }
16. cout<1) Anh/ Chị hãy cho biết độ phức tạp của các câu lệnh từ 1 đến 8. O(n)
2) Hãy xác định độ phức tạp của các câu lệnh từ 9 đến 16. Log2(n)
3) Dựa vào kết quả của các câu trên, hãy cho biết độ phức tạp của đoạn chương trình. Nêu rõ qui tắc áp dụng. O(n)+O(Log2(n))
Áp dụng quy tắc cộng ->O(max (n, Log2n)  O(n)
Câu 2: ([LO1] – 2.0 điểm)
Để quản lý thông tin các sản phẩm của một nhà máy, người ta dùng mảng một chiều.
Thông tin của sản phẩm g : Mã sản phẩm (MaSP), tên sản phẩm (TenSP), ngày
sản xuất (NgaySX), số nă bảo hành (SoNamBH). Cho trước cấu trúc dữ liệu dưới đây: struct struct SANPHAM NGAY { { int char MaSP[10]; ngay; char int TenSP[255]; thang; NGAY int NgaySX; nam; int }; SoNamBH; }; SANPHAM dsSP[10000];
Anh/chị hãy viết hàm thực hiện các công việc sau:
1. Sắp xếp danh sách sản phẩ theo thứ tự tăng dần ủa MaSP bằng thuật toán Quick sort.
int quicksort(SANPHAM dsSP[], int left, int right) { int i=left, j=right; SANPHAM x; if(left>=right) return -1; x=dsSP[(left+right)/2]; while(i<=j) {
while(strcmp(dsSP[i].MaSP, x.MaSP) < 0) i++;
while(strcmp(dsSP[j].MaSP, x.MaSP) > 0) j--; if(i<=j) { swap(dsSP[i], dsSP[j]); i++; j--; } } if(leftif(i}
void interchangeSort(SANPHAM dsSP[], int n) {
for (int i = 0; i < n-1; i++) {
for (int j = i+1; j < n; j++) {
if (strcmp(dsSP[i].MaSP, dsSP[j].MaSP) > 0) swap(dsSP[i], dsSP[j]); } } }
void bubbleSort(SANPHAM dsSP[], int n) {
for (int i = 0; i < n-1; i++) {
for (int j = n-1; j > i; j--) {
if (strcmp(dsSP[j].MaSP, dsSP[j- 1].MaSP) < 0) swap(dsSP[j], dsSP[j-1];) } } }
void selectionSort (SANPHAM dsSP[], int n) {
for (int i = 0; i < n-1; i++) { int min_idx = i;
for (int j = i+1; j < n; j++) { if(strcmp(dsSP[j].MaSP, dsSP[min_idx].MaSP) < 0) min_idx = j; } swap(dsSP[i], dsSP[min_idx]); } }
void insertionSort(SANPHAM dsSP[], int n){ SANPHAM x;
for(int i = 1; i < n; i++) { x = dsSP[i]; int j = i-1;
while(j >= 0 && strcmp(dsSP[j].MaSP, x.MaSP) > 0) { dsSP[j+1] = dsSP[j]; j--; } dsSP[j+1] = x; } }
2. Tìm k ế và in ra các sản phẩm đã hết hạn bảo hành ( nă sản xuất + số nă bảo
hành < nă h ện tạ ). Nếu không tìm thấy h ển thị thông báo. Trong đ : nă h ện tạ là
tham số ủa hàm. void xuatSP(SANPHAM sp);
void timKiemSanPhamHetHan(SANPHAM dsSP[], int n, int namHienTai) { int dem = 0;
for(int i=0; iif(dsSP[i].NgaySX.nam + dsSP[i].SoNamBH < namHienTai) { xuatSP(dsSP[i]); dem++; } } if(dem == 0)
printf("Khong co san pham het han bao hanh!\ n"); }
Câu 3: ([LO2] – 3.0 điểm)
Để quản lý thống kê số lượng của kí tự xuất hiện trong một văn bản tiếng Anh. Người
ta đã tổ chức dữ liệu bằng cây nhị phân tìm kiếm. Thông tin của từ g : kí tự
(KiTu), số lượng (SoLuong). Cấu trúc dữ liệu được cho trước bên dưới đây: struct CHARACTER { char KiTu; struct TNode { int SoLuong; CHARACTER data; }; TNode *pLeft; typedef Tnode TNode *pRight;}; *Tree;
1) Hãy v ết hàm thự h ện thêm ột kí tự X vào cây ( X là tham số ủa hàm). B ết rằng:
nếu X đã trên cây thì tăng số lượng (SoLuong) ủa kí tự này lên 1 đơn vị, ngượ lạ : thì
tạo node ớ hứa kí tự X và chèn node vào cây để cây kết quả là cây nhị phân tìm k ế . T Node*TaoNode(CHARACTER C) p-> pleft=NUll; p-> pRight=NULL; p->data=c; return p;
void Them(tree &T;char c ) { if(c==NULL){ c=TaoNode(x); } else {
if(strcmp(c->data.KiTu,x.KiTu)==0) { c->data.soluong++; } }
else if(strcmp(c->data.KiTu,x.KiTu)>0) { ThemNode(c->pLeft,x) }
else if(strcmp(c->data.KiTu,x.KiTu)<0) { ThemNode(c->pRight,x) } else { return ; } }
void insertOrUpdate(Tree &root, char X) { if (root == NULL) { Tree newNode = new TNode; newNode->data.KiTu = X; newNode->data.SoLuong = 1;
newNode->pLeft = newNode->pRight = NULL; root = newNode; } else {
if (X < root->data.KiTu) {
insertOrUpdate(root->pLeft, X);
} else if (X > root->data.KiTu) {
insertOrUpdate(root->pRight, X); } else {
// X đã có trong cây, tăng số´lượng lên 1 đơn vị root->data.SoLuong++; } } }
2) V ết hàm trả số lượng kí tự X trên cây node gố T. Nếu không kí tự X thì hàm trả về 0.
int CountNode(Tree T;char x) { if(T==NULL) return 0; if(x==T->data.KiTu) return T->data.SoLuong if(xdata.KiTu)
return CountNode(T->pLeft;X)
return CountNode(T->pRight;X) }
int countChar(Tree T, char X) { if (T == NULL) {
return 0; // Khống tìm t h â ´y ký tự X trên cây } if (T->data.KiTu == X) { return T->data.SoLuong;
} else if (X < T->data.KiTu) {
return countChar(T->pLeft, X); } else {
return countChar(T->pRight, X); } }
3) Hãy cho b ết độ phứ tạp trung bình ủa hàm mà anh/ hị đã v ết ở câu câu 3.2. Anh/Chị
hãy đ ều hỉnh ấu trúc dữ l ệu h ện tạ để độ phứ tạp là O(log2 n). B ết rằng: n là số
node ủa cây T, h ều cao ủa cây là h. h=log2n O(log2n)
Câu 4: (3.0 điểm)
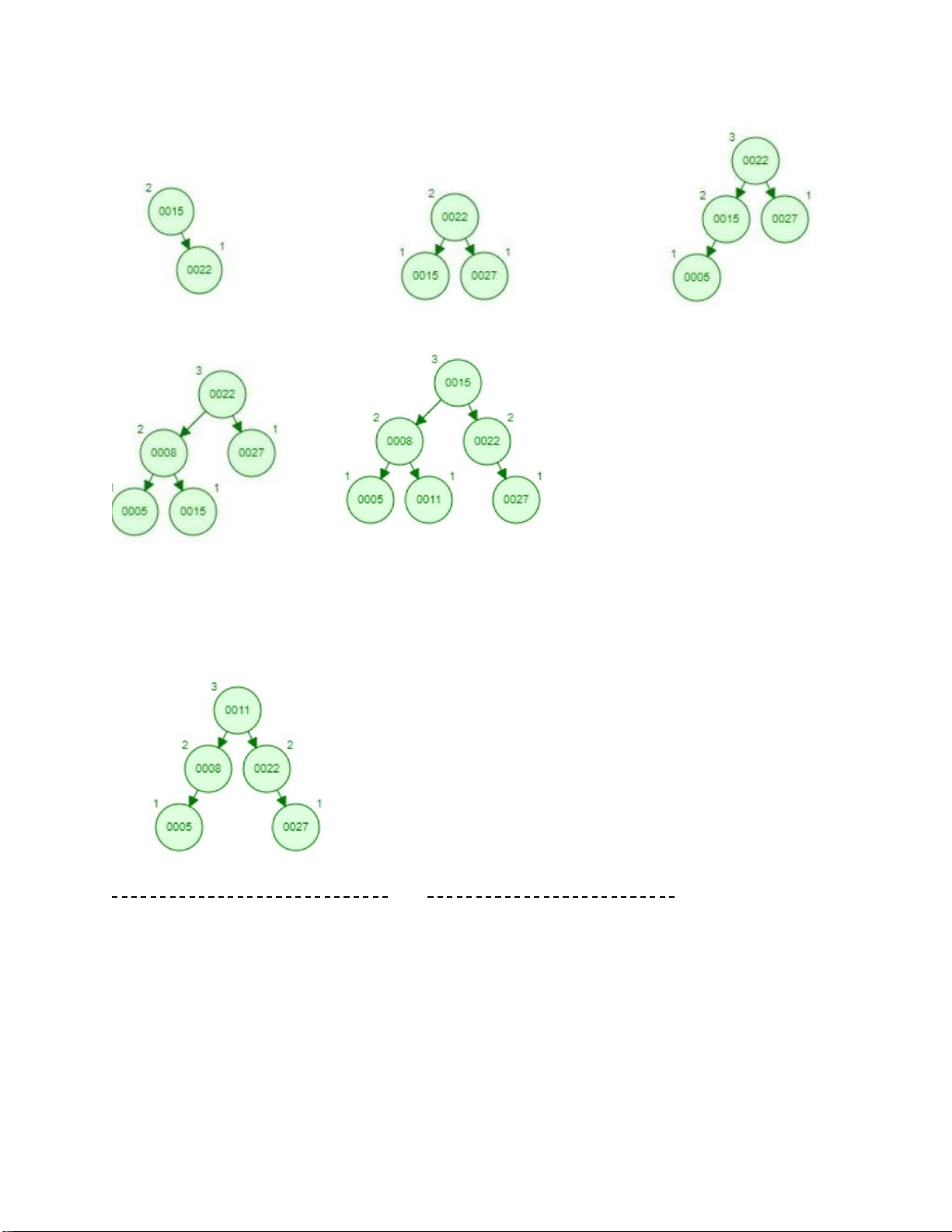
Cho dãy các số sau: 15, 22, 27, 5, 8, 11
1) Hãy vẽ cây cân bằng khi chèn liên t ếp các số theo thứ tự từ trái sang phả . Trình bày
kết quả cân bằng lạ cây trong trường hợp cây ất ần bằng tạ bướ chèn node bất kỳ.
2) Vẽ cây AVL, khi x a node Xi ( cân bằng lạ cây nếu sau khi x a cây ất cân bằng)
B ết i = K % 3 +1 (K: hai số uố ủa mã sinh viên. VD: Mã SV là 21023391 thì K = 91 => i =
91 % 3 + 1 = 2, Xi = 8) i 1 2 3 Xi 15 8 22 Hết
- Đề thi không được sử dụng tài liệu.
- Cán bộ coi thi không giải thích gì thêm.