2. Bán kính qua tiêu và tâm sai của parabol:  Lý thuyết
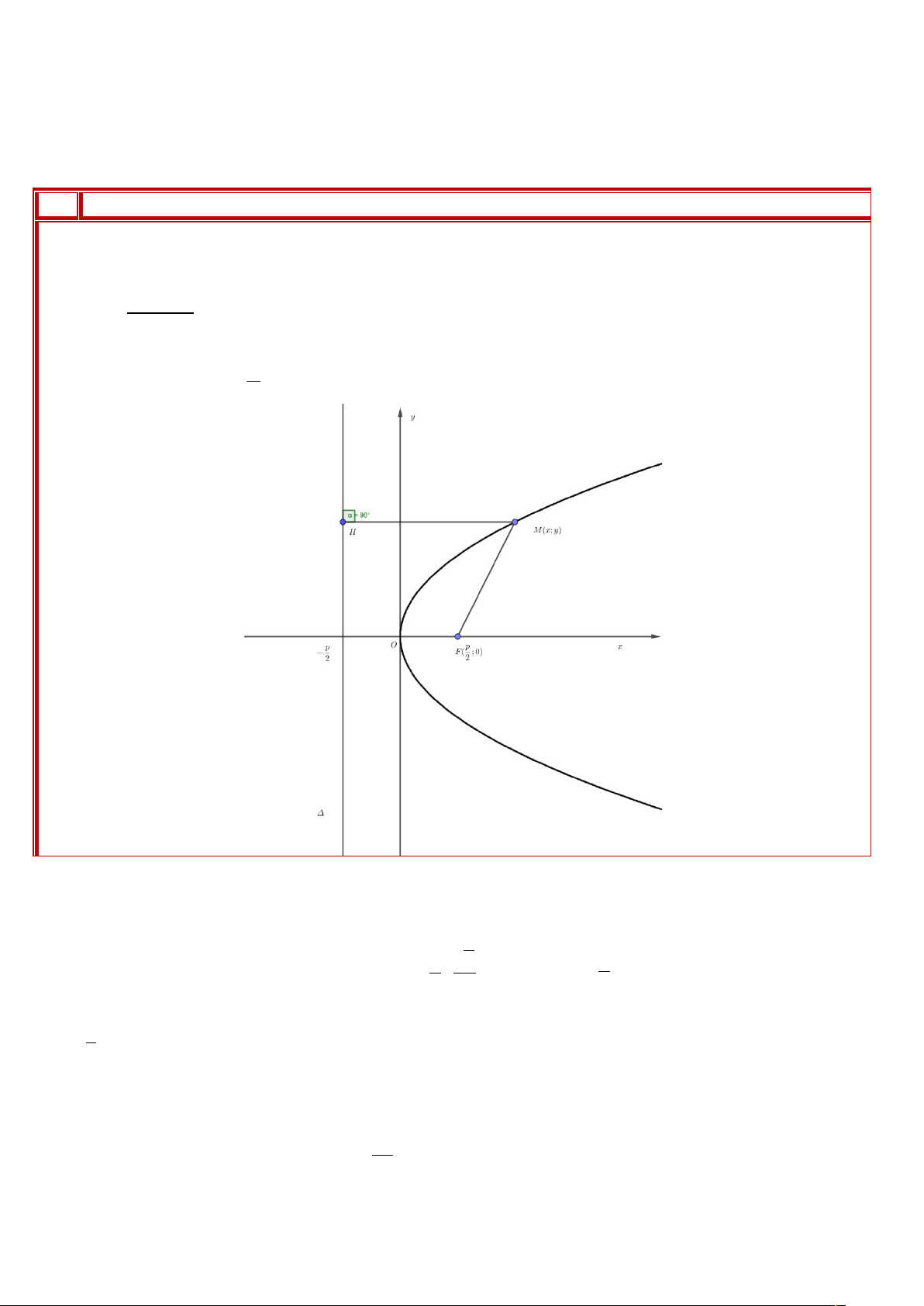
Cho điểm M thuộc parabol (P) có tiêu điểm F và đường chuẩn ∆: Ta gọi:
- Đoạn FM là bán kính qua tiêu của điểm M.
- Tỉ số e= FM
d(M ,∆) là tâm sai của parabol (P).
Mọi parabol đều có tâm sai e = 1 và parabol chính tắc (P):y2=2 px có độ dài bán kính qua tiêu của
điểm M(x ; y) là FM =x+ p . 2
Ví dụ 2.1: Tính bán kính qua tiêu của điểm M trên các parabol tương ứng sau:
a) M(1;4) trên (P):y2=16 x b) M( 1 ; √7 ¿ trên (P): y2=7 x 2 2 2
Ví dụ 2.2: Trong mặt phẳng tọa độ Oxy, cho parabol có phương trình chính tắc y2=32 x
a) Xác định tọa độ tiêu điểm phương trình đường chuẩn của parabol và bán kính qua tiêu của điểm M( 1;4√2). b) Vẽ parabol. Ví dụ 2.3:
a) Viết phương trình chính tắc của parabol (P) có tiêu điểm F(3;0).
b) Tính bán kính qua tiêu của điểm M(5;25 12). Ví dụ 2.4:
a) Lập phương trình chính tắc của parabol (P), biết phương trình đường chuẩn là x=−2
b) Tìm tọa độ tiêu điểm F và tính bán kính qua tiêu của điểm M( 5 ; 25 ¿ 2 32 .
Ví dụ 2.5: Cho parabol có phương trình y2=8 x. Tìm toạ độ tiêu điểm và phương trình đường chuẩn
của parabol. Tính bán kính qua tiêu của điểm M thuộc parabol biết điểm M có tung độ bằng 4.
Luyện tập 2.1: Tính bán kính qua tiêu của các điểm dưới đây trên parabol tương ứng:
a) A(1;2) trên parabol (P): y2=4 x b) B(5;5√2¿ trên parabol (P): y2=10 x
Luyện tập 2.2: Trong mặt phẳng tọa độ Oxy, cho parabol có phương trình chính tắc y2=8 x
a) Xác định tọa độ tiêu điểm, phương trình đường chuẩn của parabol và bán kính qua tiêu của điểm M(2;4). b) Vẽ parabol. Luyện tập 2.3:
a)Viết phương trình chính tắc của parabol (P) có tiêu điểm F(10;0).
b)Tính bán kính qua tiêu của điểm M(5;10).
Luyện tập 2.4: Trong mặt phẳng toạ độ Oxy, parabol (P) có phương trình chính tắc và đi qua điểm M(
3;3√2¿. Tìm bán kính qua tiêu và khoảng cách từ tiêu điểm tới đường chuẩn của (P).
Luyện tập 2.5: Cho parabol có phương trình y2=12 x. Tìm tiêu điểm và đường chuẩn của parabol.
Tính bán kính qua tiêu của điểm M thuộc parabol và có hoành độ bằng 5.
Luyện tập 2.6: Cho parabol có phương trình y2=18 x. Tìm tiêu điểm và đường chuẩn của parabol.
Tính bán kính qua tiêu của điểm M thuộc parabol và có hoành độ bằng 12.
Luyện tập 2.7: Cho parabol có phương trình y2=16 x. Tìm toạ độ tiêu điểm và phương trình đường
chuẩn của parabol. Tính bán kính qua tiêu của điểm M thuộc parabol biết điểm M có tung độ bằng 10.
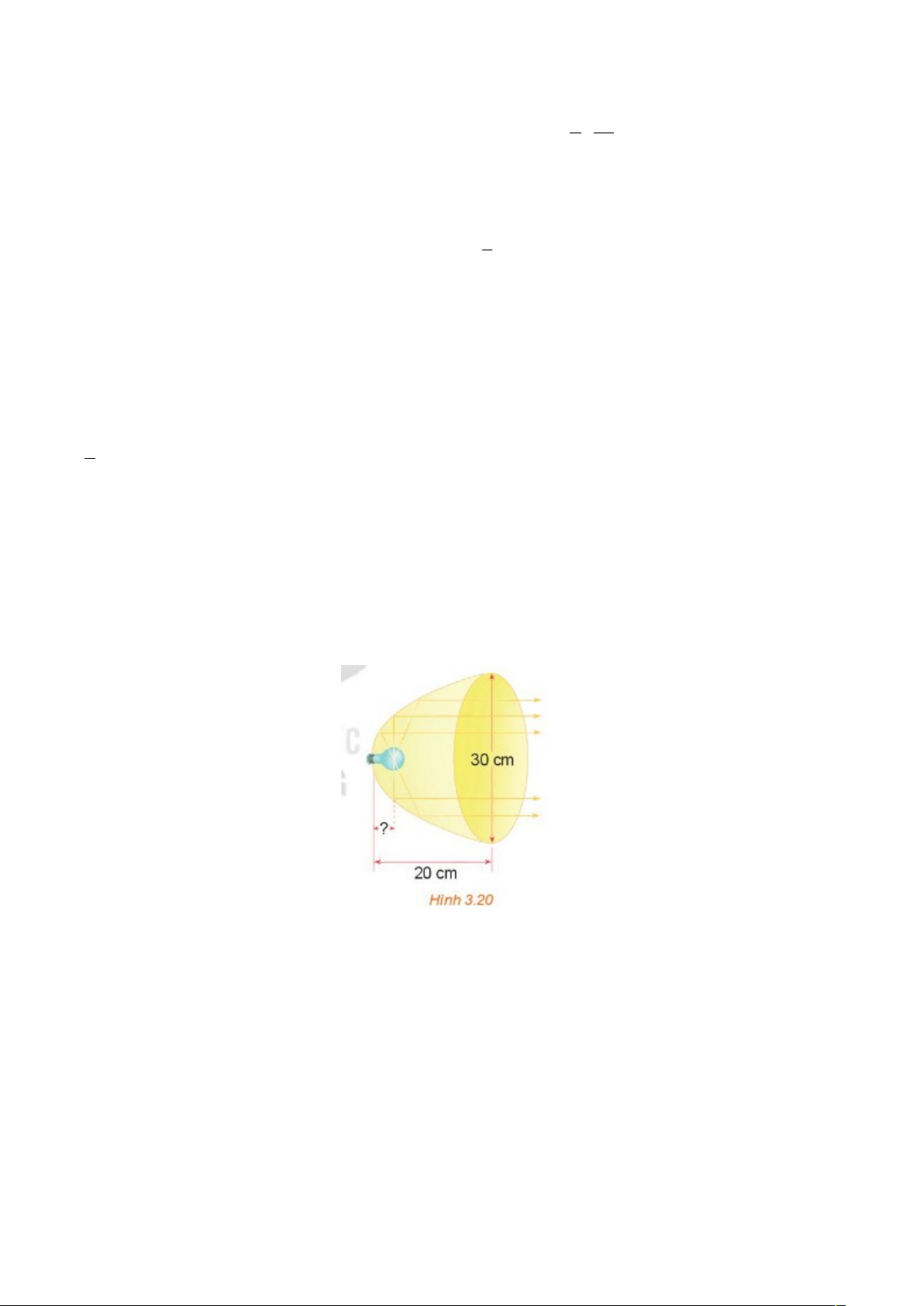
Luyện tập 2.8: Xét đèn có bát đáy parabol với kích thước được thể hiện như hình vẽ dưới đây. Dây tóc
bóng đèn được đặt ở vị trí tiêu điểm. Tính khoảng cách từ dây tóc tới đỉnh bát đáy.
Luyện tập 2.9: Anten vệ tinh parabol ở Hình 3.21 có đầu thu đặt tại tiêu điểm, đường kính miệng
enten là 240 cm, khoảng cách từ vị tri đặt đầu thu tới miệng anten là 130 cm. Tính khoảng cách từ vị trí
đặt đầu thu tới đỉnh anten.
Luyện tập 2.10: Một sao chổi chuyền động theo quỹ đạo parabol nhận tâm Mặt Trời làm tiêu điểm.
Khoảng cách ngắn nhất từ sao chổi đến tâm Mặt Trời là 106 km. Lập phương trình chính tắc của quỹ
đạo theo đơn vị kilômét. Hỏi khi sao chổi nằm trên đường vuông góc với trục đối xứng của quỹ đạo tại
tâm Mặt Trời, thì khoảng cách từ sao chổi đến tâm Mặt Trời là bao nhiêu kilômét?
VD 2.1, 2.2, 2.3, 2.4 tự làm
VD 2.5 sách chuyên đề toán 10 kết nối tri thức LT 2.1 tự làm
LT 2.2 sách chuyên đề toán 10 cánh diều LT 2.3 tự làm
LT 2.4 sách kết nối tri thức LT 2.5, 2.6, 2.7 tự làm
LT 2.8, 2.9, 2.10 sách chuyên đề kết nối tri thức
Document Outline

• 2. Bán kính qua tiêu và tâm sai của parabol: