-
Thông tin
-
Quiz
Phần I - Xác suất - Chương 4 - Xác suất thống kê | Trường Đại học Khoa học Tự nhiên, Đại học Quốc gia Thành phố Hồ Chí Minh
Biến ngẫu nhiên X của một phép thử τ với không gian mẫu Ω là một ánh xạ X : Ω → R, ω 7→ X(ω). Biến ngẫu nhiên được gọi là liên tục nếu tập hợp các giá trị mà nó có thể nhận X(Ω) là một khoảng dạng (a, b) hoặc toàn bộ R. Tài liệu được sưu tầm giúp bạn tham khảo, ôn tập và đạt kết quả cao trong kì thi sắp tới. Mời bạn đọc đón xem !
Môn:
Xác suất thống kê (Hus) 27 tài liệu
Trường:
Trường Đại học Khoa học tự nhiên, Đại học Quốc gia Thành phố Hồ Chí Minh 290 tài liệu
Thông tin:
32 trang
3 tháng trước
Tác giả:
Phần I - Xác suất - Chương 4 - Xác suất thống kê | Trường Đại học Khoa học Tự nhiên, Đại học Quốc gia Thành phố Hồ Chí Minh
Biến ngẫu nhiên X của một phép thử τ với không gian mẫu Ω là một ánh xạ X : Ω → R, ω 7→ X(ω). Biến ngẫu nhiên được gọi là liên tục nếu tập hợp các giá trị mà nó có thể nhận X(Ω) là một khoảng dạng (a, b) hoặc toàn bộ R. Tài liệu được sưu tầm giúp bạn tham khảo, ôn tập và đạt kết quả cao trong kì thi sắp tới. Mời bạn đọc đón xem !
37
19 lượt tải
Tải xuống
Môn: Xác suất thống kê (Hus) 27 tài liệu
Trường: Trường Đại học Khoa học tự nhiên, Đại học Quốc gia Thành phố Hồ Chí Minh 290 tài liệu
Thông tin:
32 trang
3 tháng trước
Tác giả:
lOMoARcPSD|46958826
≥
.
2
CHƯƠNG 4
BIẾN NGẪU NHIÊN LIÊN
TỤC
VÍ DỤ 1.1. Tìm k để hàm sau là hàm m tậ đ .ộ
®
f (x) =
k(1 + 2x)khi 0 ≤ x ≤ 2,
0
chỗ khác.
1. MỘT SỐ KHÁI NIỆM
1.1. ĐỊNH NGHĨA
Bi nế ng uẫ nhiên
X
c aủ m tộ phép thử τ v iớ không gian m uẫ Ω là m tộ ánh xạ
X
: Ω → R
ω ›→ X(ω)
Biến ngẫu nhiên đ c g i là ượ ọ liên tục n u t p h p các giá tr mà nó có th nh n ế ậ ợ ị ể ậ X(Ω) là m tộ
kho ngả d ngạ (a, b) ho cặ toàn bộ R.
1.2. HÀM MẬT ĐỘ XÁC SUẤT
Hàm mật độ xác suất (probability density function) c aủ m tộ bi nế ng uẫ nhiên liên t cụ
X
là hàm số th aỏ
i)
f
(x) 0
∫
∞
ii)
f (x)dx = 1
−∞
∫
b
iii)
P(a ≤
X
≤ b)
=
f (x)dx.
a
✍ L IỜ GI I.Ả
V iớ 0 ≤ x ≤ 2, ta có 1 + 2x > 0. Do đó, để f (x) ≥ 0, ∀x thì k ≥ 0.
Ta
có
∫
+∞
−∞
f (x)dx
=
∫
0
f (x)dx
+
−∞
∫ ∫
∫
2
f (x)dx
+
0
∫
+∞
2
∫
f (x)dx
0
=
0dx +
−∞
2
k(1 + 2x)dx
+
0
+∞
0dx
2
=
0
+
=
6k.
lOMoARcPSD|46958826
.
k
(2x + 1)
2
.
+ 0
2 0
1
.
−
.
x
lOMoARcPSD|46958826
Hàm phân phối tích lũy (cumulative distribution function) c aủ bi nế ng uẫ nhiên liên t cụ X là:
∫ a
F (a) = P(X ≤ a) =
−∞
f (x)dx,x ∈ R.
M tặ khác, để f là hàm m tậ độ thì
∫
+
∞
f (x)dx = 1, do đó 6k = 1 ⇒ k =
1
.
V yậ hàm m tậ độ đ cượ xác đ nhị
là
−∞
6
(1
+
2x) khi 0
≤
x
≤
2,
f (x) =
6
0 chỗ khác.
Q
1.3.
HÀM PHÂN PHỐI TÍCH LŨY
VÍ DỤ 1.2. Cho
X
là bi nế ng uẫ nhiên liên t cụ có hàm m tậ độ
1
f (x) =
6
(1
+
2x) khi 0
≤
x
≤
2,
0 chỗ khác.
Tìm hàm phân ph iố tích lũy c aủ
X.
✍ L IỜ GI I.Ả
∗ V iớ x
<
0, khi đó
∗ V iớ 0
≤
x
<
2, khi
đó
F (x) = P(X ≤ x)
=
∫
x
f (t)dt
=
−∞
∫
x
0dt
=
0.
−∞
F (x) = P(X ≤ x)
=
=
∫
x
f (t)dt
−∞
∫
0
∫
x
f (t)dt +
−∞ 0
∫
0
∫
x
1
f (t)dt
=
0dt +
−∞ 0
(1 + 2t)dt
6
=
0
+
1
(2t + 1)
2
.
24 0
∗ V iớ
x ≥
2, khi
đó
=
1
(2x + 1)
2
1
.
24
F (x) = P(X ≤ x)
=
=
∫
x
f (t)dt
−∞
∫
0
f (t)dt
+
∫
2
f (t)dt +
0
lOMoARcPSD|46958826
∫
x
f (t)dt
−∞
∫
0
=
0dt
+
−∞
∫
2
1
0
6
2
x
(1 + 2t)dt +
2
0dt
CH NGƯƠ 4. BI NẾ NG UẪ NHIÊN LIÊN T CỤ
1. Một số khái niệm
|
49
∫
.
X X
.
2
lOMoARcPSD|46958826
V yậ hàm phân ph iố tích tũy c aủ
X
là
=
0
+
=
1.
1
(2t + 1)
2
.
+ 0
24 0
0 n uế x
<
0
F (x) =
1
24
(2x + 1)
2
− 1
n uế 0
< x ≤
2
1 n uế 2
≤ x.
Q
2. MỘT SỐ ĐẶC TRƯNG CỦA BIẾN NGẪU NHIÊN
1)
Trung trình (kỳ vọng) c aủ bi nế ng uẫ nhiên liên t cụ X có hàm m tậ độ f (x) đ cượ đ nhị nghĩa
là
E(X) ≡ µ
X
=
∫
+∞
−∞
xf (x)dx.
2)
Kỳ vọng của hàm của biến ngẫu nhiên
Cho g là hàm số th cự b tấ kỳ, kỳ v ngọ c aủ hàm g c aủ bi nế ng uẫ nhiên r iờ r cạ
X,
ký hi uệ là
E(g(X)) xác đ nhị theo công th c:ứ
Đ cặ
bi t,ệ
E(g(X))
=
∫
+∞
−∞
g(x)f (x)dx.
N u ế g(x)
=
x
r
, ta g i ọ E(g(X)) là moment bậc r.
N uế g(x)
=
e
tx
thì ta g iọ E(g(X)) là hàm sinh moment.
N uế g(x) = e
−itx
thì ta g iọ E(g(X)) là hàm đặc trưng c aủ bi nế ng uẫ nhiên X.
3) Phương sai c aủ bi nế ng uẫ nhiên liên t cụ X có hàm m tậ độ f (x) đ cượ đ nhị nghĩa là
V ar(X) ≡ σ
2
∫
+∞
=
−∞
(x − µ
X
)
2
f (x)dx =
∫
+∞
−∞
x
2
f (x)dx − µ
2
.
4)
Độ lệch
tiêu
chuẩn c aủ bi nế ng uẫ
nhiên
liên t cụ
X
đ cượ
đ nhị nghĩa là căn b cậ hai c aủ
ph ngươ sai
σ
X
=
»
V ar(X).
VÍ DỤ 2.1. Cho
X
là bi nế ng uẫ nhiên liên t cụ có hàm m tậ độ
1
f (x) =
6
(1
+
2x) khi 0
≤
x
≤
2,
0 chỗ khác.
a)
Tính E(X) và E(X
2
).
b) Tính ph ngươ sai và độ l chệ tiêu chu nẩ c aủ
X.
lOMoARcPSD|46958826
X
X
·
9
— −
lOMoARcPSD|46958826
✍ L IỜ GI I.Ả
a)
Ta có E(X) ≡ µ
X
=
∫
+∞
∫
+∞
−∞
xf (x)dx
=
∫
∫
2
1
x ·
6
(1 + 2x)dx
=
11
.
9
E(X
2
) =
x
2
f (x)dx
=
−∞
2
1
x
2
(1 + 2x)dx
=
0
6
16
.
9
16
Å
11
ã
2
23
b)
Ph ngươ sai c aủ
X
là V
ar(X)
≡ σ
2
= E(X
2
) [E(X)]
2
= = .
81
Lưu
j:
Ta cũng có thể tính ph ngươ sai c aủ
X
như sau
V ar(X) ≡ σ
2
∫
+∞
=
−∞
(x − µ)
2
f (x)dx
=
∫
2
Å
x
0
11
ã
2
9
·
1 23
(1 + 2x)dx =
.
6 81
Độ l ch tiêuệ chu n c a ẩ ủ
X
là
σ
X
=
…
23 23
V ar(X) = = .
81 9
Q
BÀI 4.1. Dòng đi nệ trong m tộ m chạ nh tấ đ nhị đ cượ đo b ngằ m tộ ampe kế là bi nế ng uẫ nhiên liên
t cụ
X
v i hàm m t đớ ậ ộ
sau
f (x)
=
®
0,075x + 0,2
khi 3
≤ x ≤
5,
0 chỗ khác.
a) Hãy vẽ hàm m tậ độ c aủ phân ph iố và ki mể tra ph nầ di nệ tích bên d iướ đ ngườ cong c aủ hàm
m tậ độ là 1.
b)
Tính
P(X ≤
4) và so sánh v iớ
P(X >
4).
c) Tính P(3,5
≤ X ≤
4,5) và P(X
>
4,5).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
BÀI 4.2. L iỗ liên quan đ nế vi cệ th cự hi nệ m tộ phép đo nh tấ đ nhị là m tộ bi nế ng uẫ nhiên
X
liên
t cụ
v iớ hàm m tậ
độ
f (x)
=
−
0
9
»
2
lOMoARcPSD|46958826
®
0,09375(4 − x )
khi
−2 ≤ x ≤ 2,
0 chỗ khác.
a) Hãy vẽ hàm m tậ độ c aủ phân ph i.ố
b)
Tính P(−1 < X < 1).
CH NGƯƠ 4. BI NẾ NG UẪ NHIÊN LIÊN T CỤ
2. Một số đặc trưng của biến ngẫu nhiên
|
51
∼
lOMoARcPSD|46958826
c)
Tính P(X
>
0).
d)
Tính P(X
<
−0,5 ho cặ
X >
0,5).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
3. MỘT SỐ PHÂN PHỐI THƯỜNG GẶP
3.1.
PHÂN PHỐI ĐỀU
Bi nế ng uẫ nhiên liên t cụ X đ cượ g iọ là có phân phối đều trên đo nạ [a; b], ký hi uệ X
U [a;
b],
n uế hàm m tậ độ xác su tấ c aủ
X
có d ngạ
1
f (x) =
b
−
a
khi x ∈ [a; b]
0 n iơ khác
Từ đ nhị nghĩa trên ta có đ cượ hàm phân ph iố xác su tấ c aủ X ∼ U [a; b]
0 khi x
<
a
F (x) =
x
−
a
b − a
khi
x ∈ [a; b]
1 khi
x >
b
BÀI 4.3. Giả
sử
nhi tệ độ ph nả ngứ
X
(tính theo
◦
C) trong m tộ quá trình ph nả ngứ hóa h cọ nh tấ
đ nhị có phân ph iố đ uề v iớ a
=
−5
và
b
=
5.
a)
Tính P(X
<
0).
b) Tính P(−2,5 < X < 2,5).
c)
Tính P(−2
≤ X ≤
3).
d)
V iớ k th aỏ −5
<
k
<
k
+
4
<
5, hay tính P(k
< X <
k
+
4).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
—
x
≤ ≤
lOMoARcPSD|46958826
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
BÀI 4.4. M t bài báo: “Second Moment Reliability Evaluation vs. Monte Carlo Simulations for Weldộ
Fatigue Strength (Quality and Reliability Engr. Intl., 2012: 887-896)” xem xét vi c s d ng phân ph iệ ử ụ ố
đ uề v iớ a
=
0,20 và b
=
4,25 cho đ ngườ kính
X
c aủ nh ngữ m iố hàn (mm).
a)
Tìm và vẽ hàm m tậ độ c aủ
X.
b) Xác su tấ đ ngườ kính v tượ quá 3 mm là bao nhiêu?
c) Xác su tấ đ ngườ kính trong vòng 1 mm c aủ đ ngườ kính trung bình là bao nhiêu?
d)
V iớ a th aỏ đi uề ki nệ 0,2 < a < a + 1 < 4,5 thì xác su tấ P(a < X < a + 1) bao nhiêu?
BÀI 4.5. Khi đi làm, m tộ giáo sư tr cướ tiên ph iả lên xe buýt g nầ nhà cô và sau đó chuy nể sang
tuy nế xe buýt thứ hai. N uế th iờ gian chờ đ iợ (tính b ngằ phút) t iạ m iỗ đi mể d ngừ có phân bố đ uề
v iớ a
=
0 và b
=
5, khi đó có thể th yấ r ngằ t ngổ th iờ gian chờ đ iợ Y có hàm m tậ độ
1
y khi 0 y 5,
25
f
(y)
=
2 1
5
−
25
y
khi 5
≤
y
≤
10,
0
ch
ỗ
kh
á
c
.
a)
Vẽ hàm m tậ độ c aủ Y .
∫
+∞
b) Ki mể tra tính ch tấ
−∞
f (y)dy = 1.
c) Xác su tấ t ngổ th iờ gian chờ t iố đa 3 phút là bao nhiêu?
d) Xác su tấ t ngổ th iờ gian chờ t iố đa 8 phút là bao nhiêu?
e) Xác su tấ t ngổ th iờ gian chờ từ 3 đ nế 8 phút là bao nhiêu?
f) Xác su tấ mà t ngổ th iờ gian chờ đ iợ là ít h nơ 2 phút ho cặ l nớ h nơ 6 phút?
BÀI 4.6. G i ọ
X
bi u th ng su t rung (v i đ n v psi) trên l i tuabin gió t c đ gió c th trongể ị ứ ấ ớ ơ ị ưỡ ở ố ộ ụ ể
đ ng h m gió. Bài báo “Blade Fatigue Life Assessment with Application to VAWTS”ườ ầ
(J.
of Solar
Energy Engr., 1982: 107–111) đề xu tấ phân ph iố Rayleigh, v iớ hàm m tậ độ
f (x; θ) =
x
e
θ
2
2
2θ
2
khi x
>
0,
là mô hình cho phân ph iố c aủ
X.
a) Ki mể tra tính h pợ lí c aủ hàm f (x;
θ).
0 chỗ khác.
lOMoARcPSD|46958826
CH NGƯƠ 4. BI NẾ NG UẪ NHIÊN LIÊN T CỤ
3. Một số phân phối thường gặp
|
53
≥
lOMoARcPSD|46958826
b)
Giả sử θ
=
100 (m tộ giá trị đ cượ đề xu tấ b ngằ m tộ đồ thị có trong bài báo). Tính xác su tấ
X
nhi uề nh tấ là 200? Ít h nơ 200? Nhi uề h nơ 200?
c) Tính xác su tấ
X
n mằ gi aữ 100 và 200 (v nẫ v iớ giả thi tế về θ như trên).
d)
Tính hàm P(X ≤ x).
BÀI
4.7. D a trên c s phân tích d li u, m t bài báo trên: “Pedestrians’ Crossing Behaviors andự ơ ở ữ ệ ộ
Safety at Unmarked Roadways in China (Accident Analysis and Prevention, 2011: 1927-1936)” đã đề
xu t hàm m t đ ấ ậ ộ
f (x) =
0,15e
−
0
,
15(
x−
1)
v i ớ
x
1 làm mô hình cho phân ph i c a ố ủ
X =
th i gian (giây)ờ
đ cượ sử d ngụ ở dòng trung bình.
a) Xác su tấ mà th iờ gian chờ t iố đa là 5 giây là bao nhiêu? H nơ 5 giây?
b) Xác su tấ mà th iờ gian chờ đ iợ là từ 2 đ nế 5 giây là bao nhiêu?
BÀI 4.8. G iọ
X
là tu iổ thọ c aủ con ng i.ườ M tộ công trình nghiên c uứ cho bi tế hàm m tậ độ c aủ
X
là
®
2 2
f (x) =
cx (100 − x)
khi 0 ≤ x ≤ 100,
0 khi x
<
0 hay x
>
100.
a)
Xác đ nhị h ngằ số c.
b)
Tính trung bình và ph ngươ sai c aủ
X.
c)
Tính xác su tấ c aủ m tộ ng iườ có tu iổ thọ
≥
60.
d) Tính xác su tấ c aủ m tộ ng iườ có tu iổ thọ
≥
60, bi tế r ngằ ng iườ đó hi nệ nay đã 50 tu i.ổ
(Đs: 3,10
−
9
; 50, 2500/7; 0,31744; 0,63548)
BÀI 4.9. M t giáo s đ i h c không bao gi k t thúc bài gi ng c a mình tr c khi h t gi và luônộ ư ạ ọ ờ ế ả ủ ướ ế ờ
hoàn thành bài gi ngả c aủ mình trong vòng 2 phút sau giờ h c.ọ Cho
X
là th iờ gian trôi qua gi aữ th iờ
đi mể h tế ti tế h cọ và k tế thúc bài gi ngả c aủ giáo s .ư Giả sử hàm m tậ độ c aủ
X
là
®
2
kx
f (x) =
khi 0
≤ x ≤
2,
0 chỗ khác.
a) Tìm k và vẽ hàm m tậ độ t ngươ ng.ứ
b) Hãy tính xác su tấ bài gi ngả k tế thúc trong vòng 1 phút sau khi giờ h cọ k tế thúc.
c) Hãy tính xác su tấ bài gi ngả ti pế t cụ di nễ ra sau khi giờ h cọ k tế thúc từ 60 s t iớ 90 s.
d) Xác su tấ mà bài gi ngả ti pế t cụ trong ít nh tấ 90 s ngoài giờ k tế thúc là bao nhiêu?
BÀI 4.10. Tỷ lệ th iờ gian Y mà m tộ rô b tố công nghi pệ ho tạ đ ngộ trong su tố m tộ tu nầ 40 giờ là m tộ
bi nế ng uẫ nhiên có hàm m tậ độ xác su tấ
f (y) =
®
2y khi 0
≤ x ≤
1,
0 chỗ khác.
a)
Tìm E(Y ) và V ar(Y ).
−
lOMoARcPSD|46958826
b)
Đ iố v iớ các rô b tố đang đ cượ nghiên c u,ứ l iợ nhu nậ
X
m iỗ tu nầ đ cượ cho b iở
X =
200Y
60. Tìm
E(X)
và V
ar(X).
BÀI 4.11. Cho
X
là bi n ng uế ẫ nhiên liên t cụ v i hàm phânớ ph i tích lũyố
0
Å
ã
khi
x ≤
0,
x
F (x) =
4
4
1
+
ln
x
khi 0
<
x
≤
4,
1 khi
x ≥
4.
(Hàm phân ph iố tích lũy này đ cượ đề xu tấ trong bài báo “Variability in Measured Bedload Transport
Rates (Water Resources Bull., 1985: 39–48)” đ cượ xem như mô hình cho bi nế ng uẫ nhiên về th yủ văn.
Hãy tính
a) P(X ≤ 1).
b) P(1
≤ X ≤
3).
c)
Xác đ nhị hàm m tậ độ c aủ
X.
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
BÀI 4.12. Cho
X
là bi n ng uế ẫ nhiên liên t cụ v i hàm phânớ ph i tích lũyố
0
Å ã
khi x
<
−2,
1 3
x
3
F (x) =
+
2
32
4x −
3
khi
−2
≤
x
<
2,
1
kh
i
x
≥
2
.
a)
Tính P(X
<
0).
b)
Tính P(−1
< X <
1).
c)
Tính P(X > 0,5).
d) Ki mể tra l iạ hàm m tậ độ f (x) là đ oạ hàm c aủ F
′
(x).
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
lOMoARcPSD|46958826
CH NGƯƠ 4. BI NẾ NG UẪ NHIÊN LIÊN T CỤ
3. Một số phân phối thường gặp
|
55
khi ,
lOMoARcPSD|46958826
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
BÀI 4.13. Cho
X
là m tộ bi nế ng uẫ nhiên có hàm phân ph iố tích lũy như sau
0 khi x
<
0,
F (x) =
x
2
4
0
≤ x <
2
a) Tính P(X ≤ 1).
c) Tính P(X ≥ 1,5).
e) Tính E(X).
1 khi
x ≥
2.
b) Tính P(0,5
≤ X ≤
1).
d) Tìm hàm m tậ độ f (x).
f) Tính V ar(X) và σ
X
.
BÀI 4.14. Trong bài báo: “Modeling Sediment and Water Column Interactions for Hydrophobic Pollu-
tant (Water Research, 1984: 1169 - 1174)”đề xu tấ phân bố đ ngồ đ uề trên kho ngả (7,5, 20) làm mô
hình
cho độ sâu (cm) c aủ l pớ sinh h cọ trong tr mầ tích ở m tộ khu v cự nh tấ đ nh.ị
a) Tính trung bình và ph ngươ sai c aủ độ sâu.
b) Tính hàm phân ph iố tích lũy c aủ độ sâu.
c) Xác su tấ quan sát độ sâu t iố đa là 10? Từ 10 đ nế 15?
d) Xác su tấ mà độ sâu quan sát đ cượ trong ph mạ vi 1 l nầ độ l chệ chu nẩ c aủ giá trị trung bình
là bao nhiêu? Trong vòng 2 l nầ độ l chệ chu n?ẩ
BÀI 4.15. G i ọ
X
là l ng không gian b chi m b i m t văn ki n đ c đ t trong m t thùngượ ị ế ở ộ ệ ượ ặ ộ
container lo iạ 1 ft
3
. Hàm m tậ độ xác su tấ c aủ
X
là
®
f (x) =
90x
8
(1
−
x) khi 0
<
x
<
1,
0 chỗ khác.
a)
Vẽ hàm m tậ độ c aủ
X.
Tìm hàm phân ph iố tích lũy c aủ
X
và vẽ hàm này.
b)
Tìm P(X ≤ 0.5)? So sánh v iớ F (0,5).
c)
Sử d ngụ k tế quả từ câu a tính xác su tấ P(0,25 < X ≤ 0,5). K tế quả có khác v iớ P(0,25 ≤ X ≤ 0,5).
d)
Hãy tìm vị trí x khi xác su tấ đ tạ 75%.
e)
Tính E(X) và σ
X
.
3.2.PHÂN PHỐI CHUẨN
√
2
—
z
H
à
m
m
ậ
t
đ
ộ
củ
a
∈
∼ ≤
1
−
≈
lOMoARcPSD|46958826
1
2
Định nghĩa: Bi nế ng uẫ nhiên liên t cụ
X
đ cượ
g iọ là có phân phối chuẩn n uế hàm m tậ
độ xác su tấ có d ngạ
f (x) =
σ
1
−
(x−µ)
2
e
2σ
, x ,
2π
trong đó µ = E(X) và σ
2
= V ar(X), ký hi uệ X ∼ N (µ, σ
2
).
Đặc biệt,
n uế
µ
=
0 và
σ
2
=
1
thì ta
g iọ
Z
là bi nế ng uẫ nhiên có
phân phối chuẩn tắc,
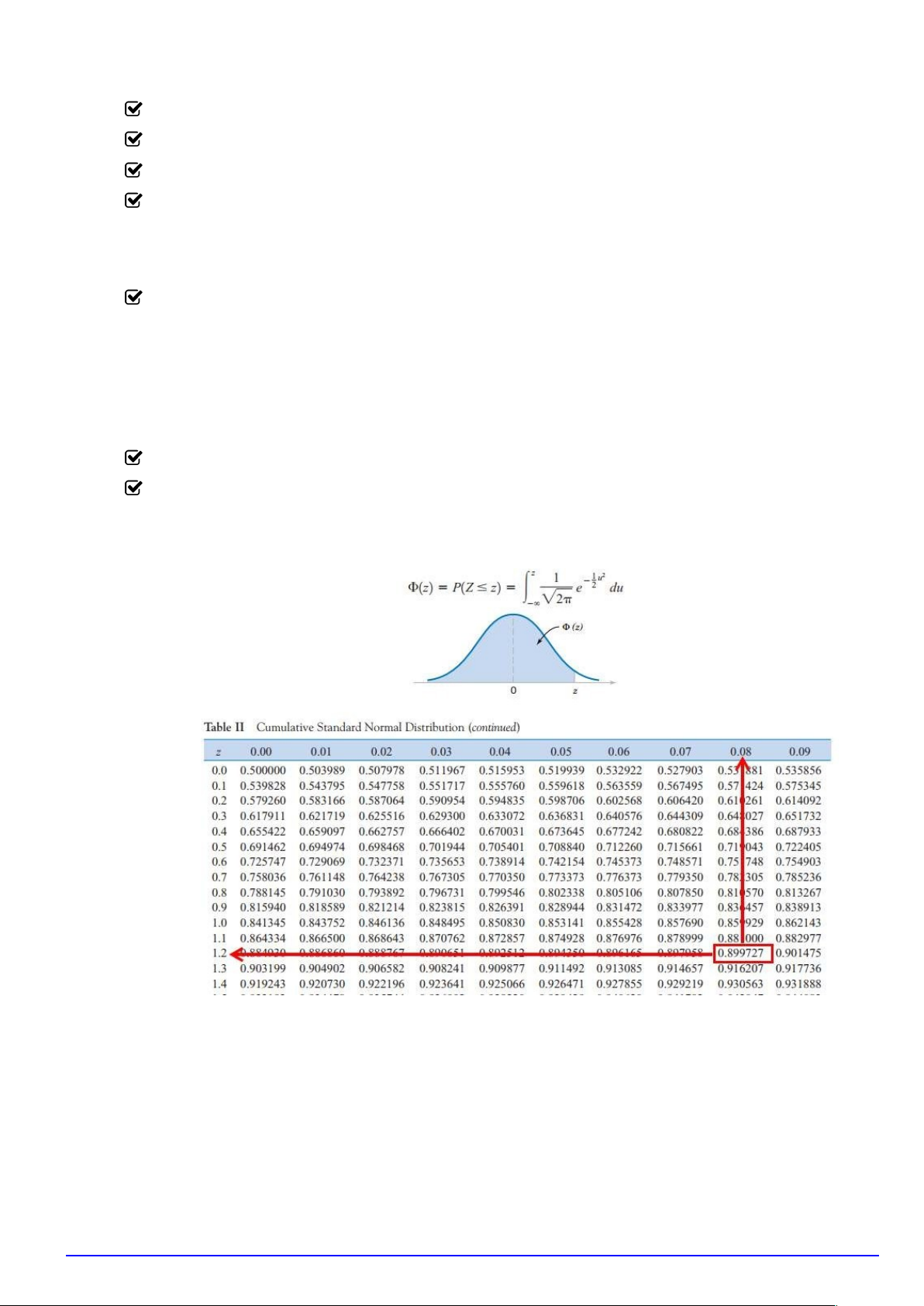
ký hi uệ Z ∼ N (0; 1) và đ tặ Φ là hàm phân ph iố tích lũy có d ngạ
Φ(z) = P(Z
≤
z).
Tính chất:
∫
a
i)
Hàm phân ph iố xác su tấ c aủ Z
N (0; 1) là Φ(a)
=
P(Z a)
=
−∞
trị c aủ hàm này đ cượ tra trong b ng.ả
2
e
2
dz. Giá
2π
ii)
Φ(z)
=
1
−
Φ(−z). Công th cứ này dùng để tìm giá trị c aủ hàm Φ t iạ m tộ z âm.
iii)
N uế
X
∼ N (µ; σ
2
) thì
Z =
X
−
µ
∼ N (0; 1).
σ
iv)
N uế
X
∼ N (µ; σ
2
)
thì
P(X
≤
x)
=
P
Å ã
X
−
µ
≤
x
−
µ
= P(Z ≤ z) = Φ(z).
v)
N uế
X
∼ N (µ; σ
2
) thì
P(a ≤
X
≤ b)
=
Φ
σ
Å ã
b − µ
σ
σ
a µ
— Φ
σ
.
BÀI 4.16. Sử d ngụ b ngả phân ph iố chu nẩ t cắ ho cặ máy tính, tính các xác su tấ sau
a) P(Z
<
1,32)
d) P(Z
>
−2,15)
b) P(Z
<
3)
e) P(−2,34 < Z <
1,76)
c) P(Z
>
1,45)
✍ L IỜ GI I.Ả
Ta có Z ∼ N (0; 1) ⇒ µ = 0; σ
2
= 1.
1
Z
f
(z)
=
e
2π
—
z
2
2
a) P(Z
<
1,32)
=
∫
1,32
−∞
f (z)dz
=
∫
1,32
−∞
1
−
z
2
e
2
dz
2π
∫
1,32
1
—
z
2
Ti nế hành b mấ máy ho cặ tra b ng,ả ta tính đ cượ P(Z < 1,32) =
−∞
e
2
dz 0,90658.
2π
Q
√
.
√
.
√
lOMoARcPSD|46958826
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
CH NGƯƠ 4. BI NẾ NG UẪ NHIÊN LIÊN T CỤ
3. Một số phân phối thường gặp
|
57
H
à
m
m
ậ
t
đ
ộ
củ
a
lOMoARcPSD|46958826
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
BÀI 4.17. Sử d ngụ b ngả phân ph iố chu nẩ t cắ ho cặ máy tính, tính các xác su tấ sau
a) P(−1
< Z <
1)
d) P(Z
>
3)
b) P(−2 < Z < 2)
e) P(0
< Z <
1)
c) P(−3 < Z < 3)
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
. . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . . .
BÀI 4.18 (Bài toán z−value). Sử d ngụ b ngả phân ph iố chu nẩ t cắ ho cặ máy tính, vẽ và tính các
z−value n uế bi tế
a) P(Z
<
z)
=
0,9
d) P(Z
>
z)
=
0,9
b) P(Z
<
z)
=
0,5
e) P(−1,24
< Z <
z)
=
0,8
c) P(Z
>
z)
=
0,1
✍ L IỜ GI I.Ả
Ta có Z ∼ N (0; 1) ⇒ µ = 0; σ
2
= 1.
1
Z
f
(z)
=
e
2π
—
z
2
2
a) Ta có
P(Z
<
z)
=
0,9
∫
z
f (t)dt = 0,9
−∞
Cách 1: Dùng máy tính cầm tay có chfíc năng tra cfíu DIST.
B cướ 1: Vào môi tr ngườ DIST/ Phân Ph iố
.
⇔
lOMoARcPSD|46958826
•
Ở
m
á
y
570
V
N
PL
U
S
/
V
I
N
A
CA
L
:
_
→
g
→
3
:
D
I
S
T.
≈
∫
lOMoARcPSD|46958826
•
Ở máy 580VN: w → g → 7:Distribution.
B cướ 2: Truy c pậ tra ng cượ phân ph iố chu n:ẩ 3: Inverse Normal
B cướ 3: Area
=
xác su tấ c nầ tra (ở câu a) này là
=
0,9).
B cướ 4: Nh pậ giá trị cho µ và σ. L uư ý: Z ∼ N (0; 1) nên µ = 0 và σ = 1.
B cướ 5: Ghi k tế quả c nầ tìm.
Ta đ cượ z 1,28155.
Cách 2: Tra bảng phân phối
B cướ 1: Đ aư xác su tấ c nầ tính về hàm Φ(a)
= P(Z ≤
a)
= P(Z < a).
P(Z
<
z)
=
0,9
∫
z
f (t)dt = 0,9
−∞
⇔ Φ(z)
=
0,9.
B cướ 2: Tìm xác su tấ bên trong b ngả g nầ v iớ 0,9 nh ngư không l nớ h n.ơ
B cướ 3: Từ vị trí xác su tấ xác đ nhị ở B cướ 2, ta gióng theo hàng, theo c tộ sẽ đ cượ k tế
quả
z ≈ 1,28.
Lưu
j:
Dù dùng cách nào, thì vi cệ tra ng cượ chỉ tra đ cượ cho tr ngườ h pợ tích phân có d ngạ
z
Φ(a) = P(Z ≤ a) = P(Z < a)
=
c) H ngướ d nẫ
f (t)dt.
−∞
P(Z
>
z)
=
0,1
⇔ 1
−
P(Z
≤
z)
=
0,1
⇔ P(Z
≤
z)
=
0,9
CH NGƯƠ 4. BI NẾ NG UẪ NHIÊN LIÊN T CỤ
3. Một số phân phối thường gặp
|
59
⇔
Bấm Tải xuống để xem toàn bộ.