Phân loại và phương pháp giải bài tập hàm số bậc nhất và bậc hai

Tài liệu gồm 102 trang, được biên soạn bởi thầy giáo Trần Đình Cư, tóm tắt lý thuyết, phân loại và phương pháp giải bài tập hàm số bậc nhất và bậc hai, giúp học sinh lớp 10 tham khảo khi học chương trình Đại số 10 chương 2 (Toán 10).

46 23 lượt tải Tải xuống
Chia sẻ Báo cáo tài liệu

Chủ đề: Chương 6: Hàm số, đồ thị và ứng dụng (KNTT)

Môn: Toán 10

Thông tin:

102 trang 8 tháng trước

Tác giả:

Profile Mai Nguyệt
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang81
BÀI 1. ĐẠI CƯƠNG VỀ HÀM SỐ
A. KIẾN THỨC CẦN NẮM
I. Ôn tập về hàm số
1. Hàm số. Tập xác định của hàm số
Định nghĩa: Cho D R, D . Hàm số f xác định trên D là một qui tắc đặt tương ứng mỗi số x
D với một và chỉ một số , kí hiệu là
fx(), số fx() được gọi là giá trị của hàm số f tại
x
. Kí
hiệu:
y
fx().
x
được gọi là biến số
D được gọi là tập xác định của hàm số.
T =

y
fxx D() được gọi là tập giá trị của hàm số.
2. Cách cho hàm số
Cho bằng bảng
Cho bằng biểu đồ
Cho bằng công thức
y
fx.
Tập xác định của hàm số
y
fx ()
) là tập hợp tất cả các số thực x sao cho biểu thức f có nghĩa.
Chú ý: Trong kí hiệu
y
fx()
, ta còn gọi
x
là biến số độc lập,
là biến số phụ thuộc của hàm số
f . Biến số độc lập và biến số phụ thuộc của một hàm số có thể được kí hiệu bởi hai chữ cái tùy ý
khác nhau. Chẳng hạn,
 yx x
32
41; và
ut t
32
41;
là hai cách viết biểu thị cùng một hàm
số.
3. Đồ thị của hàm số: Đồ thị của hàm số
y
fx xác định trên tập D là tập hợp tất cả các điểm

M
xfx;() trên mặt phẳng toạ độ với mọi x D.
Chú ý: Ta thường gặp đồ thị của hàm số
y
fx là một đường. Khi đó ta nói
y
fx là
phương trình của đường đó.
II. Sự biến thiên của hàm số
1. Hàm số đồng biến, hàm số nghịch biến
Định nghĩa: Cho hàm số f xác định trên K.
Hàm số
y
fx đồng biến trên K nếu

x
xKxx fx fx
12 1 2 1 2
,: ()()
Hàm số
y
fx
nghịch biến trên K nếu

x
x K x x fx fx
12 1 2 1 2
,: ()()
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang82
Nhận xét: Nếu một hàm số đồng biến trên K thì trên đó, đồ thị hàm số nó đi lên; ngược lại hàm số
nghịch biến trên K thì đồ thị hàm số đi xuống.
Chú ý: Nếu
fx fx
12
() ()với mọi
x
xK
12
, , tức là
fx c x K() , thì ta gọi là hàm số không
đổi hay hàm số hằng trên K.
2. Khảo sát sự biến thiên của hàm số:
Khảo sát sự biến thiên của hàm số là xét xem hàm số đồng biến, nghịch biến, không đổi trên các
khoảng nào trong tập xác định.
Đối với hàm số cho bằng biểu thức, để khảo sát sự biến thiên của hàm số ta có thể dựa vào định
nghĩa hoặc dựa vào nhận xét sau:
y
fx đồng biến trên K

fx fx
xx Kx x
xx
21
12 1 2
21
() ()
,: 0
y
fx nghịch biến trên K

fx fx
xx Kx x
xx
21
12 1 2
21
() ()
,: 0
III. Hàm số chẵn, hàm số lẻ
1. Khái niệm hàm số chẵn, hàm số lẻ
Định nghĩa: Cho hàm số
y
fx có tập xác định D.
Hàm số f được gọi là hàm số chẵn nếu với
x D thì –x D và
fx fx–.
Hàm số f được gọi là hàm số lẻ nếu với
x D thì –x D và
fx fx–– .
2. Đồ thị của hàm số chẵn và hàm số lẻ
Đồ thị của hàm số chẵn nhận trục tung làm trục đối xứng.
Đồ thị của hàm số lẻ nhận gốc toạ độ làm tâm đối xứng.
3. Sơ lượt tịnh tiến đồ thị song song với trục tọa độ
Trong mặt phẳng tọa độ
Oxy , cho đồ thị của hàm số
y
fx();
p
và q là hai số dương tùy ý. Khi
đó
Tịnh tiến lên trên q đơn vị thì được đồ thị hàm số
y
fx q()
Tịnh tiến xuống dưới q đơn vị thì được đồ thị hàm số
y
fx q()
Tịnh tiến sang trái p đơn vị thì được đồ thị hàm số
y
fx p()
Tịnh tiến sang phải p đơn vị thì được đồ thị hàm số
y
fx p()
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang83
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1: Tính giá trị của hàm số tại một điểm
1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
3. Bài tập trắc nghiệm
Câu 1. Cho hàm số
1
1
x
y
x
. Tìm tọa độ điểm thuộc đồ thị của hàm số và có tung độ bằng
2
.
A.
0; 2 . B.
1
;2
3



. C.
2; 2
. D.
1; 2 .
Hướng dẫn giải
Chọn B.
Gọi
00
;2Mx là điểm thuộc đồ thị hàm số có tung độ bằng
2
.
Khi đó:
0
0
1
2
1
x
x

00
121
x
x
0
31x
0
1
3
x
1
;2
3
M




.
Câu 2. Điểm nào sau đây thuộc đồ thị của hàm số
2
(1)
x
y
xx
A.
0; 1M . B.
2;1M . C.
2; 0M . D.

1; 1M .
Hướng dẫn giải
Chọn C.
Thử trực tiếp thấy tọa độ của
2; 0M thỏa mãn phương trình hàm số.
Câu 4. Cho hàm số

2
223
khi 2
1
2 khi 2
x
x
fx
x
xx


. Tính
22Pf f

.
A. 3P . B.
2P
. C.
7
3
P
. D. 6P .
Hướng dẫn giải
Chọn A.
Ta có:
 
2
22 2 3
22 22
21
ff


3P
.
Câu 5. Đồ thị của hàm số

21khi 2
3 khi 2
xx
yfx
x

đi qua điểm nào sau đây:
A.
0; 3
. B.
3; 7
. C.
(2; 3)
. D.
0;1
.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang84
Hướng dẫn giải
Chọn D.
Thử lần lượt từng phương án A,B,C,D với chú ý về điều kiện ta được:
02.0113f , đồ thị không đi qua điểm
0; 3
.
337f 
, đồ thị không đi qua điểm
3; 7
.
22.215 3f , đồ thị không đi qua điểm
2; 3
.
02.011f , đồ thị không đi qua điểm
0;1
.
Câu 6. Cho hàm số:


2
2 3 khi 1 1
1 khi 1
x
x
fx
xx


. Giá trị của
1f
;

1
f
lần lượt là
A.
8
và
0
. B.
0
và
8
. C.
0
và
0
. D.
8
và 4 .
Hướng dẫn giải
Chọn A.
Ta có:
12138f 
;

2
1110f

.
Câu 7. Cho hàm số
21khi 3
7
khi 3
2
xx
y
x
x


. Biết
0
5fx
thì
0
x
là
A. 2 . B.
3
. C.
0
. D. 1.
Hướng dẫn giải
Chọn B.
TH1.
0
3x  : Với

0
5fx
0
215x

0
2x
 .
TH2.
0
3x  : Với

0
5fx
0
0
7
53
2
x
x
 .
Câu 8. Cho hàm số

3
23
khi 0
1
23
khi 2 0
2
x
x
x
fx
x
x
x

. Ta có kết quả nào sau đây đúng?
A.

1
1;
3
f 

7
2
3
f
. B.
02;f
37f 
.
C.

1f
: không xác định;

11
3
24
f

. D.
18;30ff
.
Hướng dẫn giải
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang85
Chọn A.

3
23 1
1
12 3
f


;

2.2 3 7
2
21 3
f
.
Dạng 2: Tìm tập xác định của hàm số
1. Phương pháp
Tìm tập xác định D của hàm số
y
fx
là tìm tất cả những giá trị của biến số x sao cho
biểu thức f(x) có nghĩa:

D
x R f x coù nghóa()
.
Điều kiện xác định của một số hàm số thường gặp:
1) Hàm số
Ax
y
B
x
()
()
. Khi đó :
 Dx Ax
| ( ) xaùc ñònh vaø A(x) 0
2) Hàm số 
k
yAxk
*
2
(), .
Khi đó :
 Dx Ax
| ( ) xaùc ñònh vaø A(x) 0
3) Hàm số 
k
Ax
yk
Bx
*
2
()
,
()
.
Khi đó :
Dx AxBx
| ( ), ( ) xaùc ñònh vaø B(x)>0
Chú ý:
Đôi khi ta sử dụng phối hợp các điều kiện với nhau.
A.B
0
A
B
0
0
.
Nếu
y
fx() có tập xác định là
D
. Khi đó:
y
fx() xác định trên tập
X

X
D
y
fx() xác định trên tập
X
fx() xác định với mọi
x
X
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1 :
Tìm tập xác định của hàm số
1yx
Hướng dẫn giải
Hàm số
1yx
xác định
10x

1
x
.
Ví dụ 2: Tìm tập xác định của hàm số
12 6yxx

Hướng dẫn giải
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang86
Hàm số đã cho xác định khi
12 0
60
x
x
1
2
6
x
x


1
2
x

.
Vậy tập xác định của hàm số là
1
;
2
D

.
Ví dụ 3: Tập xác định của hàm số
2
x
y
x
Hướng dẫn giải
Hàm số xác định khi:
0
20
x
x

0
2
x
x
.
Vậy tập xác định của hàm số
0; \ 2D 
.
Ví dụ 4: Tìm tập xác định của hàm số
1
1
3
yx
x

.
Hướng dẫn giải
Điều kiện để hàm số xác định:
30
13
10
x
x
x



.
Vậy tập xác định của hàm số đã cho là
1; \ 3D 
.
Ví dụ 5: Tìm m để hàm số
23 1yx xm xác định trên tập
1;
?
Lời giải
ĐK:
11
;
33
mm
xD




.
Để hàm số xác định trên
1;
thì

11
1; ; 1 1 3 2
33
mm
mm


 

.
Ví dụ 6. Xác định tham số m để hàm số
y
xm3 xác định trên tập
1;
Hướng dẫn:
Tập xác định của hàm số



m
D ;
3
. Do đó hàm số xác định trên tập
1;
khi và chỉ khi


 

mm
Dm1; ; 1 3
33
Ví dụ 7. Xác định tham số m để hàm số
y
xm
2
xác định trên tập

;3
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang87
Hướng dẫn:
hàm số xác định khi và chỉ khi 
xm xm
22
0(1)




m
m
xmm
x
0
0
(1) hoaëc
;;
.
Vậy tập xác định của hàm số là



khi m
D
mm khim
0
;; 0
Do đó hàm số xác định trên tập

;3 khi và chỉ khi



m
m
Dm
m
m
0
0
;3 9
09
3
.
3. Bài tập trắc nghiệm
Câu 1.
Tìm tập xác định
D
của hàm số

1
1fx x
x

.
A.
\0D . B.
\1;0D  . C.
1; \ 0D  . D.
1;D  .
Hướng dẫn giải
Chọn C.
Điều kiện xác định:
10 1
00
xx
xx





. Vậy tập xác định:

1; \ 0D  .
Câu 2. Cho hàm số:
1
0
1
20
x
x
y
xx

. Tập xác định của hàm số là tập hợp nào sau đây?
A.
2;. B.
.
C.
\1 . D.
\1và 2xx x .
Hướng dẫn giải
Chọn B.
Với 0x
ta có:
1
1
y
x
xác định với mọi 1
x
nên xác định với mọi 0x .
Với
0x ta có:
2yx
xác định với mọi 2x  nên xác định với mọi 0x .
Vậy tập xác định của hàm số là
D
.
Câu 3. Tập xác định của hàm số
1
3
x
y
x
là
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang88
A.
3; 
. B.
1; +
. C.
1; 3 3;

. D.
\3
.
Hướng dẫn giải
Chọn C.
Hàm số
1
3
x
y
x
.
Điều kiện xác định:
10 1
30 3
xx
xx





.
Vậy tập xác định của hàm số
1; 3 3;D
.
Câu 4. Tập xác định của hàm số
2
2
4
x
y
x
x
là
A.
\ 0;2;4
. B.
\0;4
. C.
\0;4
. D.
\0;4
.
Hướng dẫn giải
Chọn D.
Hàm số xác định
2
0
40
4
x
xx
x

. Vậy
\0;4D .
Câu 5. Tìm tập xác định
D
của hàm số

1
1fx x
x

.
A.
\0D . B.
1;D
 .
C.
\1;0D  . D.
1; \ 0D  .
Hướng dẫn giải
Chọn D.
Điều kiện:
10
0
x
x

.
Vậy tập xác định của hàm số là
1; \ 0D  .
Câu 6. Tìm tập xác định của hàm số
2
441yxx
.
A.
1
;
2



. B.
1
;
2



. C. . D.
.
Hướng dẫn giải
Chọn C.
Điều kiện xác định:
2
4410xx

2
21 0x

.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang89
Do đó tập xác định D .
Câu 7. Tập xác định của hàm số

1
3
1
fx x
x

là
A.
1; 3D
. B.
;1 3;D
 
.
C.
1; 3D
. D.
D
.
Hướng dẫn giải
Chọn A.
Hàm số xác định khi
30
10
x
x


3
1
x
x
13x
.
Vậy tập xác định của hàm số là
1; 3D
.
Câu 8. Tập hợp nào sau đây là tập xác định của hàm số
15
72
x
yx
x

?
A.
17
;
52



. B.
17
;
52
. C.
17
;
52
. D.
17
;
52


Hướng dẫn giải
Chọn D.
Hàm số xác đinh khi và chỉ khi
1
15 0
17
5
72 0
7
52
2
x
x
x
x
x





.
Câu 9. Tập xác định của hàm số
2
2
9
68
x
y
x
x
là
A.

3; 8 \ 4 . B.
3; 3 \ 2 . C.
3; 3 \ 2 . D.

;3 \ 2 .
Hướng dẫn giải
Chọn B.
Ta có
2
9033033xxx x .
Hàm số xác định khi và chỉ khi
2
2
33
90 33
4
2
680
2
x
xx
x
x
xx
x






. Vậy
3; 3 \ 2x  .
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang90
Câu 10. Tập xác định của hàm số

3 8 khi 2
7 1 khi 2
xx x
yfx
xx



là
A. . B.
\2
. C.
8
;
3



. D.
7;
.
Hướng dẫn giải
Chọn A.
Ta có:
• Khi
2x :
38yfx x x
xác định khi 380x

8
3
x
.
Suy ra
1
;2D 
.
• Khi
2x :

71yfx x
xác định khi 70x
7x
 .
Suy ra
1
2;D 
.
Vậy TXĐ của hàm số là
12
;DD D
 
.
Câu 11. Tìm tập xác định của hàm số
2
43
3
x
yx x
x

.
A.

;1 3; . B.
;1 3;
. C.
3;
. D.

1; 3 .
Hướng dẫn giải
Chọn A.
Hàm số
2
43
3
x
yx x
x

xác định
2
430
30
xx
x


1v 3
3
xx
x

1
x
hoặc
3x
.
Câu 12. Tập xác định của hàm số
2
31
56
x
x
y
xx


là
A.
1; 3 \ 2
. B.
1; 2
. C.
1; 3
. D.
2; 3
.
Hướng dẫn giải
Chọn A.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang91
Hàm số
2
31
56
x
x
y
xx


có nghĩa khi
2
30
13
10
2; 3
560
x
x
x
xx
xx






1; 3 \ 2x 
.
Câu 13. Tìm tập xác định của hàm số
2
252yxx

.
A.
1
;2;
2



. B.
2;
. C.
1
;
2



. D.
1
;2
2



.
Hướng dẫn giải
Chọn A.
Hàm số xác định
2
2520xx
1
2
2
x
x
.
Câu 14. Tìm
m
để hàm số
23 31
5
xm x
y
xm
xm



xác định trên khoảng
0;1 .
A.
3
1;
2
m



. B.
3; 0m  .
C.
3; 0 0;1m 
. D.

3
4; 0 1;
2
m

.
Hướng dẫn giải
Chọn D.
*Gọi
D
là tập xác định của hàm số
23 31
5
xm x
y
xm
xm



.
*Dx
0
230
50
xm
xm
xm


23
5
m
xm
x
xm

.
*Hàm số
23 31
5
xm x
y
xm
xm



xác định trên khoảng
0;1
0;1 D

230
51
0;1
m
m
m


3
2
4
1
0
m
m
m
m


3
4; 0 1;
2
m

.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang92
Dạng 3: Tính đồng biến, nghịch biến của hàm số
1. Phương pháp
Cho hàm số f xác định trên K .
y = f(x) đồng biến trên K

x
xKxx fx fx
12 1 2 1 2
,: ()()
y = f(x) nghịch biến trên K

x
x K x x fx fx
12 1 2 1 2
,: ()()
Từ đó, ta có hai cách để xét tính đồng biến nghịch biến:
Cách 1:

x
xKxx
12 1 2
,:
. Xét hiệu số

A
fx fx
21
() ()
-
Nếu
A 0
thì hàm số đồng biến
-
Nếu
A
0 thì hàm số nghịch biến
Cách 2:

x
xKxx
12 1 2
,:
. Xét tỉ số
fx fx
A
xx
21
21
() ()
-
Nếu A 0 thì hàm số đồng biến
-
Nếu
A 0
thì hàm số nghịch biến
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1.
Khảo sát sự biến thiên của hàm số sau



ay x x
by x x
2
2
) 4 6 treân moãi khoaûng ;2 ; 2
) 6 5 treân moãi khoaûng ; 3 ; 3;
Hướng dẫn








ax
fx fx
xx x x
xx
xxxxxxA
xxxxxxA
12
21
21 2 1
21
12 1 2 1 2 1 2
12 1 2 1 2 1 2
) Vôùi x , ta coù:
() ()
A= 4 2 2
Do ñoù:
x, ;2,x 2; 2 2 0, 2 0 0
Vaäy, haøm soá nghòch bieán treân ;2
x , 2; ,x 2; 2 2 0, 2 0 0
Vaäy,

 haøm soá ñoàng bieán treân 2; .
Ví dụ 2.
Khảo sát sự biến thiên của hàm số sau




ay
x
x
by
x
3
) treân moãi khoaûng ;1 ; 1;
1
1
) treân moãi khoaûng ; 2 ; 2;
24
Hướng dẫn
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang93








ax
fx fx
xx
xx
xxxxxxA
xxxxxxA
12
21
21
12
12 1 2 1 2 1 2
12 1 2 1 2 1 2
) Vôùi x , ta coù:
() ()
3
A=
11
Do ñoù:
x, ;1,x 1; 1 1 0, 1 0 0
Vaäy, haøm soá nghòch bieán treân ;1
x, 1; ,x 1; 1 1 0, 1 0 0
Vaäy, haøm s

oá nghòch bieán treân 1; .
Ví dụ 3.
Khảo sát sự biến thiên và lập bảng biến thiên của hàm số sau

ay x by
x
3
1
)3; )
1
Hướng dẫn

a
x
x x x x x x fx fx
33 3 3
12 1 2 1 2 1 2 1 2
)Taäp xaùc ñònh:D=
x, : 3 3 ( ) ( )
Vaäy, haøm soá ñoàng bieán treân .





 

b
xD x
fx fx
xx
xxxx
xxxxxxA
x
12 1 2
21
21
1212
12 1 2 1 2 1 2
12 1
) Taäp xaùc ñònh: D= 0; \{1}
x, ,x , ta coù:
() ()
1
A=
11
Do ñoù:
x, 0;1,x 0 1;0 1 1 0, 1 0 0
Vaäy, haøm soá nghòch bieán treân 0;1
x, 1; ,x



xx x x x A
21 2 1 2
1; 1 1 0 , 1 0 0
Vaäy, haøm soá nghòch bieán treân 1; .
Ví dụ 5:
Tìm a để hàm số

1
f
xax a đồng biến trên
Hướng dẫn giải
Hàm số

1
f
xax a đồng biến trên khi và chỉ khi
0
01
10
a
a
a


3. Bài tập trắc nghiệm
Câu 1:
Hàm số nào sau đây đồng biến trên tập xác định của nó?
A.
3yx
. B.
31yx
.
C.
4y
. D.
2
23
y
xx

.
Lời giải
Chọn B
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang94
31yx
có
30a 
hàm số đồng biến trên TXĐ.
Câu 2: Xét sự biến thiên của hàm số

3
fx
x
trên khoảng
0;
. Khẳng định nào sau đây
đúng?
A. Hàm số nghịch biến trên khoảng
0;
.
B. Hàm số vừa đồng biến, vừa nghịch biến trên khoảng
0;
.
C. Hàm số đồng biến trên khoảng
0;
.
D. Hàm số không đồng biến, không nghịch biến trên khoảng
0;
.
Lời giải
Chọn A


12 1 2
21 2 1
21
2 1 21 2 1 21
,0;:
3
33 3
0



xx x x
xx fx fx
fx fx
xx xx xx xx
Vậy hàm số nghịch biến trên khoảng
0;
.
Câu 3: Trong các hàm số sau, hàm số nào nghịch biến trên ?
A.
yx
. B.
2
y
x
. C.
2
y
x
. D.
1
2
yx
Lời giải
Chọn B
Hàm số
y
ax b
với
0a
nghịch biến trên khi và chỉ khi
0a
.
Câu 4. Chọn khẳng định đúng ?
A.
Hàm số
()yfx
được gọi là nghịch biến trên K nếu
12 1 2 1 2
;, ()()
x
x Kx x fx fx .
B.
Hàm số
()yfx
được gọi là đồng biến trên K nếu
12 1 2 1 2
;, ()()
x
x Kx x fx fx .
C.
Hàm số
()yfx
được gọi là đồng biến trên K nếu
12 1 2 1 2
;, ()()
x
x Kx x fx fx .
D. Hàm số
()yfx
được gọi là đồng biến trên K nếu
12 1 2 1 2
;, ()()
x
x Kx x fx fx .
Lời giải
Chọn D
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang95
Lí thuyết định nghĩa hàm số đồng biến, nghịch biến
Câu 5. Tìm
m
để hàm số
21 7ymx
đồng biến trên
.
A.
1
2
m
. B.
1
2
m
. C.
1
2
m
. D.
m
.
Lời giải
Chọn A
hàm số
21 7ymx
đồng biến trên
khi
210m
.
Câu 6. Tìm tất cả các giá trị của tham số
m
để hàm số
23 3ymxm

nghịch biến trên
.
A.
3
2
m

. B.
3
2
m

. C.
3
2
m

. D.
3
2
m

.
Lời giải
Chọn D
Hàm số

23 3ymxm
có dạng hàm số bậc nhất.
Để hàm số nghịch biến trên
3
230
2
mm

.
Câu 7. Tổng tất cả các giá trị nguyên dương của tham số
m
để hàm số

2
213yxmx
nghịch biến trên khoảng
1;5 là
A.
6
. B.
3
. C.
1
. D.
15
.
Lời giải
Chọn A
Hàm số

2
213yxmx
nghịch biến trên khoảng
1
;
4
m



.
Để hàm số

2
213yxmx
nghịch biến trên khoảng
1;5
thì ta phải có

1
1;5 ;
4
m




1
13
4
m
m

.
Các giá trị nguyên dương của tham số
m
để hàm số
2
213yxmx

nghịch biến
trên khoảng
1;5
là
1, 2, 3mm m
.
Tổng tất cả các giá trị nguyên dương của tham số
m
để hàm số

2
213yxmx
nghịch biến trên khoảng
1;5
là
123 6S

.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang96
Câu 8. Cho hàm số
22ym x m 
. Có bao nhiêu giá trị nguyên của m để hàm số đồng
biến trên
?
A. 2 . B.
3
. C. 4 . D.
5
.
Hướng dẫn giải
Chọn C.
Hàm số có dạng
yaxb, nên để hàm số đồng biến trên
khi và chỉ khi
20
20
m
m
2
2
m
m

. Mặt khác do
m
nên
1; 0; 1; 2m 
. Vậy có 4 giá trị nguyên của m .
Câu 9. Tìm các giá trị thực của tham số
m
để hàm số
2xm
y
x
m
xác định trên
1; 2 .
A.
1
2
m
m

.
B.
1
2
m
m
.
C.
1
2
m
m
.
D. 12m .
Hướng dẫn giải
Chọn B.
Hàm số
2xm
y
x
m

xác định khi
x
m
.
Để hàm số
2xm
y
x
m

xác định trên
1; 2
khi và chỉ khi
1
2
m
m
.
Dạng 4: Dựa vào đồ thị tìm các khoảng đồng biến, nghịch biến
1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
3. Bài tập trắc nghiệm
Câu 1:
Cho hàm số có đồ thị như hình bên dưới.
Khẳng định nào sau đây là đúng?
A. Hàm số nghịch biến trên khoảng
0; 3 .
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang97
B. Hàm số đồng biến trên khoảng
;1
.
C. Hàm số nghịch biến trên khoảng
0; 2 .
D. Hàm số đồng biến trên khoảng
;3
.
Lời giải
Chọn C
Trên khoảng

0; 2
, đồ thị hàm số đi xuống từ trái sang phải nên hàm số nghịch biến.
Câu 2. Cho hàm số
yfx có tập xác định là
3; 3 và có đồ thị được biểu diễn bởi hình
bên. Khẳng định nào sau đây là đúng?
A.
Hàm số

2018yfx đồng biến trên các khoảng
3; 1
và
1; 3 .
B. Hàm số

2018yfx
đồng biến trên các khoảng
2;1
và
1; 3
.
C. Hàm số

2018yfx nghịch biến trên các khoảng
2; 1
và
0;1 .
D. Hàm số

2018yfx
nghịch biến trên khoảng
3; 2
.
Lời giải
Chọn A
Gọi
:Cy fx
,
2018Cy fx

. Khi tịnh tiến đồ thị
C
theo phương song
song trục tung lên phía trên
2018
đơn vị thì được đồ thị
C
. Nên tính đồng biến,
nghịch biến của hàm số
yfx
,
2018yfx
trong từng khoảng tương ứng không
thay đổi.
Dựa vào đồ thị ta thấy:
Hàm số

2018yfx
đồng biến trên các khoảng
3; 1
và
1; 3
.
Hàm số

2018yfx đồng biến trên các khoảng
2;1 và
1; 3 .
Hàm số

2018yfx
nghịch biến trên các khoảng
2; 1
và
0;1
.
Hàm số

2018yfx
nghịch biến trên khoảng
3; 2
.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang98
Câu 3. Cho hàm số có đồ thị như hình bên dưới.
Khẳng định nào sau đây là
đúng?
A. Hàm số nghịch biến trên khoảng
0;3
.
B. Hàm số đồng biến trên khoảng
;1
.
C. Hàm số nghịch biến trên khoảng
0; 2 .
D. Hàm số đồng biến trên khoảng
;3
.
Lời giải
Chọn C
Trên khoảng
0; 2 , đồ thị hàm số đi xuống từ trái sang phải nên hàm số nghịch biến.
Câu 4. Cho hàm số có đồ thị như hình vẽ.
Chọn đáp án sai.
A.
Hàm số nghịch biến trên khoảng
;1

.
B. Hàm số đồng biến trên khoảng
1;
.
C. Hàm số nghịch biến trên khoảng
1;1
.
D. Hàm số đồng biến trên khoảng
1; 0
.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang99
Lời giải
Chọn C
Từ đồ thị hàm số ta thấy:
Hàm số nghịch biến trong các khoảng:
;1
 và
0;1 .
Hàm số đồng biến trong các khoảng:
1; 0
và
1;
.
Câu 5.
Hàm số
f
x có tập xác định và có đồ thị như hình vẽ
Mệnh đề nào sau đây
đúng ?
A. Đồ thị hàm số cắt trục hoành theo một dây cung có độ dài bằng
2
.
B.
Hàm số đồng biến trên khoảng
0; 5
.
C.
Hàm số nghịch biến trên khoảng
0; 3 .
D.
2019 2017ff .
Lời giải
Chọn A
Nhìn vào đồ thị hàm số ta có :
Đồ thị hàm số cắt trục hoành tại hai điểm
1; 0 , 3; 0 2
M
NMNA
đúng.
Trên khoảng
0; 2
đồ thị hàm số đi xuống nên hàm số nghịch biến trên khoảng
0; 2
và
trên khoảng
2; 5 đồ thị hàm số đi lên nên hàm số đồng biến trên khoảng

2;5 B sai.
Trên khoảng
0; 2
đồ thị hàm số đi xuống nên hàm số nghịch biến trên khoảng
0; 2
và
trên khoảng
2;3
đồ thị hàm số đi lên nên hàm số đồng biến trên khoảng
2;3 C
sai.
Ta có :
2019, 2017 2; và trên khoảng
2;
hàm số đồng biến nên

2019 2017
2019 2017
D
ff
sai.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang100
Dạng 5: Xét tính chẵn lẻ của hàm số
1. Phương pháp
Để xét tính chẵn lẻ của hàm số y = f(x) ta tiến hành các bước như sau:
- Tìm tập xác định D của hàm số và xét xem D có là tập đối xứng hay không.
-
Nếu D là tập đối xứng thì so sánh f(–x) với f(x) (x bất kì thuộc D).
+ Nếu f(–x) = f(x),
x
D thì f là hàm số chẵn.
+ Nếu f(–x) = –f(x),
x
D thì f là hàm số lẻ.
Chú ý:
Tập đối xứng là tập thoả mãn điều kiện: Với
x
D thì –x
D.
Nếu
x
D mà f(–x)
f(x) thì f là hàm số không chẵn không lẻ.
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1.
Xét tính chẵn lẻ của các hàm số sau
a.

3
2
1
x
fx
x
.
b.

2
f
xxx
.
c.
3
1
f
xxx.
d.

1
x
fx
x
.
Lời giải
+ Hàm số

3
2
1
x
fx
x
có TXĐ
D
nên
x
DxD
 và
f
xfx nên
hàm số lẻ.
+ Hàm số

2
f
xxx
có TXĐ D
nên
x
DxD

và

f
xfx
nên
hàm số chẵn.
+ Hàm số
3
1
f
xxx
có TXĐ
D
nên
x
DxD

và



3
1
f
xfx
fx xx
f
xfx



nên hàm số không chẵn không lẻ.
+ Hàm số

1
x
fx
x
có TXĐ
\1D
. Ta có
1
x
D
nhưng
1
x
D
nên
hàm số không chẵn không lẻ.
Ví dụ 2. Xét tính chẵn lẻ của các hàm số sau
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang101
a)
2
20yx
,
b)
4
721yxx ,
c)
4
10x
y
x
,
d)
22yx x
,
e)
44
4
x
xxx
y
x

Lời giải:
Xét
2
20yx có tập xác định
25;25D

,
  
2
2
20 20
f
xxx
f
x
Nên
2
20yx
là hàm số chẵn.
Xét
4
721yxx có tập xác định D
,
  
4
721
f
xxxfx
Nên
4
721yxx
là hàm số chẵn.
Xét
4
10x
y
x
có tập xác định
\0D
,



4
10x
f
xfx
x


.
Nên
4
10x
y
x
là hàm số lẻ.
Xét 22yx x có tập xác định D
,
22
f
xx x fx .
Nên
22yx x
là hàm số chẵn.
Xét
44
4
x
xxx
y
x

có tập xác định
;1 1; 0D  .




44
4
xx xx
f
xfx
x



nên
44
4
x
xxx
y
x

là hàm số
chẵn.
Ví dụ 3. Cho hàm số
2016 9 2016 9
x
x
y
x

. Tính giá trị của biểu thức:
220 221 222 223 220 221 222 223 224Sf f f f f f f f f    
Lời giải
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang102
Tập xác định

2016 2016
;\0
99
D



.
x
D
, ta có
x
D
và

2016 9 2016 9 2016 9 2016 9
()
xx xx
f
xfx
xx
 

.
Do đó
f
x
là hàm số lẻ, và

()0fx f x

.
  

220 221 222 223 220 221 222 223 224
220 220 221 221 222 222 223 223 224
37
224 .
28
Sf f f f f f f f f
ff f fff f ff
f
   


Ví dụ 4. Tìm điều kiện của
m
để hàm số
4322
1yx mm x x mxm
 là hàm số chẵn.
Lời giải
Hàm
4322
1yx mm x x mxm
có tập xác định là R nên hàm số chẵn khi:
10
0
0
mm
m
m


.
Vậy
0m
.
Ví dụ 5: Tìm m thì hàm số
32 2
12 1fx x m x x m
là hàm số lẻ.
Lời giải
Hàm số có tập xác định là
D
do đó
x
DxD

.
Theo đề bài, ta có

f
xfx
,
x
D
nghĩa là
32 2 32 2
12 1 12 1xm x xm xm x xm  
,
x
D
. Điều này xảy ra khi
22
11
1
11
mm
m
mm



.
3. Bài tập trắc nghiệm
Câu 1.
Cho hàm số

yfx
xác định trên tập
D
. Mệnh đề nào sau đây đúng?
A.
Nếu
f
x không là hàm số lẻ thì
f
x là hàm số chẵn.
B. Nếu
f
xfx
,
x
D
thì
f
x
là hàm số lẻ.
C. Đồ thị hàm số lẻ nhận trục tung làm trục đối xứng.
D. Nếu
f
x
là hàm số lẻ thì
f
xfx
,
x
D
.
Lời giải
Chọn
D.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang103
A sai vì có những hàm số không chẵn, không lẻ.
B sai vì
0fx
thì
f
xfx
nhưng
f
x
cũng là hàm số chẵn.
C sai vì đồ thị hàm số lẻ nhận gốc tọa độ làm tâm đối xứng.
Câu 2. Cho đồ thị hàm số
yfx
như hình vẽ. Kết luận nào trong các kết luận sau là đúng?
A.
Đồng biến trên . B. Hàm số chẵn.
C. Hàm số lẻ. D. Cả ba đáp án đếu sai
Lời giải
Chọn B
Đồ thị hàm số đối xứng qua trục Oy nên hàm số đã cho là hàm số chẵn.
Câu 3. Hàm số
42
3yx x là
A. hàm số vừa chẵn, vừa lẻ. B. hàm số không chẵn, không lẻ.
C. hàm số lẻ. D. hàm số chẵn.
Lời giải
Chọn D
Đặt
42
3fx x x
.
Tập xác định
D .
Ta có
xx 
.

42
3fx x x
42
3xx

f
x
.
Vậy hàm số đã cho là hàm số chẵn.
Câu 4: Hàm số nào sau đây là hàm số lẻ?
A.
g
xx
. B.
2
kx x x
.
C.

1
hx x
x

. D.

2
12fx x
.
Lời giải
Chọn C
Câu 5:
Cho hàm số
42
343yfx x x
. Trong các mệnh đề sau, mệnh đề nào đúng?
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang104
A.
yfx
là hàm số chẵn. B.
yfx
là hàm số lẻ.
C.
yfx
là hàm số không có tính chẵn lẻ. D.
yfx
là hàm số vừa chẵn vừa lẻ.
Lời giải
Chọn A
Tập xác định
D
.
Ta có
  
42
42
3–4 33–43 ,
xD xD
fx xxx x Dxfx



Do đó hàm số
yfx
là hàm số chẵn.
Câu 6: Trong các hàm số sau, hàm số nào không phải là hàm số lẻ:
A.
3
yx x. B.
3
1yx
. C.
3
yx x
. D.
1
y
x
Lời giải
Chọn B
Hàm số lẻ phải triệt tiêu số hạng tự do
Câu 7. Trong các hàm số sau, hàm số nào là hàm số chẵn?
A.
2
1
yx
x

. B.
42
21
x
y
xx
.
C.
3
1
4
y
x
. D.

2018 2018
21 21yx x
.
Lời giải
Chọn D
Đặt

2018 2018
21 21yfx x x
.
Tập xác định của hàm số
yfx
là
D
.
Ta có
.xx 
.
Lại có:
 


2018 2018
2018 2018
2121 21 21
f
xx x x x
f
x
.
Vậy hàm số
yfx
là số chẵn.
Câu 8: Hàm số nào dưới đây là hàm số lẻ?
A.
44yx x
. B.
33
y
xx

.
C.
y
x
. D.
2
51yx x

.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang105
Lời giải
Chọn A
Xét hàm số
44yfx x x
+ TXĐ:
D
Ta có
x
DxD
.
+
44 44
f
xx x x x fx
với
x
D
Vậy hàm số
44yfx x x
là hàm số lẻ.
Câu 9. Cho hàm số

2018 2018 .yfx x x
Mệnh đề nào sau đây sai?
A. Hàm số

yfx có tập xác định là
R
.
B. Đồ thị hàm số

yfx
nhận trục tung làm trục đối xứng.
C. Hàm số

yfx là hàm số chẵn.
D. Đồ thị hàm số

yfx
nhận gốc tọa độ
O
làm tâm đối xứng.
Lời giải
Chọn D
Tập xác định của hàm số là , x
thì x
ta có:

2018 2018 2018 2018
f
xx x x x fx
Hàm số đã cho là hàm số chẵn, đồ thị nhận
O
y
làm trục đối xứng. Do vậy các phương án
,,
A
BC
đều đúng. Đáp án
D
sai.
Câu 10. Trong các hàm số dưới đây, hàm số nào là hàm số chẵn?
A.
3
2yx x=- . B.
42
35yxx=++. C.
1yx=+
. D.
2
2yxx=+.
Lời giải
Chọn B
Ta thấy hàm số
42
35yxx=++ có tập xác định
D =
,
() ()() ()
42
42
3535
f
xxx xx fx-=-+-+= ++=
. Vậy hàm số
42
35yxx=++ là
hàm số chẵn.
Câu 11. Cho đồ thị hàm số

yfx
như hình vẽ
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang106
Kết luận nào trong các kết luận sau là đúng:
A.
Hàm số lẻ. B. Hàm số vừa chẵn vừa lẻ.
C. Đồng biến trên
. D. Hàm số chẵn.
Lời giải
Chọn
D.
Hàm số xác định với mọi
x
và đối xứng nhau qua trục tung nên hàm số đã cho là
hàm số chẵn.
Câu 12. Đồ thị hàm số nào sau đây có tâm đối xứng?
A.
3
yx x. B.
2
yx
. C.
42
31yx x
. D. yx
.
Lời giải
Chọn A
+ Ba hàm số:
2
yx ;
42
31yx x ;
yx
đều là hàm số chẵn trên
nên đồ thị của
chúng nhận trục
O
y
làm trục đối xứng, đồ thị không có tâm đối xứng.
+ Hàm số:
3
yx x có:
3
33
()
() ()
()() () ( )
fx x x
f
xfx
fx x x x x


 
3
yx x
là hàm số lẻ trên
.
Nên đồ thị hàm số
3
yx x nhận gốc toạ độ
O
làm tâm đối xứng.
Câu 13.
Cho hàm số
 
2
3; 3 3fx xx gx x x
. Khẳng định nào sau đây là đúng?
A.
f
x
là hàm chẵn;
g
x
là hàm lẻ. B. Cả f và
g
x
là hàm chẵn.
C. Cả

f
x và
g
x là hàm lẻ D.
f
x là hàm lẻ;

g
x là hàm chẵn.
Lời giải
Chọn D
Xét

2
3fx xx
có TXĐ: D
Ta thấy
x thì x và
 
2
2
33
f
xxx xx fx
Vậy nên

f
x là hàm lẻ.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang107
Xét
33gx x x có TXĐ:
D
.
Ta thấy
x thì x và
33 3 333
g
xx x x x x x gx
Vậy nên
g
x là hàm chẵn.
Câu 14: Trong các hàm số sau, hàm số nào là hàm chẵn?
A.
22
y
xx
. B.
22yx x

.
C.
22yx x
. D.
4
1yx x
.
Lời giải
Chọn A
Hàm số
22
y
xx
có tập xác định là
2;2D  .
Suy ra:
x
D
thì
x
D
.
Ta có :
  
22
f
xxx 
22 ()
x
x
f
x
.
Vậy hàm số
22
y
xx
là hàm số chẵn.
Hàm số
22yx x
có tập xác định là
2;D

.
Ta có:
2 D nhưng
2 D
nên hàm số trên không là hàm số chẵn cũng không là hàm
số lẻ.
Hàm số
22yx x
có tập xác định là D
.
Suy ra:
x
D
thì
x
D
.
Ta có :
2222
f
xx x x x fx
.
Vậy hàm số
22yx x là hàm số lẻ.
Hàm số
4
1yx x có tập xác định là D
.
Suy ra:
x
D
thì
x
D
.
Ta có:
13f
và
11f 
. Do
11ff
và

11ff

nên hàm số trên
không là hàm số chẵn cũng không là hàm số lẻ.
Câu 15: Trong các hàm số sau, hàm số nào là hàm số lẻ?
A.
2
y
x
. B.
32
yx x
. C.
3
1yx
. D. 1yx.
Lời giải
Chọn A
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang108
Hàm số
2
y
x
có tập xác định là D
. Ta có:
xx

.
Với
2
x
fx x fx  
Do đó hàm số
2yx
là hàm số lẻ.
Hàm số
32
yx x
và
3
1yx
không là hàm số chẵn cũng không là hàm số lẻ.
Hàm số
1yx
là hàm số chẵn.
Câu 16. Cho hàm số
22fx x x và
3
5
g
xx x
. Khi đó:
A.
f
x
và
g
x
đều là hàm số lẻ. B.
f
x
và
g
x
đều là hàm số chẵn.
C.
f
x
lẻ,
g
x
chẵn. D.
f
x
chẵn,
g
x
lẻ.
Lời giải
Chọn
D.
Ta có
D
khi đó
x
DxD
2222
f
xx xxxfx
f
x
là hàm số chẵn


33
55
g
xxxxx fxfx
là hàm số lẻ
Câu 17. Nêu tính chẵn, lẻ của hai hàm số
22fx x x

,
g
xx
?
A.
f
x
là hàm số chẵn,
g
x
là hàm số chẵn.
B.
f
x là hàm số lẻ,
g
x là hàm số chẵn.
C.
f
x
là hàm số lẻ,
g
x
là hàm số lẻ.
D.
f
x
là hàm số chẵn,
g
x
là hàm số lẻ.
Lời giải
Chọn B
 Xét
f
x
có TXĐ: D .
x
DxD
.
22fx x x
22xx

f
x .
Nên
f
x
là hàm số lẻ.
 Xét
g
x
có TXĐ: D .
x
DxD
.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang109

g
xxxgx .
Nên
g
x là hàm số chẵn.
Câu 18: Cho hai hàm số

22fx x x
,
g
xx
. Trong các mệnh đề sau, mệnh đề nào
đúng?
A.

f
x là hàm số chẵn,
g
x là hàm số chẵn.
B.

f
x
là hàm số lẻ,
g
x
là hàm số chẵn.
C.

f
x là hàm số lẻ,
g
x là hàm số lẻ.
D.

f
x
là hàm số chẵn,
g
x
là hàm số lẻ.
Lời giải
Chọn B
 Xét

f
x có TXĐ. D .
x
DxD
.
22fx x x
22xx

f
x
.
Nên

f
x là hàm số lẻ.
 Xét
g
x
có TXĐ. D .
x
DxD
.
 
g
xxxgx
.
Nên
g
x
là hàm số chẵn.
Câu 19: Cho hai hàm số
f
x
đồng biến và
g
x
nghịch biến trên khoảng
;ab
. Có thể kết luận
gì về chiều biến thiên của hàm số
yfx gx
trên khoảng
;ab
?
A.
đồng biến. B. nghịch biến.
C. không đổi. D. không kết luận được
Lời giải
Chọn D
Lây hàm số
f
xx
và
gx x
trên
0;1
thỏa mãn giả thiết
Ta có
 
0yfxgx xx 
không kết luận được tính đơn điệu.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang110
Câu 20: Cho hai hàm số

11
x
x
fx
x

và
3
4
g
xx x
. Mệnh đề nào dưới đây
đúng?
A.
f
x
là hàm số chẵn và
g
x
là hàm số lẻ.
B.
f
x và

g
x là hàm số chẵn.
C.
f
x
và

g
x
là hàm số lẻ.
D.
f
x
là hàm số lẻ và
g
x
là hàm số chẵn.
Lời giải
Chọn D
Xét hàm số

11
x
x
fx
x

có
Tập xác định:
1; 1 \ 0D 
.
Ta có:
x
DxD
và
 
11xx
f
xfx
x


. Vậy nên;hàm số

11
x
x
fx
x

là hàm số lẻ.
Xét hàm số có
Tập xác định:
D
.
Ta có:
x
DxD
và
 
3
3
44
g
xx xxx
g
x
. Vậy nên;hàm số
3
4
g
xx x
là hàm số chẵn.
Câu 21. Cho hàm số
yfx
có tập xác định là
5; 5
và đồ thị của nó được biểu diễn bởi
hình dưới đây.
Trong các khẳng định sau, khẳng định nào là
sai?
A. Hàm số nghịch biến trên khoảng
2; 2
.
B. Đồ thị cắt trục hoành tại 3 điểm phân biệt.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang111
C. Hàm số đồng biến trên khoảng
5; 2
và
2; 5 .
D. Hàm số chẵn.
Lời giải
Chọn D
Đồ thị hàm số chẵn nhận
Oy
làm trục đối xứng.
Câu 22. Chọn khẳng định sai trong các khẳng định sau:
A.
Hàm số
2
22yx x
xác định trên
.
B.
Hàm số
3
yx
là hàm số lẻ.
C. Hàm số

2
1yx
là hàm số chẵn.
D.
Hàm số
2
1yx
là hàm số chẵn.
Lời giải
Chọn C
Xét hàm số

2
1yfx x
có tập xác định
.
Ta có


2
1
xx
f
x
fx x fx



không là hàm số chẵn.
Câu 23. Cho hàm số
4
1yx có đồ thị
C
. Khẳng định nào sau đây đúng?
A.
C
nhận gốc tọa độ
O
làm tâm đối xứng.
B.
C qua
0; 2A .
C.
C
tiếp xúc
Ox
.
D
.
C
nhận trục tung làm trục đối xứng.
Lời giải
Chọn D
4
:1Cyfx x
, TXĐ: D
.
+
x
DxD .
+

4
1,fxx fx x
.
Nên

yfx
là hàm số chẵn, nên
C
nhận trục tung làm trục đối xứng.
Câu 24: Cho các khẳng định:
.
I
Hàm số
42
12 5yx x là hàm số chẵn.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang112
.
I
I
Hàm số
2
1
x
y
x
là hàm số lẻ.

.
I
II
Hàm số
20 20yxx
là hàm số chẵn.

.
I
V Hàm số 20 20yx x là hàm số lẻ.
Số khẳng định đúng trong các khẳng định trên là bao nhiêu?
A.
2
. B.
4
. C.
1
. D.
3
.
Lời giải
Chọn D
Xét hàm số
42
() 12 5yfx x x
.
Tập xác định
D
.
Với mọi
xx
và
4242
( ) ( ) 12( ) 5 12 5 ( )
f
xx x xx fx
.
Do đó
42
() 12 5yfx x x là hàm số chẵn. Vậy đúng.
Xét hàm số
2
()
1
x
yfx
x

.
Tập xác định
\1D
.
Tồn tại
1 D
mà
1
D
.
Do đó
2
()
1
x
yfx
x

không là hàm số chẵn cũng không là hàm số lẻ. Vậy sai.
Xét hàm số
( ) 20 20yfx x x.
Tập xác định

20;20D 
.
Với mọi
x
DxD
và
( ) 20 ( ) 20 ( ) 20 20 ( )
f
xxxxxfx  .
Do đó
( ) 20 20yfx x x là hàm số chẵn. Vậy đúng.
Xét hàm số ( ) 20 20yfx x x.
Tập xác định
D
.
Với mọi
xx
và
( ) ( ) 20 ( ) 20 20 20 20 20 ( )
f
xx x x x x x
f
x
Do đó
( ) 20 20yfx x x là hàm số lẻ. Vậy đúng.
Câu 25. Hàm số
f
x
có tập xác định và có đồ thị như hình vẽ
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang113
Tnh giá trị biểu thức
2018 2018ff
A.
2018
. B.
0
. C.
2018
. D.
4036
.
Lời giải
Chọn B
Dựa vào hình dáng của đồ thị ta thấy rằng hàm số đối xứng qua
(0;0)O
nên là hàm số lẻ.
Suy ra
0fx fx fx fx
Vì vậy

2018 2018 0ff .
Câu 26. Hàm số
f
x
có tập xác định và có đồ thị như hình vẽ
Mệnh đề nào sau đây
sai ?
A.

111ff
. B. Đồ thị hàm số có tâm đối xứng.
C.
Hàm số đồng biến trên khoảng
1; 5
. D. Hàm số nghịch biến trên khoảng

6; 1
.
Lời giải
Chọn B
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang114
Nhìn đồ thị ta có :

111ff
A đúng.
Đồ thị không có tâm đối xứng nên B sai.
Trên khoảng
1; 5
đồ thị hàm số đi lên nên hàm số đồng biến trên khoảng
1; 5
C
đúng.
Trên khoảng

6; 1
đồ thị hàm số đi xuống nên hàm số nghịch biến trên khoảng
6; 1D đúng.
Câu 27. Cho hàm số

3
3
6khi 2
khi 2 2.
6khi 2
xx
fx x x
xx



Khẳng định nào sau đây đúng?
A.
Đồ thị hàm số
f
x
đối xứng nhau qua gốc tọa độ.
B. Đồ thị của hàm số
f
x đối xứng qua trục hoành.
C.
f
x
là hàm số lẻ.
D.
f
x
là hàm số chẵn
Lời giải
Chọn D
Hàm số có tập xác định
.D
Với
2; 2x 
ta có

f
xxx
f
x
Với
;2 2; ;xx

3
3
66
f
xx x
f
x
và ngược lại
Do đó hàm số đã cho là hàm số chẵn.
Câu 28. Cho hàm số
220172
34 7fx m m x m
. Gọi
S
là tập hợp tất cả các giá trị của
tham số
m
để hàm số
f
là hàm số lẻ trên
. Tính tổng các phần tử của
S
.
A.
0
. B.
3
. C. 7. D. 27.
Lời giải
Chọn A
Tập xác định:
D
. Suy ra:
x
D
thì
x
D
.
Ta có:


220172
34 7fx m m x m .
Để
f
là hàm số lẻ thì
x
D
,
f
xfx

.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang115
220172220172
34 7 34 7mm x m mm x m 
2
77mm
. Vậy tổng các phần tử của
S
là
770

.
Câu 29. Tìm tất cả các giá trị của tham số
m
để hàm số


322
22 4 4 36yx m x mxm
là một hàm số lẻ
A.
2m 
. B.
2m
. C.
4m
. D.
2m 
.
Lời giải
Chọn B


322
22 4 4 36yfx x m x mx m.
TXĐ:
D
Có
x
x 
Hàm số
y
fx
là hàm số lẻ
,fx fx x




322 322
22 4 4 36 22 4 4 36,x m x mxm x m x mxm x





22
24360,mxm x
Câu 30. Cho hàm số

2
2
2018 ( 2) 2018
(1)
mxm x
yfx
mx


có đồ thị là ( )
m
C (
m
là tham
số). Số giá trị của
m
để đồ thị ()
m
C nhận trục O
y
làm trục đối xứng là
A. 0. B. 1. C. 2. D. 3.
Lời giải
Chọn B
ĐK :
2
1
10
1
m
m
m


.
Vì đồ thị ()
m
C nhận trục
O
y
làm trục đối xứng nên hàm số
f
x
là hàm số chẵn, suy ra

f
xfx
.
Ta có :



2
2
2
2
2 2018 2018
2018 ( 2) 2018
(1)
1
mxmx
mxm x
fx
mx
mx




.
Đồng nhất, ta được :
2
2
2
21
20
2
2
mm m
mm
m
mm



.
Kết hợp điều kiện, suy ra
2m
thỏa mãn.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang116
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang117
BÀI 2. HÀM SỐ BẬC NHẤT
A. KIẾN THỨC CẦN NẮM
I. Ôn tập về hàm số bậc nhất
Hàm số bậc nhất y = ax + b
Tập xác định: D = R.
Sự biến thiên:
- Khi a > 0, hàm số đồng biến trên R.
- Khi a < 0, hàm số nghịch biến trên R.
Đồ thị là đường thẳng có hệ số góc bằng a, cắt trục tung tại điểm B.
Chú ý: Cho hai đường thẳng : y = ax + b và : y = a
x + b
song song với
a = a
và b
b
.
trùng với
a = a
và b = b
.
cắt
a
a
.
II. Hàm số hằng
y
b
Đồ thị của hàm số
y
b là một đường thẳng song song hoặc trùng với trục hoành và cắt trục tung
tại điểm

0;b . Đường thẳng này gọi là đường thẳng
y
b
III. Hàm số
y
x
1. TXĐ:
D
2. Chiều biến thiên


0
0
xkhix
yx
xkhix
3. Đồ thị
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1: Xét tính đồng biến, nghịch biến của hàm số
1. Phương pháp
Cho hàm số
 yaxba,0
- Khi a > 0, hàm số đồng biến trên R.
- Khi a < 0, hàm số nghịch biến trên R.
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1. Tìm các giá trị của tham số
m
để hàm số
23 3ymxm

nghịch biến trên
Hướng dẫn giải
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang118
Hàm số

23 3ymxm có dạng hàm số bậc nhất.
Để hàm số nghịch biến trên
3
230
2
mm

.
Ví dụ 2. Tìm các giá trị của tham số để
12ym x m
 đồng biến trên khoảng

; 
Hướng dẫn giải
Hàm số
12ym x m 
có dạng hàm số bậc nhất.
Để hàm số đồng biến trên
10 1mm

.
3. Bài tập trắc nghiệm
Câu 1.
Khẳng định nào về hàm số 35yx
là sai:
A. Hàm số đồng biến trên
. B. Đồ thị cắt Ox tại
5
;0
3



.
C. Đồ thị cắt Oy tại
0; 5 . D. Hàm số nghịch biến trên
.
Hướng dẫn giải
Chọn D.
Hàm số 35yx có hệ số 30a
nên đồng biến trên
, suy ra đáp án D sai.
Câu 2. Tìm m để hàm số

32ymx nghịch biến trên .
A. 0m . B. 3m
. C. 3m . D. 3m .
Hướng dẫn giải
Chọn C.
Hàm số

32ymx có dạng hàm số bậc nhất.
Để hàm số nghịch biến trên
thì 30 3mm
 .
Câu 3. Tìm
m
để hàm số
21 3ymxm đồng biến trên
.
A.
1
2
m
. B.
1
2
m
. C. 3m
. D. 3m .
Hướng dẫn giải
Chọn A.
Khi 2 1 0m
1
2
m
5
0
2
y
nên nghịch biến trên
Vậy hàm số
21 3ymxm đồng biến trên
khi và chỉ khi
1
210
2
mm
.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang119
Câu 4. Cho hàm số
21
f
xm x
. Với giá trị nào của m thì hàm số đồng biến trên
?;
nghịch biến trên
?
A. Với
2m
thì hàm số đồng biến trên
;
2m
thì hàm số nghịch biến trên
.
B. Với 2m thì hàm số đồng biến trên
; 2m
thì hàm số nghịch biến trên
.
C. Với 2m thì hàm số đồng biến trên
; 2m
thì hàm số nghịch biến trên
.
D. Với
2m
thì hàm số đồng biến trên
;
2m
thì hàm số nghịch biến trên
.
Hướng dẫn giải
Chọn D.
Hàm số
21
f
xm x
đồng biến khi
20m
2m
.
Hàm số
21
f
xm x nghịch biến khi 20m
2m
.
Câu 5. Cho hàm số

73
f
xmx
. Có bao nhiêu số tự nhiên
m
để

f
x
đồng
biến trên
?
A.
2
. B.
4
. C. 3. D. vô số.
Hướng dẫn giải
Chọn C.
Để hàm số

() 7 3
f
xmx
đồng biến trên
70 7mm
Vậy
0;1; 2m
thỏa mãn
7m
để hàm số
() 7 3
f
xmx

đồng biến trên
.
Dạng 2: Đồ thị hàm số bậc nhất
1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
3. Bài tập trắc nghiệm
Câu 1.
Hệ số góc của đồ thị hàm số
2018 2019yx
bằng
A.
2019
2018
. B. 2018 . C. 2019
. D.
2018
2019
.
Hướng dẫn giải
Chọn B.
Câu 2. Đồ thị của hàm số
21
33
yx
là
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang120
A. . B. .
C. . D. .
Hướng dẫn giải
Chọn C.
Từ giả thiết hàm số đồng biến nên loại đáp án A và B.
Mặt khác cho
0x
vào
211
333
yx

nên loại đáp án D.
Câu 3. Hàm số
21yx
có đồ thị là hình nào trong các hình sau?
x
y
O
1
-1
x
y
O
1
-1
x
y
O
1
-1
x
y
O
1
-1
Hình 1 Hình 2 Hình 3 Hình 4
A. Hình 2 B. Hình 4. C. Hình 3. D. Hình 1.
Hướng dẫn giải
Chọn D.
Đồ thị hàm số
21yx
đi qua hai điểm có tọa độ
0; 1
và
1
;0
2



.
Do đó chỉ có hình 1 thỏa mãn.
Câu 4. Hàm số nào cho dưới đây có đồ thị như hình vẽ bên:
O
x
1
2
1
3
y

d
O
x
y
1
3
1
2
d
O
x
y
1
2
1
3
d
O
x
y
1
1
3

d
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang121
A.
22yx
. B.
2yx
. C.
2yx

. D.
22yx
.
Lời giải
Chọn A.
Đồ thị hàm số cắt Ox và
Oy
lần lượt tạ
1; 0A và
0;Bb.
Câu 5. Đồ thị của hàm số
2
2
x
y 
là hình nào?
A. B.
C. D.
Lời giải
Chọn C
Đồ thị hàm số
2
2
x
y 
đi qua
0; 2 , 4; 0AB
. Quan sát đồ thị ta được đáp án C thỏa
yêu cầu.
Câu 6.
Hình vẽ bên là đồ thị của hàm số nào sau đây?
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang122
A.
22
y
x
. B.
22yx
. C.
21
y
x
. D.
1
1
2
y
x

.
Lời giải
Chọn B
Đồ thị hàm số là đường thẳng đi qua 2 điểm
1; 0 , 0; 2AB
. Hàm số có dạng
yaxb ta được:
02
22
2.0 2
ab a
yx
ab b






.
Câu 7 Hình vẽ sau đây là đồ thị của hàm số nào?
.
A.
–2yx=
. B.
–
–2yx=
. C.
–
2–2yx=
. D.
2–2yx=
.
Lời giải
Chọn D
Giả sử hàm số cần tìm có dạng:
(
)
0yaxba=+ ¹
.
Đồ thị hàm số đi qua hai điểm
()()
0; 2 , 1; 0-
nên ta có:
22
02
ba
ab b
ìì
ïï
-= =
ïï
íí
ïï
=+ =-
ïï
îî
.
Vậy hàm số cần tìm là
2–2yx=
.
Câu 8: Điểm nào sau đây không thuộc đồ thị hàm số
31
y
x
?
A.
2; 6M
. B.
1; 4N
. C.
0;1P
. D.
1; 2Q 
.
Lời giải
Chọn
A
Ta có
3.2 1 7 6
, do đó
2; 6M
không thuộc đồ thị hàm số
31yx
.
Câu 9: Đường thẳng trong hình bên là đồ thị của một hàm số nào?
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang123
A.
53yx
. B.
3yx
. C.
33yx
. D.
32yx
.
Lời giải
Chọn D
Gọi
yaxb
. Dựa vào đồ thị có
30.
2
3
3
0
2
xb
a
b
ab



.
Câu 10.
Đường gấp khúc trong hình vẽ là dạng đồ thị của một trong bốn hàm số được liệt kê
trong các phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
A.
1yx. B. 1yx
. C. 1yx
. D. 1yx .
Lời giải
Chọn D
Đồ thị hàm số đi qua các điểm
0;1
và
1; 0
nên chỉ có hàm số
1yx
thỏa mãn.
Câu 11. Hàm số nào sau đây có đồ thị như hình vẽ?
x
y
O
1
A.
2, 1
, 1
x
khi x
y
xkhix

.
B.
2, 1
, 1
x
khi x
y
xkhix

.
C.
2, 1
, 1
x
khi x
y
xkhix


.
D.
, 1
, 1
xkhix
y
x
khi x
.
Lời giải
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang124
Chọn C
Bảng biến thiên:
∞
+
∞
x
y
1
+
∞
∞
1
Câu 12. Đồ thị bên là đồ thị của hàm số nào?
x
y
3
1
O
1
A.
1yx
. B.
21yx
. C.
21yx
. D.
1yx
Lời giải
Chọn B
Đồ thị nhận trục Oy là trục đối xứng nên hàm số tương ứng là hàm chẵn nên loại
phương án C, D.
Đồ thị hàm số đi qua điểm
1; 3 . Thay vào B thấy thỏa mãn nên chọn B.
Câu 13. Đồ thị của hàm số
2
2
x
y 
là hình nào?
A.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang125
B.
C.
D.
Lời giải
Chọn C
Đồ thị hàm số
2
2
x
y 
cắt trục hoành tại điểm
4; 0
và cắt trục tung tại điểm
0; 2
nên chọn đáp án C.
Câu 14. Hình vẽ sau đây là đồ thị hàm số nào?
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang126
A. 1yx. B. 1
yx . C. 1
yx . D. yx.
Lời giải
Chọn
A
Nhìn vào đồ thị hàm số đã cho ta thấy:
-Đồ thị đi qua điểm
(0;1)A
nên loại trừ đáp án C, D.
-Đồ thị đi qua điểm
B( 1;0)
,
C(1;0)
nên loại trừ đáp án B.
Chọn đáp án A
Câu 15.
Hàm số nào trong các hàm số dưới đây có đồ thị như hình vẽ?
A.
3.yx B. 23.yx C. 46.yx
D. 46.yx
Lời giải
Chọn B
Đồ thị là một đường thẳng qua điểm

3
0; 3 à ; 0
2
v



Nên hàm số có dạng:
y
ax b
thỏa:
3.0
3
0
2
ab
ab

2
3
a
b
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang127
Câu 16. Cho hàm số
yfx
có tập xác định là
3; 3
và có đồ thị như hình vẽ. Khẳng định
nào sau đây đúng?
A.
Hàm số đồng biến trên khoảng
3;1
và
1; 4 .
B.
Hàm số nghịch biến trên khoảng
2;1 .
C. Hàm số đồng biến trên khoảng
3; 1
và
1; 3 .
D.
Đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt.
Lời giải
Chọn C
+) Dựa vào đồ thị nhận thấy: Hàm số đồng biến trên khoảng
3; 1
và
1; 3 .
Câu 17.
Hàm số nào trong bốn phương án liệt kê ở A, B, C, D có đồ thị như hình bên
A.
2yx=- +
. B.
21yx=+
. C.
1yx=+
. D.
1yx=- +
.
Lời giải
Chọn D
Gọi
:d
y
ax b=+
Đồ thị hàm số cắt các trục tọa độ lần lượt tại
()
0;1A
và
()
1; 0B
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang128
()
()
0;1
1; 0
d
d
A
B
ì
Î
Î
ï
ï
í
ï
ï
î
1
0
b
ab
ì
=
ï
ï
í
ï
+=
ï
î
1
1
b
a
ì
=
ï
ï
í
ï
=-
ï
î
:1dy x=-+
.
Dạng 3: Vị trí tương đối của hai đường thẳng
1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
3. Bài tập trắc nghiệm
Câu 1.
Cho hai đường thẳng

1
1
:100
2
dy x
và

2
1
:100
2
dy x
. Mệnh đề nào sau đây
đúng?
A.

1
d
và

2
d
trùng nhau. B.
1
d
và
2
d
vuông góc nhau.
C.

1
d
và

2
d
cắt nhau. D.
1
d
và
2
d
song song với nhau.
Hướng dẫn giải
Chọn C.
Cách 1: Gọi
1
k ,
2
k lần lượt là hệ số gốc của
1
d
và
2
d
. Khi đó
21
11
,
22
kk 
21
1
.
4
kk
nên
1
d
và
2
d
không vuông góc nhau.
Xét hệ:
1
100
2
1
100
2
yx
yx


1
100
2
1
100
2
xy
xy


0
100
x
y
Vậy

1
d
và
2
d
cắt nhau.
Cách 2: Ta thấy
11
22

nên
1
d
và
2
d
cắt nhau.
Câu 2. Biết ba đường thẳng
1
:21dy x
,
2
:8dy x
,
3
:32 2dy mx

đồng quy. Giá
trị của
m
bằng
A.
3
2
m 
. B.
1m
. C.
1m
. D.
1
2
m
.
Hướng dẫn giải
Chọn B.
+ Gọi
M
là giao điểm của
1
d và
2
d .
Xét hệ:
21
8
yx
yx


21
8
xy
xy


3
5
x
y
3; 5M
.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang129
+
3
M
d
nên ta có:
532.32m 596 2m
 66m
1m.
Câu 3. Tìm các giá trị thực của tham số
m
để đường thẳng
2
331ym xm

song song
với đường thẳng
5yx?
A. 2m  . B. 2m  . C. 2m
. D. 2m .
Hướng dẫn giải
Chọn D.
Đường thẳng
2
331ym xmsong song với đường thẳng 5yx
khi và chỉ khi
22
2vm=2
31 4
2
2
315 3 6
m
mm
m
m
mm








.
Câu 4. Các đường thẳng

51yx ; 3yxa
; 3yax
đồng quy với giá trị của
a
là
A.
11
. B. 10
. C.
12
. D. 13 .
Hướng dẫn giải
Chọn D.
Gọi
1
:55dy x
,
2
:3dy xa
,
3
:3dyax
3a
.
Phương trình hoành độ giao điểm của
1
d
và
2
d
: 5 5 3
x
xa

5
8
a
x


.
Giao điểm của
1
d
và
2
d
là
55 15
;
88
aa
A




.
Đường thẳng
1
d
,
2
d
và
3
d
đồng qui khi
3
A
d
515 5
.3
88
aa
a


2
10 39 0aa 
3
13
a
a
13a
 .
Dạng 4: Xác định hàm số bậc nhất
1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1:
Biết đồ thị hàm số
yaxb
đi qua điểm
1; 4M
và có hệ số góc bằng
3
. Tìm ,.ab
Lời giải
Vì
yaxb
có hệ số góc bằng
3
nên
3a
.
Mà
yaxb
đi qua
1; 4M
nên
3yxb

43.1b

7b
.
Ví dụ 2: Đồ thị hàm số
yaxb
là một đường thẳng đi qua
3;4A
và song song với đường
thẳng
31yx
. Tìm ,.ab
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang130
Lời giải
Đường thẳng
yaxb
đi qua
3;4A
và song song với đường thẳng
31yx
;suy
ra
34
5
3
3
1
ab
b
a
a
b





.
Ví dụ 3: Đồ thị hàm số
yaxb
cắt trục hoành tại điểm có hoành độ
3x
và đi qua điểm

2; 4M
. Tìm ,.ab
Hướng dẫn giải
Đồ thị hàm số cắt trục hoành tại điểm có hoành độ
3x
30ab

.
Đồ thị hàm số đi qua điểm
2; 4M
24ab

.
Ta có hệ
4
30
5
24 12
5
a
ab
ab
b



.
3. Bài tập trắc nghiệm
Câu 1.
Đường thẳng nào sau đây song song với đường thẳng
2yx
?
A.
2
5
2
yx
. B. 12
y
x . C.
1
3
2
yx
. D. 22yx .
Hướng dẫn giải
Chọn A.
Hai đường thẳng song song khi hai hệ số góc bằng nhau.
Câu 2. Hàm số
122fx m x m là hàm số bậc nhất khi và chỉ khi
A. 1m  . B. 1m . C. 1m
. D. 0m .
Hướng dẫn giải
Chọn C.
Hàm số
122fx m x m là hàm số bậc nhất khi và chỉ khi 1 0m  1m.
Câu 3. Tìm
m
để
221fx m x m
là nhị thức bậc nhất.
A.
2m
. B.
2
1
2
m
m
. C.
2m
. D.
2m
.
Hướng dẫn giải
Chọn A.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang131
Để
221fx m x m là nhị thức bậc nhất thì
20m
2m
.
Câu 4. Một hàm số bậc nhất
yfx có
–1 2f
và
2–3f
. Hàm số đó là
A.
–2 3yx
. B.

51
3
x
fx
.
C.
2–3yx
. D.

51
3
x
fx
.
Hướng dẫn giải
Chọn B.
Hàm số đã cho có dạng
x
byfx a
.
Ta có


–1 2
2–3
f
f
.
.2
–1 2
–3
ab
ab
5
3
a
,
1
3
b
.
Vậy

51
3
x
fx

.
Câu 5. Biết đồ thị hàm số
yaxb
đi qua điểm
1; 4M
và có hệ số góc bằng
3
. Tích
P
ab
?
A.
13P
. B. 21P
. C. 4P
. D. 21P  .
Hướng dẫn giải
Chọn D.
Vì
yaxb
có hệ số góc bằng
3
nên
3a
.
Mà
yaxb
đi qua
1; 4M nên
3yxb

43.1b

7b .
Do đó
.3.721Pab
.
Câu 6. Đồ thị hàm số nào sau đây đi qua 2 điểm
1; 2A
và
0; 1B
.
A.
1yx
. B.
1yx
. C.
31yx
D.
31yx
.
Hướng dẫn giải
Chọn D.
Gọi đường thẳng đi qua hai điểm
1; 2A và
0; 1B
có dạng:
yaxb

d .
Do
1; 2A
và
0; 1B
thuộc đường thẳng
d
nên
a
,
b
là nghiệm của hệ phương
trình:
23
11
ab a
bb
 




.
Vậy đồ thị hàm số đi qua hai điểm
1; 2A
và
0; 1B
là
31yx

.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang132
Câu 7. Đường thẳng
yaxb
có hệ số góc bằng 2 và đi qua điểm
3;1A là
A.
21yx
. B.
27yx
. C.
25yx
. D.
25yx
.
Hướng dẫn giải
Chọn B.
Đường thẳng có hệ số góc bằng
222ayxb

và đi qua điểm
3;1A .
Nên

12.3 7bb
. Vậy hàm số cần tìm là
27yx
.
Câu 8. Đường thẳng đi qua điểm
2; 1M
và vuông góc với đường thẳng
1
5
3
yx
có
phương trình là
A.
37yx
. B.
35yx
. C.
37yx

. D.
35yx
.
Hướng dẫn giải
Chọn A.
Gọi
d
là đường thẳng cần tìm.
Do
d
vuông góc với đường thẳng
1
5
3
yx

nên
:3dy x m
.
Do
d
đi qua điểm
2; 1M
nên
13.2 7mm

.
Vậy
:37dy x
.
Câu 9. Điểm
A
có hoành độ 1
A
x và thuộc đồ thị hàm số
23ymx m

. Tìm
m
để điểm
A
nằm trong nửa mặt phẳng tọa độ phía trên trục hoành .
A.
0m
.
B.
0m
. C.
1m
. D.
0m
.
Hướng dẫn giải
Chọn C.
Từ giả thiết điểm
A
nằm trong nửa mặt phẳng tọa độ phía trên trục hoành nên 0
A
y ta
có 2 3 .1 2 3 3 3 0 1
A
ymxm m m m m .
Câu 10. Tìm phương trình đường thẳng
:dy ax b
. Biết đường thẳng
d
đi qua điểm
1;3I
và tạo với hai tia
Ox
,
Oy
một tam giác có diện tích bằng
6
?
A.
36yx
. B.
972 726yx
.
C.

972 726yx . D.
36yx
.
Hướng dẫn giải
Chọn A.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang133
Do đường thẳng d đi qua điểm
1;3I nên 3ab
3ab.
Giao điểm của
d
và các tia
Ox
,
Oy
lần lượt là
;0
b
M
a



và
0;Nb
.
Do đó:
1
..
2
OMN
SOMON
2
1
..
22
bb
b
aa

. Mà
6
OMN
S
2
12ba
2
12 3bb
2
2
36 12
36 12
bb
bb



6
672L
672(L)
b
b
b


.
Với
6b 3a
:36dy x
.
Câu 11. Tìm điểm
;
M
ab với 0a
nằm trên :10xy
 và cách

1; 3N một khoảng
bằng 5 . Giá trị của ab là
A.
3
.
B. 1 . C. 11
. D. 1
.
Hướng dẫn giải
Chọn C.
(;1 ) 1 ; 2MMttMN tt

.
Ta có:

2
22
51(2)25MN MN t t


2
22;1
26200 5;6 11
55;6
tM
tt M ab
tM



Câu 12. Cho hàm số bậc nhất
2
44 32ym m xm

có đồ thị là

d
. Tìm số giá trị
nguyên dương của
m
để đường thẳng
d
cắt trục hoành và trục tung lần lượt tại hai
điểm
A
,
B
sao cho tam giác OAB là tam giác cân ( O là gốc tọa độ).
A.
3
. B. 1. C. 2 . D.
4
.
Hướng dẫn giải
Chọn B.
Đường thẳng

d tạo với trục hoành và trục tung một tam giác
OAB
là tam giác vuông
cân đường thẳng

d
tạo với chiều dương trục hoành bằng
45
hoặc
135
hệ số
góc tạo của

d
bằng 1 hoặc 1
2
2
441
441
mm
mm


2
2
430
450
mm
mm


1
5
27
m
m
m



.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang134
Thử lại:
5m
thì
d
không đi qua
O
.
Vậy có duy nhất một giá trị
5m
nguyên dương thỏa ycbt.
Câu 13. Đường thẳng

:321dy m x m cắt hai trục tọa độ tại hai điểm
A
và
B
sao cho
tam giác
OAB
cân. Khi đó, số giá trị của m thỏa mãn là
A. 1. B.
0
.
C.
3
.
D. 2 .
Hướng dẫn giải
Chọn D.
A
dOx
nên tọa độ
A
là nghiệm của hệ:

21
321
3
0
0
m
ym xm
x
m
y
y



nên
21
; 0
3
m
A
m



.
B
dOy nên tọa độ
B
là nghiệm của hệ:

321
0
21
0
ym xm
x
ym
x



nên
0; 2 1Bm
.
Ta có OA OB
21 1
21 21 10
33
m
mm
mm






1
210
2
31
4, 2
m
m
m
mm




.
Nhận xét: Với
1
2
m
thì
0; 0ABO nên không thỏa mãn.
Vậy
4, 2mm.
Câu 14: Biết rằng với mọi giá trị thực của tham số
m
, các đường thẳng
:(2)23
m
dym xm cùng đi qua một điểm cố định là (; )Iab. Tính giá trị của biểu
thức:
Sab
A.
3S 
. B.
1S
. C.
1S
. D.
3S
.
Lời giải
Chọn B
Ta có phương trình của đường thẳng đã cho:
:(2)23(2)23
m
dym xm x mx
Vì các đường thẳng
m
d luôn đi qua điểm I nên ta tìm x để m bị triệt tiêu
⇒
(2;1) 1IS
⇒ Chọn B
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang135
Câu 15. Đồ thị hàm số 21yx m tạo với hệ trục tọa độ Oxy tam giác có diện tích bằng
25
2
.
Khi đó
m
bằng
A.
2m
;
3m
. B.
2m
;
4m
. C.
2m
;
3m
. D.
2m 
.
Hướng dẫn giải
Chọn A.
Gọi:
A
,
B
lần lượt là giao điểm của đồ thị hàm số
21yx m

với trục hoành và trục
tung
Suy ra
21;0Am
;
0;1 2Bm
.
Theo giả thiết thì tam giác có diện tích bằng
25
2
là tam giác
OAB
vuông tại
O
.
Do đó:
125
..
22
OAB
SOAOB
.25
OA OB21.12 25mm 21.2125mm


2
21 25m
215
215
m
m


3
2
m
m
.
Dạng 4: Bài toán thực tế
1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
3. Bài tập trắc nghiệm
Câu 1.
Một giá đỡ được gắn vào bức tường như hình vẽ. Tam giác
A
BC vuông cân ở đỉnh C .
Người ta treo vào điểm
A
một vật có trọng lượng
10 N
. Khi đó lực tác động vào bức
tường tại hai điểm
B
và C có cường độ lần lượt là:
A.
10 2 N
và 10 N . B. 10 N và 10 N . C. 10 N và
10 2 N
. D.
10 2 N
và
10 2 N
.
Hướng dẫn giải
Chọn A.
10N
A
B
C
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang136
Cường độ lực tại C bằng cường độ lực tại
A
và bằng
10 N
.
Cường độ lực tại
B
bằng
10 2 N
.
Câu 2. Một hộ nông dân định trồng đậu và cà trên diện tích 800 m
2
. Nếu trồng đậu thì cần 20
công và thu
3.000.000
đồng trên
100
m
2
nếu trồng cà thì cần
30
công và thu
4.000.000
đồng trên
100
m
2
Hỏi cần trồng mỗi loại cây trên diện tích là bao nhiêu để thu được
nhiều tiền nhất khi tổng số công không quá 180 . Hãy chọn phương án đúng nhất trong
các phương án sau:
A. Trồng 600 m
2
đậu, 200 m
2
cà. B. Trồng 500 m
2
đậu, 300 m
2
cà.
C. Trồng 400 m
2
đậu, 200 m
2
cà. D. Trồng 200 m
2
đậu, 600 m
2
cà.
Hướng dẫn giải
Chọn A.
Gọi
x
là số 00
x
m
2
đất trồng đậu,
y
là số 00y m
2
đất trồng cà. Điều kiện 0x , 0y .
Số tiền thu được là
34Txy
triệu đồng.
Theo bài ra ta có
8
20 30 180
0
0
xy
xy
x
y


8
2318
0
0
xy
xy
x
y

Đồ thị:
Dựa đồ thị ta có tọa độ các đỉnh
0; 6A ,
6; 2B ,
8; 0C ,
0; 0O .
Thay vào
34Txy
ta được
max
26T
triệu khi trồng 600 m
2
đậu và 200 m
2
cà.
Câu 3. Một nông dân định trồng đậu và cà trên diện tích
8
ha trong vụ Đông Xuân. Nếu trồng
đậu thì cần
20
công và thu
3
triệu đồng trên diện tích mỗi ha. Nếu trồng đậu thì cần
30
công và thu
4
triệu đồng trên diện tích mỗi ha. Hỏi cần trồng mỗi loại cây trên với diện
tích bao nhiêu để thu được nhiều tiền nhất. Biết rằng tổng số công không quá
180
.
A. 1 ha đậu và
7
ha cà. B.
6
ha đậu và 2 ha cà.
C.
2
ha đậu và
6
ha cà. D.
3
ha đậu và
5
ha cà.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang137
Lời giải
Chọn B
Gọi diện tích trồng đậu là
x
, , vậy diện tích trồng cà là
8
.
Số công phải bỏ ra là:
20 30 8
x
x
240 10
x
.
Do tổng số công không quá
180 nên ta có: 240 10 180 6xx
.
Số tiền thu được là
348 32
g
xx x x 
;
g
x
nghịch biến trên đoạn
6;8
nên

6;8
max 26gx
tại 6x . Vậy cần trồng 6 ha đậu và
2
ha cà.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang138
BÀI 3. HÀM SỐ BẬC HAI
A. KIẾN THỨC CẦN NHỚ
Hàm số bậc hai là hàm số được cho bằng biểu thức có dạng

y
ax bx c
2
, trong đó abc,, là
những hằng số và
a 0
.
I. Đồ thị của hàm số bậc hai

y
ax bx c
2
Tập xác định: D = R
Đồ thị là một parabol có đỉnh




b
I
aa
;
24
, nhận đường thẳng

b
x
a2
làm trục đối
xứng, hướng bề lõm lên trên khi a > 0, xuông dưới khi a < 0.
Chú ý: Để vẽ đường parabol ta có thể thực hiện các bước như sau:
- Xác định toạ độ đỉnh




b
I
aa
;
24
.
- Xác định trục đối xứng

b
x
a2
và hướng bề lõm của parabol.
- Xác định một số điểm cụ thể của parabol .
- Căn cứ vào tính đối xứng, bề lõm và hình dáng parabol để vẽ parabol.
II. Sự biến thiên của hàm số bậc hai
Bảng biến thiên:
Như vậy:
Khi
a 0 hàm nghịch biến trên khoảng




b
a
;
2
, đồng biến trên khoảng




b
a
:
2
và có GTNN là
a4
khi

b
x
a2
Khi
a 0 hàm đồng biến trên khoảng




b
a
;
2
, nghịch biến trên khoảng




b
a
:
2
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang139
và có GTLN là
a4
khi

b
x
a2
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1: Bảng biến thiên, tính đơn điệu, GTLN và GTNN của hàm số
1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1: Tìm giá trị lớn nhất
M
và giá trị nhỏ nhất
m
của hàm số
2
3
yf
xx x

trên đoạn

0; 2 .
Lời giải
Hàm số
2
3yx x
có
10a 
nên bề lõm hướng lên.
Hoành độ đỉnh

3
0; 2
22
b
x
a

.
Vậy



39
min
24
.
max max 0 , 2 max 0, 2 0
myf
My ff





Ví dụ 2:
Tìm giá trị lớn nhất
M
và giá trị nhỏ nhất
m
của hàm số
2
43
yf
xxx

trên
đoạn

0; 4 .
Lời giải
Hàm số
2
43yx x
có
10a

nên bề lõm hướng xuống.
Hoành độ đỉnh

20;4
2
b
x
a
 
.
Ta có

 
429
min 4 29; max 0 3.
03
f
myf M yf
f


Ví dụ 3:
Tìm giá trị thực của tham số
0m
để hàm số
2
232ymx mx m

có giá trị nhỏ nhất
bằng
10
trên
.
Lời giải
Ta có
2
1
22
bm
x
am

, suy ra
42ym

.
Để hàm số có giá trị nhỏ nhất bằng
10
khi và chỉ khi
00
2
m
m
0
2
4210
m
m
m


.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang140
3. Bài tập trắc nghiệm
Câu 1.
Bảng biến thiên nào dưới đây là của hàm số
2
21yx x
 :
A.
B.
C.
D.
Hướng dẫn giải
Chọn C.
Xét hàm số
2
21yx x
có 1 0a
 , tọa độ đỉnh
1; 2I do đó hàm số trên tăng
trên khoảng
;1 và giảm trên khoảng
1;
.
Câu 2. Trục đối xứng của parabol
2
53yx x

là đường thẳng có phương trình
A.
5
4
x
. B.
5
2
x
. C.
5
4
x
. D.
5
2
x
.
Hướng dẫn giải
Chọn D.
Trục đối xứng của parabol
2
yax bxc

là đường thẳng
2
b
x
a

.
Trục đối xứng của parabol
2
53yx x

là đường thẳng
5
2
x
.
Câu 3. Cho hàm số
2
23yx x. Chọn câu đúng.
A. Hàm số nghịch biến trên khoảng
1;
.
B. Hàm số nghịch biến trên khoảng
;1
.
x

1
y

2
x

y

x

1
y
2

x

y

Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang141
C. Hàm số đồng biến trên .
D. Hàm số đồng biến trên khoảng
;1
.
Hướng dẫn giải
Chọn B.
Ta có
10a 
,
2b 
,
3c
nên hàm số có đỉnh là
1; 2I
. Từ đó suy ra hàm số nghịch
biến trên khoảng
;1
và đồng biến trên khoảng
1;
.
Câu 4. Xét tính đồng biến, nghịch biến của hàm số
2
45
f
xx x

trên các khoảng
;2
và
2; 
. Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên
;2 , đồng biến trên
2;
.
B. Hàm số nghịch biến trên các khoảng
;2
và
2;
.
C. Hàm số đồng biến trên
;2
, nghịch biến trên
2;
.
D. Hàm số đồng biến trên các khoảng
;2 và
2;
.
Hướng dẫn giải
Chọn A.
2
45
f
xx x
TXĐ: D .
Tọa độ đỉnh

2;1I .
Hàm số nghịch biến trên

;2
, đồng biến trên
2;
.
Câu 5. Tìm giá trị nhỏ nhất của hàm số
2
41yx x

.
A.
3
. B.
1
. C.
3
. D.
13
.
Hướng dẫn giải
Chọn A.
2
41yx x

2
233x
.
Dấu
"" xảy ra khi và chỉ khi
2x
.
Vậy hàm số đã cho đạt giá trị nhỏ nhất là
3
tại
2x
.
Câu 6. Giá trị lớn nhất của hàm số

2
2
59
fx
xx
bằng
A.
11
8
. B.
11
4
. C.
8
11
. D.
4
11
.
Hướng dẫn giải
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang142
Chọn C.
Ta có
2
2
511
59
24
xx x




11
4
2
22
11
59
4
xx


8
11
2
28 5
5911 2
x
xx


Vậy giá trị lớn nhất của hàm số

2
2
59
fx
xx
bằng
8
11
.
Câu 8.
Hàm số
2
43yx x đồng biến trên khoảng nào?
A.
1; 3
. B.
;2
. C.
;

. D.
2; 
.
Hướng dẫn giải
Chọn D.
Trục đối xứng
2x . Ta có 10a
nên hàm số nghịch biến trên khoảng

;2 và
đồng biến trên khoảng
2;
.
Câu 9. Cho parabol
P
có phương trình
2
324
yx x. Tìm trục đối xứng của parabol
A.
2
3
x
. B.
1
3
x
. C.
2
3
x
. D.
1
3
x
.
Hướng dẫn giải
Chọn D.
+ Có
3a
;
2b
;
4c
.
+ Trục đối xứng của parabol là
2
b
x
a
1
3
.
Câu 10. Cho hàm số
2
243yx x có đồ thị là parabol
P
. Mệnh đề nào sau đây sai?
A.
P
không có giao điểm với trục hoành. B.
P
có đỉnh là
1; 1S
.
C.
P
có trục đối xứng là đường thẳng
1y
. D.
P
đi qua điểm

1; 9M
.
Hướng dẫn giải
Chọn C.
P
có đỉnh là
1; 1S
; trục đối xứng là đường thẳng
1
x
nên C sai.
và
P
đi qua điểm

1; 9M B, D đều đúng.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang143
Xét phương trình
2
2430xx
vô nghiệm trên nên
P
không có giao điểm với
trục hoành
A đúng.
Câu 11. Hàm số
2
25yx x đồng biến trên khoảng:
A.
1;. B.
;1
 . C.
1;
. D.
;1 .
Hướng dẫn giải
Chọn D.
Ta có đồ thị hàm số là một parabol có hoành độ đỉnh:
1
2
b
x
a

Mà hệ số
10a  nên đồ thị hàm số có bề lõm quay xuống
Vậy hàm số đồng biến trên
;1
.
Câu 12. Cho hàm số
2
24yx x có đồ thị
P
. Tìm mệnh đề sai.
A.
P
có đỉnh

1; 3I . B.
min 4, 0;3yx .
C.
P
có trục đối xứng
1
x
. D.
max 7, 0;3yx
.
Hướng dẫn giải
Chọn B.
8
6
4
2
5
(
P
)
x
y
x
= 1
O
1
3
7
I
(1; 3)
3
Dựa vào đồ thị của hàm số
2
24yx x
:
P
, ta nhận thấy:
P
có đỉnh

1; 3I
nên A đúng.

min 3, 0;3yx
, đạt được khi
1
x
nên B sai.
P
có trục đối xứng
1
x
nên C đúng.
max 7, 0;3yx
, đạt được khi
3x
nên D đúng.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang144
Câu 13. Hàm số nào dưới đây đồng biến trên
3; 4 ?
A.
2
1
21
2
yxx
. B.
2
72yx x
.
C.
31yx
. D.
2
1
1
2
yxx

.
Hướng dẫn giải
Chọn A.
+ Hàm số
2
1
21
2
yxx

đồng biến trên
2;
nên đồng biến trên
3; 4
. Chọn A
+ Hàm số
2
72yx x
 đồng biến trên
7
;
2



. Loaị B.
+ Hàm số
31yx

nghịc biến trên . Loaị C.
+ Hàm số
2
1
1
2
yxx

đồng biến trên
;1
. Loaị D.
Câu 14. Hàm số nào sau đây có bảng biến thiên như hình bên?
A.
2
52yx x . B.
2
1
2
yxx

.
C.
2
31yx x. D.
2
1
3
4
yxx

.
Hướng dẫn giải
Chọn B.
Dựa vào bảng biến thiên ta thấy đồ thị có bề lõm hướng xuống nên loại C,
D.
Đồ thị hàm số
2
1
2
yxx
có tọa độ đỉnh
1
1;
2
I



.
Câu 16. Bảng biến thiên của hàm số
2
241yxx
 là bảng nào sau đây?
A. . B. .
x
1
y

1
2
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang145
C. D. .
Hướng dẫn giải
Chọn B
Do hệ số
20a 
nên parabol có bề lõm hướng xuống và đỉnh có tọa độ

1; 3I
.
Câu 17. Tìm
m
để hàm số
2
22 3yx x m có giá trị nhỏ nhất trên đoạn

2;5 bẳng
3
.
A. 3m  . B. 9m
. C. 1m
. D. 0m .
Hướng dẫn giải
Chọn A.
Ta có bảng biến thiên của hàm số
2
22 3yx x m
 trên đoạn
2;5
:
Do đó giá trị nhỏ nhất trên đoạn
2;5 của hàm số
2
22 3yx x m

bằng 2 3m
.
Theo giả thiết
233m  3m
 .
Câu 18. Cho hàm số
2
1
2yx m xm
m




0m xác định trên
1; 1 . Giá trị lớn nhất, giá
trị nhỏ nhất của hàm số trên
1; 1 lần lượt là
1
y
,
2
y
thỏa mãn
12
8yy
. Khi đó giá trị
của
m
bằng
A. 1m . B. m
. C. 2m
. D. 1m , 2m
.
Hướng dẫn giải
Chọn A.
Đặt

2
1
2yfx x m xm
m




.
Hoành độ đỉnh của đồ thị hàm số là
1
xm
m
2
.
Vì hệ số 1a
0 nên hàm số nghịch biến trên
1
;m
m




.
Suy ra, hàm số nghịch biến
1; 1 .
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang146
1
1yf
2
31m
m

.
2
1yf
2
1 m
m

.
Theo đề bài ta có:
12
8yy
22
311 8mm
mm

0m
2
210mm
 1m
.
Câu 19. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số
432
4103
yx x x x
trên đoạn

1; 4
là
A.
min
37
4
y
,
max
21y
. B.
max
37
4
y
,
min
21y
.
C.
min
37
4
y ,
max
21y . D.
max
5
y ,
min
37
4
y .
Hướng dẫn giải
Chọn A.
Ta có
432
4103
y
xxx x
4322
4451052
xxxx x

2
2
2
2512 xx x
 
2
22
11 5 1 2

 

xx
.
Đặt

2
1tx ,

1; 4 0; 9 xt
.

2
152 yt t
2
73tt
2
737
24




t
.
Cách 1: Ta có
2
7121
0
24




t
37
21
4
y .
Cách 2: Vẽ BBT
Vậy
min
37
4
y
,
max
21y
.
Dạng 2: Xác định hàm số bậc hai
1. Phương pháp

M
x y P y ax bx c
2
00 0 0 0
;()
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang147
(P) có đỉnh








b
b
x
x
a
Ix y
a
y
y
ax bx c
a
0
0
00
2
0
000
2
; hoaëc:
2
4
(P) nhận
x
x
0
làm trục đối xứng 
b
x
a
0
2
(P) có giá trị nhỏ nhất (hay lớn nhất) bằng
y
y
a
00
4
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1.
Xác định Parabol
2
yax bxc đạt cực tiểu bằng 4 tại
2x
và đồ thị đi qua
0; 6A
Hướng dẫn giải
Parabol có đỉnh
2; 4I và đi qua
0; 6A nên ta có
42 4
6
2
2
abc
c
b
a


1
2
2
6
a
b
c

. Vậy
2
1
26
2
yxx

.
Ví dụ 2. Parabol
2
yax bxc đi qua
8; 0A
và có đỉnh
6; 12I
. Xác định
,,abc
Hướng dẫn giải
Từ giả thiết ta có hệ
64 8 0
36 6 12
6
2
abc
abc
b
a



3
36
96
a
b
c

.
Ví dụ 3. Tìm các hệ số abc,, của
 Py bxca
2
(): ax , 0
a) (P) đi qua
ABC1;0; 2;0; 0; 4;
b) (P) đi qua
A 1; 2 và có đỉnh
I 1; 2 .
Giải
a) Ta có:





APabc
BPabc
CPc
1; 0 0
2;0 4 2 0
0; 4 4
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang148
Giải hệ phương trình:






 

abc a
abc b
cc
02
42 0 2
44
Vậy 
ab c2, 2, 4
b) Vì (P) đi qua
A 1; 2 nên
abc 2
Mặt khác, vì (P) có đỉnh là
I 1; 2 nên
I
P1; 2 hay
abc2
Và

b
ab
a
12 0
2
Giải hệ phương trình:

 






abc a
abc b
ab c
21
22
20 1
Vậy
 abc1; 2; 1
Ví dụ 4. Tìm các hệ số abc,, của
 Py bxca
2
(): ax , 0
a) y nhận giá trị bằng -3 khi
x
2 và (P) cắt
dy x:1 tại hai điểm có hoành độ bằng 0 và bằng
5.
b) (P) đi qua hai điểm

A 1; 6 ,

B 4;3 và có trục đối xứng là
x
2
.
Giải
a) Theo đề : y nhận giá trị bằng -3 khi
x
2 nên
abc42 3
Gọi (P) cắt
dy x:1 tại hai điểm M và N. Suy ra:
MN0;1 , 1;6



MPc
NPabc
0;1 1
1; 6 6
Giải hệ phương trình:

 






abc a
abc b
cc
42 3 7
612
11
Vậy
 abc7, 12, 1
b) (P) đi qua hai điểm
A 1; 6 ,
B 4;3 nên
APabc1; 6 6
BPabc4;3 16 4 3
(P) và có trục đối xứng là
x
2 nên

b
ab
a
24 0
2
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang149
Giải hệ phương trình:






a
abc
abc b
ab
c
3
5
6
12
16 4 3
5
40
3
Vậy
 ab c
312
;;3.
55
3. Bài tập trắc nghiệm
Câu 1.
Tìm khẳng định đúng trong các khẳng định sau?
A.

2
325
f
xxx
là tam thức bậc hai.
B.
24fx x
là tam thức bậc hai.
C.
3
321
f
xxx là tam thức bậc hai.
D.
42
1fx x x
là tam thức bậc hai.
Hướng dẫn giải
Chọn A.
* Theo định nghĩa tam thức bậc hai thì
2
325
f
xxx

là tam thức bậc hai.
Câu 2. Xác định parabol
P
:
2
yax bxc
,
0a
biết
P
cắt trục tung tại điểm có tung độ
bằng
1
và có giá trị nhỏ nhất bằng
3
4
khi
1
2
x
A.
P
:
2
1yxx . B.
P
:
2
1yx x
.
C.
P
:
2
221yx x. D.
P
:
2
0yx x
.
Hướng dẫn giải
Chọn B.
Ta có
P
cắt trục tung tại điểm có tung độ bằng 1: Khi
0x
thì
1
y
1c
.
P
có giá trị nhỏ nhất bằng
3
4
khi
1
2
x
nên:
13
24
1
22
y
b
a



11 3
1
42 4
1
22
ab
b
a

11 1
42 4
0
ab
ab


1
1
a
b
.
Vậy
P
:
2
1yx x
.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang150
Câu 3. Đồ thị của hàm số nào sau đây là parabol có đỉnh
1; 3I .
A.
2
243yx x. B.
2
1yx x
.
C.
2
245yx x. D.
2
221yx x
.
Hướng dẫn giải
Chọn C.
Đỉnh Parabol là
2
4
;;
24 2 4
bbbac
I
aa a a



 




.
Do đó chỉ có đáp án C thoả.
Câu 4. Cho parabol
P
:
2
yax bxc có trục đối xứng là đường thẳng 1
x
. Khi đó
42ab
bằng
A. 1 . B.
0
. C. 1. D. 2 .
Hướng dẫn giải
Chọn B.
Do parabol
P
:
2
yax bxc có trục đối xứng là đường thẳng 1
x
nên
1
2
b
a

2ab 20ab 420ab
.
Câu 5. Đồ thị hàm số
22
22ymx mxm
0
m
là parabol có đỉnh nằm trên đường thẳng
3
y
x
thì
m
nhận giá trị nằm trong khoảng nào dưới đây?
A.
1; 6
. B.
;2

. C.
3; 3
. D.
0; 
.
Hướng dẫn giải
Chọn C.
Ta có đồ thị hàm số
22
22ymx mxm là parabol có đỉnh
2
1; 2Imm
.
:3Id
y
x
2
213 mm
2
0
mm
0
1
m
m
3; 3m
.
Câu 6. Xác định
a
,
b
,
c
biết Parabol có đồ thị hàm số
2
yax bxc
đi qua các điểm
0; 1M
,
1; 1N
,
1; 1P
.
A.
2
1yx x . B.
2
1
yx x .
C.
2
21 yx. D.
2
1
yxx.
Hướng dẫn giải
Chọn A.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang151
Vì
M
P ,
NP,
P
P nên ta có hệ phương trình
1
1
1



c
abc
abc
1
1
1


a
b
c
.
Vậy
2
:1
P
yxx
.
Câu 7. Tìm parabol
2
:32
P
yax x, biết rằng parabol có trục đối xứng 3.x 
A.
2
32yx x. B.
2
1
2
2
yxx

.
C.
2
1
32
2
yxx
. D.
2
1
32
2
yxx

.
Hướng dẫn giải
Chọn D.
Trục đối xứng của
P
có dạng:
3
2
b
x
a
 
3
3
2a
 
36a

1
2
a
.
Vậy
P
có phương trình:
2
1
32
2
yxx

.
Câu 8. Biết rằng hàm số
2
0yax bxca
đạt cực tiểu bằng
4
tại
2x
và có đồ thị hàm
số đi qua điểm
0; 6A
. Tính tích
P
abc
.
A.
6P 
. B.
3P
. C.
6P
. D.
3
2
P
.
Hướng dẫn giải
Chọn A.
Nhận xét: Hàm số đi qua điểm
0; 6A
; đạt cực tiểu bằng 4 tại
2x
nên đồ thị hàm số
đi qua
2; 4I
và nhận
2x
làm trục đối xứng, hàm số cũng đi qua điểm
0; 6A
suy ra:
2
2
42 4
6
b
a
abc
c

1
2
2
6
a
b
c

6abc.
Câu 9. Xác định phương trình của Parabol có đỉnh
0; 1I
và đi qua điểm
2; 3A
.
A.

2
1yx
. B.
2
1yx
. C.

2
1yx
. D.
2
1yx.
Hướng dẫn giải
Chọn D.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang152
Parabol
P
có dạng
2
yax bxc
0a
.
Do
1IP c.
0; 1I là đỉnh của
P
0
2
b
a

0b.
Lại có

2;3
A
P 34 2abc 1a
.
Nên
2
:1Pyx.
Câu 10. Đồ thị dưới đây là của hàm số nào sau đây?
A.
2
23yx x . B.
2
22yx x
.
C.
2
242yx x. D.
2
21yx x
.
Hướng dẫn giải
Chọn D.
Do parabol có bề lõm quay lên nên
0a
, từ đó ta loại A.
Trục đối xứng của parabol là
1
2
b
x
a

nên ta loại B.
Khi
0x thì
1y 
nên loại C.
Vậy đồ thị trên là của hàm số
2
21yx x
.
Câu 11. Tìm
m
để Parabol
2
:23
P
ymx x
 có trục đối xứng đi qua điểm
2;3A .
A.
2m
. B.
1m
. C.
1m
. D.
1
2
m
.
Hướng dẫn giải
Chọn D.
Với
0m
ta có phương trình
23
y
x

là phương trình đuồng thẳng nên loại
0m
.
Với
0m
. Ta có phương trình của Parabol:
Trục đối xứng:
2
2
x
m

1
x
m

.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang153
Trục đối xứng đi qua điểm
2;3A
nên
1
2
m
1
2
m
.
Câu 12. Cho parabol

2
:,0P y ax bx c a có đồ thị như hình bên. Khi đó 22ab c có
giá trị là
x
y
3
-4
-1
2
O
1
A. 9 . B. 9. C. 6
. D. 6 .
Hướng dẫn giải
Chọn C.
Parabol

2
:,0Pyax bxca đi qua các điểm
1; 0A ,
1; 4B ,
3; 0C
nên có hệ phương trình:
0
4
93 0
abc
abc
abc



1
2
3
a
b
c

.
Khi đó:
222.12236ab c 
.
Câu 13. Cho hàm số
2
21yx x . Chọn câu sai.
A. Đồ thị hàm số có trục đối xứng
1x
.
B. Hàm số không chẵn, không lẻ.
C. Hàm số tăng trên khoảng
;1

.
D. Đồ thị hàm số nhận
1; 4I
làm đỉnh.
Hướng dẫn giải
Chọn D.
Ta có
1a 
,
2b 
,
1c
nên đồ thị có trục đối xứng là

2
1
2. 1
x

và tọa độ
đỉnh của parabol là
1; 2I
.
Câu 14. Cho parabol
2
4yax bx
có trục đối xứng là đường thẳng
1
3
x
và đi qua điểm

1; 3A . Tổng giá trị 2ab là
A.
1
2
. B.
1
. C.
1
2
. D.
1
.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang154
Hướng dẫn giải
Chọn B.
Vì parabol
2
4yax bx
có trục đối xứng là đường thẳng
1
3
x
và đi qua điểm
1; 3A
Nên ta có:
a43
a1 3
1
230 2
23
b
ba
b
ab b
a

 






Do đó: 2 3 4 1ab
Câu 15. Để đồ thị hàm số
22
21ymx mxm
0m
có đỉnh nằm trên đường thẳng
2yx
thì m nhận giá trị nằm trong khoảng nào dưới đây?
A.

2; 6 . B.
;2
 . C.
0; 2 . D.
2; 2 .
Hướng dẫn giải
Chọn D.
Đồ thị hàm số
22
21ymx mxm
0m
có đỉnh là
2
1; 1Imm
.
Để
2
1; 1Imm nằm trên đường thẳng 2yx
thì
2
11mm
2
0mm

0
1
ml
mn

. Vậy
1m
2; 2
.
Câu 16. Cho parabol

2
:2.P y ax bx
Xác định hệ số
a
, b biết
P
có đỉnh
2; 2I .
A. 1a  , 4b . B. 1a
, 4b
. C. 1a
, 4b
. D. 4a , 1b
.
Hướng dẫn giải
Chọn C.
+ Điều kiện:
0a
.
+
P
có đỉnh
2; 2I nên ta có hệ:
2
2
2
2.2 .22
b
a
ab


40
42 4
ab
ab


1
4
a
b
.
Câu 17. Parabol
2
:2
P
yxaxb có điểm
1; 3M với tung độ lớn nhất. Khi đó giá trị của
b là
A. 5. B.
1
. C.
2
. D. 3 .
Hướng dẫn giải
Chọn B.
Do bề lõm của
P
quay xuống và
M
có tung độ lớn nhất nên
M
là đỉnh của
P
.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang155
Ta có
1; 3M là đỉnh của parabol nên
14
4
a
a

.
Suy ra
2
24
y
xxb
qua
1; 3M nên 1b
.
Câu 18. Xác định các hệ số
a
và b để Parabol
2
:4
P
yax xb
 có đỉnh
1; 5I  .
A.
3
.
2
a
b

B.
3
.
2
a
b
C.
2
.
3
a
b
D.
2
.
3
a
b

Hướng dẫn giải
Chọn C.
Ta có:
4
112.
2
I
xa
a
  
Hơn nữa:
IP nên 54 3.abb
Câu 19. Cho hàm số
2
yf
xaxbxc
có đồ thị như hình vẽ. Đặt
2
4bac , tìm dấu
của
a
và .
A. 0a , 0 . B. 0a
, 0
.
C. 0a , 0 . D. 0a
,
, 0
.
Hướng dẫn giải
Chọn A.
* Đồ thị hàm số là một Parabol quay lên nên
0a và đồ thị hàm số cắt trục Ox tại hai
điểm phân biệt nên
0 .
Câu 20. Cho hàm số
2
yf
xaxbxc
. Biểu thức
33 23 1fx fx fx

có giá trị
bằng
A.
2
ax bx c. B.
2
ax bx c
. C.
2
ax bx c
. D.
2
ax bx c.
Lời giải
Chọn D

2
2
33 3 693
f
xax bxcaxabxabc
.

2
2
22 2 442
f
x ax bx c ax abx a bc
.
O
x
y
4
41
yfx
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang156

2
2
11 1 2
f
x ax bx c ax abxabc .
2
33 23 1
f
x
f
x
f
xaxbxc
.
Dạng 3: Đồ thị hàm số bậc hai
1. Phương pháp
Để vẽ đường parabol 
y
bx c
2
ax ta có thể thực hiện các bước như sau:
–
Xác định toạ độ đỉnh




b
I
aa
;
24
.
–
Xác định trục đối xứng 
b
x
a2
và hướng bề lõm của parabol.
–
Xác định một số điểm cụ thể của parabol (chẳng hạn, giao điểm của parabol với các
trục toạ độ và các điểm đối xứng với chúng qua trục trục đối xứng).
–
Căn cứ vào tính đối xứng, bề lõm và hình dáng parabol để vẽ parabol.
Để vẽ đồ thị hàm số

y
bx c
2
ax ta lần lượt làm như sau:
Trước hết ta vẽ đồ thị
P y ax bx c
2
():
Ta có:

 


ax bx c khi ax bx c
yax bxc
ax bx c khi ax bx c
22
2
22
,0
,0
Vậy đồ thị hàm số

y
bx c
2
ax
bao gồm hai phần
Phần 1: Chính là đồ thị (P) lấy phần phía trên trục Ox
Phần 2: Lấy đối xứng phần đồ thị (P) phía dưới trục Ox qua trục Ox.
Vẽ đồ thị hàm số
P
1
()
và
P
2
()
2. Các ví dụ rèn luyện kĩ năng
3. Bài tập trắc nghiệm
Câu 1. Cho hàm số
2
yax bxc
có đồ thị như hình bên dưới. Khẳng định nào sau đây
đúng?
`
x
y
O
A. 0, 0, 0abc. B. 0, 0, 0abc.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang157
C.
0, 0, 0abc
. D.
0, 0, 0abc

.
Hướng dẫn giải
Chọn A.
Parabol có bề lõm quay lên 0
a loại D.
Parabol cắt trục tung tại điểm có tung độ âm nên
0
c
loại B, C. Chọn A.
Câu 2. Parabol
2
23
y
xx
có phương trình trục đối xứng là
A. 1x  . B. 2x
. C. 1
x
. D. 2x  .
Hướng dẫn giải
Chọn C.
Parabol
2
23yx x có trục đối xứng là đường thẳng
2
b
x
a

1
x

.
Câu 3. Cho hàm số:
2
21
y
xx
, mệnh đề nào sai:
A. Đồ thị hàm số nhận
1; 2I
làm đỉnh.
B. Hàm số nghịch biến trên khoảng
;1
.
C. Hàm số đồng biến trên khoảng
1;
.
D. Đồ thị hàm số có trục đối xứng: 2x
.
Hướng dẫn giải
Chọn D.
Trục đối xứng của đồ thị hàm số là đường thẳng
1
2
b
x
a

.
Câu 4. Parabol
2
:263
P
yxx có hoành độ đỉnh là?
A. 3x  . B.
3
2
x
. C.
3
2
x
. D. 3x .
Hướng dẫn giải
Chọn A.
Hoành độ đỉnh của parabol
P
là:
63
242
b
x
a

.
Câu 5. Viết phương trình trục đối xứng của đồ thị hàm số
2
24yx x
.
A. 1
x
. B. 1y
. C. 2y
. D. 2x .
Hướng dẫn giải
Chọn A.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang158
Đồ thị hàm số
2
yax bxc
với 0a
có trục đối xứng là đường thẳng có phương
trình
2
b
x
a

.
Vậy đồ thị hàm số
2
24yx x
có trục đối xứng là đường thẳng có phương trình
1
x
.
Câu 6. Trục đối xứng của parabol
2
221yx x
 là đường thẳng có phương trình
A.
1
x
. B.
1
2
x
. C.
2x
. D.
1
2
x 
.
Hướng dẫn giải
Chọn D.
Phương trình của trục đối xứng là
21
2.2 2
x

.
Câu 7. Tọa độ đỉnh
I
của parabol
2
27yx x
 là
A.
1; 4I  . B.
1; 6I . C.
1; 4I
. D.

1; 6I .
Hướng dẫn giải
Chọn B.
Đỉnh
I
:
2
1
2.1
x 
,
2
12.176y 
. Vậy
1; 6I .
Câu 8. Cho parabol
2
:321
P
yx x. Điểm nào sau đây là đỉnh của
P
?
A.
0;1I . B.
12
;
33
I



. C.
12
;
33
I



. D.
12
;
33
I



.
Hướng dẫn giải
Chọn B.
Ta có:
1
23
b
x
a

nên loại A và C.
Khi
12
33
xy
. Do đó, Chọn B.
Câu 9. Cho hàm số bậc hai
2

y
ax bx c
0
a có đồ thị
P
, đỉnh của
P
được xác định
bởi công thức nào?
A.
;
24




b
I
aa
. B.
;
4




b
I
aa
.
C.
;
4



b
I
aa
. D.
;
22




b
I
aa
.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang159
Hướng dẫn giải
Chọn A.
Đỉnh của parabol
2
: 
P
yax bxc
0
a là điểm
;
24




b
I
aa
.
Câu 10. Cho hàm số
2
0yax bxca
. Khẳng định nào sau đây là sai?
A. Đồ thị của hàm số có trục đối xứng là đường thẳng
2
b
x
a

.
B. Đồ thị của hàm số luôn cắt trục hoành tại hai điểm phân biệt.
C. Hàm số đồng biến trên khoảng
;
2
b
a




.
D. Hàm số nghịch biến trên khoảng ;
2
b
a




.
Hướng dẫn giải
Chọn B.
Dựa vào sự biến thiên của hàm số
2
0yax bxca
 ta thấy các khẳng định A, C,
D đúng
Khẳng định B sai vì có những hàm số bậc hai không cắt trục hoành như hàm
2
9
23
8
yxx
Câu 11. Cho hàm số
2
122 31ym x m xm m
P
. Đỉnh của
P
là
1; 2S
thì
m
bằng bao nhiêu:
A.
3
2
. B. 0 . C.
2
3
. D.
1
3
.
Hướng dẫn giải
Chọn A.
Do đỉnh của
P
là
1; 2S 
suy ra
2
1
1
m
m

3
2
m
.
Câu 12. Đồ thị hình bên dưới là đồ thị của hàm số nào?
A.
2
231yxx . B.
2
31yx x
 .
O
x
y
1
1
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang160
C.
2
231yx x
. D.
2
31yx x

.
Hướng dẫn giải
Chọn C.
Đồ thị cắt trục tung tại điểm có tung độ bằng 1
Đồ thị cắt trục hoành tại điểm có hoành độ bằng 1, phương trình hoành độ giao điểm phải
có nghiệm
1
x
, ta chỉ có phương trình
2
1
2310
1
2
x
xx
x

Câu 13. Đồ thị hình bên dưới là đồ thị của hàm số nào?
A.
2
31yx x. B.
2
231yx x
.
C.
2
31yx x . D.
2
231yxx
.
Hướng dẫn giải
Chọn B.
Vì bề lõm hướng lên trên nên
0a
loại đáp án C, D
Đồ thì giao trục
Ox
tại điểm
1; 0
và
1
;0
2



loại A.
Câu 14. Cho hàm số
2
yax bxc có đồ thị như hình vẽ, thì dấu các hệ số của nó là
A.
0, 0, 0abc
. B.
0, 0, 0abc

.
C.
0, 0, 0abc
. D.
0, 0, 0abc

.
O
x
y
1
1
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang161
Hướng dẫn giải
Chọn B.
Đồ thị là parabol có bề lõm hướng xuống dưới nên
0a
.
Đồ thị cắt chiều dương trục
O
y
nên
0c
.
Trục đối xứng
0
2
b
x
a

, mà
0a
, nên
0b
.
Câu 15. Hàm số
2
23yx x
có đồ thị là hình nào trong các hình sau?
A. B.
C. D.
Hướng dẫn giải
Chọn A.
Do
1a 
nên đồ thị lõm xuống dưới Loại C.
Đồ thị có đỉnh

;1;4
24
b
II
aa




Câu 16. Cho hàm số
2
yax bxc có đồ thị như hình bên. Khẳng định nào sau đây đúng?
A.
0, 0, 0ab
. B.
0, 0, 0ab

.
C.
0, 0, 0ab
. D.
0, 0, 0ab
.
Hướng dẫn giải
1
1
3
4
1
1
2
5
4
2
O
x
y
3
5
6
1
1
3
4
1
1
2
3
4
2
O
x
y
3
1
1
3
4
1
1
2
3
4
2
O
x
y
3
1
1
3
4
1
1
2
3
4
2
O
x
y
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang162
Chọn B.
Quan sát bề lõm của parabol như hình vẽ ta có
0a
loại C. và D. , parabol cắt trục
Ox
tại hai điểm phân biệt nên
0
. Cho
0x
thì giao của parabol với trục tung
O
y
là
0b .
Câu 17. Hàm số nào có đồ thị như hình vẽ sau
A.
2
31yx x. B.
2
251yxx
.
C.
2
251yx x. D.
2
25yxx
.
Hướng dẫn giải
Chọn B.
Do bề lõm parabol hướng xuống nên
0a
và qua
0; 1A
.
Câu 18. Cho hàm số
2
yax bxc có đồ thị như hình vẽ dưới đây. Mệnh nào sau đây đúng?
A.
0a
,
0b
,
0c
. B.
0a
,
0b
,
0c
.
C.
0a
,
0b
,
0c
. D.
0a
,
0b
,
0c
.
Hướng dẫn giải
Chọn B.
Đồ thị có bề lõm quay lên trên
0a. Loại đáp án D.
Trục đối xứng
0.0 0
2
b
xabb
a
 
.
Câu 19. Cho hàm số
2
yax bxc có đồ thị như hình dưới đây. Khẳng định nào sau đây là
đúng?
O
x
y
O
x
y
1
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang163
A.
0a
,
0b
,
0c
. B.
0a
,
0b
,
0c
.
C. 0a , 0b , 0c . D. 0a , 0b , 0c .
Hướng dẫn giải
Chọn C.
Nhìn vào đồ thị ta có:
 Bề lõm hướng xuống
0a
.
 Hoành độ đỉnh
0
2
b
x
a
 0
2
b
a

0b
.
Đồ thị hàm số cắt trục tung tại điểm có tung độ âm
0c
.
Do đó:
0a , 0b , 0c .
Câu 20. Hàm số nào sau đây có đồ thị như hình bên?
2
2
4
6
5
y
x
3
-3
1
2
O
1
A.
2
23yx x . B.
2
43yx x
 .
C.
2
43yx x. D.
2
23yx x
.
Hướng dẫn giải
Chọn B
Dựa vào đồ thị suy ra:
0a
và hoành độ đỉnh là 2.
2
43 1;2;1yx x a I 
Câu 21. Hàm số nào sau đây có đồ thị như hình bên
y
x
y
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang164
y
1
2
3
4
5
1
2
3
5
4
3
2
1
1
2
3
A.
2
33yx x. B.
2
53yx x

.
C.
2
33yx x
. D.
2
53yx x
 .
Hướng dẫn giải
Chọn B.
Quan sát đồ thị ta loại A. và D. Phần đồ thị bên phải trục tung là phần đồ thị
P
của
hàm số
2
53yx x với
0x
, tọa độ đỉnh của
P
là
513
;
24



, trục đối xứng là
2, 5x
. Phần đồ thị bên trái trục tung là do lấy đối xứng phần đồ thị bên phải của
P
qua trục tung
O
y
. Ta được cả hai phần là đồ thị của hàm số
2
53yx x
.
Câu 22. Đồ thị hàm số
2
65yx x
.
A. có tâm đối xứng
3; 4I
.
B. có tâm đối xứng
3; 4I
và trục đối xứng có phương trình
0x
.
C. không có trục đối xứng.
D. có trục đối xứng là đường thẳng có phương trình
0x
.
Hướng dẫn giải
Chọn D.
Ta có:

2
11
2
2
22
6 5 khi 0
65
6 5 khi 0
yx x x C
yx x
yx x x C



Đồ thị
C
của hàm số
2
65yx x
gồm hai phần
Phần đồ thị
1
C
: là phần đồ thị của hàm số
2
1
65yx x

nằm bên phải trục tung
Phần đồ thị
2
C
: là phần đồ thị của hàm số
2
2
65yx x

có được bằng cách lấy đối
xứng phần đồ thị
1
C qua trục tung
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang165
Ta có đồ thị
C như hình vẽ
Vậy: đồ thị
C
có trục đối xứng có phương trình
0x
.
Câu 23. hàm số
2
yax bxc có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng?
A.
0a
,
0b
,
0c
. B.
0a
,
0b
,
0c
.
C. 0a , 0b , 0c . D. 0a
,
b
0 , c0 .
Hướng dẫn giải
Chọn D.
Quan sát đồ thị ta có:
Đồ thị quay bề lõm xuống dưới nên
0a
; có hoành độ đỉnh
000
2
I
bb
xb
aa
 .
Lại có: đồ thị cắt
Ox
tại điểm có tung độ âm nên
0c
.
Vậy
0a
,
b
0
,
c0
.
Câu 24. Cho parabol

2
:
P
yax bxc
0a
có đồ thị như hình bên. Tìm các giá trị m để
phương trình
2
ax bx c m có bốn nghiệm phân biệt.
O
x
y
1
1
C
2
C
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang166
1
2
3
1
2
3
x
y
1
O
2
3
1
2
3
4
I
A.
13m
. B.
03m
. C.
03m
. D.
13m
.
Hướng dẫn giải
Chọn B.
Quan sát đồ thị ta có đỉnh của parabol là
2; 3I nên
4
2
2
42 3
34 2
b
ba
a
abc
abc





.
Mặt khác
P
cắt trục tung tại
0; 1
nên 1c
. Suy ra
41
424 4
ba a
ab b





.
2
:41
P
yx x suy ra hàm số
2
41yxx
 có đồ thị là là phần đồ thị phía trên
trục hoành của
P
và phần có được do lấy đối xứng phần phía dưới trục hoành của
P
,
như hình vẽ sau:
1
2
3
1
2
3
x
y
1
O
2
3
1
2
3
4
I
ym
Phương trình
2
ax bx c m
hay
2
41
x
xm

có bốn nghiệm phân biệt khi đường
thẳng
ym
cắt đồ thị hàm số hàm số
2
41yxx
 tại bốn điểm phân biệt.
Suy ra 0 3m.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang167
Dạng 4: Sự tương giao
1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1:
Cho parabol

2
:21Pyx xm
. Tìm tất cả các giá trị thực của
m
để parabol cắt
Ox
tại hai điểm phân biệt có hoành độ dương.
Lời giải
Phương trình hoành độ giao điểm của
P
và trục
Ox
là
2
210.xxm

1
Để parabol cắt
Ox
tại hai điểm phân biệt có hoành độ dương khi và chỉ khi

1
có hai
nghiệm dương
20
2
20 1 2
1
10
m
m
Sm
m
Pm




.
Ví dụ 2: Tìm tất cả các giá trị thực của tham số
m
để đường thẳng
:dy mx
cắt đồ thị hàm số
32
:69
Py
xxx
tại ba điểm phân biệt.
Lời giải
Phương trình hoành độ giao điểm của
P
với
d
là
32
69
x
xxmx


2
2
0
69 0
69 0. 1
x
xx x m
xx m


Để
P
cắt
d
tại ba điểm phân biệt khi và chỉ
1
có hai nghiệm phân biệt khác
0
2
0
00
90 9
06.09 0
mm
mm
m








.
Ví dụ 2: Tìm tất cả các giá trị thực của tham số
m
để phương trình
2
572 0xx m

có nghiệm
thuộc đoạn

1; 5
.
Lời giải
Ta có
22
572 0 57 2.
x
xm xx m 
*
Phương trình
*
là phương trình hoành độ giao điểm của parabol
2
:57Px x
và
đường thẳng
2ym
(song song hoặc trùng với trục hoành).
Ta có bảng biến thiên của hàm số
2
57yx x

trên
1; 5
như sau:
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang168
Dựa vào bảng biến ta thấy
1; 5x
thì
3
;7
4
y
.
Do đo để phương trình
*
có nghiệm

337
1; 5 2 7 .
482
xmm

3. Bài tập trắc nghiệm
Câu 1.
Cho hàm số
2
0yax bxca có đồ thị là parabol
P
. Xét phương trình
2
0ax bx c
1 . Chọn khẳng định sai:
A. Số giao điểm của parabol
P
với trục hoành là số nghiệm của phương trình
1 .
B. Số nghiệm của phương trình
1 là số giao điểm của parabol
P
với trục hoành.
C. Nghiệm của phương trình
1 là giao điểm của parabol
P
với trục hoành.
D. Nghiệm của phương trình
1 là hoành độ giao điểm của parabol
P
với trục hoành.
Hướng dẫn giải
Chọn C.
Câu 2.
Tọa độ giao điểm của đường thẳng
:4dy x

và parabol
2
712yx x
 là
A.
2; 6
và
4;8
. B.
2; 2
và
4;8
.
C.
2; 2
và

4; 0
. D.
2; 2
và
4; 0
.
Hướng dẫn giải
Chọn D.
Phương trình hoành độ giao điểm:
22
22
712 4 680
40
xy
xx x xx
xy



Câu 3. Nghiệm của phương trình
2
–8 5 0xx
có thể xem là hoành độ giao điểm của hai đồ
thị hàm số:
A.
2
yx
và
85yx
. B.
2
yx
và
85
y
x

.
C.
2
yx
và
85
y
x
. D.
2
yx
và
85
y
x
.
Hướng dẫn giải
7
3
5
1
x
y
-¥
+¥
5
2
3
4
+¥
+¥
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang169
Chọn C.
Ta có
2
–8 5 0xx
2
85
x
x
.
Do đó nghiệm của phương trình
2
–8 5 0xx
có thể xem là hoành độ giao điểm của hai
đồ thị hàm số
2
yx
và
85yx
.
Câu 4. Giao điểm của parabol

2
:32Pyx x

với đường thẳng
1yx
là
A.
1; 2 ;
2;1 . B.
1; 0 ;
3; 2 .
C.
2;1
;
0; 1
. D.
0; 1
;
2; 3
.
Hướng dẫn giải
Chọn B.
Phương trình hoành độ giao điểm của
P
và
d
là
2
32 1
x
xx 
2
430xx

1
3
x
x
.
Vậy hai giao điểm của
P
và
d
là
1; 0
;
3; 2
.
Câu 5. Cho đường thẳng
:1d
y
x
và Parabol
2
:2
P
yx x
. Biết rằng d cắt
P
tại
hai điểm phân biệt
A
,
B
. Khi đó diện tích tam giác
OAB
bằng
A.
4
. B.
2
. C.
3
2
. D.
5
2
.
Hướng dẫn giải
Chọn C.
Phương trình hoành độ giao điểm của
d
và
P
là
2
21
x
xx

2
230xx
.
Phương trình này có
0abc
nên có hai nghiệm
1
1x
,
2
3x
.
Suy ra
1; 0A
và
3; 4B
.
Diện tích tam giác
OAB bằng
13
.1.3
22
.
Câu 6. Biết đường thẳng
:d
y
mx
cắt Parabol
2
:1
P
yx x

tại hai điểm phân biệt
A
,
B
.
Khi đó tọa độ trung điểm
I của đoạn thẳng
A
B là
A.
2
1
;
22
mm m
I




. B.
2
123
;
24
mm m
I




.
C.
13
;
24
I



. D.
1
;
22
m
I



.
Hướng dẫn giải
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang170
Chọn A.
Xét phương trình hoành độ giao điểm của
d
và
P
:
2
1mx x x
2
110xmx
Vì hoành độ giao điểm
A
x
,
B
x
là hai nghiệm của phương trình nên ta có tọa độ trung
điểm
I
là
2
2
A
B
I
A
B
I
x
x
x
yy
y

2
2
AB
I
A
B
I
xx
x
mx x
y
2
1
2
2
I
I
m
x
mm
y
2
1
;
22
mm m
I




.
Câu 7. Tìm tất cả các giá trị của tham số
m
để đường thẳng
:23d
y
x
cắt parabol

2
2yx m xm tại hai điểm phân biệt nằm cùng phía với trục tung
.O
y
A.
3m 
. B.
3m
. C.
3m
. D.
0m
.
Hướng dẫn giải
Chọn B.
Xét phương trình hoành độ giao điểm:
2
223
x
mxmx
2
30xmxm

.
1
Để đường thẳng
d
cắt parabol tại hai điểm phân biệt nằm cùng phía với trục tung
O
y
thì
phương trình

1
có hai nghiệm phân biệt cùng dấu
0
0
c
a
2
4120
30
mm
m


3m
.
Câu 8. Hỏi có bao nhiêu giá trị m nguyên trong nửa khoảng
10; 4
để đường thẳng

:12dy m x m
cắt Parabol
2
:2Pyx x

tại hai điểm phân biệt cùng phía
với trục tung?
A.
6
. B.
5
. C.
7
. D.
8
.
Hướng dẫn giải
Chọn A.
Xét phương trình:
22
12 2 240mxm xx xxm m
Để đường thẳng
d
cắt Parabol
P
tại hai điểm phân biệt cùng phía với trục tung vậy
điều kiện là

2
2
0
8200,
24 40
0
4
40
mm m
mm
P
m
m







Vậy trong nửa khoảng
10; 4
có
6
giá trị nguyên
m
.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang171
Câu 9. Tìm
m
để Parabol

22
:21 3Pyx m xm
 cắt trục hoành tại 2 điểm phân biệt
có hoành độ
1
x
,
2
x
sao cho
12
.1xx
.
A.
2m
. B. Không tồn tại
m
. C.
2m
. D.
2m 
.
Hướng dẫn giải
Chọn A.
Phương trình hoành độ giao điểm của
P
với trục hoành:
22
21 30xmxm


1
.
Parabol

P
cắt trục hoành tại 2 điểm phân biệt có hoành độ
1
x
,
2
x
sao cho
12
.1xx

1
có 2 nghiệm phân biệt
1
x
,
2
x
thỏa
12
.1xx

2
2
2
130
2
2
2
31
mm
m
m
m
m






.
Câu 10. Cho hai hàm số
2
1
1yx m xm
,
2
21yxm
. Khi đồ thị hai hàm số cắt nhau
tại hai điểm phân biệt thì
m có giá trị là
A.
0m
. B.
0m
. C.
m
tùy ý. D. không có giá
trị nào.
Hướng dẫn giải
Chọn C.
Phương trình hoành độ giao điểm:
2
121xmxmxm
2
3101xm x
.
Khi đồ thị hai hàm số cắt nhau tại hai điểm phân biệt thì pt
1
có hai nghiệm phân biệt

2
340m
luôn đúng
m
.
Câu 11. Đường thẳng
:2 6
m
dm xmy
luôn đi qua điểm:
A.
3; 3
B.
2;1
C.
1; 5
D.

3;1
Hướng dẫn giải
Chọn A.
26mxmy

2 6 0 xym x
Phương trình
luôn đúng với mọi
m
khi
0
260
xy
x


3
3
x
y
Vậy
m
d luôn đi qua điểm cố định
3; 3
.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang172
Câu 12. Tìm tất cả các giá trị m để đường thẳng
32
y
mx m

cắt parabol
2
35yx x
tại
2 điểm phân biệt có hoành độ trái dấu.
A. 3m  . B. 34m
. C. 4m
. D. 4m .
Hướng dẫn giải
Chọn C.
Phương trình hoành độ giao điểm:
2
35 32
x
xmx m

2
3280*xm xm
.
Đường thẳng cắt parabol tại hai điểm phân biệt có hoành độ trái dấu khi và chỉ khi
phương trình
*
có hai nghiệm trái dấu
.0ac
280m
4m
.
Câu 13. Cho parabol
2
0yax bxca ,
P
có đồ thị như hình vẽ:
Biết đồ thị

P
cắt trục Ox tại các điểm lần lượt có hoành độ là
2
,
2
. Tập nghiệm của
bất phương trình
0y
là
A.
;2 2;
. B.
2; 2
.
C.

2; 2 . D.
;2 2;
 .
Hướng dẫn giải
Chọn B
Dựa vào đồ thị ta thấy
0y
khi
2; 2x  .
Câu 14. Giá trị nào của
m
thì phương trình
2
3310mxmxm
 

1
có hai nghiệm
phân biệt?
A.
\3m
. B.

3
;1;\3
5
m




.
C.
3
;1
5
m




. D.
3
;
5
m




.
Hướng dẫn giải
Chọn B.
Phương trình có hai nghiệm phân biệt

2
30
34 3 10
m
mmm


O
x
y
2
2
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang173
2
3
5230
m
mm

3
3
5
1
m
x
x

3
;1;\3
5
m




.
Câu 15. Có bao nhiêu giá trị thực của m để đường thẳng
:42d
y
xm
tiếp xúc với parabol
2
:2231Py m x mx m 
A.
3
. B. 1. C. 2 . D.
0
.
Hướng dẫn giải
Chọn B.
Phương trình hoành độ giao điểm của
d
và
P
là
2
223142mxmxm xm
2
222 10mx mxm .
d
tiếp xúc với
P
phương trình hoành độ giao điểm của
d
và
P
có nghiệm kép.

2
20
2210
m
mmm


2
2
3
2
m
m
m
3
2
m
.
Vậy có
1 giá trị
m
để đường thẳng
d
tiếp xúc với
P
.
Câu 16. Cho hàm số
f
x xác định trên
có đồ thị như hình vẽ.
Phương trình

210fx
có bao nhiêu nghiệm?
A.
1
. B.
3
. C.
2
. D.
4
.
Hướng dẫn giải
Chọn B.
 
1
210
2
fx fx
.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang174
Số nghiệm phương trình

1 là số giao điểm của đồ thị hàm số
yfx và đường thẳng
1
2
y
.
Dựa vào đồ thị hàm số suy ra phương trình đã cho có
3
nghiệm phân biệt.
Câu 17. Cho hàm số
yfx có bảng biến thiên như sau:
Với giá trị nào của tham số
m thì phương trình
1
f
xm
có bốn nghiệm phân biệt.
A. 1m . B. 13m
. C. 01m
. D. 3m .
Hướng dẫn giải
Chọn B.
Dựa vào bảng biến thiên của hàm số
yfx , suy ra bảng biến thiên của hàm số

1yfx
.
Từ BBT suy ra phương trình
1
f
xm
có bốn nghiệm phân biệt khi
13m
.
Vậy 1 3m
.
Câu 18. Cho hàm số

2
f
xaxbxc đồ thị như hình bên dưới. Hỏi với những giá trị nào của
tham số
m
thì phương trình
1
f
xm
có đúng 3 nghiệm phân biệt.
x
y
O
2
-1
3
A. 22m . B. 3m
. C. 3m . D. 2m .
Hướng dẫn giải
Chọn D.
x
f
x

0
0
0
1



1
3
0
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang175
Hàm số

2
f
xaxbxc có đồ thị là
C , lấy đối xứng phần đồ thị nằm bên phải Oy
của

C qua Oy ta được đồ thị
C
của hàm số
yfx .
Dựa vào đồ thị, phương trình
1
f
xm
1xm

có đúng
3
nghiệm phân biệt
khi
13 2mm
.
Câu 19. Cho hàm số

2
f
xaxbxc đồ thị như hình bên dưới. Hỏi với những giá trị nào của
tham số m thì phương trình
1
f
xm
có đúng 2 nghiệm phân biệt.
x
y
O
2
-1
3
A.
0
1
m
m

. B.
0
1
m
m
. C. 1m  . D. 0m .
Hướng dẫn giải
Chọn B.
+ Phương trình
1fx m
.
+ Đồ thị hàm số

yfx có dạng:
+ Dựa vào đồ thị, để phương trình
1fx m
có hai nghiệm phân biệt thì:
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang176
11
10
m
m


0
1
m
m

.
Câu 20. Hỏi có bao nhiêu giá trị
m
nguyên trong nửa khoảng
0; 2017
để phương trình
2
45 0xx m
có hai nghiệm phân biệt?
A.
2016
. B.
2008
. C.
2009
. D.
2017
.
Hướng dẫn giải
Chọn B.
PT:
22
45 0 45
x
xm xxm
.
Số nghiệm phương trình
1
số giao điểm của đồ thị hàm số
2
45yx x P
và
đường thẳng
ym
.
Xét hàm số
2
1
45yx x P
có đồ thị như hình 1.
Xét hàm số
2
2
45yx x P
là hàm số chẵn nên có đồ thị nhận
Oy
làm trục đối
xứng. Mà
22
45 45yx x x x

nếu
0x
. Suy ra đồ thị hàm số

2
P
gồm hai
phần:
 Phần
1
: Giữ nguyên đồ thị hàm số
1
P
phần bên phải
Oy
.
 Phần
2
: Lấy đối xứng phần
1
qua trục
Oy
.
Ta được đồ thị
2
P
như hình 2.
Xét hàm số
2
45yx x P
, ta có:


2
2
45 0
45 0
xx y
y
xx y


.
Suy ra đồ thị hàm số

P
gồm hai phần:
 Phần
1
: Giữ nguyên đồ thị hàm số
2
P
phần trên
Ox
.
 Phần
2
: Lấy đối xứng đồ thị hàm số
2
P
phần dưới
Ox
qua trục
Ox
.
O
x
y
5
9
2
5
1
O
x
y
5
9
22
55
O
x
y
5
9
55
1
Hình1. Hình2. Hình3.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang177
Ta được đồ thị

P
như hình 3.
Quan sát đồ thị hàm số

P
ta có: Để
2
45 1xx m
có hai nghiệm phân
biệt
9
0
m
m
.
Mà

10;11;12;...; 2017
0; 2017
m
m
m

.
Câu 21. Hỏi có bao nhiêu giá trị m nguyên trong nửa khoảng
0; 2017
để phương trình
2
45 0xx m có hai nghiệm phân biệt?
A.
2016
. B.
2008
. C.
2009
. D.
2017
.
Hướng dẫn giải
Chọn B.
PT:
22
45 0 45 1xx m xx m
. Số nghiệm phương trình

1 số giao
điểm của đồ thị hàm số
2
45yx x P
và đường thẳng
ym
.
Xét hàm số
2
1
45yx x P có đồ thị như hình 1.
Xét hàm số
2
2
45yx x P là hàm số chẵn nên có đồ thị nhận Oy làm trục đối
xứng. Mà
22
45 45yx x x x
 nếu
0x
. Suy ra đồ thị hàm số
2
P
gồm hai
phần:
 Phần
1
: Giữ nguyên đồ thị hàm số
1
P
phần bên phải Oy .
 Phần
2
: Lấy đối xứng phần
1
qua trục Oy .
Ta được đồ thị

2
P
như hình 2.
Xét hàm số
2
45yx x P
, ta có:


2
2
45 0
45 0
xx y
y
xx y


.
Suy ra đồ thị hàm số
P
gồm hai phần:
O
x
y
5
9
2
5
1
O
x
y
5
9
22
55
O
x
y
5
9
55
1
Hình1. Hình2. Hình3.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang178
 Phần 1: Giữ nguyên đồ thị hàm số
2
P
phần trên
Ox
.
 Phần
2
: Lấy đối xứng đồ thị hàm số
2
P
phần dưới Ox qua trục Ox .
Ta được đồ thị
P
như hình 3.
Quan sát đồ thị hàm số

P
ta có: Để
2
45 1xx m có hai nghiệm phân
biệt
9
0
m
m
.
Mà

10;11;12;...; 2017
0; 2017
m
m
m

.
Dạng 4: Toán thực tế
1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1:
Khi nuôi cá thí nghiệm trong hồ, một nhà sinh học thấy rằng: Nếu trên mỗi đơn vị diện
tích của mặt hồ có
n
con cá thì trung bình mỗi con cá sau một vụ cân nặng
360 10
P
nn. Hỏi phải thả bao nhiêu con cá trên một đơn vị diện tích để trọng lương
cá sau một vụ thu được nhiều nhất?
Hướng dẫn giải
Trọng lượng cá trên đơn vị diện tích là
2
360 10 360 10Tnnnn
2
10 36 324 324nn

2
10 18 3240n
max
3240T khi 18n .
Ví dụ 2: Cổng Arch tại thành phố St Louis của Mỹ có hình dạng là một parabol . Biết khoảng
cách giữa hai chân cổng bằng
162 m
. Trên thành cổng, tại vị trí có độ cao
43m
so với
mặt đất , người ta thả một sợi dây chạm đất . Vị trí chạm đất của đầu sợi dây này cách
chân cổng A một đoạn
10 m
. Giả sử các số liệu trên là chính xác. Hãy tính độ cao của
cổng Arch .
Hướng dẫn giải
Chọn hệ trục tọa độ
Oxy như hình vẽ. Phương trình Parabol
P
có dạng
2
yax bxc
.
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang179
Parabol
P
đi qua điểm
0; 0A
,
162;0B
,
10; 43M
nên ta có
2
2
0
162 162 0
10 10 43
c
abc
abc


0
43
1520
3483
760
c
a
b


2
43 3483
:
1520 760
P
yxx
.
Do đó chiều cao của cổng là
4
h
a

2
4
4
bac
a

185,6
m.
3. Bài tập trắc nghiệm
Câu 1.
Một chiếc cổng hình parabol có phương trình
2
1
2
yx
. Biết cổng có chiều rộng
5d
mét . Hãy tính chiều cao h của cổng.
A. 4, 45h mét. B. 3,125h
mét. C. 4,125h
mét. D. 3, 25h mét.
Hướng dẫn giải
Chọn B.
Gọi
A
và
B
là hai điểm ứng với hai chân cổng như hình vẽ.
Vì cổng hình parabol có phương trình
2
1
2
yx
và cổng có chiều rộng 5d mét nên:
5AB và
525
;
28
A




;
525
;
28
B



.
Vậy chiều cao của cổng là
25 25
3,125
88

mét.
Câu 2. Một của hàng buôn giày nhập một đôi với giá là 40 đôla. Cửa hàng ước tính rằng nếu
đôi giày được bán với giá
x
đôla thì mỗi tháng khách hàng sẽ mua

120
x
đôi. Hỏi của
hàng bán một đôi giày giá bao nhiêu thì thu được nhiều lãi nhất?
A. 80 USD. B. 160 USD. C. 40 USD. D. 240 USD.
Hướng dẫn giải
Chọn A.
Gọi
y
là số tiền lãi của cửa hàng bán giày.
O
y
x
5m
h
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang180
Ta có

120 40yxx
2
160 4800xx

2
80 1600 1600x
.
Dấu
""
xảy ra 80x .
Vậy cửa hàng lãi nhiều nhất khi bán đôi giày với giá
80
USD.
Câu 3. Dây truyền đỡ trên cầu treo có dạng Parabol
A
CB
như hình vẽ. Đầu, cuối của dây được
gắn vào các điểm
A
,
B
trên mỗi trục
A
A
và
BB
với độ cao 30 m . Chiều dài đoạn
A
B

trên nền cầu bằng 200 m . Độ cao ngắn nhất của dây truyền trên cầu là 5mOC
.
Gọi
Q
,
P
,
H
,
O
, I
,
J
,
K
là các điểm chia đoạn
A
B
thành các phần bằng nhau.
Các thanh thẳng đứng nối nền cầu với đáy dây truyền:
QQ
,
P
P
,
H
H
, OC ,
II
,
J
J
,
K
K
gọi là các dây cáp treo. Tính tổng độ dài của các dây cáp treo?
A.
Đáp án khác. B. 36,87 m . C. 73,75 m . D. 78, 75m .
Hướng dẫn giải
Chọn D.
Giả sử Parabol có dạng:
2
yax bxc
,
0a
.
Chọn hệ trục
Oxy như hình vẽ, khi đó parabol đi qua điểm

100; 30A , và có đỉnh

0;5C
. Đoạn
A
B
chia làm 8 phần, mỗi phần 25m .
Suy ra:
30 10000 100
0
2
5
abc
b
a
c

1
400
0
5
a
b
c


2
1
:5
400
Py x
.
Khi đó, tổng độ dài của các dây cáp treo bằng
123
222OC
yyy

222
111
52 .25 5 2 .50 5 2 .75 5
400 400 400

 


A
B
Q
P
H
C
I
J
K
B
Q
P
H
I
J
K
A
O
y
x
30m
5m
200m
2
y
1
y
3
y
A
B
Q
P
H
C
I
J
K
B
Q
P
H
C
I
J
K
A
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang181

78, 75 m
.
Câu 4. Một doanh nghiệp tư nhân A chuyên kinh doanh xe gắn máy các loại. Hiện nay doanh
nghiệp đang tập trung chiến lược vào kinh doanh xe hon đa Future Fi với chi phí mua vào
một chiếc là 27
và bán ra với giá là 31
triệu đồng. Với giá bán này thì số lượng xe mà
khách hàng sẽ mua trong một năm là
600 chiếc. Nhằm mục tiêu đẩy mạnh hơn nữa
lượng tiêu thụ dòng xe đang ăn khách này, doanh nghiệp dự định giảm giá bán và ước
tính rằng nếu giảm
1
triệu đồng mỗi chiếc xe thì số lượng xe bán ra trong một năm là sẽ
tăng thêm 200 chiếc. Vậy doanh nghiệp phải định giá bán mới là bao nhiêu để sau khi đã
thực hiện giảm giá, lợi nhuận thu được sẽ là cao nhất.
A. 30 triệu đồng. B. 29 triệu đồng.
C. 30,5 triệu đồng. D. 29,5 triệu đồng.
Hướng dẫn giải
Chọn C.
Gọi
x
đồng là số tiền mà doanh nghiệp A dự định giảm giá;
04x
.
Khi đó:
Lợi nhuận thu được khi bán một chiếc xe là 31 27x
4
x
.
Số xe mà doanh nghiệp sẽ bán được trong một năm là
600 200
x
.
Lợi nhuận mà doanh nghiệp thu được trong một năm là
4 600 200
f
xx x
2
200 200 2400xx .
Xét hàm số

2
200 200 2400fx x x trên đoạn
0; 4 có bảng biến thiên
Vậy


0;4
max 2 450fx
1
2
x
.
Vậy giá mới của chiếc xe là
30,5
triệu đồng thì lợi nhuận thu được là cao nhất.
Câu 5. Khi quả bóng được đá lên, nó sẽ đạt độ cao nào đó rồi rơi xuống đất. Biết rằng quỹ đạo
của quả là một cung parabol trong mặt phẳng với hệ tọa độ
Oth
,trong đó t là thời gian ,
kể từ khi quả bóng được đá lên;
h là độ cao của quả bóng. Giả thiết rằng quả bóng được
đá lên từ độ cao
1, 2m . Sau đó
1
giây, nó đạt độ cao 8, 5m và
2
giây sau khi đá lên, nó ở
độ cao 6m . Hãy tìm hàm số bậc hai biểu thị độ cao h theo thời gian
t và có phần đồ thị
trùng với quỹ đạo của quả bóng trong tình huống trên.
A.
2
4,9 12, 2 1, 2yt t
. B.
2
4, 9 12, 2 1, 2yt t
.
C.
2
4, 9 12, 2 1, 2yt t
. D.
2
4, 9 12, 2 1, 2yt t
.
Hướng dẫn giải
Giáoviêncónhucầusởhữufilewordvuilòngliênhệ.Face:
TrầnĐìnhCư.SĐT:0834332133
Trang182
Chọn B.
Tại 0t ta có 1, 2yh ; tại 1t
ta có 8, 5yh
; tại 2t
, ta có 6yh.
Chọn hệ trục Oth như hình vẽ.
Parabol
P
có phương trình:
2
yat btc
, với
0a
.
Giả sử tại thời điểm t
thì quả bóng đạt độ cao lớn nhất h
.
Theo bài ra ta có: tại
0t
thì
1, 2h
nên
0; 1, 2
A
P .
Tại 1t thì
8, 5h nên
1; 8, 5BP .
Tại
2t
thì
6h
nên
2; 6CP .
Vậy ta có hệ:
1, 2 1, 2
8, 5 4, 9
42 6 12,2
cc
abc a
abc b








.
Vậy hàm số Parabol cần tìm có dạng:
2
4, 9 12, 2 1, 2yt t
.
O
t
h
12
6
8,5
C
B
h
| 1/102
| | Tải xuống

Có thể bạn quan tâm:

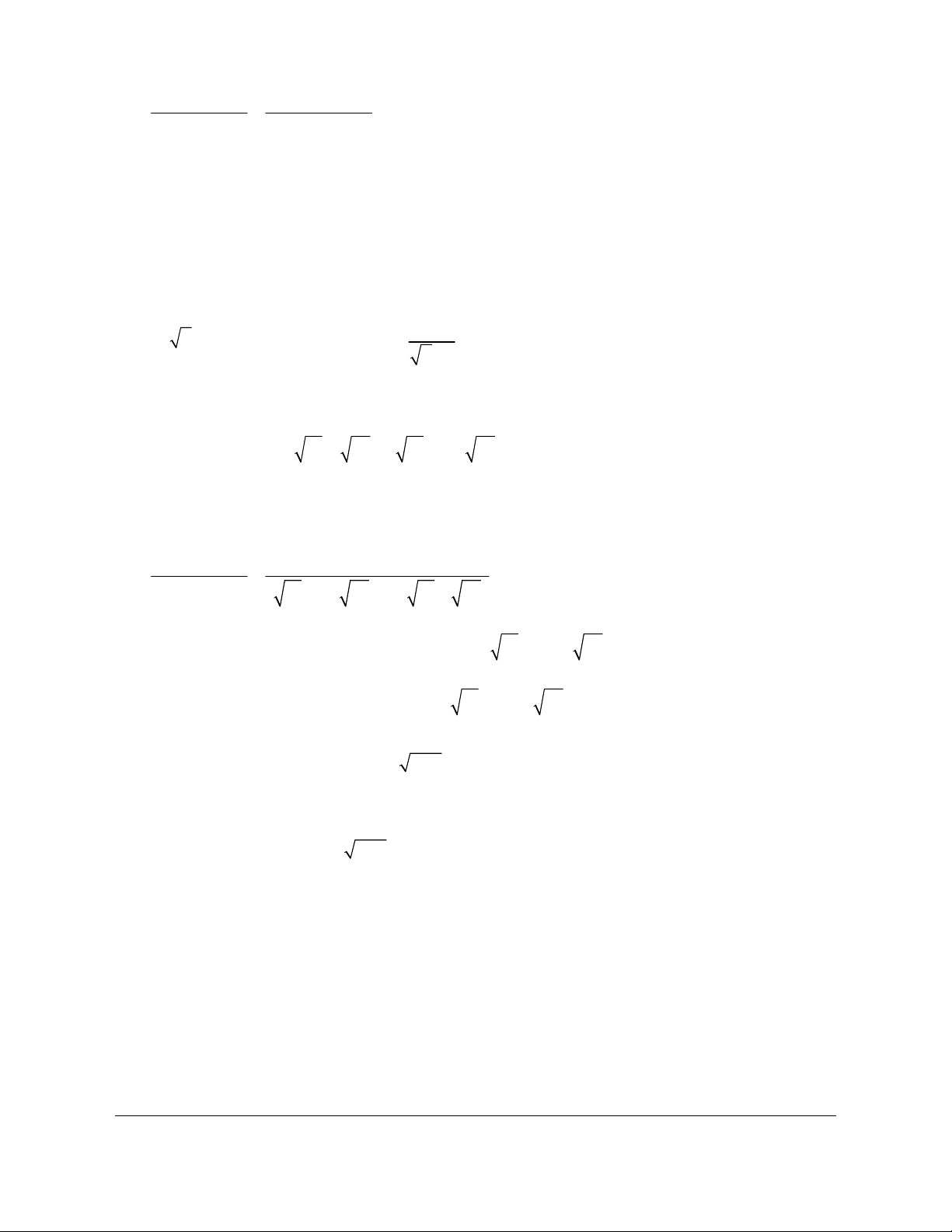
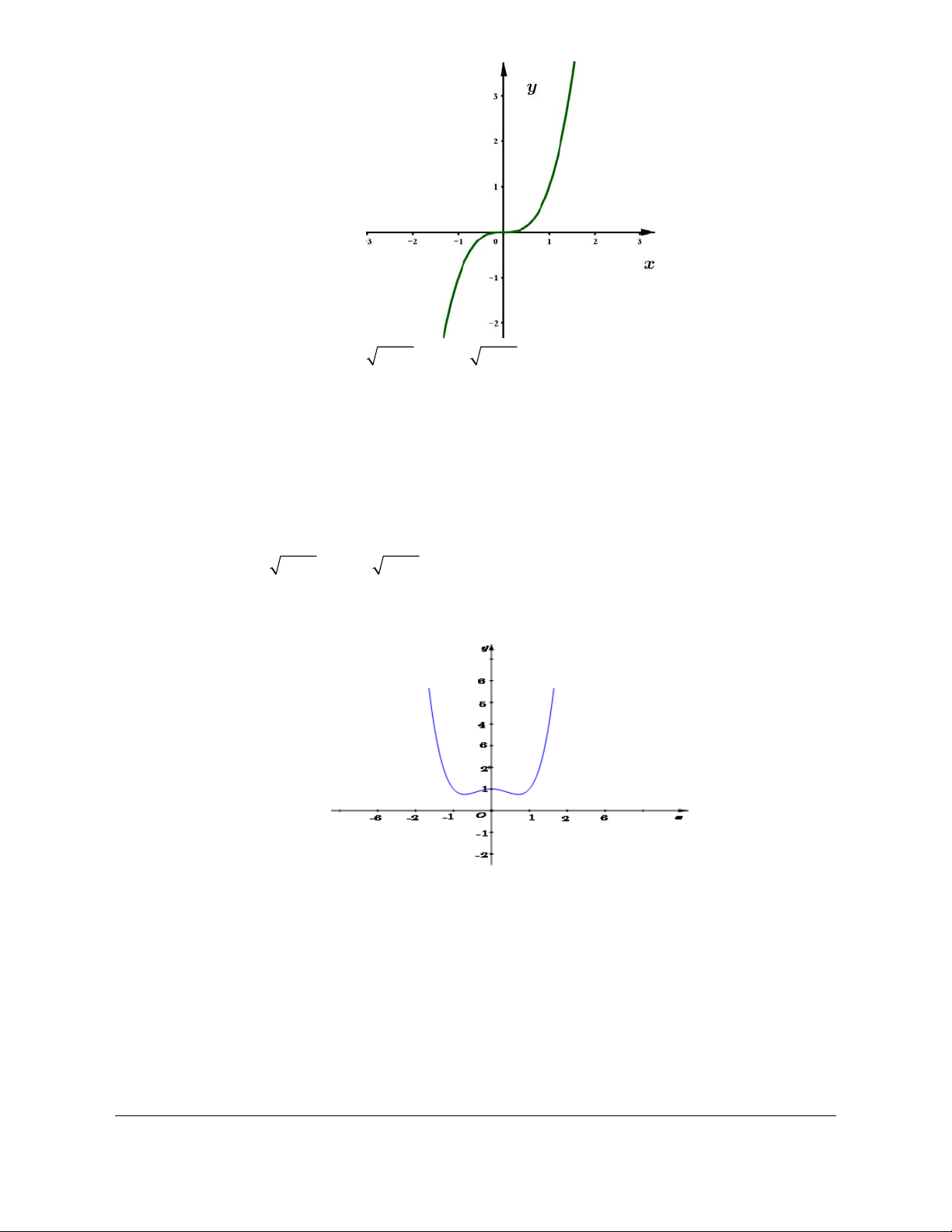
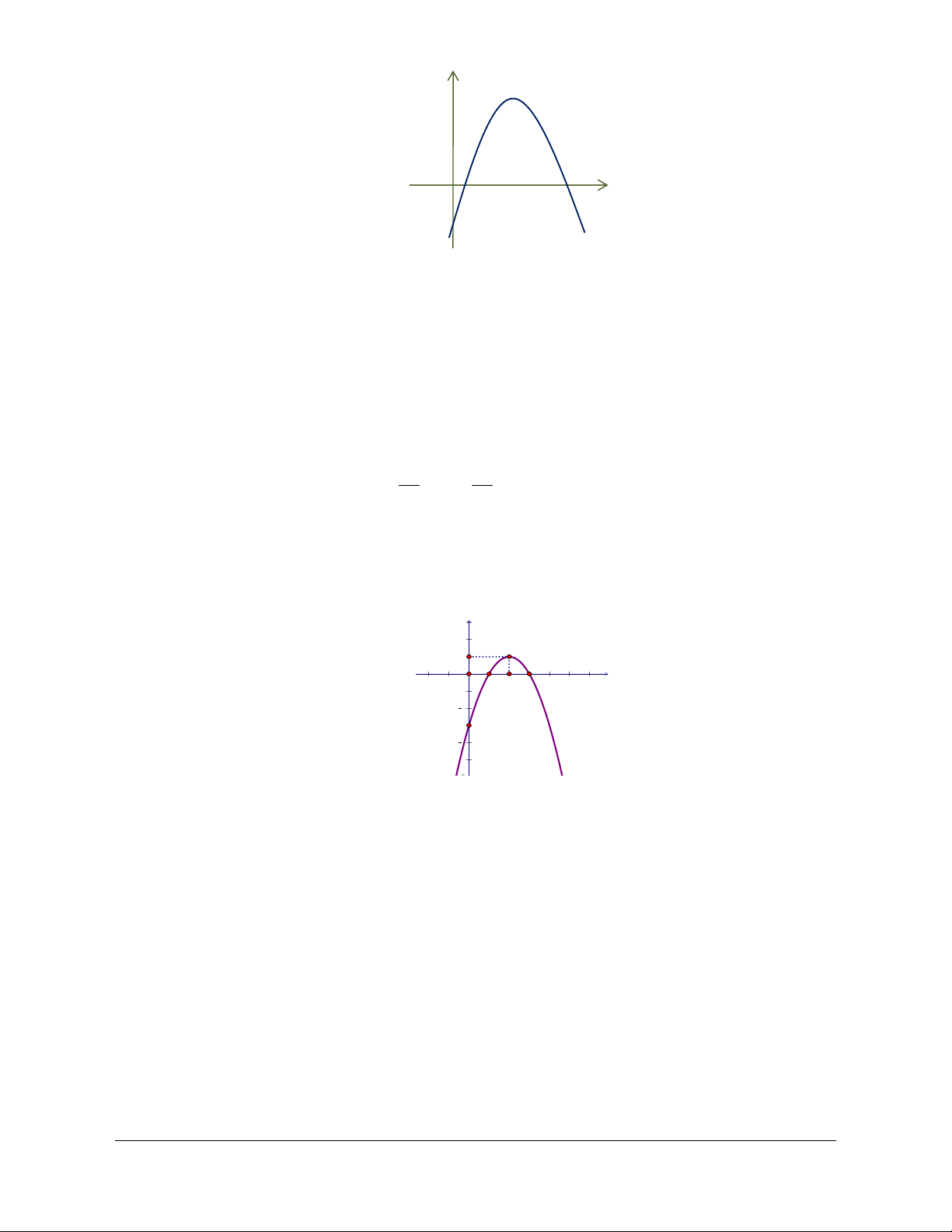
Preview text:

BÀI 1. ĐẠI CƯƠNG VỀ HÀM SỐ
A. KIẾN THỨC CẦN NẮM
I. Ôn tập về hàm số
1. Hàm số. Tập xác định của hàm số
Định nghĩa: Cho D  R, D  . Hàm số f xác định trên D là một qui tắc đặt tương ứng mỗi số x
D với một và chỉ một số , kí hiệu là f (x) , số f (x) được gọi là giá trị của hàm số f tại x . Kí
hiệu: y f (x) .
x được gọi là biến số
 D được gọi là tập xác định của hàm số.
 T = y f (x) x  
D được gọi là tập giá trị của hàm số. 2. Cách cho hàm số  Cho bằng bảng  Cho bằng biểu đồ
 Cho bằng công thức y f x.
Tập xác định của hàm số y
f (x)) là tập hợp tất cả các số thực x sao cho biểu thức f có nghĩa.
Chú ý: Trong kí hiệu y f (x) , ta còn gọi x là biến số độc lập, y là biến số phụ thuộc của hàm số
f . Biến số độc lập và biến số phụ thuộc của một hàm số có thể được kí hiệu bởi hai chữ cái tùy ý
khác nhau. Chẳng hạn, y x3  x2
4 1; và u t3  t2
4 1; là hai cách viết biểu thị cùng một hàm số.
3. Đồ thị của hàm số: Đồ thị của hàm số yfx xác định trên tập D là tập hợp tất cả các điểm
M x; f (x) trên mặt phẳng toạ độ với mọi x  D.
Chú ý: Ta thường gặp đồ thị của hàm số yfxlà một đường. Khi đó ta nói yfx là
phương trình của đường đó.
II. Sự biến thiên của hàm số
1. Hàm số đồng biến, hàm số nghịch biến
Định nghĩa: Cho hàm số f xác định trên K.
 Hàm số yfxđồng biến trên K nếu
x , x K : x x f (x )  f (x 1 2 1 2 1 2 )
 Hàm số yfxnghịch biến trên K nếu
x , x K : x x f (x )  f (x 1 2 1 2 1 2 )
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 81
Trần Đình Cư. SĐT: 0834332133
Nhận xét: Nếu một hàm số đồng biến trên K thì trên đó, đồ thị hàm số nó đi lên; ngược lại hàm số
nghịch biến trên K thì đồ thị hàm số đi xuống.
Chú ý: Nếu f (x )  f (x 1
2 ) với mọi x , x K 1 2
, tức là f (x)  c,x K thì ta gọi là hàm số không
đổi hay hàm số hằng trên K.
2. Khảo sát sự biến thiên của hàm số:
Khảo sát sự biến thiên của hàm số là xét xem hàm số đồng biến, nghịch biến, không đổi trên các
khoảng nào trong tập xác định.
Đối với hàm số cho bằng biểu thức, để khảo sát sự biến thiên của hàm số ta có thể dựa vào định
nghĩa hoặc dựa vào nhận xét sau:
yfxđồng biến trên K
f (x )  f (x )
 x , x K : x x  2 1  1 2 1 2 0 x x 2 1
yfx nghịch biến trên K
f (x )  f (x )
 x , x K : x x  2 1  1 2 1 2 0 x x 2 1
III. Hàm số chẵn, hàm số lẻ
1. Khái niệm hàm số chẵn, hàm số lẻ
Định nghĩa: Cho hàm số yfx có tập xác định D.
 Hàm số f được gọi là hàm số chẵn nếu với x  D thì –x  D và f –x  f x.
 Hàm số f được gọi là hàm số lẻ nếu với x  D thì –x  D và f –x  –f x.
2. Đồ thị của hàm số chẵn và hàm số lẻ
Đồ thị của hàm số chẵn nhận trục tung làm trục đối xứng.
Đồ thị của hàm số lẻ nhận gốc toạ độ làm tâm đối xứng.
3. Sơ lượt tịnh tiến đồ thị song song với trục tọa độ
Trong mặt phẳng tọa độ Oxy , cho đồ thị của hàm số y f (x) ; p và q là hai số dương tùy ý. Khi đó
 Tịnh tiến lên trên q đơn vị thì được đồ thị hàm số y f (x)  q
 Tịnh tiến xuống dưới q đơn vị thì được đồ thị hàm số y f (x)  q
 Tịnh tiến sang trái p đơn vị thì được đồ thị hàm số y f (x p)
 Tịnh tiến sang phải p đơn vị thì được đồ thị hàm số y f (x p)
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 82
Trần Đình Cư. SĐT: 0834332133
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1: Tính giá trị của hàm số tại một điểm 1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
3. Bài tập trắc nghiệm x 1 Câu 1.
Cho hàm số y
. Tìm tọa độ điểm thuộc đồ thị của hàm số và có tung độ bằng 2  . x 1  1  A. 0;2 . B. ; 2    . C.  2;  2  . D.  1  ; 2  .  3  Hướng dẫn giải Chọn B. Gọi M x ; 2
 là điểm thuộc đồ thị hàm số có tung độ bằng 2  . 0  0  x 1 1   Khi đó: 0  2
  x 1  2 1 x  3x 1  x  1  M ; 2 . 0  0    x 1 0 0 3  3  0 x  2 Câu 2.
Điểm nào sau đây thuộc đồ thị của hàm số y x(x 1)
A. M 0;  1 . B. M 2;  1 .
C. M 2;0 . D. M 1;  1 . Hướng dẫn giải Chọn C.
Thử trực tiếp thấy tọa độ của M 2;0 thỏa mãn phương trình hàm số. 2 x  2  3  khi x  2 Câu 4.
Cho hàm số f x   x 1
. Tính P f 2  f  2  .  2 x  2 khi x  2 7 A. P  3 . B. P  2 . C. P  . D. P  6 . 3 Hướng dẫn giải Chọn A. 2 2  2  3
Ta có: f 2  f  2      2
 2  2  P  3. 2 1  x x Câu 5.
Đồ thị của hàm số y f x 2 1 khi 2  
đi qua điểm nào sau đây:  3  khi x  2 A. 0;  3 . B. 3; 7  . C. (2;  3) . D. 0;  1 .
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 83
Trần Đình Cư. SĐT: 0834332133 Hướng dẫn giải Chọn D.
Thử lần lượt từng phương án A,B,C,D với chú ý về điều kiện ta được:
f 0  2.0 1 1  3
 , đồ thị không đi qua điểm 0;  3 . f 3  3
  7 , đồ thị không đi qua điểm 3; 7  .
f 2  2.2 1  5  3
 , đồ thị không đi qua điểm 2;  3 .
f 0  2.0 1 1, đồ thị không đi qua điểm 0;  1 .  2    x  3 khi 1   x 1 Câu 6.
Cho hàm số: f x  
. Giá trị của f   1 ; f   1 lần lượt là 2  x 1 khi x  1 A. 8 và 0 . B. 0 và 8 . C. 0 và 0 . D. 8 và 4 . Hướng dẫn giải Chọn A. Ta có: f   1  2   1
  3  8; f   2 1  1 1  0 .  2
x 1 khi x  3   Câu 7.
Cho hàm số y   x  7
. Biết f x  5 thì x là 0  khi x  3  0  2 A. 2  . B. 3 . C. 0 . D. 1. Hướng dẫn giải Chọn B. TH1. x  3
 : Với f x  5  2
x 1  5  x  2  . 0  0 0 0 x  7 TH2. x  3
 : Với f x  5 0   5  x  3 . 0  0 0 2 2x  3 khi x  0  x 1 Câu 8.
Cho hàm số f x  
. Ta có kết quả nào sau đây đúng? 3 2  3x  khi 2  x  0  x  2
A. f   1 1  ; f   7 2  .
B. f 0  2; f 3  7 . 3 3 C. f  
1 : không xác định; f   11 3   . D. f  
1  8; f 3  0 . 24 Hướng dẫn giải
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 84
Trần Đình Cư. SĐT: 0834332133 Chọn A.   f   3 2 3 1 1   ; f   2.2 3 7 2   . 1   2 3 2 1 3
Dạng 2: Tìm tập xác định của hàm số 1. Phương pháp
Tìm tập xác định D của hàm số y f x là tìm tất cả những giá trị của biến số x sao cho
biểu thức f(x) có nghĩa:
D  x R f (x) coùnghóa .
Điều kiện xác định của một số hàm số thường gặp: A(x)
1) Hàm số y
. Khi đó : D  x  | A(x) xaùc ñònh vaø A(x)   0 B(x)
2) Hàm số  2k y
A(x),k  *.
Khi đó : D  x  | A(x) xaùc ñònh vaø A(x)   0 A(x)
3) Hàm số y
,k  *. 2k B(x)
Khi đó : D  x  | A(x),B(x) xaùc ñònh vaø B(x)  >0 Chú ý:
Đôi khi ta sử dụng phối hợp các điều kiện với nhau. A  0
A.B 0 B  0.
 Nếu y f (x) có tập xác định là D . Khi đó: y f (x) xác định trên tập X X D
y f (x) xác định trên tập X f (x) xác định với mọi x X
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1 : Tìm tập xác định của hàm số y x 1 Hướng dẫn giải
Hàm số y x 1 xác định  x 1  0  x  1.
Ví dụ 2: Tìm tập xác định của hàm số y  1 2x  6  x Hướng dẫn giải
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 85
Trần Đình Cư. SĐT: 0834332133  1 1   2x  0 x   1
Hàm số đã cho xác định khi    2  x   . 6  x  0  2 x  6   1 
Vậy tập xác định của hàm số là D   ;    .  2  x
Ví dụ 3: Tập xác định của hàm số y x  2 Hướng dẫn giảix  0 x  0
Hàm số xác định khi:    . x  2  0 x  2
Vậy tập xác định của hàm số D  0; \  2 . 1
Ví dụ 4: Tìm tập xác định của hàm số y   x 1 . x  3 Hướng dẫn giảix  3  0
Điều kiện để hàm số xác định:   1  x  3. x 1  0
Vậy tập xác định của hàm số đã cho là D  1;   \  3 .
Ví dụ 5: Tìm m để hàm số y   x  2 3x m 1 xác định trên tập 1; ? Lời giải m  1  m 1  ĐK: x   D  ;    . 3  3 
Để hàm số xác định trên 1; thì   m 1  m 1 1;  ;  
 1  m 1  3  m  2   .  3  3
Ví dụ 6. Xác định tham số m để hàm số y  3x m xác định trên tập 1; Hướng dẫn: m
Tập xác định của hàm số D  ; 
 . Do đó hàm số xác định trên tập 1; khi và chỉ khi  3  1;  mm   D  ;  1   m    3  3  3
Ví dụ 7. Xác định tham số m để hàm số y x2  m xác định trên tập ;3
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 86
Trần Đình Cư. SĐT: 0834332133 Hướng dẫn:
hàm số xác định khi và chỉ khi x2  m   x2 0  m (1) m  m  0  0 (1)   hoaëc  x  x ; m m; .              khi m   0
Vậy tập xác định của hàm số là D   ; m     m; khi m 0      
Do đó hàm số xác định trên tập ;3 khi và chỉ khi  m  0 m
    D   0 ; 3  m     9 . 3   m 0  m  9
3. Bài tập trắc nghiệm Câu 1.
Tìm tập xác định D của hàm số f x 1  x 1  . x
A. D   \  0 .
B. D   \  1  ;  0 . C. D   1;   \ 
0 . D. D   1;   . Hướng dẫn giải Chọn C. x 1 0 x  1 
Điều kiện xác định:   
. Vậy tập xác định: D   1;   \  0 . x  0 x  0  1  x  0 Câu 2.
Cho hàm số: y   x 1
. Tập xác định của hàm số là tập hợp nào sau đây?
 x  2 x  0 A.  2;   . B.  . C.  \  1 .
D. x  \ x  1và x  2   . Hướng dẫn giải Chọn B. 1 Với 0
x  ta có: y  xác định với mọi 1
x  nên xác định với mọi 0 x  . x 1
Với x  0 ta có: y x  2 xác định với mọi x  2
 nên xác định với mọi x  0 .
Vậy tập xác định của hàm số là D   . x 1 Câu 3.
Tập xác định của hàm số y  là x  3
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 87
Trần Đình Cư. SĐT: 0834332133 A. 3;   . B. 1; + . C.  1
 ; 3 3;   . D.  \  3 . Hướng dẫn giải Chọn C. x 1 Hàm số y  . x  3 x 1 0 x  1 
Điều kiện xác định:    . x  3  0 x  3
Vậy tập xác định của hàm số D   1;
 3 3;   . 2  x Câu 4.
Tập xác định của hàm số y  là 2 x  4x A.  \ 0;2;  4 . B.  \ 0;4. C.  \ 0;4 . D.  \ 0;  4 . Hướng dẫn giải Chọn D. x  0 Hàm số xác định 2
x  4x  0  
. Vậy D   \0;  4 . x  4 Câu 5.
Tìm tập xác định D của hàm số f x 1  x 1  . x
A. D   \  0 .
B. D  1;  .
C. D   \  1  ;  0 .
D. D  1;  \  0 . Hướng dẫn giải Chọn D. x 1  0 Điều kiện:  . x  0
Vậy tập xác định của hàm số là D  1;  \  0 .
Câu 6. Tìm tập xác định của hàm số 2
y  4x  4x 1 . 1   1  A. ;    . B. ;   . C.  . D.  . 2  2   Hướng dẫn giải Chọn C. Điều kiện xác định: 2
4x  4x 1  0   x  2 2 1  0 .
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 88
Trần Đình Cư. SĐT: 0834332133
Do đó tập xác định D   . Câu 7.
Tập xác định của hàm số f x 1  3 x  là x 1
A. D  1;  3 .
B. D    ;1 3; .
C. D  1;  3 . D. D   . Hướng dẫn giải Chọn A. 3   x  0 x  3 Hàm số xác định khi    1 x  3. x 1  0 x 1
Vậy tập xác định của hàm số là D  1;  3 . x Câu 8.
Tập hợp nào sau đây là tập xác định của hàm số y  1 5x  ? 7  2x  1 7   1 7   1 7   1 7  A. ;    . B.  ; . C.  ;    . D.  ;    5 2   5 2    5 2   5 2  Hướng dẫn giải Chọn D.  1   1   5  0 x x  5 1 7
Hàm số xác đinh khi và chỉ khi       x  . 7  2x  0 7 5 2 x   2 2 9  x Câu 9.
Tập xác định của hàm số y  là 2 x  6x  8 A. 3;8 \  4 . B.  3;  3\  2 . C.  3;  3 \  2 . D.  ;3   \  2 . Hướng dẫn giải Chọn B. Ta có 2
9  x  0  3 x3 x  0  3   x  3 .
Hàm số xác định khi và chỉ khi  3   x  3 2 9   x  0   3   x  3   x  4   . Vậy x  3;  3\  2 . 2
x  6x  8  0  x  2 x  2 
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 89
Trần Đình Cư. SĐT: 0834332133
  x   x x
Câu 10. Tập xác định của hàm số y f x 3 8 khi 2   là  x  7 1 khi x  2  8 A.  . B.  \  2 . C. ;   . D.  7;   . 3   Hướng dẫn giải Chọn A. Ta có:
• Khi x  2 : y f x  3
x  8  x xác định khi 3  x  8  8 0  x  . 3 Suy ra D   ;2  . 1  
• Khi x  2 : y f x  x  7 1 xác định khi x  7  0  x  7  .
Suy ra D  2;  . 1  
Vậy TXĐ của hàm số là D D D  ;     . 1 2   x
Câu 11. Tìm tập xác định của hàm số 2
y x  4x  3  . x  3 A.  
;1 3;  . B.  
;1 3;  . C. 3;  . D. 1;3 . Hướng dẫn giải Chọn A. x Hàm số 2
y x  4x  3  xác định x  3 2
x  4x  3  0
x 1 v x  3    
x 1 hoặc x  3. x  3  0 x  3
3  x x 1
Câu 12. Tập xác định của hàm số y  là 2 x  5x  6 A.  1  ;3 \  2 . B.  1  ;2. C.  1  ;  3 . D. 2;3. Hướng dẫn giải Chọn A.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 90
Trần Đình Cư. SĐT: 0834332133
3  x x 1 Hàm số y  có nghĩa khi 2 x  5x  6 3  x  0  1  x  3 x 1  0    x  1  ;3 \  2 . 
x  2; x  3 2
x  5x  6  0
Câu 13. Tìm tập xác định của hàm số 2
y  2x  5x  2 .  1   1  1  A. ;  2;  
 . B. 2;  . C. ;  . D. ; 2 . 2    2    2    Hướng dẫn giải Chọn A.  1 x  Hàm số xác định 2
 2x  5x  2  0   2 .  x  2 x  2m  3 3x 1
Câu 14. Tìm m để hàm số y  
xác định trên khoảng 0;  1 . x mx m  5  3 A. m  1;  .
B. m 3;0 . 2      C. m  3;  00;  1 . D. m   3 4;0  1;  . 2    Hướng dẫn giải Chọn D. x  2m  3 3x 1
*Gọi D là tập xác định của hàm số y   . x mx m  5
x  2m  3  0
x  2m  3  
* x  D  x m  0
 x  m .
x m 5  0   x m  5  x  2m  3 3x 1 *Hàm số y  
xác định trên khoảng 0;  1 x mx m  5  3    2m  3  0 m  2       0; 
1  D  m  5 1  m  4   m   3 4;0  1;   .   2 m    0;  1 m 1  m  0
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 91
Trần Đình Cư. SĐT: 0834332133
Dạng 3: Tính đồng biến, nghịch biến của hàm số 1. Phương pháp
Cho hàm số f xác định trên K .
y = f(x) đồng biến trên K x , x K : x x f (x )  f (x 1 2 1 2 1 2 )
y = f(x) nghịch biến trên K x , x K : x x f (x )  f (x 1 2 1 2 1 2 )
Từ đó, ta có hai cách để xét tính đồng biến nghịch biến:
Cách 1: x , x K : x x 1 2 1
2 . Xét hiệu số A f (x )  f (x 2 1)
- Nếu A  0 thì hàm số đồng biến
- Nếu A  0 thì hàm số nghịch biến
f (x )  f (x )
Cách 2: x , x K : x x 2 1 1 2 1
2 . Xét tỉ số A x x 2 1
- Nếu A  0 thì hàm số đồng biến
- Nếu A  0 thì hàm số nghịch biến
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1. Khảo sát sự biến thiên của hàm số sau
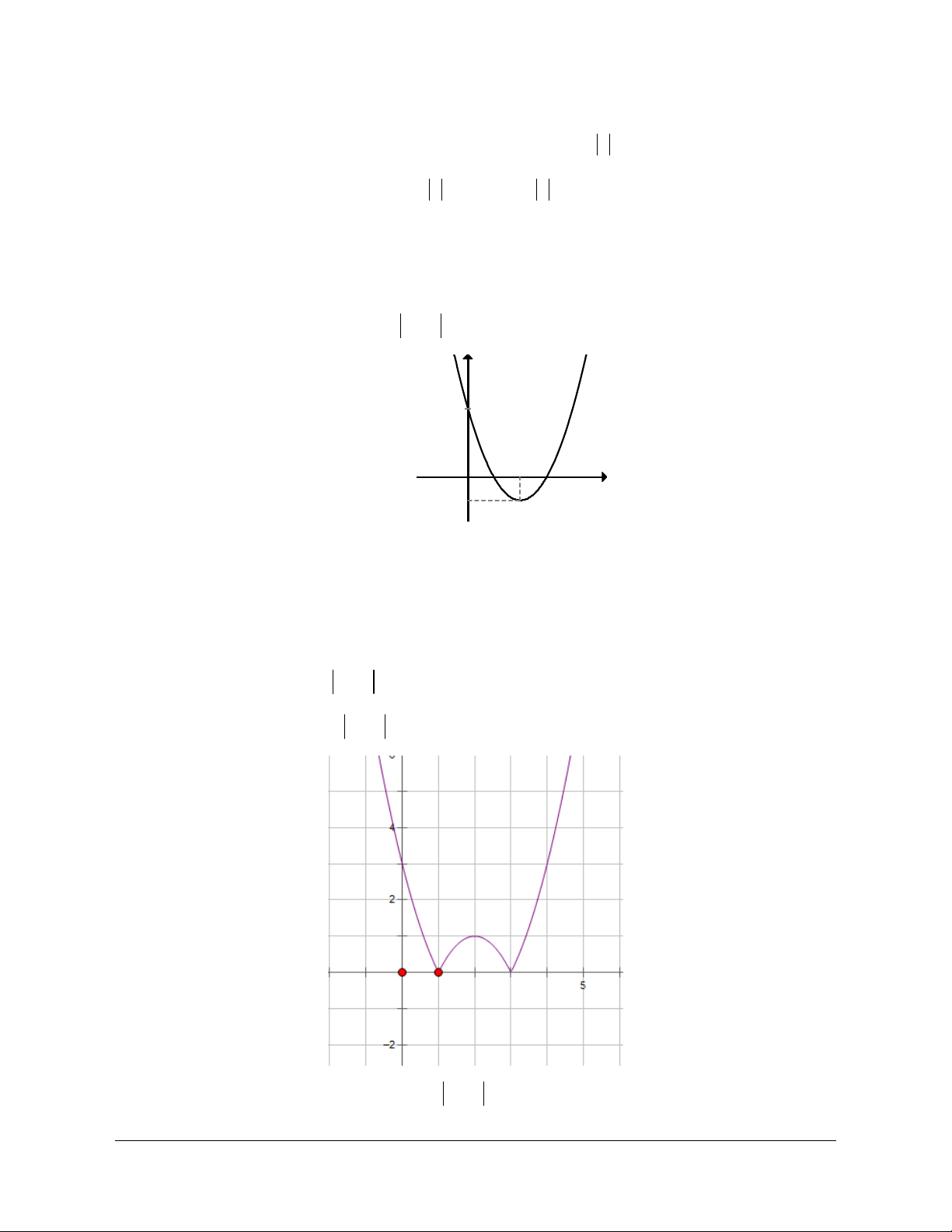
a) y x2  4x  6 treân moãi khoaûng ;2;2  
b) y  x2  6x  5 treân moãi khoaûng ;3;3; Hướng dẫn
a) Vôùi x  x 1 2, ta coù:
f (x )  f (x 2 1) A=
x x  4  2 1 x  2 2  x  1 2 x x 2 1 Do ñoù:  x , x  1 2
;2,x  x x  2;x  2  x 2  0,x 2  0  A  1 2 1 2 1 2 0
Vaäy, haøm soá nghòch bieán treân ;2  x , x  1 2
2;,x  x x  2;x  2  x 2  0,x 2  0  A  1 2 1 2 1 2 0
Vaäy, haøm soá ñoàng bieán treân 2;.
Ví dụ 2. Khảo sát sự biến thiên của hàm số sau a y 3 ) 
treân moãi khoaûng ;  1 ;1; x 1 x b y 1 ) 
treân moãi khoaûng ;2;2; 2x  4 Hướng dẫn
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 92
Trần Đình Cư. SĐT: 0834332133
a) Vôùi x  x 1 2, ta coù:
f (x )  f (x )  2 1 3 A=  x x 2 1 x  1 1x  2 1 Do ñoù:  x , x  1 2
; 1,x  x x 1;x 1 x 1 0,x 1 0  A  1 2 1 2 1 2 0
Vaäy, haøm soá nghòch bieán treân   ;1  x , x  1 2
1;,x  x x 1;x 1 x 1 0,x 1 0  A  1 2 1 2 1 2 0
Vaäy, haøm soá nghòch bieán treân 1;.
Ví dụ 3. Khảo sát sự biến thiên và lập bảng biến thiên của hàm số sau a y 1 )  3 x  3; b)y x 1 Hướng dẫn
a)Taäp xaùc ñònh:D=
x , x  : x x  3 x  3 x  3 x  3  3 x  3  f (x )  f (x 1 2 1 2 1 2 1 2 1 2 )
Vaäy, haøm soá ñoàng bieán treân .
b) Taäp xaùc ñònh: D= 0;  \{1}
x , x D, x  x 1 2 1 2, ta coù:
f (x )  f (x )  2 1 1 A=  x x 2 1
x 1 1 x  2 1 x x 1 2  Do ñoù:  x , x   1 2 0; 
1 ,x  x  0  x  1;0  x  1 x 1  0, x 1  0  A   1 2 1 2 1 2 0
Vaäy, haøm soá nghòch bieán treân 0; 1  x , x  1 2
1;, 1x  x x 1;x 1 x 1 0, x 1 0 A  2 1 2 1 2 0
Vaäy, haøm soá nghòch bieán treân 1;.
Ví dụ 5: Tìm a để hàm số f x  ax  1 a đồng biến trên  Hướng dẫn giải a  0
Hàm số f x  ax  1 a đồng biến trên  khi và chỉ khi   0  a  1 1   a  0
3. Bài tập trắc nghiệm
Câu 1: Hàm số nào sau đây đồng biến trên tập xác định của nó?
A. y  3 x .
B. y  3x 1.
C. y  4 . D. 2
y x  2x  3 . Lời giải Chọn B
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 93
Trần Đình Cư. SĐT: 0834332133
y  3x 1 có a  3  0 hàm số đồng biến trên TXĐ.
Câu 2: Xét sự biến thiên của hàm số f x 3
 trên khoảng 0;. Khẳng định nào sau đây x đúng?
A. Hàm số nghịch biến trên khoảng 0; .
B. Hàm số vừa đồng biến, vừa nghịch biến trên khoảng 0; .
C. Hàm số đồng biến trên khoảng 0;.
D. Hàm số không đồng biến, không nghịch biến trên khoảng 0; . Lời giải Chọn Ax x   x  1, 2 0; : 1 2x f  3 3 3  x x f x f x 3 x f x        2   1  2 1  2  1 0 x x x x x  2 1 2 1 2 1 x 2 x 1 x
Vậy hàm số nghịch biến trên khoảng 0;.
Câu 3: Trong các hàm số sau, hàm số nào nghịch biến trên  ? 1
A. y x .
B. y  2x .
C. y  2x .
D. y x 2 Lời giải Chọn B
Hàm số y ax b với a  0 nghịch biến trên  khi và chỉ khi a  0 . Câu 4.
Chọn khẳng định đúng ? A. Hàm số
y f (x)
được gọi là nghịch biến trên K nếu x  ; x K,
x x f (x )  f (x ) . 1 2 1 2 1 2 B. Hàm số
y f (x)
được gọi là đồng biến trên K nếu x  ; x K,
x x f (x )  f (x ) . 1 2 1 2 1 2 C. Hàm số
y f (x)
được gọi là đồng biến trên K nếu x  ; x K,
x x f (x )  f (x ) . 1 2 1 2 1 2 D. Hàm số
y f (x)
được gọi là đồng biến trên K nếu x  ; x K,
x x f (x )  f (x ) . 1 2 1 2 1 2 Lời giải Chọn D
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 94
Trần Đình Cư. SĐT: 0834332133
Lí thuyết định nghĩa hàm số đồng biến, nghịch biến
Câu 5. Tìm m để hàm số y  2m  
1 x  7 đồng biến trên  . 1 1 1 A. m  . B. m  . C. m  . D. m  . 2 2 2 Lời giải Chọn A
hàm số y  2m  
1 x  7 đồng biến trên  khi 2m 1  0 . Câu 6.
Tìm tất cả các giá trị của tham số m để hàm số y  2m  3 x m  3 nghịch biến trên  . 3 3 3 3 A. m   . B. m   . C. m   . D. m   . 2 2 2 2 Lời giải Chọn D
Hàm số y  2m  3 x m  3 có dạng hàm số bậc nhất. 3
Để hàm số nghịch biến trên   2m  3  0  m   . 2 Câu 7.
Tổng tất cả các giá trị nguyên dương của tham số m để hàm số 2 y  2
x  m   1 x  3
nghịch biến trên khoảng 1; 5 là A. 6 . B. 3 . C. 1. D. 15 . Lời giải Chọn Am 1  Hàm số 2 y  2
x  m  
1 x  3 nghịch biến trên khoảng ;     .  4  Để hàm số 2 y  2
x  m  
1 x  3 nghịch biến trên khoảng 1; 5 thì ta phải có    m1  m 1 1; 5  ;      1  m  3.  4  4
Các giá trị nguyên dương của tham số m để hàm số 2 y  2
x  m  
1 x  3 nghịch biến
trên khoảng 1; 5 là m 1, m  2, m  3.
Tổng tất cả các giá trị nguyên dương của tham số m để hàm số 2 y  2
x  m   1 x  3
nghịch biến trên khoảng 1; 5 là S  1 2  3  6 .
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 95
Trần Đình Cư. SĐT: 0834332133 Câu 8.
Cho hàm số y  m  2 x  2  m . Có bao nhiêu giá trị nguyên của m để hàm số đồng biến trên  ? A. 2 . B. 3 . C. 4 . D. 5 . Hướng dẫn giải Chọn C. m  2  0
Hàm số có dạng y ax b , nên để hàm số đồng biến trên  khi và chỉ khi  2  m  0 m  2   
. Mặt khác do m  nên m  1;  0; 1; 
2 . Vậy có 4 giá trị nguyên của m . m  2 x m  2 Câu 9.
Tìm các giá trị thực của tham số m để hàm số y  xác định trên  1;  2 . x mm  1  m  1  m  1 A.  . B.  . C.  . D. 1   m  2 . m  2 m  2 m  2 Hướng dẫn giải Chọn B. x m  2 Hàm số y
xác định khi x m . x m x m  2 m  1  Để hàm số y  xác định trên  1;  2 khi và chỉ khi . x m  m  2
Dạng 4: Dựa vào đồ thị tìm các khoảng đồng biến, nghịch biến 1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
3. Bài tập trắc nghiệm
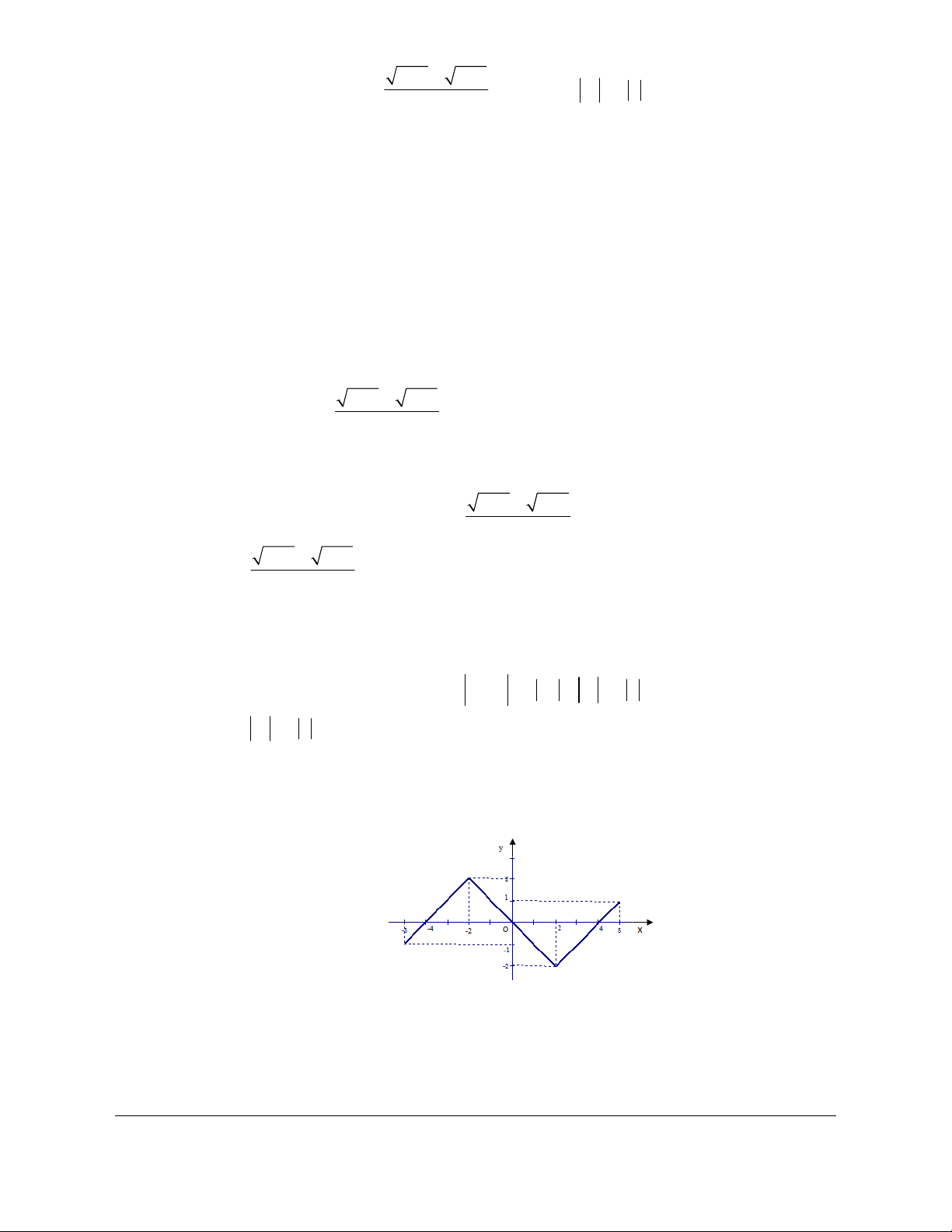
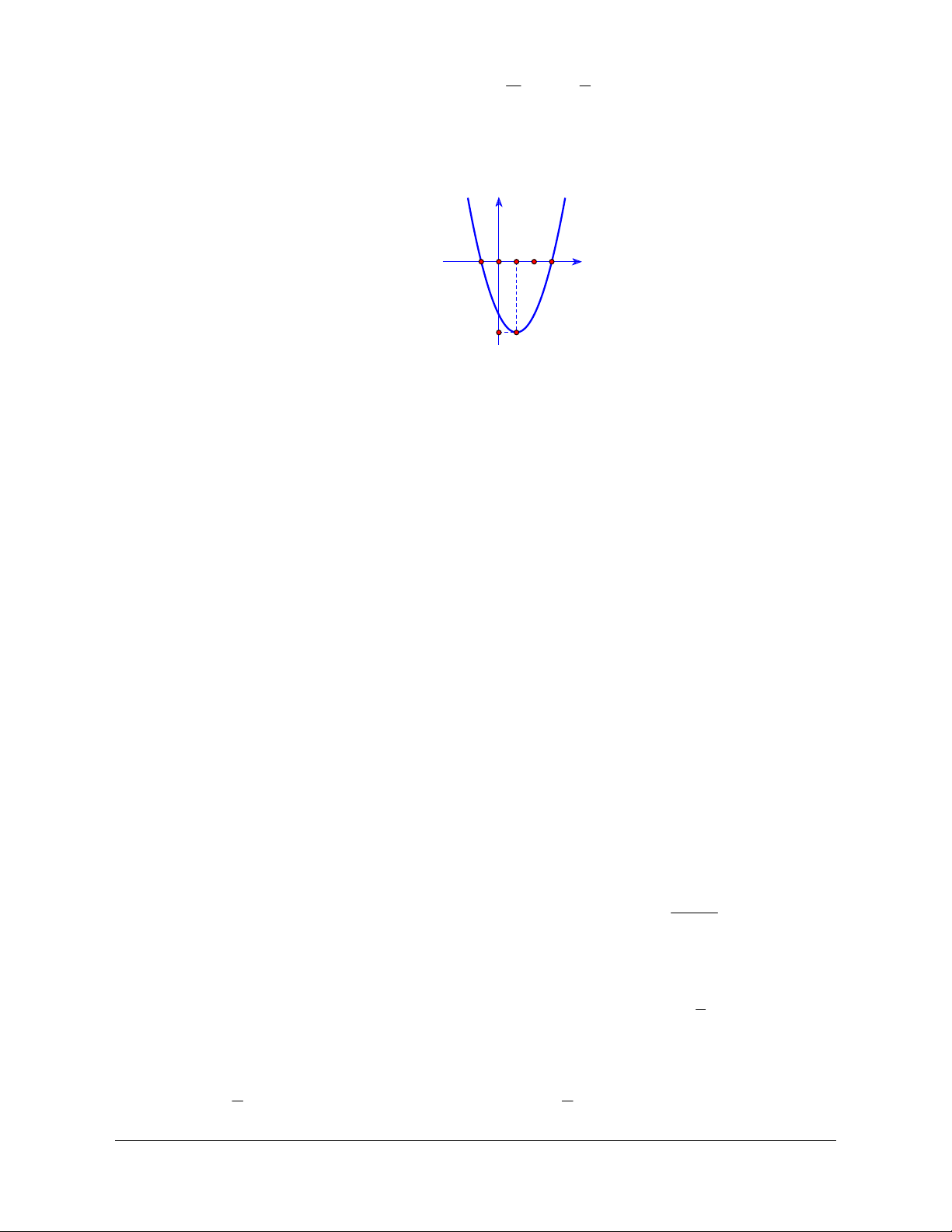
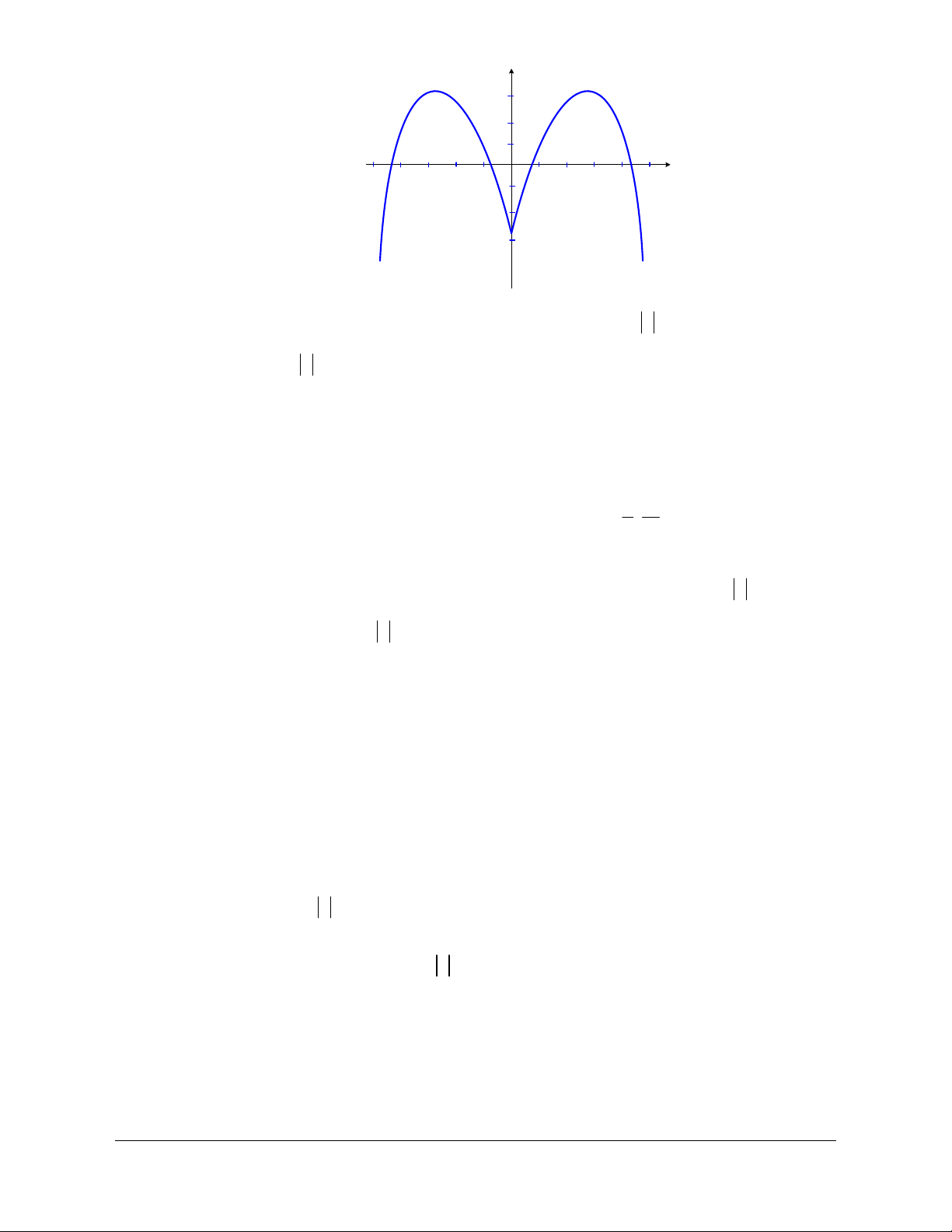
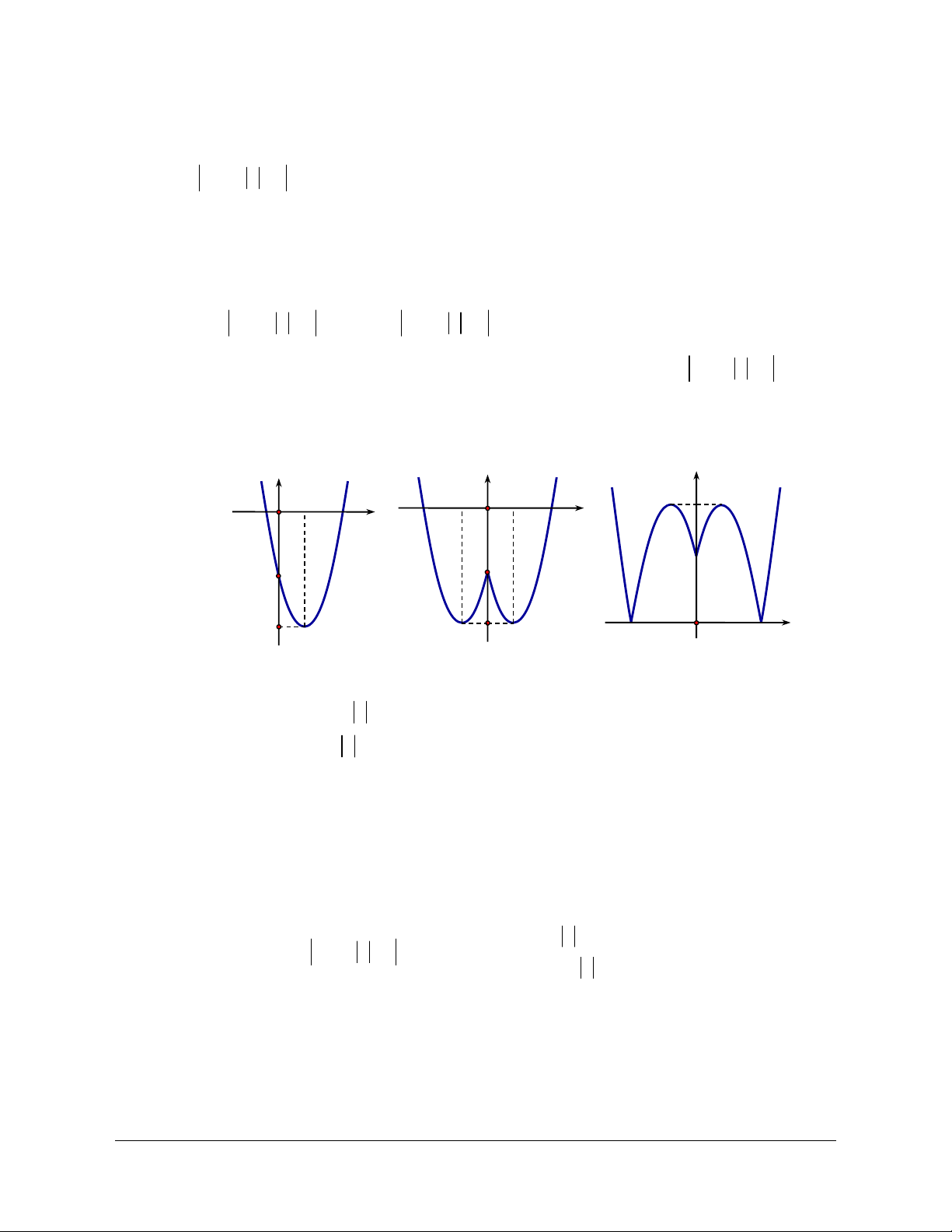
Câu 1: Cho hàm số có đồ thị như hình bên dưới.
Khẳng định nào sau đây là đúng?
A. Hàm số nghịch biến trên khoảng 0;3 .
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 96
Trần Đình Cư. SĐT: 0834332133
B. Hàm số đồng biến trên khoảng   ;1 .
C. Hàm số nghịch biến trên khoảng 0;2 .
D. Hàm số đồng biến trên khoảng  ;3   . Lời giải Chọn C
Trên khoảng 0;2 , đồ thị hàm số đi xuống từ trái sang phải nên hàm số nghịch biến. Câu 2.
Cho hàm số y f x có tập xác định là  3; 
3 và có đồ thị được biểu diễn bởi hình
bên. Khẳng định nào sau đây là đúng?
A. Hàm số y f x  2018 đồng biến trên các khoảng  3;    1 và 1;3 .
B. Hàm số y f x  2018 đồng biến trên các khoảng  2;   1 và 1;3 .
C. Hàm số y f x  2018 nghịch biến trên các khoảng  2;    1 và 0;  1 .
D. Hàm số y f x  2018 nghịch biến trên khoảng  3;  2   . Lời giải Chọn A
Gọi C : y f x,C y f x  2018. Khi tịnh tiến đồ thị C theo phương song
song trục tung lên phía trên 2018 đơn vị thì được đồ thị C . Nên tính đồng biến,
nghịch biến của hàm số y f x , y f x  2018 trong từng khoảng tương ứng không thay đổi.
Dựa vào đồ thị ta thấy:
Hàm số y f x  2018 đồng biến trên các khoảng  3;    1 và 1;3 .
Hàm số y f x  2018 đồng biến trên các khoảng  2;   1 và 1;3 .
Hàm số y f x  2018 nghịch biến trên các khoảng  2;    1 và 0;  1 .
Hàm số y f x  2018 nghịch biến trên khoảng  3;  2   .
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 97
Trần Đình Cư. SĐT: 0834332133 Câu 3.
Cho hàm số có đồ thị như hình bên dưới.
Khẳng định nào sau đây là đúng?
A. Hàm số nghịch biến trên khoảng 0;3 .
B. Hàm số đồng biến trên khoảng   ;1 .
C. Hàm số nghịch biến trên khoảng 0;2 .
D. Hàm số đồng biến trên khoảng  ;3   . Lời giải Chọn C
Trên khoảng 0;2 , đồ thị hàm số đi xuống từ trái sang phải nên hàm số nghịch biến.
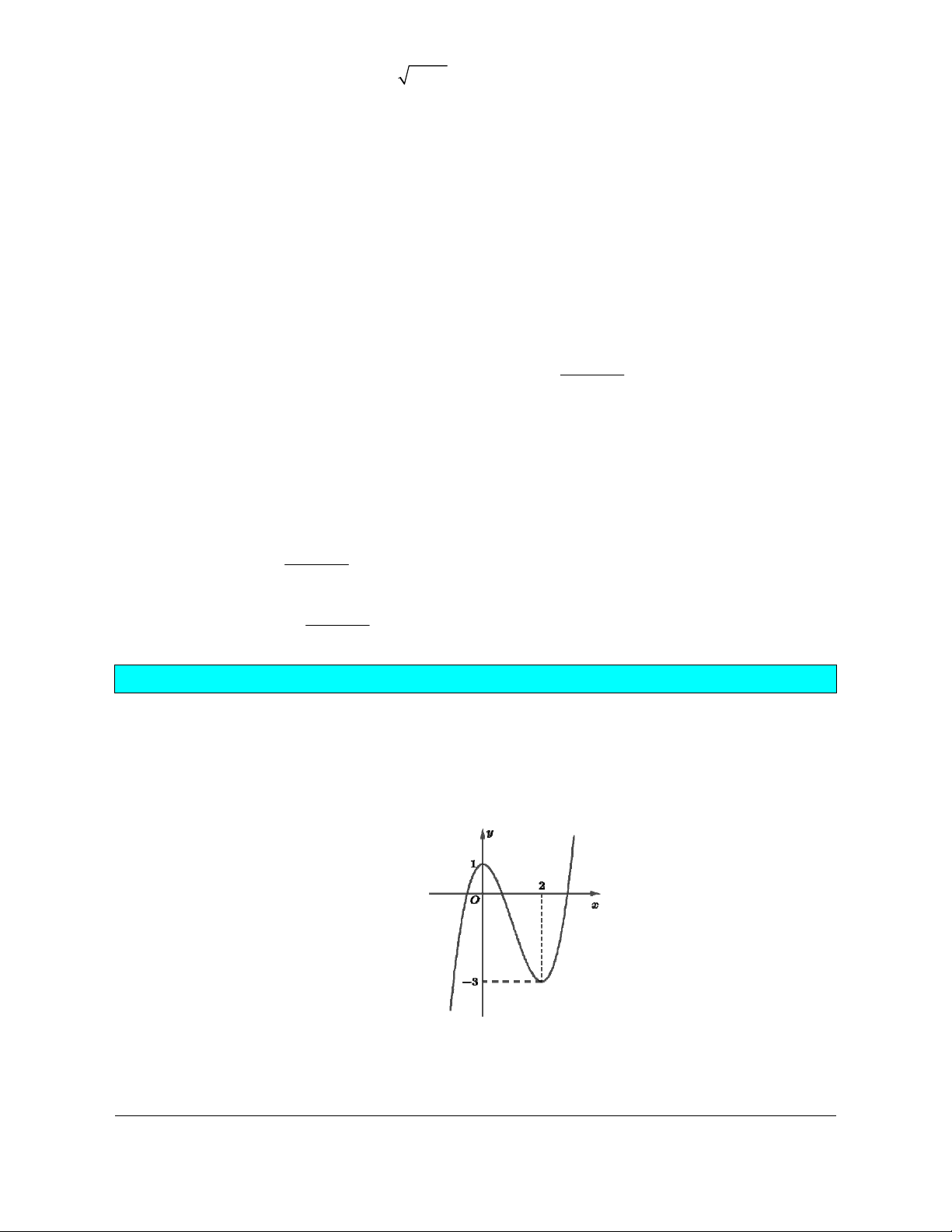
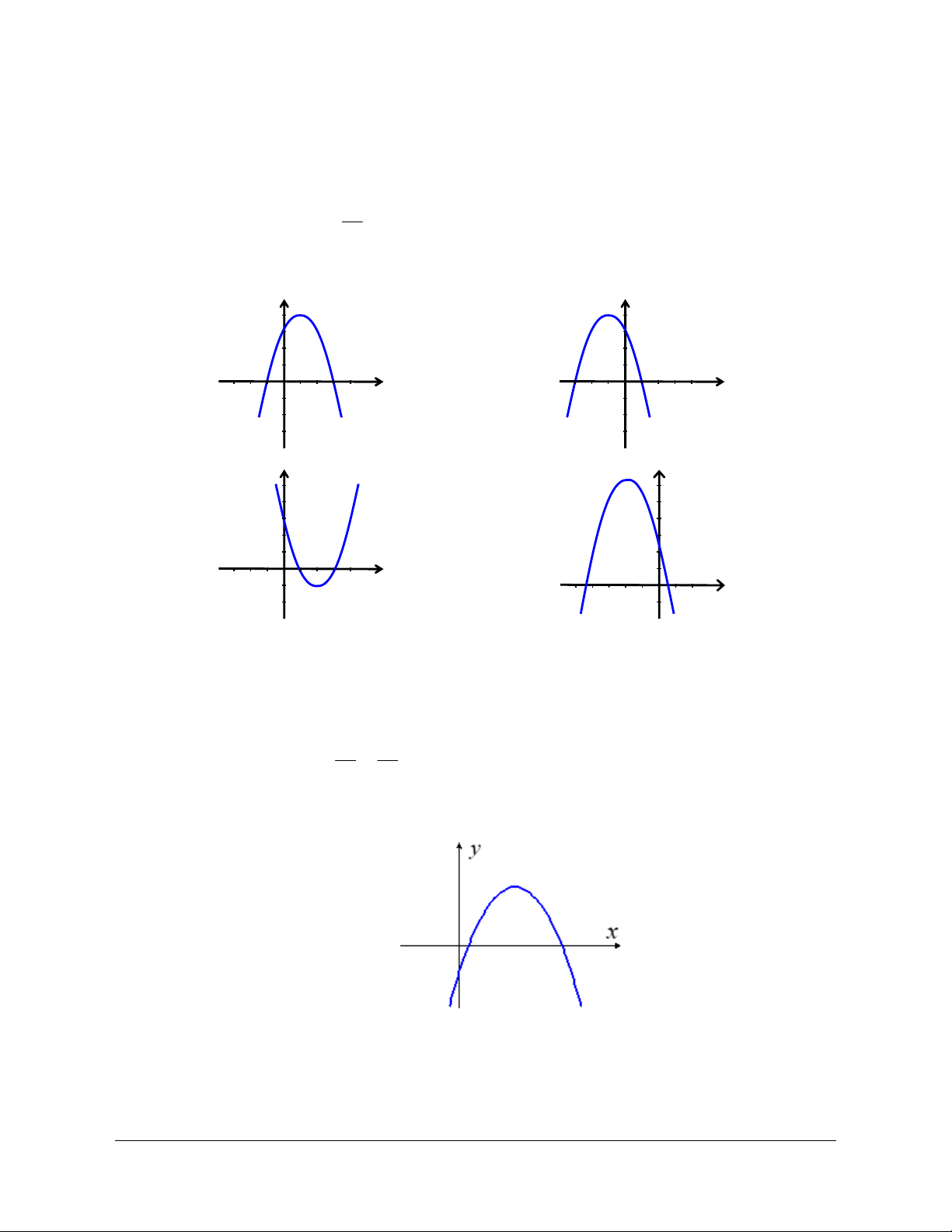
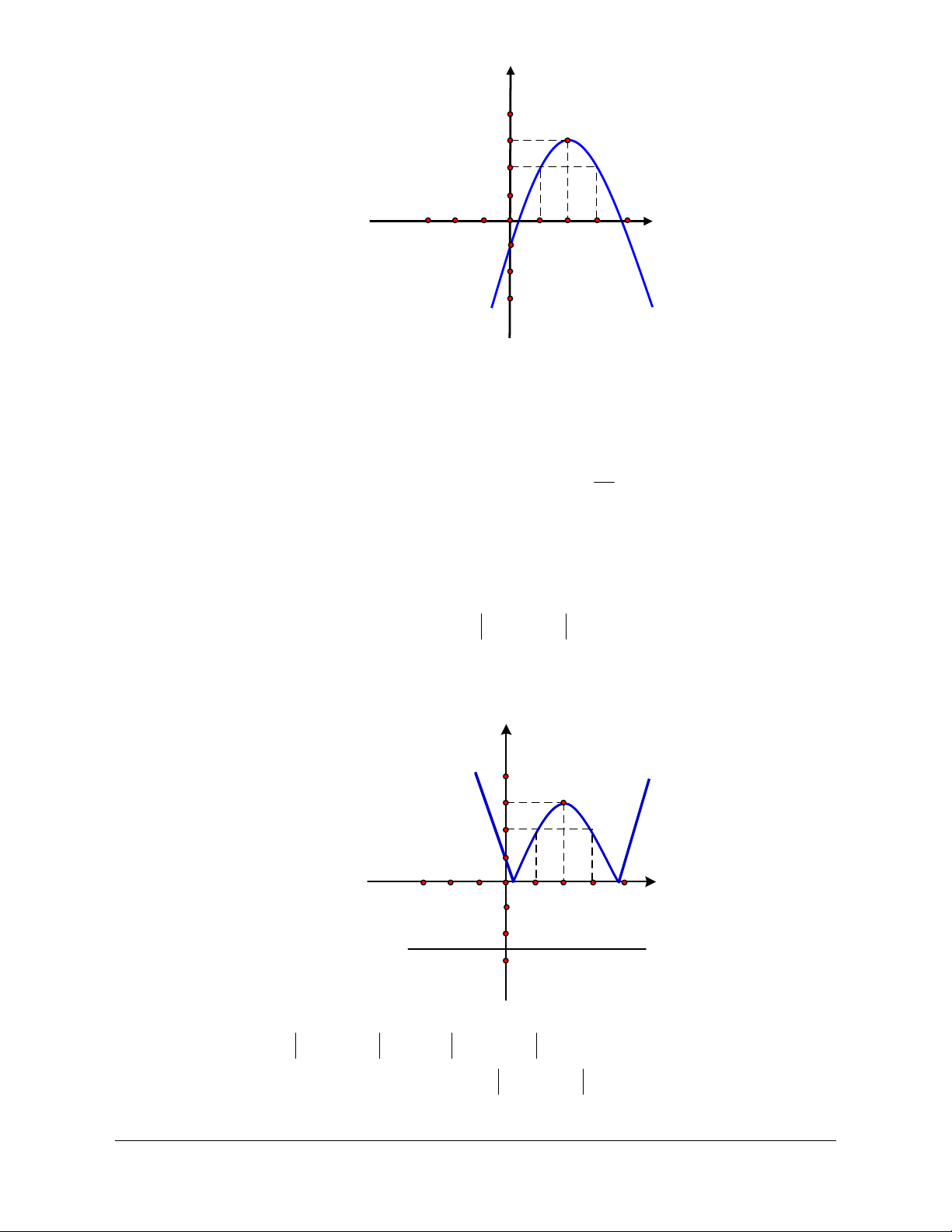
Câu 4. Cho hàm số có đồ thị như hình vẽ. Chọn đáp án sai.
A. Hàm số nghịch biến trên khoảng  ;    1 .
B. Hàm số đồng biến trên khoảng 1; .
C. Hàm số nghịch biến trên khoảng  1;   1 .
D. Hàm số đồng biến trên khoảng  1  ;0 .
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 98
Trần Đình Cư. SĐT: 0834332133 Lời giải Chọn C
Từ đồ thị hàm số ta thấy:
Hàm số nghịch biến trong các khoảng:  ;    1 và 0;  1 .
Hàm số đồng biến trong các khoảng:  1
 ;0 và 1; . Câu 5.
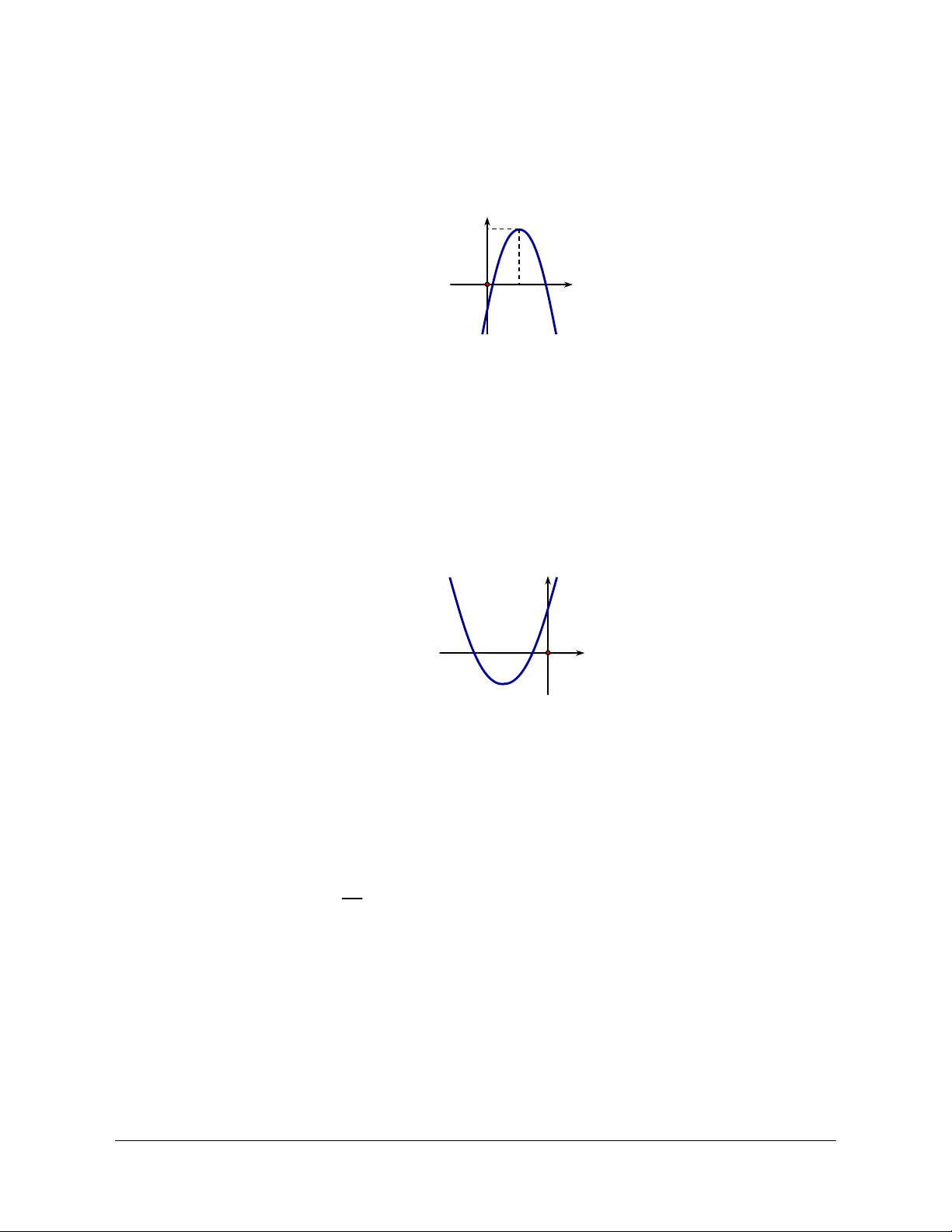
Hàm số f x có tập xác định  và có đồ thị như hình vẽ
Mệnh đề nào sau đây đúng ?
A. Đồ thị hàm số cắt trục hoành theo một dây cung có độ dài bằng 2 .
B. Hàm số đồng biến trên khoảng 0;5 .
C. Hàm số nghịch biến trên khoảng 0;3 .
D. f  2019  f  2017  . Lời giải Chọn A
Nhìn vào đồ thị hàm số ta có :
Đồ thị hàm số cắt trục hoành tại hai điểm M 1;0, N 3;0 MN  2 A đúng.
Trên khoảng 0;2 đồ thị hàm số đi xuống nên hàm số nghịch biến trên khoảng 0;2 và
trên khoảng 2;5 đồ thị hàm số đi lên nên hàm số đồng biến trên khoảng 2;5 B sai.
Trên khoảng 0;2 đồ thị hàm số đi xuống nên hàm số nghịch biến trên khoảng 0;2 và
trên khoảng 2;3 đồ thị hàm số đi lên nên hàm số đồng biến trên khoảng 2;3C sai.
Ta có : 2019, 20172;  và trên khoảng 2;  hàm số đồng biến nên  2019  2017   sai.    D f
2019   f  2017
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 99
Trần Đình Cư. SĐT: 0834332133
Dạng 5: Xét tính chẵn lẻ của hàm số 1. Phương pháp
Để xét tính chẵn lẻ của hàm số y = f(x) ta tiến hành các bước như sau:
- Tìm tập xác định D của hàm số và xét xem D có là tập đối xứng hay không.
- Nếu D là tập đối xứng thì so sánh f(–x) với f(x) (x bất kì thuộc D). +
Nếu f(–x) = f(x), x D thì f là hàm số chẵn. +
Nếu f(–x) = –f(x), x D thì f là hàm số lẻ. Chú ý:
Tập đối xứng là tập thoả mãn điều kiện: Với x D thì –x D.
Nếu x D mà f(–x) f(x) thì f là hàm số không chẵn không lẻ.
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1. Xét tính chẵn lẻ của các hàm số sau 3 x
a. f x  . 2 x 1 b.   2
f x x x .
c. f x 3
x x 1. x
d. f x  . x 1 Lời giải 3 x
+ Hàm số f x 
có TXĐ D   nên x
  D  xD và f x   f x nên 2 x 1 hàm số lẻ. + Hàm số   2
f x x x có TXĐ D   nên x
  D  xD và f x  f x nên hàm số chẵn.
+ Hàm số f x 3
x x 1có TXĐ D   nên x
  D  xD và  f
 x  f xf x 3
 x x 1 
nên hàm số không chẵn không lẻ.  f
 x   f xx
+ Hàm số f x 
có TXĐ D   \  
1 . Ta có x 1 D nhưng x  1   D nên x 1
hàm số không chẵn không lẻ.
Ví dụ 2. Xét tính chẵn lẻ của các hàm số sau
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 100
Trần Đình Cư. SĐT: 0834332133 a) 2
y  20  x , b) 4 y  7
x  2 x 1, 4 x 10 c) y  , x d)
y x  2  x  2 , 4 4
x x x x e) y x  4 Lời giải:  Xét 2
y  20  x có tập xác định D   2  5;2 5   , f x   x2 2 20
 20  x f x Nên 2
y  20  x là hàm số chẵn.  Xét 4
y  7x  2 x 1 có tập xác định D   , f x   x4 7
 2 x 1  f x Nên 4 y  7
x  2 x 1 là hàm số chẵn. 4 4 x 10 x 10  Xét y
có tập xác định D   \  
0 , f x   
  f x . xx 4 x 10 Nên y  là hàm số lẻ. x
 Xét y x  2  x  2 có tập xác định D   , f x  x  2  x  2  f x .
Nên y x  2  x  2 là hàm số chẵn. 4 4
x x x x  Xét y
có tập xác định D   ;   
1 1;    0 . x  4 4 4 4 4      
x x  x  x x x x x f x
f x nên y  là hàm số x  4 x  4 chẵn.
2016  9x  2016  9x
Ví dụ 3. Cho hàm số y
. Tính giá trị của biểu thức: x
S f 22  0  f  2   21  f 22  2  f  2   23  f  22  0 f 2  21  f  22  2 f 2  23  f 22  4 Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 101
Trần Đình Cư. SĐT: 0834332133  2016 2016
Tập xác định D  ; \   0  . 9 9    x
  D , ta có x D và
2016  9x  2016  9x
2016  9x  2016  9x f (x)   
  f x . x x Do
đó f x là hàm số lẻ, và f x  f (x)  0 .
S f 220  f  
221  f 222  f  223   f  220   f   221  f  222 
 f 223  f 224
f 220  f  220    f   221  f  
221  f 222  f  222   f  223 
 f 223  f 224  f   3 7 224  . 28
Ví dụ 4. Tìm điều kiện của m để hàm số 4
y x mm   3 2 2
1 x x mx m là hàm số chẵn. Lời giải Hàm 4
y x mm   3 2 2
1 x x mx m có tập xác định là R nên hàm số chẵn khi:
mm   1  0   m  0 . m  0 Vậy m  0 .
Ví dụ 5: Tìm m thì hàm số f x 3  x   2 m   2
1 x  2x m 1 là hàm số lẻ. Lời giải
Hàm số có tập xác định là D   do đó x D  x D .
Theo đề bài, ta có f x   f x , x D nghĩa là 3 x   2 m   2 3
x x m   x   2 m   2 1 2 1
1 x  2x m 1 , x D . Điều này xảy ra khi  2 2
m 1  m 1  m 1
m 1  m  . 1
3. Bài tập trắc nghiệm Câu 1.
Cho hàm số y f x xác định trên tập D . Mệnh đề nào sau đây đúng?
A. Nếu f x không là hàm số lẻ thì f x là hàm số chẵn.
B. Nếu f x   f x , x
  D thì f x là hàm số lẻ.
C. Đồ thị hàm số lẻ nhận trục tung làm trục đối xứng.
D. Nếu f x là hàm số lẻ thì f x   f x , x   D . Lời giải Chọn D.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 102
Trần Đình Cư. SĐT: 0834332133
A sai vì có những hàm số không chẵn, không lẻ.
B sai vì f x  0 thì f x   f x nhưng f x cũng là hàm số chẵn.
C sai vì đồ thị hàm số lẻ nhận gốc tọa độ làm tâm đối xứng. Câu 2.
Cho đồ thị hàm số y f x như hình vẽ. Kết luận nào trong các kết luận sau là đúng?
A. Đồng biến trên  . B. Hàm số chẵn. C. Hàm số lẻ.
D. Cả ba đáp án đếu sai Lời giải Chọn B
Đồ thị hàm số đối xứng qua trục Oy nên hàm số đã cho là hàm số chẵn. Câu 3. Hàm số 4 2
y x x  3 là
A. hàm số vừa chẵn, vừa lẻ.
B. hàm số không chẵn, không lẻ. C. hàm số lẻ. D. hàm số chẵn. Lời giải Chọn D
Đặt f x 4 2
x x  3.
Tập xác định D   . Ta có x
   x  .
f x  x4  x2  3 4 2
x x  3  f x.
Vậy hàm số đã cho là hàm số chẵn.
Câu 4: Hàm số nào sau đây là hàm số lẻ?
A. g x  x . B.   2
k x x x . C.   1 h x x  .
D. f x 2  x 1  2 . x Lời giải Chọn C
Câu 5: Cho hàm số y f x 4 2
 3x  4x  3 . Trong các mệnh đề sau, mệnh đề nào đúng?
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 103
Trần Đình Cư. SĐT: 0834332133
A. y f x là hàm số chẵn.
B. y f x là hàm số lẻ.
C. y f x là hàm số không có tính chẵn lẻ. D. y f x là hàm số vừa chẵn vừa lẻ. Lời giải Chọn A
Tập xác định D   .  x
  D  x D  Ta có   f
 x  x4 x2 4 2 3 – 4
 3  3x – 4x  3  f x, x   D
Do đó hàm số y f x là hàm số chẵn.
Câu 6: Trong các hàm số sau, hàm số nào không phải là hàm số lẻ: 1 A. 3
y x x . B. 3 y x 1. C. 3
y x x . D. y x Lời giải Chọn B
Hàm số lẻ phải triệt tiêu số hạng tự do Câu 7.
Trong các hàm số sau, hàm số nào là hàm số chẵn? 1 x A. 2 y x  . B. y  . x 4 2 x  2x 1 1 C. y  .
D. y   x  2018   x  2018 2 1 2 1 . 3 4x Lời giải Chọn D
Đặt y f x   x  2018   x  2018 2 1 2 1 .
Tập xác định của hàm số y f x là D   . Ta có x
   x  .  .
Lại có: f x   x  2018   x  2018   x  2018   x  2018 2 1 2 1 2 1 2 1  f x .
Vậy hàm số y f x là số chẵn.
Câu 8: Hàm số nào dưới đây là hàm số lẻ?
A. y x  4  x  4 .
B. y  3  x  3  x .
C. y x . D. 2
y x 5x 1.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 104
Trần Đình Cư. SĐT: 0834332133 Lời giải Chọn A
Xét hàm số y f x  x  4  x  4 + TXĐ: D   Ta có x
  D  x D .
+ f x  x  4  x  4   x  4  x  4    f x với x D
Vậy hàm số y f x  x  4  x  4 là hàm số lẻ. Câu 9.
Cho hàm số y f x  x  2018  x  2018 . Mệnh đề nào sau đây sai?
A. Hàm số y f x có tập xác định là R .
B. Đồ thị hàm số y f x nhận trục tung làm trục đối xứng.
C. Hàm số y f x là hàm số chẵn.
D. Đồ thị hàm số y f x nhận gốc tọa độ O làm tâm đối xứng. Lời giải Chọn D
Tập xác định của hàm số là  , x
  thì x ta có:
f x  x  2018  x  2018  x  2018  x  2018  f x
Hàm số đã cho là hàm số chẵn, đồ thị nhận Oy làm trục đối xứng. Do vậy các phương án ,
A B,C đều đúng. Đáp án D sai.
Câu 10. Trong các hàm số dưới đây, hàm số nào là hàm số chẵn? A. 3
y = x -2x . B. 4 2
y = 3x + x + 5 . C.
y = x +1 . D. 2
y = 2x + x . Lời giải Chọn B Ta thấy hàm số 4 2
y = 3x + x + 5 có tập xác định D =  ,
f (-x) = (-x)4 +(-x)2 4 2 3
+ 5 = 3x + x + 5 = f (x). Vậy hàm số 4 2
y = 3x + x + 5 là hàm số chẵn.
Câu 11. Cho đồ thị hàm số y f x như hình vẽ
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 105
Trần Đình Cư. SĐT: 0834332133
Kết luận nào trong các kết luận sau là đúng: A. Hàm số lẻ.
B. Hàm số vừa chẵn vừa lẻ.
C. Đồng biến trên  . D. Hàm số chẵn. Lời giải Chọn D.
Hàm số xác định với mọi x   và đối xứng nhau qua trục tung nên hàm số đã cho là hàm số chẵn. Câu 12.
Đồ thị hàm số nào sau đây có tâm đối xứng? A. 3
y x x . B. 2
y x . C. 4 2
y x  3x 1 . D.
y x . Lời giải Chọn A + Ba hàm số: 2 y x ; 4 2
y x  3x 1; y x đều là hàm số chẵn trên  nên đồ thị của
chúng nhận trục Oy làm trục đối xứng, đồ thị không có tâm đối xứng. + Hàm số: 3
y x x có: 3
 f (x)  x x
f (x)   f (x)  3
y x x là hàm số lẻ trên  . 3 3
 f (x)  (x)  (x)  (x x) Nên đồ thị hàm số 3
y x x nhận gốc toạ độ O làm tâm đối xứng.
Câu 13. Cho hàm số f x 2
x x  3; g x  x  3  x  3 . Khẳng định nào sau đây là đúng?
A. f x là hàm chẵn; g x là hàm lẻ.
B. Cả f và g x là hàm chẵn.
C. Cả f x và g x là hàm lẻ
D. f x là hàm lẻ; g x là hàm chẵn. Lời giải Chọn D Xét f x 2
x x  3 có TXĐ: D   Ta thấy x
   thì x   và f x  x x2 2
 3  x x  3   f x
Vậy nên f x là hàm lẻ.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 106
Trần Đình Cư. SĐT: 0834332133
Xét g x  x  3  x  3 có TXĐ: D   . Ta thấy x
   thì x   và
g x  x  3  x  3   x  3   x  3  x  3  x  3  g x
Vậy nên g x là hàm chẵn.
Câu 14: Trong các hàm số sau, hàm số nào là hàm chẵn?
A. y  2  x  2  x .
B. y x  2  x  2 .
C. y x  2  x  2 . D. 4
y x x 1. Lời giải Chọn A
 Hàm số y  2  x  2  x có tập xác định là D   2;  2. Suy ra: x
  D thì x D .
Ta có : f x  2  x  2  x  2  x  2  x f (x) .
Vậy hàm số y  2  x  2  x là hàm số chẵn.
 Hàm số y x  2  x  2 có tập xác định là D  2;  .
Ta có: 2  D nhưng 2
  D nên hàm số trên không là hàm số chẵn cũng không là hàm số lẻ.
 Hàm số y x  2  x  2 có tập xác định là D   . Suy ra: x
  D thì x D .
Ta có : f x  x  2  x  2  x  2  x  2   f x .
Vậy hàm số y x  2  x  2 là hàm số lẻ.  Hàm số 4
y x x 1 có tập xác định là D   . Suy ra: x
  D thì x D . Ta có: f  
1  3 và f   1  1. Do f   1  f   1 và f   1   f   1 nên hàm số trên
không là hàm số chẵn cũng không là hàm số lẻ.
Câu 15: Trong các hàm số sau, hàm số nào là hàm số lẻ?
A. y  2x . B. 3 2
y x x . C. 3 y x 1.
D. y x 1. Lời giải Chọn A
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 107
Trần Đình Cư. SĐT: 0834332133
 Hàm số y  2x có tập xác định là D   . Ta có: x
   x  . Với x
   f x  2
x   f x
Do đó hàm số y  2x là hàm số lẻ.  Hàm số 3 2
y x x và 3
y x 1 không là hàm số chẵn cũng không là hàm số lẻ.
 Hàm số y x 1 là hàm số chẵn.
Câu 16. Cho hàm số f x  x  2  x  2 và g x 3
x  5x . Khi đó:
A. f x và g x đều là hàm số lẻ.
B. f x và g x đều là hàm số chẵn.
C. f x lẻ, g x chẵn.
D. f x chẵn, g x lẻ. Lời giải Chọn D.
Ta có D   khi đó x
  D  xD
f x  x  2  x  2  x  2  x  2  f x  f x là hàm số chẵn g x 3
 x x   3 5
x  5x   f x  f x là hàm số lẻ
Câu 17. Nêu tính chẵn, lẻ của hai hàm số f x  x  2  x  2 , g x   x ?
A. f x là hàm số chẵn, g x là hàm số chẵn.
B. f x là hàm số lẻ, g x là hàm số chẵn.
C. f x là hàm số lẻ, g x là hàm số lẻ.
D. f x là hàm số chẵn, g x là hàm số lẻ. Lời giải Chọn B
Xét f x có TXĐ: D   .
x D  x D .
f x  x  2  x  2   x  2  x  2    f x.
Nên f x là hàm số lẻ.
Xét g x có TXĐ: D   .
x D  x D .
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 108
Trần Đình Cư. SĐT: 0834332133
g x   x   x g x .
Nên g x là hàm số chẵn.
Câu 18: Cho hai hàm số f x  x  2  x  2 , g x   x . Trong các mệnh đề sau, mệnh đề nào đúng?
A. f x là hàm số chẵn, g x là hàm số chẵn.
B. f x là hàm số lẻ, g x là hàm số chẵn.
C. f x là hàm số lẻ, g x là hàm số lẻ.
D. f x là hàm số chẵn, g x là hàm số lẻ. Lời giải Chọn B
Xét f x có TXĐ. D   .
x D  x D .
f x  x  2  x  2   x  2  x  2    f x .
Nên f x là hàm số lẻ.
Xét g x có TXĐ. D   .
x D  x D .
g x   x   x g x .
Nên g x là hàm số chẵn.
Câu 19: Cho hai hàm số f x đồng biến và g x nghịch biến trên khoảng a;b . Có thể kết luận
gì về chiều biến thiên của hàm số y f x  g x trên khoảng a;b ? A. đồng biến. B. nghịch biến. C. không đổi.
D. không kết luận được Lời giải Chọn D
Lây hàm số f x  x và g x  x trên 0;  1 thỏa mãn giả thiết
Ta có y f x  g x  x x  0 
 không kết luận được tính đơn điệu.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 109
Trần Đình Cư. SĐT: 0834332133 x   x
Câu 20: Cho hai hàm số f x 1 1  và g x 3
x  4 x . Mệnh đề nào dưới đây x đúng?
A. f x là hàm số chẵn và g x là hàm số lẻ.
B. f x và g x là hàm số chẵn.
C. f x và g x là hàm số lẻ.
D. f x là hàm số lẻ và g x là hàm số chẵn. Lời giải Chọn Dx   x
Xét hàm số f x 1 1  có x
Tập xác định: D   1  ;  1 \  0 .
1 x  1 x
Ta có: x D  x D và f x 
  f x . Vậy nên;hàm số x  
1 x  1 x f x  là hàm số lẻ. x Xét hàm số có
Tập xác định: D   .
Ta có: x D  x D và g x  x3 3
 4 x x  4 x g x . Vậy nên;hàm số g x 3
x  4 x là hàm số chẵn.
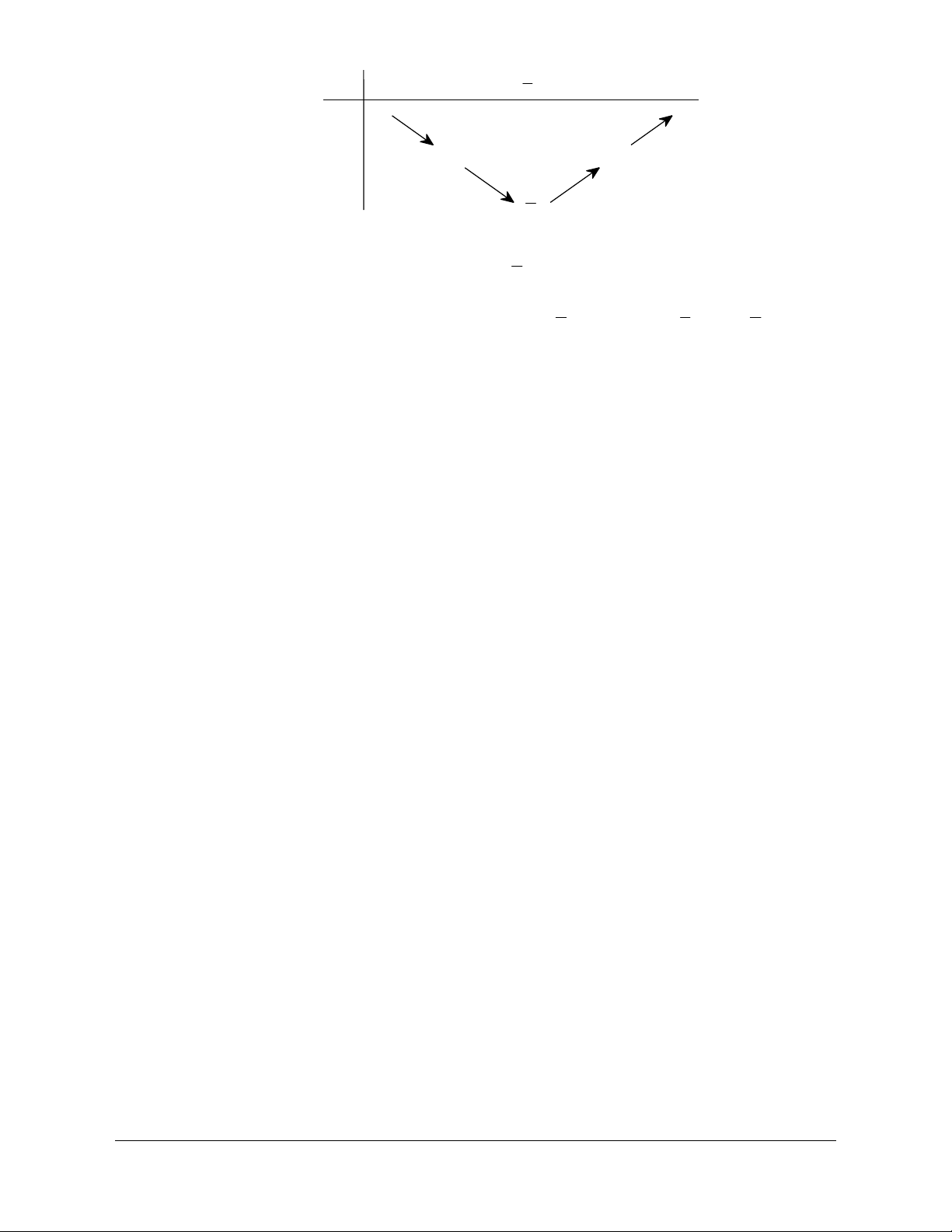
Câu 21. Cho hàm số y f x có tập xác định là  5; 
5 và đồ thị của nó được biểu diễn bởi hình dưới đây.
Trong các khẳng định sau, khẳng định nào là sai?
A. Hàm số nghịch biến trên khoảng  2;  2 .
B. Đồ thị cắt trục hoành tại 3 điểm phân biệt.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 110
Trần Đình Cư. SĐT: 0834332133
C. Hàm số đồng biến trên khoảng  5;  2   và 2;5 . D. Hàm số chẵn. Lời giải Chọn D
Đồ thị hàm số chẵn nhận Oy làm trục đối xứng.
Câu 22. Chọn khẳng định sai trong các khẳng định sau: A. Hàm số 2
y x  2x  2 xác định trên  . B. Hàm số 3
y x là hàm số lẻ.
C. Hàm số y   x  2
1 là hàm số chẵn. D. Hàm số 2
y x 1 là hàm số chẵn. Lời giải Chọn C
Xét hàm số y f x   x  2
1 có tập xác định  .  x
    x    Ta có 
f x không là hàm số chẵn. 2    f
 x  x   1  f xCâu 23. Cho hàm số 4
y x 1 có đồ thị C . Khẳng định nào sau đây đúng?
A. C nhận gốc tọa độ O làm tâm đối xứng.
B. C qua A0;2 .
C. C tiếp xúc Ox .
D. C nhận trục tung làm trục đối xứng. Lời giải Chọn D
Cy f x 4 :
x 1, TXĐ: D   . + x
  D  xD . + f x 4
x 1  f x, x   .
Nên y f x là hàm số chẵn, nên C nhận trục tung làm trục đối xứng.
Câu 24: Cho các khẳng định:
I . Hàm số 4 2
y x 12x  5 là hàm số chẵn.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 111
Trần Đình Cư. SĐT: 0834332133 x  2
II . Hàm số y  là hàm số lẻ. x 1
III . Hàm số y  20 x  20  x là hàm số chẵn.
IV . Hàm số y x 20  x  20 là hàm số lẻ.
Số khẳng định đúng trong các khẳng định trên là bao nhiêu? A. 2 . B. 4 . C. 1. D. 3 . Lời giải Chọn D 4 2
Xét hàm số y f (x)  x 12x  5 .
Tập xác định D   .
Với mọi x    x   và 4 2 4 2
f (x)  (x) 12(x)  5  x 12x  5  f (x) . Do đó 4 2
y f (x)  x 12x  5 là hàm số chẵn. Vậy đúng.   x 2
Xét hàm số y f (x)  . x 1
Tập xác định D   \  1 . Tồn tại 1
  D mà 1 D . x  2
Do đó y f (x) 
không là hàm số chẵn cũng không là hàm số lẻ. Vậy sai. x 1
 Xét hàm số y f (x)  20  x  20  x .
Tập xác định D   20  ;20 .
Với mọi x D  x D và
f (x)  20  (x)  20  (x)  20  x  20  x f (x) .
Do đó y f (x)  20  x  20  x là hàm số chẵn. Vậy đúng.
 Xét hàm số y f (x)  x  20  x  20 .
Tập xác định D   .
Với mọi x    x   và
f (x)  (x)  20  (x)  20  x  20  x  20    x  20  x  20    f (x)
Do đó y f (x)  x  20  x  20 là hàm số lẻ. Vậy đúng.
Câu 25. Hàm số f x có tập xác định  và có đồ thị như hình vẽ
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 112
Trần Đình Cư. SĐT: 0834332133
Tnh giá trị biểu thức f  2018  f  2018 A. 2018 . B. 0 . C. 2018 . D. 4036 . Lời giải Chọn B
Dựa vào hình dáng của đồ thị ta thấy rằng hàm số đối xứng qua O(0;0) nên là hàm số lẻ.
Suy ra f x   f x  f x  f x  0
Vì vậy f  2018  f  2018  0 .
Câu 26. Hàm số f x có tập xác định  và có đồ thị như hình vẽ
Mệnh đề nào sau đây sai ? A. f   1  f   1 1 . B.
Đồ thị hàm số có tâm đối xứng.
C. Hàm số đồng biến trên khoảng 1;5 . D. Hàm số nghịch biến trên khoảng  6;    1 . Lời giải Chọn B
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 113
Trần Đình Cư. SĐT: 0834332133 Nhìn đồ thị ta có : f   1  f   1 1 A đúng.
Đồ thị không có tâm đối xứng nên B sai.
Trên khoảng 1;5 đồ thị hàm số đi lên nên hàm số đồng biến trên khoảng 1;5 C đúng. Trên khoảng  6;   
1 đồ thị hàm số đi xuống nên hàm số nghịch biến trên khoảng  6;    1  D đúng. 3
x  6 khi x  2  
Câu 27. Cho hàm số f x   x
khi  2  x  2. Khẳng định nào sau đây đúng?  3
x  6 khi x  2
A. Đồ thị hàm số f x đối xứng nhau qua gốc tọa độ.
B. Đồ thị của hàm số f x đối xứng qua trục hoành.
C. f x là hàm số lẻ.
D. f x là hàm số chẵn Lời giải Chọn D
Hàm số có tập xác định D  .  Với x  2;
 2 ta có f x  x x f x Với x  ;  2
   x2;; f x  x3 3
 6  x  6  f x và ngược lại
Do đó hàm số đã cho là hàm số chẵn.
Câu 28. Cho hàm số f x   2
m m   2017 2 3 4 x
m  7 . Gọi S là tập hợp tất cả các giá trị của
tham số m để hàm số f là hàm số lẻ trên  . Tính tổng các phần tử của S . A. 0 . B. 3 . C. 7 . D. 2 7 . Lời giải Chọn A
Tập xác định: D   . Suy ra: x D thì x D .
Ta có: f x   2
m m   2017 2 3 4 xm  7 .
Để f là hàm số lẻ thì x D , f x   f x .
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 114
Trần Đình Cư. SĐT: 0834332133   2
m m   2017 2 xm    2
m m   2017 2 3 4 7 3 4 xm  7 2
m  7  m   7 . Vậy tổng các phần tử của S là 7   7  0.
Câu 29. Tìm tất cả các giá trị của tham số m để hàm số 3
y x   2 m   2 2 2
4 x  4  mx 3m 6 là một hàm số lẻ A. m  2  .
B. m  2 . C. m  4  . D. m  2  . Lời giải Chọn B
y f x 3  x   2 m   2 2 2
4 x  4  mx 3m 6. TXĐ: D   Có x
   x 
Hàm số y f x là hàm số lẻ  f x   f x, x   3   x   2 m   2
x    m 3
x m     x   2 m   2 2 2 4 4 3 6 2 2
4 x  4  mx 3m 6, x        2 m   2 2
4 x  3m 6  0, x    2
m 2018  x  (m  2) 2018  x
Câu 30. Cho hàm số y f x 
có đồ thị là (C ) ( m là tham 2 (m 1)x m
số). Số giá trị của m để đồ th ị (C ) nhận trục Oy làm trục đối xứng là m A. 0. B. 1. C. 2. D. 3. Lời giải Chọn B m  1 ĐK : 2 m 1  0   . m  1 
Vì đồ th ị (C ) nhận trục Oy làm trục đối xứng nên hàm số f x là hàm số chẵn, suy ra m
f x  f x .
m 2018  x  (m  2) 2018  x  2 2
2  m  2018  x m 2018  x
Ta có : f x   . 2
(m 1)x  2 m   1 x 2
2  m mm  1 Đồng nhất, ta được : 2 
m m  2  0   . 2
m  2  mm  2
Kết hợp điều kiện, suy ra m  2  thỏa mãn.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 115
Trần Đình Cư. SĐT: 0834332133
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 116
Trần Đình Cư. SĐT: 0834332133
BÀI 2. HÀM SỐ BẬC NHẤT
A. KIẾN THỨC CẦN NẮM
I. Ôn tập về hàm số bậc nhất
Hàm số bậc nhất y = ax + b
 Tập xác định: D = R.  Sự biến thiên:
- Khi a > 0, hàm số đồng biến trên R.
- Khi a < 0, hàm số nghịch biến trên R.
 Đồ thị là đường thẳng có hệ số góc bằng a, cắt trục tung tại điểm B.
Chú ý: Cho hai đường thẳng : y = ax + b và : y = ax + b
song song với a = a và b b.
trùng với a = a và b = b.
cắt a a.
II. Hàm số hằng y b
Đồ thị của hàm số y b là một đường thẳng song song hoặc trùng với trục hoành và cắt trục tung
tại điểm 0;b . Đường thẳng này gọi là đường thẳng y b
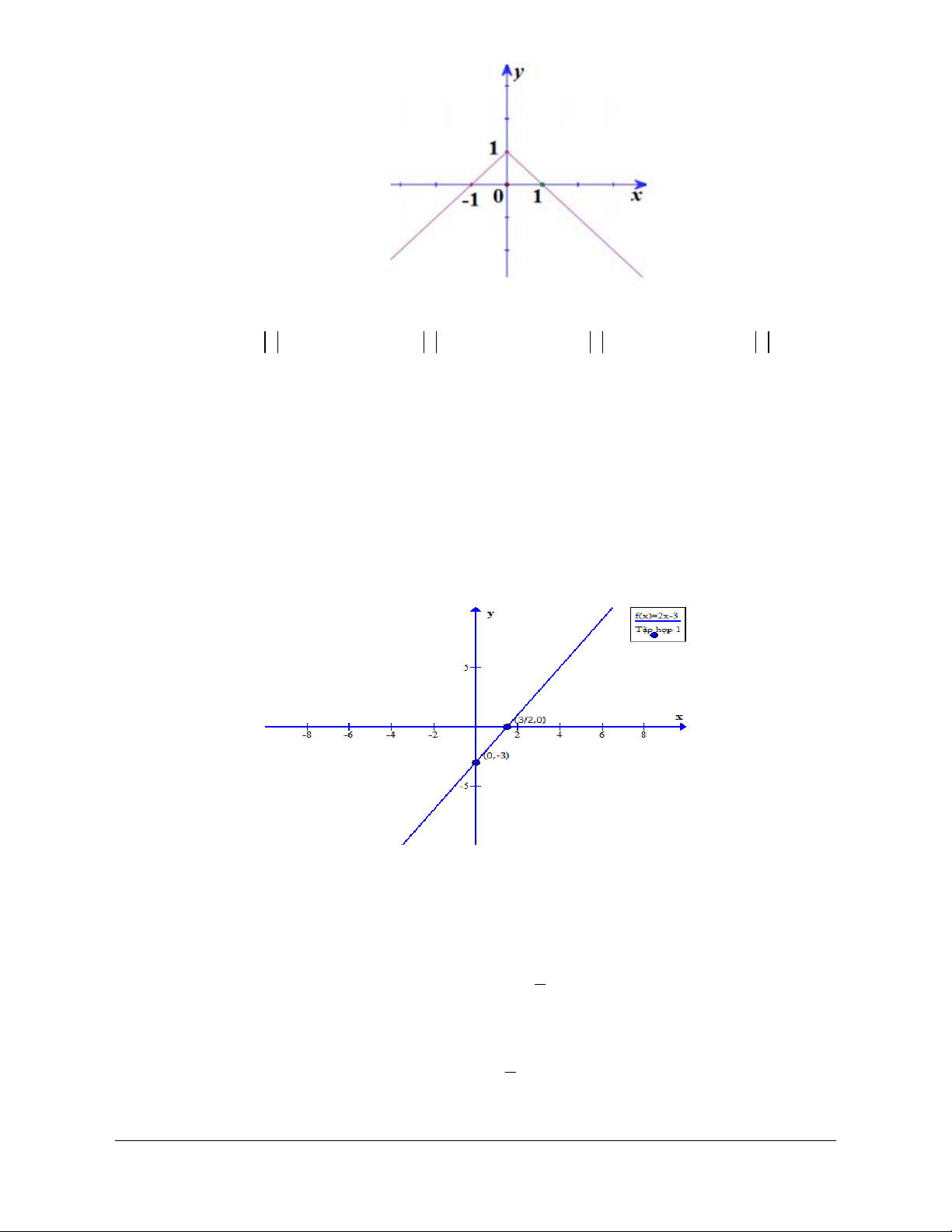
III. Hàm số y x
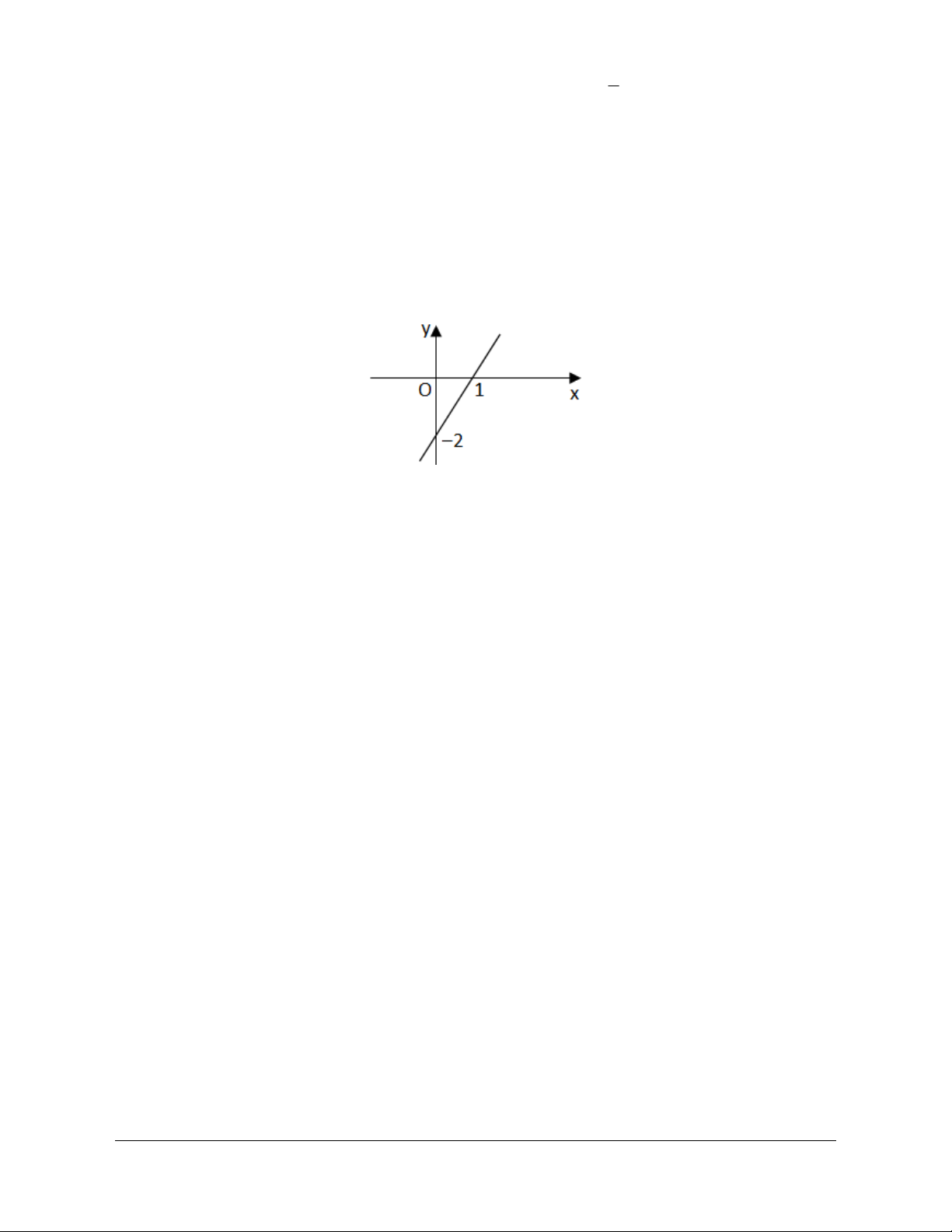
1. TXĐ: D  
2. Chiều biến thiên x khi x y x  0  x khi x  0 3. Đồ thị
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1: Xét tính đồng biến, nghịch biến của hàm số 1. Phương pháp
Cho hàm số y ax b, a  0
- Khi a > 0, hàm số đồng biến trên R.
- Khi a < 0, hàm số nghịch biến trên R.
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1. Tìm các giá trị của tham số m để hàm số y  2m  3 x m  3 nghịch biến trên  Hướng dẫn giải
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 117
Trần Đình Cư. SĐT: 0834332133
Hàm số y  2m  3 x m  3 có dạng hàm số bậc nhất. 3
Để hàm số nghịch biến trên   2m  3  0  m   . 2
Ví dụ 2. Tìm các giá trị của tham số để y  m  
1 x  2  m đồng biến trên khoảng  ;   Hướng dẫn giải
Hàm số y  m  
1 x  2  m có dạng hàm số bậc nhất.
Để hàm số đồng biến trên   m 1  0  m 1.
3. Bài tập trắc nghiệm Câu 1.
Khẳng định nào về hàm số y  3x  5 là sai:  5 
A. Hàm số đồng biến trên  .
B. Đồ thị cắt Ox tại  ;0   .  3 
C. Đồ thị cắt Oy tại 0;5.
D. Hàm số nghịch biến trên  . Hướng dẫn giải Chọn D.
Hàm số y  3x  5 có hệ số a  3  0 nên đồng biến trên  , suy ra đáp án D sai. Câu 2.
Tìm m để hàm số y  3 mx  2 nghịch biến trên  . A. m  0 . B. m  3 . C. m  3 . D. m  3 . Hướng dẫn giải Chọn C.
Hàm số y  3 mx  2 có dạng hàm số bậc nhất.
Để hàm số nghịch biến trên  thì 3  m  0  m  3 . Câu 3.
Tìm m để hàm số y   2  m  
1 x m  3 đồng biến trên  . 1 1 A. m  . B. m  . C. m  3 . D. m  3 . 2 2 Hướng dẫn giải Chọn A. Khi 2  m 1  1 0  m  5
y    0 nên nghịch biến trên  2 2
Vậy hàm số y   2  m  
1 x m  3 đồng biến trên  khi và chỉ khi 1 2
m 1  0  m  . 2
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 118
Trần Đình Cư. SĐT: 0834332133 Câu 4.
Cho hàm số f x  m  2 x 1. Với giá trị nào của m thì hàm số đồng biến trên  ?; nghịch biến trên  ?
A. Với m  2 thì hàm số đồng biến trên  ; m  2 thì hàm số nghịch biến trên  . B. Với 2
m  thì hàm số đồng biến trên  ; 2
m  thì hàm số nghịch biến trên  . C. Với 2
m  thì hàm số đồng biến trên  ; 2
m  thì hàm số nghịch biến trên  .
D. Với m  2 thì hàm số đồng biến trên  ; m  2 thì hàm số nghịch biến trên  . Hướng dẫn giải Chọn D.
Hàm số f x  m  2 x 1 đồng biến khi m  2  0  m  2 .
Hàm số f x  m  2 x 1 nghịch biến khi m  2  0  m  2 . Câu 5.
Cho hàm số f x   7  mx  3. Có bao nhiêu số tự nhiên m để f x đồng biến trên  ? A. 2 . B. 4 . C. 3. D. vô số. Hướng dẫn giải Chọn C.
Để hàm số f (x)   7  mx  3 đồng biến trên   7  m  0  m  7 Vậy m0;1; 
2 thỏa mãn m  7 để hàm số f (x)   7  mx  3 đồng biến trên  .
Dạng 2: Đồ thị hàm số bậc nhất 1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
3. Bài tập trắc nghiệm Câu 1.
Hệ số góc của đồ thị hàm số y  2018x  2019 bằng 2019 2018 A.  . B. 2018 . C. 20  19 . D.  . 2018 2019 Hướng dẫn giải Chọn B. 2 1 Câu 2.
Đồ thị của hàm số y x  là 3 3
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 119
Trần Đình Cư. SĐT: 0834332133 y yd  1 3 1 O x 1 3 2 O 1  xd A. . B. . yd yd  1 1 3 3 O x 1  2 1  O x 2 C. . D. . Hướng dẫn giải Chọn C.
Từ giả thiết hàm số đồng biến nên loại đáp án A và B. 2 1 1
Mặt khác cho x  0 vào y x   nên loại đáp án D. 3 3 3 Câu 3.
Hàm số y  2x 1 có đồ thị là hình nào trong các hình sau? y y y y x x x x O 1 O 1 O 1 O 1 -1 -1 -1 -1 Hình 1 Hình 2 Hình 3 Hình 4 A. Hình 2 B. Hình 4. C. Hình 3. D. Hình 1. Hướng dẫn giải Chọn D.  1 
Đồ thị hàm số y  2x 1 đi qua hai điểm có tọa độ 0;  1  và ;0   .  2 
Do đó chỉ có hình 1 thỏa mãn. Câu 4.
Hàm số nào cho dưới đây có đồ thị như hình vẽ bên:
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 120
Trần Đình Cư. SĐT: 0834332133
A. y  2x  2 .
B. y x  2 .
C. y  x  2 .
D. y  2x  2 . Lời giải Chọn A.
Đồ thị hàm số cắt Ox và Oy lần lượt tạ A1;0 và B0;b . x Câu 5.
Đồ thị của hàm số y    2 là hình nào? 2 A. B. C. D. Lời giải Chọn C x
Đồ thị hàm số y    2 đi qua A0;2, B4;0 . Quan sát đồ thị ta được đáp án C thỏa 2 yêu cầu.
Câu 6. Hình vẽ bên là đồ thị của hàm số nào sau đây?
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 121
Trần Đình Cư. SĐT: 0834332133 1 A. y  2  x  2 .
B. y  2x  2 . C. y  2x 1. D. y   x 1. 2 Lời giải Chọn B
Đồ thị hàm số là đường thẳng đi qua 2 điểm A 1;
 0, B0;2 . Hàm số có dạng
0  a ba  2
y ax b ta được:   
y  2x  2 . 2  . a 0  b b   2 Câu 7
Hình vẽ sau đây là đồ thị của hàm số nào? .
A. y = x – 2 .
B. y = –x – 2 .
C. y = –2x – 2 .
D. y = 2x – 2 . Lời giải Chọn D
Giả sử hàm số cần tìm có dạng: y = ax + b (a ¹ 0) . ìï-2 = b a ìï = 2
Đồ thị hàm số đi qua hai điểm (0;- ) 2 , (1; ) 0 nên ta có: ï ï í  í . 0 ï = a + b b ï = -2 ïî ïî
Vậy hàm số cần tìm là y = 2x – 2 .
Câu 8: Điểm nào sau đây không thuộc đồ thị hàm số y  3x 1?
A. M 2;6 .
B. N 1;4. C. P 0;  1 .
D. Q 1;2 . Lời giải Chọn A
Ta có 3.2 1  7  6 , do đó M 2;6 không thuộc đồ thị hàm số y  3x 1.
Câu 9: Đường thẳng trong hình bên là đồ thị của một hàm số nào?
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 122
Trần Đình Cư. SĐT: 0834332133 A. y  5  x  3. B.
y x  3 . C.
y  3 3x . D.
y  3 2x . Lời giải Chọn D 3
  0.x b  a  2
Gọi y ax b . Dựa vào đồ thị có  3   . 0  a b  b  3  2
Câu 10. Đường gấp khúc trong hình vẽ là dạng đồ thị của một trong bốn hàm số được liệt kê
trong các phương án A, B, C, D dưới đây. Hỏi hàm số đó là hàm số nào?
A. y x 1.
B. y   x 1 .
C. y   x 1 .
D. y  1 x . Lời giải Chọn D
Đồ thị hàm số đi qua các điểm 0; 
1 và 1;0 nên chỉ có hàm số y  1 x thỏa mãn.
Câu 11. Hàm số nào sau đây có đồ thị như hình vẽ? y 1 x O x  2, khi x  1 x  2, khi x  1 A. y   . B. y   . x, khi x  1 x, khi x  1 x  2, khi x  1 x, khi x  1 C. y   . D. y   . x, khi x  1 x, khi x  1 Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 123
Trần Đình Cư. SĐT: 0834332133 Chọn C Bảng biến thiên: x ∞ 1 +∞ ∞ +∞ y 1
Câu 12. Đồ thị bên là đồ thị của hàm số nào? y 3 1 x O 1
A. y x 1.
B. y  2 x 1.
C. y  2x 1 .
D. y x 1 Lời giải Chọn B
Đồ thị nhận trục Oy là trục đối xứng nên hàm số tương ứng là hàm chẵn nên loại phương án C, D.
Đồ thị hàm số đi qua điểm 1;3 . Thay vào B thấy thỏa mãn nên chọn B. x Câu 13.
Đồ thị của hàm số y    2 là hình nào? 2 A.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 124
Trần Đình Cư. SĐT: 0834332133 B. C. D. Lời giải Chọn C x
Đồ thị hàm số y    2 cắt trục hoành tại điểm 4;0 và cắt trục tung tại điểm 0;2 2 nên chọn đáp án C.
Câu 14. Hình vẽ sau đây là đồ thị hàm số nào?
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 125
Trần Đình Cư. SĐT: 0834332133
A. y  1 x . B. y x 1. C. y x 1. D. y x . Lời giải Chọn A
Nhìn vào đồ thị hàm số đã cho ta thấy:
-Đồ thị đi qua điểm A(0;1) nên loại trừ đáp án C, D.
-Đồ thị đi qua điểm B(1; 0) , C(1; 0) nên loại trừ đáp án B.
Chọn đáp án A
Câu 15. Hàm số nào trong các hàm số dưới đây có đồ thị như hình vẽ?
A. y x  3.
B. y  2x  3.
C. y  4x  6.
D. y  4x  6. Lời giải Chọn B  
Đồ thị là một đường thẳng qua điểm    3 0; 3 à v ;0    2  3  . a 0  b  a  2
Nên hàm số có dạng: y ax b thỏa:  3   0  a bb   3   2
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 126
Trần Đình Cư. SĐT: 0834332133
Câu 16. Cho hàm số y f x có tập xác định là  3; 
3 và có đồ thị như hình vẽ. Khẳng định nào sau đây đúng?
A. Hàm số đồng biến trên khoảng 3;  1 và 1;4.
B. Hàm số nghịch biến trên khoảng 2;  1 .
C. Hàm số đồng biến trên khoảng 3;  1 và 1;3.
D. Đồ thị hàm số cắt trục hoành tại 3 điểm phân biệt. Lời giải Chọn C
+) Dựa vào đồ thị nhận thấy: Hàm số đồng biến trên khoảng 3;  1 và 1;3.
Câu 17. Hàm số nào trong bốn phương án liệt kê ở A, B, C, D có đồ thị như hình bên
A. y = -x + 2 . B. y = 2x +1. C. y = x +1. D. y = -x +1. Lời giải Chọn D
Gọi d : y = ax + b
Đồ thị hàm số cắt các trục tọa độ lần lượt tại A(0; ) 1 và B(1;0)
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 127
Trần Đình Cư. SĐT: 0834332133 ìïA(0; ) 1 Î d ï b ìï =1 b ìï =1 í ï  ï 
d : y = -x +1. ï í í B ï (1; ) 0 Î d ï ï î a + b = 0 ïî a = 1 - ïî
Dạng 3: Vị trí tương đối của hai đường thẳng 1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
3. Bài tập trắc nghiệm 1 1 Câu 1.
Cho hai đường thẳng d : y x 100 và d : y   x 100 . Mệnh đề nào sau đây 2  1  2 2 đúng?
A. d và d trùng nhau.
B. d và d vuông góc nhau. 2  1  2  1 
C. d và d cắt nhau.
D. d và d song song với nhau. 2  1  2  1  Hướng dẫn giải Chọn C.
Cách 1: Gọi k , k lần lượt là hệ số gốc của d và d . Khi đó 2  1  1 2 1 1 1
k  , k    k .k   nên d và d không vuông góc nhau. 2  1  1 2 2 2 1 2 4  1  1 y x 100 
x y  100   x  0 Xét hệ: 2 2      1  1  y 100
y   x 100     x y 100  2 2
Vậy d và d cắt nhau. 2  1  1 1
Cách 2: Ta thấy   nên d và d cắt nhau. 2  1  2 2 Câu 2.
Biết ba đường thẳng d : y  2x 1, d : y  8  x , d : y  3  2m x  2 đồng quy. Giá 3   1 2 trị của m bằng 3 1 A. m   . B. m 1. C. m  1  . D. m  . 2 2 Hướng dẫn giải Chọn B.
+ Gọi M là giao điểm của d và d . 1 2
y  2x 1
2x y  1  x  3 Xét hệ:       M 3;5 .
y  8  xx y  8  y  5
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 128
Trần Đình Cư. SĐT: 0834332133
+ M d nên ta có: 5  3 2m.3 2  5  9  6m  2  6m  6  m 1. 3 Câu 3.
Tìm các giá trị thực của tham số m để đường thẳng y   2
m  3 x  3m 1 song song
với đường thẳng y x  5 ? A. m  2  .
B. m   2 . C. m  2  . D. m  2 . Hướng dẫn giải Chọn D.
Đường thẳng y   2
m  3 x  3m 1song song với đường thẳng y x  5 khi và chỉ khi 2 2 m  3 1 m  4 m  2  v m = 2       m  2 . 3  m 1  5 3  m  6 m  2 Câu 4.
Các đường thẳng y  5  x  
1 ; y  3x a ; y ax  3 đồng quy với giá trị của a là A. 11. B. 10  . C. 12 . D. 13  . Hướng dẫn giải Chọn D.
Gọi d : y  5
x  5, d : y  3x a , d : y ax  3 a  3 . 1 2 3 a
Phương trình hoành độ giao điểm của d và d : 5
x  5  3x  5 a x  . 1 2 8
 a  5 5a 15 
Giao điểm của d và d là A ; . 1 2    8 8 
Đường thẳng d , d và d đồng qui khi Ad 1 2 3 3 5a 15 a  5 a  3   . a  3 2
a 10a  39  0  13  a   . 8 8  a  13 
Dạng 4: Xác định hàm số bậc nhất 1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1: Biết đồ thị hàm số y ax b đi qua điểm M 1; 4 và có hệ số góc bằng 3  . Tìm a, . b Lời giải
Vì y ax b có hệ số góc bằng 3  nên a  3  .
Mà y ax b đi qua M 1; 4 nên y  3x b  4  3
 .1 b b  7 .
Ví dụ 2: Đồ thị hàm số y ax b là một đường thẳng đi qua A3;4 và song song với đường
thẳng y  3x 1 . Tìm a, . b
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 129
Trần Đình Cư. SĐT: 0834332133 Lời giải
Đường thẳng y ax b đi qua A3;4 và song song với đường thẳng y  3x 1;suy 3
a b  4  b   5  ra a  3   .  a  3 b  1  
Ví dụ 3: Đồ thị hàm số y ax b cắt trục hoành tại điểm có hoành độ x  3 và đi qua điểm
M 2;4. Tìm a, . b Hướng dẫn giải
Đồ thị hàm số cắt trục hoành tại điểm có hoành độ x  3  3a b  0 .
Đồ thị hàm số đi qua điểm M 2;4  2a b  4 .  4 a   3
a b  0  Ta có hệ 5    .  2
a b  4 12 b    5
3. Bài tập trắc nghiệm Câu 1.
Đường thẳng nào sau đây song song với đường thẳng y  2x ? 2 1 A. y x  5 .
B. y  1 2x . C. y x  3 .
D. y   2x  2 . 2 2 Hướng dẫn giải Chọn A.
Hai đường thẳng song song khi hai hệ số góc bằng nhau. Câu 2.
Hàm số f x  m  
1 x  2m  2 là hàm số bậc nhất khi và chỉ khi A. m  1  . B. m  1. C. m  1. D. m  0 . Hướng dẫn giải Chọn C.
Hàm số f x  m  
1 x  2m  2 là hàm số bậc nhất khi và chỉ khi m 1  0  m  1. Câu 3.
Tìm m để f x  m  2 x  2m 1 là nhị thức bậc nhất. m  2  A. m  2 . B.  1 . C. m  2 . D. m  2 . m    2 Hướng dẫn giải Chọn A.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 130
Trần Đình Cư. SĐT: 0834332133
Để f x  m  2 x  2m 1 là nhị thức bậc nhất thì m  2  0  m  2 . Câu 4.
Một hàm số bậc nhất y f x có f  
–1  2 và f 2  –3 . Hàm số đó là  x
A. y  –2x  3.
B. f x 5 1  . 3  x
C. y  2x – 3 .
D. f x 5 1  . 3 Hướng dẫn giải Chọn B.
Hàm số đã cho có dạng y f x  x a b .  f    –1  2  . a   –1  b  2 5 1 Ta có   
a   , b  .  f  2  –3  .2 a b  –3 3 3  x  Vậy f x 5 1  . 3 Câu 5.
Biết đồ thị hàm số y ax b đi qua điểm M 1; 4 và có hệ số góc bằng 3  . Tích P ab ? A. P  13 . B. P  21. C. P  4 . D. P  21. Hướng dẫn giải Chọn D.
Vì y ax b có hệ số góc bằng 3  nên a  3  .
Mà y ax b đi qua M 1; 4 nên y  3x b  4  3
 .1 b b  7 . Do đó P  . a b  3  .7  2  1. Câu 6.
Đồ thị hàm số nào sau đây đi qua 2 điểm A 1
 ;2 và B0;  1 .
A. y x 1.
B. y x 1.
C. y  3x 1
D. y  3x 1. Hướng dẫn giải Chọn D.
Gọi đường thẳng đi qua hai điểm A 1
 ;2 và B0; 
1 có dạng: y ax b d  . Do A 1;
 2 và B0; 
1 thuộc đường thẳng d  nên a , b là nghiệm của hệ phương trình:
2  a ba  3     .  1   b b   1 
Vậy đồ thị hàm số đi qua hai điểm A 1
 ;2 và B0; 
1 là y  3x 1.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 131
Trần Đình Cư. SĐT: 0834332133 Câu 7.
Đường thẳng y ax b có hệ số góc bằng 2 và đi qua điểm A 3;   1 là
A. y  2x 1.
B. y  2x  7 .
C. y  2x  5 .
D. y  2x  5 . Hướng dẫn giải Chọn B.
Đường thẳng có hệ số góc bằng 2  a  2  y  2x b và đi qua điểm A 3;   1 . Nên 1  2. 3
   b b  7. Vậy hàm số cần tìm là y  2x  7 . 1 Câu 8.
Đường thẳng đi qua điểm M 2;  
1 và vuông góc với đường thẳng y   x  5 có 3 phương trình là
A. y  3x  7 .
B. y  3x  5 .
C. y  3x  7 .
D. y  3x  5 . Hướng dẫn giải Chọn A.
Gọi d là đường thẳng cần tìm. 1
Do d vuông góc với đường thẳng y   x  5 nên d : y  3x m . 3
Do d đi qua điểm M 2;   1 nên 1
  3.2  m m  7  .
Vậy d : y  3x  7 . Câu 9.
Điểm A có hoành độ x  1 và thuộc đồ thị hàm số y mx  2m  3. Tìm m để điểm A A
nằm trong nửa mặt phẳng tọa độ phía trên trục hoành . A. m  0 . B. m  0 . C. m 1. D. m  0 . Hướng dẫn giải Chọn C.
Từ giả thiết điểm A nằm trong nửa mặt phẳng tọa độ phía trên trục hoành nên y  0 ta A có 2
y mx m  3  .1
m  2m  3  3m  3  0  m  1. A
Câu 10. Tìm phương trình đường thẳng d : y ax b . Biết đường thẳng d đi qua điểm I 1;3
và tạo với hai tia Ox , Oy một tam giác có diện tích bằng 6 ?
A. y  3x  6 .
B. y  9  72 x  72  6.
C. y  9  72 x  72  6.
D. y  3x  6 . Hướng dẫn giải Chọn A.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 132
Trần Đình Cư. SĐT: 0834332133
Do đường thẳng d đi qua điểm I 1;3 nên a b  3  a  3b .  b
Giao điểm của d và các tia Ox , Oy lần lượt là M  ;0 
 và N 0;b  a  . 1 2 1 b b Do đó: S
 .OM.ON  . . b  . Mà OMN  2 2 a 2 ab  6 2
b  36 12bS  6 2  b 12 a 2
b 12 3 b   b  6   72 L . OMN  2
b  36 12b  b  6   72 (L)
Với b  6  a  3
  d : y  3x  6 .
Câu 11. Tìm điểm M a;b với 0
a  nằm trên  : x y 1  0 và cách N  1  ;3 một khoảng
bằng 5 . Giá trị của a b là A. 3 . B. 1  . C. 11  . D. 1 . Hướng dẫn giải Chọn C. 
M    M (t;1 t)  MN   1
  t;t  2 .
Ta có: MN   MN    t2 2 2 5 1  (2  t)  25
t  2  M 2;  1 2
 2t  6t  20  0    M  5  ;6    
t    M    a b 11 5 5;6
Câu 12. Cho hàm số bậc nhất y   2
m  4m  4 x  3m  2 có đồ thị là d  . Tìm số giá trị
nguyên dương của m để đường thẳng d  cắt trục hoành và trục tung lần lượt tại hai
điểm A , B sao cho tam giác OAB là tam giác cân ( O là gốc tọa độ). A. 3 . B. 1. C. 2 . D. 4 . Hướng dẫn giải Chọn B.
Đường thẳng d  tạo với trục hoành và trục tung một tam giác OAB là tam giác vuông
cân  đường thẳng d  tạo với chiều dương trục hoành bằng 45 hoặc 135  hệ số 2
m  4m  4  1 2
m  4m  3  0
góc tạo của d  bằng 1 hoặc 1     2
m  4m  4  1 2
m  4m  5  0 m  1    m  5  .  m  2  7
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 133
Trần Đình Cư. SĐT: 0834332133
Thử lại: m  5 thì d không đi qua O .
Vậy có duy nhất một giá trị m  5 nguyên dương thỏa ycbt.
Câu 13. Đường thẳng d : y  m  3 x  2m 1 cắt hai trục tọa độ tại hai điểm A và B sao cho
tam giác OAB cân. Khi đó, số giá trị của m thỏa mãn là A. 1. B. 0 . C. 3 . D. 2 . Hướng dẫn giải Chọn D.
A d Ox nên tọa độ A là nghiệm của hệ:  
y  m   2m 1 3 x  2m 1 x   2m 1     m  3 nên A ; 0   . y  0   m  3  y  0
B d Oy nên tọa độ B là nghiệm của hệ:
y  m 3 x  2m 1 x  0   
nên B 0;2m   1 . x  0 y  2  m 1 m    Ta có OA  2 1 1 OB   2
m 1  2m 1  1  0 m 3  m 3       1 2m 1  0 m      2 . m  3  1   m  4, 2 m  1
Nhận xét: Với m  thì A B O 0; 0 nên không thỏa mãn. 2 Vậy m  4, 2 m  .
Câu 14: Biết rằng với mọi giá trị thực của tham số m , các đường thẳng
d : y  (m  2)x  2m  3 cùng đi qua một điểm cố định là I (a; b) . Tính giá trị của biểu m
thức: S a b A. S  3 .
B. S  1 . C. S  1 . D. S  3 . Lời giải Chọn B
Ta có phương trình của đường thẳng đã cho:
d : y  (m  2)x  2m  3  (x  2)m  2x  3 m
Vì các đường thẳng d luôn đi qua điểm I nên ta tìm x để m bị triệt tiêu m
⇒ I (2; 1)  S  1 ⇒ Chọn B
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 134
Trần Đình Cư. SĐT: 0834332133 25
Câu 15. Đồ thị hàm số y x  2m 1 tạo với hệ trục tọa độ Oxy tam giác có diện tích bằng . 2 Khi đó m bằng
A. m  2 ; m  3 .
B. m  2 ; m  4 . C. m  2  ; m  3. D. m  2  . Hướng dẫn giải Chọn A.
Gọi: A , B lần lượt là giao điểm của đồ thị hàm số y x  2m 1 với trục hoành và trục tung
Suy ra A2m 1;0 ; B0;1 2m . 25
Theo giả thiết thì tam giác có diện tích bằng
là tam giác OAB vuông tại O . 2 1 25 Do đó: S  .O . A OB OAB 2 2  .
OA OB  25  2m 1 . 1 2m  25  2m 1 . 2m 1  25 2m 1  5 m  3   m  2 2 1  25     . 2m 1  5  m  2 
Dạng 4: Bài toán thực tế 1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
3. Bài tập trắc nghiệm Câu 1.
Một giá đỡ được gắn vào bức tường như hình vẽ. Tam giác ABC vuông cân ở đỉnh C .
Người ta treo vào điểm A một vật có trọng lượng 10 N . Khi đó lực tác động vào bức
tường tại hai điểm B và C có cường độ lần lượt là: B A C 10N A. 10 2 N và 10 N . B. 10 N và 10 N .
C. 10 N và 10 2 N . D. 10 2 N và 10 2 N . Hướng dẫn giải Chọn A.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 135
Trần Đình Cư. SĐT: 0834332133
Cường độ lực tại C bằng cường độ lực tại A và bằng 10 N .
Cường độ lực tại B bằng 10 2 N . Câu 2.
Một hộ nông dân định trồng đậu và cà trên diện tích 800 m2. Nếu trồng đậu thì cần 20
công và thu 3.000.000 đồng trên 100 m2 nếu trồng cà thì cần 30 công và thu 4.000.000
đồng trên 100 m2 Hỏi cần trồng mỗi loại cây trên diện tích là bao nhiêu để thu được
nhiều tiền nhất khi tổng số công không quá 180 . Hãy chọn phương án đúng nhất trong các phương án sau:
A. Trồng 600 m2 đậu, 200 m2 cà.
B. Trồng 500 m2đậu, 300 m2cà.
C. Trồng 400 m2 đậu, 200 m2 cà.
D. Trồng 200 m2 đậu, 600 m2 cà. Hướng dẫn giải Chọn A.
Gọi x là số x00 m2 đất trồng đậu, y là số y00 m2 đất trồng cà. Điều kiện x  0 , y  0 .
Số tiền thu được là T  3x  4y triệu đồng. x y  8 x y  8  
20x  30y 180
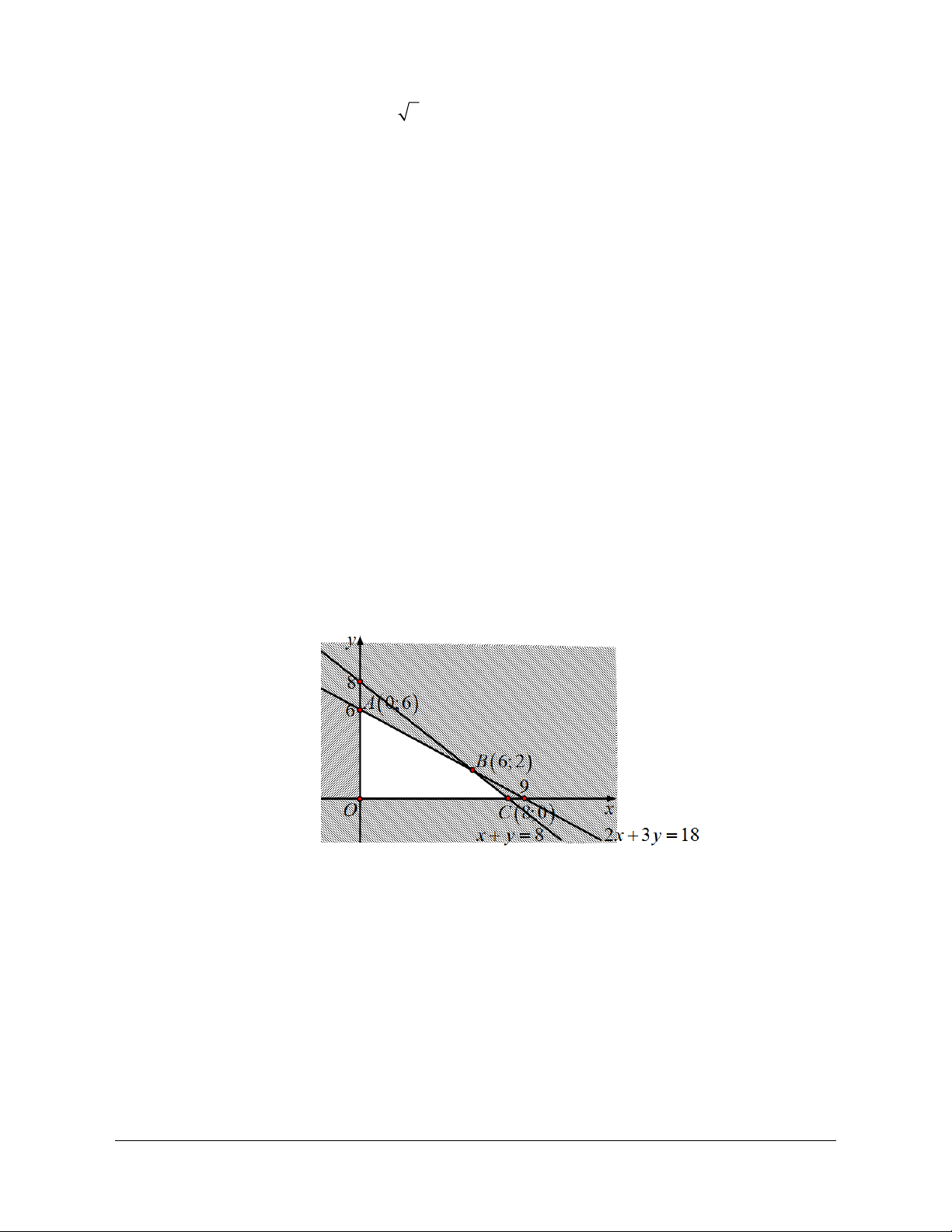
2x  3y 18 Theo bài ra ta có    x  0  x  0  y  0 y  0 Đồ thị:
Dựa đồ thị ta có tọa độ các đỉnh A0;6, B6;2 , C 8;0 , O0;0 .
Thay vào T  3x  4 y ta được T
 26 triệu khi trồng 600 m2 đậu và 200 m2 cà. max
Câu 3. Một nông dân định trồng đậu và cà trên diện tích 8 ha trong vụ Đông Xuân. Nếu trồng
đậu thì cần 20 công và thu 3 triệu đồng trên diện tích mỗi ha. Nếu trồng đậu thì cần 30
công và thu 4 triệu đồng trên diện tích mỗi ha. Hỏi cần trồng mỗi loại cây trên với diện
tích bao nhiêu để thu được nhiều tiền nhất. Biết rằng tổng số công không quá 180 .
A. 1 ha đậu và 7 ha cà. B. 6 ha đậu và 2 ha cà.
C. 2 ha đậu và 6 ha cà.
D. 3 ha đậu và 5 ha cà.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 136
Trần Đình Cư. SĐT: 0834332133 Lời giải Chọn B
Gọi diện tích trồng đậu là x , , vậy diện tích trồng cà là 8  x .
Số công phải bỏ ra là: 20x  308  x  240 10x .
Do tổng số công không quá 180 nên ta có: 240 10x  180  x  6 .
Số tiền thu được là g x  3x  48  x  32  x ; g x nghịch biến trên đoạn 6;  8 nên
max g x  26 tại x  6 . Vậy cần trồng 6 ha đậu và 2 ha cà. 6;8
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 137
Trần Đình Cư. SĐT: 0834332133
BÀI 3. HÀM SỐ BẬC HAI
A. KIẾN THỨC CẦN NHỚ
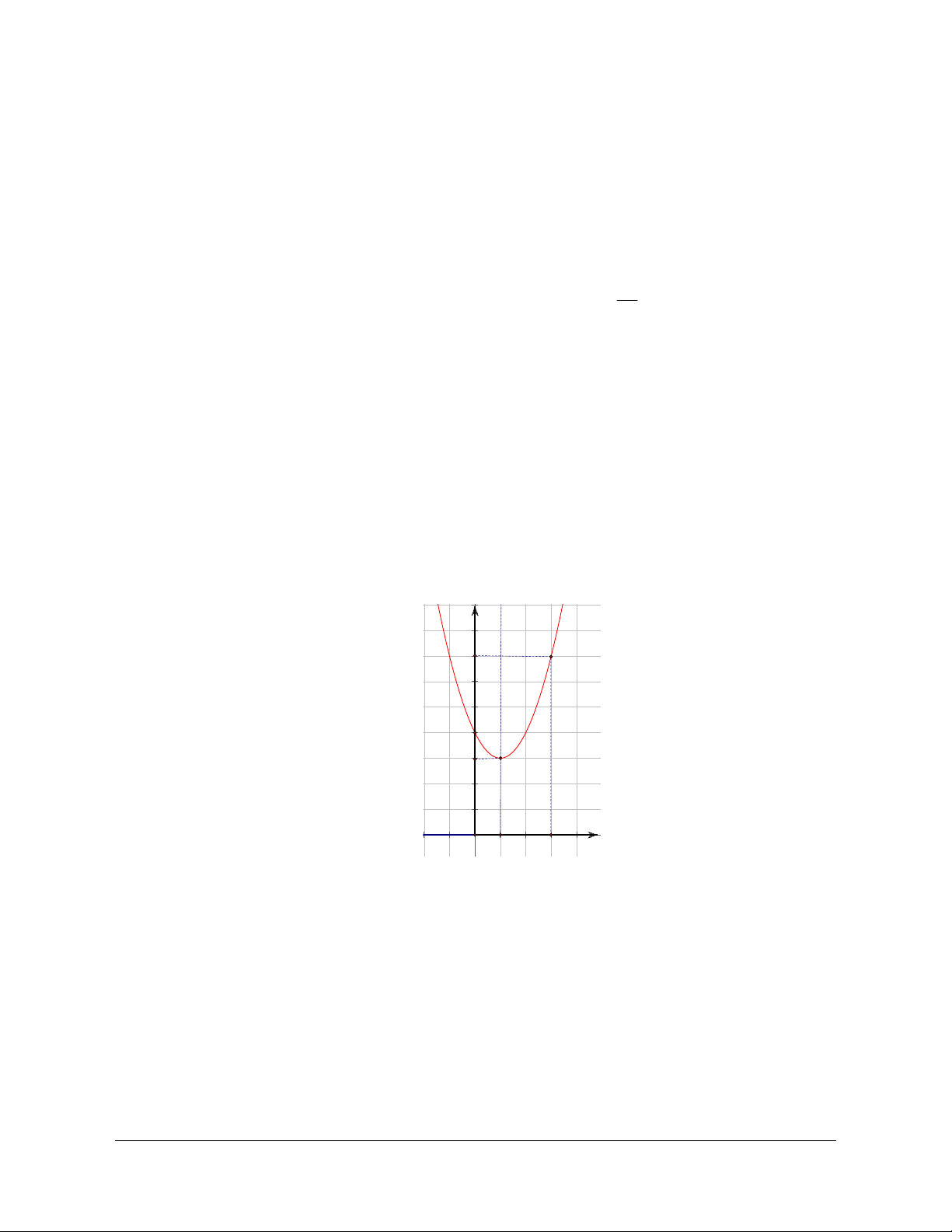
Hàm số bậc hai là hàm số được cho bằng biểu thức có dạng y ax2  bx c , trong đó a,b,c là
những hằng số và a  0 .
I. Đồ thị của hàm số bậc hai
y ax2  bx c  Tập xác định: D = R  b   b
 Đồ thị là một parabol có đỉnh I   ;
 , nhận đường thẳng x   làm trục đối  2a 4a  2a
xứng, hướng bề lõm lên trên khi a > 0, xuông dưới khi a < 0.
Chú ý: Để vẽ đường parabol ta có thể thực hiện các bước như sau: b  
- Xác định toạ độ đỉnh I   ;  .  2a 4a b
- Xác định trục đối xứng x  
và hướng bề lõm của parabol. 2a
- Xác định một số điểm cụ thể của parabol .
- Căn cứ vào tính đối xứng, bề lõm và hình dáng parabol để vẽ parabol.
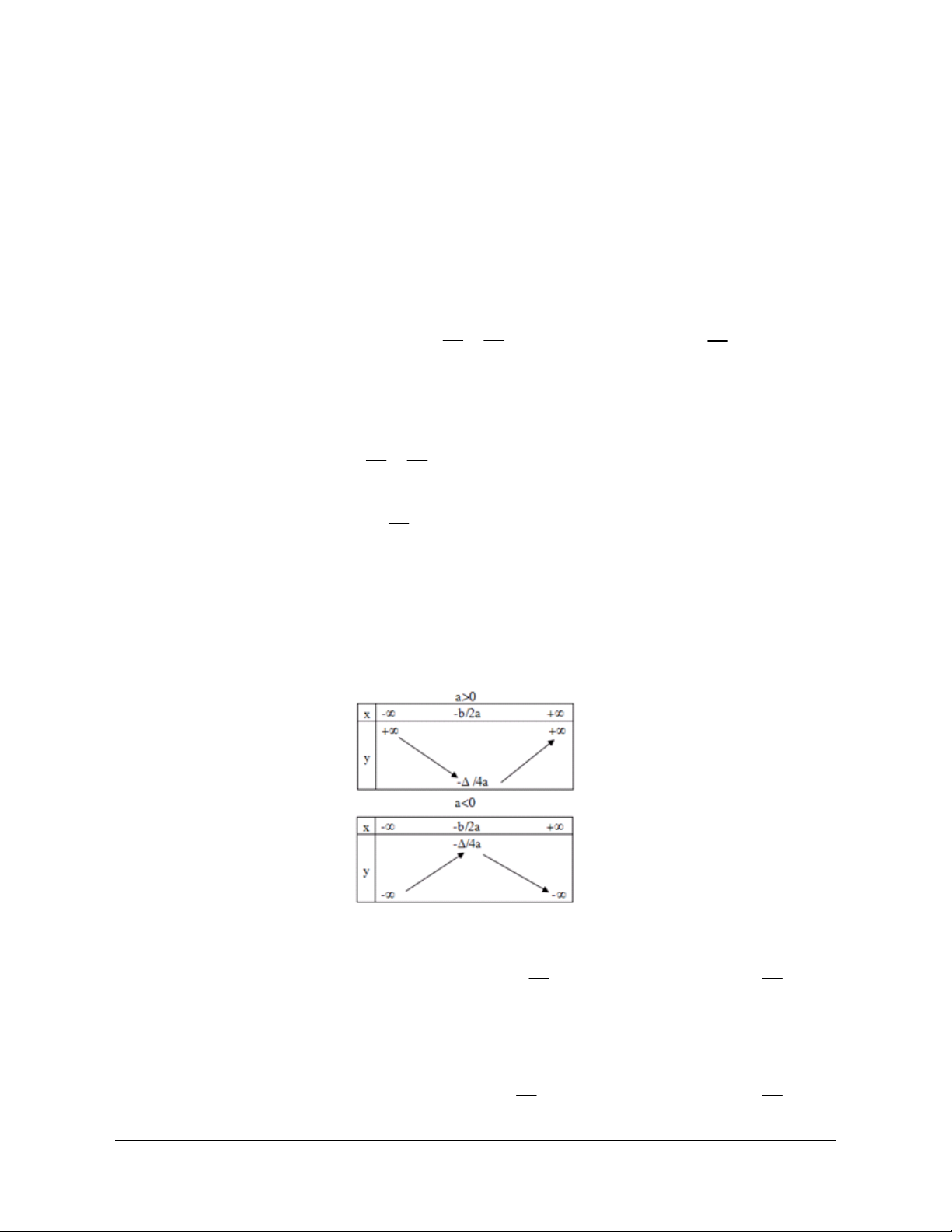
II. Sự biến thiên của hàm số bậc hai Bảng biến thiên: Như vậy:  b   b
 Khi a  0 hàm nghịch biến trên khoảng ; 
, đồng biến trên khoảng  :     2a   2a   b và có GTNN là khi x   4a 2ab   b
 Khi a  0 hàm đồng biến trên khoảng ; 
 , nghịch biến trên khoảng  :     2a   2a
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 138
Trần Đình Cư. SĐT: 0834332133  b và có GTLN là khi x   4a 2a
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1: Bảng biến thiên, tính đơn điệu, GTLN và GTNN của hàm số 1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
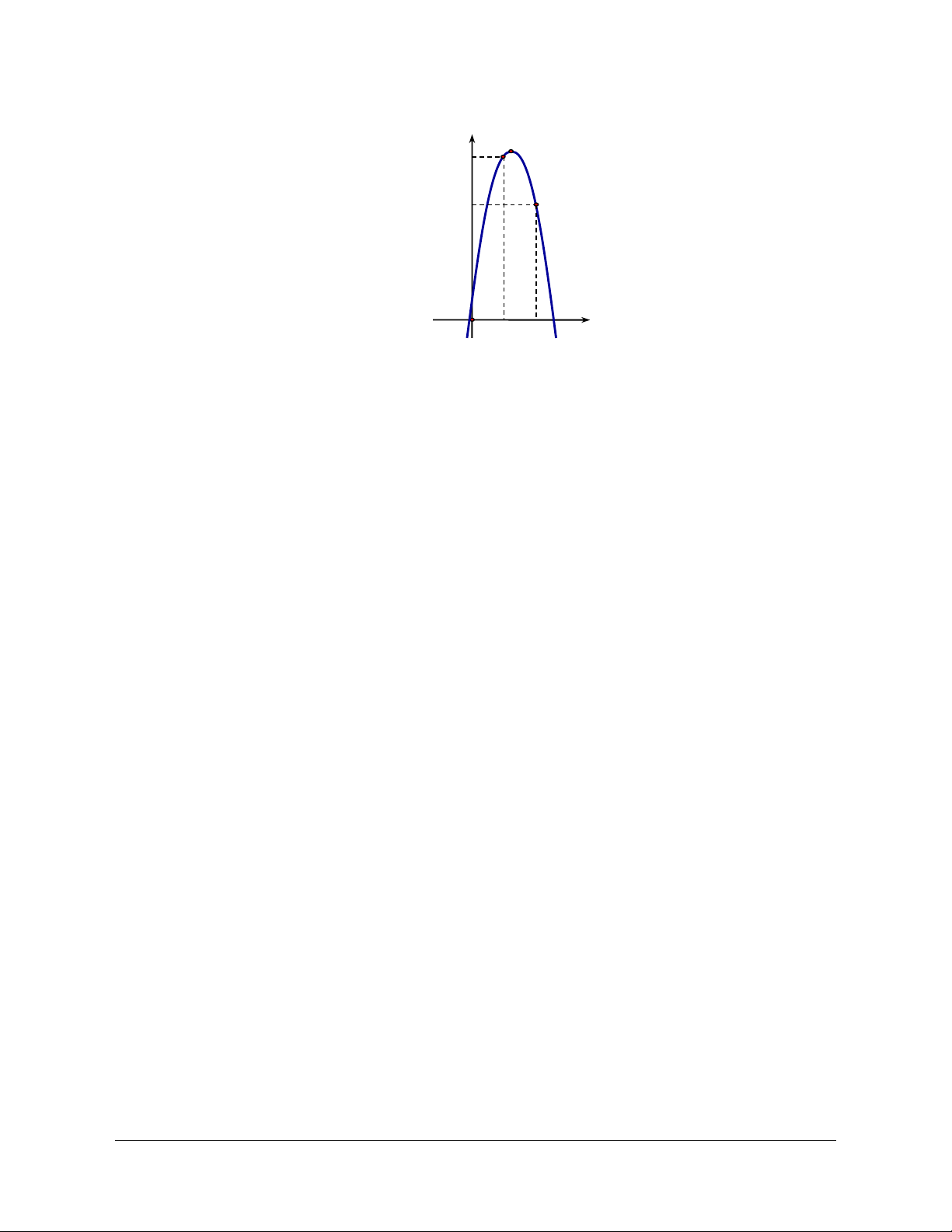
Ví dụ 1: Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y f x 2
x  3x trên đoạn 0;2. Lời giải Hàm số 2
y x  3x có a 1  0 nên bề lõm hướng lên. b 3
Hoành độ đỉnh x    0;2 . 2a 2   3  9
m  min y f      Vậy   2  4 .
M  max y  max 
f 0, f 2  max0,  2  0
Ví dụ 2: Tìm giá trị lớn nhất M và giá trị nhỏ nhất m của hàm số y f x 2
 x  4x  3 trên đoạn 0;4. Lời giải Hàm số 2
y  x  4x  3 có a  1
  0 nên bề lõm hướng xuống. b
Hoành độ đỉnh x    2  0;4. 2af  4  2  9 Ta có  
m  min y f 4  2  9; ma M
x y f 0  f    3. 0  3
Ví dụ 3: Tìm giá trị thực của tham số m  0 để hàm số 2
y mx  2mx  3m  2 có giá trị nhỏ nhất bằng 10  trên .  Lời giải b 2m Ta có x   
1, suy ra y  4m  2 . 2a 2m m
Để hàm số có giá trị nhỏ nhất bằng 10
 khi và chỉ khi  0  m  0 2 m  0    m  2 .  4  m  2  1  0
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 139
Trần Đình Cư. SĐT: 0834332133 3. Bài tập trắc nghiệm Câu 1.
Bảng biến thiên nào dưới đây là của hàm số 2
y  x  2x 1: x  1    y A. 2 x    y B.  x  1  2 y C.   x    y D.  Hướng dẫn giải Chọn C. Xét hàm số 2
y  x  2x 1 có a  1
  0 , tọa độ đỉnh I 1;2 do đó hàm số trên tăng trên khoảng   ;1
 và giảm trên khoảng 1; . Câu 2.
Trục đối xứng của parabol 2
y  x  5x  3 là đường thẳng có phương trình 5 5 5 5 A. x  . B. x   . C. x   . D. x  . 4 2 4 2 Hướng dẫn giải Chọn D. b
Trục đối xứng của parabol 2
y ax bx c là đường thẳng x   . 2a 5
Trục đối xứng của parabol 2
y  x  5x  3 là đường thẳng x  . 2 Câu 3. Cho hàm số 2
y x  2x  3 . Chọn câu đúng.
A. Hàm số nghịch biến trên khoảng 1; .
B. Hàm số nghịch biến trên khoảng   ;1 .
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 140
Trần Đình Cư. SĐT: 0834332133
C. Hàm số đồng biến trên  .
D. Hàm số đồng biến trên khoảng   ;1 . Hướng dẫn giải Chọn B.
Ta có a  1  0 , b  2 , c  3 nên hàm số có đỉnh là I 1; 2 . Từ đó suy ra hàm số nghịch
biến trên khoảng  
;1 và đồng biến trên khoảng 1; . Câu 4.
Xét tính đồng biến, nghịch biến của hàm số f x 2
x  4x  5 trên các khoảng  ;2  
và 2;  . Khẳng định nào sau đây đúng?
A. Hàm số nghịch biến trên  ;2
  , đồng biến trên 2;  .
B. Hàm số nghịch biến trên các khoảng  ;2
  và 2;  .
C. Hàm số đồng biến trên  ;2
  , nghịch biến trên 2;  .
D. Hàm số đồng biến trên các khoảng  ;2
  và 2;  . Hướng dẫn giải Chọn A. f x 2
x  4x  5 TXĐ: D   .
Tọa độ đỉnh I 2;  1 .
Hàm số nghịch biến trên  ;2
  , đồng biến trên 2;  . Câu 5.
Tìm giá trị nhỏ nhất của hàm số 2
y x  4x 1. A. 3  . B. 1. C. 3 . D. 13 . Hướng dẫn giải Chọn A. 2
y x  4x 1   x  2 2  3  3 .
Dấu "  " xảy ra khi và chỉ khi x  2 .
Vậy hàm số đã cho đạt giá trị nhỏ nhất là 3  tại x  2 . 2 Câu 6.
Giá trị lớn nhất của hàm số f x  bằng 2 x  5x  9 11 11 8 4 A. . B. . C. . D. . 8 4 11 11 Hướng dẫn giải
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 141
Trần Đình Cư. SĐT: 0834332133 Chọn C. 2  5  11 11 2 2 8 Ta có 2
x  5x  9  x          2  4 4 2 x  5x  9 11 11 4 2 8 5   x  2
x  5x  9 11 2 2 8
Vậy giá trị lớn nhất của hàm số f x  bằng . 2 x  5x  9 11 Câu 8. Hàm số 2
y x  4x  3 đồng biến trên khoảng nào? A. 1;3 . B.  ;2   . C.  ;    . D. 2;  . Hướng dẫn giải Chọn D.
Trục đối xứng x  2 . Ta có a  1  0 nên hàm số nghịch biến trên khoảng  ;2   và
đồng biến trên khoảng 2;  . Câu 9.
Cho parabol P có phương trình 2
y  3x  2x  4 . Tìm trục đối xứng của parabol 2 1 2 1 A. x   . B. x   . C. x  . D. x  . 3 3 3 3 Hướng dẫn giải Chọn D.
+ Có a  3; b  2  ; c  4 .  1
+ Trục đối xứng của parabol là  b x  . 2a 3 Câu 10. Cho hàm số 2
y  2x  4x  3 có đồ thị là parabol P . Mệnh đề nào sau đây sai?
A. P không có giao điểm với trục hoành.
B. P có đỉnh là S 1;  1 .
C. P có trục đối xứng là đường thẳng y  1. D. P đi qua điểm M  1  ; 9. Hướng dẫn giải Chọn C.
P có đỉnh là S 1; 1 ; trục đối xứng là đường thẳng x 1 nên C sai.
và P đi qua điểm M  1
 ; 9  B, D đều đúng.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 142
Trần Đình Cư. SĐT: 0834332133 Xét phương trình 2
2x  4x  3  0 vô nghiệm trên  nên P không có giao điểm với trục hoành  A đúng. Câu 11. Hàm số 2
y  x  2x  5 đồng biến trên khoảng: A.  1  ; . B.  ;    1 . C. 1; . D.   ;1  . Hướng dẫn giải Chọn D. b
Ta có đồ thị hàm số là một parabol có hoành độ đỉnh: x    1 2a Mà hệ số a  1
  0 nên đồ thị hàm số có bề lõm quay xuống
Vậy hàm số đồng biến trên   ;1 . Câu 12. Cho hàm số 2
y x  2x  4 có đồ thị P . Tìm mệnh đề sai.
A. P có đỉnh I 1;3 .
B. min y  4, x  0;  3 .
C. P có trục đối xứng x 1.
D. max y  7, x  0;  3 . Hướng dẫn giải Chọn B. y 8 (P) x = 1 7 6 4 3 I(1; 3) 2 O 1 3 x 5
Dựa vào đồ thị của hàm số 2
y x  2x  4 : P , ta nhận thấy:
P có đỉnh I 1;3 nên A đúng. min y  3, x  0; 
3 , đạt được khi x  1 nên B sai.
P có trục đối xứng x 1 nên C đúng. max y  7, x  0; 
3 , đạt được khi x  3 nên D đúng.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 143
Trần Đình Cư. SĐT: 0834332133
Câu 13. Hàm số nào dưới đây đồng biến trên 3;4? 1 A. 2
y x  2x 1 . B. 2
y x  7x  2 . 2 1
C. y  3x 1. D. 2
y   x x 1. 2 Hướng dẫn giải Chọn A. 1 + Hàm số 2
y x  2x 1 đồng biến trên 2; nên đồng biến trên 3;4. Chọn A 2  7  + Hàm số 2
y x  7x  2 đồng biến trên ;   . Loaị B.  2 
+ Hàm số y  3x 1 nghịc biến trên . Loaị C. 1 + Hàm số 2
y   x x 1 đồng biến trên   ;1 . Loaị D. 2
Câu 14. Hàm số nào sau đây có bảng biến thiên như hình bên? x  1  1 y 2   1 A. 2
y  x  5x  2 . B. 2
y   x x . 2 1 C. 2
y x  3x 1 . D. 2
y x x  3 . 4 Hướng dẫn giải Chọn B.
Dựa vào bảng biến thiên ta thấy đồ thị có bề lõm hướng xuống nên loại C, D. 1  1  Đồ thị hàm số 2
y   x x có tọa độ đỉnh I 1;   . 2  2 
Câu 16. Bảng biến thiên của hàm số 2 y  2
x  4x 1 là bảng nào sau đây? A. . B. .
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 144
Trần Đình Cư. SĐT: 0834332133 C. D. . Hướng dẫn giải Chọn B Do hệ số a  2
  0 nên parabol có bề lõm hướng xuống và đỉnh có tọa độ I 1;3 .
Câu 17. Tìm m để hàm số 2
y x  2x  2m  3 có giá trị nhỏ nhất trên đoạn 2;5 bẳng 3  . A. m  3  . B. m  9  . C. m  1. D. m  0 . Hướng dẫn giải Chọn A.
Ta có bảng biến thiên của hàm số 2
y x  2x  2m  3 trên đoạn 2;5:
Do đó giá trị nhỏ nhất trên đoạn 2;5 của hàm số 2
y x  2x  2m  3 bằng 2m  3 .
Theo giả thiết 2m  3  3  m  3.  1  Câu 18. Cho hàm số 2
y x  2 m x m  
m  0 xác định trên  1  ; 
1 . Giá trị lớn nhất, giá  m
trị nhỏ nhất của hàm số trên  1  ; 
1 lần lượt là y , y thỏa mãn y y  8 . Khi đó giá trị 1 2 1 2 của m bằng A. m  1. B. m  . C. m  2 . D. m  1, 2 m  . Hướng dẫn giải Chọn A.  1 
Đặt y f x 2
x  2 m x m   .  m  1
Hoành độ đỉnh của đồ thị hàm số là x m   2 . m  1 
Vì hệ số a  1  0 nên hàm số nghịch biến trên ;  m    .  m
Suy ra, hàm số nghịch biến  1  ;  1 .
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 145
Trần Đình Cư. SĐT: 0834332133 y f 1  2  3m  1. 1   m y  2
f 1  1 m  . 2   m
Theo đề bài ta có: y y  8 1 2  2 2 3m  11 m   8 m  0 2
m  2m 1  0  m 1. m m
Câu 19. Giá trị lớn nhất và giá trị nhỏ nhất của hàm số 4 3 2
y x  4x x 10x  3 trên đoạn  1  ;4 là 37 37 A. y   , y  21. B. y  , y  21  . min 4 max max 4 min 37 37 C. y  , y  21. D. y  5, y   . min 4 max max min 4 Hướng dẫn giải Chọn A. Ta có 4 3 2
y x  4x x 10x  3 4 3 2 2
x  4x  4x  5x 10x  5  2 2
 x x2  x  2 2 2 5
1  2   x  2     x  2 1 1 5 1  2   .
Đặt t   x  2 1 , x  1
 ;4  t 0;9. 2  7  37
y  t  2 1  5t  2 2
t  7t  3  t     .  2  4 2  7  121 37
Cách 1: Ta có 0  t        y  21.  2  4 4
Cách 2: Vẽ BBT 37 Vậy y   , y  21. min 4 max
Dạng 2: Xác định hàm số bậc hai 1. Phương pháp  2 M x ;y
0 0   (P)  y ax bx c 0 0 0
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 146
Trần Đình Cư. SĐT: 0834332133 b x     b  0 x    2a
(P) có đỉnh I x ; y    hoaëc:  0 0 0 2a   y  
y ax2  bx  0  c  4a 0 0 0 b
 (P) nhận x x0 làm trục đối xứng  x   0 2a 
 (P) có giá trị nhỏ nhất (hay lớn nhất) bằng y   y 0 a 0 4
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1. Xác định Parabol 2
y ax bx c đạt cực tiểu bằng 4 tại x  2  và đồ thị đi qua A0;6 Hướng dẫn giải
Parabol có đỉnh I  2;
 4 và đi qua A0;6 nên ta có   1  
4a  2b c  4 a   2  1 c  6  b   2 . Vậy 2
y x  2x  6 .  2 b      c 6 2    2aVí dụ 2. Parabol 2
y ax bx c đi qua A8;0 và có đỉnh I 6; 1
 2 . Xác định a, , b c Hướng dẫn giải
64a 8b c  0 a  3  
Từ giả thiết ta có hệ 36
a  6b c  1  2  b   36  .  b      c 96 6   2a
Ví dụ 3. Tìm các hệ số a,b,c của P y  2 ( ) :
ax  bx c,a  0
a) (P) đi qua A1;0;B2;0;C 0;4 ;
b) (P) đi qua A1;2 và có đỉnh I 1;2 . Giải a) Ta có:
A1;0P  a b c  0
B2;0P  4a  2b c  0
C 0;4P  c  4
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 147
Trần Đình Cư. SĐT: 0834332133
a b c  0 a  2  
Giải hệ phương trình: 4a  2b c  0  b  2 c  4 c     4
Vậy a  2,b  2,c  4
b) Vì (P) đi qua A1;2 nên a b c  2
Mặt khác, vì (P) có đỉnh là I 1;2 nên I 1;2P hay a b c  2 b Và
 1  2a b  0 2a
a b c  2 a  1  
Giải hệ phương trình: a b c  2  b  2
2a b  0 c    1
Vậy a  1;b  2;c  1
Ví dụ 4. Tìm các hệ số a,b,c của P y  2 ( ) :
ax  bx c,a  0
a) y nhận giá trị bằng -3 khi x  2 và (P) cắt d : y x 1 tại hai điểm có hoành độ bằng 0 và bằng 5.
b) (P) đi qua hai điểm A1;6, B4;3 và có trục đối xứng là x  2 . Giải
a) Theo đề : y nhận giá trị bằng -3 khi x  2 nên 4a  2b c  3
Gọi (P) cắt d : y x 1 tại hai điểm M và N. Suy ra: M 0;  1 , N 1;6 M 0; 
1 P  c 1
N 1;6P  a b c  6
4a  2b c  3 a  7  
Giải hệ phương trình: a b c  6  b 12 c  1 c    1
Vậy a  7, b  12, c  1
b) (P) đi qua hai điểm A1;6, B4;3 nên
A1;6P  a b c  6
B4;3P 16a  4b c  3 b
(P) và có trục đối xứng là x  2 nên 
 2  4a b  0 2a
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 148
Trần Đình Cư. SĐT: 0834332133 a 3  
a b c   5 6   12
Giải hệ phương trình: 16a  4b c  3  b  
4a b  0  5  c   3  3 12
Vậy a  ;b   ;c  3. 5 5
3. Bài tập trắc nghiệm Câu 1.
Tìm khẳng định đúng trong các khẳng định sau?
A. f x 2
 3x  2x  5 là tam thức bậc hai.
B. f x  2x  4 là tam thức bậc hai.
C. f x 3
 3x  2x 1 là tam thức bậc hai.
D. f x 4 2
x x 1 là tam thức bậc hai. Hướng dẫn giải Chọn A.
* Theo định nghĩa tam thức bậc hai thì f x 2
 3x  2x  5 là tam thức bậc hai. Câu 2.
Xác định parabol P : 2
y ax bx c , a  0 biết P cắt trục tung tại điểm có tung độ 3 1
bằng 1 và có giá trị nhỏ nhất bằng khi x  4 2 A. P : 2
y  x x 1. B. P : 2
y x x 1. C. P : 2
y  2x  2x 1. D. P : 2
y x x  0 . Hướng dẫn giải Chọn B.
Ta có P cắt trục tung tại điểm có tung độ bằng 1: Khi x  0 thì y  1  c 1.  3 1
P có giá trị nhỏ nhất bằng khi x  nên: 4 2   1  3 1 1 3 y     a b 1  1 1 1   2  4 4 2 4
a b   a  1     4 2 4   .  b  1 b  1 b   1    
a b  0 2a 2 2a 2 Vậy P : 2
y x x 1.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 149
Trần Đình Cư. SĐT: 0834332133 Câu 3.
Đồ thị của hàm số nào sau đây là parabol có đỉnh I  1  ;3. A. 2
y  2x  4x  3 . B. 2
y x x 1. C. 2
y  2x  4x  5 . D. 2
y  2x  2x 1. Hướng dẫn giải Chọn C. 2  b    b b  4ac
Đỉnh Parabol là I  ;       ;   .  2a 4a   2a 4a
Do đó chỉ có đáp án C thoả. Câu 4.
Cho parabol P : 2
y ax bx c có trục đối xứng là đường thẳng x  1. Khi đó
4a  2b bằng A. 1. B. 0 . C. 1. D. 2 . Hướng dẫn giải Chọn B. b Do parabol P : 2
y ax bx c có trục đối xứng là đường thẳng x  1 nên   1 2a  2a b
  2a b  0  4a  2b  0. Câu 5. Đồ thị hàm số 2 2
y mx  2mx m  2 m  0 là parabol có đỉnh nằm trên đường thẳng
y x  3 thì m nhận giá trị nằm trong khoảng nào dưới đây? A. 1;6 . B.  ;   2 . C.  3;  3 . D. 0; . Hướng dẫn giải Chọn C. Ta có đồ thị hàm số 2 2
y mx  2mx m  2 là parabol có đỉnh I  2
1; m m  2 . m  0
I d : y x  3 2
 m m  2  1 3 2
m m  0    m 3;  3 . m  1  Câu 6.
Xác định a , b , c biết Parabol có đồ thị hàm số 2
y ax bx c đi qua các điểm M 0;  1 , N 1;  1 , P  1  ;  1 . A. 2
y x x 1. B. 2
y x x 1. C. 2 y  2  x 1. D. 2
y  x x 1. Hướng dẫn giải Chọn A.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 150
Trần Đình Cư. SĐT: 0834332133 c  1  a  1  
Vì M P , N P , P P nên ta có hệ phương trình a b c  1   b  1  .
a b c 1   c  1   Vậy P 2
: y  x x 1. Câu 7.
Tìm parabol P 2
: y ax  3x  2 , biết rằng parabol có trục đối xứng x  3.  1 A. 2
y x  3x  2 . B. 2
y x x  2 . 2 1 1 C. 2
y x  3x  2 . D. 2
y x  3x  2 . 2 2 Hướng dẫn giải Chọn D.
Trục đối xứng của P có dạng: b x     3 3    3  3   6  1 a a  . 2a 2a 2 1
Vậy P có phương trình: 2
y x  3x  2 . 2 Câu 8.
Biết rằng hàm số 2
y ax bx c a  0 đạt cực tiểu bằng 4 tại x  2 và có đồ thị hàm
số đi qua điểm A0;6 . Tính tích P abc . 3 A. P  6  . B. P  3  . C. P  6 . D. P  . 2 Hướng dẫn giải Chọn A.
Nhận xét: Hàm số đi qua điểm A0;6 ; đạt cực tiểu bằng 4 tại x  2 nên đồ thị hàm số
đi qua I 2;4 và nhận x  2 làm trục đối xứng, hàm số cũng đi qua điểm A0;6 suy ra:  b    1 2  a  2a   2 
4a  2b c  4  b   2   abc  6  . c  6   c  6    Câu 9.
Xác định phương trình của Parabol có đỉnh I 0; 
1 và đi qua điểm A2;3 .
A. y   x  2 1 . B. 2 y x 1.
C. y   x  2 1 . D. 2 y x 1. Hướng dẫn giải Chọn D.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 151
Trần Đình Cư. SĐT: 0834332133
Parabol P có dạng 2
y ax bx c a  0 .
Do I P  c  1  . b I 0; 
1 là đỉnh của P   0  b  0 . 2a
Lại có A2;3P  3  4a  2b c a 1. Nên P 2 : y x 1.
Câu 10. Đồ thị dưới đây là của hàm số nào sau đây? A. 2
y  x  2x  3 . B. 2
y x  2x  2 . C. 2
y  2x  4x  2 . D. 2
y x  2x 1. Hướng dẫn giải Chọn D.
Do parabol có bề lõm quay lên nên a  0 , từ đó ta loại A. b
Trục đối xứng của parabol là x  
1 nên ta loại B. 2a
Khi x  0 thì y  1 nên loại C.
Vậy đồ thị trên là của hàm số 2
y x  2x 1.
Câu 11. Tìm m để Parabol P 2
: y mx  2x  3 có trục đối xứng đi qua điểm A2;3 . 1 A. m  2 . B. m  1  . C. m 1. D. m  . 2 Hướng dẫn giải Chọn D.
Với m  0 ta có phương trình y  2x  3 là phương trình đuồng thẳng nên loại m  0 .
Với m  0 . Ta có phương trình của Parabol: 2  1
Trục đối xứng: x    x  . 2m m
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 152
Trần Đình Cư. SĐT: 0834332133 1
Trục đối xứng đi qua điểm A2;3 nên 2  1  m  . m 2
Câu 12. Cho parabol P 2
: y ax bx c,a  0 có đồ thị như hình bên. Khi đó 2a b  2c có giá trị là y 1 -1 O 2 3 x -4 A. 9  . B. 9 . C. 6  . D. 6 . Hướng dẫn giải Chọn C. Parabol P 2
: y ax bx c,a  0 đi qua các điểm A 1  ; 0 , B1;
 4 , C 3; 0
a b c  0 a  1  
nên có hệ phương trình: a b c  4   b   2  . 9
a 3b c  0   c  3  
Khi đó: 2a b  2c  2.1 2  2 3    6  . Câu 13. Cho hàm số 2
y  x  2x 1. Chọn câu sai.
A. Đồ thị hàm số có trục đối xứng x  1 .
B. Hàm số không chẵn, không lẻ.
C. Hàm số tăng trên khoảng ;  1 .
D. Đồ thị hàm số nhận I 1;4 làm đỉnh. Hướng dẫn giải Chọn D. 2 
Ta có a  1 , b  2 , c  1 nên đồ thị có trục đối xứng là x    và tọa độ    1  2. 1
đỉnh của parabol là I 1;2 . 1 Câu 14. Cho parabol 2
y ax bx  4 có trục đối xứng là đường thẳng x  và đi qua điểm 3
A1;3 . Tổng giá trị a  2b là 1 1 A.  . B. 1. C. . D. 1  . 2 2
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 153
Trần Đình Cư. SĐT: 0834332133 Hướng dẫn giải Chọn B. 1 Vì parabol 2
y ax bx  4 có trục đối xứng là đường thẳng x  và đi qua điểm A1;3 3 a  b  4  3  a  b  1  a  3  Nên ta có:  b 1       
2a  3b  0 b   2  2a 3 Do đó: 2 a b  3   4 1
Câu 15. Để đồ thị hàm số 2 2
y mx  2mx m 1 m  0 có đỉnh nằm trên đường thẳng
y x  2 thì m nhận giá trị nằm trong khoảng nào dưới đây? A. 2; 6 . B.  ;   2. C. 0; 2 . D.  2;  2 . Hướng dẫn giải Chọn D. Đồ thị hàm số 2 2
y mx  2mx m 1 m  0 có đỉnh là I  2
1;  m m   1 . Để I  2
1;  m m  
1 nằm trên đường thẳng y x  2 thì 2
m m 1  1 
m  0 l 2
m m  0   . Vậy m  1   2;  2 . m  1   n
Câu 16. Cho parabol P 2
: y ax bx  2. Xác định hệ số a , b biết P có đỉnh I 2; 2   . A. a  1  , 4 b  . B. a  1, 4 b  . C. a  1, 4 b   . D. a  4 , 1 b   . Hướng dẫn giải Chọn C.
+ Điều kiện: a  0 .  b   2
4a b  0 a 1
+ P có đỉnh I 2; 2
  nên ta có hệ:  2a     .
4a  2b  4  b   4  2  2   . a 2  . b 2  2
Câu 17. Parabol P 2 : y  2
x ax b có điểm M 1;3 với tung độ lớn nhất. Khi đó giá trị của b là A. 5 . B. 1. C. 2  . D. 3  . Hướng dẫn giải Chọn B.
Do bề lõm của P quay xuống và M có tung độ lớn nhất nên M là đỉnh của P .
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 154
Trần Đình Cư. SĐT: 0834332133 a
Ta có M 1;3 là đỉnh của parabol nên  1  a  4  . 4  Suy ra 2 y  2
x  4x b qua M 1;3 nên b 1.
Câu 18. Xác định các hệ số a và b để Parabol P 2
: y ax  4x b có đỉnh I  1  ; 5   . a  3 a  3 a  2 a  2 A.  . B.  . C.  . D.  . b   2  b   2 b   3 b   3  Hướng dẫn giải Chọn C. 4 Ta có: x  1     1   a  2. I 2a
Hơn nữa: I P nên 5
  a  4  b b  3.
Câu 19. Cho hàm số    2 y
f x ax bx c có đồ thị như hình vẽ. Đặt 2
  b  4ac , tìm dấu của a và . y
y f x 4 O x 1 4
A. a  0 ,   0 .
B. a  0 ,   0 .
C. a  0 ,   0 . D. a  0 , ,   0 . Hướng dẫn giải Chọn A.
* Đồ thị hàm số là một Parabol quay lên nên a  0 và đồ thị hàm số cắt trục Ox tại hai
điểm phân biệt nên   0 .
Câu 20. Cho hàm số    2 y
f x ax bx c . Biểu thức f x  3  3 f x  2  3 f x   1 có giá trị bằng A. 2
ax bx c . B. 2
ax bx c . C. 2
ax bx c . D. 2
ax bx c . Lời giải Chọn D
f x    ax  2  bx   2 3 3
3  c ax  6a bx  9a  3b c .
f x    ax  2  bx   2 2 2
2  c ax  4a bx  4a  2b c .
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 155
Trần Đình Cư. SĐT: 0834332133
f x    ax  2  bx   2 1 1
1  c ax  2a bx a b c .
f x    f x    f x   2 3 3 2 3
1  ax bx c .
Dạng 3: Đồ thị hàm số bậc hai 1. Phương pháp
Để vẽ đường parabol y  2
ax  bx c ta có thể thực hiện các bước như sau:  b  
– Xác định toạ độ đỉnh I   ;  .  2a 4a b
– Xác định trục đối xứng x  
và hướng bề lõm của parabol. 2a
– Xác định một số điểm cụ thể của parabol (chẳng hạn, giao điểm của parabol với các
trục toạ độ và các điểm đối xứng với chúng qua trục trục đối xứng).
– Căn cứ vào tính đối xứng, bề lõm và hình dáng parabol để vẽ parabol.
Để vẽ đồ thị hàm số y  2
ax  bx c ta lần lượt làm như sau:
Trước hết ta vẽ đồ thị P y ax2 ( ) :  bx c Ta có:  2
ax2  bx c,
khi ax2  bx c  0
y ax bx c  ax2 bxc,
khi ax2  bx c   0
Vậy đồ thị hàm số y  2
ax  bx c bao gồm hai phần
 Phần 1: Chính là đồ thị (P) lấy phần phía trên trục Ox
 Phần 2: Lấy đối xứng phần đồ thị (P) phía dưới trục Ox qua trục Ox.
Vẽ đồ thị hàm số (P1) và (P2)
2. Các ví dụ rèn luyện kĩ năng 3. Bài tập trắc nghiệm Câu 1. Cho hàm số 2
y ax bx c có đồ thị như hình bên dưới. Khẳng định nào sau đây đúng? y x O ` A. a  0, 0 b  , c  0 . B. a  0, 0 b  , c  0 .
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 156
Trần Đình Cư. SĐT: 0834332133 C. a  0, 0 b  , c  0 . D. a  0, 0 b  , c  0 . Hướng dẫn giải Chọn A.
Parabol có bề lõm quay lên  a  0 loại D.
Parabol cắt trục tung tại điểm có tung độ âm nên c  0 loại B, C. Chọn A. Câu 2. Parabol 2
y  x  2x  3 có phương trình trục đối xứng là A. x  1  . B. x  2 . C. x  1. D. x  2  . Hướng dẫn giải Chọn C. b Parabol 2
y  x  2x  3 có trục đối xứng là đường thẳng x    x  1. 2a Câu 3. Cho hàm số: 2
y x  2x 1, mệnh đề nào sai:
A. Đồ thị hàm số nhận I 1; 2   làm đỉnh.
B. Hàm số nghịch biến trên khoảng   ;1 .
C. Hàm số đồng biến trên khoảng 1; .
D. Đồ thị hàm số có trục đối xứng: x  2  . Hướng dẫn giải Chọn D. b
Trục đối xứng của đồ thị hàm số là đường thẳng x    1. 2a Câu 4.
Parabol P 2 : y  2
x  6x  3 có hoành độ đỉnh là? 3 3 A. x  3  . B. x  . C. x   . D. x  3 . 2 2 Hướng dẫn giải Chọn A. b 6 3
Hoành độ đỉnh của parabol P là: x     . 2a 4 2 Câu 5.
Viết phương trình trục đối xứng của đồ thị hàm số 2
y x  2x  4 . A. x  1. B. y  1. C. y  2 . D. x  2 . Hướng dẫn giải Chọn A.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 157
Trần Đình Cư. SĐT: 0834332133 Đồ thị hàm số 2
y ax bx c với 0
a  có trục đối xứng là đường thẳng có phương b trình x   . 2a Vậy đồ thị hàm số 2
y x  2x  4 có trục đối xứng là đường thẳng có phương trình x 1. Câu 6.
Trục đối xứng của parabol 2
y  2x  2x 1 là đường thẳng có phương trình 1 1 A. x  1. B. x  . C. x  2 . D. x   . 2 2 Hướng dẫn giải Chọn D. 2 1
Phương trình của trục đối xứng là x     . 2.2 2 Câu 7.
Tọa độ đỉnh I của parabol 2
y x  2x  7 là A. I  1  ; 4   .
B. I 1; 6 . C. I 1; 4   . D. I  1  ; 6 . Hướng dẫn giải Chọn B. 2
Đỉnh I : x   1, 2
y  1  2.1 7  6 . Vậy I 1; 6 . 2.1 Câu 8.
Cho parabol P 2
: y  3x  2x 1. Điểm nào sau đây là đỉnh của P ?  1 2   1  2   1 2   A. I 0;  1 . B. I ;   . C. I ;   . D. I ;   .  3 3   3 3   3 3  Hướng dẫn giải Chọn B. b  1 Ta có: x   nên loại A và C. 2a 3 1 2
Khi x   y  . Do đó, Chọn B. 3 3 Câu 9.
Cho hàm số bậc hai 2
y ax bx c a  0 có đồ thị P , đỉnh của P được xác định bởi công thức nào?  b    b   A. I  ;    . B. I  ;    .  2a 4a   a 4a   b    b   C. I ;   . D. I  ;    .  a 4a   2a 2a
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 158
Trần Đình Cư. SĐT: 0834332133 Hướng dẫn giải Chọn A. b  
Đỉnh của parabol P 2
: y ax bx c a  0 là điểm I  ;    .  2a 4a
Câu 10. Cho hàm số 2
y ax bx c a  0 . Khẳng định nào sau đây là sai? b
A. Đồ thị của hàm số có trục đối xứng là đường thẳng x   . 2a
B. Đồ thị của hàm số luôn cắt trục hoành tại hai điểm phân biệt.  b
C. Hàm số đồng biến trên khoảng  ;    .  2a   b
D. Hàm số nghịch biến trên khoảng ;     .  2a Hướng dẫn giải Chọn B.
Dựa vào sự biến thiên của hàm số 2
y ax bx c a  0 ta thấy các khẳng định A, C, D đúng
Khẳng định B sai vì có những hàm số bậc hai không cắt trục hoành như hàm 9 2
y  2x  3x  8
Câu 11. Cho hàm số y  m   2
1 x  2m  2 x m  3 m  
1 P . Đỉnh của P là S  1  ; 2  
thì m bằng bao nhiêu: 3 2 1 A. . B. 0 . C. . D. . 2 3 3 Hướng dẫn giải Chọn A. m  2 3
Do đỉnh của P là S  1  ; 2   suy ra 1   m  . m 1 2
Câu 12. Đồ thị hình bên dưới là đồ thị của hàm số nào? y 1 O x 1 A. 2 y  2
x  3x 1. B. 2
y  x  3x 1.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 159
Trần Đình Cư. SĐT: 0834332133 C. 2
y  2x  3x 1. D. 2
y x  3x 1 . Hướng dẫn giải Chọn C.
Đồ thị cắt trục tung tại điểm có tung độ bằng 1
Đồ thị cắt trục hoành tại điểm có hoành độ bằng 1, phương trình hoành độ giao điểm phải x 1
có nghiệm x  1, ta chỉ có phương trình 2 2x 3x 1 0      1  x   2
Câu 13. Đồ thị hình bên dưới là đồ thị của hàm số nào? y 1 O x 1 A. 2
y x  3x 1 . B. 2
y  2x  3x 1. C. 2
y  x  3x 1. D. 2 y  2
x  3x 1. Hướng dẫn giải Chọn B.
Vì bề lõm hướng lên trên nên a  0  loại đáp án C, D  1 
Đồ thì giao trục Ox tại điểm 1;0 và ;0    loại A.  2  Câu 14. Cho hàm số 2
y ax bx c có đồ thị như hình vẽ, thì dấu các hệ số của nó là
A. a  0,b  0, c  0 .
B. a  0,b  0, c  0 .
C. a  0,b  0, c  0 .
D. a  0,b  0, c  0 .
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 160
Trần Đình Cư. SĐT: 0834332133 Hướng dẫn giải Chọn B.
Đồ thị là parabol có bề lõm hướng xuống dưới nên a  0 .
Đồ thị cắt chiều dương trục Oy nên c  0 . b
Trục đối xứng x  
 0 , mà a  0 , nên b  0. 2a Câu 15. Hàm số 2
y  x  2x  3 có đồ thị là hình nào trong các hình sau? y y 4 4 3 3 1 1 2 1 O 1 2 3 4 x 3 2 1 O 1 2 3 4 x 1 1 A. B. y y 6 4 5 3 4 3 1 1 3 2 1  O 1 2 3 4 x 1   3 2 1  5  4 O 1 2 x 1  C. D. Hướng dẫn giải Chọn A. Do a  1
 nên đồ thị lõm xuống dưới  Loại C. b  
Đồ thị có đỉnh I  ;   I   1;4  2a 4a Câu 16. Cho hàm số 2
y ax bx c có đồ thị như hình bên. Khẳng định nào sau đây đúng?
A. a  0,b  0,   0 .
B. a  0,b  0,   0 .
C. a  0,b  0,   0 .
D. a  0,b  0,   0 . Hướng dẫn giải
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 161
Trần Đình Cư. SĐT: 0834332133 Chọn B.
Quan sát bề lõm của parabol như hình vẽ ta có a  0 loại C. và D. , parabol cắt trục Ox
tại hai điểm phân biệt nên   0 . Cho x  0 thì giao của parabol với trục tung Oy là b  0 .
Câu 17. Hàm số nào có đồ thị như hình vẽ sau y O x 1  A. 2
y x  3x 1. B. 2 y  2
x  5x 1. C. 2
y  2x  5x 1. D. 2 y  2  x  5x . Hướng dẫn giải Chọn B.
Do bề lõm parabol hướng xuống nên a  0 và qua A0;  1 . Câu 18. Cho hàm số 2
y ax bx c có đồ thị như hình vẽ dưới đây. Mệnh nào sau đây đúng? y O x
A. a  0 , b  0 , c  0 .
B. a  0 , b  0 , c  0 .
C. a  0 , b  0 , c  0 .
D. a  0 , b  0 , c  0 . Hướng dẫn giải Chọn B.
Đồ thị có bề lõm quay lên trên  a  0 . Loại đáp án D. b
Trục đối xứng x    0  .
a b  0  b  0 . 2a Câu 19. Cho hàm số 2
y ax bx c có đồ thị như hình dưới đây. Khẳng định nào sau đây là đúng?
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 162
Trần Đình Cư. SĐT: 0834332133 y y x
A. a  0 , b  0 , c  0 .
B. a  0 , b  0 , c  0 .
C. a  0 , b  0 , c  0 .
D. a  0 , b  0 , c  0 . Hướng dẫn giải Chọn C.
Nhìn vào đồ thị ta có:
Bề lõm hướng xuống  a  0 . b b
Hoành độ đỉnh x    0   0  b  0 . 2a 2a
Đồ thị hàm số cắt trục tung tại điểm có tung độ âm  c  0 .
Do đó: a  0 , b  0 , c  0 .
Câu 20. Hàm số nào sau đây có đồ thị như hình bên? y 2 1 x 5 O 1 2 3 2 -3 4 6 A. 2
y  x  2x  3 . B. 2
y  x  4x  3 . C. 2
y x  4x  3 . D. 2
y x  2x  3 . Hướng dẫn giải Chọn B
Dựa vào đồ thị suy ra: a  0 và hoành độ đỉnh là 2. 2
y  x  4x  3  a  1  ; I 2;  1
Câu 21. Hàm số nào sau đây có đồ thị như hình bên
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 163
Trần Đình Cư. SĐT: 0834332133 y 3 2 1 x 5  4 3  2 1 1 2 3 4 5 1 2 3  A. 2
y x  3x  3 . B. 2
y  x  5 x  3. C. 2
y  x  3 x  3 . D. 2
y  x  5x  3 . Hướng dẫn giải Chọn B.
Quan sát đồ thị ta loại A. và D. Phần đồ thị bên phải trục tung là phần đồ thị P của  5 13  hàm số 2
y  x  5x  3 với x  0 , tọa độ đỉnh của P là ; 
 , trục đối xứng là  2 4 
x  2,5 . Phần đồ thị bên trái trục tung là do lấy đối xứng phần đồ thị bên phải của
Pqua trục tung Oy . Ta được cả hai phần là đồ thị của hàm số 2
y  x  5 x  3.
Câu 22. Đồ thị hàm số 2
y x  6 x  5 .
A. có tâm đối xứng I 3; 4  .
B. có tâm đối xứng I 3; 4
  và trục đối xứng có phương trình x  0 .
C. không có trục đối xứng.
D. có trục đối xứng là đường thẳng có phương trình x  0 . Hướng dẫn giải Chọn D. 2
y x  6x  5 khi x  0 C  1  1 Ta có: 2
y x  6 x  5   2
y x  6x  5 khi x  0 C  2  2 
Đồ thị C của hàm số 2
y x  6 x  5 gồm hai phần
Phần đồ thị C : là phần đồ thị của hàm số 2
y x  6x  5 nằm bên phải trục tung 1  1
Phần đồ thị C : là phần đồ thị của hàm số 2
y x  6x  5 có được bằng cách lấy đối 2  2
xứng phần đồ thị C qua trục tung 1 
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 164
Trần Đình Cư. SĐT: 0834332133
Ta có đồ thị C như hình vẽ C2 C1
Vậy: đồ thị C có trục đối xứng có phương trình x  0 . Câu 23. hàm số 2
y ax bx c có đồ thị như hình vẽ bên. Mệnh đề nào dưới đây đúng? y O x 1 
A. a  0 , b  0 , c  0 .
B. a  0 , b  0 , c  0 .
C. a  0 , b  0 , c  0 .
D. a  0 , b  0 , c  0 . Hướng dẫn giải Chọn D. Quan sát đồ thị ta có:
Đồ thị quay bề lõm xuống dưới nên a  0 ; có hoành độ đỉnh b b x  
 0   0  b  0 . I 2a a
Lại có: đồ thị cắt Ox tại điểm có tung độ âm nên c  0 .
Vậy a  0 , b  0 , c  0 .
Câu 24. Cho parabol P 2
: y ax bx c a  0 có đồ thị như hình bên. Tìm các giá trị m để phương trình 2
ax bx c m có bốn nghiệm phân biệt.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 165
Trần Đình Cư. SĐT: 0834332133 y 4 I 3 2 1 3  1  O 2  1 2 3 x 1 2  3  A. 1   m  3 .
B. 0  m  3 .
C. 0  m  3 . D. 1   m  3 . Hướng dẫn giải Chọn B. b   2 b   4  a
Quan sát đồ thị ta có đỉnh của parabol là I 2;3 nên  2a   . 
4a  2b c  3
3  4a  2b c b   4  aa  1 
Mặt khác P cắt trục tung tại 0;  1  nên c  1  . Suy ra    .
4a  2b  4 b   4 P 2
: y  x  4x 1 suy ra hàm số 2
y  x  4x 1 có đồ thị là là phần đồ thị phía trên
trục hoành của P và phần có được do lấy đối xứng phần phía dưới trục hoành của P , như hình vẽ sau: y 4 I 3 2 1 3  1  O 2 1 2 3 x 1 y m 2 3 Phương trình 2
ax bx c m hay 2
x  4x 1  m có bốn nghiệm phân biệt khi đường
thẳng y m cắt đồ thị hàm số hàm số 2
y  x  4x 1 tại bốn điểm phân biệt. Suy ra 0  m  3.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 166
Trần Đình Cư. SĐT: 0834332133
Dạng 4: Sự tương giao 1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1: Cho parabol P 2
: y x  2x m 1. Tìm tất cả các giá trị thực của m để parabol cắt Ox
tại hai điểm phân biệt có hoành độ dương. Lời giải
Phương trình hoành độ giao điểm của P và trục Ox là 2
x  2x m 1  0.   1
Để parabol cắt Ox tại hai điểm phân biệt có hoành độ dương khi và chỉ khi   1 có hai
  2  m  0  m  2
nghiệm dương  S  2  0    1  m  2.  m  1
P m 1  0 
Ví dụ 2: Tìm tất cả các giá trị thực của tham số m để đường thẳng d : y mx cắt đồ thị hàm số P 3 2
: y x  6x  9x tại ba điểm phân biệt. Lời giải
Phương trình hoành độ giao điểm của P với d là 3 2
x  6x  9x mx    xx 0 2
x  6x  9  m  0   2
x  6x  9  m  0.   1
Để P cắt d tại ba điểm phân biệt khi và chỉ  
1 có hai nghiệm phân biệt khác 0   0 m  0 m  0       . 2
0  6.0  9  m  0 9   m  0 m  9
Ví dụ 2: Tìm tất cả các giá trị thực của tham số m để phương trình 2
x  5x  7  2m  0 có nghiệm thuộc đoạn 1;5 . Lời giải Ta có 2 2
x  5x  7  2m  0  x  5x  7  2 . m *
Phương trình * là phương trình hoành độ giao điểm của parabol P 2
: x  5x  7 và
đường thẳng y  2m (song song hoặc trùng với trục hoành).
Ta có bảng biến thiên của hàm số 2
y x  5x  7 trên 1;5 như sau:
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 167
Trần Đình Cư. SĐT: 0834332133 5 x -¥ 1 5 +¥ 2 +¥ +¥ y 7 3 3 4 3 
Dựa vào bảng biến ta thấy x 1;  5 thì y  ;7  . 4   
Do đo để phương trình * có nghiệm x   3 3 7 1;5   2
m  7    m   . 4 8 2
3. Bài tập trắc nghiệm Câu 1. Cho hàm số 2
y ax bx c a  0 có đồ thị là parabol P . Xét phương trình 2
ax bx c  0  
1 . Chọn khẳng định sai:
A. Số giao điểm của parabol P với trục hoành là số nghiệm của phương trình  1 .
B. Số nghiệm của phương trình  
1 là số giao điểm của parabol P với trục hoành.
C. Nghiệm của phương trình  
1 là giao điểm của parabol P với trục hoành.
D. Nghiệm của phương trình  
1 là hoành độ giao điểm của parabol P với trục hoành. Hướng dẫn giải Chọn C. Câu 2.
Tọa độ giao điểm của đường thẳng d : y  x  4 và parabol 2
y x  7x 12 là A.  2;  6 và  4;  8 .
B. 2;2 và 4;8. C. 2; 2   và 4;0 .
D. 2;2 và 4;0 . Hướng dẫn giải Chọn D.
Phương trình hoành độ giao điểm:
x  2  y  2 2 2
x  7x 12  x  4  x  6x  8  0  
x  4  y  0 Câu 3.
Nghiệm của phương trình 2
x – 8x  5  0 có thể xem là hoành độ giao điểm của hai đồ thị hàm số: A. 2
y x và y  8x  5 . B. 2
y x và y  8x 5. C. 2
y x và y  8x  5. D. 2
y x và y  8x  5. Hướng dẫn giải
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 168
Trần Đình Cư. SĐT: 0834332133 Chọn C. Ta có 2
x – 8x  5  0  2
x  8x  5 .
Do đó nghiệm của phương trình 2
x – 8x  5  0 có thể xem là hoành độ giao điểm của hai đồ thị hàm số 2
y x và y  8x 5. Câu 4.
Giao điểm của parabol P 2
: y x  3x  2 với đường thẳng y x 1 là A.  1  ;2 ; 2;  1 .
B. 1;0 ; 3;2. C. 2;  1 ; 0;  1  . D. 0;  1  ;  2;  3   . Hướng dẫn giải Chọn B.
Phương trình hoành độ giao điểm của P và d  là x  1 2
x  3x  2  x 1 2
x  4x  3  0   . x  3
Vậy hai giao điểm của P và d  là 1;0 ; 3;2. Câu 5.
Cho đường thẳng d : y x 1 và Parabol P 2
: y x x  2 . Biết rằng d cắt P tại
hai điểm phân biệt A , B . Khi đó diện tích tam giác OAB bằng 3 5 A. 4 . B. 2 . C. . D. . 2 2 Hướng dẫn giải Chọn C.
Phương trình hoành độ giao điểm của d và P là 2
x x  2  x 1 2
x  2x  3  0 .
Phương trình này có a b c  0 nên có hai nghiệm x  1  , x  3 . 1 2 Suy ra A 1
 ;0 và B3;4 . 1 3
Diện tích tam giác OAB bằng .1.3  . 2 2 Câu 6.
Biết đường thẳng d : y mx cắt Parabol P 2
: y x x 1 tại hai điểm phân biệt A , B .
Khi đó tọa độ trung điểm I của đoạn thẳng AB là 2
1 m m m  2
1 m m  2m  3  A. I ;   . B. I ;   .  2 2   2 4   1 3   1 m C. I ;   . D. I ;   .  2 4   2 2  Hướng dẫn giải
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 169
Trần Đình Cư. SĐT: 0834332133 Chọn A.
Xét phương trình hoành độ giao điểm của d và P : 2
mx x x 1 2
x  m   1 x 1  0
Vì hoành độ giao điểm x , x là hai nghiệm của phương trình nên ta có tọa độ trung A Bx xx xm 1 A B x A Bx x I   I   I  2 2
1 m m m  điểm 2 I là 2       I ;   . y ym  x x 2 m m  2 2 A B A B y   y   Iy  2 I  2 I  2 Câu 7.
Tìm tất cả các giá trị của tham số m để đường thẳng d : y  2x  3 cắt parabol 2
y x  m  2 x m tại hai điểm phân biệt nằm cùng phía với trục tung Oy. A. m  3  . B. m  3  . C. m  3 . D. m  0 . Hướng dẫn giải Chọn B.
Xét phương trình hoành độ giao điểm: 2
x  m  2 x m  2x  3  2
x mx m  3  0 .   1
Để đường thẳng d cắt parabol tại hai điểm phân biệt nằm cùng phía với trục tung Oy thì   0  2
m  4m 12  0 phương trình  
1 có hai nghiệm phân biệt cùng dấu   c    0  m  3  0 am  3  . Câu 8.
Hỏi có bao nhiêu giá trị m nguyên trong nửa khoảng  10  ; 4
  để đường thẳng
d : y  m  
1 x m  2 cắt Parabol P 2
: y x x  2 tại hai điểm phân biệt cùng phía với trục tung? A. 6 . B. 5 . C. 7 . D. 8 . Hướng dẫn giải Chọn A.
Xét phương trình: m   2 2
1 x m  2  x x  2  x x m  2  m  4  0
Để đường thẳng d cắt Parabol P tại hai điểm phân biệt cùng phía với trục tung vậy   
 m  22  4m  4 2 0  0
m  8m  20  0, m  điều kiện là      P  0 m  4  0 m  4 
Vậy trong nửa khoảng 10  ; 4
  có 6 giá trị nguyên m .
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 170
Trần Đình Cư. SĐT: 0834332133 Câu 9.
Tìm m để Parabol P 2
y x  m   2 : 2
1 x m  3 cắt trục hoành tại 2 điểm phân biệt
có hoành độ x , x sao cho x .x  1. 1 2 1 2 A. m  2 .
B. Không tồn tại m . C. m  2  . D. m  2  . Hướng dẫn giải Chọn A.
Phương trình hoành độ giao điểm của P với trục hoành: 2
x  m   2 2
1 x m  3  0   1 .
Parabol P cắt trục hoành tại 2 điểm phân biệt có hoành độ x , x sao cho x .x 1 1 2 1 2   
1 có 2 nghiệm phân biệt x , x thỏa x .x  1 1 2 1 2
  m  2 1   2 m  3  0 m  2       m  2 . 2    m  2 m 3 1 
Câu 10. Cho hai hàm số 2
y x m 1 x m , y  2x m 1. Khi đồ thị hai hàm số cắt nhau 1   2
tại hai điểm phân biệt thì m có giá trị là A. m  0 . B. m  0 . C. m tùy ý. D. không có giá trị nào. Hướng dẫn giải Chọn C.
Phương trình hoành độ giao điểm: 2
x  m  
1 x m  2x m 1 2
x  m 3 x 1 0  1 .
Khi đồ thị hai hàm số cắt nhau tại hai điểm phân biệt thì pt  
1 có hai nghiệm phân biệt
   m  2
3  4  0 luôn đúng m   .
Câu 11. Đường thẳng d : m  2 x my  6  luôn đi qua điểm: m A. 3; 3   B. 2;  1 C. 1; 5   D. 3;  1 Hướng dẫn giải Chọn A.
m2 x my  6
  x ym  2x  6  0  x y  0 x  3
Phương trình  luôn đúng với mọi m khi     2  x  6  0 y  3 
Vậy d luôn đi qua điểm cố định 3; 3   . m
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 171
Trần Đình Cư. SĐT: 0834332133
Câu 12. Tìm tất cả các giá trị m để đường thẳng y mx  3  2m cắt parabol 2
y x  3x  5 tại
2 điểm phân biệt có hoành độ trái dấu. A. m  3  . B. 3   m  4. C. m  4 . D. m  4 . Hướng dẫn giải Chọn C.
Phương trình hoành độ giao điểm: 2
x  3x  5  mx  3  2m  2
x  m  3 x  2m 8  0   * .
Đường thẳng cắt parabol tại hai điểm phân biệt có hoành độ trái dấu khi và chỉ khi phương trình  
* có hai nghiệm trái dấu  .
a c  0  2m 8  0  m  4 . Câu 13. Cho parabol 2
y ax bx c a  0 , P có đồ thị như hình vẽ: y 2  O 2 x
Biết đồ thị P cắt trục Ox tại các điểm lần lượt có hoành độ là 2 , 2 . Tập nghiệm của
bất phương trình y  0 là A.  ;
  22; . B.  2;  2 . C.  2;  2. D.  ;
  2 2;  . Hướng dẫn giải Chọn B
Dựa vào đồ thị ta thấy y  0 khi x  2;  2.
Câu 14. Giá trị nào của m thì phương trình m   2
3 x  m  3 x  m   1  0   1 có hai nghiệm phân biệt?  3 
A. m   \   3 . B. m   ;    1;     \  3 .  5   3   3  C. m   ;1   .
D. m   ;     .  5   5  Hướng dẫn giải Chọn B.m  3  0 
Phương trình có hai nghiệm phân biệt     
m 32  4m 3m  1  0
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 172
Trần Đình Cư. SĐT: 0834332133 m  3 m  3    3  3  
  x    m ;  1;     \  3 . 2 5
m  2m  3  0  5   5  x 1
Câu 15. Có bao nhiêu giá trị thực của m để đường thẳng d : y  4x  2m tiếp xúc với parabol
Py  m   2 :
2 x  2mx  3m 1 A. 3 . B. 1. C. 2 . D. 0 . Hướng dẫn giải Chọn B.
Phương trình hoành độ giao điểm của d và P là m   2
2 x  2mx  3m 1  4x  2m  m   2
2 x  2m  2 x m 1  0 .
d tiếp xúc với P  phương trình hoành độ giao điểm của d và P có nghiệm kép. m  2 m  2  0    m  2 3     m  .    
m  22 m  2m  1  0  3  2 m   2
Vậy có 1 giá trị m để đường thẳng d tiếp xúc với P .
Câu 16. Cho hàm số f x xác định trên có đồ thị như hình vẽ.
Phương trình 2 f x 1  0 có bao nhiêu nghiệm? A. 1. B. 3. C. 2 . D. 4 . Hướng dẫn giải Chọn B.
f x    f x 1 2 1 0  . 2
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 173
Trần Đình Cư. SĐT: 0834332133
Số nghiệm phương trình  
1 là số giao điểm của đồ thị hàm số y f x và đường thẳng 1 y  . 2
Dựa vào đồ thị hàm số suy ra phương trình đã cho có 3 nghiệm phân biệt.
Câu 17. Cho hàm số y f x có bảng biến thiên như sau:
Với giá trị nào của tham số m thì phương trình f x 1  m có bốn nghiệm phân biệt. A. m  1.
B. 1  m  3.
C. 0  m  1. D. m  3 . Hướng dẫn giải Chọn B.
Dựa vào bảng biến thiên của hàm số y f x , suy ra bảng biến thiên của hàm số
y f x 1 . x  0 1    1 3 f x 0 0 0
Từ BBT suy ra phương trình f x 1  m có bốn nghiệm phân biệt khi 1 m  3. Vậy 1  m  3.
Câu 18. Cho hàm số   2
f x ax bx c đồ thị như hình bên dưới. Hỏi với những giá trị nào của
tham số m thì phương trình f x  1  m có đúng 3 nghiệm phân biệt. y 3 x O 2 -1 A. 2   m  2 . B. m  3 . C. m  3 . D. m  2 . Hướng dẫn giải Chọn D.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 174
Trần Đình Cư. SĐT: 0834332133 Hàm số   2
f x ax bx c có đồ thị là C , lấy đối xứng phần đồ thị nằm bên phải Oy
của C qua Oy ta được đồ thị C của hàm số y f x  .
Dựa vào đồ thị, phương trình f x  1  m   x   m 1 có đúng 3 nghiệm phân biệt khi
m 1  3  m  2 .
Câu 19. Cho hàm số   2
f x ax bx c đồ thị như hình bên dưới. Hỏi với những giá trị nào của
tham số m thì phương trình f x 1  m có đúng 2 nghiệm phân biệt. y 3 x O 2 -1 m  0 m  0 A.  . B.  . C. m  1  . D. m  0 . m  1  m  1  Hướng dẫn giải Chọn B.
+ Phương trình  f x  m 1.
+ Đồ thị hàm số y f x có dạng:
+ Dựa vào đồ thị, để phương trình f x  m 1 có hai nghiệm phân biệt thì:
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 175
Trần Đình Cư. SĐT: 0834332133 m 1  1 m  0    . m 1  0 m  1 
Câu 20. Hỏi có bao nhiêu giá trị m nguyên trong nửa khoảng 0;2017 để phương trình 2
x  4 x  5  m  0 có hai nghiệm phân biệt? A. 2016 . B. 2008 . C. 2009 . D. 2017 . Hướng dẫn giải Chọn B. PT: 2 2
x  4 x  5  m  0  x  4 x  5  m .
Số nghiệm phương trình  
1  số giao điểm của đồ thị hàm số 2
y x  4 x  5 P và
đường thẳng y m . Xét hàm số 2
y x  4x  5 P có đồ thị như hình 1. 1  y y y 1  2 5 5 2  2 5 9 O x O x 5 5 5 9 9 5 O x 5 Hình 1. Hình 2. Hình 3. Xét hàm số 2
y x  4 x  5 P là hàm số chẵn nên có đồ thị nhận Oy làm trục đối 2  xứng. Mà 2 2
y x  4 x  5  x  4x  5 nếu x  0 . Suy ra đồ thị hàm số P gồm hai 2  phần:
Phần 1: Giữ nguyên đồ thị hàm số P phần bên phải Oy . 1 
Phần 2 : Lấy đối xứng phần 1 qua trục Oy .
Ta được đồ thị P như hình 2. 2  2
x  4 x  5   y  0 Xét hàm số 2
y x  4 x  5 P , ta có: y   .    2
x  4 x  5  y  0
Suy ra đồ thị hàm số P gồm hai phần:
Phần 1: Giữ nguyên đồ thị hàm số P phần trên Ox . 2 
Phần 2 : Lấy đối xứng đồ thị hàm số P phần dưới Ox qua trục Ox . 2 
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 176
Trần Đình Cư. SĐT: 0834332133
Ta được đồ thị P như hình 3.
Quan sát đồ thị hàm số P ta có: Để 2 x  4 x 5   m   1 có hai nghiệm phân m  9 biệt   . m  0 m   Mà    . m    m 10;11;12;...;  2017 0; 2017
Câu 21. Hỏi có bao nhiêu giá trị m nguyên trong nửa khoảng 0;2017 để phương trình 2
x  4 x 5  m  0 có hai nghiệm phân biệt? A. 2016 . B. 2008 . C. 2009 . D. 2017 . Hướng dẫn giải Chọn B. PT: 2 2 x  4 x 5
  m  0  x  4 x 5   m 
1 . Số nghiệm phương trình   1  số giao
điểm của đồ thị hàm số 2
y x  4 x  5 P và đường thẳng y m . Xét hàm số 2
y x  4x  5 P có đồ thị như hình 1. 1  y y y 1  2 5 5 2  2 5 9 O x O x 5 5 5 9 9 5 O x 5 Hình 1. Hình 2. Hình 3. Xét hàm số 2
y x  4 x  5 P là hàm số chẵn nên có đồ thị nhận Oy làm trục đối 2  xứng. Mà 2 2
y x  4 x  5  x  4x  5 nếu x  0 . Suy ra đồ thị hàm số P gồm hai 2  phần:
Phần 1: Giữ nguyên đồ thị hàm số P phần bên phải Oy . 1 
Phần 2 : Lấy đối xứng phần 1 qua trục Oy .
Ta được đồ thị P như hình 2. 2  2
x  4 x  5   y  0 Xét hàm số 2
y x  4 x  5 P , ta có: y   .    2
x  4 x  5  y  0
Suy ra đồ thị hàm số P gồm hai phần:
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 177
Trần Đình Cư. SĐT: 0834332133
Phần 1: Giữ nguyên đồ thị hàm số P phần trên Ox . 2 
Phần 2 : Lấy đối xứng đồ thị hàm số P phần dưới Ox qua trục Ox . 2 
Ta được đồ thị P như hình 3.
Quan sát đồ thị hàm số P ta có: Để 2
x  4 x 5  m   1 có hai nghiệm phân m  9 biệt   . m  0 m   Mà    . m    m 10;11;12;...;  2017 0; 2017
Dạng 4: Toán thực tế 1. Phương pháp
2. Các ví dụ rèn luyện kĩ năng
Ví dụ 1: Khi nuôi cá thí nghiệm trong hồ, một nhà sinh học thấy rằng: Nếu trên mỗi đơn vị diện
tích của mặt hồ có n con cá thì trung bình mỗi con cá sau một vụ cân nặng
P n  360 10n . Hỏi phải thả bao nhiêu con cá trên một đơn vị diện tích để trọng lương
cá sau một vụ thu được nhiều nhất? Hướng dẫn giải
Trọng lượng cá trên đơn vị diện tích là T    n 2
360 10 n  360n 10n    2
10 n  36n  324  324   n  2 10 18  3240  T  3240 khi n 18. max
Ví dụ 2: Cổng Arch tại thành phố St Louis của Mỹ có hình dạng là một parabol . Biết khoảng
cách giữa hai chân cổng bằng 162 m . Trên thành cổng, tại vị trí có độ cao 43m so với
mặt đất , người ta thả một sợi dây chạm đất . Vị trí chạm đất của đầu sợi dây này cách
chân cổng A một đoạn 10 m . Giả sử các số liệu trên là chính xác. Hãy tính độ cao của cổng Arch . Hướng dẫn giải
Chọn hệ trục tọa độ Oxy như hình vẽ. Phương trình Parabol P có dạng 2
y ax bx c .
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 178
Trần Đình Cư. SĐT: 0834332133
Parabol P đi qua điểm A0;0, B162;0 , M 10;43 nên ta có   c  0 c  0   2  43 43 3483 162 
a 162b c  0  a    P 2 : y   x x .  1520 1520 760 2
10 a 10b c  43    3483 b   760  2 b  4ac
Do đó chiều cao của cổng là h      185,6 m. 4a 4a
3. Bài tập trắc nghiệm 1 Câu 1.
Một chiếc cổng hình parabol có phương trình 2
y   x . Biết cổng có chiều rộng d  5 2
mét . Hãy tính chiều cao h của cổng. y O x h 5 m
A. h  4, 45 mét.
B. h  3,125 mét.
C. h  4,125 mét.
D. h  3, 25 mét. Hướng dẫn giải Chọn B.
Gọi A và B là hai điểm ứng với hai chân cổng như hình vẽ. 1
Vì cổng hình parabol có phương trình 2
y   x và cổng có chiều rộng d  5 mét nên: 2  5 25   5 25 
AB  5 và A  ;    ; B ;   .  2 8   2 8  25 25
Vậy chiều cao của cổng là    3,125 mét. 8 8 Câu 2.
Một của hàng buôn giày nhập một đôi với giá là 40 đôla. Cửa hàng ước tính rằng nếu
đôi giày được bán với giá x đôla thì mỗi tháng khách hàng sẽ mua 120  x đôi. Hỏi của
hàng bán một đôi giày giá bao nhiêu thì thu được nhiều lãi nhất? A. 80 USD. B. 160 USD. C. 40 USD. D. 240 USD. Hướng dẫn giải Chọn A.
Gọi y là số tiền lãi của cửa hàng bán giày.
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 179
Trần Đình Cư. SĐT: 0834332133
Ta có y  120  x x  40 2
 x 160x  4800  x  2 80 1600  1600 .
Dấu "  " xảy ra  x  80 .
Vậy cửa hàng lãi nhiều nhất khi bán đôi giày với giá 80 USD. Câu 3.
Dây truyền đỡ trên cầu treo có dạng Parabol ACB như hình vẽ. Đầu, cuối của dây được
gắn vào các điểm A , B trên mỗi trục AA và BB với độ cao 30 m . Chiều dài đoạn
AB trên nền cầu bằng 200 m . Độ cao ngắn nhất của dây truyền trên cầu là OC  5 m .
Gọi Q , P , H , O , I , J  , K là các điểm chia đoạn A B
  thành các phần bằng nhau.
Các thanh thẳng đứng nối nền cầu với đáy dây truyền: QQ , PP , HH  , OC , II , JJ  ,
KK gọi là các dây cáp treo. Tính tổng độ dài của các dây cáp treo? B A Q K P J H C I BQ
PH C I
J K A A. Đáp án khác. B. 36,87 m . C. 73, 75 m . D. 78, 75 m . Hướng dẫn giải Chọn D. y B A Q K P J H C I y y 30m 5m y 3 2 1 BQ
PH O I
J K Ax 200m
Giả sử Parabol có dạng: 2
y ax bx c , a  0 .
Chọn hệ trục Oxy như hình vẽ, khi đó parabol đi qua điểm A100; 30 , và có đỉnh
C 0;5. Đoạn AB chia làm 8 phần, mỗi phần 25m .  1 30
 10000a 100b c a    400  b   1 Suy ra:   0  b   0  P 2 : y x  5 . 2a   400 c  5 5   c   
Khi đó, tổng độ dài của các dây cáp treo bằng OC  2y  2y  2y 1 2 3  1 2   1 2   1 2   5  2 .25  5  2 .50  5  2 .75  5        400   400   400 
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 180
Trần Đình Cư. SĐT: 0834332133  78,75m . Câu 4.
Một doanh nghiệp tư nhân A chuyên kinh doanh xe gắn máy các loại. Hiện nay doanh
nghiệp đang tập trung chiến lược vào kinh doanh xe hon đa Future Fi với chi phí mua vào
một chiếc là 27 và bán ra với giá là 31 triệu đồng. Với giá bán này thì số lượng xe mà
khách hàng sẽ mua trong một năm là 600 chiếc. Nhằm mục tiêu đẩy mạnh hơn nữa
lượng tiêu thụ dòng xe đang ăn khách này, doanh nghiệp dự định giảm giá bán và ước
tính rằng nếu giảm 1 triệu đồng mỗi chiếc xe thì số lượng xe bán ra trong một năm là sẽ
tăng thêm 200 chiếc. Vậy doanh nghiệp phải định giá bán mới là bao nhiêu để sau khi đã
thực hiện giảm giá, lợi nhuận thu được sẽ là cao nhất. A. 30 triệu đồng. B. 29 triệu đồng.
C. 30,5 triệu đồng.
D. 29,5 triệu đồng. Hướng dẫn giải Chọn C.
Gọi x đồng là số tiền mà doanh nghiệp A dự định giảm giá; 0  x  4 . Khi đó:
Lợi nhuận thu được khi bán một chiếc xe là 31 x  27  4  x .
Số xe mà doanh nghiệp sẽ bán được trong một năm là 600  200x .
Lợi nhuận mà doanh nghiệp thu được trong một năm là
f x  4  x600  200x 2
 200x  200x  2400 .
Xét hàm số f x 2  200 
x  200x  2400 trên đoạn 0;4 có bảng biến thiên
Vậy max f x  1 2 450  x  . 0;4 2
Vậy giá mới của chiếc xe là 30,5 triệu đồng thì lợi nhuận thu được là cao nhất. Câu 5.
Khi quả bóng được đá lên, nó sẽ đạt độ cao nào đó rồi rơi xuống đất. Biết rằng quỹ đạo
của quả là một cung parabol trong mặt phẳng với hệ tọa độ Oth ,trong đó t là thời gian ,
kể từ khi quả bóng được đá lên; h là độ cao của quả bóng. Giả thiết rằng quả bóng được
đá lên từ độ cao 1, 2m . Sau đó 1 giây, nó đạt độ cao 8,5m và 2 giây sau khi đá lên, nó ở
độ cao 6m . Hãy tìm hàm số bậc hai biểu thị độ cao h theo thời gian t và có phần đồ thị
trùng với quỹ đạo của quả bóng trong tình huống trên. A. 2
y  4,9t 12, 2t 1, 2 . B. 2 y  4,
 9t 12,2t 1,2 . C. 2 y  4,
 9t 12,2t 1,2. D. 2 y  4,
 9t 12,2t 1,2. Hướng dẫn giải
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 181
Trần Đình Cư. SĐT: 0834332133 Chọn B.
Tại t  0 ta có y h  1, 2 ; tại t  1 ta có y h  8,5 ; tại t  2 , ta có y h  6 . h B h  8 , 5 6 C O 1 2 t
Chọn hệ trục Oth như hình vẽ.
Parabol P có phương trình: 2
y at bt c , với a  0 .
Giả sử tại thời điểm t thì quả bóng đạt độ cao lớn nhất h .
Theo bài ra ta có: tại t  0 thì h  1, 2 nên A0; 1,2P . Tại 1
t  thì h  8,5 nên B 1; 8,5P.
Tại t  2 thì h  6 nên C 2; 6P . c 1,2 c  1, 2  
Vậy ta có hệ:  a b c  8,5   a  4  ,9 . 4a 2b c 6     b  12, 2  
Vậy hàm số Parabol cần tìm có dạng: 2 y  4,
 9t 12,2t 1,2 .
Giáo viên có nhu cầu sở hữu file word vui lòng liên hệ. Face: Trang 182
Trần Đình Cư. SĐT: 0834332133