
































































































































Preview text:
CHƯƠNG III PHƯƠNG PHÁP TỌA ĐỘ TRONG MẶT PHẲNG
BÀI 1. PHƯƠNG TRÌNH ĐƯỜNG THẲNG
A. KIẾN THỨC CƠ BẢN CẦN NẮM
1. Vectơ chỉ phương của đường thẳng
Vectơ u được gọi là vectơ chỉ phương của đường thẳng D nếu u ¹ 0 và giá của u song song hoặc trùng với D .
Nhận xét. Một đường thẳng có vô số vectơ chỉ phương.
2. Phương trình tham số của đường thẳng
Đường thẳng D đi qua điểm M x ; y và có VTCP u = ( ; a b) 0 ( 0 0 )
ìïx = x + at ¾¾
phương trình tham số của đường thẳng D có dạng ï 0 í t Î .
ïy = y + bt ïî 0
Nhận xét. Nếu đường thẳng b D có VTCP u = ( ;
a b) thì có hệ số góc k = . a
3. Vectơ pháp tuyến của đường thẳng
Vectơ n được gọi là vectơ pháp tuyến của đường thẳng D nếu n ¹ 0 và n vuông góc với vectơ chỉ phương của D . Nhận xét.
● Một đường thẳng có vô số vectơ pháp tuyến. ● Nếu u = ( ;
a b) là một VTCP của D ¾¾ n = ( ; b a - ) là một VTPT của D .
● Nếu n = (A;B) là một VTPT của D ¾¾
u = (B;-A) là một VTPCT của D .
4. Phương trình tổng quát của đường thẳng
Đường thẳng D đi qua điểm M x ; y và có VTPT n = (A;B) 0 ( 0 0 ) ¾¾
phương trình tổng quát của đường thẳng D có dạng
A (x - x + B y - y = 0 hay Ax + By +C = 0 với C = -Ax - By . 0 ) ( 0 ) 0 0 Nhận xét. ● Nếu đường thẳng A
D có VTPT n = (A;B) thì có hệ số góc k = - . B
● Nếu A, B, C đều khác 0 thì ta có thể đưa phương trình tổng quát về dạng x y + = 1 với C C a = - , b = - . a b 0 0 A B 0 o
Phương trình này được gọi là phương trình đường thẳng theo đoạn chắn, đường thẳng này cắt Ox và
Oy lần lượt tại M (a ;0 và N (0;b . 0 ) 0 )
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 731
hệ. Face: Trần Đình Cư. SĐT: 0834332133
5. Vị trí tương đối của hai đường thẳng
Xét hai đường thẳng có phương trình tổng quát là
D : a x + b y + c = 0 và D : a x + b y + c = 0 . 1 1 1 1 2 2 2 2 ìï + + =
Tọa độ giao điểm của a x b y c 0
D và D là nghiệm của hệ phương trình: ï 1 1 1 í . 1 2
ïa x + b y + c = 0 ïî 2 2 2
● Nếu hệ có một nghiệm (x ; y thì D cắt D tại điểm M x ; y . 0 ( 0 0 ) 0 0 ) 1 2
● Nếu hệ có vô số nghiệm thì D trùng với D . 1 2
● Nếu hệ vô nghiệm thì D và D không có điểm chung, hay D song song với D . 1 2 1 2
Cách 2. Xét tỉ số ● Nếu a b c 1 1 1 = = thì D trùng với D . a b c 1 2 2 2 2 ● Nếu a b c 1 1 1 = ¹ thì D song song D . a b c 1 2 2 2 2 ● Nếu a b 1 1 ¹ thì D cắt D . a b 1 2 2 2
6. Góc giữa hai đường thẳng Cho hai đường thẳng
D : a x + b y + c = 0 có VTPT n = a ;b ; 1 ( 1 1) 1 1 1 1
D : a x + b y + c = 0 có VTPT n = a ;b . 2 ( 2 2 ) 2 2 2 2
Gọi a là góc tạo bởi giữa hai đường thẳng D và D . 1 2 Khi đó n n a a + b b
cos a = cos(n ,n ) . 1 2 . . 1 2 1 2 = = . 1 2 2 2 2 2 n . n
a + b . a + b 1 2 1 1 2 2
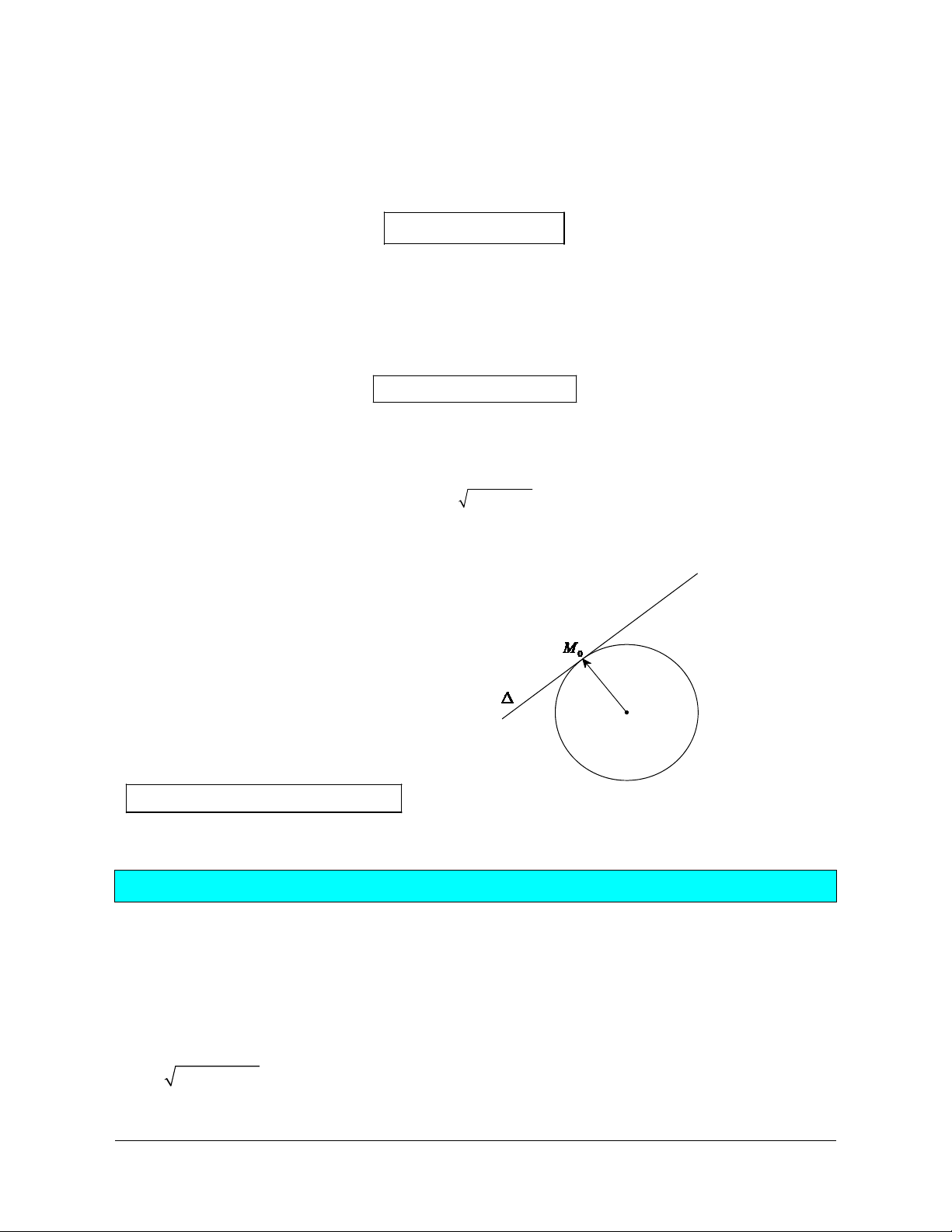
7. Khoảng cách từ một điểm đến một đường thẳng
Khoảng cách từ M x ; y đến đường thẳng D : ax +by + c = 0 được tính theo công thức 0 ( 0 0 ) + + ( ax by c d M , D) 0 0 = . 0 2 2 a + b
Nhận xét. Cho hai đường thẳng D : a x +b y + c = 0 và D : a x +b y + c = 0 cắt nhau thì phương trình 1 1 1 1 2 2 2 2
hai đường phân giác của góc tạo bởi hai đường thẳng trên là:
a x + b y + c
a x + b y + c 1 1 1 2 2 2 = . 2 2 2 2 a + b a + b 1 1 2 2
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 732
hệ. Face: Trần Đình Cư. SĐT: 0834332133
B. CÁC DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI.
Dạng 1: viết phương trình tổng quát của đường thẳng.
1. Phương pháp giải:
Để viết phương trình tổng quát của đường thẳng D ta cần xác định - Điểm ( A x ;y ) Î D 0 0
- Một vectơ pháp tuyến n (a;b ) của D
Khi đó phương trình tổng quát của D là a (x - x + b y - y = 0 0 ) ( 0 ) Chú ý:
o Đường thẳng D có phương trình tổng quát là 2 2
ax + by + c = 0, a + b ¹ 0 nhận n (a;b ) làm vectơ pháp tuyến.
o Nếu hai đường thẳng song song với nhau thì VTPT đường thẳng này cũng là VTPT của đường thẳng kia.
o Phương trình đường thẳng D qua điểm M (x ;y có dạng 0 0 )
D : a (x - x + b y - y = 0 với 2 2 a + b ¹ 0 0 ) ( 0 )
hoặc ta chia làm hai trường hợp
+ x = x : nếu đường thẳng song song với trục Oy 0
+ y - y = k x - x : nếu đường thẳng cắt trục Oy 0 ( 0 ) x y
o Phương trình đường thẳng đi qua A(a; 0),B ( 0;b ) với ab ¹ 0 có dạng + = 1 a b
Ví dụ 1: Cho tam giác ABC biết A(2;0), B (0;4), C(1;3). Viết phương trình tổng quát của a) Đường cao AH
b) Đường trung trực của đoạn thẳng BC .
c) Đường thẳng AB .
d) Đường thẳng qua C và song song với đường thẳng AB . Lời giải
a) Vì AH ^ BC nên BC là vectơ pháp tuyến của AH
Ta có BC (1;-1) suy ra đường cao AH đi qua A và nhận BC là vectơ pháp tuyến có phương trình
tổng quát là 1.(x - 2) - 1.(y - 0) = 0 hay x - y - 2 = 0 .
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 733
hệ. Face: Trần Đình Cư. SĐT: 0834332133
b) Đường trung trực của đoạn thẳng BC đi qua trung điểm BC và nhận vectơ BC làm vectơ pháp tuyến. x + x 1 y + y 7 æ 1 7 ö
Gọi I là trung điểm BC khi đó B C x , B C y I ç = = = = ç ; ÷÷ I 2 2 I 2 2 çè2 2 ÷ø æ 1 ö æ 7 ö
Suy ra phương trình tổng quát của đường trung trực BC là 1.ççx ÷÷ 1.ç - - çy ÷ - ÷ = 0 ç hay è 2 ÷ø çè 2 ÷ø x - y + 3 = 0 x y
c) Phương trình tổng quát của đường thẳng AB có dạng +
= 1 hay 2x + y - 4 = 0 . 2 4
d) Cách 1: Đường thẳng AB có VTPT là n (2;1) do đó vì đường thẳng cần tìm song song với đường
thẳng AB nên nhận n (2;1) làm VTPT do đó có phương trình tổng quát là
2.(x - 1) + 1.(y - 3) = 0 hay 2x + y - 5 = 0 .
Cách 2: Đường thẳng D song song với đường thẳng AB có dạng 2x + y + c = 0 .
Điểm C thuộc D suy ra 2.1 + 3 + c = 0 c = 5 - .
Vậy đường thẳng cần tìm có phương trình tổng quát là 2x + y - 5 = 0 .
Ví dụ 2: Cho đường thẳng d : x - 2y + 3 = 0 và điểm M ( 1
- ;2) . Viết phương trình tổng quát của đường thẳng D biết:
a) D đi qua điểm M và có hệ số góc k = 3
b) D đi qua M và vuông góc với đường thẳng d
c) D đối xứng với đường thẳng d qua M Lời giải:
a) Đường thẳng D có hệ số góc k = 3 có phương trình dạng y = 3x + m . Mặt khác M Î D 2 = 3.( 1
- ) + m m = 5
Suy ra phương trình tổng quát đường thẳng D là y = 3x + 5 hay 3x - y + 5 = 0 . 1 3 1
b) Ta có x - 2y + 3 = 0 y = x + do đó hệ số góc của đường thẳng d là k = . 2 2 d 2
Vì D ^ d nên hệ số góc của D là k thì k .k = -1 k = -2 D d D D Do đó D : y = 2
- x + m , M Î D 2 = 2 - .( 1
- ) + m m = 2 -
Suy ra phương trình tổng quát đường thẳng D là y = -2x - 2 hay 2x + y + 2 = 0 . c) Cách 1: Ta có 1
- - 2.2 + 3 ¹ 0 do đó M Ï d vì vậy đường thẳng D đối xứng với đường thẳng
d qua M sẽ song song với đường thẳng d suy ra đường thẳng D có VTPT là n (1; 2 - ).
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 734
hệ. Face: Trần Đình Cư. SĐT: 0834332133
Ta có A(1;2) Î d , gọi A' đối xứng với A qua M khi đó A' Î D
Ta có M là trung điểm của AA' . ìï x + x ï A A' ïx = ì M
ïx = 2x - x = 2. -1 - 1 = -3 ï ï A' M A ( ) 2 í í A'(-3;2) ï y + y ï
y = 2y - y = 2.2 - 2 = 2 ï A A' ï A' M A ïy = î M ïî 2
Vậy phương trình tổng quát đường thẳng D là 1.(x + 3) - 2(y - 2) = 0 hay x - 2y + 7 = 0 .
Cách 2: Gọi A(x ;y là điểm bất kỳ thuộc đường thẳng d , A'(x;y ) là điểm đối xứng với A qua 0 0 ) M . ìï x + x ìï x + x ï 0 ï 0 ïx = ï-1 = ì M ïx = -2 - x
Khi đó M là trung điểm của AA' suy ra ï ï ï 0 2 2 í í í ï y + y ï y + y ï y = 4 - y ï 0 ï 0 ï 0 ïy = ï 2 = î M ïî 2 ïî 2
Ta có A Î d x - 2y + 3 = 0 suy ra ( 2
- - x ) - 2.(4 - y ) + 3 = 0 x - 2y + 7 = 0 0 0
Vậy phương trình tổng quát của D đối xứng với đường thẳng d qua M là x - 2y + 7 = 0 .
Ví dụ 3: Biết hai cạnh của một hình bình hành có phương trình x - y = 0 và x + 3y - 8 = 0 , tọa độ
một đỉnh của hình bình hành là (-2;2). Viết phương trình các cạnh còn lại của hình bình hành. Lời giải
Đặt tên hình bình hành là ABCD với A( 2;
- 2), do tọa độ điểm A không là nghiệm của hai phương
trình đường thẳng trên nên ta giả sử BC : x - y = 0 , CD : x + 3y - 8 = 0
Vì AB / /CD nên cạnh AB nhận n (1;3 làm VTPT do đó có phương trình là CD )
1.(x + 2) + 3.(y - 2) = 0 hay x + 3y - 4 = 0
Tương tự cạnh AD nhận n
(1;-1 làm VTPT do đó có phương trình là 1.(x + 2) -1.(y - 2) = 0 BC )
hay x - y + 4 = 0
Ví dụ 4: Cho điểm M (1;4) . Viết phương trình đường thẳng qua M lần lượt cắt hai tia Ox , tia Oy tại
A và B sao cho tam giác OAB có diện tích nhỏ nhất . Lời giải: x y
Giả sử A(a;0), B (0;b ) với a > 0, b > 0 . Khi đó đường thẳng đi qua A, B có dạng + = 1. Do a b 1 4 M Î AB nên + = 1 a b 1 1 Mặt khác S = O . AOB = ab . OAB 2 2
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 735
hệ. Face: Trần Đình Cư. SĐT: 0834332133 1 4 4
Áp dụng BĐT Côsi ta có 1 = + ³ 2
ab ³ 16 S ³ 8 OAB a b ab 1 4 1 4 Suy ra S nhỏ nhất khi = và +
= 1 do đó a = 2;b = 8 OAB a b a b x y
Vậy phương trình đường thẳng cần tìm là +
= 1 hay 4x + y - 8 = 0 2 8
Dạng 2: xét vị trí tương đối của hai đường thẳng.
1. Phương pháp giải:
Để xét vị trí tương đối của hai đường thẳng d : a x + b y + c =
0; d : a x + b y + c = 0 . 1 1 1 1 2 2 2 2
ìïa x + b y + c = 0 Ta xét hệ ï 1 1 1 í (I)
ïa x + b y + c = 0 ï 2 2 2 î
+ Hệ (I) vô nghiệm suy ra d / /d . 1 2
+ Hệ (I) vô số nghiệm suy ra d º d 1 2
+ Hệ (I) có nghiệm duy nhất suy ra d1 và d2 cắt nhau và nghiệm của hệ là tọa độ giao điểm.
Chú ý: Với trường hợp a .b .c ¹ 0 khi đó 2 2 2 a b + Nếu 1 1 ¹
thì hai đường thẳng cắt nhau. a b 2 2 a b c + Nếu 1 1 1 = ¹
thì hai đường thẳng song song nhau. a b c 2 2 2 a b c + Nếu 1 1 1 = =
thì hai đường thẳng trùng nhau. a b c 2 2 2 2. Các ví dụ:
Ví dụ 1: Xét vị trí tương đối các cặp đường thẳng sau
a) D : x + y - 2 = 0;
D : 2x + y - 3 = 0 1 2 b) D : x - - 2y + 5 = 0;
D : 2x + 4y - 10 = 0 1 2
c) D : 2x - 3y + 5 = 0; D : x - 5 = 0 1 2
d) D : 2x + 3y + 4 = 0; D : -4x - 6y = 0 1 2 Lời giải: 1 1 a) Ta có ¹ suy ra D cắt D 2 1 1 2
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 736
hệ. Face: Trần Đình Cư. SĐT: 0834332133 -1 -2 5 b) Ta có = = suy ra D trùng D 2 4 -10 1 2 1 0 c) Ta có ¹ suy ra D cắt D 2 -3 1 2 -4 -6 0 d) Ta có = ¹ suy ra D / /D 2 3 4 1 2
Ví dụ 2: Cho tam giác ABC có phương trình các đường thẳng , AB BC,CA là
AB : 2x - y + 2 = 0 ; BC : 3x + 2y + 1 = 0 ; CA : 3x + y + 3 = 0 .
Xác định vị trí tương đối của đường cao kẻ từ đỉnh A và đường thẳng D : 3x - y - 2 = 0 Lời giải
ìï2x - y + 2 = 0 ìïx = -1
Tọa độ điểm A là nghiệm của hệ ï ï í í A(-1;0) ï3x + y + 3 = 0 ï y = 0 ïî ïî
Ta xác định được hai điểm thuộc đường thẳng BC là M (-1;1), N (1;-2)
Đường cao kẻ từ đỉnh A vuông góc với BC nên nhận vectơ MN (2; 3
- ) làm vectơ pháp tuyến nên có
phương trình là 2(x + 1) - 3y = 0 hay 2x - 3y + 2 = 0 3 -1 Ta có ¹
suy ra hai đường thẳng cắt nhau. 2 -3
Ví dụ 3: Cho hai đường thẳng 2
D : (m - 3)x + 2y + m - 1 = 0 và 1 2 D : x
- + my + (m - 1) = 0 . 2
a) Xác định vị trí tương đối và xác định giao điểm (nếu có) của D và D trong các trường hợp 1 2 m = 0, m = 1
b) Tìm m để hai đường thẳng song song với nhau. Lời giải:
ìï-3x + 2y - 1 = 0 ìïx = 1
a) Với m = 0 xét hệ ï ï í í
suy ra D cắt D tại điểm có tọa độ (1;2) ï x - + 1 = 0 ïy = 2 1 2 ïî ïî ìï-2x + 2y = 0 ìïx = 0
Với m = 1 xét hệ ï ï í í
suy ra D cắt D tại gốc tọa độ ï x - + y = 0 ïy = 0 1 2 ïî ïî
b) Với m = 0 hoặc m = 1 theo câu a hai đường thẳng cắt nhau nên không thỏa mãn
Với m ¹ 0 và m ¹ 1 hai đường thẳng song song khi và chỉ khi 2 m - 3 2 m - 1 = ¹ m = 2 1 - m (m - 1)2
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 737
hệ. Face: Trần Đình Cư. SĐT: 0834332133
Vậy với m = 2 thì hai đường thẳng song song với nhau.
Ví dụ 4: Cho tam giác ABC , tìm tọa độ các đỉnh của tam giác trong trường hợp sau
a) Biết A(2;2) và hai đường cao có phương trình d : x + y - 2 = 0 ;
d : 9x - 3y + 4 = 0 . 1 2 b) Biết (4
A ;-1) , phương trình đường cao kẻ từ B là D : 2x - 3y = 0 ; phương trình trung tuyến đi
qua đỉnh C là D ' : 2x + 3y = 0. Lời giải
a) Tọa độ điểm A không là nghiệm của phương trình d ,d suy ra A Ï d , A Ï d nên ta có thể giả sử 1 2 1 2
B Î d , C Î d 1 2
Ta có AB đi qua A và vuông góc với d nên nhận u (3;9) làm VTPT nên có phương trình là 2
3(x - 2) + 9(y - 2) = 0 hay 3x + 9y - 24 = 0 ; AC đi qua A và vuông góc với d nên nhận 1
v(-1;1) làm VTPT nên có phương trình là 1.
- (x - 2) + 1.(y - 2) = 0 hay x - y = 0
B là giao điểm của d và AB suy ra tọa độ của B là nghiệm của hệ 1
ìï x + y - 2 = 0 ìïx = -1 ï ï í í B (-1;3)
ï3x + 9y - 24 = 0 ï y = 3 ïî ïî ìï 2 ìï9 - 3 + 4 = 0 ïx x y = - ï æ ï ï 2 2 ö
Tương tự tọa độ C là nghiệm của hệ 3 í í C ç ç- ; ÷ - ÷ ï x - y = 0 ï 2 çè 3 3 ÷ø ïî ïïy = - ïî 3 æ 2 2 ö
Vậy A(2;2), B ( 1 - ;3) và C çç- ; ÷ - ÷ ç è 3 3 ÷ø b) Ta có AC đi qua (4
A ;-1) và vuông góc với D nên nhận u (3;2) làm VTPT nên có phương trình là
3(x - 4) + 2(y + 1) = 0 hay 3x + 2y - 10 = 0
ìï3x + 2y - 10 = 0 ìïx = 6
Suy ra toạ độ C là nghiệm của hệ ï ï í í C (6;-4) ï2x + 3y = 0 ïy = -4 ïî ïî æ x + 4 y - 1ö
Giả sử B (x ;y suy ra trung điểm ç B I ç ; B
÷÷ của AB thuộc đường thẳng D' do đó B B ) çè 2 2 ÷÷ø x + 4 y - 1 2. B + 3. B
= 0 hay 2x + 3y + 5 = 0 (1) 2 2 B B
Mặt khác B Î D suy ra 2x - 3y = 0 (2) B B
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 738
hệ. Face: Trần Đình Cư. SĐT: 0834332133 æ 5 5 ö
Từ (1) và (2) suy ra B çç- ; ÷ - ÷ ç è 4 6 ÷ø æ 5 5 ö Vậy (4
A ;-1) , B çç- ; ÷ - ÷ - ç và C (6; 4). è 4 6 ÷ø
Dạng 3: viết phương trình tham số và chính tắc của đường thẳng.
1. Phương pháp giải:
Để viết phương trình tham số của đường thẳng D ta cần xác định - Điểm ( A x ;y ) Î D 0 0
- Một vectơ chỉ phương u (a;b ) của D
ìïx = x + at
Khi đó phương trình tham số của D là ï 0 í , t Î R .
ï y = y + bt ï 0 î
Để viết phương trình chính tắc của đường thẳng D ta cần xác định - Điểm ( A x ;y ) Î D 0 0
- Một vectơ chỉ phương u (a;b ), ab ¹ 0 của D x - x y - y
Phương trình chính tắc của đường thẳng D là 0 0 = a b
(trường hợp ab = 0 thì đường thẳng không có phương trình chính tắc) Chú ý:
o Nếu hai đường thẳng song song với nhau thì chúng có cùng VTCP và VTPT.
o Hai đường thẳng vuông góc với nhau thì VTCP của đường thẳng này là VTPT của đường thẳng kia và ngược lại
o Nếu D có VTCP u = (a;b) thì n = (- ;
b a) là một VTPT của D . 2. Các ví dụ:
Ví dụ 1: Cho điểm A(1; 3 - ) và B ( 2;
- 3). Viết phương trình tham số của đường thẳng trong mỗi trường hợp sau:
a) D đi qua A và nhận vectơ n (1;2) làm vectơ pháp tuyến
b) D đi qua gốc tọa độ và song song với đường thẳng AB
c) D là đường trung trực của đoạn thẳng AB Lời giải:
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 739
hệ. Face: Trần Đình Cư. SĐT: 0834332133
a) Vì D nhận vectơ n (1;2) làm vectơ pháp tuyến nên VTCP của D là u ( 2; - 1) . ìïx = 1 - 2t
Vậy phương trình tham số của đường thẳng D là : ï D í ïy = -3 + t ïî
b) Ta có AB (-3;6) mà D song song với đường thẳng AB nên nhận u ( 1 - ;2) làm VTCP ìïx = t -
Vậy phương trình tham số của đường thẳng D là : ï D í ïy = 2t ïî
c) Vì D là đường trung trực của đoạn thẳng AB nên nhận AB 3;
6 làm VTPT và đi qua trung điểm
I của đoạn thẳng AB . 1 Ta có I ;0
và nhận u 1
;2 làm VTCP nên phương trình tham số của đường thẳng D là 2 ìï 1 ïx = - - t : ï D í 2 . ïïy = 2t ïî
Ví dụ 2: Viết phương trình tổng quát, tham số, chính tắc (nếu có) của đường thẳng trong mỗi trường hợp sau:
a) đi qua điểm A(3;0) và B (1;3) ìïx = 1 - 3t
b) đi qua N (3;4) và vuông góc với đường thẳng d ' : ïí . ïy = 4 + 5t ïî Lời giải:
a) Đường thẳng đi qua hai điểm A và B nên nhận AB = (-2;3) làm vectơ chỉ phương do đó ìïx = 3 - 2t x - 3 y
phương trình tham số là ïí
; phương trình chính tắc là
= ; phương trình tổng quát ï y = 3t ïî -2 3 là 3(x - 3) = 2
- y hay 3x + 2y - 9 = 0
b) D ^ d ' nên VTCP của d ' cũng là VTPT của D nên đường thẳng D nhận u (-3;5) làm VTPT và v(-5; 3
- ) làm VTCP do đó đó phương trình tổng quát là 3
- (x - 3) + 5(y - 4) = 0 hay ìïx = 3 - 5t x - 3 y - 4
3x - 5y + 11 = 0 ; phương trình tham số là ïí
; phương trình chính tắc là = ïy = 4 - 3t ïî -5 -3
Ví dụ 3: Cho tam giác ABC có A(-2;1), B (2;3) và C (1; 5 - ).
a) Viết phương trình đường thẳng chứa cạnh BC của tam giác.
b) Viết phương trình đường thẳng chứa đường trung tuyến AM.
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 740
hệ. Face: Trần Đình Cư. SĐT: 0834332133
c) Viết phương trình đường thẳng đi qua hai điểm D, G với D là chân đường phân giác trong góc A và
G là trọng tâm của DABC . Lời giải: ìï x = 2 - t a) Ta có BC ( 1 - ; 8
- ) suy ra đường thẳng chứa cạnh BC có phương trình là ïí ïy = 3 - 8t ïî æ 3 ö
b) M là trung điểm của BC nên M çç ; 1÷ - ÷ ç
do đó đường thẳng chứa đường trung tuyến AM nhận è 2 ÷ø ì æ ï 7 7 ö ïx = -2 + t AM çç ;-2÷÷ ï ç
làm VTCP nên có phương trình là í 2 è 2 ÷ø ïï y = 1 - 2t ïî
c) Gọi D(x ;y ) là chân đường phân giác hạ từ A của tam giác ABC D D AB Ta có BD = DC AC
MàAB = (- - )2 + ( - )2 2 2 3 1 = 2 5 và AC = ( + )2 + (- - )2 1 2 5 1 = 3 5 suy ra ìï 2 ìï 8
ïx - 2 = (1 - x ) ï AB 2 x = ï D D ï D ï ï 8 1 3 5 æ 1 1 ö BD = DC = DC í í
D( ;- ) G çç ; ÷ - ÷ là AC 3 ï 2 ï 1 - 5 5 ç ÷ ï è 3 3 ø ïy 3 ( 5 y ) ï - = - - ïy = D ïî 3 D D ïî 5
trọng tâm của tam giác ABC æ 19 2 ö Ta có DG çç- ; ÷ - ÷ ç
suy ra đường thẳng DG nhận u (19;2) làm VTCP nên có phương trình là è 15 15 ÷ø ìï 1 ï x = + 19t ïï 3 í . ï 1 ïïy = - + 2t ïî 3
Ví dụ 4: Cho tam giác ABC biết AB : x + y - 1 = 0 , AC : x - y + 3 = 0 và trọng tâm G (1;2) .
Viết phương trình đường thẳng chứa cạnh BC. Lời giải:
ìïx + y - 1 = 0 ìïx = -1
Ta có tọa độ điểm A là nghiệm của hệ ï ï í í A( 1 - ;2) ïx - y + 3 = 0 ï y = 2 ïî ïî
Gọi M (x;y ) là trung điểm của BC
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 741
hệ. Face: Trần Đình Cư. SĐT: 0834332133
Vì G là trọng tâm nên AG = 2.GM , AG (2;0), GM (x - 1;y - 2) suy ra ìï2 = 2.(x - 1) ïí M (2;2) ï0 = 2.(y - 2) ïî
B (x ;y ) Î AB x + y - 1 = 0 y = 1 - x do đó B (x ;1 - x B B ) B B B B B B
C (x ;y ) Î AC x - y + 3 = 0 y = x + 3 do đó C (x ;x + 3 C C ) C C C C C C ìï x + x ï B C ïx = ìï + = ì M x x 4 ïx = 2
Mà M là trung điểm của BC nên ta có ï 2 ï B C ï B í í í ï y + y ïx - x = 0 ïx = 2 ï B C ï C B ï = î ï C y î M ïî 2 ìï x = 2 Vậy B (2; 1
- ), C (2;5) BC (0;6) suy ra phương trình đường thẳng BC là ïí . ïy = -1 + 6t ïî
Dạng 4. Xác định tọa độ điểm thuộc đường thẳng.
1. Phương pháp giải.
Để xác định tọa độ điểm thuộc đường thẳng ta dựa vào nhận xét sau:
ìïx = x + at x - x y - y ï
Điểm A thuộc đường thẳng 0 D : í
, t Î R ( hoặc 0 0 D : = ) có dạng
ï y = y + bt ï a b 0 î
A(x + at; y + bt 0 0 ) æ - - ö at c
Điểm A thuộc đường thẳng D : ax + by + c = 0 (ĐK: 2 2
a + b ¹ 0 ) có dạng Aççt; ÷÷ ç è b ÷ø æ bt - - c ö
với b ¹ 0 hoặc Açç ;t ÷÷ ç với a ¹ 0 è a ÷ø 2. Các ví dụ.
Ví dụ 1: Cho đường thẳng D : 3x - 4y - 12 = 0
a) Tìm tọa độ điểm A thuộc D và cách gốc tọa độ một khoảng bằng bốn
b) Tìm điểm B thuộc D và cách đều hai điểm E (5;0) , F (3; 2 - )
c) Tìm tọa độ hình chiếu của điểm M (1;2) lên đường thẳng D Lời giải: a) Dễ thấy M (0; 3
- ) thuộc đường thẳng D và u (4;3) là một vectơ chỉ phương của D nên có ìï x = 4t
phương trình tham số là ïí . ïy = -3 + 3t ïî
Điểm A thuộc D nên tọa độ của điểm A có dạng A(4t; 3 - + 3t ) suy ra
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 742
hệ. Face: Trần Đình Cư. SĐT: 0834332133 é t = 1 ê
OA = 4 (4t )2 + (-3 + 3t )2 2
= 4 25t - 18t - 7 = 0 ê -7 êt = êë 25 æ-28 -96 ö
Vậy ta tìm được hai điểm là A 4;0 và A çç ; ÷÷ 1 ( ) 2 çè 25 25 ÷ø
b) Vì B Î D nênB (4t; 3 - + 3t )
Điểm B cách đều hai điểm E (5;0) , F (3; 2 - ) suy ra
EB = FB (4t - 5)2 + (3t - 3)2 = (4t - 3)2 + (3t - 1)2 6 2 2 t = 7 æ 24 3 ö Suy ra B çç ; ÷ - ÷ ç è 7 7 ÷ø
c) Gọi H là hình chiếu của M lên D khi đó H Î D nên H (4t; 3 - + 3t )
Ta có u (4;3)là vectơ chỉ phương của D và vuông góc với HM (4t - 1;3t - 5) nên HM u =
( t - ) + ( t - ) 19 . 0 4 4 1 3 3 5 = 0 t = 25 æ 76 18 ö Suy ra H çç ; ÷ - ÷ ç è 25 25 ÷ø ìïx = -1 - t
Ví dụ 2: Cho hai đường thẳng D : x - 2y + 6 = 0 và ' : ï D í . ï y = t ïî
a) Xác định tọa độ điểm đối xứng với điểm A( 1 - ;0) qua đường thẳng D
b) Viết phương trình đường thẳng đối xứng với D ' qua D Lời giải:
a) Gọi H là hình chiếu của A lên D khi đó H (2t - 6;t )
Ta có u (2;1) là vectơ chỉ phương của D và vuông góc với AH (2t - 5;t ) nên
AH.u = 0 2(2t - 5) + t = 0 t = 2 H (-2;2)
A' là điểm đối xứng với A qua D suy ra H là trung điểm của AA' do đó
ìïx = 2x - x ìïx = -3 ï A' H A ï A' í í
ïy = 2y - y ï y = 4 ï A' H A î ï A' î
Vậy điểm cần tìm là A'( 3 - ;4)
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 743
hệ. Face: Trần Đình Cư. SĐT: 0834332133 ìïx = -1 - t 5 b) Thay ïí
vào phương trình D ta được -1 - t - 2t + 6 = 0 t = suy ra giao điểm ï y = t ïî 3 æ 8 5 ö
của D và D ' là K çç- ; ÷÷ ç è 3 3 ÷ø
Dễ thấy điểm A thuộc đường thẳng D ' do đó đường thẳng đối xứng với D ' qua D đi qua điểm A' và æ 1 7 ö 1 ìïx = -3 + t
điểm K do đó nhận A' K ç = ç ; ÷ - ÷ = (1;-7) ï ç
nên có phương trình là í è 3 3 ÷ø 3 ï y = 4 - 7t ïî
Nhận xét: Để tìm tọa độ hình chiếu H của A lên D ta có thể làm cách khác như sau: ta có đường thẳng
AH nhận u (2;1) làm VTPT nên có phương trình là 2x + y + 2 = 0 do đó tọa độ H là nghiệm của hệ
ìïx - 2y + 6 = 0 ïí H (-2;2) ï2x + y + 2 = 0 ïî
Ví dụ 3: Cho tam giác ABC vuông ở A. Biết A(-1;4), B (1;-4), đường thẳng BC đi qua điểm æ 7 ö K çç ;2÷÷
çè 3 ÷ø. Tìm toạ độ đỉnh C. Lời giải: æ 4 ö Ta có BK çç ;6÷÷ ç
suy ra đường thẳng BC nhận u (2;9) làm VTCP nên có phương trình là è 3 ÷ø ìï x = 1 + 2t ïí ïy = -4 + 9t ïî
C Î BC C (1 + 2t; 4 - + 9t )
Tam giác ABC vuông tại A nên AB.AC = 0 , AB (2; 8
- ), AC (2 + 2t; 8 - + 9t ) suy ra
2(2 + 2t ) - 8(9t - 8) = 0 t = 1 Vậy C (3;5) æ 7 5 ö æ 3 ö
Ví dụ 4: Cho hình bình hành ABCD . Biết I çç ; ÷÷ ç ÷ ç
là trung điểm của cạnh CD, D ç3; ÷và đường phân è 2 2 ÷ø çè 2 ÷ø
giác góc BAC có phương trình là D : x - y + 1 = 0 . Xác định tọa độ đỉnh B. Lời giải:
ìïx = 2x - x = 4 ï C I D æ 7 ö
Cách 1: Điểm I là trung điểm của CD nên ïí C ç ç4; ÷ 7 ÷
ïïy = 2x - y ç = è 2 ÷ø C I D ïî 2
Vì A Î D nên tọa độ điểm A có dạng A(a;a + 1)
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 744
hệ. Face: Trần Đình Cư. SĐT: 0834332133
Mặt khác ABCD là hình bình hành tương đương với ,
DA DC không cùng phương và AB = DC ì ï x - a = 4 - 3 ï B ìïx = a + 1 ï ï B AB = DC í í
B (a + 1;a + 3 7 3 ) ïïy -a - 1 = - ïy = a + 3 ï 2 2 B B î ïî 3 a + 1 a 3 - - 11 ,
DA DC không cùng phương khi và chỉ khi 2 ¹ a ¹ 1 2 2
Đường thẳng D là phân giác góc BAC nhận vectơ u = (1;1) làm vec tơ chỉ phương nên ( AB u ) = (AC u) AB.u AC.u cos ; cos ;
= (*) AB u AC u æ ö Có AB ( ) 5
1;2 , AC çç4 - a; - a ÷÷ ç nên è 2 ÷ø 13 - 2a é a = 1 ( ê *) 3 2 2 =
2a - 13a + 11 = 0 ê 11 2 5 ê æ ö a = (l) (4 -a )2 5 ç + ç - a ÷ ê ÷ ë 2 çè2 ÷ø
Vậy tọa độ điểm B (2;4) æ 7 ö
Cách 2: Ta có C çç4; ÷÷ ç . è 2 ÷ø
Đường thẳng d đi qua C vuông góc với D nhận u (1;1) làm vectơ pháp tuyến nên có phương trình là ( æ ö x ) 7 1. 4 1.ç - + çy ÷ - ÷ = 0 ç
hay 2x + 2y - 15 = 0 è 2 ÷ø
Tọa độ giao điểm H của D và d là nghiệm của hệ: ìï 13 ìï - + 1 = 0 ïx x y = ï æ ï ï 13 17 4 ö í í H ç ç ; ÷÷
ï2x + 2y - 15 = 0 ï 17 çè 4 4 ÷ø ïî ïïy = ïî 4
Gọi C' là điểm đối xứng với C qua D thì khi đó C' thuộc đường thẳng chứa cạnh AB và H là trung điểm ìï 5
ìïx = 2x - x ï = æ ö ï C H C x 5 của CC' do đó ' ï C ' í í 2 C 'ç ç ;5÷÷
ïy = 2y - y ï ç ÷ è ø ï C H C 2 ' î ïy = 5 ï C ' î
Suy ra đường thẳng chứa cạnh AB đi qua C' và nhận DC (1;2) làm vectơ chỉ phương nên có phương trình
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 745
hệ. Face: Trần Đình Cư. SĐT: 0834332133 ìï 5 ï x = + t là ïí 2 ïïy = 5 + 2t ïî
Thay x, y từ phương trình đường thẳng chứa cạnh AB vào phương trình đường thẳng D ta được 5 3
+ t - 5 - 2t + 1 = 0 t = - suy ra A(1;2) 2 2 ìïx - 1 = 1 ìïx = 2
ABCD là hình bình hành nên ï B ï B AB = DC í í ïy - 2 = 2 ïy = 4 ï B î ï B î Suy ra B (2;4)
Chú ý: Bài toán có liên quan đến đường phân giác thì ta thường sử dụng nhận xét " D là đường phân giác
của góc tạo bởi hai đường thẳng cắt nhau D và D khi đó điểm đối xứng với điểm M Î D qua D 1 2 1 thuộc D " 2
Ví dụ 5: Cho đường thẳng d : x - 2y - 2 = 0 và 2 điểm A(0;1) và B (3;4) . Tìm tọa độ điểm M
trên d sao cho MA + 2MB là nhỏ nhất. Lời giải:
M Î d M (2t + 2;t ), MA( 2
- t - 2;1 - t ), MB (1 - 2t;4 - t ) do đó
MA + 2MB = (-6t; 3 - t + 9) 2 2 æ 3 ö 314 314 Suy ra MA 2MB ( 6t ) ( 3t 9) 45ç + = - + - + = çt ÷ - ÷ + ³ ç è 5 ÷ø 5 5 3 æ16 3 ö
MA + 2MB nhỏ nhất khi và chỉ khi t = do đó M çç ; ÷÷ là điểm cần tìm. 5 çè 5 5 ÷ø
Dạng 5. Bài toán liên quan đến khoảng cách từ một điểm tới một đường thẳng.
1.Phương pháp giải.
Để tính khoảng cách từ điểm M (x ;y đến đường thẳng :
ax + by + c = 0 ta dùng công thức 0 0 )
ax + by + c 0 0 d(M , ) = 0 2 2 a + b 2. Các ví dụ.
Ví dụ 1: Cho đường thẳng : 5x + 3y - 5 = 0
a) Tính khoảng cách từ điểm A( 1
- ;3) đến đường thẳng D
b) Tính khoảng cách giữa hai đường thẳng song song D và ':
5x + 3y + 8 = 0
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 746
hệ. Face: Trần Đình Cư. SĐT: 0834332133 Lời giải: 5.( 1 - ) + 3.3 - 5 1
a) Áp dụng công thức tính khoảng cách ta có: d( , B ) D = = 2 2 5 + 3 34 5.1 + 3.0 + 8 13
b) Do M (1;0) Î nên ta có d ( ;
D D') = d(M,D') = = 2 2 5 + 3 34
Ví dụ 2: Cho 3 đường thẳng có phương trình
: x + y + 3 = 0; : x - y - 4 = 0; : x - 2y = 0 1 2 3
Tìm tọa độ điểm M nằm trên sao cho khoảng cách từ M đến bằng 2 lần khoảng cách từ M đến 3 1 . 2 Lời giải:
M Î D M 2t;t 3 ( )
Khoảng cách từ M đến bằng 2 lần khoảng cách từ M đến nên ta có 1 2 + + - - d ( 2t t 3 2t t 4 M;D = 2d M;D = 2 1 ) ( 2 ) 2 2
é 3t + 3 = 2(t - 4) ét = -11 ê ê ê 3t 3 2 ê (t 4) ê + = - - t = 1 ë êë
Vậy có hai điểm thỏa mãn là M -22;-11 , M 2;1 1 ( ) 2 ( )
Ví dụ 3: Cho ba điểm A(2;0), B (3;4) và P (1;1) . Viết phương trình đường thẳng đi qua P đồng thời
cách đều A và B Lời giải:
Đường thẳng D đi qua P có dạng a (x - ) + b (y - ) = ( 2 2 1 1
0 a + b ¹ 0) hay
ax + by - a - b = 0
D cách đều A và B khi và chỉ khi ( - +
A D) = d (B D) a b 2a 3b d ; ; = 2 2 2 2 a + b a + b
éa - b = 2a + 3b é a = -4b ê ê ê b a 2a 3b ê - = + 3a = -2b êë êë
+ Nếu a = -4b , chọn a = 4, b = 1
- suy ra D : 4x - y - 3 = 0
+ Nếu 3a = -2b . chọn a = 2, b = 3
- suy ra D : 2x - 3y + 1 = 0
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 747
hệ. Face: Trần Đình Cư. SĐT: 0834332133
Vậy có hai đường thẳng thỏa mãn bài toán là D : 4x - y - 3 = 0 và D : 2x - 3y + 1 = 0 1 2
Ví dụ 4: Cho tam giác ABC có ( A 1; 2 - ), ( B 5;4), C( 2
- , 0) . Hãy viết phương trình đường phân giác trong góc A. Lời giải:
Cách 1: Dễ dàng viết đường thẳng AB, AC có phương trình
AB: 3x - 2y - 7 = 0 , AC:2x + 3y + 4 = 0
Ta có phương trình đường phân giác góc A là é 3x - 2y - 7 2x + 3y + 4 êD : = 1 é ê
D : x - 5y - 11 = 0 1 13 13 ê ê ê 3x 2y 7 2x 3y 4 ê - - + +
D : 5x + y - 3 = 0 ê 2 êD : = - ë 2 êë 13 13
Ta thấy (5 - 5.4 - 11)(-2 - 5.0 - 11) > 0 nên 2 điểm B,C nằm về cùng 1 phía đối với đường
thẳng D . Vậy D : 5x + y - 3 = 0 là phương trình đường phân giác trong cần tìm. 1 2
Cách 2: Gọi D(x;y) là chân đường phân giác hạ từ A của tam giác ABC AB Ta có BD = DC AC
MàAB = 2 13, AC = 13 ìï 1 ï AB ìï - 5 = 2(-2 - ) x x x = ï ï ï 3 1 4 BD = DC í í suy ra D( ; ) AC
ïy - 4 = 2(0 - y) ï 4 ïî ï 3 3 ïy = ïî 3 y + 2 x - 1
Ta có phương trình đường phân giác AD: = hay 5x + y - 3 = 0 4 1 + 2 - 1 3 3
Cách 3: Gọi M(x;y) thuộc đường thẳng D là đường phân giác góc trong góc A
Ta có (AB,AM ) = (AC,AM )
Do đó cos(AB,AM ) = cos(AC,AM ) (*)
Mà AB = (4;6); AC = (-3;2) ;AM = (x - 1;y + 2) thay vào (*) ta có
4(x - 1) + 6(y + 2) 3(
- x - 1) + 2(y + 2) = 2 2 2 2 2 2 2 2 4 + 6
(x - 1) + (y + 2) ( 3
- ) + 2 (x - 1) + (y + 2)
2(x - 1) + 3(y + 2) = -3(x - 1) + 2(y + 2) 5x + y - 3 = 0
Vậy đường phân giác trong góc A có phương trình là: 5x + y - 3 = 0
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 748
hệ. Face: Trần Đình Cư. SĐT: 0834332133
Ví dụ 5: Cho điểm C 2;
5 và đường thẳng :3x 4y 4 0 . Tìm trên hai điểm , A B đối xứng 5 với nhau qua I 2;
và diện tích tam giác ABC bằng 15 . 2 Lời giải:
Dễ thấy đường thẳng đi qua M 0;
1 và nhận u 4;3 làm vectơ chỉ phương nên có phương trình x 4t tham số là y 1 3t
Vì A nên A4t;1 3t, t R . 4t x 2 B 5
x 4 4t Hai điểm ,
A B đối xứng với nhau qua I 2; 2 suy ra B 2 5 1 3t y y 4 3t B B 2 2
Do đó B 4 4t;4 3t 3. 2 4.5 4 22
Ta có AB t2 t2 4 8 3 6
5 2t 1 và d C; 5 5 1 1 22 Suy ra S A . B d C t t ABC ; .5 2 1 . 11 2 1 2 2 5 15 13 2
Diện tích tam giác ABC bằng 15 11 2t 1 15 2t 1 t hoặc t . 12 11 11 13 52 50 8 5 Với t A ; , B ; 11 11 11 11 11 2 8 5 52 50 Với t A ; , B ; 11 11 11 11 11 52 50 8 5 8 5 52 50 Vậy A ; , B ; hoặc A ; , B ; . 11 11 11 11 11 11 11 11
Dạng 6: bài toán liên quan đến góc giữa hai đường thẳng.
1.Phương pháp giải:
Trong mặt phẳng toạ độ Oxy , góc giữa hai đường thẳng D ;D có phương trình 1 2
(D ) : a x + b y + c = 0, ( 2 2 a + b ¹ 0 1 1 1 1 1 1 )
(D ) : a x + b y + c = 0, ( 2 2 a + b ¹ 0 2 2 2 2 2 2 )
được xác định theo công thức: a a + b b cos(D ,D ) 1 2 1 2 = 1 2 2 2 2 2 a + b a + b 1 1 2 2
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 749
hệ. Face: Trần Đình Cư. SĐT: 0834332133
Để xác định góc giữa hai đường thẳng ta chỉ cần biết véc tơ chỉ phương( hoặc vectơ pháp tuyến
) của chúng cos(D ,D = cos u ,u = cos n ,n . 1 2 ) ( 1 2) ( 1 2) 2. Các ví dụ.
Ví dụ 1: Xác định góc giữa hai đường thẳng trong các trường hợp sau: ìï x = t a) : 3x 2y 1 0; : ï D - + = D í t Î R 1 2 ( ) ïy = 7 - 5t ïî ìï x = 1 - t ìïx = 2 - 4t ' b) : ïí t R : ï D Î D í t ' Î R 1 ( ) 2 ( ) ïy = 1 + 2t ïy = 5 - 2t ' ïî ïî Lời giải: a) n 3; 2
- , n 5;1 lần lượt là vectơ pháp tuyến của đường thẳng D và D suy ra 1 ( ) 2 ( ) 1 2 ( 3.5 - 2.1 2 cos D , D = = do đó (D ;D = 45 1 2 ) 0 1 2 ) 13. 26 2 b) u 1 - ;2 , u 4 - ; 2
- lần lượt là vectơ chỉ phương của đường thẳng D và D suy ra 1 ( ) 2 ( ) 1 2 -1.(-4) + 2.(-2) cos(D ,D = = 0 do đó (D ;D = 90 1 2 ) 0 1 2 ) 17. 8
Ví dụ 2: Tìm m để góc hợp bởi hai đường thẳng : 3x - y + 7 = 0 và 1
: mx + y + 1 = 0 một góc bằng 0 30 2 Lời giải: m 3 - 1 Ta có: cos(D , D ) = 1 2 2 2 2 2 ( 3) + (-1) . m + 1
Theo bài ra góc hợp bởi hai đường thẳng , bằng 0 30 nên 1 2 m 3 - 1 m 3 - 1 3 0 2 cos 30 = =
3(m + 1) = m 3 - 1 2 2 2. m + 1 2 2. m + 1 1 Hay 2 2 2 2
3(m + 1) = (m 3 - 1) 3m + 3 = 3m - 2m 3 + 1 m = - 3 1 Vậy m = - là giá trị cần tìm. 3
Ví dụ 3: Cho đường thẳng d : 3x - 2y + 1 = 0 và M (1;2). Viết phương trình đường thẳng D đi qua
M và tạo với d một góc 45o .
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 750
hệ. Face: Trần Đình Cư. SĐT: 0834332133 Lời giải.
Đường thẳng D đi qua M có dạng D a (x - ) + b (y - ) 2 2 : 1
2 = 0, a + b ¹ 0 hay
ax + by - a - 2b = 0
Theo bài ra D tạo với d một góc 0 45 nên: 3a + (-2b) 2 3a - 2b 0 cos 45 = = 2 2 2 2 2 2 3 + (-2) . a + b 2 13. a + b é a = 5b 2 2 2 2 26(a b ) 2 3a 2b 5a 24ab 5b 0 ê + = - - - = ê 5a = b - êë
+ Nếu a = 5b , chọn a = 5, b = 1 suy ra D : 5x + y - 7 = 0 + Nếu 5a = b
- , chọn a = 1, b = 5
- suy ra D : x - 5y + 9 = 0
Vậy có 2 đường thẳng thoả mãn D : x - 5y + 9 = 0 và D : 5x + y - 7 = 0 1 2
Ví dụ 4: Cho 2 đường thẳng D : 2x - y + 1 = 0; D : x + 2y - 7 = 0 . Viết phương trình đường 1 2
thẳng D qua gốc toạ độ sao cho D tạo với D và D tam giác cân có đỉnh là giao điểm D và D . 1 2 1 2 Lời giải:
Đường thẳng D qua gốc toạ độ có dạng ax + by = 0 với 2 2 a + b ¹ 0
Theo giả thiết ta có cos( ; D D = cos ; D D hay 1 ) ( 2 ) 2a - b a + 2b
é2a - b = a + 2b é a = 3b ê ê = 2 2 2 2 êb 2a a 2b ê - = + 3 5. 5. a = b a b a b - + + êë êë
+ Nếu a = 3b , chọn a = 3, b = 1 suy ra D : 3x + y = 0 + Nếu 3a = b
- , chọn a = 1, b = 3
- suy ra D : x - 3y = 0
Vậy có hai đường thẳng thỏa mãn là D : 3x + y = 0 và D : x - 3y = 0 1 2
C. CÂU HỎI TRẮC NGHIỆM
Vấn đề 1. VECTƠ CHỈ PHƯƠNG – VECTƠ PHÁP TUYẾN
Câu 1: Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng song song với trục Ox ? A. u = 1;0 u = 0;-1 . u = -1;1 . u = 1;1 . 4 ( ) 3 ( ) 2 ( ) 1 ( ) . B. C. D. Lời giải Chọn A.
Trục Ox: y = 0 có VTCP i (1; )
0 nên một đường thẳng song song với Ox cũng có VTCP là
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 751
hệ. Face: Trần Đình Cư. SĐT: 0834332133 i(1;0).
Câu 2: Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng song song với trục Oy ? A. u = 1;-1 . u = 0;1 . u = 1;0 . u = 1;1 . 4 ( ) 3 ( ) 2 ( ) 1 ( ) B. C. D. Lời giải Chọn B.
Trục Oy: x = 0 có VTCP j (0; )
1 nên một đường thẳng song song với Oy cũng có VTCP là j(0; )1.
Câu 3: Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua hai điểm A (-3;2) và B (1;4)? A. u = -1;2 . u = 2;1 . u = -2;6 . u = 1;1 . 4 ( ) 3 ( ) 2 ( ) 1 ( ) B. C. D. Lời giải Chọn B.
Đường thẳng đi qua hai điểm
A (-3;2) và B(1; 4) có VTCP là AB = (4;2) hoặc u (2; ) 1 .
Câu 4: Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua gốc tọa độ O(0;0) và điểm M (a;b)?
A. u = 0;a + b . u = ; a b . u = ; a b - . u = - ; a b . 4 ( ) 3 ( ) 2 ( ) 1 ( ) B. C. D. Lời giải Chọn B.
OM = (a;b) ¾¾
đường thẳng OM có VTCP: u = OM = (a;b).
Câu 5: Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng đi qua hai điểm A ( ;0 a ) và B (0;b)? A. u = ; a b - u = ; a b u = ; b a u = - ; b a 4 ( ) 3 ( ) 2 ( ) 1 ( ) . B. . C. . D. . Lời giải Chọn A. AB = ( a - ;b) ¾¾
đường thẳng AB có VTCP: AB = ( a
- ;b) hoặc u = -AB = (a; b - ).
Câu 6: Vectơ nào dưới đây là một vectơ chỉ phương của đường phân giác góc phần tư thứ nhất? A. u = ; 1 1 . u = 0;-1 . u = 1;0 . u = -1;1 . 4 ( ) 3 ( ) 2 ( ) 1 ( ) B. C. D. Lời giải Chọn A.
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 752
hệ. Face: Trần Đình Cư. SĐT: 0834332133
Đường phân giác góc phần tư (I): x - y = 0 ¾¾ VTPT: n (1;- ) 1 ¾¾ VTCP: u (1; ) 1 .
Câu 7: Vectơ nào dưới đây là một vectơ pháp tuyến của đường thẳng song song với trục Ox ? A. n = 0;1 . n = 1;0 . n = -1;0 . n = 1;1 . 4 ( ) 3 ( ) 2 ( ) 1 ( ) B. C. D. Lời giải Chọn A.
Đường thẳng song song với Ox:
y + m = 0 (m = / 0) ¾¾ VTPT: n (0; ) 1 .
Câu 8: Vectơ nào dưới đây là một vectơ pháp tuyến của đường thẳng song song với trục Oy ? A. n = 1;1 . n = 0;1 . n = -1;1 . n = 1;0 . 4 ( ) 3 ( ) 2 ( ) 1 ( ) B. C. D. Lời giải Chọn D.
Đường thẳng song song với Oy:
x + m = 0 (m = / 0) ¾¾
VTPT: n (1;0).
Câu 9: Vectơ nào dưới đây là một vectơ pháp tuyến của đường thẳng đi qua hai điểm A (2;3) và B (4; ) 1 ? A. n = 2;-2 . n = 2;-1 . n = 1;1 . n = 1;-2 . 4 ( ) 3 ( ) 2 ( ) 1 ( ) B. C. D. Lời giải Chọn C. AB = (2;-2) ¾¾
đường thẳng AB có VTCP u (1;- ) 1 ¾¾ VTPT n (1; ) 1 .
Câu 10: Vectơ nào dưới đây là một vectơ pháp tuyến của đường thẳng đi qua gốc tọa độ và điểm A (a;b)? A. n = - ; a b . n = 1;0 . n = ; b a - . n = ; a b . 4 ( ) 3 ( ) 2 ( ) 1 ( ) B. C. D. Lời giải Chọn C.
OA = (a;b) ¾¾
đường thẳng AB có VTCP u = AB = (a;b) ¾¾ VTPT n( ; b a - ).
Câu 11: Vectơ nào dưới đây là một vectơ pháp tuyến của đường thẳng đi qua hai điểm phân biệt A ( ;0
a ) và B (0;b)? A. n = ; b a - . n = - ; b a . n = ; b a . n = ; a b . 4 ( ) 3 ( ) 2 ( ) 1 ( ) B. C. D. Lời giải Chọn C. AB = ( a - ;b) ¾¾
đường thẳng AB có VTCP u = (-a;b) ¾¾ VTPT n = ( ; b a).
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 753
hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 12: Vectơ nào dưới đây là một vectơ pháp tuyến của đường phân giác góc phần tư thứ hai? A. n = ; 1 1 . n = 0;1 . n = 1;0 . n = -1;1 . 4 ( ) 3 ( ) 2 ( ) 1 ( ) B. C. D. Lời giải Chọn A. Góc phần tư (II): x + y = 0 ¾¾ VTPT n = (1; ) 1 .
Câu 13: Đường thẳng d có
một vectơ chỉ phương là u = (2;- )
1 . Trong các vectơ sau, vectơ nào là
một vectơ pháp tuyến của ? d A. n = -1;2 . n = 1;-2 . n = -3;6 . n = 3;6 . 4 ( ) 3 ( ) 2 ( ) 1 ( ) B. C. D. Lời giải Chọn D.
Đường thẳng d có VTCP: u (2;- ) 1 ¾¾
VTPT n (1; 2) hoặc 3n = (3;6).
Câu 14: Đường thẳng d có
một vectơ pháp tuyến là n = (4;-2) . Trong các vectơ sau, vectơ nào là
một vectơ chỉ phương của ? d A. u = 2;-4 . u = -2;4 . u = 1;2 . u = 2;1 . 4 ( ) 3 ( ) 2 ( ) 1 ( ) B. C. D. Lời giải Chọn C.
Đường thẳng d có VTPT: 1 n (4;-2) ¾¾
VTCP u (2; 4) hoặc u = ( ; 1 2). 2
Câu 15: Đường thẳng d có
một vectơ chỉ phương là u = (3;-4). Đường thẳng D vuông góc với d có
một vectơ pháp tuyến là: A. n = 4;3 . n = -4;-3 . n = 3;4 . n = 3;-4 . 4 ( ) 3 ( ) 2 ( ) 1 ( ) B. C. D. Lời giải Chọn D. u ìïï = - d (3; 4) í ¾¾ n = u = - d (3; 4). ïïD ^ d D î
Câu 16: Đường thẳng d có
một vectơ pháp tuyến là n = (-2;-5) . Đường thẳng D vuông góc với d
có một vectơ chỉ phương là: A. u = 5;-2 . u = -5;2 . u = 2;5 . u = 2;-5 . 4 ( ) 3 ( ) 2 ( ) 1 ( ) B. C. D. Lời giải Chọn C. ì ïn ï = - - d ( 2; ) 5 í ¾¾
u = n = - - hay chọn n - = D (2;5). d ( 2; ) 5 ïD ï ^ d D î
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 754
hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 17: Đường thẳng d có
một vectơ chỉ phương là u = (3;-4). Đường thẳng D song song với d có
một vectơ pháp tuyến là: A. n = 4;3 . n = -4;3 . n = 3;4 . n = 3;-4 . 4 ( ) 3 ( ) 2 ( ) 1 ( ) B. C. D. Lời giải Chọn A. u ìïï = - d (3; 4) í ¾¾ u = u = - ¾¾ n = d (3; 4) (4; ) 3 . ïïD || d D D î
Câu 18: Đường thẳng d có một vectơ pháp tuyến là n = (-2;-5) . Đường thẳng D song song với d
có một vectơ chỉ phương là: A. u = 5;-2 . u = -5;-2 . u = 2;5 . u = 2;-5 . 4 ( ) 3 ( ) 2 ( ) 1 ( ) B. C. D. Lời giải Chọn A. ì ïn ï = - - d ( 2; ) 5 í ¾¾
n = u = - - ¾¾ u = - d ( 2; ) 5 (5; 2). D ïï || d D D î
Câu 19: Một đường thẳng có bao nhiêu vectơ chỉ phương? A. 1 . B. 2 . C. 4 . D. Vô số. Lời giải Chọn D.
Câu 20: Đường thẳng d đi qua điểm M (1;-2) và có vectơ chỉ phương u = (3;5) có phương trình tham số là: ìïx = 3+ t ìïx = 1+3t ìïx = 1+5t ìïx = 3 + 2t A. d : ïí . B. d : ïí . C. d : ïí . D. d : ïí . ïy = 5-2t ïî ïy = -2 + 5t ïî ïy = -2 -3t ïî ïy = 5 + t ïî Lời giải Chọn B. ìïM (1; 2 - )Î d ï ìïx =1+3t í ¾¾ d : ïí (t Î ). u ïï ï = - + d (3; ) 5 î = PTTS y 2 5t ïî
Câu 21: Đường thẳng
d đi qua gốc tọa độ O và có vectơ chỉ phương u = (-1;2) có phương trình tham số là: ìïx = 1 - ìïx = 2t ìïx = t ìïx = -2t A. d : ïí . B. d : ïí . C. d : ïí . D. d : ïí . ïy = 2 ïî ïy = t ïî ïy = -2t ïî ïy = t ïî Lời giải Chọn C.
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 755
hệ. Face: Trần Đình Cư. SĐT: 0834332133 O ìï (0;0)Î d ï ìïx = t í ¾¾ d :ïí (t Î ). u ïï = u - = (1; 2 ï = - d ) î - PTTS y 2t ïî
Câu 22: Đường thẳng
d đi qua điểm M (0;-2) và có vectơ chỉ phương u = (3;0) có phương trình tham số là: ìïx = 3+ 2t ìïx = 0 ìïx = 3 ìïx = 3t A. d : ïí . B. d : ïí . C. d : ïí . D. d : ïí . ïy = 0 ïî ïy = -2 +3t ïî ïy = -2t ïî ïy = -2 ïî Lời giải Chọn D. ìïM (0; 2 - )Î d ï ìïx = 3t í ¾¾ d :ïí (t Î ). u ïï = u = ï = - d ( ; 3 0) î PTTS y 2 ïî ìïx = 2
Câu 23: Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng ?
d : ïíïy =-1+6t ïî A. u = 6;0 u = -6;0 u = 2;6 u = 0;1 4 ( ) 3 ( ) 2 ( ) 1 ( ) . B. . C. . D. . Lời giải Chọn D. ìïx = 2 = d : ï u = 0;6 6 0;1 u = 0;1 . í ¾¾ VTCP ( ) ( ) hay chọn ( ) ïy = 1 - + 6t ïî ìï 1 ïx = 5- t
Câu 24: Vectơ nào dưới đây là một vectơ chỉ phương của đường thẳng ? : ï D í 2 ïïïy =-3+3t î æ ö A. 1 u = -1;6 . u = çç ;3÷÷ u = 5;-3 u = -5;3 4 ( ) 3 ( ) 1 ( ) B. 2 . C. . D. . çè2 ÷ø Lời giải Chọn A. ìï 1 ïx = 5- t : ï D í 2 ¾¾ æ 1 ö 1 ï = ç ÷ ï u - ç ;3÷ = ( 1 - ; ) 6 ïy = 3 - + 3t î ç ÷ VTCP è 2 ø 2
hay chọn u(-1;6).
Câu 25: Viết phương trình tham số của đường thẳng đi qua hai điểm A (2;- ) 1 và B (2;5) . ìïx = 2 ìïx = 2t ìïx = 2 + t ìïx = 1 A. ïí . B. ïí . C. ïí . D. ïí . ïy = -1+ 6t ïî ïy = -6t ïî ïy = 5 + 6t ïî ïy = 2 + 6t ïî Lời giải Chọn A. ìïA(2;- ) 1 Î AB ì ï ïx = 2 ïí AB : ï ¾¾ í (t Î ). u ïï AB = 0;6 ïy = -1+ 6t ï ï AB ( ) î = î
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 756
hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 26: Viết phương trình tham số của đường thẳng đi qua hai điểm A (–1;3) và B (3; ) 1 . ìïx = -1+ 2t ìïx = -1-2t ìïx = 3 + 2t ìïx = -1-2t A. ïí . B. ïí . C. ïí . D. ïí . ïy = 3 + t ïî ïy = 3-t ïî ïy = -1+ t ïî ïy = 3 + t ïî Lời giải Chọn D. ìïA(-1; ) 3 Î AB ì ï ïx = -1- 2t ïí AB : ï ¾¾ í (t Î ). u ïï
= AB = (4;-2) = -2(-2; ) 1 ïy = 3+ t ï AB î ïî
Câu 27: Đường thẳng đi qua hai điểm A (1; )
1 và B (2;2) có phương trình tham số là: ìïx = 1+ t ìïx = 1+ t ìïx = 2 + 2t ìïx = t A. ïí . B. ïí . C. ïí . D. ïí . ïy = 2 + 2t ïî ïy = 1+ 2t ïî ïy = 1+ t ïî ïy = t ïî Lời giải Chọn D. ìïA(1; ) 1 Î AB ì ï ïx = 1+ ï t í AB : ï ¾¾ í (t Î ) ïïu AB = y t AB (1; ) 1 ï = 1+ ïî î = ï ìïx = t t 1 =- ¾ ¾¾ O( ; 0 ) 0 AB AB : ï Î ¾¾ í (t Î ). îïy = ï t
Câu 28: Đường thẳng đi qua hai điểm A (3;-7) và B(1;-7) có phương trình tham số là: ìï x = t ìï x = t ìï x = 3-t ìïx = t A. ïí . B. ïí . C. ïí . D. ïí . ïy = -7 ïî ïy = -7 -t ïî ïy = 1-7t ïî ïy = 7 ïî Lời giải Chọn A. ìïA(3;-7)Î AB ì ï ïx = 3+ ï t í AB : ï ¾¾ í
ïïu = AB = -2;0 = -2 1;0 ïy = -7 Ta có: AB ( ) ( ) ïî ïî ìïx = t t 3 =- ¾¾¾ M (0; 7 - ) AB AB : ï Î ¾¾ í . ïy = 7 ïî -
Câu 29: Phương trình nào dưới đây không phải là phương trình tham số của đường thẳng đi qua hai điểm O(0;0) và M (1;-3) ? ìïx = 1-t ìïx = 1+ t ìïx = 1-2t ìïx = t - A. ïí . B. ïí . C. ïí . D. ïí . ïy = 3t ïî ïy = -3-3t ïî ïy = -3 + 6t ïî ï y = 3t ïî Lời giải Chọn A.
Kiểm tra đường thẳng nào không chứa O(0;0) ¾¾ loại A.
Nếu cần thì có thể kiểm tra đường thẳng nào không chứa điểm M (1;- ) 3 .
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 757
hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 30: Trong mặt phẳng với hệ tọa độ Oxy , cho ba điểm ¸ A (2;0) B (0;3) và C (-3;- ) 1 . Đường thẳng
đi qua điểm B và song song với AC có phương trình tham số là: ìïx = 5t ìïx = 5 ìïx = t ìïx = 3 +5t A. ïí . B. ïí . C. ïí . D. ïí . ïy = 3 + t ïî ïy = 1+ 3t ïî ïy = 3-5t ïî ïy = t ïî Lời giải Chọn A.
Gọi d là đường thẳng qua B và song song với AC. Ta có ìïB(0; ) 3 Î d ì ï ïx = 5t ïí d : ï ¾¾ í (t Î ) u ïï = AC =(-5;- ) 1 = -1.(5; ) 1 ïy = 3+t ï d î ïî
Câu 31: Trong mặt phẳng với hệ tọa độ , Oxy cho ba điểm ¸ A (3;2) P (4;0) và Q (0;-2) . Đường thẳng
đi qua điểm A và song song với PQ có phương trình tham số là: ìïx = 3 + 4t ìïx = 3-2t ìïx = -1+ 2t ìïx = -1+ 2t A. ïí . B. ïí . C. ïí . D. ïí . ïy = 2 -2t ïî ïy = 2 + t ïî ïy = t ïî ïy = -2 + t ïî Lời giải Chọn C.
Gọi d là đường thẳng qua A và song song với PQ. ìïA(3;2)Î d ì ï ïx = + Ta có: 3 2 ï t í d : ï í ïïu = PQ = y t d ( 4;-2) -2(2; ) 1 ï = 2 + ï ï = î - î ìïx = 1 - + 2t t 2 =- ¾¾¾ M ( 1 - ;0) d d :ï Î í (t Î ). ïy = ïî t
Câu 32: Trong mặt phẳng với hệ tọa độ Oxy , cho hình bình hành ABCD có đỉnh A (–2 ; ) 1 và phương ìïx = 1+ 4t
trình đường thẳng chứa cạnh CD là ïí
. Viết phương trình tham số của đường thẳng ïy = 3t ïî chứa cạnh . AB ìïx = -2 +3t ìïx = -2 -4t ìïx = -2 -3t ìïx = -2 -3t A. ïí . B. ïí . C. ïí . D. ïí . ïy = -2 -2t ïî ïy = 1-3t ïî ïy = 1- 4t ïî ïy = 1+ 4t ïî Lời giải Chọn B. ì ïA( 2; - ) 1 Î AB, u = ìï = - - CD (4; ) 3 x 2 4t ïí AB :ï ¾¾ í (t Î ).
ïïAB || CD u = u - = - - ïy = - t AB CD ( 4; ) 3 1 3 î ïî
Câu 33: Viết phương trình tham số của đường thẳng
d đi qua điểm M (-3;5) và song song với
đường phân giác của góc phần tư thứ nhất. ìïx = -3 + t ìïx = -3 + t ìïx = 3 + t ìïx = 5-t A. ïí . B. ïí . C. ïí . D. ïí . ïy = 5-t ïî ïy = 5 + t ïî ïy = -5 + t ïî ïy = -3 + t ïî Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 758
hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn B. ìïx = - +t x - y = 0 ¾¾ VTCP : u ( ) 3 1;1 u d :ï = ¾¾ í (t Î ). d Góc phần tư (I) : ïy = 5+t ïî
Câu 34: Viết phương trình tham số của đường thẳng
d đi qua điểm M (4;-7) và song song với trục Ox . ìïx = 1+ 4t ìïx = 4 ìïx = -7 + t ìïx = t A. ïí . B. ïí . C. ïí . D. ïí . ïy = -7t ïî ïy = -7 + t ïî ïy = 4 ïî ïy = -7 ïî Lời giải Chọn D. ìïx = +t ìïx = t u = ¾¾ u = ¾¾ d ï =- í ¾¾¾ A - d d ï Î í Ox (1; ) 0 d (1; ) 4 t 4 0 : (0; 7) : . ïy = 7 - ïy = 7 ïî - ïî
Câu 35: Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có A(1;4) , B(3;2) và C (7;3). Viết
phương trình tham số của đường trung tuyến CM của tam giác. ìïx = 7 ìïx = 3-5t ìïx = 7 + t ìïx = 2 A. ïí . B. ïí . C. ïí . D. ïí . ïy = 3 + 5t ïî ïy = -7 ïî ïy = 3 ïî ïy = 3-t ïî Lời giải Chọn C. ìïA(1;4) ï ìï = + í M ( x t 2; ) 3 MC ( ) ( ) 7 5;0 5 1;0 CM : ï = = í (t Î ). ïïB(3; ) 2 ïy = 3 î ïî
Câu 36: Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có A (2;4), B(5;0) và C (2; ) 1 . Trung tuyến
BM của tam giác đi qua điểm N có hoành độ bằng 20 thì tung độ bằng: A. - 25 12. B. - . C. - 27 13. D. - . 2 2 Lời giải Chọn B. ìïA(2;4) æ ï 5ö æ 5ö 1 ìïx = + t í ¾¾
M çç2; ÷÷ MB = 3; ç ÷ ç - ÷ = (6;- ) 5 6 5 ¾¾ MB :ïí . C ïï (2; ) 1 çè 2÷ø çè 2÷ø 2 ïy = 5 - t î ïî ìï 5 ï = ìï20 = 5+6 t t ï Ta có: ï ï N ( ; 20 y BM Î ¾¾ í í N ) 2 ïy = 5 - t ï 25 ïî N ïïy =- N ïïî 2
Câu 37: Một đường thẳng có bao nhiêu vectơ pháp tuyến? A. 1. B. 2. C. 4. D. Vô số.
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 759
hệ. Face: Trần Đình Cư. SĐT: 0834332133 Lời giải Chọn D.
Câu 38: Vectơ nào dưới đây là một vectơ pháp tuyến của ?
d : x -2 y + 2017 = 0 A. n = 0;-2 n = 1;-2 n = -2;0 n = 2;1 4 ( ) 3 ( ) 2 ( ) 1 ( ) . B. . C. . D. . Lời giải Chọn B.
d : x - 2 y + 2017 = 0 ¾¾ n = (1;-2). d
Câu 39: Vectơ nào dưới đây là một vectơ pháp tuyến của ?
d : -3x + y + 2017 = 0 A. n = -3;0 n = -3;-1 n = 6;2 n = 6;-2 4 ( ) 3 ( ) 2 ( ) 1 ( ) . B. . C. . D. . Lời giải Chọn D.
d : -3x + y + 2017 = 0 ¾¾ n = (-3; ) 1 -2n = ; 6 -2 . d hay chọn d ( ) ìïx = -1+ 2t
Câu 40: Vectơ nào dưới đây là một vectơ pháp tuyến của d : ïí ? ïy = 3-t ïî A. n = 2;-1 n = -1;2 n = 1;-2 n = 1;2 4 ( ) 3 ( ) 2 ( ) 1 ( ) . B. . C. . D. . Lời giải Chọn D. ìïx = 1 - + 2t d : ïí ¾¾ u = (2;- ) 1 ¾¾ n = (1; ) 2 . ïy = 3 d d -t ïî
Câu 41: Vectơ nào dưới đây là một vectơ chỉ phương của
d : 2x -3y + 2018 = 0 ? A. u = -3;-2 u = 2;3 u = -3;2 u = 2;-3 4 ( ) 3 ( ) 2 ( ) 1 ( ) . B. . C. . D. . Lời giải Chọn A.
d : 2x - 3y + 2018 = 0 ¾¾ n = (2;- ) 3 ¾¾ u = (3; 2 n - = -3;-2 . d d ) hay chọn d ( )
Câu 42: Đường trung trực của đoạn thẳng AB với , A = (-3;2) B = (-3;3) có một vectơ pháp tuyến là: A. n = 6;5 n = 0;1 n = -3;5 n = -1;0 4 ( ) 3 ( ) 2 ( ) 1 ( ) . B. . C. . D. . Lời giải Chọn B.
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 760
hệ. Face: Trần Đình Cư. SĐT: 0834332133 ì ï Gọi ïAB = 0;1
d là trung trực đoạn AB, ta có: ( ) í ¾¾
n = AB = (0; ) 1 . d ïïd ^ AB î
Câu 43: Cho đường thẳng .
D : x -3y -2 = 0 Vectơ nào sau đây không phải là vectơ pháp tuyến của D ? æ ö A. 1 n = 1; –3 n = –2;6 n = çç ;-1÷÷ n = 3;1 4 ( ) 2 ( ) 1 ( ). B. . C. 3 . D. . çè3 ÷ø Lời giải Chọn D. ì ïn 1;-3 = ï n 1 ( ) d ï
D : x -3y - 2 = 0 ¾¾ n = n n d (1;- ) 3 ï ¾¾ ïï (-2; ) 6 = -2 . 2 í d ïï æ1 ö 1 ï ç
ïn ç ;-1÷÷ = n 3 ï çè3 ÷ø d ï 3 î
Câu 44: Đường thẳng
d đi qua điểm A (1;-2) và có vectơ pháp tuyến n = (-2;4) có phương trình tổng quát là:
A. d : x + 2y + 4 = 0.
B. d : x -2y -5 = 0.
C. d : -2x + 4 y = 0.
D. d : x -2y + 4 = 0. Lời giải Chọn B. ìïA(1; 2 - ) ï Î d í ¾¾ d : 2 - (x- ) 1 + 4( y + 2) = 0 ïïn = d ( 2; - 4) î
d :-2x + 4y +10 = 0 d : x-2y -5 = 0.
Câu 45: Đường thẳng
d đi qua điểm M (0;-2) và có vectơ chỉ phương u = (3;0) có phương trình tổng quát là:
A. d : x = 0.
B. d : y +2 = 0.
C. d : y -2 = 0.
D. d : x -2 = 0. Lời giải Chọn B. ìïM (0;- ) 2 Î d ïí ¾¾
d : y + 2 = 0. u ï = ï n d (3; ) 0 3(1;0) d (0; ) 1 î = =
Câu 46: Đường thẳng
d đi qua điểm A (-4;5) và có vectơ pháp tuyến n = (3;2) có phương trình tham số là: ìïx = -4 -2t ìïx = -2t ìïx = 1+ 2t ìïx = 5-2t A. ïí . B. ïí . C. ïí . D. ïí . ïy = 5 +3t ïî ïy = 1+3t ïî ïy = 3t ïî ïy = -4 +3t ïî Lời giải Chọn A.
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 761
hệ. Face: Trần Đình Cư. SĐT: 0834332133 ìïA( 4; - ) 5 Î d ì ï ïx = 4 - -2t í d : ï ¾¾ í (t Î ). ïïn = u ïy = + t d (3; ) 2 d ( 2; ) 3 5 3 î = - ïî ìïx = 3-5t
Câu 47: Phương trình nào sau đây là phương trình tổng quát của đường thẳng ?
d : ïíïy =1+4t ïî
A. 4x +5y +17 = 0 .
B. 4x -5y +17 = 0 .
C. 4x +5y -17 = 0 .
D. 4x -5y -17 = 0 . Lời giải Chọn C. ìïx = 3-5 ì t ïA(3; ) 1 Î d Ta có: d :ï ï í í ¾¾ d : 4(x- ) 3 + 5(y - ) 1 = 0 ï
d : 4x + 5y -17 = 0. y =1+ 4t ï ï u = î ï n d ( 5; - ) 4 = d (4; ) 5 î ìïx = 15
Câu 48: Phương trình nào sau đây là phương trình tổng quát của đường thẳng ?
d : ïíïy = 6+7t ïî A. x -15 = 0 . B. x +15 = 0 .
C. 6x -15y = 0 .
D. x - y -9 = 0 . Lời giải Chọn A. ìïx =15 ìïA(15; ) 6 Î d d : ï ï í í ¾¾
d : x -15 = 0. ïy = 6+ 7t ïî u ïï = = n = d (0;7) 7(0; ) 1 d (1 ) ;0 î
Câu 49: Phương trình nào sau đây là phương trình tham số của đường thẳng ?
d : x - y + 3 = 0 ìïx = t ìïx = t ìïx = 3 ìïx = 2 + t A. ïí . B. ïí . C. ïí . D. ïí . ïy = 3 + t ïî ïy = 3-t ïî ïy = t ïî ïy = 1+ t ïî Lời giải Chọn A.
ìïx = 0 y = 3 ìïA(0; ) 3 Î d ì ï ï ïx = t d : x y 3 0 í í d : ï - + = ¾¾ í (t Î ). n ï = - ï u ï = ïy = +t d (1; ) 1 î ï (1 ) ;1 3 d î ïî
Câu 50: Phương trình nào sau đây là phương trình tham số của đường thẳng
d : 3x - 2 y + 6 = 0 ? ì ì ì ì ïx = t ïx = t ïx = 2t ïx = 3t ï ï ï A. ïí . B. ïí ï ï 3 . C. í 3 . D. í 3 . ïy = 2t + 3 ïî ïy = t + 3 ï ïy = - t +3 ïy = t + 3 ï ï ï î 2 ïî 2 ïî 2 Lời giải Chọn B.
ìïx = 0 y = 3
d : 3x 2 y 6 0 ï - + = íïn = d (3;-2) ïî
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 762
hệ. Face: Trần Đình Cư. SĐT: 0834332133 ìïA(0; ) 3 Î d ì ï ïx = t ï ï ï ï í æ 3ö ¾¾ d :í 3 (t Î ). ïu = y t d (2; ) 3 = 2 1 çç ; ÷ ï ÷ = 3+ ï ç ÷ ï ï è 2ø ï ïî î 2
Câu 51: Cho đường thẳng .
d : 3x + 5y + 2018 = 0 Tìm
mệnh đề sai trong các mệnh đề sau:
A. d có vectơ pháp tuyến . n = (3;5)
B. d có vectơ chỉ phương . u = (5;-3) C. 5
d có hệ số góc k = . 3
D. d song song với đường thẳng . D : 3x + 5y = 0 Lời giải Chọn C. ìï ì ï ï ï ï n = ïïn = = ï n d (3; ) 5 (3; ) 5 d ïï ï ï
d : 3x 5y 2018 0 u ïí u ï + + = = - ¾¾ í = - = u ¾¾ d (5; ) 3 (5; ) 3 d ïï ï ï ï 3 ï 5 ïïk ï = - ïk = = / k d ïïî 5 ïîï 3 d
d : 3x + 5y + 2018 = 0 d | D : 3x + 5y = 0 ¾¾ D đúng.
Câu 52: Đường thẳng
d đi qua điểm M (1;2) và song song với đường thẳng
D : 2x + 3y -12 = 0 có
phương trình tổng quát là:
A. 2x +3y -8 = 0 .
B. 2x +3y +8 = 0 .
C. 4x + 6y +1 = 0 .
D. 4x -3y -8 = 0 . Lời giải Chọn A. ìïM (1;2) ì Î d ïM (1;2) ï ï Î d í í
ïïd || D: 2x+3y-12 = 0 ï î
ïd : 2x + 3y + c = 0(c / = 12 - ) î
2.1+ 3.2 + c = 0 c = -8. Vậy d : 2x +3y -8 = 0.
Câu 53: Phương trình tổng quát của đường thẳng
d đi qua O và song song với đường thẳng
D : 6x - 4x +1 = 0 là: A. 3x - 2 y = 0. B. 4x + 6 y = 0. C. 3x +12 y -1 = 0. D.
6x - 4 y -1 = 0. Lời giải Chọn A. O ìï (0; ) 0 Î d O ìï (0; ) 0 Î d ï ï í í ¾¾
6.0-4.0 + c = 0 c = 0. d
ï || D : 6x-4x +1= 0 d ï ïî
ï : 6x -4x + c = 0 (c = / ) 1 î
Vậy d : 6x-4y = 0 d : 3x-2y = 0.
Câu 54: Đường thẳng
d đi qua điểm M (-1;2) và vuông góc với đường thẳng
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 763
hệ. Face: Trần Đình Cư. SĐT: 0834332133
D : 2x + y -3 = 0 có phương trình tổng quát là:
A. 2x + y = 0 .
B. x -2y -3 = 0 .
C. x + y -1 = 0 .
D. x -2y +5 = 0 . Lời giải Chọn D. ìïM (-1;2)Î d ìïM (-1;2)Î d ï ï í ¾¾ í ¾¾
-1- 2.2 + c = 0 c = 5.
ïïd ^ D : 2x + y-3 = 0 ï î
ïd : x - 2 y + c = 0 î
Vậy d : x-2y +5 = 0.
Câu 55: Viết phương trình đường thẳng
D đi qua điểm A (4;-3) và song song với đường thẳng ìïx = 3-2t d : ïí . ïy = 1+3t ïî
A. 3x + 2y + 6 = 0 .
B. -2x +3y +17 = 0 . C. 3x + 2y -6 = 0 .
D. 3x -2y + 6 = 0 . Lời giải Chọn C. ìïA(4;- ) 3 Î d ïï ì ïA(4;- ) 3 Î d Ta có: u ïí = - ï í d ( 2; ) 3 ï ï u ï = - = ï D ( 2; ) 3 nD (3;2) D || d î ïïî
D : 3(x-4)+ 2(y + )
3 = 0 D : 3x + 2 y -6 = 0.
Câu 56: Cho tam giác ABC có A (2;0), B( 0 ;3), C ( –3; ) 1 . Đường thẳng
d đi qua B và song song với
AC có phương trình tổng quát là:
A. 5x – y +3 = 0 .
B. 5x + y – 3 = 0 .
C. x +5y –15 = 0 .
D. x –15y +15 = 0 . Lời giải ìïB(0; ) 3 Î d ïï ì ï ïB(0; ) 3 Î d u ïí = AC ï = - í AC ( 5 ) ;1 ï ï ï ïn = d (1; ) 5 ïd || AC î ïïî d ( :1 x -0)+5(y - )
3 = 0 d : x +5y -15 = 0.
Câu 57: Viết phương trình tổng quát của đường thẳng
d đi qua điểm M (-1;0) và vuông góc với ìïx = t đường thẳng : ï D í . ïy = -2t ïî
A. 2x + y + 2 = 0 .
B. 2x - y + 2 = 0 .
C. x -2y +1 = 0 .
D. x + 2y +1 = 0 . Lời giải Chọn C. ìïM (-1;0)Î d ïï ì ïM ( 1; - 0)Î d u ï ï í = - í + - - = - + = D (1; 2) d ( :1 x ) 1 2( y 0) 0
d : x 2y 1 0. ï ï ï ïn = (1;-2 d ) ïd î î ^ D ï
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 764
hệ. Face: Trần Đình Cư. SĐT: 0834332133 ìïx = 1-3t
Câu 58: Đường thẳng
d đi qua điểm M (-2; )
1 và vuông góc với đường thẳng : ï D í có ïy = -2 +5t ïî
phương trình tham số là: ìïx = -2 -3t ìïx = -2 +5t ìïx = 1-3t ìïx = 1+ 5t A. ïí . B. ïí . C. ïí . D. ïí . ïy = 1+5t ïî ïy = 1+3t ïî ïy = 2 + 5t ïî ïy = 2 + 3t ïî Lời giải Chọn B. ìïM ( 2; - ) 1 Î d ïï ì ïM ( 2; - ) 1 Î d ì ï ï ïx = - + t u í = - ï í í Î D ( 2 5 3; ) 5 d : (t ). ï ï ï ïn = ( 3; - ) 5 u = (5; ïy = + t d d ) 3 1 3 î ïî ïd ïî ^ D
Câu 59: Viết phương trình tham số của đường thẳng
d đi qua điểm A (-1;2) và song song với đường thẳng .
D : 3x -13y +1 = 0 ìïx = -1+13t ìïx = 1+13t ìïx = -1-13t ìïx = 1+3t A. ïí . B. ïí . C. ïí . D. ïí . ïy = 2 + 3t ïî ïy = -2 +3t ïî ïy = 2 +3t ïî ïy = 2 -13t ïî Lời giải Chọn A. ìïA( 1 - ;2)Î d ïï ì ïA(-1;2)Î d ì ï ï = - + ín = - ï ï í í Î D ( x 1 13t 3; 1 ) 3 d : (t ). ï ï ï ïn = (3; 1 - ) 3 u = (13; ) 3 ïy = 2 +3t î ïî ïd || d d ïî D
Câu 60: Viết phương trình tham số của đường thẳng d qua
điểm A (-1;2) và vuông góc với đường thẳng .
D : 2x - y + 4 = 0 ìïx = -1+ 2t ìïx = t ìïx = -1+ 2t ìïx = 1+ 2t A. ïí . B. ïí . C. ïí . D. ïí . ïy = 2 -t ïî ïy = 4 + 2t ïî ïy = 2 + t ïî ïy = 2 -t ïî Lời giải Chọn A. ìïA(-1;2)Î d ïï ì ïA(-1;2)Î d ì ï ï = - + ín ï ï = - í Î D ( x t 2; ) 1 2 1 d :í (t ). ïï u ïï =(2;- ) 1 ïy = 2-t d î ïî ïd ï ^ D î
Câu 61: Viết phương trình tổng quát của đường thẳng
d đi qua điểm M (-2;-5) và song song với
đường phân giác góc phần tư thứ nhất.
A. x + y -3 = 0 .
B. x - y -3 = 0 .
C. x + y +3 = 0 .
D. 2x - y -1 = 0 . Lời giải Chọn B.
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 765
hệ. Face: Trần Đình Cư. SĐT: 0834332133 ìïM ( 2; - - ) 5 Î d ïï ìïM (-2;- ) 5 = 0 (I
ïí ): x- y = 0 ( ) D ï í 2 - -(- )
5 + c = 0 c = 3 - . ï
ïd : x- y +c = ï ï 0 (c = / 0) d || î ïï D î
Vậy d : x- y -3 = 0.
Câu 62: Viết phương trình tổng quát của đường thẳng
d đi qua điểm M (3;- ) 1 và vuông góc với
đường phân giác góc phần tư thứ hai.
A. x + y -4 = 0 .
B. x - y -4 = 0 .
C. x + y + 4 = 0 .
D. x - y + 4 = 0 . Lời giải Chọn B. ìïM (3;- ) 1 ï Î d ï ìïM (3;- ) 1 (
ïí II): x+ y = 0 (D) ï í ï ï ï
ïd : x - y + c = 0 î ïïîd ^ D 3-(- )
1 + c = 0 c = -4 d : x - y - 4 = 0. Choïn B.
Câu 63: Viết phương trình tham số của đường thẳng
d đi qua điểm M (-4;0) và vuông góc với
đường phân giác góc phần tư thứ hai. ìïx = t ìïx = -4 + t ìïx = t ìïx = t A. ïí . B. ïí . C. ïí . D. ïí . ïy = -4 + t ïî ïy = t - ïî ïy = 4 + t ïî ïy = 4 -t ïî Lời giải Chọn C. ìïx = - + ì t ïM (-4;0) 4 ï t=4 Î d í ¾¾ A(0;4) ï Î d ïï ïy = t ( ïî
í II): x + y = 0 (D) n = D (1; ) 1 ïïï d ^ D u = ï d (1; ) 1 î ìïx = t d : ï í
(t Î ). Choïn . C ïy = 4 + ïî t
Câu 64: Viết phương trình tổng quát của đường thẳng
d đi qua điểm M (-1;2) và song song với trục Ox . A. y +2 = 0 . B. x +1 = 0 . C. x -1 = 0 . D. y -2 = 0 . Lời giải Chọn D. ìïM (-1;2)Î d ïí ¾¾ d : y = 2.
ïïd || Ox : y = 0 î
Câu 65: Viết phương trình tham số của đường thẳng
d đi qua điểm M (6;-10) và vuông góc với trục Oy . ìïx =10 +t ìïx = 2 + t ìïx = 6 ìïx = 6 A. ïí . B. d : ïí . C. d : ïí . D. d : ïí . ïy = 6 ïî ïy = -10 ïî ïy = -10 -t ïî ïy = -10 + t ïî
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 766
hệ. Face: Trần Đình Cư. SĐT: 0834332133 Lời giải Chọn B.
ìïM (6;-10)Î d ìïx = 6 + ï ï t t=-4 í ¾¾ d : í ¾¾¾ A(2;-10)Î d ïd ^ ï
Oy : x = 0 u = y d (1;0) ï = -10 î îï ìïx = 2 +t d : ïí . Choïn B. ïy = -10 ïî
Câu 66: Phương trình tổng quát của đường thẳng đi qua hai điểm A (3;- ) 1 và B (1;5) là: A. -x + 3y + 6 = 0. B. 3x - y +10 = 0. C. 3x - y + 6 = 0. D. 3x + y -8 = 0. Lời giải Chọn D. ìïA(3;- ) 1 Î ï AB í ï ïu = AB = n AB (-2;6) = AB (3; ) 1 ïî AB : 3(x - ) 3 + ( 1 y + )
1 = 0 AB : 3x + y -8 = 0. Choïn D.
Câu 67: Phương trình đường thẳng cắt hai trục tọa độ tại A (–2;0) và B(0;3) là:
A. 2x -3y + 4 = 0 .
B. 3x – 2y + 6 = 0 .
C. 3x – 2 y -6 = 0 .
D. 2x – 3y -4 = 0 . Lời giải Chọn B. ìïA( 2; - 0)Î Ox ï x y í ¾¾ AB :
+ =1 3x - 2y + 6 = 0. ïïB(0; ) 3 Î Oy 2 - 3 î
Câu 68: Phương trình tổng quát của đường thẳng đi qua hai điểm A (2;- ) 1 và B (2;5) là: A. x + y -1 = 0. B.
2x -7 y + 9 = 0. C. x + 2 = 0. D. x - 2 = 0. Lời giải Chọn D. ìïA(2;- ) 1 Î AB ï í ¾¾
AB : x - 2 = 0. u ïï
= AB = (0;6) n = (1;0 ï AB AB ) î
Câu 69: Phương trình tổng quát của đường thẳng đi qua hai điểm A (3;-7) và B(1;-7) là: A. y -7 = 0. B. y +7 = 0. C. x + y + 4 = 0. D. x + y + 6 = 0. Lời giải Chọn B. ìïA(3;-7)Î AB ï í ¾¾
AB : y + 7 = 0. u ïï = AB = ( 4;0) n (0; ) 1 ï AB AB î - =
Câu 70: Cho tam giác ABC có A (1; ) 1 , 0 B( ;-2), C (
4;2). Lập phương trình đường trung tuyến của tam
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 767
hệ. Face: Trần Đình Cư. SĐT: 0834332133 giác ABC kẻ từ A A. x + y -2 = 0. B. 2x + y -3 = 0. C. x + 2 y -3 = 0. D.
x - y = 0. Lời giải Chọn A.
Gọi M là trung điểm của BC. Ta cần viết phương trình đường thẳng AM. Ta có : ìïB(0; 2 - ) ï í
M (2;0) u = AM = - n =
AM x + y - = AM (1; ) 1 AM (1; ) 1 : 2 0. C ïï (4;2) î
Câu 71: Đường trung trực của đoạn
AB với A (1;-4) và B(5;2) có phương trình là: A. 2x + 3y -3 = 0. B.
3x + 2 y +1 = 0. C. 3x - y + 4 = 0. D. x + y -1 = 0. Lời giải Chọn A.
Gọi I là trung điểm của AB và d là trung trực đoạn AB. Ta có
ìïA(1;-4), B(5;2) I (3;- ) 1 Î d ï í ¾¾
d : 2x + 3y -3 = 0. ï
ïd ^ AB n = AB = (4;6) = 2(2; ï d ) 3 î
Câu 72: Đường trung trực của đoạn
AB với A (4;- )
1 và B (1;-4) có phương trình là: A. x + y = 1. B. x + y = 0. C. y - x = 0. D. x - y = 1. Lời giải Chọn B.
Gọi I là trung điểm của AB và d là trung trực đoạn AB. Ta có ìï æ ö
ïïA( - ) B( - ) 5 5 4; 1 , 1; 4 I çç ; ÷ - ÷ Î d ï çè2 2÷ø í ¾¾
d : x + y = 0. ïï ï
d ^ AB n = AB = - ï - = - d ( 3; ) 3 3(1; ) 1 î
Câu 73: Đường trung trực của đoạn
AB với A (1;-4) và B(1;2) có phương trình là: A. y +1 = 0. B. x +1 = 0. C. y -1 = 0. D. x - 4 y = 0. Lời giải Chọn A.
Gọi I là trung điểm của AB và d là trung trực đoạn AB. Ta có
ìïA(1;-4), B(1;2) I (1;- ) 1 Î d ï í ¾¾
d : y +1 = 0. ï
ïd ^ AB n = AB ï = = d (0;6) 6(0; ) 1 î
Câu 74: Đường trung trực của đoạn
AB với A (1;-4) và B(3;-4) có phương trình là :
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 768
hệ. Face: Trần Đình Cư. SĐT: 0834332133 A. y + 4 = 0. B. x + y -2 = 0. C. x - 2 = 0. D. y - 4 = 0. Lời giải Chọn C.
Gọi I là trung điểm của AB và d là trung trực đoạn AB. Ta có
ìïA(1;-4), B(3;-4) I (2;-4)Î d ï í ¾¾
d : x - 2 = 0. ï
ïd ^ AB n = AB = = ï d (2;0) 2(1;0) î
Câu 75: Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có A (2;- ) 1 , B (
4;5) và C (-3;2) . Lập
phương trình đường cao của tam giác ABC kẻ từ A.
A. 7x +3y -11 = 0. B.
-3x +7 y +13 = 0. C.
3x + 7 y +1 = 0. D. 7x + 3y +13 = 0. Lời giải Chọn A.
Gọi h là đường cao kẻ từ A của tam giác ABC. Ta có A ìïA(2;- ) 1 Î hA ï í
h : 7x + 3y -11 = 0. ï
ïh ^ BC n = BC = - - = - A h ( 7; ) 3 (7; ) 3 A ïî A
Câu 76: Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có A (2;- ) 1 , B (
4;5) và C (-3;2). Lập
phương trình đường cao của tam giác ABC kẻ từ . B
A. 3x -5y -13 = 0. B. 3x + 5y -20 = 0. C.
3x + 5y -37 = 0. D.
5x -3y -5 = 0. Lời giải Chọn D.
Gọi h là đường cao kẻ từ B của tam giác ABC. Ta có B ìïB(4; ) 5 Î hB ï í
h : 5x -3y -5 = 0. B
ïïh ^ AC n = AC = - = - - B h ( 5; ) 3 (5; ) 3 ïî B
Câu 77: Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có A (2;- ) 1 , B (
4;5) và C (-3;2). Lập
phương trình đường cao của tam giác ABC kẻ từ C.
A. x + y -1 = 0. B. x + 3y -3 = 0. C.
3x + y +11 = 0. D.
3x - y +11 = 0. Lời giải Chọn B.
Gọi h là đường cao kẻ từ C của tam giác ABC. Ta có C C ìï (-3;2)Î h ï C ïí
h : x + 3y -3 = 0. ï
ïh ^ AB n = AB = = C h (2;6) 2(1; ) 3 C ïî C
Câu 78: Xét vị trí tương đối của hai đường thẳng
d : x -2 y +1 = 0
d : -3x + 6 y -10 = 0 1 và 2 .
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 769
hệ. Face: Trần Đình Cư. SĐT: 0834332133 A. Trùng nhau. B. Song song.
C. Vuông góc với nhau.
D. Cắt nhau nhưng không vuông góc nhau. Lời giải Chọn B.
ìïd : x-2y +1= 0 ï 1 1 -2 1 í = = / ¾¾
d || d . 1 2
ïd :-3x + 6y -10 = 0 -3 6 10 ïî - 2
Câu 79: Xét vị trí tương đối của hai đường thẳng
d : 3x -2 y -6 = 0
d : 6x -2 y -8 = 0 1 và 2 . A. Trùng nhau. B. Song song.
C. Vuông góc với nhau.
D. Cắt nhau nhưng không vuông góc nhau. Lời giải Chọn D. ìï3 ìï -
d : 3x - 2 y -6 = 0 n = 3; 2 2 - ï ï = / 1 1 ( ) ï í í6 -2 ¾¾
d , d cắt nhau nhưng không vuông góc. 1 2
ïïd : 6x-2y-8 = 0 n = 6;-2 ï 2 2 ( ) î ïïn ⋅n = 0 ïî / 1 2 Câu 80: x y
Xét vị trí tương đối của hai đường thẳng d : - = 1
d : 3x + 4 y -10 = 0 1 và 2 . 3 4 A. Trùng nhau. B. Song song.
C. Vuông góc với nhau.
D. Cắt nhau nhưng không vuông góc nhau. Lời giải Chọn C. ìï x y æ1 1ö
ïïd : - =1 n =çç ; ÷ - ÷ 1 1 ï í 3 4 çè3 4÷ø
n ⋅n = 0 d ^ d . 1 2 1 2 ïï
ïd : 3x + 4y 1 - 0 = 0 n = 3;4 ï 2 2 ( ) î ìïx = 1 - +t ìïx = 2- 2t¢
Câu 81: Xét vị trí tương đối của hai đường thẳng d : ïí d : ïí 1 và 2 . ïy = 2 - -2t ïî ïy = -8+ 4t¢ ïî A. Trùng nhau. B. Song song.
C. Vuông góc với nhau.
D. Cắt nhau nhưng không vuông góc nhau. Lời giải Chọn A. ìïx = -1+t ü ï d : ïí u 1; 2 ï = - ï 1 1 ( ) ì ï ï ï 1 -2 y = -2- 2t ïî ï ï = ï ï ý í-2 4
d º d . 1 2 ìïx = 2-2t¢ ï ï d : ïí
B 2;-8 Î d , u = -2;4 ï ï ï
ïB Î d « t = 3 ï î 2 ( ) 2 2 ( ) 1 ïy = -8+ 4t¢ ï ïî þï
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 770
hệ. Face: Trần Đình Cư. SĐT: 0834332133 ìïx = 3 - + 4t ìïx = 2- 2t¢
Câu 82: Xét vị trí tương đối của hai đường thẳng d : ïí d : ïí 1 và 2 . ïy = 2-6t ïî ïy = -8+ 4t¢ ïî A. Trùng nhau. B. Song song.
C. Vuông góc với nhau.
D. Cắt nhau nhưng không vuông góc nhau. Lời giải Chọn B. ìïx = -3+ 4t ü ï d : ïí A 3; 2 Î d , u 2; 3 ï - = - ï 1 ( ) 1 1 ( ) ì ï ï ï 2 -3 y = 2-6t ïî ï ï = ï ï ý í-2
3 d || d . 1 2 ìïx =1-2t¢ ï ï d : ïí = -2;3 ï ï ï ïA Î / d u ï î 2 2 ( ) 2 ïy = 4 +3t¢ ï ïî ïþ
Câu 83: Xác định vị trí tương đối của hai đường thẳng ìï 3 ì ï ï 9 x = 3 + t ï ïx = + 9t ¢ ï ï ï 2 ï D : 2 í D : í 1 và 2 . ï 4 ï ï 1 ïy = 1 - + t ïï = + ¢ ï y 8t ïî 3 ïïî 3 A. Trùng nhau. B. Song song.
C. Vuông góc với nhau.
D. Cắt nhau nhưng không vuông góc nhau. Lời giải Chọn A. ìï 3 üï ïx = 3+ t ï ï ï ï 2 æ3 4öï D :í A 3; 1
- Î D , u = çç ; ÷ï ÷ 1 ( ) 1 1 ï ì ï ç ÷ ï 3 4 4 è2 3 ï ø ï ïïy = -1+ t ï ï ï ï ï ï 2 3 ïî 3 ï ï = ï ï ý í 9 8 D º D . 1 2 ìï 9 ï ï x = + 9t ï ï ï ¢ ï ï 1 ï ï 2 ï ï ï A Î D « t ï ï ¢ = - 2 D :í u = 9;8 ï ïî 6 2 2 ( ) 1 ï ï ï ïïy = +8t¢ ïï ïîï 3 ïïþ
Câu 84: Xác định vị trí tương đối của hai đường thẳng ìïx = 4+t
D : 7x + 2 y -1 = 0 : ï D í . 1 và 2 ïy =1-5t ïî A. Trùng nhau. B. Song song.
C. Vuông góc với nhau.
D. Cắt nhau nhưng không vuông góc nhau. Lời giải Chọn D.
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 771
hệ. Face: Trần Đình Cư. SĐT: 0834332133 D : 7x + 2y 1 - = 0 n = 7;2 üï 1 1 ( ) ì ï ï7 2 ï ï ï ï = / ìïx = 4+t ï ý í5 1
D , D cắt nhau nhưng không vuông D :ïí u = 1; 5 - n = 5;1 ï ï 2 2 ( ) 2 ( ) 1 2 ï ï ïy =1-5 ï n ï ⋅n = / 0 t ï ï î ï î 1 2 þ góc.
Câu 85: Xét vị trí tương đối của hai đường thẳng ìïx = 4 +2t d : ïí
d : 3x + 2 y -14 = 0 1 và . ïy =1-3t 2 ïî A. Trùng nhau. B. Song song.
C. Vuông góc với nhau.
D. Cắt nhau nhưng không vuông góc nhau. Lời giải Chọn A. ìïx = 4+ 2t ü ï d : ïí
A 4;1 Î d , u = 2; 3 ï - ï ì = 1 ( ) 1 1 ( ) u ï u ï ï ï 1 2 y =1-3t ïî ý í d º d . 1 2 ï ï A Î d
d : 3x + 2y -14 = 0 n = (3;2) u = 2; 3 ï ïî - ï 2 ( ) 2 2 2 ïþ
Câu 86: Xét vị trí tương đối của hai đường thẳng ìïx = 4 +2t d : ïí
d : 5x + 2 y -14 = 0 1 và 2 . ïy =1-5t ïî A. Trùng nhau. B. Song song.
C. Vuông góc với nhau.
D. Cắt nhau nhưng không vuông góc nhau. Lời giải Chọn B. ìïx = 4+ 2t ü ï d : ïí
A 4;1 Î d , u = 2; 5 ï - ï ì = 1 ( ) 1 1 ( ) u ï u ï ï ï 1 2 y = 1-5t ïî ý í
d || d . 1 2 ï ï A Î / d
d : 5x + 2y -14 = 0 n = (5;2) u = (2;- )ï ïî 2 5 ï 2 2 2 ïþ ìïx = 2 +3t ìïx = 2t¢
Câu 87: Xét vị trí tương đối của hai đường thẳng d : ïí d : ïí 1 và 2 . ïy = 2 - t ïî ïy = -2 +3t¢ ïî A. Trùng nhau. B. Song song.
C. Vuông góc với nhau.
D. Cắt nhau nhưng không vuông góc nhau. Lời giải Chọn C.
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 772
hệ. Face: Trần Đình Cư. SĐT: 0834332133 ìïx = 2 +3t ü ï d : ïí u 3; 2 ï = - ï 1 1 ( ) ïy = -2t ï ïî ïï
ý u ⋅u = 0 d ^ d . 1 2 1 2 ìïx = 2t¢ ï d : ïí u = 2;3 ïï 2 2 ( ) y = -2 + 3t ï ï ¢ ï ïî ïþ ìïx = 2 +t ìïx = 5-t
Câu 88: Cho hai đường thẳng d : ïí ï 1 d : í 1 và 2 . ïy = 3 - +2t ïî ïy = -7 + 3t ïî 1
Khẳng định nào sau đây là đúng:
A. d song song d . B.
d và d cắt nhau tại . M (1; –3) 1 2 1 2 C. d d d d M (3;– ) 1 1 trùng với . 2
D. 1 và 2 cắt nhau tại . Lời giải Chọn D. Ta có ìïx = 2 +t üï d : ïí d : 2x y 7 0 ï - - = ï 1 1 ïy = -3+ 2 ï t ïî ïïý ìïx = 5-t ï ï 1 d : í
d : 3x + y -8 = 0ïï 2 2 y = -7 + 3 ï ï t ï ïî 1 ïþ
ìïd : 2x- y -7 = 0 ìïx = 3 ï 1 ï í í
d Ç d = M 3; 1 - . 1 2 ( )
ïd : 3x + y -8 = 0 ïy = 1 - ïî 2 ïî ìïx =1-t
Câu 89: Cho hai đường thẳng d : ïí
d : x – 2 y +1 = 0 1 và 2 . ïy = 5 +3t ïî
Khẳng định nào sau đây là đúng: A. d d d Ox 1 song song 2 .
B. 2 song song với trục . æ ö æ ö C. 1 1 3 d Oy M çç0; ÷÷ d d M çç ; ÷÷ 2 cắt trục tại .
D. và 2 cắt nhau tại . çè 2÷ø 1 çè8 8÷ø Lời giải Chọn C. ìï 15 ïx = ìïx =1-t
ìïd : 3x + y-8 = 0 ï ï ï 1 ï d : ï 7 í
d : 3x + y -8 = 0 í í A, B, D sai. 1 1 ïy = 5+3t
ïd : x – 2y +1= 0 ï 11 ïî ïî 2 ïïy = îïï 7 1 æ 1ö
Oy Ç d : x – 2y +1= 0 « x = 0 y = d ÇOy = M çç0; ÷÷. 2 2 2 çè 2÷ø
Câu 90: Cho bốn điểm , A (4;-3) B (5; ) 1 , C (2;3) và D (-2; 2) . Xác
định vị trí tương đối của hai đường thẳng AB và CD . A. Trùng nhau. B. Song song.
C. Vuông góc với nhau.
D. Cắt nhau nhưng không vuông góc nhau.
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 773
hệ. Face: Trần Đình Cư. SĐT: 0834332133 Lời giải Chọn D. ì ì u ï = AB ï = ï ï AB ( ) 1 4 1; 4 ï ï = / í í-4 -1 AB, CD
cắt nhau nhưng không vuông góc. u ï = CD = - - ï ï ï ï CD ( 4; ) 1 î u ï ⋅u = / 0 î AB CD
Câu 91: Cho bốn điểm ,
A (1;2) B(4;0) , C (1;-3) và D (7;-7) . Xác
định vị trí tương đối của hai đường thẳng AB và CD . A. Trùng nhau. B. Song song.
C. Vuông góc với nhau.
D. Cắt nhau nhưng không vuông góc nhau. Lời giải Chọn B. ì ì
ïïA(1;2)Î AB, u = AB = - n = AB x + y - = ï - ï AB (3; 2) AB (2; ) 3 : 2 3 8 8 3 2 = ï ï í í6 -4
nên AB || C . D C ï (1;- ) 3 Î CD, u CD ï ï = = - ï ï CD (6; 4) î C ï AB î Î /
Câu 92: Các cặp đường thẳng nào sau đây vuông góc với nhau? ìïx = t A. d : ïí
d : 2x + y – 1 = 0. 1 và ïy = 1 - -2t 2 ïî ìïx = t
B. d : x -2 = 0 và d : ïí . 2 1 ïy = 0 ïî
C. d : 2x - y +3 = 0
d : x -2 y +1 = 0. 1 và 2
D. d : 2x - y +3 = 0
d : 4x -2 y +1 = 0. 1 và 2 Lời giải Chọn B. ìï ìïx = t d ïï :ïí u = 1; 2 - 1 1 ( ) (i) ï í ïy = 1 - -2t ï î u ⋅u = / 0 loại A. 1 2 ï d
ïï : 2x+ y –1= 0 n = 2;1 u = 1; 2 - ï 2 2 ( ) 2 ( ) î ì
ïd : x -2 = 0 n = 1;0 1 1 ( ) ïï (ii) ï í ìïx = t
n ⋅n = 0 d ^ d . 1 2 ïd : d :ïí
. u = 1;0 n = ï 0;1 2 2 2 ( ) 2 ( ) 1 2 ï ïy = 0 ïî ïî
Tương tự, kiểm tra và loại các đáp án C, D.
Câu 93: Đường thẳng nào sau đây song song với đường thẳng ? 2x + 3y -1 = 0
A. 2x +3y +1 = 0 .
B. x -2y +5 = 0 .
C. 2x -3y +3 = 0 .
D. 4x -6y -2 = 0 . Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 774
hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn A. d
ìï : 2x +3y-1= 0 Xét đáp án A: 2 3 1 ï - í = = /
d || d . d ï : 2x +3y +1= 0 2 3 1 A ïî - A
Để ý rằng một đường thẳng song song với 2x +3y -1 = 0 sẽ có dạng 2x + 3y + c = 0 (c =/ - ) 1 .
Do đó kiểm tra chỉ thấy có đáp án A thỏa mãn, các đáp án còn lại không thỏa mãn.
Câu 94: Đường thẳng nào sau đây không có điểm chung với đường thẳng ? x -3y + 4 = 0 ìïx =1+t ìïx =1-t ìïx =1-3t ìïx =1-3t A. ïí . B. ïí . C. ïí . D. ïí . ïy = 2 +3t ïî ïy = 2 +3t ïî ïy = 2 +t ïî ïy = 2-t ïî Lời giải Chọn D. Kí hiệu
d : x -3y + 4 = 0 n = (1;- ) 3 . d ìïx =1+t (i) Xét đáp án A: d : ïí
n = 1;3 n , n không cùng phương nên loại A. 1 1 ( ) 1 ïy = 2+3t ïî ìïx =1-t (ii) Xét đáp án B: d : ïí
n = 3;1 n , n không cùng phương nên loại B. 2 2 ( ) 2 ïy = 2+3t ïî ìïx =1-3t (iii) Xét đáp án C: d :ïí
n = 1;3 n , n không cùng phương nên loại C. 3 3 ( ) 3 ïy = 2+t ïî ì ïx =1-3t ìïM (1;2)Î d ìïn = n (iv) Xét đáp án D: 4 ï ï ï 4 d : í í í d | d . 4 ïy = 2-t ï ïî ïn = (1;- ) 4 3 ïM d 4 î ï Î / î
Câu 95: Đường thẳng nào sau đây vuông góc với đường thẳng ? 4x -3y +1 = 0 ìïx = 4t ìïx = 4t ìïx = 4 - t ìïx = 8t A. ïí . B. ïí . C. ïí . D. ïí . ïy = 3 - -3t ïî ïy = 3 - +3t ïî ïy = 3 - -3t ïî ïy = 3 - +t ïî Lời giải Chọn A. Kí hiệu
d : 4x - 3y +1 = 0 n = (4;- ) 3 . d ìïx = 4t (i) Xét đáp án A: d : ïí
n = 3;4 n ⋅ n = 0 1 1 ( ) 1 ïy = 3 - -3 d ïî t
(ii) Tương tự kiểm tra và loại các đáp án B, C, D. ìïx = t
Câu 96: Đường thẳng nào sau đây có vô số điểm chung với đường thẳng ? ïíïy = 1 - ïî ìïx = 0 ìïx = 1 - + t ìïx = 1 - + 2018t ìïx =1 A. B ïí . . ïí . C. ïí . D. ïí . ïy = 1 - + 2018t ïî ïy = 0 ïî ïy = 1 - ïî ïy = 1 - + t ïî Lời giải Chọn C.
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 775
hệ. Face: Trần Đình Cư. SĐT: 0834332133
Hai đường thẳng có hai điểm chung thì chúng trùng nhau. Như vậy bài toán trở thành tìm
đường thẳng trùng với đường thẳng đã cho lúc đầu. Ta có ì ì ïx = t ïA(0;- ) 1 Î d d : ï ï í ¾¾ í ¾¾
kiểm tra đường thẳng nào chứa điểm A(0;- ) 1 và có VTCP ïy = 1 - ï ïî ïu = (1;0) î d
cùng phương với u ¾¾ Chọn C. d ìïx = 2 - +3t
Câu 97: Đường thẳng nào sau đây có đúng một điểm chung với đường thẳng ? ïíïy =5-7t ïî
A. 7x +3y -1 = 0.
B. 7x +3y +1 = 0.
C. 3x -7y +2018 = 0.
D. 7x +3y +2018 = 0. Lời giải Chọn C. ìïx = 2 - +3t
Ta cần tìm đường thẳng cắt d :ïí ¾¾
d : 7x +3y 1 - = 0. ïy = 5-7 ïî t
d : 7x +3y 1 - = 0 ¾¾ d º d ¾¾ loại A. 1 1
d : 7x +3y +1= 0 & d : 7x +3y + 2018 = 0 ¾¾
d , d | d ¾¾ loại B, D. 2 3 2 3
Câu 98: Với giá trị nào của m thì hai đường thẳng
d : 3x + 4 y +10 = 0
d : 2m -1 x + m y +10 = 0 2 ( ) 2 1 và trùng nhau? A. m 2 . B. m = 1 . C. m = 2 . D. m = -2 . Lời giải Chọn C. ìïd :(2m- ) 2 2
1 x + m y +10 = 0 d d m - ï 2 º 2 1 m 10 1 2 í ¾¾¾ = =
ïïd :3x+4y +10 = 0 3 4 10 î 1 ìï2m-1= 3 ï í
m = 2. Choïn . C 2 ïm = 4 ïî
Câu 99: Trong mặt phẳng với hệ tọa độ , Oxy cho hai
đường thẳng có phương trình
d : mx + m -1 y + 2m = 0
d : 2x + y -1 = 0 d d 1 ( ) và 2 . Nếu 1 song song 2 thì: A. m = 2. B. m = -1. C. m = -2. D. m = 1. Lời giải Chọn A.
ìïd : mx + m-1 y + 2m = 0 ï 1 ( ) d d m m -1 2m 1 || 2 í ¾¾¾ = = /
ïd : 2x + y -1= ï 0 2 1 -1 î 2 ì- ï 1 = / 2 ï í
m = 2. Choïn A. ïm = 2m-2 ïî
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 776
hệ. Face: Trần Đình Cư. SĐT: 0834332133 ìïx = 2-3t
Câu 100: Tìm m để hai đường thẳng d : 2x -3y + 4 = 0 và d : ïí 2 cắt nhau. 1 ïy =1-4mt ïî A. 1 1 m ¹ - . B. m ¹ 1 2. C. m ¹ . D. m = . 2 2 2 Lời giải Chọn C.
ìïd : 2x-3y + 4 = 0 1 ï ì ï ïn = 2; 3 - 1 ( ) ï ï d Çd =M 4m 3 - 1 1 2 í ìïx = 2-3t ¾¾ í ¾¾¾¾ = / m = / . d :ï ïï í ïn = ï 4 ; m 3 - 2 3 - 2 2 2 ( ) ï ïy =1-4 î ïî ïî mt
Câu 101: Với giá trị nào của a thì hai đường thẳng ìïx = -1+ at
d : 2x – 4 y +1 = 0 d : ïí 1 và 2 vuông góc với nhau? ïy = 3-(a + ) 1 t ïî A. a = -2. B. a = 2. C. a = -1. D. a = 1. Lời giải Chọn D. Ta có
ìïd : 2x – 4y +1= 0 1 ï ì ï ïn = 1;-2 ï ï 1 ( ) 1 d ^d2 í ìïx = -1+ at ¾¾ í
¾¾¾ n ⋅ n = 0 a +1- 2a = 0 a =1. ï 1 2 ïd : ï í
ïïn = a +1;a 2 ï ïy = 3-(a + ) 2 ( ) 1 ïî ï î î t
Câu 102: Với giá trị nào của m thì hai đường thẳng ìïx = 2 - + 2t ìïx = 2 + mt d : ïí d : ïí 1 và 2 trùng nhau? ïy = 3 - t ïî
ïy = -6 +(1-2m)t ïî A. 1 m = . B. m = -2 . C. m = 2 . D. m ¹ 2 . 2 Lời giải Chọn C. ìïx = 2 - + 2t ü ï d : ïí u = 2;-3 ïï 1 1 ( ) ï ì ï ïA Î d1 y = -3 ïî t ï ï ï d d ï 1 º 2 ý ¾¾¾ím
1- 2m m = 2. ìïx = 2+ mt ï ï = d : ï ï ï í
A 2;-6 Î d , u = ; m 1- 2m ï ï ï î 2 3 - 2 ( ) 2 2 ( ) ïy = -6 +(1-2m) ïî t ïïþ
Câu 103: Tìm tất cả các giá trị của
m để hai đường thẳng ìïx = 2 +2t d : ïí
d : 4x -3y + m = 0 1 và trùng nhau. ïy = 1+ mt 2 ïî A. 4 m = -3 . B. m = 1 . C. m = . D. m Î Æ . 3
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 777
hệ. Face: Trần Đình Cư. SĐT: 0834332133 Lời giải Chọn D. ìïx = 2+ 2t ü ï ï ì ï ïA Î d 5 ìï + m = 0 2 d : í
A 2;1 Î d ,u = 2;m ï ï ï 1 ( ) 1 1 ( ) ï ï d d ï ï 1 º 2 y =1+ ïî mt ý ¾¾¾í2 m í 8 m Î . Æ ï ï = ïm =
d : 4x -3y + m = 0 u = 3;4 ï ï ï ï ï ï î3 4 ïî 3 2 2 ( ) þ
Câu 104: Với giá trị nào của m thì hai đường thẳng
d : 2x + y + 4 - m = 0 và d : m + 3 x + y + 2m -1 = 0 2 ( ) song song? 1 A. m = 1. B. m = -1. C. m = 2. D. m = 3. Lời giải Chọn B.
ìïd : 2x + y = 0 Với ï 1 m = 4 ¾¾ í ¾¾ d Ç d = / Æ ¾¾
loại m = 4. 1 2
ïd : 7x + y + 7 = 0 ïî 2 Với m =/ 4 thì
ìïd : 2x + y + 4-m = 0 m m m d d + -2 -1 ìï = 1 - 1 3 1 ï ï 1 || 2 í ¾¾¾ = = / í m = -1.
ïd : m +3 x + y -2m-1= 0 2 1 4- m ïm = / 5 - ï 2 ( ) î ïî
Câu 105: Tìm tất cả các giá trị của
m để hai đường thẳng
D : 2x -3my +10 = 0
D : mx + 4 y +1 = 0 1 và 2 cắt nhau.
A. 1 < m <10 . B. m = 1 .
C. Không có m . D. Với mọi . m Lời giải Chọn D. é ìïD : x +5 = 0 ê ï 1 m = 0 í
m = 0 (thoaû maõn) ìD ï
: 2x -3my +10 = 0 ê ï ï 1 D : 4y +1= 0 í ê ïî 2 .
ïD : mx + 4y +1= 0 ê ïî 2 ê D ÇD = 2 -3m 1 2 m = / 0 ¾¾¾¾ = / "m / = 0 ê M ë m 4
Câu 106: Với giá trị nào của m thì hai đường thẳng
D : mx + y -19 = 0
D : m -1 x + m +1 y - 20 = 0 2 ( ) ( ) 1 và vuông góc? A. Với mọi . m B. m = 2 .
C. Không có m . D. m = 1 . Lời giải Chọn C. ì
ïD : mx + y -19 = 0 n = ; m 1 1 1 ( ) Ta có :ïí ï
D : m-1 x + m +1 y - 20 = 0 n = m-1;m + ï 1 2 ( ) ( ) 2 ( ) î 1 D ^ 1 D ¾¾¾ m(m- ) 1 + ( 1 m + ) 1 = 0 m Î . Æ Choïn . C
Câu 107: Với giá trị nào của m thì hai đường thẳng
d : 3mx + 2 y + 6 = 0 và d : ( 2
m + 2 x + 2my + 6 = 0 2 ) cắt nhau? 1
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 778
hệ. Face: Trần Đình Cư. SĐT: 0834332133 A. m ¹ -1. B. m ¹ 1 . C. m Î .
D. m ¹1 và m ¹ 1 - . Lời giải Chọn D. ì
ïd : 3mx + 2 y + 6 = 0 n = 3 ; m 2 ï 1 1 ( ) Ta có: ïí ï d :( 2
m + 2)x + 2my + 6 = 0 n = ( 2 m + ï 2; 2m 2 2 ) ïî é ìïd : y +3 = 0 ê ï 1 m = 0 í m = 0(thoaû maõn) ê
ïd : x + y +3 = 0 ê ïî 2 . ê 2 ê d Çd =M m + 2 2m 1 2 êm = / 0 ¾¾¾¾ = / m = / 1 êë 3m 2
Câu 108: Với giá trị nào của m thì hai đường thẳng ìï x = 2-3t
d : 2x -3y -10 = 0 và d : ïí 2 vuông góc? 1 ïy =1-4mt ïî A. 1 9 9 5 m = . B. m = . C. m = - . D. m = - . 2 8 8 4 Lời giải Chọn C. ì
ïd : 2x -3y -10 = 0 n = 2; 3 - 1 1 ( ) ïïï d ^d 9 í ìï x = 2-3 1 2 ¾¾¾ 2.4m +(- ) 3 .(- ) 3 = 0 m = - . ï t ïd :ïí n = 4 ; m 3 - 8 2 2 ( ) ï ïy =1-4 ïî ïî mt
Câu 109: Với giá trị nào của m thì hai đường thẳng ìï x =1+ 2t
d : 4x -3y + 3m = 0 và d : ïí 2 trùng nhau? 1 ïy = 4 + mt ïî A. 8 8 4 4 m = - . B. m = . C. m = - . D. m = . 3 3 3 3 Lời giải Chọn B. ì
ïd : 4x -3y +3m = 0 n = 4; 3 - 1 1 ( ) ïïïí ìï x=1+2 ï t ïd :ïí
A 1;4 Î d , n = ; m 2 - 2 ( ) 2 2 ( ) ï ïy = 4+ ïî ïî mt ìïA Î d 3 ìï m-8 = 0 1 ï ï d ºd ï ï 8 1 2 ¾¾¾ím -2 í 8 m = . ï = ïm = 3 ï ï ïî 4 -3 ïî 3
Câu 110: Với giá trị nào của m thì hai đường thẳng
d : 3mx + 2 y -6 = 0 và d : ( 2
m + 2 x + 2my -3 = 0 2 ) song song? 1
A. m =1; m = 1 - . B. m Î Æ . C. m = 2 . D. m = -1. Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 779
hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn A. ì
ïd : 3mx + 2y -6 = 0 n = 3 ; m 2 1 1 ( ) Ta cóïí ï d :( 2
m + 2)x + 2my -3 = 0 n = ( 2 m + ï 2; 2m 2 2 ) ïî é ìïd : y -3 = 0 ê ï 1 m = 0 í
m = 0(khoâng thoaû maõn) ê
ïd : 2x + 2y -3 = 0 ê ïî 2 . ê Choïn A. 2 ê d d m + 2 2m -3 1 | 2 êm = / 0 ¾¾¾ = = / m = 1 êë 3m 2 6 -
Câu 111: Với giá trị nào của m thì hai đường thẳng ìïx = 8-(m + ) 1 t d : ïí
d : mx + 2 y -14 = 0 1 và song song? ï 2 ïy = 10 + t î ém = 1 A. ê . B. m = 1 . C. m = -2 . D. m Î Æ . êm = -2 ë Lời giải Chọn A. ìï ìïx = 8-(m + ) 1 ï t ïd : ïí
A 8;10 Î d , n = 1;m +1 1 ( ) 1 1 ( ) Ta có:ï ï í ïy = 10 + î t ïïï
d : mx + 2y -14 = 0 n = ï ; m 2 2 2 ( ) î ìïA Î/ d2 ïïïé ï ìïn = 1;1 8 ìï m + 6 =/ 0 ïê ï 1 ( ) m d d ï m = ï ê í khoâng thoaû maõn ï é =1 0 ï 1 || 2 ¾¾¾ í ï n ím = / 0 ê = ê ï ï 0; 2 . 2 ( ) î ï êm = -2 ïê ïïm =1 ë ïïê 1 m +1 ïî ïê ï m = / 0 = ïê ïîë m 2
Câu 112: Với giá trị nào của m thì hai đường thẳng
d : m - 3 x + 2 y + m -1 = 0 2 d : x
- +my +m -2m +1 = 0 1 ( ) 2 và 2 cắt nhau? m ìï ¹1 ém ¹ 1 A. m ¹ 1 . B. ïí . C. m ¹ 2 . D. ê . m ï ¹ 2 ïî êm ¹ 2 ë Lời giải Chọn B. ìïd :(m- ) 2
3 x + 2y + m 1 - = 0 ï 1 í 2
ïïd :-x+my +m -2m+1= 0 î 2 é
ìïd :-3x + 2y -1= 0 ê ï 1 m = 0 í thoaû maõn ê ïd :-x +1= 0 d Çd =M ê ïî 2 1 2 ¾¾¾¾ . ê ê m -3 2 ìïm =/1 êm 0 ï = / = / í ê -1 m ïm = / 2 ë ïî
Câu 113: Với giá trị nào của m thì hai đường thẳng
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 780
hệ. Face: Trần Đình Cư. SĐT: 0834332133
ìïx = m + 2t ìïx =1+mt : ï D í và : ï D í 2 trùng nhau? 1 ïy = 1+( 2 m + ï ) 1 t ï ïî y = m + t ïî A. Không có 4 m . B. m = . C. m = 1 . D. m = -3 . 3 Lời giải Chọn C. ìï ìïx = m + 2 ï ï t 2 ïD : ï í A ;
m 1 Î d , u = 2; m +1 ì 1 ïA Î ï ï d y = 1+ ï ( 2 m + ï ) ( ) 1 1 ( ) 2 1 t ï ïî d d ï 1 º 2 í ¾¾¾ím 1 ïï ìïx =1 ï = + mt ï ï ï ï D ï í u = m î 2 m +1 : ;1 2 2 ( ) 2 ï ï ï y = m + î ïî t . ìïm =1+ ï mt ìïm =1+ ï m(1-m) 2 ì ï ï ïm -1= 0 1 ï ï í = m +t í í m =1. ïï ( ïï m- ) 1 ( 2 m + m + 2 = 0 ïm-1= 0 3 ) ï ï m + m - 2 = 0 ï î î ïî
Câu 114: Tìm tọa độ giao điểm của đường thẳng
D : 5x + 2 y -10 = 0 và trục hoành. A. (0;2). B. (0;5). C. (2;0). D. (-2;0). Lời giải Chọn C. ìïy = 0 ìïx = 2
Ox Ç : 5x 2y 10 0 ï ï D + - = ¾¾ í í . 5 ï x + 2y 1 - 0 = 0 ïy = 0 ïî ïî ìïx = 2t
Câu 115: Tìm tọa độ giao điểm của đường thẳng d : ïí và trục tung. ïy = 5 - +15t ïî æ ö A. 2 çç ;0÷÷ . B. (0;-5). C. (0;5) . D. (-5;0). çè3 ÷ø Lời giải Chọn A. ìï 1 ìïy = 0 ït = ìïx = 2 ï ï ï t ï ï ï ï 3 Oy Ç d : í ¾¾ íx = 2t í . ïy = 5 - +15t ï ï 2 ïî ïïy = 5 - +15 ï t ïx = , y = 0 ïî ïïî 3
Câu 116: Tìm tọa độ giao điểm của hai đường thẳng
7x -3y +16 = 0 và x +10 = 0 . A. (-10;-18) . B. (10;18) . C. (-10;18). D. (10;-18). Lời giải Chọn A.
ìïd : 7x-3y +16 = 0 ìïx = -10 ï 1 ï í í . ïd : x +10 = 0 ïy = -18 ïî 2 ïî
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 781
hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 117: Tìm toạ độ giao điểm của hai đường thẳng ìïx = 3 - + 4t ìïx = 1+ 4t ¢ d : ïí d : ïí . 1 và 2 ï y = 2 +5t ïî ïy = 7 -5t ¢ ïî A. (1;7). B. (-3;2). C. (2;-3). D. (5; ) 1 . Lời giải Chọn A. ìï ìïx = -3+ 4 ï t ïd : ïí ìï ìx d ï = 1 1 ï ï ï y = + t ì ï ïî - ï + t = + t¢ ì ï ï 1 2 5 3 4 1 4
ït -t¢ = 1 ït = 1 ¾¾¾ í ï ï ï í í í ï í y = 7. ïî ï ì ï ï x = 1+ 4t¢ ï2 +5t = 7-5t¢ ït +t¢ =1 ï ïd :ï ïî ïî ï ï í ït¢ = 0 2 ï y = 7 -5 ïî ï t¢ ïî ïî ìïx = 22 +2t
Câu 118: Cho hai đường thẳng
d : 2x + 3y -19 = 0 và d : ïí 2
. Tìm toạ độ giao điểm của hai 1 ïy = 55+5t ïî đường thẳng đã cho. A. (2;5). B. (10;25). C. (-1;7). D. (5;2). Lời giải Chọn A. ìï
d : 2x +3y -19 = 0 1 ïï ìx d d ï = 2 ï ï 1 Ç 2 í ìïx = 22+ 2t ¾¾¾
2(22 + 2t)+3(55+5t) 1 - 9 = 0 t = 1 - 0 í . d : ï ïï í ïy = 5 2 ï y = 55+5 ïî ï ïî ïî t
Câu 119: Trong mặt phẳng với hệ tọa độ Oxy , cho hai điểm A (–2 ;0), B ( 1;4) và đường thẳng ìïx = t - d : ïí
. Tìm tọa độ giao điểm của đường thẳng AB và d . ïy = 2-t ïî A. (2;0). B. (–2;0) . C. (0;2). D. (0;– 2) . Lời giải Chọn B. ìïA(–2; ) 0 , B( 1; )
4 AB : 4x -3y +8 = 0 ïï ìï4x-3y +8 = 0 ìïx = 2 ï ABÇd ï ï í ìïx = -t ¾¾¾ í í . ïïd :ïí
d : x - y + 2 = 0 ïx- y + 2 = 0 ïy = 0 ïî ïî ï ïy = 2- ïî ïî t ìïx = 1 - + t Câu 120: Xác định
a để hai đường thẳng
d : ax + 3y – 4 = 0 và d : ïí 2
cắt nhau tại một điểm 1 ïy = 3+3t ïî nằm trên trục hoành. A. a = 1. B. a = -1. C. a = 2. D. a = -2. Lời giải Chọn D.
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 782
hệ. Face: Trần Đình Cư. SĐT: 0834332133 ìïx = 1 - +t ìïx = 2 - Ox Ç ï ï d « í í
Ox Ç d = A - ; 2 0 Î d 2 2 ( ) 1 ïy = 3+3t = 0 ïy = 0 ïî îï 2
- a - 4 = 0 a = 2 - . ìïx = 2 +t
Câu 121: Tìm tất cả các giá trị của tham số m để hai đường thẳng 2
d : 4x +3my – m = 0 d : ïí 1 và 2 ïy = 6 +2t ïî
cắt nhau tại một điểm thuộc trục tung.
A. m = 0 hoặc . m = -6
B. m = 0 hoặc . m = 2
C. m = 0 hoặc . m = -2
D. m = 0 hoặc . m = 6 Lời giải Chọn D. ìïx = 2+t = 0 ìïx = 0 Oy Ç ï ï d « í í
Oy Ç d = A 0;2 Î d 2 2 ( ) 1 ïy = 6+ 2t ïy = 2 ïî ïî ém = 0 2
6m-m = 0 ê . êm = 6 ë
Câu 122: Cho ba đường thẳng ,
d : 3x – 2 y + 5 = 0
d : 2x + 4 y – 7 = 0
d : 3x + 4 y – 1 = 0 1 , . 3 Phương trình 2 đường thẳng
d đi qua giao điểm của d d d 1 và 2 , và song song với 3 là:
A. 24x +32y – 53 = 0 .
B. 24x +32y +53 = 0 . C. 24x – 32y +53 = 0 . D. 24x – 32y – 53 = 0 . Lời giải Chọn A. ìï 3 ïx = -
ìïd : 3x – 2y +5 = 0 ï æ ö 1 ï ï ï 8 3 31 í í d Ç d = ç A - ç ; ÷÷. Ta có 1 2
ïd : 2x + 4y – 7 = 0 ï 31 çè 8 16÷ ïî ø 2 ïïy = îïï 16 ìïA Î d ìïA Î d 9 31 53 ï ï í í - +
+ c = 0 c = - .
ïd || d : 3x + 4y –1= 0
ïd : 3x + 4y + c = 0 c 1 8 4 8 ï 3 ( ) ï / - î = î Vậy 53
d : 3x + 4 y –
= 0 d : 24x + 32 y -53 = 0. 3 8
Câu 123: Lập phương trình của đường thẳng
D đi qua giao điểm của hai đường thẳng ,
d : x +3y -1 = 0 1
d : x -3y -5 = 0
d : 2x - y +7 = 0 2
và vuông góc với đường thẳng . 3
A. 3x + 6y -5 = 0 .
B. 6x +12y -5 = 0 .
C. 6x +12y +10 = 0 .
D. x + 2 y +10 = 0 . Lời giải Chọn A. ìïx = 3
ìïd : x +3y -1= 0 ï ï æ ö 1 ï 2 í í
2 d Ç d = A 3 çç ; ÷ - ÷. Ta có 1 2
ïd : x -3y -5 = 0 ïy = - çè 3÷ ïî ø 2 ïïî 3
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 783
hệ. Face: Trần Đình Cư. SĐT: 0834332133 ìïA Î d ìïA Î d æ 2ö 5 ï ï í í 3+ 2.ç ÷ - ç
÷+ c = 0 c = - .
ïd ^ d : 2x- y +7 = 0
ïd : x 2y +c = 0 çè 3÷ø 3 ïî + 3 ïî Vậy 5
d : x + 2y - = 0 d : 3x + 6y -5 = 0. 3
Câu 124: Trong mặt phẳng với hệ tọa độ , Oxy cho ba
đường thẳng lần lượt có phương trình
d : 3x - 4 y +15 = 0 d : 5x + 2 y -1 = 0
d : mx - 2m -1 y + 9m -13 = 0 3 ( ) 1 , 2 và . Tìm tất cả các giá trị
của tham số m để ba đường thẳng đã cho cùng đi qua một điểm. A. 1 1 m = . B. m = -5. C. m = - . D. m = 5. 5 5 Lời giải Chọn D.
ìïd : 3x-4y +15 = 0 ìïx = 1 - Ta có:ï 1 ï í í
d Ç d = A -1;3 Î d 1 2 ( ) 3
ïd : 5x + 2y -1= 0 ïy = 3 ïî 2 ïî
-m-6m +3+ 9m-13 = 0 m = 5.
Câu 125: Nếu ba đường thẳng d :
2x + y – 4 = 0 d : 5x – 2 y + 3 = 0
d : mx + 3y – 2 = 0 1 , 2 và 3
đồng quy thì m nhận giá trị nào sau đây? A. 12 12 . B. - . C. 12. D. -12. 5 5 Lời giải Chọn D. ìï 5 ïx = ìï d : 2x + y – 4 = 0 ï æ ö 1 ï ï ï 9 5 26 í í d Ç d = ç Aç ; ÷÷Î d 1 2 3
ïd : 5x – 2y +3 = 0 ï 26 çè9 9 ÷ ïî ø 2 ïïy = ïïî 9 5m 26 +
- 2 = 0 m = -12. 9 3
Câu 126: Với giá trị nào của m thì ba đường thẳng ,
d : 3x – 4 y +15 = 0
d : 5x + 2 y – 1 = 0 1 2 và
d : mx – 4 y +15 = 0 3 đồng quy? A. m = -5 . B. m = 5 . C. m = 3 . D. m = -3 . Lời giải Chọn C.
ìïd : 3x – 4y +15 = 0 ìïx = -1 ï 1 ï í í
d Ç d = A 1 - ;3 Î d 1 2 ( )
ïd : 5x + 2y –1= 0 ïy = 3 ïî 2 ïî
-m-12 +15 = 0 m = 3.
Câu 127: Với giá trị nào của m thì ba đường thẳng ,
d : 2x + y –1 = 0 d : x + 2 y +1 = 0
d : mx – y – 7 = 0 1 2 và 3
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 784
hệ. Face: Trần Đình Cư. SĐT: 0834332133 đồng quy? A. m = -6 . B. m = 6 . C. m = -5 . D. m = 5 . Lời giải Chọn B.
ìïd : 2x + y –1= 0 ìïx =1 ï 1 ï í í
d Ç d = A 1;-1 Î d m +1-7 = 0 m = 6. 1 2 ( ) 3
ïd : x + 2y +1= 0 ïy = 1 - ïî 2 ïî
Câu 128: Đường thẳng
d : 51x -30y +11 = 0 đi qua điểm nào sau đây? æ ö æ ö æ ö æ ö A. 4 4 3 3 M çç 1; - - . ÷÷ B. N çç 1; - . ÷÷ C. P 1; çç . ÷÷ D. Qç- ç 1; ÷ - ÷. çè 3÷ø çè 3÷ø çè 4÷ø çè 4 ÷ø Lời giải Chọn A. ìï æ ö ïï f (M ) 4 = f ç- ç 1; ÷
- ÷ = 0 M Î d ï çè 3÷ø ïïïï æ 4ö Đặt f ( ;
x y) = 51x -30y +11 ï ¾¾
f (N ) = f ç- í ç 1; ÷÷ = -80 = / 0 N Î / ç ÷ d . ï è 3ø ïïïïf (P)=/0 ïïïïf (Q)=/0 ïî ìïx =1+2t
Câu 129: Điểm nào sau đây thuộc đường thẳng d : ïí ? ïy = 3-t ïî A. M (2; ) –1 . B. N (–7;0) . C. P(3;5) . D. Q(3; 2) . Lời giải Chọn D. ìï 1 ì t t x y d ï = + ï M ( = 2; – ) 2 1 2 =2, = 1 1 - ï ï ¾¾¾¾¾í í 2 (VN ) M Î / d. ï-1= 3-t ï ïî ïït = 4 î ì- t t x y d ï = + ìï = - N (–7;0) 7 1 2 4 7, =- =0 ï ï ¾¾¾¾¾í í
(VN) N Î/ d. 0 ï = 3-t ït = 3 ïî ïî ì t t x y d ï = + ìï = P(3; ) 3 1 2 1 =3, =5 5 ï ï ¾¾¾¾¾ í í
(VN) P Î/ d. 5 ï = 3-t ït = 2 - ïî ïî ì t x y d ï = + Q(3; ) 3 1 2 =3, =2 2 Î ï ¾¾¾¾í
t =1 Q Î d. 2 ï = 3- ïî t
Câu 130: Đường thẳng
12x -7 y + 5 = 0 không đi qua điểm nào sau đây? æ ö æ ö A. 5 17 M (1; ) 1 . B. N (-1;- ) 1 . C. Pç- ç ;0÷÷ . D. Q 1; ç ÷ ç ÷ . çè 12 ÷ø çè 7 ÷ø Lời giải Chọn A.
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 785
hệ. Face: Trần Đình Cư. SĐT: 0834332133
Gọi 12x -7y +5 = 0 .
ìïï f (M (1; )1)=10 =/ 0 M Î/ d ïï Đặt f ( ;
x y) 12x 7 y 5 ï = - + ¾¾ í f (N ( 1 - ;- )
1 ) = 0 N Î d .
ïïïïf (P)=0, f (Q)=0 ïî ìïx = 1 - +2t
Câu 131: Điểm nào sau đây không thuộc đường thẳng ïí ? ïy = 3-5t ïî A. M (-1;3) . B. N (1;-2). C. P (3; ) 1 . D. Q(-3;8) . Lời giải Chọn C. ìïx = 1 - + 2t ì t x y d ï 1 - = 1 - + 2 Gọi d :ïí . M ( 1; ) 1, =- =3 3 ï - ¾¾¾¾¾ í
t = 0 M Î d. ïy = 3-5 ïî t 3 ï = 3-5 îï t ì t x y d ï = - + N (1; ) 1 1 2 1, = = 2 2 - ï - ¾¾¾¾¾ í
t =1 N Î d. ï 2 - = 3-5 ïî t ìït = 2 ì t x y d ï = - + ï P(3; ) 3 1 2 =3, 1 1 = ï ï ¾¾¾¾¾ í í 2 P Î / d. 1 ï = 3-5t ït = ïî ïïî 5 ì- t x y d ï = - + Q( 3; ) 3 1 2 3, =- 8 8 = ï - ¾¾¾¾¾í t = 1
- Q Î d. 8 ï = 3-5 ïî t
Câu 132: Tính góc tạo bởi giữa hai đường thẳng
d : 2x - y -10 = 0
d : x -3y + 9 = 0. 1 và 2 A. o 30 . B. o 45 . C. o 60 . D. o 135 . Lời giải Chọn B. Ta có ì
ïd : 2x - y -10 = 0 n = 2; 1 - 2.1+ 1 - . 3 ï - 1 1 ( ) j= ( ) ( ) (d d 1 1 ; 2 ) í ¾¾¾¾ cosj = =
ïd x- y + = n = - 2 2 ï : 3 9 0 1; 3 2 2 ( ) î 2 +(- )2 1 . 1 +(- )2 2 3
j = 45 .
Câu 133: Tính góc tạo bởi giữa hai đường thẳng
d : 7x -3y + 6 = 0
d : 2x -5y - 4 = 0. 1 và 2 A. p . B. p . C. 2p . D. 3p . 4 3 3 4 Lời giải Chọn A. Ta có
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 786
hệ. Face: Trần Đình Cư. SĐT: 0834332133 ì
ïd : 7x -3y + 6 = 0 n = 7; 3 - + ï 1 1 ( ) j (= 14 15 d d 1 p 1 ; 2 ) í ¾¾¾¾ cosj = = j = .
ïd : 2x-5y-4 = 0 n = 2; 5 - ï 49 +9. 4 + 25 2 4 2 2 ( ) î
Câu 134: Tính góc tạo bởi giữa hai đường thẳng
d : 2x + 2 3y + 5 = 0 và d : y -6 = 0. 1 2 A. o 30 . B. o 45 . C. o 60 . D. o 90 . Lời giải Chọn A. Ta có ìï
ïd : 2x + 2 3y +5 = 0 n = 1; 3 3 1 1 ï ( ) j (=d d 3 1 ; 2 ) í ¾¾¾¾ cosj = = j = 30. ï
ïd : y -6 = 0. n = 0;1 1+3. 0 1 2 ï + 2 2 ( ) î
Câu 135: Tính góc tạo bởi giữa hai đường thẳng
d : x + 3y = 0 và d : x +10 = 0. 2 1 A. o 30 . B. o 45 . C. o 60 . D. o 90 . Lời giải Chọn C. ìï
ïd : x + 3y = 0 n = 1; 3 + 1 1 ï ( ) j (=d d 1 0 1 1 ; 2 ) í ¾¾¾¾ cosj = = ï
ïd : x +10 = 0 n 1;0 1+ 3. 1+ 0 2 ï 2 2 ( ) î =
j = 60 .
Câu 136: Tính góc tạo bởi giữa hai đường thẳng ìïx =10-6t
d : 6x -5y +15 = 0 d : ïí . 1 và 2 ïy =1+5t ïî A. o 30 . B. o 45 . C. o 60 . D. o 90 . Lời giải Chọn D. ì
ïd : 6x-5y +15 = 0 n = 6; 5 - 1 1 ( ) ïï j ï ( = 1 d ;d2 ) í ìïx =10-6t
n ⋅n = 0 ¾¾¾¾ j = 90. ïïd :ïí n = 5;6 2 ( ) 1 2 2 ï ïy =1+5 ïî ïî t
Câu 137: Cho đường thẳng d : x + 2y -7 = 0
d : 2x - 4 y + 9 = 0 1 và 2
. Tính cosin của góc tạo bởi giữa hai đường thẳng đã cho. A. 3 2 3 3 - . B. . C. . D. . 5 5 5 5 Lời giải Chọn C. ì
ïd : x + 2y -7 = 0 n = 1;2 - 1 1 ( ) ï j ( = 1 4 d d 3 1 ; 2 ) í ¾¾¾¾ cosj = = .
ïïd : 2x-4y +9 = 0 n 1; 2 1 4. 1 4 5 2 2 ( ) î = - + +
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 787
hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 138: Cho đường thẳng d : x +2y -2 = 0
d : x - y = 0 1 và 2
. Tính cosin của góc tạo bởi giữa hai đường thẳng đã cho. A. 10 . B. 2 . C. 3 . D. 3 . 10 3 3 Lời giải Chọn A. ì
ïd : x + 2y -2 = 0 n = 1;2 - 1 1 ( ) ï j ( = 1 2 d d 1 1 ; 2 ) í ¾¾¾¾ cosj = = .
ïïd : x- y = 0 n 1; 1 1 4. 1 1 10 2 2 ( ) î = - + + ìïx = 2 +t
Câu 139: Cho đường thẳng d :10x +5y -1 = 0 d : ïí 1 và 2
. Tính cosin của góc tạo bởi giữa hai ï y =1-t ïî đường thẳng đã cho. A. 3 10 . B. 3 . C. 10 . D. 3 . 10 5 10 10 Lời giải Chọn A. ì
ïd :10x +5y -1= 0 n = 2;1 1 1 ( ) ïïï + j ( = 2 1 d d 3 1 ; 2 ) í ìïx = 2+t ¾¾¾¾ cosj = = . ïïd :ïí n = 1;1 4 +1. 1+1 10 2 2 ( ) ï ï y =1- ïî ïî t ìïx =15+12t
Câu 140: Cho đường thẳng
d : 3x + 4 y +1 = 0 và d : ïí 2 . 1 ïy =1+5t ïî
Tính cosin của góc tạo bởi giữa hai đường thẳng đã cho. A. 56 . B. 33 6 33 - . C. . D. . 65 65 65 65 Lời giải Chọn D. ì
ïd : 3x + 4y +1= 0 n = 3;4 1 1 ( ) ïïï - j ( = 15 48 d d 33 1 ; 2 ) í ìïx =15+12t ¾¾¾¾ cosj = = . ïïd :ïí n = 5; 1 - 2 9 +16. 25 +144 65 2 2 ( ) ï ïy =1+5 ïî ïî t
ìïx = 2m -1+ t
Câu 141: Cho đường thẳng 2
d : 2x +3y +m 1 - = 0 d : ïí 1 và 2 . 4
ïy = m -1+ 3t ïî
Tính cosin của góc tạo bởi giữa hai đường thẳng đã cho. A. 3 2 3 . B. . C. . D. 1 - . 130 5 5 5 2 Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 788
hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn A. 2
ìïd : 2x +3y + m -1= 0 n = 2;3 ï 1 1 ( ) ïï - j ( = d d 6 3 3 1 ; 2 ) í
ìïx = 2m-1+t ¾¾¾¾ cosj = = . ïïd :ïí n = 3;-1 4 + 9. 9 +1 130 2 4 2 ( ) ï ï ï y = m -1+ 3 î ïî t ìïx = 2 +at
Câu 142: Cho hai đường thẳng d : 3x + 4 y +12 = 0 và d : ïí a 2
. Tìm các giá trị của tham số để 1 ïy =1-2t ïî d d 0 45 . 1 và
2 hợp với nhau một góc bằng A. 2 2 a = hoặc a = - 7 14. B. a = hoặc a = 3.
C. a = 5 hoặc a = -14. D. a = hoặc 7 2 7 a = 5. Lời giải Chọn A. Ta có ì
ïd : 3x + 4y +12 = 0 n = 3;4 1 1 ( ) ïïï + a j= d d = 6 4 ( 1 1 ; 2 ) 45 í ìïx = 2+ at ¾¾¾¾¾ = cos 45 = cosj = ïïd :ïí n = 2;a 2 2 ( ) 2 2 25. a + 4 ï ïy =1-2 ïî ïî t éa = -14 ê 25( 2 a + 4) = 8( 2 4a +12a + 9) 2
7a + 96a - 28 = 0 ê 2 . êa = êë 7
Câu 143: Đường thẳng
D đi qua giao điểm của hai đường thẳng
d : 2x + y -3 = 0
d : x -2 y +1 = 0 1 và 2
đồng thời tạo với đường thẳng d : y -1 = 0 0 45 3 một góc có phương trình:
A. D : 2x + y = 0 hoặc .
D : x - y -1 = 0
B. D : x + 2y = 0 hoặc . D : x - 4 y = 0
C. D : x - y = 0 hoặc .
D : x + y -2 = 0
D. D : 2x +1 = 0 hoặc . D : x -3y = 0 Lời giải Chọn C.
ìïd : 2x + y -3 = 0 ìïx =1 ï 1 ï í í
d Ç d = A 1;1 Î . D 1 2 ( )
ïd : x-2y +1= 0 ïy =1 ïî 2 ïî Ta có
d : y -1 = 0 n = 0;1 , gọi n = (a;b), j = D d . Khi đó D ( ; 3) 3 3 ( ) 1 b
éa = b a = b = 1 D : x + y - 2 = 0 2 2 2 = cosj =
a + b = 2b ê . 2 2 2
êa = -b a =1,b = -1 D : x- y = a + b + 0 . 0 1 ë
Câu 144: Trong mặt phẳng với hệ tọa độ Oxy , có bao nhiêu đường thẳng đi qua điểm A (2;0) và tạo
với trục hoành một góc 45? A. Có duy nhất. B. 2 . C. Vô số. D. Không tồn tại. Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 789
hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn B.
Cho đường thẳng d và một điểm . A Khi đó. (i)
Có duy nhất một đường thẳng đi qua A song song hoặc trùng hoặc vuông góc với d. (ii) Có
đúng hai đường thẳng đi qua A và tạo với d một góc 0 < a < 90 .
Câu 145: Đường thẳng
D tạo với đường thẳng
d : x + 2 y -6 = 0 một góc 0
45 . Tìm hệ số góc k của đường thẳng . D A. 1 1 1 1 k = hoặc k = -3.
B. k = hoặc k = 3. C. k = - hoặc k = -3. D. k = - hoặc 3 3 3 3 k = 3. Lời giải Chọn A. a
d : x + 2 y - 6 = 0 n =
gọi n = a b k = - Ta có D ( ; ) . d (1;2), D b a + 1 2b = cos 45 = 5( 2 2 a + b ) 2 2
= 2a +8ab +8b 2 2 2 a + b . 5 é 1 1
êa = - b k = 2 2
3a -8ab -3b = 0 ê 3 D 3 . ê
êa = 3b k = -3 ë D
Câu 146: Biết rằng có đúng hai giá trị của tham số k để đường thẳng
d : y = kx tạo với đường thẳng
D : y = x một góc 0
60 . Tổng hai giá trị của k bằng: A. -8. B. -4. C. -1. D. -1. Lời giải Chọn B. ì
ïd : y = kx n = k d ( ;- ) 1 ï 1 k +1 2 2 í ¾¾ = cos 60 =
k +1= 2k + 4k + 2 ïD
ï : y = x n = - D (1; ) 2 1 2 k +1. 2 î 2 sol:k= 1 k , k=k2
k + 4k +1= 0 ¾¾¾¾¾ k + k = -4. 1 2
Câu 147: Trong mặt phẳng với hệ tọa độ , Oxy cho đường thẳng
D : ax + by + c = 0 và hai điểm M (x ; y N (x ; y D n n ) m m ) , không thuộc .
Chọn khẳng định đúng trong các khẳng định sau:
A. M , N khác phía so với D khi
(ax + by + c ax + by + c > m m ).( n n ) 0.
B. M , N cùng phía so với D khi
(ax + by + c ax + by + c ³ m m ).( n n ) 0.
C. M , N khác phía so với D khi
(ax + by + c ax + by + c £ m m ).( n n ) 0.
D. M , N cùng phía so với D khi
(ax + by + c ax + by + c > m m ).( n n ) 0. Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 790
hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn D.
Câu 148: Trong mặt phẳng với hệ tọa độ , Oxy cho đường thẳng
d : 3x + 4 y -5 = 0 và hai điểm , A (1;3)
B (2;m) . Tìm tất cả các giá trị của tham số m để A và B
nằm cùng phía đối với . d A. m < 1 0 . B. m > - . C. m > - 1 1 . D. m = - . 4 4 Lời giải Chọn B.
A (1;3) , B (2;m) nằm cùng phía với d : 3x + 4 y -5 = 0 khi và chỉ khi ( x + y - x y m m A A )( + - B B )> ( + ) 1 3 4 5 3 4 5 0 10 1 4 > 0 > - . 4
Câu 149: Trong mặt phẳng với hệ tọa độ , Oxy cho
đường thẳng d : 4x -7y + m = 0 và hai điểm , A (1;2)
B (-3;4) . Tìm tất cả các giá trị của tham số m để d và đoạn thẳng AB có điểm chung. ém > 40
A. 10 £ m £ 40 . B. ê .
C. 10 < m < 40 . D. m <10 . êm <10 ë Lời giải Chọn A.
Đoạn thẳng AB và d : 4x -7y +m = 0 có điểm chung khi và chỉ khi
(4x -7 y + m x y m m m m A A )(4 -7 + B B
)£ 0 ( -10)( - 40)£ 0 10 £ £ 40. ìïx = 2 +t
Câu 150: Trong mặt phẳng với hệ tọa độ , Oxy cho
đường thẳng d : ïí và hai điểm , A (1;2) ïy =1-3t ïî
B (-2;m). Tìm tất cả các giá trị của tham số m để A và
B nằm cùng phía đối với . d A. m >13. B. m ³13 . C. m < 13. D. m = . 13 Lời giải Chọn C. ìïx = 2+t d : ïí ¾¾
d : 3x + y -7 = 0. Khi đó điều kiện bài toán trở thành ïy =1-3 ïî t
(3x + y -7 x y m m A A )(3 + - 7 B B )> 0 -2( - ) 13 > 0 <13.
ìïx = m +2t
Câu 151: Trong mặt phẳng với hệ tọa độ , Oxy cho
đường thẳng d : ïí và hai điểm , A (1;2) ïy =1-t ïî
B (-3;4) . Tìm m để d cắt đoạn thẳng AB . A. m < 3 . B. m = 3 . C. m > 3 . D. Không tồn tại . m Lời giải Chọn B.
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 791
hệ. Face: Trần Đình Cư. SĐT: 0834332133
ìïx = m+ 2t d : ïí
d : x + 2y -m-2 = 0. Đoạn thẳng AB cắt d khi và chỉ khi ïy =1- ïî t
(x + 2y -m-2 x y m m m A A )( + 2 - -2 B B )£ (3- )2 0 £ 0 = 3.
Câu 152: Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có A (1;3) , B(-2;4) và C (-1;5) . Đường thẳng
d : 2x -3y + 6 = 0 cắt cạnh nào của tam giác đã cho? A. Cạnh . AC B. Cạnh . AB C. Cạnh . BC D. Không cạnh nào. Lời giải Chọn D.
ìïï f (A(1; )3)=-1< 0 ïï Đặt f ( ;
x y) 2x 3y 6 ï = - + ¾¾ í f (B( 2 - ;4)) = -10 < 0 ¾¾
d không cắt cạnh nào của tam giác ïïïïf (C( 1; - ) 5 ) = -11< 0 ïî ABC .
Câu 153: Cặp đường thẳng nào dưới đây là phân giác của các góc hợp bởi hai đường thẳng
D : x + 2 y -3 = 0
D : 2x - y + 3 = 0 1 và 2 .
A. 3x + y = 0 và x -3y = 0 .
B. 3x + y = 0 và x +3y -6 = 0 .
C. 3x + y = 0 và x - +3y -6 = 0 .
D. 3x + y + 6 = 0 và x -3y -6 = 0 . Lời giải Chọn C.
Điểm M (x; y) thuộc đường phân giác của các góc tạo bởi D ; D khi và chỉ khi 1 2 x + 2y -3 2x - y +3 é3x + y = 0
d (M;D = d M;D = ê . 1 ) ( 2 ) 5 5 êx-3y +6 = 0 ë
Câu 154: Cặp đường thẳng nào dưới đây là phân giác của các góc hợp bởi đường thẳng D : x + y = 0 và trục hoành.
A. (1+ 2)x + y = 0 ; . x -(1- 2) y = 0
B. (1+ 2)x + y = 0 ; . x +(1- 2) y = 0
C. (1+ 2)x - y = 0 ; . x +(1- 2) y = 0
D. x +(1+ 2) y = 0 ; . x +(1- 2) y = 0 Lời giải Chọn D.
Điểm M (x; y) thuộc đường phân giác của các góc tạo bởi ;
D Ox : y = 0 khi và chỉ khi éx+ x + y y ê (1+ 2)y = 0
d (M ;D)= d (M ;Ox) = ê . 2 1 êx+ ê (1- 2)y = 0 ë æ ö Câu 155: 7
Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có Açç ;3÷÷, B (1;2) và C (-4;3) . çè4 ÷ø
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 792
hệ. Face: Trần Đình Cư. SĐT: 0834332133
Phương trình đường phân giác trong của góc A là:
A. 4x +2y -13 = 0.
B. 4x -8y +17 = 0.
C. 4x -2y -1 = 0.
D. 4x +8y -31 = 0. Lời giải Chọn B. ìï æ7 ö ïAç
ï ç ;3÷÷, B(1;2) AB : 4x -3y + 2 = 0 ï çè4 ÷ø ïí . ï æ7 ö
ïïAçç ;3÷÷,C( 4 - ; )
3 AC : y -3 = 0 ï ç ï è4 ÷ø ïî
Suy ra các đường phân giác góc A là: 4x -3y + 2 y -3
é4x + 2y -13 = 0 f ( ;
x y) = 4x + 2y -13 = ê 5 1 ê4x-8y +17 = 0 ë ì
ïï f (B(1;2))= 5 - < 0 ï
íïïf (C(-4; )3)= 2 - 3 < 0 ïî
suy ra đường phân giác trong góc A là 4x -8y +17 = 0.
Câu 156: Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có A (1;5) , B(-4;-5) và C (4;- ) 1 .
Phương trình đường phân giác ngoài của góc A là: A. y +5 = 0. B. y -5 = 0. C. x +1 = 0. D. x -1 = 0. Lời giải Chọn B. ìïA(1; ) 5 , B( 4 - ;- )
5 AB : 2x - y + 3 = 0 ïí . ïA(1; ) 5 ,C(4;- )
1 AC : 2x + y -7 = ï 0 î
Suy ra các đường phân giác góc A là: 2x - y + 3 2x + y -7
éx-1= 0 f ( ; x y) = x -1
ìïï f (B(-4;- ) 5 ) = -5 < 0 = ê ï í 5 5 ê y-5 = 0 ï ë ï f (C(4;- ) 1 ) = 3 > 0 ïî
suy ra đường phân giác trong góc A là y -5 = 0.
Câu 157: Trong mặt phẳng với hệ tọa độ , Oxy cho hai đường thẳng
d : 3x - 4 y -3 = 0 1 và
d : 12x + 5y -12 = 0 d 2
. Phương trình đường phân giác góc nhọn tạo bởi hai đường thẳng 1 và d2 là:
A. 3x +11y -3 = 0.
B. 11x -3y -11 = 0.
C. 3x -11y -3 = 0.
D. 11x +3y -11 = 0. Lời giải Chọn B.
Các đường phân giác của các góc tạo bởi
d : 3x - 4 y -3 = 0 và d : 12x + 5y -12 = 0 là: 1 2
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 793
hệ. Face: Trần Đình Cư. SĐT: 0834332133 3x -4y -3 12x +5y 1 - 2 é3x +11y -3 = 0 = ê . 5 13 11 ê x-3y-11= 0 ë
Gọi I = d Ç d I 1;0 ; d : 3x +11y -3 = 0 M -10;3 Î d, 1 2 ( ) ( )
Gọi H là hình chiếu của M lên d . 1 30 - -12-3
Ta có: IM = 130, MH = = 9, suy ra 5 MH 9 sin MIH = =
MIH > 52 MI 2 H > 90 . IM 130
Suy ra d : 3x +11y -3 = 0 là đường phân giác góc tù, suy ra đường phân giác góc nhọn là 11x-3y 1 - 1= 0 .
Câu 158: Trong mặt phẳng với hệ tọa độ , Oxy cho điểm M (x ; y
D : ax + by + c = 0 0 0 ) và đường thẳng . Khoảng cách từ điểm M đến
D được tính bằng công thức: ax + by + A. ax by d (M ,D) 0 0 = .
B. d (M , ) 0 0 D = . 2 2 a + b 2 2 a +b
ax + by + c + + C. ax by c d (M ,D) 0 0 = .
D. d(M , ) 0 0 D = . 2 2 a + b 2 2 a +b Lời giải Chọn C.
Câu 159: Khoảng cách từ điểm M (-1; ) 1 đến đường thẳng
D : 3x - 4 y -3 = 0 bằng: A. 2 4 4 . B. 2 . C. . D. . 5 5 25 Lời giải Chọn B. 3 - -4-3 d (M ; ) D = = 2. 9 +16
Câu 160: Khoảng cách từ giao điểm của hai đường thẳng
x -3y + 4 = 0 và 2x + 3y -1 = 0 đến đường thẳng
D : 3x + y + 4 = 0 bằng: A. 3 10 10 2 10 . B. . C. . D. 2 . 5 5 Lời giải Chọn C. ìïx-3y + 4 = 0 ìïx = 1 - - + + ï ï í í
A(- ) d (A ) 3 1 4 2 1;1 ;D = = . ï2x +3y -1= 0 ïy =1 ïî ïî 9 +1 10
Câu 161: Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có A(1;2), B(0;3) và C(4;0) . Chiều
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 794
hệ. Face: Trần Đình Cư. SĐT: 0834332133
cao của tam giác kẻ từ đỉnh A bằng: A. 1 . B. 1 3 3 . C. . D. . 5 25 5 Lời giải Chọn A. ìïA(1;2) 3+8-12 ïí h = d A BC A ( ) 1 ; = = . ïïB(0; )
3 , C(4;0) BC : 3x + 4y -12 = 0 9 +16 5 î
Câu 162: Trong mặt phẳng với hệ tọa độ Oxy , cho tam giác ABC có A (3;-4), B(1;5) và C (3; ) 1 . Tính
diện tích tam giác ABC . A. 10. B. 5. C. 26. D. 2 5. Lời giải Chọn B. ìïA(3;-4) ìïA( ï 3;-4) ï ìï ï ï BC = 2 5 Cách 1: ï í íBC 2 5 ï = í ïïB(1; ) 5 ,C (3; ) 1 ï ï î ï ïh = d A BC A ( ; )= 5
ïBC : 2x + y -7 = 0 ïî ïïî 1 S = .2 5. 5 = 5. ABC 2 Cách 2: 1 S =
AB .AC - AB⋅ AC DABC ( )2 2 2 . 2
Câu 163: Khoảng cách từ điểm
M (0;3) đến đường thẳng
D : x cos a + y sin a + 3(2 - sin a) = 0 bằng: A. 3 6. B. 6. C. 3sin . a D. . cos a + sin a Lời giải Chọn B.
3sin a + 3(2-sin a) d (M ;D) = = 6. 2 2 cos a + sin a ìï x =1+3t
Câu 164: Khoảng cách từ điểm
M (2;0) đến đường thẳng : ï D í bằng: ïy = 2 + 4t ïî A. 2 10 5 2. B. . C. . D. . 5 5 2 Lời giải Chọn A.
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 795
hệ. Face: Trần Đình Cư. SĐT: 0834332133 ìï x =1+3t 8+0+ 2 :ï D í
D : 4x-3y + 2 = 0 d (M; ) D = = 2. ïy = 2+ 4 ïî t 16 +9
Câu 165: Khoảng cách nhỏ nhất từ điểm M (15; ) 1
đến một điểm bất kì thuộc đường thẳng ìïx = 2 +3t : ï D í bằng: ïy = t ïî A. 1 16 10. B. . C. . D. 5. 10 5 Lời giải Chọn A. ìïx = 2+3t 15-3-2 :ï D í
D : x-3y -2 = 0 "NÎD ¾¾¾MN = d M;D = = 10. min ( ) ïy = ïî t 1+9
Câu 166: Tìm tất cả các giá trị của tham số m để khoảng cách từ điểm
A (-1;2) đến đường thẳng
D : mx + y -m + 4 = 0 bằng . 2 5 ém = -2 ê A. 1 m = 2. B. ê 1 . C. m = - . D. Không tồn tại . m êm = ê 2 ë 2 Lời giải Chọn B. -m + -m + d ( ; A ) 2 4 2 2 D =
= 2 5 m-3 = 5. m +1 4m + 6m-4 = 0 2 m +1 ém = -2 ê ê 1 . êm = êë 2
Câu 167: Tìm tất cả các giá trị của tham số m để khoảng cách từ giao điểm của hai đường thẳng ìïx = t d : ïí
d : x -2 y + m = 0 2 1 và
đến gốc toạ độ bằng . ïy = 2-t 2 ïî ém = 4 - ém = 4 - ém = 4 ém = 4 A. ê . B. ê . C. ê . D. ê . êm = 2 ë êm = 2 - ë êm = 2 ë êm = 2 - ë Lời giải Chọn C. ìï ìïx = ï t ïd :ïí
ìïd : x + y -2 = 0 ìïx = 4- ï m 1 ï 1 í y = 2 ï ï -t ïî í í ï
ïd : x-2y + m = 0 ïy = m-2 ï ïî 2 ï
ïd : x-2y + m = 0 î ïî 2 M (4- ; m m- )
2 = d Ç d . 1 2
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 796
hệ. Face: Trần Đình Cư. SĐT: 0834332133 ém = 2
Khi đó: OM = 2 (4- )2 m +(m- )2 2
2 = 4 m -6m +8 = 0 ê . ê m = 4 ë
Câu 168: Đường tròn (C) có tâm là gốc tọa độ O(0;0) và tiếp xúc với đường thẳng D : 8x +6y +100 = 0
. Bán kính R của đường tròn (C) bằng: A. R = 4 . B. R = 6 . C. R = 8 . D. R =10 . Lời giải Chọn D.
R = d (O ) 100 ;D = =10. 64 +36
Câu 169: Đường tròn (C) có tâm I (-2;-2) và tiếp xúc với đường thẳng .
D : 5x +12 y -10 = 0 Bán kính
R của đường tròn (C) bằng: A. 44 24 7 R = . B. R = . C. R = 44 . D. R = . 13 13 13 Lời giải Chọn A. - - - R = d (I ) 10 24 10 44 ;D = = . 25+144 13 Câu 170: 2 2
Với giá trị nào của m thì đường thẳng D : x -
y + m = 0 tiếp xúc với đường tròn 2 2 (C) 2 2 : x + y = 1 ? A. 2 m = 1 . B. m = 0 . C. m = 2 . D. m = . 2 Lời giải Chọn A. ( )
D tiếp xúc đường tròn ìïI = O(0;0) m (C) 2 2 : x y 1: ï + = í
« d (I;D) = R
= 1 m = 1. ïïR = 1 1 î
Câu 171: Cho đường thẳng d : 21x -11y -10 = 0. Trong các điểm , M (21;-3) N (0;4) , P (-19;5) và
Q (1;5) điểm nào gần đường thẳng d nhất? A. M . B. N . C. P . D. Q . Lời giải Chọn D.
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 797
hệ. Face: Trần Đình Cư. SĐT: 0834332133
ìïï f (M (21;- )3)= 464
ïïïïf (N(0;4))=54 f ( ; x y) 21x 11y 10 ï = - - í . ï ï f (P( 19 - ; ) 5 ) = 464
ïïïïïf(Q(1; )5)=44 î
Câu 172: Cho đường thẳng d : 7x +10y -15 = 0. Trong các điểm ,
M (1;-3) N (0;4) , P (-19;5) và Q (1;5)
điểm nào cách xa đường thẳng d nhất? A. M . B. N . C. P . D. Q . Lời giải Chọn C.
ìïï f (M (1;- )3)= 38
ïïïïf (N(0;4))=25 f ( ; x y) 7x 10y 15 ï = + - í . ï ï f (P( 19 - ; ) 5 ) = 98
ïïïïïf(Q(1; )5)=42 î
Câu 173: Trong mặt phẳng với hệ tọa độ Oxy , cho hai điểm A (2;3) và . B (1;4) Đường thẳng nào sau
đây cách đều hai điểm A và ? B
A. x - y + 2 = 0.
B. x + 2y = 0.
C. 2x -2y +10 = 0.
D. x - y +100 = 0. Lời giải
Đường thẳng cách đều hai điểm ,
A B thì đường thẳng đó hoặc song song (hoặc trùng) với
AB , hoặc đi qua trung điểm I của đoạn AB . Chọn A. ìï æ ö ìïA(2; ) 3 7 3 ï ç ïI ç ; ÷÷ Ta có: ï ï ç í è2 2÷ø í
AB || d : x - y -2 = 0. ïB(1;4) ï ï î ïï AB = (-1; ) 1 n = AB (1 ) ;1 ïî
Câu 174: Trong mặt phẳng với hệ tọa độ , Oxy cho ba điểm A ( ) 0;1 , B (12;5) và C (-3;0). Đường thẳng
nào sau đây cách đều ba điểm A, B và C .
A. x -3y + 4 = 0 . B. x - + y +10 = 0 .
C. x + y = 0 .
D. 5x - y +1 = 0 . Lời giải Chọn A. Dễ thấy ba điểm ,
A B, C thẳng hàng nên đường thẳng cách điều ,
A B, C khi và chỉ khi chúng
song song hoặc trùng với AB . Ta có:
AB = (12; 4) n = AB d x y AB (1;- ) 3 | : - 3 + 4 = 0.
Câu 175: Trong mặt phẳng với hệ tọa độ , Oxy cho hai điểm A (1; ) 1 , B (-2;4) và đường thẳng
D : mx - y + 3 = 0 . Tìm tất cả các giá trị của tham số m để D cách đều hai điểm . A, B
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 798
hệ. Face: Trần Đình Cư. SĐT: 0834332133 ém =1 ém = 1 - ém = 1 - ém = 2 A. ê . B. ê . C. ê . D. ê . êm = 2 - ë êm = 2 ë êm =1 ë êm = 2 - ë Lời giải Chọn C. ìï æ 1 5ö ï ç ïI - ç ; ÷÷ Gọi ï ç ÷
I là trung điểm đoạn AB è 2 2ø í . ïï ï AB = (-3; ) 3 n = (1; ) 1 ïî AB Khi đó:
D : mx - y + 3 = 0 (n = (m;- ) 1 cách đều , A B D ) éI Î D é m 5 ê ê- - + = ém = 3 0 1 ê m -1 ê 2 2 ê . ê = ê êm = -1 ê êm = -1 ë ë 1 1 ë
Câu 176: Khoảng cách giữa hai đường thẳng song song
D : 6x – 8y +3 = 0
D : 3x – 4 y – 6 = 0 1 và 2 bằng: A. 1 . B. 3 . C. 5 2 . D. . 2 2 2 Lời giải Chọn B. ìïA(2;0)Î D 12 + 3 ï 2 í d ( 3 D ;D = d ; A D = = . 1 2 ) ( 1 )
ïïD || D : 6x-8y +3 = 0 100 2 î 2 1 ìïx = 2 - + t
Câu 177: Tính khoảng cách giữa hai đường thẳng
d : 7x + y -3 = 0 và : ï D í . ïy = 2-7t ïî A. 3 2 . B. 9 15 . C. 9 . D. . 2 50 Lời giải Chọn A. ì ïA( 2; - 2)Î , D n = D (7; ) 1 ïí ï
d : 7x + y -3 = 0 n = ï d (7; ) 1 î 14 - + 2-3
D d d (d ) D = d (A d) 3 ; ; = = . 50 2
Câu 178: Khoảng cách giữa hai đường thẳng song song
d : 6x – 8y -101 = 0
d : 3x – 4 y = 0 1 và 2 bằng: A. 10,1. B. 1,01. C. 101 . D. 101 . Lời giải Chọn A.
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 799
hệ. Face: Trần Đình Cư. SĐT: 0834332133 ìïA(4; ) 3 Î d 24- 24-101 ï 2 í d ( 101 d ; d = = = 10,1. 1 2 )
ïd || d : 6x – 8y -101= ï 0 100 10 î 2 1
Câu 179: Trong mặt phẳng với hệ tọa độ , Oxy cho hai điểm , A (1; ) 1 B (4;-3) và đường thẳng
d : x -2 y -1 = 0 . Tìm điểm M thuộc d có
tọa độ nguyên và thỏa mãn khoảng cách từ M đến đường thẳng AB bằng . 6 æ ö A. 27 M (3;7). B. M (7;3). C. M (-43;-27). D. M 3; ç ÷ ç - ÷. çè 11÷ø Lời giải Chọn B.
ìïM Î d : x-2y -1= 0 M (2m +1;m), m Î ï í . Khi đó
ïïAB : 4x +3y-7 = 0 î ém = 3 m + + m - ê = d (M AB) 8 4 3 7 6 ; = 11m-3 = 30 ê 27 M (7; ) 3 . 5 êm = (l) êë 11 ìïx = 2 +2t
Câu 180: Trong mặt phẳng với hệ tọa độ , Oxy cho điểm A ( ) 0;1 và đường thẳng . d : ïí Tìm ïy = 3+t ïî điểm M thuộc d và cách A một khoảng bằng , 5 biết M có hoành độ âm. éM (-4;4) ê æ ö A. 24 2 M (4;4). B. ê æ ç ÷ ê 24 2ö. C. M - ç ;- ÷. D. M (-4;4). M ç- ç ÷ ê ç ; ÷ - ÷ è ø ç 5 5 ê è 5 5÷ø ë Lời giải Chọn C. ìïx = 2+ 2t M Î d :ïí
M (2+ 2t;3+t) với 2+ 2t < 0 t < 1 - . Khi đó ïy = 3 î + ï t ét =1 (l) ê æ ö
5 = AM (2t + 2)2 +(t + 2)2 24 2 2
= 25 5t +12t -17 = 0 ê ç M - ç ;; ÷ - ÷. 17 ê ç t = - è 5 5÷ø êë 5
Câu 181: Biết rằng có đúng hai điểm thuộc trục hoành và cách đường thẳng
D : 2x - y + 5 = 0 một
khoảng bằng 2 5 . Tích hoành độ của hai điểm đó bằng: A. 75 25 225 - . B. - . C. - . D. Đáp số khác. 4 4 4 Lời giải Chọn A. Gọi M (x )
;0 Î Ox thì hoành độ của hai điểm đó là nghiệm của phương trình:
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 800
hệ. Face: Trần Đình Cư. SĐT: 0834332133 é 5 êx = = x1 2x + 5 d (M D) ê 2 75 ; = 2 5 = 2 5 ê ¾¾ x ⋅ x = - . 1 2 5 ê 15 4 êx = - = x2 êë 2
Câu 182: Trong mặt phẳng với hệ tọa độ Oxy , cho hai điểm A (3;- )
1 và B (0;3) . Tìm điểm M thuộc
trục hoành sao cho khoảng cách từ M đến đường thẳng AB bằng . 1 é é é æ ö æ ö æ 14 14 7 ö ê ç ÷ é æ ö ê ç ÷ ê M ç ;0÷ 7 M - ç ;0÷ M çç ;0÷÷ ê çè 3 ÷ø êM ç- ç ;0÷÷ ê çè 3 ÷ø A. ê çè2 ÷ø. B. ê . C. ê çè 2 ÷ø. D. ê . ê ê ê ê ê æ4 ö æ 4 ö M ê ê (1;0) ê ç ÷ ê ç ÷ ë M ç ;0÷ ê ç M ê (-1;0) M - ç ;0÷ è3 ÷ø ë ê ç ÷ ë è 3 ø ë Lời giải Chọn A. é æ ö ìïM ( ;0 x ) 7 7 4x -9
êx = M çç ;0÷÷ ïí
1= d (M ; AB) ê = 2 çè2 ÷ø.
ïïAB : 4x +3y-9 = 0 5 ê î êx =1 ê M (1;0) ë
Câu 183: Trong mặt phẳng với hệ tọa độ Oxy , cho hai điểm A (3;0) và B (0;-4) . Tìm điểm M thuộc
trục tung sao cho diện tích tam giác MAB bằng 6. éM (0;0) éM (0;0) A. ê . B. M (0;-8). C. M (6;0). D. ê . êM (0;- ê ê 8) ë êM (0;6) ë Lời giải Chọn A. Ta có
ìïAB : 4x-3y -12 = 0 ïï 1 3y +12
é y = 0 M (0;0) ïAB = 5 6 = S = .5. ê . ï DMAB 2 5 ê í y = 8 - M (0;- ê ) 8 ï ë ï y +
ïM ( y) h = d (M AB) 3 12 0; ; = ïïî M 5
Câu 184: Trong mặt phẳng với hệ tọa độ Oxy , cho hai đường thẳng
D : 3x -2 y -6 = 0 1 và
D : 3x -2 y + 3 = 0 M M 2 . Tìm điểm thuộc trục hoành sao cho
cách đều hai đường thẳng đã cho. æ ö æ ö æ ö A. 1 1 1 M çç0; .÷÷
B. M çç ;0 .÷÷ C. M ç- ç ;0 . ÷÷ D. M ( 2;0). çè 2÷ø çè2 ÷ø çè 2 ÷ø Lời giải Chọn B. ìïM ( ;0 x ) 3x -6 3x + 3 1 æ1 ö ïí =
x = M çç ;0÷÷.
ïïd(M;D = d M;D 13 13 2 çè2 ÷ø 1 ) ( 2 ) î
Câu 185: Trong mặt phẳng với hệ tọa độ , Oxy cho hai điểm A (-2;2), B (4;-6) và đường thẳng
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 801
hệ. Face: Trần Đình Cư. SĐT: 0834332133 ìïx = t d : ïí . Tìm điểm
M thuộc d sao cho M cách đều hai điểm A, B. ïy =1+2t ïî A. M (3;7). B. M (-3;-5). C. M (2;5). D. M (-2;-3) Lời giải Chọn B. ìï ìïx = ï t ïM Î d : ïí
M (t;1+ 2t) ïí ïy =1+ 2t ï
(t + 2)2 +(2t - )2
1 = (t - 4)2 +(2t + 7)2 î ïïïMA= ïî MB
20t +60 = 0 t = 3 - M ( 3 - ;- ) 5 .
Câu 186: Trong mặt phẳng với hệ tọa độ Oxy , cho hai điểm A (-1;2), B (-3;2) và đường thẳng
d : 2x - y +3 = 0 . Tìm điểm
C thuộc d sao cho tam giác ABC cân tại C. æ ö A. 3 C (-2;- ) 1 . B. Cç- ç ;0 . ÷÷ C. C (-1; ) 1 . D. C (0;3) çè 2 ÷ø Lời giải Chọn A.
ìïM Î d : 2x- y +3 = 0 M ( ; m 2m + ) 3 ïí (m + )2 1 +(2m + )2 1 = (m + )2 3 +(2m + )2 1 ïïMA = î MB m = 2 - M ( 2 - ;- ) 1 .
Câu 187: Trong mặt phẳng với hệ tọa độ Oxy , cho hai điểm
A (1;2), B (0;3) và đường thẳng . d : y = 2 Tìm điểm
C thuộc d sao cho tam giác ABC cân tại . B C é (1;2) A. C (1;2). B. C (4;2). C. ê . D. C (-1;2). C ê (- ê 1;2) ë Lời giải Chọn C.
ìïC d : y = 2 C( ; c 2) é Î C(1;2) ï 2 í
2 = c +1 c = 1 ê . ê ïïBA = BC C(- î ê 1; 2) ë
Câu 188: Đường thẳng D song song với đường thẳng
d : 3x - 4 y +1 = 0 và cách d một khoảng bằng 1 có phương trình:
A. 3x -4 y + 6 = 0 hoặc . 3x - 4 y - 4 = 0
B. 3x -4 y -6 = 0 hoặc . 3x - 4 y + 4 = 0
C. 3x -4 y + 6 = 0 hoặc . 3x - 4 y + 4 = 0
D. 3x -4 y -6 = 0 hoặc .
3x - 4 y - 4 = 0
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 802
hệ. Face: Trần Đình Cư. SĐT: 0834332133 Lời giải Chọn A.
ìïd : 3x -4y +1= 0 M (1; ) 1 Î d c -1 éc = - ïí
= d (d D) = d (M D) 4 1 ; ; = ê . ïD
ï || d D : 3x - 4 y + c = 0 5 êc = 6 î ë
Câu 189: Tập hợp các điểm cách đường thẳng
D : 3x - 4 y + 2 = 0 một khoảng bằng 2 là hai đường
thẳng có phương trình nào sau đây?
A. 3x -4 y +8 = 0 hoặc .
3x - 4 y +12 = 0
B. 3x -4 y -8 = 0 hoặc . 3x - 4 y +12 = 0
C. 3x -4 y -8 = 0 hoặc .
3x - 4 y -12 = 0
D. 3x -4 y +8 = 0 hoặc .
3x - 4 y -12 = 0 Lời giải Chọn B. x- y + é d ( x- y + = M (x y) ) 3 4 2 3 4 12 0 ; ;D = 2 = 2 ê . 5 ê3x-4y-8 = 0 ë
Câu 190: Trong mặt phẳng với hệ tọa độ , Oxy cho hai đường thẳng
d : 5x + 3y -3 = 0 1 và
d : 5x + 3y +7 = 0 d , d 2
song song nhau. Đường thẳng vừa song song và cách đều với 1 2 là:
A. 5x +3y -2 = 0.
B. 5x +3y + 4 = 0.
C. 5x +3y + 2 = 0.
D. 5x +3y -4 = 0. Lời giải Chọn C. d ( 5x + 3y -3 5x + 3y + 7 M ( ;
x y);d = d M ; x y ;d =
5x +3y + 2 = 0. 1 ) ( ( ) 2) 34 34
Giáo viên có nhu cầu sở hữu file word vui lòng liên Trang 803
hệ. Face: Trần Đình Cư. SĐT: 0834332133
BÀI 2. PHƯƠNG TRÌNH ĐƯỜNG TRÒN
A. KIẾN THỨC CƠ BẢN CẦN NẮM
1. Phương trình đường tròn có tâm và bán kính cho trước Trong mặt phẳng , Oxy
đường tròn (C) tâm I ( ;
a b), bán kính R có phương trình:
(x -a)2 +(y -b)2 2 = R .
Chú ý. Phương trình đường tròn có tâm là gốc tọa độ O và bán kính R là 2 2 2
x + y = R . 2. Nhận xét
● Phương trình đường tròn (x -a)2 + (y -b)2 2
= R có thể viết dưới dạng 2 2
x + y -2ax -2by + c = 0 trong đó 2 2 2
c = a +b - R . ● Phương trình 2 2
x + y - 2ax - 2by + c = 0 là phương trình của đường tròn (C) khi 2 2
a + b -c > 0. Khi
đó, đường tròn (C) có tâm I ( ; a b), bán kính 2 2
R = a + b -c.
3. Phương trình tiếp tuyến của đường tròn
Cho đường tròn (C) có tâm I ( ;
a b) và bán kính R. Đường thẳng D là tiếp tuyến với (C) tại điểm . M x ; y 0 ( 0 0 ) Ta có ● M x ; y D 0 ( 0 0 ) thuộc . ● IM = x - ; a y -b D 0 ( 0 0
) là vectơ pháp tuyến của . I
Do đó D có phương trình là
(x – a x – x + y – b y – y = 0. 0 )( 0 ) ( 0 )( 0 )
B. PHÂN LOẠI VÀ PHƯƠNG PHÁP GIẢI BÀI TẬP
Dạng 1: nhận dạng phương trinh dường tron. Tim tam va ban kinh dường tron.
1. Phương pháp giải.
Cách 1: + Đưa phương trình về dạng: (C ) 2 2
: x + y - 2ax - 2by + c = 0 (1) + Xét dấu biểu thức 2 2
P = a + b - c
Nếu P > 0 thì (1) là phương trình đường tròn (C ) có tâm I (a;b ) và bán kính 2 2
R = a + b - c
Nếu P £ 0 thì (1) không phải là phương trình đường tròn.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 804
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Cách 2: Đưa phương trình về dạng: 2 2
(x - a) + (y - b) = P (2).
Nếu P > 0 thì (2) là phương trình đường tròn có tâm I (a;b ) và bán kính R = P
Nếu P £ 0 thì (2) không phải là phương trình đường tròn. 2. Các ví dụ.
Ví dụ 1: Trong các phương trình sau, phương trình nào biểu diễn đường tròn? Tìm tâm và bán kính nếu có. 2 2
a) x + y + 2x - 4y + 9 = 0 (1) 2 2
b) x + y - 6x + 4y + 13 = 0 (2) 2 2
c) 2x + 2y - 6x - 4y - 1 = 0 (3) 2 2
d) 2x + y + 2x - 3y + 9 = 0 (4) Lời giải:
a) Phương trình (1) có dạng 2 2
x + y - 2ax - 2by + c = 0 với a = 1
- ; b = 2; c = 9 Ta có 2 2
a + b - c = 1 + 4 - 9 < 0
Vậy phương trình (1) không phải là phương trình đường tròn. b) Ta có: 2 2
a + b - c = 9 + 4 - 13 = 0
Suy ra phương trình (2) không phải là phương trình đường tròn. 2 1 æ 3 ö 5 c) Ta có: (3) x y 3x 2y 0 ç + - - - = çx ÷ - ÷ + (y - 1)2 2 2 = 2 çè 2 ÷ø 2 æ 3 ö 10
Vậy phương trình (3) là phương trình đường tròn tâm I çç ;1÷÷ ç bán kính R = è 2 ÷ø 2
d) Phương trình (4) không phải là phương trình đường tròn vì hệ số của 2 x và 2 y khác nhau.
Ví dụ 2: Cho phương trình 2 2
x + y - 2mx - 4(m - 2)y + 6 - m = 0 (1)
a) Tìm điều kiện của m để (1) là phương trình đường tròn.
b) Nếu (1) là phương trình đường tròn hãy tìm toạ độ tâm và bán kính theo m Lời giải:
a) Phương trình (1) là phương trình đường tròn khi và chỉ khi 2 2
a + b - c > 0
Với a = m; b = 2(m - 2); c = 6 - m
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 805
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 ém > 2 Hay m 4(m 2)2 2 2 6 m 0 5m 15m 10 0 ê + - - + > - + > ê m < 1 êë
b) Với điều kiện trên thì đường tròn có tâm I ( ;2
m (m - 2)) và bán kính: 2
R = 5m - 15m + 10
Ví dụ 3: Cho phương trình đường cong (C ): 2 2
x + y + (m + 2)x - (m + 4)y + m + 1 = 0 (2) m
a) Chứng minh rằng (2) là phương trình một đường tròn
b) Tìm tập hợp tâm các đường tròn khi m thay đổi
c) Chứng minh rằng khi m thay đổi họ các đường tròn (C ) luôn đi qua hai điểm cố định. m Lời giải: æm + 2 ö æ m + 4 ö (m + 2)2 2 2 + 4 a) Ta có 2 2 a + b - c ç ÷ ç ÷ = ç ÷ + ç- ÷ - m - 1 = > 0 ç è 2 ÷ø çè 2 ÷ø 2
Suy ra (2) là phương trình đường tròn với mọi m ìï m + 2 ïx = - ï I
b) Đường tròn có tâm I : ï 2 í
suy ra x + y - 1 = 0 ï m + 4 I I ïï y = I ïî 2
Vậy tập hợp tâm các đường tròn là đường thẳng D : x + y - 1 = 0
c) Gọi M (x ;y là điểm cố định mà họ (C ) luôn đi qua. 0 0 ) m Khi đó ta có: 2 2
x + y + m + 2 x - m + 4 y + m + 1 = 0, m " o 0 ( ) 0 ( ) 0 (x - y - 1) 2 2
m + x + y + 2x - 4y + 1 = 0, m " 0 0 o 0 0 0
ìïx - y + 1 = 0 ìïx = -1 ì ï ïx = 1 0 0 ï 0 í í hoặc ï 0 í 2 2
ïx + y + 2x - 4y + 1 = 0 ïy = 0 ï ïy = 2 0 0 0 0 î ï 0 î ï 0 î
Vậy có hai điểm cố định mà họ (C ) luôn đi qua với mọi m là M 1 - ;0 và M 1;2 2 ( ) 1 ( ) m
Dạng 2: Viết Phương Trinh Dường Tron
1. Phương pháp giải.
Cách 1: + Tìm toạ độ tâm I (a;b ) của đường tròn (C)
+ Tìm bán kính R của đường tròn (C)
+ Viết phương trình của (C) theo dạng 2 2 2
(x - a) + (y - b) = R .
Cách 2: Giả sử phương trình đường tròn (C) là: 2 2
x + y - 2ax - 2by + c = 0 (Hoặc 2 2
x + y + 2ax + 2by + c = 0 ).
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 806
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
+ Từ điều kiện của đề bài thành lập hệ phương trình với ba ẩn là a, b, c.
+ Giải hệ để tìm a, b, c từ đó tìm được phương trình đường tròn (C). Chú ý:
* A Î (C ) IA = R
* (C ) tiếp xúc với đường thẳng D tại A IA = d (I;D) = R
* (C ) tiếp xúc với hai đường thẳng D và D d I;D = d I;D = R 2 ( 1 ) ( 2 ) 1 2. Các ví dụ.
Ví dụ 1 : Viết phương trình đường tròn trong mỗi trường hợp sau: a) Có tâmI (1; 5
- ) và đi qua O (0;0).
b) Nhận AB làm đường kính với A(1;1), B (7;5).
c) Đi qua ba điểm: M (-2;4), N (5;5), P (6;-2) Lời giải:
a) Đường tròn cần tìm có bán kính là 2 2
OI = 1 + 5 = 26 nên có phương trình là
(x - )2 + (y + )2 1 5 = 26
b) Gọi I là trung điểm của đoạn AB suy ra I (4;3) AI = ( - )2 + ( - )2 4 1 3 1 = 13
Đường tròn cần tìm có đường kính làAB suy ra nó nhận I (4;3) làm tâm và bán kính
R = AI = 13 nên có phương trình là (x - )2 + (y - )2 4 3 = 13
c) Gọi phương trình đường tròn (C) có dạng là: 2 2
x + y - 2ax - 2by + c = 0 .
Do đường tròn đi qua ba điểm M,N,P nên ta có hệ phương trình:
ìï4 + 16 + 4a - 8b + c = 0 ìïa = 2 ï ï ï ï ïí25 25 10a 10b c 0 b ï + - - + = í = 1 ï ï
ïï36 4 12a 4b c 0 ï + - + + = ïc = -20 ïî ïî
Vậy phương trình đường tròn cần tìm là: 2 2
x + y - 4x - 2y - 20 = 0
Nhận xét: Đối với ý c) ta có thể làm theo cách sau
Gọi I (x;y ) và R là tâm và bán kính đường tròn cần tìm 2 2 ìïIM = IN Vì IM IN IP ï = = í nên ta có hệ 2 2 ï IM = IP ïî
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 807
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
ìïï(x + 2)2 + (y - 4)2 = (x - 5)2 + (y - 5)2 ìïx = 2 ï ï í í
ïï(x + )2 + (y - )2 = (x - )2 + (y + )2 ïy = 1 2 4 6 2 ïî ïî
Ví dụ 2: Viết phương trình đường tròn (C) trong các trường hợp sau: a) (C) có tâm I ( 1
- ;2) và tiếp xúc với đường thẳng D : x - 2y + 7 = 0 b) (C) đi qua A(2; 1
- ) và tiếp xúc với hai trục toạ độ Ox và Oy
c) (C) có tâm nằm trên đường thẳng d : x - 6y - 10 = 0 và tiếp xúc với hai đường thẳng có
phương trình d : 3x + 4y + 5 = 0 và d : 4x - 3y - 5 = 0 1 2 Lời giải:
a) Bán kính đường tròn (C) chính là khoẳng cách từ I tới đường thẳng D nên - - -
R = d (I D) 1 4 7 2 ; = = 1 + 4 5
Vậy phương trình đường tròn (C) là : (x + )2 + (y - )2 4 1 2 = 5
b) Vì điểm A nằm ở góc phần tư thứ tư và đường tròn tiếp xúc với hai trục toạ độ nên tâm của
đường tròn có dạng I ( ; R R
- ) trong đó R là bán kính đường tròn (C). é R = 1 Ta có:R IA R (2 R)2 ( 1 R)2 2 2 2 2 R 6R 5 0 ê = = - + - + - + = ê R = 5 êë
Vậy có hai đường tròn thoả mãn đầu bài là: (x - )2 + (y + )2 1 1 = 1 và
(x - )2 + (y + )2 5 5 = 25
c) Vì đường tròn cần tìm có tâm K nằm trên đường thẳng d nên gọi K (6a + 10;a )
Mặt khác đường tròn tiếp xúc với d , d nên khoảng cách từ tâm I đến hai đường thẳng này bằng 1 2
nhau và bằng bán kính R suy ra é
3(6a + 10) + 4a + 5
4(6a + 10) - 3a - 5 a = 0 ê =
22a + 35 = 21a + 35 ê - 5 5 70 êa = êë 43
- Với a = 0 thì K (10;0) và R = 7 suy ra (C ) (x - )2 2 : 10 + y = 49 70 - æ 10 70 - ö 7 2 2 2 æ 10 ö æ 70 ö æ 7 ö - Với a = thì K çç ; ÷÷ và R =
suy ra (C ) : ççx ÷ ç - ÷ + çy ÷ ç ÷ + ÷ = ç ÷ 43 çè 43 43 ÷ø 43 çè 43 ÷ø çè 43 ÷ø çè 43÷ø
Vậy có hai đường tròn thỏa mãn có phương trình là
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 808
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 2 2 ( æ 10 ö æ 70 ö æ 7 ö C ) (x - )2 2 :
10 + y = 49 và (C ) : ççx ÷ ç - ÷ + çy ÷ ç ÷ + ÷ = ç ÷ ç è 43 ÷ø çè 43 ÷ø çè 43÷ø
Ví dụ 3: Cho hai điểm A(8;0) và B (0;6).
a) Viết phương trình đường tròn ngoại tiếp tam giác OAB
b) Viết phương trình đường tròn nội tiếp tam giác OAB Lời giải:
a) Ta có tam giác OAB vuông ở O nên tâm I của đường tròn ngoại tiếp tam giác là trung điểm của
cạnh huyền AB suy ra I (4;3) và Bán kính R = IA = ( - )2 + ( - )2 8 4 0 3 = 5
Vậy phương trình đường tròn ngoại tiếp tam giác OAB là: (x - )2 + (y - )2 4 3 = 25 b) Ta có 2 2
OA = 8; OB = 6; AB = 8 + 6 = 10 1 Mặt khác .
OAOB = pr (vì cùng bằng diện tích tam giác ABC ) 2 . OAOB Suy ra r = = 2
OA + OB + AB
Dễ thấy đường tròn cần tìm có tâm thuộc góc phần tư thứ nhất và tiếp xúc với hai trục tọa độ nên
tâm của đường tròn có tọa độ là (2;2)
Vậy phương trình đường tròn nội tiếp tam giác OAB là: (x - )2 + (y - )2 2 2 = 4
Ví dụ 4: Trong mặt phẳng tọa độ Oxy , cho hai đường thẳng d
d : 3x + y = 0 . và d : 3x - y = 0 . Gọi (C) là đường tròn tiếp xúc 2 A 1 2
với d tại A, cắt d tại hai điểm B, C sao cho tam giác ABC vuông tại B. d 1 2 1 B 3
Viết phương trình của (C), biết tam giác ABC có diện tích bằng và 2 C
điểm A có hoành độ dương. Hình 3.1
Lời giải (hình 3.1)
Vì A Î d A a;- 3a , a > 0; ,
B C Î d B ; b 3b , C ; c 3c 1 ( ) 2 ( ) ( )
Suy ra AB (b -a; 3(a + b )), AC (c - a; 3(c + a ))
Tam giác ABC vuông tại B do đó AC là đường kính của đường tròn C.
Do đó AC ^ d AC.u = 0 -1. c - a + 3. 3 a + c = 0 2a + c = 0 (1) 1 ( ) ( ) 1
AB ^ d AB.u = 0 1. b - a + 3 a + b = 0 2b + a = 0 (2) 2 ( ) ( ) 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 809
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 3 1 1 a 3 Mặt khác S = d A d BC c - b + c - b =
2a c - b = 1 ABC ( ; ). . ( )2 3( )2 2 2 2 2 2 (3) 3
Từ (1), (2) suy ra 2(c -b ) = 3
- a thế vào (3) ta được a 3 - a = 1 a = 3 3 2 3 æç 3 ö æ ÷ ç 2 3 ö Do đó b = - , c = - Aç ;-1÷, C ç- ;-2÷÷ ç ÷ ç ÷ ç ÷ 6 3 è 3 ÷ø çè 3 ÷ø æç 3 3 ö AC Suy ra (C) nhận I ç- ; ÷ - ÷ ç
÷ là trung điểm AC làm tâm và bán kính là R = = 1 çè 6 2 ÷ø 2 2 2 æç 3 ö æ ÷ 3 ö
Vậy phương trình đường tròn cần tìm là (C ) : çx + ÷ ç + ç ÷ çx ÷ + ÷ = 1 çè 6 ÷ ç ø è 2 ÷ø
Dạng 3: Vị Trí Tương Đối Của Điểm; Đường Thẳng; Đường Tròn Với Đường Tròn
1. Phương pháp giải.
Vị trí tương đối của điểm M và đường tròn (C)
Xác định tâm I và bán kính R của đường tròn (C) và tính IM
+ Nếu IM < R suy ra M nằm trong đường tròn
+ Nếu IM = R suy ra M thuộc đường tròn
+ Nếu IM > R suy ra M nằm ngoài đường tròn
Vị trí tương đối giữa đường thẳng D và đường tròn (C)
Xác định tâm I và bán kính R của đường tròn (C) và tính d (I;D)
+ Nếu d (I;D) < R suy ra D cắt đường tròn tại hai điểm phân biệt
+ Nếu d (I;D) = R suy ra D tiếp xúc với đường tròn
+ Nếu d (I;D) > R suy ra D không cắt đường tròn
Chú ý: Số nghiệm của hệ phương trình tạo bởi phương trình đường thẳng D và đường tròn (C)
bằng số giao điểm của chúng. Tọa độ giao điểm là nghiệm của hệ.
Vị trí tương đối giữa đường tròn (C) và đường tròn (C')
Xác định tâm I, bán kính R của đường tròn (C) và tâm I', bán kính R' của đường tròn (C') và tính
II ' , R + R ', R - R '
+ Nếu II ' > R + R ' suy ra hai đường tròn không cắt nhau và ở ngoài nhau + Nếu II ' '
= R + R suy ra hai đường tròn tiếp xúc ngoài với nhau
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 810
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 + Nếu II ' '
< R - R suy ra hai đường tròn không cắt nhau và lồng vào nhau + Nếu II ' '
= R - R suy ra hai đường tròn tiếp xúc trong với nhau
+ Nếu R - R ' < II ' < R + R ' suy ra hai đường tròn cắt nhau tại hai điểm phân biệt
Chú ý: Số nghiệm của hệ phương trình tạo bởi phương trình đường thẳng (C) và đường tròn (C')
bằng số giao điểm của chúng. Tọa độ giao điểm là nghiệm của hệ. 2. Các ví dụ.
Ví dụ 1: Cho đường thẳng D : x - y + 1 = 0 và đường tròn (C ) 2 2
: x + y - 4x + 2y - 4 = 0
a) Chứng minh điểm M (2;1) nằm trong đường tròn
b) Xét vị trí tương đối giữa D và (C )
c) Viết phương trình đường thẳng D ' vuông góc với D và cắt đường tròn tại hai điểm phân biệt
sao cho khoảng cách của chúng là lớn nhất. Lời giải:
a) Đường tròn (C) có tâm I (2; 1
- ) và bán kính R = 3 .
Ta có IM = ( - )2 + ( + )2 2 2 1 1
= 2 < 3 = R do đó M nằm trong đường tròn. + + b) Vì d (I D) 2 1 1 ; =
= 2 2 < 3 = R nên D cắt (C ) tại hai điểm phân biệt. 1 + 1
c) Vì D ' vuông góc với D và cắt đường tròn tại hai điểm phân biệt sao cho khoảng cách của chúng
là lớn nhất nên D ' vuông góc với D và đi qua tâm I của đường tròn (C).
Do đó D ' nhận vectơ u =
làm vectơ pháp tuyến suy ra D' : 1(x - 2) + 1(y + 1) = 0 hay D (1;1) x + y - 1 = 0
Vậy phương trình đường thẳng cần tìm là D ' : x + y - 1 = 0
Ví dụ 2: Trong mặt phẳng Oxy , cho hai đường tròn (C ) 2 2
: x + y - 2x - 6y - 15 = 0 và (C ) 2 2
' : x + y - 6x - 2y - 3 = 0
a) Chứng minh rằng hai đường tròn cắt nhau tại hai điểm phân biệt A, B
b) Viết phương trình đường thẳng đi qua A và B
c) Viết phương trình đường tròn đi qua ba điểm A, B và O Lời giải
a) Cách 1: (C ) có tâm I (1;3) và bán kính R = 5 , (C ) có tâm I '(3;1) và bán kính R = 13 II = ( - )2 + ( - )2 ' 3 1 1 3 = 2 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 811
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Ta thấy R - R < I I < R + R suy ra hai đường tròn cắt nhau. 1 2 1 2 1 2
Cách 2: Xét hệ phương trình 2 2 2 2
ìïx + y - 2x - 6y - 15 = 0
ìïx + y - 2x - 6y - 15 = 0 ï ï í í 2 2
ï x + y - 6x - 2y - 3 = 0 ï x - y - 3 = 0 ïî ïî ìï éy = -2 ìï
ï(y + 3)2 + y - 2(y + 3) 2 2 - 6y - 15 = 0
ìïy - y - 6 = 0 ï ê ï ï ï ê í í í y = 3 ê ï x = y + 3 ï x = y + 3 ï ë ï ï ïî î ïïx = y + 3 ïî
Suy ra hai đường tròn cắt nhau tại hai điểm có tọa độ là A(1;-2) và B (6;3)
b) Đường thẳng đi qua hai điểm A, B nhận AB (5;5) làm vectơ chỉ phương suy ra phương trình ìï x = 1 + 5t
đường thẳng cần tìm là ïí ïy = -2 + 5t ïî
c) Cách 1: Đường tròn cần tìm (C") có dạng 2 2
x + y - 2ax - 2by + c = 0 ìï 7 ïa = ï
ìï 1 + 4 - 2a + 4b + c = 0 ï 2 ï ï ï ï ï ï 1
(C") đi qua ba điểm A, B và O nên ta có hệ í36 9 12a 6b c 0 ï + - - + = íb = ï ï 2 ïï c 0 ï = ï ïî ïc = 0 ïïïî Vậy (C") : 2 2
x + y - 7x - y = 0
Cách 2: Vì A, B là giao điểm của hai đường tròn (C) và (C') nên tọa độ đều thỏa mãn phương trình 2 2
x + y - x - y - + m ( 2 2 2 6 15
x + y - 6x - 2y - 3) = 0 (*)
Tọa độ điểm O thỏa mãn phương trình (*) khi và chỉ khi 15 - + m.( 3 - ) = 0 m = 5 -
Khi đó phương trình (*) trở thành 2 2
x + y - 7x - y = 0
Vậy phương trình đường tròn cần tìm là 2 2
x + y - 7x - y = 0
Ví dụ 3: Cho đường tròn 2 2
(C ) : x + y - 2x + 4y - 4 = 0 có tâm I và đường thẳng
D : 2x + my + 1 - 2 = 0
a) Tìm m để đường thẳng D cắt đường tròn (C) tại hai điểm phân biệt A, B
b) Tìm m để diện tích tam giác IAB là lớn nhất
Lời giải (hình 3.2)
a) Đường tròn (C) có tâm I (1; 2 - ), bán kính R = 3
D cắt (C) tại hai điểm phân biệt khi và chỉ khi I B
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 812 H
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A Hình 3.2 2 - 2m + 1 - 2
d (I;D) < R < 3 2 2 + m 2
5m + 5m + 17 > 0 (đúng với mọi m) 1 9 9 b) Ta có S = I .
A IB.sin AIB = sin AIB £ IAB 2 2 2 9 Suy max S = khi và chỉ khi 0
sin AIB = 1 AIB = 90 IAB 2 3
Gọi H là hình chiếu của I lên D khi đó 0 0
AIH = 45 IH = I . A cos 45 = 2 1 - 2m 3 Ta có d (I;D) 2 = IH =
m + 8m + 16 = 0 m = 4 - 2 2 + m 2
Vậy với m = -4 thỏa mãn yêu cầu bài toán.
Dạng 4: Viết Phương Trinh Tiếp Tuyến Với Dường Tron
1. Phương pháp giải.
Cho đường tròn (C) tâm I (a;b ), bán kính R
Nếu biết tiếp điểm là M (x ;y thì tiếp tuyến đó đi qua M và nhận vectơ 0 0 )
IM (x - a;y - b làm vectơ pháp tuyến nên có phương trình là 0 0 )
(x -a x - x + y -b y - y = 0 0 )( 0 ) ( 0 )( 0 )
Nếu không biết tiếp điểm thì dùng điều kiện: Đường thẳng D tiếp xúc đường tròn (C) khi
và chỉ khi d (I;D) = R để xác định tiếp tuyến. 2. Các ví dụ.
Ví dụ 1: Cho đường tròn (C) có phương trình 2 2
x + y - 6x + 2y + 6 = 0 và điểm hai điểm
A(1;-1); B (1;3)
a) Chứng minh rằng điểm A thuộc đường tròn, điểm B nằm ngoài đường tròn
b) Viết phương trình tiếp tuyến của (C) tại điểm A
c) Viết phương trình tiếp tuyến của (C) kẻ từ B. Lời giải:
Đường tròn (C) có tâm I (3; 1 - ) bán kính 2 R = 3 + 1 - 6 = 2 .
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 813
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 a) Ta có: IA = 2 = ;
R IB = 2 5 > R suy ra điểm A thuộc đường tròn và điểm B nằm ngoài đường tròn
b) Tiếp tuyến của (C) tại điểm A nhận IA = (2;0) làm vectơ pháp tuyến nên có phương trình là
2(x - 1) + 0(y + 1) = 0 hay x = 1
b) Phương trình đường thẳng D đi qua B có dạng:
a (x - 1) + b(y - 3) = 0 (với 2 2
a + b ¹ 0 ) hay ax + by - a - 3b = 0
Đường thẳng D là tiếp tuyến của đường tròn d (I;D) = R
3a - b - a - 3b é b = 2 (a 2b)2 0 2 2 2 a b 3b 4ab 0 ê = - = + - = 2 2 ê 3b = 4a a + b êë
+ Nếu b = 0 , chọn a = 1 suy ra phương trình tiếp tuyến là x = 1.
+ Nếu 3b = 4a , chọn a = 3, b = 4 suy ra phương trình tiếp tuyến là 3x + 4y - 15 = 0
Vậy qua A kẻ được hai tiếp tuyến với (C) có phương trình là x = 1 và 3x + 4y - 15 = 0
Ví dụ 2: Viết phương trình tiếp tuyến D của đường tròn (C ) 2 2
: x + y - 4x + 4y - 1 = 0 trong trường
a) Đường thẳng D vuông góc với đường thẳng D ' : 2x + 3y + 4 = 0
b) Đường thẳng D hợp với trục hoành một góc 0 45 Lời giải:
a) Đường tròn (C) có tâm I (2; 2 - ), bán kính R = 3
Vì D ^ D ' nên D nhận u (-3;2) làm VTPT do đó phương trình có dạng
-3x + 2y + c = 0
Đường thẳng D là tiếp tuyến với đường tròn (C) khi và chỉ khi ( D) -10 + c d I; = 3
= 3 c = 10 3 13 13
Vậy có hai tiếp tuyến là D : 3
- x + 2y + 10 3 13 = 0
b) Giả sử phương trình đường thẳng 2 2
D : ax + by + c = 0, a + b ¹ 0
Đường thẳng D là tiếp tuyến với đường tròn (C) khi và chỉ khi ( D)
2a - 2b + c d I; = 3
= 3 (2a - 2b + c )2 = 9( 2 2 a + b )(*) 2 2 a + b
Đường thẳng D hợp với trục hoành một góc 0 45 suy ra
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 814
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 b b cos( ; D Ox ) 0 = cos 45 =
a = b hoặc a = b - 2 2 2 2 a + b a + b
TH1: Nếu a = b thay vào (*) ta có 2 2
18a = c c
= 3 2a , chọn a = b = 1 c = 3 2
suy ra D : x + y 3 2 = 0 é c = 3 2 - 4 a 2 2 ê ( ) TH2: Nếu a = b
- thay vào (*) ta có 18a = (4a + c ) ê
êc = -(3 2 + 4)a ë
Với c = (3 2 - 4)a , chọn a = 1, b = -1, c = (3 2 - 4) D : x - y + 3 2 - 4 = 0
Với c = -(3 2 + 4)a , chọn a = 1, b = -1, c = -(3 2 + 4) D : x - y - 3 2 - 4 = 0
Vậy có bốn đường thẳng thỏa mãn là D : x + y 3 2 = 0, D : x - y + 3 2 - 4 = 0 và 1,2 3
D : x - y - 3 2 - 4 = 0 4
Ví dụ 3: Lập phương trình tiếp tuyến chung của hai đường tròn sau: (C ) 2 2
: x + y - 4y - 5 = 0 và (C : x + y - 6x + 8y + 16 = 0 2 ) 2 2 1 Lời giải:
Đường tròn (C có tâm I 0;2 bán kính R = 3 1 ( ) 1 ) 1
Đường tròn (C có tâm I 3; 4 - bán kính R = 3 2 ( ) 2 ) 2
Gọi tiếp tuyến chung của hai đường tròn có phương trình D : ax + by + c = 0 với 2 2 a + b ¹ 0 ìïd(I , ) D = 3 ì 2 2
ï 2b + c = 3 a + b ï (*)
D là tiếp tuyến chung của (C và (C ï 1 í ï í 2 ) 1 ) ïd(I , ) D = 3 ï 2 2 ï - + = + 2 î 3a 4b c 3 a b ïïî éa = 2b ê
Suy ra 2b + c = 3a - 4b + c ê -3a + 2b êc = êë 2
TH1: Nếu a = 2b chọn a = 2, b = 1 thay vào (*) ta được c = 2
- 3 5 nên ta có 2 tiếp tuyến là
2x + y - 2 3 5 = 0 -3a + 2b TH2: Nếu c = thay vào (*) ta được 2 2
2b - a = 2 a + b a = 0 hoặc 2 3a + 4b = 0
+ Với a = 0 c = b , chọn b = c = 1 ta được D : y + 1 = 0
+ Với 3a + 4b = 0 c = 3b , chọn a = 4, b = 3 - , c = 9
- ta được D : 4x - 3y - 9 = 0
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 815
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Vậy có 4 tiếp tuyến chung của hai đường tròn là :
2x + y - 2 3 5 = 0,y + 1 = 0, 4x - 3y - 9 = 0
C. CÂU HỎI TRẮC NGHIỆM
Câu 1: Tọa độ tâm I và bán kính R của đường tròn (C) (x - )2 +(y + )2 : 1 3 = 16 là: A. I (-1;3), 4 R = . B. I (1;-3), 4 R = . C. I (1;-3), 16. R = D. I (-1;3), 1 R = 6. Lời giải Chọn B
Ta có (C) (x - )2 +(y + )2 : 1 3 = 16 ¾¾ I (1;- ) 3 , R = 16 = 4.
Câu 2: Tọa độ tâm I và bán kính R của đường tròn (C) x +(y + )2 2 : 4 = 5 là: A. I (0;-4), 5 R = . B. I (0;-4), 5 R = . C. I (0;4), 5 R = . D. I (0;4), 5 R = . Lời giải Chọn A
Ta có (C) x +(y + )2 2 : 4 = 5 ¾¾
I (0;-4), R = 5.
Câu 3: Tọa độ tâm I và bán kính R của đường tròn (C) (x + )2 2 : 1 + y = 8 là: A. I (-1;0), 8 R = . B. I (-1;0), 6 R = 4. C. I (-1;0), 2 R = 2. D. I (1;0), 2 R = 2. Lời giải Chọn C
Ta có (C) (x + )2 2 : 1 + y = 8 ¾¾
I (-1;0), R = 8 = 2 2.
Câu 4: Tọa độ tâm I và bán kính R của đường tròn (C) 2 2
: x + y = 9 là: A. I (0;0), 9 R = . B. I (0;0), 8 R = 1. C. I (1; ) 1 , 3 R = . D. I (0;0), 3 R = . Lời giải Chọn D Ta có (C) 2 2 : x + y = 9 ¾¾
I (0;0), R = 9 = 3.
Câu 5: Đường tròn (C) 2 2
: x + y - 6x + 2 y + 6 = 0 có tâm I và bán kính R lần lượt là: A. I (3;- ) 1 , 4 R = . B. I (-3; ) 1 , 4 R = . C. I (3;- ) 1 , 2 R = . D. I (-3; ) 1 , 2 R = . Lời giải Chọn C
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 816
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Ta có ( - C) 6 2 2 2
: x + y -6x + 2 y + 6 = 0 a = = 3, b = = -1, c = 6 -2 -2 I ( - ) R = +(- )2 2 3; 1 , 3 1 - 6 = 2 .
Câu 6: Đường tròn (C) 2 2
: x + y - 4 x + 6 y -12 = 0 có tâm I và bán kính R lần lượt là: A. I (2;-3), 5 R = . B. I (-2;3), 5 R = . C. I (-4;6), 5 R = . D. I (-2;3), 1 R = . Lời giải Chọn A Ta có (C) 2 2
: x + y -4x + 6y 1
- 2 = 0 a = 2,b = 3 - ,c = 1 - 2 I (2;- )
3 , R = 4 + 9 +12 = 5 .
Câu 7: Tọa độ tâm I và bán kính R của đường tròn (C) 2 2
: x + y - 4x + 2 y - 3 = 0 là: A. I (2;- ) 1 , 2 R = 2. B. I (- ) 2;1 , 2 R = 2. C. I (2;- ) 1 , 8 R = . D. I (- ) 2;1 , 8 R = . Lời giải Chọn A Ta có (C) 2 2
: x + y -4x + 2y -3 = 0 a = 2,b = 1 - ,c = 3 - I (2;- )
1 , R = 4 +1+ 3 = 2 2 . Câu 8:
Tọa độ tâm I và bán kính R của đường tròn (C) 2 2
: 2x + 2 y - 8x + 4 y -1 = 0 là: A. I (- ) 21 2;1 , . R = B. I ( - ) 22 2; 1 , . R = 2 2 C. I (4;-2), 21 R = . D. I (-4;2), 19 R = . Lời giải Chọn B ìïa = 2,b = -1 ï Ta có (C) 1 2 2 2 2
: 2x + 2 y -8x + 4y -1 = 0 x + y - 4x + 2 y - = 0 ï í 1 . 2 c ï = - ïïî 2 I ( - ) 1 22 2; 1 , R = 4 +1+ = . 2 2 Câu 9:
Tọa độ tâm I và bán kính R của đường tròn (C) 2 2
: 16x +16 y +16x - 8 y -11 = 0 là: A. I (-8;4), 9 R = 1. B. I (8;-4), 9 R = 1. æ ö C. 1 1 I (-8;4), 6 R = 9. D. I ç- ç ; ÷÷, R = 1. çè 2 4÷ø Lời giải Chọn D Ta có (C) 1 11 2 2 2 2
:16x +16 y +16x -8y -11 = 0 x + y + x - y - = 0 2 16
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 817
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 æ 1 1ö 1 1 11 I ç- ç ; ÷÷, R = + + = 1 ç . è 2 4÷ø 4 16 16
Câu 10: Tọa độ tâm I và bán kính R của đường tròn (C) 2 2
: x + y – 10x -11 = 0 là:
A. I (-10;0), 111 R = . B. I ( 10 - ;0), 8 R =
9. C. I (-5;0), 6 R = . D. I (5;0), 6 R = . Lời giải Chọn C Ta có (C) 2 2
: x + y –10x -11 = 0 I (-5;0), R = 25 + 0 +11 = 6.
Câu 11: Tọa độ tâm I và bán kính R của đường tròn (C) 2 2
: x + y – 5y = 0 là: A. I (0;5), 5 R = . B. I (0;-5), 5 R = . æ ö æ ö C. 5 5 5 5 I çç0; ÷÷, . R = D. ç ÷ ç I ç0;- ÷, . R = è 2÷ø 2 çè 2÷ø 2 Lời giải Chọn C æ ö Ta có (C) 5 25 5 2 2
: x + y – 5y = 0 ç
I ç0; ÷÷, R = 0 + -0 = . ç è 2÷ø 4 2
Câu 12: Đường tròn (C) (x - )2 +(y + )2 : 1
2 = 25 có dạng khai triển là: A. (C) 2 2
: x + y - 2x + 4 y + 30 = 0. B. (C) 2 2
: x + y + 2x - 4 y - 20 = 0. C. (C) 2 2
: x + y - 2x + 4 y - 20 = 0. D. (C) 2 2
: x + y + 2x - 4 y + 30 = 0. Lời giải Chọn C
Ta có (C) (x- )2 +(y + )2 2 2 : 1
2 = 25 x + y - 2x + 4 y - 20 = 0.
Câu 13: Đường tròn (C) 2 2
: x + y +12x -14 y + 4 = 0 có dạng tổng quát là:
A. (C) (x + )2 +(y - )2 : 6 7 = 9.
B. (C) (x + )2 +(y - )2 : 6 7 = 81.
C. (C) (x + )2 +(y - )2 : 6 7 = 89.
D. (C) (x + )2 +(y - )2 : 6 7 = 89. Lời giải Chọn B ìïI ( 6; - 7) Ta có (C) 2 2 : x y 12x 14y 4 0 ï + + - + = í
(C) (x + )2 +(y - )2 : 6 7 = 81. ïïR = 36+49-4 = 9 ïî
Câu 14: Tâm của đường tròn (C) 2 2
: x + y -10x +1 = 0 cách trục
Oy một khoảng bằng: A. 5 - . B. 0 . C. 10 . D. 5 . Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 818
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn D Ta có (C) 2 2 : x + y 1
- 0x +1= 0 I (5;0) d [I;Oy]= 5.
Câu 15: Cho đường tròn (C) 2 2
: x + y + 5x + 7 y - 3 = 0 . Tính khoảng cách từ tâm của (C) đến trục Ox . A. 5 . B. 7 . C. 3,5 . D. 2,5 . Lời giải Chọn C æ ö Ta có (C) 5 7 7 7 2 2
: x + y + 5x + 7 y -3 = 0 ç I - ç ; ÷
- ÷ d [I;Ox]= - = . ç è 2 2÷ø 2 2
Câu 16: Đường tròn có tâm trùng với gốc tọa độ, bán kính R =1 có phương trình là:
A. x +(y + )2 2 1 = 1. B. 2 2 x + y = 1.
C. (x - )2 +(y - )2 1 1 = 1.
D. (x + )2 +(y + )2 1 1 = 1. Lời giải Chọn B ìïI (0;0) Ta có (C):ïí (C) 2 2 : x + y = 1. ïïR =1 î
Câu 17: Đường tròn có tâm I (1;2) , bán kính R = 3 có phương trình là: A. 2 2
x + y + 2x + 4 y - 4 = 0. B. 2 2
x + y + 2x - 4 y - 4 = 0. C. 2 2
x + y - 2x + 4 y - 4 = 0. D. 2 2
x + y - 2x - 4 y - 4 = 0. Lời giải Chọn A ìïI (1;2) Ta có (C):ïí (C):(x - )2 1 +( y - 2)2 2 2
= 9 x + y - 2x - 4y -4 = 0. ïïR = 3 î
Câu 18: Đường tròn (C) có tâm I (1;-5) và đi qua O(0;0) có phương trình là:
A. (x + )2 +(y - )2 1 5 = 26.
B. (x + )2 +(y - )2 1 5 = 26.
C. (x - )2 +(y + )2 1 5 = 26.
D. (x - )2 +(y + )2 1 5 = 26. Lời giải Chọn C ìïI (1;- ) 5 Ta có (C):ïí (C):(x- )2 1 +(y + )2 5 = 26. ïïR = OI = 26 ïî
Câu 19: Đường tròn (C) có tâm I (-2;3) và đi qua M (2;-3) có phương trình là:
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 819
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
A. (x + )2 +(y - )2 2 3 = 52.
B. (x - )2 +(y + )2 2 3 = 52. C. 2 2
x + y + 4x - 6 y -57 = 0. D. 2 2
x + y + 4x -6 y -39 = 0. Lời giải Chọn D ìïI ( 2; - ) 3 Ta có (C) ï : ïí
(C):(x + 2)2 +(y - )2 3 = 52.
ïïR = IM = (2+2)2 +(-3- )2 3 = 52 ïî (C) 2 2
: x + y + 4x -6y -39 = 0.
Câu 20: Đường tròn đường kính AB với A (3;- ) 1 , B (
1;-5) có phương trình là:
A. (x + )2 +(y - )2 2 3 = 5.
B. (x + )2 +(y + )2 1 2 = 17.
C. (x - )2 +(y + )2 2 3 = 5.
D. (x - )2 +(y + )2 2 3 = 5. Lời giải Chọn D ìïI (2;- ) 3 ï Ta có (C):ïí
(C):(x-2)2 +( y + )2 3 = 5. 1 1 ïïR = AB = (1- )2 3 +( 5 - + )2 1 = 5 ïïî 2 2
Câu 21: Đường tròn đường kính AB với A (1; ) 1 , B ( 7;5) có ph ương trình là: A. 2 2
x + y – 8x –6 y +12 = 0 . B. 2 2
x + y + 8x –6 y – 12 = 0 . C. 2 2
x + y + 8x + 6 y +12 = 0 . D. 2 2
x + y – 8x –6 y – 12 = 0 . Lời giải Chọn A ìïI (4; ) 3 Ta có (C) ï : ïí
(C):(x -4)2 +( y - )2 3 =13
ïïR = IA = (4- )2 1 +(3- )2 1 = 13 ïî 2 2
x + y -8x - 6 y +12 = 0.
Câu 22: Đường tròn (C) có tâm I (2;3) và tiếp xúc với trục Ox có phương trình là:
A. (x - )2 +(y )2 2 – 3 = 9.
B. (x - )2 +(y )2 2 – 3 = 4.
C. (x - )2 +(y )2 2 – 3 = 3.
D. (x + )2 +(y + )2 2 3 = 9. Lời giải Chọn A ìïI (2; ) 3 Ta có (C):ïí
(C):(x-2)2 +(y - )2 3 = 9.
ïïR = d[I;Ox]= 3 î
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 820
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 23: Đường tròn (C) có tâm I (2;-3) và tiếp xúc với trục Oy có phương trình là:
A. (x + )2 +(y )2 2 – 3 = 4.
B. (x + )2 +(y )2 2 – 3 = 9.
C. (x - )2 +(y + )2 2 3 = 4.
D. (x - )2 +(y + )2 2 3 = 9. Lời giải Chọn C ìïI (2;- ) 3 Ta có (C):ïí (C):(x- )2 2 +(y + )2 3 = 4.
ïR = d[I;Oy]= ï 2 î
Câu 24: Đường tròn (C) có tâm I (- )
2;1 và tiếp xúc với đường thẳng
D : 3x – 4 y + 5 = 0 có phương trình là:
A. (x + )2 +(y )2 2 – 1 = 1.
B. (x + )2 +(y )2 1 2 – 1 = . 25
C. (x - )2 +(y + )2 2 1 = 1.
D. (x + )2 +(y )2 2 – 1 = 4. Lời giải Chọn A ìïI (-2; ) 1 ïï Ta có (C):ïí -6- 4 + 5
(C):(x + 2)2 +(y - )2 1 = 1.
ïïR = d[I;D]= = 1 ïïî 9 +16
Câu 25: Đường tròn (C) có tâm I (-1;2) và tiếp xúc với đường thẳng
D : x – 2 y +7 = 0 có phương trình là:
A. (x + )2 +(y )2 4 1 – 2 = .
B. (x + )2 +(y )2 4 1 – 2 = . 25 5
C. (x + )2 +(y )2 2 1 – 2 = .
D. (x + )2 +(y )2 1 – 2 = 5. 5 Lời giải Chọn B ìïI (-1;2) ïï Ta có (C) ïí -1- 4 + 7
2 (C) (x + )2 +( y - )2 4 : : 1 2 = .
ïïR = d[I;D]= = 5 ïïî 1+ 4 5
Câu 26: Tìm tọa độ tâm I của đường tròn đi qua ba điểm ,
A (0;4) B (2;4) , C (4;0) . A. I (0;0) . B. I (1;0) . C. I (3;2). D. I (1; ) 1 . Lời giải Chọn D
Ta có . A B C Î(C) 2 2 , ,
: x + y + 2ax + 2by + c = 0
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 821
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 16 ìï +8b +c = 0 ìïa = 1 - ï ï ï ï í20 4a 8b c 0 + +
+ = íb = -1 I (1; ) 1 . ï ï 16 ï +8a +c = 0 ï ï ïc = -8 ïî ïî
Câu 27: Tìm bán kính R của đường tròn đi qua ba điểm A (0;4) , , . B(3;4) C (3;0) A. 5 R = 5 . B. R = 3 . C. R = 10 . D. R = . 2 Lời giải Chọn D ì ïïBA =(- ) AC ( - )2 +( - )2 3;0 3 0 0 4 Ta có 5 ïí
BA ^ BC R = = = . ïïBC =( - ) 2 2 2 0; 4 ïî
Câu 28: Đường tròn (C) đi qua ba điểm A (-3;- )
1 , B (-1;3) và C (-2;2) có phương trình là: A. 2 2
x + y - 4x + 2 y - 20 = 0. B. 2 2
x + y + 2x - y - 20 = 0.
C. (x + )2 +(y - )2 2 1 = 25.
D. (x - )2 +(y + )2 2 1 = 20. Lời giải Chọn A 10
ìï -6a-2b +c = 0 ìïa = 2 - ï ï Ta có ï ï ,
A B,C (C) 2 2 : x y 2ax 2by c 0 1 í 0 2a 6b c 0 Î + + + + = - + + = íb =1 . ï ï 8
ï -4a +4b+c = 0 ï ï ïc = 2 - 0 ïî ïî Vậy (C) 2 2
: x + y -4x + 2y -20 = 0.
Câu 29: Cho tam giác ABC có A (-2;4), B( 5;5), C (
6;-2) . Đường tròn ngoại tiếp tam giác ABC có phương trình là: A. 2 2
x + y - 2x - y + 20 = 0.
B. (x - )2 +(y - )2 2 1 = 20. C. 2 2
x + y - 4x - 2 y + 20 = 0. D. 2 2
x + y - 4x - 2 y - 20 = 0. Lời giải Chọn D
ìï20-4a +8b +c = 0 ìïa = -2 ï ï Ta có ï ï ,
A B,C (C) 2 2 : x y 2ax 2by c 0 50 í 10a 10b c 0 Î + + + + = + +
+ = íb = -1 . ï ï
ï40+12a-4b+c = 0 ï ï ïc = -20 ïî ïî Vậy (C) 2 2
: x + y -4x -2y -20 = 0.
Câu 30: Cho tam giác ABC có A (1;-2), B( -3;0), C (
2;-2) . Tam giác ABC nội tiếp đường tròn có phương trình là:
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 822
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A. 2 2
x + y + 3x + 8 y +18 = 0. B. 2 2
x + y -3x -8 y -18 = 0. C. 2 2
x + y -3x -8 y +18 = 0. D. 2 2
x + y + 3x + 8 y -18 = 0. Lời giải Chọn B
Ta có A B C Î(C) 2 2 , ,
: x + y + 2ax + 2by + c = 0 5
ìï + 2a-4b +c = 0 ìï 3 ï ï ï a = - 9 ï
í -6a + c = 0 ï í 2 . Vậy (C) 2 2
: x + y -3x -8y 1 - 8 = 0. ï ï 8
ïï +4a-4b+c = 0 ïïb =-4,c = 1 - 8 ïî î
Câu 31: Đường tròn (C) đi qua ba điểm , O(0;0) A (8;0) và B (0;6) có phương trình là:
A. (x - )2 +(y - )2 4 3 = 25.
B. (x + )2 +(y + )2 4 3 = 25.
C. (x - )2 +(y - )2 4 3 = 5.
D. (x + )2 +(y + )2 4 3 = 5. Lời giải Chọn A ìïI (4; ) 3 ï
Ta có O(0;0), A(8;0), B(0;6) ï
OA ^ OB í AB
(C):(x-4)2 +(y - )2 3 = 25. ïïR = = 5 ïïî 2
Câu 32: Đường tròn (C) đi qua ba điểm O(0;0), A ( ; a 0), B (
0;b) có phương trình là: A. 2 2
x + y -2ax -by = 0 . B. 2 2
x + y - ax -by + xy = 0 . C. 2 2
x + y - ax -by = 0. D. 2 2
x - y - ay + by = 0 . Lời giải Chọn C
Ta có O(0;0), A( ; a ) 0 , B(
0;b) OA ^ OB ìï æa bö ï ç ïI ç ; ÷÷ ï ç ÷ 2 2 2 2 è2 2ø æ aö æ bö ï a b í (C) + :ç ÷ çx - ÷ +ç ÷ y ï ç ÷ ç - ÷ = è ø ç ÷ 2 2 2 è 2ø 4 ï AB a + ï b ïR = = ïî 2 2 ¾¾ (C) 2 2
: x + y -ax -by = 0.
Câu 33: Đường tròn (C) đi qua hai điểm A (1; )
1 , B (5;3) và có tâm I thuộc trục hoành có phương trình là: A. (x + )2 2 4 + y = 10. B. (x - )2 2 4 + y = 10. C. (x - )2 2 4 + y = 10. D. (x + )2 2 4 + y = 10. Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 823
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn B ìïa = 4 ïï Ta có I (a;0) IA IB R R (a )2 1 1 (a )2 2 2 2 5 3 ï = = = - + = - +
íI (4;0) . ïï 2 ïïR =10 î
Vậy đường tròn cần tìm là: (x- )2 2 4 + y = 10.
Câu 34: Đường tròn (C) đi qua hai điểm A (1; )
1 , B (3;5) và có tâm I thuộc trục tung có phương trình là: A. 2 2
x + y -8 y + 6 = 0.
B. x +(y - )2 2 4 = 6.
C. x +(y + )2 2 4 = 6. D. 2 2
x + y + 4 y + 6 = 0. Lời giải Chọn B ìïa = 4 ïï Ta có I (0;a) IA IB R R 1 (a )2 1 3 (a )2 2 2 2 5 ï = = = + - = + - íI (0;4) ïï 2 ïïR =10 î
Vậy đường tròn cần tìm là: x +(y - )2 2 4 = 10.
Câu 35: Đường tròn (C) đi qua hai điểm A(-1;2), B( 2
- ;3) và có tâm I thuộc đường thẳng
D : 3x - y +10 = 0. Phương trình của đường tròn (C) là:
A. (x + )2 +(y - )2 3 1 = 5. 2 2
B. (x -3) +(y + ) 1 = 5.
C. (x - )2 +(y + )2 3 1 = 5.
D. (x + )2 +(y - )2 3 1 = 5. Lời giải Chọn D
Ta có : I Î D I ( ;3
a a +10) IA = IB = R ìïa = 3 - ïï
R = (a + )2 +( a + )2 = (a + )2 +( a + )2 2 1 3 8 2 3 7 ï íI ( 3; - ) 1 . ïï 2 ïïR = 5 î
Vậy đường tròn cần tìm là: (x + )2 +(y - )2 3 1 = 5.
Câu 36: Đường tròn (C) có tâm I thuộc đường thẳng ,
d : x + 3y + 8 = 0 đi qua điểm A (- ) 2;1 và
tiếp xúc với đường thẳng .
D :3x - 4 y +10 = 0 Phương trình của đường tròn (C) là:
A. (x - )2 +(y + )2 2 2 = 25 .
B. (x + )2 +(y + )2 5 1 = 16 .
C. (x + )2 +(y + )2 2 2 = 9 .
D. (x - )2 +(y + )2 1 3 = 25 .
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 824
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Lời giải Chọn D
Dễ thấy A Î D nên tâm I của đường tròn nằm trên đường thẳng qua A vuông góc với D là
ìï4x +3y +5 = 0 ìïx =1 ìïI (1;- ) 3
D : 4x +3y +5 = 0 I = D Ç d :ï ï ï ¢ ¢ í í í . ïx +3y +8 = 0 ïy = -3 ï ïî ïî ïR = IA = 5 î
Vậy phương trình đường tròn là: (x- )2 +(y + )2 1 3 = 25.
Câu 37: Đường tròn (C) có tâm I thuộc đường thẳng d : x +3y -5 = 0 , bán kính R = 2 2 và tiếp
xúc với đường thẳng .
D : x - y -1 = 0 Phương trình của đường tròn (C) là:
A. (x + )2 +(y - )2 1 2 = 8 hoặc . (x - )2 2 5 + y = 8
B. (x + )2 +(y - )2 1 2 = 8 hoặc . (x + )2 2 5 + y = 8
C. (x - )2 +(y + )2 1 2 = 8 hoặc . (x - )2 2 5 + y = 8
D. (x - )2 +(y + )2 1 2 = 8 hoặc . (x + )2 2 5 + y = 8 Lời giải Chọn A 4-4a éa = 0 éI (5;0)
Ta có I Î d I (5-3 ;
a a) d [I;D] = R = 2 2 = 2 2 ê ê . 2 êa = 2 ê ë êI ( 1 - ;2) ë
Vậy các phương trình đường tròn là: (x- )2 2
5 + y = 8 hoặc (x + )2 +( y - )2 1 2 = 8.
Câu 38: Đường tròn (C) có tâm I thuộc đường thẳng d : x +2y -2 = 0 , bán kính R = 5 và tiếp xúc với đường thẳng .
D :3x - 4 y -11 = 0 Biết tâm I có hoành độ dương. Phương trình của
đường tròn (C) là:
A. (x + )2 +(y - )2 8 3 = 25 .
B. (x - )2 +(y + )2 2 2 = 25 hoặc . (x + )2 +(y - )2 8 3 = 25
C. (x + )2 +(y - )2 2 2 = 25 hoặc . (x - )2 +(y + )2 8 3 = 25
D. (x - )2 +(y + )2 8 3 = 25 . Lời giải Chọn D
Ta có I Î d I (2-2a;a), a <1 d [I;D]= R = 5 . 10a + 5 éa = 2 (l) = 5 ê I (8;- ) 3 5 êa = -3 ë
Vậy phương trình đường tròn là: (x- )2 +(y + )2 8 3 = 25.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 825
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 39: Đường tròn (C) có tâm I thuộc đường thẳng d : x +5y -12 = 0 và tiếp xúc với hai trục tọa
độ có phương trình là:
A. (x - )2 +(y - )2 2 2 = 4 .
B. (x - )2 +(y + )2 3 3 = 9 .
C. (x - )2 +(y - )2 2 2 = 4 hoặc . (x - )2 +(y + )2 3 3 = 9
D. (x - )2 +(y - )2 2 2 = 4 hoặc . (x + )2 +(y - )2 3 3 = 9 Lời giải Chọn D
Ta có I Î d I (12-5a;a) R = d [I;Ox]= d [I;Oy]= 12-5a = a
éa = 3 I (-3; ) 3 , R = 3 ê .
êa = 2 I (2;2),R = ê 2 ë
Vậy phương trình các đường tròn là : (x- )2 +(y - )2 2
2 = 4 hoặc (x + )2 +( y - )2 3 3 = 9.
Câu 40: Đường tròn (C) có tâm I thuộc đường thẳng D : x = 5 và tiếp xúc với hai đường thẳng
d : 3x – y + 3 = 0, d : x – 3y + 9 = 0 1 2 có phương trình là:
A. (x - )2 +(y + )2 5 2 = 40 ho ặc (x - )2 +(y - )2 5 8 = 10.
B. (x - )2 +(y + )2 5 2 = 40.
C. (x - )2 +(y - )2 5 8 = 10.
D. (x - )2 +(y - )2 5
2 = 40 hoặc (x -5)2 +(y + 8)2 = 10. Lời giải Chọn A 18- a 14-3a
Ta có I Î D I (5;a) R = d [I;d = d I;d = = 1 ] [ 2 ] 10 10
éa = 8 I (5; ) 8 , R = 10 ê ê .
êa = -2 I (5; 2 - ), R = 2 10 ë
Vậy phương trình các đường tròn: (x- )2 +(y - )2 5
8 = 10 hoặc (x - )2 +( y + )2 5 2 = 40.
Câu 41: Đường tròn (C) đi qua điểm A (1;-2) và
tiếp xúc với đường thẳng
D : x - y +1 = 0 tại
M (1;2) . Phương trình của đường tròn (C) là: A. (x - )2 2 6 + y = 29. B. (x - )2 2 5 + y = 20. C. (x - )2 2 4 + y = 13. D. (x - )2 2 3 + y = 8. Lời giải Chọn D
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 826
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Ta có Tâm I của đường tròn nằm trên đường thẳng qua M vuông góc với D là
D¢ : x + y -3 = 0 I ( ; a 3-a).
Ta có: R = IA = IM = (a - )2 +(a - )2 = (a - )2 +(a - )2 2 2 2 1 5 1 1 ìïI (3;0) a 3 ï = í (C):(x- )2 2 3 + y = 8. 2 ïïR = 8 î
Câu 42: Đường tròn (C) đi qua điểm M ( )
2;1 và tiếp xúc với hai trục tọa độ Ox, Oy có phương trình là:
A. (x - )2 +(y - )2 1 1 = 1 hoặc
(x -5)2 +(y -5)2 = 25.
B. (x + )2 +(y + )2 1 1 = 1 hoặc
(x +5)2 +(y +5)2 = 25.
C. (x -5)2 +(y -5)2 = 25.
D. (x - )2 +(y - )2 1 1 = 1. Lời giải Chọn A Vì M (2; )
1 thuộc góc phần tư (I) nên A( ; a a), a > 0.
Khi đó: R = a = IM = (a - )2 +(a- )2 2 2 2 1
éa =1 I (1; )
1 , R = 1 (C):(x - )2 1 +( y - )2 1 = 1 ê ê .
êa = 5 I (5; )
5 , R = 5 (C):(x - )2 5 +( y - )2 5 = 25 ë
Câu 43: Đường tròn (C) đi qua điểm M (2;- )
1 và tiếp xúc với hai trục tọa độ Ox, Oy có phương trình là:
A. (x + )2 +(y - )2 1 1 = 1 hoặc
(x +5)2 +(y -5)2 = 25.
B. (x - )2 +(y + )2 1 1 = 1 .
C. (x -5)2 +(y +5)2 = 25.
D. (x - )2 +(y + )2 1
1 = 1 hoặc (x -5)2 +(y + 5)2 = 25. Lời giải Chọn D Vì M (2; ) 1
- thuộc góc phần tư (IV) nên A( ;
a -a), a > 0.
Khi đó: R = a = IM = (a- )2 +(a- )2 2 2 2 1
éa =1 I (1;- )
1 , R = 1 (C):(x - )2 1 +( y + )2 1 = 1 ê ê .
êa = 5 I (5;- )
5 , R = 5 (C):(x - )2 5 +( y + )2 5 = 25 ë
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 827
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 44: Đường tròn (C) đi qua hai điểm A (1;2), B ( 3;4) và
tiếp xúc với đường thẳng
D : 3x + y -3 = 0 . Viết phương trình đường tròn (C), biết tâm của (C) có tọa độ là những số nguyên. A. 2 2
x + y -3x – 7 y +12 = 0. B. 2 2
x + y - 6x – 4 y + 5 = 0. C. 2 2
x + y -8x – 2 y -10 = 0. D. 2 2
x + y -8x – 2 y + 7 = 0. Lời giải Chọn D
Ta có AB : x- y +1= 0, đoạn AB có trung điểm M (2; )
3 trung trực của đoạn AB
là d : x + y -5 = 0 I ( ;5
a -a), a Î . a +
Ta có: R = IA = d [I D]= (a- )2 +(a- )2 2 2 ; 1 3 =
a = 4 I (4; ) 1 , R = 10. 10
Vậy phương trình đường tròn là: (x- )2 +(y - )2 2 2 4
1 = 10 x + y -8x - 2 y + 7 = 0.
Câu 45: Đường tròn (C) đi qua hai điểm A (–1; ) 1 , B (3;3) và
tiếp xúc với đường thẳng
d : 3x – 4 y + 8 = 0 . Viết phương trình đường tròn (C), biết tâm của (C) có hoành độ nhỏ hơn 5.
A. (x - )2 +(y + )2 3 2 = 25.
B. (x + )2 +(y - )2 3 2 = 5.
C. (x + )2 +(y + )2 5 2 = 5.
D. (x - )2 +(y - )2 5 2 = 25 . Lời giải Chọn A
Ta có AB : x-2y +5 = 0, đoạn AB có trung điểm M (1; )
2 trung trực của đoạn AB là
d : 2x + y -4 = 0 I ( ;4
a -2a), a < . 5 Ta có a -
R = IA = d [I D]= (a + )2 +( a- )2 11 8 ; 1 2 3 =
a = 3 I (3;- ) 2 , R = 5. 5
Vậy phương trình đường tròn là: (x- )2 +(y + )2 3 2 = 25.
Câu 46: Cho phương trình 2 2
x + y - 2ax - 2by + c = 0 ( ) 1 . Điều kiện để ( ) 1 là phương trình đường tròn là: A. 2 2
a -b >c . B. 2 2
a + b >c . C. 2 2
a + b <c . D. 2 2
a -b <c . Lời giải Chọn B
Câu 47: Trong các phương trình sau, phương trình nào là phương trình của một đường tròn?
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 828
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A. 2 2
4x + y -10x -6 y -2 = 0. B. 2 2
x + y -2x -8 y + 20 = 0. C. 2 2
x + 2 y - 4x -8 y +1 = 0. D. 2 2
x + y - 4x + 6 y -12 = 0. Lời giải Chọn D
Xét phương trình dạng : 2 2
x + y - 2ax - 2by + c = 0, lần lượt tính các hệ số a,b, c và kiểm tra điều kiện 2 2
a +b -c > 0. 2 2 2 2
x + y - 4x + 6 y -12 = 0 a = 2,b = -3, c = -12 a + b - c > 0. Các phương trình 2 2 2 2
4x + y -10x - 6 y - 2 = 0, x + 2 y - 4x -8y +1 = 0 không có dạng đã nêu
loại các đáp án A và C. Đáp án 2 2
x + y - 2x -8y + 20 = 0 không thỏa mãn điều kiện 2 2
a +b -c > 0.
Câu 48: Trong các phương trình sau, phương trình nào là phương trình của một đường tròn? A. 2 2
x + y + 2x - 4 y + 9 = 0. B. 2 2
x + y - 6x + 4 y +13 = 0. C. 2 2
2x + 2 y -8x - 4 y - 6 = 0. D. 2 2
5x + 4 y + x - 4 y +1 = 0. Lời giải Chọn D
Ta có Loại các đáp án D vì không có dạng 2 2
x + y - 2ax - 2by + c = 0. Xét đáp án A : 2 2 2 2
x + y + 2x - 4 y + 9 = 0 a = -1,b = 2, c = -9 a + b - c < 0 loại A. Xét đáp án B : 2 2 2 2
x + y - 6x + 4 y +13 = 0 a = 3,b = -2, c = 13 a + b - c < 0 loại B. Xét đáp án D : ìïa = 2 ï 2 2 2 2 ï 2 2
2x + 2y -8x - 4y -6 = 0 x + y - 4x - 2 y -3 = 0 íb =1 a +b -c > 0. ïïïc = 3 - ïî
Câu 49: Trong các phương trình sau, phương trình nào là phương trình của một đường tròn? A. 2 2
x + y - x - y + 9 = 0 . B. 2 2
x + y - x = 0 . C. 2 2
x + y -2xy -1 = 0. D. 2 2
x - y - 2x + 3y -1 = 0. Lời giải Chọn B
Loại các đáp án C và D vì không có dạng 2 2
x + y - 2ax - 2by + c = 0. Xét đáp án A : 1 1 2 2 2 2
x + y - x - y + 9 = 0 a = , b = ,c = 9 a + b -c < 0 loại A. 2 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 829
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Xét đáp án B : 1 2 2 2 2
x + y - x = 0 a = ,b = c = 0 a + b -c > 0 . 2
Câu 50: Trong các phương trình sau, phương trình nào không phải là phương trình của đường tròn? A. 2 2
x + y - x + y + 4 = 0. B. 2 2
x + y – 100 y +1 = 0. C. 2 2
x + y – 2 = 0. D. 2 2
x + y - y = 0. Lời giải Chọn A Xét A : 1 1 2 2 2 2
x + y - x + y + 4 = 0 a = ,b = - ,c = 4 a + b -c < 0 . 2 2
Các đáp án còn lại các hệ số a, b, c thỏa mãn 2 2
a +b -c > 0.
Câu 51: Cho phương trình 2 2
x + y + mx + (m ) 2 2 2
– 1 y + 2m = 0 ( ) 1 . Tìm điều kiện của m để ( ) 1 là
phương trình đường tròn. A. 1 1 m < . B. m £ . C. m > 1 . D. m = 1 . 2 2 Lời giải Chọn A Ta có: 2 2
x + y + mx + (m ) 2 2 2 –1 y + 2m = 0 ìïa = - ï m ï 1 ï 2 2
íb =1-m a +b -c > 0 -2m +1> 0 m < . ï 2 ï 2 ïc = 2 ïî m
Câu 52: Cho phương trình 2 2
x + y - 2mx - 4(m - 2) y + 6 - m = 0 ( ) 1 . Tìm điều kiện của m để ( ) 1 là
phương trình đường tròn. A. m Î . B. m Î (-¥ ) ;1 È(2;+¥). æ ö C. 1 m Î (-¥ ] ;1 È[2;+¥). D. m Îç- ç ; ÷ ¥ ÷È(2;+ ) ¥ . çè 3÷ø Lời giải Chọn B ìïa = ï m Ta có: ï 2 2 x y mx (m ) ï + - - -
y + - m = íb = (m- ) 2 2 2 4 2 6 0 2
2 a + b -c > 0 ïïïc =6- ïî m ém < 1 2
5m -15m +10 > 0 ê . êm > 2 ë
Câu 53: Cho phương trình 2 2
x + y - 2x + 2my + 10 = 0 ( )
1 . Có bao nhiêu giá trị m nguyên dương
không vượt quá 10 để ( )
1 là phương trình của đường tròn?
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 830
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A. Không có. B. 6 . C. 7 . D. 8 . Lời giải Chọn C ìïa =1 ï Ta có: 2 2 ï 2 2 2
x + y - 2x + 2my + 10 = 0 íb = -m a +b -c > 0 m -9 > 0 ïïïc =10 ïî ém < -3 ê m = 4;5¼;10. êm > 3 ë
Câu 54: Cho phương trình 2 2
x + y – 8x +10 y + m = 0 ( ) 1 . Tìm điều kiện của m để ( ) 1 là phương
trình đường tròn có bán kính bằng . 7
A. m = 4 . B. m = 8 . C. m = –8 . D. m = – 4 . Lời giải Chọn C ìïa = 4 ï Ta có 2 2 ï 2 2 2
x + y – 8x +10y + m = 0 íb = -5 a +b -c = R = 49 m = -8. ïïïc = ïî m
Câu 55: Cho phương trình 2 2
x + y - 2(m + )
1 x + 4 y -1 = 0 ( )
1 . Với giá trị nào của m để ( ) 1 là
phương trình đường tròn có bán kính nhỏ nhất? A. m =2. B. m = -1. C. m = 1. D. m = -2. Lời giải Chọn B ìïa = m +1 ï Ta có: 2 2 ï x y 2(m ) 1 x 4y 1 0 + - + + - = íb = 2 - ïïïc = 1 - ïî
R = a + b -c = (m + )2 2 2 2 1 + 5 R = 5 m = -1. min
Câu 56: Phương trình tiếp tuyến
d của đường tròn (C): (x + 2)2 +(y + )2 2 = 25 tại điểm M ( ) 2;1 là:
A. d : -y +1 = 0.
B. d : 4x +3y +14 = 0.
C. d : 3x -4 y -2 = 0.
D. d : 4x +3y -11 = 0. Lời giải Chọn D
Đường tròn (C) có tâm I ( 2; - - )
2 nên tiếp tuyến tại M có VTPT là n = IM = (4; ) 3 , nên có
phương trình là: 4(x-2)+3(y - )
1 = 0 4x +3y 1 - 1= 0.
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 831
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 57: Cho đường tròn (C) (x - )2 +(y + )2 : 1
2 = 8 . Viết phương trình tiếp tuyến d của (C) tại điểm A (3;-4) .
A. d : x + y +1 = 0.
B. d : x -2y -11 = 0.
C. d : x - y -7 = 0.
D. d : x - y +7 = 0. Lời giải Chọn C
Đường tròn (C) có tâm I (1; ) 2
- nên tiếp tuyến tại A có VTPT là n = IA = (2;-2) = 2(1;- ) 1 ,
Nên có phương trình là: ( 1. x - ) 3 1 - (
. y + 4) = 0 x- y -7 = 0.
Câu 58: Phương trình tiếp tuyến
d của đường tròn (C) 2 2
: x + y - 3x - y = 0 tại điểm N (1;- ) 1 là:
A. d : x +3y -2 = 0.
B. d : x -3y + 4 = 0.
C. d : x -3y -4 = 0.
D. d : x +3y +2 = 0. Lời giải Chọn D æ ö
Đường tròn (C) có tâm 3 1 ç I ç ; ÷÷ ç
nên tiếp tuyến tại N có VTPT là è2 2÷ø æ 1 3ö 1 n = IN = ç- ç ; ÷ - ÷ = - (1; ) 3 , ç è 2 2÷ø 2
Nên có phương trình là: ( 1 x - ) 1 +3(y + )
1 = 0 x +3y + 2 = 0.
Câu 59: Viết phương trình tiếp tuyến của đường tròn (C): (x - )2 +(y + )2 3
1 = 5 , biết tiếp tuyến song
song với đường thẳng .
d : 2x + y +7 = 0
A. 2x + y +1 = 0 hoặc 2x + y -1 = 0.
B. 2x + y = 0 hoặc 2x + y -10 = 0.
C. 2x + y +10 = 0 hoặc 2x + y -10 = 0.
D. 2x + y = 0 hoặc 2x + y +10 = 0. Lời giải Chọn B
Đường tròn (C) có tâm I (3;- )
1 , R = 5 và tiếp tuyến có dạng D : 2x + y + c = 0 (c = / 7). c + éc = Ta có 5
R = d [I D] 0 ; = 5 ê . 5 êc = -10 ë
Câu 60: Viết phương trình tiếp tuyến của đường tròn (C) 2 2
: x + y + 4 x + 4 y -17 = 0 , biết tiếp tuyến
song song với đường thẳng .
d : 3x - 4 y -2018 = 0
A. 3x – 4 y + 23 = 0 hoặc 3x – 4y – 27 = 0. B.
3x – 4 y + 23 = 0 hoặc 3x – 4 y + 27 = 0.
C. 3x – 4 y -23 = 0 hoặc
3x – 4 y + 27 = 0.
D. 3x – 4 y -23 = 0 hoặc 3x – 4y – 27 = 0. Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 832
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn A
Đường tròn (C) có tâm I ( 2; - - )
2 , R = 5 và tiếp tuyến có dạng D : 3x-4y + c = 0 (c = / 20 - ) 18 . c + éc = Ta có 2
R = d [I D] 23 ; = 5 ê . 5 êc = -27 ë
Câu 61: Viết phương trình tiếp tuyến của đường tròn (C): (x -2)2 +(y - )2
1 = 25 , biết tiếp tuyến
song song với đường thẳng .
d : 4x + 3y +14 = 0
A. 4x +3y +14 = 0 hoặc 4x + 3y -36 = 0.
B. 4x +3y +14 = 0.
C. 4x +3y -36 = 0.
D. 4x +3y -14 = 0 hoặc 4x +3y -36 = 0. Lời giải Chọn C
Đường tròn (C) có tâm I (2; )
1 , R = 5 và tiếp tuyến có dạng D : 4x +3y + c = 0 (c = / 1 ) 4 . c +11 éc =14(l)
Ta có R = d [I;D] = 5 ê . 5 êc = -36 ë
Câu 62: Viết phương trình tiếp tuyến của đường tròn (C): (x -2)2 +(y + )2
4 = 25 , biết tiếp tuyến
vuông góc với đường thẳng .
d : 3x - 4 y + 5 = 0
A. 4x – 3y +5 = 0 hoặc 4x – 3y – 45 = 0. B.
4x + 3y + 5 = 0 hoặc 4x + 3y + 3 = 0. C.
4x + 3y + 29 = 0. D.
4x + 3y + 29 = 0 hoặc 4x +3y – 21 = 0. Lời giải Chọn D
Đường tròn (C) có tâm I (2; 4
- ), R = 5 và tiếp tuyến có dạng D : 4x +3y + c = 0. c - éc =
Ta có R = d [I D] 4 29 ; = 5 ê . 5 êc = -21 ë
Câu 63: Viết phương trình tiếp tuyến của đường tròn (C) 2 2
: x + y + 4 x - 2 y - 8 = 0 , biết tiếp tuyến
vuông góc với đường thẳng .
d : 2x -3y + 2018 = 0
A. 3x + 2y -17 = 0 hoặc 3x + 2 y -9 = 0.
B. 3x +2y +17 = 0 hoặc
3x + 2 y + 9 = 0.
C. 3x +2y +17 = 0 hoặc 3x + 2 y -9 = 0.
D. 3x + 2y -17 = 0 hoặc 3x + 2y + 9 = 0. Lời giải Chọn C
Đường tròn (C) có tâm I (-2; )
1 , R = 13 và tiếp tuyến có dạng D : 3x + 2y + c = 0. c - éc =
Ta có R = d [I D] 4 17 ; = 13 ê . 13 êc = -9 ë
Câu 64: Viết phương trình tiếp tuyến của đường tròn (C) 2 2
: x + y - 4 x - 4 y + 4 = 0 , biết tiếp tuyến
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 833
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
vuông góc với trục hoành. A. x = 0 .
B. y = 0 hoặc . y - 4 = 0 C. x = 0 hoặc x - 4 = 0 D. y = 0 . Lời giải Chọn C
Đường tròn (C) có tâm I (2; )
2 , R = 2 và tiếp tuyến có dạng D : x + c = 0. éc =
Ta có R = d [I D] 0 ; c + 2 = 2 ê . êc = -4 ë
Câu 65: Viết phương trình tiếp tuyến
D của đường tròn (C) (x - )2 +(y + )2 : 1 2 = 8 , biết tiếp tuyến đi qua điểm . A (5;-2)
A. D : x -5 = 0 .
B. D : x + y -3 = 0 hoặc . D : x - y -7 = 0
C. D : x -5 = 0 hoặc .
D : x + y -3 = 0
D. D : y +2 = 0 hoặc . D : x - y -7 = 0 Lời giải Chọn B
Đường tròn (C) có tâm I (1;-2), R = 2 2 và tiếp tuyến có dạng
D ax + by - a + b = ( 2 2 : 5 2 0 a + b = / 0). 4a
éa = b a = b =1 Ta có: d [I;D] 2 2 = R
= 2 2 a -b = 0 ê . 2 2
êa = -b a =1,b = - a + 1 b ë
Câu 66: Viết phương trình tiếp tuyến
D của đường tròn (C) 2 2
: x + y - 4 x - 4 y + 4 = 0 , biết tiếp tuyến đi qua điểm . B (4;6)
A. D : x -4 = 0 hoặc .
D : 3x + 4 y -36 = 0
B. D : x -4 = 0 hoặc . D : y -6 = 0
C. D : y -6 = 0 hoặc .
D : 3x + 4 y -36 = 0
D. D : x - 4 = 0 hoặc .
D : 3x - 4 y +12 = 0 Lời giải Chọn D
Đường tròn (C) có tâm I (2; )
2 , R = 2 và tiếp tuyến có dạng
D ax + by - a - b = ( 2 2 : 4 6 0 a + b = / 0). 2a + 4b
éb = 0 a =1,b = 0
Ta có: d [I;D]= R
= 2 b(3b + 4a) = 0 ê . 2 2 ê3b = 4
- a a = 3,b = 4 - a + b ë
Câu 67: Cho đường tròn (C) (x + )2 +(y - )2 : 1 1 = 25 và điểm .
M (9;-4) Gọi D là tiếp tuyến của , (C) biết
D đi qua M và không song song với các trục tọa độ. Khi đó khoảng cách từ điểm P (6;5) đến D bằng: A. 3 . B. 3 . C. 4 . D. 5 .
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 834
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Lời giải Chọn B
Đường tròn (C) có tâm I ( 1 - ; )
1 , R = 5 và tiếp tuyến có dạng D : ax +by -9a + 4b = 0 (ab = / ) 0 . 10a -5b
Ta có: d [I;D]= R
= 5 a(3a -4b) = 0 2 2 a +b + -
3a = 4b a = 4,b = 3 D : 4x +3y -24 = 0. Suy ra d [P D] 24 15 24 ; = = 3. 5
Câu 68: Có bao nhiêu đường thẳng đi qua gốc tọa độ O và
tiếp xúc với đường tròn (C) 2 2
: x + y - 2x + 4 y -11 = 0 ? A. 0. B. 2. C. 1. D. 3. Lời giải Chọn A
Đường tròn (C) có tâm I (1;-2), R = 4 OI = 5 < R không có tiếp tuyến nào của đường tròn kẻ từ O.
Câu 69: Cho đường tròn (C) (x - )2 +(y + )2 : 3
3 = 1 . Qua điểm M (4 ;-3) có thể kẻ được bao nhiêu
đường thẳng tiếp xúc với đường tròn (C)? A. 0. B. 1. C. 2. D. Vô số. Lời giải Chọn C
Ta có Vì M Î(C) nên có đúng 1 tiếp tuyến của đường tròn kẻ từ M .
Câu 70: Có bao nhiêu đường thẳng đi qua điểm N (-2 ;0)
tiếp xúc với đường tròn
(C) (x - )2 +(y + )2 : 2 3 = 4 ? A. 0. B. 1. C. 2. D. Vô số. Lời giải Chọn C
Đường tròn (C) có tâm I (2;- )
3 , R = 2 IN = 16 + 9 = 5 > R có đúng hai tiếp tuyến của
đường tròn kẻ từ N .
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 835
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
BÀI 3. PHƯƠNG TRÌNH ELIP
A. KIẾN THỨC CƠ BẢN CẦN NẮM
1. Định nghĩa: Cho hai điểm cố định
F F = 2 (c > 0) . Tập hợp các điểm 1 F và 2 F với 1 2 c M
thỏa mãn MF + MF = 2 ( > > ) là một 1 2 a
a không đổi và a c 0 đường Elip. y B2 ● F , 1 2
F là hai tiêu điểm. M ● A1 A2
F F = 2 là tiêu cự của Elip. 1 2 c F O x 1 F2
2. Phương trình chính tắc của Elip B1 2 2 ( ): x y Hình 3.3 E + = 1 với 2 2 2
a = b + c . 2 2 a b 2 2 Do đó điểm ( x y
M x ; y ) Î (E ) 0 0 + = 1 và £ , £ . 0 0 x a y b 2 2 0 0 a b
3. Tính chất và hình dạng của Elip
● Trục đối xứng Ox (chứa trục lớn), Oy (chứa trục bé).
● Tâm đối xứng O .
● Tọa độ các đỉnh A - ; a 0 , A ; a 0 , B 0; b - , B 0; . 1 ( ) 2 ( ) 1 ( ) 2 ( b)
● Độ dài trục lớn 2a . Độ dài trục bé 2b .
● Tiêu điểm F - ;0 c , ;0 . 1 ( ) 2 F (c ) ● Tiêu cự 2c .
B. CÁC DẠNG TOÁN VÀ PHƯƠNG PHÁP GIẢI.
Dạng 1. Xác định các yếu tố của elip khi biết phương trình chính tắc của elip.
1.Phương pháp giải.
Từ phương trình chính tắc ta xác định các đại lượng a,b và 2 2 2
b = a - c ta tìm được c elip từ đó
ta suy ra được các yếu tố cần tìm. 2. Các ví dụ.
Ví dụ 1. Xác định các đỉnh, độ dài trục, tiêu cự, tiêu điểm , tâm sai của elip có phương trình sau: 2 2 x y a) + = 1 b) 2 2 4x + 25y = 100 4 1 Lời giải:
a) Từ phương trình của (E) ta có 2 2
a = 2, b = 1 c = a - b = 3 .
Suy ra tọa độ các đỉnh là A -2; 0 ; A 2; 0 ; B 0;-1 ; B 0;1 1 ( ) 2 ( ) 1 ( ) 2 ( )
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 836
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Độ dài trục lớn A A = 4 , độ dài trục bé B B = 2 1 2 1 2
Tiêu cự F F = 2c = 2 3 , tiêu điểm là F - 3; 0 ; F 3;0 , 1 ( ) 2( ) 1 2 c 3
Tâm sai của (E) là e = = a 2 2 2 x y b) Ta có 2 2
4x + 25y = 100 + = 1 suy ra 2 2
a = 5; b = 2 c = a - b = 21 25 4
Do đó tọa độ các đỉnh là A -5; 0 ; A 5; 0 ; B 0;-2 ; B 0;-2 1 ( ) 2 ( ) 1 ( ) 2 ( )
Độ dài trục lớn A A = 10 , độ dài trục bé B B = 4 1 2 1 2
Tiêu cự F F = 2c = 2 21 , tiêu điểm là F - 21; 0 ; F 21; 0 , 1 ( ) 2 ( ) 1 2 c 21
Tâm sai của (E) là e = = a 5
Dạng 2. Viết phương trình chính tắc của đường elip.
1. Phương pháp giải.
Để viết phương trình chính tắc của elip ta làm như sau: 2 2 x y
+ Gọi phương trình chính tắc elip là +
= 1(a > b > 0) 2 2 a b
+ Từ giả thiết của bài toán ta thiết lập các phương trình, hệ phương trình từ giải thiết của bài toán để
tìm các đại lượng a,b của elip từ đó viết được phương trình chính tắc của nó. 2. Các ví dụ.
Ví dụ 1. Viết phương trình chính tắc của elip (E) trong mỗi trường hợp sau: 2
a) (E) có độ dài trục lớn là 6 và tâm sai e = 3 æç4 10 ö
b) (E)có tọa độ một đỉnh là (0; 5) và đi qua điểm M ç ;-1÷÷ ç ÷ çè 5 ÷ø 4 33
c) (E) có tiêu điểm thứ nhất (- 3;0) và đi qua điểm M(1; ) . 5
d) Hình chữ nhật cơ sở của (E) có một cạnh nằm trên đường thẳng y + 2 = 0 và có diện tích bằng 48. 5 e) (E) có tâm sai bằng
và hình chữ nhật cơ sở của (E) có chu vi bằng 20. 3 Lời giải:
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 837
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 2 x y
Phương trình chính tắc của (E) có dạng: +
= 1(a > b > 0) 2 2 a b 2
a) (E) có độ dài trục lớn là 6 suy ra 2a = 6 a = 3 , Tâm sai e = nên 3 c 2 2 2 2 =
c = 2, b = a - c = 5 a 3 2 2 x y
Vậy phương trình chính tắc (E) là + = 1 9 5
b) (E) có một đỉnh có tọa độ là (0; 5) nằm trên trục tung nên b = 5 do đó phương trình chính 2 2 x y tắc của (E) có dạng: + = 1 a > 5 . 2 ( ) a 5 æç4 10 ö 160 1
Mặt khác (E) đi qua điểm M ç ;-1÷÷ ç ÷ nên 2 + = 1 a = 8 çè 5 ÷ø 2 25a 5 2 2 x y
Vậy phương trình chính tắc (E) là + = 1 8 5
c) (E) có tiêu điểm F (- 3;0) nên c = 3 suy ra 2 2 2 2
a = b + c = b + 3 (1) 1 4 33 1 528 Mặt khác M(1; ) Î (E) + = 1 (2) 2 2 5 a 25b
Thế (1) vào (2) ta được 1 528 4 2 +
= 1 25b - 478b - 1584 = 0 2 2
b = 22 a = 25 2 2 b + 3 25b 2 2 x y
Vậy phương trình chính tắc (E) là + = 1 25 22
d) (E) có hình chữ nhật cơ sở có một cạnh nằm trên đường thẳng y + 2 = 0 suy ra b = 2
Mặt khác hình chữ nhật cơ sở diện tích bằng 48 nên 2a.2b = 48 b = 6 2 2 x y
Vậy phương trình chính tắc (E) là + = 1 36 4 5 2 2 a - b 5 e) (E) có tâm sai bằng suy ra = hay 2 2 4a = 9b (3) 3 a 3
Hình chữ nhật cơ sở của (E) có chu vi bằng 20 suy ra 4(a + b ) = 20 (4).
Từ (3) và (4) suy ra a = 3, b = 2 2 2 x y
Vậy phương trình chính tắc (E) là + = 1 9 4
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 838
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Dạng 3. Xác định điểm nằm trên đường elip thỏa mãn điều kiện cho trước.
1. Phương pháp giải.
Để xác định tọa độ điểm M thuộc elip có phương trình chính tắc là 2 2 ( ) x y E : +
= 1(a > b > 0) ta làm như sau 2 2 a b 2 2 x y
Giả sử M (x ;y , điểm M Î (E ) M M +
= 1 ta thu được phương trình thứ nhất. M M ) 2 2 a b
Từ điều kiện của bài toán ta thu được phương trình thứ hai; giải phương trình, hệ phương
trình ẩn x , y ta tìm được tọa độ của điểm M M M 2. Các ví dụ: 2 2 x y
Ví dụ 1. Trong mặt phẳng Oxy , cho elip (E): +
= 1 có tiêu điểm F và F . 25 9 1 2
Tìm điểm M trên (E) sao cho
a) Điểm M có tung gấp ba lần hoành độ b) MF = 2MF 1 2 c) 0 F MF = 60 1 2
d) Diện tích tam giác OA D
M lớn nhất với A(1;1) Lời giải 2 2 x y
Giả sử M (x ;y Î E suy ra M M + = 1(*) M M ) ( ) 25 9
a) Điểm M có tung gấp ba lần hoành độ do đó y = 3x thay vào (*) ta được M M x (3x M M )2 2 5 2 +
= 1 26x = 25 x = 25 9 M M 26 æ 5 15 ö æ 5 15 ö
Vậy có hai điểm thỏa mãn là M çç ; ÷÷ và M çç- ; ÷ - ÷ 1 ç ÷ è ç ÷ 26 26 ÷ø 2 è 26 26 ø
b) Từ phương trình (E) có 2 2
a = 25, b = 9 nên 2 2
a = 5, b = 3,c = a - b = 4
Theo công thức tính bán kính qua tiêu điểm ta có : c 4 c 4
MF = a + x
= 5 + x và MF = a - x = 5 - x 1 M a 5 M 2 M a 5 M 4 æ 4 ö 25
Theo giải thiết MF = 2MF suy ra 5 x 2ç +
= ç5 - x ÷÷ x = 1 2 5 M çè 5 M ÷ø M 12
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 839
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 25 y 119 Thay vào (*) ta có : M + = 1 y = 144 9 M 4 æç25 119 ö æç25 119 ö
Vậy có hai điểm M thỏa mãn là: M ç ; ÷÷ và M ç ; ÷ - ÷ 1 ç ÷ ç ç ÷ è12 4 ÷ø 2 çè12 4 ÷ø
c) Ta có F -4; 0 , F 4; 0 MF x + 4;y , MF x - 4;y 1 ( ) 2 ( ) 1 ( M M ) 2 ( M M )
2 2 MF .MF x + y - 16 Vì 0 F MF = 60 nên 0 1 2 cos 60 M M
= = 1 2 æ 4 öæ 4 MF . MF ö ç ÷ç ÷ 1 2
ç5 + x ÷ç5 - x ÷ çè 5 M ÷øçè 5 M ÷ø 1 æ 16 ö 2 2 ç 2
x + y - 16 = ç25 - x ÷÷ M M 2 çè 25 M ÷ø 2 2 x 57 y 2 2 57 y y 3 3 Suy ra M M = - thế vào (*) ta được M M - + = 1 y = và 25 66 33 66 33 9 M 4 5 13 x = M 4 æç5 13 3 3 ö
Vậy có bốn điểm thỏa mãn là M ç ; ÷÷, 1 ç ÷ çè 4 4 ÷ø æç 5 13 3 3 ö æ ÷ ç 5 13 3 3 ö æç 5 13 3 3 ö M ç- ; ÷,M ç ; ÷ - ÷ và M ç- ; ÷ - ÷ 2 ç ÷ 3 ç ÷ ç ÷ ç ÷ è 4 4 ÷ø çè 4 4 ÷ø 4 çè 4 4 ÷ø
d) Ta có OA(1;1) nên đường thẳng đi qua hai điểm O, A nhận n ( 1
- ;1) làm vectơ pháp tuyến có phương trình là x - + y = 0 1 x - + y S = OAd M OA = = x - + y OAM ( ) 1 M M 1 . ; 2 2 2 2 2 M M
Áp dụng bất đẳng thức Bnhiacốpxki ta có 2 2 1 x y 1 æ x y ö 34 S =
-5. M + 3. M £ .34.ç M M ÷ ç + ÷ = OAM 2 5 3 2 çè 25 9 ÷÷ø 2 x y
Dấu bằng xảy ra khi và chỉ khi M M - =
kết hợp với (*) ta được 25 9 ìï 25 ì ï ï 25 x = ï ïx = - M ï ï M ï ï 34 í hoặc 34 ï í 9 ï ï 9 ïy = - ïï y = M ïïî 34 M ïïî 34
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 840
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 æ 25 9 ö æ 25 9 ö
Vậy có hai điểm M çç ; ÷ - ÷ và M çç- ;
÷÷ thỏa mãn yêu cầu bài toán 1 ç ÷ è ç ÷ 34 34 ÷ø 2 è 34 34 ø 2 2 x y
Ví dụ 2: Cho elip (E) : + = 1 và C (2;0). Tìm ,
A B thuộc (E) biết ,
A B đối xứng nhau qua 4 1
trục hoành và tam giác ABC đều. Lời giải
Giả sử A(x ;y . Vì ,
A B đối xứng nhau qua trục hoành nên B (x ; y - với y > 0 . 0 0 ) 0 0 ) 0 2 2 2 x y x
Vì A Î (E ) nên 0 0 2 0 + = 1 y = 1 - (1) 0 4 1 4
Vì tam giác ABC đều nên AB = AC ( 2
- y )2 = (2 - x )2 + ( y - )2 2 2 0 0 0 2 2
3y = 4 - 4x + x (2) 0 0 0 Thay (1) vào (2) ta có é x = 2 2 æ ö 0 x ê ç 0 ÷ 2 2 3ç1 -
÷ = 4 - 4x + x 7x - 16x + 4 = 0 ê ç ÷ 0 0 0 0 2 çè 4 ÷ø êx = 0 êë 7
+ Nếu x = 2 thay vào (1) ta cóy = 0 . Trường hợp này loại vì A º C 0 0 2 4 3 + Nếu x =
thay vào (1) ta có y = 0 7 0 7 æç2 4 3 ö æç2 4 3 ö æç2 4 3 ö æç2 4 3 ö Vậy Aç ; ÷÷ ÷ ÷ ÷ ç ÷ , B ç ;- ÷ hoặc Aç ;- ÷ , B ç ; ÷ . ç ç ÷ ç ÷ ç ÷ è 7 7 ÷ø çè 7 7 ÷ø çè 7 7 ÷ø çè7 7 ÷ø
C. CÂU HỎI TRẮC NGHIỆM 2 2 Câu 1: x y Elip (E): +
= 1 có độ dài trục lớn bằng: 25 9 A. 5. B. 10. C. 25. D. 50. Lời giải Chọn B 2 2
Gọi phương trình của Elip là x y +
= 1, có độ dài trục lớn A A = 2 . a 2 2 1 2 a b 2 2 2 ìï = ì Xét ï = ( ï ï E ) x y a 25 a 5 : + = 1 í í ¾¾
A A = 2.5 = 10. 1 2 2 25 9 b ïï = 9 b ï = 3 î ïî
Câu 2: Elip (E ) 2 2
: 4x +16 y = 1 có độ dài trục lớn bằng:
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 841
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A. 2. B. 4. C. 1. D. 1 . 2 Lời giải Chọn C 2 2
Gọi phương trình của Elip là x y +
= 1, có độ dài trục lớn A A = 2 . a 2 2 1 2 a b ìï 1 2 ï = 2 2 a ï Xét ( ï E ) x y 4 1 1 2 2
: 4x +16 y = 1 + = 1 í a = ¾¾ A A = 2. = 1. 1 2 1 1 ï 1 ï 2 2 2 b ï = 4 16 ïïî 16
Câu 3: Elip (E ) 2 2
: x + 5y = 25 có độ dài trục lớn bằng: A. 1. B. 2. C. 5. D. 10. Lời giải Chọn D 2 2
Gọi phương trình của Elip là x y +
= 1, có độ dài trục lớn A A = 2 . a 2 2 1 2 a b 2 2 2 ìï Xét = ( ï E ) x y a 25 2 2
: x + 5y = 25 + = 1 í a = 5 ¾¾ A A = 2.5 = 10. 1 2 2 25 5 b ïï = 5 î 2 2 Câu 4: x y Elip (E): +
= 1 có độ dài trục bé bằng: 100 64 A. 8. B. 10. C. 16. D. 20. Lời giải Chọn C 2 2
Gọi phương trình của Elip là x y +
= 1, có độ dài trục bé B B = 2 . b 2 2 1 2 a b 2 2 2 ìï Xét = ( ï E ) x y a 100 : + = 1 í b = 8 ¾¾
B B = 2.8 = 16. 1 2 2 100 64 b ïï = 64 î 2 Câu 5: x Elip (E) 2 :
+ y = 4 có tổng độ dài trục lớn và trục bé bằng: 16 A. 5. B. 10. C. 20. D. 40. Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 842
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn C 2 2
Gọi phương trình của Elip là x y +
= 1, có độ dài trục lớn A A = 2a và độ dài trục bé là 2 2 1 2 a b 2 2 2 x x y
B B = 2 . Khi đó, xét (E ) 2 : + y = 4 + = 1. 1 2 b 16 64 4 2 ìïa = 64 ï a ìï = 8 í ï í ¾¾
A A + B B = 2.8 + 2.2 = 20. 2 1 2 1 2 b ïï = 4 î b ï = 2 ïî 2 2 Câu 6: x y Elip (E): + = 1 có tiêu cự bằng: 25 16 A. 3. B. 6. C. 9. D. 18. Lời giải Chọn B 2 2
Gọi phương trình của Elip là x y + = 1, có tiêu cự là 2 . c 2 2 a b 2 2 2 ìï Xét = ( ï E ) x y a 25 2 2 2 : + = 1 í
c = a -b = 9 c = 3 ¾¾ 2c = 6. 2 25 16 b ïï =16 î 2 2 Câu 7: x y Elip (E): + = 1 có tiêu cự bằng: 9 4 A. 5. B. 5. C. 10. D. 2 5. Lời giải Chọn D 2 2
Gọi phương trình của Elip là x y + = 1, có tiêu cự là 2 . c 2 2 a b 2 2 2 ìï Xét = ( ï E ) x y a 9 2 2 2 : + = 1 í
c = a -b = 5 c = 5 ¾¾
2c = 2 5. Chọn D. 2 9 4 b ïï = 4 î 2 2 Câu 8: x y Elip (E): +
= 1 , với p > q > 0 có tiêu cự bằng: 2 2 p q
A. p +q . B. p-q . C. 2 2 p - q . D. 2 2 2 p - q . Lời giải Chọn D 2 2
Gọi phương trình của Elip là x y + = 1, có tiêu cự là 2 . c 2 2 a b
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 843
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 2 2 2 ìï Xét = ( ï E ) x y a p 2 2 2 2 2 2 2 : + = 1 í
c = p - q c = p - q ¾¾
2c = 2 p - q . 2 2 2 2 p q b ïï = q î 2 2 Câu 9: x y Elip (E): +
= 1 có một đỉnh nằm trên trục lớn là: 100 36 A. (100;0) . B. (-100;0) . C. (0;10) . D. (-10;0) . Lời giải Chọn D
Gọi M là điểm nằm trên trục lớn của (E) M ÎOx M (m;0). 2 é é m m = 10 M (10;0)
Mặt khác M Î (E ) suy ra 2 2 = 1 = ê ê m 10 . 100 ê ê m = -10 M (- ë ê 10;0) ë 2 2 Câu 10: x y Elip (E ): +
= 1 có một đỉnh nằm trên trục bé là: 16 12 A. (4;0) . B. (0;12) . C. (0;2 3) . D. (4;0) . Lời giải Chọn C
Gọi N là điểm nằm trên trục bé của (E) N ÎOy N (0;n). é 2 é N 0;2 3 2 n n = 2 3 ê ( ) Mặt khác ê
N Î (E ) suy ra 2 = 1 n = (2 3) ê . 12 ê ê ên = -2 3 ë N ê (0;-2 3) ë 2 2 Câu 11: x y Elip (E ): +
= 1 có một tiêu điểm là: 9 6 A. (0;3). B. (0 ; 6). C. (- 3;0). D. (3;0). Lời giải Chọn C 2 2 Gọi phương trình của ( x y E ) là +
= 1, có tọa độ tiêu điểm F ( ;0 c ). 2 2 a b 2 2 2 ìï Xét = ( ï E ) x y a 9 2 2 2 : + = 1 í
c = a -b = 3 c = 3. 2 9 6 b ïï = 6 î
Vậy tiêu điểm của Elip là F
3;0 , F - 3;0 . 1 ( ) 2 ( )
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 844
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 2 Câu 12: x y
Cặp điểm nào là các tiêu điểm của elip (E ): + = 1 ? 5 4
A. F -1;0 và F 1;0 .
B. F -3;0 và F 3;0 . 2 ( ) 1 ( ) 2 ( ) 1 ( )
C. F 0;-1 và F 0;1 .
D. F -2;0 và F 2;0 . 2 ( ) 1 ( ) 2 ( ) 1 ( ) Lời giải Chọn A 2 2 Gọi phương trình của ( x y E ) là +
= 1, có tọa độ tiêu điểm F ( ;0 c ). 2 2 a b 2 2 2 ìï Xét = ( ï E ) x y a 5 2 2 2 : + = 1 í
c = a -b = 1 c = 1. 2 5 4 b ïï = 4 î
Vậy tiêu điểm của Elip là F 1;0 , F -1;0 . 1 ( ) 2 ( ) 2 2 Câu 13: x y Elip (E ): +
= 1 . Tỉ số e của tiêu cự và độ dài trục lớn của elip bằng: 16 9 A. e =1. B. 7 e = . C. 3 e = . D. 5 e = . 4 4 4 Lời giải Chọn B 2 2 2 2 ìï = ì x y a 16 a ï = 16 a ìï = 4 Xét ( ï ï ï E ) c 7 : + = 1 í í í ¾¾ e = = . 2 2 16 9 b ïï = 9 c ï î ï = 7 c ï î ï = 7 a 4 î 2 2 Câu 14: x y Elip (E ): +
= 1 . Tỉ số f của độ dài trục lớn và tiêu cự của elip bằng: 9 4 A. 3 f = . B. 3 f = . C. 2 f = . D. 5 f = . 2 5 3 3 Lời giải Chọn B 2 2 2 2 ìï = ì x y a 9 ïa = 9 ìïa = 3 Xét ( ï ï ï E ) : + = 1 í í í . 2 2 9 4 b ïï = 4 ï î ïc = 5 ï î ïc = 5 î Vậy tỉ số a f cần tính là 2 3 f = = . 2c 5 2 2 Câu 15: x y Elip (E ): +
= 1 . Tỉ số k của tiêu cự và độ dài trục bé của elip bằng: 16 8
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 845
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 A. k = 8 . B. k = 8 . C. k =1 . D. k = 1 - . Lời giải Chọn C 2 2 2 2 ìï = ì ì ï = ï Xét = ( ï ï ï E ) x y a 16 b 8 b 2 2 : + = 1 í í í . 2 2 16 8 b ïï = 8 ï î ïc = 8 ï î c ï = 2 2 ïî Vậy tỉ số c k cần tính là 2 2 2 k = = = 1. Chọn C. 2b 2 2 2 2 Câu 16: x y Cho elip (E ): +
= 1 . Trong các khẳng định sau, khẳng định nào sai? 25 9
A. (E) có các tiêu điểm F -4;0 và F 4;0 . 2 ( ) 1 ( ) B. ( c E ) có tỉ số 4 = . a 5
C. (E) có đỉnh A -5;0 . 1 ( )
D. (E) có độ dài trục nhỏ bằng 3. Lời giải Chọn D ìa ïï = 5 2 2 2 2 ï Ta có ( ): x y + = 1 ( ): x y ï E E + = 1 ¾¾ b í = 3 2 2 25 9 5 3 ïïï 2 2 2 2 c
ï = a -b = 5 -3 = 4 ïî
Do đó, độ dài trục nhỏ của (E) là 6.
Câu 17: Cho elip (E ) 2 2
: x + 4 y = 1 . Khẳng định nào sau đây là đúng?
A. Elip có tiêu cự bằng 3.
B. Elip có trục nhỏ bằng 2. æ ö
C. Elip có một tiêu điểm là ç 2 ÷ F ç0; ÷ ç ÷.
D. Elip có trục lớn bằng 4. ç è 3 ÷ø Lời giải Chọn A ìïa = 1 ïïï 1 2 2 ï Ta có ( ) ï = 2 2 : + 4 = 1 ( ): x y ï E x y E + = 1 b ¾¾ í 2 . 2 2 1 æ1ö ï ç ÷ ï ç ÷ ï 3 ç ÷ ï 2 2 è2ø c ï = a -b = ïïî 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 846
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Do đó:
(E) có tiêu cự F F = 2c = 3 . 1 2
(E) có trục nhỏ bằng 1, trục lớn bằng 2. æ ö æ ö ( ç 3 ÷ ç 3 ÷
E ) có tiêu điểm là F ç- ;0÷ và F ç ;0÷ . 1 ç ÷ ç ç ÷ è 2 ÷ø 2 çè 2 ÷ø
Câu 18: Cho elip (E) 2 2
: 4x + 9 y = 36 . Tìm mệnh đề sai trong các mệnh đề sau:
A. (E) có trục lớn bằng 6.
B. (E) có trục nhỏ bằng 4. C. ( c
E ) có tiêu cự bằng 5.
D. (E) có tỉ số 5 = . a 3 ìa ïï = 3 2 2 ï Ta có ( ) 2 2 : 4 + 9 = 36 ( ): x y ï E x y E + = 1 ¾¾ b í = 2 . 2 2 3 2 ïïï 2 2 c ï = a -b = 5 ïî
Do đó, (E) có tiêu cự bằng 2 5 .
Câu 19: Phương trình của elip (E ) có độ dài trục lớn bằng 8, độ dài trục nhỏ bằng 6 là: A. 2 2 9x +16 y = 144. B. 2 2
9x +16 y = 1. 2 2 2 2 C. x y + = 1. D. x y + = 1. 9 16 64 36 Lời giải Chọn A 2 2 x y a ìï = 4 Xét đáp án A. Ta có ( ï E ) 2 2
: 9x +16 y = 144 (E ): + = 1 ¾¾ í . 2 2 4 3 b ï = 3 ïî
Do đó (E) có độ dài trục lớn là 8, độ dài trục nhỏ là 6.
Câu 20: Tìm phương trình chính tắc của elip có tiêu cự bằng 6 và trục lớn bằng 10. 2 2 2 2 2 2 2 2 A. x y + = 1. B. x y + = 1. C. x y - = 1. D. x y + = 1. 25 9 100 81 25 16 25 16 Lời giải Chọn D ìï = = ìï = Elip F F 6 2 ( c c 3 ï ï E ) có 1 2 2 2 í í
b = a - c = 4 . ïA A = 10 = 2a a ï = 5 ïî 1 2 ïî
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 847
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 2
Do đó, phương trình chính tắc của Elip là ( ): x y E + = 1 . 25 16
Câu 21: Elip có độ dài trục lớn là 10 và có một tiêu điểm F (-3;0). Phương trình chính tắc của elip là: 2 2 2 2 2 2 2 2 A. x y + = 1. B. x y + = 1. C. x y + = 1. D. x y + = 1. 25 9 100 16 100 81 25 16 Lời giải Chọn D
Elip (E) có độ dài trục lớn là 10 ¾¾
2a =10 a = 5 .
Elip (E) có một tiêu điểm F (-3;0) ¾¾ c = 3 . Khi đó, 2 2
b = a - c = 4 . 2 2
Phương trình chính tắc của Elip là ( ): x y E + = 1 . 25 16
Câu 22: Elip có độ dài trục nhỏ là 4 6 và có một tiêu điểm F (5;0) . Phương trình chính tắc của elip là: 2 2 2 2 2 2 2 2 A. x y + = 1. B. x y + = 1. C. x y + = 1. D. x y + = 1. 121 96 101 96 49 24 29 24 Lời giải Chọn C
Elip (E) có độ dài trục nhỏ là 4 6 ¾¾
2b = 4 6 b = 2 6 .
Elip (E) có một tiêu điểm F (5;0) ¾¾ c = 5 . Khi đó, 2 2 a = b + c = 7 . 2 2
Phương trình chính tắc của Elip là ( ): x y E + =1 . 49 24
Câu 23: Elip có một đỉnh là A(5;0) và có một tiêu điểm F -4;0 . Phương trình chính tắc của elip là: 1 ( ) 2 2 2 2 2 2 A. x y + = 1. B. x y + = 1. C. x y + = 1. D. x y + =1. 25 16 5 4 25 9 5 4 Lời giải Chọn C
Elip (E) có một đỉnh là A (5;0)ÎOx ¾¾ a = 5 .
Elip (E) có một tiêu điểm F (-4;0) ¾¾ c = 4 . Khi đó, 2 2 b = a - c = 3 .
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 848
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 2
Phương trình chính tắc của Elip là ( ): x y E + = 1 . 25 9
Câu 24: Elip có hai đỉnh là (-3;0);(3;0) và có hai tiêu điểm là (-1;0); (1;0). Phương trình chính tắc của elip là: 2 2 2 2 2 2 2 2 A. x y + = 1. B. x y + = 1. C. x y + = 1. D. x y + = 1. 9 1 8 9 9 8 1 9 Lời giải Chọn C
Elip (E) có hai đỉnh là (-3;0)Î Ox và (3;0)ÎOx ¾¾ a = 3 .
Elip (E) có hai tiêu điểm là F -1;0 và F 1;0 ¾¾ c = 1 . 2 ( ) 1 ( ) Khi đó, 2 2 b = a - c = 2 2 . 2 2
Phương trình chính tắc của Elip là ( ): x y E + = 1 . 9 8
Câu 25: Tìm phương trình chính tắc của elip nếu trục lớn gấp đôi trục bé và có tiêu cự bằng 4 3 . 2 2 2 2 2 2 2 2
A. x + y =1. B. x y + = 1. C. x y + = 1.
D. x + y = 1. 16 4 36 9 36 24 24 16 Lời giải Chọn A
Elip (E) có trục lớn gấp đôi trục bé A A = 2B B 2a = 2.2b a = 2 . 1 2 1 2 b
Elip (E) có tiêu cự bằng 4 3 ¾¾
2c = 4 3 c = 2 3 .
Ta có a = b +c ( ) b = b +( )2 2 2 2 2 2 2
2 3 b = 2 . Khi đó, a = 2b = 4 . 2 2
Phương trình chính tắc của Elip là ( ): x y E + = 1 . 16 4
Câu 26: Lập phương trình chính tắc của elip biết độ dài trục lớn hơn độ dài trục nhỏ 4 đơn vị, độ
dài trục nhỏ hơn độ dài tiêu cự 4 đơn vị. 2 2 2 2 2 2 2 2 A. x y + = 1. B. x y + = 1. C. x y + = 1. D. x y + = 1. 64 60 25 9 100 64 9 1 Lời giải Chọn C
Elip (E) có độ dài trục lớn hơn độ dài trục nhỏ 4 đơn vị ¾¾ 2a-2b = 4 .
Elip (E) có độ dài trục nhỏ hơn độ dài tiêu cự 4 đơn vị ¾¾ 2b-2c = 4 . Ta có
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 849
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 a ìï -b = 2 ïï a ìï -b = 2 a ìï = b + 2 a ìï = b + 2 a ì ï ï ï ï = 10 ï ï b í -c = 2 í í í í 2 2 ïï a ï = ï b +(b - 2)2 ( ï ï î ï b + 2)2 2 2 = 2b - 4b + 4 b ï -8b = 0 b ï = 8 2 2 2 î ïî ïî a = b + c ïî 2 2
Phương trình chính tắc của Elip là ( ): x y E + = 1 . 100 64
Câu 27: Lập phương trình chính tắc của elip biết tỉ số giữa độ dài trục nhỏ và tiêu cự bằng 2 ,
tổng bình phương độ dài trục lớn và tiêu cự bằng 64 . 2 2 2 2 2 2 2 2 A. x y + = 1. B. x y + = 1. C. x y + = 1. D. x y + = 1. 12 8 8 12 12 4 8 4 Lời giải Chọn A Elip ( b b
E ) có tỉ số độ dài trục nhỏ và tiêu cự bằng 2 2 2 ¾¾ = 2 c = . 2c 2
Mặt khác, ( a)2 +( c)2 2 2 2 2
= 64 a + c = 16 . ìï b 2 ï ìï 1 2 2 ïc = a ï + b =16 2 ï ï ì ï ï ï = Ta có 2 a 12 ï 2 ï í í í . 2 2 2 a ï + c = 16 ï 3 ï ï ï 2 2 b ï = 8 ï a ï - b = 0 î ï 2 2 2 ï a ï = b + c ïî 2 ïî 2 2
Phương trình chính tắc của Elip là ( ): x y E + = 1 . 12 8
Câu 28: Elip có một tiêu điểm F (-2;0) và tích độ dài trục lớn với trục bé bằng 12 5 . Phương trình chính tắc của elip là: 2 2 2 2 2 2 2 2 A. x y + = 1. B. x y + = 1. C. x y + = 1. D. x y + = 1. 9 5 36 20 144 5 45 16 Lời giải Chọn A
Elip (E) có một tiêu điểm F (-2;0) ¾¾ c = 2 .
Elip (E) có tích độ dài trục lớn với trục bé bằng 12 5 ¾¾ 2 .
a 2b = 12 5 ab = 3 5 . ìï 3 5 ïa ï = ì ï ab ï = 3 5 ï b a ìï = 3 Ta có ï ï ï í í 2 í . 2 2 2 ï æ ï ö a ï -b = c î ïç3 5 ÷ b ïï = 5 2 ïç ÷ î ïç ÷ -b = 4 ç ïè b ÷ø ïî 2 2
Phương trình chính tắc của Elip là ( ): x y E + = 1 . 9 5
Câu 29: Lập phương trình chính tắc của elip có độ dài trục lớn bằng 26 và tỉ số của tiêu cự với độ dài trục lớn bằng 12 . 13
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 850
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 2 2 2 2 2 2 2 A. x y + = 1. B. x y + = 1. C. x y + = 1. D. x y + = 1. 26 25 169 25 52 25 169 5 Lời giải Chọn B
Elip (E) có độ dài trục lớn bằng 26 ¾¾
2a = 26 a =13 . Elip ( c
E ) có tỉ số của tiêu cự với độ dài trục lớn bằng 12 2 12 12 ¾¾ = c = a = 12 . 13 2a 13 13 Do đó, 2 2 b = a - c = 5 . 2 2
Phương trình chính tắc của Elip là ( ): x y E + = 1 . 169 25
Câu 30: Lập phương trình chính tắc của elip có độ dài trục lớn bằng 6 và tỉ số của tiêu cự với độ dài trục lớn bằng 1 . 3 2 2 2 2 2 2 2 2
A. x + y =1. B. x y + = 1. C. x y + = 1.
D. x + y =1. 9 8 9 5 6 5 9 3 Lời giải Chọn A
Elip (E) có độ dài trục lớn bằng 6 ¾¾
2a = 6 a = 3 . Elip ( c
E ) có tỉ số của tiêu cự với độ dài trục lớn bằng 1 2 1 1 ¾¾
= c = a = 1 . 3 2a 3 3 Do đó, 2 2 b = a - c = 2 2 . 2 2
Phương trình chính tắc của Elip là ( ): x y E + = 1 . 9 8
Câu 31: Lập phương trình chính tắc của elip có độ dài trục nhỏ bằng 12 và tỉ số của tiêu cự với độ dài trục lớn bằng 4 . 5 2 2 2 2 2 2 2 2 A. x y + = 1. B. x y + = 1. C. x y + = 1. D. x y + = 1. 36 25 25 36 64 36 100 36 Lời giải Chọn D 2 2
Gọi phương trình chính tắc của Elip là ( ): x y E +
= 1, với a > b > 0. 2 2 a b
Độ dài trục nhỏ của Elip là 12 suy ra 2b =12 b = 6. Tiêu cự của Elip là 2 , c
c độ dài trục lớn là 2a suy ra tỉ số 4 4 = c = . a a 5 5
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 851
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Mặt khác 16 9 2 2 2 2 2 2 2 2
a -b = c a -6 = a
a = 36 a = 100. 25 25 2 2
Vậy phương trình cần tìm là ( ): x y E + = 1. 100 36
Câu 32: Elip có tổng độ dài hai trục bằng 18 và tỉ số của tiêu cự với độ dài trục lớn bằng 3 . 5
Phương trình chính tắc của elip là: 2 2 2 2 2 2 2 2 A. x y + = 1. B. x y + = 1. C. x y + = 1. D. x y + = 1. 25 16 5 4 25 9 9 4 Lời giải Chọn A 2 2
Gọi phương trình chính tắc của Elip là ( ): x y E +
= 1, với a > b > 0. 2 2 a b
Tổng độ dài hai trục của Elip là 2a +2b =18 a +b = 9 b = 9- . a Tiêu cự của Elip là 2 , c
c độ dài trục lớn là 2a suy ra tỉ số 3 3 = c = . a a 5 5 Mà 2 2 2
a -b = c suy ra: a -(9 -a)2 9 2 2 =
a a = 5 ( a = 45 loại vì b = 9 - 45 = -36 < 0 ) 25 2 2
Vậy phương trình cần tìm là ( ): x y E + = 1. 25 16
Câu 33: Elip có tổng độ dài hai trục bằng 10 và tỉ số của tiêu cự với độ dài trục lớn bằng 5 . 3
Phương trình chính tắc của elip là: 2 2 2 2 2 2 2 2 A. x y + = 1. B. x y + = 1. C. x y + = 1. D. x y + = 1. 25 16 5 4 25 9 9 4 Lời giải Chọn D 2 2
Gọi phương trình chính tắc của Elip là ( ): x y E +
= 1, với a > b > 0. 2 2 a b
Tổng độ dài hai trục của Elip là .. Tiêu cự của Elip là 2 , c
c độ dài trục lớn là 2a suy ra tỉ số 5 5 = c = . a a 3 3 Mà 5 2 2 2
a -b = c suy ra a -(5-a)2 2 2
= a a = 3 ( a =15 loại vì b = 5-15 = 1 - 0 < 0 ) 9 2 2
Vậy phương trình cần tìm là ( ): x y E + = 1. 9 4
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 852
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 34: Lập phương trình chính tắc của elip, biết elip đi qua hai điểm A(7;0) và B(0;3) . 2 2 2 2 2 2 2 2 A. x y + = 1. B. x y + = 1. C. x y + = 1. D. x y + = 1. 40 9 16 9 9 49 49 9 Lời giải Chọn D 2 2
Gọi phương trình chính tắc của Elip là ( ): x y E +
= 1, với a > b > 0. 2 2 a b 2 Elip đi qua điểm 7 2 A (7;0) suy ra = 1 a = 49. 2 a 2 Elip đi qua điểm 3 B (0;3) suy ra 2 = 1 b = 9. 2 b 2 2
Vậy phương trình cần tìm là ( ): x y E + = 1. 49 9 æ ö
Câu 35: Elip đi qua các điểm ç ÷ M (0;3) và 12 N 3; ç - ÷ ç
có phương trình chính tắc là: è 5 ÷ø 2 2 2 2 2 2 2 2 A. x y + = 1 . B. x y + = 1 . C. x y + = 1 . D. x y - = 1 . 16 9 25 9 9 25 25 9 Lời giải Chọn B 2 2
Gọi phương trình chính tắc của Elip là ( ): x y E +
= 1, với a > b > 0. 2 2 a b 2 2 Elip đi qua điểm 0 3 2 M (0;3) suy ra + = 1 b = 9. 2 2 a b 2 æ 12ö ç ÷ - æ ö ç ÷ 2 ç ÷ Elip đi qua điểm 12 3 è 5 ø 9 144 1 N 3; ç ÷ ç - ÷ 2 ç suy ra + = 1 = 1- . a = 25. è 5 ÷ø 2 2 2 2 a b a 25 b 2 2
Vậy phương trình cần tìm là ( ): x y E + = 1. 25 9 æ ö
Câu 36: Elip đi qua các điểm ç ÷ A (0; ) 1 và 3 N 1; ç ÷ ç
÷ có phương trình chính tắc là: çè 2 ÷ø 2 2 2 2 2 2 2 2 A. x y + = 1. B. x y + = 1. C. x y + = 1. D. x y + = 1. 16 4 8 4 4 1 2 1 Lời giải Chọn C 2 2
Gọi phương trình chính tắc của Elip là ( ): x y E +
= 1, với a > b > 0. 2 2 a b
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 853
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 2 Elip đi qua điểm 0 1 2 A ( ) 0;1 suy ra + = 1 b = 1. 2 2 a b 2 æç 3ö÷ ç ÷ æ ö ç ÷ 2 1 çè 2 ÷ Elip đi qua điểm ç 3 ÷ ø 1 3 1 N 1; ç ÷ 2 ç ÷ suy ra + = 1 = 1- . a = 4. çè 2 ÷ø 2 2 2 2 a b a 4 b 2 2
Vậy phương trình cần tìm là ( ): x y E + = 1. 4 1
Câu 37: Tìm phương trình chính tắc của elip nếu nó có trục lớn gấp đôi trục bé và đi qua điểm M (2;-2) . 2 2 2 2 2 2 2 2
A. x + y =1. B. x y + = 1. C. x y + = 1.
D. x + y =1. 20 5 36 9 24 6 16 4 Lời giải Chọn A 2 2
Gọi phương trình chính tắc của Elip là ( ): x y E +
= 1, với a > b > 0. 2 2 a b
Elip có độ dài trục lớn gấp đôi trục bé suy ra 2a = 2.2b a = 2 . b 2 (-2)2 2 Elip đi qua điểm 1 1 1 M (2;-2) suy ra + = 1 + = . 2 2 2 2 a b a b 4 2 2 a ìï = 2b a ìï = 4b 2 ï ï a ìï = ï ï 20
Do đó, ta có hệ phương trình ï ï í 1 1 1 í í . 1 1 1 2 ï + = ï ï ï + = b ïï = 5 2 2 2 2 î ïîa b 4 ïî4b b 4 2 2
Vậy phương trình cần tìm là ( ): x y E + = 1. 20 5
Câu 38: Tìm phương trình chính tắc của elip, biết elip có tiêu cự bằng 6 và đi qua A(5;0). 2 2 2 2 2 2 2 2 A. x y - = 1 .
B. x + y = 1 .
C. x + y = 1 .
D. x + y =1 . 25 16 25 16 25 9 100 81 Lời giải Chọn B 2 2
Gọi phương trình chính tắc của Elip là ( ): x y E +
= 1, với a > b > 0. 2 2 a b
Elip có tiêu cự bằng 6 suy ra 2 2 2
2c = 6 c = 3 a -b = c = 9. 2 2 Elip đi qua điểm 5 0 A (5;0) suy ra 2 + = 1 a = 25. 2 2 a b 2 2 2 ìï - = ìï
Do đó, ta có hệ phương trình a b 9 a = 25 ï ï í í . 2 2 ïïa = 25 b ï î ï = 16 î 2 2
Vậy phương trình cần tìm là ( ): x y E + = 1. 25 16
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 854
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Câu 39: Tìm phương trình chính tắc của elip, biết elip có tiêu cự bằng 2 3 và đi qua A ( ) 2;1 . 2 2 2 2 2 2 2 2
A. x + y =1. B. x y + = 1. C. x y + = 1.
D. x + y =1. 6 3 8 2 8 5 9 4 Lời giải Chọn A 2 2
Gọi phương trình chính tắc của Elip là ( ): x y E +
= 1, với a > b > 0. 2 2 a b
Elip có tiêu cự bằng 2 3 suy ra 2 2 2
2c = 2 3 c = 3 a -b = c = 3 ( ) 1 . 2 2 Elip đi qua điểm 2 1 4 1 A ( ) 2;1 suy ra + = 1 + = 1 (2). 2 2 2 2 a b a b 2 2 2 2 a ìï -b = 3 a ìï = b +3 2 2 2 ï ï ï ï a ìï = b +3 a ìï = 6 Từ ( ) 1 , (2) suy ra ï ï ï í 4 1 í 4 1 í í . 4 2 2 ïï + =1 ï + = 1 ï b ïï -2b -3 = 0 b ï î ï = 3 2 2 2 2 î ïîa b ïïîb +3 b 2 2
Vậy phương trình cần tìm là ( ): x y E + = 1. 6 3
Câu 40: Tìm phương trình chính tắc của elip, biết elip có tiêu cự bằng 8 và đi qua điểm M ( 15;- ) 1 . 2 2 2 2 2 2 2 2 A. x y + = 1. B. x y + = 1. C. x y + = 1. D. x y + = 1. 12 4 16 4 18 4 20 4 Lời giải Chọn D 2 2
Gọi phương trình chính tắc của Elip là ( ): x y E +
= 1, với a > b > 0. 2 2 a b
Elip có tiêu cự bằng 8 suy ra 2 2 2
2c = 8 c = 4 a -b = c =16 ( ) 1 . ( 15)2 (- )2 1 Elip đi qua điểm 15 1 M ( 15;- ) 1 suy ra + =1 + =1 (2). 2 2 2 2 a b a b 2 2 2 2 a ìï -b =16 a ìï = b +16 2 2 2 ï ï ï ï a ìï = b +16 a ìï = 20 Từ ( ) 1 , (2) suy ra ï ï ï í15 1 í 15 1 í í . 4 2 ïï + =1 ï + = 1 ï b ïï =16 b ï î ï = 4 2 2 2 2 î ïîa b ïïîb +16 b 2 2
Vậy phương trình cần tìm là ( ): x y E + = 1. 20 4 æ ö
Câu 41: Elip qua điểm 5 M çç2; ÷÷ ç
và có một tiêu điểm F (-2;0) . Phương trình chính tắc của elip là: è 3÷ø 2 2 2 2 2 2 2 2 A. x y + = 1 . B. x y + = 1 . C. x y + = 1 . D. x y + = 1 . 9 5 9 4 25 16 25 9 Lời giải
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 855
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Chọn A 2 2
Gọi phương trình chính tắc của Elip là ( ): x y E +
= 1, với a > b > 0. 2 2 a b
Elip có một tiêu điểm là F (-2;0) suy ra 2 2 2 2
c = 2 a = b + c = b + 4 ( ) 1 . 2 æ5ö ç ÷ æ ö ç ÷ 2 ç ÷ Elip đi qua điểm 5 2 è3ø 4 25 M çç2; ÷÷ ç suy ra + = 1 + = 1 (2). è 3÷ø 2 2 2 2 a b a 9b 2 2 2 2 a ìï = b + 4 a ìï = b + 4 2 ï ï ï ï a ìï = 9 Từ ( ) 1 , (2) suy ra ï ï í 4 25 í 4 25 í . 2 ïï + = 1 ï + = 1 ï b ïï = 5 2 2 2 2 î ïîa 9b ïïîb + 4 9b 2 2
Vậy phương trình cần tìm là ( ): x y E + = 1. 9 5
Câu 42: Phương trình chính tắc của elip có hai tiêu điểm F -2;0 , 2; F
0 và đi qua điểm M (2;3) 1 ( ) 2 ( ) là: 2 2 2 2 2 2 2 2 A. x y + = 1. B. x y + = 1. C. x y + = 1. D. x y + = 1. 16 12 16 9 16 4 16 8 Lời giải Chọn A 2 2
Gọi phương trình chính tắc của Elip là ( ): x y E +
= 1, với a > b > 0. 2 2 a b
Elip có hai tiêu điểm là F -2;0 , F 2;0 2 2 2 2
c = 2 a = b + c = b + 4 ( ) 1 . 1 ( ) 2 ( ) 2 2 Elip đi qua điểm 2 3 4 9 M (2;3) suy ra + = 1 + = 1 (2). 2 2 2 2 a b a b 2 2 2 2 a ìï = b + 4 a ìï = b + 4 2 2 2 ï ï ï ï a ìï = b + 4 a ìï =16 Từ ( ) 1 , (2) suy ra ï ï ï í 4 9 í 4 9 í í . 4 2 2 ïï + =1 ï + = 1 ï b ïï -4b -36 = 0 b ï î ï = 12 2 2 2 2 î ïîa b ïïîb + 4 b 2 2
Vậy phương trình cần tìm là ( ): x y E + = 1. 16 12
Câu 43: Tìm phương trình chính tắc của elip nếu nó đi qua điểm A(6;0) và tỉ số của tiêu cự với độ dài trục lớn bằng 1 . 2 2 2 2 2 2 2 2 2
A. x + y =1. B. x y + = 1.
C. x + y =1.
D. x + y =1. 36 27 6 3 36 18 6 2 Lời giải Chọn A 2 2
Gọi phương trình chính tắc của Elip là ( ): x y E +
= 1, với a > b > 0. 2 2 a b
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 856
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 2 Elip đi qua điểm 6 0 A (6;0) suy ra 2 + = 1 a = 36. 2 2 a b 2
Tỉ số của tiêu cực với độ dài trục lớn bằng 1 suy ra 2c 1 c 1 2 a = = c = . 2 2a 2 a 2 4 2
Kết hợp với điều kiện a 3 3 2 2 2
b = a - c , ta được 2 2 2 b = a - = a = .36 = 27. 4 4 4 2 2
Vậy phương trình cần tìm là ( ): x y E + = 1. 36 27 æ ö
Câu 44: Tìm phương trình chính tắc của elip nếu nó đi qua điểm 5 N çç2; ÷ - ÷ ç
và tỉ số của tiêu cự với è 3÷ø
độ dài trục lớn bằng 2 . 3 2 2 2 2 2 2 2 2 A. x y + = 1. B. x y + = 1. C. x y + = 1. D. x y + = 1. 9 4 9 5 9 6 9 3 Lời giải Chọn B 2 2
Gọi phương trình chính tắc của Elip là ( ): x y E +
= 1, với a > b > 0. 2 2 a b 2 æ 5ö ç ÷ - æ ö ç ÷ 2 ç ÷ Elip đi qua điểm 5 2 è 3ø 4 25 N çç2; ÷ - ÷ ç suy ra + = 1 + = 1 ( ) 1 . è 3÷ø 2 2 2 2 a b a 9b
Tỉ số của tiêu cực với độ dài trục lớn bằng 2 suy ra 2c 2 c 2 4 2 2
= = c = a . 3 2a 3 a 3 9
Kết hợp với điều kiện 4 5 2 2 2
b = a - c , ta được 2 2 2 2 2 2 b = a - a =
a 9b = 5a (2). 9 9 ìï 4 25 ìï 4 25 ìï 9 2 ï + = 1 ï + = 1 ï = 1 a ìï = ï ï ï 9 Từ ( ) 1 , (2) suy ra 2 2 2 2 ï 2 ï ía 9b ía 5a ía í . 2 ï ï ï ï ï 2 2 ï 2 2 ï 2 2 b ï = 5 9 ï b = 5a 9 ï ï b = 5a 9 î ï ï b = 5a î î ïî 2 2
Vậy phương trình cần tìm là ( ): x y E + = 1. 9 5
Câu 45: Tìm phương trình chính tắc của elip nếu nó đi qua điểm A(2; 3) và tỉ số của độ dài trục
lớn với tiêu cự bằng 2 . 3 2 2 2 2 2 2 2 2 A. x y + = 1. B. x y + = 1. C. x y + = 1. D. x y + = 1. 16 4 4 3 3 4 4 16 Lời giải Chọn A 2 2
Gọi phương trình chính tắc của Elip là ( ): x y E +
= 1, với a > b > 0. 2 2 a b
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 857
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 ( 3 2 )2 2 Elip đi qua điểm 4 3 A (2; 3) suy ra + =1 + =1 ( ) 1 . 2 2 2 2 a b a b
Tỉ số của độ dài trục lớn với tiêu cự bằng 2 suy ra 2a 2 3 2 2 = c = a . 3 2c 3 4 2
Kết hợp với điều kiện 3 2 2 2 a
b = a - c , ta được 2 2 2 2 2 b = a - a = a = 4b (2). 4 4 ìï 4 3 ìï 4 3 ìï 4 2 ï + = 1 ï + = 1 ï = 1 a ìï = ï ï ï 16 Từ ( ) 1 , (2) suy ra 2 2 2 2 ï 2 ï ía b í4b b íb í . 2 ï ï ï ï ï 2 2 ï 2 2 ï 2 2 b ï = 4 a ï = 4b a ï ï = 4b a î ï ï = 4b î î ïî 2 2
Vậy phương trình cần tìm là ( ): x y E + = 1. 16 4 2 2 Câu 46: x y Cho elip (E ): +
= 1 với a > b > 0. Gọi 2c là tiêu cự của (E) . Trong các mệnh đề sau, 2 2 a b mệnh đề nào đúng? A. 2 2 2
c = a + b . B. 2 2 2
b = a + c . C. 2 2 2
a = b + c .
D. c = a+ . b Lời giải Chọn C Ta có 2 2 2 2 2 2
c = a -b ¬¾
a = b +c .
Câu 47: Cho elip có hai tiêu điểm F , 1 2
F và có độ dài trục lớn bằng 2a . Trong các mệnh đề sau, mệnh đề nào đúng?
A. 2a = F F .
B. 2a > F F .
C. 2a < F F .
D. 4a = F F . 1 2 1 2 1 2 1 2 Lời giải Chọn B
Ta có a > c¬¾2a > 2c
¬¾ 2a > F F . 1 2 2 2 Câu 48: x y Cho elip (E ): +
= 1 . Hai điểm A, B là hai đỉnh của elip lần lượt nằm trên hai trục 25 9
Ox , Oy . Khi đó độ dài đoạn thẳng AB bằng: A. 34. B. 34. C. 5. D. 136. Lời giải Chọn B
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 858
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 Ta có 2 a = 25 ¾¾ a = 5 và 2 b = 9 ¾¾ b = 3
Tam giác OAB vuông, có 2 2 AB = OA + OB = 34. Vậy AB = 34 .
Câu 49: Một elip (E) có trục lớn dài gấp 3 lần trục nhỏ. Tỉ số e của tiêu cự với độ dài trục lớn bằng: A. 1 e = . B. 2 e = . C. 3 e = . D. 2 2 e = . 3 3 3 3 Lời giải Chọn D
. Ta có A A = 3B B ¾¾ a = 3 1 2 1 2 b 2 2 ¾¾ a = b = ( 2 2 a - c ) 2 2 9 9 ¾¾ 9c = 8a 2 c 8 c 2 2 ¾¾ = ¾¾ = . 2 a 9 a 3 Vậy 2 2 e = . 3
Câu 50: Một elip (E) có khoảng cách giữa hai đỉnh kế tiếp nhau gấp 3 lần tiêu cự của nó. Tỉ số e 2
của tiêu cự với độ dài trục lớn bằng: A. 5 e = . B. 2 e = . C. 3 e = . D. 2 e = . 5 5 5 5 Lời giải Chọn A Ta có 3 2 2 AB = F F ¾¾ a + b = 3 1 2 c 2
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 859
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 2 2 2 ¾¾
a + b = 9c ¾¾ a +( 2 2 a - c ) 2 = 9c 2 2 ¾¾ 2a = 10c 2 c 1 c 5 ¾¾ = ¾¾ = . 2 a 5 a 5 Vậy 5 e = . 5 2 2 Câu 51: x y
Cho điểm M (2;3) nằm trên đường elip (E ) có phương trình chính tắc: + = 1 . Trong 2 2 a b
các điểm sau đây điểm nào không nằm trên (E): A. M -2;3 . B. M 2;-3 . C. M -2;-3 . D. M 3;2 . 4 ( ) 3 ( ) 2 ( ) 1 ( ) Lời giải Chọn D
Ta có điểm M đối xứng qua Ox có tọa độ là (2;- ) 3 .
Điểm M đối xứng qua Oy có tọa độ là (-2; ) 3 .
Điểm M đối xứng qua gốc tọa độ O có tọa độ là (-2;- ) 3 . 2 2 Câu 52: x y Cho elip (E ): +
= 1 . Khẳng định nào sau đây là đúng? 2 2 a b
A. (E) không có trục đối xứng.
B. (E) có một trục đối xứng là trục hoành.
C. (E) có hai trục đối xứng là trục hoành và trục tung.
D. (E) có vô số trục đối xứng. Lời giải Chọn C
Ta có (E) có hai trục đối xứng là trục hoành và trục tung. 2 2 Câu 53: x y Cho elip (E ): +
= 1 . Khẳng định nào sau đây là đúng? 2 2 a b
A. (E) không có tâm đối xứng.
B. (E) có đúng một tâm đối xứng.
C. (E) có hai tâm đối xứng . D. (E) có vô số tâm đối xứng. Lời giải Chọn B
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 860
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
Ta có (E) có đúng một tâm đối xứng là gốc tọa độ O .
Câu 54: Elip (E) có độ dài trục bé bằng tiêu cự. Tỉ số e của tiêu cự với độ dài trục lớn của (E) bằng: A. e =1 . B. e = 2 . C. 1 e = . D. 1 e = . 2 3 Lời giải Chọn C
Ta có B B = F F ¬¾b = 1 2 1 2 c 2 2 b c ( 2 2 a c ) 2 ¾¾ = ¾¾ - = c 2 c 1 c 1 ¾¾ = ¾¾ = . 2 a 2 a 2 Vậy 1 e = . 2
Câu 55: Elip (E) có hai đỉnh trên trục nhỏ cùng với hai tiêu điểm tạo thành một hình vuông. Tỉ số
e của tiêu cự với độ dài trục lớn của (E ) bằng: A. e =1 . B. e = 2 . C. 1 e = . D. 1 e = . 2 3 Lời giải Chọn C Ta có 0 1 F 2 = F F B F 90 ¾¾ OB = ¾¾ b = 1 1 2 1 c 2 2 2 b c ( 2 2 a c ) 2 ¾¾ = ¾¾ - = c 2 c 1 c 1 ¾¾ = ¾¾ = . 2 a 2 a 2 Vậy 1 e = . 2
Câu 56: Elip (E) có độ dài trục lớn bằng 4 2 , các đỉnh trên trục nhỏ và các tiêu điểm của elip
cùng nằm trên một đường tròn. Độ dài trục nhỏ của (E) bằng: A. 2. B. 4. C. 8. D. 16. Lời giải Chọn B Ta có A A = 4 2 ¾¾ a = 2 2 1 2
Và bốn điểm F , B , F , 1 1 2 2
B cùng nằm trên một đường tròn
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 861
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 2 ¾¾ b = c ¾¾ b = c 2 2 2 ¾¾ = - ¾¾ = a b a b b = 2. 2
Vậy độ dài trục nhỏ của (E) là 4. 2 2 Câu 57: x y Cho elip (E ): +
= 1 và M là một điểm tùy ý trên (E) . Khi đó: 16 9 A. 3 £OM £ 4. B. 4 £OM £ 5. C. OM ³ 5. D. OM £ 3. Lời giải Chọn A Ta có 2 a = 16 ¾¾ a = 4 và 2 b = 9 ¾¾ b = 3.
Mà OB £ OM £ OA¬¾3 £ OM £ 4. 2 2 Câu 58: x y Cho elip (E ): +
= 1 và điểm M nằm trên (E) . Nếu M có hoành độ bằng 13 - thì 169 144
khoảng cách từ M đến hai tiêu điểm bằng: A. 10 và 6. B. 8 và 18. C. 13 5 . D. 13 10 . Lời giải Chọn B Ta có 2 a = 169 ¾¾ a =13 , 2 b = 144 ¾¾ b =12 và 2 2 2 c = a - b = 5
Tọa độ hai tiêu điểm F -5;0 , F 5;0 1 ( ) 2 ( )
M có hoành độ bằng -13 ¾¾
y = 0, M (-13;0). ¾¾
MF = 8, MF = 18. 1 2 2 2 Câu 59: x y Cho elip (E ): +
= 1 và điểm M nằm trên (E) . Nếu M có hoành độ bằng 1 thì 16 12
khoảng cách từ M đến hai tiêu điểm bằng: A. 3,5 và 4,5 . B. 3 và 5 . C. 4 2 . D. 2 4 . 2 Lời giải Chọn A Ta có 2 a = 16 ¾¾ a = 4 , 2 b = 12 ¾¾ b = 2 3 và 2 2 2 c = a - b = 2
Tọa độ hai tiêu điểm F -2;0 , F 2;0 1 ( ) 2 ( )
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 862
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133
M có hoành độ bằng 3 5 1 ¾¾ y = . 2 æ ö Do tính đối xứng của ( ç ÷ E ) nên chọn 3 5 M 1 ç ; ÷ ç ÷. çè 2 ÷ø 9 7 ¾¾
MF = , MF = . 1 2 2 2
Câu 60: Cho elip có phương trình 2 2
16x + 25y = 100 . Tính tổng khoảng cách từ điểm M thuộc
elip có hoành độ bằng 2 đến hai tiêu điểm. A. 3. B. 2 2. C. 5 . D. 4 3. Lời giải Chọn C 2 2 Ta có 2 2 16 + 25
= 100¬¾ x + y x y =1 25 4 4 25 5 2 a = ¾¾ a = , 2 b = 4 ¾¾ b = 2 4 2
MF + MF = 2a = 5. 1 2 2 2 Câu 61: x y Cho elip (E ): +
= 1 . Qua một tiêu điểm của (E) dựng đường thẳng song song với 100 36
trục Oy và cắt (E) tại hai điểm M và N . Tính độ dài MN . A. 48 . B. 36 . C. 25 . D. 25 . 5 5 2 Lời giải Chọn A 2 2 2 ìï Xét = ( ï E ) x y a 100 2 2 2 : + = 1 í
c = a -b = 100 -36 = 64. 2 100 36 b ïï = 36 î
Khi đó, Elip có tiêu điểm là F -8;0 đường thẳng d //Oy và đi qua 1 ( ) 1 F là x = -8.
Giao điểm của d và (E) là nghiệm của hệ phương trình ìïx = -8 ìïx = -8 ï ï ï ï 2 2 í x y í 24 . ïï + = 1 ïy = ï 100 ïî 36 ïî 5 æ ö æ ö Vậy tọa độ hai điểm 24 24 48 M ç- ç 8; ÷÷, N ç- ç 8; ÷ - ÷ MN = ç è 5 ÷ø çè 5 ÷ø 5
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 863
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 2 2 Câu 62: x y Cho (E ): +
= 1 . Một đường thẳng đi qua điểm A (2;2) và song song với trục hoành 20 16
cắt (E) tại hai điểm phân biệt M và N . Tính độ dài MN . A. 3 5. B. 15 2. C. 2 15. D. 5 3. Lời giải Chọn C
Phương trình đường thẳng d đi qua điểm A(2;2) và song song trục hoành có phương trình là y = 2. ì 2 2 ìï ì ïy = 2 x y ïy = 2 ï ìï ïï + =1 ï ìï = ï ïM y ( 15;2 2 ) Ta có ï ï ï ïé ï d Ç(E ) 2 2 í20 16 íx 2 í í x = 15 í 2 ï ï + = 1 ê ï ï ïx =15 ï ï ïî ïê ïN - ïy = ï ï î ï ï ( 15;2 2 ) î20 16 ïêx = - 15 ïî ïîë
Vậy độ dài đoạn thẳng MN = 2 15. 2 2 Câu 63: x y
Dây cung của elip (E ): +
= 1 (0 < b < a) vuông góc với trục lớn tại tiêu điểm có độ 2 2 a b dài bằng: 2 2 2 2 A. 2c . B. 2b . C. 2a . D. a . a a c c Lời giải Chọn B
Hai tiêu điểm có tọa độ lần lượt là F - ;0 c , F ; c 0 . 1 ( ) 2 ( )
Đường thẳng chứa dây cung vuông góc với trục lớn (trục hoành ) tại tiêu điểm F có
phương trình là D: x = .c 2 2 ìï ì ì x y ïx = c ïx = c ìïx = c ï ï ï ï Suy ra ( ï + = ï ï ï ï ï ï D Ç E ) 1 2 2 2 2 2 ía b íc y í b ( 2 2 a - c ) 2 4 b í b ï ï ï ï + = ï 2 1 ï ïy = = ïy = 2 2 ïx = c ï ï î ï 2 2 îa b ïî a a ïî a 2 2 2 æ ö æ ö
Vậy tọa độ giao điểm của D và ( b ç ÷ b ç ÷ 2b E ) là M ç ; c ÷, N ç ; c - ÷ MN = . ç ÷ ç ÷ ç ÷ è a ø çè a ÷ø a 2 2 Câu 64: x y
Đường thẳng d : 3x + 4 y -12 = 0 cắt elip (E ): +
= 1 tại hai điểm phân biệt M và N . 16 9
Khi đó độ dài đoạn thẳng MN bằng: A. 3. B. 4. C. 5. D. 25. Lời giải Chọn C
Tọa độ giao điểm của đường thẳng d và (E) là nghiệm của hệ
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 864
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133 ìï 3 ï = 3 x y - ìï 3x 3 ï
ìï x + 4 y -12 = 0 ï 4 ìï 3 ï = - ï ï ï y 3 ï ï ï = 3 x y - ï ï 4 2 ï ï 2 2 í x y í æ 3 ö í 4 í . ïï + =1 ïï 3 x ç ÷ ç - ï ÷ ïéx = 0 ï ï ï ï ç ÷ ï 2 2 î16 9 ê x è 4 ø ïx - 4x = 0 ï ï ï + = 1 ïî ïê ï x = 4 ï îë ïî16 9 ìïM (0;3)
Vậy tọa độ giao điểm là ïí MN = 5. ïïN (4;0) î
Giáo viên có nhu cầu sở hữu file word vui lòng Trang 865
liên hệ. Face: Trần Đình Cư. SĐT: 0834332133




