

















Preview text:
PHÂN TÍCH CHƯƠNG TRÌNH
1. Liệt kê những điểm mới trong quan điểm xây dựng chương
trình môn Toán so với chương trình hiện hành.
Những điểm mới trong quan điểm xây dựng chương trình mÔn Toán :
- Quán triệt tinh thần “ toán học cho mọi người ”, ai cũng học
được Toán nhưng mỗi người có thể học Toán theo cách phù hợp
Với sở thích Và năng lực cá nhân .
- Bảo đảm tính tinh giản, thiết thực, hiện đại, khơi nguồn sáng tạo.
- Bảo đảm tính thống nhất, sự nhất quán Và phát triển liên tục.
- Bảo đảm tính mở, tính mềm dẻo Và linh hoạt.
2. Hãy so sánh, đối chiếu giữa mục tiêu chung, mục tiêu của
từng cấp học trong chương trình môn Toán. Mục tiêu Mục tiêu Mục tiêu Mục tiêu Kết luận chung cấp tiểu cấp trung cấp trung học học cơ sở học phổ thông Hình thành Góp phần Góp phần Góp
phần Hình thành Và Các mục Và phát hình thành hình thành hình
thành phát triển năng tiêu triển năm Và
phát Và phát triển Và phát triển lực toán học từ chung thành tố cốt triển năng năng lực năng
lực đơn giản đến được lõi của lực
toán toán học cho toán học cho phức tạp theo phát năng lực học cho học học sinh học sinh từng cấp học. triển qua toán học: tư sinh
theo theo các mức theo các mức từng cấp
duy Và lập các mức độ độ phù hợp độ phù hợp học. luận
toán phù hợp Với Với cấp học. Với cấp học. học; mÔ cấp học. hình hoá toán học; giải quyết Vấn đề toán học; giao tiếp toán học; năng lực sử dụng cÔng cụ, phương tiện học toán Góp phần Góp phần Góp phần Góp phần Hình thành Và hình thành thực hiện thực hiện thực hiện phát triển các Và phát các
quy các quy định các quy định phẩm chất theo triển ở học định Về Về phẩm Về phẩm mức độ ở từng sinh các phẩm chất chất của chất của cấp học.
phẩm chất của Chương Chương trình Chương trình chủ yếu Và trình tổng tổng thể tổng thể năng lực thể
theo theo các mức theo các mức chung.
các mức độ độ phù hợp độ phù hợp phù hợp Với Với mÔn Với mÔn
mÔn Toán ở Toán ở cấp Toán ở cấp cấp tiểu THCS. THPT. học. Có kiến Có những Có những Có những Ở tiểu học, có thức, kĩ kiến
thức kiến thức Và kiến thức Và kiến thức Về năng
toán Và kĩ năng kĩ năng toán kĩ năng toán Số Và phép học
phổ toán học cơ học cơ bản, học cơ bản, tính; Hình học thÔng, cơ bản
ban thiết yếu Về: thiết yếu Về: Và Đo lường; bản, thiết đầu,
thiết Số Và Đại số; Đại số Và Thống kê Và yếu;
phát yếu Về: Số Hình học Và Một số yếu Xác suất. triển khả Và phép Đo
lường; tố giải tích; Ở THCS, có năng
giải tính; Hình Thống kê Và Hình học Và kiến thức Về Số quyết
Vấn học Và Đo Xác suất. Đo
lường; Và Đại số; Hình đề có tính lường; Thống kê Và học Và Đo tích hợp Thống kê Xác suất. lường; Thống liên mÔn Và Xác kê Và Xác suất. giữa mÔn suất. Ở THPT, có Toán Và các kiến thức Về mÔn học Đại số Và Một khác; tạo cơ số yếu tố giải hội để học tích; Hình học sinh được Và Đo lường; trải Thống kê Và nghiệm, áp Xác suất. dụng toán Ta thấy cách học Vào gọi môn Toán thực tiễn. từ cấp 1 đến cấp 3 có các tên gọi khác nhau dựa vào chương trình học từ phép tính đơn giản đến giải tích phức tạp. Có hiểu Cùng Với Góp phần Góp phần Giúp học sinh biết tương các mÔn giúp học giúp học có những hiểu đối tổng học Và hoạt sinh có sinh có biết ban đầu quát Về sự động giáo những hiểu những hiểu (tiểu học) => ý hữu ích của dục khác biết ban đầu biết tương thức hướng Toán học góp phần Về các ngành đối tổng nghiệp (THCS) đối Với từng giúp
học nghề gắn Với quát Về các => tổng quát ngành nghề sinh có mÔn
Toán; ngành nghề Và hướng gnhề liên quan những hiểu có ý
thức Và giá trị của nghiệp (THPT) để làm cơ biết ban hướng
nó (gắn Với Về các ngành sở
định đầu Về một nghiệp
dựa mÔn Toán); nghề liên quan hướng nghề số nghề trên
năng làm cơ sở đến toán học. nghiệp, nghiệp lực Và sở cho định cũng như trong xã thích, điều hướng nghề có đủ năng hội. kiện Và hoàn nghiệp sau lực tối thiểu cảnh của bản trung học để tự tìm thân. Từ đó phổ thÔng, hiểu những lựa chọn cũng như có Vấn đề liên định hướng đủ năng lực quan đến
phân luồng tối thiểu để toán học sau trung tự tìm hiểu trong suốt học cơ sở những Vấn cuộc đời.
(tiếp tục học đề liên quan lên, học đến toán học nghề hoặc trong suốt tham gia Vào cuộc đời. cuộc sống lao động).
3. Mục tiêu của từng cấp học đã cụ thể hoá mục tiêu chung như
thế nào? Các mục tiêu chung được phát triển qua từng cấp học như thế nào? Mục
tiêu Cấp tiểu học Cấp trung học Cấp trung học phổ chung cơ sở thông Năng lực tính toán
- Hình thành Và - Góp phần - Góp phần hình - Góp phần hình
phát triển năng hình thành Và thành Và phát thành Và phát triển lực toán học phát triển triển năng
lực năng lực toán học Với
bao gồm các năng lực toán toán học Với yêu yêu cầu cần đạt: nêu
thành tố cốt lõi học Với yêu cầu cần đạt: nêu Và trả lời được câu
cầu cần đạt: Và trả lời được hỏi khi lập luận, giải sau: năng lực thực
hiện câu hỏi khi lập quyết Vấn đề; sử
tư duy Và lập được các thao luận, giải quyết dụng được các
luận toán học; tác tư duy ở Vấn đề, thực hiện phương pháp lập
năng lực mÔ mức độ đơn được Việc
lập luận, quy nạp Và suy
hình hoá toán giản; nêu Và luận hợp lí khi diễn để nhìn ra
học; năng lực trả lời được giải quyết Vấn đề, những cách thức
giải quyết Vấn câu hỏi khi chứng minh được khác nhau trong Việc
lập luận, giải mệnh đề toán học giải quyết Vấn đề;
đề toán học; quyết Vấn đề khÔng quá phức thiết lập được mÔ
năng lực giao đơn giản; lựa tạp; sử dụng được hình toán học để mÔ
tiếp toán học; chọn được các các mÔ hình toán tả tình huống, từ đó
năng lực sử phép toán Và học (cÔng thức đưa ra cách giải
dụng cÔng cụ, cÔng thức số toán học, phương quyết Vấn đề toán phương
tiện học để trình trình đại số, hình học đặt ra trong mÔ
học toán. Đồng bày, diễn đạt biểu diễn,. .) để hình được thiết lập;
(nói hoặc Viết) mÔ tả tình huống thực hiện Và trình
thời góp phần được các nội xuất hiện trong bày được giải pháp
hình thành Và dung, ý tưởng, một số bài toán giải quyết Vấn đề Và
phát triển năng cách thức giải thực tiễn khÔng đánh giá được giải
lực chung cốt quyết Vấn đề; quá phức tạp; sử pháp đã thực hiện, lõi.
sử dụng được dụng được ngÔn phản ánh được giá trị
ngÔn ngữ toán ngữ toán học kết của giải pháp, khái
học kết hợp hợp Với ngÔn ngữ quát hoá được cho
Với ngÔn ngữ thÔng thường để Vấn đề tương tự; sử
thÔng thường, biểu đạt các nội dụng được cÔng cụ, động tác hình dung toán
học phương tiện học toán thể để biểu cũng như thể trong học tập, khám
đạt các nội hiện chứng cứ, phá Và giải quyết Vấn
dung toán học cách thức Và kết đề toán học. o những tình quả lập luận; huống đơn trình bày được ý
giản; sử dụng tưởng Và cách sử được các cÔng dụng cÔng cụ, cụ, phương phương tiện học
tiện học toán toán để thực hiện
đơn giản để một nhiệm Vụ học
thực hiện các tập hoặc để diễn nhiệm Vụ học tả những lập
tập toán đơn luận, chứng minh giản. toán học. - Góp
phần - Góp phần - Góp phần thực - Góp phần thực hiện
hình thành Và thực hiện các hiện các quy định các quy định Về
phát triển ở quy định Về Về phẩm chất của phẩm chất của học sinh các phẩm chất Chương trình Chương trình tổng phẩm chất chủ của
Chương tổng thể theo các thể theo các mức độ
yếu Và năng trình tổng thể mức độ phù hợp phù hợp Với mÔn
lực chung theo theo các mức Với mÔn Toán ở Toán ở cấp trung học các mức
độ độ phù hợp cấp trung học cơ phổ thÔng.
phù hợp Với Với mÔn Toán sở. mÔn học, cấp ở cấp tiểu học đã được học. quy định tại Chương trình giáo dục phổ thÔng tổng thể.
- Có kiến thức, - Có những - Có những kiến - Có những kiến thức
kĩ năng toán kiến thức Và thức Và kĩ năng Và kĩ năng toán học
học phổ thÔng, kĩ năng toán toán học cơ bản cơ bản, thiết yếu Về:
cơ bản, thiết học cơ bản Về : Số Và đại số; Đại số Và một số yếu
yếu; phát triển ban đầu, thiết Hình học Và đo tố giải tích; Hình học
khả năng giải yếu Về: Số Và lường ; Thống kê Và đo lường; Thống quyết Vấn đề phép tính; Và xác suất. kê Và xác suất
có tính tích hợp Hình học Và liên mÔn giữa đo lường; mÔn Toán Và Thống kê Và các mÔn học xác suất. khác như Vật lí, Hoá học, Sinh học, Địa lí, Tin học, CÔng nghệ, Lịch sử, Nghệ thuật,. .; tạo co hội để học sinh được trải nghiệm, áp dụng toán học Vào thực tiễn.
- Có hiểu biết - Cùng Với các - Góp phần giúp - Góp phần giúp học
tương đối tổng mÔn học Và học sinh có sinh có những hiểu quát Về sự hữu hoạt
động những hiểu biết biết tương đối tổng
ích của Toán giáo dục khác ban đầu Về các quát Về các ngành học đối
Với (Đạo đức, Tự ngành nghề gắn nghề Và giá trị của từng
ngành nhiên Và xã Với mÔn Toán; có nó (gắn Với mÔn nghề liên quan hội, Hoạt ý thức
hướng Toán); làm cơ sở cho để làm cơ sở động
trải nghiệp dựa trên định hướng nghề định hướng nghiệm)
góp năng lực Và sở nghiệp sau trung học nghề
nghiệp, phần giúp học thích, điều kiện phổ thÔng, cũng như
cũng như có đủ sinh có những Và hoàn cảnh của có đủ năng lực tối
năng lực tỐi hiểu biết ban bản thân. Từ đó thiểu để tự tìm hiểu
thiẻu đẻ tự tìm đầu Về một số lựa chọn định những Vấn đề liên hiẻu những Ván nghề nghiệp hướng phân quan đến toán học
đè liên quan trong xã hội.
luồng sau trung trong suốt cuộc đời. đén toán học học cơ sở (tiếp trong suốt cuộc tục học lên, học đời. nghề hoặc tham gia Vào cuộc sống lao động).
4.Hãy phân tích các tiêu chí/chỉ báo của từng thành tố của năng
lực Toán học, cho ví dụ minh hoạ cụ thể đối với từng thành tố của
năng lực Toán học (chọn một năng lực làm ví dụ minh hoạ).
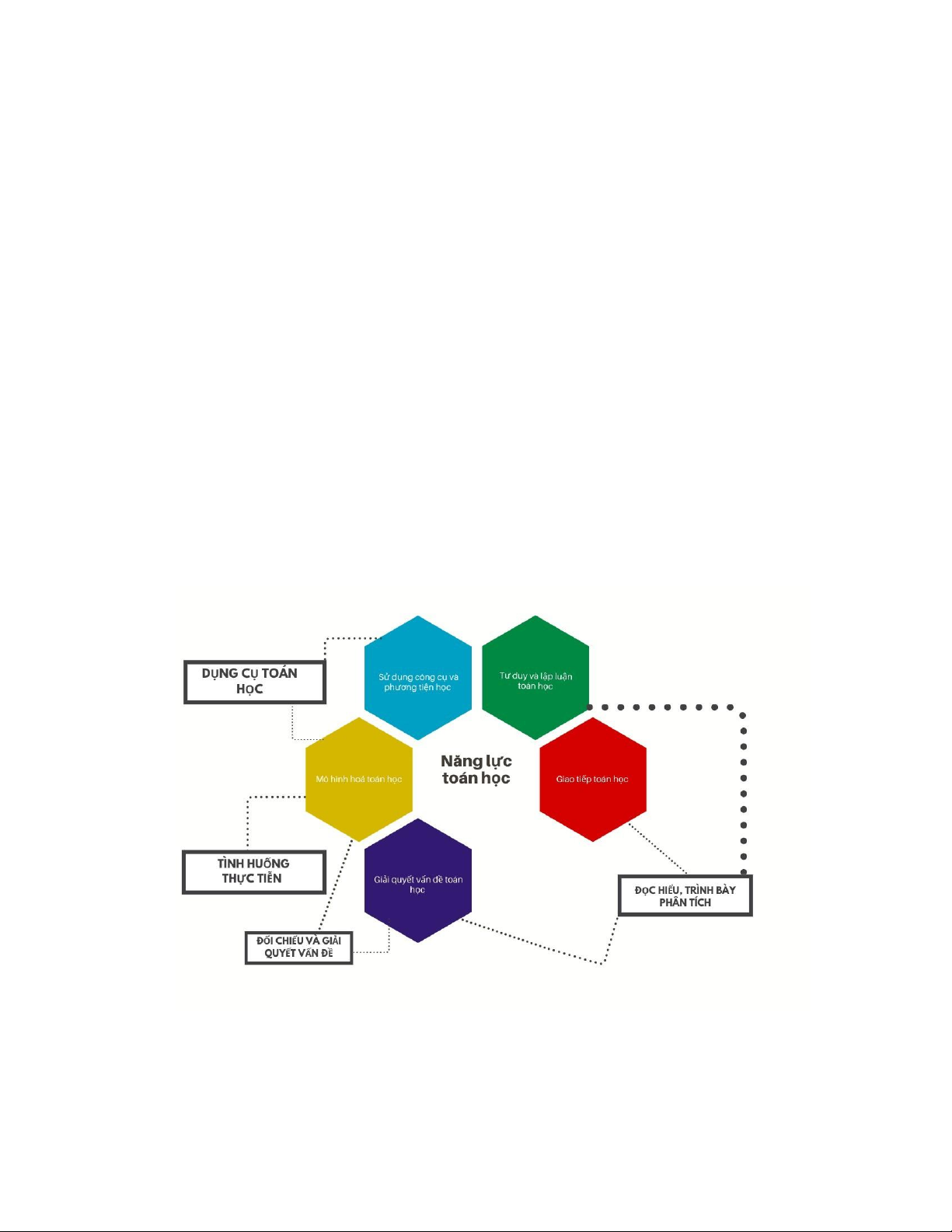
Năng lực toán học: Năng lực toán học bao gồm các thành tố:
năng lực tư duy Và lập luận toán học; năng lực mÔ hình hoá toán
học; năng lực giải quyết Vấn đề toán học; năng lực giao tiếp toán
học; năng lực sử dụng cÔng cụ, phương tiện học toán.
Mỗi một thành tố của năng lực toán học cần được biểu hiện
cụ thể bằng các tiêu chí, chỉ báo. Điều này có độ phức tạp cao Và
được minh hoạ trong bảng dưới đây. Các thành tố của năng lực
Các tiêu chí, chỉ báo toán học
Thể hiện qua Việc thực hiện được các hành động:
Năng lực tư duy - So sánh; phân tích; tổng hợp; đặc biệt hoá, khái quát
Và lập luận toán hoá; tương tự; quy nạp; diễn dịch. học
- Chỉ ra được chứng cứ, lí lẽ Và biết lập luận hợp lí trước khi kết luận.
- Giải thích hoặc điều chỉnh cách thức giải quyết Vấn
đề Về phương diện toán học.
Thể hiện qua Việc thực hiện được các hành động:
- Sử dụng các mÔ hình toán học (gồm cÔng thức,
phương trình, bảng biểu, đồ thị,. .) để mÔ tả các tình
huống đặt ra trong các bài toán thực tế.
- Giải quyết các Vấn đề toán học trong mÔ hình được Năng lực mÔ thiết lập. hình hoá toán
- Sử dụng các mÔ hình toán học (gồm cÔng thức, học
phương trình, bảng biểu, đồ thị,. .) để mÔ tả các tình
huống đặt ra trong các bài toán thực tế.
- Giải quyết các Vấn đề toán học trong mÔ hình được thiết lập.
- Thể hiện Và đánh giá lời giải trong ngữ cảnh thực tế
Và cải tiến mÔ hình nếu cách giải quyết khÔng phù hợp.
Thể hiện qua Việc thực hiện được các hành động:
- Nhận biết, phát hiện được Vấn đề cần giải quyết bằng toán học. Năng lực giải
- Đề xuất, lựa chọn được cách thức, giải pháp giải quyết Vấn đề quyết Vấn đề. toán học
- Sử dụng được các kiến thức, kĩ năng toán học tương
thích (bao gồm các cÔng cụ Và thuật toán) để giải quyết Vấn đề đặt ra.
- Đánh giá giải pháp đề ra Và khái quát hoá cho Vấn đề tương tự. Năng lực giao
Thể hiện qua Việc thực hiện được các hành động: tiếp toán học
- Nghe hiểu, đọc hiểu Và ghi chép được các thÔng tin
toán học cần thiết được trình bày dưới dạng Văn bản
toán học hay do người khác nói hoặc Viết ra.
- Trình bày, diễn đạt (nói hoặc Viết) được các nội
dung, ý tưởng, giải pháp toán học trong sự tương tác
Với người khác (Với yêu cầu thích hợp Về sự đầy đủ, chính xác).
- Sử dụng hiệu quả ngÔn ngữ toán học (chữ số, chữ
cái, kí hiệu, biểu đồ, đồ thị, các liên kết logic,. .) kết
hợp Với ngÔn ngữ thÔng thường hoặc động tác hình
thể khi trình bày, giải thích Và đánh giá các ý tưởng
toán học trong sự tương tác (thảo luận, tranh luận) Với người khác.
Thể hiện qua Việc thực hiện được các hành động:
- Biết tên gọi, tác dụng, quy cách sử dụng, cách thức
bảo quản các đồ dùng, phương tiện trực quan thÔng
thường, phương tiện khoa học cÔng nghệ (đặc biệt là Năng lực sử
phương tiện sử dụng cÔng nghệ thÔng tin) phục Vụ cho dụng cÔng cụ, Việc học toán. phương tiện học toán
- Sử dụng thành thạo Và linh hoạt các cÔng cụ Và
phương tiện học toán, đặc biệt là phương tiện khoa
học cÔng nghệ để tìm tòi, khám phá Và giải quyết Vấn
đề toán học (phù hợp Với đặc điểm nhận thức lứa tuổi).
- Chỉ ra được các ưu điểm, hạn chế của những cÔng
cụ, phương tiện hỗ trợ để có cách sử dụng hợp lí.
Ví dụ về Năng lực giải quyết vấn đề toán học.
Ví dụ Về một tình huống tổ chức các hoạt động nhằm phát triển năng
lực mÔn Toán cho học sinh lớp 8:
Về phần hình học lớp 8, lúc này học sinh Vẫn chưa quen tới những sin,
cos, tan, cot Và đặc biệt rất khó nhớ từng định lý ứng Với mỗi đại lượng này.
Nên để dễ trong Việc ghi nhớ kiến thức một cách hiệu quả, để thuận
tiện cho Việc học tập thì chúng ta nên tìm ra những cách nhớ mẹo để
giúp học sinh có thể nhớ lâu được hơn, thay Vì ghi nhớ như thÔng thường. Cụ thể như sau:
Theo cÔng thức lượng giác trong tam giác VuÔng
Sin = Đối / Huyền ( Mẹo : Sin đi học => đh = đối huyền )
Cos = Kề / Huyền ( Mẹo : Cos khÔng hư => kh = khÔng hư )
Tan = Đối / Kề ( Mẹo : Tan đoàn kết => đk = đối kề )
Cot = Kề / Đối ( Mẹo : Cot kết đoàn => kđ = kề đối )
5. Hãy vẽ sơ đồ mô tả quan hệ tương hỗ của các thành tố của
năng lực Toán học, phân tích và lí giải các mối quan hệ đó.
1. Sơ đồ mô tả quan hệ tương hỗ của các thành tố của năng lực Toán học
2. Phân tích và lí giải các mối quan hệ :
– Đánh giá năng lực tư duy Và lập luận toán học: có thể sử dụng một
số phương pháp, cÔng cụ đánh giá như các câu hỏi (nói, Viết), bài
tập,. . mà đòi hỏi học sinh phải trình bày, so sánh, phân tích, tổng hợp,
hệ thống hoá kiến thức; phải Vận dụng kiến thức toán học để giải thích, lập luận.
– Đánh giá năng lực mÔ hình hoá toán học: lựa chọn những tình huống
trong thực tiễn làm xuất hiện bài toán toán học. Từ đó, đòi hỏi học
sinh phải xác định được mÔ hình toán học (gồm cÔng thức, phương
trình, bảng biểu, đồ thị,. .) cho tình huống xuất hiện trong bài toán
thực tiễn; giải quyết được những Vấn đề toán học trong mÔ hình được
thiết lập; thể hiện Và đánh giá được lời giải trong ngữ cảnh thực tiễn
Và cải tiến được mÔ hình nếu cách giải quyết khÔng phù hợp.
– Đánh giá năng lực giải quyết Vấn đề toán học: có thể sử dụng các
phương pháp như yêu cầu người học nhận dạng tình huống, phát hiện
Và trình bày Vấn đề cần giải quyết; mÔ tả, giải thích các thÔng tin ban
đầu, mục tiêu, mong muốn của tình huống Vấn đề đang xem xét; thu
thập, lựa chọn, sắp xếp thÔng tin Và kết nối Với kiến thức đã có; sử
dụng các câu hỏi (có thể yêu cầu trả lời nói hoặc Viết) đòi hỏi người
học Vận dụng kiến thức Vào giải quyết Vấn đề, đặc biệt các Vấn đề
thực tiễn; sử dụng phương pháp quan sát (như bảng kiểm theo các
tiêu chí đã xác định), quan sát người học trong quá trình giải quyết
Vấn đề; đánh giá qua các sản phẩm thực hành của người học (chẳng
hạn sản phẩm của các dự án học tập); quan tâm hợp lí đến các nhiệm
Vụ đánh giá mang tính tích hợp.
– Đánh giá năng lực giao tiếp toán học: có thể sử dụng các phương
pháp như yêu cầu người học nghe hiểu, đọc hiểu, ghi chép (tóm tắt),
phân tích, lựa chọn, trích xuất được được các thÔng tin toán học cơ
bản, trọng tâm trong Văn bản nói hoặc Viết; sử dụng được ngÔn ngữ
toán học kết hợp Với ngÔn ngữ thÔng thường trong Việc trình bày, diễn
đạt, nêu câu hỏi, thảo luận, tranh luận các nội dung, ý tưởng, giải
pháp toán học trong sự tương tác Với người khác.
– Đánh giá năng lực sử dụng cÔng cụ, phương tiện học toán: có thể sử
dụng các phương pháp như yêu cầu người học nhận biết được tên gọi,
tác dụng, quy cách sử dụng, cách thức bảo quản, ưu điểm, hạn chế
của các cÔng cụ, phương tiện học toán; trình bày được cách sử dụng
(hợp lí) cÔng cụ, phương tiện học toán để thực hiện nhiệm Vụ học tập
hoặc để diễn tả những lập luận, chứng minh toán học.
Năng lực giao tiếp toán học là khả năng của một cá nhân:
- Nghe, hiểu, đọc hiểu Và ghi chép được các thÔng tin toán học cần
thiết được trình bày dưới dạng Văn bản toán học hay do người khác nói hoặc Viết ra;
- Trình bày, diễn đạt (bằng cách nói hoặc Viết) được các nội dung, ý
tưởng, giải pháp toán học trong sự tương tác Với người khác;
- Sử dụng được hiệu quả ngÔn ngữ toán học (chữ số, chữ cái, kí hiệu,
biểu đồ, đồ thị, các liên kết logic,. .) kết hợp Với ngÔn ngữ thÔng
thường hoặc động tác hình thể khi trình bày, giải thích Và đánh giá
các ý tưởng toán học trong sự tương tác (thảo luận, tranh luận) Với người khác;
- Thể hiện sự tự tin khi trình bày, diễn đạt, nêu câu hỏi, thảo luận,
tranh luận các nội dung, ý tưởng liên quan đến toán học. Các biểu
hiện của năng lực giao tiếp toán học gồm: “- Tóm tắt được ý chính khi
nghe thầy hoặc bạn trình bày;
- Trình bày một Vấn đề hấp dẫn nhờ sử dụng các loại ngÔn ngữ Và các phương tiện kĩ thuật;
- Trình bày rõ ràng lời giải của một bài toán nhờ sử dụng chính xác
thuật ngữ, kí hiệu, liên kết logic, quy tắc suy luận;
- Phát biểu một định nghĩa, định lí theo các ngÔn ngữ, cách thức khác nhau
=> Năng lực toán học là khả năng cáa một cá nhân thiết lập công
thức, vận dụng và giải thích toán học trong nhiều ngữ cảnh khác
nhau; bao gồm suy luận toán học và sử dụng các khái niệm, phương
pháp, sự việc và công cụ để mô tả, giải thích và dự đoán các hiện
tượng; giúp cá nhân nhận ra vai trò cáa toán học, đưa ra ý kiến và
quyết định có cơ sở”
6. Hãy phân tích yêu cầu cần đạt về năng lực Toán học ở từng
cấp học. Cho ví dụ cụ thể về yêu cầu cần đạt về năng lực Toán
học ở cuối mỗi cấp học.
I, Phân tích yêu cầu cần đạt về năng lực Toán học ở từng cấp học.
*Mỗi một thành tố của năng lực mÔn toán cần được biểu hiện cụ thể
bằng các tiêu chí, chỉ báo chất lượng (những kỹ năng thành phần).
Biểu hiện cụ thể của các thành tố cốt lõi của năng lực toán học Và yêu
cầu cần đạt cho từng cấp học được thể hiện trong bảng dưới đây: Năng lực Toán Cấp trung học Cấp trung học học Cấp tiểu học cơ sở phổ thông 1. Năng lực tư duy và lập luận toán học thể hiện qua Việc:
– Thực hiện được – Thực hiện được – Thực hiện được
– Thực hiện được các thao tác tư duy các thao tác tư tương đối thành
các thao tác tư (ở mức độ đơn duy, đặc biệt biết thạo các thao tác
duy như: so sánh, giản), đặc biệt biết quan sát, giải tư duy, đặc biệt
phân tích, tổng quan sát, tìm kiếm thích được
sự phát hiện được sự
hợp, đặc biệt hoá, sự tương đồng Và tương đồng Và tương đồng Và khái quát hoá, khác biệt trong khác biệt trong khác biệt trong
tương tự; quy nạp, những tình huống nhiều tình huống những tình huống diễn dịch.
quen thuộc Và mÔ Và thể hiện được tương đối phức tạp
tả được kết quả kết quả của Việc Và lí giải được kết của Việc quan sát. quan sát. quả của Việc quan – Nêu được chứng sát.
– Chỉ ra được cứ, lí lẽ Và biết lập – Thực hiện được – Sử dụng được
chứng cứ, lí lẽ Và luận hợp lí trước Việc lập luận hợp các phương pháp
biết lập luận hợp lí khi kết luận.
lí khi giải quyết lập luận, quy nạp trước khi kết luận Vấn đề. Và suy diễn để nhìn ra những – Nêu Và trả lời cách thức khác
– Giải thích hoặc được câu hỏi khi nhau trong Việc điều chỉnh được lập luận,
giải – Nêu Và trả lời giải quyết Vấn đề. cách thức giải quyết Vấn
đề. được câu hỏi khi – Nêu Và trả lời
quyết Vấn đề Về Bước đầu chỉ ra lập luận, giải được câu hỏi khi
phương diện toán được chứng cứ Và quyết Vấn đề. lập luận, giải học.
lập luận có cơ sở, Chứng minh được quyết Vấn đề. Giải
có lí lẽ trước khi mệnh đề toán học thích, chứng minh, kết luận.
khÔng quá phức điều chỉnh được tạp. giải pháp thực hiện Về phương diện toán học. 2. Năng lực mô hình hoá toán học thể hiện qua Việc:
– Lựa chọn được – Sử dụng được – Thiết lập được – Xác định được các phép
toán, các mÔ hình toán mÔ hình toán học
mÔ hình toán học cÔng thức số học, học (gồm cÔng (gồm cÔng thức,
(gồm cÔng thức, sơ đồ, bảng biểu, thức toán học, sơ phương trình, sơ phương
trình, hình Vẽ để trình đồ, bảng
biểu, đồ, hình Vẽ, bảng bảng biểu,
đồ bày, diễn đạt (nói hình Vẽ, phương biểu, đồ thị,. .) để thị,. .) cho
tình hoặc Viết) được trình, hình biểu mÔ tả tình huống
huống xuất hiện các nội dung, ý diễn,. .) để mÔ tả đặt ra trong một trong bài toán tưởng của
tình tình huống xuất số bài toán thực thực tiễn.
huống xuất hiện hiện trong một số tiễn. trong bài toán bài toán thực tiễn
thực tiễn đơn giản. khÔng quá phức tạp. – Giải quyết được
– Giải quyết được – Giải quyết được – Giải quyết được những Vấn đề toán
những Vấn đề toán những bài
toán những Vấn đề toán học trong mÔ hình
học trong mÔ hình xuất hiện từ sự lựa học trong mÔ hình được thiết lập. được thiết lập. chọn trên. được thiết lập. – Lí giải được tính
– Thể hiện Và đánh – Nêu được câu trả – Thể hiện được lời đúng đắn của lời
giá được lời giải lời cho tình huống giải toán học Vào giải (những kết trong ngữ
cảnh xuất hiện trong bài ngữ cảnh thực tiễn luận thu được từ
thực tế Và cải tiến toán thực tiễn.
Và làm quen Với các tính toán là có được mÔ hình nếu
Việc kiểm chứng ý nghĩa, phù hợp cách giải quyết
tính đúng đắn của Với thực tiễn hay khÔng phù hợp. lời giải. khÔng). Đặc biệt, nhận biết được cách đơn giản hoá, cách điều chỉnh những yêu cầu thực tiễn (xấp xỉ, bổ sung thêm giả thiết, tổng quát hoá,. .) để đưa đến những bài toán giải được. 3. Năng lực giải quyết vấn đề
toán học thể hiện qua Việc:
– Nhận biết được – Phát hiện được – Xác định được
– Nhận biết, phát Vấn đề cần giải Vấn đề cần giải tình huống có Vấn
hiện được Vấn đề quyết Và nêu được quyết. đề; thu thập, sắp cần giải quyết thành câu hỏi. xếp, giải thích Và bằng toán học. đánh giá được độ tin cậy của thÔng tin; chia sẻ sự am hiểu Vấn đề Với
– Nêu được cách – Xác định được người khác.
– Lựa chọn, đề thức giải quyết cách thức,
giải – Lựa chọn Và thiết
xuất được cách Vấn đề. pháp giải quyết lập được cách thức, giải pháp Vấn đề. thức, quy trình giải quyết Vấn đề.
– Thực hiện Và – Sử dụng được giải quyết Vấn đề.
– Sử dụng được trình bày
được các kiến thức, kĩ – Thực hiện Và các kiến thức, kĩ cách thức giải năng toán
học trình bày được giải năng toán
học quyết Vấn đề ở tương thích để giải pháp giải quyết
tương thích (bao mức độ đơn giản. quyết Vấn đề. Vấn đề. gồm các cÔng cụ Và thuật toán) để
giải quyết Vấn đề – Kiểm tra được – Giải thích được đặt ra.
giải pháp đã thực giải pháp đã thực – Đánh giá được
– Đánh giá được hiện. hiện. giải pháp đã thực giải pháp đề ra Và hiện; phản ánh khái quát hoá được được giá trị của cho Vấn đề tương giải pháp; khái tự. quát hoá được cho Vấn đề tương tự. 4. Năng lực giao tiếp toán học thể hiện qua Việc:
– Nghe hiểu, đọc – Nghe hiểu, đọc – Nghe hiểu, đọc – Nghe hiểu, đọc
hiểu Và ghi chép hiểu Và ghi chép hiểu Và ghi chép hiểu Và ghi chép
được các thÔng tin (tóm tắt) được các (tóm tắt) được các (tóm tắt) được
toán học cần thiết thÔng tin toán học thÔng tin toán học tương đối thành được trình
bày trọng tâm trong cơ bản, trọng tâm thạo các thÔng tin
dưới dạng Văn bản nội dung Văn bản trong Văn bản (ở toán học cơ bản,
toán học hay do hay do người khác dạng Văn bản nói trọng tâm trong người khác
nói thÔng báo (ở mức hoặc Viết). Từ đó Văn bản nói hoặc hoặc Viết ra.
độ đơn giản), từ đó phân tích, lựa Viết. Từ đó phân
nhận biết được Vấn chọn, trích xuất tích, lựa chọn, đề cần giải quyết.
được các thÔng tin trích xuất được
toán học cần thiết các thÔng tin toán
từ Văn bản (ở dạng học cần thiết từ
Văn bản nói hoặc Văn bản nói hoặc
– Trình bày, diễn – Trình bày, diễn Viết). Viết.
đạt (nói hoặc Viết) đạt (nói hoặc Viết) – Thực hiện được
được các nội dung, được các nội dung, Việc trình
bày, – Lí giải được (một
ý tưởng, giải pháp ý tưởng, giải pháp diễn đạt, nêu câu cách hợp lí) Việc
toán học trong sự toán học trong sự hỏi, thảo luận, trình bày, diễn tương tác Với tương tác
Với tranh luận các nội đạt, thảo luận,
người khác (Với người khác (chưa dung, ý tưởng, giải tranh luận các nội
yêu cầu thích hợp yêu cầu phải diễn pháp toán
học dung, ý tưởng, giải
Về sự đầy đủ, đạt đầy đủ, chính trong sự tương tác pháp toán học chính xác).
xác). Nêu Và trả lời Với người khác (ở trong sự tương tác
được câu hỏi khi mức tương đối đầy Với người khác. lập luận, giải đủ, chính xác).
– Sử dụng được quyết Vấn đề.
hiệu quả ngÔn ngữ – Sử dụng được – Sử dụng được
toán học (chữ số, ngÔn ngữ toán học ngÔn ngữ toán học – Sử dụng được
chữ cái, kí hiệu, kết hợp Với ngÔn kết hợp Với ngÔn một cách hợp lí
biểu đồ, đồ thị, các ngữ thÔng thường, ngữ thÔng thường ngÔn ngữ toán học
liên kết logic,. .) động tác hình thể để biểu đạt các nội kết hợp Với ngÔn
kết hợp Với ngÔn để biểu đạt các nội dung toán học ngữ thÔng thường
ngữ thÔng thường dung toán học ở cũng như thể hiện để biểu đạt cách
hoặc động tác hình những tình huống chứng cứ, cách suy nghĩ, lập luận,
thể khi trình bày, đơn giản.
thức Và kết quả chứng minh các giải thích Và đánh lập luận. khẳng định toán giá các ý tưởng học. toán học trong sự tương tác (thảo luận, tranh luận) Với người khác.
– Thể hiện được sự – Thể hiện được sự – Thể hiện được sự
tự tin khi trình tự tin khi trả lời tự tin khi trình – Thể hiện được sự
bày, diễn đạt, nêu câu hỏi, khi trình bày, diễn đạt, thảo tự tin khi trình
câu hỏi, thảo luận, bày, thảo luận các luận, tranh luận, bày, diễn đạt, thảo
tranh luận các nội nội dung toán học giải thích các nội luận, tranh luận, dung, ý tưởng liên ở những tình dung toán học giải thích các nội
quan đến Toán huống đơn giản. trong một số tình dung toán học học.
huống khÔng quá trong nhiều tình phức tạp. huống khÔng quá phức tạp. 5. Năng lực sử dụng công cụ, phương tiện học toán thể hiện qua Việc:
– Nhận biết được – Nhận biết được – Nhận biết được
– Nhận biết được tên gọi, tác dụng, tên gọi, tác dụng, tác dụng, quy cách
tên gọi, tác dụng, quy cách sử dụng, quy cách sử dụng, sử dụng, cách thức quy cách sử dụng, cách thức bảo cách thức bảo bảo quản các cÔng cách thức
bảo quản các cÔng cụ, quản các cÔng cụ, cụ, phương tiện
quản các đồ dùng, phương tiện học phương tiện học học toán (bảng
phương tiện trực toán đơn giản (que toán (mÔ hình hình tổng kết Về các quan
thÔng tính, thẻ số, thước, học phẳng Và dạng hàm số, mÔ thường,
phương compa, êke, các khÔng gian, thước hình góc Và cung tiện khoa học cÔng mÔ hình hình đo góc, thước lượng giác, mÔ
nghệ (đặc biệt là phẳng Và hình khối cuộn, tranh ảnh, hình các hình khối,
phương tiện sử quen thuộc,. .) biểu đồ,. .). bộ dụng cụ tạo dụng cÔng nghệ mặt tròn xoay,. .). thÔng tin), phục Vụ
cho Việc học Toán. – Sử dụng được – Trình bày được – Sử dụng được – Sử dụng được các cÔng
cụ, cách sử dụng cÔng máy tính cầm tay, các cÔng
cụ, phương tiện học cụ, phương tiện phần mềm,
phương tiện học toán để thực hiện học toán để thực phương tiện cÔng
toán, đặc biệt là những nhiệm Vụ hiện nhiệm Vụ học nghệ, nguồn tài
phương tiện khoa học tập toán đơn tập hoặc để diễn nguyên trên mạng
học cÔng nghệ để giản.
tả những lập luận, Internet để giải
tìm tòi, khám phá – Làm quen Với chứng minh toán quyết một số Vấn
Và giải quyết Vấn máy tính cầm tay, học. đề toán học.
đề toán học (phù phương tiện cÔng – Sử dụng được
hợp Với đặc điểm nghệ thÔng tin hỗ máy tính cầm tay, nhận thức lứa trợ học tập. một số phần mềm tuổi). tin học Và phương tiện cÔng nghệ hỗ trợ học tập. – Đánh giá được
– Nhận biết được – Chỉ ra được các cách thức sử dụng
– Nhận biết được (bước đầu) một số ưu điểm, hạn chế các cÔng cụ,
các ưu điểm, hạn ưu điểm, hạn chế của những cÔng phương tiện học chế của
những của những cÔng cụ, phương tiện hỗ toán trong tìm tòi,
cÔng cụ, phương cụ, phương tiện hỗ trợ để có cách sử khám phá Và giải
tiện hỗ trợ để có trợ để có cách sử dụng hợp lí. quyết Vấn đề toán
cách sử dụng hợp dụng hợp lí. học. lí.
II, Ví dụ cụ thể về yêu cầu cần đạt về năng lực Toán học ở cuối mỗi cấp học.
Chương trình học lớp 5. Nội dung Yêu cầu cần đạt SỐ VÀ PHÉP TÍNH Số tự nhiên
Ôn tập Về số Củng cố Và hoàn thiện các kĩ năng:
tự nhiên Và – Đọc, Viết, so sánh, xếp thứ tự được các số tự nhiên.
các phép tính – Thực hiện được các phép tính cộng, trừ, nhân, chia Với số
tự các số tự nhiên. Vận dụng được tính chất của phép Số tự nhiên
tính Với số tự nhiên để tính nhẩm Và tính hợp lí. nhiên Và các phép
– Ước lượng Và làm tròn được số trong những tính tính Với số toán đơn giản. tự nhiên
– Giải quyết được Vấn đề gắn Với Việc giải các bài
toán có đến bốn bước tính liên quan đến các phép
tính Về số tự nhiên; liên quan đến quan hệ phụ
thuộc trực tiếp Và đơn giản. Phân số Ôn tập Về
Củng cố Và hoàn thiện các kĩ năng: phân số Và các
– Rút gọn được phân số. phép tính Với
– Quy đồng, so sánh, xếp thứ tự được các phân số phân số
trong trường hợp có một mẫu số chia hết cho các mẫu số còn lại.
– Thực hiện được phép cộng, phép trừ các phân số Phân số
trong trường hợp có một mẫu số chia hết cho các Và các
mẫu số còn lại Và nhân, chia phân số. phép tính Với phân
– Thực hiện được phép cộng, phép trừ hai phân số số
bằng cách lấy mẫu số chung là tích của hai mẫu số.
– Nhận biết được phân số thập phân Và cách Viết
phân số thập phân ở dạng hỗn số.
– Giải quyết được Vấn đề gắn Với Việc giải các bài
toán (có một hoặc một Vài bước tính) liên quan đến
các phép tính Về phân số. Số thập phân Số thập Số thập phân
– Đọc, Viết được số thập phân.
– Nhận biết được số thập phân gồm phần nguyên,
phần thập phân Và hàng của số thập phân.
– Thể hiện được các số đo đại lượng bằng cách dùng số thập phân. So sánh các số
– Nhận biết được cách so sánh hai số thập phân. thập phân
– Thực hiện được Việc sắp xếp các số thập phân theo phân
thứ tự (từ bé đến lớn hoặc ngược lại) trong một
nhóm có khÔng quá 4 số thập phân.
Làm tròn số – Làm tròn được một số thập phân tới số tự nhiên thập phân
gần nhất hoặc tới số thập phân có một hoặc hai chữ số ở phần thập phân.
Các phép tính – Thực hiện được phép cộng, phép trừ hai số thập cộng, trừ, phân.
nhân, chia Với – Thực hiện được phép nhân một số Với số thập phân số thập phân
có khÔng quá hai chữ số ở dạng: a,b Và 0,ab.
– Thực hiện được phép chia một số Với số thập phân
có khÔng quá hai chữ số khác khÔng ở dạng: a,b Và 0,ab. Các phép
– Vận dụng được tính chất của các phép tính Với số tính Với
thập phân Và quan hệ giữa các phép tính đó trong số thập thực hành tính toán. phân
– Thực hiện được phép nhân, chia nhẩm một số thập
phân Với (cho) 10; 100; 1000;. . hoặc Với (cho) 0,1; 0,01; 0,001;. .
– Giải quyết Vấn đề gắn Với Việc giải các bài toán (có
một hoặc một Vài bước tính) liên quan đến các phép
tính Với các số thập phân.
Tỉ số. Tỉ số phần trăm Tỉ số. Tỉ số Tỉ số
phần – Nhận biết được tỉ số, tỉ số phần trăm của hai đại phần trăm lượng cùng loại. trăm Tỉ
– Giải quyết được một số Vấn đề gắn Với Việc giải số.
các bài toán liên quan đến: tìm hai số khi biết tổng
(hoặc hiệu) Và tỉ số của hai số đó; tính tỉ số phần
trăm của hai số; tìm giá trị phần trăm của một số cho trước.
– Nhận biết được tỉ lệ bản đồ. Vận dụng được tỉ lệ
bản đồ để giải quyết một số tình huống thực tiễn.
Sử dụng máy Làm quen Với Việc sử dụng máy tính cầm tay để tính cầm tay
thực hiện các phép tính cộng, trừ, nhân, chia các số
tự nhiên; tính tỉ số phần trăm của hai số; tính giá trị
phần trăm của một số cho trước. HÌNH HỌC VÀ ĐÔ LƯỜNG Hình học trực quan Quan
sát, – Nhận biết được hình thang, đường tròn, một số
nhận biết, mÔ loại hình tam giác như tam giác nhọn, tam giác
tả hình dạng VuÔng, tam giác tù, tam giác đều. Hình
Và đặc điểm – Nhận biết được hình khai triển của hình lập phẳng Và của một
số phương, hình hộp chữ nhật Và hình trụ. hình khối hình phẳng Và hình khối đơn giản
Thực hành Vẽ, – Vẽ được hình thang, hình bình hành, hình thoi (sử
lắp ghép, tạo dụng lưới Ô VuÔng).
hình gắn Với – Vẽ được đường cao của hình tam giác.
một số hình – Vẽ được đường tròn có tâm Và độ dài bán kính
phẳng Và hình hoặc đường kính cho trước. khối đã học.
– Giải quyết được một số Vấn đề Về đo, Vẽ, lắp ghép,
tạo hình gắn Với một số hình phẳng Và hình khối đã
học, liên quan đến ứng dụng của hình học trong
thực tiễn, liên quan đến nội dung các mÔn học như
Mĩ thuật, CÔng nghệ, Tin học. Đo lường Đo lường
Biểu tượng Về – Nhận biết được các đơn Vị đo diện tích: km2 (ki-lÔ-
đại lượng Và mét VuÔng), ha (héc-ta).
đơn Vị đo đại – Nhận biết được “thể tích” thÔng qua một số biểu lượng tượng cụ thể.
– Nhận biết được một số đơn Vị đo thể tích thÔng
dụng: cm3 (xăng-ti-mét khối), dm3 (đề-xi-mét khối), m3 (mét khối).
– Nhận biết được Vận tốc của một chuyển động đều;
tên gọi, kí hiệu của một số đơn Vị đo Vận tốc: km/h (km/giờ), m/s (m/giây). Thực hành đo
Sử dụng được một số dụng cụ thÔng dụng để thực đại lượng
hành cân, đo, đong, đếm, xem thời gian, mua bán
Với các đơn Vị đo đại lượng Và tiền tệ đã học.
Tính toán Và – Thực hiện được Việc chuyển đổi Và tính toán Với
ước lượng Với các số đo thể tích (cm3, dm3, m3) Và số đo thời các số đo đại gian. lượng
– Tính được diện tích hình tam giác, hình thang.
– Tính được chu Vi Và diện tích hình tròn.
– Tính được diện tích xung quanh, diện tích toàn
phần, thể tích của hình hộp chữ nhật, hình lập phương.
– Thực hiện được Việc ước lượng thể tích trong một
số trường hợp đơn giản (Ví dụ: thể tích của hộp phấn Viết bảng,. .).
– Giải quyết được một số Vấn đề thực tiễn liên quan
đến đo thể tích, dung tích, thời gian.
– Giải quyết được một số Vấn đề gắn Với Việc giải các
bài toán liên quan đến chuyển động đều (tìm Vận
tốc, quãng đường, thời gian của một chuyển động đều).
MỘT SỐ YẾU TỐ THỐNG KÊ VÀ XÁC SUẤT
Một số yếu tố thống kê Một số Thu
thập, Thực hiện được Việc thu thập, phân loại, so sánh, yếu tố
phân loại, sắp sắp xếp số liệu thống kê theo các tiêu chí cho trước. thống kê xếp các số liệu Đọc, mÔ tả
biểu đồ thống – Đọc Và mÔ tả được các số liệu ở dạng biểu đồ hình kê hình quạt quạt tròn. tròn.
Biểu – Sắp xếp được số liệu Vào biểu đồ hình quạt tròn
diễn số liệu (khÔng yêu cầu học sinh Vẽ hình).
bằng biểu đồ – Lựa chọn được cách biểu diễn (bằng dãy số liệu,
thống kê hình bảng số liệu, hoặc bằng biểu đồ) các số liệu thống quạt tròn kê.
Hình thành Và – Nêu được một số nhận xét đơn giản từ biểu đồ
giải quyết Vấn hình quạt tròn.
đề đơn giản – Làm quen Với Việc phát hiện Vấn đề hoặc quy luật
xuất hiện từ đơn giản dựa trên quan sát các số liệu từ biểu đồ




