





















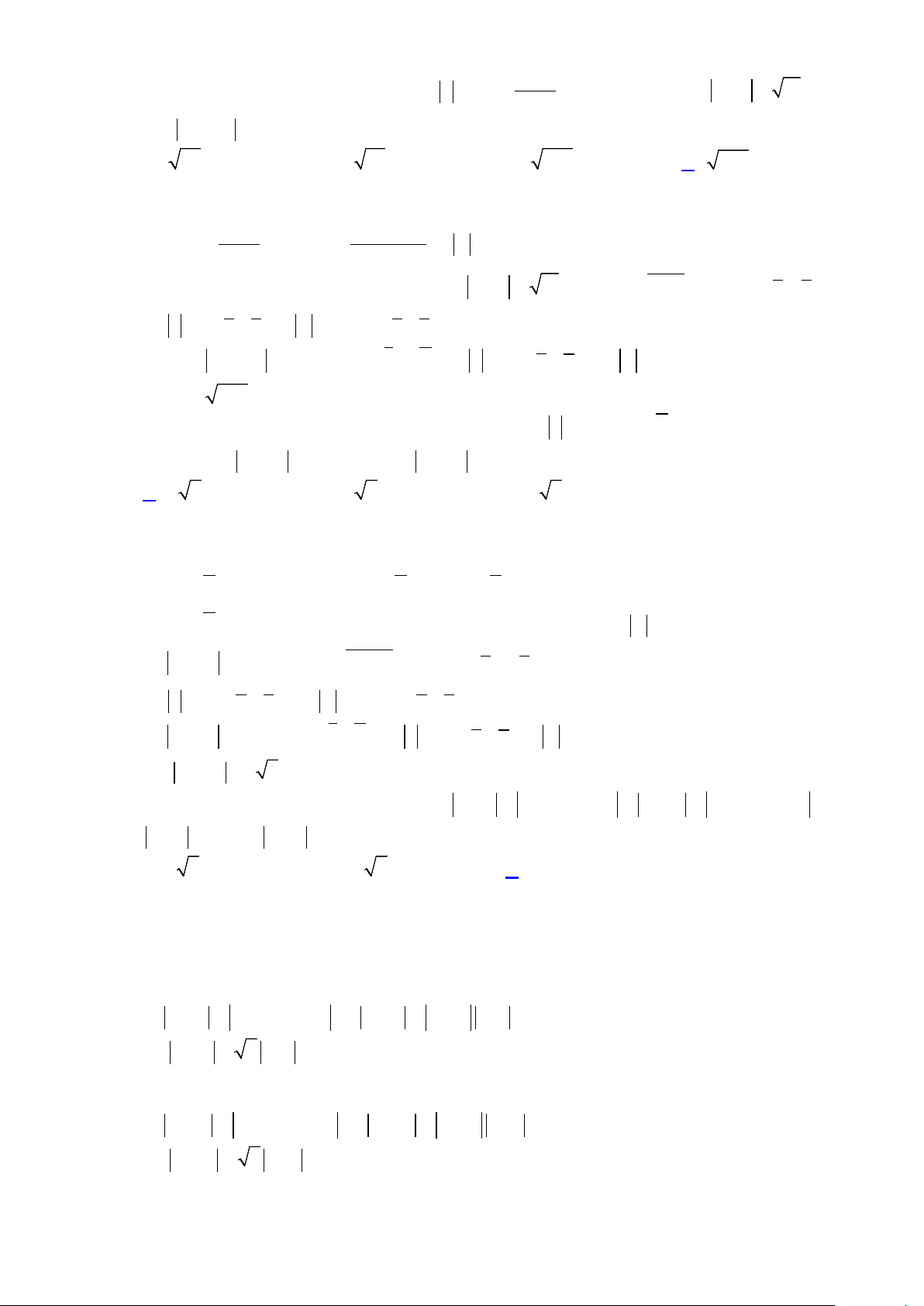







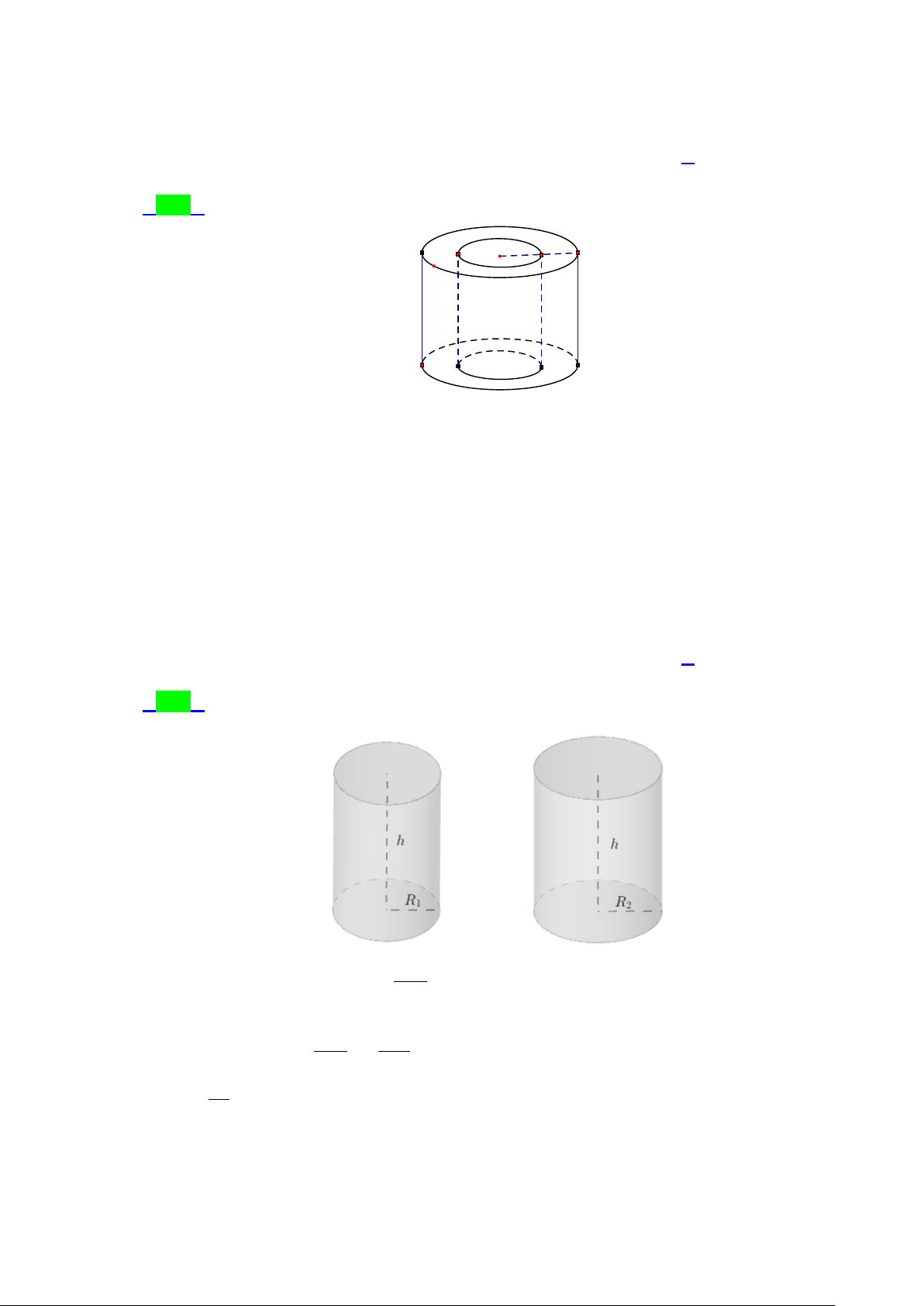





















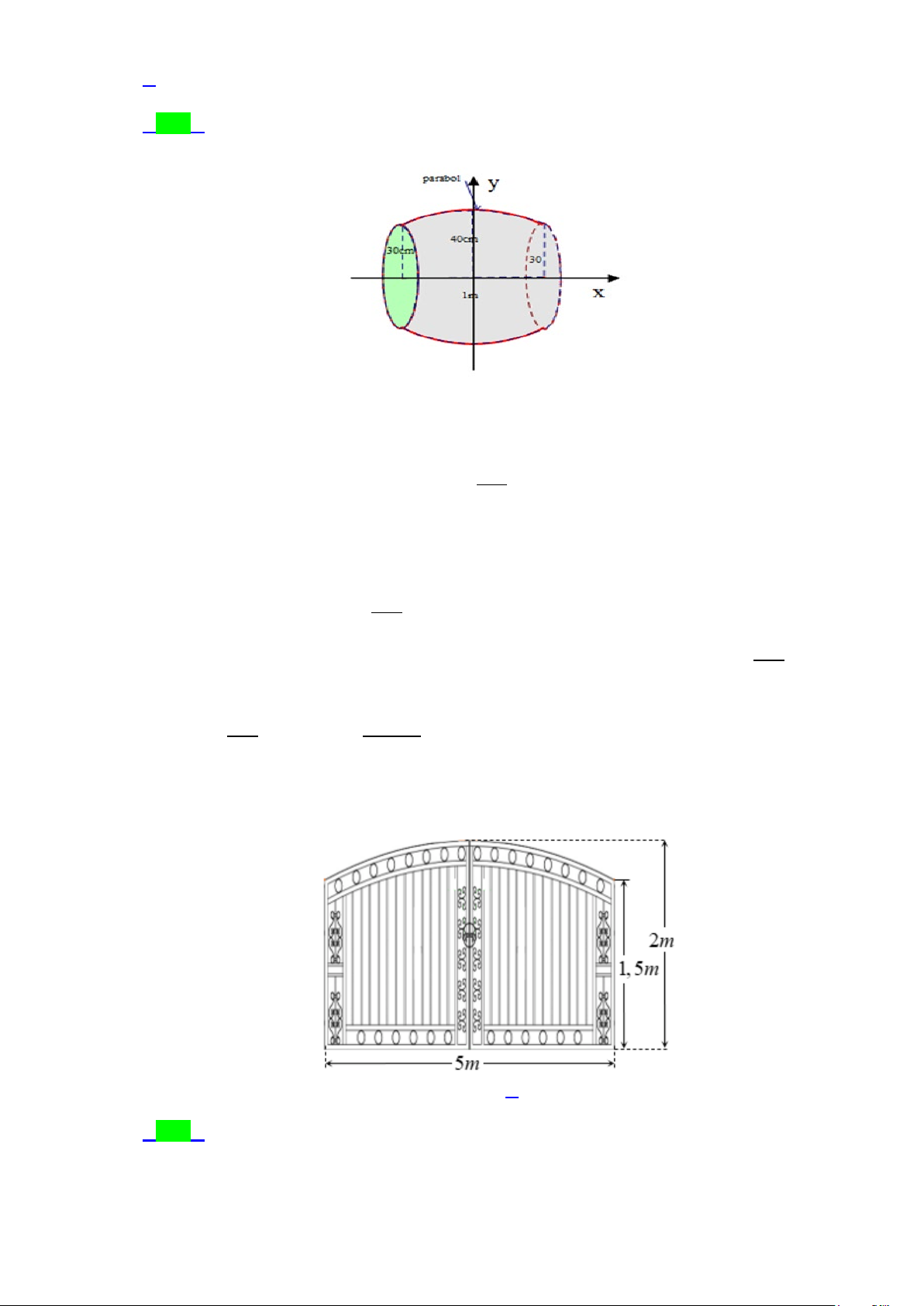



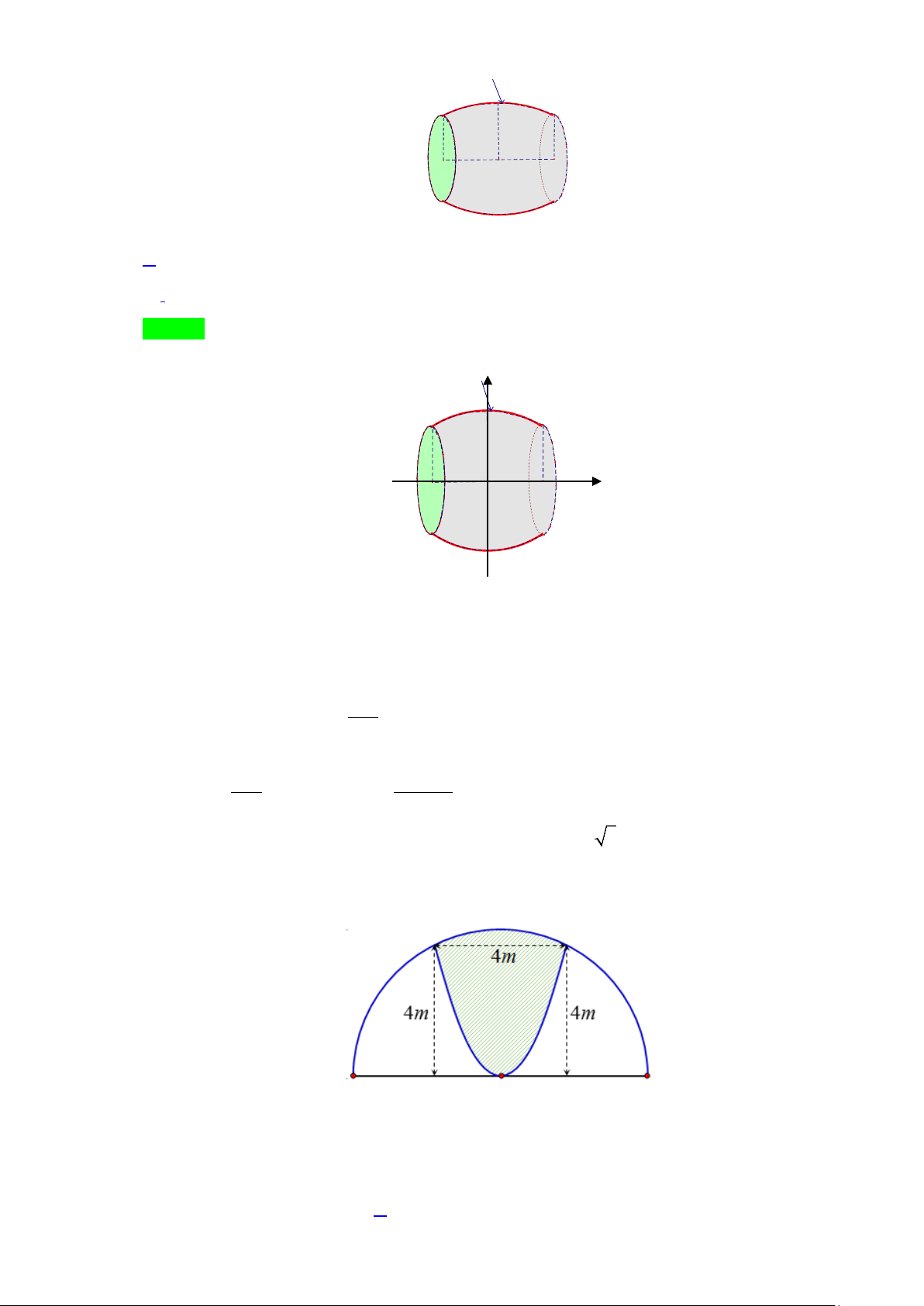

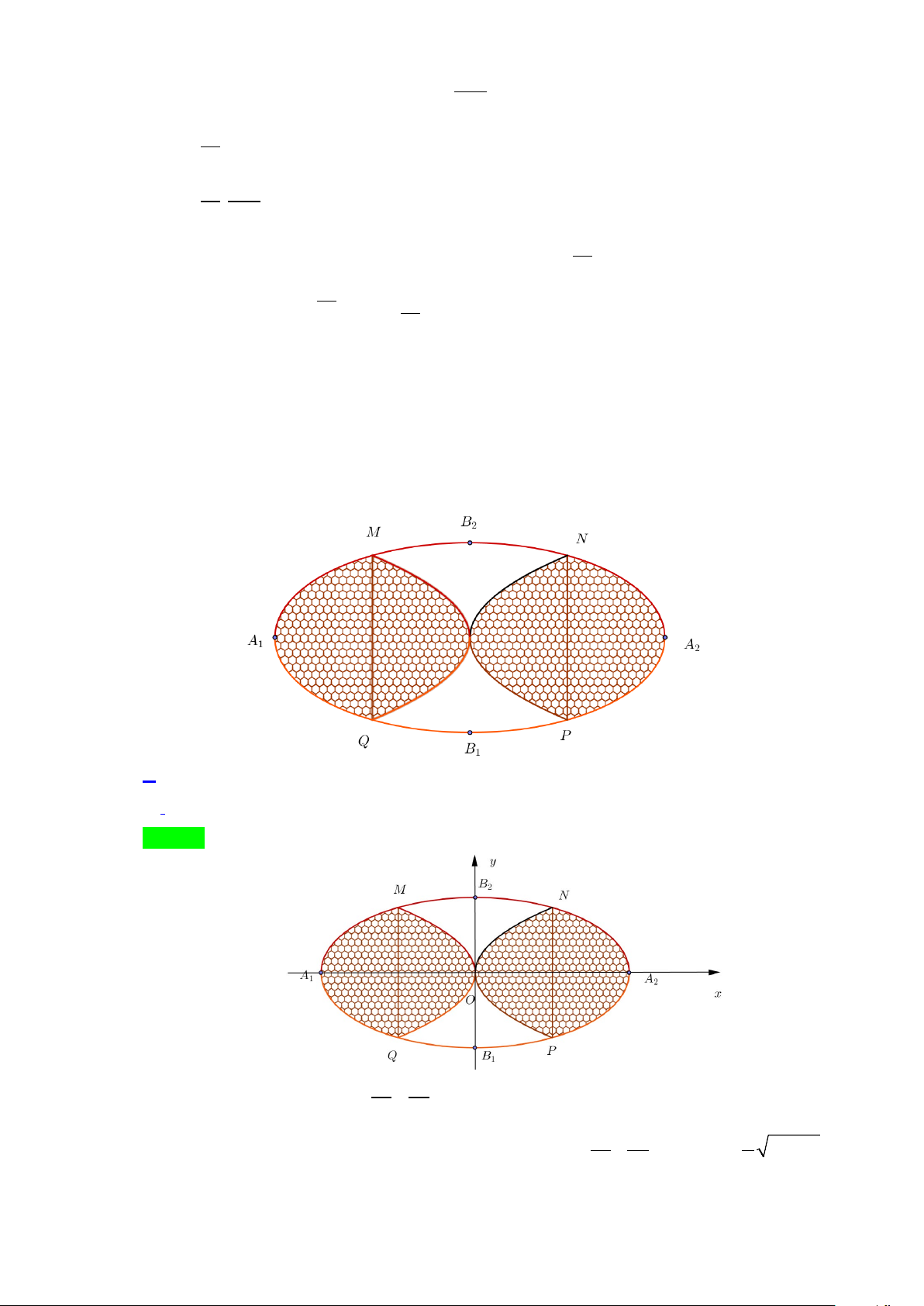







Preview text:
CÂU TƯƠNG TỰ CÂU 39 ĐỀ THAM KHẢO 2024 Câu 39.1: Cho b
a và b là hai số thực dương phân biệt, khác 1 và thỏa mãn log a b + = . a ( ) 2 2 3 .loga 27 0 3 a
Giá trị của log a bằng b A. 9 . B. 9 − . C. 2 − . D. 2 . 2 2 9 9 Lời giải Chọn C 2 Ta có 2 log b a b + = ⇔ b + b − + = . a ( 3 ).loga 27 0 loga 3 2loga 3 27 0 3 ( )2 ( ) a
Đặt t = log b t ≠ . Ta có phương trình a ; 0
(t + )2 ( t − ) + = ⇔ ( 2 3 2 3 27 0
t + 6t + 9)(2t −3) + 27 = 0 t = 0 (L) 3 2 2 3 2
2t 12t 18t 3t 18t 27 27 0 2t 9t 0 ⇔ + + − − − + = ⇔ + = ⇔ 9 . t = − 2 Vậy 9 2 log b = − ⇔ a = − . a log 2 b 9
Câu 39.2: Cho a và b là hai số thực dương phân biệt, khác 1 và thỏa mãn 2 a b b −
a b + = . Giá trị của biểu thức 7 2024 log a + bằng a ( 2 3 ) 3 2 a a ( 2 3 log .log log ) 4 0 5 b 5 A. 2038 . B. 2024 . C. 2031 . D. 2017 . 5 5 5 5 Lời giải Chọn D Ta có 2 a b b − a b + = a ( 2 3 ) 3 2 a a ( 2 3 log .log log ) 4 0 2 ⇔ a b b − + = ⇔ b + b − + = . a ( 2 3 ) ( 3 log . loga
)1 4 0 (3loga 2)2 (3loga ) 1 4 0
Đặt t = log b t ≠ . Ta có phương trình a ; 0
( t + )2 ( t − ) + = ⇔ ( 2 3 2 3 1 4 0
9t +12t + 4)(3t − ) 1 + 4 = 0 t = 0 (L) 3 2 2 3 2
⇔ 27t + 36t +12t − 9t −12t − 4 + 4 = 0 ⇔ 27t + 27t = 0 ⇔ . t = 1 − Suy ra log b = − ⇔ a = − a 1 logb 1 Vậy 7 2024 2017 log a + = . 5 b 5 5
Câu 39.3: Cho a và b là hai số thực dương thỏa mãn 2
log a + log b = 2 . Giá trị của a bằng 3 1 3 b A. 3 . B. 9 . C. 1 . D. 1 . 3 9 Lời giải Chọn A Cách 1: Tự luận
Với a và b là hai số thực dương, ta có: 2 2 2 2 a a 2 log + log = 2 ⇔ log − log = 2 ⇔ log = 2 ⇔ = 3 a a b a b ⇔ = 3 3 1 3 3 3 . b b 3 b
Cách 2: Sử dụng máy tính cầm tay
Chọn a hoặc b . Dùng chức năng SOLVE để tìm giá trị còn lại. Tính giá trị và thay vào đáp án để kiểm tra. Cụ thể: Trang 1/54 - WordToan
+ Chọn b = 3 (chọn tùy ý thỏa điều kiện bài toán). + Bấm: 2 log + log 3 = 2 SOLVE
→ ≈ 5.196152423 STO x x → A 3 1 3 + Tính a A =
= 3 ta được đáp án A . b 3 Câu 39.4:
Cho a,b,c là các số thực dương, khác 1 và thỏa mãn 2 log b = x
c = y . Giá trị của a ;log 2b log c bằng a A. 2xy . B. xy . C. 2 . D. 1 . 2 xy 2xy Lời giải Chọn A Cách 1: Tự luận
Với a,b,c là các số thực dương, khác 1, ta có: 2 log x b = x ⇔ b = x ⇔ b = . a 2loga loga 2 1 log
c = y ⇔ log c = y ⇔ log c = 4y . 2 b 4 b b Khi đó: log x b c = y = xy ⇔ c = xy . a .logb .4 2 loga 2 2
Cách 2: Sử dụng máy tính:
Chọn b = 3, x = 4, y = 2 (bạn đọc chọn tùy ý các số thỏa mãn điều kiện bài toán).
Dùng chức năng SOLVE để tìm a,c và dùng chức năng STO để gán vào biến , A C Cụ thể: + Bấm 2 log 3 = 4 SOLVE
→ x ≈1,732050808 STO → A ta được: x + Bấm log = 2 SOLVE → = 6561 STO x x →C ta được: 2 3 + Bấm log C = A 16
+ Kiểm tra bằng cách thay x = 4, y = 2 (đã chọn) vào đáp án ta được đáp án A .
Câu 39.5: Biết phương trình 2
log x + 3log x = 4 có hai nghiệm phân biệt là a ,b với a < b . Tìm khẳng 2 1 2 định sai.
A. b >10 .
B. 2a + b =17 .
C. a <1.
D. b =16a . Lời giải Chọn D
Điều kiện: x > 0 . Phương trình đã cho ⇔ 2
log x − 3log x − 4 = 0 . 2 2 t = 1 −
Đặt log x = t , ta suy ra phương trình: 2t − 3t − 4 = 0 ⇔ . 2 t = 4 Với 1 t = 1 − ⇒ log x = 1
− ⇔ x = , thỏa mãn đk x > 0 . 2 2 Trang 2/54 - WordToan
Với t = 4 ⇒ log x = 4 ⇔ x =16 , thỏa mãn đk x > 0 . 2 Khi đó 1
a = , b =16 nên khẳng định b =16a là sai. 2
Câu 39.6: Biết phương trình log 3x −1 . 1+ log 3x −1 = 6
x < x và tỉ số x a 1 = log 3 ( ) 3 ( ) có hai nghiệm là 1 2 x b 2 trong đó *
a,b∈ và a , b có ước chung lớn nhất bằng 1. Tính a + b .
A. a + b = 55.
B. a + b = 37 .
C. a + b = 56 .
D. a + b = 38 . Lời giải Chọn A log 3x −1 = 3 − 28 3 ( ) x = log
Ta có log 3x −1 . 1+ log 3x −1 = 6 ⇔ 1 3 ⇔ 3 ( ) 3 ( ) 27 log 3x −1 = 2 3 ( ) x = log 10 2 3 x 28 1 ⇒ = log
⇒ a = 28, b = 27 ⇒ a + b = 55. x 27 2
Câu 39.7: Phương trình 2 6 6 log x log 1 log + = +
log x có số nghiệm bằng 2 3 3 2 x x A. 2 nghiệm. B. 3 nghiệm.
C. vô nghiệm. D. 1 nghiệm. Lời giải Chọn D
Điều kiện x > 0. PT đã cho ⇔ 2 6 6 log x + log − log x − log . x log = 0 2 3 2 2 3 x x ⇔ 6
log x(log x −1) + log (1− log x) = 0 2 2 3 2 x log x −1 = 0 (1) 2 ⇔ 6
(log x −1)(log x − log ) = 0 ⇔ 2 2 3 x 6
log x − log = 0 (2) 2 3 x
Giải(1) : (1) ⇔ x = 2 (t / m) 6 log2 Giải (2) : 6 (2) ⇔ log x = log ⇔ log x x =
⇔ log 3.log x = log 6 − log x 2 3 x 2 log 3 2 2 2 2 2 ⇔ log .(
x 1+ log 3) = log 6 ⇔ log .(
x log 2 + log 3) = log 6 ⇔ log x =1 ⇔ x = 2 (t / m) 2 2 2 2 2 2 2 2
Vậy PT đã cho có nghiệm duy nhất x = 2. 2 Câu 39.8: Cho x,y x
là các số thực dương thoản mãn 2 2 2
log x = log y = log (x + y ). Giá trị của bằng 5 2 9 y A. 5 log . 5 log . . 5 B. C. 5 D. 2 . 2 2 2 2 Lời giải Chọn C 2 x = 5t Đặt 2 2 2
log x = log y = log (x + y ) = t ⇒ y = 2t
⇔ 5t + 4t = 9t (1) 5 2 9 . 2 2
x + y = 9t
4 t 5 t t t t t (1) ⇔ + = 1.Đặt 4 5 4 4 5 5 f (t) = + ⇒ f (′t) = ln + ln < 0 . 9 9 9 9 9 9 9 9
Hàm số f (t) nghịch biến nên phương trình (1) có duy nhất 1 nghiệm Trang 3/54 - WordToan 2 2 x 5
t = 1 ⇔ x = 5; y = 2 ⇒ = . y 2 Câu 39.9: Cho b
a và b là hai số thực dương phân biệt, khác 1 và thỏa mãn a b ⋅ − = . Giá a ( 2 ) 2 log loga 2 0 a trị của ( a)2 log bằng bao nhiêu? b A. 1 . B. 3. C. 1 . D. 3. 3 9 Lời giải Chọn A Ta có log b a b ⋅ − = ⇔ b + b − − = . a ( 2 ) 2 loga 2 0 (loga 2)(loga )2 1 2 0 a
Đặt t = log b t ≠ . Ta có phương trình a ; 0 t = 0 (L) (
t + )(t − )2 − = ⇔ (t + )( 2 2 1 2 0 2 t − 2t + ) 1 − 2 = 0 3
⇔ t − 3t = 0 ⇔ t = − 3 . t = 3 Vậy ( b = ⇔ a = . a )2 ( b )2 1 log 3 log 3 2 Câu 39.10: Cho a
a và b là hai số thực dương phân biệt, khác 1 và thỏa mãn 2 log ⋅ ab − = . a loga 4 0 b
Giá trị của log a bằng bao nhiêu? b A. 1 . B. 3. C. 1 − . D. 3 − . 3 3 Lời giải Chọn A 2 Ta có 2 log a ⋅ ab − = ⇔ − b b + − = . a loga 4 0 (2 loga )2 (loga ) 1 4 0 b
Đặt t = log b t ≠ . Ta có phương trình a ; 0 ( t = 0 (L)
− t)2 (t + ) − = ⇔ ( 2 2 1 4 0
t − 4t + 4)(t + ) 1 − 4 = 0 3 2
⇔ t − 3t = 0 ⇔ . t = 3 Vậy 1 log b = ⇔ a = . a 3 logb 3 2 log a b⋅ ab − a loga 2
Câu 39.11: Cho a và b là hai số thực dương phân biệt, khác 1 và thỏa mãn = 5 . log b a
Giá trị của log a bằng bao nhiêu? b A. 1 . B. 4 . C. 1 − . D. 4 − . 4 4 Lời giải Chọn C 2 2 log a b⋅ ab − a loga 2 Ta có = 5 ⇔ (2 + log b + b − = b a ) (1 loga )2 2 5log . log a b a
Đặt t = log b t ≠ . Ta có phương trình a ; 0 ( t = L 2 + t)(t + )2 1 − 2 = 5t ⇔ ( 0 ( ) 2 t + 2t + ) 1 (t + 2) 3 2
− 2 = 5t ⇔ t + 4t = 0 ⇔ . t = 4 − Trang 4/54 - WordToan Vậy 1 log b = − ⇔ a = − . a 4 logb 4 1 loga Câu 39.12: Cho b
a và b là hai số thực dương phân biệt, khác 1 và thỏa mãn log b = . Giá trị a a log b − a 4
của log a bằng bao nhiêu? b A. 1 − . B. 2 . C. 1 . D. 2 − . 2 2 Lời giải Chọn C 1 loga b b −log Ta có log = ⇔ log b b − = . a 1 a a a log b − b − a 4 loga 4
Đặt t = log b t ≠ . Ta có phương trình t − 2 t −1 =
⇔ t − 4t + 4 = 0 ⇔ t = 2 . a ; 0 t − 4 Vậy 1 log b = ⇔ a = . a 2 logb 2
CÂU TƯƠNG TỰ CÂU 40 ĐỀ THAM KHẢO 2024
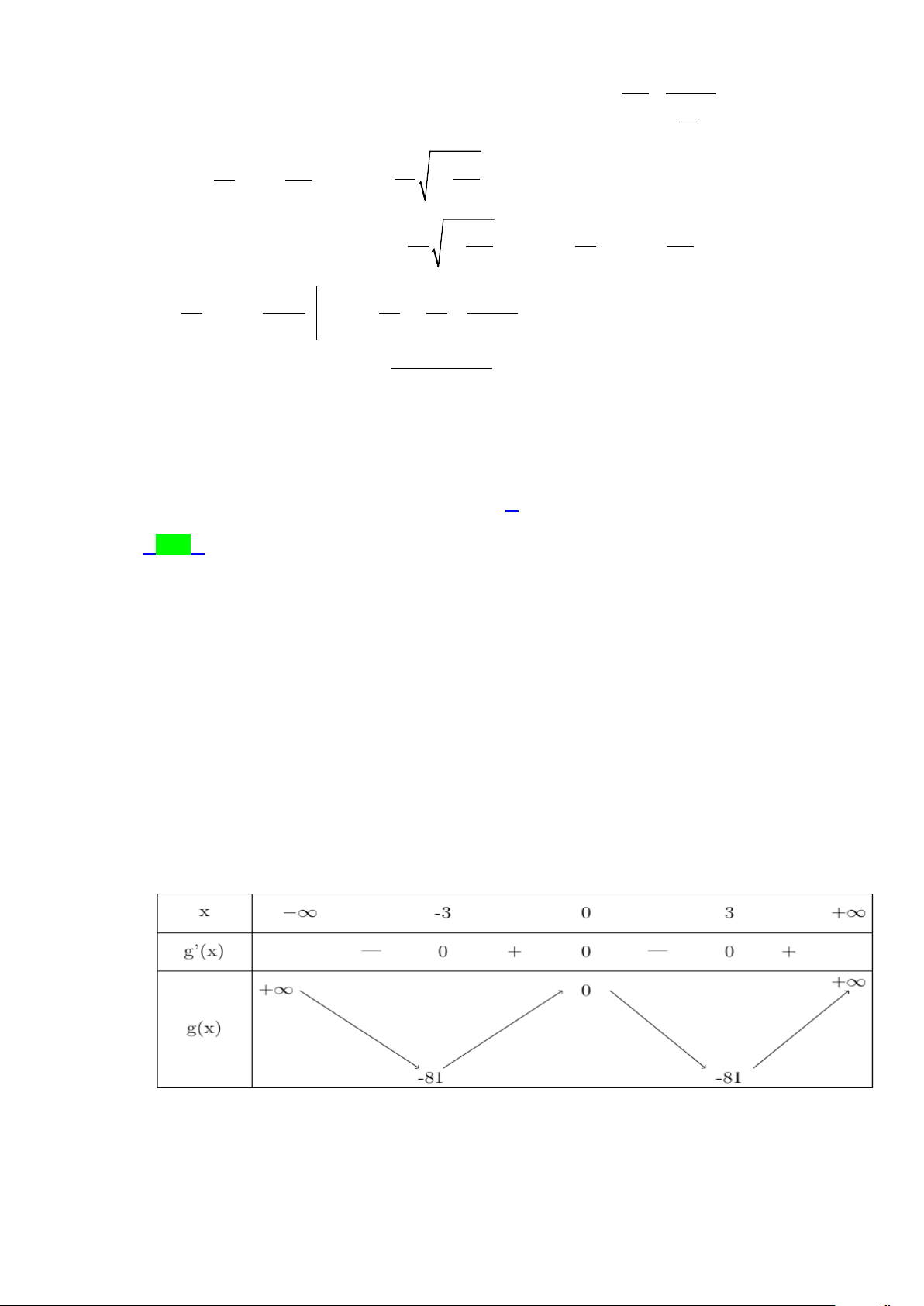
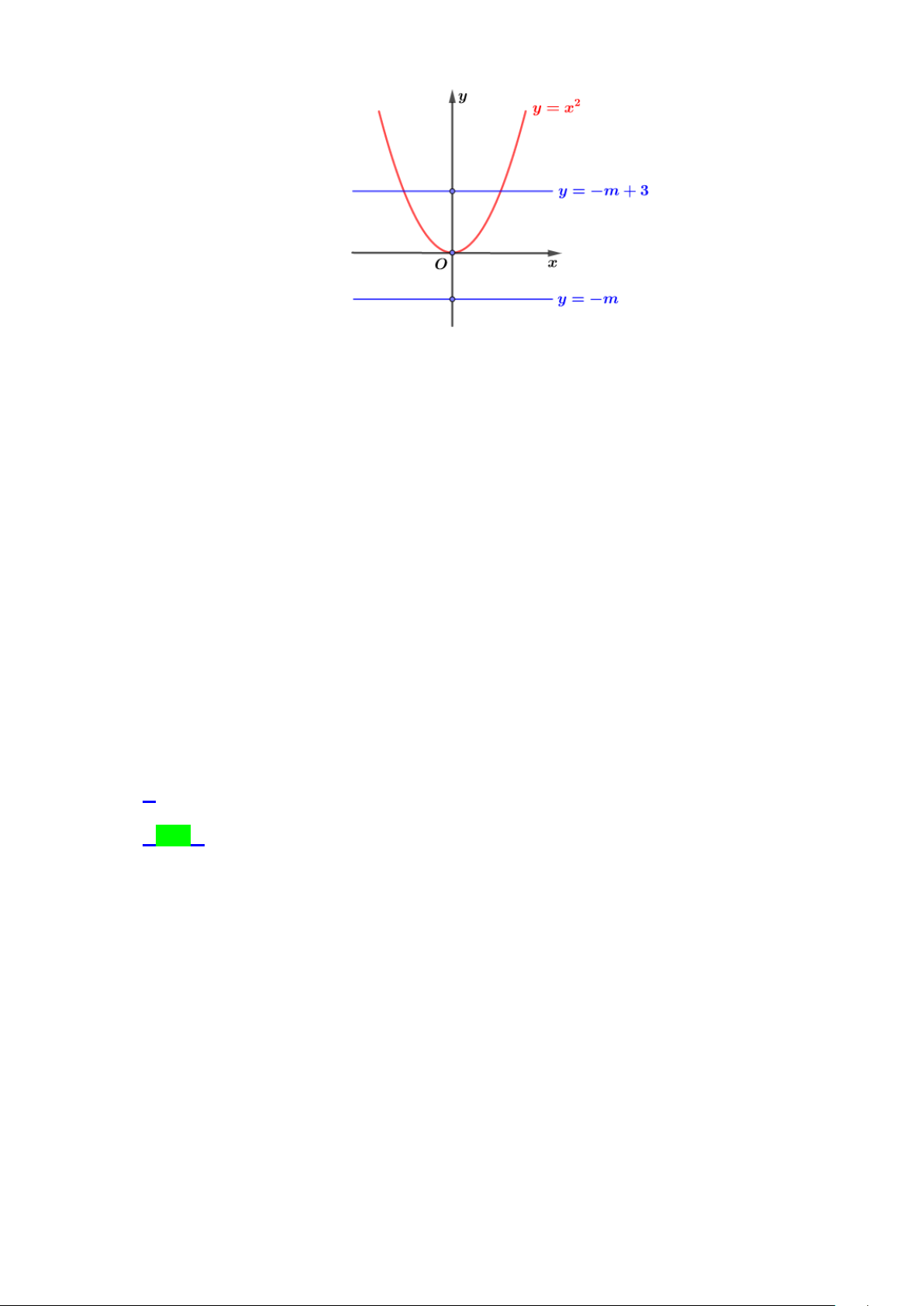
Câu 40.1: Gọi S là tập hợp các giá trị nguyên dương của m để hàm số 3
y = x − ( m + ) 2 3 2
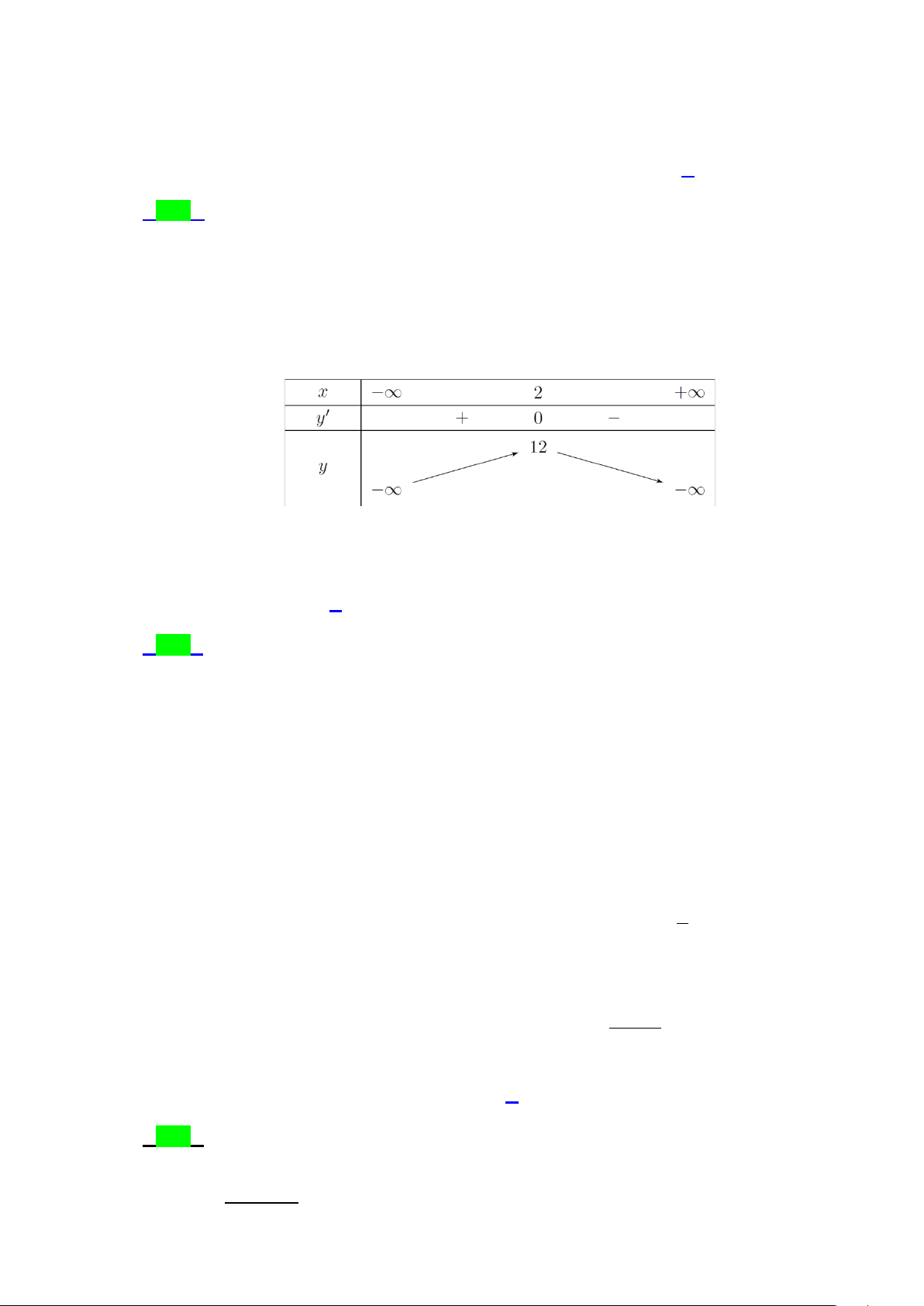
1 x + (12m + 5) x + 2 đồng biến trên khoảng (2;+ ∞) . Số phần tử của S bằng A. 1. B. 2 . C. 3. D. 0 . Lời giải Chọn D
Tập xác định D = . 2
y′ = 3x − 6(2m + ) 1 x +12m + 5 .
Hàm số đồng biến trong khoảng (2;+ ∞) khi y′ ≥ 0 , x ∀ ∈(2;+ ∞) 2
⇔ 3x − 6(2m + )
1 x +12m + 5 ≥ 0 , x ∀ ∈(2;+∞) . 2 3x − 6x + 5 2 3x − 6(2m + )
1 x +12m + 5 ≥ 0 ⇔ m ≤ 12(x − ) 1 2 − +
Xét hàm số g (x) 3x 6x 5 = với x∈(2;+ ∞). 12(x − ) 1 2
g′(x) 3x − 6x +1 = > 0 với x
∀ ∈(2;+ ∞) ⇒ hàm số g ( x) đồng biến trên khoảng (2;+ ∞) . 12(x − )2 1
Do đó m ≤ g (x) , x
∀ ∈(2;+ ∞) ⇒ m ≤ g (2) 5 ⇔ m ≤ . 12
Vậy không có giá trị nguyên dương nào của m thỏa mãn bài toán.
Câu 40.2: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [ 2024 −
;2024] để ứng với mỗi m hàm x − số hàm số cos 2 y π =
đồng biến trên khoảng 0; cos x − m 2 A. 4046 B. 2022 C. 2026 D. 2023 Lời giải Chọn B Đặt t π π = cos x . Do x 0; ∈ nên t ∈(0; )
1 . Nhận thấy hàm số t = cos x nghịch biến trên 0; 2 2 Trang 5/54 - WordToan t − 2
ta phát biểu lại bài toán như sau: Tìm m để hàm số y = nghịch biến trên (0; ) 1 . t − m
Ycbt thỏa mãn khi y′ < 0 t ∀ ∈(0; ) 1 m > 2 −m + 2 −m + 2 < 0 ⇔ y' = < 0 t ∀ ∈ 0;1 ⇔ ⇒ m ∈ ;0 −∞ ⇒ m > 2 2 ( ) ( − ) m t m ∉ (0; ) ( 1 m∈ 1; +∞ )
Do m nguyên thuộc đoạn [ 2024 −
;2024] nên có 2022 giá trị của m thỏa mãn ycđb
Câu 40.3: Gọi T là tập hợp tất cả các giá trị nguyên dương của tham số m để hàm số 4 2
y = x − 2mx +1
đồng biến trên khoảng (3;+∞) . Tổng giá trị các phần tử của T bằng A. 9. B. 45 . C. 55. D. 36. Lời giải Chọn B
+ Tập xác định: D = . + Ta có 3
y′ = x − mx = x( 2 4 4 4 x − m)
Theo đề m > 0 nên y′ = 0 có 3 nghiệm phân biệt x = − m, x = 0, x = m .
Để hàm số đồng biến trên khoảng (3;+∞) thì y′ ≥ 0, x
∀ ∈(3;+∞) ⇔ m ≤ 3 ⇔ m ≤ 9
Vì m nguyên dương nên m =1, 2, 3, 4, 5, 6, 7, 8, 9 ( là cấp số cộng )
Vậy Tổng giá trị các phần tử của 9 T bằng (1+ 9) = 45. 2
Câu 40.4: Tìm tất cả các giá trị thực của m để hàm số 3 2 1 2x x mx y − + + = đồng biến trên (1;2) . A. m > 8 − . B. m ≤ 8 − . C. m ≥ 1 − . D. m < 1 − . Lời giải Chọn C Ta có: y ( x x m) 3 2 2
x −x +mx 1 3 2 .2 + ′ = − + .ln 2
Hàm số đồng biến trên (1;2) ⇔ y′ ≥ 0, x ∀ ∈(1;2) ( x x m) 3 2 2
x −x +mx 1 3 2 .2 + ⇔ − + .ln 2 ≥ 0 , x ∀ ∈(1;2) 2
⇔ 3x − 2x + m ≥ 0 , x ∀ ∈(1;2) 2 ⇔ m ≥ 3
− x + 2x , x ∀ ∈(1;2)
Xét hàm số f (x) 2 = 3
− x + 2x , với x ∈(1;2).
Ta có: f ′(x) = 6 − x + 2 . Cho 1
f ′(x) = 0 ⇔ 6
− x + 2 = 0 ⇔ x = . 3 Bảng biến thiên: Trang 6/54 - WordToan
Từ BBT ta có m ≥ f (x) , x
∀ ∈(1;2) khi m ≥ 1 − .
Câu 40.5: Tìm tất cả các giá trị của tham số m để hàm số 3 2
y = x − 6x + mx + 3 đồng biến trên khoảng (0;+∞) A. m ≤12 . B. m ≥ 0 . C. m ≤ 0 . D. m ≥12 . Lời giải Chọn D 2
y′ = 3x −12x + m
Hàm số đã cho đồng biến trên khoảng (0;+∞) khi và chỉ khi y′ ≥ 0 , với mọi x∈(0;+∞) 2 ⇔ m ≥ 3
− x +12x , ∀x > 0 . Xét 2 f (x) = 3
− x +12x với x > 0 .
Ta có f (′x) = 6
− x +12 ; f (′x) = 0 ⇔ x = 2 . Bảng biến thiên:
Dựa vào bảng biến thiên, ta được giá trị m thỏa mãn yêu cầu bài toán là m ≥12 .
Câu 40.6: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [ 100 − ;100] sao cho hàm số
f (x) = (m − ) 3 x + (m − ) 2 1 1 x + (2m + )
1 x + 3m −1 đồng biến trên ? A. 99. B. 100. C. 200 . D. 154. Lời giải Chọn B
Tập xác định: D = .
Ta có: f ′(x) = (m − ) 2 3 1 x + 2(m − ) 1 x + 2m +1
Để hàm số đã cho đồng biến trên thì f ′(x) ≥ 0,∀x∈ (*)
( Dấu " = " xảy ra tại hữu hạn x∈ )
TH1: m −1 = 0 ⇔ m =1
Ta có : f ′(x) = 3 > 0,∀x∈ nên hàm số đồng biến trên ⇒ m =1 (nhận). TH2 : m ≠ 1.
Để hàm số đã cho đồng biến trên thì f ′(x) ≥ 0,∀x∈ 3 m >1 (m − ) 1 > 0 m > 1 ⇔ ⇔ ⇔ 4 ⇔ m >1. ( m − )2 1 − 3(m − ) 1 (2m + ) 1 ≤ 0 ( m − ) 1 ( 5 − m − 4) ≤ 0
m ≤ − ∨ m ≥ 1 5 Kết hợp 2 TH m [ ∈ 100 − ;100]
⇒ m ≥1 →m∈{1;2;..; }
100 : có 100 giá trị m thỏa mãn yêu cầu bài toán.
Câu 40.7: Có bao nhiêu giá trị nguyên của tham số m để hàm số x + 6 y =
nghịch biến trên khoảng x + 5m (10;+∞)? A. 3 B. Vô số C. 4 D. 5 Lời giải Chọn C
Tập xác định D = \{ 5 − } m . Ta có 5m − 6 y′ = . (x +5m)2 Trang 7/54 - WordToan 5 m − 6 < 0
Hàm số nghịch biến trên (10;+∞) khi và chỉ khi y′ < 0,∀x∈(10;+∞) ⇔ 5 − m∉ (10;+∞) 5 6 m − 6 < 0 m < ⇔ ⇔
5 . Mà m∈ nên m∈{ 2; − 1 − ;0; } 1 . 5 − m ≤10 m ≥ 2 −
Câu 40.8: Tập hợp tất cả các giá trị thực của tham số m để hàm số mx − 9 y =
đồng biến trên khoảng x − m (0;+∞) là A. ( 3 − ;0]. B. ( 3; − 0) . C. [ 3; − 0]. D. [ 3 − ;0). Lời giải Chọn A TXĐ: D = \{ } m . 2 Ta có −m + 9 y′ = . (x − m)2 2 −m + 9 > 0 3 − < m < 3 Yêu cầu bài toán ⇔ ⇔ ⇔ 3 − < m ≤ 0 . m ≤ 0 m ≤ 0
Câu 40.9: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [1;25] sao cho ứng với mỗi m, hàm số 2
−x + 2x − m + 5 y =
đồng biến trên khoảng (1;3) . 2x − m A. 24 . B. 2. C. 20 . D. 6 . Lời giải Chọn C m
Tập xác định: D \ = . 2 2 2
− x + 2mx −10 Ta có y ' = . (2x − m)2
Hàm số đồng biến trên khoảng (1;3) thì y ' ≥ 0, x ∀ ∈(1;3) . 2 x + 5 m ≥ , x
∀ ∈(1;3) (Do x > 0, x ∀ ∈ (1;3)) 2 2 − + 2 −10 ≥ 0,∀ ∈(1;3) x x mx x tức là m m ⇔ ≤ . x , x (1;3) 1 ≠ ∀ ∈ 2 2 m ≥ 3 2 2 x + 5
Xét hàm số g (x) = , x ∀ ∈[1; ] 3 . x 2 x − 5 x = 5 Ta có g '(x) =
. g '(x) = 0 ⇔ (x ≠ 0). 2 x x = − 5 Bảng biến thiên Trang 8/54 - WordToan 2 x + 5 m ≥ , x ∀ ∈ (1;3) x m ≥ 6 m ≤ 1
⇔ m ≤ 2 ⇔ m ≥ 6
Từ bảng biến thiên, ta có 2 . m ≥ 6 m ≥ 3 2
Mà m là số nguyên thuộc đoạn [1;25] nên m∈{6;7;8;9;10;....; } 25 .
Vậy có 20 giá trị nguyên của tham số m thuộc đoạn [1;25] thỏa mãn yêu cầu bài toán.
Câu 40.10: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [ 2;
− 25] sao cho ứng với mỗi m , 2
x + 5x − m −1 hàm số y =
nghịch biến trên khoảng (1;4) . 5x − m A. 8. B. 15. C. 14. D. 6 . Lời giải Chọn D m
Tập xác định: D \ = . 5 2 5x − 2mx + 5 Ta có y ' = . (5x − m)2
Hàm số nghịch biến trên khoảng (1;4) thì y ' ≤ 0, x ∀ ∈(1;4) . 2 5x + 5 m ≥ , x
∀ ∈(1;4) (Do 2x > 0, x ∀ ∈ (1;4)) 2 − + ≤ ∀ ∈( ) 2 5 2 5 0, 1;4 x x mx x tức là m m ⇔ ≤ . x , x (1;4) 1 ≠ ∀ ∈ 5 5 m ≥ 4 5 2 5x + 5
Xét hàm số g (x) = , x ∀ ∈[1;4]. 2x 2 5x − 5 Ta có g '(x) = > 0, x
∀ ∈ 1;4 . Hàm số đồng biến trên (1;4) . 2 [ ] 2x 85
Suy ra Max g (x) = g (4) = . x [ ∈ 1;4] 8 Trang 9/54 - WordToan 2 5x + 5 m ≥ , x ∀ ∈ (1;4) 85 2x m ≥ m 8 Khi đó, ta có ≤ 1 ⇔ ⇔ m ≥ 20 . m ≤ 5 5 m m ≥ 20 ≥ 4 5
Mà m là số nguyên thuộc đoạn [ 2;
− 25] nên m∈{20;21;22;23;24; } 25 .
Vậy có 6 giá trị nguyên của tham số m thuộc đoạn [ 2;
− 25] thỏa mãn yêu cầu bài toán.
Câu 40.11: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [ 2 − 5; ]
3 sao cho ứng với mỗi m , 2
−x + 4x − m − 5 hàm số y =
đồng biến trên khoảng ( 3 − ;− ) 1 . 4x − m A. 17. B. 15. C. 14. D. 16. Lời giải Chọn D m
Tập xác định: D \ = . 4 2 4 − x + 2mx + 20 Ta có y ' = . (4x − m)2
Hàm số đồng biến trên khoảng ( 3 − ;− )
1 thì y ' ≥ 0, x ∀ ∈( 3 − ;− ) 1 . tức là 2 2x −10 m ≤ , x ∀ ∈( 3 − ;− )
1 (Do x < 0, x ∀ ∈( 3 − ; 2 4 − + 2 + 20 ≥ 0,∀ ∈( 3 − ;− ) 1 x x mx x m m ⇔ ≤ − x , x ( 3; ) 3 1 ≠ ∀ ∈ − − 4 4 m ≥ 1 − 4 . 2 2x −10
Xét hàm số g (x) = , x ∀ ∈[ 3 − ;− ] 1 . x 2 2x +10 Ta có g '(x) = > 0, x ∀ ∈ 3 − ; 1
− . Suy ra hàm số đồng biến trên ( 3 − ;− ) 1 . 2 [ ] x 8
Suy ra Min g (x) = g ( 3 − ) = − . [ 3; − − ] 1 3 Khi đó, ta có 2 2x −10 m ≤ , x ∀ ∈( 3 − ;− ) 1 8 x m ≤ − m 3 ≤ 3 − ⇔ ⇔ m∈(−∞ − ] 8 ; 12 ∪ 4; . m ≤ 12 − − 4 − 3 m m ≥ 4 − ≥ 1 − 4 Trang 10/54 - WordToan
Mà m là số nguyên thuộc đoạn [ 2 − 5; ] 3 nên m∈{ 25 − ; 24 − ; 23 − ;...;− } 12 ∪{ 4 − ;− } 3 .
Vậy 16 giá trị nguyên của tham số m thuộc đoạn [ 2 − 5; ]
3 thỏa mãn yêu cầu bài toán.
Câu 40.12: Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [ 2024 − ;2024] sao cho ứng với mx − 6m + 5
mỗi m , hàm số y =
nghịch biến trên khoảng (2;7) . x − m A. 1027. B. 4045. C. 4043. D. 2025. Lời giải Chọn C
Tập xác định: D = \{ } m . 2 − + 6 − 5 Ta có ' m m y = . (x − m)2
Hàm số nghịch biến trên khoảng (2;7) thì y ' < 0, x ∀ ∈(2;7) . m <1 2
−m + 6m − 5 < 0 m > 5 tức là ⇔ ⇔ m∈( ; −∞ ) 1 ∪[7;+∞) . x ≠ , m x ∀ ∈ (2;7) m ≤ 2 m ≥ 7 Mà m là số nguyên thuộc đoạn [ 2024 − ;2024] nên m∈{ 2024 − ; 2023 − ;...; } 0 ∪{7;8;9;...; } 2024 .
Vậy có 4043 giá trị nguyên của tham số m thuộc đoạn [ 2024 −
;2024] thỏa mãn yêu cầu bài toán.
CÂU TƯƠNG TỰ CÂU 41 ĐỀ THAM KHẢO 2024
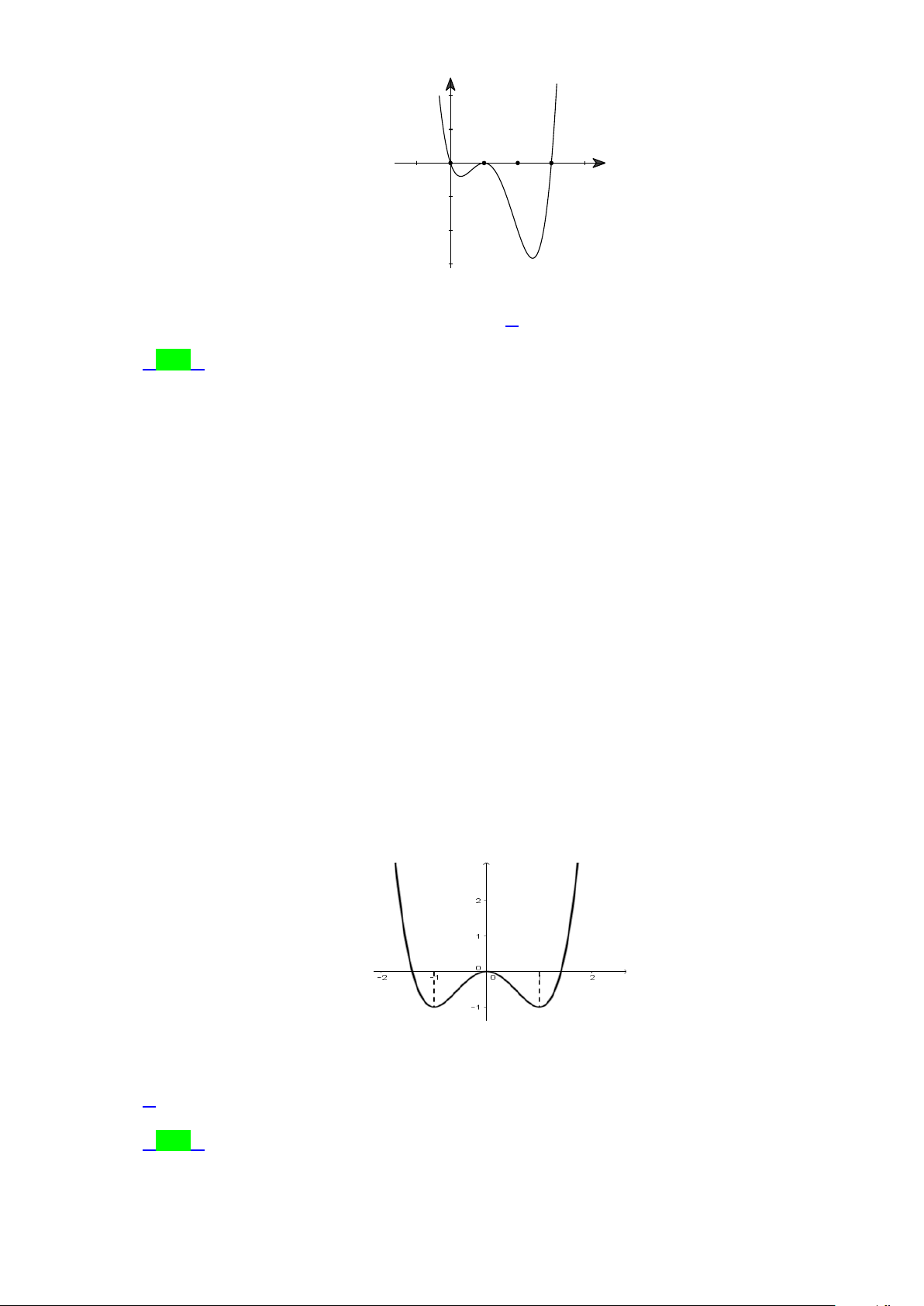
Câu 41.1. Cho hai hàm số f (x) 3 2 5
= mx + nx + px − ( ,
m n, p ∈ ) và g (x) 2
= x + 2x −1 có đồ thị cắt nhau 2
tại ba điểm có hoành độ lần lượt là 3
− ; −1; 1 (tham khảo hình vẽ bên dưới).
Diện tích hình phẳng giới hạn bởi đồ thị hàm số f (x) và g (x) bằng A. 18 . B. 4 . C. 5. D. 9 . 5 2 Lời giải Chọn B
Xét phương trình hoành độ giao điểm:
f (x) = g (x) ⇔ f (x) − g (x) 3
= ⇔ mx + (n − ) 2 x + ( p − ) 3 0 1 2 x − = 0 . 2
Vì hai đồ thị cắt nhau tại ba điểm có hoành độ lần lượt là 3
− ; −1; 1 nên ta có: 3 mx + (n − ) 2 x + ( p − ) 3 1
2 x − = m(x + 3)(x + ) 1 (x − ) 1 2 Trang 11/54 - WordToan 3
⇔ mx + (n − ) 2 1 x + ( p − 2) 3 3 2
x − = mx + 3mx − mx − 3m (*). 2 1 m = 2 n −1 = 3m
Đồng nhất thức hai vế phương trình (*) ta được 5
p − 2 = −m ⇔ n = . 2 3 − = 3 − m 3 2 p = 2
Suy ra f (x) − g (x) 1 3 3 2 1 3
= x + x − x − . 2 2 2 2
Khi đó Diện tích hình phẳng giới hạn bởi đồ thị hàm số f (x) và g (x) là 1 − 1 1 3 3 2 1 3 1 3 3 2 1 3 S x x x dx x x x = + − − − + − − dx = 2 + 2 = ∫ ∫ 4. − 2 2 2 2 − 2 2 2 2 3 1
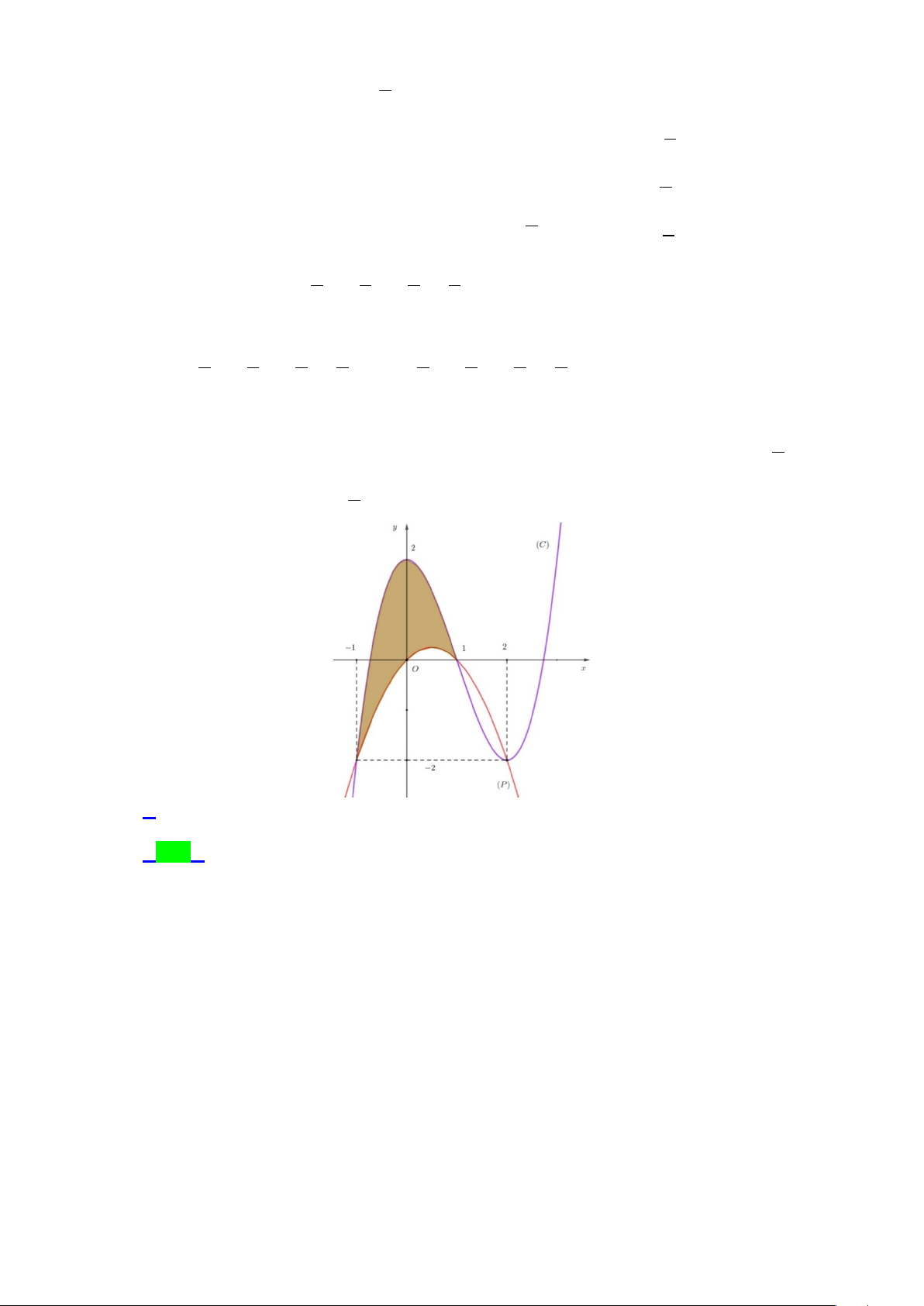
Câu 41.2. Cho hình phẳng (H ) được giới hạn bởi đồ thị (C) của hàm đa thức bậc ba và parabol (P) có
trục đối xứng vuông góc với trục hoành. Phần tô đậm như hình vẽ có diện tích bằng a , với a,b b
là các số nguyên dương và a là phân số tối giản. Tính T = a − b . b A. 5. B. 7 . C. 11. D. 25 . Lời giải Chọn A
Gọi dạng của hàm số bậc ba có đồ thị (C) là f (x) 3 2
= ax + bx + cx + d (a ≠ 0) . Dựa vào hình
vẽ, đồ thị (C) đi qua các điểm A(0;2) , B( 1; − 2
− ),C (1;0), D(2; 2
− ) . Suy ra hệ phương trình: d = 2 d = 2 d = 2 a b c d 2 a b c 4 − + − + = − − + − = − a =1 ⇔ ⇔ . Hay f (x) 3 2
= x − 3x + 2 . a b c d 0 a b c 2 b + + + = + + = − = 3 − 8
a + 4b + 2c + d = 2 − 8
a + 4b + 2c = 4 − c = 0
Gọi dạng của parabol (P) có trục đối xứng vuông góc với trục hoành là g (x) 2
= mx + nx + p (m ≠ 0) . Dựa vào hình vẽ, (P) đi qua ba điểm O(0;0) , p = 0 p = 0 p = 0 B( 1; − 2
− ),C (1;0) . Suy ra hệ phương trình: m n p 2 m n 2 − + = − ⇔ − = − ⇔ m = 1 − . Hay m n p 0 m n 0 + + = + = m = 1 ( ) 2
g x = −x + x . Trang 12/54 - WordToan 1 1
Diện tích của hình phẳng (H ) là: S = f (x) − g (x) dx = ∫ 3 2 x − 3x + 2 − ∫ ( 2
−x + x) dx 1 − 1 − 1 1 3 2
= x − 2x − x + 2 dx ∫ = ( 3 2
x − x − x + ) 8 2 2 dx = ∫ . − 3 1 − 1
Suy ra a = 8, b = 3.
Vậy T = 8 − 3 = 5 .
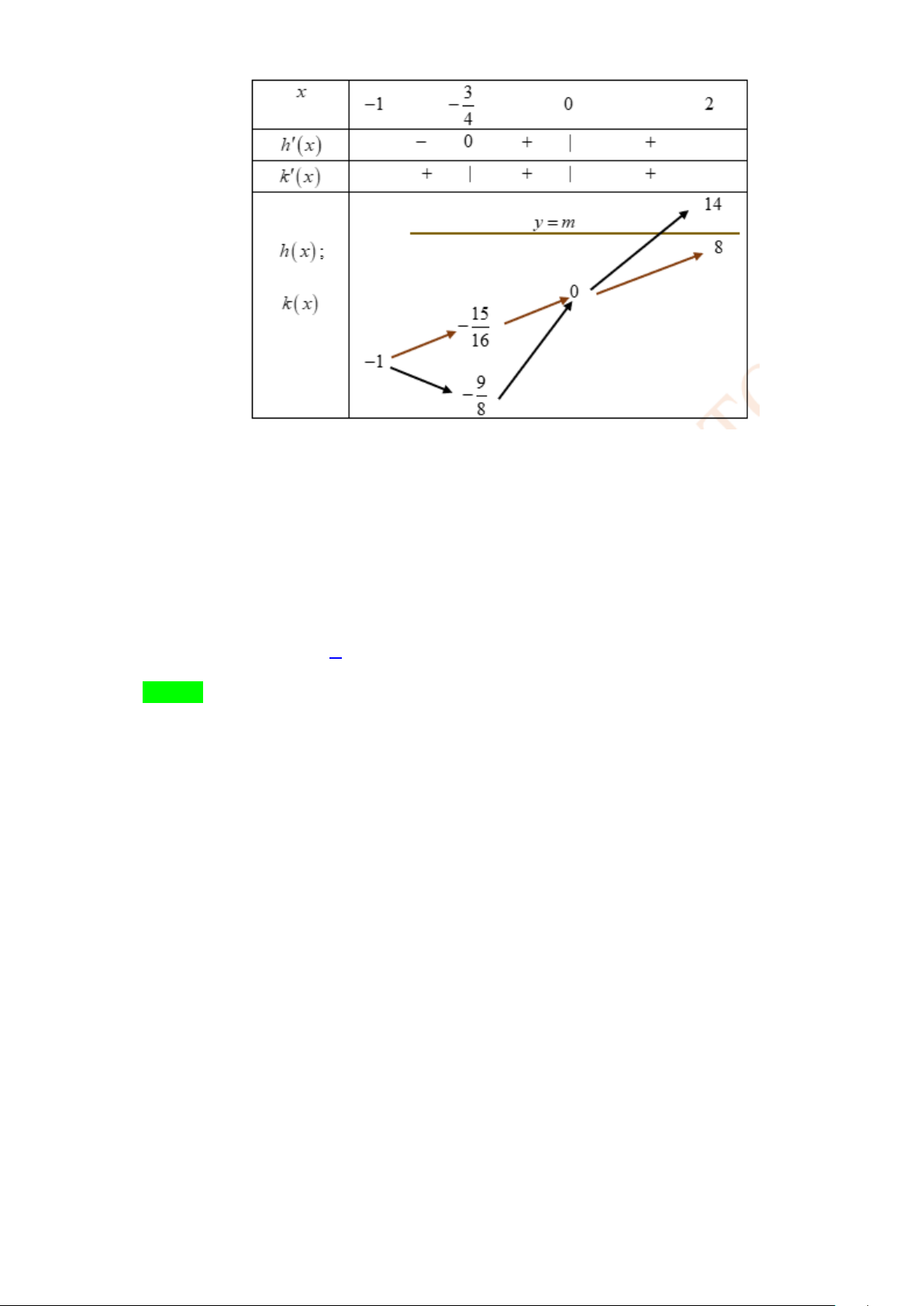
Câu 41.3. Cho hàm số bậc ba y = f (x) có đồ thị như hình vẽ, biết f (x) đạt cực tiểu tại điểm x =1 và
thỏa mãn f (x) +1
và f ( x) −1
lần lượt chia hết cho ( x − )2 1 và (x + )2
1 . Gọi S , S lần lượt 1 2
là diện tích như trong hình bên. Tính 2S + 8S 2 1 A. 1 . B. 3 . C. 4 . D. 9. 2 5 Lời giải Chọn C
+ Đồ thị hàm số y = f (x) là hàm số bậc ba và đi qua gốc tọa độ O , nên có dạng y = f (x) 3 2
= ax + bx + cx (a ≠ ) ⇒ f ′(x) 2 0
= 3ax + 2bx + c
+ Hàm số f (x) đạt cực tiểu tại điểm x =1 ⇒ f ′( )
1 = 3a + 2b + c = 0 ( ) 1
+ Ta có f (x) +1
và f ( x) −1
lần lượt chia hết cho ( x − )2 1 và (x + )2 1
f (x)+1= (x − )2 1 h(x) f ( ) 1 +1 = 0 f ( ) 1 = 1 −
a + b + c = 1 − ⇒ ⇒ ⇒ ⇒ (2) f
( x) −1 = ( x + )2 1 g (x) f (− ) 1 −1 = 0 f (− )
1 =1 −a + b − c =1 1 3 + 2 + = 0 a a b c = 2 Từ ( )
1 ,(2) ta có hệ phương trình: a + b + c = − ⇔ b = ⇒ f (x) 1 3 3 1 0
= x − x 2 2 a b c 1 − + − = 3 c = − 2 x = 0
f (x) = 0 ⇔ x = − 3 x = 3 1 1 4 2 1 3 3 x 3x 3
S = ∫ x − x +1 dx = − + x = 1 2 2 8 4 8 + Từ đồ thị ta có: 0 0
⇒ 2S + 8S = 4 . 2 1 3 3 4 2 1 3 3 x 3x 1 S = −
∫ x + x dx = − + = 2 2 2 8 4 2 1 1
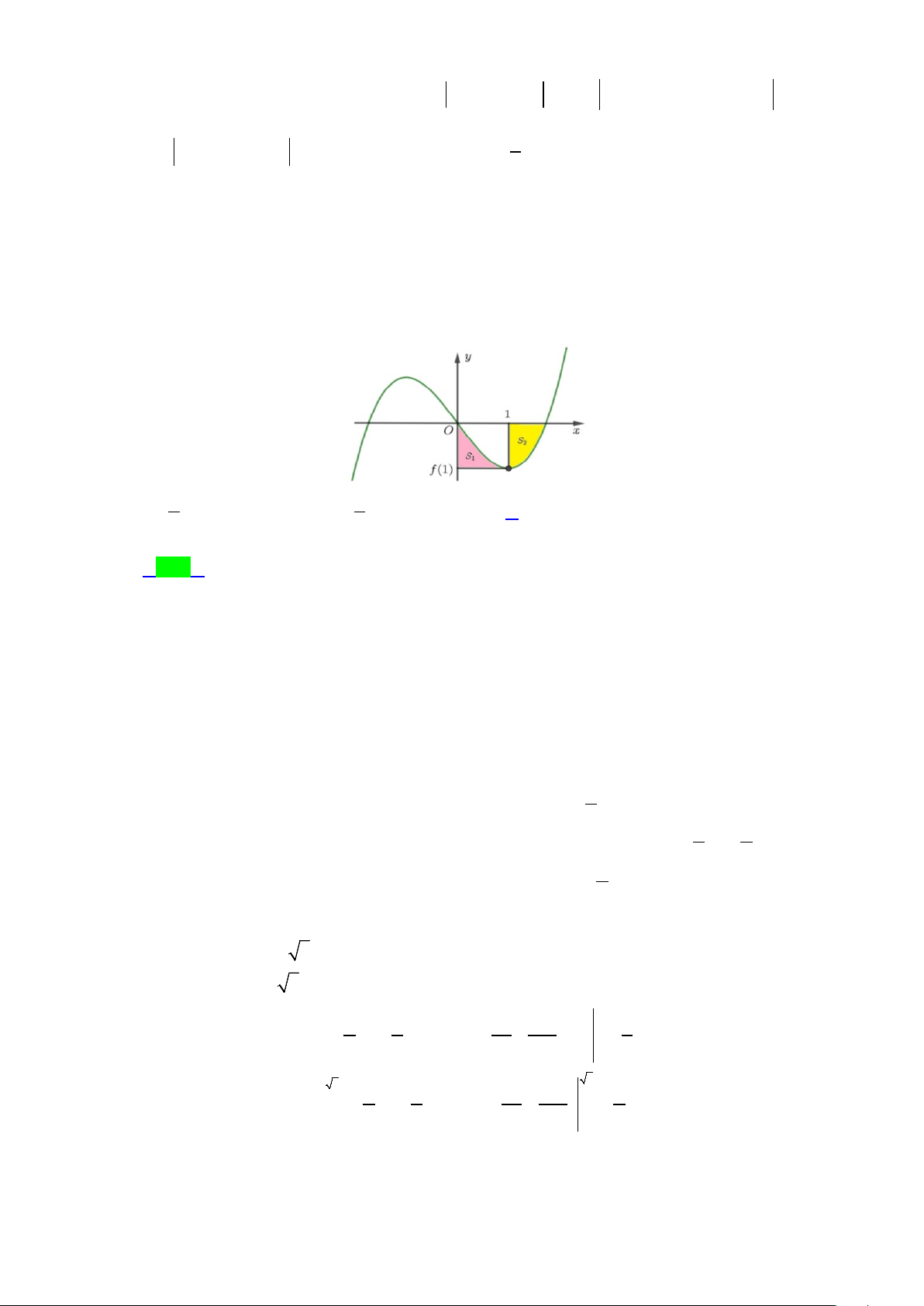
Câu 41.4. Cho hàm số y = f (x) . Đồ thị y = f ′(x) trên [ 3
− ;0] như hình vẽ sau (phần đường cong của đồ
thị là một phần của parabol 2
y = ax + bx + c ). Trang 13/54 - WordToan 1 f (ln x) Cho 2 dx = ∫
, giá trị f (0) bằng − x 3 3 e A. 1. B. 7 − . C. 2 . D. 14 . 9 9 Lời giải Chọn D - Xét 2
y = ax + bx + c , đồ thị đi qua 3 điểm có tọa độ ( 3 − ;0),( 2 − ; ) 1 ,( 1 − ;0) ta có: 9
a − 3b + c = 0 a = 1 − 2
4a − 2b + c =1 ⇔ b = 4
− ⇒ y = −x − 4x − 3 ⇒ f ′(x) 2
= −x − 4x − 3 trên 3 − ≤ x ≤ 0 a b c 0 − + = c = 3 −
- Xét y = ax + b , đồ thị hàm số đi qua 2 điểm có tọa độ ( 1; − 0),(0;2) ta có: −a + b = 0 a = 2 ⇔
⇒ y = 2x + 2 ⇒ f ′(x) = 2x + 2 trên 1 − < x ≤ 0 b = 2 b = 2 3 2
−x − 4x − 3, 3 − ≤ x ≤ 1 − x 2 −
− 2x − 3x + C , 3 − ≤ x ≤ 1 −
Khi đó: f ′(x) = , suy ra f (x) 1 = 3 2x + 2, 1 − ≤ x ≤ 0 2
x + 2x + C , 1 − ≤ x ≤ 0 2 1 f (ln x) Xét: 2 dx = ∫ − x 3 3 e
Đặt t = ln x , 3 x e− = ⇒ t = 3,
− x =1⇒ t = 0 Khi đó 0 0 1 − 0 1 − 3 0 f
∫ (t)dt = f
∫ (x)dx = f
∫ (x)dx+ f ∫ (x) x 2
dx = ∫ − −2x −3x +C dx + ∫ ( 2x + 2x +C dx 1 2 ) − − − − − 3 3 3 3 1 3 1 − 4 1 − 2 0 2 2 = + C x + − + C x = + C
− + 3C + 0 + C = + 2C + C . 1 3 − 2 ( 1 − 1 1 ) ( 2 ) 1 2 3 3 3 3 Theo đề bài: 2 2
+ 2C + C = ⇒ 2C + C = 0 1 . 1 2 1 2 ( ) 3 3
Mặt khác hàm số f (x) liên tục tại x = 1 − nên f (x) = f (x) 4 7 lim lim ⇔ + C = 1
− + C ⇒ C − C = − 2 + − 1 2 1 2 ( ) x→ 1 − x→ 1 − 3 3 3 7 x 2 7 C = − 1 −
− 2x − 3x − , 3 − ≤ x ≤ 1 − Từ ( ) 1 , (2) ta có: 9 ⇒ f (x) 3 9 = 14 2 14 C = 2 x + 2x + , 1 − ≤ x ≤ 0 9 9 Trang 14/54 - WordToan Suy ra: f ( ) 2 14 14 0 = 0 + 2.0 + = . 9 9
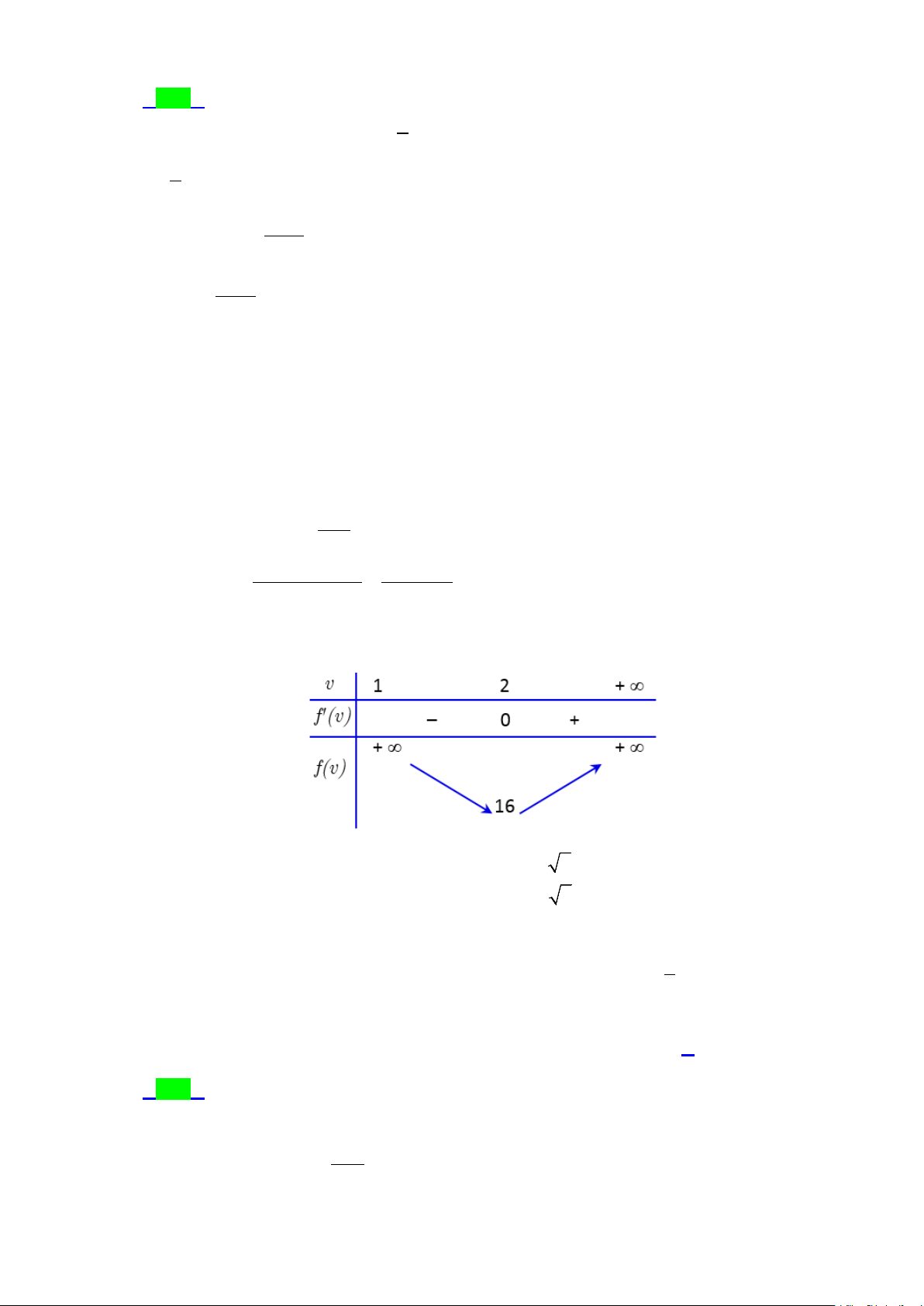
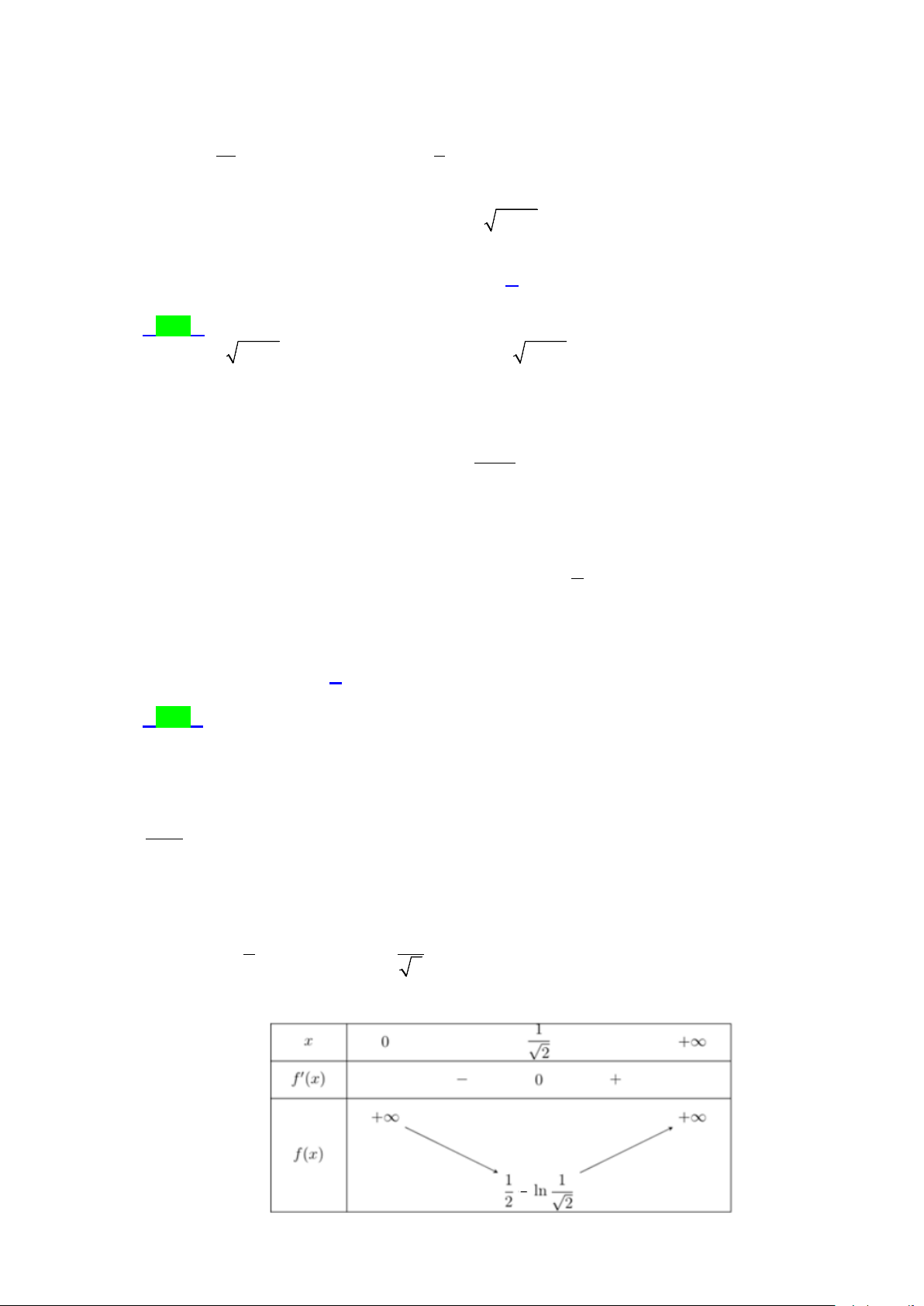
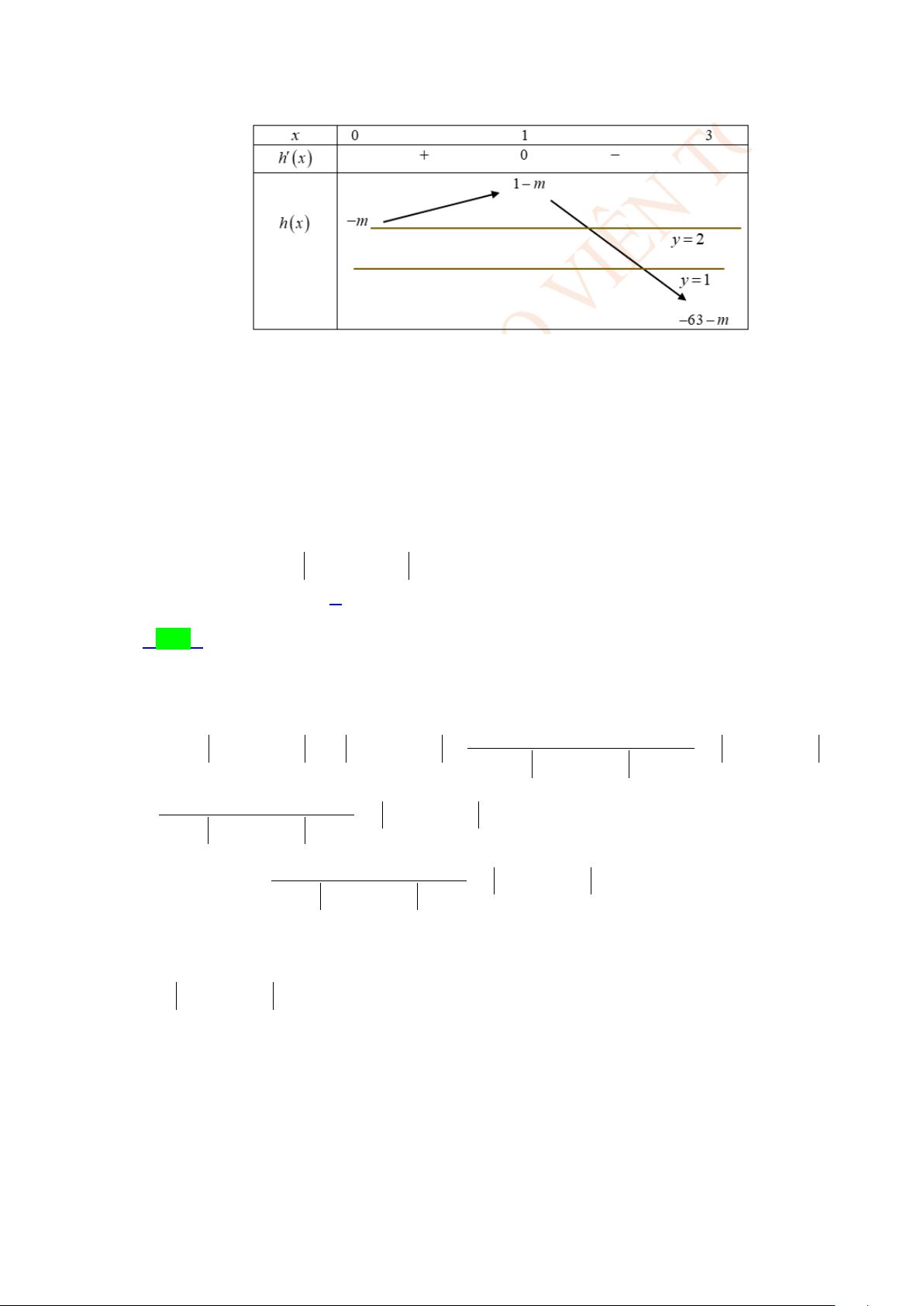
Câu 41.5: Xét f (x) 4 2
= ax + bx + c(a, ,
b c ∈,a > 0) sao cho đồ thị hàm số y = f (x) có ba điểm cực trị là ,
A B và C (2;− )
1 . Gọi y = g (x) là hàm số bậc hai có đồ thị đi qua ba điểm ,
A B và C . Khi
hình phẳng giới hạn bởi đồ thị của hai hàm số y = f (x), y = g (x) và hai đường thẳng 2
x = 0, x = 2 có diện tích bằng 64 , tích phân f
∫ (x)dx bằng 15 0 A. 226 . B. 25 . C. 17 − . D. 226 − . 15 13 15 5 1 Lời giải Chọn A
Dễ thấy f (′x) có ba nghiệm x = 0, x = 2, x = 2 − suy ra 2
f (′x) = 4ax(x − 4). Từ đó ta có 4 2
f (x) = ax −8ax + c .
Đồ thị hàm số y = f (x) đi qua điểm C (2;− ) 1 nên ta có: 1
− = 16a − 32a + c ⇔ c =16a −1.
Mặt khác, từ giả thiết đồ thị hàm số y = f (x) và y = g(x) cắt nhau tại hai điểm có hoành độ x = 2
± và tiếp xúc tại điểm có hoành độ x = 0 nên 2 2
f (x) − g(x) = ax (x − 4) .
Từ hình phẳng giới hạn bởi đồ thị của hai hàm số y = f (x), y = g (x) và hai đường thẳng 2 64
x = 0, x = 2 có diện tích bằng 64 ta có phương trình 2 2
ax (x − 4) dx = 15 ∫ . 15 0 2 4 2 64
⇔ a x − 4x dx = ∫
⇔ a =1 ⇒c =15 ⇒ f (x) 4 2 = x −8x +15 . 15 0 2 2
Ta có: f (x)dx = ( 4 2 x − x + ) 226 8 15 dx = ∫ ∫ . 15 0 0
Câu 41.6: Xét f (x) 4 2
= ax + bx + c(a, ,
b c ∈,a < 0) sao cho đồ thị hàm số y = f (x) có ba điểm cực trị là , A B và C (2; )
1 . Gọi y = g (x) là hàm số bậc hai có đồ thị đi qua ba điểm ,
A B và C . Khi
hình phẳng giới hạn bởi đồ thị của hai hàm số y = f (x), y = g (x) và hai đường thẳng 2
x = 0, x = 2 có diện tích bằng 64 , tích phân f
∫ (x)dx bằng 15 0 A. 226 . B. 25 . C. 17 − . D. 226 − . 15 13 15 5 1 Lời giải Chọn D
Dễ thấy f (′x) có ba nghiệm x = 0, x = 2, x = 2 − suy ra 2
f (′x) = 4ax(x − 4). Từ đó ta có 4 2
f (x) = ax −8ax + c .
Đồ thị hàm số y = f (x) đi qua điểm C (2; )
1 nên ta có: 1 =16a − 32a + c ⇔ c =16a +1.
Mặt khác, từ giả thiết đồ thị hàm số y = f (x) và y = g(x) cắt nhau tại hai điểm có hoành độ x = 2
± và tiếp xúc tại điểm có hoành độ x = 0 nên 2 2
f (x) − g(x) = ax (x − 4) .
Từ hình phẳng giới hạn bởi đồ thị của hai hàm số y = f (x), y = g (x) và hai đường thẳng 2 64
x = 0, x = 2 có diện tích bằng 64 ta có phương trình 2 2
ax (x − 4) dx = 15 ∫ . 15 0 2 4 2 64
⇔ −a x − 4x dx = ∫ ⇔ a = 1 − ⇒c = 15 − ⇒ f (x) 4 2
= −x + 8x −15 15 0 Trang 15/54 - WordToan 2 2
Ta có: f (x)dx = ( 4 2 −x + x − ) 226 8 15 dx = − ∫ ∫ . 15 0 0
Câu 41.7: Cho hai hàm số f (x) 4 3 2
= ax + bx + cx + 3x và g (x) 3 2
= mx + nx − x, với a,b,c, , m n ∈ . Biết
hàm số y = f (x) − g (x) có ba điểm cực trị là 1,
− 2 và 3. Diện tích hình phẳng giới hạn bởi
hai đường y = f ′(x) và y = g′(x) bằng A. 32 ⋅ B. 71⋅ C. 71⋅ D. 64 ⋅ 3 9 6 9 Lời giải Chọn B
Ta có : f ′(x) 3 2
= 4ax + 3bx + 2cx + 3 và g′(x) 2
= 3mx + 2nx −1.
Suy ra: h′(x) = f ′(x) − g′(x) = 0 có 3 nghiệm phân biệt là 1, − 2 và 3.
Nên f ′(x) − g′(x) = 4a(x + )
1 (x − 2)(x −3) (∗).
Thay x = 0 vào hai vế của (*) ta được: f ′( ) − g′( ) 1 0 0 = 4 ⇔ a = . 6 3
Vậy diện tích hình phẳng giới hạn: 2
S = ∫ (x + )1(x −2)(x −3) d 71 x = . − 3 9 1
Câu 41.8: Cho hàm số ( ) 3 2
f x = x + ax + bx + c với a , b , c là các số thực. Biết hàm số
g (x) = f (x) + f ′(x) + f ′′(x) có hai giá trị cực trị là 5
− và 3. Diện tích hình phẳng giới hạn bởi f (x) các đường y =
và y =1 bằng g (x) + 6 A. 2ln3. B. ln 2 . C. ln15. D. 3ln 2 . Lời giải Chọn A ( ) 3 2
f x = x + ax + bx + c ⇒ f ′(x) 2
= 3x + 2ax + b , f ′′(x) = 6x + 2a , f ′′′(x) = 6 .
g (x) = f (x) + f ′(x) + f ′′(x) ⇒ g′(x) = f ′(x) + f ′′(x) + f ′′′(x) = f ′(x) + f ′′(x) + 6. x = x
Do g (x) có hai cực trị là 5
− và 3 nên g′(x) 1 = 0 ⇔ với g (x = 5 − , g (x = 3. 2 ) 1 ) x = x2 f (x)
− f ′(x) − f ′′(x) − 6 x = x Ta có: = ⇔ = 1 ⇔ . g (x) 1 + g (x) 0 6 + 6 x = x2 f (x)
Diện tích hình phẳng giới hạn bởi các đường y = và y =1 là g (x) + 6 2
x f (x) 2 x
− f ′(x) − f ′′(x) − 6 S = ∫ − x = x g x + ∫ g x + x ( ) 1 d x ( ) d 6 6 1 1 2 x 1 x = d g x + 6 = ∫ (ln g x +6) 2 g x + x ( ) ( ( ) ) ( ) 6 1 x 1
= ln g (x + 6 − ln g x + 6 = ln1− ln9 = 2ln3 . 2 ) ( 1)
Câu 41.9: Xét f (x) 4 2
= ax + bx + c(a, ,
b c ∈,a > 0) sao cho đồ thị hàm số y = f (x) có ba điểm cực trị là , A B và 3 C 1; −
. Gọi y = g (x) là hàm số bậc hai có đồ thị đi qua ba điểm ,
A B và C . Khi 5 Trang 16/54 - WordToan
hình phẳng giới hạn bởi đồ thị của hai hàm số y = f (x), y = g (x) và hai đường thẳng x = 0, x =1 1
có diện tích bằng 2 , tích phân f
∫ (x)dx bằng 5 0 A. 27 . B. 44 . C. 1. D. 94 . 20 15 30 Lời giải Chọn C
Phương trình hàm số bậc hai đi qua 3 điểm ,
A B và C . là: 2
y = g(x) = mx + nx + p .
Hàm số bậc hai đi qua điểm (0
A : c) suy ra p = c 2 −
Hàm số bậc hai có trục tung là trục đối xứng n b b = 0 và đi qua C ;− + c suy ra 1 m = b 2 a 4a 2 . Suy ra 1 2
y = g(x) = bx + c 2 3 3 f (1) = −
a + b + c = − Ta có: 5 ⇔ 5 (II) f '(1) = 0
4a + 2b = 0 1 Theo đề ta có: 2
g(x) − f (x).dx = ∫ 5 0 1 4 1 2 2 a b 2 ⇔
−ax − bx .dx = ⇔ − − = (III) ∫ 2 5 5 6 5 0 Từ (II) và (III) ta có: 12 a = 3:b = 6 − : c = 5 1 Vậy f ∫ (x)dx=1. 0
Câu 41.10: Xét f (x) 4 2
= ax + bx + c(a,b,c ∈,a < 0) sao cho đồ thị hàm số y = f (x) có ba điểm cực trị là , A B và 7 2; 2 C − .
y = g x là hàm số bậc hai có đồ thị đi qua ba điểm , A B và C . 7 Gọi ( )
Khi hình phẳng giới hạn bởi đồ thị của hai hàm số y = f (x), y = g (x) và hai đường thẳng 2 x = 2,
− x = 0 có diện tích bằng 16 , tích phân f
∫ (x)dx bằng 15 0 A. 27 . B. 44 . C. 362 . D. 94 . 20 15 105 30 Lời giải Chọn C
Phương trình hàm số bậc hai đi qua 3 điểm ,
A B và C . là: 2
y = g(x) = mx + nx + p .
Hàm số bậc hai đi qua điểm (0
A : c) suy ra p = c 2 −
Hàm số bậc hai có trục tung là trục đối xứng n b b = 0 và đi qua C ;− + c suy ra 1 m = b 2 a 4a 2 . Suy ra 1 2
y = g(x) = bx + c 2 Trang 17/54 - WordToan 3 27 f (2) = − 16
a + 4b + c = Ta có: 5 ⇔ 7 (II) f '(2) = 0 8 a +b = 0 0 Theo đề ta có: 16
g(x) − f (x).dx = ∫ − 15 2 0 4 1 2 16 4a b 2 ⇔
ax + bx .dx = ⇔ + 2 = (III) ∫ − 2 15 5 6 15 2 Từ (II) và (III) ta có: 1 1
a = − :b = 2 : c = − 4 7 2 Vậy f (x) 36 d 2 x= ∫ 105 0
Câu 41.11: Xét f (x) 4 2
= ax + bx + c(a,b,c ∈,a < 0) sao cho đồ thị hàm số y = f (x) có ba điểm cực trị là , 2 1 A B và C ;
. Gọi y = g (x) là hàm số bậc hai có đồ thị đi qua ba điểm , A B và C 2 0 2
. Khi hình phẳng giới hạn bởi đồ thị của hai hàm số y = f (x), y = g (x) và hai đường thẳng 2 2 2 x = 0, x =
có diện tích bằng 2 , tích phân f (x)dx ∫ bằng 2 60 0 A. 27 . B. 44 . C. 2 − . D. 94 . 20 15 24 30 Lời giải Chọn C
Phương trình hàm số bậc hai đi qua 3 điểm ,
A B và C . là: 2
y = g(x) = mx + nx + p .
Hàm số bậc hai đi qua điểm (0
A : c) suy ra p = c 2 −
Hàm số bậc hai có trục tung là trục đối xứng n b b = 0 và đi qua C ;− + c suy ra 1 m = b 2 a 4a 2 . Suy ra 1 2
y = g(x) = bx + c 2 2 1 f ( ) = 1 1 1
a + b + c = Ta có: 2 20 ⇔ 4 2 20 (II) 2 f '( ) = 0 a +b = 0 2 1 Theo đề ta có: 2
g(x) − f (x).dx = ∫ 5 0 2 2 4 1 2 2 a b 1 ⇔ ax bx .dx = ⇔ + = (III) ∫ 2 60 40 24 60 0 Từ (II) và (III) ta có: 1 a 1:b 1: c − = − = = 5 2 2 Vậy f (x) 2 dx= − ∫ 24 0 Trang 18/54 - WordToan
Câu 41.12: Xét f (x) 4 2
= ax + bx + c(a,b,c ∈ ,a > 0) sao cho đồ thị hàm số y = f (x) có ba điểm cực trị là , A B và 2 C 2; −
. Gọi y = g (x) là hàm số bậc hai có đồ thị đi qua ba điểm , A B và C 3
. Khi hình phẳng giới hạn bởi đồ thị của hai hàm số y = f (x), y = g (x) và hai đường thẳng 2
x = 0, x = 2 có diện tích bằng 2 2 , tích phân f (x)dx ∫ bằng 15 0 A. 27 . B. 44 . C. 2 2 − . D. 94 . 20 15 15 30 Lời giải Chọn C
Phương trình hàm số bậc hai đi qua 3 điểm ,
A B và C . là: 2
y = g(x) = mx + nx + p .
Hàm số bậc hai đi qua điểm (0
A : c) suy ra p = c 2 −
Hàm số bậc hai có trục tung là trục đối xứng n b b = 0 và đi qua C ;− + c suy ra 1 m = b 2 a 4a 2 . Suy ra 1 2
y = g(x) = bx + c 2 2 2 f ( 2) = −
4a + 2b + c = − Ta có: 3 ⇔ 3 (II) f '( 2) = 0 4a +b = 0 2 Theo đề ta có: 2
g(x) − f (x).dx = ∫ 5 0 2 4 1 2 2 2 4a b 2 ⇔
−ax − bx .dx = ⇔ − − = (III) ∫ 2 15 5 3 15 0 Từ (II) và (III) ta có: 1 1 a = :b = 1 − : c = 4 3 2 2 2
Vậy f (x)dx= − ∫ 15 0
Câu 41.13: Cho hàm số f (x) 4 3 2
= 3x + ax + bx + cx + d (a, ,
b c,d ∈ ) có ba điểm cực trị là 2 − , 1 − và
1. Gọi y = g (x) là hàm số bậc hai có đồ thị đi qua ba điểm cực trị của đồ thị hàm số y = f (x) .
Diện tích hình phẳng giới hạn bởi hai đường y = f (x) và y = g (x) bằng A. 500 . B. 36 . C. 2932 . D. 2948 . 81 5 405 405 Lời giải Chọn D x = 2 −
Theo đề ta có f (x) 3 2 12x 3ax 2bx c 0 ′ = + + + = ⇔ x = 1 − x = 1 Suy ra f ′(x) 3 2
= 12x + 3ax + 2bx + c =12(x + 2)(x + ) 1 (x − ) 3 2
1 =12x + 24x −12x − 4 2 . 3 a = 24 a = 8
Đồng nhất hệ số ta được 2b = − 2 1 ⇒ b = 6 − . c = 24 − c = 24 − Trang 19/54 - WordToan Suy ra f (x) 4 3 2
= 3x + 8x − 6x + 24x + d .
Theo đề, ta có đồ thị hàm số y = f (x) có ba điểm cực trị là ( 2; − 8 + d ) , ( 1; − 13+ d ) , (1; 1 − 9 + d ).
Gọi (P) là Parabol đi qua ba điểm ( 2; − 8) , ( 1; − 13) , (1; 1 − 9). Khi đó (P) 2 : y = 7
− x −16x + 4 . Suy ra g (x) 2 = 7
− x −16x + 4 + d . x = 2 − x = 1 −
Xét phương trình f (x) − g (x) 4 3 2
= 0 ⇔ 3x + 8x + x −8x − 4 = 0 ⇔ 2 . x = − 3 x =1
Diện tích hình phẳng giới hạn bởi hai đường y = f (x) và y = g (x) là 1 1
S = ∫ f (x)− g(x) 4 3 2 2948
dx = 3x + 8x + x −8x − 4 dx = ∫ . − − 5 40 2 2
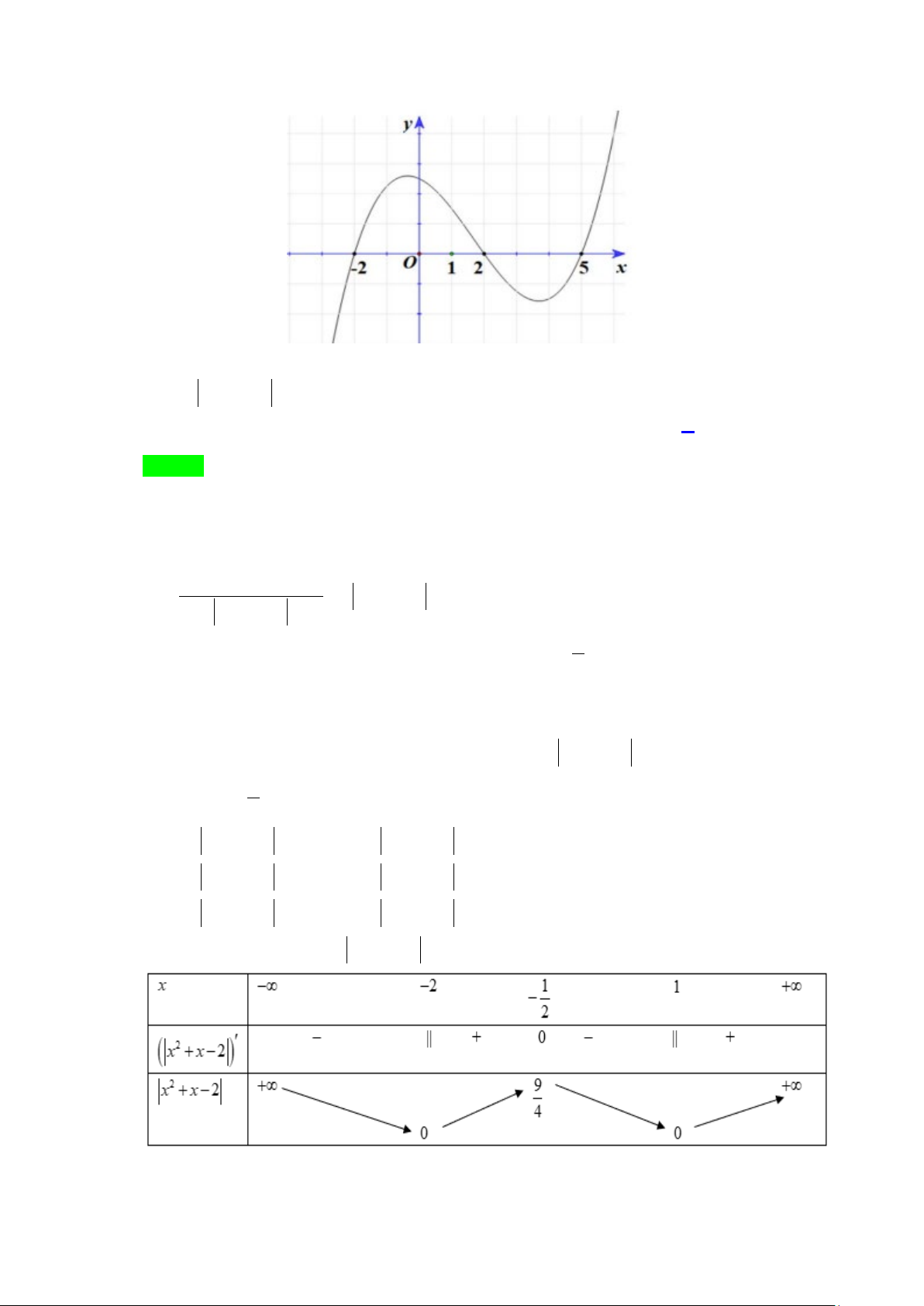
Câu 41.14: Cho hàm số 3 2
y = x + ax + bx + c (a,b,c∈) có đồ thị (C) và 2
y = mx + nx + p ( , m ,
n p ∈ ) có đồ thị (P) như hình vẽ. Tính diện tích hình phẳng giới hạn
bởi (C) và (P) có giá trị nằm trong khoảng nào sau đây? A. (0; ) 1 . B. (1;2) . C. (2;3). D. (3;4). Lời giải Chọn B
Căn cứ đồ thị ta thấy + Hàm số 3 2
y = x + ax + bx + c đạt cực trị tại x = 1 ± nên ta có y′( ) 1 = 0
2a + b + 3 = 0 a = 0 ⇔ ⇔ . y′ (− ) 1 = 0 2
− a + b + 3 = 0 b = 3 − + Hàm số 2
y = mx + nx + p đạt cực đại tại x = 1
− và (P) cắt (C) tại hai điểm có hoành độ x = 1 ± nên ta có 2 − m + n = 0 n = 2 − 1 a b c m n p + + + = + + ⇔ m = 1 − 1 a b c m n p − + − + = − + p − c = 1 1 1 Suy ra S = ( 2 3 2
mx + nx + p − x − ax − bx − c) x = ( 3 2
−x − x + x + ) 4 d 1 dx = ∈ ∫ ∫ (1;2). − − 3 1 1 Trang 20/54 - WordToan
Câu 41.15: Xét f (x) 4 2
= ax + bx + c(a,b,c ∈,a > 0) sao cho đồ thị hàm số y = f (x) có ba điểm cực trị là , A B và 3 C 1; −
. Gọi y = g (x) là hàm số bậc hai có đồ thị đi qua ba điểm , A B và C . 5
Khi hình phẳng giới hạn bởi đồ thị của hai hàm số y = f (x), y = g (x) và hai đường thẳng 1
x = 0, x =1 có diện tích bằng 2 , tích phân f
∫ (x)dx bằng 5 0 A. 1. B. -1. C 17 . − . D 17 . . 15 15 Lời giải Chọn A
Dễ thấy f (′x) có ba nghiệm x = 0, x =1, x = 1 − suy ra 2
f (′x) = 4ax(x −1) . Từ đó ta có 4 2
f (x) = ax − 2ax + c .
Mặt khác, từ giả thiết đồ thị hàm số y = f (x) và y = g(x) cắt nhau tại hai điểm có hoành độ x = 1
± và tiếp xúc tại điểm có hoành độ x = 0 nên 2 2
f (x) − g(x) = ax (x −1) .
Từ hình phẳng giới hạn bởi đồ thị của hai hàm số y = f (x), y = g (x) và hai đường thẳng 1 x 2
= 0, x =1 có diện tích bằng 2 ta có phương trình 2 2
ax (x −1) dx = 5 ∫ 5 0 1 ⇔ a ( 2 4 x − x ) 2 dx = ∫
⇔ a = 3 ⇒ f (x) 4 2 12 = 3x − 6x + 5 5 0 1 1 f ∫ (x) 4 2 12 dx 3x 6x ⇒ = − + dx = ∫ 1. 5 0 0
Câu 41.16: Xét f (x) 4 2
= ax + bx + c(a,b,c ∈,a > 0) sao cho đồ thị hàm số y = f (x) có ba điểm cực trị là ,
A B và C (1;− )
1 . Gọi y = g (x) là hàm số bậc hai có đồ thị đi qua ba điểm , A B và C .
Khi hình phẳng giới hạn bởi đồ thị của hai hàm số y = f (x), y = g (x) và hai đường thẳng 1
x = 0, x =1 có diện tích bằng 4 , tích phân f
∫ (x)dx bằng 5 0 A. 1. B. 3. C. 8 − . D. 8 . 15 15Lời giải Chọn B
Dễ thấy f '(x) có ba nghiệm x = 0, x =1, x = 1 − suy ra 2
f '(x) = 4ax(x −1) . Từ đó ta có 4 2
f (x) = ax − 2ax + c .
Mặt khác, từ giả thiết đồ thị hàm số y = f (x) và y = g(x) cắt nhau tại hai điểm có hoành độ x = 1
± và tiếp xúc tại điểm có hoành độ x = 0 nên 2 2
f (x) − g(x) = ax (x −1) .
Từ hình phẳng giới hạn bởi đồ thị của hai hàm số y = f (x), y = g (x) và hai đường thẳng 1 x 4
= 0, x =1 có diện tích bằng 4 ta có phương trình 2 2
ax (x −1) dx = 5 ∫ 5 0 1 1 1 ⇔ ( 2 4 − ) 4 a x x dx = ∫
⇔ a = 6 ⇒ f (x) 4 2
= 6x −12x + 5 ⇒ f
∫ (x)dx = ∫( 4 2
6x −12x + 5)dx = 3 5 0 0 0
Câu 41.17: Xét f (x) 4 2
= ax + bx + c(a,b,c ∈,a > 0) sao cho đồ thị hàm số y = f (x) có ba điểm cực trị là ,
A B và C (1;6) . Gọi y = g (x) là hàm số bậc hai có đồ thị đi qua ba điểm ,
A B và C . Khi Trang 21/54 - WordToan
hình phẳng giới hạn bởi đồ thị của hai hàm số y = f (x), y = g (x) và hai đường thẳng x = 0, x =1 1
có diện tích bằng 4 , tích phân 1 f
∫ (x)dx bằng 15 2 0 A. 1. B. 3. C. 53 − . D. 53 . 5 1 15Lời giải Chọn D
Dễ thấy f (′x) có ba nghiệm x = 0, x =1, x = 1 − suy ra 2
f (′x) = 4ax(x −1) . Từ đó ta có 4 2
f (x) = ax − 2ax + c .
Mặt khác, từ giả thiết đồ thị hàm số y = f (x) và y = g(x) cắt nhau tại hai điểm có hoành độ x = 1
± và tiếp xúc tại điểm có hoành độ x = 0 nên 2 2
f (x) − g(x) = ax (x −1) .
Từ hình phẳng giới hạn bởi đồ thị của hai hàm số y = f (x), y = g (x) và hai đường thẳng 1 x 4
= 0, x =1 có diện tích bằng 4 ta có phương trình 2 2
ax (x −1) dx = 15 ∫ 15 0 1 ⇔ a ( 2 4 x − x ) 4 dx = ∫
⇔ a = 2 ⇒ f (x) 4 2 = 2x − 4x + 8 15 0 1 1 1 ⇒
f (x)dx = ( 4 2 x − x + ) 53 2 4 dx = ∫ ∫ 2 15 0 0
Câu 41.18: Xét f (x) 4 2
= ax + bx + c(a,b,c ∈,a > 0) sao cho đồ thị hàm số y = f (x) có ba điểm cực trị là , A B và C (1; 5
− ). Gọi y = g (x) là hàm số bậc hai có đồ thị đi qua ba điểm , A B và C .
Khi hình phẳng giới hạn bởi đồ thị của hai hàm số y = f (x), y = g (x) và hai đường thẳng 1
x = 0, x =1 có diện tích bằng 14 , tích phân f
∫ (x)dx bằng 15 0 A. 5.
B. 3. C. 23 . D. 53 . 15 15Lời giải Chọn C
Dễ thấy f '(x) có ba nghiệm x = 0, x =1, x = 1 − suy ra 2
f '(x) = 4ax(x −1) . Từ đó ta có 4 2
f (x) = ax − 2ax + c .
Mặt khác, từ giả thiết đồ thị hàm số y = f (x) và y = g(x) cắt nhau tại hai điểm có hoành độ x = 1
± và tiếp xúc tại điểm có hoành độ x = 0 nên 2 2
f (x) − g(x) = ax (x −1) .
Từ hình phẳng giới hạn bởi đồ thị của hai hàm số y = f (x), y = g (x) và hai đường thẳng 1 x 14
= 0, x =1 có diện tích bằng 14 ta có phương trình 2 2
ax (x −1) dx = 15 ∫ 15 0 1 ⇔ ( 2 4 − ) 14 a x x dx = ∫
⇔ a = 7 ⇒ f (x) 4 2 = 7x −14x + 2 15 0 0 0
⇒ f (x)dx = ( 4 2 x − x + ) 23 7 14 2 dx = ∫ ∫ − − 15 1 1
Câu 41.19: Xét f (x) 4 2
= ax + bx + c(a, ,
b c ∈,a > 0) sao cho đồ thị hàm số y = f (x) có ba điểm cực trị là , A B và C (1; 5
− ). Gọi y = g (x) là hàm số bậc hai có đồ thị đi qua ba điểm , A B và C . Trang 22/54 - WordToan
Khi hình phẳng giới hạn bởi đồ thị của hai hàm số y = f (x), y = g (x) và hai đường thẳng 0
x = 0, x =1 có diện tích bằng 14 , tích phân f
∫ (x)dx bằng 15 1 − A. 5.
B. 3. C. 23 . D. 53 . 15 15Lời giải Chọn C
Dễ thấy f '(x) có ba nghiệm x = 0, x =1, x = 1 − suy ra 2
f '(x) = 4ax(x −1) . Từ đó ta có 4 2
f (x) = ax − 2ax + c .
Mặt khác, từ giả thiết đồ thị hàm số y = f (x) và y = g(x) cắt nhau tại hai điểm có hoành độ x = 1
± và tiếp xúc tại điểm có hoành độ x = 0 nên 2 2
f (x) − g(x) = ax (x −1) .
Từ hình phẳng giới hạn bởi đồ thị của hai hàm số y = f (x), y = g (x) và hai đường thẳng 1 x 14
= 0, x =1 có diện tích bằng 14 ta có phương trình 2 2
ax (x −1) dx = 15 ∫ 15 0 1 ⇔ ( 2 4 − ) 14 a x x dx = ∫
⇔ a = 7 ⇒ f (x) 4 2 = 7x −14x + 2 15 0 0 0
⇒ f (x)dx = ( 4 2 x − x + ) 23 7 14 2 dx = ∫ ∫ − − 15 1 1
Câu 41.20: Xét f (x) 4 2
= ax + bx + c(a, ,
b c ∈,a > 0) sao cho đồ thị hàm số y = f (x) có ba điểm cực trị là , A B và C (2; 1
− 2) . Gọi y = g (x) là hàm số bậc hai có đồ thị đi qua ba điểm , A B và C .
Khi hình phẳng giới hạn bởi đồ thị của hai hàm số y = f (x), y = g (x) và hai đường thẳng 1
x = 0, x = 2 có diện tích bằng 64 , tích phân f
∫ (x)dx bằng 15 0 A. 5.
B. 3. C. 26 . D. 23 . 15 15Lời giải Chọn D
Dễ thấy f (′x) có ba nghiệm x = 0, x = 2, x = 2 − suy ra 2
f (′x) = 4ax(x − 4). Từ đó ta có 4 2
f (x) = ax −8ax + c .
Mặt khác, từ giả thiết đồ thị hàm số y = f (x) và y = g(x) cắt nhau tại hai điểm có hoành độ x = 2
± và tiếp xúc tại điểm có hoành độ x = 0 nên 2 2
f (x) − g(x) = ax (x − 4) .
Từ hình phẳng giới hạn bởi đồ thị của hai hàm số y = f (x), y = g (x) và hai đường thẳng 2
x = 0, x = 2 có diện tích bằng 64 ta có phương trình 2 2 64
ax (x − 4) dx = 15 ∫ 15 0 2 1 1 ⇔ ( 2 4 − ∫ ) 6 4 4 a x x dx = ⇔ a =1 23 ⇒ f (x) 4 2
= x −8x + 4 ⇒ f
∫ (x)dx = ∫( 4 2
x −8x + 4)dx = 15 15 0 0 0
CÂU TƯƠNG TỰ CÂU 42 ĐỀ THAM KHẢO 2024
Câu 42.1: Cho hai số phức z , z ≠ 2 thỏa mãn các điều kiện z + = 2 , z 2 2
là số thuần ảo và z + 2z = 4 1 2 1 z − 2 1 2 2
. Giá trị của 2z − z bằng 1 2 A. 2 6 . B. 6 . C. 3 6 . D. 8 . Lời giải Trang 23/54 - WordToan Chọn A
Đặt z = a + bi, a,b ∈ , 2 ( ) Ta có:
z + 2 (a + 2) + bi (a + 2) + bi
(a − 2) − bi ( 2 2
a − 4 + b ) ((a − 2)b −(a + 2)b)i 2 = = = +
z − 2 (a − 2) + bi (a − 2)2 2 + b (a − 2)2 2 + b (a − 2)2 2 2 + b z + 2 2 là số thuần ảo 2 2 ⇒ a + b = 4 2 ⇒ z = 4. z − 2 2 2 2
z + 2z = 4 ⇒16 = z + 2z ⇔ z + 2z z + 2z =16 1 2 1 2 ( 1 2 ) ( 1 2 ) 2 2
⇒ z + 4 z + 2 z z + z z =16 ⇒ (z z + z z = 2 − 1 2 2 1 ) 1 2 ( 1 2 2 1) Ta có 2
2z − z = 2z − z 2z − z = 4 z + z − 2 z z + z z = 24 1 2 ( 2 ) ( 2 2 1 1 2 ) 1 2 ( 1 2 2 1)
⇒ 2z − z = 2 6 1 2
Câu 42.2: Cho M là tập hợp các số phức z thỏa 2z −i = 2 + iz . Gọi z , z là hai số phức thuộc tập hợp 1 2
M sao cho z − z = 3 . Tính giá trị của biểu thức P = z + z . 1 2 1 2 A. P = 3 . B. P =1. C. 1 P = . D. 3 P = . 2 2 Lời giải Chọn B
Đặt z = x + yi với x , y ∈ .
Ta có: z − i = + iz ⇔ x + ( y − ) 2 2 2 2 2 2
1 i = 2 − y + xi ⇔ x + y =1.
Suy ra tập hợp các điểm biểu diễn số phức z trên mặt phẳng phức là đường tròn ( ) ;1 O ⇒ z = z =1. 1 2 Ta có: 2 2
z + z + z − z = 2( 2 2 z + z ) 2
⇒ P =1⇒ P =1. 1 2 1 2 1 2
Câu 42.3: Xét hai số phức z , z thỏa mãn z = z = 2 và 2z − 3z = 2 7 . Giá trị của 2z − z bằng: 1 2 1 2 1 2 1 2 A. 2 3 . B. 12 . C. 2 7 . D. 28 . Lời giải Chọn A Ta có: 2 2 2 2
2z − 3z − 3 2z − z = 4 z + 9 z − 6(z z + z z ) 2 2
− 12 z − 3 z + 6 z z + z z 1 2 1 2 1 2 1 2 2 1 1 2 ( 1 2 2 1) 2
⇔ 28 − 3 2z − z = 32
− + 24 ⇔ 2z − z = 12 1 2 1 2
Câu 42.4: Cho số phức 12
z thay đổi thoả mãn z = z − 6 − 6i . Gọi S là tập hợp các số phức w z = . Biết rằng 2 z
w ,w là hai số thuộc S sao cho w − w = 2 , mô đun của số phức w + w − 2 − 2i bằng 1 2 1 2 1 2 A. 4. B. 2. C. 2 2 . D. 1. Lời giải Chọn B
12z 12z 12z 12 w 12 = = = = ⇒ z = 2 2 z z . z z z w
Theo giả thiết ta có z = z − 6 − 6i 12 12 ⇒ = − 6 − 6i w w Trang 24/54 - WordToan 12
⇔ 12 = 12 − (6 + 6i)w ⇔
= 1 − i − w 6 2
⇔ w − 1− i = 2
Đặt t = w −1− i ⇒ t = 2
t − t = w − w = 2 1 2 1 2 2 2
⇒ w + w − 2 − 2i = t + t = 2( 2 2 t + t − t − t = 2(2 + 2) − 4 = 4 1 2 ) 2 1 2 1 2 1 2
⇒ w + w − 2 − 2i = 2 . 1 2
Câu 42.5: Xét các số phức z, w thỏa mãn z = 2 và (w −3+ 4i)(w +3+ 4i) là số thuần ảo. Khi
z − w = 3 2 , giá trị của 2z + w bằng A. 41 . B. 47 . C. 63 . D. 4 3 . Lời giải Chọn C
Đặt w = a + bi,(a,b ∈ ), P = 2z + w Ta có:
(w −3+ 4i)(w +3+ 4i) = (a −3+(b+ 4)i)(a +3+( b − + 4)i)
(w −3+ 4i)(w +3+ 4i)là số thuần ảo 2 2
⇒ a + b = 25 ⇒ w = 5. 2
z − w = 3 2 ⇒18 = z − w = (z − w)(z − w) 2 ⇒ = − ( + ) 2 18 z zw zw + w
⇔ 18 = 4 − (zw + zw) + 25 ⇒ zw + zw =11 2 2
P = 2z + w = (2z + w )( 2z + w) 2
= z + (zw + zw) 2 4 2 + w =16 + 22 + 25 = 63 ⇒ P = 63 .
Câu 42.6: Xét các số phức z, w thỏa mãn z −1+ 2i =1 và (w −1+ 2i)(w −1− 2i) = 4. Khi z − w = 2 , giá
trị của z + w − 2 + 4i bằng A. 2 3 . B. 5 . C. 6 . D. 2 3 . Lời giải Chọn C
Đặt u = z −1+ 2i suy ra z −1+ 2i = 1 ⇔ u = 1
Đặt v = w −1+ 2i suy ra (w −1+ 2i)(w −1− 2i) 2 = 4 ⇔ .
v v = 4 ⇔ v = 4 ⇔ v = 2 .
z − w = 2 ⇔ ( z −1+ 2i) − (w −1+ 2i) ⇔ u − v = 2 . 2
⇒ = u − ( + v) 2 4
uv u + v ⇒ uv + uv =1 2 2
P = z + w − 2 + 4i = (z − + i) + (w − + i) 2 2 1 2 1 2 = u + v 2 2
= u + v + uv + uv = 6 .
Vậy P = z + w − 2 + 4i = 6 1z = z2 = 3 z =1 Câu 42.7: Cho ba số phức 2 1
z , z2 , 3z thỏa mãn điều kiện 1z = z2 3z
, với M = z2 − 3 z − 3 z − 1z . 6 + 2 1 z − z2 = 2 Tính 2 M . Trang 25/54 - WordToan
A. 3+ 6 − 3 − 2 . B. 6 − 3 − 2 . C. 6 + 2 − 2 . D. − 6 − 2 + 2 . 2 2 Lời giải Chọn A Ta có 2 2 z − z + z + z = 2( 2 2 1 2 1 2 1 z + z2 ) ( 6 + 2)2 ( 6 + 2)2 2
⇔ 1z + z2 = 4 −
⇔ 1z + z2 = 4 − 4 4 2 Khi đó, 1 z M = z2 − 3 z − 3
z − 1z = z2 − − 1z 3 z − 1z z2 2 2 z2 − 1z 2 1
z − z2 . 1z + z2
z − z . z + z = − 1z 3 z − 1z = − 1z 3 z − z2 3 z 1 2 1 2 =
− z . z − z z 3 1 2 2 z2 z2 ( + + )2 6 2 6 2 6 + 2 − 6 − 2 + 2 = . 4 − − = . 2 4 2 2 Khi đó 2 M = 3+ 6 − 3 − 2 .
Câu 42.8: Gọi z , z là hai trong các số phức z thỏa mãn z − 3+ 5i = 5 và z − z = 6 . Tìm bình phương 1 2 1 2
của môđun số phức w = z + z − 6 +10i . 1 2 A. 16. B. 36. C. 8 . D. 64 . Lời giải Chọn D
Giả sử z = x + yi với (x, y ∈) . Khi đó M ( ;
x y) là điểm biểu diễn số phức z trên mặt phẳng tọa độ Oxy .
Ta có: z − 3+ 5i = 5 ⇒ M ( ;
x y) thuộc đường tròn (C) có tâm I (3; 5
− ) , bán kính R = 5. w Xét + +
w = z + z − 6 +10i z z 6 10i z z 1 2 1 2 ⇒ = − + = − 3+ 5i . 1 2 2 2 2 2 2 Gọi +
A , B lần lượt biểu diễn z , z ; Khi đó điểm
z z là trung điểm của 1 2 K biểu diễn 1 2 AB . 2
Ta có z − z = 6 ⇒ AB = 6 , KB = 3. 1 2 w Do z + z 1 2 =
− 3+ 5i nên w = 2IK . 2 2
Vì IK ⊥ AB nên 2 2
IK = IB − KB = 4.
Vậy w = 2IK = 8. Khi đó bình phương của môđun số phức w = z + z − 6 +10i bằng 64. 1 2 Trang 26/54 - WordToan
Câu 42.9: Xét các số phức w +
z, w(w ≠ 4) thỏa mãn z = 3 và
4 là số thuần ảo. Khi z −w = 13, giá trị w − 4
của 3z + 2w bằng A. 74 . B. 73 . C. 219 . D. 217 . Lời giải Chọn D w+4 4 − (1+ ai) +) Ta có: = ai ⇒ w = ⇒ w = 4 w − 4 1− ai +)
z − w = 13 ⇒ (z − w)(z − w) = (z − w)(z − w) =13 2
⇒ z − (zw + zw) 2
+ w =13 ⇒ zw + zw =12 +) 2 2
P = z + w = ( z + w)( z + w) 2
= z + (zw + zw) 2 2 3 2 3 2 3 2 9 6
+ 4 w = 9.9 + 6.12 + 4.4 = 217 ⇒ P = 217 .
Câu 42.10: Cho hai số phức z , z thỏa mãn các điều kiện z = 2,(w + i)(w+i)+(4+i)(1+ 7i) là số 1 2
thuần ảo và z + 2w = 4. Giá trị của 2z − w bằng A. 2 6 . B. 6 . C. 3 6 . D. 8 . Lời giải Chọn A
Gọi w = a + bi , ( a , b∈ )
(w+i)(w+i)+( +i)( + i) = ww− +i(w+ w) 2 2 4 1 7 . 1
− 3+ 29i = a + b − 4 + (2a + 29)i
(w+i)(w+i)+(4+i)(1+7i) là số thuần ảo 2 2
⇒ a + b − 4 = 0 ⇒ w = 2
+) z + 2w = 4 ⇒ (z + 2w)(z + 2w) = (z + w)(z + 2w) =16 2
⇒ z + (zw + zw) 2 2
+ 4 w =16 ⇒ zw + zw = 2 − +) 2
2z − w = (2z − w)( 2z − w) 2
= 4 z − 2(zw + zw) 2 + w = 4.4 − 2.( 2 − ) + 4 = 24
⇒ 2z − w = 2 6 .
Câu 42.11: Cho hai số phức z ; z
z − 2i = i −1 z +1+ i
w − 2i = i +1 w +1− i 1 2 thỏa mãn: ( ) ; ( ) . Biết
z − w =1, tính z + w A. 3 2 . B. 2 2 . C. 7 . D. 3. Lời giải Chọn C
z = a + bi Đặt:
( a, ,bc,d ∈).
w = c + di Ta có:
z − 2i = (i − )
1 z +1+ i ⇔ z − 2i = (i − ) 1 z −i
⇔ z − 2i = 2 z − i 2
⇔ a + (b − )2 2
2 = 2 a + (b − )2 1 2 2
⇔ a + b = ( ) 2 1
w − 2i = (i + )
1 w +1− i ⇔ w − 2i = (i + ) 1 w − i
⇔ w − 2i = 2 w − i 2
⇔ a + (b − )2 2
2 = 2 a + (b − )2 1 2 2
⇔ a + b = ( 2 2) Trang 27/54 - WordToan
Mà: z − w =1 ⇔ (a − c)2 + (b − d )2 =1 ⇔ 2ac + 2bd = 3 (do ( ) 1 và (2) )
Vậy: z + w = (a + c)2 + (b + d )2 = ( 2 2 a + b ) + ( 2 2
c + d ) + 2(ac + bd ) = 7 .
Câu 42.12: Cho hai số phức z , w thỏa mãn điều kiện 2z − 3i = 3 2 + iz và z − w = 2 . Môđun 2z + 3w bằng A. 52 . B. 53 . C. 5 2 . D. 51. Lời giải Chọn D
2z − 3i = 3 2 + iz ⇔ 2x + (2y −3)i = 3 (2 − y) + ai
⇔ ( x)2 + ( y − )2 = ( − y)2 2 2 2 2 2 3 3 2
+ 3x ⇔ x + y = 3 ⇒ z = w = 3
Giả sử z = a + bi , ( a , b∈ ); w = c + di , ( c , d ∈ ). Theo giả thiết ta có: z = 3 2 2 a + b = 3 2 2 a + b = 3 ( ) 1 w = 3 2 2 ⇔ c + d = 3 2 2
⇔ c + d = 3 (2)
z −w = 2 2 2 2 2 2 2 ( a − c ) +(b − d) = 4 a + b +
(c +d )−2(ac+bd) = 4 (3) Thay ( )
1 ,(2) vào (3) ta được ac + bd =1 (4) .
Ta có 2z + 3w = ( a + c)2 + ( b + d )2 2 3 2 3 = ( 2 2 a + b ) + ( 2 2 4
9 c + d ) +12(ac + bd ) = 4.3+ 9.3+12.1 = 51 .
CÂU TƯƠNG TỰ CÂU 43 ĐỀ THAM KHẢO 2024
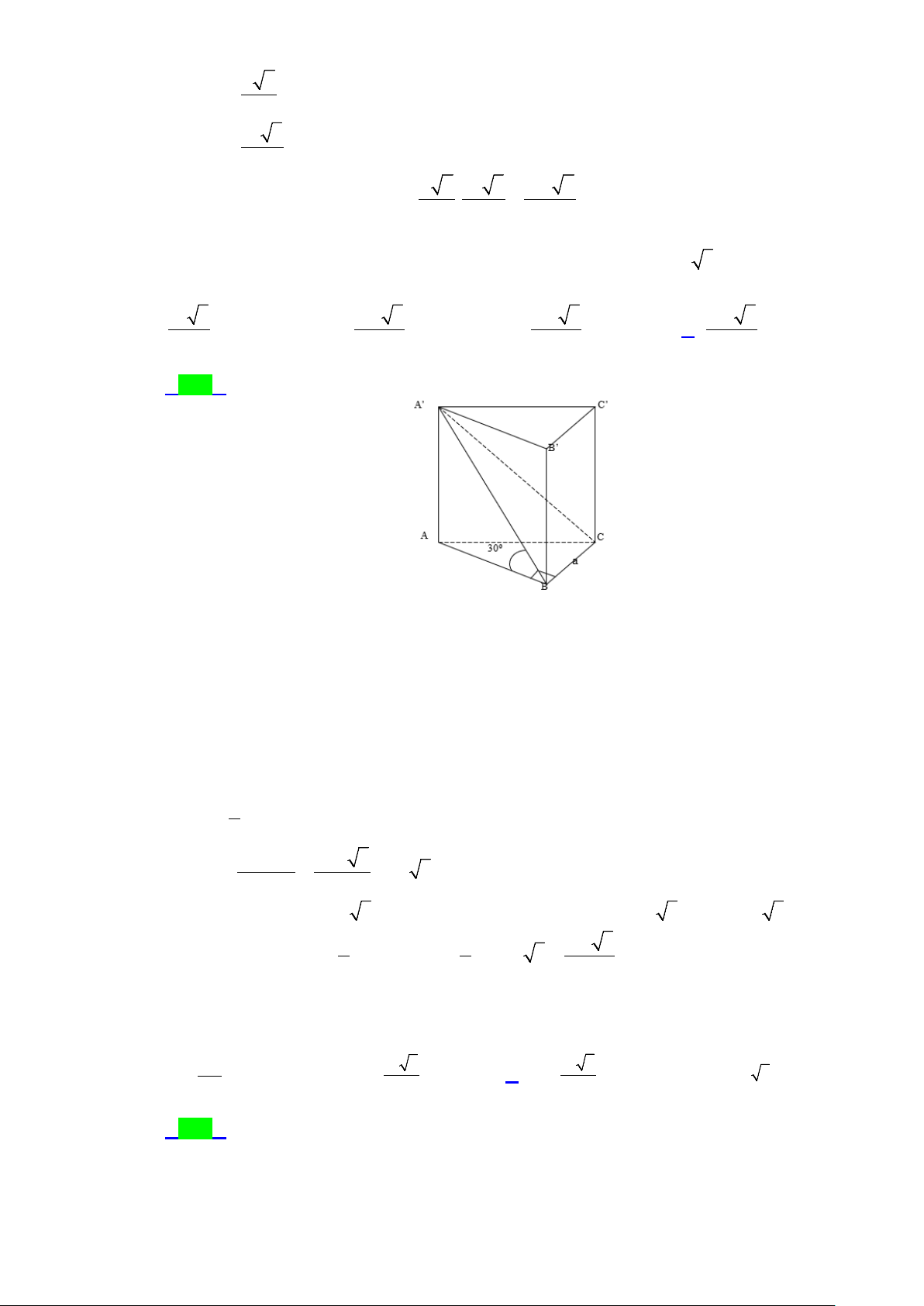
Câu 43.1: Cho hình hộp ABC . D A′B C ′ D
′ ′ có các cạnh bằng 2a . Biết BAD = A′AB =
A′AD = 60 . Tính thể
tích V của khối hộp ABC . D A′B C ′ D ′ ′ . A. 3 4 2a . B. 3 2 2a . C. 3 8a . D. 3 2a . Lời giải Chọn A
Từ giả thuyết ta có các tam giác A ∆ BD , A
∆ ′AD và A′AB là các tam giác đều.
⇒ A′A = A′B = A′D nên hình chiếu H của A′ trên mặt phẳng ( ABCD) là tâm đường tròn ngoại
tiếp tam giác đều ABD . 2 3 2 3 ⇒ AH = .2 . a = a 3 2 3 2 2 2 6
⇒ A′H = A′A − AH = a . 3 2
Thể tích của khối hộp ABC . D A′B C ′ D ′ ′ : 2 6 4a . 3 3
V = A′H.S = a = a . ABCD .2. 4 2 3 4 Trang 28/54 - WordToan 2 3
thể tích khối lăng trụ ABC.A′B C ′ ′ là a 3 a 6 V = a 2 = .
ABC.A′B C ′ ′ 4 3 4
Câu 43.2: Cho hình lăng trụ đều ABC.AB C
. Biết khoảng cách từ điểm C đến mặt phẳng ABC bằng 1
a , góc giữa hai mặt phẳng ABC và BCC B
bằng α với cosα . Tính thể tích khối 2 3
lăng trụ ABC.AB C . 3 3 3 3 A. 3a 2 V 3a 2 a 2 3a 2 . B. V . C. V . D. V . 4 2 2 8 Lời giải Chọn B A' C' y B' K E α a A C M x B
Gọi M là trung điểm của AB . Do AB CC
AB MCCABC MCC. AB CM
Kẻ CK vuông góc với CM tại K thì ta được CK ABC , do đó CK d C;ABC a . Đặt x
BC x,CC y,x 0, y 0, ta được: 3 CM 2 1 1 1 4 1 1 1 . 2 2 2 2 2 2 CM CC CK 3x y a Kẻ KC a
CE BC tại E , ta được KEC α , 12 EC a . sinα 1 11 112 1 1 1 11 Lại có 2. 2 2 2 2 x y CE 12a Giải a 1 ,2 ta được 6
x 2a, y . 2
Thể tích khối lăng trụ ABC.AB C là: 2 2 3 x 3 a 6 4a 3 3 2 . . a V y . 4 2 4 2
Câu 43.3: Cho hình lăng trụ đứng ABC.A′B C
′ ′ có đáy là tam giác ABC vuông cân tại A , cạnh BC = a 6
. Góc giữa mặt phẳng ( AB C
′ ) và mặt phẳng (BCC B
′ ′) bằng 60°. Tính thể tích V của khối đa diện AB C ′ A′C′. 3 3 3 A. 3 a 3 . B. 3a 3 . C. a 3 . D. a 3 . 2 2 3 Lời giải Chọn A Trang 29/54 - WordToan Khối đa diện AB C
′ A′C′ là hình chóp B .′ACC A
′ ′ có A′B′ ⊥ ( ACC A ′ ′) .
Từ giả thiết tam giác ABC vuông cân tại A , cạnh BC = a 6 ta suy ra AB = AC = a 3 .
Gọi M là trung điểm của a
BC , suy ra AM ⊥ BC và 6 AM = . 2 AM ⊥ BC Ta có
⇒ AM ⊥ (BCC B
′ ′) ⇒ AM ⊥ B C ′ (1). AM ⊥ BB′
Gọi H là hình chiếu vuông góc của M lên B C
′ , suy ra MH ⊥ B C ′ (2).
Từ (1) và (2) ta suy ra B C
′ ⊥ ( AMH ) . Từ đó suy ra góc giữa mặt phẳng ( AB C ′ ) và mặt phẳng
(BCC B′′) là góc giữa AH và MH . Mà tam giác AMH vuông tại H nên ⇒ AHM = 60°. a 6 1 a 2
⇒ MH = AM.cot 60° = . = . 2 3 2 a 2 MH 2 1 sin HCM = = = MC a 6 3 2 2 ⇒ + 1 1 3 = = = ⇒ 2 1 tan MCH tan MCH = 2 − 1 sin MCH 1 2 2 1− 3 ⇒ ′ = 2
BB BC.tan MCH = a 6. = a 3 2 1 1 3 ⇒ V = = ′ ′ ′ = = . ′ ′ ′ V ′ ′ ′ B A AC BB a a a a AB CA C B ACC A . . . 3. 3. 3 3 . 3 3
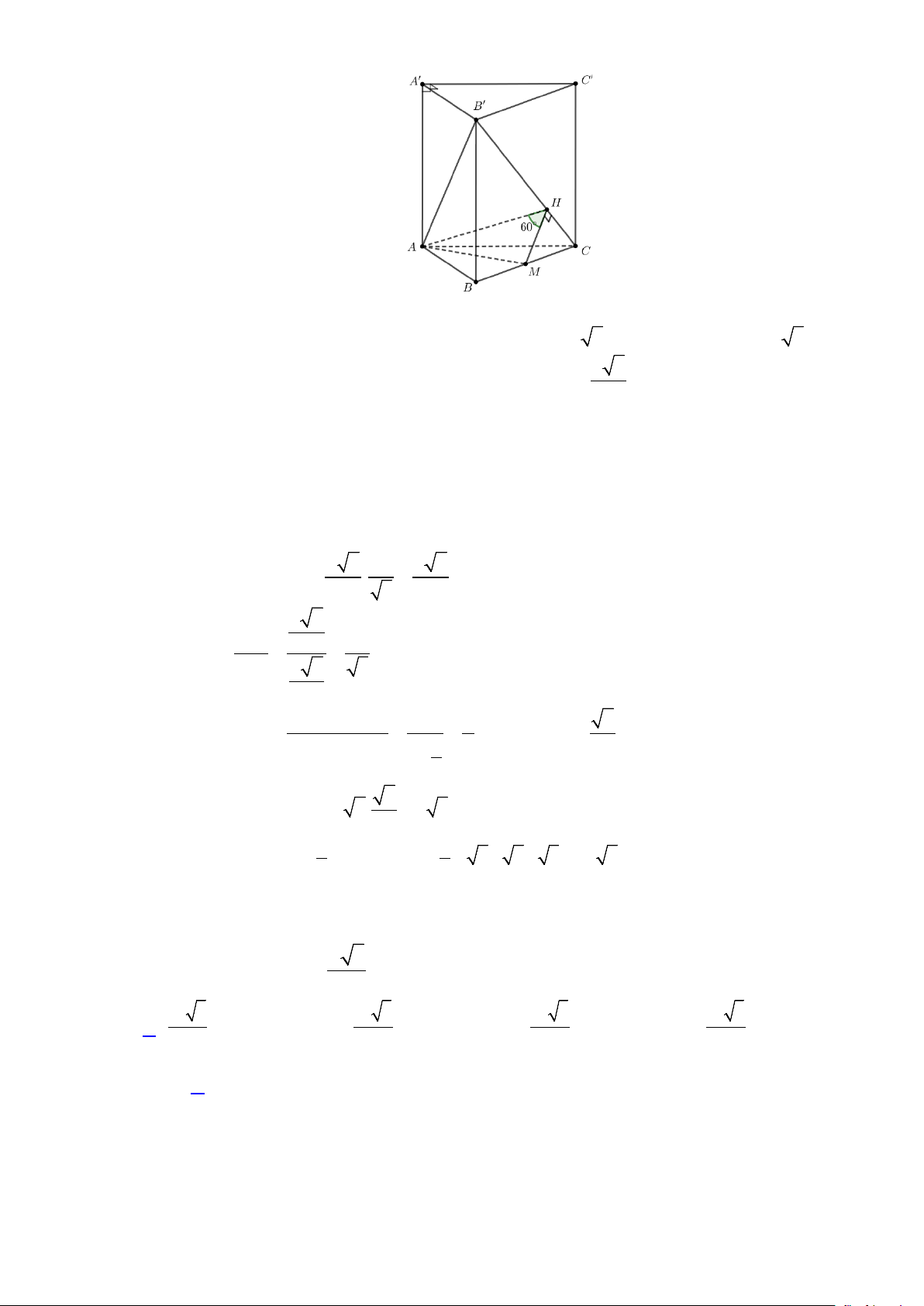
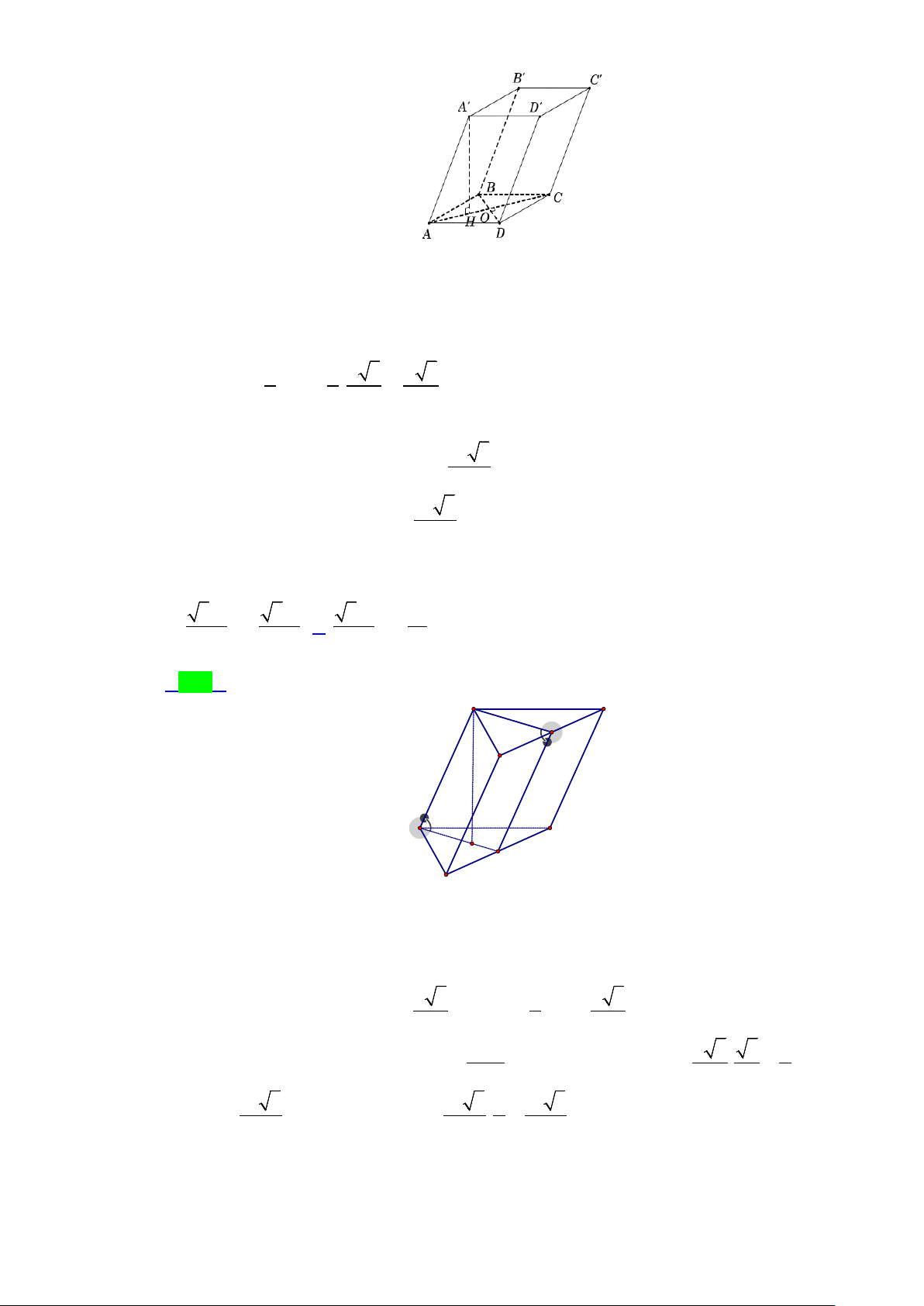
Câu 43.4: Cho lăng trụ ABC.A'B'C ' có đáy là tam giác đều cạnh a , hình chiếu vuông góc của điểm A'
lên mặt phẳng ( ABC) trùng với trọng tâm tam giác ABC . Biết khoảng cách giữa hai đường a 3
thẳng AA'và BC bằng
. Tính theo a thể tích khối lăng trụ đó. 4 3 a 3 3 a 3 3 a 3 3 a 3 A. . B. . C. . D. . 12 6 3 24 Lời giải Chọn A Trang 30/54 - WordToan
+ Gọi M là trung điểm BC , H là trọng tâm tam giác ABC ⇒ A'H ⊥ ( ABC).
+ AM ⊥ BC và AH ⊥ BC ⇒ BC ⊥ ( AA'M ).
+ Trong tam giác AA'M , kẻ MN ⊥ AA' tại N A
MN ⊥ BC tại M vì BC ⊥ ( AA'M ) . 3 c b
⇒ MN là đoạn vuông góc chung của AA'và BC ⇒ = a MN . 4 a
+ Tam giác AA'M có 1 1 B C S
= A H AM = MN AA ∆AA M ' . . ' ' M 2 2 2 2
⇒ A'H.AM = MN.AA' ⇔ A'H.AM = MN. A'H + AH 2 2 a 3 a a 2 2 3 2 3 A'H + A'H + 2 2
MN. A'H + AH 4 3 2 3 A' ⇒ H = = = . AM a 3 2 2 2 a 2 2 3 ⇒ 4 ' = ' + a A H A H ⇒ A' H = . 3 3 2 3 a a 3 a 3
Vậy thể tích khối lăng trụ V = A'H.S = = ABC A B C ∆ABC . . ' ' ' . 3 4 12
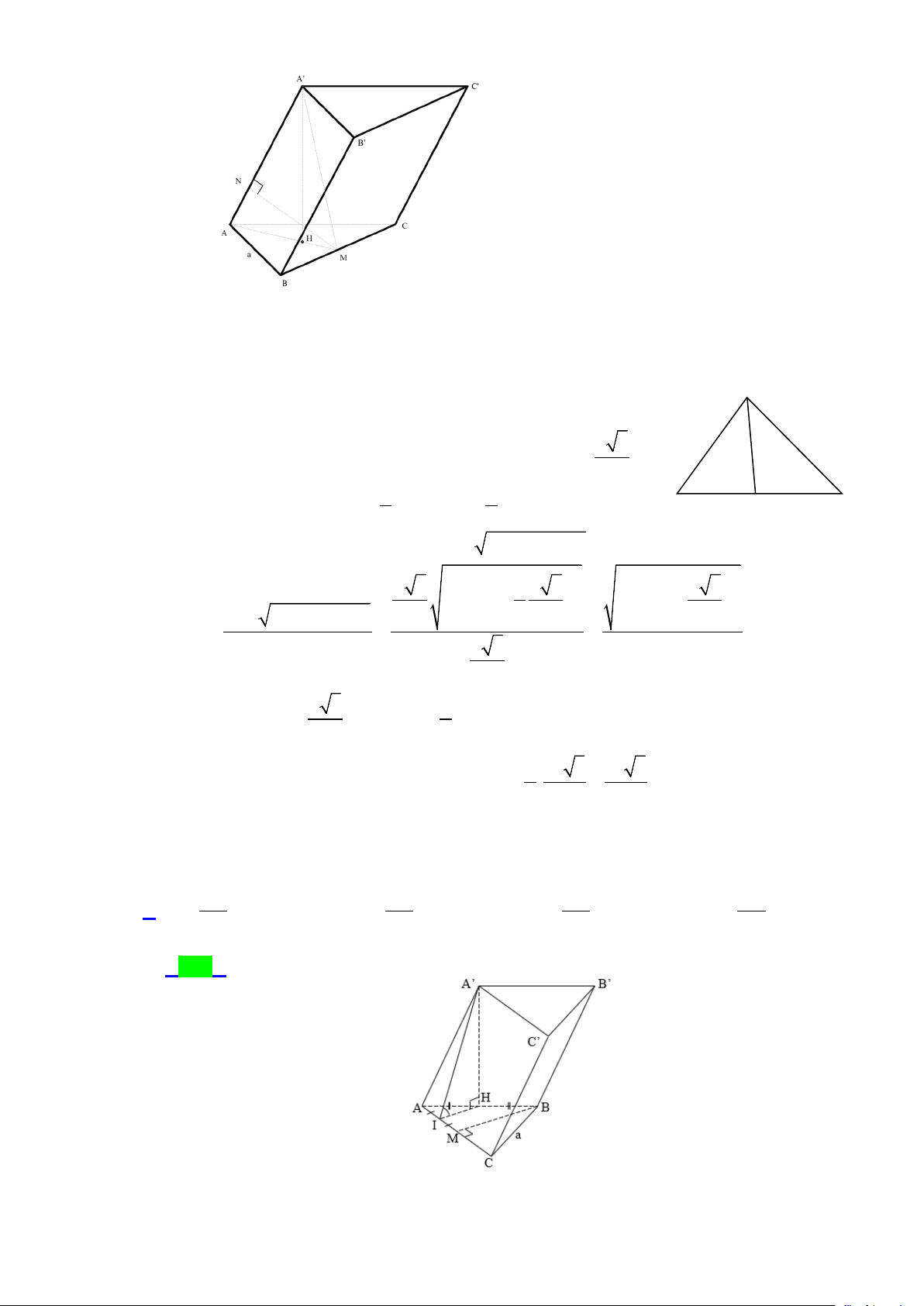
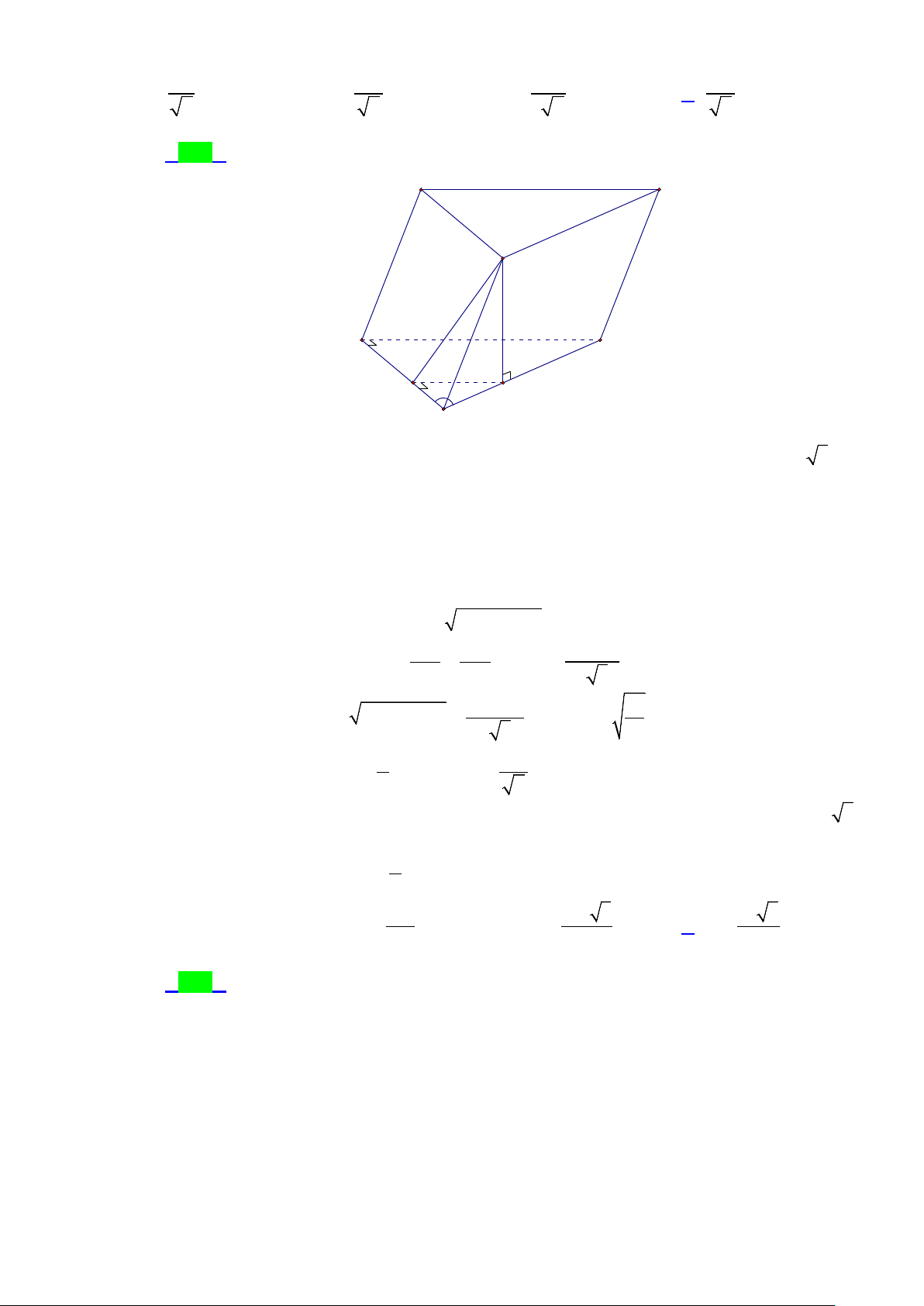
Câu 43.5: Cho hình lăng trụ ABC.A'B 'C ' có đáy ABC là tam giác đều cạnh bằng a . Hình chiếu vuông
góc của A' trên ( ABC) là trung điểm của AB . Mặt phẳng ( AA'C 'C) tạo với đáy một góc bằng
45°. Thể tích V của khối lăng trụ ABC.A'B 'C ' bằng 3 3 3 3 A. 3a V = . B. 3a V = . C. 3a V = . D. 3a V = . 16 8 4 2 Lời giải Chọn A
Gọi H, M, I lần lượt là trung điểm của AB, AC, AM.
Ta có IH là đường trung bình của tam giác AMB , MB là trung tuyến của tam giác đều ABC. Trang 31/54 - WordToan IH // MB Do đó: ⇒ IH ⊥ AC . MB ⊥ AC
AC ⊥ A' H Có:
⇒ AC ⊥ ( A'HI ) ⇒ AC ⊥ A'I AC ⊥ IH
(ABC) ∩ (ACC ' A') = AC
Có: (ABC) : AC ⊥ IH ⇒
A'IH là góc nhọn và là góc gữa hai mặt phẳng ( AA'C 'C)
(ACC ' A'): AC ⊥ A'I và ( ABCD) ⇒ A'IH = 45° .
Trong tam giác A'HI vuông tại H, ta có: ' tan 45 A H ° = HI o 1 a 3
⇒ A' H = IH.tan 45 = IH = MB = 2 4 2 3 Vậy a 3 a 3 3 . a V = = 4 4 16
Câu 43.6: Cho hình lăng trụ đứng ABC.A'B 'C ', biết đáy ABC là tam giác đều cạnh a . Khoảng cách từ tâm O a
của tam giác ABC đến mặt phẳng ( A'BC) bằng . Thể tích khối lăng trụ ABC.A'B 'C ' 6 bằng 3 3 3 3
A. 3a 2 .
B. 3a 2 .
C. 3a 2 . D. 3a 2 . 8 28 4 16 Lời giải Chọn D A' C' B' A H C O M B
Gọi M là trung điểm của BC . Ta có ( A' AM ) ⊥ ( A'BC) theo giao tuyến A'M .
Trong ( A' AM ) kẻ OH ⊥ A'M (H ∈ A'M ).
⇒ OH ⊥ ( A'BC). Suy ra: ( ,( ' )) a
d O A BC = OH = . 6
Xét hai tam giác vuông A' AM và OHM có góc
M chung nên chúng đồng dạng. a 1 a 3 . Suy ra: OH OM 6 3 2 1 3 = ⇒ = ⇒ = . 2 2 2 A' A A'M A' A A' A + AM A' A 2 a 3 A' A + 2 Trang 32/54 - WordToan a 6 ⇒ A' A = . 4 2 + a 3 S = . ABC ∆ 4 2 3 Thể tích:
a 6 a 3 3a 2 V = S = = . ∆ A A ABC A B C ABC . ' . . ' ' ' 4 4 16
Câu 43.7: Cho hình lăng trụ đứng ABC.A'B 'C ' có đáy ABC là tam giác vuông tại B , BC = a , mặt phẳng
( A'BC) tạo với đáy một góc 30° và tam giác A'BC có diện tích bằng 2a 3 . Tính thể tích khối
lăng trụ ABC.A'B 'C '. 3 3 3 3 A. a 3 B. 3a 3 C. 3a 3 D. 3a 3 8 4 8 2 Lời giải Chọn D BC ⊥ AB Do
⇒ BC ⊥ (AA′B B
′ ) ⇒ BC ⊥ A′B BC ⊥ AA′
BC = (ABC) ∩ (A' BC)
Và (ABC) : BC ⊥ AB
(A′BC) : BC ⊥ A' B ⇒ ( ABC A BC )= (AB A B)= 0 ( ),( ' ) , ' ABA' = 30 Ta có: 1 S = ′ ∆ ′ A B BC A BC . 2 . 2 2.S∆ ′ a A BC 2. 3 ⇒ A′B = = = 2a 3 BC a = ′ 0 ′ = = ′ = ′ 0 AB A .
B cos ABA 2a 3.cos30 3 ; a AA A .
B sin ABA′ = 2a 3.sin 30 = a 3 1 3 V = S
AA′ = AB BC AA′ 1 3a 3 = .3 . a . a a 3 = . ABC A B C ABC . . . . . ' ' ' 2 2 2
Câu 43.8: Cho lăng trụ ABCD.A'B'C ' D' có đáy ABCD là hình thoi cạnh a , tâm O và 0
ABC 120 . Góc giữa
cạnh bên AA' và mặt đáy bằng 0
60 . Đỉnh A' cách đều các điểm ,
A B, D . Tính theo a thể tích
V của khối lăng trụ đã cho. 3 3 A. 3 3a a 3 a 3 V . B. V . C. V . D. 3 V a 3 . 2 6 2 Lời giải Chọn C Trang 33/54 - WordToan
Từ giả thiết suy ra tam giác ABD đều cạnh a .
Gọi H là tâm của tam giác ABD .
Vì A' cách đều các điểm ,
A B, D nên A' H ABD .
Do đó AA ABCD AA H 0 ',
', A A' AH 60 . Ta có 2 2 a 3 a 3 AH AO . . 3 3 2 3
Tam giác vuông A' AH , có
A'H AH.tan A' AH a . 2 Diện tích hình thoi a 3 S S . ABCD 2 ABD 2 3 Vậy a 3 V S A H ABCD A B C D ABCD . ' . . ' ' ' ' 2
Câu 43.9: Cho khối lăng trụ ABC ⋅ ′
A B′C′ có đáy ABC là tam giác đều, AA' = AB' = AC ' = a . Biết góc
giữa hai mặt phẳng (BCC′B′) và ( ABC) bằng 30 , thể tích của khối lăng trụ đã cho bằng 3 3 3 3 A 3 . a . B 3 . a . C 3
. a . D. a . 24 8 12 8 Lời giải Chọn C A C 300 J B A' C' H I B'
I là trung điểm của B'C ', H là trọng tâm ∆A'B'C ' Chớp .
A A'B'C ' đều nên ta có AH ⊥ ( A'B'C ') . Suy ra AH là chiều cao và BC ⊥ ( AA'IJ )
Suy ra góc giữa hai mặt phẳng (BCC′B′) và ( ABC) là = ' = 30 AJI AA I ,
∆A'B'C ' đều cạnh a nên a 3 2 a 3 A'I =
⇒ A'H = A'I = 2 3 3 AH a a
∆AA'H vuông tại H ta có 0 3 3 tan AA'H =
⇔ AH = A'H.tan30 = . = A'H 3 3 3 2 2 3 a 3 a 3 a a 3 S = ⇒ V = B h = = ∆A B C ABC A B C . . ' ' ' . ' ' ' 4 4 3 12
Câu 43.10: Cho hình lăng trụ ABC. ′
A B′C′ có đáy ABC là tam giác vuông tại A , cạnh BC = 2a và
ABC = 60° . Biết tứ giác BCC′B′ là hình thoi có
B′BC nhọn. Biết (BCC′B′) vuông góc với
( ABC) và ( ABB′ ′
A ) tạo với ( ABC) góc 45°. Thể tích của khối lăng trụ ABC. ′
A B′C′bằng Trang 34/54 - WordToan 3 3 3 3 A. a . B. 6a . C. a . D. 3a . 7 7 3 7 7 Lời giải Chọn D A' C' B' A 2a C 2a K 60° H B
Do ABC là tam giác vuông tại ,
A cạnh BC = 2a và
ABC = 60° nên AB = a , AC = a 3 .
Gọi H là hình chiếu vuông góc của B′ lên BC ⇒ H thuộc đoạn BC (do B′BC nhọn)
⇒ B′H ⊥ ( ABC) (do (BCC′B′) vuông góc với ( ABC)).
Kẻ HK song song AC (K ∈ AB) ⇒ HK ⊥ AB (do ABC là tam giác vuông tại A ). ⇒ ( ABB′ ′ A ) ( ABC) = ,
B′KH = 45° ⇒ B′H = KH (1)
Ta có ∆BB′H vuông tại H 2 2
⇒ BH = 4a − B′H (2) Mặt khác .2
HK song song AC ⇒ BH = HK ⇒ = HK a BH (3) BC AC a 3 ′ Từ (1), (2) và (3) suy ra 2 2 .2 4 − ′ = B H a a B H 12
⇒ B′H = a . a 3 7 3 Vậy 1 3 = ′ = ′ = a V S B H AB AC B H . ABC A B C′ ABC . . . . ' ' 2 7
Câu 43.11: Cho hình lăng trụ ABC.A′B C
′ ′ có đáy ABC là tam giác vuông tại A , AB = a , AC = a 3
, A′A = A′B = A′C . Trên cạnh AC lấy điểm M sao cho CM = 2MA. Biết khoảng cách giữa hai đường thẳng a
A′M và BC bằng . Tính thể tích V của khối lăng trụ đã cho. 2 3 3 A. 3 3 3 V a 2a 3 a 3 = a . B. V = . C. V = . D. V = . 2 3 2 Lời giải Chọn D Trang 35/54 - WordToan
( ′ ; ) = ( ;( ′ )) = ( ;( ′ )) a d A M BC d BC A MN
d H A MN = HI ⇒ HI = . 2 Kẻ 2
AT // HK , AT ∩ MN = P ⇒ HK = PT = AT 3 Tam giác 1 1 1 4 2 a
ABC vuông tại A ⇒ = + = ⇒ HK = AT = . 2 2 2 2 AT AB AC 3a 3 3 Tam giác 1 1 1 4 3 1
A′HK vuông tại H ⇒ = − = − =
⇒ A′H = a . 2 2 2 2 2 2 A′H HI HK a a a 3
Vậy thể tích khối lăng trụ đã cho là: 1 a 3
V = A′H.S = a a a = . ABC . . . 3 2 2
Câu 43.12: Cho hình lăng trụ ABC.A′B C
′ ′ có đáy là tam giác đều cạnh a . Hình chiếu vuông góc của
điểm A′ lên mặt phẳng ( ABC) trùng với trọng tâm tam giác ABC . Biết khoảng cách giữa hai
đường thẳng AA′ và BC bằng a 3 . Tính theo a thể tích V của khối lăng trụ ABC.A′B C ′ ′. 4 3 3 3 3 A. a 3 V = . B. a 3 V = . C. a 3 V = . D. a 3 V = . 12 6 3 24 Lời giải Chọn A
Ta có A′G ⊥ ( ABC) nên A′G ⊥ BC ; BC ⊥ AM ⇒ BC ⊥ (MAA′) Kẻ MI a
⊥ AA′ ; BC ⊥ IM nên d ( AA′ BC) 3 ; = IM = 4 Trang 36/54 - WordToan
Kẻ GH ⊥ AA′ , ta có AG GH 2 2 a 3 a 3 = = ⇔ GH = . = AM IM 3 3 4 6 a 3 a 3 . 1 1 1 A . G HG 3 6 a = + ⇔ A′G = = = 2 2 2 ′ 2 2 2 2 HG A G AG AG − HG a a 3 − 3 12 2 2 a a 3 a 3 V = ′ = = ( đvtt). ′ ′ ′ A G S ABC A B C . ABC . . 3 4 12
CÂU TƯƠNG TỰ CÂU 44 ĐỀ THAM KHẢO 2024 Câu 44.1: − −
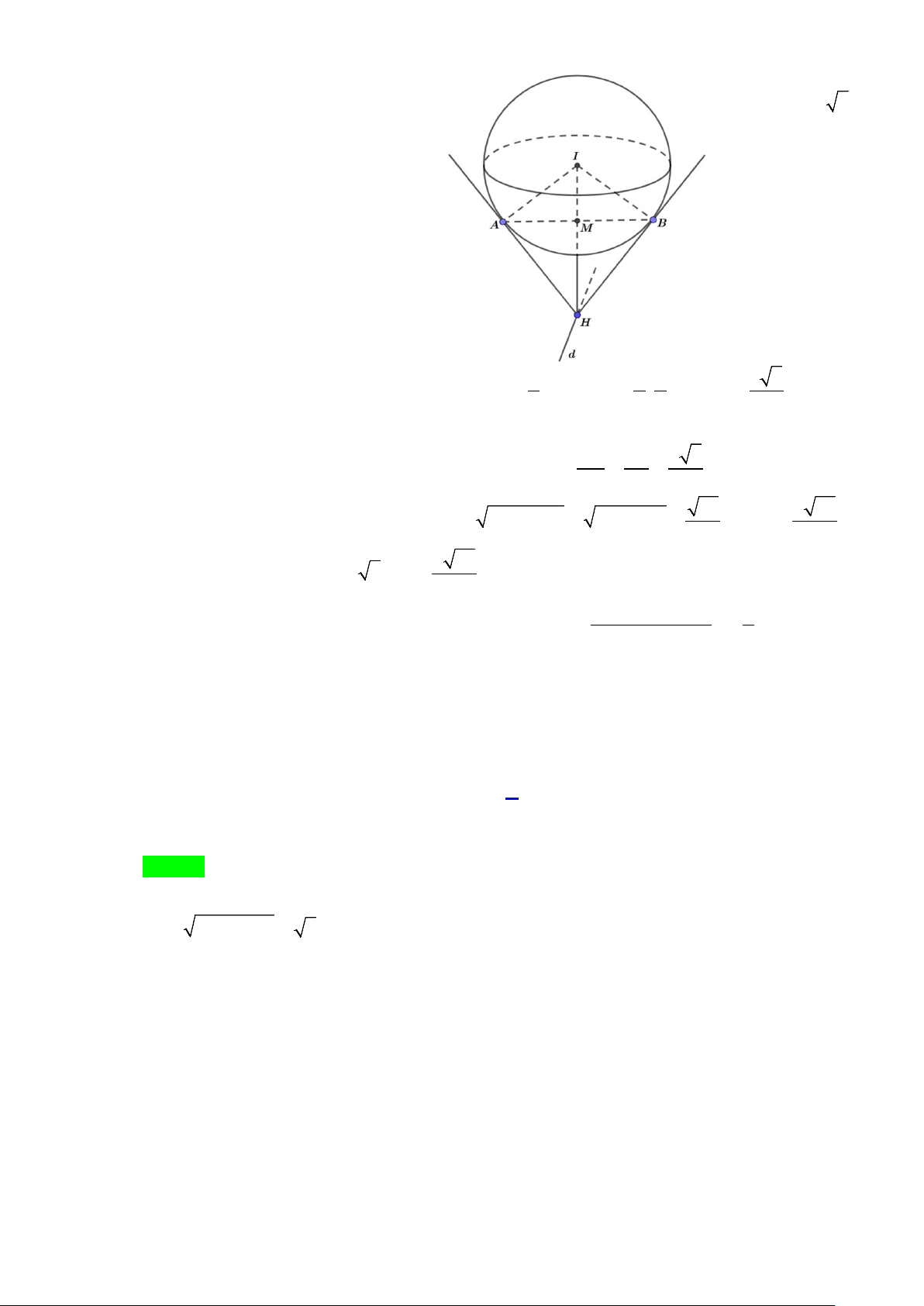
Trong không gian với hệ trục toạ độ x y z
Oxyz , cho dường thẳng 1 2 d : = = và mặt cầu 2 1 − 2 (S) (x − )2 2 :
2 + y + (z − )2
1 =1. Gọi (P) và (Q) là hai mặt phẳng chứa đường thẳng d và tiếp
xúc với mặt cầu (S ) lần lượt tại M và N . Độ dài dây cung MN có giá trị bằng A. 4 . B. 3 . C. 2 . D. 1. 2 Lời giải Chọn C
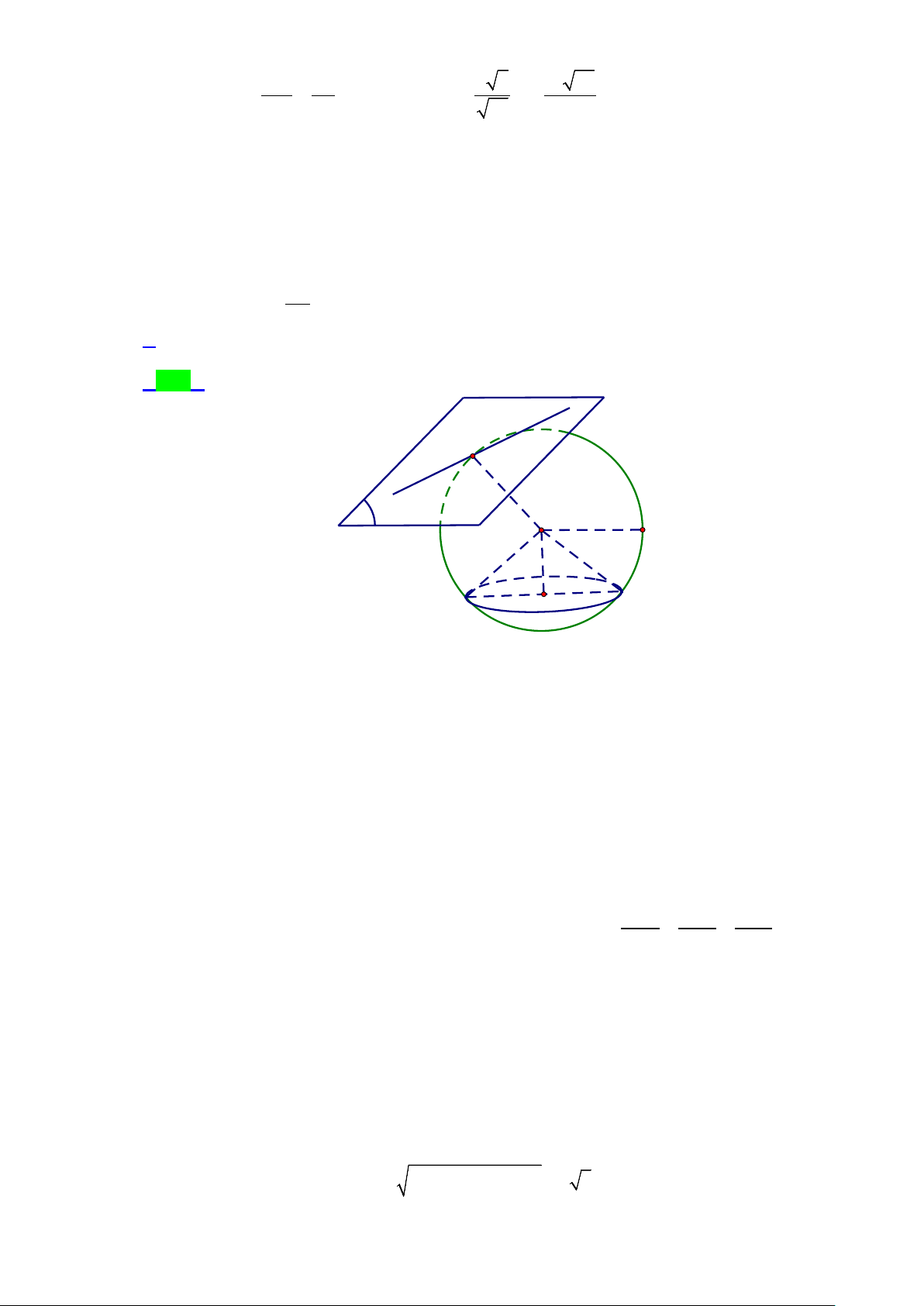
Nếu gọi H là hình chiếu vuông góc của tâm I (2;0; )
1 lên đường thẳng d , thì ta có hình vẽ minh
họa hai mặt phẳng (P) và (Q) đi qua d , tiếp xúc với mặt cầu (S ) như sau: x =1+ 2t
Phương trình tham số đường thẳng d : y = t −
; VTCP của d : u = − . d (2; 1;2) z = 2+ 2t
Gọi H (1+ 2t; t
− ;2 + 2t). Suy ra: IH = (2t −1; t − ;2t + ) 1 . Có IH ⊥ ⇔ 2(2t − ) 1 −1( t − ) + 2(2t + )
⇒ t = 0 ⇒ H (1;0;2) (
u ) ⇔ IH. (u ) = 0 1 = 0 . d d
Độ dài đoạn IH = (2 − )2 2 1 + 0 + (1− 2)2 = 2 .
Áp dụng định lý Pythago suy ra: HM = HN = IH − IM = ( 2)2 2 2 −1 =1. Suy ra: HM.IM 1.1 MN = 2MK = 2. = 2. = 2 . IH 2 Trang 37/54 - WordToan
Câu 44.2: Trong không gian với hệ trục toạ độ Oxyz , cho mặt cầu (S ) (x − )2 + ( y + )2 + (z − )2 : 1 1 2 = 9 và điểm M (1;3;− )
1 , biết rằng các tiếp điểm của các tiếp tuyến kẻ từ M tới các mặt cầu đã cho luôn
thuộc một đường tròn (C) có tâm J (a; ;
b c) . Giá trị T = 2a + b + c bằng A. 134 T = . B. 62 T = . C. 84 T = . D. 116 T = . 25 25 25 25 Lời giải Chọn C A M J I
Ta có (S ) (x − )2 + ( y + )2 + (z − )2 : 1 1 2 = 9 ⇒ I (1; 1; − 2); R = 3 . M ( − ) 2 2
1;3; 1 ⇒ IM = 0 + 4 + ( 3 − )2 = 5.
Gọi A là một tiếp điểm nên 2 2 2 2
AM = MI − IA = 5 − 3 = 4 .
Mặt cầu tâm M bán kính AM = 4 dạng (x − )2 + ( y − )2 + (z + )2 1 3 1 =16 . (x − )2
1 + ( y −3)2 + (z + )2 1 =16
Toạ độ A là nghiệm của hệ
⇒ 4y − 3z +1 = 0. (x − )2 1 + ( y + )2 1 + (z − 2)2 = 9
Hay A∈(P) : 4y −3z +1= 0 . x =1
J là hình chiếu của
I lên mặt phẳng (P) . Đường thẳng IJ dạng y = 1 − + 4t . z = 2− 3t
4y − 3x +1 = 0 x =1 x =1
J = IJ ∩(P) ⇒ J là nghiệm của hệ 11 ⇒ y = 11 23 ⇒ J 1; ; . y = 1 − + 4t 25 25 25
z = 2−3t 23 z = 25 Nên 84
T = 2a + b + c = . 25
Câu 44.3: Trong không gian + + −
Oxyz , cho đường thẳng
x 1 y 2 z 1 d : = = và mặt cầu 1 1 1 (S) 2 2 2
: x + y + z − 2x − 4y + 6z −13 = 0. Lấy điểm M (a; ;
b c) với a < 0 thuộc đường thẳng d
sao cho từ M kẻ được ba tiếp tuyến MA , MB , MC đến mặt cầu (S ) ( ,
A B,C là tiếp điểm) thỏa mãn góc AMB = 60° , BMC = 90°,
CMA =120° . Tổng a + b + c bằng A. 2 − . B. 2 . C. 10 . D. 1. 3 Lời giải Chọn A Trang 38/54 - WordToan M B C H A I
Mặt cầu (S ) có tâm I (1;2; 3
− ) , bán kính R = 3 3 .
Gọi MA = MB = MC = m .
Tam giác MAB đều ⇒ AB = m .
Tam giác MBC vuông cân tại M ⇒ BC = m 2 .
Tam giác MAC cân tại
M ,CMA =120° ⇒ AC = m 3 . Ta có: 2 2 2
AB + BC = AC ⇒ A
∆ BC vuông tại B .
Gọi H là trung điểm của AC , suy ra, H là tâm đường tròn ngoại tiếp tam giác ABC
Vì MA = MB = MC , IA = IB = IC nên M , H , I thẳng hàng.
Áp dụng hệ thức lượng cho tam giác AI MAI vuông tại ,
A ta nhận được MI = = 6 . sin 60°
M ∈d ⇒ M (t −1;t − 2;t + )
1 ⇒ IM = (t − 2;t − 4;t + 4).
t = 0 ⇒ M ( 1; − 2 − ; ) 1 (t / m) 2 2 IM 36 3t 4t 0 = ⇒ − = ⇔ 4 1 2 − 7 ⇒
a + b + c = − .
t = ⇒ M ; ; (l) 2 3 3 3 3 Câu 44.4: + +
Trong không gian với hệ trục tọa độ x y z
Oxyz , cho đường thẳng 2 1 d : = = và mặt cầu 2 3 − 1
(S) (x − )2 +( y + )2 +(z + )2 : 2 1
1 = 6 . Hai mặt phẳng (P), (Q) chứa d và cùng tiếp xúc với (S ) lần lượt tại ,
A B . Gọi I tà tâm mặt cầu (S ) . Giá trị cos AIB bằng A. 1 − . B. 1 . C. 1 − . D. 1 . 9 9 3 3 Lời giải Chọn A Trang 39/54 - WordToan
Mặt cầu (S ) có tâm I (2; 1 − ;− ) 1 và bán kính R = 6 .
Phương trình tham số của đường thẳng x = 2 − + 2t d : y = 1 − − 3t , u = − . d (2; 3; )1 z = t
Gọi H là hình chiếu của I lên d.
Vì H ∈d ⇒ H ( 2 − + 2t; 1 − − 3t;t) ⇒ IH = ( 4 − + 2t; 3 − t;t + ) 1 . Khi đó,
IH u = ⇔ − + t − − t + t + = ⇔ t = ⇒ 5 1 H 1; ; − − và 3 6 IH = . d ( ) ( ) ( ) 1 . 0 2 4 2 3 3 1 0 2 2 2 2
Gọi M là hình chiếu của A lên IH . 2 2
Xét tam giác AIH vuông tại A có: 2 IA R 2 6
IA = IM.IH ⇒ IM = = = . IH IH 3
Xét tam giác AIM vuông tại M có 2 2 2 2 2 30
AM = IA − IM = R − IM = ⇒ 2 30 AB = . 3 3 Tam giác AIB có 2 30
IA = IB = 6, AB = . 3
Áp dụng định lý côsin trong tam giác AIB ta có: 2 2 2
IA + IB − AB 1 cos AIB = = − . 2 . IA IB 9
Câu 44.5: Trong không gian Oxyz , cho điểm E (2;1;3), mặt phẳng (P) : 2x + 2y − z −3 = 0 và mặt cầu
(S) (x − )2 +( y − )2 +(z − )2 : 3 2
5 = 36 . Gọi ∆ là đường thẳng đi qua E , nằm trong (P) và cắt
(S) tại hai điểm có khoảng cách nhỏ nhất. Phương trình của ∆ là x = 2 + 9t x = 2 − 5t x = 2 + t x = 2 + 4t A. y = 1+ 9t .
B. y =1+ 3t .
C. y =1−t .
D. y =1+ 3t . z = 3+ 8t z = 3 z = 3 z = 3− 3t Lời giải Chọn C
Mặt cầu (S ) có tâm I (3;2;5) và bán kính R = 6 . 2 2 2
IE = 1 +1 + 2 = 6 < R ⇒ điểm E nằm trong mặt cầu (S ) .
Gọi H là hình chiếu của I trên mặt phẳng (P) , A và B là hai giao điểm của ∆ với (S ) .
Khi đó, AB nhỏ nhất ⇔ AB ⊥ IE , mà AB ⊥ IH nên AB ⊥ (HIE) ⇒ AB ⊥ IE . Suy ra: u = = − = − . ∆ n EI P ; (5; 5;0) 5(1; 1;0) x = 2 + t Vậy phương trình của
∆ là y =1− t . z = 3 Trang 40/54 - WordToan x =1+ t
Câu 44.6: Trong không gian Oxyz , cho mặt cầu 2 2 2
x + y + z = 9 và điểm M (x ; y ; z d :
∈ y =1+ 2t . Ba 0 0 0 ) z = 2− 3t
điểm A , B , C phân biệt cùng thuộc mặt cầu sao cho MA , MB , MC là tiếp tuyến của mặt cầu.
Biết rằng mặt phẳng ( ABC) đi qua điểm D(1;1;2) . Tổng 2 2 2
T = x + y + z bằng 0 0 0 A. 30. B. 26 . C. 20 . D. 21. Lời giải Chọn B x =1+ t
Ta có: M (x ; y ; z d :
∈ y =1+ 2t ⇒ x + y + z = 4. 0 0 0 ) 0 0 0 z = 2− 3t
Mặt cầu có phương trình 2 2 2
x + y + z = 9 ⇒ tâm O(0;0;0) , bán kính R = 3.
MA , MB , MC là tiếp tuyến của mặt cầu ⇒ MO ⊥ ( ABC).
⇒ ( ABC) đi qua D(1;1;2) có vectơ pháp tuyến OM = (x ; y ; z có phương trình dạng: 0 0 0 )
x x −1 + y y −1 + z z − 2 = 0. 0 ( ) 0 ( ) 0 ( )
MA là tiếp tuyến của mặt cầu tại A ⇒ MO ∆ A vuông tại 2 2
A ⇒ OH.OM = OA = R = 9 .
Với H là hình chiếu của O lên ( ABC) ( OH + HM = OM ) , ta có: (
−x − y − z
x + y + z + z z + d ; O ( ABC)) 2 4 0 0 0 0 0 0 0 0 = OH = = =
⇒ OH.OM = z + 4 . 0 2 2 2 2 2 2 x + y + z x + y + z OM 0 0 0 0 0 0
⇒ z + 4 = 9 ⇔ z = 5∨ z = 13 − . 0 0 0 z + 4
* Với z = 5 ⇒ M (0;−1;5) ⇒ T = 26 nhận do: 0 9 OM = 26;OH = = ; 0 OM 26
pt ( ABC) − y + z − = ⇒ MH = d (M ( ABC)) 17 : 5 9 0 ; = . 26
⇒ OH + HM = OM * Với z = 13
− ⇒ M 6;11;−13 ⇒ loại do: 9 OM = 326;OH = ; 0 ( ) 326
( ABC) x + y − z + = ⇒ MH = d (M (ABC)) 335 :6 11 13 9 0 ; = . 326
⇒ OH + HM ≠ OM (loại)
Câu 44.7: Trong không gian với hệ tọa độ Oxyz , cho mặt cầu (S ) (x − )2 + ( y − )2 + (z − )2 : 1 1 1 =1 và điểm
A(2;2;2) . Xét các điểm M thuộc mặt cầu (S ) sao cho đường thẳng AM luôn tiếp xúc với (S ) Trang 41/54 - WordToan
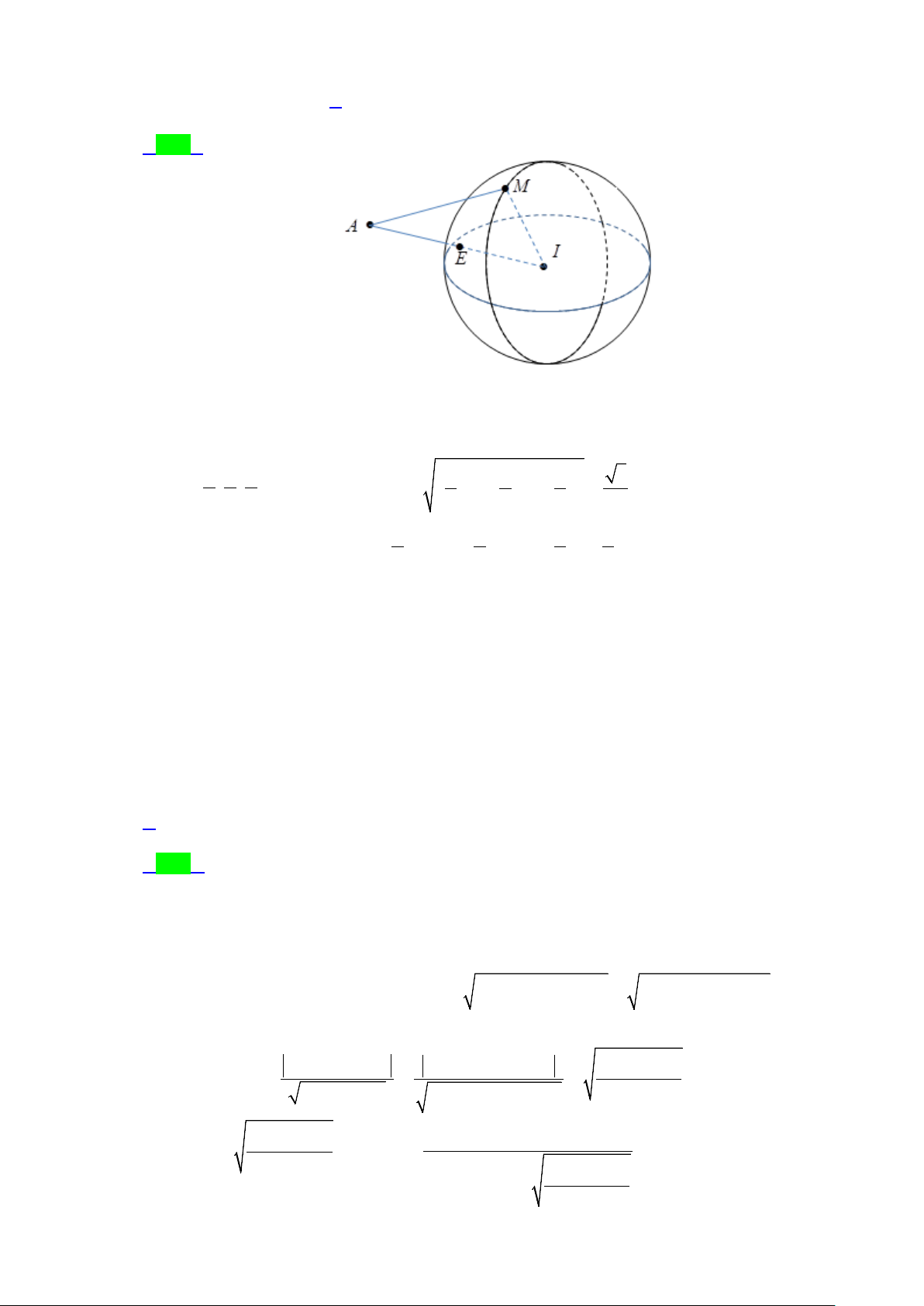
. Khi đó M luôn thuộc mặt phẳng cố định có phương trình là
A. x + y + z − 6 = 0 .
B. x + y + z − 4 = 0. C. 3x + 3y + 3z −8 = 0 . D. 3x + 3y + 3z − 4 = 0 . Lời giải Chọn B
Mặt cầu (S ) có tâm I (1;1; )
1 , bán kính R =1. A(2;2;2) Ta luôn có o
AMI = 90 , suy ra điểm M thuộc mặt cầu (S tâm 1 )
E là trung điểm của AI đường kính AI . 2 2 2 Với 3 3 3 E ; ; 1 1 1 3 , bán kính R IE = = + + = . 2 2 2 1 2 2 2 2 2 2 2
Phương trình mặt cầu (S : 3 3 3 3 x − + y − + z − = 1 ) 2 2 2 4 2 2 2
⇔ x + y + z − 3x − 3y − 3z + 6 = 0 .
Vậy điểm M có tọa độ thỏa mãn hệ: ( x − )2 1 + ( y − )2 1 + (z − )2 2 2 2 1 =1
x + y + z − 2x − 2y − 2z + 2 = 0 ⇔ 2 2 2 2 2 2
x + y + z − 3x − 3y − 3z + 6 = 0
x + y + z − 3x − 3y − 3z + 6 = 0
Trừ theo vế hai phương trình cho nhau ta được: x + y + z − 4 = 0.
Câu 44.8: Trong không gian với hệ tọa độ Oxyz , cho hai điểm A(3; 2;
− 6), B(0;1;0) và mặt cầu
(S) (x − )2 +( y − )2 +(z − )2 : 1 2
3 = 25 . Mặt phẳng (P) : ax + by + cz − 2 = 0 đi qua , A B và cắt
(S) theo giao tuyến là đường tròn có bán kính nhỏ nhất. Tính T = a +b + c A. T = 3. B. T = 4 . C. T = 5 .
D. T = 2 . Lời giải Chọn A
Mặt cầu (S ) có tâm I (1;2;3) và bán kính R = 5 A∈(P) 3
a − 2b + 6c − 2 = 0 a = 2 − 2c Ta có ⇔ ⇔ B ∈ (P) b − 2 = 0 b = 2
Bán kính của đường tròn giao tuyến là r = R − d (I (P)) 2 = − d (I (P)) 2 2 ; 25 ;
Bán kính của đường tròn giao tuyến nhỏ nhất khi và chỉ khi d (I;(P)) lớn nhất
a + 2b + 3c − 2
2 − 2c + 4 + 3c − 2 (c + 4)2
Ta có d (I,(P)) = = = 2 2 2 a + b + c (2 2 − 2c)2 2 2 + 2 + c 5c −8c + 8 c + 4 2 − − + c = Xét 48c 144c 192 f (c) ( )2 = ⇒ f ′(c) = ; f ′(c) 1 = 0 ⇔ 2 5c −8c + 8 2 ( c + c = 4 − 5c −8c + 8)2 4 2 ( ) 2 5c −8c + 8 Bảng biến thiên Trang 42/54 - WordToan
Vậy d (I;(P)) lớn nhất bằng 5 khi và chỉ khi c =1⇒ a = 0,b = 2 ⇒ a + b + c = 3.
Câu 44.9: Trong không gian với hệ trục toạ độ Oxyz , cho hai điểm A(3;5; 2 − ), B( 1; − 3;2) và mặt phẳng
(P): 2x + y − 2z +9 = 0 . Mặt cầu (S) đi qua hai điểm A, B và tiếp xúc với (P) tại điểm C .
Gọi M , m lần lượt là giả trị lớn nhất, nhỏ nhất của độ dài OC . Giá trị 2 2 M + m bằng A. 76 . B. 78. C. 72 . D. 74 . Lời giải Chọn A x = 3 − 2t
Ta có AB : y = 5−t . Gọi M (3− 2t;5−t; 2
− + 2t) là giao điểm của AB và mặt phẳng (P) . z = 2 − + 2t −
M ∈(P) nên ( − t) + ( − t) − (− + t) 8 7 7 10 2 3 2 5
2 2 2 + 9 = 0 ⇔ t = ⇒ M ; ; ⇒ OM = 22 . 3 3 3 3 16 − 8 − 16 AM ; ; = 3 3 3 AM = 8 2 ⇒ ⇒ ⇒ MC = .
MA MB =16 ⇔ MC = 4
do MC là tiếp tuyến 4 − 2 − 4 BM = 2 BM = ; ; 3 3 3
của mặt cầu (S ).
Khi đó tập hợp điểm C là đường tròn giao tuyến (
C) nằm trên (P) có tâm là 7 7 10 M − ; ; 3 3 3 và bán kính là 4 .
Gọi C′ và C′ lần lượt là hai điểm trên đường tròn (C) sao cho OC′ và OC′ lần lượt là giả trị
lớn nhất, nhỏ nhất của độ dài OC , khi đó C′ , M và C′ theo thứ tự thẳng hàng. 2 2 ′ ′′ Do đó C C 2 2 2 2 2 2 8
M + m = OC′ + OC′′ = 2OM + = 2. 22 + = 76 . 2 2
Câu 44.10: Trong không gian Oxyz , cho mặt cầu (S):(x − )2 + ( y + )2 + (z − )2 1 2 3 = 27 . Gọi (α ) là
mặt phẳng đi qua hai điểm A(0;0; 4
− ), B(2;0;0) và cắt (S ) theo giao tuyến là đường tròn (C)
sao cho khối nón đỉnh là tâm của (S ) và đáy là (C) có thể tích lớn nhất. Biết phương trình của
(α ) có dạng ax +by − z + c = 0,(a, ,bc∈) . Giá trị của a −b + c bằng A. 4 − . B. 0. C. 8. D. 2. Lời giải Chọn A
Mặt cầu (S ) có tâm I (1;− 2;3) và bán kính R = 3 3 . Điểm A(0;0; 4
− )∈(α ) ⇒ 4 + c = 0 ⇒ c = 4 − .
Điểm (2;0;0)∈(α ) ⇒ 2 + = 0 c B a c ⇒ a = − = 2 . 2
Mặt phẳng (α ) có dạng 2x + by − z − 4 = 0 .
Gọi d là khoảng cách từ tâm I đến mặt phẳng (α ) và r là bán kính của đường tròn (C). Trang 43/54 - WordToan
Khi đó khối nón có đỉnh I và đáy là đường tròn (C) có thể tích là: 1 2 1
V = π r d = π ( 2 2 R − d ) 1 d = π ( 2 27 − d )d 3 3 3
Đặt f (d ) = ( 2 − d ) 3 27
d = −d + 27d, (0 < d < 3 3) . Suy ra f ′(d ) 2 = 3
− d + 27 và f ′(d ) 2 = 0 ⇔ 3
− d + 27 = 0 ⇔ d = 3(vì 0 < d < 3 3 ). Bảng biến thiên:
Dựa vào bảng biến thiên, ta thấy f (d ) đạt giá trị lớn nhất khi d = 3 hay thể tích khối nón đạt giá trị lớn nhất khi 2
d = 3 ⇔ d = 9 . 5 − − 2b ( 5 − − 2b)2
Mà d = d (I,(α )) = nên 2
= 9 ⇔ 5b − 20b + 20 = 0 ⇔ b = 2 . 2 5 + b 2 5 + b
Vậy a − b + c = 4 − .
Câu 44.11: Trong không gian với hệ trục toạ độ Oxyz , cho hai mặt cầu (S ) (x − )2 2 :
1 + y + (z −3)2 = 36
và (S′) (x + )2 + ( y − )2 + (z − )2 : 1 1
1 = 81. Gọi d là đường thẳng tiếp xúc với cả hai mặt cầu trên
và cách điểm M (4; 1 − ; 7
− ) một khoảng lớn nhất. Gọi E ( ; m ;
n p) là giao điểm của d với mặt
phẳng (P) : 2x − y + z −17 = 0. Biểu thức T = m + n + p có giá trị bằng A. T = 81. B. T = 92 . C. T = 79 . D. T = 88. Lời giải Chọn D
Mặt cầu (S ) có tâm I (1;0;3) và có bán kính R = 6 .
Mặt cầu (S′) có tâm K ( 1; − 1; )
1 và có bán kính R′ = 9 . Lại có KI = ( − ) 2 ⇒ KI = + (− )2 2 2; 1;2 2
1 + 2 = 3 ⇒ KI = R′ − R suy ra hai mặt cầu tiếp xúc a +1 = 6 a = 5
trong tại điểm A( ; a ;
b c) , mà KA = R = 9 = 3KI ⇒ KA = 3KI ⇒ b −1 = 3 − ⇒ b ′ = 2 − . c 1 6 − = c = 7 Do đó A(5; 2
− ;7) . Vì d là đường thẳng tiếp xúc với cả hai mặt cầu trên nên d đi qua A và
vuông góc với KI . Kẻ MH ⊥ d ⇒ MH ≤ MA, nên MH lớn nhất khi và chỉ khi H trùng A .
Khi đó d là đường thẳng đi qua A và vuông góc với KI và AM suy ra d có một véc tơ chỉ
phương u = KI, AM . Ta có AM = ( 1 − ;1; 14 − ) ⇒ u = (12;26; ) 1 . Trang 44/54 - WordToan x = 5 +12t
Nên phương trình tham số của d là y = 2 − + 26t . z = 7 + t
Vì E = d ∩(P) suy ra E (5+12t; 2
− + 26t;7 + t) .
Vì E ∈(P) suy ra 2(5+12t) −( 2
− + 26t) + (7 + t) −17 = 0 ⇔ t = 2 suy ra E (29;50;9) . m = 29 Mà E ( ; m ;
n p) suy ra n = 50 . Vậy T = 88. p = 9 Câu 44.12: − − − −
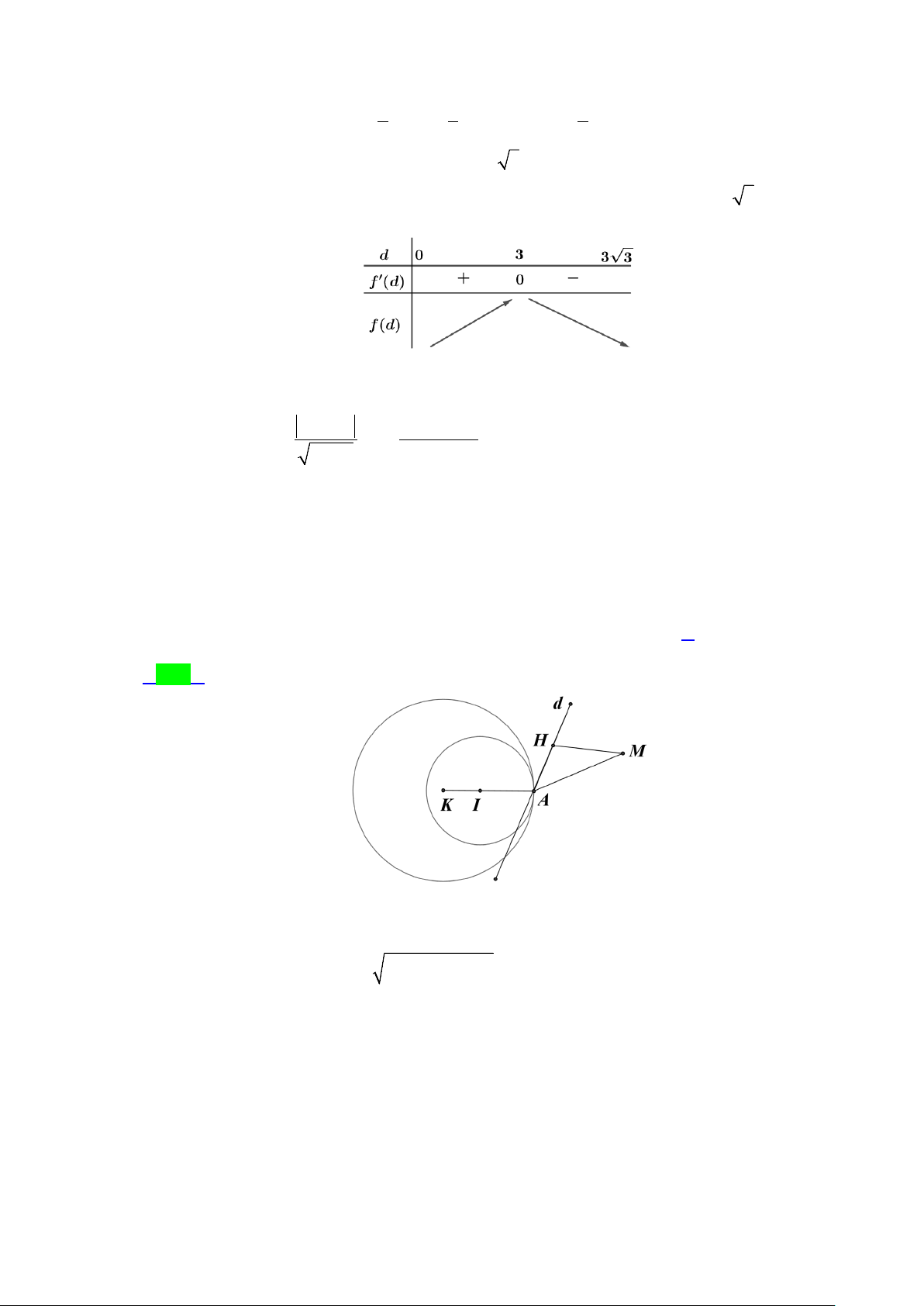
Cho hai đường thẳng (d ) x y 2 z 3 : = =
và (d′) x 1 y z 1 : = = . Gọi I ( ; a ; b c) là tâm 4 1 1 1 1 1
mặt cầu đi qua A(3;2;2) và tiếp xúc với đường thẳng (d ). Biết I nằm trên (d′) và a < 2 . Tính
T = a + b + c A. 8 . B. 4 . C. 0 . D. 2 . Lời giải Chọn D
Ta có M (0;2;3)∈d , I = (1+ t;t;1+ t)∈d′ ⇒ AI = (t − t − t − ) 2
2; 2; 1 ⇒ AI = 3t −10t + 9 . MI,u
MI = (t +1;t − 2;t − 2) ⇒ MI,u = (0;3t −9;−3t + 9) d
⇒ d (I,d ) = = t − 3 . ud
Mặt khác mặt cầu đi qua A(3;2;2) và tiếp xúc với đường thẳng (d ) nên AI = d (I,d ) t = 0 2 2
3t −10t + 9 = t − 3 ⇔ 2t − 4t = 0 ⇔ t = 2 (loai)
Khi đó: a =1,b = 0,c =1⇒ T = 2
CÂU TƯƠNG TỰ CÂU 45 ĐỀ THAM KHẢO 2024
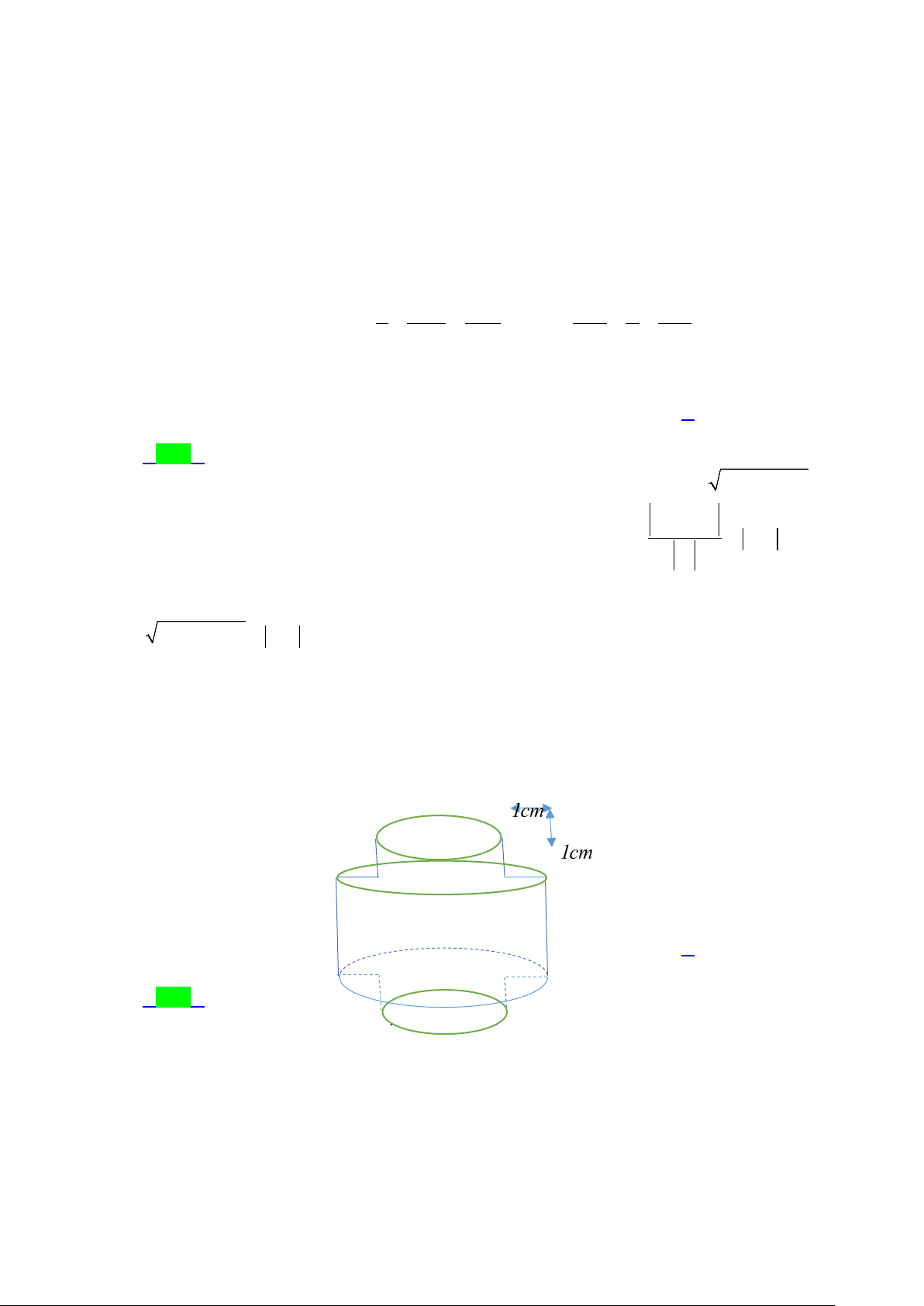
Câu 45.1: Để chế tạo một chi tiết máy, từ một khối thép hình trụ có đường kính 10cm và chiều cao 30cm,
người ta tiện bỏ xung quanh hai đầu rộng 1cm và sâu 1cm (tham khảo hình vẽ). Tinh thể tích
của chi tiết máy đó, làm tròn kết quả đến hàng phần trăm? A. 3 2326,47 cm B. 3 2236,74 cm C. 3 2623,47 cm D. 3 2326,74 cm Lời giải Chọn D
Giả thiết cho bán kính khối thép r 5cm và chiều cao h 30cm Thể tích khối thép là 2
V π.r .h π 5 .30 . 1 2
Sau khi tiện thì phần thép hai đầu có bán kính là r' 4cm và chiều cao phần tiện là h' 1cm
Thể tích khối thép ở hai đầu bị tiện bỏ là 2 2
V π.r .hπ.r .h π.h 2 2
r r =π 2 2 .1 5 4 9π . 2
Thể tích chi tiết máy là: 3
V V V 750π 9π 741π 2326,74 (cm ) 1 2 Trang 45/54 - WordToan
Câu 45.2: Người ta cần đổ một ống cống thoát nước hình trụ với chiều cao 2m , độ dày thành ống là 10cm
. Đường kính ống là 50cm . Tính lượng bê tông cần dùng để làm ra ống thoát nước đó (làm tròn
đến 2 chữ số thập phân sau dấu phẩy). A. 3 0,57 m . B. 3 0,14 m . C. 3 1,57 m . D. 3 0,25 m . Lời giải Chọn D r R
Gọi R,r lần lượt là bán kính đáy của hình trụ lớn và hình trụ nhỏ
R 0,25m và r 0,15m .
Thể tích hình trụ lớn là 2
V π.R .h π 0,25 .2 . 1 2
Thể tích hình trụ nhỏ là 2
V π.r .h π. 0,15 .2 2 2
Lượng bê tông cần dùng là V V V 2π 0,2 2 5 2π 0,1 2 5 0,25 3 m . 1 2
Câu 45.3: Một cơ sở sản xuất có hai bể nước hình trụ có chiều cao bằng nhau, bán kính đáy lần lượt bằng
1m và 1,2m . Chủ cơ sở dự định làm một bể nước mới hình trụ, có cùng chiều cao và có thể tích
bằng tổng thể tích của hai bể nước trên. Bán kính đáy của bể nước dự định làm gần nhất với kết
quả nào dưới đây? A. 1,8 . m . B. 1,4 . m . C. 2,2 . m . D. 1,6 . m Lời giải Chọn D 2 π
V = π R h = π h và 2 36 V = π R h = . h 1 1 2 2 25 Theo đề bài: 36π 61π 2
V = V +V = V = π h + h = h = π R . h 1 2 1 25 25 2 61 ⇔ R =
⇔ R =1,56(m) (V, R lần lượt là thể tích và bán kính của bể nước cần tính) 25
Câu 45.4: Một cốc hình trụ có bán kính đáy bằng 3cm , chiều cao 20cm , trong cốc đang có một ít nước,
khoảng cách giữa đáy cốc và mặt nước là 12cm . Một con quạ muốn uống được nước trong cốc
thì mặt nước phải cách miệng cốc không quá 6cm . Con quạ thông minh đã mổ những viên sỏi Trang 46/54 - WordToan
hình cầu có bán kính 0,8cm thả vào cốc để mực nước dâng lên. Hỏi để uống được nước, con
quạ cần thả ít nhất bao nhiêu viên sỏi? A. 26 . B. 27 . C. 28 . D. 29 . Lời giải Chọn B
Con quạ uống được nước đựng trong cốc khi mặt nước cách miệng cốc không quá 6cm nên mực
nước dâng lên tối thiểu là 20 −12 − 6 = 2cm .
Thể tích nước tối thiểu cần tăng thêm là 2 2 V = π R h = π = π ( 3 .3 .2 18 cm ) .
Thể tích nước tăng lên khi con quạ thả x viên sỏi là: 4 3 4 3 256 V = . x π r = . x .π.0,8 = π x ( 3 cm . 1 ) 3 3 375
Để con quạ uống được nước ta có điểu kiện 256 V ≥ V ⇔
π x ≥18π ⇔ x ≥ 26,37. 1 375
Vâỵ con quạ cần thả ít nhất 27 viên sỏi để uống được nước trong cốc.
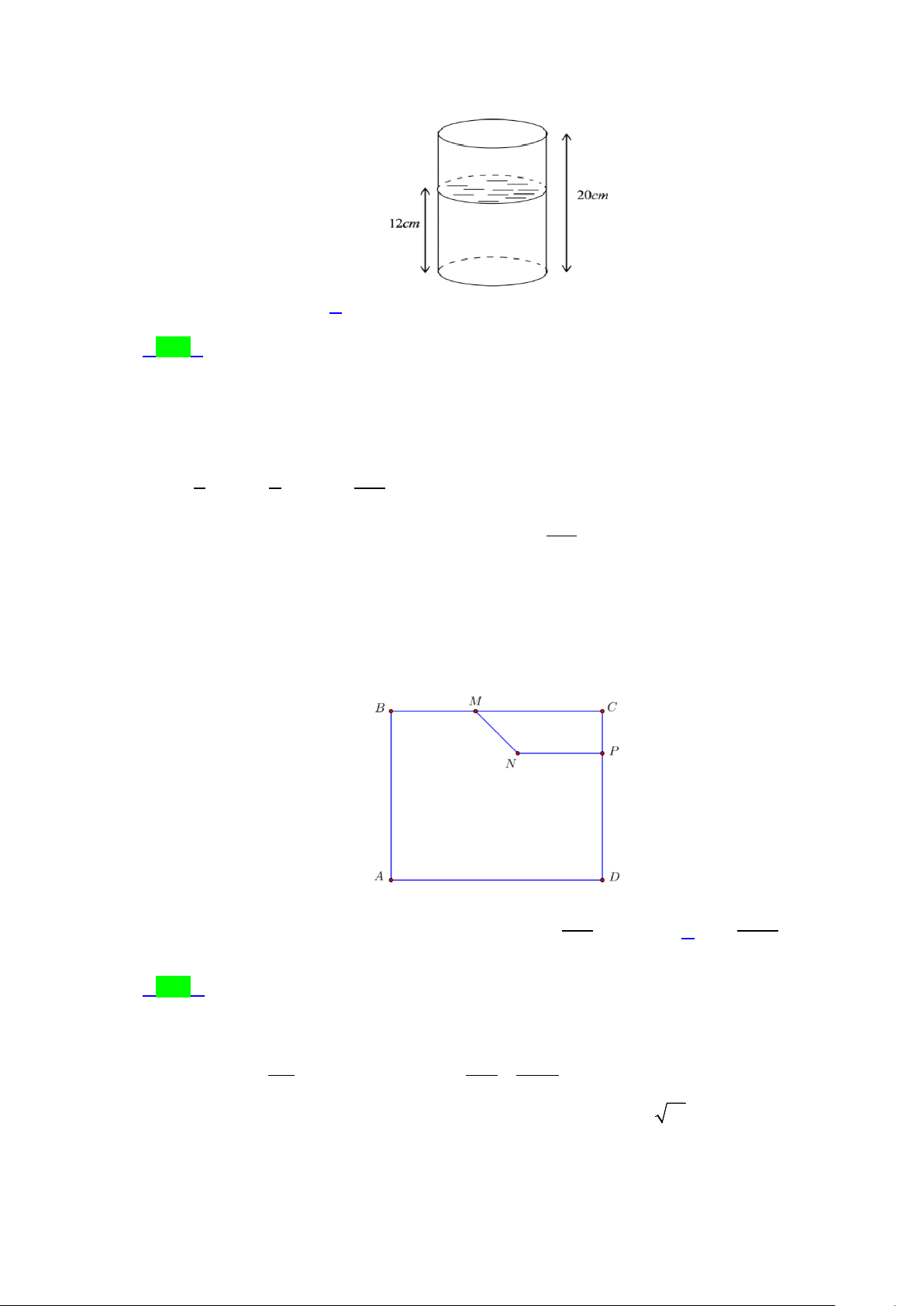
Câu 45.5: Cho hình chữ nhật ABCD với AB = 4c ,
m AD = 5cm . Cắt hình chữ nhật đã cho theo đường gấp
khúc MNP như hình vẽ bên với BM = 2c , m NP = 2c ,
m PD = 3cm và giữ lại hình phẳng lớn
(H ) . Tính thể tích V của vật thể tròn xoay tạo thành khi quay (H ) quanh trục AB . A. 94 244 V = π 3 75 cm . B. V = π 3 94 cm . C. π V = 3 cm . D. π V = 3 cm . 3 3 Lời giải Chọn D
Thể tích vật thể tròn xoay tạo thành bằng tổng thể tích của khối trụ có r = 5 cm , h = 3 cm và
thể tích của khối nón cụt có r = 2 cm, r = 3 cm, 1 h = cm . 1 2 π π π Vậy 2 .1 V = π 5 .3+ ( 2 2 2 + 3 + 2.3) 19 244 3 = 75π + = cm . 3 3 3
Câu 45.6: Người ta cắt hai hình cầu có bán kính lần lượt là R 13cm và r 41cm để làm hồ lô đựng rượu như hình vẽ sau. Trang 47/54 - WordToan
Biết đường tròn giao của hai hình cầu có bán kính r 5cm và nút uống rượu là một hình trụ
có bán kính đáy bằng 5cm , chiều cao bằng 4cm . Giả sử độ dày vỏ hồ lô không đáng kể. Hỏi
hồ lô đựng được bao nhiêu lít rượu? (Kết quả làm tròn đến một chữ số sau dấu phẩy). A. 9,5. B. 10,2 . C. 8,2. D. 11,4 . Lời giải Chọn B
Thể tích khối trụ trên cùng là V 52 .4 20 3 cm . 3
Phần dưới cùng là một chỏm cầu.
Khoảng cách từ tâm của cầu lớn đến đường tròn giao của hai cầu là 2 2 2 2
R r 13 5 12cm
Do đó khối chỏm cầu lớn có chiều cao h R 12 1312 25cm và có thể tích 2 h 2 25 8750
V h R .25 13 3 cm . 1 3 3 3
Phần ở giữa có thể tích bằng thể tích khối cầu nhỏ trừ đi thể tích hai khối chỏm cầu có chiều cao lần lượt là 2 2
h r r r 41 4125 414 ; 1 2 2
h r r 5 41 415 416 . 2 Do đó 4 V 3 2 41 4 2 41 6 41 41 4 41 41 6 41 2 3 3 3 Suy ra 3
V V V V 10220,648cm 10,2 l . 1 2 3
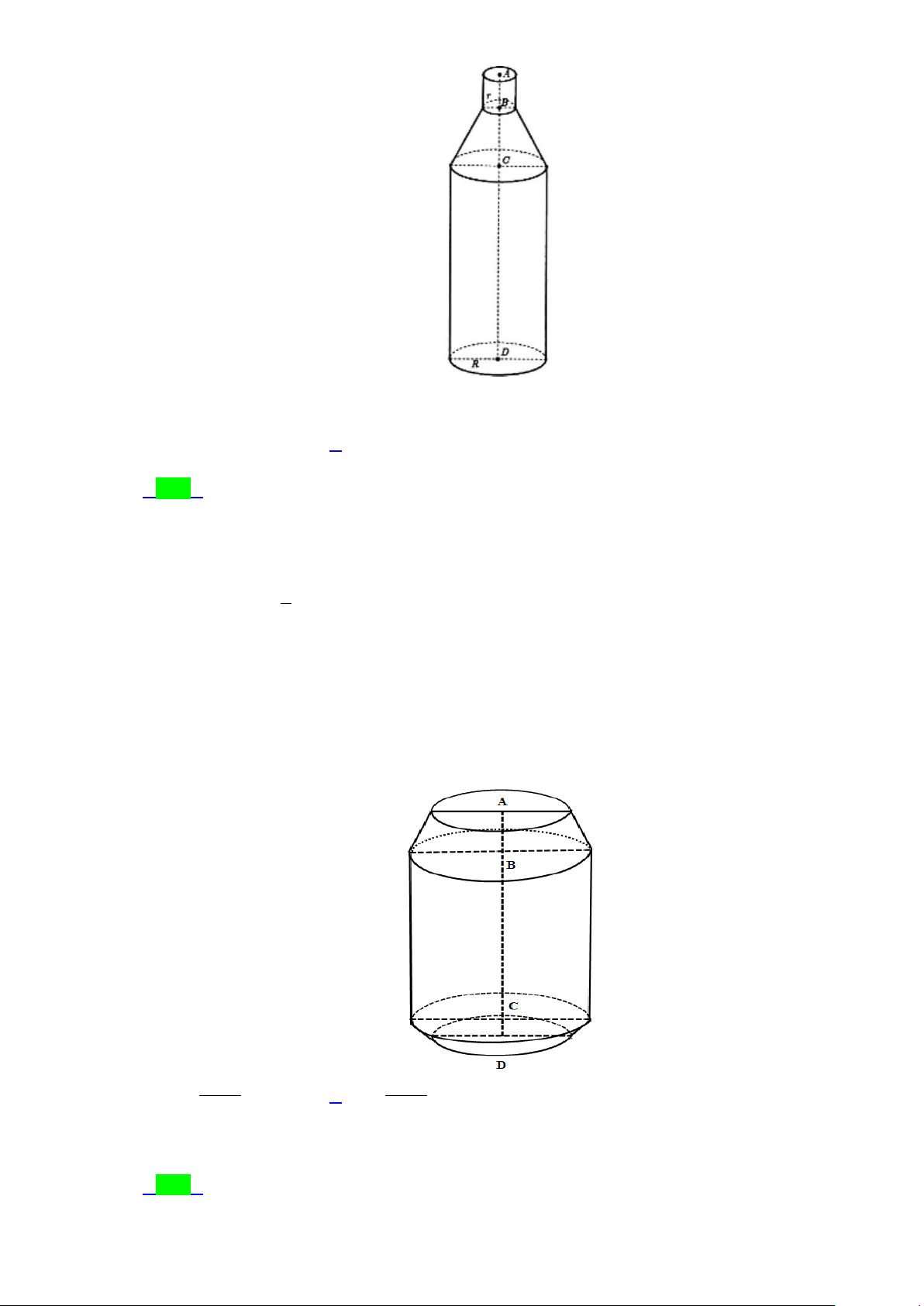
Câu 45.7: Phần không gian bên trong của chai nước ngọt có hình dạng như hình vẽ bên dưới. Trang 48/54 - WordToan
Biết bán kính đáy chai R = 5cm , bán kính cổ chai r = 2cm , AB = 3cm , BC = 6cm và
CD =16cm. Tính thể tích phần không gian bên trong của chai nước ngọt đó. A. 3 V = 495π cm . B. 3 V = 490π cm . C. 3 V = 462π cm . D. 3 V = 412π cm . Lời giải Chọn B
+ Khối trụ có bán kính đáy r = 2cm và chiều cao AB = 3cm nên có thể tích là 2 3
V = π.2 .3 =12π cm . 1
+ Khối nón cụt có bán kính đáy lần lượt là R = 5cm , r = 2cm và chiều cao h = BC = 6cm nên có thể tích là 1 V = π h( 2 2
R + r + Rr) 3 = 78π cm . 2 3
+ Khối trụ có bán kính đáy R = 5cm và chiều cao DC =16cm nên có thể tích là 2 3
V = π.5 .16 = 400π cm . 3
Vậy thể tích phần không gian bên trong của chai nước ngọt đó là 3
V = V +V +V = 490π cm . 1 2 3
Câu 45.8: Tính thể tích V của một lon nước ngọt có hình dạng là một vật thể tròn xoay như hình vẽ bên.
Biết bán kính nắp và đáy lon bằng nhau và bằng 2,5 cm ; bán kính thân chai bằng 3 cm và AB =1,5 c , m BC = 8 c , m CD = 0,5 c ,
m (giả thiết độ dày vỏ lon không đáng kể). π π A. 379 V = ( 3 cm ) . B. 523 V = ( 3 cm ). 4 6 C. V = π ( 3 95 cm ) . D. V = π ( 3 79 cm ) . Lời giải Chọn B Trang 49/54 - WordToan
Thể tích lon nước bằng tổng thể tích của khối nón cụt có r = 2,5c , m r = 3c ,
m h =1,5cm ; thể 1 2
tích khối trụ có r = 3c ,
m h = 8cm ; thể tích của khối nón cụt có r = 2,5c , m r = 3c , m h = 0,5cm . 1 2 π 1,5 + 0,5 2 ( ) π
Thể tích lon nước là V = π + ( 2 2 + + ) 523 3 .8 2,5 3 2,5.3 = ( 3 cm ) . 3 6
Câu 45.9: Để chế tạo dụng cụ như hình, từ một khối thép hình trụ có bán kính 10 cm và chiều cao 20 cm
người ta khoét bỏ một hình nón có bán kính đáy 10 cm và chiều cao 10 cm (tham khảo hình vẽ
sau). Tính thể tích của dụng cụ đó, làm tròn kết quả đến hàng phần nghìn. A. 3 6235,988 cm . B. 3 5235,988 cm . C. 3 5325,988 cm . D. 3
4235,988 cm . Lời giải Chọn B
Thể tích của khối trụ là: 2 V = .10 π .20 = 2000π. 1
Thể tích của khối nón bị khoét là: 1 2 1000 V .10 .10 π = π = . 2 3 3
Vậy thể tích của dụng cụ là: 1000π 5000 V V V 2000 π = − = π − = = 5235,988 ( 3 cm ). 1 2 3 3
Câu 45.10: Để định vị một trụ điện, người ta cần đúc một khối bê tông có chiều cao là h 1,8m gồm
+ Phần dưới có dạng hình trụ bán kính đáy R 1m và có chiều cao bằng 1 h ; 3
+ Phần trên có dạng hình nón bán kính đáy bằng R đã bị cắt bỏ bớt một phần hình nón có bán
kính đáy bằng 1 R ở phía trên (người ta thường gọi hình đó là hình nón cụt); 2
+ Phần ở giữa rỗng có dạng hình trụ bán kính đáy bằng 1 R (tham khảo hình vẽ bên dưới). 4
Thể tích của khối bê tông (làm tròn đến chữ số thập phân nghìn) bằng A. 3 3,881m B. 3 2,731m C. 3 3,203m D. 3 3,731m Lời giải Chọn D Trang 50/54 - WordToan
Thể tích hình trụ bán kính đáy h h 1
R và có chiều cao bằng : 2 2
V R . R h . 3 1 3 3
Thể tích hình nón cụt bán kính đáy lớn R h
R , bán kính đáy bé và có chiều cao bằng 2 : 2 3 2 1 2 4h 1 R 2h 7 2 V R . . R h . 2 3 3 3 4 3 18
Thể tích hình trụ bán kính đáy R và có chiều cao bằng h (phần rỗng ở giữa): 4 2 R 1 2 V .h R h . 3 16 16
Thể tích của khối bê tông bằng: V 95
V V V 2 1 7 1 R . h 2 3
R .h 3,731m . 1 2 3 3 18 16 144
Câu 45.11: Một chiếc bút chì có dạng hình trụ có chiều cao 200 mm và bán kính đáy 3 mm . Thân bút
chì được làm bằng gỗ và phần lõi được làm bằng than chì. Phần lõi có dạng hình trụ có chiều cao
bằng chiều cao của bút và đáy là hình tròn có bán kính bằng 1 mm . Tính thể tích của phần thân
bút chì làm bằng gỗ ( với π = 3,14 ) A. 3 502 m . B. 6 − 3 5,024.10 m . C. 3 5,024 m . D. 6 − 3
6,024.10 m . Lời giải Chọn B
Thể tích phần phần lõi được làm bằng than chì: 2 6 − 6 V π R h π − = = = π ( 3 m ). r .10 .0,2 0,2.10
Thể tích chiếc bút chì: 2 6 − 6
V π R h π.9.10 .0,2 1,8.10− = = = π ( 3 m ).
Thể tích phần thân bút chì được làm bằng gỗ: 6 − 6 − 6 V V V π π − = − = − = ( 3 m ). t r 1,8.10 0,2.10 5,024.10
Câu 45.12: Để chế tạo một khuôn như hình từ một khối thép hình trụ có chiều cao 20 cm và bán kính
đáy 20 cm , người ta khoét bỏ một hình nón có bán kính đáy 15 cm và chiều cao 10 cm và một
hình trụ có chiều cao bán kính đáy 10 cm và chiều cao 10 cm . Tính thể tích của dụng cụ đó, với π = 3,14 . A. 3 8988 cm . B. 3 19625 cm . C. 3 588 cm . D. 3 9625 cm . Lời giải Chọn B
Thể tích của khối trụ thép là: 2 V = .20 π .20 = 8000π . 1
Thể tích của khối nón bị khoét là: 1 2 2250 V .15 .10 π = π = . 2 3 3
Thể tích của khối trụ bị khoét là: 2 V = .10 π .10 =1000π . 3 Trang 51/54 - WordToan
Vậy thể tích của dụng cụ là: 2250 V V V V 8000 π = − − = π − −1000π = 6250π =19625 ( 3 cm ). 1 2 3 3
Câu 45.13: Người ta làm tạ tập cơ tay như hình vẽ với hai đầu là hai khối trụ bằng nhau và tay cầm cũng
là khối trụ. Biết hai đầu là hai khối trụ đường kính đáy bằng 12, chiều cao bằng 6 , chiều dài tạ
bằng 30 và bán kính tay cầm là 2 . Hãy tính thể tích vật liệu làm nên tạ tay đó. A. 108π . B. 6480π . C. 502π . D. 504π . Lời giải Chọn D Gọi h R V
1 , 1 , 1 lần lượt là chiều cao, bán kính đáy, thể tích khối trụ nhỏ mỗi đầu. 2 2
V = h .π.R = 6.π.6 = 216π . 1 1 1 Gọi h R V
2 , 2 , 2 lần lượt là chiều cao, bán kính đáy, thể tích của tay cầm. 2
V = h .π.R = (30−2.6) 2 .π.2 = 72π . 2 2 2
Thể tích vật liệu làm nên tạ tay bằng V = 2V + V = 504π 1 2 .
Câu 45.14: Một chiếc tạ tay có hình dạng gồm 3 khối trụ, trong đó hai khối trụ ở hai đầu bằng nhau và
khối trụ làm tay cầm ở giữa. Gọi khối trụ làm đầu tạ là (T và khối trụ làm tay cầm là (T lần 2 ) 1 )
lượt có bán kính và chiều cao tương ứng là r , h , r , h thỏa mãn r = 4r , 1
h = h (tham khảo 1 1 2 2 1 2 1 2 2 hình vẽ).
Biết rằng thể tích của khối trụ tay cầm (T bằng 30 ( 3
cm ) và chiếc tạ làm bằng inox có khối 2 ) lượng riêng là 3
D = 7,7g / cm . Khối lượng của chiếc tạ tay bằng A. 3,927(kg) . B. 2,927(kg) . C. 3,279(kg) . D. 2,279(kg) . Lời giải Chọn A
Thể tích của hai khối trụ làm đầu tạ (T : 1 ) 2
V = 2π r h = 2π (4r )2 1 2
h =16π r h =16.30 = 480( 3 cm . 1 1 1 2 2 2 2 ) 2
Tổng thể tích của chiếc tạ tay: V = V +V = 480+ 30 = 510( 3 cm 1 2 ).
Khối lượng của chiếc tạ: m = .
DV = 7,7.510 = 3927(g) = 3,927(kg).
Câu 45.15: Một hộp đựng bóng tennis có dạng hình trụ. Biết rằng hộp chứa vừa khít ba quả bóng tennis
được xếp theo chiều dọc, các quả bóng tennis có kích thước như nhau. Thể tích phần không gian
còn trống chiếm tỉ lệ a% so với hộp đựng bóng tennis. Số a gần đúng với số nào sau đây? A. 50. B. 66 . C. 30. D. 33. Lời giải Chọn D Trang 52/54 - WordToan Đặt ,
h R lần lượt là đường cao và bán kính hình tròn đáy của hộp đựng bóng tennis.
Dễ thấy mỗi quả bóng tennis có cùng bán kính R với hình tròn đáy của hộp đựng bóng tennis và h = 6R . Do đó ta có:
Tổng thể tích của ba quả bóng là 4 3 3
V = 3. π R = 4π R ; 1 3
Thể tích của hình trụ (hộp đựng bóng) là 2 3
V = π R h = 6π R ; 0
Thể tích phần còn trống của hộp đựng bóng là 3
V = V −V = 2π R . 2 0 1
Khi đó tỉ lệ phần không gian còn trống so với hộp đựng bóng là V 1 2 = ≈ 0,33. V 3 0 Suy ra a ≈ 33.
Câu 45.16: Một công ty sản xuất bút chì có dạng hình lăng trụ lục giác đều có chiều cao 18cm và đáy
là hình lục giác nội tiếp đường tròn đường kính 1cm . Bút chì được cấu tạo từ hai thành phần
chính là than chì và bột gỗ ép, than chì là một khối trụ ở trung tâm có đường kính 1 cm , giá 4 thành 540 đồng 3
/ cm . Bột gỗ ép xung quanh có giá thành 100 đồng 3
/ cm . Tính giá của một cái
bút chì được công ty bán ra biết giá nguyên vật liệu chiếm 15,58% giá thành sản phẩm. A. 10000 đồng. B. 8000 đồng. C. 5000 đồng. D. 3000 đồng. Lời giải Chọn A
Gọi R và r lần lượt là bán kính đường tròn ngoại tiếp lục giác đều và bán kính của lõi than chì. Ta có 1 R = cm và 1 r = cm . 2 8
Suy ra diện tích của lục giác đều là 2 3 1 3 3 3 S = 6.R = 6. . = . 4 4 4 8 Trang 53/54 - WordToan
Gọi V là thể tích của khối lăng trụ lục giác đều. V V
1 , 2 lần lượt là thể tích của khối than chì và
bột gỗ dùng để làm ra một cây bút chì. Ta có 3 3 27 3 V = S.h = .18 = ( 3 cm ) ; 2 1 9 V r h . .18 π = π = π = ( 3 cm . 1 2 ) 8 4 8 32 27 3 9 V V V π ⇒ = − = − ( 3 cm . 2 1 ) 4 32
Do đó, giá nguyên vật liệu dùng để làm một cây bút chì là 540V +100V 1 2 (đồng).
Vậy giá bán ra của cây bút chì là ( 100 9π 27 3 9π 100 540V +100V . = 540. +100 − . ≈ 10000 (đồng). 1 2 ) 15,58 32 4 32 15,58 Trang 54/54 - WordToan
CÂU TƯƠNG TỰ CÂU 46 ĐỀ THAM KHẢO 2024
Câu 46.1: Cho a là số nguyên dương lớn nhất thỏa mãn 3log ( 3
1+ a + a > 2log a . Tìm phần nguyên 3 ) 2 của log 2024a . 2 ( ) A. 14. B. 22 . C. 16. D. 19. Lời giải Chọn B Đặt 6
t = a,t > 0 , từ giả thiết ta có 3log ( 3 2 1+ t + t ) 3 > 2log t 3 2
⇔ f (t) = log ( 3 2 1+ t + t ) 2 − log t > 0 3 2 2 3 2 + − + − − f ′(t) 1 3t 2t
2 1 (3ln 2 2ln 3)t (2ln 2 2ln 3)t 2ln 3 = . − . = 3 2
ln 3 t + t +1 ln 2 t ln 2.ln 3.( 4 3
t + t + t)
Vì đề xét a nguyên dương nên ta xét t ≥1. Xét g (t) = ( − ) 3t +( − ) 2 3ln 2 2ln 3
2ln 2 2ln 3 t − 2ln 3 Ta có g (t) 8 2 4 8 4 3ln t
2ln t t 3ln t 2ln ′ = + = + 9 9 9 9 9 2ln 4 = ≈ − < g′(t) t 4,59 0 = 0 ⇔ 8 3ln . 9 t = 0
Lập bảng biến thiên suy ra hàm số g (t) ta được:
Suy ra g (t) ≤ g ( )
1 = 5ln 2 − 6ln 3 < 0 ⇒ f ′(t) < 0 .
Suy ra hàm số f (t) luôn giảm trên khoảng [1;+∞) .
Lại có f (4) = 0 nên t = 4 là nghiệm duy nhất của phương trình f (t) = 0.
Suy ra f (t) > ⇔ f (t) > f ( ) 6 0
4 ⇔ t < 4 ⇔ a < 4 ⇔ a < 4096 .
Nên số nguyên a lớn nhất thỏa mãn giả thiết bài toán là a = 4095 .
Lúc đó log 2024a ≈ 22,9826. Nên phần nguyên của log 2024a bằng 22. 2 ( ) 2 ( ) Câu 46.2: Cho 2x + y +1
x , y là các số thực dương thỏa mãn log
= x + 2y . Tìm giá trị nhỏ nhất của biểu 3 x + y thức 1 2 T = + . x y A. 3+ 3 . B. 4 . C. 3+ 2 3 . D. 6 . Lời giải Chọn A Ta có 2x + y +1 log
= x + 2y ⇔ log 2x + y +1 − log x + y = x + 2y 3 ( ) 3 ( ) 3 x + y
⇔ log 2x + y +1 = log 3x + 3y + x + 2y −1 3 ( ) 3 ( )
⇔ log 2x + y +1 + 2x + y +1 = log 3x + 3y + 3x + 3y 3 ( ) 3 ( ) (*)
Xét hàm số f (t) = log t + t với t > 0. 3 Trang 1/53 - WordToan
Khi đó f ′(t) 1 = +1 > 0, t
∀ > 0 , suy ra hàm số f (t) liên tục và đồng biến trên (0;+∞). t ln 3
Do đó (*) ⇔ 2x + y +1= 3x + 3y ⇔ x + 2y =1⇔ x =1− 2y . Vì 1
x, y > 0 ⇒ 0 < y < . 2 Xét 1 2 1 2 1 1 1 T = + = + = + + x y 1− 2y y 1− 2y y y
Áp dụng bất đẳng thức Cô si ta có 1 2 3 T ≥ 3.3 = ≥ = .
y ( − y) 3.3 y( − y) 3. 8 6 1 2 2 1 2 x = 1− 2y 1 x = Dấu " = " xảy ra 2 ⇔ 1
− 2y = y ⇔ . 1 2y =1−2y y = 4
Câu 46.3: Cho a, ,
b c là các số thực lớn hơn 1. Tìm giá trị nhỏ nhất của biểu thức: 4 1 8 P = + + 3 log a log b c bc ac 3logab A. P = 20 . B. P =10 . C. P =18. D. P =12 . min min min min Lời giải Chọn A Ta có: 4 1 8 P = + + = 2log bc + ac + ab a 2logb 8log 2log a 1 log c c bc log ab b 2 ac = 2log b + c + a + c + a + b a 2loga 2logb 2logb 8logc 8logc = (2log b + a + c + a + c + b . a 2logb ) (2loga 8logc ) (2logb 8logc ) Vì a, ,
b c là các số thực lớn hơn 1 nên: log b log a log c log a log c log b > . Do đó c 0 b , c , a , b , a ,
áp dụng bất đẳng thức Cauchy, ta có: P ≥ 2 2log b a + c a + c b = + + = . a .2 logb 2 2loga .8logc 2 2logb .8logc 4 8 8 20 log b = a a = b a logb
Dấu “=” xảy ra khi và chỉ khi 2 log c =
a ⇔ c = a ⇔ a = b = c > . a 4logc 1 2 log c = b b 4logc c = b Vậy P = 20 . min
Câu 46.4: Gọi x, y là các số thực lớn hơn 1 thỏa mãn đẳng thức 1 x + log x = x và A = đạt giá trị y log 2 y 3 y
nhỏ nhất. Khi đó điểm M ( ;
x y) thuộc đồ thị hàm số nào trong các hàm số sau? A. 3 2
y = x − 4x + x −1 B. 2
y = x − 4x +1. C. x + 2 y = . D. 4 2
y = x −18x +12. x −1 Lời giải Chọn C Ta có log x log x 2 2 1+ log x = x ⇔ + = y logy 1 2 log 2y log y 2 ( ) 2
⇔ log y 1+ log y + log .
x log y = log x 1+ log y 2 ( 2 ) 2 2 2 ( 2 )
⇔ log y + (log y)2 + log .xlog y = log x + log .xlog y 2 2 2 2 2 2 2
⇔ log y + (log y)2 = log x 2 2 2 Trang 2/53 - WordToan
Đặt t = log y , suy ra 2 log = + 2 x t t 2 Khi đó ta có x 3 2 A =
⇒ log A = log x − log y = t − 2t ≥ 1 − 3 2 2 2 y
Dấu “=” xảy ra khi t =1 ứng với x = 4; y = 2 . Suy ra M (4;2) .
Ta thấy M (4;2) thuộc đồ thị của x + 2 y = . x −1
Câu 46.5: Gọi x, y là các số thực dương thỏa mãn log x + log y +1≥ log ( 2 x + 2y 2 2 2
). Giá trị nhỏ nhất của
biểu thức x + 2y là bao nhiêu? A. 2 2 + 3 B. 2 + 3 2 C. 3+ 3 D. 9 Lời giải Chọn A
Với x > 0, y > 0 ta có
log x + log y +1≥ log ( 2
x + 2y) ⇔ log 2xy ≥ log ( 2 x + 2y 2 2 2 2 2 ) 2 2
⇔ 2xy ≥ x + 2y ⇔ y (x − ) 2 2
1 ≥ x ⇔ −1 x x ≥ > 0 ⇒ x >1 2y
Đặt m = x + 2y 2 Ta có ( − − ) 2
x m x ≥ x − x + m 2x x ⇔ m ≥ x −1 2
Xét hàm số ( ) 2x − x g x = , x >1 x −1 2 − 2 2 x = < 1
Ta có g′(x) 2x − 4x −1 = , g′(x) 1 2 = 0 ⇔ (x − )2 1 2 + 2 x = > 1 2 2
Ta có bảng biến thiên của g ( x)
Xét sự biến thiên của hàm g ( x) trên (1;+∞) + Ta có
g (x) = g ( 2 2 min x = g = 3 + 2 2 khi 2 2 x + = 2 ) (1;+∞) 2 2 2 + 2 x = Vậy m ≥ 3+ 2 2 2 Dấu = xảy ra khi (thỏa mãn) 4 + 3 2 y = 4
Vậy GTNN của x + 2y là 3+ 2 2
Câu 46.6: Gọi x, y là các số thực dương thỏa mãn (x − y) 1 ln
+ ln (xy) = ln (x + y) . Giá trị nhỏ nhất của 2
biểu thức M = x + y là bao nhiêu? A. 2 2 B. 2 C. 4 D. 16 Trang 3/53 - WordToan Lời giải Chọn C
Với x > 0, y > 0 ta có (x − y) 1 ln
+ ln (xy) = ln (x + y) 2 1
⇔ ln (xy) = ln (x + y) − ln (x − y) 2 2 + ⇔ ln ( ) = ln x y xy x y − 2 x + y ⇔ xy = x y −
⇔ (x − y)2 xy = (x + y)2 ( ) 1 u
= x + y > 0 Đặt v = xy > 0 Ta có ( ) ⇔ ( 2 u − v) 2
v = u ⇔ (v − ) 2 2 1 4 1 u = 4v Vì v > 0 nên 2
4v > 0. Do đó (v − ) 2
1 .u > 0 . Suy ra v −1 > 0 hay v >1. Ta có 2 ( − ) 2 2 2 4 1 = 4 v v u v ⇔ u =
= f (v), (v > ) 1 v −1 2 8v v −1 − 4v 4v(v − 2) Ta có f ′(v) ( ) = = (v − )2 1 (v − )2 1
f ′(v) = 0 ⇔ v = 2 (vì v >1) Ta có bảng biến thiên x + y = 4 x = 2 + 2
Vậy min (x + y) = min u = 4 ⇔ xy = 2 ⇔ . y = 2 − 2 x > y > 0
Khi đó x + y = 4 .
Câu 46.7: Gọi S là tập hợp các giá trị nguyên của y để tồn tại số thực 1 x ,9 ∈ thỏa mãn đẳng thức 3 2.9y log 3x y y x x x + + + =
+1 . Tổng các phần tử của S là 3 ( ) A. 36. B. 35. C. 28 . D. 21. Lời giải Chọn D Ta có 2.9y log 3x y y x x x + + + =
+1 ⇔ ( .3y )2 + log .3y = .3y.3x + log 3x x x x 3 ( ) 3 ( ) 3 y ⇔ x ( y x x − ) 3x .3 .3 3 = log (*) . 3 .3y x
Nếu .3y > 3x x
⇒ VT (*) > 0 > VP(*) . Trang 4/53 - WordToan
Nếu .3y < 3x x
⇒ VT (*) < 0 < VP(*) . Nếu .3y = 3x x
⇒ VT (*) = 0 = VP(*) . x Vậy y 3 3 =
⇒ y = x − log x mà 1 x ,9 ∈
nên y ∈{1,2,3,4,5, } 6 . 3 x 3
Tổng các phần tử của S là 21.
Câu 46.8: Cho hai số thực x , y thỏa mãn hệ thức 2 4 y 1 − 2 log x +1 = 2
− 2x + 2y − 3. Giá trị nhỏ nhất của 2 biểu thức 4 2 2 4 y T x + = − bằng A. (0;+∞). B. 9760 − . C. 1088 − . D. 2530 . Lời giải Chọn C Ta có 2 4 y 1 − 2 log x +1 = 2
− 2x + 2y − 3 2 4 y 2
⇔ 2log x +1 = 2 − 4x + 4y − 6 2 2 ⇔ log ( 2 x + ) 4 y 2
1 = 2 − 4x + 4y − 6 ⇔ 2 + log ( 2 + ) 4 1 = 2 y x − 4( 2 x +1 + 4y 2 ) 2 ⇔ 4( 2 + ) 1 + log 4( 2 + ) 4 1 = 2 y x x + 4y ⇔ 4( 2 x + ) 1 + log 4( 2
x +1 = t + log t (với 4 2 y t = ) 2 ) 2 2
Xét hàm số f (u) = u + log u ⇒ f ′(u) 1 = 1+
> 0 nên hàm số f (u) đồng biến trên 2 u ln 2 (0;+∞) suy ra 2 4 y 2
t = 4x + 4 ⇔ 2 = 4x + 4 . Vậy y+ y T = x − = x −
= x − ( x + ) = x − x − = (x − )2 4 2 2 4 4 4 2 4 2 2 4 16.2 16 4 4 64 64 32 −1088 ≥ 1088 −
Vậy giá trị nhỏ nhất của 1 T là 1088 − khi 2
x = 32 và y = log 132 . 2 4
Câu 46.9: Có bao nhiêu giá trị nguyên y ≤ 2024 để ứng với mỗi y tồn tại hai số thực x thỏa mãn bất
phương trình 2x + ( + ) y+lnx ≤ ( 3 ln . + ) y e y x e x x e ? A. 2023 B. 2024 C. 2025 D. 2026 Lời giải Chọn B
Điều kiện x > 0 . Ta có: 2x + ( + ) y+lnx ≤ ( 3 ln . + ). y e y x e x x e Chia 2 vế cho y
e .x ta được 2 x − y e 2
+ y + ln x ≤ x +1 2
x − y−ln x ⇔ e − ( 2
x − y − ln x) ≤1. x
Mà 2x−y−lnx e − ( 2
x − y − ln x) ≥1 vì te ≥ t +1, t ∀ ∈ Từ đó suy ra 2 2
x − y − ln x = 0 ⇒ y = x − ln x = f (x) . f ′(x) 1
= 2x − ; f ′(x) 1 = 0 ⇒ x = (vì x > 0 ). x 2 Bảng biến thiên Trang 5/53 - WordToan
Dựa vào bảng biến thiên, ta có 1 1 y ln ≥ − ≈ 0,85 . 2 2
Vậy có 2024 giá trị nguyên của y thỏa bất phương trình đã cho. 2
Câu 46.10: Xét các số thực dương x , x − y+ 4x + y y thỏa mãn 2019( 4) 2020 =
. Khi biểu thức y − 2x đạt (x + 2)2
giá trị nhỏ nhất, giá trị của biểu thức x − 2y bằng A. 6 − . B. 7 − . C. 8 − . D. 9 − . Lời giải Chọn D 2019(x+2)2 2 2 Ta có 2019(x −y+4) 4x + y
2019 (x+2) −(4x+ y) + + 4x y 2020 4 2020 = ⇔ 2020 x y = ⇔ = (x + 2)2 (x + 2)2 2019(4x+ y) 2020 (x + 2)2 2019(x+2)2 ⇔ 2020 (x + 2)2 2019(4x+ y) = 2020 (4x + y) ( )1 Xét hàm số ( ) 2019 = 2020 t f t
t với t > 0. t Ta có f ′(t) 2019 2019t 2019 = 2020 + 2020 t ln 2020 > 0 , t ∀ > 0 . Khi đó ( ) 1 ⇔ (x + )2 2
2 = 4x + y ⇔ y = x + 4 . Nên 2
P = y − 2x = x + 4 − 2x = (x − )2 1 + 3 ≥ 3. x =1 min P = 3 khi y = 5
Vậy x − 2y =1− 2.5 = 9 − .
Câu 46.11: Xét các số thực không âm x , y thỏa mãn log 4 + 4 − =1+ 2x y x
− y . Khi biểu thức 2x y + 2 ( )
đạt giá trị nhỏ nhất, giá trị của biểu thức 2y x + bằng A. 1. B. 2 . C. 3. D. 4 . Lời giải Chọn A
log 4 + 4 + = +1+ 2x ⇔ log 4 + log +1 + = +1+ 2x y y x y y x 2 ( ) 2 2 ( ) ⇔ log +1 + +1 = 2x y y + x 2 ( ) ( ) ⇔ log
+1 + +1 = log 2x + 2x y y ( ) 1 2 ( ) ( ) 2
Xét hàm số f u log u u , với u 1. 2 Ta có f u 1 ' 1
0 với u 1 f u đồng biến trên [1;+ ∞) u ln 2 Khi đó ( )
1 1 2x 2x y y 1. Nên = 2x
P y + = 2.2x −1≥1. x = 0 min P =1 khi y = 0 Vậy y 0 x + 2 = 0 + 2 =1.
Câu 46.12: Xét các số thực không âm x , y thỏa mãn log y ( x 2)( y ) 1 1 + + +
= 125 − x −1 y +1 . Khi 5 ( )( )
biểu thức x + 5y đạt giá trị nhỏ nhất, giá trị của biểu thức 5x + y bằng A. 117 . B. 118. C. 119. D. 120. Lời giải Chọn C Ta có: log y ( x 2)( y ) 1 1 + + +
= 125 − x −1 y +1 5 ( )( ) Trang 6/53 - WordToan ⇔ ( y + )
1 log x + 2 y +1 =125− x + 2 −3 y +1 5 ( )( ) ( ) ( ) 125
⇔ log x + 2 y +1 = − x + 2 − 3 5 ( )( ) ( ) y 1 + 125
⇔ log x + 2 + log y +1 = − x + 2 + 3 5 ( ) 5 ( ) ( ) y +1 (x ) (x ) 125 log 2 2 log ( y ) 1 1 − ⇔ + + + = + + + log 125 5 5 5 y +1 125 1
⇔ log x + 2 + x + 2 = + log + log 125 5 ( ) ( ) 5 5 y +1 y +1 125 125
⇔ log x + 2 + x + 2 = log + ( )1 5 ( ) ( ) 5 y 1 + y +1
Xét hàm số f (t) = log t + t 5 Ta có: f ′(t) 1 = +1 > 0, t ∀ ∈(0;+∞) t ln 5
Suy ra f (t) = log t + t đồng biến trên (0;+∞). 5 Khi đó ( ) 1 125 ⇔ x + 2 = 125 ⇔ x = − 2 y +1 y +1 Nên 125 125
P = x + y = − + y = + ( y + ) 125 5 2 5 5 1 − 7 ≥ 2 ⋅5( y + ) 1 − 7 = 43, y ∀ ≥ 0 . y +1 y +1 y +1
min P = 43 khi 125 = 5( y + )
1 ⇔ y = 4 ⇒ x = 23 y +1
Vậy 5x + y = 5.23+ 4 =119 .
Câu 46.13: Cho các số thực x, y thỏa mãn 0 ≤ x, y ≤ 1 và log x + y + x +1 y +1 − 2 = 0 . Tìm giá trị 3 ( )( ) 1− xy
nhỏ nhất của P = 2x + y . A. 2 . B. 1. C. 1 . D. 0. 2 Lời giải Chọn B
Với điều kiện biểu thức đề bài có nghĩa, ta có
log x + y + x +1 y +1 − 2 = 0 ⇔ log x + y − log 1− xy + xy + x + y −1 = 0 3 ( )( ) 3 ( ) 3 ( ) 1− xy
⇔ log x + y + x + y = log 1− xy + 1− xy * 3 ( ) ( ) 3 ( ) ( )( )
Xét hàm số f (x) = log t + t trên (0;2) 3 f ′(t) 1 = ln 3 +1 > 0, t
∀ ∈(0;2) nên hàm số f (t) đồng biến trên (0;2) . t Do đó từ ( ) − x
* ta có x + y = − xy ⇔ y ( + x) 1 1 1 = 1− x ⇔ y = 1+ x 1 = 2 + = 2 − x P x y x + 1+ x P′(x) 2 = 2 − ≥ 0,∀x ∈ 0;1 2 [ ] (1+ x)
Suy ra min P = P(0) = 1 đạt được khi x = 0, y = 1. Trang 7/53 - WordToan Câu 46.14: + + Cho 4a 2b 5
a , b là hai số thực dương thỏa mãn log = a +3b− 4 . Tìm giá trị nhỏ 5 a + b nhất của biểu thức 2 2
T = a + b A. 1 . B. 1. C. 3 . D. 5 . 2 2 2 Lời giải Chọn D 4a + 2b + 5 log
= a +3b−4 ⇔ log 4a + 2b+5 = log a +b + a +3b− 4 5 5 ( ) 5 ( ) a + b
⇔ log 4a + 2b + 5 + 4a + 2b + 5 = log 5 a + b + 5 a + b 5 ( ) ( ) 5 ( ) ( ) (*).
Xét hàm f (x) = log x + x, x > 0. 5
Đạo hàm f ′(x) 1 =
+1 > 0,∀x > 0. Suy ra hàm số f (x) đồng biến trên (0;+∞) . . x ln5
Phương trình (*) viết lại:
f (4a + 2b + 5) = f (5(a + b)) ⇔ 4a + 2b + 5 = 5(a + b) ⇔ a + 3b = 5.
Mặt khác: 2 = (a + b)2 ≤ ( 2 2 + ) ( 2 2 a + b ) 2 2 5 5 3 1 3 .
⇒ T = a + b ≥ . 2 Dấu " = " xảy ra a b ⇔ = ⇒ 1 3
a = ;b = . 1 3 2 2 1− y
Câu 46.15: Xét các số thực dương x, y thỏa mãn log
= 3xy + x + 3y − 4 3
. Tìm giá trị nhỏ nhất x + 3xy P = + min của P x y . A. 4 3 4 P − = B. 4 3 4 P + = min 3 min 3 C. 4 3 4 P + = D. 4 3 4 P − = min 9 min 9 Lời giải Chọn A 1−y Điều kiện
> 0 ⇒ 1− y > 0 ⇔ y <1. Vậy điều kiện xác định của bài toán là: x + 3xy
x > 0;0 < y <1. 1− y 1− y 3(1− y) Ta có: log
= 3xy + x + 3y − 4 ⇔
= 3 xy+x+ y−
3xy+x+3y−3 ⇔ = 3 3 3 3 4 x + 3xy x + 3xy x + 3xy 3(1− y) 3 3 xy+x ⇔ = ⇔ (3− 3y) 3−3
.3 y = (3xy + x) 3xy+x 3 −3 x .3 (*) + 3xy 3 y Xét ( ) = .3t f t
t với t > 0 . Ta có ′( ) = 3t + .3t f t
t .ln 3 > 0 với t
∀ > 0 , suy ra f (t) đồng biến trên
khoảng(0;+∞). Từ (*) ta có f (3−3y) = f (3xy + x) với 3−3y > 0,3xy + x > 0 nên 3 3−3 = 3 − x y
xy + x ⇔ y = . 3(x +1) − − Ta có 3 x 3 x 1 4
P = x + y = x + ( = + + + − x ) (x ) 1 3 1 3 ( x )1 3 + + 3 P = (x + ) 4 4 4 4 4 3 − 4 1 + ( − ≥ + − = . x + ) 2 (x ) 1 . 3 1 3 3(x + ) 1 3 3 Trang 8/53 - WordToan 4 x +1 = 3(x + ) 1 2 3 − 3 x = − − Vậy 4 3 4 3 x 3 P = ⇔ y = ⇔ . min 3 3 (x ) 1 + 2 3 −1 y =
x 0;0 y 1 > < < 3
CÂU TƯƠNG TỰ CÂU 47 ĐỀ THAM KHẢO 2024
Câu 47.1: Gọi M +
và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của 2z i P = với z z là số phức
khác 0 và thỏa mãn z ≥ 2 . Tỉ số M được xác định bởi công thức nào dưới đây? m A. M = 3. B. M 4 = . C. M 5 = . D. M = 2 . m m 3 m 3 m Lời giải
Chọn C 2z+i 2z+i 2z − i 2z + i Ta có 1 1 3 5 P = = ⇒ ≤ P ≤ ⇔ 2 − ≤ P ≤ 2 + ⇔ ≤ P ≤ . z z z z z z 2 2 Vậy M 5 = . m 3
Câu 47.2: Trong các số phức z thỏa mãn điều kiện z −i = z − 2 + 3i , số phức z0 có mô đun nhỏ nhất.
Phần ảo của z0 là A. 2 . B. 4 . 3 3 C. 3 . D. 3 . 2 4 Lời giải Chọn C
Giả sử z = x + yi, x, y ∈ 0 ( ).
Ta có: z − i = z − 2 + 3i ⇔ x + ( y − )
1 i = (x − 2) + (− y + ) 3 i 2
⇔ x + ( y − )2
1 = (x − 2)2 + (− y + )2
3 ⇔ y = −x + 3. 2 2 2 2
z = x + y = x + (−x + )2 2 3 9 3
3 = 2x − 6x + 9 = 2 x − + ≥ . 0 2 2 2 3 Vậy z = 3 3 3 3 z 0
khi và chỉ khi x = ⇒ y = ⇒ z = + i , suy ra phần ảo của bằng 3 . min 2 0 2 2 2 2 0 2
Câu 47.3: Cho tất cả các số phức z = x + i,
y (x, y ∈) thỏa mãn z + 2i −1 = z + i . Biết z được biểu diễn
bởi điểm M sao cho MA ngắn nhất với A(1;3) . Tìm P = 2x + 3y . A. 9 B. 11 C. 3 − D. 5 Lời giải Chọn A Gọi M ( ;
x y) là điểm biểu diễn số phức z = x + i,
y (x, y ∈) .
Ta có: z + 2i −1 = z + i Trang 9/53 - WordToan ⇔ x + i
y + 2i −1 = x + i
y + i ⇔ (x − )
1 + ( y + 2)i = x + ( y + ) 1 i
⇔ ( x − )2 + ( y + )2 2 1 2 = x + ( y + )2
1 ⇔ x − y − 2 = 0 .
Dễ thấy tập hợp các điểm M biểu diễn số phức z là đường thẳng: x − y − 2 = 0 ⇒ M ( ; x x − 2)
MA = (x −1;x−5) ⇒ MA = (x − ) + (x − ) = x − x + = (x − )2 2 2 2 1 5 2 12 26 2 3 2 + 8 ≥ 8 Suy ra: MA = 8 − = ⇔ = ⇒ = = + = + = min khi x 2 3 2 0 x 3
y 1. Vậy P 2x 3y 2.3 3.1 9
Câu 47.4: Cho số phức z thỏa mãn z =1. Gọi M và m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức 2
P = z +1 + z − z +1 . Tính M.m . A. 13 3 . B. 39 . C. 3 3 . D. 13 . 4 4 4 Lời giải Chọn A
Giả sử z = x + yi , (x, y ∈ R) . Do z =1 2 2 ⇔ x + y =1 2 2
⇔ x + y =1. Suy ra x, y ∈[ 1; − ] 1 . Ta có 2
z.z = z =1. Thay vào P ta được: 2
P = z +1 + z − z + z.z = z +1 + z (z −1+ z) = z +1 + z . z + z −1 = z +1 + z + z −1 = ( x + )2 2
1 + y + 2x −1 = 2x + 2 + 2x −1 .
Xét hàm số y = f ( x) = 2x + 2 + 2x −1 1
2x + 2 − 2x +1 khi 1 − ≤ x <
Ta có y = f (x) 2 = . 1
2x + 2 + 2x −1 khi ≤ x ≤1 2 1 1 − 2 khi 1 − < x <
f ′(x) 2x + 2 2 = 1 1 + 2 khi < x ≤1 2x + 2 2 1 1 − < x < 1 1 − < x < f (x) 2 ' = 0 ⇔ 2 7 ⇔ ⇔ = − 1 x − 2 = 0 1 2x + 2 = 8 2x + 2 2
Bảng biến thiên của hàm số f (x) trên [ 1; − ] 1 7 1 x 1 1 8 2 y' + 0 + 13 3 y 4 3 3 Trang 10/53 - WordToan
m = min f (x) = 3 [ 1 − ; ] 1 Suy ra . Vậy 13 3 M.m = . M = f (x) 13 max = 4 [ 1 − ; ] 1 4
Câu 47.5: Xét các số phức w , z thỏa mãn 3 5 w + i =
và 5w = (2 + i)(z − 4) . Giá trị lớn nhất của biểu 5
thức P = z − 2i + z − 6 − 2i thuộc khoảng nào dưới đây? A. (12;13) . B. (13;14). C. (15;16). D. (14;15). Lời giải Chọn C
Ta có: 5w = (2 + i)(z − 4) ⇔ 5w + 5i = (2 + i)(z − 4) + 5i
⇒ 5w + 5i = (2 + i)(z − 4) + 5i
⇒ 5 w + i = (2 + i)(z − 4 +1+ 2i) = 5 z − 3 + 2i 3 5 ⇒ 5.
= 5 z − 3+ 2i ⇒ z − 3+ 2i = 3 . 5 Ta có: 2 2
z + z + z − z = 2( 2 2 z + z ; z ∀ , z . (1) 1 1 1 ) 1 ( z + z )2 2 2 1 z + z ≥ ; z ∀ , z . (2) 1 1 2
Ta có: P = z − 2i + z − 6 − 2i = z − 3− 2i + 3 + z − 3− 2i − 3 .
Áp dụng (1) và (2), ta có: 2 2 z − − i +
+ z − − i − = ( 2 3 2 3 3 2 3
2 z − 3− 2i + 9).
( z − − i + + z − − i − )2 ( z − i + z − − i )2 2 2 3 2 3 3 2 3 2 6 2
z − 3− 2i + 3 + z − 3− 2i − 3 ≥ = . 2 2 Vậy, ta có:
( z −2i + z −6−2i )2 ≤2( 2
z − 3− 2i + 9) ⇒ ( z − 2i + z −6− 2i )2 ≤ 4( 2
z − 3− 2i + 9) . 2 2 ⇒ P ≤ 4( 2
z − 3− 2i + 9). Do ( 2
z − − i + ) = ( 2 4 3 2 9
4 z − 3+ 2i − 4i + 9) nên P ≤ ( z − + i + − i )2 2 4 3 2 4 + 9) 2 ⇒ P ≤ ( 2
4 7 + 9) = 232 ⇒ P ≤ 2 58 ≈15,23.
Ta có thể làm theo phương pháp hình học như sau
Biến đổi suy ra z − 3+ 2i = 3 , vậy quỹ tích các điểm M biểu diễn số phức z là đường tròn tâm I (3; 2
− ), R = 3. Đặt A(0;2), B(6;2) ta có = − + − − = + ≤ ( + )( + ) 2 2 2 2 2 2 2 6 2 1 1 = 22 AB P z i z i MA MB MA MB MH + , trong đó H là 2
trung điểm AB . Do đó P ⇔ MH ⇔ M ≡ M 3; 5 − max max 1 ( ) Trang 11/53 - WordToan
Khi đó P = 58 + 58 = 2 58 ≈15,23 . min
Câu 47.6: Xét các số phức z, w thỏa mãn z + w =10; z =1 và số phức z.w có phần thực bằng 2 . Giá trị
nhỏ nhất của P = z − w + 3− 4i thuộc khoảng nào dưới đây? A. (7;8). B. (3;4). C. (5;6). D. ( 6;7) . Lời giải Chọn B
Đặt z.w = 2 + bi;b∈ , suy ra z.w = z.w = 2 + bi = 2 −bi nên z.w + z.w = 4. Ta có: 2
z + w =10 ⇒10 = z + w = (z + w)(z + w) = (z + w)(z + w) = .zz + .
w w + ( .zw+ .zw) 2 2
= z + w + (z.w+ z.w) 2 2
= 1+ w + 4 = w + 5 ⇒ w = 5
z − w = (z − w) (z − w) = (z − w) (z − w) 2 2 2 . .
= z + w − (z.w+ z.w) =1+5− 4 = 2 ⇒ z − w = 2
Khi đó: P = z − w + 3− 4i = (z − w) + (3− 4i) ≥ z − w − 3− 4i = 2 −5 ≈ 3,6 .
Câu 47.7: Xét các số phức z, w thỏa mãn z − w = 2 z = 2 và số phức z.w có phần thực bằng 2 . Giá trị
lớn nhất của P = z + w + 2 − 3i thuộc khoảng nào dưới đây? A. (7;8). B. (8;9) . C. (5;6). D. ( 6;7) . Lời giải Chọn A
Đặt z.w = 2 + bi;b∈ , suy ra z.w = z.w = 2 + bi = 2 −bi nên z.w + z.w = 4. Ta có: 2
z − w = 2 ⇒ 4 = z − w = (z − w)(z − w) = (z − w)(z − w) = z.z + .
w w − (z.w+ z.w) 2 2
= z + w − (z.w+ z.w) 2 2
= 1+ w − 4 = w − 3 ⇒ w = 7 2
z + w = (z + w) (z + w) = (z + w) (z + w) 2 2 . .
= z + w + ( .zw+ .zw) =1+ 7 + 4 =12 ⇒ z + w = 2 3
Khi đó: P = z + w + 2 − 3i = (z + w) + (2 −3i) ≤ z + w + 2 −3i = 2 3 + 13 ≈ 7,07 . − + =
Câu 47.8: Cho số phức z thỏa mãn đồng thời hai điều kiện z 2 3i 2 và biểu thức 2 2
T = z + 7 + 2i + z −1− 6i đạt giá trị lớn nhất. Tính giá trị biểu thức S = z − (2023− 2024i) A. 2020 2 . B. 2021 2 . C. 2022 2 . D. 2023 2 . Lời giải Chọn A Trang 12/53 - WordToan
Gọi M (x, y) là điểm biểu diễn cho số phức z ⇒ M thuộc đường tròn tâm I (2; 3 − ) bán kính R = 2 . Gọi A( 7 − ; 2 − ), B(1;6) 2 2
⇒ T = MA + MB .
Gọi H là trung điểm của AB ⇒ H ( 3 − ;2) .
MH là đường trung tuyến trong tam giác MAB nên ta có 2( 2 2 MA + MB ) 2 − AB 2 2 2 2 1 2 MH =
⇒ MA + MB = 2MH + AB 4 2
AB = 8 2 không đổi nên T lớn nhất ⇔ MH lớn nhất ⇔ MH = IH + R với HI = 5 2 Dấu “=” xảy ra
HI 5 = 5(x − 2) x = 3 ⇔ HI =
.IM ⇒ HI = 5IM ⇒ ⇒ ⇒ M (3; 4 − ) R 5 − = 5(y + 3) y = 4 −
⇒ S = z − (2023− 2024i) = 2020 −
+ 2020i = 2020 2 .
Câu 47.9: Cho hai số phức z và w thỏa mãn z + 2w = 8 + 6i và z − w = 4. Giá trị lớn nhất của biểu thức
z + w bằng A. 4 6 . B. 2 26 . C. 66 . D. 3 6 . Lời giải Chọn C
Giả sử M , N lần lượt là các điểm biểu diễn cho z và w . Gọi E là điểm biểu diễn cho số phức
2w. Suy ra OM + 2ON = OM + OE = OF = 2OI với F (8;6) là đỉnh thứ 4 của hình bình hành
MOEF , I(4;3) là trung điểm của OF .
Ta có z − w = MN = 4 và OF = 2OI =10 . Đặt a
z = ON = ; w = OM = . b 2 Trang 13/53 - WordToan E F I N a O b M Xét tam giác O ∆ MF và O ∆ ME 2 2 2 a + b ME − = 25 Ta có 2 4 2 2
⇒ a + 2b = 88 . 2 2 2 b + ME a − = 16 2 4 2 ( )2 a z w b ( 2 2 a b ) 1 1 2 + = + ≤ + + = 66 . 2 4 2
Suy ra z + w ≤ 66, dấu “=” xảy ra khi 2 66 a = b = . 3
Vậy ( z + w ) = 66 . max
Câu 47.10: Cho các số phức w, z thỏa mãn w −1+ i = 5 và (1+ 2i)(z −5) = 5w . Giá trị lớn nhất của
biểu thức P = 2 z − 3− 2i − z + 4 − 3i là A. 53 . B. 2 53 C. 5 2 . D. 3 5 . Lời giải Chọn A
Ta có: (1+ 2i)(z −5) = 5w ⇔ (1+ 2i) z −5 −10i = 5w
⇔ (1+ 2i) z −10 − 5i = 5w − 5 + 5i ⇔ (1+ 2i)(z − 4 + 3i) = 5(w −1+ i)
⇒ 5 z − 4 + 3i = 5 w −1+ i = 5 5
⇒ z − 4 + 3i = 5
Gọi M là điểm biểu diễn của số phức z
Vì z − + = ⇒ M ∈(C) (x − )2 + ( y + )2 4 3 5 : 4 3 = 25 có tâm I (4; 3
− ) , bán kính R = 5.
Gọi A(3;2); B( 4 − ;3) , khi đó:
P = 2MA − MB Trang 14/53 - WordToan I A D C M O B
Nhận xét O(0;0) là trung điểm của IB và O∈(C), ,
A B nằm ngoài (C). 3 Gọi
C, D là trung điểm của IO, IM 1
⇒ DO = MB với C 2;− 2 2
Vì tam giác IMO cân tại I nên MC = OD ⇒ MB = 2MC .
M = AC ∩(C)
Khi đó P = 2MA − MB = 2MA − 2MC ≤ 2AC . Dấu “=” xảy ra khi
MA = k.MC;k > 0 2 P AC ( )2 3 2 2 3 2 2 ⇒ = = − + + = 53 . max 2
Câu 47.11: Cho số phức z thỏa mãn z −3− 4i = 5 . Gọi M ,m lần lượt là giá trị lớn nhất, giá trị nhỏ nhất của biểu thức 2 2
P = z + 2 − z − i . Khi đó modun của số phức w = M + mi A. 2 314 . B. 1258 . C. 3 137 . D. 2 309 . Lời giải Chọn B
Cách 1: Giả sử z = x + yi(x, y ∈) ta có z −3− 4i = 5 ⇔ (x − )2 + ( y − )2 3 4 = 5 Ta có 2 2
P = z + 2 − z − i ⇔ P = 4x + 2y + 3 ⇔ 4(x − 3) + 2( y − 4) = P − 23
Ta có (x − )+ ( y − ) 2 ≤
(x − )2 +( y − )2 4 3 2 4 20 3 4 =100 Suy ra 10
− ≤ P − 23 ≤10 ⇔ 13 ≤ P ≤ 33 suy ra M = 33,m =13 do đó ta được w = 33+13i vậy w = 1258 .
Cách 2: Gọi z = x + yi với x, y ∈ .
Ta có: z − − i =
⇔ (x − )2 + ( y − )2 3 4 5 3
4 = 5 . Suy ra, tập hợp điểm M ( ; x y) biểu diễn cho
số phức z trên hệ tọa độ Oxy là đường tròn(C) tâm I (3;4) và bán kính R = 5 . Lại có: 2 2 P = z +
− z − i ⇔ (x + )2 2 2 2
2 + y − x − ( y − )2
1 − P = 0 ⇔ 4x + 2y + 3− P = 0 , đây là
phương trình của đường thẳng ∆ : 4x + 2y + 3− P = 0 .
Ta thấy M = ∆ (C) . − P
Điều kiện để ∆ cắt (C) là: d (I ∆) 23 , ≤ R ⇔ ≤ 5 ⇔ 10
− ≤ 23− P ≤10 ⇔ 13 ≤ P ≤ 33 . 2 5 Trang 15/53 - WordToan
Suy ra: m =13, M = 33 và w = 33+13i ⇒ w = 1258 .
Câu 47.12: Cho số phức z thỏa mãn z − 3 + z + 3 = 8 . Gọi M , m lần lượt giá trị lớn nhất và nhỏ nhất
z . Khi đó M + m bằng A. 4 − 7 . B. 4 + 7. C. 7 − 4. D. 2 7 . Lời giải Chọn B
Cách 1 : Gọi z = x + yi với ; x y ∈ .
Ta có 8 = z − 3 + z + 3 ≥ z − 3+ z + 3 = 2z ⇔ z ≤ 4 .
Do đó M = max z = 4.
Mà z − + z + = ⇔ x − + yi + x + + yi = ⇔ (x − )2 2 + y + (x + )2 2 3 3 8 3 3 8 3 3 + y = 8 .
Áp dụng bất đẳng thức Bunhiacopxki, ta có = (x − )2 2 + y + (x + )2 2 + y ≤ ( 2 2 + )(x − )2 2 + y + (x + )2 2 8 1. 3 1. 3 1 1 3 3 + y ⇔ ≤ ( 2 2
x + y + ) ⇔ ( 2 2 8 2 2 2 18
2 2x + 2y +18) ≥ 64 2 2 2 2
⇔ x + y ≥ 7 ⇔ x + y ≥ 7 ⇔ z ≥ 7 .
Do đó M = min z = 7 .
Vậy M + m = 4 + 7 .
Cách 2: Tập hợp các điểm biểu diễn số phức z là elip F 3 − ;0 , F 0,3 1 ( ) 2 ( ) 2 2 x y 8 1 a 4 + = = = 16 7 2 2 2 2 2 b
= a − c = 4 − 3 = 7 z = a = 4 Do vậy Max
⇒ M + m = 4 + 7 . z = b = 7 Min
Câu 47.13: Xét các số phức z, w thỏa mãn z = 2 w = 2 . Biết P = iz + w + 3− 4i đạt giá trị nhỏ nhất.
Khi đó z − w bằng A. 2 5 . B. 29 . C. 5 . D. 1 . 5 5 Lời giải Chọn C
Cách 1: Ta có iz + w + 3− 4i ≥ 3− 4i − iz + w ≥ 5 − ( iz + w ) ≥ 5−(2 + ) 1 = 2
w = k 3− 4i khi k < 0 w = 1 1 ( ) ( 1 ) Dấu bằng xảy ra khi và .
.iz = k 3 − 4i khi k < 0 iz = z = 2 2 ( ) ( 2 ) Giải hệ trên suy ra 2 k = − ; 1 k = − . 2 5 1 5 3 4 w = − + i 5 5 Hay 2 − iz = (3− 4i) 5 2 − i ⇒ −z = ( − i) 8 6
3 4 ⇒ z = − − i 5 5 5 Trang 16/53 - WordToan
Khi đó z − w = 1
− − 2i ⇒ z − w = 5 .
Cách 2: Trong mặt phẳng Oxy :
Gọi M là điểm biểu diễn của số phức iz ⇒ OM = 2 ⇒ M thuộc đường tròn (C1) tâm O bán kính R = 2 1 .
Gọi N là điểm biểu diễn của số phức w ⇒ ON =1 ⇒ N thuộc đường tròn (C2 ) tâm O bán kính R =1 2 .
Gọi E (3; 4
− ) . Khi đó, ta có P = iz + w+ 3− 4i = OM + ON + OE .
Ta thấy P đạt giá trị nhỏ nhất khi M , N, E thẳng hàng và OM và ON ngược hướng với OE
Đường thẳng OE có phương trình là 4 y − = x . 3
Tọa độ giao điểm của đường thẳng OE và đường tròn (C1) là nghiệm của hệ phương trình: 6 x = 5 4 − 8 − 4 − y = x 4 − y = y x = 3 y = x 5 3 ⇔ ⇔ ⇔ . 2 3 2 2 2 4 6 x + y = 4 x − + x = 4 2 25x = 36 = − x 3 5 8 y = 5 Vậy 6 8 M ; − . 5 5
Tọa độ giao điểm của đường thẳng OE và đường tròn (C2 ) là nghiệm của hệ phương trình: Trang 17/53 - WordToan 3 x = 5 4 − 4 − 4 − y = x 4 − y = y x = 3 y = x 5 3 ⇔ ⇔ ⇔ 2 3 2 2 2 4 3 x + y = 1 x − + x = 1 2 25x = 9 = − x 3 5 4 y = 5 Vậy 3 4 N ; − . 5 5 Do đó: 3 4
w = − + i và 6 8 8 6
.iz = − + i ⇔ z = − − i . 5 5 5 5 5 5 Vậy z − w = 1 − − 2i = 5 .
Câu 47.14: Cho hai số phức z , z thỏa mãn z
z − z = 3, z = 2 và số phức 1 là số thuần ảo. Giá trị 1 2 1 2 1 z2
lớn nhất của P = z + z − 3+ 2i bằng 1 2 A. 3+ 2 . B. 3+ 13 . C. 3+ 5 . D. 5 + 3 . Lời giải Chọn B Cách 1.
Gọi A(x ; y , B x ; y z và z 1 1 )
( 2 2 ) lần lượt là các điểm biểu diễn số phức 1 2
z − z = 3 AB = 3 Ta có: 1 2 ⇔ z = 2 OA = 2 1 z z z 1 1 2 =
là số thuần ảo nên x x + y y = 0 ⇔ .
OAOB = 0. Suy ra OA ∆
B vuông tại O 2 z 1 2 1 2 2 z2
Gọi là I trung điểm của AB
Ta có 1 3
OA + OB = 2OI, OI = AB = 2 2 Số phức z = 3
− + 2i được biểu diễn bởi điểm C ( 3 − ;2) Khi đó 3
P = 2OI + OC ≤ 2 OI + OC ⇒ P ≤ 2. + ( 3 − )2 2 + 2 = 3+ 13 2
Vậy max P = 3+ 13 khi OI và OC cùng hướng. Cách 2. Ta có z z .z 1 1 2 =
là số thuần ảo suy ra z .z thuần ảo 2 z 1 2 2 z2
Mà z .z và z z là hai số phức liên hợp của nhau, do đó z .z + z z = 2.0 = 0 1 2 1 2 1 2 1 2 Xét 2
z + z = (z + z )(z + z ) 2 2 2 2
= z + z + z z + z z = z + z 1 2 1 2 1 2 1 2 1 2 1 2 1 2 2 2
z + z − z − z = 2 z z + z z = 0 ⇒ z + z = z − z = 3 1 2 1 2 ( 1 2 1 2) 1 2 1 2
P = z + z −3+ 2i ≤ z + z + 3
− + 2i = 3+ 13 ⇒ max P = 3+ 13 1 2 1 2
Câu 47.15: Cho hai số phức z , z thỏa mãn z − z = z = 3 và số phức z z có phần thực bằng 9 . 1 2 1 2 1 1 2 2
Giá trị lớn nhất của P = 2z + z +1− 2i thuộc khoảng nào dưới đây? 1 2 Trang 18/53 - WordToan A. 3 5 + 7 . B. 3 7 + 5 . C. 3 2 + 7 . D. 6 7 + 5 . Lời giải Chọn B Cách 1.
Gọi A(x ; y , B x ; y z và z 1 1 )
( 2 2 ) lần lượt là các điểm biểu diễn số phức 1 2
z − z = 3 AB = 3 Ta có: 1 2 ⇔ z = 3 OA = 3 1
z z có phần thực bằng 9 9 9 x x + y y = ⇒ . = . 1 2 OAOB 2 nên 1 2 1 2 2 2 Ta có 2 2 2 2
AB = OB − OA = 9 ⇔ OB − 2 .
OB OA + OA = 9 ⇒ OB = 3 Suy ra OA ∆
B đều có cạnh bằng 3.
Gọi C là điểm biểu diễn số phức 2z = 1 suy ra OC 2OA Khi đó OB ∆
C vuông tại B có OC = 6;OB = 3.
Gọi là I trung điểm của BC. Ta có OC + OB = 2OI 2 2 2 1 1 1
I = OB + OC = OB + OA = ( 2 2
OB + OB OA + OA ) 3 7 O 2 4 . 4 ⇒ OI = 4 4 4 2
Số phức z =1− 2i được biểu diễn bởi điểm D(1; 2 − )
Khi đó 3 7 2
P = 2OA + OB + OD ≤ 2 OI + OD ⇒ P ≤ 2. + 1 + ( 2 − )2 = 3 7 + 5 Vậy 2
max P = 3 7 + 5 khi OI và OD cùng hướng. Cách 2.
Ta có z .z và z z là hai số phức liên hợp của nhau, do đó 9
z .z + z z = 2. = 9 1 2 1 2 1 2 1 2 2 Xét 2
z − z = (z − z )(z − z ) 2 2
= z + z − (z z + z z ) 2 = 9 ⇒ z = 9 1 2 1 2 1 2 1 2 1 2 1 2 2 2
2z + z = (2z + z )(2z + z ) 2 2
= 4 z + z + 2 z z + z z = 63 1 2 1 2 1 2 1 2 ( 1 2 1 2)
P = 2z + z +1− 2i ≤ 2z + z + 1− 2i = 3 7 + 5 ⇒ max P = 3 7 + 5 1 2 1 2 .
Câu 47.16: Cho hai số phức z , z thỏa mãn z − z −1 = 3 z −i = 3 và số phức (z +i z +1−i 1 )( 2 ) có 1 2 1 2 1
phần thực bằng 3. Giá trị nhỏ nhất của P = z + 2z + 3− i bằng 1 2 A. 69 + 5 . B. 69 − 5 . C. 69 + 10 . D. 69 − 10 . 2 2 Lời giải Chọn B Cách 1.
Ta có: z − z −1 = z − i − z +1− i 1 2 ( 1 ) ( 2 )
Gọi A(x ; y , B x ; y
z − i và z +1− i 1 1 )
( 2 2 ) lần lượt là các điểm biểu diễn số phức 1 2 AB = 3
Ta có: z − z −1 = 3 z − i = 3 ⇔ 1 2 1 OA =1
Xét (z +i z +1−i = z −i z +1−i 1 )( 2 ) ( 1 )( 2 ) có phần thực bằng 3
Do đó x x + y y = 3 ⇒ . OAOB = 3. 1 2 1 2 Ta có 2 2 2 2
AB = OB − OA = 9 ⇔ OB − 2 .
OB OA + OA = 9 ⇒ OB = 14 Trang 19/53 - WordToan
P = z − i + 2 z +1− i +1+ 2i 1 ( 2 )
Gọi C là điểm biểu diễn số phức 2(z +1−i suy ra OC = 2OB 2 ) Khi đó OA ∆
C có OA =1;OC = 2 14.
Gọi là I trung điểm của AC. Ta có OA + OC = 2OI 2 2 2 1 1 1
I = OA + OC = OA + OB = ( 2 2
OA + OAOB + OB ) 69 O 2 4 . 4 ⇒ OI = 4 4 4 2
Số phức z =1+ 2i được biểu diễn bởi điểm D(1;2) Khi đó 69 2 2
P = OA + 2OB + OD ≥ 2 OI − OD ⇒ P ≥ 2. − 1 + 2 = 69 − 5 2
Vậy min P = 69 − 5 khi OI và OD ngược hướng. Cách 2.
Ta có: z − z −1 = z − i − z +1− i 1 2 ( 1 ) ( 2 )
Đặt w = z − i và w = z +1− i 1 1 2 2
Suy ra (z +i z +1−i = w w 1 )( 2 ) 1 2
Ta có w .w và w w là hai số phức liên hợp của nhau, do đó w .w + w w = 2.3 = 6 1 2 1 2 1 2 1 2 Xét 2 w − w = (w − w )(w − w ) 2 2 = w + w − (w w + w w ) 2 = 9 ⇒ w =14 1 2 1 2 1 2 1 2 1 2 1 2 2 2 w + 2w = (w + 2w )(w + w ) 2 2 = w + 4 w + 2 w w + w w = 69 1 2 1 2 1 2 1 2 ( 1 2 1 2)
P = z − i + 2 z +1− i +1+ 2i ≤ w + 2w − 1+ 2i = 69 − 5 ⇒ min P = 69 − 5 1 ( 2 ) 1 2
Câu 47.17. Xét các số phức z, w thỏa mãn z + w = 2 z = 4 và số phức z.w có phần thực bằng 2 . Giá trị
lớn nhất của P = z − w + 3− 4i thuộc khoảng nào dưới đây? A. (4;5) . B. (7;8). C. (5;6). D. ( 6;7) . Lời giải Chọn B
Đặt z.w = 2 + bi , suy ra z.w = z.w = 2 + bi = 2 − bi nên z.w + z.w = 4. Ta có: 2
z + w = 4 ⇒16 = z + w = (z + w)(z + w) = (z + w)(z + w) = z.z + .
w w + (z.w+ z.w) 2 2
= z + w + (z.w+ z.w) 2 2
= 4 + w + 4 = w + 8 ⇒ w = 2 2 2
z − w = (z − w) (z − w) = (z − w) (z − w) 2 2 . .
= z + w − (z.w+ z.w) = 4 +8− 4 = 8 ⇒ z − w = 2 2
Khi đó: P = z − w + 3− 4i = (z − w) + (3− 4i) ≤ z − w + 3− 4i = 2 2 + 5 .
Câu 47.18. Xét các số phức z, w thỏa mãn z − w = 2 z = 6 và số phức z.w có phần thực bằng 3. Giá trị
lớn nhất của P = 2z + 2w −1+ 3i thuộc khoảng nào dưới đây? A. (16;18). B. (14;16) . C. (12;14) . D. ( 10;12) . Lời giải Chọn A
Đặt z.w = 3+ bi , suy ra z.w = z.w = 3+ bi = 3− bi nên z.w + z.w = 6 . Ta có: 2
z − w = 6 ⇒ 36 = z − w = (z − w)(z − w) = (z − w)(z − w) = z.z + .
w w − (z.w+ z.w) 2 2
= z + w − (z.w+ z.w) 2 2
= 9 + w − 6 = w + 3 ⇒ w = 33 Trang 20/53 - WordToan 2
z + w = (z + w) (z + w) = (z + w) (z + w) 2 2 . .
= z + w + ( .zw+ .zw) = 9 + 33+ 6 = 48 ⇒ z + w = 4 3
Khi đó: P = 2z + 2w −1+ 3i = 2(z + w) + ( 1
− + 3i) ≤ 2(z + w) + 1 − + 3i = 8 3 + 10 .
Câu 47.19. Xét các số phức z, w thỏa mãn z + w = 3 z = 6 và số phức z.w có phần thực bằng 4 . Giá trị
lớn nhất của P = 3z − 3w + 2 − i thuộc khoảng nào dưới đây? A. (16;18). B. (14;16) . C. (12;14) . D. ( 18;20) . Lời giải Chọn B
Đặt z.w = 4 + bi , suy ra z.w = z.w = 4 + bi = 4 − bi nên z.w + z.w = 8 . Ta có: 2
z + w = 6 ⇒ 36 = z + w = (z + w)(z + w) = (z + w)(z + w) = .zz + .
w w + ( .zw+ .zw) 2 2
= z + w + (z.w+ z.w) 2 2
= 4 + w + 8 = w +12 ⇒ w = 2 6 2
z − w = (z − w) (z − w) = (z − w) (z − w) 2 2 . .
= z + w − (z.w+ z.w) = 4 + 24 −8 = 20 ⇒ z − w = 2 5
Khi đó: P = 3z − 3w + 2 − i = 3(z − w) + (2 −i) ≤ 3 z − w + 2 −i = 6 5 + 5 = 7 5 .
CÂU TƯƠNG TỰ CÂU 48 ĐỀ THAM KHẢO 2024
Câu 48.1: Chuẩn bị cho đêm hội diễn văn nghệ chào đón năm mới, bạn An đã làm một chiếc mũ “cách
điệu” cho ông già Noel có dáng một khối tròn xoay. Mặt cắt qua trục của chiếc mũ như hình vẽ
bên dưới. Biết rằng OO′ = 5 cm , OA =10 cm , OB = 20 cm , đường cong AB là một phần của
parabol có đỉnh là điểm A . Thể tích của chiếc mũ bằng π π π π A. 2750 3 cm B. 2500 3 cm C. 2050 ( 3 cm ) D. 2250 3 cm 3 ( ) 3 ( ) 3 3 ( ) Lời giải Chọn B
Ta gọi thể tích của chiếc mũ là V . Trang 21/53 - WordToan
Thể tích của khối trụ có bán kính đáy bằng OA =10 cm và đường cao OO′ = 5 cm là V . 1
Thể tích của vật thể tròn xoay khi quay hình phẳng giới hạn bởi đường cong AB và hai trục tọa
độ quanh trục Oy là V . 2
Ta có V = V +V 1 2 2 V = 5.10 π = 500π ( 3 cm ). 1
Chọn hệ trục tọa độ như hình vẽ.
Do parabol có đỉnh A nên nó có phương trình dạng 2
(P) : y = a(x −10) .
Vì (P) qua điểm B(0;20) nên 1 a = . 5 Do đó, (P) 1
: y = (x −10)2 . Từ đó suy ra x =10 − 5y (do x <10). 5 20
Suy ra V = π ∫ ( − y)2 8000 1000 10 5 dy = π 3000 − = π ( 3 cm ). 2 3 3 0 Do đó 1000 2500
V = V +V = π + 500π = π ( 3 cm ). 1 2 3 3
Câu 48.2: Một cốc rượu có hình dạng tròn xoay và kích thước như hình vẽ, thiết diện dọc của cốc (bổ dọc
cốc thành 2 phần bằng nhau) là một đường Parabol. Tính thể tích tối đa mà cốc có thể chứa được
(làm tròn 2 chữ số thập phân). A. 3 V = 320cm . B. 3
V =1005,31cm . C. 3 V = 251,33cm . D. 3 V = 502,65cm . Lời giải Chọn C Parabol có phương trình 5 2 2 8
y = x ⇔ x = y 8 5 Trang 22/53 - WordToan 10 Thể tích tối đa cốc 8 V π y . = dy ≈ ∫ 251,33 . 5 0
Câu 48.3: Một viên gạch hoa hình vuông cạnh 40cm . Người thiết kế đã sử dụng bốn đường parabol có
chung đỉnh tại tâm viên gạch để tạo ra bốn cánh hoa (được tô mầu sẫm như hình vẽ bên).
Diện tích mỗi cánh hoa của viên gạch bằng A. 2 800cm . B. 800 2 cm . C. 400 2 cm . D. 2 250cm . 3 3 Lời giải Chọn C
Chọn hệ tọa độ như hình vẽ (1 đơn vị trên trục bằng 10cm =1dm ), các cánh hoa tạo bởi các đường 2 2 2 2 parabol có phương trình x y = , x y = − , y x = − , y x = . 2 2 2 2
Diện tích một cánh hoa (nằm trong góc phàn tư thứ nhất) bằng diện tích hình phẳng giới hạn bởi 2 hai đồ thị hàm số x y =
, y = 2x và hai đường thẳng x = 0; x = 2 . 2
Do đó diện tích một cánh hoa bằng 2 2 2 3 ∫ 2 2 3 x 4 400 4 400 2 x x − dx = (2x) − = ( 2 dm ) = ( 2 cm ) = ( 2 dm ) = ( 2 cm ). 2 3 6 3 3 3 3 0 0
Câu 48.4: Cho hai hàm số f (x) 3 2 1
= ax + bx + cx − và g (x) 2
= dx + ex +1 (a,b,c,d,e∈) . Biết rằng đồ 2
thị của hàm số y = f (x) và y = g (x) cắt nhau tại ba điểm có hoành độ lần lượt là 3 − ; 1; − 1 (tham khảo hình vẽ). Trang 23/53 - WordToan
Hình phẳng giới hạn bởi hai đồ thị đã cho có diện tích bằng A. 9 . B. 8 . C. 4 . D. 5. 2 Lời giải Chọn C Cách 1: 1 − 1
Diện tích hình phẳng cần tìm là: S = f
∫ (x)− g(x)dx+ g
∫ (x)− f (x)dx 3 − 1 − 1 − 1 3 ax ∫
(b d ) 2x (c e) 3 3 x x ax ∫
(b d ) 2x (c e) 3 d x = + − + − − − + − + − − dx . − 2 − 2 3 1 Trong đó phương trình 3
ax + (b − d ) 2
x + (c − e) 3
x − = 0 (*) là phương trình hoành độ giao 2
điểm của hai đồ thị hàm số y = f (x) và y = g (x) .
Phương trình (*) có nghiệm 3 − ; 1 − ; 1 nên
− a + (b−d)− (c−e) 3 27 9 3 − = 0 3 1 27
− a + 9(b − d ) − 3(c − e) = a = 2 2 2 3 3
−a + (b − d ) − (c − e) 3 − = 0
⇔ −a + (b − d ) −(c − e) = ⇔ ( b − d ) = . 2 2 2 a+ 3 1
(b − d )+(c −e) 3 − = 0 a +
(b − d)+(c −e) = (c −e ) = − 2 2 2 1 − 1 Vậy 1 3 3 2 1 3 1 3 3 2 1 3 S x x x dx x x x = + − − − + − − dx ∫ ∫ = 2 − ( 2 − ) = 4. − 2 2 2 2 − 2 2 2 2 3 1 Cách 2:
Phương trình hoành độ giao điểm của f (x) và g (x) là: a(x + 3)(x + ) 1 (x − ) 1 = 0 .
Dựa vào các hệ số tự do suy ra: 1 1 3
− a = − −1⇒ a = . 2 2
Từ đó suy ra: f (x) − g (x) 1 = (x + 3)(x + ) 1 (x − ) 1 . 2
Diện tích hình phẳng giới hạn bởi hai hàm số f (x) và g (x) là: 1 − 1 1
S = ∫ (x + )(x + )(x − ) 1 3 1
1 dx − ∫ (x +3)(x + )1(x − )1dx = 2−( 2 − ) = 4 . − 2 − 2 3 1
Câu 48.5: Một cái trống trường có bán kính các đáy là 30cm, thiết diện vuông góc với trục và cách đều hai
đáy có diện tích là 1600π(cm2), chiều dài của trống là 1m. Biết rằng mặt phẳng chứa trục cắt mặt
xung quanh của trống là các đường Parabol. Hỏi thể tích của cái trống gần với giá trị nào trong 4 giá trị sau? Trang 24/53 - WordToan A. 425,2 (lít). B. 42,52 (lít). C. 4,252 (lít). D. 212,5(lít). Lời giải Chọn A
Ta có chọn hệ trục tọa độ như hình vẽ.
Vì thiết diện vuông góc với trục cách đều 2 đáy là một hình tròn và cách đều 2 đáy có diện tích là 2
1600π (cm ) nên ta có bán kính 2 2
r π =1600π (cm ) ⇒ r = 40(cm) . Lại có Parabol 2
P : y = ax + bx + c có đỉnh I (0;40) và qua các điểm A( 50 − ;30) , B(50;30) 1 = 40 a c = − 250
nên ta có hpt: 2500a + 50b = 10 − ⇒ b = 0
2500a 50b 10 − = − c = 40 Vậy Parabol có dạng 1 2 P : y = − x + 40 250
Nên thể tích của cái trống là thể tích khối tròn xoay giới hạn bởi parabol 1 2 P : y = − x + 40 250
quay quanh trục ox và các đường x = 50 − ; x = 50 50 1 2 2 406000 3 3 V = π (− x + 40) dx =
π (cm ) ≈ 425,2(dm ) = 425,2(lít) ∫ − 250 3 50
Câu 48.6: Ông An muốn làm cửa rào sắt có hình dạng và kích thước như hình vẽ bên, biết đường cong phía
trên là một Parabol. Giá 1 (m2) của rào sắt là 700.000 đồng. Hỏi ông An phải trả bao nhiêu tiền
để làm cái cửa sắt như vậy (làm tròn đến hàng phần nghìn). A. 6.520.000 đồng. B. 6.320.000 đồng. C. 6.417.000 đồng. D. 6.620.000 đồng. Lời giải Chọn C
Chọn hệ trục tọa độ như hình vẽ. Trong đó A( 2
− ,5; 1,5), B(2,5; 1,5), C (0; 2). Trang 25/53 - WordToan
Giả sử đường cong trên là một Parabol có dạng 2
y = ax + bx + c với a, b, c∈ R
Do Parabol đi qua các điểm đó A( 2
− ,5; 1,5), B(2,5; 1,5), C (0; 2).nên ta có hệ phương trình: 2 2 ( 2, − 5) − 2,5 + =1,5 a a b c = − 25 2
(2,5) a + 2,5b + c =1,5 ⇒ b = 0 c 2 = c = 2
Khi đó phương trình Parabol là: 2 2 y = − x + 2 25
Diện tích S của cửa rào sắt là diện tích phần hình phẳng giới bởi đồ thị hàm số: 2 2 y = − x + 2 25
trục hoành và hai đường thẳng x = − 2,5; x = 2,5. 2,5 3 x ,5 Ta có : 2 2 2 2
S = ∫ − x + 2 dx = − + 2 55 x = − − 25 25 3 2,5 6 2,5
Vậy ông An phải trả số tiền để làm cái cửa sắt là 55 S.700000 =
.700000 ≈ 6.417.000(đồng) 6
Câu 48.7: Một vật trang trí có dạng khối tròn xoay tạo thành khi quay miền (R) (phần gạch chéo trong hình
vẽ) quay xung quanh trục AB . Biết ABCD là hình chữ nhật cạnh AB = 3cm , AD = 2cm ; F là
trung điểm của BC ; điểm E cách AD một đoạn bằng 1cm .
Thể tích của vật thể trang trí trên là (quy tròn đến hàng phần mười) A. 3 16,4cm . B. 3 16,5cm . C. 3 5,2cm . D. 3 3,8cm . Lời giải Chọn B
Chọn hệ trục Oxy có O ≡ A; B ∈ ; Ox D ∈Oy .
Ta có: A(0;0); D(0;2); B(3;0); E (1; ) 1 Trang 26/53 - WordToan
Đường tròn tâm I (0; )
1 chứa cung ED có phương trình là: 2 x + ( y − )2 1 =1.
Nên cung trên của đường tròn tâm I là: 2 y =1+ 1− x .
Thể tích của vật thể trang trí là: 1
V = π ∫(1+ 1− x ) 3 2 2 2 3
dx +π 1 dx ≈16,5(cm ) ∫ . 0 1
Câu 48.8: Một chiếc đinh tán có dạng khối tròn xoay được tạo thành khi cho phần tô đậm quay xung quanh
cạnh AB . Biết ABCD là hình chữ nhật có AB = 20mm , AD = 6mm , cung AE là cung một
phần tư của đường tròn có bán kính bằng 6mm , điểm F cách AB một đoạn bằng 3mm
Thể tích của đinh tán là (quy tròn đến hàng phần mười) A. 3 270mm . B. 3 848,2mm . C. 3 220,8mm . D. 3 584,3mm . Lời giải Chọn B
Chọn hệ trục Oxy có A ≡ O ; B(20;0); D(0;6) .
Khi đó: F là trung điểm của EI và I (6;0); E (6;6); F (6;3);G(20;3).
+ Đường tròn tâm I (6;0) bán kính bằng 6 có phương trình là: (x − )2 2 6 + y = 36 .
Nên nửa cung phía trên của trục Ox có phương trình là: 2
y = 36 − (x − 6) .
+ Phương trình đường thẳng FG là: y = 3. Trang 27/53 - WordToan 6 20
Vậy thể tích của đinh tán là: V = π 36 − ∫ (x −6)2 2
dx +π 3 dx ≈ 848,2 ∫ ( 3 mm ) 0 6
Câu 48.9: Một viên gạch hoa hình vuông có cạnh bằng 80cm . Người ta thiết kế sử dụng 4 đường parabol
cùng chung đỉnh tại tâm của viên gạch và đi qua hai đỉnh kề nhau của viên gạch để tạo thành bông hoa như hình vẽ.
Diện tích của bông hoa (phần tô đậm trong hình vẽ) là 64 16 A. 2 dm . B. 2 dm . C. 3 16dm . D. 3 64dm . 3 3 Lời giải Chọn A
Ta có: 80cm = 8dm.
Chọn hệ trục Oxy như hình vẽ.
Ta có: A(4;0); B(4;4);C (0;4) .
Các cánh hoa được tạo thành bởi 4 đường parabol có phương trình là: 2 2 2 2 x = ; x = − ; y = ; y y y x x = − . 4 4 4 4 2
Diện tích của cánh hoa nằm trong góc phần tư thứ nhất được giới hạn bởi các đường: x y = 4
y = 2 x ; x = 0; x = 4 , nên diện tích một cánh hoa bằng: 4 2 x 16 2
S = ∫2 x − dx = (dm ) . 4 3 0
Vậy diện tích bông hoa là: 64 4S = ( 2 dm ). 3
Câu 48.10. Cho hai đường tròn (O ;5 O ;3 1
) và ( 2 ) cắt nhau tại hai điểm ,A B sao cho AB là một
đường kính của đường tròn (O . D 2 ) Gọi (
) là hình thẳng được giới hạn bởi hai đường tròn (ở
ngoài đường tròn lớn, phần được gạch chéo như hình vẽ). Quay (D) quanh trục O O 1 2 ta
được một khối tròn xoay. Tính thể tích V của khối tròn xoay được tạo thành. Trang 28/53 - WordToan A (D) O O 1 2 B A. 14π π V = . B. 68 V = . 3 3 C. 40π V = . D. V = 36π. 3 Lời giải Chọn B
Chọn hệ tọa độ Oxy với O ≡ O, O C ≡ Ox, . O A ≡ Oy 2 2 2 Đoạn 2 2 2 2
O O = O A − O A = 5 − 3 = 4 ⇒ (O ) :( x + 4)2 2 + y = 25. 1 2 1 2 1
Kí hiệu (H1) là hình phẳng giới hạn bởi các đường (O ):(x + 4)2 2 + y = 25, : Oy x = 0, x ≥ 0. 1 Kí hiệu (H
O : x + y = 9, : Oy x = 0, x ≥ 0.
2 ) là hình phẳng giới hạn bởi các đường ( ) 2 2 2 y A (D) C O x O ≡ O 1 2 B
Khi đó thể tích V cần tìm chính bằng thể tích V2 của khối tròn xoay thu được khi quay hình (H V H
2 ) xung quanh trục Ox trừ đi thể tích 1 của khối tròn xoay thu được khi quay hình ( 1 ) xung quanh trục . Ox Ta có 1 4 3 2 3
V = . π r = π.3 =18π. 2 2 3 3 x + 4 14π Lại có 2
V = π y dx = π 25 − x + 4 dx = π 25x − = . 1 ∫ ∫ ( ) ( )3 1 1 1 2 3 3 0 0 0 Do đó 14π 40π
V = V −V =18π − = . 2 1 3 3
Câu 48.11. Một cái trống trường có bán kính các đáy là 30cm, thiết diện vuông góc với trục và cách
đều hai đáy có diện tích là π ( 2
1600 cm ) , chiều dài của trống là1m. Biết rằng mặt phẳng chứa
trục cắt mặt xung quanh của trống là các đường Parabol. Hỏi thể tích của cái trống là bao nhiêu? Trang 29/53 - WordToan parabol 40cm 30cm 30 1m . A. 425,2 (lít). B. 425162 (lít). C. 212,6(lít). D. 212581(lít). Lời giải Chọn A
Ta có chọn hệ trục Oxy như hình vẽ. parabol y 40cm 30cm 30 1m x .
Thiết diện vuông góc với trục và cách đều hai đáy là hình tròn.
có bán kính r có diện tích là π ( 2 1600 cm ) , nên. 2
r π = 1600π ⇒ r = 40cm .
Ta có: Parabol có đỉnh I (0;40) và qua A(50;30) . Nên có phương trình 1 2 y = − x + 40 . 250
Thể tích của trống là. 50 2 1 2 406000 3 3 V = π − x + 40 dx = π. cm ≈ 425,2dm = ∫ 425,2 (lít). − 250 3 50
Câu 48.12. Một khuôn viên dạng nửa hình tròn có đường kính bằng 4 5 (m). Trên đó người thiết kế hai
phần để trồng hoa có dạng của một cánh hoa hình parabol có đỉnh trùng với tâm nửa hình tròn
và hai đầu mút của cánh hoa nằm trên nửa đường tròn (phần tô màu), cách nhau một khoảng
bằng 4 (m), phần còn lại của khuôn viên (phần không tô màu) dành để trồng cỏ Nhật Bản. .
Biết các kích thước cho như hình vẽ và kinh phí để trồng cỏ Nhật Bản là 100.000 đồng/m2. Hỏi
cần bao nhiêu tiền để trồng cỏ Nhật Bản trên phần đất đó? (Số tiền được làm tròn đến hàng nghìn).
A. 2.388.000 (đồng). B. 3.895.000 (đồng).
C. 1.194.000 (đồng). D.1.948.000 (đồng). Lời giải Trang 30/53 - WordToan Chọn D .
Đặt hệ trục tọa độ như hình vẽ. Khi đó phương trình nửa đường tròn là.
y = R − x = ( )2 2 2 2 2
2 5 − x = 20 − x .
Phương trình parabol (P) có đỉnh là gốc O sẽ có dạng 2
y = ax . Mặt khác (P) qua điểm
M (2;4) do đó: = a(− )2 4 2 ⇒ a =1.
Phần diện tích của hình phẳng giới hạn bởi (P) và nửa đường tròn.( phần tô màu). 2 Ta có công thức 2 2 2 S =
20 − x − x dx ≅11,94m . 1 ∫ ( ) 2 −
Vậy phần diện tích trồng cỏ là 1 S = S −S ≈ co hinhtron 1 19,47592654 . 2
Vậy số tiền cần có là S × ≈ (đồng).đồng. co 100000 1.948.000
Câu 48.13: Từ một tấm tôn hình chữ nhật ABCD với 55π AB = 30c , m AD =
cm . Người ta cắt miếng tôn 3
theo đường hình sin như hình vẽ bên để được hai miếng tôn nhỏ. Biết AM = 20cm ,CN =15cm
, BE = 5π cm .Tính thể tích của lọ hoa được tạo thành bằng cách quay miếng tôn lớn quanh trục AD
(kết quả làm tròn đến hàng trăm). A. 3 81788cm . B. 3 87388cm C. 3 83788cm D. 3 7883cm Lời giải Chọn C
Chọn hệ trục Oxy sao cho A ≡ O , D ∈Ox , B ∈Oy .
Ta có BE = 5π suy ra hàm số tuần hoàn với chu kì T = 20π .
Suy ra phương trình đồ thị hình sin cần tìm có dạng: sin x y a = + b . 10 Trang 31/53 - WordToan
Do đồ thị hình sin đi qua π M (0;20) , 55 N ;15 nên ta có: 3 1 a sin .0 + b = 20 10 a =10 ⇔ . 1 55π b = 20 asin . + b = 15 10 3
Ta có phương trình đồ thị hình sin cần tìm là 10sin x y = + 20 . 10 π 2 55 Thể tích cần tìm là: x 3 3 π ∫ 10sin +
20 dx 83788cm . 0 10
Câu 48.14: Mảnh vườn nhà ông An có dạng hình elip với bốn đỉnh A , A , B , B như hình vẽ bên. 1 2 1 2
Ông dùng 2 đường Parabol có đỉnh là tâm đối xứng của elip cắt elip tại 4 điểm M,N, , P Q như
hình vẽ sao cho tứ giác MNPQ là hình chữ nhật có MN = 4 để chia vườn. Phần tô đậm dùng
để trồng hoa và phần còn lại để trồng rau. Biết chi phí trồng hoa là 600.000 đồng/ 2 m và trồng rau là 50.000 đồng/ 2
m . Hỏi số tiền phải chi gần nhất với số tiền nào dưới đây, biết A A = 8 m 1 2 , B B = 4 m ? 1 2 A. 4.889.000 đồng. B. 5.675.000 đồng. C. 3.526.000 đồng. D. 7.120.000 đồng. Lời giải Chọn A 2 2
Giả sử phương trình elip ( ) : x + y E = 1. 2 2 a b A A = 8 2a = 8 a = 4 2 2 Theo giả thiết ta có 1 2 x y 1 ⇔ ⇔ ⇒ (E) 2 : + =1⇒ y = ± 16 − x . B B 4 2b 4 = = a = 2 16 4 2 1 2
Diện tích của elip (E) là S 2 ( π ab π (m ) . E) = = 8 Trang 32/53 - WordToan M = (P)∩(E) Ta có: MN = 4 ⇒
⇒ N (2;y . Do N ∈(E) ⇒ N(2; 3). 0 ) N = (P)∩(E)
(P) đỉnh O và đi qua N ⇒ (P) 2 2 6
: x = y ⇒ y = ± x 3 2 2
Khi đó, diện tích phần không tô màu là 1 2 6 π S − = 4∫ 16− x − x d 2 x 2 3 = 4 (m ). 2 2 3 0
Diện tích phần tô màu là π π S′ = S − 16 + 4 3 ( ) − S 2 3 = 8π − 4 = . E 3 3
Số tiền phải chi theo yêu cầu bài toán là 16π + 4 3 2π − 3 T = 600.000× + 50.000× 4 ≈ 4.889.000 đồng. 3 3
Câu 48.15. Cho khối trụ có hai đáy là hai hình tròn ( ;
O R) và (O ;′ R), OO′ = 4 .
R Trên đường tròn ( ; O R) lấy hai điểm ,
A B sao cho AB = R 3. Mặt phẳng (P) đi qua ,
A B cắt đoạn OO′ và tạo với đáy một góc bằng 0
60 . (P) cắt khối trụ theo thiết diện là một phần của hình elip. Diện tích thiết diện đó bằng. A. 4π 3 2 2π 3 + R . B. 2 − R . 3 2 3 4 C. 2π 3 2 4π 3 − R . D. 2 − R . 3 4 3 2 Lời giải Chọn A y R -R R R - x 2 -R 2 2 2
OA + OB − AB 1 cos AOB = = − ⇒ 0 = 120 ⇒ = R AOB OH . 2. . OAOB 2 2
Chọn hệ trục như hình vẽ bên ⇒ Phương trình đường tròn đáy là 2 2 2 2 2
x + y = R ⇔ y = ± R − x .
Hình chiếu của phần elip xuống đáy là miền sọc xanh như hình vẽ. R π Ta có 2 2 S = 2 R − x d . x ∫ Đặt x = . R sin t 2 3 2 ⇒ S = + R . R 3 4 − 2
Gọi diện tích phần elip cần tính là S .′ π
Theo công thức hình chiếu, ta có S 4 3 2 S′ = = 2 S = + R . 0 cos60 3 2 Trang 33/53 - WordToan
Câu 48.16. Người ta làm một cái lu đựng nước bằng cách cắt bỏ 2 chỏm của một khối cầu có bán kính
5 dm bằng 2 mặt phẳng vuông góc với đường kính và cách tâm khối cầu3 dm . Tính thể tích của chiếc lu. 3 dm 5 dm 3 dm A. π ( 3 41 dm ). B. π ( 3 132 dm ) C. π ( 3 43 dm ) D. 100π ( 3 dm ) 3 Lời giải Chọn B y 5 x -5 -3 O 3 5 -5
Đặt hệ trục với tâm O là tâm của mặt cầu, đường thẳng đứng là Ox , đường ngang là Oy .
Ta có phương trình của đường tròn lớn là 2 2 x + y = 25 .
Thể tích cái lu là thể tích của vật tròn xoay tạo thành khi quay hình giới hạn bởi các đường cong 2
y = 25 − x , trục Ox , đường thẳng x = 3,
− x = 3 quay quanh Ox . 3
V = π ∫ (25− x ) 3 x 3
2 dx = π 25x − = 132π ( 3 dm ) . − − 3 3 3 Câu 48.17.
Một cái trống trường có bán kính các đáy là 30 cm, thiết diện vuông góc với trục và cách đều hai đáy có diện tích là π ( 2
1600 cm ) , chiều dài của trống là1m. Biết rằng mặt phẳng chứa trục cắt mặt
xung quanh của trống là các đường Parabol. Hỏi thể tích của cái trống là bao nhiêu? Trang 34/53 - WordToan parabol 40cm 30cm 30 1m . A. 425,2 (lít). B. 425162 (lít). C. 212,6(lít). D. 212581(lít). Lời giải Chọn A
Ta có chọn hệ trục Oxy như hình vẽ. parabol y 40cm 30cm 30 1m x .
Thiết diện vuông góc với trục và cách đều hai đáy là hình tròn.
có bán kính r có diện tích là π ( 2 1600 cm ) , nên. 2
r π = 1600π ⇒ r = 40cm .
Ta có: Parabol có đỉnh I (0;40) và qua A(50;30) . Nên có phương trình 1 2 y = − x + 40 . 250
Thể tích của trống là. 50 2 1 2 406000 3 3 V = π − x + 40 dx = π. cm ≈ 425,2dm = ∫ 425,2 (lít). − 250 3 50
Câu 48.18. Bổ dọc một quả dưa hấu ta được thiết diện là hình elip có trục lớn 28cm , trục nhỏ 25cm . Biết cứ 3
1000cm dưa hấu sẽ làm được cốc sinh tố giá 20000 đồng. Hỏi từ quả dưa hấu trên có thể
thu được bao nhiêu tiền từ việc bán nước sinh tố? Biết rằng bề dày vỏ dưa không đáng kể. A. 180000 đồng.
B. 183000 đồng. C. 185000 đồng. D.190000 đồng.. Lời giải Chọn B Trang 35/53 - WordToan 2 2
Đường elip có trục lớn 28cm , trục nhỏ 25cm có phương trình x y + = 1 2 2 14 25 2 2 2 2 25 x 2 25 ⇔ = 1 x y − ⇔ y = ± 1− . 2 2 14 2 2 14 2 14 2 2 14 2
Do đó thể tích quả dưa là 25 = π 1 x V − dx ∫ 25 = π ∫ 1 x − dx 2 2 2 − 14 − 2 14 14 14 14 2 3 25 x 2 π = π ⋅ 25 56 8750 x − π = ⋅ 3 = cm . 2 2 3.14 2 3 3 14 −
Do đó tiền bán nước thu được là 8750π.20000 ≈183259 đồng. 3.1000
CÂU TƯƠNG TỰ CÂU 49 ĐỀ THAM KHẢO 2024
Câu 49.1: Cho hàm số f (x) có đạo hàm 2
f '(x) = x −82x . Có bao nhiêu giá trị nguyên dương của tham số m để hàm số 4 2
y = f (x −18x + m) có đúng 7 cực trị. A. 83 B. 81 C. 80. D. 84 Lời giải Chọn C Ta có: 3 4 2
y ' = (4x − 36x). f '(x −18x + m). 4 2
f '(x −18x + m) = 0 y ' = 0 ⇔ . 3 4x − 36x = 0 Với x = 0 +) 3
4x − 36x = 0 ⇔ có 3 nghiệm đơn. x = 3 ± 4 2 4 2
x −18x + m = 0
x −18x = −m +) 4 2
f '(x −18x + m) = 0 ⇔ ⇔ . 4 2 4 2
x −18x + m = 82
x −18x = −m + 82 x = 0 Xét hàm số: 4 2
g(x) = x −18x có g '(x) = 0 ⇔ . x = 3 ± Ta có BBT của hàm số 4 2
g(x) = x −18x Để hàm số 4 2
y = f (x −18x + m) có đúng 7 cực trị thì 4 2
y = f '(x −18x + m) = 0 có 4 nghiệm bội lẻ phân biệt khác 0, 3 ± . −m ≤ 81 − 82 < m <163 ⇔ 81
− < −m + 82 < 0 ⇔ m ≤ 0
−m +82 > −m ≥ 0 Trang 36/53 - WordToan Mà *
m∈ N nên m∈{83,84,........,161, }
162 . Nên có 80 giá trị m thỏa ycbt.
Câu 49.2: Cho hàm số y = f (x) có đạo hàm f ′(x) = ( 2 x − )( 2 3 x + )
1 với x ∈ . Có bao nhiêu giá trị
nguyên của tham số m để hàm số y = f (x) − mx có 4 điểm cực trị? A. 0. B. 1. C. 2. D. 3. Lời giải Chọn A
Xét đạo hàm y′ = f ′(x) − m = ( 2 x − )( 2 3 x + )
1 − m ; y′ = ⇔ ( 2 x − )( 2 0 3 x + ) 1 = m
YCBT ⇔ y′ = 0 có 4 nghiệm bội lẻ phân biệt
Đặt g (x) = ( 2 x − )( 2 x + ) 4 2 3
1 = x − 2x − 3 ; g′(x) 3
= x − x = x( 2 4 4 4 x − ) 1 ; BBT x –∞ 1 − 0 1 +∞ y′ – 0 + 0 – 0 + +∞ 3 − +∞ y 4 − 4 − Vậy 4 − < m < 3
− , mà m nguyên nên không c ó m nào.
Câu 49.3: Cho hàm số y f x có đạo hàm f x 2 x x 2 ' x 4x 3 , x .
Tính tổng tất cả các
giá trị nguyên của tham số m để hàm số 2 g x
f x m có 3 điểm cực trị. A. 0 . B. 6 . C. 3. D. 2 . Lời giải Chọn C x 0
Ta có f 'x xx 2 1 x
3 ; f 'x 0 x 1
( x 0, x 3 là nghiệm đơn; x 1 là x 3 nghiệm bội chẵn). x 0 x 0 2 2 x 0 x m 0 x m 1
Lại có g 'x 2 .x f ' 2
x m; g 'x 0 f ' 2 x m 2 2 0 x m 1
x 1m 2 2 2 x m 3 x 3 m 3
Do 2 có nghiệm luôn là nghiệm bội chẵn; các phương trình 1 , 3 có nghiệm không chung nhau và m 3 . m
Hàm số gx có 3 điểm cực trị g 'x 0 có ba nghiệm bội lẻ phân biệt m 0 0 m 3. 3 m 0
Vì m m 0;1; 2 .
Vậy tổng các giá trị nguyên của tham số m bằng 3.
Câu 49.4: Cho hàm số y = f (x). Hàm số y = f (′x) có đồ thị như hình vẽ dưới đây. Trang 37/53 - WordToan y x 0 1 2 3
Có nhiêu giá trị nguyên của m để hàm số 2
y = f (x + m) có 3 điểm cực trị. A. 1. B. 0 . C. 3. D. 2. Lời giải Chọn C Do hàm số 2
y = f (x + m) là hàm chẵn nên hàm số có 3 cực trị khi và chỉ khi hàm số này có
đúng 1 điểm cực trị dương. 2
y = f x + m ⇒ y′ = xf ′( 2 ( ) 2 x + m). x = 0 x = 0 2 2 x = 0 x + m = 0 x = −m y 0 ′ = ⇔ ⇔ ⇔ f ′ ( . 2 x + m) = 2 2 0 x + m =1 x =1− m 2 2 x + m = 3 x = 3− m
Đồ thị hàm số y = f ′(x) tiếp xúc trục hoành tại điểm có hoành độ là x =1 nên các nghiệm của pt 2
x = 1− m (nếu có) không làm ′( 2
f x + m) đổi dấu khi x đi qua, do đó các điểm cực x = 0 trị của hàm số 2
y = f (x + m) là các điểm nghiệm của hệ 2 x = −m . 2 x = 3 − m −m ≤ 0
Hệ trên có duy nhất nghiệm dương khi và chỉ khi ⇔ 0 ≤ m < 3. 3 − m > 0
Vậy có 3giá trị nguyên của thoả mãn.
Câu 49.5: Cho hàm số y = f (x) có đạo hàm y = f ′(x) với mọi x∈ .
và có đồ thị như hình vẽ.
Có bao nhiêu giá trị nguyên của tham số m để hàm số g (x) = f ( 2
x − 4x + m) có đúng hai điểm
cực trị thuộc khoảng (1;4) ? A. 4 . B. 3. C. 0 . D. 5. Lời giải Chọn A
Ta có g′(x) = (x − ) f ′( 2 2 2 .
x − 4x + m). Trang 38/53 - WordToan x = 2∈(1;4) x = 2
g′(x) = 0 ⇔ 2(x − 2). f ′( 2
x − 4x + m) 2 2
= 0 ⇔ x − 4x + m =1 ⇔ x − 4x −1= −m. 2 2
x − 4x + m = 1 −
x − 4x +1 = − m
Vẽ đồ thị hai hàm số 2
y = x − 4x −1 và 2
y = x − 4x +1 lên cùng một mặt phẳng tọa độ.
Yêu cầu bài toán tương đương f ′( 2
x − 4x + m) = 0 có đúng một nghiệm đơn khác 2 trong 4 − ≤ −m ≤ 3 − 3 ≤ m ≤ 4 khoảng (1;4) suy ra: ⇔ . 1 m 1 − ≤ − < 1 − < m ≤1
Vậy có tất cả 4 giá trị.
Câu 49.6: Cho hàm số 4 3 2
y = 3x − 4x −12x + m −1 có 7 điểm cực trị. Tổng các giá trị nguyên của m là: A. 21 B. 15 C. 7 D. 14 Lời giải Chọn D Xét hàm số 4 3 2
f (x) = 3x − 4x −12x + m −1,
Có lim f (x) = +∞ , lim f (x) = . +∞ x→+∞ x→−∞ ′ 3 2
f x = x − x − x = x( 2 ( ) 12 12 24
12 x − x − 2). x = 0 f ′(x) 0 = ⇔ x = 1 − . x = 2 Bảng biến thiên:
Từ bảng biến thiên, ta có hàm số y = f (x) có 7 điểm cực trị ⇔ đồ thị hàm số y = f (x) cắt
Ox tại 4 điểm phân biệt ⇔ m − 6 < 0 < m −1 ⇔ 1< m < 6 mà m∈ Z ⇒ m∈{2,3,4, } 5
Tổng các giá trị nguyên của m là 14. Trang 39/53 - WordToan
Câu 49.7: Cho hàm số y = f (x) liên tục trên và có f ′(x) = (x − )2 ( 2 2
x + 3x − 4) . Gọi S là tập các số
nguyên m ∈[−10;10]để hàm số y = f ( 2
x − 4x + m) có đúng 3 điểm cực trị. Số phần tử của S bằng A. 5. B. 14. C. 4. D. 10. Lời giải: Chọn A (x − 2)2 = 0
Ta có: f (′x) = 0 ⇔ . 2
x + 3x − 4 = 0
Đặt y = g x = f ( 2 ( )
x − 4x + m)
g′ x = ( x − ) 2 ( ) 2
4 f (′x − 4x + m) x = 2 2x − 4 = 0
(x −4x + m−2)2 2 = 0
g (′x) = 0 ⇔ ⇔ . 2
f (′x − 4x + m) = 0 h (x) 2 1
= x − 4x + m −1 = 0 (1) 2 2
h (x) = x − 4x + m + 4 = 0 (2)
Hàm số có 3 cực trị khi một trong 2 phương trình và có 2 nghiêm phân biệt khác 2 và phương
trình có lại có 1 nghiệm hoặc vô nghiệm. 1 h (2) ≠ 0 1∆ > 0 0 ≤ m < 5 ∆2 ≤ 0 ⇔
⇔ m ≥ 3 ⇔ 0 ≤ m < 5. 2 h (2) ≠ 0 m < 0 1 ∆ ≤ 0 ∆ 2 > 0
Mà m ∈[−10;10] do đó m∈{0;1;2;3 } ;4 có 5 phần tử.
Câu 49.8: Cho hàm số y = f (x) có đạo hàm f ′(x) = (x − )2 ( 2
1 x − 2x), với x
∀ ∈ . Số giá trị nguyên của
tham số m để hàm số g (x) = f ( 3 2
x − 3x + m) có 8 điểm cực trị là A. 1. B. 4 . C. 2 . D. 3. Lời giải Chọn A
Ta có g′(x) = ( 2
x − x) f ′( 3 2 3 6 .
x − 3x + m) . x = 0 2 3x − 6x = 0 x = 2 3 2 − + = g′(x) x 3x m 1 3 2 = 0 ⇔
⇔ x − 3x + m =1 . 3 2
x − 3x + m = 0 3 2
x − 3x + m = 0 3 2
x −3x + m = 2 3 2
x − 3x + m = 2
Vì khi đi qua các nghiệm của phương trình 3 2
x − 3x + m =1 (nếu có) dấu của f ′( 3 2
x − 3x + m)
không đổi nên dấu của g′(x) chỉ phụ thuộc các nghiệm của hai phương trình còn lại.
Vậy hàm số y = g (x) có 8 điểm cực trị khi và chỉ khi mỗi phương trình 3 2
x − 3x + m = 0 và 3 2
x − 3x + m = 2 phải có ba nghiệm phân biệt (khác 0 và khác 2 ). Trang 40/53 - WordToan x =
Xét hàm số h(x) 3 2
= −x + 3x , ta có h′(x) 2 = 3
− x + 6x ; h′(x) 0 = 0 ⇔ . x = 2
Bảng biến thiên của hàm số y = h(x)
Dựa vào bảng biến thiên, ta thấy điều kiện để mỗi phương trình 3 2
−x + 3x = m và 3 2
−x + 3x = m − 2 phải có ba nghiệm phân biệt (khác 0 và khác 2 ) là
0 < m − 2 < m < 4 ⇔ 2 < m < 4 .
Vậy chỉ có một giá trị nguyên của m thỏa mãn là m = 3 .
Câu 49.9: Cho hàm số f (x) có đạo hàm liên tục trên và đồ thị hàm số f ′(x) như hình vẽ. Có bao nhiêu
số nguyên m để hàm số = ( 2
y f x + m) có đúng 3 điểm cực trị? A. Vô số. B. 4 C. 3. D. 2 . Lời giải Chọn C
y′ = x f ′( 2 2 . x + m). x = 0 x = 0 2 2 x = 0 x + m = 0 x = −m y 0 ′ = ⇔ ⇔ ⇔ . f ′ ( 2 x + m) = 2 2 0 x + m =1 x + m =1 2 2 x + m = 3
x = −m + 3
Đồ thị hàm số f ′(x) tiếp xúc với trục hoành tại điểm có hoành độ bằng 1. Do đó hoặc phương trình 2
x + m =1 vô nghiệm hoặc nghiệm của phương trình 2x + m =1 là nghiệm bội chẵn của
phương trình y′ = 0 . −m ≠ 0 m ≠ 0 Nếu ⇔
thì x = 0 là nghiệm đơn của phương trình y′ = 0 . m 3 0 − + ≠ m ≠ 3 −m = 0 m = 0 Nếu ⇔
thì nghiệm x = 0 là nghiệm bội ba của phương trình y′ = 0 . m 3 0 − + = m = 3
Suy ra x = 0 là một điểm cực trị của hàm số = ( 2
y f x + m) , m ∀ . Xét các phương trình: 2
x = −m (1) và 2
x = −m + 3 (2).
Nhận xét: Phương trình (1) và (2) không có nghiệm chung; −m < −m + 3, m ∀ Trang 41/53 - WordToan Minh họa đồ thị
Xét −m > 0 thì phương trình (1) có 2 nghiệm phân biệt x x
1 ; 2 và phương trình (2) có 2 nghiệm phân biệt x x x x x x
3 ; 4 . Khi đó y′ đổi dấu 5 lần qua các nghiệm 1 ; 2 ; 3 ; 4 và 0 nên hàm số = ( 2
y f x + m) có 5 điểm cực trị.
Xét −m + 3 ≤ 0 thì phương trình (1) vô nghiệm; phương trình (2) hoặc vô nghiệm hoặc có nghiệm
kép x = 0 . Khi đó hàm số = ( 2
y f x + m) có 1 điểm cực trị. −m ≤ 0 m ≥ 0 Xét ⇔
⇔ 0 ≤ m < 3. Khi đó phương trình (1) vô nghiệm hoặc có nghiệm kép −m + 3 > 0 m < 3
x = 0 ; phương trình (2) có 2 nghiệm phân biệt khác 0. Suy ra hàm số = ( 2
y f x + m) có 3 điểm cực trị. Do đó, để hàm số = ( 2 y f x + m) ≤ <
có 3 điểm cực trị thì 0 m 3.
Mặt khác m nguyên nên m∈{0;1; } 2 .
Vậy có 3 giá trị nguyên của m để hàm số có đúng 3 điểm cực trị.
Câu 49.10: Cho hàm số y = f (x) có đạo hàm f ′(x) 2
= x − 3x + 2, x
∀ ∈ . Có bao nhiêu giá trị nguyên
của tham số m sao cho ứng với mỗi m , hàm số g (x) = f ( 4 2
−x + 2x − m) có đúng ba điểm cực trị thuộc khoảng (0;3)? A. 62 . B. 60 . C. 61. D. 64 . Lời giải Chọn A = f ′(x) x 1 2
= x − 3x + 2 = 0 ⇔ x = 2 *) Xét trên (0;3) x = 0∉(0;3) x =1∈(0;3) g′(x) = ( 3 4
− x + 4x) f ′( 4 2
−x + 2x − m) = 0 ⇔ x = 1 − ∉(0;3) f ′ ( 4 2
−x + 2x − m) = 0 = x =1∈(0;3) x 1 ⇔ 4 2
⇔ −x + 2x − m =1 f ′ ( 4 2
−x + 2x − m) = 0 4 2
−x + 2x − m = 2
Xét hàm số h(x) 4 2
= −x + 2x − m trên (0;3) Trang 42/53 - WordToan x = 0 h′(x) 3 = 4
− x + 4x , h′(x) 3 = 4
− x + 4x = 0 ⇔
trên (0;3) chỉ lấy nghiệm x =1 x = 1 ±
Để hàm số g (x) có 3 cực trị điều kiện g′(x) = 0 có 3 nghiệm bậc lẻ khi đó 1 m 2 1 m m 11m 1 m 0 1 m 0 63m 1 64 m 64 m 2 2 m m 2
Do m nguyên nên m 63;62;...;
2 có 62 giá trị thoả mãn bài toán.
Câu 49.11: Cho hàm số y = f (x) có đạo hàm f ′(x) 3 2
= x − x , x
∀ ∈ . Biết tham số m∈(a;b) thì hàm
số hàm số g (x) = f ( 3 2
−x + 3x + m ) đạt nhiều cực trị nhất là c cực trị. Tính tổng a + b + c ? A. 9. B. 7. C. 6 . D. 11. Lời giải Chọn B = f ′(x) x 0 3 2
= x − 3x = 0 ⇔
trong đó x = 0 là nghiệm bậc hai không cho được cực trị x =1 3 2 3 2 ′ − + + − + + g′(x) = ( ′
x 3x m . x 3x m 3 2
−x + 3x + m ) f ′( 3 2
−x + 3x + m ) ( ) ( ) = f ′( 3 2
−x + 3x + m 3 2 )
−x + 3x + m ( 3 2
−x + x + m) ( 2 3 . 3 − x + 6x) = f ′( 3 2
−x + 3x + m 3 2 )
−x + 3x + m ( 3 2
−x + 3x + m).( 2 3 − x + 6x)
Cho g′(x) = 0 ⇔
f ′ −x + 3x + m = 0 3 2 ( 3 2 )
−x + 3x + m 3 2 3 2
−x + 3x + m ≠ 0
−x + 3x + m ≠ 0 2 3x 6x = 0 ⇔ − + ⇔ x = 0; x = 2 3 2 3 2 −
x + 3x + m =1 −
x + 3x + m = 1 ± x = 0
Xét hàm số h(x) 3 2
= −x + 3x + m; h′(x) 2 = 3
− x + 6x = 0 ⇔
lập được bảng biến thiên x = 2 Trang 43/53 - WordToan
Để có nhiều cực trị nhất thì g′(x) phải có nhiều nghiệm và điểm làm g′(x) không xác định
nhất. Dựa bảng biến thiên ta có m < 1
− < 1< m + 4 ⇔ 3 − < m < 1 − ⇒ m∈( 3 − ;− ) 1 Khi đó a = 3 − ; b = 1;
− c =11 có a + b + c = 7 .
Câu 49.12: Cho hàm số y = f (x) có đạo hàm f ′(x) 3
= x + x, x
∀ ∈ . Có bao nhiêu giá trị nguyên của
tham số m sao cho ứng với mỗi m , hàm số g (x) = f ( 4 3 2
x + 2x − mx ) có đúng hai điểm cực trị thuộc khoảng ( 1; − 2) ? A. 6 . B. 8 . C. 7 . D. 9. Lời giải Chọn C
f ′(x) = x( 2 x + ) 1 = 0 ⇔ x = 0 *) Xét trên ( 1; − 2) x = 0∉( 1; − 2) g′(x) = ( 3 2
x + x − 2mx) f ′( 4 3 2 4 6
x + 2x − mx ) = 0 2
⇔ 4x + 6x − 2m = 0 4 3 2 x 2x mx 0 + − = x = 0∉( 1; − 2) 2
⇔ 2x + 3x = m ( ) 1 2
x + 2x = m (2)
Xét hàm số h(x) 2
= 2x + 3x ; k (x) 2
= x + 2x trên ( 1;
− 2) có h′(x) 3
= 4x + 3 = 0 ⇔ x = − ; 4
k′(x) = 2x + 2 = 0 ⇔ x = 1
− lập bảng biến thiên của cả hai hàm h(x);k (x) trên cùng một hình
ta được kết quả như sau: Trang 44/53 - WordToan
Để hàm số g (x) có 2 cực trị điều kiện g′(x) = 0 có 2 nghiệm bậc lẻ mà g′(x) đã có nghiệm
x = 0 nên tổng hai phương trình
1 ;2 có thêm một nghiệm khác 0 , dựa vào bảng biến thiên trên ta có m 1 m 1
mà m là số nguyên nên m 1;8;9;10;11;12; 13 có 7 giá trị 8 m 14 8 m 14
Câu 49.13: Cho hàm số y = f (x) có đạo hàm f ′(x) 2 = x (x + )( 2
1 x + 2mx − 2m − ) 1 . Có bao nhiêu giá
trị nguyên của m không vượt quá 2024 để hàm số y = f ( 2 x + )
1 có đúng 1 điểm cực trị? A. 2 . B. 2026 . C. 2024 . D. 2025 . Lời giải Chọn B
Ta có: y = ( f (x + ) ′ = x f (x + ) = x (x + )2 (x + )2 (x + )2 2 2 2 2 2 + m( 2 1 2 . 1 2 . 1 2 1 2 x + ) 1 − 2m −1 ′ ′ x = 0
Khi đó: y′ = 0 ⇔ .
(x + )1 + 2m(x + ) 2 2 2 2 t=x 1 + (t≥ ) 1 2
1 − 2m −1 = 0 →t + 2mt − 2m −1 = 0 ( ) 1 Ta thấy nghiệm của ( )
1 nếu có sẽ khác 0 . Nên x = 0 là 1 cực trị của hàm số.
Do đó để hàm số có 1 điểm cực trị thì ( )
1 hoặc vô nghiệm hoặc có nghiệm kép, hoặc có 2 t −1 ≤ 0 nghiệm 1 t ;t ≤1 ⇔ 1 2 t −1≤ 0 2 2
∆ ' = m + 2m +1≤ 0 m = 1 − 2 ' m 2m 1 0 ∆ = + + > m ≠ 1 − ⇔ ( ⇔
t −1 + t −1 ≤ 0 t + t ≤ 2 1 ) ( 2 ) 1 2 (
t −1 t −1 ≥ 0 t
t − t +t +1≥ 0 1 )( 2 ) 1 2 ( 1 2 ) . m = 1 − m = 1 − m 1 ≠ − m ≠ 1 − m = 1 − ⇔ ⇔ ⇔ ⇔ m ≥ 1 − 2 − m ≤ 2 m ≥ 1 − m > 1 − 2m 1 ( 2m) 1 0 − − − − + ≥ 0 ≥ 0
Vậy tập hợp các giá trị m thỏa đề là S = { 1 − ;0;1;...; }
2024 nên có 2026 giá trị m . Trang 45/53 - WordToan
Câu 49.14: Cho hàm số bậc bốn y = f (x) có đồ thị y = f ′(x) như hình vẽ
Gọi S là tập hợp các giá trị nguyên thuộc đoạn [ 2024 −
;2024] của tham số m để hàm số
y = f ( 2x + x − 2 − m) có đúng 3 điểm cực trị. Số phần tử của tập hợp S bằng A. 2026 . B. 2022 . C. 2024 . D. 2020 . Lời giải Chọn D x = 2 − f (x) 0 ′ = ⇔ x = 2 x = 5 (2x + ) 1 ( 2 x + x − 2) y′ = f ′( 2
x + x − 2 − m 2 ) x + x − 2 1 x = − 2
Điểm đặc biệt: y ' = 0 hoặc y ' không xác định x = ⇔ 1 x = 2 − f ′ ( 2
x + x − 2 − m) = 0 (1) Ta thấy 1
x = − ; x =1; x = 2
− là các nghiệm đơn của y′. 2 2 2
x + x − 2 − m = 2 −
x + x − 2 = m − 2 2 2
(1) ⇔ x + x − 2 − m = 2 ⇔ x + x − 2 = m + 2 2 2
x + x − 2 − m = 5
x + x − 2 = m + 5 Ta có BBT của hàm số 2
t = x + x − 2 như sau:
Để hàm số có đúng 3 điểm cực trị thì phương trình (1) không có nghiệm đơn.
Dựa vào BBT trên, phương trình (1) không có nghiệm đơn ⇔ m + 5 ≤ 0 ⇔ m ≤ 5 −
Vì m∈ , m ∈[ 2024 − ;2024] ⇒ m ∈{ 2024 − ; 2023 − ;...... − }
5 . Vậy tập S có 2020 phần tử. Trang 46/53 - WordToan
Câu 49.15: Cho hàm số bậc năm y = f (x) có đồ thị y = f ′(x) như hình vẽ dưới đây
Có bao nhiêu giá trị nguyên của m 2024;2024 để số điểm cực trị của hàm số
g (x) = f ( 2
x − 3x + m) là 5. A. 2025 . B. 2 . C. 2027 . D. 2024 . Lời giải Chọn C
Ta có: g′(x) = ( x − ) f ′( 2 2 3 .
x − 3x + m) . 2x − 3 = 0 g′(x) ( ) 1 = 0 ⇔ . f ′ ( 2
x − 3x + m) = 0 (2) Ta có: ( ) 3 1 ⇔ x = . 2 2 2
x − 3x + m = 0
m = −x + 3x Và ( 2) 2 2
⇔ x − 3x + m = 2 2
⇔ m − = −x + 3x . 2 2
x − 3x + m = a, a > 2
m − a = −x + 3x Với 2
x − 3x + m = 2 thì g′(x) = 0 có nghiệm kép. Xét hàm số 2
y x 3x ta có đồ thị Trang 47/53 - WordToan Do a > 2 , suy ra 9
m < .phương trình g′(x) = 0 có 5 nghiệm đơn phân biệt nên g (x) có 5 4
điểm cực trị khi và chỉ khi 9 m < . 4
Vì m∈ , m ∈[ 2024 − ;2024] ⇒ m ∈{ 2024 − ; 2023 − ;......; }
2 . Vậy tập S có 2027 phần tử.
CÂU TƯƠNG TỰ CÂU 50 ĐỀ THAM KHẢO 2024
Câu 50.1: Trong không gian Oxyz , cho hình nón (Ν) có đỉnh A(1;4;0) , độ dài đường sinh bằng 6 và
đường tròn đáy nằm trên mặt phẳng (P) : 2x + y + 2z −3 = 0 . Gọi (C) là giao tuyến của mặt xung
quanh của (N ) với mặt phẳng (Q) : x − 4y + z + 3 = 0 và M là một điểm di động trên (C). Hỏi
giá trị nhỏ nhất của độ dài đoạn thẳng AM thuộc khoảng nào dưới đây? A. 3 ;2 . B. (0; ) 1 . C. 3 1; . D. (2;3). 2 2 Lời giải Chọn D
Gọi l,h,r lần lượt là độ dài đường sinh, chiều cao và bán kính của hình nón.
Theo đề bài ta có l = 6 và h = d ( , A (P)) =1. Suy ra 2 2
r = l − h = 35 . n = P (2;1;2) Mặt khác
⇒ n n = ⇒ P ⊥ Q . P . Q 0 ( ) ( ) n = − Q (1; 4; ) 1
Khi đó giao tuyến (C) là một parabol có đỉnh H (như hình vẽ). Q A E H M I K B P
Gọi E là hình chiếu vuông góc của A lên (Q) . Và d ( ,
A (Q)) = AE = 2 2 (= IK ) do IA∥(Q) . Ta có: 2 2 2
AM = AE + EM = 8 + EM
Đồng thời EM ≥ EH . Do đó AM
⇔ AM = AH hay ≡ . min M H
Gọi K là hình chiếu vuông góc của H lên IB . Trang 48/53 - WordToan Vì AH IK IA∥HK ⇒ = (Thales) 2 2 12 70 ⇒ AH = .6 = ≈ 2,87∈(2;3) . AB IB 35 35
Vậy giá trị nhỏ nhất của độ dài đoạn thẳng AM thuộc khoảng (2;3) .
Câu 50.2: Trong không gian Oxyz , cho đường thẳng ∆ đi qua E (1+ 3 ; a 2;
− 2 + 3a) và có một vectơ chỉ phương u = ( ; a 1;a + )
1 . Biết khi a thay đổi luôn tồn tại một mặt cầu (S ) cố định có tâm I ( ; m ;
n p) bán kính R đi qua điểm M (1;1; )
1 và tiếp xúc với đường thẳng ∆ . Một khối nón (N )
có đỉnh I và đường tròn đáy của khối nón nằm trên mặt cầu (S ) . Thể tích lớn nhất của khối nón ( π N ) là max q + + + ( V =
. Khi đó tổng m n p q bằng N ) 3 A. 250. B. 256. C. 252. D. 225. Lời giải Chọn A Δ A P I M O
x =1+ 3a + at
Từ giả thiết ta có phương trình đường thẳng ∆ : y = 2 − + t .
z = 2+3a +(a + ) 1 t
Ta có đường thẳng ∆ luôn đi qua điểm cố định A(1; 5 − ;− ) 1 , a ∀ ∈ . (t = 3 − ) .
Nhận thấy đường thẳng ∆ luôn nằm trên mặt phẳng (P) : x + y − z + 3 = 0 .
Nếu (P) cắt (S ) theo giao tuyến là một đường tròn thì ∆ chính là tiếp tuyến của đường tròn,
mà từ một điểm chỉ có thể kẻ tối đa hai tiếp tuyến với đường tròn, nên khi đó chỉ có thể tồn tại
tối đa hai tiếp tuyến ∆ với (S ) . Do từ A kẻ được vô số tiếp tuyến ∆ với (S ) nên (P) phải tiếp
xúc với (S ) tại A .
Ta có AI ⊥ (P) nên − + +
AI cùng phương với n =
− , do đó m 1 n 5 p 1 = = P (1;1; )1 1 1 1 − m + p = 0 ⇔ ( )1. n + p = 6 − Ta lại có 2 2
MI = IA ⇔ MI = IA ⇔ (m − )2 1 + (n − )2 1 + ( p − )2 1 = (m − )2
1 + (n + 5)2 + ( p + )2 1 ⇔ 3n + p = 6 − (2) . m + p = 0 m = 6 Từ ( )
1 ,(2) ta có hệ phương trình: n p 6 + = − ⇒ n = 0 . 3 n p 6 + = − p = 6 −
Bán kính mặt cầu (S ): 2
R = IM = 5 + (− )2 1 + ( 7 − )2 = 5 3 . Trang 49/53 - WordToan
Gọi O là tâm của hình tròn đáy của hình nón, đặt x = IO, x > 0 , khi đó hình nón có bán kính đáy là 2 2 2
r = R − IO = 75 − x . Thể tích khối nón: 1 2 π
V = π.r .x = . x − x . N ( 3 75 ) ( ) 3 3
Xét hàm số: f (x) 3
= 75x − x , x ∈(0;+∞) , f ′(x) 2
= 75 − 3x với x ∈(0;5 3) . x = 5(n) Cho f '(x) 2
= 0 ⇔ 75 − 3x = 0 ⇔ . x = 5 − (l) Bảng biến thiên:
Dựa vào bảng biến thiên, suy ra max f (x) = 250 tại x = 5. (0;5 3) Do đó 250π max (V = ⇒ q = . N ) 250 3
Vậy m + n + p + q = 6 + 0 + ( 6 − ) + 250 = 250.
Câu 50.3: Trong không gian tọa độ Oxyz , cho hai mặt cầu (S ) 2
: x + y −1 + z − 2 =16, 1 ( )2 ( )2 (S ):(x − )2 1 + ( y + )2 2 1 + z =1 và điểm 4 7 14 A ; ; −
. Gọi I là tâm của mặt cầu (S và (P) 1 ) 2 3 3 3
là mặt phẳng tiếp xúc với cả hai mặt cầu (S và (S . Xét các điểm 2 ) 1 )
M thay đổi và thuộc mặt
phẳng (P) sao cho đường thẳng IM tiếp xúc với mặt cầu (S . Khi đoạn thẳng 2 ) AM ngắn nhất thì M (a; ;
b c) . Tính giá trị của T = a + b + c . A. T =1. B. T = 1 − . C. 7 T = . D. 7 T = − . 3 3 Lời giải Chọn B N M H I K Trang 50/53 - WordToan
Ta có mặt cầu (S có tâm I (0;1;2) bán kính R = 4 và mặt cầu (S có tâm K (1; 1; − 0) bán 2 ) 1 ) 1 kính R =1. 2
Có IK = 3 , suy ra IK = R − R nên hai mặt cầu (S và (S tiếp xúc trong tại 2 ) 1 ) 1 2 H . Suy ra 4 4 5 2 IH IK H ; ; = ⇒ − − và IK = (1; 2 − ; 2 − ) . 3 3 3 3
Vì (P) là mặt phẳng tiếp xúc với cả hai mặt cầu (S và (S nên (P) qua 2 ) 1 ) H và nhận vectơ IK = (1; 2 − ; 2
− ) là một vectơ pháp tuyến. Suy ra ra phương trình mặt phẳng (P) là
x − 2y − 2z − 6 = 0 .
Giả sử điểm M thay đổi trên (P) thỏa mãn đường thẳng IM tiếp xúc với mặt cầu (S , tiếp 2 )
điểm tương ứng là N . Ta có IK ∆ N và IMH IN NK ∆ đồng dạng suy ra = (*). IH HM Với 2 2
NK = R =1; IH = 4; IK = 3; IN = IK − NK = 2 2 nên (*) ⇔ 2 2 2 1 = ⇔ HM = 2 . 4 HM H 2 M A (P)
Mặt khác ta lại có A∈(P) và M thay đổi thuộc đường tròn (C) tâm H bán kính R = 2 nên
AM ngắn nhất bằng HA − R = 4 2 − 2 = 3 2 khi điểm M thoả mãn 3 AM = AH 4 4 2 5 M ; ; ⇒ − − 3 3 3 Suy ra 4 2 5
a = ;b = − ;c = − ⇒ T = a + b + c = 1 − . 3 3 3
Câu 50.4: Trong không gian với hệ tọa độ Oxyz, cho hai điểm ( A 3; 2; − 6), (
B 0;1;0) và mặt cầu 2 2 2
(S) : (x −1) + (y − 2) + (z −3) = 25 . Mặt phẳng (P) : ax + by + cz − 2 = 0 đi qua A, B và cắt theo
giao tuyến là đường tròn có bán kính nhỏ nhất. Tính T = a + b + c . A. T = 3
B. T = 5
C. T = 2 D. T = 4 Lời giải I B H K A
Mặt cầu (S) có tâm I (1;2;3), bán kính R = 5. Trang 51/53 - WordToan
Mặt phẳng (P) có vec-tơ pháp tuyến n = a b c P ( ; ; )
Theo giả thiết B(0;1;0)∈(P) :b − 2 = 0 ⇔ b = 2. Ta có: AB = ( 3 − ;3; 6
− ) cùng phương với u = (1; 1; − 2) . x = t
Phương trình đường thẳng AB : y =1− t z = 2t
Gọi r là bán kính đường tròn giao tuyến. K là hình chiếu vuông góc của I lên đường thẳng
AB, H là hình chiếu vuông góc của I lên (P)
Ta có: K ∈ AB ⇒ K (t;1−t;2t) ⇒ IK = (t −1; t − −1;2t −3)
IK ⊥ AB ⇒ A .
B IK = 0 ⇒ t =1⇒ IK = (0; 2; − − ) 1 . 2 2
r = R − d (I (P)) 2 =
− d (I (P)) 2 , 25 , = 25 − IH . Ta có: r ⇔ IH min max . Mà
IH ≤ IK ⇒ IH
= IK ⇔ H ≡ K ⇒ P ⊥ IK ⇒ n và IK cùng phương. max ( ) P a = 0 a = 0 a = 0
⇒ n = k IK ⇒ b
= − k ⇒ k = − ⇒
⇒ t = a + b + c = 0 + 2 +1 = 3. P . 2 1 c =1 c = −k c = 1
Câu 50.5: Trong không gian hệ tọa độ Oxyz , cho hai điểm A(0;3;0) , B(0; 3
− ;0) . Mặt cầu (S ) nhận AB
là đường kính. Hình trụ (H ) là hình trụ có trục thuộc trục tung, nội tiếp với mặt cầu và có thể
tích lớn nhất. Khi đó mặt phẳng chứa đáy của hình trụ đi qua điểm nào sau đây? A. ( 3;0;0). B. ( 3; 3;0). C. ( 3;2; ) 1 . D. ( 3; 2; 3). Lời giải Chọn B
Bán kính của mặt cầu là AB R = = 3 . 2
Gọi chiều cao của hình trụ là 2h , h > 0 . Do đó bán kính của hình trụ là 2 2 2
r = R − h = 9 − h . Thể tích khối trụ là 2 V = π r h = π ( 2 − h ) h = π ( 2 − h )( 2 − h ) 2 . .2 . 9 .2 2 9 9 .2h . 3 2 2 2
9 − h + 9 − h + 2 ≤ 2. h V π = π 2.6 6 = 12π 3 . 3 Dấu đẳng thức xảy ra 2 2
⇔ 9 − h = 2h ⇔ h = 3 .
Khi đó hình trụ có thể tích lớn nhất là 12π 3 . Trang 52/53 - WordToan
Vậy hai mặt đáy của trụ có phương trình tương ứng là y = 3; y = − 3 .
Câu 50.6: Trong không gian với hệ tọa độ Oxyz , cho mặt cầu (S) có đường kính AB , I(3;2; 2 − ) là trung
điểm AB . Gọi (P) là mặt phẳng vuông góc với đoạn AB tại H sao cho khối nón đỉnh A và
đáy là đường tròn (C) ( (C) là giao của (S) và (P) ) có thể tích lớn nhất. Biết (C) có bán kính 2 10 r = S
3 , viết phương trình mặt cầu ( ). A. 2 2 2
(x −3) + (y − 2) + (z + 2) = 40 . B. 2 2 2
(x −3) + (y − 2) + (z + 2) = 5 . C. 2 2 2
(x + 3) + (y + 2) + (z − 2) = 5. D. 2 2 2
(x − 3) + (y − 2) + (z + 2) = 5 . Lời giải Chọn B
Mặt cầu (S) có tâm I , bán kính R , (C) có tâm H , bán kính r . Đặt AH = x (0 < x < 2R) , ta có 1 1 2
V = AH ⋅ S = AH ⋅π r N C . ( ) ( ) 3 3
Do AB là đường kính nên ta có 2
r = AH ⋅ HB = x(2R − x) . Khi đó π 2 π 3 2 π V = x R − x = −x + Rx = f x . N (2 ) ( 2 ) ( ) ( ) 3 3 3 x = 0 Xét hàm số 3 2
f (x) = −x + 2Rx trên (0;2R) , 2 f (′x) = 3
− x + 4Rx , f (′x) = 0 ⇔ 4 x = . R 3
Bảng biến thiên f (x) :
Dựa vào bảng biến thiên, ta có V lớn nhất khi 4 = hay 2 = . Mà ( N ) x R AH AB 3 3 2 40
AH ⋅ HB = r = . Suy ra 9 2 1 40 AB ⋅ AB =
⇒ AB = 2 5 ⇒ R = 5. 3 3 9 Suy ra 2 2 2
(S) : (x −3) + (y − 2) + (z + 2) = 5. Trang 53/53 - WordToan
Document Outline
- từ câu 39 đến câu 45
- từ câu 46 đến câu 50
- Lời giải




