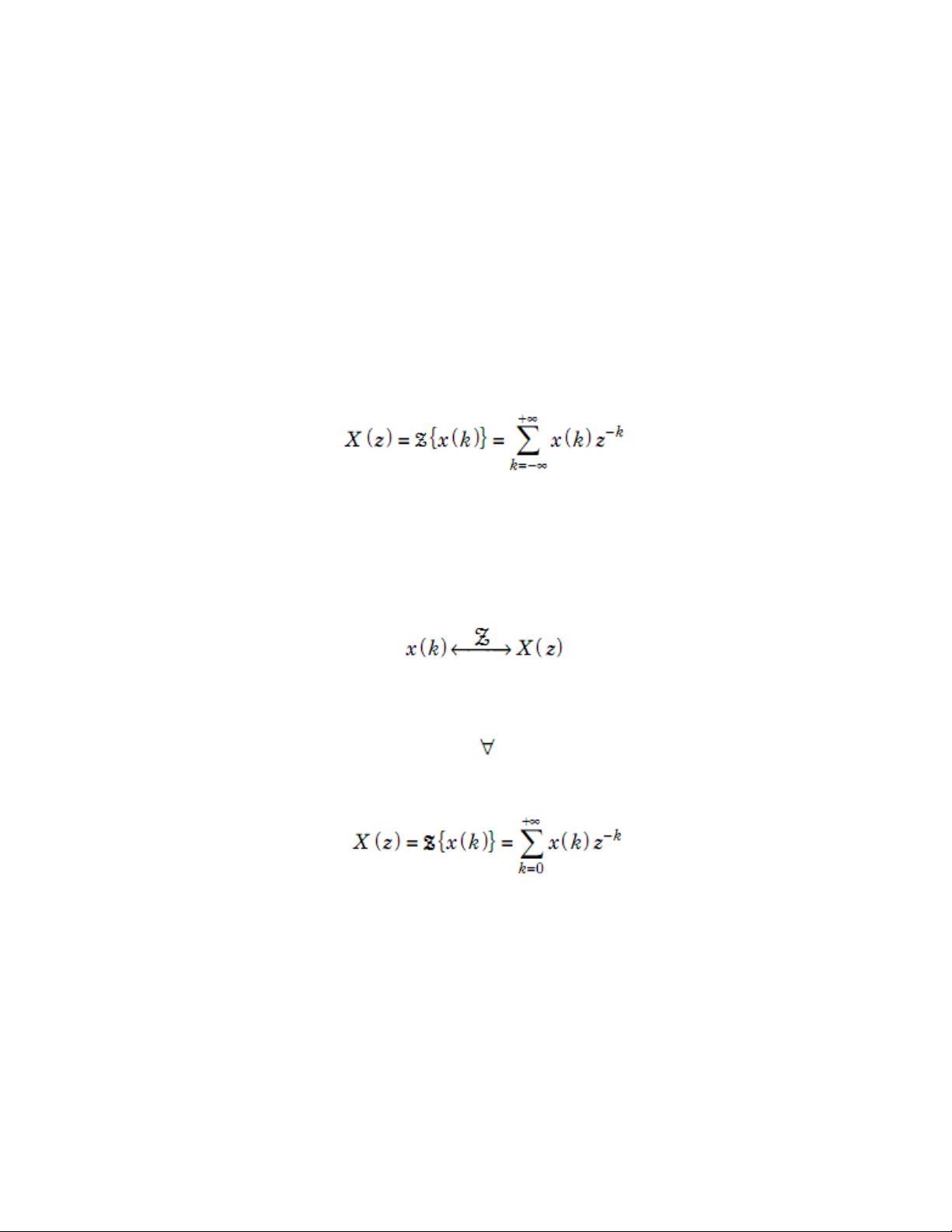
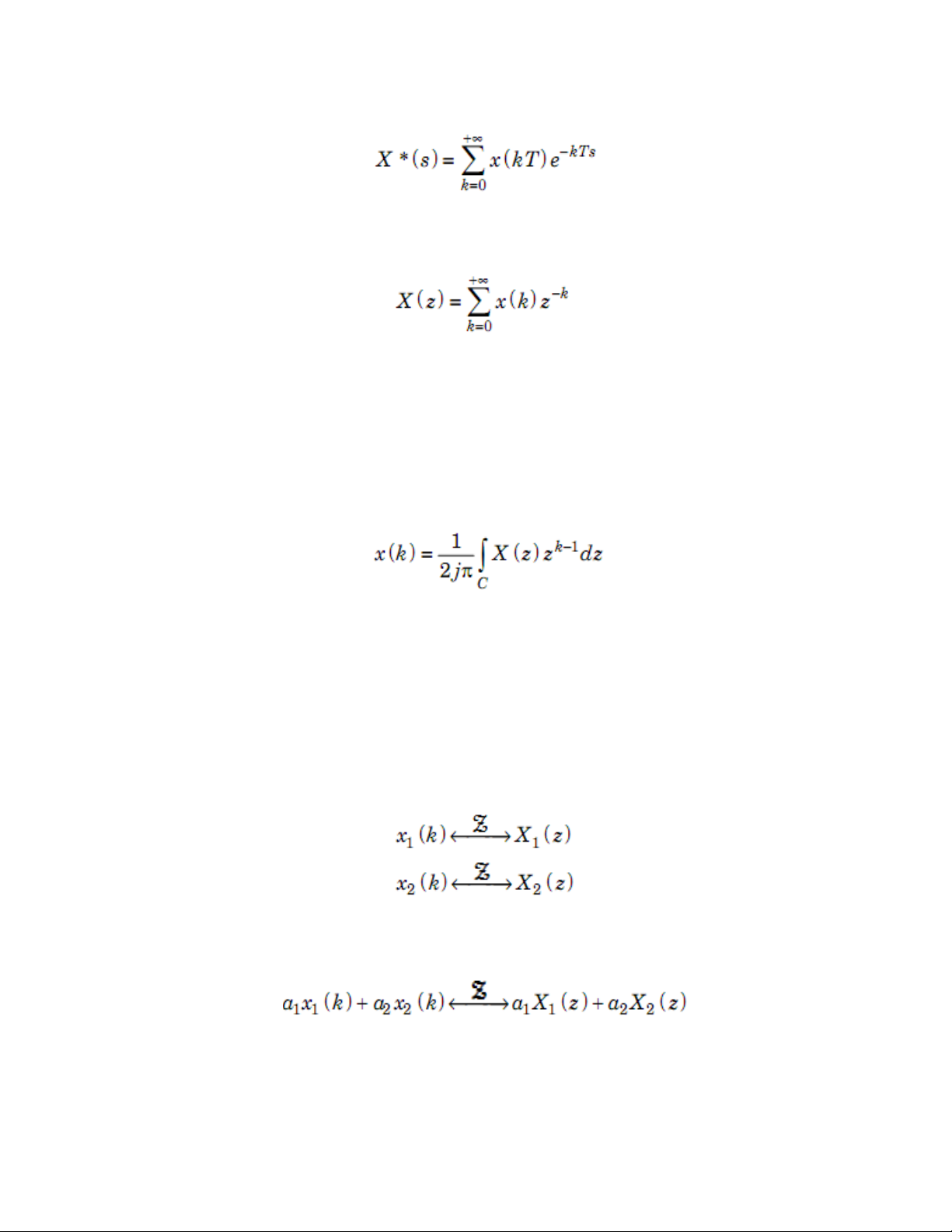
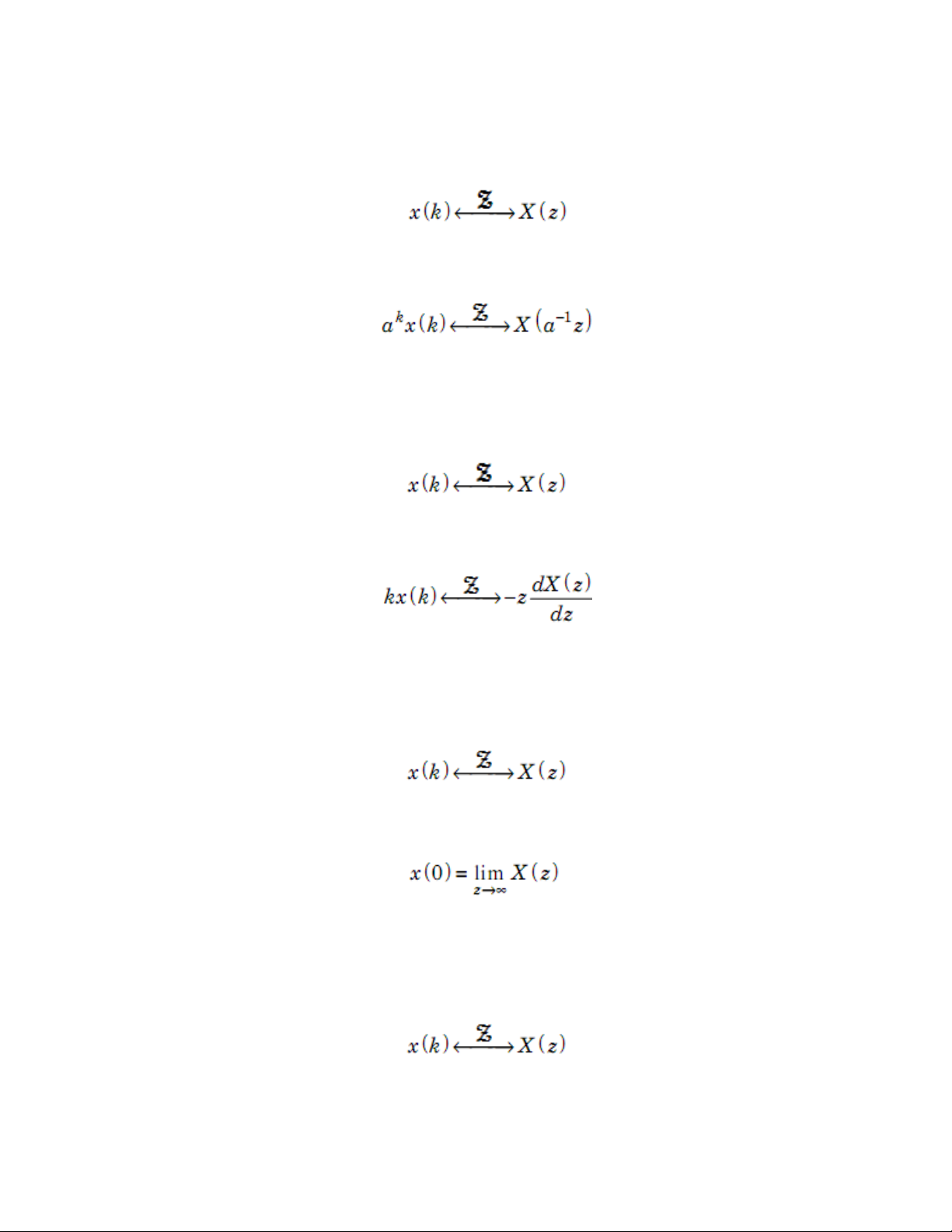





Preview text:
Phép biến đổi Z Phép biến đổi Z Bởi: Khoa CNTT ĐHSP KT Hưng Yên Định nghĩa
Cho x(k) là chuỗi tín hiệu rời rạc. Biến đổi Z của x(k) là: (7.7)
trong đó: z = eTs (s là biến Laplace) Ký hiệu: Nếu x(k) = 0,
k < 0thì biểu thức định nghĩa trở thành:
Miền hội tụ (Region of Convergence - ROC)
ROC là tập hợp tất cả các giá trị z sao cho X(z) hữu hạn.
Ý nghĩa của phép biến đổi Z
Giả sử x(t) là tín hiệu liên tục trong miền thời gian, lấy mẫu x(t) với chu kỳ lấy mẫu T ta
được chuỗi rời rạc x(k) = x(kT). 1/12 Phép biến đổi Z
Biểu thức lấy mẫu x(t): Biểu thức biến đổi Z:
Vì z = eTs nên vế phải của hai biểu thức (7.9) và (7.10) là như nhau, do đó bản chất của
việc biến đổi Z một tín hiệu chính là rời rạc hóa tín hiệu đó.
Phép biến đổi Z ngược
Cho X(z) là hàm theo biến phức z. Biến đổi Z ngược của X(z) là:
với C là đường cong kín bất kỳ nằm trong miền hội tụ ROC của X(z) và bao gốc tọa độ.
Tính chất của phép biến đổi Z Tính tuyến tính Nếu: Thì: 2/12 Phép biến đổi Z
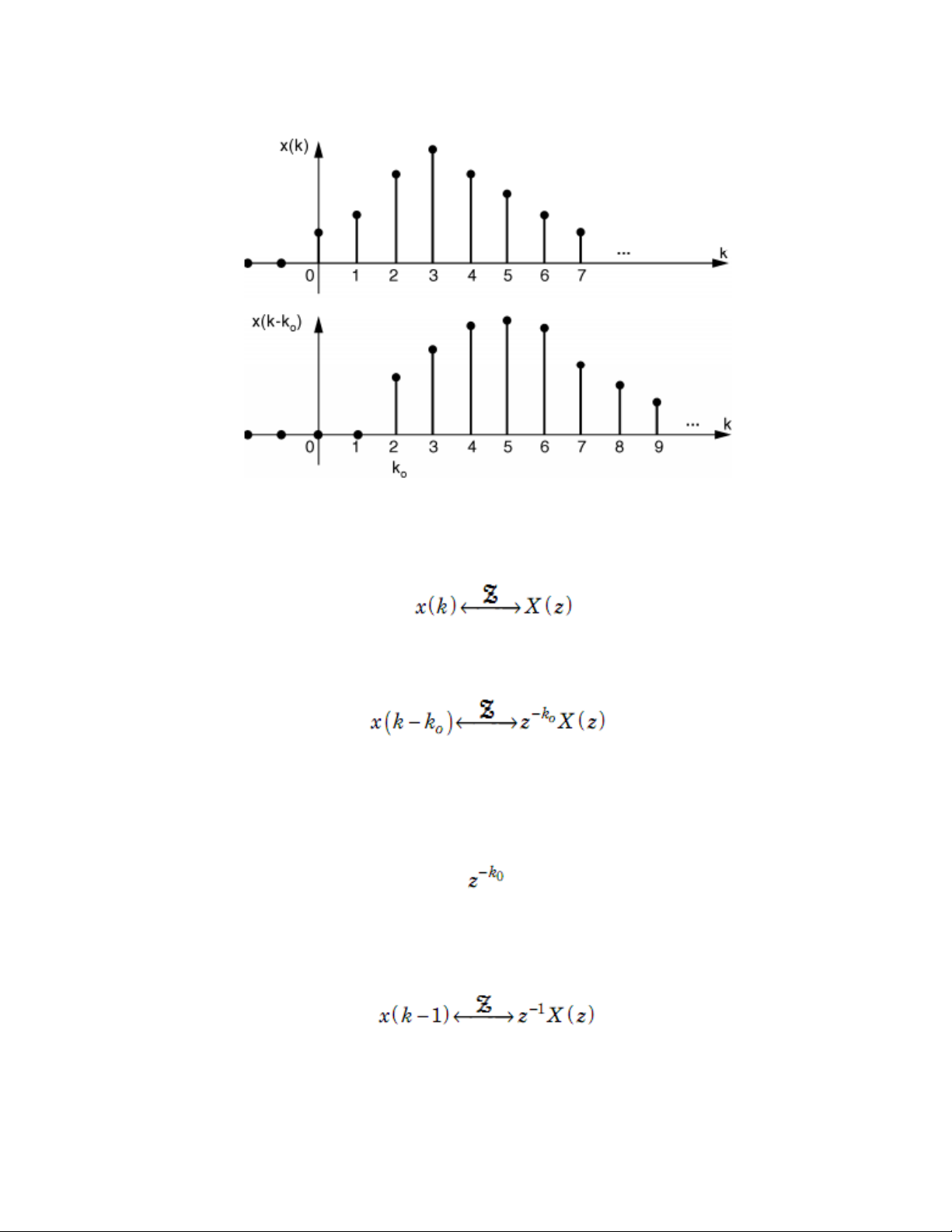
Dời trong miền thời gian
Làm trễ tín hiệu Ko mẫu Nếu: Thì: Nhận xét:
Nếu trong miền Z ta nhân X(z) với
thì tương đương với trong miền thời gian là trễ tín hiệu x(k) ko chu kỳ lấy mẫu. Vì:
nên z–1 được gọi là toán tử làm trễ một chu kỳ lấy mẫu. 3/12 Phép biến đổi Z
Tỉ lệ trong miền Z Nếu: Thì:
Đạo hàm trong miền Z Nếu: Thì:
Định lý giá trị đầu Nếu: Thì:
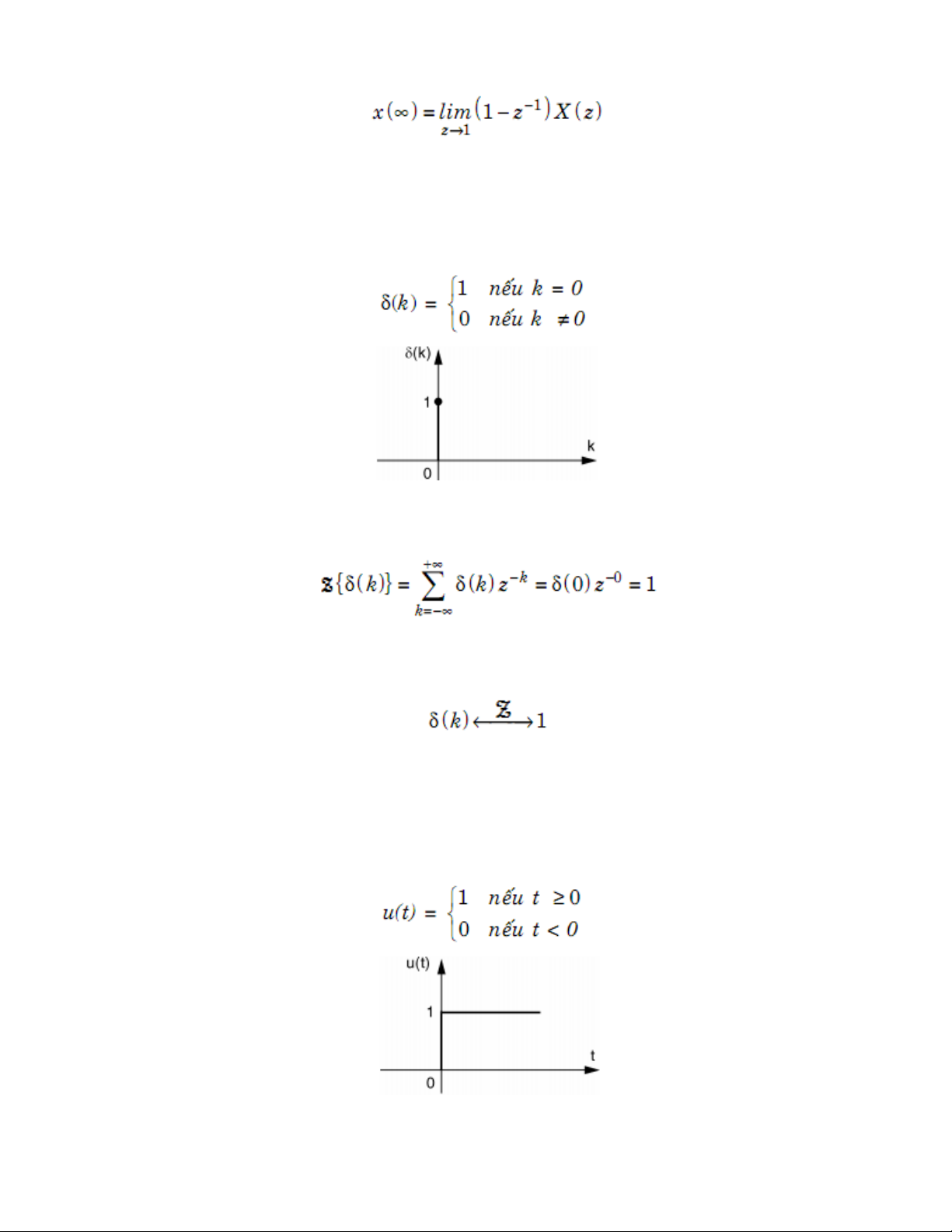
Định lý giá trị cuối Nếu: Thì: 4/12 Phép biến đổi Z
Biến đổi Z của các hàm cơ bản Hàm dirac Theo định nghĩa: Vậy:
(ROC: toàn bộ mặt phẳng Z) Hàm nấc đơn vị
Hàm nấc đơn vị (liên tục trong miền thời gian): 5/12 Phép biến đổi Z
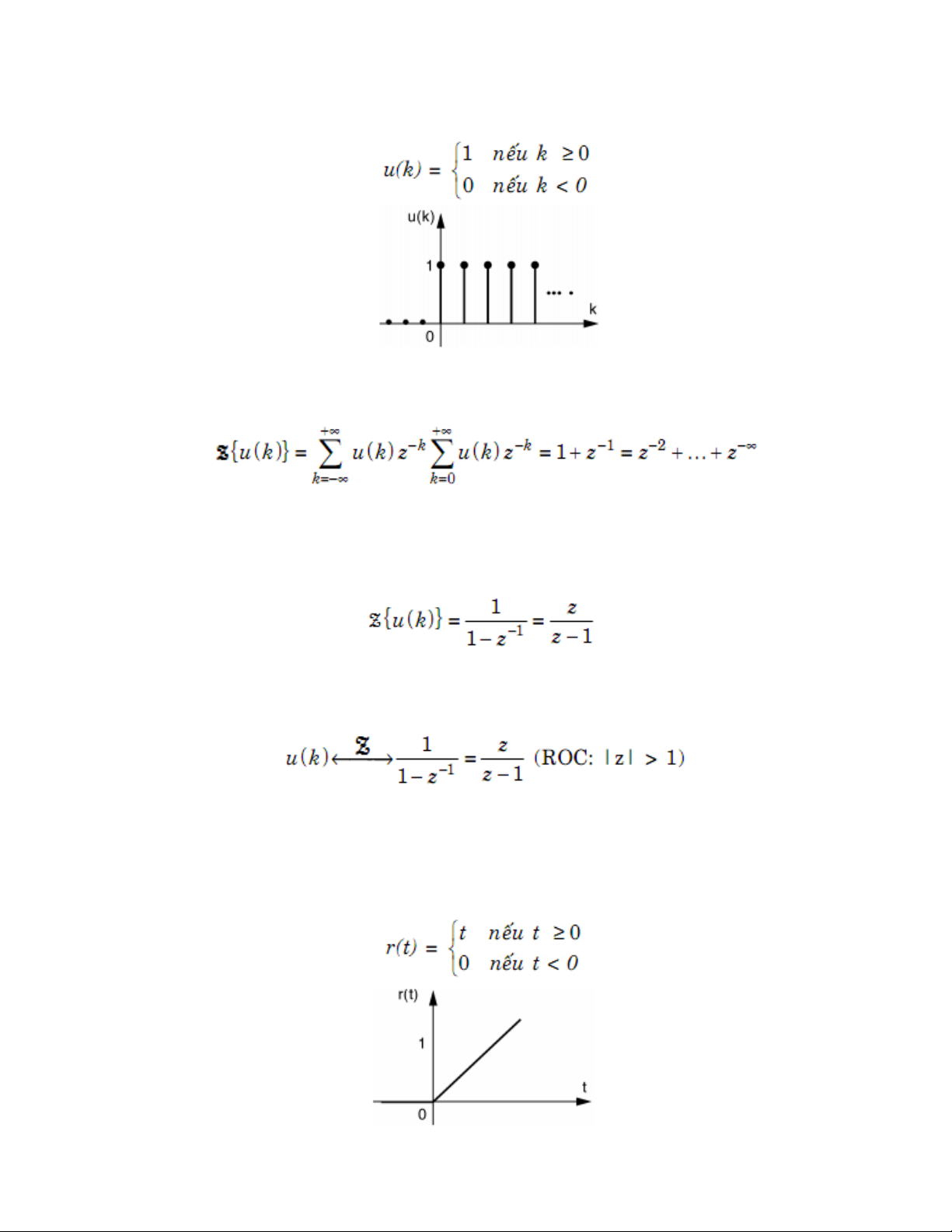
Lấy mẫu u(t) với chu kỳ lấy mẫu là T, ta được: Theo định nghĩa:
Nếu |z-1| < 1thì biểu thức trên là tổng của cấp số nhân lùi vô hạn. Áp dụng công thức
tính tổng của cấp số nhân lùi vô hạn, ta dễ dàng suy ra: Vậy: Hàm dốc đơn vị
Hàm dốc đơn vị (liên tục trong miền thời gian): 6/12 Phép biến đổi Z
Lấy mẫu r(t) với chu kỳ lấy mẫu là T, ta được:
Ta tìm biến đổi Z của r(k) bằng cách áp dụng tính chất tỉ lệ trong miền Z: Ta có: Vậy: Hàm mũ
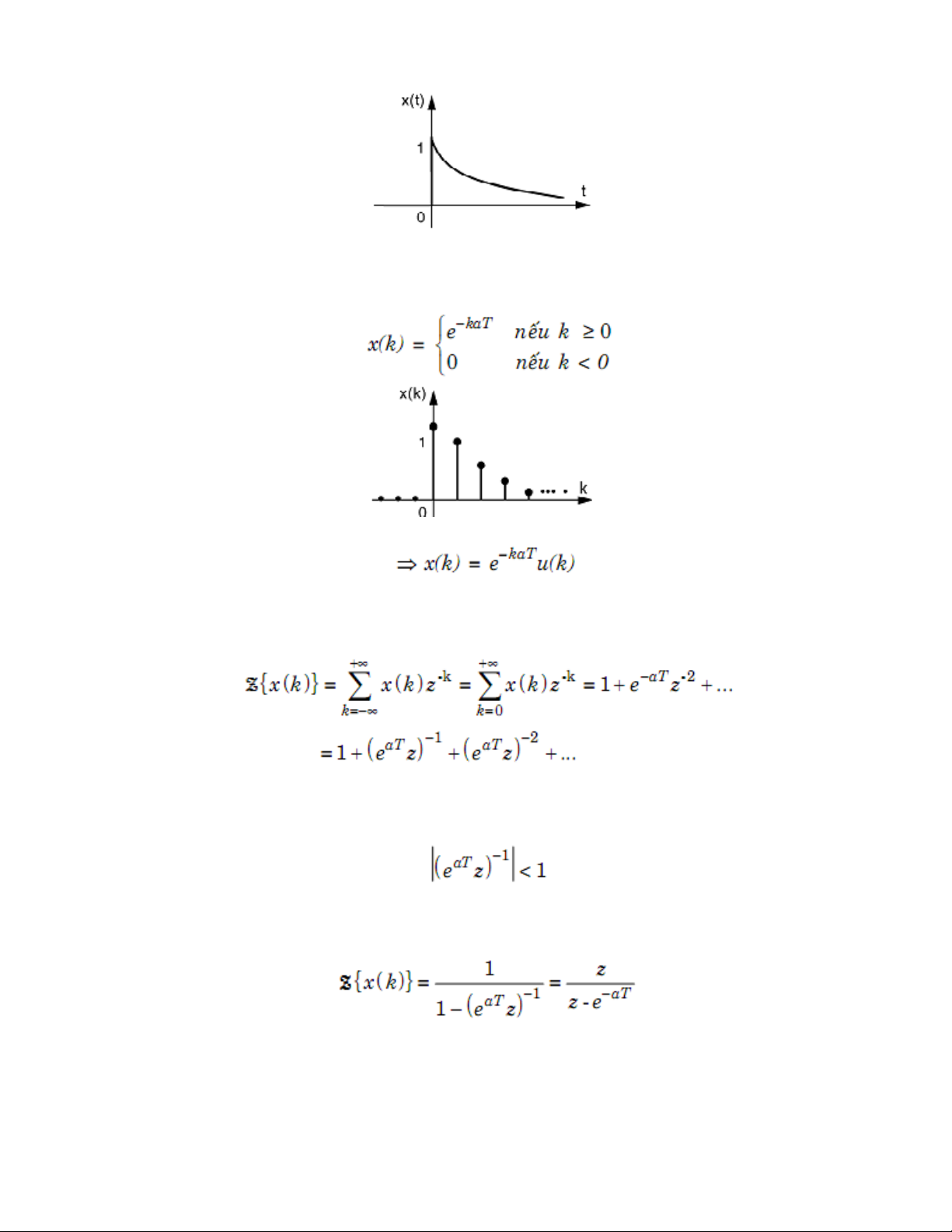
Hàm mũ liên tục trong miền thời gian: 7/12 Phép biến đổi Z
Lấy mẫu r(t) với chu kỳ lấy mẫu là T, ta được: Theo định nghĩa: Nếu
thì biểu thức trên là tổng của cấp số nhân lùi vô hạn. Áp dụng công thức tính tổng của
cấp số nhân lùi vô hạn, ta suy ra: Vậy: 8/12 Phép biến đổi Z
Kết quả trên ta dễ dàng suy ra:
Các phương pháp tìm biến đổi Z ngược
Cho hàm ( ) X z , bài toán đặt ra là tìm ( ) x k . Theo công thức biến đổi Z ngược, ta có:
với C là đường cong kín bất kỳ nằm trong ROC của và bao gốc tọa độ.
Tìm x(k) bằng công thức trên rất phức tạp, thực tế ta thường áp dụng các cách sau:
Cách 1: Phân tích X( z ) thành tổng các hàm cơ bản, sau đó tra bảng biến đổi Z Ví dụ 7.1. Cho: Tìm x(k). Giải. Phân tích , ta được: 9/12 Phép biến đổi Z Tra bảng biến đổi Z:
Suy ra: x(k) = (–2k + 3k) u(k)
Cách 2: Phân tích ( ) X z thành chuỗi lũy thừa
Theo định nghĩa biến đổi z:
Do đó nếu phân tích X(z) thành tổng của chuỗi lũy thừa ta sẽ được giá trị x(k) chính là
hệ số của thành phần z–k. Ví dụ :. Cho: Tìm x(k). Giải: Chia đa thức ta được:
Suy ra: x(0) = 0; x(1) = 1; x(2) = 5; x(3) = 19; x(4) = 65,...
Cách 3: Tính x(k) bằng công thức đệ qui Ví dụ :. Cho: 10/12 Phép biến đổi Z Tìm x(k). Giải: Ta có:
Biến đổi Z ngược hai vế phương trình trên (để ý tính chất dời trong miền thời gian), ta được:
Với điều kiện đầu: x( k – 1) = 0; x(k – 2) = 0
Thay vào công thức trên ta tìm được:
x(0) = 0; x(1) = 1; x(2) = 5; x(3) = 19; x(4) = 65,...
Cách 4: Áp dụng công thức thặng dư Nếu là cực bậc một thì: Nếu là cực bậc p thì: 11/12 Phép biến đổi Z Ví dụ : Cho: Tìm x(k).
Giải. Áp dụng công thức thặng dư, ta được: Mà:
Do đó: x(k) = –2k + 3k 12/12
Document Outline
- Phép biến đổi Z
- Định nghĩa
- Ý nghĩa của phép biến đổi Z
- Phép biến đổi Z ngược
- Tính chất của phép biến đổi Z
- Tính tuyến tính
- Dời trong miền thời gian
- Tỉ lệ trong miền Z
- Đạo hàm trong miền Z
- Định lý giá trị đầu
- Định lý giá trị cuối
- Biến đổi Z của các hàm cơ bản
- Hàm dirac
- Hàm nấc đơn vị
- Hàm dốc đơn vị
- Hàm mũ
- Các phương pháp tìm biến đổi Z ngược