4 cách xác định một số chia hết cho 7 1. CÁCH THỨ NHẤT
Quy tắc chung: Để nhận biết một số có thể chia hết cho 7, ta cắt giảm chữ số cuối cùng
đi 1 số, nhân đôi số đó và lấy số cắt giảm trừ đi số đã nhân đôi. Điều này cần được thực
hiện lặp đi lặp lại một vài lần, đến khi thu được một số có thể chia hết cho 7 (như: 14, 7,
0, – 7, v.v…), thì số đã cho chia hết cho 7. Sơ đồ tóm tắt: Giả sử có số M=a1a2a3...an−1an― cắt an còn a1a2a3...an−1―
a1a2a3...an−1―−2an lặp lại cho đến khi còn axbx― Nếu
axbx― chia hết cho 7 thì số M chia hết cho 7.
Thí dụ: Số 3 101 có chia hết cho 7 hay không?
Các bước thực hiện:
• Giảm chữ số cuối cùng của số 3 101 đi chữ số 1 còn 310
• Nhân đôi chữ số cắt giảm (2 . 1 = 2) và lấy số còn lại sau cắt giảm trừ đi nó: 310 – 2 = 308
• Lặp lại quy trình bằng cách giảm đi 8 của 308 còn 30
• Nhân đôi số 8 cho (2 . 8 = 16) và trừ đi số đó: 30 – 16 = 14
• Nhận được Số là 14 là số chia hết cho 7
→ Kết luận: Số 3 101 chia hết cho 7 2. CÁCH THỨ HAI
Quy tắc: (cách này đơn giản dễ nhớ hơn)
Lấy chữ số đầu tiên nhân với 3 rồi cộng thêm chữ số tiếp theo, được bao nhiêu lại nhân
với 3 rồi cộng thêm chữ số tiếp theo… cứ như vậy cho đến chữ số cuối cùng của số cần
nhận biết. Nếu kết quả cuối cùng này chia hết cho 7 thì số đó chia hết cho 7.
Để nhanh gọn, cứ mỗi lần nhân với 3 và cộng thêm chữ số tiếp theo nếu có số ≥ 7 thì ta
lấy kết quả trừ đi 7 hoặc trừ đi các số là bội số của 7 (14, 21…) rồi tiếp tục như trên.
Thí dụ: Số cần nhận biết là 203:
Lấy 2 . 3 = 6 → 6 + 0 = 6 → 3 . 6 = 18 → 18 + 3 = 21 → 203 chia hết cho 7 3. CÁCH THỨ BA
Lấy chữ số đầu tiên bên phải nhân với 5 rồi cộng với chữ số thứ hai sau đó trừ cho bội
của 7; được bao nhiêu nhân với 5 cộng với chữ số thứ 3 rồi trừ cho bội của 7; được bao
nhiêu nhân với 5 cộng với chữ số thứ 4 rồi trừ cho bội của 7; …. Nếu kết quả cuối cùng
là một số chia hết cho 7 thì số đã cho chia hết cho 7. Ví dụ:
a) Số 2 275 có chia hết cho 7 không?
Ta có: (5 . 5 + 7) – 7 . 4 = 4
→ có (4 . 5 + 2) – 7 . 3 = 1 → có (1 . 5 + 2) – 7 = 0
Vậy 2 275 chia hết cho 7. Kiểm tra thấy: 2 275 = 7 . 325
b) số 35 742 có chia hết cho 7 không? có (2 . 5 + 4) – 7 . 2 = 0 → có (0 . 5 + 7) – 7 = 0
→ có (0 . 5 + 5) – 7 . 0 = 5
→ có (5 . 5 + 3) – 7 . 4 = 0
Vậy 35 742 chia hết cho 7. Kiểm tra thấy: 35 742 = 7 x 5 106
4. CÁCH THỨ TƯ (với số có 6 chữ số)
• Biết rằng: Các số có 6 chữ số khác nhau abcdeg― chia hết cho 7 nếu
(abc―−deg―) chia hết cho 7 [*]. (a, b, c, d, e, g ∈ N và khác nhau) →
Chỉ việc lấy 3 số đầu trừ đi 3 số cuối, nếu hiệu này chia hết cho 7 thì số đó chia hết cho 7. Chứng minh: Ta có:
abcdeg―=abc― . 1 000+deg―
⇒abcdeg―=abc― . 1 001−abc―+deg―
⇒abcdeg―=abc― . 1 001−(abc―−deg―)
⇒abcdeg―=abc― . 7.143−(abc―−deg―) chia hết cho 7 Vậy abcdeg― chia hết cho 7.
• Lưu ý rằng tính chất [*] còn có thể tổng quát hơn:
Các số có 6 chữ số chia hết cho 7 nếu hiệu của 3 số liền nhau trừ cho 3 số liền nhau còn
lại chia hết cho 7 thì số đó chia hết cho 7 [**]
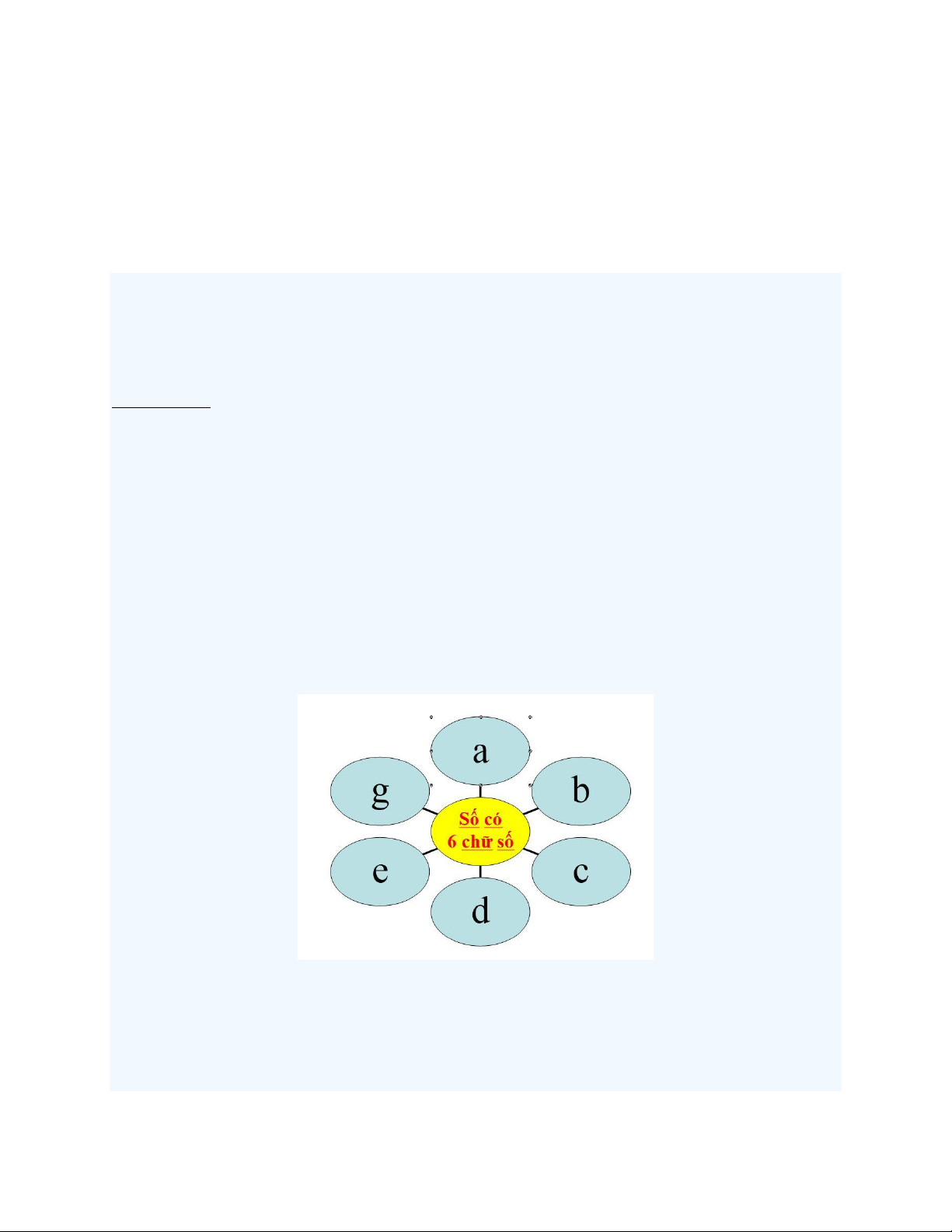
Theo Sơ đồ: Có thể tính các cặp hiệu theo chiều kim đồng hồ:
Nếu (abc – deg) Chia hết cho 7 ⇒ abcdeg chia hết cho 7
(bcd – ega) Chia hết cho 7 ⇒ abcdeg chia hết cho 7
(gab – cde) Chia hết cho 7 ⇒ abcdeg chia hết cho 7
(cde – gab) Chia hết cho 7 ⇒ abcdeg chia hết cho 7
(deg – abc) Chia hết cho 7 ⇒ abcdeg chia hết cho 7
(ega – bcd) Chia hết cho 7 ⇒ abcdeg chia hết cho 7
⇒ Như vậy, để xác định số có 6 chữ số có chia hết cho 7 hay không ta lấy hiệu của 3 số
liền nhau trừ 3 số liền nhau còn lại mà hiệu này nhỏ nhất để dễ so với 1 bội số của 7.
Thí dụ 1: Số 523 152, ta lấy 315 – 252 = 63 → dễ thấy 63 là bội của 7
Nếu theo [*] ta lấy 523 – 152 = 371 → Để xác định 371 có là bội của 7 hay không ta lại
phải áp dụng CÁCH THỨ HAI (phần trên) phức tạp hơn
Thí dụ 2: Số 203 203. Nếu theo [*] ta lấy 203 – 203 = 000.
→ Trường hợp này ta coi 0 cũng là số chia hết cho 7 → 203 203 chia hết cho 7
KẾT LUẬN: Tùy trường hợp phải Số xác định lớn hay nhỏ, các em có thể áp dụng 1 trong
4 cách trên để biết số đó có chia hết cho 7 hay không.