Probability and Statistics Exercises K63TOAE201 môn Xác suất thống kê| Trường Đại học Ngoại Thương

20:55, 27/01/2026
Probability and Statistics Exercises K63TOAE201 - Comprehensive Review - Studocu
Probability and Statistics exercises
1. In a school, 48% of the students take a foreign language class and 19% of students
take both foreign language and technology. What is the probability that a student
takes technology given that the students takes foreign language?
2. The test contains 10 questions, each one with available four different answers,
among which just one is correct. To pass the test at least 5 questions must be
answered correctly. What is the probability that completely unprepared student will pass the test ?
3. In the class of 30 students, seven of them don't have done the homework. The
teacher choosed randomly 6 students. What is the chance that at least four of them have done their homework ?
4. Three shooters shoot at the same target, each of them shoots just once. The first
one hits the target with a probability of 70%, the second one with a probability
of 80% and the third one with a probability of 90%. What is the probability that
the shooters will hit the target a) at least once b) at least twice ?
5. Based on incidence rate, the following table presents the corresponding numbers per 100,000 people. Cancer Symptom Total No Yes No 99989 0 99989 Yes 10 1 11 Total 99999 1 100000
Which can then be used to calculate the probability of having cancer when you have the symptoms:
6. A factory produces an item using three machines—A, B, and C—which account
for 20%, 30%, and 50% of its output, respectively. Of the items produced by 20:55, 27/01/2026
Probability and Statistics Exercises K63TOAE201 - Comprehensive Review - Studocu
machine A, 5% are defective; similarly, 3% of machine B's items and 1% of
machine C's are defective. If a randomly selected item is defective, what is the
probability it was produced by machine C?
7. X is a discrete random variable. The table below defines a probability distribution for X X 0 1 2 3 P 0.17 0.14 0.36 0.33
What is the expected value of X? What is the variance value of X?
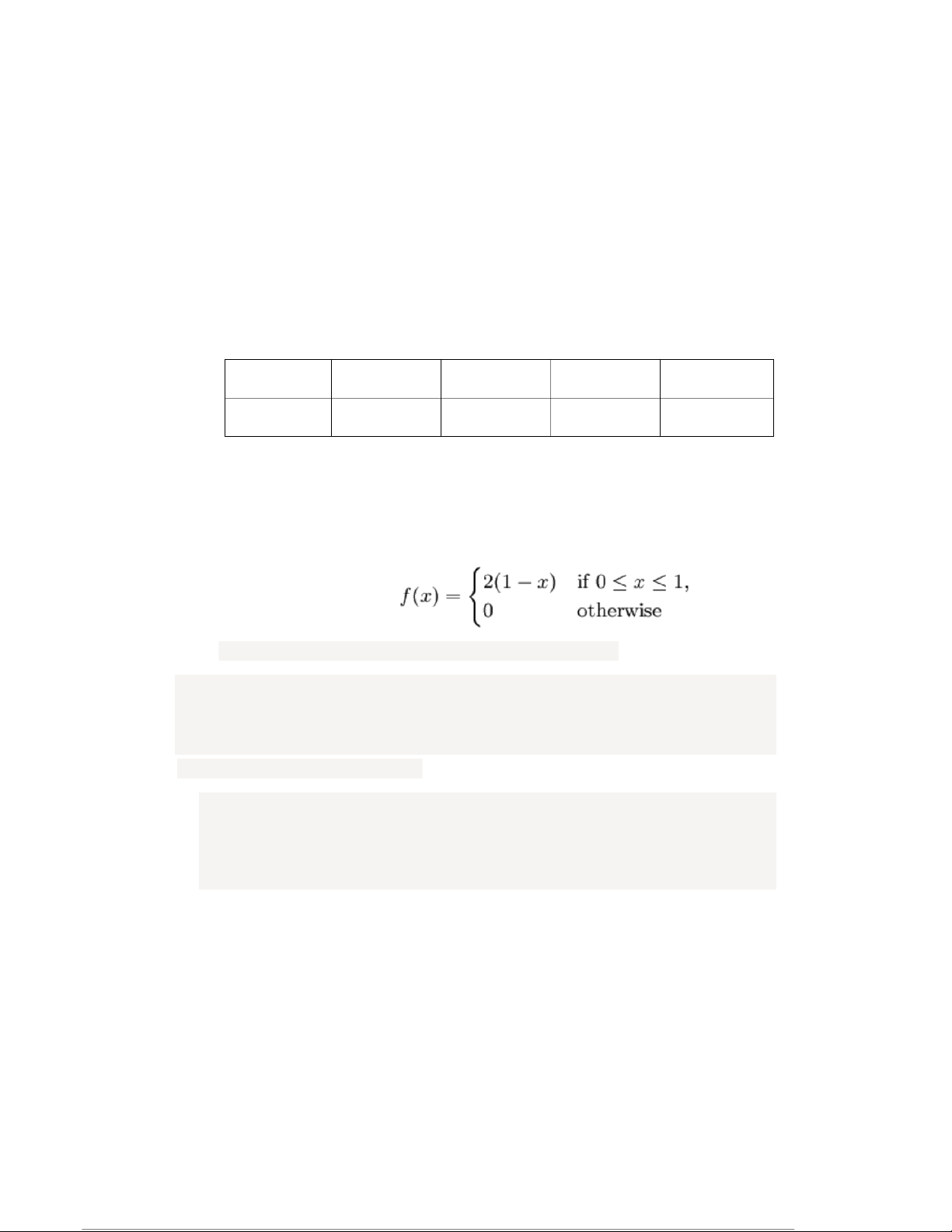
8. The random variable X is given by the following PDF. Check that this is a valid
PDF and calculate the expected, the variance, the standard deviation values of X.
9. Let X be a continuous random variable with the following
𝑓(𝑥)={𝑐𝑒−𝑥 𝑖𝑓 𝑥 ≥ 0
0 𝑜𝑡ℎ𝑒𝑟𝑤𝑖𝑠𝑒
where c is a positive constant. a. Find c.
b. Find the cumulative distribution function of X.
c. Find P(110. Let X be a random variable following a normal distribution model N(10,2). a. Calculate P(X≤10). b. Calculate P(8≤X≤14).
11. Let Z be a random variable following a standard normal distribution model.
Determine the value of x in the following cases using the table of the distribution function: a. P(Zb. P(Z>x)=0.0606. 20:55, 27/01/2026
Probability and Statistics Exercises K63TOAE201 - Comprehensive Review - Studocu c. P(0≤Z≤x)=0.4783. d. P(−1.5≤Z≤x)=0.2313. e. P(−x≤Z≤x)=0.5467.
12. It is known that the glucose level in blood of diabetic persons follows a normal
distribution model with mean 106 mg/100 ml and standard deviation 8 mg/100 ml.
a. Calculate the probability of a random diabetic person having a glucose level less than 120 mg/100 ml.
b. What percentage of persons have a glucose level between 90 and 120 mg/100 ml?
13. It is known that the cholesterol level in males 30 years old follows a normal
distribution with mean 220 mg/dl and standard deviation 30 mg/dl. If there are
20000 males 30 years old in the population,
a. How many of them have a cholesterol level between 210 and 240 mg/dl?
b. If a cholesterol level greater than 250 mg/dl can provoke a thrombosis, how
many of them are at risk of thrombosis?
c. Calculate the cholesterol level above which 20% of the males are?
14. In a population with 40000 persons, 2276 have between 0.8 and 0.84 milligrams of
bilirubin per deciliter of blood, and 11508 have more than 0.84. Assuming that the
level of bilirubin in blood follows a normal distribution model,
a. Calculate the mean and the standard deviation.
b. How many persons have more than 1 mg of bilirubin per dl of blood?
15. . If 95% of households have a TV and 8 houses are surveyed, what is the probability that more than 6 have a TV?
16. A manufacturer knows that an average of 1 out of 10 of his products are faulty.
What is the probability that a random sample of 5 articles will contain: a. No faulty products b. Exactly 1 faulty products c. At least 2 faulty products
d. No more than 3 faulty products 20:55, 27/01/2026
Probability and Statistics Exercises K63TOAE201 - Comprehensive Review - Studocu
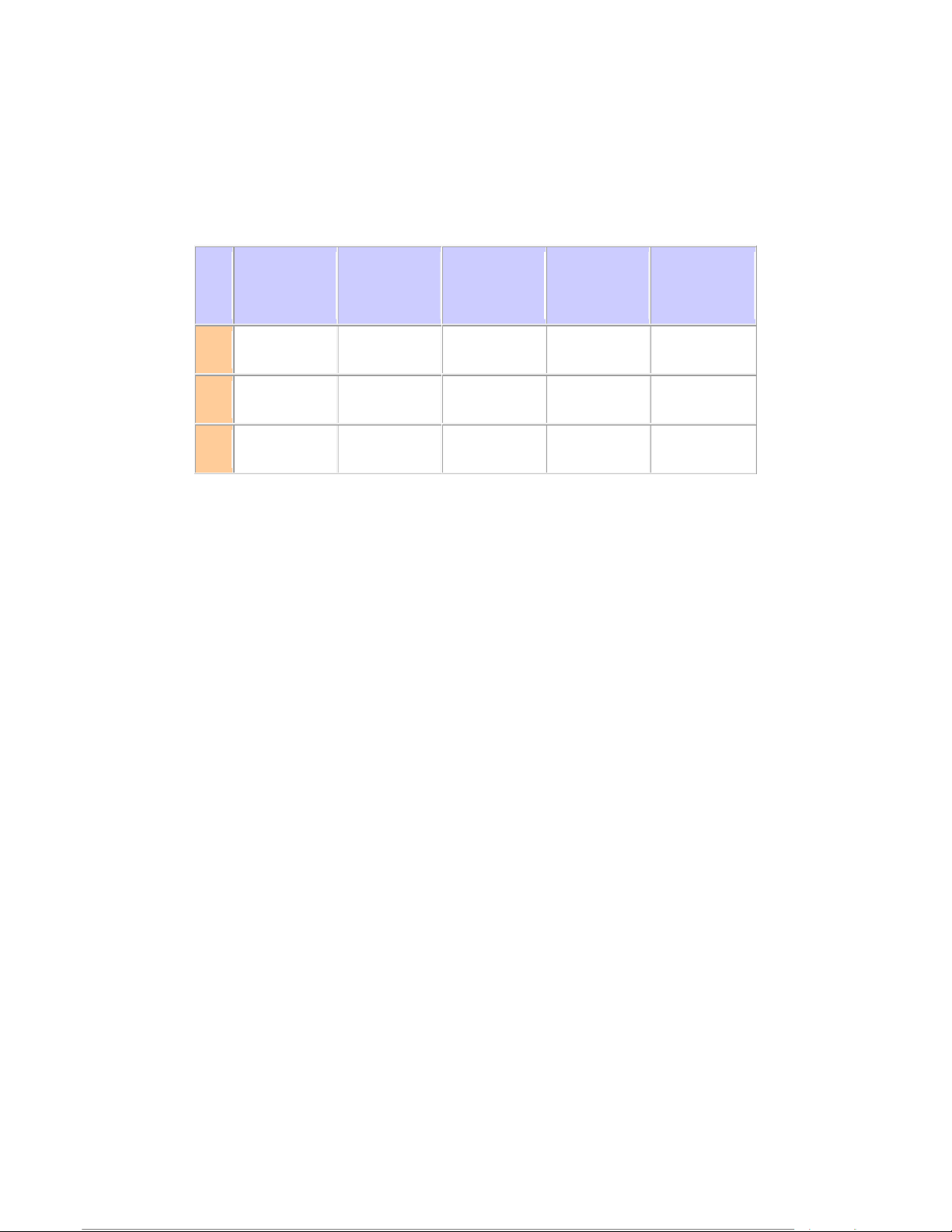
17. Complete the table for the following binomial distributions: standard N p mean Variance deviation a 50 0.5 b 20 5 c 0.4 100
where n = number of trials and p = probability of a success.
18. The probability that cars passing a speed camera are speeding is 0.23. If 750 cars
pass the camera, how many of the cars would you expect to be speeding and what
would be the standard deviation?
19. A normal population has a mean of 60 and a standard deviation of 12 . You select a
random sample of 9 . Compute the probability the sample mean is: a. Greater than 63. b. Less than 56. c. Between 56 and 63.
20. The mean rent for a one-bedroom apartment in Southern California is $2,200 per
month. The distribution of the monthly rent does not follow the normal distribution.
In fact, it is positively skewed. What is the probability of selecting a sample of 50
onebedroom apartments and finding the mean to be at least $1,950 per month? The
population standard deviation is $250.
21. A population is known to be normally distributed with a standard deviation of 2.8.
a. Compute the 95% confidence interval on the mean based on the
following sample of nine: 8, 9, 10, 13, 14, 16, 17, 20, 21.
b. Now compute the 99% confidence interval using the same data.
22. You do a study of hypnotherapy to determine how effective it is in increasing the
number of hours of sleep subjects get each night. You measure hours of sleep for 12
subjects with the following results. Construct a 95% confidence interval for the
mean number of hours slept for the population (assumed normal) from which you took the data. 20:55, 27/01/2026
Probability and Statistics Exercises K63TOAE201 - Comprehensive Review - Studocu
8.2; 9.1; 7.7; 8.6; 6.9; 11.2; 10.1; 9.9; 8.9; 9.2; 7.5; 10.5
23. A random sample of 20 nominally measured 2mm diameter steel ball bearings is
taken and the diameters are measured precisely. The measurements, in mm, are as
follows: 2.02 1.94 2.09 1.95 1.98 2.00 2.03 2.04 2.08 2.07 1.99 1.96 1.99 1.95 1.99
1.99 2.03 2.05 2.01 2.03 Assuming that the diameters are normally distributed with
unknown mean, µ, and unknown variance σ 2 ,
a. Find a two-sided 95% confidence interval for the variance
b. Find a two-sided confidence interval for the standard deviation.
24. In a typical car, bell housings are bolted to crankcase castings by means of a series
of 13 mm bolts. A random sample of 12 bolt-hole diameters is checked as part of
a quality control process and found to have a variance of 0.0013 mm2 .
a. Construct the 95% confidence interval for the variance of the holes.
b. Find the 95% confidence interval for the standard deviation of the holes.
25. Harris Interactive conducted a poll of American adults in August of 2011 to study
the use of online medical information. Of the 1,019 randomly chosen adults, 60%
had used the Internet within the past month to obtain medical information. Use the
results of this survey to create an approximate 95% confidence interval estimate for
the percentage of all American adults who have used the Internet to obtain medical
information in the past month.
26. The following is an excerpt from an August 2011 Just the Facts publication from
the Public Policy Institute for California, “Because neither of the major political
parties has a majority of California’s registered voters, independents are influential
in statewide elections. For example, in the previous gubernatorial election, 54% of
the independents in our post-election survey said they voted for Republican Arnold
Schwarzenegger. But in the 2008 presidential election, most independents (59%)
said they supported Democrat Barack Obama. In each case, the outcome reflected
the choice of the majority of independents.”
Suppose that the survey included 1011 independents. Find and interpret 99% confidence
interval for the proportion of California independents who supported Barack Obama in
the 2008 presidential election. 20:55, 27/01/2026
Probability and Statistics Exercises K63TOAE201 - Comprehensive Review - Studocu
27. Find the sample size given 99% confidence, Margin of Error = 0.25 and f =0.30.
28. A group of researchers want to test the possible effect of an epilepsy medication
taken by pregnant mothers on the cognitive development of their children. As
evidence, they want to estimate the IQ scores of three-year-old children born to
mothers who where on this medication during pregnancy.
Previous studies suggest that the SD of IQ scores of three-year-old chilren is 18
points. How many such children should the researchers sample in order to obtain a
90% confidence interval with a margin of error less than or equal to 4 points?
29. An inventor has developed a new, energy-efficient lawn mower engine. He claims
that the engine will run continuously for 5 hours (300 minutes) on a single gallon of
regular gasoline. From his stock of 2000 engines, the inventor selects a simple
random sample of 50 engines for testing. The engines run for an average of 295
minutes, with a population standard deviation of 20 minutes. Test the null hypothesis
that the mean run time is 300 minutes against the alternative hypothesis that the
mean run time is not 300 minutes. Use a 0.05 level of significance. (Assume that run
times for the population of engines are normally distributed.)
30. Bon Air Elementary School has 1000 students. The principal of the school thinks
that the average IQ of students at Bon Air is at least 110. To prove her point, she
administers an IQ test to 20 randomly selected students. Among the sampled
students, the average IQ is 108 with a sample standard deviation of 10. Based on
these results, should the principal accept or reject her original hypothesis? Assume
a significance level of 0.01. (Assume that test scores in the population of engines are normally distributed.)
31. A particular brand of tires claims that its deluxe tire averages 50,000 miles before it
needs to be replaced. From past studies of this tire, the standard deviation is known
to be 8,000. A survey of owners of that tire design is conducted. From the 28 tires
surveyed, the mean lifespan was 46,500 miles with a standard deviation of 9,800
miles. Using α=0.05, is the data highly inconsistent with the claim?
32. A Nissan Motor Corporation advertisement read, “The average man’s I.Q. is 107.
The average brown trout’s I.Q. is 4. So why can’t man catch brown trout?” Suppose 20:55, 27/01/2026
Probability and Statistics Exercises K63TOAE201 - Comprehensive Review - Studocu
you believe that the brown trout’s mean I.Q. is greater than four. You catch 12 brown
trout. A fish psychologist determines the I.Q.s as follows: 5; 4; 7; 3; 6; 4; 5; 3; 6; 3;
8; 5. Using α=0.05, conduct a hypothesis test of your belief.
33. The television habits of 30 children were observed. The sample mean was found
to be 48.2 hours per week, with a standard deviation of 12.4 hours per week.
Using α=0.05, test the claim that the standard deviation was at least 16 hours per week.
34. After many years of teaching, a statistics pro- fessor computed the variance of the
marks on her final exam and found it to be a2 = 250. She recently made changes to the
way in which the final exam is marked and wondered whether this would result in a
reduction in the variance. A random sample of this year’s final exam marks are listed
here. Can the pro- fessor infer at the 10% significance level that the variance has
decreased? 57 92 99 73 62 64 75 70 88 60
35. The US Department of Energy reported that 51.7% of homes were heated by natural
gas. A random sample of 221 homes in Kentucky found that 115 were heated by
natural gas. Does the evidence support the claim for Kentucky at the α=0.05 level in Kentucky? 20:55, 27/01/2026
Probability and Statistics Exercises K63TOAE201 - Comprehensive Review - Studocu