Quang học lượng tử | Bài giảng môn Vật lý đại cương 3 | Trường Đại học Bách Khoa Hà Nội
Quang học lượng tử | Bài giảng môn Vật lý đại cương 3 | Trường Đại học Bách Khoa Hà Nội. Tài liệu gồm 17 trang giúp bạn tham khảo ôn tập đạt kết quả cao trong kỳ thi sắp tới. Mời bạn đọc đón xem.
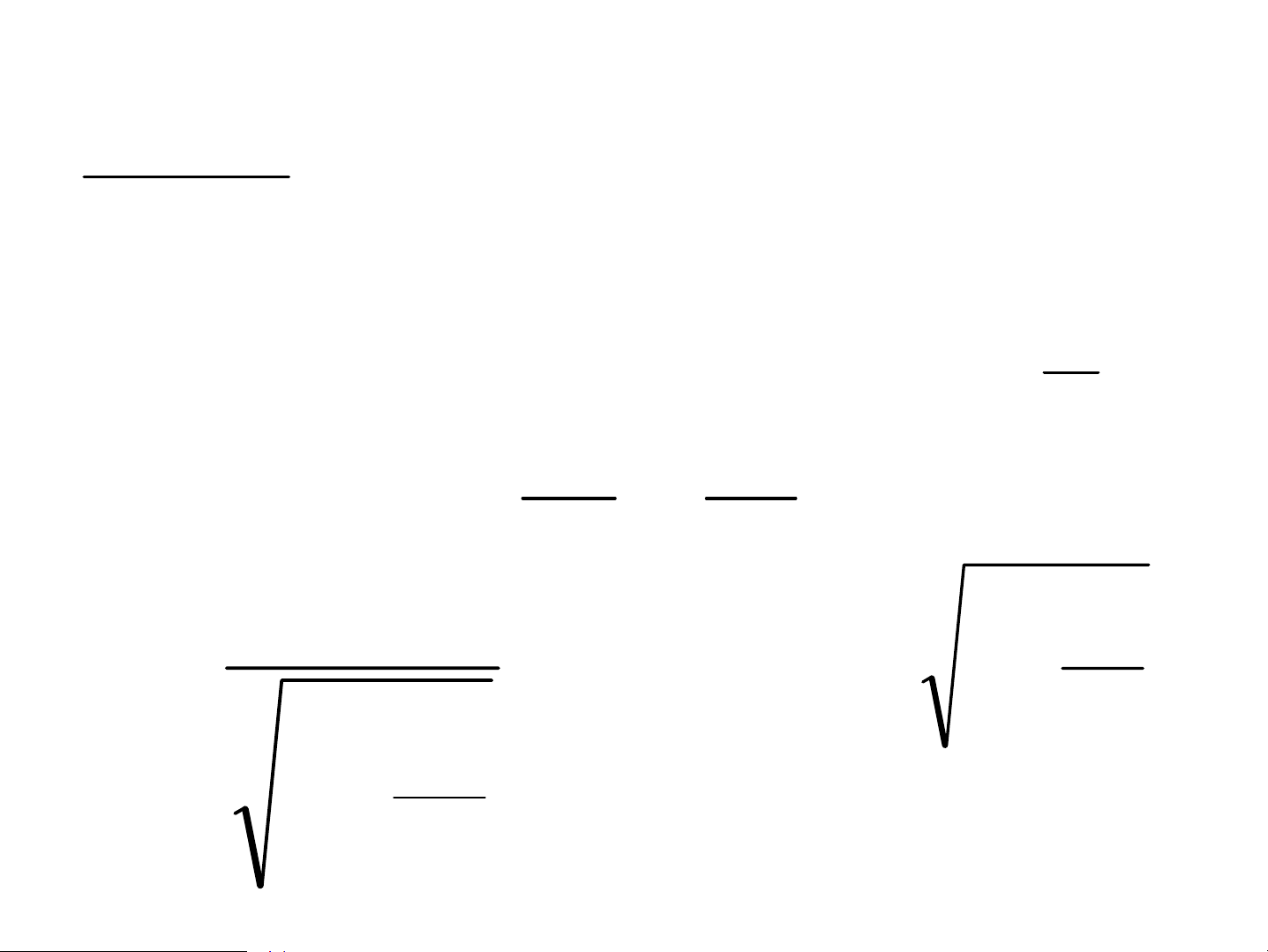
Preview text:
Bμi gi¶ng VËt lý ®¹i c−¬ng
T¸c gi¶: PGS. TS §ç Ngäc UÊn ViÖn VËt lý kü thuËt
Tr−êng §H B¸ch khoa Hμ néi Ch−¬ng 5 Quang häc l−îng tö 1. Bøc x¹ nhiÖt
1.1.C¸c kh¸i niÖm më ®Çu:
C¸c nguyªn tö bÞ kÝch thÝch ph¸t ra bøc x¹ ®iÖn
tõ, bøc x¹ do kÝch thÝch nhiÖt ->Bøc x¹ nhiÖt
N¨ng l−îng bøc x¹ ph¸t ra=n¨ng l−îng thu vμo
b»ng hÊp thô bøc x¹ =>Tr¹ng th¸i c©n b»ng
nhiÖt ®éng øng víi nhiÖt ®é x¸c ®Þnh
1.2.C¸c ®¹i l−îng ®Æc tr−ng
N¨ng l−îng bøc x¹ ph¸t ra tõ dS trong dS
®¬n vÞ thêi gian (n¨ng th«ng bøc x¹ tõ
dS) bëi c¸c bøc x¹ cã tÇn sè trong
kho¶ng ν ÷ ν + dν lμ dW (ν,T) p dW (ν,T)=r(ν,T)dS.d ν p
r(ν,T)N¨ng suÊt ph¸t x¹ ®¬n s¾c øng víi tÇn sè ν ∞
R(T) = ∫ r(ν,T)dν N¨ng suÊt ph¸t x¹ toμn phÇn hay ®é tr−ng cña vËt 0 ν HÖ sè hÊp thô ®¬n s¾c dW ( , T) a(ν, T) t = dW(ν,T) dW (ν,T) do dS hÊp thô t dW(ν,T) chiÕu ®Õn dS a(ν,T)<1
a(ν,T)=1 VËt ®en tuyÖt ®èi
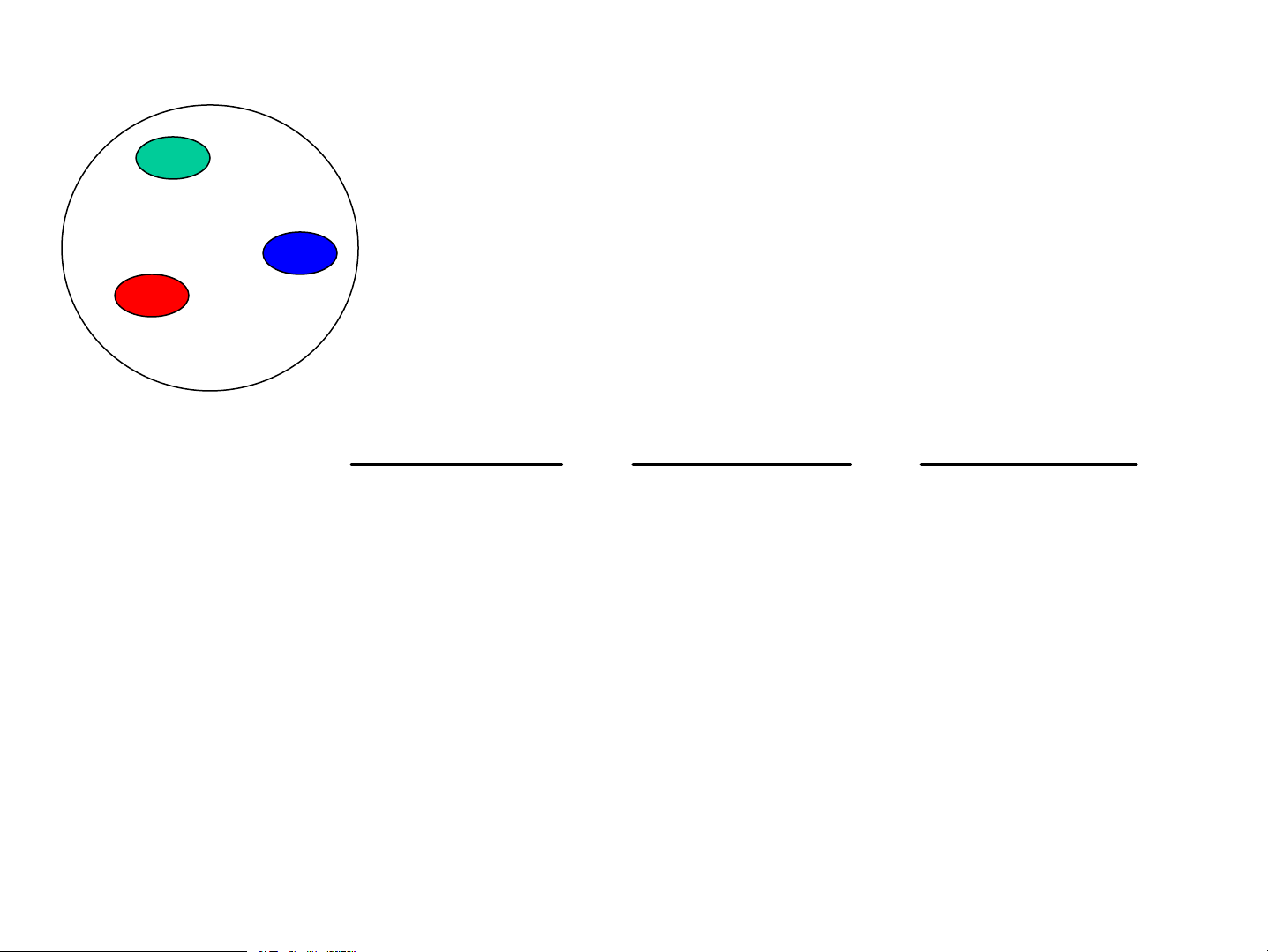
1.3. §Þnh lý Kirkhèp (Kirchoff) 1
Trong b×nh kÝn c¸ch nhiÖt cã 3 2
vËt -> HÊp thô m¹nh còng bøc x¹ 3 m¹nh r(ν,T)~a(ν,T) r (ν, T) r (ν, T) r (ν, T) f (ν, T) 1 2 3 = = = a (ν, T) a (ν, T) a (ν, T) 1 2 3
§Þnh lý: Tû sè gi÷a n¨ng suÊt ph¸t x¹ ®¬n s¾c vμ
hÖ sè hÊp thô ®¬n s¾c cña cïng mét vËt ë nhiÖt
®é nhÊt ®Þnh lμ mét hμm chØ phô thuéc vμo tÇn
sè bøc x¹ ν vμ nhiÖt ®é T mμ kh«ng phô thuéc vμo b¶n chÊt cña vËt ®ã Hμm ph©n bè lμ n¨ng suÊt r(ν, T) f (ν, T) =
ph¸t x¹ ®¬n s¾c cña vËt ®en a(ν, T) tuyÖt ®èi
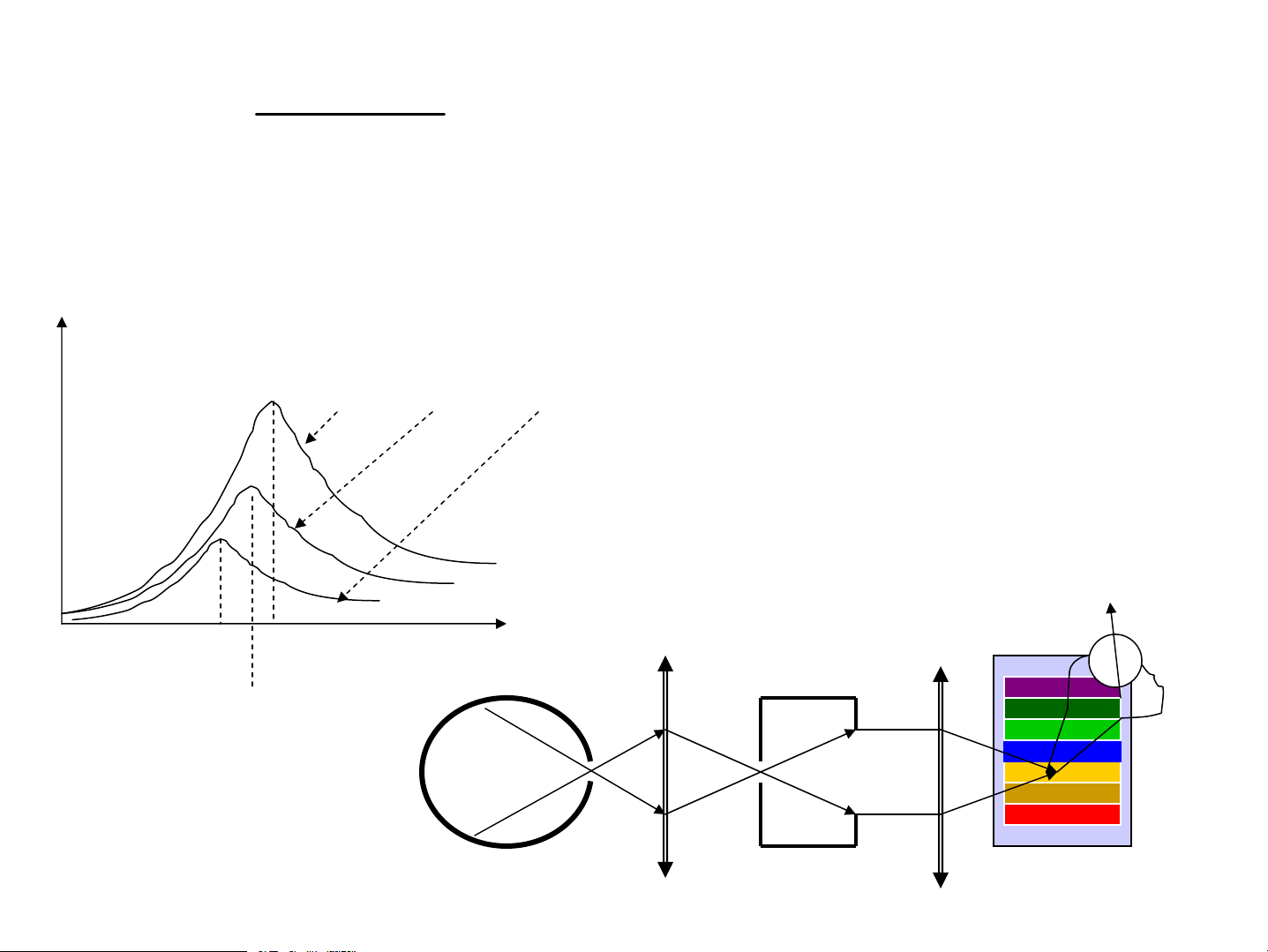
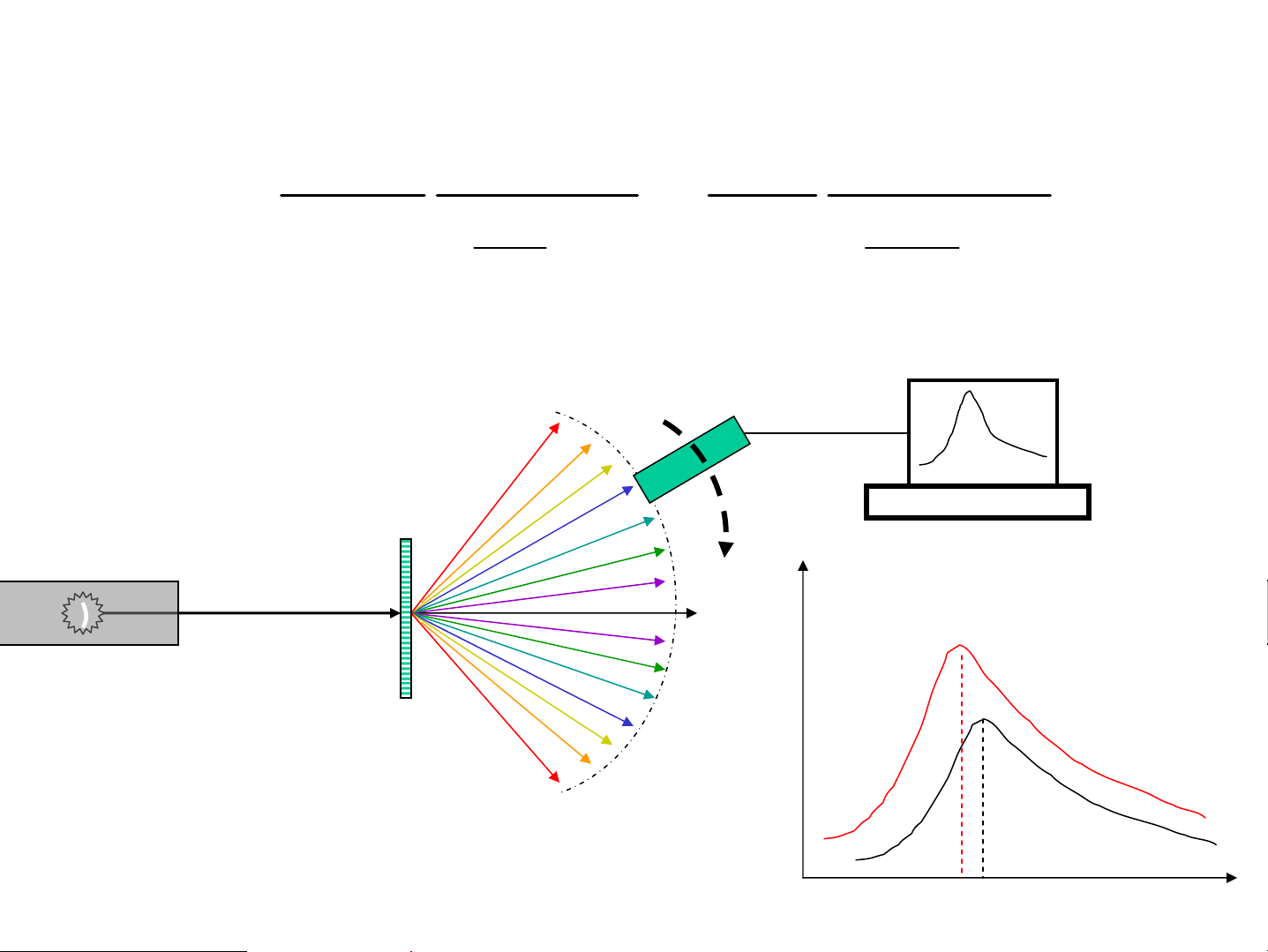
NÕu a(ν,T)=1 th× r(ν,T)= f(ν,T) f(ν,T) T >T >T 1 2 3 f(ν,T) x©y dùng b»ng thùc nghiÖm ν ®o T ν ν ν m3 m1 m2 vËt ®en tuyÖt ®èi HÖ t¸ch phæ bøc x¹
X©y dùng f(ν,T) b»ng thùc nghiÖm (ngμy É) 2 2 πν hν 2 c π h f (ν, T) = = ν c2 h 3 hc λ λ e k T B −1 e k T B −1 Detector M¸y C¸ch tö tÝnh AS tr¾ng f(ν,T) T §Ìn sîi ®èt 2 thay ®æi ®−îc ®iÖn ¸p T1 λ λ m
2. ThuyÕt l−îng tö cña Planck
2.1. Sù thÊt b¹i cña sãng ¸nh s¸ng trong viÖc gi¶i
thÝch hiÖn t−îng bøc x¹ nhiÖt
Hμm ph©n bè theo thuyÕt ®iÖn tõ cæ ®iÓn cña Relay vμ Jeans k =1,38.10-23J/K 2 B 2πν f (ν, T) = k T H»ng sè Boltzmann c2 B ∞ R(T) = r(ν, T)dν = ∞ ∫ 0
“Sù khñng ho¶ng vïng tö ngo¹i” vμo cuèi thÕ kû 19
2.2. ThuyÕt l−îng tö cña Planck
1900 Planck ®−a ra thuyÕt LT:
a. C¸c nguyªn tö, ph©n tö ph¸t x¹ hay hÊp thô
n¨ng l−îng ®iÖn tõ mét c¸ch gi¸n ®o¹n. PhÇn
n¨ng l−îng ph¸t x¹ hay hÊp thô lμ béi nguyªn
lÇn cña mét l−îng n¨ng l−îng nhá gäi lμ l−îng
tö n¨ng l−îng hay Quantum n¨ng l−îng
b. §èi víi bøc x¹ ®iÖn tõ ®¬n s¾c tÇn sè ν, b−íc
sãng λ l−îng tö n¨ng l−îng t−¬ng øng b»ng ε = hν = c h λ
h=6,625.10-34Js H»ng sè Planck
c. C«ng thøc hμm ph©n bè Planck:ph¸t x¹ ®¬n
s¾c cña vËt ®en tuyÖt ®èi 2 2 πν hν f (ν, T) = 2 hν
2.3. C¸c ®Þnh luËt bøc x¹ c k T B − cña vËt ®en tuyÖt ®èi e 1
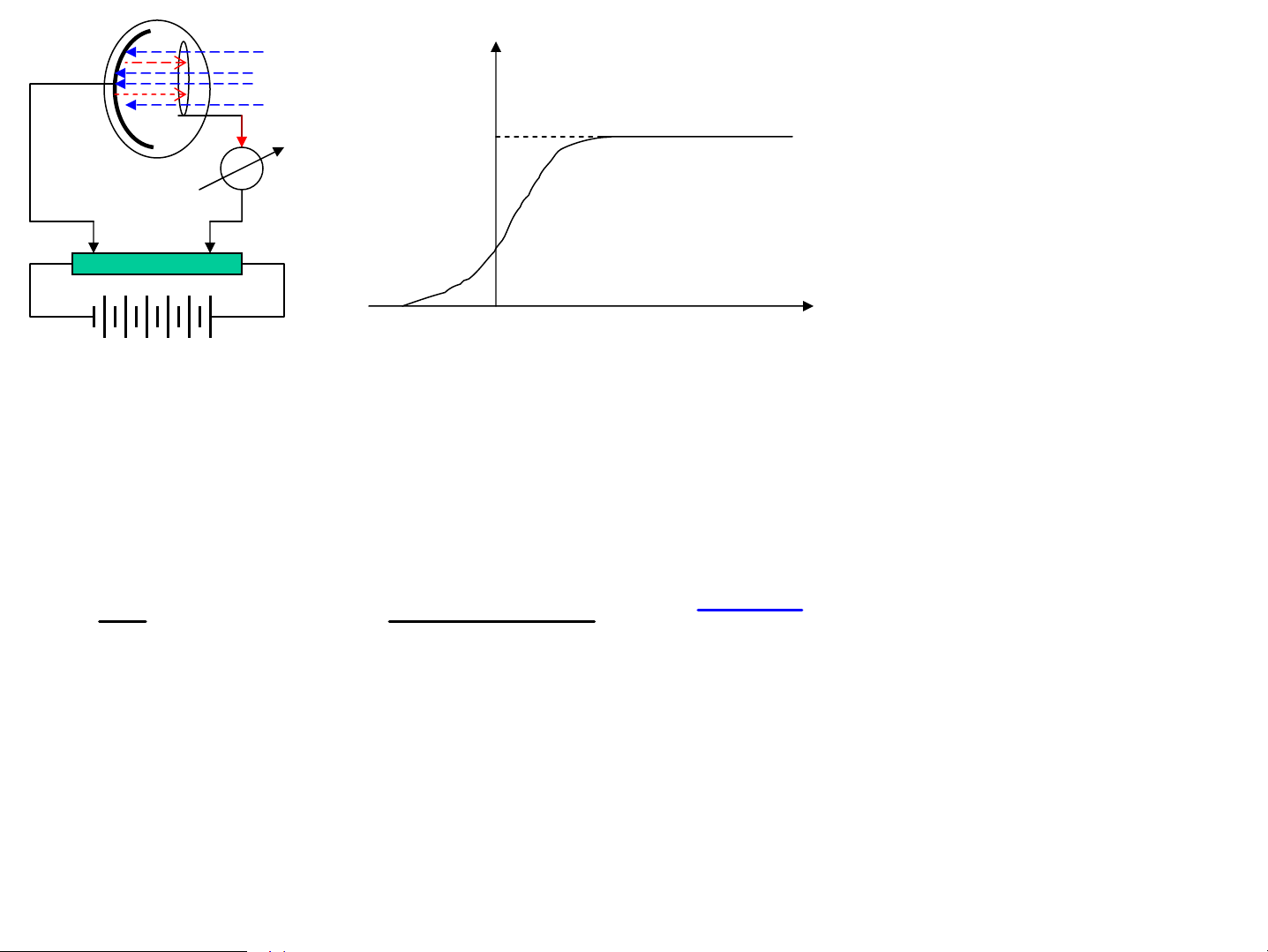
a. N¨ng suÊt ph¸t x¹ toμn phÇn ∞ hν 4 R(T) = ∫ f (ν,T)dν x = R(T) = T σ 4 4 ∞ k T 0 3 B 2π 4 4 R = k T x 2 k T B dx 5 , 6 T T 2 3 ∫ π = B = σ 4 x c h e − 2 3 1 c h 0
σ=5,67.10-8W/m2K4 h»ng sè Steffan-Boltzmann
§L1: N¨ng suÊt ph¸t x¹ toμn phÇn cña vËt ®en tuyÖt ®èi ~ T4 cña nã
b. §L Vin(Wien): §èi víi vËt ®en tuyÖt ®èi b−íc
sãng λ cña chïm bøc x¹ mang nhiÒu n¨ng m
l−îng nhÊt tû lÖ nghÞch víi nhiÖt ®é tuyÖt cña vËt λ T=b b=2,898.10-3m.K H»ng sè Vin m (LÊy df/dν=0)
3. ThuyÕt photon cña Anhxtanh (Einstein)
ThuyÕt Planck ch−a nªu lªn ®−îcb¶n chÊt gi¸n
®o¹n cña bøc x¹ ®iÖn tõ
3.1. ThuyÕt photon cña Anhxtanh
a. Bøc x¹ ®iÖn tõ cÊu t¹o bëi v« sè c¸c h¹t gäi lμ
l−îng tö ¸nh s¸ng hay photon
b. Víi mét bøc x¹ ®iÖn tõ ®¬n s¾c x¸c ®Þnh
c¸c photon ®Òu gièng nhau vμ cã n¨ng l−îng x¸c ®Þnh b»ng ε = hν = c h λ
c. Trong mäi m«i tr−êng c¸c photon cã cïng vËn tèc b»ng: c=3.108m/s
d. Khi mét vËt ph¸t x¹ hay hÊp thô bøc x¹ ®iÖn
tõ -> ph¸t hay hÊp thô c¸c photon
e. C−êng ®é cña chïm bøc x¹ tû lÖ víi sè photon
ph¸t ra trong 1 ®¬n vÞ thêi gian
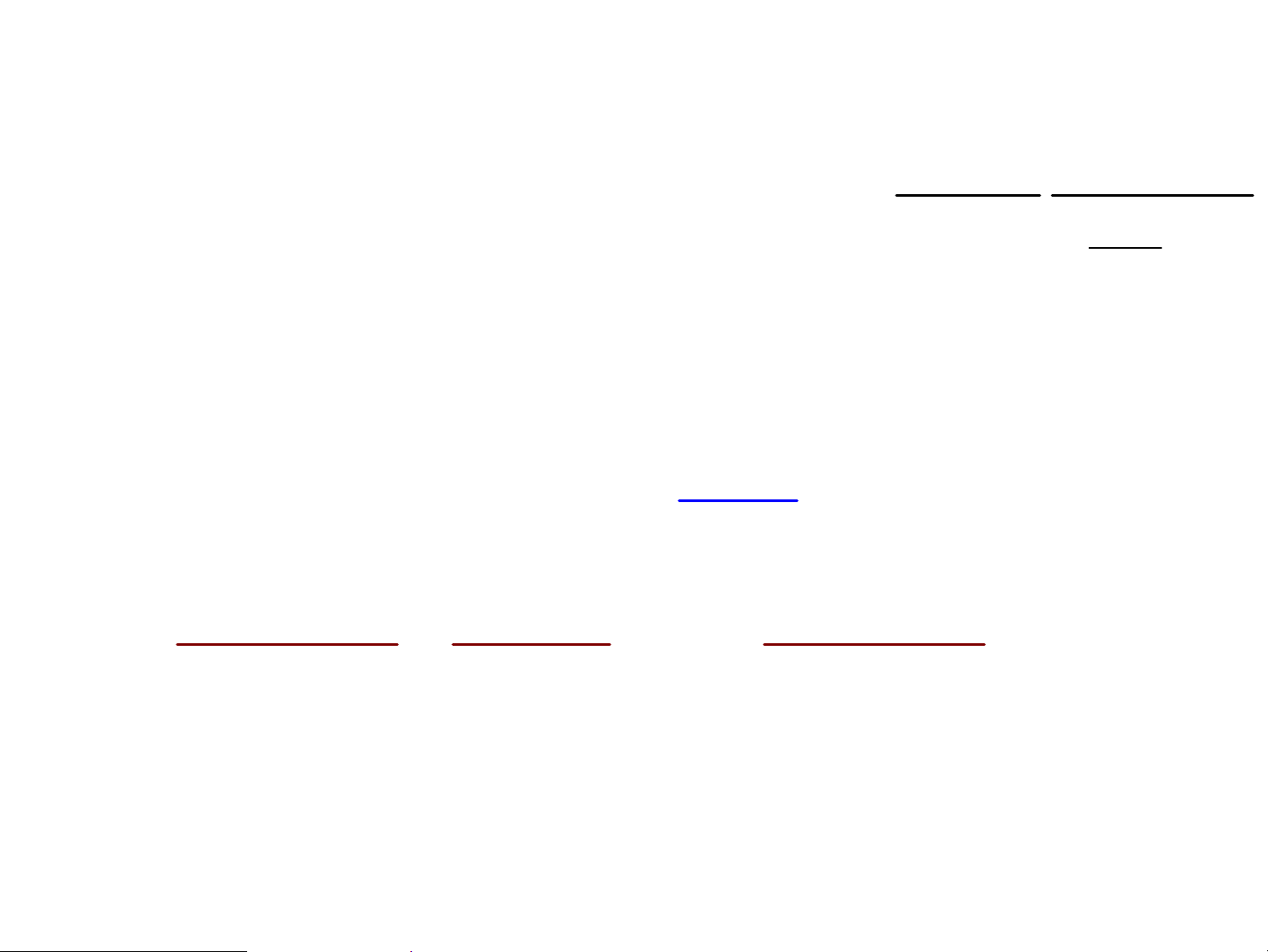
3.2. HiÖn t−îng quang ®iÖn:
HiÖu øng b¾n ra c¸c ®iÖn tö tõ mét tÊm kim lo¹i
khi däi lªn tÊm KL ®ã mét bøc x¹ ®iÖn tõ thÝch
hîp -> c¸c ®iÖn b¾n ra: Quang ®iÖn tö K *I~U ->Ib·o hoμ λ<λ I 0 I *U=0, I ≠0 b·o hoμ 0 U I -> mv 2/2 - + 0 0 U U C 2 0 *eU = mv /2 C 0
3.3. Gi¶i thÝch c¸c ®Þnh luËt quang ®iÖn: a. Giíi h¹n quang ®iÖn c mv2 hc h = A 0 max + = λ λ<λ0 th λ 0 2 Ath
b. Dßng quang ®iÖn b·o hoμ tû lÖ víi I¸nh s¸ng I
~ sè ®iÖn tö b¾n ra ~ Sè photon b¾n vμo K ~ ®iÖn I => I ~ I ¸nh s¸ng ®iÖn ¸nh s¸ng
c. §éng n¨ng ban ®Çu cña quang ®iÖn tö mv2 hν=hν +eU 0 C 0 max = h(ν − ν ) eU =h(ν-ν ) 2 0 C 0 3.4. §éng lùc häc photon c N¨ng l−îng photon ε = ν h = h hν h λ 2 ε = mc m = = c2 λc m 2 v 0 m = m = m 1 − 0 2 2 v c 1 − v=c => m =0 khèi l−îng 2 0 c nghØ cña photon b»ng 0 §éng l−îng photon hν P = mc = = h c λ
§éng l−îng photon tû lÖ thuËn víi tÇn sè hoÆc tû lÖ nghÞch víi b−íc sãng
3.4. HiÖu øng K«ngt¬n (Compton) λ
λ λ’ 1892: Khi chiÕu tia X lªn GraphÝt
Ngoμi ph¶n x¹ Bragg cßn ghi GraphÝt ®−îc λ’> λ
λ’ kh«ng phô thuéc vμo chÊt tinh thÓ, chØ phô
thuéc vμo gãc t¸n x¹ θ: θ Λ Δλ = λ =2,426.10-12m '−λ = 2Λ sin2 C C 2 B−íc sãng Compton
Ph¶n x¹ Bragg x¶y ra khi tia X t¸n x¹ trªn c¸c
®iÖn tö trong Ion t¹i nót m¹ng.
T¸n x¹ Compton x¶y ra khi photon tia X va ®Ëp víi c¸c ®iÖn tö tù do:
§iÖn tö cã vËn tèc tr−íc va ®Ëp v=0 Tr−íc va ®Ëp Sau va ®Ëp m v 2 e m c p ' = e §iÖn tö p =0, E=m c2 = e E' e e 2 v 2 v 1 − 1 − 2 c 2 c hν hν' Photon p = ε = hν p' = ε' = hν' ph c ph c
HÖ c« lËp: B¶o toμn n¨ng l−îng, ®éng l−îng B¶o toμn n¨ng l−îng: 2 m c 2 e hν + m c = hν'+ e 2 v B¶o toμn ®éng l−îng 1 − 2 r r r , c p = p + p ph ph e r r r , 2 2 (p − p ) = p 2 ,2 , 2 p + rp − 2p p cos θ = p ph ph e ph ph ph ph e 2 2 2 hν hν' h νν' m v 2 2 ( ) + ( ) − 2 cos θ = 2 2 c c c v 2 4 m c 1 − 2 2 e θ (hν + m c − hν' ) = 2 e c 2 v 1 − 2 c θ m c2 (ν − ν' ) = hνν' 1 ( − cos ) θ = 2hνν'sin2 e 2 h θ λ h B−íc sãng Compton: '−λ = 2 sin2 Λ = C m c 2 Λ =2,426.10-12m m c e e C