Quy Tắc Hình Bình Hành Trong Giải Toán Vectơ - Tài Liệu Tập Huấn

BÀI 5+6: PHÉP CỘNG, TRỪ CÁC VECTƠ
ĐẲNG THỨC VECTƠ GIẢI BẰNG QUY TẮC HÌNH BÌNH HÀNH PHƯƠNG PHÁP
Cho hình bình hành ABCD, ta có quy tắc hình bình hành: AB  AD  AC Bài 1.
Cho hình bình hành ABCD tâm O , gọi N là trung điểm BC . Tổng OB OC bằng Bài 2.
Cho hình bình hành ABCD. Chứng minh BA BC  DA DC . Bài 3.
Cho hình vuông ABCDcạnh a . Tính AB  AC . Bài 4.
Cho tam giác ABC đều cạnh a. Tính độ dài của vectơ AB  AC . Bài 5.
Cho hình chữ nhật ABCD. Chứng minh AB  AD  AB  AD . Bài 6.
Cho hình bình hành ABCD, tâm O , gọi G là trọng tâm tam giác ABC . Chứng minh rằng:
GA  GC  GD  BA  BC . B C O G A D Bài 7.
Cho hình bình hành ABCD. Dựng bên ngoài hình bình hành hai tam giác đều ABM và CDN .
Tính DA  DN  NC . Trang 1 Bài 8.
Cho hình bình hành ABCD . Gọi O là điểm bất kì trên đường chéo AC . Qua O kẻ các đường
thẳng song song với các cạnh của hình bình hành.Các đường thẳng này cắt AB và DC lần lượt
tại M và N, cắt AD và BC tại E và F . Chứng minh rằng: BD  ME  FN . Bài 9.
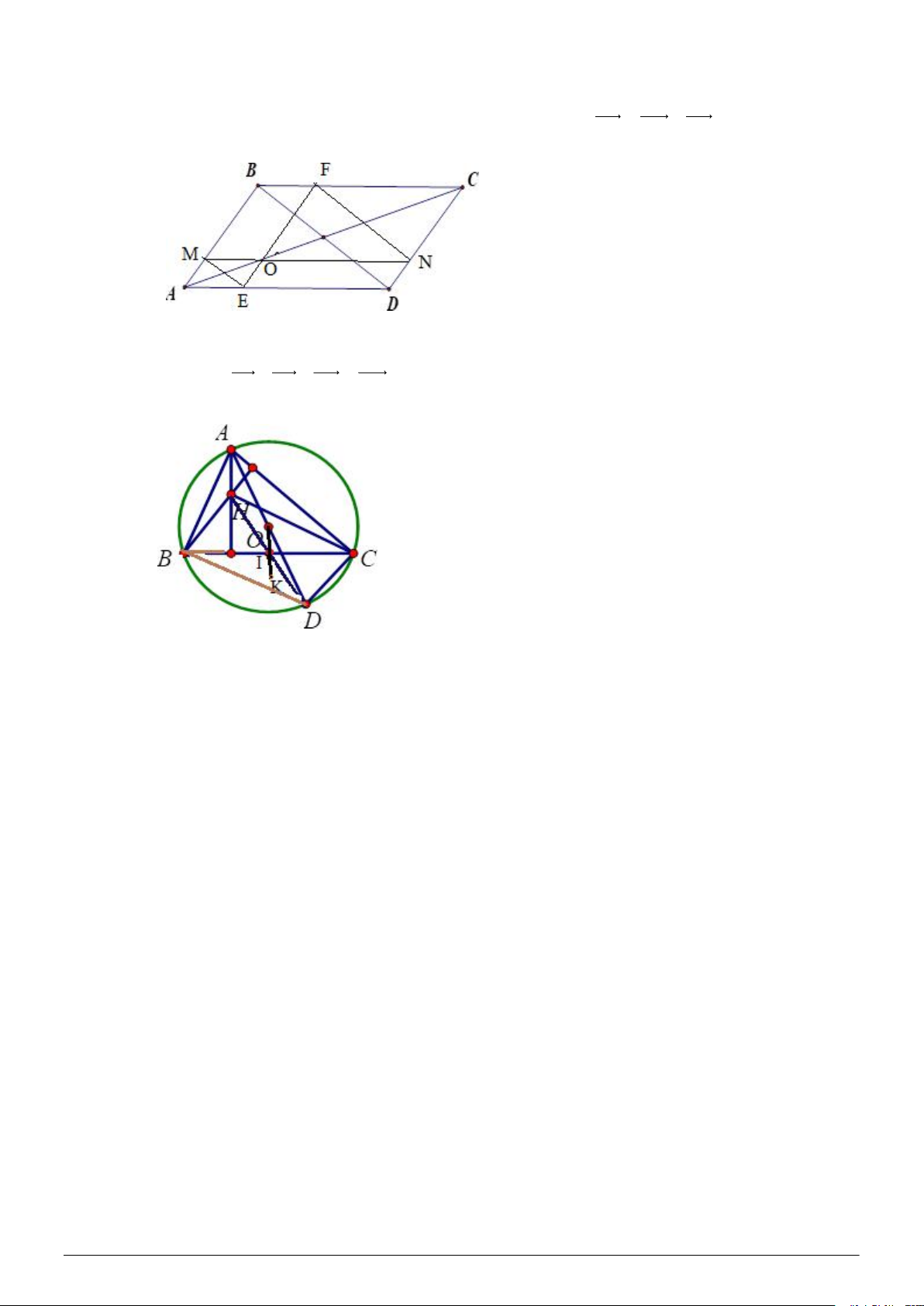
Cho tam giác ABC nhọn có trực tâm H , trọng tâm G và tâm đường tròn ngoại tiếp O . Chứng
minh rằng: OAOB OC  OH . Trang 2
Document Outline

• ĐẲNG THỨC VECTƠ GIẢI BẰNG QUY TẮC HÌNH BÌNH HÀNH